Предел функции с корнями
Среди примеров пределов функции часто встречаются функции с корнями, которые не всегда понятно как раскрывать. Проще когда есть пример границе с корневой функцией вида
Решение подобных пределов просто и понятно каждому.
Трудности возникают если есть следующие примеры функций с корнями.
Пример 1. Вычислить предел функции
При прямой подстановке точки x = 1 видно что и числитель и знаменатель функции
превращаются в ноль, то есть имеем неопределенность вида 0/0.
Для раскрытия неопределенности следует умножить выражение, содержащее корень на сопряженное к нему и применить правило разности квадратов. Для заданного примера преобразования будут следующими
Предел функции с корнями равен 6. Без приведенного правила ее трудно было бы найти.
Рассмотрим подобные примеры вычисления границы с данным правилом
Пример 2. Найти предел функции
Убеждаемся что при подстановке x = 3 получаем неопределенность вида 0/0.
Ее раскрываем умножением числителя и знаменателя на сопряженное к числителю.
Далее числитель раскладываем согласно правилу разности квадратов
Вот так просто нашли предел функции с корнями.
Пример 3. Определить предел функции
Видим, что имеем неопределенность вида 0/0.
Избавляемся ирациональносьти в знаменателе
Предел функции равна 8.
Теперь рассмотрим другой тип примеров, когда переменная в переделе стремится к бесконечности.
Пример 4. Вычислить предел функции
Много из Вас не знают как найти предел функции. Ниже будет раскрыта методика вычислений.
Имемем предел типа бесконечность минус бесконечность. Умножаем и делим на сопряженный множитель и используем правило разности квадратов
Границ функции равна -2,5.
Вычисление подобных пределов фактически сводится к раскрытию иррациональности , а затем подстановке переменной
Пример 5. Найти предел функции
Предел эквивалентен – бесконечность минус бесконечность
.
Умножим и разделим на сопряженное выражение и выполним упрощение
Пример 6. Чему равен предел функции?
Имеем неопределенность вида бесконечность минус бесконечность
Выполняем преобразования с корневыми функциями
предел функции равен -2.
Хорошо ознакомьтесь с методикой раскрытия неопределенностей, алгоритм достаточно прост и поможем найти сложную границу функции.
Решение пределов с корнями онлайн · Как пользоваться Контрольная Работа РУ
Есть два вида выражений-функций с корнями, для которых надо найти предел.
- Функции, содержащие корень (sqrt) в числителе или знаменателе дроби:
- Функции, имеющие разность двух корней:
Оба этих случая легко решает калькулятор пределов.
Как ввести корень в форму?
К примеру, если вы хотите ввести разность двух корней, то укажите следующее выражение:
sqrt(x^2 + 2*x) – sqrt(-3 + x^2)
Для этого примера вы получите подробное решение:
Возьмём предел
::
__________ _________
/ 2 / 2
lim \/ x + 2*x - \/ -3 + x
x->oo
Устраним неопределённость oo - oo
Домножим и разделим на
::
_________ __________
/ 2 / 2
\/ -3 + x + \/ x + 2*x
тогда
::
__________ _________
/ 2 / 2
lim \/ x + 2*x - \/ -3 + x =
x->oo
::
/ __________ _________\ / _________ __________\
| / 2 / 2 | | / 2 / 2 |
\\/ x + 2*x - \/ -3 + x /*\\/ -3 + x + \/ x + 2*x /
lim ------------------------------------------------------------- =
x->oo _________ __________
/ 2 / 2
\/ -3 + x + \/ x + 2*x
::
2 2
__________ _________
/ 2 / 2
\/ x + 2*x - \/ -3 + x
lim ------------------------------ =
x->oo _________ __________
/ 2 / 2
\/ -3 + x + \/ x + 2*x
::
2 2
x + 2*x + 3 - x
lim ----------------------------
x->oo _________ __________ =
/ 2 / 2
\/ -3 + x + \/ x + 2*x
::
3 + 2*x
lim ----------------------------
x->oo _________ __________
/ 2 / 2
\/ -3 + x + \/ x + 2*x
Разделим числитель и знаменатель на x:
::
3
2 + -
x
lim ----------------------------
x->oo _________ __________ =
/ 2 / 2
\/ -3 + x \/ x + 2*x
------------ + -------------
x x
::
3
2 + -
x
lim ----------------------------------
x->oo _________ __________
/ 2 / 2 =
/ -3 + x / x + 2*x
/ ------- + / --------
/ 2 / 2
\/ x \/ x
::
3
2 + -
x
lim ---------------------------
x->oo ________ _______
/ 3 / 2
/ 1 - -- + / 1 + -
/ 2 \/ x
\/ x
Сделаем замену
::
1
u = -
x
тогда
::
3
2 + -
x
lim ---------------------------
x->oo ________ _______ =
/ 3 / 2
/ 1 - -- + / 1 + -
/ 2 \/ x
\/ x
::
2 + 3*u
lim ---------------------------
u->0+ __________ =
/ 2 _________
\/ 1 - 3*u + \/ 1 + 2*u
::
2 + 3*0
--------------------------- = 1
= __________
/ 2 _________
\/ 1 - 3*0 + \/ 1 + 2*0
Получаем окончательный ответ:
::
__________ _________
/ 2 / 2
lim \/ x + 2*x - \/ -3 + x = 1
x->oo
Для случая, когда корень находится в числителе или знаменателе дроби, то, к примеру, введите так:
(sqrt(x + 1) – sqrt(2*x – 2))/(x – 3)
Не забудьте указать к чему стремится переменная x.
Для указанного примера Вы также получите подробное решение, но с применением правила Лопиталя.
Ещё раз приводим ссылку на калькулятор:
>> решение пределов функций <<
Как решать пределы с корнями с примерами решения
Содержание:
- Примеры с решением
- Раскрытие неопределенностей вида
При вычислении предела вначале проверяют принадлежит ли точка области определения. Если то предел равен значению функции в точке
(это объясняется непрерывностью элементарной функции на своей области определения)
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Примеры с решением
Пример 1:
Вычислить:
a)
б)
в)
Решение:
а)
б)
в)
Правило сохраняет силу, если Запись например, означает, что когда абсолютное значение
неограниченно возрастает, функция стремится к нулю (это ясно из графика функции).
Возможно вам будут полезны данные страницы:
Пример 2:
Найти:
а)
в)
Решение:
а)
б)
в)
Пример 3:
Найти
Решение:
При подстановке в значение функции вместосимвола бесконечности, результат может оказаться не конечным числом. Например:
Что считать ответом в этом случае?
При вычислении подобных пределов пользуются одним из следующих правил (в приводимых ниже формулах с означает число):
Приведенные формулы следуют из соображений здравого смысла. Например, первая из приведенных формул по существу утверждает, что если одна из функций становится очень большой и положительной, а другая ограничена, то сумма их становится очень большой и положительной.
Те же соображения приводят и к формальному доказательству: надо только вместо «очень больших» значений говорить о «больших любого заданного числа».
Применим эти правила для вычисления пределов, которые были оставлены без вычисления:
Соображениями здравого смысла руководствуются и при вычислении пределов от функций при Надо проследить ио графику функции куда стремится значение функции, если аргумент стремится к
Пример 4:
Вычислить:
а)
б)
в)
Решение:
а) При знаменатель неограниченно растет, т.е. является величиной бесконечно большой, а обратная величина бесконечно малой. Произведение бесконечно малой на ограниченную величину (постоянная — частный случай ограниченной еличины) есть величина бесконечно малая, и предел ее при равен нулю. Следовательно,
Этот же ответ получается при применении последнего из приведенных выше правил
б)
в)
Приведенные рассуждения не являются строгими.
Выражение взято в скобки, чтобы подчеркнуть условность записи.
Пример 5:
Найти:
а)
б)
в)
Решение:
а)
б)
в)
Имеются случаи, не охватываемые правилами из предыдущего параграфа. Не существует «общей формулы» для выражения . В самом деле, пусть где —целое число. Частное этих функций. при является частным бесконечно малых. Оно может стремиться к нулю (при), или (при ), или (при ). Поэтому выражение и подобные ему называются неопределенностями. К неопределенностям относятся следующие выражения:
Как для случая неопределенности вида встретившейся при сравнении бесконечно малых, здесь для раскрытия неопределенности уже недостаточно знать лишь пределы функций и а нужно учесть и закон их изменения. Примеры раскрытия неопределенностей приведены ниже.
Примеры раскрытия неопределенностей приведены ниже.
Пример 6:
Найти
Решение:
Непосредственной подстановкой вместо аргумента его предельного значения вычислить предел нельзя, поскольку получается неопределенность вида
Разложим числитель и знаменатель на множители, чтобы сократить дробь на общий множитель, стремящийся к нулю. Нужно иметь в виду, что здесь не производится сокращение на нуль, что недопустимо. По определению предела функции аргумент стремится к своему предельному значению, никогда не принимая этого значения (вспомним, что в определении предела по Коши оэтому до перехода к пределу можно произвести сокращение на множитель, стремящийся к нулю. Имеем:
Пример 7:
Найти
Решение:
Пределы числителя и знаменателя при равны нулю
Разложим квадратный трехчлен в числителе на линейные множители по формуле где и – корни трехчлена. Разложив на множители и знаменатель, сократим на получим
Пример 8:
Найти
Решение:
и
Пример 9:
Найти
Решение:
Пределы числителя и знаменателя при равны нулю. Умножим числитель и знаменатель на сопряженный знаменателю множитель и затем, сократив дробь на получим:
Умножим числитель и знаменатель на сопряженный знаменателю множитель и затем, сократив дробь на получим:
Пример 10:
Найти
Решение:
Когда числитель и знаменатель дроби стремятся к нулю, получается неопределенность вида Желая избавится от иррациональности в знаменателе, преобразуем данное выражение:
Перейдя к пределу, получим
В предыдущих примерах неопределенность вида раскрывалась путем выделения в числителе и знаменателе общего множителя. Однако этот прием «срабатывает» не во всех случаях. Например, в случае предела неясно, как выделить общий множитель. Этот предел можно вычислить с помощью принципа замены эквивалентных. Вычислим этот предел другим способом — сведением к пределу
называемому 300 лет назад первым замечательным пределом. Доказательство равенства нетрудно и опирается оно не приводится.
Заметим, что выражение взято в скобки, поскольку писать нельзя! Скобки в записи подчеркивают ее условность. Равенство означает, что в данном конкретном случае неопределенность раскрыта и значение соответствующего предела равно единице.
Равенство означает, что в данном конкретном случае неопределенность раскрыта и значение соответствующего предела равно единице.
Пример 11:
Найти
Решение:
Пример 12:
Найти
Решение:
Пример 13:
Найти
Решение:
При числитель и знаменатель — величины бесконечно большие. Поэтому при непосредственной подстановке символа вместо получаем выражение которое представляет собой неопределенность. Для вычисления предела этой функции нужно и числитель и знаменатель разделить на (наивысшую степень аргумента в знаменателе):
Пример 14:
Найти
Решение:
При непосредственной подстановке символа вместо получаем неопределенность вида Для вычисления предела этой функции нужно и числитель и знаменатель разделить на (наивысшую степень аргумента в знаменателе):
(при слагаемые — величины бесконечно малые и, следовательно, их пределы равны нулю).
Пример 14:
Наити
Решение:
Вообще, предел отношения полиномов при равен отношению коэффициентов при старших членах, если степени числителя и знаменателя одинаковы, и равен нулю или бесконечности, если степень числителя соответственно меньше или больше знаменателя.
Пример 15:
Найти
Решение:
Пример 16:
Найти
Решение:
В подобных примерах полезно иметь в виду, что функция где — многочлен степени стремится к бесконечности так же, как и функция Это позволяет выделить высшую степень входящую в данное выражение, и разделить числитель и знаменатель на эту степень В данном примере надо делить на
Неопределенности вида и путем преобразования можно привести к неопределенности вида или которая раскрывается уже известными способами.
Покажем на примерах, как находятся такие пределы.
Пример 17:
Найти
Решение:
Произведем вычитание дробей, получим
Пример 18:
Найти
Решение:
Пример 19:
Найти
Решение:
(сделали замену ).
Пример 20:
Найти
Ответ:
Раскрытие неопределенностей вида
Рассмотрим последовательность где
Может показаться, что неограниченное возрастание показателя степени должно повлечь неограниченное возрастание целочисленной функции Но рост показателя компенсируется тем, что основание стремится к В результате последовательность оказывается возрастающей и ограниченной. А всякая ограниченная и возрастающая последовательность имеет конечный предел. Предел, к торому стремится при обозначается
Обозначением числа и его широким применением во многих вопросах математики мы обязаны Эйлеру. Это число иррационально и с точностью до шестой значащей цифры равно
Это число иррационально и с точностью до шестой значащей цифры равно
Функция имеет пределом число не только при целочисленных значениях но и тогда, когда стремится к бесконечности, пробегая числовую прямую непрерывно. Более того, аргументможет принимать как положительные, так и отрицательные значения, лишь бы неограниченно росло по абсолютному значению. Чтобы отмстить это обстоятельство, заменим букву буквой и напишем:
или короче
Этот предел часто используется в математике для раскрытия неопределенности и именуется вторым замечательным пределом
Пример 21:
Найти пределы:
а)
б)
Решение:
а)
б)
Пример 22:
Найти пределы
а)
б)
Решение:
а) При основание степени стремится к единице, а показатель стремится к бесконечности. Следовательно, имеем неопределенность вида Представим основание в виде суммы единицы и некоторой бесконечно малой величины:
Следовательно, имеем неопределенность вида Представим основание в виде суммы единицы и некоторой бесконечно малой величины:
тогда
б)
Число во многих случаях выгодно брать за основание логарифмов. Логарифм от с основанием носит название натурального логарифма и обозначается Показательная функция широко используется в науке и называется экспоненциальной. Другое обозначение этой функции –
Неопределенности вида и можно свести к неопределенности вида следующим образом:
Пределы с корнями: примеры с решением
Поиск значений пределов с корнями мало чем отличается от каких-либо других пределов.
Замечание 1
Основная цель в данном случае — это избавление от знака корня с помощью тождественных преобразований.
Например, если необходимо иметь дело с дробью с корнем в знаменателе, можно домножить всё выражение на такой множитель, который позволит получить в знаменателе разность квадратов.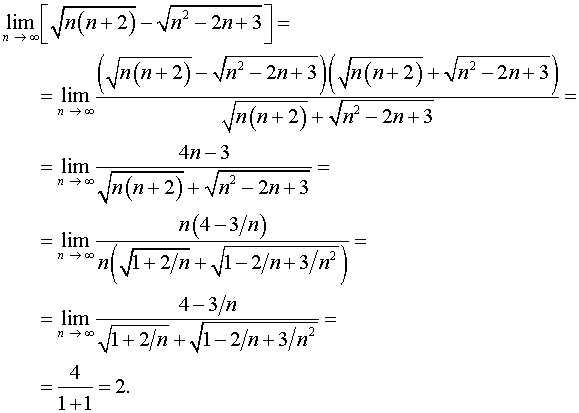 2-4x} + x}=-\frac{4}{\sqrt{1-\frac{4}{x}} + 1} = -\frac{4}{\sqrt{1-0}+1} = -2$.
2-4x} + x}=-\frac{4}{\sqrt{1-\frac{4}{x}} + 1} = -\frac{4}{\sqrt{1-0}+1} = -2$.
Пределы с иррациональностями. Примеры раскрытия неопределённостей. Первая часть.
Пределы, содержащие иррациональности (или, попросту говоря, корни) крайне популярны у составителей типовых расчётов и контрольных работ по высшей математике. Обычно рассматриваются три группы неопределённостей:
В данной теме мы рассмотрим все три перечисленные выше группы пределов с иррациональностями. Начнём с пределов, содержащих неопределенность вида $\frac{0}{0}$.
Раскрытие неопределенности $\frac{0}{0}$.
Схема решения стандартных примеров такого типа обычно состоит из двух шагов:
- Избавляемся от иррациональности, вызвавшей неопределенность, домножая на так называемое “сопряжённое” выражение;
- При необходимости раскладываем выражение в числителе или знаменателе (или и там и там) на множители;
- Сокращаем множители, приводящие к неопределённости, и вычисляем искомое значение предела.
 2+bx+c=a\cdot(x-x_1)\cdot(x-x_2)
\end{equation}
$$
2+bx+c=a\cdot(x-x_1)\cdot(x-x_2)
\end{equation}
$$Формул (1)-(5) вполне хватит для решения стандартных задач, к которым мы сейчас и перейдём.
Пример №1
Найти $\lim_{x\to 3}\frac{\sqrt{7-x}-2}{x-3}$.
Решение
Найдём отдельно пределы числителя и знаменателя:
$$ \begin{aligned} & \lim_{x\to 3}(\sqrt{7-x}-2)=\sqrt{7-3}-2=\sqrt{4}-2=0;\\ & \lim_{x\to 3} (x-3)=3-3=0. \end{aligned} $$В заданном пределе мы имеем неопределённость вида $\frac{0}{0}$. Раскрыть эту неопределённость нам мешает разность $\sqrt{7-x}-2$. Для того, чтобы избавляться от подобных иррациональностей, применяют умножение на так называемое “сопряжённое выражение”. Как действует такое умножение мы сейчас и рассмотрим. Умножим $\sqrt{7-x}-2$ на $\sqrt{7-x}+2$:
$$(\sqrt{7-x}-2)(\sqrt{7-x}+2)$$Чтобы раскрыть скобки применим формулу №1, подставив в правую часть упомянутой формулы $a=\sqrt{7-x}$, $b=2$:
$$(\sqrt{7-x}-2)(\sqrt{7-x}+2)=(\sqrt{7-x})^2-2^2=7-x-4=3-x. $$
$$Как видите, если умножить числитель на $\sqrt{7-x}+2$, то корень (т.е. иррациональность) в числителе исчезнет. Вот это выражение $\sqrt{7-x}+2$ и будет сопряжённым к выражению $\sqrt{7-x}-2$. Однако мы не вправе просто взять и умножить числитель на $\sqrt{7-x}+2$, ибо это изменит дробь $\frac{\sqrt{7-x}-2}{x-3}$, стоящую под пределом. Умножать нужно одовременно и числитель и знаменатель:
$$ \lim_{x\to 3}\frac{\sqrt{7-x}-2}{x-3}= \left|\frac{0}{0}\right|=\lim_{x\to 3}\frac{(\sqrt{7-x}-2)\cdot(\sqrt{7-x}+2)}{(x-3)\cdot(\sqrt{7-x}+2)}$$Теперь вспомним, что $(\sqrt{7-x}-2)(\sqrt{7-x}+2)=3-x$ и раскроем скобки. А после раскрытия скобок и небольшого преобразования $3-x=-(x-3)$ сократим дробь на $x-3$:
$$ \lim_{x\to 3}\frac{(\sqrt{7-x}-2)\cdot(\sqrt{7-x}+2)}{(x-3)\cdot(\sqrt{7-x}+2)}= \lim_{x\to 3}\frac{3-x}{(x-3)\cdot(\sqrt{7-x}+2)}=\\ =\lim_{x\to 3}\frac{-(x-3)}{(x-3)\cdot(\sqrt{7-x}+2)}= \lim_{x\to 3}\frac{-1}{\sqrt{7-x}+2} $$Неопределенность $\frac{0}{0}$ исчезла.
 2
2
Каков предел дроби внутри квадратного корня
Мне нужно найти предел sqrt ((3x-1)/(x+2)), Когда x – >бесконечность
Кто-нибудь может мне помочь, пожалуйста?
math limits fractions sqrt
Поделиться Источник Jan Vorisek 16 сентября 2012 в 12:222 ответа
- Отправка знака квадратного корня в textarea
Когда пользователь нажимает на метку кнопки со знаком квадратного корня, он посылает знак квадратного корня внутри textarea. Есть ли способ сделать это с php? Если нет, то javascript-это нормально?
- Квадратный корень внутри квадратного корня python
Мне было интересно, как написать код, показывающий квадратный корень внутри квадратного корня. Это то, что у меня есть до сих пор: number=float(input(Please enter a number: )) square = 2*number**(1/2)**(1/3) print(square) Но это неправильно, так как я получаю другое число из калькулятора.
 0 ) становятся незначительными, таким образом оставляя:
0 ) становятся незначительными, таким образом оставляя:sqrt(3x/x)Как вы можете видеть, это сводится к:
sqrt(3)И это больше не зависит от
xи, следовательно, является ответом.Примечание
Математические вопросы лучше всего подходят на математической странице Stack Exchange .
Поделиться mjgpy3 16 сентября 2012 в 12:31
Поделиться duffymo 16 сентября 2012 в 12:36
Похожие вопросы:
символ квадратного корня / символМне было интересно, каков код символа квадратного корня в java? То есть я хочу иметь возможность печатать знак квадратного корня на экране внутри строки других символов или в качестве метки на…
Как реализуется функция квадратного корня?Как реализуется функция квадратного корня?
Нормализация пространственных векторов без квадратного корняИтак, я узнал, что использование квадратного корня в программировании-это всегда плохая практика, особенно на каждом этапе обновления.
 Я пытаюсь сделать реалистичные упругие столкновения между…
Я пытаюсь сделать реалистичные упругие столкновения между…
Отправка знака квадратного корня в textareaКогда пользователь нажимает на метку кнопки со знаком квадратного корня, он посылает знак квадратного корня внутри textarea. Есть ли способ сделать это с php? Если нет, то javascript-это нормально?
Квадратный корень внутри квадратного корня pythonМне было интересно, как написать код, показывающий квадратный корень внутри квадратного корня. Это то, что у меня есть до сих пор: number=float(input(Please enter a number: )) square =…
вычисление квадратного корня без использования функции квадратного корня в c++Вы должны написать свой собственный алгоритм вычисления квадратного корня. Сначала напишите псевдокод, прежде чем продолжить и написать программу C++. Не используйте функцию sqrt из математической…
Поддержка Z3 и извлечения квадратного корняЯ искал функциональность квадратного корня, предоставляемую z3.
 Например, для добавления ограничения относительно действительного числа x, которое x*x = 2, каков наилучший способ его кодирования? Я…
Например, для добавления ограничения относительно действительного числа x, которое x*x = 2, каков наилучший способ его кодирования? Я…
OpenCL половина квадратного корняЯ разрабатываю для GPU под управлением OpenCL 1.2. Я пытаюсь использовать функцию половины квадратного корня, чтобы вычислить квадратный корень из моего типа данных половины. Однако для всех функций…
Можно ли отображать числа внутри символа квадратного корня в HTML? (Javascript?)Этот вопрос не требует объяснений. Мне нужно отобразить числа внутри символа квадратного корня в html. Возможно ли это вообще? Если это не так, то какова лучшая альтернатива? (помимо проектирования…
Можно ли использовать функцию 32-битного квадратного корня для вычисления квадратного корня 64-bit?Чтобы развить эту идею, предположим, что у меня есть 2 32-битных регистра, представляющих верхний и Нижний биты 64-bit с плавающей запятой. Я хочу вычислить на них квадратный корень 64-bit.
 Однако,…
Однако,…Поиск пределов: свойства пределов
Определение предела суммы, разницы и произведения
Построение графика функции или изучение таблицы значений для определения предела может быть обременительным и трудоемким. По возможности более эффективно использовать свойств пределов , которые представляют собой набор теорем для нахождения пределов.
Знание свойств пределов позволяет нам вычислять пределы напрямую. Мы можем складывать, вычитать, умножать и делить пределы функций, как если бы мы выполняли операции над самими функциями, чтобы найти предел результата.Точно так же мы можем найти предел функции, возведенной в степень, подняв предел до этой степени. Мы также можем найти предел корня функции, взяв корень предела. Используя эти операции над пределами, мы можем найти пределы более сложных функций, найдя пределы их более простых компонентных функций.
Общее примечание: свойства пределов
Пусть [latex] a, k, A [/ latex] и [latex] B [/ latex] представляют действительные числа, а [latex] f [/ latex] и [latex] g [/ latex] являются функциями, например что [латекс] \ underset {x \ to a} {\ mathrm {lim}} f \ left (x \ right) = A [/ latex] и [latex] \ underset {x \ to a} {\ mathrm {lim }} g \ left (x \ right) = B [/ латекс].
 Для существующих и конечных пределов свойства пределов приведены в таблице ниже.
Для существующих и конечных пределов свойства пределов приведены в таблице ниже.Константа, k [латекс] \ underset {x \ to a} {\ mathrm {lim}} k = k [/ latex] Постоянно раз функция [латекс] \ underset {x \ to a} {\ mathrm {lim}} \ left [k \ cdot f \ left (x \ right) \ right] = k \ underset {x \ to a} {\ mathrm { lim}} f \ left (x \ right) = kA [/ латекс] Сумма функций [латекс] \ underset {x \ to a} {\ mathrm {lim}} \ left [f \ left (x \ right) + g \ left (x \ right) \ right] = \ underset {x \ to a } {\ mathrm {lim}} f \ left (x \ right) + \ underset {x \ to a} {\ mathrm {lim}} g \ left (x \ right) = A + B [/ latex] Различие функций [латекс] \ underset {x \ to a} {\ mathrm {lim}} \ left [f \ left (x \ right) -g \ left (x \ right) \ right] = \ underset {x \ to a } {\ mathrm {lim}} f \ left (x \ right) – \ underset {x \ to a} {\ mathrm {lim}} g \ left (x \ right) = AB [/ latex] Произведение функций [латекс] \ underset {x \ to a} {\ mathrm {lim}} \ left [f \ left (x \ right) \ cdot g \ left (x \ right) \ right] = \ underset {x \ to a} {\ mathrm {lim}} f \ left (x \ right) \ cdot \ underset {x \ to a} {\ mathrm {lim}} g \ left (x \ right) = A \ cdot B [/ латекс ] Частное число функций [латекс] \ underset {x \ to a} {\ mathrm {lim}} \ frac {f \ left (x \ right)} {g \ left (x \ right)} = \ frac {\ underset {x \ в a} {\ mathrm {lim}} f \ left (x \ right)} {\ underset {x \ to a} {\ mathrm {lim}} g \ left (x \ right)} = \ frac {A} {B}, B \ ne 0 [/ латекс] Функция, возведенная в степень [латекс] \ underset {x \ to a} {\ mathrm {lim}} {\ left [f \ left (x \ right) \ right]} ^ {n} = {\ left [\ underset {x \ to \ infty} {\ mathrm {lim}} f \ left (x \ right) \ right]} ^ {n} = {A} ^ {n} [/ latex], где [latex] n [/ latex] – это положительное целое число n -й корень функции, где n – положительное целое число [латекс] \ underset {x \ to a} {\ mathrm {lim}} \ sqrt [n] {f \ left (x \ right)} = \ sqrt [n] {\ underset {x \ to a} { \ mathrm {lim}} \ left [f \ left (x \ right) \ right]} = \ sqrt [n] {A} [/ latex] Полиномиальная функция [латекс] \ underset {x \ to a} {\ mathrm {lim}} p \ left (x \ right) = p \ left (a \ right) [/ latex] Пример 1: Алгебраическая оценка предела функции
Вычислить [латекс] \ underset {x \ to 3} {\ mathrm {lim}} \ left (2x + 5 \ right) [/ latex].

Решение
[латекс] \ begin {array} {ll} \ underset {x \ to 3} {\ mathrm {lim}} \ left (2x + 5 \ right) = \ underset {x \ to 3} {\ mathrm {lim }} \ left (2x \ right) + \ underset {x \ to 3} {\ mathrm {lim}} \ left (5 \ right) \ hfill & \ text {Свойство суммы функций} \ hfill \\ \ text { } = \ underset {x \ to 3} {2 \ mathrm {lim}} \ left (x \ right) + \ underset {x \ to 3} {\ mathrm {lim}} \ left (5 \ right) \ hfill & \ text {Постоянное время свойство функции} \ hfill \\ \ text {} = 2 \ left (3 \ right) +5 \ hfill & \ text {Evaluate} \ hfill \\ \ text {} = 11 \ hfill & \ hfill \ end {array} [/ latex]
Попробуйте 1
Оцените следующий предел: [латекс] \ underset {x \ to -12} {\ mathrm {lim}} \ left (-2x + 2 \ right) [/ latex].
Решение
Нахождение предела многочлена
Не все функции или их пределы включают простое сложение, вычитание или умножение. Некоторые могут включать многочлены. Напомним, что многочлен – это выражение, состоящее из суммы двух или более членов, каждое из которых состоит из константы и переменной, возведенных в неотрицательную целую степень.
 Чтобы найти предел полиномиальной функции, мы можем найти пределы отдельных членов функции, а затем сложить их вместе.Кроме того, предел полиномиальной функции по мере приближения [latex] x [/ latex] к [latex] a [/ latex] эквивалентен простому вычислению функции для [latex] a [/ latex].
Чтобы найти предел полиномиальной функции, мы можем найти пределы отдельных членов функции, а затем сложить их вместе.Кроме того, предел полиномиальной функции по мере приближения [latex] x [/ latex] к [latex] a [/ latex] эквивалентен простому вычислению функции для [latex] a [/ latex].Как: дана функция, содержащая многочлен, найдите ее предел.
- Используйте свойства пределов, чтобы разбить многочлен на отдельные члены.
- Найдите пределы отдельных условий.
- Сложите пределы вместе.
- В качестве альтернативы оцените функцию для [latex] a [/ latex].{3} +5 \ right) [/ латекс].
Решение
Поиск предела мощности или корня
Когда предел включает степень или корень, нам нужно другое свойство, которое поможет нам его оценить. Квадрат предела функции равен пределу квадрата функции; то же самое и с высшими силами. Точно так же квадратный корень из предела функции равен пределу из квадратного корня из функции; то же самое верно и для высших корней.
 {5} [/ latex].{2} + 6x + 8} {x – 2} \ right) [/ latex], можем ли мы определить предел функции, когда [latex] x [/ latex] приближается к [latex] a [/ latex]?
{5} [/ latex].{2} + 6x + 8} {x – 2} \ right) [/ latex], можем ли мы определить предел функции, когда [latex] x [/ latex] приближается к [latex] a [/ latex]?Да. Некоторые функции могут быть перегруппированы алгебраически, чтобы можно было оценить предел упрощенной эквивалентной формы функции.
Определение предела частного
Найти предел функции, выраженной как частное, может быть сложнее. Нам часто нужно переписать функцию алгебраически, прежде чем применять свойства предела.Если знаменатель равен 0, когда мы применяем свойства предела напрямую, мы должны переписать частное в другой форме. Один из подходов – записать частное в факторизованной форме и упростить.
Практическое руководство. Учитывая предел функции в форме частного, используйте факторинг для ее оценки.
- Полностью разложите числитель и знаменатель на множители.
- Упростите, разделив любые множители, общие для числителя и знаменателя.
- Оцените полученный предел, не забывая использовать правильный домен.
 {2} -6x + 8} {x – 2} \ right) = \ underset {x \ to 2} {\ mathrm {lim}} \ left (\ frac {\ left (x – 2 \ right) \ left ( x – 4 \ right)} {x – 2} \ right) \ hfill & \ text {Разложите числитель на множители}. \ hfill \\ \ text {} = \ underset {x \ to 2} {\ mathrm {lim}} \ left (\ frac {\ overline {) \ left (x – 2 \ right)} \ left (x – 4 \ right)} {\ overline {) x – 2}} \ right) \ hfill & \ text {Отмена общие факторы}. \ hfill \\ \ text {} = \ underset {x \ to 2} {\ mathrm {lim}} \ left (x – 4 \ right) \ hfill & \ text {Evaluate}. \ hfill \ \ \ text {} = 2 – 4 = -2 \ hfill & \ hfill \ end {array} [/ latex]
{2} -6x + 8} {x – 2} \ right) = \ underset {x \ to 2} {\ mathrm {lim}} \ left (\ frac {\ left (x – 2 \ right) \ left ( x – 4 \ right)} {x – 2} \ right) \ hfill & \ text {Разложите числитель на множители}. \ hfill \\ \ text {} = \ underset {x \ to 2} {\ mathrm {lim}} \ left (\ frac {\ overline {) \ left (x – 2 \ right)} \ left (x – 4 \ right)} {\ overline {) x – 2}} \ right) \ hfill & \ text {Отмена общие факторы}. \ hfill \\ \ text {} = \ underset {x \ to 2} {\ mathrm {lim}} \ left (x – 4 \ right) \ hfill & \ text {Evaluate}. \ hfill \ \ \ text {} = 2 – 4 = -2 \ hfill & \ hfill \ end {array} [/ latex]Анализ решения
Когда предел рациональной функции не может быть вычислен напрямую, факторизованные формы числителя и знаменателя могут упроститься до результата, который может быть вычислен.{2} -11x + 28} {7-x} \ right) [/ latex].
Решение
Пример 6: Оценка предела частного по ЖК-дисплею
Вычислить [латекс] \ underset {x \ to 5} {\ mathrm {lim}} \ left (\ frac {\ frac {1} {x} – \ frac {1} {5}} {x – 5} \ справа) [/ латекс].

Решение
Найдите ЖК-дисплей для знаменателей двух членов в числителе и преобразуйте обе дроби так, чтобы ЖК-дисплей был их знаменателем.
Рисунок 3
Анализ решения
При определении предела рациональной функции, в которой добавлены или вычтены члены в числителе или знаменателе, первым шагом является поиск общего знаменателя добавленных или вычтенных членов; затем преобразуйте оба члена в этот знаменатель или упростите рациональную функцию, умножив числитель и знаменатель на наименьший общий знаменатель.Затем проверьте, есть ли у числителя и знаменателя общие множители.
Попробуй 6
Вычислить [латекс] \ underset {x \ to -5} {\ mathrm {lim}} \ left (\ frac {\ frac {1} {5} + \ frac {1} {x}} {10 + 2x} \ справа) [/ латекс].
Решение
Практическое руководство. Учитывая предел функции, содержащей корень, для вычисления используйте конъюгат.
- Если данное частное не в неопределенной [латексной] \ левой (\ frac {0} {0} \ правой) [/ латексной] форме, оцените напрямую.

- В противном случае перепишите сумму (или разность) двух частных как одинарное частное, используя наименьший общий знаменатель (LCD) .
- Если числитель включает корень, рационализируйте числитель; умножьте числитель и знаменатель на , сопряженное числителя. Напомним, что [latex] a \ pm \ sqrt {b} [/ latex] являются конъюгатами.
- Упростить.
- Оцените полученный предел.
Пример 7: Оценка предела, содержащего корень, с помощью конъюгата
Вычислить [латекс] \ underset {x \ to 0} {\ mathrm {lim}} \ left (\ frac {\ sqrt {25-x} -5} {x} \ right) [/ latex].
Решение
[латекс] \ begin {array} {ll} \ underset {x \ to 0} {\ mathrm {lim}} \ left (\ frac {\ sqrt {25-x} -5} {x} \ right) = \ underset {x \ to 0} {\ mathrm {lim}} \ left (\ frac {\ left (\ sqrt {25-x} -5 \ right)} {x} \ cdot \ frac {\ left (\ sqrt {25-x} +5 \ right)} {\ left (\ sqrt {25-x} +5 \ right)} \ right) \ hfill & \ text {Умножьте числитель и знаменатель на сопряжение}.
 \ hfill \\ \ text {} = \ underset {x \ to 0} {\ mathrm {lim}} \ left (\ frac {\ left (25-x \ right) -25} {x \ left (\ sqrt { 25-x} +5 \ right)} \ right) \ hfill & \ text {Умножение:} \ left (\ sqrt {25-x} -5 \ right) \ cdot \ left (\ sqrt {25-x} + 5 \ right) = \ left (25-x \ right) -25. \ Hfill \\ \ text {} = \ underset {x \ to 0} {\ mathrm {lim}} \ left (\ frac {-x} {x \ left (\ sqrt {25-x} +5 \ right)} \ right) \ hfill & \ text {Объединить похожие термины}. \ hfill \\ \ text {} = \ underset {x \ to 0} { \ mathrm {lim}} \ left (\ frac {- \ overline {) x}} {\ overline {) x} \ left (\ sqrt {25-x} +5 \ right)} \ right) \ hfill & \ текст {Упростить} \ frac {-x} {x} = – 1.\ hfill \\ \ text {} = \ frac {-1} {\ sqrt {25-0} +5} \ hfill & \ text {Evaluate}. \ hfill \\ \ text {} = \ frac {-1} {5 + 5} = – \ frac {1} {10} \ hfill & \ hfill \ end {array} [/ latex]
\ hfill \\ \ text {} = \ underset {x \ to 0} {\ mathrm {lim}} \ left (\ frac {\ left (25-x \ right) -25} {x \ left (\ sqrt { 25-x} +5 \ right)} \ right) \ hfill & \ text {Умножение:} \ left (\ sqrt {25-x} -5 \ right) \ cdot \ left (\ sqrt {25-x} + 5 \ right) = \ left (25-x \ right) -25. \ Hfill \\ \ text {} = \ underset {x \ to 0} {\ mathrm {lim}} \ left (\ frac {-x} {x \ left (\ sqrt {25-x} +5 \ right)} \ right) \ hfill & \ text {Объединить похожие термины}. \ hfill \\ \ text {} = \ underset {x \ to 0} { \ mathrm {lim}} \ left (\ frac {- \ overline {) x}} {\ overline {) x} \ left (\ sqrt {25-x} +5 \ right)} \ right) \ hfill & \ текст {Упростить} \ frac {-x} {x} = – 1.\ hfill \\ \ text {} = \ frac {-1} {\ sqrt {25-0} +5} \ hfill & \ text {Evaluate}. \ hfill \\ \ text {} = \ frac {-1} {5 + 5} = – \ frac {1} {10} \ hfill & \ hfill \ end {array} [/ latex]Анализ решения
При определении предела функции с корнем в качестве одного из двух членов, где мы не можем вычислить напрямую, подумайте о умножении числителя и знаменателя на сопряжение членов.

Попробуйте 7
Оцените следующий предел: [латекс] \ underset {h \ to 0} {\ mathrm {lim}} \ left (\ frac {\ sqrt {16-h} -4} {h} \ right) [/ latex] .
Решение
Пример 8: Оценка предела частного значения функции путем факторинга
Вычислить [латекс] \ underset {x \ to 4} {\ mathrm {lim}} \ left (\ frac {4-x} {\ sqrt {x} -2} \ right) [/ latex].
Решение
[латекс] \ begin {array} {ll} \ underset {x \ to 4} {\ mathrm {lim}} \ left (\ frac {4-x} {\ sqrt {x} -2} \ right) = \ underset {x \ to 4} {\ mathrm {lim}} \ left (\ frac {\ left (2+ \ sqrt {x} \ right) \ left (2- \ sqrt {x} \ right)} {\ sqrt {x} -2} \ right) \ hfill & \ text {Factor.} \ hfill \\ \ text {} = \ underset {x \ to 4} {\ mathrm {lim}} \ left (\ frac {\ left (2+ \ sqrt {x} \ right) \ overline {) \ left (2- \ sqrt {x} \ right)}} {- \ overline {) \ left (2- \ sqrt {x} \ right) }} \ right) \ hfill & \ text {Factor} -1 \ text {вне знаменателя} \ text {.{2} [/ латекс]
и может быть разложен на
[латекс] \ left (a + b \ right) \ left (a-b \ right) [/ латекс].

Попробуй 8
Оцените следующий предел: [latex] \ underset {x \ to 3} {\ mathrm {lim}} \ left (\ frac {x – 3} {\ sqrt {x} – \ sqrt {3}} \ right) [/латекс].
Решение
Практическое руководство. Получив частное с абсолютными значениями, оцените его предел.
- Попробуйте разложить на множители или найти ЖК-дисплей.
- Если предел не может быть найден, выберите несколько значений, близких и по обе стороны от входа, где функция не определена.
- Используйте числовое свидетельство, чтобы оценить пределы с обеих сторон.
Пример 9: Оценка предела частного с помощью абсолютных значений
Вычислить [латекс] \ underset {x \ to 7} {\ mathrm {lim}} \ frac {| x – 7 |} {x – 7} [/ latex].
Решение
Функция не определена при [latex] x = 7 [/ latex], поэтому мы попробуем значения, близкие к 7 слева и справа.
Предел слева: [латекс] \ frac {| 6.9 – 7 |} {6.
 9 – 7} = \ frac {| 6.99 – 7 |} {6.99 – 7} = \ frac {| 6.{+}} {\ mathrm {lim}} \ frac {6-x} {| x – 6 |} [/ latex].
9 – 7} = \ frac {| 6.99 – 7 |} {6.99 – 7} = \ frac {| 6.{+}} {\ mathrm {lim}} \ frac {6-x} {| x – 6 |} [/ latex].Решение
Ключевые концепции
- Свойства ограничений могут использоваться для выполнения операций с пределами функций, а не с самими функциями.
- Предел полиномиальной функции можно найти, найдя сумму пределов отдельных членов.
- Предел функции, возведенный в степень, равен той же степени, что и предел функции. Другой метод – прямая подмена.
- Предел корня функции равен соответствующему корню предела функции.
- Один из способов найти предел функции, выраженной как частное, – это записать частное в факторизованной форме и упростить.
- Другой метод определения предела сложной дроби – найти ЖК-дисплей.
- Предел, содержащий функцию, содержащую корень, может быть вычислен с использованием конъюгата.
- Пределы некоторых функций, выраженные в виде частных, можно найти с помощью факторинга.

- Один из способов оценить предел частного, содержащего абсолютные значения, – использовать числовое свидетельство. Также может быть полезна его настройка по частям.
Глоссарий
- свойства пределов
- Сборник теорем для нахождения пределов функций путем выполнения математических операций над пределами
Упражнения по разделу
1. Приведите пример типа функции [latex] f [/ latex], предел которой, когда [latex] x [/ latex] приближается к [latex] a [/ latex], составляет [latex] f \ left (a \ справа) [/ латекс].
2. Когда прямая подстановка используется для оценки предела рациональной функции, поскольку [латекс] x [/ латекс] приближается к [латексу] a [/ латексу], и в результате получается [латекс] f \ left (a \ right) = \ frac {0} {0} [/ latex], означает ли это, что предел [latex] f [/ latex] не существует?
3. Что означает утверждение, что предел [латекса] f \ left (x \ right) [/ latex], поскольку [latex] x [/ latex] приближается к [latex] c [/ latex], не определен?
Для следующих упражнений оцените пределы алгебраически.

4.{2}} {x – 2} \ right) [/ латекс]
Для следующего упражнения используйте данную информацию для оценки пределов: [латекс] \ underset {x \ to c} {\ mathrm {lim}} f \ left (x \ right) = 3 [/ latex], [latex ] \ underset {x \ to c} {\ mathrm {lim}} g \ left (x \ right) = 5 [/ latex]
31. [латекс] \ underset {x \ to c} {\ mathrm {lim}} \ left [2f \ left (x \ right) + \ sqrt {g \ left (x \ right)} \ right] [/ латекс]
32. [латекс] \ underset {x \ to c} {\ mathrm {lim}} \ left [3f \ left (x \ right) + \ sqrt {g \ left (x \ right)} \ right] [/ латекс]
33. [латекс] \ underset {x \ to c} {\ mathrm {lim}} \ frac {f \ left (x \ right)} {g \ left (x \ right)} [/ latex]
Для следующих упражнений оцените следующие пределы.{2}} [/ латекс]
51. [латекс] f \ left (x \ right) = \ sqrt {x} [/ latex]
52. Найдите уравнение, которое может быть представлено на рисунке 2.
Рисунок 2
53. Найдите уравнение, которое можно представить на рис.
 3.
3.Рисунок 4
Следующие упражнения см. На рис. 4.
Рисунок 5
54. Каков правый предел функции, когда [latex] x [/ latex] приближается к 0?
55.{0,0425t} [/ latex], где [latex] {A} _ {0} [/ latex] – начальная сумма инвестиций. Найдите среднюю скорость изменения баланса аккаунта с [latex] t = 1 [/ latex] года до [latex] t = 2 [/ latex] лет, если первоначальная сумма инвестиций составляет 1000 долларов США.
Calculus – Решение пределов с квадратными корнями
Calculus – Решение пределов с квадратными корнями – Mathematics Stack ExchangeСеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange
- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange – это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 37k раз
$ \ begingroup $Мне сложно понять, как решить этот предел путем рационализации.
 2 + 11} +6} \\ [2ex]
& = \ frac {10} {12} \\ [2ex]
& = \ frac {5} {6}
\ end {align} $$
2 + 11} +6} \\ [2ex]
& = \ frac {10} {12} \\ [2ex]
& = \ frac {5} {6}
\ end {align} $$Создан 08 июля ’15 в 4: 362015-07-08 04:36
Рори ДолтонРори Долтон31.2 + 11} – 6} {y} = \ frac {\ frac {5} {6} y + o (y)} {y} = \ frac {5} {6} + o (1) \ xrightarrow [y \ по 0] {} \ frac {5} {6}. $$
Создан 08 июл.
Клемент К.61.9k33 золотых знака5555 серебряных знаков126126 бронзовых знаков
$ \ endgroup $ Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.

Принимать все файлы cookie Настроить параметры
Предел на бесконечности Задачи с квадратными корнями – Matheno.com
По мере того, как $ x \ to \, – \ infty $, член $ x $ становится все больше и больше в отрицательном направлении, а член квадратного корня становится все больше и больше в положительном направлении.2}}} \\ [8 пикселей] & = \ lim_ {x \ to \, – \ infty} \ frac {-a} {1 + \ sqrt {1 + \ frac {a} {x}}} \\ [8px] & = \ frac {-a} {1 + \ sqrt {1}} \\ [8px] & = \ frac {-a} {2} \ quad \ cmark
\ end {align *} \]Обратите внимание, что во второй предпоследней строке мы использовали тот факт, что $ \ displaystyle {\ lim_ {x \ to \, – \ infty} \ frac {a} {x} = 0}. $
[свернуть]
Пределы на бесконечности — Корни и абсолютные значения
Краткий обзор
- Во-первых, если есть квадратный корень, вычтите за скобки наибольшую степень $$ x $$, которая находится под корнем.
 2} = | a | $$
2} = | a | $$ - $$ | а | = a $$, если $$ a $$ положительно, но $$ | a | = -a $$, если значение $$ 4a $$ отрицательное.
Примеры
Пример 1
Вычислить $$ \ displaystyle \ lim_ {x \ to \ infty} \, \ frac {| x | +2} {4x + 3} $$
Шаг 1Упростите абсолютное значение.
Поскольку предел учитывает положительные значения $$ x $$, мы знаем, что $$ | x | = x $$.Таким образом, мы можем переписать предел как
$$ \ displaystyle \ lim_ {x \ to \ infty} \, \ frac {\ blue {| x |} +2} {4x + 3} % = \ displaystyle \ lim_ {x \ to \ infty} \, \ frac {\ blue x + 2} {4x + 3}. $$
Шаг 2Выносим за скобки числитель и знаменатель $$ x $$.
 Затем разделите общий множитель.
Затем разделите общий множитель.$$ \ begin {align *}% \ lim_ {x \ to \ infty} \, \ frac {\ blue x + 2} {4 \ blue x + 3} % & = \ lim_ {x \ to \ infty} \, \ frac {% \ синий x \ left (% 1 + \ frac 2 {\ blue x} \верно) } {% \ синий x \ left (% 4 + \ frac 3 {\ blue x} \верно) } \\ [6pt] % & = \ lim_ {x \ to \ infty} \, \ frac {% 1 + \ гидроразрыва 2 х } {% 4 + \ гидроразрыва 3 х } \ end {выровнять *} $$
Шаг 3Оцените предел.

$$ \ Displaystyle \ lim_ {х \ к \ infty} \, \ гидроразрыва {% 1 + \ синий {\ frac 2 x} } {% 4 + \ красный {\ frac 3 x} } % = \ frac {1 + \ blue 0} {4 + \ red 0} % = \ frac 1 4 $$
Отвечать$$ \ displaystyle \ lim_ {x \ to \ infty} \, \ frac {| x | + 2} {4x + 3} = \ frac 1 4 $$
Пример 2
Вычислить $$ \ displaystyle \ lim_ {x \ to- \ infty} \, \ frac {| x | +2} {4x + 3} $$
Обратите внимание, что это та же функция, что и в примере 1, но на этот раз $$ x $$ становится отрицательным.
Шаг 1
Упростите абсолютное значение.
Поскольку этот предел учитывает отрицательные значения $$ x $$, мы знаем, что $$ | x | = -x $$. Это означает, что мы можем переписать предел как
$$ \\ \ displaystyle \ lim_ {x \ to- \ infty} \, \ frac {\ blue {| x |} + 2} {4x + 3} % = \ lim_ {x \ to- \ infty} \, \ frac {\ blue {-x} + 2} {4x + 3} \\ $$
Шаг 2Выносим за скобки числитель и знаменатель наибольшей степени $$ x $$.Затем разделите общий множитель.
$$ \ begin {align *}% \ lim_ {x \ to- \ infty} \, \ frac {- \ blue x + 2} {4 \ blue x + 3} % & = \ lim_ {x \ to- \ infty} \, \ frac {% \ синий x \ left (% -1 + \ frac 2 {\ blue x} \верно) } {% \ синий x \ left (% 4+ \ frac 3 {\ blue x} \верно) } \\ [6pt] % & = \ lim_ {x \ to- \ infty} \, \ frac {-1 + \ frac 2 x} {4+ \ frac 3 x} \ end {выровнять *} $$
Шаг 3Оцените предел.
Продолжайте практиковать задачи 2-4}} {8x +3} = \ frac 5 8 $$
2-4}} {8x +3} = \ frac 5 8 $$Ошибка: Нажмите «Не робот», затем повторите попытку.
Пределы на бесконечности. Независимо от того, какие у вас ограничения… | Соломон Се | Основы исчисления
Независимо от того, какие типы пределов вы ищете,
, чтобы лучше понять это,
лучший способ – прочитать пошаговое решениеSymbolab:
Калькулятор пределов от Symbolab.)КЛЮЧЕВОЙ момент – посмотреть на степени и коэффициенты числителя и доминатора.
То же самое сПоиск асимптоты.Обратитесь к предыдущему примечанию к
Как найти Asymptote.Решить:
КЛЮЧЕВОЙ пункт – вычислить числитель
и доминатор, а затем вычислить предел КАЖДОГО члена с помощью квадратного корня.
Решите:
См. Пошаговое решение Symbolab.)- Разделите на наивысшую мощность , чтобы получить:
- Рассчитайте отдельно предел
ЧислительиДоминатор:
- Вычислите
Квадратный корень: Необходимо найти пределы для КАЖДОГО члена внутри квадратного корня.
- Тогда легко получить результат.
КЛЮЧЕВОЙ момент – применить теорему
о сжатии, и это ОБЯЗАТЕЛЬНО.Решить:
- Знайте, что
-1 cos (x) ≦ 1, поэтому мы можем настроить его, чтобы применить теоремуо сжатии, чтобы получить его предел. - Сделайте неравенство:
3 / -1 ≦ 3 / cos (x) / - 1 ≦ 3/1 - Получите правую часть
3 / -1 = -1и левую3/1 = 1не равно.
- Значит, лимита не существует.
Шаги более простого решения :
- Знать неравенство
-1 ≦ cos (x) ≦ 1 - Заменить
cos (x)на± 1в уравнении,3 / ± 1. - Вычислить пределы двух сторон.
- Если результаты точно такие же, то предел – это результат; В противном случае ограничения не существует.
Решить:
- Знайте, что
-1 ≦ sin (x) ≦ 1 - Замените
sin (x)как± 1 - Левая сторона станет
(5x + 1) / (x- 5), правая сторона становится(5x-1) / (x-5) - Пределы обеих сторон равны
5, поэтому предел существует, и он равен5.2−6x − 7} {x − 7} \ nonumber \]Функцию можно разложить следующим образом:
\ [f (x) = \ dfrac {\ cancel {(x − 7)} (x + 1)} {\ cancel {x − 7}} \ nonumber \]
, что дает нам
\ [f (x) = x + 1, x ≠ 7.
 \ nonumber \]
\ nonumber \]Означает ли это, что функция \ (f (x) \) такая же, как функция \ (g (x) = x + 1? \)
Ответ – нет. Функция \ (f (x) \) не имеет \ (x = 7 \) в своей области определения, но \ (g (x) \) имеет. Графически мы видим, что в графике \ (f (x) \) есть дыра в точке \ (x = 7 \), как показано на рисунке, и нет такой дыры в графике \ (g (x) \), как показано на рисунке.
(слева) График функции \ (f \) содержит разрыв в точке \ (x = 7 \) и, следовательно, не является непрерывным в точке \ (x = 7 \). (Справа) График функции \ (g \) непрерывен.
Итак, эти две разные функции также имеют разные ограничения, поскольку \ (x \) приближается к 7? Не обязательно. Помните, что при определении предела функции, когда \ (x \) приближается к \ (a \), важно то, приближается ли результат к действительному числу, когда мы приближаемся к \ (x = a \). Существование предела не зависит от того, что происходит, когда \ (x \) равно \ (a \).
Посмотрите еще раз на рисунок и рисунок.
. Обратите внимание, что на обоих графиках, когда \ (x \) приближается к 7, выходные значения приближаются к 8. Это означает
Обратите внимание, что на обоих графиках, когда \ (x \) приближается к 7, выходные значения приближаются к 8. Это означает\ [\ lim \ limits_ {x \ to 7} f (x) = \ lim \ limits_ {x \ to 7} g (x). \ nonumber \]
Помните, что при определении предела важно то, что происходит рядом с \ (x = a \), а не с \ (x = a \). В этом разделе мы будем использовать различные методы, такие как переписывание функций на множители, чтобы оценить предел. Эти методы дадут нам формальную проверку того, что мы раньше делали интуитивно.
Определение предела суммы, разницы и произведения
Построение графика функции или изучение таблицы значений для определения предела может быть обременительным и трудоемким. По возможности более эффективно использовать свойств пределов , которые представляют собой набор теорем для нахождения пределов.
Знание свойств пределов позволяет нам вычислять пределы напрямую. Мы можем складывать, вычитать, умножать и делить пределы функций, как если бы мы выполняли операции над самими функциями, чтобы найти предел результата.
 Точно так же мы можем найти предел функции, возведенной в степень, подняв предел до этой степени. Мы также можем найти предел корня функции, взяв корень предела. Используя эти операции над пределами, мы можем найти пределы более сложных функций, найдя пределы их более простых компонентных функций.
Точно так же мы можем найти предел функции, возведенной в степень, подняв предел до этой степени. Мы также можем найти предел корня функции, взяв корень предела. Используя эти операции над пределами, мы можем найти пределы более сложных функций, найдя пределы их более простых компонентных функций.свойства лимитов
Пусть \ (a, k, A, \) и \ (B \) представляют действительные числа, а \ (f \) и \ (g \) будут функциями, такими, что \ (\ lim \ limits_ {x \ to a } f (x) = A \) и \ (\ lim \ limits_ {x \ to a} g (x) = B.\) Для существующих и конечных пределов свойства пределов сведены в Таблицу
.Константа, k \ (\ lim \ limits_ {x \ to a} k = k \) Постоянно раз функция \ (\ lim \ limits_ {x \ to a} [k⋅f (x)] = k \ lim \ limits_ {x \ to a} f (x) = kA \) Сумма функций \ (\ lim \ limits_ {x \ to a} [f (x) + g (x)] = \ lim \ limits_ {x \ to a} f (x) + \ lim \ limits_ {x to a} g (х) = А + В \) Различие функций \ (\ lim \ limits_ {x \ to a} [f (x) −g (x)] = \ lim \ limits_ {x \ to a} f (x) – \ lim \ limits_ {x \ to a} г (х) = A − B \) Произведение функций \ (\ lim \ limits _ {x \ to a} [f (x) ⋅g (x)] = \ lim \ limits _ {x \ to a} f (x) ⋅ \ lim \ limits_ {x \ to a} g (x) = A⋅B \) Частное число функций \ (\ lim \ limits _ {x \ to a} \ frac {f (x)} {g (x)} = \ frac {\ lim \ limits _ {x \ to a} f (x)} {\ lim \ limits _ {x \ to a} g (x)} = \ frac {A} {B}, B ≠ 0 \) Функция, возведенная в степень \ (\ lim \ limits _ {x \ to a} [f (x)] ^ n = [\ lim \ limits _ {x \ to ∞} f (x)] ^ n = A ^ n \), где \ (n \) – натуральное число n -й корень функции, где n – положительное целое число \ (\ lim \ limits _ {x \ to a} f (x) \ sqrt [n] {f (x)} = \ sqrt [n] {\ lim \ limits _ {x \ to a} [f ( x)]} = \ sqrt [n] {A} \) Полиномиальная функция \ (\ lim \ limits _ {x \ to a} p (x) = p (a) \) Пример \ (\ PageIndex {1} \): алгебраическое вычисление предела функции
Вычислить \ [\ lim \ limits _ {x \ to 3} (2x + 5).
 \ nonumber \]
\ nonumber \]Решение
\ [\ begin {align} \ lim \ limits _ {x \ to 3} (2x + 5) & = \ lim \ limits _ {x \ to 3} (2x) + \ lim \ limits _ {x \ to 3} (5) && \ text {Свойство суммы функций} \\ & = 2 \ lim \ limits_ {x \ to 3} (x) + \ lim \ limits _ {x \ to 3} (5) && \ text {Постоянное время свойство функции} \\ & = 2 (3) +5 && \ text {Evaluate} \\ & = 11 \ end {align} \ nonumber \]
Упражнение \ (\ PageIndex {1} \):
Оцените следующий предел: \ [\ lim \ limits_ {x \ to −12} (- 2x + 2).\ nonumber \]
Решение
26
Нахождение предела многочлена
Не все функции или их пределы включают простое сложение, вычитание или умножение. Некоторые могут включать многочлены. Напомним, что многочлен – это выражение, состоящее из суммы двух или более членов, каждое из которых состоит из константы и переменной, возведенных в неотрицательную целую степень. Чтобы найти предел полиномиальной функции, мы можем найти пределы отдельных членов функции, а затем сложить их вместе.
 5.2 + 6x + 8} {x − 2}) \), можем ли мы определить предел функции, когда \ (x \) приближается к \ (a \)?
5.2 + 6x + 8} {x − 2}) \), можем ли мы определить предел функции, когда \ (x \) приближается к \ (a \)?Да. Некоторые функции могут быть перегруппированы алгебраически, чтобы можно было оценить предел упрощенной эквивалентной формы функции.
Определение предела частного
Найти предел функции, выраженной как частное, может быть сложнее. Нам часто нужно переписать функцию алгебраически, прежде чем применять свойства предела. Если знаменатель равен 0, когда мы применяем свойства предела напрямую, мы должны переписать частное в другой форме.2−6x + 8} {x − 2}) & = \ lim \ limits_ {x \ to 2} (\ dfrac {(x − 2) (x − 4)} {x − 2}) && \ text {Фактор числитель.} \\ & = \ lim \ limits_ {x \ to 2} (\ dfrac {\ cancel {(x − 2)} (x − 4)} {\ cancel {x − 2}}) && \ text {Отмените общие множители.} \\ & = \ lim \ limits_ {x \ to 2} (x − 4) && \ text {Evaluate.} \\ & = 2−4 = −2 \ end {align} \ nonumber \]
Анализ
Когда предел рациональной функции не может быть вычислен напрямую, факторизованные формы числителя и знаменателя могут упроститься до результата, который может быть вычислен.
 2−11x + 28} {7 − x} \ right). \ nonumber \]
2−11x + 28} {7 − x} \ right). \ nonumber \]Решение
\ (- 3 \)
Пример \ (\ PageIndex {5} \): оценка предела коэффициента по ЖК-дисплею
Вычислить \ [\ lim \ limits_ {x \ to 5} \ left (\ dfrac {\ frac {1} {x} – \ frac {1} {5}} {x − 5} \ right). \ nonumber \]
Решение
Найдите ЖК-дисплей для знаменателей двух членов в числителе и преобразуйте обе дроби так, чтобы ЖК-дисплей был их знаменателем.
Анализ
При определении предела рациональной функции, в которой члены добавляются или вычитаются либо в числителе, либо в знаменателе, первый шаг – найти общий знаменатель добавленных или вычтенных членов; затем преобразуйте оба члена в этот знаменатель или упростите рациональную функцию, умножив числитель и знаменатель на наименьший общий знаменатель.Затем проверьте, есть ли у числителя и знаменателя общие множители.
Упражнение \ (\ PageIndex {5} \):
Вычислить \ [\ lim \ limits_ {x \ to −5} \ left (\ dfrac {\ frac {1} {5} + \ frac {1} {x}} {10 + 2x} \ right). \ nonumber \]
Решение
\ (- \ frac {1} {50} \)
как: Учитывая предел функции, содержащей корень, используйте сопряжение для вычисления
- Если данное частное не имеет неопределенной формы \ ((\ frac {0} {0}) \), оцените напрямую.
- В противном случае перепишите сумму (или разность) двух частных как одинарное частное, используя наименьший общий знаменатель (LCD).
- Если числитель включает корень, рационализируйте числитель; умножьте числитель и знаменатель на , сопряженное числителя. Напомним, что \ (a ± \ sqrt {b} \) сопряжены.
- Упростить.
- Оцените полученный предел.
Пример \ (\ PageIndex {6} \): оценка предела, содержащего корень, с помощью конъюгата
Вычислить \ [\ lim \ limits_ {x \ to 0} \ left (\ dfrac {\ sqrt {25 − x} −5} {x} \ right).\ nonumber \]
Решение
\ [\ begin {align} \ lim \ limits_ {x \ to 0} \ left (\ dfrac {\ sqrt {25 − x} −5} {x} \ right) & = \ lim \ limits_ {x \ to 0} \ left (\ dfrac {(\ sqrt {25 − x} −5)} {x} ⋅ \ frac {(\ sqrt {25 − x} +5)} {(\ sqrt {25 − x} +5 )} \ right) && \ text {Умножьте числитель и знаменатель на сопряжение.} \\ & = \ lim \ limits_ {x \ to 0} \ left (\ dfrac {(25 − x) −25} {x (\ sqrt {25 − x} +5)} \ right) && \ text {Умножить:} (\ sqrt {25 − x} −5) ⋅ (\ sqrt {25 − x} +5) = (25 − x) – 25. \\ & = \ lim \ limits_ {x \ to 0} \ left (\ dfrac {- \ cancel {x}} {\ cancel {x} (25 − x + 5)} \ right) && \ text {Объединить как термины.} \\ & = \ lim \ limits_ {x \ to 0} \ left (\ dfrac {- \ cancel {x}} {\ cancel {x} (\ sqrt {25 − x} +5)} \ right) && \ text {Упростить} \ dfrac {−x} {x} = – 1. \\ & = \ dfrac {−1} {\ sqrt {25−0} +5} && \ text {Оценить.} \\ & = \ dfrac {−1} {5 + 5} = – \ dfrac {1} {10} \ end {align} \ nonumber \]
Анализ
При определении предела функции с корнем в качестве одного из двух членов, где мы не можем вычислить напрямую, подумайте о умножении числителя и знаменателя на сопряжение членов.
Упражнение \ (\ PageIndex {6} \)
Оцените следующий предел: \ (\ lim \ limits_ {h \ to 0} \ left (\ dfrac {\ sqrt {16 − h} −4} {h} \ right) \).
Решение
\ (- \ frac {1} {8} \)
Пример \ (\ PageIndex {7} \): Оценка предела коэффициента функции путем факторинга
Вычислить \ [\ lim \ limits_ {x \ to 4} \ left (\ frac {4 − x} {\ sqrt {x − 2}} \ right). \ nonumber \]
Решение
\ [\ begin {align} \ lim \ limits_ {x \ to 4} (\ dfrac {4 − x} {\ sqrt {x} −2}) & = \ lim \ limits_ {x \ to 4} (\ dfrac {(2+ \ sqrt {x}) (2 − x)} {\ sqrt {x} −2}) && \ text {Фактор.} \\ & = \ lim \ limits_ {x \ to 4} (\ dfrac {(2+ \ sqrt {x}) (\ cancel {2− \ sqrt {x}})} {- \ cancel {(2− \ sqrt {x})}}) && \ text {Выделяем -1 из знаменателя. Упростить.} \\ & = \ lim \ limits_ {x \ to 4} – (2 + x) && \ text {Evaluate.} \\ & = – (2+ \ sqrt {4}) \\ & = – 4 \ end {align} \ nonumber \]
Анализ
Умножение на конъюгат расширит числитель; вместо этого ищите множители в числителе. Четыре – это полный квадрат, поэтому числитель имеет вид
. 2 \ nonumber \]и может быть разложен на
\ [(a + b) (a − b).\ nonumber \]
Упражнение \ (\ PageIndex {7} \)
Оцените следующий предел: \ [\ lim \ limits_ {x \ to 3} \ left (\ frac {x − 3} {\ sqrt {x} – \ sqrt {3}} \ right). \ nonumber \]
Решение
\ (2 \ sqrt {3} \)
как сделать: учитывая частное с абсолютными значениями, оценить его предел
- Попробуйте разложить на множители или найти ЖК-дисплей.
- Если предел не может быть найден, выберите несколько значений, близких и по обе стороны от входа, где функция не определена.
- Используйте числовое свидетельство, чтобы оценить пределы с обеих сторон.
Пример \ (\ PageIndex {8} \): оценка предела коэффициента с абсолютными значениями
Вычислить \ [\ lim \ limits_ {x \ to 7} \ frac {| x − 7 |} {x − 7}. \ nonumber \]
Решение
Функция не определена в \ (x = 7 \), поэтому мы попробуем значения, близкие к 7 слева и справа.
Левый предел: \ [\ frac {| 6.9-7 |} {6.9-7} = \ frac {| 6.99-7 |} {6.99-7} = \ frac {| 6.+} \ frac {6 − x} {| х − 6 |}. \ nonumber \]
Решение
Ключевые концепции
- Свойства ограничений могут использоваться для выполнения операций с пределами функций, а не с самими функциями. См. Пример.
- Предел полиномиальной функции можно найти, найдя сумму пределов отдельных членов. См. Пример и Пример.
- Предел функции, возведенный в степень, равен той же степени, что и предел функции.Другой метод – прямая подмена. См. Пример.
- Предел корня функции равен соответствующему корню предела функции.
- Один из способов найти предел функции, выраженной как частное, – это записать частное в факторизованной форме и упростить. См. Пример.
- Другой метод определения предела сложной дроби – найти ЖК-дисплей. См. Пример.
- Предел, содержащий функцию, содержащую корень, может быть вычислен с использованием конъюгата.См. Пример.
- Пределы некоторых функций, выраженные в виде частных, можно найти с помощью факторинга. См. Пример.
- Один из способов оценить предел частного, содержащего абсолютные значения, – использовать числовое свидетельство. Также может быть полезна его настройка по частям. См. Пример.
Глоссарий
- свойства пределов
- Сборник теорем для нахождения пределов функций путем выполнения математических операций над пределами
Видео с вопросом: Определение предела функций, включающих квадратные корни, с использованием рационализации
Стенограмма видео
Найдите предел квадратного корня плюс девять минус квадратный корень минус 𝑥 плюс девять над 𝑥, когда 𝑥 стремится к нулю.
Снова выписываем лимит. Мы видим, что, поскольку знаменатель равен, мы не можем просто заменить. Точно так же мы не можем записать предел этого частного как частное от пределов, поскольку это правило применяется только тогда, когда значение предела в знаменателе не равно нулю.
Если бы это была рациональная функция с полиномом в числителе, а не что-то, включающее радикалы, как у нас, то мы бы надеялись найти множитель 𝑥 в числителе, чтобы сократить его с в знаменателе.
К сожалению, в числителе стоят радикалы. И нет очевидного множителя 𝑥. Нам нужно будет его создать. И мы делаем это, умножая числитель и знаменатель на сопряжение числителя. Сопряжение минус 𝑏 есть 𝑎 плюс 𝑏. Итак, мы умножаем числитель и знаменатель на квадратный корень плюс девять плюс квадратный корень минус плюс девять.
Затем мы можем упростить числитель, используя разность двух квадратов идентичности, либо расширив, а затем отменив.И мы можем еще больше упростить: квадратный корень из плюс девять в квадрате составляет всего 𝑥 плюс девять. А другой член, квадратный корень минус плюс девять в квадрате, равен минус 𝑥 плюс девять.
Опять же, мы оставляем знаменатель как есть и упрощаем числитель, на этот раз собирая одинаковые термины. 𝑥 минус минус 𝑥 дает два 𝑥. А девять минус девять ничего не дают. Значит, в числителе всего два 𝑥. А теперь мы замечаем общий множитель в числителе и знаменателе, который мы сокращаем.
И вот мы подошли к моменту, когда мы можем напрямую заменить.Подставляя ноль вместо, мы что-то получаем. Мы можем оценить как вручную, так и с помощью калькулятора. Двое больше шести, или одна треть. Основным приемом решения этой проблемы было умножение на сопряжение числителя, чтобы рационализировать числитель.
После некоторой алгебры это позволило нам найти множитель в числителе, который затем мы могли бы сократить множителем в знаменателе. Конечно, это изменяет область определения функции внутри предела. Исходная функция не была определена при, равном нулю.Но для всех других значений 𝑥 эти две функции, исходная функция и упрощенная функция, имеют одинаковый результат.
И поскольку предел, когда стремится к нулю, зависит только от значений 𝑥, близких к нулю, а не 𝑥, сам равен нулю, эти два предела равны.
- Если данное частное не в неопределенной [латексной] \ левой (\ frac {0} {0} \ правой) [/ латексной] форме, оцените напрямую.
- Отправка знака квадратного корня в textarea


 2+bx+c=a\cdot(x-x_1)\cdot(x-x_2)
\end{equation}
$$
2+bx+c=a\cdot(x-x_1)\cdot(x-x_2)
\end{equation}
$$ $$
$$ 2
2
 0 ) становятся незначительными, таким образом оставляя:
0 ) становятся незначительными, таким образом оставляя: Я пытаюсь сделать реалистичные упругие столкновения между…
Я пытаюсь сделать реалистичные упругие столкновения между… Например, для добавления ограничения относительно действительного числа x, которое x*x = 2, каков наилучший способ его кодирования? Я…
Например, для добавления ограничения относительно действительного числа x, которое x*x = 2, каков наилучший способ его кодирования? Я… Однако,…
Однако,… Для существующих и конечных пределов свойства пределов приведены в таблице ниже.
Для существующих и конечных пределов свойства пределов приведены в таблице ниже.
 Чтобы найти предел полиномиальной функции, мы можем найти пределы отдельных членов функции, а затем сложить их вместе.Кроме того, предел полиномиальной функции по мере приближения [latex] x [/ latex] к [latex] a [/ latex] эквивалентен простому вычислению функции для [latex] a [/ latex].
Чтобы найти предел полиномиальной функции, мы можем найти пределы отдельных членов функции, а затем сложить их вместе.Кроме того, предел полиномиальной функции по мере приближения [latex] x [/ latex] к [latex] a [/ latex] эквивалентен простому вычислению функции для [latex] a [/ latex]. {5} [/ latex].{2} + 6x + 8} {x – 2} \ right) [/ latex], можем ли мы определить предел функции, когда [latex] x [/ latex] приближается к [latex] a [/ latex]?
{5} [/ latex].{2} + 6x + 8} {x – 2} \ right) [/ latex], можем ли мы определить предел функции, когда [latex] x [/ latex] приближается к [latex] a [/ latex]? {2} -6x + 8} {x – 2} \ right) = \ underset {x \ to 2} {\ mathrm {lim}} \ left (\ frac {\ left (x – 2 \ right) \ left ( x – 4 \ right)} {x – 2} \ right) \ hfill & \ text {Разложите числитель на множители}. \ hfill \\ \ text {} = \ underset {x \ to 2} {\ mathrm {lim}} \ left (\ frac {\ overline {) \ left (x – 2 \ right)} \ left (x – 4 \ right)} {\ overline {) x – 2}} \ right) \ hfill & \ text {Отмена общие факторы}. \ hfill \\ \ text {} = \ underset {x \ to 2} {\ mathrm {lim}} \ left (x – 4 \ right) \ hfill & \ text {Evaluate}. \ hfill \ \ \ text {} = 2 – 4 = -2 \ hfill & \ hfill \ end {array} [/ latex]
{2} -6x + 8} {x – 2} \ right) = \ underset {x \ to 2} {\ mathrm {lim}} \ left (\ frac {\ left (x – 2 \ right) \ left ( x – 4 \ right)} {x – 2} \ right) \ hfill & \ text {Разложите числитель на множители}. \ hfill \\ \ text {} = \ underset {x \ to 2} {\ mathrm {lim}} \ left (\ frac {\ overline {) \ left (x – 2 \ right)} \ left (x – 4 \ right)} {\ overline {) x – 2}} \ right) \ hfill & \ text {Отмена общие факторы}. \ hfill \\ \ text {} = \ underset {x \ to 2} {\ mathrm {lim}} \ left (x – 4 \ right) \ hfill & \ text {Evaluate}. \ hfill \ \ \ text {} = 2 – 4 = -2 \ hfill & \ hfill \ end {array} [/ latex]

 \ hfill \\ \ text {} = \ underset {x \ to 0} {\ mathrm {lim}} \ left (\ frac {\ left (25-x \ right) -25} {x \ left (\ sqrt { 25-x} +5 \ right)} \ right) \ hfill & \ text {Умножение:} \ left (\ sqrt {25-x} -5 \ right) \ cdot \ left (\ sqrt {25-x} + 5 \ right) = \ left (25-x \ right) -25. \ Hfill \\ \ text {} = \ underset {x \ to 0} {\ mathrm {lim}} \ left (\ frac {-x} {x \ left (\ sqrt {25-x} +5 \ right)} \ right) \ hfill & \ text {Объединить похожие термины}. \ hfill \\ \ text {} = \ underset {x \ to 0} { \ mathrm {lim}} \ left (\ frac {- \ overline {) x}} {\ overline {) x} \ left (\ sqrt {25-x} +5 \ right)} \ right) \ hfill & \ текст {Упростить} \ frac {-x} {x} = – 1.\ hfill \\ \ text {} = \ frac {-1} {\ sqrt {25-0} +5} \ hfill & \ text {Evaluate}. \ hfill \\ \ text {} = \ frac {-1} {5 + 5} = – \ frac {1} {10} \ hfill & \ hfill \ end {array} [/ latex]
\ hfill \\ \ text {} = \ underset {x \ to 0} {\ mathrm {lim}} \ left (\ frac {\ left (25-x \ right) -25} {x \ left (\ sqrt { 25-x} +5 \ right)} \ right) \ hfill & \ text {Умножение:} \ left (\ sqrt {25-x} -5 \ right) \ cdot \ left (\ sqrt {25-x} + 5 \ right) = \ left (25-x \ right) -25. \ Hfill \\ \ text {} = \ underset {x \ to 0} {\ mathrm {lim}} \ left (\ frac {-x} {x \ left (\ sqrt {25-x} +5 \ right)} \ right) \ hfill & \ text {Объединить похожие термины}. \ hfill \\ \ text {} = \ underset {x \ to 0} { \ mathrm {lim}} \ left (\ frac {- \ overline {) x}} {\ overline {) x} \ left (\ sqrt {25-x} +5 \ right)} \ right) \ hfill & \ текст {Упростить} \ frac {-x} {x} = – 1.\ hfill \\ \ text {} = \ frac {-1} {\ sqrt {25-0} +5} \ hfill & \ text {Evaluate}. \ hfill \\ \ text {} = \ frac {-1} {5 + 5} = – \ frac {1} {10} \ hfill & \ hfill \ end {array} [/ latex]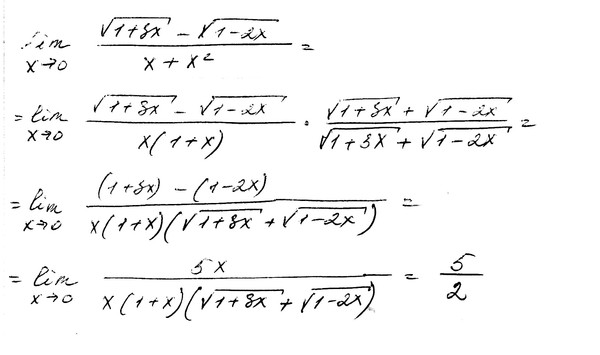

 9 – 7} = \ frac {| 6.99 – 7 |} {6.99 – 7} = \ frac {| 6.{+}} {\ mathrm {lim}} \ frac {6-x} {| x – 6 |} [/ latex].
9 – 7} = \ frac {| 6.99 – 7 |} {6.99 – 7} = \ frac {| 6.{+}} {\ mathrm {lim}} \ frac {6-x} {| x – 6 |} [/ latex].

 3.
3.
 2 + 11} +6} \\ [2ex]
& = \ frac {10} {12} \\ [2ex]
& = \ frac {5} {6}
\ end {align} $$
2 + 11} +6} \\ [2ex]
& = \ frac {10} {12} \\ [2ex]
& = \ frac {5} {6}
\ end {align} $$
 2} = | a | $$
2} = | a | $$ Затем разделите общий множитель.
Затем разделите общий множитель.

 2-4}} {8x +3} = \ frac 5 8 $$
2-4}} {8x +3} = \ frac 5 8 $$

 \ nonumber \]
\ nonumber \] Обратите внимание, что на обоих графиках, когда \ (x \) приближается к 7, выходные значения приближаются к 8. Это означает
Обратите внимание, что на обоих графиках, когда \ (x \) приближается к 7, выходные значения приближаются к 8. Это означает Точно так же мы можем найти предел функции, возведенной в степень, подняв предел до этой степени. Мы также можем найти предел корня функции, взяв корень предела. Используя эти операции над пределами, мы можем найти пределы более сложных функций, найдя пределы их более простых компонентных функций.
Точно так же мы можем найти предел функции, возведенной в степень, подняв предел до этой степени. Мы также можем найти предел корня функции, взяв корень предела. Используя эти операции над пределами, мы можем найти пределы более сложных функций, найдя пределы их более простых компонентных функций. \ nonumber \]
\ nonumber \] 5.2 + 6x + 8} {x − 2}) \), можем ли мы определить предел функции, когда \ (x \) приближается к \ (a \)?
5.2 + 6x + 8} {x − 2}) \), можем ли мы определить предел функции, когда \ (x \) приближается к \ (a \)? 2−11x + 28} {7 − x} \ right). \ nonumber \]
2−11x + 28} {7 − x} \ right). \ nonumber \]