принцип, теорема и примеры решения задач
Задание. Решить СЛАУ $\left\{\begin{array}{l} 2 x_{1}+x_{2}+x_{3}=2 \\ x_{1}-x_{2}=-2 \\ 3 x_{1}-x_{2}+2 x_{3}=2 \end{array}\right.$ методом Гаусса.
Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент $a_{11}$ равнялся 1 (это мы делаем для упрощения вычислений):
$$\tilde{A}=A \mid B=\left(\begin{array}{rrr|r} 2 & 1 & 1 & 2 \\ 1 & -1 & 0 & -2 \\ 3 & -1 & 2 & 2 \end{array}\right) \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 2 & 1 & 1 & 2 \\ 3 & -1 & 2 & 2 \end{array}\right)$$Далее делаем нули под главной диагональю в первом столбце.
Все элементы третьей строки делим на два (или, что тоже самое, умножаем на $\frac{1}{2}$ ):
$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 3 & 1 & 6 \\ 0 & 1 & 1 & 4 \end{array}\right)$$Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:
От третьей строки отнимаем вторую, умноженную на 3:
$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 0 & -2 & -6 \end{array}\right)$$Умножив третью строку на $\left(-\frac{1}{2}\right)$ , получаем:
$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 0 & 1 & 3 \end{array}\right)$$Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю.
Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:
$$\tilde{A} \sim\left(\begin{array}{ccc|c} 1 & 0 & 0 & -1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 3 \end{array}\right)$$Полученной матрице соответствует система
Ответ. $\left\{\begin{array}{l} x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3 \end{array}\right.$
Решение систем линейных уравнений методом Гаусса
1.
 Решение систем линейных уравнений методом Гаусса
Решение систем линейных уравнений методом Гаусса2. Метод Гаусса – это метод последовательного исключения переменных
• Систему уравнений приводят кэквивалентной ей системе с
треугольной матрицей. Это называется
прямым ходом.
• Из полученной треугольной системы
переменные находят с помощью
последовательных подстановок. Это
называется обратным ходом.
3. При выполнении прямого хода используют следующие преобразования:
1. Умножение или деление коэффициентов2. Сложение и вычитание уравнений;
3. Перестановка уравнений системы;
4. Исключение из системы уравнений, в
которых все коэффициенты при
неизвестных и свободные члены равны
нулю.
4. Решить систему уравнений методом Гаусса
x y 52 x y 7
Нужно записать расширенную матрицу системы
1 1 5
2 1 7
Вертикальная черта внутри матрицы не несёт
никакого математического смысла – это
просто отчеркивание для удобства
оформления.

Матрица системы – это матрица,
составленная только из
коэффициентов при неизвестных.
Расширенная матрица системы – это
столбец свободных членов, в
данном случае.
6. Решение. Умножим первую строку на (-2)
1 1 52 1 7
2 2 10
2 1 7
7. ко второй строке прибавим первую строку умноженную на -2
1 1 52 1 7
2 2 10
0 3 3
2 2 10
2 1 7
8. Разделим опять первую строку на (-2)
1 1 52 1 7
2 2 10
0 3 3
2 2 10
2 1 7
1 1 5
0 3 3
строка, которую ПРИБАВЛЯЛИ – не изменилась.
Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ.
9. Цель элементарных преобразований –
Цель элементарных преобразований–
привести матрицу к ступенчатому виду.
Сам термин «ступенчатый вид» не
вполне теоретический, в научной и
учебной литературе он часто
называется трапециевидный
вид или треугольный
10.
 В результате элементарных преобразований получена эквивалентная исходной система уравнений В результате элементарных преобразований
В результате элементарных преобразований получена эквивалентная исходной система уравнений В результате элементарных преобразованийx y 5
2 x y 7
x y 5
y 1
Выполняем обратный ход, т.е. подстановку в первое
уравнение вместо у,
х =-5+у
х=-5+1
х=-4
Ответ: (-4; 1)
11. Решить систему уравнений методом Гаусса
3 x 2 y z 42 x y 3z 9
x 2 y 2z 3
Решение.
Переставим третье уравнение на место первого и запишем расширенную
матрицу:
x 2 y 2z 3
3 x 2 y z 4
2 x y 3z 9
1 2 2 3
3 2 1 4
2 1 3 9
12. Чтобы в первом столбце получить а2=а3=0, умножим 1-ю строку сначала на 3, а затем на 2 и вычтем результаты из 2-й и 3-й строк
1 2 2 33 2 1 4
2 1 3 9
1 2 2 3
0 8 7 5
0 3 1 3
13. Разделим 2-ю строку на 8, полученные результаты умножим на 3 и вычтем из 3-й строки
1 2 2 33 2 1 4
2 1 3 9
1 2 2 3
0 1 7 5
8 8
0 3 1 3
1 2 2 3
0 8 7 5
1 2 2 3
0 3 21 15
8
8
0 3 1 3
1 2 2
3
21
15
0
3
8
8
39
0 0 13
8
8
14.
 Запишем новую эквивалентную систему с учетом расширенной матрицы x 2 y 2z 3
Запишем новую эквивалентную систему с учетом расширенной матрицы x 2 y 2z 37
5
y z
8
8
13
39
z
8
8
x 2 y 2z 3
7
5
y z
8
8
13
39
z
8
8
Выполняем обратный ход, с помощью
последовательных подстановок находим
неизвестные
13
39
z
z 3
8
8
7
5
5 21 16
y 3
y
2
8
8
8 8
8
x 2 2 2 3 3 x 3 4 6 1
Ответ: (1; 2; 3)
Численные методы решения систем линейных алгебраических уравнений. Метод Гаусса
Библиографическое описание: 05.2021).
05.2021). В статье рассматривается алгоритм метода Гаусса для решения систем линейных алгебраических уравнений. Выбран язык Maple, как наиболее оптимальный для реализации алгоритма. В статье содержится листинг программного кода.
Ключевые слова: система линейных алгебраических уравнений, метод Гаусса, алгоритм реализации метода Гаусса, прямой и обратный ход, программный код.
В прикладных задачах довольно часто приходится решать системы линейных алгебраических уравнений (СЛАУ). Это не удивительно, поскольку математические модели тех или иных процессов либо сразу строятся как СЛАУ, либо сводятся к таковым посредством дискретизации или линеаризации.
Метод Гаусса прекрасно подходит для решения СЛАУ. Являясь наиболее мощным и универсальным инструментом для нахождения решения СЛАУ, он обладает рядом преимуществ: 1) нет необходимости предварительно исследовать систему уравнений на совместность; 2) методом Гаусса можно решать не только СЛАУ, в которых число уравнений совпадает с количеством неизвестных переменных и основная матрица системы невырожденная, но и системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равен нулю; 3) метод Гаусса приводит к результату при сравнительно небольшом количестве вычислительных операций.
Но главное, что было отмечено в работе «Метод Гаусса в школе» М. Ю. Шонина и Л. А. Мамедалиной, «Метод Гаусса решения СЛАУ с числовыми коэффициентами в силу простоты и однотипности выполняемых операций пригоден для счета на электронно-вычислительных машинах» [3].
Настоящая статья посвящена составлению и апробации алгоритма численного решения СЛАУ в соответствии с алгоритмом метода Гаусса. Рассмотрим следующую задачу.
Задача. Решить систему линейных алгебраических уравнений [1]
Решение:
Для численного решения СЛАУ воспользуемся математическим пакетом Maple 15. В соответствии с условием задачи имеем:
и
Для эффективной работы в необходимо разбираться в тонкостях языка. К ним относится, например, команда и переменная .
Команда — очищает память . Это означает, что все определенные для этого в программе переменные и другие объекты будут стерты. При этом текст программы останется неизменным. Данная функция необходима для осуществления компиляции.
Данная функция необходима для осуществления компиляции.
Переменная возвращает необходимое количество знаков после запятой . Установим точность вычисления . Поскольку нам придется иметь дело с матрицей и вектор-столбцом, то необходимо подключить библиотеку линейной алгебры — . Введем данные в программу.
>
>
>
>
>
>
>
В соответствии с логикой метода Гаусса, программа должна привести матрицу к треугольному виду (Прямой ход). Целесообразно воспользоваться циклом со счетчиком . Цикл предназначен для реализации итерационных (повторяющихся) действий [2].
>
>
>
>
>
Следующий этап — обратный ход, построчное вычисление входящих в систему переменных и их вывод на экран.
>
>
>
Заключительным этапом программы служит проверка адекватности найденного решения. Для этого воспользуемся командой решения СЛАУ — .
>
Найдем абсолютную погрешность (модуль разности значений переменных, полученных путем численного решения и при помощи встроенной команды соответственно). Команда выполняет операции над матрицами. Команда возвращает абсолютные значения.
>
Анализируя последние результаты, можно констатировать высокую точность вычисления. Таким образом, разработанная программа вполне адекватна для решения СЛАУ.
Литература:
- Ильин В. А. Линейная алгебра: Учебник для вузов / В. А. Ильин, Э. Г. Позняк. — 6-е изд., стер. — М.: Физматлит, 2004. — 280 с.
- Кирсанов М. Н. Практика программирования в системе Maple. — М.: Издательский дом МЭИ, 2011.
 — 208 с.
— 208 с. - Мамедалина Л. А. Метод Гаусса в решении СЛАУ в школе / Л. А. Мамедалина, М. Ю. Шонин // Весенний школьный марафон: материалы III Междунар. науч.-практ. конф. школьников (Чебоксары, 31 мая 2016 г.) / редкол.: О. Н. Широков [и др.] — Чебоксары: ЦНС «Интерактив плюс», 2016. — С. 139–143.
Основные термины (генерируются автоматически): метод Гаусса, численное решение, алгоритм метода Гаусса, обратный ход, переменная, программный код, система уравнений, число уравнений.
Систем линейных уравнений: исключение Гаусса
Системы
линейных уравнений:
Решение методом исключения Гаусса (стр.
6 из 7)
Разделы: Определения, Решение по графику, Подстановка, Исключение / добавление, исключение по Гауссу.
Решение трех переменных,
линейных систем с тремя уравнениями сложнее, по крайней мере, на начальном этапе, чем
решение систем с двумя переменными, потому что требуемые вычисления
более грязный. Вам нужно будет очень аккуратно работать, и вам следует
планируйте использовать много бумаги для заметок. Метод решения этих систем
является расширением метода сложения двух переменных, поэтому сделайте
конечно ты знаешь это
метод хорошо и
можно использовать его последовательно правильно.
Вам нужно будет очень аккуратно работать, и вам следует
планируйте использовать много бумаги для заметок. Метод решения этих систем
является расширением метода сложения двух переменных, поэтому сделайте
конечно ты знаешь это
метод хорошо и
можно использовать его последовательно правильно.
Хотя метод решения основан на добавлении / исключении, попытка выполнить фактическое добавление имеет тенденцию становится очень запутанным, поэтому существует систематизированный метод решения трех или более переменных системы.Этот метод называется «исключением по Гауссу» (с уравнения заканчиваются так называемой «строковой формой»).
Начнем с простого, и работаем над более сложными примерами.
- Решите следующие проблемы система уравнений.
Достаточно легко увидеть
как действовать в этом случае. Я просто подставлю обратно значение z -value
из третьего уравнения во второе, решите результат для л , г. а затем подключите z и y в
первое уравнение и решите результат для x .
а затем подключите z и y в
первое уравнение и решите результат для x .
10 л 3 (3) = 11
10 y 9 = 11
10 y = 20
y = 2
5x +
4 (2) (3) = 0
5 x + 8 3 = 0
5 x + 5 = 0
5 x = 5
x = 1
Тогда решение ( х , y , z ) = (1, 2, 3).
Причина, по которой эта система была Легко решить, что система была «треугольной»; это относится к уравнениям, имеющим форму треугольника, из-за нижних уравнений содержащий только более поздние переменные.
Дело в том, что в этом
формат, система проста в решении. А гауссовское исключение – это
метод, который мы будем использовать для преобразования систем в эту верхнетреугольную форму, используя
операции со строками, которые мы изучили, когда применили метод сложения.
- Решите следующие проблемы система уравнений с использованием исключения Гаусса.
Уравнение не решается для переменной, поэтому мне нужно будет выполнить умножение и сложение чтобы упростить эту систему. Чтобы отслеживать свою работу, напишу вниз на каждом шагу, когда я иду. Но я буду делать свои вычисления на бумаге для заметок. Вот как я это сделал:
Первое, что нужно сделать
состоит в том, чтобы избавиться от ведущих x -термов
в два ряда.А пока я просто посмотрю, какие строки будут легко
расчистить; Я могу поменять строки позже, чтобы перевести систему в “верхний
треугольной “формы. Нет правила, которое гласит, что я должен использовать x – срок
из первой строки, и в этом случае, думаю, будет проще
используйте термин x из третьей строки, так как его коэффициент просто «1».
Так что я умножу третью строку на 3,
и добавьте его в первую строку. Я делаю вычисления на бумаге для заметок:
Я делаю вычисления на бумаге для заметок:
… а потом записываю результатов:
(Когда мы решали системы с двумя переменными, мы могли умножить строку, переписав систему в сторону, а затем добавить. Для этого нет места в система с тремя переменными, поэтому нам и нужна бумага для заметок.)
Предупреждение: поскольку я не на самом деле ничего не делаю с третьей строкой, я скопировал ее без изменений, в новую матрицу уравнений.Я б / у третий ряд, но я на самом деле не менял Это. Не путайте «использование» с «изменением».
Чтобы получить меньшие числа для коэффициентов умножу первую строку пополам:
Теперь умножу третий ряд на 5 и добавьте это ко второму строка. Работаю на бумаге для заметок:
. .. а потом записываю
результаты: Авторские права
Элизабет Стапель 2003-2011 Все права защищены
.. а потом записываю
результаты: Авторские права
Элизабет Стапель 2003-2011 Все права защищены
Я ничего не делал с первым рядом, поэтому я скопировал его без изменений. Я работал с третий ряд, но я работал только на вторая строка, поэтому вторая строка обновляется, а третья строка копируется более без изменений.
Хорошо, теперь x – столбец удаляется, за исключением ведущего члена в третьей строке.Так что дальше Приходится работать над колонкой и .
Предупреждение: С третьего уравнение имеет член x , Я больше не могу использовать его ни в одном из двух других уравнений (или я отменить мой прогресс). Я могу работать с уравнением, но не с Это.
Если я добавлю в два раза больше первого
строки во вторую строку, это даст мне ведущую 1
во втором ряду. Я не буду
избавились от ведущего y -терм
во втором ряду, но я его преобразовал (не вмешиваясь
дробями) в более простую форму. (Вы должны сохранить
обратите внимание на такого рода упрощения.) Сначала я делаю царапину
работа:
Я не буду
избавились от ведущего y -терм
во втором ряду, но я его преобразовал (не вмешиваясь
дробями) в более простую форму. (Вы должны сохранить
обратите внимание на такого рода упрощения.) Сначала я делаю царапину
работа:
… а потом записываю результатов:
Теперь могу использовать второй ряд, чтобы убрать и -семестр в первом ряду.Вторую строку умножу на 7 и добавить. Сначала я царапаю работа:
… а потом записываю результатов:
Я могу сказать что z сейчас, но для большей точности я разделю первую строку на 43. Затем я переставляю ряды, чтобы придать им верхнетреугольную форму:
Теперь я могу начать процесс обратного решения:
Тогда решение ( х , y , z ) = ( 2,
3, 1 ) .
Примечание: нет ничего священного о шагах, которые я использовал при решении указанной выше системы; там ничего не было особенно о том, как я решил эту систему. Вы могли бы работать в другом упорядочивайте или упрощайте разные строки, и все равно получите правильный ответ. Эти системы достаточно сложны, поэтому вряд ли один правильный способ вычисления ответа. Так что не беспокойтесь о том, “как она знала, что делать дальше? », потому что здесь нет правила.я просто делал все, что пришло мне в голову; Я делал то, что казалось самым простым или что-то еще пришла в голову первая. Не волнуйтесь, если бы вы использовали совершенно другой шаги. Если каждый шаг на этом пути верен, вы придумаете Такой же ответ.
В приведенном выше примере я мог
пошли дальше в своих вычислениях и более тщательно проработали
строковые операции, очищая все термины и кроме этого во втором ряду и во всех терминах z кроме того, что в первой строке. Это то, что процесс тогда
посмотрели так:
Это то, что процесс тогда
посмотрели так:
Так я могу просто читать от значений x , л , г. и z , и мне не нужно возиться с обратной заменой. Это более полное метод решения называется «методом исключения Гаусса-Жордана» (с уравнения, заканчивающиеся тем, что называется “эшелон сокращенного ряда” форма”).Многие тексты доходят до исключения Гаусса, но я всегда было легче продолжать и делать Гаусс-Джордан.
Обратите внимание, что я выполнил две строковые операции сразу на этом последнем шаге перед переключением строк. Пока я не работая с и работая на в той же строке на том же шаге, это нормально. В этом случае я работал с первой строкой и рабочая по второй и третий ряды.
<< Предыдущая Вверх | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Вернуться к указателю Далее >>
Цитируйте эту статью как: | Стапель, Елизавета. |
Системы линейных уравнений: исключение Гаусса
Решение линейной системы с матрицами с использованием исключения Гаусса
После нескольких уроков, в которых мы неоднократно упоминали, что мы охватываем основы, необходимые для последующего изучения того, как решать системы линейных уравнений, пришло время для нашего урока сосредоточиться на полной методологии, которой нужно следовать, чтобы найти решения. для таких систем.
Что такое гауссовское исключение
Исключение Гаусса – это название метода, который мы используем для выполнения трех типов операций со строками матрицы над расширенной матрицей, полученной из линейной системы уравнений, чтобы найти решения для такой системы. Этот метод также называется сокращением строк и состоит из двух этапов: прямого исключения и обратной замены.
Этот метод также называется сокращением строк и состоит из двух этапов: прямого исключения и обратной замены.
Эти два шага метода исключения Гаусса различаются не операциями, которые вы можете использовать с их помощью, а результатом, который они производят.Шаг прямого исключения относится к сокращению строки, необходимому для упрощения рассматриваемой матрицы до ее эшелонированной формы. Такой этап имеет целью продемонстрировать, имеет ли система уравнений, изображенная в матрице, единственное возможное решение, бесконечное множество решений или просто отсутствие решения. Если обнаружено, что система не имеет решения, то нет причин продолжать сокращение строки матрицы на следующем этапе.
Если возможно получить решения для переменных, входящих в линейную систему, то выполняется этап исключения Гаусса с обратной подстановкой.На этом последнем шаге будет получена сокращенная форма матрицы, которая, в свою очередь, дает общее решение системы линейных уравнений.
Правила исключения Гаусса такие же, как правила для трех элементарных операций со строками, другими словами, вы можете алгебраически оперировать строками матрицы следующими тремя способами (или комбинацией):
- Перестановка двух рядов
- Умножение строки на константу (любую константу, отличную от нуля)
- Добавление строки к другой строке
Итак, решение линейной системы с матрицами с использованием исключения Гаусса оказывается структурированным, организованным и довольно эффективным методом.
Как выполнить исключение по Гауссу
На самом деле это не установленный набор шагов исключения Гаусса, которым нужно следовать, чтобы решить систему линейных уравнений, это все о матрице, которая у вас есть в ваших руках, и необходимых операциях со строками для ее упрощения. Для этого давайте поработаем над нашим первым примером исключения Гаусса, чтобы вы могли начать изучать весь процесс и интуицию, которая необходима при работе с ними:
Пример 1
Обратите внимание, что в этот момент мы можем заметить, что эта система линейных уравнений разрешима с единственным решением для каждой из ее переменных.То, что мы выполнили до сих пор, – это первый этап сокращения строк: прямое исключение. Мы можем продолжить упрощение этой матрицы еще больше (что приведет нас ко второму этапу обратной подстановки), но нам это действительно не нужно, поскольку на этом этапе система легко разрешима. Таким образом, мы смотрим на получившуюся систему, чтобы решить ее напрямую:
- Уравнение 5: Полученная линейная система уравнений для решения
Из этого набора мы можем автоматически заметить, что значение переменной z равно: z = -2. Мы используем это знание, чтобы подставить его во вторые уравнения для решения относительно y, и подставить значения y и z в первые уравнения для решения относительно x:
Мы используем это знание, чтобы подставить его во вторые уравнения для решения относительно y, и подставить значения y и z в первые уравнения для решения относительно x:
В последний раздел этого урока добавлено больше задач исключения Гаусса. Обязательно проработайте их, чтобы практиковаться.
Разница между исключением по Гауссу и по Гауссу Иордану
Разница между методом исключения Гаусса и исключением Гаусса Жордана заключается в том, что один создает матрицу в форме эшелона строк, а другой – матрицу в форме уменьшенного ряда.Матрица формы эшелона строк имеет верхнюю треугольную композицию, где любые нулевые строки находятся внизу, а ведущие члены находятся справа от ведущего члена из строки выше. Уменьшенная форма эшелона выходит за рамки еще большего упрощения (иногда даже достигая формы единичной матрицы).
Уравнение 8: Разница между формой эшелона и формой ряда эшелонов История исключения Гаусса и его названия довольно интересны, вы будете удивлены, узнав, что название «Гауссовский» было присвоено этой методологии по ошибке в прошлом веке. В действительности было обнаружено, что алгоритм одновременного решения системы линейных уравнений с использованием матриц и редукции строк записан в той или иной форме в древних китайских текстах, которые датируются еще до нашей эры. Затем в конце 1600-х годов Исаак Ньютон провел по этому уроку, чтобы заполнить то, что он считал пробелом в книгах по алгебре. После того, как название «Гауссиан» было уже установлено в 1950-х годах, термин Гаусса-Иордана был принят, когда геодезист У. Джордан усовершенствовал технику, чтобы он мог использовать такие вычисления для обработки своих наблюдаемых данных топографической съемки.Если вы хотите продолжить чтение увлекательной истории математиков исключения Гаусса, не бойтесь щелкнуть ссылку и прочитать.
В действительности было обнаружено, что алгоритм одновременного решения системы линейных уравнений с использованием матриц и редукции строк записан в той или иной форме в древних китайских текстах, которые датируются еще до нашей эры. Затем в конце 1600-х годов Исаак Ньютон провел по этому уроку, чтобы заполнить то, что он считал пробелом в книгах по алгебре. После того, как название «Гауссиан» было уже установлено в 1950-х годах, термин Гаусса-Иордана был принят, когда геодезист У. Джордан усовершенствовал технику, чтобы он мог использовать такие вычисления для обработки своих наблюдаемых данных топографической съемки.Если вы хотите продолжить чтение увлекательной истории математиков исключения Гаусса, не бойтесь щелкнуть ссылку и прочитать.
На самом деле нет никакой физической разницы между исключением Гаусса и исключением Гаусса Джордана, оба процесса следуют одному и тому же типу операций со строками и их комбинациям, их различие зависит от результатов, которые они производят. Многие математики и учителя во всем мире будут относиться к исключению Гаусса и исключению Гаусса Джордана как к методам создания матрицы эшелонированной формы по сравнению с методом создания матрицы уменьшенной эшелонированной формы, но на самом деле они говорят о двух стадиях сокращения строк. мы объяснили это в самом первом разделе этого урока (прямое исключение и обратная подстановка), и поэтому вы просто применяете операции со строками, пока не упростите рассматриваемую матрицу.Если вы дойдете до формы эшелона, вы обычно можете решить с ней систему линейных уравнений (до сих пор это то, что называлось бы исключением Гаусса). Если вам нужно продолжить упрощение такой матрицы, чтобы напрямую получить общее решение для системы уравнений, над которой вы работаете, в этом случае вы просто продолжаете работать с матрицей по строкам, пока не упростите ее до сокращенной формы эшелона. (это будет то, что мы называем частью Гаусса-Жордана, и которую можно рассматривать также как поворотное исключение Гаусса).
Многие математики и учителя во всем мире будут относиться к исключению Гаусса и исключению Гаусса Джордана как к методам создания матрицы эшелонированной формы по сравнению с методом создания матрицы уменьшенной эшелонированной формы, но на самом деле они говорят о двух стадиях сокращения строк. мы объяснили это в самом первом разделе этого урока (прямое исключение и обратная подстановка), и поэтому вы просто применяете операции со строками, пока не упростите рассматриваемую матрицу.Если вы дойдете до формы эшелона, вы обычно можете решить с ней систему линейных уравнений (до сих пор это то, что называлось бы исключением Гаусса). Если вам нужно продолжить упрощение такой матрицы, чтобы напрямую получить общее решение для системы уравнений, над которой вы работаете, в этом случае вы просто продолжаете работать с матрицей по строкам, пока не упростите ее до сокращенной формы эшелона. (это будет то, что мы называем частью Гаусса-Жордана, и которую можно рассматривать также как поворотное исключение Гаусса).
Мы оставим подробное объяснение форм сокращения строк и эшелонирования для следующего урока, поскольку сейчас вам нужно знать, что, если у вас нет единичной матрицы в левой части расширенной матрицы, которую вы решаете (в этом случае вы не используете не нужно ничего делать для решения системы уравнений, относящейся к матрице), метод исключения Гаусса (регулярное сокращение строк) всегда будет использоваться для решения линейной системы уравнений, которая была записана в виде матрицы.
Примеры исключения Гаусса
В качестве последнего раздела давайте поработаем еще несколько упражнений по исключению Гаусса (сокращение строк), чтобы вы могли больше попрактиковаться в этой методологии.На протяжении многих будущих уроков этого курса линейной алгебры вы обнаружите, что сокращение строк является одним из самых важных инструментов при работе с матричными уравнениями. Поэтому убедитесь, что вы понимаете все этапы решения следующих проблем.
Пример 2
Пример 3
Мы знаем, что для этой системы мы получим расширенную матрицу с тремя строками (поскольку система содержит три уравнения) и тремя столбцами слева от вертикальной линии (поскольку есть три разных переменных). В этом случае мы перейдем непосредственно к сокращению строк, и поэтому первая матрица, которую вы увидите в этом процессе, – это та, которую вы получите, преобразовав систему линейных уравнений в расширенную матрицу.
В этом случае мы перейдем непосредственно к сокращению строк, и поэтому первая матрица, которую вы увидите в этом процессе, – это та, которую вы получите, преобразовав систему линейных уравнений в расширенную матрицу.
- Уравнение 15: Строка, уменьшающая расширенную матрицу
Обратите внимание, как мы можем сразу сказать, что переменная z равна нулю для этой системы, поскольку третья строка результирующей матрицы показывает уравнение -9z = 0 . Мы используем это знание и проверяем вторую строку матрицы, которая предоставит уравнение 2y – 6z = 0 , подставив в это уравнение значение z = 0 \, получится y \, также равное нулю.Таким образом, мы, наконец, подставляем оба значения y и z \ в уравнение, которое получается из первой строки матрицы: x + 4y + 3z = 1 , поскольку и y , и z \ , равны нулю, то это дает нам x = 1 . Итак, окончательное решение этой системы уравнений выглядит следующим образом:
- Уравнение 16: Окончательное решение системы уравнений
Пример 4
Из чего видно, что последняя строка дает уравнение: 6z = 3 и, следовательно, z = 1/2. Мы подставляем это в уравнения, полученные во второй и первой строках (в указанном порядке), чтобы вычислить значения переменных x и y:
Мы подставляем это в уравнения, полученные во второй и первой строках (в указанном порядке), чтобы вычислить значения переменных x и y:
Пример 5
- Решите следующую линейную систему, используя метод исключения Гаусса: Уравнение 21: Система линейных уравнений с двумя переменными
- Транскрипция линейной системы в виде расширенной матрицы и редукции строк: Уравнение 22: Строка, уменьшающая расширенную матрицу
Что автоматически говорит нам y = 8 .Итак, подставляя это значение в уравнение из первой строки, получаем: 4x – 5y = 4x – 5 (8) = 4x – 40 = -6 4x = 34 \, и поэтому значение x равно: x = 172 \ frac {\ small17} {\ small2} 217 . И окончательное решение этой системы уравнений:
Уравнение 23: Окончательное решение системы уравнений
Пример 6
Чтобы завершить наш урок на сегодня, у нас есть рекомендация по ссылке для дополнения ваших исследований: Исключение Гаусса – статья, которая содержит некоторую дополнительную информацию о сокращении строк, включая введение в тему и еще несколько примеров. Как мы упоминали ранее, будьте готовы продолжать использовать сокращение строк почти на протяжении всего курса линейной алгебры, так что до встречи на следующем уроке!
Как мы упоминали ранее, будьте готовы продолжать использовать сокращение строк почти на протяжении всего курса линейной алгебры, так что до встречи на следующем уроке!
Решение систем с исключением Гаусса – College Algebra
Цели обучения
В этом разделе вы:
- Напишите расширенную матрицу системы уравнений.
- Напишите систему уравнений из расширенной матрицы.
- Выполнение операций со строками в матрице.
- Решите систему линейных уравнений, используя матрицы.
Немецкий математик Карл Фридрих Гаусс (1777–1855).
Карл Фридрих Гаусс жил в конце 18-го и начале 19-го веков, но он по-прежнему считается одним из самых плодовитых математиков в истории. Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика.Его открытия в области теории матриц изменили способ работы математиков за последние два столетия.
Мы впервые столкнулись с методом исключения Гаусса в системах линейных уравнений: две переменные. В этом разделе мы еще раз вернемся к этой технике решения систем, на этот раз с использованием матриц.
Написание расширенной матрицы системы уравнений
Матрица может служить средством представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы.Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по сути заменяя знаки равенства. Когда система написана в такой форме, мы называем ее расширенной матрицей.
Например, рассмотрим следующую систему уравнений.
Мы можем записать эту систему в виде расширенной матрицы:
Мы также можем написать матрицу, содержащую только коэффициенты. Это называется матрицей коэффициентов.
Система уравнений три на три, например
имеет матрицу коэффициентов
и представлена расширенной матрицей
Обратите внимание, что матрица написана таким образом, что переменные выстраиваются в свои собственные столбцы: x -термы идут в первый столбец, – -термы во втором столбце и z -термы в третьем столбце. Очень важно, чтобы каждое уравнение было написано в стандартной форме, чтобы переменные совпадали. Если в уравнении отсутствует член переменной, коэффициент равен 0.
Очень важно, чтобы каждое уравнение было написано в стандартной форме, чтобы переменные совпадали. Если в уравнении отсутствует член переменной, коэффициент равен 0.
Для данной системы уравнений напишите расширенную матрицу.
- Запишите коэффициенты членов x в виде чисел в первом столбце.
- Запишите коэффициенты членов y в виде чисел во втором столбце.
- Если имеется z -термов, запишите коэффициенты в виде чисел в третьем столбце.
- Нарисуйте вертикальную линию и напишите константы справа от нее.
Написание расширенной матрицы для системы уравнений
Напишите расширенную матрицу для данной системы уравнений.
Расширенная матрица отображает коэффициенты переменных и дополнительный столбец для констант.
Запишите расширенную матрицу данной системы уравнений.
Написание системы уравнений из расширенной матрицы
Мы можем использовать расширенные матрицы, чтобы помочь нам решать системы уравнений, потому что они упрощают операции, когда системы не обременены переменными.Однако важно понимать, как переключаться между форматами, чтобы поиск решений был более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.
Напишите систему уравнений из расширенной матрицы.
Выполнение операций со строками в матрице
Теперь, когда мы можем писать системы уравнений в форме расширенной матрицы, мы рассмотрим различные операции со строками, которые могут выполняться с матрицей, такие как сложение, умножение на константу и перестановка строк.
Выполнение строковых операций над матрицей – это метод, который мы используем для решения системы уравнений. Чтобы решить систему уравнений, мы хотим преобразовать матрицу в форму строки-эшелона, в которой есть единицы вниз по главной диагонали от верхнего левого угла до нижнего правого угла и нули в каждой позиции ниже главной диагонали. как показано.
Чтобы решить систему уравнений, мы хотим преобразовать матрицу в форму строки-эшелона, в которой есть единицы вниз по главной диагонали от верхнего левого угла до нижнего правого угла и нули в каждой позиции ниже главной диагонали. как показано.
Мы используем операции со строками, соответствующие операциям с уравнениями, чтобы получить новую матрицу, эквивалентную строкам в более простой форме.Вот рекомендации по получению формы рядного эшелона.
- В любой ненулевой строке первым ненулевым числом является 1. Оно называется ведущим 1.
- Любые нулевые строки помещаются внизу матрицы.
- Любая ведущая 1 находится ниже и правее предыдущей ведущей 1.
- Любой столбец, в котором в начале стоит 1, имеет нули во всех остальных позициях в столбце.
Чтобы решить систему уравнений, мы можем выполнить следующие операции со строками, чтобы преобразовать матрицу коэффициентов в форму ряда строк и выполнить обратную подстановку, чтобы найти решение.
- Поменять местами ряды. (Обозначение 🙂
- Умножить строку на константу. (Обозначение 🙂
- Добавить произведение одной строки на константу к другой строке. (Замечание:
Каждая из строковых операций соответствует операциям, которые мы уже научились решать системы уравнений с тремя переменными. С помощью этих операций есть несколько ключевых шагов, которые быстро достигнут цели написания матрицы в виде эшелона строк. Чтобы получить матрицу в виде эшелона строк для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, чтобы строку 1 можно было использовать для преобразования оставшихся строк.
Исключение по Гауссу
Метод исключения Гаусса относится к стратегии, используемой для получения матрицы в виде строки-эшелона. Цель состоит в том, чтобы записать матрицу с номером 1 в качестве записи по главной диагонали и иметь все нули внизу.
Первый шаг стратегии Гаусса включает получение 1 в качестве первой записи, так что строка 1 может использоваться для изменения строк ниже.
Учитывая расширенную матрицу, выполните операции со строками для получения формы «строка-эшелон».
- Первое уравнение должно иметь старший коэффициент 1. При необходимости поменяйте местами строки или умножьте на константу.
- Используйте операции со строками, чтобы получить нули в первом столбце под первой записью 1.
- Используйте операции со строками, чтобы получить 1 в строке 2, столбце 2.
- Используйте операции со строками, чтобы получить нули в нижнем столбце 2, ниже записи 1.
- Используйте операции со строками, чтобы получить 1 в строке 3, столбце 3.
- Продолжайте этот процесс для всех строк, пока в каждой записи по главной диагонали не будет 1, а внизу будут только нули.
- Если какие-либо строки содержат все нули, поместите их внизу.

Решите данную систему методом исключения Гаусса.
Решите данную систему методом исключения Гаусса.
Использование исключения Гаусса для решения системы уравнений
Используйте метод исключения Гаусса для решения данной системы уравнений.
Решение зависимой системы
Решите систему уравнений.
Выполнение операций со строками в расширенной матрице 3×3 для получения формы Row-Echelon
Выполняет строковые операции с заданной матрицей для получения формы “строка-эшелон”.
Запишите систему уравнений в виде строк.
Решение системы линейных уравнений с использованием матриц
Мы видели, как написать систему уравнений с расширенной матрицей, а затем как использовать строковые операции и обратную подстановку для получения строчно-эшелонированной формы.Теперь мы перейдем на шаг дальше от строковой формы, чтобы решить систему линейных уравнений 3 на 3. Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.
Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.
Решение системы линейных уравнений с использованием матриц
Решите систему линейных уравнений с помощью матриц.
Решение зависимой системы линейных уравнений с использованием матриц
Решите следующую систему линейных уравнений, используя матрицы.
Решите систему, используя матрицы.
Можно ли решить любую систему линейных уравнений методом исключения Гаусса?
Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.
Для данной системы уравнений решите с помощью матриц с помощью калькулятора.
- Сохранить расширенную матрицу как матричную переменную
- Используйте функцию ref ( в калькуляторе, вызывая каждую матричную переменную по мере необходимости.

Решение систем уравнений с матрицами с помощью калькулятора
Решите систему уравнений.
Применение матриц 2 × 2 к финансам
Кэролайн инвестирует в общей сложности 12 000 фунтов стерлингов в две муниципальные облигации, одна из которых выплачивает 10,5% годовых, а другая – 12%. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 евро. Сколько было вложено по каждой ставке?
Применение матриц 3 × 3 к финансам
Ava инвестирует в общей сложности 10 000 фунтов стерлингов в три счета, один из которых платит 5% годовых, другой – 8%, а третий – 9%.Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 фунтов стерлингов. Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?
У нас есть система трех уравнений с тремя переменными. Пусть будет сумма, вложенная под 5%, пусть будет сумма, вложенная под 8%, пусть будет сумма, вложенная под 9%. Таким образом,
Таким образом,
В качестве матрицы имеем
Теперь мы выполняем исключение Гаусса, чтобы получить форму строки-эшелон.
Третья строка сообщает usthus
Вторая строка сообщает нам Подставляя, мы получаем
Первая строка говорит нам, что подставляем и получаем
Ответ: 3000 евро вложены под 5%, 1000 евро вложены под 8% и 6000 евро вложены под 9%.
Небольшая обувная компания взяла ссуду в размере 1 500 000 фунтов стерлингов для расширения своих запасов. Часть денег была взята под 7%, часть – под 8%, часть – под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла 130 500 фунтов стерлингов. Используйте матрицы, чтобы найти сумму займа по каждой ставке.
– 150 000 фунтов стерлингов при 7%, 750 000 фунтов стерлингов при 8%, 600 000 фунтов стерлингов при 10%
Ключевые понятия
- Расширенная матрица – это матрица, которая содержит коэффициенты и константы системы уравнений.
 См. (Рисунок).
См. (Рисунок). - Матрица, дополненная постоянным столбцом, может быть представлена как исходная система уравнений. См. (Рисунок).
- Операции со строками включают в себя умножение строки на константу, добавление одной строки к другой строке и замену строк местами.
- Мы можем использовать метод исключения Гаусса для решения системы уравнений. См. (Рисунок), (Рисунок) и (Рисунок).
- Операции со строками выполняются над матрицами для получения формы «строка-эшелон». См. (Рисунок).
- Чтобы решить систему уравнений, запишите ее в форме дополненной матрицы.Выполните операции со строками, чтобы получить форму эшелона строк. Обратно-заменитель, чтобы найти решения. См. (Рисунок) и (Рисунок).
- Калькулятор можно использовать для решения систем уравнений с использованием матриц. См. (Рисунок).
- Многие реальные проблемы можно решить с помощью расширенных матриц. См. (Рисунок) и (Рисунок).
Упражнения по разделам
Устный
Можно ли записать любую систему линейных уравнений в виде расширенной матрицы? Объясните, почему да или почему нет. Объясните, как написать эту расширенную матрицу.
Объясните, как написать эту расширенную матрицу.
Да. Для каждой строки коэффициенты переменных записываются поперек соответствующей строки и помещается вертикальная черта; затем константы помещаются справа от вертикальной полосы.
Можно ли записать любую матрицу в виде системы линейных уравнений? Объясните, почему да или почему нет. Объясните, как написать эту систему уравнений.
Есть только один правильный метод использования операций со строками в матрице? Попытайтесь объяснить две различные операции со строками, которые можно выполнить для расширенной матрицы
.Нет, существует множество правильных методов использования строковых операций над матрицей.Есть два возможных способа: (1) Поменять местами строки 1 и 2. Затем (2) Разделить строку 1 на 9.
Можно ли решить матрицу с нулевым элементом на диагонали? Объясните, почему да или почему нет. Что бы вы сделали, чтобы исправить ситуацию?
Может ли матрица с 0 элементами для всей строки иметь одно решение? Объясните, почему да или почему нет.
Нет. Матрица с 0 элементами для всей строки будет иметь либо ноль, либо бесконечно много решений.
Алгебраические
Для следующих упражнений напишите расширенную матрицу для линейной системы.
Для следующих упражнений запишите линейную систему из расширенной матрицы.
Для следующих упражнений решите систему методом исключения Гаусса.
Расширения
Для следующих упражнений используйте метод исключения Гаусса для решения системы.
Реальные приложения
Для следующих упражнений настройте расширенную матрицу, описывающую ситуацию, и найдите желаемое решение.
Ежедневно в магазине кексов продается 5 000 кексов со вкусом шоколада и ванили. Если вкус шоколада в 3 раза популярнее, чем аромат ванили, сколько кексов продается в день?
В конкурирующем магазине кексов ежедневно продаются кексы на сумму 4520 фунтов стерлингов.Шоколадные кексы стоят 2,25 евро, а кексы из красного бархата – 1,75 евро. Если общее количество кексов, проданных в день, составляет 2200, сколько штук каждого вкуса продается каждый день?
860 красный бархат, 1340 шоколадный
Вы вложили 10 000 евро в два счета: один с простой процентной ставкой 3%, а другой – с процентной ставкой 2,5%. Если ваша общая сумма процентов по истечении одного года составила 283,50 фунтов стерлингов, какая сумма была на каждом счете по истечении года?
Вы вложили 2300 евро на счет 1 и 2700 евро на счет 2. Если общая сумма процентов по истечении одного года составляет 254 евро, а на счете 2 процентная ставка в 1,5 раза выше, чем на счете 1, каковы процентные ставки? Предположим простые процентные ставки.
Если общая сумма процентов по истечении одного года составляет 254 евро, а на счете 2 процентная ставка в 1,5 раза выше, чем на счете 1, каковы процентные ставки? Предположим простые процентные ставки.
4% на счет 1, 6% на счет 2
Bikes’R’Us производит велосипеды по 250 фунтов стерлингов. Производитель обошелся в 180 фунтов стерлингов за велосипед плюс стартовый взнос в размере 3500 фунтов стерлингов. Через сколько проданных велосипедов производитель выйдет на уровень безубыточности?
Крупный магазин бытовой техники рассматривает возможность приобретения пылесосов у небольшого производителя.Магазин сможет приобрести пылесосы по 86 фунтов стерлингов каждый, со стоимостью доставки 9 200 фунтов стерлингов, независимо от того, сколько пылесосов продано. Если магазин должен начать получать прибыль после продажи 230 единиц, сколько они должны взимать за пылесосы?
Три самых популярных вкуса мороженого – это шоколад, клубника и ваниль, составляющие 83% вкусов, продаваемых в магазине мороженого. Если ваниль продается на 1% больше, чем в два раза больше клубники, а шоколад продается на 11% больше, чем ваниль, сколько в общем потреблении мороженого приходится на ароматы ванили, шоколада и клубники?
Если ваниль продается на 1% больше, чем в два раза больше клубники, а шоколад продается на 11% больше, чем ваниль, сколько в общем потреблении мороженого приходится на ароматы ванили, шоколада и клубники?
В магазине мороженого возрастает спрос на три вкуса.В прошлом году банановое, тыквенное и мороженое с каменистой дорогой составили 12% от общего объема продаж мороженого. В этом году на те же три вида мороженого пришлось 16,9% продаж мороженого. Продажи по каменистой дороге увеличились вдвое, продажи бананов увеличились на 50%, а продажи тыквы – на 20%. Если у мороженого по каменистой дороге было на один процент меньше продаж, чем у бананового мороженого, узнайте, какой процент продаж мороженого было произведено каждым отдельным мороженым в прошлом году.
Банан – 3%, тыква – 7%, а каменистая дорога – 2%
Пакет с ореховой смесью содержит кешью, фисташки и миндаль.Всего в сумке 1000 орехов, а миндаля на 100 меньше, чем фисташек. Кешью весит 3 г, фисташки – 4 г, миндаль – 5 г. Если мешок весит 3,7 кг, узнайте, сколько орехов каждого вида в нем.
Если мешок весит 3,7 кг, узнайте, сколько орехов каждого вида в нем.
Пакет с ореховой смесью содержит кешью, фисташки и миндаль. Изначально в сумке было 900 орехов. Было съедено 30% миндаля, 20% кешью и 10% фисташек, и теперь в сумке осталось 770 орехов. Изначально кешью было на 100 штук больше, чем миндаля.Для начала выясните, сколько орехов каждого типа было в пакете.
100 миндальных орехов, 200 кешью, 600 фисташек
Глоссарий
- дополненная матрица
- матрица коэффициентов, примыкающая к столбцу констант, разделенному вертикальной линией в скобках матрицы
- матрица коэффициентов
- матрица, содержащая только коэффициенты из системы уравнений
- Гауссово исключение
- с использованием элементарных операций со строками для получения матрицы в виде эшелона строки
- главная диагональ
- записей из левого верхнего угла по диагонали в правый нижний угол квадратной матрицы
- рядная форма
- после выполнения строковых операций матричная форма, содержащая единицы по главной диагонали и нули в каждом пробеле ниже диагонали
- эквивалент строки
- две матрицы и эквивалентны строкам, если одна может быть получена из другой путем выполнения основных операций со строками
- строковые операции
- : добавление одной строки к другой, умножение строки на константу, перестановка строк и т.
 Д. С целью получения формы «строка-эшелон»
Д. С целью получения формы «строка-эшелон»
Решающих систем с исключением Гаусса – алгебра и тригонометрия
Цели обучения
В этом разделе вы:
- Напишите расширенную матрицу системы уравнений.
- Напишите систему уравнений из расширенной матрицы.
- Выполнение операций со строками в матрице.
- Решите систему линейных уравнений, используя матрицы.
Карл Фридрих Гаусс жил в конце 18-го и начале 19-го веков, но он по-прежнему считается одним из самых плодовитых математиков в истории. Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика.Его открытия в области теории матриц изменили способ работы математиков за последние два столетия.
Мы впервые столкнулись с методом исключения Гаусса в системах линейных уравнений: две переменные. В этом разделе мы еще раз вернемся к этой технике решения систем, на этот раз с использованием матриц.
В этом разделе мы еще раз вернемся к этой технике решения систем, на этот раз с использованием матриц.
Написание расширенной матрицы системы уравнений
Матрица может служить средством представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы.Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по сути заменяя знаки равенства. Когда система написана в такой форме, мы называем ее расширенной матрицей.
Например, рассмотрим следующую систему уравнений.
Мы можем записать эту систему в виде расширенной матрицы:
Мы также можем написать матрицу, содержащую только коэффициенты. Это называется матрицей коэффициентов.
Система уравнений три на три, например
имеет матрицу коэффициентов
и представлена расширенной матрицей
Обратите внимание, что матрица написана так, что переменные выстраиваются в свои собственные столбцы: x -термы идут в первый столбец, – -термы во втором столбце и z -термы в третьем столбце. Очень важно, чтобы каждое уравнение было написано в стандартной форме, чтобы переменные совпадали. Если в уравнении отсутствует член переменной, коэффициент равен 0.
Очень важно, чтобы каждое уравнение было написано в стандартной форме, чтобы переменные совпадали. Если в уравнении отсутствует член переменной, коэффициент равен 0.
Как сделать
Для данной системы уравнений напишите расширенную матрицу.
- Запишите коэффициенты членов x в виде чисел в первом столбце.
- Запишите коэффициенты членов y в виде чисел во втором столбце.
- Если имеется z -термов, запишите коэффициенты в виде чисел в третьем столбце.
- Нарисуйте вертикальную линию и напишите константы справа от нее.
Написание расширенной матрицы для системы уравнений
Напишите расширенную матрицу для данной системы уравнений.
[show-answer q = ”fs-id1165137727716 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137727716 ″]
Расширенная матрица отображает коэффициенты переменных и дополнительный столбец для констант.
Попробуй
Запишите расширенную матрицу данной системы уравнений.
[show-answer q = ”fs-id1165134301343 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134301343 ″]
[/ hidden-answer]
Написание системы уравнений из расширенной матрицы
Мы можем использовать расширенные матрицы, чтобы помочь нам решать системы уравнений, потому что они упрощают операции, когда системы не обременены переменными. Однако важно понимать, как переключаться между форматами, чтобы поиск решений был более плавным и интуитивно понятным.Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.
Написание системы уравнений из расширенной матричной формы
Найдите систему уравнений из расширенной матрицы.
[show-answer q = ”fs-id1165137737608 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137737608 ″]
Когда столбцы представляют переменные [latex] y, \, [/ latex] и
[/ скрытый-ответ]Попробуй
Напишите систему уравнений из расширенной матрицы.
[скрытый-ответ a = ”fs-id1165135528897 ″]
[/ hidden-answer]
Выполнение операций со строками в матрице
Теперь, когда мы можем писать системы уравнений в форме расширенной матрицы, мы рассмотрим различные операции со строками, которые могут выполняться с матрицей, такие как сложение, умножение на константу и перестановка строк.
Выполнение строковых операций над матрицей – это метод, который мы используем для решения системы уравнений.Чтобы решить систему уравнений, мы хотим преобразовать матрицу в форму строки-эшелона, в которой есть единицы вниз по главной диагонали от верхнего левого угла до нижнего правого угла и нули в каждой позиции ниже главной диагонали. как показано.
Мы используем операции со строками, соответствующие операциям с уравнениями, чтобы получить новую матрицу, эквивалентную строкам в более простой форме. Вот рекомендации по получению формы рядного эшелона.
- В любой ненулевой строке первым ненулевым числом является 1.Он называется ведущим 1.
- Любые нулевые строки помещаются внизу матрицы.
- Любая ведущая 1 находится ниже и правее предыдущей ведущей 1.
- Любой столбец, в котором в начале стоит 1, имеет нули во всех остальных позициях в столбце.
Чтобы решить систему уравнений, мы можем выполнить следующие операции со строками, чтобы преобразовать матрицу коэффициентов в форму ряда строк и выполнить обратную подстановку, чтобы найти решение.
- Поменять местами ряды.(Обозначение 🙂
- Умножить строку на константу. (Обозначение 🙂
- Добавить произведение одной строки на константу к другой строке. (Замечание:
Каждая из строковых операций соответствует операциям, которые мы уже научились решать системы уравнений с тремя переменными. С помощью этих операций есть несколько ключевых шагов, которые быстро достигнут цели написания матрицы в виде эшелона строк. Чтобы получить матрицу в виде эшелона строк для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, чтобы строку 1 можно было использовать для преобразования оставшихся строк.
Чтобы получить матрицу в виде эшелона строк для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, чтобы строку 1 можно было использовать для преобразования оставшихся строк.
Исключение по Гауссу
Метод исключения Гаусса относится к стратегии, используемой для получения матрицы в виде строки-эшелона. Цель состоит в том, чтобы записать матрицу с номером 1 в качестве записи по главной диагонали и иметь все нули внизу.
Первый шаг стратегии Гаусса включает получение 1 в качестве первой записи, так что строка 1 может использоваться для изменения строк ниже.
Как сделать
Учитывая расширенную матрицу, выполните операции со строками для получения формы «строка-эшелон».
- Первое уравнение должно иметь старший коэффициент 1. При необходимости поменяйте местами строки или умножьте на константу.
- Используйте операции со строками, чтобы получить нули в первом столбце под первой записью 1.

- Используйте операции со строками, чтобы получить 1 в строке 2, столбце 2.
- Используйте операции со строками, чтобы получить нули в нижнем столбце 2, ниже записи 1.
- Используйте операции со строками, чтобы получить 1 в строке 3, столбце 3.
- Продолжайте этот процесс для всех строк, пока в каждой записи по главной диагонали не будет 1, а внизу будут только нули.
- Если какие-либо строки содержат все нули, поместите их внизу.
Решение системы методом исключения Гаусса
Решите данную систему методом исключения Гаусса.
Попробуй
Решите данную систему методом исключения Гаусса.
[show-answer q = ”fs-id1165137732121 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137732121 ″]
[/ hidden-answer]
Использование исключения Гаусса для решения системы уравнений
Используйте метод исключения Гаусса для решения данной системы уравнений
.
Решение зависимой системы
Решите систему уравнений.
Выполнение операций со строками в расширенной матрице 3 × 3 для получения формы Row-Echelon
Выполняет строковые операции с заданной матрицей для получения формы “строка-эшелон”.
Попробуй
Запишите систему уравнений в виде строк.
[show-answer q = ”fs-id1165134189887 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134189887 ″]
[/ hidden-answer]
Решение системы линейных уравнений с использованием матриц
Мы видели, как написать систему уравнений с расширенной матрицей, а затем как использовать строковые операции и обратную подстановку для получения строчно-эшелонированной формы.Теперь мы перейдем на шаг дальше от строковой формы, чтобы решить систему линейных уравнений 3 на 3. Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.
Решение системы линейных уравнений с использованием матриц
Решите систему линейных уравнений с помощью матриц.
Решение зависимой системы линейных уравнений с использованием матриц
Решите следующую систему линейных уравнений, используя матрицы.
Попробуй
Решите систему, используя матрицы.
[show-answer q = ”fs-id1165135172200 ″] Показать решение [/ show-answer][hidden-answer a = ”fs-id1165135172200 ″]
[/ hidden-answer]
Можно ли решить любую систему линейных уравнений методом исключения Гаусса?
Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.
Как сделать
Для данной системы уравнений решите с помощью матриц с помощью калькулятора.
- Сохранить расширенную матрицу как матричную переменную
- Используйте в калькуляторе функцию ref (, вызывая каждую матричную переменную по мере необходимости.

Решение систем уравнений с матрицами с помощью калькулятора
Решите систему уравнений.
Применение матриц 2 × 2 к финансам
Кэролайн инвестирует в общей сложности 12 000 долларов в две муниципальные облигации, одна из которых выплачивает 10,5% годовых, а другая – 12%.Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов. Сколько было вложено по каждой ставке?
Применение матриц 3 × 3 к финансам
Ava инвестирует в общей сложности 10 000 долларов в три счета, один из которых платит 5%, другой – 8%, а третий – 9%. Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 долларов. Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?
[show-answer q = ”fs-id1165134589597 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134589597 ″]
У нас есть система трех уравнений с тремя переменными. Пусть будет сумма, вложенная под 5%, пусть будет сумма, вложенная под 8%, пусть будет сумма, вложенная под 9%. Таким образом,
Пусть будет сумма, вложенная под 5%, пусть будет сумма, вложенная под 8%, пусть будет сумма, вложенная под 9%. Таким образом,
В качестве матрицы имеем
Теперь мы выполняем исключение Гаусса, чтобы получить форму строки-эшелон.
Третья строка сообщает usthus
Вторая строка сообщает нам Подставляя, мы получаем
Первая строка говорит нам, что подставляем и получаем
Ответ: 3000 долларов вложены под 5%, 1000 долларов вложены под 8% и 6000 долларов вложены под 9%.[/ hidden-answer]
Попробуй
Небольшая обувная компания взяла ссуду в размере 1 500 000 долларов на расширение своего ассортимента. Часть денег была взята под 7%, часть – под 8%, часть – под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла 130 500 долларов. Используйте матрицы, чтобы найти сумму займа по каждой ставке.
[show-answer q = ”fs-id1165137547014 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137547014 ″]
150 000 долларов США под 7%, 750 000 долларов США под 8%, 600 000 долларов США под 10%
[/ hidden-answer]
Ключевые понятия
- Расширенная матрица – это матрица, которая содержит коэффициенты и константы системы уравнений.
 См. (Рисунок).
См. (Рисунок). - Матрица, дополненная постоянным столбцом, может быть представлена как исходная система уравнений. См. (Рисунок).
- Операции со строками включают в себя умножение строки на константу, добавление одной строки к другой строке и замену строк местами.
- Мы можем использовать метод исключения Гаусса для решения системы уравнений. См. (Рисунок), (Рисунок) и (Рисунок).
- Операции со строками выполняются над матрицами для получения формы «строка-эшелон». См. (Рисунок).
- Чтобы решить систему уравнений, запишите ее в форме дополненной матрицы.Выполните операции со строками, чтобы получить форму эшелона строк. Обратно-заменитель, чтобы найти решения. См. (Рисунок) и (Рисунок).
- Калькулятор можно использовать для решения систем уравнений с использованием матриц. См. (Рисунок).
- Многие реальные проблемы можно решить с помощью расширенных матриц. См. (Рисунок) и (Рисунок).
Упражнения по разделам
Устный
Можно ли записать любую систему линейных уравнений в виде расширенной матрицы? Объясните, почему да или почему нет. Объясните, как написать эту расширенную матрицу.
Объясните, как написать эту расширенную матрицу.
[скрытый-ответ a = ”fs-id1165134155093 ″]
Да. Для каждой строки коэффициенты переменных записываются поперек соответствующей строки и помещается вертикальная черта; затем константы помещаются справа от вертикальной полосы.
[/ hidden-answer]
Можно ли записать любую матрицу в виде системы линейных уравнений? Объясните, почему да или почему нет. Объясните, как написать эту систему уравнений.
Есть только один правильный метод использования операций со строками в матрице? Попытайтесь объяснить две различные операции со строками, которые можно выполнить для расширенной матрицы
. [show-answer q = ”fs-id1165134036654 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134036654 ″]
Нет, существует множество правильных методов использования строковых операций над матрицей.Есть два возможных способа: (1) Поменять местами строки 1 и 2. Затем (2) Разделить строку 1 на 9.
Затем (2) Разделить строку 1 на 9.
[/ hidden-answer]
Можно ли решить матрицу с нулевым элементом на диагонали? Объясните, почему да или почему нет. Что бы вы сделали, чтобы исправить ситуацию?
Может ли матрица с 0 элементами для всей строки иметь одно решение? Объясните, почему да или почему нет.
[show-answer q = ”fs-id1165137639609 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137639609 ″]
№Матрица с 0 элементами для всей строки будет иметь либо ноль, либо бесконечно много решений.
[/ hidden-answer]
Алгебраические
Для следующих упражнений напишите расширенную матрицу для линейной системы.
[show-answer q = ”fs-id1165133145058 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165133145058 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165137418199 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137418199 ″]
[/ hidden-answer]
Для следующих упражнений запишите линейную систему из расширенной матрицы.
[скрытый-ответ a = ”fs-id11651374 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165137836994 ″] Показать решение [/ show-answer][hidden-answer a = ”fs-id1165137836994 ″]
[/ hidden-answer] [show-answer q = ”fs-id1165135440480 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135440480 ″]
[/ hidden-answer]
Для следующих упражнений решите систему методом исключения Гаусса.
[show-answer q = ”fs-id1165135151213 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135151213 ″]
Нет решений
[/ hidden-answer]
[show-answer q = ”fs-id1165134329612 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134329612 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165135473768 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135473768 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165135580980 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135580980 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165137843205 ″] Показать решение [/ show-answer][hidden-answer a = ”fs-id1165137843205 ″]
[/ hidden-answer] [show-answer q = ”fs-id1165133243532 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165133243532 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165137501549 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137501549 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165135551136 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135551136 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165133141313 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165133141313 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165135620833 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135620833 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165134188796 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134188796 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165135496208 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135496208 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165134138496 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134138496 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165135407366 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135407366 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165135665476 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135665476 ″]
[/ hidden-answer]
Расширения
Для следующих упражнений используйте метод исключения Гаусса для решения системы.
[скрытый-ответ a = ”fs-id1165137471175 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165135263629 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135263629 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165135354918 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135354918 ″]
Решения отсутствуют.
[/ hidden-answer]
Реальные приложения
Для следующих упражнений настройте расширенную матрицу, описывающую ситуацию, и найдите желаемое решение.
Ежедневно в магазине кексов продается 5 000 кексов со вкусом шоколада и ванили. Если вкус шоколада в 3 раза популярнее, чем аромат ванили, сколько кексов продается в день?
В конкурирующем магазине кексов ежедневно продаются кексы на сумму 4520 долларов.Шоколадные кексы стоят 2,25 доллара, а кексы из красного бархата – 1,75 доллара. Если общее количество кексов, проданных в день, составляет 2200, сколько штук каждого вкуса продается каждый день?
Если общее количество кексов, проданных в день, составляет 2200, сколько штук каждого вкуса продается каждый день?
[show-answer q = ”fs-id1165137767240 ″] Показать решение [/ show-answer]
[hidden-answer a =” fs-id1165137767240 ″] 860 красный бархат, 1340 шоколад [/ hidden-answer]
Вы вложили 10 000 долларов в два счета: один с простой процентной ставкой 3%, а другой – с процентной ставкой 2,5%. Если ваша общая сумма процентов по истечении одного года составила 283 доллара.50, сколько было на каждом счете по прошествии года?
Вы инвестировали 2300 долларов на счет 1 и 2700 долларов на счет 2. Если общая сумма процентов по истечении одного года составляет 254 доллара, а на счете 2 процентная ставка в 1,5 раза выше, чем на счете 1, каковы процентные ставки? Предположим простые процентные ставки.
[show-answer q = ”fs-id1165134254294 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134254294 ″]
4% на счет 1, 6% на счет 2
[/ hidden-answer]
Bikes’R’Us производит велосипеды по 250 долларов. Он стоит производителю 180 долларов за велосипед плюс стартовый взнос в размере 3500 долларов. Через сколько проданных велосипедов производитель выйдет на уровень безубыточности?
Он стоит производителю 180 долларов за велосипед плюс стартовый взнос в размере 3500 долларов. Через сколько проданных велосипедов производитель выйдет на уровень безубыточности?
Крупный магазин бытовой техники рассматривает возможность приобретения пылесосов у небольшого производителя. Магазин сможет приобрести пылесосы по 86 долларов каждый, со стоимостью доставки 9 200 долларов, независимо от того, сколько пылесосов будет продано. Если магазин должен начать получать прибыль после продажи 230 единиц, сколько они должны взимать за пылесосы?
[show-answer q = ”fs-id1165135456730 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135456730 ″]
$ 126
[/ hidden-answer]
Три самых популярных вкуса мороженого – это шоколад, клубника и ваниль, составляющие 83% вкусов, продаваемых в магазине мороженого.Если ваниль продается на 1% больше, чем в два раза больше клубники, а шоколад продается на 11% больше, чем ваниль, сколько в общем потреблении мороженого приходится на ароматы ванили, шоколада и клубники?
В магазине мороженого возрастает спрос на три вкуса. В прошлом году банановое, тыквенное и мороженое с каменистой дорогой составили 12% от общего объема продаж мороженого. В этом году на те же три вида мороженого пришлось 16,9% продаж мороженого. Продажи по каменистой дороге увеличились вдвое, продажи бананов увеличились на 50%, а продажи тыквы – на 20%.Если у мороженого по каменистой дороге было на один процент меньше продаж, чем у бананового мороженого, узнайте, какой процент продаж мороженого было произведено каждым отдельным мороженым в прошлом году.
В прошлом году банановое, тыквенное и мороженое с каменистой дорогой составили 12% от общего объема продаж мороженого. В этом году на те же три вида мороженого пришлось 16,9% продаж мороженого. Продажи по каменистой дороге увеличились вдвое, продажи бананов увеличились на 50%, а продажи тыквы – на 20%.Если у мороженого по каменистой дороге было на один процент меньше продаж, чем у бананового мороженого, узнайте, какой процент продаж мороженого было произведено каждым отдельным мороженым в прошлом году.
[скрытый-ответ a = ”fs-id1165135255463 ″]
Банан – 3%, тыква – 7%, а каменистая дорога – 2%
[/ hidden-answer]
Пакет с ореховой смесью содержит кешью, фисташки и миндаль. Всего в сумке 1000 орехов, а миндаля на 100 меньше, чем фисташек.Кешью весит 3 г, фисташки – 4 г, миндаль – 5 г. Если мешок весит 3,7 кг, узнайте, сколько орехов каждого вида в нем.
Пакет с ореховой смесью содержит кешью, фисташки и миндаль. Изначально в сумке было 900 орехов. Было съедено 30% миндаля, 20% кешью и 10% фисташек, и теперь в сумке осталось 770 орехов. Изначально кешью было на 100 штук больше, чем миндаля. Для начала выясните, сколько орехов каждого типа было в пакете.
[show-answer q = ”fs-id1165133294879 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165133294879 ″]
100 миндальных орехов, 200 кешью, 600 фисташек
[/ hidden-answer]
Глоссарий
- дополненная матрица
- матрица коэффициентов, примыкающая к столбцу констант, разделенному вертикальной линией в скобках матрицы
- матрица коэффициентов
- матрица, содержащая только коэффициенты из системы уравнений
- Гауссово исключение
- с использованием элементарных операций со строками для получения матрицы в виде эшелона строки
- главная диагональ
- записей из левого верхнего угла по диагонали в правый нижний угол квадратной матрицы
- рядная форма
- после выполнения строковых операций матричная форма, содержащая единицы по главной диагонали и нули в каждом пробеле ниже диагонали
- эквивалент строки
- две матрицы и эквивалентны строкам, если одна может быть получена из другой путем выполнения основных операций со строками
- строковые операции
- : добавление одной строки к другой, умножение строки на константу, перестановка строк и т. Д. С целью получения формы «строка-эшелон»
15.4 Решение неоднородных уравнений: исключение Гаусса
15.4 Решение неоднородных уравнений: исключение Гаусса
|
Имея систему уравнений, можно выполнить несколько операций.
на них, что не влияет на их содержание.
Их:
1. Складываем одно к другому (добавляем левые части к левым и правым к прав.)
Проба
2. Переупорядочить их.
Комментарий
3. Умножьте обе части любого из них на ненулевое число.
Они называются операциями элементарной строки .
Решение уравнений означает поиск эквивалентной системы уравнений, имеющей
очень простая форма: в каждом уравнении есть только одна переменная, ее коэффициент
равно 1, и переменная появляется одна в левой части уравнения.Затем уравнение предоставляет явное выражение для соответствующей переменной.
Решаем линейные уравнения по , выполняя последовательность элементарных
строковые операции, которые преобразуют исходную матрицу коэффициентов в единицу
матрица. Эта процедура называется Гауссовское исключение .
Обсуждение:
1. Предположим, у нас есть матрица коэффициентов 3 на 3 C , мы определяем столбец
вектор v , чтобы правая часть j-го уравнения была его j-й компонентой,
и пусть вектор-столбец r имеет компоненты x, y и z.
Тогда линейные уравнения принимают вид C r = v , где
левая часть представляет собой матричное произведение матрицы 3 на 3 C и
матрица 3 на 1 r .
2. Если матрица коэффициентов C является единичной матрицей, мы имеем решение: C = I подразумевает C r = I r = r = v .
3. Исключение Гаусса – это в точности обычный стандартный метод решения уравнений, который выглядит следующим образом: решите первое уравнение для любой переменной, которая встречается в нем с точки зрения остального.Используйте это уравнение, чтобы исключить эту переменную из все остальные уравнения. Повторите эти шаги для другого уравнения и переменной. Повторить пока у вас не будет явного выражения для последней переменной. Замена для эту переменную во всех уравнениях, исключив ее из них; взять следующий переменную и повторяйте, пока не получите явное выражение для всех переменных.
Решение уравнения означает, помимо перестановки правой и левой частей, умножение уравнение константой, чтобы коэффициент связанной переменной в 1.Исключение переменной из других уравнений означает добавление или вычитание строка, соответствующая уравнению, к другим строкам, чтобы коэффициент переменной, решаемой в этом уравнении, в ноль во всех остальных уравнениях. Таким образом, стандартный метод – это метод исключения по Гауссу.
Пример
Как решить линейные системы с помощью исключения Гаусса – Видео и стенограмма урока
Расширенная матрица
Помните, что матрица – это просто прямоугольный массив значений, помещенных в строки и столбцы.Сначала нам нужно превратить нашу линейную систему в матричную форму, превратив ее в расширенную матрицу. Расширенная матрица – это комбинация двух матриц. В нашем случае у нас есть матрица для коэффициентов левой части уравнения и еще одна матрица для правой части уравнения.
Напомним, что преобразование системы уравнений в матричную форму включает в себя выделение только коэффициентов вместе с их соответствующими знаками после их организации таким образом, что за членом x сначала следует член y , за которым следует член z , т.е. знак равенства, а затем константа.Мы можем использовать вертикальную линию или несколько точек на вертикальной линии, чтобы обозначить наш знак равенства. Наша линейная система уже организована должным образом, поэтому все, что нам нужно сделать, это выделить наши коэффициенты. В нашей первой строке будет 1, 1, 1, | а затем 5. Во второй строке 2, 0, -1, | и 4. В нашей третьей строке 0, 3, 1, | и 2. Наша матрица выглядит так:
Исключение Гаусса
Теперь мы можем использовать метод исключения Гаусса, чтобы помочь нам решить эту линейную систему.Исключение Гаусса – это манипулирование расширенной матрицей до тех пор, пока мы не получим матрицу, которая представляет левую часть уравнений в верхней треугольной форме . Это означает, что мы хотим, чтобы все нули находились ниже главной диагонали. Эта главная диагональ начинается в верхнем левом углу и заканчивается в правом нижнем углу матрицы коэффициентов. Другими словами, мы хотим манипулировать матрицей так, чтобы 2 во второй строке и 0 и 3 в третьей строке были равны 0.
Чтобы заменить эти числа на нули, мы будем использовать наши операции со строками матрицы.Чтобы превратить наши первые 2 в 0, мы умножаем нашу первую строку на -2, а затем добавляем ее ко второй строке, чтобы создать новую вторую строку. Получаем новую вторую строку 0, -2, -3, | и -6. Теперь, чтобы заменить 3 в третьей строке на 0, мы будем использовать эту новую вторую строку в сочетании с третьей строкой. Мы умножим вторую строку на 3 и прибавим ее к третьей строке, умноженной на 2. Мы получим новую третью строку 0, 0, -7, | и -14.
Мы не переписывали первую строку, потому что нам не нужно менять это уравнение.Мы только умножили первую строку на 3, чтобы вычесть ее из второй строки. Помните, что в алгебре всякий раз, когда мы умножаем уравнение на любую константу, уравнение вообще не меняется; числа просто увеличиваются в разы.
Теперь, когда у нас есть нули под главной диагональю, мы закончили с помощью исключения Гаусса. Теперь мы можем продолжить и решить нашу линейную систему.
Решение системы
Обратите внимание, как легко теперь решить эту проблему. Если мы выпишем наши линейные уравнения, мы получим x + y + z = 5, -2 y -3 z = -6 и -7 z = -14.Мы можем немедленно решить третье уравнение для z , чтобы получить z = -14 / -7 = 2. Затем мы можем заменить это значение на z во второе уравнение, чтобы найти следующую переменную, y . Получаем -2 y -3 (2) = -6. Получается -2 y – 6 = -6. Чтобы решить для y , мы прибавляем 6 к обеим сторонам и получаем -2 y = 0. Разделив обе стороны на -2, мы получаем y = 0. Итак, теперь у нас есть y = 0 и . z = 2.Чтобы решить нашу последнюю переменную, x , мы можем использовать наше самое первое уравнение. Подставляя эти два значения, мы получаем x + 0 + 2 = 5. Решая это для x , мы получаем x = 3. Итак, наш окончательный ответ: x = 3, y = 0, и z = 2. Мы также можем записать это в точечной форме, например: (3, 0, 2).
Резюме урока
Давайте рассмотрим то, что мы узнали. Мы узнали, что линейных систем представляют собой наборы линейных уравнений.Линейная система имеет такое же количество уравнений, как и переменных, поскольку нам нужно по одному уравнению для каждой переменной, чтобы решить такую систему уравнений. В методе, о котором мы говорили в этом уроке, используется метод исключения Гаусса , метод решения системы уравнений, который включает манипулирование матрицей так, чтобы все элементы ниже главной диагонали равнялись нулю. Верхний треугольник – это термин, используемый для описания матрицы, в которой все нули находятся ниже главной диагонали. Затем мы используем алгебру и подстановку, чтобы завершить решение нашей системы уравнений.
Результаты обучения
Завершение этого урока может подготовить вас к:
- Чтению определений линейных систем, расширенной матрицы и верхней треугольной формы
- Продемонстрировать использование метода исключения Гаусса для решения системы уравнений
Решение линейных систем – математический Python
импортировать numpy как np
импортировать matplotlib.pyplot как plt
импорт scipy.линалг как ла
% matplotlib встроенный
Линейные системы
Линейная система уравнений представляет собой набор линейных уравнений
\ begin {align} a_ {0,0} x_0 + a_ {0,1} x_2 + \ cdots + a_ {0, n} x_n & = b_0 \\ a_ {1,0} x_0 + a_ {1,1} x_2 + \ cdots + a_ {1, n} x_n & = b_1 \\ & \ vdots \\ a_ {m, 0} x_0 + a_ {m, 1} x_2 + \ cdots + a_ {m, n} x_n & = b_m \\ \ end {align}
В матричной записи линейной системой является $ A \ mathbf {x} = \ mathbf {b} $, где
$$ A = \ begin {bmatrix} a_ {0,0} & a_ {0,1} & \ cdots & a_ {0, n} \\ a_ {1,0} и a_ {1,1} & \ cdots & a_ {1, n} \\ \ vdots & & & \ vdots \\ a_ {m, 0} & a_ {m, 1} & \ cdots & a_ {m, n} \\ \ end {bmatrix} \ \, \ \ \ mathbf {x} = \ begin {bmatrix} x_0 \\ x_1 \\ \ vdots \\ x_n \ end {bmatrix} \ \, \ \ \ mathbf {b} = \ begin {bmatrix} b_0 \\ b_1 \\ \ vdots \\ b_m \ end {bmatrix} $
Исключение по Гауссу
Общая процедура решения линейной системы уравнений называется исключением Гаусса.Идея состоит в том, чтобы выполнить элементарные операции со строками, чтобы привести систему к ее эшелонированной форме, а затем решить.
Операции с элементарными строками
Элементарные операции со строками включают:
- Добавить $ k $, умноженное на строку $ j $, в строку $ i $.
- Умножить строку $ i $ на скаляр $ k $.
- Переключить строки $ i $ и $ j $.
Каждая из элементарных операций со строкой является результатом умножения матрицы на элементарную матрицу (слева). Чтобы добавить $ k $, умноженное на строку $ i $, в строку $ j $ в матрице $ A $, мы умножаем $ A $ на матрицу $ E $, где $ E $ равно единичной матрице, за исключением $ i, j $ запись $ E_ {i, j} = k $.Например, если $ A $ равно 3 на 3, и мы хотим добавить 3 раза строку 2 к строке 0 (с использованием 0-индексации), тогда
$$ E_1 = \ begin {bmatrix} 1 и 0 и 3 \\ 0 & 1 & 0 \\ 0 и 0 и 1 \ end {bmatrix} $
Проверим расчет:
A = np.array ([[1,1,2], [- 1,3,1], [0,5,2]])
печать (A)
[[1 1 2]
[-1 3 1]
[0 5 2]]
E1 = np.array ([[1,0,3], [0,1,0], [0,0,1]])
печать (E1)
[[1 0 3]
[0 1 0]
[0 0 1]]
E1 @ A
массив ([[1, 16, 8],
[-1, 3, 1],
[0, 5, 2]])
Чтобы умножить $ k $ на строку $ i $ в матрице $ A $, мы умножаем $ A $ на матрицу $ E $, где $ E $ равно единичной матрице, за исключением того, что запись $, i, j $ равна $ E_ {i, i} = k $.Например, если $ A $ равно 3 на 3, и мы хотим умножить строку 1 на -2, тогда
$$ E_2 = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & -2 & 0 \\ 0 и 0 и 1 \ end {bmatrix} $
Проверим расчет:
E2 = np.array ([[1,0,0], [0, -2,0], [0,0,1]])
печать (E2)
[[1 0 0]
[0–2 0]
[0 0 1]]
E2 @ A
массив ([[1, 1, 2],
[2, -6, -2],
[0, 5, 2]])
Наконец, чтобы поменять местами строку $ i $ и строку $ j $ в матрице $ A $, мы умножаем $ A $ на матрицу $ E $, где $ E $ равно единичной матрице, за исключением $ E_ {i, i} = 0 $, $ E_ {j, j} = 0 $, $ E_ {i, j} = 1 $ и $ E_ {j, i} = 1 $.3 = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 и 1 и 0 \ end {bmatrix} $
Проверим расчет:
E3 = np.array ([[1,0,0], [0,0,1], [0,1,0]])
печать (E3)
[[1 0 0]
[0 0 1]
[0 1 0]]
E3 @ A
массив ([[1, 1, 2],
[0, 5, 2],
[-1, 3, 1]])
Реализация
Напишем функцию для реализации простейших строковых операций.Прежде всего, давайте напишем функцию с именем add_rows , которая принимает входные параметры $ A $, $ k $, $ i $ и $ j $ и возвращает массив NumPy, полученный в результате добавления $ k $ times row $ j $ к строке $ i $ в матрице $ A $. Если $ i = j $, то предположим, что функция масштабирует строку $ i $ на $ k + 1 $, поскольку это будет результатом того, что $ k $ умножается на строку $ i $, добавленную к строке $ i $.
def add_row (A, k, i, j):
«Добавить k раз строку j к строке i в матрице A.»
n = A.shape [0]
E = np.eye (n)
если я == j:
E [i, i] = k + 1
еще:
E [i, j] = k
вернуть E @ A
Давайте протестируем нашу функцию:
M = np.массив ([[1,1], [3,2]])
печать (M)
[[1 1]
[3 2]]
add_row (M, 2,0,1)
массив ([[7., 5.],
[3., 2.]])
add_row (M, 3,1,1)
массив ([[1., 1.],
[12., 8.]])
Давайте напишем функцию с именем scale_row , которая принимает 3 входных параметра $ A $, $ k $ и $ i $ и возвращает матрицу, которая получается из $ k $, умноженного на строку $ i $ в матрице $ A $.
def scale_row (A, k, i):
«Умножить строку i на k в матрице A.»
n = A.shape [0]
E = np.eye (n)
E [i, i] = k
вернуть E @ A
M = np.array ([[3,1], [- 2,7]])
печать (M)
[[3 1]
[-2 7]]
scale_row (M, 3,1)
массив ([[3., 1.],
[-6., 21.]])
A = np.array ([[1,1,1], [1, -1,0]])
печать (A)
[[1 1 1]
[1–1 0]]
scale_row (A, 5,1)
массив ([[1., 1., 1.],
[5., -5., 0.]])
Давайте напишем функцию с именем switch_rows , которая принимает 3 входных параметра $ A $, $ i $ и $ j $ и возвращает матрицу, полученную в результате переключения строк $ i $ и $ j $ в матрице $ A $.
def switch_rows (A, i, j):
«Поменяйте местами строки i и j в матрице A.»
n = A.shape [0]
E = np.eye (n)
E [i, i] = 0
E [j, j] = 0
E [i, j] = 1
E [j, i] = 1
вернуть E @ A
A = np.array ([[1,1,1], [1, -1,0]])
печать (A)
[[1 1 1]
[1–1 0]]
switch_rows (A, 0,1)
массив ([[1., -1., 0.],
[1., 1., 1.]])
Примеры
Найдите обратное
Применим наши функции к расширенной матрице $ [M \ | \ I] $, чтобы найти обратную матрицу $ M $:
M = np.array ([[5,4,2], [- 1,2,1], [1,1,1]])
печать (M)
[[5 4 2]
[-1 2 1]
[1 1 1]]
A = np.hstack ([M, np.eye (3)])
печать (A)
[[5. 4. 2. 1. 0. 0.]
[-1. 2. 1. 0. 1. 0.]
[1. 1. 1. 0. 0. 1.]]
A1 = switch_rows (A, 0,2)
печать (A1)
[[1. 1. 1. 0. 0. 1.]
[-1. 2. 1. 0. 1. 0.]
[5. 4. 2. 1. 0. 0.]]
A2 = add_row (A1,1,1,0)
печать (A2)
[[1. 1. 1. 0. 0. 1.]
[0. 3. 2. 0. 1. 1.]
[5. 4. 2. 1. 0. 0.]]
A3 = add_row (A2, -5,2,0)
печать (A3)
[[1. 1. 1. 0. 0. 1.]
[0. 3. 2. 0. 1.1.]
[0. -1. -3. 1. 0. -5.]]
A4 = switch_rows (A3,1,2)
печать (A4)
[[1. 1. 1. 0. 0. 1.]
[0. -1. -3. 1. 0. -5.]
[0. 3. 2. 0. 1. 1.]]
A5 = scale_row (A4, -1,1)
печать (A5)
[[1. 1. 1. 0. 0. 1.]
[0. 1. 3. -1. 0. 5.]
[0. 3. 2. 0. 1. 1.]]
A6 = add_row (A5, -3,2,1)
печать (A6)
[[1. 1. 1. 0. 0.1.]
[0. 1. 3. -1. 0. 5.]
[0. 0. -7. 3. 1. -14.]]
A7 = scale_row (A6, -1 / 7,2)
печать (A7)
[[1. 1. 1. 0. 0. 1.]
[0. 1. 3. -1. 0. 5.]
[0. 0. 1. -0.42857143 -0.14285714 2.]]
A8 = add_row (A7, -3,1,2)
печать (A8)
[[1. 1.1. 0. 0. 1.]
[0. 1. 0. 0,28571429 0,42857143 -1. ]
[0. 0. 1. -0.42857143 -0.14285714 2.]]
A9 = add_row (A8, -1,0,2)
печать (A9)
[[1. 1. 0. 0.42857143 0.14285714 -1. ]
[0. 1. 0. 0,28571429 0,42857143 -1. ]
[0. 0. 1. -0.42857143 -0.{-1} $ правильно:
Minv = A10 [:, 3:]
печать (Minv)
[[0,14285714 -0,28571429 0.]
[0,28571429 0,42857143 -1. ]
[-0,42857143 -0,14285714 2.]]
результат = Minv @ M
печать (результат)
[[1.00000000e + 00 4.44089210e-16 2.22044605e-16]
[-6.66133815e-16 1.00000000e + 00 -2.22044605e-16]
[0.00000000e + 00 0.00000000e + 00 1.00000000e + 00]]
Успех! Мы сможем увидеть результат более четко, если округлим до 15 знаков после запятой:
нп.round (результат, 15)
массив ([[1.e + 00, 0.e + 00, 0.e + 00],
[-1.e-15, 1.e + 00, -0.e + 00],
[0.e + 00, 0.e + 00, 1.e + 00]])
Решите систему
Давайте воспользуемся нашими функциями для выполнения исключения Гаусса и решения линейной системы уравнений $ A \ mathbf {x} = \ mathbf {b} $.
A = np.array ([[6,15,1], [8,7,12], [2,7,8]])
печать (A)
[[6 15 1]
[8 7 12]
[2 7 8]]
б = нп.массив ([[2], [14], [10]])
печать (б)
[[2]
[14]
[10]]
Форма расширенной матрицы $ M $:
M = np.hstack ([A, b])
печать (M)
[[6 15 1 2]
[8 7 12 14]
[2 7 8 10]]
Выполнение операций со строками:
M1 = scale_row (M, 1 / 6,0)
печать (M1)
[[1. 2.5 0.16666667 0.33333333]
[8. 7. 12. 14.]
[2. 7.8. 10.]]
M2 = add_row (M1, -8,1,0)
печать (M2)
[[1. 2.5 0.16666667 0.33333333]
[0. -13. 10,66666667 11,33333333]
[2. 7. 8. 10.]]
M3 = add_row (M2, -2,2,0)
печать (M3)
[[1. 2.5 0.16666667 0.33333333]
[0. -13. 10,66666667 11,33333333]
[0.2. 7.66666667 9.33333333]]
M4 = scale_row (M3, -1 / 13,1)
печать (M4)
[[1. 2.5 0.16666667 0.33333333]
[0,1,1 -0,82051282 -0,87179487]
[0. 2. 7.66666667 9.33333333]]
M5 = add_row (M4, -2,2,1)
печать (M5)
[[1. 2.5 0.16666667 0.33333333]
[0,1,1 -0,82051282 -0,87179487]
[0. 0.9.30769231 11.076]]
M6 = scale_row (M5,1 / M5 [2,2], 2)
печать (M6)
[[1. 2.5 0.16666667 0.33333333]
[0,1,1 -0,82051282 -0,87179487]
[0. 0. 1. 1.164]]
M7 = add_row (M6, -M6 [1,2], 1,2)
печать (M7)
[[1. 2,5 0,16666667 0,33333333]
[0. 1. 0. 0.1046832]
[0. 0. 1.1.164]]
M8 = add_row (M7, -M7 [0,2], 0,2)
печать (M8)
[[1. 2,5 0. 0,13498623]
[0. 1. 0. 0.1046832]
[0. 0. 1. 1.164]]
M9 = add_row (M8, -M8 [0,1], 0,1)
печать (M9)
[[1. 0. 0. -0.12672176]
[0. 1. 0. 0.1046832]
[0. 0. 1. 1.164]]
Успех! Решение $ Ax = b $ -
x = M9 [:, 3] .reshape (3,1)
печать (х)
[[-0,12672176]
[0.1046832]
[1.164]]
Или мы можем сделать это простым способом ...
x = la.solve (A, b)
печать (х)
[[-0,12672176]
[0.1046832]
[1.164]]
scipy.linalg.solve Нас больше всего интересуют линейные системы $ A \ mathbf {x} = \ mathbf {b} $, в которых существует единственное решение $ \ mathbf {x} $.Это тот случай, когда $ A $ - квадратная матрица ($ m = n $) и $ \ mathrm {det} (A) \ not = 0 $. Чтобы решить такую систему, мы можем использовать функцию scipy.linalg.solve .
Функция возвращает решение системы уравнений $ A \ mathbf {x} = \ mathbf {b} $. Например:
A = np.array ([[1,1], [1, -1]])
печать (A)
[[1 1]
[1 -1]]
b1 = np.array ([2,0])
печать (b1)
[2 0]
И решаем:
x1 = la.решить (A, b1)
печать (x1)
[1. 1.]
Обратите внимание, что выходные данные $ \ mathbf {x} $ возвращаются как одномерный массив NumPy, когда вектор $ \ mathbf {b} $ (правая часть) вводится как одномерный массив NumPy. Если мы введем $ \ mathbf {b} $ как 2D-массив NumPy, то на выходе получится 2D-массив NumPy. Например:
A = np.array ([[1,1], [1, -1]])
b2 = np.array ([2,0]). reshape (2,1)
x2 = la.solve (A, b2)
печать (x2)
[[1.]
[1.]]
Наконец, если правая часть $ \ mathbf {b} $ представляет собой матрицу, то на выходе получается матрица того же размера.Это решение $ A \ mathbf {x} = \ mathbf {b} $, когда $ \ mathbf {b} $ - матрица. Например:
A = np.array ([[1,1], [1, -1]])
b3 = np.array ([[2,2], [0,1]])
x3 = la.solve (A, b3)
печать (x3)
[[1. 1.5]
[1. 0,5]]
Простой пример
Вычислим решение системы уравнений
\ begin {align}
2х + у & = 1 \\
х + у & = 1
\ end {align}
Создайте матрицу коэффициентов:
A = np.массив ([[2,1], [1,1]])
печать (A)
[[2 1]
[1 1]]
И вектор $ \ mathbf {b} $:
b = np.array ([1, -1]). Reshape (2,1)
печать (б)
[[1]
[-1]]
И решаем:
x = la.solve (A, b)
печать (х)
[[2.]
[-3.]]
Мы можем проверить решение, вычислив обратную величину $ A $:
Ainv = la.inv (A)
печать (Ainv)
[[1.{-1} $ для решения $ A \ mathbf {x} = \ mathbf {b} $, если $ A $ большой. Это слишком дорого с точки зрения вычислений. Давайте создадим большую случайную матрицу $ A $ и вектор $ \ mathbf {b} $ и вычислим решение $ \ mathbf {x} $ двумя способами:
N = 1000
A = np.random.rand (N, N)
b = np.random.rand (N, 1)
Проверить первые записи $ A $:
A [: 3,: 3]
массив ([[0.35754719, 0.63135432, 0.6572258],
[0,18450506, 0,14639832, 0,23528745],
[0,27576474, 0.46264005, 0,26589724]])
А для $ \ mathbf {b} $:
б [: 4 ,:]
массив ([[0.82726751],
[0,96946096],
[0,31351176],
[0.63757837]])
Теперь сравним скорость scipy.linalg.solve с scipy.linalg.inv :
%% timeit
х = la.solve (A, b)
2,77 с ± 509 мс на цикл (среднее ± стандартное отклонение из 7 прогонов, по 1 циклу в каждом)
%% timeit
х = ла.inv (A) @ b
4,46 с ± 2,04 с на цикл (среднее ± стандартное отклонение из 7 прогонов, по 1 циклу в каждом)
Решение с scipy.linalg.solve примерно в два раза быстрее!
Упражнения
Строится
.

 — 208 с.
— 208 с. «Системы линейных уравнений, решаемые методом исключения Гаусса». Purplemath
«Системы линейных уравнений, решаемые методом исключения Гаусса». Purplemath 
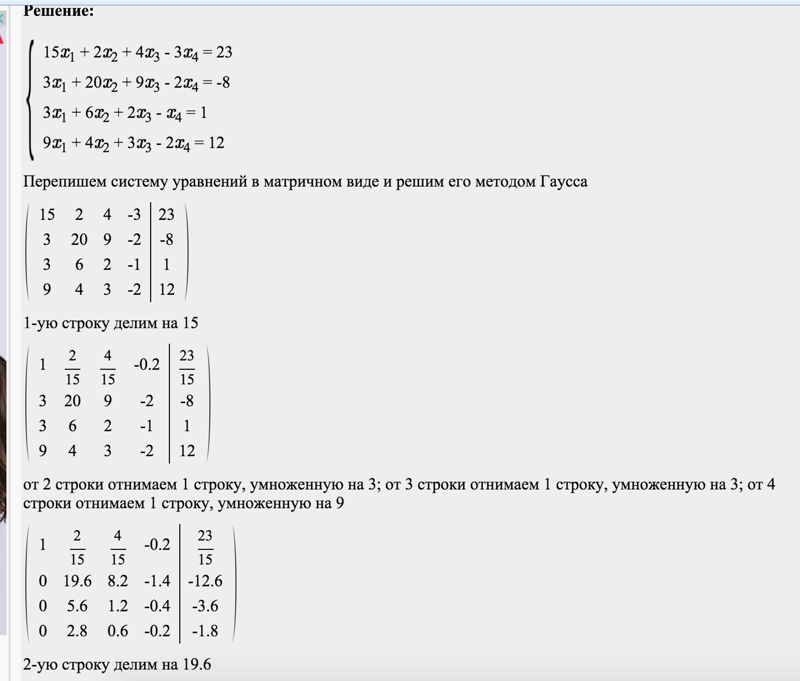
 См. (Рисунок).
См. (Рисунок). Д. С целью получения формы «строка-эшелон»
Д. С целью получения формы «строка-эшелон»

 См. (Рисунок).
См. (Рисунок).