Как скорость связана с ускорением и перемещением: Ускорение через перемещение и время. Формулы ускорения в физике: линейное и центростремительное ускорение

Средняя скорость по перемещению определение. Средняя скорость перемещения. Средняя путевая скорость

Все задачи, в которых присутствует движение объектов, их перемещение или вращение, так или иначе связаны со скоростью.

Данный термин характеризует перемещение объекта в пространстве за определенный отрезок времени – число единиц расстояния за единицу времени. Он является частым «гостем» как разделов математики, так и физики. Исходное тело может менять свое расположение как равномерно, так и с ускорением. В первом случае величина скорости статична и в ходе движения не меняется, во втором наоборот – увеличивается или уменьшается.

Как найти скорость – равномерное движение

Если скорость движения тела оставалась неизменной от начала перемещения и до окончания пути, то речь идет о перемещении с постоянным ускорением – равномерном движении. Оно может быть прямолинейным или же криволинейным. В первом случае траекторией перемещения тела является прямая.

Тогда V=S/t, где:

• V – искомая скорость,
• S – пройденное расстояние (общий путь),
• t – общее время движения.

Как найти скорость – ускорение постоянно

Если объект двигался с ускорением, то его скорость по мере движения менялась. В таком случае найти искомую величину поможет выражение:

V=V (нач) + at, где:

• V (нач) – первоначальная скорость движения объекта,
• a – ускорение тела,
• t – общее время пути.

Как найти скорость – неравномерное движение

В данном случае имеет место ситуация, когда разные участки пути тело проходило за разное время.
S(1) – за t(1),
S(2) – за t(2) и т.д.

На первом участке движение происходило в “темпе” V(1), на втором – V(2) и т.д.

Чтобы узнать скорость перемещения объекта на всем пути (ее среднее значение) воспользуйтесь выражением:

Как найти скорость – вращение объекта

В случае вращения речь идет об угловой скорости, определяющей угол, на который поворачивается элемент за единицу времени. Обозначается искомая величина символом ω (рад/с).

• ω = Δφ/Δt, где:

Δφ – пройденный угол (приращение угла),
Δt – прошедшее время (время движения – приращение времени).

• В случае, если вращение равномерное, искомая величина (ω) связана с таким понятием как период вращения – за какое время наш объект совершит 1 полный оборот. В таком случае:

ω = 2π/T, где:
π – константа ≈3,14,
T – период.

Или ω = 2πn, где:
π – константа ≈3,14,
n – частота обращения.

• При известной линейной скорости объекта для каждой точки на пути движения и радиусе окружности, по которой она перемещается, для нахождения скорости ω потребуется следующее выражение:

ω = V/R, где:
V – численное значение векторной величины (линейной скорости),
R – радиус траектории следования тела.

Как найти скорость – сближение и отдаление точек

В подобного рода задачах уместным будет использование терминов скорость сближения и скорость отдаления.

Если объекты направляются друг к другу, то скорость сближения (отдаления) будет следующей:
V (сближ) = V(1) + V(2), где V(1) и V(2) – скорости соответствующих объектов.

Если одно из тел догоняет другое, то V (сближ) = V(1) – V(2), V(1) больше V(2).

Как найти скорость – движение по водоему

Если события разворачиваются на воде, то к собственной скорости объекта (движение тела относительно воды) добавляется еще и скорость течения (т.е. движение воды относительно неподвижного берега). Как взаимосвязаны эти понятия?

В случае перемещения по течению V=V(собст) + V(теч).
Если против течения – V=V(собств) – V(теч.).

Средней скоростью называется скорость, которая получается, если весь путь поделить на время, за которое объект преодолел этот путь. Формула средней скорости:

• V ср = S/t.

• S = S1 + S2 + S3 = v1*t1 + v2*t2 + v3*t3
• V ср = S/t = (v1*t1 + v2*t2 + v3*t3) / (t1 + t2 + t3)

Чтобы не путаться с часами и минутами, переводим все минуты в часы: 15 мин. = 0,4 час, 36 мин. = 0,6 час. Подставляем числовые значения в последнюю формулу:

• V ср = (20*0,4 + 0,5*6 + 0,6*15) / (0,4 + 0,5 + 0,6) = (8 + 3 + 9) / (0,4 + 0,5 + 0,6) = 20 / 1,5 = 13,3 км/час

Ответ: средняя скорость V ср = 13,3 км/час.

Как найти среднюю скорость движения с ускорением

Если скорость в начале движения отличается от скорости в его конце, такое движение называют ускоренным. Причём далеко не всегда тело действительно двигается всё быстрее и быстрее. Если движение замедляется, всё равно говорят, что оно движется с ускорением, только ускорение будет уже отрицательным.

Иными словами, если автомобиль, трогаясь с места, через секунду разогнался до скорости 10 м/сек, то его ускорение а равно 10 м в секунду за секунду а = 10 м/сек². Если в следующую секунду автомобиль остановился, то его ускорение тоже равно 10 м/сек², только уже со знаком минус: а = -10 м/сек².

Скорость движения с ускорением в конце временного отрезка вычисляется по формуле:

• V = V0 ± at,

где V0 – начальная скорость движения, a – ускорение, t – время, за которое наблюдалось данное ускорение. Плюс или минус в формуле ставится в зависимости от того, увеличивалась скорость или уменьшалась.

Средняя скорость за отрезок времени t вычисляется как среднее арифметическое начальной и конечной скорости:

• V ср = (V0 + V) / 2.

Находим среднюю скорость: задача

Шарик толкнули по ровной плоскости с начальной скоростью V0 = 5 м/сек. Через 5 сек. шарик остановился. Чему равны ускорение и средняя скорость?

Конечная скорость шарика V = 0 м/сек. Ускорение из первой формулы равно

• а = (V – V0)/ t = (0 – 5)/ 5 = – 1 м/сек².

Средняя скорость V ср = (V0 + V) / 2= 5 /2 = 2,5 м/сек.

Механическим движением

тела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики.

Раздел механики, описывающий геометрические свойства движения без учета причин, его вызывающих, называется кинематикой.

В более общем значении движением называется любое пространственное или временное изменение состояния физической системы. Например, можно говорить о движении волны в среде.

Относительность движения

Относительность – зависимость механического движения тела от системы отсчёта Не указав систему отсчёта, не имеет смысла говорить о движении.

Траектория материальной точки – линия в трёхмерном пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве. Существенно, что понятие о траектории имеет физический смысл даже при отсутствии какого-либо по ней движения. Кроме того, и при наличии движущегося по ней объекта, траектория сама по себе не может ничего дать в отношении причин движения, то есть о действующих силах.

Путь – длина участка траектории материальной точки, пройденного ею за определённое время.

Скорость (часто обозначается , от англ. velocity или фр. vitesse) – векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта (например, угловая скорость). Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

В науке используется также скорость в широком смысле, как быстрота изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще изменения во времени, но также в пространстве или любой другой). Так, например, говорят о скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения, угловой скорости и т. д. Математически характеризуется производной функции.

Единицы измерения скорости

Метр в секунду, (м/с), производная единица системы СИ

Километр в час, (км/ч)

узел (морская миля в час)

Число Маха, 1 Мах равен скорости звука в данной среде; Max n в n раз быстрее.

Как единица, зависящая от конкретных условий среды, должна дополнительно определяться.

Скорость света в вакууме (обозначается c )

В современной механике движение тела подразделяется на виды, и существует следующая классификация видов движения тела :

Поступательное движение, при котором любая прямая линия, связанная с телом, остаётся при движении параллельной самой себе

Вращательное движение или вращение тела вокруг своей оси, считающейся неподвижной.

Сложное движение тела, состоящее из поступательного и вращательного движений.

Каждое из этих видов может быть неравномерным и равномерным (с не постоянной и постоянной скоростью соответственно).

Средняя скорость неравномерного движения

Средняя путевая скорость – это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден:

Средняя путевая скорость, в отличие от мгновенной скорости не является векторной величиной.

Средняя скорость равна среднему арифметическому от скоростей тела во время движения только в том случае, когда тело двигалось с этими скоростями одинаковые промежутки времени.

В то же время если, например, половину пути автомобиль двигался со скоростью 180 км/ч, а вторую половину со скоростью 20 км/ч, то средняя скорость будет 36 км/ч. В примерах, подобных этому, средняя скорость равна среднему гармоническому всех скоростей на отдельных, равных между собой, участках пути.

Средняя скорость по перемещению

Можно также ввести среднюю скорость по перемещению, которая будет вектором, равным отношению перемещения ко времени, за которое оно совершено:

Средняя скорость, определённая таким образом, может равняться нулю даже в том случае, если точка (тело) реально двигалась (но в конце промежутка времени вернулась в исходное положение).

Если перемещение происходило по прямой (причём в одном направлении), то средняя путевая скорость равна модулю средней скорости по перемещению.

Прямолинейное равномерное движение – это движение, при котором тело (точка) за любые равные промежутки времени совершает одинаковые перемещения. Вектор скорости точки остаётся неизменным, а её перемещение есть произведение вектора скорости на время:

Если направить координатную ось вдоль прямой, по которой движется точка, то зависимость координаты точки от времени является линейной: , где – начальная координата точки, – проекция вектора скорости на координатную ось x.

Точка, рассматриваемая в инерциальной системе отсчёта, находится в состоянии равномерного прямолинейного движения, если равнодействующая всех сил, приложенных к точке, равна нулю.

Вращательное движение – вид механического движения. При вращательном движении абсолютно твердого тела его точки описывают окружности, расположенные в параллельных плоскостях.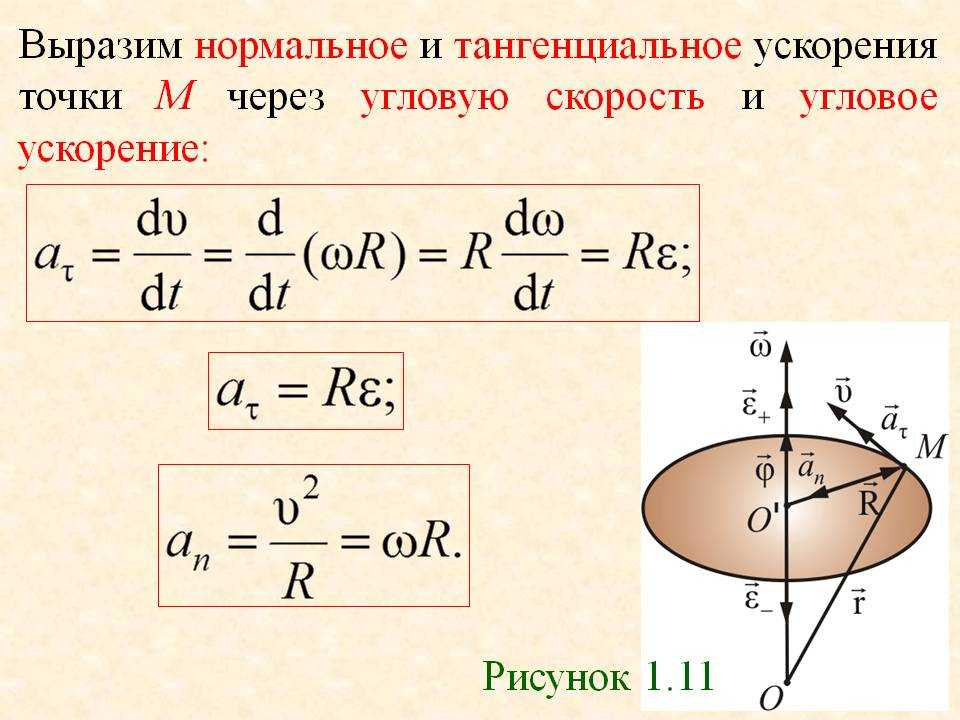 Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землей, ось вращения ротора генератора на электростанции неподвижна.

Характеристики вращения тела

При равномерном вращении (N оборотов в секунду),

Частота вращения – число оборотов тела в единицу времени,

Период вращения – время одного полного оборота. Период вращения T и его частота v связаны соотношением T = 1 / v.

Линейная скорость точки, находящейся на расстоянии R от оси вращения

,
Угловая скорость вращения тела.

Кинетическая энергия вращательного движения

Где I z – момент инерции тела относительно оси вращения. w – угловая скорость.

Гармонический осциллятор (в классической механике) – это система, которая при смещении из положения равновесия испытывает действие возвращающей силы, пропорциональной смещению.

Если возвращающая сила – единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение – синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.

Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.

Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами смещения), груз на пружине, торсионный маятник и акустические системы. Среди других аналогов гармонического осциллятора стоит выделить электрический гармонический осциллятор (см. LC-цепь).

Звук , в широком смысле – упругие волны, продольно распространяющиеся в среде и создающие в ней механические колебания; в узком смысле – субъективное восприятие этих колебаний специальными органами чувств животных или человека.

Как и любая волна, звук характеризуется амплитудой и спектром частот. Обычно человек слышит звуки, передаваемые по воздуху, в диапазоне частот от 16 Гц до 20 кГц. Звук ниже диапазона слышимости человека называют инфразвуком; выше: до 1 ГГц, – ультразвуком, более 1 ГГц – гиперзвуком. Среди слышимых звуков следует также особо выделить фонетические, речевые звуки и фонемы (из которых состоит устная речь) и музыкальные звуки (из которых состоит музыка).

Физические параметры звука

Колебательная скорость – величина, равная произведению амплитуды колебаний А частиц среды, через которую проходит периодическая звуковая волна, на угловую частоту w :

где В – адиабатическая сжимаемость среды; р – плотность.

Как и световые волны, звуковые тоже могут отражаться, преломляться и т.д.

Если Вам понравилась эта страница, и Вам захотелось, чтобы Ваши друзья тоже её увидели, то выберите внизу значок социальной сети, где вы имеете свою страницу, и выразите своё мнение о содержании.

Ваши друзья и случайные посетители благодаря этому добавят Вам и моему сайту рейтинг

Понятие скорости − одно из главных понятий в кинематике.
 Многим наверняка известно, что скорость − это физическая величина, показывающая насколько быстро (или насколько медленно) перемещается в пространстве движущееся тело. Разумеется, речь идет о перемещении в выбранной системе отсчета. Известно ли, однако, Вам, что используются не одно, а три понятия скорости? Есть скорость в данный момент времени, называемая мгновенной скоростью, и есть два понятия средней скорости за данный промежуток времени − средняя путевая скорость (по английски speed) и средняя скорость по перемещению (по-английски velocity).
 Будем рассматривать материальную точку в системе координат x , y , z (рис. а).

Положение A точки в момент времени t характеризуем координатами x(t) , y(t) , z(t) , представляющими три составляющих радиуса-вектора (t ). Точка движется, ее положение в выбранной системе координат с течением времени изменяется − конец радиуса-вектора (t ) описывает кривую, называемую траекторией движущейся точки.
 Траектория, описанная за промежуток времени от t до t + Δt , показана на рисунке б.

 Через B обозначено положение точки в момент t + Δt (его фиксирует радиус-вектор (t + Δt )). Пусть Δs − длина рассматриваемой криволинейной траектории, т. е. путь, пройденный точкой за время от t до t + Δt .
 Среднюю путевую скорость точки за данный промежуток времени определяют соотношением

 Очевидно, что v п − скалярная величина; она характеризуется только числовым значением.
 Показанный на рисунке б вектор

называют перемещением материальной точки за время от t до t + Δt .
 Среднюю скорость по перемещению за данный промежуток времени определяют соотношением

 Очевидно, что v ср − векторная величина. Направление вектора v ср совпадает с направлением перемещения Δr .
 Заметим, что в случае прямолинейного движения средняя путевая скорость движущейся точки совпадает с модулем средней скорости по перемещению.
 Движение точки по прямолинейной либо криволинейной траектории называют равномерным, если в соотношении (1) величина vп не зависит от Δt . Если, например, уменьшить Δt в 2 раза, то и длина пройденного точкой пути Δs уменьшится в 2 раза. При равномерном движении точка проходит за равные промежутки времени пути равной длины.
 Вопрос :
 Можно ли считать, что при равномерном движении точки от Δt не зависит также вектор ср средней скорости по перемещению?

 Ответ :
 Так можно считать только в случае прямолинейного движения (при этом, напомним, модуль средней скорости по перемещению равен средней путевой скорости). Если же равномерное движение совершается по криволинейной траектории, то с изменением промежутка усреднения Δt будут изменяться как модуль, так и направление вектора средней скорости по перемещению. При равномерном криволинейном движении равным промежуткам времени Δt будут соответствовать разные векторы перемещения Δr (а значит, и разные векторы v ср ).
 Правда, в случае равномерного движения по окружности равным промежуткам времени будут соответствовать равные значения модуля перемещения |r| (а значит, и равные |v ср | ). Но направления перемещений (а значит, и векторов v ср ) и в данном случае будут различными для одинаковых Δt . Это видно на рисунке,

 Где равномерно движущаяся по окружности точка описывает за равные промежутки времени равные дуги AB , BC , CD . Хотя векторы перемещений 1 , 2 , 3 имеют одинаковые модули, однако направления у них различны, так что о равенстве этих векторов говорить не приходится.
 Примечание
 Из двух средних скоростей в задачах обычно рассматривают среднюю путевую скорость, а среднюю скорость по перемещению используют довольно редко. Однако она заслуживает внимания, так как позволяет ввести понятие мгновенной скорости.

1. Материальная точка прошла половину окружности. Найти отношение средней путевой скорости к модулю средней векторной скорости.

Решение . Из определения средних значений путевой и векторной скоростей с учетом того, что путь, пройденный материальной точкой за время движенияt , равенR , а величина перемещения 2R , гдеR – радиус окружности, получим:

2. Автомобиль проехал первую треть пути со скоростью v 1 = 30 км/ч, а оставшуюся часть пути – со скоростью v 2 = 40 км/ч. Найти среднюю скорость на всем пройденном пути.

Решение . По определению =гдеS – путь, пройденный за времяt . Очевидно, что
Поэтому искомая средняя скорость равна

3. Студент проехал половину пути на велосипеде со скоростьюv 1 = 12 км/ч. Далее половину оставшегося времени он ехал со скоростьюv 2 = 10 км/ч, а оставшуюся часть пути шел пешком со скоростьюv 3 = 6 км/ч. Определить среднюю скорость движения студента на всем пути.

Решение . По определению
гдеS – путь, аt – время движения. Ясно, чтоt =t 1 +t 2 +t 3 . Здесь
– время движения на первой половине пути,t 2 – время движения на втором участке пути иt 3 – на третьем. По условию задачиt 2 =t 3 . Кроме того,S /2 =v 2 t 2 + v 3 t 3 = (v 2 +v 3)t 2 . Отсюда следует:

Подставив t 1 и t 2 +t 3 = 2t 2 в выражение для средней скорости, получим:

4. Расстояние между двумя станциями поезд прошел за времяt 1 = 30 мин. Разгон и торможение длилисьt 2 = 8 мин, а остальное время поезд двигался равномерно со скоростью v = 90 км/ч.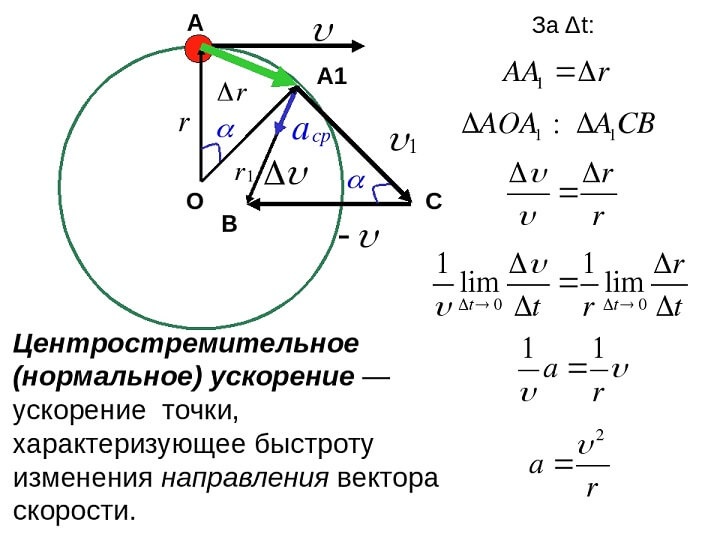 Определить среднюю скорость поезда , считая, что при разгоне скорость увеличивалась с течением времени по линейному закону, а при торможении уменьшалась тоже по линейному закону.

Р

ешение . Построим график зависимости скорости поезда от времени (см. рис.). Этот график описывает трапецию с длинами оснований, равнымиt 1 иt 1 –t 2 и высотой, равной v. Площадь этой трапеции численно равна пути, пройденному поездом от начала движения до остановки. Поэтому средняя скорость равна:

Задачи и упражнения

1.1. Мяч упал с высотыh 1 = 4 м, отскочил от пола и был пойман на высотеh 2 = 1 м. Чему равен путьS и величина перемещения
?

1.2. Материальная точка переместилась на плоскости из точки с координатамиx 1 = 1 см иy 1 = 4cм в точку с координатамиx 2 = 5 см иy 2 = 1 см. Построить вектор перемещения и с помощью линейки определить модуль вектора перемещения и проекции вектора перемещения на осиx иy . Найти эти же величины аналитически и сравнить результаты.

1.3. Первую половину пути поезд шел со скоростью вn = 1,5 раза большей, чем вторую половину пути. Средняя скорость поезда на всем пути = 43,2 км/ч. Каковы скорости поезда на первой и второй половинах пути?

1.4. Первую половину времени своего движения велосипедист проехал со скоростью v 1 = 18 км/ч, а вторую половину времени – со скоростью v 2 = 12 км/ч. Определить среднюю скорость движения велосипедиста.

1.5. Движение двух автомобилей описывается уравнениями
и
, где все величины измеряются в системе СИ. Запишите закон изменения расстояния
между автомобилями от времени и найдите
через время
с. после начала движения.

Варенье из бузины: польза и вред

Узнать встретимся ли мы. Сонник дома солнца. Как правильно сформулировать вопрос в процессе гадания

Равноускоренное прямолинейное движение. Графики зависимости кинематических величин от времени в равноускоренном движении.

Переменное движение. Средняя скорость. Ускорение. Единицы измерения ускорения все тела состоят из частиц: атомов, молекул и ионов

(тема «Форматирование шрифта и абзаца »)

Текст 1

Второй закон Ньютона

Масса тела

Сила

вторым законом Ньютона

Текст 2

Второй закон Ньютона

Свойства тела, от которого зависит его ускорение при взаимодействии с другими телами, называется инертностью.

Количественной мерой инертности тела является масса тела. Масса тела – это физическая величина, характеризующая инертность.

При неравномерном поступательном движении скорость тела изменяется с течением времени. Процесс изменения скорости тела характеризуется ускорением.

Для количественного выражения действия одного тела на другое вводится понятие «сила». Сила – векторная величина, т.е. характеризуется направлением. Для количественной характеристики процесса движения тела вводится понятие скорости движения. Скорость выражается в метрах в секунду.

Связь между силой и ускорением тела устанавливается вторым законом Ньютона . Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение.

Фрагмент	Отличия
	Текст 1	Текст 2
Заголовок	Выравнивание по левому краю	Выравнивание по центру
Первый абзац	Нет красной строки	Красная строка – отступ
Слово инертность	Разреженный межсимвольный интервал	Обычный межсимвольный интервал
Фраза Масса тела	Полужирное начертание	Начертание курсив
Третий абзац	Выравнивание по левому краю	Выравнивание по правому краю
Четвертый абзац	Выравнивание по ширине Красная строка – отступ	Выравнивание по левому краю Красная строка – выступ
Слово Сила	Начертание – полужирный курсив	Начертание – курсив с подчеркиванием
Пятый абзац	Полуторный междустрочный интервал	Одинарный междустрочный интервал
Фраза Второй закон Ньютона	Подчеркивание – только слова	Одинарное подчеркивание

Рис. 4

Система координат, тело отсчета, с которым она связана, и указание начала отсчета времени образуют систему отсчета, относительно которой рассматривается движение тела.

Траектория движения тела, пройденный путь и перемещение зависят от выбора системы отсчета. Другими словами, механическое движение относительно.

Скорость. Для количественной характеристики процесса движения тела вводится понятие скорости движения.

Мгновенной скоростью поступательного движения тела в момент времени называется отношение очень малого перемещения к малому промежутку времени , за который произошло это перемещение:

Мгновенная скорость – векторная величина.

При последовательном уменьшении длительности промежутка времени направление вектора перемещения приближается к касательной в точке A траектории движения, через которую проходит тело в момент времени (рис. 5). Поэтому вектор скорости лежит на касательной к траектории движения тела в точке A и направлен в сторону движения тела.

Рис. 5

Формула (1.1) позволяет установить единицу скорости.

В Международной системе (СИ) единицей расстояния является метр, единицей времени – секунда; поэтому скорость выражается в метрах в секунду:

Метр в секунду равен скорости прямолинейно и равномерно движущейся точки, при которой точка за время 1 с перемещается на расстояние 1 м.

Равномерное прямолинейное движение. Движение с постоянной по модулю и направлению скоростью называется равномерным прямолинейным движением. При равномерном прямолинейном движении тело движется по прямой и за любые равные промежутки времени проходит одинаковые пути.

Выясним, как связаны между собой скорости движения тела в различных системах отсчета. Рассмотрим такой пример. Вагон движется по прямолинейному участку железнодорожного пути равномерно со скоростью относительно Земли. Пассажир движется относительно вагона со скоростью , векторы скоростей и имеют одинаковое направление. Найдем скорость пассажира относительно Земли. Перемещение пассажира относительно Земли за малый промежуток времени равно сумме перемещений за этот промежуток времени вагона относительно Земли и пассажира относительно вагона (рис. 6):

или .

Рис. 6

Отсюда скорость пассажира относительно Земли равна

Мы получили, что скорость пассажира в системе отсчета, связанной с Землей, равна сумме скоростей пассажира в системе отсчета, связанной с вагоном, и вагона относительно Земли.

Этот вывод справедлив для любых направлений векторов скорости и скорости . Закон, выражаемый формулой (1.2), называется классическим законом сложения скоростей.

Движение любого тела в реальных условиях никогда не бывает строго равномерным и прямолинейным. Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным движением.

Ускорение. При неравномерном поступательном движении скорость тела изменяется с течением времени. Процесс изменения скорости тела характеризуется ускорением. Ускорением называется векторная величина, равная отношению очень малого изменения вектора скорости к малому промежутку времени , за которое произошло это изменение.

Работа №9

Разработка гипертекстового документа

Вариант 1

Используя приведенные ниже фрагменты, разработать гипертекстовый документ по теме “Второй закон Ньютона”, определив ключевые слова и установив связи между фрагментами.

Фрагмент 1. Свойство тела, от которого зависит его ускорение при взаимодействии с другими телами, называется инертностью.

Фрагмент 2. Количественной мерой инертности тела является масса тела. Масса тела – это физическая величина, характеризующая инертность.

Фрагмент 3. При неравномерном поступательном движении скорость тела изменяется с течением времени. Процесс изменения скорости тела характеризуется ускорением.

Фрагмент 4. Для количественного выражения действия одного тела на другое вводится понятие “сила”. Сила – векторная величина, т. е. характеризуется направлением. За единицу силы принимается сила, которая телу массой 1 кг сообщает ускорение 1 м/с.

Фрагмент 5. Для количественной характеристики процесса движения тела вводится понятие скорости движения. Скорость выражается в метрах в секунду.

Фрагмент 6. Связь между силой и ускорением тела устанавливается вторым законом Ньютона. Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение.

Вариант 2

Используя приведенные ниже фрагменты, разработать гипертекстовый документ по теме “Музыкальный звукоряд”, упорядочив фрагменты от более простых понятий к более сложным, определив ключевые слова и установив связи между фрагментами:

Фрагмент 1. Музыкальный звук отличается следующими свойствами: высотой, силой, длительностью и тембром. Высота звука зависит от частоты колебаний упругого тела; сила (громкость) – от широты размаха колебаний; длительность – от того, как долго возбуждается упругое тело; тембр – это своеобразная окраска звуков.

Фрагмент 2. Все музыкальные звуки, если их расположить по высоте от самого низкого к самому высокому, образуют музыкальный звукоряд. Каждому звуку музыкального звукоряда соответствуют подобные по звучанию, но разные по высоте звуки. Они называются октавными, а группа звуков между ними – октавой.

Фрагмент 3. Звук – это явление, возникающее вследствие быстрого колебания упругого тела и воспринимающееся органом слуха – ухом.

Фрагмент 4. Весь звукоряд делится на девять октав: семь полных и две неполных. Названия октав по порядку их расположения: субконтроктава, контроктава, большая октава, малая октава, первая октава, вторая октава, третья октава, четвертая октава, пятая октава.

Фрагмент 5. Полная октава содержит двенадцать различных по высоте звуков. Из них только семь основных имеют самостоятельные названия: до, ре, ми, фа, соль, ля, си.

Фрагмент 6. Кратчайшее расстояние между двумя соседними звуками называется полутоном. Два полутона составляют целый тон. Расстояние между звуками до-ре, ре-ми, фа-соль, ля-си равно целому тону, а между звуками ми-фа и си-до – полутону.

Вариант 3

Разработать тестирующий гипертекстовый документ по теме “Полтавская битва”. На экран должны выводиться вопросы и предлагаться варианты ответа. В случае верного ответа выводить соответствующий фрагмент текста с сообщением, а в случае неверного – выводить верный ответ, после чего – возвращаться к текущему вопросу. Организовать связь между фрагментами, выделив ключевые слова, по которым будет производиться переход от фрагмента к фрагменту.

Фрагмент 1. Армии каких стран участвовали в Полтавской битве?

1. Россия и Франция 2. Россия и Польша 3. Швеция и Россия

Фрагмент 2. В каком году произошла Полтавская битва?

Фрагмент 3. Кто стоял во главе шведской армии?

Фрагмент 4. Какова была численность русской армии?

1. 20 000 2. 32 000 3. 56 000

Фрагмент 5. Ответ верный.

Возврат к вопросу: 1 2 3 4

Фрагмент 6. В Полтавской битве участвовали армии России и Швеции.

Фрагмент 7. Полтавская битва произошла в 1709 году.

Фрагмент 8. Во главе шведской армии стоял король Карл XII.

Фрагмент 9. Численность русской армии составляла 32 000 человек.

Назначение теста

Методика предназначена для оценки знаний , по разделу “Механика”. Материал предназначен для студентов первого курса СПО.

Инструкция к тесту

На выполнение теста дается ровно 60 мин . Не задерживайтесь слишком долго над одним заданием. Быть может, вы находитесь на ложном пути и лучше перейти к следующей задаче. Но и не сдавайтесь слишком легко; большинство заданий поддается решению, если вы – проявите немного настойчивости. Ответ на задание состоит из выбора на ваш взгляд правильного ответа. Иногда нужно произвести выбор из нескольких возможностей. Ответ напишите в указанном месте. Если вы не в состоянии решить, задачу – не следует писать ответ наугад. Тест не содержит «каверзных» заданий, но всегда приходится рассмотреть несколько путей решения. Прежде чем приступить к решению, удостоверьтесь, что вы правильно поняли, что от вас требуется. Вы напрасно потеряете время, если возьметесь за решение, не уяснив, в чем состоит задача.

Оформление работ

Ответы на тест вам необходимо записать в тетради для проверочных работ в виде:

1 а

2 а,б

ЗАДАНИЯ ПО МЕХАНИКЕ

а) перемещением

б) траекторией

в) линией движения

а) система координат

б) тело отсчёта

в) часы

г) перемещение точки

а) перемещение

б) время поездки

в) пройденный путь

б) он имеет небольшой рост.

5. Система часов совершает:

а) вращательное движение

б) поступательное движение

в) прямолинейное движение

а) 11 м/с

б) 9 м/с

в) 1 м/с

а) перемещением.

б) мгновенной скоростью

в) координатами тела

г) ускорением

а) постоянным по направлению

б) постоянным по модулю

а) -2 м\с

б) 2 м/с

в) 50 м/с

а) кинематикой

б) динамикой

в) статикой

а) инерцией

б) инертностью

в) равноускоренным движением

а) первый закон Ньютона

б) второй закон Ньютона

в) третий закон Ньютона

а) внутреннее строение

б) особенности внешней среды

а) муха

б) человек

в) троллейбус

а) перемещения

б) ускорение

в) приложения силы

а) 0,5 м/с2

б)200 м/с2

в)2 м/с2

а) -20 Н

б) 0 Н

в) 40 Н

19. Гравитационная постоянная G равна:

а)6,67×10

б)6,67×10

в)9,8

а) силой упругости

б) силой тяжести

в) весом тела

а) перегрузкой

б) невесомостью

в) свободным падением

а) силу тяжести

б) вес тела

в) силу упругости

а) силой тяжести

б) силой упругости

в) весом тела

г) равна силе тяжести

а) 1 м/с

б) 2 м/с

в) 0 м/с

а) с землёй

б) с вакуумом

27. Работа совершаемая силой F, положительна, если угол между вектором F и S:

а)

б)

в)

а) 3 с

б) 40 с

в) 160 с

а) 50 Дж

б)200Дж

в)2000Дж

а) 10 Дж

б)100 Дж

в)1000 Дж

а) кинетическую энергию

б) потенциальную энергию

в) механическую работу

а) 2000 Дж

б) 10000 Дж

в) -2000 Дж

а)0,5 м/с

б)1,5 м/с

в)2 м/с

а)0,5 Дж

б)2 Дж

в)5000 Дж

а) 0,4 Н

б)2,5 Н

в)10 Н

а) 98 кг

б)100 кг

в)9800 кг

а) 0,1 м/с

б) 10 м/с

в) 90 м/с

а) 0 м

б) 2,5 м

в) 5 м

39. Уравнение для определения координат материальной точки имеет вид Определите с его помощью ускорение.

а)-3 м/с2

б)4 м/с2

в)8 м/с2

а) равномерное

б) равноускоренное

в) равнозамедленное

Ключ к тесту

1.Линия, по которой движется точка тела, называется-

а) перемещением

б) траекторией

в) линией движения

2. Что образует систему отчёта.

а) система координат

б) тело отсчёта

в) часы

г) перемещение точки

3.Что оплачивает пассажир такси:

а) перемещение

б) время поездки

в) пройденный путь

4. Велосипедист едет по дороге. В каком случае его можно рассматривать как материальную точку:

а) он движется без остановки 60 метров.

б) он имеет небольшой рост.

в) он проезжает расстояние 60 км.

5. Система часов совершает:

а) вращательное движение

б) поступательное движение

в) прямолинейное движение

6. Поезд едет со скоростью . Пассажир идет против движения поезда со скоростью 1м/с, относительно вагона. Определите скорость пассажира относительно земли.

а) 11 м/с

б) 9 м/с

в) 1 м/с

7. Процесс изменения скорости тела характеризуется:

а) перемещением.

б) мгновенной скоростью

в) координатами тела

г) ускорением

8. Равноускоренным называется движение с ускорением:

а) постоянным по направлению

б) постоянным по модулю

в) постоянным по направлению и модулю

9. Скорость автомобиля за 5 секунд меняется с 20м/с, до 10м/с. Определите ускорение автомобиля.

а) -2 м\с

б) 2 м/с

в) 50 м/с

10. С помощью уравнения х=х можно определить:

а) перемещение при равноускоренном движении

б) координаты тела при равномерном движении

в) координаты тела при равноускоренном движении

11. Раздел механики, изучающий законы взаимодействия тел называется:

а) кинематикой

б) динамикой

в) статикой

12. Явления сохранения скорости движения тела при отсутствии внешних воздействий называется:

а) инерцией

б) инертностью

в) равноускоренным движением

13. Какой из законов Ньютона имеет следующую формулировку: существуют такие системы отчёта, относительно которой поступательно движущиеся тело сохраняет свою скорость постоянной, если на них не действуют другие тела, или их действия скомпенсированы.

а) первый закон Ньютона

б) второй закон Ньютона

в) третий закон Ньютона

14.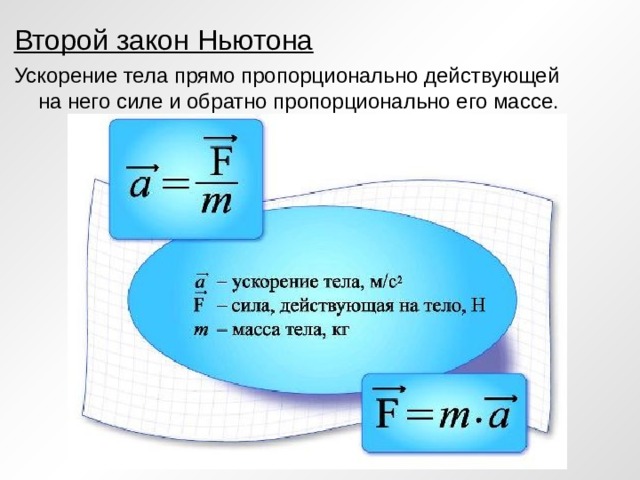 Причиной изменения скорости движения тела является:

а) внутреннее строение

б) особенности внешней среды

в) взаимодействие с другими телами

15. Какое тело более инертно:

а) муха

б) человек

в) троллейбус

а) перемещения

б) ускорение

в) приложения силы

17. На тело массой 10 кг. действует сила 20Н. Определите, с каким ускорение движется тело.

а) 0,5 м/с 2

б)200 м/с 2

в)2 м/с 2

18. Гиря действует на весы с силой 20 Н. С какой силой весы действуют на гирю.

а) -20 Н

б) 0 Н

в) 40 Н

19. Гравитационная постоянная G равна:

а)6,67 x 10

б)6,67 x 10

в)9,8

20. Сила с которой тело действует на горизонтальную опору или вертикальный подвес называют:

а) силой упругости

б) силой тяжести

в) весом тела

21. Исчезновение веса при движении опоры с ускорением свободного падения называется:

а) перегрузкой

б) невесомостью

в) свободным падением

22.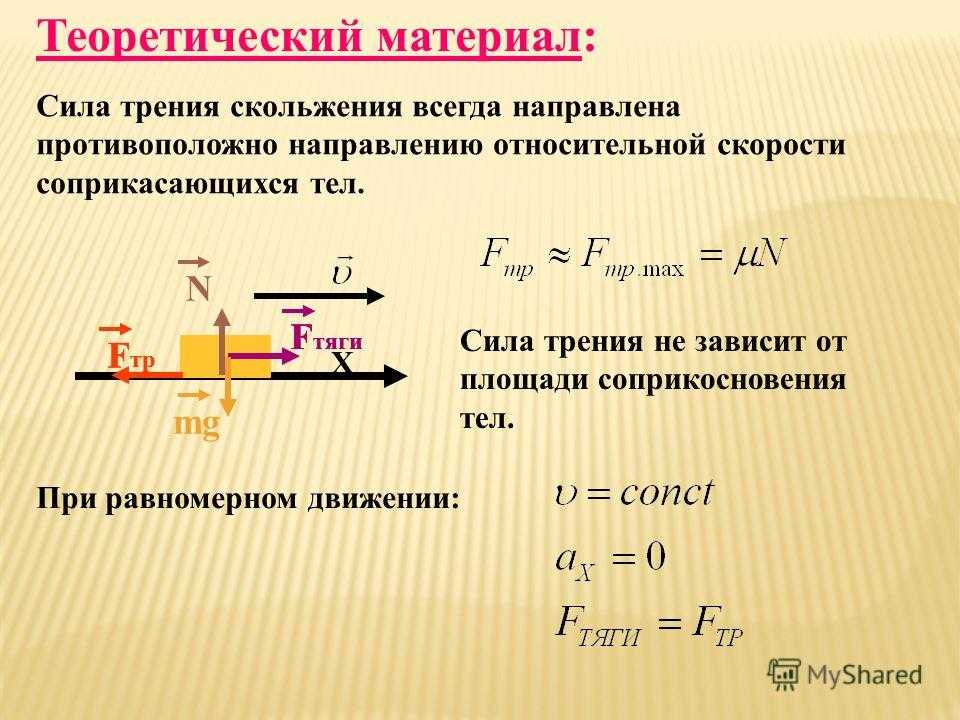 С помощью данной формулы можно определить:

а) силу тяжести

б) вес тела

в) силу упругости

23. Сила, возникающая в результате деформации и направленная в сторону, противоположную перемещением частиц тела при деформации, называется:

а) силой тяжести

б) силой упругости

в) весом тела

24. Выберете все верные варианты ответа. Сила трения:

а) равна по модулю внешней силе

б) направлена в сторону движения тела.

в) направлена в противоположную сторону движения

г) равна силе тяжести

25.Две тележки массами по 200 кг. движутся навстречу друг другу со скоростями 1м/с. С какой скоростью они будут двигаться после неупругого удара.

а) 1 м/с

б) 2 м/с

в) 0 м/с

26. С чем взаимодействует реактивная ракета при движении:

а) с землёй

б) с вакуумом

в) с газами, образующимися при сгорании.

27. Работа совершаемая силой F , положительна, если угол между вектором F и S :

а)

б)

в)

28. Подъёмный кран мощностью 2 кВт., совершил работу 0,08МДж. За какое время была совершена работа?

а) 3 с

б) 40 с

в) 160 с

29. Определите потенциальную энергию человека массой 100 кг, на высоте 2 метра

а) 50 Дж

б)200Дж

в)2000Дж

30.Определите кинетическую энергию пули массой 2 грамма, летящей со скоростью 100 м/с.

а) 10 Дж

б)100 Дж

в)1000 Дж

31. Формула позволяет определить:

а) кинетическую энергию

б) потенциальную энергию

в) механическую работу

32. Кинетическая энергия тела изменилась с 4000Дж до 6000Дж. Определите работу тела:

а) 2000 Дж

б) 10000 Дж

в) -2000 Дж

33. Железнодорожный вагон массой 15 т движется со скоростью 2 м/с, догоняет не подвижный вагон массой 5 т. Какой будет скорость вагонов после их столкновения?

а)0,5 м/с

б)1,5 м/с

в)2 м/с

34. Сани, двигающиеся равномерно под действием силы 50 Н, переместились на 100 метров. Какую работу они совершают при этом?

а)0,5 Дж

б)2 Дж

в)5000 Дж

35. Определите силу, под действием которой тело массой 5 кг. Приобретает ускорение 2м/с?

а) 0,4 Н

б)2,5 Н

в)10 Н

36. Определите массу тела, если сила тяжести равна 980 Н.

а) 98 кг

б)100 кг

в)9800 кг

37.Автомобиль, двигаясь равномерно за 3 секунды проехал 30 метров. Определите его скорость.

а) 0,1 м/с

б) 10 м/с

в) 90 м/с

38.Мальчик, подбросил мяч на высоту 2,5м снова поймал его. Определите перемещение мяча.

а) 0 м

б) 2,5 м

в) 5 м

39. Уравнение для определения координат материальной точки имеет вид .Определите с его помощью ускорение.

а)-3 м/с 2

б)4 м/с 2

в)8 м/с 2

40. Проекция скорости движущегося тела изменяется по закону. Опишите характер движения:

а) равномерное

б) равноускоренное

в) равнозамедленное

Движение любого тела в реальных условиях никогда не бывает строго равномерным и прямолинейным. При неравномерном поступательном движении скорость тела изменяется с течением времени. Процесс изменения скорости тела характеризуется ускорением.

Ускорение – это величина, которая определяет быстроту изменения скорости тела, и равна пределу, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:

Равнопеременное движение может быть равноускоренным или равнозамедленным.

Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения за любые равные промежутки времени скорость увеличивается на одну и ту же величину и направление ускорения совпадает с направлением скорости движения.

­­ ∆ и а > 0

Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.

­¯ ∆ и а ˂ 0

В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.

Измеряют ускорение в метрах на секунду в квадрате

При равноускоренном движении с начальной скоростью 0 ускорение равно .

где – скорость в момент времени t, тогда скорость равнопеременного движения равна

0 + t илиυ= ±υ 0 ±a t(3.3)

Пройденный путь при прямолинейном равноускоренном движении равен модулю перемещения и определяется по формуле:

где знак “плюс” относится к ускоренному, а “минус” – к замедленному движению.

Если время движения тела неизвестно, можно использовать другую формулу перемещения:

где υ – конечная скорость движения;

υ 0 – начальная скорость движения

Координаты тела при равноускоренном движении в любой момент времени можно определить по формулам:

где х 0 ; у 0 – начальные координаты тела; υ 0 -скорость тела в начальный момент времени; а – ускорение движения. Знак «+» и «-» зависят от направления оси ОХ и направления векторов и .

Проекция перемещение

на ось ОХ равна: S х = х-х 0

на ось ОУ равна: S у = у-у 0

График зависимости перемещения тела от времени при

υ 0 = 0 показан на рис. 1.9.

Скорость тела в данный момент времени t 1 равна тангенсу угла наклона между касательной к графику и осью времени υ=tgα.

Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При

а

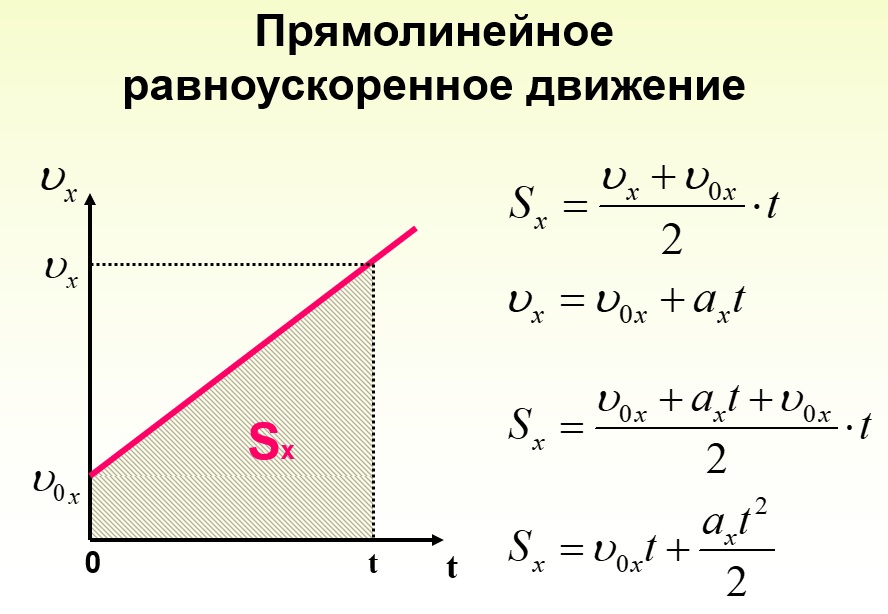
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия

(рис. 1.11). Тангенс угла наклона прямой к оси времени численно равен ускорению.

При этом перемещение численно равно площади фигуры 0abc (рис. 1.11). Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны: 0a = υ 0 bc = υ.

Формула t при равноускоренном движении.

Равноускоренное движение. Задачи и формулы

Прямолинейное равномерное движение – это такое движение, при котором за одинаковые промежутки времени, тело проходит одинаковое расстояние.

Равномерное движение – это такое движение тела, при котором его скорость остается постоянной (),то есть все время движется с одной скоростью, а ускорение или замедление не происходит ().

Прямолинейное движение – это движение тела по прямой линии, то есть траектория у нас получается – прямая.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор скорости совпадает с вектором перемещения. При всем этом средняя скорость в любой промежуток времени равна начальной и мгновенной скорости:

Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела за любой промежуток времен к значению этого промежутка t:

Из данной формулы. мы легко можем выразить перемещение тела при равномерном движении:

Рассмотрим зависимость скорости и перемещения от времени

Так как тело у нас движется прямолинейно и равноускоренно (), то график с зависимостью скорости от времени будет выгладить, как параллельная прямая оси времени.

В зависимости проекции скорости тела от времени ничего сложного нет. Проекция перемещения тела численно равна площади прямоугольника АОВС, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

На графике мы видим зависимость перемещения от времени .

Из графика видно, что проекция скорости равна:

Рассмотрев эту формулу. мы можем сказать, чем больше угол, тем быстрей движется наше тело и оно проходит больший путь за меньшее время

Как, зная тормозной путь, определить начальную скорость автомобиля и как, зная характеристики движения, такие как начальная скорость, ускорение, время, определить перемещение автомобиля? Ответы мы получим после того, как познакомимся с темой сегодняшнего урока: «Перемещение при равноускоренном движении, зависимость координаты от времени при равноускоренном движении»

При равноускоренном движении график имеет вид прямой линии, уходящей вверх, так как его проекция ускорения больше нуля.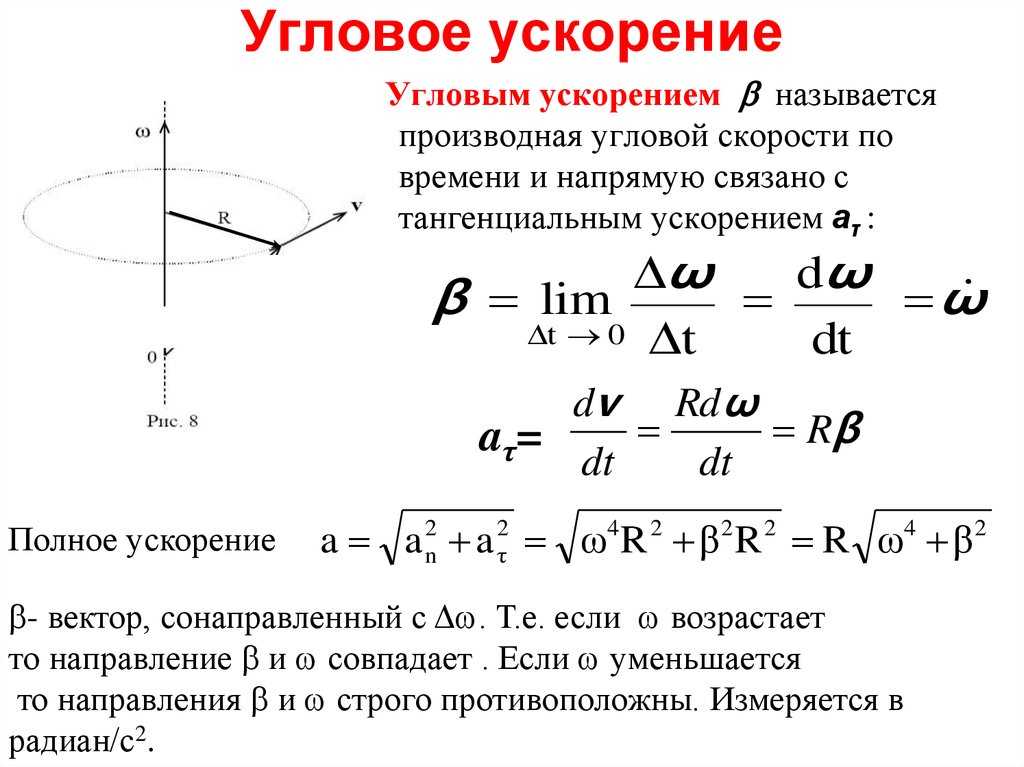

При равномерном прямолинейном движении площадь численно будет равна модулю проекции перемещения тела. Оказывается, этот факт можно обобщить для случая не только равномерного движения, но и для любого движения, то есть показать, что площадь под графиком численно равна модулю проекции перемещения. Это делается строго математически, но мы воспользуемся графическим способом.

Рис. 2. График зависимости скорости от времени при равноускоренном движении ()

Разобьем график проекции скорости от времени для равноускоренного движения на небольшие промежутки времени Δt. Предположим, что они так малы, что на их протяжении скорость практически не менялась, то есть график линейной зависимости на рисунке мы условно превратим в лесенку. На каждой ее ступеньке мы считаем, что скорость практически не поменялась. Представим, что промежутки времени Δt мы сделаем бесконечно малыми. В математике говорят: совершаем предельный переход. В этом случае площадь такой лесенки будет неограниченно близко совпадать с площадью трапеции, которую ограничивает график V x (t).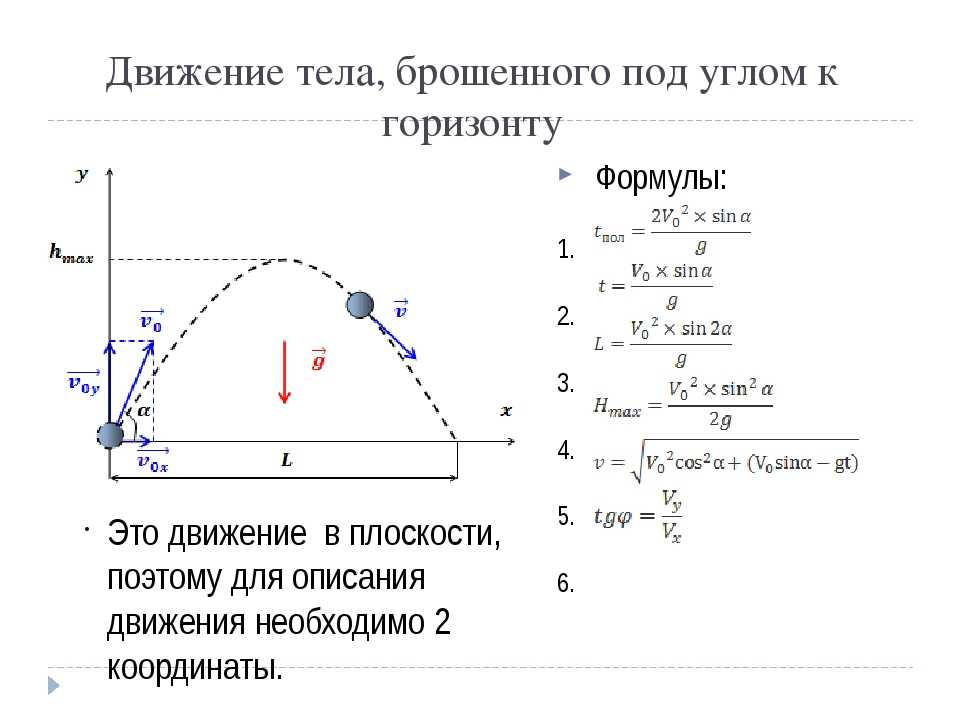 А это значит, что и для случая равноускоренного движения можно сказать, что модуль проекции перемещения численно равен площади, ограниченной графиком V x (t): осями абсцисс и ординат и перпендикуляром, опущенным на ось абсцисс, то есть площади трапеции ОАВС, которую мы видим на рисунке 2.

Задача из физической превращается в математическую задачу – поиск площади трапеции. Это стандартная ситуация, когда ученые физики составляют модель, которая описывает то или иное явление, а затем в дело вступает математика, которая обогащает эту модель уравнениями, законами – тем, что превращает модель в теорию.

Находим площадь трапеции: трапеция является прямоугольной, так как угол между осями – 90 0 , разобьем трапецию на две фигуры – прямоугольник и треугольник. Очевидно, что общая площадь будет равна сумме площадей этих фигур (рис. 3). Найдем их площади: площадь прямоугольника равна произведению сторон, то есть V 0x · t, площадь прямоугольного треугольника будет равна половине произведения катетов – 1/2АD·BD, подставив значения проекций, получим: 1/2t·(V x – V 0x), а, вспомнив закон изменения скорости от времени при равноускоренном движении: V x (t) = V 0x + а х t, совершенно очевидно, что разность проекций скоростей равна произведению проекции ускорения а х на время t, то есть V x – V 0x = а х t.

Рис. 3. Определение площади трапеции (Источник)

Учитывая тот факт, что площадь трапеции численно равна модулю проекции перемещения, получим:

S х(t) = V 0 x t + а х t 2 /2

Мы с вами получили закон зависимости проекции перемещения от времени при равноускоренном движении в скалярной форме, в векторной форме он будет выглядеть так:

(t) = t + t 2 / 2

Выведем еще одну формулу для проекции перемещения, в которую не будет входить в качестве переменной время. Решим систему уравнений, исключив из нее время:

S x (t) = V 0 x + а х t 2 /2

V x (t) = V 0 x + а х t

Представим, что время нам неизвестно, тогда выразим время из второго уравнения:

t = V x – V 0x / а х

Подставим полученное значение в первое уравнение:

Получим такое громоздкое выражение, возведем в квадрат и приведем подобные:

Мы получили очень удобное выражение проекции перемещения для случая, когда нам неизвестно время движения.

Пусть у нас начальная скорость автомобиля, когда началось торможение, составляет V 0 = 72 км/ч, конечная скорость V = 0, ускорение а = 4 м/с 2 . Узнаем длину тормозного пути. Переведя километры в метры и подставив значения в формулу, получим, что тормозной путь составит:

S x = 0 – 400(м/с) 2 / -2 · 4 м/с 2 = 50 м

Проанализируем следующую формулу:

S x = (V 0 x + V x) / 2 · t

Проекция перемещения- это полусумма проекций начальной и конечной скоростей, умноженная на время движения. Вспомним формулу перемещения для средней скорости

S x = V ср · t

В случае равноускоренного движения средняя скорость будет:

V ср = (V 0 + V к) / 2

Мы вплотную подошли к решению главной задачи механики равноускоренного движения, то есть получению закона, по которому меняется координата со временем:

х(t) = х 0 + V 0 x t + а х t 2 /2

Для того чтобы научиться пользоваться этим законом, разберем типичную задачу.

Автомобиль, двигаясь из состояния покоя, приобретает ускорение 2 м/с 2 . Найти путь, который прошел автомобиль за 3 секунды и за третью секунду.

Дано: V 0 x = 0

Запишем закон, по которому меняется перемещение со временем при

равноускоренном движении: S х = V 0 x t + а х t 2 /2. 2 c

Мы можем ответить на первый вопрос задачи, подставив данные:

t 1 = 3 c S 1х = а х t 2 /2 = 2· 3 2 / 2 = 9 (м) – это путь, который прошел

c автомобиль за 3 секунды.

Узнаем сколько он проехал за 2 секунды:

S х (2 с) = а х t 2 /2 = 2· 2 2 / 2 = 4 (м)

Итак, мы с вами знаем, что за две секунды автомобиль проехал 4 метра.

Теперь, зная два эти расстояния, мы можем найти путь, который он прошел за третью секунду:

S 2х = S 1х + S х (2 с) = 9 – 4 = 5 (м)

Механическое движение

Механическое движение -это процесс изменения положения тела в пространстве с течением времени относительно другого тела, которое мы считаем неподвижным.

Тело, условное принятое за неподвижное- тело отсчета.

Тело отсчета -это тело, относительно которого определяется положение другого тела.

Система отсчета -это тело отсчета, система координат, жестко связанная с ним, и прибор для измерения времени движения.

Траектория движения

Траектория движения тела -это непрерывная линия, которую описывает движущееся тело(рассматриваемое как материальная точка) по отношению к выбранной системе отсчета.

Пройденный путь

Пройденный путь -скалярная величина, равная длине дуги траектории, пройденной телом за некоторое время.

Перемещение

Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением, векторная величина.

Средняя и мгновенная скорости движения.Направление и модуль скорости.

Скорость – физическая величина, которая характеризует быстроту изменения координаты.

Средняя скорость движения – это физическая величина, равная отношению вектора перемещения точки к интервалу времени, за которое это перемещение произошло. Направление вектора средней скорости совпадает с направлением вектора перемещения ∆S

Мгновенная скорость -это физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени ∆t. Вектор мгновенной скорости направлен по касательной к траектории. Модуль равен первой производной пути по времени.

Формула пути при равноускоренном движении.

Равноускоренное движение – это движение, при котором ускорение постоянно по модулю и направлению.

Ускорение движения

Ускорение движения – векторная физическая величина, определяющая быстроту изменения скорости тела, то есть первая производная от скорости по времени.

Тангенциальное и нормальное ускорения.

Тангенциальное(касательное) ускорение -это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Направление вектора тангенциального ускорения a лежит на одной оси с касательной окружности, которая является траекторией движения тела.

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела.

Вектор перпендикулярен линейной скорости движения, направлен по радиусу кривизны траектории.

Формула скорости при равноускоренном движении

Первый закон Ньютона (или закон инерции )

Существуют такие системы отсчета, относительно которых изолированные поступательно движущиеся тела сохраняют свою скорость неизменной по модулю и направлению.

Инерциальной системой отсчёта является такая система отсчёта, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется прямолинейно и равномерно (т.е. с постоянной скоростью).

В при­ро­де су­ще­ству­ют че­ты­ре вида вза­и­мо­дей­ствия

1. Гра­ви­та­ци­он­ное (сила тя­го­те­ния) – это вза­и­мо­дей­ствие между те­ла­ми, ко­то­рые об­ла­да­ют мас­сой.

2. Элек­тро­маг­нит­ное- спра­вед­ли­во для тел, об­ла­да­ю­щих элек­три­че­ским за­ря­дом, от­вет­ствен­но за такие ме­ха­ни­че­ские силы, как сила тре­ния и сила упру­го­сти.

3.Силь­ное- вза­и­мо­дей­ствие ко­рот­ко­дей­ству­ю­щее, то есть дей­ству­ет на рас­сто­я­нии по­ряд­ка раз­ме­ра ядра.

4. Сла­бое. Такое вза­и­мо­дей­ствие от­вет­ствен­но за неко­то­рые виды вза­и­мо­дей­ствия среди эле­мен­тар­ных ча­стиц, за неко­то­рые виды β-рас­па­да и за дру­гие про­цес­сы, про­ис­хо­дя­щие внут­ри атома, атом­но­го ядра.

Масса – является количественной характеристикой инертных свойств тела. Она показывает, как тело реагирует на внешнее воздействие.

Сила – является количественной мерой действия одного тела на другое.

Второй закон Ньютона.

Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение: F=ma

Измеряется в

Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела (или количеством движения ). Импульс тела – векторная величина. Единицей измерения импульса в СИ является килограмм-метр в секунду (кг·м/с) .

Выражение второго закона Ньютона через изменение импульса тела

Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равноускоренное движение – движение, при котором ускорение постоянно по модулю и направлению.

Третий закон Ньютона. Примеры.

Плечо силы.

Плечо силы – это длина перпендикуляра из некоторой вымышленной точки О к силе. Вымышленный центр, точку О, будем выбирать произвольно, моменты каждой силы определяем относительно этой точки. Нельзя для определения моментов одних сил выбрать одну точку О, а для нахождения моментов других сил выбрать ее в другом месте!

Выбираем точку О в произвольном месте, больше ее местоположение не изменяем.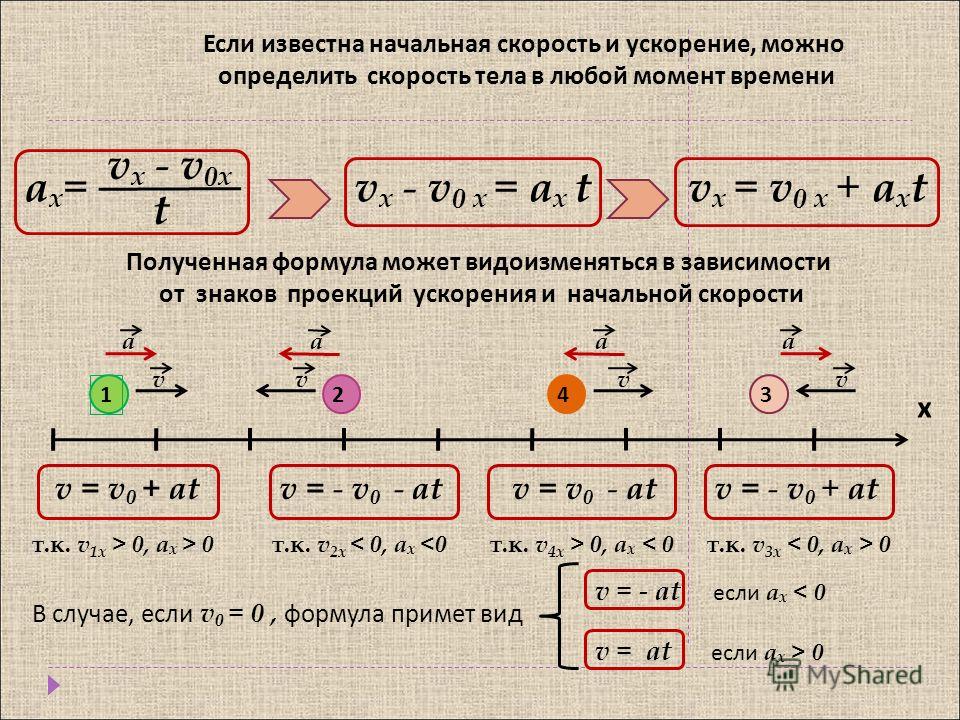 Тогда плечо силы тяжести – это длина перпендикуляра (отрезок d) на рисунке

Момент инерции тел.

Момент инерции J (кгм 2) – параметр, аналогичный по физическому смыслу массе при поступательном движении. Он характеризует меру инерции тел, вращающихся относительно фиксированной оси вращения. Момент инерции материальной точки с массой m равен произведению массы на квадрат расстояния от точки до оси вращения: .

Момент инерции тела есть сумма моментов инерции материальных точек, составляющих это тело. Он может быть выражен через массу тела и его размеры

Теорема Штейнера.

Момент инерции J тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела Jc относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:

Jc – известный момент инерции относительно оси, проходящей через центр масс тела,

J – искомый момент инерции относительно параллельной оси,

m – масса тела,

d – расстояние между указанными осями.

Закон сохранения момента импульса. Примеры.

Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса) :
.

Очень нагляден закон сохранения момента импульса в опытах с уравновешенным гироскопом – быстро вращающимся телом, имеющим три степени свободы (рис. 6.9).

Именно закон сохранения момента импульса используется танцорами на льду для изменения скорости вращения. Или еще известный пример – скамья Жуковского (рис. 6.11).

Работа силы.

Работа силы – мера действия силы при превращении механического движения в другую форму движения.

Примеры формул работы сил.

работа силы тяжести; работа силы тяжести наклонной пов-ти

работа силы упругости

Работа силы трения

Механическая энергия тела.

Механическая энергия – это физическая величина, являющаяся функцией состояния системы и характеризующая способность системы совершать работу.

Характеристика колебаний

Фаза определяет состояние системы, а именно координату, скорость, ускорение, энергию и др.

Циклическая частота характеризует скорость изменения фазы колебаний.

Начальное состояние колебательной системы характеризует начальная фаза

Амплитуда колебаний A – это наибольшее смещение из положения равновесия

Период T – это промежуток времени, в течение которого точка выполняет одно полное колебание.

Частота колебаний – это число полных колебаний в единицу времени t.

Частота, циклическая частота и период колебаний соотносятся как

Физический маятник.

Физический маятник – твёрдое тело способное совершать колебания относительно оси, не совпадающей с центром масс.

Электрический заряд.

Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.

Электрический заряд обычно обозначается буквами q или Q .

Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:

· Существует два рода электрических зарядов, условно названных положительными и отрицательными.

· Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.

· Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.

Закон Кулона.

Модуль силы взаимодействия двух точечных неподвижных электрических зарядов в вакууме прямо пропорционален произведению величин этих зарядов и обратно пропорционален квадрату расстояния между ними.

Г – расстояние между ними, k – коэффициент пропорциональности, зависящий от выбора системы единиц, в СИ

Величина, показывающая, во сколько раз сила взаимодействия зарядов в вакууме больше, чем в среде, называется диэлектрической проницаемостью среды Е. Для среды с диэлектрической проницаемостью е закон Кулона записывается следующим образом:

В СИ коэффициент k принято записывать следующим образом:

Электрическая постоянная, численно равная

Использованием электрической постоянной закон Кулона имеет вид:

Электростатическое поле.

Электростатическое поле – поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов). Электрическое поле представляет собой особый вид материи, связанный с электрическими зарядами и передающий действия зарядов друг на друга.

Основные характеристики электростатического поля:

· напряженность

· потенциал

Примеры формул напряженности поля заряженных тел.

1. Напряженность электростатического поля, создаваемого равномерно заряженной сферической поверхностью.

Пусть сферическая поверхность радиуса R (рис. 13.7) несет на себе равномерно распределенный заряд q, т. е. поверхностная плотность заряда в любой точке сферы будет одинакова.

Заключим нашу сферическую поверхность в симметричную поверхность S с радиусом r>R. Поток вектора напряженности через поверхность S будет равен

По теореме Гаусса

Следовательно

Сравнивая это соотношение с формулой для напряженности поля точечного заряда, можно прийти к выводу, что напряженность поля вне заряженной сферы такова, как если бы весь заряд сферы был сосредоточен в ее центре.

Для точек, находящихся на поверхности заряженной сферы радиуса R, по аналогии с вышеприведенным уравнением, можно написать

Проведем через точку В, находящуюся внутри заряженной сферической поверхности, сферу S радиусом г

2. Электростатическое поле шара.

Пусть имеем шар радиуса R, равномерно заряженный с объемной плотностью.

В любой точке А, лежащей вне шара на расстоянии r от его центра (r>R), его поле аналогично полю точечного заряда,расположенного в центре шара.

Тогда вне шара

а на его поверхности (r=R)

В точке В, лежащей внутри шара на расстояний r от его центра (r>R), поле определяется лишь зарядом , заключенным внутри сферы радиусом r. Поток вектора напряженности через эту сферу равен

с другой стороны, в соответствии с теоремой Гаусса

Из сопоставления последних выражений следует

где – диэлектрическая проницаемость внутри шара.

3. Напряженность поля равномерно заряженной бесконечной прямолинейной нити (или цилиндра).

Предположим, что полая цилиндрическая поверхность радиуса R заряжена с постоянной линейной плотностью .

Проведем коаксиальную цилиндрическую поверхность радиуса Поток вектора напряженности через эту поверхность

По теореме Гаусса

Из последних двух выражений определяем напряженность поля, создаваемого равномерно заряженной нитью:

Пусть плоскость имеет бесконечную протяженность и заряд на единицу площади равен σ. Из законов симметрии следует, что поле направлено всюду перпендикулярно плоскости, и если не существует никаких других внешних зарядов, то поля по обе стороны плоскости должны быть одинаковы. Ограничим часть заряженной плоскости воображаемым цилиндрическим ящиком, таким образом, чтобы ящик рассекался пополам и его образующие были перпендикулярны, а два основания, имеющие площадь S каждое, параллельны заряженной плоскости (рис 1.10).

Суммарный поток вектора; напряженности равен вектору , умноженному на площадь S первого основания, плюс поток вектора через противоположное основание. Поток напряженности через боковую поверхность цилиндра равен нулю, т.к. линии напряженности их не пересекают.

Таким образом, с другой стороны по теореме Гаусса

Следовательно

Но тогда напряженность поля бесконечной равномерно заряженной плоскости будет равна

В это выражение не входят координаты, следовательно электростатическое поле будет однородным, а напряженность его в любой точке поля одинакова.

5. Напряженность поля, создаваемого двумя бесконечными параллельными плоскостями, заряженными разноименно с одинаковыми плотностями.

Как видно из рисунка 13.13, напряженность поля между двумя бесконечными параллельными плоскостями, имеющими поверхностные плотности зарядов и , равны сумме напряженностей полей, создаваемых пластинами, т.е.

Таким образом,

Вне пластины векторы от каждой из них направлены в противоположные стороны и взаимно уничтожаются. Поэтому напряженность поля в пространстве, окружающем пластины, будет равна нулю Е=0.

Электрический ток.

Электри́ческий ток – направленное (упорядоченное) движение заряженных частиц

Сторонние силы.

Сторонние силы – силы неэлектрической природы, вызывающие перемещение электрических зарядов внутри источника постоянного тока. Сторонними считаются все силы отличные от кулоновских сил.

Э.д.с. Напряжение.

Электродвижущая сила (ЭДС) – физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.

ЭДС можно выразить через напряжённость электрического поля сторонних сил

Напряжение (U) равно отношению работы электрического поля по перемещению заряда
к величине перемещаемого заряда на участке цепи.

Единица измерения напряжения в системе СИ:

Сила тока.

Сила тока (I)- скалярная величина, равная отношению заряда q , прошедшего через поперечное сечение проводника, к промежутку времени t , в течение которого шел ток. Сила тока показывает, какой заряд проходит через поперечное сечение проводника за единицу времени.

Плотность тока.

Плотность тока j – вектор, модуль которого равен отношению силы тока, протекающего через некоторую площадку, перпендикулярно направлению тока, к величине этой площадки.

В СИ единицей плотности тока является ампер на квадратный метр (А/м2).

Закон Ома.

Ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.

Закон Джоуля-Ленца.

При прохождении электрического тока по проводнику количество теплоты, выделяемое в проводнике, прямо пропорционально квадрату тока, сопротивлению проводника и времени, в течение которого электрический ток протекал по проводнику.

Магнитное взаимодействие.

Магнитное взаимодействие – это взаимодействие упо­рядочение движущихся электричес­ких зарядов.

Магнитное поле.

Магнитное поле – это особый вид материи, посредством которой осуществляется взаимодействие между движущимися электрически заряженными частицами.

Сила Лоренца и сила Ампера.

Сила Лоренца – сила, действующая со стороны магнитного поля на движущийся со скоростью положительный заряд (здесь – скорость упорядоченного движения носителей положительного заряда).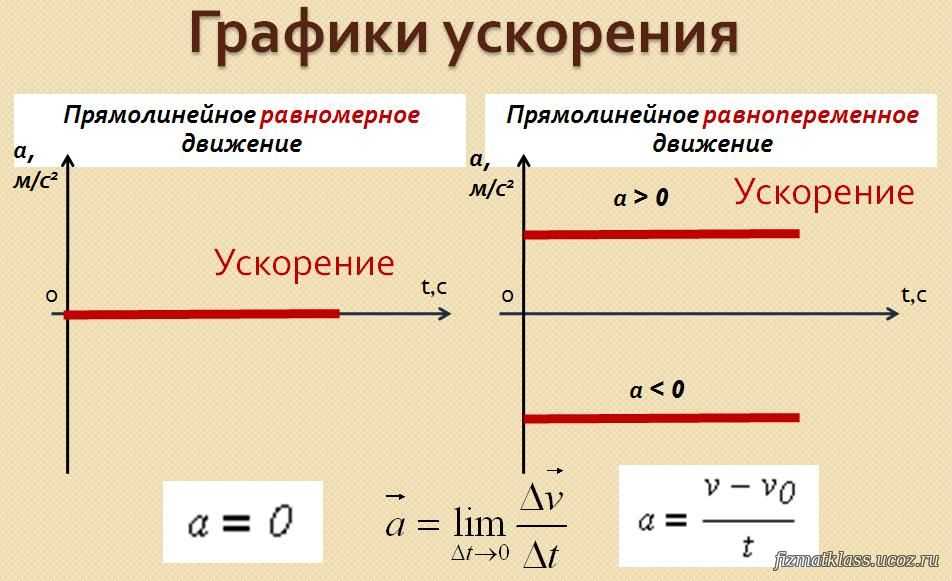 Модуль лоренцевой силы:

Сила Ампера – это сила, с которой магнитное поле действует на проводник с током.

Модуль силы Ампера равен произведению силы тока в проводнике на модуль вектора магнитной индукции, длину проводника и синус угла между вектором магнитной индукции и направлением тока в проводнике.

Сила Ампера максимальна, если вектор магнитной индукции перпендикулярен проводнику.

Если вектор магнитной индукции параллелен проводнику, то магнитное поле не оказывает никакого действия на проводник с током, т.е. сила Ампера равна нулю.

Направление силы Ампера определяется по правилу левой руки.

Закон Био-Савара-Лапласа.

Закон Био Савара Лапласа – Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов.

Формулировка

Пусть постоянный ток течёт по контуру γ, находящемуся в вакууме, -точка, в которой ищется поле, тогда индукция магнитного поля в этой точкевыражается интегралом (в системе СИ)

Направление перпендикулярно и , то есть перпендикулярноплоскости, в которой они лежат, и совпадает с касательной к линиимагнитной индукции. Это направление может быть найдено по правилунахождения линий магнитной индукции (правилу правого винта):направление вращения головки винта дает направление , еслипоступательное движение буравчика соответствует направлению тока вэлементе. Модуль вектора определяется выражением (в системе СИ)

Векторный потенциал даётся интегралом (в системе СИ)

Индуктивность контура.

Индуктивность – физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду.
Также индуктивность можно рассчитать по формуле:

где Ф – магнитный поток через контур, I – сила тока в контуре.

Единицы измерения индуктивности в системе СИ:

Энергия магнитного поля.

Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии.

Электромагнитная индукция.

Электромагнитная индукция – явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.

Правило Ленца.

Правило Ленца

Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует изменению магнитного потока, которым он вызван.

Первое уравнение Максвелла

2. Всякое перемещенное магнитное поле порождает вихревое электрическое (основной закон электромагнитной индукции).

Второе уравнение Максвелла:

Электромагнитное излучение.

Электромагни́тные во́лны, электромагни́тное излуче́ние – распространяющееся в пространстве возмущение (изменение состояния) электромагнитного поля.

3.1. Волна – это колебания, распространяющиеся в пространстве в течение времени.
Механические волны могут распространяться только в какой-нибудь среде (веществе): в газе, в жидкости, в твердом теле. Источником волн являются колеблющиеся тела, которые создают в окружающем пространстве деформацию среды. Необходимым условием для появления упругих волн является возникновение в момент возмущения среды препятствующих ему сил, в частности, упругости. Они стремятся сблизить соседние частицы, когда они расходятся, и оттолкнуть их друг от друга в момент сближения. Силы упругости, действуя на удаленные от источника возмущения частицы, начинают выводить их из равновесия. Продольные волны характерны только газообразным и жидким средам, а вот поперечные – также и твердым телам: причина этого заключается в том, что частицы, составляющие данные среды, могут свободно перемещаться, так как жестко не зафиксированы, в отличие от твердых тел. Соответственно, поперечные колебания принципиально невозможны.

Продольные волны возникают тогда, когда частицы среды колеблются, ориентируясь вдоль вектора распространения возмущения. Поперечные волны распространяются в перпендикулярном вектору воздействия направлении. Короче: если в среде деформация, вызванная возмущением, проявляется в виде сдвига, растяжения и сжатия, то речь идет о твердом теле, для которого возможны как продольные, так и поперечные волны. Если же появление сдвига невозможно, то среда может быть любой.

Каждая волна распространяется с какой-то скоростью. Под скоростью волны понимают скорость распространения возмущения. Поскольку скорость волны – величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:

Длина́ волны́ – расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой «проходит» за интервал времени, равный периоду колебаний, поэтому

Волновое число (также называемое пространственной частотой ) – это отношение 2π радиан к длине волны: пространственный аналог круговой частоты.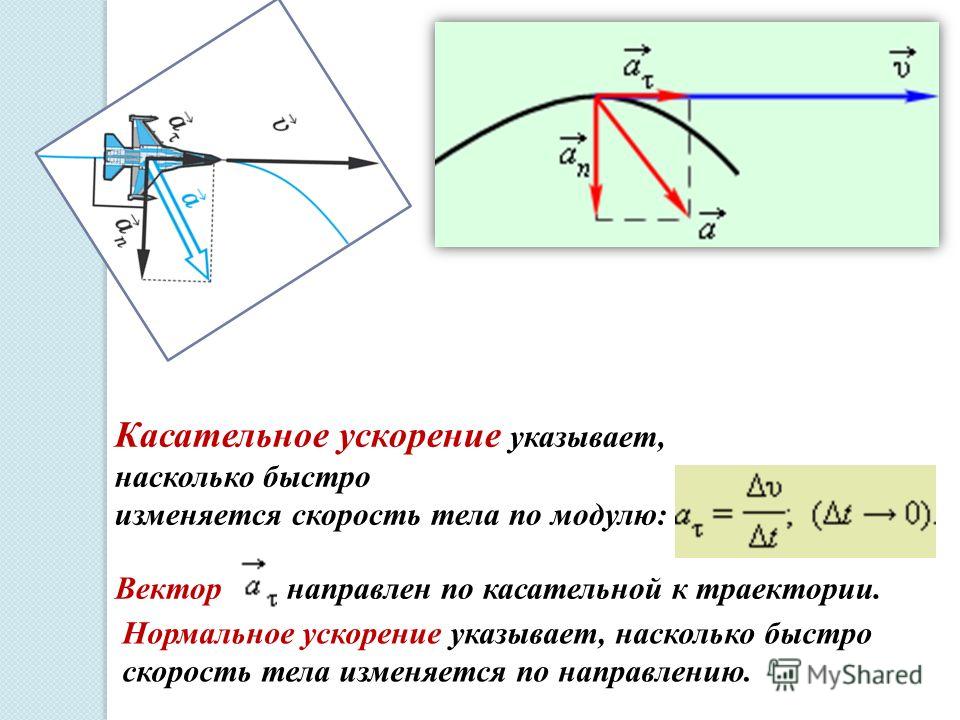

Определение : волновым числом k называется быстрота роста фазы волны φ по пространственной координате.

3.2. Плоская волна – волна, фронт которой имеет форму плоскости.

Фронт плоской волны неограничен по размерам, вектор фазовой скорости перпендикулярен фронту. Плоская волна является частным решением волнового уравнения и удобной моделью: такая волна в природе не существует, так как фронт плоской волны начинается в и заканчивается в , чего, очевидно, быть не может.

Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Волновое уравнение для функции записывается в виде:

где

· – оператор Лапласа;

· – искомая функция;

· – радиус вектора искомой точки;

· – скорость волны;

· – время.

Волновая поверхность – геометрическое место точек, испытывающих возмущение обобщенной координаты в одинаковой фазе. Частный случай волновой поверхности – волновой фронт.

А) Плоская волна – это волна, волновые поверхности которой представляют собой совокупность параллельных друг другу плоскостей.

Б) Сферическая волна – это волна, волновые поверхности которой представляют собой совокупность концентрических сфер.

Луч – линия, нормальной и волновой поверхности. Под направлением распространения волн понимают направление лучей. Если среда распространения волны однородная и изотропная, лучи прямые (причём, если волна плоская – параллельные прямые).

Понятием луч в физике обычно пользуются только в геометрической оптике и акустике, так как при проявлении эффектов, не изучаемых в данных направлениях, смысл понятия луч теряется.

3.3. Энергетические характеристики волны

Среда, в которой распространяется волна, обладает механической энергией, складывающейся из энергий колебательного движения всех ее частиц. Энергия одной частицы с массой m 0 находится по формуле: Е 0 = m 0 Α 2 ω 2 /2. В единице объема среды содержится n = p /m 0 частиц (ρ – плотность среды). Поэтому единица объема среды обладает энергией w р = nЕ 0 = ρ Α 2 ω 2 /2.

Объемная плотность энергии (W р)- энергия колебательного движения частиц среды, содержащихся в единице ее объема:

Поток энергии (Ф) – величина, равная энергии, переносимой волной через данную поверхность за единицу времени:

Интенсивность волны или плотность потока энергии (I) – величина, равная потоку энергии, переносимой волной через единичную площадку, перпендикулярную направлению распространения волны:

3.4. Электромагнитная волна

Электромагнитная волна – процесс распространения электромагнитного поля в пространстве.

Условие возникновения электромагнитных волн. Изменения магнитного поля происходят при изменении силы тока в проводнике, а сила тока в проводнике изменяется при изменении скорости движения электрических зарядов в нем, т. е. при движении зарядов с ускорением. Следовательно, электромагнитные волны должны возникать при ускоренном движении электрических зарядов. При скорости заряда, равной нулю, существует только элект­рическое поле. При постоянной скорости заряда возникает электромаг­нитное поле. При ускоренном движении заряда происходит излучение электромагнитной волны, кото­рая распространяется в про­странстве с конечной скоро­стью.

Электромагнитные волны распространяются в веществе с конечной скоростью. Здесь ε и μ – диэлектрическая и магнитная проницаемости вещества, ε 0 и μ 0 – электрическая и магнитная постоянные: ε 0 = 8,85419·10 –12 Ф/м, μ 0 = 1,25664·10 –6 Гн/м.

Скорость электромагнитных волн в вакууме (ε = μ = 1):

Основными характеристиками электромагнитного излучения принято считать частоту, длину волны и поляризацию. Длина волны зависит от скорости распространения излучения. Групповая скорость распространения электромагнитного излучения в вакууме равна скорости света, в других средах эта скорость меньше.

Электромагнитное излучение принято делить по частотам диапазонам (см. таблицу). Между диапазонами нет резких переходов, они иногда перекрываются, а границы между ними условны. Поскольку скорость распространения излучения постоянна, то частота его колебаний жёстко связана с длиной волны в вакууме.

Интерференция волн. Когерентные волны. Условия когерентности волн.

Оптическая длина пути (о.д.п.) света. Связь разности о.д.п. волн с разностью фаз колебаний, вызываемых волнами.

Амплитуда результирующего колебания при интерференции двух волн. Условия максимумов и минимумов амплитуды при интерференции двух волн.

Интерференционные полосы и интерференционная картина на плоском экране при освещении двух узких длинных параллельных щелей: а) красным светом, б) белым светом.

Теперь мы должны выяснить самое главное – как изменяется координата тела при его прямолинейном равноускоренном движении. Для этого, как мы знаем, нужно знать перемещение тела, потому что проекция вектора перемещения как раз и равна изменению координаты.

Формулу для вычисления перемещения проще всего получить графическим методом.

При равноускоренном движении тела вдоль оси X скорость изменяется со временем согласно формуле v x = v 0х + a x t Так как время в эту формулу входит в первой степени, то график для проекции скорости в зависимости от времени представляет собой прямую, как это показано на рисунке 39. Прямая 1 на этом рисунке соответствует движению с положительной проекцией ускорения (скорость растет), прямая 2 – движению с отрицательной проекцией ускорения (скорость убывает). Оба графика относятся к случаю, когда в момент времени t = О тело имеет некоторую начальную скорость v 0 .

Перемещение выражается площадью. Выделим на графике скорости равноускоренного движения (рис. 40) маленький участок ab и опустим из точек а и Ь перпендикуляры на ось t. Длина отрезка cd на оси t в выбранном масштабе равна тому малому промежутку времени, за который скорость изменилась от ее значения в точке а до ее значения в точке Ь. Под участком ab графика получилась узкая полоска abсd.

Если промежуток времени, соответствующий отрезку cd, достаточно мал, то в течение этого малого времени скорость не может заметно измениться – движение в течение этого малого промежутка времени можно считать равномерным. Полоска abсd поэтому мало отличается от прямоугольника, а ее площадь численно равна проекции перемещения за время, соответствующее отрезку cd (см. § 7).

Но на такие узкие полоски можно разбить всю площадь фигуры, расположенной под графиком скорости. Следовательно, перемещение за все время t численно равно площади трапеции ОАВС. Площадь же трапеции, как известно из геометрии, равна произведению полусуммы ее оснований на высоту. В нашем случае длина одного из оснований численно равна v ox , другого-v x (см. рис. 40). Высота же трапеции численно равна t. Отсюда следует, что проекция s x перемещения выражается формулой

3с 15.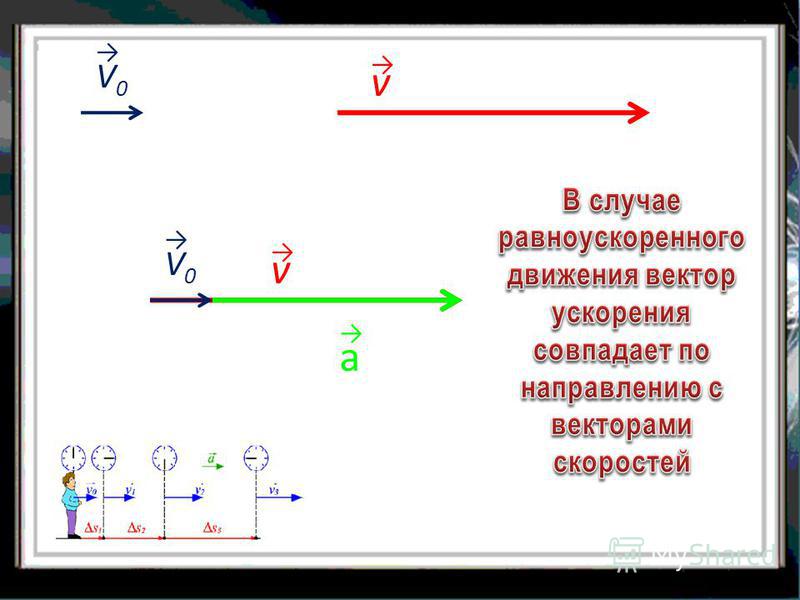 09

Если проекция v ox начальной скорости равна нулю (в начальный момент времени тело покоилось!), то формула (1) принимает вид:

График скорости такого движения показан на рисунке 41.

При пользовании формулами (1) и (2) НУЖНО ПОМНИТЬ, ЧТО S x , V ox и v x могут быть как положительным», так и отрицательными – ведь это проекции векторов s, v o и v на ось X.

Таким образом, мы видим, что при равноускоренном движении перемещение растет со временем не так, как при равномерном движении: теперь в формулу входит квадрат времени. Это значит, что перемещение со временем растет быстрее, чем при равномерном движении.

Как зависит от времени координата тела? Теперь легко получить и формулу для вычисления координаты х в любой момент времени для тела, движущегося равноускоренно.

проекция s x вектора перемещения равна изменению координаты х-х 0 . Поэтому можно записать

Из формулы (3) видно, что, для того чтобы вычислить координату х в любой момент времени t, нужно знать начальную координату, начальную скорость и ускорение.

Формула (3) описывает прямолинейное равноускоренное движение, подобно тому как формула (2) § 6 описывает прямолинейное равномерное движение.

Другая формула для перемещения. Для вычисления перемещения можно получить и другую полезную формулу, в которую время не входит.

Из выражения v x = v 0x + a x t. получим выражение для времени

t = (v x – v 0x): a x и подставим его в формулу для перемещения s x , приведенную выше. Тогда получаем:

Эти формулы позволяют найти перемещение тела, если известны ускорение, а также начальная и конечная скорости движения. Если начальная скорость v o равна нулю, формулы (4) принимают вид:

На предыдущих уроках мы обсуждали, как определить пройденный путь при равномерном прямолинейном движении. Настало время узнать, как определить координату тела, пройденный путь и перемещение при прямолинейном равноускоренном движении. Это можно сделать, если рассмотреть прямолинейное равноускоренное движение как набор большого количества очень малых равномерных перемещений тела.

Первым решил задачу местоположения тела в определенный момент времени при ускоренном движении итальянский ученый Галилео Галилей (рис. 1).

Рис. 1. Галилео Галилей (1564-1642)

Свои опыты он проводил с наклонной плоскостью. По желобу он запускал шар, мушкетную пулю, а затем определял ускорение этого тела. Как же он это делал? Он знал длину наклонной плоскости, а время определял по биению своего сердца или по пульсу (рис. 2).

Рис. 2. Опыт Галилея

Рассмотрим график зависимости скорости равноускоренного прямолинейного движения от времени. Эта зависимость вам известна, она представляет собой прямую линию: .

Рис. 3. Определение перемещения при равноускоренном прямолинейном движении

График скорости разбиваем на маленькие прямоугольные участки (рис. 3). Каждый участок будет соответствовать определенной скорости, которую можно считать постоянной в данный промежуток времени. Надо определить пройденный путь за первый промежуток времени. Запишем формулу: . Теперь посчитаем суммарную площадь всех имеющихся у нас фигур.

Сумма площадей при равномерном движении – это полный пройденный путь.

Обратите внимание: от точки к точке скорость будет изменяться, тем самым мы получим путь, пройденный телом именно при прямолинейном равноускоренном движении.

Заметим, что при прямолинейном равноускоренном движении тела, когда скорость и ускорение направлены в одну сторону (рис. 4), модуль перемещения равен пройденному пути, поэтому, когда мы определяем модуль перемещения – определяем пройденный путь . В данном случае можем говорить, что модуль перемещения будет равен площади фигуры, ограниченной графиком скорости и времени.

Рис. 4. Модуль перемещения равен пройденному пути

Воспользуемся математическими формулами для вычисления площади указанной фигуры.

Рис. 5 Иллюстрация для вычисления площади

Площадь фигуры (численно равная пройденному пути), равна полусумме оснований, умноженной на высоту. Обратите внимание, что на рисунке одним из оснований является начальная скорость, а вторым основанием трапеции будет конечная скорость, обозначенная буквой . Высота трапеции равна , это промежуток времени, за который произошло движение.

Конечную скорость, рассмотренную на предыдущем уроке, мы можем записать как сумму начальной скорости и вклада, обусловленного наличием у тела постоянного ускорения. Получается выражение:

Если раскрыть скобки, то становится удвоенным. Мы можем записать следующее выражение:

Если по отдельности записать каждое из этих выражений, итогом будет следующее:

Это уравнение впервые было получено благодаря экспериментам Галилео Галилея. Поэтому можно считать, что именно этот ученый впервые дал возможность определить местоположение тела при прямолинейном равноускоренном движении в любой момент времени. Это и есть решение главной задачи механики.

Теперь давайте вспомним, что пройденный путь, равный в нашем случае модулю перемещения , выражается разностью:

Если это выражение подставить в уравнение Галилея , то получим закон, по которому меняется координата тела при прямолинейном равноускоренном движении:

Следует помнить, что величины – это проекции скорости и ускорения на выбранную ось. Поэтому они могут быть как положительными, так и отрицательными.

Заключение

Следующим этапом рассмотрения движения станет исследование движения по криволинейной траектории.

Список литературы

1. Кикоин И.К., Кикоин А.К. Физика: учебник для 9 класса средней школы. – М.: Просвещение.
2. Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений/А. В. Перышкин, Е. М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300.
3. Соколович Ю.А., Богданова Г.С . Физика: Справочник с примерами решения задач. 2 .
4. Чем отличаются зависимости перемещения от времени при равномерном и равноускоренном движениях?

кинематика – Как ускорение, скорость и смещение влияют друг на друга?

$\begingroup$

Я задавался этим вопросом с тех пор, как узнал о графиках положения, скорости и ускорения в зависимости от времени, но не могу сопоставить числа/уравнения.

Я знаю, что ускорение влияет на изменение скорости, о чем свидетельствует влияние гравитации на объект, когда его подбрасывают вверх. Точно так же, когда вы едете в автомобиле, ваша скорость изменяется/воздействует на ваш рабочий объем. Но как же тогда ускорение влияет на смещение? Как бы вы показали это каким-то количественным способом? Как ваша средняя скорость и мгновенная скорость связаны с вашим перемещением (та же идея с соотношением для ускорения)? 9{2} \propto $ или есть какие-то другие интуитивные отношения, которые можно представить с помощью чисел?

Это так же просто, как $v = \frac{\Delta s}{\Delta t}$ так же, как $ v\Delta t \propto \Delta s $?

Подобие, $a = \frac{\Delta v}{\Delta t}$, поэтому $ a\Delta t \propto \Delta v $?

Но как бы вы связали между собой ускорение и смещение? Я знаю, что они должны быть связаны, но я не уверен, как именно.

Могу ли я сделать что-то вроде $\Delta t = \frac{\Delta s}{v}$ и $\Delta t = \frac{\Delta v}{a}$, так что $v\frac{\Delta v} {a} \propto \Delta s$? Но это не дает большого понимания с первого взгляда… 92t} $ может быть? Проще говоря, как эти три понятия связаны и связаны друг с другом, а также как они влияют друг на друга?

• кинематика
• ускорение
• скорость
• исчисление
• перемещение

$\endgroup$

1

$\begingroup$

Ответ состоит в том, что они буквально определяются как дифференциалы/интегранты друг друга.

Скорость определяется как скорость изменения смещения во времени. Ускорение определяется как скорость изменения скорости во времени. То есть, как они связаны.

В ситуациях, когда есть постоянное ускорение (или нет), это приводит к набору хорошо известных формул, связывающих их. Но эти формулы применимы только для постоянного ускорения. Что-нибудь еще, и вы обычно возвращаетесь к определениям, основанным на дифференциалах/интегрантах.

Чтобы ответить на некоторые ваши вопросы:

Я знаю, что ускорение влияет на изменение скорости, о чем свидетельствует влияние гравитации на объект, когда его подбрасывают вверх. Точно так же, когда вы едете в автомобиле, ваша скорость изменяется/воздействует на ваш рабочий объем. Но как же тогда ускорение влияет на смещение?

Буквально – ускорение меняет вашу скорость (по определению), а разная скорость означает, что вы путешествуете на разное расстояние/смещение за время сейчас и в другое время (также по определению). Вот и все. Практически нет более прямого способа сказать это. Мы определяем эти термины, потому что они полезны таким образом. Это все, что есть.

Как ваша средняя скорость и мгновенная скорость связаны с вашим перемещением.

Как и прежде. Мгновенная скорость — это способ узнать, как меняется ваше смещение за более короткие и короткие периоды времени. Это предел в том смысле, что всякое дифференцирование является пределом, поскольку ∆x или ∆t стремится к нулю. Средняя скорость спрашивает, как изменяется ваше перемещение при усреднении за ненулевой интервал времени – какой была бы эквивалентная постоянная скорость, чтобы пройти такое же общее перемещение за то же общее время.

Для ускорения, очевидно, что по мере того, как вы ускоряетесь, ваше перемещение также будет быстро увеличиваться, верно?

Не обязательно. Предположим, вы ускоряетесь со скоростью +10 м/с ² от начальной скорости -100 м/с до +0 м/с, это ускорение. Но ваши абсолютные размеры смещения будут замедляться. Или предположим, что ваше ускорение происходит по кругу или по внутренней спирали. В обоих случаях вы не увидите, что смещения в единицу времени становятся «быстро большими». Это потому, что ускорение буквально есть скорость изменения скорости, не более того. Даже движение по кругу с постоянной скоростью является ускорением, потому что, хотя ваша скорость постоянна, ваши скорость непостоянна. (*) Таким образом, ускорение не означает, что смещения «становятся больше» (быстро или каким-либо другим образом) или вообще имеет какое-либо другое значение. Это просто скорость изменения скорости, не более того.

(*) Поскольку скорость – это заявленная скорость в указанном направлении , поэтому изменение скорости или направления меняет скорость, а изменение скорости означает, что она ускоряется.

Но как бы вы связали ускорение и перемещение вместе? Я знаю, что они должны быть связаны, но я не уверен, как именно.

Вторая производная или второй интеграл по времени. Это и ничего больше……

$\endgroup$

$\begingroup$

Вот как мне нравится думать о положении, скорости (т. е. изменении положения) и ускорении (т.е. изменении скорости):

Предположим, что при t=0 (в секундах или любых других единицах)

Положение = [0, 0, 0] Скорость = [10, 20, 30] Ускорение = [1, 0, 0]

Тогда при t=1, если ускорение постоянно, движение объекта будет полностью описано по:

Положение = [10, 20, 30] Скорость = [11, 20, 30] Ускорение = [1, 0, 0]

При t=2,

Положение = [21, 40, 60] Скорость = [12, 20, 30] Ускорение = [1, 0, 0]

При t=3,

Положение = [33, 60, 80] Скорость = [13, 20, 30] Ускорение = [ 1, 0, 0]

Мы можем думать об исчислении как о том, что происходит, когда время очень мало, например, когда тик составляет не 1 секунду, а 0,0000001 секунду. Соотношения те же самые между положением, скоростью и ускорением. 9п}$.

$\endgroup$

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Перемещение, скорость и ускорение | бартлби

Что такое перемещение, скорость и ускорение?

В классической механике кинематика имеет дело с движением частицы. Он имеет дело только с положением, скоростью, ускорением и смещением частицы. Он не имеет никакого отношения к источнику движения.

Перемещение

Расстояние и перемещение — это две величины, которые указывают длину между двумя точками, но они совершенно разные.

Расстояние означает общую длину пути, пройденного объектом независимо от направления, и является скалярной величиной. Смещение означает общее изменение положения объекта или частицы. Это векторная величина, что означает, что она имеет как направление, так и величину.

Рассмотрим объект, помещенный в точку A, он перемещается из своего положения в положение B. Смещенное положение объекта называется смещением. Перемещение измеряется вдоль линейной или прямой линии.

Перемещение, AB→ =OB→- OA→

Это разница векторов между начальным этапом или начальным положением и этапом завершения или конечным положением. Если A — начальная позиция, а B — конечная позиция. Тогда смещение равно

∆x=xf-xi

где ∆x=перемещение 

xf= конечное положение

xi=начальное положение

Единицей перемещения является метр (м).

Скорость

Скорость изменения смещения объекта по отношению ко времени и системе отсчета называется скоростью. Это векторная величина.

Velocity=DisplacementTimev=dsdt

где ds=изменение смещения

dt= изменение во времени

Единицей скорости является м/с или мс-1.

Подобно расстоянию и смещению, скорость и скорость имеют разные значения. Скорость является скалярной величиной и относится к тому, насколько быстро объект движется или скорость, с которой объект преодолевает расстояние. Если объект движется с большой скоростью, он преодолевает большое расстояние за малое время. Напротив, если объект движется медленно, это означает медленную скорость, он покрывает лишь небольшое расстояние за одно и то же время.

Мгновенная скорость

Мгновенная скорость определяется как скорость движущегося объекта в определенный момент времени, которая почти равна нулю.

vi=lim∆t→∞dsdt

Где vi= мгновенная скорость

ds= изменение смещения

dt= интервал времени

Средняя скорость

Средняя скорость. Формула:

vav=d2-d1t2-t1

Где vav= средняя скорость

d2 и d1= конечное и начальное положение.

t2 и t1 = конечное и начальное время.

Ускорение

Описывается как скорость изменения скорости объекта во времени. Это векторная величина. Кроме того, если есть изменение скорости объекта, то говорят, что объект ускоряется. Формула:

Ускорение = Изменение velocityTimea=dvdt

Единицей измерения ускорения является м/с2 или мс-2.  

 Если скорость объекта увеличивается с постоянной скоростью, то объект имеет неизменное ускорение или постоянное ускорение.

Если отношение скорости ко времени оценивается для конечного интервала времени, то оно называется средним ускорением. Если отношение оценивается для бесконечно малого интервала времени, оно называется мгновенным ускорением.

Ускорение при движении снаряда

Если объект брошен вверх, то единственной основной силой, действующей на объект, является гравитация. На него действуют и некоторые другие вторичные силы, но по сравнению с гравитацией их влияние невелико. Сила, которая тянет объект вниз, называется ускорением силы тяжести. Когда объект бросают наискось с поверхности земли, он создает траекторию, которая выглядит как кривая и достигает центра земли. Путь, созданный частицей во время движения, называется снарядом, а движение называется снарядным движением.

СС-BY| Авторы изображений:
https://www.saratogaschools.org/webpages/tsanders/notes.cfm?subpage=1381204

Уравнение движения                     

Это так называемые кинематические уравнения движения. Это также объясняет взаимосвязь между смещением, скоростью и ускорением. Она объясняет движение частицы, которая перемещается в одномерных, двухмерных или трехмерных областях. Движение может быть равномерным или неравномерным, ускоряющимся или неускоряющимся. Эти уравнения связывают параметры и помогают признать движение объекта. Четыре основных уравнения:

v= u +ats=ut+12at2v2-u2=2as

Вывод

Представим себе частицу, которая совершает перемещение s за время t. Пусть u — начальная скорость, а v — конечная скорость. Движение объекта равноускорено в интервале времени t со скоростью (а) для системы отсчета. Используя дифференциальное и интегральное исчисление, мы можем вывести уравнения.

Первое уравнение движения

Из определения ускорения a определяется как

a=dvdt

Интегрируя уравнение, получаем первое уравнение движения.

v=dsdtds= v dtds=(u+at)dt

При интегрировании

(2)    

Третье уравнение движения

Третье уравнение получено из ускорения. Это дается как,

A = DVDT

Умножение и делите на DS на правой стороне,

A = DVDTDSDSA = VDVDSVDV = A DS

при интегрировании,

∫UVVDV = ∫0SADSV22UV = AS0SV2-U22 = ASV2-U 2ASV2 = aUVV2-U 2ASV22.

Перемещение, скорость, ускорение при простом гармоническом движении

В классической механике для одномерной СГМ уравнение движения представляет собой дифференциальное уравнение второго порядка с постоянными коэффициентами. Эти константы выводятся из закона Гука и второго закона Ньютона для массы, помещенной на пружину. Дифференциальное уравнение:

m d2xdt2=-kx       (5)

где m = инерционная масса тела.

x= смещение массы от среднего положения.

k = жесткость пружины.

Следовательно,

d2xdt2=-kmx         (6)

при решении приведенного выше дифференциального уравнения мы получаем синусоидальное уравнение.

x(t)=c1cos(ωt)+c2sin(ωt)     (7)

Где ω=km

c1 и c2 — дифференциальные константы.

Чтобы найти значения этих констант, положим t=0,

x(0)=c1cos(0)+c2sin(0)x(0)=c1c1=x0

Где c1 — начальное положение частицы.

Дифференцируя уравнение (7), находим константу c2,

v(t)≡dxdt=-ωx0cosωt+c2ωsin(ωt)

при t=0,

v(0)=ωc2c2=v0ω

Подставьте все значения в уравнение (7):

x(t)=x0coskmt+v0ωsinkmt         (8)

Другая форма уравнения:

x(t)=Acos(ωt-φ)

Где A=c12+c22 и tanφ=c2c1

, где A = амплитуда.

ω=угловая частота.

φ= фазовый угол или начальная фаза.

В этом решении константы определяются из их начальных условий, а их исходное положение устанавливается в положение равновесия. Эти две константы несут физическое значение этого движения.

Используя метод исчисления, мы можем найти скорость и ускорение колебаний.

Из уравнения смещения мы можем определить скорость,

v(t)=dxdt=ddt(Acos(ωt-φ)v(t)=-A sin(ωt-φ)

Первым производным скорости является ускорение.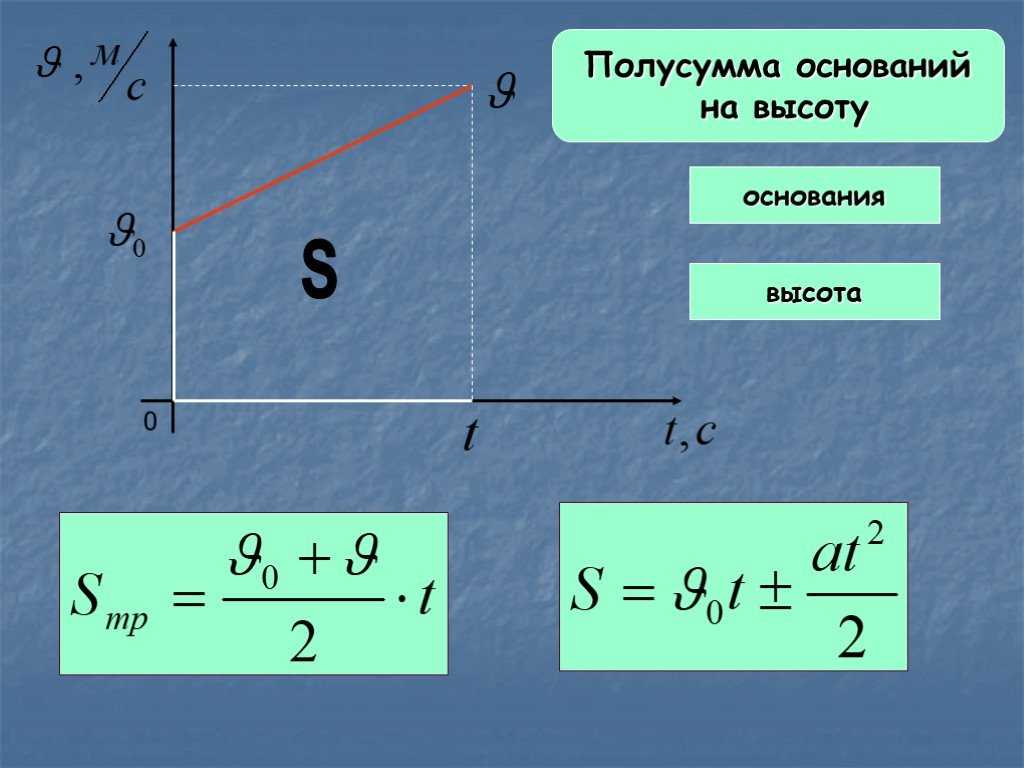 Следовательно, путем дифференцирования

a( t)=dvdt=ddt(-Asin(ωt-φ))a(t)=-Aω2cos(ωt-φ)

Ускорение, найденное из приведенного выше уравнения, находится в положении равновесия. В крайних точках максимальное ускорение is Aω2

Интерпретируется, что когда масса подвергается колебаниям, ускорение прямо пропорционально смещению.

a(x)=ωx

График показывает взаимосвязь между смещением, скоростью и ускорением в простом гармоническом движении. Всякий раз, когда скорость максимальна, ускорение равно нулю.

Скорость опережает смещение на фазовый угол (π/2). Ускорение опережает на (π/2) скорость или π смещения.

Формулы

Формула скорости,

v=dxdt

Формула средней скорости,

vav=d2-d1t2-t1

Формула мгновенной скорости

vi=lim∆t→∞dsdt

Формула ускорения

a=dvdt

Уравнения движения

v= u +ats=ut+12at2v2-u2= 2as

Контекст и приложения

Это основная и необходимая тема для всех выпускников и аспирантов, особенно для бакалавров и магистров естественных наук (физики).

Практические задачи

Вопрос 1: Автомобиль движется из состояния покоя. Он достигает скорости 20 мс-1 за 10 секунд. Найдите ускорение автомобиля.

а. 2 мс-2                   b. 0,2 мс-2   c. 4 мс-2                     d. 20 мс-2   

Данные:

Начальная скорость, u=0 мс-1

Конечная скорость, v=20 мс-1

Время, t=10 с

3 Пояснение: первое уравнение движения,

v-u=at20 мс-1-0=a×10sa=20 мс-110sa=2 мс-2

Ускорение автомобиля равно 2 мс-2.

Ответ: Правильный вариант a.

Вопрос 2: Мяч движется со скоростью 0,3 м/с. Его скорость уменьшается со скоростью 0,05 м/с2. Найдите скорость мяча через 5 с.

а. 0,05 мс-1                     b. 0,5 мс-1 в. 5 мс-1                     d. 50 мс-1

Присвоенные данные:

Начальная скорость, U = 0,3 мс-1

Ускорение, A = 0,05 MS-2

, T = 5S

Раствор:

по первым кинематичным уравнение,

v=u+atv=(0,3 мс-1)+(-0,05 мс-2)(5с)v=0,3 мс-1 -0,25 мс-1 v=0,05 мс-1

Скорость мяча 0,05 м/с.

Ответ: Правильный вариант b.

Вопрос 3: Грузовик трогается с места с равномерным ускорением 7 м/с2. Найдите путь, пройденный грузовиком за 5 с.

а. 75м б. 95м

в. 87,5м д. 75,5м

Данные:

Начальная скорость, u=0 мс-1

Ускорение, a=7мс-2

Время, t=5 с

Решение:

Из второго кинематического уравнения

s=ut+12at2s=(0)(5s)+12(7ms-2)(5s)2 s=87,5 м

Расстояние, пройденное грузовиком составляет 87,5 м.

Ответ: Правильный вариант c.

Вопрос 4: Средняя скорость ______.

а. Общее расстояние/время

b. Общее водоизмещение/общее время

c. Расстояние/скорость

д. Скорость/время

Ответ: Правильный вариант (б).

Объяснение: Средняя скорость определяется как общее перемещение тела, деленное на общее время.

             vav=∆d∆t=d2-d1t2-t1

Вопрос 5: Движение объекта из одного положения в другое называется ________.

а. Скорость

б. Скорость

в. Рабочий объем

д. Расстояние

Ответ: Правильный вариант (c).

Объяснение: Перемещение определяется как перемещение объекта из одного места в другое. И это кратчайшее расстояние между начальным положением объекта и конечным положением.

Скорость и скорость: определение, формула, единицы измерения, различия

В нашей повседневной жизни скорость и скорость — это то, с чем мы сталкиваемся, перемещаясь из одного места в другое, что дает нам возможность приводить в действие эти два термина. Скорость и скорость связаны таким образом, что связаны расстояние и перемещение. Скорость — это скаляр, а скорость — это вектор. v  (курсив) — это символ скорости, а скорость получает символ V (жирный шрифт). Кроме того, средние значения получают полосу над символом. В этой статье вы получите глубокие знания об определении, формуле, единицах измерения, символах и примерах скорости и скорости. Вы также узнаете разницу между скоростью и скоростью.

Подробнее: Расстояние и перемещение

Содержание

• 1 Что такое скорость?
• 2 Что такое скорость?
• 3 Единицы
  • 3.1 Подпишитесь на нашу рассылку новостей
• 4 Различия между скоростью и скоростью
  • 4.1 Скорость
  • 4.2 Скорость
    • 4.2.1 Посмотрите видео ниже, чтобы узнать больше о скорости и скорости.
• 5 Примеры скорости и скорости
• 6 Заключение
  • 6.1 Пожалуйста, поделитесь!

Что такое скорость?

Скоростью называется скорость, с которой объект прошел определенное расстояние. мы также можем сказать, что скорость — это скорость, с которой объект движется, чтобы покрыть расстояние. Скорость известна как скалярная величина, это всего лишь величина. Когда два одинаковых объекта движутся с разной скоростью, в чем их различие? Отличие их лишь в том, что один из них движется быстрее (тот, у кого больше скорость) и проедет дальше, чем тот, который движется медленнее, за то же время. Это также говорит о том, что объект, движущийся быстрее, доберется до места назначения быстрее, чем объект, движущийся медленнее.

При любой скорости речь идет как о расстоянии, так и о времени. А «Быстрее» описывает большее расстояние, а «дальше и раньше» означает меньшее время. Увеличение скорости означает удвоение пройденного расстояния за заданный промежуток времени. Это также означает наличие времени, необходимого для прохождения заданного расстояния. Эти утверждения распространены и полезны в математике. Символ v в курсиве используется для обозначения скорости из-за связи между скоростью и скоростью:

• Скорость прямо пропорциональна расстоянию, когда время постоянно: v ∝s (t константа)
• Скорость обратно пропорциональна времени при постоянном расстоянии: v ∝ ¹ t (с константа)

Объединив эти два правила, мы получим определение скорости в символической форме. Хотя это не окончательное определение.

v  =	с
	т

Вот еще один способ определения скорости без использования символов. Скорость – это скорость изменения расстояния со временем.

Подробнее: Понимание ускорения

Давайте быстро посчитаем скорость, но чтобы добиться этого, мы должны знать, как далеко он ушел и сколько времени потребовалось, чтобы добраться туда. хотя «дальше» и «ранее» соответствуют «быстрее», обратите внимание! Предположим, вы проехали на машине из Нью-Йорка в Чикаго. Расстояние по дороге составляет примерно 300 км (200 миль). Если путешествие занимает четыре часа, с какой скоростью вы ехали?

Применяя приведенную выше формулу, получаем

v  =	с	≈	300 км	= 75 км/ч
	т		4 часа

 

Вычисленное выше число — это не скорость автомобиля, а средняя скорость на всем пути. Чтобы подчеркнуть этот момент, уравнение иногда можно изменить следующим образом:

v  =	∆ с
	∆ т

Черта над v означает среднее или среднее значение, а символы ∆ (дельта) описывают изменение. Это может выглядеть как «V-образная планка — это дельта-эсс над дельта-тройником». Это количество мы рассчитали для нашей гипотетической поездки. Напротив, спидометр автомобиля показывает его мгновенную скорость, то есть скорость, определяемую за очень небольшой промежуток времени — мгновение. В норме этот интервал должен быть как можно ближе к нулю, однако в реальности мы ограничены чувствительностью наших измерительных приборов. Но можно представить вычисление средней скорости за меньшие интервалы времени, пока мы не вычислим мгновенную скорость. Это можно записать символически как:

90 604  = 90 607

v  =	лим ∆ t →0	∆ с	дс
		∆ т	дт

Подробнее: Понимание плавучести

Для тех, кто знаком с исчислением, скорость исчисления – это первая производная расстояния по времени. Ну, это не то, о чем стоит беспокоиться, если вы не имели дело с исчислением. Есть и другие более простые способы определения мгновенной скорости движущегося объекта. На графике расстояние-время скорость соответствует наклону, и, таким образом, мгновенная скорость объекта с непостоянной скоростью может быть найдена по наклону линии, касательной к его кривой. Это будет обсуждаться в другой теме.

Что такое скорость?

Скорость просто означает скорость, с которой объект меняет свое положение. Скорость — векторная величина; она имеет как величину, так и направление. например, объект, движущийся быстро и все еще в своем исходном положении. Допустим, объект движется вперед со скоростью 2 метра и в то же время движется назад с той же скоростью 2 метра, что показывает, что человек движется с нулевой скоростью, а объект движется вперед со скоростью 2 м/. с, такой объект движется со скоростью, а скорость — это скорость, с которой объект меняет свое положение, потому что положение этого объекта меняется на 2 метра каждую секунду.

Рассчитать скорость можно, зная, как далеко ушел объект и сколько времени потребовалось, чтобы туда добраться. затем вы должны знать, требуется ли расстояние или смещение, или скорость или скорость должны быть рассчитаны. Здесь

• Средняя скорость — это скорость изменения расстояния со временем.
• Средняя скорость — это скорость изменения смещения во времени.

И для исчисления,

• Мгновенная скорость есть первая производная расстояния по времени.
• Мгновенная скорость – это первая производная смещения по времени.

По сути, скорость говорит вам, как быстро, в то время как скорость говорит вам, как быстро, а также определяет направление.

Подробнее: Связь между силой и движением

Единицы

Скорость и скорость измеряются в одних и тех же единицах измерения. Для расстояния и смещения их единицей СИ является метр, а для времени единицей СИ является секунда. Единицей СИ для скорости и скорости является метр в секунду. Эта единица часто используется вне научных и академических кругов. Большинство людей измеряют скорость в километрах в час (км/ч или км/ч). В Соединенных Штатах используется более старая миля в час (миль в час или миль в час).

Подпишитесь на нашу рассылку новостей

Разница между скоростью и скоростью

В таблице ниже показана разница между скоростью и скоростью.

		Скорость	Скорость
	1.	Скорость — это скорость, с которой объект прошел определенное расстояние	Скорость — это скорость, с которой объект меняет свое положение
	2.	Скорость — скалярная величина; у него есть величина и нет направления	Скорость — векторная величина; у него есть и величина, и направление
	3.	Скорость всегда положительная	Скорость может быть положительной, отрицательной или равной нулю
	4.	Единица измерения скорости в системе СИ м/с	Единица измерения скорости в системе СИ м/с

Подробнее: Как Force изменяет состояние движения

Посмотрите видео ниже, чтобы узнать больше о скорости и скорости.

Примеры скорости и скорости

Ниже приведены примеры скорости и скорости:

• Устройство, событие, явление, процесс
• Сперматозоиды человека
• Рост волос, рост ногтей
• Улитки
• Выливание кетчупа из бутылки
• Тараканы
• Ленивцы, черепахи, черепахи.
• Океанские течения.
• Человеческий типичный темп ходьбы.
• Самый быстрый человек – плавание (Сезар Сьело).
• Максимальная комфортная скорость лифта.
• Дельфины, морские свинки, киты.
• Падающие капли дождя.
• Самый быстрый человек – бег (Усэйн Болт).
• Стадионная волна.
• Пробка от шампанского.
• Кролики, зайцы, лошади, борзые, тунец, акулы.
• Гепарды
• Падающие градины.
• Сокол-сапсан в пике.
• Очень быстрый мяч для гольфа.
• Ураган, максимальная устойчивая скорость ветра.
• Торнадо, максимальная устойчивая скорость ветра.
• Коммерческий реактивный самолет.
• Скорость звука в воздухе, ст.
• Скорость звука в воде.
• Сейсмические волны.
• Самый быстрый самолет (SR-71 Blackbird).

Подробнее: Формы энергии: кинетическая и потенциальная энергия

Заключение

Скорость и скорость — это то, с чем мы должны столкнуться, перемещаясь из одного места в другое, что дает нам возможность приводить в действие эти два термина.