Как умножать большие числа быстро: Эта инструкция научит вас умножать тысячи в уме. Сколько будет 5185 на 8018?

Как научиться перемножать большие числа и зачем вам это нужно

В школе было важно правильно писать слова «задача» и «решение» и красиво рисовать скобки. В итоге для многих алгебра и геометрия остались набором непонятных формул, которые нужно заучивать наизусть. Профессор математики Нелли Литвак и продюсер Алла Кечеджан написали об этом книгу «Математика для безнадежных гуманитариев. Для тех, кто учил языки, литературу и прочую лирику». Публикуем отрывок о разных способах умножения и о том, почему раскрытие скобок — это естественный закон о разрывании вещей.

Математика для безнадежных гуманитариев. Для тех, кто учил языки, литературу и прочую лирику

Нелли Литвак, Алла Кечеджан

АСТ. 2019

18 × 5

Начнем с задания из книги Джо Боулер «Математическое мышление». Это одно из ее любимых заданий. Оно очень простое, пожалуйста, выполните его полностью.

Задание: Умножьте в уме 18 на 5. Напишите подробно, как именно вы это сделали. То есть что на что умножили сначала, что потом, что складывали. Или, может, вы помнили ответ наизусть? Удачи!

Это простенькое задание Джо Боулер задавала многим, в том числе ребятам из технологического стартапа, у которых с умножением все в порядке. Тем не менее, они бурно обсуждали задание, горячились, выбегали к доске, а потом даже предложили выпустить футболку с надписью 18 × 5.

Что их так потрясло? То, что все они решили эту простую задачку разными способами! Наверное, многие из вас посчитали вот так:

18 × 5 = 10 × 5 + 8 × 5 = 50 + 40 = 90.

Кто-то посчитал по-другому:

18 × 5 = 20 × 5 — 2 × 5 = 100 — 10 = 90.

А можно еще вот так:

9 × 2 × 5 = 9 × 10 = 90.

Еще один удобный способ умножить на 5 — это сначала умножить на 10, а потом поделить пополам. Вот так:

18 × 5 = (18 × 10) / 2 = 180 / 2 = 90.

Знаете ли вы, что во французском языке считают не десятками, а двадцатками? Число 90 по-французски звучит так: quatre vingt dix, что в буквальном переводе означает «четырежды двадцать десять». И мы могли бы посчитать на французский манер:

18 × 5 = 4(4 × 5) + 2 × 5 = 4 × 20 + 10 = 90.

Надеемся, мы вас убедили, что даже при элементарном умножении нет единственно правильного подхода. Прийти к ответу можно самыми разными способами, и все они правильные.

Путь к решению — это и есть самое интересное в математике. А вовсе не правильный ответ!

Решение важнее ответа

«Одна из самых первых и самых сложных задач, с которой я сталкиваюсь как университетский преподаватель, — это заставить студентов (да, именно заставить!) правильно записывать математику. Их первые домашние задания — это обычно нечитабельная коллекция цифр и символов… „Зачем писать полные предложения? — удивляется первокурсник. — Я же нашел правильный ответ, вот, смотрите, внизу страницы!“»

Автор этих строк — профессор математики Кевин Хьюстон из Лидского университета в Англии и автор книги «Думать как математик» (How to Think Like a Mathematician). Под его словами подпишется подавляющее большинство университетских преподавателей.

В школе на уроках математики мы привыкли, что самое главное — это правильный ответ и что учитель из обрывков формул поймет, как мы до него добрались. Но на самом деле в математике, по словам того же Хьюстона, главное — «получить ответ с помощью обоснованных аргументов и убедить других, что ваши аргументы обоснованы».

В этом еще один колоссальный разрыв между школьной математикой и математикой на самом деле. Главное не ответ, главное — решение. Математические статьи в основном состоят из слов, а не из формул. И даже формулы, если приглядеться внимательно, это просто часть предложения! Мы могли бы это все записать словами, но формулы просто короче. Как пишет Джейсон Уилкс в книге «Математика в огне», формулы — это всего-навсего сокращения.

Работа по математике — это связное рассуждение. В этом смысле она ничем не отличается от работы, скажем, по истории.

Муж Нелли тоже университетский преподаватель математики. И, конечно, он тоже тратит много сил и времени, чтобы убедить студентов записывать решения подробно, с помощью полных предложений. Убедить бывших школьников, что решение важнее ответа, очень непросто! На рисунке его любимый пример, который он приводит на своих занятиях.

Ответ совершенно правильный, можете сами проверить. Но если рассуждать так, то можно получить и много всякой ерунды, например, что ¹²/₂₄ тоже равно ¼, или что ¹³/₃₉ равно ⅑.

На всякий случай приведем правильное решение. Можете в нем не разбираться, мы просто хотим показать, что оно выглядит совершенно по-другому.

Как видите, правильный ответ мало что значит. Получилась одна четвертая — ну и что. Это может посчитать любой калькулятор. Для математиков самое важное — это подход. Если нам нужно упростить дробь, то нельзя взять и зачеркнуть шестерку, а нужно искать общие множители!

Главное не ответ, а решение. И мы уже видели, что даже такую простую задачку, как 18 × 5, можно решить самыми разными способами. Поэтому математика — это не набор стандартных приемов, а творческий процесс.

В математике есть понятие вкуса: кому-то больше нравится одно решение, кому-то другое. У математиков могут быть свои любимые способы доказательств, теоремы, алгоритмы. И уж конечно, в математике есть мода и даже устаревшие задачи и устаревшие методы решения!

Устаревшая математика?

В блестящем TED-выступлении в октябре 2014 года Эдуардо Саенц де Кабесон сказал: «Если вы хотите сделать подарок навечно, не дарите бриллианты, подарите теорему!»

Если математический результат доказан, то он верен всегда. Любая теорема — на века. В других науках это не так. Например, сначала люди считали, что земля плоская; потом стали полагать, что круглая. Сначала думали, что брожение вина — это химический процесс, потом Луи Пастер доказал, что брожение происходит из-за бактерий (кстати, именно в честь Пастера мы называем молоко пастеризованным). Математика в этом плане занимает особенное место.

Если математический результат доказан, то он — как ни крути — всегда останется верным.

Тем не менее, в математике, как в искусстве, что-то становится классикой, а что-то устаревает. Например, теорема Пифагора — это золотая классика, которая не устареет никогда! Не случайно профессор математики и популяризатор Алексей Савватеев сказал, что именно эту теорему он передал бы в капсуле инопланетянам как одно из основных достижений человеческого разума.

Что же такое устаревшая теорема? Нелли запомнилась история, которую ей рассказал коллега из университета Твенте, профессор по вычислительным методам.

Вычислительные методы — это область математики, которая разрабатывает алгоритмы, чтобы решать задачи приблизительно, с помощью вычислений, а не с помощью формул. Коллега Нелли рассказал ей, как лет двадцать назад уходил на пенсию старый профессор и оставил ему журналы по вычислительным методам 60-х годов. Это были отличные журналы, в них публиковались известные авторы. Но только тогда еще не было общедоступных быстрых компьютеров. Ученые пользовались так называемыми специальными функциями и таблицами, которые занимали целые тома.

С появлением компьютеров все изменилось, потому что машины считают очень быстро. Обычный ноутбук выполняет 2 миллиарда операций в секунду! Многие результаты и подходы докомпьютерной эпохи безнадежно устарели. Коллега Нелли глубоко вздохнул и отнес все эти журналы в макулатуру.

Вы уже раскрыли скобки!

Посмотрим снова на пример 18 × 5. Допустим, вы подсчитали так:

18 × 5 = 10 × 5 + 8 × 5 = 50 + 40 = 90.

Когда мы умножаем в уме, мы очень легко и естественно разбиваем числа на части и умножаем по отдельности. Это и есть раскрытие скобок. Скобки нам нужны, просто чтобы записать то, что мы делаем в уме:

(10 + 8) × 5 = 10 × 5 + 8 × 5 = 50 + 40 = 90.

Математики называют раскрытие скобок великими и ужасными словами «распределительный закон».

Звучит умно, но терминология не так важна. В книге «Математика в огне» Уилкс называет раскрытие скобок «естественным законом о разрывании вещей». Мы «разрываем» 18 на две части — 10 и 8, умножаем каждую из них на 5, а потом складываем.

Две скобки

Скобок может быть и больше. Принцип остается тот же самый.

Задание: Умножьте 12 на 13. Объясните, как это можно сделать с помощью раскрытия скобок. Считать в столбик, на калькуляторе или пользоваться Интернетом можно, только чтобы проверить ответ. Удачи!

Начать можно, как и раньше:

12 × 13 = (10+ 2) × 13 = 10 × 13 + 2 × 13.

В принципе теперь можно сразу посчитать ответ:

130 + 26 = 156.

Но, если подумать: как мы умножаем на 13? Может, кто-то делает это на автомате. Но обычно (может, даже незаметно для себя) мы все-таки разрываем 13 на 10 и 3. Тогда получается:

10 × 13 + 2 × 13 = 10 × (10 + 3) + 2 × (10 + 3) = 10 × 10 + 10 × 3 + 2 × 10 + 2 × 3 = 100 + 30 + 20 + 6 = 156.

Конечно, скобок может быть и больше:

12 × 13 × 14 = (10 + 2) × (10 + 3) × (10 + 4).

И чисел в скобках тоже может быть больше:

112 × 113 = (100 + 10 + 2) × (100 + 10 + 3).

Принцип тот же, просто вычисления длиннее. Сколько бы ни было скобок.

Скобки и площади

Со школы мы привыкли считать, что есть две математики — алгебра и геометрия, и каждая тема сама по себе. На самом деле в математике все взаимосвязано и наука движется вперед, как раз когда идеи из одного раздела проникают в другой.

Площадь прямоугольника — скорее геометрия. Раскрытие скобок — типичная алгебра. Но площадь прямоугольника — это одна сторона, умноженная на другую. И скобки мы раскрываем тоже, когда умножаем числа. Значит, связь есть!

Алла долго воевала со скобками, пока не решила их нарисовать. Когда она увидела связь между скобками, умножением и площадью прямоугольника, все встало на свои места.

Нелли долго удивлялась: неужели на числах было непонятно? Но многим детям и взрослым — в точности как Алле — гораздо проще работать с рисунками, фигурами и площадями, чем с абстрактными числами и скобками. Классическая школьная программа обычно не рассчитана на визуалов. Мы постараемся немножко восполнить этот пробел и нарисовать тему скобок.

Нарисуйте прямоугольник 12 на 13 см. Ничего страшного, если у вас под рукой нет бумаги с карандашом — на своем любимом пляже в Варне Алла начертила прямоугольник, конечно же, пером чайки на песке.

Теперь сделайте десять «насечек» для десятков по вертикали и горизонтали, а потом две и три для единиц соответственно. Теперь проведем линию раздела между десятками и единицами. Получилось 4 прямоугольника.

Теперь перемножаем длину и ширину в каждом из прямоугольников между собой:

10 × 10 = 100

2 × 10 = 20

2 × 3 = 6

3 × 10 = 30

Потом складываем все результаты и получаем 156.

Это работает всегда! Фактически Алла предложила геометрическую трактовку раскрытия скобок. Когда мы раскрывали скобки без рисунка, мы разбивали 12 × 13 на те же самые числа:

12 × 13 = (10 + 2) × (10 + 3) = 10 × (10 + 3) + 2 × (10 + 3) = 100 + 30 + 20 + 6 = 156.

Задание: С помощью площадей прямоугольников умножьте 21 на 33. Удачи!

a плюс b в квадрате

Может быть, вы помните (а может, и нет) знаменитую формулу для вычисления (a + b) в квадрате:

a-квадрат-плюс-два-ab-плюс-b-квадрат

Мы написали эту формулу на рисунке. У кого-то она вызовет легкую ностальгию, у кого-то — давно забытое, но знакомое смятение.

Задание: Получите сами формулу для вычисления (a + b)². У нас для этого уже все есть! Вспомните, что (a + b) — это всего лишь число. А квадрат — это число, умноженное на само себя! То есть (a + b)² = (a + b)(a + b). Получив формулу, проверьте ее на числах. Удачи!

Надеемся, вы увидели связь этой формулы с предыдущей. Это в точности то же самое, что (a + b)(a + b), но только скобки одинаковые. Заметим, что когда мы перемножаем букву саму на себя, например, a × a, то знак умножения упускать не принято. На письме aa смотрится как-то некрасиво и неуместно, как крик о помощи или заикание. Принято писать a × a или a². Давайте попробуем применить эту формулу. Вот что получилось:

(a + b)² = (a + b)(a + b) = a × a + ab + ba + b × b.

Что тут можно заметить? Во-первых, a × a — это a², а b × b — это b². Кроме того, ab и ba — это одно и то же, потому что буквы просто обозначают числа, и перемножать их можно в любом порядке. Тогда ab + ba = ab + ab = 2ab. В результате выходит:

(a + b)² = (a + b)(a + b) = a × a + ab + ba + b × b = a² + 2ab + b².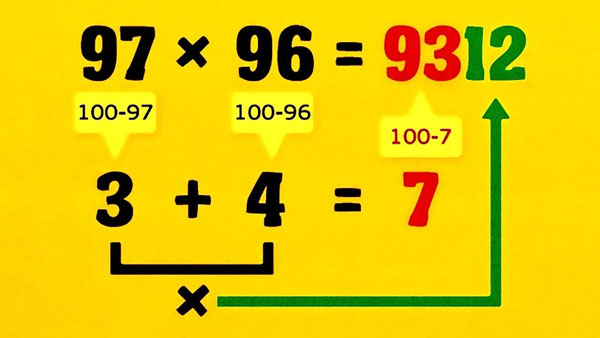

То, что слева, равно тому, что справа, то есть:

(a + b)² = a² + 2ab + b².

Что и требовалось доказать.

Естественно, геометрическая интерпретация через площади по-прежнему в силе. Мы приводим рисунок ниже, но сначала попробуйте выполнить задание сами!

Задание: Объясните формулу (a + b)² = a² + 2ab + b² с помощью площадей. Удачи!

Если у вас получилось выполнить это задание, то можете снять видео и выложить его на «Ютьюбе». Как вы думаете, сколько просмотров оно наберет? Не стоит недооценивать интерес людей к раскрытию скобок. В 2012 году тридцатисекундное видео учителя математики из Индии Кхуршеда Батливалы про (a + b)² взорвало Интернет, собрав более миллиона просмотров! И это всего лишь визуализация того, как раскрыть скобки с помощью площадей.

Давайте попробуем повторить успех Батливалы. Нарисуем горизонтальную линию, состоящую из двух отрезков — a и b.

Так как в формуле мы возводим a и b в квадрат, то и рисуем квадрат — проводим вертикальную линию, также состоящую из отрезков — a и b (помните, что у квадрата все стороны равны?), и достраиваем чертеж до нужной нам фигуры. Площадь такого квадрата равна (a + b)(a + b), или (a + b)².

А теперь разделим квадрат изнутри на 4 части, соединив между собой противоположные стороны.

Из чего состоит эта площадь? a² и b² — это площади внутренних заштрихованных квадратов. Осталось два одинаковых внутренних прямоугольника, у каждого из которых площадь равна ab. Сложим четыре площади вместе и получим a × a + ab + ab + b × b. Узнаете? Это же та же формула, a² + 2ab + b²!

Если вам, как и Алле, непросто раскрывать скобки, то по картинке всегда можно вспомнить формулу или даже вывести ее заново! К этому волшебному квадрату мы еще не раз вернемся. Именно он позволит нам добраться до самых глубоких корней квадратного уравнения и доказать теорему Пифагора.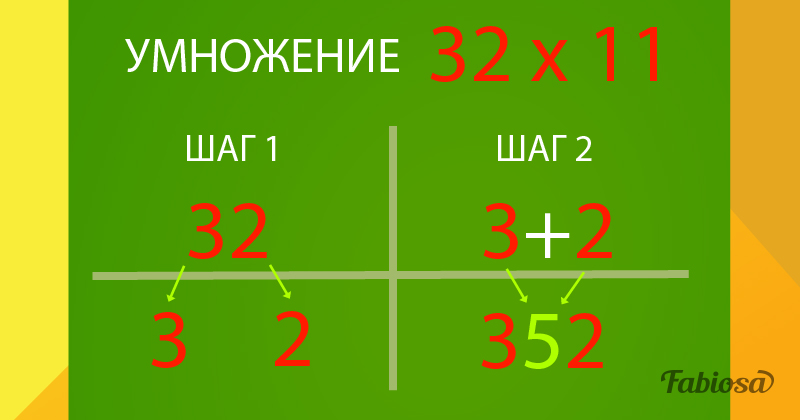

Ну и наконец, подставим числа. Давайте a примем за 4, а b — за 3. Тогда (4 + 3)² = 7² = 7 × 7 = 49. А по формуле (4 + 3)² = 42 + 2 × 4 × 3 + 32 = 16 + 24 + 9 = 49. Красота!

Игры с умножением

В Интернете можно найти много интересных игр и примеров с умножением чисел. Вот один забавный.

Задание: Возьмите калькулятор, умножьте 481 на 21 и на ваш возраст. Понимаете, как получился результат? Для самых любознательных вопрос посложнее: всегда ли это работает? Удачи!

Конечно, числа 481 и 21 выбраны не случайно. Если их перемножить, то получится 10101. Допустим вам 34 года. Тогда 10101 × 34 = 343434. Это работает, если вам от 10 до 99. Кстати, этот трюк напрямую связан с раскрытием скобок.

Смотрите, мы можем разорвать 10101 на части:

10101 = 10000 + 100 + 1. Перемножим по частям:

10000 × 34 = 340000

100 × 34 = 3400

1 × 34 = 34.

Сложим и получим 343434.

Стихия скобок

Тему раскрытия скобок можно продолжать бесконечно. Если бы мы не ограничились (a + b)², а добавили побольше скобок, например, (a + b)³ = (a + b) (a + b) (a + b), то очень быстро столкнулись бы с комбинаторикой, биномом Ньютона, треугольником Паскаля и теорией вероятностей. И предела этому нет…

Наш гуманитарий Алла, находясь под впечатлением от скобок в математике, стояла на черноморском берегу и смотрела на отплывающие от берега судна. Она заметила, что паруса издалека выглядят как скобки, и можно представить, что это числа ходят под парусами: те, что побольше, отплывают на шхунах, поменьше — на утлых лодочках. С берегом расставаться всегда немного грустно. Вот на какие стихи Аллу вдохновила математика:

Мне жалко цифры разрывать,

Они, как лодки от причала,

Не отрываются сначала,

На помощь нужно ветер звать.

И гнутся скобки — столько ветра,

А на борту одно весло.

От круглых чисел словно ветка

Откалывается колесо.

В рубрике «Открытое чтение» мы публикуем отрывки из книг в том виде, в котором их предоставляют издатели. Незначительные сокращения обозначены многоточием в квадратных скобках. Мнение автора может не совпадать с мнением редакции.

Читайте нас в Facebook, VK, Twitter, Instagram, Telegram (@tandp_ru) и Яндекс.Дзен.

Какой самый быстрый способ сложить в уме большие числа? – Обзоры Вики

Как я могу быстро умножить свой ум? Правило простое. Умножать слева направо. Одна цифра за раз. Умножение слева направо выполняется быстрее, потому что вам нужно запомнить меньше чисел, чтобы вспомнить и использовать их позже.

Во-вторых, как я могу улучшить свой расчет? Улучшите навыки расчета за 7 шагов

1. Начните с простого вычисления: во-первых, начните с небольшого и простого вычисления, такого как 300 + 550 = 850, небольшого умножения и простого деления и т. д. …
2. Изучите приемы большого умножения или деления:…
3. Записать все вычисления:…
4. Может использовать палец:…
5. Игра: …
6. Упражняться: …
7. Интернет:

Как умножать большие числа в C++?

Алгоритм

1. Инициализировать числа в строке.
2. Инициализирует строку длины number_one_length + number_two_length.
3. Перебрать первое число с конца. …
4. Преобразуйте символы в цифры, добавив 0 символов к каждому символу в результате.
5. Верните результат, игнорируя начальный ноль.

Как научить ребенка складывать большие числа?

Как сложить два больших числа? 1) Перевернуть обе строки. 2) Продолжайте добавлять цифры одну за другой от 0-го индекса (в перевернутых строках) до конца меньшей строки, добавляйте сумму% 10 до конца результата и отслеживайте перенос как сумму/10. 3) Наконец, измените результат.

Каковы стратегии умножения?

Девять стратегий умножения включают в себя:

• повторное добавление.
• массив.
• равные группы.
• числовая строка.
• коммутативное право.
• удвоение и деление пополам.
• удвоение.
• используйте дружественные факты.

Что можно умножить, чтобы получить 20? Множители 20 — это числа, которые при перемножении пары множителей дают результат 20. Эти факторы 1,2,4,5,10 и 20.

Что такое умственное умножение?

При умственном умножении люди обычно нравится делать большие или важные объемы в первую очередь. Это дает оценку ожидаемой стоимости. Такой подход представляет собой передний конец или умножение слева направо. Студенты, использующие этот метод, умножают десятки перед единицами и сотни перед десятками и так далее.

Легок ли метод Трахтенберга?

Система состоит из ряда легко запоминается операции, которые позволяют очень быстро выполнять арифметические вычисления.

Как я могу научить свой мозг считать быстрее? В основном, есть 3 типа упражнений. ; 1) Запоминать как можно больше; 2) Изучите различные техники; 3) Практика.

1. Запоминание определенно сделает это быстрее. …
2. Есть много методов, которые могут помочь сделать расчет быстрее. …
3. Практика делает это все легче и легче, а также быстрее и быстрее.

Есть ли дислексия для математики? Исследования показывают, что это так же распространено, как дислексия — расстройство чтения, но не так хорошо изучено. На самом деле, дети и родители иногда называют это «математической дислексией», но это может сбивать с толку, потому что дискалькулия — это совсем другое состояние.

Могу ли я умножить строку в C?

Вы не можете умножать строки в c.

Как вы умножаете большие числа в Java? умножить (значение BigInteger) используется для вычисления умножения двух BigIntegers. Поскольку класс BigInteger внутренне использует для обработки массив целых чисел, операции с объектом BigInteger выполняются не так быстро, как с примитивами.

Как вы умножаете большие числа в Python?

Вы можете умножать большие числа в python напрямую, не беспокоясь о скорости. Python поддерживает «бигнум» целочисленный тип, который может работать с произвольно большими числами. В Python 2.5+ этот тип называется long и отделен от типа int, но интерпретатор автоматически использует тот из них, который больше подходит.

Любые 5 умножаются? Умножение на 5: если число умножается на 5, затем разделите число на 2 и умножьте на 10. Пример: 8 × 5: 8 разделить на 2 = 4, 4 умножить на 10, 4 × 10 = 40. Умножение на 9: Прибавить +1 к 9 и вычесть число с самим собой, которое нужно умножить.

Как я могу быстро освоить ментальную арифметику?

Как улучшить навыки умственной математики

1. 1 Разбейте задачи на сложение и вычитание на части.
2. 2 Измените задачу, сделав круглые числа.
3. 3 Научитесь складывать сразу много чисел.
4. 4 Умножайте слева направо.
5. 5 Попробуйте уловку быстрого умножения, которая лучше всего подходит для чисел от 11 до 19.
6. 6 Упростите задачи, используя числа, оканчивающиеся на ноль.

Что такое японское умножение? Японский метод умножения на самом деле является просто визуальным способом представления этих четыре шага. Каждая группа пересечений соответствует одному из четырех меньших произведений, используемых при умножении двух чисел (например, левая группа, 3×1, дает вам 300 или 3 сотни).

Как умножать большие числа | Более быстрый способ умножения

• Умножать большие числа сложно. В 1971 году два немецких профессора предсказали алгоритм, который упростит задачу, но никто так и не доказал его.
• До сих пор.
• Математики из Австралии и Франции говорят, что их алгоритм может значительно повысить эффективность умножения и других видов арифметики.

---

Начиная со школы сложное умножение было головной болью. Но доцент из Сиднейского университета Нового Южного Уэльса в Австралии разработал новый метод умножения гигантских чисел, который более эффективен, чем «длинное умножение», которому многие учат в раннем возрасте.

«С технической точки зрения мы доказали гипотезу Шёнхаге и Штрассена 1971 года о сложности целочисленного умножения», — говорит доцент Дэвид Харви в видео ниже.

Посмотреть полный пост на Youtube

Алгоритм Шёнхаге-Штрассена, разработанный двумя немецкими математиками, был фактически самым быстрым методом умножения с 1971 по 2007 год. Хотя более быстрый метод был разработан в 2007 году, сегодня он редко используется.

Шёнхаге и Штрассен предсказали, что алгоритм, умножающий n -значные числа с использованием n * log( n ) должны существовать основные операции, говорит Харви. Его статья является первым известным доказательством того, что это так.

Харви приводит пример 314, умноженного на 159 — большое уравнение, конечно, но в реальных сценариях каждый день используются гораздо более крупные уравнения. Чтобы решить эту задачу, большинство людей учат перемножать каждое отдельное число вместе, а затем складывать суммы:

9 умножается на 4, 1 и 3; затем 5 умножается на 4, 1 и 3 и так далее. В результате получается 9поразрядные продукты.

Этот метод называется n ² или n в квадрате, потому что нужно несколько раз умножить n на n . Он даст правильный ответ, но Шенхаге и Штрассен разработали более быстрый метод. Он смог перейти от n ² к чему-то меньшему, но проблема все же возникла в виде n * log( n ).

Некоторым достаточно увидеть слово в середине математической задачи, чтобы глаза затуманились, как на уроке алгебры. Напомню: log — это сокращение от logarithm, которое помогает людям расшифровывать показатели степени, при которых числа возводятся в квадрат или в куб, или даже выше. Таким образом, 2⁵ равно 32, но в логарифмическом выражении это будет выглядеть как log₂(32)=5. Хотя это может показаться пустяком, логарифмы имеют решающее значение, когда числа становятся намного больше.

Еще математика

• Как решить возмутительную вирусную математическую задачу
• 10 самых сложных математических задач, которые когда-либо решались
• 10 самых сложных математических задач, которые остаются нерешенными

Метод Шёнхаге-Страса очень быстрый. Если бы компьютер использовал метод возведения в квадрат, которому учили в школе, для решения задачи, в которой два числа состоят из миллиарда цифр каждое, это заняло бы месяцы. Компьютер, использующий метод Шёнхаге-Штрассена, может сделать это за 30 секунд.

Но если числа будут продолжать расти до триллионов и выше, алгоритм, разработанный Харви и его коллегой Йорисом ван дер Хувеном из Политехнической школы во Франции, сможет находить решения быстрее, чем алгоритм Шенхаге-Штрассена 1971 года.

«Это означает, что вы можете более эффективно выполнять все виды арифметических операций, например, деление и вычисление квадратных корней», — говорит он. «Вы также можете более эффективно, чем раньше, вычислять цифры числа пи. У него даже есть приложения к задачам, связанным с огромными простыми числами.

«Люди охотились за таким алгоритмом почти 50 лет», — продолжает он. Это не было забытым выводом, что кто-то в конце концов добьется успеха.

«Но теперь мы знаем лучше», — говорит он.

Дэвид Гроссман

Дэвид Гроссман — штатный автор PopularMechanics.com. Ранее он писал для The Verge, Rolling Stone, The New Republic и ряда других изданий. Он живет в Бруклине.0012

Мы нашли более быстрый способ умножать очень большие числа

Умножать два числа легко, верно?

В начальной школе мы учимся выполнять длинное умножение следующим образом:

Долгий путь умножения (Дэвид Харви)

Методы, подобные этому, известны тысячи лет назад, по крайней мере, древние шумеры и египтяне.

Но действительно ли это лучший способ перемножить два больших числа?

При длинном умножении мы должны умножить каждую цифру первого числа на каждую цифру второго числа. Если каждое из двух чисел имеет N цифр, то есть N ^² (или N x N ) умножений вместе взятых. В приведенном выше примере N равно 3, и нам нужно было сделать 3 ^² = 9 умножений.

Примерно в 1956 году известный советский математик Андрей Колмогоров предположил, что это наилучший способ умножения двух чисел.

Другими словами, как бы вы ни организовали свои расчеты, объем работы, который вам придется сделать, будет пропорционален как минимум Н ^² . В два раза больше цифр означает, что в четыре раза больше .

Колмогоров чувствовал, что если бы был возможен короткий путь, он бы наверняка уже был обнаружен. Ведь люди умножают числа уже тысячи лет.

Это прекрасный пример логической ошибки, известной как «аргумент от незнания».

Более быстрый путь

Всего несколько лет спустя гипотеза Колмогорова оказалась в корне неверной.

В 1960 году Анатолий Карацуба, 23-летний студент-математик из России, открыл хитрый алгебраический трюк, позволяющий сократить количество необходимых умножений.

Например, чтобы умножить четырехзначные числа, вместо 4 ^² = 16 умножений метод Карацубы обходится только девятью. При использовании его метода вдвое больше цифр означает только в три раза больше работы.

Это дает впечатляющее преимущество по мере увеличения числа. Для тысячезначных чисел метод Карацубы требует примерно в 17 раз меньше умножений, чем длинное умножение.

Но с какой стати кому-то нужно перемножать такие большие числа?

На самом деле приложений огромное количество. Одним из наиболее заметных и экономически значимых является криптография.

Встреча Битлз с математикой

Начальные аккорды A Hard Day’s Night – загадка. Математика поможет решить?

Читать дальше

Большие числа в реальной жизни

Каждый раз, когда вы участвуете в зашифрованном обмене данными в Интернете — например, заходите на веб-сайт своего банка или выполняете поиск в Интернете — ваше устройство выполняет головокружительное количество умножений, включая числа с сотнями или даже тысячи цифр.

Скорее всего, ваше устройство использует трюк Карацубы для этой арифметики. Все это является частью удивительной программной экосистемы, которая обеспечивает максимально быструю загрузку наших веб-страниц.

Для некоторых более эзотерических приложений математикам приходится иметь дело с еще большими числами, с миллионами, миллиардами или даже триллионами цифр. Для таких огромных чисел даже алгоритм Карацубы слишком медленный.

Настоящий прорыв произошел в 1971 году благодаря работе немецких математиков Арнольда Шёнхаге и Фолькера Штрассена. Они объяснили, как использовать недавно опубликованное быстрое преобразование Фурье (БПФ) для эффективного умножения огромных чисел. Их метод обычно используется сегодня математиками для обработки чисел, состоящих из миллиардов цифр.

БПФ — один из самых важных алгоритмов 20-го века. Одним из приложений, знакомых в повседневной жизни, является цифровое аудио: всякий раз, когда вы слушаете MP3, службы потоковой передачи музыки или цифровое радио, БПФ выполняет декодирование звука за кулисами.

На преодоление гендерного разрыва в таких академических областях, как физика и математика, могут уйти столетия, согласно новому исследованию, которое показало, что женщины по-прежнему недостаточно представлены в точных науках.

Еще более быстрый способ?

В своей статье 1971 года Шёнхаге и Штрассен также сделали поразительное предположение. Чтобы объяснить, мне придется на мгновение углубиться в технические подробности.

Первая половина их гипотезы состоит в том, что должно быть возможно умножать N -значных чисел, используя количество основных операций, пропорциональное не более чем N log ( N ) (это N умножить на натуральный логарифм N ).

Их собственный алгоритм не совсем достиг этой цели; они были слишком медленными в логарифмическом разе (log N ) (логарифм логарифма N ). Тем не менее их интуиция заставляла их подозревать, что они что-то упустили, и что N log ( N ) должно быть осуществимо.

За десятилетия, прошедшие с 1971 года, несколько исследователей нашли улучшения в алгоритме Шёнхаге и Штрассена. Примечательно, что алгоритм, разработанный Мартином Фюрером в 2007 году, был мучительно близок к неуловимому журналу N ( N ).

Вторая (и гораздо более сложная) часть их предположения состоит в том, что N log ( N ) должно быть фундаментальным ограничением скорости — ни один возможный алгоритм умножения не может работать лучше этого.

Знакомо?

Мы достигли предела?

Несколько недель назад мы с Йорисом ван дер Хувеном опубликовали исследовательскую работу, описывающую новый алгоритм умножения, который, наконец, достигает святого Грааля N log ( N ), таким образом определяя «легкую» часть уравнения Шёнхаге-Штрассена. предположение.

Статья еще не прошла рецензирование, поэтому требуется некоторая осторожность. Стандартной практикой в ​​математике является распространение результатов исследований до того, как они подверглись рецензированию.

Вместо использования одномерных БПФ — основы всей работы над этой проблемой с 1971 года — наш алгоритм опирается на многомерных БПФ. В этих гаджетах нет ничего нового: широко используемый формат изображения JPEG зависит от 2-мерного БПФ, а 3-мерное БПФ имеет множество приложений в физике и технике.

В нашей статье мы используем БПФ с 1729 измерениями. Это сложно визуализировать, но математически это не более проблематично, чем двумерный случай.

Присоединяйтесь к Вирджинии каждые выходные

Подпишитесь, чтобы присоединиться к Вирджинии Триоли каждое субботнее утро, чтобы получать лучшие лонгриды, анализ и статьи от ABC.

Читать дальше

Очень, очень большие числа

Новый алгоритм не совсем практичен в его нынешнем виде, потому что доказательство, приведенное в нашей статье, работает только для смехотворно больших чисел. Даже если бы каждая цифра была записана на атоме водорода, в наблюдаемой Вселенной не хватило бы места для их записи.

С другой стороны, мы надеемся, что с дальнейшими уточнениями алгоритм может стать практичным для чисел, состоящих всего лишь из миллиардов или триллионов цифр. Если это так, то он вполне может стать незаменимым инструментом в арсенале вычислительного математика.