Как умножать двузначные числа на двузначные в уме: Как быстро научиться умножать в уме двузначные числа? — Блог Викиум

Как быстро умножать трехзначные числа в уме? –

Как быстро считать в уме трехзначные числа?

Рекомендуемый клип · 107 сек.

Тренажер умножения в уме трехзначных чисел — YouTube

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как можно быстро умножать в уме?

Рекомендуемый клип · 119 сек.

Быстрое умножение в уме. Метод «Соты» — YouTube

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как умножать трехзначные числа на трехзначное?

Рекомендуемый клип · 69 сек.

Письменное умножение на трёхзначное число. Видеоурок по

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как умножать трехзначные числа на двузначное?

0:06

9:51

Рекомендуемый клип · 99 сек.

умножение на двузначное и трехзначное число — YouTube

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как научить ребенка быстро считать в уме?

Рекомендуемый клип · 109 сек.

Как научить школьника быстро считать в уме? Методика

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как быстро в уме делить?

Рекомендуемый клип · 110 сек.

Тренажер быстрого деления в уме — YouTube

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как умножить двузначное на двузначное в уме?

0:02

2:05

Рекомендуемый клип · 102 сек.

Умножение двузначных чисел в уме. Быстрый счет. — YouTube

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как считать без калькулятора?

Рекомендуемый клип · 119 сек.

Как научиться считать без калькулятора | Осторожно, спойлер

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как умножить четырехзначное число на двузначное?

0:04

3:15

Рекомендуемый клип · 38 сек.

Умножение четырехзначных чисел на однозначные. Пример

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как быстро умножать двузначные числа в уме?

Умение мгновенно считать в уме может стать бесценным подспорьем в работе и в условиях скоростных темпов жизни современного человека.

Как быстро умножать большие числа, как овладеть такими полезными навыками? У большинства вызывает затруднения устное перемножение двузначных чисел на однозначные. А о сложных арифметических расчетах и говорить нечего. Но при желании способности, заложенные в каждом человеке, можно развить. Регулярные тренировки, немного усилий и применение, разработанных учеными, эффективных методик позволят достичь потрясающих результатов.

Выбираем традиционные методы

Проверенные десятилетиями способы перемножения двузначных чисел не теряют своей актуальности. Простейшие приемы помогают миллионам обычных школьников, учащихся специализированных ВУЗов и лицеев, а также людям, занимающимся саморазвитием, усовершенствовать вычислительное мастерство.

Умножение с помощью разложения чисел

Наиболее легким способом, как быстро научиться умножать большие числа в уме, является перемножение десятков и единиц. Сначала умножаются десятки двух чисел, затем поочередно единицы и десятки. Четыре полученных числа суммируются. Для использования этого метода важно уметь запоминать результаты перемножения и складывать их в уме.

Например, для умножения 38 на 57 необходимо:

• разложить число на
  (30+8)*(50+7);
• 30*50 = 1500 – запомнить результат;
• 30*7 + 50*8 = 210 + 400 = 610 – запомнить;
• (1500 + 610) + 8*7 = 2110 + 56 = 2166

Естественно, необходимо отлично знать таблицу умножения, так как быстро умножать в уме этим способом не удастся без соответствующих умений.

Умножение в столбик в уме

Визуальное представление привычного перемножения в столбик многие используют при расчетах. Этот метод подойдет тем, кто умеет надолго запоминать вспомогательные числа и выполнять с ними арифметические действия. Но процесс значительно упрощается, если вы научились, как быстро умножать двузначные числа на однозначные. Для перемножения, например, 47*81 нужно:

• 47*1 = 47 – запомнить;
• 47*8 = 376 – запоминаем;
• 376*10 + 47 = 3807.

Запоминать промежуточные результаты поможет проговаривание их вслух с одновременным суммированием в уме. Несмотря на сложность мысленных вычислений, после непродолжительных тренировок этот метод станет вашим любимым.

Приведенные выше способы умножения универсальны. Но знание более эффективных алгоритмов для некоторых чисел намного сократит количество расчетов.

Умножение на 11

Это, пожалуй, самый простой способ, который используется для умножения любых двузначных чисел на 11.

Достаточно между цифрами множителя вставить их сумму:
13*11 = 1(1+3)3 = 143

Если в скобках получается число больше 10, то к первой цифре добавляется единица, а из суммы в скобках вычитается 10.
28*11 = 2 (2+8) 8 = 308

Умножение больших чисел

Очень удобно перемножать числа, близкие к 100 разложением их на составляющие. Например, необходимо умножить 87 на 91.

• Каждое число необходимо представить как разницу 100 и еще одного числа:
  (100 — 13)*(100 — 9)
  Ответ будет состоять из четырех цифр, две первые из которых – разница первого множителя и вычитаемого из второй скобки или наоборот – разница второго множителя и вычитаемого из первой скобки.
  87 – 9 = 78
  91 – 13 = 78
• Вторые две цифры ответа — результат перемножения вычитаемых из двух скобок.13*9 = 144
• В результате получаются числа 78 и 144. Если при записывании окончательного результата получается число из 5 цифр вторую и третью цифру суммируем. Результат: 87*91 = 7944.

Это самые простые способы перемножения. После многократного их применения, доведения вычислений до автоматизма можно осваивать более сложные техники. И через некоторое время проблема, как быстро умножить двузначные числа перестанет вас волновать, а память и логика существенно улучшатся.

Как научиться быстро считать в уме взрослому

Зачем считать в уме, если решить любую арифметическую задачу можно на калькуляторе. Современная медицина и психология доказывают, что устный счет — это тренаж для серых клеточек. Выполнять такую гимнастику необходимо для развития памяти и математических способностей.

Известно множество приёмов для упрощения вычислений в уме. Все, кто видел знаменитую картину Богданова-Бельского «Устный счёт», всегда удивляются — как крестьянские дети решают такую непростую задачу, как деление суммы из пяти чисел, которые предварительно ещё надо возвести в квадрат?

Оказывается, эти дети — ученики известного педагога-математика Сергея Александровича Рачицкого (он также изображен на картине). Это не вундеркинды — ученики начальных классов деревенской школы XIX века. Но все они уже знают приёмы упрощения арифметических расчетов и выучили таблицу умножения! Поэтому решить такую задачку этим детишкам вполне под силу!

Секреты устного счёта

Существуют приемы устного счета — простые алгоритмы, которые желательно довести до автоматизма. После овладения простыми приёмами можно переходить к освоению более сложных.

Прибавляем числа 7,8,9

Для упрощения вычислений числа 7,8,9 сначала надо округлять до 10, а затем вычитать прибавку. К примеру, чтобы прибавить 9 к двузначному числу, надо сначала прибавить 10, а затем вычесть 1 и т.

д.

Быстро складываем двузначные числа

Если последняя цифра двузначного числа больше пяти, округляем его в сторону увеличения. Выполняем сложение, из полученной суммы отнимаем «добавку».

Если последняя цифра двузначного числа меньше пяти, то складываем по разрядам: сначала прибавляем десятки, затем — единицы.

Если слагаемые поменять местами, то сначала можно округлить число 57 до 60, а потом вычесть из общей суммы 3:

Складываем в уме трехзначные числа

Быстрый счет и сложение трехзначных чисел — это возможно? Да. Для этого надо разобрать трехзначные числа на сотни, десятки, единицы и поочередно их приплюсовать.

Особенности вычитания: приведение к круглым числам

Вычитаемые округляем до 10, до 100. Если надо вычесть двузначное число, надо округлить его до 100, вычесть, а затем к остатку прибавить поправку. Это актуально если поправка невелика.

Вычитаем в уме трехзначные числа

Если в свое время был хорошо усвоен состав чисел от 1 до 10, то вычитание можно производить по частям и в указанном порядке: сотни, десятки, единицы.

Умножить и разделить

Моментально умножать и делить в уме? Это возможно, но без знания таблицы умножения не обойтись. Таблица умножения — это золотой ключик к быстрому счету в уме! Она применяется и при умножении, и при делении. Вспомним, что в начальных классах деревенской школы в дореволюционной Смоленской губернии (картина «Устный счет») дети знали продолжение таблицы умножения — с 11 до 19!

Хотя на мой взгляд достаточно знать таблицу от 1 до 10, чтобы мочь перемножать бо´льшие числа. Например:

Умножаем и делим на 4, 6, 8, 9

Овладев таблицей умножения на 2 и на 3 до автоматизма, сделать остальные расчеты будет проще простого.

Для умножения и деления двух- и трехзначных чисел применяем простые приёмы:

умножить на 4 — это дважды умножить на 2;

умножить на 6 — это значит умножить на 2, а потом на 3;

умножить на 8 — это трижды умножить на 2;

умножить на 9 — это дважды умножить на 3.

разделить на 4 — это дважды разделить на 2;

разделить на 6 — это сначала разделить на 2, а потом на 3;

разделить на 8 — это трижды разделить на 2;

разделить на 9 — это дважды разделить на 3.

Как умножать и делить на 5

Число 5 — это половина от 10 (10:2). Поэтому сначала умножаем на 10, затем полученное делим пополам.

Еще проще правило деления на 5. Сначала умножаем на 2, а затем полученное делим на 10.

Умножение на 9

Чтобы умножить число на 9, необязательно его дважды умножать на 3. Достаточно его умножить на 10 и вычесть из полученного умножаемое число. Сравним, что быстрее:

Также давно замечены частные закономерности, которые значительно упрощают умножение двузначных чисел на 11 или на 101. Так, при умножении на 11, двузначное число как бы раздвигается. Составляющие его цифры остаются по краям, а в центре оказывается их сумма. Например: 24*11=264. При умножении на 101, достаточно приписать к двузначному числу такое же. 24*101= 2424. Простота и логичность таких примеров вызывает восхищение. Встречаются такие задачи очень редко — это примеры занимательные, так называемые маленькие хитрости.

Счет на пальцах

Сегодня еще можно встретить много защитников «пальчиковой гимнастики» и методики устного счета на пальцах. Нас убеждают, что учиться складывать и отнимать, загибая и разгибая пальцы — это очень наглядно и удобно. Диапазон таких вычислений очень ограничен. Как только расчеты выходят за рамки одной операции возникают трудности: надо осваивать следующий прием. Да и загибать пальцы в эпоху айфонов как-то несолидно.

Например, в защиту «пальчиковой» методики приводится приём умножения на 9. Хитрость приёма такова:

• Чтобы умножить любое число в пределах первой десятки на 9, надо развернуть ладони к себе.
• Отсчитывая слева направо, загнуть палец, соответствующий умножаемому числу. К примеру, чтобы умножить 5 на 9, надо загнуть мизинец на левой руке.
• Оставшееся количество пальцев слева будет соответствовать десяткам, справа — единицам. В нашем примере — 4 пальца слева и 5 справа. Ответ: 45.

Да, действительно, решение быстрое и наглядное! Но это — из области фокусов. Правило действует только при умножении на 9. А не проще ли, для умножения 5 на 9 выучить таблицу умножения? Этот фокус забудется, а хорошо выученная таблица умножения останется навсегда.

Также существует еще множество подобных приемов с применением пальцев для каких-то единичных математических операций, но это актуально пока вы этим пользуетесь и тут же забывается при прекращении применения. Поэтому лучше выучить стандартные алгоритмы, которые останутся на всю жизнь.

Устный счёт на автомате

Во-первых, необходимо хорошо знать состав числа и таблицу умножения.

Во-вторых, надо запомнить приемы упрощения расчётов. Как выяснилось, таких математических алгоритмов не так уж много.

В-третьих, чтобы приём превратился в удобный навык, надо постоянно проводить краткие «мозговые штурмы» — упражняться в устных вычислениях, используя тот или иной алгоритм.

Тренировки должны быть короткими: решить в уме по 3-4 примера, используя один и тот же приём, затем переходить к следующему. Надо стремиться использовать любую свободную минутку — и полезно, и нескучно. Благодаря простым тренировкам все вычисления со временем будут совершаться молниеносно и без ошибок. Это очень пригодится в жизни и выручит в непростых ситуациях.

Как давно вы считали в уме, а не столбиком, и уж тем более не с помощью калькулятора? Между прочим, считать в уме не только модно, но и полезно: так вы развиваете краткосрочную память, концентрацию и внимание. А ещё, какой же кайф испытываешь, когда можешь посчитать, сколько тебе должны дать сдачи, пока стоишь в очереди, м-м-м…

Всего несколько месяцев ежедневных тренировок по 5-10 минут, и вы почувствуете, как ускорился ваш мозг.

Сложение

Начнём с простого — сложения однозначных чисел. Научившись мгновенно складывать однозначные числа, вы сможете легко складывать и многозначные числа, потому что все расчёты сводятся к выполнению типовых действий. Вы в этом скоро убедитесь.

Сложение однозначных чисел

С примерами, результаты которых находятся в пределах 10 проблем нет. Эти комбинации чисел нужно просто запомнить, как основу основ.

А вот для примеров «с переходом через 10» уже есть методика — «опора на десяток». Суть в том, чтобы довести одно слагаемое до 10, а потом из второго слагаемого вычесть столько же, сколько мы прибавили к первому.

Например, нам нужно сложить 5 и 8:

1. Числу 5 не хватает до 10 ещё столько же — 5.
2. Теперь представим 8 как сумму 5 и ещё какого-то числа (это 3).
3. И прибавим к 5 ту часть числа 8, которой недостаёт до 10, а затем и остаток. Получится 10 и 3, то есть 13.

Сложение многозначных чисел

Принцип сложения многозначных чисел — складывать друг с другом одинаковые разряды: тысячи с тысячами, сотни с сотнями, десятки с десятками, единицы с единицами.

Например, нам нужно сложить 245 и 917:

245 состоит из трёх разрядов — 200, 40 и 5. А 917 из 900, 10 и 7.

Сложим разрядные части друг с другом:

200 + 900 = 1100, 40 + 10 = 50, 5 + 7 = 12.

А теперь сложим получившиеся числа в обратном порядке, «закрывая» нули:

Вычитание

Как и со сложением, с вычитанием однозначных чисел из однозначных ничего сложного нет. А при вычитании однозначного числа из двузначного удобно пользоваться тем же правилом «опоры на десяток».

Вычитание однозначных числа

Например, нужно вычесть 13 − 7:

1. Убираем у 13 столько, чтобы получилось 10 — то есть 3.
2. Столько же убираем и у 7 — получается 4.
3. Теперь просто вычитаем 4 из 10.

Вычитание многозначных чисел

Здесь всё даже проще, чем со сложением многозначных чисел, потому что на разрядные части нужно разложить только то число, которое вычитаем.

Например, нужно вычесть 734 − 427:

1. Раскладываем 427 на разряды: 400, 20 и 7. Теперь последовательно вычитаем их из 734.
2. Вычесть 734 − 400 очень просто, потому что действие происходит только с сотнями. Грубо говоря, мы вычитаем 4 из 7 — получаем 3, вернее, 334.
3. С десятками всё аналогично: вычитаем 30 − 20, получаем 10 — 314.

Теперь вычитаем единицы через десяток: 314 − 7.

Убираем 4 из 314 и 7, получаем 310 − 3. Ну а тут уже совсем просто — ответ 307.

Чтобы вычитать 7, 8 и 9 было проще, часто прибегают к следующим правилам:

При отнимании 9 из числа сначала вычитают 10, а затем добавляют 1:

321 − 9 = 321 − 10 + 1 = 312

При отнимании 8 из числа сначала вычитают 10, а затем добавляют 2:

321 − 8 = 321 − 10 + 2 = 313

При отнимании 7 из числа сначала вычитают 10, а затем добавляют 3:

321 − 7 = 321 − 10 + 3 = 314

Умножение

Это когда несколько раз складывают одно и то же. Например, 7 × 3 = 7 + 7 + 7 = 21.

Чтобы научиться быстро умножать любые числа в уме (кроме совсем уж космических), нужно идеально умножать однозначные числа, то есть знать таблицу умножения.

Причём идеально знать её необязательно, достаточно запомнить для себя опорные числа, которые будут помогать в вычислениях. Умножим 6 × 7. Мнемотехнически мы знаем что 6 × 6 = 36. То есть к 36 нужно прибавить ещё 6, чтобы получился ответ — 42.

Считается, что из всех примеров в таблице умножения 7 × 8 самый сложный. Чтобы запомнить ответ есть отличное правило «пять шесть семь восемь»: 56 = 7 × 8.

Умножение однозначного числа на двузначное

В первую очередь мы раскладываем 387 на разряды — 300, 80 и 7 — и умножаем каждый из них на 8.

Начинаем с сотен: 300 × 8 — это то же самое, что умножить 3 × 8, а потом к результату дописать два нуля. То есть:

3 × 8 × 100 = 24 × 100 = 2400.

По аналогии, 80 × 8 = 640, 7 × 8 = 56.

А теперь мы складываем получившиеся числа, объединяя их по разрядам:

2400 + 640 + 56 = 2000 + 400 + 600 + 40 + 50 + 6 = 2000 + (400 + 600) + (40 + 50) + 6 = 2000 + 1000 + 90 + 6 = 3000 + 90 + 6 = 3096

Любое число легко умножить на 9: нужно просто умножить на 10 (или дописать в конце ноль), а затем отнять исходное число.

47 × 9 = (47 × 10) − 47 = 470 − 47 = 423

Некруглое число можно легко умножить на 2, сначала округлив его до удобного ближайшего значения.

Например, 237 × 2. Сначала проще умножить 240 × 2 = 480. А потом вычесть из результата 6 (3 × 2 = 6 — ведь 3 нам не хватало до 240). Итого:

237 × 2 = 240 × 2 − (3 × 2) = 476

Чтобы умножить любое двузначное число на 11, нужно сложить две цифры этого двузначного числа друг с другом, а затем вписать её между цифрами исходного числа:

Правда, если сумма двух цифр исходного числа больше 10, нужно поставить разряд единиц между цифрами исходного числа, а десяток прибавить к левой цифре:

Умножение двузначных чисел

Хотя кажется, что умножать двузначные числа — вершина ментальных вычислений, решать такие примеры не сильно сложнее, чем в предыдущем пункте. Давайте разберём на примере.

Разобьём 34 на 30 и 4, чтобы было проще, а затем умножим каждое на 83.

83 умножить на 30 просто — это как умножить 83 × 3, а потом умножить результат ещё на 10. Как умножать однозначные и двузначные числа мы разобрались. Считаем:

83 × 3 = 80 × 3 + 3 × 3 = 240 + 9 = 249. Значит, 84 × 30 = 2490.

83 × 4 = 80 × 4 + 3 × 4 = 320 + 12 = 332.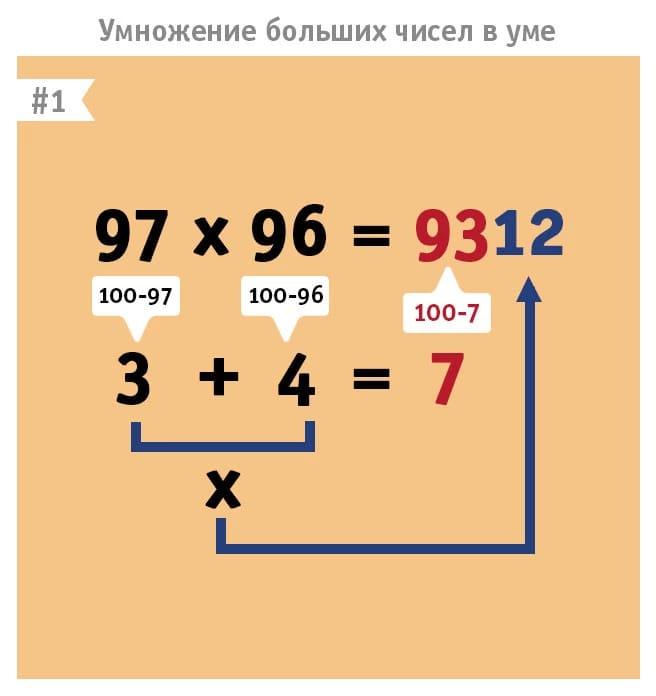

2490 + 332 = 2000 + 400 + 300 + 90 + 30 + 2 = 2000 + 700 + 120 + 2 = 2822.

Деление

Это операция, обратная умножению. Начнём снова с самого простого.

Деление двузначного числа на однозначное

Разделим 48 : 3. Основная задача — подобрать число, которое можно умножить на 3 и получить 48. Из таблицы умножения мы помним, что единственное число, результат умножения которого на 3 в конце имеет цифру 8 — это 6. А 3 × 6 = 18. То есть, у нас остаётся 30 : 3 = 10. Итого, получается 48 : 3 = 16.

Деление многозначного числа на однозначное

Разделим 6475 : 7. В подобных примерах главная задача — «взять» максимальные «круглые» части, которые можно разделить на 6 без остатка.

1. Выделим из 6475 самую большую часть, которую можно разделить на 7 без остатка. 6475 близко к 7000 (то есть 7 × 1000), значит, можно попробовать взять 900 × 7 = 6300. Отлично!
2. Остаётся 175. Таким же образом, выделяем из 175 самое большое число, которое можно разделить на 7 по таблице умножения — это 140. А 140 : 7 = 20. Запомним это число и вычтем 175 − 140. Сотни в результате дают ноль, а 7 − 4 = 3. То есть остаток на данный момент — 35.
3. Вспоминаем, что по таблице умножения 7 × 5 = 35, и складываем все получившиеся числа: 900 + 20 + 5 = 925.

Деление на двузначное число

С делением на двузначное число всё гораздо интереснее. Задача в том, чтобы найти пределы, в которых лежит результат.

Например, разделим 6351 : 73:

1. Сначала попробуем угадать, в каком десятке находится результат. Помним, что по таблице умножения 7 × 8 = 56, поэтому пробуем умножить 73 × 80 = 5840. Это максимально близкий десяток, потому что если прибавить ещё 730 (то есть 73 × 10), получится уже 6570 — больше чем нужно. Следовательно, наше число лежит в пределах между 80 и 90.
2. Теперь посмотрим на последние цифры наших чисел — 1 и 3. Из таблицы умножения мы помним, что только одно число при умножении на 3 на на конце даёт 1 — это 7. Пробуем умножить 73 × 7 = 511. Складываем 5840 + 511 = 6351. Ура, ответ 87!

Некруглые числа можно легко делить на 2, округляя их. Например, 358 делим на 2. Округлим 358 до 360, а затем уже его разделим на 2 — получим 130. А затем вычтем и этого числа 1 (получились в результате деления на 2 прибавленной 2).

358 : 2 = 360 : 2 − 2 : 2 = 130 − 1 = 129

Чтобы умножить число на 25, порой проще разделить его на 4, а затем умножить на 100 (или дописать два нуля):

12 × 25 = 12 : 4 × 100 = 3 × 100 = 300

Этих способов достаточно, чтобы тренироваться уверенно считать в уме. Помните, что делать это нужно регулярно, уделяя всего по 5–10 минут каждый день. Постарайтесь поймать свой ритм, чтобы решение таких задачек приносило удовольствие. И упирайте на правильность ответов, а не скорость — она придёт со временем. И не бросайте.

А если вам нужна помощь в решении более сложных задач, которые уже нельзя просчитать в уме, вам с радостью помогут специалисты Мультиворка

Эта статья навеяна топиком «Как и насколько быстро вы считаете в уме на элементарном уровне?» и призвана распространить приёмы С. А. Рачинского для устного счёта.
Рачинский был замечательным педагогом, преподававшим в сельских школах в XIX веке и показавшим на собственном опыте, что развить навык быстрого устного счёта можно. Для его учеников не было особой проблемой посчитать подобный пример в уме:

Используем круглые числа

Один из самых распространённых приёмов устного счёта заключается в том, что любое число можно представить в виде суммы или разности чисел, одно или несколько из которых «круглое»:

Т.к. на 10, 100, 1000 и др. круглые числа умножать быстрее, в уме нужно сводить всё к таким простым операциям, как 18 x 100 или 36 x 10. Соответственно, и складывать легче, «отщепляя» круглое число, а затем добавляя «хвостик»: 1800 + 200 + 190.
Еще пример:

Упростим умножение делением

При устном счёте бывает удобнее оперировать делимым и делителем нежели целым числом (например, 5 представлять в виде 10:2, а 50 в виде 100:2):

Аналогично выполняется умножение или деление на 25, ведь 25 = 100:4. Например,

Теперь не кажется невозможным умножить в уме 625 на 53:

Возведение в квадрат двузначного числа

Оказывается, чтобы просто возвести любое двузначное число в квадрат, достаточно запомнить квадраты всех чисел от 1 до 25. Благо, квадраты до 10 мы уже знаем из таблицы умножения. Остальные квадраты можно посмотреть в нижеприведённой таблице:

Приём Рачинского заключается в следующем. Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю. Например,

В общем случае (M — двузначное число):

Попробуем применить данный трюк при возведении в квадрат трёхзначного числа, разбив его предварительно на более мелкие слагаемые:

Хм, я бы не сказала, что это сильно легче, чем возведение в столбик, но, возможно, со временем можно приноровиться.
И начинать тренировки, конечно, следует с возведения в квадрат двузначных чисел, а там уже и до дизассемблирования в уме можно дойти.

Умножение двузначных чисел

Этот интересный приём был придуман 12-летним учеником Рачинского и является одним из вариантов добавления до круглого числа.
Пусть даны два двузначных числа, у которых сумма единиц равна 10:

Составив их произведение, получим:

Например, вычислим 77 x 13. Сумма единиц этих чисел равна 10, т.к. 7 + 3 = 10. Сначала ставим меньшее число перед большим: 77 x 13 = 13 x 77.
Чтобы получить круглые числа, мы забираем три единицы от 13 и добавляем их к 77. Теперь перемножим новые числа 80 x 10, а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10:

У этого приёма есть частный случай: всё значительно упрощается, когда у двух сомножителей одинаковое число десятков. В этом случае число десятков умножается на следующее за ним число и к полученному результату приписывается произведение единиц этих чисел. Посмотрим, как элегантен этот приём на примере.
48 x 42. Число десятков 4, последующее число: 5; 4 x 5 = 20. Произведение единиц: 8 x 2 = 16. Значит,
99 x 91. Число десятков: 9, последующее число: 10; 9 x 10 = 90. Произведение единиц: 9 x 1 = 09. Значит,
Ага, то есть, чтобы перемножить 95 x 95, достаточно посчитать 9 x 10 = 90 и 5 x 5 = 25 и ответ готов:

Тогда предыдущий пример можно вычислить немного проще:

Вместо заключения

Казалось бы, зачем уметь считать в уме в 21 веке, когда можно просто подать голосовую команду смартфону? Но если задуматься, что будет с человечеством, если оно будет взваливать на машины не только физическую работу, но и любую умственную? Не деградирует ли оно? Даже если не рассматривать устный счёт как самоцель, для закалки ума он вполне подходит.

Использованная литература:
«1001 задача для умственного счёта в школе С.А. Рачинского».

Умножение двузначных цифр. Алгоритм перемножения двузначных чисел. Умножение в столбик в уме

С лучшей бесплатной игрой учится очень быстро. Проверьте это сами!

Учить таблицу умножения – игра

Попробуйте нашу обучающую электронную игру. Используя её, вы уже завтра сможете решать математические задачи в классе у доски без ответов, не прибегая к табличке, чтобы умножить числа. Стоит только начать играть, и уже минут через 40 будет отличный результат. А для закрепления результата тренируйтесь несколько раз, не забывая о перерывах. В идеале – каждый день (сохраните страницу, чтобы не потерять). Игровая форма тренажера подходит как для мальчиков, так и для девочек.

Смотрите ниже шпаргалки в полной форме.

Умножение прямо на сайте (онлайн)

*
Таблица умножения (числа от 1 до 20)

×	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
2	2	4	6	8	10	12	14	16	18	20	22	24	26	28	30	32	34	36	38	40
3	3	6	9	12	15	18	21	24	27	30	33	36	39	42	45	48	51	54	57	60
4	4	8	12	16	20	24	28	32	36	40	44	48	52	56	60	64	68	72	76	80
5	5	10	15	20	25	30	35	40	45	50	55	60	65	70	75	80	85	90	95	100
6	6	12	18	24	30	36	42	48	54	60	66	72	78	84	90	96	102	108	114	120
7	7	14	21	28	35	42	49	56	63	70	77	84	91	98	105	112	119	126	133	140
8	8	16	24	32	40	48	56	64	72	80	88	96	104	112	120	128	136	144	152	160
9	9	18	27	36	45	54	63	72	81	90	99	108	117	126	135	144	153	162	171	180
10	10	20	30	40	50	60	70	80	90	100	110	120	130	140	150	160	170	180	190	200
11	11	22	33	44	55	66	77	88	99	110	121	132	143	154	165	176	187	198	209	220
12	12	24	36	48	60	72	84	96	108	120	132	144	156	168	180	192	204	216	228	240
13	13	26	39	52	65	78	91	104	117	130	143	156	169	182	195	208	221	234	247	260
14	14	28	42	56	70	84	98	112	126	140	154	168	182	196	210	224	238	252	266	280
15	15	30	45	60	75	90	105	120	135	150	165	180	195	210	225	240	255	270	285	300
16	16	32	48	64	80	96	112	128	144	160	176	192	208	224	240	256	272	288	304	320
17	17	34	51	68	85	102	119	136	153	170	187	204	221	238	255	272	289	306	323	340
18	18	36	54	72	90	108	126	144	162	180	198	216	234	252	270	288	306	324	342	360
19	19	38	57	76	95	114	133	152	171	190	209	228	247	266	285	304	323	342	361	380
20	20	40	60	80	100	120	140	160	180	200	220	240	260	280	300	320	340	360	380	400

Как умножать числа столбиком (видео по математике)

Чтобы потренироваться и быстро выучить, можно также попробовать умножать числа столбиком.

Как быстро умножать большие числа, как овладеть такими полезными навыками? У большинства вызывает затруднения устное перемножение двузначных чисел на однозначные. А о сложных арифметических расчетах и говорить нечего. Но при желании способности, заложенные в каждом человеке, можно развить. Регулярные тренировки, немного усилий и применение, разработанных учеными, эффективных методик позволят достичь потрясающих результатов.

Выбираем традиционные методы

Проверенные десятилетиями способы перемножения двузначных чисел не теряют своей актуальности. Простейшие приемы помогают миллионам обычных школьников, учащихся специализированных ВУЗов и лицеев, а также людям, занимающимся саморазвитием, усовершенствовать вычислительное мастерство.

Умножение с помощью разложения чисел

Наиболее легким способом, как быстро научиться умножать большие числа в уме, является перемножение десятков и единиц. Сначала умножаются десятки двух чисел, затем поочередно единицы и десятки. Четыре полученных числа суммируются. Для использования этого метода важно уметь запоминать результаты перемножения и складывать их в уме.

Например, для умножения 38 на 57 необходимо:

• разложить число на (30+8)*(50+7) ;
• 30*50 = 1500 – запомнить результат;
• 30*7 + 50*8 = 210 + 400 = 610 – запомнить;
• (1500 + 610) + 8*7 = 2110 + 56 = 2166

Естественно, необходимо отлично знать таблицу умножения, так как быстро умножать в уме этим способом не удастся без соответствующих умений.

Умножение в столбик в уме

Визуальное представление привычного перемножения в столбик многие используют при расчетах. Этот метод подойдет тем, кто умеет надолго запоминать вспомогательные числа и выполнять с ними арифметические действия. Но процесс значительно упрощается, если вы научились, как быстро умножать двузначные числа на однозначные. Для перемножения, например, 47*81 нужно:

• 47*1 = 47 – запомнить;
• 47*8 = 376 – запоминаем;
• 376*10 + 47 = 3807.

Запоминать промежуточные результаты поможет проговаривание их вслух с одновременным суммированием в уме. Несмотря на сложность мысленных вычислений, после непродолжительных тренировок этот метод станет вашим любимым.

Приведенные выше способы умножения универсальны. Но знание более эффективных алгоритмов для некоторых чисел намного сократит количество расчетов.

Умножение на 11

Это, пожалуй, самый простой способ, который используется для умножения любых двузначных чисел на 11.

Достаточно между цифрами множителя вставить их сумму:
13*11 = 1(1+3)3 = 143

Если в скобках получается число больше 10, то к первой цифре добавляется единица, а из суммы в скобках вычитается 10.
28*11 = 2 (2+8) 8 = 308

Умножение больших чисел

Очень удобно перемножать числа, близкие к 100 разложением их на составляющие. Например, необходимо умножить 87 на 91.

• Каждое число необходимо представить как разницу 100 и еще одного числа:
  (100 – 13)*(100 – 9)
  Ответ будет состоять из четырех цифр, две первые из которых – разница первого множителя и вычитаемого из второй скобки или наоборот – разница второго множителя и вычитаемого из первой скобки.
  87 – 9 = 78
  91 – 13 = 78
• Вторые две цифры ответа – результат перемножения вычитаемых из двух скобок.13*9 = 144
• В результате получаются числа 78 и 144. Если при записывании окончательного результата получается число из 5 цифр вторую и третью цифру суммируем. Результат: 87*91 = 7944 .

Это самые простые способы перемножения. После многократного их применения, доведения вычислений до автоматизма можно осваивать более сложные техники. И через некоторое время проблема, как быстро умножить двузначные числа перестанет вас волновать, а память и логика существенно улучшатся.

Умножение двузначных чисел | Онлайн-тренажёр

Упражнение считается выполенным после 7 правильных ответов

Норма выполнения упражнения – 3 минуты

Для успешного выполнения упражнения ознакомьтесь с теорией и проработайте предыдущие уроки

Умножение двузначных чисел | Теория

В общем случае умножение в уме двузначных чисел удобно выполнять в следующем порядке:

1. за базовое (первое или находящееся слева) число примите число с наибольшей второй цифрой;
2. умножьте базовое (первое) двузначное число на десятки другого (второго) двузначного числа;
3. умножьте базовое (первое) двузначное число на единицы другого (второго) двузначного числа;
4. сложите два результата.

Задача: 42 x 36

1) 36 x 42 (число 36 принято за базовое (первое) число, так как 6>1)

2) 36 x 40 = (30+6) x 4 x 10

30 x 4 = 120; 6 x 4 = 24; 120 + 24 = 144; 144 x 10 = 1440*

3) 36 x 2 = (30+6) x 2

30 x 2 = 60; 6 x 2 = 12; 60 + 12 = 72

4) 1440 + 72 = 1752

Задача: 47 x 52

1) 47 x 52 (число 47 принято за базовое (первое) число, так как 7>2)

2) 47 x 50 = 2350

4) 2350 + 94 = 2444

Если одно из чисел заканчивается на 9, то задачу удобнее решать в следующем порядке:

1. за второе (находящееся справа) число примите число, заканчивающееся на 9;
2. округлите второе число в большую сторону до десятков, прибавив к нему 1;
3. умножьте первое число на округлённое второе число;
4. вычтите из результата пункта 3 первое число.

Задача: 39 x 56

1) 56 x 39 (число 39 принято за второе (находящееся справа) число, так как оно заканчивается на 9)

2) 56 x 39(40-1)

3) 56 x 40 = (50+6) x 4 x 10

50 x 4 = 200; 6 x 4 = 24; 200 + 24 = 224; 224 x 10 = 2240

4) 2240 – 56 = 2184

Если одно из двузначных чисел равно 11, то решить такую задачу будет намного проще, если вы воспользуетесь методикой, изложенной в Уроке 1.

Во многих случаях решение задачи умножения двузначных чисел в уме намного упрощается, если воспользоваться методом факторизации.

Факторизация – это преобразование числа в произведение более простых чисел. Например, число 24 можно преобразовать в произведение 8 и 3 (24 = 8 x 3) или 6 и 4 (24 = 6 x 4). Число 24 также можно представить в виде произведения 12 и 2 (24 = 12 x 2), но при выполнении арифметических операций в уме удобнее иметь дело с однозначными числами.

Отдельные двузначные числа также можно представить в виде произведения трёх однозначных чисел. Например, 84 = 7 x 6 x 2 = 7 x 4 x 3.

Решим задачу умножения с помощью факторизации.

Задача: 34 x 42

Факторизация числа 24 даёт 8 и 3 или 6 и 4. Для решения задачи представим число 24 в виде произведения 6 и 4, но, если вам удобнее, вы можете выбрать произведение 8 и 3.

Умножаем первое число на 6, после чего умножаем результат на 4:

34 x 6 = 204

204 x 4 = 816

Чтобы знать, какие из двузначных чисел поддаются факторизации, необходимо тщательно изучить таблицу умножения. Можно выписать все двузначные числа, поддающиеся факторизации, с указанием возможных способов их факторизации.

Если оба из перемножаемых двузначных чисел поддаются факторизации, то в большинстве случае удобнее факторизовать меньшее число.

Задача: 36 x 72

Число 36 можно представить в виде произведения 6 и 6, а число 72 – в виде произведения 9 и 8.

Так как 36

72 x 6 = 432

432 x 6 = 2592

Пример с факторизацией на три числа.

Задача: 57 x 75

В случае, если одно из перемножаемых двузначных чисел состоит из одинаковых цифр (22, 33, 44 и т.д.), то его удобнее факторизовать на 11 и 2, 3, 4 и т.д.), так как умножение на 11 не представляет труда, как было показано в уроке 11.

Задача: 81 x 44

Если числа близки по значению с круглым числом, то при их перемножении в уме удобно пользоваться следующими формулами: (C+a)(C+b) = (C+a+b)C+ab; (C-a)(C-b) = (C-a-b)C+ab; (C+a)(C-b) = (C+a-b)C-ab**, где “C” – близкое к двум перемножаемым числам круглое число, а “а” и “b” – это разницы между перемножаемыми числами и круглым числом.

Задача: 67 x 64

(60 + 7) x (60 + 4) = (60 + 7 + 4) x 60 + 7 x 4 = 71 x 60 + 28 = 4260 + 28 = 4288

Задача: 39 х 38

(40 – 1) x (40 – 2) = (40 – 1 – 2) x 40 + 1 x 2 = 37 x 40 + 2 = 1480 + 2 = 1482

Задача: 41 x 38

(40 + 1) x (40 – 2) = (40 + 1 – 2) x 40 + 1 x 2 = 39 x 40 – 2 = 1558

Умножение двузначных чисел, первые цифры (десятки) которых равны, а вторые цифры (единицы) дают в сумме 10, удобнее производить в следующем порядке:

1. умножьте первую цифру двузначных чисел на эту же цифру, увеличенную на единицу;
2. перемножить вторые цифры двузначных чисел;
3. поместите один за другим результаты пункта 1 и пункта 2.

Задача: 76 x 74

Не расстраивайтесь и не сдавайтесь, если на первых порах у вас возникнут трудности с умножением двузначных чисел. Для уверенного выполнения такой операции в уме необходима практика, а также творческий подход.

* Для запоминания в уме промежуточных результатов вычислений можете применять мнемотехники, основанные на ассоциации цифр с образами.

** Доказательства формул путём преобразования: (C+a)(C+b) = (C+a)C+(C+a)b = C 2 +Ca+Cb+ab = (C+a+b)C+ab; (C-a)(C-b) = (C-a)C-(C-a)b = C 2 -Ca-Cb+ab = (C-a-b)C+ab; (C+a)(C-b) = (C+a)C-(C+a)b = C 2 +Ca-Cb-ab = (C+a-b)C-ab.

*** Доказательство метода: согласно формуле, применяемой в предудущем методе (C+a)(C+b) = (C+a+b)C+ab; так как a+b=10, то (C+a)(C+b) = (C+10)C+ab; поскольку произведение двузначных круглых чисел С и С+10 даёт число с двумя нулями на конце, а произведение a и b даёт двузначное число, то для нахождения суммы этих двух выражений достаточно поставить произведение a и b вместо двух последних нулей первого выражения.

Существуют три общих способа: прямое умножение, метод опорного числа и метод Трахтенберга.

Освойте их все, так как каждый может быть более предпочтительным в той или иной ситуации.

Отрабатывать полученные навыки можно с помощью тренировочной таблицы.

Прямое умножение

Этот метод удобен, когда один из множителей находится в диапазоне 12-18 или заканчивается на 1, а другой значительно от него отличается.

Один из множителей мысленно разбивают на десятки и единицы. Затем умножают другой множитель на десятки, потом на единицы и складывают.

Например, 62×13 = 62×10 + 62×3 = 620 + 186 = 806.

Иногда удобно разбивать на десятки и единицы больший множитель: 42×17 = 17×40 + 17×2 = 714.

Метод опорного числа

Для освоения метода требуется небольшая практика, однако он очень удобен, когда два множителя — близкие числа. В частности, это основной способ для возведения двузначных чисел в квадрат.

Опорное число — это круглое число, близкое к обоим множителям. Оно может быть меньше обоих множителей, больше обоих множителей или находится между ними.

В качестве опорного числа следует выбирать числа, на которые легко умножать. Например, 50 или 100, если они близки к двум множителям.

В зависимости от того, как соотносятся опорное число и множители, техника умножения немного различается.

а. Опорное число меньше двух множителей. Например, нужно умножить 32 на 36.

• Опорное число — 30. Множители больше опорного числа на 2 и 6.
• Добавьте к первому множителю 6 и умножьте на опорное число: 38 × 30 = 1140.
• Добавьте произведение 2 и 6: 1140 + 2×6 = 1152.

б. Опорное число больше двух множителей. Например, нужно умножить 43 на 48.

• Опорное число — 50. Множители меньше опорного числа на 7 и 2.
• Вычтите из первого множителя 2 и умножьте на опорное число: 41 × 50 = 2050.
• Добавьте произведение 7 и 2: 2050 + 7×2 = 2064.

в. Опорное число — между множителями. Например, нужно умножить 37 на 42.

• Опорное число — 40. Первый множитель меньше на 3, второй — больше на 2.
• Добавьте к меньшему множителю 2 и умножьте на опорное число: 39 × 40 = 1560.
• Вычтите произведение 3 и 2: 1440 − 3×2 = 1554.

Метод Трахтенберга

Метод Трахтенберга — самый общий. Им удобно пользоваться всегда, когда не работают специальные приемы. Он также распространяется на умножение многозначных чисел.

Поскольку метод Трахтенберга не совсем привычен, при его освоении лучше иметь множители перед глазами. В дальнейшем практикуйтесь без записи исходных чисел.

Разберем метод на примере умножения 87 на 32.

• Представьте числа последовательно: 8732. Перемножьте два внутренних числа (7 и 3), два внешних числа (8 и 2) и сложите. Получается 37.
• Перемножьте десятки: 80×30 = 2400. Добавьте 37×10. Получается 2770.
• Добавьте произведение единиц (7 и 2). Итого 2784.

Например: 98 х 97 = 9506

Здесь я пользуюсь таким алгоритмом: если хочешь перемножить два

двузначных числа, близких к 100, то поступай так:

1) найди недостатки сомножителей до сотни;

2) вычти из одного сомножителя недостаток второго до сотни;

3) к результату припиши двумя цифрами произведение недостатков

сомножителей до сотни.

2.9 Умножение трёхзначного числа на 999

Любопытная особенность числа 999 проявляется при умножении на него всякого другого трёхзначного числа. Тогда получается шестизначное произведение: первые три цифры есть умножаемое число, только уменьшенное на единицу, а остальные три цифры (кроме последней) – «дополнения » первых до 9. Например:

385 * 999 = 384615

573 * 999 = 572427 943 * 999 = 942057

2.10 Умножение на шесть (по Трахтенбергу)

Нужно прибавить к каждой цифре половину «соседа ».

Пример: 0622084 * 6

0622084 * 6 4 является правой цифрой этого числа и, так 4 как «соседа » у неё нет, прибавлять нечего.

06222084 * 6 Вторая цифра 8, е «сосед » – 4. Мы берём 8 04 прибавляем половину 4 (2) и получаем 10, ноль пишем, 1 в перенос.

06222084 * 6 Следующая цифра ноль. Мы прибавляем к ней

504 половину «соседа » 8 (4), то есть 0 + 4 = 4 плюс

перенос (1).

Остальные цифры аналогичны.

Ответ: 06222084 * 6

Правило умножения на 6: является «сосед » чётным или не чётным – никакой роли не играет. Мы смотрим только на саму цифру: если она чётная, прибавляем к ней её целую часть половины «соседа », если нечётная, то кроме половины «соседа » прибавляем еще 5.

Пример: 0443052 * 6

0443052 * 6 2 – чётная и не имеет «соседа », напишем её снизу

0443052 * 6 5 – нечётная: 5+5 и плюс половина «соседа » 2 (1)

12 будет 11. Запишем 1 и в перенос 1

0443052 * 6 половина от 5 будет 2, и прибавим перенос 1, то будет 3

0443052 * 6 3 – нечетная, 3 + 5 = 8

0443052 * 6 4 + половина от 3 (1) будет 5

0443052 * 6 4 + половина от 4 (2) будет 6

0443052 * 6 ноль + половина от 4 (2) будет 2

2658312 Ответ: 2658312.

Выводы

Знание приемов быстрого счета позволяет упрощать вычисления, экономить время, развивает логическое мышление и гибкость ума.

В школьных учебниках практически нет приемов быстрого счета, поэтому результат данной работы – памятка для быстрого счета будет очень полезной для учащихся 5-6 классов.

Как мы видим, быстрый счёт это уже не тайна за семью печатями, а научно разработанная система. Раз есть система, значит, её можно изучать, ей можно следовать, ею можно овладевать.

Все рассмотренные мною методы устного умножения говорят о многолетнем интересе ученых, и простых людей к игре с цифрами.

Используя некоторые из этих методов на уроках или дома, можно развить скорость вычислений, привить интерес к математике, добиться успехов в изучении всех школьных предметов.

Заключение

Описывая старинные способы вычислений и современные приёмы быстрого счёта, я попытался показать, что как в прошлом, так и в будущем, без математики, науки созданной разумом человека, не обойтись.

Изучение старинных способов вычислений показало, что эти арифметические действия были трудными и сложными из-за многообразия способов и их громоздкости выполнения.

Современные способы вычислений просты и доступны всем.

При знакомстве с научной литературой обнаружил более быстрые и надежные способы вычислений.

Результаты своей работы я оформил в памятку (Приложение 2), которую предложу всем своим одноклассникам. Возможно, что с первого раза не у всех получится быстро, с ходу выполнять вычисления с применением этих приемов, даже если сначала не получится использовать прием, показанный в памятке, ничего страшного, просто нужна постоянная вычислительная тренировка. Она и поможет приобрести полезные навыки.

Список использованной литературы

1. Ванцян А.Г. Математика: Учебник для 5 класса. – Самара: Издательский дом «Фёдоров », 1999г.

2. Зайкин М.Н. Математический тренинг. – Москва, 1996.

3. Зимовец К.А., Пащенко В.А. Интересные приемы устных вычислений. //Начальная школа. – 1990, №6.

4. Иванова Т. Устный счёт. // Начальная школа. – 1999, №7.

5. Кордемский Б.А., Ахадов А.А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986г.

6. Минских Е.М. «От игры к знаниям », М., «Просвещение », 1982г.

7. Перельман Я.И. Живая математика. – Екатеринбург, Тезис, 1994.

8. Свечников А.А. Числа, фигуры, задачи. М., Просвещение, 1977г.

Интернет-источники

1. school.edu.ru

в столбец и в уме

Умножение двузначных чисел – навык, крайне необходимый для нашей повседневной жизни. Люди постоянно сталкиваются с потребностью перемножить что-либо в уме: ценник в магазине, массу продуктов или размер скидки. Но как умножать двузначные числа быстро и без проблем? Давайте разберемся.

Как умножить двузначное число на однозначное?

Начнем с простой задачи – как умножать двузначные числа на однозначные.

Для начала, двузначное число – это такое число, которое состоит из определенного количества десятков и единиц.

Для того чтобы умножить двузначное число на однозначное в столбец, нужно написать нужное двузначное число, а под ним соответствующее однозначное. Далее следует поочередно умножить на заданное число сначала единицы, а потом – десятки. Если при умножении единиц получилось число больше 10, то количество десятков нужно просто перенести в следующий разряд, прибавив их.

Умножение двузначных чисел на десятки

Умножение двузначных чисел на десятки – задача ненамного сложнее, чем умножение на однозначные числа. Основной порядок действий остается тем же:

• Выписать числа друг под другом в столбец, при этом нуль должен находиться как бы «сбоку», чтобы не мешать при арифметических действиях.
• Умножить двузначное число на количество десятков, не забыть про перенос некоторых цифр в следующие разряды.
• Единственное, что отличает этот пример от предыдущего – в конце получившегося ответа нужно добавить нуль, так что десятки, которые были опущены в начале, становятся учтенными.

Как перемножить два двузначных числа?

После того как вы полностью разобрались с умножением двузначных и однозначных чисел, можно начинать думать, как умножать столбиком двузначные числа друг на друга. На самом деле это действие тоже не должно потребовать от вас больших усилий, так как принцип все еще остается тем же.

• Выписываем данные числа в столбец – единицы под единицами, десятки под десятками.
• Начинаем умножение с единицы точно так же, как в примерах с однозначными числами.
• После того как вы получили первое число, умножив единицы на данную цифру, нужно таким же образом умножить десятки на эту же цифру. Внимание: ответ нужно записывать строго под десятками. Пустое место под единицами – это неучтенный нуль. Вы можете записывать его, если вам так удобнее.
• Перемножив и десятки, и единицы и получив два числа, записанных одно под одним, их нужно сложить в столбец. Получившееся значение и является ответом.

Как правильно умножать двузначные числа? Для этого недостаточно просто прочитать или выучить приведенную инструкцию. Помните, для того чтобы освоить принцип, как умножать двузначные числа, в первую очередь нужно постоянно практиковаться – решать как можно больше примеров, как можно реже пользоваться калькулятором.

Как умножать в уме

Научившись блестяще умножать на бумаге, можно задаться вопросом, как быстро умножить двузначные числа в уме.

Конечно, это не самая простая задача. Она требует некоторой концентрации, хорошей памяти, а также способности удерживать в голове некоторое количество информации. Однако и этому можно научиться, приложив достаточно усилий, тем более если подобрать правильный алгоритм. Очевидно, что легче всего умножать на круглые числа, поэтому самым простым способом является разложение чисел на множители.

• Для начала следует разбить одно из данных двузначных чисел на десятки. Например, 48 = 4 × 10 + 8.
• Далее нужно последовательно перемножить сначала единицы, а потом десятки со вторым числом. Это достаточно сложные для выполнения в уме операции, так как нужно одновременно умножать числа друг на друга и держать в уме уже получившийся результат. Вероятнее всего, вам будет трудно справиться с этой задачей с первого раза, но, если быть достаточно усердным, этот навык можно развить, ведь понять, как правильно умножать двузначные числа в уме, можно только на практике.

Некоторые хитрости при умножении двузначных чисел

Но существует ли более легкий способ в уме умножать двузначные числа, и как это сделать?

Есть несколько хитростей. Они помогут вам легко и быстро умножать двузначные числа.

• При умножении на одиннадцать нужно просто поставить сумму десятков и единиц в середину данного двузначного числа. К примеру, нам понадобилось умножить 34 на 11.

3 + 4 = 7

Ставим 7 в середину, 374. Это и есть ответ.

Если при сложении получается число больше 10, то следует просто добавить единицу к первому числу. Например, 79 × 11.

7 + 9 = 16

(7 + 1)69 = 869

• Иногда легче разложить число на множители и последовательно умножить их. Например, 16 = 2 × 2 × 2 × 2, поэтому можно просто 4 раза умножить исходное число на 2.

14 = 2 × 7, поэтому при выполнении математических операций можно умножить сначала на 7, а потом на 2.

• Для того чтобы умножить число на числа, кратные 100, например, 50 или 25, можно умножить это число на 100, а потом разделить на 2 или 4 соответственно.
• Еще нужно помнить, что иногда при умножении легче не складывать, а отнимать числа друг от друга.

Например, чтобы умножить число на 29, можно сначала умножить его на 30, а потом отнять от полученного числа данное число один раз. Это правило справедливо для любых десятков.

Умножение двузначных чисел | Ментальная арифметика онлайн бесплатно

Упражнение считается выполенным после 7 правильных ответов

Для успешного выполнения упражнения ознакомьтесь с теорией и проработайте предыдущие уроки

Умножение двузначных чисел | Теория

В общем случае умножение в уме двузначных чисел удобно выполнять в следующем порядке:

1. за базовое (первое или находящееся слева) число примите число с наибольшей второй цифрой;
2. умножьте базовое (первое) двузначное число на десятки другого (второго) двузначного числа;
3. умножьте базовое (первое) двузначное число на единицы другого (второго) двузначного числа;
4. сложите два результата.

Задача: 42 x 36

Решение:

1) 36 x 42 (число 36 принято за базовое (первое) число, так как 6>1)

36 x 42(40+2)

2) 36 x 40 = (30+6) x 4 x 10

 30 x 4 = 120; 6 x 4 = 24; 120 + 24 = 144[120+20=140;140+4=144]; 144 x 10 = 1440*

3) 36 x 2 = (30+6) x 2

 30 x 2 = 60; 6 x 2 = 12; 60 + 12 = 72[60+10=70;70+2=72]

4) 1440 + 72 = 1752 [1440+70=1510;1510+2=1512]

Задача: 47 x 52

Решение:

1) 47 x 52 (число 47 принято за базовое (первое) число, так как 7>2)

2) 47 x 50 = 2350

3) 47 x 2 = 94

4) 2350 + 94 = 2444

Если одно из чисел заканчивается на 9, то задачу удобнее решать в следующем порядке:

1. за второе (находящееся справа) число примите число, заканчивающееся на 9;
2. округлите второе число в большую сторону до десятков, прибавив к нему 1;
3. умножьте первое число на округлённое второе число;
4. вычтите из результата пункта 3 первое число.

Задача: 39 x 56

Решение:

1) 56 x 39 (число 39 принято за второе (находящееся справа) число, так как оно заканчивается на 9)

2) 56 x 39(40-1)

3) 56 x 40 = (50+6) x 4 x 10

 50 x 4 = 200; 6 x 4 = 24; 200 + 24 = 224; 224 x 10 = 2240

4) 2240 – 56 = 2184[2240-50=2190;2190-6=2184]

Если одно из двузначных чисел равно 11, то решить такую задачу будет намного проще, если вы воспользуетесь методикой, изложенной в Уроке 1.

Во многих случаях решение задачи умножения двузначных чисел в уме намного упрощается, если воспользоваться методом факторизации.

Факторизация – это преобразование числа в произведение более простых чисел. Например, число 24 можно преобразовать в произведение 8 и 3 (24 = 8 x 3) или 6 и 4 (24 = 6 x 4). Число 24 также можно представить в виде произведения 12 и 2 (24 = 12 x 2), но при выполнении арифметических операций в уме удобнее иметь дело с однозначными числами.

Отдельные двузначные числа также можно представить в виде произведения трёх однозначных чисел. Например, 84 = 7 x 6 x 2 = 7 x 4 x 3.

Решим задачу умножения с помощью факторизации.

Задача: 34 x 42

Решение:

Факторизация числа 24 даёт 8 и 3 или 6 и 4. Для решения задачи представим число 24 в виде произведения 6 и 4, но, если вам удобнее, вы можете выбрать произведение 8 и 3.

34 x 24(6×4)

Умножаем первое число на 6, после чего умножаем результат на 4:

34 x 6 = 204[30×6=180;4×6=24;180+24=204]

204 x 4 = 816[200×4=800;4×4=16;800+16=816]

Чтобы знать, какие из двузначных чисел поддаются факторизации, необходимо тщательно изучить таблицу умножения. Можно выписать все двузначные числа, поддающиеся факторизации, с указанием возможных способов их факторизации.

Если оба из перемножаемых двузначных чисел поддаются факторизации, то в большинстве случае удобнее факторизовать меньшее число.

Задача: 36 x 72

Решение:

Число 36 можно представить в виде произведения 6 и 6, а число 72 – в виде произведения 9 и 8.

Так как 36

72 x 36(6×6)

72 x 6 = 432[70×6=420;2×6=12;420+12=432]

432 x 6 = 2592[400×6=2400;30×6=180;2×6=12; 2400+180=2580;2580+12=2592]

Пример с факторизацией на три числа.

Задача: 57 x 75

Решение:

75 = 5 x 5 x 3

57 x 75(5x5x3)

57 x 5 = 285

285 x 5 = 1425

1425 x 3 = 4275

В случае, если одно из перемножаемых двузначных чисел состоит из одинаковых цифр (22, 33, 44 и т.д.), то его удобнее факторизовать на 11 и 2, 3, 4 и т.д.), так как умножение на 11 не представляет труда, как было показано в уроке 11.

Задача: 81 x 44

Решение:

81 x 44(11×4)

81 x 11 = 891;

891 x 4 = 3564

Если числа близки по значению с круглым числом, то при их перемножении в уме удобно пользоваться следующими формулами: (C+a)(C+b) = (C+a+b)C+ab; (C-a)(C-b) = (C-a-b)C+ab; (C+a)(C-b) = (C+a-b)C-ab**, где “C” – близкое к двум перемножаемым числам круглое число, а “а” и “b” – это разницы между перемножаемыми числами и круглым числом.

Задача: 67 x 64

Решение:

(60 + 7) x (60 + 4) = (60 + 7 + 4) x 60 + 7 x 4 = 71 x 60 + 28 = 4260 + 28 = 4288

Задача: 39 х 38

Решение:

(40 – 1) x (40 – 2) = (40 – 1 – 2) x 40 + 1 x 2 = 37 x 40 + 2 = 1480 + 2 = 1482

Задача: 41 x 38

Решение:

(40 + 1) x (40 – 2) = (40 + 1 – 2) x 40 + 1 x 2 = 39 x 40 – 2 = 1558

Умножение двузначных чисел, первые цифры (десятки) которых равны, а вторые цифры (единицы) дают в сумме 10, удобнее производить в следующем порядке:

1. умножьте первую цифру двузначных чисел на эту же цифру, увеличенную на единицу;
2. перемножить вторые цифры двузначных чисел;
3. поместите один за другим результаты пункта 1 и пункта 2.

Задача: 76 x 74

Решение:

1) 7 x 8 = 56

2) 6 x 4 = 24

3) 5624

Не расстраивайтесь и не сдавайтесь, если на первых порах у вас возникнут трудности с умножением двузначных чисел. Для уверенного выполнения такой операции в уме необходима практика, а также творческий подход.

* Для запоминания в уме промежуточных результатов вычислений можете применять мнемотехники, основанные на ассоциации цифр с образами (смотрите теорию для запоминания чисел).

** Доказательства формул путём преобразования: (C+a)(C+b) = (C+a)C+(C+a)b = C²+Ca+Cb+ab = (C+a+b)C+ab; (C-a)(C-b) = (C-a)C-(C-a)b = C²-Ca-Cb+ab = (C-a-b)C+ab; (C+a)(C-b) = (C+a)C-(C+a)b = C²+Ca-Cb-ab = (C+a-b)C-ab.

*** Доказательство метода: согласно формуле, применяемой в предудущем методе (C+a)(C+b) = (C+a+b)C+ab; так как a+b=10, то (C+a)(C+b) = (C+10)C+ab; поскольку произведение двузначных круглых чисел С и С+10 даёт число с двумя нулями на конце, а произведение a и b даёт двузначное число, то для нахождения суммы этих двух выражений достаточно поставить произведение a и b вместо двух последних нулей первого выражения.

Как быстро умножать на 11: легкий способ

Здравствуйте, мои юные (и не очень) любители умножения! Сегодня у нас занимательная математика по плану. Будем с вами разбираться как быстро  умножать на 11. Умножать будем двузначные числа.

Давайте, готовьте свои головушки к работе. Расскажу вам об очень интересном способе поиска произведений.

Готовы? Ну тогда начинаем!

Давайте рассмотрим все способы.

Точно, но долго

Можно просто сложить умножаемое число 11 раз с самим собой.

Да уж, не так уж просто и не так уж быстро. Пока все сложишь, полдня пройдет! Нам требуется что-нибудь более скоростное.

Немного быстрее

Можно поступить проще. Сначала умножить число на 10, то есть дописать к нему нолик, а потом прибавить к результату само число.

Так, конечно, проще уже, но все равно не достаточно быстро. И вот мы подбираемся к разгадке, которая поможет нам не прибегать к счету в столбик и помощи калькулятора.

Самый быстрый

Следите внимательно!

Умножим 43 на 11.

Напишем 43 с пробелом по серединке

4  _ 3

Теперь сложим 4 и 3.

4+3=7

И семерку вставим в серединку вместо пробела.

4 7 3

Это и есть результат! Можете проверить на калькуляторе.

Согласитесь, так намного проще!

Теперь попробуем умножить на 76 на 11.

Так же пишем 76 с пробелом по серединке.

7 _ 6

Затем складываем между собой 7 и 6.

7 + 6 = 13

Теперь смотрите внимательно.

Тройку вставим вместо пробела, а единичку прибавим к семерке.

8 3 6.

Готово!

И таким образом будем поступать со всеми числами, сумма цифр в которых больше 9.

Еще пара примеров.

А теперь попробуйте сами! Внизу на картинках увидите примеры, которые нужно решить. Сделайте это в уме. А чтобы проверить себя, просто нажмите на картинку, она перевернется и вы увидите правильный ответ.

Получается? Отлично! Можете рассказать об этом способе друзьям или удивить их своими способностями к молниеносным вычислениям в уме.

Устный счет развивает мышление и прививает любовь к математике. Оказывается, она может быть не только точной и сухой наукой, но еще и веселым, полным разных чудесных штуковин занятием.

А постоянные читатели блога, кстати, уже узнали как можно супербыстро делить на пять. А вы в курсе? Если нет, то советую заглянуть сюда и узнать этот математический трюк.

А еще у нас есть для вас занимательные тесты, которые помогут проверить ваши знания в самых разных областях, например,

Эти тесты будут интересны не только маленьким школьникам, но и их родителям. Советую проходить их вместе, так намного веселее!

На сегодня все!

Заходите в гости снова, «ШколаЛа» всегда рада вас чем-нибудь удивить!

Математический трюк

– умножение двухзначных чисел

(последнее обновление: 1 июня 2018 г.)

Большинство людей вынимают калькуляторы каждый раз, когда сталкиваются с математической задачей, но это не обязательно должны быть вы. Существуют различные математические приемы, которые помогут быстрее и эффективнее решать математические задачи. Вот несколько приемов, которые вы можете использовать для умножения двузначных чисел размером до 19 x 19.

Этот математический трюк чрезвычайно быстр и прост. Всего за два шага вы можете умножить двузначные числа от 11 до 19.

Шаг # 1: Умножьте единичные цифры в каждом множителе вместе. Запишите ответ и при необходимости укажите числа.

Шаг № 2: Определите, какая цифра меньше между каждым множителем. Используйте это число и прибавьте его к целому числу большего множителя. Если есть какие-либо перенесенные числа, добавьте и их. Запишите эти числа рядом с вашим первым числом.

Вуаля! У вас есть решенное уравнение. Давайте посмотрим на это с цифрами.

Уравнение: 14 x 15

Шаг 1: Умножьте 4 на 5, что равно 20.Запишите ноль и несите 2.

Шаг № 2: Найдите меньшую цифру в множителе, равном 4, и прибавьте ее к большему множителю – 15. Добавьте 2, которые вы взяли из первого шага. Это означает, что ваше уравнение 4 + 15 + 2 = 21. Добавьте 21 рядом с нулем.

Ваш окончательный ответ: 210.

Этот математический трюк по-прежнему быстр, но требует нескольких дополнительных шагов. Ключ к этому методу – составить уравнение таким образом, чтобы каждый фактор располагался один над другим.

Шаг # 1: Умножьте единичные цифры и запишите свой ответ. При необходимости возьмите с собой любые продукты.

Шаг № 2: Перемножьте крестиком и сложите числа. Если вам приходилось носить с собой номер из первого шага, обязательно включите его в свое дополнение. При необходимости перенесите любые продукты снова.

Шаг № 3: Умножьте только цифры десятков. Если вы взяли продукт из шага № 2, добавьте это к своему ответу.

Шаг № 4: Объедините все свои ответы.

Давайте сейчас проверим.

Уравнение: 14 x 15

Шаг №1: Умножьте 4 на 5, что равно 20. Запишите ноль и перенесите 2.

Шаг № 2: Умножьте 5 на 1 и 4 на 1. Вам нужно будет прибавить 2 к вашему ответу из уравнения 5 × 1. Это из-за 2, которую вы перенесли с шага №1. Ваше уравнение должно выглядеть так: 7 + 4 = 11. Напишите 1 и перенесите 1.

Шаг 3: Умножьте 1 на 1, что равно 1.Затем вы добавите 1 из шага №2. Это означает, что ваш ответ – 2. Запишите его.

Шаг № 4: Объедините свои ответы.

Ваш окончательный ответ: 210

Вот та же задача, записанная по-другому:

Если один из ваших факторов – 11, используйте этот трюк, чтобы ускорить процесс. Это займет всего несколько простых шагов, и вы получите ответ в кратчайшие сроки.

Шаг 1: Найдите множитель, НЕ равный 11.Разделите каждое число пробелом между ними.

Шаг № 2: Используя тот же коэффициент, сложите десятки и единицы вместе. Поместите продукт в пустое пространство между двумя цифрами на шаге №1.

И это ваш ответ. Давай попробуем с числами. Это может иметь немного больше смысла.

Уравнение: 14 x 11

Шаг № 1: Определите, какой коэффициент не равен 11. В этом уравнении это 14. Разделите цифры, чтобы ваш ответ выглядел так: 1_4.

Шаг # 2: Сложите цифры множителя из шага 1. Это означает, что 1 + 4 = 5. Поместите 5 в пустое место в своем ответе.

Ваш окончательный ответ: 154

На шаге № 2, если вы сложите свои числа, а их больше 10, вам нужно будет нести продукт и добавить его к своей первой цифре. Давайте посмотрим на пример.

Уравнение: 19 x 11

Шаг 1: Найдите множитель, НЕ равный 11.В данном случае это 19. Разделите числа пробелом между ними. Ваш ответ должен выглядеть так: 1_9

Шаг 2: Сложите цифры множителя. Это означает, что сложите 1 и 9. Это даст вам 10. Запишите ноль в пустое место. Вам нужно перенести 1 и прибавить ее к разряду сотен.

Ваш окончательный ответ: 209

Немного потренировавшись, вы, возможно, научитесь умножать двузначные числа в уме.

Проверьте свои навыки, сыграв несколько математических викторин на Sporcle.

Комментарии

комментария

Умножение двузначных чисел Быстрые приемы

Умножение двухзначных чисел

Быстрые приемы очень важны на конкурсных экзаменах. Время – главный фактор при проведении конкурсных экзаменов. Если вы знаете, как управлять временем, вы наверняка отлично сдадите экзамен. Большинство из нас скучает по этому поводу. Несколько примеров быстрого доступа к умножению двухзначных чисел приведены на этой странице ниже.Здесь представлены все уловки по умножению двузначных чисел. Мы просим всех посетителей внимательно прочитать все примеры. Эти примеры помогут вам понять хитрые приемы умножения двузначных чисел.

Перед тем, как что-либо начинать, просто выполните набор упражнений по математике. Затем найдите двадцать математических задач, связанных с этой темой, и запишите их на бумаге. Решите первые десять математических задач по основной математической формуле. Также нужно следить за временем. После решения всех десяти математических вопросов запишите, сколько времени вы потратили на их решение.Теперь пройдемся по нашей странице для быстрого трюка умножения двухзначных чисел. После этого вернитесь к оставшимся десяти вопросам и решите их, используя методы быстрого доступа. Снова следите за временем. На этот раз время наверняка будет улучшено. Но это еще не все. Вам нужно больше практиковаться, чтобы больше улучшать свое время.

Несколько важных вещей, которые следует помнить

Математический раздел на конкурсном экзамене – самая важная часть экзамена. Это не значит, что другие разделы не так важны.Но если вам нужен хороший результат на экзамене, вы должны получить хороший результат по математике. Вы можете получить хороший результат, только тренируясь все больше и больше. Все, что вам нужно сделать, это правильно решать математические задачи в течение времени, а этого можно достичь только с помощью трюков. Но это не значит, что без использования быстрых клавиш вы не сможете решать математические задачи. Вы можете решать математические задачи вовремя, не прибегая к каким-либо трюкам. У вас может быть такой потенциал.

Но другие народы не могут делать то же самое. Итак, умножение двухзначных чисел – это краткие уловки для этих людей.Здесь, на этой странице, мы пытаемся применить все виды уловок для умножения двузначных чисел. Но если вы видите, что какие-то трюки отсутствуют в списке, сообщите нам. Ваша небольшая помощь поможет другим.

Традиционно умножение двузначных чисел занимает очень много времени. Но вы можете очень легко рассчитать это, используя трюки с ярлыками. Главное, чтобы вы просто выполняли указанные шаги. Если вы выучите это мысленно, вы будете выполнять это очень быстро и быстро с двузначными числами.

---

Пример №1 – Умножение двухзначных чисел

43 x 63 =?

1. 2661
2. 2689
3. 2709
4. 2733

Показать ответ Показать Как решить открытую черновую рабочую область

Ответ: Вариант (C)

Как решить 3 x 3

1. . Затем запишите 9,
2. Сделайте перекрестное умножение (4 x 3) = 12 и (6 x 3) = 18.
3. Сложите оба результата (4 x 3 + 6 x 3) = 30 и запишите 0 в слева от 9 и нести 3.
4. Умножим числа в левой части (4 x 6) = 24 и прибавим перенос (24 + 3) = 27 и запишем слева от 0.
   В итоге мы получим 2709 . (Попробуйте рассчитать все четыре шага в уме).

Черновая рабочая область

---

Пример № 2 – Умножение двухзначных чисел

59 x 42 =?

1. 2478
2. 2499
3. 2519
4. 2548

Показать ответ Показать Как решить открытую черновую рабочую область

Ответ: Вариант (A)

Как решить

1. .Запишите 8 и перенесите 1, затем
2. Сделайте перекрестное умножение (2 x 5) = 10 и (4 x 9) = 36.
3. Сложите оба результата с переносом (10 + 36 + 1) = 47 и запишите 7 перенос 4.
4. Умножаем числа в левой части (4 x 5) = 20 и прибавляем перенос (20 + 4) = 24 и записываем слева от 7.
   В итоге мы получаем 2478 . (Попробуйте рассчитать все четыре шага в уме).

Черновая рабочая область

---

Пример № 3 – Умножение двухзначных чисел

13 x 13 =?

1. 144
2. 169
3. 172
4. 189

Показать ответ Показать Как решить открытую черновую рабочую область

Ответ: Вариант (B)

Как решить 3

1. умножить.Затем запишите 9,
2. Произведите перекрестное умножение (1 x 3) = 3 и (1 x 3) = 3.
3. Сложите оба результата (1 x 3 + 1 x 3) = 6 и запишите слева из 9.
4. Умножаем числа в левой части (1 x 1) = 1 и записываем слева от 6.
   В итоге мы получаем 169 . (Попробуйте рассчитать все четыре шага в уме).

Черновая рабочая область

---

Пример №4 – Умножение двухзначных чисел

87 x 33 =?

1. 2841
2. 2859
3. 2871
4. 2899

Показать ответ Показать Как решить открытую черновую рабочую область

Ответ: Вариант (C)

Как решить 3 x 214

1. . Запишите 1 и перенесите 2, затем
2. Сделайте перекрестное умножение (3 x 8) = 24 и (3 x 7) = 21.
3. Сложите оба результата с переносом (24 + 21 + 2) = 47 и запишите 7 перенос 4.
4. Умножаем числа в левой части (3 x 8) = 24 и прибавляем перенос (24 + 4) = 28 и записываем слева от 7
   В итоге получаем 2871 . (Попробуйте рассчитать все четыре шага в уме).

Черновая рабочая область

---

Пример № 5

38 x 27 =?

1. 1026
2. 1042
3. 1061
4. 1087

Показать ответ Показать Как решить открытую черновую рабочую область

Ответ: Вариант (A)

Как решить

7 8 x 562.Запишите 6 и перенесите 5, затем
1. Сделайте перекрестное умножение (7 x 3) = 21 и (2 x 8) = 16.
2. Сложите оба результата с переносом (21 + 16 + 5) = 42 и запишите 2 переносится 4.
3. Умножаем числа в левой части (2 x 3) = 6 и прибавляем перенос (6 + 4) = 10 и записываем слева от 2
   В итоге получаем 1026 . (Попробуйте рассчитать все четыре шага в уме).

Черновая рабочая область

---

Пример № 6

17 x 19 =?

1. 292
2. 303
3. 313
4. 323

Показать ответ Показать Как решить открытую черновую рабочую область

Ответ: Вариант (D)

Как решить

1. .Запишите 3 и перенесите 6, затем
2. Сделайте перекрестное умножение (1 x 9) = 9 и (7 x 1) = 7.
3. Сложите оба результата с переносом (9 + 7 + 6) = 22 и запишите 2 переносится 2.
4. Умножаем числа в левой части (1 x 1) = 1 и прибавляем перенос (1 + 2) = 3, записываем слева от 2
   В итоге получаем 323 . (Попробуйте рассчитать все четыре шага в уме).

Rough Workspace

---

Еще несколько примеров быстрых приемов умножения

Мы предлагаем несколько быстрых приемов умножения двухзначных чисел. Посетите эту страницу, чтобы получать новости о других математических трюках. Вы также можете лайкнуть нашу страницу в Facebook, чтобы получать обновления.

Если у вас есть какие-либо вопросы относительно умножения двузначных чисел, прокомментируйте, пожалуйста, раздел ниже. Вы также можете отправить нам сообщение на facebook.

Ментальная математика – БУДЬТЕ ИЛИ B2: КВАДРАТ ДВУХЗНАЧНЫХ ЧИСЕЛ

Я рад представить новую функцию CompAct. Начиная с этого выпуска, мы будем включать отрывки из книги «Секреты ментальной математики: Руководство математика по вычислению молний и удивительных математических трюков» Артура Бенджамина и Майкла Шермера.Random House, Inc. любезно предоставила нам разрешение воспроизводить отрывки из этой книги каждый квартал в CompAct. Большая часть знаний, которые можно почерпнуть из этой книги, зависит от накопления определенных навыков в предыдущих главах; однако я постараюсь включить отдельные разделы. Приведенный ниже выбор включает упрощенный метод вычисления квадрата двузначного числа на основе некоторой базовой алгебры.

—Пол Рамирес, соредактор

Возведение чисел в квадрат (умножение числа на само) – одно из самых простых, но самых впечатляющих умений в уме.Я до сих пор помню, где был, когда узнал, как это делать. Мне было 13 лет, я ехал в автобусе навестить отца на работе в центре Кливленда. Я часто совершал это путешествие, поэтому мои мысли начали блуждать. Не знаю почему, но я начал думать о числах, которые в сумме дают 20, и мне стало интересно, насколько большим может быть произведение двух таких чисел?

Я начал с середины с 10 × 10 (или 10 ² ), произведение которого равно 100. Затем я умножил 9 × 11 = 99, 8 × 12 = 96, 7 × 13 = 91, 6 × 14. = 84, 5 × 15 = 75, 4 × 16 = 64 и т. Д.Я заметил, что продукты становились все меньше, и их разница от 100 составляла 1, 4, 9, 16, 25, 36,… – или 1 ² , 2 ² , 3 ² , 4 ² , 5 ² , 6 ² ,… (см. Таблицу ниже).

Числа, которые добавляют к 20		Расстояние от 10	Их продукт	Отличия товара от 100
10	10	0	100	0
9	11	1	99	1
8	12	2	96	4
7	13	3	91	9
6	14	4	84	16
5	15	5	75	25
4	16	6	64	36
3	17	7	51	49
2	18	8	36	64
1	19	9	19	81

Этот узор меня поразил. Затем я попробовал числа, которые складываются с 26, и получил аналогичные результаты. Сначала я вычислил 13 ² = 169, затем вычислил 12 × 14 = 168, 11 × 15 = 165, 10 × 16 = 160, 9 × 17 = 153 и так далее. Как и раньше, расстояния, на которые эти продукты находились 169, составляли 1 ² , 2 ² , 3 ² , 4 ² и так далее (см. Таблицу ниже).

На самом деле существует простое алгебраическое объяснение этого явления (см. Почему эти уловки работают). В то время я недостаточно хорошо знал свою алгебру, чтобы доказать, что эта закономерность всегда будет иметь место, но я экспериментировал с достаточным количеством примеров, чтобы убедиться в этом.

Затем я понял, что этот шаблон может помочь мне легче возводить числа в квадрат. Предположим, я хочу возвести в квадрат число 13. Вместо умножения 13 × 13,

Числа, которые добавляют к 26		Расстояние от 13	Их продукт	Отличия товара от 169
13	13	0	169	0
12	14	1	168	1
11	15	2	165	4
10	16	3	160	9
9	17	4	153	16
8	18	5	144	25

Почему бы не получить приблизительный ответ, используя два числа, которые легче умножить, но которые также можно добавить к 26? Я выбрал 10 × 16 = 160. Чтобы получить окончательный ответ, я просто добавил 32 = 9 (поскольку 10 и 16 – это каждые 3 от 13). Таким образом, 132 = 160 + 9 = 169. Отлично!

Схема этого метода выглядит следующим образом:

Теперь посмотрим, как это работает для другого квадрата:

Чтобы возвести в квадрат 41, вычтите 1, чтобы получить 40, и прибавьте 1, чтобы получить 42. Затем умножьте 40 × 42. Не паникуйте! Это просто замаскированная задача умножения 2 на 1 (в частности, 4 × 42). Поскольку 4 × 42 = 168, 40 × 42 = 1680. Почти готово! Все, что вам нужно сложить, это квадрат 1 (число, на которое вы поднялись или уменьшились с 41), что даст вам 1680 + 1 = 1681.

Можно ли возвести в квадрат двузначное число так просто? Да, с помощью этого метода и небольшой практики это возможно. И это работает независимо от того, округляете ли вы сначала в меньшую или большую сторону. Например, давайте рассмотрим 77 ² , вычислив его как округлением в большую, так и в меньшую сторону:

или

В этом случае преимущество округления в большую сторону состоит в том, что вы практически закончили, как только завершили задачу умножения, потому что к числу, оканчивающемуся на 0, просто прибавить 9!

На самом деле, для всех двузначных квадратов я всегда округляю в большую или меньшую сторону до ближайшего кратного 10. Итак, если число, которое нужно возвести в квадрат, оканчивается на 6, 7, 8 или 9, округляйте в большую сторону, а если число, которое нужно возвести в квадрат, заканчивается на 1, 2, 3 или 4, округляйте в меньшую сторону. (Если число заканчивается на 5, вы делаете и то, и другое!) С помощью этой стратегии вы добавите только числа 1, 4, 9, 16 или 25 к вашему первому вычислению.

Давайте попробуем другую задачу. Вычислите 56 ² в своей голове, прежде чем смотреть, как мы это сделали, ниже:

Возвести в квадрат числа, оканчивающиеся на 5, еще проще. Поскольку вы всегда будете округлять в большую и меньшую сторону на 5, оба числа для умножения будут кратны 10.Следовательно, умножение и сложение особенно просты. Мы отработали 85 ² и 35 ² , ниже:

Как вы видели в главе 0, когда вы возводите в квадрат число, оканчивающееся на 5, округление вверх и вниз позволяет сразу же выпалить первую часть ответа, а затем закончить ее числом 25. Например, если вы хотите вычислить 75 ² , округляя до 80 и до 70, вы получите «Пятьдесят шестьсот… двадцать пять!»

Для чисел, оканчивающихся на 5, у вас не должно возникнуть проблем с тем, чтобы победить кого-нибудь с помощью калькулятора, а немного потренировавшись с другими квадратами, скоро вы сможете обыграть калькулятор с любым двузначным квадратным числом.Не стоит опасаться даже большого числа. Вы можете попросить кого-нибудь дать вам действительно большое двузначное число, что-то около 90-х, и это будет звучать так, как если бы вы выбрали для вычисления невозможную задачу. Но на самом деле это еще проще, потому что они позволяют округлить до 100.

Допустим, ваша аудитория дает вам 96 ² . Попробуйте сами, а потом проверьте, как мы это сделали.

Разве не все было просто? Вы должны были округлить в большую сторону от 4 до 100 и от 4 до 92, а затем умножить 100 × 92, чтобы получить 9200.На этом этапе вы можете сказать вслух: «Девяносто двести», а затем закончить «шестнадцать» и наслаждаться аплодисментами!

Почему эти уловки работают

Этот раздел предназначен для учителей, студентов, любителей математики и всех, кому интересно, почему наши методы работают. Некоторые люди могут найти теорию столь же интересной, как и ее применение. К счастью, вам не нужно понимать, почему работают наши методы, чтобы понимать, как их применять. У всех фокусов есть рациональное объяснение, и математические фокусы ничем не отличаются.Именно здесь математик раскрывает свои самые сокровенные секреты!

В этой главе, посвященной задачам умножения, закон распределения – это то, что позволяет нам разбивать задачи на их составные части. Распределительный закон гласит, что для любых чисел a, b и c:

(b + c) × a = (b × a) + (c × a)

То есть внешний термин a распределяется или применяется отдельно к каждому из внутренних терминов b и c. Например, в нашей первой мысленной задаче умножения 42 × 7 мы пришли к ответу, рассматривая 42 как 40 + 2, а затем распределив 7 следующим образом:

42 × 7 = (40 + 2) × 7 = (40 × 7) + (2 × 7) = 280 + 14 = 294

Вы можете задаться вопросом, почему вообще действует закон о распределении.Чтобы понять это интуитивно, представьте, что у вас есть 7 сумок, каждая из которых содержит 42 монеты, 40 из которых золотые и 2 серебряные. Сколько всего у вас монет? Есть два способа прийти к ответу. Во-первых, по самому определению умножения есть монеты 42 × 7. С другой стороны, есть золотые монеты 40 × 7 и серебряные монеты 2 × 7. Следовательно, всего у нас есть (40 × 7) + (2 × 7) монет. Ответив на наш вопрос двумя способами, мы получаем 42 × 7 = (40 × 7) + (2 × 7). Обратите внимание, что числа 7, 40 и 2 можно заменить любыми числами (a, b или c), и применима та же логика.Вот почему действует закон распределения!

Используя аналогичные рассуждения для золотых, серебряных и медных монет, мы можем получить:

(b + c + d) × a = (b × a) + (c × a) + (d × a)

Следовательно, чтобы решить задачу 326 × 7, мы разбиваем 326 на 300 + 20 + 6, а затем распределяем 7 следующим образом: 326 × 7 = (300 + 20 + 6) × 7 = (300 × 7) + (20 × 7) + (6 × 7), которые затем складываем, чтобы получить ответ. Что касается возведения в квадрат, следующая алгебра оправдывает мой метод. Для любых чисел A и d

A2 = (A + d) × (A – d) + d ²

Здесь A – возведенное в квадрат число; d может быть любым числом, но я выбрал расстояние от A до ближайшего числа, кратного 10. Следовательно, для 77 ² я установил d = 3, и наша формула говорит нам, что 772 = (77 + 3) × (77 – 3) + 32 = (80 × 74) + 9 = 5929. Следующее алгебраическое соотношение также работает, чтобы объяснить мой метод возведения в квадрат:

(z + d) ² = z ² + 2zd + d ² = z (z + 2d) + d ²

Следовательно, в квадрате 41 мы устанавливаем z = 40 и d = 1, чтобы получить:

41 & sup2 = (40 + 1) 2 = 40 × (40 + 2) + 1 ² = 1681

Аналогично (z – d) ² = z (z – 2d) + d ²

Чтобы найти 77 ² , когда z = 80 и d = 3,

77 & sup2 = (80–3) ² = 80 × (80–6) + 3 ² = 80 × 74 + 9 = 5929

Как возвести двузначные числа в квадрат в голове

Купить сейчас

Как партнер Amazon и книжный магазин.org, QDT зарабатывает на соответствующих покупках.

Несколько дней назад мой друг спросил, видел ли я когда-нибудь в голове трюк для вычисления квадратов двузначных чисел. В свое время я видел много умственных математических уловок, но оказалось, что по какой-то причине я никогда раньше не сталкивался с этим. После того, как мой друг показал мне, как это работает – и увидев, насколько это быстро, легко и совершенно круто, – я убедился, что это уловка, которую должны увидеть поклонники математики во всем мире.Именно поэтому я собираюсь показать это вам сегодня.

Обзор: что такое идеальные квадраты?

Мы уже много раз говорили о возведении чисел и точных квадратов в квадрат, поэтому всем, кто следит за ними некоторое время, следует быть в курсе. Но на всякий случай, если вы немного запутались, краткое изложение состоит в том, что возведение числа в квадрат – это просто процесс умножения этого числа на само себя. И в результате получается число, которое называется идеальным квадратом. Таким образом, квадрат 5 равен 5 x 5, что равняется идеальному квадрату 25.

Есть ли способ быстро возвести 2-значные числа в квадрат?

Хотя легко вычислить в уме квадраты однозначных чисел, таких как 5 (поскольку эти квадраты являются частью базовой таблицы умножения, которую мы узнали много лун назад), перемножить двузначные числа в уме не так просто. . Или… на самом деле… это так? Как вы думаете: если бы я попросил вас быстро найти квадрат числа вроде 32, вы бы смогли это сделать? По правде говоря, вероятно, нет, но это просто потому, что ты не знаешь трюка, который показал мне мой друг.Пришло время открыть вам этот математический секрет.

Как возвести в квадрат 2-значные числа, заканчивающиеся на 5

Давайте начнем с особого случая возведения в квадрат двузначного числа, заканчивающегося на 5. Например, что такое квадрат 35? Что ж, оказывается, что результат возведения в квадрат любого двухзначного числа, заканчивающегося на 5, начинается с числа, которое вы получаете, умножая первую цифру числа, которое вы возводите в квадрат, на следующую наивысшую цифру и заканчивается числом 25. Что означает, что ответ на 35 x 35 должен начинаться с числа 3 x 4 = 12 (так как 3 – первая цифра в 35, а 4 – следующее число больше 3) и заканчиваться числом 25.Итак, как вы можете проверить вручную (просто чтобы убедиться, что это работает!), Ответ на 35 x 35 составляет 1225.

Как насчет квадрата 75? Что ж, ответ должен начинаться с 7 x 8 = 56 и заканчиваться 25. Значит, 5625, не так ли? Как вы можете проверить вручную или с помощью калькулятора, это так! И, как вы можете проверить с остальными двузначными числами, оканчивающимися на 5, этот трюк всегда работает – мысленно возвести в квадрат двузначные числа, оканчивающиеся на 5, – это несложно. Но что, если число не заканчивается на 5?

Мысленно возвести в квадрат двузначные числа, оканчивающиеся на 5, – это несложно.

Как возвести в квадрат любое двузначное число в голове

Возвести в квадрат любое двузначное число, скажем, 32 x 32, немного сложнее. У нас нет времени вдаваться в подробности того, почему это работает прямо сейчас, но первый шаг – вычислить расстояние (точнее абсолютное значение) от числа, которое вы возводите в квадрат, до ближайшего кратного десяти. В нашем примере ближайшее кратное от 10 до 32 равно 30, а расстояние между 32 и 30 равно 2. Если вместо этого вы возведете 77 в квадрат, ближайшее кратное 10 будет 80, а расстояние между 80 и 77 равно 3. Теперь, когда мы вычислили это расстояние, все, что нам нужно сделать, чтобы найти ответ на проблему, – это умножить число, которое мы получим, когда мы вычтем это расстояние из исходного числа, на число, которое мы получим, когда добавим это расстояние к исходное число, а затем прибавьте к результату квадрат расстояния.

Я знаю, это звучит глупо, но на самом деле не так уж и плохо. В нашем примере метод говорит, что 32 x 32 должны быть равны 30 (это исходное число минус расстояние 2) умножить на 34 (это исходное число плюс расстояние 2) плюс 4 (это квадрат расстояния 2).Другими словами, 32 x 32 = (30 x 34) + 4. Подождите, это на самом деле выглядит более сложным! Чем именно лучше? Поскольку, если вы используете тот факт, что 30 = 3 x 10, чтобы упростить задачу умножения (например, 30 x 34 = 3 x 10 x 34 = 3 x 340 = 1020), теперь эту задачу легко решить! Немного потренируйтесь, и вы увидите, что прелесть этого метода в том, что он превращает одну проблему, которую трудно решить в вашей голове, в несколько простых.

Практические задачи

Чтобы убедиться, что вы понимаете, как все это работает, давайте выполним пару практических задач.Я начну с того, что покажу вам еще один рабочий пример, а затем оставлю вас, чтобы вы испробовали все остальное на себе.

1. 77 х 77 = 5929 Расстояние от 80 до 77 равно 3, поэтому 77 x 77 = (74 x 80) + 9 = (8 x 10 x 74) + 9 = (8 x 740) + 9 = 5,920 + 9 = 5,929

2. 21 х 21 = _____

3. 54 х 54 = _____

4. 98 х 98 = _____

Заключение

Хорошо, это все математические вычисления, на которые у нас есть время.Не забудьте стать поклонником Math Dude на Facebook, где вы найдете новые популярные числа или математические головоломки, публикуемые каждый будний день. И если вы в Твиттере, подпишитесь на меня и там. Наконец, если у вас есть вопросы по математике, не стесняйтесь присылать их мне через Facebook, Twitter или по электронной почте [email protected] com.

До следующего раза это Джейсон Маршалл с «Быстрые и грязные советы по упрощению математики» из «Чувака по математике». Спасибо за чтение, любители математики!

2- и 3-значное умножение

В этом посте мы расскажем о , чтобы узнать, как умножать на двузначные и трехзначные числа .

Прежде чем мы начнем, давайте рассмотрим, что такое члены умножения :

• Факторы: Факторы – это числа, которые умножаются.
• Произведение: Произведение является результатом умножения.
• Множаемое: Множаемое – это число (множитель), которое умножается.
• Множитель: Множитель – это число (множитель), на которое вы умножаете.

Обычно первым записывается множитель с большим числом цифр.Обычно множимое больше множителя.

Теперь посмотрим, что такое шага, чтобы умножить на двузначные и трехзначные числа.

Первый шаг: Умножьте цифру единиц нижнего множителя (множителя) на верхний множитель (множимое) и запишите результат в строке ниже.

Давайте посмотрим на пример. Если мы умножаем 781 x 95, первое, что нужно сделать, это умножить на 5, что находится в разряде единиц 95, на каждую из цифр верхнего множителя справа налево и поместить результат 3905 на строку ниже, как показано на изображении.

Второй шаг: Умножьте цифру в разряде десятков нижнего множителя на верхний множитель и напишите результат в строке ниже, но поставьте 0 в разряде единиц, так как эта часть умножения является числом десятков. Продолжим пример. Теперь мы умножаем 9, учитывая, что оно находится в разряде десятков нижнего множителя 95, на верхний множитель 781. Результат, 7029, должен быть записан под 3905, но перемещен на одну позицию влево.

Третий этап: Добавьте продукты.Как мы видим на изображении, мы складываем продукты, и результат умножения равен 74,195.

Если нижний коэффициент (множитель) представляет собой трехзначное число , то за результатом умножения разряда сотен будут два 0. Давайте посмотрим на другой пример. Если мы умножаем 367 x 251, первое, что нужно сделать, – это умножить цифру в разряде единиц 251, то есть 1, на 367. Результатом будет 367, и мы поместим его в строку ниже.

После того, как мы умножим цифру в разряде десятков 251, то есть 5, на 367.Результатом будет 1835, и мы поместим его в строку ниже, после чего поставим 0 вместо единиц.

Затем мы умножаем цифру в разряде сотен 251, то есть 2, на 367. Результатом будет 734, и мы помещаем его в строку ниже, за которой следует 0 в разрядах десятков и 0 в разрядах единиц. место.

Наконец, мы производим сложение, и получаем результат 92,117.

Если вы хотите попрактиковаться в умножении на 2- и 3-значные числа и заняться более элементарной математикой, попробуйте Smartick бесплатно!

Подробнее:

Развлечение – любимый способ обучения нашего мозга

Дайан Акерман

Smartick – увлекательный способ изучения математики

• 15 веселых минут в день
• Адаптируется к уровню вашего ребенка
• Миллионы учеников с 2009 года

Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.

Энтузиаст математики показывает, как быстро умножать двузначные числа в уме

Игра с числами может дать потрясающие, хотя иногда и сомнительные результаты. Математика привела к развитию технологий и прогресса в том виде, в каком мы их знаем. Итак, это навык, которому должен научиться каждый.

В наши дни у каждого есть калькулятор, например, с мобильного телефона.

Однако изучение новых математических трюков может быть интересным. Это также отличный способ произвести впечатление на друзей.

Pexels – Каролина Грабовская Источник: Pexels – Каролина Грабовская

Вот простой способ умножить двузначные числа до 100.

Давайте заставим этот мозг работать. Что 21 умножить на 31?

Конечно, 651. У вас есть калькулятор! И если вы не использовали его, а вместо этого полагались на силу в своей голове, примите наши поздравления!

YouTube – tecmath Источник: YouTube – tecmath

Вот tecmath с классным трюком для решения уравнения без использования калькулятора.

Умножьте первые две цифры вместе. Итак, это 2, умноженное на 3. Это просто, это 6. Поставьте пробел после 6 и умножьте последние две цифры, которые равны 1 на 1. В результате вы должны увидеть 6_1. Ты понял?

Посмотрите, как он теперь получает среднюю цифру.

YouTube – tecmath Источник: YouTube – tecmath

Вам нужно будет умножить 1 на 2 и 1 на 3. Сложите два ответа, 2 и 3, чтобы получить в сумме 5. Получается 651.

Вот еще один.

Он вычисляет 43 х 21 =?

На этот раз нет ничего постыдного. Есть ли у вас калькулятор или нет, посмотрите, что у вас получится. 903?

YouTube – tecmath Источник: YouTube – tecmath

Мы берем 4 из 43 и 2 из 21. В результате 4 x 2 = 8. Далее следует еще один пробел, за которым следуют 3 из 43 и 1 из 21, что дает 3 x 1 = 3.

Это та же уловка. 4 из 43 и 1 из 21, умножьте получится 4.Тогда 3 из 43 плюс 2 из 21 будет 3 x 2 = 6. У вас есть 4 и 6. Когда вы сложите их все, вы получите в сумме десять.

Но нельзя ставить 10 между 8 и 3.

YouTube – tecmath Источник: YouTube – tecmath

Вставьте ноль между числами 8 и 3. Как показано в его примере, возьмите 1 и прибавьте его к 8, чтобы получить 9.

Вот и все, 903.

Один из зрителей по имени Джим Си выражает благодарность.

«Мне 38 лет, и я не очень хорошо разбираюсь в математике.Я ни в чем не виню себя. Я просмотрел несколько ваших видео и узнал по математике больше, чем за последние 36 лет моего образования. Вы развлекаете меня с математикой. Единственное, что меня сейчас сдерживает, – это мысленная математика и выполнение ее в голове. Но я над этим работаю. Спасибо!”

Мы тоже должны быть!

Третий пример можно найти на Tecmath.

Я уверен, что вы уже освоили это, но ради обучения попробуйте этот.

YouTube – tecmath Источник: YouTube – tecmath

42, умноженное на 63. Становится выше, а?

Возьмите ответ и оставьте место. Начнем с 4 x 6 = 24. Затем 2 x 3 = 6, что дает нам 24_6.

Мы размножаемся по схеме, которую он нам показал еще раз. 4 x 3 равно 12, а 2 x 6 равно 12. Сложите оба вместе, так что 12 + 12 = 24.

Поместите 4 между 24 и 6, затем сложите 2 и 4, чтобы получить 6. Правильный ответ: 2 646.

YouTube – tecmath Источник: YouTube – tecmath

Я понимаю, о чем вы думаете.Не все хорошо разбираются в математике, хотя у всех есть телефоны с калькуляторами. Но в том-то и дело. Зачем быть обычным, когда можно быть необычным?

Вот еще три примера, над которыми вы можете поработать.

Пригласите своих детей или друзей попробовать и решить эти задачи!

YouTube – tecmath Источник: YouTube – tecmath

Вы знали, кто стоит за этим трюком?

Ведет энтузиаст математики Джош.

«Ученики, обучающиеся наглядно, оценят этот канал на YouTube, который раскрывает принципы математики с помощью удобоваримых клипов, примеров и анимаций.”

Tecmath помогает зрителям изучать геометрию, тригонометрию, статистику и многое другое!

Посмотрите видео ниже, чтобы увидеть классный математический трюк!

Пожалуйста, ПОДЕЛИТЕСЬ этим со своими друзьями и семьей!

Источники: YouTube – tecmath, AMSER

5 советов по ускорению умственного умножения

Теперь, когда мы изучили основы молниеносного умственного сложения, умственного вычитания и умственного умножения, пора обратить наше внимание на несколько советов, которые помогут вам поднять свои навыки на новый уровень.

Сегодня мы собираемся начать с изучения 5 советов, которые помогут вам быстро умножать числа в своей голове и стать волшебником умственной математики в своей семье.

Совет №1: Умножение на 5 степеней
Бывают в жизни моменты, когда просто везет. Оказывается, один из тех счастливых моментов случается каждый раз, когда вам нужно умножить одно число на другое, которое оказывается степенью 5. Например, скажем, вам нужно найти 36 x 5 (что, конечно, , отвечает всем требованиям, поскольку 5 – это первая степень числа 5).2 это конечно. Так как же это работает в этом случае? Уловка здесь состоит в том, чтобы распознать, что 25 = 100/4. И вообще, уловка со степенями 5 состоит в том, чтобы распознать, что они всегда кратны 10, деленному на целое число. Это говорит нам, что 36 x 25 = 36 x 100/4. Поскольку мы можем быстро вычислить, что 36 x 100 = 3600, легко найти, что 36 x 25 = 3600/4 = 900.

Совет № 2: возведение чисел в квадрат, заканчивающиеся на 5
На этом наше веселье с пятерками не заканчивается.