Трюки для простого умножения чисел
1. Умножение на 10, 100, 1000 и т.д.
По-моему, это самый простой трюк. Для того, чтобы получить результат умножения числа на 10, нужно к этому числу дописать 0 (нолик) справа.
Например:
15 · 10 = 150
372 · 10 = 3720
Если умножаем на 100, 1000 и другие подобные числа, то просто дописываем справа столько же нулей:
15 · 100 = 1500
15 · 1000 = 15000…
5789 · 1000 = 5789000
27 · 10000 = 270000
2. Умножение на 11
Для того, чтобы умножить любое двухзначное число на 11, нужно сложите две цифры этого числа вместе и поместить их сумму посередине.
Например:
13 · 11 = 1(1+3)3 = 143
54 · 11 = 5(5+4)4 = 594
Если сумма двух цифр равняется двухзначному числу (10 или более), нужно прибавить это число к левой цифре.
Например:
29 · 11 = 2(2+9)9 = 2(11)9 = (2+1)19 = 319
65 · 11 = 6(6+5)5 = 6(11)5 = (6+1)15 = 715
88 · 11 = 8(8+8)8 = 8(16)8 = (8+1)68 = 968
3. Умножение на 5
Если нужно посчитать по-быстрому, то разделите Ваше число на 2, а затем умножьте то, что получилось на 10.
Например:
628 · 5 = 628 : 2 · 10 = 314 · 10 = 3140
2460 · 5 = 2460 : 2 · 10 = 1230 · 10 = 12300
4261 · 5 = 4261 : 2 · 10 = 2130,5 · 10 = 21305
4. Умножение на 4
Умножение на
Например:
52 · 4 = 52 · 2 · 2 = 104 · 2 = 208
133 · 4 = 133 · 2 · 2 = 266 · 2 = 532
5. Возведение в квадрат чисел, оканчивающихся на 5
Например, 152 = 15 · 15.
Казалось бы, сложная штука, но есть специальный прием для упрощения:
Берем число, стоящее перед цифрой 5 (в нашем случае единица), прибавляем к нему 1 (получаем два) и перемножаем
Несколько примеров:
35 · 35 = (3 · (3+1))25 = (3 · 4)25 = 1225
85 · 85 = (8 · (8+1))25 = (8 · 9)25 = 7225
125 · 125 = (12 · (12+1))25 = (12 · 13)25 = 15625
6. Деление на 5
Эта операция делается обратно операции умножения на 5. Берем число, умножаем его на 2, затем делим на 10.
Например:
250 : 5 = 250 · 2 : 10 = 500 : 10 = 50
340 : 5 = 340 · 2 : 10 = 680 : 10 = 68
351 : 5 = 351 · 2 : 10 = 702 : 10 = 70,2
7. Извлечение квадратного корня
Выполняется путем примерного подбора.
Возьмем число 576 и попробуем извлечь из него корень.
Для начала определим к какому десятку относится искомое число:
10 · 10 = 100
20 · 20 = 400
30 · 30 = 900
Значит наше число лежит между числами 20 и 30.
Идем дальше, число 576 оканчивается на 6. Наша цель подобрать однозначное число, квадрат которого оканчивается
1 · 1 = 1
2 · 2 = 4
3 · 3 = 9
4 · 4 = 16 (подходит)
5 · 5 = 25
6 · 6 = 36 (подходит)
7 · 7 = 49
8 · 8 = 64
9 · 9 = 81
Итак, нам подошли 4 и 6. значит наше число это или 24 или 26. Проверка дает нам 24 · 24 = 576.
Нашли!
Давайте разберем еще один пример: 4489
Если 30 · 30 = 900 – это маловато.
Возьмем 60 · 60 = 3600 – уже ближе.
70 · 70 =
4900 – а это уже больше. Значит больше, чем 60, но меньше, чем 70.
Теперь подберем вторую цифру, которая в квадрате оканчивается на 9. Для этого воспользуемся табличкой выше.
Из нее мы видим, что на девять оканчивается 3 · 3 = 9 и 7 · 7 = 49. Значит подходят 63 и 67.
Так как наше число находится ближе к числу 4900, чем к числу 3600, то искомое число почти на 100% является числом 67.
Проверяем 67 · 67 = 4489.
Ура!
Ничего сложного, зато сколько сэкономили времени!
На этом пока все, если знаете еще какие-то комбинации легких вычислений, пишите в комментариях!
И не забывайте, что вычисления в уме тренируют Ваш мозг и не дают ему засохнуть!
Устный счет – раскрываем секреты гибкого ума
Люди, обладающие неординарными способностями, всегда вызывают восхищение.
Чаще всего мы склоны приписывать удивительные навыки природным способностям. На самом деле, это не всегда так. Ведь многим вещам можно просто обучиться и затем привыкнуть применять на практике. Классический устный счет является довольно важным элементом общего развития. Хорошее освоение вполне ординарных методик позволит значительно ускорить многие вычислительные операции. Секреты устного счета могут быть полезны абсолютно всем – от домохозяек и школьников до менеджеров серьезных компаний.
Устный счет можно осуществлять быстро
Если под рукой нет калькулятора, то можно воспользоваться несколькими приемами упрощения таких вычислительных операций, как сложение, вычитание, умножение и деление.
Навыки быстрого счета чрезвычайно полезны. Не многие люди могут производить вычислительные операции одновременно правильно и быстро.
С целью понимания потребности людей в быстром счете
социологи провели опрос. Людям задавали такой вопрос: «Зачем надо уметь быстро
считать?».
- Чтобы подсчитывать денежные расходы.
- Для хорошей учебы.
- Для изучения многих наук (математика, физика, химия).
При этом, все опрошенные указали, что они либо не владеют секретами, упрощающими устный счет, либо не применяют техники быстрых вычислений на практике.
Как научиться быстро считать
Существует несколько очень простых и эффективных приемов, упрощающих устный счет. Пожалуй, самым интересным и простым приемом является секрет таблицы умножения чисел первого десятка на девять:
Считать нужно, применяя пальцы обеих рук. К примеру, нам нужно вычислить значение операции 5х9. Для этого нужно развернуть ладони к себе и загнуть 5-й палец. Если считать, начиная слева, то им будет мизинец на левой руке.
Четыре пальца, которые окажутся слева от загнутого – это десятки, а пальцы, оказавшиеся справа (все пальцы правой руки) – единицы искомого числа 45.
Эта операция работает во всех случаях, когда требуется
какое-то число до 10 умножить на 9.
Для умножения чисел второго десятка применяется способ разложения. Для примера, проведем умножение числа 15 на 13. Простой и понятный алгоритм выглядит так:
- Разложим число 13 на 10 и 3.
- К 15 добавим количество единиц числа 13 (это 3). Получим 18.
- Умножим 18 на 10 – получим 180.
- Перемножим между собой единицы числа 15 (это 5) и 13 (это 3). Результат перемножения (это 15) прибавим к 180.
- Искомое число – 195.
Еще несколько способов быстрого умножения
Как быстро считать, не используя калькулятор и приемы умножения в столбик? Еще несколько полезных правил от наших репетиторов по математике:
- Любое двузначное число, кроме 10 легко умножить
на 11. Для этого надо раздвинуть двузначное число и вставить между его цифрами
сумму его цифр. Например, необходимо умножить число 45 на 11. Получаем 4 (4+5)
5. Результатом будет 495. Посложнее будет умножить 89 на 11, потому что мы
получаем: 8 (8+9)9. Если сумма цифр выше 9, то к сотням добавляем 1, а
оставшееся число будет вторым в итоговом результате.
- При умножении на двузначные числа, кроме 11, вида аа (когда цифра десятков и единиц совпадает), то существует очень удобный способ вычислений. О состоит из двух этапов: а) нужно представить число вида аа в виде множителей, где одним из множителей является 11: 22=2х11, 55=5х11. б) затем найти произведение числа, которое надо умножить, на тот множитель, который отличается от 11; в) использовать схему умножения на 11, рассмотренную выше. Пример 1: 35х22==35х2х11=70х11=770. Пример 2: 21х33=21х3х11=63х11=693. Пример 3: 18х44=18х4х11=72х11=792.
Разобраться, как быстро считать, займет у пытливого ума немного времени. Зато потом вычисления будут проще и интереснее.
Как быстро считать в уме при умножении и делении на 5, 25, 50, 125
Гибкий ум анализирует особенности различных чисел и
применяет к ним свои правила упрощения вычислений. К слову, все предлагаемые
секреты устного счета были разработаны математиками, которые, ввиду отсутствия
компьютеров, вынуждены были производить множество сложнейших операций на
бумаге.
Гибкость ума – первейшее требование для математика.
Предлагаем несколько правил быстрого счета на числа, включающие «5». Для этого воспользуемся способами разложения чисел:
Ах5=Ах10:2
Ах50=Ах100:2
Ах25=Ах100:4
Ах125=Ах1000:8
Согласно таким правилам, вычислим следующие выражения: 28х5=28х10:2=140, 36х50=36х100:2=1800, 36Х25=36х100:4=900, 64х125=64х1000:8=8000.
Чтобы разделить на эти же числа, их нужно представить в виде операции умножения:
А:5 = Ах2:10
А:50 = Ах2:100
А:25=Ах4:100
Произведем расчеты: 450:5=450Х2:10=90, 4800:50=4800х2:100=96, 2800:25=2800х4:100=70.
Быстрый счет по приведенным нами правилам – всего лишь, небольшая часть из огромного багажа весьма интересных возможностей.
Устный счет — зачем он нужен
Гибкий ум тренируется в изучении логики приведенных процессов. А использование правил того, как быстро считать в уме, будет полезным в практической жизни:
- Поможет в развитии аналитических способностей.
- Будет подспорьем в решении многих задач без подручных средств, как калькулятор.
- Позволит производить несложные расчеты в уме при решении бытовых вопросов.
В общем, секреты быстрого счета предоставляют огромные возможности. Чтобы познакомиться со всеми правилами и развить гибкий ум, читайте книги наблюдайте за цифрами, анализируйте получаемые результаты.
Возможно, вы откроете огромное количество собственных способов быстрого счета. А наши репетиторы по математике знают не менее 100 приемов быстрого счета. И могут этому научить.
в столбец и в уме
Как быстро умножать большие числа, как овладеть такими полезными навыками? У большинства вызывает затруднения устное перемножение двузначных чисел на однозначные. А о сложных арифметических расчетах и говорить нечего. Но при желании способности, заложенные в каждом человеке, можно развить. Регулярные тренировки, немного усилий и применение, разработанных учеными, эффективных методик позволят достичь потрясающих результатов.
Выбираем традиционные методы
Проверенные десятилетиями способы перемножения двузначных чисел не теряют своей актуальности. Простейшие приемы помогают миллионам обычных школьников, учащихся специализированных ВУЗов и лицеев, а также людям, занимающимся саморазвитием, усовершенствовать вычислительное мастерство.
Умножение с помощью разложения чисел
Наиболее легким способом, как быстро научиться умножать большие числа в уме, является перемножение десятков и единиц. Сначала умножаются десятки двух чисел, затем поочередно единицы и десятки. Четыре полученных числа суммируются. Для использования этого метода важно уметь запоминать результаты перемножения и складывать их в уме.
Например, для умножения 38 на 57 необходимо:
- разложить число на (30+8)*(50+7) ;
- 30*50 = 1500 – запомнить результат;
- 30*7 + 50*8 = 210 + 400 = 610 – запомнить;
- (1500 + 610) + 8*7 = 2110 + 56 = 2166
Естественно, необходимо отлично знать таблицу умножения, так как быстро умножать в уме этим способом не удастся без соответствующих умений.
Умножение в столбик в уме
Визуальное представление привычного перемножения в столбик многие используют при расчетах. Этот метод подойдет тем, кто умеет надолго запоминать вспомогательные числа и выполнять с ними арифметические действия. Но процесс значительно упрощается, если вы научились, как быстро умножать двузначные числа на однозначные. Для перемножения, например, 47*81 нужно:
- 47*1 = 47 – запомнить;
- 47*8 = 376 – запоминаем;
- 376*10 + 47 = 3807.
Запоминать промежуточные результаты поможет проговаривание их вслух с одновременным суммированием в уме. Несмотря на сложность мысленных вычислений, после непродолжительных тренировок этот метод станет вашим любимым.
Приведенные выше способы умножения универсальны. Но знание более эффективных алгоритмов для некоторых чисел намного сократит количество расчетов.
Умножение на 11
Это, пожалуй, самый простой способ, который используется для умножения любых двузначных чисел на 11.
Достаточно между цифрами множителя вставить их сумму:
13*11 = 1(1+3)3 = 143
Если в скобках получается число больше 10, то к первой цифре добавляется единица, а из суммы в скобках вычитается 10.
28*11 = 2 (2+8) 8 = 308
Умножение больших чисел
Очень удобно перемножать числа, близкие к 100 разложением их на составляющие. Например, необходимо умножить 87 на 91.
- Каждое число необходимо представить как разницу 100 и еще одного числа:
(100 – 13)*(100 – 9)
Ответ будет состоять из четырех цифр, две первые из которых – разница первого множителя и вычитаемого из второй скобки или наоборот – разница второго множителя и вычитаемого из первой скобки.
87 – 9 = 78
91 – 13 = 78 - Вторые две цифры ответа – результат перемножения вычитаемых из двух скобок.13*9 = 144
- В результате получаются числа 78 и 144. Если при записывании окончательного результата получается число из 5 цифр вторую и третью цифру суммируем. Результат: 87*91 = 7944 .
Результат: 87*91 = 7944 .Это самые простые способы перемножения. После многократного их применения, доведения вычислений до автоматизма можно осваивать более сложные техники. И через некоторое время проблема, как быстро умножить двузначные числа перестанет вас волновать, а память и логика существенно улучшатся.
Родители школяров очень часто сталкиваются с довольно сложной проблемой: как помочь ребенку выучить таблицу умножения? Таблицу Пифагора дети изучают во втором классе начальной школы. В этом возрасте отлично работает механическая память, поэтому многие просто «зазубривают» материал. Но не всем детям удается выучить таблицу умножения таким способом. Сегодня в Интернете представлен исчерпывающий список различных методик, позволяющих с комфортом для ребенка и с особым вниманием к его индивидуальным особенностям выучить таблицу умножения.
Существуют различные способы запоминания таблицы Пифагора: пословицы-поговорки, стихи, песни, сказки, игры, а также различные визуальные материалы.
Однако, какой бы вы не выбрали путь изучения, стоит помнить одно: ребенок должен понять сам принцип таблицы умножения!
Это важно! На тот момент, когда ваш ребенок приступит к изучению таблицы умножения,он уже будет знать логику такого арифметического действия, как сложение. Прежде всего, стоит объяснить ребенку сам процесс умножения. К примеру, 3 умножить на 4 означает сложить число 3 четыре раза или 3+3+3+3. Применяйте ассоциации, пусть это будет не просто число 3, а три машины или три куклы. Ребенок должен хорошопонимать само арифметическое действие – умножение. Если вы объясните ребенку, что, по сути, умножение – это краткая запись сложения указанного количества одинаковых слагаемых.
Только после того, как ребенок поймет суть арифметического действия, приступайте к изучению самой таблицы.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Изучаем таблицу умножения вместе с ребенком
Научите ребенка разбираться в таблице Пифагора.
Объясните, что при умножении числа из левого крайнего столбца на любое из чисел получается их произведение, которое находится на пересечении искомых строки и столбца. Когда ребенок научится без труда ориентироваться в самой таблице, необходимо приступать к самому главному-заучиванию самой таблицы.
Играючи запоминаем таблицу умножения!
К сожалению, очень многим детям довольно сложно со всей ответственностью подойти к вопросу заучивания таблицы. Гораздо проще вести обучения, используя при этом элемент игры. Детям будет гораздо легче запоминать ту информацию, которая по-настоящему покажется им интересной.
Довольно простой и действенной игрой является занятие с карточками. Нарисуйте или распечатайте вместе с ребенком различные варианты примеров из таблицы умножения вида:
- 3х7=?
- 2х4=?
- 5х8=?
Начинайте тренировку. Те карточки, на которые ребенок ответил без труда и с первого раза, откладывайте в сторону.
Примеры, вызвавшие у вашего школьника затруднение, откладывайте в низ стопки, чтобы потом ребенок смог вытянуть их снова. Продолжайте игру до тех пор, пока ваш ученик не даст ответ на все вопросы. Такую викторину можно проводить ежедневно, к примеру, после ужина. Не нужно заставлять ребенка или ругать его за неправильные ответы. Придумайте вместе особое поощрение, которое ждет вашего сына или дочь, если те ответят на все вопросы абсолютно верно.
Вариантов такой игры можно придумать великое множество. К примеру, ваш ребенок выучил все примеры умножения на 2 и 3. Сделайте вместе с малышом только эти карточки, а после разбавляйте их новыми. Еще одним вариантом лучшего заучивания таблицы может быть составление карточек вида:
- 3х?=15
- ?х2=6
- 10х?=10
Это интересно! Включите свое воображение! Ребенку будет гораздо проще, а главное, интереснее запоминать материал, если карточки с примерами будут яркими и красочными. Вместо скучных вопросов появятся веселые зверушки или любимые сказочные герои малыша.
Пофантазируйте, и тогда ваш ребенок будет с удовольствием угадывать, какое число спрятано за спиной благородного Кота в сапогах или смешного Карлсона.
Заучиваем таблицу умножения с ребенком – основные правила!
Чтобы ребенку было не сложно заучивать таблицу Пифагора, а полученная информация не превратилась в кашу, требуется соблюдать несколько простых правил:
- Увидев таблицу Пифагора, даже самый смышленый малыш может напугаться. Объясните ребенку, что в понимании этой информации нет ничего сложного, и в свое время, и мама и папа, и бабушка и дедушка, учили эту таблицу.
- Выучите сначала простое умножение, к примеру, на единицу. Объясните своему малышу, что при умножении на 1, всегда получается то же число, что мы умножали на единицу. К примеру, 1х1=1, 5х1=5, 10х1=10 и т.д. Умножение на десять также нетрудно донести до ребенка: это, то же самое, что каждый раз приписывать ноль к числу. К примеру, 2х10=20, 3х10=30. Главное – чтобы ассоциация с появлением нуля у числа отложилась у ребенка в голове, и он мог решать примеры не только на бумаге, но и в уме.
- Когда вы выучили и повторили наиболее простые примеры, начинайте продвигаться с малышом далее по таблице.
- После каждого заучивания арифметического действия – умножения на 2,3,4,5,6 и т.д. не забывайте повторять с ребенком пройденный материал (можно в виде игры, которая была описана выше).
- Очень часто ребенок, выучив умножение на 2, начинает теряться, если взрослый спрашивает его: « сколько будет 2х5»? В такой ситуации нужно быть внимательным, объясняя ученику коммуникативное правило умножения: при перемене мест множителей произведение не меняется.
Пальчиковые игры – учим таблицу умножения весело!
Есливашему ребенку непросто дается изучение таблицы умножения. Можно задействовать пальчики юного счетовода. Отличным примером будет изучение умножения на 9. Пусть ребенок положит обе руки на стол, ладонями вниз. Каждый пальчик будет означать число от одного до десяти. К примеру, мы хотим умножить 9 на 4. Считаем слева направо до 4 – получается указательный палец левой руки.
Загибаем его, и считаем число пальчиков слева. Их всего 3 – это десятки. Чисто пальчиков справа – 6 – единицы. Ответ 36. Такой вариант запоминания привнесет в процесс обучения капельку волшебства, и ваш юный счетовод обязательно увлечется столь интересным процессом обучения.
Игра в ассоциации
У многих детей хорошо развита моторная и образная память, поэтому им легче будет запомнить табличные примеры при помощи различных ассоциаций. К примеру, цифра 2 похожа на лебедя, а цифра 1 на гнома с любопытным носом. Например, на случай умножения 2х1=2 можно придумать следующую историю: Один прекрасный лебедь был очень одинок. Он так хотел найти себе друга, что искал его везде-везде. И вот однажды он встретил гнома со смешным крючковатым носом. Однако, гном был очень хитрый и коварный, что лебедь еле спасся от него. Так и остался лебедь в гордом одиночестве…
Таких рассказов можно придумать великое множество. Пусть ребенок сам пофантазирует, главное, чтобы история объединяла двух персонажей-множителей, а произведение было логическим завершением этого сюжета.
Чем эмоциональней и увлекательней будут истории, тем ребенку будет проще запомнить тот или иной пример.
Как только причинно-следственные связи при помощи сказки будут отработаны, можно вычленить самое главное: «Лебедь встретил гномика, подружился ли он с ним или остался один?» Если ваш ребенок все ответил правильно, тогда необходимо попросить его составить данный пример в числах.
Стихи, песни, рассказы
Такой способ запоминания таблицы умножения подойдет детям, которые отлично запоминают стихи и песни. Детям можно предложить заучивание примеров из таблицы умножения при помощи стихов. Отличным вариантом являются произведения А. Усачева «Умножение» и М. Казариной «Про умножение». Таким образом, решая тот или иной пример, ребенок будет проводить ассоциацию с рифмованной строчкой.
Как бы вы не объясняли ребенку таблицу умножения, главное – никогда не сердиться на своего малыша, если ему что-то непонятно! Проявите терпение, а также свое воображение, и тогда ваш ребенок с удовольствием будет учить таблицу умножения!
В определенный момент перед родителями обязательно встанет вопрос: как быстро выучить таблицу умножения ребенку ? Сам он с этой задачей не справится, нужна помощь взрослых.
А еще – правильно выбранные методы запоминания.
Азы обучения
Чтобы помочь ребенку быстро выучить таблицу умножения, лучше всего сначала объяснить ему суть этого действия. Понятие о сложении и вычитании он уже имеет. Поясняем, что 2 умножить на 2 – это значит сложить две двойки, то есть 2+2.
Можно и более сложные примеры привести: 3 умножить на 4 означает сложить тройку 4 раза – 3+3+3+3.
Хорошо свои объяснения подкреплять реальными, понятными ребенку примерами: «Дедушка принес 2 набора фломастеров тебе и Ксюше. В каждом по 5 штук. А всего сколько фломастеров получится? Как будем считать: 5 плюс 5 или 2 умножим на 5? И так, и так получим 10».
Игровые приемы
Как быстро выучить таблицу умножения ребенку? Конечно, использовать игровые наглядные приемы. Берем коробку и мячики. Кладем их в коробку парой. Потом следующие два мячика, затем еще и еще. Получилось вот так:
Методы изучения таблицы умножения
Быстро выучить таблицу умножения ребенку помогут разные методы.
Дело в том, что кто-то из деток хорошо заучивает цифры просто механическим путем (в этом возрасте такой тип памяти у них развит достаточно неплохо).
Кому-то понадобится визуальное подкрепление: видеосюжеты, рисунки, эмоциональная подпитка, хорошо работают игровые приемы и такие средства, как онлайн-игры и стихи.
Таблица умножения – с чего начать?
Ребенку нужно объяснить, как устроена таблица Пифагора: есть числа в столбиках и в строчках, а там, где они пересекаются, ищем ответ – произведение чисел, например, шесть на восемь будет сорок восемь (6×8=48).
Можно начинать изучение таблицы с обычного ее варианта. Сразу объясните ребенку – не стоит пугаться того, что она такая большая на первый взгляд. Многие примеры там уже известны и не требуют запоминания.
Например, умножение на 1 и на 10. Что значит умножить число на 1 – взять его 1 раз. Два так и останется двойкой, четыре – четверкой и так далее. То есть число не изменится. А умножать на 10 тоже просто – всего лишь добавить нолик к цифре: 5×10=50.
Умножаем на 2, на 5 и учим квадраты чисел
Как быстро выучить таблицу умножения ребенку – запоминать вначале более простые варианты. Умножать на 2 детям обычно не трудно. Это как к числу прибавить еще одно такое же.
После этого можно выучить, как умножать на 5. Ответы будут заканчиваться или на 0 (четные числа) или на 5 (нечетные).
Следующий этап – запоминание квадратов чисел. Без повторения и закрепления здесь не обойтись. Ребенку предстоит просто запомнить, что 8 на 8 — это 64, а 9 на 9 – 81.
Обычно с умножения на 3 начинаются первые сложности. Здесь пора вводить дополнительные методы запоминания – визуальные приемы, например, игры в карточки или ассоциации с использованием стихов. О них – чуть ниже.
Как умножать на 6, 7, 8 и 9
Этот этап самый сложный, и некоторые примеры нужно просто запомнить. Повторять эти несколько самых трудных произведений вместе с ребенком придется постоянно, пока цифры не дойдут до автоматизма.
Главное, показать ребенку, что он уже знает практически всю таблицу, а остались сущие пустяки.
Вот эти коварные значения, которые так трудно запоминать:
6×7=42
6×8=48
6×9=54
7×8=56
7×9=63
8×9=72
О перемене сомножителей
Взрослым-то понятно, что 4х3=3х4. А вот ребенку нужно объяснить, что если поменять местами сомножители, результат не изменится.
Тогда вашему ученику будет гораздо проще вспомнить, сколько будет, к примеру, 7 на 4. Если забыл, пусть вспомнит умножение 4 на 7. Это важный момент в изучении таблицы умножения.
Разные методики изучения таблицы умножения
Разнообразие способов изучения таблицы умножения помогает найти подходящий именно вашему ребенку.
Карточки для запоминания
Всякие онлайн-игры в Интернете тоже способствуют запоминанию, но самым надежным и проверенным остается визуальный метод, использующий карточки для запоминания.
Изготовьте карточки с примерами: например, на одной стороне пишите 7х8, а на другой – ответ. Как играем – ребенок берет карточку, отвечает на вопрос и переворачивает, чтобы посмотреть ответ.
Ответил правильно – оставляет карточку себе, если нет – берет другую карточку. Побеждает тот, у кого наберется больше карточек. В процессе игры происходит повторение и запоминание, но в веселой игровой форме.
Один из подобных вариантов – цифровое лото. В карточки вписываете ответы из таблицы, изготавливаете карточки с заданиями-примерами. Игровой процесс стимулирует запоминание.
Умножаем на пальцах
Есть такой способ счета – на пальцах. Подходит для умножения на 9. Нужно опустить руки вниз ладонями и выпрямить пальцы. Нам нужно умножить 7 на 9. Загибаем 7-й по счету палец и смотрим – количество пальцев до него будет равно десяткам в ответе – 6, а после 7-го пальчика – единицам, то есть трем. Получаем 63.
Для умножения на 9 есть еще один интересный метод. Нужно умножить заданное число, к примеру 6, на 10 (6 на 10 = 60). А теперь отнимем 6, получится 54.
Повторение – залог запоминания
Чтобы ребенку было легче запоминать, сделайте ему наглядные пособия.
Он должен постоянно видеть примеры перед глазами и повторять их. Можно ярко и красочно оформить таблицу и повесить ее в детской комнате и на кухне. Так информация будет запоминаться легче.
Обучающие стихи
Многим деткам, особенно гуманитариям, гораздо легче запоминать таблицу, используя стихотворную форму. Самые известные подобные стихи написали Марина Казарина и Александр Усачев:
Пять на шестерку умножаем,
В итоге ТРИДЦАТЬ получаем.
И пятью семь – легко считать —
Ответ короткий: ТРИДЦАТЬ ПЯТЬ!
Раз олень спросил у лося:
— Сколько будет семью восемь? —
Лось не стал в учебник лезть:
— Пятьдесят, конечно, шесть!
Мультфильмы для запоминания
Если задаться целью, то можно найти массу интересных мультов в помощь изучающим азы умножения. Дети всегда хорошо воспринимают такую форму подачи материала, так что мы советуем активно ее использовать. Пример – в этом видео:
Забирай себе, расскажи друзьям!
Читайте также на нашем сайте:
Показать еще
Думаете, изображать людей на бумаге сложно, и это искусство доступно только одаренным? Ничего подобного! Мы расскажем, как нарисовать человека, разбив процесс на этапы и максимально упростив его.
Следуя нашей инструкции, изобразить homo sapiens сможет даже ребенок.
1:506
Все родители рано или поздно оказываются в непростой ситуации, выход из которой найти бывает достаточно трудно. Эта проблема возникает, когда ребенку нужно помочь выучить таблицу умножения.
1:863 1:868
Родителям данная проблема знакома с детства, но раньше справиться с ней было намного сложнее. Ведь современный интернет предоставляет в помощь родителям и детям разнообразные методы освоения таблицы Пифагора, помогающие в игровой форме запомнить таблицу умножения. Для занятий с ребенком в интернете можно найти стишки, песенки, видео и аудио-уроки, сценарии игр, что может помочь облегчить задачу родителей и детей в этом непростом деле.
1:1679
Но среди предложенных способов родителям предстоит выбрать наиболее подходящий и эффективный именно для их ребенка, так как каждый ребенок требует индивидуального подхода к обучению, поэтому применяемые методики должны опираться на особенности характера и способности ребенка.
1:520 1:525
В представленной статье проанализированы наиболее популярные методики запоминания таблицы умножения, среди которых каждый из родителей найдет подходящий для своего ребенка.
1:853 1:858
Изначально следует акцентировать внимание на том, что ребенку необходимо объяснить смысл арифметического действия умножения.
2:1608
2:4
Как известно, дети, приступающие к изучению таблицы умножения, уже имеют представление о таких самых простых арифметических действиях как сложение и вычитание.
2:304
Именно на эти знания ребенка следует опираться при разъяснении ему принципа умножения, то есть, что арифметическое действие 2х3 тождественно примеру 2+2+2.
2:590 2:595
Нужно добиться, чтобы ребенок усвоил данное правило, что поможет преодолеть все возможные сложности, возникающие в ходе запоминания примеров таблицы.
2:877 2:882
Также необходимо растолковать ребенку какова система таблицы умножения, о том, что число, находящееся в левом столбце умножается на число, расположенное на верхней строчке, при этом ответ – их произведение нужно искать в точке пересечения столбца и строки, где находятся данные числа.
2:1409
Игра
Всегда нужно помнить о том, что даже самое скучное и нудное дело для ребенка можно превратить в интересное занятие, скрасив его игрой. Изучение таблицы умножения – не исключение. В этом помогут игровые методики, которые привлекут внимание ребенка к обучению, раскроют смысл умножения и облегчат задачу родителей. При занятиях с ребенком следует придерживаться правила о том, что интересное всегда запомнить проще и быстрее, то есть изначально нужно заинтересовать ребенка предметом изучения и сконцентрировать его внимание на арифметическом действии умножения.
7 правил запоминания информации
2:2599
- Пробудите интерес.
- Делайте ассоциации.
- Запоминайте частями.
- Повторяйте запомнившееся.
- Попытайте понять.
- Поставьте цель «запомнить».
- Примените знание данной информации.
Например, пять умножить на восемь равно сорок (5×8=40)
2:446
3:958
Это один из наиболее востребованных и эффективных методов запоминания таблицы умножения с помощью игры. В данной статье раскрывается суть игры и последовательность действий.
Карточки, на которых приведены примеры и их ответы
3:1431 3:1436
Смысл игровой таблицы умножения сводится к тому, что ребенку нужно предложить доставать из пачки в случайном порядке карточки, на которых он обнаружит пример из таблицы умножения без ответа, то есть после знака «равно» стоит вопросительный знак. Если ребенок озвучит верный ответ, то данная карточка больше не участвует в игре, но при неверном ответе карточка кладется между другими карточками и ребенок сможет вытянуть ее вновь.
3:2230 3:4
Таким образом, игра длится до тех пор, пока ребенок не переберет все карточки и не даст по всем карточкам правильные ответы. Когда игра приближается к концу остается совсем мало карточек и они, чаще всего, оказываются самыми сложными, на которые ребенок не смог ответить с легкостью. Если в конце игры ребенок вновь обратится к ним и попробует найти правильный ответ, то он запомнит эти примеры.
Данная игра является фактически тренажером по таблице умножения. Игра становится интереснее и проще для освоения, если разбить ее на последовательные этапы, связанные с учебным материалом. Так, можно начать импровизированное занятие с самых простых карточек примеров умножения на 2, а далее, постепенно добавлять к ним новые более сложные освоенные примеры. Можно разработать различные варианты игры, которые можно выбрать в зависимости от способностей и знаний ребенка.
Также подкрепить игру в ходе изучения таблицы умножения помогут различные специальные программы, онлайн-игры и оригинальные звуковые плакаты, которые предлагает интернет.
Однако игра в карточки считается самой простой и результативной.
3:2052
Начиная обучение ребенка азам умножения, этот процесс могут упростить некоторые специальные приемы.
3:293 3:298
Так, необходимо начать обучение с самых простых и элементарных примеров таблицы умножения , которые ребенок решит без особых трудностей. Ведь, если ребенок сразу увидит таблицу целиком, состоящую из множества сложных примеров он может отчаяться и подумать, что выучить эту таблицу нереально. Поэтому задача родителей успокоить ребенка и показать ему, что всё на самом деле гораздо проще и что он сразу может решить несколько несложных примеров.
1. Самые простые примеры – умножение на 1 , которые всегда в результате имеют то число, на которое умножали. Так, 1х1=1, 2х1=2 и так далее.
2. Также простыми являются примеры умножения на 10 , так как это то же самое что приписать ноль к числу, которое умножается.
Так, результатом умножения 3 на 10 будет 30.
Таким образом, выучив самые простые примеры таблицы умножения на 1 и на 10, ребенок поймет, что он уже освоил самые крайние столбцы и строки таблицы умножения.
3:1974
4:505 4:512
Родителям следует уметь правильно распределять нагрузку ребенка и если он устал после первого этапа обучения, то следует отложить дальнейшее занятие на следующий раз. Но в случае, когда ребенок готов сейчас продолжать обучение можно попробовать продолжить занятие.
4:1122
3. На первых этапах занятия мы убедились, что примеры умножения на 2 являются самыми простыми для ребенка , так как тождественны простому сложению двух чисел. Обычно, дети, начинающие изучение таблицы умножения, уже обладают навыками складывания чисел, поэтому простые примеры умножения на 2 освоят легко.
4:1687
4.
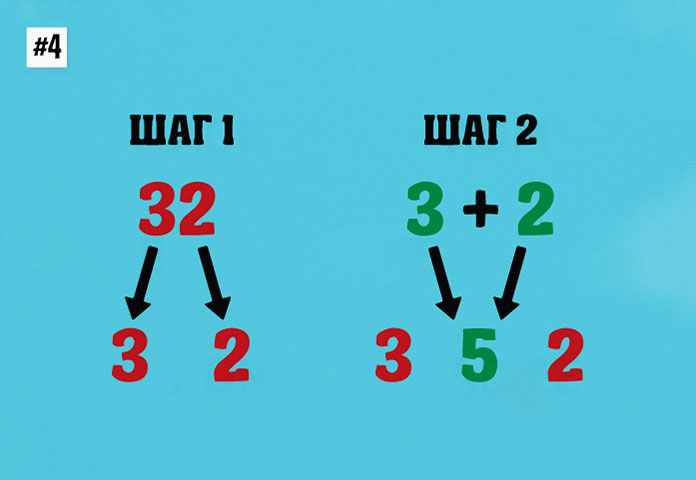Следующий этап изучения таблицы умножения будет связан с правилом о замене множителя, основанный на переместительном законе умножения,
который может быть понятен родителям, но весьма сложен для ребенка. Это закон хорошо знаком родителям, потому что они уже когда-то сталкивались с ним в процессе школьного обучения. Он гласит – от перемены множителей произведение не меняется. Иными словами, ребенку следует объяснить, что пример 2х4 тождественен примеру 4х2.
4:854
Ребенку необходимо доходчиво разъяснить, каким образом получилось так, что вторая строка и второй столбец таблицы имеют одни и те же числа, как и все остальные строки и столбцы, совпадающие по порядковому номеру.
4:1303 4:1308
Таким образом, ребенок, зная все примеры умножения на 2, будет знать умножение всех чисел таблицы на 2, то есть задача ребенка предельно упрощается.
4:1580
Исходя из этого, в результате применения представленных методов изучения таблицы умножения, родители могут существенно облегчить задачу ребенка в процессе запоминания многочисленных примеров таблицы умножения.
4:399 4:404
Завершая каждый этап обучения, в результате которого ребенком выучено определенное количество примеров, родителям рекомендуется выделять их в таблице зеленым цветом, чтобы ребенок четко видел свои достижения и убедился в том, что ничего нереального в запоминании таблицы умножения нет, и она ему не будет представлять такой огромной и непостижимой, как вначале занятий.
5:1606
После освоения ребенком азов умножения и самых простых примеров таблицы следует переходить к следующим этапам обучения с более сложными множителями.
5:335 5:340
На этом этапе необходимо применять не только игровые приемы, но и различные эффективные приемы запоминания, основанные на ассоциациях, на методе повторения, на разделении на части, на решении проверочных задач и применение знаний ребенка на практике.
5:805 5:810
Большинство примеров таблицы ребенку придется специально заучивать и для закрепления знаний многократно повторять их для достижения такого результата, когда ребенок сможет называть примеры и правильные ответы без запинки.
Для этого необходимо терпеливо соблюдать последовательность и торопить ребенка.
5:1382 5:1387
Эффективнее всего начинать данный этап обучения с квадратов, содержащих примеры умножения на 3 и 4 , понемногу передвигаясь к следующим числам.
5:1654
Зачастую можно услышать мнение педагогов о том, что лучше и правильнее всего изучать таблицу умножения двигаясь от конца к началу, то есть от сложных примеров – к более простым.
5:331
Однако данный вариант обучение представляется достаточно сомнительным, так как он может быть эффективен не для каждого ребенка, так как определенные трудности могут быть связаны с растерянностью ребенка в связи с непониманием того, каким образом получились те сложные значения, которые он видит в ответах к примерам.
5:920 5:925
Поэтому начинать нужно с примера 3х3, при решении которого, ребенок сможет самостоятельно проверить себя, посчитав пример на пальцах, в результате чего ребенку станет понятно, каким образом в ответе получается число 9.
Если же ребенку дать задание умножить, например, 8 на 7 и потребовать, чтобы он просто зазубрил правильный ответ, то это может просто напугать ребенка невозможностью проверки данного примера на практике, а в результате сокрытия от него самого процесса решения ребенок может утратить мотивацию и интерес к обучению, так как посчитает, что у него нет способностей к математике.
5:2016
На следующем этапе обучения понадобится знание и применение данного термина. Ребенку следует объяснить, что он означает произведение числа на самого себя. Таблица умножения содержит 10 квадратов, необходимые для запоминания. Практика показывает, что квадраты до примера 6х6=36 запоминаются детьми просто прекрасно. Следующие за ним 3 квадрата также чаще всего не представляют особых сложностей.
5:765
С данного этапа начинаются трудности у ребенка при запоминании примеров из таблицы. При возникновении трудностей такого плана следует обратиться к игре с карточками.
Однако если даже эти приемы окажутся неэффективными, например, из-за того, что у ребенка гуманитарный склад ума, то можно использовать для запоминания специальные стишки, которые в простой форме представят ребенку примеры из таблицы.
5:1558
При изучении примеров из таблицы умножения на 4 вероятно также придется применять в занятиях карточки и стихи . Чтобы упростить ребенку задачу следует объяснить ему, что умножение на 4 – всё равно, что умножение 2 раза на 2.
5:471
Этот этап изучения таблицы умножения проходит обычно без трудностей, так как примеры на 5 запоминаются достаточно просто. Ребенку следует объяснить, что все значения данного ряда умножения находятся через 5 по отношению друг к другу, а крайним числом будет или 5 или 0, также, что умножая четные числа на 5, в результате с краю получаем 0, а умножая нечетные – с краю получаем 5.
5:1214
Умножение на 6,7, 8 и 9 считаются самыми сложными для запоминания.
Поэтому на данном этапе ребенку необходимо объяснить, что после того как он выучил квадраты и таблицу умножения до 5, ему предстоит приложить совсем немного усилий, ведь все последующие примеры он, фактически, уже выучил.
5:1817
5:8 5:13
Итак, ребенку осталось выучить самые сложные примеры из таблицы умножения, их 6 и именно им следует уделить особое внимание, сделать последний рывок и выполнить до конца данное задание.
5:440
6×7=42
6×8=48
6×9=54
7×8=56
7×9=63
8×9=72
5:625
Чтобы их запомнить эффективнее всего обратиться к игре в карточки для того, чтобы ребенок мог дать ответ на любой пример не задумываясь. При этом лучше всего использовать в игре 12 карточек, содержащие произведения с переменой мест множителей.
Таким образом, применяя специальные методики и приемы можно быстро и просто выучить таблицу умножения, которая изначально казалась детям и родителям непостижимой для запоминания.
5:1415
Очевидно, что одного конкретного метода изучения таблицы умножения, подходящего для всех, не существует. Ведь проводя занятия с ребенком, необходимо подходить к ним индивидуально, исходя из подготовки ребенка и его характера.
5:1930
Поэтому родителям следует овладеть несколькими методиками и знать не один способ запоминания таблицы умножения, чтобы выбрать подходящий для своего ребенка.
5:296
Вот некоторые из них.
Применение на практике
Обучение будет более простым и эффективным, если все примеры из таблицы умножения проиллюстрировать ребенку на практике.
5:629
Например, изучая примеры на 5 мальчику можно задать вопрос сколько колес понадобится для 5 машин. Так, ребенок представит машину с четырьмя колесами и успешно запомнит пример 5×4=20. У девочки можно спросить сколько ленточек потребуется, чтобы сделать трем куклам по два хвостика.
С помощью такой иллюстрации ребенок запомнит, что 3х2=6.
Сложные примеры
В ходе изучения таблицы умножения у ребенка могут возникнуть некоторые проблемы при попытке запоминания самых сложных примеров, на которых следует акцентировать внимание ребенка и помочь ему их выучить, тем самым преодолеть самые трудные этапы задания.
5:1765
6:515
Запоминание таблицы умножения с помощью пальцев
Для упрощения процесса запоминания отдельных произведений из таблицы умножения можно подсказать ребенку, что их можно посчитать с помощью пальцев.
6:898
При этом, примеры, которые можно посчитать таким способом могут быть не только самыми простыми, но и, например, из умножения на 9. Для этого понадобятся обе руки. Следует загибать при умножении любого числа на 9 выпрямленные пальцы под номером умножаемого числа.
Таким образом, количество пальцев до загнутого – это десятки, а после него – единицы.
Для начала нужно сделать две вещи: распечатать саму таблицу умножения и объяснить принцип умножения.
Для работы нам понадобится таблица Пифагора. Раньше её публиковали на обороте тетрадей. Выглядит она так:
Также вы можете увидеть таблицу умножения в таком формате:
Так вот, это не таблица. Это просто столбики из примеров, в которых невозможно найти логические связи и закономерности, поэтому ребёнку приходится учить всё наизусть. Чтобы облегчить ему работу, найдите или распечатайте настоящую таблицу.
2. Объясните принцип работы
psyh-olog.ru
Когда ребёнок самостоятельно находит закономерность (например, видит симметрию в таблице умножения), он запоминает её навсегда, в отличие от того, что он вызубрил или что ему сказал кто-то другой. Поэтому постарайтесь превратить изучение таблицы в интересную игру.
Приступая к изучению умножения, дети уже знакомы с простыми математическими действиями: сложением и умножением.
Вы сможете объяснить ребёнку принцип умножения на простом примере: 2 × 3 – то же самое, что 2 + 2 + 2, то есть 3 раза по 2.
Объясните, что умножение – это короткий и быстрый путь провести вычисления.
Дальше нужно разобраться с устройством самой таблицы. Покажите, что числа из левого столбика умножаются на числа из верхней строки, а правильный ответ – на месте их пересечения. Найти результат очень просто: нужно только провести рукой по таблице.
3. Учите небольшими порциями
ytimg.com
Не нужно пытаться за один присест выучить всё. Начните с колонок 1, 2 и 3. Так вы постепенно подготовите ребёнка к усвоению более сложной информации.
Хорошая методика: взять пустую распечатанную или нарисованную таблицу и самостоятельно её заполнить. На этом этапе ребёнок будет не запоминать, а считать.
Когда он разобрался и достаточно хорошо усвоил самые простые столбцы, переходите к числам посложнее: сначала к умножению на 4–7, а затем на 8–10.
4. Объясните свойство коммутативности
blogspot.com
То самое известное правило: от перестановки множителей произведение не меняется.
Ребёнку станет понятно, что на деле ему нужно выучить не всю, а только половину таблицы, и некоторые примеры он уже знает. Например, 4 × 7 – то же самое, что 7 × 4.
5. Находите закономерности в таблице
secretwomans.ru
Как мы уже говорили ранее, в таблице умножения можно обнаружить множество закономерностей, которые упростят её запоминание. Вот некоторые из них:
- При умножении на 1 любое число остаётся тем же.
- Все примеры на 5 оканчиваются на 5 или 0: если число чётное, приписываем 0 к половине числа, если нечётное – 5.
- Все примеры на 10 оканчиваются на 0, а начинаются с числа, на которое мы умножаем.
- Примеры на 5 вполовину меньше, чем примеры на 10 (10 × 5 = 50, а 5 × 5 = 25).
- Чтобы умножать на 4, можно просто дважды удваивать число. Например, чтобы умножить 6 × 4, нужно удвоить 6 два раза: 6 + 6 = 12, 12 + 12 = 24.
- Чтобы запомнить умножение на 9, запишите ряд ответов в столбик: 09, 18, 27, 36, 45, 54, 63, 72, 81, 90. Запомнить нужно первое и последнее число. Все остальные можно воспроизвести по правилу: первая цифра в двузначном числе увеличивается на 1, а вторая уменьшается на 1.
Например, чтобы умножить 6 × 4, нужно удвоить 6 два раза: 6 + 6 = 12, 12 + 12 = 24.6. Повторяйте
medaboutme.ru
Чаще занимайтесь повторением. Сначала спрашивайте по порядку. Когда заметите, что ответы стали уверенными, начинайте спрашивать вразброс. Следите и за темпом: сначала давайте побольше времени на размышление, но постепенно увеличивайте темп.
7. Играйте
utahpubliceducation.org
Пользуйтесь не только стандартными методами . Обучение должно увлекать, интересовать ребёнка. Поэтому используйте наглядные средства, играйте, применяйте разные методики.
Карточки
Игра проста: подготовьте карточки с примерами умножения без ответов.
Перемешайте их, а ребёнок должен вытягивать по одной. Если он даёт правильный ответ, откладываем карточку в сторону, неправильный – возвращаем в стопку.
Игру можно разнообразить. Например, давать ответы на время. И каждый день подсчитывать количество правильных ответов, чтобы у ребёнка появилось желание побить свой вчерашний рекорд.
Играть можно не только на время, но и до тех пор, пока не кончится вся стопка примеров. Тогда за каждый неправильный ответ можно поручать ребёнку задание: рассказать стихотворение или прибрать вещи на столе. Когда же все карточки разгаданы, вручить небольшой подарок.
От обратного
Игра похожа на предыдущую, только вместо карточек с примерами вы готовите карточки с ответами. Например, на карточке написано число 30. Ребёнок должен назвать несколько примеров, которые в результате дадут 30 (например, 3 × 10 и 6 × 5).
Примеры из жизни
Обучение становится интереснее, если обсуждать с ребёнком вещи, которые ему нравятся. Так, у мальчика можно спрашивать, сколько колёс нужно четырём машинам.
Также можно использовать наглядные средства: палочки для счёта, карандаши, кубики. Например, возьмите два стакана, в каждом из которых по четыре карандаша. И наглядно покажите, что количество карандашей равно количеству карандашей в одном стакане, помноженному на количество стаканов.
Стихи
Рифма поможет запомнить даже сложные примеры, которые никак не даются ребёнку. Самостоятельно придумывайте незамысловатые стихи. Подбирайте самые простые слова, ведь ваша цель – упростить процесс запоминания. Например: «Восемь медведей рубили дрова. Восемью девять – семьдесят два».
8. Не нервничайте
Обычно в процессе некоторые родители забываются и совершают одни и те же ошибки. Вот список вещей, которые нельзя делать ни в коем случае:
- Заставлять ребёнка , если он не хочет. Вместо этого пытайтесь его мотивировать.
- Ругать за ошибки и пугать плохими оценками.
- Ставить в пример одноклассников. Когда тебя с кем-то сравнивают, это неприятно. К тому же нужно помнить, что все дети разные, поэтому к каждому нужно найти правильный подход.
- Учить сразу всё. Ребёнка легко напугать и утомить большим объёмом материала. Учитесь постепенно.
- Игнорировать успехи. Хвалите ребёнка, когда он справляется с заданиями. В такие моменты у него появляется желание учиться дальше.
Умножение на 11 – Математика 3-го класса
Вы проделали большую работу, изучив умножение от 1 до 10.
Давайте повторим
Умножение любого числа на 1 ‘ число не меняется.
8 x 1 = 8
К умножьте число на 10 , просто прибавьте к
8 0 0 , и в конце ответ!
5 х 10 = 5 0
Так что же такое 6 х 10?
Верно! Это 60!
Умножение на 11
Есть несколько способов умножения на 11.
Чтобы получить , умножьте число на 11 , вы можете пропустить счет на это число 11 раз!
Это довольно медленно, но давайте попробуем:
7 x 11 = ?
Это сокращение для записи:
7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7
Мы можем пропустить счет в уме, чтобы получить ответ:
7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77
А теперь научимся фокусу!
Секретный трюк номер 1
Чтобы умножить любое однозначное число, например, 5 или 3, на 11, просто продублируйте цифру , и это ваш ответ.
😀 Дублировать означает скопировать или написать заново.
Итак, используя трюк, мы видим, что:
7 x 11 = 77
3 x 11 = 33
Это намного быстрее, чем считать 11 раз. 👍
Секретный трюк номер 2
Теперь, вот трюк для умножение 11 на 2 – цифры чисел.
11 x 12 = ?
Во-первых, добавьте две цифры числа, которое не равно 11.
👉 Цифры для 12 это 1 и 2.
Давайте сложим их.
1 + 2 = 3
😀 Далее, поместите этот ответ между двумя цифрами вашего номера.
👉 Опять же, наш номер 12 и его цифры 1 и 2.
Если мы поместим наш ответ между этими двумя цифрами, что мы получим?
Получаем 132! 👏
Давайте проверим нашу таблицу умножения и посмотрим, получили ли мы правильный ответ.
Сделали!
🤔 Почему этот трюк работает?
Умножение на 11
Умножение на 11 равносильно умножению на 10 и прибавлению к этому числу еще одного.
Например:
11 x 15 = 10 x 15 + 15
11 x 15 = 1 6 5
🤔 Видите, что 5 + 16 равно 16?
👉 Это так, потому что вы добавляете число 10 раз к самому себе!
Всякий раз, когда вы умножаете любое двузначное число на 11, вы в конечном итоге складываете первую и вторую цифры и кладете их в середину, чтобы получить ответ!
Так что же такое 11 х 42?
Просто добавьте 1-ю и 2-ю цифры 42:
4 6 2!
Отличная работа! 🎉
Теперь завершите практику! 💪 Это поможет вам дольше помнить то, что вы узнали.
Кратность 11 – Что такое кратность 11? [Решено]
УзнатьПрактикаСкачать
Число, кратное 11 – это целое число. Они являются произведением n натуральных чисел и 11. Другими словами, мы можем сказать, что числа, кратные 11, — это числа, которые можно разделить на 11 без остатка. Мы можем создать n число, кратное 11, просто умножив 11 на n натуральных чисел. Определить число, кратное 11, очень просто.
В этом мини-уроке мы вычислим числа, кратные 11, и узнаем некоторые интересные факты об этих кратных.
- Первые пять кратных 11 : 11, 22, 33, 44 и 55
- Разложение числа 11 на простые множители : 11 = 1 × 11
| 1. | Сколько кратно 11? |
| 2. | Первые 20 кратных 11 |
| 3. | Советы и рекомендации |
| 4. | Часто задаваемые вопросы о числах, кратных 11 |
Сколько кратно 11?
Интересно отметить, что первые 9 кратных 11 могут быть удобно получены и очень легко запоминаются.
Когда 11 умножается на любое однозначное натуральное число, произведение этого натурального числа записывается дважды. Например, 11 × n = nn; здесь n – натуральное число. Таким образом, мы получили первые девять кратных 11.
- 11 × 1 = 11
- 11 × 2 = 22
- 11 × 3 = 33
- 11 × 4 = 44
- 11 × 5 = 55
- 11 × 6 = 66
- 11 × 7 = 77
- 11 × 8 = 88
- 11 × 9 = 99
Следовательно, Первые девять малистов из 11 – 11, 22, 33, 44, 55, 66, 77, 88 и 99.
Первые 20 -кратные из 11
Первые 20 200256 числа, кратные 11 – это те числа, которые мы получаем в результате умножения натуральных чисел от 1 до 20 на 11. Мы только что получили первые 9 кратных 11. Давайте попробуем небольшой трюк, чтобы получить кратные 11 для натуральных чисел 10–20. . Первые 20, кратные 11 , также можно получить с помощью метода подсчета пропусков. Чтобы вычислить числа, кратные 11 для двузначных чисел, возьмите сумму цифр числа и поместите сумму между двумя цифрами исходного двузначного числа.
Например, когда 11 умножается на 10, возьмите сумму 1 и 0, то есть 1. Теперь поместите сумму 1 между 1 и 0. Получившееся число равно 110. Произведение 11 и 10 равно 110, т. е. 11 × 10 = 110. Будьте осторожны при умножении 11 × 19.используя этот трюк. Первые 20 кратных 11 перечислены в таблице ниже.
| Первые 20 кратных 11 | |
|---|---|
| 11 × 1 = 11 | 11 × 11 = 121 |
| 11 × 2 = 22 | 11 × 12 = 132 |
| 11 × 3 = 33 | 11 × 13 = 143 |
| 11 × 4 = 44 | 11 × 14 = 154 |
| 11 × 5 = 55 | 11 × 15 = 165 |
| 11 × 6 = 66 | 11 × 16 = 176 |
| 11 × 7 = 77 | 11 × 17 = 187 |
| 11 × 8 = 88 | 11 × 18 = 198 |
| 11 × 9 = 99 | 11 × 19 = 209 |
| 11 × 10 = 110 | 11 × 20 = 220 |
Чтобы понять концепцию поиска кратных, давайте возьмем еще несколько примеров.
- Кратные 12. Первые пять кратных 12: 12, 24, 36, 48 и 60.
- Кратность 3 — первые пять кратных 3 равны 3, 6, 9, 12 и 15.
- Кратность 10. Первые пять чисел, кратных 10, равны 10, 20, 30, 40 и 50.
- Число, кратное 14. Первые пять чисел, кратных 14, равны 14, 28, 42, 56 и 70.
- Число, кратное 13. Первые пять чисел, кратных 13, равны 13, 26, 39, 52 и 65.
Советы и подсказки:
- При умножении 11 на любое натуральное число, состоящее из одной цифры, произведение этого натурального числа записывается дважды.
- Чтобы вычислить кратность 11 для двузначных чисел, возьмите сумму цифр числа и поместите сумму между двумя цифрами полученного произведения.
Пример 1: Помогите Xin найти сумму первых 9 кратных 11. Укажите, кратно ли полученное число 11 или нет.
Решение :
Первые 9 кратных 11 = 11, 22, 33, 44, 55, 66, 77, 88 и 99.
Сумма 9кратные 11 = 11 + 22 + 33 + 44 + 55 + 66 + 77 + 88 + 99 = 495
495 — это 45 th , кратное 11.Пример 2: Найти первые 5 нечетных чисел, кратных 11.
Решение :
Чтобы определить первые пять нечетных чисел, кратных 11, нам нужно умножить 11 на нечетные числа.
11 × 1 = 11
11 × 3 = 33
11 × 5 = 55
11 × 7 = 77
11 × 9 = 99
Первые пять нечетных чисел, кратных 11, равны 11, 33, 55, 77 и 99.
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о числах, кратных 11
Как найти числа, кратные 11?
Умножьте любое натуральное число на 11.
Например, 11 × 2 = 22
Чему равны первые 9 кратных 11?
Первые 9 кратных 11 – это 11, 22, 33, 44, 55, 66, 77, 88 и 99.
Все ли кратные 11 четные?
Нет, все числа, кратные 11, нечетные. Некоторые числа, кратные 11, четные, а некоторые нечетные.
Например, 11 × 11 = 121, 121 — это нечетное число
.
11 × 12 = 132, 132 — четное число
Чему равно наименьшее общее кратное 11 и 111?
Здесь мы должны сначала взять множители обоих чисел.
11 = 11 × 1
111= 3 × 37
Следовательно, наименьшее общее кратное чисел 11 и 111 3 × 11 × 37 = 1221
. Каковы первые 5 кратных 11?
Первые 5 кратных 11 – это 11, 22, 33, 44 и 55.
Рабочие листы по математике и
наглядный учебный план
Кратные 11 — Математика с мамой
Что такое кратные 11
- 9021 Числа, кратные 11, — это числа, которые можно разделить точно на 11. Они образуются путем умножения любого целого числа на 11.
- 1 × 11 = 11
- 2 × 11 = 22
- 3 × 11 = 33
- 4 × 11 = 44
- 5 × 11 = 55
- 6 × 11 = 66
- 7 × 11 = 77
- 8 × 11 = 88
- 9 × 11 = 99
- 10 × 11 = 110
- 11 × 11 = 121
- 12 × 11 = 132
- Начиная с первой цифры числа, добавьте каждую вторую цифру, чтобы получить общее количество.
- Начиная со второй цифры, добавьте каждую вторую цифру, чтобы получить сумму.
- Найдите разницу между двумя суммами.
- Если эта разница кратна 11 (включая 0), исходное число кратно 11.
- Если эта разница не кратна 11, исходное число не кратно 11.
Например, третье кратное 11 равно 33, потому что 3 × 11 = 33, Первые числа, кратные 11, показаны в таблице умножения на 11. Вот плакат, показывающий таблицу умножения на 11.
Первые 12 кратны 11:
При обучении числам, кратным 11, полезно показать шаблон в первых 9 кратных 11. Первые кратные 11 легко запомнить, потому что они просто повторяют одну и ту же цифру.
Как найти числа, кратные 11
Чтобы найти числа, кратные 11, умножьте любое целое число на 11. Самый простой способ сделать это — умножить число на 10, написав в конце цифру ноль, а затем прибавив еще 1 часть числа. Например, 14-е число, кратное 11, равно 154, потому что 140 + 14 = 154,9.
0489
В качестве альтернативы числа, кратные 11, можно найти, начав с 0 и прибавив одиннадцать.
0 + 11 = 11. 11 + 11 = 22. 22 + 11 = 33. 33 + 11 = 44 и так далее.
Эти числа, кратные 11, показаны ниже на числовой диаграмме. Таблица с числами может быть полезным способом обучения числам, кратным 11, потому что мы можем легко увидеть диагональный рисунок, образованный числами.
Мы видим, что каждая цифра повторяется на этом графике. Это верно только для первых 9кратно 11.
Если мы знаем число, кратное 11, мы можем легко найти следующее число, кратное 11, прибавив 11.
Из 99 имеем 99 + 11 = 110, а затем 110 + 11 = 121.
Мы видим, что после 99 числа, кратные 11, больше не повторяют свои цифры.
Двузначные числа, кратные 11, можно определить по повторению их цифр. Трехзначное число, кратное 11, можно определить, поскольку первая и последняя цифры в сумме образуют среднюю цифру.
Например, 1 + 1 = 2 в 121, что кратно 11.
Какие числа кратны от 11 до 100
Есть 9 кратных 11 до 100. Это:
11, 22, 33, 44, 55, 66, 77, 88 и 99. Все эти числа, кратные 11, содержат повторяющуюся цифру.
Вот первые кратные 11, показанные на числовой диаграмме.
Вот список первых 100 кратных 11:
11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132, 143, 154, 165, 176, 187, 198, 209, 220, 231, 242, 253, 264, 275, 286, 297, 308, 319, 330, 341, 352, 363, 374, 385, 396, 407, 418, 429, 440, 451, 462, 473, 484, 495, 506, 517, 528, 539, 550, 561, 572, 583, 594, 605, 616, 627, 638, 649, 660, 671, 682, 693, 704, 715, 726, 737, 748, 759, 770, 781, 792, 803, 814, 825, 836, 847, 858, 869, 880, 891, 902, 913, 924, 935, 946, 957, 968, 979, 990, 1001, 1012, 1023, 1034, 1045, 1056, 1067, 1078, 1089, 1100.
Правило определения числа, кратного 11
Чтобы определить, является ли число кратным 11, выполните следующие действия.
Например, вот 2937. Мы будем использовать правило, чтобы проверить, является ли это число кратным 11.
Первый шаг — начать с первой цифры и добавить каждую вторую цифру.
Первая цифра — 2. Мы пропускаем 9 и добавляем следующую цифру 3.
2 + 3 = 5.
Второй шаг — начать со второй цифры и добавить каждую вторую цифру.
Вторая цифра — 9. Мы пропускаем следующую цифру 3 и добавляем следующую цифру 7.
9 + 7 = 16.
Третий шаг — найти разницу между этими двумя суммами. Мы делаем это, вычитая меньшее число из большего числа.
16 – 5 = 11.
Если разница между суммами кратна 11, исходное число кратно 11.
Поскольку разница равна 11, исходное число делится на 11.