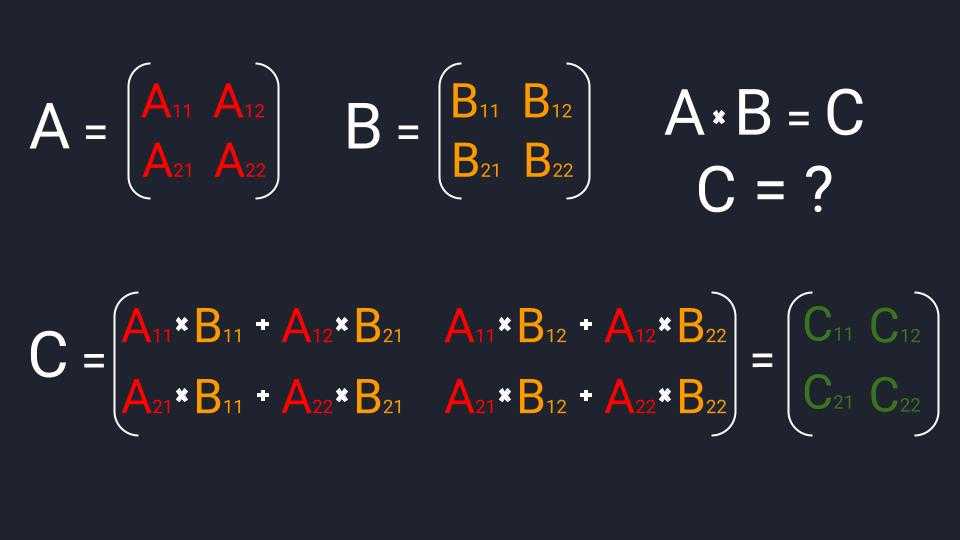[Перевод] Матричное умножение. Медленное достижение мифической цели
19:17
Balloon Fight: перенос с VS system на NES
19:17
«Ниеншанц-Автоматики» протестировало различные системы «Байкала»
21:02
KODI: собираем удобный и функциональный медиацентр для дома. Часть 4. Архив IPTV
22:17
Red Hat отказалась финансировать FSF за возврат Столлмана
22:17
Избавляемся от постоянного написания конструкторов для инжекта зависимостей с помощью C# Source Generators
19:17
[Перевод] Матричное умножение. Медленное достижение мифической цели
19:17
QGit, улучшения
19:17
Умелец попробовал майнить биткойны на Game Boy — получилось в 125 трлн раз медленнее современных устройств
19:17
Технологический журналист: как стать и куда убежать
16:32
Apollo.
На входе в плотные слои атмосферы
16:32
[Перевод] Под капотом у Emoji
В недавней работе был установлен новый рекорд скорости по умножению двух матриц. Она также знаменует и конец эпохи для метода, который ученые применяли для исследований на протяжении десятилетий.
Математики стремятся к достижению мифической цели — второй степени (exponent two), то есть к умножению пары матриц n х n всего за n2 шагов. Исследователи подбираются все ближе к своей цели, но получится ли у них когда-нибудь достичь ее?
Для специалистов в области Computer Science и математиков сама идея о «второй степени» связана с представлениями о совершенном мире.
«Трудно разграничить научное мышление и беспочвенные мечтания», — признается Крис Уманс из Калифорнийского технологического института. «Я хочу, чтобы степень была равна двум, потому что это красиво».
С точки зрения необходимого количества шагов «вторая степень» — это идеальная скорость выполнения одной из самых фундаментальных математических операций — матричного умножения. Если вторая степень достижима, то матричное умножение получится выполнять максимально быстро, насколько это физически возможно. Если это не так, то мы застряли в мире, который не соответствует нашим мечтам.
Матрицы представляют собой массивы чисел. Когда две матрицы согласованы (число столбцов в первом сомножителе равно числу строк во втором), их можно перемножить, чтобы получить третью. Например, если вы начнете с пары матриц 2×2, их произведение также будет матрицей 2×2, содержащей четыре элемента. В более общем смысле, произведение пары матриц размером n х n представляет собой другую матрицу размером n х n с n2 элементами.
Поэтому наименьшее возможное количество шагов для умножения пар матриц это n2, то есть количество шагов, необходимое просто для записи ответа. Отсюда и название «вторая степень».
И хотя никто точно не знает, можно ли этого достичь, исследователи продолжают продвигаться в этом направлении.
Статья, опубликованная в октябре, подбирается к цели еще ближе и описывает самый быстрый на данный момент метод умножения двух матриц. Результат, который получили Джош Алман, докторант Гарвардского университета, и Вирджиния Василевска Уильямс из Массачусетского технологического института, уменьшает степень предыдущего лучшего показателя примерно на одну стотысячную. Это действительно большое достижение в данной области, добытое кропотливым трудом.
Чтобы получше разобраться в этом процессе и понять, как его можно усовершенствовать, давайте начнем с пары матриц 2×2, A и B. При вычислении каждого элемента их произведения вы используете соответствующую строку из A и соответствующий столбец из B. Чтобы получить верхний правый элемент, умножьте первое число в первой строке A на первое число во втором столбце B, затем умножьте второе число в первой строке A на второе число во втором столбце B и сложите эти два произведения.
Самуэль Веласко / Quanta Magazine
Эта операция известна как получение «скалярного произведения» строки со столбцом (иногда называется «внутренним произведением»). Чтобы вычислить другие элементы в произведении матриц, повторите процедуру с соответствующими строками и столбцами.
В целом, классический метод умножения матриц 2×2 состоит из восьми умножений и нескольких сложений. Как правило, этот способ умножения двух матриц размера n х n требует n3 умножений.
С увеличением размера матриц количество умножений, необходимых для нахождения их произведения, растет намного быстрее, чем количество сложений. Чтобы найти произведение матриц 2×2 требуется всего восемь промежуточных умножений, а чтобы найти произведение матриц 4×4 их требуется уже 64. Однако количество сложений, необходимых для получения суммы этих матриц, не так значительно отличается. Обычно количество сложений равно количеству элементов в матрице, то есть четыре для матриц 2×2 и 16 для матриц 4×4.
Эта разница между сложением и умножением позволяет понять, почему исследователи измеряют скорость умножения матриц исключительно с точки зрения количества требуемых умножений.
«Умножения — это наше всё, — утверждает Уманс, — Показатель степени в итоге полностью зависит только от количества умножений. Сложения в некотором смысле исчезают».
На протяжении веков люди считали, что n3 — это самый быстрый способ умножения матриц. По имеющимся сведениям, в 1969 году Фолькер Штрассен намеревался доказать, что невозможно умножить матрицы 2×2, используя менее восьми умножений. Видимо, он все-таки не смог найти доказательства, а через некоторое время и понял почему: на самом деле, существует способ сделать это с помощью семи умножений!
Штрассен придумал сложный набор соотношений, которые позволили заменить одно из этих восьми умножений 14 дополнительными сложениями. Может показаться, что разница совершенно незначительна, но она оправдывает себя, так как умножение вносит больший вклад, чем сложение.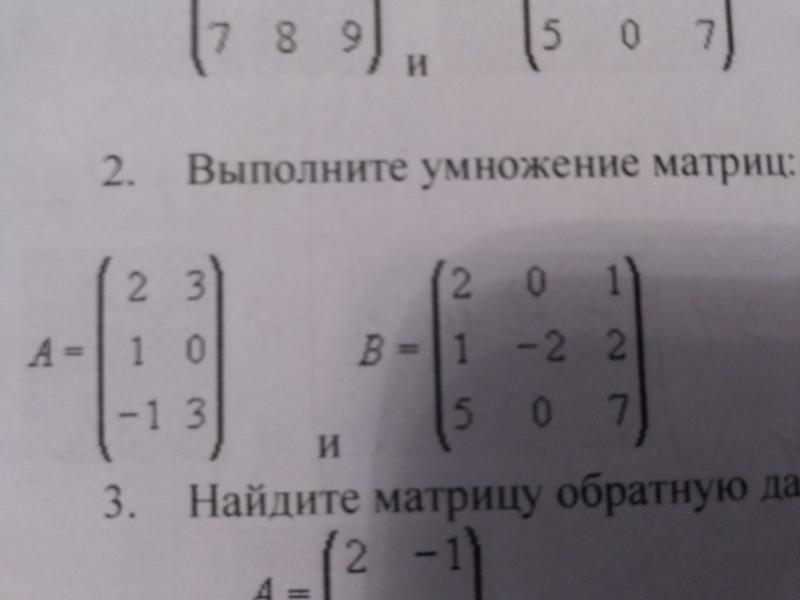
Найдя способ избавиться от одного умножения для маленьких матриц 2×2, Штрассен открыл возможность, которую он мог использовать при умножении бOльших матриц.
«Это крошечное изменение приводит к огромным улучшениям в работе с большими матрицами», — говорит Уильямс.
Вирджиния Василевска Уильямс из Массачусетского технологического института и Джош Алман из Гарвардского университета открыли самый быстрый способ перемножения двух матриц за n2.3728596 шагов. Джаред Чарни; Ричард Т.К. Хоук
Предположим, вы хотите перемножить пару матриц 8×8. Один из способов сделать это — разбить каждую большую матрицу на четыре матрицы размером 4×4 так, чтобы каждая имела по четыре элемента. Поскольку элементы матрицы также могут являться матрицами, вы можете считать исходные матрицы парой матриц 2×2, каждый из четырех элементов которых сам по себе является матрицей 4×4. Посредством некоторых манипуляций каждая из этих матриц размером 4×4 может быть разбита на четыре матрицы размером 2×2.
Смысл этого многократного разбиения больших матриц на более мелкие заключается в том, что можно снова и снова применять алгоритм Штрассена к меньшим матрицам и с помощью его метода сокращать количество шагов на каждом этапе. В целом алгоритм Штрассена увеличил скорость умножения матриц с n3 до n2.81 мультипликативных шагов.
Следующий важный шаг в развитии идеи произошел в конце 1970-х, когда появился принципиально новый подход к решению этой задачи. Он подразумевает перевод матричного умножения в другую вычислительную задачу линейной алгебры с использованием объектов, называемых тензорами. Тензоры, используемые в этой задаче, представляют собой трехмерные массивы чисел, состоящие из множества различных частей, каждая из которых выглядит как небольшая задача на умножение матриц.
Умножение матриц и эта задача, связанная с тензорами, в определенном смысле эквивалентны друг другу, но для решения последней исследователи уже имели более быстрые процедуры. Таким образом, перед ними встала задача определить «обменный курс» между ними: Матрицы какого размера можно перемножить при тех же вычислительных затратах, которые требуются для решения тензорной задачи?
«Это очень распространенная в теоретической информатике концепция: преобразовывать задачи и проводить аналогию между ними, чтобы показать, что они одинаково простые или сложные», — сказал Алман.
В 1981 году Арнольд Шёнхаге использовал этот подход, чтобы доказать, что умножение матриц возможно выполнить за n2.522 шагов. Позднее Штрассен назвал этот подход «лазерным методом» (laser method).
За последние несколько десятилетий каждое улучшение в процессе умножения матриц происходило за счет усовершенствования лазерного метода, поскольку исследователи находили все более эффективные способы трансформации задачи. В своем новом доказательстве Алман и Уильямс стирают различие между 2 задачами и показывают, что уменьшить число умножений возможно. «В целом Джош и Вирджиния нашли способ применить машинные вычисления в рамках лазерного метода и получили лучшие на настоящий момент результаты», — сказал Генри Кон из Microsoft Research.
В их статье теоретическое ограничение скорости умножения матриц улучшено до n2.3728596.
Также благодаря этому исследованию Уильямс может вернуть себе корону в области матричного умножения, которую она по праву получила в 2012 году (n2. 372873), а затем уступила в 2014 году Франсуа Ле Галлю (n2.3728639).
Но, несмотря на все эти гонки и победы, становится ясно, что в случае с этим подходом действует закон убывающей доходности, или убывающей отдачи. Скорее всего, усовершенствование Алмана и Уильямс почти полностью исчерпало возможности лазерного метода, но так и не позволило достичь конечной теоретической цели.
«Маловероятно, что получится приблизиться ко второй степени, используя это семейство методов», — отметил Уманс.
Для этого потребуется открытие новых методов и стойкая вера в то, что это вообще возможно.
Уильямс вспоминает один из разговоров со Штрассеном об этом: «Я спросила его, считает ли он, что возможно получить вторую степень для матричного умножения, и он ответил: «Нет, нет, нет, никогда!».
© Habrahabr.ru
Умножение матриц в Matlab | Как выполнить умножение матриц?
Слово «Matlab» означает лабораторию Matrix. Изначально Matlab предназначался для выполнения матричных операций.
Используя Matlab, мы можем очень легко реализовать сложные операции и задачи. Как мы знаем, в матричных операциях умножение является одной из сложных и сложных операций, но с помощью простой команды «mtimes» мы умножаем две матрицы.
Есть некоторые правила умножения матриц, как и в математике. Если матриц две, то количество столбцов первой матрицы должно быть равно количеству строк второго столбца. Предположим, что размеры первой матрицы составляют 2 строки и 3 столбца, а размеры второй матрицы — 4 строки и 3 столбца, тогда мы не можем выполнить умножение, поскольку количество столбцов в первой матрице и количество строк во второй матрице не совпадают.
Как выполнить умножение матриц в Matlab?
Существует два способа умножить матрицу на единицу с помощью оператора умножения «*». И во-вторых, с помощью команды «mtimes».
Использование оператора «*»
Чтобы сначала умножить две матрицы, нам нужны две матрицы. мы можем напрямую объявить матрицы или принять ввод от пользователя.
Вот некоторые из шагов, которые нам нужно выполнить, как указано ниже:
- Шаг 1: принять две матрицы, объявив две переменные.
- Шаг 2: назначьте 3 rd переменную для вывода и запишите оператор как матрица 1 * матрица 2.
- Шаг 3: Отображение выходных данных.
Использование команды «mtimes»
В этом методе нет необходимости в операторах, мы можем дать прямую команду входной матрице. Оператор может быть записан как mtimes (матрица 1, матрица 2)
- Шаг 1: принять две матрицы, объявив две переменные.
- Шаг 2: назначить переменную 3 rd для вывода и дать команду mtimes.
- Шаг 3: Отображение выходных данных.
Примеры выполнения умножения матриц
Ниже приведены некоторые примеры умножения матриц в Matlab:
Пример №1
Рассмотрим две матрицы mat1 и mat2, 3
3 4 2
3 2 1
мат 2 =
1 1 1
3 4 2
3 2 1
Использование оператора «*»
В следующей таблице показан приведенный выше пример с использованием оператора «*».
Редактор Matlab | Выход |
| мат1 = [ 1 2 3 ; 3 4 2 ; 3 2 1 ] мат2=[ 1 1 1; 3 4 2 ; 3 2 1 ] мат3 = мат1 * мат2 | мат1 = 1 2 3 3 4 2 3 2 1 мат2 = 1 1 1 3 4 2 3 2 1 мат3 = 16 15 8 21 23 13 12 13 8 |
Выходные данные:
Использование команды «mtimes»
В следующей таблице показан приведенный выше пример с использованием команды «mtimes».
Редактор Matlab | Выход |
| мат1= [ 1 2 3 ; 3 4 2 ; 3 2 1 ] мат2=[ 1 1 1 ; 3 4 2 ; 3 2 1 ] мат4= mtimes ( мат1 , мат2 ) | мат1 = 1 2 3 3 4 2 3 2 1 мат2 = 1 1 1 3 4 2 3 2 1 мат4 = 16 15 8 21 23 13 12 13 8 |
Выход:
Пример № 2
Давайте рассмотрим два матричных мат и мат 2,
MAT1 =
23 32 110003
22 3 2
16 39 21
32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 3222 2 2 2 2
9000 21 21 2002 9000 2 23 4 1mat2 =
41 11 43
32 41 32
3 2 1
вторые 1
3 столбца, поэтому количество столбцов первой матрицы равно количеству строк второй матрицы, поэтому можно выполнить умножение.
Использование оператора «*»
В следующей таблице показан приведенный выше пример с использованием оператора «*».
Редактор Matlab | Выход |
| мат1 = [ 23 , 32 , 11 ; 22 3 2 ; 16 39 21 ; 32 4 1 ] мат2 = [ 4 1 11 43 ; 32 41 32 ; 3 2 1 ] мат3 = мат1 * мат 2 | мат1 = 23 32 11 22 3 2 16 3921 32 4 1 мат2 = 41 11 43 32 41 32 3 2 1 мат3 = 2000 1587 2024 1004 369 1044 1967 1817 1957 1443 518 1505 |
Вывод:
Использование команды «mtimes»
В следующей таблице показан приведенный выше пример с использованием команды «mtimes».
Редактор Matlab | Выход |
| мат1 = [ 23 , 32 , 11 ; 22 3 2 ; 16 39 21 ; 32 4 1 ] мат2 = [ 41 11 43 ; 32 41 32 ; 3 2 1 ] мат4 = mtimes ( мат1 , мат2 ) | мат1 = 23 32 11 22 3 2 16 39 21 32 4 1 мат2 = 41 11 43 32 41 32 3 2 1 мат4 = 2000 1587 2024 1004 369 1044 1967 1817 1957 1443 518 1505 |
Выход:
Пример № 3
Предположим, что две матрицы – MAT1 и MAT2,
MAT1 =
5 6 3 2
3 2 4 5
3 2 2 2 2 2 2
3 4 5
3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 100020003
mat2 =
3 4 2
2 3 4
3 3 4
поэтому количество столбцов первой матрицы не равно количеству строк второй матрицы, поэтому умножение не может быть выполнено.
Редактор Matlab | Выход |
| мат1= [ 5 6 3 2 ; 3 2 4 5 ; 3 2 1 1 ] мат2= [ 3 4 2 ; 2 3 4 ; 3 3 4 ] мат3= мат1 * мат2 | мат1 = 5 6 3 2 3 2 4 5 3 2 1 1 мат2 = 3 4 2 2 3 4 3 3 4 Ошибка при использовании * Внутренние размеры матрицы должны совпадать. |
Вывод:
Заключение
Умножение матриц – очень сложная и сложная операция в математике, но мы реализуем то же самое в Matlab, мы можем легко получить вывод без ошибок. Оба метода, используемые для умножения матриц, легки и просты в реализации. Это делает программу более эффективной.
Рекомендуемые статьи
Это руководство по умножению матриц в Matlab. Здесь мы обсуждаем, как выполнить умножение матриц в Matlab вместе с примерами.
Вы также можете прочитать следующие статьи, чтобы узнать больше –
- Умножение матриц в Java
- 3D Матрица в MATLAB
- Матрица в Matlab
- Matlab И Оператор
– Как умножать матрицы?
В этом посте вы увидите, как вычислить умножение матриц. Мы объясним процедуру умножения матриц шаг за шагом на примере, а затем вы найдете решенные упражнения, чтобы вы могли также попрактиковаться. Наконец, вы узнаете, когда две матрицы нельзя перемножить, и все свойства этой матричной операции.
Содержание
Как перемножить две матрицы?
На умножьте две матрицы , умножьте строки матрицы слева на столбцы матрицы справа.
Давайте рассмотрим процедуру умножения двух матриц на примере:
Прежде всего, мы должны умножить первую строку матрицы слева на первый столбец матрицы справа. Для этого мы умножаем каждый элемент в первой строке на каждый элемент в первом столбце один за другим, а затем складываем результаты.
Так что все это будет первым элементом в первой строке результирующей матрицы. Взгляните на процедуру:
Делаем вычисления:
Во-вторых, мы должны умножить первой строки на второй столбец . Итак, повторяем процедуру: умножаем каждый элемент в первой строке на каждый элемент во втором столбце один за другим, а затем складываем результаты. И все это будет вторым элементом первой строки результирующей матрицы:
Выполняем операции:
После того, как вычислили первую строку результирующей матрицы, переходим ко второй строке. Итак, мы умножаем вторую строку на первый столбец повторяем процедуру: умножаем каждый элемент второй строки на каждый элемент первого столбца по одному, а затем складываем результаты:
Таким образом:
Наконец умножаем вторая строка вторым столбцом . Всегда применяя одну и ту же процедуру: мы умножаем каждый элемент во второй строке на каждый элемент во втором столбце один за другим, а затем складываем результаты:
В результате получается следующая матрица:
И здесь заканчивается произведение двух матриц.
Как вы видели, строки нужно умножать на столбцы, всегда повторяя одну и ту же процедуру: мы умножаем каждый элемент в строке на каждый элемент в столбце один за другим, а затем складываем результаты умножения.
Практика умножения матриц
Задача 1
Решите следующее умножение матриц 2×2:
См. решение
Произведение матриц порядка 2:
Чтобы решить произведение матриц, мы должны умножить строки матрицы слева на столбцы матрицы справа.
Поэтому сначала умножаем первую строку на первый столбец. Для этого мы умножаем каждый элемент в первой строке на каждый элемент в первом столбце один за другим и складываем результаты.
Теперь умножим первую строку на второй столбец, чтобы найти второй элемент первой строки получившейся матрицы:
Переходим ко второй строке, поэтому умножаем вторую строку на первый столбец:
Наконец, умножаем вторую строку на второй столбец, чтобы вычислить последний элемент матрицы:
Таким образом, результат матричного произведения матриц 2×2 выглядит следующим образом:
Задача 2
Умножьте следующие матрицы 2×2:
См.
решение
Чтобы решить матрицу умножьте строки матрицы слева на столбцы матрицы справа:
Задача 3
Вычислите следующее умножение матрицы 3×3:
См. решение
Чтобы выполнить умножение матрицы 3×3, мы должны умножить строки матрицы слева из матрицы справа:
Проблема 4
Учитывая Матрица А:
Рассчитайте:
См. Раствор
Сначала мы рассчитываем переход из Matrix A в порядке. умножение. И чтобы транспонировать матрицу, мы должны поменять местами ее строки на ее столбцы, другими словами, первая строка матрицы становится первым столбцом матрицы, а вторая строка матрицы становится вторым столбцом матрицы.
Итак, матричная операция:
Теперь мы можем произвести вычисления. Сначала умножим матрицу A на скаляр 2 (хотя мы могли бы также сначала вычислить A·A T ):
И, наконец, решим произведение матриц:
083
Имея следующие матрицы:
Рассчитать:
См.
решение
Это операция, которая объединяет вычитание и умножение квадратных матриц порядка 2:
Сначала мы вычисляем умножение слева:
Теперь мы решаем умножение справа:
И, наконец, мы вычитаем матрицы:
Когда нельзя перемножить две матрицы?
Из-за правил умножения матриц не все матрицы можно перемножать. Две матрицы можно перемножить только в том случае, если количество столбцов матрицы слева равно количеству строк матрицы справа.
Например, следующее умножение невозможно, потому что первая матрица имеет 3 столбца, а вторая матрица имеет 2 строки:
Однако, если мы изменим порядок, их можно умножить. Так как первая матрица имеет два столбца, а вторая матрица имеет две строки:
Свойства умножения матриц
Этот тип матричной операции имеет следующие характеристики:
- Умножение матриц является ассоциативным , поэтому всегда выполняется следующее уравнение:
- Произведение матриц не коммутативно , то есть результат умножения двух матриц зависит от порядка их умножения:
Например, следующее умножение матриц дает результат:
Но результат произведения будет другим, если мы изменим порядок умножения матриц:
Когда умножение двух матриц дает одно и то же результат независимо от порядка умножения, они являются коммутирующими матрицами.
