Умножение на единичную матрицу
На основании правила умножения матриц получаем:
АЕ = | а11 | а12 . | 1 | 0 | = | а11 | а12 |
а21 | а22 | 0 | 1 | а21 | а22 | ||
EA= | 1 | 0 . | а11 | а12 | = | а11 | а12 |
1 | а21 | а22 | а21 | а22, | |||
т.е. АЕ = ЕА = А (11)
Произведение
квадратной матрицы любого порядка на
соответствующую единичную матрицу
равняется первоначальной матрице. Таким
образом, при умножении матриц единичная
матрица играет роль единицы, поэтому и
называется единичной.
Понятие обратной матрицы
Если А – квадратная матрица, то обратной по отношению к А называется матрица, которая, будучи умноженной на А (как справа, так и слева), даёт единичную матрицу. Обозначив обратную матрицу через А-1, запишем
А-1А = АА-1 = Е (12)
Если обратная
матрица А-1 существует,
то матрица А называется
Нахождение матрицы, обратной данной
Пусть дана невырожденная матрица
а11 | а12 | а13 | ||
А= | а21 | а22 | а23 | |
а31 | а32 | а33 |
а11 | а12 | ||||
DА = | а21 | а22 | а23 | ≠ 0 | |
а31 | а32 | а33 | |||
Обратной матрицей А-1 будет матрица
A11/DА | A21/DА | A31/DА | ||||
A-1 = | A12/DА | A22/DА | , | ( 13 ) | ||
A13/DА | A23/DА | A33/DА |
где Аij – алгебраическое дополнение элемента аij определителя DA

Убедиться в этом можно, умножая матрицу А на матрицу А-1. Например, элементы с11 и с23 определяются так:
···
c23=a21···=
== 0
В итоге
а11 | а12 | а13 | A11/DА | A21/DА | A31/DА | 1 | 0 | 0 | |||
С=AA-1= | а21 | а22 | а23 | A22/DА | A32/DА | = | 0 | 1 | 0 | =E | |
а31 | а32 | а33 | A13/DА | A23/DА | A33/DА | 0 | 0 | 1 |
Матрица
A11 | A21 | A31 | ||||
= | A12 | A22 | A32 | ( 14 ) | ||
A13 | A23 | A33 |
называется матрицей, присоединённой к А. (Используется также обозначение ).
Обратная матрица А-1 через присоединённую выражается так:
(Используется также обозначение ).
Обратная матрица А-1 через присоединённую выражается так:
= | 1 | ( 15 ) | |
DA |
Обратную матрицу будем находить по следующей схеме:
1. Находим определитель матрицы А.
2. Находим алгебраическое дополнение всех элементов аij матрицы и записываем новую матрицу.
3. Меняем местами строки и столбцы полученной матрицы (транспонируем матрицу).
4. Умножаем полученную
матрицу на 1/DA.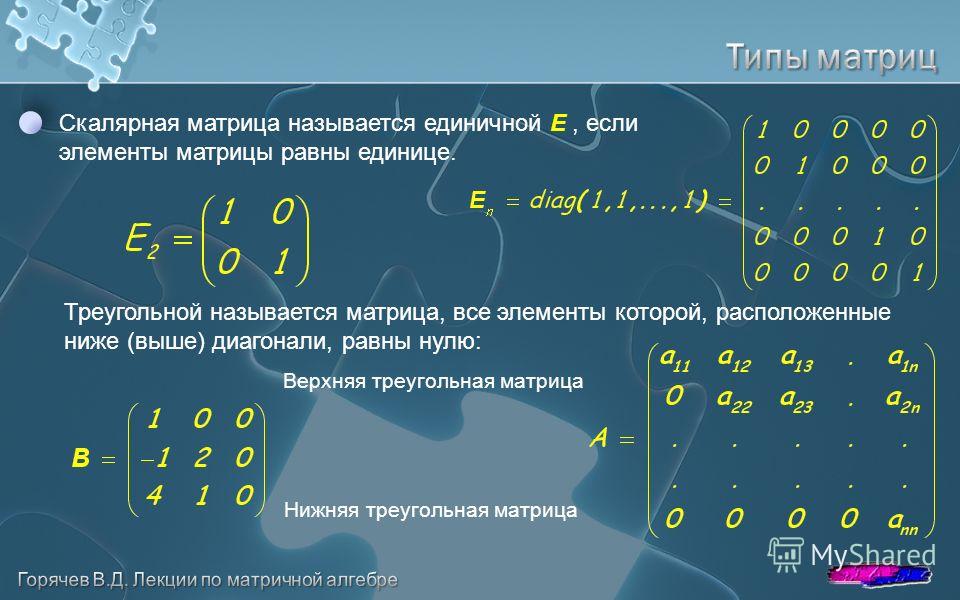
Пример 6. (Лена Иванова, КШ-061).
Дана матрица
Найти обратную матрицу.
1. Вычисляем определитель матрицы А:
2 | 5 | 7 | 2 | 5 | 7 | ||||
DA = | 6 | 3 | 4 | = | 0 | -12 | -17 | = | (492 – 493) = -1 |
5 | -2 | -3 | 0 | -29/2 | -41/2 |
Так как DA ≠ 0, то матрица А является невырожденной, и, значит, можно
найти матрицу А-1.
2. Находим алгебраические дополнения элементов этого определителя:
A11 = | 3 | 4 | = -1, | A21= – | 5 | 7 | = 1, | A31= | 5 | 7 | = -1, |
-2 | -3 | -2 | -3 | 3 | 4 |
A12= – | 6 | 4 | = 38, | A22= | 2 | 7 | = -41, | A32= – | 2 | 7 | = 34, |
5 | -3 | 5 | -3 | 6 | 4 |
A13 = | 6 | 3 | = -27, | A23=- | 2 | 5 | = 29, | A33= | 2 | 5 | =
-24. |
5 | -2 | 5 | -2 | 6 | 3 |
Следовательно,
-1 | 1 | -1 | 1 | -1 | 1 | ||
A-1 = -1 | 38 | -41 | 34 | = | -38 | 41 | -34 |
-27 | 29 | -24 | 27 | -29 | 24 |
Лекция 4.
определение, свойства и примеры решения задач
Задание. Вычислить $AB$ и $BA$, если $ A=\left( \begin{array}{rr}{1} & {-1} \\ {2} & {0} \\ {3} & {0}\end{array}\right) $ , $ B=\left( \begin{array}{ll}{1} & {1} \\ {2} & {0}\end{array}\right) $
Решение. Так как $ A=A_{3 \times 2} $ , а $ B=B_{2 \times 2} $ , то произведение возможно и результатом операции умножения будет матрица $ C=C_{3 \times 2} $ , а это матрица вида $ C=\left( \begin{array}{ll}{c_{11}} & {c_{12}} \\ {c_{21}} & {c_{22}} \\ {c_{31}} & {c_{32}}\end{array}\right) $ .
Вычислим элементы матрицы $C$ :
$ c_{11}=a_{11} \cdot b_{11}+a_{12} \cdot b_{21}=1 \cdot 1+(-1) \cdot 2=-1 $
$ c_{12}=a_{11} \cdot b_{12}+a_{12} \cdot b_{22}=1 \cdot 1+(-1) \cdot 0=1 $
$ c_{21}=a_{21} \cdot b_{11}+a_{22} \cdot b_{21}=2 \cdot 1+0 \cdot 2=2 $
$ c_{22}=a_{21} \cdot b_{12}+a_{22} \cdot b_{22}=2 \cdot 1+0 \cdot 0=2 $
$ c_{31}=a_{31} \cdot b_{11}+a_{32} \cdot b_{21}=3 \cdot 1+0 \cdot 2=3 $
$ c_{32}=a_{31} \cdot b_{12}+a_{32} \cdot b_{22}=3 \cdot 1+0 \cdot 0=3 $
Итак, $ C=A B=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right) $ .
Выполним произведения в более компактном виде:
$ C=A B=\left( \begin{array}{rr}{1} & {-1} \\ {2} & {0} \\ {3} & {0}\end{array}\right)_{3 \times 2} \cdot \left( \begin{array}{ll}{1} & {1} \\ {2} & {0}\end{array}\right)_{2 \times 2}= $
$ =\left( \begin{array}{ccc}{1 \cdot 1+(-1) \cdot 2} & {1 \cdot 1+(-1) \cdot 0} \\ {2 \cdot 1+0 \cdot 2} & {2 \cdot 1+0 \cdot 0} \\ {3 \cdot 1+0 \cdot 2} & {3 \cdot 1+0 \cdot 0}\end{array}\right)=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right) $
Найдем теперь произведение $ D=B A=B_{2 \times 2} \cdot A_{3 \times 2} $. Так как количество столбцов матрицы $B$ (первый сомножитель) не совпадает с количеством строк матрицы $A$ (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. $ A B=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right) $ . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы
$B$ не совпадает с количеством строк матрицы $A$ .
В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы
$B$ не совпадает с количеством строк матрицы $A$ .
как найти произведение двух или трех разных размеров, условия и формулы
Мы помним, что матрицы – это таблицы взаимосвязанных элементов, которые позволяют упростить математические вычисления и систематизировать определённую информацию. Их можно складывать, вычитать, умножать между собой. В этой статье подробнее остановимся на последнем алгоритме – матричном произведении.
Умножение матриц — определение
Матричное умножение – это одна из основных операций, которая проводится исключительно с согласованными матрицами.
При произведении матриц A и B получается новая матрица C. В математическом виде формула будет выглядеть так:
Но для начала разберёмся, что такое согласованные матрицы.
Согласованные матрицы
Согласованными матрицами называют матрицы вида A = [m ☓ n] и B = [n ☓ k], где количество столбцов А равно количеству строк В.
Индексы показывают координаты равных элементов.
Для того, чтобы умножить А и В, нужно взять строку в первой матрице и столбец во второй, перемножить одинаковые элементы и сложить полученные произведения.
Основные свойства матричного произведения
Размеры, то есть количество строк (m) и столбцов (n), влияют на особенности матричного произведения. Следовательно, для двух главных видов – квадратных и прямоугольных – действуют разные свойства произведения. Однако умножение любого вида всегда некоммуникативное. Это означает, что матрицы нельзя менять местами (АВ ≠ ВА).
Умножение квадратных матриц
Для квадратных матриц существует единичная матрица Е. В ней элементы по главной диагонали равны единице, а оставшиеся – нулю. Произведение любой квадратной матрицы на неё не влияет на результат.
Произведение любой квадратной матрицы на неё не влияет на результат.
В математическом виде это выглядит так: ЕА = АЕ = А
Также существует обратная матрица А (-1), при умножении на которую исходная A = [m ☓ n] даёт в результате единичную матрицу E.
Следовательно, формула такова: АА(-1) = Е
Умножение прямоугольных матриц
Существуют четыре основных свойства умножения:
- Сочетательное свойство, или ассоциативность: (AB)C = A(BC)
- Распределительное свойство, или дистрибутивность: А(В+С) = АВ + АС / (А+В)С = АС + ВС
- Умножение на единичную матрицу: ЕА = А
- Умножение на нулевую матрицу: 0А = 0
Напомним, что у нулевой матрицы все элементы равны нулю.
Произведение трех матриц
Произведение АВС можно получить двумя альтернативными способами:
- Найти АВ и умножить на С
- Найти ВС и умножить на А
(АВ) С = А (ВС)
Данное свойство называется ассоциативностью матричного умножения и действует на все виды согласованных матриц. Сами они не переставляются, меняется только порядок их умножения.
Сами они не переставляются, меняется только порядок их умножения.
Умножение матрицы на число
Для умножения на число необходимо умножить каждый матричный элемент на это число:
Дроби вносить не нужно, поскольку они могут затруднить дальнейшие операции.
Умножение матрицы на вектор
Здесь работает правило «строка на столбец».
При умножении на вектор-столбец важно, чтобы количество столбцов в матрице совпадало с количеством строк в векторе-столбце. Результатом произведения будет вектор-столбец.
При умножении на вектор-строку матрица должна быть только вектором-столбцом. Важно, чтобы количество строк в векторе-столбце совпадало с количеством столбцов в векторе-строке. Результатом произведения будет квадратная матрица.
Примеры задач на умножение матриц
Задача №1: выполнить умножение и найти С, если A = [m ☓ n] и B = [n ☓ k] равны.
Решение:
c11 = a11·b11 + a12·b21 = 4·3 + 2·(-3) = 12 – 6 = 6
c12 = a11·b12 + a12·b22 = 4·1 + 2·4 = 4 + 8 = 12
c21 = a21·b11 + a22·b21 = 9·3 + 0·(-3) = 27 + 0 = 27
c22 = a21·b12 + a22·b22 = 9·1 + 0·4 = 9 + 0 = 9
Ответ:
Задача №2: вычислить С, если А = [m ☓ n] и вектор-столбец В равны.
Решение:
c11 = a11·b11 + a12·b21 = 2·1 + (-1)·2 + 3·(-1) = -3
c21 = a11·b12 + a12·b22 = 4⋅1 + 2⋅2 + 0⋅2 = 8
c31 = a21·b11 + a22·b21 = −1⋅1 + 1⋅2 + 1⋅(−1) = 0
Ответ:
Изучение матричных операций очень увлекательное, но сложное занятие. Если у вас нет времени на учёбу, ФениксХэлп может помочь в решении контрольных и самостоятельных работ, написании статей и диссертаций.
двух матриц умножение
Вы искали двух матриц умножение? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и двух умножение матриц, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение. Например, «двух матриц умножение».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как двух матриц умножение,двух умножение матриц,единичную матрицу умножить на матрицу,как матрицу умножить на дробь,как матрицу умножить на матрицу,как матрицу умножить на столбец,как найти произведение матриц,как перемножать матрицы,как перемножать матрицы 3х3,как перемножаются матрицы,как перемножить две матрицы,как перемножить матрицы разных размеров,как перемножить три матрицы,как умножать матрицы 2 на 2,как умножать матрицы друг на друга,как умножать матрицы разных размеров,как умножить две матрицы,как умножить единичную матрицу на матрицу,как умножить матрицу,как умножить матрицу 2х3 на 2х3,как умножить матрицу на единичную матрицу,как умножить матрицу на матрицу,как умножить матрицу на матрицу 3 на 3,как умножить матрицу на обратную матрицу,как умножить матрицы,как умножить на матрицу столбец,как умножить столбец на матрицу,как умножить три матрицы,какие можно матрицы складывать,матриц двух умножение,матриц умножение двух,матрица примеры умножение,матрица умножение,матрица умножение на матрицу,матрицу умножить на единичную матрицу,матрицы примеры умножение,матрицы произведение,матрицы умножение,матрицы умножение примеры,матричное умножение,перемножение двух матриц,перемножение матриц примеры,правила перемножения матриц,правила умножения матриц,правила умножения матрицы на матрицу,правило перемножения матриц,правило умножение матриц,правило умножения матриц,правило умножения матрицы на матрицу,примеры матриц умножения,примеры матрицы умножение,примеры произведение матриц,примеры умножение матрицы,примеры умножение матрицы на матрицу,примеры умножения матриц,произведение матриц примеры,произведение матриц примеры и решения,произведение матриц формула,произведение матрицу на матрицу,произведение матрицы,произведения матриц,свойства матриц умножение,свойства умножение матриц,свойства умножения матриц,сложение и умножение матриц,умножение 2х2 матриц,умножение двух матриц,умножение и сложение матриц,умножение квадратных матриц,умножение матриц 2х2,умножение матриц 2х2 на 2х2,умножение матриц 3 на 3,умножение матриц 3х3,умножение матриц двух,умножение матриц друг на друга,умножение матриц квадратных,умножение матриц на матрицу,умножение матриц правила,умножение матриц правило,умножение матриц пример,умножение матриц примеры,умножение матриц примеры с решением,умножение матриц разных размеров,умножение матриц свойства,умножение матриц третьего порядка,умножение матриц формула,умножение матрица на матрицу,умножение матрицы,умножение матрицы 2х2 на 2х2,умножение матрицы на матрицу,умножение матрицы на матрицу примеры,умножение матрицы на столбец,умножение матрицы примеры,умножение на единичную матрицу,умножения матриц,умножения матриц правила,умножения матриц примеры,умножения матриц свойства,умножения матриц формула,умножить матрицу на единичную матрицу,умножить матрицу на матрицу столбец,формула произведение матриц,формула умножение матриц,формула умножения матриц,формула умножения матрицы. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и двух матриц умножение. Просто введите задачу в окошко и нажмите
«решить» здесь (например, единичную матрицу умножить на матрицу).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и двух матриц умножение. Просто введите задачу в окошко и нажмите
«решить» здесь (например, единичную матрицу умножить на матрицу).
Где можно решить любую задачу по математике, а так же двух матриц умножение Онлайн?
Решить задачу двух матриц умножение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
5
55. Умножение матриц.
Рассмотрим правило умножения двух
квадратных матриц второго и третьего
порядков. Пусть даны две матрицы
Пусть даны две матрицы
Произведением матрицы А на матрицу В называется матрица С= А В, элементы которой составляются следующим образом:
Как видим, элемент матрицы-произведения, находящийся на пересечении i-й строки и k-го столбца, представляет собой сумму парных произведений элементов i-й строки первой матрицы на элементы k-го столбца второй матрицы.
Например, элемент, стоящий во второй строке и первом столбце матрицы произведения АВ, равен сумме парных произведений элементов второй строки матрицы А на элементы первого столбца матрицы В.
Это правило сохраняется для умножения
квадратных матриц третьего и более высокого порядка, а
также для умножения прямоугольных матриц, в которых число
столбцов матрицы-множимого равно числу строк матрицы-множителя.
Пример1
Пример2
Пример3.
Видим , что в результате перемножения двух матриц получается матрица, содержащая столько строк, сколько имеет их матрица-множимое, и столько столбцов, сколько имеет матрица-множитель. Рассмотрим еще пример:
С другой стороны, как установлено выше,
Следовательно, произведение двух матриц, вообще говоря, не подчиняется переместительному закону:
АВ ВА.
Можно проверить, что умножение матриц подчиняется сочетательному закону:
А(ВС) = (АВ)С.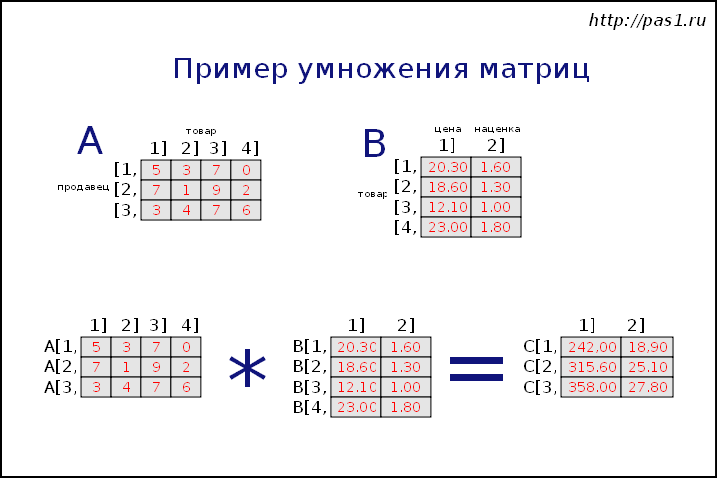
Отметим любопытный факт. Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, т.е. произведение двух ненулевых матриц может оказаться равным нуль-матрице.
Пример 4. Если
то
При умножении матриц второго порядка особое значение имеет квадратная матрица
При умножении любой квадратной матрицы
второго порядка на матрицу Е снова получается матрица А.
Действительно,
Аналогично EA =A.
Матрица Е называется единичной матрицей. Единичная матрица n-го
порядка имеет вид
Единичная матрица n-го
порядка имеет вид
Если в матрице (1), обозначаемой буквой А, сделать все строки столбцами с тем же номером, то получим матрицу
называемую транспонированной к матрице А.
Понятие о матрице | Сложение матриц | Вычитание матриц и умножение матриц на число |
Умножение матриц | Контакты первого и второго порядков в эпидемиологии | Матрицы и сети |
Главная
Произведение двух матриц: формула, решения, свойства
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Определение. Произведением двух матриц А и В называется матрица С, элемент
которой, находящийся на пересечении i-й строки и j-го столбца, равен сумме произведений элементов
i-й строки матрицы А на соответствующие (по порядку) элементы j-го столбца матрицы В.
Из этого определения следует формула элемента матрицы C:
Произведение матрицы А на матрицу В обозначается АВ.
Пример 1. Найти произведение двух матриц А и B, если
,
.
Решение. Удобно нахождение произведения двух матриц А и В записывать так, как на рис.2:
На схеме серые стрелки показывают, элементы какой строки матрицы А на элементы какого столбца матрицы В нужно перемножить для получения элементов матрицы С , а линиями цвета элемента матрицы C соединены соответствующие элементы матриц A и B, произведения которых складываются для получения элемента матрицы C.
В результате получаем элементы произведения матриц:
Теперь у нас есть всё, чтобы записать произведение двух матриц:
.
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Произведение двух матриц АВ имеет смысл только в том случае, когда число столбцов матрицы А совпадает с числом строк матрицы В .
Эту важную особенность будет легче запомнить, если почаще пользоваться следующими памятками:
Имеет место ещё одна важная особенность произведения матриц относительно числа строк и столбцов:
В произведении матриц АВ число строк равно числу строк матрицы А , а число столбцов равно числу столбцов матрицы В .
Пример 2. Найти число строк и столбцов матрицы C, которая является произведением двух матриц A и B следующих размерностей:
а) 2 Х 10 и 10 Х 5;
б) 10 Х 2 и 2 Х 5;
в) 4 Х 4 и 4 Х 10.
Решение:
а) 2 Х 5;
б) 10 Х 5;
в) 4 Х 10.
Пример 3. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A – 2, число столбцов в матрице B – 2. Следовательно, размерность матрицы C = AB – 2 X 2.
Вычисляем элементы матрицы C = AB.
Найденное произведение матриц: .
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Пример 5. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A – 2, число столбцов в матрице B – 1. Следовательно, размерность матрицы C = AB – 2 X 1.
Следовательно, размерность матрицы C = AB – 2 X 1.
Вычисляем элементы матрицы C = AB.
Произведение матриц запишется в виде матрицы-столбца: .
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Пример 6. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A – 3, число столбцов в матрице B – 3. Следовательно, размерность матрицы C = AB – 3 X 3.
Вычисляем элементы матрицы C = AB.
Найденное произведение матриц: .
Проверить решение этой и других подобных задач можно на
калькуляторе произведения
матриц онлайн.
Пример 7. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A – 1, число столбцов в матрице B – 1. Следовательно, размерность матрицы C = AB – 1 X 1.
Вычисляем элемент матрицы C = AB.
Произведение матриц является матрицей из одного элемента: .
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Программная реализация произведения двух матриц на С++ разобрана в соответствующей статье в блоке “Компьютеры и программирование”.
Возведение матрицы в степень определяется как умножение матрицы на ту же самую матрицу.
Так как произведение матриц существует только тогда, когда число столбцов первой матрицы совпадает с
числом строк второй матрицы, то возводить в степень можно только квадратные матрицы. n-ая
степень матрицы путём умножения матрицы на саму себя n раз:
n-ая
степень матрицы путём умножения матрицы на саму себя n раз:
Пример 8. Дана матрица . Найти A² и A³.
Решение:
Найти произведение матриц самостоятельно, а затем посмотреть решение
Пример 9. Дана матрица
Найти произведение данной матрицы и транспонированной матрицы , произведение транспонированной матрицы и данной матрицы.
Правильное решение и ответ.
Свойство 1. Произведение любой матрицы А на единичную матрицу Е соответствующего порядка как справа, так и слева, совпадает с матрицей А , т.е. АЕ = ЕА = А .
Иными словами, роль единичной матрицы при умножении матриц такая же, как и единицы при умножении чисел.
Пример 10. Убедиться в справедливости свойства 1, найдя произведения матрицы
Убедиться в справедливости свойства 1, найдя произведения матрицы
на единичную матрицу справа и слева.
Решение. Так как матрица А содержит три столбца, то требуется найти произведение АЕ , где
–
единичная матрица третьего порядка. Найдём элементы произведения С = АЕ :
Получается, что АЕ = А .
Теперь найдём произведение ЕА , где Е – единичная матрица второго порядка, так как матрица А содержит две строки. Найдём элементы произведения С = ЕА :
Доказано: ЕА = А .
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Свойство 2. Произведение матрицы А на нуль-матрицу является нуль-матрицей. Это свойство очевидно, так как все элементы нуль-матрицы равны нулю.
Свойство 3. Произведение матриц некоммутативно:
.
Для этого достаточно показать, что равенство АВ = ВА не выполняется для каких-либо двух матриц.
Пример 11. Найти произведения матриц АВ и ВА, если
,
,
и убедиться в том, что эти произведения не равны друг другу:
.
Решение. Находим:
И действительно, найденные произведения не равны:
.
Проверить решение этой и других подобных задач можно на
калькуляторе произведения
матриц онлайн.
Свойство 4. Произведение матриц ассоциативно: (АВ)С = А(ВС) .
Свойство 5. Для произведения матриц выполняется дистрибутивный закон: (А + В) С = АС + ВС , С (А + В) = СА + СВ .
Свойство 6. Определитель произведения двух квадратных матриц равен произведению их определителей: если С = АВ , то
.
Поделиться с друзьями
Начало темы “Матрицы”
Продолжение темы “Матрицы”
Другие темы линейной алгебры
Умножение матриц » ProcMem.Ru Линейная Алгебра
Определение. Произведением строки длины n на столбец высоты n называется скаляр, вычисляемый по правилу:
.
Замечание. Из определения следует, что для умножения строки на столбец необходимо, чтобы длина строки была равна высоте столбца. В противном случае произведение строки на столбец не определено.
В противном случае произведение строки на столбец не определено.
Пример.
Определение. Произведением матрицы размера на матрицу размера называют матрицу размера , где элемент является результатом произведения – й строки матрицы А на – й столбец матрицы В для всех значений индексов , , т.е.
или
.
Обозначение: .
Другими словами, чтобы умножить две матрицы, нужно каждую строку первой матрицы умножить на каждый столбец второй матрицы. Умножая первую строку первой матрицы на каждый столбец второй матрицы мы получим все элементы первой строки матрицы произведения, затем делаем то же самое для второй строки первой матрицы и т.д.
Замечание. Из определения следует, что умножение матриц возможно только тогда, когда ширина первой матрицы (т.е. число ее столбцов) равна высоте второй (т.е. числу ее строк)
Пример.
.
Определение. Квадратную матрицу – го порядка называют единичной матрицей n-го порядка и обозначают буквой Е, если для любой квадратной матрицы А – го порядка справедливо равенство: .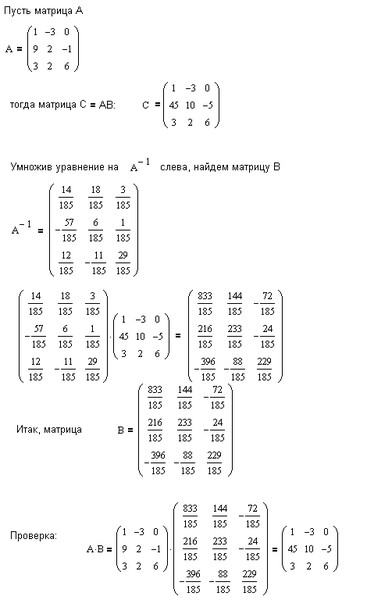
Множество всех квадратных матриц n-го порядка будем обозначать через .
Теорема. Множество содержит единичную матрицу n-го порядка, которой является матрица
.
Доказательство этой теоремы предоставляется читателю.
Теорема. Единичная матрица Е является единственной в множестве .
Доказательство. Пусть еще одна единичная матрица. Тогда, по определению, . Положим , тогда . Далее, по определению, . Положим здесь . Получаем равенство, отсюда имеем , ч.т.д.
Заметим, что точно также доказывается единственность нейтрального элемента (при условии его существования) в любой алгебраической структуре.
Теорема доказана.
Из теоремы следует, что никакая другая матрица, кроме матрицы не является единичной.
Теорема. (Свойства умножения матриц.)
Умножение матриц подчиняется следующим законам:
9) ассоциативность:
;
10) существование единичной матрицы:
: ;
дистрибутивность умножения относительно сложения матриц:
11) дистрибутивность умножения относительно сложения матриц:
и
12) умножение матриц связано с умножением матрицы на число естественным законом: и верно равенство:
.
Замечание. Для квадратных матриц одного порядка выполняются все 12 свойств. Это говорит о том, что множество всех квадратных матриц одного и того же порядка образует алгебру матриц над полем К.
Замечание. Умножение матриц не обладает свойством коммутативности. Для доказательства достаточно привести один контрпример.
Пусть , . Тогда , .
Аналогичный пример можно привести для квадратных матриц любого порядка.
Последнее равенство говорит о том, что квадратные матрицы имеют делители нуля.
Следствие. Множество всех квадратных матриц n-го порядка над полем K является некоммутативным кольцом с единицей и с делителями нуля.
Доказательство. На множестве всех квадратных матриц n-го порядка над полем K определены две операции: сложение матриц и их умножение, которые подчиняются законам 1) – 4) и 9) – 11), откуда и следует, по определению, что является кольцом с единицей (см. лекцию 1, п.14 и п.15). Пример, приведенный перед формулировкой данного следствия, показывает, что кольцо имеет делители нуля.
Следствие доказано.
Определение. Натуральной степенью квадратной матрицы А называется матрица .
Нулевую степень квадратной матрицы А – го порядка по определению полагают равной единичной матрице того же порядка: .
Еще записи по теме
Умножение матриц
Вы можете умножить только два матрицы если их Габаритные размеры являются совместимый , что означает, что количество столбцов в первой матрице совпадает с количеством строк во второй матрице.
Если А знак равно [ а я j ] является м × п матрица и B знак равно [ б я j ] является п × п матрица, продукт А B является м × п матрица.
А
B
знак равно
[
c
я
j
]
, куда
c
я
j
знак равно
а
я
1
б
1
j
+
а
я
2
б
2
j
+
. ..
+
а
я
п
б
п
j
.
..
+
а
я
п
б
п
j
.
(Запись в я th ряд и j th столбец обозначается двойным индексом а я j , б я j , и c я j .Например, запись а 23 – запись во второй строке и третьем столбце.)
Определение матричного умножения указывает на построчное умножение, где записи в я th ряд А умножаются на соответствующие записи в j th столбец из B а затем добавляем результаты.
Умножение матриц НЕ коммутативно. Если ни то, ни другое А ни B – единичная матрица, А B ≠ B А .
Умножение строки на столбец
Мы начнем с того, что покажем вам, как умножить
1
×
п
матрица
п
×
1
матрица. Первый – это всего лишь одна строка, а второй – один столбец. По приведенному выше правилу товар является
1
×
1
матрица; другими словами, одно число.
Первый – это всего лишь одна строка, а второй – один столбец. По приведенному выше правилу товар является
1
×
1
матрица; другими словами, одно число.
Сначала назовем записи в строке р 1 , р 2 , … , р п , а записи в столбце c 1 , c 2 , … , c п . Тогда произведение строки и столбца – это 1 × 1 матрица
[ р 1 c 1 + р 2 c 2 + … + р п c п ] .
Пример:
Найдите товар.
[ 1 4 0 ] ⋅ [ 2 – 1 5 ]
Мы должны умножить
1
×
3
матрица
1
×
3
матрица. Количество столбцов в первом равно количеству строк во втором, поэтому они совместимы.
Количество столбцов в первом равно количеству строк во втором, поэтому они совместимы.
Товар есть:
[ ( 1 ) ( 2 ) + ( 4 ) ( – 1 ) + ( 0 ) ( 5 ) ] знак равно [ 2 + ( – 4 ) + 0 ] знак равно [ – 2 ]
Умножение больших матриц
Теперь, когда вы знаете, как умножать строку на столбец, умножать матрицы большего размера очень просто. Для входа в
я
th
ряд и
j
th
столбец матрицы продукта, умножьте каждую запись в
я
th
строку первой матрицы на соответствующую запись в
j
th
столбец второй матрицы и складываем результаты.
Для входа в
я
th
ряд и
j
th
столбец матрицы продукта, умножьте каждую запись в
я
th
строку первой матрицы на соответствующую запись в
j
th
столбец второй матрицы и складываем результаты.
Возьмем следующую задачу, умножая 2 × 3 матрица с 3 × 2 матрица, чтобы получить 2 × 2 матрица как продукт.Элементы матрицы продукта называются е я j когда они в я th ряд и j th столбец.
[ 1 0 1 0 1 2 ] ⋅ [ 3 5 – 1 0 2 – 1 ] знак равно [ е 11 е 12 е 21 год е 22 ]
Получить
е
11
, умножить строку
1
первой матрицы по столбцу
1
второй.
е 11 знак равно [ 1 0 1 ] ⋅ [ 3 – 1 2 ] знак равно 1 ( 3 ) + 0 ( – 1 ) + 1 ( 2 ) знак равно 5
Получить е 12 , умножить строку 1 первой матрицы по столбцу 2 второй.
е 12 знак равно [ 1 0 1 ] ⋅ [ 5 0 – 1 ] знак равно 1 ( 5 ) + 0 ( 0 ) + 1 ( – 1 ) знак равно 4
Получить
е
21 год
, умножить строку
2
первой матрицы по столбцу
1
второй.
е 21 год знак равно [ 0 1 2 ] ⋅ [ 3 – 1 2 ] знак равно 0 ( 3 ) + 1 ( – 1 ) + 2 ( 2 ) знак равно 3
Получить е 22 , умножить строку 2 первой матрицы по столбцу 2 второй.
е 22 знак равно [ 0 1 2 ] ⋅ [ 5 0 1 ] знак равно 0 ( 5 ) + 1 ( 0 ) + 2 ( – 1 ) знак равно – 2
Записывая матрицу продуктов, получаем:
[ е 11 е 12 е 21 год е 22 ] знак равно [ 5 4 3 – 2 ]
Таким образом, мы показали:
[ 1 0 1 0 1 2 ] ⋅ [ 3 5 – 1 0 2 – 1 ] знак равно [ 5 4 3 – 2 ]
4.Умножение матриц
Важно: Мы можем перемножать матрицы, только если количество столбцов в первой матрице совпадает с количеством строк во второй матрице.
Пример 1
a) Умножение матрицы 2 × 3 на матрицу 3 × 4 возможно, и это дает матрицу 2 × 4 в качестве ответа.
b) Допускается умножение матрицы 7 × 1 на матрицу 1 × 2; это дает матрицу 7 × 2
c) НЕЛЬЗЯ умножить матрицу 4 × 3 на матрицу 2 × 3.
Как умножить 2 матрицы
Сначала мы используем буквы, чтобы увидеть, что происходит. Позже мы увидим пример чисел.
В качестве примера возьмем обычную матрицу 2 × 3, умноженную на матрицу 3 × 2.
`[(a, b, c), (d, e, f)] [(u, v), (w, x), (y, z)]`
Ответом будет матрица 2 × 2.
Умножаем и складываем элементы следующим образом. Мы обрабатываем по 1-й строке первой матрицы, поэлементно умножая на 1-го столбца второй матрицы.Складываем к полученным продуктам . Наш ответ находится в позиции a 11 (вверху слева) матрицы ответов.
Мы делаем аналогичный процесс для 1-й строки первой матрицы и 2-го столбца второй матрицы. Результат помещается в позицию a 12 .
Теперь перейдем к 2-й строке первой матрицы и 1-му столбцу второй матрицы. Результат помещается в позицию a 21 .
Наконец, мы делаем вторую строку первой матрицы и второй столбец второй матрицы. Результат помещается в позицию a 22 .
Итак, результат умножения наших двух матриц будет следующим:
`[(a, b, c), (d, e, f)] [(u, v), (w, x), (y, z)]` `= [(au + bw + cy, av + bx + cz), (du + ew + fy, dv + ex + fz)] `
Теперь давайте посмотрим на числовой пример.
Телефонные пользователи
ПРИМЕЧАНИЕ. Если вы разговариваете по телефону, вы можете прокрутить любую матрицу шириной на этой странице вправо или влево, чтобы увидеть все выражение.
Пример 2
Умножить:
`((0, -1,2), (4,11,2)) ((3, -1), (1,2), (6,1))`
Ответ
Это 2 × 3 умножить на 3 × 2, что даст нам 2 × 2 отвечать.
`((0, -1,2), (4,11,2)) ((3, -1), (1,2), (6,1))`
`= ((0xx3 + -1xx1 + 2xx6,0xx-1 + -1xx2 + 2xx1), (4xx3 + 11xx1 + 2xx6,4xx -1 + 11xx2 + 2xx1))`
`= ((0-1 + 12,0-2 + 2), (12 + 11 + 12, -4 + 22 + 2))`
`= ((11,0), (35,20))`
Наш ответ – матрица 2 × 2.
Умножение матриц 2 × 2
Процесс одинаков для матрицы любого размера. Мы умножаем на строки первой матрицы и на столбца второй матрицы поэлементно. Затем мы добавляем продукты:
`((a, b), (c, d)) ((e, f), (g, h))` `= ((ae + bg, af + bh), (ce + dg, cf + dh )) `
В этом случае мы умножаем матрицу 2 × 2 на матрицу 2 × 2 и в результате получаем матрицу 2 × 2.
Пример 3
Умножить:
`((8,9), (5, -1)) ((- 2,3), (4,0))`
Ответ
`((8,9), (5, -1)) ((- 2,3), (4,0))`
`= ((8 xx -2 + 9xx4,8xx3 + 9xx0), (5xx-2 + -1xx4,5xx3 + -1xx0))`
`= ((-16 + 36,24 + 0), (- 10+ -4,15 + 0))`
`= ((20,24), (- 14,15))`
Матрицы и системы одновременных линейных уравнений
Теперь мы видим, как написать систему линейных уравнений, используя умножение матриц.
Пример 4
Система уравнений
−3 x + y = 1
6 x -3 y = −4
можно записать как:
Матрицы`((-3,1), (6, -3)) ((x), (y)) = ((1), (- 4))`
идеальны для компьютерного решения задач, потому что компьютеры легко формируют массивы . Мы можем опустить алгебраические символы. Компьютеру требуются только первая и последняя матрицы для решения системы, как мы увидим в разделе «Матрицы и линейные уравнения».
Примечание 1 – Обозначение
Care с записью и умножением матриц .
Следующие выражения имеют различное значение:
AB – это матричное умножение
A × B – это перекрестное произведение , которое возвращает вектор
A * B используется в компьютерной нотации, но не на бумаге
A • B точечное произведение , которое возвращает скаляр .
[Дополнительную информацию о векторных и скалярных величинах см. В главе «Вектор».]
Примечание 2 – Коммутативность умножения матриц
Есть ли `AB = BA`?
Посмотрим, правда ли это на примере.
Пример 5
Если
`A = ((0, -1,2), (4,11,2))`
и
`B = ((3, -1), (1,2), (6,1))`
найдите AB, и BA.
Ответ
Мы выполнили AB выше, и ответ был:
`AB = ((0, -1,2), (4,11,2)) ((3, -1), (1,2), (6,1))`
`= ((11,0), (35,20))`
Теперь BA – это (3 × 2) (2 × 3), что даст 3 × 3:
`BA = ((3, -1), (1,2), (6,1)) ((0, -1,2), (4,11,2))`
`= ((0-4, -3-11,6-2), (0 + 8, -1 + 22,2 + 4), (0 + 4, -6 + 11,12 + 2))`
`= ((-4, -14,4), (8,21,6), (4,5,14))`
Итак, в этом случае AB НЕ равно BA.
Фактически, для большинства матриц нельзя изменить порядок умножения и получить тот же результат.
В общем случае при умножении матриц закон коммутативности не выполняется, т.е. AB ≠ BA . Есть два распространенных исключения:
.- Идентификационная матрица: IA = AI = A .?
- инверсия матрицы: A -1 A = AA -1 = I.
В следующем разделе мы узнаем, как найти обратную матрицу.
Пример 6 – Умножение на идентификационную матрицу
Учитывая, что
`A = ((- 3,1,6), (3, -1,0), (4,2,5))`
найдите AI .
Ответ
`AI = ((-3,1,6), (3, -1,0), (4,2,5)) ((1,0,0), (0,1,0), (0 , 0,1)) `
`= ((- 3 + 0 + 0,0 + 1 + 0,0 + 0 + 6), (3 + 0 + 0,0 + -1 + 0,0 + 0 + 0), (4 + 0 + 0,0 + 2 + 0,0 + 0 + 5)) `
`= ((- 3,1,6), (3, -1,0), (4,2,5))`
`= A`
Мы видим, что умножение на единичную матрицу не меняет значения исходной матрицы.
То есть
AI = A
Упражнения
1. Если возможно, найдите BA и AB .
`A = ((- 2,1,7), (3, -1,0), (0,2, -1))`
`B = (4 \ \ -1 \ \ \ 5)`
Ответ
`BA = (4 \ \ -1 \ \ \ 5) ((- 2,1,7), (3, -1,0), (0,2, -1))`
`= (-8 + (- 3) +0 \ \ \ 4 + 1 + 10 \ \ \ 28 + 0 + (- 5))`
`= (- 11 \ \ 15 \ \ 23)`
AB невозможно.(3 × 3) × (1 × 3).
2. Определите, если B = A -1 , учитывая:
`A = ((3, -4), (5, -7))`
`B = ((7,4), (5,3))`
Ответ
Если B = A -1 , то AB = I.
`AB = ((3, -4), (5, -7)) ((7,4), (5,3))`
`= ((21-20,12-12), (35-35,20-21))`
`= ((1,0), (0, -1))`
`! = I`
Таким образом, B НЕ является инверсией A.2 + 0)) `
`= ((1,0), (0,1))`
`= I`
4. Оцените следующее умножение матриц, которое используется для управления движением роботизированного механизма.
`((cos \ 60 °, -sin \ 60 °, 0), (sin \ 60 °, cos \ 60 °, 0), (0,0,1)) ((2), (4), ( 0)) `
Ответ
`((cos \ 60 °, -sin \ 60 °, 0), (sin \ 60 °, cos \ 60 °, 0), (0,0,1)) ((2), (4), ( 0)) `
`= ((2 (0,5) -4 (0,866) +0), (2 (0,866) +4 (0,5) +0), (0 + 0 + 0))`
`= ((- 2,464), (3,732), (0))`
Интерпретация этого заключается в том, что рука робота движется из позиция (2, 4, 0) в позицию (-2.46, 3.73, 0). То есть это перемещается в плоскости x-y , но его высота остается на уровне z = 0 . Матрица 3 × 3, содержащая sin и Значения cos говорят, на сколько градусов нужно переместиться.
Интерактивные элементы умножения матриц
6.2 – Операции с матрицами
6.2 – Операции с матрицамиРавенство
Две матрицы равны тогда и только тогда, когда
- Порядок матриц такой же
- Соответствующие элементы матриц одинаковые
Дополнение
- Порядок матриц должен быть таким же
- Сложите соответствующие элементы вместе
- Матричное сложение коммутативно
- Матрица сложения ассоциативна
Вычитание
- Порядок матриц должен быть одинаковым
- Вычесть соответствующие элементы
- Матричное вычитание не коммутативно (как и вычитание действительных чисел)
- Матричное вычитание не ассоциативное (как и вычитание действительных чисел)
Скалярное умножение
Скаляр – это число, а не матрица.
- Матрица может быть любого порядка
- Умножить все элементы в матрице на скаляр
- Скалярное умножение коммутативно
- Скалярное умножение ассоциативно
Нулевая матрица
- Матрица любого заказа
- Состоит из всех нулей
- Обозначается заглавной буквы O
- Аддитивный идентификатор для матриц
- Любая матрица плюс нулевая матрица является исходной матрицей
Умножение матриц
A m × n × B n × p = C m × p
- Количество столбцов в первой матрице должно быть равно количество строк во второй матрице.То есть внутренние размеры должны быть одинаковыми.
- Порядок произведения – это количество строк в первой матрице на количество столбцов в вторая матрица. То есть габариты изделия – это габариты внешние.
- Поскольку количество столбцов в первой матрице равно количеству строк во второй матрицу, вы можете объединить записи в пары.
- Каждый элемент в строке i из первой матрицы объединяется в пару с элементом в столбце j из вторая матрица.
- Элемент в строке i , столбце j продукта формируется путем умножения этих парных элементов. и суммируя их.
- Каждый элемент в продукте представляет собой сумму произведений элементов из строка i первой матрицы и столбец j второй матрицы.
- Будет n продуктов, которые суммируются для каждого элемента в продукте.
См. Полный пример умножения матриц.
Умножение матриц некоммутативное
- Умножение действительных чисел.
- Внутренние размеры могут не совпадать при изменении порядка матриц.
Не просто перемножайте соответствующие элементы вместе
- Поскольку порядок (размеры) матриц не обязательно должны быть одинаковыми, может не быть соответствующие элементы умножаются вместе.
- Умножьте строки первого столбца на столбцы второго и сложите.
Нет матричного деления
- Не существует определенного процесса деления матрицы на другую матрицу.
- Матрица может быть разделена скаляром.
Идентификационная матрица
- Квадратная матрица
- Единицы по главной диагонали
- Нули везде
- Обозначается I. Если указан нижний индекс, это порядок единичной матрицы.
- I – мультипликативное тождество для матриц
- Любая матрица, умноженная на единичную матрицу, является исходной матрицей.
- Умножение на единичную матрицу коммутативно, хотя порядок единицы может изменить
Идентификационная матрица размера 2
Идентификационная матрица размера 3
| I 3 = | 1 | 0 | 0 | ||
| 0 | 1 | 0 | |||
| 0 | 0 | 1 |
Свойства матриц
| Имущество | Пример |
|---|---|
| Коммутативность сложения | А + В = В + А |
| Ассоциативность сложения | А + (В + С) = (А + В) + С |
| Ассоциативность скалярного умножения | (кд) А = с (дА) |
| Скалярная идентичность | 1А = А (1) = А |
| Распределительный | c (A + B) = cA + cB |
| Распределительный | (с + г) А = сА + дА |
| Аддитивный идентификатор | А + О = О + А = А |
| Ассоциативность умножения | A (BC) = (AB) C |
| Распределительный левый | A (B + C) = AB + AC |
| Распределитель правый | (A + B) C = AC + BC |
| Скалярная ассоциативность / коммутативность | c (AB) = (cA) B = A (cB) = (AB) c |
| Мультипликативная идентичность | IA = AI = A |
Свойства действительных чисел, не являющиеся свойствами матриц
Коммутативность умножения
- Вы не можете изменить порядок задачи умножения и ожидать получить то же самое товар.AB ≠ BA
- Вы должны быть осторожны при разложении общих множителей, чтобы убедиться, что они такой же боковая сторона. AX + BX = (A + B) X и XA + XB = X (A + B), но AX + XB не учитывается.
Свойство нулевого продукта
- Тот факт, что произведение двух матриц является нулевой матрицей, не означает, что одна из им была нулевая матрица.
Мультипликативное свойство равенства
- Если A = B, то AC = BC. Это свойство все еще верно, но обратное не обязательно верно.То, что AC = BC, не означает, что A = B.
- Поскольку умножение матриц не коммутативно, вы должны умножение до или после умножения с обеих сторон уравнения. То есть, если A = B, тогда AC = BC или CA = CB, но AC ≠ CB.
Нет матричного деления
- Надо умножить на обратную матрицу
Оценка функции с помощью матрицы
Рассмотрим функцию f (x) = x 2 – 4x + 3 и матрицу A
Первоначальная попытка оценить f (A) будет заключаться в замене каждого x с помощью A, чтобы получить f (A) = A 2 – 4A + 3.Есть одно небольшое проблема, однако. Константа 3 равна не матрица, и вы не можете добавить матрицы и скаляры вместе. Итак, умножаем константа матрицей идентичности.
f (A) = A 2 – 4A + 3I.
Оцените каждый член функции, а затем сложите их.
| А 2 = | 1 | 2 | * | 1 | 2 | = | 7 | 10 | ||||||
| 3 | 4 | 3 | 4 | 15 | 22 |
| -4 А = -4 | 1 | 2 | = | -4 | -8 | ||||
| 3 | 4 | -12 | -16 |
| 3I = 3 | 1 | 0 | = | 3 | 0 | ||||
| 0 | 1 | 0 | 3 |
| f (А) = | 7 | 10 | + | -4 | -8 | + | 3 | 0 | = | 6 | 2 | ||||||||
| 15 | 22 | -12 | -16 | 0 | 3 | 3 | 9 |
Факторинговые выражения
Показаны некоторые примеры факторинга.Упрощайте и решайте как обычно, но помните эта матрица умножение не коммутативно и нет матричного деления.
2X + 3X = 5X
AX + BX = (A + B) X
ХА + ХВ = Х (А + В)
AX + 5X = (A + 5I) X
AX + XB не учитывает
Решение уравнений
Систему линейных уравнений можно записать как AX = B, где A – коэффициент матрица, X – вектор-столбец, содержащий переменные, а B – правая боковая сторона. В следующем разделе мы узнаем, как решить это уравнение.
Если существует более одной системы линейных уравнений с одним и тем же коэффициентом матрица, то вы можете расширить матрицу B, чтобы она содержала более одного столбца. Положил каждую правую часть в свой столбец.
Умножение матриц
Умножение матриц включает суммирование произведения. Это уместно там, где вы нужно умножайте вещи вместе, а затем добавлять. Например, умножение количества единиц на стоимость единицы будет дать общую Стоимость.
Единицы по продукту найдены путем выполнения модульного анализа на матрицы.Этикетки для продукта – это этикетки строк первого матрица и метки столбцов вторая матрица.
Умножение вектора на матрицу
Чтобы умножить вектор-строку на вектор-столбец, вектор-строка должен иметь столько столбцов, сколько строк в векторе-столбце.
Определим умножение матрицы А и вектор Икс в котором количество столбцов в А равно количеству строк в Икс .
Так что если А является м × п матрица, то произведение А Икс определяется для п × 1 векторы-столбцы Икс . Если мы позволим А Икс знак равно б , потом б является м × 1 вектор-столбец. Другими словами, количество строк в А определяет количество строк в продукте б .
Общая формула для произведения матрица-вектор:
А Икс знак равно [ а 11 а 12 ⋯ а 1 п а 21 год а 22 ⋯ а 2 п ⋮ ⋮ ⋮ ⋮ а м 1 а м 2 ⋯ а м п ] [ Икс 1 Икс 2 ⋮ Икс п ] знак равно [ а 11 Икс 1 + а 12 Икс 2 + ⋯ + а 1 п Икс п а 21 год Икс 1 + а 22 Икс 2 + ⋯ + а 2 п Икс п ⋮ а м 1 Икс 1 + а м 2 Икс 2 + ⋯ + а м п Икс п ]
Пример :
Найти А у куда у знак равно [ 2 1 3 ] и А знак равно [ 1 2 3 4 5 6 7 8 9 ] .
По определению, количество столбцов в А равно количеству строк в у .
А у знак равно [ 1 2 3 4 5 6 7 8 9 ] [ 2 1 3 ]
Сначала умножьте строку 1 матрицы по столбцу 1 вектора.
[ 1 2 3 ] [ 2 1 3 ] знак равно [ 1 ⋅ 2 + 2 ⋅ 1 + 3 ⋅ 3 ] знак равно 13
Далее умножаем строку 2 матрицы по столбцу 1 вектора.
[ 4 5 6 ] [ 2 1 3 ] знак равно [ 4 ⋅ 2 + 5 ⋅ 1 + 6 ⋅ 3 ] знак равно 31 год
Наконец умножьте строку 3 матрицы по столбцу 1 вектора.
[ 7 8 9 ] [ 2 1 3 ] знак равно [ 7 ⋅ 2 + 8 ⋅ 1 + 9 ⋅ 3 ] знак равно 49
Записывая матрично-векторное произведение, получаем:
А у знак равно [ 13 31 год 49 ]
Матрица идентичности – Концепция
При вычислении матрицы важно понимать единичную матрицу .Мы можем думать об единичной матрице как о мультипликативной единице квадратных матриц или как о единичной матрице. Любая квадратная матрица, умноженная на единичную матрицу равных размеров слева или справа, не меняется. Единичная матрица часто используется в доказательствах и при вычислении обратной матрицы.
Мы говорим о квадратных матрицах, и одна действительно важная квадратная матрица – это единичная матрица, о которой мы поговорим чуть позже.Во-первых, давайте посмотрим на матрицу a, b и i, я сначала хочу умножить на i, чтобы перебрать 1 умножить на 1, чтобы 1 плюс 0, было 1, 0-1 это -1, 3 + 0 это 3 и 0+ 0 равно 0, поэтому обратите внимание: 1, -1,3,0 1, -1,3,0 Я получаю ту же матрицу, полученную из этого продукта, на самом деле это просто матрица a.
А теперь позвольте мне умножить i на b, так вот i и вот b, я получаю 2 + 0 2, здесь 3 + 0 3, я получаю 0-1 -1, и я получаю 0 + 4 4 и снова 2,3 -1 , 4 точно так же, это матрица b, поэтому мы замечаем, что когда мы умножаем на эту специальную матрицу i, мы получаем матрицу, с которой мы начали, так что 8 раз i будет просто a, i умножить b будет просто b, i называется единичной матрицей.Это единичная матрица порядка 2, поэтому единичная матрица – это матрица, в которой по диагонали стоят единицы, а во всем остальном – нули. У других других порядков квадратных матриц они тоже есть. Вот единичная матрица порядка 3, вот единичная матрица порядка 4, и, как вы видели раньше, если я умножу матрицу 3 на 3 на эту матрицу, она останется неизменной, так что это вроде как умножение единицы действительных чисел, которое это число 1, которое вы умножаете 5 на 1, вы получаете 5, поэтому при умножении число остается неизменным.
Единичная матрица действительно важна в алгебре матриц, как вы увидите в следующем выпуске.
Identity Matrix – обзор
6 Решение жестких систем ODE
Как описано в предыдущих разделах, временное интегрирование реагирующих газовых смесей является основой многих вычислительных подходов в численном сгорании [12]. Примеры включают моделирование идеальных реакторов (реакторы периодического действия, PSR, PFR, ударные трубы и т. Д.) И точечное интегрирование по времени членов химических источников как часть стратегии разделения операторов для решения многомерных уравнений переноса [ 57].Таким образом, предположим, что реагирующая газовая смесь определяется следующей системой связанных ОДУ первого порядка:
(66) dydt = Sytyt0 = y0
В приведенном ранее уравнении y – это вектор неизвестных ( концентрации веществ, температуры, давления и т. д., в зависимости от конкретной исследуемой проблемы), размером n y , t – время (или пространственная координата, например, в PFR) и S ( y , t ) – нелинейная функция неизвестных из-за химических реакций.Система ODE (66) обычно жесткая, поскольку эволюция химических частиц в большинстве случаев происходит в широком диапазоне характерных времен. Более того, в случае больших кинетических механизмов количество решаемых уравнений может быть очень большим (тысячи уравнений).
В этом абзаце краткий обзор методов, обычно используемых для решения уравнения. (66) сообщается. Более подробный анализ доступен у Имрена и Хауорта [58].
Нелинейная задача, представленная уравнением. (66) обычно решается путем деления времени на небольшие интервалы Δ t ODE .Чтобы продвинуть решение через такой интервал, то есть от времени t n (где y n = y ( t n ) известно) до времени t n + 1 = t n + Δ t ODE (где y n + 1 = 2 y ( t n + 1 ), уравнение линеаризуется следующим образом:
(67) yn + 1 = yn + ∫tntn + 1Sn + Jnyn + 1 − yndt≈yn + SnΔtODE + Jnyn + 1 − ynΔtODE
, который можно переставить как
(68) I − JnΔtODEyn + 1 − yn = SnΔtODE
В предыдущем уравнении I – это единичная матрица, а Jn = ∂S∂yn – так называемая матрица Якоби, вычисляемая на временном уровне. н. .Окончательная формула. (68) представляет собой основу для итерационной процедуры, которую можно использовать для оценки нового решения y n + 1 из решения y n на предыдущем временном уровне. На каждой итерации исходный член S пересчитывается на основе самого последнего значения y , и матрица Якоби J обновляется (можно принять несколько стратегий для выбора того, как и когда обновлять J ) .При правильном выборе шага по времени ожидается, что решение сходится к решению нелинейной задачи. Методы, основанные на решении уравнения. (67) являются довольно дорогостоящими в вычислительном отношении, так как требуют повторных решений линейных систем, содержащих матрицу Якоби. Их можно классифицировать по разным семействам в соответствии с применяемыми ими стратегиями:
- –
выбор временного шага и порядка точности;
- –
вычислить матрицу Якоби;
- –
решите линейную систему (68).
6.1 Варианты интегрирования по времени: BDF и методы экстраполяции
Сегодня приняты две основные стратегии интегрирования: методы обратного дифференцирования с переменным коэффициентом (BDF) [59] и методы экстраполяции [58].
Методы BDF были внедрены в вычислительную химию с 1970-х годов и до сих пор остаются наиболее популярными методами временной интеграции жестких механизмов реакций. В методах BDF в начале интегрирования принимается аппроксимация первого порядка с очень малым временным шагом Δ t ODE .Затем, по мере того, как интеграция продолжается, используется средневзвешенное значение информации из предыдущих внутренних шагов для увеличения порядка схемы интегрирования по времени ad для увеличения временного шага. Как порядок интеграции, так и временные шаги могут значительно увеличиться во время интеграции. В частности, если интеграция может продолжаться до установившегося состояния, методы BDF чрезвычайно эффективны. В методах BDF вычислительные усилия сосредоточены в начале интеграции. Более того, при переходе от временного уровня t n к t n + 1 = t n + Δ t ODE , информация из нескольких предыдущих временных уровней обычно требуется и должен быть правильно сохранен (если порядок интеграции больше 1).Наиболее популярные решатели BDF перечислены ниже:
• CVODE [60]: это решатель для жестких и нежестких задач. Методы, используемые в CVODE, представляют собой многошаговые методы переменного порядка с переменным шагом. Для нежестких задач CVODE включает формулы Адамса – Моултона с порядком, изменяющимся от 1 до 12. Для жестких задач CVODE включает BDF в форме так называемых фиксированных ведущих коэффициентов с порядком, изменяющимся от 1 до 5. Для любого выбора формулы, полученная нелинейная система решается (приближенно) на каждом шаге интегрирования;
• ДАСПК [61]: решатель для систем дифференциально-алгебраических уравнений.Он включает варианты как прямого, так и итерационного (Крылова) методов решения линейных систем, возникающих на каждом (неявном) временном шаге;
• DVODE [59]: это решатель общего назначения, очень похожий на DLSODE [62]. Однако вместо методов интерполяции с фиксированным шагом в DLSODE используются методы с переменными коэффициентами (форма с фиксированными ведущими коэффициентами). Эта и другие особенности часто делают его более эффективным, чем DLSODE;
• DLSODE [62]: решает жесткие и нежесткие системы. В нежестком случае приняты методы Адамса (предсказатель-корректор), а в жестком – методы BDF (методы Гира).Возникающие линейные системы решаются прямыми методами (LU-факторизация / решение). DLSODE заменил старые пакеты GEAR и GEARB с некоторыми улучшениями алгоритмов;
• DLSODA [62]: это вариантная версия пакета DLSODE. Он автоматически переключается между жесткими и нежесткими методами. Это означает, что пользователю не нужно определять, является ли проблема сложной или нет, и решатель автоматически выберет наиболее подходящий метод. Он всегда начинается с нежесткого метода;
• OdeSMOKE ++ [15]: это программа для решения очень жестких задач, основанная на BDF в форме так называемых фиксированных ведущих коэффициентов с порядком, изменяющимся от 1 до 5.При любом выборе формулы результирующая нелинейная система решается (приблизительно) на каждом шаге интегрирования. OdeSMOKE ++ основан на том же численном подходе, который используется библиотекой BzzMath [63];
• RADAU5 [64]: он использует неявный метод Рунге – Кутта порядка 5 (три этапа) с контролем размера шага и непрерывным выводом.
В методах экстраполяции [58] каждый временной шаг Δ t ODE последовательно делится на подинтервалы, метод низкого порядка применяется для каждого подинтервала, а рекурсивная процедура используется для проецирования с точностью более высокого порядка. по каждому Δ т ODE .Разделение продолжается до тех пор, пока не будет достигнут заданный пользователем уровень точности. Как и в случае с методами BDF, следующий временной шаг оценивается во время интегрирования на основе теоретических и эвристических аргументов. В методах экстраполяции вычислительные усилия не концентрируются в начале временного интервала, а для перехода от временного уровня t n к t n + 1 = t n + Δ t ODE , нужна только информация с уровня t n .Один из самых популярных методов экстраполяции – SEULEX, который подробно описан в работе. [58].
6.2 Оценка якобиана: численные и аналитические методы
Можно выделить три основных подхода к вычислению элементов матрицы Якоби: метод конечных разностей, полуаналитические методы и полностью аналитические методы [58]. В первом случае каждый столбец J вычисляется путем возмущения одного элемента y на небольшую величину ɛ и вычисления частных производных численно, обычно с использованием прямых разностей первого порядка.Поскольку для этого требуется n y оценок S , численное дифференцирование требует больших вычислительных ресурсов и сегодня применяется только для небольших кинетических механизмов.
Аналитические методы основаны на том факте, что скорость образования большинства химических соединений обычно определяется лишь небольшим набором реакций. Отражая это физическое поведение, большинство крупных химических кинетических механизмов в литературе чрезвычайно редки с точки зрения взаимодействий между различными видами.Другими словами, каждый вид вступает в реакцию с небольшим количеством из общего числа видов, имеющихся в смеси. В частности, аналитические методы вычисляют некоторые (в случае полуаналитического) или все (в случае полностью аналитического) частные производные химического исходного члена S аналитически. Эта операция относительно проста для элементарных реакций, но становится гораздо более сложной для реакций, зависящих от давления, реакций на основе полиномов Чебышева, реакций с эффективностью третьего тела и т. Д.Это причина популярности полуаналитических методов для сложных механизмов: только простые реакции рассматриваются в рамках полностью аналитического подхода, в то время как сложные реакции (обычно присутствующие в небольшом проценте) обрабатываются методом конечных разностей.
6.3 Линейные системы: прямые и итерационные методы
Решение линейных систем требуется на каждой итерации, и эта операция требует больших вычислительных ресурсов, особенно когда используются большие механизмы. Доступны два основных варианта: прямые и итерационные линейные решатели.Прямые решатели (факторизация Гаусса, разложение LU и т. Д.) Очень точны и, в принципе, могут дать точное решение линейной системы. Вычислительные затраты масштабируются с n y 3 для больших n y . Итерационные решатели (например, методы Крылова) дают приближенное решение линейной системы в пределах заданного пользователем допуска. Предобуславливатель обычно связан с каждым итеративным методом, и неполное разложение LU является одним из наиболее распространенных вариантов.Вычислительные затраты масштабируются как n y до n y 2 для больших n y [12,65,66]. Ожидается, что для больших систем итерационные решатели будут более эффективными, чем прямые решатели, особенно когда приняты высокооптимизированные библиотеки [67]. Поскольку приближения, сделанные в оценке Якоби, не влияют на решение связанной нелинейной системы (до тех пор, пока она сходится), можно использовать дополнительные численные методы для снижения вычислительных затрат.Одним из наиболее многообещающих подходов является фильтрация матрицы Якоби, которая заключается в установке значений, меньших заданного порога, равными нулю, чтобы увеличить разреженность матрицы.
6.4 Ускорение численных расчетов
Согласно Smooke et al. [68], в типичных расчетах потока реагирования с подробными кинетическими схемами более ~ 80% времени ЦП тратится на численную оценку матриц Якоби. Поскольку построение матрицы Якоби включает в себя оценку термодинамических свойств и вычисление скоростей образования каждого вида большое количество раз, важно обеспечить максимально быстрое вычисление этих свойств.Эта цель достигается с помощью нескольких методов:
- •
кэширование : код написан так, чтобы кэшировать как можно больше, что означает сохранение элементов для будущего использования, чтобы избежать их извлечения или пересчета. На лету выполняются только строго необходимые расчеты. Если некоторые переменные можно вычислить только один раз, они сохраняются, чтобы быть доступными для будущих нужд;
- •
оптимизированные функции : численные алгоритмы часто переформулируются, чтобы использовать автоматическую векторизацию, предлагаемую современными компиляторами;
- •
переформулировка кода : многие части численных алгоритмов переформулированы менее интуитивно, чтобы минимизировать количество флопов (т.е.например, элементарные операции), необходимые для выполнения некоторых вычислений или для того, чтобы избежать использования дорогостоящих CPU функций [2]. Например, кинетические константы не оцениваются с использованием обычного прямого подхода, то есть как k j = A j T β j ехр (- E j / RT ). Напротив, они рассчитываются по следующей формуле: k j = exp (ln ( A j ) + β j – E j / РТ ).Первая формулировка требует двух дорогостоящих функций для вычисления кинетической постоянной: степенной и экспоненциальной. Вторая формулировка только одна дорогостоящая экспоненциальная функция. Коэффициент ln ( A j ) должен оцениваться только один раз и сохраняться, и его не нужно повторно вычислять каждый раз. Совершенно очевидно, что, используя эту простую переформулировку, пользователь может сэкономить время процессора, учитывая, что подробные кинетические схемы включают тысячи реакций.
единичная матрица · Tea & Stats
Сколько различных способов создать единичную матрицу в R? Это была небольшая интересная задача, поставленная Гийомом Никуло в Twitter.
Найдите как можно больше способов создать единичную матрицу с помощью #rstats. pic.twitter.com/HlhIM6mSrx
– Гийом Никуло (@ordrespontane) 3 февраля 2018 г.
В гольф-коде программисты пытаются написать алгоритм, используя как можно более короткую программу, часто используя менее известные эксцентричности каждого языка программирования.
Однако эта задача R не столько сводится к минимизации вашего гандикапа в гольф, сколько к демонстрации некоторых особенностей и функций в R, о которых другие могут не знать. Выбираем живописный маршрут и учимся по пути. Безумный гольф код, если хотите.
Идентификационная матрица
Напоминаем, что единичная матрица является линейным алгебраическим эквивалентом числа 1. Это диагональная матрица из единиц, в которой все недиагональные элементы равны нулю. Например, трехмерная единичная матрица имеет вид $$ \ mathbf {I} = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}.{-1} \ mathbf {M} = \ mathbf {I} $$
Идентификационные матрицы в R
Сейчас я покажу вам множество способов создания пятимерной единичной матрицы в R, от простых до более эзотерических.
Легкий путь
Есть функция, предназначенная именно для этой цели, так что используйте ее.
n <- 5 л
диаг (п)
[, 1] [, 2] [, 3] [, 4] [, 5]
[1,] 1 0 0 0 0
[2,] 0 1 0 0 0
[3,] 0 0 1 0 0
[4,] 0 0 0 1 0
[5,] 0 0 0 0 1
Функция diag () при передаче матрицы извлекает диагональные элементы из этой матрицы.При передаче вектора он создает диагональную матрицу с элементами, равными этому вектору.
Когда передается скаляр, как здесь, он создает единичную матрицу размером n на n .
Если вы действительно искали функцию для создания матриц идентичности в R, вы ее нашли и можете перестать читать здесь.
Путь оптимистичного математика
В приведенном выше уравнении мы видели, что единичная матрица равна любой матрице, умноженной на ее собственную обратную.Итак, давайте сделаем это, используя матрицу случайных нормальных выборок.
x <- матрица (rnorm (n * n), n, n)
x% *% решить (x)
[, 1] [, 2] [, 3] [, 4] [, 5]
[1,] 1.000000e + 00 -1.387779e-16 -1.196959e-16 -2.498002e-16 -3.330669e-16
[2,] 0.000000e + 00 1.000000e + 00 2.775558e-17 0.000000e + 00 2.220446e-16
[3,] 0.000000e + 00 0.000000e + 00 1.000000e + 00 0.000000e + 00 0.000000e + 00
[4,] -2.220446e-16 5.551115e-17 -6.938894e-18 1.000000e + 00 0,000000e + 00
[5,] -5.551115e-16 1.387779e-16 -3.816392e-17 0.000000e + 00 1.000000e + 00
К сожалению, компьютеры не обладают бесконечной точностью, поэтому здесь есть небольшая ошибка с плавающей запятой. Результатом является почти , равное единичной матрице. Немного округления должно позаботиться об этом:
раунд (x% *% решить (x))
[, 1] [, 2] [, 3] [, 4] [, 5]
[1,] 1 0 0 0 0
[2,] 0 1 0 0 0
[3,] 0 0 1 0 0
[4,] 0 0 0 1 0
[5,] 0 0 0 0 1
Отлично!
Векторизованный индексный путь
Диагональные записи - это те записи, у которых индексы строки и столбца равны.То есть единичная матрица - это матрица $ \ mathbf {D} $, элементами которой являются $$ d_ {ij} = \ begin {cases} 1 & i = j, \\ 0 & i \ neq j \ end {cases}. $$
Или в терминах R:
.col (c (n, n)) == .row (c (n, n))
[, 1] [, 2] [, 3] [, 4] [, 5]
[1,] ИСТИНА ЛОЖЬ ЛОЖЬ ЛОЖЬ ЛОЖЬ
[2,] FALSE TRUE FALSE FALSE
[3,] FALSE FALSE TRUE FALSE FALSE
[4,] FALSE FALSE FALSE TRUE FALSE
[5,] FALSE FALSE FALSE FALSE TRUE
Умножьте этот результат на 1 или добавьте 0, чтобы преобразовать логические значения в двоичные.Если у вас уже есть матрица $ n \ times n $, вы можете быть еще более кратким:
x <- матрица (nrow = n, ncol = n)
1 * (столбец (x) == строка (x))
[, 1] [, 2] [, 3] [, 4] [, 5]
[1,] 1 0 0 0 0
[2,] 0 1 0 0 0
[3,] 0 0 1 0 0
[4,] 0 0 0 1 0
[5,] 0 0 0 0 1
Просто помните, что функции нижнего уровня .col () и .row () , в отличие от всего остального во вселенной R, действительно заботятся о разнице между целым числом и числом с плавающей запятой.Команда .col (c (5, 5)) вызывает бесполезную ошибку,
Ошибка в .col (c (5, 5)):
объект, подобный матрице, требуется в качестве аргумента для 'col'
, в то время как .col (c (5L, 5L)) , где размеры являются явно целыми числами, дает желаемый результат.
Внешний путь продукта
Аналогично предыдущему, но более элегантно.
внешний (1: n, 1: n, '==') + 0
Спасибо Флориану Приве за это. Функция внешнего произведения применяет все возможные комбинации элементов первых двух аргументов и возвращает результаты в виде матрицы.
Если это непонятно, вот сетка Battleship :
внешний (БУКВЫ [1: 5], 1: 5, paste0)
[, 1] [, 2] [, 3] [, 4] [, 5]
[1,] «A1» «A2» «A3» «A4» «A5»
[2,] «B1» «B2» «B3» «B4» «B5»
[3,] «C1» «C2» «C3» «C4» «C5»
[4,] «D1» «D2» «D3» «D4» «D5»
[5,] «E1» «E2» «E3» «E4» «E5»
Путь с петельным указателем
То же, что и выше, но с использованием циклов, которые в R довольно медленны, и их следует избегать.
x <- матрица (nrow = n, ncol = n)
для (я в 1: п)
для (j в 1: n)
если (я == j)
x [i, j] <- 1
саппли путьЕсли вы хотите использовать петли, убеждая себя, что вы не используете петли.
sapply (1: n, функция (i) as.integer (1: n == i))
Аккуратный путь
tidyverse побуждает нас хранить все в длинных фреймах данных, поэтому давайте не будем делать здесь исключения. Вот набор данных, описывающий положение всех.
data.frame (значение = 1, row_index = 1: n, column_index = 1: n)
row_index column_index значение
1 1 1 1
2 2 2 1
3 3 3 1
4 4 4 1
5 5 5 1
Теперь мы можем использовать удобную функцию xtabs () для создания двусторонней таблицы непредвиденных обстоятельств.Dimnames теряет актуальность, поэтому мы можем удалить их, пока работаем.
unname (xtabs (data.frame (1, 1: n, 1: n)))
Edit: Еще более простая версия -
таблица (data.frame (1: n, 1: n))
Редкий путь
Единичная матрица - это то же самое, что и матрица перестановок, в которой порядок элементов не изменяется:
$$ \ {1, \ dots, n \} \ rightarrow \ {1, \ dots, n \}. $$
Пакет Matrix имеет специальный класс pMatrix для матриц разреженных перестановок.
библиотека (матрица)
как (1: n, 'pMatrix')
5 x 5 разреженная матрица класса "pMatrix"
[1,] | . . . .
[2,]. | . . .
[3,]. . | . .
[4,]. . . | .
[5,]. . . . |
Трудный путь
Матрицы - это просто измененные векторы. Элементами единичной матрицы являются (либо по столбцам, либо по строкам; это не имеет значения, потому что они симметричны) $$ \ {1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, \ dots, 1 \} $$ то есть единица, затем $ n $ обнуляет, еще одну, еще $ n $ обнуляет и так далее, заканчивая $ n $ ой единицей.
Мы можем записать такую последовательность, а затем изменить ее форму.
матрица (c (rep (c (1, rep (0, n)), n - 1), 1), n)
В принципе не читается, но работает!
Собственная версия Гийома не умещается в одной строке, но немного более разумна:
x <- rep (0, n * n)
x [seq (1, n * n, n + 1)] <- 1
dim (х) <- с (п, п)
Колин Фэй делает более читаемое решение, используя преимущества матричного вещания. То есть R будет повторять вектор, чтобы он соответствовал выделенному пространству, если он уже недостаточно длинный.2 $ не является точным кратным $ n + 1 $, R выдаст предупреждение, которое можно проигнорировать.
[, 1] [, 2] [, 3] [, 4] [, 5]
[1,] 1 0 0 0 0
[2,] 0 1 0 0 0
[3,] 0 0 1 0 0
[4,] 0 0 0 1 0
[5,] 0 0 0 0 1
Предупреждение:
В матрице (c (1, rep (0, n)), nrow = n, ncol = n):
длина данных [6] не является кратной или кратной количеству строк [5]
Если это вас раздражает, скройте это с помощью suppressWarnings () .2, 1, 1/5)
Этот великолепный код будет многократно выполнять выборку записей m из биномиального распределения, пока в результате не будет единичная матрица.
Пожалуй, это лучшее решение.
Решив эту задачу, какие еще задачи по игре в гольф с кодом R вы бы хотели увидеть? Возможно, все разные способы решения общей задачи обработки данных или создания определенного вида визуализации - пожалуйста, дайте мне знать, если у вас есть какие-либо идеи.
.

