Как умножить матрицу: примеры, алгоритм умножения на вектор, число, свойства произведения

примеры, алгоритм умножения на вектор, число, свойства произведения

Произведение двух матриц

Определение 1

Произведение матриц (С= АВ) — операция только для согласованных матриц А и В, у которых число столбцов матрицы А равно числу строк матрицы В:

C⏟m×n=A⏟m×p×B⏟p×n

Пример 1

 Даны матрицы:

• A=a(ij) размеров m×n;
• B=b(ij) размеров p×n

Матрицу C, элементы cij которой вычисляются по следующей формуле:

cij=ai1×b1j+ai2×b2j+…+aip×bpj, i=1,…m, j=1,…m

Пример 2

Вычислим произведения АВ=ВА:

А=121012, В=100111

Решение, используя правило умножения матриц:

А⏟2×3×В⏟3×2=121012×100111=1×1+2×0+1×11×0+2×1+1×10×1+1×0+2×10×0+1×1+2×1==2323⏟2×2

В⏟3×2×А⏟2×3=100111×121012=1×1+0×01×2+0×11×1+0×20×1+1×00×2+1×10×1+1×21×1+1×01×2+1×11×1+1×2=121012133⏟3×3

Произведение АВ и ВА найдены, но являются матрицами разных размеров: АВ не равна ВА.

Свойства умножения матриц

Свойства умножения матриц:

• (АВ)С = А(ВС) — ассоциативность умножения матриц;
• А(В+С) = АВ + АС — дистрибутивность умножения;
• (А+В)С = АС + ВС — дистрибутивность умножения;
• λ(АВ)=(λА)В

Пример 1

Проверяем свойство №1: (АВ)С = А(ВС):

(А×В)×А=1234×5678×1002=19224350×1002=194443100,

А(В×С)=1234×56781002=1234×512716=194443100.

Пример 2

Проверяем свойство №2: А(В+С) = АВ + АС:

А×(В+С)=1234×5678+1002=1234×66710=20264658,

АВ+АС=1234×5678+1234×1002=19224350+1438=20264658.

Произведение трех матриц

Произведение трех матриц АВС вычисляют 2-мя способами:

• найти АВ и умножить на С: (АВ)С;
• либо найти сначала ВС, а затем умножить А(ВС).

​​​​​Пример 3

Перемножить матрицы 2-мя способами:

4375×-289338-126×7321

Алгоритм действий:

• найти произведение 2-х матриц;
• затем снова найти произведение 2-х матриц.

1). АВ=4375×-289338-126=4(-28)+3×384×93+3(-126)7(-28)+5×387×93+5(-126)=2-6-621

2). АВС=(АВ)С=2-6-6217321=2×7-6×22×3-6×1-6×7+21×2-6×3+21×1=2003.

Используем формулу АВС=(АВ)С:

1). ВС=-289338-1267321=-28×7+93×2-28×3+93×138×7-126×238×3-126×1=-10914-12

2). АВС=(АВ)С=7321-10914-12=4(-10)+3×144×9+3(-12)7(-10)+5×147×9+5(-12)=2003

Ответ: 4375-289338-1267321=2003

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Умножение матрицы на число

Определение 2

Произведение матрицы А на число k — это матрица В=Аk того же размера, которая получена из исходной умножением на заданное число всех ее элементов:

bi,j=k×ai,j

Свойства умножения матрицы на число:

• 1×А=А
• 0×А=нулевая матрица
• k(A+B)=kA+kB
• (k+n)A=kA+nA
• (k×n)×A=k(n×A)

Пример 4

Найдем произведение матрицы А=4290   на 5.

Решение:

5А=542905×45×25×95×0=2010450

Умножение матрицы на вектор

Определение 3

Чтобы найти произведение матрицы и вектора, необходимо умножать по правилу «строка на столбец»:

• если умножить матрицу на вектор-столбец число столбцов в матрице должно совпадать с числом строк в векторе-столбце;
• результатом умножения вектора-столбца является только вектор-столбец:

АВ=а11а12⋯а1nа21а22⋯а2n⋯⋯⋯⋯аm1аm2⋯аmnb1b2⋯b1n=a11×b1+a12×b2+⋯+a1n×bna21×b1+a22×b2+⋯+a2n×bn⋯⋯⋯⋯am1×b1+am2×b2+⋯+amn×bn=c1c2⋯c1m

• если умножить матрицу на вектор-строку, то умножаемая матрица должна быть исключительно вектором-столбцом, причем количество столбцов должно совпадать с количеством столбцов в векторе-строке:

АВ=аа⋯аbb⋯b=a1×b1a1×b2⋯a1×bna2×b1a2×b2⋯a2×bn⋯⋯⋯⋯an×b1an×b2⋯an×bn=c11c12⋯c1nc21c22⋯c2n⋯⋯⋯⋯cn1cn2⋯cnn

Пример 5

Найдем произведение матрицы А и вектора-столбца В:

АВ=240-213-10112-1=2×1+4×2+0×(-1)-2×1+1×2+3×(-1)-1×1+0×2+1×(-1)=2+8+0-2+2-3-1+0-1=10-3-2

Пример 6

Найдем произведение матрицы А и вектора-строку В:

А=320-1, В=-1102

Решение:

АВ=3201×-1102=3×(-1)3×13×03×22×(-1)2×12×02×20×(-1)0×10×00×21×(-1)1×11×01×2=-3306-22040000-1102

Ответ: АВ=-3306-22040000-1102

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

определение, свойства и примеры решения задач

Содержание:

Определение

Произведением матрицы $A$ на ненулевое число $ \lambda $ называется матрица $ B=\lambda A $ того же порядка, полученная из исходной умножением на заданное число всех ее элементов:

$$ B=\lambda A \Longrightarrow b_{i j}=\lambda a_{i j} $$

Итак, в результате умножения матрицы на число получается матрица такой же размерности, что и исходная, каждый элемент которой является результатом произведения соответствующего элемента исходной матрицы на заданное число.

Мы получим одинаковый результат, умножая число на матрицу, или матрицу на число, то есть $ \lambda A = A \lambda $.

Из определения следует, что общий множитель всех элементов матрицы можно выносить за знак матрицы.

Данная операция, вместе с операцией сложения матриц, относится к линейным операциям над матрицами.

Пример

Задание. Чему равна матрица $-3A$, если матрица $ A=\left( \begin{array}{rr}{-1} & {3} \\ {0} & {2}\end{array}\right) $ ?

Решение. $ -3 A=3 \cdot \left( \begin{array}{rr}{-1} & {3} \\ {0} & {2}\end{array}\right)=\left( \begin{array}{rr}{-3 \cdot(-1)} & {-3 \cdot 3} \\ {-3 \cdot 0} & {-3 \cdot 2}\end{array}\right)=\left( \begin{array}{cc}{3} & {-9} \\ {0} & {-6}\end{array}\right) $

Ответ. $ -3 A=\left( \begin{array}{ll}{3} & {-9} \\ {0} & {-6}\end{array}\right) $

Свойства умножения матрицы на число:

1. $ 1 \cdot A=A $
2. $ 0 \cdot A=\Theta $
3. $ \lambda(A+B)=\lambda A+\lambda B $
4. $ (\lambda+\mu) A=\lambda A+\mu A $
5. $ (\lambda \mu) A=\lambda(\mu A) $

Читать дальше: сложение и вычитание матриц.

Слишком сложно?

Умножение матрицы на число не по зубам? Тебе ответит эксперт через 10 минут!

Умножение матриц

Расчет умножения матриц онлайн. Умножьте матрицы порядка 2×3, 1×3, 3×3, 2×2 с 3×2, 3×1, 3×3, 2×2. Динамические расчеты, нахождения произведения матриц.

Умножение матриц возможно когда число столбцов первой матрицы равно числу строк второй матрицы.

Матрица 1

X

Матрица 2

3x33x22x33x11x32x2

X

3x33x22x33x11x32x2

В первой части мы рассмотрим умножение квадратных матриц. В следующей части Вы узнаете, как умножить разные матрицы (например, 2х3 до 3х3).

Здесь мы будем умножать матрицу 3х3 (3 ряда, 3 колонки) на другую матрицу 3х3 (3 ряда, 3 колонки).

Матрица A		Матрица B
a11 a12 a13 a21 a22 a23 a31 a32 a33	x	b11 b12 b13 b21 b22 b23 b31 b32 b33

В результате мы получим матрицу 3х3. Нам придется рассчитать каждую клетку результатов матрицы отдельно. Результат выразим через X.

Шаг 1:Рассчитаем x11
Для того, чтобы вычислить результат  x11 мы будем использовать первую строку матрицы А и первый столбец матрицы В.

Результат X		Матрица A		Матрица B
x11 x12 x13 x21 x22 x23 x31 x32 x33	=	a11 a12 a13 a21 a22 a23 a31 a32 a33	x	b11 b12 b13 b21 b22 b23 b31 b32 b33

Мы можем представить результат  x11 = a11 x b11 + a12 x b21 + a13 x b31

Шаг 2: Рассчитаем x12
Для того, чтобы вычислить результат x12 мы будем использовать первую строку матрицы А и втором столбце матрицы В.

Результат X		Матрица A		Матрица B
x11 x12 x13 x21 x22 x23 x31 x32 x33	=	a11 a12 a13 a21 a22 a23 a31 a32 a33	x	b11 b12 b13 b21 b22 b23 b31 b32 b33

Мы можем представить резальтат x12 = a11 x b12 + a12 x b22 + a13 x b32

По той же методике мы вычислим значения для всех ячеек.

Результат Матрица

a11xb11 + a12xb21 + a13xb31 a11xb12 + a12xb22 + a13xb32 a11xb13 + a12xb23 + a13xb33 a21xb11 + a22xb21 + a23xb31 a21xb12 + a22xb22 + a23xb32 a21xb13 + a22xb23 + a23xb33 a31xb11 + a32xb21 + a33xb31 a31xb12 + a32xb22 + a33xb32 a31xb13 + a32xb23 + a33xb33

Умножение матриц, формулы и примеры

ОПРЕДЕЛЕНИЕ Произведением матрицы размером на матрицу размером называется матрица () размером элементы которой определяются формулой:

   

Иначе говоря, элемент матрицы стоящий в -той строке и -том столбце, равен сумме произведений элементов -той строки матрицы на соответствующие элементы -го столбца матрицы Таким образом, умножение осуществляется по правилу умножения строки на столбец.

Не всякие две матрицы можно перемножить. Произведение двух матриц возможно только в том случае, если число столбцов матрицы совпадает с числом строк в матрице . Для того чтобы перемножить две квадратные матрицы необходимо, чтобы они были одного порядка. При этом в результате получится матрица того же порядка, что и перемножаемые матрицы.

Как умножать матрицы, примеры

ПРИМЕР 1

Задание	Найти произведение матрицы и вектора-столбца .
Решение	Матрица имеет размерность матрица имеет размерность значит размерность произведения будет Действительно,         Заметим, что произведение этих матриц в обратном порядке невозможно.
Ответ

Произведение двух матриц в общем случае зависит от порядка сомножителей, то есть оно не коммутативно:

   

ПРИМЕР 2

Задание	Заданы матрицы и . Найти их произведения и
Решение	Матрица имеет размерность а матрица – размерность тогда размерность произведения будет . Действительно, умножая по принципу, строка первой матрицы на столбец второй, получим         Произведение так же будет существовать и его размерность будет .
Ответ

Но бывают матрицы, для которых выполняется равенство

   

такие матрицы называются перестановочными или коммутирующими. Такие матрицы будут обязательно квадратными.

ПРИМЕР 3

Задание	Проверить являются ли перестановочными матрицы и , если
Решение	Найдем произведения этих матриц и .                 Таким образом, для заданных матриц выполняется равенство поэтому они являются перестановочными.
Ответ	Матрицы и перестановочные.

Читайте также:

Определитель матрицы и способы вычисления

Обратная матрица и способы вычисления

Ранг матрицы

Транспонирование матрицы

Сложение матриц

Единичная матрица

Умножить матрицу на вектор онлайн

Результат умножения вектора-строки на матрицу с*A

Результат умножения матрицы на вектор-столбец A*b

Каждый вектор можно рассматривать как одностолбцовую или однострочную матрицу. Одностолбцовую матрицу будем называть вектор-столбцом, а однострочную матрицу – вектор-строкой.

Если A-матрица размера m*n, то вектор столбец b имеет размер n, а вектор строка b имеет размер m.

Таким образом, что бы умножить матрицу на вектор, надо рассматривать вектор как вектор-столбец. При умножении вектора на матрицу, его нужно рассматривать как вектор -строку.

Пример.

Умножить матрицу

\(\begin{pmatrix} 1+2i & 2+i & 1+3i \\ 2 & 4+2i & 2+5i \end{pmatrix}\)

на комплексный вектор

\(\begin{pmatrix} 2+2i  \\ 1+4i \\ 2+2i \end{pmatrix}\)

Получаем результат

Результат умножения матрицы на вектор A*b

Результат умножения вектора на матрицу b*A

 

Как видите при неизменной размерности вектора, у нас могут существовать два решения.

Хотелось бы обратить Ваше внимание на то что матрица в первом и втором варианте, несмотря на одинаковые значения, совершенно разные (имеют различную размерность)

 

В первом случае вектор считается как столбец и тогда необходимо  умножать матрицу на вектор, а во втором случае у нас вектор-строка и тогда у нас произведение вектора на матрицу.

 

 

Свойства умножения матрицы на вектор

 – матрица   – вектор столбец   – вектор-строка  – произвольное число

1. Произведение матрицы на сумму векторов-столбцов равна сумме произведений матрицы на каждый из векторов

2. Произведение суммы векторов-строк на матрицу  равна сумме произведений векторов на матрицу

3. Общий множитель вектора  можно вынести за пределы произведения матрицы на вектор/вектора на матрицу

4.Произведение вектора-строки на произведение матрицы и вектора столбца, равноценно произведению произведения вектора-строки на матрицу и вектора-столбца.

 

Удачных расчетов!!

 

Как умножить матрицу на число: правило, свойства, примеры

В данной публикации мы рассмотрим, каким образом матрицу можно умножить на определенное число. Также мы приведем практические примеры и перечислим основные свойства рассматриваемого произведения.

Правило умножения матрицы на число

Результатом умножения матрицы (A) на любое число (m), не равное нулю, является матрица того же порядка (размера), элементы которой равны произведению соответствующих элементов исходной матрицы на данное число.

B = m ⋅ A

В общем виде это выглядит примерно так:

Согласно законам умножениям, порядок сомножителей неважен, т.е.:

m ⋅ A = A ⋅ m = B

Следствие: если у всех элементов матрицы есть общий множитель, его можно вынести за пределы матрицы.

Свойства произведения матрицы и числа

1. Если матрицу умножить на единицу (или наоборот), в результате получится та же самая матрица.

1 ⋅ A = A ⋅ 1 = A

2. Результатом произведения матрицы на ноль является Θ, где Θ – нулевая матрица (все ее элементы равны нулю).

0 ⋅ A = A ⋅ 0 = Θ

3. Умножение числа на сумму матриц – это то же самое, что и сумма произведений данного числа с каждой матрицей по отдельности.

m ⋅ (A + B) = mA + mB

4. Произведение суммы чисел и матрицы – это то же самое, что и сумма произведений каждого числа и матрицы.

(m + n ) ⋅ A = mA + nA

5. Сочетательный закон при умножении применим и к матрицам:

(m ⋅ n ) ⋅ A = m ⋅ (n ⋅ A)

Примеры задач

Пример 1
Определите, чему равняется 4A, если исходная матрица A выглядит так:

Решение:

Пример 2
Выясните, есть ли у матрицы ниже общий множитель, и, если да, вынесите его за ее пределы.

Решение:
Наименьшим общим делителем всех элементом заданной матрицы является число 2, следовательно, его можно вынести за скобки.

Линейная алгебра на Python. [Урок 3]. Действия над матрицами

Тема третьего урока: действия над матрицами. В рамках нее будут рассмотрены следующие вопросы: умножение матрицы на число, сложение и умножение матриц.

Действия над матрицами

Умножение матрицы на число

При умножении матрицы на число, все элементы матрицы умножаются на это число:

➣ Численный пример

➤ Пример на Python

>>> A = np. matrix('1 2 3; 4 5 6')
>>> C = 3 * A
>>> print(C)
[[ 3  6 9]
[12 15 18]]

 

Рассмотрим свойства операции умножения матрицы на число.

Свойство 1. Произведение единицы и любой заданной матрицы равно заданной матрице:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> L = 1 * A
>>> R = A
>>> print(L)
[[1 2]
[3 4]]

>>> print(R)
[[1 2]
[3 4]]

 

Свойство 2. Произведение нуля и любой матрицы равно нулевой матрице, размерность которой равна исходной матрицы:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> Z = np.matrix('0 0; 0 0')
>>> L = 0 * A
>>> R = Z

>>> print(L)
[[0 0]
[0 0]]

>>> print(R)
[[0 0]
[0 0]]

 

Свойство 3. Произведение матрицы на сумму чисел равно сумме произведений матрицы на каждое из этих чисел:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> p = 2
>>> q = 3

>>> L = (p + q) * A
>>> R = p * A + q * A

>>> print(L)
[[ 5 10]
[15 20]]

>>> print(R)
[[ 5 10]
[15 20]]

 

Свойство 4. Произведение матрицы на произведение двух чисел равно произведению второго числа и заданной матрицы, умноженному на первое число:

➣ Численный пример

➤Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> p = 2
>>> q = 3

>>> L = (p * q) * A
>>> R = p * (q * A)

>>> print(L)
[[ 6 12]
[18 24]]

>>> print(R)
[[ 6 12]
[18 24]]

 

Свойство 5. Произведение суммы матриц на число равно сумме произведений этих матриц на заданное число:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> k = 3

>>> L = k * (A + B)
>>> R = k * A + k * B

>>> print(L)
[[18 24]
[30 36]]

>>> print(R)
[[18 24]
[30 36]]

 

Сложение матриц

Складывать можно только матрицы одинаковой размерности — то есть матрицы, у которых совпадает количество столбцов и строк.

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 6 3; 8 2 7')
>>> B = np.matrix('8 1 5; 6 9 12')
>>> C = A + B

>>> print(C)
[[ 9  7 8]
[14 11 19]]

 

Рассмотрим свойства сложения матриц.

Свойство 1. Коммутативность сложения. От перестановки матриц их сумма не изменяется:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')

>>> L = A + B
>>> R = B + A

>>> print(L)
[[ 6  8]
[10 12]]

>>> print(R)
[[ 6  8]
[10 12]]

 

Свойство 2. Ассоциативность сложения. Результат сложения трех и более матриц не зависит от порядка, в котором эта операция будет выполняться:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> C = np.matrix('1 7; 9 3')

>>> L = A + (B + C)
>>> R = (A + B) + C
>>> print(L)

[[ 7 15]
[19 15]]

>>> print(R)
[[ 7 15]
[19 15]]

 

Свойство 3. Для любой матрицы существует противоположная ей , такая, что их сумма является нулевой матрицей :

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> Z = np.matrix('0 0; 0 0')

>>> L = A + (-1)*A

>>> print(L)
[[0 0]
[0 0]]

>>> print(Z)
[[0 0]
[0 0]]

 

Умножение матриц

Умножение матриц это уже более сложная операция, по сравнению с рассмотренными выше. Умножать можно только матрицы, отвечающие следующему требованию: количество столбцов первой матрицы должно быть равно числу строк второй матрицы.

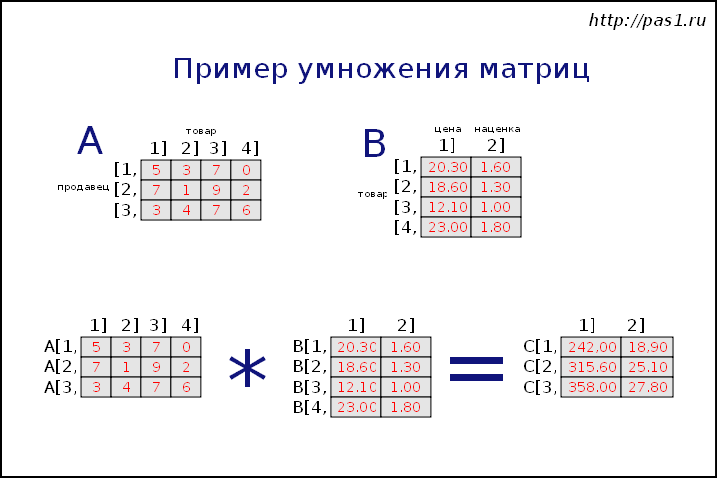
Для простоты запоминания этого правила можно использовать диаграмму умножения, представленную на рисунке 1.

Рисунок 1 — Диаграмма матричного умножения

Рассмотрим умножение матриц на примере.

➣ Численный пример

Каждый элемент c_ij новой матрицы является суммой произведений элементов i-ой строки первой матрицы и j-го столбца второй матрицы. Математически это записывается так:

➤Пример на Python

Решим задачу умножения матриц на языке Python. Для этого будем использовать функцию dot() из библиотеки Numpy:

>>> A = np.matrix('1 2 3; 4 5 6')
>>> B = np.matrix('7 8; 9 1; 2 3')

>>> C = A.dot(B)

>>> print(C)
[[31 19]
[85 55]]

 

Ниже представлены свойства произведения матриц. Примеры свойств будут показаны для квадратной матрицы.

Свойство 1. Ассоциативность умножения. Результат умножения матриц не зависит от порядка, в котором будет выполняться эта операция:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> C = np.matrix('2 4; 7 8')

>>> L = A.dot(B.dot(C))
>>> R = (A.dot(B)).dot(C)

>>> print(L)
[[192 252]
[436 572]]

>>> print(R)
[[192 252]
[436 572]]

 

Свойство 2. Дистрибутивность умножения. Произведение матрицы на сумму матриц равно сумме произведений матриц:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> C = np.matrix('2 4; 7 8')

>>> L = A.dot(B + C)
>>> R = A.dot(B) + A.dot(C)

>>> print(L)
[[35 42]
[77 94]]
>>> print(R)
[[35 42]
[77 94]]

 

Свойство 3. Умножение матриц в общем виде не коммутативно. Это означает, что для матриц не выполняется правило независимости произведения от перестановки множителей:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')

>>> L = A.dot(B)
>>> R = B.dot(A)

>>> print(L)
[[19 22]
[43 50]]

>>> print(R)
[[23 34]
[31 46]]

 

Свойство 4. Произведение заданной матрицы на единичную равно исходной матрице:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> E = np.matrix('1 0; 0 1')

>>> L = E.dot(A)
>>> R = A.dot(E)

>>> print(L)
[[1 2]
[3 4]]

>>> print(R)
[[1 2]
[3 4]]

>>> print(A)
[[1 2]
[3 4]]

 

Свойство 5. Произведение заданной матрицы на нулевую матрицу равно нулевой матрице:

➣ Численный пример

➤ Пример на Python

>>> A = np.matrix('1 2; 3 4')
>>> Z = np.matrix('0 0; 0 0')

>>> L = Z.dot(A)
>>> R = A.dot(Z)

>>> print(L)
[[0 0]
[0 0]]

>>> print(R)
[[0 0]
[0 0]]

>>> print(Z)
[[0 0]
[0 0]]

 

P.S.

Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.

Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas.  Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.

Как перемножить две матрицы

Умножение матриц

Есть ровно два способа умножения матриц. Первый способ – умножить матрицу на скаляр. Это называется скалярным умножением. Второй способ – умножить матрицу на другую матрицу. Это известно как матричное умножение.

Скалярное умножение

скалярное умножение на самом деле очень простая матричная операция. Чтобы умножить скаляр на матрицу, мы просто берем скаляр и умножаем его на каждую запись в матрице.Приведем пример.

Вопрос 1 : Вычислить 2A2A2A, если

Уравнение 1: пример скалярного умножения 1, часть 1

Вопрос просит нас узнать, что такое 2A2A2A. Другими словами, мы находим

Уравнение 1: пример скалярного умножения 1, часть 2

Обратите внимание, что если мы умножим 2 на каждую запись в матрице, мы получим:

Уравнение 1: пример скалярного умножения 1, часть 3

Очень просто! Давай сделаем еще один.

Вопрос 2 : Рассчитать 0A0A0A, если

Уравнение 2: Пример скалярного умножения 2 pt.1

Опять пытаемся найти 0A0A0A. Это означает, что мы будем искать ответ на

. Уравнение 2: пример скалярного умножения 2, часть 2

Матрица будет необычной формы, но концепция останется прежней. Мы по-прежнему умножаем скаляр 0 на каждую запись в матрице. Так мы получим:

Уравнение 2: пример скалярного умножения 2, часть 3

Обратите внимание, что все элементы в матрице равны 0. Это известно как нулевая матрица 3 x 2.

Теперь, когда мы хорошо знакомы со скалярным умножением, почему бы нам не перейти к матричному умножению?

Как умножить матрицы

Чтобы умножить матрицу на другую матрицу, нам сначала нужно узнать, что такое скалярное произведение.

Что такое скалярное произведение?

Точечное произведение (также известное как умножение векторов) – это способ вычисления произведения двух векторов. Например, пусть два вектора будут:

Уравнение 3: Пример скалярного произведения, часть 1

Как мне умножить эти два вектора? Просто умножьте соответствующие записи и сложите продукты. Другими словами,

Уравнение 3: Пример скалярного произведения, часть 2

Итак, умножая векторы, мы получаем одно значение. Однако обратите внимание на то, что два вектора имеют одинаковое количество записей.Что, если один из векторов имеет другое количество входов, чем другой? Например, пусть

Уравнение 4: Пример отказа скалярного произведения ч.1

Если бы я умножил соответствующие записи и сложил их все вместе, то получил бы:

Уравнение 4: Пример отказа скалярного продукта, часть 2

Здесь проблема. Первые три записи имеют соответствующие записи для умножения, но последняя запись не имеет. Итак, что нам здесь делать? Ответ: мы ничего не можем здесь сделать. Это просто означает, что мы не можем вычислить скалярное произведение этих двух векторов.

Итак, в заключение, мы не можем найти скалярное произведение двух векторов с разным количеством элементов. У них должно быть и одинаковое количество записей.

Умножение матриц 2 x 2

Так в чем был смысл изучения скалярного произведения? Что ж, мы будем использовать скалярное произведение, когда умножим две матрицы вместе. При умножении матрицы на другую матрицу мы хотим рассматривать строки и столбцы как вектор. Более конкретно, мы хотим обрабатывать каждую строку в первой матрице как векторы, а каждый столбец во второй матрице как векторы.Приведем пример.

Вопрос 3 : Найдите A ∙ BA \ bullet BA ∙ B, если

Уравнение 5: пример умножения матрицы 2 x 2, часть 1

Умножение двух матриц даст нам:

Уравнение 5: Пример умножения матрицы 2 x 2, часть 2

Теперь количество строк и столбцов, на которые мы обращаем внимание, равно

. Уравнение 5: пример умножения матрицы 2 x 2, часть 3

, где r1r_ {1} r1 – первая строка, r2r_ {2} r2 – вторая строка, а c1, c2c_ {1}, c_ {2} c1, c2 – первый и второй столбцы.Теперь мы будем рассматривать каждую строку и столбец, которые мы видим здесь, как вектор.

Обратите внимание, что умножение матрицы 2 x 2 на другую матрицу 2 x 2 дает матрицу 2 x 2. Другими словами, в матрице должно быть 4 элемента.

Уравнение 5: Пример умножения матрицы 2 x 2, часть 4

Как именно мы получаем первую запись? Обратите внимание, что первая запись находится в первой строке и первом столбце. Поэтому мы просто берем скалярное произведение r1r_ {1} r1 и c1c_ {1} c1. Таким образом, первая запись будет

. Уравнение 5: Пример умножения матрицы 2 x 2 pt.{nd} 2-й столбец. Итак, мы берем скалярное произведение r2r_ {2} r2 и c1c_ {1} c1 и скалярное произведение r2r_ {2} r2 и c2c_ {2} c2. Это дает нам:

Уравнение 5: пример умножения матрицы 2 x 2, часть 7

Вот и все! Это то, что мы получаем, когда умножаем матрицы 2 x 2. В общем, формула умножения матриц для матриц 2 x 2 составляет

Формула 1: Формула умножения матрицы 2 x 2

Умножение матриц 3×3

Теперь процесс умножения матриц 3 x 3 очень похож на процесс умножения матриц 2 x 2.Опять же, почему бы нам не сделать пример умножения матриц?

Вопрос 4 : Найдите A ∙ BA \ bullet BA ∙ B, если

Уравнение 6: Пример умножения матрицы 3 x 3, часть 1

Во-первых, обратите внимание, что их умножение должно дать нам еще одну матрицу 3 x 3. Другими словами,

Уравнение 6: Пример умножения матрицы 3 x 3, часть 2

Теперь давайте пометим все наши строки в первой матрице и столбцы во второй матрице. {st}, поэтому мы берем скалярное произведение r1r_ {1} r1 и c1c_ {1} c1.{nd} 2-й столбец. Таким образом, мы берем скалярное произведение r1r_ {1} r1 и c2c_ {2} c2. Это дает нам:

Уравнение 6: пример умножения матрицы 3 x 3, часть 5

Если мы продолжим находить все записи и производить скалярное произведение, соответствующее строкам и столбцам, то мы получим окончательный результат.

Уравнение 6: Пример умножения матрицы 3 x 3, часть 6

Готово! Обратите внимание, что чем больше матрицы, тем более утомительным становится умножение матриц. Это потому, что нам приходится иметь дело со все большим количеством цифр! Как правило, формула умножения матриц для матриц 3 x 3 составляет

Формула 2: Формула умножения матрицы 3 x 3

Как умножить матрицы разной размерности?

Пока что у нас есть перемноженные матрицы одинаковой размерности.Кроме того, мы знаем, что умножение двух матриц одинаковой размерности дает матрицу одинаковой размерности. Но что будет, если мы умножим матрицу разных размеров? Как мы узнаем размеры вычисленной матрицы? Во-первых, нам нужно увидеть, как умножение матриц дает вам определенную матрицу.

Определена ли матрица?

Бывают случаи, когда невозможно перемножить две матрицы. В таких случаях мы называем матрицу undefined .Как мы можем определить, не определены ли они?

Произведение двух матриц определяется только в том случае, если количество столбцов в первой матрице равно количеству строк второй матрицы .

Давайте попробуем использовать это определение в этом примере.

Вопрос 5 : Пусть

Уравнение 7: Пример определенной матрицы, часть 1

Определено ли A ∙ BA \ bullet BA ∙ B?

Во-первых, обратите внимание, что первая матрица имеет 3 столбца . Также вторая матрица имеет 3 строки .Поскольку они оба равны 3, то я знаю, что определено A ∙ BA \ bullet BA ∙ B.

Теперь, когда мы знаем, что оно определено, как мы можем узнать размеры A ∙ BA \ bullet BA ∙ B?

Размер собственности

Чтобы найти размеры A ∙ BA \ bullet BA ∙ B, нам нужно сначала взглянуть на размеры и отдельно.

Уравнение 7: Пример определенной матрицы, часть 2

Теперь поместим размеры матриц рядом, вот так:

Уравнение 7: Пример определенной матрицы pt.3

Теперь мы возьмем первое число и последнее число и объединим их, чтобы получить размеры A ∙ BA \ bullet BA ∙ B. Посмотрите, что первое число – 2 , а последнее – 4 . Таким образом, габариты A ∙ BA \ bullet BA ∙ B будут:

Уравнение 7: Пример определенной матрицы, часть 4

Теперь, когда мы знаем размеры матрицы, мы можем просто вычислить каждую запись, используя скалярные произведения. Это даст нам:

Уравнение 7: Пример определенной матрицы pt.5

Теперь, когда мы очень хорошо знаем, как умножать матрицы, почему бы не взглянуть на некоторые правила умножения матриц?

Свойства умножения матриц

Итак, какими свойствами на самом деле обладает матричное умножение? Во-первых, давайте все формально определим.

Пусть X, Y, ZX, Y, ZX, Y, Z – матрицы, InI_ {n} In – единичная матрица, а OnO_ {n} On – нулевая матрица. Если все пять из этих матриц имеют равные размеры, то у нас будет следующая матрица для свойств умножения матриц:

Формула 3: свойства умножения матриц

Ассоциативное свойство утверждает, что порядок умножения не имеет значения.Другими словами, вычисление X ∙ YX \ bullet YX ∙ Y, а затем умножение на ZZZ даст вам тот же результат, что и вычисление Y ∙ ZY \ bullet ZY ∙ Z, а затем умножение на XXX. Приведем пример.

Вопрос 6 : Показать, что ассоциативное свойство работает с этими матрицами:

Уравнение 8: Пример ассоциативного свойства, часть 1

Глядя на левую часть уравнения в ассоциативном свойстве, мы видим, что (XY) Z (XY) Z (XY) Z дает:

Уравнение 8: Пример ассоциативного свойства pt.2

Теперь, глядя на правую часть уравнения в ассоциативном свойстве, мы видим, что X (YZ) X (YZ) X (YZ) дает:

Уравнение 8: Пример ассоциативного свойства, часть 3

Посмотрите, как равны левая и правая части уравнения. Следовательно, мы знаем, что ассоциативное свойство действительно работает! Опять же, это означает, что порядок умножения матриц не имеет значения!

Теперь следующее свойство – распределительное свойство . В распределительной собственности указано, что:

Формула 4: Распределительная собственность

Мы видим, что нам разрешено использовать технику фольги и для матриц.Чтобы показать, что это свойство работает, давайте рассмотрим пример.

Вопрос 7 : Показать, что свойство распределения работает для следующих матриц:

Уравнение 9: Пример распределительного свойства, часть 1

Посмотрите, что левая часть уравнения – это X (Y + Z) X (Y + Z) X (Y + Z). Отсюда вычисления, которые дают нам:

Уравнение 9: Пример распределительного свойства, часть 2

Теперь давайте проверим, дает ли правая часть уравнения то же самое. Обратите внимание, что правая часть уравнения – это XY + XZXY + XZXY + XZ.Вычисление дает нам:

Уравнение 9: Пример распределительного свойства, часть 3

Обратите внимание, что левая часть уравнения в точности совпадает с правой частью уравнения. Следовательно, мы можем подтвердить, что свойство распределения действительно работает.

Коммутативно ли матричное умножение?

Мы знаем, что умножение матриц удовлетворяет как ассоциативным, так и дистрибутивным свойствам, однако мы вообще не говорили о коммутативности. Означает ли это, что умножение матриц его не удовлетворяет? На самом деле это не так, и мы можем проверить это на примере.

Вопрос 8 : Если матричное умножение коммутативно, то должно выполняться следующее:

Уравнение 10: Нарушение коммутативного свойства ч.1

Покажите, что XYeqYXXY eq YXXYeqYX, если

Уравнение 10: Нарушение коммутативного свойства ч. 2

Сначала мы вычисляем левую часть уравнения. Расчет XYXYXY дает нам:

Уравнение 10: Нарушение коммутативного свойства ч. 3

Теперь вычисляя правую часть уравнения, мы имеем:

Уравнение 10: Нарушение коммутативного свойства pt.4

Как видите,

Уравнение 10: Нарушение коммутативного свойства ч. 5

Потому что у нас

Уравнение 10: Нарушение коммутативного свойства ч. 6

Эти две матрицы совершенно разные.

Теперь есть еще несколько свойств умножения матриц. Однако эти свойства имеют дело с нулевой и единичной матрицами.

Умножение матрицы на нулевую матрицу

Свойство умножения матриц для нулевой матрицы утверждает следующее:

Формула 5: умножение матрицы для нулевой матрицы

, где ООО – нулевая матрица.

Это означает, что если вы умножите нулевую матрицу на другую ненулевую матрицу, то вы получите нулевую матрицу. Давайте проверим, так ли это на примере.

Вопрос 9 : Покажите, что уравнение OX = OOX = OOX = O и XO = OXO = OXO = O выполняется, если:

Уравнение 11: Умножение матрицы для примера с нулевой матрицей, часть 1

Давайте сначала посмотрим на уравнение

Уравнение 11: Умножение матриц для нулевой матрицы, пример, часть 2

Обратите внимание, что вычисление OXOXOX дает нам:

Уравнение 11: Умножение матрицы для примера с нулевой матрицей pt.3

Мы видим, что OX = OOX = OOX = O, поэтому уравнение выполняется. Аналогично, если мы посчитаем XOXOXO, мы получим:

Уравнение 11: Умножение матрицы для примера с нулевой матрицей, часть 4

Мы видим, что уравнение XO = OXO = OXO = O выполняется, так что мы закончили.

Умножение матриц для идентификационной матрицы

А как насчет свойства умножения матриц для единичных матриц? Что ж, в собственности указано следующее:

Формула 6: умножение матрицы для матрицы идентичности

, где InI_ {n} In – единичная матрица размера n × nn \ умноженная на nn × n.Опять же, мы можем видеть, что следующие уравнения действительно выполняются на примере.

Вопрос 10 : Покажите, что уравнения XI2 = XX I_ {2} = XXI2 = X и I2X = XI_ {2} X = XI2 X = X выполняются со следующими матрицами

Уравнение 12: Умножение матриц для примера единичной матрицы, часть 1

Итак, для уравнения XI2 = XX I_ {2} = XXI2 = X имеем:

Уравнение 12: Умножение матриц для примера единичной матрицы, часть 2

Итак, уравнение верно. Аналогично уравнению I2X = XI_ {2} X = XI2 X = X, имеем:

Уравнение 12: Умножение матриц для примера единичной матрицы pt.3

Опять же, уравнение верно. Итак, мы закончили с вопросом, и оба уравнения верны. На этом завершаются все свойства умножения матриц. Теперь, если вы хотите взглянуть на реальное применение умножения матриц, я рекомендую вам взглянуть на эту статью.

https://www.mathsisfun.com/algebra/matrix-multiplying.html

Умножение матриц – Примеры | Как умножить матрицы?

Умножение матриц или умножение матриц – одна из операций, которые могут выполняться над матрицами в линейной алгебре.Умножение матрицы A на матрицу B возможно, когда обе заданные матрицы A и B совместимы. Умножение матриц – это бинарная операция, которая дает матрицу из двух заданных матриц.

Матричное умножение было впервые введено в 1812 году французским математиком Жаком Филиппом Мари Бине для представления линейных карт с использованием матриц. Давайте разберемся с правилом умножения матриц и формулой умножения матриц подробно в следующих разделах.

Что такое умножение матриц?

Умножение матриц – это двоичная операция, вывод которой также является матрицей при умножении двух матриц.В линейной алгебре умножение матриц возможно только тогда, когда матрицы совместимы. В общем, умножение матриц, в отличие от арифметического умножения, не является коммутативным, что означает, что умножение матриц A и B, заданных как AB, не может быть равно BA, то есть AB ≠ BA. Поэтому порядок умножения матриц важен.

Умножение матриц Определение

Предположим, у нас есть две матрицы A и B, умножение матрицы A на матрицу B может быть задано как (AB).Это означает, что результирующая матрица для умножения любой матрицы «A» размера m × n на матрицу «B» размера n × p, результат может быть задан как матрица «C» порядка m × p. Давайте разберемся с этой концепцией подробно в следующем разделе.

Совместимость матриц:

Две матрицы A и B называются совместимыми, если количество столбцов в A равно количеству строк в B. Это означает, что если A – матрица порядка m × n, а B – матрица порядка n × p. , то можно сказать, что матрицы A и B совместимы.

Правила умножения матриц

Как мы исследовали, две матрицы могут быть перемножены только тогда, когда они совместимы, что означает, что для существования умножения матриц количество столбцов в первой матрице должно быть равно количеству строк во второй матрице, в приведенном выше случае ‘п’. Если A – матрица порядка m × n, а B – матрица порядка n × p, то порядок матрицы произведения равен m × p.

Например,

a) Умножение матрицы 4 × 3 на матрицу 3 × 4 допустимо и дает матрицу порядка 4 × 4

б) матрица 7 × 1 и матрицы 1 × 2 совместимы; произведение дает матрицу 7 × 2.

c) Умножение матрицы 4 × 3 и матрицы 2 × 3 НЕ возможно.

Формула умножения матриц

Мы можем понять общий процесс умножения матриц с помощью техники: «Сначала строки умножаются на столбцы (элемент за элементом), а затем строки заполняются». Рассмотрим две матрицы порядка 3 × 3, как указано ниже,

\ (\ begin {pmatrix}
a & b & c \\
d & e & f \\
g & h & i
\ end {pmatrix}
%
\ begin {pmatrix}
j & k & l \\
m & n&o \\
p & q & r
\ end {pmatrix}
\)

Здесь матрицы имеют одинаковые размеры, поэтому результирующая матрица также будет иметь такую ​​же размерность 3 × 3

Умножение матриц 2 × 2

Процесс одинаков для матрицы любого порядка.Мы умножаем элементы каждой строки первой матрицы на элементы каждого столбца второй матрицы (элемент за элементом), как показано на изображении. Наконец, мы добавляем товары.

Умножение матриц 3 × 3

Умножение матриц 3 × 3 может быть выполнено с использованием формулы умножения матриц, чтобы указанные матрицы были совместимы. Процесс точно такой же для матрицы любого порядка.

Свойства умножения матриц

Есть определенные свойства умножения матриц операция в линейной алгебре в математике.Эти свойства приведены ниже:

.

• Некоммутативно: Умножение матриц некоммутативно, т. Е. Для умножения двух матриц A и B AB ≠ BA.
• Дистрибутивность: Умножение матриц следует свойству распределения, то есть умножению матрицы A и матрицы B на другую матрицу C, A (B + C) = AB + BC, при условии, что A, B и c совместимы.
• Произведение со скаляром: Если произведение матриц A и B, AB определено, то c (AB) = (cA) B = A (Bc), так что c является скаляром.
• Транспонирование: Транспонирование произведения матриц A и B может быть задано как, (AB) ^T = B ^T A ^T , где ^T обозначает транспонирование.
• Комплексное сопряжение: Если A и B – сложные записи, то (AB) ^* = B ^* A ^*
• Ассоциативность: Для трех матриц A, B и C, таких, что произведения (AB) C и A (BC) определены, тогда (AB) C = A (BC).

Как умножить матрицы?

Умножение двух совместимых матриц может быть выполнено с использованием некоторых общих шагов, как описано выше. шага в матричном умножении задаются как,

• Убедитесь, что количество столбцов в матрице 1 ^st равно количеству строк в матрице 2 ^nd (совместимость матриц).
• Умножьте элементы каждой строки первой матрицы на элементы каждого столбца второй матрицы.
• Добавьте товары.
• Поместите добавленные продукты в соответствующие столбцы.

Давайте лучше поймем эти шаги для умножения матриц на примере.

Пример: умножьте указанные ниже матрицы, чтобы найти их произведение на \ (\ begin {pmatrix}
1 и 2 \
3 и 4 \ 5 и 1 \
\ end {pmatrix} \ text {and} \ begin {pmatrix}
2 \
4 \
\ end {pmatrix}
\)

Решение: Указанные матрицы имеют порядок 3 × 2 и 2 × 1. ∵ Приведенные матрицы совместимы, мы можем выполнить матричное умножение, и матрица произведения будет иметь порядок 3 × 1.

\ (\ begin {pmatrix}
1 и 2 \
3 и 4 \ 5 и 1 \
\ end {pmatrix}. \ begin {pmatrix}
2 \
4 \
\ end {pmatrix} \\\\
= \ begin {pmatrix}
(1 \ times2) + (2 \ times4) \
(3 \ times2) + (4 \ times4) \\ (5 \ times2) + (1 \ times4) \\
\ end {pmatrix} \\\\ = \ begin {pmatrix}
2 + 8 \
6 + 16 \ 10 + 4 \
\ end {pmatrix}
\\\\
= \ begin {pmatrix}
10 \
22 \ 14 \
\ end {pmatrix} \).

Ответ: Матрица продуктов – \ (\ begin {pmatrix}
10 \
22 \ 14 \
\ end {pmatrix}
\)

Мыслить нестандартно:

• Используя матрицы, показанные ниже, проверьте, является ли матричное умножение коммутативным или нет.
  \ (\ begin {pmatrix}
  1 & 0 \\
  2 и 4 \
  \ end {pmatrix} \ text {and} \ begin {pmatrix}
  6 и 8 \
  4 и 3 \
  \ end {pmatrix}
  \)
• Ассоциативно ли матричное умножение?

Важные замечания по умножению матриц:

• Для умножения матриц указанные матрицы должны быть совместимыми.
• Порядок матрицы продуктов может быть получен по следующему правилу:
  Если A – матрица порядка m × n, а B – матрица порядка n × p, то порядок матрицы произведения равен m × p.
• Умножение матриц указывает умножение строк на столбцы.

Часто задаваемые вопросы по умножению матриц

Что такое умножение матриц в линейной алгебре?

Умножение – это одна из двоичных операций, которые можно применять к матрицам в линейной алгебре.Чтобы матричное умножение существовало для двух матриц A и B, количество столбцов в матрице A должно быть равно количеству строк в матрице B. ⇒AB существует.

Как умножить матрицы порядка 3 × 3?

матриц 3×3 в математике могут быть умножены путем умножения строк первой матрицы, умноженных на столбцы второй матрицы, чтобы получить соответствующие элементы матрицы произведения.

Какова формула умножения матриц?

Формула умножения матриц используется для умножения матриц в целом.Для умножения матриц 2×2 эта формула получается путем умножения элементов в строках на элементы в столбцах.

Можно ли перемножить матрицы порядка 2×3 и 2×2?

Нет, мы не можем умножить матрицу 2×3 и 2×2, потому что для выполнения матричного умножения две матрицы должны быть совместимы. Поскольку количество столбцов в первой матрице (3) не равно количеству строк во второй матрице (2), мы не можем выполнить матричное умножение для этого случая.

Какова цель умножения матриц?

Умножение матриц важно для облегчения вычислений в линейной алгебре и используется для представления линейных карт.Это важный инструмент во многих областях математики, а также в прикладной математике, статистике, физике, экономике и технике.

Можно ли перемножить матрицы порядка 2 × 1 и 2 × 2?

Нет, их нельзя перемножить, так как эти матрицы несовместимы. Количество столбцов первой матрицы не равно количеству строк второй матрицы.

Когда возможно умножение матриц?

Умножение матриц возможно, только если матрицы совместимы i.е., матричное умножение допустимо, только если количество столбцов первой матрицы равно количеству строк второй матрицы.

Всегда ли матричное умножение коммутативно?

Умножение матриц, как правило, не коммутативно. Это означает, что порядок умножения матриц важен.

Всегда ли определяется умножение матриц?

Умножение матриц возможно только тогда, когда матрицы совместимы. Чтобы умножение матриц существовало, количество столбцов в первой матрице должно быть равно количеству строк во второй матрице

Умножение матриц

– объяснение и примеры

Есть 3 $ общих операций с матрицами.Это:

• Сложение матриц
• Вычитание матриц
• Умножение матриц

Сложение и вычитание матриц – простые операции. Вы можете узнать больше о сложении матриц здесь и о вычитании матриц здесь.

Матричное умножение имеет 2 типа $:

• Скалярное умножение
• Матричное умножение

Скалярное умножение не очень сложно и просто.Тем не менее, умножение матриц может сначала показаться немного пугающим. После прочтения этого урока это станет так же просто, как и другие операции с матрицами.

Давайте посмотрим на определение умножения матриц:

Умножение матриц – это операция, которая включает в себя умножение матрицы на скаляр или умножение двух матриц вместе (после выполнения определенных условий).

Этот урок покажет, как умножать матрицы, умножать $ 2 \ times 2 $ матрицы, умножать $ 3 \ times 3 $ матрицы, умножать другие матрицы, а также проверять, определено ли матричное умножение, и некоторые свойства матричного умножения.

Как умножить матрицы

Чтобы умножить две матрицы вместе, нам сначала нужно убедиться, что количество столбцов 1-й матрицы равно количеству строк 2-й матрицы. Если они не равны , тогда умножение матриц будет undefined .

Если они равны, мы можем перемножить матрицы по $ 2 $ вместе. Результирующая матрица будет иметь размерность, равную количеству строк 1-й матрицы и количеству столбцов 2-й матрицы.

Если первая матрица имеет размерность $ a \ times b $, а размерность второй матрицы равна $ m \ times n $, для умножения матриц определено , количество столбцов первой матрицы ($ б $) должно равняться количеству строк второй матрицы ($ m $). Результирующая матрица будет иметь размеры $ a \ times n $.

Чтобы умножить матрицы на 2 доллара, нам нужно понимать скалярное произведение . Рассмотрим две матрицы размером $ 1 \ times 3 $, показанные ниже:

$ \ begin {bmatrix} {1} & {2} & 1 \ end {bmatrix} $

$ \ begin {bmatrix} {2} & {0 } & 4 \ end {bmatrix} $

Чтобы получить его скалярное произведение, мы умножаем каждый соответствующий элемент матриц $ 2 $ друг на друга и получаем сумму. Показано ниже:

$ = (1) (2) + (2) (0) + (1) (4) = 2 + 0 + 4 = 6 $

Обратите внимание, что скалярное произведение – это только число! Помните, что для существования скалярного произведения обе матрицы должны иметь одинаковое количество записей! Следовательно, количество столбцов первой матрицы должно равняться количеству строк второй матрицы, когда мы умножаем матрицы на $ 2 $. Мы увидим это в ближайшее время.

Шаги для умножения двух матриц

1. Проверьте, ли количество столбцов первой матрицы равно количеству строк второй матрицы .Если это так, мы можем выполнить матричное умножение. В противном случае операция undefined . Обратите внимание, что размер результирующей матрицы будет равен номеру строки первой матрицы и номеру столбца второй матрицы.
2. Возьмем скалярное произведение первой строки первой матрицы с первым столбцом второй матрицы. Поместите ответ в первую строку, заполнитель первого столбца в результирующей матрице.
3. Возьмите скалярное произведение первой строки первой матрицы со вторым столбцом второй матрицы.{th} $ столбец результирующей матрицы.

Как умножить матрицы 2 x 2

Рассмотрим матрицу $ A $ и матрицу $ B $, показанные ниже:

$ A = \ begin {bmatrix} {1} & {3} \\ 1 & {- 2 } \ End {bmatrix} $

$ B = \ begin {bmatrix} {0} & {- 3} \\ 1 & {1} \ end {bmatrix} $

Обе матрицы $ A $ и $ B $ являются Матрицы $ 2 \ times 2 $. Мы будем следовать шагам, описанным выше, чтобы выполнить умножение между Matrix $ A $ и Matrix $ B $. Поскольку номер столбца первой матрицы равен номеру строки второй матрицы, мы можем продолжить и выполнить умножение. Процесс показан ниже:

$ A \ times B = \ begin {bmatrix} {1} & {3} \\ 1 & {- 2} \ end {bmatrix} \ times \ begin {bmatrix} {0} & {- 3} \\ 1 & {1} \ end {bmatrix} $

$ = \ begin {bmatrix} {(1) (0) + (3) (1)} & {(1) (- 3 ) + (3) (1)} \\ {(1) (0) + (- 2) (1)} & {(1) (- 3) + (-2) (1)} \ end {bmatrix} $

$ = \ begin {bmatrix} {3} & {0} \\ {- 2} & {- 5} \ end {bmatrix} $

Таким образом,

$ A \ times B = \ begin {bmatrix } {3} & {0} \\ {- 2} & {- 5} \ end {bmatrix} $

Процесс умножения матриц $ 3 \ times 3 $ аналогичен.Мы рассмотрим это ниже.

Как умножить матрицы 3 x 3

Рассмотрим матрицу $ A $ и матрицу $ B $, показанные ниже:

$ A = \ begin {bmatrix} {1} & {3} & {- 1} \\ 1 & {- 2} & 0 \\ 1 & {- 1} & 2 \ end {bmatrix} $

$ B = \ begin {bmatrix} {- 2} & {6} & {0} \\ 1 & {- 5} & 1 \\ 0 & {- 1} & {- 4} \ end {bmatrix} $

И Matrix $ A $, и $ B $ являются матрицами размером $ 3 \ times 3 $. Мы будем следовать шагам, описанным выше, чтобы выполнить умножение между Matrix $ A $ и Matrix $ B $. Поскольку номер столбца первой матрицы равен номеру строки второй матрицы, мы можем продолжить и выполнить умножение. Процесс показан ниже:

$ A \ times B = \ begin {bmatrix} {1} & {3} & {- 1} \\ 1 & {- 2} & 0 \\ 1 & {- 1} & 2 \ end {bmatrix} \ times \ begin {bmatrix} {- 2} & {6} & {0} \\ 1 & {- 5} & 1 \\ 0 & {- 1} & {- 4} \ конец {bmatrix} $

$ = \ begin {bmatrix} {(1) (- 2) + (3) (1) + (-1) (0)} & {(1) (6) + (3) (-5) + (-1) (- 1)} & {(1) (0) + (3) (1) + (-1) (- 4)} \\ {(1) (- 2) + (-2) (1) + (0) (0)} & {(1) (6) + (-2) (- 5) + (0) (- 1)} & {(1) (0) + (-2) (1) + (0) (- 4)} \\ {(1) (- 2) + (-1) (1) + (2) (0)} & {(1) (6) + (-1) (- 5) + (2) (- 1)} & {(1) (0) + (-1) (1) + (2) (- 4)} \ end {bmatrix} $

$ = \ begin {bmatrix} {1} & {- 8} & {7} \\ {- 4} & {16} & {- 2} \\ {- 3} & {9} & {- 9} \ end {bmatrix} $

Таким образом,

$ A \ times B = \ begin {bmatrix} {1} & {- 8} & {7} \\ {- 4} & {16} & {- 2} \\ {- 3} & {9} & {- 9} \ end {bmatrix} $

Умножение матриц с разными размерностями

Мы рассмотрели умножение только квадратной матрицы (например,грамм. Матрица $ 2 \ times 2 $ с другой матрицей $ 2 \ times 2 $ и матрица $ 3 \ times 3 $ с другой матрицей $ 3 \ times 3 $).

Что делать, если обе матрицы, которые нужно перемножить, находятся в разном порядке?

Не проблема! Просто проверьте , равно ли количество столбцов первой матрицы количеству строк второй матрицы . Если это так, мы следуем шагам, описанным выше, и умножаем матрицы на $ 2 $. Также помните, что размер результирующей матрицы будет $ a \ times n $, где $ a $ – количество строк первой матрицы, а $ n $ – количество столбцов второй матрицы .Позже мы рассмотрим этот пример.

Правила умножения матриц

Мы рассмотрим 5 $ свойства умножения матриц. Они изложены в таблице ниже ($ A $ и $ B $ – это матрицы $ n \ times n $, $ I $ – единичная матрица $ n \ times n $, а $ 0 $ – матрица $ n \ times n $ zero matrix):

Теперь давайте рассмотрим несколько примеров, чтобы прояснить наше понимание умножения матриц.

Пример 1

Укажите, можно ли перемножать следующие матрицы.Если да, то каков будет размер итоговой матрицы?

1. Матрица $ 2 \ times 2 $ с другой матрицей $ 2 \ times 2 $
2. Матрица $ 1 \ times 4 $ с матрицей $ 4 \ times 1
3. Матрица $ 3 \ times 3 $ с матрицей $ 2 \ times 3 $ matrix

Решение

Напомним, что если номер столбца первой матрицы равен номеру строки второй матрицы, две матрицы можно перемножить. Результирующая матрица будет иметь размерность $ a \ times b $, где $ a $ – количество строк первой матрицы, а $ b $ – количество столбцов второй матрицы.

1. Да, обе матрицы можно перемножить, и результирующая матрица будет иметь размерность $ 2 \ times 2 $.
2. Да, обе эти матрицы можно перемножить, и результирующая матрица будет иметь порядок 1. Это будет матрица $ 1 \ times 1 $.
3. Нет, эти две матрицы нельзя перемножить, поскольку количество столбцов первой матрицы ($ 3 $) не равно количеству строк второй матрицы ($ 2 $). Умножение матриц между этими $ 2 $ матрицами не определено.

Пример 2

Умножение матрицы $ A $ и матрицы $ B $ показано ниже:

$ A = \ begin {bmatrix} {0} & {- 3} \\ 2 & {0} \ end {bmatrix} $

$ B = \ begin {bmatrix} {1} & {1} \\ 5 & {- 2} \ end {bmatrix} $

Решение

Обе матрицы $ A $ и $ B $ представляют собой матрицы размером $ 2 \ times 2 $. Поскольку номер столбца первой матрицы равен номеру строки второй матрицы, мы можем продолжить и выполнить умножение. Процесс показан ниже:

$ A \ times B = \ begin {bmatrix} {0} & {- 3} \\ 2 & {0} \ end {bmatrix} \ times \ begin {bmatrix} {1} & {1} \\ 5 & {- 2} \ end {bmatrix} $

$ = \ begin {bmatrix} {(0) (1) + (-3) (5)} & {(0) (1 ) + (-3) (- 2)} \\ {(2) (1) + (0) (5)} & {(2) (1) + (0) (- 2)} \ end {bmatrix} $

$ = \ begin {bmatrix} {-15} & {6} \\ {2} & {2} \ end {bmatrix} $

Пример 3

Умножение матрицы $ \ begin { bmatrix} {3} & {2} \\ {1} & {-4} \ end {bmatrix} $ с единичной матрицей $ 2 \ times 2 $.Какое свойство умножения матриц он иллюстрирует?

Решение

Выполним указанное умножение, используя правила умножения матриц:

$ \ begin {bmatrix} {3} & {2} \\ {1} & {-4} \ end {bmatrix} \ times \ begin { bmatrix} {1} & {0} \\ 0 & 1 \ end {bmatrix} $

$ = \ begin {bmatrix} {(3) (1) + (2) (0)} & {(3) ( 0) + (2) (1)} \\ {(1) (1) + (-4) (0)} & {(1) (0) + (-4) (1)} \ end {bmatrix} $

$ = \ begin {bmatrix} {3} & {2} \\ {1} & {-4} \ end {bmatrix} $

Результирующая матрица равна исходной матрице.Эта задача проиллюстрировала мультипликативную идентичность умножения матриц.

Теперь ваша очередь опробовать некоторые задачи.

Практические вопросы

1. Укажите, можно ли перемножать следующие матрицы. Если да, то каков будет размер итоговой матрицы?

   1. Матрица $ 3 \ times 1 $ с матрицей $ 1 \ times 4 $
   2. Матрица $ 4 \ times 4 $ с другой матрицей $ 4 \ times 4 $
   3. Матрица $ 2 \ times 4 $ с матрицей $ 3 \ times 4 $ matrix
2. Для двух матриц, показанных ниже, $ AB = BA $?

   $ A = \ begin {bmatrix} {1} & {0} \\ 3 & {0} \ end {bmatrix} $

   $ B = \ begin {bmatrix} {1} & {-1} \\ 0 & {1} \ end {bmatrix} $

3. Умножение матрицы $ C $ и матрицы $ D $ показано ниже:

   $ C = \ begin {bmatrix} {1} & {- 4} & 1 \\ 1 & 2 & 3 \\ -1 & 2 & -1 \ end {bmatrix} $

   $ D = \ begin {bmatrix} {0} & 1 & 7 \\ 1 & -1 & -1 \\ 1 & { 0} & 2 \ end {bmatrix} $

Ответы

1. Напомним, что если номер столбца первой матрицы равен номеру строки второй матрицы, две матрицы можно умножить.Результирующая матрица будет иметь размерность $ a \ times b $, где $ a $ – количество строк первой матрицы, а $ b $ – количество столбцов второй матрицы.

   1. Да, обе матрицы можно перемножить, и результирующая матрица будет иметь размерность $ 3 \ times 4 $.
   2. Да, обе эти матрицы можно перемножить, и результирующая матрица будет иметь порядок 4. Это будет матрица $ 4 \ times 4 $.
   3. Нет, эти две матрицы нельзя перемножить, поскольку количество столбцов первой матрицы (4 доллара США) не равно количеству строк второй матрицы (3 доллара США).Умножение матриц между этими $ 2 $ матрицами не определено.
2. Сначала найдем $ AB $:

   $ \ begin {bmatrix} {1} & {0} \\ 3 & {0} \ end {bmatrix} \ times \ begin {bmatrix} {1} & { -1} \\ 0 & {1} \ end {bmatrix} $

   $ = \ begin {bmatrix} {(1) (1) + (0) (0)} & {(1) (- 1) + (0) (1)} \\ {(3) (1) + (0) (0)} & {(3) (- 1) + (0) (1)} \ end {bmatrix} $

   $ = \ begin {bmatrix} {1} & {-1} \\ {3} & {-3} \ end {bmatrix} $

   Следовательно,
   $ A \ times B = \ begin {bmatrix} {1} & {-1} \\ {3} & {-3} \ end {bmatrix} $

   Теперь давайте найдем $ BA $:

   $ \ begin {bmatrix} {1} & {-1} \\ 0 & {1} \ end {bmatrix} \ times \ begin {bmatrix} {1} & {0} \\ 3 & {0} \ end {bmatrix} $

   $ = \ begin {bmatrix} {(1) (1 ) + (-1) (3)} & {(1) (0) + (-1) (0)} \\ {(0) (1) + (1) (3)} & {(0) ( 0) + (1) (0)} \ end {bmatrix} $

   $ = \ begin {bmatrix} {-2} & {0} \\ {3} & {0} \ end {bmatrix} $

   Следовательно,
   $ B \ times A = \ begin {bmatrix} {-2} & {0} \\ {3} & {0} \ end { bmatrix} $

   Таким образом, мы видим, что $ AB \ neq BA $.Умножение матриц не коммутативно!

3. Давайте умножим две матрицы $ 3 \ times 3 $, следуя этапам умножения матриц. Показано ниже:

   $ C \ times D = \ begin {bmatrix} {1} & {- 4} & 1 \\ 1 & 2 & 3 \\ -1 & 2 & -1 \ end {bmatrix} \ times \ begin {bmatrix} {0} & 1 & 7 \\ 1 & -1 & -1 \\ 1 & {0} & 2 \ end {bmatrix} $

   $ = \ begin {bmatrix} {(1) (0) + (-4) (1) + (1) (1)} & {(1) (1) + (-4) (- 1) + (1) (0)} & {(1) (7) + (-4) (- 1) + (1) (2)} \\ {(1) (0) + (2) (1) + (3) (1)} & {(1) (1) + ( 2) (- 1) + (3) (0)} & {(1) (7) + (2) (- 1) + (3) (2)} \\ {(-1) (0) + ( 2) (1) + (-1) (1)} & {(-1) (1) + (2) (- 1) + (-1) (0)} & {(-1) (7) + (2) (- 1) + (-1) (2)} \ end {bmatrix} $

   $ = \ begin {bmatrix} {-3} & {5} & 13 \\ 5 & {-1} & {11} \\ 1 & {-3} & {-11} \ end {bmatrix} $

   Таким образом,

   $ C \ times D = \ begin {bmatrix} {-3} & {5} & 13 \ \ 5 & {-1} & {11} \\ 1 & {-3} & {-11} \ end {bmatrix} $

Предыдущий урок | Главная страница | Следующий урок

Умножение матриц

В матричной алгебре существует два вида умножения матриц: умножение матрицы на число и умножение матрица другой матрицей.

Как умножить матрицу на число

Когда вы умножаете матрицу на число, вы умножаете каждый элемент в матрице по тому же номеру. Эта операция создает новую матрицу, которая называется скалярное кратное .

Например, если x равно 5, а матрица A будет:

Тогда x A = 5 A и

5 A = 2
	5 * 100	5 * 200
	5 * 300	5 * 400

4 5 90 A

В приведенном выше примере каждый элемент A умножается на 5, чтобы получить скалярное кратное, B .

Примечание. В некоторых текстах эта операция называется умножением матрицы на скаляр. (Скаляр – это действительное число или символ, представляющий действительное число.)

Как умножить матрицу на матрицу

Матричный продукт A B определен только когда количество столбцов в A равно количество строк в B . Сходным образом, матричный продукт B A определяется только когда количество столбцов в B равно количество строк в A .

Предположим, что A – это матрица i x j , и B – это матрица j x k . Тогда матрица продукт A B приводит к матрице C , который имеет i строк и k столбцов; а также каждый элемент в C может быть вычислен в соответствии с по следующей формуле.

C _{i k} = Σ _j A _{i j} B _{j k}

, где

C _{i k} = элемент в строке i и столбец k из матрицы C
A _{i j} = элемент в строке i и столбец j из матрицы A
B _{j k} = элемент в строке j и столбце k из матрицы B
Σ _j = знак суммы, который указывает, что a _{i j} b _{j k} термины должны быть суммировано j

Давайте рассмотрим пример, чтобы показать, как работает приведенная выше формула.Предположим, мы хотим вычислить A B , учитывая матрицы ниже.

Пусть A B = C . Поскольку A имеет 2 строки, мы знаем, что C будет иметь два ряда; и поскольку B имеет 2 столбца, мы знаем, что C будет иметь 2 столбца. Чтобы вычислить значение каждого элемента в матрице 2 x 2 C , мы используем формулу C _{i k} = Σ _j A _{i j} B _{j k} , как показано ниже.

• C _{1 1} = Σ A _{1 j} B _{j 1} = 0 * 6 + 1 * 8 + 2 * 10 = 0 + 8 + 20 = 28
• C _{1 2} = Σ A _{1 j} B _{j 2} = 0 * 7 + 1 * 9 + 2 * 11 = 0 + 9 + 22 = 31
• C _{2 1} = Σ A _{2 j} B _{j 1} = 3 * 6 + 4 * 8 + 5 * 10 = = 18 + 32 + 50 = 100
• C _{2 2} = Σ A _{2 j} B _{j 2} = 3 * 7 + 4 * 9 + 5 * 11 = 21 + 36 +55 = 112

Основываясь на приведенных выше расчетах, мы можем сказать, что

То, что мы сделали для вычисления Matrix C , не было сложный.Все, что мы сделали, это умножили элементы строки в Матрица A по соответствующим элементам столбца в Матрица B .

Порядок умножения

Как мы уже упоминали, в некоторых случаях умножение матриц определен для A B , но не для B A ; наоборот. Тем не мение, даже если умножение матриц возможно в обоих направлениях, результаты могут быть разными. То есть, A B не всегда равно В А .

Поскольку порядок важен, жаргон матричной алгебры превратился в четко указать порядок, в котором матрицы перемножаются.

• Для описания матричного продукта A B , мы можем сказать, что – это после умножения по B ; или мы можем сказать, что B – это предварительно умножили на A .
• Аналогично для описания матричного произведения B A , мы можем сказать, что B – это после умножения по А ; или мы можем сказать, что A – это умножил на B .

Итог: при умножении двух матриц порядок имеет значение.

Идентификационная матрица

Идентификационная матрица является n x n диагональная матрица с единицами по диагонали и нулями везде. Единичная матрица обозначается I или I _n . Ниже представлены две матрицы идентичности.

Идентификационная матрица обладает уникальным талантом. Любая матрица, которая может быть умноженное на предварительное или постмноженное на I остается тем же; то есть:

A I = I A = A

Проверьте свое понимание

Проблема 1

Рассмотрим матрицы, показанные ниже – A , B , и C

Предположим, что A B = C .Какие из следующих утверждений верны?

(A) w = a * e + b * h
(B) x = a * f + b * h
(C) y = c * g + d * h
(D) Все вышеперечисленное
( E) Ни один из вышеперечисленных

Решение

Правильный ответ – (B). Чтобы вычислить значение любого элемента в матрица C , воспользуемся формулой C _{i k} = Σ _j A _{i j} B _{j k} .

В матрице C x – это элемент в строке 1 и столбце 2, который представлен в формуле как C _{1 2} .Поэтому, чтобы найти x, мы используем формулу для вычисления C _{1 2} , как показано ниже.

x = C _{1 2} = Σ _j A _{1 j} B _{j 2} = A _{1 1} B _{1 2} + A _{1 2} B _{2 2} = a * f + b * h

Все остальные ответы неверны.

Умножение матриц Excel | Top 2 Method

Что такое умножение матриц в Excel?

В Excel у нас есть встроенная функция для умножения матриц, и это функция MMULT, она принимает два массива в качестве аргумента и возвращает произведение двух массивов, учитывая, что оба массива должны иметь одинаковое количество строк и одинаковое количество столбцы.

Пояснение

Умножение матриц

– одна из полезных функций Excel. Основные функции MS excel: горячие клавиши, суммирование значений, фильтрация данных, специальная вставка, вставка случайных чисел, инструмент анализа поиска цели, вставка серийных номеров и т. Д.подробнее представлены для выполнения математических операций. Это помогает получить произведение двух матриц. Матрицы, которые нужно умножить, имеют определенное количество строк и столбцов для представления данных. Размер полученной матрицы берется из количества строк первого массива и количества столбцов второго массива. Есть условие умножения матриц; количество столбцов в первой матрице должно быть равно количеству строк во второй матрице.

Для выполнения матричного умножения используется предопределенная функция MMULT, представленная в программном обеспечении Excel.Умножение матриц в Excel сокращает время, затрачиваемое на вычисление произведения матриц вручную.

Обычно умножение матриц выполняется двумя способами. Простое скалярное умножение выполняется с использованием основных арифметических операций, а расширенное умножение матриц управляется с помощью функции массива в Excel.

Формула Excel, используемая для умножения В Excel нет специальной функции умножения. Тем не менее, вы можете выполнить операцию умножения, используя символ звездочки (*), функцию ПРОИЗВОДИТ и функцию СУММПРОИЗВ, чтобы получить умножение.Вы можете выполнить определенный набор вычислений в ячейке, столбце или строке, используя это. Подробнее вводится двумя способами, включая ручной ввод функции MMULT после знака равенства или выбор библиотеки функций Math и Trig, представленной в разделе «Формулы» таб. Математическая функция MMULT помогает вернуть умножение двух массивов. Это одна из предопределенных функций Excel. Функции Excel помогают пользователям экономить время и поддерживать обширные рабочие листы. Существует более 100 функций Excel, разделенных на финансовые, логические, текстовые, функции даты и времени, функции поиска и справки, математические, статистические и информационные функции.читать больше используется в рабочих таблицах для выполнения расчетов за короткое время.

Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т.д.

Синтаксис

Требуемый синтаксис умножения матриц:

• Параметры: Array1 и Array2 – два параметра, необходимые для умножения
• Правило: Столбцы array1 должны быть равны строкам array2, а размер продукта равен количеству строк в array1 и количество столбцов в массиве2
• Возвращает: Функция ММУЛЬТ генерирует числа в матрице произведения.Он вводится как формула или функция рабочего листа в вычислениях Excel.

Рассмотрим,

Тогда произведение A * B выглядит следующим образом.

Как сделать умножение матриц в Excel? (с примерами)

Умножение матриц в Excel имеет некоторое приложение в реальном времени. Есть два способа выполнить матричное умножение. Ниже приведены несколько примеров умножения матриц Excel.

Пример №1 – Умножение матрицы на скалярное число.

Пример № 2 – Матричное умножение двух отдельных массивов

• Шаг 1: Прежде всего, данные должны быть введены в массив A размером 3 × 3

• Шаг 2: Введите данные во второй массив под названием B размером 3 × 3

Введите значения для расчета произведения A и B.

После ввода формулы нажмите Ctrl + Shift + Enter , чтобы получить результат. Результаты получены путем умножения двух массивов следующим образом, и размер результирующего массива составляет 3×3.

Пример # 3

Матрица Умножение между массивами с одной строкой и одним столбцом. Рассмотрим элементы матриц как

Матрица A имеет размер 1 × 3, а матрица B – 3 × 1. Размер матрицы продукта A * B [AB] равен 1 × 1. Итак, введите в ячейку формулу умножения матриц.

Нажмите Enter, чтобы получить результат.

Пример № 4 – Умножение матриц между массивами с одним столбцом и одной строкой

Матрица A имеет размер 3 × 1, а матрица B – 1 × 3. Размер матрицы произведения A * B [AB] составляет 3 × 3.

Итак, ответ будет:

Пример № 5 – Определение квадрата матрицы с помощью MMULT в ExcelMMULT – это встроенная функция математики и тригонометрии в Excel, которая выполняет матричное умножение двух массивов, где столбцы массива 1 эквивалентны строкам для массива 2.читать далее

Квадрат матрицы A определяется умножением A на A.

Результирующая матрица получается как

Что нужно помнить

• Для выполнения матричного умножения количество столбцов, представленных в массиве 1 и количество строк, представленных в массиве 2, равны.
• Трудно изменить часть массива, так как массив представляет собой группу элементов.
• При выполнении умножения массива следует использовать CTRL + SHIFT + ENTER для создания всех элементов матрицы результатов.В противном случае производится только один элемент.
• Элементы массива не должны быть нулевыми, а текст не должен использоваться в матрицах, чтобы избежать ошибок.
• Размер массива товаров равен строкам первого массива и столбцам второго массива.
• Умножение A * B не равно умножению B * A в матричном умножении.
• Умножение матрицы на единичную матрицу дает ту же матрицу (например, [A] * [Модульная матрица] = [A])

Рекомендуемые статьи

Это руководство по умножению матриц Excel.Здесь мы обсудили, как выполнить умножение матриц в Excel с помощью скалярного метода и функции MMULT (), с примерами и загружаемым шаблоном Excel. Вы можете узнать больше об Excel из следующих статей –

Пакет All in One Excel VBA (35 курсов с проектами)

• 35+ курсов
• 120+ часов
• Полный пожизненный доступ
• Свидетельство о завершении

ПОДРОБНЕЕ >>

Как быстро и правильно умножить матрицы за шесть простых шагов

Допустим, нам даны две матрицы A и B, где

, и нас попросили найти продукт AB.Чтобы увидеть, имеет ли смысл AB, запишите размеры матриц в тех позициях, на которые вы хотите их умножить. В этом случае пишем

Чтобы убедиться, что продукт имеет смысл, просто проверьте , совпадают ли два числа на внутренней стороне. Если они это сделают, продукт можно принять, если они не согласны, продукт не имеет смысла. Например, даже если продукт AB имеет смысл, продукт BA – нет. Действительно, внутренние номера

не совпадают.

Опять же, мы можем использовать технику записи размеров по порядку.Возьмем те же A и B сверху. Записываем

Внешние числа по порядку указывают размеры продукта. Читая внешние числа слева направо, мы получаем 1 × 3, что соответствует размерности

.

или продукт AB. Мы сами вычислим это через минуту! Напомним,

• Запишите размеры двух матриц A и B.

• Проверьте соответствие внутренних чисел.

• Если они согласны, прочтите размеры ответа на внешних числах

Особый случай – умножение вектора-строки на матрицу

В нашем примере мы бы написали

Убедитесь, что вы пишете их в том порядке, в котором они появились!

Умножьте первую строку B на первую запись A, вторую строку на вторую запись и так далее.

, что равно

Сложите строки, полученные на шаге 3, чтобы получить ответ

Общий случай – две матрицы

Теперь предположим, что мы хотим умножить новую матрицу A ‘на ту же матрицу B, где

Выполняя шаги 0 и 1, видим

, продукт имеет смысл, и результат должен быть 3 X 3. Мы найдем результат строка за строкой.

В нашем примере мы бы написали

Чтобы найти первую строку нашего ответа 3×3, вычислите произведение, первую строку из A ‘умножить на B.

, это проблема, которую мы только что решили. Итак, первая строка нашего ответа –

.

Чтобы найти вторую строку нашего ответа 3×3, вычислите, который я оставлю читателю для проверки, это

Наконец, третья строка нашего ответа 3×3, поэтому мы умножаем

, а затем прибавить

Мы нашли три строки нашей матрицы решений и заключаем

Обычно эту перспективу формулируют так, что при умножении AB A действует на B операциями со строками.Мы рассматриваем B как набор векторов-строк, и строки A заставляют нас брать линейные комбинации векторов-строк в B, чтобы сформировать строки решения. Существует эквивалентная перспектива операций с колонками. У каждого свое место. Следите за обновлениями, и мы расскажем, как каждая из этих точек зрения вступает в игру при решении матричного уравнения Ax = b.

Вы заинтересованы в сотрудничестве с репетитором математики, таким как Джесси?

Скалярное и матричное умножение

Скалярный и матричное умножение (стр. 1 из 3) Есть два типа умножение для матриц: скалярное умножение и умножение матриц.Скалярное умножение – это просто. Вы просто набираете обычный номер (называется «скаляр») и умножьте его на каждую запись в матрице. Для следующей матрицы А , найти 2 A и 1 A . Сделать первый скаляр умножение, чтобы найти 2 А , Я просто умножаю 2 на каждую запись в матрице: Другое скалярное умножение, найти 1 A , работает аналогично: Итак, окончательный ответ: авторское право Элизабет Стапель 2003-2011 Все права защищены Скалярное умножение легкий.Однако умножение матриц – это совсем другая история. По факту, это королевская боль. Ваш текст, вероятно, дал вам сложную формулу для процесс, и эта формула, вероятно, не имела для вас никакого смысла. Это Ладно. Процесс грязный, и эта сложная формула – лучшее, что они может пригодиться для объяснения в формальной обстановке, например, в учебнике. Вот как работает процесс: Найдите продукт AB для следующих матриц: Для расчета AB , Записываю А и B рядом друг с другом вот так: Теперь мне нужно умножить РЯД А КОЛОННАМИ Б .Под этим я подразумеваю, что сначала беру первый ряд A и первый столбец B , и я умножаю первые записи, затем вторые записи, а затем третьи записи, а затем я добавляю три продукта. Сумма одна запись в матрице продуктов AB ; фактически, будучи произведением строки 1 и столбец 1, результатом является 1,1-запись из AB .Затем я продолжаю в том же духе. Например, сумма произведений из 2-го ряда из А и столбец 1 из Б 2,1-запись из AB . Когда я умножаю матрицы, Я использую пальцы, чтобы следить за тем, что я делаю. Следующая анимация это моя попытка проиллюстрировать этот процесс. (Не смейтесь, я не художник!) (Итак, класс; что я сказать про смех?) Окончательный ответ: Как вы видели в приведенном выше примере, по общему правилу продукт i -й ряд А и j -й колонка Б это i , j -й запись матрицы продукта AB .Это общее правило по большей части представляет собой сложную формулу в ваш текст был о. Например, когда я, в в приведенном выше примере сначала умножили ряд (из А ) и второй столбец (из Б ), это дало мне первая строка – вторая колонка запись в матрице продукта AB . Верх | 1 | 2 | 3 | Вернуться к указателю Далее >> Цитируйте эту статью как: Стапель, Елизавета.«Скалярное и матричное умножение». Purplemath . Доступно по номеру https://www.purplemath.com/modules/mtrxmult.htm . Дата обращения [Дата] [Месяц] 2016 г.

.