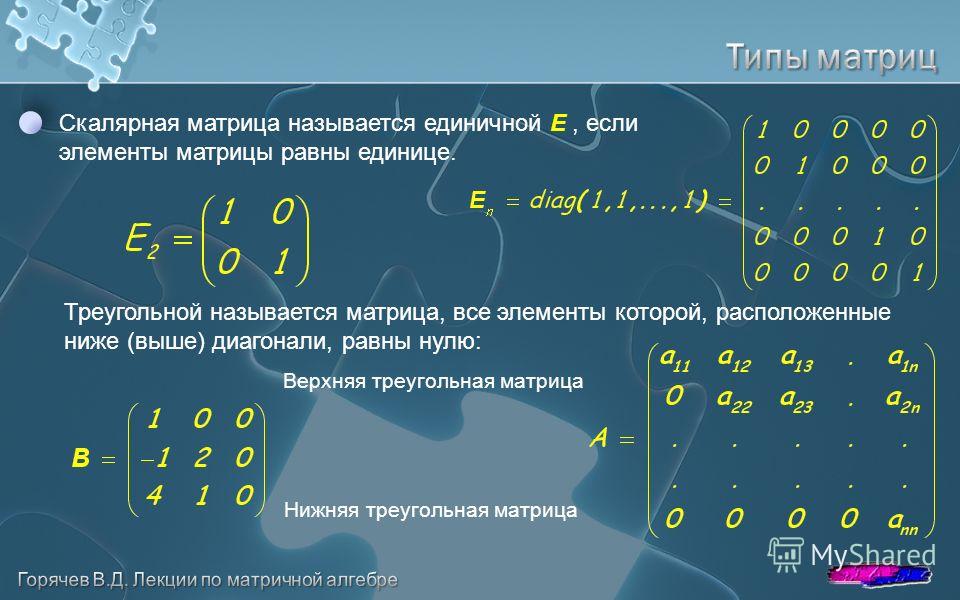
примеры, алгоритм умножения на вектор, число, свойства произведения
Произведение двух матриц
Определение 1Произведение матриц (С= АВ) — операция только для согласованных матриц А и В, у которых число столбцов матрицы А равно числу строк матрицы В:
C⏟m×n=A⏟m×p×B⏟p×n
Пример 1Даны матрицы:
- A=a(ij) размеров m×n;
- B=b(ij) размеров p×n
Матрицу C, элементы cij которой вычисляются по следующей формуле:
cij=ai1×b1j+ai2×b2j+…+aip×bpj, i=1,…m, j=1,…m
Пример 2Вычислим произведения АВ=ВА:
А=121012, В=100111
Решение, используя правило умножения матриц:
А⏟2×3×В⏟3×2=121012×100111=1×1+2×0+1×11×0+2×1+1×10×1+1×0+2×10×0+1×1+2×1==2323⏟2×2
В⏟3×2×А⏟2×3=100111×121012=1×1+0×01×2+0×11×1+0×20×1+1×00×2+1×10×1+1×21×1+1×01×2+1×11×1+1×2=121012133⏟3×3
Произведение АВ и ВА найдены, но являются матрицами разных размеров: АВ не равна ВА.
Свойства умножения матриц
Свойства умножения матриц:
- (АВ)С = А(ВС) — ассоциативность умножения матриц;
- А(В+С) = АВ + АС — дистрибутивность умножения;
- (А+В)С = АС + ВС — дистрибутивность умножения;
- λ(АВ)=(λА)В
Проверяем свойство №1: (АВ)С = А(ВС):
(А×В)×А=1234×5678×1002=19224350×1002=194443100,
А(В×С)=1234×56781002=1234×512716=194443100.
Проверяем свойство №2: А(В+С) = АВ + АС:
А×(В+С)=1234×5678+1002=1234×66710=20264658,
АВ+АС=1234×5678+1234×1002=19224350+1438=20264658.
Произведение трех матриц
Произведение трех матриц АВС вычисляют 2-мя способами:
- найти АВ и умножить на С: (АВ)С;
- либо найти сначала ВС, а затем умножить А(ВС).
Перемножить матрицы 2-мя способами:
4375×-289338-126×7321
- найти произведение 2-х матриц;
- затем снова найти произведение 2-х матриц.
1). АВ=4375×-289338-126=4(-28)+3×384×93+3(-126)7(-28)+5×387×93+5(-126)=2-6-621
2). АВС=(АВ)С=2-6-6217321=2×7-6×22×3-6×1-6×7+21×2-6×3+21×1=2003.
Используем формулу АВС=(АВ)С:
1). ВС=-289338-1267321=-28×7+93×2-28×3+93×138×7-126×238×3-126×1=-10914-12
2). АВС=(АВ)С=7321-10914-12=4(-10)+3×144×9+3(-12)7(-10)+5×147×9+5(-12)=2003
Ответ: 4375-289338-1267321=2003
Умножение матрицы на число
Определение 2Произведение матрицы А на число k — это матрица В=Аk того же размера, которая получена из исходной умножением на заданное число всех ее элементов:
bi,j=k×ai,j
Свойства умножения матрицы на число:
- 1×А=А
- 0×А=нулевая матрица
- k(A+B)=kA+kB
- (k+n)A=kA+nA
- (k×n)×A=k(n×A)
Найдем произведение матрицы А=4290 на 5.
Решение:
5А=542905×45×25×95×0=2010450
Умножение матрицы на вектор
Определение 3Чтобы найти произведение матрицы и вектора, необходимо умножать по правилу «строка на столбец»:
- если умножить матрицу на вектор-столбец число столбцов в матрице должно совпадать с числом строк в векторе-столбце;
- результатом умножения вектора-столбца является только вектор-столбец:
АВ=а11а12⋯а1nа21а22⋯а2n⋯⋯⋯⋯аm1аm2⋯аmnb1b2⋯b1n=a11×b1+a12×b2+⋯+a1n×bna21×b1+a22×b2+⋯+a2n×bn⋯⋯⋯⋯am1×b1+am2×b2+⋯+amn×bn=c1c2⋯c1m
- если умножить матрицу на вектор-строку, то умножаемая матрица должна быть исключительно вектором-столбцом, причем количество столбцов должно совпадать с количеством столбцов в векторе-строке:
АВ=аа⋯аbb⋯b=a1×b1a1×b2⋯a1×bna2×b1a2×b2⋯a2×bn⋯⋯⋯⋯an×b1an×b2⋯an×bn=c11c12⋯c1nc21c22⋯c2n⋯⋯⋯⋯cn1cn2⋯cnn
Пример 5Найдем произведение матрицы А и вектора-столбца В:
АВ=240-213-10112-1=2×1+4×2+0×(-1)-2×1+1×2+3×(-1)-1×1+0×2+1×(-1)=2+8+0-2+2-3-1+0-1=10-3-2
Пример 6А=320-1, В=-1102
Решение:
АВ=3201×-1102=3×(-1)3×13×03×22×(-1)2×12×02×20×(-1)0×10×00×21×(-1)1×11×01×2=-3306-22040000-1102
Ответ: АВ=-3306-22040000-1102
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта
примеры, алгоритм умножения на вектор, число, свойства произведения
Произведение двух матриц
Определение 1Произведение матриц (С= АВ) — операция только для согласованных матриц А и В, у которых число столбцов матрицы А равно числу строк матрицы В:
C⏟m×n=A⏟m×p×B⏟p×n
Пример 1Даны матрицы:
- A=a(ij) размеров m×n;
- B=b(ij) размеров p×n
Матрицу C, элементы cij которой вычисляются по следующей формуле:
cij=ai1×b1j+ai2×b2j+…+aip×bpj, i=1,…m, j=1,…m
Пример 2Вычислим произведения АВ=ВА:
А=121012, В=100111
Решение, используя правило умножения матриц:
А⏟2×3×В⏟3×2=121012×100111=1×1+2×0+1×11×0+2×1+1×10×1+1×0+2×10×0+1×1+2×1==2323⏟2×2
В⏟3×2×А⏟2×3=100111×121012=1×1+0×01×2+0×11×1+0×20×1+1×00×2+1×10×1+1×21×1+1×01×2+1×11×1+1×2=121012133⏟3×3
Произведение АВ и ВА найдены, но являются матрицами разных размеров: АВ не равна ВА.
Свойства умножения матриц
Свойства умножения матриц:
- (АВ)С = А(ВС) — ассоциативность умножения матриц;
- А(В+С) = АВ + АС — дистрибутивность умножения;
- (А+В)С = АС + ВС — дистрибутивность умножения;
- λ(АВ)=(λА)В
Проверяем свойство №1: (АВ)С = А(ВС):
(А×В)×А=1234×5678×1002=19224350×1002=194443100,
А(В×С)=1234×56781002=1234×512716=194443100.
Проверяем свойство №2: А(В+С) = АВ + АС:
А×(В+С)=1234×5678+1002=1234×66710=20264658,
АВ+АС=1234×5678+1234×1002=19224350+1438=20264658.
Произведение трех матриц
Произведение трех матриц АВС вычисляют 2-мя способами:
- найти АВ и умножить на С: (АВ)С;
- либо найти сначала ВС, а затем умножить А(ВС).
Перемножить матрицы 2-мя способами:
4375×-289338-126×7321
Алгоритм действий:
- найти произведение 2-х матриц;
- затем снова найти произведение 2-х матриц.
1). АВ=4375×-289338-126=4(-28)+3×384×93+3(-126)7(-28)+5×387×93+5(-126)=2-6-621
2). АВС=(АВ)С=2-6-6217321=2×7-6×22×3-6×1-6×7+21×2-6×3+21×1=2003.
Используем формулу АВС=(АВ)С:
1). ВС=-289338-1267321=-28×7+93×2-28×3+93×138×7-126×238×3-126×1=-10914-12
2). АВС=(АВ)С=7321-10914-12=4(-10)+3×144×9+3(-12)7(-10)+5×147×9+5(-12)=2003
Ответ: 4375-289338-1267321=2003
Умножение матрицы на число
Определение 2Произведение матрицы А на число k — это матрица В=Аk того же размера, которая получена из исходной умножением на заданное число всех ее элементов:
bi,j=k×ai,j
Свойства умножения матрицы на число:
- 1×А=А
- 0×А=нулевая матрица
- k(A+B)=kA+kB
- (k+n)A=kA+nA
- (k×n)×A=k(n×A)
Найдем произведение матрицы А=4290 на 5.
Решение:
5А=542905×45×25×95×0=2010450
Умножение матрицы на вектор
Определение 3Чтобы найти произведение матрицы и вектора, необходимо умножать по правилу «строка на столбец»:
- если умножить матрицу на вектор-столбец число столбцов в матрице должно совпадать с числом строк в векторе-столбце;
- результатом умножения вектора-столбца является только вектор-столбец:
АВ=а11а12⋯а1nа21а22⋯а2n⋯⋯⋯⋯аm1аm2⋯аmnb1b2⋯b1n=a11×b1+a12×b2+⋯+a1n×bna21×b1+a22×b2+⋯+a2n×bn⋯⋯⋯⋯am1×b1+am2×b2+⋯+amn×bn=c1c2⋯c1m
- если умножить матрицу на вектор-строку, то умножаемая матрица должна быть исключительно вектором-столбцом, причем количество столбцов должно совпадать с количеством столбцов в векторе-строке:
АВ=аа⋯аbb⋯b=a1×b1a1×b2⋯a1×bna2×b1a2×b2⋯a2×bn⋯⋯⋯⋯an×b1an×b2⋯an×bn=c11c12⋯c1nc21c22⋯c2n⋯⋯⋯⋯cn1cn2⋯cnn
Пример 5Найдем произведение матрицы А и вектора-столбца В:
АВ=240-213-10112-1=2×1+4×2+0×(-1)-2×1+1×2+3×(-1)-1×1+0×2+1×(-1)=2+8+0-2+2-3-1+0-1=10-3-2
Пример 6Найдем произведение матрицы А и вектора-строку В:
А=320-1, В=-1102
Решение:
АВ=3201×-1102=3×(-1)3×13×03×22×(-1)2×12×02×20×(-1)0×10×00×21×(-1)1×11×01×2=-3306-22040000-1102
Ответ: АВ=-3306-22040000-1102
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта
Матрицы: основные операции OTUS
В математике и информатике полно разнообразных объектов, с которыми нужно уметь работать. Некоторые из них изучаются в школьных программах, а какие-то в университетах. В данной статье будет рассказано о том, что такое матрица. А еще – как найти произведение двух матриц, умножить соответствующий объект на число, выполнить иные основные операции.
Определение термина
Матрица – это некий математический объект. Он представлен таблицей чисел, которая включает в себя определенное количество столбцов и срок.
Под матрицами принято понимать прямоугольную или квадратную табличку элементов, в которой строчки получают нумерацию по направлению «сверху-вниз», а столбцы – «слева-направо».
При помощи таких математических объектов можно решать разного рода задачи. С рассматриваемыми компонентами должен уметь справляться любой математик. Программистам и работникам сферы IT тоже пригодятся подобные навыки.
Основные операции
Стоит запомнить, что с матричными объектами удается выполнять разнообразные действия. В основном – алгебраического характера:
- перемножать между собой;
- находить обратные матрицы и транспонированные;
- складывать;
- вычитать;
- обнаруживать произведение матрицы на число.
Также человек сможет отыскать детерминант при необходимости. Все это удается сделать как вручную, так и через специальные онлайн калькуляторы.
Сложение
Правило сложения матриц напоминает принцип сложения в линейных уравнениях (примерах). Но соответствующая операция доступна только относительно объектов с одинаковым количеством чисел. На выходе получится мат. объект аналогичного «объема».
Для сложения нескольких матричных составляющих, необходимо просто сложить их соответствующие элементы.
Вычитание
Перед тем, как умножать заданные матрицы, рекомендуется изучить более простые операции над ними. Все это пригодится в будущем каждому.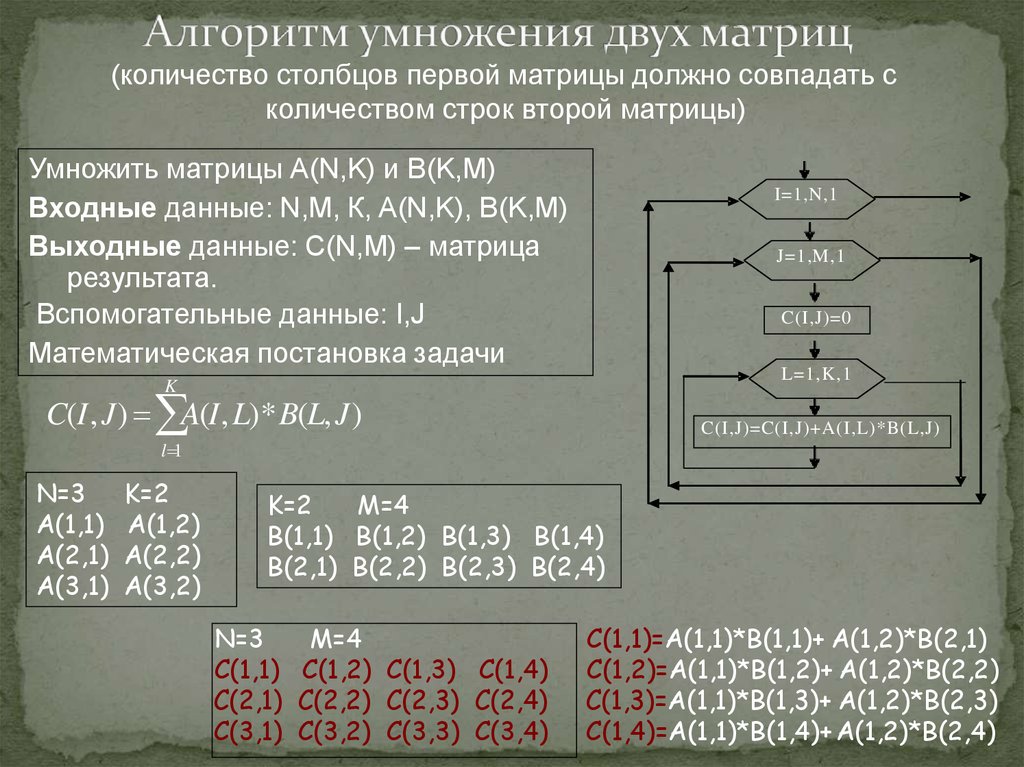
В случае с вычитанием действует точно такое же правило, как и со сложением – манипуляции возможны над объектами одинакового размера. На выходе получим результат с таким же количеством составляющих. И для этого достаточно от чисел матрицы a отнять соответствующие элементы матрицы b.
Обнаружение транспонированной матрицы
Для некоторых задач в математике имеет смысл транспонирование. Это – операция, при которой строки и столбцы заданного объекта будут меняться местами. Столбик станет строкой и наоборот.
Умножение на число
Теперь можно задуматься над тем, как умножать заданные изначально задачей матрицы. Первый вариант – на число.
С этой операцией проблем возникнуть не должно. Каждый элемент имеющихся матриц нужно просто последовательно умножить на заданное число. Принцип здесь точно такой же, как и в обычных алгебраических примерах.
Друг с другом
Умножать (cdot) матричные объекты можно не всегда. Здесь необходимо запомнить следующие моменты:
- удастся найти результат умножения рассматриваемых объектов, когда количество у первой матрицы количество строк точно такое же, как и количество столбцов у второй матрицы;
- результатом перемножения (cdot) матричного объекта A размером m cdot n и B с параметрами n*k будет C «объемом» m*k;
- каждый компонент в C будет равен сумме произведений элементов i-строки матрицы A на соответствующие составляющие в j-строке от матрицы B.

Найти произведение рассматриваемых мат. объектов можно, осуществив cdot (умножение) строк на столбцы.
Пошаговый алгоритм
Для того, чтобы у матрицы умножение на «себе подобную» прошло успешно, стоит соблюдать следующий алгоритм действий:
- Определить размеры каждого матричного объекта.
- Сравнить строки и столбцы в оных.
- Если соблюдено правило перемножения – применить cdot (умножение) строки матрицы на столбец.
- Записать результаты и сложить их, согласно действующим принципам математики.
Это – самый верный вектор направления по изучению рассматриваемой тематики. Если в процессе возникли какие-то проблемы, можно воспользоваться разнообразными онлайн-калькуляторами. В режиме реального времени они помогут перемножить между собой разного рода матричные объекты, а также осуществить с ними иные операции. Там нередко рассматриваемая манипуляция помечена как cdot.
Определители
После того, как у матриц умножение оказалось позади, можно рассмотреть связанные с этим действием операции. Первое, что должен знать математик после изученного материала – это нахождение определителя.
Первое, что должен знать математик после изученного материала – это нахождение определителя.
Здесь актуальны следующие моменты:
- определитель носит название детерминанта;
- это – численная характеристика заданного квадратного матричного объекта;
- помогает решать разного рода задачи;
- вычисляется путем разности произведений элементов главной и побочных диагоналей.
В случае единичной матрицы результатом будет служить единственный элемент мат. объекта. Когда разговор заходит о более крупных составляющих, ситуация меняется. Здесь предстоит вспомнить принципы cdot.
Для матричного объекта размером 3 на 3 детерминантом станет сумма произведений элементов главной диагонали, а также произведений компонентов на треугольниках с гранью которая идет параллельно главной. После этого от последней нужно отнять произведение (cdot) побочной диагонали и результат умножения числовых составляющих, лежащих на треугольниках с гранью параллельной побочной диагонали.
На практике искать детерминант крупных рассматриваемых элементов требуется редко. Если с этим процессом возникли затруднения, cdot сможет выполнить практически любой специализированный онлайн калькулятор. В нем достаточно выставить команду «определитель» или «детерминант», после чего ввести изначальные параметры.
Обратные
Для каждого числа a, не равного нулю, существует обратное a-1. Если к ним применить cdot, результатом послужит единица. Запись данного правила: a cdot a-1 = 1 = E. Соответствующее утверждение актуально и для матричных квадратных компонентов.
Нужно запомнить, что:
- A-1 – обратная к A, если при cdot ее на соответствующую матрицу, как справа, так и слева, будет единица.
- Не у каждой матрицы есть обратная ей.
- Когда a не равно 0 – это условие, которое является достаточным и необходимым для существования a-1, для получения A-1 требованием будет условие, что модуль A не равен 0.

Транспонирование и обратные матричные элементы, а также cdot – это база, без которой более сложные задачи решать не выйдет. Особенно тогда, когда речь заходит об уравнениях.
О минорах
Вектор направления в рассматриваемой теме в основном крутится вокруг cdot. Это – элементарная, но очень важная операция, с которой предстоит столкнуться не только математику, но и работнику в IT-сфере. Особенно если он хочет попытаться составить собственный калькулятор.
Для более полного раскрытия темы необходимо изучить миноры и алгебраические дополнения:
- Минор – это детерминант (n-1) порядка, который получается из определителя n-го порядка. В последнем нужно вычеркнуть i-строку и k-столбец, на пересечении которых находится aik. Обозначение минора – Mik.
- Алгебраическое дополнение – это минор с определенным знаком. Последний зависит от четности суммы i+k номеров строки и столбца, на пересечении которых находится aik.

- Обозначение алгебраического дополнения: Aik = (-1)i+k cdot Mik.
- Если у детерминанта n-го порядка все элементы последней строки/столбца, исключая составляющую, которая находится в правом нижнем углу, равны 0, то определителем будет cdot этого значения на минор.
- Когда определитель состоит из нулей за исключением одного компонента – детерминантом будет cdot соответствующего значения на алгебраическое дополнение.
В этой теории без матриц, умножение которых было рассмотрено ранее, разобраться не получится. Миноры и алгебраические дополнения тоже иногда удается получить через специализированные онлайн калькуляторы.
Об уравнениях
Математика – точная наука, в которой иногда требуется не только нарисовать вектор или фигуру, совершить элементарные операции, но и обнаружить неизвестное. В рассматриваемой теме речь зайдет о матрицах и уравнениях с ними.
Без cdot справиться с этой задачей не получится, ведь существуют различные варианты развития событий. В них может потребоваться воспользоваться перемножением строки одного компонента на второй, а также cdot на число. В некоторых ситуациях нужно искать обратные мат. составляющие.
В них может потребоваться воспользоваться перемножением строки одного компонента на второй, а также cdot на число. В некоторых ситуациях нужно искать обратные мат. составляющие.
Для матричных уравнений будут действовать те же правила, что и у линейных, но с некоторыми оговорками. Здесь у матриц умножение окажется одним из самых важных принципов.
Правила решения уравнений
Далее, когда транспонирование и иные важные аспекты тематики изучены, будут даны возможные примеры матричных уравнений с решениями. Пусть дано условие A cdot X = B, где A и B – известны, а X- нет.
Принцип решения зависит от ситуации:
- A cdot X = B. Здесь обе части перемножаются на обратную А-1 слева. На выходе будет E cdot X = A-1 cdot B. Итог – X = A-1 * B.
- X cdot A = B. Здесь действует тот же принцип, что и в предыдущем примере. Но перемножение на обратную A осуществляется справа. Результат – X = B cdot A-1.
- A * X * B = C.
 Известная матрица в левой части перемножается на обратную той, что расположена слева в уравнении. Далее – с правой стороны на матрицу, обратную той, что находилась справа. Результат: X = A-1 * C * B-1.
Известная матрица в левой части перемножается на обратную той, что расположена слева в уравнении. Далее – с правой стороны на матрицу, обратную той, что находилась справа. Результат: X = A-1 * C * B-1.
Когда в заданном примере X – это обычное число, правило умножения заданных матриц не работает. Здесь будет применяться простой принцип – решение линейных уравнений.
Быстрое решение
Чтобы не приходилось думать, каким размером матрицу на матрицу можно перемножить, а также как строить векторные графики при необходимости, стоит посмотреть школьную программу по алгебре и геометрии (старшее звено), а также заглянуть в пособия для учеников ВУЗов.
Если же нужно быстро получить решение по матрицам, в интернете удастся отыскать немало калькуляторов на любой случай. А это видео объяснит, как у матриц проводить умножение на наглядных примерах.
Чтобы применять cdot, а также матричные компоненты в программировании, стоит пройти дистанционные специализированные курсы. Предложения есть как для новичков, так и для продвинутых программистов и математиков.
Предложения есть как для новичков, так и для продвинутых программистов и математиков.
Хотите освоить современную IT-специальность? Огромный выбор курсов по востребованным IT-направлениям есть в Otus!
Также, возможно, вам будет интересен следующий курс:
Умножение матриц 3х3 формула
Чтобы можно было умножить две матрицы, количество столбцов первой матрицы должно быть равно количеству строк второй матрицы.
Алгоритм умножения матриц
Умножаем элементы в строках первой матрицы на элементы в столбцах второй матрицы.
- Умножаем элементы первой строки на элементы первого столбца.
- Умножаем первый элемент первой строки на первый элемент первого столбца.
- Умножаем второй элемент первой строки на второй элемент первого столбца.
- Делаем то же самое с каждым элементом, пока не дойдем до конца как первой строки первой матрицы, так и первого столбца второй матрицы.
- Складываем полученные произведения.
- Полученный результат будет первым элементом первой строки произведения матриц.

- Умножаем элементы первой строки первой матрицы на элементы второго столбца второй матрицы.
- Умножаем первый элемент первой строки на первый элемент второго столбца.
- Умножаем второй элемент первой строки на второй элемент второго столбца.
- Делаем то же самое с каждым элементом, пока не дойдем до конца как первой строки первой матрицы, так и второго столбца второй матрицы.
- Складываем полученные произведения.
- Полученный результат будет вторым элементом первой строки произведения матриц.
- Применяя тот же самый алгоритм, умножаем элементы первой строки первой матрицы на элементы остальных столбцов второй матрицы. Полученные числа составят первую строку вычисляемой матрицы.
- Вторая строка вычисляемой матрицы находится аналогично умножением элементов второй строки первой матрицы на элементы каждого столбца второй матрицы: результаты записываются в новую матрицу после каждого суммирования.
- Делаем это с каждой строкой первой матрицы, пока все строки новой матрицы не будут заполнены.

Пример 7
$A= egin 1 & 2 & 2\ 3 & 1 & 1 end$
$B=egin4 & 2 \ 3 & 1 \ 1 & 5\ end$
Заметим, что матрица A имеет 3 столбца, а матрица B имеет 3 строки, значит, их можно перемножить.
$B cdot A = egin color4 &color2 \ color3 & color1 \ color1 & color5 endegincolor1 &color2 & color2\ color3 &color1 & color1 end=$
Заметим, что $A cdot B
eq B cdot A$
Пример 8
$A= egin 5 & 2 \ 3 & 1 endB= egin4 & 6 \ 5 & 2 end$
Опять-таки $A cdot B
eq B cdot A$.
Пример 9
$A= egin 1 & 4 & 3 \ 2 & 1 & 5\ 3 & 2 & 1 endB= egin5 & 2 & 1 \ 4 & 3 & 2 \ 2 & 1 & 5 end$
Опять-таки $A cdot B
eq B cdot A$.
Заметим, что $A cdot I_ <2>= I_ <2>cdot A=A$.
Пример 11
$A=egin 1 & 4 & 3 \ 2 & 1 & 5\ 3 & 2 & 1 endI_<3>= egin1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 end$
Опять-таки $A cdot I_ <3>= I_ <3>cdot A = A$.
Примечание:
- В общем случае умножение матриц некоммуникативно.
- $Acdot I_ = I_cdot A = A$ для любой матрицы A, имеющей n столбцов.
Расчет умножения матриц онлайн. Динамические расчеты, нахождения произведения матриц.
Расчет умножения матриц онлайн. Умножьте матрицы порядка 2×3, 1×3, 3×3, 2×2 с 3×2, 3×1, 3×3, 2×2. Динамические расчеты, нахождения произведения матриц.
Умножение матриц возможно когда число столбцов первой матрицы равно числу строк второй матрицы.
В первой части мы рассмотрим умножение квадратных матриц. В следующей части Вы узнаете, как умножить разные матрицы (например, 2х3 до 3х3).
Здесь мы будем умножать матрицу 3х3 (3 ряда, 3 колонки) на другую матрицу 3х3 (3 ряда, 3 колонки).
| Матрица A | Матрица B |
| a11 | a12 | a13 |
| a21 | a22 | a23 |
| a31 | a32 | a33 |
В результате мы получим матрицу 3х3. Нам придется рассчитать каждую клетку результатов матрицы отдельно. Результат выразим через X.
Нам придется рассчитать каждую клетку результатов матрицы отдельно. Результат выразим через X.
Шаг 1:Рассчитаем x11
Для того, чтобы вычислить результат x11 мы будем использовать первую строку матрицы А и первый столбец матрицы В.
| Результат X | Матрица A | Матрица B |
| x11 | x12 | x13 |
| x21 | x22 | x23 |
| x31 | x32 | x33 |
Мы можем представить результат x11 = a11 x b11 + a12 x b21 + a13 x b31
Шаг 2: Рассчитаем x12
Для того, чтобы вычислить результат x12 мы будем использовать первую строку матрицы А и втором столбце матрицы В.
| Результат X | Матрица A | Матрица B |
| x11 | x12 | x13 |
| x21 | x22 | x23 |
| x31 | x32 | x33 |
Мы можем представить резальтат x12 = a11 x b12 + a12 x b22 + a13 x b32
По той же методике мы вычислим значения для всех ячеек.
Свойства умножения матриц
- (A · B) · C= A · (B · C) – произведение матриц ассоциативно;
- ( z · A) · B= z · (A · B), где z – число;
- A · (B + C) = A · B + A · C – произведение матриц дистрибутивно;
- E n · A nm = A nm · E m = A nm – умножение на единичную матрицу;
- A · B ≠ B · A – в общем случае произведение матриц не коммутативно.

- Произведением двух матриц есть матрица, у которой столько строк, сколько их у левого сомножителя, и столько столбцов, сколько их у правого сомножителя.
Примеры задач на умножение матриц
С = A · B = 4 2 9 0 · 3 1 -3 4 = 6 12 27 9
Элементы матрицы C вычисляются следующим образом:
C = A · B = 2 1 -3 0 4 -1 · 5 -1 6 -3 0 7 = 7 -2 19 -15 3 -18 23 -4 17
Элементы матрицы C вычисляются следующим образом:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
#11. Произведение матриц и векторов, элементы линейной алгебры
Смотреть материал на видео
Пришло время
познакомиться с одной из фундаментальных возможностей пакета NumPy–матричных и
векторных вычислений. На одном из прошлых занятий мы с вами уже видели, как
можно поэлементно умножать один вектор на другой или одну матрицу на другую:
На одном из прошлых занятий мы с вами уже видели, как
можно поэлементно умножать один вектор на другой или одну матрицу на другую:
a = np.arange(1, 10).reshape(3, 3) b = np.arange(10, 19).reshape(3, 3) a*b
В консоли увидим результат:
array([[
10, 22, 36],
[ 52, 70, 90],
[112, 136,
162]])
Матричное умножение
Но если нам нужно выполнить именно матричное умножение, то есть, строки одной матрицы умножать на столбцы другой и результаты складывать:
то для этого следует использовать специальные функции и операторы. Начнем с функций. Итак, чтобы перемножить две матрицы a иbпо всем правилам математики, запишем следующую команду:
np.dot(a, b)
Эта функция возвращает новую матрицу (двумерный массив) с результатом умножения:
array([[ 84, 90, 96],
[201,
216, 231],
[318, 342,
366]])
Тот же результат можно получить и с помощью функции:
np.matmul(a, b)
Считается, что этот вариант предпочтительнее использовать при умножении матриц.
Векторное умножение
Аналогичные операции можно выполнять и с векторами. Математически, если у нас имеются два вектора:
то их умножение можно реализовать в двух видах:
и
Первое умножение реализуется либо через функцию:
a = np.arange(1, 10) b = np.ones(9) np.dot(a, b) # значение 45
Либо, более предпочтительной функцией для внутреннего умножения векторов:
np.inner(a, b) # 45
Второй вариант умножения (внешнее умножение векторов) реализуется с помощью функции:
np.outer(a, b)
получим результат в виде следующей матрицы:
array([[1.,
1., 1., 1., 1., 1., 1., 1., 1.],
[2., 2., 2., 2. , 2., 2., 2., 2., 2.],
, 2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5., 5., 5., 5., 5.],
[6., 6., 6., 6., 6., 6., 6., 6., 6.],
[7., 7., 7., 7., 7., 7., 7., 7., 7.],
[8., 8., 8., 8., 8., 8., 8., 8., 8.],
[9., 9., 9., 9., 9., 9., 9., 9., 9.]])
Операция умножения матриц и векторов используется довольно часто, поэтому в пакете NumPy имеется весьма полезный перегруженный оператор, заменяющий функцию matmul:
a @ b # значение 45
или, с использованием матриц:
a.resize(3, 3) b.resize(3, 3) a @ b # аналог np.matmul(a, b)
Умножение вектора на матрицу
Наконец, рассмотрим умножение вектора на матрицу. Это также можно записать двумя способами:
или
Для реализации первого способа, зададим одномерный вектор и двумерную матрицу:
a = np.array([1,2,3]) b = np.arange(4,10).reshape(3,2) # матрица 3x2
И, затем, воспользуемся уже знакомой нам функцией dot:
np.dot(a, b) # array([40, 46])
При такой записи, когда одномерный массив записан первым аргументом, а матрица – вторым, получаем умножение вектора-строки на матрицу, то есть, первый способ.
Для реализации второго способа аргументы нужно поменять местами: сначала указать матрицу, а затем, вектор. Но, если мы сейчас это сделаем с нашими массивами, то получим ошибку:
np.dot(b, a) # несогласованность размеров
Дело в том, что массив a должен представлять вектор длиной два элемента, так как матрица b имеет размер в 3 строки и 2 столбца:
Определим массивa в два элемента и умножим на матрицу b:
a = np.array([1, 2]) np.dot(b, a) # array([14, 20, 26])
Получаем
вектор-строку (одномерный массив) как результат умножения. Обратите внимание,
по правилам математики вектор aдолжен быть вектором-столбцом, то есть,
быть представленным в виде:
Обратите внимание,
по правилам математики вектор aдолжен быть вектором-столбцом, то есть,
быть представленным в виде:
a.shape = -1, 1 # вектор-столбец 2x1
Но мы использовали вектор-строку. В NumPyтак тоже можно делать и это не приведет к ошибке. Результат будет именно умножение матрицы как бы на вектор-столбец. Ну а если использовать вектор-столбец, то и на выходе получим вектор-столбец:
np.dot(b, a) # вектор-столбец 3x1
Этого же результат можно достичь, используя оператор @ (перегрузка функции matmul):
a @ b # вектор-столбец 3x1
Результат будет тем же. Вот так в NumPyвыполняется умножение матриц, векторов и вектора на матрицу.
Элементы линейной алгебры
Из высшей
математики хорошо известно, что матрицы можно использовать для решения систем
линейных уравнений. Для этого в NumPyсуществует модуль linalg. Давайте
рассмотрим некоторые из его функций.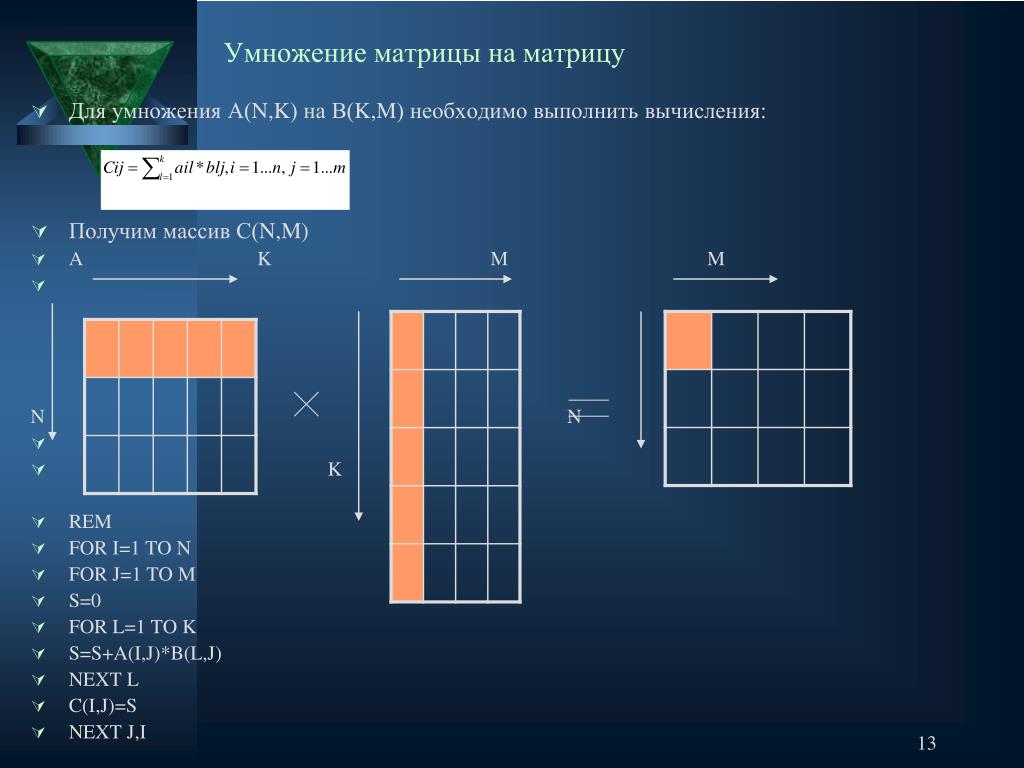
Предположим, имеется квадратная матрица 3×3:
a = np.array([(1, 2, 3), (1, 4, 9), (1, 8, 27)])
Первым делом вычислим ранг этой матрицы, чтобы быть уверенным, что она состоит из линейно независимых строк и столбцов:
np.linalg.matrix_rank(a) # рангравен 3
Если ранг матрицы совпадает с ее размерностью, значит, она способна описывать систему из трех независимых линейных уравнений. В нашем случае, система уравнений будет иметь вид:
Здесь - некие числа линейного уравнения. Например, возьмем их равными:
y = np.array([10, 20, 30])
Тогда корни уравнения можно вычислить с помощью функции solve:
np.linalg.solve(a, y) # array([-5. , 10. , -1.66666667])
Другой способ решения этой же системы линейных уравнений возможен через вычисление обратной матрицы. Изначально, уравнение можно записать в векторно-матричном виде:
Откуда получаем решения :
На уровне пакета NumPy это делается так:
invA = np.linalg.inv(a) # вычисление обратной матрицы invA @ y # вычисление корней
Конечно, я здесь представил лишь примеры использования модуля linalg. Приводить все функции нет смысла, так как они имеют довольно специализированное назначение и специалисты в своих областях без труда смогут ими воспользоваться. Для полноты картины я лишь приведу список наиболее характерных функций, чтобы вы знали возможности расширения linalg.
|
Функция |
Описание |
|
linalg.cholesky() |
Разложение Холецкого |
|
linalg.qr() |
QR-разложение матрицы |
|
linalg.svd() |
Сингулярное (SVD) разложение матрицы |
|
linalg. |
Норма матрицы или вектора |
|
linalg.cond() |
Число обусловленности матрицы |
|
linalg.det() |
Определитель (детерминант) матрицы |
|
linalg.matrix_rank() |
Вычисление ранга матрицы по алгоритму SVD |
|
np.trace() |
Сумма диагональных элементов массива |
|
linalg.eig() |
Вычисление собственных значений и правых собственных векторов |
|
linalg. |
Вычисление собственных значений матрицы |
|
linalg.solve() |
Решение линейного матричного уравнения |
|
linalg.tensorsolve() |
Решение линейного тензорного уравнения |
|
linalg.lstsq() |
Решает задачу поиска наименьших квадратов для линейного матричного уравнения |
|
linalg.inv() |
Вычисление обратной матрицы |
|
linalg.pinv() |
Вычисление псевдообратной (Мура-Пенроуза) матрицы |
|
linalg. |
Вычисление обратного тензора (N-мерного массива) |
Конечно, это не все математические функции пакета NumPy. Полное описание смотрите на сайте с официальной документацией:
https://numpy.org/doc/stable/
Видео по теме
#1. Пакет numpy – установка и первое знакомство | NumPy уроки
#2. Основные типы данных. Создание массивов функцией array() | NumPy уроки
#3. Функции автозаполнения, создания матриц и числовых диапазонов | NumPy уроки
#4. Свойства и представления массивов, создание их копий | NumPy уроки
#5. Изменение формы массивов, добавление и удаление осей | NumPy уроки
#6. Объединение и разделение массивов | NumPy уроки
#7. Индексация, срезы, итерирование массивов | NumPy уроки
#8. Базовые математические операции над массивами | NumPy уроки
Базовые математические операции над массивами | NumPy уроки
#9. Булевы операции и функции, значения inf и nan | NumPy уроки
#10. Базовые математические функции | NumPy уроки
#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy уроки
#12. Множества (unique) и операции над ними | NumPy уроки
#13. Транслирование массивов | NumPy уроки
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Основы обеспечения единства измерений: Обеспечение единства измерений – деятельность метрологических служб, направленная на достижение… Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре. Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации – обмен информацией между организацией и её внешней средой… Интересное: Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
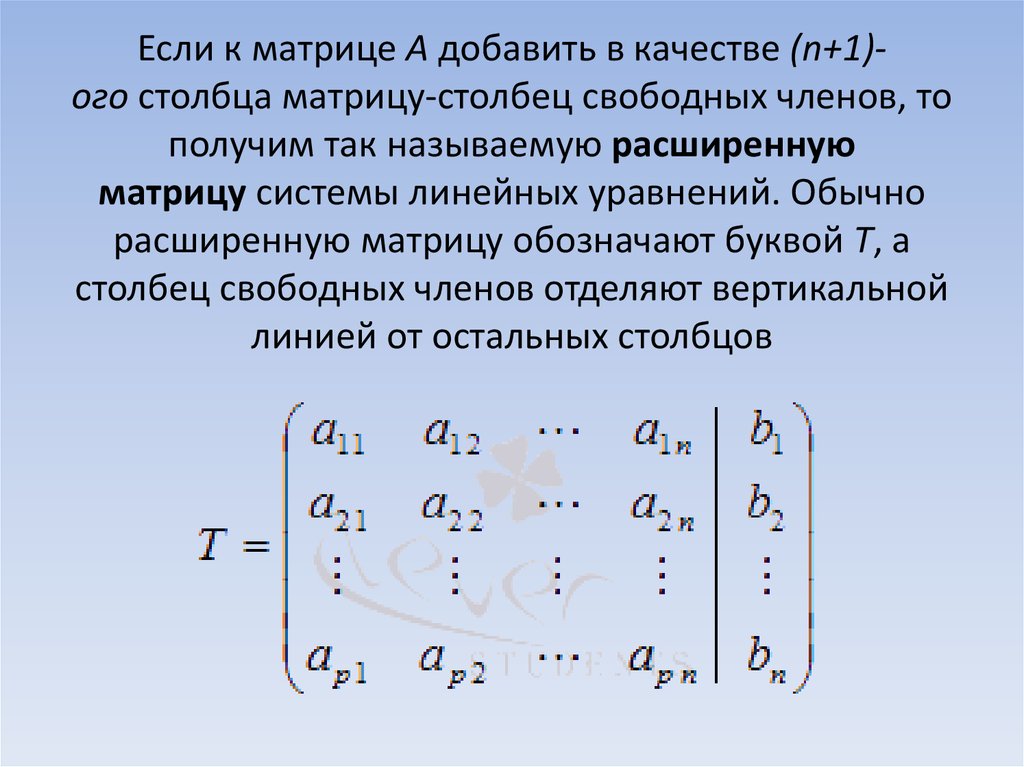
⇐ ПредыдущаяСтр 2 из 8Следующая ⇒ Матрицей называется прямоугольная таблица чисел. А – матрица, – элемент матрицы, номер строки, в которой стоит данный элемент, номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов. Определение.Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.
Определение. Матрица вида: = E, называетсяединичной матрицей. Операции над матрицами: Сложение (вычитание) матриц – складывать (вычитать) по элементам и только над матрицами одинаковой размерности. Например: Сложить матрицы и Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы: Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов. 2) Транспонирование матрицы. Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы. Пример: Транспонировать матрицу
Умножение матрицы на число , произведение. Пример: Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку. Умножение матриц. mxnи nxq, называется матрица размерности mxq. Количество столбцов 1-ой матрицы должно совпадать с количеством строк 2-ой матрицы. Умножение происходит таким образом, берется 1 строка 1-ой матрицы и умножается на 1 столбец 2-ой матрицы, далее 1 строка 1-ой матрицы умножается на 2 столбец 2-ой матрицы и т.д и получится 1 строка НОВОЙ МАТРИЦЫ. Пример: Свойства умножения матриц: · 1.ассоциативность (AB)C = A(BC); · 2.некоммутативность (в общем случае): AB BA; · 3.произведение коммутативно в случае умножения с единичной матрицей: AI = IA; · 4. 5.ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB) Коммуникативность: Умножение матриц не коммуникативно, и даже в том случае, когда матрицы квадратные все равно , например имеется 2 матрицы и результатом умножения матрицы А на матрицу Bбудет матрица , а если мы матрицу Bумножим на матрицу А получится . Множество квадратный матриц mxn замкнуто относительно умножения . Множество матриц nxm обладают мультипликативной единицей , , . Действительно, если перемножить матрицу и , то получим => Ассоциативность: Вопрос 3. Определители. Теорема Лапласа. Свойства определителей. Определитель– это число, которое считается по определенному правилу. Минор – это определитель, составленный из первоночального определителя, путем вычеркивания k-строк и k- любых столбцов. Алгебраическим дополнением Аij элемента аij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:
1)Определитель можно посчитать только у квадратной матрицы. 2) Определитель матрицы |An|=An 3)Определитель матрицы 5) Для вычисления матрицы 3×3 существует правило треугольников (Правило Саррюса) Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой . ⇐ Предыдущая12345678Следующая ⇒ Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Индивидуальные и групповые автопоилки: для животных. |
3 способа понять умножение матриц | by Glenn Henshaw
Развивайте свою интуицию в матричном умножении с нуля
Photo by Markus Spiske на UnsplashКогда я впервые узнал о матричном умножении, я был удивлен тем, как трудно мне было развить интуицию в отношении этой операции. Обычное определение матричного умножения скрывает множество интересных фактов, которые легче распознать, если посмотреть с разных точек зрения. В этом посте я опишу умножение матриц с трех точек зрения: столбцы, строки и их комбинации. Я также расскажу о некоторых простых фактах, которые помогут проверить вашу интуицию. Мы надеемся, что после прочтения вы получите более глубокое представление об умножении матриц, строках и столбцах. Этот пост был вдохновлен курсом линейной алгебры, который вел великий Гилберт Странг (MIT) .
В этом посте перечислены три способа интерпретации умножения матриц. Для каждой из этих интерпретаций мы обсудим следующее.
Для каждой из этих интерпретаций мы обсудим следующее.
- Интерпретация: Что это значит?
- Почему это работает?: Как эта интерпретация возникает из определения умножения матриц?
- Проверьте свою интуицию: Список фактов, которые вы можете использовать, чтобы проверить свою интуицию для интерпретации, которую мы рассматриваем.
Иногда я упоминаю понятия линейной комбинации , линейной зависимости, линейной независимости, скалярного произведения . Если вы хотите быстро освежить свою память по этим темам, посмотрите мою статью 3 основных понятия в линейной алгебре.
Пример. Допустим, у нас есть три завсегдатая: Ларс, Фатима и Джорджия. На вечеринке Ларс купил 2 пива и 1 коктейль, Фатима купила 1 пиво и 2 коктейля, а у Джорджии было 4 пива и никаких коктейлей. Пиво стоит 7 долларов, а коктейли — 10 долларов. Мы можем смоделировать их расходы на ночь с помощью матричного умножения.
Как были вычислены числа справа?
Наша цель — понять свойства матричного умножения в более общем виде, поэтому в этом посте мы будем рассматривать произведение матрицы 3×3 A и матрицы 3×2 B . Результатом будет матрица 3×2 C .
Жак Филипп Мари Бине … признан первым, кто вывел правило умножения матриц в 1812 году. — Оливер Книлл
Обычный способ определить умножение матриц – это суммирование или, более компактно, скалярное произведение строк A и столбцов B. Скалярное произведение строки 1 A и столбца 1 B даст первую запись C.
В общем случае ij-я запись C представляет собой i-ю строку A , разделенную точками с j-м столбцом B .
Пример. Найдите третью строку и второй столбец произведения C .
Ответ: (1)(1)+(2)(2) +(3)(1) = 8. Попробуйте использовать определение, чтобы найти остальные элементы С .
Попробуйте использовать определение, чтобы найти остальные элементы С .
Интерпретация: Запись C является скалярным произведением строки A и столбца B . Нулевые записи в C соответствуют строке A и столбцу B , которые ортогональны (под прямым углом друг к другу).
Проверьте свою интуицию: С этой точки зрения некоторые факты становятся яснее .
- Количество столбцов A должно равняться количеству строк B . В противном случае суммы в определении не будут определены.
- Произведение AB будет матрицей с тем же количеством столбцов, что и A , и таким же количеством строк, как B.

- Нулевая запись в C соответствует ряду A и столбец B ортогональны. Ортогональные векторы линейно независимы . Но не все пары линейно независимых векторов ортогональны.
Первое, на что следует обратить внимание относительно AB = C , это то, что столбцы матрицы C связаны со столбцами матрицы A важным образом.
Интерпретация Каждый из столбцов C является матрицей A , умноженный на колонку B. Влияние этого заключается в том, что Колонны C являются линейными сочетаниями из колонн A с весами, принесенные весами из колонн A с весами. столбцы B.
Почему это работает? Чтобы понять, почему столбцы C являются линейными комбинациями столбцов A , давайте внимательно посмотрим, как мы вычисляем первый столбец C.
Проверьте свою интуицию: С этой точки зрения некоторые факты становятся яснее .
- Матрица, умноженная на вектор, Ax , представляет собой просто линейную комбинацию столбцов a с элементами x. Таким образом, столбцы A линейно независимы тогда и только тогда, когда уравнение Ax = 0 имеет только нулевое решение.
- Мы можем просмотреть столбцы C как результат применения линейного преобразования, определенного B , к столбцам A .
- Предположим, что столбцы A линейно независимы. Тогда, если C имеет столбец нулей, B также должен иметь столбец нулей.
- Если столбцы C линейно зависимы и столбцы B линейно независимы, тогда столбцы A зависимы.
 Это следует из того факта, что если x является нетривиальным решением Cx = 0 , затем BX -нетривиальное решение из AX = 0,
Это следует из того факта, что если x является нетривиальным решением Cx = 0 , затем BX -нетривиальное решение из AX = 0, - Если уравнение Ax = b не имеет решения, то уравнение ABx = Cx = b не имеет решения. Ведь столбцы C – это просто комбинации столбцов A .
- Пролет колонн C содержится в пролете колонн A . Следовательно, ранг(AB) ≤ ранг(A) .
- Если B обратим с обратным B’ , то столбцы A и AB имеют одинаковый диапазон. Мы можем доказать это из предыдущего факта, ранг(AB) ≤ ранг(A) в сочетании с тем фактом, что ранг(A) = ранг(AI) = ранг(ABB’) ≤ ранг(AB).

Итак, умножение матриц с точки зрения столбцов. Теперь перейдем к рядам?
Интерпретация Строки C являются строками A , умноженными на матрицу B . Следовательно, строки C являются линейными комбинациями строк B с весами, указанными в строках A.
Почему это работает? Чтобы понять, почему строки C являются линейными комбинациями строк B , давайте внимательно посмотрим, как мы вычисляем первую строку C , используя определение умножения матриц.
Проверьте свою интуицию: Еще раз перечислим некоторые факты о строках, которые выводятся из этой интерпретации умножения матриц.
- Для AB = C , если строки C линейно независимы, то строки B линейно независимы.
 Предупреждение: обратное не обязательно верно.
Предупреждение: обратное не обязательно верно. - Если A имеет ряд нулей, то AB имеет ряд нулей.
- Диапазон строк B содержит диапазон строк C .
- Если Е — обратимая матрица n×n , а B — любая матрица n×m . Тогда EB имеет то же место в строке, что и E . В частности, элементарные операции со строками сохраняют пространство строк.
Мы можем использовать интерпретацию строки и столбца, чтобы помочь набросать доказательство интересного результата о размерности пространства строки и пространства столбца m×n матрица. Размерность размаха столбцов матрицы называется ее рангом . Размер промежутка строк называется rowrank .
Претензия: Ранг и Rowrank из M × N Матрица C – равны.
Есть много m×r матриц A и r×n матрицы B такие, что C = AB. Выберите A и B так, чтобы r было минимальным. The R Колонны из A SPAN The Column Пространство C. R 9005 C. R 9005 C. 9005 R 9005 C. 9005 R 9005 C. 9005 R C. C. 0043 строк B охватывают пространство строк C. Поскольку мы выбрали r как наименьшее такое число, rank(C) = rowrank(C) = r.
C. 0043 строк B охватывают пространство строк C. Поскольку мы выбрали r как наименьшее такое число, rank(C) = rowrank(C) = r.
Претензия: , если A и B – квадратные матрицы, а AB = I , затем BA = I. Следовательно, B – это обратно A.
Мы имеем . АВ = I . Поэтому столбцы A линейно независимы. Следовательно, уравнение Ax = 0 имеет только тривиальное решение. умножьте первое уравнение справа на A , чтобы получить ABA = A . Тогда АВА-А = А(ВА-I)=0 . Следовательно, ВА = I .
Наша последняя интерпретация дает нам способ разложить произведение двух матриц на сумму матриц.
Интерпретация Матрица C представляет собой сумму матриц, состоящих из столбцов A , умноженных на строки B. Матрицы, составляющие сумму, имеют столбцы, скалярно кратные столбцу A.
Почему это работает? Чтобы понять, почему это так, рассмотрим, что происходит, когда вы записываете матрицу A как сумму матриц и вычисляете AB путем распределения B .
Проверь свою интуицию:
- Каждая из матриц в слагаемом имеет одномерные столбцы.
- Вы можете поменять местами два столбца A и получить тот же продукт AB , если вы поменяете местами соответствующие строки B .
Мы говорили о трех разных способах понимания умножения матриц.
- Матрица, умноженная на столбцы
- Строки, умноженная на матрицы
- И столбцы, умноженные на строки
Мы использовали эти различные интерпретации для обзора некоторых основных фактов о матричном умножении, независимости и интервале.
Умножение матриц и векторов — Math Insight
Произведение матрицы на вектор
Для определения умножения между матрицей $A$ и вектором $\vc{x}$ (т. е. произведение матрицы на вектор), нам нужно просмотреть вектор как матрица-столбец. Определим матрично-векторное произведение только для случая, когда число столбцов в $A$ равно количеству строк в $\vc{x}$. Итак, если $A$ матрица $m \times n$ (т.е. с $n$ столбцами), то произведение $A \vc{x}$ определено для $n \times 1$ векторов-столбцов $\vc{x}$. Если мы пусть $A \vc{x} = \vc{b}$, тогда $\vc{b}$ — столбец $m \times 1$ вектор. Другими словами, количество строк в $A$ (которое может быть что угодно) определяет количество строк в произведении $\vc{b}$.
Общая формула для матрично-векторного произведения:
\начать{выравнивать*}
А\ВК{х}=
\оставил[
\begin{массив}{cccc}
а_{11} и а_{12} и \ldots и а_{1n}\\
a_{21} & a_{22} & \ldots & a_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
a_{m1} & a_{m2} & \ldots & a_{mn}
\конец{массив}
\Правильно]
\оставил[
\начать{массив}{с}
х_1\\
х_2\\
\vdots\\
х_n
\конец{массив}
\Правильно]
знак равно
\оставил[
\начать{массив}{с}
a_{11}x_1+a_{12}x_2 + \cdots + a_{1n} x_n\\
a_{21}x_1+a_{22}x_2 + \cdots + a_{2n} x_n\\
\vdots\\
a_{m1}x_1+a_{m2}x_2 + \cdots + a_{mn} x_n\\
\конец{массив}
\Правильно]. \конец{выравнивание*}
Хотя поначалу это может показаться запутанным, процесс матрично-векторного
умножение на самом деле очень просто. Берется скалярное произведение
$\vc{x}$ с каждой строкой $A$. (Вот почему количество
столбцов в $A$ должно быть равно количеству компонентов в $\vc{x}$.)
первый компонент матрично-векторного произведения является скалярным произведением
$\vc{x}$ с первой строкой $A$ и т. д. На самом деле, если $A$ имеет только один
row, произведение матрицы на вектор на самом деле является замаскированным точечным произведением.
\конец{выравнивание*}
Хотя поначалу это может показаться запутанным, процесс матрично-векторного
умножение на самом деле очень просто. Берется скалярное произведение
$\vc{x}$ с каждой строкой $A$. (Вот почему количество
столбцов в $A$ должно быть равно количеству компонентов в $\vc{x}$.)
первый компонент матрично-векторного произведения является скалярным произведением
$\vc{x}$ с первой строкой $A$ и т. д. На самом деле, если $A$ имеет только один
row, произведение матрицы на вектор на самом деле является замаскированным точечным произведением.
Например, если
\начать{выравнивать*}
А = \ влево[
\начать{массив}{ррр}
1 и -1 и 2\\
0 и -3 и 1
\конец{массив}
\Правильно]
\конец{выравнивание*}
и $\vc{x} = (2,1,0)$, то
\начать{выравнивать*}
A \vc{x} &= \left[
\начать{массив}{ррр}
1 и -1 и 2\\
0 и -3 и 1
\конец{массив}
\Правильно]
\оставил[
\начать{массив}{л}
2\\1\\0
\конец{массив}
\Правильно]\\
знак равно
\оставил[
\начать{массив}{г}
2 \cdot 1 – 1\cdot 1 + 0 \cdot 2\\
2 \cdot 0 – 1 \cdot 3 +0 \cdot 1
\конец{массив}
\Правильно]
\\
знак равно
\оставил[
\начать{массив}{г}
1\\
-3
\конец{массив}
\Правильно]. \конец{выравнивание*}
\конец{выравнивание*}
Произведение матрицы на матрицу
Поскольку мы рассматриваем векторы как матрицы-столбцы, произведение матрицы на вектор равно просто частный случай матрично-матричного произведения (т. е. произведения между двумя матрицами). Так же, как и для матрично-векторного произведения, Произведение $AB$ между матрицами $A$ и $B$ определено, только если количество столбцов в $A$ равно количеству строк в $B$. Говоря математическим языком, мы говорим, что можем умножить матрицу $m \times n$ $A$ на $n \times p$-матрицу $B$. (Если $p$ равно 1, то $B$ будет вектор-столбец $n\times 1$, и мы вернемся к матрично-векторное произведение.)
Произведение $AB$ представляет собой матрицу $m \x p$, которую мы будем называть $C$, т.е.
$АВ=С$. Чтобы вычислить произведение $B$, мы рассматриваем $B$ как группу из $n
\times 1$ векторов-столбцов, выстроенных рядом друг с другом:
\начать{выравнивать*}
\оставил[
\begin{массив}{cccc}
b_{11} & b_{12} & \ldots & b_{1p}\\
b_{21} & b_{22} & \ldots & b_{2p}\\
\vdots & \vdots & \vdots & \vdots\\
b_{n1} & b_{n2} & \ldots & b_{np}
\конец{массив}
\Правильно]
знак равно
\оставил[
\оставил[
\начать{массив}{с}
б_{11}\\
б_{21}\\
\vdots\\
b_{n1}\\
\конец{массив}
\Правильно]
\оставил[
\начать{массив}{с}
б_{12}\\
б_{22}\\
\vdots\\
b_{n2}\\
\конец{массив}
\Правильно]
\cdots
\оставил[
\начать{массив}{с}
б_{1п}\\
б_{2п}\\
\vdots\\
b_{np}\\
\конец{массив}
\Правильно]
\Правильно]
\конец{выравнивание*}
Тогда каждый столбец таблицы $C$ является векторным произведением матрицы $A$ с
соответствующий столбец $B$. Другими словами, компонент в $i$th
строка и $j$-й столбец $C$ — это скалярное произведение между $i$-й строкой
$A$ и $j$-й столбец $B$. В математике мы пишем этот компонент
$C$ как $c_{ij} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots +
a_{in}b_{nj}$.
Другими словами, компонент в $i$th
строка и $j$-й столбец $C$ — это скалярное произведение между $i$-й строкой
$A$ и $j$-й столбец $B$. В математике мы пишем этот компонент
$C$ как $c_{ij} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots +
a_{in}b_{nj}$.
Пример справки делает процесс понятным. Пусть $A$ будет $2 \times 3$
матрица
\начать{выравнивать*}
А=\влево[
\начать{массив}{ррр}
0 и 4 и -2\\
-4 и -3 и 0
\конец{массив}
\Правильно]
\конец{выравнивание*}
и $B$ — матрица $3 \times 2$
\начать{выравнивать*}
B= \влево[
\begin{массив}{rr}
0 &1\\
1 и -1\\
2 и 3
\конец{массив}
\Правильно].
\конец{выравнивание*}
Затем,
\начать{выравнивать*}
АБ &=\влево[
\начать{массив}{ррр}
0 и 4 и -2\\
-4 и -3 и 0
\конец{массив}
\Правильно]
\оставил[
\begin{массив}{rr}
0 &1\\
1 и -1\\
2 и 3
\конец{массив}
\Правильно]
\\
знак равно
\оставил[
\начать{массив}{ррр}
0 \cdot 0+4 \cdot 1-2\cdot 2 && 0 \cdot 1 +4 \cdot (-1) -2\cdot 3\\
-4 \cdot 0-3\cdot 1 + 0 \cdot 2 && -4 \cdot 1 -3 \cdot (-1) + 0\cdot 3
\конец{массив}
\Правильно]
\\
знак равно
\оставил[
\начать{массив}{ррр}
0+4-4 && 0-4-6\\
0-3+0 && -4 +3 +0
\конец{массив}
\Правильно]
\\
знак равно
\оставил[
\begin{массив}{rr}
0 и -10\\
-3 и -1
\конец{массив}
\Правильно]. \конец{выравнивание*}
\конец{выравнивание*}
Хотите больше примеров?
Умножение матриц в R – GeeksforGeeks
Умножение матриц — самая полезная операция над матрицами. В настоящее время он широко используется в таких областях, как теория сетей, преобразование координат и во многих других областях. Матрица в R может быть создана с помощью функции matrix() , и эта функция принимает входной вектор, nrow, ncol, byrow, dimnames в качестве аргументов.
Создание матрицы
Матрицу можно создать с помощью функции matrix().
Python3
|
Вывод:
[1] [2] [3] [4] [1,] 1 3 5 7 [2,] 2 4 6 8
Умножение матриц
Оператор умножения * используется для умножения матрицы скалярным или поэлементным умножением двух матриц.
Умножение на скаляр
Если вы умножаете матрицу на скалярное значение, то каждый элемент матрицы будет умножен на этот скаляр.
Example:
Python3
|
Вывод:
[1] [2] [3] [4] [1,] 2 6 10 14 [2,] 4 8 12 16
В приведенном выше коде скаляр умножается на каждый элемент исходной матрицы. Вот как происходит процесс умножения:
2*1=2 2*3=6 2*5=10 2*7=14 2*2=4 2*4=8 2*6=12 2*8=16
Умножение между матрицами
Когда матрица умножается на другую матрицу, происходит поэлементное умножение двух матриц. Все соответствующие элементы обеих матриц будут перемножены при условии, что обе матрицы будут одной размерности.
Все соответствующие элементы обеих матриц будут перемножены при условии, что обе матрицы будут одной размерности.
Пример:
Python3
|
Output:
[1] [2] [3] [4] [1,] 8 30 60 98 [2,] 18 44 78 120
Вот как происходит процесс умножения:
1*8=8 3*10=30 5*12=60 7*14=98 2*9=18 4*11=44 6*13=78 8*15=120
Умножение на вектор
Если матрица умножается на вектор, то вектор будет преобразован в матрицу строк или столбцов, чтобы получилось два аргументы созвучны.
Пример:
Python3
|
Output:
[1] [2] [3] [4] [1,] 1 3 5 7 [2,] 4 8 12 16
Вот как происходит процесс умножения:
1*1=1 1*3=3 1*5=5 1*7=7 2*2=4 2*4=8 2*6=12 2*8=16
Умножение с использованием оператора %*%
Оператор %*% используется для умножения матриц, удовлетворяющих условию, что число столбцов в первой матрице равно количеству строк во второй. Если перемножить матрицу A[M, N] и матрицу B[N, Z], то результирующая матрица будет иметь размерность M*N.
Если перемножить матрицу A[M, N] и матрицу B[N, Z], то результирующая матрица будет иметь размерность M*N.
Example:
Python3
|
.
[1,] 162 226
[2,] 200 280 Вот как происходит умножение: В матричной алгебре есть два виды умножения матриц:
умножение матрицы на число и умножение
матрица на другую матрицу. Когда вы умножаете матрицу на число, вы умножаете каждый элемент матрицы
по тому же номеру. Эта операция создает новую матрицу, которая называется
скалярное число , кратное . For example, if x is 5, and the matrix A is: Then, x A = 5 A and В приведенном выше примере каждый элемент A умножается
на 5, чтобы получить скалярное число, Б . Примечание. В некоторых текстах эта операция упоминается как умножение матрицы на
скаляр. (Скаляр — это действительное число или символ, представляющий действительное число.) Реклама Произведение матриц A B определено только
когда количество столбцов в A равно
количество строк в B . Сходным образом,
произведение матрицы B A определяется только
когда количество столбцов в B равно
количество строк в A . Предположим, что A является матрицей i x j , и B — это матрица j x k . Затем матрица
продукт A B приводит к матрице C , который имеет i строк и k столбцов; а также
каждый элемент в C может быть вычислен в соответствии с
следующую формулу. С я к =
Σ j A i j B j k where C i k = the element in row i and
столбец k из матрицы C Давайте рассмотрим пример, чтобы показать, как работает приведенная выше формула.
Предположим, мы хотим вычислить A B , учитывая приведенные ниже матрицы. Пусть А В 6. 0 J 2 9900 J 2 0 На основе вышеуказанных расчетов, мы можем сказать, 1*8+3*9+5*10+7*11 = 162 1*12+3*13+5*14+7*15 =226
2*8+4*9+6*10+8*11 = 200 2*12+4*13+6*14+8*15=280
Умножение матриц

Как умножить матрицу на число
A = 100 200 300 400 5 A = 5 100 200 300 400 5 * 300 5 * 400 5 A = 500 1000 1500 2000 = B 
Как умножить матрицу на матрицу

A i j = элемент в строке i и
столбец j из матрицы A
B j k =
элемент в строке j и столбец k из матрицы B
Σ j = знак суммы, что указывает на то, что
a i j b j k условия должны быть
суммируется по j А = 0 1 2 3 4 5 B = 6 7 8 9 10 11  Поскольку A имеет 2 строки, мы знаем, что С будет
иметь два ряда; и поскольку B имеет 2 столбца, мы знаем, что C будет иметь 2 столбца.
Чтобы вычислить значение каждого элемента в матрице 2 x 2 C ,
мы используем формулу С я к =
Σ j A i j B j k ,
как показано ниже.
Поскольку A имеет 2 строки, мы знаем, что С будет
иметь два ряда; и поскольку B имеет 2 столбца, мы знаем, что C будет иметь 2 столбца.
Чтобы вычислить значение каждого элемента в матрице 2 x 2 C ,
мы используем формулу С я к =
Σ j A i j B j k ,
как показано ниже. = 3*6 + 4*8 +5*10 = = 18 + 32 + 50 = 100
= 3*6 + 4*8 +5*10 = = 18 + 32 + 50 = 100
.0005 С не было
сложный. Все, что мы сделали, это умножили элементы строки в
Матрица A соответствующими элементами столбца в
Матрица Б . A B = C = 6 B = C = B = C = B = C = B = C = B = =. 28 31 100 
Порядок умножения
Как мы уже упоминали, в некоторых случаях умножение матриц определено для A B , но не для Б А ; наоборот. Однако, даже если умножение матриц возможно в обоих направлениях, результаты могут быть разными. То есть, А B не всегда равно Б А .
Поскольку порядок важен, жаргон матричной алгебры превратился в четко указать порядок умножения матриц.
- Для описания матричного произведения A B , мы можем сказать, что равно , умноженному на . по В ; или мы можем сказать, что B есть предварительно умножить на A .
- Аналогично, для описания матричного произведения Б А ,
мы можем сказать, что B равно , умноженному на .
 по А ; или мы можем сказать, что A есть предварительно умножить на B .
по А ; или мы можем сказать, что A есть предварительно умножить на B .
Суть: когда вы перемножаете две матрицы, порядок имеет значение.
Идентификационная матрица
Идентификационная матрица является н х н диагональная матрица с единицами по диагонали и нулями везде. Матрица идентичности обозначается I или I n . Ниже показаны две матрицы идентичности.
|
Матрица идентичности обладает уникальным талантом. Любая матрица, которая может быть
предварительно умноженное или постумноженное на I остается
такой же; то есть:
Любая матрица, которая может быть
предварительно умноженное или постумноженное на I остается
такой же; то есть:
А I = I А = A
Проверьте свое понимание
Задача 1
Рассмотрим приведенные ниже матрицы - A , B , и C
Предположим, что A B = C . Какие из следующих утверждений верны?
(A) w = a*e + b*h
(B) x = a*f + b*h
(C) y = c*g + d*h
(D) Все вышеперечисленное
(E) Ничего из перечисленного
Решение
Правильный ответ (B). Чтобы вычислить значение любого элемента в
матрица C используем формулу C i k = Σ j A i j B j 9.
В матрице C x — это элемент в строке 1 и столбце 2, что представлено в формуле как C 1 2 . Поэтому, чтобы найти x, мы используем формулу для вычисления C 1 2 , как показано ниже.
х = С 1 2 = Σ j A 1 j B j 2 = А 1 1 В 1 2 + А 1 2 Б 2 2 = а*ф + б*ч
Все остальные ответы неверны.
Последний урок Следующий урок
Как выполнять умножение матриц
Изображение ARENA Creative на Shutterstock
Линейная алгебра может быть сложной для изучения. Однако очень важно, чтобы вы понимали это, а не просто запоминали, как выполняется каждая операция в линейной алгебре.
Понимание того, почему и как выполняются операции в линейной алгебре, требует логики и практики. Умножение матриц — это лишь одна из операций, охватываемых при изучении линейной алгебры в колледже, и для сдачи экзаменов требуется понимание того, как выполнять эту операцию вручную.
Давайте посмотрим, как выполнить матричное умножение между матрицей и скалярным числом, вектором или матрицей.
Что такое умножение матриц?
Линейная алгебра — относительно новая область изучения математики. В 1812 году французский математик Жак Филипп Мари Бине первым описал умножение матриц. Однако некоторые ученые ставят эту дату под сомнение, поскольку первая матрица не была полностью описана до 1857 года Артуром Кейли в Великобритании.
Чтобы понять, насколько «молодой» является линейная алгебра, приведем описание теоремы Пифагора в геометрии между 400 и 800 годами до нашей эры.
Матрица — это прямоугольный массив чисел или выражений. Он расположен в строках и столбцах. Количество строк представлено «m», а количество столбцов — «n».
Он расположен в строках и столбцах. Количество строк представлено «m», а количество столбцов — «n».
Каждый элемент в матрице может быть представлен как «ai,j», где «j» увеличивается по отношению к столбцу, а «i» увеличивается по количеству строк, как вы можете видеть на рисунке ниже.
Фото Кредит
Как умножить матрицу на число
г. Умножить матрицу на число очень просто. Просто каждый элемент в матрице умножается на число. Стратегия не меняется в зависимости от количества строк и столбцов.
Когда число умножается на матрицу, это называется скалярным умножением. Скаляр — это величина, полностью описываемая одной величиной или числовым значением. В приведенном выше примере 3 является скаляром.
Как умножить матрицу на матрицу
Умножение между матрицами более сложное. Хотя вычисление результата умножения матриц вручную, вероятно, нецелесообразно в реальном мире, понимание процесса углубит ваше понимание линейной алгебры.
При умножении матрицы на матрицу количество столбцов в первой матрице должно равняться количеству строк во второй матрице, иначе операция не может быть определена.
Результатом будет матрица с m столбцами и p строками. Это представлено следующим уравнением:
[mn ][np] [mp]
Чтобы вычислить результат умножения матрицы на матрицу, вычислите «точечный продукт» каждой строки и столбца.
Скалярное произведение — это алгебраическая операция, при которой два списка чисел (векторов), равных по длине, возвращают одно число. Скалярный продукт также называется скалярным произведением, поскольку в результате вычисления получается одно число.
Матрицы разных размеров можно перемножать. Здесь у нас есть матрица A с «m» строками и «n» столбцами и матрица B с «n» строками и «p» столбцами.
Результатом матричного произведения является матрица C с «m» строк и «p» столбцов.
Для вычисления каждого элемента в матрице C используются приведенные ниже формулы.
Давайте рассмотрим пример. Здесь у нас есть матрица с 2 строками и 3 столбцами, умноженная на матрицу с 3 столбцами и 2 строками. В результате получится матрица с 2 строками и 2 столбцами.
Чтобы вычислить c1,1, мы должны определить скалярное произведение 1-й строки 1-й матрицы и 1-го столбца 2-й матрицы.
Формула выглядит следующим образом:
c1,1=2 (-1) +(-2) 3 +7 1 =-1 строку и 2-й столбец 2-й матрицы.
Формула выглядит следующим образом:
c1,2=2 5 +(-2)7 +7 9 =59
Для расчета c2,1 и c2,2 используются следующие уравнения:
c2,1=1 (-1) +8 3 +4 1 =27
c2,2=1 5 +8 7 +4 9 =97
Произведение матрицы на матрицу:
Как умножить матрицу на вектор
Вектор — это матрица только с одной строкой или только с одним столбцом. Умножение матрицы на вектор выполняется аналогично процедуре умножения матрицы на матрицу.
Умножение матрицы на вектор выполняется аналогично процедуре умножения матрицы на матрицу.
Здесь у нас есть вектор x=(4,-2,1), и мы умножаем его на матрицу A.
Вычислите c1,1, определив скалярное произведение 1-й строки, умноженное на вектор.
См. приведенное ниже уравнение для расчета c1,1.
c1,1=64 +2(-2) +41=24
Аналогично, вот уравнения для расчета c2,1 и c3,1.
c2,1 =-14 +4(-2) +31 =-9
c3,1 =-24 +9(-2) +31 =-23
Решение умножения матрицы на вектор выглядит следующим образом: следующим образом:
В целом, умножение матрицы на вектор следует той же процедуре, что и умножение матрицы на матрицу. Тем не менее, важно соблюдать соглашения об именах.
Каков порядок операций?
В отличие от умножения действительных чисел, умножение матриц не является коммутативным. Например, результат не зависит от порядка элементов.
Например, результат не зависит от порядка элементов.
Например, в приведенном ниже расчете:
123=312=36
Обе части уравнения равны 36 независимо от порядка чисел. Это верно не для всех матриц. Коммутативные матрицы возникают, когда матрица умножается сама на себя или когда она умножается на единичную матрицу.
Например, у нас есть матрица A, умноженная на матрицу B, в результате получается матрица C.
Но если у нас есть матрица B, умноженная на матрицу A, конечным результатом будет другая матрица D.
Давайте сравним вычисление первого скалярного произведения, чтобы понять, почему существует разница.
При вычислении первого значения c1,1 используется формула: 23 =0
Из того, как вычисляется скалярное произведение, ясно, что порядок имеет значение при умножении матриц. Обратите внимание, как подсвечиваются разные числа в матрицах при переключении порядка умножения матриц.
Как применять умножение матриц к реальным задачам
Умножение матриц имеет применение в реальном мире, даже если мы не можем думать об этих ситуациях как об умножении матриц.
Например, умножение матриц можно использовать для расчета прибыли магазина.
В таблице ниже указана стоимость каждого предмета, выставленного на продажу в магазине одежды.
В таблице ниже показано, сколько рубашек, свитеров и брюк было продано в понедельник, вторник и среду.
Прибыль в понедельник можно рассчитать по следующей формуле.
Прибыль за понедельник = Цена проданных рубашек + Цена проданных свитеров и свитеров
+ Цена проданных брюк Брюки
=122 + 304 + 604 =384
Знакомо? Мы только что рассчитали скалярный продукт для продаж в понедельник.
Представим эти данные в виде матрицы и вектора.
После умножения матриц мы можем рассчитать продажи в понедельник, вторник и среду ниже.
Приведенное ниже уравнение можно использовать для расчета прибыли во вторник.
Прибыль во вторник = c2,1=412 +1530 +1160 =1158
Аналогично, прибыль в среду можно рассчитать по приведенной ниже формуле.
Прибыль среды = c3,1= 412 + 230 + 160 = 168
Результирующая матрица 1 на 3 приведена ниже.
Матрицы и их операции также играют фундаментальную роль в понимании логики между массивами в программировании. Матрицы хранятся в виде массива массивов в программировании. Их также называют многомерными массивами.
Линейная алгебра лежит в основе многих передовых математических инструментов, таких как ряды Фурье и решение линейных уравнений. Он также играет ключевую роль в других областях, таких как статистика.
Краткий обзор специальных матриц
Некоторые матрицы неоднократно появляются в ходе исследований, и им присвоены определенные имена, чтобы их можно было легко идентифицировать.
Например, в нулевой матрице все значения просто равны 0.
Единичная матрица — это еще одна специальная матрица. Это квадратная матрица, в которой количество столбцов и строк равно. Диагональные значения, где «m» и «m» равны, равны 1.
Конкретные условия для единичной матрицы обозначаются:
Квадратная матрица, умноженная на единичную матрицу, не приведет к изменению квадратной матрицы. Например:
Для демонстрации расчета скалярного произведения первого значения используется следующая формула:
c1,1=91 + 40 + (-2)0 = 9 базовое упражнение по линейной алгебре и является обязательным курсом для большинства специальностей STEM. Освоение этой операции позволяет учащимся глубже понять линейную алгебру.
Убедитесь, что вы практикуете умножение матриц вручную. Легко пропустить число при вычислении скалярного произведения во время экзамена или теста. Практика должна помочь вам снизить вероятность ошибок, которых можно было бы избежать, если бы вы лучше знали метод расчета.
Практика должна помочь вам снизить вероятность ошибок, которых можно было бы избежать, если бы вы лучше знали метод расчета.
Если у вас проблемы с линейной алгеброй, онлайн-курсы охватывают различные операции и линейные преобразования, чтобы вы были готовы к экзаменам. Эти курсы знакомят с новыми обозначениями и абстрактными способами мышления, которые могут быть чужды некоторым студентам.
Чтобы получить индивидуальную помощь в умножении матриц, вы можете найти лучших преподавателей на HeyTutor.
Умножение матриц и обратные матрицы
Это третий пост в серии статей о курсе линейной алгебры Массачусетского технологического института. В этом посте я рассмотрю третью лекцию о пяти способах умножения матриц , обратных матриц и алгоритме нахождения обратных матриц под названием Исключение Гаусса-Жордана .
Первая лекция была посвящена геометрии линейных уравнений, а вторая лекция была посвящена исключению матриц.
Вот третья лекция.
Третья лекция начинается с пяти способов умножения матриц .
Первый способ - классический. Предположим, нам дана матрица A размера m x n с элементами a ij и матрица B размера n x p с элементами b jk , и мы хотим найти произведение А · Б . Умножение матриц A и B даст матрицу C размером m x p с элементами .
Вот как работает эта сумма. Чтобы найти первый элемент c 11 матрицы C , мы суммируем по 1-й строке A и 1-му столбцу B . The sum expands to c 11 = a 11 ·b 11 + a 12 ·b 21 + a 13 ·b 31 + ... + a 1n ·b №1 . Вот визуализация суммирования:
Продолжаем таким образом, пока не найдем все элементы матрицы С . Вот еще одна визуализация нахождения c 23 :
Вот еще одна визуализация нахождения c 23 :
Второй способ - взять каждый столбец B , умножить на всю матрицу A и поместить полученный столбец в матрицу C . Столбцы C представляют собой комбинации столбцов A . (Помните из предыдущей лекции, что матрица, умноженная на столбец, является столбцом.)
Например, чтобы получить столбец 1 матрицы C , мы умножаем на ·(столбец 1 матрицы B ):
Третий способ — взять каждую строку в A , умножить на всю матрицу B и полученную строку поместить в матрицу C . Ряды C являются комбинациями рядов B . (Опять же, помните из предыдущей лекции, что произведение строки на матрицу является строкой.)
Например, чтобы получить строку 1 матрицы C , мы умножаем строку 1 матрицы A на всю матрицу B :
Четвертый способ посмотреть на произведение A · B как сумма (столбцы A ) раз (строки B ).
Вот пример:
Пятый способ - рубить матрицы на блоки и умножать блоки любым из предыдущих способов.
Вот пример. Matrix A gets subdivided in four submatrices A 1 A 2 A 3 A 4 , matrix B gets divided in four submatrices B 1 B 2 B 3 B 4 , и блоки обрабатываются как простые матричные элементы.
Here is the visualization:
Element C 1 , for example, is obtained by multiplying A 1 · B 1 + A 2 · B 3 .
Далее лекция переходит к нахождению обратных матриц . Обратной матрицей A является другая матрица, такая, что A -1 · A = I , где I — единичная матрица. На самом деле, если A -1 является обратной матрицей квадратной матрицы A , то это и левая, и правая обратная матрица, то есть A -1 · A = A · А -1 = I .
На самом деле, если A -1 является обратной матрицей квадратной матрицы A , то это и левая, и правая обратная матрица, то есть A -1 · A = A · А -1 = I .
Если матрица A имеет обратную, то она называется обратимой или невырожденной .
Матрица A является сингулярной, если мы можем найти ненулевой вектор x такой, что A · x = 0 . Доказательство легко. Предположим, что A невырождена, т. е. существует матрица A -1 . Тогда A -1 · A · x = 0 · A -1 , что приводит к ложному утверждению, что x = 0 . Следовательно, A должно быть в единственном числе.
Другой способ сказать, что матрица A является сингулярной, это сказать, что столбцы матрицы A линейно зависимы (один или несколько столбцов могут быть выражены как линейная комбинация других).
Наконец, в лекции показан детерминированный метод нахождения обратной матрицы. Этот метод называется методом исключения Гаусса-Жордана . Короче говоря, исключение Гаусса-Жордана преобразует расширенную матрицу ( A | I ) в ( I | A -1 ), используя только исключения строк.
Пожалуйста, посмотрите лекцию, чтобы узнать, как это работает во всех деталях:
Прямая ссылка: http://www.youtube.com/watch?v=FX4C-JpTFgY
Темы третьей лекции:
- [00:51] Первый способ умножения матриц.
- [04:50] Когда нам разрешено перемножать матрицы?
- [06:45] Второй способ умножения матриц.
- [10:10] Третий способ умножения матриц.





 Известная матрица в левой части перемножается на обратную той, что расположена слева в уравнении. Далее – с правой стороны на матрицу, обратную той, что находилась справа. Результат: X = A-1 * C * B-1.
Известная матрица в левой части перемножается на обратную той, что расположена слева в уравнении. Далее – с правой стороны на матрицу, обратную той, что находилась справа. Результат: X = A-1 * C * B-1.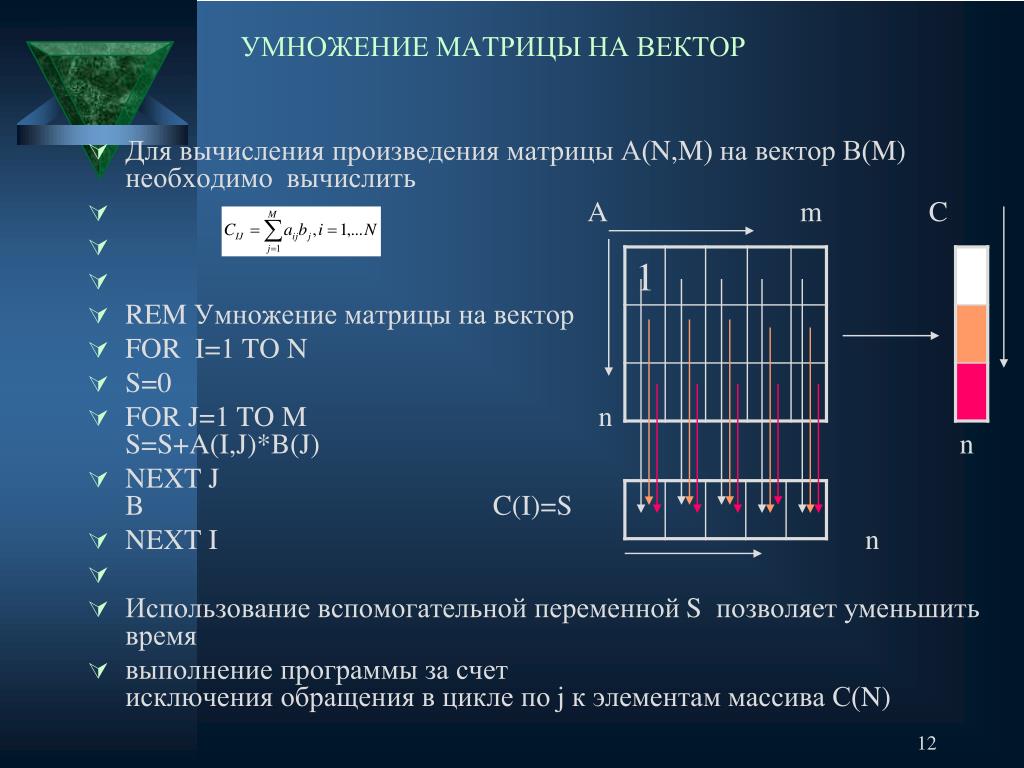

 matmul(a, b)
matmul(a, b) array([1,2,3])
b = np.arange(4,10).reshape(3,2) # матрица 3x2
array([1,2,3])
b = np.arange(4,10).reshape(3,2) # матрица 3x2 linalg.inv(a) # вычисление обратной матрицы
invA @ y # вычисление корней
linalg.inv(a) # вычисление обратной матрицы
invA @ y # вычисление корней norm()
norm()
 eigvals()
eigvals()
 tensorinv()
tensorinv()
 ..
..

 дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC;
дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC;
 Схемы и конструкции…
Схемы и конструкции…
 Это следует из того факта, что если x является нетривиальным решением Cx = 0 , затем BX -нетривиальное решение из AX = 0,
Это следует из того факта, что если x является нетривиальным решением Cx = 0 , затем BX -нетривиальное решение из AX = 0, 
 Предупреждение: обратное не обязательно верно.
Предупреждение: обратное не обязательно верно.