Как перемножить матрицы в Excel
Одной из частых операций, которую выполняют при работе с матрицами, является перемножение одной из них на другую. Программа Excel является мощным табличным процессором, который предназначен, в том числе и для работы над матрицами. Поэтому у него имеются инструменты, которые позволяют перемножить их между собой. Давайте узнаем, как это можно выполнить различными способами.
Процедура перемножения матриц
Сразу нужно сказать, что перемножить между собой можно далеко не все матрицы, а только те, которые соответствуют определенному условию: число столбцов одной матрицы должно быть равным числу строк другой и наоборот. Кроме того, исключается наличие в составе матриц пустых элементов. В этом случае тоже выполнить требуемую операцию не получится.
Способов перемножить матрицы в Экселе все-таки не так уж и много — всего два. И оба они связаны с применением встроенных функций Excel. Разберем в деталях каждый из данных вариантов.
Способ 1: функция МУМНОЖ
Наиболее простым и популярным вариантом среди пользователей является применение функции МУМНОЖ. Оператор МУМНОЖ относится к математической группе функций. Как раз его непосредственной задачей и является нахождение произведения двух матричных массивов. Синтаксис МУМНОЖ имеет такой вид:
=МУМНОЖ(массив1;массив2)
Таким образом этот оператор имеет два аргумента, которые представляют собой ссылки на диапазоны двух перемножаемых матриц.
Теперь давайте посмотрим, как используется функция МУМНОЖ на конкретном примере. Имеется две матрицы, число строк одной из которых, соответствует количеству столбцов в другой и наоборот. Нам нужно перемножить два этих элемента.
- Выделяем диапазон, где будет отображаться результат умножения, начиная с его верхней левой ячейки. Размер данного диапазона должен соответствовать числу строк у первой матрицы и числу столбцов у второй.
 Клацаем по пиктограмме «Вставить функцию».
Клацаем по пиктограмме «Вставить функцию». - Активируется Мастер функций. Перемещаемся в блок «Математические», кликаем по наименованию «МУМНОЖ» и клацаем по кнопке «OK» в нижней части окна.
- Будет выполнен запуск окна аргументов требуемой функции. В этом окне имеется два поля для ввода адресов матричных массивов. Ставим курсор в поле
После того, как оба аргумента внесены, не спешим жать на кнопку «OK», так как мы имеем дело с функцией массива, а это значит, что для получения корректного результата обычный вариант завершения работы с оператором не подойдет. Данный оператор предназначен не для того, чтобы выводить результат в одну ячейку, так как выводит его в целый диапазон на листе.

- Как видим, после этого предварительно выделенный диапазон был заполнен данными. Это и есть результат умножения матричных массивов. Если взглянуть на строку формул, после выделения любого из элементов данного диапазона, то мы увидим, что сама формула обернута в фигурные скобки. Это и есть признак функции массива, который добавляется после нажатия сочетания клавиш Ctrl+Shift+Enter перед выводом результат на лист.
Урок: Функция МУМНОЖ в Экселе
Способ 2: использование составной формулы
Кроме того, существует ещё один способ умножения двух матриц. Он более сложный, чем предыдущий, но тоже заслуживает упоминания, как альтернативный вариант. Данный способ предполагает использование составной формулы массива, которая будет состоять из функции
- На этот раз выделяем на листе только левый верхний элемент массива пустых ячеек, который рассчитываем использовать для вывода результата.
 Щелкаем по значку «Вставить функцию».
Щелкаем по значку «Вставить функцию». - Мастер функций запускается. Перемещаемся в блок операторов
- Происходит открытие окна аргументов вышеуказанной функции. Данный оператор предназначен для перемножения различных массивов между собой. Его синтаксис следующий:
=СУММПРОИЗВ(массив1;массив2;…)В качестве аргументов из группы «Массив» используется ссылка на конкретный диапазон, который нужно перемножить. Всего может быть использовано от двух до 255 таких аргументов. Но в нашем случае, так как мы имеем дело с двумя матрицами, нам понадобится как раз два аргумента.
Ставим курсор в поле «Массив1». Тут нам нужно будет ввести адрес первой строки первой матрицы. Для этого, зажав левую кнопку мыши, нужно просто выделить её на листе курсором. Тут же координаты данного диапазона будут отображены в соответствующем поле окна аргументов.

- После этого устанавливаем курсор в поле «Массив2». С этим аргументом будет посложнее, так как по правилам умножения матриц, вторую матрицу нужно «перевернуть». Для этого используем вложенную функцию ТРАНСП.
Чтобы перейти к ней, клацаем по значку в виде треугольника, направленного острым углом вниз, который размещен слева от строки формул. Открывается список недавно используемых формул. Если вы в нем найдете наименование «ТРАНСП», то щелкайте по нему. Если же вы давно использовали данный оператор или вообще никогда не применяли его, то в этом списке указанное наименование вы не отыщите.

- Открывается уже хорошо знакомое нам окно Мастера функций. На этот раз перемещаемся в категорию «Ссылки и массивы» и выбираем наименование «ТРАНСП». Щелкаем по кнопке «OK».
- Производится запуск окна аргументов функции ТРАНСП. Данный оператор предназначен для транспонирования таблиц. То есть, попросту говоря, он меняет местами столбцы и строки. Это нам и нужно сделать для второго аргумента оператора СУММПРОИЗВ. Синтаксис функции ТРАНСП предельно простой:
=ТРАНСП(массив)То есть, единственным аргументом данного оператора является ссылка на тот массив, который следует «перевернуть». Вернее, в нашем случае даже не на весь массив, а только на его первый столбец.
Итак, устанавливаем курсор в поле «Массив» и выделяем первый столбец второй матрицы на листе с зажатой левой кнопкой мыши. Адрес отобразится в поле.
 Как и в предыдущем случае, тут тоже нужно сделать определенные координаты абсолютными, но на этот раз не координаты столбцов, а адреса строк. Поэтому ставим знак доллара перед цифрами в ссылке, которая отображается в поле. Можно также выделить всё выражение и дважды кликнуть по клавише
Как и в предыдущем случае, тут тоже нужно сделать определенные координаты абсолютными, но на этот раз не координаты столбцов, а адреса строк. Поэтому ставим знак доллара перед цифрами в ссылке, которая отображается в поле. Можно также выделить всё выражение и дважды кликнуть по клавише - Но на этот раз у нас заполнился не массив, а только одна ячейка, которую мы ранее выделили при вызове Мастера функций.
- Нам нужно заполнить данными такой же по размеру массив, как и в первом способе. Для этого следует скопировать формулу, полученную в ячейке, на равнозначный диапазон, который будет равен количеству строк первой матрицы и количеству столбцов второй. В конкретно нашем случае получается три строки и три столбца.
 Наводим курсор на нижний правый угол ячейки, в которой расположена формула. Курсор преобразуется в черный крестик. Это и есть маркер заполнения. Зажимаем левую кнопку мыши и протягиваем курсор по всему вышеуказанному диапазону. Сама начальная ячейка с формулой должна стать левым верхним элементом данного массива.
Наводим курсор на нижний правый угол ячейки, в которой расположена формула. Курсор преобразуется в черный крестик. Это и есть маркер заполнения. Зажимаем левую кнопку мыши и протягиваем курсор по всему вышеуказанному диапазону. Сама начальная ячейка с формулой должна стать левым верхним элементом данного массива. - Как видим, выделенный диапазон заполнен данными. Если их сравнить с тем результатом, который мы получили благодаря применению оператора МУМНОЖ, то увидим, что значения полностью идентичны. Это означает, что умножение двух матриц выполнено верно.
Урок: Работа с массивами в Экселе
Как видим, несмотря на то, что был получен равнозначный результат, использовать функцию для умножения матриц МУМНОЖ значительно проще, чем применять для этих же целей составную формулу из операторов СУММПРОИЗВ и ТРАНСП. Но все-таки данный альтернативный вариант тоже нельзя оставить без внимания при изучении всех возможностей перемножения матриц в Microsoft Excel.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТБиблиотека NumPy в Python матрицы в питон
В этом уроке мы разберём действия с матрицами в модуле NumPy в Python Питон.
NumPy это модуль для Python, предназначенный для научных расчётов. NumPy позволяет использовать в Питоне математические функции, такие как работа с матрицами, векторами, все тригонометрические функции, возведение в экспоненту и действия с логарифмами. NumPy в Питон позволяет работать с матрицами гораздо быстрее, чем стандартные алгоритмы работы с матрицами.
Для более удобного использования NumPy импортируем этот модуль, используя постфикс as np.
import numpy as np
as np означает, что когда мы вызываем процедуры и функции из NumPy в Python, перед названиями этих процедур и функций вместо numpy мы будем писать np. Это позволит не только удобнее писать код, но и быстрее читать его. Например, вместо numpy.array([1, 2]) мы будем писать np.array([1, 2]).
Матрицы в NumPy в Питоне задаются с помощью команды np.array([]). В круглых скобках находится сам массив, в квадратных скобках находятся элементы массива.
Пример. Задание одномерного массива в python
import numpy as np
arr = np.array([1, 2])
Матрица в Python задаётся с помощью двумерного массива. Матрица это таблица состоящая из строк и столбцов. Двумерный массив задаётся с помощью той же команды, что и одномерный массив.
Пример. Задание матрицы двумерного массива и вывод различных его элементов на экран в python
import numpy as np
matrix = np. array([ [‘first’, ‘second’], [‘third’, ‘fourth’] ])
array([ [‘first’, ‘second’], [‘third’, ‘fourth’] ])
print(matrix[0, 0])
print(matrix[1, 1])
print(matrix[0, 0]) выведет первый элемент из первого массива внутри – first. print(matrix[1, 1]) выведет второй элемент внутреннего второго массива – fourth.
NumPy в Питоне может выполнять различные действия с матрицами, такие как сложение, умножение, возведение матрицы в степень и вычисление определителя матрицы.
Для сложения матриц в Питоне не используются никакие команды, матрицы в Python складываются так же, как и числа.
Пример. Сложение матриц.
import numpy as np
matrix1 = np.array([ [3, 5, 1], [8, 7, 2] ])
matrix2 = np.array([ [5, 3, 4], [1, 10, 9] ])
total = matrix1 + matrix2
print(total)
NumPy в Питоне позволяет складывать только матрицы одинаковых размеров.
Матрицы складываются с помощью сложения всех элементов массива с одинаковыми индексами. Матрица с суммами этих элементов является результатом сложения.
Матрица с суммами этих элементов является результатом сложения.
Умножение матрицы на вектор в Python выполняется с помощью команды A.dot(B), где A и B это матрицы. Для выполнения умножения в Питоне нужно, чтобы количество столбцов матрицы A было равно количеству строк матрицы B.
Пример. Умножение матрицы на вектор в python
import numpy as np
a = np.array([ [2, 1], [2, 2], [4, 3] ])
b = np.array([ [1], [3] ])
total = a.dot(b)
print(total)
Умножение вектора на матрицу определено только тогда, когда число столбцов матрицы равно числу строк вектора. В этом примере была рассмотрена матрица размером 3×2 и вектор-строка размером 2×1. Число столбцов матрицы (2) равно числу строк вектора (2). В результате умножения матрицы на вектор получается вектор, у кторого число строк равно числу строк матрицы
Определитель матрицы в Python вычисляется с помощью с помощью команды
np. linalg.det(A), где A это квадратная матрица. У квадратной матрицы количество строк равно количеству столбцов.
linalg.det(A), где A это квадратная матрица. У квадратной матрицы количество строк равно количеству столбцов.
Пример. Вычисление определителя матрицы в python
import numpy as np
a = np.array([ [2, 1], [4, 3] ])
print(np.linalg.det(a))
Определитель может быть вычислен только для матриц с одинаковым количеством строк и столбцов – квадратных матриц. В этом примере с матрицей размерами 2×2 определитель матрицы равен разнице произведений диагоналей (2 * 3 – 1 * 4 = 2.0)
Умножение матрицы на матрицу в Питоне выполняется с помощью команды A.dot(B), где A и B это матрицы. Умножение определено, если количество столбцов A равно количеству строк B.
Пример. Умножение матрицы на матрицу в python
import numpy as np
a = np.array([ [2, 1, 3], [2, 2, 4] ])
b = np.array([ [1, 1], [3, 2], [2, 4] ])
total = a. dot(b)
dot(b)
print(total)
Чтобы умножение было определено, количество столбцов первой матрицы должно быть равно количеству строк второй матрицы. В этом примере умножаются матрицы размерами 2×3 и 3×2, результатом умножения является матрица размером 2×2.
Возведение матрицы в степень в Питоне выполняется с помощью команды np.linalg.matrix_power(A, P), где A – квадратная матрица, P – степень, в которую возводится матрица, допускаются только целочисленные степени. Возводить в степень можно только квадратные матрицы, так как количество строк должно быть равно количеству столбцов матрицы.
Пример. Возведение матрицы в степень в python
import numpy as np
a = np.array([[1, 3], [2, 1]])
result = np.linalg.matrix_power(a, 2)
print(result)
Для решения системы двух линейных уравнений нужно задать два массива.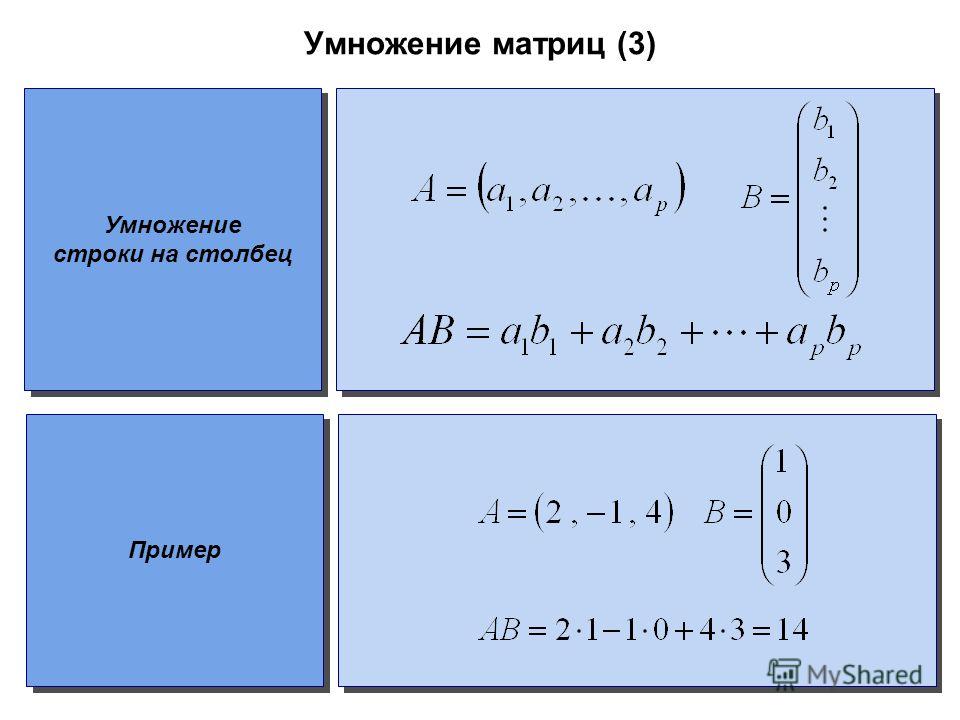 Один массив будет содержать коэффициенты для x и y в каждом уравнении, второй массив будет содержать правые части уравнений. Для решения линейных уравнений используется команда в Python np.linalg.solve(матрица левой части, вектор правой части)
Один массив будет содержать коэффициенты для x и y в каждом уравнении, второй массив будет содержать правые части уравнений. Для решения линейных уравнений используется команда в Python np.linalg.solve(матрица левой части, вектор правой части)
Решение системы линейных уравнений в python
import numpy as np
a = np.array([[1, 2], [3, 2]])
b = np.array([5, 6])
result = np.linalg.solve(a, b)
print(result)
Эта программа на Python решает два линейных уравнения.
1x + 2y = 5
3x + 2y = 6
Для вычисления экспоненты числа или массива в Питоне используется команда np.exp(A), где A – число или массив. Если возводится в экспоненту массив, то все элементы массива будут возведены в экспоненту.
Пример. Возведение вектора в экспоненту.
import numpy as np
a = np.array([2, 1, 5])
print(np. 5], где e это основание натурального логарифма.
5], где e это основание натурального логарифма.
Вернуться к содержанию Следующая тема Графики функций и поверхностей в Python
Полезно почитать по теме матрицы и массивы в python:
Матрицы в python
Массивы в python
Поделиться:
Три способа умножения матриц в Excel
Дата публикации Jul 2, 2019
Часть-2 изФастай «Из фондов»наконец-то вышел. Я не помню, когда в последний раз я был так взволнован по поводу MOOC. Как только курс был обнародован, я начал копаться в нем, чтобы углубить свое понимание глубокого обучения и основополагающих концепций.
На этот раз я решил последовать совету Джереми и Рэйчел и написать блоги. Эта конкретная статья объясняетразличные методы умножения матриц,что Джереми реализует в Уроке-8. Я буду использоватьМайкрософт Эксельдля иллюстрации.
Итак, начнем!
Умножение матриц
Отличное и интерактивное место для понимания умножения матриц, на которое ссылается Джереми, доступно по адресу:
matrixmultiplication.xyzПо сути, как видно из изображения, мы берем транспонирование второй матрицы, умножаем и складываем элементы вместе, чтобы получить результат. Как пример, самый первый пункт15в результирующей матрице происходит от1*2 + 6*2 + 1*1 = 2 + 12 + 1 = 15,
Хотя это объяснение визуально приятно, по моему скромному мнению, его трудно преобразовать в код. Так что давайте использовать Excel и понимать матричное умножение по-другому!
Умножение матриц в EXCEL
Рассмотрим две матрицыа такжеВразмера4x3а также3x4,
Примечание: я буду использовать жирный шрифта такжеВсослаться на матрицы в этой статье. Обычная практика – ссылаться на векторы и матрицы, используя жирный шрифт.
Из изображения, которое мы видели раньше, если вы помните, мы взяли транспонированиеВи умноженные строкис колоннамиВчтобы получить результирующую матрицу. Скорее, давайте пропустим этот шаг, сделав транспонирование на этот раз, и сразу умножим строки и столбцы.
Поэтому строка 0 изумножается на столбец 0Впоэлементные и результирующие поэлементные продукты добавляются для получения первого элемента в результирующей матрицеСв положении[0][0],
Вот как это выглядит в Excel:
C [0] [0] = 1 * 1 + 10 * 5 + 100 * 9 = 1 + 50 + 900 = 951Точно так же мы получаемC[0][3]поэлементно умножая строку 0 изи кол 3 изB.В Excel это выглядит так:
И, наконец, мы следуем тому же процессу, чтобы пройти каждый пустой ящик вСчтобы получить окончательный результат.
Вот и мы! Вот так мы делаем матричное умножение! Это было легко, не так ли? Мы теперь не только поняли умножение матриц, но и внедрили его в Excel! Как это круто?
Я лично считаю, что теперь вы готовы работать с некоторыми правилами, связанными с умножением матрицMatMul):
- Позволять
ar,acбыть количеством строк и столбцов вA.Точно так же, пустьbr, bcбыть количеством строк и столбцов вB.Тогда для выполнения умножения матриц необходимо, чтобыac == br, Зачем? Итак, как вы видели в Excel, мы умножили строки и столбцы поэлементно, а затем добавили промежуточные продукты, чтобы получить конечный результат. Если есть несоответствие в размерах, и один вектор длиннее другого, мы больше не можем выполнять поэлементное умножение! - Размеры результирующей матрицы всегда будут
ar,bc, То есть количество строк исходит оти количество столбцов исходит отB.
Способ 1: использование 3-х циклов FOR
Вот еще один отказ от ответственности, при реализации умножения матриц в Excel, мы не только поняли это, но и повторили первый метод Джереми, который использовал 3 цикла FOR. Вот как это выглядит в коде:
def matmul1(a,b):
ar,ac = a.shape
br,bc = b.shape
assert ac==br
c = torch.zeros(ar, bc)
for i in range(ar):
for j in range(bc):
for k in range(ac): #or br
c[i,j] += a[i,k]*b[k,j]
return c
Надеюсь, теперь вы сможете лучше понять это. Если нет, то сейчас самое время сделать паузу, поэкспериментировать с кодом и посмотреть, что на самом деле происходит. Я обещаю вам, это так же, как наша версия Excel!
Хорошо, я предполагаю, что вы потратили некоторое время на размышления о коде, поэтому давайте обсудим это!
- Почему первые две петли в
range(ar)а такжеrange(bc)? Ну, как вы помните изПравило-2наша результирующая матрица будет иметь размерыar,bc, И из Excel мы увидели, что мы пересекаем каждый элементСследовательно, один за другим, чтобы пройтиarстроки иbcстолбцы нам нужно 2 цикла вrange(ar)а такжеrange(bc), - Итак, почему третий цикл FOR в
range(ac) #or br? Ну изПравило-1, мы знаем этоac==brтак что на самом деле не имеет значения, ставим ли мыrange(ac)илиrange(br)в третьем цикле. По сути, именно здесь отдельные элементы умножаются вместе и добавляются. Из нашего предыдущего примера Excel, для
По сути, именно здесь отдельные элементы умножаются вместе и добавляются. Из нашего предыдущего примера Excel, дляC[0][0]это где шагC[0][0] = 1*1 + 10*5 + 100*9 = 1 + 50 + 900 = 951произойдет, и, наконец, мы перейдем к следующей коробке. Количество предметов, которые умножаются и складываются вместе, равноac or br,
Это действительно так! Это метод-1 для вас! Вот песня, чтобы помнить Матричное Умножение. (Я узнал об этом первым из fast.ai, оригинальный автор неизвестен)
Надеюсь, теперь вы понимаете, как две матрицы умножаются друг на друга. Если не,Вотэто еще один учебник Хан Академии
Метод 2: Использование поэлементного умножения
Так что до сих пор мы разбираем каждую позицию в результирующей матрицеC,найти отдельные элементы, а затем суммировать их вместе. Если вы помните, что-то вродеC[0][0] = 1*1 + 10*5 + 100*9 = 1 + 50 + 900 = 951, Конечно, должен быть другой путь? Что если вместо того, чтобы делать отдельные продукты, а затем суммировать их, мы умножаем векторы за один раз, чтобы получить результирующий вектор, и суммируем полученный вектор, чтобы получить конечный элемент?
m = tensor([1, 2, 3])
n = tensor([10, 10, 10])
m*n>>tensor([10, 20, 30])
До сих пор мы находили отдельные продукты10, 20, 30и сложить их вместе10 + 20 + 30 = 60, Но, действительно, все это можно заменить на:
m = tensor([1, 2, 3])
n = tensor([10, 10, 10])
(m*n).sum()>>tensor(60)
Если вы помните, самый внутренний цикл вrange(ac) #or brнаходил отдельные продукты и добавлял их. Ну, мы можем заменить этот цикл, чтобы выполнить векторное поэлементное произведение и положить.sum()в конце концов, и PyTorch / NumPy имеют возможность выполнять поэлементные операции для нас!
Вот как это выглядит в Excel:
C [0] [0] = сумма (A [строка 0] * B [столбец 0])Точно так же мы получаемC[0][3]путем умножения вектора в строке 0с вектором на цв 3Ви суммируя полученный вектор.
И, наконец, мы следуем тому же процессу, чтобы пройти каждый пустой ящик вСчтобы получить окончательный результат.
C [3] [3] = сумма (A [строка 3] * B [столбец 3])Обратите внимание, как это отличается отМетод-1? На этот раз мы просто говорим Excel или PyTorch: умножьте строку 0с col 0 изВи суммируем полученный вектор, чтобы дать нам ответ. Вместо того чтобы делать
Вместо того чтобы делать1*1 + 10*5 + 100*9, Например, дляC[0][0]этот метод умножает Vector на строку 0tensor([1,10,100])с вектором в столбце 0 изВtensor{[1,5,9])чтобы получить промежуточный продукт Векторtensor([1,50,900])и суммирует это, чтобы дать результат в положенииC[0][0]какtensor(951),
В коде это выглядит так:
def matmul2(a,b):
ar,ac = a.shape
br,bc = b.shape
assert ac==br
c = torch.zeros(ar,bc)
for i in range(ar):
for j in range(bc):
c[i,j] = (a[i,:]*b[:,j]).sum()
return c
Таким образом, мы просто анализируем каждую позициюC,используя две петли FOR и введите соответствующий результат в этой позиции. Еслиi,jпредставляют строки и столбцы вСэто выглядит примерно так …
i:0,j:0
a:tensor([ 1, 10, 100]),b:tensor([1, 5, 9])
tensor([[951., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
---
i:0,j:1
a:tensor([ 1, 10, 100]),b:tensor([ 2, 6, 10])
tensor([[ 951., 1062., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
---
i:0,j:2
a:tensor([ 1, 10, 100]),b:tensor([ 3, 7, 11])
tensor([[ 951., 1062., 1173., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
---
i:0,j:3
a:tensor([ 1, 10, 100]),b:tensor([ 4, 8, 12])
tensor([[ 951., 1062., 1173., 1284.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
---
i:1,j:0
a:tensor([ 2, 20, 200]),b:tensor([1, 5, 9])
tensor([[ 951., 1062., 1173., 1284.],
[1902., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
И так далее .. пока мы не получим полную матрицуС,
tensor([[ 951., 1062., 1173., 1284.],
[1902., 2124., 2346., 2568.],
[2853., 3186., 3519., 3852.],
[3804., 4248., 4692., 5136.]])
Метод 3: вещание
Заметили общую тему здесь? Каждый раз мы должны умножить каждый рядс каждым столбцомВполучитьС, Вы замечаете повторение? Мы умножаем один и тот же вектор строки вbcраз! И мы повторяем этот процессarраз!
Есть ли способ умножить вектор строкисо всеми столбцамиВполучить соответствующий ряд вC?Да, есть! Войдите в трансляцию …
Примечание: я не буду объяснять вещание, Джереми делает это очень хорошоВот,
Вместо этого давайте посмотрим, что это за волшебный кусок кода
for i in range(ar):
c[i] = (a[i,:].unsqueeze(-1).expand_as(b)*b).sum(dim=0)
Как обычно, давайте повторим в Excel! Это сделает вещи действительно легкими. Давайте сделаем это поэтапно.
Шаг 1)Выберите i-й рядa[i,:], Мы выбираем строку 0 в качестве примера.
Шаг 2)Возьмите егоТранспонированиеa[i,:].unsqueeze(-1)
Шаг 3)Развернуть матрицу столбца какВa[i,:].unsqueeze(-1).expand_as(b)
Шаг-4)Элемент мудрый умножить наВa[i,:].unsqueeze(-1).expand_as(b)*b
Шаг-5)Суммируйте по строкам, чтобы получить строку 0 C
Суммируйте по измерению боковой строки, чтобы получить строку 0 CПолный процесс вещания для каждого рядавыглядит примерно так:
Вещание в целомЯ надеюсь, что теперь вы получитевещания!Итак, давайте посмотрим, как это выглядит в коде ..
def matmul3(a,b):
ar,ac = a.shape
br,bc = b.shape
assert ac==br
c = torch.zeros(ar,bc)
for i in range(ar):
c[i] = (a[i,:].unsqueeze(-1).expand_as(b)*b).sum(dim=0)
print(f"i:{i}")
print(c)
return c
Вывод выглядит так:
i:0
tensor([[ 951., 1062., 1173., 1284.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
i:1
tensor([[ 951., 1062., 1173., 1284.],
[1902., 2124., 2346., 2568.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
i:2
tensor([[ 951., 1062., 1173., 1284.],
[1902., 2124., 2346., 2568.],
[2853., 3186., 3519., 3852.],
[ 0., 0., 0., 0.]])
i:3
tensor([[ 951., 1062., 1173., 1284.],
[1902., 2124., 2346., 2568.],
[2853., 3186., 3519., 3852.],
[3804., 4248., 4692., 5136.]])
Это именно то, как мы ожидаем, что это будет так же, как нашиВерсия Excel!
Вот и все! Мы успешно рассмотрели три метода умножения матриц, включая вещание.
Google лист для вышеупомянутой иллюстрации можно найтиВот, Спасибо за чтение! Если у вас есть какие-либо вопросы, пожалуйста, не стесняйтесь обращаться ко мне по адресуhttps://linkedin. com/in/aroraaman/,
com/in/aroraaman/,
Оригинальная статья
Узнаем как находить произведение матриц. Умножение матриц. Скалярное произведение матриц. Произведение трех матриц
С матрицами (таблицами с числовыми элементами) могут проводиться различные вычислительные действия. Одни из них – умножение на число, вектор, другую матрицу, несколько матриц. Произведение иногда получается неверным. Ошибочный результат – итог незнания правил выполнения вычислительных действий. Давайте разберемся, как следует осуществлять умножение.
Матрица и число
Начнем с самого простого – с умножения таблицы с числами на конкретную величину. Например, мы имеем матрицу A с элементами aij (i – это номера строк, а j – это номера столбцов) и число e. Произведением матрицы на число e будет матрица B с элементами bij, которые находятся по формуле:
bij = e × aij.
Т. е. для получения элемента b11 нужно взять элемент a11 и умножить его на нужное число, для получения b12 требуется найти произведение элемента a12 и числа e и т.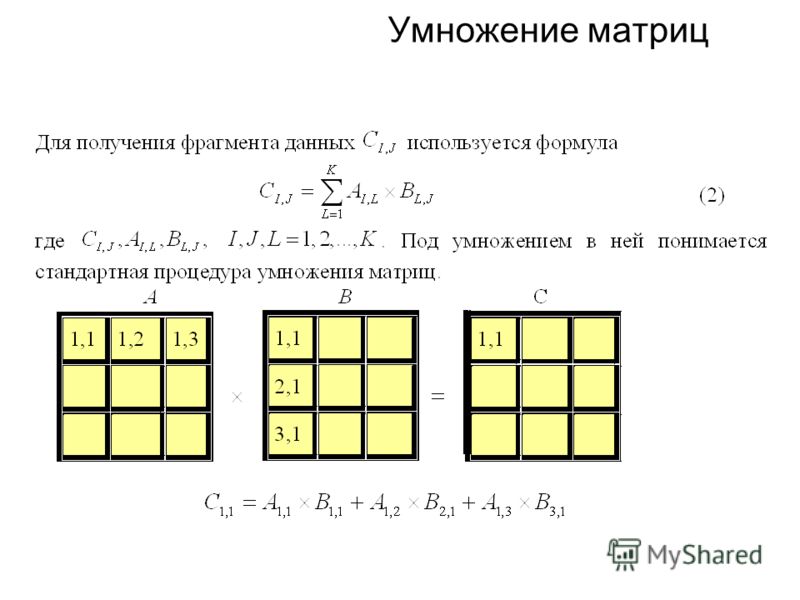 д.
д.
Решим задачу № 1, представленную на картинке. Для получения матрицы B просто умножим элементы из A на 3:
- a11 × 3 = 18. Это значение записываем в матрицу B в то место, где пересекаются столбец № 1 и строка № 1.
- a21 × 3 = 15. Мы получили элемент b21.
- a12 × 3 = –6. Мы получили элемент b12. Записываем его в матрицу B в место, где пересекаются столбец № 2 и строка № 1.
- a22 × 3 = 9. Данный результат – это элемент b22.
- a13 × 3 = 12. Данное число вносим в матрицу на место элемента b13.
- a23 × 3 = –3. Последнее полученное число – это элемент b23.
Таким образом, мы получили прямоугольный массив с числовыми элементами.
Векторы и условие существования произведения матриц
В математических дисциплинах существует такое понятие, как «вектор». Под этим термином понимается упорядоченный набор величин от a1 до an. Они называются координатами векторного пространства и записываются в виде столбца. Еще есть термин «транспонированный вектор». Его компоненты располагаются в виде строки.
Они называются координатами векторного пространства и записываются в виде столбца. Еще есть термин «транспонированный вектор». Его компоненты располагаются в виде строки.
Векторы можно называть матрицами:
- вектор-столбец – это матрица, построенная из одного столбца;
- вектор-строчка – это матрица, которая включает в себя только одну строку.
При выполнении над матрицами операций умножения важно помнить о том, что есть условие существования произведения. Вычислительное действие A × B может быть выполнено только тогда, когда число столбцов в таблице A равно числу строчек в таблице B. Итоговая матрица, получаемая в результате вычисления, всегда имеет число строк таблицы A и число столбцов таблицы B.
При умножении не рекомендуется переставлять местами матрицы (множители). Их произведение обычно не соответствует коммутативному (переместительному) закону умножения, т. е. результат операции A × B не равен результату операции B × A. Такая особенность именуется некоммутативностью произведения матриц. В некоторых случаях результат умножения A × B равен результату умножения B × A, т. е. произведение коммутативно. Матрицы, при которых равенство A × B = B × A выполняется, называются перестановочными. С примерами таких таблиц можно ознакомиться ниже.
В некоторых случаях результат умножения A × B равен результату умножения B × A, т. е. произведение коммутативно. Матрицы, при которых равенство A × B = B × A выполняется, называются перестановочными. С примерами таких таблиц можно ознакомиться ниже.
Умножение на вектор-столбец
При выполнении умножения матрицы на вектор-столбец обязательно учитываем условие существования произведения. Число столбцов (n) в таблице должно совпадать с количеством координат, из которых составлен вектор. Результат вычисления – преобразованный вектор. Его количество координат равно числу строчек (m) из таблицы.
Как вычисляются координаты вектора y, если есть матрица A и вектор x? Для расчетов созданы формулы:
y1 = a11x1 + a12x2 + … + a1nxn,
y2 = a21x1 + a22x2 + … + a2nxn,
…………………………………,
ym = am1x1 + am2x2 + … + amnxn,
где x1, …, xn – координаты из x-вектора, m – число строк в матрице и количество координат в новом y-векторе, n – число столбцов в матрице и количество координат в x-векторе, a11, a12, …, amn – элементы матрицы A.
Таким образом, для получения i-й компоненты нового вектора выполняется скалярное произведение. Из матрицы A берется i-я вектор-строка, и она умножается на имеющийся вектор x.
Решим задачу № 2. Произведение матрицы на вектор найти можно, ведь A имеет 3 столбца, и x состоит из 3 координат. В результате мы должны получить вектор-столбец с 4 координатами. Воспользуемся вышеуказанными формулами:
- Вычислим y1. 1 × 4 + (–1) × 2 + 0 × (–4). Итоговое значение равно 2.
- Вычислим y2. 0 × 4 + 2 × 2 + 1 × (–4). При расчете получим 0.
- Вычислим y3. 1 × 4 + 1 × 2 + 0 × (–4). Сумма произведений указанных множителей равна 6.
- Вычислим y4. (–1) × 4 + 0 × 2 + 1 × (–4). Координата равна –8.
Умножение вектор-строки на матрицу
Нельзя умножить матрицу, состоящую из нескольких столбцов, на вектор-строку. В таких случаях не выполняется условие существования произведения. А вот умножение вектор-строки на матрицу возможно. Эта вычислительная операция выполняется при совпадении количества координат в векторе и числа строк в таблице. Результат произведения вектора на матрицу – новая вектор-строка. Ее количество координат должно равняться числу столбцов в матрице.
Эта вычислительная операция выполняется при совпадении количества координат в векторе и числа строк в таблице. Результат произведения вектора на матрицу – новая вектор-строка. Ее количество координат должно равняться числу столбцов в матрице.
Вычисление первой координаты нового вектора подразумевает умножение вектор-строки и первого вектор-столбца из таблицы. Аналогичным способом производится расчет второй координаты, но вместо первого вектор-столбца берется уже второй вектор-столбец. Вот общая формула для вычисления координат:
yk = a1kx1 + a2kx2 + … + amkxm,
где yk – координата из y-вектора, (k находится в промежутке от 1 до n), m – число строк в матрице и количество координат в x-векторе, n – число столбцов в матрице и количество координат в y-векторе, a с буквенно-цифровыми индексами – элементы матрицы A.
Произведение прямоугольных матриц
Это вычислительное действие может показаться сложным. Однако умножение легко выполняется. Начнем с определения. Произведение матрицы A с m строками и n столбцами и матрицы B с n строками и p столбцами – это матрица C с m строками и p столбцами, в которой элемент cij представляет собой сумму произведений элементов i-й строки из таблицы A и j-го столбца из таблицы B. Если говорить более простым языком, то элемент cij – это скалярное произведение i-й вектор-строчки из таблицы A и j-го вектор-столбца из таблицы B.
Однако умножение легко выполняется. Начнем с определения. Произведение матрицы A с m строками и n столбцами и матрицы B с n строками и p столбцами – это матрица C с m строками и p столбцами, в которой элемент cij представляет собой сумму произведений элементов i-й строки из таблицы A и j-го столбца из таблицы B. Если говорить более простым языком, то элемент cij – это скалярное произведение i-й вектор-строчки из таблицы A и j-го вектор-столбца из таблицы B.
Теперь разберемся на практике в том, как находить произведение матриц прямоугольного вида. Решим для этого задачу № 3. Условие существования произведения выполняется. Приступим к расчету элементов cij:
- Матрица C будет состоять из 2 строк и 3 столбцов.
- Рассчитаем элемент c11. Для этого выполним скалярное произведение строки № 1 из матрицы A и столбца № 1 из матрицы B. c11 = 0 × 7 + 5 × 3 + 1 × 1 = 16. Далее поступаем аналогичным образом, меняя только строки, столбцы (в зависимости от индекса элемента).

- c12 = 12.
- c13 = 9.
- c21 = 31.
- c22 = 18.
- c23 = 36.
Элементы рассчитаны. Теперь осталось только составить прямоугольный блок из полученных чисел.
Умножение трех матриц: теоретическая часть
Можно ли найти произведение трех матриц? Эта вычислительная операция выполнима. Результат можно получить несколькими способами. Например, есть 3 квадратных таблицы (одного порядка) – A, B и C. Чтобы вычислить произведение, можно:
- Умножить сначала A и B. Результат затем умножить на C.
- Найти сначала произведение B и C. Далее матрицу A умножить на полученный результат.
Если требуется перемножить матрицы прямоугольного вида, то сначала нужно удостовериться в том, что данная вычислительная операция возможна. Должны существовать произведения A × B и B × C.
Поэтапное умножение не является ошибкой. Есть такое понятие, как «ассоциативность умножения матриц». Под этим термином понимается равенство (A × B) × C = A × (B × C).
Под этим термином понимается равенство (A × B) × C = A × (B × C).
Умножение трех матриц: практика
Квадратные матрицы
Начнем с умножения небольших квадратных матриц. Ниже на рисунке представлена задача № 4, которую нам предстоит решить.
Будем пользоваться свойством ассоциативности. Перемножим сперва либо A и B, либо B и C. Помним только одно: нельзя переставлять местами множители, т. е. нельзя умножать B × A или C × B. При таком умножении мы получим ошибочный результат.
Ход решения.
Шаг первый. Для нахождения общего произведения умножим сначала A на B. При умножении двух матриц будем руководствоваться теми правилами, которые были изложены выше. Итак, результатом умножения A и B будет матрица D с 2 строчками и 2 столбцами, т. е. прямоугольный массив будет включать в себя 4 элемента. Найдем их, выполнив расчет:
- d11 = 0 × 1 + 5 × 6 = 30;
- d12 = 0 × 4 + 5 × 2 = 10;
- d21 = 3 × 1 + 2 × 6 = 15;
- d22 = 3 × 4 + 2 × 2 = 16.

Промежуточный результат готов.
Шаг второй. Теперь умножим матрицу D на матрицу C. Результатом должна быть квадратная матрица G с 2 строками и 2 столбцами. Рассчитаем элементы:
- g11 = 30 × 8 + 10 × 1 = 250;
- g12 = 30 × 5 + 10 × 3 = 180;
- g21 = 15 × 8 + 16 × 1 = 136;
- g22 = 15 × 5 + 16 × 3 = 123.
Таким образом, результатом произведения квадратных матриц является таблица G с вычисленными элементами.
Прямоугольные матрицы
Ниже на рисунке представлена задача № 5. Требуется перемножить прямоугольные матрицы и найти решение.
Проверим, выполняется ли условие существования произведений A × B и B × C. Порядки указанных матриц позволяют нам выполнять умножение. Приступим к решению задачи.
Ход решения.
Шаг первый. Умножим B на C для получения D. Матрица B содержит 3 строчки и 4 столбца, а матрица C – 4 строчки и 2 столбца. Это значит, что матрица D у нас получится с 3 строчками и 2 столбцами. Рассчитаем элементы. Вот 2 примера вычислений:
Рассчитаем элементы. Вот 2 примера вычислений:
- d11 = 3 × 0 + 0 × 0 + 1 × 0 + 0 × 1 = 0;
- d12 = 3 × 2 + 0 × 3 + 1 × 1 + 0 × 6 = 7.
Продолжаем решать задачу. В результате дальнейших вычислений мы находим значения d21, d22, d31 и d32. Эти элементы равны 0, 19, 1 и 11 соответственно. Запишем найденные значения в прямоугольный массив.
Шаг второй. Умножим A на D, чтобы получить итоговую матрицу F. В ней будет 2 строчки и 2 столбца. Рассчитаем элементы:
- f11 = 2 × 0 + 6 × 0 + 1 × 1 = 1;
- f12 = 2 × 7 + 6 × 19 + 1 × 11 = 139;
- f21 = 0 × 0 + 1 × 0 + 3 × 1 = 3;
- f22 = 0 × 7 + 1 × 19 + 3 × 11 = 52.
Составим прямоугольный массив, являющийся конечным результатом умножения трех матриц.
Знакомство с прямым произведением
Достаточно сложным для понимания материалом является кронекеровское произведение матриц. У него есть еще дополнительное название – прямое произведение. Что же понимается под этим термином? Допустим, у нас есть таблица A порядка m × n и таблица B порядка p × q. Прямым произведением матрицы A на матрицу B является матрица порядка mp × nq.
У него есть еще дополнительное название – прямое произведение. Что же понимается под этим термином? Допустим, у нас есть таблица A порядка m × n и таблица B порядка p × q. Прямым произведением матрицы A на матрицу B является матрица порядка mp × nq.
У нас есть 2 квадратные матрицы A, B, которые представлены на картинке. Первая из них состоит из 2 столбцов и 2 строк, а вторая – из 3 столбцов и 3 строк. Мы видим, что матрица, полученная в результате прямого произведения, состоит из 6 строк и точно такого же количества столбцов.
Как при прямом произведении вычисляют элементы новой матрицы? Найти ответ на этот вопрос очень легко, если проанализировать рисунок. Сначала заполняют первую строку. Берут первый элемент из верхней строчки таблицы A и последовательно умножают на элементы первой строки из таблицы B. Далее берут второй элемент первой строчки таблицы A и последовательно умножают на элементы первой строки таблицы B. Для заполнения второй строки снова берут первый элемент из первой строки таблицы A и умножают его на элементы второй строки таблицы B.
Итоговую матрицу, получаемую прямым произведением, называют блочной. Если вновь проанализировать рисунок, то можно заметить, что наш результат состоит из 4 блоков. Все они включают элементы матрицы B. Дополнительно элемент каждого блока умножен на конкретный элемент матрицы A. В первом блоке все элементы умножены на a11, во втором – на a12, в третьем – на a21, в четвертом – на a22.
Определитель произведения
При рассмотрении темы, касающейся умножения матриц, стоит еще рассмотреть такой термин, как «определитель произведения матриц». Что такое определитель? Это важная характеристика квадратной матрицы, определенное значение, которое ставится в соответствие этой матрице. Буквенное обозначение определителя – det.
Для матрицы A, состоящей из двух столбцов и двух строчек, определитель легко найти. Существует небольшая формула, представляющая собой разность произведений конкретных элементов:
det A = a11 × a22 – a12 × a21.
Рассмотрим пример вычисления определителя для таблицы второго порядка. Существует матрица A, в которой a11 = 2, a12 = 3, a21 = 5 и a22 = 1. Для вычисления определителя воспользуемся формулой:
det A = 2 × 1 – 3 × 5 = 2 – 15 = –13.
У матриц 3 × 3 определитель вычисляется по более сложной формуле. Она представлена ниже для матрицы A:
det A = a11a22a33 + a12a23a31 + a13a21a32 – a13a22a31 – a11a23a32 – a12a21a33.
Для запоминания формулы придумали правило треугольника, которое проиллюстрировано на картинке. Сначала умножаются элементы главной диагонали. К полученному значению прибавляются произведения тех элементов, на которые указывают углы треугольников с красными сторонами. Далее отнимается произведение элементов побочной диагонали и отнимаются произведения тех элементов, на которые указывают углы треугольников с синими сторонами.
Теперь поговорим об определителе произведения матриц. Существует теорема, которая гласит, что данный показатель равен произведению определителей таблиц-сомножителей. Убедимся в этом на примере. У нас есть матрица A с элементами a11 = 2, a12 = 3, a21 = 1 и a22 = 1 и матрица B с элементами b11 = 4, b12 = 5, b21 = 1 и b22 = 2. Найдем определители для матриц A и B, произведение A × B и определитель этого произведения.
Ход решения.
Шаг первый. Вычислим определитель для A: det A = 2 × 1 – 3 × 1 = –1. Далее вычислим определитель для B: det B = 4 × 2 – 5 × 1 = 3.
Шаг второй. Найдем произведение A × B. Новую матрицу обозначим буквой C. Вычислим ее элементы:
- c11 = 2 × 4 + 3 × 1 = 11;
- c12 = 2 × 5 + 3 × 2 = 16;
- c21 = 1 × 4 + 1 × 1 = 5;
- c22 = 1 × 5 + 1 × 2 = 7.
Шаг третий. Вычислим определитель для C: det C = 11 × 7 – 16 × 5 = –3. Сравним со значением, которое могло бы получиться при умножении определителей исходных матриц. Числа одинаковые. Вышеуказанная теорема верна.
Вычислим определитель для C: det C = 11 × 7 – 16 × 5 = –3. Сравним со значением, которое могло бы получиться при умножении определителей исходных матриц. Числа одинаковые. Вышеуказанная теорема верна.
Ранг произведения
Ранг матрицы – это характеристика, отражающая максимальное количество линейно независимых строк или столбцов. Для вычисления ранга выполняют элементарные преобразования матрицы:
- перестановку местами двух параллельно лежащих рядов;
- умножение всех элементов определенного ряда из таблицы на число, не равняющееся нулю;
- прибавление к элементам одного ряда элементов из другого ряда, умноженных на конкретное число.
После элементарных преобразований смотрят на количество ненулевых строк. Их число – это и есть ранг матрицы. Рассмотрим предыдущий пример. В нем было представлено 2 матрицы: A с элементами a11 = 2, a12 = 3, a21 = 1 и a22 = 1 и B с элементами b11 = 4, b12 = 5, b21 = 1 и b22 = 2. Также будем использовать матрицу C, полученную в результате умножения. Если мы выполним элементарные преобразования, то в упрощенных матрицах нулевых строк не будет. Это значит, что и ранг таблицы A, и ранг таблицы B, и ранг таблицы C равен 2.
Также будем использовать матрицу C, полученную в результате умножения. Если мы выполним элементарные преобразования, то в упрощенных матрицах нулевых строк не будет. Это значит, что и ранг таблицы A, и ранг таблицы B, и ранг таблицы C равен 2.
Теперь особое внимание уделим рангу произведения матриц. Существует теорема, которая гласит, что ранг произведения таблиц, содержащих числовые элементы, не превышает ранга любого из сомножителей. Это можно доказать. Пусть A – это матрица размера k × s, а B – это матрица размера s × m. Произведение A и B равно C.
Изучим рисунок, представленный выше. На нем изображен первый столбец матрицы C и его упрощенная запись. Этот столбец – линейная комбинация столбцов, входящих в матрицу A. Аналогичным образом можно сказать о любом другом столбце из прямоугольного массива C. Таким образом, подпространство, образованное векторами-столбцами таблицы C, имеется в подпространстве, образованном векторами-столбцами таблицы A. По этой причине размерность подпространства № 1 не превосходит размерности подпространства № 2. Отсюда следует вывод, что ранг по столбцам таблицы C не превышает ранга по столбцам таблицы A, т. е. r(C) ≤ r(A). Если рассуждать аналогичным образом, то можно убедиться в том, что строчки матрицы C – это линейные комбинации строчек матрицы B. Из этого следует неравенство r(C) ≤ r(B).
Отсюда следует вывод, что ранг по столбцам таблицы C не превышает ранга по столбцам таблицы A, т. е. r(C) ≤ r(A). Если рассуждать аналогичным образом, то можно убедиться в том, что строчки матрицы C – это линейные комбинации строчек матрицы B. Из этого следует неравенство r(C) ≤ r(B).
Как находить произведение матриц – достаточно сложная тема. Ее можно легко освоить, но для достижения такого результата придется уделить немало времени заучиванию всех существующих правил и теорем.
2.2: Умножение матриц — Mathematics LibreTexts
Следующая важная операция с матрицами, которую мы рассмотрим, — это умножение матриц. Операция умножения матриц — одна из самых важных и полезных из матричных операций. В этом разделе мы также покажем, как умножение матриц связано с линейными системами уравнений.
Во-первых, мы даем формальное определение векторов строк и столбцов.
Определение \(\PageIndex{1}\): векторы строк и столбцов
Матрицы размера \(n\times 1\) или \(1\times n\) называются векторами . {th}\) столбец матрицы-строки.
{th}\) столбец матрицы-строки.
Матрица \(n\times 1\) \[X=\left[ \begin{array}{c} x_{1} \\ \vdots \\ x_{n} \end{array} \right]\nonumber \] называется вектор-столбцом . Матрица \(1\times n\) \[X = \left[ \begin{array}{ccc} x_{1} & \cdots & x_{n} \end{array} \right]\nonumber \] называется вектором-строкой .
Мы можем просто использовать термин вектор в этом тексте для обозначения либо столбца, либо вектора-строки. Если мы это сделаем, то из контекста будет ясно, о чем мы говорим.
В этой главе мы снова будем использовать понятие линейной комбинации векторов, как в определении 9.2.2. В этом контексте линейная комбинация представляет собой сумму, состоящую из векторов, умноженных на скаляры. Например, \[\left[ \begin{array}{r} 50 \\ 122 \end{array} \right] = 7\left[ \begin{array}{r} 1 \\ 4 \end{array} \right] +8\left[ \begin{array}{r} 2 \\ 5 \end{array} \right] +9\left[ \begin{array}{r} 3 \\ 6 \end{array} \right]\nonumber \] представляет собой линейную комбинацию трех векторов.
Оказывается, любую систему линейных уравнений можно представить в виде линейной комбинации векторов.На самом деле векторы, которые мы будем использовать, — это всего лишь столбцы соответствующей расширенной матрицы!
Определение \(\PageIndex{2}\): векторная форма системы линейных уравнений
Предположим, у нас есть система уравнений, заданная \[\begin{array}{c} a_{11}x_{1}+\cdots +a_{1n}x_{n}=b_{1} \\ \vdots \ \ a_{m1}x_{1}+\cdots +a_{mn}x_{n}=b_{m} \end{array}\nonumber \] Мы можем выразить эту систему в векторной форме , которая выглядит следующим образом: \[x_1 \left[ \begin{array}{c} a_{11}\\ a_{21}\\ \vdots \\ a_{m1} \end{array} \right] + x_2 \left[ \begin{ array}{c} a_{12}\\ a_{22}\\ \vdots \\ a_{m2} \end{array} \right] + \cdots + x_n \left[ \begin{array}{c} a_ {1n}\\ a_{2n}\\ \vdots \\ a_{mn} \end{array} \right] = \left[ \begin{array}{c} b_1\\ b_2\\ \vdots \\ b_m \end{массив} \right]\nonumber \]
Обратите внимание, что каждый используемый здесь вектор представляет собой один столбец соответствующей расширенной матрицы. Существует один вектор для каждой переменной в системе вместе с постоянным вектором.
Существует один вектор для каждой переменной в системе вместе с постоянным вектором.
Первая важная форма матричного умножения — умножение матрицы на вектор. Рассмотрим произведение, заданное \[\left[ \begin{array}{rrr} 1 & 2 & 3 \\ 4 & 5 & 6 \end{array} \right] \left[ \begin{array}{r} 7 \\ 8 \\ 9 \end{array} \right]\nonumber \] Вскоре мы увидим, что это равно \[7\left[ \begin{array}{c} 1 \\ 4 \end{array} \right ] +8\left[ \begin{array}{c} 2 \\ 5 \end{массив} \right] +9\left[ \begin{array}{c} 3 \\ 6 \end{массив} \right ] =\left[ \begin{array}{c} 50 \\ 122 \end{array} \right]\nonnumber \]
В общих чертах, \[\begin{aligned} \left[ \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_ {23} \end{массив} \right] \left[ \begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{массив} \right] &= \ x_ {1}\left[ \begin{array}{c} a_{11} \\ a_{21} \end{array} \right] +x_{2}\left[ \begin{array}{c} a_{ 12} \\ a_{22} \end{массив} \right] +x_{3}\left[ \begin{array}{c} a_{13} \\ a_{23} \end{массив} \right] \\ &=\left[ \begin{array}{c} a_{11}x_{1}+a_{12}x_{2}+a_{13}x_{3} \\ a_{21}x_{1 }+a_{22}x_{2}+a_{23}x_{3} \end{array} \right] \end{aligned}\] Таким образом, вы берете \(x_{1}\) раз первый столбец, добавьте к \(x_{2}\) раз второй столбец и, наконец, \(x_{3}\) раз третий столбец. {n}x_{j}A_{j}\номер\]
{n}x_{j}A_{j}\номер\]
Если мы запишем столбцы \(A\) в терминах их записей, они будут иметь вид \[A_{j} = \left[ \begin{array}{c} a_{1j} \\ a_{2j } \\ \vdots \\ a_{mj} \end{array} \right]\nonumber \] Тогда мы можем записать произведение \(AX\) как \[AX = x_{1}\left[ \begin{ array}{c} a_{11} \\ a_{21} \\ \vdots \\ a_{m1} \end{array} \right] + x_{2}\left[ \begin{array}{c} a_ {12} \\ a_{22} \\ \vdots \\ a_{m2} \end{array} \right] +\cdots + x_{n}\left[ \begin{array}{c} a_{1n} \\ a_{2n} \\ \vdots \\ a_{mn} \end{массив} \right]\nonumber \]
Обратите внимание, что умножение матрицы \(m \times n\) на вектор \(n \times 1\) дает вектор \(m \times 1\).
Вот пример.
Пример \(\PageIndex{1}\): вектор, умноженный на матрицу
Вычислить произведение \(AX\) для \[A = \left[ \begin{array}{rrrr} 1 & 2 & 1 & 3 \\ 0 & 2 & 1 & -2 \\ 2 & 1 & 4 & 1 \end{массив} \right], X = \left[ \begin{array}{r} 1 \\ 2 \\ 0 \\ 1 \end{массив} \right]\nonumber \]
Раствор
Мы будем использовать определение \(\PageIndex{3}\) для вычисления произведения. Поэтому мы вычисляем произведение \(AX\) следующим образом.\[\begin{align} & 1\left[ \begin{array}{r} 1 \\ 0 \\ 2 \end{array} \right] + 2\left[ \begin{array}{r} 2 \ \ 2 \\ 1 \end{array} \right] + 0\left[ \begin{array}{r} 1 \\ 1 \\ 4 \end{array} \right] + 1 \left[ \begin{array }{r} 3 \\ -2\\ 1 \end{массив} \right] \\ &= \left[ \begin{array}{r} 1 \\ 0 \\ 2 \end{массив} \right] + \left[ \begin{array}{r} 4 \\ 4 \\ 2 \end{array} \right] + \left[ \begin{array}{r} 0 \\ 0 \\ 0 \end{array } \right] + \left[ \begin{array}{r} 3 \\ -2\\ 1 \end{array} \right] \\ &= \left[ \begin{array}{r} 8 \\ 2 \\ 5 \конец{массив} \справа]\конец{выровнено}\]
Поэтому мы вычисляем произведение \(AX\) следующим образом.\[\begin{align} & 1\left[ \begin{array}{r} 1 \\ 0 \\ 2 \end{array} \right] + 2\left[ \begin{array}{r} 2 \ \ 2 \\ 1 \end{array} \right] + 0\left[ \begin{array}{r} 1 \\ 1 \\ 4 \end{array} \right] + 1 \left[ \begin{array }{r} 3 \\ -2\\ 1 \end{массив} \right] \\ &= \left[ \begin{array}{r} 1 \\ 0 \\ 2 \end{массив} \right] + \left[ \begin{array}{r} 4 \\ 4 \\ 2 \end{array} \right] + \left[ \begin{array}{r} 0 \\ 0 \\ 0 \end{array } \right] + \left[ \begin{array}{r} 3 \\ -2\\ 1 \end{array} \right] \\ &= \left[ \begin{array}{r} 8 \\ 2 \\ 5 \конец{массив} \справа]\конец{выровнено}\]
Используя описанную выше операцию, мы также можем написать систему линейных уравнений в матричной форме .В этой форме мы выражаем систему как матрицу, умноженную на вектор. Рассмотрим следующее определение.
Определение \(\PageIndex{4}\): матричная форма системы линейных уравнений
Предположим, у нас есть система уравнений, заданная \[\begin{array}{c} a_{11}x_{1}+\cdots +a_{1n}x_{n}=b_{1} \\ a_{21 }x_{1}+ \cdots + a_{2n}x_{n} = b_{2} \\ \vdots \\ a_{m1}x_{1}+\cdots +a_{mn}x_{n}=b_ {m} \end{array}\nonumber \] Тогда мы можем выразить эту систему в матричной форме следующим образом. \[\left[ \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \ \ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right] \left[ \begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{массив} \right] = \left[ \begin{массив}{c} b_{1}\\ b_{2} \\ \vdots \\ b_{m} \end{массив} \right]\nonumber \]
\[\left[ \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \ \ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right] \left[ \begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{массив} \right] = \left[ \begin{массив}{c} b_{1}\\ b_{2} \\ \vdots \\ b_{m} \end{массив} \right]\nonumber \]
Выражение \(AX=B\) также известно как Matrix Form соответствующей системы линейных уравнений.Матрица \(A\) – это просто матрица коэффициентов системы, вектор \(X\) – вектор-столбец, построенный из переменных системы, и, наконец, вектор \(B\) – это вектор-столбец, построенный из константы системы. Важно отметить, что в таком виде можно записать любую систему линейных уравнений.
Обратите внимание, что если мы запишем однородную систему уравнений в матричной форме, она будет иметь вид \(AX=0\) для нулевого вектора \(0\).
Из этого определения видно, что вектор \[X = \left[ \begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array} \right]\nonumber \] будет удовлетворять уравнению \(AX=B\) только тогда, когда элементы \(x_{1}, x_{2}, \cdots, x_{n}\) вектора \(X\ ) являются решениями исходной системы.
Теперь, когда мы рассмотрели, как умножать матрицу на вектор, мы хотим рассмотреть случай, когда мы умножаем две матрицы более общих размеров, хотя, как мы увидим, эти размеры все еще должны быть подходящими. Например, в примере \(\PageIndex{1}\) мы умножили матрицу \(3 \times 4\) на вектор \(4 \times 1\). Мы хотим исследовать, как умножать другие размеры матриц.
Мы еще не дали никаких условий, когда возможно умножение матриц! Для матриц \(A\) и \(B\), чтобы образовать произведение \(AB\), количество столбцов \(A\) должно равняться количеству строк \(B.\) Рассмотрим произведение \(AB\), где \(A\) имеет размер \(m\times n\), а \(B\) имеет размер \(n \times p\). Затем произведение с точки зрения размера матриц определяется как \[(m\times\overset{\text{они должны совпадать!}}{\widehat{n)\;(n}\times p})=m\ раз p\номер\]
Обратите внимание, что две внешние цифры обозначают размер продукта. Одно из важнейших правил умножения матриц заключается в следующем. Если два средних числа не совпадают, вы не можете умножать матрицы!
Когда количество столбцов \(A\) равно количеству строк \(B\), говорят, что две матрицы созвучны , а произведение \(AB\) получается следующим образом. {th}\) столбец \(AB\).
{th}\) столбец \(AB\).
Рассмотрим следующий пример.
Пример \(\PageIndex{2}\): умножение двух матриц
Найдите \(AB\), если возможно. \[A = \left[ \begin{array}{rrr} 1 & 2 & 1 \\ 0 & 2 & 1 \end{array} \right], B = \left[ \begin{array}{rrr} 1 & 2 & 0 \\ 0 & 3 & 1 \\ -2 & 1 & 1 \end{массив} \right]\nonumber \]
Раствор
Первое, что вам нужно проверить при вычислении произведения, это возможно ли умножение.Первая матрица имеет размер \(2\times 3\), а вторая матрица имеет размер \(3\times 3\). Внутренние числа равны, поэтому матрицы \(A\) и \(B\) созвучны. Согласно приведенному выше обсуждению, \(AB\) будет матрицей \(2\times 3\). Определение \(\PageIndex{5}\) дает нам способ вычислить каждый столбец \(AB\) следующим образом.
\[\left[ \overset{ \text{Первый столбец}}{\overbrace{\left[ \begin{array}{rrr} 1 & 2 & 1 \\ 0 & 2 & 1 \end{массив} \right ] \left[ \begin{array}{r} 1 \\ 0 \\ -2 \end{массив} \right] }},\overset{\text{Второй столбец}}{\overbrace{\left[ \begin {array}{rrr} 1 & 2 & 1 \\ 0 & 2 & 1 \end{array} \right] \left[ \begin{array}{r} 2 \\ 3 \\ 1 \end{array} \ right] }},\overset{\text{Третий столбец}}{\overbrace{\left[\begin{array}{rrr} 1 & 2 & 1 \\ 0 & 2 & 1 \end{array} \right] \left[ \begin{array}{r} 0 \\ 1 \\ 1 \end{array} \right] }}\right]\nonumber \] Вы знаете, как умножить матрицу на вектор, используя Определение \( \PageIndex{3}\) для каждого из трех столбцов. Таким образом, \[\left[ \begin{array}{rrr} 1 & 2 & 1 \\ 0 & 2 & 1 \end{array} \right] \left[ \begin{array}{rrr} 1 & 2 & 0 \\ 0 & 3 & 1 \\ -2 & 1 & 1 \end{array} \right] = \ \left[ \begin{array}{rrr} -1 & 9 & 3 \\ -2 & 7 & 3 \end{массив} \right]\nonumber \]
Таким образом, \[\left[ \begin{array}{rrr} 1 & 2 & 1 \\ 0 & 2 & 1 \end{array} \right] \left[ \begin{array}{rrr} 1 & 2 & 0 \\ 0 & 3 & 1 \\ -2 & 1 & 1 \end{array} \right] = \ \left[ \begin{array}{rrr} -1 & 9 & 3 \\ -2 & 7 & 3 \end{массив} \right]\nonumber \]
Поскольку векторы представляют собой просто \(n \times 1\) или \(1 \times m\) матрицы, мы также можем умножить вектор на другой вектор.
Пример \(\PageIndex{3}\): умножение вектора на вектор
Умножить, если возможно \(\left[ \begin{array}{r} 1 \\ 2 \\ 1 \end{array} \right] \left[ \begin{array}{rrrr} 1 & 2 & 1 & 0 \end{массив} \right] .\)
Раствор
В этом случае мы умножаем матрицу размера \(3 х 1\) на матрицу размера \(1 х 4). Внутренние числа совпадают, поэтому произведение определено. Обратите внимание, что произведение будет матрицей размера \(3 x 4\). Используя определение \(\PageIndex{5}\), мы можем вычислить это произведение следующим образом \(\:\) \[\left[ \begin{array}{r} 1 \\ 2 \\ 1 \end{array} \right] \left[ \begin{array}{rrrr} 1 & 2 & 1 & 0 \end{array} \right] = \left[ \overset{ \text{Первый столбец}}{\overbrace{\left[ \begin{array}{r} 1 \\ 2 \\ 1 \end{массив} \right] \left[ \begin{array}{r} 1 \end{массив} \right] }},\overset{\ text{Второй столбец}}{\overbrace{\left[ \begin{array}{r} 1 \\ 2\\ 1 \end{массив} \right] \left[ \begin{array}{r} 2 \end {массив} \right] }},\overset{\text{Третий столбец}}{\overbrace{\left[ \begin{array}{r} 1 \\ 2 \\ 1 \end{массив} \right] \ left[ \begin{array}{r} 1 \end{array} \right] }}, \overset {\text{Четвертый столбец}}{\overbrace{\left[ \begin{array}{r} 1\\ 2\\ 1 \end{массив} \right] \left[ \begin{array}{r} 0 \end{массив} \right]}} \right]\nonumber \]
Вы можете использовать определение \(\PageIndex{3}\), чтобы убедиться, что этот продукт является \[\left[ \begin{array}{cccc} 1 & 2 & 1 & 0 \\ 2 & 4 & 2 & 0 \ \ 1 & 2 & 1 & 0 \end{массив} \right]\nonumber \]
Пример \(\PageIndex{4}\): умножение, которое не определено
Найдите \(BA\), если возможно. \[B = \left[ \begin{array}{ccc} 1 & 2 & 0 \\ 0 & 3 & 1 \\ -2 & 1 & 1 \end{array} \right], A = \left[ \ begin{array}{ccc} 1 & 2 & 1 \\ 0 & 2 & 1 \end{array} \right]\nonumber \]
\[B = \left[ \begin{array}{ccc} 1 & 2 & 0 \\ 0 & 3 & 1 \\ -2 & 1 & 1 \end{array} \right], A = \left[ \ begin{array}{ccc} 1 & 2 & 1 \\ 0 & 2 & 1 \end{array} \right]\nonumber \]
Раствор
Сначала проверьте, возможно ли это. Это произведение имеет вид \(\влево( 3\умножить на 3\вправо) \влево( 2\умножить на 3\вправо).\) Внутренние числа не совпадают, поэтому вы не можете выполнить это умножение.
В этом случае мы говорим, что умножение не определено.Обратите внимание, что это те же матрицы, которые мы использовали в примере \(\PageIndex{2}\). В этом примере мы попытались вычислить \(BA\) вместо \(AB\). Это демонстрирует еще одно свойство матричного умножения. Хотя произведение \(AB\) может быть определено, мы не можем предполагать, что произведение \(BA\) будет возможно. Поэтому важно всегда проверять, определено ли произведение, прежде чем выполнять какие-либо расчеты.
Ранее мы определили нулевую матрицу \(0\) как матрицу (соответствующего размера), содержащую нули во всех элементах. Рассмотрим следующий пример умножения на нулевую матрицу.
Рассмотрим следующий пример умножения на нулевую матрицу.
Пример \(\PageIndex{5}\): умножение на нулевую матрицу
Вычислите произведение \(A0\) для матрицы \[A= \left[ \begin{array}{rr} 1 & 2 \\ 3 & 4 \end{array} \right]\nonumber \] и \ (2 \times 2\) нулевая матрица, заданная \[0= \left[ \begin{array}{rr} 0 & 0 \\ 0 & 0 \end{array} \right]\nonumber \]
Раствор
В этом продукте мы вычисляем \[\left[ \begin{array}{rr} 1 & 2 \\ 3 & 4 \end{array} \right] \left[ \begin{array}{rr} 0 & 0 \\ 0 & 0 \end{массив} \right] = \left[ \begin{array}{rr} 0 & 0 \\ 0 & 0 \end{массив} \right]\nonumber \]
Следовательно, \(A0=0\).
Обратите внимание, что мы также можем умножить \(A\) на \(2 \times 1\) нулевой вектор, заданный как \(\left[ \begin{array}{r} 0 \\ 0 \end{array} \right ]\). Результатом будет \(2 \times 1\) нулевой вектор. Поэтому всегда имеет место \(A0=0\) для нулевой матрицы или вектора соответствующего размера.
Умножить столбец чисел на одно и то же число
Предположим, вы хотите умножить столбец чисел на то же число в другой ячейке. Хитрость умножения столбца чисел на одно число заключается в добавлении символов $ к адресу ячейки этого числа в формуле перед копированием формулы.
Хитрость умножения столбца чисел на одно число заключается в добавлении символов $ к адресу ячейки этого числа в формуле перед копированием формулы.
В приведенном ниже примере таблицы мы хотим умножить все числа в столбце A на число 3 в ячейке C2. Формула =A2*C2 даст правильный результат (4500) в ячейке B2. Но копирование формулы вниз по столбцу B не сработает, потому что ссылка на ячейку C2 изменится на C3, C4 и так далее. Поскольку в этих ячейках нет данных, результат в ячейках с B3 по B6 будет равен нулю.
Чтобы умножить все числа в столбце A на ячейку C2, добавьте символы $ к ссылке на ячейку следующим образом: $C$2 , что вы можете увидеть в примере ниже.
Использование символов $ сообщает Excel, что ссылка на C2 является «абсолютной», поэтому при копировании формулы в другую ячейку ссылка всегда будет на ячейку C2. Чтобы создать формулу:
В ячейке B2 введите знак равенства (=).

Щелкните ячейку A2, чтобы ввести ячейку в формулу.
Введите звездочку (*).
Щелкните ячейку C2, чтобы ввести ячейку в формулу.
Теперь введите символ $ перед C и символ $ перед 2: $C$2 .
Нажмите Enter.
Совет: Вместо того, чтобы вводить символ $, вы можете поместить точку вставки до или после ссылки на ячейку, которую вы хотите сделать «абсолютной», и нажать клавишу F4, чтобы добавить символы $.
Теперь вернемся немного назад, чтобы увидеть простой способ скопировать формулу вниз по столбцу после того, как вы нажмете Enter в ячейке B2.
Выберите ячейку B2.
Дважды щелкните маленький зеленый квадратик в правом нижнем углу ячейки.

Формула автоматически копируется вниз по ячейке B6.
И с скопированной формулой столбец B возвращает правильные ответы.
матриц
матрицДалее: Детерминанты Вверх: линейная_алгебра Предыдущая: Векторы Матрица — это прямоугольный набор чисел (опять же, возможно, сложных). Он может представлять собой набор векторов строк/столбцов или преобразование который изменяет вектор на другой вектор. Например, вращение реального 2D-вектора на угол вокруг оси может быть представлен в виде матрицы 2×2,
Влияние этого поворота на двумерный вектор на плоскости может определяется путем умножения вектора на эту матрицу преобразования,
| (9) |
где и .

В более общем случае произведение матрицы и вектор-столбца может быть
написано как
| (10) |
где
Обратите внимание, что каждый элемент произведения , является просто скалярное произведение й строки матрицы на вектор. Также можно думать о векторе-столбце как будучи линейной комбинацией столбцов матрицы , с каждым столбцом, имеющим вес.
Также возможно «умножить влево» матрицу на вектор-строку, например
это:
| (12) |
где
На этот раз каждый элемент произведения , является точечным произведением вектора слева с th столбцом матрицы.Вектор-строку можно рассматривать как линейную комбинацию строк матрицы , каждая строка имеет вес из .

Из приведенной информации должно быть очевидно, что вектор-строка умножение матрицы на вектор-столбец дает число (скаляр).
Теперь рассмотрим умножение двух матриц и ,
что дает новую матрицу:
где
| (15) |
То есть каждый элемент матрицы продукта является результатом скалярного произведения между строку матрицы и столбец матрицы.Умножение матриц можно рассматривать как обобщение произведения матрицы на вектор, где теперь вместо одного вектор-столбец справа, у нас есть ряд из них. Это также можно думать об умножении матриц как об обобщении произведение вектора-строки на матрицу, где теперь вместо один вектор-строка слева, у нас есть ряд из них.
транспонирует матрицы , обычно обозначается
, получается простой перестановкой элементов по диагонали, .Например,
| (16) |
Для комплексных чисел обычно комплексное сопряжение транспонирует или примыкает к , более полезно. Сопряженная матрица часто
обозначенный
. Например,
Сопряженная матрица часто
обозначенный
. Например,
| (17) |
Если матрица равна своей присоединенной , это называется эрмитовой матрицей . Ясно, что это может произойти только в том случае, если диагональные элементы действительны (иначе никогда не будут равны , Например).Можно также взять сопряжение вектора, т. е. эффективно то, что нужно сделать, чтобы взять скалярное произведение двух сложных векторы (см. выше):
| (18) |
Далее: Детерминанты Вверх: линейная_алгебра Предыдущая: Векторы Дэвид Шерил 2006-08-15
Три способа умножения матриц в Excel — фастай часть-2, урок-8 | Аман Арора
Обратите внимание, чем это отличается от Method-1 ? На этот раз мы просто говорим Excel или PyTorch, чтобы они умножили строку 0 из A на столбец 0 из B и просуммировали полученный вектор, чтобы дать нам ответ. Вместо
Вместо 1*1 + 10*5 + 100*9 . Например, для C[0][0] этот метод умножает вектор в строке 0 A tensor([1,10,100]) на вектор в столбце 0 B tensor{[1, 5,9]) , чтобы получить промежуточный продукт Vector tensor([1,50,900]) и суммировать его, чтобы получить результат в позиции C[0][0] как tensor(951) .
В коде это выглядит так:
def matmul2(a,b):
ar,ac = a.shape
br,bc = b.shape
assert ac==br
c = torch.zeros(ar,bc)
для i в диапазоне (ar):
для j в диапазоне (bc):
c[i,j] = (a[i,: ]*b[:,j]).sum()
return c
Итак, мы просто анализируем каждую позицию C, , используя два цикла FOR, и вводим соответствующий результат в эту позицию. Если i,j представляют позицию строки и столбца в C , это выглядит примерно так..
i:0,j:0
a:tensor([ 1, 10, 100]),b:tensor([ 1, 5, 9])
тензор([[951., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
- --
i:0,j:1
a:tensor([ 1, 10, 100]),b:tensor([ 2, 6, 10])
tensor([[ 951., 1062., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
---
i:0,j:2
a:tensor([ 1, 10, 100]),b:tensor([ 3, 7, 11])
tensor([[ 951., 1062., 1173 ., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
---
i:0,j:3
a:tensor([ 1, 10, 100 ]),b:tensor([ 4, 8, 12])
tensor([[ 951., 1062., 1173., 1284.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
---
i:1,j:0
a:tensor([ 2, 20 , 200]),b:tensor([1, 5, 9])
tensor([[ 951., 1062., 1173., 1284.],
[1902., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
И так далее.. пока не получим полную матрицу C .
тензор([[ 951., 1062., 1173., 1284.],
[1902., 2124., 2346., 2568.],
[2853., 3186., 3519., 3852.],
[3804., 4248., 4692., 5136.]])
Метод-3: Трансляция
Заметили здесь общую тему? Каждый раз мы должны умножать каждую строку A на каждый столбец B , чтобы получить C . Вы замечаете повторение? Мы умножаем один и тот же вектор строки в A bc раз! И повторяем этот процесс или раз!
Есть ли способ умножить вектор-строку A на все столбцы B , чтобы получить соответствующую строку в C? Да, есть! Включить трансляцию…
Примечание: я не буду объяснять трансляцию, Джереми отлично с ней справляется.
Вместо этого давайте посмотрим, что представляет собой этот волшебный фрагмент кода
для i в диапазоне (ar):
c[i] = (a[i,:].unsqueeze(-1).expand_as(b)*b) .sum(dim=0)
Как обычно, реплицируем в Excel! Это действительно упростит задачу. Давайте сделаем это по шагам.
Давайте сделаем это по шагам.
Шаг-1) Выберите i-ю строку A a[i,:] . Мы выбираем строку 0 в качестве примера.
Шаг 2) Возьмите его Транспонируйте a[i,:].unsqueeze(-1)
Как умножить столбцы в Excel
Microsoft Excel в первую очередь предназначен для работы с числами, поэтому он предоставляет несколько различных способов выполнения основных математических операций, а также более сложных вычислений. В нашем последнем уроке мы обсуждали, как умножать ячейки в Excel. В этом уроке мы сделаем еще один шаг и посмотрим, как можно быстро умножать целые столбцы.
- Как умножить два столбца в Excel
- Как умножить столбец на число в Excel
Как умножить два столбца в Excel
Как и в случае со всеми основными математическими операциями, в Excel существует несколько способов умножения столбцов. Ниже мы покажем вам три возможных решения, чтобы вы могли выбрать то, которое лучше всего подходит для вас.
Ниже мы покажем вам три возможных решения, чтобы вы могли выбрать то, которое лучше всего подходит для вас.
Как умножить один столбец на другой с помощью оператора умножения
Самый простой способ умножить 2 столбца в Excel — создать простую формулу с символом умножения (*). Вот как:
- Умножьте две ячейки в первой строке.
Предположим, ваши данные начинаются со строки 2, где столбцы B и C должны быть умножены. Формула умножения, которую вы поместили в D2, проста:
= B2 * C2. - Дважды щелкните маленький зеленый квадратик в нижнем правом углу D2, чтобы скопировать формулу вниз по столбцу до последней ячейки с данными.Сделанный!
Поскольку в формуле используются относительные ссылки на ячейки (без знака $), ссылки будут меняться в зависимости от относительного положения строки, в которую копируется формула. Например, формула в D3 изменится на =B3*C3 , формула в D3 станет =B4*C4 и так далее.
Как умножить два столбца с помощью функции ПРОИЗВЕД
Если вы предпочитаете работать с функциями Excel, а не с выражениями, вы можете умножить 2 столбца с помощью функции ПРОИЗВЕД, которая специально разработана для выполнения умножения в Excel.
Для нашего примера набора данных формула выглядит следующим образом:
=ПРОДУКТ(B2:C2)
Как и в случае с символом умножения, ключевым моментом является использование относительных ссылок на ячейки, чтобы формула могла правильно корректироваться для каждой строки.
Вы вводите формулу в первую ячейку, а затем копируете ее вниз по столбцу, как показано в приведенном выше примере:
Как умножить два столбца на формулу массива
Еще один способ умножить целые столбцы в Excel — использовать формулу массива.Пожалуйста, не расстраивайтесь и не пугайтесь слов «формула массива». Этот очень прост и удобен в использовании. Вы просто записываете диапазоны, которые хотите умножить, разделяя их знаком умножения, например:
.
=B2:B5*C2:C5
Чтобы вставить эту формулу умножения в свои рабочие листы, выполните следующие действия:
- Выберите весь диапазон, в который вы хотите ввести формулу (D2:D5).
- Введите формулу в строке формул и нажмите Ctrl + Shift + Enter.Как только вы это сделаете, Excel заключит формулу в {фигурные скобки}, что указывает на формулу массива. Ни в коем случае нельзя набирать фигурные скобки вручную, это не сработает.
В результате Excel будет умножать значение в столбце B на значение в столбце C в каждой строке без необходимости копировать формулу вниз.
Этот подход может быть полезен, если вы хотите предотвратить случайное удаление или изменение формулы в отдельных ячейках. При такой попытке Excel выдаст предупреждение о том, что нельзя изменить часть массива.
Как умножить несколько столбцов в Excel
Чтобы умножить более двух столбцов в Excel, вы можете использовать формулы умножения, аналогичные рассмотренным выше, но включающие несколько ячеек или диапазонов.
Например, чтобы умножить значения в столбцах B, C и D, используйте одну из следующих формул:
- Оператор умножения:
=A2*B2*C2 - Функция ПРОИЗВЕД:
=ПРОИЗВЕД(A2:C2) - Формула массива (Ctrl + Shift + Enter):
=A2:A5*B2:B5*C2:C5
Как показано на скриншоте ниже, формулы умножают на числа и на проценты одинаково хорошо.
Как умножить столбец на число в Excel
В ситуациях, когда вы хотите умножить все значения в столбце на одно и то же число, выполните одно из следующих действий.
Умножение столбца на число по формуле
Как оказалось, самый быстрый способ выполнить умножение в Excel — использовать символ умножения (*), и эта задача не является исключением. Вот что вы делаете:
- Введите число для умножения в какой-либо ячейке, например, в ячейке B1.
В этом примере мы собираемся умножить столбец чисел на проценты.
 Поскольку во внутренней системе Excel проценты хранятся в виде десятичных чисел, мы можем вставить либо 11%, либо 0,11 в ячейку B1.
Поскольку во внутренней системе Excel проценты хранятся в виде десятичных чисел, мы можем вставить либо 11%, либо 0,11 в ячейку B1. - Напишите формулу для самой верхней ячейки столбца, зафиксировав ссылку на постоянное число знаком $ (например, $B$1).
В нашей типовой таблице числа, которые нужно умножить, находятся в столбце B, начиная с строки 4, поэтому формула выглядит следующим образом:
=B4*$B$1 - Введите формулу умножения в самую верхнюю ячейку (C4).
- Дважды щелкните маленький зеленый квадратик в нижнем правом углу ячейки формулы, чтобы скопировать формулу вниз по столбцу до тех пор, пока в левой части есть какие-либо данные. Вот и все!
Как работает эта формула
Вы используете абсолютную ссылку на ячейку (например, $B$1), чтобы зафиксировать координаты столбца и строки ячейки с числом, на которое нужно умножить, чтобы эта ссылка не менялась при копировании формулы в другие ячейки.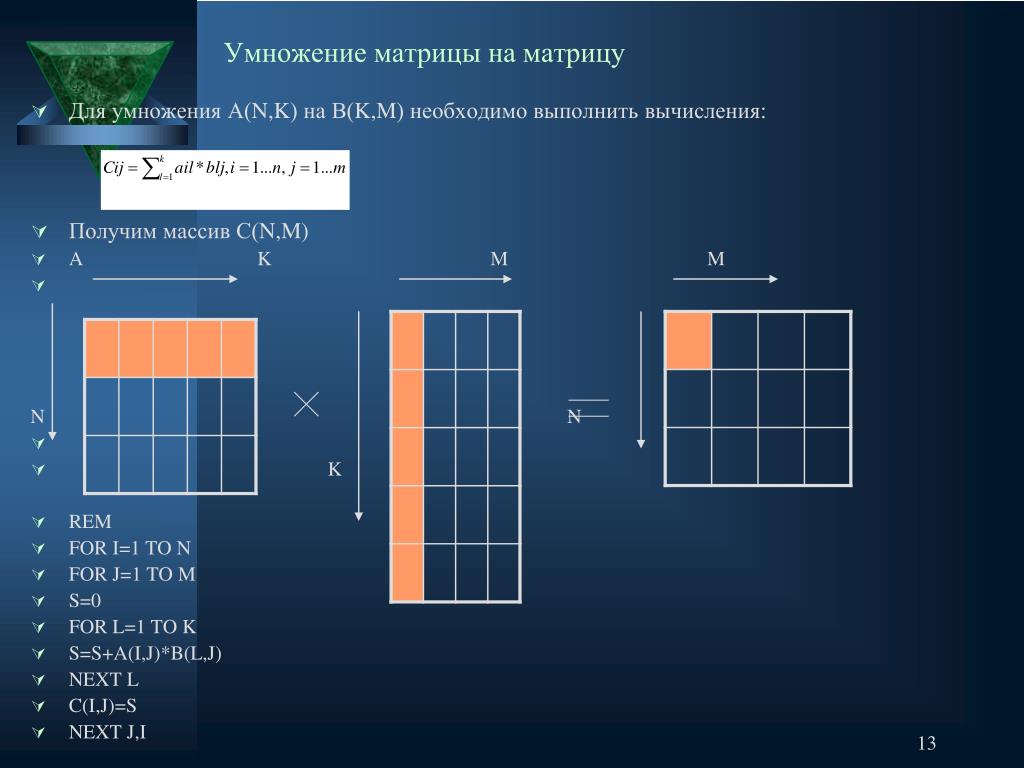
Вы используете относительную ссылку на ячейку (например, B4) для самой верхней ячейки в столбце, чтобы эта ссылка менялась в зависимости от относительного положения ячейки, в которую копируется формула.
В результате формула в C5 изменится на =B5*$B$1 , формула в C6 изменится на =B6*$B$1 и так далее.
Наконечник. Если вы умножаете столбец на постоянное число, которое вряд ли изменится в будущем, вы можете указать это число непосредственно в формуле, например: =B4*11% или =B4*0,11
Умножение столбца чисел на одно и то же число с помощью специальной вставки
Если вы хотите получить результат в виде значений, а не формул, выполните умножение с помощью функции Специальная вставка > Умножение .
- Скопируйте числа, которые вы хотите умножить, в столбец, где вы хотите вывести результаты. В этом примере мы копируем значения продаж (B4:B7) в столбец НДС (C4:C7), потому что мы не хотим переопределять исходные данные о продажах.

- Введите постоянное число для умножения в какую-нибудь пустую ячейку, например B1. На данный момент ваши данные будут выглядеть примерно так:
- Выберите ячейку с постоянным номером (B1) и нажмите Ctrl + C, чтобы скопировать ее в буфер обмена.
- Выберите ячейки, которые вы хотите умножить (C4:C7).
- Нажмите Ctrl + Alt + V, затем M, что является ярлыком для Специальная вставка > Умножение , а затем нажмите Enter.
Или щелкните правой кнопкой мыши выделение, выберите Специальная вставка… в контекстном меню, выберите Умножение в разделе Операции и нажмите OK.
В любом случае Excel будет умножать каждое число в диапазоне C4:C7 на значение в ячейке B1 и возвращать результаты в виде значений, а не формул:
 Чтобы исправить это, выберите получившиеся ячейки и примените к ним нужный числовой формат, в данном случае Валюта .
Чтобы исправить это, выберите получившиеся ячейки и примените к ним нужный числовой формат, в данном случае Валюта .Умножение столбца на число с помощью Ultimate Suite для Excel
Как и специальная вставка, этот метод умножения возвращает значения, а не формулы.В отличие от специальной вставки, Ultimate Suite for Excel удобен и интуитивно понятен. Вот как можно в пару кликов умножить столбец чисел на другое число:
- Выберите все ячейки, которые вы хотите умножить. Если вы хотите сохранить исходные значения, скопируйте их в другой столбец, где вы хотите получить результаты, и выберите эти ячейки.
- На ленте Excel перейдите на вкладку Ablebits Tools > группу Calculate .
- Выберите знак умножения (*) в поле Операция , введите число для умножения в поле Значение и нажмите кнопку Вычислить .
В качестве примера рассчитаем бонус в размере 5% от наших продаж. Для этого мы копируем значения продаж из столбца B в столбец C, а затем либо:
Для этого мы копируем значения продаж из столбца B в столбец C, а затем либо:
- Выберите знак умножения (*) в поле Операция и введите 0,05 в поле Значение (0,05 представляет 5%, поскольку 5 процентов составляют пять частей от ста).
- Выберите знак процента (%) в поле Операция и введите 5 в поле Значение .
Оба метода умножают правильно и дают идентичные результаты:
В отличие от специальной функции вставки Excel, Ultimate Suite сохраняет исходный формат валюты, поэтому дальнейшая корректировка результатов не требуется.Если вам интересно попробовать параметры расчета Ultimate Suite в своих рабочих листах, вы можете загрузить ознакомительную версию, используя ссылку ниже.
Благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Доступные загрузки
Excel Multiply Columns — примеры формул (файл .xlsx)
Ultimate Suite — 14-дневная пробная версия (файл . zip)
zip)
Вас также может заинтересовать
поэлементное умножение | Практичный R
Это основной пост об операциях умножения в R.Мы рассматриваем поэлементное умножение против матричного умножения . Сначала давайте сделаем некоторые данные:
# Сделать некоторые данные
а = с (1,2,3)
б = с (2,4,6)
с = ссвязать (а, б)
х = с (2,2,2)
Если мы посмотрим на результат (c и x), то увидим, что c — это матрица 3×2, а x — матрица 1×3 (которую я также буду называть вектором).
# Посмотреть наши данные
с
## а б
## [1,] 1 2
## [2,] 2 4
## [3,] 3 6
Икс
## [1] 2 2 2
В R звездочка (*) используется для поэлементного умножения.Здесь элементы в одной строке умножаются друг на друга.
#Это даст тот же результат
с*х
х * с
Мы видим, что выходные данные c*x и x*c одинаковы, а вектор x удваивает матрицу c.
#Посмотрите вывод поэлементного умножения
## а б
## [1,] 2 4
## [2,] 4 8
## [3,] 6 12
## а б
## [1,] 2 4
## [2,] 4 8
## [3,] 6 12
В R знаки процента в сочетании со звездочками используются для умножения матриц (%*%).
# Это работает (умножение матриц)
х%*%с
## а б
## [1,] 12 24
Если вы покопаетесь и вспомните умножение матриц, вы обнаружите, что матрица 1×3, умноженная на матрицу 3×2, дает матрицу 1×2. Она будет иметь то же количество строк, что и первая матрица (x имеет 1 строку), и то же количество столбцов, что и вторая матрица (c имеет 2 столбца). Теперь давайте попробуем это, поменяв местами x и c.
# Это не работает. Неправильные размеры.
с%*%х
## Ошибка в c %*% x : несоответствующие аргументы
R дает нам ошибку, потому что вы не можете перемножить матрицу 3×2 и 1×3.Чтобы умножение матриц работало, количество столбцов в первой матрице (c = 3 столбца) должно быть равно количеству строк во второй матрице (x = 1 строка).
Предыдущие операции выполнялись с использованием массивов R по умолчанию, которые являются матрицами. Мы можем подтвердить это, используя команду class и typeof ниже:
# Получить тип данных
класс (с)
тип(с)
класс (х)
тип(х)
Вот вывод этих функций.
# Вывод
## [1] "матрица"
## [1] "двойной"
## [1] "числовой"
## [1] "двойной"
Это показывает нам, что наша матрица c имеет тип данных матрицы R с форматированием «двойное», что означает, что это числа (в отличие от чего-то вроде «символа»).Это также показывает нам, что наша матрица или вектор 1 × 3 имеет тип данных R «числовой», а также имеет форматирование «двойной».
Теперь предположим, что ваши данные находятся во фрейме данных, а не в матрице. Давайте посмотрим, что происходит, когда мы выполняем умножение фреймов данных. Помните, что фреймы данных в R могут содержать данные разных типов (числа, буквы и т. д.), тогда как матрицы могут содержать данные только одного типа.
***Для получения дополнительной информации см. мой пост здесь под названием CBIND2***
Давайте преобразуем наши матрицы во фреймы данных, используя данные функции.Рамка.
c1 = data.frame(c)
x1 = данные.кадр(х)
Теперь давайте посмотрим на наши данные. Обратите внимание, что есть дополнительный столбец чисел от 1 до 3 как для c1, так и для x1. Это просто особенность вывода фрейма данных в R, где подсчитываются строки с 1 по 3.
Обратите внимание, что есть дополнительный столбец чисел от 1 до 3 как для c1, так и для x1. Это просто особенность вывода фрейма данных в R, где подсчитываются строки с 1 по 3.
с1
## а б
## 1 1 2
## 2 2 4
## 3 3 6
х1
## Икс
## 1 2
## 2 2
## 3 2
И чтобы быть дотошнее, давайте проверим тип данных R, чтобы убедиться, что они не являются матрицами.
# Проверить тип данных
класс (с1)
тип(c1)
класс(x1)
тип(x1)
Вот вывод этих типов данных.Обратите внимание, что класс теперь называется «data.frame», а не «matrix» или «numeric».
# Вывод
## [1] "data.frame"
## [1] "список"
## [1] "data.frame"
## [1] "список"
Теперь давайте снова попробуем наше простое поэлементное умножение. Возможно, вы уже догадались, что эти функции больше не будут работать.
# Оба не работают
с1*х1
х1*с1
Вот результат умножения (т. е. ошибки, которые выдает R).
## Ошибка в операции. data.frame(c1, x1):
## ‘*’ определено только для фреймов данных одинакового размера
## Ошибка в Ops.data.frame(c1, x1):
## ‘*’ определено только для фреймов данных одинакового размера
data.frame(c1, x1):
## ‘*’ определено только для фреймов данных одинакового размера
## Ошибка в Ops.data.frame(c1, x1):
## ‘*’ определено только для фреймов данных одинакового размера
Согласно ошибке R, мы можем умножать кадры данных только одного размера. Итак, давайте попробуем это, создав некоторые новые данные.
# Сделать некоторые данные
ч = с (2,2)
к=с(4,4)
j = cbind (ч, к)
л=j*2
df1 = data.frame(j)
df2 = data.frame(l)
Теперь давайте посмотрим на данные, чтобы увидеть, что у нас есть
# Просмотр новых фреймов данных
df1
## ч к
## 1 2 4
## 2 2 4
дф2
## ч к
## 1 4 8
## 2 4 8
Наконец, давайте умножим df1*df2 и посмотрим, что получится.
# Умножение кадра данных
дф1*дф2
## ч к
## 1 8 32
## 2 8 32
R выполнил поэлементное умножение кадров данных. Это имеет смысл, поскольку мы используем только команду (*). Если мы попробуем это еще раз с обратным порядком кадров данных, мы получим тот же ответ.
# Обратный порядок умножения
дф2*дф1
## ч к
## 1 8 32
## 2 8 32
На этом пока все. Надеюсь, это пролило больше света на то, как R выполняет умножение, особенно на основе типа данных.
Нравится:
Нравится Загрузка…
Умножение матриц
Умножение матриц: Дальше по кроличьей норе
До сих пор мы имели дело с достаточно простыми операциями: сложение и вычитание матриц ограничено одним и тем же -матрицы, а скалярное умножение просто пропускает одно число через всю матрицу.
Но поймите: настоящие матрицы тоже можно перемножать друг с другом. Это немного сложнее, но в основном вам просто нужно помнить самое главное: размер имеет значение — по крайней мере, для перемножения матриц.
Размер задействованных матриц является наиболее важным фактором, поэтому будьте осторожны: для перемножения матриц количество столбцов в первой матрице должно быть таким же, как количество строк во второй . И это сделает вашу жизнь намного, намного проще, если вы потратите секунду, чтобы освежить в памяти разницу между строкой и столбцом. Помните, что строк — это горизонтальных (слева направо), а столбцов — это вертикальных (сверху вниз).
И это сделает вашу жизнь намного, намного проще, если вы потратите секунду, чтобы освежить в памяти разницу между строкой и столбцом. Помните, что строк — это горизонтальных (слева направо), а столбцов — это вертикальных (сверху вниз).
Пример задачи
Допустим, у нас есть матрица A и матрица B :
И размер матриц, и порядок умножения имеют значение.
AB — это то, что мы не можем сделать, потому что в A есть два столбца и три строки в B . Игра окончена, чувак.
BA мы можем сделать, потому что B имеет два столбца, а A имеет две строки. Идеально. Следующее, что нужно помнить, это то, что матрица продукта будет иметь то же количество строк, что и первая матрица, и то же количество столбцов, что и вторая матрица .Да, это так важно, что мы выделили всю чертову штуку курсивом.
Далее до BA . Вот как это выглядит:
Вот как это выглядит:
Мы знаем, что произведение будет иметь три строки, как B , и два столбца, как A :
Мы уже знаем, что первая матрица здесь B , и второй – A . Назовем наш продукт P . В этом случае записи в матрицах могут быть помечены следующим образом:
Вам нужно пройтись по ним и вниз, чтобы понять это: )( A 11 ) + ( B 12 )( A 21 )
Умножаем и складываем первые элементы первой строки первой строки вторая матрица.Поэтому размеры должны совпадать, чтобы ничего не осталось. Тогда, для следующей записи в нашем продукте:
P 12 = ( B 11 ) ( A 12 ) + ( B 12 ) ( A 22 )
Теперь переходим к следующей части. Вы умножаете и складываете элементы второй строки первой матрицы с элементами первого столбца второй матрицы. Пристегнитесь.
Пристегнитесь.
P P 21 = ( B 21 ) ( A 11 ) + ( B 22 ) ( A 21 )
Тогда вы разбили вторые строку первой матрицы со вторым столбцом второй матрицы.Это дает вам второй ряд вашего продукта.
P P 22 = ( B 21 ) ( A 12 ) + ( B 22 ) ( A 22 )
. Всего еще один ряд, и вы, вероятно, можете догадаться, как он идет:
P P 31 = ( B 31 ) ( A 11 ) + ( B 32 ) ( 21 )
P P 32 = ( B 31 ) ( A 12 ) + ( B 32 ) ( A 22 )
Подключив весь этот хлам к общей картине, мы получим следующее:
Вот еще один взгляд на это. Из правил мы знаем, что P будет иметь три строки, как B , и два столбца, как A . Попробуйте визуализировать три из них вместе следующим образом:
Из правил мы знаем, что P будет иметь три строки, как B , и два столбца, как A . Попробуйте визуализировать три из них вместе следующим образом:
Глядя на пересечения, мы можем увидеть, какая строка B и какой столбец A сталкиваются, чтобы получить один из P записи. Ниже мы видим, что X отмечает место, где первая строка B и первый столбец A разбиваются:
Мы знаем, что эти четыре числа нужно объединить в одно.Как они это делают? Ну, читаем строки слева направо, как книгу. Читаем столбцы сверху вниз. Следовательно, умножаем первое число из B в первой строке на первое число из A в первом столбце:
(1)(2) = 2
Затем умножаем второе число из B первая строка со вторым числом из A первый столбец:
(3)(3) = 9
И мы складываем их вместе:
(1)(2) + (3)(3) = 2 + 9 = 11
Затем мы проверяем коллизию между первой строкой B и вторым столбцом A :
Да; X отмечает место, и мы делаем то же самое.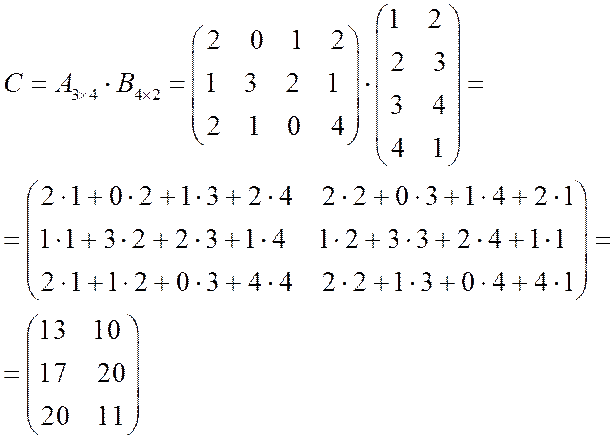 Читаем ряды слева направо, как книгу. И мы читаем столбцы сверху вниз. Умножаем первое число из первой строки B на первое число из второго столбца A : (1)(1) = 1. Затем умножаем второе число из первой строки B на второе число из Второй столбец : (3)(2) = 6. Сложите их вместе, чтобы получить нашу запись для X:
Читаем ряды слева направо, как книгу. И мы читаем столбцы сверху вниз. Умножаем первое число из первой строки B на первое число из второго столбца A : (1)(1) = 1. Затем умножаем второе число из первой строки B на второе число из Второй столбец : (3)(2) = 6. Сложите их вместе, чтобы получить нашу запись для X:
(1)(1) + (3)(2) = 1 + 6 = 7
Мы знаем, мы знаем.Мы как заезженная пластинка, но Х снова ставит точку, и мы делаем то же самое. Мы читаем строку слева направо и читаем столбец сверху вниз. На этот раз мы делаем вторую строку произведения, поэтому мы умножаем первое число из второй строки B на первое число из первого столбца A : (2)(2) = 4. Тогда умножьте второе число из второй строки B на второе число из первого столбца A : (1)(3) = 3. Теперь сложите их:
(2)(2) + (1 )(3) = 4 + 3 = 7
Теперь мы действительно к чему-то пришли.Почти на месте.
Теперь это выглядит так, и мы можем видеть, что будет дальше:
X отмечает точку, друг, и мы делаем то же самое. Строка идет слева направо, столбец сверху вниз. На этот раз мы все еще делаем второй ряд в продукте, но мы переходим ко второму месту в нем. Умножаем первое число из второй строки B на первое число из второго столбца A : (2)(1) = 2. Затем умножаем второе число из второй строки B на второе число из второго столбца A : (1)(2) = 2.Добавьте этих парней:
(2)(1) + (1)(2) = 2 + 2 = 4
И мы повторим все сначала, на этот раз с третьей строкой в B , один раз для каждой записи в первом столбце A .
(4)(2) + (2)(3) = 8 + 6 = 14
И, наконец, мы объединяем третью строку B со вторым столбцом A 9 (4)(1) + (2)(2) = 4 + 4 = 8 У-у-у! Мы сделали это! Мы не растерялись, и становится только легче, пока мы помним самые важные правила: Эй, помните, мы говорили, что даже когда у нас есть две матрицы одинакового размера, порядок имеет значение? Конечно, вы можете умножать в любом порядке, но ответ будет другим. Смотреть: Сначала мы можем сделать это в следующем порядке: (2)(1) + (4)(4) = 2 + 16 = 18 Итак, это наш продукт: А если мы поменяемся местами? Расположим так, чтобы было легче увидеть: (1)(2) + (0)(3) = 2 + 0 = 2 3) = 4 + 0 = 4 Это наш продукт: Совершенно другой.Странно, да? Придержите прессы. Помните единичную матрицу и нулевую матрицу? Единственный случай, когда число может быть умножено и останется прежним, это умножение на число 1. 3 × 1 = 3 В Стране матриц единичная матрица представляет собой матричную версию 1. Все матрицы идентичности равны 0, за исключением диагональной линии из 1, проходящей от верхнего левого угла к нижнему правому.Они могут быть любых размеров, главное, чтобы они были квадратными: Вот что важно: всякий раз, когда матрица умножается на единичную матрицу, получается то же самое, что и неединичная матрица. И мы можем это доказать. Действуем так же, как при умножении ранее. Мы назовем единичную матрицу I , произведение P , а другую матрицу назовем T для Теда. Нам просто нравится это имя, хорошо? Попробуйте визуализировать три из них вместе следующим образом:
Образец задачи
(2)(0) + (4) )(2) = 0 + 8 = 8
(3)(1) + (3)(4) = 3 + 12 = 15
(3)(0) + (3)(2) = 0 + 6 = 6
(4)(2) + (2)(3) = 8 + 6 = 14
(4)(4) + (2)(3) = 16 + 6 = 22 Двоичное мышление

100 × 1 = 100
457 820 × 1 = 457 820 Пример задачи
Итак, мы комбинируем первую строку T с I , первый столбец, чтобы найти X:
(2) )(0) + (2)(0) = 2 + 0 + 0 = 2 Мы продолжаем действовать по этому шаблону и получаем произведение, точно такое же, как T , потому что умножение матрицы на I похоже на умножение числа на число 1.
Правило: Всякий раз, когда мы умножаем матрицу на единичную матрицу, ответ всегда такой же, как и у неединичной матрицы. Да, мы вернули курсив для этого очень важного правила.
А нулевая матрица? Ну, мы же помним, что любое число, умноженное на ноль, равно нулю. Точно так же нулевая матрица действует при умножении матриц. Это все нулевые матрицы:
Правило: Всякий раз, когда мы умножаем матрицу на нулевую матрицу, ответ всегда будет нулевой матрицей, которая имеет то же количество строк, что и первая матрица, и то же количество столбцов, что и вторая матрица.
Пример задачи
Мы знаем, что их можно перемножить, потому что количество столбцов в первой матрице (3) совпадает с количеством строк во второй (тоже 3). Мы также знаем, что матрица произведения будет матрицей 3 × 3, потому что матрица произведения будет иметь то же количество строк, что и первая матрица, и то же количество столбцов, что и вторая матрица.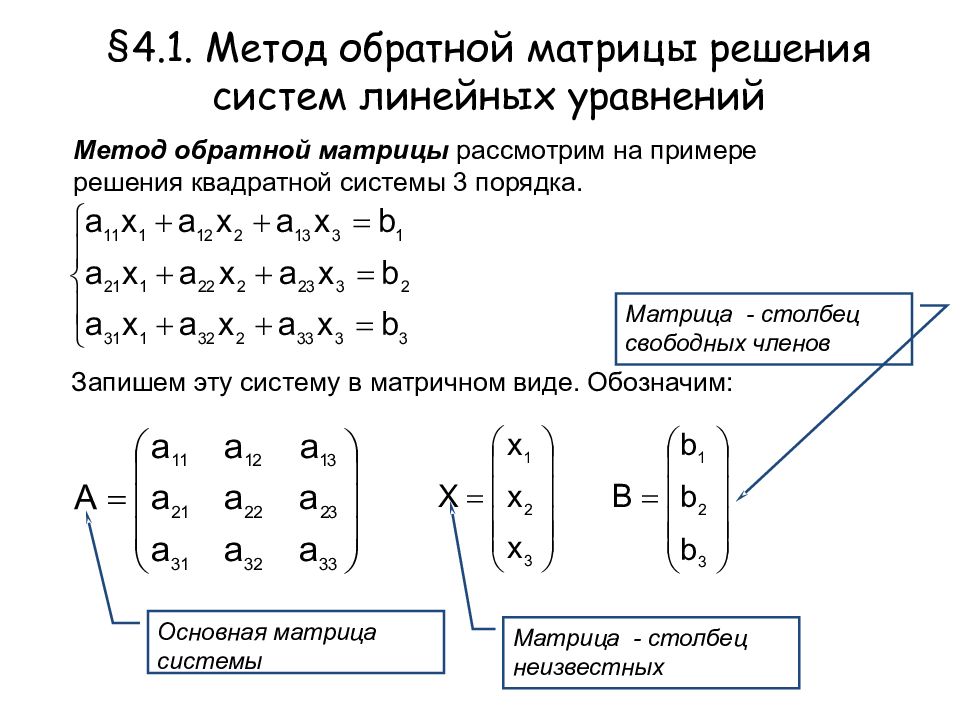

 Клацаем по пиктограмме «Вставить функцию».
Клацаем по пиктограмме «Вставить функцию».
 Щелкаем по значку «Вставить функцию».
Щелкаем по значку «Вставить функцию».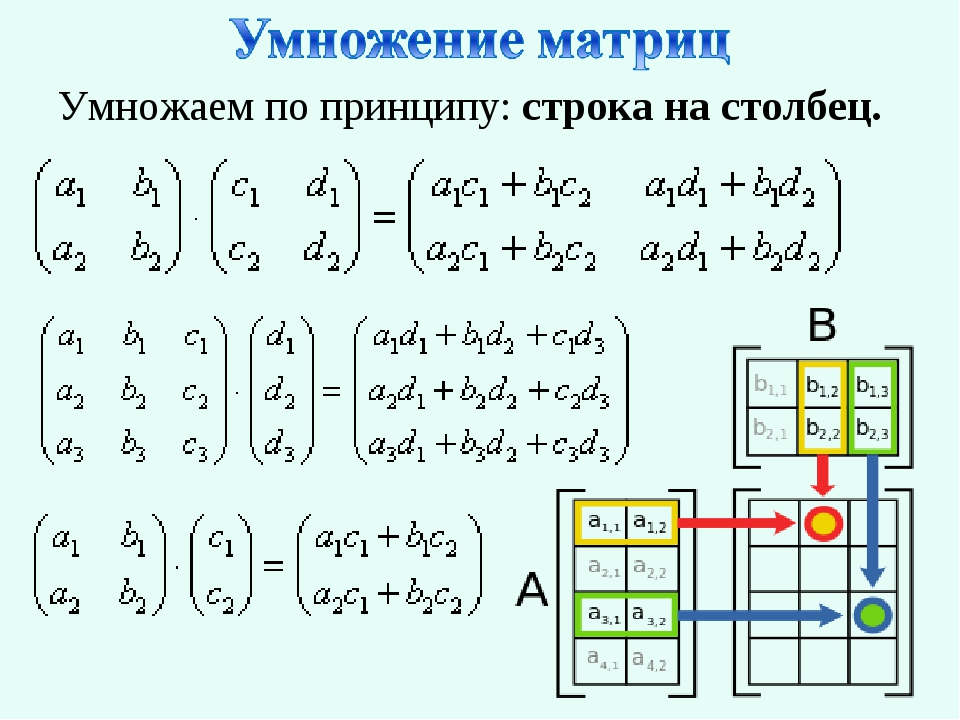

 Как и в предыдущем случае, тут тоже нужно сделать определенные координаты абсолютными, но на этот раз не координаты столбцов, а адреса строк. Поэтому ставим знак доллара перед цифрами в ссылке, которая отображается в поле. Можно также выделить всё выражение и дважды кликнуть по клавише
Как и в предыдущем случае, тут тоже нужно сделать определенные координаты абсолютными, но на этот раз не координаты столбцов, а адреса строк. Поэтому ставим знак доллара перед цифрами в ссылке, которая отображается в поле. Можно также выделить всё выражение и дважды кликнуть по клавише  Наводим курсор на нижний правый угол ячейки, в которой расположена формула. Курсор преобразуется в черный крестик. Это и есть маркер заполнения. Зажимаем левую кнопку мыши и протягиваем курсор по всему вышеуказанному диапазону. Сама начальная ячейка с формулой должна стать левым верхним элементом данного массива.
Наводим курсор на нижний правый угол ячейки, в которой расположена формула. Курсор преобразуется в черный крестик. Это и есть маркер заполнения. Зажимаем левую кнопку мыши и протягиваем курсор по всему вышеуказанному диапазону. Сама начальная ячейка с формулой должна стать левым верхним элементом данного массива.
 По сути, именно здесь отдельные элементы умножаются вместе и добавляются. Из нашего предыдущего примера Excel, для
По сути, именно здесь отдельные элементы умножаются вместе и добавляются. Из нашего предыдущего примера Excel, для sum()>>tensor(60)
sum()>>tensor(60) ],
], , 1062., 1173., 1284.],
, 1062., 1173., 1284.], zeros(ar,bc)
zeros(ar,bc)
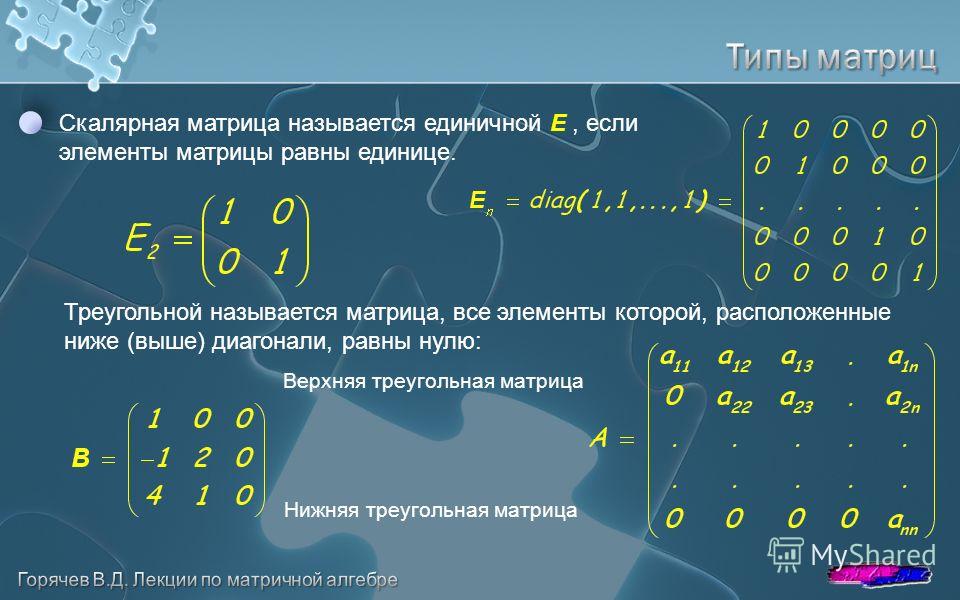

 , 0., 0., 0.],
, 0., 0., 0.],  , 2124., 2346., 2568.],
, 2124., 2346., 2568.],  Поскольку во внутренней системе Excel проценты хранятся в виде десятичных чисел, мы можем вставить либо 11%, либо 0,11 в ячейку B1.
Поскольку во внутренней системе Excel проценты хранятся в виде десятичных чисел, мы можем вставить либо 11%, либо 0,11 в ячейку B1.
 data.frame(c1, x1):
## ‘*’ определено только для фреймов данных одинакового размера
## Ошибка в Ops.data.frame(c1, x1):
## ‘*’ определено только для фреймов данных одинакового размера
data.frame(c1, x1):
## ‘*’ определено только для фреймов данных одинакового размера
## Ошибка в Ops.data.frame(c1, x1):
## ‘*’ определено только для фреймов данных одинакового размера