Как в физике обозначается: Как обозначается ширина длина высота в физике

Какой буквой в физике обозначается путь?

Какой буквой в физике обозначается путь?

Напомним, что обозначается он буквой S (иногда встречается обозначение L) и измеряется в СИ в метрах. Пройденный путь – это скалярная величина, т. е. величина, которая характеризуется только числовым значением.

Чему равно перемещение в физике?

Перемещение – направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю: Δr=0.

Что такое пройденный путь в физике?

Пройденный путь — это скалярная величина, которая обозначает расстояние, пройденное телом, в процессе перемещения. … Перемещение же представляет собой направленный отрезок, соединяющий начальную и конечную точки. А если тело в процессе движения вернулось в исходную точку, то его перемещение будет равно нулю.

Какой буквой в физике обозначается длина?

Для обозначений могут быть использованы и соответствующие заглавные буквы, в литературе часто встречается сочетание L, B, H (L – длина, В – ширина, Н — высота). Эти же буквы приняты и в физике для обозначения длины, ширины, высоты объектов.

Какой буквой обозначают ширину?

Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет.

Какой буквой обозначить длину?

Как обозначаются различные параметры В единой системе измерения используется обозначение латинскими буквами: длину буквой l, если речь идет об одной прямой линии: маятнике, рычаге, отрезке, прямой.

Какой буквой обозначается давление в физике?

— от лат. pressūra «давление». . Осмотическое давление часто обозначается буквой π.

Чему равняется давление?

Чтобы определить давление, надо силу, действующую перпендикулярно поверхности, разделить на площадь поверхности: давление = сила / площадь.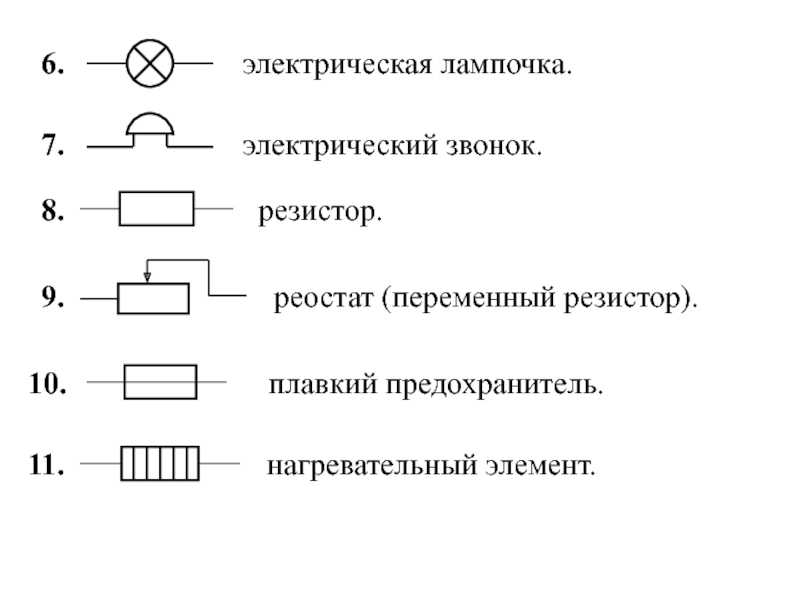 Обозначим величины, входящие в это выражение: давление – p, сила, действующая на поверхность, – F и площадь поверхности – S.

Как обозначается давление у человека?

Артериальное давление измеряется в миллиметрах ртутного столба (мм рт. ст.). Показатель систолического артериального давления всегда указывается первым, а диастолического – вторым. Нормальный показатель артериального давления находится в рамках 85.

Что значит давление 100 на 60?

Артериальная гипотония – патологическое снижение артериального давления (АД) менее 100/60 мм рт. ст., сопровождаемое головокружением, нарушением зрения, снижением мыслительных способностей и обмороками.

Что такое верхнее и нижнее давление?

Известно, что 120/70 или 120/80 – это оптимальные показатели АД здорового человека («как у космонавтов»), где первая цифра 120 – это верхнее или систолическое давление, а 70 или 80 – это диастолическое или нижнее давление.

Что означают цифры при измерении артериального давления?

Артериальное давление измеряют в миллиметрах ртутного столба. В карточку пациента, историю болезни вносят два показателя, разделенные наклонной чертой: 130/90 мм рт. ст. Первое число — это систолическое давление, второе — диастолическое.

Что означает вторая цифра в артериальном давлении?

Систолическое давление всегда выше второй цифры — значения диастолического давления, которое обозначает давление крови, когда желудочки расслаблены. В нашем примере диастолическое давление — 80. Измерять же давление крови в миллиметрах ртутного столба — дань традиции.

Какое низкое давление является критическим?

Пониженное давление хронического характера (гипотония) также может стать причиной того, что человек умрет. В случае гипотонии сложно сказать, при каком низком давлении человек умирает. Но показатели в 70/40 считаются критичными.

Что может быть из за низкого давления?

В большинстве случаев пациенты с низким давлением жалуются на значительное ухудшение самочувствия. Для гипотоников характерна сонливость, слабость, частые головные боли, ощущение холода в конечностях, озноб, тошнота. Возможно нарушение сердечного ритма, его учащение, головокружения, обмороки.

Почему бывает низкое давление?

Причинами такой гипотонии могут быть обезвоживание, слабость при длительном постельном режиме, беременность, диабет, высокая температура воздуха, заболевания сосудов (варикоз) , пожилой возраст. Такую симптоматику дают и некоторые серьезные неврологические заболевания . Постпрандиальная гипотониядостаточно редка.

Как повысить низкое давление у пожилых людей?

Что съесть, чтобы повысить давление

1. есть часто, от четырех до шести раз в день, но небольшими порциями;
2. плотно завтракать, вводя в рацион такие продукты как сыр, масло, творог, яйца, каша;
3. взять в привычку выпивать с утра чашку хорошего кофе или чая;
4. выпивать не менее 1,5 л воды в сутки;

Какие таблетки пить при низком давлении?

В некоторых случаях могут применяться более серьезные препараты.

• Кофеин Препарат выпускается в таблетках и растворах для введения подкожно. …
• Гутрон Выпускается в форме таблеток и капель для приема внутрь, отпускается по рецепту врача. …
• Экдистен …
• Кофетамин …
• Апилак

Как понять что низкое давление?

Симптомы низкого давления:

1. головокружение, потеря сознания, слабость, снижение памяти, внимания, работоспособности,
2. головная боль (в висках, в области лба),
3. тахикардия (учащенный пульс),
4. боли в области сердца (длится больше 30 минут),
5. тошнота, рвота, метеоризм, запоры.

Как определить высокое или низкое давление?

Посмотрите внимательно в зеркало. Если кожа на лице ярко розового цвета, с возможными пятнами красного цвета – это признак повышенного давления. При низких показателях АД лицо становится бледным и выглядит болезненно.

Что пить от головной боли при пониженном давлении?

Можно выпить чашку горячего сладкого кофе, лечь в кровать с опущенным головным концом и приподнятыми ногами, выпить таблетку безрецептурного «Цитрамона», так как в нём содержатся кофеин, который повышает артериальное давление, и парацетамол, который облегчает головную боль.

Как обозначается совершенная работа в физике. Механическая работа

Содержание:

Электрический ток вырабатывается для того, чтобы в дальнейшем использовать его в определенных целях, для совершения какой-либо работы. Благодаря электричеству, функционируют все приборы, устройства и оборудование. Сама работа представляет собой определенные усилия, прилагаемые для перемещения электрического заряда на установленное расстояние. Условно, такая работа в пределах участка цепи, будет равна численному значению напряжения на данном участке.

Для выполнения необходимых расчетов необходимо знать, в чем измеряется работа тока. Все расчеты проводятся на основании исходных данных, полученных с помощью измерительных приборов. Чем больше величина заряда, тем больше усилий требуется для его перемещения, тем большая работа будет совершена.

Что называют работой тока

Электрический ток, как физическая величина, сам по себе не имеет практического значения. Наиболее важным фактором является действие тока, характеризующееся выполняемой им работой. Сама работа представляет собой определенные действия, в процессе которых один вид энергии превращается в другой. Например, электрическая энергия с помощью вращения вала двигателя, превращается в механическую энергию. Работа самого электрического тока заключается в движении зарядов в проводнике под действием электрического поля. Фактически вся работа по перемещению заряженных частиц выполняется электрическим полем.

С целью выполнения расчетов должна быть выведена формула работы электрического тока. Для составления формул понадобятся такие параметры, как сила тока и . Поскольку работа электрического тока и работа электрического поля – это одно и то же, она будет выражаться в виде произведения напряжения и заряда, протекающего в проводнике. То есть: A = Uq. Данная формула была выведена из соотношения, определяющего напряжение в проводнике: U = A/q. Отсюда следует, что напряжение представляет собой работу электрического поля А по переносу заряженной частицы q.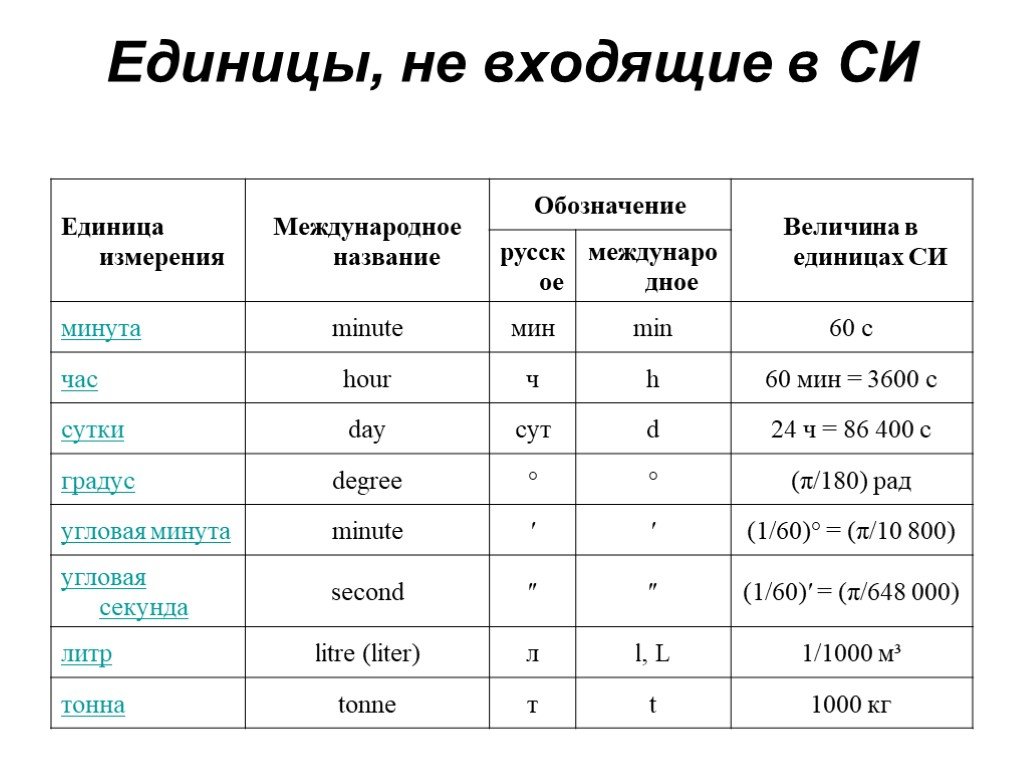

Сама заряженная частица или заряд отображается в виде произведения силы тока и времени, затраченного на движение этого заряда по проводнику: q = It. В этой формуле было использовано соотношение для силы тока в проводнике: I = q/t. То есть, является отношением заряда к промежутку времени, за которое заряд проходит через поперечное сечение проводника. В окончательном виде формула работы электрического тока будет выглядеть, как произведение известных величин: A = UIt.

В каких единицах измеряется работа электрического тока

Прежде чем непосредственно решать вопрос, в чем измеряется работа электрического тока, необходимо собрать единицы измерений всех физических величин, с помощью которых вычисляется этот параметр. Любая работа , следовательно, единицей измерения данной величины будет 1 Джоуль (1 Дж). Напряжение измеряется в вольтах, сила тока – в амперах, а время – в секундах. Значит единица измерения будет выглядеть следующим образом: 1 Дж = 1В х 1А х 1с.

Исходя из полученных единиц измерения, работа эл тока будет определяться, как произведение силы тока на участке цепи, напряжения на концах участка и промежутка времени, за которое ток протекает по проводнику.

Измерение проводятся с помощью , вольтметра и часов. Эти приборы позволяют эффективно решить проблему, как найти точное значение данного параметра. При включении амперметра и вольтметра в цепь, необходимо следить за их показаниями в течение установленного промежутка времени. Полученные данные вставляются в формулу, после чего выводится конечный результат.

Функции всех трех приборов объединяются в электросчетчиках, учитывающих потребленную энергию, а фактически работу, совершенную электротоком. Здесь используется уже другая единица – 1 кВт х ч, что также означает, сколько работы было совершено в течение единицы времени.

В повседневной жизни часто приходится встречаться с таким понятием как работа. Что это слово означает в физике и как определить работу силы упругости? Ответы на эти вопросы вы узнаете в статье.

Механическая работа

Работа – это скалярная алгебраическая величина, которая характеризует связь между силой и перемещением. При совпадении направления этих двух переменных она вычисляется по следующей формуле:

• F – модуль вектора силы, которая совершает работу;
• S – модуль вектора перемещения.

Не всегда сила, которая действует на тело, совершает работу. Например, работа силы тяжести равна нулю, если ее направление перпендикулярно перемещению тела.

Если вектор силы образует отличный от нуля угол с вектором перемещения, то для определения работы следует воспользоваться другой формулой:

A=FScosα

α – угол между векторами силы и перемещения.

Значит, механическая работа – это произведение проекции силы на направление перемещения и модуля перемещения, или произведение проекции перемещения на направление силы и модуля этой силы.

Знак механической работы

В зависимости от направления силы относительно перемещения тела работа A может быть:

• положительной (0°≤ α
• отрицательной (90°
• равной нулю (α=90°).

Если A>0, то скорость тела увеличивается. Пример – падение яблока с дерева на землю. При A

Единица измерения работы в СИ (Международной системе единиц) – Джоуль (1Н*1м=Дж). Джоуль – это работа силы, значение которой равно 1 Ньютону, при перемещении тела на 1 метр в направлении действия силы.

Работа силы упругости

Работу силы можно определить и графическим способом. Для этого вычисляется площадь криволинейной фигуры под графиком F s (x).

Так, по графику зависимости силы упругости от удлинения пружины, можно вывести формулу работы силы упругости.

Она равна:

A=kx 2 /2

• k – жесткость;
• x – абсолютное удлинение.

Что мы узнали?

Механическая работа совершается при действии на тело силы, которая приводит к перемещению тела. В зависимости от угла, который возникает между силой и перемещением, работа может быть равна нулю или иметь отрицательный или положительный знак. На примере силы упругости вы узнали о графическом способе определения работы.

1.5. МЕХАНИЧЕСКАЯ РАБОТА И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ

Понятие энергии. Механическая энергия. Работа – количественная мера изменения энергии. Работа равнодействующей сил. Работа сил в механике. Понятие мощности. Кинетическая энергия как мера механического движения. Связь изменения ки нетической энергии с работой внутренних и внешних сил. Кинетическая энергия системы в различных системах отсчета. Теорема Кенига.

Энергия – это универсальная мера различных форм движения и взаимодействия.

Механи́ческая эне́ргия описывает сумму потенциальной и кинетической энергии , имеющихся в компонентах механической системы . Механическая энергия – это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.

Работа силы – это количественная характеристика процесса обмена энергией между взаимодействующими телами.

Пусть частица под действием силы совершает перемещение по некоторой траектории 1-2 (рис. 5.1). В общем случае сила в процессе

движения частицы может изменяться как по модулю, так и по направлению.

Рассмотрим, как показано на рис.5.1, элементарное перемещение , в пределах которого силу можно считать постоянной.

Действие силы на перемещении характеризуют величиной, равной скалярному произведению , которую называют элементарной работой силы на перемещении . Ее можно представить и в другом виде:

,

где – угол между векторами и – элементарный путь, проекция вектора на векторобозначена (рис. 5.1).

Итак, элементарная работа силы на перемещении

.

Величина – алгебраическая: в зависимости от угла между векторами силы и или от знака проекции вектора силы на вектор перемещения она может быть как положительной, так и отрицательной и, в частности, равной нулю, если т.е. . Единицей измерения работы в вивтеме СИ служит Джоуль, сокращенное обозначение Дж.

Суммируя (интегрируя) выражение (5.1) по всем элементарным участкам пути от точки 1 до точки 2, найдем работу силы на данном перемещении:

видно, что элементарная работа A численно равна площади заштрихованной полоски, а работа А на пути от точки 1 до точки 2 – площади фигуры, ограниченной кривой, ординатами 1 и 2 и осью s. При этом площадь фигуры над осью s берется со знаком плюс (она соответствует положительной работе), а площадь фигуры под осью s – со знаком минус (она соответствует отрицательной работе).

Рассмотрим примеры на вычисление работы. Работа упругой силы где – радиус-вектор частицы А относительно точки О (рис. 5.3).

Переместим частицу A, на которую действует эта сила, по произвольному пути из точки 1 в точку 2. Найдем сначала элементарную работу силы на элементарном перемещении :

.

Скалярное произведение где проекция вектора перемещения на вектор . Эта проекция равна приращению модуля вектора Поэтому и

Теперь вычислим работу данной силы на всем пути, т. е. проинтегрируем последнее выражение от точки 1 до точки 2:

Вычислим работу гравитационной (или аналогичной ей математически силы кулоновской) силы. Пусть в начале вектора (рис. 5.3) находится неподвижная точечная масса (точечный заряд). Определим работу гравитационной (кулоновской) силы при перемещении частицы А из точки 1 в точку 2 по произвольному пути. Сила, действующая на частицу А, может быть представлена так:

где параметр для гравитационного взаимодействия равен , а для кулоновского взаимодействия его значение равно . Вычислим сначала элементарную работу этой силы на перемещении

Как и в предыдущем случае, скалярное произведение поэтому

.

Работа же этой силы на всем пути от точки 1 до точки 2

Рассмотрим теперь работу однородной силы тяжести . Запишем эту силу в виде где орт вертикальной оси z с положительным направлением обозначен (рис.5.4). Элементарная работа силы тяжести на перемещении

Скалярное произведение гдепроекция на орт равная – приращению координаты z. Поэтому выражение для работы приобретает вид

Работа же данной силы на всем пути от точки 1 до точки 2

Рассмотренные силы интересны в том отношении, что их работа, как видно из формул (5. 3) – (5.5), не зависит от формы пути между точками 1 и 2, а зависит только от положения этих точек. Эта весьма важная особенность данных сил присуща, однако, не всем силам. Например, сила трения этим свойством не обладает: работа этой силы зависит не только от положения начальной и конечной точек, но и от формы пути между ними.

До сих пор речь шла о работе одной силы. Если же на частицу в процессе движения действуют несколько сил, результирующая которых то нетрудно показать, что работа результирующей силы на некотором перемещении равна алгебраической сумме работ, совершаемых каждой из сил в отдельности на том же перемещении. Действительно,

Введем в рассмотрение новую величину – мощность. Она используется для характеристики скорости, с которой совершается работа. Мощность , по определению, – это работа, совершаемая силой за единицу времени . Если за промежуток времени сила совершает работу , то мощность, развиваемая этой силой в данный момент времени, есть Учитывая, что , получим

Единица мощности в системе СИ – Ватт, сокращенное обозначение Вт.

Таким образом, мощность, развиваемая силой , равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения данной силы. Как и работа, мощность – величина алгебраическая.

Зная мощность силы , можно найти и работу, которую совершает эта сила за промежуток времени t. В самом деле, представив подынтегральное выражение в (5.2) в виде получим

Следует также обратить внимание на одно весьма существенное обстоятельство. Когда говорят о работе (или мощности), то необходимо в каждом конкретном случае четко указывать или представлять себе, работа какой именно силы (или сил) имеется в виду. В ином случае, как правило, неизбежны недоразумения.

Рассмотрим понятие кинетической энергии частицы . Пусть частица массы т движется под действием некоторой силы (в общем случае эта сила может быть результирующей нескольких сил). Найдем элементарную работу, которую совершает эта сила на элементарном перемещении . Имея в виду, что и , запишем

.

Скалярное произведение где проекция вектора на направление вектора . Эта проекция равна – приращению модуля вектора скорости. Поэтому и элементарная работа

Отсюда видно, что работа результирующей силы идет на приращение некоторой величины стоящей в скобках, которую называют кинетической энергией частицы.

а при конечном перемещении из точки 1 в точку 2

(5. 10 )

т. е. приращение кинетической энергии частицы на некотором перемещении равно алгебраической сумме работ всех сил , действующих на частицу на том же перемещении. Если то т. е. кинетическая энергия частицы увеличивается; если же то то есть кинетическая энергия уменьшается.

Уравнение (5.9) можно представить и в другой форме, поделив обе части его на соответствующий промежуток времени dt:

(5. 11 )

Это значит, что производная кинетической энергии частицы по времени равна мощности N результирующей силы, действующей на частицу.

Теперь введем понятие кинетической энергии системы . Рассмотрим в некоторой системе отсчета произвольную систему частиц. Пусть частица системы имеет в данный момент кинетическую энергию . Приращение кинетической энергии каждой частицы равно, согласно (5.9), работе всех сил, действующих на эту частицу: Найдем элементарную работу, которую совершают все силы, действующие на все частицы системы:

где – суммарная кинетическая энергия системы. Заметим, что кинетическая энергия системы – величина аддитивная : она равна сумме кинетических энергий отдельных частей системы независимо от того, взаимодействуют они между собой или нет.

Итак, приращение кинетической энергии системы равно работе, которую совершают все силы, действующие на все частицы системы . При элементарном перемещении всех частиц

(5.1 2 )

а при конечном перемещении

т. е. производная кинетической энергии системы по времени равна суммарной мощности всех сил, действующих на все частицы системы ,

Теорема Кенига: кинетическую энергию K системы частиц можно представить как сумму двух слагаемых: а) кинетической энергии mV c 2 /2 воображаемой материальной точки, масса которой равна массе всей системы, а скорость совпадает со скоростью центра масс; б) кинетической энергии K отн системы частиц, вычисленной в системе центра масс.

Практически все, не задумываясь, ответят: во втором. И будут неправы. Дело обстоит как раз наоборот. В физике механическая работа описывается следующими определениями: механическая работа совершается тогда, когда на тело действует сила, и оно движется. Механическая работа прямо пропорциональна приложенной силе и пройденному пути.

Формула механической работы

Определяется механическая работа формулой:

где A – работа, F – сила, s – пройденный путь.

ПОТЕНЦИА́Л (потенциальная функция), понятие, характеризующее широкий класс физических силовыхполей (электрических, гравитационных и т. п.) и вообще поля физических величин, представляемыхвекторами (поле скоростей жидкости и т. п.). В общем случае потенциал векторного поля a(x ,y ,z ) – такаяскалярная функция u (x ,y ,z ), что a=grad

35. Проводники в электрическом поле. Электроемкость. Проводники в электрическом поле. Проводники – это вещества, характеризующиеся наличием в них боль­шого количества свободных носителей зарядов, способ­ных перемещаться под действием электрического поля. К проводникам относятся металлы, электролиты, уголь. В металлах носителями свободных зарядов являются электроны внешних оболочек атомов, которые при взаи­модействии атомов полностью утрачивают связи со «своими» атомами и становятся собственностью всего проводника в целом. Свободные электроны участвуют в тепловом движении подобно молекулам газа и могут перемещаться по металлу в любом направлении. Электри́ческая ёмкость – характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками

36. Емкость плоского конденсатора.

Емкость плоского конденсатора.

Т.о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости. Для создания конденсатора большой емкости необходимо увеличить площадь пластин и уменьшить толщину слоя диэлектрика.

37. Магнитное взаимодействие токов в вакууме. Закон Ампера. Закон Ампера. В 1820 году Ампер (французский ученый (1775-1836)) установил экспериментально закон, по которому можно рассчитать силу, действующую на элемент проводника длины с током .

где – вектор магнитной индукции,– вектор элемента длины проводника, проведенного в направлении тока.

Модуль силы , где– угол между направлением тока в проводнике и направлением индукции магнитного поля.Для прямолинейного проводника длиной с токомв однородном поле

Направление действующей силы может быть определено с помощью правила левой руки :

Если ладонь левой руки расположить так, чтобы нормальная (к току) составляющая магнитного поля входила в ладонь, а четыре вытянутых пальца направлены вдоль тока, то большой палец укажет направление, в котором действует сила Ампера.

38.Напряженность магнитного поля. Закон Био-Савара-Лапласа Напряжённость магни́тного по́ля (стандартное обозначение Н ) – векторная физическая величина , равная разности вектора магнитной индукции B и вектора намагниченности J .

В Международной системе единиц (СИ) : где-магнитная постоянная .

Закон БСЛ. Закон, определяющий магнитное поле отдельного элемента тока

39. Приложения закона Био-Савара-Лапласа. Для поля прямого тока

Для кругового витка.

И для соленоида

40. Индукция магнитного поля Магнитное поле характеризуется векторной величиной, которая носит название индукции магнитного поля (векторная величина, являющаяся силовой характеристикой магнитного поля в данной точке пространства). МИ. (В) это не сила, действующая на проводники, это величина, которая находится через данную силу по следующей формуле: B=F / (I*l) (Словестно: Модуль вектора МИ. (B) равен отношению модуля силы F, с которой магнитное поле действует на расположенный перпендикулярно магнитным линиям проводник с током, к силе тока в проводнике I и длине проводника l . Магнитная индукция зависит только от магнитного поля. В связи с этим индукцию можно считать количественной характеристикой магнитного поля. Она определяет, с какой силой(Сила Лоренца) магнитное поле действует назаряд, движущийся со скоростью. 2/R играет роль центростремительной силы. Период обращения равен T=2пиR/V=2пиm/qB и он не зависит от скорости частицы (Это справедливо только при V

Сила Л. определяется соотношением: Fл = q·V·B·sina (q – величина движущегося заряда; V – модуль его скорости; B – модуль вектора индукции магнитного поля; aльфа – угол между вектором V и вектором В) Сила Лоренца перпендикулярна скорости и поэтому она не совершает работы, не изменяет модуль скорости заряда и его кинетической энергии. Но направление скорости изменяется непрерывно. Сила Лоренца перпендикулярна векторам В и v , и её направление определяется с помощью того же правила левой руки, что и направление силы Ампера: если левую руку расположить так, чтобы составляющая магнитной индукции В, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца F л.

Физика | Определение, типы, темы, важность и факты

Модель давления газа Бернулли

Смотреть все СМИ

Ключевые люди:

Райнер Вайс Донна Стрикленд Артур Эшкин Эдвард Александр Буше Барри С. Бэриш

Похожие темы:

механика оптика квантовая механика сила тяжести космология

Просмотреть весь связанный контент →

Популярные вопросы

Что такое физика?

Физика — это отрасль науки, изучающая структуру материи и то, как взаимодействуют фундаментальные составляющие Вселенной. Он изучает объекты, начиная от очень маленьких, используя квантовую механику, и заканчивая всей вселенной, используя общую теорию относительности.

Почему физика работает в единицах СИ?

Физики и другие ученые используют в своей работе Международную систему единиц (СИ), потому что они хотят использовать систему, принятую учеными всего мира. С 2019 годаединицы СИ были определены в терминах фундаментальных физических констант, а это означает, что ученые, где бы они ни использовали СИ, могут договориться о единицах, которые они используют для измерения физических явлений.

Сводка

Прочтите краткий обзор этой темы

физика , наука, изучающая структуру материи и взаимодействия между фундаментальными составляющими наблюдаемой вселенной. В самом широком смысле физика (от греческого physikos ) касается всех аспектов природы как на макроскопическом, так и на субмикроскопическом уровнях. Область его изучения охватывает не только поведение объектов под действием заданных сил, но и природу и происхождение гравитационных, электромагнитных и ядерных силовых полей. Его конечной целью является формулировка нескольких всеобъемлющих принципов, которые объединяют и объясняют все такие разрозненные явления.

(Читайте эссе Эйнштейна «Британика» 1926 года о пространстве-времени. )

Физика является фундаментальной физической наукой. До сравнительно недавнего времени физика и натурфилософия взаимозаменяемо обозначали науку, целью которой является открытие и формулировка фундаментальных законов природы. По мере того как современные науки развивались и становились все более специализированными, физика стала обозначать ту часть физической науки, которая не включалась в астрономию, химию, геологию и инженерию. Физика, однако, играет важную роль во всех естественных науках, и во всех таких областях есть разделы, в которых физические законы и измерения получают особое внимание, носящие такие названия, как астрофизика, геофизика, биофизика и даже психофизика. Физику можно, по сути, определить как науку о материи, движении и энергии. Его законы обычно выражаются экономно и точно на языке математики.

Как эксперимент, наблюдение за явлениями в максимально точно контролируемых условиях, так и теория, формулировка единой концептуальной основы, играют существенную и взаимодополняющую роль в развитии физики. Физические эксперименты приводят к измерениям, которые сравниваются с результатом, предсказанным теорией. Говорят, что теория, которая надежно предсказывает результаты экспериментов, к которым она применима, воплощает закон физики. Однако закон всегда может быть изменен, заменен или ограничен более ограниченной областью, если более поздний эксперимент сделает это необходимым.

Викторина “Британника”

Как много вы знаете о физике?

Конечная цель физики — найти единый набор законов, управляющих материей, движением и энергией на малых (микроскопических) субатомных расстояниях, в человеческом (макроскопическом) масштабе повседневной жизни и на самых больших расстояниях (например, во внегалактическом масштабе). Эта амбициозная цель была достигнута в значительной степени. Хотя полностью единая теория физических явлений еще не создана (и, возможно, никогда не будет), кажется, что удивительно небольшой набор фундаментальных физических законов может объяснить все известные явления. Совокупность физики, разработанная примерно к началу 20-го века и известная как классическая физика, может в значительной степени объяснить движения макроскопических объектов, движущихся медленно относительно скорости света, а также такие явления, как тепло, звук, электричество, магнетизм и свет. Современные разработки теории относительности и квантовой механики видоизменяют эти законы в той мере, в какой они применимы к более высоким скоростям, очень массивным объектам и к крошечным элементарным составляющим материи, таким как электроны, протоны и нейтроны.

Объем физики

Традиционно организованные разделы или области классической и современной физики описаны ниже.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подписаться сейчас

Под механикой обычно понимают изучение движения объектов (или отсутствия их движения) под действием заданных сил. Классическую механику иногда считают разделом прикладной математики. Он состоит из кинематики, описания движения и динамики, изучения действия сил при создании либо движения, либо статического равновесия (последнее составляет науку о статике). Предметы 20-го века квантовой механики, имеющие решающее значение для изучения структуры материи, субатомных частиц, сверхтекучести, сверхпроводимости, нейтронных звезд и других важных явлений, и релятивистской механики, важной, когда скорости приближаются к скорости света, являются формами механики, которые будут будут обсуждаться далее в этом разделе.

В классической механике законы изначально формулируются для точечных частиц, в которых не учитываются размеры, форма и другие внутренние свойства тел. Таким образом, в первом приближении даже такие большие объекты, как Земля и Солнце, рассматриваются как точечные, например, при расчете планетарного орбитального движения. В динамике твердого тела также учитываются протяженность тел и распределение их масс, но предполагается, что они не способны деформироваться. Механика деформируемых твердых тел — это упругость; гидростатика и гидродинамика рассматривают, соответственно, жидкости в состоянии покоя и в движении.

Три закона движения, сформулированные Исааком Ньютоном, составляют основу классической механики вместе с признанием того, что силы являются направленными величинами (векторами) и соответственно комбинируются. Первый закон, также называемый законом инерции, гласит, что, если на него не действует внешняя сила, покоящийся объект остается в покое или, если он движется, он продолжает двигаться по прямой линии с постоянной скоростью. Следовательно, равномерное движение не требует причины. Соответственно, механика сосредотачивается не на движении как таковом, а на изменении состояния движения объекта, которое является результатом действующей на него результирующей силы. Второй закон Ньютона приравнивает результирующую силу, действующую на объект, к скорости изменения его количества движения, которое является произведением массы тела на его скорость. Третий закон Ньютона, закон действия и противодействия, гласит, что при взаимодействии двух частиц силы, действующие друг на друга, равны по величине и противоположны по направлению. В совокупности эти законы механики в принципе позволяют определить будущие движения множества частиц, если известно их состояние движения в какой-то момент, а также силы, действующие между ними и на них извне. Из этого детерминированного характера законов классической механики в прошлом делались глубокие (и, вероятно, неверные) философские выводы, которые даже применялись к человеческой истории.

Лежащие на самом базовом уровне физики, законы механики характеризуются определенными свойствами симметрии, примером которых является вышеупомянутая симметрия между силами действия и противодействия. Другие симметрии, такие как инвариантность (т. е. неизменная форма) законов при отражениях и вращениях, совершаемых в пространстве, обращение времени или переход в другую часть пространства или в другую эпоху времени, присутствуют как в классических механике и в релятивистской механике, а с некоторыми ограничениями и в квантовой механике. Можно показать, что свойства симметрии теории имеют в качестве математических следствий основные принципы, известные как законы сохранения, которые утверждают постоянство во времени значений определенных физических величин при заданных условиях. Сохраняющиеся величины являются наиболее важными в физике; к ним относятся масса и энергия (в теории относительности масса и энергия эквивалентны и сохраняются вместе), импульс, угловой момент и электрический заряд.

Научное определение – Школа физики

Резюме

• Объясните, как объект должен быть смещен, чтобы сила, действующая на него, совершила работу.
• Объясните, как относительные направления силы и перемещения определяют, будет ли совершенная работа положительной, отрицательной или равной нулю.

Научное определение труда несколько отличается от его повседневного значения. Некоторые вещи, которые мы считаем тяжелой работой, например, написание экзамена или переноска тяжелого груза по ровной поверхности, не являются работой в том смысле, в каком ее определяют ученые. Научное определение работы раскрывает ее связь с энергией: всякий раз, когда работа выполняется, энергия передается.

Чтобы работа в научном смысле была совершена, должна быть приложена сила и должно быть смещение в направлении силы.

Формально работа , совершаемая над системой постоянной силой, определяется как произведение составляющей силы в направлении движения, умноженной на расстояние, на котором действует сила . Для одностороннего движения в одном измерении это выражается в виде уравнения как

.

, где работа, перемещение системы и угол между вектором силы и вектором смещения, как на рисунке 1. Мы также можем записать это как

Чтобы найти работу, совершаемую над системой, совершающей движение не в одном направлении или в двух или трех измерениях, мы разделим движение на односторонние одномерные сегменты и сложим работу, выполненную на каждом сегменте.

ЧТО ТАКОЕ РАБОТА?

Работа, совершаемая над системой постоянной силой, равна произведению составляющей силы в направлении движения, умноженной на расстояние, на котором действует сила . Для одностороннего движения в одном измерении это выражается в форме уравнения как

где работа, величина силы, действующей на систему, величина смещения системы, угол между вектором силы и вектором смещения

 

Рисунок 1. Примеры работы. (a) Работа, совершаемая силой F на этой газонокосилке, равна Fd cosθ . Обратите внимание, что F cosθ — это составляющая силы в направлении движения. (b) Человек, держащий портфель, не работает над ним, потому что перемещения нет. Никакая энергия не передается в портфель или из него. в) Человек, перемещающий портфель горизонтально с постоянной скоростью, не совершает над ним работы и не передает ему никакой энергии. (d) Над портфелем совершается работа, когда он поднимается по лестнице с постоянной скоростью, потому что обязательно присутствует составляющая силы F по направлению движения. Энергия передается в портфель и, в свою очередь, может быть использована для выполнения работы. (e) Когда портфель опускается, энергия передается из портфеля в электрический генератор. Здесь работа, проделанная над портфелем генератором, отрицательна, удаляя энергию из портфеля, потому что F и d направлены в противоположные стороны.

Чтобы понять, что означает определение работы, давайте рассмотрим другие ситуации, показанные на рисунке 1. Например, человек, держащий портфель на рисунке 1(b), не работает. Вот так Почему ты устаешь просто держать груз? Ответ в том, что ваши мышцы работают друг против друга, , но они не работают с интересующей нас системой («портфель-Земля» — см. главу 7.3 «Потенциальная гравитационная энергия» для более подробной информации). Для совершения работы должно быть перемещение, и должна быть составляющая силы в направлении движения. Например, человек, несущий портфель на ровной поверхности на рис. 1(с), не совершает над ним работы, потому что сила перпендикулярна движению. То есть и так

Напротив, когда сила, действующая на систему, имеет составляющую в направлении движения, например, на рисунке 1(d), работа — это — энергия передана в портфель. Наконец, на рис. 1(e) энергия передается от портфеля к генератору. Есть два хороших способа интерпретировать эту передачу энергии. Одна интерпретация состоит в том, что вес портфеля действует на генератор, давая ему энергию. Другая интерпретация состоит в том, что генератор совершает отрицательную работу над портфелем, тем самым удаляя из него энергию. На чертеже показан последний с усилием генератора вверх на портфеле и смещением вниз. Это делает и, следовательно, является отрицательным.

Работа и энергия имеют одни и те же единицы измерения. Из определения работы мы видим, что эти единицы равны силе, умноженной на расстояние. Таким образом, в единицах СИ работа и энергия измеряются в ньютон-метрах . Ньютон-метру дается специальное название джоулей (Дж), а один джоуль не является большим количеством энергии; он поднимет небольшое 100-граммовое яблоко на расстояние около 1 метра.

Пример 1. Расчет работы, которую необходимо совершить, чтобы толкнуть газонокосилку по большой лужайке

Какую работу совершает на газонокосилке человек на рис. 1(а), если он прикладывает постоянную силу под углом ниже горизонтально и толкает косилку по ровной поверхности? Преобразуйте количество работы из джоулей в килокалории и сравните его со средним ежедневным потреблением этим человеком (около ) пищевой энергии. Один калория (1 кал) тепла — это количество тепла, необходимое для нагревания 1 г воды и эквивалентное ему, в то время как одна пищевая калория (1 ккал) эквивалентна

Стратегия

Мы можем решить эту задачу следующим образом: подставляя данные значения в определение работы, совершаемой над системой, выраженной в уравнении. Сила, угол и перемещение заданы, так что неизвестна только работа.

Решение

Уравнение работы

Подстановка известных значений дает

Преобразование работы в джоулях в килокалории Отношение выполненной работы к суточному потреблению составляет типичный. Очень небольшая часть энергии, высвобождаемой при потреблении пищи, используется для выполнения работы. Даже когда мы «работаем» весь день, менее 10% энергии, потребляемой с пищей, используется для выполнения работы, а более 90% преобразуется в тепловую энергию или запасается в виде химической энергии в жире.

• Работа — это передача энергии силой, действующей на объект при его перемещении.