Как в физике пишется сила: Сила в физике — что такое? В чем измеряется? Определение

Сила в физике — что такое? В чем измеряется? Определение

Какие ассоциации возникают у вас со словом «сильный» или «сильная»? Возможно, вы представляете себе спортсмена, который с легкостью поднимает тяжелую штангу или гирю. Или большого африканского слона, который может нести в хоботе огромный ствол дерева. А может, вам на ум приходит ваша мама, которая занимается домашними делами каждый день, без выходных и отпуска?

В каждом случае мы характеризуем человека или животное, но можно ли рассчитать силу количественно? Есть ли разница между силами? Как можно измерить эту величину? На эти и многие другие вопросы вы получите ответы в этой статье.

Определение силы

Начнем с самого главного — со слова «сила» в физике.

Сила — векторная физическая величина, которая является мерой воздействия на данное тело со стороны других тел или полей.

Представьте, что вы ходите по супермаркету и выбираете продукты, бережно складывая их в тележку. Вы передвигаете ее с помощью силы ваших мускулов, и чем сильнее вы напряжете руки и толкнете тележку, тем на большее расстояние она укатится (только аккуратно, не попадите в стенд с газировкой!).

Или вспомните урок физкультуры, где соревнуются в перетягивании каната: команда соперников может даже потерять равновесие, если вы одновременно с вашими друзьями потянете канат на себя.

Результаты действия сил мы можем видеть постоянно: любой подброшенный предмет падает на землю, тела плавают на поверхности жидкости, пружины растягиваются под весом груза. Даже Вселенная подчиняется законам сил: астероиды летают по определенным траекториям, а черные дыры со всей своей мощью поглощают свет далеких звезд. 💫

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Обозначение и единица измерения

У любой физической величины есть свое обозначение и единица измерения. Как же сила обозначается в физике?

Все просто. Сила обозначается латинской буквой F (кстати, на английском языке «сила» — force), а измеряется в ньютонах [H] — в честь великого английского ученого сэра Исаака Ньютона.

Возможно, вы слышали легенду про Ньютона: как он сидел под деревом и размышлял о физических законах, как ему на голову упало яблоко, и это зародило в нем новые гипотезы… Так вот, спешим развеять этот миф: на самом деле такого не происходило. Исаак Ньютон действительно сделал открытия о законах движения и всемирном тяготении, но в этом ему помогли отнюдь не яблоки!

Вернемся к единице измерения силы. Интересно, что ньютоны — это не основная, а производная единица международной системы СИ.

1 Н = 1 кг · м/с².

А значит, сила, равная одному ньютону, определяется как взаимодействие, которое за 1 секунду изменяет скорость тела массой 1 кг на 1 м/с в направлении действия силы.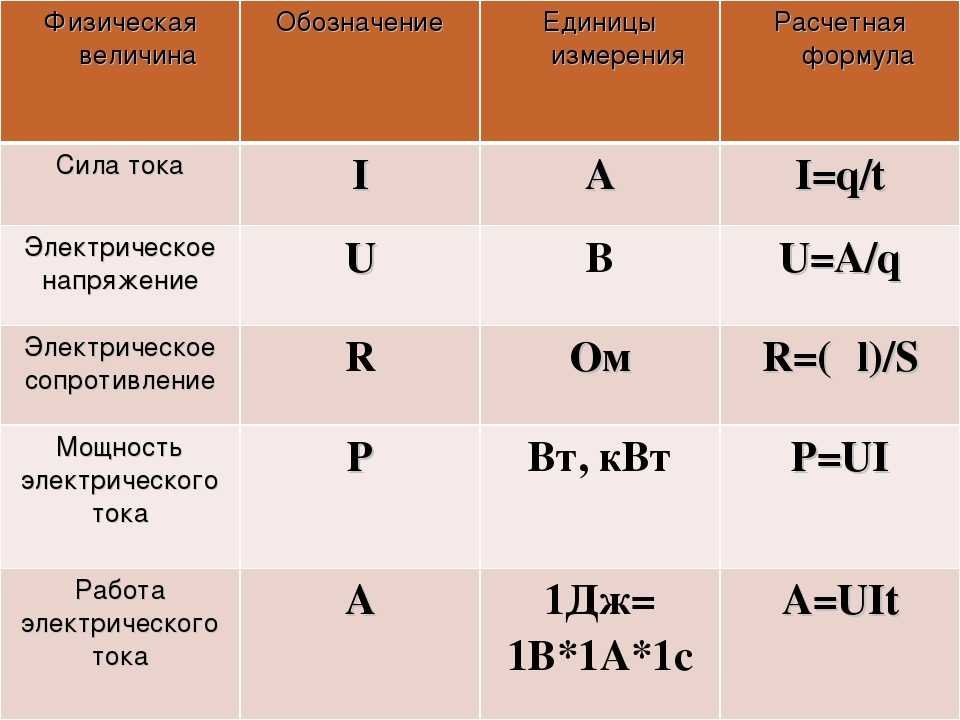

К ньютонам можно прибавлять дольные и кратные приставки, чтобы выразить величину как можно удобнее, не используя при этом огромное количество нулей.

Так, 1 кН = 1 000 Н; 1 гН = 100 Н; 1 мН = 0,001 Н.

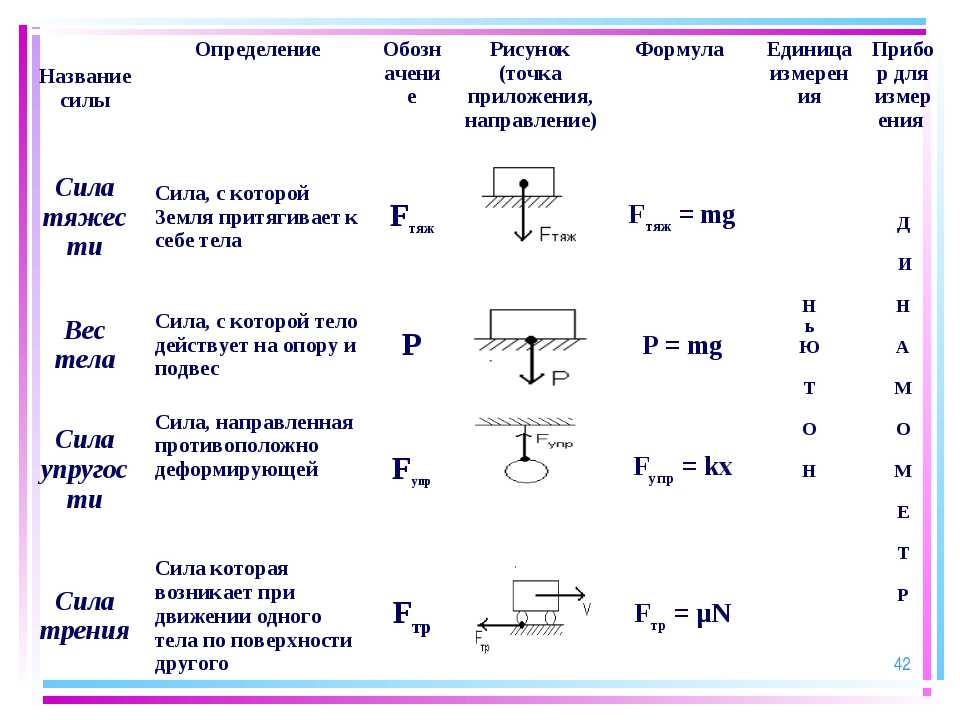
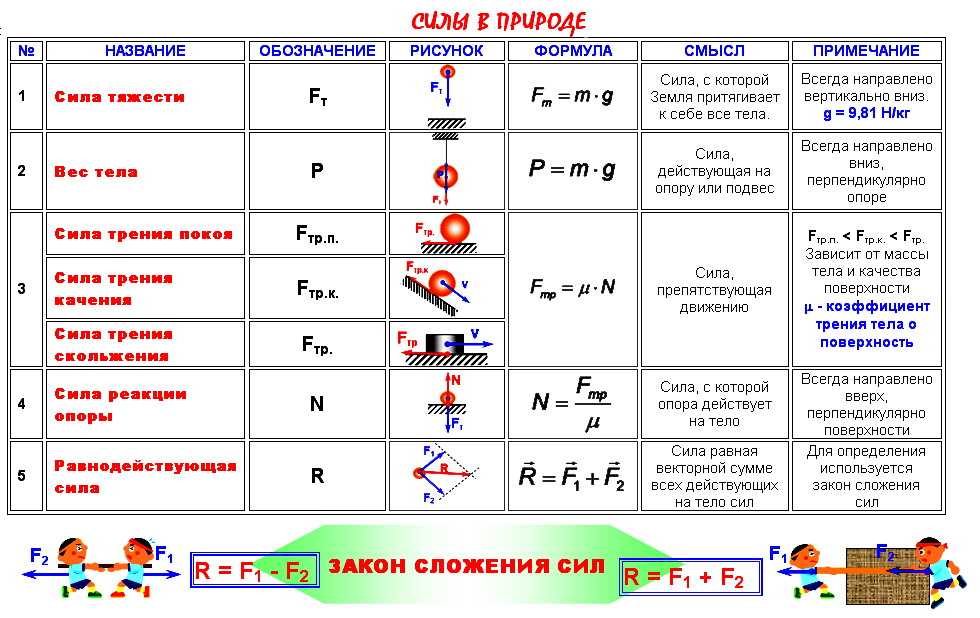
Классификация сил

А какие силы вообще существуют? Давайте разберемся вместе.

На фундаментальном уровне ученые выделяют четыре типа сил: слабые, сильные, гравитационные и электромагнитные.

1. Слабое взаимодействие происходит при распаде атомных ядер и элементарных частиц.

2. Сильное взаимодействие отвечает за притяжение между нуклонами — протонами и нейтронами в ядре атомов.

3. К гравитационным силам принято относить тот тип взаимодействий, которые происходят между материальными телами, имеющими массу. Сила тяготения и сила тяжести по праву относятся к такому типу, так как зависят прямо пропорционально от массы тела.

4. Электромагнитные силы действуют между всеми частицами, у которых есть электрические заряды. К ним можно отнести силу упругости, трения, вес тела, силу Архимеда и другие.

Сила как физическая величина характеризуется:

Рассмотрим таблицу и сравним некоторые силы по их направлению и точке приложения:

Сила	Направление	Точка приложения
Сила тяжести	Вертикально вниз	Центр массы тела
Вес	Противоположно силе реакции опоры	Точка на опоре/подвесе
Сила упругости	Вдоль пружины противоположно силе, вызвавшей деформацию	Точка соединения тела и пружины
Сила трения	Противоположно действующей силе	Точка соприкосновения тела с поверхностью
Сила Архимеда	Вертикально вверх	Центр массы тела

Бесплатные занятия по английскому с носителем

Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.

На все ли тела действуют силы?

Смотря какие. Думаем, для вас не секрет, что все тела состоят из молекул и атомов. На таком уровне между частицами существуют силы притяжения и отталкивания, от них никуда не деться. Если бы отсутствовали силы притяжения, молекулы бы разлетались друг от друга и не могли формировать тела. Уберите силы отталкивания, и все частицы слепятся в один большой комок.

На все тела в пределах планеты Земля действует сила тяжести. Именно поэтому все предметы, которые вы подбросите в воздух, устремятся вниз, а не вверх. Выйдя в открытый космос, мы попадем в состояние невесомости: на нас не будет действовать сила притяжения Земли. Но не спешите радоваться свободе! Во-первых, на космический корабль будет действовать аэродинамическая сила, а во-вторых, мы легко можем стать зависимы от силы притяжения другой планеты, как только приблизимся к ней.

Некоторые силы возникают только при определенных условиях. Возьмем любой предмет и начнем его деформировать, растягивать или сжимать — возникнет сила упругости. Погрузим тело в жидкость — появится сила Архимеда, начнем катить по дороге — движению будет препятствовать сила трения качения.

Измерение силы

Как можно измерить силу? Есть два верных способа: практически, с помощью измерительного прибора, и через формулы.

Прибор для измерения силы носит название

динамометр (от латинского «динамос» — сила). В зависимости от типа конструкции и применения динамометры бывают ручными, тяговыми, электронными, гидравлическими и пружинными.

В вопросе измерения сил с помощью формул есть множество нюансов. Какую формулу выбрать? Как научиться выражать неизвестное из формул? Где можно взять дополнительную информацию о величинах, значений которых нет в задаче? Ответы на все эти вопросы можно получить на онлайн-курсах физики в школе Skysmart! Уроки на интерактивной платформе проходят увлекательно, живо, с большим количеством опытов и экспериментов.

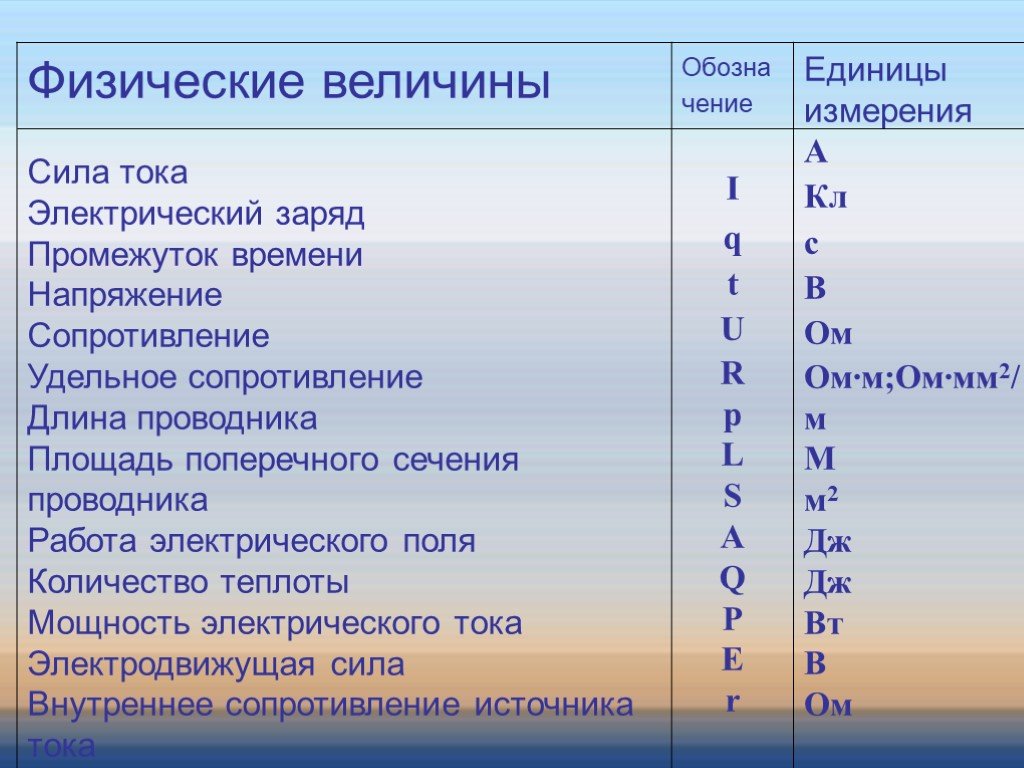
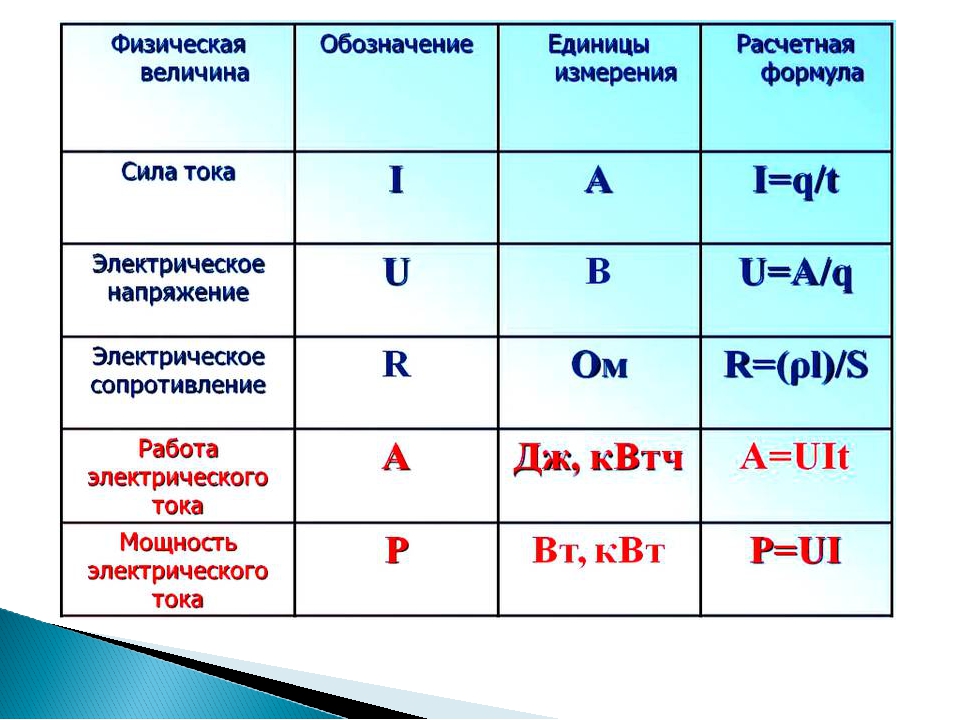
Сила тока в физике — что это такое?

Электрический ток

По проводам течет электрический ток. Причем он именно «течет», практически как вода. Представим, что вы — счастливый фермер, который решил полить свой огород из шланга. Вы чуть-чуть приоткрыли кран, и вода сразу же побежала по шлангу. Медленно, но все-таки побежала.

Сила струи очень слабая. Потом вы решили, что напор нужен побольше и открыли кран на полную катушку. В результате струя хлынет с такой силой, что ни один помидор не останется без внимания, хотя в обоих случаях диаметр шланга одинаков.

А теперь представьте, что вы наполняете два ведра из двух шлангов. У зеленого напор сильнее, у желтого — слабее. Быстрее наполнится то ведро, в которое льется вода из шланга с сильным напором. Все дело в том, что объем воды за равный промежуток времени из двух разных шлангов тоже разный. Иными словами, из зеленого шланга количество молекул воды выбежит намного больше, чем из желтого за равный период времени.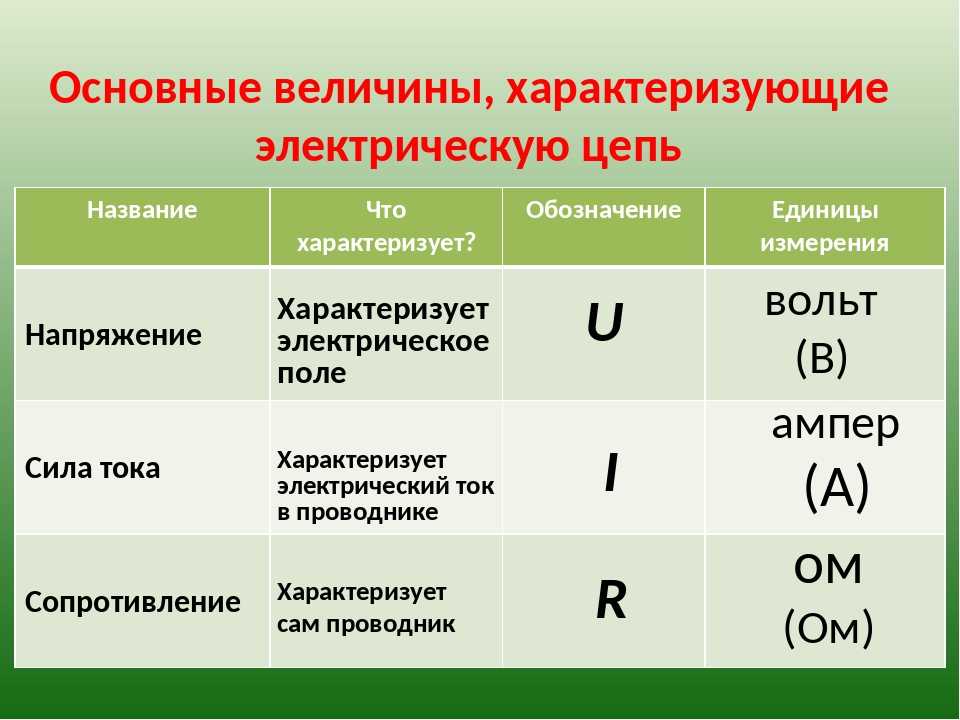

Если мы возьмем проводник с током, то будет происходить то же самое: заряженные частицы будут двигаться по проводнику, как и молекулы воды. Если больше заряженных частиц будет двигаться по проводнику, то «напор» тоже увеличится.

• Электрический ток — это направленное движение заряженных частиц.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Сила тока

Сразу возникает потребность в величине, которой мы будем «напор» электрического тока измерять. Такая, чтобы она зависела от количества частиц, которые протекают по проводнику.

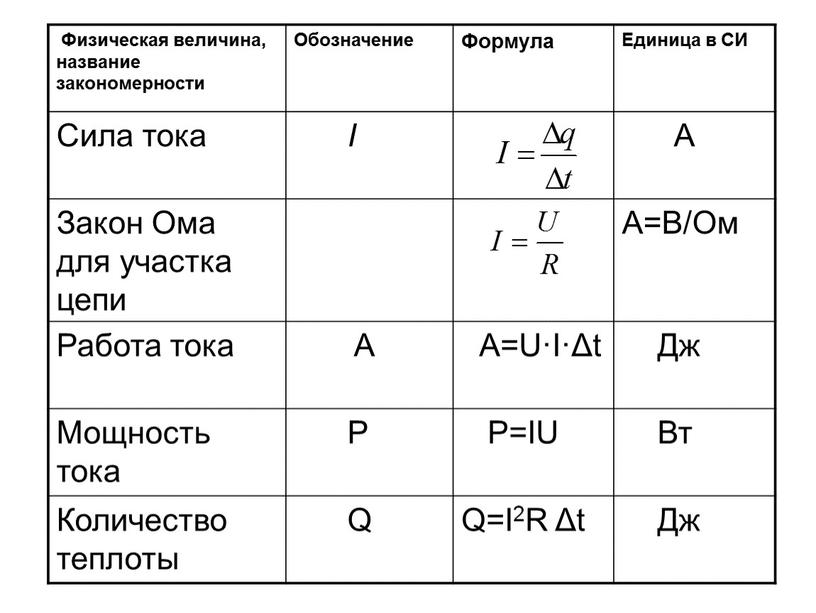
Сила тока — это физическая величина, которая показывает, какой заряд прошел через проводник за единицу времени.

Как обозначается сила тока?

Сила тока обозначается буквой I

Сила тока I = q/t I — сила тока [A] q — заряд [Кл] t — время [с]

Сила тока измеряется в амперах.

Единица измерения выбрана не просто так.

Во-первых, она названа в честь физика Андре-Мари Ампера, который занимался изучением электрических явлений. А во-вторых, единица этой величины выбрана на основе явления взаимодействия двух проводников.

Здесь аналогии с водопроводом провести, увы, не получится. Шланги с водой не притягиваются и не отталкиваются вблизи друг друга (а жаль, было бы забавно).

Когда ток проходит по двум параллельным проводникам в одном направлении, проводники притягиваются. А когда в противоположном направлении (по этим же проводникам) — отталкиваются.

За единицу силы тока 1 А принимают силу тока, при которой два параллельных проводника длиной 1 м, расположенные на расстоянии 1 м друг от друга в вакууме, взаимодействуют с силой 0,0000002 Н.

Задача

Найти силу тока в цепи, если за 2 секунды в ней проходит заряд, равный 300 мКл.

Решение:

Возьмем формулу силы тока

I = q/t

Подставим значения

I = 300 мКл / 2 с = 150 мА

Ответ: сила тока в цепи равна 150 мА

Чтобы хорошо запомнить теорию, нужно много практики. Классический курс по физике для 10 класса в онлайн-школе Skysmart — отличная возможность попрактиковаться в решении задач.

Проводники и диэлектрики

Некоторые делят мир на черное и белое, а мы — на проводники и диэлектрики.

• Проводники — это материалы, которые проводят электрический ток. Самыми лучшими проводниками являются металлы.
• Диэлектрики — материалы, которые не проводят электрический ток. Изи!

Проводники	Диэлектрики
Медь, железо, алюминий, олово, свинец, золото, серебро, хром, никель, вольфрам	Воздух, дистиллированная вода, поливинилхлорид, янтарь, стекло, резина, полиэтилен, полипропилен, полиамид, сухое дерево, каучук

То, что диэлектрик не проводит электрический ток, не значит, что он не может накапливать заряд. Накопление заряда не зависит от возможности его передавать.

Бесплатные занятия по английскому с носителем

Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.

Направление тока

Раньше в учебниках по физике писали так: когда-то давно решили, что ток направлен от плюса к минуса, а потом узнали, что по проводам текут электроны. Но электроны эти — отрицательные, а значит к минусу идти не могут. Но раз уже условились о направлении, поэтому оставим, как есть. Вопрос тогда возникал у всех: почему нельзя поменять направление тока? Но ответ так никто и не получил.

Сейчас пишут немного иначе: положительные частицы текут по проводнику от плюса к минусу, туда и направлен ток. Здесь вопросов ни у кого не возникает.

Так и какая версия верна? На самом деле, обе. Носители заряда в каждом типе материала разные. В металлах — это электроны, в электролитах — ионы. У каждого типа частиц свои знаки и потребность в том, чтобы бежать к противоположно заряженному полюса источника тока. Не будем же мы для каждого типа материала выбирать направление тока, чтобы решить задачу! Поэтому принято направлять ток от плюса к минусу. В большинстве задач школьного курса направление тока роли не играет, но есть то самое коварное меньшинство, где этот момент будет очень важным. Поэтому запомните — направляем ток от плюса к минусу.

Источник тока

Вода в шланге берется из водопровода, ключа с водой в земле — в общем, не из ниоткуда. Электрический ток тоже имеет свой источник.

В качестве источника может выступить, например, гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. Эти реакции выделяют энергию, которая потом передается электрической цепи.

У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения. По сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «-».

Амперметр

Мы знаем, куда ток направлен, в чем измеряется сила тока, как ее вычислить, зная заряд и время, за которое этот заряд прошел. Осталось только измерить.

Прибор для измерения силы тока называется амперметр. Его включают в электрическую цепь последовательно с тем проводником, в котором ток измеряют.

Амперметры бывают очень разными по принципу действия: электромагнитные, магнитоэлектрические, электродинамические, тепловые и индукционные — и это только самые распространенные.

Мы рассмотрим только принцип действия теплового амперметра, потому что для понимания принципа действия других устройств необходимо знать, что такое магнитное поле и катушки.

Тепловой амперметр основан на свойстве тока нагревать провода. Устроен так: к двум неподвижным зажимам присоединена тонкая проволока. Эта тонкая проволока оттянута вниз шелковой нитью, связанной с пружиной. По пути эта нить петлей охватывает неподвижную ось, на которой закреплена стрелка. Измеряемый ток подводится к неподвижным зажимам и проходит через проволоку (на рисунке стрелками показан путь тока).

Под действием тока проволока немного нагреется, из-за чего удлинится, вследствие этого шелковая нить, прикрепленная к проволоке, оттянется пружиной. Движение нити повернет ось, а значит и стрелку. Стрелка покажет величину измерения.

Сила: определение, уравнение, единица измерения и типы

Сила — это термин, который мы постоянно используем в повседневном языке. Иногда люди говорят о «силе природы», а иногда мы ссылаемся на авторитеты, такие как полиция. Возможно, ваши родители «заставляют» вас пересмотреть прямо сейчас? Мы не хотим навязывать вам понятие силы, но было бы определенно полезно узнать, что мы подразумеваем под силой в физике для ваших экзаменов! Это то, что мы обсудим в этой статье. Сначала мы рассмотрим определение силы и ее единиц, затем поговорим о типах сил и, наконец, рассмотрим несколько примеров сил в нашей повседневной жизни, чтобы улучшить наше понимание этой полезной концепции.

Определение силы

Сила определяется как любое воздействие, которое может изменить положение, скорость и состояние объекта.

Сила также может быть определена как толчок или тяга, воздействующая на объект. Действующая сила может остановить движущийся объект, вывести объект из состояния покоя или изменить направление его движения. Это основано на законе движения Ньютона 1 ^st , который гласит, что объект продолжает находиться в состоянии покоя или двигаться с постоянной скоростью, пока на него не действует внешняя сила. Сила является векторной величиной, поскольку она имеет направление и величину .

Формула силы

Уравнение для силы дается законом Ньютона 2 , в котором утверждается, что ускорение, создаваемое движущимся объектом, прямо пропорционально действующей на него силе и обратно пропорционально массе тела. объект. Закон Ньютона 2 ^й можно представить следующим образом:

его также можно записать как

Или прописью

где сила в ньютонах, масса объекта в , и ускорение тела в . Другими словами, по мере увеличения силы, действующей на объект, его ускорение будет увеличиваться при условии, что масса остается постоянной.

Какое ускорение вызывается телом массой , когда к нему приложена сила ?

Мы знаем, что

Результирующая сила вызовет ускорение объекта.

Единица силы в физике

Единицей силы в системе СИ является ньютон и обычно обозначается символом . можно определить как силу, которая вызывает ускорение в объекте массы. Поскольку силы являются векторами, их величины могут быть сложены вместе в зависимости от их направления.

Результирующая сила представляет собой единую силу, имеющую тот же эффект, что и две или более независимых сил.

Рис. 1. Силы можно сложить или отнять друг от друга, чтобы найти результирующую силу в зависимости от того, действуют ли силы в одном или противоположном направлении соответственно

Взгляните на изображение выше, если силы действуют в противоположных направлениях, то результирующий вектор силы будет разницей между ними и направлением силы, которая имеет большую величину. Две силы, действующие в одной точке в одном и том же направлении, можно сложить вместе, чтобы получить результирующую силу в направлении двух сил.

Какова результирующая сила, действующая на объект, когда на него действуют сила толкания и сила трения?

Сила трения всегда будет противоположна направлению движения, поэтому результирующая сила равна

Результирующая сила, действующая на объект, направлена ​​по направлению движения тела.

Типы силы

Мы говорили о том, как можно определить силу как толчок или притяжение. Толчок или вытягивание может произойти только тогда, когда два или более объекта взаимодействуют друг с другом. Но силы могут также испытываться объектом без какого-либо прямого контакта между объектами. Таким образом, силы можно разделить на контактных и бесконтактных сил.

Контактные силы

Это силы, которые действуют, когда два или более объектов соприкасаются друг с другом. Рассмотрим несколько примеров контактных сил.

Нормальная сила реакции

Нормальная сила реакции — это название, данное силе, действующей между двумя объектами, находящимися в контакте друг с другом. Нормальная сила реакции отвечает за силу, которую мы чувствуем, когда нажимаем на объект, и именно эта сила не дает нам провалиться сквозь пол! Нормальная сила реакции всегда будет действовать нормально к поверхности, поэтому ее называют нормальной силой реакции.

Нормальная сила реакции – это сила, испытываемая двумя объектами, соприкасающимися друг с другом и действующая перпендикулярно поверхности контакта между двумя объектами. Его происхождение связано с электростатическим отталкиванием между атомами двух объектов, соприкасающихся друг с другом.

Рис. 2 – Мы можем определить направление нормальной силы реакции, рассматривая направление, перпендикулярное поверхности контакта. Слово «нормальный» — это еще одно слово, означающее «перпендикулярный» или «под прямым углом» 9.0003

Нормальная сила, действующая на ящик, равна нормальной силе, действующей на ящик, на землю, это результат закона Ньютона 3 ^rd . Закон Ньютона 3 ^rd гласит, что для каждой силы существует равная сила, действующая в противоположном направлении.

Поскольку объект неподвижен, мы говорим, что коробка находится в равновесии. Когда объект находится в равновесии, мы знаем, что общая сила, действующая на объект, должна быть равна нулю. Следовательно, сила тяжести, притягивающая ящик к поверхности Земли, должна быть равна нормальной силе реакции, удерживающей его от падения к центру Земли.

Сила трения

Сила трения — это сила, действующая между двумя поверхностями, которые скользят или пытаются скользить друг относительно друга.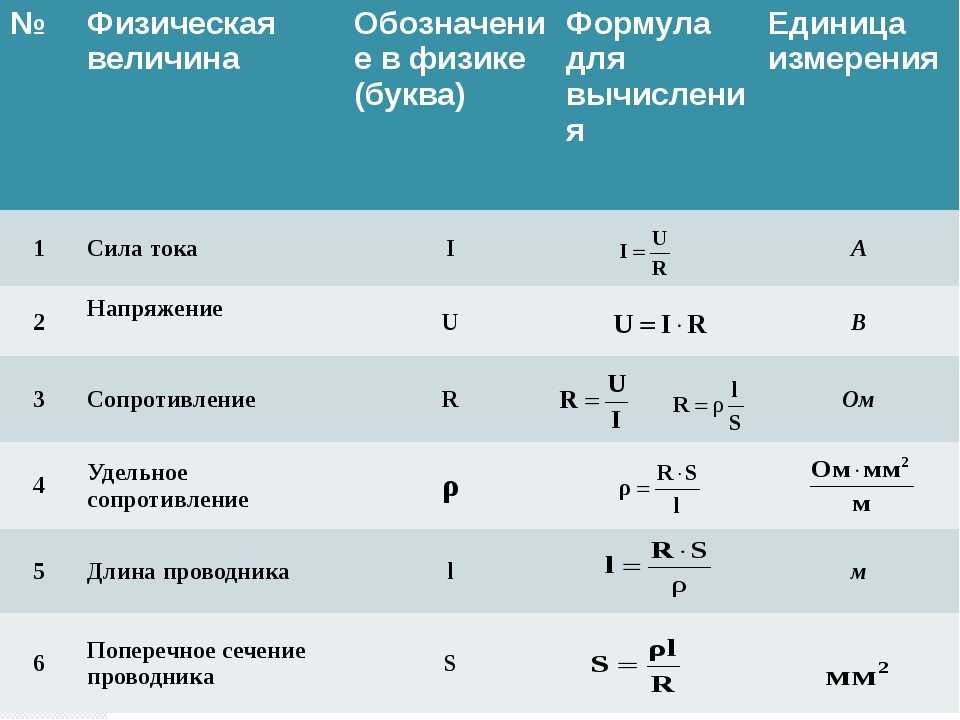

Даже кажущаяся гладкой поверхность будет испытывать некоторое трение из-за неровностей на атомарном уровне. Без трения, противодействующего движению, объекты продолжали бы двигаться с той же скоростью и в том же направлении, что и закон движения Ньютона. От простых вещей, таких как ходьба, до сложных систем, таких как автомобильные тормоза, большинство наших повседневных действий возможны только благодаря трению.

Рис. 3. Сила трения на движущийся объект действует из-за шероховатости поверхности

Бесконтактные силы

Бесконтактные силы действуют между объектами, даже когда они физически не соприкасаются друг с другом. Давайте рассмотрим несколько примеров бесконтактных сил.

Сила гравитации

Сила притяжения, испытываемая всеми объектами, имеющими массу в гравитационном поле, называется гравитацией. Эта гравитационная сила всегда притягивает и на Земле действует по направлению к ее центру. Средняя напряженность гравитационного поля Земли равна . Вес объекта – это сила, с которой он действует под действием силы тяжести, и определяется по следующей формуле:

Или прописью

Где – вес объекта, – его масса, – напряженность гравитационного поля. у поверхности Земли. На поверхности Земли напряженность гравитационного поля примерно постоянна. Мы говорим, что гравитационное поле однородно в определенной области , когда напряженность гравитационного поля имеет постоянное значение. Величина напряженности гравитационного поля у поверхности Земли равна .

Рис. 4 – Сила притяжения Земли на Луну действует по направлению к центру Земли. Это означает, что Луна будет вращаться по почти идеальной окружности, мы говорим почти идеальной, потому что орбита Луны на самом деле слегка эллиптическая, как и у всех вращающихся тел

Магнитная сила

Магнитная сила — это сила притяжения между одинаковыми и разными полюсами. магнита. Северный и южный полюса магнита обладают силой притяжения, а два одинаковых полюса обладают силой отталкивания.

Рис. 5 – Магнитная сила

Другими примерами бесконтактных сил являются ядерные силы, сила Ампера и электростатическая сила, возникающая между заряженными объектами.

Примеры сил

Давайте рассмотрим несколько примеров ситуаций, в которых действуют силы, о которых мы говорили в предыдущих разделах.

Книга, помещенная на столешницу, испытывает силу, называемую нормальной силой реакции , которая нормальна к поверхности, на которой она лежит. Эта нормальная сила является реакцией на нормальную силу книги, действующую на столешницу. (Ньютон 3 ^-й закона). Они равны, но противоположны по направлению.

Даже когда мы идем, сила трения постоянно помогает нам двигаться вперед. Сила трения между землей и подошвами наших ног помогает нам сохранять сцепление при ходьбе. Если бы не трение, передвижение было бы очень сложной задачей. Объект может начать двигаться только тогда, когда внешняя сила преодолеет силу трения между объектом и поверхностью, на которой он покоится.

Рис. 6 – Сила трения при ходьбе по разным поверхностям

Нога толкает по поверхности, поэтому сила трения здесь будет параллельна поверхности пола. Вес действует вниз, а нормальная сила реакции действует против веса. Во второй ситуации трудно ходить по льду из-за небольшого трения между подошвами ног и землей, из-за чего мы скользим.

Спутник, возвращающийся в атмосферу Земли, испытывает сильное сопротивление воздуха и трение. Когда он падает на Землю со скоростью тысячи километров в час, тепло от трения сжигает спутник.

Другими примерами контактных сил являются сопротивление воздуха и напряжение. Сопротивление воздуха — это сила сопротивления, которую испытывает объект при движении в воздухе. Сопротивление воздуха возникает из-за столкновений с молекулами воздуха. Натяжение — это сила, которую объект испытывает при растяжении материала. Натяжение альпинистских веревок — это сила, которая удерживает скалолазов от падения на землю при скольжении.

Силы — ключевые выводы

• Сила определяется как любое воздействие, которое может изменить положение, скорость и состояние объекта.
• Сила также может быть определена как толчок или тяга, воздействующая на объект.
• Ньютоновский 1 ^st закон движения гласит, что объект продолжает находиться в состоянии покоя или двигаться с постоянной скоростью, пока на него не действует внешняя сила.
• Закон Ньютона 2 ^nd движения гласит, что сила, действующая на объект, равна его массе, умноженной на его ускорение.
• Единицей силы в системе СИ является Ньютон () и задается , или прописью.
• Ньютон 3 ^rd закон движения гласит, что для каждой силы существует равная сила, действующая в противоположном направлении.
• Сила является величиной вектора , поскольку она имеет направление и величину .
• Мы можем разделить силы на контактные и бесконтактные.
• Примерами контактных сил являются силы трения, силы реакции и напряжения.
• Примерами бесконтактных сил являются гравитационная сила, магнитная сила и электростатическая сила.

FIRCE-вектор-DUMMIES

BY: Стивен Холцнер и

Обновлено: 03-26-2016

Из книги: Physics I Рабочие Для чайников с онлайн-практикой

Изучите книгу Купить на Amazon

Сила, как и смещение, скорость и ускорение, является векторной величиной, поэтому второй закон Ньютона записывается как сигма 9.0241 F = м а. Проще говоря, это говорит о том, что векторная сумма сил, действующих на объект, равна его массе (скаляр), умноженной на его ускорение (вектор).

Поскольку сила является векторной величиной, вы складываете силы как векторы. Это соответствует второму закону Ньютона.

Пример вопроса

1. Предположим, что у вас есть две силы, как показано: A = 5,0 Н при 40 градусах и B = 7,0 Н при 125 градусах. Какова чистая сила, сигма Ф ?

   Правильный ответ: звездная величина 8,9 N, угол 91 градус.

   1. Преобразование силы A в векторное обозначение компонентов. Используйте уравнение A _x = A cos theta, чтобы найти координату силы x : 5,0 cos 40 градусов = 3,8.

   2. Используйте уравнение A _y = A sin theta, чтобы найти y координата силы: 5.0 sin 40 градусов, или 3.2. Это делает вектор A (3.8, 3.2) в координатной форме.

   3. Преобразовать вектор B в компоненты. Используйте уравнение B _x = B cos theta, чтобы найти координату ускорения x : 7,0 cos 125 градусов = -4,0.

   4. Используйте уравнение B _y = B sin тета, чтобы найти y координата второй силы: 7. 0 sin 125 градусов или 5.7. Это делает силу B (–4,0, 5,7) в координатной форме.

   5. Выполните сложение векторов, чтобы найти результирующую силу: (3.8, 3.2) + (–4.0, 5.7) = (–0.2, 8.9).

   6. Преобразование вектора (–0,2, 8,9) в форму модуля/угла. Используйте уравнение theta = tan ^–1 ( y / x ), чтобы найти угол: tan ^–1 (–44,5) = 91 градус.

   7. Применить уравнение

      , чтобы найти величину чистой силы, что дает вам 8,9 Н.

Практические вопросы

1. Добавьте две силы: A равна 8,0 Н при 53 градусах, а B равна 9,0 Н при 19 градусах.

2. Добавьте две силы: A равна 16,0 Н при 39 градусах, а B равна 5,0 Н при 125 градусах.

3. Добавьте две силы: A равна 22,0 Н при 68 градусах, а B равна 6,0 Н при 24 градусах.

4. Добавьте две силы: A равна 12,0 Н при 129 градусах, а B равна 3,0 Н при 225 градусах.

Ниже приведены ответы на практические вопросы:

1. Величина: 16 с.ш.; Угол: 35 градусов

   1. Преобразование силы A в векторное обозначение компонентов. Используйте уравнение A _x = A cos тета, чтобы найти x координату силы A : 8,0 cos 53 градуса = 4,8 Н.

   2. Используйте уравнение A _y = A sin theta, чтобы найти y координату силы A : 8,0 sin 53 градуса = 6,4 0,90 909 Н. )N в координатной форме.

   3. Преобразование вектора B в компоненты. Используйте уравнение B _x = B кос-тета, чтобы найти x координата силы B : 9,0 cos 19 градусов = 8,5 Н.

   4. Используйте уравнение B _y = B sin тета, чтобы найти y координату второй силы: 9,0 sin 19 градусов = 2,9 Н. Это дает силу B 9,5, 10 (. 8,5, 10) N в координатной форме.

   5. Выполните сложение векторов, чтобы найти результирующую силу: (4.8, 6.4)Н + (8.5, 2.9)Н = (13.3, 9.3)Н.

   6. Преобразование вектора силы (13.3, 9.3) Н в форму величины/угла. Используйте уравнение тета = тангенс ^–1 ( y / x ), чтобы найти угол: тангенс ^–1 (0,70) = 35 градусов.

   7. Применить уравнение

      , чтобы найти величину чистой силы, что даст вам 16 Н.

2. Величина: 17 с.ш.; Угол: 56 градусов

   1. Преобразование силы A в виде компонентов вектора. Используйте уравнение A _x = A cos тета, чтобы найти x координату силы A : 16,0 cos 39 градусов = 12,4 Н.

   2. Используйте уравнение A _Y = A SIN THETA, чтобы найти Y Координата силы A : 16. 0 SIN 39 DEGREES = 10,0 N., которая создает силу A : 16.0 SIN 39 DEGREES = 10,0 N., которая создает силу A (12 10.0. )N в координатной форме.

   3. Преобразовать силу B в компоненты. Используйте уравнение B _x = B cos тета, чтобы найти x координату силы B : 5,0 cos 125 градусов = -2,9 Н.

   4. Используйте уравнение B _y = B sin theta , чтобы найти y координату второй силы: 9,0 sin 4,15 N.0009 B (–2.9, 4.1)N в координатной форме.

   5. Выполните сложение векторов, чтобы найти результирующую силу: (12,4, 10,0)Н + (–2,9, 4,1)Н = (9,5, 14,1)Н.

   6. Преобразование вектора силы (9.5, 14.1) Н в форму величины/угла. Используйте уравнение theta = tan ^–1 ( y / x ), чтобы найти угол: tan ^–1 (1,5) = 56 градусов.

   7. Применить уравнение

      , чтобы найти величину чистой силы, что даст вам 17 Н.

3. Величина: 27 с.ш.; Угол: 59 градусов

   1. Преобразование силы A в векторное обозначение компонентов. Используйте уравнение A _x = A cos тета, чтобы найти x координату силы A : 22,0 cos 68 градусов = 8,24 Н.

   2. Используйте уравнение A _y = A sin theta , чтобы найти y координату силы A : 22,0 sin 68 градусов = 20,4 Н. Это дает силу A (8,24, 20,4) Н в координатной форме.

   3. Преобразовать силу B в компоненты. Используйте уравнение B _x = B cos theta , чтобы найти x координату силы B : 6,0 cos 24 градуса = 5,5 Н.

   4. Используйте уравнение B _y = B sin theta найти y координату силы B : 6,0 sin 24 градуса = 2,4 дюйма (N)9. форма координат.

   5. Выполните сложение векторов, чтобы найти результирующую силу: (8.24, 20.3)Н + (5.5, 2.4)Н = (13.7, 22.7)Н.

   6. Преобразование вектора силы (13.7, 22.7)Н в форму модуля/угла. Используйте уравнение тета = тангенс ^–1 ( y / x ), чтобы найти угол: tan ^–1 (1,66) = 59 градусов.

   7. Применить уравнение

      , чтобы найти величину чистой силы, что даст вам 27 Н.

4. Величина: 12 с.ш.; Угол: 143 градуса

   1. Преобразование силы A в векторное обозначение компонентов. Используйте уравнение A _x = A cos тета, чтобы найти x координату силы A : 12,0 cos 129 градусов = –7,6.

   2. Используйте уравнение A _Y = A SIN THETA , чтобы найти Y координата FIRCE A : 12.0 SIN 129 DEGEES n . 7.6, 9.3)N в координатной форме.

   3. Преобразовать силу B в компоненты. Используйте уравнение B _x = B cos theta найти координату силы x B : 3,0 cos 225 градусов = –2,1 Н.

   4. Use the equation B _y = B sin theta to find the y coordinate of force B : 3.0 sin 225 degrees = –2.1 N. That makes force B ( –2.1, –2.1)N в координатной форме.

   5. Выполните сложение векторов, чтобы найти результирующую силу: (–7,6, 9,3)Н + (–2,1, –2,1)Н = (–9,7, 7,2)Н.

   6. Преобразование вектора силы (–9,7, 7,2) Н в форму величины/угла.