Урок 35. задачи на движение – Математика – 5 класс
Математика
5 класс
Урок № 35
Задачи на движение
Перечень вопросов, рассматриваемых в теме:
- Понятия скорости, времени, расстояния.
- Формулы нахождения скорости, времени, расстояния.
- Понятия скорости сближения, скорости удаления.
Глоссарий по теме
Расстояние – это длина от одного пункта до другого.
Большие расстояния, в основном, измеряются в метрах и километрах.
Расстояние обозначается латинской буквой S.
Чтобы найти расстояние, надо скорость умножить на время движения:
S = v ∙ t
Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Скорость обозначается латинской буквой v.
Чтобы найти скорость, нужно расстояние разделить на время движения:
v = S : t
Время – это продолжительность каких-то действий, событий.
Время движения обозначается маленькой латинской буквой t.
Чтобы найти время, нужно расстояние разделить на скорость движения:
t = S : v
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Основная литература
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К., Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
2. Потапов М. К., Шевкин А. В. Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010
Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010
Дополнительная литература
1. Чесноков А. С., Нешков К. И. Дидактические материалы по математике 5 кл. – М.: Академика учебник, 2014
2. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5–6 классы // Составитель Бурмистрова Т. А.
3. Потапов М. К. Математика: дидактические материалы. 6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010
Теоретический материал для самостоятельного изучения
Очень часто нам встречаются задачи на нахождение скорости, времени и расстояния. Что же всё это такое? Сейчас нам предстоит в этом разобраться.
Расстояние – это длина от одного пункта до другого. (Например, расстояние от дома до школы 2 километра). В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. Скорость обозначается маленькой латинской буквой v.
Скорость обозначается маленькой латинской буквой v.
Рассмотрим задачу:
Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?
Решение:
Быстрее бежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. Чтобы найти скорость, нужно расстояние разделить на время движения.
Давайте найдём скорость первого школьника. Для этого разделим 200 метров на время движения первого школьника, то есть на 50 секунд:
200 м : 50 с = 4
Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит, скорость измеряется в метрах в секунду:
200 м : 50 с = 4 (м/с)
Скорость движения первого школьника составляет 4 метра в секунду.
Теперь найдём скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника:
200 м : 100 c = 2 (м/с)
Скорость движения первого школьника – 4 (м/с).
Скорость движения второго школьника – 2 (м/с).
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит, он бежал до спортплощадки быстрее.
Иногда возникает ситуация, когда требуется узнать, за какое время тело преодолеет то или иное расстояние. Время движения обозначается маленькой латинской буквой t.
Рассмотрим задачу:
От дома до спортивной секции 1200 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 600 метров в минуту. За какое время мы доедем до спортивной секции?
Решение:
Если за одну минуту мы будем проезжать 600 метров, то сколько таких минут нам понадобится для преодоления тысячи двухсот метров? Очевидно, что надо разделить 1200 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 600 метров.
1200 : 600 = 2 (мин)
Ответ: мы доедем до спортивной секции за 2 минуты.
Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
S = v ∙ t
Рассмотрим задачу:
Решение:
Если за одну минуту мы прошли 60 метров, то сколько таких отрезков по шестьдесят метров мы пройдём за 15 минут? Очевидно, что умножив 60 метров на 15 минут, мы определим расстояние от дома до магазина:
v = 60 (м/мин)
t = 15 (минут)
S = v ∙ t = 60 ∙ 15 = 900 (метров)
Ответ: мы прошли 900 метров.
Если известно время и расстояние, то можно найти скорость:
v = S : t
Рассмотрим задачу:
Расстояние от дома до школы 800 метров.
Скорость движения школьника – это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 800 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот вопрос, нужно разделить расстояние на время движения школьника:
S = 800 метров
t = 8 минут
v = S : t = 800 : 8 = 100 (м/мин)
Ответ: скорость школьника была 100 м/мин.
Если известна скорость и расстояние, то можно найти время:
t = S : v
Рассмотрим задачу:
От дома до спортивной секции 600 метров. Мы должны дойти до неё пешком. Наша скорость будет 120 метров в минуту (120 м/мин). За какое время мы дойдём до спортивной секции?
Если за одну минуту мы будем проходить 120 метров, то сколько таких минут со ста двадцатью метрами будет в шестистах метрах?
Чтобы ответить на этот вопрос, нужно 600 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 120. Тогда мы получим время, за которое мы дойдём до спортивной секции:
Тогда мы получим время, за которое мы дойдём до спортивной секции:
S = 600 метров
v = 120 (м/мин)
t = S : v = 600 : 120 = 5 (минут).
Ответ: мы дойдём до спортивной секции за 5 минут.
Итак, все рассмотренные нами формулы мы можем представить в виде треугольника для лучшего запоминания:
Теперь рассмотрим типы задач на движение.
Задачи на сближение.
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причём скорость первого будет 100 метров в минуту, а второго – 105 метров в минуту, то скорость сближения будет составлять 100 плюс 105, то есть 205 метров в минуту. Значит, каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Задача.
 Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.
Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.Решение:
- Найдём скорость сближения велосипедистов:
13 км/ч + 15 км/ч = 28 км/ч
- Определим расстояние между населёнными пунктами. Для этого скорость сближения умножим на время движения:
28 ∙ 3 = 84 км
Ответ: расстояние между населёнными пунктами 84 км.
Задачи на скорость удаления.
Скорость удаления
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причём скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4 плюс 6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Рассмотрим задачу:
С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?
Решение:
- Определим скорость удаления. Для этого сложим их скорости:
60 + 130 = 190 км/ч.
Получили скорость удаления равную 190 км/ч. Данная скорость показывает, что за час расстояние между теплоходом и катером будет увеличиваться на 190 километров.
- Чтобы узнать какое расстояние будет между ними через два часа, нужно 190 умножить на 2:
190 ∙ 2 = 380 км.
Ответ: через 2 часа расстояние между теплоходом и катером будет составлять 380 километров.
Задачи на движение объектов в одном направлении.
В предыдущих пунктах мы рассматривали задачи, в которых объекты (люди, машины, лодки) двигались либо навстречу друг другу, либо в противоположных направлениях. В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.
В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Рассмотрим задачу:
Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?
Решение:
- Найдём скорость удаления. Для этого из большей скорости вычтем меньшую:
130 км/ч − 90 км/ч = 40 км/ч
- Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 3 часа в три раза больше:
40 ∙ 3 = 120 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через три часа – 120 км.
Рассмотрим ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном направлении.
Задача.
Пусть на одной улице имеется дом, школа и аттракцион. Дом находится на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Решение:
- Определим расстояние, пройденное первым пешеходом за 3 минуты. Он двигался со скоростью 90 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 270 метров:
90 ∙ 3 = 270 метров
- Определим расстояние, пройденное вторым пешеходом за 3 минуты. Он двигался со скоростью 85 метров в минуту.
 За три минуты он пройдёт в три раза больше, то есть 255 метров:
За три минуты он пройдёт в три раза больше, то есть 255 метров:
85 ∙ 3 = 255 метров
- Теперь найдём расстояние между пешеходами. Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (900м) прибавить расстояние, пройденное вторым пешеходом (255м), и из полученного результата вычесть расстояние, пройденное первым пешеходом (270м):
900 + 255 = 1155 м
1155 – 270 = 885 м
Либо из расстояния от дома до школы (900 м) вычесть расстояние, пройденное первым пешеходом (270 м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (255 м):
900 – 270 = 630 м
630 + 255 = 885 м
Таким образом, через три минуты расстояние между пешеходами будет составлять 885 метров.
- Теперь давайте ответим на вопрос: через сколько минут после начала движения первый пешеход догонит второго?
В самом начале пути между пешеходами было расстояние 900 м. Через минуту после начала движения расстояние между ними будет составлять 895 метров, поскольку первый пешеход двигается на 5 метров в минуту быстрее второго:
90 ∙ 1 = 90 м
85 ∙ 1 = 85 м
900 + 85 – 90 = 985 – 90 = 895 м
Через три минуты после начала движения расстояние уменьшится на 15 метров и будет составлять 885 метров.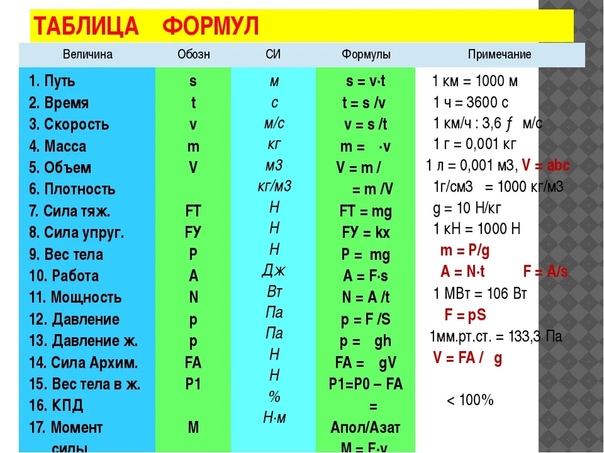 Это был наш ответ на первый вопрос задачи:
Это был наш ответ на первый вопрос задачи:
90 ∙ 3 = 270 м
85 ∙ 3 = 255 м
900 + 255 – 270 = 1155 – 270 = 885 м
Можно сделать вывод, что каждую минуту расстояние между пешеходами будет уменьшаться на 5 метров.
А раз изначальные 900 метров с каждой минутой уменьшаются на одинаковые 5 метров, то мы можем узнать сколько раз 900 метров содержат по 5 метров, тем самым определяя через сколько минут первый пешеход догонит второго:
900 : 5 = 180 минут.
Ответ: через три минуты расстояние между пешеходами будет составлять 885 метров, первый пешеход догонит второго через 180 минут = 3 часа.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Заполните таблицу:
S | v | t | |
1. | 135 км | 9 км/ч | ____ ч |
2. | ____ м | 12 м/с | 4 с |
3. | 132 м | ____ м/мин | 11 мин |
Для заполнения пропусков воспользуемся формулами нахождения скорости, времени, расстояния:
- Надо найти время: t = S : v
135 : 9 = 15 часов.
- Надо найти расстояние: S = v ∙ t
12 ∙ 4 = 48 м.
- Надо найти скорость: v = S : t
132 : 11 = 12 м/мин.
Верный ответ:
S | v | t | |
1. | 135 км | 9 км/ч | 15 часов |
2. | 48 м | 12 м/с | 4 с |
3. | 132 м | 12 м/мин | 11 мин |
№2. Тип задания: единичный / множественный выбор
Выберите верный ответ к задаче:
Из пунктов А и В, расстояние между которыми 300 км, отправились одновременно навстречу друг другу мотоциклист и автомобилист. Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?
Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?
Варианты ответов:
- 70
- 30
- 270
- 240
Эта задача относится к типу задач на сближение, т.е. нам надо:
- сложить скорости мотоциклиста и автомобилиста:
60 + 30 = 90 км/ч – скорость сближения;
- узнать, сколько километров они пройдут за 3 часа вместе. Для этого:
90 ∙ 3 = 270 км;
- из общего расстояния нам осталось вычесть пройденное:
300 – 270 = 30 км
Верный ответ: 2. 30 км.
|
Предмет |
Класс |
Время выполнения работы |
Печать вариантов ВПР Не допускается печать двух страниц на одну сторону листа А4 |
|
Русский язык (1 часть) |
4 |
45 минут |
формат печати – А4, чёрно-белая, односторонняя |
|
Русский язык (2 часть) |
4 |
45 минут |
|
|
Математика |
4 |
45 минут |
формат печати – А4, чёрно-белая, допускается печать на обеих сторонах листа |
|
Окружающий мир |
4 |
45 минут |
|
|
Математика |
5 |
60 минут |
формат печати – А4, чёрно-белая, допускается печать на обеих сторонах листа |
|
Русский язык |
5 |
60 минут |
|
|
Биология |
5 |
45 минут |
|
|
История |
5 |
45 минут |
|
|
Математика |
6 |
60 минут |
формат печати – А4, чёрно-белая, допускается печать на обеих сторонах листа |
|
Русский язык |
6 |
90 минут |
|
|
Биология |
6 |
45 минут |
|
|
География |
6 |
60 минут |
|
|
Обществознание |
6 |
45 минут |
|
|
История |
6 |
60 минут |
|
|
Математика |
7 |
90 минут |
формат печати – А4, чёрно-белая, допускается печать на обеих сторонах листа |
|
Русский язык |
7 |
90 минут |
|
|
Биология |
7 |
60 минут |
|
|
География |
7 |
90 минут |
|
|
Физика |
7 |
45 минут |
|
|
Обществознание |
7 |
45 минут |
|
|
История |
7 |
60 минут |
|
|
Английский язык, французский язык, немецкий язык (в компьютерной форме) |
7 |
45 минут (включая пятиминутный перерыв для выполнения комплекса упражнений гимнастики глаз) |
– |
|
Математика |
8 |
90 минут |
формат печати – А4, чёрно-белая, допускается печать на обеих сторонах листа |
|
Русский язык |
8 |
90 минут |
|
|
Биология |
8 |
60 минут |
|
|
География |
8 |
90 минут |
|
|
Обществознание |
8 |
45 минут |
|
|
История |
8 |
90 минут |
|
|
Физика |
8 |
45 минут |
|
|
Химия |
8 |
90 минут |
|
|
Английский язык, французский язык, немецкий язык (в компьютерной форме) |
11 |
75 минут (включая 2 пятиминутных перерыва для выполнения комплекса упражнений гимнастики глаз) |
– |
|
История |
11 |
90 минут |
формат печати – А4, чёрно-белая, допускается печать на обеих сторонах листа |
|
Физика |
11 |
90 минут |
|
|
Химия |
11 |
90 минут |
|
|
География |
11 |
90 минут |
|
|
Биология |
11 |
90 минут |
Импульс – Физика – Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Импульс тела
К оглавлению.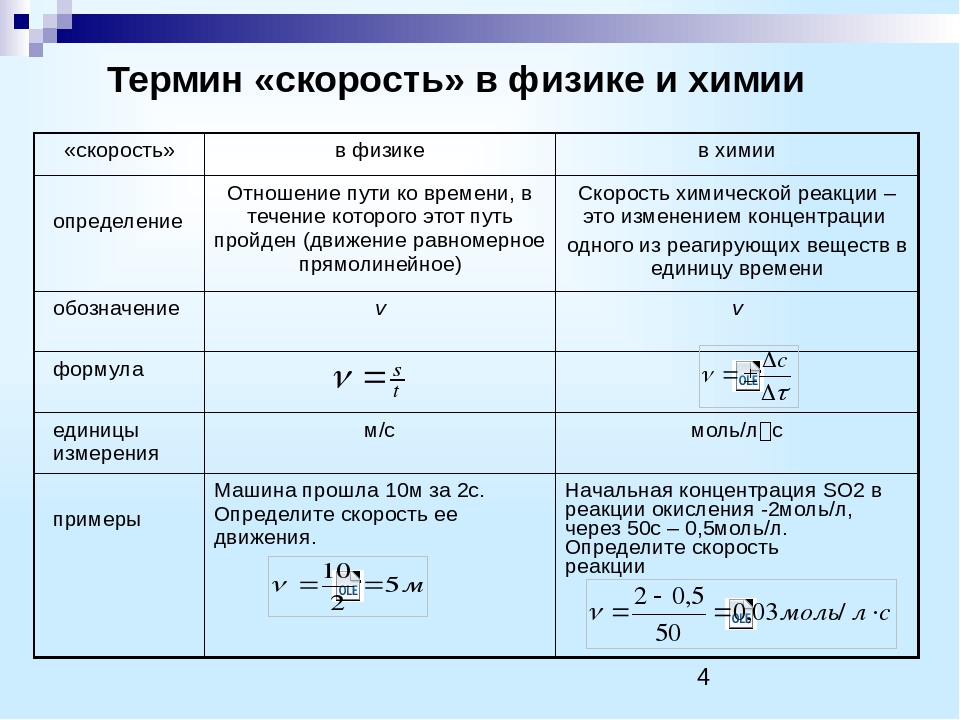 ..
..
Импульсом (количеством движения) тела называют физическую векторную величину, являющуюся количественной характеристикой поступательного движения тел. Импульс обозначается р. Импульс тела равен произведению массы тела на его скорость, т.е. он рассчитывается по формуле:
Направление вектора импульса совпадает с направлением вектора скорости тела (направлен по касательной к траектории). Единица измерения импульса – кг∙м/с.
Общий импульс системы тел равен векторной сумме импульсов всех тел системы:
Изменение импульса одного тела находится по формуле (обратите внимание, что разность конечного и начального импульсов векторная):
где: pн – импульс тела в начальный момент времени, pк – в конечный. Главное не путать два последних понятия.
Абсолютно упругий удар – абстрактная модель соударения, при которой не учитываются потери энергии на трение, деформацию, и т. п. Никакие другие взаимодействия, кроме непосредственного контакта, не учитываются. При абсолютно упругом ударе о закрепленную поверхность скорость объекта после удара по модулю равна скорости объекта до удара, то есть величина импульса не меняется. Может поменяться только его направление. При этом угол падения равен углу отражения.
п. Никакие другие взаимодействия, кроме непосредственного контакта, не учитываются. При абсолютно упругом ударе о закрепленную поверхность скорость объекта после удара по модулю равна скорости объекта до удара, то есть величина импульса не меняется. Может поменяться только его направление. При этом угол падения равен углу отражения.
Абсолютно неупругий удар – удар, в результате которого тела соединяются и продолжают дальнейшее своё движение как единое тело. Например, пластилиновый шарик при падении на любую поверхность полностью прекращает свое движение, при столкновении двух вагонов срабатывает автосцепка и они так же продолжают двигаться дальше вместе.
Закон сохранения импульса
К оглавлению…
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой.
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называется законом сохранения импульса (ЗСИ). Следствием его являются законы Ньютона. Второй закон Ньютона в импульсной форме может быть записан следующим образом:
Этот фундаментальный закон природы называется законом сохранения импульса (ЗСИ). Следствием его являются законы Ньютона. Второй закон Ньютона в импульсной форме может быть записан следующим образом:
Как следует из данной формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Аналогично можно рассуждать для равенства нулю проекции силы на выбранную ось. Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Аналогичные записи можно составить и для остальных координатных осей. Так или иначе, нужно понимать, что при этом сами импульсы могут меняться, но именно их сумма остается постоянной. Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны.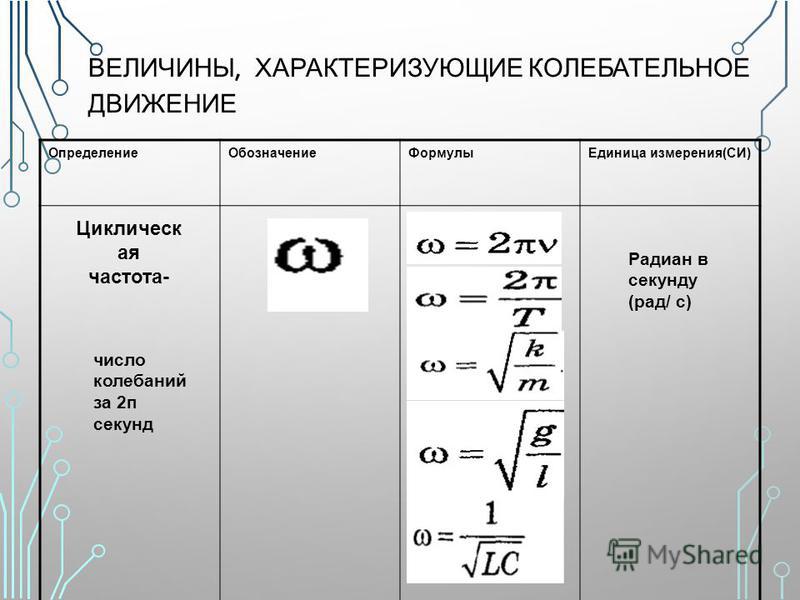
Сохранение проекции импульса
К оглавлению…
Возможны ситуации, когда закон сохранения импульса выполняется только частично, то есть только при проектировании на одну ось. Если на тело действует сила, то его импульс не сохраняется. Но всегда можно выбрать ось так, чтобы проекция силы на эту ось равнялась нулю. Тогда проекция импульса на эту ось будет сохраняться. Как правило, эта ось выбирается вдоль поверхности по которой движется тело.
Многомерный случай ЗСИ. Векторный метод
К оглавлению…
В случаях если тела движутся не вдоль одной прямой, то в общем случае, для того чтобы применить закон сохранения импульса, нужно расписать его по всем координатным осям, участвующим в задаче. Но решение подобной задачи можно сильно упростить, если использовать векторный метод. Он применяется если одно из тел покоится до или после удара. Тогда закон сохранения импульса записывается одним из следующих способов:
В этих формулах буквой υ обозначены скорости тел до соударения, а буквой u обозначены скорости тел после соударения. Из правил сложения векторов следует, что три вектора в этих формулах должны образовывать треугольник. Для треугольников применяется теорема косинусов. Если правильно записать соответствующую теорему косинусов, то зачастую получается уравнение из которого можно найти нужную величину. Однако, иногда к правильно записанной теореме косинусов еще нужно будет добавить правильно записанный закон сохранения энергии (смотрите следующий раздел). В этом случае получится система уравнений из которых наверняка можно будет найти нужную величину.
Из правил сложения векторов следует, что три вектора в этих формулах должны образовывать треугольник. Для треугольников применяется теорема косинусов. Если правильно записать соответствующую теорему косинусов, то зачастую получается уравнение из которого можно найти нужную величину. Однако, иногда к правильно записанной теореме косинусов еще нужно будет добавить правильно записанный закон сохранения энергии (смотрите следующий раздел). В этом случае получится система уравнений из которых наверняка можно будет найти нужную величину.
время, взаимодействие квантовые парадоксы и прочие занятные зверюшки / Хабр
Ок, раз почтенной публике (хотя, это пишется не для публики) так важно наличие краткого описания, то это будет сообщение с поиском ответа на вопросы: (1) есть ли в теоретико-физической картине мира время? (2) есть ли в ней место взаимодействию? (3) может ли вообще формальное описание схватить подобные явления? Текст будет скучным, невозможным для чтения, сложным для восприятия. Лучше не читайте. Потом не пишите в комментариях, что не предупреждал
Лучше не читайте. Потом не пишите в комментариях, что не предупреждал
ОК. Мои познания в физике ограничены. Так уж сложилось, что я в своё время не пошёл на физический факультет, а выбрал математику. Поэтому, я не могу утверждать, что следующие заявления верны вообще для всей физики, но с основопологающие книги я осилил. Это Пространство, время, материя’ Г.Вейля — замечательная книжка, всем рекомендую. И ‘Квантовая теория поля’ С.Вайнберга.
Так вот, чем оперируют изложенные в этих книгах общая теория относительности и квантовая физика? Они описывают мир в терминах функций от времени. Нечто вроде x(t) = sin(t), и у нас есть колебание. Даже в страшной и ужасной (действительно страшной для мозгов, и те физики, которые это всё придумали — гении и заслуживают восхищения) квантовой теории поля, которая самозабвенно оперирует группами симметрий, пятимерными интегралами от операторных выражений, пространством Миньковского и прочими высокотехнологичными математическими инструментами, в основании лежит скромное понятие функции.
Потому что группы — это группы симметрий, в которых должны сохраняться свойства операторов, а операторы работают над пространством волновых функций. Интегралы считаются по путям в полях, а векторное поле это тоже нечто, имеющее вид A(t). Ну и что, что A — заглавная буква?
Кривизна пространства-времени? Так это тоже функция, в каждой точке (x, y, z, t) имеющая определённое значение.
Но тут возникает вопрос, а что из того, что это функция от времени от t? Ну, назван её аргумент этой замечательной буквой, но от этого функция не меняет свой математический смысл, который заключается в том, что функция f: M -> N, отображающая элементы множества M в элементы множества N, является ‘всего лишь’ множеством пар (m, n), таких что m из M, n из N, с тем свойством что, в этом множестве нет двух таких пар, у которых n-компоненты одинаковые, а m-компоненты разные.
Но… А где здесь время? Где динамика и изменение? Где вся замечательная подвижность? Не видно. Вообще, может быть подумано, что ну, и нормально, даже так жить можно, подвижность всего — это как в кино. Лента с кучей картинок протягивается через лампу, мы способны видеть только одну картинку, от сюда и эффект… Но кто протягивает вселенную для… для каждого живого существа персонально? Или для всех живых существ вместе взятых? Каков лентопротяжный механизм.
Лента с кучей картинок протягивается через лампу, мы способны видеть только одну картинку, от сюда и эффект… Но кто протягивает вселенную для… для каждого живого существа персонально? Или для всех живых существ вместе взятых? Каков лентопротяжный механизм.
Кроме того, мы знаем, что теория информации работает в этом реальном мире. А, как известно мера информации требует наличия канала, состояние которого может меняться. Хм… Но такой канал сконструировать в многомерном и статичном множестве без лентопротяжного механизма опять же невозможно. Минимум, что нужно — это некая ползающая по этому множеству граница, описывающая то, что нужно считать каналом. Но по какой траектории это должно ползать? По заранее предопределённой и статичной?
Собственно, это причина для второй части моего персонального когнитивного диссонанса. Потому что, если эти описания верны, то можно запросто менять направление течения времени и верить в то, что возможны путешевствия во времени. А что? Ведь ничего не останавливает, кроме смутного интуитивного ощущения того, что решения с отрицательным t физически неверны.
Что же на самом деле исследуется в теоретической физике? Статичные множества подобные, мы можем видеть только лишь в истории процессов. В следах. Мы и сами физические законы воссоздаём по результатам экспериментов, по истрии произошедшего. Но сейчас самое время показать простой фокус.
Предположим, что мы наблюдаем за случайным процессом, который принимает значения 0 или 1. Предположим, что мы можем наблюдать только лишь за самим этим процессом, что мы увидим? Ничего, хаос и среднестатистическое непонятно, что. Но если мы видим не только голову процесса, но ещё и предыдущие два значения, не важно как, помним ли мы их, или не помним, а просто видим, за счёт своего особого восприятия времени, и что мы увидим?
Например, если мы помним 01, то набор следующих возможных воспринимаемах состояний для нас ограничен двумя значениями 10 и 11. То есть, имеет место присутствовать некая закономерность, наблюдаемая в случайном процессе, если мы решаемся запоминать его значения.
Хм. Занятно, да? Закон для случайного процесса. В том числе возникает и время, как определённая смена состояний.
Занятно, да? Закон для случайного процесса. В том числе возникает и время, как определённая смена состояний.
Приближает ли это разум ещё ближе к восприятию концепции Дао, которая определялась, как нечто подвижное и неформальное, формы и предметы в котором определялись только через восприятие? На мой взгляд — определённо.
При этом, в квантовой физике есть нечто похожее на подобный процесс — это коллапс волновой функции. Когда система принимает одно из возможных состояний без каких-либо видимых причин, и без какого-либо видимого течения времени… Но, к сожалению, вместо построения теории вокруг того, что это означает и какое отношение имеет к понятию времени, физики, в основной массе своей пытаются выразить этот процесс через уже знакомый им инструмент функции и унитарной эволюции (ну, можно сказать, что через функцию от времени, значением своим имеющую волновую функцию, то же самое множество пар, только не численных). Хм… Вот. Это теория суперотбора. Насколько мне известно, пока она не общепринята, но тем не менее, работы усиленно ведутся.
ОК. Следующая проблема в том, что в физике нет никакой модели восприятия. Более того, лучшая модель наблюдателя в физике — это точечный наблюдатель в теории относительности. Мне очень интересно представить, как это так? Точечный наблюдатель, способный следить за путешевствием фотона в световых часах? Эйнштейн определённо был гением, раз додумался до такого мысленного эксперимента.
Восприятие легко бы удалось определить через взаимодействие, но со взаимодействием так же туго. Лучшее, что есть на сегодняшний день — это концепция обмена медиаторами между элементарными частицами (электроны воздействуют друг с другом через постоянный обмен фотонами). Хм… И ещё раз хм… Потому что, это действительно нетривиально: точечная частица, которая не имеет определённого местоположения в пространстве-времени, меняет своё состояние, когда к ней подходит другая точечная частица с неопределённым местом пребывания… При этом, изменение в принципе невозможно, или возможно, но заранее предопределено. Логический ужас, если попытаться это всё применять к подвижным и изменчивым системам… На мой взгляд.
Логический ужас, если попытаться это всё применять к подвижным и изменчивым системам… На мой взгляд.
При этом, с математической точки зрения всё очень просто: у фотона есть вероятности оказаться в некоторой области пространства-времени, у электрона тоже своя область со своими вероятностями, на пересечении этих областей с некоторой вероятностью возможно взаимодействие. И теория может в этих терминах предсказывать результаты экспериментов… Но. Но… И ещё раз но. Чтобы это всё сделать нужен математик. Что заставляет нас верить в то, что электроны действительно существуют?
OK. Хорошо… Теперь немного о квантовой механике. И небезизвестном (популяризованном, в частности, в Квантовой психологии) эксперименте с ERP-парами. Суть эксперимента (мысленного, предложенного Эйнштейном) вот в чём. Предположим у нас есть система из двух фотонов, находящаяся в одном квантовом состоянии. Теперь, не измеряя это квантовое состояние мы эти фотоны разносим на произвольное расстояние, измеряем один из фотонов в паре, получаем случайное значение (с некоторой вероятность то или иное), но что самое занятное, неизмеренный фотон при этом тоже займёт определённое состояние, такое, которое должен был бы занимать в общем квантовом состоянии, если бы другой фотон занимал то состояние, в которое его измеряли.
Множество копьев было сломано об интерпретацию этого эксперимента, который был реально проведён. Как это вдруг? Фотоны узнают друг о друге мгновенно? Так не бывает. Давайте, чтобы так не было, придумаем, что наше измерение меняет наше прошлое — говорят горячие головы. Давайте откажемся от здравого смысла — говорят они.
Хм. ОК. А теперь представим себе такой эксперимент: некто берёт, два шарика, один чёрный, другой белый, с закрытыми глазами перемешивает, и отправляет в два разных города. А потом сидит и ждёт звонка от своих друзей, чтобы те рассказали ему, какого же цвета они получили шарики. Из Екатеринбурга ему звонят и говорят: Марья Петровна (соблюдём равенство полов), а у нас тут чёрный шарик. Звонят из Зеленограда и говорят: а у нас белый. Хм… И Марья Петровна удивлена — как же это может быть так!? Как екатеринбуржский шарик узнал о шарике зеленоградском?
При этом, что занятно, для измерителей, в Зеленограде, Екатеринбурге и самой Марьи Ивановны из Днепропетровска, любой шарик посланный по почте имел неопределённое состояние до того, как его измеряли. В мире не существовало информации о том (ну, мы верим в честность почтовых работников), какой именно шарик куда летит, поэтому, о них можно было рассуждать только в терминах волновых функций. Но такое волновое поведение — плод условий проведения эксперимента.
В мире не существовало информации о том (ну, мы верим в честность почтовых работников), какой именно шарик куда летит, поэтому, о них можно было рассуждать только в терминах волновых функций. Но такое волновое поведение — плод условий проведения эксперимента.
Чем фотоны отличаются от шариков? Многие настаивают, что всем. Но лично я не понимаю. Этот эксперимент с ERP — просто изощрённый способ передать себе и так, наперёд известный факт: два фотона в спутанной ERP-паре будут в разных состояниях. Два шарика будут покрашены в разный цвет…
Риторический вопрос, если бы информация, полученная при измерении не попала бы потом в одно место, где бы её сравнили и удивились тому, как ведут себя фотоны, то кто бы этому эксперименту удивился бы? Поведение фотонов определяет не вариативное прошлое, и не какакая не контрфактуальность и антиинтуитивность (скорее это всё относиться к классическим описаниям физических систем в виде траекторий, материальных точек и комплексных векторных связок над комплексными же гладкими многообразиями), а не к очевидным фактам, что поведение вседенной в виде фотонов определяется нашим способом за ним наблюдать и обрабатывать информацию, то есть самим экспериментом.
При этом, эксперимент всегда конечен во времени и в пространстве, его история конечна, поэтому мы можем рассуждать о его симметриях, траекториях и прочих явлениях, на которых построена современная теоретическая физика. Но как устроена природа там, где нет синхрофазатрона?
Хм… Вот. То есть, вполне возможно, что электроны, фотоны, протоны и так далее — это действительно лишь модели. Термины, которые появляются при применении определённой конфигурации оборудования ко Вселенной, конфигурации которая ограничивает варианты поведения вселенной, которая позволяет кое-что запомнить, и таким образом сформулировать закон… Хм, наверное, я в этом всём не прав, но иное не приходит в голову.
И это не противоречит нашему успеху в инженерном искусстве. Пользуясь понятиями о симметричности различных конечных форм во Вселенной, полученное в экспериментальной установке поведение мы можем смасштабировать, развернуть, повернуть, растянуть, потрясти, покрутить и так далее, и получить транзистор. Но означает ли это, что в транзисторе существуют дырки? Вообще, означает ли наша возможность пронаблюдать существование наблюдаемого? Или это особенность нашего наблюдения?
Но означает ли это, что в транзисторе существуют дырки? Вообще, означает ли наша возможность пронаблюдать существование наблюдаемого? Или это особенность нашего наблюдения?
И, напоследок, взаимодействие. В физике со взаимодействием туго. Для меня, по крайней мере. А есть ли формальная система, в которой взаимодействие очевидно? Не поленитесь, скачайте Game of Life Конвэя. Желательно, тот вариант, который укомплектован коллекцией различных конфигураций, в том числе и космическими кораблями. www.ibiblio.org/lifepatterns тут можно посмотреть, заветная кнопка enjoy life в верхнем левом углу.
Так вот. Что в ней занятного? При всей её отрешённости от мира комплексных чисел, при всей простоте правил в ней: (1) очевидно существуют структуры, которые сохраняя своё устройства могут перемещаться с определённой скоростью — космические корабли (spaceships). При этом, эта структура не состоит из строительных блоков, она не состоит за самих клеток, которые эволюционируют, она состоит из свойств этих клеток. Просто группка перекрашенных в чёрное элементов. (2) известна простейшая структура, способная двигаться — glider. Можете столкнуть два spaceship’а и посмотреть на возникающий взрыв.
Просто группка перекрашенных в чёрное элементов. (2) известна простейшая структура, способная двигаться — glider. Можете столкнуть два spaceship’а и посмотреть на возникающий взрыв.
Взаимодействие на лицо. И для этого взаимодействия не нужны пространства Калаби-Яу. Нужно лишь принять очень простую установку — существующее это лишь сохраняющийся признак эволюционирующей группы клеток (прямо как сохраняющееся свойство в аксиоматике натуральных чисел, в последней аксиоме индукции). Когда два свойства сблизятся, они начнут меняться и образовывать новые свойства. Потому что сами клеточки изменчивы, как изменчиво Дао.
Всё просто. Но опять же… Сложности с математикой. Эту игру математически так и не проанализировали, сам Конвэй пытался, и в процессе даже изобрёл замечательные сюрреалистичные числа, но… особых значимых выводов найдено не было. Ещё один гвоздь, приколачивающий к стене надпись о том, что математика в одиночку не способна справиться с подвижными системами. Для их анализа нужен человек, или компьютер. Соответственно, вполне возможно, это опровергает гипотезу Пенроуза о том, что для интеллекта нужны некие загадочные квантовые эффекты, путешевствующие из будущего в прошлое. Для существования интеллекта нужна динамика — вот альтернативный тезис. Естсественно, никакая машина Тьюринга динамикой не обладает. Это лишь последовательность состояний, всегда определённая начальнм состоянием ленты и самой машины… Но всё меняется, когда в процессе вычисления машина способна получать данные, независящие от её внутреннего состояния — машина с регистром ввода\вывода. Вот эта штука, вполне возможно, вполне динамична. Компьютер, естественно, является именно такой машиной.
Соответственно, вполне возможно, это опровергает гипотезу Пенроуза о том, что для интеллекта нужны некие загадочные квантовые эффекты, путешевствующие из будущего в прошлое. Для существования интеллекта нужна динамика — вот альтернативный тезис. Естсественно, никакая машина Тьюринга динамикой не обладает. Это лишь последовательность состояний, всегда определённая начальнм состоянием ленты и самой машины… Но всё меняется, когда в процессе вычисления машина способна получать данные, независящие от её внутреннего состояния — машина с регистром ввода\вывода. Вот эта штука, вполне возможно, вполне динамична. Компьютер, естественно, является именно такой машиной.
Ладно. Ещё одно замечание. Если в Жизни взять пустое пространство без каких-либо отклонений от симметрии, а потом вокруг него построить некую установку, то вполне возможны ситуации, когда внутри этого пространства со временем возникнут, например, глайдеры (существует glidergun). Таким образом, можно говорить о том, что возникающий глайдер — это не элемент вселенной, а элемент эксперимента. Хотя, существовать и возникать эта структура может где угодно, но не обязательно, что она существует везде, например, между двумя электронами в молекуле. Не существует, пока мы не полезем туда со своим экспериментом, или со своим измерением.
Хотя, существовать и возникать эта структура может где угодно, но не обязательно, что она существует везде, например, между двумя электронами в молекуле. Не существует, пока мы не полезем туда со своим экспериментом, или со своим измерением.
Но почему только мы должны обладать этим правом? Вот ведь в чём проблема. А современная математическая картинка говорит именно об этом. Чтобы столкнуть два электрона, нужен человек, чтобы указать электронам, как фотоны поглащать, нужен человек. Сами они этого не умеют. Точнее, умеют, но качественного описания процесса у нас нет. Возможно, оно и не появиться никогда, потому что возможности математики ограничены, но существование формальной Game of Life даёт надежду на то, что это не так.
На самом деле, это всё тесно перекликается с квантовой теорией поля, которая работает в ускорителях.
Поэтому, на мой взгляд, физикам сейчас надо не LHC строить, не генерировать чёрные дыры и стрэйнджлеты, а попытаться понять, что же они такое делают в своих теориях. К чему идут. Ввести в них, наконец, аккуратно понятия взаимодействия и понятия времени. Или показать, что это невозможно сделать. Но из самой невозможности это сделать, тоже последуют интересные результаты, наверняка. Этому учит нас квантовая теория — результат эксперимента зависит от того, что можно измерять.
К чему идут. Ввести в них, наконец, аккуратно понятия взаимодействия и понятия времени. Или показать, что это невозможно сделать. Но из самой невозможности это сделать, тоже последуют интересные результаты, наверняка. Этому учит нас квантовая теория — результат эксперимента зависит от того, что можно измерять.
Возможно, вообще, нужно начать говорить на языке информации. Потому что в ERP-эксперименте поток информации имеет определённую структуру, и во всех других квантовых экспериментах, если принять частицу как то, что переносит информацию, которая разделённая на части не имеет смысла, то многие парадоксы перестают таковыми быть.
Да и в конце концов — общая теория всего, к которой стремяться физики — это чисто информационная теория. Когда, не нужно ничего, кроме символов, написанных ручкой, чтобы объяснить всё богатство вселенной. А только информация обладает тем свойством, что ей не важен носитель, важно лишь то свойство, что носитель способен принимать различные состояния. И информация может образовывать сущности, как показывает Game of Life и многие другие клеточные автоматы.
И информация может образовывать сущности, как показывает Game of Life и многие другие клеточные автоматы.
Возможно, это способно приблизить сознание к пониманию того, из чего же построена вселенная. И возможно, это способ приблизиться к пониманию того, что же такое Дао. Но скорее всего — это просто флуктуации, которое моё сознание выловило непонять от куда, и решило обнародовать. Обнародовало, успокоилось и теперь может спокойно вернуться к общественно полезной деятельности в виде программирования.
Вот, надеюсь, больше меня эта каша не будет беспокоить.
Время Present Simple в английском языке
Наиболее часто употребляемое время — Present Simple Tense (настоящее простое время). Можно сказать, что это основное время в английском языке, и поэтому его необходимо понять и уметь правильно применять в своей речи.
The Present Simple Tense или the Present Simple Indefinite?
На уроках английского в школе мы, как правило, первым делом узнаем, что такое презент симпл в английском языке, — именно с этого времени начинается изучение грамматики.
Для начала давайте поймем, почему при изучении английского языка, а также в лингвистической литературе the Present Simple Tense (настоящее простое время) часто могут называть the Present Simple Indefinite (настоящее простое неопределенное) и есть ли разница между этими понятиями.
Present Simple часто описывает действие, при котором время не определено.
- I enjoy eating seafood. — Я люблю есть морепродукты.
- He plays tennis. — Он играет в теннис.
Мы видим, что в данных примерах глагол выражает действие вообще, время, как таковое, не уточняется. Именно поэтому Present Simple еще называют Present Indefinite, то есть неопределенное (indefinite переводится как «неопределенный». Это название в некоторых случаях точнее передает смысл этого времени. Итак, Present Simple и Present Indefinite — это просто разные названия для одного и того же времени. При переводе на русский язык тоже применяют оба термина: настоящее простое время в английском языке и настоящее неопределенное время.
При переводе на русский язык тоже применяют оба термина: настоящее простое время в английском языке и настоящее неопределенное время.
Употребление Present Simple в английском языке
В каких случаях мы используем в речи настоящее простое время Present Simple?
- обычные ситуации, события, что-то постоянное, не привязанное к конкретному моменту
People in Moscow speak Russian. — Люди в Москве говорят по-русски.
She works as a doctor. — Она работает врачом.
- регулярно повторяющиеся действия, привычки
I go to Australia every spring. — Я езжу в Австралию каждую весну.
I get up at 7 a.m. — Я встаю в 7 часов утра.
He never eats fish. — Он никогда не ест рыбу.
- неизменные факты, правда, законы природы
Doctors study for many years. — Врачи учатся много лет.
My teacher always arrives early. — Мой учитель всегда приходит рано.
Water freezes at 0 C.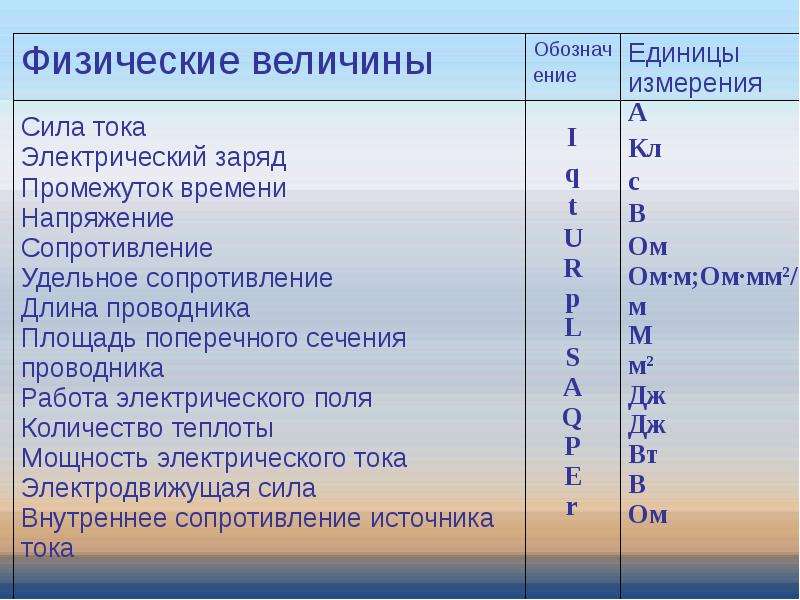 — Вода замерзает при нуле градусов.
— Вода замерзает при нуле градусов.
- расписание и программа, время в этом случае выбрано не нами
The train from Sochi arrives at 6:15 p.m. — Поезд из Сочи прибывает в 18:15.
School begins at 9:00 and ends at 3:00. — Уроки в школе начинаются в 9 утра и заканчиваются в 3 дня.
- рецензии, а также спортивные комментарии
Pele scores a goal. — Пеле забивает гол.
Meryl Streep acts brilliantly in this film. — Мэрил Стрип великолепно играет в этом фильме.
- когда рассказываем, что произошло в фильме, книге или пьесе
An old Irish man decides to revenge the death of his dear friend by hunting down the members of the criminal gang. He kills them one by one. — Старый ирландец решает отомстить за смерть своего дорогого друга охотой на членов криминальной группировки. Он убивает их одного за другим.
- мнение или отношение
I like jazz. — Я люблю джаз.
My sister loves movies. — Моя сестра обожает кино.
Формула Present Simple. Объяснение основных правил
Грамматика английского времени Present Simple довольно проста. Даже для детей объяснение должно быть понятным. Рассмотрим, как образуется Present Simple в английском языке, как строится Present Simple в утвердительных, отрицательных и вопросительных предложениях. При изучении всех форм Present Simple правила и таблицы будут необходимы, поэтому ниже вы найдете всю нужную информацию в виде таблиц.
Утвердительная форма Present Simple
Образование Present Simple в утвердительной форме: убираем у глагола в инфинитиве частицу «to» и ставим глагол после подлежащего. Подлежащим может быть и существительное, и местоимение. Это и будет утвердительная конструкция Present Simple.
| Подлежащее | Основной глагол |
| I / We / You / They | Основная форма глагола |
| He / She / It | Основная форма глагола + -s(-es) |
I / We / You / They + V
He / She / It + V + s (es)
I play drums. — Я играю на барабанах.
— Я играю на барабанах.
Jacob and Francis get a coffee together every week. — Джейкоб и Фрэнсис встречаются на кофе каждую неделю.
Every month I have to submit a new assignment. — Каждый месяц я должна сдать новое задание.
В Present Simple форма глагола почти всегда совпадает с изначальной, но есть исключения:
- в третьем лице единственного числа (he / she / it) у глагола появляется окончание -s.
I work at the factory. — She works at the factory.
I love my work. — He loves his work.
- в случае, если в конце глагола стоит -ss, -sh, -ch, -x, или -o, к нему нужно добавить окончание -es.
| Глагол в начальной форме | Глагол + окончание -es/s |
| kiss | kisses |
| wish | wishes |
| breach | breaches |
| relax | relaxes |
| go | goes |
- Если последние две буквы в глаголе — это согласная + -y, к нему прибавляется окончание -es.
 -Y надо заменить на -i.
-Y надо заменить на -i.
| Глагол в начальной форме | Глагол + окончание -es/s |
| try | tries |
| deny | denies |
| breach | breaches |
| embody | embodies |
- если в конце глагола есть гласная + -y, то к нему также прибавляется окончание -s. -Y остается на своем месте.
| Глагол в начальной форме | Глагол + окончание -es/s |
| play | plays |
| enjoy | enjoys |
| buy | buys |
Отрицательная форма Present Simple
Отрицательные предложения в Present Simple строятся с помощью вспомогательного глагола to do.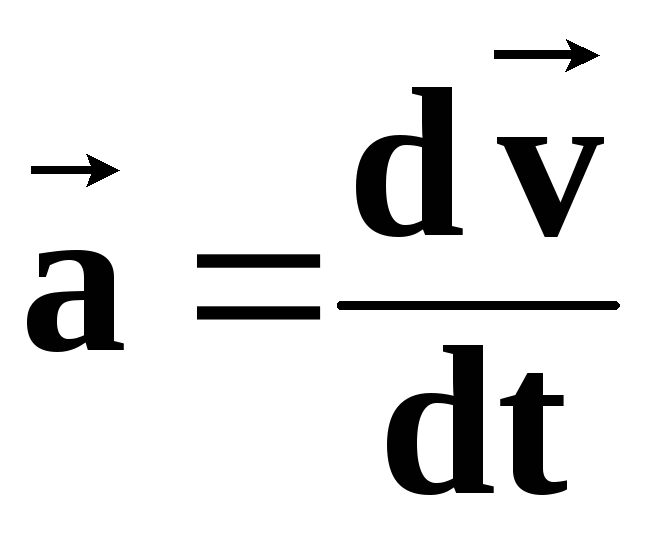 Вообще, для построения предложений в английском языке часто используется какой-либо вспомогательный глагол. Present Simple — не исключение.
Схема построения: используем вспомогательный глагол to do и частицу not. В третьем лице единственного числа do, присоединяя к себе окончание -es, превращается в does.
Вообще, для построения предложений в английском языке часто используется какой-либо вспомогательный глагол. Present Simple — не исключение.
Схема построения: используем вспомогательный глагол to do и частицу not. В третьем лице единственного числа do, присоединяя к себе окончание -es, превращается в does.
| Подлежащее | Вспомогательный глагол | Основной глагол |
| I / We / You /They | do not = don’t | основная форма глагола |
| He / She / It | does not = doesn’t |
I / We / You / They + do not + V
He / She / It + does not + V
Вспомогательные глаголы do not и does not в разговорной речи можно использовать в сокращенной форме: don’t и doesn’t. Обратите внимание, что, если мы используем does, окончание -s у основного глагола исчезает. Вспомогательные глаголы всегда берут на себя -s (do + es = does), и нам не надо использовать это окончание еще раз.
Вспомогательные глаголы всегда берут на себя -s (do + es = does), и нам не надо использовать это окончание еще раз.
I don’t go to the office on Mondays. — Я не хожу на работу по понедельникам.
They never drink alcohol. — Они никогда не пью алкоголь.
Chloe doesn’t like the climate in France. — Хлое не нравится климат во Франции.
My brother doesn’t know much about physics. — Мой брат мало что знает о физике.
Отрицание в английском языке, как и в русском, можно выразить отрицательными местоимениями и наречиями.
Nobody eats beef ribs for breakfast. — Никто ест говяжьи ребрышки на завтрак.
The President does nothing to improve the situation. — Президент не делает ничего, чтобы улучшить ситуацию.
Вопросительная форма Present Simple
Вопросительная форма Present Simple также требует использования вспомогательного глагола do (does). Мы ставим в начале предложения do (does), потом подлежащее и основной глагол.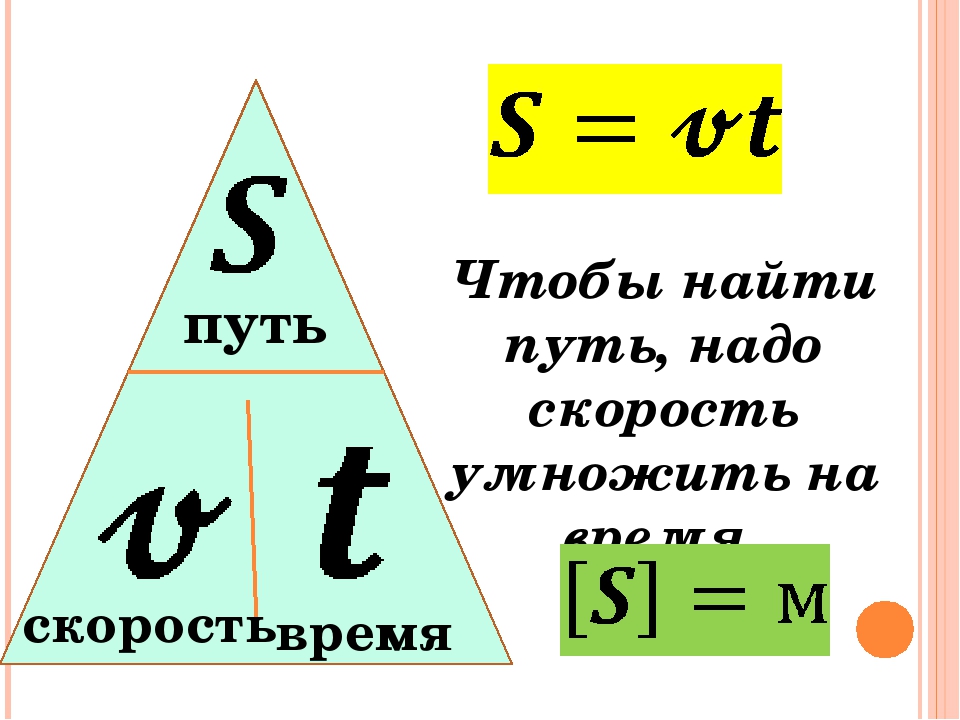 Помните, если появляется does, окончание -s (-es) у основного глагола исчезает.
Помните, если появляется does, окончание -s (-es) у основного глагола исчезает.
| Вспомогательный глагол | Подлежащее | Основной глагол |
| Do | I / we / you / they | основная форма глагола |
| Does | he / she / it |
Do + I / we / you / they + V ?
Does + he / she / it + V ?
Do I believe in God? — Я верю в Бога?
Do we go to the coast or not? — Мы собираемся ехать на побережье или нет?
Do you like pizza? — Ты любишь пиццу?
Do boys eat fish? — Мальчики едят рыбу?
Does she like spending time at home? — Она любит проводить время дома?
Does he speak Chinese fluently? — Он в совершенстве владеет китайским?
В вопросительном предложении часто употребляются вопросительные слова и фразы, так называемые question words. Они помогут более точно и корректно передать мысль в Present Simple.
Они помогут более точно и корректно передать мысль в Present Simple.
К таким словам относятся: how long, how, why, where и другие. Вопросительные слова стоят в начале предложения перед уже известной нам вопросительной конструкцией Present Simple.
QW + do (does) + I / We / You / They / He / She / It + V ?
Where does the road lead? — Куда ведет дорога?
How long does it take to make the soup? — Как долго готовится суп?
Глагол to be в Present Simple
Глагол to be (быть, есть) в английском языке не такой, как все глаголы. Present Simple требует специальной формы его использования, она зависит от подлежащего.
| I | He / She / It | We / you / they |
| am | is | are |
Утверждение
I + am
He / She / it + is
We / you / they + are
I am a student. — Я студент.
— Я студент.
My brothers are drivers. — Мои братья водители.
Her garden is beautiful. — Ее сад прекрасен.
Отрицание
I + am not
We / you / they + are not (aren’t)
He / She / it + is not (isn’t)
I am not a lawyer. — Я не юрист.
We are not travelers. — Мы не путешественники.
He is not my husband. — Он не мой муж.
Вопрос
Am + I
Are + we / you / they
Is + she / he / it
Am I healthy? — Я здоров?
Are we free? — Мы свободные?
Is Dan your younger brother? — Дэн — твой младший брат?
Показатели Present Simple
Слова-маркеры
В английском языке существуют своеобразные подсказки, которые раскрывают контекст предложения, указывая на время. Эти слова-маркеры встречаются в большинстве предложений и выражают конкретное время или его периоды. Вспомогательные слова помогут нам точнее определить Present Simple. Как объяснить даже ребенку, какое предложение образовано в Present Simple? Покажите ему основные маркеры презент симпл — обстоятельства времени и служебные слова, указывающие на повторяемость действия, и тогда найти предложения в Present Simple будет легко:
Вспомогательные слова помогут нам точнее определить Present Simple. Как объяснить даже ребенку, какое предложение образовано в Present Simple? Покажите ему основные маркеры презент симпл — обстоятельства времени и служебные слова, указывающие на повторяемость действия, и тогда найти предложения в Present Simple будет легко:
I usually drink matcha latte. — Я обычно пью матча латте.
We often go ocean swimming in the morning. — Мы часто ходим купаться в океан по утрам.
People always help if others are in trouble.— Люди всегда помогают, если другие попали в беду.
- daily — ежедневно
Children read daily at school. — Дети в школе читают ежедневно.
- every day — каждый день
I go out every day. — Я гуляю каждый день.
The guests arrive in Moscow today. — Гости приезжают в Москву сегодня.
- once a week — раз в неделю
I let myself have a cheat meal once a week. — Я позволяю себе нарушать диету один раз в неделю.
— Я позволяю себе нарушать диету один раз в неделю.
- sometimes — иногда
Sometimes he sleeps a long time. — Иногда он долго спит.
I seldom have rest. — Я редко отдыхаю.
Our director is never late. — Наш директор никогда не опаздывает.
Глаголы-маркеры
Указателями времени могут быть не только обстоятельства и служебные слова, но и сами глаголы. В английском языке есть целый ряд глаголов, которые описывают состояние объекта, его умственные процессы и чувства. Они называются stative verbs — статичные глаголы.
В противовес им существуют active verbs — активные глаголы (to sleep, to run, to row…). Если за действием активного глагола мы можем наблюдать — например смотреть, как кто-то бежит, — то нельзя увидеть, как кто-то верит или чего-то хочет, потому что это не физический процесс, а результат когнитивной деятельности человека.
Статичные глаголы или глаголы состояния часто можно увидеть в предложениях с Present Simple.
Stative verbs выражают:
- эмоции и чувства: love — любить, like — нравится, want — хотеть, wish — желать, hate — ненавидеть, need — нуждаться, prefer — предпочитать;
- мыслительную деятельность: know — знать, agree — соглашаться, believe — верить, forget — забывать, expect — ожидать, understand — понимать, suppose — полагать, remember — помнить, respect — уважать, think — полагать
- обладание, отношение: be — быть, belong — принадлежать, consist — состоять, have — иметь.
Примеры предложений:
She is short and has long hair. — У нее маленький рост и длинные волосы.
They like strawberries. — Они любят клубнику.
We want a new car. — Мы хотим машину.
I promise I will help you. — Я обещаю, что помогу тебе.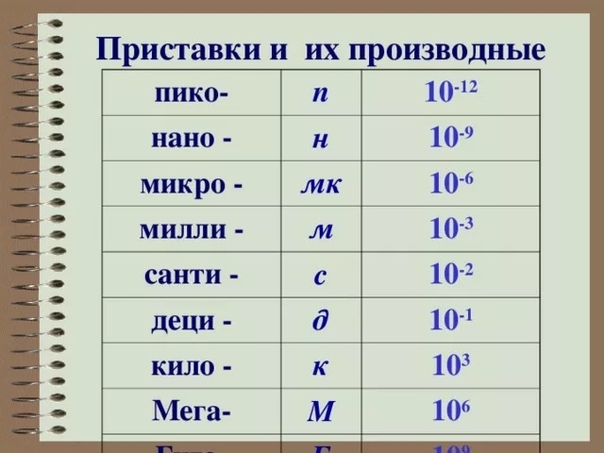
You look fantastic. — Ты потрясающе выглядишь.
They belong to the yacht club. — Они члены яхт-клуба.
I don’t know the answer. — Я не знаю ответа.
Заключение
Итак, теперь мы знаем, что такое настоящее простое время Present Simple. Грамматика Present Simple, правила и примеры употребления достаточно просты и понятны. Вы уже убедились в этом, не так ли?
Читайте также:
Future Simple
Past Simple
Времена Simple: согласование
Все времена английского глагола
Время, отведенное на выполнение тестов ЗНО – Освіта.UA
Сколько времени получат участники внешнего независимого оценивания на выполнение заданий тестов |
В 2022 году в программу проведения внешнего независимого оценивания включены 12 тестовых предметов. В частности, абитуриентам во время регистрации было предложено выбрать тесты по украинскому языку, украинскому языку и литературе, математике, истории Украины, биологии, географии, физике, химии, а также по английскому, немецкому, французскому и испанскому языкам.
Учитывая разное количество заданий и их форм, на выполнение каждого теста внешнего независимого оценивания отводится разное время.
Время, отведенное на выполнение заданий тестов ЗНО в 2022 году:
-
Предмет
Время на выполнение заданий теста
Английский язык
150 минут
Билогия
150 минут
География
150 минут
Испанский язык
150 минут
История Украины
150 минут
Математика
120 минут (уровень стандарта)
180 минут (профильный уровень)
Немецкий язык
150 минут
Украинский язык и литература
210 минут
Украинский язык
150 минут
Физика
180 минут
Французский язык
150 минут
Химия
150 минут
С целью дистанционной подготовки к тестированию участники ЗНО могут использовать сайт ЗНО онлайн, на котором представлены все задания тестов внешнего оценивания, которые были предложены абитуриентам Украинским центром оценивания качества образования со времен введения независимого тестирования.
Для получения информации о внешнем независимом оценивании и вступительной кампании присоединяйтесь к группе Абитуриент или Освіта.ua на Facebook.
Освіта.ua
04.11.2021
8.1: Время не абсолютное
Когда Эйнштейн впервые начал разрабатывать теорию относительности, примерно в 1905 году, единственные наблюдения реального мира, на которые он мог опираться, были неоднозначными и косвенными. Сегодня доказательства стали частью повседневной жизни. Например, каждый раз, когда вы используете GPS-приемник a, вы используете теорию относительности Эйнштейна. Где-то между 1905 годом и сегодня технологии стали достаточно хороши, чтобы позволить концептуально простых экспериментов , которые студенты в начале 20-го века могли обсуждать только в терминах типа «Представьте, что мы могли бы… »
Рисунок a: / Эта система глобальной системы позиционирования (GPS), работающая на смартфоне, прикрепленном к рулю велосипеда, зависит от теории относительности Эйнштейна. На спутнике GPS время течет с другой скоростью, чем на велосипеде, и программное обеспечение GPS должно это учитывать.
На спутнике GPS время течет с другой скоростью, чем на велосипеде, и программное обеспечение GPS должно это учитывать.
Хорошая отправная точка – 1971 год. В этом году J.C. Hafele и R.E. Китинг привез атомные часы на борт коммерческих авиалайнеров b и совершил кругосветное путешествие – один раз с востока на запад, другой – с запада на восток.Хафеле и Китинг заметили несоответствие между временем, измеренным ходовыми часами, и временем, измеренным аналогичными часами, которые оставались дома в Военно-морской обсерватории США в Вашингтоне. Часы, идущие на восток, отстают от времени, заканчивая \ (- 59 \ pm10 \) наносекунд, в то время как часы, идущие на запад, показывают \ (273 \ pm7 \) нс.
б / Часы заняли два места, и на них было куплено два билета на имя «Mr. Часы.”
7.1.1 Принцип соответствия
Это устанавливает, что время не работает так, как полагал Ньютон, когда писал, что «Абсолютное, истинное и математическое время само по себе и из своей собственной природы течет равномерно, независимо от чего-либо внешнего. … »Мы привыкли думать о времени как о абсолютном и универсальном, поэтому очень неприятно обнаруживать, что оно может течь с разной скоростью для наблюдателей в разных системах отсчета. Тем не менее эффекты, которые наблюдали Хафеле и Китинг, были небольшими. В этом есть смысл: законы Ньютона уже были тщательно проверены экспериментами в самых разных условиях, поэтому новая теория, такая как теория относительности, должна в хорошем приближении согласовываться с теорией Ньютона в пределах применимости ньютоновской теории.Это требование обратной совместимости известно как принцип соответствия.
… »Мы привыкли думать о времени как о абсолютном и универсальном, поэтому очень неприятно обнаруживать, что оно может течь с разной скоростью для наблюдателей в разных системах отсчета. Тем не менее эффекты, которые наблюдали Хафеле и Китинг, были небольшими. В этом есть смысл: законы Ньютона уже были тщательно проверены экспериментами в самых разных условиях, поэтому новая теория, такая как теория относительности, должна в хорошем приближении согласовываться с теорией Ньютона в пределах применимости ньютоновской теории.Это требование обратной совместимости известно как принцип соответствия.
7.1.2 Причинно-следственная связь
Также обнадеживает то, что влияние на время было небольшим по сравнению с трехдневной продолжительностью перелетов. Следовательно, не было возможности для парадоксальных сценариев, таких как тот, в котором экспериментатор, идущий на восток, возвращался в Вашингтон перед отъездом, а затем убеждал себя не совершать поездку. Говорят, что теория, которая поддерживает такого рода упорядоченные отношения между причиной и следствием, удовлетворяет причинно-следственную связь.
Причинность похожа на голодную воду лужайку перед перед домом в Лос-Анджелесе: мы знаем, что хотим, но нелегко объяснить почему. Даже в простой старой ньютоновской физике нет четкого различия между прошлым и будущим. На рисунке c цифра 18 перебрасывает футбольный мяч на номер 25, и мяч подчиняется законам движения Ньютона. Если бы мы сняли на видео передачу и воспроизвели ее в обратном направлении, мы бы увидели, как мяч летит от 25 до 18, и законы Ньютона все равно будут выполняться. Тем не менее, у нас сложилось сильное психологическое впечатление, что время идет вперед.
c / Законы Ньютона не различают прошлое и будущее. Мяч мог двигаться в любом направлении, подчиняясь законам Ньютона.
Я могу вспомнить, что делала фондовая биржа в прошлом году, но не могу вспомнить, что она будет делать в следующем году. Военные победы Жанны д’Арк против Англии заставили англичан сжечь ее на костре; Трудно согласиться с тем, что законы Ньютона дают одинаково хорошее описание процесса, в котором ее казнь в 1431 году побудила ее выиграть битву в 1429 году.На данный момент среди физиков нет единого мнения о происхождении и значении стрелы времени, и для наших нынешних целей нам не нужно разгадывать эту загадку. Вместо этого мы просто отмечаем эмпирический факт, что независимо от того, что на самом деле означает причинность и откуда она на самом деле исходит, ее поведение непротиворечиво. В частности, эксперименты показывают, что если наблюдатель в определенной системе отсчета наблюдает, что событие A вызывает событие B, то наблюдатели в других системах отсчета соглашаются, что A вызывает B, а не наоборот.Это просто обобщение большого количества экспериментальных результатов, а не логически необходимое предположение. Если бы Китинг объехал весь мир и вернулся в Вашингтон перед отъездом, это опровергло бы это утверждение о причинно-следственной связи.
7.1.3 Искажение времени, вызванное движением и гравитацией
Хафеле и Китинг проверяли конкретные количественные предсказания относительности, и они подтвердили их с точностью до планки ошибок своего эксперимента. Вместо этого давайте вернемся назад и проверим эмпирические результаты, чтобы понять, как работает время.
Два бегущих часа испытывают эффекты в противоположных направлениях, и это предполагает, что скорость, с которой течет время, зависит от движения наблюдателя. Часы, идущие на восток, двигались в том же направлении, что и вращение Земли, поэтому их скорость относительно центра Земли была больше, чем у часов, оставшихся в Вашингтоне, в то время как скорость часов, идущих на запад, была соответственно уменьшена. Тот факт, что часы, идущие на восток, отстали, а часы, идущие на запад, опередили, показывает, что эффект движения заставляет время идти медленнее.Этот эффект движения во времени был предсказан Эйнштейном в его оригинальной статье 1905 года по теории относительности, написанной, когда ему было 26 лет.
Рисунок d : Все три часа движутся на восток. Несмотря на то, что летящий на запад самолет движется на запад относительно воздуха, воздух движется на восток из-за вращения Земли.
Если бы это был единственный эффект в эксперименте Хафеле-Китинга, то мы ожидали бы увидеть эффекты на двух летающих часах, равных по размеру.Составив несколько простых чисел, чтобы сделать арифметику прозрачной, предположим, что Земля вращается с запада на восток со скоростью 1000 км / час, а самолеты летают со скоростью 300 км / час. Тогда скорость часов на земле составляет 1000 км / час, скорость часов на восточном самолете составляет 1300 км / час, а скорость часов на западе составляет 700 км / час. Поскольку скорости 700, 1000 и 1300 км / ч имеют равные интервалы по обе стороны от 1000, мы ожидаем, что расхождения движущихся часов относительно часов в лаборатории будут одинаковыми по размеру, но противоположными по знаку.
e / График, показывающий разницу во времени между двумя атомными часами. Одни часы хранились в обсерватории Митака на высоте 58 м над уровнем моря. Другой перемещался взад и вперед ко второй обсерватории, станции Норикура Корона, на вершине вулкана Норикура, на высоте 2876 м над уровнем моря. Плато на графике – это данные тех периодов, когда часы сравнивались бок о бок в Митаке. Разница между одним плато и другим показывает гравитационный эффект на скорость течения времени, накопленный за период, когда мобильные часы находились на вершине Норикуры.Ср. проблема 25, с. 443.
На самом деле, два эффекта не равны по размеру: \ (- 59 \) нс и 273 нс. Это означает, что есть второй эффект, просто из-за того, что самолеты находятся в воздухе. Это было подтверждено более прямо в эксперименте 1978 года, проведенном Иидзимой и Фудзиварой (рис. E), в котором идентичные атомные часы находились в покое на вершине и внизу горы недалеко от Токио. Этот эксперимент, в отличие от эксперимента Хафеле-Китинга, выделяет один эффект во времени, гравитационный: скорость течения времени увеличивается с высотой в гравитационном поле.Эйнштейн не придумал, как включить гравитацию в теорию относительности до 1915 года, после многих разочарований и множества неудачных попыток. Более простая версия теории без гравитации известна как специальная теория относительности, а полная версия – как общая теория относительности. {- 15} \) – намного меньше, чем часы способны обнаружить.{-10} \). Общая идея здесь в том, что все физические законы являются приближениями, а приближения не просто правильны или неправильны в разных ситуациях. Приближения лучше или хуже в разных ситуациях, и вопрос в том, достаточно ли конкретное приближение в данной ситуации, чтобы служить определенной цели. Чем быстрее движение, тем хуже ньютоновское приближение абсолютного времени. Достаточно ли хорошее приближение зависит от того, чего вы пытаетесь достичь. Принцип соответствия гласит, что приближение должно было быть достаточно хорошим, чтобы объяснить все эксперименты, проведенные за столетия до того, как Эйнштейн придумал теорию относительности.
Между прочим, не делайте преувеличенного представления о важности эксперимента Хафеле-Китинга. Специальная теория относительности уже была подтверждена многочисленными и разнообразными экспериментами за десятилетия до 1971 года. Единственная причина, по которой я придаю столь важную роль этому эксперименту, который на самом деле был более важен как проверка общей теории относительности, заключается в том, что он концептуально очень прямо.
Колебание крошечной частицы может изменить известные законы физики
Появляется все больше свидетельств того, что крошечная субатомная частица, похоже, не подчиняется известным законам физики, объявили ученые в среду, открытие, которое откроет огромную и мучительную дыру в нашем понимании. Вселенной.
Результат, говорят физики, предполагает, что существуют формы материи и энергии, жизненно важные для природы и эволюции космоса, которые еще не известны науке. По их словам, новая работа может в конечном итоге привести к более драматичным прорывам, чем объявленное в 2012 году открытие бозона Хиггса, частицы, которая наделяет другие частицы массой.
«Это момент посадки нашего марсохода», – сказал Крис Полли, физик из Национальной ускорительной лаборатории Ферми (Фермилаб) в Батавии, штат Иллинойс., который работал над этим открытием большую часть своей карьеры.
Селебра частица – это мюон, который похож на электрон, но намного тяжелее и является неотъемлемым элементом космоса. Доктор Полли и его коллеги – международная группа из 200 физиков из семи стран – обнаружили, что мюоны ведут себя не так, как предсказывалось, когда они проходят через сильное магнитное поле в Фермилабе.
Аберрантное поведение бросает серьезный вызов Стандартной модели, набору уравнений, которые перечисляют фундаментальные частицы во Вселенной (17, по последним подсчетам) и то, как они взаимодействуют.
«Это убедительное доказательство того, что мюон чувствителен к чему-то, что не входит в нашу лучшую теорию», – сказала Рене Фатеми, физик из Университета Кентукки.
Результаты, первые из эксперимента под названием «Мюон g-2», согласуются с аналогичными экспериментами в Брукхейвенской национальной лаборатории в 2001 году, которые с тех пор дразнят физиков. «После 20 лет того, как люди размышляли об этой загадке из Брукхейвена, заголовок любой новости здесь гласит, что мы подтвердили результаты экспериментов в Брукхейвене», – сказал доктор.- сказала Полли.
На виртуальном семинаре и пресс-конференции в среду доктор Полли указала на график, показывающий пустое пространство, где результаты Фермилаб отклоняются от теоретического предсказания. «Мы можем сказать с довольно высокой уверенностью, что должно быть что-то, способствующее образованию этого белого пространства», – сказал он. «Какие монстры могут там прятаться?»
«Сегодня необычный день, долгожданный не только для нас, но и для всего международного сообщества физиков», – сказал Грациано Венанцони, представитель коллаборации и физик Итальянского национального института ядерной физики, в заявлении, опубликованном Фермилаб.Результаты также публикуются в серии статей, представленных в Physical Review Letters, Physical Review A, Physical Review D и Physical Review Accelerators and Beams.
По словам ученых, измерения имеют примерно один шанс из 40 000 оказаться случайностью, что намного меньше золотого стандарта, необходимого для признания официального открытия по физическим стандартам. В науке многообещающие сигналы все время исчезают, но появляются новые данные. Результаты среды представляют лишь 6 процентов от общего объема данных, которые, как ожидается, получит мюонный эксперимент в ближайшие годы.
На протяжении десятилетий физики полагались на Стандартную модель и были связаны ею, которая успешно объясняет результаты экспериментов с частицами высоких энергий в таких местах, как Большой адронный коллайдер ЦЕРНа. Но эта модель оставляет без ответа многие глубокие вопросы о Вселенной.
Большинство физиков полагают, что их ждут богатые сокровища новой физики, если бы они могли заглядывать глубже и дальше. Дополнительные данные эксперимента Фермилаб могут стать серьезным стимулом для ученых, стремящихся построить следующее поколение дорогостоящих ускорителей частиц.
Это может также привести со временем к объяснениям тех космических загадок, которые долгое время занимали наш одинокий вид. Что такое темная материя, невидимое вещество, которое, по словам астрономов, составляет четверть Вселенной по массе? В самом деле, почему вообще существует материя во Вселенной?
В Твиттере и других местах физики отреагировали на объявление среды со смесью энтузиазма и осторожности.
Фабиола Джанотти, генеральный директор ЦЕРН, направила свои поздравления и назвала результаты «интригующими».Но Сабина Хоссенфельдер, физик из Франкфуртского института перспективных исследований, написала в Твиттере: «Конечно, существует возможность, что это новая физика. Но я бы не стал на это ставить.
Марсела Карена, руководитель отдела теоретической физики в Fermilab, которая не участвовала в эксперименте, сказала: «Я очень взволнована. Я чувствую, что это крошечное колебание может пошатнуть основы того, что, как мы думали, мы знали ».
«Кто это заказал?»
Мюоны – маловероятная частица, занимающая центральное место в физике.Иногда их называют «толстыми электронами», они напоминают знакомые элементарные частицы, которые питают наши батареи, свет и компьютеры и вращаются вокруг ядер атомов; у них отрицательный электрический заряд, и у них есть свойство, называемое вращением, которое заставляет их вести себя как крошечные магниты.
Но они в 207 раз массивнее своих более известных собратьев. Они также нестабильны, радиоактивно распадаясь на электроны и сверхлегкие частицы, называемые нейтрино, за 2,2 миллионных долей секунды.
Какую роль в общей структуре космоса играют мюоны, все еще остается загадкой. «Кто это заказал?» физик Колумбийского университета И.И. Раби сказал, когда они были впервые обнаружены в 1936 году. В настоящее время мюоны в больших количествах образуются в таких местах, как Большой адронный коллайдер, когда более обычные частицы сталкиваются вместе при высоких энергиях.
Мюоны обязаны своей нынешней известностью причуде квантовой механики, неинтуитивным правилам, лежащим в основе атомного царства. Среди прочего, квантовая теория утверждает, что пустое пространство на самом деле не пусто, а на самом деле кипит «виртуальными» частицами, которые то появляются, то исчезают.
«Вы можете подумать, что частица может быть одна в мире», – сказал доктор Полли в биографическом заявлении, опубликованном Fermilab. «Но на самом деле здесь совсем не одиноко. Благодаря квантовому миру мы знаем, что каждая частица окружена свитой из других частиц ».
Этот антураж влияет на поведение существующих частиц, в том числе на свойство мюона, называемое его магнитным моментом, которое выражается в уравнениях фактором, называемым g. Согласно формуле, полученной в 1928 году Полем Дираком, английским физиком-теоретиком и основателем квантовой теории, g-фактор одиночного мюона должен быть равен 2.
Но мюоны не одиноки, поэтому формулу необходимо скорректировать с учетом квантового шума, возникающего от всех других потенциальных частиц во Вселенной. Это приводит к тому, что коэффициент g для мюона больше 2, отсюда и название эксперимента: Мюон g-2.
Степень отклонения g-2 от теоретических предсказаний является одним из показателей того, сколько еще неизвестно о Вселенной – сколько монстров, как выразился доктор Полли, скрываются в темноте, чтобы физики могли их обнаружить.
В 1998 году физики из Брукхейвена, в том числе д-р.Полли, которая тогда была аспирантом, намеревалась исследовать это космическое невежество, фактически измерив g-2 и сравнив его с предсказаниями.
В эксперименте ускоритель, называемый синхротроном с переменным градиентом, создавал пучки мюонов и отправлял их в накопительное кольцо шириной 50 футов, гигантскую гоночную трассу, управляемую сверхпроводящими магнитами.
Полученное ими значение g расходилось с предсказанием Стандартной модели настолько, чтобы взволновать воображение физиков, но без достаточной уверенности, чтобы заявить о достоверном открытии.Более того, эксперты не смогли прийти к согласию с точным предсказанием Стандартной модели, что еще больше омрачает обнадеживающие воды.
Не имея денег на повторение эксперимента, Брукхейвен в 2001 году снял с эксплуатации 50-футовое накопительное кольцо для мюонов. Вселенная осталась висеть.
В Фермилабе строился новый кампус, посвященный изучению мюонов.
«Это открыло мир возможностей», – вспоминал доктор Полли в своей биографической статье. К этому времени доктор Полли уже работала в Фермилабе; он призвал лабораторию повторить эксперимент с g-2.Они поставили его главным.
Однако для проведения эксперимента им потребовалась 50-футовая магнитная беговая дорожка из Брукхейвена. Итак, в 2013 году магнит отправился в одиссею протяженностью 3200 миль, в основном на баржах, вниз по Восточному побережью, вокруг Флориды и вверх по реке Миссисипи, а затем на грузовике через Иллинойс в Батавию, где проживает Фермилаб.
Магнит напоминал летающую тарелку и привлекал внимание, когда он двигался на юг через Лонг-Айленд со скоростью 10 миль в час. «Я шел и разговаривал с людьми о науке, которой мы занимаемся», – сказал д-р.Написала Полли. «Он провел одну ночь на стоянке Costco. Более тысячи человек пришли посмотреть на это и услышать о науке ».
Эксперимент начался в 2018 году с более интенсивного мюонного пучка и с целью собрать в 20 раз больше данных, чем в версии для Брукхейвена.
Между тем, в 2020 году группа из 170 экспертов, известная как Muon g-2 Theory Initiative, опубликовала новое согласованное значение теоретического значения магнитного момента мюона, основанное на трехлетних семинарах и расчетах с использованием Стандартной модели.Этот ответ подтвердил исходное несоответствие, о котором сообщает Brookhaven.
В понедельник, за два дня до объявления, позвонили по телефону. Аида Х. Эль-Хадра, физик из Университета Иллинойса и сопредседатель инициативы по теории мюона g-2, сказала, что они ждали этого результата. долгое время.
«Раньше у меня не было ощущения сидения на горячих углях», – сказала она.
В день объявления Фермилаба другая группа, использовавшая другую технику, известную как расчет решетки, для вычисления магнитного момента мюона, получила другой ответ, чем доктор Др.Группа Эль-Хадры, добавляющая новую нотку неуверенности в разбирательстве.
«Да, мы утверждаем, что нет никаких расхождений между Стандартной моделью и результатом Брукхейвена, нет новой физики», – сказал в интервью Золтан Фодор из Университета штата Пенсильвания, один из авторов отчета, опубликованного в Nature в среду. .
Доктор Эль-Хадра назвал это «удивительным расчетом», но добавил, что его необходимо сравнить с независимой работой других групп.
В темноту
Бригаде пришлось исправить еще одну морщинку.Чтобы избежать предвзятости со стороны человека – и предотвратить любое мошенничество – экспериментаторы использовали практику, называемую ослеплением, которая является обычной для больших экспериментов. В этом случае главные часы, которые отслеживают колебание мюонов, были установлены на частоту, неизвестную исследователям. Фигура была запечатана в конверты, которые были заперты в офисах Фермилаба и Вашингтонского университета в Сиэтле.
На церемонии 25 февраля, которая была записана на видео и просмотрена по всему миру на Zoom, доктор Полли открыла конверт Fermilab, а Дэвид Герцог из Вашингтонского университета открыл конверт из Сиэтла.Число внутри было введено в электронную таблицу, предоставляя ключ ко всем данным, и результат выскочил на хор вау.
«Это действительно привело к действительно захватывающему моменту, потому что никто из участников сотрудничества не знал ответа до того же момента», – сказала Саския Чарити, научный сотрудник Fermilab, работавшая удаленно из Ливерпуля, Англия, во время пандемии.
Была гордость за то, что им удалось выполнить такое сложное измерение, и затем радость, что результаты совпадают с результатами из Брукхейвена.
«Похоже, это подтверждение того, что Брукхейвен не был случайностью», – сказал теоретик доктор Карена. «У них есть реальный шанс сломать Стандартную модель».
Физики говорят, что аномалия дала им идеи, как искать новые частицы. Среди них есть частицы, достаточно легкие, чтобы их мог дотянуть Большой адронный коллайдер или его предполагаемый преемник. В самом деле, некоторые из них, возможно, уже были записаны, но настолько редки, что еще не вышли из потока данных, записанных прибором.
Другой кандидат по имени Z-prime может пролить свет на некоторые загадки Большого взрыва, по словам Гордана Крняика, космолога из Фермилаба.
Результат g-2, как он сказал в электронном письме, может определить повестку дня для физики следующего поколения.
«Если центральное значение наблюдаемой аномалии останется неизменным, новые частицы не смогут скрываться вечно», – сказал он. «В будущем мы узнаем гораздо больше о фундаментальной физике».
Ученые измеряют самый короткий интервал времени в «зептосекундах»
Blink, и вы обязательно его пропустите.
Ученые измерили самый короткий из когда-либо зарегистрированных интервалов времени, подсчитывая, сколько времени требуется частице света, чтобы пересечь единственную молекулу водорода.
По данным группы немецких исследователей, сверхбыстрое путешествие заняло 247 зептосекунд, причем зептосекунда представляет собой триллионную миллиардную долю секунды. Это эквивалентно цифре 1, записанной после десятичной точки и 20 нулей.
Результаты являются кульминацией глобальных усилий по измерению все более и более коротких промежутков времени в физике, и они предлагают ученым способ точно измерить атомные изменения с помощью так называемого фотоэлектрического эффекта.
Альберт Эйнштейн предложил теорию фотоэлектрического эффекта в 1905 году, описав явление, при котором электроны могут выбрасываться из атомов после того, как на них попадает свет. В 1999 году египетский химик Ахмед Зеваил использовал ультракороткие лазерные импульсы, чтобы наблюдать, как молекулы меняют свою форму. Зевайл, который впоследствии получил Нобелевскую премию за свои исследования, измерял эти незначительные изменения в фемтосекундах; фемтосекунда – одна миллионная миллиардной секунды.
Теперь ученые из Университета Гете во Франкфурте, Института Фрица Габера Общества Макса Планка в Берлине и DESY, ускорителя элементарных частиц в Гамбурге, измерили еще более короткое деление времени.Их результаты были опубликованы 16 октября в журнале Science.
Исследователи выпустили рентгеновские лучи из ускорителя PETRA III на молекулу водорода (h3), которая состоит из двух протонов и двух электронов. Ученые сказали, что они использовали одну частицу света или один фотон, чтобы освободить электроны. Затем они использовали быстрые вспышки второго лазера ближнего инфракрасного диапазона, чтобы обнаружить последующие взаимодействия.
Когда фотон попадает в молекулу водорода, он сначала выбрасывает один электрон, а затем второй быстро после этого, как если бы камешек попал по поверхности воды, сказали они.Эффект создавал волны так называемой «интерференционной картины», которая позволяла ученым точно измерять убегающие электроны.
«Поскольку мы знали пространственную ориентацию молекулы водорода, мы использовали интерференцию двух электронных волн, чтобы точно вычислить, когда фотон достиг первого и второго атома водорода», – сказал Свен Грундманн, доктор философии. В заявлении говорится, что кандидат Университета Гете, диссертация которого легла в основу нового исследования.
От начала до конца фотону потребовалось 247 зептосекунд, чтобы пересечь молекулу водорода, хотя есть некоторые вариации в зависимости от того, насколько далеко друг от друга находятся атомы в молекуле водорода, когда они попадают под фотон, согласно Грундманну.
«Мы впервые заметили, что электронная оболочка в молекуле не реагирует на свет одновременно и повсюду», – говорится в заявлении Рейнхарда Дёрнера, профессора атомной физики в Гете. «Задержка по времени возникает из-за того, что информация внутри молекулы распространяется только со скоростью света.”
Дениз Чоу, репортер NBC News Science, специализируется на общей науке и изменении климата.
Оригинал Usenet FAQ по физике
Оригинальный Usenet FAQ по физикеДата версии: июнь 2020 г.
Этот список ответов на часто задаваемые вопросы по физике был составлен Скоттом Чейзом в 1992 году. цель состояла в том, чтобы дать хорошие ответы на вопросы, которые часто обсуждались в sci.physics и связанных Группы новостей в Интернете. Статьи в этом FAQ основаны на этих обсуждениях и на информации из хорошие справочные источники.Позже они были поддержаны и расширены Майклом Вайсом и Филипом Гиббсом. Остальные, написавшие для FAQ, указаны в верхней части отправленных элементов, в то время как многие другие, кто внесли меньшие взносы были поблагодарили в частном порядке.
Большинство статей, которые вы найдете здесь, были написаны в те дни, когда Интернет был совсем новым. Но вместо того, чтобы указывать их возраст, это означает, что они были написаны в то время, когда большинство вкладов в Интернет пришел от авторов, которые хорошо разбирались в своем предмете.То же самое уже не верно современный Интернет, где огромное количество авторитетных страниц вики-типа написано кем угодно кто хочет, независимо от их знаний.
Таким образом, из-за своего возраста записи в FAQ, которые вы найдете здесь, имеют большое академическое значение. достоверность – но они не всегда безупречны и полны. Если у вас есть исправления, обновления или Чтобы сделать дополнительные замечания, отправьте электронное письмо редактору (его резюме здесь). Если вы хотите написать статья по часто задаваемому вопросу по физике, не стесняйтесь предлагать ее редактору.
Авторские права на этот документ принадлежат. Пожалуйста, прочтите авторские права уведомление об авторских правах и архивной информации.
Общая физика
Физика элементарных частиц и ядерная физика
Квантовая физика
Теория относительности и космология
Скорость света
Специальная теория относительности
Общая теория относительности и космология
Черные дыры
Справочные темы
Есть много других мест, где вы можете найти ответы на свой вопрос.Вот список других часто задаваемых вопросов. и архивы ответов, которые могут быть полезны.
Этот FAQ в настоящее время доступен на следующих веб-сайтах:
- Австралия:
- http://hermes.physics.adelaide.edu.au/~dkoks/Faq
- Англия:
- http://physicsfaq.co.uk/Faq
- Нидерланды:
- http://www.xs4all.nl/~johanw/PhysFAQ
- США:
- http: // math.ucr.edu/home/baez/physics
- http://www.obscure.org/physics-faq
- http://www.edu-observatory.org/physics-faq
- http://www.ronen.net/physics
- http://www.obscure.org/physics-faq
Спасибо Джону Баезу, Ронену Бен-Хай, Филиппу Гиббсу, Крису Хиллману, Чунг-руи Као, Мэтту МакИрвину, Джо Мирандо, Мэтью Парри, Хан-Цонг Су, Натан Урбан, Йохан Веверс, Сэм Уормли и различные организации, принимающие гостей нас! Если другие некоммерческие сайты захотят отразить этот FAQ, пожалуйста, свяжитесь с редактором.
Физика 100 Лекция 2
Эйнштейн в Ньютон
В первые годы 20 века имя Альберта Эйнштейна достигнуто известность в массовой культуре. Немногие, кто узнал это имя, понимали теории что он разработал. Идеи, захватившие всеобщее воображение обеспокоенный относительность пространства и времени. Он сказал, что время и пространство не абсолютный но относительно системы отсчета наблюдателя. Другими словами, человек, двигающийся по отношению к другому, испытает другие Космос и время.Эти новые теории начали разрушать классический часовой мир. сформулирован в 17-18 веках Галилей, Ньютон, Декарт и другие. Их прочная, предсказуемая механика могла быть легко согласована с общий чувственные восприятия пространства и времени. Эйнштейн сказал, что эти здравый смысл идеи были ошибочными.
Теория относительности Эйнштейна казалась странной. Но его выводы не были простыми полеты фантазии.Они следовали из строгий анализ наблюдаемых фактов. Эйнштейн был вынужден выводы логикой так же, как детектив может быть вынужден доказательствами подозревать его лучший друг в крупном преступлении.
Путь от Ньютона до Эйнштейна занял немногим более 200 лет. траверс. Это было едва ли 1/10 времени от первых попыток рационального понимание физический мир до первых шагов по пути современного физика были приняты.Как только эти первые шаги будут найдены, продвигайтесь по пути. было наверное неизбежно. Методы измерения и анализа пространства, времени и движение были ключом, который открыл дверь в современную физику и полностью новое видение Вселенной. Галилео Галилею обычно приписывают создание наука об измерении движения называется Кинематика , однако курс, многие другие внесли свой вклад в его развитие
Давайте посмотрим, что это было.
Мера пространства
Сначала мы должны установить точные определения терминов, которые будут использоваться, если мы находятся понимать друг друга. В физике это означает определение в терминах процесс с помощью которого можно измерить количество: список операций, ведущих к количество. Такое определение называется операционным определением .
Стандарт расстояния
Возьмите палку и назовите ее своим стандартом длины .Считать как много раз вы можете положить его конец в конец по прямой между два очка. Этот счет называется расстоянием между двумя точки.Позвольте мне предупредить вас об общей проблеме: циркуляр определение . В моем определении расстояния я не сказал, что я имею в виду под прямым линия. Это часто определяется как кратчайшее расстояние между двумя точками. Теперь вернись и перечитайте оба мои определения расстояния.Ты видишь проблему!Прямая линия определяется расстоянием и расстояние определяется в плане прямой. Это как кошка гонится за собственным хвостом – она не будет пойти куда угодно, делая это. Чтобы избежать этой округлости (которая часто встречается в плохо написанных учебниках физики) нужно использовать другое определение для прямая линия. Возможно, это можно было бы определить как путь, по которому следует нить плотно растянуты между точками.
Возвращаясь к расстоянию, определяющая процедура дала бы расстояние до ближайшая «палка». Допустим, мы измеряли длину стола. Мы можем получить что-то вроде “длина стола больше, чем три палки, но меньше 4 “. Затем возьмите палку 1/10 длину первого и посчитайте, сколько «решёток» уместится между конец третьей палки и конец стола. Если бы мы получили, для пример, между шестью и семью из них, мы могли бы сказать, что за столом было 3.6 или 3,7 «Децистики» долго смотря какие казались ближе. Тогда мы могли возьмите другую палку на 1/100 длины оригинала и продолжайте процесс. Таким образом, мы можем уточнять измерения до все более значимых цифр. пока мы не достигли практического предела нашего оборудования.
[ Значимые цифры: Мы делаем это указать на пишите только цифры, в которых мы уверены. Таким образом, если бы мы только измерили до ближайшего решающего значения, было бы бессмысленно писать 3.654. Что будет означать, что мы знаем что-то, чего на самом деле не знаем. Мы бы писать четыре значащих цифры, когда мы знали только две.Иногда количество значащих цифр в числе неочевидно когда нули в начале в конце числа. Следующий правила поможет избежать путаницы: ведущие нули не считаются значимыми цифры. Таким образом, 0,036 будет иметь только две значащие цифры. Завершающие нули до десятичная точка не считается, если десятичная точка не указана явно написано после них.Таким образом, 3600 состоит из двух значащих цифр, а 3600 – из четырех. Трейлинг нули после десятичной точки. Таким образом, 3600.0 имеет пять значимых цифры.]
Стандарт длины, который мы используем, не влияет на физический реальность, которую мы измеряем. Однако, как только мы выберем стандарт, мы должны палка с этим! Законы физики одинаковы, если они выражены в метры, ярды, цепи или фарлонги. До Французской революции в каждой стране а также часто в каждом городе была своя система измерений.Короли и правители бы измерить степень своего могущества по количеству городов и деревень усыновленный его (или, реже, ее) система мер. Создатели французов революция не хотел больше такой ерунды. Пусть правит логика! Поэтому они учредил единица длины, не зависящая от какого-либо конкретного человека. Счетчик был определенный быть одной десятимиллионной расстояния от северного полюса до экватор по меридиану, проходящему через Париж.Это определение было скорее сложно применить на практике. Так что они также поставили метровый платино-иридиевый бар в Севре, городе недалеко от Парижа, для людей, которые приезжают и сравни их с правителями.
Слово о написании: Официальное написание единицы длины в Канада и многие другие страны составляют метров . Это добавлено преимущество быть правильным французским тоже. Однако в нашей культуре западного побережья усыновленный американское написание, метр, до такой степени, что официальное орфография выглядит странно.Название гаджета, который сообщает нам, что число всегда метров как в Америке, так и в Великобритании. использование; например, вольтметр.
Степени десяти
Меньшие и большие единицы были определены следующим образом:| дециметр | 0,1 метр | км | 1000 метров |
| сантиметр | 0.01 метр | мегаметр | 1 000 000 метров |
| миллиметр | 0,001 метр | гигаметр | 1 000 000 000 метров |
| мкм | 0 .000001 метр | | |
| нм | 0.000000001 метр | | |
| пикометров | 0.0000000000001 метр | | |
Как видите, писать числа с большим количеством нулей становится немного сбивает с толку. Один теряет счет нулей. Чтобы преодолеть расстояние от микроскопический к космическому с большой легкостью записи другой способ записи чисел является часто используется.Кто пишет числа, несколько раз больше или меньше десяти. чем 1 с числом, близким к единице (обычно от 0,1 до 10) умноженный на 10 в целой степени. Вот несколько примеров:
Для больших чисел
100 = 1 × 10 2
1000 = 1 × 10 3
10 000 = 1 × 10 4
100 000 = 1 × 10 5
1000000 = 1 × 10 6
3465,3 = 3,4653 × 10 3
Для малых чисел
0.01 = 1 × 10 –2
0,0000001 = 1 × 10 –7
0,0034653 = 3,4653 × 10 –3
Префиксы, используемые на счетчике, также используются для других единиц измерения. определенный. Они соответствуют степени десяти при умножении числа. Большинство общий префиксы и соответствующие целочисленные степени следующие:
(единицы, отмеченные знаком *, не совсем официальные.)
Единицы менее одного метра
| блок с префиксом | с десятичной степенью | a bbreviation |
| дециметров * | 10 -1 м | дм |
| сантиметр * | 10 -2 м | см |
| миллиметр | 10 -3 м | мм |
| мкм | 10 -6 м | мкм |
| нм | 10 -9 м | нм |
| пикометров | 10 -12 м | вечера |
| фемтометр | 10 -15 м | фм |
| аттометр | 10 -18 м | утра |
Установки размером более одного метра
| блок с префиксом | с десятичной степенью | a bbreviation |
| декаметр * | 10 1 м | плотина |
| гектометров * | 10 2 м | гм |
| км | 10 3 м | км |
| мегаметр | 10 6 м | мм |
| гигаметр | 10 9 м | Гм |
| тераметр | 10 12 м | ТМ |
| петаметр | 10 15 м | мкм |
| экзамен | 10 18 м | Em |
Мы проиллюстрируем методы измерения очень маленьких и очень больших длина и дистанции с двумя демонстрациями.Сначала мы измеряем диаметр волос просматривается под микроскопом. Используемый метод зависит от первого калибровка измерительной системы путем измерения чего-либо, что может быть измеренный как новым, так и старым методами. Известно, что старый метод надежный, новый метод может привести нас к меньшим размерам.
Рабочий лист микроскопа
В этом месяце истории физики
Декабрь 1706: Рождение Эмили дю Шатле
Эмили дю Шатле
Эмили дю Шатле, известная тем, что была любовницей Вольтера, на самом деле была талантливым ученым и интеллектуалом.Преодолевая проблемы, которые мешали женщинам становиться учеными в то время, она получила образование и проводила эксперименты по физике, а также завершила перевод и комментарии к Принципам Ньютона.
Габриэль Эмили ле Тоннелье де Бретей (позже Эмили дю Шатле) родилась 17 декабря 1706 года в Париже. Ее отец, Луи Николя ле Тоннелье де Бретей, был высокопоставленным чиновником двора Людовика XIV. Семья де Бретей была частью французского аристократического общества, и поэтому они часто развлекались.В доме частыми гостями были выдающиеся ученые и математики.
Получив домашнее образование, юная Эмили к двенадцати годам выучила шесть языков, получила уроки фехтования и других видов спорта. Даже с юных лет она увлекалась наукой и математикой, к большому неудовольствию матери. Такие интересы считались неприемлемыми для юных леди, и ее мать даже угрожала отправить ее в монастырь. К счастью, ее отец признал ее ум и поддержал ее интересы, организовав для нее обсуждение астрономии с известными ему известными учеными.
Эмили также была склонна к азартным играм, применяя свой математический талант, чтобы получить преимущество. На свой выигрыш она покупала книги и лабораторное оборудование для своих научных исследований.
Когда ей исполнилось 18 лет, она знала, что должна выйти замуж, и приняла предложение маркиза Флорана-Клода дю Шатле, выдающегося армейского офицера. Это было удобно для Эмили, потому что Шатле часто бывала вдали от дома, давая ей возможность самостоятельно заниматься математикой и естественными науками.
Она также могла иметь дело с писателем Вольтером, одним из немногих мужчин, которые ценили ее ум и поощряли ее научные поиски. Эмили дю Шатле и Вольтер отремонтировали большой особняк Шатле в сельской местности. В доме было несколько комнат для научного оборудования и места для экспериментов, а также большая библиотека с более чем 20 000 книг, больше, чем во многих университетах того времени.
Хотя она была разочарована тем, что ее исключили из научного общества и образования из-за того, что она была женщиной, она смогла изучить математику и естественные науки у нескольких известных ученых, включая Пьера-Луи Мопертюи и Сэмюэля Кенига, пригласив их к себе домой.
В 1737 году, после нескольких месяцев проведения тайных исследований, она приняла участие в организованном Французской Академией наук конкурсе по природе света, тепла и огня, представив свою работу «Диссертация на тему природы и распространения жизни». В нем она предположила, что разные цвета света несут разную тепловую мощность, и предвосхитила существование того, что сейчас известно как инфракрасное излучение. Она не выиграла конкурс, но ее статья была опубликована и была положительно воспринята научным сообществом.
Она также сильно заинтересовалась работами Исаака Ньютона, которые в то время вызывали споры во Франции, где картезианская философия предпочитала идеи Ньютона. Эмили и Вольтер совместно написали книгу «Элементы философии Ньютона», которая ясно объяснила астрономию и оптику Ньютона для широкого французского читателя. В книге фигурировало только имя Вольтера, но он признал ее важную роль.
Эмили также работала над другой рукописью, «Основы физики», в которой она рассматривала философскую основу науки и пыталась объединить противоречащие друг другу взгляды Ньютона, Декарта и Лейбница.
Одним из самых важных ее вкладов в науку было разъяснение концепций энергии и энергосбережения. После экспериментов, ранее проведенных Виллемом Грейвзандом, она бросила тяжелые свинцовые шары в слой глины. Она показала, что шары, ударяющие по глине с удвоенной скоростью, проникают в глину в четыре раза глубже; те, у кого скорость была втрое выше, достигли глубины в девять раз большей. Это предполагает, что энергия пропорциональна mv 2 , а не mv, как предполагал Ньютон.
Эмили дю Шатле, выполняя свою научную работу, продолжала выполнять свои обязанности матери для своих троих детей и хозяйки для своих многочисленных посетителей, поэтому она всегда была занята, и у нее было мало времени для сна.
В 42 года Эмили дю Шатле обнаружила, что беременна. В то время беременность в столь преклонном возрасте была крайне опасной. Зная, что она, скорее всего, умрет, она начала работать по 18 часов в день, чтобы завершить свой самый большой проект – французский перевод «Начала Ньютона», прежде чем она умерла.
«Начала» Эмили дю Шатле – это не просто перевод, оно включало ее собственные примечания, примеры, выводы и пояснения к часто непонятным произведениям Ньютона, а также примеры экспериментов, подтвердивших теории Ньютона. Ее современные обозначения и ясный стиль вскоре помогли французским ученым понять идеи Ньютона и развить их.
С упорными усилиями она достигла своей цели – закончить рукопись незадолго до своей смерти в сентябре 1749 года. Полная работа была опубликована десятью годами позже, когда возвращение кометы Галлея возродило интерес к ньютоновской механике.
Книга Эмили дю Шатле в течение многих лет была единственным доступным переводом «Начала Ньютона» на французский язык, и этот перевод и содержательные комментарии, вероятно, помогли продвинуть науку во Франции. Тем не менее сама Эмили дю Шатле была в значительной степени забыта историей (или вспоминалась в основном как любовница Вольтера), и лишь недавно ее научные достижения были обнаружены.
История физики
Этот месяц в истории физики
Новости APS Архив
Инициатива по историческим местам
Места и подробности исторических физических событий
Квантовый эксперимент показывает, как время «выходит» из запутанности | Автор: The Physics Блог arXiv | The Physics arXiv Blog
Время – это возникающее явление, которое, по словам физиков, является побочным эффектом квантовой запутанности.И у них есть первые экспериментальные результаты, подтверждающие это.
Когда новые идеи квантовой механики распространились по науке со скоростью лесного пожара в первой половине 20-го века, физики первым делом применили их к гравитации и общей теории относительности. Результаты не были хорошими.
Сразу стало ясно, что эти две основы современной физики совершенно несовместимы. Когда физики попытались объединить подходы, полученные уравнения были запутаны бесконечностями, что сделало невозможным понимание результатов.
Затем, в середине 1960-х, произошел прорыв. Физики Джон Уиллер и Брайс ДеВитт успешно объединили ранее несовместимые идеи в ключевом результате, который с тех пор стал известен как уравнение Уиллера-ДеВитта. Это важно, потому что позволяет избежать неприятных бесконечностей – огромный прогресс.
Но физикам не потребовалось много времени, чтобы понять, что, хотя уравнение Уиллера-ДеВитта решает одну важную проблему, оно порождает другую. Новая проблема заключалась в том, что время не играло роли в этом уравнении.По сути, в нем говорится, что во Вселенной ничего никогда не происходит, и это предсказание явно расходится с данными наблюдений.
Эта загадка, которую физики называют «проблемой времени», оказалась занозой в плоти для современных физиков, которые пытались ее игнорировать, но без особого успеха.
Затем в 1983 году теоретики Дон Пейдж и Уильям Вуттерс предложили новое решение, основанное на квантовом феномене запутанности. Это экзотическое свойство, при котором две квантовые частицы имеют одно и то же существование, даже если они физически разделены.
Запутывание – это глубокая и мощная связь, и Пейдж и Вуттерс показали, как ее можно использовать для измерения времени. Их идея заключалась в том, что способ эволюции пары запутанных частиц – это своего рода часы, которые можно использовать для измерения изменений.
Но результаты зависят от того, как проводится наблюдение. Один из способов сделать это – сравнить изменение запутанных частиц с внешними часами, которые полностью не зависят от Вселенной. Это эквивалентно богоподобному наблюдателю за пределами Вселенной, измеряющему эволюцию частиц с помощью внешних часов.
В этом случае Пейдж и Вуттерс показали, что частицы будут казаться совершенно неизменными – в этом сценарии времени не будет.
Но есть другой способ, который дает другой результат. Это для наблюдателя внутри Вселенной, чтобы сравнить эволюцию частиц с остальной Вселенной. В этом случае внутренний наблюдатель увидит изменение, и эта разница в эволюции запутанных частиц по сравнению со всем остальным является важной мерой времени.
Это элегантная и мощная идея. Это предполагает, что время – это возникающее явление, которое возникает из-за природы запутанности. И он существует только для наблюдателей во Вселенной. Любой богоподобный наблюдатель снаружи видит статичную, неизменную Вселенную, как и предсказывают уравнения Уиллера-ДеВитта.
Конечно, без экспериментальной проверки идеи Пейджа и Вуттера представляют собой не более чем философское любопытство. А поскольку иметь наблюдателя за пределами Вселенной невозможно, казалось мало шансов когда-либо проверить эту идею.
До сих пор. Сегодня Екатерина Морева из Istituto Nazionale di Ricerca Metrologica (INRIM) в Турине, Италия, и несколько приятелей провели первую экспериментальную проверку идей Пейджа и Вуттерса. И они подтверждают, что время действительно является новым явлением для «внутренних» наблюдателей, но отсутствует для внешних.
Эксперимент включает создание игрушечной вселенной, состоящей из пары запутанных фотонов и наблюдателя, который может измерить их состояние одним из двух способов. В первом наблюдатель измеряет эволюцию системы, запутавшись в ней.Во втором случае богоподобный наблюдатель измеряет эволюцию по внешним часам, которые полностью не зависят от игрушечной вселенной.
Детали эксперимента просты. Каждый запутанный фотон имеет поляризацию, которую можно изменить, пропустив ее через двулучепреломляющую пластину. В первом случае наблюдатель измеряет поляризацию одного фотона, тем самым запутываясь с ним. Затем он или она сравнивает это с поляризацией второго фотона. Разница – это мера времени.
Во второй установке оба фотона снова проходят через двулучепреломляющие пластины, которые меняют свою поляризацию. Однако в этом случае наблюдатель измеряет только общие свойства обоих фотонов, сравнивая их с независимыми часами.
В этом случае наблюдатель не может обнаружить никакой разницы между фотонами, не запутавшись ни с одним, ни с другим. И если разницы нет, система выглядит статичной. Другими словами, время не появляется.
«Несмотря на то, что наша модель чрезвычайно проста, она отражает два, казалось бы, противоречивых свойства механизма Пейджа-Вуттерса», – говорят Морева и его компания.
Это впечатляющий эксперимент. Эмерджентность – популярная идея в науке. В частности, физиков недавно увлекла идея о том, что гравитация – это возникающее явление. Так что это относительно небольшой шаг, чтобы предположить, что время может появиться аналогичным образом.
Чего, конечно, не хватало возникающей гравитации, так это экспериментальной демонстрации, показывающей, как она работает на практике.

 За три минуты он пройдёт в три раза больше, то есть 255 метров:
За три минуты он пройдёт в три раза больше, то есть 255 метров:
 -Y надо заменить на -i.
-Y надо заменить на -i.