Как в физике выводить формулы: Выражение неизвестной, учимся выражать - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Как выводить формулы по физике. Как выразить одну переменную через другую? Как выразить переменную из формулы? Как вывести формулу из формулы онлайн

В каждой задаче по физике требуется из формулы выразить неизвестную, следующим шагом подставить численные значения и получить ответ, в некоторых случаях необходимо только выразить неизвестную величину. Способов выведения неизвестной из формулы много. Если посмотреть страницы Интернета, то мы увидим множество рекомендаций по этому поводу. Это говорит о том, что единого подхода к решению этой проблемы научное сообщество еще не выработало, а те способы, которые используются, как показывает опыт работы в школе – все они малоэффективны. До 90% учащихся выпускных классов не умеют правильно выразить неизвестное. Те же, кто умеют это делать – выполняют громоздкие преобразования. Очень странно, но физики, математики, химики имеют разные подходы, объясняя методы переноса параметров через знак равенства (предлагают правила треугольника, креста или пропорций др. ) Можно сказать, что имеют разную культуру работы с формулами. Можно представить, что происходит с большинством учеников, которые встречается с разными трактовками решения данной проблемы, последовательно посещая уроки этих предметов. Эту ситуацию описывает типичный диалог в сети:

Научите выражать из формул величины. 10 класс, мне стыдно не знать, как из одной формулы делать другую.

Да не переживай – это проблема многих моих одноклассников, хоть я и в 9 кл. Учителя показывают это чаще всего методом треугольника, но мне кажется, что это неудобно, да и запутаться легко. Покажу наиболее простой способ, которым я пользуюсь…

Допустим, дана формула:

Ну более простая….тебе из этой формулы нужно найти время. Ты берешь и в эту формулу подставляешь числа только разные, исходя из алгебры. Допустим:

и тебе наверное хорошо видно, что чтобы найти время в алгебраическом выражении 5 нужно 45/9 т.е переходим к физике: t=s/v

У большинства учащихся формируется психологический блок. Часто учащиеся отмечают, что при чтении учебника трудности в первую очередь вызывают те фрагменты текста, в которых много формул, что «длинные выводы все равно не понять», но при этом возникает чувство неполноценности, неверия в свои силы.

Я, предлагаю следующее решение данной проблемы – большинство учащихся все – таки могут решать примеры и, следовательно, расставлять порядок действий. Используем это их умение.

1. В той части формулы, где содержится переменная, которую нужно выразить, надо расставь порядок действий, причем в одночленах, не содержащих искомую величину этого делать не будем.

2. Затем в обратной последовательности вычислений перенесите элементы формулы в другую часть формулы (через знак равенства) с противоположным действием (« минус» – «плюс», «разделить» – « умножить», « возведение в квадрат» – «извлечение корня квадратного»).

То есть найдем в выражении последнее действие и перенесем одночлен или многочлен, исполняющий это действие, через знак равенства первым, но уже с противоположным действием.

Таким образом, последовательно, находя последнее действие в выражении, перенесите из одной части равенства в другую все известные величины. В заключение перепишем формулу так, чтобы неизвестная переменная стояла слева.

Получаем четкий алгоритм работы, точно знаем, сколько преобразований необходимо выполнить. Можем для тренировки использовать уже известные формулы, можем выдумывать свои. Для начала работы над усвоением данного алгоритма была создана презентация.

Опыт работы с учащимися показывает, что данный способ хорошо воспринимается ими. Реакция учителей на мое выступление на фестивале «Учитель профильной школы» также говорит о положительном зерне, заложенном в этой работе.

Этот урок – полезное дополнение к предыдущей теме ” “.

Умение делать такие вещи – штука не просто полезная, она – необходимая . Во всех разделах математики, от школьной до высшей. Да и в физике тоже. Именно по этой причине задания подобного рода обязательно присутствуют и в ЕГЭ и в ОГЭ. Во всех уровнях – как базовом, так и профильном.

Собственно, вся теоретическая часть подобных заданий представляет собой одну единственную фразу. Универсальную и простую до безобразия.

Удивляемся, но запоминаем:

Любое равенство с буквами, любая формула – это ТОЖЕ УРАВНЕНИЕ!

А где уравнение, там автоматически и . Вот и применяем их в удобном нам порядке и – готово дело.) Читали предыдущий урок? Нет? Однако… Тогда эта ссылочка – для вас.

Ах, вы в курсе? Отлично! Тогда применяем теоретические знания на практике.

Начнём с простого.

Как выразить одну переменную через другую?

Такая задача постоянно возникает при решении систем уравнений. Например, имеется равенство:

3 x – 2 y = 5

Здесь две переменные – икс и игрек.

Допустим, нас просят выразить x через y .

Что означает это задание? Оно означает, что мы должны получить некоторое равенство, где слева стоит чистый икс.

В гордом одиночестве, безо всяких соседей и коэффициентов. А справа – что уж получится.

И как же нам получить такое равенство? Очень просто! С помощью всё тех же старых добрых тождественных преобразований! Вот и применяем их в удобном нам порядке, шаг за шагом добираясь до чистого икса.

Анализируем левую часть уравнения:

3 x – 2 y = 5

Здесь нам мешаются тройка перед иксом и –2 y . Начнём с –2у , это попроще будет.

Перекидываем –2у из левой части в правую. Меняя минус на плюс, разумеется. Т.е. применяем первое тождественное преобразование:

3 x = 5 + 2 y

Полдела сделано. Осталась тройка перед иксом. Как от неё избавиться? Разделить обе части на эту самую тройку! Т.е. задействовать второе тождественное преобразование.

Вот и делим:

Вот и всё. Мы выразили икс через игрек . Слева – чистый икс, а справа – что уж получилось в результате “очищения” икса.

Можно было бы сначала поделить обе части на тройку, а затем – переносить. Но это привело бы к появлению дробей в процессе преобразований, что не очень удобно. А так, дробь появилась лишь в самом конце.

Напоминаю, что порядок преобразований никакой роли не играет. Как нам удобно, так и делаем. Самое главное – не порядок применения тождественных преобразований, а их правильность!

А можно из этого же равенства

3 x – 2 y = 5

выразить y через x ?

А почему – нет? Можно! Всё то же самое, только на этот раз нас интересует слева чистый игрек. Вот и очищаем игрек от всего лишнего.

Первым делом избавляемся от выражения 3х

. Перебрасываем его в правую часть:

–2 y = 5 – 3 x

Осталась двойка с минусом. Делим обе части на (-2):

И все дела.) Мы выразили y через х. Переходим к более серьёзным заданиям.

Как выразить переменную из формулы?

Не проблема! Точно так же! Если понимать, что любая формула – тоже уравнение .

Например, такое задание:

Из формулы

выразить переменную с.

Формула – тоже уравнение! Задание означает, что через преобразования из предложенной формулы нам надо получить какую-то

новую формулу. В которой слева будет стоять чистая с , а справа – что уж получится, то и получится…

Однако… Как нам эту самую с вытаскивать-то?

Как-как… По шагам! Ясное дело, что выделить чистую с сразу невозможно: она в дроби сидит. А дробь умножается на r … Значит, первым делом очищаем выражение с буквой с , т.е. всю дробь целиком. Здесь можно поделить обе части формулы на r .

Получим:

Следующим шагом надо вытащить с из числителя дроби. Как? Легко! Избавимся от дроби. Нету дроби – нету и числителя. ) Умножаем обе части формулы на 2:

Осталась элементарщина. Обеспечим справа букве с гордое одиночество. Для этого переменные a и b переносим влево:

Вот и всё, можно сказать. Осталось переписать равенство в привычном виде, слева направо и – ответ готов:

Это было несложное задание. А теперь задание на основе реального варианта ЕГЭ:

Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость погружения батискафа вычисляется по формуле

где с = 1500 м/с – скорость звука в воде,

f 0 – частота испускаемых импульсов (в МГц),

f – частота отражённого от дна сигнала, регистрируемая приёмником (в МГц).

Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 2 м/с.

“Многа букафф”, да… Но буквы – это лирика, а общая суть всё равно та же самая . Первым делом надо выразить эту самую частоту отражённого сигнала (т.е. букву f ) из предложенной нам формулы. Вот этим и займёмся. Смотрим на формулу:

Напрямую, естественно, букву f никак не выдернешь, она снова в дробь запрятана. Причём и в числитель и в знаменатель. Поэтому самым логичным шагом будет избавиться от дроби. А там – видно будет. Для этого применяем второе преобразование – умножаем обе части на знаменатель.

Получим:

А вот тут – очередные грабли. Прошу обратить внимание на скобки обеих частях! Частенько именно в этих самых скобочках и кроются ошибки в подобных заданиях. Точнее, не в самих скобочках, а в их отсутствии.)

Скобки слева означают, что буква v умножается на весь знаменатель целиком . А не на его отдельные кусочки…

Справа же, после умножения, дробь исчезла и остался одинокий числитель. Который, опять же, весь целиком умножается на буковку с .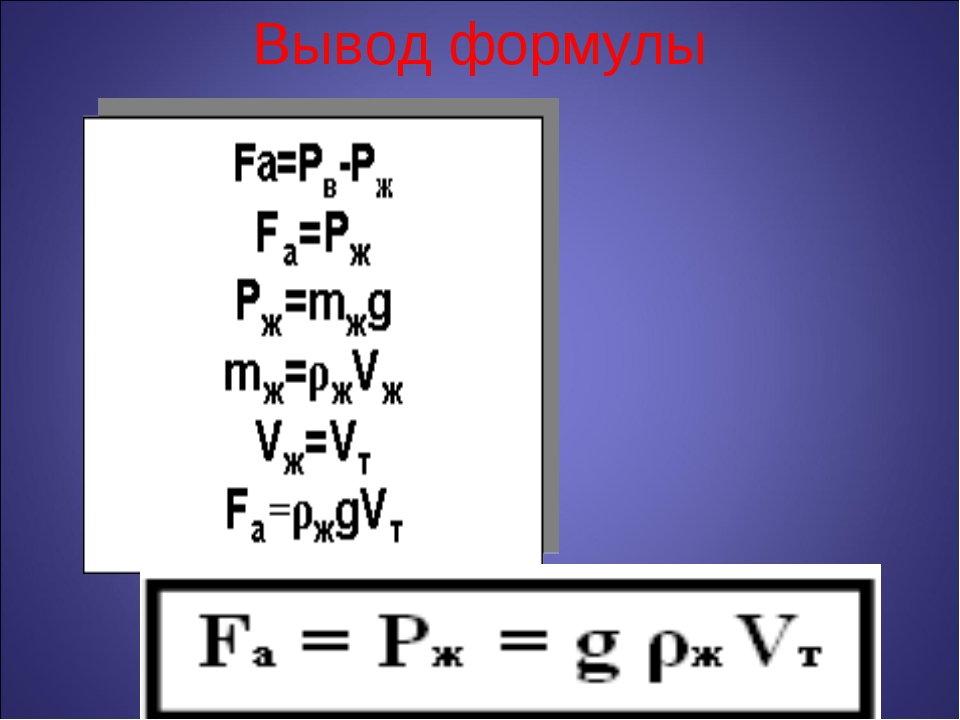 Что и выражается скобками в правой части.)

А вот теперь скобки и раскрыть можно:

Отлично. Процесс идёт.) Теперь буковка f слева стала общим множителем . Выносим её за скобки:

Осталось всего ничего. Делим обе части на скобку (v – c ) и – дело в шляпе!

В принципе, всё готово. Переменная f уже выражена . Но можно дополнительно “причесать” полученное выражение – вынести f 0 за скобку в числителе и сократить всю дробь на (-1), тем самым избавившись от лишних минусов:

Вот такое выражение. А вот теперь и числовые данные подставить можно. Получим:

Ответ: 751 МГц

Вот и всё. Надеюсь, общая идея понятна.

Делаем элементарные тождественные преобразования с целью уединить интересующую нас переменную. Главное здесь – не последовательность действий (она может быть любой), а их правильность.

В этих двух уроках рассматриваются лишь два базовых тождественных преобразования уравнений.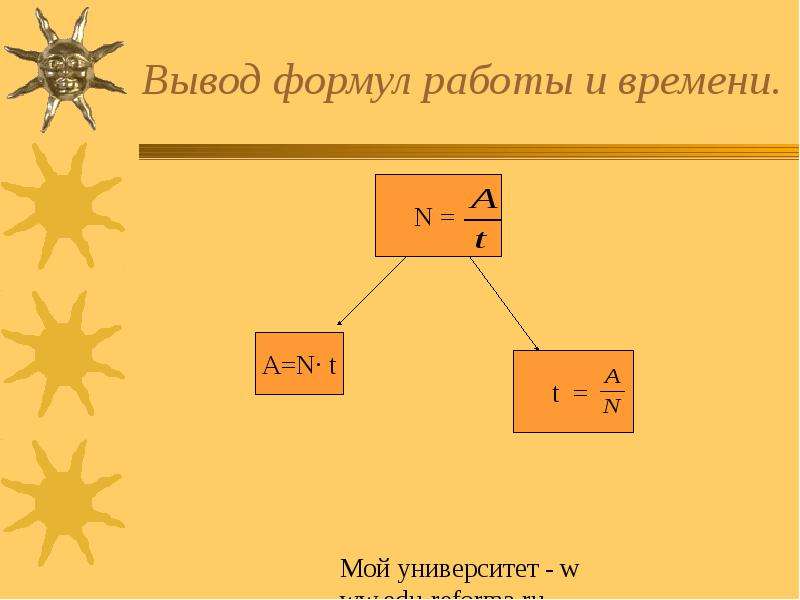 Они работают всегда . На то они и базовые. Помимо этой парочки, существует ещё множество других преобразований, которые тоже будут тождественными, но не всегда, а лишь при определённых условиях.

Например, возведение обеих частей уравнения (или формулы) в квадрат (или наоборот, извлечение корня из обеих частей) будет тождественным преобразованием, если обе части уравнения заведомо неотрицательны .

Или, скажем, логарифмирование обеих частей уравнения будет тождественным преобразованием, если обе части заведомо положительны. И так далее…

Подобные преобразования будут рассматриваться в соответствующих темах.

А здесь и сейчас – примеры для тренировки по элементарным базовым преобразованиям.

Простенькая задачка:

Из формулы

выразить переменную а и найти её значение при S =300, V 0 =20, t =10.

Задачка посложнее:

Средняя скорость лыжника (в км/ч) на дистанции в два круга рассчитывается по формуле:

где V 1 и V 2 – средние скорости (в км/ч) на первом и втором кругах соответственно. Какова была средняя скорость лыжника на втором круге, если известно, что первый круг лыжник пробежал со скоростью 15 км/ч, а средняя скорость на всей дистанции оказалась равной 12 км/ч?

Задача на основе реального варианта ОГЭ:

Центростремительное ускорение при движении по окружности (в м/с 2) можно вычислить по формуле a =ω 2 R , где ω – угловая скорость (в с -1), а R – радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с -1 , а центростремительное ускорение равно 289 м/с 2 .

Задача на основе реального варианта профильного ЕГЭ:

К источнику с ЭДС ε=155 В и внутренним сопротивлением r =0,5 Ом хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, даётся формулой:

При каком сопротивлении нагрузки напряжение на ней будет 150 В? Ответ выразите в омах.

Ответы (в беспорядке): 4; 15; 2; 10.

А уж где числа, километры в час, метры, омы – это как-нибудь сами…)

Чтобы вывести формулу сложного , нужно прежде всего путем анализа установить, из каких элементов состоит вещество и в каких весовых отношениях соединены друг с другом входящие в него элементы. Обычно состав сложного выражают в процентах, но он может быть выражен и в любых других числах, указывающих отношение между весовыми количествами элементов, образующих данное вещество. Например, состав окиси алюминия, содержащей 52,94% алюминия и 47,06% кислорода, будет вполне определен, если мы скажем, что и соединены в весовом отношении 9:8, т. е. что на 9 вес. ч. алюминия приходится 8 вес. ч. кислорода. Понятно, что отношение 9: 8 должно равняться отношению 52,94: 47,06.

Зная весовой состав сложного и атомные веса образующих его элементов, нетрудно найти относительное число атомов каждого элемента в молекуле взятого вещества и таким образом установить его простейшую формулу.

Положим, например, что требуется вывести формулу хлористого кальция, содержащего 36% кальция и 64% хлора. Атомный вес кальция 40, хлора 35,5.

Обозначим число атомов кальция в молекуле хлористого кальция через х, а число атомов хлора через у. Так как атом кальция весит 40, а атом хлора 35,5 кислородных единиц, общий вес атомов кальция, входящих в состав молекулы хлористого кальция, будет равен 40 х, а вес атомов хлора 35,5 у. Отношение этих чисел, очевидно, должно равняться отношению весовых количеств кальция и хлора в любом количестве хлористого кальция. Но последнее отношение равно 36: 64.

Приравняв оба отношения, получим:

40x: 35,5y = 36:64

Затем освободимся от коэффициентов при неизвестных х и у путем деления первых членов пропорции на 40, а вторых на 35,5:

Числа 0,9 и 1,8 выражают относительное число атомов в молекуле хлористого кальция, но они дробны, тогда как в молекуле может содержаться только целое число атомов. второго отношения на наименьший из них. Получаем

х: у = 1:2

Следовательно, в молекуле хлористого кальция на один атом кальция приходятся два атома хлора. Этому условию удовлетворяет целый ряд формул: СаСl 2 , Са 2 Сl 4 , Са 3 Сl 6 и т. д. Так как у нас нет данных, чтобы судить, какая из написанных формул отвечает действительному атомному составу молекулы хлористого кальция, мы остановимся на простейшей из них СаСl 2 , указывающей наименьшее возможное число атомов в молекуле хлористого кальция.

Однако произвол в выборе формулы отпадает, если наряду с весовым составом вещества известен также его молекулярный вес. В этом случае нетрудно вывести формулу, выражающую истинный состав молекулы. Приведем пример.

Путем анализа установлено, что глюкоза содержит на 4,5 вес. ч. углерода 0,75 вес. ч. водорода и 6 вес. ч. кислорода. Молекулярный вес ее был найден равным 180. Требуется вывести формулу глюкозы.

Как и в предыдущем случае, находим сперва отношение между числом атомов углерода (атомный вес 12), водорода и кислорода в молекуле глюкозы. Обозначив число атомов углерода через х, водорода через у и кислорода через z, составляем пропорцию:

2х :у: 16z = 4,5: 0,75: 6

откуда

Разделив все три члена второй половины равенства на 0,375, получаем:

х :у: z= 1: 2: 1

Следовательно, простейшая формула глюкозы будет СН 2 O. Но вычисленный по ней равнялся бы 30, тогда как в действительности глюкозы 180, т. е. в шесть раз больше. Очевидно, что для глюкозы нужно принять формулу C 6 H 12 O 6 .

Формулы, основанные, кроме данных анализа, также и на определении молекулярного веса и указывающие действительное число атомов в молекуле, называются истинными или молекулярнымиформулами; формулы же, выведенные только из данных анализа, называются простейшими или эмпирическими.

Познакомившись с выводом химических формул,» легко понять, как устанавливаются точные молекулярные веса. Как мы уже упоминали, существующие методы определения молекулярных весов в большинстве случаев не дают вполне точных результатов. Но, зная хотя бы приблизительный и процентный состав вещества, можно установить его формулу, выражающую атомный состав молекулы. Так как вес молекулы равняется сумме весов образующих ее атомов, сложив веса атомов, входящих в состав молекулы, мы определим ее вес в кислородных единицах, т. е. молекулярный вес вещества. Точность найденного молекулярного веса будет такой же, как и точность атомных весов.

Нахождение формулы химического соединения во многих случаях может быть значительно упрощено, если воспользоваться понятием овалентности элементов.

Напомним, что валентностью элемента называется свойство его атомов присоединять к себе или замещать определенное число атомов другого элемента.

Что такое валентность

элемента определяется числом, показывающим, сколько атомов водорода (или другого одновалентного элемента) присоединяет или замещает атом данного элемента.

Понятие о валентности распространяется не только на отдельные атомы, но и на целые группы атомов, входящие в состав химических соединений и участвующие как одно целое в химических реакциях. Такие группы атомов получили название радикалов. В неорганической химии наиболее важными радикалами являются: 1) водный остаток, или гидроксил ОН; 2) кислотные остатки; 3) основные остатки.

Водный остаток, или гидроксил, получается, если отмолекулы воды отнять один атом водорода. В молекуле воды гидроксил связан с одним атомом водорода, следовательно, группа ОН одновалентна.

Кислотными остатками называются группы атомов (аиногда и один атом), «остающиеся» от молекул кислот, если мысленно отнять от них один или несколько атомов водорода, замещаемых металлом. этих групп определяется числом отнятых атомов водорода. Например, дает два кислотных остатка – один двухвалентный SO 4 и другой одновалентный HSO 4 , входящий в состав различных кислых солей. Фосфорная кислотаН 3 РО 4 может дать три кислотных остатка: трехвалентный РО 4 , двухвалентный НРО 4 и одновалентный

Н 2 РО 4 и т. д.

Основными остатками мы будем называть; атомы или группы атомов, «остающиеся» от молекул оснований, если мысленно отнять от них один или несколько гидроксилов. Например, последовательно отнимая от молекулы Fe(OH) 3 гидроксилы, получаем следующие основные остатки: Fe(OH) 2 , FeOH и Fe. их определяется числом отнятых гидроксильных групп:Fe(OH) 2 – одновалентен; Fe(OH)-двухвалентен; Fe – трехвалентен.

Основные остатки, содержащие гидроксильные группы, входят в состав так называемых основных солей. Последние можно рассматривать как основания, в которых часть гидроксилов замещенакислотными остатками. Так, при замещении двух гидроксилов вFe(OH)3 кислотным остатком SO 4 получается основная соль FeOHSO 4 , при замещении одного гидроксила в Bi(OH) 3

кислотным остатком NO 3 получается основная соль Bi(OH) 2 NO 3 и т.д.

Знание валентностей отдельных элементов и радикалов позволяет в простых случаях быстро составлять формулы очень многих химических соединений, что освобождает химика от необходимости механически их заучивать.

Химические формулы

Пример 1. Составить формулу гидрокарбоната кальция – кислой соли угольной кислоты.

В состав этой соли должны входить атомы кальция и одновалентные кислотные остатки НСО 3 . Так как двухвалентен, то на один атом кальция надо взять два кислотных остатка. Следовательно, формула соли будет Са(НСО 3)г.

Физика – наука о природе. Она описывает процессы и явления окружающего мира на макроскопическом ярусе – ярусе маленьких тел, сравнимых с размерами самого человека. Для изложения процессов физика использует математический агрегат.

Инструкция

1. Откуда берутся физические формулы ? Упрощенно схему приобретения формул дозволено представить так: ставится вопрос, выдвигаются догадки, проводится серия экспериментов. Итоги обрабатываются, появляются определенные формулы , и это дает предисловие новой физической теории либо продолжает и развивает теснее имеющуюся.

2. Человеку, постигающему физику, не нужно снова проходить каждый данный непростой путь. Довольно освоить центральные представления и определения, ознакомиться со схемой эксперимента, обучиться выводить основополагающие формулы . Безусловно, без крепких математических познаний не обойтись.

3. Выходит, выучите определения физических величин, относящихся к рассматриваемой теме. У всякой величины есть свой физический толк, тот, что вы обязаны понимать. Скажем, 1 кулон – это заряд, проходящий через поперечное сечение проводника за 1 секунду при силе тока в 1 ампер.

4. Уясните физику рассматриваемого процесса. Какими параметрами он описывается, и как эти параметры меняются на протяжении времени? Зная основные определения и понимая физику процесса, легко получить простейшие формулы . Как водится, между величинами либо квадратами величин устанавливаются прямо пропорциональные либо обратно пропорциональные зависимости, вводится показатель пропорциональности.

5. Путем математических реформирований дозволено из первичных формул вывести вторичные. Если вы обучитесь делать это легко и стремительно, последние дозволено будет не запоминать. Стержневой способ реформирований – способ подстановки: какая-нибудь величина выражается из одной формулы и подставляется в иную. Главно лишь, дабы эти формулы соответствовали одному и тому же процессу либо явлению.

6. Также уравнения дозволено складывать между собой, разделять, перемножать. Функции по времени дюже зачастую интегрируют либо дифференцируют, получая новые зависимости. Логарифмирование подойдет для степенных функций. При итоге формулы опирайтесь на итог, тот, что вы хотите в результате получить.

Каждая человеческая жизнь окружена большинством разновидных явлений. Ученые-физики занимаются постижением этих явлений; их инструментарием выступают математические формулы и достижения предшественников.

Природные явления

Изучение природы помогает умней относиться к имеющимся источникам, открывать новые источники энергии. Так, геотермальные источники обогревают примерно всю Гренландию. Само слово «физика» восходит к греческому корню «физис», что обозначает «природа». Таким образом, сама физика – наука о природе и природных явлениях.

Вперед, в грядущее!

Часто физики в прямом смысле «опережают время», открывая законы, которые находят использование лишь десятками лет (и даже столетиями) позднее. Никола Тесла открывал законы электромагнетизма, которые находят использование в наши дни. Пьер и Мария Кюри открыли радий фактически без поддержки, в невероятных для современного ученого условиях. Их открытия помогли спасти десятки тысяч жизней. Теперь физики каждого мира сосредоточены на вопросах Вселенной (макрокосмос) и мельчайших частиц вещества (нанотехнологии, микрокосмос).

Понимание мира

Важнейшим мотором общества является любознательность. Вот отчего эксперименты в Большом Андронном Коллайдере имеют такую высокую важность и спонсируются союзом из 60 государств. Имеется настоящая вероятность раскрыть тайны общества.Физика – наука фундаментальная. Это значит, что всякие открытия физики дозволено применять в иных сферах науки и техники. Небольшие открытия в одной ветви могут поразительно повлиять на всю «соседнюю» ветвь целиком. В физике знаменита практика изыскания группами ученых из различных стран, принята политика помощи и сотрудничества.Тайна мироздания, материи волновала великого физика Альберта Эйнштейна. Он предложил теорию относительности, поясняющую, что поля гравитации искривляют пространство и время. Апогеем теории стала известная формула E = m * C * C, объединяющая энергию с массой.

Союз с математикой

Физика опирается на новейшие математические инструменты. Нередко математики открывают абстрактные формулы, выводя новые уравнения из существующих, применяя больше высокие ярусы абстракции и законы логики, делая храбрые догадки. Физики следят за становлением математики, и изредка научные открытия абстрактной науки помогают пояснять незнакомые дотоле природные явления.Бывает и напротив – физические открытия толкают математиков на создание догадок и нового логичного агрегата. Связь физики и математики – одной из важнейших научных дисциплин подкрепляет авторитет физики.

Воспользовавшись записью первого начала термодинамики в дифференциальной форме (9.2), получим выражение для теплоёмкости произвольного процесса:

Представим полный дифференциал внутренней энергии через частные производные по параметрам и :

После чего формулу (9. 6) перепишем в виде

Соотношение (9.7) имеет самостоятельное значение, поскольку определяет теплоёмкость в любом термодинамическом процессе и для любой макроскопической системы, если известны калорическое и термическое уравнения состояния.

Рассмотрим процесс при постоянном давлении и получим общее соотношение между и .

Исходя из полученной формулы, можно легко найти связь между теплоемкостями и в идеальном газе. Этим мы и займемся. Впрочем, ответ уже известен, мы его активно использовали в 7.5.

Уравнение Роберта Майера

Выразим частные производные в правой части уравнения (9.8), с помощью термического и калорического уравнений, записанных для одного моля идеального газа. Внутренняя энергия идеального газа зависит только от температуры и не зависит от объёма газа, следовательно

Из термического уравнения легко получить

Подставим (9.9) и (9.10) в (9.8), тогда

Окончательно запишем

Вы, надеюсь, узнали (9.11). Да, конечно, это уравнение Майера. Еще раз напомним, что уравнение Майера справедливо только для идеального газа.

9.3. Политропические процессы в идеальном газе

Как отмечалось выше первое начало термодинамики можно использовать для вывода уравнений процессов, происходящих в газе. Большое практическое применение находит класс процессов, называемых политропическими. Политропическим называется процесс, проходящий при постоянной теплоемкости .

Уравнение процесса задается функциональной связью двух макроскопических параметров, описывающих систему. На соответствующей координатной плоскости уравнение процесса наглядно представляется в виде графика – кривой процесса. Кривая, изображающая политропический процесс, называется политропой. Уравнение политропического процесса для любого вещества может быть получено на основе первого начала термодинамики с использованием его термического и калорического уравнений состояния. Продемонстрируем, как это делается на примере вывода уравнения процесса для идеального газа.

Вывод уравнения политропического процесса в идеальном газе

Требование постоянства теплоёмкости в процессе позволяет записать первое начало термодинамики в виде

Используя уравнение Майера (9.11) и уравнение состояния идеального газа, получаем следующее выражение для

Разделив уравнение (9.12) на T и подставив в него (9.13) придем к выражению

Разделив () на , находим

Интегрированием (9.15), получаем

Это уравнение политропы в переменных

Исключая из уравнения () , с помощью равенства получаем уравнение политропы в переменных

Параметр называется показателем политропы, который может принимать согласно () самые разные значения, положительные и отрицательные, целые и дробные. За формулой () скрывается множество процессов. Известные вам изобарный, изохорный и изотермический процессы являются частными случаями политропического.

К этому классу процессов относится также адиабатный или адиабатический процесс . Адиабатным называется процесс, проходящий без теплообмена (). Реализовать такой процесс можно двумя способами. Первый способ предполагает наличие у системы теплоизолирующей оболочки, способной изменять свой объем. Второй – заключается в осуществлении столь быстрого процесса, при котором система не успевает обмениваться количеством теплоты с окружающей средой. Процесс распространения звука в газе можно считать адиабатным благодаря его большой скорости.

Из определения теплоемкости следует, что в адиабатическом процессе . Согласно

где – показатель адиабаты.

В этом случае уравнение политропы принимает вид

Уравнение адиабатного процесса (9.20) называют также уравнением Пуассона, поэтому параметр часто именуют постоянной Пуассона. Постоянная является важной характеристикой газов. Из опыта следует, что ее значения для разных газов лежат в интервале 1,30 ÷ 1,67, поэтому на диаграмме процессов адиабата «падает» более круто, чем изотерма.

Графики политропических процессов для различных значений представлены на рис. 9.1.

На рис. 9.1 графики процессов пронумерованы в соответствии с табл. 9.1.

Как выводить формулы по физике

Как выводить формулы по физике.
Путем математических преобразований можно из первичных формул вывести вторичные.
Если вы научитесь делать это легко и быстро, последние можно будет не запоминать.
Как выводить формулы по физике – версия для памяти.
Добавить комментарий сможете и вы, если позвоните репетитору.
Урок математики и физики.
Уроки математики. Сдать ГИА на 100 баллов
Как сдать гиа на 100 баллов. ГИА математика.
Сдать онлайн урок.
Видео – YouTube http://youtu.be/CCHgckh2ICQ
Разложение многочленов на множители.
Способ группировки
http://razlozhenie-mnogochlena-sposobom.blogspot.ru/
Тесты ГИА онлайн – 5 #ballov

Экзамен на отлично или как сдать ЕГЭ и ГИА.

Экзамен сдадим на отлично или как сдать ГИА и ОГЭ.
Теперь ученики, не прибегая к услугам репетиторов, сами готовиться к сдаче экзаменов с помощью раздела ГИА.

Достаточно выбрать нужный предмет и пройти тест.
ГИА — 2015: Решения.
Обучающая система без Дмитрия Гущина «СДАМ ГИА»
Система тестов для подготовки и самоподготовки к ГИА.
По окончании работы вы увидите правильные решения заданий и узнаете свой балл по сто-балльной шкале.
Учителю Об экзамене
Государственная итоговая аттестация (ГИА) по математике (алгебре) 2015.
#examen Все о ГИА #gia -po-matematike
Математику необходимо сдавать для перевода в 10-й класс и получения аттестата о неполном среднем образовании.
Если же вы собираетесь продолжать обучение в физ-мат-классе, то потребуется сдать математику на высокий балл.

Как запомнить формулы математики Методы Султанова Видео YouTube

ГИА был введен в 9-м классе специально для ГИА.
Чаще всего нам приходится запоминать формулы математические, химические и физические.
Названия формул, особенно химических, удобно запоминать, используя метод Султанова.
(Такая математика не для меня).
В данной статье нет приведенных точных указаний.

Как быстро запомнить формулы по физике?
– Способов и методов для запоминания математических формул и законов существует множество.
Здравствуйте!

На портале «Репетитор» АРепетитор.рф появился новый заказ на обучение в Вашем городе и по Вашему предмету.
Детали заказа:
Заказ №: 495-345-20-61
Имя заказчика: Тихон Дипломов

Имя ученика: Даниела Курсовая
Предмет: Математика
Где будут проводиться занятия: На территории преподавателя
Район: Москва – Котловка – Марьино
Продолжительность занятия: 45 минут.
Цена занятий (за 60 минут): 3000 RUR
Цель занятий, пожелания, комментарии: Ученик – девочка, 11 класс.
Переводим ребенка в более сильную школу. Училась по программе “Школы России”.

Необходимо за месяц подтянуть математику до нужного уровня.
Программа – Петерсон, Шклярова.

Если Вы заинтересованы в этом заказе, зайдите в раздел Заказы на обучение и подайте заявку на этот заказ.

Узнать подробно, как работать с поступающими заказами, получить ответы на вопросы Вы сможете, прочитав раздел “Как это вообще у репетиторов работает”.
Общая, весёлая и экспериментальная физика Механика.
“А путин предпочтительнее не только потому, что умнее”,- сказал эббот из австралии

Формулы по математике и физике: инструкция по запоминанию

Помните ли вы формулу Закона всемирного притяжения или скорости с постоянным ускорением? Остались ли у вас в памяти формулы суммы кубов или произведения косинусов? Наверняка, вы либо вовсе не помните, что означает этот набор слов, либо что-то припоминаете, либо не помните формулы, но понимаете, о чем мы. Если же вы без проблем сможете написать хотя бы пару из этих формул, значит, вы скорее всего, технарь, и ваша работа связана с математическими или физическими расчетами. Конечно, есть еще вариант, что у вас феноменальная память, но это встречается довольно редко.

Совершенно логично у вас может возникнуть вопрос: а зачем мне вообще помнить эту информацию, если она никак не пригодится мне в жизни? Что ж, здесь нам есть, что ответить:

Во-первых, главная причина – это тренировка памяти, а это в свою очередь развитие системного, аналитического, ассоциативного мышления. Более подробно о пользе и способах развития памяти читайте здесь.
Во-вторых, запоминая формулы, вы способны быстрее выполнять вычисления, что заметно облегчает работу, особенно связанную с какими-либо подсчетами.
В-третьих, несмотря на то, что ваша работа никак не связана с вычислениями и подсчетами, в бытовой жизни вам нет-нет да приходится что-то складывать, вычитать, умножать или делить, и чтобы не попасть впросак, нужно тренировать этот навык.

Кстати, отличным бонусом развития памяти становится выясненное канадскими учеными замедление процессов старения головного мозга. Любое упражнение, в том числе заучивание стихотворений, воспоминание прошедших событий, изучение иностранных слов и т.д. этому способствует.

Итак, давайте приступим к способам запоминания формул. Сначала перечислим наиболее общеизвестные способы запоминания формул по математике и физике.

Решаем, решаем и еще раз решаем

Конечно! А как вы думали? Давайте порассуждаем: конечная цель запоминания формул – это решение поставленной задачи. Следовательно, идем от противного: чтобы запомнить формулу, её нужно как можно чаще применять. Соответственно, практика – лучшее средство.

С каждым разом формула запоминается все лучше и лучше, оседает в памяти, ведь напоминание – это лучшая техника при борьбе с забыванием. Еще лучше, если вы будете выполнять задания с перерывами в полчаса, 8 часов, день, 5 дней и т.д. Тогда формула навсегда останется с вами. Более подробно о кривой забывания можно почитать в этой статье.

Плюсом данного метода является и то, что с наработанными примерами по одной формуле вы прокачиваете умение решать задачи подобного вида. Особенно актуально это для школьников и студентов.

Давайте посмотрим, какие еще способы можно применять при запоминании математических и физических формул.

Пишем на карточках

Не преуменьшайте значение визуального контакта. Чем чаще вы встречаетесь глазами со своей формулой, тем более родной она становится для вас, и собственно вероятность её забывания снижается.

Также очень полезно среди большого количества разных формул сгруппировать их по определенному критерию и составить «тематические» карточки. К примеру, вы можете сделать заготовки формул квадратного уравнения, составить список карточек по тригонометрии или начертить трапецию с поясняющими равенствами. Точно так же это работает и с физикой. В этой области знаний можете выбрать, допустим, формулы, начинающиеся с ½, или все равенства, где есть масса. Так запоминать будет увлекательнее и эффективнее!

Карточки желательно не сложить в одно место и забыть, а разложить по разным местам комнаты или даже квартиры (только предупредите домочадцев, чтобы они не удивились). Нежданная встреча с той или иной формулой добавит в процесс запоминания эмоции (неожиданность), а это всегда усиливает воздействие.

Более стандартным подходом является использование карточек с целью проверки. Для этого одна их сторона должна быть подписана названием, а другая (перевернутая и не видная вам) должна содержать непосредственно саму формулу. Когда вам попадается, к примеру, «Потенциальная энергия тела, поднятого на высоту», вы пытаетесь вспомнить, что же там было (если что, это Ep = mgh). Если вспоминаете без труда, значит, откладываете её в сторону. С теми карточками, с которыми возникают сложности, вы не прощаетесь, а берете их на вооружение и обязательно возвращаетесь к ним впоследствии.

«Сейчас будет метод для умных», – подумаете вы.

Выводим сами

Но на самом деле, этот способ подвластен всем. Если уж вы решили изучать формулы, то наверняка вам знакомы базовые знания по элементарным арифметическим операциям. Если же нет, советуем вам этому научиться, это совершенно просто.

А работает это так. Допустим, вы однозначно знаете, что формула Закона всеобщего тяготения – это F = G(Mm/r2), G = 6,673 × 10 в -11-й степени , поэтому вам не составит труда вычислить массу первого объекта: M = Fr²/Gm².

Чтобы прийти к этому результату, необходимо стремиться к тому, чтобы m₁с каждым последующим шагом оставался в одиночестве в левой (или правой) стороне уравнения. Следовательно, мы перенесли r²к F в числитель, а G и m₂отправились в знаменатель. Собственно, так и получилась новая формула.

Или, к примеру, вы позабыли формулу нахождения высоты правильной четырехугольной пирамиды. Изобразив пирамиду (ABCDS), прочертив её высоту (SO) и соединив точку пересечения высоты и основания (O) с одной из точек нижнего квадрата (возьмем B) получится прямоугольный треугольник (SOB) (см. рис. 1). Далее вы можете вывести формулу высоты пирамиды из площади прямоугольного треугольника либо как высоту равнобедренного треугольника, либо из теоремы Пифагора.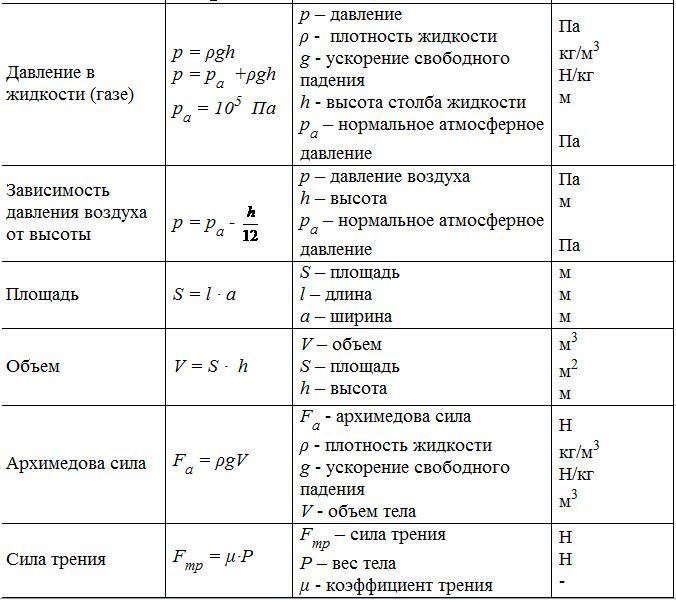 Выбирайте и считайте:

Таким образом, данный способ заставляет не только тренировать память, но и развивать логическое мышление, мыслить структурированно и рационально. Минусом этого метода является то, что у вас должны быть все же какие-то знания, ведь выводить новую формулу нужно из чего-то, из уже имеющихся равенств, которыми можно воспользоваться.

Медитируем над формулой

Не переживайте, благовония или успокаивающая музыка вам не понадобятся. Достаточно лишь хорошо вглядеться в формулу, разобраться, какой символ что означает, подумать над тем, почему эти символы связаны именно таким путем, и – вуаля! – вы придете к осознанному пониманию того, что пытаетесь вычислить.

Снова не обойтись без примера. Возьмем формулу связи давления, площади и силы, выглядит она так: p = F/S . Теперь вдумайтесь, ведь на самом деле когда мы на что-то давим, нужно, главным образом, учитывать три фактора:

То, с какой силой мы давим (F).
То, какая поверхность оказывается под воздействием этой силы (S).
То, что чем больше площадь поверхности, на которую оказывают действие, тем менее заметно это воздействие, т.е. сила обратно пропорциональна площади поверхности (F/S).

Аналогично можно проанализировать и разобрать остальные не слишком комплексные формулы. Но что же делать, если формула гораздо более сложная, длинная и содержащая большее количество параметров? В таком случае обычно применяют мнемотехники.

Даем волю фантазии

Слово мнемоника (равнозначна мнемотехнике) – это совокупность специальных приемов, помогающих увеличить объем запоминаемой информации, подчас в разы. Может показаться, что это панацея для забывчивых и ленивых товарищей, однако мнемотехника требует активного включения воображения, фантазии, креативности, долгих часов тренировок и, конечно же, самой памяти. Посмотрим, как мнемоника помогает на практике с математическими и физическими формулами.

Суть этой техники заключается в присвоении какой-либо единице информации определенного образа, его последующем кодировании, запоминании связей между кодированными данными и последовательной расшифровке. В этом сложно сформулированном алгоритме на самом деле все очень просто.

Помните, сколько цветов и какие конкретно заложены в радуге? Наверняка в ответе на этот вопрос вам поможет детская присказка «Каждый Охотник Желает Знать, Где Сидит Фазан». Таким образом, посредством акростиха (как вариант мнемотехники) вы запомнили, что радуга содержит красный, оранжевый, желтый и другие цвета.

Точно так же можно пофантазировать и на тему формул, а именно придумать символические образы для каждого параметра или цифры, соединить их каким-либо действием или ситуацией и запомнить. Допустим, мы говорим о цифрах, тогда мы можем использовать следующие образы:

1 — свеча;

2 – лебедь;

3 – скрученная змея;

4 – перевернутый стул;

5 – дяденька с пузом, стоящий вбок;

6 – вишенка;

7 – флаг;

8 – бесконечность;

9 – рыбка.

Все это нужно хорошенько визуализировать, представить и запомнить.

Далее мы начинаем вводить параметры. Чтобы быть более конкретными, давайте выберем формулу механической работы, которая выглядит следующим образом:

Какую тут можно придумать технику? Можно подобрать какие-нибудь слова, фразу, связывающую параметры. В конце концов, это буквы, и, связав их, можно получить что-то со смыслом. Например, буквы «А», «Ф», «С» содержатся в имени АФанаСий. Если у Афанасия появляется коза, то и запоминать становится почти нечего: только лишь рельсы (знак равенства) со звездой (знак умножения).

Теперь представьте: стоит некий Афанасий на железнодорожных путях рядом с козой вечерком, а над ними ярко-ярко горит звезда и освещает их. Представили? Подержите у себя в голове Афанасия с козой секунд пять, постарайтесь разглядеть их подробно, увидеть то, как свет играет по шерсти козы и волосам Афанасия. Теперь вероятность того, что вы вспомните формулу механической работы гораздо выше.

Если вдруг вы обладаете знаниями в английском языке или латыни, это может помочь во многом. В частности, вышеупомянутая формула давления содержит в себе первые буквы таких слов как pressure (давление), force (сила), square (площадь поверхности). Другие слова, такие как volume (объем), height (высота), mass (масса), time (время), acceleration (ускорение) несомненно будут большой подсказкой. Учите иностранный язык, эти знания пригодятся в нужный момент.

Техниками мнемоники пользуется большое количество людей, существуют даже специальные школы по подготовке именно с использованием этой методики. На 4brain также есть онлайн-программа «Мнемотехника», благодаря которой вы сможете в увлекательной форме научиться запоминать большой массив данных, перестанете забывать имена, адреса, телефоны, дни рождения и многое другое.

Другие мнемотехники, связанные с ассоциативным мышлением, поэтапным запоминанием, можно посмотреть в этом видеоролике:

Тренируйте память, учите формулы, заставляйте работать головной мозг, потому что, как показывает практика, это идет только на пользу организму, да и жизни в целом.

Желаем вам успехов!

Формулы по физике 8 класс

Путь	$S=Vt$	метр
Скорость	$V=S/t$	метр/секунда
Плотность	$p=\frac{m}{v}$	килограмм/метр3
Масса	$m=pv$	килограмм
Сила тяжести	$F=mg$	Ньютон
Давление твердых тел	$p=\frac{F}{S}$	Паскаль
Давление в жидкостях	$p=\rho gh$	Паскаль
Гидравлический пресс	$\frac{F_1}{F_2}=\frac{S_2}{S_1}$
Закон Архимеда	$F=p_ж V_т g$	Ньютон
Механическая работа	$A=FS$	Джоуль
Мощность	$N=\frac{A}{t}$	Ватт
$КПД=\frac{А_п}{A_з}100\% = \frac{Q_п}{Q_з}100\%$		%
Кинетическая энергия	$E=\frac{mv^2}{2}$	Джоуль
Потенциальная энергия	$E=mgh$	Джоуль
Количество теплоты	$Q=cm(t_2 – t_1)$	Джоуль
Теплота сгорания	$Q=qm$	Джоуль
Теплота парообразования	$Q=Lm$	Джоуль
Закон Ома	$I=\frac{U}{R}$	Ампер
Сопротивление проводника	$R=\frac{pl}{s}$	Ом
Последовательное соединение проводников
Сила тока	$I=I_1=I_2$	Ампер
Напряжение	$U=U_1 + U_2$	Вольт
Сопротивление	$R=R_1 + R_2$	Ом
Параллельное соединение проводников
Сила тока	$I=I_1 + I_2$	Ампер
Напряжение	$U=U_1=U_2$	Вольт
Сопротивление	$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}$	Ом
Работа тока	$A=IUt$	Джоуль
Мощность тока	$P=\frac{A}{t}=UI$	Ватт
Тепловое действие тока	$Q=I_2 Rt$	Джоуль

что делать, если забыл математическую формулу?

Иногда случается, что нужная для решения задачи формула начисто вылетает из головы. Это не страшно, когда под рукой справочники или интернет, но что если это произошло на олимпиаде, когда дорога каждая минута, а нервы и без того на пределе?

Физики, если им нужно восстановить формулу, исходят из соображений размерности входящих в неё величин. Я на двух примерах покажу, как довольно быстро восстановить математическую формулу, если вы хотя бы в общих чертах помните её вид.

Начнём с формулы Эйлера, связывающей количества граней, рёбер и вершин многогранника. Допустим, мы забыли, как эти величины соотносятся друг с другом, а помним только, что отношение линейное.

Запишем формулу в виде xГ+yВ+zР=t, где Г, В и Р – количества, соответственно, граней, вершин и рёбер, а x, y, z и t – коэффициенты, которые нам необходимо вспомнить. Рассмотрим 4 тела: тетраэдр, куб, четырёхугольную пирамиду и треугольную призму (для облегчения дальнейших вычислений выбираем тела, в которых поменьше граней, вершин и рёбер).

Подставив в формулу количества граней, вершин и рёбер каждого многогранника, получим систему из четырёх уравнений:

4x+4y+6z-t=0 //тетраэдр
6x+8y+12z-t=0 //куб
5x+5y+8z-t=0 // четырёхугольная пирамида
5x+6y+9z-t=0 //треугольная призма

Вычитая из третьего уравнения четвёртое, получим
y+z=0
И третьего первое:
x+y+2z=0
Учитывая предыдущий результат, получим
x+z=0
Теперь в какое бы уравнение ни подставить x=-z и y=-z, будем получать:
-2z-t=0
Таким образом формула Эйлера будет иметь вид:

-zГ+-zВ+zР+2z=0

Подставив вместо z минус единицу и перенеся свободный член вправо, получим формулу Эйлера:
Г+В-Р=2

Можно для проверки попробовать, действует ли она, скажем, для икосаэдра.

Имеем: 20 граней (на то он и икосаэдр), вершин – 12 (2 полюса и 10 в поясе), рёбер–30 (по 5 из каждого полюса, по 5 вокруг верхнего и нижнего краёв пояса и ещё 10 змейкой в самом поясе). 20+12-30=2. Сошлось! Мы таки вспомнили её!

Теперь формулу можно применить при решении задачи. Однако обратите внимание, что такой способ лишь помогает вспомнить забытую формулу, но никак не является её доказательством.

Другая полезная формула – формула Пиля, она позволяет вычислить площадь выпуклого многоугольника с вершинами в узлах сетки клетчатого листа бумаги. Попробуем вспомнить и её.

Итак, имеем, что площадь многоугольника выражается как линейная комбинация числа узлов сетки, лежащих внутри многоугольника, на его сторонах и на углах. Запишем её как
S=xI+yB+zC+t
где S – площадь, I, B и C – количества узлов сетки внутри, на сторонах и на углах многоугольника, а x, y, z и t – неизвестные коэффициенты и свободный член.

Рассмотрим четыре небольших фигуры: треугольник в половину клетки, единичный квадрат, прямоугольник 1х2 и квадрат 2х2. Получим систему из четырёх уравнений:

0.5=3z+t // треугольник в половину клетки
1=4z+t // единичный квадрат
2=2y+4z+t // прямоугольник 1х2
4=x+4y+4z+t // квадрат 2х2

Вычитаем из второго первое:
z=0.5
Вычитаем из третьего второе:
y=0.5
Далее из первого:
t=-1
а из четвёртого:
x=1

Таким образом, формула имеет вид:
S=I+0.5(B+C)-1

Ещё раз повторю, это не доказательство! И если суть задачи сводится к тому, что нужно доказать формулу Пиля, то данный метод не поможет. А вот если данную формулу предполагается использовать как вспомогательную и доказывать её по пути не требуется, то так вполне можно для себя восстановить забытое на черновике. И, разумеется, на абсолютно пустом месте этот метод также не сработает, нужно иметь хотя бы представление о том, что хочешь вспомнить.

Как быстро запомнить формулы по физике?

Физика это интересный предмет, который, как правило, нравится большинство ученикам. Все это верно, за исключение формул, которые доставляют немало хлопот всем. Вот если бы не они, то физика нравилась бы всем без исключения. Остается тогда эту проблему решить, пытаться выучить все формулы. Но как? Существует множество методик это делать. Одна из них подразумевает запоминание формул по приемам, которые используются для запоминания любой другой информации. Другая методика, более специфическая именно для физики, заключается в том, чтобы самому выводить эти формулы, но для этого, конечно же, нужно физику понимать. Этот метод подойдет тем, кому легко дается физика, но тяжело запоминаются формулы, особенно те, что очень сложные. Кроме этого, есть определенные фишки, которые позволяют быстрее выучить формулы и запомнить их надолго.

Правила запоминания формул по физике:

Перед изучением формул необходимо запомнить их содержание и назначение.
Необходимо выучить символы формул. Это не так сложно делать, учитывая тот факт, что те же самые символы используются в нескольких формулах.
Один из способов гласит, что нужно написать на листочки формулы, с одной стороны формулу, а с другой название закона, положить в карман, потом по очереди доставать и учить, переложить в другой карман то, что уже выучили.
Можно придумать для формулы образ или название, использовать ассоциации.
Нужно стараться запоминать последовательность символов в формуле. Можно для этого использовать аббревиатуры.
Записывать формулы на листочке бумаги для того, чтобы запомнить получше. Написать название законов или формул буквами на листке, а потом из памяти написать формулы. Выделить при проверке ошибки красным, чтобы запомнилось.
Запишите формулы везде, так чтобы они были на глазах, и запомнились таким образом. Только не игнорируйте их, и каждый раз, когда вы их видите, не поленитесь прочитать их.
Записывайте в блонкноте формулы разными цветами. Отведите специальный блокнот только для формул.
При прочтении материала из книги не пропускайте формулы, постарайтесь сразу в них вникать.
Попробуйте привязать формулу к вопросам: «Что? Где? Когда?».
Тренируйте зрительную память.
Включите логику. Не учите наизусть, а старайтесь понять.

Заметка: Экономить потребление электроэнергии помогут современные однофазные и трехфазные счетчики. Установка электросчетчика (http://fazaa.ru/ustanovka-elektroschetchika/) профессионалом поможет избежать потери, и обеспечит четкий контроль затрат электричества.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Как запомнить формулы по физике | Контрольные, курсовые, решение задач для студентов

Как можно быстро запомнить физические формулы?
Физика — очень интересный и занимательный предмет, который с удовольствием изучают многие школьники. Однако немало учащихся испытывает объективные трудности, связанные с усвоением физических формул. Но без них никак не обойтись при решении простейших задач уровня А, поэтому проблему необходимо устранять. Но как это сделать?
Сегодня существует целый ряд техник и методик, позволяющих добиться нужного результата. Одни предлагают использовать мнемотехнические приемы, аналогичные запоминанию любой другой информации. Другие советуют самостоятельно выводить формулы, но для этого требуются глубокие знания предмета. Поэтому данный метод хорошо подойдет тем, кто хорошо разбирается в физике, но не может воспроизводить точные формулировки. Кроме того, в процессе усвоения существует ряд нюансов, позволяющих ускорить запоминание и сделать его более прочным.

Правила запоминания физических формул

• Привязать каждую формулу к конкретному содержанию (закону или явлению), определить назначение и привязать к разделу физики.
• Выучить символические обозначения, представленные в формулах. На самом деле их не очень большое количество и во многих формулах они повторяются.
• Выписать все нужные формулы на листочек (а лучше красивый и стильный блокнот). Затем отдельно написать названия законов или физических явлений и к ним попытаться на память указать формулы. После этого проверить правильность ответов, а ошибки выделить цветом.
• Подобрать к каждой формуле некий образ или оригинальное название, которое будет ассоциироваться с содержанием.
• Сформировать в отдельном блокноте перечень формул, выделяя их отдельным цветами.
• Написать на отдельных листочках, с одной стороны, название закона или явления, а с другой — саму формулу. Затем по очереди начать учить, перекладывая листки с запомнившимся содержанием в соседний карман.
• Читая книги или учебники, стараться вникнуть в суть формул и ни в коем случае их не пропускать.
• Свяжите по смыслу формулы с тремя вопросами —”Что? Где? Когда?”.
• Постараться выучить последовательность встречающихся символов. В этом могут хорошо пригодиться аббревиатуры.
• Растиражировать формулы и разместите их легкодоступных местах. При взгляде не поленитесь прочитать их и постарайтесь запомнить.
• Развивать и тренировать зрительную память.
• Стараться избежать механического заучивания. Необходимо запоминать логически, пытаясь вникнуть в суть формулы.

Новая книга может научить любого, как вывести формулу | Имперские новости

Два имперских академика написали книгу, чтобы помочь студентам глубже понять математику с помощью искусства вывода формул.

В эпоху машинного обучения, искусственного интеллекта, «Интернета вещей» и массового компьютерного моделирования вы можете спросить, нужны ли нам еще формулы для описания физических законов.

Профессор Алексей Корнышев и Доминик О’Ли с кафедры химии страстно верят, что формулы по-прежнему имеют свое место, и надеются вдохновить студентов на изучение искусства формул и понимание того, как они могут помочь проверить научное моделирование и эксперименты.

Мы поговорили с профессором Корнышевым о мотивации книги Как вывести формулу и о том, чем она отличается от большинства математических текстов.

Почему вы захотели написать книгу о научных формулах?

Великие формулы, ставшие решениями великих уравнений, полностью изменили наш мир. Например, решение уравнений Максвелла означает, что мир теперь подключен через Интернет; аэродинамические формулы, объясняющие происхождение подъемной силы и форму крыльев, чтобы усилить ее, физически связали мир через полет; формула для выпрямления тока на p-n переходе транзистора открыла путь к вычислениям; а формула, описывающая модели рассеяния рентгеновских лучей ДНК, помогла расшифровать структуру ДНК, положив начало молекулярной биологии – и это лишь некоторые из них!

Получение формул – это настоящее искусство.Разве это искусство – прерогатива интеллектуальных гигантов? На самом деле, его основы можно изучить с усердием, логической дисциплиной и аналитическими способностями. Насколько важными и полезными будут ваши формулы – это, конечно, другой вопрос; они могут не принести вам Нобелевскую премию, но, по крайней мере, они должны быть правильными! Этот двухтомный проект представляет собой попытку обучить этому искусству практически от средней школы / A-level до бакалавриата и аспирантуры. Том 1 посвящен необходимым основам. В томе 2, который будет опубликован в ближайшее время (работа в стадии разработки), рассматриваются более продвинутые и сложные методы вывода формул.

Почему получение формул – важный навык?

За годы обучения мы поняли, что многие, в основном студенты, не занимающиеся математикой, даже те, кто усердно изучает математику, часто не могут понять, как это работает. У них нет ощущения того, как вещи связаны, и часто они проверяют свои результаты путем изучения вывода, а не анализа прогнозов, порядка величины результатов или их ограничивающего поведения в известных случаях.

Таким образом, книга предназначена не только для вывода формул, но и для обучения студентов тому, как понимать, что они получили; имеют ли результаты смысл, как они проявляются в очевидных хорошо известных случаях и каковы их ограничения – в какой области параметров они должны работать, а где нет.

В книге не обошлось без введения математической основы, но это сделано с намерением систематически «упростить» ее, сделать ее очевидной и простой, с упором на обучающие навыки, развитие интуиции и здравого смысла. понимание того, что вы получили.

На кого рассчитана книга?

Особо амбициозные старшеклассники / ученики A-level, специализирующиеся на естественных науках; студенты бакалавриата, факультеты физики, химии и инженерии, и даже биологи, интересующиеся количественными методами; и аспиранты, теоретики и экспериментаторы.

Мы также надеемся, что книга будет полезна лекторам, преподающим математические методы нематематикам; математики, за исключением прикладных математиков, имеют собственное мышление, и мы не хотим вмешиваться и возиться с ним.

С Томом 1 мы начинаем практически с нуля, что требует только знания элементарной алгебры, геометрии и исчисления, постепенно увеличивая сложность материала. В этом отношении книга самодостаточна.

Вы бы порекомендовали книгу людям, которые боятся математики?

Совершенно верно! Это было одной из мотиваций написать его, так как, к сожалению, многие молодые студенты испытывают фобию к математике, потому что не понимают, как ее различные части работают вместе, и с трудом видят лес за деревьями.

Также, имея возможность решать проблемы, нажимая клавиши на вашем компьютере, используя готовые программы, можно соблазнить оставить работу компьютеру. Однако для понимания этих результатов может оказаться очень полезным изучение того, что описано в книге.

Для творческого научного программирования, которое требует большой дисциплины, но других навыков и мышления, изучение аналитических навыков, описанных в этой книге, может принести дополнительные силы по тем же причинам, и особенно для отладки результатов, которые не воспроизводят сформулированные законы, которые как ожидается, будут работать.

Что отличает вашу книгу от других?

Начиная этот проект, мы были мотивированы типичными ошибками студентов, их неспособностью соответствовать различным концепциям и их недостаточной подготовкой к пониманию своих результатов.Кроме того, мы помнили подход, применявшийся великими лекторами Фейнмана по физике. Мы хотели сделать что-то подобное для прикладной математики.

Мы надеемся, что профессиональные математики не будут винить нас в этом. Книгу написали математики, которые в прошлом испытывали те же трудности, что и наши нынешние ученики, и благодаря своим великим учителям смогли пройти через нее.

По возможности, мы хотели сделать книгу забавной и забавной. Мы хотели показать красоту некоторых конструкций и логических процедур в надежде, что наши читатели будут ими очарованы.В книге есть исторические забавы и юмор, подкрепленные забавными карикатурами и аллегориями (не судите нас!), Чтобы сделать ее менее сухой и увлекательной для молодежи и разделить нашу любовь к этой технике.

И последнее, но не менее важное: в нем используются решенные примеры – чисто математические (то, что мы называем «игровыми гаммами»), и физические приложения, разделенные упражнениями для очевидных промежуточных выводов или побочных случаев. Систематически приближенные аналитические формулы сравниваются с точными численными решениями.Физические примеры обычно вполне естественны, но некоторые, предназначенные для демонстрации определенного математического трюка, в конечном итоге выглядят немного надуманными (простите нас за это, хотя Фейнман, возможно, не стал бы!). Половина этой 700-страничной книги – это те примеры.

Удалось ли нам сделать эту книгу действительно другой, ни в коей мере не конкурирующей с строгими математическими книгами, – судить читатели. Мы сделали то, что, по нашему мнению, крайне необходимо в настоящее время, и сделали все, что могли, в то ограниченное время, которое у нас было.

–

Если вы являетесь преподавателем, студентом или выпускником Имперского химического факультета, издатели предлагают 30-процентную скидку при заказе до 30 июня 2020 года. За дополнительной информацией обращайтесь к профессору Алексею Корнышеву.

Вывод уравнений силы тяжести скорость-время, Рон Куртус

SfC Home> Физика> Гравитация>

Рона Куртуса

можно вывести общие уравнения гравитации для скорости падающего объекта за заданное время , а также для времени, необходимого для достижения заданной скорости.Уравнения включают начальную скорость объекта.

Основа для вывода уравнений гравитации скорость-время начинается с предположения, что ускорение свободного падения является постоянной величиной.

Так как ускорение – это также изменение скорости с приращением времени, вы используете Calculus, чтобы интегрировать это изменение, чтобы получить скорость для заданного истекшего времени. Затем из уравнения скорости можно определить уравнение для времени, которое требуется объекту, чтобы достичь заданной скорости из начальной точки.

На производные уравнения влияет начальная скорость объекта. Это важно в более поздних приложениях уравнений.

Вопросы, которые могут у вас возникнуть:

На чем основаны деривации?
Какова скорость для данного уравнения времени?
Сколько времени для данного уравнения скорости?

Этот урок ответит на эти вопросы. Полезный инструмент: Конвертация единиц

Основа для расчета скорости-времени

Выводы начинаются с предположения, что ускорение свободного падения g является константой для смещений относительно близко к Земле.Кроме того, ускорение определяется как приращение скорости во времени:

а = дв / дт

где

a – ускорение
dv – первая производная от скорости v (небольшое изменение скорости)
dt – первая производная от времени t (небольшой приращение времени)

( Дополнительные сведения см. В разделе «Векторы в уравнениях силы тяжести».)

Соотношение скорость-время

Начиная с g – это ускорение свободного падения:

а = г

дв / дт = г

Умножьте обе части уравнения на dt , чтобы получить:

dv = g * dt

Используя Calculus для интегрирования этого уравнения, вы можете получить уравнения для скорости и времени, как показано ниже.

Расчет скорости для заданного времени

Интегрируйте dv = g * dt по обе стороны от знака равенства.

Сначала проинтегрируйте dv в интервале от v = v _i _{до v = v :}

∫dv = v – v _i

где

∫ – знак интеграла, используемый в исчислении
v – вертикальная скорость объекта
v _i – начальная вертикальная скорость объекта

Примечание : Начальная скорость – это скорость, с которой объект отпускается после ускорения с нулевой скорости.Начальная скорость не возникает мгновенно.

Затем проинтегрируйте g * dt за интервал времени от t = 0 до t = t :

∫g * dt = gt – 0

Результат двух интеграций:

v – v _i = gt

Таким образом, общее уравнение гравитации для скорости относительно времени:

Расчет времени для заданной скорости

Время, необходимое для достижения заданной скорости, получается путем преобразования уравнения v = gt + v _i и решения для t :

v – v _i = gt

Сводка

Исходя из того факта, что ускорение свободного падения g считается постоянным и зная, что ускорение – это изменение скорости при изменении во времени, вы можете вывести уравнения гравитации для скорости относительно времени.Затем вы можете определить уравнение времени для достижения заданной скорости.

Производные уравнения:

v = GT + v _i
t = (v – v _i) / г

Знайте, откуда берутся уравнения

Ресурсы и ссылки

Полномочия Рона Куртуса

Сайты

Гравитационные ресурсы

Падающие тела – Гипертекст по физике

Уравнения падающего тела – Википедия

Расчет силы тяжести – Земля – Калькулятор

Книги

(Примечание: Школа чемпионов может получать комиссионные от покупки книг)

Книги с самым высоким рейтингом по простой науке о гравитации

Книги с самым высоким рейтингом по продвинутой физике гравитации

Вопросы и комментарии

Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте.Я постараюсь вернуться к вам как можно скорее.

Поделиться страницей

Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:

Студенты и исследователи

Веб-адрес этой страницы:
www.school-for-champions.com/science/
gravity_derivations_velocity_time.htm

Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или диссертации.

Где ты сейчас?

Школа чемпионов

Гравитационные темы
Вывод уравнений силы тяжести скорость-время

Простой метод вывода формул относительности

[1] Ю.Л. Сюй, Исследование описания электромагнитных волн, PIERS ONLINE, Vol. 6, № 1, 2010, с. 41-45, DOI: 10. 2529 / PIERS 0110025.

[2] Дж.Ф. Ян, Ядерная физика, издательство Фуданьского университета, Шанхай, 2002, с. 211.

[3] X.T. Лу, Ядерная физика, Издательство по атомной энергии, Пекин, 2008 г., стр.375.

[4] Б.С. Ву, Physics, Science Press, Пекин, 2008 г., стр.307.

[5] Дж.Дж. Чжао, З.С. Инь, Технология ускорителей частиц, High Education Press, Пекин, 2006 г., стр. 172.

[6] H.C. Оганян, Р. Руффини, Гравитация и пространство-время, У.W. Norton & Company, Inc. 1994. Глава 9, раздел 3.

Mr Toogood Physics – Вывод уравнений движения

$ \ newcommand {\ amount} [2] {# 1 \; \ mathrm {# 2}} $ $ \ newcommand {\ units} [1] {\ mathrm {# 1}} $

Вывод уравнений движения

Ожидается, что вы будете знать только, как использовать четыре уравнения SUVAT, и хотя вам не нужно знать, как вывести их, первые принципы (т.е. научитесь записывать их, исходя из самых простых предположений, чтобы показать, откуда они берутся) полезно увидеть, как они возникают, чтобы полностью их понять.

Термин первые принципы означает самые основные предположения, которые можно сделать о физической системе. Это может быть физический закон, например законы движения Ньютона, или определения, например, для скорости и ускорения

$$ \ large v = \ frac {\ Delta s} {\ Delta t} $$

$$ \ large a = \ frac {\ Delta v} {\ Delta t} $$

Уравнение 1

Это простейший вывод, основанный на понимании определения ускорения,

$$ a = \ frac {\ Delta v} {\ Delta t} $$

Δ v может быть указано как (v-u) или конечная скорость объекта за вычетом его начальной скорости.Итак:

$$ a = \ frac {\ left (v-u \ right)} {t} $$

Теперь обе стороны можно умножить на t :

$$ at = \ left (v-u \ right) $$

Чтобы сделать это равным v , необходимо добавить u к обеим сторонам, что приведет к окончательному уравнению:

$$ \ large v = u + at $$

Уравнение 2

Если объект движется от точки a до b , его скорость может изменяться.Его средняя скорость между двумя точками может быть вычислена путем добавления мгновенной скорости при a ( u ) к мгновенной скорости при b ( v ) и деления на 2:

$$ \ frac {\ left (u + v \ right)} {2} $$

Уравнение скорости может быть преобразовано в с , так что с = vt , что приводит к:

$$ \ large s = \ frac {\ left (u + v \ right) t} {2} $$

Уравнение 3

Мы знаем, что из графика скорость-время смещение представлено областью под линией.

Рис. 1: Использование графика скорость-время для вывода уравнений сувата.

Площадь под нижней частью графика можно рассчитать, умножив начальную скорость u на время t :

$$ s = ut $$

Площадь под верхней частью графика находится путем вычитания начальной скорости и из конечной скорости v и умножения на время:

$$ s = \ frac {1} {2} \ left (v-u \ right) t $$

Таким образом, выражение для полного смещения может быть следующим: $ s = ut + \ frac {1} {2} \ left (v-u \ right) t $

Однако член (v-u) также появляется в уравнении для ускорения, поэтому его можно заменить на на , что приводит к:

$$ \ large s = ut + \ frac {1} {2} в ^ {2} $$

Уравнение 4

Это самое сложное для вывода, но часто самое полезное из четырех уравнений.{2} +2 за $

Калькулятор равномерно ускоренного движения

Использование калькулятора

Калькулятор равномерно ускоренного движения использует уравнения движения для решения расчетов движения, включающих постоянное ускорение в одном измерении, по прямой. Он может найти начальную скорость u, конечную скорость v, смещение s, ускорение a и время t.

Выберите расчет, чтобы найти неизвестные переменные, и введите переменные, указанные в вашей задаче.Этот калькулятор вычислит неизвестные значения и предоставит производные уравнения, которые использовались для поиска решения. Уравнения решения выводятся из приведенных ниже уравнений равноускоренного движения.

Обратите внимание, что при решении для нескольких переменных обычно существует более одного способа решения для ваших неизвестных. Вы можете вывести несколько наборов уравнений, чтобы решить вашу проблему разными способами. 2 \ tag {4} \)

Где:

u = начальная скорость вращения
v = конечная скорость
a = ускорение
с = рабочий объем
t = время

Используйте стандартную гравитацию, a = 9.80665 м / с ², для уравнений, учитывающих гравитационную силу Земли как скорость ускорения объекта.

Уравнения с 1 по 4 являются ключевыми уравнениями, используемыми для решения переменных в этом калькуляторе, однако иногда вы можете увидеть другое количество уравнений равномерно ускоренного движения в зависимости от ресурса. Вы обнаружите, что уравнение 1 получается при подстановке уравнения 1b в уравнение 1a ниже.

\ (s = \ overline {v} t \ tag {1a} \)

\ (\ overline {v} = \ dfrac {1} {2} (v + u) \ tag {1b} \)

8 лучших советов по запоминанию математических и физических формул

В этой статье вы получите несколько важных советов и предложений о том, как вы можете легко и быстро выучить сложные математические и физические формулы.Изучите различные приемы запоминания, которые помогут вам освоить так называемые самые сложные предметы; По математике и физике и получайте хорошие оценки на текущих экзаменах.

В. Я очень плохо запоминаю математические формулы. Пожалуйста, предложите несколько советов о том, как изучать математические и физические формулы и удерживать их в мозгу.

Отв. Вы проводите долгие ночи, чтобы узнать сложные, длинные математические формулы, но уже на следующий день, когда вы пытаетесь их вспомнить, вы обнаруживаете, как будто все вычистили из вашего мозга.Собственно, так бывает с каждым вторым учеником. Так что вам не нужно беспокоиться об этом. Все, что вам нужно, – это следовать нескольким стратегиям, чтобы с легкостью запомнить все фолмулы по математике и физике.

Поговорив и обсудив вышеупомянутую проблему с ветеранами в области образования и некоторыми руководителями экзаменов, мы собрали несколько советов, которые будут полезны для понимания и сохранения различных математических или физических формул в мозгу.

Ниже приведены основные советы по легкому изучению различных математических и физических формул:

1.Практика концентрации: математических и физических терминов и формул требуют интенсивного сосредоточения и глубокой концентрации, чтобы они могли быть поглощены умом. Поэтому вам нужно работать над уровнем концентрации, чтобы все сложные или длинные формулы запоминались.

2. Расслабьте свой мозг: Задачи математики и физики невозможно решить в условиях стресса, поскольку напряженный мозг теряет свой рабочий потенциал и ему становится трудно работать над сложными задачами. Итак, вам нужно сначала расслабить свой ум.Поступая так, вы сможете больше сосредоточиться на своей задаче.

3. Практикуйтесь как можно больше: Это может показаться очевидным, но чем больше вы практикуетесь в использовании формул, которые вам нужно знать, тем больше вероятность, что вы запомните то же самое. Перечислите все важные формулы на листе и, когда будете свободны, взгляните на них один раз. Ведь повторение ведет к запоминанию.

4. Сведите к минимуму контрольные проверки : Многие студенты думают, что, взглянув на формулу, они уже мыслят, но на следующее утро, когда они пытаются вспомнить то же самое, они шокированы, узнав, что формула просочилась. ночью.Чтобы избежать такой ситуации, попробуйте попрактиковаться в решении проблемы с формулой, не заглядывая в нее.

5. Разберитесь с основной концепцией формулы: Постарайтесь прояснить свои основные концепции, прежде чем переходить к формулам. Это поможет вам понять смысл формулы.

Например: В формуле a = F / m, где ускорение (a) выражается через силу (F) и массу (м), F находится в верхней части дроби. Это имеет смысл, поскольку, если вы приложите больше силы к объекту, он ускорится быстрее.Принимая во внимание, что масса находится в нижней части фракции, что означает, что скорость объекта будет уменьшаться, поскольку больше массы означает больше инерции, что затрудняет ускорение объекта.

6. Держитесь подальше от всех отвлекающих факторов: Под этим заголовком следует говорить не только о гаджетах, которые вы используете, но и о ваших физических желаниях, таких как голод, жажда, сонливость и т. Д., Также необходимо избегать.

7. Изучите вывод каждой формулы. Вывод формулы поможет вам познакомиться с корнями и концепциями этой формулы, что поможет вам сохранить ее в течение длительного времени в вашем мозгу.Более того, когда вы выводите формулу, вы сталкиваетесь с рядом других формул. Таким образом, вы сможете запомнить только минимальное количество формул, из которых вам нужно вывести остальные.

8. Используйте уловки запоминания: Постарайтесь создать рассказ, включающий в себя все, что вы пытаетесь выучить. Последовательность рассказа может помочь вам запомнить вещи в определенном порядке.

Например: Чтобы узнать тригонометрические отношения; P / H = sin, B / H = cos, P / B = tan , вы можете использовать фразу «пандит бадри прасад хар хар боле сона чанди толе» , а затем установить такие слова, как:

Поработайте над такими фразами, которые помогут вам вспомнить длинные сложные формулы.

Таким образом, все приведенные выше советы и уловки, если следовать им с умом, определенно помогут вам овладеть математикой и физикой, и вы получите отличный результат на экзаменах.

Вы также можете прочитать:

Семь лучших приемов для овладения математикой

Концептуальное отображение: инструмент обучения

Тренируйте свой мозг для здоровой памяти

Основы СИ: базовые и производные единицы

Для простота понимания и удобство, даны 22 производные единицы СИ специальные имена и символы, как показано в Таблице 3.

Полученное количество	Имя	Символ	Выражение в терминах других единиц СИ	Выражение в терминах базовых единиц СИ
Таблица 3. Производные единицы СИ со специальными названиями и обозначениями
	Производная единица СИ
плоский угол	радиан ^(а)	рад	–	м · м ^-1 = 1 ^(б)
телесный угол	стерадиан ^(а)	ср ^(в)	–	м ² · м ^-2 = 1 ^(б)
частота	герц	Гц	–	с ^-1
сила	ньютон	N	–	м · кг · с ^-2
давление, напряжение	паскаль	Па	Н / м ²	м ^-1 · кг · с ^-2
энергия, работа, количество тепла	джоуль	Дж	Н · м	м ² · кг · с ^-2
мощность, лучистый поток	ватт	Вт	Дж / с	м ² · кг · с ^-3
электрический заряд, количество электроэнергии	кулон	С	–	с · A
разность электрических потенциалов, электродвижущая сила	вольт	В	Вт /	м ² · кг · с ^-3 · A ^-1
емкость	фарад	F	C / V	м ^-2 · кг ^-1 · с ⁴ · A ²
электрическое сопротивление	Ом		В / А	м ² · кг · с ^-3 · A ^-2
Электропроводность	siemens	S	Аудио / видео	м ^-2 · кг ^-1 · с ³ · A ²
магнитный поток	Вебер	Wb	В · с	м ² · кг · с ^-2 · A ^-1
плотность магнитного потока	тесла	Т	Вт / м ²	кг · с ^-2 · A ^-1
индуктивность	генри	H	Вт / A	м ² · кг · с ^-2 · A ^-2
Температура Цельсия	градусов Цельсия	° С	–	К
световой поток	люмен	лм	кд · sr ^(к)	м ² · м ^-2 · cd = cd
освещенность	люкс	лк	лм / м ²	м ² · м ^-4 · cd = m ^-2 · cd
активность (радионуклида)	беккерель	Бк	–	с ^-1
Поглощенная доза, удельная энергия (переданная), керма	серый	Гр	Дж / кг	м ² · с ^-2
эквивалент дозы ^(d)	зиверт	Sv	Дж / кг	м ² · с ^-2
каталитическая активность	катал	кат		с ^-1 · моль
^(а) Радиан и стерадиан можно выгодно использовать в выражениях для производных единиц, чтобы различать количества различной природы, но того же размера; некоторые примеры приведены в таблице 4. ^(b) На практике символы rad и sr используются там, где уместно, но производная единица “1” обычно опускается. ^(c) В фотометрии название единицы стерадиан и единица измерения символ sr обычно сохраняется в выражениях для производных единиц. ^(d) Прочие величины, выраженные в зивертах, относятся к окружающей среде. эквивалент дозы, эквивалент направленной дозы, эквивалент индивидуальной дозы, и органная эквивалентная доза.

Примечание о градусах Цельсия. Производная единица в таблице 3 со специальным названием градус Цельсия и специальный символ ° C заслуживает комментария. Из-за температуры шкалы, которые раньше определялись, остается обычной практикой выражать термодинамические температура, условное обозначение T , по отличию от эталонной температура Т ₀ = 273,15 К, ледяная точка. Эта температура разница называется температурой Цельсия, символ t , и составляет определяется количественным уравнением

т = т – т ₀.

Единицей измерения температуры по Цельсию является градус Цельсия, символ ° C. В числовое значение температуры Цельсия t , выраженное в градусах Цельсия –

t / ° C = T / K – 273,15.

Из определения t следует, что градус Цельсия равен по величине до кельвина, что, в свою очередь, означает, что числовой значение заданной разницы температур или температурного интервала, значение выражается в градусах Цельсия (° C) равно числовое значение той же разницы или интервала, когда его значение выражается в единицах кельвина (К).Таким образом, перепады температур или температура интервалы могут быть выражены либо в градусах Цельсия, либо в кельвинах. используя то же числовое значение. Например, температура по Цельсию разница т и термодинамический перепад температур T между точкой плавления галлия и тройной точкой воды может можно записать как t = 29,7546 ° C = T = 29,7546 К.

Специальные наименования и символы 22 производных единиц СИ со специальными наименованиями и символами приведенные в таблице 3, сами могут быть включены в названия и символы другие производные единицы СИ, как показано в таблице 4.

Полученное количество	Имя	Символ
Таблица 4. Примеры производных единиц СИ, названия и обозначения которых включать производные единицы СИ со специальными названиями и обозначениями
	Производная единица СИ
динамическая вязкость	паскаль-секунда	Па · с
момент силы	Ньютон-метр	Н · м
поверхностное натяжение	ньютон на метр	Н / м
угловая скорость	радиан в секунду	рад / с
угловое ускорение	радиан на секунду в квадрате	рад / с ²
плотность теплового потока, энергетическая освещенность	Вт на квадратный метр	Вт / м ²
теплоемкость, энтропия	джоуль на кельвин	Дж / К
удельная теплоемкость, удельная энтропия	джоуль на килограмм кельвина	Дж / (кг · К)
удельная энергия	джоуль на килограмм	Дж / кг
теплопроводность	ватт на метр кельвин	Вт / (м · К)
плотность энергии	джоуль на кубический метр	Дж / м ³
Напряженность электрического поля	вольт на метр	В / м
плотность электрического заряда	кулонов на кубический метр	С / м ³
Плотность электрического потока	кулонов на квадратный метр	С / м ²
диэлектрическая проницаемость	фарад на метр	Ф / м
проницаемость	генри на метр	Г / м
молярная энергия	джоуль на моль	Дж / моль
мольная энтропия, мольная теплоемкость	джоуль на моль кельвина	Дж / (моль · К)
экспозиция (x и лучи)	кулонов на килограмм	C / кг
Мощность поглощенной дозы	серого в секунду	Гр / с
интенсивность излучения	Вт на стерадиан	Вт / ср
сияние	Вт на квадратный метр стерадиан	Вт / (м ² · ср)
каталитическая (активность) концентрация	катал на кубический метр	кат / м ³

Продолжить до префиксов SI

Путь	\(S=Vt\)	метр
Скорость	\(V=S/t\)	метр/секунда
Плотность	\(p=\frac{m}{v}\)	килограмм/метр3
Масса	\(m=pv\)	килограмм
Сила тяжести	\(F=mg\)	Ньютон
Давление твердых тел	\(p=\frac{F}{S}\)	Паскаль
Давление в жидкостях	\(p=\rho gh\)	Паскаль
Гидравлический пресс	\(\frac{F_1}{F_2}=\frac{S_2}{S_1}\)
Закон Архимеда	\(F=p_ж V_т g\)	Ньютон
Механическая работа	\(A=FS\)	Джоуль
Мощность	\(N=\frac{A}{t}\)	Ватт
\(КПД=\frac{А_п}{A_з}100\% = \frac{Q_п}{Q_з}100\%\)		%
Кинетическая энергия	\(E=\frac{mv^2}{2}\)	Джоуль
Потенциальная энергия	\(E=mgh\)	Джоуль
Количество теплоты	\(Q=cm(t_2 – t_1)\)	Джоуль
Теплота сгорания	\(Q=qm\)	Джоуль
Теплота парообразования	\(Q=Lm\)	Джоуль
Закон Ома	\(I=\frac{U}{R}\)	Ампер
Сопротивление проводника	\(R=\frac{pl}{s}\)	Ом
Последовательное соединение проводников
Сила тока	\(I=I_1=I_2\)	Ампер
Напряжение	\(U=U_1 + U_2\)	Вольт
Сопротивление	\(R=R_1 + R_2\)	Ом
Параллельное соединение проводников
Сила тока	\(I=I_1 + I_2\)	Ампер
Напряжение	\(U=U_1=U_2\)	Вольт
Сопротивление	\(\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}\)	Ом
Работа тока	\(A=IUt\)	Джоуль
Мощность тока	\(P=\frac{A}{t}=UI\)	Ватт
Тепловое действие тока	\(Q=I_2 Rt\)	Джоуль