Главная
Как в компасе перевести чертеж из 3д в 2д: Быстрое создание 3D модели по 2D эскизу

Как в компасе перевести чертеж из 3д в 2д: Быстрое создание 3D модели по 2D эскизу

Содержание

Создание чертежа в Компас 3D по модели детали.: pavel_samuta — LiveJournal

Трехмерное моделирование можно просто определить как процесс создания трехмерного цифрового визуального представления реального объекта с использованием специализированного компьютерного программного обеспечения. Думайте об этом как о реалистичном рисовании, но с гораздо большей сложностью, потому что вы можете включать в модель данные в реальном времени и взаимодействовать с объектом с помощью компьютера. Как и физическая модель, объект можно вращать, переворачивать, взрывать или манипулировать различными способами на экране.

Из 3D-модели можно быстро создать чертеж. Некоторые производители программного обеспечения продают свои 3D-программы и 2D-программы в виде отдельных пакетов, но есть много таких, которые объединяют их в один, как Компас 3D. Здесь стоит отметить, что Компас позволяет работать с чертежом, не закрывая и редактировать при необходимости 3D модель, пользоваться некоторыми преимуществами по оформлению чертежей: создавать 2D проекции, включая изометрию, выполняя всевозможные разрезы и виды трехмерной детали.

Программа открывает файлы других форматов трехмерных моделей, но желательно чтобы трехмерная модель была выполнена в Компас 3D, чтобы не возникло вопросов  при построении разрезов.

Создание чертежа в Компас 3D по модели детали.

Из 3D в 2D

Помимо графического изображения, чертеж содержит рамку, основную надпись, знак неуказанной шероховатости и технические требования. Геометрическая характеристика листа— формат. Она включает в себя собственно формат (А4, А3 и т.д), а также кратность и ориентацию.

При создании нового чертежа в нем автоматически создается первый лист. При необходимости вы можете добавить листы. Это можно сделать в любой момент работы над чертежом. Если чертеж включает несколько листов, то для каждого из них можно задать собственный формат в Менеджере документа, а также выбрать нужный тип основной надписи.

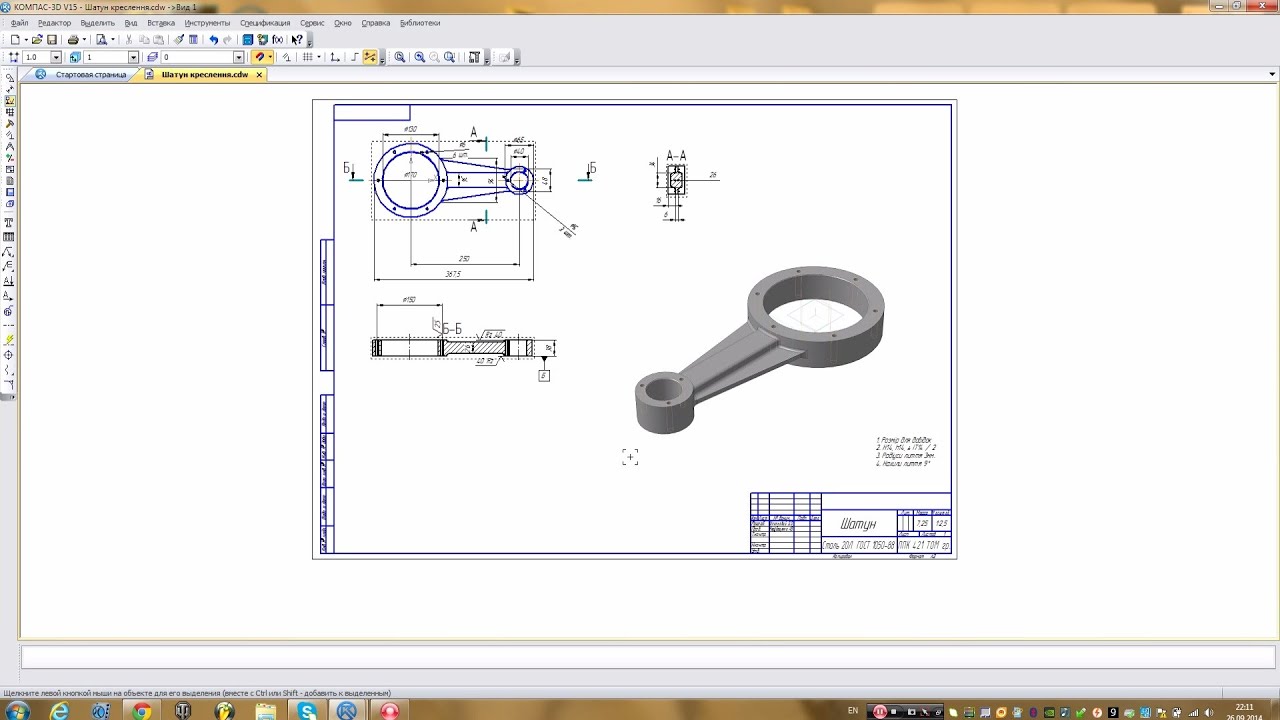
Если создан документ, типа «Чертеж», сначала выбираем формат чертежа и его ориентацию, оформление, количество листов в «Менеджере документов», далее в меню «Вставка» – «Вид с модели» – «Стандартные» создаем стандартные виды чертежа.

Менеджер документов в Компас 3D, выбираем формат, ориентацию и оформление.

Команда «Стандартные виды» позволяет выбрать существующую (сохраненную на диске) трехмерную модель и создать в активном документе чертеж этой модели, состоящий из одного или нескольких стандартных ассоциативных видов.

Ассоциативный вид — вид чертежа, ассоциативно связанный с существующей моделью (деталью или сборкой). При изменении формы, размеров и топологии модели изменяется и изображение во всех связанных с ней видах.

Для вызова команды нажмите кнопку Стандартные виды на инструментальной панели Виды или выберите ее название в меню «Вставка» — «Вид с модели».

На экране появится диалог, в котором следует выбрать модель. После того, как модель выбрана, в окне чертежа показывается фантом изображения в виде габаритных прямоугольников видов.

Вставка видов детали с 3D модели

Кнопка «Схема» видов на вкладке «Параметры» Панели свойств позволяет изменить набор стандартных видов выбранной модели.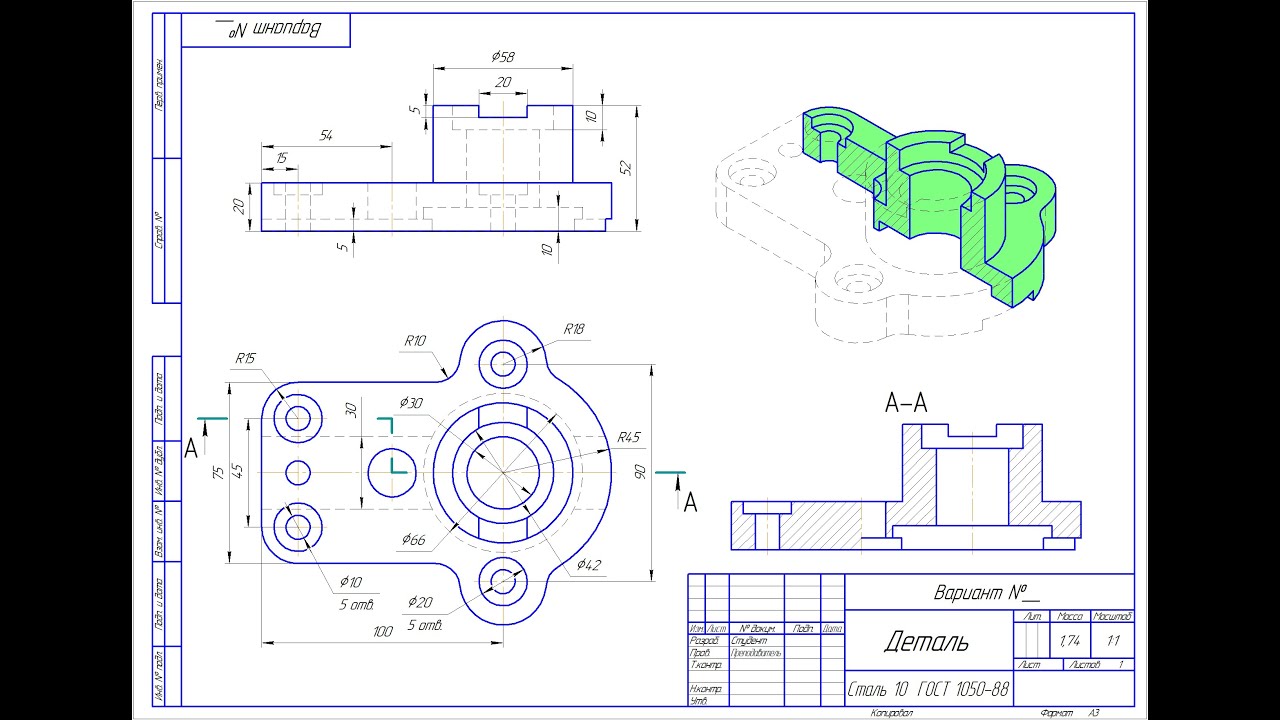

В поле Файл-источник отображается полное имя файла выбранной модели. С помощью кнопки Выбрать другую модель вы можете указать другой файл модели, виды которой требуется разместить в чертеже.

При создании стандартных видов вы может воспользоваться автоматическим подбором масштаба. Для этого нажмите кнопку «Подобрать». Из стандартного ряда будет выбран масштаб, при котором все виды, указанные для построения, полностью умещаются на чертеже выбранного формата. При подборе коэффициента масштабирования учитываются области чертежа, занятые основной надписью и другими элементами оформления.

После выбора нужных стандартных видов и их настройки укажите положение точки привязки изображения — начала координат главного вида.

Свойства трехмерной детали.

В активный документ будут вставлены виды модели, в основную надпись чертежа передадутся следующие сведения из трехмерной модели:

  1. обозначение чертежа детали,
  2. наименование чертежа детали,
  3. масса детали считается автоматизированно или принудительно,
  4. материал изделия.

Для того чтобы масштаб был привязан к виду модели два нужно добавить во вкладке «Масштаб» активную ссылку на вид требуемый модели.

Указание масштаба активной ссылкой с вида модели

Преимущества трёхмерных элементов оформления модели

Возможность создания трёхмерных элементов оформления позволяет внести в 3D модель не только геометрическую (тверды тела, поверхности, точки, поверхности), но и технологическую и другую информацию, которая впоследствии может быть использована при построении чертежей по 2D проекциям, а также в других приложениях, например, в модулях технологического проектирования или создания управляющих программ для ЧПУ. 

Графические и другие данные перенос с трехмерной модели.

*Почему в Компасе не создается чертеж из 3D модели?

Модель состоит из поверхностей.

В основном вопрос возникает из того что по умолчанию в отображении модели включены только твердые тела, если ваша модель состоит из поверхностей то следует включить функцию Поверхности в окошке Объекты интерфейса КОМПАС 3D

.

Например, если какой-то размер между гранями или размер на цилиндрической грани (радиус или диаметр) имеет допуск или дополнительные текстовые строки, то при построении размера на чертеже при выборе соответствующих линий на проекции эта информация будет автоматически передаваться размеру на 2D проекции через функцию Эллементы оформления интерфейса КОМПАС 3D. То же самое происходит при простановке обозначения шероховатости на грань – в случае создания обозначения шероховатости на соответствующих линиях изображения 2D проекции, параметры шероховатости будут взяты с 3D модели

Функции местный разрез, разрыв вида, выносной вид, вид по стрелке доступны в меню Вставка Компаса 3D, виды автоматически строятся в проекционной связи.

Вставка Компаса 3D

Все виды связаны с моделью: изменения в модели приводят к изменению изображения в ассоциативном виде.

Функции местный разрез, разрыв вида, выносной вид, вид по стрелке доступны в меню Вставка Компаса 3D, виды автоматически строятся в проекционной связи.

Для любого вида можно указать, какие объекты модели не требуется отображать в нем. Это могут быть тела, поверхности или созданные в модели элементы оформления (условные изображения резьбы, размеры, обозначения).

Для удобства управления видами рекомендуется использовать Дерево построения чертежа.

Технические требования являются частью чертежа. Они дополняют графическую информацию, содержащуюся в видах и сечениях, и позволяют изготовить деталь или узел в точном соответствии с замыслом инженера конструктора и требованиям нормативных документов.

Закончите оформление чертежа  по уже готовой 3D модели, оформлением технических требований: Меню — Вставка — Технические требования — Ввод. Вы можете настроить параметры технических требований документа, которые будут использоваться по умолчанию. 

Вставка технических требований чертежа.

Знак неуказанной шероховатости практически всегда присутствует на чертежах машиностроительных деталей. Для простановки знака неуказанной шероховатости на чертеже вызовите команду: Вставка — Неуказанная шероховатость — Ввод.

Знак неуказанной шероховатости практически всегда присутствует на чертежах машиностроительных деталей.

Все, чертеж трехмерной детали в программе Компас 3D готов! 

Чертежа в Компас 3D по модели детали готов.

You can choose several answers

Poll results is visible to all

Одна машина может сделать работу пяти обычных людей; ни одна машина не сделает работу одного незаурядного человека.

Я стремлюсь предоставлять клиентам опыт, который обретает доверие и заставляет возвращаться для дальнейшего сотрудничества.

Инженерная поддержка ваших идей, инициативность и предоставление социально ответственных и культурно значимых ответов на самые сложные запросы.

Моя миссия – принять потребности и видение клиента и воплотить его в реальность, которая является конструктивной, реализуемой, соответствует его бюджету. Если у вас есть необходимость в создании высококачественного чертежа ISO, DIN, ANSI, ЕСКД или трехмерной модели в Автокад, Компас 3D?  Для обсуждения именно вашего варианта чертежа, Вы можете связаться и поддерживать со мной связь с помощью электронной почты. И мы детально обсудим ваш проект. Контакты указаны в профиле блога. Испытайте мои навыки и опыт обслуживания клиентов – свяжитесь удобным способом, чтобы обсудить ваш следующий проект сегодня.

Инженер конструктор – Ремонт и строительство, Компьютеры и IT, … – Яндекс.Услуги

yandex.ru

Если у вас есть, что добавить по теме, не стесняйтесь. Делитесь тем, что вам интересно!

Главная » Все статьи » Создание чертежа в Компас 3D по модели детали.

Не удается найти страницу | Autodesk Knowledge Network

(* {{l10n_strings. REQUIRED_FIELD}})

{{l10n_strings.CREATE_NEW_COLLECTION}}*

{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}

{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}  

{{l10n_strings.DRAG_TEXT_HELP}}

{{l10n_strings. LANGUAGE}} {{$select.selected.display}}

{{article.content_lang.display}}

{{l10n_strings.AUTHOR}}  

{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}

{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}

Конвертация файлов КОМПАС-3D в формат AutoCAD

Одними из самых актуальных и используемых САПР являются КОМПАС-3D компании Аскон и всем известный AutoCAD. В этой статье мы расскажем, как можно перенести данные из КОМПАСа в AutoCAD.

Экспорт 2D-моделей

Для того что бы конвертировать 2D-файлы Компас в AutoCAD, не зависимо от того, чертеж это, фрагмент или спецификация. Достаточно выполнить команду Меню: Файл > Сохранить как, и в проводнике выбрать соответствующий формат AutoCAD.

Стоит отметить, что при экспорте документов из Компаса в AutoCAD большая часть элементов чертежа передается в виде блоков. Для последующей корректной работы с данными чертежами в AutoCAD может потребовать их переопределение или разрушение.

Экспорт 3D-моделей

В Компас отсутствует возможность прямого сохранения моделей в формате *.DWG, это касается и сборки и детали отдельно. Обходным путем является сохранение моделей в универсальных форматах, как вариант формат *.SAT — данный формат позволяет экспортировать как отдельные детали так и сборки.

Для того что бы сохранить документ в формате *. SAT  достаточно выполнить команду  Меню: Файл > Сохранить как, и в проводнике выбрать соответствующий формат.

После указания формата, пути сохранения файла и его имени, нажмите клавишу Сохранить, далее будет выведено окно Запись файла формата …, где опять же будет указан путь к файлу Компас (по умолчанию текущий) и путь к файлу в который будет осуществляться запись (по умолчанию файл создается в указанной вами папке).

Стоит все же отметить что экспорт и импорт документов между программами не всегда проходит «гладко», а потому, старайтесь избегать редактирования импортированных объектов.

 

P.S. Для тех, кто хочет стать Мастером КОМПАС-3D! Новый обучающий видеокурс позволит вам легко и быстро освоить систему КОМПАС-3D с нуля до уровня опытного пользователя.

Другие интересные материалы

Мы не можем найти эту страницу

(* {{l10n_strings. REQUIRED_FIELD}})

{{l10n_strings.CREATE_NEW_COLLECTION}} *

{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}

{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}

{{l10n_strings.DRAG_TEXT_HELP}}

{{l10n_strings.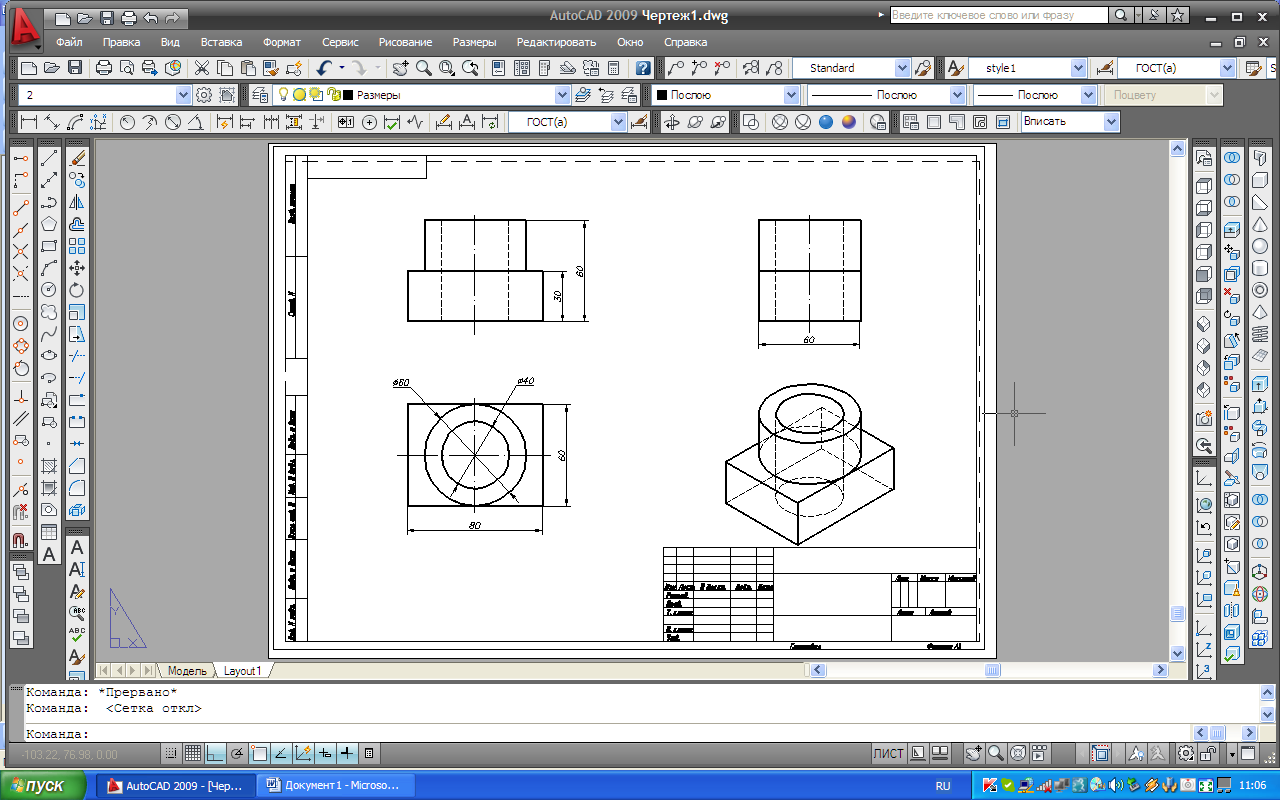 ЯЗЫК}} {{$ select.selected.display}}

{{article.content_lang.display}}

{{l10n_strings.AUTHOR}}

{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}

{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}

Регулировка осей рисования | Справка SketchUp

Регулировка осей рисования SketchUp упрощает рисование 3D-модели в нескольких сценариях:

  • Использование инструментов, таких как инструмент «Масштаб», которые изменяют геометрию на основе осей рисования: Когда вы выравниваете ребра, которые вы хотите изменить, с осями, вы можете немного легче изменить свою геометрию.
  • Отслеживание плана этажа для создания его трехмерной модели: Когда края прямоугольного плана этажа совпадают с красной и зеленой осями, вы можете легче проследить план этажа. Это связано с тем, что механизм вывода SketchUp выделяет ребра, параллельные оси, когда вы рисуете их с помощью инструмента «Линия», как показано на рисунке.
  • Геолокация модели на местности (чаще всего выполняется по TIN или триангулированной нерегулярной сети): Если вы рисуете геолокационную модель, вы, вероятно, захотите выровнять оси чертежа по сторонам света, которые эти оси представляют.Это поможет вам правильно расположить модель на местности. (Если вы не знакомы с этими методами моделирования, узнайте больше о моделировании ландшафта и работе с TIN.)
  • Создание реалистичных теней: Если вы определите географическое местоположение своей модели, вы также сможете увидеть, как она выглядит в разное время дня. Это еще одна ситуация, когда полезно совмещение осей по сторонам света.

SketchUp позволяет изменять положение осей чертежа несколькими способами:

  • Щелкните мышью.
  • Совместите оси с гранью.
  • Перемещайте и вращайте оси относительно их текущего положения.

В других случаях вы можете скрыть оси рисования. Например, в готовой модели стула или даже дома или улицы оси рисования могут отвлекать от вашей окончательной модели, а не помогать вам ее рисовать.

Подробнее о настройке или скрытии осей рисования см. В соответствующих разделах этой статьи.

Перемещение и вращение осей рисования

Здесь вы найдете подробные инструкции по настройке осей рисования с помощью мыши или с помощью параметров в контекстном меню осей рисования.

Совет: Прежде чем настраивать оси рисования, найдите наилучший вид вашей модели. Часто это угол, по которому вы хотите выровнять оси сверху или сбоку. Вы можете вращаться вокруг или выбрать опцию в подменю Камера> Стандартные виды. (См. Раздел Просмотр модели для более подробного ознакомления с вашими параметрами просмотра.)

Чтобы настроить оси с помощью мыши, выполните следующие действия:

  1. Выберите инструмент Оси (). Инструмент «Оси» находится на панели инструментов «Построение», на панели инструментов «Большой набор инструментов» или на палитре инструментов (только для macOS).Кроме того, вы можете активировать инструмент «Оси», выбрав «Инструменты »> «Оси », или щелкнув в контекстном меню пустое место на оси и выбрав «Поместить» в появившемся меню.
  2. Щелкните, чтобы разместить исходную точку осей. Обычно вы хотите установить исходную точку в нижнем углу объекта в вашей модели, как показано на следующем рисунке. После щелчка от курсора мыши выйдет красная пунктирная ось.

    Совет : После того, как вы разместите начало координат или выберете первое направление, вы можете нажать клавишу Alt (Microsoft Windows) или клавишу Command (macOS), чтобы изменить ориентацию оси, ведущей к курсору мыши.

  3. Щелкните, чтобы разместить красную ось. Вероятно, вы захотите выровнять красную ось по краю вашей модели. Когда положение красной оси выровнено по краю, механизм вывода SketchUp отображает на экране подсказку, как показано на рисунке. После того, как вы щелкнете мышью, чтобы разместить красную ось, другая пунктирная ось, представляющая зеленую ось, выйдет из курсора мыши.
  4. Щелкните, чтобы разместить красную ось, или ось, которую вы выбрали, если вы используете наконечник выше. Вероятно, вы захотите выровнять красную ось по краю вашей модели.Когда положение красной оси выровнено по краю, механизм вывода SketchUp отображает на экране подсказку, как показано на рисунке. После того, как вы щелкнете мышью, чтобы разместить красную ось, другая пунктирная ось, представляющая зеленую ось, выйдет из курсора мыши.
  5. Щелкните, чтобы разместить зеленую ось. Если вы настроили вид, чтобы увидеть край, который вы хотите выровнять по красной оси, то зеленая пунктирная ось может быть плохо видна. Однако механизм вывода SketchUp отображает вывод «Параллельно краю» при наведении курсора на край, даже если этот край скрыт в текущем виде.

Совет: При изменении ориентации осей рисования следите за синей осью. Если вы не хотите перевернуть модель (а функции переворота и поворота предлагают более эффективные способы сделать это), убедитесь, что синяя ось указывает вверх. Он может указывать вниз или в сторону при наведении курсора мыши на поиск новых точек оси.

Чтобы выровнять оси по грани, щелкните грань в контексте и выберите Выровнять оси в появившемся меню.

На следующем рисунке показано, как лицо, которое вы нажимаете в контексте, меняет ориентацию осей:

  • Если вы выберете грань в сине-красной или сине-зеленой плоскости (выноска 1), вы повернете оси на 90 градусов. Обратите внимание, как зеленая ось направлена ​​вверх (выноска 2), а синяя ось поворачивается на бок относительно прямоугольника.
  • Если выбрать грань в красно-зеленой плоскости (выноска 3), оси не поворачиваются, но базовая плоскость выравнивается по выбранной плоскости (выноска 4).

Из-за такого поведения команда «Выровнять оси» часто бывает полезна, когда вы рисуете 3D-модель из 2D-фигуры, которая в данный момент находится на базовой плоскости. Выберите 2D-грань на базовой плоскости, и оси рисования будут выровнены по нижнему левому углу, прежде чем вы начнете рисовать в 3D, как показано на следующем рисунке.

Чтобы переместить и повернуть оси относительно их текущего положения, выполните следующие действия:

  1. Щелкните контекстным щелчком пустую область на оси и выберите Переместить в появившемся меню.
  2. В появившемся диалоговом окне «Перемещение осей» (показанном на следующем рисунке) введите, как далеко вы хотите переместить и повернуть каждую ось. SketchUp использует единицы измерения, указанные в вашем шаблоне. (Чтобы просмотреть или изменить единицы измерения, выберите Окно > Информация о модели , выберите Единицы на боковой панели слева и выберите новую единицу измерения.)
  3. Нажмите кнопку ОК .
  1. Щелкните контекстным щелчком пустую область на оси и выберите Переместить в появившемся меню.
  2. В появившемся диалоговом окне «Переместить контекст эскиза» (показанном на следующем рисунке) введите, как далеко вы хотите переместить и повернуть каждую ось. SketchUp использует единицы измерения, указанные в вашем шаблоне. (Чтобы просмотреть или изменить единицы измерения, выберите Окно > Информация о модели и выберите Единицы на боковой панели слева. Затем выберите новую единицу измерения.)
  3. Нажмите кнопку ОК .

В следующем видео вы увидите, как работает изменение положения осей рисования, и получите несколько советов, которые помогут вам использовать различные методы.

Сброс осей рисования

Если вы перемещали оси рисования из стороны в сторону, вы можете легко вернуть оси в их положение по умолчанию. Просто щелкните в контекстном меню ось и выберите «Сброс» в появившемся меню, как показано на рисунке.

Скрытие осей рисования

SketchUp позволяет скрыть оси рисования двумя способами:

  • Щелкните контекстным щелчком по открытой области на оси и выберите Скрыть в появившемся меню.
  • Выберите View> Axes в строке меню. Когда рядом с пунктом меню «Оси» появляется галочка, при выборе этого параметра пункт меню «Оси» очищается, и оси скрываются из поля зрения.

Чтобы снова увидеть скрытые оси рисования, выберите View> Axes , который выберет параметр Axes.

Выравнивание осей чертежа по сторонам света

Каждая ось имеет сплошную линию с одной стороны от начала координат и пунктирную линию с другой стороны от начала координат.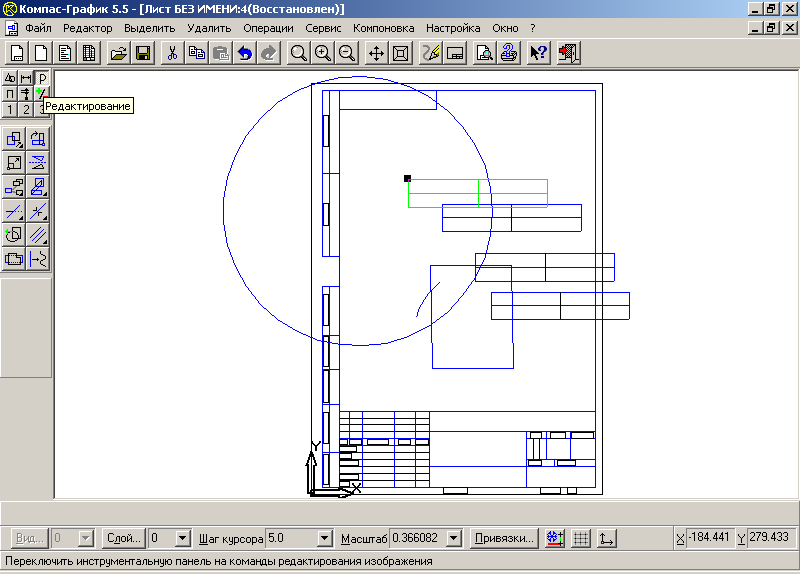 Сплошная синяя линия ведет вверх от начала координат, а синяя пунктирная линия – вниз. Остальные линии соответствуют одному из сторон света (север, юг, восток, запад). В следующей таблице показано, как каждая линия соответствует кардинальному направлению, ведущему от точки начала координат осей.

Линия Направление
Сплошная зеленая линия Север
Пунктирная зеленая линия Юг
Сплошная красная линия Восток
Красная пунктирная линия Запад

Геометрия

Геометрия – это всего фигур, и их свойства.

Если вам нравится играть с объектами или рисовать, то геометрия для вас!

Геометрию можно разделить на:


Плоская геометрия – это плоские формы, такие как линии, круги и треугольники … фигуры, которые можно нарисовать на листе бумаги


Solid Geometry – это трехмерные объекты, такие как кубы, призмы, цилиндры и сферы.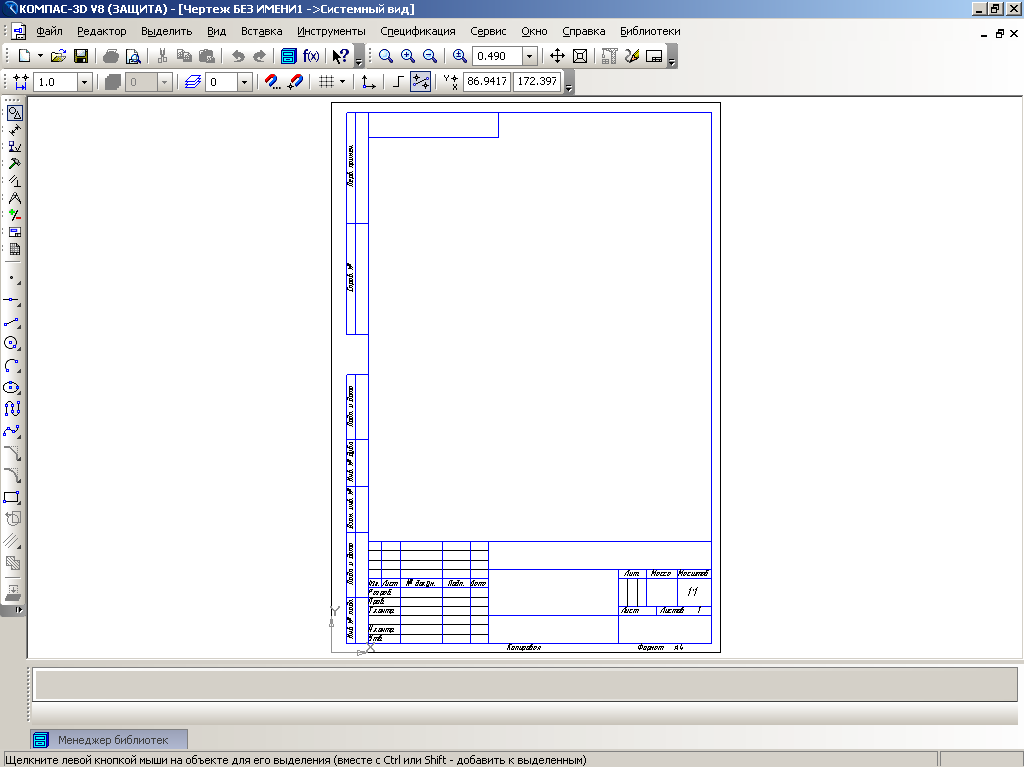

Совет: попробуйте нарисовать некоторые формы и углы по мере обучения… это помогает.

Точка, линия, плоскость и твердое тело

Точка не имеет размеров, только позиция
Линия одномерная
Плоскость двухмерная (2D)
Твердое тело трехмерное (3D)

Почему?

Почему мы делаем геометрию? Чтобы открывать закономерности, находить площади, объемы, длины и углы, а также лучше понимать мир вокруг нас.

Плоская геометрия

Плоская геометрия – это все о формах на плоской поверхности (например, на бесконечном листе бумаги).




Полигоны

Многоугольник – это двумерная фигура, состоящая из прямых линий. Треугольники и прямоугольники – это многоугольники.

Вот еще несколько:

Круг

Теоремы о круге (расширенная тема)

Символы

В геометрии используется много специальных символов.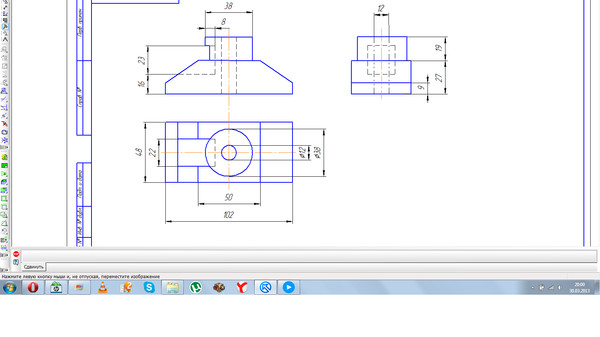 Вот вам краткая справка:

Геометрические символы

Конгруэнтные и похожие

Уголки

Типы углов


Использование инструментов для рисования

Преобразования и симметрия

Преобразований:

Симметрия:


Координаты

Более сложные темы по геометрии плоскости

Пифагор

Конические секции

Теоремы о круге

Центры треугольника

Тригонометрия

Тригонометрия – отдельная тема, поэтому вы можете посетить:

Твердая геометрия

Solid Geometry – это геометрия трехмерного пространства, в котором мы живем…

… давайте начнем с самых простых форм:


Общие 3D-формы

Многогранники и неполигранники

Есть два основных типа твердых тел: «Многогранники» и «Неполиэдры»:

Многогранники (у них должны быть плоские грани) :

Non-Polyhedra (когда любая поверхность не плоский) :

Заявка на патент США на КОМПЬЮТЕРНО-РЕАЛИЗУЕМЫЙ СПОСОБ ПОМОЩИ ПОЗИЦИОНИРОВАНИЮ 3D-ОБЪЕКТА В 3D-СЦЕНЕ Заявка на патент (Заявка №202100

, выданная 25 марта 2021 г.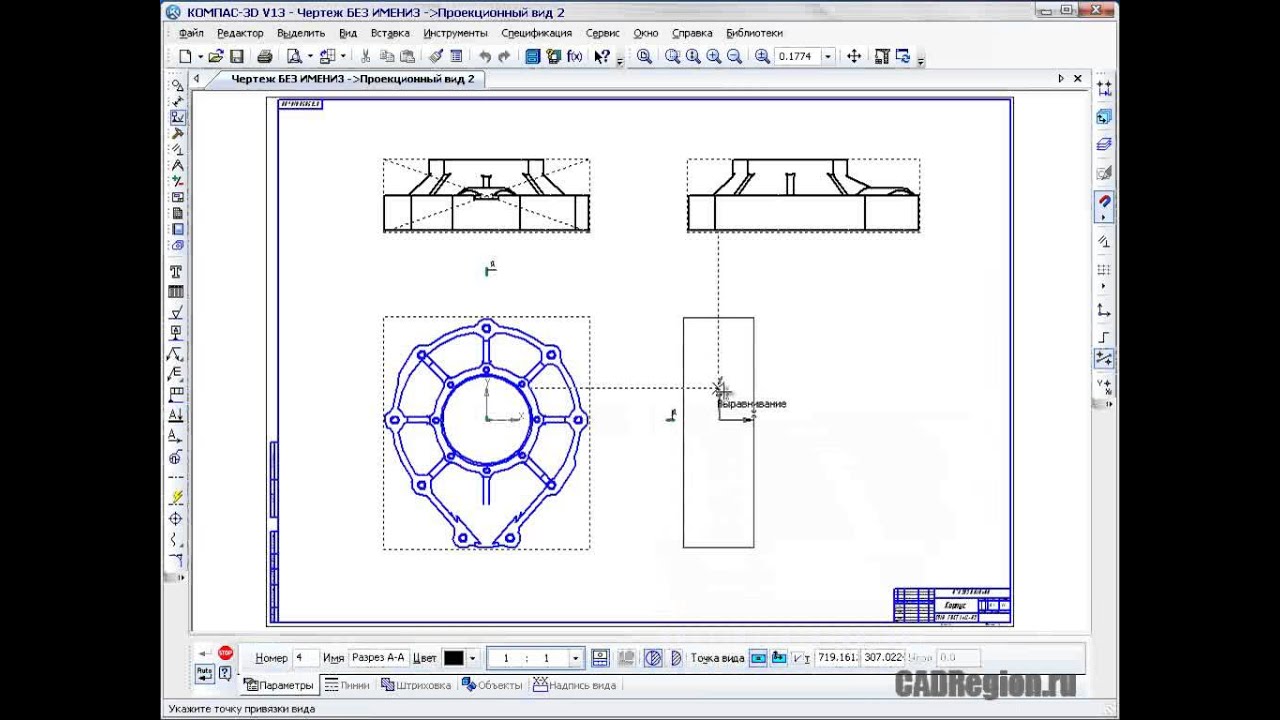 ) ПЕРЕКРЕСТНАЯ ССЫЛКА НА РОДСТВЕННЫЕ ЗАЯВКИ

Эта заявка испрашивает приоритет согласно 35 U.S.C. §119 или 365 к европейской заявке № 19306172.8, поданной 23 сентября 2019 г. Все содержание вышеуказанной заявки (заявок) включено в настоящий документ посредством ссылки.

FIELD

Раскрытие относится к реализованному на компьютере способу оказания помощи в позиционировании смоделированного в цифровой форме трехмерного объекта в трехмерной сцене. Например, изобретение позволяет делать снимок объекта, такого как мебель, создавать трехмерную модель объекта или, начиная с существующего изображения объекта, сохранять его и / или совместно использовать его для дальнейших операций САПР.

ИСТОРИЯ ВОПРОСА

Создание цифровой модели сложного трехмерного физического объекта (например, стола, состоящего из плоской поверхности и одной или нескольких ножек) на основе одного изображения – сложная задача. Действительно, изображение имеет перспективу, которая определяется углом обзора и положением камеры, и при моделировании всех частей объекта необходимо учитывать перспективу. В противном случае трехмерная модель не будет отражать реалистичное расположение физического объекта. В дальнейшем любая ссылка на трехмерный объект будет относиться к трехмерному объекту, смоделированному в цифровой форме, а не к физическому, если иное не указано явно.Точно так же любая ссылка на трехмерную сцену будет относиться к компьютерной цифровой трехмерной сцене, а не к сцене в физическом мире, если иное не указано явно.

В системах автоматизированного проектирования (CAD), таких как система, предоставляемая Dassault Systemes под торговой маркой CATIA, пользователь может создать сложный трехмерный объект, состоящий из нескольких трехмерных частей, на основе одного изображения. Для этого он создает 3D-части, рисуя 3D-части поверх 2D-изображения (например, рисуя первый параллелепипед на плоской поверхности стола, а другой – на опорной плите).В качестве альтернативы он может начать с существующих 3D-деталей. Из-за того, что трехмерные части собираются только в соответствии с одной точкой обзора виртуальной камеры системы CAD, относительное расположение трехмерных частей с этой точки зрения может не соответствовать желаемому относительному расположению. Например, с первой точки обзора пользователь видит, что трехмерная часть, представляющая плоский верх стола, и трехмерная часть, представляющая ножку стола, выровнены. С другой стороны, обе трехмерные части могут не совпадать.

Чтобы исправить неправильное относительное расположение трехмерных деталей, пользователь может манипулировать графическим манипулятором, например трехмерным компасом в CATIA. Трехмерный компас представляет собой компактное представление множества функций, которые могут быть связаны с объектом, на котором эти функции будут реализованы, например, вращение, перемещение, масштабирование.

Пользователь перетаскивает трехмерный компас к одной из трехмерных частей (например, той, которая представляет собой плоскую вершину), и отпускает указатель на трехмерной части, которая привязывает трехмерный компас к трехмерной части.При изменении точки обзора виртуальной камеры пользователь перемещает трехмерную часть, на которой закреплен трехмерный компас, перетаскивая одну из стрелок трехмерного компаса.

Однако, как только пользователь снова меняет точку обзора и возвращается к исходной, оказывается, что размеры проекции на экране трехмерной части, которая была переведена, изменились из-за перевода. Переведенная трехмерная деталь либо больше, либо меньше по сравнению с исходными размерами. Поэтому пользователь перетаскивает 3D-компас на переведенную 3D-часть; затем он нажимает кнопку масштабирования трехмерного компаса, не отпуская ее, и перемещает указатель до тех пор, пока не считает, что трехмерная деталь была правильно запечатана.

Таким образом, использование пользователя происходит в два этапа, то есть один для перевода, другой для повторного запечатывания, что отнимает много времени. Кроме того, эти два шага можно повторять, чтобы итеративно получать желаемое относительное позиционирование, дополнительно увеличивая время разработки.

Решения, использующие технику фотограмметрии, позволяют выполнять очень точную трехмерную реконструкцию, как это реализовано, например, в приложении «Catia Photo To Shape» (продается Dassault Systemes). Однако для этого метода необходимо начинать как минимум с двух изображений с двух разных точек обзора.Следовательно, это не удовлетворительное решение для моделирования физического трехмерного объекта, начиная с его единственного изображения.

Академические исследования также недавно были сосредоточены на оценке трехмерной позы, как это раскрывается, например, в статье «Трехмерные позирующие машины человека с самоконтролируемым обучением» (Кезе Ван и др., Транзакции IEEE по шаблону, анализу и машинному интеллекту, 2019) . В этом контексте, начиная с двухмерной позы человека, можно восстановить трехмерную позу, используя 1) глубокое обучение.Однако эта статья относится к определенному классу, то есть к человеческому телу, и не может быть распространена на другой класс объектов. В более общем плане каждая нейронная сеть адаптирована к определенному классу объектов.

Следовательно, существует потребность в помощи пользователю в быстром размещении трехмерного объекта в трехмерной сцене на основе единственного изображения объекта, что не требует предварительного знания сборки.

СУЩНОСТЬ ИЗОБРЕТЕНИЯ

Таким образом, объектом настоящего изобретения является реализованный на компьютере способ оказания помощи в позиционировании смоделированного в цифровой форме трехмерного объекта, включающий следующие этапы:

S 1 : создание первого смоделированного цифровым способом трехмерного объекта, имеющего 3D-положение в 3D-сцене;

S 2 : визуализация проекции упомянутого первого смоделированного в цифровой форме трехмерного объекта на экране в соответствии с первой осью и первой точкой обзора;

S 3 : при изменении под действием пользователя трехмерного положения первого трехмерного объекта, смоделированного цифровым способом, вдоль первой оси, автоматическое масштабирование первого трехмерного объекта для сохранения постоянной проекции перемещаемого объекта на экране.

В варианте осуществления этап S 3 содержит отображение упомянутого первого смоделированного цифровым способом трехмерного объекта со второй точки обзора согласно второй оси, причем упомянутая вторая точка обзора и упомянутая вторая ось соответственно отличаются от первой точки обзора и от первой оси.

В варианте осуществления первая ось и вторая ось взаимно ортогональны.

В варианте осуществления первая ось представлена ​​пунктирной или непрерывной линией, причем указанная пунктирная или непрерывная линия совпадает с первой осью.

В варианте осуществления:

этап S 1 содержит предоставление второго трехмерного объекта, смоделированного в цифровой форме, имеющего предварительно определенные размеры и трехмерное положение в трехмерной сцене;

этап S 3 содержит фиксированное трехмерное положение и размеры второго трехмерного объекта, смоделированного в цифровой форме.

В варианте осуществления, этап S 3 содержит отображение на первой оси по меньшей мере одной точки привязки относительно второго смоделированного цифровым способом трехмерного объекта, чтобы обеспечить быстрое позиционирование первого смоделированного цифровым способом трехмерного объекта относительно второго. 3D-объект, смоделированный в цифровой форме.

В варианте осуществления точка привязки соответствует:

проекции на первую ось центра минимального ограничивающего прямоугольника, охватывающего второй смоделированный цифровым способом 3D-объект, или

проекции на первую ось край минимального ограничивающего прямоугольника, охватывающего второй 3D-объект, смоделированный цифровым способом.

В варианте осуществления этап S 3 содержит выделение первого трехмерного объекта, смоделированного в цифровой форме.

В варианте осуществления этап S 1 содержит прием пользовательского ввода для, по меньшей мере, частичного согласования упомянутого первого трехмерного объекта, смоделированного в цифровой форме, с частью двумерного изображения на экране.

Раскрытие также относится к компьютерному программному продукту, хранящемуся на машиночитаемом носителе данных, содержащему исполняемые компьютером инструкции, побуждающие компьютерную систему выполнять вышеупомянутый способ.

Раскрытие также относится к машиночитаемому носителю данных, содержащему исполняемые компьютером инструкции, чтобы заставить компьютерную систему выполнять вышеупомянутый способ.

Раскрытие также относится к компьютерной системе, содержащей процессор, соединенный с памятью, экраном, памятью, хранящей исполняемые компьютером инструкции, чтобы заставить компьютерную систему выполнять вышеупомянутый способ.

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

Дополнительные признаки и преимущества настоящего изобретения станут очевидными из последующего описания, взятого вместе с прилагаемыми чертежами, которые показывают:

Фиг. 1 – блок-схема способа согласно изобретению;

РИС. 2, изображение, содержащее сборку, которая должна быть смоделирована в трех измерениях, в данном случае плоская вершина стола и опорная плита стола – выбор трехмерной формы в соответствии с первой точкой обзора;

РИС.3 – схематическая иллюстрация изменения масштаба объекта;

РИС. 4, трехмерная сцена, отображающая первый и второй трехмерные объекты, со второй точки обзора;

РИС. 5 – перетаскивание по первой оси виртуальной камеры;

РИС. 6 – точки фиксации;

РИС. 7, трехмерная сборка, содержащая исправленные положения трехмерных объектов.

РИС. 8 – блок-схема компьютерной системы, подходящей для реализации способа согласно изобретению.

ПОДРОБНОЕ ОПИСАНИЕ

На первом этапе способа (этап S 1 блок-схемы на фиг. 1) предоставляется первый (смоделированный в цифровой форме) трехмерный объект OBJ 1 . Первый объект OBJ 1 находится в (созданной компьютером) трехмерной сцене в соответствии с трехмерной позицией. Он создается пользователем или может уже находиться в 3D-сцене до того, как пользователь начнет манипулировать.

На втором этапе (этап S 2 блок-схемы на фиг. 1) проекция первого 3D-объекта OBJ 1 визуализируется на экране электронного вычислительного устройства пользователя (компьютер, ноутбук , планшет, смартфон), как показано на фиг.2.

Изображение IM содержит сборку для моделирования в 3D. В данном случае двухмерное изображение состоит из стола, состоящего из трех частей: плоской поверхности, опорной ножки и ножки, на которой поддерживается плоская поверхность, лежащая на опоре пластины. Далее раскрывается правильное расположение только двух 3D-объектов. Размещение остальных 3D-объектов, составляющих сборку, выполняется так же, как для двух объектов.

В случае, если пользователь начинает с двухмерного изображения, необходимо определить перспективу рисования.Предлагаемый способ особенно подходит для изображений, которые соответствуют гипотезе

Манхэттена, поскольку перспективу рисования можно легко обнаружить. Гипотеза Манхэттена раскрыта в статье « Манхэттенское слово: направление компаса из единственного изображения с помощью байесовского вывода » (Coughla, et al.). Изображение соответствует гипотезе Манхэттена, если на изображении есть три ортогональных доминирующих направления, то есть три основных набора параллельных линий.

Затем, как только будет получена правая перспектива рисования, пользователь может нарисовать трехмерный объект (также называемый трехмерной формой) на двумерном изображении на основе трех обнаруженных ортогональных доминирующих направлений для изображений, соответствующих гипотезе Манхэттена.Принимается пользовательский ввод по меньшей мере частичного согласования первого 3D-объекта OBJ 1 с частью 2D-изображения на экране.

Перспектива рисования может быть обнаружена на двухмерном изображении посредством идентификации по меньшей мере одной точки схода. Точка схода соответствует точке схождения двумерных перспективных проекций взаимно параллельных линий в трехмерном пространстве. Следовательно, перспектива рисования принимает форму точки (точек) схода. Одна точка схода P 1 показана в правой части фиг.2. Еще один может быть идентифицирован в левой части фиг. 2, но для ясности он не проиллюстрирован.

Первый 3D-объект OBJ 1 нарисован в соответствии с перспективой чертежа. В данном случае пользователь рисует прямоугольник, перетаскивая указатель (мышь, палец или стилус) из первой точки экрана в другую, которая определяется как противоположные углы прямоугольника. Затем пользователь выполняет операцию выдавливания прямоугольника, чтобы создать параллелепипед.Создается первый объект OBJ 1 , который представляет собой трехмерный объект, нарисованный поверх двухмерного изображения. Это соответствует плоской поверхности стола. Те же шаги выполняются, чтобы нарисовать второй объект OBJ 2 . Однако способ согласно изобретению может быть реализован даже для одного трехмерного объекта.

Трехмерный объект OBJ 1 (персонаж на фиг. 3) предоставляется в трехмерной сцене, которая визуализируется виртуальной камерой CAM в соответствии с первой осью AX 1 и первой точкой обзора VP 1 .Первая точка обзора VP 1 соответствует трехмерному положению камеры. Первая ось AX 1 соединяет первую точку обзора VP 1 и центр масс ограничивающих прямоугольников всех трехмерных объектов, которые расположены в трехмерной сцене. На фиг. 3 считается, что трехмерная сцена содержит только один трехмерный объект, то есть трехмерный объект OBJ 1 .

Затем, на третьем этапе (этап S 3 блок-схемы на фиг. 1), пользователь перетаскивает (нажимает, не отпуская) первый объект OBJ 1 вдоль первой оси AX 1 .При перетаскивании первого объекта OBJ 1 вдоль первой оси AX 1 масштаб первого объекта OBJ 1 изменяется, чтобы сохранить неизменной проекцию первого объекта OBJ 1 на экране SCR.

Повторное запечатывание выполняется сначала путем вычисления расстояния D OldPosition между первой точкой обзора и центром минимальной ограничивающей рамки CBB, охватывающей первый объект OBJ 1 . На фиг. 3, до манипулирования первым объектом OBJ 1 , расстояние между первой точкой обзора VP 1 , т.е.е. положение виртуальной камеры и первого объекта OBJ 1 отмечено как D OldPosition . Когда пользователь перетаскивает первый объект OBJ 1 вдоль первой оси AX 1 , отметьте D NewPosition расстояние между первой точкой обзора VP 1 и перемещенным первым объектом OBJ 1 . Также отметим H OldPosition одно измерение первого объекта OBJ 1 , например его высоту, когда первый объект OBJ 1 удален от первой точки обзора VP 1 на расстояние D OldPosition , и отметим H NewPosition того же размера, когда первый объект OBJ 1 удален от первой точки обзора VP 1 на расстояние D NewPosition .Размер H NewPosition вычисляется в соответствии со следующим соотношением:

HNewPosition = DNewPositionDOldPosition × HOldPosition

Затем масштабируется первый объект OBJ 1 .

Когда пользователь перетаскивает первый объект OBJ 1 от первой точки обзора VP 1 , первый объект OBJ 1 увеличивается, а когда пользователь перетаскивает первый объект OBJ 1 ближе к первой точке обзора VP 1 , первый объект OBJ 1 становится меньше.Следовательно, проекция первого объекта OBJ 1 остается постоянной, и пользователю не нужно вручную изменять масштаб первого объекта OBJ 1 с помощью компаса.

В варианте осуществления первый 3D-объект OBJ 1 отображается согласно второй точке обзора VP 2 и второй оси AX 2 виртуальной камеры. С этой целью, когда первый объект OBJ 1 визуализируется на экране в соответствии с первой точкой обзора VP 1 и первой осью AX 1 , как показано на фиг.2, пользователь выбирает (например, щелкая выделенную кнопку в меню или контекстную кнопку) команду, которая запускает отображение первого объекта OBJ 1 в соответствии со второй точкой обзора VP 2 и второй осью AX 2 виртуальной камеры. Таким образом, пользователь может видеть изменение масштаба первого объекта OBJ 1 , а также может точно перетащить первый объект OBJ 1 .

Преимущественно первая ось AX 1 и вторая ось AX 2 взаимно ортогональны.Таким образом, пользователь может легко увидеть положение первого 3D-объекта OBJ 1 на оси AX 1 .

РИС. 4 иллюстрирует первый 3D-объект OBJ 1 , который отображается в соответствии со второй точкой обзора VP 2 . На фиг. 4 видно, что первый объект OBJ 1 и второй объект OB 2, не выровнены правильно. Следовательно, пользователь перетаскивает первый объект OBJ 1 вдоль первой оси AX 1 , пока он не оценит, что взаимное расположение обоих объектов является правильным.

В варианте осуществления, когда трехмерная сцена визуализируется в соответствии с первой точкой обзора, пользователь выбирает перемещаемый объект, щелкая по нему, и перемещаемый объект выделяется. Например, контур выбранного объекта мигает, или цвет первого объекта OBJ 1 изменяется после выбора. Если другие 3D-объекты были импортированы или нарисованы в 3D-сцене, эти объекты не выделяются. Таким образом, даже если перемещаемый объект частично скрыт другими объектами в 3D-сцене, пользователь может легко идентифицировать его в 3D-сцене.

Первая ось AX 1 предпочтительно представлена ​​пунктирной или непрерывной линией, которая совпадает с первой осью AX 1 . Следовательно, смещение первого OBJ 1 3D-объекта можно легко спрогнозировать, когда пользователь изменяет положение первого OBJ 1 3D-объекта. Без пунктирной или непрерывной линии пользователю было бы сложно оценить положение первой точки обзора по сравнению со второй точкой обзора, в частности, когда первая ось AX 1 и вторая ось AX 2 не ортогональны.Также было бы сложно оценить точную ориентацию первой оси AX 1 относительно второй оси AX 2 . Этот вариант осуществления также полезен, когда вторая ось AX 2 не может быть ортогональна первой оси AX 1 из-за трехмерного объекта, скрывающего вторую точку обзора VP 2 . Это может произойти, когда 3D-сцена содержит много 3D-объектов.

РИС. 4 показано смещение первого объекта OB 1 вдоль первой оси AX 1 .Первый объект OBJ 1 теперь ближе с первой точки обзора VP 1 , поэтому первый объект OBJ 1 становится меньше. Таким образом, проекция первого объекта OBJ 1 на экране, когда камера расположена в первой точке обзора V 1 , остается постоянной.

В варианте осуществления, когда, по меньшей мере, первый и второй трехмерные объекты должны быть расположены один относительно другого, этап S 3 содержит отображение на первой оси, по меньшей мере, одной точки привязки SP относительно второго трехмерного объекта. объект OBJ 2 .Здесь и далее точка привязки – это графический значок, который расположен на первой оси AX 1 в месте, которое соответствует проекции характеристической точки второго 3D-объекта OBJ 2 на первую ось AX 1 . Следовательно, движение первого 3D-объекта OBJ 1 в точке привязки SP происходит не так быстро, как на других частях первой оси AX 1 , так что пользователь может очень точно и точно выровнять первый 3D объект OBJ 1 относительно второго 3D.Например, при перетаскивании первого 3D-объекта OBJ 1 наведение указателя на точку привязки может происходить медленнее, чем на других частях первой оси AX 1 . В качестве альтернативы, первый объект может быть привязан к точке привязки SP при наведении на него курсора (однако, полностью не запрещая пользователю перемещать первый 3D-объект OBJ 1 ).

Преимущественно точка привязки может соответствовать:

проекции на первую ось AX 1 центра минимальной ограничивающей рамки, охватывающей второй 3D-объект OBJ 2 или

проекции на первая ось края минимального ограничивающего прямоугольника, охватывающего второй 3D-объект OBJ 2 .

Несколько точек привязки одного и того же объекта могут отображаться на первой оси AX 1 , как показано на фиг. 6. Таким образом, пользователь может выбрать выравнивание первого 3D-объекта либо по центру минимальной ограничивающей рамки, охватывающей второй 3D-объект OBJ 2 , либо по одному из краев ограничивающей рамки. Тип точек привязки можно настроить.

Пользователь может перемещаться по 3D-сцене, чтобы проверить, что первый 3D-объект OBJ 1 расположен должным образом, используя, например, комбинацию перемещения мыши с одновременным нажатием средней кнопки мыши.Например, он может снова установить виртуальную камеру в соответствии с первой точкой обзора, как показано на фиг. 7.

В любой момент он также может переключиться на 2D-изображение, как показано на фиг. 2, щелкнув (нажмите и отпустите) в 3D-сцене за пределами 3D-объектов. Таким образом, он может проверить, что размеры трехмерных объектов остаются неизменными.

В другом варианте осуществления трехмерная сцена в соответствии с другой точкой обзора камеры может отображаться в виде уменьшенных изображений при отображении в основной части экрана двухмерного изображения.Таким образом, пользователь может видеть, что необходимо переместить и выровнять один из 3D-объектов.

Способ по настоящему изобретению может выполняться соответствующим образом запрограммированным компьютером общего назначения или компьютерной системой, возможно, включающей компьютерную сеть, хранящей подходящую программу в энергонезависимой форме на машиночитаемом носителе, таком как жесткий диск, твердотельный накопитель. состояние диска или CD-ROM и выполнение указанной программы с использованием его микропроцессора (ов) и памяти.

Компьютерный CPT, подходящий для выполнения способа согласно примерному варианту осуществления, описывается со ссылкой на фиг.8. На фиг. 8, компьютер CPT включает в себя центральный процессор (ЦП) P, который выполняет этап способа, описанный выше, при запуске исполняемой программы, то есть набора машиночитаемых инструкций, хранящихся в запоминающем устройстве, таком как RAM M 1 или ROM. M 2 или жесткий диск (HDD) M 3 , привод DVD / CD M 4 или удаленное хранение. Кроме того, трехмерные объекты, созданные на этапе S 1 способа, также могут быть сохранены на одном или нескольких запоминающих устройствах с M 1 по M 4 или удаленно.

Заявленное изобретение не ограничивается формой машиночитаемого носителя, на котором хранятся машиночитаемые инструкции и / или структура данных процесса изобретения. Например, инструкции) и файлы могут храниться на компакт-дисках, DVD-дисках, во флэш-памяти, RAM, ROM, PROM, EPROM, EEPROM, на жестком диске или на любом другом устройстве обработки информации, с которым компьютер взаимодействует, например, сервер или компьютер. . Программа и файлы могут храниться на одном устройстве памяти или на разных устройствах памяти.

Кроме того, компьютерная программа, подходящая для реализации способа по настоящему изобретению, может быть предоставлена ​​в виде служебного приложения, фонового демона или компонента операционной системы, или их комбинации, выполняемой вместе с ЦП P и операционной системой, такой как Microsoft VISTA. , Microsoft Windows 10, UNIX, Solaris, LINUX, Apple MAC-OS и другие системы, известные специалистам в данной области техники.

CPU P может быть процессором Xenon от Intel из Америки или процессором Opteron от AMD из Америки или может быть процессором другого типа, например Freescale ColdFire, IMX или ARM от Freescale Corporation of America.В качестве альтернативы, ЦП может быть процессором, таким как Core2 Duo от Intel Corporation of America, или может быть реализован на ПЛИС, ASIC, PLD или с использованием дискретных логических схем, что может понять специалист в данной области техники. Кроме того, ЦП может быть реализован как несколько процессоров, совместно работающих для выполнения машиночитаемых инструкций процессов согласно изобретению, описанных выше.

Компьютер CPT на фиг. 8 также включает сетевой интерфейс NI, такой как сетевая карта Intel Ethernet PRO от Intel Corporation of America, для взаимодействия с сетью, такой как локальная сеть (LAN), глобальная сеть (WAN), Интернет и нравиться.Компьютер дополнительно включает в себя контроллер дисплея DC, такой как графический адаптер NVIDIA GeForce GTX от NVIDIA Corporation of America, для взаимодействия с дисплеем DY, например ЖК-монитор Hewlett Packard HPL2445w. Интерфейс ввода-вывода общего назначения IF взаимодействует с клавиатурой KB и указывающим устройством PD, например с роликовым шариком, мышью, сенсорной панелью и т.п. Дисплей, клавиатура и указывающее устройство вместе с контроллером дисплея и интерфейсами ввода-вывода образуют графический пользовательский интерфейс, используемый пользователем для предоставления команд ввода и компьютером для отображения трехмерных объектов.Контроллер диска DKC соединяет жесткий диск M3 и DVD / CD M4 с коммуникационной шиной CBS, которая может быть ISA, EISA, VESA, PCI или аналогичной, для соединения всех компонентов компьютера.

Описание общих характеристик и функциональных возможностей дисплея, клавиатуры, указывающего устройства, а также контроллера дисплея, контроллера диска, сетевого интерфейса и интерфейса ввода-вывода здесь опущено для краткости, поскольку эти функции известны.

Любые шаги метода, описанные в данном документе, следует понимать как представление модулей, сегментов или частей кода, которые включают в себя одну или несколько исполняемых инструкций для реализации определенных логических функций или шагов в процессе, а альтернативные реализации включены в объем примерного варианта осуществления. настоящего изобретения.

Групповые свойства 2D и 3D в Motion

2D-группы и 3D-группы ведут себя по-разному. А в инспекторе групп 2D-группы и 3D-группы имеют разные параметры.

Инспектор групп для 3D-групп содержит параметры выравнивания и порядка слоев. Установка флажка «Сглаживание» помещает слои и группы внутри 3D-группы в двухмерную плоскость. Установка флажка «Порядок слоев» объединяет слои и группы внутри 3D-группы в соответствии с их положением в списке «Слои», а не по порядку глубины (положение на холсте по оси Z).См. Раздел «Создание 3D-пересечения в движении».

Инспектор групп для 2D-групп содержит параметр «Фиксированное разрешение». Установка флажка «Фиксированное разрешение» позволяет вручную установить размер группы с помощью ползунков. По умолчанию фиксированное разрешение отключено, и размер группы определяется слоями в этой группе. См. Раздел «Ограничение размера группы в движении».

Свойства групп 2D

  • Вложенные слои и группы компонуются на холсте в порядке слоев (иерархический порядок в списке слоев).Однако смежные 3D-группы, не вложенные в 2D-группы, могут пересекаться в зависимости от порядка глубины.

    В приведенном выше примере два серых шара в группе 2D «Передний план» расположены поверх остальной части сцены. «Оранжевый A» и «Желтый B» пересекаются, потому что они являются трехмерными группами, но ни одна из них не может пересекаться с двумерными группами корневого уровня.

  • 2D-группа может быть вложена в 3D-группу.

  • 2D-группа, не вложенная в 3D-группу, фиксируется для камеры, даже если камера анимирована.Дополнительные сведения о камерах см. В разделе «Камеры и виды в движении».

  • Фильтры применяются к 2D-группе в локальном пространстве, то есть плоско к изображению.

  • При использовании источников света группа светится как единый объект; вложенные слои и группы не подсвечиваются по отдельности.

    Примечание: 2D-группы, не вложенные в 3D-группы, не подвержены влиянию света.

  • Поскольку это плоская группа, 2D-группа имеет параметры «Тень», «Четыре угла» и «Обрезка» в инспекторе свойств.

  • 2D-группы могут иметь фиксированное разрешение.

Свойства группы 3D

  • Вложенные слои и группы компонуются в порядке глубины (в соответствии с их положением по оси Z).

  • Когда группа 3D вложена в группу 2D, группа 3D становится развернутой . Это означает, что вложенная 3D-группа действует как плоская карта и игнорирует камеру. Кроме того, развернутая группа не пересекается со слоями 2D-группы или других групп в проекте.

  • Фильтры применяются к 3D-группе в пространстве просмотра. Другими словами, фильтр влияет на группу, как если бы он был применен к объективу камеры, просматривающей группу.

  • Когда источники света используются в трехмерной группе, вложенные слои и группы группы подсвечиваются индивидуально.

  • Только 3D-группа с включенным параметром Flatten имеет параметры Crop, Drop Shadow и Four Corner в инспекторе свойств.

Роботизированный блок геометрии в 3D

.
Команда
Назначение и примеры
точка (x, y) Пример: – точка (3, 4) или A = точка (3, 4), где A – метка.
линия (x1, y1, x2, y2) Пример: – линия (0,0, -2,5) или C = линия (A, B), где A, B – метки точек.
Длина может быть дополнительно задана как линия (A, B, 3), где 3 – длина сегмента.
дуга (исходная точка, радиус, угол от, до) Пример: – arc (point (2, 2), 3, 40, 20) Использует точку (2, 2) как начало координат, 3 как радиус и начинает дугу с 40 градусов, добавляя еще 20 градусов против часовой стрелки.Отрицательное значение параметра «до» будет перемещаться по часовой стрелке.
Чтобы скопировать линию, укажите первый параметр как линию или две точки, как показано здесь arc (point1, point2, originPoint, angleFrom, upto)
перп (линия, точка прохода, длина = 10) Пример: – A = perp (линия (1, 2, 3, 4), точка (1, 2)) рисует перпендикулярную линию к заданной линии (1, 2, 3, 4), проходящей через точку (1, 2) ). Последний необязательный параметр команды perp – это длина перпендикулярной линии, которая по умолчанию равна 10
параллельно (линия, passThroughPoint, длина = 10) Пример: – параллель (линия (1, 2, 3, 4), точка (1, 2))
угол (точка1, точка2, градусы) Пример: – угол (A, B, 45, 1) Две точки A и B определяют базовую линию.Соотношение – это необязательный параметр, который управляет положением транспортира. Значение 0 помещает его в A, 1 в B и 0,5 посередине.
многоугольник (точки, разделенные запятыми) Пример: – многоугольник (A, B, C) рисует треугольник, где A, B, C – точки
findangle (2 линии или многоугольник) Пример: – findangle (A, B) находит угол между двумя линиями A, B или многоугольником findangle (C) (C – метка многоугольника, в этом случае метод возвращает первый угол)
заливка (A, B) Заполняет внутреннюю часть форм A, B.Фигуры могут представлять собой дугу, многоугольник или другую заливку. Команда принимает любое количество форм. fill (A), fill (arc (0, 0, 3, 0, 360), D, многоугольник (2, 3, 4, 6, 1, 0))
след (точки, разделенные запятыми) Обводит кривую, проходящую через заданные точки. след (точка (0, 0), точка (1, sin (30)), точка (1, sin (60)), точка (1, sin (120)), B)
деталь (форма для извлечения, 2 точки на форме, необязательный индекс детали) Пример: – часть (a, D, E, 2) или A = part (a, correct (a, b, 1), point (2,3)), где A – метка фигуры, из которой нужно принять участие.Форма «а» в этом примере относится к многоугольнику, линии или дуге. 2 балла, полученные после того, как фигура должна быть на форму (т.е. если это дуга, то точка должна находиться на периметре дуги, то же самое верно для многоугольника, точки должны находиться на одной из линий многоугольника. Команда части извлекает 2 формы, поэтому мы можем указать необязательный partIndex (1 или 2) и точка для получения желаемой части, как показано здесь.part (a, correct (a, b, 1), point (2,3), 2) Последнее значение 2 извлекает вторую часть. Вы можете указать только 1 или 2 в качестве индекса части. Возвращенная часть, которая хранится в ‘A’, затем может быть использована. для создания дополнительной сложной формы, используемой для тессляций. Например polygon (2,4,6,7, A, 10,12) В этом примере будет создан новый многоугольник с использованием точек 2,4,6,7 и точек из команд части «A», которые следуют за ними
fade (этикетки формы, коэффициент выцветания) Пример: – fade (a, D, E, 0.4) Коэффициент затухания (последнее) значение, которое должно быть от 0 до 1. который определяет, насколько объекты должны исчезать или проявляться
точечный (крест) Пример: – pointtype (‘cross’) Изменяет стиль точки с «сферы» на «крест». Любая команда точки после этой команды pointtype будет отображать крест, если мы хотим просто вернуться к «сфере». введите другую команду pointtype () без значений
тире (x1, y1, x2, y2, dashLength, dashGapLength) Пример: – тире (3,4,7,8,0.5,0.6) Рисует пунктирную линию, 5-й аргумент определяет длину тире, а 0,6 (последнее значение) – промежуток. Используя эти 2 значения, мы также можем нарисовать пунктирные линии. Как и другие команды robocompass, вместо того, чтобы давать 4 значения напрямую, мы можем либо дать 2 точки или любое выражение, которое разрешается в 4 координаты, аналогичные тире (A, C, 1.2, 0.5) где A, C – точечные метки
штрих (метки формы, толщины) Пример: – stroke (a, D, E, 3) Изменяет толщину формы, указанные на этикетках.Толщина должна быть больше 0, верхний предел не ограничен
реверс (метки формы) Пример: – reverse (a) Переворачивает координаты формы. Это будет полезно при построении сложных мозаик. Обычно используется внутри многоугольника (реверс (L), 3,7,8,1), L здесь может быть частью, линией или любой формой.Вы также можете указать более одной формы в качестве аргумента
участок («выражение») Пример: – plot (“sin (x)”) или A = plot (“tan (x)”, 2,10), где A – метка. Минимальные и максимальные значения после выражения необязательны. По умолчанию график покрывает всю область графика. Как и в других функциях, переменные можно определять где угодно и ссылаться на них внутри выражения.2 не поддерживаются. Однако вы можете задайте такие уравнения, как «y = 2 * x» или «x = 2y».
para (“выражение1”, “выражение2”) Пример: – para («2 * sin (t)», «3 * cos * (t)») или A = para (“2 * sin (t)”, “3 * cos * (t)”, 0,6.29,0.1), где A – метка. В выражениях должен быть параметр “t”. Значения min, max и step после выражений необязательны.Команда pos может использоваться для получения точки в определенной точке графика, например pos (p, 0.2) где p – p = plot (“some exp”) или p = para (“some exp”)
Общее правило

Когда в выражении ожидается точка, используйте либо точку (2, 3), либо ее метку, либо вспомогательную команду, которая вычисляет и возвращает точку.Точно так же везде, где ожидается линия, дайте метку линии или метку двух точек.

Например, arc (A, B, point (2, 1), 50, 40) использует расстояние от A до B и рисует дугу из точки (2, 1).
Примечание: – вместо точки (2, 1) используйте букву «C», если есть точка с меткой C.

Полярные, цилиндрические и сферические координаты

Наша страница о декартовых координатах представляет простейший тип системы координат, в которой опорные оси ортогональны (под прямым углом) друг к другу.В большинстве повседневных приложений, таких как рисование графика или чтение карты, вы должны использовать принципы декартовых систем координат. В этих ситуациях точное уникальное положение каждой точки данных или ссылки на карту определяется парой координат (x, y) (или (x, y, z) в трех измерениях). Координаты – это «адрес» точки, ее расположение относительно известного положения, называемого исходной точкой , в двух- или трехмерной сетке на плоской поверхности или в прямоугольном трехмерном пространстве.

Однако в некоторых приложениях задействовано изогнутых линий, поверхностей и пространств.Здесь декартовы координаты трудно использовать, и возникает необходимость использовать систему, полученную из круговых форм, таких как полярные, сферические или цилиндрические системы координат.

Почему важны полярные, сферические и цилиндрические координаты?

В повседневных ситуациях гораздо более вероятно, что вы встретите декартовы системы координат, чем полярные, сферические или цилиндрические. Однако двумерные полярные координаты и их трехмерные родственники используются в широком спектре приложений от инженерии и авиации до компьютерной анимации и архитектуры.

Вам может потребоваться использовать полярные координаты в любом контексте, где существует круговая, сферическая или цилиндрическая симметрия в форме физического объекта или какое-либо круговое или орбитальное (колебательное) движение.

Что это значит?

Физически изогнутые формы или конструкции включают диски, цилиндры, шары или купола. Это может быть что угодно, от сосудов под давлением, содержащих сжиженные газы, до множества примеров купольных конструкций в древних и современных архитектурных шедеврах.

Физики и инженеры используют полярные координаты, когда они работают с криволинейной траекторией движущегося объекта (динамика), и когда это движение повторяется назад и вперед (колебания) или по кругу (вращение). Примеры включают орбитальное движение, такое как движение планет и спутников, качающийся маятник или механическая вибрация. В электрическом контексте полярные координаты используются при разработке приложений, использующих переменный ток; аудиотехники используют их для описания «зоны приема микрофонов»; и они используются при анализе температуры и магнитных полей.

Акцент на разведку

Пожалуй, наиболее привычное использование в повседневном контексте – это навигация. На протяжении всей истории исследователи полагались на понимание полярных координат.

Корабли и самолеты перемещаются с помощью компасов, которые указывают направление движения (известное как курс ) относительно известного направления, которым является магнитный север. Курс измеряется как угол относительно севера (0 °), по часовой стрелке вокруг компаса, поэтому на восток – 90 °, юг – 180 ° и запад – 270 °.

Спутники

GPS могут определять местоположение судна с большой точностью в современном мире, но даже сейчас морякам и авиаторам необходимо понимать принципы классической навигации.

Как определяются полярные, сферические и цилиндрические координаты?

В этих и многих других случаях более целесообразно использовать измерение расстояния по линии, ориентированной в радиальном направлении (с началом в центре круга, сферы или дуги) в сочетании с углом поворота, чем использовать ортогональную (декартову) систему координат.

Затем можно использовать тригонометрию

для преобразования между двумя типами системы координат. Чтобы узнать больше об этом и теории, лежащей в основе этого, взгляните на наши страницы, посвященные изогнутым формам , , трехмерным формам , и тригонометрии , .

Полярные координаты

В математических приложениях, где необходимо использовать полярные координаты, любая точка на плоскости определяется ее радиальным расстоянием \ (r \) от начала координат (центр кривизны или известное положение) и углом тета. \ (\ theta \) (измеряется в радианах).2 \ quad \ text {and} \ quad \ tan \ theta = \ frac {y} {x} $$

И обратно:

$$ x = r \ cos \ theta \ quad \ text {and} \ quad y = r \ sin \ theta $$

Сферические и цилиндрические системы координат

Эти системы являются трехмерными родственниками двумерной полярной системы координат.

Цилиндрические координаты более понятны, чем сферические, и похожи на трехмерную декартову систему (x, y, z).2, \ quad \ tan \ theta = \ frac {y} {x} \ quad \ text {и} \ quad z = z $$

$$ x = r \ cos \ theta, \ quad y = r \ sin \ theta \ quad \ text {and} \ quad z = z $$

Поверхностей в цилиндрической системе:

  • Если вы сделаете \ (z \) константой, у вас будет плоская круговая плоскость.
  • Если вы сделаете \ (\ theta \) константой, у вас будет вертикальная плоскость.
  • Если вы сделаете \ (r \) постоянным, вы получите цилиндрическую поверхность.

Сферическая система координат более сложна.Маловероятно, что вы столкнетесь с ним в повседневных ситуациях. Он в основном используется в сложных научных и инженерных приложениях. Например, электрическое и гравитационное поля демонстрируют сферическую симметрию.

Сферические координаты определяют положение точки тремя координатами rho ( \ (\ rho \) ), theta (\ (\ theta \)) и phi (\ (\ phi \)).

\ (\ rho \) – это расстояние от начала координат (аналогично \ (r \) в полярных координатах), \ (\ theta \) – это то же самое, что угол в полярных координатах, а \ (\ phi \) – это угол между осью \ (z \) и линией от начала координат до точки.2}} {z} $$

Поверхностей в сферической системе:

  • Если вы сделаете \ (\ rho \) константой, у вас будет сфера.
  • Если вы сделаете \ (\ theta \) константой, у вас будет вертикальная плоскость.
  • Если вы сделаете \ (\ phi \) константой, у вас будет горизонтальная плоскость (или конус).

Широта и долгота, карты и навигация

Наиболее известное применение сферических координат – это система широты и долготы, которая делит поверхность Земли на сетку для целей навигации.Расстояния между линиями сетки измеряются не в милях или километрах, а в градусах и минутах.

Линии широты – это горизонтальные срезы земного шара. Срез на экваторе находится на широте 0 °, а полюса – на ± 90 °. Эти линии называются параллелями.

Линии долготы подобны клиньям апельсина, измеренным радиально от вертикальной линии симметрии, соединяющей полюса. Эти линии называются меридианами. Опорная линия 0 ° долготы известна как Гринвичский меридиан, который проходит через Королевскую обсерваторию в Гринвиче, Лондон.

Однако, чтобы использовать эту трехмерную систему для навигации, изогнутая сетка должна быть перенесена на плоские «карты» (карты береговых линий и дна океана для моряков) с помощью проекции . Таким образом, диаграммы могут использоваться как обычные карты с ортогональной сеткой, и могут применяться правила декартовых координат.

Сначала представьте, что лист бумаги оборачивается вокруг земного шара, образуя цилиндр. Изображение на схеме проецируется из трехмерной сферы на двухмерный лист бумаги.Это особый метод, используемый картографами под названием Mercator Projection .

Линии сетки на морской карте по-прежнему указываются в градусах и минутах, а расстояния измеряются в морских милях. Одна морская миля равна одной минуте широты.

Заключение

Маловероятно, что вам понадобится использовать полярные или сферические координаты, если вы не работаете в роли, которая специально этого требует, но полезно знать, что они из себя представляют и как они используются.

Также интересно понять, как карту трехмерной формы, такой как земной шар, можно преобразовать в плоские карты, которые позволяли морякам путешествовать по земному шару на протяжении сотен лет.

Оставить комментарий