03. Пример решения Заданий из раздела №1
Задание 1. Для данного определителя найти миноры и алгебраические дополнения элементов . Вычислить определитель : а) разложив его по элементам I-ой строки; б) разложив его по элементам J-го столбца; в) получив предварительно нули в I-ой строки.
I = 1, J = 2
Решение: 1. Находим миноры к элементам :
Алгебраические дополнения элементов соответственно равны:
2. а). Вычислим определитель, разложив его по элементам первой строки:
Б) Вычислим определитель, разложив его по элементам второго столбца:
В) Вычисли определитель , Получив предварительно нули в первой строке. Используем свойство определителей: определитель Не ИЗмеНиТся, ЕСлИ ко всЕМ эЛеМентам кАКой-либо строки (столбца) прибавить СоотВЕтстВУющие эЛеМЕНтЫ другой строки (столбца), умноженНЫе на одно И то же произвольное число.
В опрЕДЕЛитЕЛе трЕТьЕГо порядка получили нули в ПеРвом столбце по свойству тому же свойству определителей.
Задание 2.
Даны две матрицы A и B. Найти: а) AB; б) BA; в) ; г) .
Решение: а) Произведение АВ имеет смысл, так как число столбцов матрицы А равно числу строк матрицы В.
Б) Вычислим
ОчЕВидНО, что ;
В) Обратная матрица матрицы А имеет виД
,
Где – алгебраическое дополнение, -минор, т. е. определитель полученный из основного определителя вычёркивание i-строки, j-столбца.
,
Т. е. матрица A – Невырожденная, и, значит, существуЕТ матрица . Находим:
Тогда
;
Г) Проверка
;
Задание 3. Проверить совместность линейной системы уравнений и в случае совместности решить ее а) по формулам Крамера б) методом Гаусса.
Решение: Совместность данной системы проверим по теореме Кронекера – Капелли. С помощью элементарных преобразований найдем ранг матрицы
Данной системы и ранг расширенной матрицы
Для этого умножим первую строку матрицы В на (-2) и сложим со второй, затем умножим первую строку на (-3) и сложим с третьей, поменяем местами второй и третий столбцы. Получим
.
Следовательно, (т. е. числу неизвестных). Значит, исходная система совместна и имеет единственное решение.
А) По формулам Крамера
Где -главный определитель, который мы посчитаем, например, по правилу треугольника
,
Аналогично найдем
,
,
,
Находим: .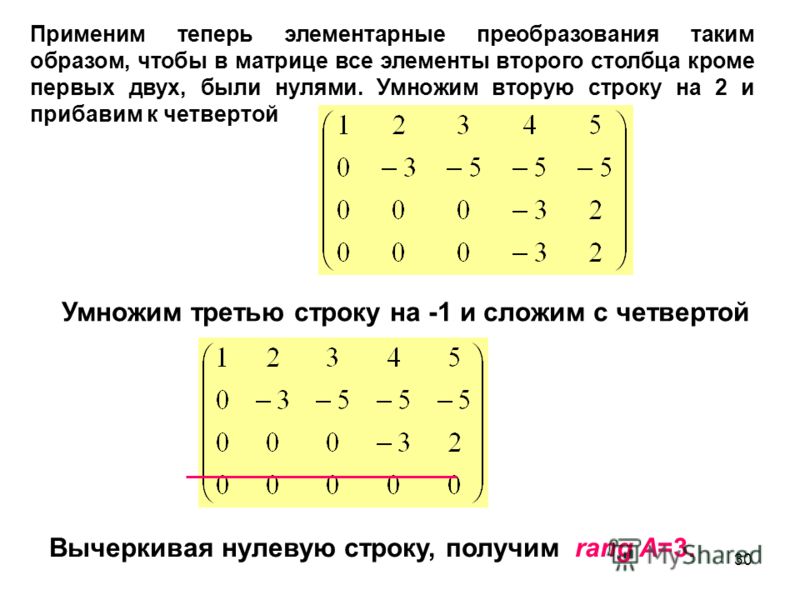
Б) Решим систему методом Гаусса. Исключим из второго и третьего уравнений. Для этого первое уравнение умножим на 2 и вычтем из второго, затем первое уравнение умножим на 3 и вычтем из третьего:
Из полученной системы находим .
Задание 4
Решить матричное уравнение
Пусть ,
решение матричного уравнения находим по формуле
Х=А -1В, где А -1 обратная матрица
– алгебраическое дополнение, где
– определитель, полученный из основного вычеркивание i-строки, j-столбца, – определитель матрицы.
Найдем обратную матрицу.
(-1)1+14=4
А12=(-1)1+23=-3
А21= (-1)2+12=-2
А22=(-1)2+21=1
DetA==1*4-2*3=4-6=-2
Итак,
Задание 5
Предприятие выпускает три вида продукции, используя сырье трёх видов: . Необходимые характеристики указаны в таблице .
Вид сырья | Нормы расхода сырья на изготовление одного вида продукции, усл. | Расход сырья за один день, усл. ед. | ||
Сапог | Кроссовок | Ботинок | ||
S1 S2 S3 | 5 2 3 | 3 1 2 | 4 1 2 | 2700 900 1600 |
Найти ежедневный объем выпуска каждого вида продукции.
Решение: Пусть ежедневно фабрика выпускает x1 – единиц продукции первого вида, x2 – единиц продукции второго вида, x3 – единиц продукции третьего вида. Тогда в соответствии с расходом сырья каждого вида имеем систему.
Решаем систему линейных уравнений любым способом. Решим данную систему, например, методом Гаусса. Составим матрицу из коэффициентов стоящих перед неизвестными и из свободных членов.
Обнуляем первый столбец, кроме первого элемента
1. Первую строчку оставляем без изменения
2. Вместо второй записываем сумму первой, умноженной на -2 и второй, умноженной на 5
Вместо второй записываем сумму первой, умноженной на -2 и второй, умноженной на 5
3. Вместо третьей записываем сумму первой, умноженной на -3 и третьей, умноженной на 5
Аналогично обнуляем второй столбец под элементом второй строки второго столбца
˜˜
Вернемся к системе
Задание 6. Решить однородную систему линейных алгебраических
Уравнений.
Решение: Так как определитель системы
,
То система ИМЕЕт бЕСчисленное множество решений. Поскольку , , возьмем любые два уравнения системы (наПРИМЕР, ПЕрвое И второе) и найдем ее рЕШение. ИмЕеМ:
Так как определитель из коэффициентов при неизвестных и не равен нулю, то в качестве базисных нЕИзвестных ВОзьмЕМ и (хотя можно брать и другие пары нЕИзвЕСтных) И ПеРЕМЕСтим члЕНы с в правые частИ УравнЕНИЙ:
РЕШаЕМ пОСлЕдНюю систЕМу по формулам КрамЕРа :
Где
,
,
.
Отсюда находим, что Полагая , где K—Произвольный коэффициент пропорциональности (произвольная постоянная), получаем решение исходной сИСтЕМы: .
| < Предыдущая | Следующая > |
|---|
теоремы и примеры нахождения определителей
Содержание:
В общем случае правило вычисления определителей $n$-го порядка является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы второго порядка, надо от произведения элементов главной диагонали отнять произведение элементов побочной диагонали:
$$\left| \begin{array}{ll}{a_{11}} & {a_{12}} \\ {a_{21}} & {a_{22}}\end{array}\right|=a_{11} \cdot a_{22}-a_{12} \cdot a_{21}$$
Пример
Задание. Вычислить определитель второго порядка
$\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|$
Вычислить определитель второго порядка
$\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|$
Решение. $\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|=11 \cdot 5-(-2) \cdot 7=55+14=69$
Ответ. $\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|=69$
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком “плюс”; аналогично, для второго определителя – соответствующие произведения берутся со знаком “минус”, т.е.
$$\left| \begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {a_{31}} & {a_{32}} & {a_{33}}\end{array}\right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$
$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$
Слишком сложно?
Методы вычисления определителей не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Вычислить определитель $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|$ методом треугольников.
Вычислить определитель $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|$ методом треугольников.
Решение. $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|=3 \cdot 1 \cdot(-2)+4 \cdot(-2) \cdot(-1)+$
$$+3 \cdot 3 \cdot 1-(-1) \cdot 1 \cdot 1-3 \cdot(-2) \cdot 3-4 \cdot 3 \cdot(-2)=54$$
Ответ. $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|=54$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком “плюс”; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком “минус”:
$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$
Пример
Задание. Вычислить определитель $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|$ с помощью правила Саррюса.
Вычислить определитель $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|$ с помощью правила Саррюса.
Решение.
$$+(-1) \cdot 4 \cdot(-2)-(-1) \cdot 1 \cdot 1-3 \cdot 3 \cdot(-2)-3 \cdot 4 \cdot(-2)=54$$
Ответ. $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|=54$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Пример
Задание. Разложив по первой строке, вычислить определитель $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|$
Решение. Ответ. $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|=0$ Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка. Пример Задание. Вычислить определитель $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|$ Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному. $$\left| \begin{array}{ccc}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|=\left| \begin{array}{ccc}{1} & {2} & {3} \\ {4-4 \cdot 1} & {5-4 \cdot 2} & {6-4 \cdot 3} \\ {7-7 \cdot 1} & {8-7 \cdot 2} & {9-7 \cdot 3}\end{array}\right|=$$ $$=\left| \begin{array}{rrr}{1} & {2} & {3} \\ {0} & {-3} & {-6} \\ {0} & {-6} & {-12}\end{array}\right|=\left| \begin{array}{ccc}{1} & {2} & {3} \\ {0} & {-3} & {-6} \\ {0} & {2 \cdot(-3)} & {2 \cdot(-6)}\end{array}\right|=0$$ Определитель равен нулю, так как вторая и третья строки являются пропорциональными. Ответ. $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|=0$ Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа. Пример Задание. Вычислить определитель
$\left| \begin{array}{llll}{9} & {8} & {7} & {6} \\ {5} & {4} & {3} & {2} \\ {1} & {0} & {1} & {2} \\ {3} & {4} & {5} & {6}\end{array}\right|$ , разложив его по элементам какой-то строки или какого-то столбца. Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй – пять третьих и от четвертой – три третьих строки, получаем: $$\left| \begin{array}{cccc}{9} & {8} & {7} & {6} \\ {5} & {4} & {3} & {2} \\ {1} & {0} & {1} & {2} \\ {3} & {4} & {5} & {6}\end{array}\right|=\left| \begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \\ {5-5} & {4-0} & {3-5} & {2-10} \\ {1} & {0} & {1} & {2} \\ {0} & {4} & {2} & {0}\end{array}\right|=\left| \begin{array}{rrrr}{0} & {8} & {-2} & {-12} \\ {0} & {4} & {-2} & {-8} \\ {1} & {0} & {1} & {2} \\ {0} & {4} & {2} & {0}\end{array}\right|$$ Полученный определитель разложим по элементам первого столбца: $$\left| \begin{array}{rrrr}{0} & {8} & {-2} & {-12} \\ {0} & {4} & {-2} & {-8} \\ {1} & {0} & {1} & {2} \\ {0} & {4} & {2} & {0}\end{array}\right|=0+0+1 \cdot(-1)^{3+1} \cdot \left| \begin{array}{rrr}{8} & {-2} & {-12} \\ {4} & {-2} & {-8} \\ {4} & {2} & {0}\end{array}\right|+0$$ Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. $$=4 \cdot(2 \cdot 8-4 \cdot 4)=0$$ Ответ. $\left| \begin{array}{cccc}{9} & {8} & {7} & {6} \\ {5} & {4} & {3} & {2} \\ {1} & {0} & {1} & {2} \\ {3} & {4} & {5} & {6}\end{array}\right|=0$ Замечание Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки. С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали. Пример Задание. Вычислить определитель
$\Delta=\left| \begin{array}{rrrr}{-2} & {1} & {3} & {2} \\ {3} & {0} & {-1} & {2} \\ {-5} & {2} & {3} & {0} \\ {4} & {-1} & {2} & {-3}\end{array}\right|$ приведением его к треугольному виду. Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный: $$\Delta=\left| \begin{array}{rrrr}{-2} & {1} & {3} & {2} \\ {3} & {0} & {-1} & {2} \\ {-5} & {2} & {3} & {0} \\ {4} & {-1} & {2} & {-3}\end{array}\right|=-\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {3} & {-1} & {2} \\ {2} & {-5} & {3} & {0} \\ {-1} & {4} & {2} & {-3}\end{array}\right|$$ Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь: $$\Delta=-\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {3} & {-1} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {2} & {5} & {-1}\end{array}\right|$$ Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. $$\Delta=\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {3} & {-1} & {2} \\ {0} & {2} & {5} & {-1}\end{array}\right|$$ Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой – две вторых строки, получаем: $$\Delta=\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {-10} & {-10} \\ {0} & {0} & {-1} & {-9}\end{array}\right|$$ Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью: $$\Delta=-10 \left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {1} & {1} \\ {0} & {0} & {-1} & {-9}\end{array}\right|=$$ $$=-10 \cdot \left| \begin{array}{cccc}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {1} & {1} \\ {0} & {0} & {0} & {-8}\end{array}\right|=(-10) \cdot 1 \cdot(-1) \cdot 1 \cdot(-8)=-80$$ Ответ. Теорема Пусть $\Delta$ – определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k \leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю. Пример Задание. Используя теорему Лапласа, вычислить определитель
$\left| \begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \\ {0} & {1} & {0} & {-1} & {2} \\ {3} & {2} & {1} & {0} & {1} \\ {0} & {4} & {0} & {-5} & {0} \\ {1} & {1} & {2} & {-2} & {1}\end{array}\right|$ Решение. Выберем в данном определителе пятого порядка две строки –
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем): $$\left| \begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \\ {0} & {1} & {0} & {-1} & {2} \\ {3} & {2} & {1} & {0} & {1} \\ {0} & {4} & {0} & {-5} & {0} \\ {1} & {1} & {2} & {-2} & {1}\end{array}\right|=\left| \begin{array}{cc}{1} & {-1} \\ {4} & {-5}\end{array}\right| \cdot(-1)^{2+4+2+4} \cdot \left| \begin{array}{ccc}{2} & {0} & {5} \\ {3} & {1} & {1} \\ {1} & {2} & {1}\end{array}\right|+$$ $$+\left| \begin{array}{ll}{1} & {2} \\ {4} & {0}\end{array}\right| \cdot(-1)^{2+4+2+5} \cdot \left| \begin{array}{rrr}{2} & {0} & {4} \\ {3} & {1} & {0} \\ {1} & {2} & {-2}\end{array}\right|+\left| \begin{array}{cc}{-1} & {2} \\ {-5} & {0}\end{array}\right| \cdot(-1)^{2+4+5} \cdot \left| \begin{array}{ccc}{2} & {3} & {0} \\ {3} & {2} & {1} \\ {1} & {1} & {2}\end{array}\right|=$$ $$=-23+128+90=195$$ Ответ. Читать дальше: обратная матрица. Такой метод порождает рекурсивный процесс, позволяющий вычислить любой определитель. Но производительность этого алгоритма оставляет желать лучшего — O(n!). Поэтому применяется такое прямое вычисление разве что при символьных выкладках (и с определителями не слишком высокого порядка). Гораздо производительнее оказывается метод Гаусса. Его суть основывается на следующих положениях: 1. Определитель верхней треугольной матрицы \begin{pmatrix}{a}_{1,1} & {a}_{1,2} &… & {a}_{1,n} \\ 0 & {a}_{2,2} &… & {a}_{2,n} \\ 0 & 0 &… & …\\ 0 & 0 &… & {a}_{n,n} \\\end{pmatrix} равен произведению ее диагональных элементов. Этот факт сразу же следует из разложения определителя по элементам первой строки или первого столбца. 2. Если в матрице к элементам одной строки прибавить элементы другой строки, умноженные на одно и то же число, то значение определителя не изменится. 3. Если в матрице поменять местами две строки (или два столбца), то значение определителя изменит знак на противоположный. Мы можем, подбирая коэффициенты, складывать первую строку матрицы со всеми остальными и получать в первом столбце нули во всех позициях, кроме первой. Для получения нуля во второй строке, нужно прибавить ко второй строке первую, умноженную на Если же в матрице элемент Далее, действуя аналогично, можно получить нули во втором столбце, затем в третьем и т.п. Важно, что при сложении строк полученные ранее нули не изменятся. Если для какой-либо строки не удастся найти ненулевой элемент для знаменателя, то определитель равен нулю и процесс можно остановить. Нормальное завершение процесса Гаусса порождает матрицу, у которой все элементы, расположенные ниже главной диагонали, равны нулю. Как говорилось выше, определитель такой матрицы равен произведению диагональных элементов. Следующая функция вычисляет строку r1 сложенную со строкой r2, умноженной поэлементно на число f: Функция search проверяет, подходит ли матрица для очередного преобразования (у нее должен быть ненулевым очередной диагональный элемент). Если это не так, матрица преобразовывается перестановкой строк. Код можно скачать здесь Научиться вычислять определители, обратные матрицы и т. За справочник возьмем сборник задач Дубовика В.П., Юрика И.И. “Высшая математика”. Позже будут добавлены примеры вычисления определителя матрицы из других источников. ——————————————– Примеры. 1) (1.4) Применим правило вычисления определителя для матрицы второго порядка. 2) (1.6) Выполним вычисления согласно правилу 3) (1.8) Данный пример выглядит сложным но со знанием следующих правил логарифма решается на удивление быстро. 4) (1.14) Вычислим данный определитель двумя способами: по правилу треугольников и через алгебраические дополнения. А сейчас разложим по элементам первого рядка, поскольку в нем больше нулей В этом примере специально выписаны дополнение у нулевых множителей, так как не все понимают откуда берутся дополнения. По правилу они равны определителю, который образуется вычеркиванием строки и столбца того элемента для которого ищутся, умноженному на минус единицу в степени . Схематически на примере матрицы четвертого порядка это выглядит так: Внимательно посмотрите, какие элементы в определителе выписаны для дополнений и Вам все станет понятно. Суть метода алгебраических дополнений заключается в том, что когда мы матрицу с нулевыми элементами может разложив ее по по строке или столбцу в котором больше нулей нам остается вычислить столько определителей на порядок меньших основной матрицы, сколько ненулевых элементов. 6) (1.19) Если вычисления проводить по правилу треугольников, то получим много нулевых произведений. В такого рода примерах целесообразно использовать алгебраические дополнения. 7) (1.21) Вычислим определитель через алгебраические дополнения третьей строки Как можно убедиться, решение с помощью алгебраических дополнений в случаях разреженных матриц можно получить быстро и без большого количества вычислений. 8) (1.58) Выполним элементарные преобразования. От другого рядка вычтем первый, а от четвертого – третий. Получим разреженную матрицу Определитель найдем через алгебраические дополнения к четвертой строке Вычислим каждый из слагаемых Подставляем в определитель 9) (1.72) Найдем определитель через расписание по строкам и столбцам, содержащие нули (выделены черным). Таким методом нахождения определителя пятого порядка свелось к простым вычислениям. ———————————————- Методические указания для выполнения лабораторных работ по дисциплине ст. преп. каф. Информатика Лабораторная работа №5 Обработка матриц. Решение систем линейных уравнений матричным способом. Цель работы: Получить практические навыки по возможностям обработки матриц в MCAD и решению систем уравнений с использованием матриц. Задание к лабораторной работе. 1. Загрузить среду MCAD и набрать там пояснения а) Включить русский шрифт. б) Установить тип шрифта Courier New Cyr. в) В появившемся окне набрать рекомендуемый текст. a. Лабораторная работа №5 в среде MathCAD b. Выполнил студент(ка) ФИО, группа, шифр 2. а) Нажать левую кнопку мыши и выделить вариант задания из таблицы 1. б) Скопировать задание в буфер обмена (Правка->копировать).в) Установить курсор( красный крестик) в нужное место и вставить из буфера (Правка->вставить). 3. Задать данную матрицу. a) Набрать имя матрицы и установить с панели инструментов знак присваивания := b) Открыть панель векторов и матриц (значок есть на панели Математика) c) Выбрать там шаблон матрицы d) Указать нужное количество строк и столбцов e) Заполнить шаблон значениями из своего варианта 4. Для получения матрицы B, умножим матрицу A на число, равное номеру вашего варианта + 1, так для 14 варианта матрицу A надо умножить на 15. 5. Для получения D умножим имеющиеся матрицы между собой. 6. Для нахождения дискриминантов матриц выбираем значок модуля на панели матриц, указываем имя и ставим знак равенства. 7. Для решения системы линейных уравнений необходимо задать матрицу коэффициентов (коэффициенты брать со знаком, если переменной нет в уравнении, значит коэффициент равен 0), вектор-столбец свободных членов 8. Решение будет найдено по формуле: 1. Решить с применением операций над матрицами. Задача. Дана матрица А: Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1. Получите матрицу D, умножив матрицы А и В друг на друга. Найти дискриминант матриц A, B, D. 2. Решить систему уравнений матричным способом. Провести проверку правильности решения. 1. Решить с применением операций над матрицами. Задача. Дана матрица А: Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1. Получите матрицу D, умножив матрицы А и В друг на друга. Найти дискриминант матриц A, B, D. 2. Решить систему уравнений матричным способом. Провести проверку правильности решения. 1. Решить с применением операций над матрицами. Задача. Дана матрица А: Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1. Получите матрицу D, умножив матрицы А и В друг на друга. Найти дискриминант матриц A, B, D. 2. Решить систему уравнений матричным способом. Провести проверку правильности решения. 1. Решить с применением операций над матрицами. Задача. Дана матрица А: Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1. Получите матрицу D, умножив матрицы А и В друг на друга. Найти дискриминант матриц A, B, D. 2. Решить систему уравнений матричным способом. Провести проверку правильности решения. 1. Задача. Дана матрица А: Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1. Получите матрицу D, умножив матрицы А и В друг на друга. Найти дискриминант матриц A, B, D. 2. Решить систему уравнений матричным способом. Провести проверку правильности решения. 1. Решить с применением операций над матрицами. Задача. Дана матрица А: Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1. Получите матрицу D, умножив матрицы А и В друг на друга. Найти дискриминант матриц A, B, D. 2. Решить систему уравнений матричным способом. Провести проверку правильности решения. 1. Решить с применением операций над матрицами. Задача. Дана матрица А: Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т. Получите матрицу D, умножив матрицы А и В друг на друга. Найти дискриминант матриц A, B, D. 2. Решить систему уравнений матричным способом. Провести проверку правильности решения. 1. Решить с применением операций над матрицами. Задача. Дана матрица А: Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1. Получите матрицу D, умножив матрицы А и В друг на друга. Найти дискриминант матриц A, B, D. 2. Решить систему уравнений матричным способом. Провести проверку правильности решения. 1. Решить с применением операций над матрицами. Задача. Дана матрица А: Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1. Получите матрицу D, умножив матрицы А и В друг на друга. Найти дискриминант матриц A, B, D. 2. Решить систему уравнений матричным способом. 1. Решить с применением операций над матрицами. Задача. Дана матрица А: Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1. Получите матрицу D, умножив матрицы А и В друг на друга. Найти дискриминант матриц A, B, D. 2. Решить систему уравнений матричным способом. Провести проверку правильности решения. 1. Решить с применением операций над матрицами. Задача. Дана матрица А: Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1. Получите матрицу D, умножив матрицы А и В друг на друга. Найти дискриминант матриц A, B, D. 2. Решить систему уравнений матричным способом. Провести проверку правильности решения. 1. Решить с применением операций над матрицами. Задача. Дана матрица А: Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т. Получите матрицу D, умножив матрицы А и В друг на друга. Найти дискриминант матриц A, B, D. 2. Решить систему уравнений матричным способом. Провести проверку правильности решения. 1. Решить с применением операций над матрицами. Задача. Дана матрица А: Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1. Получите матрицу D, умножив матрицы А и В друг на друга. Найти дискриминант матриц A, B, D. 2. Решить систему уравнений матричным способом. Провести проверку правильности решения. 1. Решить с применением операций над матрицами. Задача. Дана матрица А: Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1. Получите матрицу D, умножив матрицы А и В друг на друга. Найти дискриминант матриц A, B, D. 2. Решить систему уравнений матричным способом. В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту. Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества. Определители матриц часто используются в вычислениях, в линейной алгебре и аналитической геометрии. Вне академического мира определители матриц постоянно требуются инженерам и программистам, в особенности тем, кто работает с компьютерной графикой. Если вы уже знаете, как найти определитель матрицы размерностью 2×2, то из инструментов для нахождения определителя матрицы 3×3 вам будут необходимы только сложение, вычитание и умножение. Определитель (детерминант) квадратной матрицы A – это число, обладающее определенными свойствами, которое может быть получено из элементов матрицы рядом методов. Пусть $ A = egin 1 & 4 & 2 \ 5 & 3 & 7 \ 6 & 2 & 1 end$ $det(A) = left|A Пример 12 Пример 13 Пример 14 Пример 15 $ egin 9 & 12 & 3\ 1 & 8 & 7\ 5 & 7 & 2 end=0$ $C_<1>+C_<3>=C_<2>$ Пример 17 Пример 20 Определитель матрицы, полученной вычеркиванием некоторых строк и столбцов матрицы, называется минором этой матрицы. Пример 21 Один из миноров матрицы A есть $egin 1 & 2\ 5 & 3 end$ (он получается вычеркиванием строки 3 и столбца 3 из матрицы A) Другим минором является $egin 1 & 2 \ 6 & 1 end$ (получается вычеркиванием строки 2 и столбца 2 из матрицы A) Пример 22 Один из миноров матрицы B есть $ egin 1 & 7 & 9\ 8 & 3 & 2\ 8 & 1 & 4 end$ (получается вычеркиванием строки 1 и столбца 1 из матрицы B) Другим минором является $egin 1 & 7 \ 8 & 3 end$ (получается вычеркиванием строк 1 и 4 и столбцов 1 и 4 из матрицы B) Пусть $A= egin a_ <1,1>& a_ <1,2>& a_ <1,3>& . Можно определить минор $Delta_$, полученный вычеркиванием строки i и столбца j, для любого элемента $a_$ квадратной матрицы A. Такой минор называется дополнительным. Определить дополнительный минор элемента 2. Так как данный элемент находится в строке 2, столбце 1, видно, что это $a_<2,1>$. Нужно вычеркнуть строку 2 и столбец 1 из матрицы A, после чего получаем Минор, дополнительный к элементу 2, есть $Delta_ <2,1>= 7$. Пример 24 Нужно найти минор, дополнительный к элементу 7. Так как данный элемент находится в строке 2, столбце 3, видно, что это $a_<2,3>$. Порядок определителя матрицы равен числу ее строк и столбцов. Пример 26 Пример 27 Определитель матрицы равен сумме произведений элементов любой строки или любого столбца и их алгебраических дополнений. $left| A Можно посчитать определитель, например, используя строку i: Либо же можно посчитать определитель, используя столбец j: Используем строку 1, чтобы вычислить определитель. Заметим, что $ Delta_<1,1>= a_ <2,2>$ и $ Delta_<1,2>=a_<2,1>$ $ left| A $color < egina & b\ c & d end=a cdot d – b cdot c>$ Пример 28 Пример 29 Используем строку 1, чтобы вычислить определитель. Упростить получение последней формулы можно следующим образом. Начнем с того, что перепишем первые две строки под определителем как показано ниже. Умножаем элементы на каждой из трех красных диагоналей (на главной диагонали и на диагоналях под ней) и складываем результаты: Умножаем элементы на каждой из трех синих диагоналей (на побочной диагонали и на диагоналях под ней) и складываем результаты: Вычитая вторую сумму из первой, получаем формулу определителя: Пример 30 Пример 31 $= 3cdot4cdot9 + 1cdot1cdot1 + 7cdot5cdot2 -(1cdot4cdot7 + 2cdot1cdot3 + 9cdot5cdot1) =$ $ 108 + 1 + 70 -(28 + 6 + 45)=79-79=100$ Элементы матрицы могут быть обозначены буквами. Вычисление их определителей можно упростить, используя свойства определителей. Например, можно вычислить определитель матрицы, в которой к какой-либо строке (или столбцу) прибавлена линейные комбинация других строк (столбцов). Используя свойства определителей, модифицируем строку 1 так, чтобы два элемента обратились в 0. В этом случае, когда мы используем полученную выше формулу для определителя матрицы 3×3, нет необходимости вычислять алгебраические дополнения этих элементов, поскольку их произведение будет равно 0. Вычислить определитель матрицы 4×4 можно с использованием общей формулы для определителя матрицы 3×3. Но сначала надо использовать свойства определителей: В любом из этих случаев нам пригодятся соответствующие методы вычисления определителей матриц 3×3. Модифицируем строку или столбец так, чтобы все его элементы, кроме одного, обратились в 0. Пример 33 Замечаем, что все элементы в строке 3 равны нулю, а значит, определитель равен 0. Пример 34 Пример 35 Пример 36 Поскольку в столбце 1 только один элемент отличен от нуля, применяем общую формулу, используя этот столбец. = Пример 37 Чтобы изменить строку так, чтобы в ней стало больше нулей, нужно совершать операции со столбцами, и наоборот. Выбираем строку или столбец, содержащий элемент 1, поскольку из него можно получить любое число простым умножением. Заметим, что в строке 2 уже есть два нулевых элемента. Достаточно обратить лишь еще один элемент в 0, чтобы осталось посчитать только одно алгебраическое дополнение единичного элемента. $egin 4 & 3 & 2 & 2\ 0 & 1 & 0 & -2\ 1 & -1 & 3 & 3\ 2 & 3 & 1 & 1 endxlongequal+2C_<2>>$ $egin4>4 & 3 & 2 & 8\ 0 & color <1>& 0 & 0\ 1 & -1 & 3 & 1\ 2 & 3 & 1 & 7 end=$ $=$br /> $= 1cdot(-1)^<2+2>cdot egin 4 & 2 & 8\ 1 & 3 & 1\ 2 & 1 & 7 end=$ Пример 38 Можно вынести множитель 3 из строки 3: Поскольку в строке 3 все элементы равны 1, легко обратить получить нули. Выносим общий множитель -1 из столбца 2 и еще раз -1 из столбца 3. Пример 40 Мы видим элемент 1 в столбце 3, так что мы можем обратить остальные элементы строки 2 в нули. $egin 4 & 7 & 2 & 3\ 1 & 3 & 1 & 2\ 2 & 5 & 3 & 4\ 1 & 4 & 2 & 3 end$ $xlongequal-C_<3>, C_<2>-3C_<3>,C_<4>-2C_<3>> egin1>2 & 1 & 2 & -1\ 0 & 0 & color <1>& 0 \ -1 & -4 & 3 & -2\ -1 & -2 & 2 & -1 end=$ $=1cdot(-1)^<2+5>cdot egin2 & 1 & -1\ -1 & -4 & -2\ -1 & -2 & -1 end$ Выносим общий множитель -1 из строки 2 и еще раз -1 из строки 3. Пример 41 Заметим, что все строки и все столбцы состоят из одних и тех же элементов, но в разном порядке. В таком случае мы можем сложить все строки или все столбцы. $egin 2 & 1 & 3 & 4\ 1 & 3 & 4 & 2\ 3 & 4 & 2 & 1\ 4 & 2 & 1 & 3 end$ $xlongequal+L_<2>+L_<3>+L_<4>> egin1>10 & 10 & 10 & 10\ 1 & 3 & 4 & 2\ 3 & 4 & 2 & 1\ 4 & 2 & 1 & 3 end=$ $10cdot egin1 & 1 & 1 & 1\ 1 & 3 & 4 & 2\ 3 & 4 & 2 & 1\ 4 & 2 & 1 & 3 end$ $xlongequal – C_<4>,C_<2>-C_<4>,C_<3>-C_<4>>10cdot egin1>0 & 0 & 0 & color<1>\ -1 & 1 & 2 & 2\ 2 & 3 & 1 & 1\ 1 & -1 & -2 & 3 end=$ $=10cdot1cdot(-1)^<1+4>$ $ = (-10)cdot egin -1 & 1 & 2\ 2 & 3 & 1\ 1 & -1 & -2 end=$ $(-10)cdot((-1)cdot 3cdot (-2) +2 cdot (-1)cdot2 + 1cdot 1cdot 1$ $-(2cdot 3cdot 1 + 1cdot (-1)cdot (-1) + (-2)cdot1cdot2))$ $= -10cdot(6 -4 +1 -6 – 1 + 4) =0$ 1. Линейные системы и матрицы 1. Дать определение умножения матриц. Коммутативна ли эта операция? Ответ пояснить. Произведение C матриц A и B определяется как m p m p A B ij = A ik B kj. Операция не коммутативна. Лекция 0. Глава 4. Матрицы. В этой главе мы рассмотрим основные виды матриц, операции над ними, понятие ранга матрицы и их приложения к решению систем линейных алгебраических уравнений. 4.. Основные понятия. Московский Государственный Технический Университет им. Н.Э. Баумана Факультет Фундаментальные науки Кафедра Высшая математика Аналитическая геометрия Модуль 1. Матричная алгебра. Векторная алгебра Лекция -й семестр. РАЗДЕЛ. Линейная алгебра. Основные определения. Определение. Матрицей размера mn где m- число строк n- число столбцов называется таблица чисел расположенных в определенном порядке. Эти числа ПЕРЕСТАНОВКИ Определение 1 Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,, n в строчку одно за другим Например, 2, 4, 3, 1, 5 Это перестановка пятой степени Вообще Занятие 1 Определители 11 Матричные обозначения Основные определения Матрицей размера m n, или m n-матрицей, называется таблица чисел (или других математических выражений с m строками и n столбцами Матрица Глава Начала линейной алгебры Системы линейных уравнений Систему m линейных уравнений с n неизвестными будем записывать в следующем виде: + + + + n n = + + + + nn = m + m + m + + mnn = m () Здесь n неизвестные Министерство образования и науки РФ Нижегородский государственный университет им. Н.И. Лобачевского В.К. Вильданов Практикум по линейной алгебре Учебно-методическое пособие Нижний Новгород Издательство Примеры решений контрольных работ Л.И. Терехина, И.И. Фикс 1 Контрольная работа 1 Линейная алгебра Решить матричное уравнение ( ( 3 1 2 1 X + 2 4 2 3 3 ( 1 0 = 3 2 3 Выполним вначале умножение матриц на Линейная алгебра и аналитическая геометрия Тема: Системы линейных уравнений (Метод Гаусса. ПРИЛОЖЕНИЯ Требования к знаниям умениям навыкам Страницы даны по учебнику «Математика в экономике» [] Дополнительные задачи по данному курсу можно найти в учебных пособиях [ 6] Векторы Владеть понятиями: ООО «Резольвента», wwwresolventru, resolvent@listru, (95) 509-8-0 Учебный центр «Резольвента» Доктор физико-математических наук, профессор К Л САМАРОВ МАТЕМАТИКА Учебно-методическое пособие по разделу Установить совместность и решить систему линейных уравнений 5xx x xx 5x 0 x4x x 0 а) по формулам Крамера, б) матричным способом, в) методом Гаусса Совместность Совместность системы можно установить: а) ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра высшей математики Допущены к проведению занятий в – учгоду Заведующий кафедрой профессор АП Господариков Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Алтайская государственная педагогическая академия» Б. 1. Линейная алгебра 1.1. В 1 представлены задачи на решение линейных алгебраических крамеровских систем с определителем, отличным от нуля, вычисление определителей и действий с матрицами. Линейные алгебраические Математика (БкПл-100) М.П. Харламов 2011/2012 учебный год, 1-й семестр Лекция 3. Элементы линейной алгебры (матрицы, определители, системы линейных уравнений и формулы Крамера) 1 Тема 1: Матрицы 1.1. Понятие МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ “САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ АЛМАТИНСКИЙ ФИЛИАЛ НЕГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САНКТ-ПЕТЕРБУРГСКИЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ ПРОФСОЮЗОВ» СЖ КАРАТАБАНОВА ЛИНЕЙНАЯ АЛГЕБРА задания Государственное образовательное учреждение высшего профессионального образования «Московский авиационный институт (национальный исследовательский университет)» Кафедра «Высшая математика» ЛИНЕЙНАЯ АЛГЕБРА А А КИРСАНОВ ЗАДАЧНИК-ПРАКТИКУМ ПО ЛИНЕЙНОЙ АЛГЕБРЕ МАТРИЦЫ ДЕТЕРМИНАНТЫ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ m m n n m n ПСКОВ ББК я К Печатается по решению кафедры алгебры и геометрии, и редакционно-издательского ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» АИ Шерстнёва, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Московский государственный университет путей сообщения» Институт экономики и финансов Кафедра «Математика» Одобрено методической комиссией кафедры «Высшая математика» Пермь 2007 Задание к работе 1. Вычислить определитель 3-го порядка, используя метод Саррюса (или метод треугольников) и метод разложения по минорам какого-нибудь ряда. 2. Вычислить определитель высшего порядка. 3. Привести матрицу к ступенчатому виду и вычислить ранг матрицы. 4. Выполнить действия с матрицами. 5. Вычислить значение многочлена от матрицы . 6. Найти неизвестную матрицу из уравнения. Образец решения варианта. 1.Вычислить определитель 3-го порядка 1) по правилу Саррюса (правило треугольников). Это правило заключается в равенстве . Таким образом, 2) Второе правило вычисления называется разложением по элементам некоторой строки (или столбца). Например, разложение по элементам первой строки имеет вид . Определитель разложим по элементам третьего столбца, т.е. . Как видно из приведенных примеров, вычисление определителей значительно упрощается, если какой-нибудь ряд определителя имеет только один элемент, отличный от нуля. Это можно всегда достигнуть, используя свойства определителей. В определителе умножим первую строку на 2 и прибавим ко второй, прибавим первую строку к третьей, получим . 2. Вычислить определитель высшего порядка . Решение : Используя свойства определителя, понизим порядок определителя. С этой целью прибавим пятый столбец к первому : ; в полученном определителе 4-го порядка четвертый столбец умножим на 3 и прибавим к первому столбцу, затем умножим его на 2 и прибавим ко второму столбцу, умножим его на 8 и прибавим к третьему столбцу, получаем . Из приведенного примера очевидно, что вычисление определителей высших порядков значительно упрощается, если определитель привести к треугольному виду. 3. Привести матрицу к ступенчатому виду и вычислить ранг матрицы . Решение. Говорят, что квадратная матрица имеет ступенчатый вид, если ниже ее главной диагонали стоят нулевые элементы. Матрица приводится к ступенчатому виду с помощью элементарных преобразований : а) перестановка строк, б) умножение строки на число, в) прибавление к одной строки другой, умноженной на некоторое число. Ранг матрицы , , равен количеству ненулевых строк эквивалентной ей матрицы ступенчатого вида. В первом столбце данной матрицы ниже первого элемента получим нулевые элементы с помощью преобразования в). Последовательно умножим первую строку матрицы на (–2) и прибавим ко второй строке, умножим на (–3) и прибавим к третьей строке, умножим на (–2) и прибавим к четвертой строке, получим . В полученной матрице во втором столбце во второй строке и ниже второй строки отсутствуют единицы. . Во втором столбце полученной матрицы ниже второго элемента получим нулевые элементы. Последовательно умножим вторую строку полученной матрицы на 2 и прибавим к третьей строке, умножим на 7 и прибавим к четвертой строке, затем третью строку поделим на 9 , четвертую строку поделим на 18. Во вновь полученной матрице в третьем столбце ниже третьего элемента получим нулевой элемент: третью строку умножим на (–1) и прибавим к четвертой строке, имеем . Отсюда заключаем, что . 4. Выполнить действия с матрицами . Решение. Обозначим , , , . Произведение имеет смысл, так как число столбцов матрицы равно числу строк матрицы . Находим матрицу , элементы которой , . Имеем . Произведение имеет смысл, так как тоже число столбцов матрицы равно числу строк матрицы . Находим матрицу , элементы которой , . Имеем . Разность имеет смысл, так как матрицы и имеют одинаковую размерность . Находим искомую матрицу , элементы которой , . Имеем . Ответ : Результатом действия данных матриц является матрица . 5. Вычислить значение многочлена от матрицы , где , . Решение. При вычислении значения многочлена от матрицы вместо подставляем данную матрицу , а свободный член многочлена записываем в матричной форме, т.е. в виде , где единичная матрица того же порядка, что и данная матрица . Таким образом, , 1) , 2) , 3) . Имеем . Ответ : . 6. 1) Найти неизвестную матрицу из уравнения . Решение. , где , . Матричное уравнение вида имеет решение, если матрицы и – квадратные матрицы одинакового порядка и матрица – невырожденная, т.е. . В этом случае для матрицы существует обратная матрица . Умножая слева обе части уравнения на , получим , где единичная матрица, искомая матрица. Для данной матрицы : . Следовательно, существует . Найдем ее по формуле , где алгебраическое дополнение элемента матрицы . Для данной матрицы : . Тогда и . Ответ : . 2) Найти неизвестную матрицу из уравнения . Решение. , где , . Матричное уравнение вида имеет решение, если матрицы и – квадратные матрицы одинакового порядка и , т.е. для матрицы существует обратная матрица . искомая матрица. Для данной матрицы : . Следовательно, существует . Найдем ее по формуле, указанной в примере 1), имеем и . Тогда . Ответ : . Вариант № 1 1.1. 1.2. 1.3. 1.4. 1.5. , 1.6. Вариант № 2 2.1. 2.2. 2.3. 2.4. 2.5. , 2.6. Вариант № 3 3.1 3.2. 3.3. 3.4. 3.5. , 3.6. Вариант № 4 4. 1. 4.2. 4.3. 4.4. 4.5. , 4. 6. Вариант № 5 5.1. 5.2. 5.3. 5.4. 5.5. , 5.6. Вариант № 6 6.1. 6.2. 6.3. 6.4. 6.5. , 6.6. Вариант № 7 7.1. 7.2. 7.3. 7.4. 7.5. , 7. 6. Вариант № 8 8.1. 8. 8.4. 8.5. , 8.6. Вариант № 9 9.1. 9.2. 9.3. 9.4. 9.5. , 9.6. Вариант № 10 10.1. 10.2. 10.3. 10.4. 10.5. , 10.6. Вариант № 11 11.1. 11.2. 11.3. 11.4. 11.5. , 11. 6. Вариант № 12 12.1. 12.2. 12.3. 12.4. 12.5. , 12.6. Вариант № 13 13.1. 13.2. 13.3. 13.4. 13.5. , 13.6. Вариант № 14 14.1. 14.2. 14.3. 14.4. 14.5. , 14.6. Вариант № 15 15.1. 15.2. 15.3. 15.4. 15.5. , 15.6. Вариант № 16 16.1. 16.2. 16.3. 16.4. 16.5. , 16.6. Вариант № 17 17.1. 17.2. 17.3. 17.4. 17.5. , 17.6. Вариант № 18 18.1. 18.2. 18.3. 18.4. 18.5. , 18.6. Вариант № 19 19. 19.4. 19.5. , 19.6. Вариант № 20 20.1. 20.2. 20.3. 20.4. 20.5. , 20.6. Вариант № 21 21.1. 21.2. 21.3. 21.4. 21.5. , 21.6. Вариант № 22 22.1. 22.2. 22.3. 22.4. 22.5. , 22.6. Вариант № 23 23.1. 23.2. 23.3. 23.4. 23.5. , 23.6. Вариант № 24 24.1. 24.2. 24.3. 24.4. 24.5. , 24.6. Вариант № 25 25.1. 25.2. 25.3. 25.4. 25.5. , 25.6. Вариант № 26 26.1. 26.2. 26.3. 26.4. 26.5. , 26.6. Вариант № 27 27.1. 27.2. 27.3. 27.4. 27.5. , 27.6. Вариант № 28 28.1. 28.2. 28.3. 28.4. 28.5. , 28.6. Вариант № 29 29.1. 29.2. 29.3. 29.4. 29.5. , 29. Вариант № 30 30.1. 30.2. 30.3. 30.4. 30.5. , 30.6. . Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру. Mathematics Stack Exchange – это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях. Кто угодно может задать вопрос Кто угодно может ответить Лучшие ответы голосуются и поднимаются наверх Спросил Просмотрено
28к раз Из поручения: Пусть $ A = \ left [\ begin {matrix} 3 & -6 \\ -2 & 4 \ end {matrix} \ right] $ Построит матрицу $ 2 * 2 $ $ B $ такую, что $ AB $ является нулем. Стоимость $ AB $ будет: $
AB = \ left [
\ begin {matrix}
3b_ {11} -6b_ {12} и 3b_ {21} -6b_ {22} \\
-2b_ {11} + 4b_ {12} и -2b_ {21} + 4b_ {22}
\ end {matrix} \ right] Я думал об использовании подстановки, но следующие уравнения просто приводят к переменным, равным $ 0 $: $$ \ begin {align *}
3b_ {11} -6b_ {12} & = 0 \\
-2b_ {11} + 4b_ {12} & = 0
\ end {align *} $$ Есть подсказки, как я могу решить эту проблему? 331k4646 золотых знаков701701 серебряный знак10321032 бронзовых знака Создан 24 янв. Ваши уравнения $$ 3b_ {11} -6b_ {12} = 0, \ qquad -2b_ {11} + 4b_ {12} = 0 $$ оба говорят вам $ b_ {11} = 2b_ {12} $, что означает, что вы можете позволить $ b_ {12} $ быть вашим любимым ненулевым числом, и тогда вы также знаете, что $ b_ {11} $. Создан 24 янв. 163k1111 золотых знаков184184 серебряных знака350350 бронзовых знаков Рассмотрим решения $ A \ mathbf {x} = \ mathbf {0} $.Их легко найти методом исключения Гаусса:
$$ \ left (\ begin {array} {rr}
3 & -6 \\
-2 и 4
\ end {array} \ right) \ rightarrow \ left (\ begin {array} {rr}
1 & -2 \\
1 и -2
\ end {array} \ right) \ rightarrow \ left (\ begin {array} {rr}
1 & -2 \\
0 и 0
\ end {array} \ right). Теперь обратите внимание, что если $ B = [\ mathbf {b} _1 | \ mathbf {b} _2] $, где $ \ mathbf {b} _1 $ – это первый столбец, а $ \ mathbf {b} _2 $ – второй столбец, затем
$$ AB = [A \ mathbf {b} _1 | A \ mathbf {b} _2]. Создан 24 янв. 331k4646 золотых знаков701701 серебряный знак10321032 бронзовых знака Я думаю, что для небольших матриц, подобных приведенной выше, в такой задаче хорошо просто поискать линейную зависимость столбцов. Глядя на такую линейную зависимость между столбцами, вы быстро поймете, почему $ B $ выглядит именно так (т. Е. Возьмите 1 из столбца 1 и -2 из столбца два, и вы придете к нулевой матрице, и это это именно то, что делает умножение на $ B $)! Создан 24 янв. 2,87611 золотых знаков1919 серебряных знаков3131 бронзовый знак Ваша конфиденциальность Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie. Принимать все файлы cookie
Настроить параметры Я люблю линейную алгебру! Я понимаю, что в начале вашего курса на этот вопрос уже был дан самый простой ответ, но это может помочь вам позже, когда вам дадут матрицу A, где одна строка – все нули, тогда у вас дефицит ранга .Это означает, что размер пространства столбца не равен размеру вашей матрицы, скажем, n (что также происходит, если ваша матрица не квадратная). Это также означает, что отсутствует значение поворота. Значение поворота – это, по сути, значения на главной диагонали вашей матрицы. Если отсутствует значение поворота, вы можете выполнить метод исключения Гаусса, чтобы найти значения x, и, когда я изучал линейную алгебру, есть теорема, которая очень полезна при решении для x. Пример: Пусть A = \ begin {array} {cccc}
1 & 0 & -1 & 0 \\
0 и 1 и 2 и 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 \ end {array} b = \ begin {array} {c}
5 \\
-7 \\
0 \\
0 \ end {array} Этот пример показывает, что $ x_ {3} $ – единственная свободная переменная, и вы знаете, что: $ x_ {1} – x_ {3} = 5 $ $ x_ {2} + 2x_ {3} = -7 $ $ x_ {4} = 0 $ $ 0 = 0 $ x = \ begin {массив} {c}
х_ {1} \\
х_ {2} \\
х_ {3} \\
x_ {4} \ end {array} = \ begin {array} {c}
5 + x_ {3} \\
-7-2x_ {3} \\
х_ {3} \\
0 \ end {array} = \ begin {array} {c}
5 \\
-7 \\
0 \\
0 \ end {array} + $ x_ {3} $ * \ begin {array} {c}
1 \\
-2 \\
1 \\
0 \ end {array} Таким образом, это означает, что каждый $ x $ в вашем x-векторе, независимо от того, являются ли они переменными x или другими разными переменными, может быть записан так, что $ x_ {part} $ – это константы, оставшиеся после выполнения исключения Гаусса на A, связанном с б. Строка из всех нулей также подразумевает, что A не обратима, что важно, когда вы начинаете изучать, как взять обратную матрицу, которая всегда должна быть квадратной, чтобы получить обратную, но обратное не имеет значения при решении для x в системе уравнений, если вы не используете Matlab для решения относительно x. Боковое примечание: Вы выполнили функцию исключения по Гауссу, чтобы строка стала полностью нулевой? Если это так, то это означает, что строки вашей матрицы не были линейно независимыми, что также подразумевает, что размер вашего пространства столбцов также не является размером вашей матрицы, поэтому вы не занимаетесь полным рангом. Side Note2: Если у вас возникнут какие-либо вопросы позже, не стесняйтесь спрашивать меня. Без сохранения какой-либо внешней информации нет ничего лучше Θ (N 2 ). В более общем плане, при разработке алгоритмов обработки данных хороший способ проверить, можете ли вы добиться большего, чем определенные среды выполнения, – это использовать такого рода «состязательный анализ». Задайте себе вопрос: если я буду работать быстрее, чем некоторое время O (f (n)), может ли злоумышленник манипулировать данными таким образом, чтобы изменить ответ, но я не смог бы обнаружить? Это своего рода анализ, который вместе с более умной математикой доказывает, что алгоритмы сортировки на основе сравнения не могут работать лучше, чем Ω (n log n) в среднем случае. Если матрица имеет какие-то другие свойства (например, если она отсортирована), тогда вы можете выполнить работу лучше, чем выполнение в O (N 2 ). В качестве примера предположим, что вы знаете, что все строки матрицы отсортированы. Затем вы можете легко выполнить двоичный поиск в каждой строке, чтобы определить, сколько нулей она содержит, что занимает O (N log N) времени и быстрее. В зависимости от параметров вашей настройки вы можете заставить алгоритм работать быстрее, если вы предполагаете, что вам разрешено сканирование параллельно.Например, если на вашем компьютере есть K процессоров, которые могут быть выделены для задачи сканирования матрицы, вы можете разделить матрицу на K примерно равных по размеру групп, попросить каждый процессор подсчитать количество нулей в группе, а затем суммируем результаты этих вычислений. Это дает вам время выполнения Θ (N 2 / K), поскольку время выполнения разделено на несколько ядер. Вспомните из нашего урока по записи матриц, что матрица – это упорядоченный список чисел, заключенный в прямоугольную скобку. Таким образом, нулевая матрица – это матрица любых размеров, в которой все элементы элементов равны нулю. Математически нулевую матрицу можно представить выражением: Где m представляет количество строк, а n количество столбцов, содержащихся в матрице.Следовательно, если мы хотим записать нулевые матрицы разных размеров, нам просто нужно определить m и n в каждом случае и заполнить все записи внутри скобок матриц нулями. Примеры нулевых матриц можно увидеть ниже: Из приведенных выше примеров нотации нулевой матрицы обратите внимание, что эти матрицы могут иметь любой размер и комбинацию измерений, и они не обязательно являются квадратными матрицами. Не путайте нулевую матрицу с тем, что люди могут назвать «нулевой диагональной матрицей». Такая нулевая диагональная матрица обычно относится к полой матрице, где все диагональные элементы внутри нее равны нулю, а остальные ее элементы могут быть любым числом. Сходство между обычной нулевой матрицей и пустой матрицей происходит от их следа (сложения элементов на их диагоналях), поскольку у обоих есть все нулевые элементы, которые нужно добавить, чтобы получить след, равный нулю. Таким образом, оба этих типа матриц представляют собой то, что мы называем матрицей нулевого следа. Важные примечания относительно нулевой матрицы После того, как мы изучили определение нулевой матрицы, давайте поговорим о некоторых особых характеристиках этой матрицы. Поскольку нулевая матрица сама по себе является небольшой и конкретной концепцией, которую можно использовать во многих наших уроках линейной алгебры, теперь мы вынуждены еще раз вернуться к теме следующего урока: нулевому пространству матрицы. Если мы возьмем то, что мы знаем из наших уроков о представлении линейной системы в виде матрицы и матричного уравнения Ax = b, мы можем заметить, что при таком умножении умножаемый вектор фактически представляет собой набор решений, заданных однородной системой. В этом разделе мы сосредоточимся на демонстрации примеров операций либо с нулевыми матрицами внутри, над которыми работают, либо с проблемами, приводящими к решениям с нулевыми матрицами.Для этого давайте сразу перейдем к примерам упражнений: Пример 1 Начнем с добавления, содержащего нулевую матрицу. Каждое уравнение в системе превращается в строку. Каждая переменная в
система становится колонной. Переменные отбрасываются, а
коэффициенты помещаются в матрицу. Если правая часть включена,
это называется расширенной матрицей. Если правая сторона не указана, это
называется матрицей коэффициентов. Система линейных уравнений … становится расширенной матрицей… Элементарные операции со строками – это операции, которые могут быть выполнены с матрицей, которая даст
эквивалентная строка матрица. При работе с системами линейных уравнений вы могли выполнять три операции.
что не повлияет на набор решений. Когда система линейных уравнений преобразуется в расширенную матрицу, каждое уравнение становится
строка. Итак, теперь есть три элементарные операции со строками, которые производят эквивалент строки
матрица. Это эквивалентные строкам формы матрицы. Матрица находится в виде эшелона строк, когда выполняются следующие условия. Матрица находится в сокращенной форме строка-эшелон, когда все условия формы строка-эшелон выполнены
и все элементы выше и ниже, ведущие равны нулю. Существует три типа решений, которые возможны при решении системы линейных уравнений. Когда вы конвертируете расширенную матрицу обратно в форму уравнения, вы получаете x = 3,
y = 1 и z = 2. Первое уравнение будет x + 3z = 4. Второе уравнение будет y – 2z = 3. Решение для
y дает y = 3 + 2z. Столбец z не очищается (все нули, кроме
одно число), поэтому другие переменные будут определены через z. Следовательно,
z
будет параметром
t и решение … x = 4 – 3t, y = 3 + 2t, z = t Здесь нет решения. Язык программирования R предлагает нам множество способов создания матрицы и заполнения ее таким образом, чтобы все значения элементов были эквивалентны 0. Давайте посмотрим на эти способы – Встроенный метод matrix () в R может использоваться для создания матрицы с заданным набором значений, то есть размером nxm, и инициализировать ее заданным значением.Все элементы инициализируются одним и тем же значением. Если один из параметров m или n не указан, делается попытка вывести отсутствующее значение из длины данных и других заданных параметров. Если ни один из них не указан, то в качестве вывода возвращается матрица с одним столбцом. Затем эту матрицу можно сохранить в переменной, а затем можно будет обращаться к ее элементам и манипулировать ими. Синтаксис: matrix (0, n, m) Параметры: Тип возврата: матрица или скаляр из нулей Пример: Выход [, 1] [, 2] [, 3] [1,] 0 0 0 {1+3} \cdot \left| \begin{array}{cc}{4} & {5} \\ {7} & {8}\end{array}\right|=-3+12-9=0$
{1+3} \cdot \left| \begin{array}{cc}{4} & {5} \\ {7} & {8}\end{array}\right|=-3+12-9=0$
Разложение определителя по элементам строки или столбца
 {2+2} \cdot \left| \begin{array}{ll}{2} & {4} \\ {4} & {8}\end{array}\right|=$$
{2+2} \cdot \left| \begin{array}{ll}{2} & {4} \\ {4} & {8}\end{array}\right|=$$Приведение определителя к треугольному виду

 И снова, если
диагональный элемент будет равен $\pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
И снова, если
диагональный элемент будет равен $\pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя): $\Delta=-80$
$\Delta=-80$Теорема Лапласа
 $\left| \begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \\ {0} & {1} & {0} & {-1} & {2} \\ {3} & {2} & {1} & {0} & {1} \\ {0} & {4} & {0} & {-5} & {0} \\ {1} & {1} & {2} & {-2} & {1}\end{array}\right|=195$
$\left| \begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \\ {0} & {1} & {0} & {-1} & {2} \\ {3} & {2} & {1} & {0} & {1} \\ {0} & {4} & {0} & {-5} & {0} \\ {1} & {1} & {2} & {-2} & {1}\end{array}\right|=195$Вычисляем определитель матрицы на Хаскелле / Хабр
Решил выложить код вычисления определителей. Код рабочий, хотя и не претендует на виртуозность. Просто было интересно решить эту задачу именно на Хаскелле. Рассмотрены два подхода к решению задачи: простая рекурсия и метод Гаусса.Немного теории
Как известно, определитель квадратной матрицы n*n — это сумма n! слагаемых, каждое из которых есть произведение, содержащее ровно по одному элементу матрицы из каждого столбца и ровно по одному из каждой строки. Знак очередного произведения:
определяется чётностью подстановки:
\begin{pmatrix}1 & 2 &… & n \\ {i}_{1} & {i}_{2} &… & {i}_{n} \end{pmatrix}
Прямой метод вычисления определителя состоит в разложении его по элементам строки или столбца в сумму произведений элементов какой-либо строки или столбца на их алгебраические дополнения. В свою очередь, алгебраическое дополнение элемента матрицы есть при этом — есть минор элемента (i,j), т.е. определитель, получающийся из исходного определителя вычеркиванием i-й строки и j-го столбца.
В свою очередь, алгебраическое дополнение элемента матрицы есть при этом — есть минор элемента (i,j), т.е. определитель, получающийся из исходного определителя вычеркиванием i-й строки и j-го столбца.
 Если же в первом столбце нет ненулевых элементов, то определитель равен нулю.
Если же в первом столбце нет ненулевых элементов, то определитель равен нулю.Перейдем к программированию.
Мы работаем с данными с плавающей точкой. Матрицы представляем списками строк. Для начала определим два типа:type Row = [Double]
type Matrix = [Row]
Простая рекурсия
Ничтоже сумняшеся, мы будем раскладывать определитель по элементам первой (т.е. нулевой) строки. Нам понадобится программа построения минора, получающегося вычеркиванием первой строки и k-го столбца.
-- Удаление k-го элемента изо всех строк матрицы
deln :: Matrix -> Int -> Matrix
deln matrix k = map (\ r -> (take (k) r)++(drop (k+1) r)) matrix
А вот и минор:-- Минор k-го элемента нулевой строки
minor :: Matrix -> Int -> Double
minor matrix k = det $ deln (drop 1 matrix) k
Обратите внимание: минор — это определитель. Мы вызываем функцию det, которую еще не реализовали. Для реализации det, нам придется сформировать знакочередующуюся сумму произведений очередного элемента первой строки на определитель очередного минора. Чтобы избежать громоздких выражений, создадим для формирования знака суммы отдельную функцию:sgn :: Int -> Double
sgn n = if n `rem` 2 == 0 then 1.0 else (-1.0)
Теперь можно вычислить определитель:-- Определитель квадратной матрицы
det :: Matrix -> Double
det [[a,b],[c,d]] = a*d-b*c
det matrix = sum $ map (\c -> ((matrix !! 0)!!c)*(sgn c)*(minor matrix c)) [0. .n]
where n = length matrix - 1
.n]
where n = length matrix - 1
Код очень прост и не требует особых комментариев. Чтобы проверить работоспособность наших функций, напишем функцию main:main = print $ det [[1,2,3],[4,5,6],[7,8,(-9)]]
Значение этого определителя равно 54, в чем можно убедиться.Метод Гаусса
Нам понадобится несколько служебных функций (которые можно будет использовать и в других местах). Первая из них — взаимный обмен двух строк в матрице:-- Обмен двух строк матрицы
swap :: Matrix -> Int -> Int -> Matrix
swap matrix n1 n2 = map row [0..n]
where n=length matrix - 1
row k | k==n1 = matrix !! n2
| k==n2 = matrix !! n1
| otherwise = matrix !! k
Как можно понять по приведенному выше коду, функция проходит строку за строкой. При этом, если встретилась строка с номером n1, принудительно подставляется строка n2 (и наоборот). Остальные строки остаются на месте.
Остальные строки остаются на месте.-- Вычислить строку r1+f*r2
comb :: Row -> Row -> Double -> Row
comb r1 r2 f = zipWith (\ x y -> x+f*y) r1 r2
Здесь все предельно прозрачно: действия выполняются над строками матрицы (т.е. над списками [Double]). А вот следующая функция выполняет это преобразование над матрицей (и, естественно, получает новую матрицу):-- прибавить к строке r1 строку r2, умноженную на f
trans :: Matrix -> Int -> Int -> Double -> Matrix
trans matrix n1 n2 f = map row [0..n]
where n=length matrix - 1
row k | k==n1 = comb (matrix !! n1) (matrix !! n2) f
| otherwise = matrix !! k
Функция getNz ищет номер первого ненулевого элемента в списке. Она нужна в случае, когда очередной диагональный элемент оказался равным нулю.
-- Номер первого ненулевого в списке
getNz :: Row -> Int
getNz xs = if length tmp == 0 then (-1) else snd $ head tmp
where tmp=dropWhile (\ (x,k) -> (abs x) <= 1.0e-10) $ zip xs [0..]
Если все элементы списка равны нулю, функция вернет -1.-- Поиск ведущего элемента и перестановка строк при необходимости
search :: Matrix -> Int -> Matrix
search matrix k | (abs ((matrix !! k) !! k)) > 1.0e-10 = matrix
| nz < 0 = matrix -- матрица вырождена
| otherwise = swap matrix k p
where n = length matrix
lst = map (\ r -> r !! k) $ drop k matrix
nz = getNz lst
p = k + nz
Если ведущий (ненулевой) элемент найти невозможно (матрица вырождена), то функция вернет ее без изменений. Функция mkzero формирует нули в очередном столбце матрицы:
Функция mkzero формирует нули в очередном столбце матрицы:-- получение нулей в нужном столбце
mkzero :: Matrix -> Int -> Int -> Matrix
mkzero matrix k p | p>n-1 = matrix
| otherwise = mkzero (trans matrix p k (-f)) k (p+1)
where n = length matrix
f = ((matrix !! p) !! k)/((matrix !! k) !! k)
Функция triangle формирует верхнюю треугольную форму матрицы:-- Получение верхней треугольной формы матрицы
triangle :: Matrix -> Int -> Matrix
triangle matrix k | k>=n = matrix
| (abs v) <= 1.0e-10 = [[0.0]] -- матрица вырождена
| otherwise = triangle (mkzero tmp k k1) k1
where n = length matrix
tmp = search matrix k
v = (tmp !! k) !! k -- диагональный элемент
k1 = k+1
Если на очередном этапе не удалось найти ведущий элемент, функция возвращает нулевую матрицу 1-го порядка. Теперь можно составить парадную функцию приведения матрицы к верхней треугольной форме:
Теперь можно составить парадную функцию приведения матрицы к верхней треугольной форме:-- Парадная функция
gauss :: Matrix -> Matrix
gauss matrix = triangle matrix 0
Для вычисления определителя нам нужно перемножить диагональные элементы. Для этого составим отдельную функцию:-- Произведение диагональных элементов
proddiag :: Matrix -> Double
proddiag matrix = product $ map (\ (r,k) -> r !!k) $ zip matrix [0,1..]
Ну, и «бантик» — собственно вычисление определителя:-- Вычисление определителя
det :: Matrix -> Double
det matrix = proddiag $ triangle matrix 0
Проверим, как работает эта функция:main = print $ det [[1,2,3],[4,5,6],[7,8,-9]]
[1 of 1] Compiling Main ( main.hs, main.o )
Linking a.out ...
54.0
Спасибо тем, кто дочитал до конца!Вычисление определителей 2 – 4-го порядка
 д. – одно из основных заданий для первокурсников, которые получают образование на факультетах с математическим уклоном в обучении. Многие сервисы в интернете предлагают онлайн нахождения определителей и всего что касается матриц, однако мало программ – математических калькуляторов которые показывают ход решения. В конце статьи Вашему вниманию предлагается такой калькулятор, но об этом позже, а сейчас давайте рассмотрим несколько примеров нахождение определителя матрицы.
д. – одно из основных заданий для первокурсников, которые получают образование на факультетах с математическим уклоном в обучении. Многие сервисы в интернете предлагают онлайн нахождения определителей и всего что касается матриц, однако мало программ – математических калькуляторов которые показывают ход решения. В конце статьи Вашему вниманию предлагается такой калькулятор, но об этом позже, а сейчас давайте рассмотрим несколько примеров нахождение определителя матрицы.
 Это значительно упрощает вычисления.
Это значительно упрощает вычисления. Практикуйте и изучайте правила и через некоторое время у Вас будет выходить не хуже. До встречи в следующих уроках!
Практикуйте и изучайте правила и через некоторое время у Вас будет выходить не хуже. До встречи в следующих уроках!Как найти дискриминант матрицы
Страницы работы
Содержание работы
 Скопировать задание из таблицы 6 и вставить в среду MathCAD
Скопировать задание из таблицы 6 и вставить в среду MathCAD
Таблица 6

 Решить с применением операций над матрицами.
Решить с применением операций над матрицами. е. № варианта) плюс 1.
е. № варианта) плюс 1. Провести проверку правильности решения.
Провести проверку правильности решения. е. № варианта) плюс 1.
е. № варианта) плюс 1. Провести проверку правильности решения.
Провести проверку правильности решения.Определение
Обозначения
ight| = egin 1 & 4 & 2 \ 5 & 3 & 7 \ 6 & 2 & 1 end$Свойства определителя

$egin 1 & 4 & 2\ 0 & 0 & 0\ 3 & 9 & 5 end= 0$ или $egin1 & 4 & 0\ 4 & 2 & 0\ 3 & 9 & 0 end=0$
Если в матрице есть две одинаковых строки или два одинаковых столбца, то ее определитель равен 0.
$egin 1 & 4 & 2\ 1 & 4 & 2\ 3 & 9 & 5 end= 0$ или $egin1 & 4 & 1\ 4 & 2 & 4\ 3 & 9 & 3 end=0$
Если в матрице есть две пропорциональных строки или два пропорциональных столбца, то ее определитель равен 0.
$egin 1 & 4 & 2\ 2 & 8 & 4\ 3 & 9 & 5 end= 0$ (две первые строки пропорциональны)
или
$egin8 & 4 & 7\ 4 & 2 & 3\ 18 & 9 & 8 end=0$ (два первых столбца пропорциональны)
Если некоторая строка (столбец) является суммой или разностью других строк (столбцов), то определитель равен 0.
$egin 1 & 4 & 2\ 7 & 2 & 3\ 8 & 6 & 5 end= 0$ $R_ <1>+R_ <2>=R_<3>$ или
При вычислении определителя можно выносить общие множители целых строк или столбцов.
$egin 1 & 5\ 3 & 8 end$ $xlongequal+R_<2>> egin1>4 & 13\ 3 & 8 end$
Пример 18
$egin1 & 5\ 3 & 8 end$ $xlongequal+C_<2>> egin1>6 & 5\ 11 & 8 end$
При вычислении определителя можно прибавлять или отнимать строки и столбцы, умноженные на произвольный коэффициент .
$egin 1 & 5\ 3 & 8 end$ $xlongequal<5C_<1>-C_<2>> egin0 & 5\ 7 & 8 end$Минор матрицы
$A=egin 1 & 4 & 2 \ 5 & 3 & 7 \ 6 & 2 & 1 end$
$B=egin 2 & 5 & 1 & 3\ 4 & 1 & 7 & 9\ 6 & 8 & 3 & 2\ 7 & 8 & 1 & 4 end$ & . & a_<1,n>\ a_ <2,1>& a_ <2,2>& a_ <2,3>& . & . & a_<2,n>\ a_ <3,1>& a_ <3,2>& a_ <3,3>& . & . & a_<3,n>\ . & . & . & . & .& .\ a_ & a_ & a_ & . & . & a_ end$
& . & a_<1,n>\ a_ <2,1>& a_ <2,2>& a_ <2,3>& . & . & a_<2,n>\ a_ <3,1>& a_ <3,2>& a_ <3,3>& . & . & a_<3,n>\ . & . & . & . & .& .\ a_ & a_ & a_ & . & . & a_ end$
$B=egin 1 & 4 & 2\ 5 & 3 & 7\ 6 & 2 & 1\ end$ <7>cdotDelta_<2,5>= -Delta_ <2,5>$ соответствует элементу $a_<2,5>$.
<7>cdotDelta_<2,5>= -Delta_ <2,5>$ соответствует элементу $a_<2,5>$.Порядок определителя
$egin 1 & 4\ 6 & 2\ end$ (матрица имеет 2 строки и 2 столбца, так что порядок определителя равен 2)
$egin 4 & 7 & 9\ 6 & 3 & 2\ 7 & 1 & 4\ end$ (матрица имеет 3 строки и 3 столбца, так что порядок определителя равен 3)Вычисление определителя матрицы
ight| = egin a_ <1,1>& a_ <1,2>& a_ <1,3>& . & . & a_<1,n>\ a_ <2,1>& a_ <2,2>& a_ <2,3>& . & . & a_<2,n>\ a_ <3,1>& a_ <3,2>& a_ <3,3>& . & . & a_<3,n>\ . & . & . & . & .& .\ a_ & a_ & a_ & . & . & a_\ end$
& .& .\ a_ & a_ & a_ & . & . & a_\ end$Вычисление определителя матрицы 2×2
ight| =a_ <1.1>cdot a_<2,2>- a_ <1.2>cdot a_<2,1>$
$egin 2 & 5\ 3 & 8 end=2 cdot 8 – 3 cdot 5 = 16 -15 =1$
$egin -4 & 7\ -2 & 9 end=-4 cdot 9 – 7 cdot (-2) = -36 -(-14) =-36 + 14 = – 22$Вычисление определителя матрицы 3×3

$colorcdot a_<2,2>cdot a_<3,3>+ a_<2,1>cdot a_<3,2>cdot a_<1,3>+a_<3,1>cdot a_<1,2>cdot a_<2,3>>$
$A=egin 1 & 4 & 3 \ 2 & 1 & 5\ 3 & 2 & 1\ end$
$A=egin 3 & 5 & 1 \ 1 & 4 & 2\ 7 & 1 & 9\ end$ <2>end$
<2>end$Вычисление определителя матрицы 4×4
 Определитель будет равен произведению этого ненулевого элемента на его алгебраическое дополнение. В этом случае, алгебраическое дополнение – это определитель матрицы 3×3, который считается по уже известной формуле.
Определитель будет равен произведению этого ненулевого элемента на его алгебраическое дополнение. В этом случае, алгебраическое дополнение – это определитель матрицы 3×3, который считается по уже известной формуле.
$egin 1 & 3 & 9 & 2\ 5 & 8 & 4 & 3\ 0 & 0 & 0 & 0\ 2 & 3 & 1 & 8 end$
$egin 1 & 3 & 1 & 2\ 5 & 8 & 5 & 3\ 0 & 4 & 0 & 0\ 2 & 3 & 2 & 8 end$
Замечаем, что $C_<1>$ равно $C_<3>$, следовательно, определитель равен 0.
$egin 1 & 3 & 9 & 2\ 5 & 8 & 4 & 3\ 10 & 16 & 18 & 4\ 2 & 3 & 1 & 8 end$
Замечаем, что строки 2 и 3 пропорциональны друг другу, следовательно, определитель равен 0.
$egin color <4>& 3 & 2 & 2\ 0 & 1 & -3 & 3\ 0 & -1 & 3 & 3\ 0 & 3 & 1 & 1 end$ Алгебраические дополнения нулевых элементов считать не надо, так как их произведения на эти элементы все равно будут равны нулю.
Алгебраические дополнения нулевых элементов считать не надо, так как их произведения на эти элементы все равно будут равны нулю.
$=4(1cdot3cdot1 +(-1)cdot1cdot3+3cdot(-3)cdot3$ $-(3cdot3cdot3+3cdot1cdot1 +1cdot(-3)cdot(-1)))$ $=4(3-3-27-(27+3+3))=4cdot(-60)=-240$
$egin 4 & 3 & 2 & 2\ 0 & 1 & 0 & -2\ 1 & -1 & 3 & 3\ 2 & 3 & 1 & 1 end$
$=4cdot3cdot7 + 1cdot1cdot8 + 2cdot2cdot1$ $-(8cdot3cdot2 + 1cdot1cdot4 + 7cdot2cdot1) =$ $ 84 + 8 + 4- 48-4-14=30$
$egin 1 & -2 & 3 & 2\ 2 & 3 & 1 & -1\ 3 & 3 & 3 & 3\ -1 & 4 & 2 & 1\ end$
$3cdot egin 1 & -2 & 3 & 2\ 2 & 3 & 1 & -1\ 1 & 1 & 1 & 1\ -1 & 4 & 2 & 1\ end$ <4+1>cdot egin5 & -3 & -4\ 1 & -2 & -13\ 3 & -3 & -18 end=$ $(-1)cdot egin5 & -3 & -4\ 1 & -2 & -13\ 3 & -3 & -18 end$
<4+1>cdot egin5 & -3 & -4\ 1 & -2 & -13\ 3 & -3 & -18 end=$ $(-1)cdot egin5 & -3 & -4\ 1 & -2 & -13\ 3 & -3 & -18 end$
$ (-1)cdot(-1)cdot(-1)cdot egin 5 & 3 & 4\ 1 & 2 & 13\ 3 & 3 & 18 end=$ $(-1)cdot egin5 & 3 & 4\ 1 & 2 & 13\ 3 & 3 & 18 end=$ $-[5cdot 2cdot 18 + 1cdot 3cdot 4+ 3cdot 3cdot 13 – (4cdot 2cdot 3cdot + 13cdot 3cdot 5 + 18cdot 3cdot 1)]=$ $-(180+12+117-24-195-54)=36$
$egin 4 & 7 & 2 & 3\ 1 & 3 & 1 & 2\ 2 & 5 & 3 & 4\ 1 & 4 & 2 & 3 end$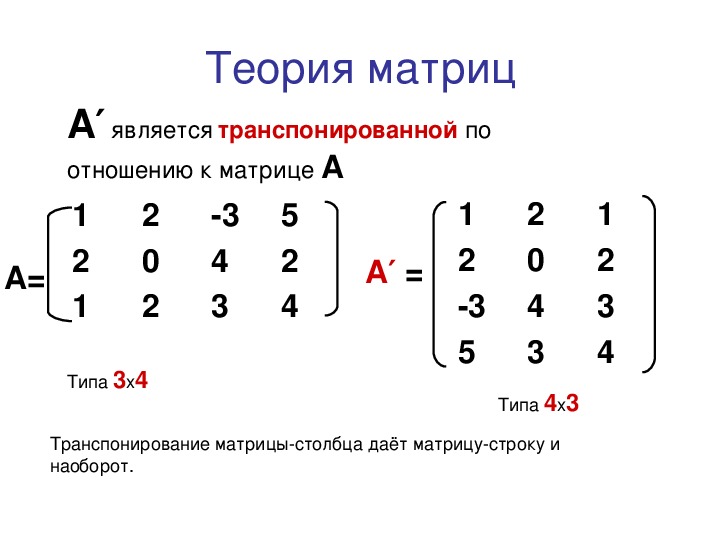
$ (-1)cdot(-1)cdot(-1)cdot egin 2 & 1 & -1\ 1 & 4 & 2\ 1 & 2 & 1 end=$ $(-1)cdot egin2 & 1 & -1\ 1 & 4 & 2\ 1 & 2 & 1 end=$ $-[2cdot 4cdot 1 + 1cdot 2cdot (-1)+ 1cdot 1cdot 2 – ((-1)cdot 4cdot 1 + 2cdot 2cdot 2 + 1cdot 1cdot 1)]=$ $-(8-2+2+4-8-1)=-3$
$egin 2 & 1 & 3 & 4\ 1 & 3 & 4 & 2\ 3 & 4 & 2 & 1\ 4 & 2 & 1 & 3\ end$МАТРИЦЫ, ОПРЕДЕЛИТЕЛИ, СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
1.
 Линейные системы и матрицы
Линейные системы и матрицы Глава 4. Матрицы. Лекция Основные понятия.
Аналитическая геометрия. Лекция 1.3
РАЗДЕЛ 1.
 Линейная алгебра.
Линейная алгебра. ПЕРЕСТАНОВКИ. Определение 1. Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,…, n в строчку одно за другим.
2 5 8 A = a) A = 2 3. ; b) B =
Глава 1.
 Начала линейной алгебры
Начала линейной алгебры Практикум по линейной алгебре
Примеры решений контрольных работ
Тема: Системы линейных уравнений
 Системы линейных однородных уравнений) Лектор Рожкова С.В. 0 г. Метод Гаусса (метод исключения неизвестных) Две
Системы линейных однородных уравнений) Лектор Рожкова С.В. 0 г. Метод Гаусса (метод исключения неизвестных) Две 1. Требования к знаниям, умениям, навыкам
МАТЕМАТИКА ЛИНЕЙНАЯ АЛГЕБРА
Теорема Кронекера-Капелли
ТЕКСТЫ ЛЕКЦИЙ по учебной дисциплине
Алгебра и аналитическая геометрия
ТИПОВЫЕ ЗАДАНИЯ ПО ВЫСШЕЙ МАТЕМАТИКЕ
 Г. Бочков Н.В. Воробьева Е.Ф. Шестакова ТИПОВЫЕ ЗАДАНИЯ ПО ВЫСШЕЙ МАТЕМАТИКЕ ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное
Г. Бочков Н.В. Воробьева Е.Ф. Шестакова ТИПОВЫЕ ЗАДАНИЯ ПО ВЫСШЕЙ МАТЕМАТИКЕ ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное 1. Линейная алгебра. a21x1 a12 x2 a13 x3 b2
Математика (БкПл-100)
АЛГЕБРА И ГЕОМЕТРИЯ. АЛГЕБРА МАТРИЦ
С.
 Ж. КАРАТАБАНОВА ЛИНЕЙНАЯ АЛГЕБРА
Ж. КАРАТАБАНОВА ЛИНЕЙНАЯ АЛГЕБРА ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
ЗАДАЧНИК-ПРАКТИКУМ ПО ЛИНЕЙНОЙ АЛГЕБРЕ
ЛЕКЦИИ ПО ВЫСШЕЙ АЛГЕБРЕ
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ.
 I часть
I частьМатрицы и определители Индивидуальные задания
Федеральное агентство по образованиюГосударственное образовательное учреждениевысшего профессионального образованияПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТМатрицы и определители
Индивидуальные заданияПособие разработано ст.
 преп. Зубко Т. Я., доцентом Седовой С. М., доцентом Сулавко Т. С..
преп. Зубко Т. Я., доцентом Седовой С. М., доцентом Сулавко Т. С..© 2007, каф. «Высшая математика» ПГТУ

 Единицу можно получить, умножив вторую строку на (), или поделив на (–5) , а затем во втором столбце ниже второго элемента получить нули с помощью преобразования в), при этом будут возникать дробные числа. Во избежание вычислений над дробями получим единицу во втором столбце второй строки иначе: ко второй строке прибавим третью строку, умноженную на (–1), результат запишем на месте второй строки. Далее, поделим третью строку на (–2), четвертую строку на (–1), имеем
Единицу можно получить, умножив вторую строку на (), или поделив на (–5) , а затем во втором столбце ниже второго элемента получить нули с помощью преобразования в), при этом будут возникать дробные числа. Во избежание вычислений над дробями получим единицу во втором столбце второй строки иначе: ко второй строке прибавим третью строку, умноженную на (–1), результат запишем на месте второй строки. Далее, поделим третью строку на (–2), четвертую строку на (–1), имеем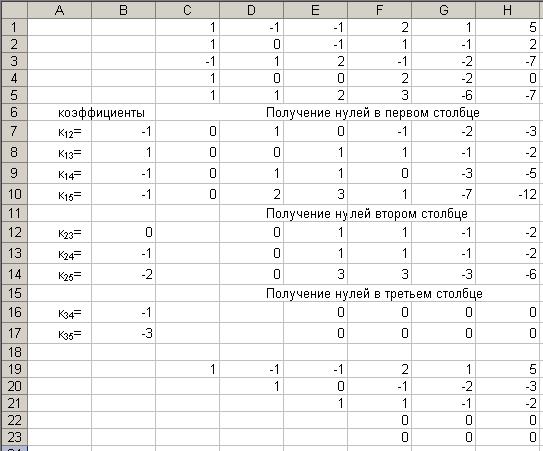

Исходное уравнение запишем в матричной форме
Исходное уравнение запишем в матричной форме
 Умножая справа обе части уравнения на , получим , где единичная матрица, или , или
Умножая справа обе части уравнения на , получим , где единичная матрица, или , или 2. 8.3.
2. 8.3. 1. 19.2. 19.3.
1. 19.2. 19.3. 6. .
6. . матриц – Создание нулевой матрицы посредством умножения матриц
матрицы – Создание нулевой матрицы посредством умножения матриц – Mathematics Stack Exchange Сеть обмена стеков
 Регистрация займет всего минуту.
Регистрация займет всего минуту. матрица.Используйте два разных ненулевых столбца для $ B $.
матрица.Используйте два разных ненулевых столбца для $ B $. Вы также получите два уравнения для $ b_ {21} $ и $ b_ {22} $; вы можете позволить $ b_ {22} $ быть вашим вторым любимым ненулевым числом и вычислить $ b_ {21} $. Тогда все готово.
Вы также получите два уравнения для $ b_ {21} $ и $ b_ {22} $; вы можете позволить $ b_ {22} $ быть вашим вторым любимым ненулевым числом и вычислить $ b_ {21} $. Тогда все готово. $$
Итак, $ \ mathbf {x} = \ left (\ begin {array} {c} r \\ s \ end {array} \ right) $ удовлетворяет $ A \ mathbf {x} = \ mathbf {0} $ тогда и только если $ r-2s = 0 $, тогда и только тогда, когда $ r = 2s $.
$$
Итак, $ \ mathbf {x} = \ left (\ begin {array} {c} r \\ s \ end {array} \ right) $ удовлетворяет $ A \ mathbf {x} = \ mathbf {0} $ тогда и только если $ r-2s = 0 $, тогда и только тогда, когда $ r = 2s $. (т.е. здесь вы можете быстро заметить, что в матрице $ A $ столбец 2 – это просто столбец 1, умноженный на -2)
(т.е. здесь вы можете быстро заметить, что в матрице $ A $ столбец 2 – это просто столбец 1, умноженный на -2)
линейная алгебра – что это значит, когда все значения строки в матрице равны 0?
 Однако мой профессор не привел теоремы, которые он обсуждал, в названиях классов, поэтому эта теорема верна, но я не совсем уверен, как она называется.{T}) $ соответственно. Вы узнаете больше об этом позже, когда будете определять, какая часть матрицы будет составлять базис (который представляет собой подпространство, которое является линейно независимыми векторами внутри него, а диапазон базиса – это все пространство). Нулевое пространство принимает ваш b-вектор равным 0 и отправляет x в 0. Это тривиально, если единственный вектор, который отправляется в 0, является нулевым вектором. Однако, если в вашей матрице есть строка со всеми нулями, это означает, что $ N (A) $ нетривиальна и есть свободная переменная.
Однако мой профессор не привел теоремы, которые он обсуждал, в названиях классов, поэтому эта теорема верна, но я не совсем уверен, как она называется.{T}) $ соответственно. Вы узнаете больше об этом позже, когда будете определять, какая часть матрицы будет составлять базис (который представляет собой подпространство, которое является линейно независимыми векторами внутри него, а диапазон базиса – это все пространство). Нулевое пространство принимает ваш b-вектор равным 0 и отправляет x в 0. Это тривиально, если единственный вектор, который отправляется в 0, является нулевым вектором. Однако, если в вашей матрице есть строка со всеми нулями, это означает, что $ N (A) $ нетривиальна и есть свободная переменная. Извините, я не мог понять, как набрать матрицу и векторы для более привлекательного просмотра.
Извините, я не мог понять, как набрать матрицу и векторы для более привлекательного просмотра. – эффективный способ найти все нули в матрице?
 Обоснование простое – если вы не посмотрите на все ячейки N 2 в матрице, то вы не сможете гарантировать, что нашли все нули и, возможно, в конечном итоге дадите неправильный ответ. Например, если я знаю, что вы просматриваете менее N 2 местоположений, я могу запустить ваш алгоритм на матрице и посмотреть, сколько нулей вы сообщаете.Затем я мог бы посмотреть места, к которым у вас не было доступа, заменить их все нулями и снова запустить ваш алгоритм. Поскольку ваш алгоритм не смотрит на эти места, он не может знать, что в них есть нули, и поэтому по крайней мере один из двух прогонов алгоритма даст неправильный ответ.
Обоснование простое – если вы не посмотрите на все ячейки N 2 в матрице, то вы не сможете гарантировать, что нашли все нули и, возможно, в конечном итоге дадите неправильный ответ. Например, если я знаю, что вы просматриваете менее N 2 местоположений, я могу запустить ваш алгоритм на матрице и посмотреть, сколько нулей вы сообщаете.Затем я мог бы посмотреть места, к которым у вас не было доступа, заменить их все нулями и снова запустить ваш алгоритм. Поскольку ваш алгоритм не смотрит на эти места, он не может знать, что в них есть нули, и поэтому по крайней мере один из двух прогонов алгоритма даст неправильный ответ.
Определение нулевой матрицы
Нулевая матрица
Что такое нулевая матрица?
 Для нулевой матрицы все упрощается, поскольку вам действительно не нужно беспокоиться о числах, содержащихся в прямоугольном массиве этой нотации, как и говорит название, есть только одно число, которое может содержаться внутри этих матриц, поскольку все его записи.
Для нулевой матрицы все упрощается, поскольку вам действительно не нужно беспокоиться о числах, содержащихся в прямоугольном массиве этой нотации, как и говорит название, есть только одно число, которое может содержаться внутри этих матриц, поскольку все его записи. Таким образом, у вас может быть нулевая матрица с любым количеством строк или столбцов, но помните, что для любого заданного размера можно получить только одну нулевую матрицу (что имеет смысл, поскольку есть только один способ иметь все нули в качестве записей в матрица определенного размера или размерной комбинации).
Таким образом, у вас может быть нулевая матрица с любым количеством строк или столбцов, но помните, что для любого заданного размера можно получить только одну нулевую матрицу (что имеет смысл, поскольку есть только один способ иметь все нули в качестве записей в матрица определенного размера или размерной комбинации).
Помните, что ранг матрицы соответствует максимальному количеству линейно независимых столбцов внутри матрицы. Мы можем определить ранг матрицы, вычислив ее форму эшелона строк, а затем подсчитав левые ненулевые строки, цель которых состоит в том, чтобы найти размерность векторного пространства для рассматриваемой матрицы.
Итак, если мы говорим о разрешимой системе линейных уравнений, преобразованной в матричную запись, определение ранга такой матрицы позволяет нам увидеть максимальное количество независимых переменных и, таким образом, размерные плоскости, для которых система может быть представлена графически.
Как же тогда получить это для нулевой матрицы? Для этого нам сначала нужно спросить себя, являются ли векторы внутри нулевой матрицы линейно независимыми друг от друга? Не совсем, все они одинаковые и все нулевые векторы.Так случилось ли, что они представляют собой какую-либо плоскость измерения? Нет. Можете ли вы на самом деле свести его к форме эшелона строк? Нет. Таким образом, если задуматься, нулевая матрица содержит нулевое количество линейно независимых столбцов и нулевое количество ненулевых строк, и поэтому наш окончательный вывод состоит в том, что ранг нулевой матрицы должен быть равен нулю.
Таким образом, если задуматься, нулевая матрица содержит нулевое количество линейно независимых столбцов и нулевое количество ненулевых строк, и поэтому наш окончательный вывод состоит в том, что ранг нулевой матрицы должен быть равен нулю.
Если вы подумаете об этой идее более глубоко, вы поймете, что любая ненулевая матрица не может иметь ранг меньше единицы, другими словами, чтобы любая матрица имела ранг нуля, она должна содержать все нулевые элементы внутри, Итак, мы пришли к выводу, что только нулевые матрицы имеют нулевой ранг.
Для практических целей мы оставим полное объяснение того, как узнать, является ли матрица обратимой или нет, и как инвертировать те, которые для наших следующих уроков будут говорить об обратимой матрице 2×2. А пока прямо скажем, что нулевая матрица необратима.
Есть несколько правил, которые могут доказать это, например, ее определитель равен нулю, а если матрица квадратная, то ее ранг меньше, чем ее размерность. Опять же, мы поговорим об этом немного больше в наших следующих уроках об инвертировании матриц.Но давайте задумаемся над этой идеей на минуту: если мы упомянули ранее, что для любой матрицы определенного размера или размеров существует только одна конфигурация, в которой все ее элементы равны нулю, поэтому не может быть другого способа, которым вы можете переставить нули, чтобы получить обратную матрицу тех же размеров. Если все записи одинаковы, матрица будет точно такой же, нет «обратного» или «противоположного» от этого.
Опять же, мы поговорим об этом немного больше в наших следующих уроках об инвертировании матриц.Но давайте задумаемся над этой идеей на минуту: если мы упомянули ранее, что для любой матрицы определенного размера или размеров существует только одна конфигурация, в которой все ее элементы равны нулю, поэтому не может быть другого способа, которым вы можете переставить нули, чтобы получить обратную матрицу тех же размеров. Если все записи одинаковы, матрица будет точно такой же, нет «обратного» или «противоположного» от этого.
Мы все еще немного далеки от нашего урока по диагонализации, но пока мы можем сказать, что да, нулевая матрица диагонализуема, поскольку ее нулевые элементы могут легко содержать линейно независимые собственные векторы.Подробнее о диагонализации в последующих уроках. Пустое пространство нулевой матрицы

Если наша рассматриваемая матрица представляет собой матрицу с именем A, которая умножается на вектор u, мы говорим, что u находится в нулевом пространстве A, если выполняется следующее условие:
Уравнение 3: Условие для того, чтобы вектор u был частью нулевого пространства A
Ну, любая нулевая матрица, умноженная на вектор, будет иметь в результате нулевой вектор. То есть, если размеры матрицы и вектора соответствуют правилам умножения матриц, другими словами, если умножение может быть определено, то результатом обязательно будет нулевой вектор.
Причина этого в том, что, учитывая, что нулевая матрица содержит только нулевые элементы, любая запись, умноженная на любой элемент в векторе, приведет к нулевому компоненту, который будет частью результирующего вектора.Итак, условие для нулевого пространства выполнено, и это приводит нас к чему-то важному, о котором мы до сих пор не упоминали: нулевая матрица – это то, что мы называем нулевой матрицей, и это можно ясно увидеть, следуя процессу, описанному выше, поскольку нет независимо от того, какой вектор к нему умножается, результат всегда будет содержать только нулевые элементы. Сложение, вычитание и скалярное умножение нулевой матрицы
 Это довольно простая операция, поэтому давайте начнем с добавления следующего вида:
Это довольно простая операция, поэтому давайте начнем с добавления следующего вида:
Пример 2
Чтобы продолжить наш следующий пример, мы работаем над вычитанием матриц, где нулевая матрица вычитается из другой матрицы равного размера. Уравнение 6: вычитание с нулевой матрицей
Операция следует тем же принципам, что и сложение в примере 1. Таким образом, решая эту операцию, мы получаем: Уравнение 7: Решение вычитания с нулевой матрицей
Как мы уже упоминали в нашем уроке о сложении и вычитании матриц, хотя сложение матриц является коммутативным (вы можете изменить порядок матриц, и результат не изменится), вычитания матриц нет, и это хорошо видно на этом примере.
Если бы у вас была нулевая матрица справа от знака минус в уравнении 6, то результат был бы равен другой матрице, участвующей в операции. Но поскольку нулевая матрица была первой, результат операции оказывается отрицательным по сравнению с ненулевой матрицей.
Пример 3
В этом примере мы добавляем следующие две следующие матрицы: Уравнение 8: сложение противоположных матриц
Заметили что-то особенное из приведенных выше матриц? Они представляют собой отрицательные матрицы друг друга, или, другими словами, если вы возьмете первую матрицу и умножите ее на отрицательную, вы получите вторую матрицу.Следовательно, эта конкретная операция эквивалентна вычитанию матрицы из самой себя. Чтобы показать это, давайте определим первую матрицу как A: Уравнение 9: Матрица A
Затем мы записываем эквивалентную операцию, которую мы объяснили минуту назад: Уравнение 10: Преобразование сложения матриц в вычитание
Обратите внимание, что скалярное умножение минус один на A было упрощено, чтобы просто записать его как вычитание двух матриц, которые к настоящему времени являются A, и поэтому то, что мы имеем в уравнении 10, можно было бы просто записать как: A – A что, очевидно, имеет нулевой результат. Но поскольку здесь речь идет не только о числах, а о матрицах, нулевой результат должен быть массивом тех же размеров, что и A, и поэтому: Уравнение 11: вычитание самой матрицы
Обратите внимание, что субиндексы в правой части уравнения обозначают размеры нулевой матрицы, что означает, что результирующая нулевая матрица должна иметь «m из A» (такое же количество строк, что и A) и «N из A». “(такое же количество столбцов, как у A).
Давайте получим результат двумя разными способами: добавлением исходной матрицы, показанным в уравнении 8, и вычитанием матрицы, найденным в конце уравнения 10, чтобы показать, как мы получим тот же результат: нулевую матрицу, чтобы доказать уравнение 11.Уравнение 12: Окончательное решение, полученное двумя разными способами
Вывод из этой проблемы состоит в том, что всякий раз, когда вы вычитаете матрицу из самой себя, вы получаете нулевую матрицу с теми же размерами, что и ваши исходные матрицы. Пример 4
Но поскольку здесь речь идет не только о числах, а о матрицах, нулевой результат должен быть массивом тех же размеров, что и A, и поэтому: Уравнение 11: вычитание самой матрицы
Обратите внимание, что субиндексы в правой части уравнения обозначают размеры нулевой матрицы, что означает, что результирующая нулевая матрица должна иметь «m из A» (такое же количество строк, что и A) и «N из A». “(такое же количество столбцов, как у A).
Давайте получим результат двумя разными способами: добавлением исходной матрицы, показанным в уравнении 8, и вычитанием матрицы, найденным в конце уравнения 10, чтобы показать, как мы получим тот же результат: нулевую матрицу, чтобы доказать уравнение 11.Уравнение 12: Окончательное решение, полученное двумя разными способами
Вывод из этой проблемы состоит в том, что всякий раз, когда вы вычитаете матрицу из самой себя, вы получаете нулевую матрицу с теми же размерами, что и ваши исходные матрицы. Пример 4
В этом примере мы увидим вычитание двух равных матриц, которые оказываются векторами-столбцами. Уравнение 13: вычитание двух равных векторов-столбцов
Здесь снова используется принцип, объясненный в предыдущем упражнении: при вычитании двух равных матриц (которые в данном случае оказываются двумя векторами-столбцами, поскольку каждая из матриц состоит только из одного столбца), результатом является нулевая матрица того же размера. как оригинальные: Уравнение 14: Решение вычитания двух равных векторов-столбцов Пример 5
Уравнение 13: вычитание двух равных векторов-столбцов
Здесь снова используется принцип, объясненный в предыдущем упражнении: при вычитании двух равных матриц (которые в данном случае оказываются двумя векторами-столбцами, поскольку каждая из матриц состоит только из одного столбца), результатом является нулевая матрица того же размера. как оригинальные: Уравнение 14: Решение вычитания двух равных векторов-столбцов Пример 5
Вычислите следующее скалярное умножение матрицы: Уравнение 15: Скалярное умножение матрицы на ноль
В этом конкретном случае должно быть ясно, что результат будет равен нулю, поскольку все, что вы умножаете на ноль, приведет к нулю.Интересная часть здесь исходит из того факта, что вы умножаете матрицу, и поэтому каждый элемент будет умножен на скаляр снаружи, в данном случае ноль, и что произойдет, вместо того, чтобы получить просто ноль в результате, это умножение даст матрицу, в которой все ее элементы равны нулю, и, таким образом, результатом будет нулевая матрица: Уравнение 16: Результат скалярного умножения матрицы на ноль
Что также можно записать как: Уравнение 17: нулевая матрица с размерами 3 x 2 Пример 6
Вычислить следующее скалярное умножение, содержащее нулевую матрицу Уравнение 18: Скалярное умножение нулевой матрицы
Как и в случае с прошлыми проблемами, мы можем интуитивно записать ответ в виде нулевой матрицы, поскольку каждый элемент в матрице равен нулю, не имеет значения, умножаете ли вы на них любой другой скаляр, результат всегда будет равен нулю в каждом дело. Чтобы расширить операцию, вот как это происходит: Уравнение 19: Результат скалярного умножения нулевой матрицы Пример 7
Чтобы расширить операцию, вот как это происходит: Уравнение 19: Результат скалярного умножения нулевой матрицы Пример 7
Давайте изменим режим наших задач, теперь вам даны матрицы, показанные ниже: Уравнение 20: матрицы B и 0
Имея это в виду, верны ли следующие матричные уравнения? Если нет, поправьте их.
Случаи e) и f) приводят к важному выводу: умножение матриц не коммутативно, если одна из двух матриц не является нулевой матрицей. Независимо от того, в каком порядке вы умножаете элементы каждой матрицы, одна из них имеет все нулевые элементы, производящие умножения, которые все приводят к нулю.
Этот случай соответствует тому, что мы видели в примере 1: наличие двух матриц с одинаковыми размерами, одна из них нулевая матрица, а другая ненулевая матрица, когда вы складываете их вместе, результат равна ненулевой матрице, поскольку нулевая матрица ничего не вносит при добавлении каждого соответствующего элемента в две матрицы, участвующие в операции.Следовательно, это выражение ПРАВИЛЬНО.
В этом случае мы можем взглянуть на пример 2 и понять, что это выражение НЕПРАВИЛЬНО.
При вычитании матрицы из нулевой матрицы той же размерности результат равен отрицательному значению ненулевой матрицы.
Следовательно, правильным выражением будет 0 – B = -B
Это выражение ПРАВИЛЬНО и соответствует тому, что мы видели в примерах 3 и 4: если вы вычитаете матрицу сама по себе, это приводит к записи путем вычитания записи самого числа, и, таким образом, результирующей матрицы в котором все его входные элементы будут равны нулю (нулевая матрица 0).
Вышеприведенное выражение НЕПРАВИЛЬНО. При добавлении нуля плюс ноль результат всегда равен нулю. Это случай для каждого элемента результирующей матрицы при добавлении нулевой матрицы и другой равной нулевой матрицы, результатом будет равная нулевая матрица. Таким образом, правильное выражение: 0 + 0 = 0.
Это выражение ПРАВИЛЬНО. Результатом умножения каждого элемента на элемент в результате этой операции будет ноль, в результате чего будет получена матрица с нулевыми элементами, то есть нулевая матрица 0.
Как и в случае e), это выражение ПРАВИЛЬНО, поскольку каждый соответствующий элемент из ненулевой матрицы будет умножен на ноль из нулевой матрицы.
Как упоминалось ранее, нулевая матрица – это очень конкретная концепция, поэтому на этом уроке действительно нечего сказать о ней, но это не значит, что она не будет использоваться во многих областях линейной алгебры. Так же, как число ноль в математике, нулевая матрица предоставляет нам представление нулевого пространства, которое мы все еще можем характеризовать, другими словами, она может содержать нулевые элементы, но ее качества остаются там, чтобы мы могли использовать их по своему усмотрению с другими матрицами.
Чтобы завершить наш урок, мы просто предоставим две дополнительные ссылки на случай, если вы захотите посетить их и посмотреть, как они определяют нулевую матрицу, и предоставим простой пример добавления с нулевой матрицей. На сегодня все, до встречи на следующем уроке!
На сегодня все, до встречи на следующем уроке! Матрицы и системы уравнений
6.1 – Матрицы и системы уравнений Определение матрицы
Терминология

Преобразование систем линейных уравнений в
Матрицы
х + у - г = 1
3х - 2у + г = 3
4x + y - 2z = 9
х y z справа 1 1 –1 1 3 -2 1 3 4 1 -2 9 Элементарные операции со строками
 Если матрица является расширенной матрицей, построенной из системы линейных
уравнений, то эквивалентная строка матрица будет иметь то же решение, что и исходная матрица.
Если матрица является расширенной матрицей, построенной из системы линейных
уравнений, то эквивалентная строка матрица будет иметь то же решение, что и исходная матрица. Формы рядов-эшелонов и сокращенных рядов-эшелонов
 Несложно решить систему линейных уравнений
когда матрицы находятся в одной из этих форм.
Несложно решить систему линейных уравнений
когда матрицы находятся в одной из этих форм. Форма рядного эшелона
Банкноты Форма Row-Echelon уменьшенная

Банкноты Исключение по Гауссу
Гаусс-Джордан Ликвидация
Поворотный
Типы решений

х y z справа 1 0 0 3 0 1 0 1 0 0 1 2 
х y z справа 1 0 3 4 0 1 -2 3 0 0 0 0  Решение относительно x дает x = 4 – 3z.
Решение относительно x дает x = 4 – 3z. х y z справа 1 0 3 4 0 1 -2 3 0 0 0 2  Вы можете записать это как нулевой набор Ø,
пустой набор {} или нет решения.
Вы можете записать это как нулевой набор Ø,
пустой набор {} или нет решения. Создание матрицы нулей в R
 рядов
рядов
R
mat = матрица 2, 3 печать (мат)
Метод replicate () используется для создания копии второго аргумента метода vec путем добавления его n раз.Он повторно применяет один и тот же указанный вектор для формирования 2D-матрицы. Метод принадлежит к набору функций apply, используемых в R, и использует его в качестве родительского или базового класса. Второй аргумент указывается заключением в числовое (целое) значение. Также числовой метод создает реальный вектор указанной длины. Все элементы вектора равны 0 в числовом приложении.
Также числовой метод создает реальный вектор указанной длины. Все элементы вектора равны 0 в числовом приложении.
Синтаксис: replicate (n, numeric (m))
Параметр:
- n – нет.рядов
- числовое (м) – шт. столбцов в матрице, заданной как числовой параметр
Тип возвращаемого значения: матрица или скаляр нулей
Пример:
R
|
|
Выход
[1] «Матрица:«
[1] 0 0 0 0 0 0 0 0 0
Использование Numeric () и integer ()
Есть несколько других методов, таких как numeric () или integer (), которые можно использовать для создания вектора нулей.Все эти методы принимают аргумент длины, указывающий количество нулей для объединения. Поведение методов integer () и numeric () практически одинаково.
Поведение методов integer () и numeric () практически одинаково.
Синтаксис:
числовой (размер)
целочисленный (размер)
Пример:
R
целое число |
Выход
[1] «Матрица с использованием метода numeric ():»
[1] 0 0 0 0 0 0 0 0
[1] «Матрица с использованием метода integer () : ”
[1] 0 0 0 0 0
Нулевая матрица - обзор
5.2 Статистический вывод для RSS
Предположим, что необходимо измерить общее количество n единиц из основной совокупности по интересующей переменной. Пусть n наборов единиц, каждый размером k, случайным образом выбирается из совокупности с использованием метода простой случайной выборки (SRS). Единицы каждого набора ранжируются любым способом, кроме фактического количественного определения переменной. Наконец, по переменной измеряется одна единица в каждом упорядоченном наборе с заранее заданным рангом. Пусть mr будет количеством измерений на блоках ранга r, r = 1,…, k, таких, что n = ∑r = 1kmr.Пусть X (r) j обозначает измерение на j-й единице измерения с рангом r. Это приводит к URSS размера n из основной популяции как {X (r) j; r = 1,…, k, j = 1,…, mr}. Когда mr = m, r = 1,…, k, URSS сводится к сбалансированному RSS. Стоит отметить, что в схемах выборки ранжированных наборов X (1) j,…, X (k) j являются статистикой независимого порядка (поскольку они получены из независимых наборов), и каждый X (r) j предоставляет информацию о различных слой населения. Структуру URSS можно представить следующим образом:
Пусть n наборов единиц, каждый размером k, случайным образом выбирается из совокупности с использованием метода простой случайной выборки (SRS). Единицы каждого набора ранжируются любым способом, кроме фактического количественного определения переменной. Наконец, по переменной измеряется одна единица в каждом упорядоченном наборе с заранее заданным рангом. Пусть mr будет количеством измерений на блоках ранга r, r = 1,…, k, таких, что n = ∑r = 1kmr.Пусть X (r) j обозначает измерение на j-й единице измерения с рангом r. Это приводит к URSS размера n из основной популяции как {X (r) j; r = 1,…, k, j = 1,…, mr}. Когда mr = m, r = 1,…, k, URSS сводится к сбалансированному RSS. Стоит отметить, что в схемах выборки ранжированных наборов X (1) j,…, X (k) j являются статистикой независимого порядка (поскольку они получены из независимых наборов), и каждый X (r) j предоставляет информацию о различных слой населения. Структуру URSS можно представить следующим образом:
Xr = {X (r) 1, X (r) 2,…, X (r) mr} ~ i. i.d.F (r), r = 1,…, k1,
i.d.F (r), r = 1,…, k1,
где F (r) - функция распределения (df) статистики r-го порядка. Второй образец может быть создан с использованием той же процедуры. Мы предполагаем, что вторая выборка сгенерирована с использованием k2, которое может отличаться от k = k1
Yr = {Y (r) 1, Y (r) 2,…, Y (r) mr} ~ iidG (r), r = 1,…, к2.
Интересно проверить H0: F (x) = dG (x − Δ). В частности, нас интересует нулевая гипотеза H0: μx = μy + Δ по сравнению с H0: μx ≠ μy + Δ. Обычно используются два выборочных теста, чтобы определить, происходят ли образцы из одного и того же неизвестного распределения.В нашей настройке мы предполагаем, что X и Y собраны с разными размерами рангов. Следовательно, даже при одних и тех же родительских распределениях дисперсия оценки не будет одинаковой.
Следующее предложение может быть использовано для установления асимптотической нормальности статистики при нулевой гипотезе.
Утверждение 1
Пусть F обозначает cdf члена семейства с ∫x2dF (x) <∞ и Fˆ (r) - эмпирическая функция распределения (edf) r-й строки. .Если ϑi = (X¯ (i) −μ (i)) , то (ϑ1,…, ϑk) сходится по распределению к многомерному нормальному распределению с нулевым средним вектором и ковариационной матрицей diag (σ (1) 2 / m1,…, σ (k) 2 / mk) , где σ (i) 2 = ∫ (x − μ (i)) 2dF (i) (x) и μ (i) = ∫xdF ( i) (x).
.Если ϑi = (X¯ (i) −μ (i)) , то (ϑ1,…, ϑk) сходится по распределению к многомерному нормальному распределению с нулевым средним вектором и ковариационной матрицей diag (σ (1) 2 / m1,…, σ (k) 2 / mk) , где σ (i) 2 = ∫ (x − μ (i)) 2dF (i) (x) и μ (i) = ∫xdF ( i) (x).
Предложение 1 предлагает следующую статистику для проверки H0: µ = µ0,
Z = 1k∑r = 1kX¯ (r) −µ0σˆ → dN (0,1),
, где σˆ2 - оценка плагина для V (1k∑r = 1kX¯ (r)),
σˆ2 = 1k2∑r = 1kσˆ (r) 2mr,
и σ (r) 2 - оценка V (X¯ (r)).Используя центральную предельную теорему, получаем доверительный интервал, где
P (μ∈ (X¯ + tα / 2, n − 1σn, X¯ + t1 − α / 2, n − 1σn)) ≈1 − α.
Для оценки дисперсии среднего требуется σ (r) 2. Следовательно, необходимо, чтобы mr≥2. Оценка дисперсии для небольших размеров выборки была бы очень неточной, что наводит на мысль о том, что основная статистика может быть ненадежной. В разделе 5.4 мы покажем, что параметрическая статистика очень консервативна. Bootstrap предоставляет непараметрическую альтернативу для оценки дисперсии.Метод начальной загрузки может использоваться для получения выборочного распределения интересующей статистики и позволяет оценить стандартную ошибку любого четко определенного функционала. Следовательно, бутстрап позволяет нам делать выводы, когда точное или асимптотическое распределение интересующей статистики недоступно. Процедура генерации повторной выборки для вычисления дисперсии обсуждается в разделе 5.3.
Bootstrap предоставляет непараметрическую альтернативу для оценки дисперсии.Метод начальной загрузки может использоваться для получения выборочного распределения интересующей статистики и позволяет оценить стандартную ошибку любого четко определенного функционала. Следовательно, бутстрап позволяет нам делать выводы, когда точное или асимптотическое распределение интересующей статистики недоступно. Процедура генерации повторной выборки для вычисления дисперсии обсуждается в разделе 5.3.
Утверждение 1 можно использовать для получения тестовой статистики для двух выборок {X1,…, Xk1} и {Y1,…, Yk2}.Можно показать, что
T (X, Y) = (1k1∑r = 1k1X¯ (r) −1k2∑r = 1k2Y¯ (r)) - (μ1 − μ2) σˆ → dN (0,1),
, где
σˆ2 = 1k12∑r1 = 1k1σˆ (r1) 2mr1 + 1k22∑r2 = 1k2σˆ (r2) 2mr2.
Мы можем рассмотреть параметрический статистический вывод для асимметричного распределения: пусть X1,…, Xn равны i.i.d. случайная величина со средним значением μ и конечной дисперсией σ2. Поскольку характеристическая функция Sn сходится к e − t2 / 2, характеристическая функция стандартной нормали nSn = n (μ − μ) / σ асимптотически нормально распределена с нулевым средним и единичной дисперсией. Чтобы учесть асимметрию выборки, следующее предложение получает разложение Эджворта для nSn.
Чтобы учесть асимметрию выборки, следующее предложение получает разложение Эджворта для nSn.
Предложение 2
Если EYi6 <∞ и условие Крамера выполняется, асимптотическая функция распределения nSn равна
P (nSn≤x) = Φ (x) + 1nγ (ax2 + b) ϕ (x) + O (n − 1),
где a и b - известные константы, γ - оцениваемая константа, а Φ и ϕ обозначают стандартное нормальное распределение и функции плотности соответственно.Холл (1992) предложил две функции:
S1 (t) = t + aγˆt2 + 13a2γˆ2t3 + n − 1bγˆ, S2 (t) = (2an − 12γˆ) −1 {exp (2an − 12γˆt) −1} + n − 1bγˆ,
, где a = 1/3 и b = 1/6.Чжоу и Динь (2005) предложили
S3 (t) = t + t2 + 13t3 + n − 1bγˆ.
Используя Si (t), для i = 1,2,3, можно построить новые доверительные интервалы для μ как
(μˆ − Si (n − 1 / 2t1 − α / 2, n − 1) σˆ, μˆ− Si (n − 1 / 2tα / 2, n − 1) σˆ),
, где t1 − α / 2, n − 1 - квартиль 1 − α / 2 распределения t. Однако использование асимптотического распределения выборки делает вывод менее надежным, особенно для параметрических методов.


 Первый аргумент определяет вектор, который будет повторяться и складываться вместе y раз, в данном случае это 0. Мы можем указать 0L вместо 0.
Первый аргумент определяет вектор, который будет повторяться и складываться вместе y раз, в данном случае это 0. Мы можем указать 0L вместо 0.