Как в уме быстро умножать: Эта инструкция научит вас умножать тысячи в уме. Сколько будет 5185 на 8018? - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Умножение на 1,5. Умножение дробей на целое число.

Альфашкола
Статьи
Как быстро умножить число на 1,5

Для того чтобы быстро умножить на \(1,5\) надо разложить число в виде суммы \(1\) и \(0,5\). Существует правило быстрого умножения на \(1,5\):

Пример 1. Умножьте \(18\) на \(1,5\).

Решение: \(18*1,5=18*1+\frac{18}{2}=18+9=27\)

Ответ: \(27\).

Пример 2. Умножьте \(\frac{1}{2}\) на \(2,5\).

Решение: \(\frac{1}{2}*1,5=\frac{1}{2}+\frac{1}{2*2}=\frac{2}{4}+\frac{1}{4}=\frac{3}{4}=0,75\)

Ответ: \(0,75\).

Пример 3. Умножьте \(52\) на \(1,5\).

Решение: \(52*1,5=52*1+\frac{52}{2}=52+26=78\)

Ответ: \(78\).

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы “Альфа”. Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку “Записаться” принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Оксана Александровна Анцыферова

Репетитор по математике

Стаж (лет)

Образование:

Саратовский государственный университет им. Н. Г. Чернышевского

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Альфинур Самерхановна Мурзабаева

Репетитор по математике

Стаж (лет)

Образование:

Стерлитамакская государственная педагогическая академия

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Тамара Анатольевна Меркулова

Репетитор по математике

Стаж (лет)

Образование:

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

Математика
Репетитор по физике
Репетитор по химии
Репетитор по русскому языку

Репетитор по английскому языку
Репетитор по обществознанию
Репетитор по истории России
Репетитор по биологии
Репетитор по географии
Репетитор по информатике

Специализации

Подготовка к ОГЭ по математике

Репетитор по геометрии
Подготовка к ЕГЭ по математике (профильный уровень)
Репетитор по английскому языку для подготовки к ОГЭ
Подготовка к олимпиадам по английскому языку
Английский язык для начинающих
Репетитор по разговорному английскому
Репетитор для подготовки к ОГЭ по истории

ВПР по математике
Репетитор по географии для подготовки к ОГЭ

Как научиться быстро считать в уме?

Если рассуждать о том, что именно из школьного курса математики пригодится нам в дальнейшей жизни, то можно смело отметить устный счёт.

Казалось бы, зачем он нам нужен? Ведь сейчас можно включить калькулятор на любом устройстве и быстренько всё вычислить, а учителя продолжают требовать считать самостоятельно. Зачем?

Дело в том, что счёт в уме тренирует память, а также активнее многих других практик способствует тренировке серого вещества, а значит и способности анализировать самостоятельно, думать, делать выводы и решать сложные жизненные задачи.

В Японии существует целая система развития памяти, основанная именно на устном счёте, и сейчас эта система признана всем миром. С годами человек перестаёт быстро запоминать, и память нуждается в тренировке.

Но устный счёт нужен не только поэтому. Кроме тренировки для мозга, это ещё и хороший практический навык, который до сих пор бывает нужен всем взрослым. Спланировать траты, посчитать сдачу наличными, узнать разницу в возрасте или быстро сориентироваться, на сколько частей нужно поделить торт – в таких ситуациях обычно редко есть время доставать калькулятор, и чаще до сих пор всё-таки быстрее посчитать в уме.

Но у многих с этим навыком есть трудности.

Перед тем, как мы расскажем о секретах быстрого счёта, хочется отметить, что это просто навык. А это значит, что его можно развить у любого человека – и у способного к математике, и у того, кому она даётся сложнее.

Для того, чтобы научиться складывать, вычитать, умножать или делить быстро, необходимо каждое из этих действий привести к определённой системе, которая будет работать чётко всегда, в любых случаях.

Во время счёта у нас всегда есть одна очень важная проблема – переход через 10. Об этом нужно помнить.

Давайте рассмотрим удобную систему сложения.

Сложение

Давайте решим пример: 775+821

Для того, чтобы легко сложить эти числа, нам нужно разложить каждое число на сотни, десятки и единицы:

775 – это 700+70+5

821 – это 800+20+1

Дальше мы складываем отдельно сотни, отдельно десятки и отдельно единицы друг с другом:

775+821= (700+800)+(70+20)+(5+1)= 1500+90+6= 1596

Безусловно, для того, чтобы делать это быстро, нужно хорошо знать таблицу сложения и уметь складывать и вычитать числа до 10.

Вычитание

Кажется, что вычитание всегда даётся нам сложнее, но на самом деле механизм проще, чем в сложении.

При вычитании раскладывать на части нужно только то число, которое мы вычитаем.

Например:

348 — 155

155 – это 100+50+5

А теперь считаем:

348 – 100 – 50 – 5 = 248 – 50 – 5 = 198 – 5 = 193

Особого внимания требуют вычисления с цифрой «9». Таблицу сложения и вычитания с девятками нужно выучить наизусть.

Интересно!

15 + 9 = 24

При сложении числа с девяткой последняя цифра в сумме слагаемых всегда будет уменьшаться на «1». В этом примере цифра «5» из первого слагаемого изменилась на «4» в ответе.

33 – 9 = 24

При вычитании с «9» последняя цифра в разности всегда будет увеличиваться на «1». В данном случае цифра «3» из уменьшаемого изменилась на «4» в ответе.

Умножение

Нет лучшего способа умножать простые числа в уме, кроме как выучить таблицу умножения. Здесь всё довольно скучно и примитивно. Но! Зато сколько возможностей открывается, когда мы умножаем наизусть, даже представить сложно!

Давайте для начала разберёмся с двузначными числами:

28*8

Чтобы быстро умножить на «8», нам нужно разложить «28»

28 – это 20 и 8.

28*8= 20*8 + 8*8 = 160 + 64 = 224

28*38

Сначала раскладываем оба числа:

28 – это 20 и 8;

38 – это 30 и 8.

28*38 = 20*30 + 20*8 + 8*30 + 8*8 = 600 + 160 + 240 + 64 = 1064

Интересно!

Умножить число на «11» намного проще, чем на другие множители.

Здесь достаточно просто сложить цифры умножаемого числа, и вписать сумму между этими цифрами.

Например: 35 * 11 = 3(3+5)5 = 385

А если в сумме получается больше 10, то первая цифра в ответе увеличивается на 1:

57 * 11

5 + 7 = 12 – число больше 10. Значит «5» увеличивается на «1», и получается «6». И дальше записываем только вторую цифру от «12», то есть «2».

57 * 11 = (5+1)(2)7 = 627

Деление

Чтобы научиться делить сложные числа в уме, важно очень хорошо знать таблицу умножения.

Давайте рассмотрим деление на однозначное число:

6728 : 6

В этом случаем на важно найти в многозначном числе самое ближайшее, что делится на «6» – это «6600».

Раскладываем: 6728 = 6600 + 128

6728 : 6 = 6600 : 6 + 128 : 6 = 1100 + 128 : 6

128 – это 120 и 8

120 : 6 = 20

8 : 6 = 1, (3)

У нас есть ответы по частям, теперь нужно сложить все эти части:

6728 : 6 = 1100 + 20 + 1, (3) = 1121, (3)

Самое сложное – это деление многозначных чисел:

Представим, что нам нужно разделить 4608 на 64.

На сколько примерно нужно умножить 64, чтобы получить число рядом с нашим? Может быть, на 70? Давайте проверим:

64 * 70 = 4480

Получилось число немного меньше того, что нам нужно, однако ясно, что искомый множитель находится в промежутке между 70 и 80.

Чтобы подобрать правильный «хвостик» к «70» нам нужно, чтобы произведение этой цифры на 4 (от «64») давало в результате число с окончанием 8 (от «4608»).

Теперь нужно подобать эту цифру:

2 * 4 = 8

«Хвостик» к 70 найден, проверяем «72»:

64 * 72 = 60 * 70 + 4*70 + 60*2 + 4*2 = 4200 + 280 + 120 + 8 = 4608.

Конечно, сразу считать в уме быстро вы не сможете. Здесь, как и в любом другом деле, необходима тренировка. Поэтому просто начните с простого и старайтесь заниматься каждый день. Тогда результат абсолютно точно вас порадует.

Для более организованной тренировки рекомендуем бесплатное приложение для мобильных устройств «Тренажёр устного счёта». С ним вам не придётся придумывать себе примеры самостоятельно, а также будет легче отследить динамику. Успехов!

20 умопомрачительных трюков с умножением, которые понравятся вашим детям

Не все дети могут выучить математические факты с помощью бездумного запоминания. Действительно, исследования показали, что механическое запоминание не помогает детям выучить связи между числами или понять правила умножения. К счастью, Mindful Math приходит на помощь с приемами умножения, помогающими детям выполнять математические действия в реальной жизни. Этот метод намного эффективнее, чем простое обучение математическим фактам или упор на запоминание.

Вот 20 трюков с умножением, которые научат детей творчески умножать.

1.

Правило девяток

Во-первых, у нас есть наши друзья, Девятки. Девятки похожи на вашего друга, у которого всегда есть немного правдоподобная теория заговора. У них обоих странные узоры, но, вероятно, это просто совпадение. Если вы посмотрите на левую часть столбца ответов, вы увидите, что в нисходящем столбце числа идут по порядку до 10. Затем прыгайте в правый столбец и поднимайтесь вверх, и числа также возрастают. Игнорируйте своего друга. Вселенная не пытается сказать вам что-то с помощью этого шаблона.

2 . Метод бабочки

Далее мы переходим к методу бабочки. Как и следовало ожидать, это метод перекрестного умножения, но для сложения и вычитания дробей. Сначала умножьте диагональ слева направо, затем умножьте диагональ справа налево. Эти два числа входят в антенну-бабочку. Вычтите их, и вы получите числитель. Умножьте два знаменателя, и вы получите знаменатель решения. Не забудьте сократить ответ!

3. Двузначный раунд

Один из моих личных фаворитов — двузначный раунд. Этот метод полезен для умножения двух двузначных чисел. Во-первых, подумайте о красивом круглом числе, к которому оба наших числа ближе всего. Возьмем, к примеру, 92 х 98. Оба числа близки к 100, поэтому мы вычтем их из 100, чтобы получить 8 и 2. Сложите их вместе, чтобы получить 10, и вот ваша разница! Вычтите 10 из 100, чтобы получить 90, что является первой частью нашего ответа. Помните 8 и 2? Умножьте их, чтобы получить 16. Следовательно, наш ответ — 9.016. Умно, правда?

4. Вспомните близнецов

Для следующего помните, что все факты умножения имеют идентичных близнецов. Итак, если вы забудете 8×2, вы можете вспомнить, что 2×8 — это 16. Нам нравится это, потому что оно разрезает стол пополам!

5. Двойной двойной

Хорошо, давайте наберем обороты со следующими трюками. Удвоить, потом еще раз удвоить. 4×9: двойная 9 — это 18, двойная 18 — это 36, то есть 4×9.

6. В два раза больше 10

Разрезать пополам, затем умножить на 10. 5×6: половина от 6 будет 3, затем умножить на 10 будет 30.

7. Шестерки любят эвенов

Шестерки смотрят на эвенов! 6x 2 = 1 2 , 6x 4 = 2 4 , 6x 6 = 3 6

8. Трюк танца

7 × 8, помните, 5,6, 5,6, 5,6, 7 и 8! 56 = 7 x 8

9. Трипл-дабл для восьмерок
(Примечание: это не заказ Dairy Queen!) Этот заказ работает только на 8 секунд. 8×6: удвоить 6 — это 12, удвоить 12 — это 24, удвоить 24 — это 48.
10. Умножить на 10, минус число (для девяток)
На полпути! Давайте снова заглянем к нашим друзьям The Nines. 9 — это десятикратное число минус число. Например, 9 x 6 = 10 x 6 – 6 = 60 – 6 = 54. Не забывайте свой порядок действий (PEMDAS)!
11. Добавим ноль к десяткам
Давайте поболтаем с нашим другом, и самое целое число, 10. Единственным ответом 10 будет «поставить ноль после него». 10 x 2 = 2 0
12. 11s Повторять до 9
Хорошо, мы набрали 10; давайте перейдем к самому нечетному числу, 11. Конечно, 11 имеет повторяющиеся цифры до 11×9. 11×4=44. А что после 9?
13. Сумма между для 11s, 10-18
Для 11×10 до 11×18: сумма цифр между цифрами. Например, 11 × 15 = 1 (1 + 5) 5 = 165.
14. Правило 12: 10 раз плюс 2 раза
12 — это весело, потому что это все подростковые гормоны без списка подростковых обязанностей ( может быть). Правило 12: 10-кратное число плюс 2-кратное число. Например, 12×4=40+8=48.
15. Правило 15 с: умножить на 10, затем прибавить половину, снова
15 умно, используя тот же метод, что и 12: умножить на 10, затем снова прибавить половину. 15×4=40+20=60. Мы любим 15-ки.
16. Правило 20-х: умножить на 10, затем удвоить
Хорошо, метод последней уникальной цифры. 20! Это как взросление, но не одновременно. Странный. Ладно, 20 умножаем на 10, потом удваиваем. 20×4=40+40=80 или 20×7 = 70+70 = 140.
17. Цифры, разделенные цифрой 2
Если вы хотите что-то запомнить, начните с квадратов. Запомните каждое число, умноженное само на себя. Здесь нет шаблона; это просто важно. Но это не было бы 17-м номером, если бы у меня не было трюка. Когда числа, которые мы умножаем, разделены на 2 (пример 7 и 5), умножьте число в середине само на себя и вычтите единицу. Например, 5×5=25 на единицу больше, чем 6×4 = 24, а 6×6 = 36 на единицу больше, чем 7×5 = 35.
18. Представьте с помощью объектов
Это одно из моих любимых заданий, потому что оно связывает математические факты с реальными объектами, а не с абстрактными идеями. Использование таких вещей, как блоки и маленькие игрушки, может помочь вашему ученику увидеть, что умножение — это способ складывать более одной группы одного и того же числа снова и снова. Например, в 6×3 попросите вашего ученика создать 6 групп по 3 блока в каждой. Тогда они увидят, что проблема на самом деле состоит в том, чтобы мы собрали 6 групп по 3 человека.0008
Подсчет пропусков на самом деле констатирует факт умножения 5 с. Пока ученик учится считать на 5, напомните ему, что он знает факты умножения на 5!
20. Если сомневаетесь, используйте множители
В качестве последнего трюка давайте приведем проверенный и верный метод: используйте кратные, чтобы найти ответ. Если сомневаетесь, используйте кратные! Допустим, вы не можете вспомнить, что такое 5 х 7, но можете вспомнить, что 5 х 5 = 25. Тогда просто продолжайте прибавлять 5 к 25: 25 + 5 = 30, 30 + 5 = 35, поэтому 5 х 7 = 35.
Большинство из этих трюков могут стать отличной разминкой перед началом математического блока и началом урока. Вовлеките учащихся, включив их камеру и следя за тем, как вы демонстрируете каждый метод. Затем предложите учащимся посмотреть, смогут ли они создать свои собственные методы.
Дополнительные советы и рекомендации можно найти в этих математических приложениях, с которыми учащиеся могут играть, ожидая еды в ресторане, вместо того, чтобы просить больше хлеба в 100 раз.
5 приемов, которые помогут улучшить математические способности учащихся
По мере того, как учащиеся продвигаются в учебе, улучшается их способность вычислять в уме математические суммы и решать задачи. От вычисления простого сложения и вычитания до запоминания квадратного корня из целых чисел, ментальная математика включает в себя специальные методы обучения, которые помогают учащимся быстро решать математические задачи.
Исследования Министерства образования Великобритании показывают, что заучивание основных математических фактов «наизусть» позволяет детям сконцентрироваться на вычислениях, что, в свою очередь, помогает им разрабатывать стратегии вычислений. Использование и применение этих стратегий на практике помогает им вырабатывать ответы и запоминать больше фактов. (источник: Национальные стратегии; Обучение детей считать в уме, 2010 г.)
Школьные программы часто включают темы, которые развивают и укрепляют математические способности учащихся в течение года. Кроме того, учителя также используют эффективные стратегии для развития навыков ментальной математики у учащихся и повышения их осведомленности и понимания ряда методов ментальной арифметики, над которыми они могут работать.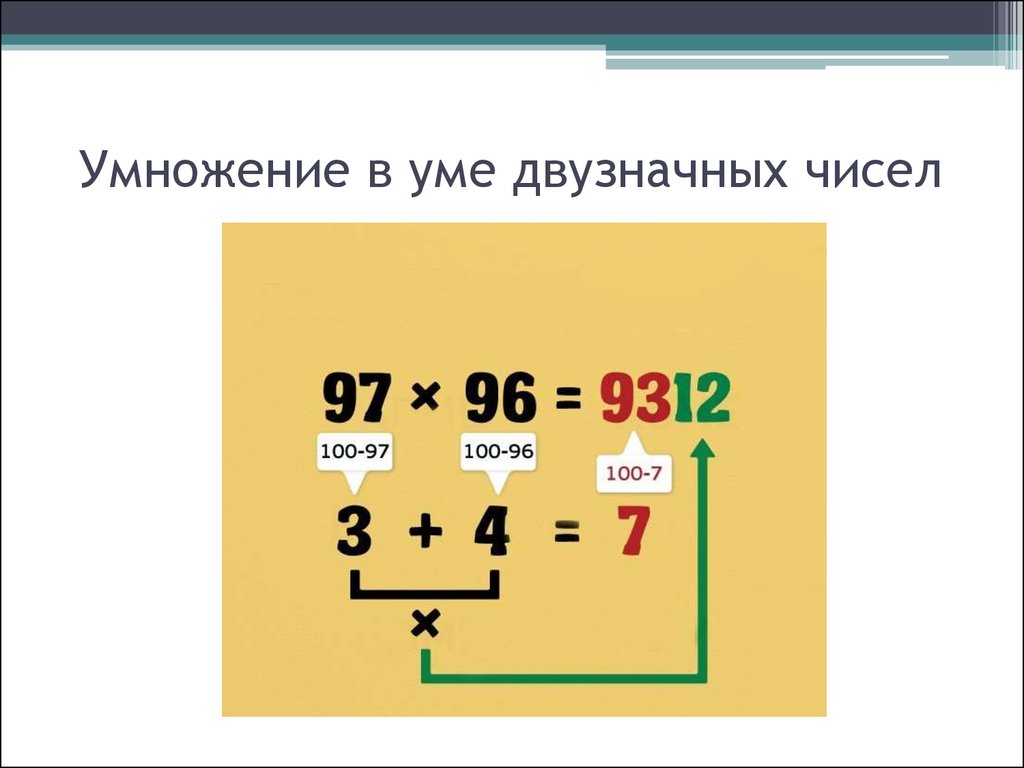 Это также помогает развить их уверенность и беглость речи, решая математические задачи с использованием этих стратегий.
Чтобы помочь учащимся улучшить свои навыки счета в уме и постепенно решать сложные математические задачи за меньшее время, учителя могут использовать ряд подходящих учебных материалов и приемов.
Вот 5 математических приемов, которые помогут улучшить математические способности ваших учеников в уме:
1. Упростите задачу
Учащимся иногда бывает сложно умножать или складывать большие номиналы. Хорошая стратегия состоит в том, чтобы помочь им упростить задачу, временно меняя значения.
Например, если задача состоит в том, чтобы вычислить 791 + 540, проще добавить 9 к 800, что делает вычисление более управляемым. Теперь вычислите 800 + 540, что равно 1340, и отнимите дополнительные 9.чтобы получить правильный ответ 1331.
Вы можете научить учащихся применять эту стратегию также и с умножением. Например, если задача состоит в том, чтобы вычислить 59 x 7, вместо этого вычислите 60 x 7, а затем вычтите эти дополнительные 7, так что 420-7 = 413
Вычисление с числами, кратными 10, станет намного проще для учащихся, поэтому всегда напоминайте им об этом. округлять числа при расчетах.
2. Вычитание путем сложения
Это очень важный принцип, основанный на связи между сложением и вычитанием. Как только эта стратегия будет правильно понята, учащимся не нужно запоминать факты вычитания.
Например, если задача состоит в том, чтобы найти разницу между 14 и 8, вместо вычитания подумайте: «8 плюс сколько будет 14?» Другими словами, подумайте о недостающем числе, которое нужно добавить; 8 + ___ = 14. Ответ на это также является ответом на 14 − 8.
Этот принцип особенно удобен при вычитании, таком как 13 − 7, 17 − 8, 16 − 9, и других основных фактах вычитания, где minuend находится между 10 и 20. Но вы также можете использовать его во множестве других ситуаций. Например, 72 − 55 легче решить, если подумать о сложении: 55 + 17 дает 72, поэтому ответ на 72 − 55 равен 17.

Читайте также: 4 Задания для учащихся по алгебре [+ Загружаемые рабочие листы для занятий]
3.
Сложные умножения стали проще
Умножение больших чисел может быть сложной задачей для учащихся. Итак, логичнее всего учить тому, как упрощать числа, а затем умножать их. Ниже приведены несколько интересных советов по умножению, которым могут следовать ваши ученики:
Самый простой способ запомнить умножение — при умножении любого числа на 10 просто добавить ноль в конце числа. Например, 62 х 10 = 620,
Если одно из чисел четное, вы можете разделить первое число пополам, а затем удвоить второе число. Например, 20 x 120 также можно решить, разделив 20 на 2, что равно 10, и удвоив 120, что составит 240. Затем умножьте два ответа; ответ 10 x 240 = 2400.
Существует также простой способ умножить любое двузначное число на 11. Все, что вам нужно сделать, это сложить две цифры множимого и вставить ответ в центр. Например, чтобы умножить 35 на 11, сложите числа 3 и 5, что равно 8, и добавьте их между двузначным множимым; ответ 385.
4.
Советы по делению
Чтобы не усложнять задачи на деление для учащихся, вы можете дать им краткий список ключевых фактов, которые они могут запомнить, чтобы легко выполнять деление. Вот быстрый способ узнать, можно ли разделить число без остатка на эти определенные числа:
Число можно разделить на 10, если оно оканчивается на 0
Число можно разделить на 9, если сложить цифры и сумма делится без остатка на 9
Число можно разделить на 8, если последние три цифры делятся на 8 без остатка или равны 000. 3
Число можно разделить на 5, если оно оканчивается на 0 или 5
Число можно разделить на 4, если оно оканчивается на 00 или на двузначное число, которое делится на 4 без остатка
5. Решение задач с процентами
По мере того, как учащиеся продвигаются в классе, такие темы, как нахождение процента от числа, становятся несколько сложными, но использование правильных математических стратегий и приемов может помочь им с легкостью справиться с этими задачами.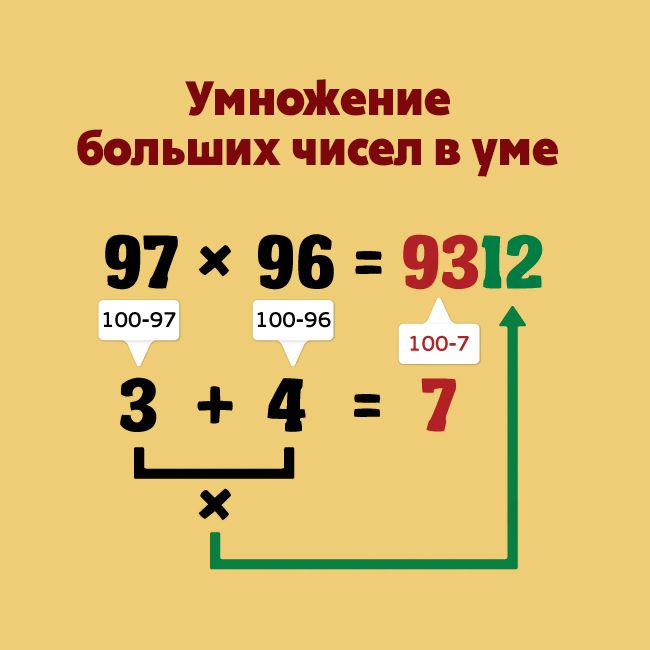
Например, найти процент 5 для любого числа можно сделать за секунды. Следуйте этому методу, чтобы найти, что составляет 5% от 235:
Шаг 1: Переместите десятичную точку на одно место, 235 станет 23,5
Шаг 2: Разделите 23,5 на 2, и ответ будет 11,75. Это также ответ на исходное уравнение.
Регулярная работа над развитием математических навыков учащихся не только помогает им совершенствоваться, но и дает им чувство уверенности, что они могут решать больше математических задач. Даже если вы не можете посвятить весь класс ментальной арифметике, преподаватели должны искать возможности ввести короткие периоды ментальных вычислений между уроками и занятиями, чтобы поддерживать умственные способности своих учеников свежими и активными.
Выполнение этих 5 полезных математических трюков в уме, несомненно, поможет вашим ученикам быстрее решать математические задачи, а также сделает изучение предмета более интересным.
Представьте Prodigy в классе
Вы также можете опробовать игровые математические платформы, которые оказывают большее влияние на улучшение математических навыков учащихся, чем любые другие стратегии обучения.