Главная
Как в уме перемножать двузначные числа: Математическая мастерская «Интересное умножение двузначных чисел»

Как в уме перемножать двузначные числа: Математическая мастерская «Интересное умножение двузначных чисел»

Как решить один и тот же пример разными способами: китайский метод умножения, египетский, метод решетки – 20 января 2023

Привычные нам способы решения примеров далеко не единственно верные

Поделиться

Складывать, вычитать, умножать и делить мы все научились еще в школьные годы. Многие даже неплохо сохранили эти навыки и до сих пор могут что-нибудь да умножить. В уме. Но что, если приходится умножать многозначные числа? Понятно, что проще всего воспользоваться калькулятором. Но мы не ищем легких путей — вместо них мы нашли несколько способов решить одни и те же примеры. Ими до сих пор пользуются в разных странах, и это не привычное нам умножение столбиком.

В качестве примера, решить который мы попробуем семью разными методами, мы взяли не самый сложный, но и не самый простой: 223 х 304. Произведение этих множителей равняется 67 792. Нам было важно, чтобы числа были не двузначные и чтобы хотя бы в одном из них был ноль (потом объясним зачем). А теперь давайте посчитаем.

Чтобы решить наш пример этим способом, сперва запишем множители. После этого нужно представить число 223 в виде суммы степеней двоек — начинаем с единицы и умножаем на два, пока не получим число, которое будет больше, чем 223. Получится 256. Это уже много. А раз много, значит нам это не нужно. Остается 128.

Поделиться

Дальше нужно число 304 умножить на все получившиеся числа. Но понадобятся нам не все. Из чисел левого столбца нам нужно собрать число 223. Идем снизу вверх. Берем 128, прибавляем к нему 64. Получается 192. Если прибавить к этой сумме 32, получится 224, а это уже перебор. Поэтому 32 пропускаем и прибавляем все остальные. Выйдет наше 223. На те числа, что остались (а это все, кроме 32), мы и будем умножать наше 304. Теперь суммируем всё, что у нас получилось. Сумма этих чисел окажется 67 792.

Поделиться

Если вам кажется, что умножать 304 на 128 в такой ситуации будет полнейшим безумием, воспользуйтесь хитростью и просто умножайте каждое предыдущее число на два — так будет проще.

Всё, что вам понадобится, чтобы решить любой пример с умножением этим крестьянским методом, — это уметь умножать и делить на два.

Для начала будем последовательно делить на два первое число, пока оно не превратится в единицу. Думаете, не получится в случае с числом 223? Только не в древнерусском способе! Если в результате будет получаться число с остатком, отбрасываем эти остатки куда подальше — они нам не пригодятся.

Поделиться

После этой нехитрой процедуры беремся за второй множитель — его будем на два умножать. Столько же раз, сколько делили первый множитель, пока он не достиг единицы. Умножили? Теперь вычеркивайте все строчки, в которых в левом столбце есть четное число. У нас такая строчка одна — с цифрой шесть.

Поделиться

Дальше — самая нелегкая задача этого метода: суммировать все числа, что стоят справа (включая 304). Сложно, но у древнерусских счетоводов не было другого выбора, и им приходилось всё считать вручную. У нас, к счастью, есть калькуляторы, так что мы с удовольствием воспользуемся этой возможностью. И калькулятор покажет 67 792. Если вы хотите проверить, действительно ли работает этот метод, можете поменять множители местами и всё пересчитать, но, забегая вперед, мы вам скажем, что от перестановки мест множителей произведение не меняется даже в этом случае.

Первым дело запишем наши числа одно над другим и подведем под ними черту. И умножим каждую цифру верхнего числа на каждую цифру нижнего. Если будут получаться двузначные числа, пишем их как есть, а вот однозначные пишем в виде «ноль и цифра» — например, 08 вместо просто 8.

Поделиться

Получив эту хитрую комбинацию, умножаем соседние цифры (2 на 0, 2 на 4) и в обратную стороны (2 на 3 и 3 на 0). Идем еще дальше и стараемся не запутаться — перемножаем первую верхнюю цифру на третью нижнюю, а третью верхнюю — на первую нижнюю. Умножение закончилось.

Поделиться

Давайте складывать то, что у нас получилось. А получилось у нас 67 792.

Выписываем наших героев и подводим под ними черту, как делали это в методе треугольника. Затем перемножим крайние цифры — 2 и 4. Результат (его мы записываем как 08) будет первой строкой нашего решения. Следом за ними умножаем вторую цифру левого множителя на первую и третью — правого. Запишем их во вторую строку. Начало ромбу положено.

Поделиться

Ну а дальше умножаем друг на друга цифры из разряда сотен, десятков и единиц и так же записываем их в одну строку. Результат заносим в третью строчку.

Теперь берем вторую цифру во втором множителе и умножаем на первую и третью из первого. Четвертая строка решения готова. Последней, пятой строкой записываем произведение последней цифры первого множителя и первой цифры второго. Наш ромб готов. Осталось только суммировать цифры, расположенные друг над другом. Метод, конечно, красивый, но совсем не простой в применении.

Поделиться

Вот мы и добрались до того момента, где объясним, зачем нам понадобились трехзначные числа, да еще и с нулем. В китайском методе нам придется считать, чертить и рисовать. Так что для начала разберем принцип его работы на простом примере и умножим 34 на 62. Для этого нарисуем черты. Сперва три горизонтальные, потом, через промежуток, еще четыре. Это три десятка и четыре единицы нашего первого числа. А число 62 по такому же принципу превращается в шесть и две вертикальные черты. Теперь нам нужно разграничить зоны единиц, десятков и сотен.

Поделиться

После этого считаем точки пересечения всех черточек. В зоне единиц их восемь, в зоне десятков — 30, в зоне сотен — 18. Теперь нужно это сложить: 1800+300+8 = 2 108. На калькуляторе, умножая 34 на 62, получится тот же результат.

Переходим к нашему изначальному примеру и умножим 223 на 304. Рисуем две, две и три горизонтальные линии, три вертикальные слева и четыре справа. Место посередине оказывается пустым, поэтому здесь у нас будет воображаемая линия. (Цифры у нас стали крупнее, поэтому и зон будет больше.) И считаем точки пересечения.

Поделиться

Складываем, начиная с единиц. Там, где получились двузначные числа, оставляем единицы, а десятки перекидываем в соседнюю область. То есть там, где стояли рядом 8 и 12, оказались 9 и 2, а соседство 6 и 17 превратилось в 7 и 7. Считаем, что у нас получилось, справа налево: 67 792.

Чтобы решить наш пример методом решетки (его еще называют древнеиндийским методом), первым делом надо нарисовать таблицу, у которой будет три столбца и три строки — по количеству цифр в умножаемых числах. Потом делим каждую ячейку по диагонали на две части. Решетка готова.

Теперь по горизонтали выписываем цифры числа 223, а по вертикали — числа 304. И перемножаем каждое число сверху на каждое число справа. Результат вписываем в наши ячейки таким образом: сверху — десятки, снизу — единицы (если десятков нет, пишем ноль).

Поделиться

Теперь складываем цифры, которые получились в наших диагоналях. По периметру, начиная с правого нижнего угла и поднимаясь до левого верхнего. Если число вышло двузначным, оставляем только единицу, а десятки плюсуются к единицам числа предыдущего — совсем как в сложении, к которому мы привыкли.

Поделиться

Выписываем ответ, начиная с левой стороны: 67 792. Что и требовалось доказать.

Этот метод похож на метод решетки, но есть отличия. Здесь мы снова рисуем таблицу на три столбца и три строки, но ни на какие ячейки не делим. А наши числа записываем не в виде отдельных цифр, а сотнями, десятками и единицами.

Поделиться

Дальше начинаем умножать те цифры, что сверху, на те, что справа.

Поделиться

Умножили? Осталось только всё сложить: 60 000 + 6000 + 900 + 800 + 80 + 12 = 67 792. Тот результат, который и получится, если умножить 223 на 304.

Разные способы решить один и тот же пример, к слову, далеко не единственная математическая причуда. На днях одна несложная на первый взгляд задачка рассорила весь интернет — скандал разгорелся из-за простого примера для 6-классников. И мы попробовали решить его с математиком.

Как решить один и тот же пример разными способами: китайский метод умножения, египетский, метод решетки – 20 января 2023

Привычные нам способы решения примеров далеко не единственно верные

Поделиться

Складывать, вычитать, умножать и делить мы все научились еще в школьные годы. Многие даже неплохо сохранили эти навыки и до сих пор могут что-нибудь да умножить. В уме. Но что, если приходится умножать многозначные числа? Понятно, что проще всего воспользоваться калькулятором. Но мы не ищем легких путей — вместо них мы нашли несколько способов решить одни и те же примеры. Ими до сих пор пользуются в разных странах, и это не привычное нам умножение столбиком.

В качестве примера, решить который мы попробуем семью разными методами, мы взяли не самый сложный, но и не самый простой: 223 х 304. Произведение этих множителей равняется 67 792. Нам было важно, чтобы числа были не двузначные и чтобы хотя бы в одном из них был ноль (потом объясним зачем). А теперь давайте посчитаем.

Чтобы решить наш пример этим способом, сперва запишем множители. После этого нужно представить число 223 в виде суммы степеней двоек — начинаем с единицы и умножаем на два, пока не получим число, которое будет больше, чем 223. Получится 256. Это уже много. А раз много, значит нам это не нужно. Остается 128.

Поделиться

Дальше нужно число 304 умножить на все получившиеся числа. Но понадобятся нам не все. Из чисел левого столбца нам нужно собрать число 223. Идем снизу вверх. Берем 128, прибавляем к нему 64. Получается 192. Если прибавить к этой сумме 32, получится 224, а это уже перебор. Поэтому 32 пропускаем и прибавляем все остальные. Выйдет наше 223. На те числа, что остались (а это все, кроме 32), мы и будем умножать наше 304. Теперь суммируем всё, что у нас получилось. Сумма этих чисел окажется 67 792.

Поделиться

Если вам кажется, что умножать 304 на 128 в такой ситуации будет полнейшим безумием, воспользуйтесь хитростью и просто умножайте каждое предыдущее число на два — так будет проще.

Всё, что вам понадобится, чтобы решить любой пример с умножением этим крестьянским методом, — это уметь умножать и делить на два.

Для начала будем последовательно делить на два первое число, пока оно не превратится в единицу. Думаете, не получится в случае с числом 223? Только не в древнерусском способе! Если в результате будет получаться число с остатком, отбрасываем эти остатки куда подальше — они нам не пригодятся.

Поделиться

После этой нехитрой процедуры беремся за второй множитель — его будем на два умножать. Столько же раз, сколько делили первый множитель, пока он не достиг единицы. Умножили? Теперь вычеркивайте все строчки, в которых в левом столбце есть четное число. У нас такая строчка одна — с цифрой шесть.

Поделиться

Дальше — самая нелегкая задача этого метода: суммировать все числа, что стоят справа (включая 304). Сложно, но у древнерусских счетоводов не было другого выбора, и им приходилось всё считать вручную. У нас, к счастью, есть калькуляторы, так что мы с удовольствием воспользуемся этой возможностью. И калькулятор покажет 67 792. Если вы хотите проверить, действительно ли работает этот метод, можете поменять множители местами и всё пересчитать, но, забегая вперед, мы вам скажем, что от перестановки мест множителей произведение не меняется даже в этом случае.

Первым дело запишем наши числа одно над другим и подведем под ними черту. И умножим каждую цифру верхнего числа на каждую цифру нижнего. Если будут получаться двузначные числа, пишем их как есть, а вот однозначные пишем в виде «ноль и цифра» — например, 08 вместо просто 8.

Поделиться

Получив эту хитрую комбинацию, умножаем соседние цифры (2 на 0, 2 на 4) и в обратную сторону (2 на 3 и 3 на 0).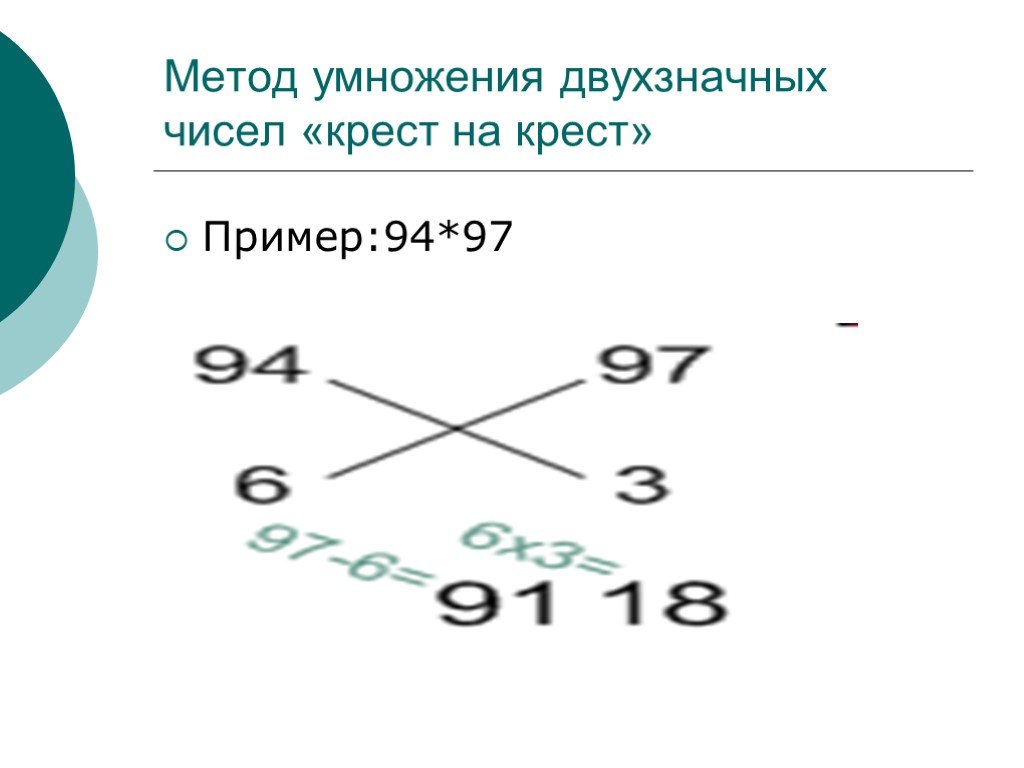 Идем еще дальше и стараемся не запутаться — перемножаем первую верхнюю цифру на третью нижнюю, а третью верхнюю — на первую нижнюю. Умножение закончилось.

Поделиться

Давайте складывать то, что у нас получилось. А получилось у нас 67 792.

Выписываем наших героев и подводим под ними черту, как делали это в методе треугольника. Затем перемножим крайние цифры — 2 и 4. Результат (его мы записываем как 08) будет первой строкой нашего решения. Следом за ними умножаем вторую цифру левого множителя на первую и третью — правого. Запишем их во вторую строку. Начало ромбу положено.

Поделиться

Ну а дальше умножаем друг на друга цифры из разряда сотен, десятков и единиц и так же записываем их в одну строку. Результат заносим в третью строчку.

Теперь берем вторую цифру во втором множителе и умножаем на первую и третью из первого. Четвертая строка решения готова. Последней, пятой строкой записываем произведение последней цифры первого множителя и первой цифры второго. Наш ромб готов. Осталось только суммировать цифры, расположенные друг над другом. Метод, конечно, красивый, но совсем не простой в применении.

Поделиться

Вот мы и добрались до того момента, где объясним, зачем нам понадобились трехзначные числа, да еще и с нулем. В китайском методе нам придется считать, чертить и рисовать. Так что для начала разберем принцип его работы на простом примере и умножим 34 на 62. Для этого нарисуем черты. Сперва три горизонтальные, потом, через промежуток, еще четыре. Это три десятка и четыре единицы нашего первого числа. А число 62 по такому же принципу превращается в шесть и две вертикальные черты. Теперь нам нужно разграничить зоны единиц, десятков и сотен.

Поделиться

После этого считаем точки пересечения всех черточек. В зоне единиц их восемь, в зоне десятков — 30, в зоне сотен — 18. Теперь нужно это сложить: 1800+300+8 = 2 108. На калькуляторе, умножая 34 на 62, получится тот же результат.

Переходим к нашему изначальному примеру и умножим 223 на 304. Рисуем две, две и три горизонтальные линии, три вертикальные слева и четыре справа. Место посередине оказывается пустым, поэтому здесь у нас будет воображаемая линия. (Цифры у нас стали крупнее, поэтому и зон будет больше.) И считаем точки пересечения.

Поделиться

Складываем, начиная с единиц. Там, где получились двузначные числа, оставляем единицы, а десятки перекидываем в соседнюю область. То есть там, где стояли рядом 8 и 12, оказались 9 и 2, а соседство 6 и 17 превратилось в 7 и 7. Считаем, что у нас получилось, справа налево: 67 792.

Чтобы решить наш пример методом решетки (его еще называют древнеиндийским методом), первым делом надо нарисовать таблицу, у которой будет три столбца и три строки — по количеству цифр в умножаемых числах. Потом делим каждую ячейку по диагонали на две части. Решетка готова.

Теперь по горизонтали выписываем цифры числа 223, а по вертикали — числа 304. И перемножаем каждое число сверху на каждое число справа. Результат вписываем в наши ячейки таким образом: сверху — десятки, снизу — единицы (если десятков нет, пишем ноль).

Поделиться

Теперь складываем цифры, которые получились в наших диагоналях. По периметру, начиная с правого нижнего угла и поднимаясь до левого верхнего. Если число вышло двузначным, оставляем только единицу, а десятки плюсуются к единицам числа предыдущего — совсем как в сложении, к которому мы привыкли.

Поделиться

Выписываем ответ, начиная с левой стороны: 67 792. Что и требовалось доказать.

Этот метод похож на метод решетки, но есть отличия. Здесь мы снова рисуем таблицу на три столбца и три строки, но ни на какие ячейки не делим. А наши числа записываем не в виде отдельных цифр, а сотнями, десятками и единицами.

Поделиться

Дальше начинаем умножать те цифры, что сверху, на те, что справа.

Поделиться

Умножили? Осталось только всё сложить: 60 000 + 6000 + 900 + 800 + 80 + 12 = 67 792. Тот результат, который и получится, если умножить 223 на 304.

Разные способы решить один и тот же пример, к слову, далеко не единственная математическая причуда. На днях одна несложная на первый взгляд задачка рассорила весь интернет — скандал разгорелся из-за простого примера для 6-классников. И мы попробовали решить его с математиком.

Трюк с двузначным умножением с одинаковыми цифрами десятков

с помощью банковских экзаменов

Вам, должно быть, интересно, что мы узнали так много приемов умножения двузначных чисел, так как же это может быть полезно. Что ж, знание новых приемов и способов их применения для быстрого получения ответа может иметь решающее значение. Трюк с двузначным умножением или трюк с двузначным умножением, у которого цифры десятков совпадают, – это один из тех трюков, которые мы рассмотрим сегодня.

Оглавление

Основное условие, необходимое для использования двузначного приема умножения 

Если разряд десятков одинаков, а разряды разряда единиц в сумме дают 10, можно применить упрощенный трюк, чтобы легко умножить любые 2 цифры числа.

Трюк с двузначным умножением, в котором разряд десятков одинаков

Теперь давайте подробно рассмотрим шаги.

Шаг 2: Чтобы получить разряд десятков, умножьте разряд десятков на его последовательный (следующий) номер.

Шаг 3: Поместите результат, полученный на шаге 2, слева от результата, полученного на шаге 1.

Теперь потренируемся на некоторых примерах

Пример 1: Умножить 26 x 24=? Используя прием двузначного умножения

, мы видим, что разряд десятков в обоих числах = 2

, и, складывая разряды единиц обоих чисел (6+4=10), мы получаем 10,9.0007

Следовательно, мы можем применить этот трюк

Шаг 1: Умножая цифры разряда единиц, получаем
Разряд разряда единиц = 6 x 4 = 24

Шаг 2: Умножая разряд десятков на его порядковый номер, получаем
Разряд десятков =2 x 3=6

Шаг 3: Разместив результат шага 2 слева от результата, полученного на шаге 1, получим
624

Ответ  26 x 24=624

Пример 2: умножить 43 х 47=? используя двузначный трюк умножения

Мы видим, что разряд десятков обоих чисел = 4
, и, сложив разряд разряда единиц обоих чисел (3 + 7 = 10) , мы получим 10

Шаг 1: Умножая разряды разрядов единиц, мы получим
Разряд разряда единиц = 3 x 7 = 21

Шаг 2. Умножив разряд десятков на его порядковый номер, мы получим
Разряд разряда десятков = 4 x 5 = 20

Шаг 3. Поместите результат шага 2 слева от результат, полученный на шаге 1, получаем
2021

Ответ 43 x 47=2021

Пример 3: Умножить 38 x 32=? Используя прием двузначного умножения

, мы видим, что разряд десятков в обоих числах = 3
, и, складывая разряды единиц обоих чисел (8+2=10), мы получаем 10

Шаг 1: Умножение разряда единиц цифр, которые мы получаем
Цифра разряда единиц = 8 x 2 = 16

Шаг 2: Умножая цифру разряда десятков на ее порядковый номер, мы получаем
Цифра разряда десятков = 3 x 4 = 12

Шаг 3: Поместите результат шага 2 в слева от результата, полученного на шаге 1, получаем
1216

Ответ 38 x 32=1216

Пример 4: Оцените это: 65 x 65=? используя 2-значный трюк умножения

Мы видим, что разряд десятков обоих чисел = 6
, и, добавляя разряд разряда единиц обоих чисел (5 + 5 = 10), мы получаем 10

Шаг 1: Умножение разрядов разрядов единиц получаем
Разряд десятков = 1 x 9 = 09

Шаг 2.

Умножая разряд десятков на его порядковый номер, получаем
Разряд десятков = 7 x 8 = 56

Шаг 3: Разместив результат шага 2 слева от результата, полученного на шаге 1, получим
5609

Ответ 71 x 79=5609

Умножение двузначных чисел на однозначные числа

Извините, вы использовали все доступные подсказки для этого урока.

Достигнут предел практики

Вы достигли ежедневного лимита практики в 12 вопросов.

Когда вы зарегистрируете бесплатную учетную запись и войдете в нее, вы сможете играть во все, что захотите.

(Для регистрации вам должно исполниться 18 лет.)

Интерактивная математическая игра – Умножение двузначных чисел на однозначные числа

В этом интерактивном математическом задании от iKnowIt.com ваши третьеклассники будут практиковать базовые навыки умножения. Учащиеся укрепят свои навыки умножения, практикуя умножение двузначных чисел на однозначные числа. Вот несколько учебных целей этого математического задания для третьего класса:

  • Решить задачи на вертикальное умножение, содержащие одно двузначное и однозначное число.
  • Решите задачи на горизонтальное умножение, содержащие одно двузначное число и одно однозначное число.
  • Решите задачи на умножение слов, содержащие одно двузначное число и одно однозначное число.
  • Умножайте единицы, умножайте десятки и перегруппировывайте при необходимости.

Вопросы в этом интерактивном математическом задании представлены в формате заполнения пробелов. Если учащимся нужна дополнительная помощь в решении задачи на умножение, они могут нажать кнопку «Подсказка». Они увидят иллюстрированную или письменную подсказку, которая подтолкнет их к первому шагу «Умножьте единицы», не выдавая ответа. Когда учащиеся дают неправильный ответ, страница с подробным объяснением покажет им шаг за шагом, как умножать, чтобы получить правильный результат. Таким образом, дети будут продвигаться по математической деятельности, учась на предыдущих ошибках.

Все математические задания на iKnowIt.com, в том числе эта игра на умножение для третьего класса, оснащены встроенными функциями, помогающими учащимся максимизировать свои математические навыки. Вот некоторые из них:

  • Отслеживание успеваемости. Учащиеся могут проверить отслеживание успеваемости, чтобы узнать, на сколько вопросов они ответили из общего числа вопросов на уроке математики.
  • Счетчик очков. Дети могут посмотреть на счетчик очков, чтобы узнать, сколько баллов они заработали за правильные ответы на вопросы.
  • Функция чтения вслух. Учащиеся могут щелкнуть значок динамика в верхнем левом углу экрана практики, чтобы вопрос был прочитан им вслух четким голосом. Это отличный ресурс для учащихся ESL/ELL и детей, которые учатся на слух.

Каждая из встроенных функций, которую учащиеся находят в своих интерактивных математических занятиях, предназначена для повышения их практического опыта по математике и помогает им достичь большего.

Подарите своим ученикам практику цифровой математики, которую они полюбят

Цифровая математическая практика, предлагаемая iKnowIt.com, — это отличная возможность помочь малышам укрепить математические навыки с помощью математической практики, которая им действительно нравится. Вот лишь несколько причин, по которым учащимся нравятся наши интерактивные математические игры:

  • Веселый, удобный для детей формат — учащимся нравятся яркие цвета и смелый дизайн наших уроков математики для начальной школы.
  • Очаровательные анимационные друзья. Причудливые анимационные персонажи готовы подбодрить учащихся в их математических занятиях хитрым трюком или милым танцем каждый раз, когда они правильно отвечают на вопрос.
  • Математические награды. Учащиеся имеют возможность зарабатывать виртуальные математические награды, которые добавляются в их ящик с трофеями за каждый новый освоенный математический навык.
  • Положительные отзывы. Множество положительных отзывов побуждают детей «Не останавливаться!» даже когда они ошибаются.

Студенты не единственные, кто любит математическую онлайн-программу «Я знаю это». Учителям тоже нравится ощущать разницу, которую интерактивная математическая практика может сделать в их классах. Вот несколько вещей, которые больше всего нравятся учителям начальных классов, школьным администраторам и воспитателям в нашей дополнительной математической программе.

  • Уроки математики, соответствующие стандарту Common Core. Математические задания в нашей коллекции соответствуют стандарту Common Core Standard и продуманно написаны такими же аккредитованными учителями начальной математики, как и вы.
  • Большое разнообразие математических тем. Учителя ценят множество математических тем, которые мы освещаем среди сотен интерактивных математических уроков на нашем веб-сайте.
  • Быстро и легко находите и назначайте практические занятия по математике. Все уроки математики на iKnowIt.com упорядочены на веб-сайте по классам и темам, что позволяет легко находить и назначать практические задания всего за несколько кликов.

Мы надеемся, что вам и вашим учащимся третьего класса понравится практиковаться в умножении двузначных и однозначных чисел в этой интерактивной математической игре! Обязательно ознакомьтесь с сотнями других уроков математики для третьего класса, которые также доступны на нашем веб-сайте.

Попробуйте базовую практику умножения в своем классе бесплатно

Хотите узнать, подходит ли я знаю это вам и вашим ученикам? Подпишитесь на нашу бесплатную 30-дневную пробную версию и попробуйте любое математическое задание на нашем веб-сайте бесплатно в течение полных 30 дней — кредитная карта не требуется! Мы уверены, что вам и вашему классу понравится разница, которую может дать интерактивная математическая практика, и мы надеемся, что вы, не колеблясь, присоединитесь к нашему сообществу в качестве члена после окончания бесплатного пробного периода. Ваша подписка I Know It дает вашему классу неограниченный доступ к интерактивным математическим играм в течение всего календарного года. У нас есть варианты членства для семей, отдельных учителей, школ и школьных округов. Посетите нашу страницу с информацией о членстве, чтобы узнать подробности: https://www.iknowit.com/order.html.

Ваше членство в программе «Я знаю это» дает вам доступ к удобным административным функциям веб-сайта, которые помогут вам максимизировать математическую практику вашего класса:

  • Создание списка класса для всех ваших учеников всем учащимся
  • Выдача конкретных заданий по математике разным учащимся
  • Изменение основных настроек урока, например, ограничение количества подсказок на уроке
  • Печать, загрузка и сохранение отчетов об успеваемости учащихся

Ваши ученики войдут в удобную для детей версию iKnowIt.com, где они смогут быстро и легко найти математические задания, которые вы им назначили для практики. Если вы хотите предоставить им возможность через свою учетную запись администратора, ваши учащиеся также могут изучать другие математические задания в своем классе и за его пределами для дополнительного повторения или дополнительной задачи. Уровни оценок в студенческом режиме I Know It помечены буквами (например, «Уровень C» для третьего класса), что упрощает назначение математических заданий в зависимости от потребностей и уровня навыков каждого учащегося.

Уровень

Этот онлайн-урок математики относится к уровню C. Он может быть идеальным для третьего класса.

Common Core Standard

4.NBT.5
Числа и операции с основанием 10
Учащиеся будут использовать свое понимание разрядного значения и свойств операций для выполнения многозначной арифметики. Учащиеся будут умножать целое число до четырех цифр на однозначное целое число и умножать два двузначных числа, используя стратегии, основанные на разрядности и свойствах операций.

Вас также может заинтересовать.

Оставить комментарий