Главная
Как в уме умножать двузначные числа: Математическая мастерская «Интересное умножение двузначных чисел»

Как в уме умножать двузначные числа: Математическая мастерская «Интересное умножение двузначных чисел»

Содержание

Как решить один и тот же пример разными способами: китайский метод умножения, египетский, метод решетки – 20 января 2023

Привычные нам способы решения примеров далеко не единственно верные

Поделиться

Складывать, вычитать, умножать и делить мы все научились еще в школьные годы. Многие даже неплохо сохранили эти навыки и до сих пор могут что-нибудь да умножить. В уме. Но что, если приходится умножать многозначные числа? Понятно, что проще всего воспользоваться калькулятором. Но мы не ищем легких путей — вместо них мы нашли несколько способов решить одни и те же примеры. Ими до сих пор пользуются в разных странах, и это не привычное нам умножение столбиком.

В качестве примера, решить который мы попробуем семью разными методами, мы взяли не самый сложный, но и не самый простой: 223 х 304. Произведение этих множителей равняется 67 792. Нам было важно, чтобы числа были не двузначные и чтобы хотя бы в одном из них был ноль (потом объясним зачем). А теперь давайте посчитаем.

Чтобы решить наш пример этим способом, сперва запишем множители. После этого нужно представить число 223 в виде суммы степеней двоек — начинаем с единицы и умножаем на два, пока не получим число, которое будет больше, чем 223. Получится 256. Это уже много. А раз много, значит нам это не нужно. Остается 128.

Поделиться

Дальше нужно число 304 умножить на все получившиеся числа. Но понадобятся нам не все. Из чисел левого столбца нам нужно собрать число 223. Идем снизу вверх. Берем 128, прибавляем к нему 64. Получается 192. Если прибавить к этой сумме 32, получится 224, а это уже перебор. Поэтому 32 пропускаем и прибавляем все остальные. Выйдет наше 223. На те числа, что остались (а это все, кроме 32), мы и будем умножать наше 304. Теперь суммируем всё, что у нас получилось. Сумма этих чисел окажется 67 792.

Поделиться

Если вам кажется, что умножать 304 на 128 в такой ситуации будет полнейшим безумием, воспользуйтесь хитростью и просто умножайте каждое предыдущее число на два — так будет проще.

Всё, что вам понадобится, чтобы решить любой пример с умножением этим крестьянским методом, — это уметь умножать и делить на два.

Для начала будем последовательно делить на два первое число, пока оно не превратится в единицу. Думаете, не получится в случае с числом 223? Только не в древнерусском способе! Если в результате будет получаться число с остатком, отбрасываем эти остатки куда подальше — они нам не пригодятся.

Поделиться

После этой нехитрой процедуры беремся за второй множитель — его будем на два умножать. Столько же раз, сколько делили первый множитель, пока он не достиг единицы. Умножили? Теперь вычеркивайте все строчки, в которых в левом столбце есть четное число. У нас такая строчка одна — с цифрой шесть.

Поделиться

Дальше — самая нелегкая задача этого метода: суммировать все числа, что стоят справа (включая 304). Сложно, но у древнерусских счетоводов не было другого выбора, и им приходилось всё считать вручную. У нас, к счастью, есть калькуляторы, так что мы с удовольствием воспользуемся этой возможностью. И калькулятор покажет 67 792. Если вы хотите проверить, действительно ли работает этот метод, можете поменять множители местами и всё пересчитать, но, забегая вперед, мы вам скажем, что от перестановки мест множителей произведение не меняется даже в этом случае.

Первым дело запишем наши числа одно над другим и подведем под ними черту. И умножим каждую цифру верхнего числа на каждую цифру нижнего. Если будут получаться двузначные числа, пишем их как есть, а вот однозначные пишем в виде «ноль и цифра» — например, 08 вместо просто 8.

Поделиться

Получив эту хитрую комбинацию, умножаем соседние цифры (2 на 0, 2 на 4) и в обратную стороны (2 на 3 и 3 на 0). Идем еще дальше и стараемся не запутаться — перемножаем первую верхнюю цифру на третью нижнюю, а третью верхнюю — на первую нижнюю. Умножение закончилось.

Поделиться

Давайте складывать то, что у нас получилось. А получилось у нас 67 792.

Выписываем наших героев и подводим под ними черту, как делали это в методе треугольника. Затем перемножим крайние цифры — 2 и 4. Результат (его мы записываем как 08) будет первой строкой нашего решения.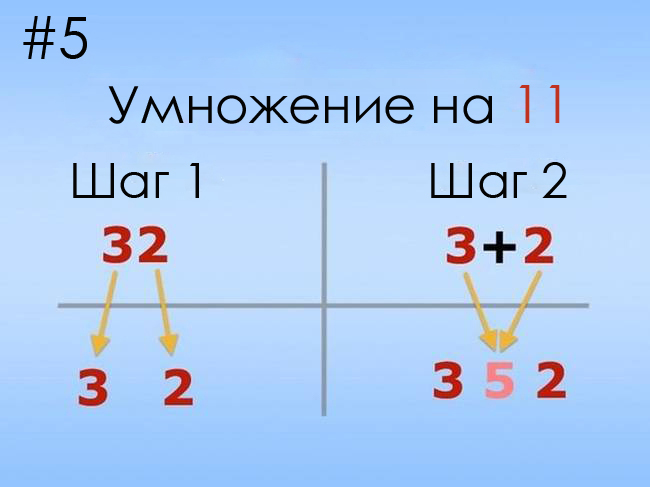 Следом за ними умножаем вторую цифру левого множителя на первую и третью — правого. Запишем их во вторую строку. Начало ромбу положено.

Поделиться

Ну а дальше умножаем друг на друга цифры из разряда сотен, десятков и единиц и так же записываем их в одну строку. Результат заносим в третью строчку.

Теперь берем вторую цифру во втором множителе и умножаем на первую и третью из первого. Четвертая строка решения готова. Последней, пятой строкой записываем произведение последней цифры первого множителя и первой цифры второго. Наш ромб готов. Осталось только суммировать цифры, расположенные друг над другом. Метод, конечно, красивый, но совсем не простой в применении.

Поделиться

Вот мы и добрались до того момента, где объясним, зачем нам понадобились трехзначные числа, да еще и с нулем. В китайском методе нам придется считать, чертить и рисовать. Так что для начала разберем принцип его работы на простом примере и умножим 34 на 62. Для этого нарисуем черты. Сперва три горизонтальные, потом, через промежуток, еще четыре. Это три десятка и четыре единицы нашего первого числа. А число 62 по такому же принципу превращается в шесть и две вертикальные черты. Теперь нам нужно разграничить зоны единиц, десятков и сотен.

Поделиться

После этого считаем точки пересечения всех черточек. В зоне единиц их восемь, в зоне десятков — 30, в зоне сотен — 18. Теперь нужно это сложить: 1800+300+8 = 2 108. На калькуляторе, умножая 34 на 62, получится тот же результат.

Переходим к нашему изначальному примеру и умножим 223 на 304. Рисуем две, две и три горизонтальные линии, три вертикальные слева и четыре справа. Место посередине оказывается пустым, поэтому здесь у нас будет воображаемая линия. (Цифры у нас стали крупнее, поэтому и зон будет больше.) И считаем точки пересечения.

Поделиться

Складываем, начиная с единиц. Там, где получились двузначные числа, оставляем единицы, а десятки перекидываем в соседнюю область. То есть там, где стояли рядом 8 и 12, оказались 9 и 2, а соседство 6 и 17 превратилось в 7 и 7. Считаем, что у нас получилось, справа налево: 67 792.

Чтобы решить наш пример методом решетки (его еще называют древнеиндийским методом), первым делом надо нарисовать таблицу, у которой будет три столбца и три строки — по количеству цифр в умножаемых числах. Потом делим каждую ячейку по диагонали на две части. Решетка готова.

Теперь по горизонтали выписываем цифры числа 223, а по вертикали — числа 304. И перемножаем каждое число сверху на каждое число справа. Результат вписываем в наши ячейки таким образом: сверху — десятки, снизу — единицы (если десятков нет, пишем ноль).

Поделиться

Теперь складываем цифры, которые получились в наших диагоналях. По периметру, начиная с правого нижнего угла и поднимаясь до левого верхнего. Если число вышло двузначным, оставляем только единицу, а десятки плюсуются к единицам числа предыдущего — совсем как в сложении, к которому мы привыкли.

Поделиться

Выписываем ответ, начиная с левой стороны: 67 792. Что и требовалось доказать.

Этот метод похож на метод решетки, но есть отличия. Здесь мы снова рисуем таблицу на три столбца и три строки, но ни на какие ячейки не делим. А наши числа записываем не в виде отдельных цифр, а сотнями, десятками и единицами.

Поделиться

Дальше начинаем умножать те цифры, что сверху, на те, что справа.

Поделиться

Умножили? Осталось только всё сложить: 60 000 + 6000 + 900 + 800 + 80 + 12 = 67 792. Тот результат, который и получится, если умножить 223 на 304.

Разные способы решить один и тот же пример, к слову, далеко не единственная математическая причуда. На днях одна несложная на первый взгляд задачка рассорила весь интернет — скандал разгорелся из-за простого примера для 6-классников. И мы попробовали решить его с математиком.

Секреты устного счета в математике

Какие существуют секреты счета в математике или как научиться быстро считать в уме? Существуют приемы устного счета (в том числе с большими числами), которые очень помогают особенно при отсутствии калькулятора. В статье описаны самые простые приемы умножения чисел и возведения чисел в квадрат, с помощью которых можно значительно увеличить скорость решения примеров: умножать двузначные и трехзначные числа в уме, возвести в квадрат большое число. Эти секреты устного счета в математике настолько просты для понимания, что их можно с легкостью использовать в повседневной жизни.

После овладения простыми приемами и доведения их до автоматизма можно переходить к освоению более сложных. Так можно научить ребенка быстро считать и без ошибок.

Умножение чисел, оканчивающихся на 0

Если множители заканчивается на 0, то нужно просто умножить числа без нолей, а потом приписать нужное количество нолей.
Например, 70*80=7*8 и 00 = 5600; 500*30 = 5*3 и 000 = 15000.

Умножение на 4

Это очень простой прием: нужно умножить число на 2, а затем опять умножить на 2:
58 х 4 = (58 х 2) х 2 = 116 х 2 = 232

Умножение на 5

Чтобы любое число умножить на 5, нужно (на примере 2682): 
Исходное число умножить на 10 и разделить пополам: 2682 х 5 = 2682х10/2=13410. 
Пример для закрепления: 4887×5 = 4887 х 10 : 2 = 24435.

Умножение на 11

Чтобы любое число умножить на 11, нужно (на примере 53):
Сложить две цифры двузначного числа: 5+3=8. 
Поместить результат между двумя цифрами двузначного числа: 5 и 8 и 3 = 583. 
Если сумма получилась 10 и больше, то единицу прибавляем к первой цифре числа. Например, для числа 59 получаем: 5 и (5+9) и 9 = 5 и 14 и 9 = (5+1) и 4 и 9 = 649.

Умножение на 9

Чтобы любое число умножить на 9, нужно (на примере 26): 
Исходное число умножить на 10 и вычесть исходное число: 26х9=26х10-26=234.

Умножение на 19

Чтобы любое число умножить на 19, нужно (на примере 26):
Исходное число умножить на 20 и вычесть исходное число: 26х19=26х20-26=494.

Умножение на 99

Чтобы любое число умножить на 99, нужно (на примере 26): 
Исходное число умножить на 100 и вычесть исходное число: 26х99=26х100-26=2574.

Квадрат двузначного числа, которое оканчивается на 5

Чтобы найти квадрат числа, которое оканчивается числом 5, нужно (на примере числа 85):

  • Умножить первую цифру числа на число, которое больше него на единицу: 8*(8+1) =72. Это будет первая часть ответа
  • Дописать число 25 – это вторая часть ответа.
  • Получаем: 85*85= 8*(8+1) и 25 = 7225
  • Пример для закрепления: 45*45= 4*(4+1) и 25 = 2025

Квадрат двузначного числа, которое оканчивается числом 1 или 9 (отличается на единицу от числа, кратного 10)

Чтобы найти квадрат двузначного числа, которое оканчивается числом 1 или 9 (отличается на единицу от числа, кратного 10), нужно (на примере числа 51):

  • Представит число в виде суммы или разности числа, кратного 10, и 1: (50+1)
  • Возвести в квадрат число, кратное 10: 502=2500
  • Прибавляем исходное число и число, кратное 10: 2500+51+50 = 2601
  • Получаем: 512 = 502 + 51 +50 = 2500 + 51 + 50 = 2601
  • Пример для закрепления: 212
    =202+20+21= 400 +20+21=441
  • Если число оканчивается на 9: 392=402−40−39 =1600−40−39=1521

 Квадрат числа, которое оканчивается на 25

Чтобы найти квадрат числа, которое оканчивается числом 25, нужно (на примере числа 425):

  • Возвести в квадрат первое исходное число и прибавить к полученному числу половину первого исходного числа: 42+4:2 = 16+2 = 18 – это первая часть ответа.
  • Записать число 0625 – это вторая часть ответа.
  • Получаем: 425*425= 42+4:2 и 0625 = 18 и 0625 = 180625
  • Пример для закрепления: 1225*1225= (12
    2    +12:2) и 0625 = (144+6) и 0625 = 1500625

Квадрат любого числа по формуле

Для возведения любого числа в квадрат можно воспользоваться формулой квадрата суммы и разности: (a+b)2=a2+2ab+b2 или (a-b)2=a2-2ab+b2. То есть любое число можно представить как сумму или разность чисел с использованием числа, кратного 10. При этом разложение числа на слагаемые, где второе слагаемое минимально, будет проще для проведения расчетов. Например, для возведения числа 28 в квадрат удобнее применить формулу к (30-2)2, чем к (20+8)2.

Пример 1: 282=(30−2)2=302-2*30*2+22 = 900-120+4=784
Пример 2: 512=(50+1)2= 502+2*50*1+12 = 2500+100+1=2601

 

Чтобы применять секреты счета в математике и научится считать быстрее, достаточно небольшой тренировки – несколько примеров в день. В итоге на подсчет любого двухзначного выражения у вас будет уходить не более пяти-шести секунд.

 

8 отличных математических трюков с умножением в уме, которые сделают вас гением математики!

Ментальная арифметика — это способ использовать только один инструмент, ваш мозг, для быстрого вычисления чисел в вашей голове. Ни калькуляторов, ни бумаги, ни ручки!

Большая часть ментальной математики на самом деле представляет собой серию стратегий — некоторые очень простые, некоторые требуют больше практики, чтобы запомнить, но все они быстрые, легкие и отличная тренировка для вашего мозга🧠! Готовы попробовать?

Трюк № 1 – Округлить вверх или вниз!

В школе учителя и родители всегда учили нас складывать и вычитать числа справа налево и всегда брать одно слева. Это прекрасно работает, когда у вас есть бумага и карандаш, но мой мозг отказывается думать вправо -> влево, и знаете что, я снова забыл взять с собой 1!

Если вашему мозгу нужно быстро сообразить, вот простой прием ментальной арифметики:  Округлите числа в большую или меньшую сторону!

Округление – пример 1:

  • Получилось: 796 + 812.
  • Шаг 1: Округлите быстро до 800 и 800. 800 + 800 = 1600.
  • Шаг 2: 796 = 800 – 4 ; 812 = 800 + 12. Сложите эти два вместе, чтобы получить -4 + 12 = 8.
  • Шаг 3: 1600 + 8 = 1608.

Как видите, округление делает числа более управляемыми и простыми для решения.

  • Шаг 1. Быстро округлите 89 до 90 и 6. 90 x 6 = 540.
  • Шаг 2: Мы использовали дополнительные 6, поэтому вычтите их из ответа. 540 – 6 = 534

    • Трюк №2 – Разбей и умножь на части

    Это важная, основополагающая вещь, которая может помочь умножать и делить довольно быстро, как только вы освоитесь.

    Не беритесь за калькулятор, пока не попробуете это!

    Пример 1:

    • Вам дано 3 x 68
    • Шаг 1: Разберем, ладно? 3 x 78 идентичен 3 x 60 + 3 x 8
    • Шаг 2: 3 x 60 + 3 x 8 = 180 + 24 = 20 4

    Почти СЛИШКОМ просто, да? Тогда давайте попробуем большее число.

    Пример 2:

    • Вам дано 7 x 328
    • Шаг 1: Разберем, ладно? 7 x 328 идентичен 7 x 300 + 7 x 20 + 7 x 8
    • Шаг 2: 7 x 300 + 7 x 20 + 7 x 8 = 2100 + 140 + 56 = 2240 + 56 = 2296

    Опять же, легко, правда? Пока не бросайте этот калькулятор — мы будем использовать его для более сложных вещей. Но это отличный способ держать свой ум активным и сосредоточенным.

    Уловка № 3. Удвоение числа

    Навык, который должен освоить каждый в математике, — это удвоение. Давайте объединим наши навыки, которые мы изучили выше (разложим и умножим на части.

    Пример 1:

    • Дано – 38 х 2 = 38 + 38
    • Сломаться — ты знаешь как! 30 + 30 + 8 + 8 = 60 + 16 = 76.

    Слишком просто? Попробуем посложнее.

    Пример 2:

    • Дано – 929 х 2 = 929 + 929
    • Сломаться — ты знаешь как! 90 0 + 900 + 20 + 20 + 9 + 9= 1800 + 40 + 18 = 1840 + 18 = 1858.

    Понял? Эй, ты хорошо разбираешься в этом!

    Трюк № 4 – Четырежды число

    Это, наверное, один из моих самых часто используемых трюков! Вы уже освоили удвоение, верно? Давайте расширим этот навык.

    Четырежды число = удвоить число + удвоить число, то есть удвоить число дважды.

    Пример 1:

    • Дано – 38 x 4 = 38 + 38 + 38 + 38
    • Разбить часть 1 – удвоить! 30 + 30 + 8 + 8 = 60 + 16 = 76.
    • Теперь удвойте еще раз – 76 + 76 = 70 + 70 + 6 + 6 = 140 + 12 = 152.

    Немного сложнее, теперь, когда вы разбираетесь в этом.

    Пример 2:

    • Дано – 929 х 4 = 929 + 929 + 929 + 929
    • Разбить часть 1 – удвоить! 90 0 + 900 + 20 + 20 + 9 + 9= 1800 + 40 + 18 = 1840 + 18 = 1858.
    • Теперь повторите еще раз, чтобы удвоить – 1858 + 1858 = 1800 + 1800 + 50 + 50 + 8 + 8 = 3600 + 100 + 16 = 3716

    Да? Что ж, ты официально гений!

    Трюк № 5 — Восемь раз число

    У вас есть это, не так ли? Умножение на 8 означает удвоение в 3 раза!

    Пример 1:

    • Дано – 38 x 8 = 38 x 2 + 38 x 2 + 38 x 2
    • Разбить часть 1 – удвоить!
      30 + 30 + 8 + 8 = 60 + 16 = 76.
    • Разобьем часть 2 – удвоим еще раз, чтобы получить 38 x 4 =   76 + 76 = 70 + 70 + 6 + 6 = 140 + 12 = 152.
    • И, наконец, еще раз удвойте это 152 + 152 = 150 + 150 + 2 + 2 = 304.

    Пример 2:

    • Дано – 929 х 9 = 929 х 2 + 929 х 2 + 929 х 2
    • Разбить часть 1 – удвоить! 90
      0 + 900 + 20 + 20 + 9 + 9= 1800 + 40 + 18 = 1840 + 18 = 1858.
    • Теперь повторите это: удвойте еще раз, чтобы получить 929 x 4 = 1858 + 1858 = 1800 + 1800 + 50 + 50 + 8 + 8 = 3600 + 100 + 16 = 3716
    • Наконец, удвойте еще раз, чтобы получить 929 x 8 = 3716 + 3716 = 3000 + 3000 + 700 + 700 + 10 + 10 + 6 + 6 = 6000 + 1400 + 20 + 12 = 7400 + 32 = 7432.

    Трюк № 6. Умножение на 5

    Это очень просто, но иногда дети не знают этого и берутся за бумагу, чтобы решить! Чтобы найти любое число, умноженное на 5, нужно сначала умножить это число на десять, а затем взять половину этого числа. Почему это легко? Потому что разделить пополам число, кратное десяти, всегда легко!

    Пример 1:

    • Дано – 38 х 5 = ?
    • Сначала умножьте на 10: 38 x 10 = 380
    • Тогда вдвое! 380 ÷ 2 = 190.
      • Если вам трудно разделить пополам, найдите ближайшее большое число, которое вы легко узнаете. В этом случае 400 ÷ 2 = 200. Теперь уменьшите его. Итак, 380 ÷ 2 = 190. 
      • Или подсчитайте из ближайшего большого числа, которое вам легко. 300 ÷ 2 = 150, тогда 320 ÷ 2 = 160, 340 ÷ 2 = 170; 360 ÷ 2 = 180, а затем 380 ÷ 2 = 19.0

    Помогает ли это? Тогда давайте попробуем более сложный пример.

    Пример 2:

    • Дано – 929 x 5= ?
    • Сначала умножьте на 10.  929 x 10 = 9290
    • Уменьшить вдвое. 9290  ÷ 2 = ?
      • Давайте разберем это, чтобы было удобнее? 9290  ÷ 2 = 9000 ÷ 2 +200 ÷ 2 + ÷ 2 2 3333333333333333333333333333333333330202020
      • 9000 
        ÷ 2 = 4500.
      • 200 ÷ 2 = 100
      • 90  ÷ 2 = 45
      • Сложите их: 4500 + 100 + 45 = 4645 .
      • Довольно понятно, верно?

    Трюк № 7. Умножение на 9

    Это очень простой способ умножить любое число на 9! Умножьте число на 10, а затем вычтите из него все число. Давай попробуем!

    Умножить на 9 – Пример 1:

    • Получилось: 77 x 9.
    • Шаг 1. Сначала идем 77 x 10 = 770.
    • Шаг 2: Теперь вычтите 77 из произведения   770 – 77 = 694

    Умножить на 9 – Пример 2:

    • Вам дано: 129 x 9.
    • Шаг 1. Сначала идем 129 x 10 = 1290.
    • Шаг 2. Теперь вычтите 129 из произведения   1290 – 129 = 1161

    Трюк № 8.

    Умножение на 11

    Это похоже на настоящий фокус — для его выполнения не требуется особых умственных способностей.

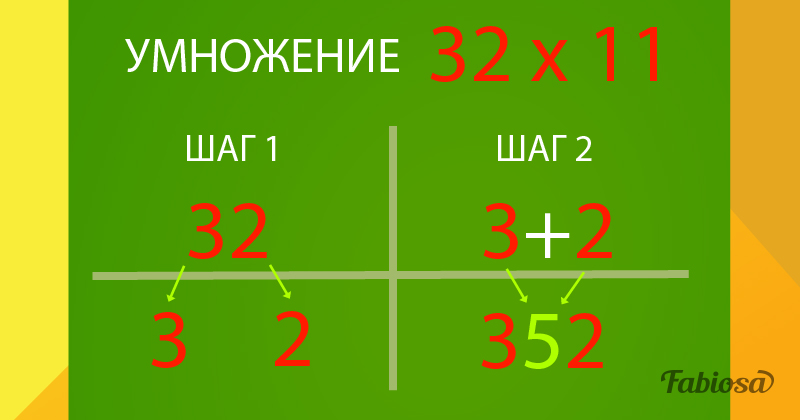
    Когда вы умножаете двузначное число на 11, возьмите исходное число и поставьте пробел между цифрами. Затем сложите оба числа и поместите это в центр. Звучит схематично, верно? Давай попробуем!

    Умножить на 11 – Пример 1:

    • Вам дано: 25 x 11.
    • Шаг 1: Сначала идем  2_5.
    • Шаг 2: Теперь мы добавляем 2 + 5 = 7 и
    • Шаг 3. Поместите это в центр   275
    • Шаг 4: Давай, проверь свой ответ! 25 х 11 = 275

    Но, подождите, что, если сумма состоит из 2 цифр. Давайте попробуем это!

    Умножить на 11 – Пример 2:

    • Вам дано: 99 x 11.
    • Шаг 1: Сначала идем 9 _9.
    • Шаг 2: Теперь мы добавляем 9 + 9 = 18
    • Поставьте 8 в центр, но не забудьте взять с собой лишнюю 1. Итак, (9+1)89.
    • 99 х 11 = 1089
    • Очень просто!
    • Автор
    • Recent Posts

    Aniruddha Pochimcherla

    Как старшеклассник и соучредитель STEAMism и TimeforAI.com, Ани нравится решать задачи и решать проблемы, технические предметы, включая искусственный интеллект и инженерное проектирование, а также сотрудничать с единомышленниками по мероприятий и хакатонов. Он проходил стажировку в городе Остин, был научным сотрудником аэрокосмической школы НАСА в 2019–2020 годах и является репетитором по математике в Mathnasium. Он ведет блог со 2-го класса и балуется веб-дизайном и программированием. Ему нравятся предметы STEM и преподавание, поэтому STEAMизм — отличный способ совместить и то, и другое.

    Последние сообщения Анируддхи Почимчерлы (посмотреть все)

    Двузначное умножение стало проще! – Caffeine Queen Teacher

    Умножение двузначных чисел — сложная задача, требующая много практики и повторения (и повторения и повторения). В прошлом я преподавал множество методов, включая ящик, частичные произведения, решетку и традиционный алгоритм.

    Некоторые учащиеся быстро и легко адаптируются к целому ряду методов, в то время как другие с трудом усваивают даже один метод.

    Многие учащиеся (и большинство родителей) с облегчением сосредотачиваются на стандартном алгоритме. Стандартный алгоритм — это традиционный метод, которым пользуется большинство людей.

    К 5-му классу в большинстве штатов требуется, чтобы учащиеся свободно владели стандартным алгоритмом. На протяжении многих лет я провел много поисков и не смог найти графический органайзер, который приносил бы пользу моим ученикам, испытывающим затруднения.

    Некоторым моим ученикам было трудно выучить шаги и выполнить их в правильном порядке. Я понял, что мои борцы, как правило, были визуальными и практическими учениками, поэтому я разработал графический органайзер, чтобы помочь студентам с алгоритмом.

    Щелкните, чтобы получить БЕСПЛАТНЫЙ набор навыков стратегии умножения!

    Визуальный органайзер для умножения на 2 цифры

    Этот органайзер представляет собой метод, который учителя могут использовать для обучения традиционному алгоритму. Органайзер удобен для учащихся и использует форм и цветов , чтобы помочь учащимся выполнять шаги по порядку.

    Во время обучения я постоянно говорю: «Кружки идут к кругам» или «Квадраты идут к квадратам». Это побуждает учащихся искать следующий шаг в этой конкретной форме. Эти утверждения помогают учащимся помнить, куда класть их продукты, когда они решают задачи на умножение. Например, учащиеся выполняют каждый шаг для красных кругов, прежде чем перейти к синим квадратам.

    Как видно на картинках, органайзеры используют не только формы, но и цвета. Цвета и формы могут быть добавлены или удалены в зависимости от уровня адаптации, в котором нуждаются ваши ученики.

    Цвета и формы помогают новичкам. По мере того, как учащиеся становятся более опытными, цвета могут быть удалены или даже добавлены учащимися, если это необходимо. Маркеры также можно использовать, чтобы подчеркнуть и сфокусировать внимание на конкретных шагах, которые необходимо укрепить учащимся.

    Якорная диаграмма визуальной стратегии

    FYI — приведенная выше якорная диаграмма — это винтаж — 2014 года, но вы поняли идею. Первоначально в этих наборах использовались треугольники, а не пятиугольники. Мне показалось, что треугольники не дают ученикам достаточно места для письма, поэтому форму заменили на пятиугольники.

     

    Умножение 2 цифр с помощью органайзера фигур

    Я ОБОЖАЮ эти Карманные диаграммы C-Line , которые можно приобрести в магазинах для учителей, Wal-Mart или Amazon. Вы просто вставляете страницу в карманную таблицу и ВУАЛЯ! Ламинировать не надо.

    Это пластиковый футляр, который можно использовать для маркеров с сухим стиранием. Студенты часто пользуются ими.

    Ученикам нравится использовать карманные рукава, потому что маркеры с сухим стиранием позволяют легко писать и стирать, не беспокоясь об ошибках.

    Органайзеры и рабочие листы для умножения двузначных чисел

    Мне было трудно найти рабочие листы без перегруппировки. Я хотел, чтобы мои ученики сосредоточились на стандартном алгоритме умножения без дополнительного шага перегруппировки.

    Когда учащиеся освоятся с умножением без перегруппировки, они готовы к изучению этого дополнительного шага. Перегруппировка должна пройти гладко после того, как вы потратите время на решение проблем без перегруппировки и изучения процесса двузначного умножения.

    Выделение или раскрашивание начальной точки помогает учащимся запомнить, с чего начать.

    Эти наборы органайзеров для умножения Shape Math содержат множество практических страниц, поэтому используйте столько страниц, сколько нужно вашим ученикам. Кроме того, наборы облегчают дифференциацию в зависимости от уникальных потребностей учащихся.

    Моим ученикам обычно требовалась дополнительная практика и МНОГО повторений, поэтому в исходный набор включено множество различных рабочих листов с перегруппировкой.

    Кроме того, в набор входят три графических органайзера разного размера. Первый и самый большой органайзер занимает целую страницу. На других страницах есть четыре органайзера; другая страница содержит девять пустых органайзеров. Эти страницы идеально подходят для вас (или ваших учеников) для решения задач. Мои ученики любят составлять рабочие листы друг для друга и быть «учителем».

    Страница ниже свернута, что является простым приспособлением для студентов, которые перегружены просмотром целой страницы задач.

    Страница свернута для учащихся, которые перегружены объемом работы, которую от них ожидают.

    Рабочие листы размеров , цветов и упрощают дифференциацию и построение лесов. Эти наборы для умножения и деления Shape Math — мои любимые, они протестированы учащимися и одобрены учителями!

    После того, как учащиеся научатся решать задачи на умножение с перегруппировкой и без нее, учащиеся готовы решать задачи без графического органайзера. Два рабочих листа на миллиметровой бумаге включены, чтобы помочь им перейти к независимости.

     

    Если вы также обучаете делению, вам понравится этот комплект, который сэкономит ваше время!

    Советы по обучению учащихся двухэтапному умножению

    В коротком (5-минутном) видео ниже показано, как я обучаю учащихся двузначному умножению с помощью шаблона Shape Multiplication.

    Нажмите, чтобы посетить Учителя Платите учителям и узнайте больше!

    Хотите узнать больше?

    Если вы хотите узнать больше об этой новой стратегии умножения (а также о стратегиях деления!), вот несколько статей, которые вы можете прочитать:

    Рабочие листы дифференцированного умножения:

    Все ресурсы по умножению  – Ознакомьтесь с все ресурсы умножения, которые я предлагаю в моем магазине учителей, платных учителям.

    Двузначное умножение – дифференцированная стратегия обучения многозначному умножению с использованием органайзеров и рабочих листов, чтобы помочь учащимся визуализировать процесс умножения.

    2-значное и 3-значное умножение — этот метод многозначного (3-х 2-значного) умножения использует цвета и формы для визуальной, конкретной стратегии.

    Статьи об умножении:

    3 идеи для обучения многозначному умножению — 3 БЫСТРЫЕ идеи для обучения многозначному умножению. Эти вмешательства просты и быстры для занятых учителей.

    Рабочие листы по умножению 2-значных чисел: дифференцированные . Ниже представлен визуальный метод обучения умножению 2-значных чисел с использованием дифференцированных визуальных подсказок, которые помогут учащимся добиться успеха в обучении.

    Двузначное умножение стало проще! – Вот как использовать организаторы двузначного умножения и рабочие листы.

    Статьи о длинном делении:

    БЕСПЛАТНЫЕ дифференцированные рабочие листы для длинного деления – БЕСПЛАТНО возьмите эти дифференцированные рабочие листы для длинного деления и значительно повысьте успеваемость учащихся и ваши успехи в обучении!

    Как преподавать многозначное умножение и деление в длинное число  – Эта статья в блоге познакомит вас с имеющимися у меня ресурсами по дифференцированному умножению и делению в длинное число.

    Оставить комментарий