Как вычесть из матрицы матрицу: определения, свойства и примеры решения задач

определения, свойства и примеры решения задач

Содержание:

Сложение и вычитание матриц, допускаются только для матриц одинакового размера.

Сумма матриц

Определение

Суммой матриц $A$ и $B$ одного размера называется матрица $C = A+B$ такого же размера, получаемая из исходных путем сложения соответствующих элементов:

$$ A_{m \times n}+B_{m \times n}=C_{m \times n} ; c_{i j}=a_{i j}+b_{i j}, i=\overline{1 ; m}, j=\overline{1 ; n} $$

Замечание

Складывать можно только матрицы одинакового размера.

Пример

Задание. Найти $A+B$, если $ A=\left( \begin{array}{ll}{1} & {4} \\ {2} & {3}\end{array}\right) $ , $ B=\left( \begin{array}{ll}{4} & {4} \\ {5} & {2}\end{array}\right) $

Решение. $ C=A+B=\left( \begin{array}{cc}{1} & {4} \\ {2} & {3}\end{array}\right)_{2 \times 2}+\left( \begin{array}{ll}{4} & {4} \\ {5} & {2}\end{array}\right)_{2 \times 2}= $

$ =\left( \begin{array}{cc}{1+4} & {4+4} \\ {2+5} & {3+2}\end{array}\right)=\left( \begin{array}{ll}{5} & {8} \\ {7} & {5}\end{array}\right) $

Ответ. $ A+B=\left( \begin{array}{ll}{5} & {8} \\ {7} & {5}\end{array}\right) $

Свойства сложения и вычитания матриц:

1.   Ассоциативность $ (A+B)+C=A+(B+C) $
2.   $ A+\Theta=\Theta+A $, где $\Theta$ – нулевая матрица соответствующего размера.
3.   $ A-A=\Theta $
4.   Коммутативность $ A+B=B+A $

Разность матриц

Разность двух матриц одинакового размера можно определить через операцию сложения матриц и через умножение матрицы на число.

Вычитание матриц вводится следующим образом: $ A-B=A+(-1) \cdot B $

То есть к матрице $A$ прибавляется матрица $B$, умноженная на (-1).

Определение

Разностью матриц $A$ и $B$ одного и того же размера называется матрица $C = A-B$ такого же размера, получаемая из исходных путем прибавления к матрице $A$ матрицы $B$, умноженной на (-1).

На практике же от элементов матрицы $A$ попросту отнимают соответствующие элементы матрицы $B$ при условии, что заданные матрицы одного размера.

Замечание

Вычитать можно только матрицы одинакового размера.

Слишком сложно?

Сложение и вычитание матриц не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Найти матрицу $ C=A-3 B $, если $ A=\left( \begin{array}{rr}{1} & {2} \\ {2} & {-1} \\ {3} & {0}\end{array}\right) $ , $ B=\left( \begin{array}{rr}{-1} & {1} \\ {1} & {2} \\ {0} & {0}\end{array}\right) $

Решение. $ C=A-3 B=\left( \begin{array}{rr}{1} & {2} \\ {2} & {-1} \\ {3} & {0}\end{array}\right)-3 \cdot \left( \begin{array}{rr}{-1} & {1} \\ {1} & {2} \\ {0} & {0}\end{array}\right)= $

$ \left( \begin{array}{rr}{1} & {2} \\ {2} & {-1} \\ {3} & {0}\end{array}\right)-\left( \begin{array}{rr}{-3} & {3} \\ {3} & {6} \\ {0} & {0}\end{array}\right)=\left( \begin{array}{rr}{1-(-3)} & {2-3} \\ {2-3} & {-1-6} \\ {3-0} & {0-0}\end{array}\right)=\left( \begin{array}{rr}{4} & {-1} \\ {-1} & {-7} \\ {3} & {0}\end{array}\right) $

Ответ. $ C=\left( \begin{array}{rr}{4} & {-1} \\ {-1} & {-7} \\ {3} & {0}\end{array}\right) $

Читать дальше: умножение матриц.

Матриц сложение – Энциклопедия по машиностроению XXL

Как и в случае матриц, сложению поворотов в случае их активного представления отвечает произведение кватернионов составляющих поворотов в обратном порядке. При этом все кватернионы заданы в исходном базисе к (/ = 1, 2, 3).  [c.46]

В кинематике механизмов операции сложения матриц и умножения их на скаляр находят применение в действиях над матрицами-столбцами.  [c.631]

При сложении двух матриц одинакового размера получается матрица того же размера, каждый элемент которой равеи сумме соответствующих элементов слагаемых матриц.  [c.104]

Над матрицами можно выполнять действия транспонирования, сложения, умножения. Матрица А, транспонированная по отношению к матрице А, образуется из матрицы А заменой каждой ее строки на столбец того же номера. Например, при транспонировании матрицы  [c.50]

Множество J n всех л-мерных векторов называют линейным алгебраическим пространством, если в нем определены операции сложения и умножения на скаляр точно так же, как для матриц. Число я называется размерностью пространства Rn- Рассмотрим помимо вектора а другой п-мерный вектор  

[c.19]

Матрица [/(], называемая глобальной матрицей жесткости или просто матрицей жесткости системы, получается сложением локальных матриц жесткости [Л ] по следующему правилу сначала к нулевой матрице размерности NxN добавляется матрица, в левом верхнем углу которой стоит локальная матрица жесткости 1-го элемента, к получившейся матрице добавляется матрица размера /V х /V, ненулевые элементы которой расположены на пересечении 2-го и 3-го столбцов и 2-й и 3-й строк и равны соответствующим элементам локальной матрицы жесткости для 2-го элемента и т. д. на -м шаге добавляется матрица, ненулевые элементы которой расположены на пересечении к и к- строк и к н k- – столбцов и равны соответствующим элементам локальной матрицы жесткости k-ro элемента.  

[c.134]

При вычислении матрицы плотности мы будем предполагать, что рассеянные волны имеют беспорядочные фазы и при сложении в среднем дают нуль. Если и г и г лежат слева от слоя, то  [c.718]

Все остальные неизвестные определяются лишь путем умножения и сложения матриц. Весь процесс вычислений при этом легко программируется с использованием стандартных программ сложения, умножения и обращения матриц.  [c.97]

Непосредственным перемножением и сложением матриц (71.29) нетрудно убедиться, что они удовлетворяют соотношениям (71.28), понимая, что в их правой части стоит единичная матрица. Например, для имеем  

[c.387]

Описанная процедура лежит в основе алгоритма формирования глобальной матрицы и глобального вектор-столбца. Как было уже отмечено выше, она реализуется путем последовательного перебора элементов следующим образом. Берется первый элемент, анализируется его строка в индексной матрице и устанавливается, в какие три уравнения этот элемент дает вклад . Далее рассчитываются его локальная матрица и вектор-столбец. При этом расчете используется информация о наличии у данного элемента граничных сторон, содержащаяся в четвертом столбце индексной матрицы. Пусть локальным номерам 1, 2, 3 соответствуют фактические номера i, j, k. Тогда первая строка локальной матрицы и первый коэффициент локального вектор-столбца участвуют в формировании i-й строки глобальной матрицы и i-ro коэффициента глобального вектор-столбца. Производится сложение найденных локальных коэффициентов с имеющимися значениями глобальных коэффициентов дц, Gij, Затем аналогичная процедура повторяется для второй и третьей строк локальной матрицы и второго и третьего коэффициентов локального столбца. Они участвуют в формировании строк глобальной матрицы и коэффициентов глобального столбца с номерами / и к, которые соответствуют локальным номерам 2 и 3.

 [c.144]

Сложение и вычитание матриц. Две матрицы можно сложить (вычесть). Для этого необходимо, чтобы порядки матриц были одинаковы, и тогда сложить (вычесть) соответствующие элементы матриц.  [c.179]

Нетрудно убедиться, что выполнение операций дифференцирование вектора [X], умножение матрицы [К] на вектор [Р] и сложение с вектором [F] —приводит к системе уравнений вида (1). Однако матричная форма записи более компактна й упрощает действия по преобразованию системы уравнений.  

[c.181]

Полное изображение типа С образуется при перемещении преобразователя в направлении, перпендикулярном к направлению электронного сканирования. При этом сигналы коорди-, нат строки вырабатываются датчиками координат, как в системе с ручным (механическим) сканированием. Более простое решение этой задачи может быть получено с применением двумерного электронного сканирования. Пьезоэлементы двумерной матрицы (например, с числом элементов 8X8) возбуждаются с задержками, обеспечивающими сложение амплитуд акустических импульсов лишь на определенных направлениях в объекте контроля. Аналогично в тракте приема принятые пьезоэлементами сигналы предварительно задерживаются так, что суммирование амплитуд соответствует направлению излучения.  

[c.271]

Матрица называется единичной матрицей. Удобство записывать совокупности значений каких-либо величин в таком виде заключается в том, что над матрицами можно производить соответствующие действия (сложение, умножение, см., например, р]).  [c.93]

Бесконечно малые повороты. Целесообразно попытаться установить соответствие между векторами и конечными поворотами, описываемыми ортогональными матрицами. Вектор, который мы поставим в соответствие некоторому повороту, должен, конечно, иметь определенное направление —направление оси вращения и определенную величину, например равную углу поворота. Мы сейчас увидим, что успешно осуществить такое соответствие оказывается невозможным. Предположим, что А и В будут двумя такими векторами , связанными с преобразованиями А и В. Тогда, поскольку это векторы, они должны обладать свойством коммутативности при сложении, т. е. для них должно выполняться равенство  [c.142]

Но сложение двух вращений, т. е. последовательное выполнение одного из них за другим, описывается, как мы знаем, произведением матриц АВ, и это умножение не коммутативно, т. е. АВ =ВА. Следовательно, векторы Л и Д не будут обладать коммутативностью сложения и поэтому их нельзя будет считать в  [c.142]

Мы имеем здесь иллюстрацию сложения вращений согласно формуле (9.13), ибо, транспонируя элементы в (11.1)—(11.3), можно получить матрицы М, М2, Mg и непосредственно убедиться, что матрица М (11.5) представима в виде  [c.47]

В алгебре матриц определяются следующие действия над матрицами а) сложение матриц б) умножение матрицы на число в) умножение матриц. Указанные действия позволяют вычислить соответственно сумму матриц, произведение матрицы на число, произведение матриц и, как следствие, разность матриц.  [c.41]

После построения /-й строки матрицы F выполняется циклический сдвиг элементов матрицы-строки R на один влево или вправо для формирования направлений штриховки, соответствующих углам 45 и 135°. Завершив формирование матрицы F, с помощью логического сложения получим матрицу содержащую описание заштрихованной области сечения  [c.123]

Логическое сложение матриц реализуется путем попарного логического сложения одноименных элементов исходных матриц  [c.123]

Сложение и вычитание матриц. Эти операции имеют смысл лишь при их одинаковой структуре (одинаковом количестве строк и одинаковом количестве столбцов) слагаемых или вычитаемых матриц. Суммой (или разностью) двух (т х п) матриц А =– а,-/ и В = ( fe(jj называется (т х п) матрица С = с у (г = 1, 2,. . ., т, / = 1, 2,. . ., п), элементы которой равны сумме (или разности) соответствующих элементов слагаемых (вычитаемых) матриц, т. е.  [c.22]

Сложение (а следовательно, и вычитание) матриц ассоциативно и коммутативно, т. е.  [c.22]

Операции сложения и вычитания матриц применяются при переносе систем координат в процессе решения задач анализа механизмов (см. гл. 17, п. 34).  [c.22]

Если учесть, что для перемножения двух матриц п-то порядка необходимо осуществить л умножений и п — 1) сложений, то для перемножения двух матриц 4-го порядка нужно произвести 64 умножения и 48 сложений или всего 112 вычислительных действий, а для матриц 3-го порядка соответственно 27 + 18 = = 45 действий.  [c.188]

В нижней траверзе пресса имеется проём для пропуска через пресс балки или двух швеллеров, сложенных стенками нижний стол, на котором устанавливается инструмент, состоит из двух частей. Подушки с матрицами для пробивания отверстий в полках устанавливаются на концах консольных выступов стола.  [c.483]

Рассмотрим, как влияет учет дисперсий на результаты расчета. Формально учет дисперсий выражается в сложении матрицы [а] [а] с диагональной матрицей [ )], имеющей положительные члены. Это способствует улучшению обусловленности матрицы [а] [а], что особенно важно в случаях, когда последняя плохо  [c.58]

Сложение матриц. Суммой матриц  [c.95]

DN — присвоение значений единицы диагональным элементам двумерного массива А+В — сложение матриц А и В  [c.163]

Необходимость применения динамического метода существенно усложняет решение неконсервативных задач устойчивости. Здесь требуется весьма эффективный метод определения частот собственных колебаний. Среди других методов в этом отношении вьщеляется МГЭ. Он позволяет получать точный спектр частот (устраняет недостаток МКЭ), а в трансцендентном частотном уравнении отсутствуют точки разрыва 2-го рода (устраняет недостаток метода перемещений). Дополнительными положительными факторами являются простая логика формирования динамической матрицы устойчивости, отсутствие операций умножения, обращения и сложения матриц, хорошая устойчивость численных операций при вычислении определителя и т.п.  [c.196]

Кватернионное сложение поворотов. Как и в случае матриц, сложению поворотов отвечает произведение кватернионов, при этом активная и пассивная точки зрения на преобразования имеют существенные отличия.  [c.46]

Сложение. Матрицы А п В могут быть сложены, если они имеют оди-накоиое число строк и столбцов.  [c.631]

Таком образом, для выполнения алгоритма (55) требуются два прямых и одно обратное преобразование Ф/рье, а также прямое умножение матрицы на матрицу. Если в качестве дижретного преобразования Фурье использовать алгоритм БПФ, число опера дай сложения составит 2N og2 , а число операций умножения -.  [c.63]

Показано, что в случае произвольных распределений наработок и времени восстановления в матрицу Гб) вводятся ооответствувщие вероятности переходов, а вместо сложения интенсивностей осуществляется умножение вероятностей независимых событий.  [c.15]

Сложение двух матриц не является такой важной операцией, как их умножение, однако оно встречается достаточно часто. Под суммойА + В понимается такая матрица С, элементы которой получаются посредством сложения соответствующих элементов А и В. Таким образом, можно написать  [c.119]

Может показаться, что скорость, большую скорости света с, можно получить с помощью двух последовательных преобразований Лоренца. Пусть, например, вторая система движется относительно первой со скоростью Vi > с/2, а третья система движется относительно второй со скоростью 02, также большей, чем с/2 (в том же направлении). Можно подумать, что скорость третьей системы относительно первой будет тогда больше чем с. Однако это не так, ибо эта скорость не равна просто V -f Ua-Чтобы убедиться в этом, достаточно найти преобразование Ло-)енца, описывающее переход от первой системы к третьей. 1еремножая для этого матрицы рассматриваемых преобразований, мы найдем полное преобразование и увидим, что оно соответствует скорости из, определяемой так называемым законом Эйнштейна для сложения скоростей. Согласно этому закону  [c.217]

Описание механических свойств композитных материалов, которые могут обладать весьма высокой прочностью (особенно статической и ударной), можно производить двумя путями. В первом случае композитные материалы рассматриваются как квазиодно-родные (гомогенные), обладающие в случае объемного дисперсного армирования изотропией деформационных и прочностных свойств, а в случае армирования волокнами, плоскими сетками или тканями — определенного типа анизотропией. Обычно применяют модели ортотропного или трансверсально-изотропного тела. При таком подходе речь идет о механических характеристиках, осред-ненных в достаточно больших объемах, содержащих много однотипных армирующих элементов. Другой, несравненно более сложный, но и более информативный путь состоит в раздельном рассмотрении механических свойств каждой фазы с последующим теоретическим прогнозированием свойств всего композита в целом. При этом приходится рассматривать фактически еще одну дополнительную фазу зоны сопряжения основных фаз, например, матрицы с армирующими волокнами. Механизм повреждений, развивающихся на границах фаз, обычно весьма сложен и определяется помимо свойств основных компонентов гетерогенной системы еще рядом дополнительных факторов, таких как адгезия фаз, технологические и температурные местные напряжения, обычно возникающие вблизи границ, наличие дефектов и др. Границы фаз как зоны концентраций напряжений играют особенно важную роль в развитии много- и малоцикловых усталостных повреждений композитов.  [c.37]

При необходимости подчеркнуть состав множеств D я Z далее будут использоваться и такие обозначения a D, Z] = a[, 2,…,d Z] = a D , 2,…,Z]== = a d I, 2, z] и T. П. С их помощью можно удобно записывать отдельные составные части (подматрицы) матрицы или новые матрицы, образованные на основе a[D, Z], Например, а , 2, k—l, k+l, d z] = a[D/ k), Z]—матрица, полученная из a[D,Z] в результате вычеркивания й-й строки, а d D — k, Z ], где Z — множество четных чисел (Z zZ)—матрица, в которой к тому же еще вычеркнуты все столбцы с нечетными номерами. В частности, a[k, Z] — k-я строка матрицы a[D, Z], а a[D, /] — ее /-Й столбец. Запись a[D 1, 2 + 3 + 5, 4] обозначает матрицу, в которой второй, третий и пятый столбцы сложены поэлементно и полученный суммарный столбец помещен на второе место. Пусть Zi сг Z и Z2 с= Z— подмножества множества Z, причем Z, 0 2=0 Z/”, Z — обозначения столбцов, полученных как результат сложения столбцов с номерами из множеств Zi и Z2. Тогда матрица а[0] Zt, Z —(Z1UZ2), Zt  [c.88]

Таким образом, на всех стадиях определения скоростей и моментов используется один и тот же алгоритм, позволяющий легко автоматизировать весь процесс вычисления. Его основной недостаток состоит в том, как уже отмечалось выше, что он производит много лишних действий, связанных с умножением и сложением нулей при вычислении определителей ред-козаполненных матриц. Применение направленных графов и соответствующего математического аппарата [2, 21] дает возможность избавиться от этого недостатка и тем са.мым значительно сократить машинное время решения задачи.  [c.98]

Порядок матриц при транспонировании в общем случае изменяется. Сложение и вычитание матрии  [c.18]

К матрицам одного и того же порядка применимы операции сложения и вычитания. Результатом сложения (вычитания) двух матрии А и В порядка n m является новая матрица С того же порядка, каждый элемент которой jj = ajj bjj, где i – номер строки, j – номер столбца. Пусть,  [c.18]

Число критических сил по МКЭ равно степени кинематической неопределимости стержневой системы, а при формировании векового уравнения используются операции сложения, умножения и траспонирования матриц.  [c.179]

---

Сложение и вычитание матриц, онлайн калькулятор

Наш онлайн калькулятор позволяет найти сумму и разность двух матриц всего в пару кликов. Для того чтобы сложить или вычесть две матрицы выберите размер матриц, введите необходимые значения в поля ввода и нажмите кнопку «Вычислить», калькулятор выдаст ответ и подробное решение! Каждый шаг будет детально расписан, это поможет вам понять, как был получен ответ.

Заполните элементы матриц  

Первая матрица:

Вторая матрица:

Решили сегодня: раз, всего раз

Понравился сайт? Расскажи друзьям!

Как найти сумму и разность матриц онлайн

Следует заметить, что данной операции поддаются только матрицы одинакового размера. При сложении двух матриц попарно суммируются все их элементы, а при вычитании мы, соответственно, имеем дело с их попарной разностью. Получив детальное и пошаговое решение, вы сможете лучше разобраться с процессом нахождения суммы и разности матриц.

Итак, перед вами две матрицы, и вам необходимо узнать их сумму, либо же разность. И то, и другое вы сможете легко и оперативно сделать, если воспользуетесь нашим онлайн калькулятором. Он будет очень вам полезен, если вы желаете разобраться в алгоритме данных операций. Теория не всегда способна дать чёткий ответ на все вопросы, куда лучше с этой задачей справляются практические расчёты. Используя онлайн калькулятор, вы получите подробную схему, по которой происходит вычитание или сложение матриц. К тому же, вы можете сначала попробовать просчитать всё самостоятельно, а затем перепроверить себя здесь.

Данный онлайн калькулятор имеет предельно простую инструкцию. Указать размеры каждой из матриц вы сможете, нажимая на иконки «+» или «-» слева от матриц и под ними. Далее вам потребуется ввести все элементы. И затем, нажав кнопку «Вычислить», вы сможете быстро получить искомое значение вместе с развёрнутым алгоритмом вычислений.

Матрицы сложение и вычитание – Справочник химика 21

    Сложение (вычитание) матриц. Две матрицы А и И можно сложить, если опи имеют одинаковое число строк и столбцов. Суммой матриц А и В размерности т X п является матрица С той же размерности, каждый элемент которой равен сумме соответствующих элементов матрицы А VI В. [c.232]

    Сложение (вычитание) строк в матрице А приводит к новой линейной комбинации узлов, а сложение строквВ – к новой системе контуров. Прибавим, к примеру, в матрице соединений (4.12) первую строку ко второй. Получим новую матрицу и схему соединений (рис. 4.4, а), в которой узел 1 + 2 соответствует области, ограниченной пунктирной кривой, т.е. [c.53]

    Квадратные матрицы обладают следующим важным свойством, вытекающим непосредственно из законов их сложения и вычитания любая квадратная матрица Л может быть представлена в виде симметричной и антисимметричной матриц. Так, если [c.43]

    Аналогично каждый элемент матрицы разности есть разность соответствующих элементов матрицы-уменьшаемого и матрицы-вычитаемого Сц = Ац — Bij. Процедура вычитания матриц аналогична процедуре сложения. [c.233]

    Интеллектуальные системы аналитических преобразований (САП). В математическом обеспечении ЭВМ в последние годы все чаще присутствуют системы аналитических преобразований (САП). Они предназначены для облегчения программирования п решения задач, связанных с преобразованием математических выражений. Автоматизированное выполнение аналитических преобразований при помощи ЭВМ стало возможным благодаря развитию методов обработки символьной информации и искусственного интеллекта соответствующих языков программирования методов трансляции и организации памяти разработке вычисленных алгоритмов [62] и т. п. Под аналитическим преобразованием понимаем формальное преобразование математического выражения, заданного в символьном виде, по определенным правилам. Наиболее часто встречающимися операциями аналитического преобразования являются дифференцирование и интегрирование функциональных выражений подстановка вместо переменных констант и выражений упрощение выражений (свертка констант, приведение подобных членов в многочленах и т. п.) разрешение уравнений относительно заданных переменных действия над матрицами, элементами которых являются символьные выражения вынолнение алгебраических действий (сложение, вычитание, умножение, деление) над арифметическими выражениями и т. п. [c.248]

    Для сложения (вычитания) матриц необходимо сложить (вычесть) их элементы, имеющие одинаковые индексы. Складывать можно матрицы, содержащие одинаковое число строк и колонок  [c.167]

    Сложение, вычитание, произведение матриц [c.383]

    Из операций сложения, вычитания и умножения матриц последняя самая сложная и наиболее часто используемая. В дальнейшем матрицы будем обозначать прописными буквами.  [c.148]

    Сложение, вычитание и равенство матриц можно определить только тогда, когда матрицы имеют одинаковую форму и размер. В этом случае [c.65]

    Элементами множества Ж обычно служат вещественные или комплексные числа, целые числа, полиномы некоторой переменной X, функции одной или нескольких переменных и т. п. Если эти элементы образуют поле, т. е. для их совокупности определены выполняющиеся однозначно операции сложения, вычитания, умножения и деления, то говорят, что матрица А задана над полем. Далее мы будем иметь дело в основном с матрицами, заданными над полем действительных или вещественных чисел. [c.9]

    Операции сложения и вычитания матриц понятны из следующих примеров  [c.695]

    Если Ьц = Ьц, то матрицу называют симметричной. А-5а. Сложение и вычитание матриц. Операцию В=А+В [c.432]

    Сложение и вычитание матриц одного размера  [c. 7]

    Сумма и разность. Суммой или разностью д матриц А и В одинаковых размеров называется матрица С, элементами которой служат суммы или разности соответствующих элементов А и В, т.е. С=А+В, если отношении действий сложения и вычитания матриц справедливы переместительный и сочетательный законы  [c.216]

    Программа на стр. 290 реализует метод унитарных преобразований для нахождения собственных значений действительных несимметрических матриц. Вычислительная часть программы оформлена в виде процедуры UNITIM, входными параметрами которой являются порядок матрицы Р, матрица U, точность расчета EPS. Выходным параметром процедуры является матрица L размерности Р X 2, строки которой содержат действительные и мнимые части найденных собственных значений исходной матрицы. В процедуре UNI TIM используются две процедуры SDM и СОМР, первая из которых реализует сложение и вычитание матриц, а вторая — преобразование комплексных чисел из алгебраической в тригонометрическую форму и обратно.  [c.295]

---

Умножение матрицы на скаляр. Сложение и вычитание матриц. Умножение матриц. Транспонирование матриц

                                         Содержание

Задание к курсовой работе ………………………….2

Теоретическая часть :

  1. Умножение матрицы на скаляр ……………………3

  2. Сложение и вычитание матриц ……………………3

  3. Умножение матриц ……………………………..4

  4. Транспонирование матриц ……………………….5

  5.Поиск максимального (минимального) элемента матрицы .6

  6. Формирование вектора из элементов матрицы ……….7

Блок-схема алгоритма решения задачи …………………9

Программа решения задачи ………………………….13

Результаты вычисления по программе . ………………..16

Краткие выводы по решению задачи …………………..17

Список используемой литературы …………………….18

Задание к курсовой работе

Составить программу вычисления и преобразования матрицы D=F(A,B,C),  где F(A,B,C) -матричное выражение А,В,С-исходные матрицы размер и значение элемнтов которых выбираются произвально.

Выражение для расчёта матрицы D и действия по её преобразованию выбираются из таблицы № 1 и №2 в соответствии с номером варианта задания.

В программе предусмотреть вывод на печать всех исходных, промежуточных  и разультирующих матриц, а также результатов преобразования 

Таблица №1

D= (2*A*B^T-С) ^T 

Таблица №2

Определить количество элементов, удовлетворяющих условиям:

1) Pij>Q1         2)Pij<Q2           3)Q2<=Pij<=Q1.

Значения Q1 и Q2 выбрать произвольно

1. Умножение матрицы на скаляр

Чтобы умножить матрицу на скаляр, необходимо каждый элемент этой матрицы умножить на скаляр. Например, если требуется вычислить А=d*В, где А и В матрицы, d – скаляр, то каждый элемент матрицы А определяется по формуле а_ij = в*в_ij; i = 1, 2,…, n;   j = 1, 2,…, m,                   (1)

где n, m – размеры матриц.

Алгоритмы умножения матрицы на скаляр представлен на рис. 1. Здесь центральный оператор вычисления очередного элемента матрицы-произведения (блок 4) является телом двойного цикла по строкам (i) и столбцам (j).

Рис. 1

Входные параметры матрица В(n,m) скаляр d                     

                                             1

ВХОД 

 

                                             2   

                                                 i=I,(1),n

            

                                              3

                                                  j=I,(1),m

 

                                              4

A_ij =d*B_ij

 

                              

 

                                               5

                                                ВЫХОД  

2. Сложение и вычитание матриц

Чтобы сложить (вычесть) две матрицы, необходимо сложить (вычесть) соответствующие элементы этих матриц. Например, если требуется вычислить С = А⁺В, где А и В – матрицы, то каждый элемент матрицы С определяется по формуле с_ij  = a _ij ⁼ b_ij  ; i = 1, 2,…, n ;   j = 1, 2,…, m,              (2)

где n, m – размеры матриц.

Из выражения (2) следует, что складывать (вычитать) можно только матрицы одинакового размера. Алгоритм сложения (вычитания) матриц будет таким же, как на рис. 1, если в блоке 4 вместо формулы (1) записать формулу (2). при этом соответственно изменятся и выходные параметры.

3. Умножение матриц

При перемножении матриц каждый элемент матрицы-произведения определяется как сумма произведений элементов строки матрицы-множителя [1]. Например, если требуется вычислить C = A*B, где A и B – матрицы, то каждый элемент матрицы С определяется по формуле

m

С_ij =       a_ik * b_kj ,  i = 1, 2,. .., n ;   j = 1, 2,…, m,    (3)

                    k=1    где n – число строк матрицы А;

i – число столбцов матрицы B;

m – число столбцов матрицы А или число строк матрицы В. Из (3) следует, что перемножать можно только такие матрицы, у которых число столбцов матрицы-множимого равно числу строк матрицы-множителя, т.е.

 a_{ij      nm}  *     b_{ij        nl}  =     c_{ij         nl}  .

Блок-схема алгоритма перемножения матриц представлена на рис. 2. Здесь каждый элемент матрицы-произведения вычисляется в блоках 4-7 как сумма произведений. В блоке 4 сумма сбрасывается в ноль, в блоке 6 производится непосредственное суммирование произведений, в блоке 7 накопленная сумма записывается в выходной массив.

Рис. 2

Входные параметры матрица А(n,m), В(n,l)         

                                                                1

ВХОД

 

                                                                 2

                                                                      i=I,(1),n     

 

                                                                 3

                                                                     j=I,(1),m          

 

                                                                 4

S=0  

                                                                 5

Обратная матрица

15 февраля 2018

Эта тема является одной из самых ненавистных среди студентов.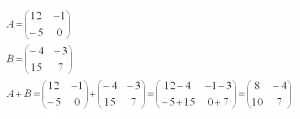 Хуже, наверное, только определители.

Фишка в том, что само понятие обратного элемента (и я сейчас не только о матрицах) отсылает нас к операции умножения. Даже в школьной программе умножение считается сложной операцией, а уж умножение матриц — вообще отдельная тема, которой у меня посвящён целый параграф и видеоурок.

Сегодня мы не будем вдаваться в подробности матричных вычислений. Просто вспомним: как обозначаются матрицы, как они умножаются и что из этого следует.

Повторение: умножение матриц

Прежде всего договоримся об обозначениях. Матрицей $A$ размера $\left[ m\times n \right]$ называется просто таблица из чисел, в которой ровно $m$ строк и $n$ столбцов:

\[A=\left[ m\times n \right]=\underbrace{\left[ \begin{matrix} {{a}_{11}} & {{a}_{12}} & … & {{a}_{1n}} \\ {{a}_{21}} & {{a}_{22}} & . .. & {{a}_{2n}} \\ … & … & … & … \\ {{a}_{m1}} & {{a}_{m2}} & … & {{a}_{mn}} \\\end{matrix} \right]}_{n}\]

Чтобы случайно не перепутать строки и столбцы местами (поверьте, на экзамене можно и единицу с двойкой перепутать — что уж говорить про какие-то там строки), просто взгляните на картинку:

Определение индексов для клеток матрицы

Что происходит? Если разместить стандартную систему координат $OXY$ в левом верхнем углу и направить оси так, чтобы они охватывали всю матрицу, то каждой клетке этой матрицы можно однозначно сопоставить координаты $\left( x;y \right)$ — это и будет номер строки и номер столбца.

Почему система координат размещена именно в левом верхнем углу? Да потому что именно оттуда мы начинаем читать любые тексты. Это очень просто запомнить.

А почему ось $x$ направлена именно вниз, а не вправо? Опять всё просто: возьмите стандартную систему координат (ось $x$ идёт вправо, ось $y$ — вверх) и поверните её так, чтобы она охватывала матрицу. Это поворот на 90 градусов по часовой стрелке — его результат мы и видим на картинке.

В общем, как определять индексы у элементов матрицы, мы разобрались. Теперь давайте разберёмся с умножением.

Определение. Матрицы $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$, когда количество столбцов в первой совпадает с количеством строк во второй, называются согласованными.

Именно в таком порядке. Можно сумничать и сказать, мол, матрицы $A$ и $B$ образуют упорядоченную пару $\left( A;B \right)$: если они согласованы в таком порядке, то совершенно необязательно, что $B$ и $A$, т.е. пара $\left( B;A \right)$ — тоже согласована.

Умножать можно только согласованные матрицы.

Определение. Произведение согласованных матриц $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$ — это новая матрица $C=\left[ m\times k \right]$, элементы которой ${{c}_{ij}}$ считаются по формуле:

\[{{c}_{ij}}=\sum\limits_{k=1}^{n}{{{a}_{ik}}}\cdot {{b}_{kj}}\]

Другими словами: чтобы получить элемент ${{c}_{ij}}$ матрицы $C=A\cdot B$, нужно взять $i$-строку первой матрицы, $j$-й столбец второй матрицы, а затем попарно перемножить элементы из этой строки и столбца. Результаты сложить.

Да, вот такое суровое определение. Из него сразу следует несколько фактов:

1. Умножение матриц, вообще говоря, некоммутативно: $A\cdot B\ne B\cdot A$;
2. Однако умножение ассоциативно: $\left( A\cdot B \right)\cdot C=A\cdot \left( B\cdot C \right)$;
3. И даже дистрибутивно: $\left( A+B \right)\cdot C=A\cdot C+B\cdot C$;
4. И ещё раз дистрибутивно: $A\cdot \left( B+C \right)=A\cdot B+A\cdot C$.

Дистрибутивность умножения пришлось отдельно описывать для левого и правого множителя-суммы как раз из-за некоммутативности операции умножения.

Если всё же получается так, что $A\cdot B=B\cdot A$, такие матрицы называются перестановочными.

Среди всех матриц, которые там на что-то умножаются, есть особые — те, которые при умножении на любую матрицу $A$ снова дают $A$:

Определение. Матрица $E$ называется единичной, если $A\cdot E=A$ или $E\cdot A=A$. В случае с квадратной матрицей $A$ можем записать:

\[A\cdot E=E\cdot A=A\]

Единичная матрица — частый гость при решении матричных уравнений. {-1}}$. Тогда эта обратная матрица — единственная.

Доказательство. Пойдём от противного: пусть у матрицы $A$ есть хотя бы два экземпляра обратных —$B$ и $C$. Тогда, согласно определению, верны следующие равенства:

\[\begin{align} & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end{align}\]

Из леммы 1 мы заключаем, что все четыре матрицы — $A$, $B$, $C$ и $E$ — являются квадратными одинакового порядка: $\left[ n\times n \right]$. Следовательно, определено произведение:

\[B\cdot A\cdot C\]

Поскольку умножение матриц ассоциативно (но не коммутативно!), мы можем записать:

\[\begin{align} & B\cdot A\cdot C=\left( B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left( A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Rightarrow B=C. \\ \end{align}\]

Получили единственно возможный вариант: два экземпляра обратной матрицы равны. Лемма доказана.

Приведённые рассуждения почти дословно повторяют доказательство единственность обратного элемента для всех действительных чисел $b\ne 0$. {-1}} \right|\ne 0.\]

Вот и получается, что $\left| A \right|\ne 0$. Лемма доказана.

На самом деле это требование вполне логично. Сейчас мы разберём алгоритм нахождения обратной матрицы — и станет совершенно ясно, почему при нулевом определителе никакой обратной матрицы в принципе не может существовать.

Но для начала сформулируем «вспомогательное» определение:

Определение. Вырожденная матрица — это квадратная матрица размера $\left[ n\times n \right]$, чей определитель равен нулю.

Таким образом, мы можем утверждать, что всякая обратимая матрица является невырожденной.

Как найти обратную матрицу

Сейчас мы рассмотрим универсальный алгоритм нахождения обратных матриц. Вообще, существует два общепринятых алгоритма, и второй мы тоже сегодня рассмотрим.

Тот, который будет рассмотрен сейчас, очень эффективен для матриц размера $\left[ 2\times 2 \right]$ и — частично — размера $\left[ 3\times 3 \right]$. {t}}$, где $t$ — это (вот сейчас внимание!) сумма номеров всех выбранных строчек и столбцов. Это и будет алгебраическое дополнение.

Взгляните на третий шаг: там вообще-то сумма $2k$ слагаемых! Другое дело, что для $k=1$ мы получим лишь 2 слагаемых — это и будут те самые $i+j$ — «координаты» элемента ${{a}_{ij}}$, для которого мы ищем алгебраическое дополнение.

Таким образом сегодня мы используем слегка упрощённое определение. Но как мы увидим в дальнейшем, его окажется более чем достаточно. Куда важнее следующая штука:

Определение. Союзная матрица $S$ к квадратной матрице $A=\left[ n\times n \right]$ — это новая матрица размера $\left[ n\times n \right]$, которая получается из $A$ заменой ${{a}_{ij}}$ алгебраическими дополнениями ${{A}_{ij}}$:

\[A=\left[ \begin{matrix} {{a}_{11}} & {{a}_{12}} & … & {{a}_{1n}} \\ {{a}_{21}} & {{a}_{22}} & … & {{a}_{2n}} \\ … & … & … & … \\ {{a}_{n1}} & {{a}_{n2}} & . {T}}=\left[ \begin{array}{*{35}{r}} 2 & -1 \\ -5 & 3 \\\end{array} \right]\]

Ну вот и всё. Задача решена.

Ответ. $\left[ \begin{array}{*{35}{r}} 2 & -1 \\ -5 & 3 \\\end{array} \right]$

Задача. Найдите обратную матрицу:

\[\left[ \begin{array}{*{35}{r}} 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end{array} \right]\]

Решение. Опять считаем определитель:

\[\begin{align} & \left| \begin{array}{*{35}{r}} 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end{array} \right|=\begin{matrix} \left( 1\cdot 2\cdot 1+\left( -1 \right)\cdot \left( -1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\left( 2\cdot 2\cdot 1+\left( -1 \right)\cdot 0\cdot 1+1\cdot \left( -1 \right)\cdot 0 \right) \\\end{matrix}= \\ & =\left( 2+1+0 \right)-\left( 4+0+0 \right)=-1\ne 0. \\ \end{align}\]

Определитель отличен от нуля — матрица обратима. А вот сейчас будет самая жесть: надо посчитать аж 9 (девять, мать их!) алгебраических дополнений. {-1}}=\frac{1}{-1}\cdot \left[ \begin{matrix} 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end{matrix} \right]=\left[ \begin{array}{*{35}{r}}-2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end{array} \right]\]

Ну и всё. Вот и ответ.

Ответ. $\left[ \begin{array}{*{35}{r}} -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end{array} \right]$

Как видите, в конце каждого примера мы выполняли проверку. В связи с этим важное замечание:

Не ленитесь выполнять проверку. Умножьте исходную матрицу на найденную обратную — должна получиться $E$.

Выполнить эту проверку намного проще и быстрее, чем искать ошибку в дальнейших вычислениях, когда, например, вы решаете матричное уравнение.

Альтернативный способ

Как я и говорил, теорема об обратной матрице прекрасно работает для размеров $\left[ 2\times 2 \right]$ и $\left[ 3\times 3 \right]$ (в последнем случае — уже не так уж и «прекрасно»), а вот для матриц больших размеров начинается прям печаль.

Но не переживайте: есть альтернативный алгоритм, с помощью которого можно невозмутимо найти обратную хоть для матрицы $\left[ 10\times 10 \right]$. Но, как это часто бывает, для рассмотрения этого алгоритма нам потребуется небольшая теоретическая вводная.

Элементарные преобразования

Среди всевозможных преобразований матрицы есть несколько особых — их называют элементарными. Таких преобразований ровно три:

1. Умножение. Можно взять $i$-ю строку (столбец) и умножить её на любое число $k\ne 0$;
2. Сложение. Прибавить к $i$-й строке (столбцу) любую другую $j$-ю строку (столбец), умноженную на любое число $k\ne 0$ (можно, конечно, и $k=0$, но какой в этом смысл? Ничего не изменится же).
3. Перестановка. Взять $i$-ю и $j$-ю строки (столбцы) и поменять местами.

Почему эти преобразования называются элементарными (для больших матриц они выглядят не такими уж элементарными) и почему их только три — эти вопросы выходят за рамки сегодняшнего урока. Поэтому не будем вдаваться в подробности.

Важно другое: все эти извращения нам предстоит выполнять над присоединённой матрицей. Да, да: вы не ослышались. Сейчас будет ещё одно определение — последнее в сегодняшнем уроке.

Присоединённая матрица

Наверняка в школе вы решали системы уравнений методом сложения. Ну, там, вычесть из одной строки другую, умножить какую-то строку на число — вот это вот всё.

Так вот: сейчас будет всё то же, но уже «по-взрослому». Готовы?

Определение. Пусть дана матрица $A=\left[ n\times n \right]$ и единичная матрица $E$ такого же размера $n$. Тогда присоединённая матрица $\left[ A\left| E \right. \right]$ — это новая матрица размера $\left[ n\times 2n \right]$, которая выглядит так:

\[\left[ A\left| E \right. \right]=\left[ \begin{array}{rrrr|rrrr}{{a}_{11}} & {{a}_{12}} & … & {{a}_{1n}} & 1 & 0 & … & 0 \\{{a}_{21}} & {{a}_{22}} & … & {{a}_{2n}} & 0 & 1 & . {-1}}\]

Вот так всё просто! Короче говоря, алгоритм нахождения обратной матрицы выглядит так:

1. Записать присоединённую матрицу $\left[ A\left| E \right. \right]$;
2. Выполнять элементарные преобразования строк до тех пор, пока права вместо $A$ не появится $E$;
3. Разумеется, слева тоже что-то появится — некая матрица $B$. Это и будет обратная;
4. PROFIT!:)

Конечно, сказать намного проще, чем сделать. Поэтому давайте рассмотрим парочку примеров: для размеров $\left[ 3\times 3 \right]$ и $\left[ 4\times 4 \right]$.

Задача. Найдите обратную матрицу:

\[\left[ \begin{array}{*{35}{r}} 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end{array} \right]\]

Решение. Составляем присоединённую матрицу:

\[\left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end{array} \right]\]

Поскольку последний столбец исходной матрицы заполнен единицами, вычтем первую строку из остальных:

\[\begin{align} & \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end{array} \right]\begin{matrix} \downarrow \\ -1 \\ -1 \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end{array} \right] \\ \end{align}\]

Больше единиц нет, кроме первой строки. Но её мы не трогаем, иначе в третьем столбце начнут «размножаться» только что убранные единицы.

Зато можем вычесть вторую строку дважды из последней — получим единицу в левом нижнем углу:

\[\begin{align} & \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end{array} \right]\begin{matrix} \ \\ \downarrow \\ -2 \\\end{matrix}\to \\ & \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right] \\ \end{align}\]

Теперь можно вычесть последнюю строку из первой и дважды из второй — таким образом мы «занулим» первый столбец:

\[\begin{align} & \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right]\begin{matrix} -1 \\ -2 \\ \uparrow \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right] \\ \end{align}\]

Умножим вторую строку на −1, а затем вычтем её 6 раз из первой и прибавим 1 раз к последней:

\[\begin{align} & \left[ \begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right]\begin{matrix} \ \\ \left| \cdot \left( -1 \right) \right. \\ \ \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right]\begin{matrix} -6 \\ \updownarrow \\ +1 \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end{array} \right] \\ \end{align}\]

Осталось лишь поменять местами строки 1 и 3:

\[\left[ \begin{array}{rrr|rrr} 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & -18 & 32 & -13 \\\end{array} \right]\]

Готово! Справа — искомая обратная матрица.

Ответ. $\left[ \begin{array}{*{35}{r}}4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end{array} \right]$

Задача. Найдите обратную матрицу:

\[\left[ \begin{matrix} 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\end{matrix} \right]\]

Решение. Снова составляем присоединённую:

\[\left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end{array} \right]\]

Немного позалимаем, попечалимся от того, сколько сейчас придётся считать… и начнём считать. Для начала «обнулим» первый столбец, вычитая строку 1 из строк 2 и 3:

\[\begin{align} & \left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end{array} \right]\begin{matrix} \downarrow \\ -1 \\ -1 \\ \ \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end{array} \right] \\ \end{align}\]

Наблюдаем слишком много «минусов» в строках 2—4. Умножим все три строки на −1, а затем «выжжем» третий столбец, вычитая строку 3 из остальных:

\[\begin{align} & \left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end{array} \right]\begin{matrix} \ \\ \left| \cdot \left( -1 \right) \right. \\ \left| \cdot \left( -1 \right) \right. \\ \left| \cdot \left( -1 \right) \right. \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\\end{array} \right]\begin{matrix} -2 \\ -1 \\ \updownarrow \\ -2 \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right] \\ \end{align}\]

Теперь самое время «поджарить» последний столбец исходной матрицы: вычитаем строку 4 из остальных:

\[\begin{align} & \left[ \begin{array}{rrrr|rrrr} 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right]\begin{matrix} +1 \\ -3 \\ -2 \\ \uparrow \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right] \\ \end{align}\]

Финальный бросок: «выжигаем» второй столбец, вычитая строку 2 из строки 1 и 3:

\[\begin{align} & \left[ \begin{array}{rrrr|rrrr} 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right]\begin{matrix} 6 \\ \updownarrow \\ -5 \\ \ \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right] \\ \end{align}\]

И снова слева единичная матрица, значит справа — обратная.:)

Ответ. $\left[ \begin{matrix} 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & -1 \\\end{matrix} \right]$

Ну вот и всё. Проверку сделайте сами — мне в лом.:)

Смотрите также:

1. Определитель
2. Угол между двумя прямыми
3. Тест к уроку «Сложные выражения с дробями» (легкий)
4. Правила комбинаторики в задаче B6
5. Пример решения задачи 15
6. Тригонометрия в задаче B15: решаем без производных

TensorFlow – Математические основы

Важно понять математические понятия, необходимые для TensorFlow, прежде чем создавать базовое приложение в TensorFlow. Математика считается сердцем любого алгоритма машинного обучения. Именно с помощью основных понятий математики определяется решение для конкретного алгоритма машинного обучения.

 

Вектор

Массив чисел, который является либо непрерывным, либо дискретным, определяется как вектор. Алгоритмы машинного обучения работают с векторами фиксированной длины для лучшего генерирования выходных данных.

Алгоритмы машинного обучения работают с многомерными данными, поэтому векторы играют решающую роль.

Графическое представление векторной модели показано ниже:

 

Скаляр

Скаляр может быть определен как одномерный вектор. Скаляры – это те, которые включают только величину и отсутствие направления. Со скалярами нас интересует только величина.

Примеры скаляров включают в себя параметры веса и роста детей.

 

Матрица

Матрица может быть определена как многомерные массивы, которые расположены в формате строк и столбцов. Размер матрицы определяется длиной строки и длиной столбца. На следующем рисунке показано представление любой указанной матрицы.

 

Рассмотрим матрицу с «m» строками и «n» столбцами, как упомянуто выше, представление матрицы будет определено как «m * n matrix», которое также определило длину матрицы.

 

Математические вычисления

В этом разделе мы узнаем о различных математических вычислениях в TensorFlow.

 

Добавление матриц

Добавление двух или более матриц возможно, если матрицы имеют одинаковое измерение. Добавление подразумевает добавление каждого элемента в соответствии с заданной позицией.

Рассмотрим следующий пример, чтобы понять, как работает сложение матриц:

Вычитание матриц

Вычитание матриц работает аналогично добавлению двух матриц. Пользователь может вычесть две матрицы при условии, что размеры равны.

 

Умножение матриц

Для того чтобы две матрицы A m * n и B p * q были умножаемыми, n должно быть равно p. Полученная матрица:

Транспонирование матрицы

Транспонирование матрицы A, m * n обычно представляется AT (транспонирование) n * m и получается путем транспонирования векторов столбцов в качестве векторов строк.

Точечное произведение векторов

Любой вектор размерности n можно представить в виде матрицы v = R ^ n * 1.

Точечное произведение двух векторов является суммой произведений соответствующих компонентов – Компонентов вдоль одного измерения и может быть выражено как

Пример точечного произведения векторов приведен ниже:

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Как складывать и вычитать матрицы

Сложение и вычитание матриц

На этом этапе нашего курса линейной алгебры мы много работали с матрицами, мы выполняли операции со строками для решения систем линейных уравнений, представляя линейную систему в виде матрицы и используя их в наших интересах посредством сокращения строк и эшелонированных форм. Мы также научились понимать не только обозначения матриц, но и их элементы, их размеры, и теперь пора подумать о них в целом и узнать, какие операции могут быть выполнены с ними (обратите внимание: «с ними», НЕ «в их”).

В этом уроке мы познакомимся с первыми двумя из четырех основных операций, которые можно выполнить с парой (или более) матриц: сложение, вычитание, скалярное умножение и умножение. Мы знаем эти базовые операции из арифметики, поэтому нам просто нужно узнать, как они работают со всей структурой матриц и с результатами, которые они производят. Обратите внимание, что мы не упомянули деление матриц, потому что деления между матрицами не существует (или, по крайней мере, процесс еще не определен), единственное деление, которое мы можем сделать, – это разделить элементы в матрице на скаляр, но разделить матрицу на другую матрицу невозможно.

Сложение и вычитание матриц

Мы начинаем с работы с двумя основными операциями, известными нам с тех пор, как мы впервые познакомились с математикой в ​​начальной школе: сложение и вычитание (или что-то «плюс» и «минус»). Чтобы проработать эти операции в этом уроке, давайте определим набор из двух матриц для сложения и вычитания. Итак, определяем матрицы A и B следующим образом:

Уравнение 1: матрицы A и B

Теперь с ними мы настроены для работы через операции сложения и вычитания матриц.К операции будут применяться несколько правил, но мы поговорим о них в следующем разделе, а пока давайте быстро пройдемся по процессу, а затем мы сможем вернуться и проверить, насколько операции были возможны. Начнем с добавления A и B:

Уравнение 2: сложение матриц A и B

Мы закодировали каждый элемент в матрицах цветом, чтобы вы могли видеть, что было сделано для каждого элемента. Обратите внимание на то, как сложение двух матриц действует в случае отдельных элементов, требуя, чтобы у вас были точно такие же элементы в матрицах, участвующих в операции, и чтобы они распределялись одинаковым образом.

Мы повторно рассмотрим эту тему в следующем разделе, но пока вы должны помнить, что при добавлении матриц вы будете добавлять элементы первой матрицы к соответствующей (той, которая находится в «том же месте», той же строке и столбце число) во второй матрице.

Теперь давайте посмотрим на матричное вычитание:

Уравнение 3: вычитание матрицы B из A

Глядя на приведенное выше вычитание, мы можем легко заключить, что этот процесс очень похож на процесс сложения, поскольку вычитание вычисляется по отдельности для каждого из элементов матриц, таким образом давая результат для каждого соответствующего пространства элементов и в результате получается матрица с таким же количеством элементов в той же организации.

Проще говоря, сложение и вычитание матриц работают одинаково, единственная разница между ними – это арифметический знак, который вы используете для работы: знак плюс для сложения и знак минус для вычитания.

Крайне важно, чтобы вы поняли этот вывод, поскольку это может помочь вам не запутаться при работе с различной литературой по данной теме. Дело в том, что некоторые математики, книги или учебные материалы в целом могут относиться к операциям сложения и вычитания как к «сложению» в целом.Эта конкретная ссылка исходит из того факта, что вычитание эквивалентно сложению чисел, в которых хотя бы одно из них отрицательно. Если у вас есть какие-либо вопросы по этому поводу, помните, что вычитание в арифметике также называется «разницей», и все потому, что когда вы складываете числа с разными знаками, результатом становится разница между ними. Мы рассмотрели эту тему в нашем уроке по вычитанию целых чисел, который, хотя и не является частью этого курса линейной алгебры, вы можете проверить в любое время на веб-сайте StudyPug.Вы также можете проверить следующую статью о сложении и вычитании целых чисел, которая содержит дополнительные упражнения и некоторые графические изображения.

Вкратце: Как складывать матрицы? Мы добавляем каждый соответствующий элемент в задействованные матрицы, чтобы создать новую матрицу, в которой такие элементы будут занимать то же место, что и их предшественники. Как вычесть матрицы? Точно так же, как мы вычисляем сложение, за исключением того, что мы используем знак минус для работы вместо знака плюс.

Правила сложения и вычитания матриц

Матричное сложение и вычитание – это две операции, которые, хотя и несложны и просты для решения (как показано выше), у вас все же есть несколько правил, которым нужно следовать, чтобы работать.

Например, когда мы добавляли матрицу A к матрице B выше, сначала обратите внимание, что A и B – очень похожие матрицы, они имеют одинаковое количество строк и столбцов каждая и операция сложения применяется к каждому «соответствующему члену» в них. Это приводит к основному правилу сложения и вычитания матриц, которое соответствует размерам матриц, с которыми работают друг с другом.

Также обратите внимание, что вычитание матриц происходит в очень похожем режиме, на самом деле единственное изменение состоит в том, что вместо знака сложения между матрицами и соответствующими элементами в каждом матричном пространстве у вас есть знак вычитания.

С учетом всего этого правила сложения и вычитания матриц следующие:

1. Вы можете складывать или вычитать только матрицы с одинаковыми размерами.
   1. Если задуматься, это происходит из-за того, что добавление матриц с разными размерами создает проблему, потому что не все элементы в каждой матрице будут иметь соответствующий элемент для работы, и, следовательно, операцию невозможно завершить.
2. Сложение матриц является коммутативным, но вычитание – нет, если сначала вы не примените знак минуса к матрице справа, таким образом сначала преобразуя операцию в сложение.
   1. Свойство коммутативности означает, что при добавлении двух матриц вы можете изменить порядок их добавления, и это не повлияет на результат.
   2. Это не так просто при вычитании. В уравнении 3 у нас есть пример вычитания матриц, обратите внимание, что если вы просто измените порядок матриц, не перемещая знак минус, результат не будет таким же, тогда как вычитание матриц может быть коммутативным? Вы должны применить отрицательный знак к матрице, которая вычитается первой! Проверьте процесс шаг за шагом ниже: Уравнение 4: Условие, чтобы сделать вычитание матрицы коммутативным = сначала преобразовать его в сложение! Обратите внимание, как для того, чтобы иметь возможность изменять порядок матриц, не влияя на результат, мы должны преобразовать вычитание в сложение, что просто означает, что вы должны сначала применить отрицательный знак ко второй матрице, тем самым сделав все отрицательные числа его элементов (которые произведут операцию вычитания, не беспокоясь о порядке элементов).Это единственный способ изменить порядок матриц при вычитании, поэтому помните об этом процессе при работе с еще более сложными проблемами: например, в случаях, когда у вас может быть более двух матриц и вы связываетесь в группах. Подробнее об ассоциации в следующем пункте.
3. Матричное сложение и вычитание ассоциативны.
   1. Свойство ассоциативности используется в задачах, включающих более двух матриц, которые складываются или вычитаются друг из друга.Это свойство позволяет вам сначала работать с операцией между двумя матрицами, а затем использовать матрицу, полученную в результате такой операции, для выполнения второй операции под рукой. Повторяйте такой процесс до тех пор, пока не выполните все необходимые операции с участием всех матриц в задаче.
4. При сложении или вычитании матриц результирующая матрица будет иметь те же размеры, что и матрица, которая ее создала.
   1. Это имеет смысл, поскольку каждый элемент в первой матрице будет работать с соответствующим элементом второй матрицы, таким образом производя результат для каждого пространства элементов.Затем такие результаты станут элементами новой матрицы.

Примеры сложения и вычитания

Далее мы покажем примеры сложения и вычитания матриц. В первом примере упражнения мы сосредоточимся на демонстрации условий, в которых такие операции возможны. Затем мы решаем несколько примеров матричных задач с пошаговым объяснением операций. Мы заканчиваем этот раздел решением матричных уравнений, которые включают либо сложение, либо вычитание матриц.

Пример 1

Можем ли мы сложить или вычесть следующие матрицы?

• Случай 1: Уравнение 5: Можете ли вы сложить эти две матрицы вместе? (Дело 1) Обратите внимание, что размеры матриц, участвующих в сложении, не совпадают. Первая матрица имеет три строки и два столбца, таким образом, это матрица 3×2, а вторая содержит две строки и три столбца, что делает ее размер равным 2×3. Наличие таких различий означает, что, хотя они имеют одинаковое количество элементов, их позиции не соответствуют друг другу, и поэтому по правилам сложения матриц сложение невозможно.
• Случай 2: Уравнение 6: Можете ли вы сложить эти две матрицы вместе? (случай 2) Учитывая, что в этом случае мы будем добавлять матрицы 2×2 (явно; обе матрицы имеют одинаковую размерность 2×2), тогда да, добавление этих двух матриц возможно путем добавления каждого из элементов в первой матрице с соответствующим ему элементом из вторая матрица. Результирующая матрица также будет иметь размеры 2×2.
• Случай 3: Уравнение 7: Можете ли вы сложить эти две матрицы вместе? (случай 3) Как вы, возможно, уже подумали, добавление двух матриц, подобных приведенным выше, невозможно.Размеры этих матриц не совпадают (одна – матрица 3×3, а другая – 2×2), поэтому это добавление невозможно.

Пример 2

Складываем следующие две матрицы:

Уравнение 8: сложение двух матриц

При добавлении двух матриц каждый элемент добавляется к соответствующему элементу в другой матрице. Процесс прост и показан ниже:

Уравнение 9: Решение для сложения двух матриц

Выполните те же действия в следующих двух упражнениях.

Пример 3

Складываем следующие две матрицы:

Уравнение 10: сложение двух матриц

Итак, мы добавляем каждый элемент в матрицах к соответствующему элементу в другой матрице. Обратите внимание, что, как упоминалось ранее, матрицы должны иметь одинаковые размеры, чтобы произошло поэлементное соответствие:

Уравнение 11: Решение для сложения двух матриц

Пример 4

Складываем следующие две матрицы:

Уравнение 12: сложение трех матриц

При добавлении более двух матриц вы можете связать две, выполнив сначала их сложение, а затем добавив полученную матрицу к оставшейся матрице.Это то, что мы называем ассоциативным свойством сложения матриц, это и другие свойства сложения матриц будут объяснены в последующих уроках, а пока проверьте процесс решения этой проблемы ниже:

Уравнение 13: Решение для сложения трех матриц

Итак, как вы можете видеть, первым шагом было добавление матриц один и два, что привело к новой матрице, которая позже добавляется к третьей. Если добавление матриц содержит больше трех матриц, тот же процесс связывания можно повторять столько раз, сколько необходимо, чтобы упростить задачу, пока вы не получите простую операцию с двумя матрицами.

Пример 5

Вычтите следующие матрицы:

Уравнение 14: Вычитание двух матриц

Еще раз обратите внимание, что матрицы, участвующие в вычитании, должны иметь одинаковые размеры, чтобы соблюдалось поэлементное соответствие.

Уравнение 15: Решение для вычитания двух матриц

Пример 6

Вычтите следующие матрицы:

Уравнение 16: Вычитание двух матриц

Неважно, насколько велики матрицы, если они имеют одинаковые размеры, вы можете выполнить вычитание.

Уравнение 17: Решение для вычитания двух матриц

Пример 7

Вычтите следующие матрицы:

Уравнение 18: Вычитание трех матриц

Обратите внимание, что для вычитания матриц с более чем двумя матрицами мы можем снова использовать свойство ассоциативности. Помните, что вычитание матриц не коммутативно (вы не можете изменить порядок матриц в операции и получить тот же результат).

Уравнение 19: Решение вычитания трех матриц

Пример 8

Решите следующее уравнение, содержащее добавление постоянной матрицы к переменной.

Уравнение 20: Найдите A в матричном уравнении (часть 1)

Мы начинаем с вычитания матрицы в левой части к обеим частям уравнения, чтобы мы могли легко найти A, выполнив вычитание матрицы:

Уравнение 21: Найдите A в матричном уравнении (часть 2)

Пример 9

Решите следующие матричные уравнения

Уравнение 22: Найдите X в матричном уравнении (часть 1)

В этом случае самый простой способ найти X – передать его в правую часть, добавив его к обеим частям уравнения, чтобы оно стало положительным.Мы также вычитаем матрицу, найденную в правой части уравнения, из обеих частей, и поэтому мы получаем вычитание матрицы, которое определяет X.

Уравнение 23: Найдите X в матричном уравнении (часть 2)

Решая вычитание матриц, находим X.

Пример 10

Найдите значения элементов a, b, c, d, e и f, решив следующее матричное уравнение наиболее эффективным способом.

Уравнение 24: Нахождение значений элементов в самой левой матрице

В этой задаче мы можем поэлементно преобразовывать регистр элемента, уравнение, которое позволит нам получить значение каждого из элементов в первой матрице.

Другими словами, вы знаете, что элемент из первой строки и первого столбца (вверху слева) в первой матрице будет добавлен к элементу в первой строке и первом столбце второй матрицы, чтобы получить элемент в этом пространстве. в получившейся матрице справа. Другими словами, мы можем легко записать следующие уравнения для каждого пространства элементов:

Уравнение 25: Набор уравнений для каждой переменной, которую необходимо решить

И из этого мы можем решить значение каждой переменной:

Уравнение 25: Решение переменных от a до f

После того, как мы научимся складывать и вычитать матрицы, пришло время изучить другие операции: скалярное умножение матриц и умножение двух или более матриц будут объяснены в следующих двух уроках.

Мы завершаем наш урок на сегодня несколькими полезными ссылками: первая содержит краткий список основных правил сложения матриц и дополнительную лекцию по матричным операциям.

И это все, до встречи на нашем следующем уроке!

Как складывать и вычитать матрицы

Матрица (множественное число матриц ) – это просто массив или таблица чисел. Что бы значило сложить две таблицы вместе? Что ж, ты скоро узнаешь! В этой короткой статье мы обсудим, как складывать и вычитать матрицы.

_{Изображение Андрея Попова}

Что такое матрица?

Во-первых, давайте поговорим о том, что такое матрица.

Матрица представляет собой прямоугольный массив чисел.

Каждая горизонтальная строка чисел в матрице является строкой . Каждая вертикальная линия представляет собой столбец . Мы часто называем отдельные числа элементами матрицы .

Если в массиве m строк и n столбцов, то мы говорим, что размер матрицы равен m × n .Это станет важным, потому что можно складывать или вычитать только матрицы с одинаковыми размерами .

Эта матрица имеет 2 строки и 3 столбца, поэтому ее размеры составляют 2 × 3.

Как складывать и вычитать матрицы

Есть два основных правила для сложения матриц вместе.

1. Можно добавить только две матрицы с одинаковыми точными размерами . Итак, вы можете сложить две матрицы 3 × 4 вместе. Но вы не можете добавить матрицу 3 × 4 к матрице 4 × 3.(Порядок размеров тоже имеет значение!)
2. Добавьте соответствующие записи. То есть левый верхний элемент первой матрицы должен быть добавлен к левому верхнему элементу второй матрицы и так далее.

Чтобы вычесть двух матриц, A – B , выполните следующие действия:

1. Измените операцию на сложение, A + (- B ), преобразовав каждую запись B в противоположную (переверните знаки).
2. Добавьте матрицы, используя описанный выше метод.

(Вместо этого вы можете просто вычесть соответствующих записей, чтобы вычислить A – B , но тогда вам иногда придется отслеживать вычитание отрицательных сумм. Мне просто легче сначала перевернуть каждый знак, а затем прибавить. С алгебраической точки зрения это то же самое.)

Примеры

Рассмотрим следующие три матрицы:

Находят:

а) А + В

б) А + С

в) В – А

г) С – С

Решения

a) Сначала проверьте размеры.И A , и B имеют две строки и два столбца. Поскольку обе они представляют собой матрицы 2 × 2, их можно складывать вместе. Не забудьте добавить соответствующие записи.

б) На этот раз при проверке размеров обнаруживаем несоответствие. A – это 2 × 2, но C – 3 × 2. Следовательно, сумма не существует. Другими словами, нет ответа .

c) Как и в части a , обе матрицы имеют одинаковые размеры.Так что нам разрешено их вычесть. Не забывайте переворачивать знаки второго!

d) Очевидно, что C имеет те же размеры, что и он сам, поэтому правила говорят, что вы можете вычесть.

Поскольку все записи одинаковы, при вычитании C – C вы получите ноль (0) в каждой точке.

(Кстати, любая матрица, в каждой записи которой нет ничего, кроме 0, называется нулевой матрицей или нулевой матрицей .)

• Шон получил докторскую степень по математике в Университете штата Огайо в 2008 году (Go Bucks !!). В 2002 году он получил степень бакалавра математики и информатику в Оберлинском колледже. Кроме того, Шон получил степень бакалавра искусств. из Консерватории Оберлина в том же году по специальности “музыкальная композиция”.Шон по-прежнему любит музыку – почти так же, как математику! – и он (думает, что он) может играть на пианино, гитаре и басу. Шон обучал и обучал студентов математике около десяти лет и надеется, что его опыт поможет вам добиться успеха!

  Просмотреть все сообщения

Вычитание матриц – Свойства

Вычитание матриц относится к вычитанию соответствующих элементов двух или более матриц.Матрица – это математический формат для размещения данных в виде строк и столбцов. Вычитание матриц можно производить посредством поэлементного вычитания матриц. К матрицам могут применяться различные операции, такие как сложение, вычитание и умножение. В этой статье мы в основном сосредоточимся на операции вычитания матриц. Вычитание матриц – это процесс вычитания соответствующих элементов матриц.

Вычитание матриц выполняется так же, как и сложение матриц.Ограничения сложения матриц применимы и к вычитанию матриц. Вычитание матриц определяется только для матриц одинакового размера. Разберем концепцию подробно на примерах.

Что такое вычитание матриц?

Вычитание матриц – это операция поэлементного вычитания матриц одного порядка, то есть матриц, имеющих одинаковое количество строк и столбцов. Если количество горизонтальных строк в матрице равно «m», а количество вертикальных столбцов – «n», то говорят, что матрица имеет размерность «m × n».Для вычитания матриц необходимо, чтобы вычитаемые матрицы имели ту же размерность, что и вычитаемые соответствующие элементы матриц.

Вычитание матриц, означающих

Вычитание матриц или вычитание матриц возможно только в том случае, если количество строк и столбцов обеих матриц одинаково. Вычитая две матрицы, мы вычитаем элементы в каждой строке и столбце из соответствующих элементов в строке и столбце другой матрицы.Рассмотрим две матрицы A и B одного порядка ‘m × n’, где m – количество строк, а n – количество столбцов двух матриц, обозначенных как A = [a _ij ] и B = [b _ij ]. Теперь разность двух матриц A и B определяется как: A – B = [a _ij ] – [b _ij ] = [a _{ij –} b _ij ], где ij обозначает положение каждого элемента в i ^{-й строке} и j ^{-й столбце} . Размерность матрицы разностей, то есть A – B, также равна m × n.

Вычитание матриц порядка 2 × 2

Как мы знаем, вычитание матриц возможно только в том случае, если матрицы имеют равное количество строк и столбцов, поэтому для вычитания матриц порядка 2 × 2 матрицы должны иметь 2 строки и 2 столбца. Теперь рассмотрим две матрицы A и B с размерами 2 × 2. Чтобы вычесть B из A, мы вычтем элементы B из соответствующих элементов A. Общая форма вычитания B из A (порядок 2 × 2): :

Чтобы лучше понять концепцию матричного вычитания размерности 2 × 2, давайте рассмотрим пример двух матриц A и B и вычтем B из A.

Вычитание матриц порядка 3 × 3

Вычитание матриц 3 × 3 означает, что вычитаемые друг из друга матрицы имеют 3 строки и 3 столбца. При вычитании матриц мы вычитаем элементы одной матрицы из соответствующих элементов другой матрицы. Общая форма вычитания матриц A и B порядка 3 × 3:

Обратите внимание, что для вычитания матриц матрицы не обязательно должны быть квадратными.Матричное вычитание прямоугольных матриц также определяется, если порядок матриц один и тот же.

Свойства матричного вычитания

Все ограничения на добавление матриц применяются также и к вычитанию матриц. Но есть определенные законы, которым вычитание матриц не следует так же, как вычитание чисел. Самая важная необходимость для вычитания матриц для сохранения всех этих свойств состоит в том, что вычитание матриц определяется только в том случае, если порядок матриц один и тот же.

• Количество строк и столбцов при вычитании матрицы должно быть одинаковым.
• Вычитание матриц не коммутативно, то есть A – B ≠ B – A
• Вычитание матриц не ассоциативно, то есть (A – B) – C ≠ A – (B – C)
• Вычитание матрицы из самой себя приводит к нулевой матрице, то есть A – A = O.
• Вычитание матриц – это добавление отрицательного значения одной матрицы к другой матрице, то есть A – B = A + (-B).

Важные примечания по вычитанию матриц

• Вычитание матриц возможно только в том случае, если матрицы имеют одинаковую размерность.
• Вычитание матриц не коммутативно и ассоциативно.
• Вычитаем соответствующие элементы матриц для матричного вычитания.

Связанные темы с матричным вычитанием

Часто задаваемые вопросы о вычитании матриц

Что такое вычитание матриц?

Вычитание матриц – это операция поэлементного вычитания матриц одного порядка, то есть матриц, имеющих одинаковое количество строк и столбцов.Вычитая две матрицы, мы вычитаем элементы в каждой строке и столбце из соответствующих элементов в строке и столбце другой матрицы.

Как выполнять вычитание матриц?

Рассмотрим две матрицы A и B одного порядка ‘m × n’, где m – количество строк, а n – количество столбцов двух матриц, обозначенных как A = [a _ij ] и B = [b _ij ]. Теперь разность двух матриц A и B определяется как: A – B = [a _ij ] – [b _ij ] = [a _{ij –} b _ij ], где ij обозначает положение каждого элемента в i ^{-й строке} и j ^{-й столбце} .Размерность матрицы разностей, то есть A – B, также равна m × n.

Является ли

вычитание матриц коммутативным?

Вычитание матриц не коммутативно, то есть A – B ≠ B – A. Как и вычитание чисел, вычитание матриц также имеет определенные ограничения.

Какое необходимое условие для вычитания матриц?

Для вычитания матриц необходимо, чтобы они имели одинаковое количество строк и столбцов.Вычитаемые матрицы должны иметь одинаковую размерность.

Можно ли вычесть две матрицы разного порядка?

Матрицы разного порядка не могут быть вычтены, так как при вычитании любых двух матриц мы вычитаем элементы одной матрицы из соответствующих элементов другой матрицы. Если порядки разные, то в одной из матриц отсутствуют соответствующие элементы.

Является ли ассоциативное вычитание матрицы?

Вычитание матриц не ассоциативно, то есть (A – B) – C ≠ A – (B – C).Как и вычитание чисел, вычитание матриц также имеет определенные ограничения.

Сложение и вычитание матриц и умножение матрицы на константу

При умножении матрицы на скаляр (константа или число) или сложении и вычитании матриц операции выполняются построчно. Давайте рассмотрим каждую операцию отдельно, чтобы увидеть, как это работает.

Содержание

1. Добавление матриц
2. Вычитание матриц
3. Умножение матрицы на константу (скалярное умножение)
4. Сочетание сложения, вычитания и скалярного умножения

реклама

Добавление матриц

Чтобы добавить две матрицы, добавьте соответствующие записи, как показано ниже.Обратите внимание, что вам нужно, чтобы матрицы были одинакового размера, чтобы это имело смысл.

Если матрицы разного размера, сложение не определено.

Матрицы вычитания

Вычитание матриц работает точно так же. Вы можете вычесть запись за записью.

Как и в случае сложения, это не было бы определено, если бы матрицы были разных размеров. В этой ситуации ваш ответ будет просто «не определен».

Умножение матрицы на константу (скалярное умножение)

Умножение матрицы на константу или число (иногда называемое скаляром) всегда определяется независимо от размера матрицы.Вам просто нужно убедиться, что каждая запись в матрице умножена на число.

Объединение операций

В некоторых вопросах вас могут попросить объединить сложение, вычитание и умножение на константу. Здесь мы рассмотрим несколько примеров, чтобы убедиться, что вы знаете, как это сделать.

Пример

Найдите \ (- 2A + B \) для:

\ (A = \ left [\ begin {array} {cc} -4 & 1 \\ 2 & -2 \\ \ end {array} \ right] \) и \ (B = \ left [\ begin {array} {cc} 9 & -4 \\ 0 & 8 \\ \ end {array} \ right] \)

Не забудьте умножать каждую запись на константу и работать с записью при сложении.

\ (\ begin {align} -2A + B & = 2 \ left [\ begin {array} {cc} -4 & 1 \\ 2 & -2 \\ \ end {array} \ right] + \ left [\ begin {array} {cc} 9 & -4 \\ 0 & 8 \\ \ end {array} \ right] \\ & = \ left [\ begin {array} {cc} -2 \ times -4 & -2 \ times 1 \\ -2 \ times 2 & -2 \ times -2 \\ \ end {array} \ right] + \ left [\ begin {array} {cc} 9 & -4 \\ 0 & 8 \\ \ end {array} \ right] \\ & = \ left [\ begin {array} {cc} 8 & -2 \\ -4 & 4 \\ \ end {array} \ right] + \ left [\ begin { массив} {cc} 9 & -4 \\ 0 & 8 \\ \ end {array} \ right] \\ & = \ left [\ begin {array} {cc} 8 + 9 & -2 + (-4) \\ -4 + 0 & 4 + 8 \\ \ end {array} \ right] \\ & = \ boxed {\ left [\ begin {array} {cc} 17 & -6 \\ -4 & 12 \\ \ end {array} \ right]} \ end {align} \)

Это также работает, когда у вас более двух матриц, как показано в следующем примере.

Пример

Найдите \ (A – 3B + 2C \) для:

\ (A = \ left [\ begin {array} {cc} 1 & 1 \\ 0 & 0 \\ \ end {array} \ right] \), \ (B = \ left [\ begin {array} {cc} 2 & 1 \\ 1 & 4 \\ \ end {array} \ right] \) и \ (C = \ left [\ begin {array} { cc} 5 & 2 \\ 3 & 0 \\ \ end {array} \ right] \)

\ (\ begin {align} A – 3B + 2C & = \ left [\ begin {array} {cc} 1 & 1 \\ 0 & 0 \\ \ end {array} \ right] – 3 \ left [\ begin {массив} {cc} 2 & 1 \\ 1 & 4 \\ \ end {array} \ right] + 2 \ left [\ begin {array} {cc} 5 & 2 \\ 3 & 0 \\ \ end { массив} \ right] \\ & = \ left [\ begin {array} {cc} 1 & 1 \\ 0 & 0 \\ \ end {array} \ right] – \ left [\ begin {array} {cc} 3 \ times2 и 3 \ times1 \\ 3 \ times1 & 3 \ times4 \\ \ end {array} \ right] + \ left [\ begin {array} {cc} 2 \ times5 & 2 \ times2 \\ 2 \ times3 & 2 \ times0 \\ \ end {массив} \ right] \\ & = \ left [\ begin {array} {cc} 1 & 1 \\ 0 & 0 \\ \ end {array} \ right] – \ left [\ begin {array} {cc} 6 & 3 \\ 3 & 12 \\ \ end {array} \ right] + \ left [\ begin {array} {cc} 10 & 4 \\ 6 & 0 \\ \ конец {массив} \ right] \\ & = \ left [\ begin {array} {cc} 1 – 6 + 10 & 1 – 3 + 4 \\ 0 – 3 + 6 & 0 – 12 + 0 \\ \ end {массив} \ right] \\ & = \ boxed {\ left [\ begin {array} {cc} 5 & 2 \\ 3 & – 12 \\ \ end {array} \ right]} \ end {align} \ )

Резюме

Запомните следующее для операций с матрицами:

• Чтобы добавить или вычесть, переходите ввод за вводом.
• Сложение и вычитание определяются только в том случае, если матрицы одинакового размера.
• Скалярное умножение всегда определяется – просто умножьте каждый элемент матрицы на скаляр.

реклама

Продолжайте изучение матричных операций

Далее: Умножение матриц

Подпишитесь на нашу рассылку новостей!

Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькулятору и пакеты задач.

Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!

Связанные

Вычитание матрицы – объяснение и примеры

Есть базовые операции стоимостью 4 доллара, которые мы можем выполнять с матрицами. Это сложение, вычитание, скалярное умножение и умножение матриц. Матричное вычитание является одним из них, и мы рассмотрим его в этой статье.

Примечание. Деление матрицы не является определенной операцией.Мы можем разделить матрицу только на скалярное число. Чтобы узнать больше о матричном делении, щелкните здесь.

Определим матричное вычитание:

Матричное вычитание – это операция вычитания двух матриц одинаковой размерности путем вычитания соответствующих элементов.

В этой статье будут показаны условия, при которых возможно вычитание матриц, вычитание матриц и несколько примеров, демонстрирующих этот процесс.

Когда можно вычитать матрицы?

Можно ли вычесть какие-либо матрицы?

Нет!

Мы можем вычесть матрицы по 2 доллара, только если они имеют одинаковую размерность. То есть, если матрицы $ 2 $ имеют одинаковое количество строк и столбцов, тогда и только тогда мы можем вычесть матрицы $ 2 $ вместе.

Напомним, что размерность матрицы – это количество строк и столбцов. Если в матрице есть $ a $ строк и $ b $ столбцов, мы можем сказать, что матрица имеет размеры $ a \ times b $ (произносится как $ a $ -by- $ b $). Чтобы узнать больше о размерах матрицы, прочтите эту статью!

Помните, что матрица, полученная в результате операции вычитания матриц, будет той же размерности, что и матрицы, которые ее создали.

Как вычесть матрицы?

После того, как мы пришли к выводу, что матрицы имеют одинаковые размеры, мы вычитаем матрицы на 2 доллара, вычитая соответствующие друг другу элементы . Рассмотрим матрицу $ A $ и матрицу $ B $, показанные ниже:

$ A = \ begin {bmatrix} {0} & {4} \\ {- 3} & {- 3} \ end {bmatrix} $

$ B = \ begin {bmatrix} {- 9} & 0 \\ 2 & {- 2} \ end {bmatrix} $

И матрица $ A $, и $ B $ имеют $ 2 $ строк и $ 2 $ столбцов.Следовательно, размеры матриц равны $ 2 \ times 2 $, что делает их равными. Это означает, что мы можем вычесть матрицы по $ 2 $, вычитая каждую соответствующую запись друг из друга. Процесс показан ниже:

$ A – B = \ begin {bmatrix} {0 – – 9} & {4 – 0} \\ {- 3 – 2} & {- 3 – – 2} \ end {bmatrix } $

$ A – B = \ begin {bmatrix} {0 + 9} & {4 – 0} \\ {- 3-2} & {- 3 + 2} \ end {bmatrix} $

$ A – B = \ begin {bmatrix} {9} & {4} \\ {- 5} & {- 1} \ end {bmatrix} $

Теперь давайте рассмотрим две матрицы, показанные ниже:

$ A = \ begin {bmatrix} {0} & {- 1} \\ 10 & 2 \ end {bmatrix} $

$ B = \ begin {bmatrix} {- 5} & 0 \\ 6 & 0 \\ 3 & 7 \ \ 4 & {- 7} \ end {bmatrix} $

Определяется ли $ A – B $?

№
Матрица $ A $ имеет размерность $ 2 \ times 2 $. Матрица $ B $ имеет размерность $ 4 \ times 2 $. Поскольку размеры обеих матриц не равны, вычитание матриц не определено! Мы не можем вычесть матрицу $ A $ и $ B $, потому что не будет соответствующей записи для каждого элемента матрицы $ A $ и матрицы $ B $.

Правила вычитания матриц

Мы можем написать правила вычитания матриц стоимостью 4 доллара. Показано ниже:

1. Вычитать можно только матрицы с одинаковыми размерами (т.е.е. количество строк первой матрицы должно равняться количеству строк второй матрицы. Кроме того, количество столбцов первой матрицы должно быть равно количеству столбцов второй матрицы.)
2. Результирующая матрица вычитания матрицы будет иметь тот же размер, что и исходные матрицы, которые ее создали.
3. Матричное вычитание НЕ коммутативно (т.е. $ A – B \ neq B – A $). Когда вы меняете порядок матриц и вычитаете, он дает другой ответ (как и действительные числа).
4. Матричное вычитание НЕ ассоциативно (т.е. $ (A – B) – C \ neq A – (B – C) $).

Давайте посмотрим на несколько примеров вычитания матриц .

Пример 1

Проверьте, определено ли вычитание матрицы между Матрицей $ A $ и Матрицей $ B $. Если да, вычтите их.

$ A = \ begin {bmatrix} {0} & {- 5} \\ {- 5} & {0} \ end {bmatrix} $

$ B = \ begin {bmatrix} {3} & {- 4} \\ {0} & {- 5} \ end {bmatrix} $

Решение

Для определения вычитания матрицы размер каждой матрицы должен быть одинаковым.
Матрица $ A $ – это матрица размером $ 2 \ times 2 $. Матрица $ B $ также является матрицей $ 2 \ times 2 $. Таким образом, определяется вычитание матриц между матрицами $ A $ и $ B $.

Теперь давайте вычтем матрицы по $ 2 $ вместе, вычтя каждую соответствующую запись матрицы $ B $ из каждой соответствующей записи матрицы $ A $. Показано ниже:

$ A – B = \ begin {bmatrix} {0 – 3} & {- 5 – – 4} \\ {- 5 – 0} & {0 – – 5} \ end {bmatrix} $

$ A – B = \ begin {bmatrix} {- 3} & {- 5 + 4} \\ {- 5} & {0 + 5} \ end {bmatrix} $

$ A – B = \ begin { bmatrix} {- 3} & {- 1} \\ {- 5} & {5} \ end {bmatrix} $

Пример 2

Для представленных ниже матриц $ 2 $ найдите $ C – D $.

$ C = \ begin {bmatrix} {1} & {- 1} \\ 1 & {- 1} \\ 7 & {- 7} \ end {bmatrix} $

$ D = \ begin {bmatrix} {1} & {- 2} & {- 1} \\ {- 1} & 0 & {- 1} \ end {bmatrix} $

Решение

Размерность матрицы $ C $ равна $ 3 \ times 2 $. Размерность Матрицы $ D $ равна $ 2 \ times 3 $. Несмотря на то, что размеры эквивалентны, мы, , не можем вычесть Matrix $ D $ из Matrix $ C $ . Порядок размеров также важен.Матрица $ 3 \ times 2 $ не равна матрице $ 2 \ times 3 $. Таким образом, мы не можем вычесть Матрицу $ D $ из Матрицы $ C $.

Мы также можем решать основные алгебраические уравнения с вычитанием матриц. Рассмотрим пример, показанный ниже.

Пример 3

Найдите значения $ a $ и $ b $ по следующему уравнению:

$ \ begin {pmatrix} {1} & {2} \\ b & {- 6} \ конец {pmatrix} – \ begin {pmatrix} {a} & {- 1} \\ 0 & {- 3} \ end {pmatrix} = \ begin {pmatrix} {7} & {3} \\ {- 2} & {- 3} \ end {pmatrix} $

Решение

Мы можем вычесть соответствующие записи, чтобы найти $ a $ и $ b $.Сначала вычтем соответствующие элементы для $ a $ и решим для переменной:

$ 1 – a = 7 $
$ a = 1-7 $
$ a = – 6 $

Теперь давайте найдем значение $ b $ путем вычитания соответствующих записей для $ b $:

$ b – 0 = – 2 $
$ b = – 2 $

Теперь вы можете попробовать несколько практических вопросов и посмотреть, правильно ли вы их ответили. Ответы ниже.

Практические вопросы

1. Рассмотрим следующие 3 $ матрицы:
   $ P = \ begin {pmatrix} {- 2} & {- 2} \\ 1 & {1} \ end {pmatrix} $
   $ Q = \ begin {pmatrix} {- 3} & {- 3} \\ {- 3} & {- 3} \ end {pmatrix} $
   $ R = \ begin {pmatrix} 1 & 1 \\ 7 & {- 2} \\ 3 & {- 7} \ end {pmatrix}
   $ Найти:
   
   1. $ P – Q $
   2. $ Q –
   R $
   3. $ Q – P $
2. Найти значения $ a $, $ b $ и $ c $ заданы следующим уравнением:

   $ \ begin {pmatrix} {3} & {2} & 0 \\ b & {- 2} & 3 \\ 11 & a & -2 \ end {pmatrix} – \ begin {pmatrix} {3} & {2} & c \\ 5 & {- 5} & 3 \\ {- 4} & {6} & 10 \ end {pmatrix } = \ begin {pmatrix} {0} & {0} & -9 \\ 12 & {3} & 0 \\ 15 & -3 & {- 12} \ end {pmatrix} $

Ответы

1. Все задачи $ 3 $ представляют собой матричное вычитание.Обратите внимание, что, поскольку матричное вычитание не коммутативно , ответ на Part $ A $ и Part $ C $ будет другим. Ответы приведены ниже.
   
   1. Обе матрицы $ P $ и $ Q $ являются матрицами размером $ 2 \ times 2 $. Таким образом, мы вычитаем матрицы размером $ 2 $, вычитая соответствующие элементы. Показано ниже:
      $ P – Q = \ begin {pmatrix} {- 2 – – 3} & {- 2 – – 3} \\ {1 – – 3} & {1 – – 3} \ end {pmatrix} $
      $ P – Q = \ begin {pmatrix} {- 2 + 3} & {- 2 + 3} \\ {1 + 3} & {1 + 3} \ end {pmatrix} $
      $ P – Q = \ begin {pmatrix} {1} & {1} \\ {4} & {4} \ end {pmatrix} $
   2. Мы не можем вычесть матрицу $ R $ из матрицы $ Q $, потому что их размеры не совпадают .Матрица $ Q $ – это матрица $ 2 \ times 2 $, а Матрица $ R $ – матрица $ 3 \ times 2 $.
   3. Ответ на эту часть вопроса будет отличаться от ответа в части $ A $, поскольку вычитание матриц не коммутативно. Вычтем Матрицу $ P $ из Матрицы $ Q $.
      $ Q – P = \ begin {pmatrix} {- 3 – – 2} & {- 3 – – 2} \\ {- 3 – 1} & {- 3 – 1} \ end {pmatrix} $
      $ Q – P = \ begin {pmatrix} {- 3 + 2} & {- 3 + 2} \\ {- 4} & {- 4} \ end {pmatrix} $
      $ Q – P = \ begin {pmatrix} { – 1} & {- 1} \\ {- 4} & {- 4} \ end {pmatrix} $
2. Мы можем вычесть соответствующие записи, чтобы найти $ a $, $ b $ и $ c $.Сначала вычтем соответствующие элементы для $ a $ и решим для переменной:

   $ a – 6 = -3 $
   $ a = – 3 + 6 $
   $ a = 3 $

   Теперь давайте найдем значение $ b $ путем вычитания соответствующих записей для $ b $:

   $ b – 5 = 12 $
   $ b = 12 + 5 $
   $ b = 17 $

   Наконец, давайте найдем значение $ c $ путем вычитания соответствующие записи для $ c $:

   $ 0 – c = -9 $
   $ c = 0 – – 9 $
   $ c = 0 + 9 $
   $ c = 9 $

Предыдущий урок | Главная страница | Следующий урок

Как складывать и вычитать матрицы | Precalculus

Сложение и вычитание матриц

Шаг 1: Найдите размеры заданных матриц.Матрицы можно складывать или вычитать только в том случае, если они имеют одинаковые размеры.

Шаг 2: Если данные матрицы имеют одинаковые размеры, чтобы добавить матрицы, добавьте соответствующие элементы каждой матрицы. Запись первого столбца и строки первой матрицы будет добавлена ​​к записи первой строки и столбца второй матрицы. Полученная сумма будет помещена в соответствующую позицию; то есть сумма записей в первой строке-столбце обеих матриц будет помещена в первый столбец первой строки результирующей матрицы.

Аналогичным образом мы вычтем соответствующие элементы в двух матрицах, если мы выполняем вычитание матриц.

Мы можем разместить матрицы в любом порядке, когда нас попросят их добавить; то есть, если нас попросят добавить матрицу {eq} A {/ eq} и матрица {eq} B {/ eq}, мы можем разместить их в любом порядке и начать добавлять. Когда нас просят вычесть матрицы, мы должны расположить их в том же порядке, в каком нам дается вычитание; то есть, если нас попросят вычесть матрицы {eq} A – B {/ eq}, тогда мы должны поместить матрицу {eq} A {/ eq} сначала, а затем вычтите матрицу {eq} B {/ eq} от него.И наоборот, быть не может.

Сложение и вычитание матриц Словарь

Матрицы: Матрицы представляют собой прямоугольное расположение чисел в строках и столбцах. «Матрица» – это единственное число «матриц». Числа в матрице заключены в скобки. Матрицу можно обозначить прописной буквой алфавита. Горизонтальная линия – это строка в матрице, а вертикальная линия – это столбец в матрице. Каждое число или выражение в матрице – это запись в матрице.

Размерность матрицы: Размерность матрицы сообщает нам количество строк и количество столбцов в матрице. Если данная матрица имеет {eq} x {/ eq} строк и {eq} y {/ eq} столбцов, размер матрицы будет записан как {eq} x \ times y {/ экв}. Это также называется {eq} x \ text {by} y {/ экв}. Помните, что {eq} \ bf {(\ times)} Знак {/ eq} не означает умножение.

Мы рассмотрим два примера и решим их вместе, используя шаги, упомянутые выше, чтобы лучше понять сложение и вычитание матриц.Первый пример покажет сложение матриц, а второй пример покажет вычитание матриц.

Сложение и вычитание матриц: пример сложения матрицы

Сложите две заданные матрицы {eq} A + B {/ eq}

{eq} A = \ begin {bmatrix} 3 и -6 и 5 \\ 4 и 5 и -2 \ end {bmatrix}, B = \ begin {bmatrix} 5 и 3 и -8 \\ 2 и 8 и -4 \ end {bmatrix} \\ {/ eq}

Шаг 1: Найдите размеры заданных матриц. Матрицы можно складывать или вычитать только в том случае, если они имеют одинаковые размеры.

• Количество строк или горизонтальных линий в матрице {eq} A {/ eq} равно двум.

• Количество столбцов в матрице {eq} A {/ eq} равно трем.

Таким образом, размерность матрицы {eq} A {/ eq} равно {eq} 2 \ times3 {/ eq}

• Количество строк или горизонтальных линий в матрице {eq} B {/ eq} равно двум.

• Количество столбцов в матрице {eq} B {/ eq} равно трем.

Таким образом, размерность матрицы {eq} B {/ eq} равно {eq} 2 \ times3 {/ eq}

Таким образом, они имеют одинаковые размеры.Мы можем добавить матрицы.

Шаг 2: Если данные матрицы имеют одинаковые размеры, чтобы добавить матрицы, добавьте соответствующие записи; то есть столбец первой строки, одна запись первой матрицы будет добавлен к столбцу первой строки, одна запись второй матрицы. Полученная сумма будет помещена в соответствующую позицию результирующей матрицы.

$$ A + B = \ begin {bmatrix} 3 и -6 и 5 \\ 4 и 5 и -2 \ end {bmatrix} + \ begin {bmatrix} 5 и 3 и -8 \\ 2 и 8 и -4 \ end {bmatrix} \\ A + B = \ begin {bmatrix} 3 + 5 и -6 + 3 и 5 + (- 8) \\ 4 + 2 и 5 + 8 и -2 + (- 4) \ end {bmatrix} \\ \ boxed {A + B = \ begin {bmatrix} 8 & -3 & -3 \\ 6 и 13 и -6 \ end {bmatrix}} $$

Сложение и вычитание матриц: пример матрицы вычитания

Вычтите две заданные матрицы {eq} A – B. {/ eq}

{eq} A = \ begin {bmatrix} 3 и -6 и 5 \\ 4 и 5 и -2 \ end {bmatrix}, B = \ begin {bmatrix} 5 и 3 и -8 \\ 2 и 8 и -4 \ end {bmatrix} \\ {/ eq}

Шаг 1: Найдите размеры заданных матриц.Матрицы можно складывать или вычитать только в том случае, если они имеют одинаковые размеры.

Размерность матрицы {eq} A \ text {and} B {/ eq} равно {eq} 2 \ times3 {/ eq}

Мы можем вычесть матрицы.

Шаг 2: Если данные матрицы имеют одинаковые размеры для вычитания матриц, вычтите соответствующие записи и поместите результат после вычитания в соответствующую позицию.

$$ A – B = \ begin {bmatrix} 3 и -6 и 5 \\ 4 и 5 и -2 \ end {bmatrix} – \ begin {bmatrix} 5 и 3 и -8 \\ 2 и 8 и -4 \ end {bmatrix} \\ А – В = \ begin {bmatrix} 3-5 и -6-3 и 5 – (- 8) \\ 4-2 и 5-8 и -2 – (- 4) \ end {bmatrix} \\ \ boxed {A – B = \ begin {bmatrix} -2 и -9 и 13 \\ 2 и -3 и 2 \ end {bmatrix}}

$ Получите доступ к тысячам практических вопросов и объяснений!

Онлайн-справка – Быстрая справка

Вычесть одно изображение из другого Последнее обновление: 05.03.2020 Да, хотя, если изображения различаются по размеру, операция немного сложнее. Импорт изображений в матрицу Нажмите кнопку Новая матрица на стандартной панели инструментов. В проводнике Windows, CTRL + выберите файлы изображений и перетащите их в окно матрицы. Если изображения имеют одинаковые размеры, они будут импортированы как отдельные объекты в окно матрицы. Если изображения имеют разные размеры, каждое будет импортировано на отдельный лист в окне матрицы. ПРИМЕЧАНИЕ. Вы также можете перетащить изображения в Origin вне любого окна. Будет создано новое окно матрицы. Вычитание изображений или матриц на одном листе Ниже предполагается, что ваши изображения имеют одинаковый размер: Если вы хотите отправить вывод в новый матричный объект на том же листе, вы должны сначала создать пустой объект, щелкнув значок изображения, а затем выбрав Добавить . В меню выберите Изображение : Арифметическое преобразование : Простая математика : Открыть диалоговое окно . Укажите входные и выходные данные с помощью кнопок со стрелками рядом с Входное изображение1 , Входное изображение2 и Выходное изображение , выбрав вновь созданный (пустой) матричный объект для выходного изображения . Щелкните раскрывающийся список Математическая функция и укажите операцию, которую необходимо выполнить (например,грамм. «Добавить», «img1 – img2» и т. Д.). Выберите канал, смещения Z и кадрируйте, если необходимо. Нажмите ОК . Вычитание изображений или матриц на разных листах или книгах Активируйте матричную книгу, содержащую два или более листов, затем выберите Изображение : Арифметическое преобразование : Простая математика : Открыть диалоговое окно . Нажмите кнопку со стрелкой рядом с Входное изображение1 и Входное изображение2 и используйте обозреватель изображений (используйте раскрывающийся список Список изображений вверху для фильтрации) и выберите, куда отправить Выходное изображение . Щелкните раскрывающийся список Математическая функция и укажите операцию, которую нужно выполнить (например, «Добавить», «img1 – img2» и т. Оставить комментарий Отменить ответ Для отправки комментария вам необходимо авторизоваться. Меню Поиск: