В начале было тяготение: как появился самый известный труд Ньютона – Наука
“Действию всегда есть равное и противоположное противодействие” — третий закон движения сэра Исаака Ньютона сейчас звучит скорее как расхожий штамп поп-психологии, чем строгая формулировка физического закона. Однако в конце XVII века “Математические начала натуральной философии” произвели революционный прорыв в науке, определив то, как человечество понимало устройство Вселенной, вплоть до появления теории относительности Эйнштейна.
Фундаментальная трехтомная работа Ньютона, заложившая основы современной физики и астрономии, впервые увидела свет в июле 1687 года (впоследствии она была переиздана в 1713 и 1726 годах). В ней ученый сформулировал три закона движения — фундамент классической механики, закон всемирного тяготения, а также привел доказательства законов планетарного движения Кеплера, которые самим Кеплером были выведены эмпирически.
Работа Ньютона считается кульминацией научной революции раннего Нового времени.
На эту тему
Успех ньютоновской теории гравитации привел к формированию новой концепции точной науки, в которой физическая теория, сопровождаемая строгими доказательствами, получила примат над эмпирическим наблюдением, а любое расхождение между ними, даже самое малое, воспринималось как важная информация об окружающем мире.
Вывод же Ньютона о том, что сила, удерживающая планеты на орбитах, — явление того же порядка, что и земная гравитация, покончил с представлением, восходящим еще к Аристотелю, что наука о небесных сферах не имеет ничего общего с наукой земной.
Используя наработки Галлея, Ньютон рассчитал массу каждой планеты, объяснил приплюснутость Земли у полюсов действием солнечной гравитации, а также связал солнечное и лунное притяжение с циклами приливов и отливов. По мысли Ньютона, вся Вселенная удерживалась сетью гравитационных сил, воздействующих на каждую звезду, планету или комету — то есть описывалась универсальным законом, доступным человеческому разуму.
По мысли Ньютона, вся Вселенная удерживалась сетью гравитационных сил, воздействующих на каждую звезду, планету или комету — то есть описывалась универсальным законом, доступным человеческому разуму.
Подробно описывая эффекты гравитации, Ньютон отказывался говорить, почему она возникает. “Я не измышляю гипотез”, — заявил он в начале третьего тома, однако все его тезисы и аргументы подтверждались математическими и экспериментальными доказательствами.
На эту тему
Публикация “Начал” произвела эффект разорвавшейся бомбы в научном сообществе — часть ученых с готовностью приняла ньютоновскую концепцию, другая (главным образом картезианцы) обрушилась с критикой на теорию притяжения.
Дискуссии продолжались и в XVIII веке, пока череда экспериментов и наглядная возможность предсказывать движения небесных тел не доказали применимость ньютоновского закона тяготения.
Ряд не решенных Ньютоном проблем потребовал длительного совершенствования математического аппарата, а по мере развития науки накапливались необъяснимые в рамках теории расхождения расчетных и эмпирических данных — пока теория относительности Эйнштейна не свергла ньютоновскую концепцию с пьедестала, низведя ее до статуса частного случая общей теории.
Нина Блейман
Полную версию материала читайте на научно-популярном портале “Чердак”
Законы Ньютона – презентация онлайн
1. Законы Ньютона
ЗАКОНЫ НЬЮТОНА1. Первый закон ньютона (закон инерции)
Повторим один из опытов, которые поставил итальянский ученый
Поставим опыт:
Будем скатывать шар по
1)
наклонной плоскости и
наблюдать за его
дальнейшим движением
по горизонтальной
2)
поверхности.
1)Если она посыпана
песком, шар остановится
очень скоро.
2)Если она покрыта
тканью, шар катится
значительно дольше.
3)А вот по стеклу шар
катится очень долго.
3)
На основании этого и подобных опытов
Галилей открыл закон инерции:
если на тело не действуют другие тела
или действия других тел
скомпенсированы, то тлело движется
равномерно и прямолинейно или
покоится.
Сохранение скорости тела, когда на него
не действуют другие тела или действия
называют явлением инерции.

Закон инерции называют
также первым законом
Ньютона, потому что
Ньютон включил его в
качестве первого закона в
систему трех законов
динамики, которые
называют «тремя
законами Ньютона».
Закон инерции
Если на тело не действуют силы
или их действие
скомпенсировано, то данное тело
находится в состоянии покоя или
равномерного прямолинейного
движения.
Существуют такие системы отсчета,
относительно которых
поступательно движущееся тело
сохраняет свою скорость
действуют другие тела (или
действия других тел
компенсируется).Такие системы
называются ИНЕРЦИАЛЬНЫМИ
СИСТЕМАМИ ОТСЧЕТА
Первый закон Ньютона называют
законом инерции.
Существуют такие системы
отсчета, относительно которых
тела сохраняют свою скорость
неизменной (по модулю и
направлению), если на них не
действуют другие тела или
действия других тел
компенсируются
11.
 Второй закон Ньютона ВТОРОЙ ЗАКОН
Второй закон Ньютона ВТОРОЙ ЗАКОННЬЮТОНА
12. 1. Кто из ученых сформулировал закон инерции?
1. Аристотель2. Галилей
3. Ньютон
4. Архимед
13. Зависимость ускорения от массы: a ~ 1/m
1)2)
Равнодействующая сила
Если на тело, которое можно считать
материальной точкой, действуют
одной силой, которая является
векторной суммой этих сил. Ее
называют равнодействующей.
На рисунке 13.4 показано, как найти
равнодействующую двух сил.
15. Сила -количественная мера действия тел друг на друга, в результате которого тела получают ускорения.
Сила определяется:• Модулем
• Направлением
• Точкой приложения
16. Сила
R F 1 F 2 … F nn число сил
17. Зависимость ускорения от силы: a ~ F
Зависимость ускорения от силы:a~F
18. Формулировка второго закона Ньютона
Ускорение тела прямо пропорциональноравнодействующей сил, приложенных к телу, и обратно
пропорционально его массе.

19. Второй закон Ньютона
ВТОРОЙ ЗАКОНПроизведение массы тела на его
ускорение равно сумме всех сил,
действующих на тело
20. Второй закон Ньютона
ВТОРОЙ ЗАКОННЬЮТОНА
21. Границы применимости
ГРАНИЦЫ ПРИМЕНИМОСТИДля макроскопических тел
Под телом подразумевается материальная точка
Движение материальной точки рассматривается в
инерциальной системе отсчета
Для скоростей, много меньших скорости света в вакууме
22. Особенности второго закона Ньютона
ОСОБЕННОСТИ ВТОРОГОЗАКОНА НЬЮТОНА
Закон справедлив для любых сил
Сила является причиной изменения скорости и
определяет ускорение тела
Если на тело действует несколько сил, то результат
действия – сила, равная геометрической сумме
приложенных сил – равнодействующая
равнодействующей силы
Если равнодействующая сила равна нулю, то ускорение
тела равно нулю, т.
 е. получаем первый закон Ньютона
е. получаем первый закон Ньютона23. Причина ускорения – равнодействующая всех сил.
ПРИЧИНА УСКОРЕНИЯ –РАВНОДЕЙСТВУЮЩАЯ
ВСЕХ СИЛ.
Вектор ускорения и вектор силы
всегда сонаправлены.
a
F
р
24. 1. Если при неизменной массе тела увеличить силу в 2 раза, то ускорение
1. ЕСЛИ ПРИ НЕИЗМЕННОЙ МАССЕТЕЛА УВЕЛИЧИТЬ СИЛУ В 2 РАЗА, ТО
УСКОРЕНИЕ
1. уменьшится в 2 раза.
2. увеличится в 2 раза.
3. не изменится.
4. увеличится в 4 раза.
25. 2. Определите силу, под действием которой велосипедист скатывается с горки с ускорением, равным 0,8 м/с2, если масса
2. ОПРЕДЕЛИТЕ СИЛУ, ПОД ДЕЙСТВИЕМ КОТОРОЙВЕЛОСИПЕДИСТ СКАТЫВАЕТСЯ С ГОРКИ С
ВЕЛОСИПЕДИСТА ВМЕСТЕ С ВЕЛОСИПЕДОМ 50 КГ.
Дано:
Решение.
a = 0,8 м/с2
m = 50 кг
F=m*a
F = 50 кг * 0,8 м/с2
F-?
= 40 Н
Ответ: 40 Н.
=
26. 3. С каким ускорением двигался при разбеге реактивный самолет массой 70 т, если сила тяги двигателей 140 кН?
3. С КАКИМ УСКОРЕНИЕМ ДВИГАЛСЯ ПРИ
С КАКИМ УСКОРЕНИЕМ ДВИГАЛСЯ ПРИРАЗБЕГЕ РЕАКТИВНЫЙ САМОЛЕТ МАССОЙ 70 Т,
ЕСЛИ СИЛА ТЯГИ ДВИГАТЕЛЕЙ 140 КН?
Дано:
Решение.
F = 140 кН = 140 000 Н
F=m*a;a=F/m
m = 70 т = 70 000 кг
a = 2 м/с2
a-?
Ответ: 2 м/с2.
27. 1. Спустившись с горки, санки с мальчиком начинают тормозить с ускорением 2 м/с2. Определите величину тормозящей силы, если
1. СПУСТИВШИСЬ С ГОРКИ, САНКИ СМАЛЬЧИКОМ НАЧИНАЮТ ТОРМОЗИТЬ С
УСКОРЕНИЕМ 2 М/С2. ОПРЕДЕЛИТЕ ВЕЛИЧИНУ
МАЛЬЧИКА И САНОК РАВНА 40 КГ.
1) 20 Н
2) 40 Н
3) 42 Н
4) 80 Н
28. 2. Легкоподвижную тележку массой 3 кг толкают с силой 6 Н. Определите ускорение тележки.
2. ЛЕГКОПОДВИЖНУЮ ТЕЛЕЖКУ МАССОЙ 3КГ ТОЛКАЮТ С СИЛОЙ 6 Н. ОПРЕДЕЛИТЕ
УСКОРЕНИЕ ТЕЛЕЖКИ.
1) 18 м/с2
2) 1,6 м/с2
3) 2 м/с2
4) 0,5 м/с2
29. 3. Как будет двигаться тело массой 4 кг под действием единственной силы 8 Н?
3. КАК БУДЕТ ДВИГАТЬСЯ ТЕЛО МАССОЙ 4КГ ПОД ДЕЙСТВИЕМ ЕДИНСТВЕННОЙ
СИЛЫ 8 Н?
1) Равномерно, со скоростью 2 м/с
2) Равноускоренно, с ускорением 2 м/с2
3) Равноускоренно, с ускорением 0,5 м/с2
4) Равномерно, со скоростью 0,5 м/с
30.
 4. В инерциальной системе отсчета сила F сообщает телу массой m ускорение а. Как изменится ускорение тела, если массу тела и 4. В ИНЕРЦИАЛЬНОЙ СИСТЕМЕ ОТСЧЕТА
4. В инерциальной системе отсчета сила F сообщает телу массой m ускорение а. Как изменится ускорение тела, если массу тела и 4. В ИНЕРЦИАЛЬНОЙ СИСТЕМЕ ОТСЧЕТАСИЛА F СООБЩАЕТ ТЕЛУ
МАССОЙ M УСКОРЕНИЕ А. КАК ИЗМЕНИТСЯ
УСКОРЕНИЕ ТЕЛА, ЕСЛИ МАССУ ТЕЛА И
РАЗА?
1) Увеличится в 4 раза
2) Уменьшится в 4 раза
3) Уменьшится в 8 раз
4) Не изменится
«Третий закон
Ньютона»
. При ударе мяча об стенку или пол,
мяч отскакивает. Почему?
•Двое стоят на одинаковых тележках.
Тянет за веревку один,
а в движение приходят обе тележки.
Почему?
Поставим опыт
Предложим первокласснику и
десятикласснику посоревноваться в
перетягивании каната, стоя на
скейтбордах: тогда трением между
колесами и полом можно пренебречь
(схема опыта показана на рисунке )
Точные опыты, подобные описанном
выше, показывают, что модули
ускорений обратно
пропорциональны массам тел:
a1/a2 = m2/m1
Поскольку ускорения направлены
противоположно, то
34.
 Третий закон Ньютона ТРЕТИЙ ЗАКОН
Третий закон Ньютона ТРЕТИЙ ЗАКОННЬЮТОНА
Силы, с которыми 2 тела
взаимодействуют друг с
другом, равны по модулю
и направлены вдоль
одной прямой в
противоположные
стороны
Кстати!
В быту третий закон
Ньютона звучит так:
“действие равно
противодействию”. Не раз,
наверное, эта фраза
звучала у вас в ушах …
36. Третий закон Ньютона
ТРЕТИЙ ЗАКОННЬЮТОНА
37. Третий закон Ньютона
ТРЕТИЙ ЗАКОННЬЮТОНА
38. Третий закон Ньютона
ТРЕТИЙ ЗАКОННЬЮТОНА
Силы, возникающие при
взаимодействии двух
тел, приложены к разным
телам.
41. Опыты и наблюдения показывают, что:
ОПЫТЫ И НАБЛЮДЕНИЯ ПОКАЗЫВАЮТ, ЧТО:Причиной изменения движения тел,
то есть причиной изменения их скорости, являются
воздействия на них других тел
Количественно действие одного тела на другое,
вызывающее изменение скорости, выражается
величиной, называемой силой
Тела взаимодействуют
Ускорение, которое получает тело при данном
взаимодействии, зависит от особого свойства всякого
тела – его инертности
F ma
Законы Ньютона для школьников | NUR.
 KZ Исаак Ньютон и его законы: Freepick
KZ Исаак Ньютон и его законы: FreepickЗаконы Ньютона описывают множество физических явлений, которые происходят во Вселенной. Со времен Ньютона наука колоссально продвинулась вперед, но и сейчас при проектировании новых автомобилей и запуске на Луну космических кораблей ученые ориентируются на эти законы. Их всего три, и каждому школьнику придется их изучить.
Первый закон Ньютона
В первом законе Ньютон обобщил информацию о том, как движется тело под действием сил. В жизни постоянно наблюдаем, как взаимодействуют тела, будь то удар по мячу или притягивание магнита к дверце холодильника. Мера каждого такого взаимодействия — сила, то есть величина, которая показывает, как и в каком направлении оно происходит.
Из наблюдений и опыта известно, что тела двигаются, когда на них действуют другие тела. Например, мяч бросаем, напрягая для толчка мышцы руки. Когда его ловим, то замедляем и останавливаем тоже рукой. Если другие тела не действуют, то тело или останется в покое, или будет совершать равномерное и прямолинейное движение.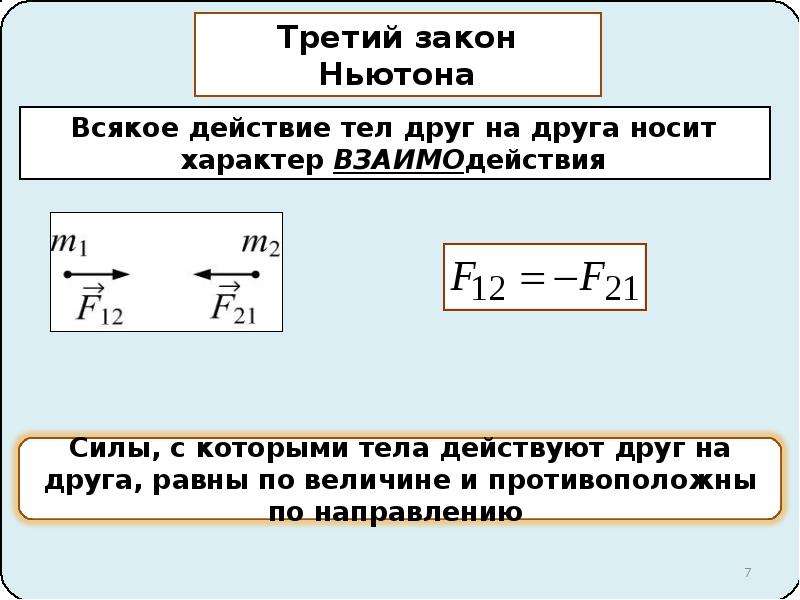
Читайте также
Почему Земля круглая и откуда возникли теории о плоской Земле
Это правило известно как закон инерции, а движение, которое в этом случае возникает, называют движением по инерции. Например:
- в случае резкого торможения пассажиры автобуса двигаются по инерции вперед;
- велосипедист вылетит вперед по инерции при резком торможении;
- спутники на земной орбите двигаются по инерции без расхода топлива.
Первым об инерции написал еще Галилей, а Исаак Ньютон сформулировал правило в форме закона. Он звучит так: существуют инерциальные системы отсчета, относительно которых тело при отсутствии на него внешнего воздействия (или при его компенсации) будет сохранять состояние покоя или равномерно прямолинейно двигаться.
Иллюстрация законов Ньютона: FreepickСуть первого закона легко продемонстрировать на примере: если на абсолютно ровной дороге толкнуть тележку и пренебречь силой трения колес и сопротивлением воздуха, то она на одинаковой скорости будет катиться бесконечно долгий период времени.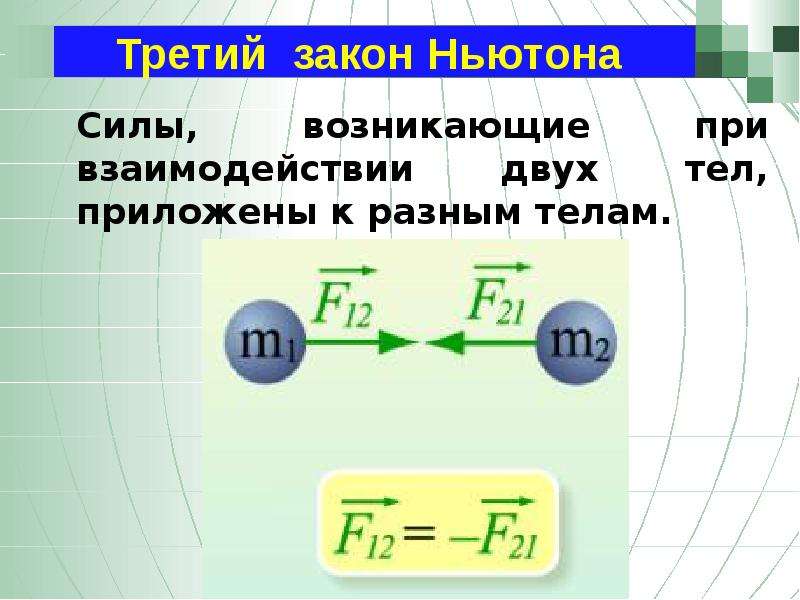
Читайте также
Что такое магнитное поле, его свойства и источники
Но существуют и неинерциальные системы, в которых скорости тел могут меняться без силы. Например, такая система — автобус, в котором пассажиры едут, не ощущая движения. Стоит ему резко затормозить, как всех бросит вперед, хотя сила при этом не действует, то есть движение относительно автобуса оказывается беспричинным. В этом случае говорят о неинерциальной системе отсчета.
Движение в таких системах происходит с ускорением. При расчетах учитываются силы инерции.
Таким образом, говоря о скорости тела, обязательно указывают, относительно какой инерциальной системы отсчета она измерялась, так как для разных систем она может быть разной. Ускорение тела во всех системах сохраняется.
Второй закон Ньютона
Основываясь на повседневных наблюдениях, можно сделать вывод, что ускорение, которое сообщается телу тем больше, чем большая сила на него действует. К примеру, мяч летит быстрее, если был сильнее удар. О количественной связи между силой, которая действует на тело, и приобретаемым ускорением говорит второй закон Ньютона.
О количественной связи между силой, которая действует на тело, и приобретаемым ускорением говорит второй закон Ньютона.
Читайте также
Сила тяжести: формула, единицы измерения, особенности
Рассмотрим такой опыт:
- Берут два мяча — легкий шар для пинг-понга и тяжелый шар из железа.
- Действуют на них с одинаковой силой.
- Тяжелый шар набирает маленькую скорость, то есть получает небольшое ускорение.
- Легкий шар двигается с большей скоростью.
Ускорение рассчитывают по формуле: a = 2S/t², где S — путь, t — время его прохождения.
Если использовать различные силы и отмечать полученное ускорение, то окажется, что отношение силы к ускорению — постоянная величина для конкретного шара. Этот показатель называют массой.
Масса — мера инертности тела. Она указывает на то, как сильно тело оказывает сопротивление изменениям скорости. Чем больше масса, тем сложнее разгонять и останавливать тело.
Читайте также
Почему Луна не падает на Землю: пояснения
Как же Ньютон сформулировал второй закон? Звучит он так: ускорение, которое получает тело, прямо пропорционально равнодействующей всех сил, действующих на него, и обратно пропорционально его массе (F = m×a).
При проведении расчетов на основании второго закона Ньютона важно выбирать единицы силы и массы. В СИ единица массы — килограмм (кг), а единица силы — ньютон (Н). Один ньютон равняется силе, под воздействием которой тело с массой 1 кг получает ускорение 1 м/с².
Третий закон Ньютона
Сила никогда не возникает самостоятельно, это явление предполагает наличие другой силы. Когда одно тело действует с определенной силой на другое («действие»), то и второе тело с определенной силой действует на первое («противодействие»):
Читайте также
Теплопроводность воды и льда и их особенности
- Когда соударяются два бильярдных шара, то оба меняют скорость.
- Земля притягивает Луну, заставляя ее двигаться по определенной траектории, но и Луна притягивает Землю. Ускорение нашей планеты под воздействием этой силы обнаруживается в приливах морей и океанов.
Что еще известно о силах, которые возникают во время взаимодействия двух тел? Рассмотрим следующий опыт:
- Берут два динамометра (приборы с пружиной для измерения сил), цепляют их друг за друга, растягивают и наблюдают за показаниями.

- Оказывается, что при любом растяжении показания обоих динамометров совпадут, то есть друг на друга они воздействуют с одинаковой силой.
Опыт показывает, что при действии одного тела на другое с определенной силой, второе также действует на первое. Сила этого действия равна первой по модулю и противоположна по направлению. При этом обе силы находятся на одной прямой. Такова формулировка закона равенства действия и противодействия, открытого Ньютоном и известного как третий закон движения.
Читайте также
Психология как наука о поведении: ученые, мнения
В жизни сталкиваемся с этим законом довольно часто. Так, в при перетягивании каната каждая из команд действует, согласно третьему закону Ньютона, на другую (через канат) с одинаковой силой. При этом выигрывают (перетягивают канат) не те, кто сильнее тянет, а те, кто лучше упирается в поверхность Земли.
Третий закон Ньютона:
- Объясняет движение транспортных средств. Лошадь двигает и везет нагруженные сани, так как на ее копыта действует большая сила трения от дороги, чем на скользкие полозья саней.
 На идеально скользких поверхностях, от которых не получится оттолкнуться, ни сани с лошадью, ни поезда, ни автомобили не смогут сдвинуться с места.
На идеально скользких поверхностях, от которых не получится оттолкнуться, ни сани с лошадью, ни поезда, ни автомобили не смогут сдвинуться с места. - Помогает рассчитать силу отдачи во время выстрела, так как в этом случае снаряд летит в одну сторону, а орудие отталкивается в другую. Отдача представляет собой противодействие снаряда, действующее на орудие. Таким образом, ускорения, получаемые пушкой и снарядом, направлены противоположно, а по модулю обратно пропорциональны массам этих тел. В результате снаряд и пушка приобретут противоположно направленные скорости, находящиеся в том же отношении.
- Описывает падение тел. Яблоко падает на поверхность Земли, так как оно притягивается земным шаром. Но при этом и само яблоко притягивает планету. Можно сказать, что яблоко с Землей падают друг на друга, но отличается скорость их падения из-за значительной разницы в массе.
Читайте также
Существует ли машина времени в действительности?
Классическая механика и ее принципы формировались длительное время. На протяжении многих веков ученые выяснили законы, по которым двигаются материальные тела. Ньютон в работе «Математические начала натуральной философии» обобщил накопленные знания. Выдающийся физик сформулировал три закона, которые известны всему миру.
На протяжении многих веков ученые выяснили законы, по которым двигаются материальные тела. Ньютон в работе «Математические начала натуральной философии» обобщил накопленные знания. Выдающийся физик сформулировал три закона, которые известны всему миру.
Оригинал статьи: https://www.nur.kz/family/school/1912208-zakony-nyutona-dlya-shkolnikov/
Что устанавливает 2 закон ньютона. Второй закон Ньютона. Формула. Формулировка. Ускорение
1 / 5
Первый закон Ньютона постулирует существование инерциальных систем отсчета. Поэтому он также известен как Закон инерции . Инерция – это свойство тела сохранять скорость своего движения неизменной (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают разной инертностью. Инертность – это свойство тел сопротивляться изменению их скорости. Величина инертности характеризуется массой тела.
Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают разной инертностью. Инертность – это свойство тел сопротивляться изменению их скорости. Величина инертности характеризуется массой тела.
Современная формулировка
В современной физике первый закон Ньютона принято формулировать в следующем виде :
где p → = m v → {\displaystyle {\vec {p}}=m{\vec {v}}} – импульс точки, v → {\displaystyle {\vec {v}}} – её скорость , а t {\displaystyle t} – время . При такой формулировке, как и при предшествующей, полагают, что масса материальной точки неизменна во времени .
Иногда предпринимаются попытки распространить сферу применения уравнения
d
p
→
d
t
=
F
→
{\displaystyle {\frac {d{\vec {p}}}{dt}}={\vec {F}}}
и на случай тел переменной массы. Однако, вместе с таким расширительным толкованием уравнения приходится существенным образом модифицировать принятые ранее определения и изменять смысл таких фундаментальных понятий, как материальная точка, импульс и сила . {n}{\vec {F_{i}}}.}
{n}{\vec {F_{i}}}.}
Второй закон Ньютона, как и вся классическая механика, справедлив только для движения тел со скоростями, много меньшими скорости света . При движении тел со скоростями, близкими к скорости света, используется релятивистское обобщение второго закона , получаемое в рамках специальной теории относительности .
Следует учитывать, что нельзя рассматривать частный случай (при F → = 0 {\displaystyle {\vec {F}}=0} ) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.
Историческая формулировка
Исходная формулировка Ньютона:
Интересно, что если добавить требование инерциальности для системы отсчёта, то в такой формулировке этот закон справедлив даже в релятивистской механике .
Третий закон Ньютона
Этот закон описывает, как взаимодействуют две материальные точки. Возьмём для примера замкнутую систему, состоящую из двух материальных точек. Первая точка может действовать на вторую с некоторой силой , а вторая – на первую с силой . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия
F
→
1
→
2
{\displaystyle {\vec {F}}_{1\to 2}}
равна по модулю и противоположна по направлению силе противодействия
F
→
2
→
1
{\displaystyle {\vec {F}}_{2\to 1}}
.
Как соотносятся силы? Третий закон Ньютона утверждает: сила действия
F
→
1
→
2
{\displaystyle {\vec {F}}_{1\to 2}}
равна по модулю и противоположна по направлению силе противодействия
F
→
2
→
1
{\displaystyle {\vec {F}}_{2\to 1}}
.
Современная формулировка
Закон утверждает, что силы возникают лишь попарно, причём любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, сила всегда есть результат взаимодействия тел. Существование сил, возникших самостоятельно, без взаимодействующих тел, невозможно .
Историческая формулировка
Ньютон дал следующую формулировку закона :
Следствия
Закон сохранения импульса
Закон сохранения импульса утверждает, что векторная сумма импульсов всех тел системы есть величина постоянная , если векторная сумма внешних сил, действующих на систему тел, равна нулю .
Закон сохранения механической энергии
Комментарии к законам Ньютона
Законы Ньютона являются основными законами механики. Из них могут быть выведены уравнения движения механических систем. Однако не все законы механики можно вывести из законов Ньютона. Например, закон всемирного тяготения или закон Гука не являются следствиями трёх законов Ньютона.
Из них могут быть выведены уравнения движения механических систем. Однако не все законы механики можно вывести из законов Ньютона. Например, закон всемирного тяготения или закон Гука не являются следствиями трёх законов Ньютона.
Силы инерции
Помимо сил, о которых идёт речь во втором и третьем законах Ньютона, в механике вводят в рассмотрение так называемые силы инерции . Обычно речь идёт о силах инерции двух различных типов . Сила первого типа (Д’Аламберова сила инерции ) представляет собой векторную величину, равную произведению массы материальной точки на её ускорение, взятое со знаком минус. Силы второго типа (Эйлеровы силы инерции ) используются для получения формальной возможности записи уравнений движения тел в неинерциальных системах отсчёта в виде, совпадающем с видом второго закона Ньютона. По определению эйлерова сила инерции равна произведению массы материальной точки на разность между значениями её ускорения в той неинерциальной системе отсчёта, для которой эта сила вводится, с одной стороны, и в какой-либо инерциальной системе отсчёта , с другой . Определяемые таким образом силы инерции силами в смысле законов Ньютона не являются . Данный факт служит основанием для утверждения о том, что они не являются физическими силами ; ту же мысль выражают, называя их фиктивными , кажущимися или псевдосилами .
Определяемые таким образом силы инерции силами в смысле законов Ньютона не являются . Данный факт служит основанием для утверждения о том, что они не являются физическими силами ; ту же мысль выражают, называя их фиктивными , кажущимися или псевдосилами .
Законы Ньютона и Лагранжева механика
Законы Ньютона – только один из способов формулирования классической механики. В рамках Лагранжевой механики имеется одна-единственная формула (запись действия) и один-единственный постулат (тела движутся так, чтобы действие было стационарным) , и из этого можно вывести все законы Ньютона, правда, только для лагранжевых систем (в частности для консервативных систем). Следует, однако, отметить, что все известные фундаментальные взаимодействия описываются именно лагранжевыми системами. Более того, в рамках Лагранжева формализма можно легко рассмотреть гипотетические ситуации, в которых действие имеет какой-либо другой вид. При этом уравнения движения станут уже непохожими на законы Ньютона, но сама классическая механика будет по-прежнему применима.
Решение уравнений движения
Уравнение F → = m a → {\displaystyle {\vec {F}}=m{\vec {a}}} является дифференциальным уравнением : ускорение есть вторая производная от координаты по времени . Это значит, что эволюцию (перемещение) механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости.
Заметим, что если бы уравнения, описывающие наш мир, были бы уравнениями первого порядка, то из нашего мира исчезли бы такие явления, как инерция , колебания , волны .
Исторический очерк
|
Ньютон также дал строгие определения таких физических понятий, как количество движения (не вполне ясно использованное у Декарта) и сила . Он ввёл в физику понятие массы как меры инерции и, одновременно, гравитационных свойств (ранее физики пользовались понятием вес ).
Завершили математизацию основ механики Эйлер и Лагранж .
Примечания
- Исаак Ньютон. Математические начала натуральной философии. Перевод с латинского и примечания А.
 Н. Крылова / под ред. Полака Л. С.. – М. : Наука, 1989. – С. 40-41. – 690 с. – («Классики науки»). – 5 000 экз.
– ISBN 5-02-000747-1 .
Н. Крылова / под ред. Полака Л. С.. – М. : Наука, 1989. – С. 40-41. – 690 с. – («Классики науки»). – 5 000 экз.
– ISBN 5-02-000747-1 . - Тарг С. М. Ньютона законы механики // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров . – М. : Большая российская энциклопедия, 1992. – Т. 3: Магнитоплазменный – Пойнтинга теорема. – С. 370. – 672 с. – 48 000 экз. – ISBN 5-85270-019-3 .
- Инерциальная система отсчёта // Физическая энциклопедия (в 5 томах) / Под редакцией акад.
Кинематика – изучает движение тел, не рассматривая причины, которые это движение обуславливает.
Мат.точка – не имеет размеров, но в мат.точке сосредоточенна масса всего тела.
Поступательное – движение при котором прямая связанная с телом остаётся || самой себе.
Кинетические ур-я движения мат.точки:
Траектория – линия описываемая мат.точкой в пространстве.
Перемещение – приращение радиуса-вектора точки за
рассматриваемый промежуток времени.
Скорость – Быстрота движения мат.точки.
Вектором средней скорости называется отношение приращения радиуса-вектора точки к промежутку времени.
Мгновенная скорость – величина, равная первой производной радиуса-вектора движущейся точки по времени.
Модуль мгновенной скорости равен первой производной пути по времени.
Компоненты равны производным от координат по времени.
Равномерное – движение при котором за равные промежутки времени тело проходит одинаковые пути.
Неравномерное – движение при котором скорость меняется как по модулю так и по направлению.
Ускорение и его составляющие.
Ускорение – физ.величина, определяющая быстроту изменения скорости, как по модулю, так и по направлению.
Средним
ускорением неравномерного движения в интервале
времени от t
до t+t
называется векторная величина равная
отношению изменения скорости
к интервалу времениt:
. Мгновенным
ускорением мат.точки в момент времени t
будет предел среднего ускорения.
..
Мгновенным
ускорением мат.точки в момент времени t
будет предел среднего ускорения.
..
определяет по модулю.
определяет по направлению.т.е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.
Нормальная составляющая ускорения направлена по нормали к траектории к центру её кривизны (поэтому её также называют центростремительным ускорением).
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих.
Если а н =?,а т =?
В основе Динамики мат.точки лежат три закона Ньютона.
Первый
закон Ньютона – всякая
материальная точка (тело) сохраняет
состояние покоя или равномерного
прямолинейного движения до тех пор,
пока воздействие со стороны других тел
не заставит её изменить это состояние.
Инертность – стремление тела сохранять состояние покоя или равномерного прямолинейного движения.
Законы Ньютона выполняются только в инерциальной системе отсчёта .
Инерциальная система отсчёта – система, которая либо покоится, либо движется равномерно и прямолинейно относительно какой то другой инерциальной системы.
Масса тела – физ.величина, являющаяся одной из основных характеристик материи, определяющая её инерционные (инертная масса) и гравитационные (гравитационная масса) св-ва.
Сила – векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.
Второй
закон Ньютона – ускорение,
приобретаемое материальной точкой
(телом), пропорционально вызывающей
его силе, совпадает с нею по направлению
и обратно пропорционально массе
материальной точки.
Импульс (кол-во движения) – векторная величина, численно равная произведению массы материальной точки на её скорость и имеющая направление скорости.
Более общая формулировка 2-го закона Н.(уравнение движения мт): скорость изменения импульса материальной точки равна действующей на неё силе.
Следствие из 2зН: принцип независимости действия сил: если на мт действует одновременно несколько сил, то каждая из этих сил сообщает мт ускорение согласно 2зН, как будто других сил не было.
Третий закон Ньютона. Всякое действие мт (тел) друг на друга, носит характер взаимодействия; силы, с которыми действуют друг на друга мт, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки.
Импульс тела, сила. Закон сохранения импульса.
Внутренние
силы –
силы взаимодействия между мт механической
системы.
Внешние силы – силы, с которыми на мт системы действуют внешние тела.
В механической системе тел, по 3-му закону Ньютона, силы, действующие между этими телами, будут равны и противоположно направлены, т.е. геометрическая сумма внутренних сил равна 0.
Запишем 2зН, для каждого из n тел механической системы(мс):
…………………
Сложим эти ур-я:
Т.к. геометрическая сумма внутренних сил мс по 3зН равна 0, то:
где – импульс системы.
В случае отсутствия внешних сил(замкнутая система):
, т.е.
Это и есть закон сохранения импульса : импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени.
Центр масс, движение центра масс.
Центр
масс (центр инерции) системы мт называется воображаемая
точка С ,
положение которой характеризует
распределение массы этой системы.
Радиус-вектор этой точки равен:
Скорость центра масс (цм):
; , т.е. импульс системы равен произведению массы системы на скорость её центра масс.
Т.к. то:, т.е.:
Закон движения центра масс: центр масс системы движется как мт, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему.
Кинематика вращательного движения материальной точки.
Угловая скорость – векторная величина, равная первой производной угла поворота тела по времени.
Вектор направлен вдоль оси вращения по правилу правого винта.
Линейная скорость точки:
В векторном виде: , при этом модуль равен:.
Если =const, то вращение равномерное.
Период вращения (Т) – время, за которое точка совершает один полный оборот. ().
Частота
вращения ( n ) – число полных оборотов, совершаемых
телом при равномерном его движении по
окружности, в единицу времени. ;.
;.
Угловое ускорение – векторная величина, равная первой производной угловой скорости по времени: . При ускоренном, при замедленном.
Тангенциальная составляющая ускорения:
Нормальная составляющая: .
Формулы связи линейных и угловых величин:
При :
Момент силы.
Момент силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r , проведённого из точки О в точку А приложения силы, на силу F.
Здесь – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении отк.
Модуль момента силы равен .
Момент
силы относительно неподвижной оси z
– скалярная величина
,
равная проекции на эту ось векторамомента силы, определённого относительно
произвольной точки О данной осиz. Значение момента не зависит от выбора
положения точки О на данной оси.
Значение момента не зависит от выбора
положения точки О на данной оси.
Момент инерции твёрдого тела. Теорема Штейнера.
Момент инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n мт системы на квадрат их расстояний до рассматриваемой оси.
При непрерывном распределении масс.
Теорема Штейнера: момент инерции тела J относительно любой оси вращения равен моменту его инерции J C относительно параллельной оси, проходящеё через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями:
Основное уравнение динамики вращательного движения.
Пусть сила F приложена к точке В. Находящейся от оси вращения на расстоянии r, -угол между направлением силы и радиус-векторомr. При повороте тела на бесконечно малый угол , точка приложения В проходит путь, и работа равна произведению проекции силы на направление смещения на величину смещения:
Учитывая, что , запишем:
Где
-момент
силы, относительно оси.
Работа при вращении тела равна произведению момента действующей силы на угол поворота.
Работа при вращении тела идёт на увеличение его кинетической энергии:
Но ,, поэтому
Учитывая, что получим:
Этот и есть относительно неподвижной оси.
Если ось вращения совпадает с главной осью инерции, проходящей через центр масс, то: .
Момент импульса. Закон сохранения момента импульса.
Момент импульса (количество движения) мт А относительно неподвижной точки О – физическая величина, определяемая векторным произведением:
где r-радиус-вектор, проведённый из точки О в точку А; – импульс мт.-псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении отк.
Модуль вектора момента импульса:
Момент
импульса относительно неподвижной оси z
называется скалярная величина L z ,
равная проекции на эту ось вектора
момента импульса, определённого
относительно произвольной точки О
данной оси.
Т.к. , то момент импульса отдельной частицы:
Момент импульса твёрдого тела относительно оси есть сумма моментов импульса отдельных частиц, а т.к. , то:
Т.о. момент импульса твёрдого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.
Продифференцируем последнее уравнение: , т.е.:
это и есть уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси: Производная момента импульса твёрдого тела относительно оси равна моменту сил относительно той же оси.
Можно показать, что имеет место векторное равенство:
В замкнутой системе момент внешних сил и, откуда:L=const, это выражение и есть закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени.
Работа силы. Мощность.
Энергия – универсальная мера различных форм
движения и взаимодействия.
Работа силы – величина, характеризующая процесс обмена энергией между взаимодействующими телами в механике.
Если тело движется прямолинейно и на него действует постоянная сила , которая составляет некоторый уголс направлением перемещения, торабота этой силы равна произведению проекции силы F s на направление перемещения, умноженной на перемещение точки приложения силы:
Элементарная работа силы на перемещенииназывается скалярная величина, равная:, где,,.
Работа силы на участке траектории от 1 до 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути:
Если на графике изображена зависимость F s от S, то работа определяется на графике площадью закрашенной фигуры.
При , то А>0
При , то А
При , то А=0.
Мощность – скорость совершения работы.
Т.е. мощность равна скалярному произведению
вектору силы на вектор скорости, с
которой движется точка приложения
силы.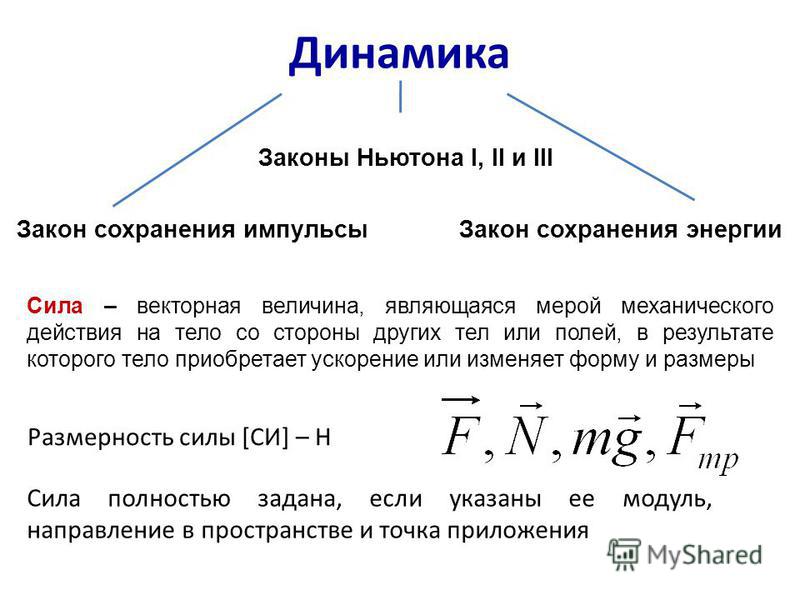
Кинетическая и потенциальная энергия поступательного и вращательного движения.
Кинетическая энергия механической системы – энергия механического движения этой системы. dA=dT. По 2зН , помножим наи получим:;
Отсюда:.
Кинетическая энергия системы – есть функция состояния её движения, она всегда , и зависит от выбора системы отсчёта.
Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Если
силовое поле характеризуется тем, что
работа совершаемая действующими силами
при перемещении тела из одного положения
в другое, не зависит от того, по какой
траектории, по которой это перемещение
произошло, а зависит только от начального
и конечного положений, то такое поле
называется потенциальным, а силы, действующие в нём – консервативными, если же работа зависит от траектории
то такая сила – диссипативная .
Т.к. работа совершается за счёт убыли потенциальной энергии, то: ;;, где С – постоянная интегрирования, т.е. энергия определяется с точностью до некоторой произвольной постоянной.
Если силы консервативны, то:
– Градиент скаляра П. (также обозначается ).
Т.к. начало отсчёта выбирается произвольно, то потенциальная энергия может иметь отрицательное значение. (при П=-mgh’).
Найдём потенциальную энергию пружины.
Сила упругости: , по 3зН:F x =-F x упр =kx;
dA=F x dx=kxdx;.
Потенциальная энергия системы является функцией состояния системы, она зависит только от конфигурации системы и от её положения по отношению к внешним телам.
Кинетическая энергия вращения
Механическая энергия. Закон сохранения механической энергии.
Полная
механическая энергия системы – энергия механического движения и
взаимодействия: Е=Т+П, т.е. равна сумме
кинетической и потенциальной энергий.
Пусть F 1 ’…F n ’ – равнодействующие внутренних консервативных сил. F 1 …F n – равнодействующие внешних консервативных сил. f 1 …f n . Запишем уравнения 2зН для этих точек:
Умножим каждое ур-е на , учтя, что.
Сложим ур-я:
Первый член левой части:
Где dT есть приращение кинетической энергии системы.
Второй член равен элементарной работе внутренних и внешних сил, взятой со знаком минус, т.е. равен элементарному приращению потенциальной энергииdП системы.
Правая часть равенства задаёт работу вешних неконсервативных сил, действующих на систему. Т.о.:
Если внешние неконсервативные силы отсутствуют, то:
d(Т+П)=0;Т+П=Е=const
Т.е. полная механическая энергия системы сохраняется постоянной. Закон сохранения механической энергии : в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т.е. не изменяется со временем.
Абсолютно
упругий удар.
Удар (соударение)
Коэффициент восстановления
абсолютно неупругими , если =1 тоабсолютно упругими.
Линия удара
Центральный удар
Абсолютно упругий удар – столкновение 2-х тел, в результате которого в обоих взаимодействующих не остаётся ни каких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию.
Для абсолютно упругого удара выполняются закон сохранения импульса и закон сохранения энергии.
Законы сохранения:
m 1 v 1 +m 2 v 2 =m 1 v’ 1 +m 2 v’ 2
после преобразований:
откуда:v 1 +v 1 ’=v 2 +v 2 ’
решая последнее ур-е и предпедпоследнее найдём:
Абсолютно неупругий удар.
Удар
(соударение) – столкновение 2-х или более тел, при
котором взаимодействие длится очень
короткое время. При ударе внешними
силами можно пренебречь.
При ударе внешними
силами можно пренебречь.
Коэффициент восстановления – отношение нормальной составляющей относительной скорости тел после и до удара.
Если для сталкивающих тел =0, то такие тела называютсяабсолютно неупругими , если =1 тоабсолютно упругими.
Линия удара – прямая проходящая через точку соприкосновения тел и нормальная к поверхности их соприкосновения.
Центральный удар – такой удар, при котором тела до удара движутся вдоль прямой, проходящей через их центр масс.
Абсолютно неупругий удар – столкновении 2-х тел, в результате которого тела объединяются, двигаясь дальше, как единое целое.
Закон сохранения импульса:
Если шары двигались навстречу друг другу, то при абсолютно неупругом ударе шары движутся в сторону большего импульса.
Поле тяготения, напряжённость, потенциал.
Закон всемирного тяготения: между любыми двумя мт действует сила взаимного притяжения, прямо пропорциональная произведению масс этих точек и обратно пропорциональная квадрату расстояния между ними:
G – Гравитационная постоянная (G=6,67*10 -11 Hm 2 /(кг) 2)
Гравитационное
взаимодействие между двумя телами
осуществляется с помощью поля
тяготения ,
или гравитационного
поля. Это
поле порождается телами и является
формой существования материи. Основное
св-во поля в том, что на всякое тело
внесённое в это поле действует сила
тяготения:
Это
поле порождается телами и является
формой существования материи. Основное
св-во поля в том, что на всякое тело
внесённое в это поле действует сила
тяготения:
Вектор не завит от массы и называется напряжённостью поля тяготения.
Напряжённость поля тяготения определяется силой действующей со стороны поля на мт единичной массы, и совпадает по направлению с действующей силой, напряжённость есть силовая хар-ка поля тяготения.
Поле тяготения однородное если напряжённость во всех точках его одинакова, и центральным , если во всех точках поля векторы напряжённости направлены вдоль прямых, которые пересекаются в одной точке.
Гравитационное поле тяготения – носитель энергии.
На расстоянии R на тело действует сила:
при перемещении этого тела на расстояние dR затрачивается работа:
Знак
минус появляется, т.к. сила и перемещение
в данном случае противоположны по
направлению.
Затраченная работа в пол тяготения не зависит от траектории перемещения, т.е. илы тяготения консервативны, а поле тяготения является потенциальным.
Если то П 2 =0, тогда запишем:,
Потенциал поля тяготения – скалярная величина, определяемая потенциальной энергией тела единичной массы в данной точке поля или работой по перемещению единичной массы из данной точки поля в бесконечность. Т.о.:
Эквипотенциальные – такие поверхности, для которых потенциал постоянен.
Взаимосвязь между потенциалом и напряженностью.
Знак мину указывает на то, что вектор напряжённости направлен в сторону убывания потенциала.
Если тело находится на высоте h, то
Неинерциальная система отсчёта. Силы инерции при ускоренном поступательном движении системы отсчёта.
Неинерциальная – система отсчёта, движущаяся относительно
инерциальной системы отсчёта с
ускорением.
Законы Н можно применять в неинерциальной системе отсчёта, если учесть силы инерции. Силы инерции при этом должны быть такими, чтобы вместе с силами, обусловленными воздействием тел друг на друга, они сообщали телу ускорение, каким оно обладает в неинерциальных системах отсчёта, т.е.:
Силы инерции при ускоренном поступательном движении системы отсчёта.
Т.е. угол отклонения нити от вертикали равен:
Относительно системы отсчёта, связанной с тележкой шарик покоится, что возможно, если сила F уравновешивается равной и противоположно направленной ей силой F ин, т.е.:
Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчёта.
Пусть
диск равномерно вращается с угловой
скоростью
вокруг вертикальной оси, проходящей
через его центр. На диске на разных
расстояниях от оси вращения установлены
маятники (на нитях подвешены шарики).
При вращении маятников вместе с диском
шарики отклоняются от вертикали на
некоторый угол.
В инерциальной системе отсчёта, связанной с помещением, на шарик действует сила, равная , и направлена перпендикулярно оси вращения диска. Она является равнодействующей силы тяжестии силы натяжения нити:
Когда движение шарика установится, то:
т.е. углы отклонения нитей маятников будут тем больше, чем больше расстояние R от шарика до оси вращения диска и чем больше угловая скорость вращения .
Относительно системы отсчёта, связанной с вращающимся диском, шарик покоится, что возможно, если сила уравновешивается равной и противоположно направленной ей силой.
Сила , называемаяцентробежной силой инерции , направлена по горизонтали от оси вращения диска и равна:.
Гидростатическое давление, закон Архимеда, закон неразрывности струи.
Гидроаэромеханика – раздел механики, изучающий равновесие и движение жидкостей и газов, их взаимодействие между собой и обтекаемыми ими твёрдыми телами.
Несжимаемая жидкость – жидкость, плотность которой всюду одинакова и не изменяется со временем.
Давление – физическая величина, определяемая нормальной силой, действующей о стороны жидкости на единицу площади:
Закон Паскаля – давление в любом месте покоящейся жидкости одинаково по всем направлениям, причём давление одинаково передаётся по всему объёму, занятому покоящейся жидкости.
Если жидкость не сжимаема, то при поперечном сечении S столба жидкости, его высоте h и плотности вес:
А давление на нижнее основание:,т.е. давление изменяется линейно с высотой. Давлениеназываетсягидростатическим давлением .
Из этого следует, что давление на нижние слои жидкости будет больше, чем на верхние, значит на тело, погружённое в жидкость действует выталкивающая сила, определяемая законом Архимеда: на тело погружённое в жидкость (газ), действует со стороны этой жидкости направленная вверх выталкивающая сила, равная весу вытесненной телом жидкости:,
Течение – движение жидкости.Поток – совокупность частиц движущейся жидкости.Линии тока – графическое изображение движения жидкости.
Течение жидкости установившееся (стационарно) , если форма расположения линий тока, а так же значения скоростей в каждой её точке со временем не изменяются.
За 1с через сечение S 1 пройдёт объём жидкости равный , а черезS 2 – , здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость не сжимаема, то через оба сечения пройдёт равный объём:
Это и есть уравнение неразрывности струи для несжимаемой жидкости.
Закон Бернулли.
Жидкость идеальна, движение стационарно.
За малый промежуток времени жидкость перемещается от сеченийS 1 и S 2 к сечениям S’ 1 и S’ 2 .
По закону сохранения энергии изменение полной энергии идеальной несжимаемой жидкости равно работе внешних сил по перемещению массы жидкости:,
где Е 1 и Е 2 – полные энергии жидкости массой m в местах сечений S 1 и S 2 соответственно.
С другой стороны А – это работа, совершаемая при перемещении всей жидкости, заключённой между сечениями S 1 и S 2 , за рассматриваемый промежуток времени . Для переноса массыm от S 1 до S’ 1 жидкость должна переместится на расстояние и отS 2 до S’ 2 на расстояние .,гдеF 1 =p 1 S 1 и F 2 =-p 2 S 2 .
Изучение явлений природы на основании эксперимента возможно только при условии соблюдения всех этапов: наблюдение, гипотеза, эксперимент, теория. Наблюдение позволит выявить и сопоставить факты, гипотеза дает возможность дать им подробное научное пояснение, требующее экспериментального подтверждения. Проведение наблюдения за движением тел привело к интересному выводу: изменение скорости тела возможно только под действием другого тела.
К примеру, если быстро бежать по лестнице, то на повороте просто необходимо ухватиться за перила (изменение направления движения), либо приостановиться (изменением величины скорости), чтобы не столкнуться с противоположной стеной.
Наблюдения за аналогичными явлениями привело к созданию раздела физики, изучающего причины изменения скорости тел или их деформации.
Основы динамики
Ответить на сакраментальный вопрос о том, почему физическое тело движется тем или иным образом или покоится, призвана динамика.
Рассмотрим состояние покоя. Исходя из понятия можно сделать вывод: нет и не может быть абсолютно неподвижных тел. Любой предмет, будучи неподвижным по отношению к одному телу отсчета, движется относительно другого. К примеру, книга, лежащая на столе, неподвижна относительно стола, но если рассмотреть ее положение по отношению к проходящему человеку, то делаем естественный вывод: книга движется.
Поэтому рассматриваются в инерциальных системах отсчета. Что это такое?
Инерциальной называется система отсчета, в которой тело покоится или выполняет равномерное и при условии отсутствия воздействия на него иных предметов или объектов.
В приведенном выше примере система отсчета, связанная со столом, может быть названа инерциальной. Человек, движущийся равномерно и прямолинейно, может служить телом отсчета ИСО. Если его движение будет ускоренным, то связать с ним инерциальную СО нельзя.
По сути, такую систему можно соотнести с телами, жестко закрепленными на поверхности Земли. Однако сама планета не может служить телом отсчета для ИСО, так как равномерно вращается вокруг собственной оси. Тела на поверхности имеют центростремительное ускорение.
Что такое инерция?
Явление инерции напрямую связано с ИСО. Вспомните, что происходит, если движущийся автомобиль резко останавливается? Пассажиры подвергаются опасности, поскольку продолжают свое движение. Остановить его может кресло впереди либо ремни безопасности. Поясняют этот процесс инерцией пассажира. Так ли это?
Инерция – явление, предполагающее сохранение постоянной скорости тела при отсутствии воздействия на него других тел. Пассажир находится под действием ремней или кресел. Явление инерции здесь не наблюдается.
Объяснение кроется в свойстве тела, и, согласно ему, мгновенно изменить скорость того или иного предмета невозможно. Это – инертность. К примеру, инертность ртути в термометре позволяет опустить столбик, если мы встряхнем градусник.
Мерой инертности называют массу тела. При взаимодействии скорость быстрее меняется у тел с меньшей массой. Столкновение автомобиля с бетонной стеной для последней протекает практически бесследно. Автомобиль чаще всего претерпевает необратимые изменения: меняется скорость, происходит значительная деформация. Получается, что инертность бетонной стены значительно превышает инертность автомобиля.
Возможно ли в природе встретиться с явлением инерции? Условие, при котором тело находится без взаимосвязи с другими телами – глубокий космос, в котором движется космический корабль с выключенными двигателями. Но даже в этом случае гравитационный момент присутствует.
Основные величины
Изучение динамики на экспериментальном уровне предполагает проведение опыта с измерениями физических величин. Наиболее интересны:
- ускорение как мера быстроты изменения скорости тел; обозначают ее буквой а, измеряют в м/с 2 ;
- масса как мера инертности; обозначена литерой m, измеряется в кг;
- сила как мера взаимного действия тел; обозначается чаще всего буквой F, измеряется в Н (ньютонах).
Взаимосвязь этих величин изложена в трех закономерностях, выведенных величайшим английским физиком. Законы Ньютона призваны объяснить сложности взаимодействия различных тел. А также процессы, ими управляющие. Именно понятия “ускорение”, “сила”, “масса” законы Ньютона связывают математическими соотношениями. Попробуем разобраться, что же это значит.
Действие только одной силы – явление исключительное. К примеру, искусственный спутник, движущийся по орбите вокруг Земли, находится под действием только силы притяжения.
Равнодействующая
Действие нескольких сил можно заменить одной силой.
Геометрическая сумма сил, воздействующих на тело, именуется равнодействующей.
Речь идет именно о геометрической сумме, поскольку сила – векторная величина, которая зависит не только от точки приложения, но и от направления действия.
К примеру, если необходимо передвинуть достаточно массивный шкаф, то можно пригласить друзей. Совместными усилиями достигается желаемый результат. Но можно пригласить только одного, очень сильного человека. Его усилие равно действию всех друзей. Сила, приложенная богатырем, может быть названа равнодействующей.
Законы движения Ньютона формулируются на основании понятия «равнодействующая».
Закон инерции
Начинают изучать законы Ньютона с наиболее часто встречающегося явления. Первый закон обычно называют законом инерции, поскольку он устанавливает причины равномерного прямолинейного движения или состояния покоя тел.
Тело перемещается равномерно и прямолинейно или покоится, если на него не осуществляют действия силы, либо это действие скомпенсировано.
Можно утверждать, что равнодействующая в этом случае равна нулю. В таком состоянии находится, к примеру, движущийся с постоянной скоростью автомобиль на прямолинейном участке дороги. Действие силы притяжения скомпенсировано силой реакции опоры, а сила тяги двигателя по модулю равна силе сопротивления движению.
Люстра на потолке покоится, так как сила тяжести скомпенсирована силой натяжения ее креплений.
Скомпенсированными могут быть только те силы, которые приложены к одному телу.
Второй закон Ньютона
Равнодействующая сил, воздействующих на тело, определяется как произведение массы тела на приобретаемое под действием сил ускорение.
2 закон Ньютона (формула: F=ma), к сожалению, не устанавливает причинно-следственных связей между и динамики. Он не может с точностью указать, что является причиной появления ускорения тел.
Сформулируем иначе: ускорение, получаемое телом, прямо пропорционально равнодействующей сил и обратно пропорционально массе тела.
Так, можно установить, что изменение скорости происходит только в зависимости от силы, приложенной к нему, и массы тела.
2 закон Ньютона, формула которого может быть и такой: a = F/m, в векторном виде считают основополагающим, поскольку он дает возможность установить связь между разделами физики. Здесь, a – вектор ускорения тела, F – равнодействующая сил, m – масса тела.
Ускоренное движение автомобиля возможно, если сила тяги двигателей превышает силу сопротивления движению. С увеличением силы тяги возрастает и ускорение. Грузовые автомобили снабжаются двигателями большой мощности, ведь их масса значительно превышает массу легкового авто.
Болиды, созданные для скоростных гонок, облегчаются таким образом, что на них закрепляется минимум необходимых деталей, а мощность двигателей увеличивается до возможных пределов. Одной из важнейших характеристик спортивных авто является время разгона до 100 км/ч. Чем меньшее этот интервал времени, тем лучше скоростные свойства болида.
Закон взаимодействия
Законы Ньютона, основанные на силах природы, утверждают, что любое взаимодействие сопровождается появлением пары сил. Если шар висит на нити, то испытывает ее действие. При этом нить также растягивается под действием шара.
Завершает законы Ньютона формулировка третьей закономерности. Вкратце это звучит так: действие равно противодействию. Что это значит?
Силы, с которыми тела воздействуют друг на друга, равны по величине, противоположны по направлению и направлены вдоль линии, соединяющей центры тел. Интересно, что скомпенсированными их назвать нельзя, ведь действуют они на разные тела.
Применение законов
Знаменитая задача «Конь и телега» может поставить в тупик. Конь, запряженный в упомянутую повозку, сдвигает ее с места. В соответствии с третьим законом Ньютона, эти два объекта действуют друг на друга с равными по модулю силами, но на практике лошадь может сдвинуть телегу, что не укладывается в основы закономерности.
Решение найдется, если учесть, что эта система тел не замкнута. Дорога оказывает свое действие на оба тела. Сила трения покоя, действующая на копыта коня, превышает по значению силу трения качения колес телеги. Ведь момент движения начинается с попытки сдвинуть повозку. Если положение изменится, то конь ни при каких условиях не сдвинет её с места. Его копыта будут проскальзывать по дороге, и движения не будет.
В детстве, катая друг друга на санках, каждый мог столкнуться с таким примером. Если на санки сядут два-три ребенка, то усилий одного явно недостаточно, чтобы сдвинуть их с места.
Падение тел на поверхность земли, объясняемое Аристотелем («Каждое тело знает свое место») можно опровергнуть на основании вышеизложенного. Предмет движется к земле под действием такой же силы, что и Земля к нему. Сравнив их параметры намного больше массы тела), в соответствии со вторым законом Ньютона, утверждаем, что ускорение предмета во столько же раз больше ускорения Земли. Мы наблюдаем именно изменение скорости тела, Земля не смещается с орбиты.
Границы применимости
Современная физика законы Ньютона не отрицает, а лишь устанавливает границы их применимости. До начала XX века физики не сомневались в том, что эти законы объясняют все явления природы.
1, 2, 3 закон Ньютона полностью выявляет причины поведения макроскопических тел. Движение объектов с незначительными скоростями полностью описывается этими постулатами.
Попытка пояснить на их основании движение тел со скоростями, близкими к обречена на провал. Полное изменение свойств пространства и времени при этих скоростях не позволяет использовать динамику Ньютона. Кроме того, законы меняют свой вид в неинерциальных СО. Для их применения вводится понятие силы инерции.
Пояснить движение астрономических тел, правила их расположения и взаимодействия могут законы Ньютона. Закон всемирного тяготения вводится с этой целью. Увидеть же результат притяжения малых тел невозможно, ведь сила мизерна.
Взаимное притяжение
Известна легенда, согласно которой господина Ньютона, сидевшего в саду и наблюдавшего падение яблок, посетила гениальная идея: объяснить движение предметов вблизи поверхности Земли и движение на основании взаимного притяжения. Это не так далеко от истины. Наблюдения и точный расчет касались не только падения яблок, но и перемещения Луны. Закономерности этого движения приводят к выводам, что сила притяжения возрастает с увеличением масс взаимодействующих тел и уменьшается с увеличением расстояния между ними.
Опираясь на второй и третий законы Ньютона, закон всемирного тяготения формулируют следующим образом: все тела во вселенной притягиваются друг к другу с силой, направленной вдоль линии, соединяющей центры тел, пропорциональной массам тел и обратно пропорциональной квадрату расстояния между центрами тел.
Математическая запись: F = GMm/r 2 , где F – сила притяжения, M, m – массы взаимодействующих тел, r – расстояние между ними. Коэффициент пропорциональности (G = 6.62 х 10 -11 Нм 2 /кг 2) получил название гравитационной постоянной.
Физический смысл: эта постоянная равна силе притяжения между двумя телами массами по 1 кг на расстоянии 1 м. Понятно, что для тел небольших масс сила столь незначительна, что ею можно пренебречь. Для планет, звезд, галактик сила притяжения настолько огромна, что полностью определяет их движение.
Именно закон притяжения Ньютона утверждает, что для запуска ракет необходимо топливо, способное создать такую реактивную тягу, чтобы преодолеть влияние Земли. Скорость, необходимая для этого – первая космическая скорость, равная 8 км/с.
Современная технология изготовления ракет позволяет запускать беспилотные станции как искусственные спутники Солнца к другим планетам, чтобы их исследовать. Скорость, развиваемая таким аппаратом, – вторая космическая скорость, равная 11 км/с.
Алгоритм применения законов
Решение задач динамики подчиняется определенной последовательности действий:
- Провести анализ задачи, выявить данные, вид движения.
- Выполнить рисунок с указанием всех сил, действующих на тело, и направления ускорения (при его наличии). Выбрать систему координат.
- Записать первый или второй законы, в зависимости от наличия ускорения тела, в векторной форме. Учесть все силы (равнодействующая сила, законы Ньютона: первый, если скорость тела не меняется, второй, если есть ускорение).
- Уравнение переписать в проекциях на выбранные оси координат.
- Если полученной системы уравнений недостаточно, то записать иные: определения сил, уравнения кинематики и т. п.
- Решить систему уравнений относительно искомой величины.
- Выполнить проверку размерностей, чтобы определиться с правильностью полученной формулы.
- Вычислить.
Обычно этих действий вполне достаточно для решения любой стандартной задачи.
Настала пора поговорить о них подробнее и затронуть в обсуждении чуть больше, чем просто основу. В этой статье мы подробно разберем основные законы классической механики. Как вы уже догадались, речь пойдет о законах Ньютона .
Основные законы классической механики Исаак Ньютон (1642-1727) собрал и опубликовал в 1687 году. Три знаменитых закона были включены в труд, который назывался «Математические начала натуральной философии».
Был долго этот мир глубокой тьмой окутан
Да будет свет, и тут явился Ньютон.
(Эпиграмма 18-го века)
Но сатана недолго ждал реванша –
Пришел Эйнштейн, и стало все как раньше.
(Эпиграмма 20-го века)
Что стало, когда пришел Эйнштейн, читайте в отдельном материале про релятивистскую динамику . А мы пока приведем формулировки и примеры решения задач на каждый закон Ньютона.
Первый закон Ньютона
Первый закон Ньютона гласит:
Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано.
Проще говоря, суть первого закона Ньютона можно сформулировать так: если мы на абсолютно ровной дороге толкнем тележку и представим, что можно пренебречь силами трения колес и сопротивления воздуха, то она будет катиться с одинаковой скоростью бесконечно долго.
Инерция – это способность тела сохранять скорость как по направлению, так и по величине, при отсутствии воздействий на тело. Первый закон Ньютона еще называют законом инерции.
До Ньютона закон инерции был сформулирован в менее четкой форме Галилео Галилеем. Инерцию ученый называл «неистребимо запечатленным движением». Закон инерции Галилея гласит: при отсутствии внешних сил тело либо покоится, либо движется равномерно. Огромная заслуга Ньютона в том, что он сумел объединить принцип относительности Галилея, собственные труды и работы других ученых в своих “Математических началах натуральной философии”.
Понятно, что таких систем, где тележку толкнули, а она покатилась без действия внешних сил, на самом деле не бывает. На тела всегда действуют силы, причем скомпенсировать действие этих сил полностью практически невозможно.
Например, все на Земле находится в постоянном поле силы тяжести. Когда мы передвигаемся (не важно, ходим пешком, ездим на машине или велосипеде), нам нужно преодолевать множество сил: силу трения качения и силу трения скольжения, силу тяжести, силу Кориолиса.
Второй закон Ньютона
Помните пример про тележку? В этот момент мы приложили к ней силу ! Интуитивно понятно, что тележка покатится и вскоре остановится. Это значит, ее скорость изменится.
В реальном мире скорость тела чаще всего изменяется, а не остается постоянной. Другими словами, тело движется с ускорением. Если скорость нарастает или убывает равномерно, то говорят, что движение равноускоренное.
Если рояль падает с крыши дома вниз, то он движется равноускоренно под действием постоянного ускорения свободного падения g . Причем любой дугой предмет, выброшенный из окна на нашей планете, будет двигаться с тем же ускорением свободного падения.
Второй закон Ньютона устанавливает связь между массой, ускорением и силой, действующей на тело. Приведем формулировку второго закона Ньютона:
Ускорение тела (материальной точки) в инерциальной системе отсчета прямо пропорционально приложенной к нему силе и обратно пропорционально массе.
Если на тело действует сразу несколько сил, то в данную формулу подставляется равнодействующая всех сил, то есть их векторная сумма.
В такой формулировке второй закон Ньютона применим только для движения со скоростью, много меньшей, чем скорость света.
Существует более универсальная формулировка данного закона, так называемый дифференциальный вид.
В любой бесконечно малый промежуток времени dt сила, действующая на тело, равна производной импульса тела по времени.
В чем состоит третий закон Ньютона? Этот закон описывает взаимодействие тел.
3 закон Ньютона говорит нам о том, что на любое действие найдется противодействие. Причем, в прямом смысле:
Два тела воздействуют друг на друга с силами, противоположными по направлению, но равными по модулю.
Формула, выражающая третий закон Ньютона:
Другими словами, третий закон Ньютона – это закон действия и противодействия.
Пример задачи на законы Ньютона
Вот типичная задачка на применение законов Ньютона. В ее решении используются первый и второй законы Ньютона.
Десантник раскрыл парашют и опускается вниз с постоянной скоростью. Какова сила сопротивления воздуха? Масса десантника – 100 килограмм.
Решение:
Движение парашютиста – равномерное и прямолинейное, поэтому, по первому закону Ньютона , действие сил на него скомпенсировано.
На десантника действуют сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.
По второму закону Ньютона , сила тяжести равна ускорению свободного падения, умноженному на массу десантника.
Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и противоположна направлена.
Кстати! Для наших читателей сейчас действует скидка 10% на
А вот еще одна физическая задачка на понимание действия третьего закона Ньютона.
Комар ударяется о лобовое стекло автомобиля. Сравните силы, действующие на автомобиль и комара.
Решение:
По третьему закону Ньютона, силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.
Другое дело, что действие этих сил на тела сильно отличаются вследствие различия масс и ускорений.
Исаак Ньютон: мифы и факты из жизни
На момент публикации своего основного труда Ньютону было 45 лет. За свою долгую жизнь ученый внес огромный вклад в науку, заложив фундамент современной физики и определив ее развитие на годы вперед.
Он занимался не только механикой, но и оптикой, химией и другими науками, неплохо рисовал и писал стихи. Неудивительно, что личность Ньютона окружена множеством легенд.
Ниже приведены некоторые факты и мифы из жизни И. Ньютона. Сразу уточним, что миф – это не достоверная информация. Однако мы допускаем, что мифы и легенды не появляются сами по себе и что-то из перечисленного вполне может оказаться правдой.
- Факт. Исаак Ньютон был очень скромным и застенчивым человеком. Он увековечил себя благодаря своим открытиям, однако сам никогда не стремился к славе и даже пытался ее избежать.
- Миф. Существует легенда, согласно которой Ньютона осенило, когда на наго в саду упало яблоко. Это было время чумной эпидемии (1665-1667), и ученый был вынужден покинуть Кембридж, где постоянно трудился. Точно неизвестно, действительно ли падение яблока было таким роковым для науки событием, так как первые упоминания об этом появляются только в биографиях ученого уже после его смерти, а данные разных биографов расходятся.
- Факт. Ньютон учился, а потом много работал в Кембридже. По долгу службы ему нужно было несколько часов в неделю вести занятия у студентов. Несмотря на признанные заслуги ученого, занятия Ньютона посещались плохо. Бывало, что на его лекции вообще никто не приходил. Скорее всего, это связано с тем, что ученый был полностью поглощен своими собственными исследованиями.
- Миф. В 1689 году Ньютон был избран членом Кембриджского парламента. Согласно легенде, более чем за год заседания в парламенте вечно поглощенный своими мыслями ученый взял слово для выступления всего один раз. Он попросил закрыть окно, так как был сквозняк.
- Факт. Неизвестно, как бы сложилась судьба ученого и всей современной науки, если бы он послушался матери и начал заниматься хозяйством на семейной ферме. Только благодаря уговорам учителей и своего дяди юный Исаак отправился учиться дальше вместо того, чтобы сажать свеклу, разбрасывать по полям навоз и по вечерам выпивать в местных пабах.
Дорогие друзья, помните – любую задачу можно решить! Если у вас возникли проблемы с решением задачи по физике, посмотрите на основные физические формулы . Возможно, ответ перед глазами, и его нужно просто рассмотреть. Ну а если времени на самостоятельные занятия совершенно нет, специализированный студенческий сервис всегда к вашим услугам!
В самом конце предлагаем посмотреть видеоурок на тему “Законы Ньютона”.
1 2 и 3 закон ньютона – Третий закон Ньютона определение. Формула третьего закона Ньютона. Третий закон Ньютона, сила
Кратко и понятно о первом, втором и третьем законах Ньютона: формулировки, примеры и формулы
Три закона Ньютона — это основа классической механики. В 1867 году Ньютон опубликовал работу под названием «Математические начала натуральной философии». Там были все знания, накопленные до него другими учёными, а также новые, открытые самим Ньютоном. Его считают одним из самых первых основоположником современной физики. Благодаря систематизированным знаниям, которые были описаны в вышеуказанном труде, он открыл множество законов механики, Закон всемирного тяготения и многое другое.
Кратко о законах Ньютона
Первый закон Ньютона
- Формулировка. В наше время встречаются несколько формулировок, вот одна из самых современных: «Существуют такие инерциальные системы отсчёта, относительно которых тело, если на него не действуют другие силы (либо действие других сил компенсируется), находится в покое либо движется равномерно и прямолинейно». Этот закон иногда называют Законом инерции.
- Трактовка. Если описать это утверждение простыми словами, то можно увидеть, что всё достаточно просто: если какое-то тело находится в покое относительно чего-либо, то оно и будет оставаться в покое до тех пор, пока на него не подействует какой-либо предмет. То же самое, если тело движется равномерно прямолинейно, то оно будет продолжать так двигаться, пока на него не подействует какая-либо сила. До Ньютона его открыл Галилео Галилей, но он не совсем точно его описал. Теперь осталось только разобраться, что такое инерциальные системы отсчёта. Проще говоря, это такая система, для которой выполняется Первый закон Ньютона.
- Пример действия. Представьте себе парашютиста, который движется прямолинейно равномерно к Земле. Это будет продолжаться до тех пор, пока притяжение к поверхности Земли будет компенсироваться сопротивлением воздуха. Если же сопротивление станет меньше либо больше, то тогда на тело начнёт действовать сила притяжения, и оно станет двигаться прямолинейно равноускоренно.
- История открытия. Существует легенда об открытии этого утверждения. Когда-то Ньютон сидел под деревом, и рядом с ним упало яблоко. Это подтолкнуло его на размышления о том, почему яблоко упало перпендикулярно земле, каковы были причины данного явления. По крайней мере, так описывал этот эпизод знаменитый биограф Уильям Стьюкли.
- Формулы у него нет.
Это интересно: система отсчета в физике – определение и ее виды.
Второй закон Ньютона
Он описывает поведение тела при действии на него других объектов. Что с ним происходит, как он начинает двигаться и прочее.
- Формулировка. «В инерциальных системах отсчёта ускорение тела с постоянной массой прямо пропорционально равнодействующей всех сил и обратно пропорционально его массе».
- Формула. Математическое описание этого утверждения такое: а = F/m, где a — это ускорение, F — равнодействующая всех сил, приложенных к телу, m — масса тела.
- Трактовка. Из формулы мы видим, что ускорение тела зависит от силы, приложенной к этому телу, и массы. А также можно увидеть, что чем больше равнодействующая всех сил, то тем больше ускорение, и чем больше масса тела, тем ускорение меньше. Говоря простым языком, если равнодействующая всех сил не равна нулю и не меньше нуля, то выполняется данное утверждение. Можно сказать ещё проще, если на тело действует сила, то оно приобретает ускорение.
- Пример действия. Возьмём бейсбольную биту и мяч. Если ударить битой по мячу, и удар будет сильнее действия всех других сил, то мяч приобретёт ускорение равное отношению равнодействующей всех сил к массе.
Это интересно: формула всемирного тяготения – определение закона.
Третий закон Ньютона
- Формулировка. «Тела взаимодействуют друг на друга с силами одинаковой природы, направленными вдоль прямой, которая соединяет центры масс этих тел, а силы равны по модулю и разнонаправленны».
- Трактовка. Это значит, что на каждое действие есть своё противодействие.
- Пример действия. Более понятно это можно рассмотреть на таком примере: представьте пушку, из которой стреляют ядром. Ядро будет действовать на пушку с той же силой, с какой пушка вытолкала ядро. Поэтому при выстреле пушка откатится чуть-чуть назад, это происходит из-за того, что размеры пушки и ядра разные. Примерно то же самое происходит и при падении яблока на землю. Земля действует на яблоко с некой силой и яблоко тоже действует на Землю. Только из-за того, что масса Земли в миллионы раз больше яблока этого действия не видно. Еще один пример действия Третьего закона для закрепления усвоенного. Возьмём довольно сложный пример: притяжение планет. Луна вертится вокруг Земли благодаря тому, что она притягивается к Земле, но по Третьему закону Ньютона Луна тоже притягивает Землю к себе. Однако, из-за того, что их массы разные, Луна не может притянуть Землю, но у неё получается вызвать отливы и приливы в морях и океанах.
- Формула. Математически это утверждение можно записать так: F1 = -F2, где F1 — это сила, с которой первое тело действует на второе, а F2 — сила, с которой второе тело действует на первое.
obrazovanie.guru
Гравитация – что это?
Гравитация (с лат. gravitas — «тяжесть») — невидимая сила, притягивающая объекты с меньшей массой к более массивным. Таким образом определяющая положение галактик, планет, спутников и всех небесных тел. В контексте Земли отвечает за то, что объекты притягиваются к поверхности и не улетают за пределы планеты. Это одно из четырех фундаментальных взаимодействий в физике, определяющих функционирование вселенной, наряду со слабым и сильным атомными взаимодействиями и электромагнетизмом.
Точного научного определения термина не существует, поскольку подходы к изучению гравитации и теории относительно её природы постоянно разрабатываются, дополняются и совершенствуются. Актуальными на сегодня являются закон всемирного тяготения Ньютона вместе с его дополнениями и общая теория относительности Эйнштейна.
Историческая справка
Год открытия Закон Ома — 1826 немецким ученым Георгом Омом. Он эмпирически определил и описал закон о соотношении силы тока, напряжения и типа проводника. Позже выяснилось, что третья составляющая – это не что иное, как сопротивление. Впоследствии этот закон назвали в честь открывателя, но законом дело не ограничилось, его фамилией и назвали физическую величину, как дань уважения его работам.
Величина, в которой измеряют сопротивление, названа в честь Георга Ома. Например, резисторы имеют две основные характеристики: мощность в ваттах и сопротивление – единица измерения в Омах, килоомах, мегаомах и т.д.
кратко и понятно о формулах и формулировках на конкретных примерах
В школьном курсе физики изучаются три закона Ньютона, являющиеся основой классической механики. Сегодня с ними знаком каждый школьник, но во времена великого ученого подобные открытия считались революционными. Законы Ньютона, кратко и понятно будут описаны ниже, они помогают не только понять основу механики и взаимодействия объектов, но и помогают записать данные в качестве уравнения.
Содержание статьи
Вводная информация
Впервые три закона Иссак Ньютон описал в труде «Математические начала натуральной философии» (1867 год), в котором были подробно изложены не только собственные выводы ученого, но все знания по этой теме открытые другими философами и математиками. Таким образом, труд стал фундаментальным в истории механики, а позднее и физики. В нем рассмотрены перемещение и взаимодействие массивных тел.
Интересно знать! Исаак Ньютон был не только талантливым физиком, математиком и астрономом, но и считался гением в механике. Занимал должность президента королевского общества Лондона.
Каждое утверждение освещает одну из сфер взаимодействия и перемещения предметов в природе, правда обращение к ним было несколько упразднено Ньютоном, и они были приняты как точки без определенного размера (математические).
Именно это упрощение позволило проигнорировать естественные физические явления: воздушное сопротивление, трение, температуру или другие физические показатели объекта.
Полученные данные могли быть описаны только по времени, массе или длине. Именно из-за этого формулировки Ньютона обеспечивают лишь подходящие, но приближенные значения, которые нельзя использовать для описания точной реакции крупных или изменяемых по форме объектов.
Перемещение массивных предметов, которые участвуют в определениях, принято исчислять в инерциальной системе отсчета, представленной в виде системы координат из трех измерений, и при этом она не увеличивает свою скорость и не оборачивается вокруг своей оси.
Ее часто называют системой отсчета Ньютона, но при этом ученый никогда не создавал и не использовал подобной системы, а использовал нерациональную. Именно в этой системе тела могут двигаться так, как описывает это Ньютон.
Первый закон
Называется законом инерции. Не существует его практической формулы, зато есть несколько формулировок. В учебниках по физике предлагается следующая формулировка первого закона Ньютона: есть инерциальные системы отсчета, в отношении которых объект, если он свободен от воздействия любых сил (или же они моментально компенсируется), находиться в полном покое или же двигается по прямой и с одинаковой скоростью. Что означает данное определение и как его понять?
Простыми словами первый закон Ньютона объясняется так: любое тело, если его не трогать и никоим образом не воздействовать на него, будет оставаться постоянно в состоянии покоя, то есть бесконечно стоять на месте. То же самое происходит и при его движении: оно будет равномерно двигаться по заданной траектории бесконечно, пока на него не воздействует что-либо.
Подобное утверждение озвучивал Галилео Галилей, но не смог уточнить и точно описать это явление. В этой формулировке важно правильно понять, что такое инерциальные системы отсчета. Если сказать совсем простыми словами, то это система, в которой выполняется действие данного определения.
Первый закон Ньютона
В мире можно увидеть огромное множество подобных систем, если понаблюдать за движением:
- поезда на заданном участке с одинаковой скоростью;
- Луны вокруг Земли;
- колеса обозрения в парке.
В качестве примера рассмотрим некоего парашютиста, который уже раскрыл парашют и движется прямолинейно и при этом равномерно по отношению к поверхности Земли. Движение человека не прекратиться до тех пор, пока земное притяжение будет компенсироваться движением и сопротивлением воздуха. Как только это сопротивление уменьшится, то притяжение увеличится, что приведет к изменению скорости парашютиста – его движение станет прямолинейным и равноускоренным.
Именно в отношении этой формулировки существует яблочная легенда: Исаак отдыхал в саду под яблоней и размышлял о физических явлениях, когда с дерева сорвалось спелое яблоко и упало в траву. Именно ровное падение заставило ученого изучить этот вопрос и выдать в итоге научное объяснение движению предмета в некой системе отсчета.
Интересно знать! Помимо трех явлений в механике, Исаак Ньютон также объяснил движение Луны как спутника Земли, создал корпускулярную теорию света и разложил радугу на 7 цветов.
Второй закон
Данное научное обоснование касается не просто движения предметов в пространстве, а взаимодействия их с другими объектами и результатов этого процесса.
Закон гласит: увеличение скорости объекта с некоторой постоянной массой в инерциальной системе отсчета прямо пропорционально силе воздействия и обратно пропорционально постоянной массе движущегося предмета.
Проще говоря, если существует некое движущиеся тело, масса которого не изменяется, и на него вдруг начнет воздействовать посторонняя сила, то оно начнет ускоряться. А вот скорость ускорения будет прямо зависеть от воздействия и обратно пропорционально зависеть от массы движущегося предмета.
Для примера можно рассмотреть снеговой шар, который катиться с горы. Если шар толкать по ходу движения, то ускорения шара будет зависеть от мощности воздействия: чем она больше, тем больше ускорение. Но, чем больше масса данного шара, тем меньше будет ускорение. Данное явление описывается формулой, в которой учитывается ускорение, или «a», равнодействующая масса всех воздействующих сил, или «F», а также масса самого предмета, или «m»:
а = F/m
Следует уточнить, что данная формула может существовать только в том случае, если равнодействующая всех сил не меньше и не равна нулю. Применяется закон только относительно тел, которые двигаются со скоростью меньше световой.
Полезное видео: первый и второй законы Ньютона
Третий закон
Многие слышали выражение: «На каждое действие есть свое противодействие». Его часто используют не только в общеобразовательных целях, но и воспитательных, объясняя, что на каждую силу найдется большая.
Эта формулировка пошла от очередного научного утверждения Исаака Ньютона, а точнее его третьего закона, который объясняет взаимодействие различных сил в природе относительно какого-либо тела.
Третий закон Ньютона определение имеет такое: предметы оказывают воздействие друг на друга с силами одинаковой природы (соединяющей массы предметов и направлены вдоль прямой), которые равны по своим модулям и при этом направлены в разные стороны. Данная формулировка звучит достаточно сложно, но простыми словами объяснить закон легко: каждая сила имеет свое противодействие или равную силу, направленную в обратную сторону.
Гораздо проще будет понять смысл закона, если в качестве примера взять пушку, из которой стреляют ядрами. Пушка воздействует на снаряд с той же силой, с которой снаряд воздействует на пушку. Подтверждением этого будет небольшое движение пушки назад во время выстрела, что подтвердит воздействие ядра на орудие. Если взять как пример тоже самое яблоко, которое падает на землю, то станет понятно, что яблоко и земля воздействуют друг на друга с равной силой.
Закон имеет также математическое определение, в котором используется сила первого тела (F1) и второго (F2):
F1 = -F2
Знак минуса сообщает о том, что векторы сил двух разных тел направлены в противоположные стороны. При этом важно помнить, что данные силы не компенсируют друг друга, поскольку направлены относительно двух тел, а не одного.
Полезное видео: 3 закона Ньютона на примере велосипеда
Вывод
Данные законы Ньютона кратко и четко необходимо знать каждому взрослому человеку, поскольку они являются основой механики и действуют в повседневной жизни, несмотря на то, что не при всех условиях данные закономерности соблюдаются. Они стали аксиомами в классической механике, и на основе их были созданы уравнения движения и энергии (сохранение импульса и сохранение механической энергии).
Вконтакте
Google+
znaniya.guru
Вводная информация
Впервые три закона Иссак Ньютон описал в труде «Математические начала натуральной философии» (1867 год), в котором были подробно изложены не только собственные выводы ученого, но все знания по этой теме открытые другими философами и математиками. Таким образом, труд стал фундаментальным в истории механики, а позднее и физики. В нем рассмотрены перемещение и взаимодействие массивных тел.
Интересно знать! Исаак Ньютон был не только талантливым физиком, математиком и астрономом, но и считался гением в механике. Занимал должность президента королевского общества Лондона.
Каждое утверждение освещает одну из сфер взаимодействия и перемещения предметов в природе, правда обращение к ним было несколько упразднено Ньютоном, и они были приняты как точки без определенного размера (математические).
Именно это упрощение позволило проигнорировать естественные физические явления: воздушное сопротивление, трение, температуру или другие физические показатели объекта.
Полученные данные могли быть описаны только по времени, массе или длине. Именно из-за этого формулировки Ньютона обеспечивают лишь подходящие, но приближенные значения, которые нельзя использовать для описания точной реакции крупных или изменяемых по форме объектов.
Перемещение массивных предметов, которые участвуют в определениях, принято исчислять в инерциальной системе отсчета, представленной в виде системы координат из трех измерений, и при этом она не увеличивает свою скорость и не оборачивается вокруг своей оси.
Ее часто называют системой отсчета Ньютона, но при этом ученый никогда не создавал и не использовал подобной системы, а использовал нерациональную. Именно в этой системе тела могут двигаться так, как описывает это Ньютон.
Видеоурок по физике – Второй закон Ньютона
Видеоурок по второму закону Ньютона
Видеоурок по второму закону Ньютона обсуждает второй закон движения Ньютона. Связь между ускорением и чистой силой, а также ускорением и массой подробно объясняется с помощью слов, уравнений и числовых данных. Подробно описаны величина и направление ускорения, а также их зависимость от массы и полезной силы.Видеоурок отвечает на следующие вопросы:
- Что утверждает второй закон Ньютона относительно ускорения объектов?
- Как можно использовать второй закон Ньютона для сравнения значений ускорения, для прогнозирования значения ускорения или для прогнозирования движения объекта?
Чтобы повысить эффективность обучения, The Physics Classroom предоставил следующие инструменты:
Примечания к уроку
Заметки к уроку предназначены для распечатки и использования при просмотре видео.Они структурированы так, чтобы студенты могли следить за видео, записывать некоторые заметки и оставлять видео с документом, который можно назвать продолжением их обучения. Примечания к уроку доступны в формате PDF. Разрешается распечатать заметки или включить на них ссылку из системы управления обучением.Просмотр заметок к уроку
Дополнительные и сопутствующие средства обучения
Обучение требует усилий. Просмотр видео – относительно пассивное занятие. Одно дело – послушать видео, представленное человеком, разбирающимся в материале.Но совсем другое дело – применить информацию из видео, чтобы лично понять материал. На этой странице перечислены различные инструменты, которые можно использовать для применения нового обучения. Инструменты включают те, которые могут использоваться учениками, и те, которые могут использоваться учителями со своими учениками в классе. Связанные ресурсы также включены в эти инструменты.Просмотр дополнительных средств обучения
Ресурсы для учителей
Так вы этому учите? Может, мы сможем помочь… мы занимаемся этим некоторое время и у нас есть несколько ресурсов, которые могут вам пригодиться. Посетите страницу ресурсов для учителей и узнайте о некоторых инструментах, которые помогут вам преподавать и разрабатывать уроки по этой теме.Просмотр ресурсов учителя
Слайды из видеоурока
Некоторым студентам полезно просматривать слайды презентации. Мы размещаем их здесь, на нашем сайте. Анимации, присутствующие в видео, преобразуются в одно статичное экранное изображение на слайдах.Просмотреть слайды
Вы можете просмотреть это видео на YouTube или здесь, на нашем сайте:
Посмотреть видеоурок
Помогите нам Помогите вам Это видео является частью нашей серии видеоуроков по законам Ньютона. Другие видеоуроки вы можете найти здесь, на нашем сайте. Чтобы получать самые свежие материалы из нашей серии видеоуроков по физике, мы предлагаем пользователям подписаться на канал The Physics Classroom на YouTube. Каждые лайков и каждые подписок помогает продвигать наше видео… так что спасибо за любую помощь, которую вы можете нам дать. Когда вы помогаете нам, мы можем помочь вам больше.Законы движения Ньютона | Физическая обработка аудиосигнала
Законы движения Ньютона
Возможно, наиболее часто используемое уравнение в физике – это секунда Ньютона. закон движения :
То есть, когда к массе приложена сила, масса испытывает ускорение пропорционально приложенной силе.Обозначая массу , сила во время на, а ускорение на у нас есть| (В.1) |
В этой формулировке приложенная сила считается положительной. в направлении положительного масс-положения. Сила и ускорение, как правило, векторов в трехмерное пространство . Другими словами, сила и ускорение обычно является векторной функцией времени. В масса – это скалярная величина, и ее можно рассматривать как меру инерция физической системы (см.1.1 ниже).
Три закона движения Ньютона
Три закона движения Ньютона можно сформулировать следующим образом:
- Каждый объект в состоянии равномерного движения останется в этом состояние движения, если на него не действует внешняя сила.
- Сила равна массе, умноженной на ускорение [ ].
- На каждое действие есть равная и противоположная реакция.
Первый закон, также называемый законом инерции , был впервые предложен Галилео.Это был довольно концептуальный скачок, потому что он был невозможен. во времена Галилея наблюдать за движущимся объектом без каких-либо силы трения, тянущиеся против движения. Фактически, более за тысячу лет до Галилея образованные люди считали Формулировка Аристотеля о том, что везде, где есть движение, есть внешняя сила, вызывающая это движение.
Второй закон, , фактически следует первый закон, так как когда (без приложенной силы) ускорение равно нулю, подразумевая постоянную скорость.(Скорость – это просто интеграл по времени .)
Третий закон Ньютона предполагает сохранение импульса [137]. Это также можно увидеть как следующее из второй закон: когда один объект “ толкает ” второй объект в какой-то (безмассовая) точка контакта, использующая приложенную силу, должна быть равная и противоположная сила от второго объекта, которая отменяет приложенная сила. В противном случае на безмассовая точка, которая по второму закону ускоряла бы точку контакт на бесконечное количество.
Таким образом, законы Ньютона сводятся к. Огромное количество физических наук была разработана с применением этого простой B.1 математический закон к разным физическим ситуации.
Масса
Масса – внутреннее свойство материи. Из второго закона Ньютона , мы имеем, что количество сила, необходимая для ускорения объекта на заданную величину, равна пропорциональна его массе.Таким образом, масса объекта количественно определяет его инерция – его сопротивление изменению скорости.
Мы можем измерить массу объекта, измерив гравитационная сила между ним и другой известной массой, как описано в следующем разделе. Это частный случай измерения его ускорение в ответ на известную силу. Какой бы ни была сила, масса делится на результирующее ускорение опять же по второму закону Ньютона.
Обычная математическая модель идеальной массы – это безразмерная точка в некотором месте в космосе. Пока нет реальных объектов безразмерные, их часто можно рассматривать математически как безразмерные точки, расположенные в их центре масс , или центроид (§B.4.1).
физическое состояние массы во времени состоит из ее позиция и скорость в трехмерном пространстве.Само количество массы рассматривается как фиксированный параметр, который не меняется. Другими словами, состояние из физическая система обычно меняется со временем, в то время как любая параметры системы, такие как масса, остаются фиксированными время (если не указано иное).
Сила гравитации
Все мы знакомы с силой тяжести . Это фундаментальное наблюдаемое свойство нашей Вселенной, что любые две массы и испытать притягивающую силу , создаваемую формула
| (Б.2) |
где – расстояние между центрами масс и в то время, а гравитация постоянная . B.2
Закон всемирного тяготения (Б.2) можно принять как экспериментальный факт , который определяет концепцию силы . B.3 Гигантский концептуальный скачок, сделанный Ньютоном, заключался в том, что закон гравитация универсальный – применяется как к небесным телам, так и к объектам на Земля.Когда груз “ уронили ” и позволили ему “ упасть ” в гравитационного поля, наблюдается – равномерное ускорение пропорционально его массе. Секунда Ньютона закон движения (§B.1) количественно определяет этот результат.
Закон Гука
Рассмотрим идеальную пружину, подвешивающую массу к жесткому потолку, как изображенный на рис.B.1. Предположим, что масса покоится, и что его расстояние от потолка фиксировано.
Если обозначает массу Земли, а – расстояние массы центр от центра масс Земли, то сила, направленная вниз от массы определяется уравнением (Б.2) как
куда называется ускорением свободного падения . Изменения в срок движению массы считаются пренебрежимо малыми по сравнению с радиуса Земли (около миль), и поэтому рассматривается как постоянная для большинства практических целей у поверхности земли.Мы видим что если мы удвоим массу, мы удвоим силу, тянущую на весна. Это экспериментальный факт , что типичные пружины демонстрируют смещение, примерно пропорциональное приложенная сила для широкого диапазона приложенных сил. Это Закон Гука для идеальных пружин:| (Закон Гука) | (В.3) |
где смещение пружины от ее естественная длина. Мы называем жесткость пружины , или жесткость пружины.Используя наши предыдущие обозначения, мы имеем где – длина пружины без массы.
Обратите внимание, что сила на пружине на рис. B.1 равна сила гравитации. Равно и противоположно силе тяжести сила пружины , приложенная пружиной вверх к массе (который не движется). Мы знаем, что сила пружины равна и против гравитационной силы, потому что в противном случае масса ускоряться чистой силой. B.4 Следовательно, как и гравитация, смещенную пружину можно рассматривать как определение приложенной силы. То есть всякий раз, когда вам нужно подумать о приложенной силе, вы можете всегда считайте это доставленным к концу какой-то идеальной весны привязан к какой-то внешней физической системе.
Заметьте, кстати, что нормальные силы взаимодействия при соприкосновении объектов возникают из кулоновской силы (электростатическая сила или отталкивание одинаковых зарядов) между электронными орбиталями.Эта электростатическая сила подчиняется закону обратных квадратов, как гравитация, и, следовательно, также ведет себя как идеальная пружина при небольших перемещениях. B.5
Конкретное значение зависит от физических единиц, принятых как а также “ жесткость ” пружины. Что самое главное в это определение силы состоит в том, что удвоение смещения пружины удваивает силу. То есть сила пружины линейная функция перемещения пружины (сжатие или растяжение).
Применение законов движения Ньютона
В качестве простого примера рассмотрим массу, движущуюся по бесконтактной поверхность идеальной пружиной, как показано на рис.B.2. Предположим, что положение массы соответствует пружине в состоянии покоя, , то есть , без растяжения и сжатия. Сила, необходимая для сжатия пружина на расстояние определяется законом Гука (§B.1.3):
Эта сила всегда уравновешивается силой инерции. из масса, т.е. , г. уступая B.6| (В.4) |
где мы определили как начальное перемещение массы вместе . Это дифференциальное уравнение , решение которого дает уравнение движения узла масс-пружина для всех время: B.7
| (В.5) |
куда обозначает частоту колебание в радианах в секунду.В более общем плане полный пространство решений уравнения (Б.4), соответствующее всем возможным начальные перемещения и начальные скорости , это совокупность всех синусоидальных колебаний на частоте: Амплитуда колебаний и сдвиг фазы равны определяется начальными условиями , т.е. , начальное положение и начальная скорость массы (это начальная состояние ), когда мы “ отпускаем это ” или “ отталкиваем ” во время.
Следующий раздел:
Работа = Сила, умноженная на Расстояние = Энергия
Предыдущий раздел:
Резюме
Второй закон Ньютона – обзор
3.4 Второй закон Ньютона
Второй закон Ньютона можно сформулировать как
Объект будет ускоряться, если неуравновешенная сила, действующая на объект, не равна нулю. Направление ускорения совпадает с направлением неуравновешенной силы. Величина ускорения прямо пропорциональна неуравновешенной силе и обратно пропорциональна массе объекта.
Мы предполагаем, что вы знакомы с массой и можете действительно так думать, но это нетривиальная концепция.Как вы скоро узнаете, масса составляет , а не . В гравитационном поле масса, безусловно, создает вес, но масса присутствует даже там, где нет гравитации, например, в космическом пространстве. Массу лучше всего рассматривать как количество материи; это свойство вещества.
Центральным элементом любого научного набора единиц является определение силы . Вероятно, вы уже знакомы с этим понятием в старшей школе. Согласно второму закону Ньютона, сила пропорциональна массе и ускорению и может быть записана как
(3.1) F∝ma
, где a – это ускорение массы м . Ускорение – это просто скорость изменения скорости (скорости), поэтому Второй закон Ньютона для тел постоянной массы можно записать как F ∝ м (Δ v / Δ t ) с Δ v – изменение скорости, а Δ t – изменение времени в течение периода ускорения. Чтобы преобразовать пропорциональность во втором законе Ньютона в «равенство», нам нужно ввести константу пропорциональности .
Чтобы сформулировать уравнение (3.1) в терминах равенства, предположим, что существует набор единиц, для которых сила F 1 ускоряет массу м 1 на a 1 . Тогда второй закон Ньютона может быть записан как
F1∝m1a1
Если мы теперь устраним пропорциональность, разделив уравнение (3.1) на это уравнение, мы получим
(3.2) FF1 = mm1aa1orF = F1m1a1ma
Ясно, что факт что константа пропорциональности, F 1 / m 1 a 1 , представляет собой отношение удельной силы к удельной массе и ускорению, что очень важно для расчетов, сделанных с помощью этого уравнения.Стало принято давать коэффициенту пропорциональности необычный символ: 1/ g c , где g c ≡ м 1 a 1 /
40 F 1 . Тогда Второй закон Ньютона принимает вид
(3.3) F = F1m1a1ma = mam1a1F1 = magc
Мы должны выбрать как величину, так и размерность константы пропорциональности g c .Любой согласованный набор единиц удовлетворяет этому уравнению. При такой степени гибкости легко увидеть, как эволюционировало большое количество различных систем единиц.
Пример 3.2Предположим, вы определяете единицу массы, называемую снарядом , довольно уродливым словом для обозначения массы, которая ускоряется «точно» на 1 фут / с 2 , когда сила «точно» составляет 1 фунт-сила (фунт-сила). применяется к нему. Какой вес у пули массой 5,00?
Потребность: Масса массы 5.00 пуля.
Знать: Вес – это сила, создаваемая гравитационным ускорением Земли 32,2 фута / с 2 .
Как: Здесь можно использовать первую часть уравнения (3.3):
F = F1m1a1ma, в котором F1m1a1 = 11 × 1 = 1 фунт-сила × s2slug × ft
Следовательно,
a Fmgm = 1 фунт-сила × s2slug × ft × 5.00slug × 32,2ft2 = 161lbfОбратите внимание, что
gc = m1a1F1 = 1slug × ftlbf × s2
с этим определением силы.
Фактически, в некоторых областях техники в Соединенных Штатах все еще предпочитают пулевую систему. Его очевидное преимущество состоит в том, что константа пропорциональности Второго закона Ньютона g c равна 1, поэтому закон можно записать в знакомой форме: F = мА, с условием, что масса м находится в пробках, а ускорение – в фут / с 2 . Его недостаток в том, что вы плохо «чувствуете» размер пули.
Система SI в некоторой степени похожа на систему пробок с выбором константы пропорциональности g c , которая одновременно проста и логична. Отношение F 1 / m 1 a 1 было выбрано таким образом, чтобы его числовое значение было точно «1» и чтобы оно фактически не имело (т. Е. [0]) размеров. 3 Тогда единица силы должна быть просто эквивалентна единицам массы, умноженным на единицы ускорения.Удобно дать этому набору единиц уникальное новое имя (в основном, чтобы избежать необходимости записывать объединенные единицы массы, умноженные на ускорение для каждой силы), а в системе СИ единица силы называется ньютон (сокращенно N ).
Другими словами, сила F 1 в 1 ньютон (Н), действующая на массу м 1 , равную ровно 1 кг, вызывает ускорение массы a 1 с точностью до 1 м / с 2 .Таким образом, в системе СИ g c = m 1 a 1 / F 1 ≡ 1 и второй закон Ньютона может быть записан
(3.4) F = ma
Это упрощение привело к знакомой форме закона движения Ньютона, которую большинство из вас видели раньше. Поскольку коэффициент преобразования г c – то есть [(кг · м / с 2 ) / Н] – в точности равен единице, мы полностью его отбросили.
Пример 3.3Какова сила в ньютонах на тело массой 102 г (0,102 кг), которое ускоряется при ускорении свободного падения 9,81 м / с 2 ?
Потребность: Сила в ньютонах на массу 0,102 кг, ускоренную со скоростью 9,81 м / с 2 .
Знать: Второй закон Ньютона применяется с использованием единиц MKS.
Как: Уравнение (3.4) – это принцип, который мы используем.
Решить: F = ma = 0.102 × 9,81 [кг] [м / с 2 ] = 1,00 [кг · м / с 2 ] = 1,00 Н .
Эти последние два примера используют ускорение, представляющее особый интерес, которое вызвано гравитацией Земли: g = 32,2 фута / с 2 = 9,81 м / с 2 . Глядя на уравнение (3.4), сила SI, действующая на 1 кг массы под действием силы тяжести, составляет не 1 Н, а 9,81 Н, что вызывает беспокойство у новичков в этом вопросе. Таким образом, вес – это просто особая сила – сила тяжести.В этом смысле уравнение (3.4) может быть специализировано для ускорения свободного падения, чтобы получить ту силу, которую мы называем массой , W , записывая ее как
(3,5) W = мг / гс
Пример 3.4Что такое вес ньютонов при массе 0,102 кг?
Потребность: Вес в ньютонах при массе 0,102 кг с ускорением 9,81 м / с 2 .
Знать: Второй закон Ньютона применяется с использованием единиц MKS.
Как: Уравнение (3.5) с g c = 1 (поскольку мы используем единицы СИ).
Решить: Арифметические операции идентичны расчетам в примере 3.2 – сила, действующая на 0,102 кг массы (что составляет около 4 унций в общепринятых английских единицах), составляет 1,00 Н; другими словами, один ньютон примерно равен весу небольшого яблока здесь, на Земле, ! Возможно, это поможет вам мысленно представить величину силы, выраженную в ньютонах.
В дополнение к единицам СИ североамериканский инженер должен владеть по крайней мере одной из других систем, которые соотносят массу и силу, одна из которых постоянство в Соединенных Штатах объясняется скорее обычаями, чем логикой: система Engineering English единиц. В этой системе коэффициент преобразования g c между силой и массой × ускорение равен , а не единицам. Из-за этого мы должны нести явную константу пропорциональности каждый раз, когда используем эту систему единиц.Кроме того, поскольку коэффициент пропорциональности не равен единице, он также требует использования явного набора единиц.
Система инженерного английского языка также выработала довольно неудачное соглашение, касающееся как единицы фунта (сокращенно фунт), так и определения силы. Было решено, что название фунт будет использоваться как , так и для массы и веса (силы) . Поскольку масса и сила являются совершенно разными величинами, к единице «фунт» нужно было добавить модификатор, чтобы различать, какая (масса или вес) используется.Это было решено простым использованием словосочетаний фунтов массы и фунтов силы с соответствующими сокращениями, фунт-сила и фунт-сила, соответственно, чтобы различать их.
В системе инженерного английского языка было решено, что «фунтовая масса» должна весить «фунт-силу» при стандартной гравитации, которая ускоряет массу на 32,174 фут / с 2 . Это дает полезное удобство, позволяя интуитивно понять, что имеется в виду, скажем, под силой в 15 фунтов силы.Это была бы сила, которую вы испытали бы, если бы подняли на поверхности Земли камень массой 15 фунтов.
Это удобство было достигнуто путем установки отношения ( F 1 / м 1 a 1 ) = 1 / 32,174 [фунт-сила · с 2 / фунт · фут]. Другими словами, 1 фунт-сила определяется как сила, которая ускоряет ровно 1 фунт-метр на 32,174 фут / с 2 . Разработчики системы Engineering English хитроумно решили определить числовое значение константы пропорциональности g c как
(3.6) gc≡32.174lbm⋅ftlbf⋅s2
Символика g c была выбрана потому, что числовое значение (но не размеров) g c такое же, как это ускорения свободного падения в системе английских инженерных единиц. Это неудобно, потому что заставляет вас думать, что g c – это то же самое (т. Е. Равно) ускорение от местной силы тяжести, g , , которое определенно не .Константа g c – это не что иное, как константа пропорциональности с размерами [масса × длина / (сила × время 2 )]. Поскольку использование g c настолько широко распространено сегодня в Соединенных Штатах, и поскольку важно, чтобы вы могли распознать значение g c , когда вы видите его в другом месте, это используются в соответствующих уравнениях в этом курсе, кроме тех случаев, когда мы используем гораздо более удобные (и универсальные) единицы СИ.Например, в английской инженерной системе единиц мы впредь будем писать Второй закон Ньютона как
(3,7) F = magc
. Последствия этого выбора для F 1 , m 1 и a 1 выражается как g c заключается в том, что вы можете легко вычислить силу в фунтах-силах, соответствующую ускорению в фут / с 2 и массе в фунтах-фунтах.
Пример 3.5Какая сила необходима для ускорения массы 65.0 фунтов на метр при скорости 15,0 фут / с 2 ?
Требуется : Сила для ускорения массы 65,0 фунтов на 15,0 фут / с 2 .
Знать : Второй закон Ньютона в инженерных английских единицах, в которых г c = 32,2 [фунт-фут] [фунт-сила с 2 ].
Как :
F = magc
Решить: Поскольку проблема выражена в единицах инженерного английского языка, предположим, что ответ требуется в этих единицах.Уравнение (3.7) является принципом, используемым здесь:
F = magc = 65,0 × 15,032,174 = фунт-фут2 фунт-сила × с2 фунт-метр × фут = 30,3 фунта-силы
Обратите внимание, как единиц , а также значение г c введите проблему; без г c наша «сила» была бы в бессмысленных единицах фунт / фут / с 2 , а наше расчетное числовое значение в этих бессмысленных единицах было бы 975.
Есть еще ряд последствий, тоже.В следующей главе вы познакомитесь с величиной кинетической энергии . Инженер, использующий систему SI, определяет кинетическую энергию как ½ мВ 2 (помните, v означает скорость). Однако инженер, использующий систему Engineering English, определяет кинетическую энергию как ½ ( м / г c ) v 2 . Удобная мнемоника для всех приложений системы инженерного английского –
. Когда вы видите массу m в системе инженерного английского языка, разделите ее на g c .
Конечно, логически безопаснее аргументировать единицы, используя ранее введенное соглашение о скобках [..]. Например, если группировка ½ mv 2 была выражена в единицах инженерного английского языка, это было бы [фунт-метр] × [фут / с] 2 , если бы g c игнорировалось. Это бессмысленный набор единиц! Но, используя коэффициент пропорциональности г c , определение кинетической энергии теперь принимает вид
фунт · м × фут / с2 фунт · фут / фунт-сила / с2 = фут · фунт
, что является допустимой единицей энергии в Система единиц инженерного английского языка.
Поймите, что константа преобразования силы г c имеет одинаковое значение во всей Вселенной, то есть 32,174 фунт-фут / (фунт-сила · с 2 ), даже если ее область принятие ограничено Соединенными Штатами! В связи с этим, как указывалось ранее, его не следует путать с физической величиной g, ускорением свободного падения, которое имеет разные числовые значения в разных местах (а также разные размеры от g c ).
Понятие веса всегда связано с понятием местной силы тяжести . Таким образом, вес меняется в зависимости от местоположения – действительно, только немного над поверхностью Земли, но значительно на внеземных телах.
Чтобы повторить то, что было изучено, вес тела массой м на поверхности Земли – это сила, действующая на него из-за ускорения « g » под действием силы тяжести; то есть
(3.8a) Вес, W = mggc
, где в системе единиц инженерного английского языка г = 32.174 фут / с 2 и г c = 32,174 (фунт-фут / фунт-сила-с 2 ), но в системе единиц СИ г = 9,81 м / с 2 и г 903 c = 1. В единицах СИ это
(3.8b) Вес, W = мг
Вес тела массой м , где местная сила тяжести г ′ равна мг ′ / г c . Человек на Международной космической станции испытывает микрогравитацию, гораздо меньшую г , чем мы на Земле; и человек на Луне испытывает примерно 1 / 6 из г по сравнению с человеком на поверхности Земли.Однако инженер, использующий систему единиц инженерного английского языка, должен использовать одно и то же числовое значение для g c , где бы он ни находился во вселенной.
Пример 3.6- а.
Какой вес на Земле в единицах инженерного английского языка 4 у объекта 10,0 фунта?
- б.
Какой вес на Земле в единицах СИ для массы 10 кг?
- г.
Какова масса 10.0 фунт-метр на Луне (предположим, что местное значение г = = 1 / 6.00, что на Земле)?
- г.
Каков вес этого объекта весом 10,0 фунтов на Луне?
Поскольку это простая задача преобразования единиц, давайте сразу перейдем к решениям:
- a.
W = мг / г c в единицах инженерного английского языка. Следовательно, W = 10,0 × 32,2 / 32,2 [фунт-метр] [фут / с 2 ] / [фунт · фут / фунт-сила · с 2 ] = 10.0 фунтов
- б.
W = мг / g c , где g c = 1 в единицах СИ. Следовательно, Вт = 10,0 × 9,81 [кг] [м / с 2 ] = 98,1 [кгм / с 2 ] = 98,1 Н. (См. Таблицу 2.2 для определения ньютонов в терминах основных единиц MKS. )
- с.
Масса – это свойство материала. Следовательно, объект по-прежнему имеет массу 10,0 фунта на Земле, на Луне или где-либо в космосе.
- г.
W = мг / г c в единицах инженерного английского языка. На Луне г = 32,2 / 6,00 = 5,37 фут / с 2 . Следовательно, на Луне W = 10 × (5,37) / 32,2 [фунт-метр] [фут / с 2 ] / [фунт · фут / фунт-сила · с 2 ] = 1,67 фунт-силы.
До середины 20 века в большинстве англоязычных стран использовалась одна или несколько форм системы единиц инженерного английского языка. Но из-за давления со стороны мировой торговли и всемирного признания системы СИ во многих инженерных учебниках сегодня представлены примеры и домашние задания как на инженерном английском, так и на системе единиц СИ.Соединенные Штаты медленно переходят на обычное использование системы СИ. Однако вполне вероятно, что это преобразование займет по крайней мере значительную часть вашей жизни. Итак, чтобы добиться успеха в качестве инженера в Соединенных Штатах, вы должны изучить систему инженерного английского языка. Это поможет вам избежать в будущем повторения таких бедствий, как неприятная потеря НАСА в 1999 году дорогостоящего и важного с научной точки зрения посадочного модуля на Марс из-за неправильного преобразования между инженерным английским языком и единицами СИ. 5
Пример 3.7Какая горизонтальная сила требуется для разгона автомобиля массой 1000 кг со скоростью 5,00 м / с 2 ?
Need: Неуравновешенная сила, необходимая для ускорения автомобиля со скоростью 5,00 м / с 2 .
Знать: Масса автомобиля 1000. кг.
Как: Второй закон Ньютона в единицах СИ.
Решите: Второй закон Ньютона связывает массу объекта, несбалансированную силу, действующую на него, и его ускорение: F = ma / g c , поэтому
F = ma / gc = 1000.× 5.00 / 1kgms2 = 5000.newtons
1.1.2: Три закона Ньютона – Physics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Примеры видео / аудио:
- Вопросы по первому закону Ньютона:
- Вопросы по второму закону Ньютона:
- Вопросы по третьему закону Ньютона:
Ньютон придумал несколько важных законов физики, три из которых мы можем найти полезный для физики звука.
Первый закон: Объекты продолжают движение в покое или по прямой с постоянной скоростью, если на них не действует неуравновешенная сила. Вы можете подумать, что если не действуют никакие силы, объект неподвижен. Но это только один случай; первый закон также гласит, что если все силы добавить к нулю, объект все еще может двигаться с постоянной скоростью. Так зачем вам запускать двигатель в машине, если вы едете по дороге в том же направлении с той же скоростью? Двигатель выдает достаточно силы, чтобы преодолеть трение.Не больше силы, чем трение, а сила точно равна трению, так что общая сила равна нулю , и вы продолжаете двигаться с постоянной скоростью. Точно так же исполнитель, играющий на духовом инструменте, должен продолжать прикладывать силу к воздуху в инструменте, чтобы преодолеть трение, когда воздух проходит через инструмент. Инерция – это термин, используемый для свойства объекта, которое заставляет его продолжать движение по прямой линии, если на него не действует неуравновешенная сила.
Второй закон: Силы вызывают ускорения (силы не вызывают скорость, но изменяет скорость ). Второй закон также известен как \ (F = ma \), где \ (F \) – полная сила, действующая на массу \ (m \), а \ (a \) – ускорение массы. Обратите внимание, что, как было сказано в первом законе, чистая общая сила не требуется для поддержания постоянной скорости; Первый закон гласит, что если что-то движется, оно будет продолжать движение, если сила (например, трение) не остановит его.Когда вы ускоряете машину, на нее действует чистая сила. Но когда вы достигнете крейсерской скорости, чистая сила упадет до нуля (моторная сила в точности компенсирует силы сопротивления). В этом случае (когда чистая сила прибавляется к нулю) объект (ваша машина) подчиняется 1-му закону Ньютона, и вы продолжаете движение по прямой с постоянной скоростью.
Третий закон: Каждый раз, когда один объект оказывает силу на второй объект, второй объект оказывает равное усилие (но в противоположном направлении) на первый объект.Силы всегда действуют парами на два разных объекта; сила действия, действующая на один объект, и сила реакции, действующая на второй объект. Другой способ сказать это: вы не можете прикоснуться к чему-либо, пока оно не коснется вас в ответ, причем так же сильно, как вы прикоснулись к нему. Это кажется простым, если вы толкаете стену; стена явно отталкивается с той же силой. Но как насчет силы, действующей на бейсбольный мяч, когда вы его бросаете (перед выпуском)? Является ли сила, отталкиваемая бейсбольным мячом, такая же, как сила, которую вы прикладываете? ДА! Законы физики всегда верны без исключений.Итак, как можно бросить бейсбольный мяч, если две силы равны по величине, но противоположны по направлению? Ключ в том, чтобы понять, что силы действия и противодействия действуют на разные объекты. Ваша сила, действующая на мяч, заставляет его идти вперед, пока он не выйдет из вашей руки. Равная сила реакции, исходящая от мяча, действует на вашу руку (не на мяч), поэтому вы можете чувствовать мяч, когда вы его бросаете.
Примеры видео / аудио:
- Первый закон Ньютона: яйцо.
- Первый закон Ньютона (автомобильные краш-тесты) один, два, три.Наблюдайте за движением тела и головы манекена, когда машина внезапно останавливается. Поскольку на голову не действует сила, она продолжает двигаться в соответствии с 1-м законом Ньютона.
- Первый и второй закон Ньютона: прыжки с парашютом. Если вы поймете этот пример, вы получите хорошее представление о том, как работают законы Ньютона.
- Первый, второй и третий закон Ньютона применимы к велосипеду.
- Третий закон Ньютона: примеры на космической станции.
Вопросы о Первом законе Ньютона:
- Если вы сидите у знака «Стоп» и вас ударили сзади, ваша голова отлетает назад и ударяется о подголовник.Объясните, используя закон инерции Ньютона, что происходит на самом деле.
- Если вы стоите в автобусе, и он внезапно останавливается, вам кажется, что вас бросают вперед. Используя закон инерции Ньютона, объясните, что происходит на самом деле.
- Объясните, используя закон инерции Ньютона, почему подголовник предотвращает хлыстовые травмы.
- Объясните, используя закон инерции Ньютона, почему использование ремня безопасности в автомобиле, самолете, американских горках и т. Д. Является хорошей идеей.
- Когда спутник находится на орбите, ему не нужно запускать ракеты, чтобы оставаться там.Почему нет? Что поддерживает это?
- Что заставляет Землю вращаться вокруг Солнца?
- Волшебный трюк, который вы можете выполнить дома, – это вытащить скатерть из-под посуды на столе, очень быстро дернув скатерть по горизонтали. Объясните, почему посуда не двигается.
- Шары для боулинга немного замедляются, катясь по дорожке. Объясните, почему это не нарушает закон инерции Ньютона?
- Если вы перестанете толкать корзину, она остановится.Объясните, как это не нарушает закон инерции Ньютона.
- Земля вращается так, что объекты на поверхности движутся со скоростью, близкой к \ (1000 \ text {км} \) в час (это немного отличается в зависимости от широты). Используя закон Ньютона, объясните, почему вас не ударит стена, если вы подпрыгнете прямо в воздух.
- Когда вы путешествуете на самолете на крейсерской высоте, почему упавший объект не летит к задней части самолета?
- Человек роняет гаечный ключ с мачты парусника, который движется вперед с постоянной скоростью.Где приземляется гаечный ключ относительно мачты, если скорость лодки \ (10 \ text {м / с} \), а высота мачты \ (20 \ text {m} \)?
- Водитель, направляющийся на левый поворот, наталкивается на лед на дороге. Опишите движение автомобиля (в этом поможет рисунок), предполагая, что лед препятствует действию на автомобиль какой-либо силы трения. Какой из законов Ньютона говорит вам, что произойдет?
- Маленький шарик катится в трубе без трения, которая расположена плоско на столе, показанном сверху на чертеже.Нарисуйте траекторию полета мяча, когда он покидает трубку, и обоснуйте свой ответ.
Рисунок \ (\ PageIndex {1} \)
Вопросы по второму закону Ньютона:
- На книгу, лежащую на столе, не действуют никакие силы? Перечислите и объясните силы, действующие на книгу.
- Автомобиль, едущий на север по дороге с постоянной скоростью, имеет нулевое ускорение. Чистая сила должна быть равна нулю, поскольку \ (F = ma \). Зачем же тогда нужно держать двигатель работающим и педаль газа нажатой?
- Можно ли заставить объект двигаться вперед с действующей на него чистой силой в противоположном направлении? Объясните и приведите пример.
- Вы прилагаете \ (800 \ text {N} \) силы, чтобы толкнуть ящик по полу с постоянной скоростью (нулевое ускорение). Сила трения больше, меньше или точно равна \ (800 \ text {N} \)? Откуда вы знаете?
- Можно ли заставить объект двигаться по кривой без приложения силы? Объяснять.
- Вы выпрыгиваете из самолета и раскрываете свой парашют. С раскрытым парашютом вы путешествуете с постоянной скоростью. Как соотносится восходящая сила парашюта с нисходящей силой тяжести?
- Пиломатериалы в кузове пикапа ускоряются с той же скоростью, что и грузовик.Что применяет силу, чтобы это произошло? Что произойдет, если этой силы недостаточно?
- Вы бросаете мяч вверх. Какая сила действует на него, когда он покидает вашу руку, на пути вверх? По пути вниз? Каково влияние этой силы на подъем? Какое влияние оказывает сила на спуск?
- Объясните, почему первый закон Ньютона на самом деле является частным случаем второго закона Ньютона.
- Автомобиль едет с постоянной \ (55 \ text {mph} \) по прямой. Какая чистая сила действует на автомобиль?
- Космонавт находится в космическом корабле вдали от воздействия гравитации.Она с одинаковой силой толкает бейсбол и шар для боулинга. Укажите, что из следующего верно, и объясните, почему:
- они оба ускоряются с одинаковой скоростью, потому что они невесомые;
- они ускоряются по-разному, поскольку их масса различна, но в конечном итоге они имеют одинаковую конечную скорость;
- у них разные разгоны.
- Максимальное натяжение гитарной струны составляет примерно \ (900 \ text {N} \) (\ (202 \) фунтов силы).{2} \))?
- Опасно ли ускорение в предыдущей задаче? Подсказка: если сила действует на половину длины гитары, скажем, \ (0.20 \ text {m} \), конечная скорость будет \ (v = \ sqrt {2ax} \), где \ (a \) – ускорение а \ (x \) – пройденное расстояние.
- Повторите предыдущие два вопроса для струны фортепиано с натяжением \ (700 \ text {N} \) и пройденным расстоянием \ (50 \ text {см} \). Предположим, что у колышка одинаковая масса.
Вопросы по третьему закону Ньютона:
- Можете ли вы толкнуть левую руку с большей силой, используя правую руку? Объяснять.
- Вы привязываете веревку к коробке, чтобы протащить ее по полу. Согласно второму закону Ньютона, ящик тянет веревку назад с той же силой, с которой вы тянете веревку. Объясните, как можно перемещать коробку, если эти силы в точности равны и направлены в противоположные стороны.
- Объясните силы действия и противодействия, когда вы толкаете ногу о землю, чтобы сделать шаг вперед.
- Каковы силы действия и противодействия в этих случаях:
- теннисная ракетка попадает в теннисный мяч;
- при ходьбе отталкивается ступня от бордюра;
- вы нажимаете на педаль велосипеда;
- во время разгона бейсбольного питчера, до тех пор, пока он не выпустит мяч?
- Для каждого случая в предыдущем вопросе укажите, какая сила больше.
- Сила \ (\ text {F} \) толкает коробку влево. Сила трения \ (\ text {f} \) между полом и коробкой препятствует перемещению коробки. Это единственные силы, действующие в горизонтальном направлении. Для следующих трех случаев укажите, что больше (или того же размера), \ (\ text {F} \) или \ (\ text {f} \) и почему.
- Ящик не двигается.
- Ящик движется влево с постоянной скоростью.
- Коробка перемещается влево и ускоряется.
- Коробка перемещается влево и замедляется.
- Шар для боулинга сталкивается с теннисным мячом. Какой объект имеет большую силу удара по другому? У кого больше ускорение? Объяснять.
- До космических путешествий некоторые люди думали, что ракеты не будут работать в космосе, потому что не было атмосферы, в которую могли бы толкать выхлопы ракеты. Объясните ошибку в этом мышлении, используя третий закон Ньютона.
- Вы в железнодорожном вагоне, но рельсы очень ровные, а окна закрыты, так что вы не можете сказать, двигаетесь вы или нет.Вы роняете теннисный мяч, и он падает прямо под вашу руку. Что вы можете сделать из этого наблюдения о движении автомобиля?
- Когда вы ударяете по стержню ксилофона молотком, он отскакивает назад. Какой из трех законов Ньютона объясняет, откуда берется сила, заставляющая молоток отскакивать обратно в воздух?
- Струна гитары натягивает механизм колышка с усилием \ (600 \ text {N} \) (\ (134 \ text {lbs} \)). Какое минимальное усилие должно иметь механизм для оттягивания, чтобы избежать изменения натяжения струны (что также меняет высоту тона)?
- Какую силу должна выдержать рама пианино, если натяжение самой тугой струны равно \ (900 \ text {N} \)?
Почему скорость звука?
Почему сегодня у звука есть скорость? В Инженерный колледж Хьюстонского университета представляет серию статей о машины, которые заставляют нашу цивилизацию работать, и люди, чья изобретательность создала их.
Может показаться удивительным, что звук движется только с одной скоростью в воздухе вокруг нас. Ни высота, ни громкость не меняют эту скорость. Исаак Ньютон пытался объяснить скорость звука и понял только ее часть. Он понял этот воздух эластичен. Попробуйте надуть щеку; затем нажмите на него пальцем. Можно подумать, что ты стучишь по резиновому мячу. Сжатый воздух очень упругий.
Пока мы думаем о подпрыгивании, что происходит с нарушениями на открытом воздухе? Воздух вокруг нас не задерживается, как воздух в наших щеках.Вместо подпрыгивания возмущение перемещается с через по воздуху. Сочетание упругости мяча сочетается с его плотностью, чтобы установить частоту подпрыгивания. Та же комбинация в открытый воздух вызывает беспокойство не потому, что он подпрыгивает, а движется с заданной скоростью.
Предположим, мы хлопаем в ладоши. Это создает внезапную область высокого давления, которая должна двигаться. Так что регион ускользает во все стороны. Но делает это со скоростью устанавливается тем, что требуется время, чтобы сжать и выпустить воздух.А вот часть, которую Ньютон ошибся: поскольку энергия движется в волне, воздух нагревается и охлаждается. по мере того, как его давление повышается и понижается.
Законы физики определяют скорость всех этих процессов. Студенты инженерных специальностей или физика научится вычислять скорость звука по этим законам. Они показывают, что скорость увеличивается как квадратный корень из абсолютной температуры. Это около 760 миль час на поверхности Земли в теплый день, но только 660 на высоте 80 000 футов.
Вот почему числа Маха могут сбивать с толку. Число Маха – это просто кратное скорость звука, которая может меняться. 2 Маха, что в два раза больше скорости звука, превышает 1500 миль в час у поверхности Земли, но в холодном воздухе на 80 000 футов.
Одна вещь, на которую мы должны обратить внимание, – это идея частоты. Все мы знаем о частота тонов – как у оркестровой А-440. Но те частоты не имеют ничего общего с воздухом.Они устанавливаются тростью в гобое, или наши голосовые связки или скрипичная струна.
С другой стороны, фейерверк или щелчок клавиатуры моего компьютера – это просто скачок давления без ритма. Звук синусоидальной волны или простой хлопок, оба движутся с одинаковой скоростью.
Кстати, та же физика работает и с другими материалами. Скорость звука намного быстрее в воде – более 3000 миль в час. В стали это более 10 000 миль в час.Оба эластичны, но оба намного жестче воздуха. Так, если друг за милю пробивает железнодорожные пути, звук занимает пять секунд, чтобы достичь нас в воздухе. Но если приложить ухо к гусенице, мы услышим удар молота после всего четыре десятых секунды.
Все это работает, потому что воздух (или сталь) подобен упругой пружине, в которой каждый кусочек звук долго отскакивает от него. Почему мы слышим скрипач, радио или друг разговаривает с нами? Это потому, что это очень физическое, очень пружинистое, очень невидимая материя, называемая воздух, одновременно разделяет нас и присоединяется к нам.
Я Джон Линхард из Хьюстонского университета, где нас интересуют изобретательные умы Работа.
(Музыкальная тема)Этот веб-сайт НАСА предлагает хорошее вводное руководство по скорости звука: http://www.grc.nasa.gov/WWW/K-12/airplane/sound.html
Скорость звука, c, является квадратным корнем из частной производной давления с относительно плотности среды (скажем, воздуха) при неизменной энтропии s.Если вычислить это для воздуха, то для c получится квадратный корень из kRT, где R – это постоянная идеального газа, T – абсолютная температура, а k – отношение удельных нагревается при постоянном давлении и объеме. k = 1,405 для воздуха при нормальных условиях.
Аналогия Джона Тиндаля для распространения звука. Мальчик A толкает мальчика B, который, в свою очередь, толкает мальчика C и т. Д., Пока мальчик E не упадет вперед. Сами мальчики остаются на месте, пока беспокойство проходит через них.Скорость возмущения определяется массой мальчиков и жесткостью, с которой они контактируют. (Из J. Tyndall, Sound. (NY: D. Appleton and Co., 1867.)
Двигатели нашей изобретательности Авторские права © 1988-2006, Джон Х. Линхард.
Сила, масса и ускорение – второй закон Ньютона
ФотографияMultiflash создает последовательные изображения через равные промежутки времени на одном кадре.
Метод 1. Использование цифровой камеры в режиме мульти-вспышки
Созданное изображение можно передавать прямо на компьютер.
Метод 2: Использование видеокамеры
Воспроизведите видео кадр за кадром и поместите прозрачный ацетатный лист на экран телевизора, чтобы записать положение объектов.
Метод 3. Использование камеры и дискового стробоскопа с приводом от двигателя
Вам нужна камера, которая будет фокусироваться на изображениях объектов на расстоянии до 1 метра. Фотокамере потребуется настройка B, при которой затвор остается открытым для непрерывной экспозиции.Используйте большую диафрагму, например f3,5. Цифровые камеры немедленно предоставляют изображение для анализа. В некоторых камерах может потребоваться закрыть фотоэлемент, чтобы затвор оставался открытым.
Установите стробоскоп перед камерой так, чтобы прорези в диске позволяли свету от объекта попадать в объектив камеры через равные промежутки времени по мере вращения диска.
Расстояние между линзой и диском может составлять всего 1 см. Диск с прорезями должен иметь привод от синхронного двигателя, чтобы интервалы времени между экспозициями были постоянными.
Вы можете изменять частоту «экспонирования», заклеивая нежелательные щели черной лентой. Делайте это симметрично. Например, диск с 2 открытыми прорезями при 300 об / мин дает 10 экспозиций в секунду.
Чем уже щель, тем резче, но темнее изображение. Сильное освещение объектов или использование источника света в качестве движущегося объекта позволяет использовать более узкую щель.
Осветите объект как можно ярче, но как можно меньше на черном матовом фоне.Слайд-проектор – хороший источник света для этой цели.
Метод 4: Использование ксенонового стробоскопа
Это обеспечивает более четкое изображение, чем при использовании дискового стробоскопа, при условии хорошего затемнения. Общие указания такие же, как для метода 3. Направьте свет от стробоскопа вдоль пути объекта.
При съемке с несколькими вспышками избегайте частоты вспышки в диапазоне 15–20 Гц и избегайте мерцания красного света. Некоторые люди могут плохо себя чувствовать из-за мерцания.Редко у некоторых людей бывает светочувствительная эпилепсия.
Общие советы по успеху
Необходимо устроить частичное затемнение. См. Инструкцию
.Управление классом в полумраке
Используйте белый или серебристый предмет, например, большой полированный стальной мяч или мяч для гольфа, на темном фоне. В качестве альтернативы можно использовать движущийся источник света, например лампу, прикрепленную к ячейке, с подходящими электрическими соединениями. В этом случае положите подушку на пол, чтобы предотвратить поломку.
Используйте видоискатель, чтобы убедиться, что объект находится в фокусе на протяжении всего своего движения, и что достаточный диапазон его движения находится в пределах поля зрения камеры.
Разместите сетку измерений на заднем плане, чтобы можно было проводить измерения. Черная карточка с полосами белой изоленты, скажем, на расстоянии 10 см, обеспечивает сильный контраст и позволяет выделяться освещенному движущемуся объекту.
В качестве альтернативы сетке можно использовать линейку счетчика. Его масштаб обычно не виден на окончательном изображении, но вы можете спроецировать фотографию на экран.Перемещайте проектор до тех пор, пока линейка метра на изображении не станет того же размера, что и линейка метра, расположенная рядом с экраном. После этого вы можете проводить измерения прямо с экрана.
Используйте штатив и / или систему зажимов и подставок для крепления оборудования. Убедитесь, что любая система максимально жесткая и устойчивая.
Работа в команде имеет значение, особенно в методе 3. Один человек может управлять камерой, другой – системой стробоскопа, если необходимо, а третий – объектом, который нужно сфотографировать.
- Включите лампу и затемните комнату.
- Проверьте фокусировку камеры, f 3,5, настройку B.
- Проверьте поле зрения, чтобы убедиться, что весь эксперимент будет записан.
- Стробоскоп Line Up.
- Обратный отсчет 3-2-1-0. Откройте заслонку непосредственно перед началом эксперимента и закройте ее по окончании эксперимента.
Что открыл Исаак Ньютон?
Исаак Ньютон, живший с 25 декабря 1642 г. по 20 марта 1727 г., был английским ученым, математиком и «натурфилософом».В свое время он сыграл жизненно важную роль в научной революции, помогая продвигать вперед области физики, астрономии, математики и естественных наук. Исходя из этого, он создал наследие, которое будет доминировать в науке в течение следующих трех столетий.
Фактически, термин «ньютоновский» стал использоваться последующими поколениями для описания совокупностей знаний, которые обязаны своим существованием его теориям. И благодаря его обширному вкладу сэр Исаак Ньютон считается одним из самых влиятельных ученых в истории науки.Но что именно он обнаружил?
Три закона движения Ньютона:
Во-первых, его magnum opus – Philosophiæ Naturalis Principia Mathematica («Математические принципы естественной философии»), впервые опубликованный в 1687 году, заложил основы классической механики. В нем он сформулировал свои три закона движения, которые были выведены из законов движения планет Иоганна Кеплера и его собственного математического описания гравитации.
Уильям Блейк Ньютон (1795), изображающий его в виде божественного геометра.Кредит изображения: Архив Уильяма Блейка / ВикипедияПервый закон, известный как «закон инерции», гласит: «Покоящийся объект будет оставаться в покое, если на него не действует неуравновешенная сила. Движущийся объект продолжает движение с той же скоростью и в том же направлении, если на него не действует неуравновешенная сила ». Второй закон гласит, что ускорение возникает, когда сила действует на массу – следовательно, чем больше масса объекта, тем больше сила, необходимая для его ускорения. Третий и последний закон гласит, что «на каждое действие есть равное, но противоположное противодействие».
Вселенская гравитация:
Он также сформулировал свой закон всемирного тяготения в Principia , в котором говорится, что каждая точечная масса притягивает каждую другую точечную массу силой, направленной вдоль линии, пересекающей обе точки. Согласно его расчетам, эта сила пропорциональна произведению двух масс и обратно пропорциональна квадрату расстояния между ними. Формула этой теории может быть выражена как:
Ньютон будет использовать эти принципы для объяснения траекторий комет, приливов, прецессии равноденствий и других астрофизических явлений.Это эффективно устранило последние сомнения в справедливости гелиоцентрической модели космоса, в которой утверждалось, что Солнце (а не Земля) находится в центре планетной системы. Его работа также продемонстрировала, что движение объектов на Земле и небесных тел можно описать одними и теми же принципами.
Саженец известного оригинального дерева, которое вдохновило сэра Исаака Ньютона на мысль о гравитации. Предоставлено: Wikipedia Commons / Loodog. Хотя вдохновение Ньютона для создания его теорий гравитации часто приписывается «инциденту с яблоком» – i.е. где он наблюдал, как яблоко упало с дерева – эта история считается апокрифической современными источниками, которые утверждают, что он пришел к своим выводам с течением времени. Однако сам Ньютон описал инцидент, и современники его отстаивают это утверждение.
Форма Земли:
Дополнительные материалы включают его предсказание о том, что Земля, вероятно, имела форму «сплюснутого сфероида», то есть сферы, которая претерпевала сплющивание на полюсах. Позднее эта теория будет подтверждена измерениями Мопертюи, Ла Кондамина и других.Это, в свою очередь, помогло убедить большинство ученых континентальной Европы в превосходстве механики Ньютона над более ранней системой Декарта.
С точки зрения математики, он внес вклад в изучение степенных рядов, обобщил биномиальную теорему на нецелые показатели, разработал метод Ньютона для аппроксимации корней функции и классифицировал большинство кривых на кубической плоскости. Он также разделяет заслуги с Готфридом Лейбницем за развитие математического анализа.
Эти открытия представляют собой огромный скачок вперед в области математики, физики и астрономии, позволяя проводить расчеты, которые более точно моделируют поведение Вселенной, чем когда-либо прежде.
Оптика:
В 1666 году Ньютон начал вносить свой вклад в область оптики, сначала обнаружив, что цвет является свойством света, измеряя его через призму. С 1670 по 1672 год он читал лекции по оптике в Кембриджском университете и исследовал преломление света, демонстрируя, что разноцветный спектр, создаваемый призмой, может быть преобразован в белый свет с помощью линзы и второй призмы.
Солнечный свет, проходящий через призму. Изображение предоставлено: NASAВ результате своего исследования он пришел к выводу, что цвет является результатом взаимодействия объектов с уже окрашенным светом, а не объектов, сами генерирующих цвет, что известно как теория цвета Ньютона.
Кроме того, он пришел к выводу, что линза любого рефракторного телескопа будет страдать от рассеивания света по цветам (хроматической аберрации). В качестве доказательства своей концепции он сконструировал телескоп, используя зеркало в качестве объектива, чтобы обойти эту проблему. Это был первый известный функциональный телескоп-рефлектор, конструкция которого теперь известна как телескоп Ньютона.
Другие достижения:
Он также сформулировал эмпирический закон охлаждения, изучил скорость звука и ввел понятие ньютоновской жидкости.Этот термин используется для описания любой жидкости, где вязкие напряжения, возникающие при ее течении в каждой точке, линейно пропорциональны скорости изменения ее деформации во времени.
Помимо работы в области математики, оптики и физики, он также посвятил значительное количество времени изучению библейской хронологии и алхимии, но большая часть его работ в этих областях оставалась неопубликованной еще долгое время после его смерти.
Так что же открыл Исаак Ньютон? Теории, которые будут доминировать в областях науки, астрономии, физики и естественного мира на столетия вперед.Его идеи впоследствии повлияли на таких корифеев, как Жозеф-Луи Лагранж и Альберт Эйнштейн, последний из которых, как считается, единственный ученый, оставивший подобное наследие.
Мы написали много интересных статей о сэре Исааке Ньютоне здесь, в Universe Today. Вот кем был сэр Исаак Ньютон? Что изобрел Исаак Ньютон? Кто открыл гравитацию? Что такое абсолютное пространство? Что такое гравитационная постоянная?
В Интернете есть и другие ресурсы, если вы хотите узнать больше об Исааке Ньютоне.На этом британском сайте есть отличная информация о его открытиях. Вы также можете посетить веб-сайт PBS.


 На идеально скользких поверхностях, от которых не получится оттолкнуться, ни сани с лошадью, ни поезда, ни автомобили не смогут сдвинуться с места.
На идеально скользких поверхностях, от которых не получится оттолкнуться, ни сани с лошадью, ни поезда, ни автомобили не смогут сдвинуться с места.
 Н. Крылова / под ред. Полака Л. С.. – М. : Наука, 1989. – С. 40-41. – 690 с. – («Классики науки»). – 5 000 экз.
– ISBN 5-02-000747-1 .
Н. Крылова / под ред. Полака Л. С.. – М. : Наука, 1989. – С. 40-41. – 690 с. – («Классики науки»). – 5 000 экз.
– ISBN 5-02-000747-1 .