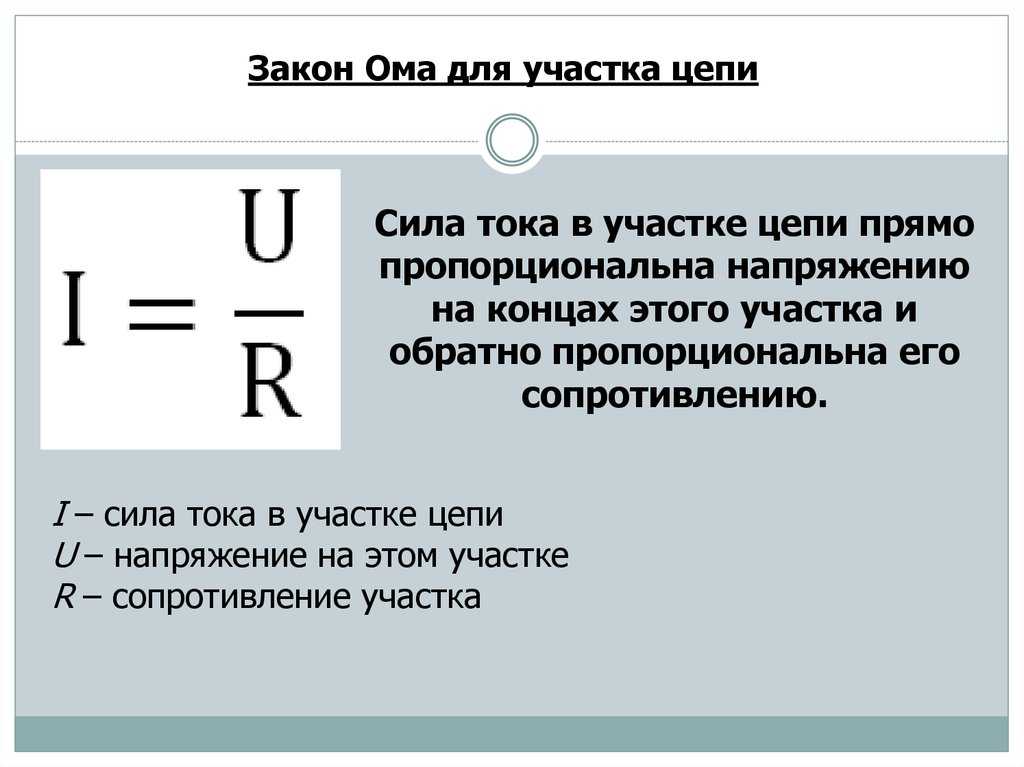
Закон Ома для однородного участка цепи: Закон Ома простым языком
Содержание
Классическая формулировка
Этот простой вариант трактовки, известный нам со школы.
Однородный открытый участок электроцепи
Формула в интегральной форме будет иметь следующий вид:
Формула в интегральной форме
То есть, поднимая напряжение, мы тем самым увеличиваем ток. В то время, как увеличение такого параметра, как «R», ведет к снижению «I». Естественно, что на рисунке сопротивление цепи показано одним элементом, хотя это может быть последовательное, параллельное (вплоть до произвольного)соединение нескольких проводников.
В дифференциальной форме закон мы приводить не будем, поскольку в таком виде он применяется, как правило, только в физике.
Свойства электрического тока
Направлением электрического тока принято считать движение свободных положительных зарядов. Ток называется постоянным, если его направление и сила постоянны во времени.
Электрическое поле величиной E действует на заряд величиной q с силой F, которая равна:
$ F = q * E $ (1).
В результате в проводнике возникает электрический ток. Для создания электрического поля E, к концам проводника должно быть приложено напряжение U, которое равно разности потенциалов φ1 и φ2 на концах проводника:
$ U = φ2 – φ1 $ (2),
при этом φ2 > φ1.
Единица электрического тока — ампер (А) — названа в честь французского физика Ампера. Эта единица является одной семи основных единиц в Международной системе СИ. Единицей измерения напряжений является вольт (В), названная в честь итальянского исследователя Алессандро Вольта.
Опыты Георга Ома
В 1826 г. Георг Ом на основании данных своих многочисленных экспериментов открыл однозначную связь между силой тока I и напряжением U. Ученый измерял зависимости тока от напряжения (вольт-амперные характеристики) и строил графики, из которых он обнаружил не просто пропорциональность (чем больше напряжение, тем больше ток), а линейную математическую зависимость тока от напряжения, т. е. I ∼ U.
е. I ∼ U.
Рис. 1. График линейной зависимости силы тока от напряжения в проводниках:.
Из графиков было видно, что угол наклона линейных зависимостей для разных материалов разный, т.е. каждый проводник обладал различной степенью сопротивляемости или проводимости. Эта величина была названа электрическим сопротивлением R. Формула закона Ома для однородного участка цепи выглядит следующим образом:
$ I = {U over R} $ (3).
Полностью формулировка закона Ома звучит так: сила тока I для проводника на однородном участке цепи прямо пропорциональна напряжению U на этом участке и обратно пропорциональна сопротивлению проводника R.
Любую электрическую цепь можно разделить на отдельные участки. Участки цепи, на которых отсутствует действие сторонних сил (т.е. участки, где отсутствуют источники тока), называются однородными. Участки цепи, на которых имеются источники тока, называются неоднородными.
Принятые единицы измерения
Необходимо учитывать, что все расчеты должны проводиться в следующих единицах измерения:
- напряжение – в вольтах;
- ток в амперах
- сопротивление в омах.

Если вам встречаются другие величины, то их необходимо будет перевести к общепринятым.
Сила тока I
Пусть в каком-то проводнике течет ток. То есть, происходит направленное движение заряженных частиц – допустим, это электроны. Каждый электрон обладает элементарным электрическим зарядом (e= -1,60217662 × 10-19 Кулона). В таком случае через некоторую поверхность за определенный промежуток времени пройдет конкретный электрический заряд, равный сумме всех зарядов протекших электронов.
Отношение заряда к времени и называется силой тока. Чем больший заряд проходит через проводник за определенное время, тем больше сила тока. Сила тока измеряется в Амперах.
Напряжение U, или разность потенциалов
Это как раз та штука, которая заставляет электроны двигаться. Электрический потенциал характеризует способность поля совершать работу по переносу заряда из одной точки в другую. Так, между двумя точками проводника существует разность потенциалов, и электрическое поле совершает работу по переносу заряда.
Физическая величина, равная работе эффективного электрического поля при переносе электрического заряда, и называется напряжением. Измеряется в Вольтах. Один Вольт – это напряжение, которое при перемещении заряда в 1 Кл совершает работу, равную 1 Джоуль.
Сопротивление R
Ток, как известно, течет в проводнике. Пусть это будет какой-нибудь провод. Двигаясь по проводу под действием поля, электроны сталкиваются с атомами провода, проводник греется, атомы в кристаллической решетке начинают колебаться, создавая электронам еще больше проблем для передвижения. Именно это явление и называется сопротивлением. Оно зависит от температуры, материала, сечения проводника и измеряется в Омах.
Памятник Георгу Симону Ому
Мощность электрического тока
Мощность электрического тока равна отношению работы тока ко времени, в течение которого она совершается.
Обозначение – ( P ), единица измерения в СИ – ватт (Вт).
Вычисляется по формуле:
Можно записать еще несколько формул для вычисления мощности электрического тока на участке цепи:
Полная мощность источника тока:
Коэффициент полезного действия источника тока:
При решении задач на тепловое действие тока нужно учитывать следующее:
1. Если на участке есть источник тока, то необходимо использовать для решения формулу закона Джоуля–Ленца:
Если на участке есть источник тока, то необходимо использовать для решения формулу закона Джоуля–Ленца:
2. Если сила тока в цепи постоянна, то удобно использовать формулу закона Джоуля–Ленца:
3. Если постоянно напряжение, то формулу:
4. Количество теплоты можно находить, используя формулы термодинамики.
Электрическое сопротивление. Удельное сопротивление вещества
Электрическое сопротивление – свойство материала проводника препятствовать прохождению через него электрического тока.
Обозначение – ( R ), единица измерения в СИ – Ом.
Объяснить наличие сопротивления можно на основе строения металлических проводников. Свободные электроны при движении по проводнику встречают на своем пути ионы кристаллической решетки и другие электроны и, взаимодействуя с ними, неизбежно теряют часть своей энергии. Различные металлические проводники, имеющие различное атомное строение, оказывают различное сопротивление электрическому току.
Чем больше сопротивление проводника, тем хуже он проводит электрический ток.
Сопротивление различных проводников зависит от материала, из которого они изготовлены, их длины, геометрической формы и температуры. Для характеристики электрического сопротивления различных материалов введено понятие так называемого удельного сопротивления.
Удельным сопротивлением называется сопротивление проводника длиной 1 м и площадью поперечного сечения 1 м².
Обозначение – ( rho ), единица измерения в СИ – Ом·м.
Каждый материал, из которого изготовляется проводник, обладает своим удельным сопротивлением.
Например, удельное сопротивление меди равно 1,7·10-8 Ом·м, т. е. медный проводник длиной 1 м и сечением 1 м2 обладает сопротивлением 1,7·10-8 Ом. На практике часто используют единицу удельного сопротивления (Ом·мм2)/м. Электрическое сопротивление проводника прямо пропорционально длине проводника и обратно пропорционально площади поперечного сечения проводника.
Формула для вычисления:
Сопротивление проводника увеличивается с ростом температуры. Удельное сопротивление зависит от температуры:
Удельное сопротивление зависит от температуры:
где ( rho_0 ) – удельное сопротивление при ( T_0 ) = 293 К (20°С), ( Delta T=T-T_0 ), ( alpha ) – температурный коэффициент сопротивления.
Единица измерения температурного коэффициента сопротивления – К-1. При нагревании увеличивается интенсивность движения частиц вещества. Это создает трудности для направленного движения электронов. Увеличивается число столкновений свободных электронов с ионами кристаллической решетки.
Свойство изменения сопротивления при изменении температуры используется в термометрах сопротивления. Эти приборы могут измерять температуру, основываясь на зависимости сопротивления от температуры. У термометров сопротивления высокая точность измерений.
Электродвижущая сила. Внутреннее сопротивление источника тока
Для создания электрического поля в проводниках используют источник тока. Внутри источника тока происходит перераспределение зарядов, в результате которого на полюсах источника возникает избыток зарядов разных знаков.
Виды источников тока:
- электрофорная машина;
- термопара;
- фотоэлемент;
- аккумулятор;
- гальванический элемент.
Сторонними называются силы неэлектрической природы, действующие внутри источника тока. Когда проводник соединяют с полюсами источника, то на внешнем участке цепи заряженные частицы движутся под действием электростатической силы. А внутри источника на заряды действуют сторонние и электростатические силы.
Под действием этих сил внутри источника происходит перемещение положительных зарядов от отрицательного полюса источника к положительному. Это перемещение происходит до тех пор, пока сторонние силы не станут равными электростатическим. При переносе заряда эти силы совершают работу. Работа сторонних сил по перемещению заряда компенсирует потери энергии заряженными частицами при их движении по цепи.
Электродвижущей силой (ЭДС) называется отношение работы сторонних сил по перемещению положительного заряда к величине этого заряда.
Обозначение – ( varepsilon ), единица измерения в СИ – вольт (В).
Формула для вычисления:
где ( Delta q ) – модуль перенесенного заряда.
Если электрическая цепь содержит несколько источников тока с ЭДС ( varepsilon_1,varepsilon_2,,…,varepsilon_T ), то суммарная ЭДС ( varepsilon=varepsilon_1+varepsilon_2+…,varepsilon_T ).
ЭДС считается положительной, если направление обхода цепи против часовой стрелки совпадает с переходом внутри источника тока от отрицательного полюса источника к положительному полюсу.
На рисунке: ( varepsilon_1>0,,varepsilon_2<0,,varepsilon_3>0. )
Суммарная ЭДС: ( varepsilon=varepsilon_1-varepsilon_2+varepsilon_3. )
При подключении проводника к полюсам источника тока происходит перераспределение заряда на поверхности проводника, а внутри проводника возникает постоянное электрическое поле. Заряды начинают перемещаться по замкнутой цепи, в которой устанавливается постоянная сила тока.
Сопротивление источника тока называется внутренним сопротивлением.
Обозначение внутреннего сопротивления – ( r ). Единица измерения в СИ – Ом.
Закон Ома для участка цепи
Взаимосвязь между силой тока, протекающей по проводнику, и напряжением на его концах была экспериментально установлена Г. Омом и носит название закона Ома для участка цепи.
Закон Ома для участка цепи
Сила тока прямо пропорциональна напряжению на концах участка и обратно пропорциональна его сопротивлению:
График зависимости силы тока от напряжения называется вольт-амперной характеристикой. Из закона Ома для участка цепи следует, что при постоянном сопротивлении сила тока прямо пропорциональна напряжению. Следовательно, вольт-амперная характеристика для металлического проводника представляет собой прямую линию, проходящую через начало координат.
Проводник с такими свойствами называется резистором.
Угол наклона графика к оси напряжений зависит от сопротивления проводника. Тангенс угла наклона графика равен проводимости резистора.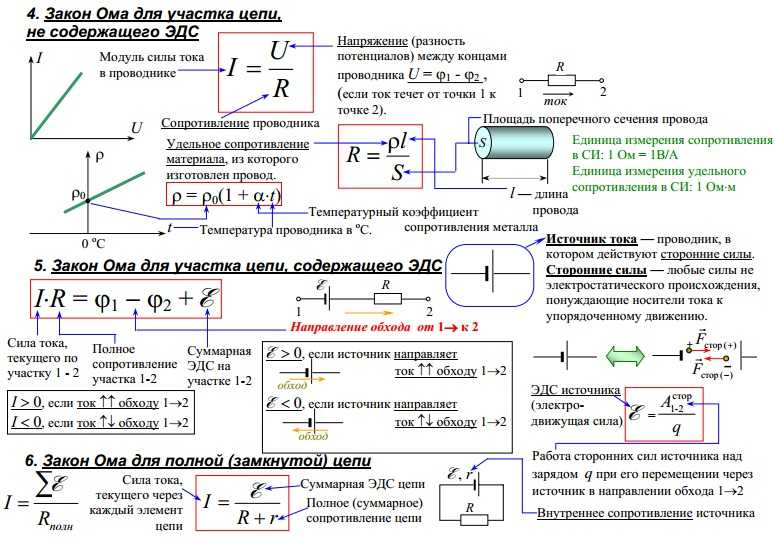
Формулировка для полной цепи
Трактовка для полной цепи будет несколько иной, чем для участка, поскольку в законе, составленном Омом, еще учитывает параметр «r», это сопротивление источника ЭДС. На рисунке ниже проиллюстрирована подобная схема.
Схема с подключенным с источником
Учитывая «r» ЭДС, формула предстанет в следующем виде:
Заметим, если «R» сделать равным 0, то появляется возможность рассчитать «I», возникающий во время короткого замыкания.
Напряжение будет меньше ЭДС, определить его можно по формуле:
Собственно, падение напряжения характеризуется параметром «I*r». Это свойство характерно многим гальваническим источникам питания.
Неоднородный участок цепи постоянного тока
Под таким типом подразумевается участок, где помимо электрического заряда производится воздействие других сил. Изображение такого участка показано на рисунке ниже.
Схема неоднородного участка
Формула для такого участка (обобщенный закон) будет иметь следующий вид:
Формула для неоднородного участка цепи
Переменный ток
Если в схема, подключенная к переменному току снабжена емкостью и/или индуктивностью (катушкой), расчет производится с учетом величин их реактивных сопротивлений. Упрощенный вид закона будет выглядеть следующим образом:
Упрощенный вид закона будет выглядеть следующим образом:
Где «Z» представляет собой импеданс, это комплексная величина, состоящая из активного (R) и пассивного (Х) сопротивлений.
Параллельное и последовательное соединение проводников
Проводники в электрических цепях могут соединяться последовательно и параллельно.
Последовательное соединение проводников
При последовательном соединении начало одного проводника соединяется с концом другого.
При последовательном соединении сила тока во всех проводниках одинакова:
Общее напряжение ( U ) на проводниках равно сумме напряжений на отдельных проводниках:
Напряжение на проводниках прямо пропорционально их сопротивлениям:
Общее сопротивление равно сумме сопротивлений проводников, образующих цепь:
Если проводники имеют одинаковое сопротивление, то общее сопротивление находится по формуле:
где ( n ) – число проводников, ( R_i ) – сопротивление проводника.
Параллельное соединение проводников
При параллельном соединении проводники подключаются между одной и той же парой точек. Если в этой точке соединяются три и более проводников, то она называется узлом электрической цепи.
При параллельном соединении напряжение на всех проводниках одинаково:
Сумма сил токов, протекающих по проводникам, равна силе тока в неразветвленной цепи:
Это следствие того факта, что в точках разветвления цепи заряды не могут накапливаться.
Силы токов в разветвленных частях цепи обратно пропорциональны их сопротивлениям:
Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников:
Если проводники имеют одинаковое сопротивление, то общее сопротивление находится по формуле:
где ( n ) – число проводников, ( R_1 ) – сопротивление проводника.
Если параллельно соединены два проводника, от общее сопротивление вычисляется по формуле:
Смешанное соединение проводников
Смешанное соединение проводников – соединение, при котором часть проводников соединена последовательно, а часть – параллельно.
Чтобы рассчитать общее сопротивление такого участка или найти силу тока и напряжение при таком соединении, нужно:
- разбить его на простые участки с последовательно или параллельно соединенными проводниками;
- найти общее (эквивалентное) сопротивление каждого из этих участков;
- составить эквивалентную схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений;
- рассчитать сопротивление полученной схемы.
Если в схеме не удается выделить участки с последовательным или параллельным соединением проводников, то можно использовать такое правило: точки с одинаковыми потенциалами можно соединять и разъединять, ток между такими точками не идет.
На рисунке, если ( R_1=R_2,R_4=R_5, ) то потенциалы точек 1 и 2 равны. Резистор ( R_3 ) можно убрать на эквивалентной схеме – ток по нему не идет. Точки с одинаковыми потенциалами есть в схемах с осью или плоскостью симметрии относительно точек подключения источника тока.
Если схема симметрична относительно оси, проходящей через точки входа и выхода тока, то точки равного потенциала находятся на концах симметричных сопротивлений (по ним идут одинаковые токи). Если схема симметрична относительно оси, перпендикулярной линии, на которой лежат точки входа и выхода тока, то точки равного потенциала находятся на пересечении этой оси с проводниками.
Если в схеме нет участков с известным видом соединения и нет точек с равным потенциалом, то для расчета таких цепей используют правила Кирхгофа.
Правила Кирхгофа:
- Алгебраическая сумма сил токов, сходящихся в узле, равна нулю:
Положительными считают токи, входящие в узел, отрицательными – выходящие из узла.
- В любом замкнутом контуре, произвольно выбранном в разветвленной цепи, алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме ЭДС, имеющихся в контуре:
Порядок расчета цепи:
- выбрать направление токов во всей цепи;
- записать уравнения токов для узлов;
- записать уравнения для выделенных контуров.
 Произвольные замкнутые контуры выделяются так, чтобы каждый новый контур содержал хотя бы один участок, не входящий в ранее рассмотренные контуры;
Произвольные замкнутые контуры выделяются так, чтобы каждый новый контур содержал хотя бы один участок, не входящий в ранее рассмотренные контуры; - решить полученную систему уравнений.
Алгоритм решения задач на определение силы тока, напряжения или сопротивления на участке цепи:
- начертить схему цепи и указать на ней все элементы;
- установить, какие элементы цепи включены последовательно, какие – параллельно;
- расставить токи и напряжения на каждом участке цепи и записать для каждой точки разветвления (если они есть) уравнения токов и уравнения, связывающие напряжения на участках цепи;
- используя закон Ома, установить связь между токами, напряжениями и ЭДС;
- если в схеме делают какие-либо переключения сопротивлений или источников, уравнения составить для каждого режима работы цепи;
- решить полученную систему уравнений относительно неизвестной величины;
- решение проверить.
Работа электрического тока. Закон Джоуля–Ленца
Работа тока – работа сил электрического поля, создающего электрический ток.
Работа тока на участке цепи вычисляется по формуле:
Используя формулу закона Ома для участка цепи, можно работу тока вычислить так:
Работа тока в замкнутой цепи находится по формуле:
При протекании постоянного тока по металлическому проводнику электроны сталкиваются с положительными ионами, расположенными в узлах кристаллической решетки. При этом электроны передают им энергию. Это приводит к нагреванию проводника. Количество теплоты, выделяющееся в проводнике за время ( t ), равно:
Эта формула выражает закон Джоуля–Ленца: количество теплоты, выделяющееся при прохождении тока по проводнику, прямо пропорционально квадрату силы тока, времени его прохождения и сопротивлению проводника.
Как понять закон Ома?
Чтобы интуитивно понять закон Ома, обратимся к аналогии представления тока в виде жидкости. Именно так думал Георг Ом, когда проводил опыты, благодаря которым был открыт закон, названный его именем.
Представим, что ток – это не движение частиц-носителей заряда в проводнике, а движение потока воды в трубе.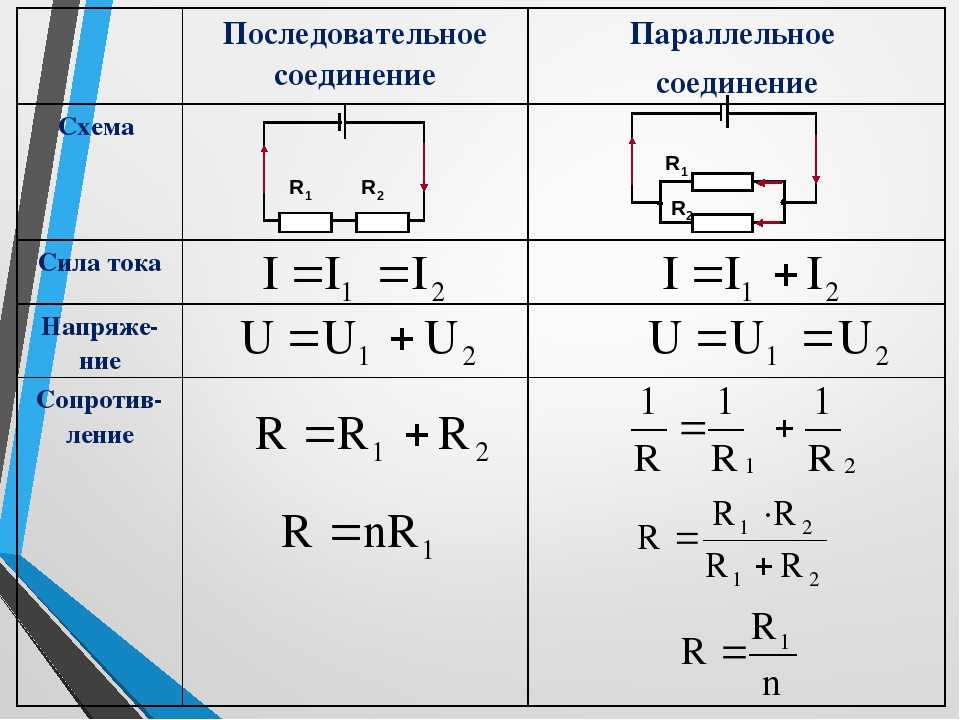 Сначала воду насосом поднимают на водокачку, а оттуда, под действием потенциальной энергии, она стремиться вниз и течет по трубе. Причем, чем выше насос закачает воду, тем быстрее она потечет в трубе.
Сначала воду насосом поднимают на водокачку, а оттуда, под действием потенциальной энергии, она стремиться вниз и течет по трубе. Причем, чем выше насос закачает воду, тем быстрее она потечет в трубе.
Отсюда следует вывод, что скорость потока воды (сила тока в проводе) будет тем больше, чем больше потенциальная энергия воды (разность потенциалов)
Сила тока прямо пропорциональна напряжению.
Теперь обратимся к сопротивлению. Гидравлическое сопротивление – это сопротивление трубы, обусловленное ее диаметром и шероховатостью стенок. Логично предположить, что чем больше диаметр, тем меньше сопротивление трубы, и тем большее количество воды (больший ток) протечет через ее сечение.
Сила тока обратно пропорциональна сопротивлению.
Такую аналогию можно проводить лишь для принципиального понимания закона Ома, так как его первозданный вид – на самом деле довольно грубое приближение, которое, тем не менее, находит отличное применение на практике.
В действительности, сопротивление вещества обусловлено колебанием атомов кристаллической решетки, а ток – движением свободных носителей заряда. В металлах свободными носителями являются электроны, сорвавшиеся с атомных орбит.
Ток в проводнике
В данной статье мы постарались дать простое объяснение закона Ома. Знание этих на первый взгляд простых вещей может сослужить Вам неплохую службу на экзамене. Конечно, мы привели его простейшую формулировку закона Ома и не будем сейчас лезть в дебри высшей физики, разбираясь с активным и реактивным сопротивлениями и прочими тонкостями.
Основные формулы раздела «Законы постоянного тока»
Магнитное поле → ← Электрическое поле Законы постоянного тока3.9 (77.5%) 8 votes
Практическое использование
Пример приведен на рисунке.
Применяем закон к любому участку цепи
Используя такой план, можно вычислить все необходимые характеристики для неразветвленного участка. Рассмотрим более детальные примеры.
Рассмотрим более детальные примеры.
Находим силу тока
Рассмотрим теперь более определенный пример, допустим, возникла необходимость узнать ток, протекающий через лампу накаливания. Условия:
- Напряжение – 220 В;
- R нити накала – 500 Ом.
Решение задачи будет выглядеть следующим образом: 220В/500Ом=0,44 А.
Рассмотрим еще одну задачу со следующими условиями:
- R=0,2 МОм;
- U=400 В.
В этом случае, в первую очередь, потребуется выполнить преобразование: 0,2 МОм = 200000 Ом,после чего можно приступать к решению: 400 В/200000 Ом=0,002 А (2 мА).
Вычисление напряжения
Для решения мы также воспользуемся законом, составленным Омом. Итак задача:
- R=20 кОм;
- I=10 мА.
Преобразуем исходные данные:
- 20 кОм = 20000 Ом;
- 10 мА=0,01 А.
Решение: 20000 Ом х 0,01 А = 200 В.
Незабываем преобразовывать значения, поскольку довольно часто ток может быть указан в миллиамперах.
Сопротивление
Несмотря на то, что общий вид способа для расчета параметра «R» напоминает нахождение значения «I», между этими вариантами существуют принципиальные различия. Если ток может меняться в зависимости от двух других параметров, то R (на практике) имеет постоянное значение. То есть по своей сути оно представляется в виде неизменной константы.
Если через два разных участка проходит одинаковый ток (I), в то время как приложенное напряжение (U) различается, то, опираясь на рассматриваемый нами закон, можно с уверенностью сказать, что там где низкое напряжение «R» будет наименьшим.
Рассмотрим случай когда разные токи и одинаковое напряжение на несвязанных между собой участках. Согласно закону, составленному Омом, большая сила тока будет характерна небольшому параметру «R».
Рассмотрим несколько примеров
Допустим, имеется цепь, к которой подведено напряжение U=50 В, а потребляемый ток I=100 мА. Чтобы найти недостающий параметр, следует 50 В / 0,1 А (100 мА), в итоге решением будет – 500 Ом.
Вольтамперная характеристика позволяет наглядно продемонстрировать пропорциональную (линейную) зависимость закона. На рисунке ниже составлен график для участка с сопротивлением равным одному Ому (почти как математическое представление закона Ома).
Изображение вольт-амперной характеристики, где R=1 Ом
Изображение вольт-амперной характеристики
Вертикальная ось графика отображает ток I (A), горизонтальная – напряжение U(В). Сам график представлен в виде прямой линии, которая наглядно отображает зависимость от сопротивления, которое остается неизменным. Например, при 12 В и 12 А «R» будет равно одному Ому (12 В/12 А).
Обратите внимание, что на приведенной вольтамперной характеристике отображены только положительные значения. Это указывает, что цепь рассчитана на протекание тока в одном направлении. Там где допускается обратное направление, график будет продолжен на отрицательные значения.
Заметим, что оборудование, вольт-амперная характеристика которого отображена в виде прямой линии, именуется — линейным. Этот же термин используется для обозначения и других параметров.
Этот же термин используется для обозначения и других параметров.
Помимо линейного оборудования, есть различные приборы, параметр «R» которых может меняться в зависимости от силы тока или приложенного напряжения. В этом случая для расчета зависимости нельзя использовать закон Ома. Оборудование такого типа называется нелинейным, соответственно, его вольт-амперные характеристики не будут отображены в виде прямых линий.
Что мы узнали?
Итак, мы узнали, что закон Ома для однородного участка цепи формулируется так: сила тока I для проводника на однородном участке цепи прямо пропорциональна напряжению U на этом участке и обратно пропорциональна сопротивлению проводника R. Участки электрической цепи, на которых отсутствуют источники тока, называются однородными. Удельное электрическое сопротивление вещества ρ — величина, характеризующая способность вещества к сопротивлению.
Вывод
Как уже упоминалось в начале статьи, вся прикладная электротехника базируется на законе, составленном Омом. Незнание этого базового догмата может привести к неправильному расчету, который, в свою очередь, станет причиной аварии.
Незнание этого базового догмата может привести к неправильному расчету, который, в свою очередь, станет причиной аварии.
Подготовка электриков как специалистов начинается с изучения теоретических основ электротехники. И первое, что они должны запомнить – это закон составленный Омом, поскольку на его основе производятся практически все расчеты параметров электрических цепей различного назначения.
Понимание основного закона электротехники поможет лучше разбираться в работе электрооборудования и его основных компонентов. Это положительно отразится на техническом обслуживании в процессе эксплуатации.
Самостоятельная проверка, разработка, а также опытное изучение узлов оборудования – все это существенно упрощается, если использовать закон Ома для участка цепи. При этом не требуется проводить всех измерений, достаточно снять некоторые параметры и, проведя несложные расчеты, получить необходимые значения.
Видеоурок
Электродинамика. Постоянный ток. Закон Ома для однородного участка цепи” src=”https://www.youtube.com/embed/q_qiSzdE0VA?feature=oembed” frameborder=”0″ allow=”accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture” allowfullscreen=””>Источники
- https://www.asutpp.ru/zakon-oma-dlya-uchastka-cepi.html
- https://obrazovaka.ru/fizika/zakon-oma-dlya-odnorodnogo-uchastka-cepi-formula.html
- https://Zaochnik.ru/blog/zakon-oma-dlya-chajnikov/
- https://fizi4ka.ru/egje-2018-po-fizike/zakony-postojannogo-toka.html
Закон ома на практике
В природе существует два основных вида материалов, проводящие ток и не проводящие диэлектрики. Отличаются эти материалы наличием условий для перемещения в них электрического тока электронов. Из токопроводящих материалов медь, алюминий, графит, и многие другие , делают электрические проводники, в них электроны не связаны и могут свободно перемещаться. В диэлектриках электроны привязаны к атомам намертво, поэтому ток в них течь не может.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Применение закона Ома
- Закон Ома для участка цепи простым языком
- Закон Ома и его применение
- Закон Ома для участка цепи теория и практика
- Закон Ома для «чайников»: понятие, формула, объяснение
- Какая формула выражает закон Ома?
- Закон Ома. Для цепей и тока.
Формулы и применение
- Закон Ома для полной цепи и для участка цепи: варианты записи формулы, описание и объяснение
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Урок 7. ЗАКОН ОМА простыми словами с примерами
Применение закона Ома
Закон Ома — основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением. Итак, строгая формулировка закона Ома записывается так: Сила тока в проводнике прямо пропорциональна напряжению на его концах разности потенциалов и обратна пропорциональна сопротивлению этого проводника.
Формула закона Ома записывается так:. Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза.
Скажите пожалуйста, какая формула выражает закон Ома? Какая формула выражает закон Ома? Елена Вечоркина ответил 1 год назад. Формула закона Ома записывается так: , где — сила тока в проводнике, единица измерения силы тока — А Ампер , — электрическое напряжение разность потенциалов , единица измерения напряжения — вольт В , — электрическое сопротивление проводника, единица измерения электрического сопротивления — ом ОМ. Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза Ответить на Какая формула выражает закон Ома?
Помощь в решении задач. Выберите город. Отправить заявку Отправить заявку. Без предоплаты. Вы вносите средства в систему, но автор получит оплату после сдачи работы.
Закон Ома для участка цепи простым языком
Электрика и электрооборудование, электротехника и электроника — информация! В этой работе Фурье представлял тепловой поток между двумя точками как разницу температур, а изменение теплового потока связывал с его прохождением через препятствие неправильной формы из теплоизолирующего материала. Аналогично этому Ом обуславливал возникновение электрического тока разностью потенциалов. Исходя из этого Ом стал экспериментировать с разными материалами проводника.
Так как же применить Закон Ома на практике? Возьмем, к примеру, светодиод, который необходимо “запитать” от 9 В. Источником питания будет.
Закон Ома и его применение
Регистрация Вход. Ответы Mail. Вопросы – лидеры Задача по физике 1 ставка. Провод КСПВ, вопрос к электрикам 1 ставка. Мощность рассеивания транзистора? Зачем электродрели нужен редуктор, точнее большая шестеренка? Лидеры категории Антон Владимирович Искусственный Интеллект.
Закон Ома для участка цепи теория и практика
Закон Ома — основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением. Итак, строгая формулировка закона Ома записывается так: Сила тока в проводнике прямо пропорциональна напряжению на его концах разности потенциалов и обратна пропорциональна сопротивлению этого проводника. Формула закона Ома записывается так:. Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза.
Содержание: Историческая справка Закон Ома для участка цепи Закон Ома для параллельной и последовательной цепи Закон Ома для полной цепи Закон Ома в дифференциальной и интегральной форме Закон Ома для переменного тока Как запомнить закон Ома. Он эмпирически определил и описал закон о соотношении силы тока, напряжения и типа проводника.
Закон Ома для «чайников»: понятие, формула, объяснение
Этот рисунок напоминает, что электрический ток — это упорядоченное движение заряженных частиц в определенной среде. Передвижение их возможно под действием приложенной внешней энергии, создающей разность потенциалов — напряжение. Однако, внутренние силы проводников и элементов схемы уменьшают величину тока, оказывают сопротивление его перемещению. Рассмотрим простую схему 2, поясняющую действие закона Ома для участка электрической цепи постоянного тока. В качестве источника напряжения U используем аккумуляторную батарею , которую подключим к сопротивлению R толстыми и одновременно короткими проводами в точках А и В.
Передвижение их возможно под действием приложенной внешней энергии, создающей разность потенциалов — напряжение. Однако, внутренние силы проводников и элементов схемы уменьшают величину тока, оказывают сопротивление его перемещению. Рассмотрим простую схему 2, поясняющую действие закона Ома для участка электрической цепи постоянного тока. В качестве источника напряжения U используем аккумуляторную батарею , которую подключим к сопротивлению R толстыми и одновременно короткими проводами в точках А и В.
Какая формула выражает закон Ома?
Теория и практика. Кейсы, схемы, примеры и технические решения, обзоры интересных электротехнических новинок. Уроки, книги, видео. Профессиональное обучение и развитие. Сайт для электриков и домашних мастеров, а также для всех, кто интересуется электротехникой, электроникой и автоматикой. Про закон Ома в популярном изложении. Электрический ток и опасное напряжение невозможно услышать за исключением гудящих высоковольтных линий и электроустановок. Токоведущие части, находящиеся под напряжением, ничем не отличаются по внешнему виду.
Токоведущие части, находящиеся под напряжением, ничем не отличаются по внешнему виду.
Закон Ома часто называют основным законом электричества. . Закон Ома широко применяется на практике при проектировании.
Закон Ома. Для цепей и тока. Формулы и применение
Вся прикладная электротехника базируется на одном догмате — это закон Ома для участка цепи. Без понимания принципа этого закона невозможно приступать к практике, поскольку это приводит к многочисленным ошибкам. Имеет смысл освежить эти знания, в статье мы напомним трактовку закона, составленного Омом, для однородного и неоднородного участка и полной цепи.
Закон Ома для полной цепи и для участка цепи: варианты записи формулы, описание и объяснение
ВИДЕО ПО ТЕМЕ: Запрещенный опыт нарушающий ЗАКОН ОМА. Все физики в ШОКЕ.
Доброго дня уважаемые радиолюбители! В школе Вы, несомненно, проходили, а, если еще нет — обязательно будете изучать Закон Ома. Он определяет соотношение между напряжением, силой тока и сопротивлением проводника в электрической цепи. Назван в честь его первооткрывателя Георга Ома. Суть закона следующая : порождаемый напряжением ток обратно пропорционален сопротивлению, которое ему приходится преодолевать, и прямо пропорционален порождающему напряжению. Именно такое определение содержит учебник по физике.
Он определяет соотношение между напряжением, силой тока и сопротивлением проводника в электрической цепи. Назван в честь его первооткрывателя Георга Ома. Суть закона следующая : порождаемый напряжением ток обратно пропорционален сопротивлению, которое ему приходится преодолевать, и прямо пропорционален порождающему напряжению. Именно такое определение содержит учебник по физике.
Все те, кто знаком с основами электротехники, представляют себе значение закона Ома в теории и практике электрических цепей.
Так давайте же узнаем вспомним , что это за закон, и смело пойдем гулять. Как понять закон Ома? Нужно просто разобраться в том, что есть что в его определении. И начать следует с определения силы тока, напряжения и сопротивления. Пусть в каком-то проводнике течет ток. То есть, происходит направленное движение заряженных частиц — допустим, это электроны. В таком случае через некоторую поверхность за определенный промежуток времени пройдет конкретный электрический заряд, равный сумме всех зарядов протекших электронов.
Многие были для меня загадкой, но некоторые просто резали глаз пренебрежением основными законами физики. Хотя видел я и талантливые, тщательно продуманные решения, когда от полубытовой полуигрушечной техники добивались всего, на что она способна и даже чуть больше. Вот я и подумал: наверное, многие уже забыли, чему их учили в школе.
Закон Ома для цепи переменного тока. Мощность
RIR=UR; 1ωCIC=UC; ωLIL=UL.
Указанные выше формулы внешне могут напоминать закон Ома на участке цепи постоянного тока, но стоит заметить, что в этом случае вместо величин постоянных токов и напряжений на участке цепи, в них входят амплитудные значения напряжений и переменных токов.
Формулы, указанные выше, выражают собой закон Ома для переменного тока, который содержит один из элементов R, L и C.
Определение 1R – активное сопротивление резистора.
1ωС – емкостное сопротивление конденсатора.
ωL – индуктивное сопротивление катушки в цепи переменного тока.
Движение переменного тока по участку цепи провоцирует электромагнитное поле выполнять работу, благодаря чему выделяется джоулево тепло.
Определение 2Мгновенной мощностью в цепи называется произведение мгновенных значений тока и напряжения: p=J·u.
Прикладной интерес у нас вызывает среднее значение мощности за некоторый период переменного тока:
P=Pcα=I0U0cos ωt cos ωt+φ.
В приведенной выше формуле I0 и U0 являются амплитудными значениями тока и напряжения на выбранном участке цепи, а φ – фазовым сдвигом между током и напряжением. Черта же представляет собой символ усреднения. В случае, когда цепь содержит только резистор с сопротивлением R, то фазовый сдвиг φ будет равен нулю:
PR=IRURcos2ωt=IRUR2=IR2R2.
Действующие значения силы тока и напряжения
Определение 3По причине необходимости совпадения с уравнением для мощности постоянного тока, нам приходится ввести определения действующих значений силы тока и напряжения:
IД=l02; UД=U02.
Мощность переменного тока на участке цепи
Определение 4Средняя величина мощности переменного тока на участке цепи, включающем в себя резистор, равняется:
PR=IДUД.
Если в цепи содержится лишь конденсатор емкости C, то φ=π2. Отсюда, справедливо следующее выражение:
PC=ICUCcos ωt cosωt+π2=ICUCcos ωt-sin ωt=0.
Таким же способом можно проиллюстрировать, что PL=0.
Исходя из описанного выше получим следующие определение.
Определение 5Мощность в цепи переменного тока выделяется только на активном сопротивлении, а среднее значение мощности переменного тока на конденсаторе и катушке индуктивности равняется нулю.
Теперь стоит рассмотреть электрическую цепь, включающую последовательно соединенные резистор, конденсатор и катушки, и подключенную к источнику переменного тока некой частоты ω. Следует выделить, что на всех участках цепи, соединенных последовательно, проходит один и тот же ток. Между напряжением внешнего источника e(t) и током J(t) проявляется фазовый сдвиг на определенный угол φ.
Исходя из приведенных выше фактов, мы можем записать:
J(t)=I0cos ωt; e(t)=δ0cos ωt+φ.
Данные формулы мгновенных значений тока и напряжения подходят к построениям, выполненным на векторной диаграмме (рис. 2.3.2).
Рисунок 2.3.2. Гармонические колебания A cos (ωt+φ1), B cos (ωt+φ2) и их суммы C cos (ωt+φ) на векторной диаграмме.
Средняя величина мощности, развиваемой источником переменного тока, может быть найдена из следующего выражения:
P=I0δ0cos ωt cos ωt+φ=I0δ02cos φ=IДδД cos φ.
Исходя из данных векторной диаграммы можно заявить, что UR=δ0·cos φ, следовательно,
В прошлых темах нами было получено выражение, являющееся соотношением амплитуд тока I0 и напряжений δ0 в условиях последовательной RLC-цепи:
I0=δ0R2+ωL-1ωC2
Определение 6Z=R2+ωL-1ωC2– это величина, имеющая название полное сопротивление цепи переменного тока.
Связь между амплитудными значениями тока и напряжения в цепи имеет вид:
ZI0=δ0.
Данное выражение представляет собой закон Ома для цепи переменного тока.
Закон Ома в условиях параллельной RLC-цепи
В различных расчетах, связанных с работой над цепями переменного тока, очень важное место занимает понятие полного сопротивления. Для его определения в цепи в большей части случаев практично использовать метод векторных диаграмм. В качестве примера, приведем параллельный подключенный к внешнему источнику переменного тока (рис. 2.4.1) RLC-контур:
Рисунок 2.4.1. Параллельный RLC-контур.
При построении диаграммы важно учесть, что в условиях параллельного соединения напряжение на всех элементах R, C и L идентично и равняется напряжению внешнего источника питания. Ток, текущий в разных ветвях цепи, различается не только по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Следовательно, полное сопротивление цепи невозможно вычислить опираясь на законы параллельного соединения цепей постоянного тока. Векторную диаграмму для параллельного RLC-контура можно увидеть на рис. 2.4.2.
Векторную диаграмму для параллельного RLC-контура можно увидеть на рис. 2.4.2.
Рисунок 2.4.2. Векторная диаграмма для параллельного RLC-контур.
Исходя из вида диаграммы, следует:
I0=δ01R2+ωL-1ωC2.
Определение 8Соответственно, полное сопротивление параллельного RLC-контура выражается в виде следующего соотношения:
Z=11R2+ωL-1ωC2.
Определение 9При параллельном резонансе (ω2=1LC) полное сопротивление цепи принимает свое максимальное значение, которое эквивалентно активному сопротивлению резистора:
Z=Zmax=R.
А значение фазового сдвига φ между током и напряжением при параллельном резонансе равняется нулю.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Открытый урок по физикев в 8 классе по теме” Закон Ома для участка цепи”
Раздел долгосрочного планирования: 8.4А Закон Ома для участка цепи | Школа: КГУ « Большенарымский сельский лицей» |
| ||||||||||||||||
Дата :24.
01. | ФИО учителя:Нечаева Н.С. |
| ||||||||||||||||
класс: 8 б | Участвовали: 12 |
| ||||||||||||||||
Тема урока | Закон Ома для участка цепи |
|
| |||||||||||||||
Цели обучения, достигаемые на этом уроке | 8.4.2.6 – применять закон Ома для участка цепи при решении задач |
| ||||||||||||||||
Цель урока | Все учащиеся: будут знать физичекие величины ;
основные понятия сила тока, напряжение, сопротивление. Большинство
учащихся: будут уметь, работать с основными единицами,
измерние силы тока, напряжения, сопротивления, и переводить в систему СИ. Некоторые ученики: Уметь, применять при решении задач математическую формулу закона Ома для участка цепи. |
| ||||||||||||||||
Критерии оценивания | -называют форму закона Ома и величины входящие в нее, -применяют формулу для решения расчетных задач -объясняют при помощи вольт-амперной характеристики зависимость силы тока от напряжения. |
| ||||||||||||||||
Языковые задачи
| Используют
ключевые слова: сила тока, напряжение, сопротивление. Полезные фразы для диалога: Сила прямо пропорциональна …… Сила тока обратно пропорциональна….. В системе Си сила тока измеряется…… Вольтамперная характеристика…. |
| ||||||||||||||||
Воспитание ценностей
| Общество всеобщего труда: сотрудничество при групповой и парной работе, трудолюбие, уметь принимать чужую точку зрения, уважение к друг другу.
|
| ||||||||||||||||
Межпредметная связь | Самопознание . Создание в классе благоприятной психологической обстановки Круг «От сердца к сердцу» |
| ||||||||||||||||
Предыдущие знания
| Электрический ток, напряжение и сопротивление, соединение проводников, схематические обозначения амперметра, вольтметра, резистора |
| ||||||||||||||||
Ход урока |
| |||||||||||||||||
Запланированные этапы урока | Виды упражнений, запланированных на урок:
| Ресурсы |
| |||||||||||||||
«Начало» 5 минут | 1. –
Ребята, я вижу, не у всех настроение в начале урока отличное, но давайте
проведём наш урок так, чтобы в конце урока у всех ребят нашего класса
настроение было прекрасное.
2.Актуализация: проверка домашнего задания: Форматиное оценивание в виде тестов из 4 вопросов: Критерии оценивания: – знает единицы измерение сила тока, -знает единицы измерения сопротивления, – знает единицы измерения напряжения, – рассчитывает силу тока по формуле, – рассчитывает напряжение по формуле, – знает
схематические обозначения приборов. |
(приложение 1) |
| |||||||||||||||
Середина урока На определение новой темы 3 минут
На обсуждение новой темы 10 минут и на оформление постера 10 минут На закрепление Т.е. решение задач 7 минут | Определение темы и целей урока Слова-подсказки: закон Ома, решение задач, объяснение взаимосвязи силы тока от напряжения, знать единицы измерения силы тока, напряжения и сопротивления
1) С помощью подсказок вы определили новую тему , решение задач на закон Ома для участка цепи. А сейчас
нам необходимо разделится на три группы.
2)Актуализация знаний
ФО:По таблице
Дифференциация: Просто: задания на уровне повторения(физические величины, термины, измерения Задания
среднего уровня; требуют обобщение нового
материала,побуждают к подведению итогов,применению знаний в новых условиях. Задания высокого уровня: требуют обобщение нового материала, подведение итога урока | Слайд 2 с портретами ученных
Раздаточный материал «Карточки с проводами»
Раздаточный материал: листы с условием задач
Приложение 2 Карточки с формативным оцени4ванием |
| |||||||||||||||
Конец урока 5 минут | Рефлексия.
Домашнее задание: по стратегии «цепочка».. Критерий оценивания: – Первые два ученика пишут дано, – вторые переводят в систему Си, – третья пара записывает
формулы решения задач по физике, находят неизвестные величины,
преобразовывают формулы для решения задач. |
Карточки для заполнения |
| |||||||||||||||
Дифференциация – каким способом вы хотите больше оказывать поддержку? Какие задания вы даете ученикам более способным по сравнению с другими? | Оценивание – как Вы планируете проверять уровень усвоения материала учащимися? | Охрана здоровья и соблюдение техники безопасности |
| |||||||||||||||
Разноуровневые задания,задачи разной сложности(простые задачи на одну формулу, задачи с переводом в систему СИ, задачи с применением графической зависимости) ,диалог и поддержка, оценивание ,группировка | Взаимооценивание
при решении тестов (обмениваются листами ответов)Формативное оценивание на
каждом этапе урока. | Ознакомление с правилами техники безопасности , используемых на данном уроке.
|
| |||||||||||||||
Краткосрочный план
1 группа ( для всех учеников)
1) заполните пустые ячейки в таблице, применяя формулу закона Ома для участка цепи.
I (А) |
| 4 | 15 | 6 |
U( В)| | 10 |
| 45 |
|
R( Ом) | 5 | 8 |
| 2,5 |
2) решите задачу, используя чертеж. ( Для некоторых
учеников)
( Для некоторых
учеников)
На чертеже изображена зависимость силы тока от напряжения. Чему равно сопротивление проводника? Назовите силу тока, которая соответствует 8 В.
(Для большинства учеников)
3)Через
проводник длиной 22 м с сечением 1 мм2, находящийся под
напряжением 220 В, протекает ток силой 10 А. Из какого материала изготовлена
проволока? ( воспользуйтесь таблицей 10, удельных cопротивлений
в конце учебника)
Дескрипторы:
-Знает
формулу , которая выражает закон
Ома
– Правильно выражает сопротивление из формулы закона Ома –
Правильно вычисляет
сопротивление
—-Правильно выражает удельное сопротивление из формулы сопротивления
-Знает формулу, по которой вычисляется
сопротивление -Переводит
мм2 в м2 ;
–
-правильно определяет по таблице вещество, из которого изготовлен проводник Дополнительное задание 4) начертить схему электрической
цепи, состоящей из источника тока, лампочки, ключа, амперметра, вольтметра, звонка.
2 группа ( для всех учеников)
1) Заполните пустые ячейки в таблице, применяя формулу закона Ома для участка цепи
I (А) |
| 4 |
| 4 |
U( В)| | 10 |
| 420 | 100 |
R( Ом) | 4 | 10 | 100 |
|
2) решите задачу, используя чертеж. ( Для некоторых
учеников)
( Для некоторых
учеников)
На чертеже изображена зависимость силы тока от напряжения. Чему равно сопротивление проводника? Назовите силу тока, которая соответствует 10 В.
(Для большинства учеников)
3)Во сколько раз уменьшится сила тока в проводнике, если при неизменном сопротивлении, напряжение уменьшится в 2 раза?
Дополнительное задание
4) начертить схему электрической цепи, состоящей из источника тока, резистора, ключа, амперметра, вольтметра
3)Группа ( для всех учеников) 1) Заполните пустые ячейки в таблице, применяя формулу закона Ома для участка цепи.
I (А) |
| 4 | 15 | 6 |
U( В)| | 10 |
| 45 |
|
R( Ом) | 5 | 8 |
| 2,5 |
2) решите задачу, используя чертеж. ( Для некоторых
учеников)
На чертеже изображена зависимость силы тока от напряжения. Чему равно сопротивление
проводника? Назовите силу тока, которая соответствует 4 В.
( Для некоторых
учеников)
На чертеже изображена зависимость силы тока от напряжения. Чему равно сопротивление
проводника? Назовите силу тока, которая соответствует 4 В.
(Для большинства учеников)
3) Известно, что через поперечное сечение проводника, включенного в цепь на 2 мин, прошел заряд, равный 36 Кл. Какова была сила тока в этом проводнике? Чему равно напряжение , если сопротивление равно 220 В А) 0,3 А ; 66 В В) 18 А; 3960 Ом С) 36 А ; 72 В Д) 72 А; 144 В
Дополнительное задание 4) начертить схему электрической цепи, состоящей из источника тока, лампочки, ключа, амперметра, вольтметра, звонка.
1 ) Закончи предложение:
1)Силой
тока называется физическая величина, которая показывает, какой величины заряд
проходит через…….
2)Напряжение- физическая величина, которая показывает, какую работу совершает электрическое поле при……..
3)Электрическим сопротивлением называется физическая величина, характеризующая способность проводника препятствовать……..
4) Сила тока, напряжение, электрическое сопротивление обозначаются ……………, и имеют единицы измерения……….
5) Сила тока, напряжение, электрическое сопротивление измеряются приборами……….
2 )Заполни таблицу:
Название физической величины | Обозначение буквой | Единица измерения | Формула вычисления | Каким прибором измеряется |
сила тока |
|
|
|
|
напряжение |
|
|
|
|
сопротивление |
|
|
|
|
3)Стратегия: верю, не верю, графический диктант
1)Силой
тока называется физическая величина, которая показывает, какой величины заряд проходит
через длинный проводник. 2)Напряжение- физическая величина, которая показывает, какую работу совершает
электрическое поле при перемещении единичного заряда по проводнику.
3)Электрическим сопротивлением называется физическая величина, характеризующая
способность проводника препятствовать прохождению тока по нему
4) Сила тока, напряжение, электрическое сопротивление обозначаются I,
U, R и имеют единицы измерения B, Oм,
А
5) Сила тока, напряжение, электрическое сопротивление измеряются приборами
амперметр, вольтметр, омметр
2)Напряжение- физическая величина, которая показывает, какую работу совершает
электрическое поле при перемещении единичного заряда по проводнику.
3)Электрическим сопротивлением называется физическая величина, характеризующая
способность проводника препятствовать прохождению тока по нему
4) Сила тока, напряжение, электрическое сопротивление обозначаются I,
U, R и имеют единицы измерения B, Oм,
А
5) Сила тока, напряжение, электрическое сопротивление измеряются приборами
амперметр, вольтметр, омметр
1 ) Закончи предложение:
1)Силой
тока называется физическая величина, которая показывает, какой величины
заряд проходит через поперечное сечение проводника за единицу
времени
2)Напряжение– физическая величина, которая показывает, какую работу
совершает электрическое поле при перемещении единичного заряда по
проводнику. 3)Электрическим сопротивлением называется физическая величина,
характеризующая способность проводника препятствовать прохождению тока по
нему 4) Сила
тока, напряжение, электрическое сопротивление обозначаются буквами I,
U , R и имеют единицы измерения A, B,
Oм. 5) Сила тока, напряжение, электрическое сопротивление измеряются приборами
амперметр, вольтметр ,
омметр.
2 )Заполни таблицу:
3)Электрическим сопротивлением называется физическая величина,
характеризующая способность проводника препятствовать прохождению тока по
нему 4) Сила
тока, напряжение, электрическое сопротивление обозначаются буквами I,
U , R и имеют единицы измерения A, B,
Oм. 5) Сила тока, напряжение, электрическое сопротивление измеряются приборами
амперметр, вольтметр ,
омметр.
2 )Заполни таблицу:
Название физической величины | Обозначение буквой | Единица измерения | Формула вычисления | Каким прибором измеряется |
сила тока | I | A( ампер) | I | амперметр |
напряжение | U | В( вольт) | U | вольтметр |
сопротивление | R | Ом( ом) | R | омметр |
3)Стратегия: верю, не верю, графический диктант
—– —–
1 группа ( для всех учеников)
1)
заполните пустые ячейки в таблице, применяя формулу закона Ома
для участка цепи.
I (А) | 2 | 4 | 15 | 6 |
U( В)| | 10 | 32 | 45 | 15 |
R( Ом) | 5 | 8 | 3 | 2,5 |
2) решите задачу, используя чертеж. ( Для некоторых учеников)
На чертеже
изображена зависимость силы тока от напряжения. Чему равно сопротивление
проводника? Назовите силу тока, которая соответствует 8 В.
Чему равно сопротивление
проводника? Назовите силу тока, которая соответствует 8 В.
R= =4 Oм, I=2A (Для большинства учеников) 3)Через
проводник длиной 22 м с сечением 0,01 мм2, находящийся под
напряжением 220 В, протекает ток силой 10 А. Из какого материала изготовлена
проволока? ( воспользуйтесь таблицей 10, удельных сопротивлений в конце
учебника. = = =
1Ом (
из железа) Дескрипторы:
-Знает
формулу , которая выражает закон
Ома
– Правильно выражает сопротивление из формулы закона
Ома
– Правильно вычисляет
сопротивление —-Правильно
выражает удельное сопротивление из формулы сопротивления
-Знает формулу, по которой вычисляется
сопротивление
-Переводит мм2 в м2 ;
– -правильно
определяет по таблице вещество, из которого изготовлен проводник Дополнительное задание : 4) начертить схему
электрической цепи, состоящей из источника тока, лампочки, ключа, амперметра,
вольтметра, звонка.
2 группа ( для всех учеников)
1)Заполните пустые ячейки в таблице, применяя формулу закона Ома для участка цепи
I (А) | 2,5 | 4 | 4,2 | 4 |
U( В)| | 10 | 40 | 420 | 100 |
R( Ом) | 4 | 10 | 100 | 25 |
2) решите задачу, используя чертеж. ( Для некоторых
учеников)
На чертеже изображена зависимость силы тока от напряжения. Чему равно
сопротивление проводника? Назовите силу тока, которая соответствует 10 В.
( Для некоторых
учеников)
На чертеже изображена зависимость силы тока от напряжения. Чему равно
сопротивление проводника? Назовите силу тока, которая соответствует 10 В.
R= =4 Oм, I=2,5A
(Для большинства учеников) 3)Во сколько раз уменьшится сила тока в проводнике, если при неизменном сопротивлении, напряжение уменьшится в 2 раза? ( Уменьшится в 2 раза, потому что сила тока прямопропорциональна напряжению)
Дополнительное задание
4) начертить схему электрической цепи, состоящей из источника тока, резистора, ключа, амперметра, вольтметра
3)Группа
( для всех
учеников)
1) Заполните пустые ячейки в таблице, применяя формулу закона Ома
для участка цепи.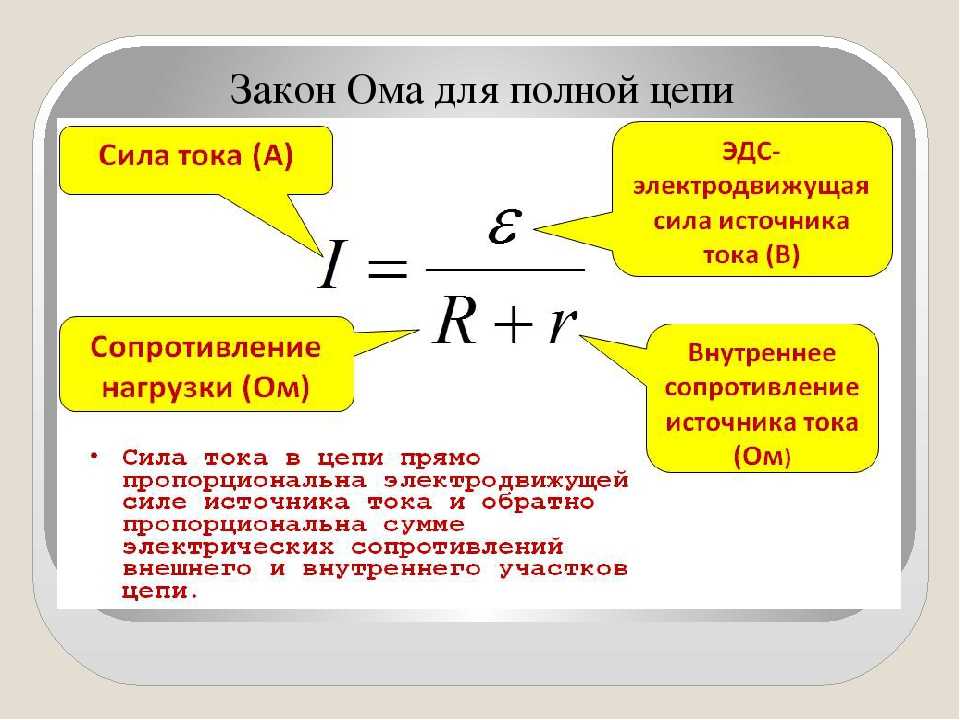
I (А) | 2 | 4 | 15 | 6 |
U( В)| | 10 | 64 | 450 | 18 |
R( Ом) | 5 | 16 | 30 | 3 |
2) решите задачу, используя чертеж. ( Для некоторых
учеников)
На чертеже изображена зависимость силы тока от напряжения. Чему равно
сопротивление проводника? Назовите силу тока, которая соответствует напряжению
4 В.
( Для некоторых
учеников)
На чертеже изображена зависимость силы тока от напряжения. Чему равно
сопротивление проводника? Назовите силу тока, которая соответствует напряжению
4 В.
R= =4 Oм, I=1 A (Для большинства учеников)
3) Известно, что через поперечное сечение проводника, включенного в цепь на 2 мин, прошел заряд, равный 36 Кл. Какова была сила тока в этом проводнике? Чему равно напряжение , если сопротивление равно 220 В А) 0,3 А ; 66 В В) 18 А; 3960 Ом С) 36 А ; 72 В Д) 72 А; 144 В ответ А
2 мин=120 с,I= = = 0,3 А, U=I66 B
Дескрипторы:-
Переводит минуты в секунды. -Записывает
формулу силы тока
-Правильно
вычисляет силу тока
-Правильно выражает из формулы закона Ома
напряжение
– Правильно вычисляет
напряжение
Дополнительное задание 4) начертить схему
электрической цепи, состоящей из источника тока, лампочки, ключа, амперметра,
вольтметра, звонка.
-Записывает
формулу силы тока
-Правильно
вычисляет силу тока
-Правильно выражает из формулы закона Ома
напряжение
– Правильно вычисляет
напряжение
Дополнительное задание 4) начертить схему
электрической цепи, состоящей из источника тока, лампочки, ключа, амперметра,
вольтметра, звонка.
Закон Ома для неоднородного участка цепи » Kupuk.net
Участки электрических цепей принято разделять на однородные и неоднородные.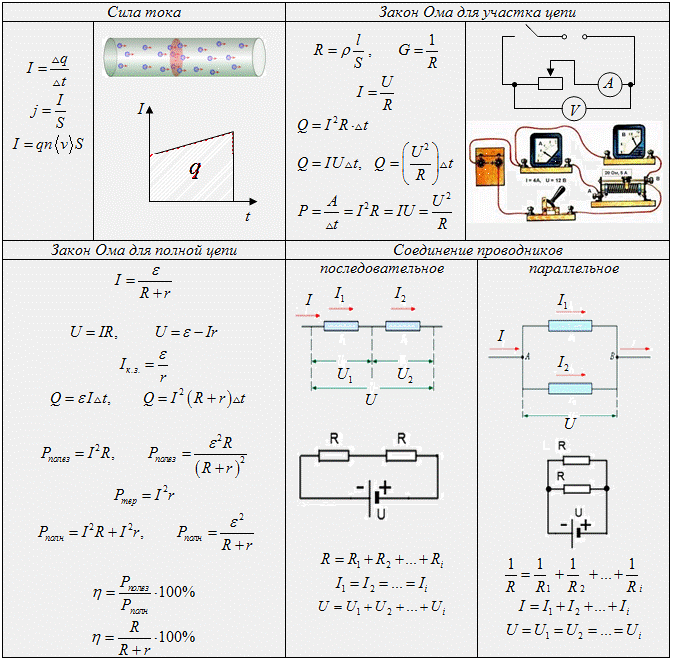 Закон Ома выполняется для обоих видов цепей. Однако математические выражения, которые отражают действие этого закона, несколько отличаются. Это связано с действием сторонних сил на электрические заряды, когда они проходят через неоднородные участки цепей.
Закон Ома выполняется для обоих видов цепей. Однако математические выражения, которые отражают действие этого закона, несколько отличаются. Это связано с действием сторонних сил на электрические заряды, когда они проходят через неоднородные участки цепей.
Стационарное электрическое поле
Электрический ток возникает при наличии электрического поля и свободных носителей заряда. Соединив проводником разноименно заряженные тела, можно получить электрический ток, протекающий в течение короткого промежутка времени. Стационарное электрическое поле — это поле постоянных во времени электрических токов при условии неподвижности проводников с электрическими токами. Участки цепи, где на заряды действует только стационарное поле, называются однородными.
Сторонние силы
Для того, чтобы в проводнике электрический ток был длительное время, необходимо создать определенные условия. Для этого на отдельных участках цепи, кроме сил стационарного поля, действуют, так называемые, сторонние силы. Участки цепи, на которых имеется действие дополнительных, сторонних, сил называются неоднородными. В этом случае перемещение зарядов возникает под действием сил не электростатической природы, действующих в устройствах, называемых источниками постоянного тока.
Участки цепи, на которых имеется действие дополнительных, сторонних, сил называются неоднородными. В этом случае перемещение зарядов возникает под действием сил не электростатической природы, действующих в устройствах, называемых источниками постоянного тока.
Силы, приводящие в движение электрические заряды внутри источника постоянного тока против направления действия сил электростатического поля, называются сторонними силами. Сторонние силы в гальваническом элементе или аккумуляторе возникают в результате электрохимических реакций, происходящих между частицами металлического электрода и молекулами электролита. В генераторах постоянного тока сторонней силой является сила, возникающая от действия магнитного поля на движущийся электрический заряд. Работа источника тока похожа на функцию насоса, который заставляет двигаться жидкость (качает) по трубам замкнутого гидравлического контура. Под воздействием сторонних сил заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи длительное время поддерживается постоянный электрический ток.
Рис. 1. Источники постоянного тока, аккумуляторы, гальванические элементы, генераторы.
В организме человека имеется множество химических веществ, которые вступая друг с другом в различные реакции, способствуют возникновению электрической энергии. Например, в сердце есть клетки, которые в процессе поддержания сердечного ритма поглощают натрий и выделяют калий, что приводит к образованию электрических зарядов. При достижении определенной величины заряда, возникает импульс электрического поля, заставляющий сокращаться сердечную мышцу. Эти импульсы регистрируют с помощью кардиографа в больницах и поликлиниках при снятии электрокардиограммы (ЭКГ), дающей информацию о работе сердца..
Закон Ома для неоднородного участка цепи
Физическая величина, равная отношению работы сторонних сил Aст при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой (ЭДС) источника Eэдс:
$ E_{эдс} = {A_{cт}over q} $ (1).
Таким образом, ЭДС равна работе, совершаемой сторонними силами при перемещении единичного положительного заряда. При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа электростатического поля равна нулю, а работа сторонних сил равна сумме всех ЭДС, действующих в этой цепи.
Работа электростатических сил по перемещению единичного заряда равна разности потенциалов $ Δφ = φ_1 – φ_2 $ между начальной и конечной точками 1 и 2 неоднородного участка. Работа сторонних сил равна, по определению, электродвижущей силе Eэдс, действующей на данном участке. Поэтому полная работа равна:
$ U_п = φ_1 – φ_2 + E_{эдc} $ (2).
Величина Uп называется напряжением на участке цепи 1–2. В случае однородного участка напряжение равно разности потенциалов:
$ U_п = φ_1 – φ_2 $ (3).
Немецкий исследователь Георг Симон Ом в начале XIX века установил, что сила тока I, текущего по однородному проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:
е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:
$ I = {U over R} $ (4).
Рис. 2. Портрет Георга Ома.
Величина R — это электрическое сопротивление. Уравнение (4) выражает закон Ома для однородного участка цепи. Для участка цепи, содержащего ЭДС, закон Ома записывается в следующем виде:
$ U_п = I * R = φ_1 – φ_2 + E_{эдс} = Δ φ_{12} + E_{эдс}$ (5).
Данное уравнение называется обобщенным законом Ома для неоднородного участка цепи.
Закон Ома для полной цепи
Если замкнутая цепь состоит из сопротивления цепи, равного R, и источника тока с электродвижущей силой Eэдс и внутренним сопротивлением r, то в этом случае ток цепи I будет равен:
$ I = {E_{эдс} over R + r} $ (6).
Выражение (6) называется законом Ома для полной цепи: сила тока в полной цепи равна ЭДС источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
Проводники, в точности соответствующие закону Ома, называются линейными, так как график зависимости тока I от напряжения U изображается прямой линией. Следует отметить, что существуют много материалов, которые не подчиняются закону Ома, например, полупроводники или газоразрядные лампы. У металлических проводников отклонения от линейной зависимости появляются при больших токах, так как сопротивление металлов возрастает с ростом температуры.
Рис. 3. График зависимости сопротивления металлических проводников от температуры.
Что мы узнали?
Итак, мы узнали, что участки электрической цепи, на которых кроме стационарного электрического поля имеется действие дополнительных, сторонних сил, называются неоднородными. Сторонние силы возникают в результате работы источников тока: аккумуляторов, гальванических элементов и электрических генераторов тока. Получены уравнения закона Ома для неоднородного участка цепи и для полной цепи.
Согласно закону ома сила тока вычисляется по формуле найти
Формулировка и объяснение
Человеком, который смог получить основной закон электротехники, стал ученый Георг Ом из Германии. Выведенный им постулат имеет довольно простое определение — сила тока на участке цепи обратно пропорциональна сопротивлению и прямо пропорциональна напряжению.
Выведенный им постулат имеет довольно простое определение — сила тока на участке цепи обратно пропорциональна сопротивлению и прямо пропорциональна напряжению.
При этом она является самой простой и применяется для внешнего однородного участка цепи, на котором отсутствуют источники ЭДС. Говоря проще, в рассматриваемой электроцепи не должно находиться батарейки, иначе формула, выражающая закон, примет слегка измененный вид: I = E / (R + r). В ней E соответствует потенциальной энергии источника ЭДС, а r представляет собой его внутреннее сопротивление. Таким образом, появилось еще несколько новых понятий:
- однородный участок электроцепи;
- полная цепь;
- внешний и внутренний участок.
Зная простейшую формулу закона Ома, на экзамене можно легко дать его определение и решать несложные практические задачи. При дальнейшем изучении электротехники предстоит углубиться в тонкости этого предмета, например, познакомиться с понятиями реактивного и активного сопротивления, а также записать более сложную формулу.
Электрический ток и его характеристики
Определение 9
Проводники, которые подчинены закону Ома, получили название линейных.
Для изображения графической зависимости силы тока I от U (графики называют вольт-амперными характеристиками, ВАХ) используется прямая линия, проходящая через начало координат.
Существуют устройства, не подчиняющиеся закону Ома. К ним относят полупроводниковый диод или газоразрядную лампу. Металлические проводники имеют отклонения от закона Ома при токах большой силы. Это связано с ростом температуры.
Определение 10
Участок цепи, содержащий ЭДС, позволяет записывать закон Ома таким образом:
IR=U12=φ1-φ2+δ=∆φ12+δ.
Формула получила название обобщенного закона Ома или закон Ома для неоднородного участка цепи.
Рисунок 1.8.2 показывает замкнутую цепь с постоянным током, причем ток цепи (cd) считается однородным.
Рисунок 1.8.2. Цепь постоянного тока.
Исходя из закона Ома IR=∆φcd, участок (ab) содержит источник тока с ЭДС, равной δ. Тогда для неоднородного участка формула примет вид Ir=∆φab+δ. Сумма обоих равенств дает в результате выражение I(R+r)=∆φcd+∆φab+δ. Но ∆φcd=∆φba=-∆φab, тогда I=δR+r.
Определение 11
Формула I=δR+r выражает закон Ома для полной цепи. Запишем ее, как определение: сила тока в полной цепи равняется электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
Рисунок 1.8.2 говорит о том, что R неоднородного тела может быть рассмотрено как внутреннее сопротивление источника тока. Тогда (ab) участок будет являться внутренним участком источника.
Определение 12
При замыкании a и b с помощью проводника с малым по сравнению с внутренним сопротивлением источника получим, что в цепи имеется ток короткого замыкания Iкз=δr.
Сила тока короткого замыкания является максимальной, получаемой от источника с ЭДС и внутренним сопротивлением r. Если внутренне сопротивление мало, тогда ток короткого замыкания может вызвать разрушение электрической цепи или источника.
Пример 1
Свинцовые аккумуляторы автомобилей имеют силу тока короткого замыкания в несколько сотен ампер. Особую опасность представляют замыкания в осветительных сетях, которые имеют подпитку от подстанций. Во избежание разрушительных действий предусмотрены предохранители или автоматы для защиты сетей.
Чтобы при превышении допустимых значений силы тока не произошло короткого замыкания, используют внешнее сопротивление. Если сопротивление r равняется сумме внутреннего и внешнего сопротивления источника, сила тока не будет превышать норму.
При наличии разомкнутой цепи разность потенциалов на полюсах разомкнутой батареи равняется ее ЭДС. Когда внешнее R включено и ток I подается через батарею, то разность потенциалов на полюсах запишется, как ∆φba=δ-Ir.
Рисунок 1.8.3 дает точное схематическое изображение источника постоянного тока с ЭДС, равной δ, внутренним r в трех режимах: «холостой ход», работа на нагрузку, режим короткого замыкания. E→ является напряженностью внутри электрического поля внутри батареи, a – силами, действующими на положительные заряды, Fст→– сторонней силой. Исчезновение электрического поля возникает при коротком замыкании.
Рисунок 1.8.3. Схематическое изображение источника постоянного тока: 1 – батарея разомкнута;2 – батарея замкнута на внешнее сопротивление R; 3 – режим короткого замыкания.
Применение и практический смысл
Непосредственное превращение электричества в тепловую энергию нельзя назвать экономически выгодным. Однако, с точки зрения удобства и доступности современного человечества к источникам электроэнергии различные нагревательные приборы продолжают массово применяться как в быту, так и на производстве.
Перечислим некоторые из них:
- электрочайники;
- утюги;
- фены;
- варочные плиты;
- паяльники;
- сварочные аппараты и многое другое.

На рисунке 3 изображены бытовые нагревательные приборы, которыми мы часто пользуемся.
Рис. 3. Бытовые нагревательные приборы
Использование тепловых мощностей в химической, металлургической и в других промышленных отраслях тесно связно с использованием электрической энергии.
Без знания физического закона Джоуля-Ленца было бы невозможно сконструировать безопасный нагревательный прибор. Для этого нужны расчёты, которые невозможно сделать без применения рассмотренных нами формул. На основе расчётов происходит выбор материалов с нужным удельным сопротивлением, влияющим на нагревательную способность устройств.
Закон Джоуля-Ленца без преувеличения можно назвать гениальным. Это один из тех законов, которые повлияли на развитие электротехники.
Почему греется проводник
Как же объясняется нагрев проводника? Почему он именно греется, а не остаётся нейтральным или охлаждается? Нагрев происходит из-за того, что свободные электроны, перемещающиеся в проводнике под действием электрического поля, бомбардируют атомы молекул металла, тем самым передавая им собственную энергию, которая переходит в тепловую. Если изъясняться совсем просто: преодолевая материал проводника, электрический ток как бы “трётся”, соударяется электронами о молекулы проводника. Ну а , как известно, любое трение сопровождается нагревом. Следовательно, проводник будет нагреваться пока по нему бежит электрический ток.
Если изъясняться совсем просто: преодолевая материал проводника, электрический ток как бы “трётся”, соударяется электронами о молекулы проводника. Ну а , как известно, любое трение сопровождается нагревом. Следовательно, проводник будет нагреваться пока по нему бежит электрический ток.
Из формулы также следует – чем выше удельное сопротивление проводника и чем выше сила тока протекающего по нему, тем выше будет нагрев . Например, если последовательно соединить проводник-медь (удельное сопротивление 0,018 Ом·мм²/м) и проводник-алюминий (0,027 Ом·мм²/м), то при протекании через цепь электрического тока алюминий будет нагреваться сильнее чем медь из-за более высокого сопротивления. Поэтому, кстати, не рекомендуется в быту делать скрутки медных и алюминиевых проводов друг с другом – будет неравномерный нагрев в месте скрутки. В итоге – подгорание с последующим пропаданием контакта.
Опыты Ленца
Перенесемся в 19 век-эпоху накопления знаний и подготовки к технологическому прыжку 20 века. Эпоха, когда по всему миру различные учёные и просто изобретатели-самоучки чуть ли не ежедневно открывают что-то новое, зачастую тратя огромное количество времени на исследования и, при этом, не представляя конечный результат.
Эпоха, когда по всему миру различные учёные и просто изобретатели-самоучки чуть ли не ежедневно открывают что-то новое, зачастую тратя огромное количество времени на исследования и, при этом, не представляя конечный результат.
Один из таких людей, русский учёный Эмилий Христианович Ленц, увлекался электричеством, на тогдашнем примитивном уровне, пытаясь рассчитывать электрические цепи. В 1832 году Эмилий Ленц “застрял” с расчётами, так как параметры его смоделированной цепи “источник энергии – проводник – потребитель энергии” сильно разнились от опыта к опыту. Зимой 1832-1833 года учёный обнаружил, что причиной нестабильности является кусочек платиновой проволоки, принесённый им с холода. Отогревая или охлаждая проводник, Ленц также заметил что существует некая зависимость между силой тока, электрическим сопротивлением и температурой проводника.
При определённых параметрах электрической цепи проводник быстро оттаивал и даже слегка нагревался. Измерительных приборов в те времена практически никаких не существовало – невозможно было точно измерить ни силу тока, ни сопротивление. Но это был русский физик, и он проявил смекалку. Если это зависимость, то почему бы ей не быть обратимой?
Но это был русский физик, и он проявил смекалку. Если это зависимость, то почему бы ей не быть обратимой?
Для того чтобы измерить количество тепла, выделяемого проводником, учёный сконструировал простейший “нагреватель” – стеклянная ёмкость, в которой находился спиртосодержащий раствор и погружённый в него платиновый проводник-спираль. Подавая различные величины электрического тока на проволоку, Ленц замерял время, за которое раствор нагревался до определённой температуры. Источники электрического тока в те времена были слишком слабы, чтобы разогреть раствор до серьёзной температуры, потому визуально определить количество испарившегося раствора не представлялось возможным. Из-за этого процесс исследования очень затянулся – тысячи вариантов подбора параметров источника питания, проводника, долгие замеры и последующий анализ.
Кулон и электрический заряд
Одна из основных единиц электрических измерений, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, – это кулон – единица измерения электрического заряда, пропорциональная количеству электронов в несбалансированном состоянии. Один кулон заряда соответствует 6 250 000 000 000 000 000 электронов. Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается «Кл». Единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этом смысле, ток – это скорость движения электрического заряда через проводник.
Один кулон заряда соответствует 6 250 000 000 000 000 000 электронов. Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается «Кл». Единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этом смысле, ток – это скорость движения электрического заряда через проводник.
Как указывалось ранее, напряжение – это мера потенциальной энергии на единицу заряда, доступная для стимулирования протекания тока из одной точки в другую. Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией».
Общей метрической единицей измерения энергии любого вида является джоуль, равный количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении). В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленному на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.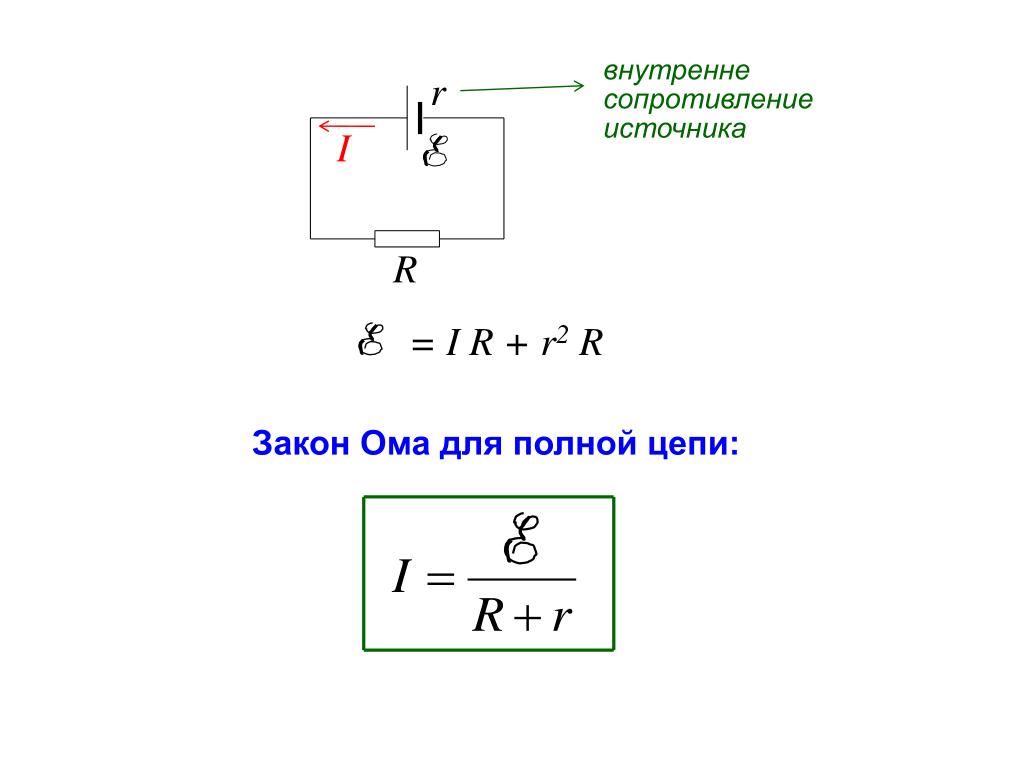
Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.
Где может пригодиться этот закон Джоуля-Ленца?
В электротехнике есть понятие длительно допустимого тока протекающего по проводам. Это такой ток, который провод способен выдержать длительное время (то есть, бесконечно долго), без разрушения провода (и изоляции, если она есть, потому что провод может быть и без изоляции). Конечно, данные вы теперь можете взять из ПУЭ (Правила устройства электроустановок), но получали эти данные исключительно на основе закона Джоуля-Ленца.
В электротехнике так же используются плавкие предохранители. Их основное качество – надёжность срабатывания. Для этого используется проводник определенного сечения. Зная температуру плавления такого проводника можно вычислить количество теплоты, которое необходимо, чтобы проводник расплавился от протекания через него больших значений тока, а вычислив ток, можно вычислить и сопротивление, которым такой проводник должен обладать. В общем, как вы уже поняли, применяя закон Джоуля-Ленца можно рассчитать сечение или сопротивление (величины взаимозависимы) проводника для плавкого предохранителя.
В общем, как вы уже поняли, применяя закон Джоуля-Ленца можно рассчитать сечение или сопротивление (величины взаимозависимы) проводника для плавкого предохранителя.
А ещё, помните, мы говорили про . Там на примере лампочки я рассказывал парадокс, что более мощная лампа в последовательном соединении светит слабее. И наверняка помните почему: падение напряжения на сопротивлении тем сильнее, чем меньше сопротивление. А поскольку мощность — это , а напряжение очень сильно падает, то и выходит, что большое сопротивление выделит большое количество тепла, то есть, току придется больше потрудиться, чтобы преодолеть большое сопротивление. И количество тепла, которое выделит ток при этом можно посчитать с помощью закона Джоуля-Ленца. Если брать последовательное соединение сопротивлений, то использовать лучше выражение через квадрат тока, то есть, изначальный вид формулы:
А для параллельного соединения сопротивлений, поскольку ток в параллельных ветвях зависит от сопротивления, в то время, как напряжение на каждой параллельной ветви одинаковое, то формулу лучше всего представить через напряжение:
Примерами работы закона Джоуля-Ленца вы все пользуетесь в повседневной жизни – в первую очередь это всевозможные нагревательные приборы. Как правило, в них используется нихромовая проволока и толщина (поперечное сечение) и длина проводника подбираются с учётом того, чтобы длительное тепловое воздействие не приводило к стремительному разрушению проволоки. Точно таким же образом добиваются свечения вольфрамовой нити в лампе накаливания. По этому же закону определяют степень возможного нагрева практически любого электротехнического и электронного устройства.
Как правило, в них используется нихромовая проволока и толщина (поперечное сечение) и длина проводника подбираются с учётом того, чтобы длительное тепловое воздействие не приводило к стремительному разрушению проволоки. Точно таким же образом добиваются свечения вольфрамовой нити в лампе накаливания. По этому же закону определяют степень возможного нагрева практически любого электротехнического и электронного устройства.
В общем, несмотря на кажущуюся простоту, закон Джоуля-Ленца играет в нашей жизни очень огромную роль. Этот закон дал большой толчок для теоретических расчётов: выделение тепла токами , вычисление конкретной температуры дуги, проводника и любого другого электропроводного материала, потери электрической мощности в тепловом эквиваленте и т.д.
Вы можете спросить, а как перевести Джоули в Ватты и это довольно частый вопрос в интернете. Хотя вопрос несколько неверный, читая далее, вы поймёте почему. Ответ довольно прост: 1 дж = 0.000278 Ватт*час, в то время, как 1 Ватт*час = 3600 Джоулей. Напомню, что в Ваттах измеряется потребляемая мгновенная мощность, то есть непосредственно используемая пока включена цепь. А Джоуль определяет работу электрического тока, то есть мощность тока за промежуток времени. Помните, в законе Ома я приводил аллегорическую ситуацию. Ток – деньги, напряжение – магазин, сопротивление – чувство меры и денег, мощность – количество продуктов, которые вы сможете на себе унести (увезти) за один раз, а вот как далеко, как быстро и сколько раз вы сможете их увезти – это работа. То есть, сравнить работу и мощность никак не получается, но можно выразить в более понятных нам единицам: Ваттах и часах.
Напомню, что в Ваттах измеряется потребляемая мгновенная мощность, то есть непосредственно используемая пока включена цепь. А Джоуль определяет работу электрического тока, то есть мощность тока за промежуток времени. Помните, в законе Ома я приводил аллегорическую ситуацию. Ток – деньги, напряжение – магазин, сопротивление – чувство меры и денег, мощность – количество продуктов, которые вы сможете на себе унести (увезти) за один раз, а вот как далеко, как быстро и сколько раз вы сможете их увезти – это работа. То есть, сравнить работу и мощность никак не получается, но можно выразить в более понятных нам единицам: Ваттах и часах.
Думаю, что теперь вам не составит труда применить закон Джоуля-Ленца в практике и теории, если таковое потребуется и даже сделать перевод Джоулей в Ватты и наоборот. А благодаря пониманию, что закон Джоуля-Ленца это произведение электрической мощности на время, вы сможете более легко его запомнить и даже, если вдруг забыли основную формулу, то помня всего лишь закон Ома можно снова получить закон Джоуля-Ленца.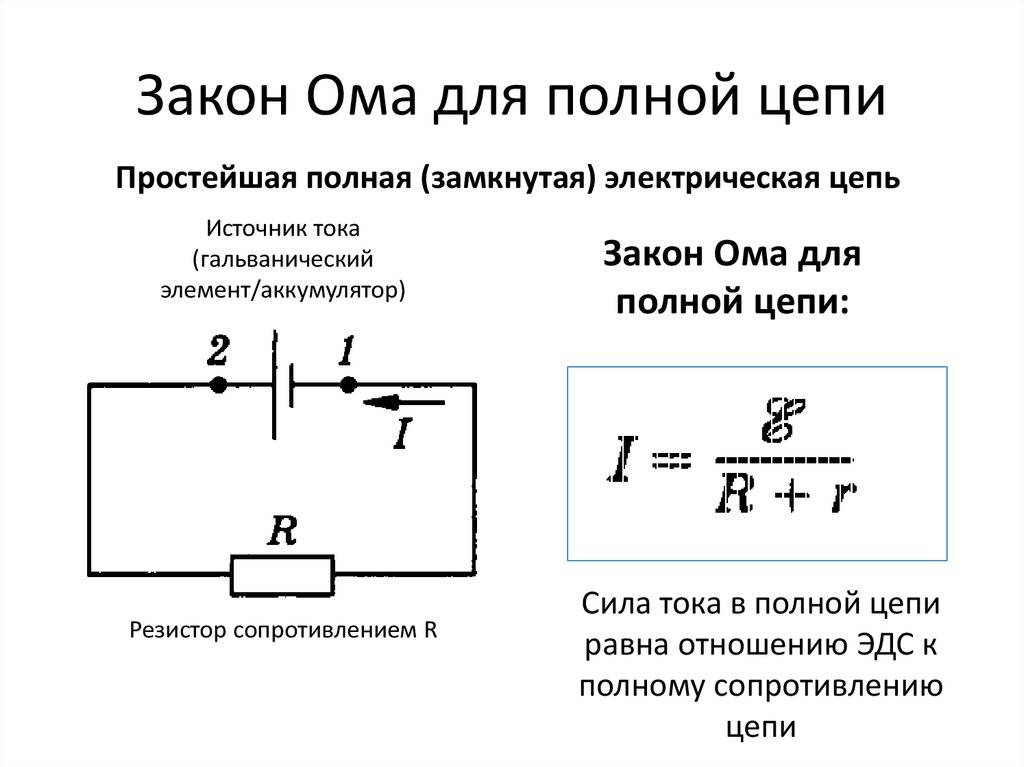 А я на этом с вами прощаюсь.
А я на этом с вами прощаюсь.
Знаменитый русский физик Ленц и английский физик Джоуль, проводя опыты по изучению тепловых действий электрического тока, независимо друг от друга вывели закон Джоуля-Ленца. Данный закон отражает взаимосвязь количества теплоты, выделяемого в проводнике, и электрического тока, проходящего по этому проводнику в течение определенного периода времени.
Простые примеры расчета
Бытовая сеть переменного тока
Пример №1. Проверка ТЭНа.
В стиральную машину встроен трубчатый электронагреватель 1,25 кВт на 220 вольт. Требуется проверить его исправность замером сопротивления.По мощности рассчитываем ток и сопротивление.
Проверяем расчет сопротивления калькулятором по току и напряжению. Данные совпали. Можно приступать к электрическим замерам.
Пример №2. Проверка сопротивления двигателя
Допустим, что мы купили моющий пылесос на 1,6 киловатта для уборки помещений. Нас интересует ток его потребления и сопротивление электрического двигателя в рабочем состоянии.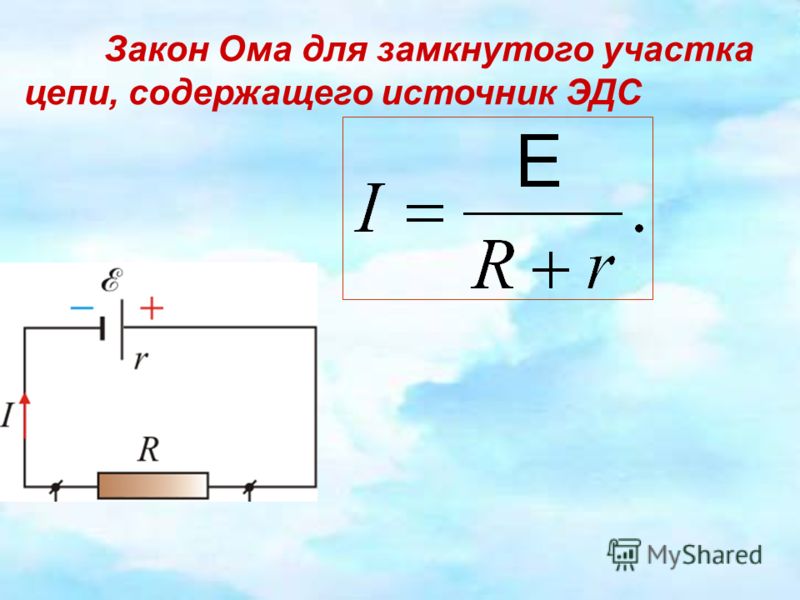 Считаем ток:
Считаем ток:
Вводим в графы калькулятора напряжение 220 вольт и ток 7,3 ампера. Запускаем расчет. Автоматически получим данные:
- сопротивление двигателя — 30,1 Ома;
- мощность 1600 ватт.
Цепи постоянного тока
Рассчитаем сопротивление нити накала галогенной лампочки на 55 ватт, установленной в фаре автомобиля на 12 вольт.
Считаем ток:
Вводим в калькулятор 12 вольт и 4,6 ампера. Он вычисляет:
- сопротивление 2,6 ома.
- мощность 5 ватт.
Здесь обращаю внимание на то, что если замерить сопротивление в холодном состоянии мультиметром, то оно будет значительно ниже. Это свойство металлов позволяет создавать простые и относительно дешевые лампы накаливания без сложной пускорегулирующей аппаратуры, необходимой для светодиодных и люминесцентных светильников
Это свойство металлов позволяет создавать простые и относительно дешевые лампы накаливания без сложной пускорегулирующей аппаратуры, необходимой для светодиодных и люминесцентных светильников.
Другими словами: изменение сопротивления вольфрама при нагреве до раскаленного состояния ограничивает возрастание тока через него. Но в холодном состоянии металла происходит бросок тока. От него нить может перегореть.
Для продления ресурса работы подобных лампочек используют схему постепенной, плавной подачи напряжения от нуля до номинальной величины.
В качестве простых, но надежных устройств для автомобиля часто используется релейная схема ограничения тока, работающая ступенчато.
При включении выключателя SA сопротивление резистора R ограничивает бросок тока через холодную нить накала. Когда же она разогреется, то за счет изменения падения напряжения на лампе HL1 электромагнит с обмоткой реле KL1 поставит свой контакт на удержание.
Он зашунтирует резистор, чем выведет его из работы. Через нить накала станет протекать номинальный ток схемы.
Закон Ома — формула
Формула закона Ома может быть использована, когда известно две из трех переменных. Соотношение между сопротивлением, током и напряжением может быть записано по-разному. Для усвоения и запоминания может быть полезен «треугольник Ома».
Для усвоения и запоминания может быть полезен «треугольник Ома».
или
или
Ниже приведены два примера использования такого треугольного калькулятора.
| Имеем резистор сопротивлением в 1 Ом в цепи с падением напряжения от 100В до 10В на своих выводах.Какой ток протекает через этот резистор?Треугольник напоминает нам, что: | |
| Имеем резистор сопротивлением в 10 Ом через который протекает ток в 2 Ампера при напряжении 120В.Какое будет падение напряжения на этом резисторе?Использование треугольника показывает нам, что:Таким образом, напряжение на выводе будет 120-20 = 100 В. |
Закон Ома для полной цепи
- Подробности
- Просмотров: 479
«Физика — 10 класс»
Сформулируйте закон Ома для участка цепи.
Из каких элементов состоит электрическая цепь?
Для чего служит источник тока?
Рассмотрим простейшую полную (т. е. замкнутую) цепь, состоящую из источника тока (гальванического элемента, аккумулятора или генератора) и резистора сопротивлением R (рис. 15.10). Источник тока имеет ЭДС Ε и сопротивление r.
15.10). Источник тока имеет ЭДС Ε и сопротивление r.
В генераторе r — это сопротивление обмоток, а в гальваническом элементе сопротивление раствора электролита и электродов.
Сопротивление источника называют внутренним сопротивлением в отличие от внешнего сопротивления R цепи.
Закон Ома для замкнутой цепи связывает силу тока в цепи, ЭДС и полное сопротивление цепи R + r. Эта связь может быть установлена теоретически, если использовать закон сохранения энергии и закон Джоуля—Ленца (15.14).
Пусть за время Δt через поперечное сечение проводника проходит электрический заряд Δq. Тогда работу сторонних сил при перемещении заряда Δq можно записать так: Аст = ΕΔq. Согласно определению силы тока (15.1) Δq = IΔt. Поэтому
Аст = ΕIΔt. (15.17)
При совершении этой работы на внутреннем и внешнем участках цепи, сопротивления которых г и Я, выделяется некоторое количество теплоты. По закону Джоуля—Ленца оно равно:
Q = I2RΔt + I2rΔt. (15.18)
(15.18)
По закону сохранения энергии Аст = Q, откуда получаем
Ε = IR + 1r. (15.19)
Произведение силы тока и сопротивления участка цепи называют падением напряжения на этом участке.
Таким образом, ЭДС равна сумме падений напряжения на внутреннем и внешнем участках замкнутой цепи.
Закон Ома для замкнутой цепи:
Сила тока в замкнутой цепи равна отношению ЭДС источника тока к полному сопротивлению цепи.
Согласно этому закону сила тока в цепи зависит от трёх величин: ЭДС Ε сопротивлений R внешнего и г внутреннего участков цепи. Внутреннее сопротивление источника тока не оказывает заметного влияния на силу тока, если оно мало по сравнению с сопротивлением внешней части цепи (R >> r). При этом напряжение на зажимах источника примерно равно ЭДС: U = IR = Ε — Ir ≈ Ε
При коротком замыкании, когда R ≈ 0, сила тока в цепи и определяется именно внутренним сопротивлением источника и при электродвижущей силе в несколько вольт может оказаться очень большой, если r мало (например, у аккумулятора r ≈ 0,1 — 0,001 Ом). Провода могут расплавиться, а сам источник выйти из строя.
Провода могут расплавиться, а сам источник выйти из строя.
Если цепь содержит несколько последовательно соединённых элементов с ЭДС Ε1, Ε2, Ε3 и т. д., то полная ЭДС цепи равна алгебраической сумме ЭДС отдельных элементов.
Для определения знака ЭДС любого источника нужно вначале условиться относительно выбора положительного направления обхода контура.
На рисунке (15.11) положительным (произвольно) считают направление обхода против часовой стрелки.
Если при обходе цепи данный источник стремится вызвать ток в направлении обхода, то его ЭДС считается положительной: Ε > 0. Сторонние силы внутри источника совершают при этом положительную работу.
Если же при обходе цепи данный источник вызывает ток против направления обхода цепи, то его ЭДС будет отрицательной: Ε < 0. Сторонние силы внутри источника совершают отрицательную работу. Так, для цепи, изображённой на рисунке 15.11, при обходе контура против часовой стрелки получаем следующее уравнение:
Εп = Ε1 + Ε2 + Ε3 = lΕ1| — |Ε2| + |Ε3|
Если Εп > 0, то согласно формуле (15. 20) сила тока I > 0, т. е. направление тока совпадает с выбранным направлением обхода контура. При Εп < 0, наоборот, направление тока противоположно выбранному направлению обхода контура. Полное сопротивление цепи Rп равно сумме всех сопротивлений (см. рис. 15.11):
20) сила тока I > 0, т. е. направление тока совпадает с выбранным направлением обхода контура. При Εп < 0, наоборот, направление тока противоположно выбранному направлению обхода контура. Полное сопротивление цепи Rп равно сумме всех сопротивлений (см. рис. 15.11):
Rп = R + r1 + r2 + r3.
Для любого замкнутого участка цепи, содержащего несколько источников токов, справедливо следующее правило: алгебраическая сумма падений напряжения равна алгебраической сумме ЭДС на этом участке (второе правило Кирхгофа):
I1R1+ I2R2 + … + InRn = Ε1 + Ε2 + … + Εm
Следующая страница «Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»»
Назад в раздел «Физика — 10 класс, учебник Мякишев, Буховцев, Сотский»
Законы постоянного тока — Физика, учебник для 10 класса — Класс!ная физика
Электрический ток. Сила тока —
Сила тока —
Закон Ома для участка цепи. Сопротивление —
Электрические цепи. Последовательное и параллельное соединения проводников —
Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» —
Работа и мощность постоянного тока —
Электродвижущая сила —
Закон Ома для полной цепи —
Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»
Классическая формулировка
Этот простой вариант трактовки, известный нам со школы.
Однородный открытый участок электроцепи
Формула в интегральной форме будет иметь следующий вид:
Формула в интегральной форме
То есть, поднимая напряжение, мы тем самым увеличиваем ток. В то время, как увеличение такого параметра, как «R», ведет к снижению «I». Естественно, что на рисунке сопротивление цепи показано одним элементом, хотя это может быть последовательное, параллельное (вплоть до произвольного)соединение нескольких проводников.
В дифференциальной форме закон мы приводить не будем, поскольку в таком виде он применяется, как правило, только в физике.
Опытное определение зависимости силы тока от сопротивления при постоянном напряжении
Для того, чтобы определить зависимость силы тока от сопротивления проводника, мы проведем еще один опыт. Теперь мы будем знать электрическое сопротивление тех проводников, которые будем использовать.
Обратите внимание, что в ходе опыта напряжение на концах используемых проводников должно быть постоянным. Эта величина не должна изменяться, чтобы мы могли корректно оценить зависимость силы тока от сопротивления
Соберем электрическую цепь из источника тока, ключа, амперметра, проводника. К проводнику параллельно подсоединим вольтметр (рисунок 1).
Проводников у нас будет три разных. Они обладают разными сопротивлениями. Мы будем поочередно подключать их в цепь. Каждый раз мы будем фиксировать показания амперметра.
По показаниям вольтметра необходимо следить, чтобы напряжение на концах каждого проводника было одинаковым.
Рисунок 1. Установление зависимости силы тока от сопротивления проводника
{"questions":,"explanations":,"answer":}}}]}Закон Ома для участка цепи – расчет цепей
Простейший вариант наглядно представлен на рисунке. Это однородный участок цепи открытого типа.
Для его описания применяется известная формула, которая будет иметь следующую форму:
I = U/R, где I является силой тока, U – напряжением, R – сопротивлением.
Данная формула является интегральной. С ее помощью хорошо видно, как при возрастании напряжения, увеличивается и сила тока. Но, если увеличить сопротивление, то сила тока, наоборот, будет понижаться.
На схеме изображен всего один элемент, обладающий сопротивлением. На практике, их может быть любое количество. Они могут соединяться последовательно, параллельно и смешанным способом.
Как найти с помощью формулы напряжение
Людей, интересующихся электричеством и физикой, всегда волнует вопрос, как найти напряжения, если известны другие характеристики. Его можно найти через многие формулы: в соответствии с законом Ома, через работу тока, путём сложения всех напряжений в электрической цепи и практическим способом – с помощью вольтметра. Как вычислить показатель с помощью последнего способа было описано выше.
Его можно найти через многие формулы: в соответствии с законом Ома, через работу тока, путём сложения всех напряжений в электрической цепи и практическим способом – с помощью вольтметра. Как вычислить показатель с помощью последнего способа было описано выше.
Важно! В цепях с последовательным соединением общее напряжение – сумма значений каждой нагрузки. При параллельном соединении общее напряжение равно значению каждой лампочки, у которых оно также эквивалентно
Вам это будет интересно WAGO соединители
Измерение напряжения
По каким формулам вычисляется напряжение через работу и сама сила тока, рассказывают на уроках физики, так как эти величины считаются базовыми. Работа тока равна произведению напряжения и заряда: A = U*q. Также, из этой формулы выводится A = U*I*t, так как заряд – произведение силы тока и времени. Из них следует, что U = A/q или U = A/(I*t). Кроме того, одной из основных является формула напряжения, выведенная из закона Ома: U = R/I.
Важно! Определить напряжение можно и через мощность электрического тока. Мощность равна A/t, и, так как A = U*I*t, конечная формула выглядит, как P = (U*I*t)/t
Мощность равна A/t, и, так как A = U*I*t, конечная формула выглядит, как P = (U*I*t)/t
Здесь t сократится, и останется P = U*I, из которой следует, что U = P/I.
Сопротивление проводника/цепи.
Термин «сопротивление» уже фактически говорит сам за себя ) Итак, сопротивление — физическая величина, характеризующая свойства проводника препятствовать (сопротивляться) прохождению электрического тока.
Рассмотрим медный проводник длиной l с площадью поперечного сечения, равной S:
Сопротивление проводника зависит от нескольких факторов:
- удельного сопротивления проводника \rho
- длины проводника l
- площади поперечного сечения проводника S
Удельное сопротивление — это табличная величина. Формула, с помощью которой можно вычислить сопротивление данного проводника выглядит следующим образом:
R = \rho\medspace \frac{l}{S}Для нашего случая \rho будет равно 0,0175 (Ом * кв. мм / м) — удельное сопротивление меди. Пусть длина проводника составляет 0.5 м, а площадь поперечного сечения равна 0.2 кв. мм. Тогда:
Пусть длина проводника составляет 0.5 м, а площадь поперечного сечения равна 0.2 кв. мм. Тогда:
R =0,0175 \cdot \frac{0.5}{0.2} = 0.04375\medspace ОмИ, как вы уже поняли из примера, единицей измерения сопротивления является Ом. Рассмотрим взаимосвязь напряжения, силы тока и сопротивления цепи.
Основные понятия закона Ома
Как понять закон Ома? Нужно просто разобраться в том, что есть что в его определении. И начать следует с определения силы тока, напряжения и сопротивления.
Сила тока I
Пусть в каком-то проводнике течет ток. То есть, происходит направленное движение заряженных частиц – допустим, это электроны. Каждый электрон обладает элементарным электрическим зарядом (e= -1,60217662 × 10-19 Кулона). В таком случае через некоторую поверхность за определенный промежуток времени пройдет конкретный электрический заряд, равный сумме всех зарядов протекших электронов.
Отношение заряда к времени и называется силой тока. Чем больший заряд проходит через проводник за определенное время, тем больше сила тока. Сила тока измеряется в Амперах.
Сила тока измеряется в Амперах.
Напряжение U, или разность потенциалов
Это как раз та штука, которая заставляет электроны двигаться. Электрический потенциал характеризует способность поля совершать работу по переносу заряда из одной точки в другую. Так, между двумя точками проводника существует разность потенциалов, и электрическое поле совершает работу по переносу заряда.
Физическая величина, равная работе эффективного электрического поля при переносе электрического заряда, и называется напряжением. Измеряется в Вольтах. Один Вольт – это напряжение, которое при перемещении заряда в 1 Кл совершает работу, равную 1 Джоуль.
Сопротивление R
Ток, как известно, течет в проводнике. Пусть это будет какой-нибудь провод. Двигаясь по проводу под действием поля, электроны сталкиваются с атомами провода, проводник греется, атомы в кристаллической решетке начинают колебаться, создавая электронам еще больше проблем для передвижения. Именно это явление и называется сопротивлением. Оно зависит от температуры, материала, сечения проводника и измеряется в Омах.
Оно зависит от температуры, материала, сечения проводника и измеряется в Омах.
Памятник Георгу Симону Ому
Закон Ома… Связь между напряжением, током и сопротивлением
Теоретические термины и определения
Следующие определения относятся к базовой теории электричества. Важно, чтобы установщики и инспекторы обладали практическими знаниями в области теории электричества. Такие знания часто необходимы для определения надлежащего размера проводников для цепей с различными нагрузками.
Вольт — единица электрического давления — это давление, необходимое для передачи одного ампера через сопротивление в один ом; сокращенно «Е», первая буква термина электродвигатель сила .
Ампер — единица электрического тока, который будет протекать через один ом под давлением в один вольт за одну секунду; сокращенно «И», первая буква термина интенсивность тока .
Ом — единица электрического сопротивления — это сопротивление, через которое один вольт действует на один ампер; сокращенно «R», первая буква термина сопротивление .
Вт — это единица измерения энергии, протекающей в электрической цепи в любой момент времени. Это также количество работы, выполняемой в электрической цепи. Термины ватт или киловатт чаще использовались для выражения количества работы, выполненной в электрической цепи, а не термин джоуль . Ватты — это произведение вольт и ампер, иногда их называют вольт-амперами. Одна тысяча вольт-ампер обозначается как один киловольт-ампер или один кВА.
Закон Ома
Джордж Саймон Ом открыл взаимосвязь между током, напряжением и сопротивлением в электрической цепи в 1826 году. Экспериментально он обнаружил, что давление равно произведению силы тока и сопротивления; эта зависимость называется законом Ома. Этот закон является практической основой, на которой основано большинство электрических расчетов. Формула может быть выражена в различных формах и по ее использованию, как в трех примерах, показанных на рисунке 1.
Рисунок 1. Основные примеры закона Ома и его применение
Основные примеры закона Ома и его применение
Если известны любые два значения, то третье можно найти по формуле. Например, если известны сопротивление и напряжение, ток можно определить, разделив напряжение на сопротивление. Это может быть полезно при определении количества тока, который будет протекать в цепи, для правильного выбора размеров проводников, а также устройств перегрузки по току.
Лошадиная сила. Механическая мощность обычно выражается в лошадиных силах, а электрическая мощность – в ваттах. Срок лошадиных сил возникла как объем работы, которую сильная лондонская упряжная (тягловая) лошадь могла выполнить за короткий промежуток времени. Он также использовался для измерения мощности паровых двигателей. Одна лошадиная сила, сокращенно «HP», равна работе, необходимой для подъема 33 000 фунтов на один фут (33 000 футо-фунтов) за одну минуту. Это то же самое, что поднять 550 фунтов на один фут за одну секунду.
Часто необходимо преобразовать мощность из одних единиц в другие, и уравнение на рисунке 2 используется для преобразования лошадиных сил в ватты или ватт в лошадиные силы.
Рисунок 2. Базовая формула HP
Формула HP применима к лабораторным условиям, поскольку двигатели потребляют больше энергии, чем выдают. Это происходит из-за того, что мощность расходуется в виде тепла в двигателе для преодоления трения в подшипниках, сопротивления ветра и других факторов. Например, двигатель мощностью 1 л.с. (746 ватт) может потреблять около 1000 ватт, разница расходуется на преодоление уже указанных факторов. Для определения фактической мощности однофазных двигателей необходимо учитывать коэффициент КПД двигателя (см. рис. 3).
Рисунок 3. Базовые формулы коэффициента мощности
Колесо Ватт
Колесо Ватта было разработано и опубликовано во многих руководствах и в нескольких вариантах для иллюстрации ватт или мощности и их связи с элементами закона Ома. Как показано в этом тексте, он точен для цепей постоянного тока и резистивных нагрузок цепей переменного тока, где коэффициент мощности близок к 100 процентам или единице (см. рис. 4). Не пытайтесь использовать его для нагрузки двигателя, так как в формулу должны быть включены как коэффициент мощности, так и КПД двигателя (см. рис. 3).
рис. 4). Не пытайтесь использовать его для нагрузки двигателя, так как в формулу должны быть включены как коэффициент мощности, так и КПД двигателя (см. рис. 3).
Рисунок 4. Колесо Ватта и закон Ома
В цепях переменного тока мы используем термин импеданс вместо омов для представления сопротивления цепи Импеданс – это полное сопротивление току, протекающему в цепи переменного тока; измеряется в омах. Полное сопротивление включает сопротивление, емкостное сопротивление и индуктивное сопротивление. Последние два фактора уникальны для цепей переменного тока и обычно могут игнорироваться в таких цепях, как нагрузки освещения с лампами накаливания и цепи нагревателей, состоящие из резистивных нагрузок. Подробное объяснение емкостного реактивного сопротивления и индуктивного сопротивления выходит за рамки этого текста, но его можно найти во многих превосходных учебниках по теории электричества.
Закон Ома и основы теории электротехники
Электрический ток, протекающий через любую электрическую цепь, можно сравнить с водой под давлением, протекающей через пожарный рукав. Вода, протекающая через пожарный шланг, измеряется в галлонах в минуту (GPM), а электричество, протекающее по цепи, измеряется в амперах (А).
Вода, протекающая через пожарный шланг, измеряется в галлонах в минуту (GPM), а электричество, протекающее по цепи, измеряется в амперах (А).
Вода течет по шлангу, когда на него оказывается давление и открывается клапан. Давление воды измеряется в фунтах на квадратный дюйм (psi). Электрический ток течет по электрическому проводнику, когда к нему приложено электрическое давление и предусмотрен путь для протекания тока. Подобно тому, как «фунты на квадратный дюйм» (давление) заставляют течь галлоны в минуту, так и «вольты» (давление) заставляют течь «ампер» (ток).
Чтобы протолкнуть такое же количество воды через маленький шланг, требуется большее давление, чем через большой шланг. Небольшой шланг при том же давлении, что и шланг большего размера, пропустит гораздо меньше воды за определенный период времени. Из этого следует, что маленький шланг оказывает большее сопротивление потоку воды.
В электрической цепи большее электрическое давление (вольты) будет пропускать ток определенной силы (ампер) через небольшой проводник (сопротивление), чем то, которое требуется для подачи того же количества тока (амперы) через проводник большего размера (сопротивление ). Проводник меньшего размера будет пропускать меньший ток (ампер), чем проводник большего размера, если к каждому проводнику будет приложено одинаковое электрическое давление (вольты) в течение того же периода времени. Можно предположить, что меньший проводник имеет большее сопротивление (Ом), чем больший проводник. Таким образом, мы можем определить сопротивление как «свойство тела, которое сопротивляется или ограничивает поток электричества через него». Сопротивление измеряется в Ом. — термин, аналогичный трению в шланге или трубе.
Проводник меньшего размера будет пропускать меньший ток (ампер), чем проводник большего размера, если к каждому проводнику будет приложено одинаковое электрическое давление (вольты) в течение того же периода времени. Можно предположить, что меньший проводник имеет большее сопротивление (Ом), чем больший проводник. Таким образом, мы можем определить сопротивление как «свойство тела, которое сопротивляется или ограничивает поток электричества через него». Сопротивление измеряется в Ом. — термин, аналогичный трению в шланге или трубе.
Взято из Электрические системы жилых домов на одну и две семьи, , 8 th Edition. Эту книгу можно приобрести по адресу www.iaei.org/web/shop или по адресу Amazon.com .
Закон Ома и начало расчета напряжения, тока и сопротивления
Независимо от того, являетесь ли вы любителем, техническим специалистом или планируете карьеру в области дизайна, вы должны начать с хорошего понимания того, с чем вы работаете. Для электроники это означает работу с законом Ома. Основной принцип закона Ома, который представляет собой взаимосвязь между напряжением, током и сопротивлением, является основой, на которой построена электроника. И точно так же, как под зданием требуется прочный фундамент, чтобы поддерживать его, ваша способность работать с электричеством и использовать его зависит от прочного фундамента закона Ома и вашего понимания его.
Для электроники это означает работу с законом Ома. Основной принцип закона Ома, который представляет собой взаимосвязь между напряжением, током и сопротивлением, является основой, на которой построена электроника. И точно так же, как под зданием требуется прочный фундамент, чтобы поддерживать его, ваша способность работать с электричеством и использовать его зависит от прочного фундамента закона Ома и вашего понимания его.
Ом — это стандартная единица электрического сопротивления, но вам может быть интересно, откуда взялся этот термин и как все это влияет на закон Ома. Все началось с немецкого физика и математика по имени Георг Ом, и термин «ом» был назван в его честь. Так откуда же взялся закон Ома и что это за закон? Давайте посмотрим поближе.
Георг Ом, создатель закона Ома
Родившийся в 1789 году, Георг Ом начал свою профессиональную жизнь в качестве учителя математики. Однако поначалу он не был доволен своей профессией, и разные школы, в которых он первоначально преподавал, тоже не были лучшими. В конце концов, он стал преподавать математику и физику в иезуитской гимназии Кёльна. Это ему больше нравилось, поскольку у школы была хорошая репутация в области естественнонаучного образования.
В конце концов, он стал преподавать математику и физику в иезуитской гимназии Кёльна. Это ему больше нравилось, поскольку у школы была хорошая репутация в области естественнонаучного образования.
Георг Ом начал экспериментировать с электричеством, что привело его к публикации статей на эту тему. В 1827 г. он опубликовал свою книгу; «Гальваническая цепь, исследованная математически», где он дал свою полную теорию электричества, включая формулу того, что в конечном итоге будет названо законом Ома. К сожалению, школа, в которой он работал, не оценила его работу, в результате чего Ом в конечном итоге ушел в отставку. Позже он перешел на должности в других школах, где его работа получила более широкое признание, а его открытие взаимосвязи между напряжением, током и сопротивлением стало известно во всем мире как закон Ома.
Формулы, используемые для описания закона Ома
Что такое закон Ома?
Георг Ом открыл и определил, как электрическое напряжение, ток и сопротивление влияют друг на друга в цепи. Цепь представляет собой замкнутый контур электричества или заряда. Компоненты, которые мы используем в цепи, будут контролировать заряд, чтобы он вел себя так, как нам нужно для работы конкретной цепи. Для начала первое, что мы сделаем, это определим эти термины:
Цепь представляет собой замкнутый контур электричества или заряда. Компоненты, которые мы используем в цепи, будут контролировать заряд, чтобы он вел себя так, как нам нужно для работы конкретной цепи. Для начала первое, что мы сделаем, это определим эти термины:
Напряжение : В цепи одна точка будет иметь больший заряд, чем другая. Эта разница заряда между двумя точками представляет собой напряжение и измеряется в вольтах.
Ток : Количество или объем заряда, протекающего по цепи за определенный период времени. Ток измеряется в амперах, которые обычно называют амперами.
Сопротивление : Некоторые материалы будут сопротивляться потоку электричества, и когда эти материалы используются в цепи, они создают сопротивление. Чем больше сопротивление в цепи, тем меньше заряда будет течь. Сопротивление измеряется в омах.

Для лучшего объяснения взаимосвязи между напряжением, током и сопротивлением может быть полезно использовать аналогию с резервуаром для воды с хостом, соединенным со дном.
Заряд будет представлен водой в баке, которая будет вытекать из шланга.
Напряжение будет представлено давлением потока воды.
Ток будет представлен объемом расхода воды.
Сопротивление будет представлено диаметром шланга.
Если наш резервуар для воды приподнят над землей, давление воды, вытекающей из шланга на дне, будет представлять собой напряжение, а объем протекающей воды будет представлять ток. Если бы диаметр шланга стал меньше, поток воды был бы сужен, что привело бы к уменьшению протекания воды. Если бы диаметр шланга стал больше, то через него могло бы пройти больше воды. Подводя итог, можно сказать, что цепь с более высоким сопротивлением будет ограничивать количество заряда, протекающего через нее.
Подводя итог, можно сказать, что цепь с более высоким сопротивлением будет ограничивать количество заряда, протекающего через нее.
Чтобы выразить закон Ома в виде формулы, в которой напряжение равно произведению силы тока на сопротивление, укажите V = напряжение в вольтах, I = ток в амперах и R = сопротивление в омах. Это позволяет легко решить для каждого из трех элементов:
В = I х R
И = В / Р
Р = В/Я
Следовательно, в цепи на 12 вольт, в которой есть компонент с сопротивлением 6 Ом, мы можем рассчитать, что 12 вольт, разделенные на сопротивление 6 Ом, дадут ток в 2 ампера для нашей цепи. Хотя это чрезвычайно простое объяснение, вы можете видеть, что закон Ома будет частью почти всего в электронике.
PSpice — это симулятор схем, который позволит вам находить параметры в вашей схеме на основе целей схемы
Почему важен закон Ома?
V=IR, или закон Ома, является наиболее фундаментальным законом в электричестве, и он будет влиять на каждую цепь, с которой вы будете работать. Усилия Георга Ома ознаменовали собой первую работу в области теории и анализа электричества, которая представляет собой процесс нахождения напряжений и токов через все компоненты цепи.
Усилия Георга Ома ознаменовали собой первую работу в области теории и анализа электричества, которая представляет собой процесс нахождения напряжений и токов через все компоненты цепи.
Хотя сначала Ом столкнулся с холодным отношением к своему открытию, он упорствовал, и в конце концов важность закона Ома была признана всеми. Он остается наиболее широко используемым из всех различных правил и законов, касающихся электрических цепей и их поведения.
По мере того, как вы применяете закон Ома и другие электронные принципы и правила в своей работе, вам потребуются инструменты анализа, которые могут моделировать ваши схемы и точно сообщать вам об их поведении. Использование надлежащих инструментов SPICE может подтвердить теоретические концепции с помощью моделирования, позволит вам создавать более сложные комбинации схем перед компоновкой, а также сэкономит огромное количество времени на ручных вычислениях.
PSpice, входящий в комплект инструментов проектирования Cadence, дает вам возможность моделировать ваши схемы в программном обеспечении, экономя ваше время на самостоятельное создание и тестирование этих схем вручную. PSpice — это предпочтительный инструмент моделирования для пользователей, независимо от того, начинаете ли вы свой бизнес или уже являетесь опытным инженером. Вы также можете полностью воссоздать схему, которая у вас есть, в инструменте создания схем OrCAD Capture, чтобы ее можно было легко смоделировать с помощью PSpice.
PSpice — это предпочтительный инструмент моделирования для пользователей, независимо от того, начинаете ли вы свой бизнес или уже являетесь опытным инженером. Вы также можете полностью воссоздать схему, которая у вас есть, в инструменте создания схем OrCAD Capture, чтобы ее можно было легко смоделировать с помощью PSpice.
Если вы хотите узнать больше о том, как инструменты моделирования от Cadence станут для вас лучшим решением, поговорите с нами и нашей командой экспертов.
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на Linkedin Посетить сайт Больше контента от Cadence PCB Solutions
Загрузка, подождите
Ошибка – что-то пошло не так!
Хотите последние новости о печатных платах?
Подпишитесь на нашу ежемесячную рассылку новостей
Спасибо!
Знакомство с законом Ома и примерами — производство печатных плат и сборка печатных плат
Вам интересно узнать, не разряжается ли аккумулятор вашего автомобиля? Сколько энергии от настенной розетки идет на вашу кофеварку? Или, может быть, вы боретесь с проектом в области электричества и нуждаетесь в переподготовке! Что бы это ни было, этот пост в блоге научит вас основам закона Ома.
При изучении электричества взаимосвязь между различными электрическими величинами играет ключевую роль. Эти электрические величины включают ток, напряжение, сопротивление, емкость, индуктивность и т. д. Мы рассмотрим взаимосвязь между сопротивлением, напряжением и током в электрической установке. Закон Ома был сформулирован в 1827 году физиком Георгом Симоном Омом, который изучал, как электродвижущая сила, сопротивление и ток связаны с электрической цепью. Его исследование привело к формулировке и публикации закона Ома, который в значительной степени опирался на вдохновение предыдущих ученых, анализировавших сопротивление и другие связанные теории. В качестве источника напряжения использовалась термопара, температура перехода которой пропорциональна напряжению на ее клеммах в этой формулировке. Мы можем начать с определения закона Ома, а затем изучить различные его принципы, а затем углубиться в его взаимосвязь с другими формулировками, его приложениями, а также его ограничениями, если они существуют.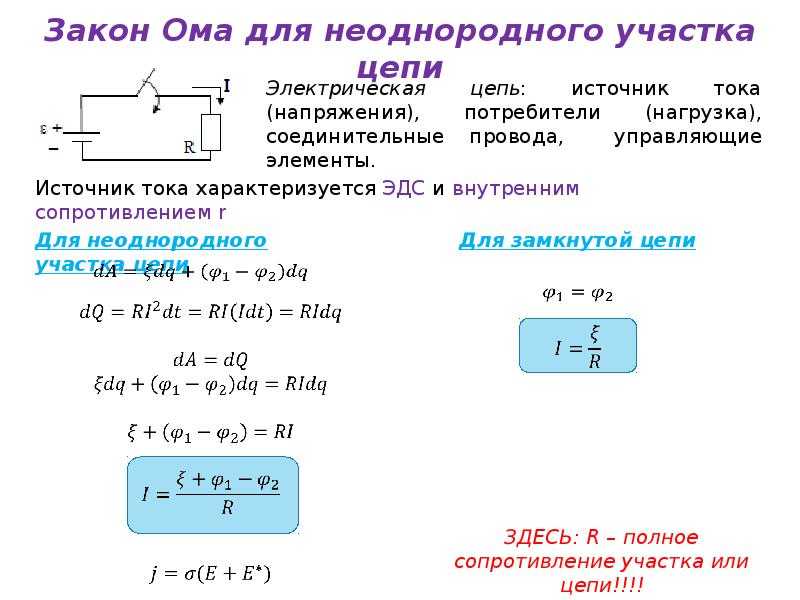
Запросить изготовление и сборку печатных плат сейчас
Что такое закон Ома?
Определение закона Ома иллюстрирует связь между разностью потенциалов, электрическим током и сопротивлением. Согласно закону Ома, величина стабильного тока, протекающего через электрический материал, прямо пропорциональна или зависит от разности потенциалов (напряжения) на его концах. Другими словами, закон Ома гласит, что разность потенциалов на концах электропроводного материала прямо пропорциональна количеству электрического тока, протекающего через него, и обратно пропорциональна его общему сопротивлению, если его температура, а также физические условия соблюдены. поддерживается постоянным. Однако в некоторых материалах, таких как нить накаливания лампы, ее температура увеличивается с увеличением тока через них, и, следовательно, закон Ома может быть неприменим.
Анализ закона Ома с использованием аналогии с водопроводной трубой
Люди придумали определенные сравнения с целью достижения ясности закона Ома. Например, представление о воде, текущей по трубам, может объяснить соотношение закона Ома в электрической цепи. В этом случае мы принимаем напряжение за давление воды, количество воды, проходящей через трубу, представляет собой общий ток в цепи, а размер трубы представляет собой сопротивление. В большой трубе (более низкое сопротивление) приложение большего давления (напряжения) заставляет больше воды (тока) течь по трубе. Следовательно, когда сопротивление поддерживается постоянным, увеличение напряжения на концах материала приводит к соответствующему увеличению количества, протекающего через материал. Ясно, что это показывает, что разность потенциалов на концах материала прямо пропорциональна количеству электрического тока, протекающего через материал.
Например, представление о воде, текущей по трубам, может объяснить соотношение закона Ома в электрической цепи. В этом случае мы принимаем напряжение за давление воды, количество воды, проходящей через трубу, представляет собой общий ток в цепи, а размер трубы представляет собой сопротивление. В большой трубе (более низкое сопротивление) приложение большего давления (напряжения) заставляет больше воды (тока) течь по трубе. Следовательно, когда сопротивление поддерживается постоянным, увеличение напряжения на концах материала приводит к соответствующему увеличению количества, протекающего через материал. Ясно, что это показывает, что разность потенциалов на концах материала прямо пропорциональна количеству электрического тока, протекающего через материал.
Какое математическое выражение закона Ома?
Математически закон Ома обозначается как V=IR,
, где V представляет собой напряжение на концах материала, измеряемое в вольтах (В), I представляет электрический ток, проходящий через материал, измеряемый в амперах (А) , а R представляет собой сопротивление материала, измеренное в омах (Ом).
Из уравнения V=IR ток (I) можно выразить через разность потенциалов (V) и сопротивление (R) следующим образом:
Мы также можем выразить сопротивление материала (R) через разность потенциалов, (В) через материал и электрический ток (I) через материал следующим образом: Теперь
Магический треугольник для формулы закона Ома
Мы представляем уравнения закона Ома в виде простого треугольника, отображающего три переменные, разность потенциалов (V), ток (I) и сопротивление (R), как показано на рисунок ниже:
С помощью этого треугольника, учитывая две переменные, третью можно легко вычислить, покрыв рассматриваемую переменную, а затем используя две другие с оператором между ними. Например, зная разность потенциалов и сопротивление в цепи, мы можем найти формулу для расчета тока в цепи, покрыв I треугольником и взяв V и R с оператором между ними. Следовательно, I=V/R.
Примеры задач по закону Ома
Пример 1
Через электрический чайник с сопротивлением 80,0 Ом протекает ток силой 4,0 А. Найдите разность потенциалов на электрическом чайнике.
Найдите разность потенциалов на электрическом чайнике.
Решение
. разница(В) 9Пример 2 Если через резистор протекает ток 5,0 А, рассчитайте значение сопротивления этого резистора. (В этом случае предположим, что проводники, используемые в установке, имели незначительное сопротивление)
Решение
Here, V= 20.0V
I= 5.0A
By Ohm’s law,
Making R the subject of this formula,
Therefore,
= 4.0 Ω
Example 3
Резистивная лампочка с сопротивлением 10,0 Ом подключена к батарее, создающей ЭДС 12,0 В. Рассчитайте количество электрического тока, протекающего через лампочку.
Решение
В этой задаче даны сопротивление (R) и разность потенциалов (V).
R= 10,0 Ом
V= 12,0 В
Применяя закон Ома: левая часть уравнения на R.
Следовательно, уравнение принимает вид:
=1.2A
Запросить производство и сборку печатных плат
Графическое представление закона Ома V) по всему материалу.
Например, при следующих данных:
| Напряжение (В) | 0,0 | 1,0 | 2,0 | 3,0 2 | |
| Current (A) | 0,0 | 1,0 | 2,0 | 3.0 | 4.0 |
График. В целом. можно описать сопротивление проводящего материала как отношение изменения разности потенциалов на его концах к соответствующему изменению электрического тока, протекающего через него.
Экспериментально проверяем закон Ома.
Давайте теперь посмотрим, как мы можем легко проверить закон Ома экспериментально.
Apparatus
- DC supply
- Connecting wires
- Ammeter
- Rheostat
- Voltmeter
- Plug key
- Resistor
Procedure
The circuit is connected as shown in the figure below :
В этом эксперименте первым шагом является замыкание ключа K и регулировка реостата для получения минимальных показаний амперметра и вольтметра. Затем вы постепенно перемещаете клемму реостата, чтобы увеличить электрический ток в цепи, и в то же время записываете значения тока, протекающего через цепь, и соответствующую разность потенциалов на проводе сопротивления. Таким образом, происходит сбор различных значений данных о напряжении и электрическом токе. Затем рассчитывается и записывается отношение V/I. Как вы заметите, это соотношение дает почти одинаковые значения для каждого набора данных.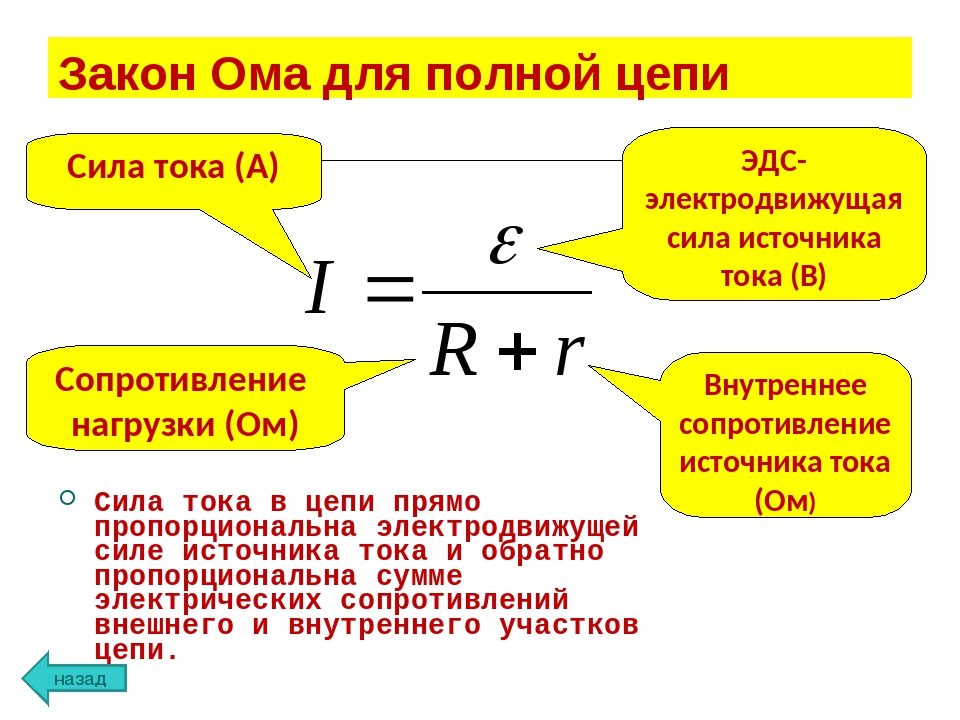 Поскольку это отношение дает константу, оно получает представление R, обозначающее сопротивление электрической цепи. Следовательно, V/I=R.
Поскольку это отношение дает константу, оно получает представление R, обозначающее сопротивление электрической цепи. Следовательно, V/I=R.
Запросить производство и сборку печатных плат
Использование закона Ома для расчета электроэнергии
Мы можем определить электрическую мощность (P) как скорость, с которой электрическая энергия в цепи преобразуется в другие формы энергии, например , тепла, механической энергии или магнитных полей. Мы выражаем электрическую мощность в единицах, известных как ватты (Вт). Применяя закон Ома, можно легко рассчитать электрическую мощность в определенной цепи при условии, что заданы значения тока, напряжения и сопротивления.
Мы используем следующую формулу для определения электрической мощности в данной цепи:
P=VI
По закону Ома, V=IR. Следовательно, мы можем выразить электрическую мощность (P) как:
P=(IR)I
Следовательно, при раскрытии скобок уравнение принимает вид:
P=I 2 R
в некоторых случаях указаны напряжение (В) и сопротивление (R). Поэтому мы рассчитываем электрическую мощность, как показано ниже:
Поэтому мы рассчитываем электрическую мощность, как показано ниже:
P=VI
, но из закона Ома текущий (i) может быть выражен как
замены в формуле для электроэнергии, P = VI
= V ()
= V 2 /R
3 =
V 2 /RТреугольник мощности
Учитывая значения разности потенциалов (В) и электрического тока (I), мы можем легко рассчитать электрическую мощность, используя простой треугольник, известный как треугольник мощности. Мы можем выразить, как показано на рисунке ниже:
Чтобы получить одну из трех переменных, учитывая две другие, вы покрываете рассматриваемую переменную и берете две другие с оператором между ними. Например, зная электрический ток и разность потенциалов, мы можем вычислить электрическую мощность, покрыв P треугольником мощности и взяв I и V с оператором между ними. Следовательно, P=V x I.
Примеры задач на электроэнергию
Пример 1
Электрический утюг подключен к источнику ЭДС 120,0В. Рассчитайте потребляемую им электрическую мощность, если сила тока через него равна 6,0 А.
Рассчитайте потребляемую им электрическую мощность, если сила тока через него равна 6,0 А.
Решение
В этой задаче V = 120,0 В и I = 6,0 А.
Используя формулу для мощности,
P= VI
=120,0 x 6,0
=720,0 Вт
Пример 2
0137Резистор с сопротивлением 20,0 Ом подключен к источнику постоянного тока, создающему ЭДС 12,0 В. Далее рассчитайте полную электрическую мощность в этой электрической цепи.
Раствор
ЗДЕСЬ. Р= В 2 /Р
= 120,0 2 / 20,0
= 720,0 Вт
Пример 3 9000
. Если общее сопротивление в цепи было 30,0 Ом, рассчитайте полную электрическую мощность, рассеиваемую в этой электрической цепи.
Раствор
Учитывая, что ток (I) = 10,0 А, а полное сопротивление (R) = 30,0 Ом, мы можем рассчитать электрическую мощность по формуле: 30,0
= 100,0 x 30,0 = 3000,0 Вт
Запросить производство и сборку печатных плат сейчас
Круговая диаграмма для закона Ома мощность и сопротивление. Например, мы представляем круговую диаграмму, как показано на рисунке ниже:
Матричная таблица для закона Ома
Мы также можем объединить все уравнения для закона Ома в простую матричную таблицу, которая упрощает использование при расчете различных значений.
| Известные | Сопротивление (R) | Ток (I) | Напряжение (В) | Мощность (P) |
| Сопротивление и ток2. . . . . . . . . . . . . . | . . . . . . . . . . . . . . | В = I x R | P = I 2 x R | |
| Ток и напряжение | R = V / I | . . . . . . . . . . . . . . . . . . . . . . . . . . . | . . . . . . . . . . . . . . | P = V x I |
| Мощность и ток | R = P/I 2 | . . . . . . . . . . . . . . | В = П/Я | . . . . . . . . . . . . . . |
| Сопротивление и напряжение | . . . . . . . . . . . . . . | И = В / Р | . . . . . . . . . . . . . . | P = V 2 / R |
| Сопротивление и мощность | . . . . . . . . . . . . . . | I = √ (P / R) | V = √ (Z x R) | . . . . . . . . . . . . . . |
| Напряжение и мощность | R = В 2 / P | I = P / V | . . . . . . . . . . . . . . | . . . . . . . . . . . . . . |
Закон Ома и Ньютона 2
-й -й закон движения В то время как закон Ома касается взаимосвязи между сопротивлением (R), напряжением (В) и током (I) в электрических цепях, 2-й -й -й закон Ньютона фокусируется на связи между силой ( F), ускорение (а) и массу (м). Однако уравнения двух отношений могут основываться на одном и том же принципе, управляющем силой, действующей на разные частицы и материю целиком. Взаимосвязь между механической энергией и электрической энергией очевидна, поскольку мы часто используем электрическую энергию для выработки энергии для работы механических систем, например, в электрических лифтах и электромобилях. Точно так же мы используем механические системы для производства электроэнергии. Из-за этого отношения были разработаны новые единицы, объединяющие их. В механических системах, например, мы измеряем движение частицы как скорость в метрах в секунду (м/с).
Однако уравнения двух отношений могут основываться на одном и том же принципе, управляющем силой, действующей на разные частицы и материю целиком. Взаимосвязь между механической энергией и электрической энергией очевидна, поскольку мы часто используем электрическую энергию для выработки энергии для работы механических систем, например, в электрических лифтах и электромобилях. Точно так же мы используем механические системы для производства электроэнергии. Из-за этого отношения были разработаны новые единицы, объединяющие их. В механических системах, например, мы измеряем движение частицы как скорость в метрах в секунду (м/с).
Усовершенствованная формула
Напротив, мы измеряем ток электрона в электрической системе как ток в амперах (А). Если мы рассматриваем заряд как волну, его амплитуда представляет собой просто смещение. В этом случае единицы кулонов (C), таким образом, могут быть преобразованы в единицы перемещения, метры (м) и, следовательно, выравнивание единиц, и поэтому связь ясна. Разрушающая и конструктивная интерференция — это свойства волн, которые позволяют зарядам объединяться или нейтрализовать друг друга в зависимости от характера интерференции. Таким образом, единицы измерения могут заменить единицы Кулон (C) для расстояния, метров (м), заряда (е). Таким образом, будут единицы. Следовательно, мы можем заменить единицы измерения всех составляющих закона Ома, как показано ниже:
Разрушающая и конструктивная интерференция — это свойства волн, которые позволяют зарядам объединяться или нейтрализовать друг друга в зависимости от характера интерференции. Таким образом, единицы измерения могут заменить единицы Кулон (C) для расстояния, метров (м), заряда (е). Таким образом, будут единицы. Следовательно, мы можем заменить единицы измерения всех составляющих закона Ома, как показано ниже:
Мы измеряем мощность в ваттах в электрической системе, P = VI. В механических системах мы измеряем мощность в ваттах. Therefore, we can express the units of power as follows:
The table below summarizes the relationship between electrical and mechanical systems and their corresponding corrected units:
| Electrical system | Механическая система | Исправлено Units | |||
| Power (P) | watts | = | watts | ||
| Voltage (V | volts | = | newtons | ||
| Ток (I) | Amperes | = | Velocity | . 0412 0412 |
В приведенной выше таблице ток был преобразован в скорость, а напряжение в силу в ньютонах (Н). Мощность сохранила свои единицы как для электрических, так и для механических систем.
Запросить производство и сборку печатных плат
Неомические и омические проводники
Согласно закону Ома, при построении тока и напряжения на оси получается прямолинейный график. Увеличение разности потенциалов на проводящем материале увеличивает электрический ток, протекающий через него. Однако некоторые проводники имеют более высокое сопротивление и поэтому требуют приложения большего напряжения для получения определенного тока. С другой стороны, другие проводники требуют применения более низкого напряжения для получения определенного количества тока. Проводники, графики которых линейны и подчиняются закону Ома, являются омическими проводниками. Однако некоторые электрические компоненты могут отображать разные характеристики тока/напряжения, и их графики могут не быть линейными. Такие проводники называются неомическими проводниками. На рисунке ниже показаны формы линейных графиков как для омических, так и для неомических проводников.
Такие проводники называются неомическими проводниками. На рисунке ниже показаны формы линейных графиков как для омических, так и для неомических проводников.
Например, медные соединительные провода, используемые для электрических компонентов, являются хорошими примерами омического проводника. Это связано с тем, что его температура остается постоянной при нормальных условиях, поскольку рассеиваемое тепло очень мало. В результате разность потенциалов между клеммами проводов мала, что приводит к меньшему сопротивлению. Однако провод по-прежнему подчиняется закону Ома. Резисторы, используемые в электронных компонентах, также являются хорошим примером омических проводников. Они состоят из омической свинцовой металлической пленки. Омические резисторы используются в электронных компонентах для обеспечения фиксированного сопротивления в цепи и, следовательно, для установки напряжения и ограничения величины тока через эти компоненты.
Есть показательный пример?
Хорошим примером неомического проводника является лампа накаливания. Эти лампы эффективно преобразуют электрическую энергию в энергию света. Однако они выделяют много тепла, поскольку нагреваются до высоких температур, раскаляются добела и излучают свет. Повышение температуры приводит к увеличению сопротивления нити накала. В результате ток через нить накала уменьшается, переводя лампу в нормальный режим работы.
Эти лампы эффективно преобразуют электрическую энергию в энергию света. Однако они выделяют много тепла, поскольку нагреваются до высоких температур, раскаляются добела и излучают свет. Повышение температуры приводит к увеличению сопротивления нити накала. В результате ток через нить накала уменьшается, переводя лампу в нормальный режим работы.
Полупроводниковый диод также является примером неомического проводника. Он состоит из p-n-перехода и позволяет току течь через него только в одном направлении. Он практически не имеет прямого сопротивления и существенно большого сопротивления в противоположном (реверсивном) направлении. Большинство полупроводниковых приборов являются неомическими проводниками. Например, варисторы, используемые для защиты от переходных процессов в сети или сетевого питания, имеют высокое сопротивление, которое падает только при превышении определенного установленного напряжения, поглощая переходные процессы и защищая блоки питания.
Применение закона Ома
- Закон Ома обычно применяется при управлении скоростью вращения вентиляторов, чего можно добиться, изменив положение регулятора с конечной точки на начальную.
 Кроме того, можно добиться тока, протекающего через вентилятор, с помощью регулятора для управления сопротивлением. Мы можем измерить мощность, сопротивление и ток, протекающий через вентилятор, применяя закон Ома.
Кроме того, можно добиться тока, протекающего через вентилятор, с помощью регулятора для управления сопротивлением. Мы можем измерить мощность, сопротивление и ток, протекающий через вентилятор, применяя закон Ома. - Автоматические выключатели и плавкие предохранители последовательно подключаются к электроприборам для защиты цепи. Следовательно, мы можем определить электрический ток, протекающий через предохранитель, применяя закон Ома.
- В электроприборах, таких как электрические утюги и чайники, многие резисторы ограничивают количество протекающего через них электрического тока и при этом обеспечивают необходимое количество тепла. Подходящий размер используемых резисторов определяется по закону Ома.
- Закон Ома применим в электрических нагревателях, которые имеют металлические катушки с высоким сопротивлением для определения мощности, потребляемой нагревателями во время их работы.
Запросить производство и сборку печатных плат сейчас
Ограничения закона Ома
- Для неметаллических проводников, таких как графит, мы не можем применить закон Ома, поскольку он работает только для металлических проводников.

- Односторонние электрические компоненты, такие как транзисторы и диоды, пропускают ток только в одном направлении. Поэтому к таким элементам нельзя применить закон Ома.
- Например, в диодах, если величина напряжения сохраняется, но вы меняете его направление, величина производимого тока будет отличаться от тока, создаваемого в противоположном направлении. Таким образом, закон Ома не будет выполняться в обоих направлениях, поскольку соотношение между током (I) и напряжением (V) зависит от характера V. То есть оно зависит от того, положительный или отрицательный знак V.
- Закон Ома нельзя применять для электрических цепей с нелинейными электрическими компонентами, такими как резисторы, конденсаторы и т. д., поскольку ток через них и разность потенциалов на них могут не быть постоянными. Для нелинейных элементов, таких как тиристоры и электрическая дуга, приложенное напряжение не пропорционально величине тока через них. Следовательно, сопротивление будет изменяться при изменении значений тока и разности потенциалов, а значит, применение закона Ома будет затруднено.

Заключение
Как мы видели в этой статье, закон Ома является основной концепцией в изучении и применении электричества, одной из областей физики. Мы часто взаимодействуем с электричеством в нашей повседневной деятельности, работая с различными электроприборами. Поэтому очень важно понимать основные принципы функционирования этих приборов. В этой статье мы рассмотрели закон Ома, его математическое и графическое выражение и то, как его можно проверить экспериментально. Мы также рассмотрели другие аналогии, объясняющие закон Ома, такие как взаимосвязь закона Ома и закона Ньютона.0092 й закон движения. Таким образом, взаимосвязь приводит к новым блокам, которые соединяют между собой механические и электрические системы. Мы также рассмотрели круговую диаграмму Ома, треугольник Ома и матрицу закона Ома как другие способы представления закона Ома.
При расчете электрической мощности мы можем использовать закон Ома для упрощения операций. Мы рассмотрели различные области, в которых мы можем применять закон Ома в нашей повседневной деятельности, и выявили его ограничения.
Очевидно, что Закон Ома невероятно важен и должен быть частью общих знаний каждого инженера. Надеюсь, теперь вы лучше понимаете закон Ома и можете применять его в своих собственных приложениях.
Преобразователь случайных чисел | Преобразователь длины и расстоянияПреобразователь массыСухой объем и общие измерения для приготовления пищиКонвертер площадиКонвертер объема и общего измерения для приготовления пищиПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь мощностиПреобразователь силыПреобразователь силыПреобразователь времениПреобразователь линейной скорости и скоростиПреобразователь углаПреобразователь эффективности использования топлива, расхода топлива и экономии топливаПреобразователь чиселКонвертер единиц информации и Хранение данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияПреобразователь ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер импульсаИмпульс крутящего моментаКонвертер удельной энергии, теплоты сгорания (в расчете на массу)Конвертер удельной энергии, теплоты сгорания (в объеме) Конвертер температуры Конвертер интервала Конвертер коэффициента теплового расширенияКонвертер теплового сопротивленияТеплопровод Конвертер удельной теплоемкостиПлотность теплоты, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер массового потокаКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяженияМодерация проницаемости, проницаемости, паропроницаемости Преобразователь скорости пропускания паровПреобразователь уровня звукаПреобразователь чувствительности микрофонаПреобразователь уровня звукового давления (SPL)Преобразователь уровня звукового давления с выбираемым эталонным давлениемПреобразователь яркостиПреобразователь силы светаПреобразователь освещенностиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической силы (диоптрий) в фокусное расстояниеПреобразователь оптической силы (диоптрий) в увеличение (X)Электрический заряд КонвертерКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаОбъемный заряд De Преобразователь электрического токаПреобразователь линейной плотности токаПреобразователь поверхностной плотности токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь удельного электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электропроводностиПреобразователь емкостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь калибров проводов в СШАПреобразование уровней в дБм, дБВ, Ватт и других единицахПреобразователь силы магнитного поля КонвертерПлотность магнитного потокаМощность поглощенной дозы излучения, Мощность общей дозы ионизирующего излучения КонвертерРадиоактивность.
Этот онлайн-конвертер единиц измерения позволяет быстро и точно преобразовать множество единиц измерения из одной системы в другую. Страница Unit Conversion предлагает решение для инженеров, переводчиков и всех, чья деятельность требует работы с величинами, измеряемыми в разных единицах. Вы можете использовать этот онлайн-конвертер для преобразования нескольких сотен единиц (включая метрические, британские и американские) в 76 категориях или нескольких тысяч пар, включая ускорение, площадь, электрическую энергию, силу, длину, свет, массу, массовый расход, плотность, удельный объем, мощность, давление, напряжение, температура, время, крутящий момент, скорость, вязкость, объем и производительность, объемный расход и многое другое. Общие конвертеры единицКонвертер длины и расстояния : метр, километр, сантиметр, миллиметр, нанометр, ярд, фут, дюйм, парсек, световой год, астрономическая единица, лунное расстояние (от Земли до Луны), лига , миля, морская миля (международная), сажень, кабельтовая (международная), точка, пиксель, калибр, планковская длина… Конвертер массы : грамм, килограмм, миллиграмм, тонна (метрическая), фунт, унция, стоун (США), стоун (Великобритания), карат, гран, талант (греческое библейское), драхма (греческое библейское), денарий ( библейский римлянин), шекель (библейский иврит), масса Планка, масса протона, единица атомной массы, масса электрона (в покое), масса Земли, масса Солнца. Конвертер площади : миллиметр², сантиметр², метр², километр², гектар, акр, дюйм², фут², ярд², миля², сарай, круговой дюйм, поселок, руд, стержень², окунь², усадьба, полюс², сабин, арпен, куэрда, верста квадратная, аршин квадратный, фут квадратный, сажень квадратная, площадь планка… Конвертер единиц объема и кулинарных единиц измерения : метр³, километр³, миллиметр³, литр, гектолитр, миллилитр, капля, баррель (масло), баррель (США) ), баррель (Великобритания), галлон (США), галлон (Великобритания), кварта (США), кварта (Великобритания), пинта (США), пинта (Великобритания), баррель (нефть), баррель (США), баррель (Великобритания ), галлон (США), галлон (Великобритания), кварта (США), кварта (Великобритания), пинта (США), пинта (Великобритания), ярд³, фут³, дюйм³, регистровая тонна, 100 кубических футов. Преобразователь температуры : кельвин, градус Цельсия, градус Фаренгейта, градус Ранкина, градус Реомюра, планковская температура. Давление, напряжение, модуль Юнга Конвертер единиц : паскаль, килопаскаль, мегапаскаль, миллипаскаль, микропаскаль, нанопаскаль, техническая атмосфера, стандартная атмосфера, тысяч фунтов/кв. дюйм, ньютон/метр², бар, миллибар, килограмм-сила/метр², грамм- сила/сантиметр², тонна-сила (короткая)/фут², фунт-сила/фут², миллиметр ртутного столба (0°C), дюйм ртутного столба (32°F), сантиметр водяного столба (4°C), фут водяного столба (4°C) , метр морской воды… Конвертер энергии и работы : джоуль, килоджоуль, мегаджоуль, миллиджоуль, мегаэлектрон-вольт, электрон-вольт, эрг, киловатт-час, мегаватт-час, ньютон-метр, килокалория (ИТ), калория (пищевая), БТЕ ( ИТ), мега БТЕ (ИТ), тонна-час (охлаждение), тонна нефтяного эквивалента, баррель нефтяного эквивалента (США), мегатонна, тонна (ВВ), килограмм тротила, дина-сантиметр, грамм-сила-сантиметр, килограмм- метр силы, килопонд-метр, фут-фунт, дюйм-фунт, планковская энергия. Мощность Перевод единиц : ватт, киловатт, мегаватт, милливатт, лошадиная сила, вольт-ампер, ньютон-метр в секунду, джоуль в секунду, мегаджоуль в секунду, килоджоуль в секунду, миллиджоуль в секунду, джоуль в час, килоджоуль в час, эрг/секунду , БТЕ (ИТ)/час, килокалория (ИТ)/час… Перевод единиц силы : ньютон, килоньютон, миллиньютон, дина, джоуль/метр, джоуль/сантиметр, грамм-сила, килограмм-сила, тонна- сила (короткая), кип-сила, килофунт-сила, фунт-сила, унция-сила, фунт-сила, фунт-фут/секунда², пруд, стен, грав-сила, миллиграв-сила… Преобразователь времени : секунда, миллисекунда, наносекунда, пикосекунда, минута, час, день, неделя, месяц, год, десятилетие, столетие, тысячелетие, планковское время, год (юлианский), год (високосный), год (тропический) , год (звездный), год (григорианский), две недели, встряска… Конвертер линейной скорости и скорости : метр/секунда, километр/час, километр/секунда, миля/час, фут/секунда, миля/секунда , узел, узел (Великобритания), Скорость света в вакууме, Космическая скорость – первая, Космическая скорость – вторая, Космическая скорость – третья, Скорость Земли, Скорость звука в чистой воде, Мах (стандарт СИ), Мах (20°C и 1 атм), ярд/сек. Конвертер углов : градус, радиан, град, гон, минута, секунда, знак, мил, оборот, окружность, поворот, квадрант, прямой угол, секстант. Конвертер топливной экономичности, расхода топлива и экономии топлива : метр/литр, километр/литр, миля (США)/литр, морская миля/литр, морская миля/галлон (США), километр/галлон (США), литр/100 км, галлон (США)/миля, галлон (США)/100 миль, галлон (Великобритания)/миля, галлон (Великобритания)/100 миль… Преобразователь чисел : двоичный, восьмеричный, десятичный, шестнадцатеричный, основание-3, основание-4, основание-5, основание-6, основание-7, основание-9, основание-10, основание-11, основание-12, основание-13, основание-14, основание-15, основание-20, основание-21, основание-22, основание-23, основание-24, основание-28, основание -30, base-32, base-34, base-36… Преобразователь единиц хранения информации и данных : бит, байт, слово, четверное слово, MAPM-слово, блок, килобит (10³ бит ), кибибит, кибибайт, килобайт (10³ байт), мегабайт (10⁶ байт), гигабайт (10⁹ байт), терабайт (10¹² байт), петабайт (10¹⁵ байт), эксабайт (10¹⁸ байт), дискета (3,5 ED), дискета диск (5,25 HD), Zip 250, Jaz 2 ГБ, CD (74 минуты), DVD (2 слоя с 1 стороны), диск Blu-ray (однослойный), диск Blu-ray (двухслойный). Курсы обмена валюты : евро, доллар США, канадский доллар, британский фунт стерлингов, японская иена, швейцарский франк, аргентинское песо, австралийский доллар, бразильский реал, болгарский лев, чилийское песо, китайский юань, чешская крона, датская крона, египетский фунт стерлингов, венгерский форинт, исландская крона, индийская рупия, индонезийская рупия, новый израильский шекель, иорданский динар, малазийский ринггит, мексиканское песо, новозеландский доллар, норвежская крона, пакистанская рупия, филиппинское песо, румынский лей, российский рубль, саудовский риал, сингапур доллар, южноафриканский ранд, южнокорейская вона, шведская крона, новый тайваньский доллар, тайский бат, турецкая лира, украинская гривна… Размеры женской одежды и обуви : Женские платья, костюмы и свитера, женская обувь, женские купальные костюмы, размер букв, бюст, дюймы, естественная талия, дюймы, заниженная талия, дюймы, бедра, дюймы, бюст, сантиметры, Естественная талия, сантиметры, Заниженная талия, сантиметры, Бедра, сантиметры, Длина стопы, мм, Торс, дюймы, США, Канада, Великобритания, Европа, Континенталь, Россия, Япония, Франция, Австралия, Мексика, Китай, Корея. Размеры мужской одежды и обуви : Мужские рубашки, мужские штаны/брюки, размер мужской обуви, буквенный размер, шея, дюймы, грудь, дюймы, рукав, дюймы, талия, дюймы, шея, сантиметры, грудь, сантиметры, рукав, сантиметры, Талия, сантиметры, Длина стопы, мм, Длина стопы, дюймы, США, Канада, Великобритания, Австралия, Европа, Континентальная, Япония, Россия, Франция, Италия, Испания, Китай, Корея, Мексика… МеханикаПреобразователь угловой скорости и частоты вращения : радиан/секунда, радиан/день, радиан/час, радиан/минута, градус/день, градус/час, градус/минута, градус/секунда, оборот/день, оборот/час, оборот/минута, оборот/секунда, оборот/год, оборот/месяц, оборот/неделя, градус/год, градус/месяц, градус/неделя, радиан/год, радиан/месяц, радиан/неделя. Преобразователь ускорения : дециметр/секунда², метр/секунда², километр/секунда², гектометр/секунда², декаметр/секунда², сантиметр/секунда², миллиметр/секунда², микрометр/секунда², нанометр/секунда², пикометр/секунда², фемтометр/секунда² , аттометр/секунда², гал, галилео, миля/секунда², ярд/секунда², фут/секунда², дюйм/секунда², ускорение свободного падения, ускорение свободного падения на Солнце, ускорение свободного падения на Меркурии, ускорение свободного падения на Венере , ускорение свободного падения на Луне, ускорение свободного падения на Марсе, ускорение свободного падения на Юпитере, ускорение свободного падения на Сатурне. Конвертер углового ускорения : радиан/секунда², радиан/минута², оборот/секунда², оборот/минута/секунда, оборот/минута². Конвертер плотности : килограмм/метр³, килограмм/сантиметр³, грамм/метр³, грамм/сантиметр³, грамм/миллиметр³, миллиграмм/метр³, миллиграмм/сантиметр³, миллиграмм/миллиметр³, эксаграмм/литр, петаграмм/литр, тераграмм/литр , гигаграмм/литр, мегаграмм/литр, килограмм/литр, гектограмм/литр, декаграмм/литр, грамм/литр, дециграмм/литр, сантиграмм/литр, миллиграмм/литр, микрограмм/литр, нанограмм/литр, пикограмм/литр, фемтограмм /литр, аттограмм/литр, фунт/дюйм³… Конвертер удельного объема : метр³/килограмм, сантиметр³/грамм, литр/килограмм, литр/грамм, фут³/килограмм, фут³/фунт, галлон (США)/фунт, галлон (Великобритания)/фунт. Преобразователь момента инерции : килограмм-метр², килограмм-сантиметр², килограмм-миллиметров², грамм-сантиметр², грамм-миллиметр², килограмм-сила-метр-секунда², унция-дюйм², унция-сила-дюйм-секунда², фунт-фут², фунт-сила-фут-секунда², фунт-дюйм² , фунт-сила, дюйм, секунда², слизняк, фут². Преобразователь момента силы : ньютон-метр, килоньютон-метр, миллиньютон-метр, микроньютон-метр, тонно-сила (короткий) метр, тонно-сила (длинный) метр, тонно-сила (метрический) метр, килограмм-сила-метр, грамм -сила-сантиметр, фунт-сила-фут, фунт-фут, фунт-дюйм. Импульс : килограмм-метр в секунду, ньютон-секунда, килоньютон-секунда, килограмм-метр в минуту, килограмм-метр в час, грамм-сантиметр в секунду, ньютон-минута, ньютон-час, дина-минута, грамм-сила-секунда, килограмм-сила-секунда, тонна-сила-минута, фунт-фут в секунду, слаг-фут в минуту, фунт-сила-час, кип-минута, планковский импульс, мегаэлектронвольт импульса… Импульс : ньютон-секунда, меганьютон-секунда, миллиньютон-секунда, килограмм-метр в секунду, килограмм-метр в минуту, килограмм-метр в час, грамм-сантиметр в секунду, ньютон-минута, ньютон-час, дина-минута, грамм-сила-секунда, килограмм-сила-секунда, тонна-сила-минута, фунт-фут в секунду, слаг-фут в минуту, фунт-сила-час, кип-секунда, кип-минута, кип- час. Преобразователь крутящего момента : ньютон-метр, ньютон-сантиметр, ньютон-миллиметр, килоньютон-метр, дина-метр, дина-сантиметр, дина-миллиметр, килограмм-сила-метр, килограмм-сила-сантиметр, килограмм-сила-миллиметр, грамм-сила метр, грамм-сила-сантиметр, грамм-сила-миллиметр, унция-сила-фут, унция-сила-дюйм, фунт-сила-фут, фунт-сила-дюйм. Термодинамика. ТеплотаУдельная энергия, теплота сгорания (на массу) Перевод единиц : джоуль/килограмм, килоджоуль/килограмм, калория (IT)/грамм, калория (th)/грамм, Btu (IT)/фунт, Btu (th)/фунт, килограмм/джоуль, килограмм/килоджоуль, грамм/калория (IT), грамм/калория (th), фунт/Btu (IT), фунт/Btu (th), фунт/лошадиная сила-час, грамм /лошадиная сила (метрическая)-час, грамм/киловатт-час. Удельная энергия, теплота сгорания (на объем) Перевод единиц : джоуль/метр³, джоуль/литр, мегаджоуль/метр³, килоджоуль/метр³, килокалория (ИТ)/метр³, калория (ИТ)/сантиметр³, терм/фут³, терм/галлон (Великобритания), БТЕ (IT)/фут³, БТЕ (терм. Преобразователь температурного интервала : кельвин, градус Цельсия, градус Цельсия, градус Фаренгейта, градус Ранкина, градус Реомюра. Преобразователь коэффициента теплового расширения : длина/длина/кельвин, длина/длина/градус Цельсия, длина/длина/градус Фаренгейта, длина/длина/градус Ранкина, длина/длина/градус Реомюра. Преобразователь теплового сопротивления : кельвин/ватт, градус Фаренгейта-час/БТЕ (IT), градус Фаренгейта-час/БТЕ (th). Преобразователь теплопроводности : ватт/метр/K, ватт/сантиметр/°C, киловатт/метр/K, калория (IT)/секунда/сантиметр/°C, калория (th)/секунда/сантиметр/°C , килокалория (ИТ)/час/метр/°C, килокалория (терм.)/час/метр/°C, БТЕ (IT) дюйм/секунда/фут²/°F, БТЕ (терм.) дюйм/секунда/фут²/°F , Btu (IT) фут/час/фут²/°F, Btu (TH) фут/час/фут²/°F, BTU (IT) дюйм/час/фут²/°F, BTU (TH) дюйм/час/фут²/ °F. Конвертер удельной теплоемкости : джоуль/килограмм/K, джоуль/килограмм/°C, джоуль/грамм/°C, килоджоуль/килограмм/K, килоджоуль/килограмм/°C, калория (ИТ)/грамм/° C, калория (IT)/грамм/°F, калория (TH)/грамм/°C, килокалория (IT)/килограмм/°C, килокалория (TH)/килограмм/°C, килокалория (IT)/килограмм/K , килокалория (терм.)/килограмм/K, килограмм-сила-метр/килограмм/K, фунт-сила-фут/фунт/°R, Btu (IT)/фунт/°F, Btu (th)/фунт/°F, Btu (IT)/фунт/°R, Btu (th)/фунт/°R, Btu (IT)/фунт/°C, CHU/фунт/°C. Плотность тепла, плотность пожарной нагрузки : джоуль/метр², калория (терм.)/сантиметр², лэнгли, БТЕ (ИТ)/фут², БТЕ (тепл.)/фут². Конвертер плотности теплового потока : ватт/метр², киловатт/метр², ватт/сантиметр², ватт/дюйм², джоуль/секунда/метр², килокалория (IT)/час/метр², килокалория (IT)/час/фут², калория (IT)/минута/сантиметр², калория (IT)/час/сантиметр², калория (й)/минута/сантиметр², калория (теплая)/час/сантиметр², дина/час/сантиметр, эрг/час/миллиметр², фут-фунт/ минута/фут², лошадиная сила/фут², лошадиная сила (метрическая)/фут², БТЕ (ИТ)/секунда/фут², БТЕ (ИТ)/минута/фут², БТЕ (ИТ)/час/фут², БТЕ (й)/секунда/дюйм² , БТЕ (й)/секунда/фут², БТЕ (й)/минута/фут², БТЕ (й)/час/фут², CHU/час/фут². Конвертер коэффициента теплопередачи : ватт/метр²/K, ватт/метр²/°C, джоуль/секунда/метр²/K, килокалория (IT)/час/метр²/°C, килокалория (IT)/час/фут² /°C, БТЕ (ИТ)/секунда/фут²/°F, БТЕ (терм.)/секунда/фут²/°F, БТЕ (ИТ)/час/фут²/°F, БТЕ (терм.)/час/фут²/° F, CHU/час/фут²/°C. Гидравлика — жидкостиПреобразователь объемного расхода : метр³/сек, метр³/день, метр³/час, метр³/минута, сантиметр³/день, сантиметр³/час, сантиметр³/минута, сантиметр³/секунда, литр/день, литр/час, литр/минута, литр/секунда, миллилитр/день, миллилитр/час, миллилитр/минута, миллилитр/секунда, галлон (США)/день, галлон (США)/час, галлон (США)/минута, галлон (США)/секунда, галлон (Великобритания)/день, галлон (Великобритания)/час, галлон (Великобритания)/минута, галлон (Великобритания)/секунда, килобаррель (США)/день, баррель (США)/день… Конвертер массового расхода : килограмм/секунда, грамм/секунда, грамм/минута, грамм/час, грамм/день, миллиграмм/минута, миллиграмм/час, миллиграмм/день, килограмм/минута, килограмм/час, килограмм /день, эксаграмм/секунда, петаграмм/секунда, тераграмм/секунда, гигаграмм/секунда, мегаграмм/секунда, гектограмм/секунда, декаграмм/секунда, дециграмм/секунда, сантиграмм/секунда, миллиграмм/секунда, микрограмм/секунда, тонна (метрическая )/секунда, тонна (метрическая)/минута, тонна (метрическая)/час, тонна (метрическая)/день. Конвертер молярного расхода : моль в секунду, экзамол в секунду, петамол в секунду, терамол в секунду, гигамоль в секунду, мегамоль в секунду, киломоль в секунду, гектомоль в секунду, декамоль в секунду, децимоль в секунду, сантимоль в секунду, миллимоль в секунду, микромоль/секунда, наномоль/секунда, пикомоль/секунда, фемтомоль/секунда, аттомоль/секунда, моль/минута, моль/час, моль/день, миллимоль/минута, миллимоль/час, миллимоль/день, киломоль/минута, киломоль/ час, киломоль/день. Конвертер массового потока : грамм в секунду/метр², килограмм/час/метр², килограмм/час/фут², килограмм/секунда/метр², грамм/секунда/сантиметр², фунт/час/фут², фунт/секунда/фут². Конвертер молярной концентрации : моль/метр³, моль/литр, моль/сантиметр³, моль/миллиметр³, киломоль/метр³, киломоль/литр, киломоль/сантиметр³, килломоль/миллиметр³, миллимоль/метр³, миллимоль/литр, миллимоль/ сантиметр³, миллимоль/миллиметр³, моль/дециметр³, молярный, миллимолярный, микромолярный, наномолярный, пикомолярный, фемтомолярный, аттомолярный, зептомолярный, йоктомолярный. Конвертер массовой концентрации в растворе : килограмм/литр, грамм/литр, миллиграмм/литр, часть/миллион, гран/галлон (США), гран/галлон (Великобритания), фунт/галлон (США), фунт/галлон галлон (Великобритания), фунт/миллион галлонов (США), фунт/миллион галлонов (Великобритания), фунт/фут³, килограмм/метр³, грамм/100 мл. Конвертер динамической (абсолютной) вязкости : паскаль-секунда, килограмм-сила-секунда/метр², ньютон-секунда/метр², миллиньютон-секунда/метр², дина-секунда/сантиметр², пуаз, экзапуаз, петапуаз, терапуаз, гигапуаз, мегапуаз, килопуаз, гектоуравновешенность, декауаз, деципуаз, сантипуаз, миллипуаз, микроуравновешенность, наноуравновешенность, пикоуравновешенность, фемтоуравновешенность, атоуравновешенность, фунт-сила-секунда/дюйм², фунт-сила-секунда/фут², фунт-сила-секунда/фут², грамм/сантиметр/секунда… Конвертер кинематической вязкости : метр²/секунда, метр²/час, сантиметр²/секунда, миллиметр²/секунда, фут²/секунда, фут²/час, дюйм²/секунда, стокс, эксастокс, петастокс, терастокс, гигастокс, мегастокс, килостокс, гектостокс, декастокс, декастокс, сантистокс, миллистокс, микростокс, наностокс, пикостокс, фемтостокс, аттостокс. Конвертер поверхностного натяжения : ньютон/метр, миллиньютон/метр, грамм-сила/сантиметр, дина/сантиметр, эрг/сантиметр², эрг/миллиметр², фунт/дюйм, фунт-сила/дюйм. Проницаемость, проницаемость, паропроницаемость Конвертер единиц : килограмм/паскаль/секунда/метр², нанограмм/паскаль/секунда/метр², проницаемость (0°C), проницаемость (23°C), фунты на 1000 кв. 24 часа. Преобразователь коэффициента пропускания паров влаги : грамм/метр²/день, грамм/100 дюймов²/день, гран/фут²/час. Акустика — звукПреобразователь уровня звука : бел, децибел, непер. Преобразователь чувствительности микрофона : децибел относительно 1 вольта на 1 паскаль, децибел относительно 1 вольта на 1 микропаскаль, децибел относительно 1 вольта на 1 дин на квадратный сантиметр, децибел относительно 1 вольта на 1 микробар, вольт на паскаль, милливольт на паскаль, микровольт на паскаль. Конвертер уровня звукового давления (SPL) : ньютон на квадратный метр, паскаль, миллипаскаль, микропаскаль, дина/квадратный сантиметр, бар, миллибар, микробар, уровень звукового давления в децибелах. Преобразователь уровня звукового давления с возможностью выбора эталонного давления : Уровень звукового давления (SPL) представляет собой логарифмическую меру абсолютного уровня звука, звукового давления или интенсивности звука по отношению к эталонному звуковому давлению (отношение амплитуд). Фотометрия — светКонвертер яркости : кандела/метр², кандела/сантиметр², кандела/фут², кандела/дюйм², килокандела/метр², стильб, люмен/метр²/стерадиан, люмен/сантиметр²/стерадиан, люмен/фут²/ стерадиан, нит, миллинит, ламберт, миллиламберт, фут-ламберт, апостильб, блондель, брил, скот. Конвертер силы света : кандела, свеча (немецкий), свеча (Великобритания), десятичная свеча, свеча (пентан), пентановая свеча (мощность 10 свечей), свеча Хефнера, единица Карселя, десятичное число бужей, люмен/стерадиан, свеча (Международный). Преобразователь освещенности : люкс, метр-свеча, сантиметр-свеча, фут-свеча, фот, нокс, кандела стерадиан/метр², люмен/метр², люмен/сантиметр², люмен/фут², ватт/сантиметр² (при 555 нм) . Преобразователь разрешения цифрового изображения : точка/метр, точка/миллиметр, точка/дюйм, пиксель/дюйм. Преобразователь частоты и длины волны : герц, экзагерц, петагерц, терагерц, гигагерц, мегагерц, килогерц, гектогерц, декагерц, децигерц, сантигерц, миллигерц, микрогерц, наногерц, пикогерц, фемтогерц, аттогерц, цикл/секунду, длина волны в экзаменах , длина волны в петаметрах, длина волны в тераметрах, длина волны в гигаметрах, длина волны в мегаметрах, длина волны в километрах, длина волны в гектометрах, длина волны в декаметрах… Конвертер оптической силы (диоптрии) в фокусное расстояние : Оптическая сила (диоптрийная сила или преломляющая сила) линзы или другой оптической системы — это степень, в которой система сводит или расходит свет. Он рассчитывается как величина, обратная фокусному расстоянию оптической системы, и измеряется в обратных метрах в СИ или чаще в диоптриях (1 диоптрия = м⁻¹) Конвертер оптической силы (диоптрии) в увеличение (X) : Этот преобразователь позволяет преобразовать оптическую силу лупы в диоптриях в увеличение (например, 10-кратное), которое обычно указывается на лупах. ЭлектротехникаПреобразователь электрического заряда : кулон, мегакулон, килокулон, милликулон, микрокулон, нанокулон, пикокулон, абкулон, EMU заряда, статкулон, ESU заряда, франклин, ампер-час, миллиампер-час, ампер- минута, ампер-секунда, фарадей (по углероду 12), элементарный заряд. Конвертер линейной плотности заряда : кулон/метр, кулон/сантиметр, кулон/дюйм, абкулон/метр, абкулон/сантиметр, абкулон/дюйм. Конвертер плотности поверхностного заряда : кулон/метр², кулон/сантиметр², кулон/дюйм², абкулон/метр², абкулон/сантиметр², абкулон/дюйм². Конвертер объемной плотности заряда : кулон/метр³, кулон/сантиметр³, кулон/дюйм³, абкулон/метр³, абкулон/сантиметр³, абкулон/дюйм³. Преобразователь электрического тока : ампер, килоампер, миллиампер, биот, абампер, ЭВС тока, статампер, ЭСУ тока, СГС э.м. ед., СГС у.с. ед., микроампер, наноампер, планковский ток. Конвертер линейной плотности тока : ампер/метр, ампер/сантиметр, ампер/дюйм, абампер/метр, абампер/сантиметр, абампер/дюйм, эрстед, гильберт/сантиметр, ампер/миллиметр, миллиампер/метр, миллиампер/дециметр , миллиампер/сантиметр, миллиампер/миллиметр, микроампер/метр, микроампер/дециметр, микроампер/сантиметр, микроампер/миллиметр. Преобразователь поверхностной плотности тока : ампер/метр², ампер/сантиметр², ампер/дюйм², ампер/мил², ампер/круговой мил, абампер/сантиметр², ампер/миллиметр², миллиампер/миллиметр², микроампер/миллиметр², килоампер/миллиметр², миллиампер/сантиметр², микроампер/сантиметр², килоампер/сантиметр², ампер/дециметр², миллиампер/дециметр², микроампер/дециметр², килоампер/дециметр². Преобразователь напряженности электрического поля : вольт/метр, киловольт/метр, киловольт/сантиметр, вольт/сантиметр, милливольт/метр, микровольт/метр, киловольт/дюйм, вольт/дюйм, вольт/мил, абвольт/сантиметр, статвольт /сантиметр, статвольт/дюйм, ньютон/кулон, вольт/микрон. Преобразователь электрического потенциала и напряжения : вольт, милливольт, микровольт, нановольт, пиковольт, киловольт, мегавольт, гигавольт, теравольт, ватт/ампер, абвольт, EMU электрического потенциала, статвольт, ESU электрического потенциала, планковское напряжение. Конвертер электрического сопротивления : ом, мегом, микроом, вольт/ампер, обратный сименс, абом, EMU сопротивления, статом, ESU сопротивления, квантованное сопротивление Холла, импеданс Планка, миллиом, килоом. Конвертер удельного электрического сопротивления : ом-метр, ом-сантиметр, ом-дюйм, микроом-сантиметр, микроом-дюйм, абом-сантиметр, статом-сантиметр, круговой мил ом/фут, ом квадратный миллиметр на метр. Преобразователь электрической проводимости : сименс, мегасименс, килосименс, миллисименс, микросименс, ампер/вольт, мхо, геммо, микромо, абмо, статмо, квантизированная холловская проводимость. Конвертер электропроводности : сименс/метр, пикосименс/метр, мОм/метр, мОм/сантиметр, абмо/метр, абмо/сантиметр, статмо/метр, статмо/сантиметр, сименс/сантиметр, миллисименс/метр, миллисименс/ сантиметр, микросименс/метр, микросименс/сантиметр, единица электропроводности, коэффициент проводимости, частей на миллион, шкала 700, частей на миллион, шкала 500, частей на миллион, шкала 640, TDS, частей на миллион, шкала 640, TDS, частей на миллион, шкала 550, TDS, частей на миллион, шкала 500, TDS, частей на миллион, шкала 700. Конвертер емкости : фарад, эксафарад, петафарад, терафарад, гигафарад, мегафарад, килофарад, гектофарад, декафарад, децифарад, сантифарад, миллифарад, микрофарад, нанофарад, пикофарад, фемтофарад, аттофарад, кулон/вольт, абфарад, EMU , статфарад, ЕСУ емкости. Преобразователь индуктивности : генри, эксагенри, петагенри, терагенри, гигагенри, мегагенри, килогенри, гектогенри, декагенри, децигенри, сантигенри, миллигенри, микрогенри, наногенри, пикогенри, фемтогенри, аттогенри, вебер/ампер EMU, индуктивности, , статенри, ЭСУ индуктивности. Преобразователь реактивной мощности переменного тока : вольт-ампер реактивный, милливольт-ампер реактивный, киловольт-ампер реактивный, мегавольт-ампер реактивный, гигавольт-ампер реактивный. Преобразователь американского калибра проводов : Американский калибр проводов (AWG) — это стандартизированная система калибров проводов, используемая в США и Канаде для определения диаметров цветных электропроводящих проводов, включая медь и алюминий. Чем больше площадь поперечного сечения провода, тем выше его пропускная способность по току. Чем больше номер AWG, также называемый калибром провода, тем меньше физический размер провода. Наибольший размер AWG — 0000 (4/0), а наименьший — 40. Преобразование уровней в дБм, дБВ, Ватт и другие единицы : децибел-милливатт, децибел-ватт, децибел-микровольт, децибел-вольт. Магнитостатика, магнетизм и электромагнетизмПреобразователь магнитодвижущей силы : ампер, ампер-виток, килоампер-виток, миллиампер-виток, абампер-виток, гильберт. Преобразователь напряженности магнитного поля : ампер/метр, ампер-виток/метр, килоампер/метр, эрстед. Преобразователь магнитного потока : вебер, милливебер, микровебер, вольт-секунда, единица полюса, мегалайн, килолин, линия, максвелл, тесла-метр², тесла-сантиметр², гаусс-сантиметр², квант магнитного потока. Конвертер плотности магнитного потока : тесла, вебер/метр², вебер/сантиметр², вебер/дюйм², максвелл/метр², максвелл/сантиметр², максвелл/дюйм², гаусс, линия/сантиметр², линия/дюйм², гамма. Радиация и радиологияМощность поглощенной дозы излучения, суммарная мощность дозы ионизирующего излучения Конвертер мощности : грей/секунда, экзагрей/секунда, петагрей/секунда, терагрей/секунда, гигагрей/секунда, мегагрей/секунда, килогрей/секунда, гектогрей/секунда, декагрей/секунда, децигрей/секунда, сантигрей/секунда, миллигрей/секунда, микрогрей/секунду, наногрей/секунду, пикогрей/секунду, фемтогрей/секунду, аттогрей/секунду, рад/секунду, джоуль/килограмм/секунду, ватт/килограмм, зиверт/секунду, миллизиверт/год, миллизиверт/час, микрозиверт/час, бэр/сек, рентген/час… Радиоактивность. Конвертер радиоактивного распада : беккерель, петабеккерель, терабеккерель, гигабеккерель, мегабеккерель, килобеккерель, миллибеккерель, кюри, килокюри, милликюри, микрокюри, нанокюри, пикокюри, резерфорд, одна/секунда, распадов/секунду, распадов/минуту. Преобразователь радиационной экспозиции : кулон/килограмм, милликулон/килограмм, микрокулон/килограмм, рентген, миллирентген, микрорентген, рентген ткани, Паркер, респ. Радиация. Конвертер поглощенной дозы : рад, миллирад, джоуль/килограмм, джоуль/грамм, джоуль/сантиграмм, джоуль/миллиграмм, грей, экзагрей, петагрей, терагрей, гигагрей, мегагрей, килогрей, гектогрей, декагрей, децигрей, сантигрей, миллигрей, микрогрей , наногрей, пикогрей, фемтогрей, аттогрей, зиверт, миллизиверт, микрозиверт… Разные конвертерыКонвертер метрических префиксов : нет, йотта, зетта, экза, пета, тера, гига, мега, кило, гекто, дека, деци, санти, милли, микро, нано, пико, фемто, атто, зепто, йокто. Преобразователь передачи данных : бит/секунду, байт/секунду, килобит/секунду (SI по умолчанию), килобайт/секунду (SI по умолчанию), кибибит/секунду, кибибайт/секунду, мегабит/секунду (SI по умолчанию) , мегабайт в секунду (по SI), мебибит в секунду, мебибайт в секунду, гигабит в секунду (по SI), гигабайт в секунду (по SI), гибибит в секунду, гибибайт в секунду, терабит в секунду (по SI по умолчанию) .), терабайт/секунду (SI по умолчанию), тебибит/секунду, тебибайт/секунду, ethernet, ethernet (быстрый), ethernet (гигабит), OC1, OC3, OC12, OC24, OC48. Конвертер единиц типографии и цифрового изображения : твип, метр, сантиметр, миллиметр, символ (X), символ (Y), пиксель (X), пиксель (Y), дюйм, пика (компьютер), пика (принтер) , точка (DTP/PostScript), точка (компьютерная), точка (принтерная), en, cicero, em, Didot точка. Конвертер единиц измерения объема пиломатериалов : кубический метр, кубический фут, кубический дюйм, досковые футы, тысяча досковых футов, шнур, шнур (80 футов³), кордовые футы, кунит, поддон, поперечная стяжка, переключающая стяжка. Калькулятор молярной массы : Молярная масса — это физическое свойство, которое определяется как масса вещества, деленная на количество вещества в молях. Другими словами, это масса одного моля определенного вещества. Периодическая таблица : Периодическая таблица представляет собой список всех химических элементов, расположенных слева направо и сверху вниз по их атомному номеру, электронным конфигурациям и повторяющимся химическим свойствам, организованным в виде таблицы, так что элементы с аналогичные химические свойства отображаются в вертикальных столбцах, называемых группами. Таблицы мер и весов Калькуляторы Вам трудно перевести единицу измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms и вы получите ответ от опытных технических переводчиков в считанные минуты. |
Сопротивление и удельное сопротивление | Физика
Цели обучения
К концу этого раздела вы сможете:
- Объясните понятие удельного сопротивления.
- Используйте удельное сопротивление для расчета сопротивления определенных конфигураций материала.

- Используйте термический коэффициент удельного сопротивления для расчета изменения сопротивления в зависимости от температуры.
Зависимость сопротивления от материала и формы
Сопротивление объекта зависит от его формы и материала, из которого он состоит. Цилиндрический резистор на рисунке 1 легко анализировать, и таким образом мы можем получить представление о сопротивлении более сложных форм. Как и следовало ожидать, электрическое сопротивление цилиндра R прямо пропорционально его длине L , подобно сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше столкновений зарядов с его атомами произойдет. Чем больше диаметр цилиндра, тем больший ток он может пропускать (опять же аналогично потоку жидкости по трубе). На самом деле R обратно пропорционально площади поперечного сечения цилиндра A .
Рис. 1. Однородный цилиндр длиной L и площадью поперечного сечения A. Его сопротивление потоку тока аналогично сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление. Чем больше его площадь поперечного сечения А, тем меньше его сопротивление.
Чем длиннее цилиндр, тем больше его сопротивление. Чем больше его площадь поперечного сечения А, тем меньше его сопротивление.
Для данной формы сопротивление зависит от материала, из которого состоит объект. Различные материалы оказывают различное сопротивление потоку заряда. Определим удельное сопротивление ρ вещества так, что сопротивление R объекта прямо пропорционально ρ . Удельное сопротивление ρ является внутренним свойством материала, не зависящим от его формы или размера. Сопротивление R однородного цилиндра длиной L , площадью поперечного сечения A , изготовленного из материала с удельным сопротивлением ρ , равно
[латекс] R = \ frac{\rho L}{A }\\[/латекс].
В таблице 1 приведены репрезентативные значения ρ . Материалы, перечисленные в таблице, разделены на категории проводников, полупроводников и изоляторов на основе широких групп удельного сопротивления.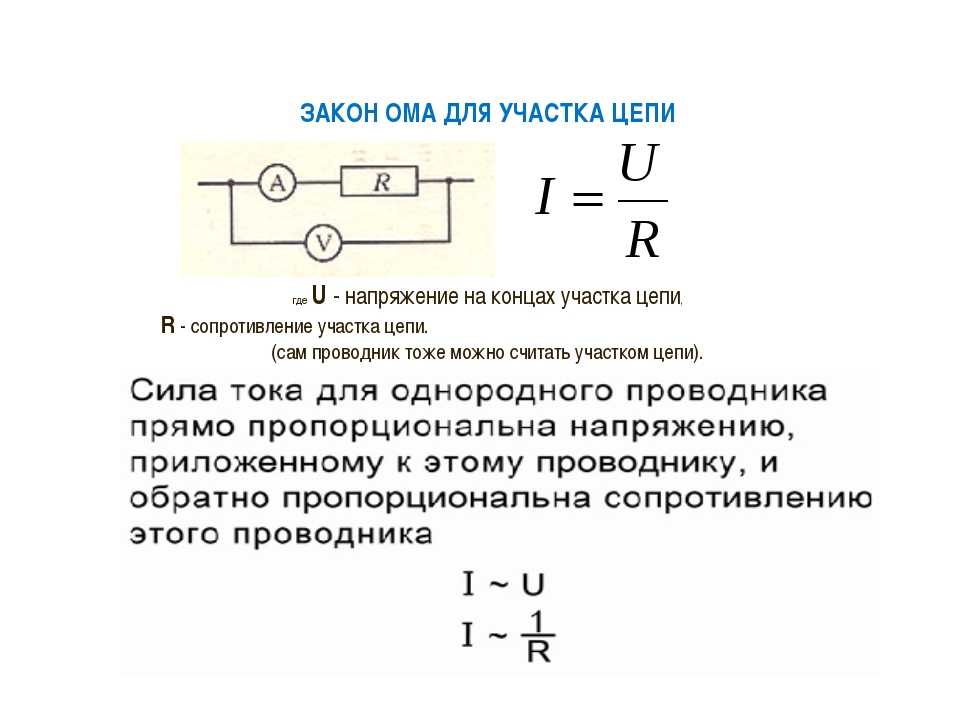 Проводники имеют наименьшее удельное сопротивление, а изоляторы – наибольшее; полупроводники имеют промежуточное сопротивление. Проводники имеют разную, но большую плотность свободного заряда, в то время как большинство зарядов в изоляторах связаны с атомами и не могут свободно перемещаться. Полупроводники занимают промежуточное положение, имея гораздо меньше свободных зарядов, чем проводники, но обладая свойствами, из-за которых количество свободных зарядов сильно зависит от типа и количества примесей в полупроводнике. Эти уникальные свойства полупроводников используются в современной электронике, что будет рассмотрено в последующих главах.
Проводники имеют наименьшее удельное сопротивление, а изоляторы – наибольшее; полупроводники имеют промежуточное сопротивление. Проводники имеют разную, но большую плотность свободного заряда, в то время как большинство зарядов в изоляторах связаны с атомами и не могут свободно перемещаться. Полупроводники занимают промежуточное положение, имея гораздо меньше свободных зарядов, чем проводники, но обладая свойствами, из-за которых количество свободных зарядов сильно зависит от типа и количества примесей в полупроводнике. Эти уникальные свойства полупроводников используются в современной электронике, что будет рассмотрено в последующих главах.
| Материал | Удельное сопротивление ρ ( Ом ⋅ м ) |
|---|---|
| Проводники | |
| Серебро | 1.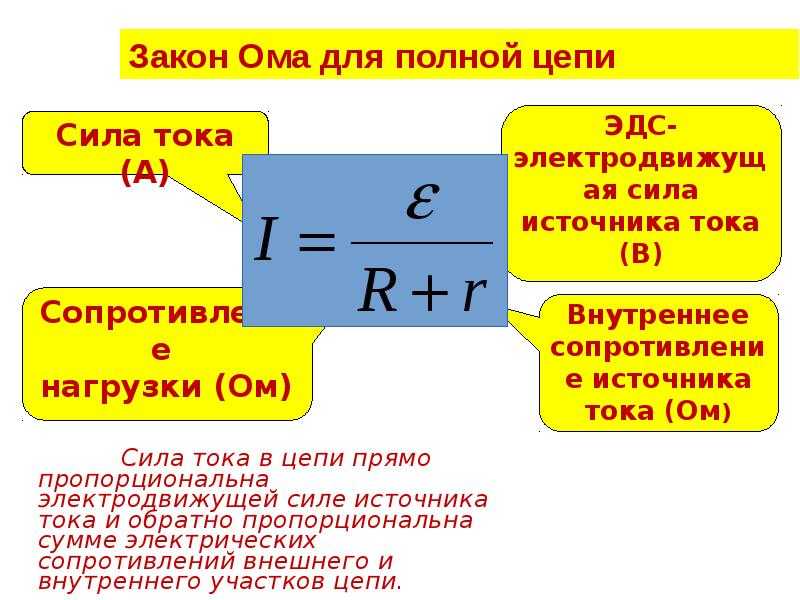 59 × 10 −8 59 × 10 −8 |
| Медь | 1. 72 × 10 −8 |
| Золото | 2. 44 × 10 −8 |
| Алюминий | 2. 65 × 10 −8 |
| Вольфрам | 5. 6 × 10 −8 |
| Железо | 9. 71 × 10 −8 |
| Платина | 10. 6 × 10 −8 |
| Сталь | 20 × 10 −8 |
| Свинец | 22 × 10 −8 |
| Манганин (сплав Cu, Mn, Ni) | 44 × 10 −8 |
| Константан (сплав Cu, Ni) | 49 × 10 −8 |
| Меркурий | 96 × 10 −8 |
| Нихром (сплав Ni, Fe, Cr) | 100 × 10 −8 |
| Полупроводники [1] | |
| Углерод (чистый) | 3,5 × 10 5 |
| Углерод | (3,5 − 60) × 10 5 |
| Германий (чистый) | 600 × 10 −3 |
| Германий | (1−600) × 10 −3 |
| Кремний (чистый) | 2300 |
| Кремний | 0,1–2300 |
| Изоляторы | |
| Янтарный | 5 × 10 14 |
| Стекло | 10 9 − 10 14 |
| Люцит | >10 13 |
| Слюда | 10 11 − 10 15 |
| Кварц (плавленый) | 75 × 10 16 |
| Резина (твердая) | 10 13 − 10 16 |
| Сера | 10 15 |
| Тефлон | >10 13 |
| Дерево | 10 8 − 10 11 |
Пример 1.
 {-9{-5}\text{m}\end{массив}\\[/latex]. Обсуждение
{-9{-5}\text{m}\end{массив}\\[/latex]. Обсуждение Диаметр чуть меньше десятой доли миллиметра. Оно приводится только с двумя цифрами, потому что ρ известно только с двумя цифрами.
Изменение сопротивления в зависимости от температуры
Удельное сопротивление всех материалов зависит от температуры. Некоторые даже становятся сверхпроводниками (нулевое сопротивление) при очень низких температурах. (См. рис. 2.)
Рис. 2. Сопротивление образца ртути равно нулю при очень низких температурах — это сверхпроводник примерно до 4,2 К. Выше этой критической температуры ее сопротивление делает резкий скачок, а затем возрастает почти до линейно с температурой.
И наоборот, удельное сопротивление проводников увеличивается с повышением температуры. Поскольку атомы вибрируют быстрее и преодолевают большие расстояния при более высоких температурах, электроны, движущиеся через металл, совершают больше столкновений, что фактически увеличивает удельное сопротивление. При относительно небольших изменениях температуры (около 100ºC или меньше) удельное сопротивление ρ изменяется с изменением температуры Δ T , как выражается в следующем уравнении
При относительно небольших изменениях температуры (около 100ºC или меньше) удельное сопротивление ρ изменяется с изменением температуры Δ T , как выражается в следующем уравнении
ρ = ρ 0 (1 + α Δ T ),
, где ρ 0 – исходное сопротивление, а α – температурный коэффициент 8. (См. значения α в Таблице 2 ниже.) Для больших изменений температуры α может варьироваться, или может потребоваться нелинейное уравнение для нахождения ρ . Обратите внимание, что α положительно для металлов, что означает, что их удельное сопротивление увеличивается с температурой. Некоторые сплавы были разработаны специально, чтобы иметь небольшую температурную зависимость. Манганин (состоящий из меди, марганца и никеля), например, имеет α близок к нулю (до трех знаков по шкале в табл. 2), поэтому его удельное сопротивление слабо зависит от температуры. Это полезно, например, для создания эталона сопротивления, не зависящего от температуры.
Это полезно, например, для создания эталона сопротивления, не зависящего от температуры.
| Материал | Коэффициент (1/°C) [2] |
|---|---|
| Проводники | |
| Серебро | 3,8 × 10 −3 |
| Медь | 3,9 × 10 −3 |
| Золото | 3,4 × 10 −3 |
| Алюминий | 3,9 × 10 −3 |
| Вольфрам | 4,5 × 10 −3 |
| Железо | 5,0 × 10 −3 |
| Платина | 3,93 × 10 −3 |
| Свинец | 3,9 × 10 −3 |
| Манганин (сплав Cu, Mn, Ni) | 0,000 × 10 −3 |
| Константан (сплав Cu, Ni) | 0,002 × 10 −3 |
| Меркурий | 0,89 × 10 −3 |
| Нихром (сплав Ni, Fe, Cr) | 0,4 × 10 −3 |
| Полупроводники | |
| Углерод (чистый) | −0,5 × 10 −3 |
| Германий (чистый) | −50 × 10 −3 |
| Кремний (чистый) | −70 × 10 −3 |
Обратите внимание, что α является отрицательным для полупроводников, перечисленных в таблице 2, а это означает, что их удельное сопротивление уменьшается с повышением температуры. Они становятся лучшими проводниками при более высокой температуре, потому что повышенное тепловое возбуждение увеличивает количество свободных зарядов, доступных для переноса тока. Это свойство уменьшения ρ с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках. Сопротивление объекта также зависит от температуры, так как R 0 прямо пропорционально ρ . Для цилиндра мы знаем, что R = ρL / A , и поэтому, если L и A не сильно изменяются с температурой, R будет иметь такую же температурную зависимость, как ρ . (Изучение коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, поэтому влияние температуры на L и A на два порядка меньше, чем на ρ .) Таким образом,
Они становятся лучшими проводниками при более высокой температуре, потому что повышенное тепловое возбуждение увеличивает количество свободных зарядов, доступных для переноса тока. Это свойство уменьшения ρ с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках. Сопротивление объекта также зависит от температуры, так как R 0 прямо пропорционально ρ . Для цилиндра мы знаем, что R = ρL / A , и поэтому, если L и A не сильно изменяются с температурой, R будет иметь такую же температурную зависимость, как ρ . (Изучение коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, поэтому влияние температуры на L и A на два порядка меньше, чем на ρ .) Таким образом,
R = R 0 (1 + α Δ T )
температурная зависимость сопротивления объекта, где R 0 — исходное сопротивление, R — сопротивление после изменения температуры Δ T . Многие термометры основаны на влиянии температуры на сопротивление. (См. рис. 3.) Одним из наиболее распространенных является термистор, полупроводниковый кристалл с сильной температурной зависимостью, сопротивление которого измеряется для получения его температуры. Устройство маленькое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается.
Многие термометры основаны на влиянии температуры на сопротивление. (См. рис. 3.) Одним из наиболее распространенных является термистор, полупроводниковый кристалл с сильной температурной зависимостью, сопротивление которого измеряется для получения его температуры. Устройство маленькое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается.
Рисунок 3. Эти известные термометры основаны на автоматизированном измерении сопротивления термистора в зависимости от температуры. (кредит: Biol, Wikimedia Commons)
Пример 2. Расчет сопротивления: сопротивление горячей нити
Хотя следует соблюдать осторожность при применении ρ = ρ 0 (1 + α 8 Δ
) и
R = R 0 (1 + α Δ T ) для изменений температуры более 100ºC, для вольфрама уравнения работают достаточно хорошо для очень больших изменений температуры. Каково же тогда сопротивление вольфрамовой нити в предыдущем примере, если ее температуру повысить с комнатной (20°С) до типичной рабочей температуры 2850°С? СтратегияЭто прямое применение R = R 0 (1 + α Δ T ), так как первоначальный сопротивление было дано R
), первоначальное сопротивление было дано R ). {-3}/º\text{C }\right)\left(2830º\text{C}\right)\right]\\ & =& {4.8\Omega}\end{массив}\\[/latex]. Обсуждение
{-3}/º\text{C }\right)\left(2830º\text{C}\right)\right]\\ & =& {4.8\Omega}\end{массив}\\[/latex]. Обсуждение Это значение согласуется с примером сопротивления фары в Законе Ома: сопротивление и простые схемы.
Исследования PhET: сопротивление в проводеУзнайте о физике сопротивления в проводе. Измените его удельное сопротивление, длину и площадь, чтобы увидеть, как они влияют на сопротивление провода. Размеры символов в уравнении меняются вместе со схемой провода.
Нажмите, чтобы запустить симуляцию.
Резюме сечения
- Сопротивление R цилиндра длиной L и площадью поперечного сечения A равно [латекс]R=\frac{\rho L}{A}\\[/latex], где ρ — удельное сопротивление материала.
- Значения ρ в таблице 1 показывают, что материалы делятся на три группы: проводники, полупроводники и изоляторы .

- Температура влияет на удельное сопротивление; для относительно небольших изменений температуры Δ T , удельное сопротивление равно [латекс]\rho ={\rho }_{0}\left(\text{1}+\alpha \Delta T\right)\\[/latex] , где ρ 0 исходное удельное сопротивление, а [латекс]\текст{\альфа}[/латекс] – температурный коэффициент удельного сопротивления.
- В таблице 2 приведены значения α , температурного коэффициента удельного сопротивления.
- Сопротивление R объекта также зависит от температуры: [латекс]R={R}_{0}\left(\text{1}+\alpha \Delta T\right)\\[/latex], где R 0 — исходное сопротивление, а R — сопротивление после изменения температуры.
Концептуальные вопросы
1. В каком из трех полупроводниковых материалов, перечисленных в таблице 1, примеси создают свободные заряды? (Подсказка: изучите диапазон удельного сопротивления для каждого из них и определите, имеет ли чистый полупроводник более высокую или более низкую проводимость. )
)
2. Зависит ли сопротивление объекта от пути прохождения тока через него? Рассмотрим, например, прямоугольный стержень — одинаково ли его сопротивление по длине и по ширине? (См. рис. 5.)
Рис. 5. Встречает ли ток, проходящий двумя разными путями через один и тот же объект, разное сопротивление?
3. Если алюминиевый и медный провода одинаковой длины имеют одинаковое сопротивление, какой из них имеет больший диаметр? Почему?
4. Объясните, почему [латекс]R={R}_{0}\left(1+\alpha\Delta T\right)\\[/latex] для температурного изменения сопротивления R объекта не так точен, как [латекс]\rho ={\rho }_{0}\left({1}+\alpha \Delta T\right)\\[/latex], что дает температурное изменение удельного сопротивления р .
Задачи и упражнения
1. Каково сопротивление отрезка медной проволоки 12-го калибра диаметром 2,053 мм длиной 20,0 м?
2. Диаметр медной проволоки нулевого калибра 8,252 мм. Найти сопротивление такого провода длиной 1,00 км, по которому осуществляется передача электроэнергии.
3. Если вольфрамовая нить диаметром 0,100 мм в электрической лампочке должна иметь сопротивление 0,200 Ом при 20ºC, то какой длины она должна быть?
4. Найдите отношение диаметра алюминиевого провода к медному, если они имеют одинаковое сопротивление на единицу длины (как в бытовой электропроводке).
5. Какой ток протекает через стержень из чистого кремния диаметром 2,54 см и длиной 20,0 см, если к нему приложено напряжение 1,00 × 10 3 В? (Такой стержень можно использовать, например, для изготовления детекторов ядерных частиц). ? (б) Происходит ли это в бытовой электропроводке при обычных обстоятельствах?
7. Резистор из нихромовой проволоки используется в тех случаях, когда его сопротивление не может измениться более чем на 1,00% от его значения при 20,0ºC. В каком диапазоне температур его можно использовать?
8. Из какого материала изготовлен резистор, если его сопротивление при 100°С на 40,0% больше, чем при 20,0°С?
9. Электронное устройство, предназначенное для работы при любой температуре в диапазоне от –10,0ºC до 55,0ºC, содержит резисторы из чистого углерода.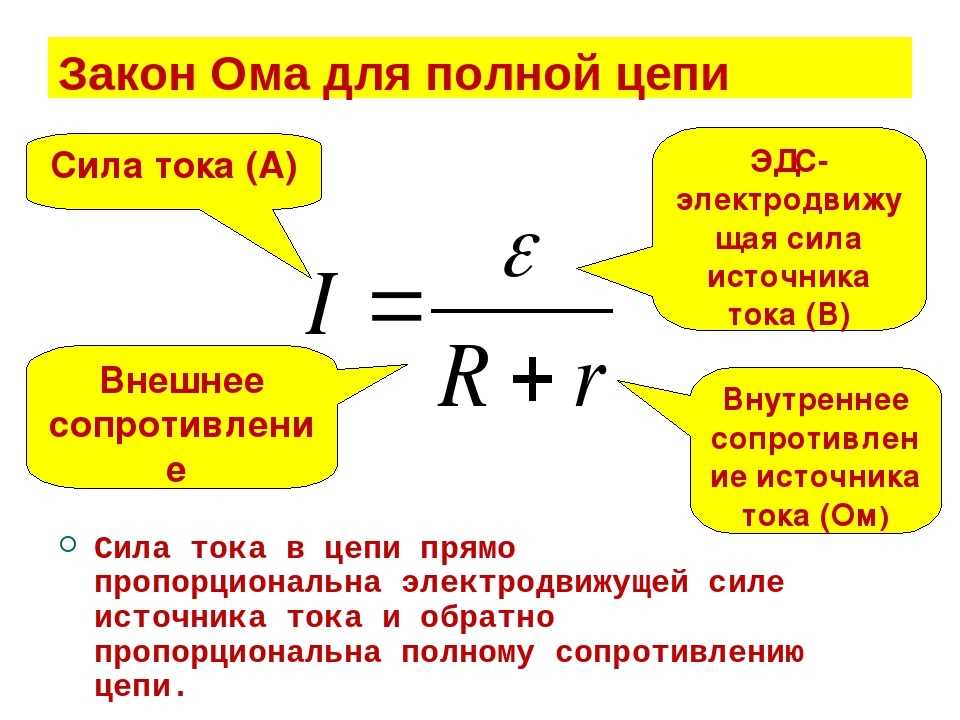 Во сколько раз увеличивается их сопротивление в этом диапазоне?
Во сколько раз увеличивается их сопротивление в этом диапазоне?
10. (a) Из какого материала сделан провод, если он имеет длину 25,0 м, диаметр 0,100 мм и сопротивление 77,7 Ом при 20,0ºC? б) Каково его сопротивление при 150°С?
11. При постоянном температурном коэффициенте удельного сопротивления, каково максимальное уменьшение сопротивления константановой проволоки в процентах, начиная с 20,0ºC?
12. Проволоку протягивают через матрицу, растягивая ее в четыре раза по сравнению с первоначальной длиной. Во сколько раз увеличивается его сопротивление?
13. Медный провод имеет сопротивление 0,500 Ом при 20,0°С, а железный провод имеет сопротивление 0,525 Ом при той же температуре. При какой температуре их сопротивления равны?
14. (a) Цифровые медицинские термометры определяют температуру путем измерения сопротивления полупроводникового устройства, называемого термистором (которое имеет α = –0,0600/ºC), когда оно имеет ту же температуру, что и пациент. Какова температура тела пациента, если сопротивление термистора при этой температуре составляет 82,0% от его значения при 37,0°С (нормальная температура тела)? (b) Отрицательное значение для α может не поддерживаться при очень низких температурах. Обсудите, почему и так ли это, здесь. (Подсказка: сопротивление не может стать отрицательным.)
Какова температура тела пациента, если сопротивление термистора при этой температуре составляет 82,0% от его значения при 37,0°С (нормальная температура тела)? (b) Отрицательное значение для α может не поддерживаться при очень низких температурах. Обсудите, почему и так ли это, здесь. (Подсказка: сопротивление не может стать отрицательным.)
15. Комплексные концепции (a) Повторите упражнение 2 с учетом теплового расширения вольфрамовой нити. Вы можете принять коэффициент теплового расширения равным 12 × 10 −6 /ºC. б) На сколько процентов ваш ответ отличается от ответа в примере?
16. Необоснованные результаты (a) До какой температуры нужно нагреть резистор из константана, чтобы удвоить его сопротивление при постоянном температурном коэффициенте удельного сопротивления? б) Разрезать пополам? в) Что неразумного в этих результатах? (d) Какие предположения неразумны, а какие предпосылки противоречивы?
Сноски
- 1 Значения сильно зависят от количества и типов примесей
- 2 Значения при 20°C.

Глоссарий
- Удельное сопротивление:
- внутреннее свойство материала, независимое от его формы или размера, прямо пропорциональное сопротивлению, обозначаемому ρ
- температурный коэффициент удельного сопротивления:
- эмпирическая величина, обозначаемая α , которая описывает изменение сопротивления или удельного сопротивления материала при температуре
Выбранные решения для проблем и упражнений
1. 0,104 ω
3. 2,8 × 10 −2 M
5. 1,10 × 10 – 3 A
7. – 5ºC до 45ºC
9. 1,03
11. 0,06%
13,-17ºC
15. (а) 4,7 Ом (всего) (б) уменьшение на 3,0%
Значения сильно зависят от количества и типа примесей °С. ↵
Закон Кирхгофа для сложных цепей | ОРЕЛ
Закон Ома — ваш золотой билет для расчета напряжения, тока или сопротивления в простой последовательной или параллельной цепи, но что происходит, когда ваша цепь более сложная? Вы можете проектировать электронику, которая имеет как параллельное, так и последовательное сопротивление, и закон Ома начинает нарушаться. Или что, если у вас нет источника постоянного тока? В этих ситуациях, когда вы не можете использовать только V = IR, пришло время встать на плечи Ома и использовать закон Кирхгофа. Здесь мы рассмотрим, что такое закон Кирхгофа о цепях и как его использовать для анализа напряжения и тока в сложных электрических цепях.
Или что, если у вас нет источника постоянного тока? В этих ситуациях, когда вы не можете использовать только V = IR, пришло время встать на плечи Ома и использовать закон Кирхгофа. Здесь мы рассмотрим, что такое закон Кирхгофа о цепях и как его использовать для анализа напряжения и тока в сложных электрических цепях.
Что такое закон Кирхгофа?
Когда вы строите сложную схему, включающую мосты или тройники, вы не можете полагаться исключительно на закон Ома для определения напряжения или тока. Здесь пригодится закон Кирхгофа о цепях, который позволяет рассчитать как ток, так и напряжение для сложных цепей с помощью системы линейных уравнений. Есть два варианта закона Кирхгофа, в том числе:
- Закон тока Кирхгофа: Для анализа полного тока сложной цепи
- Закон Кирхгофа о напряжении : для анализа полного напряжения сложной цепи
- Если объединить эти два закона, получится Закон Кирхгофа о цепях
Как и любой другой научный или математический закон, названный в честь его создателя, Закон Кирхгофа был изобретен немецким физиком Густавом Кирхгофом. Густав был известен многими достижениями при жизни, в том числе теорией спектрального анализа, которая доказала, что элементы излучают уникальный световой узор при нагревании. Когда Кирхгоф и химик Роберт Бунзен проанализировали эти световые узоры через призму, они обнаружили, что каждый элемент в периодической таблице имеет свою уникальную длину волны. Открытие этой закономерности позволило дуэту открыть два новых элемента, цезий и рубидий.
Густав был известен многими достижениями при жизни, в том числе теорией спектрального анализа, которая доказала, что элементы излучают уникальный световой узор при нагревании. Когда Кирхгоф и химик Роберт Бунзен проанализировали эти световые узоры через призму, они обнаружили, что каждый элемент в периодической таблице имеет свою уникальную длину волны. Открытие этой закономерности позволило дуэту открыть два новых элемента, цезий и рубидий.
Густав Кирхгоф (слева) и Роберт Бунзен (справа)
Позже Кирхгоф применил свою теорию спектрального анализа для изучения состава Солнца, где он обнаружил много темных линий в солнечном спектре длин волн. Это было вызвано поглощением солнечным газом световых волн определенной длины, и это открытие ознаменовало начало новой эры исследований и исследований в области астрономии.
Чуть ближе к дому в мире электроники Кирхгоф объявил свой свод законов для анализа тока и напряжения в электрических цепях в 1845 году, известный сегодня как Закон Кирхгофа о цепях. Эта работа основана на фундаменте, изложенном в законе Ома, и помогла проложить путь для анализа сложных цепей, на который мы полагаемся сегодня.
Эта работа основана на фундаменте, изложенном в законе Ома, и помогла проложить путь для анализа сложных цепей, на который мы полагаемся сегодня.
Первый закон – Текущий закон Кирхгофа
Закон тока Кирхгофа гласит, что количество тока, входящего в узел, равно количеству тока, выходящего из узла. Почему? Потому что, когда ток входит в узел, ему некуда идти, кроме выхода. То, что входит, должно выйти. Вы можете определить узел, в котором два или более пути соединены через общую точку. На схеме это будет точка соединения, соединяющая два пересекающихся сетевых соединения.
Взгляните на изображение ниже, чтобы наглядно понять этот Закон. Здесь у нас есть два тока, входящие в узел, и три тока, выходящие из узла. Согласно закону токов Кирхгофа отношение между этими токами, входящими в узел и выходящими из узла, можно представить как I 1 + I 2 = I 3 + I 4 + I 9,90
Закон тока Кирхгофа, ток на входе должен равняться току на выходе. (Источник изображения)
(Источник изображения)
Когда вы сбалансируете это уравнение как алгебраическое выражение, вы сделаете вывод, что ток входа и выхода из узла всегда будет равен 0, или56 3 + -I 4 + -I 5 ) = 0 Все должно уравновеситься, и Кирхгоф назвал этот принцип Сохранение заряда .
Давайте посмотрим на пример схемы, чтобы увидеть, как это работает. Ниже у нас есть схема с четырьмя узлами: A, C, E и F. Ток сначала течет от источника напряжения и разделяется в узле A, который затем течет через резисторы R1 и R2. Оттуда ток рекомбинирует в узле C и снова разделяется, чтобы течь через резисторы R3, R4 и R5 , где он встречается с узлом E и узлом F.
(Источник изображения)
Чтобы подтвердить действие закона тока Кирхгофа в этой цепи, нам нужно предпринять следующие шаги:
- Расчет полного тока цепи
- Рассчитать ток, протекающий через каждый узел
- Сравните входной и выходной токи в определенных узлах, чтобы подтвердить закон Кирхгофа о токе.

1. Расчет общего тока
Здесь мы используем закон Ома, чтобы получить общий ток нашей цепи с I = В/Р . У нас уже есть общее напряжение 132 В, и теперь нам просто нужно найти общее сопротивление во всех наших узлах. Для этого требуется простой метод расчета общего сопротивления резисторов, соединенных параллельно, которое составляет:
Начиная с узла AC, мы получаем следующее сопротивление для параллельных резисторов R1 и R2:
И переходя к Node CEF, мы получаем следующее сопротивление для параллельных резисторов R3, R4 и R5:
Теперь у нас есть общее сопротивление 11 Ом для всей цепи, которое мы затем можем подставить в закон Ома I = V/R , чтобы получить полный ток в нашей цепи:
2. Расчет узловых токов
Теперь, когда мы знаем, что из нашей цепи вытекает 12 ампер, мы можем рассчитать ток в каждом наборе узлов. Мы снова воспользуемся законом Ома в виде I = V/R , чтобы получить ток для каждой ветви узла.
Сначала нам нужны напряжения узловых ветвей AC и CF:
Затем мы можем рассчитать ток для каждой ветки узла:
3. Подтвердить действующий закон Кирхгофа
После расчета тока для каждой ветви узла у нас теперь есть две различные контрольные точки, которые мы можем использовать для сравнения наших входных и выходных токов. Это позволит нам проанализировать нашу схему и подтвердить закон тока Кирхгофа следующим образом:
Второй закон – закон напряжения Кирхгофа
Закон Кирхгофа о напряжении гласит, что в любой цепи с замкнутым контуром общее напряжение всегда будет равно сумме всех падений напряжения в контуре. Вы обнаружите, что падение напряжения происходит всякий раз, когда ток протекает через пассивный компонент, такой как резистор, и Кирхгоф назвал этот закон Законом сохранения энергии . Опять же, то, что входит, должно выйти.
Взгляните на изображение ниже, чтобы понять это визуально. В этой схеме у нас есть источник напряжения и четыре области в цепи, где напряжение будет встречаться с пассивной составляющей, что вызовет отчетливое падение напряжения.
В этой схеме у нас есть источник напряжения и четыре области в цепи, где напряжение будет встречаться с пассивной составляющей, что вызовет отчетливое падение напряжения.
Поскольку эти пассивные компоненты соединены последовательно, вы можете просто сложить общее падение напряжения и сравнить его с общим напряжением, чтобы получить соотношение, которое выглядит следующим образом:
Давайте начнем с простой схемы, чтобы продемонстрировать, как это работает. В приведенном ниже примере у нас есть две известные переменные: общее напряжение и падение напряжения на резисторе R1.
(Источник изображения)
Что нам нужно вычислить, так это падение напряжения на R2, и мы можем использовать закон Кирхгофа о напряжении, чтобы вычислить это со следующим соотношением:
Поскольку общее падение напряжения в цепи должно равняться общему напряжению источника, это обеспечивает простой способ вычисления отсутствующей переменной. Если бы вы хотели выразить это соотношение в виде правильного алгебраического выражения, вы бы получили сумму всех падений напряжения и общее напряжение, равное нулю, как показано здесь:
Если бы вы хотели выразить это соотношение в виде правильного алгебраического выражения, вы бы получили сумму всех падений напряжения и общее напряжение, равное нулю, как показано здесь:
Давайте посмотрим на другой пример. В схеме ниже у нас есть три резистора, соединенных последовательно с 12-вольтовой батареей.
Чтобы подтвердить закон Кирхгофа о напряжении в этой схеме, нам нужно предпринять следующие шаги:
- Расчет полного сопротивления цепи
- Рассчитать полный ток цепи
- Рассчитать ток через каждый резистор
- Вычислить падение напряжения на каждом резисторе
Сравните источник напряжения с полным падением напряжения , чтобы подтвердить закон Кирхгофа о напряжении
1. Рассчитать общее сопротивление
Поскольку все наши резисторы соединены последовательно, мы можем легко найти общее сопротивление, просто сложив все значения сопротивления вместе:
2.
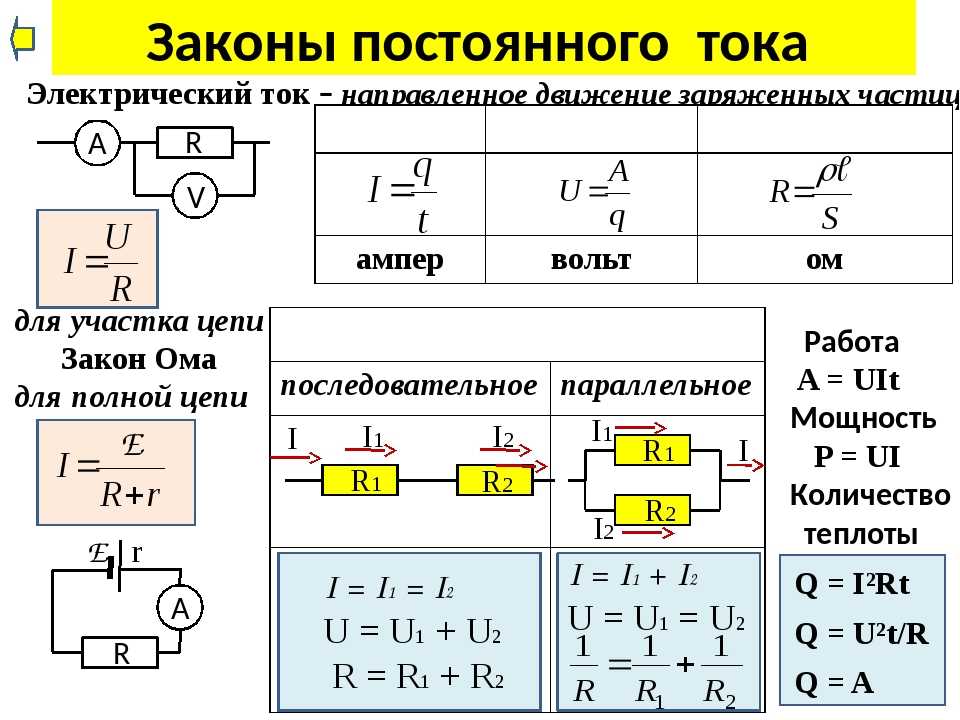 Рассчитать общий ток
Рассчитать общий токТеперь, когда мы знаем наше общее сопротивление, мы можем снова использовать закон Ома, чтобы получить полный ток нашей цепи в виде I = V/R, , что выглядит так:
3. Рассчитать ток через каждый резистор
Поскольку все наши резисторы соединены последовательно, все они будут иметь одинаковую величину тока, протекающего через них, что мы можем выразить как:
4. Рассчитайте падение напряжения на каждом резисторе
Наш окончательный расчет снова будет использовать закон Ома, чтобы дать нам общее падение напряжения для каждого резистора в виде В = IR , что выглядит следующим образом:
5. Проверка закона Кирхгофа о напряжении
Теперь у нас есть все необходимые данные, включая общее напряжение нашей цепи, а также каждое падение напряжения на каждом из наших резисторов. Собрав все это вместе, мы можем легко подтвердить закон Кирхгофа о напряжении с помощью этого соотношения:
Это также может быть выражено как:
Как видите, общее напряжение равно общему падению напряжения в нашей схеме. То, что входит, должно выйти наружу, и закон Кирхгофа снова работает!
То, что входит, должно выйти наружу, и закон Кирхгофа снова работает!
Процесс использования Закона о цепях Кирхгофа
Теперь, когда вы понимаете, как работает закон Кирхгофа о цепях, у вас есть новый инструмент для анализа напряжения и тока в полных цепях. При использовании этих законов в дикой природе рассмотрите возможность использования следующего пошагового процесса:
- Во-первых, начните с маркировки всех известных напряжений и сопротивлений в вашей цепи.
- Затем назовите каждую ветвь вашей цепи текущей меткой, например I1, I2, I3 и т. д. Ветвь – это один или группа компонентов, соединенных между двумя узлами.
- Затем найдите закон тока Кирхгофа для каждого узла в вашей цепи.
- Затем найдите закон Кирхгофа для напряжения для каждого из независимых контуров в вашей цепи.
После того, как вы вычислили законы тока и напряжения Кирхгофа, вы можете использовать ваши уравнения, чтобы найти недостающие токи. Готовы попробовать сами? Взгляните на схему ниже и посмотрите, сможете ли вы проверить закон Кирхгофа для тока и закон напряжения с небольшой помощью Ома!
Пишите свои ответы в комментариях ниже!Стоя на плечах Ома
Имея в руках закон Кирхгофа о цепях, у вас теперь есть все инструменты, необходимые для анализа напряжения и тока в сложных цепях.



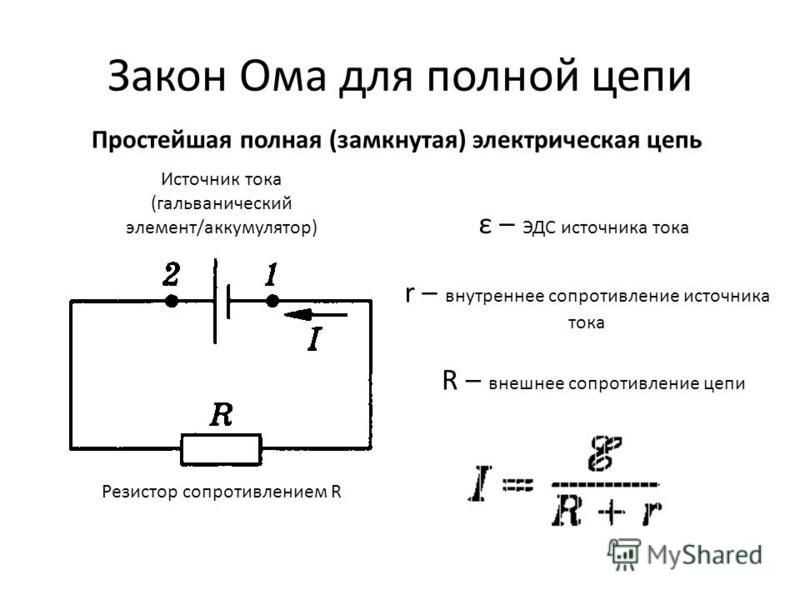 Произвольные замкнутые контуры выделяются так, чтобы каждый новый контур содержал хотя бы один участок, не входящий в ранее рассмотренные контуры;
Произвольные замкнутые контуры выделяются так, чтобы каждый новый контур содержал хотя бы один участок, не входящий в ранее рассмотренные контуры; Формулы и применение
Формулы и применение 2019 г
2019 г измерение физических
величин, решать простые задачи на формулу закона Ома и формулу сопротивления
проводника
измерение физических
величин, решать простые задачи на формулу закона Ома и формулу сопротивления
проводника
 Организационный момент. Создание
в классе благоприятной психологической обстановки Доброе утро,
ребята! Пусть оно действительно будет для нас сегодня добрым.
Организационный момент. Создание
в классе благоприятной психологической обстановки Доброе утро,
ребята! Пусть оно действительно будет для нас сегодня добрым. 
 Стратегия «мозаика»
Стратегия «мозаика»

 Оценивание самим учителем (решение задач),самооценивание,и
взаимооценивание при работе с изучением новой темы и составлением постера
Оценивание самим учителем (решение задач),самооценивание,и
взаимооценивание при работе с изучением новой темы и составлением постера

 Кроме того, можно добиться тока, протекающего через вентилятор, с помощью регулятора для управления сопротивлением. Мы можем измерить мощность, сопротивление и ток, протекающий через вентилятор, применяя закон Ома.
Кроме того, можно добиться тока, протекающего через вентилятор, с помощью регулятора для управления сопротивлением. Мы можем измерить мощность, сопротивление и ток, протекающий через вентилятор, применяя закон Ома.

 Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица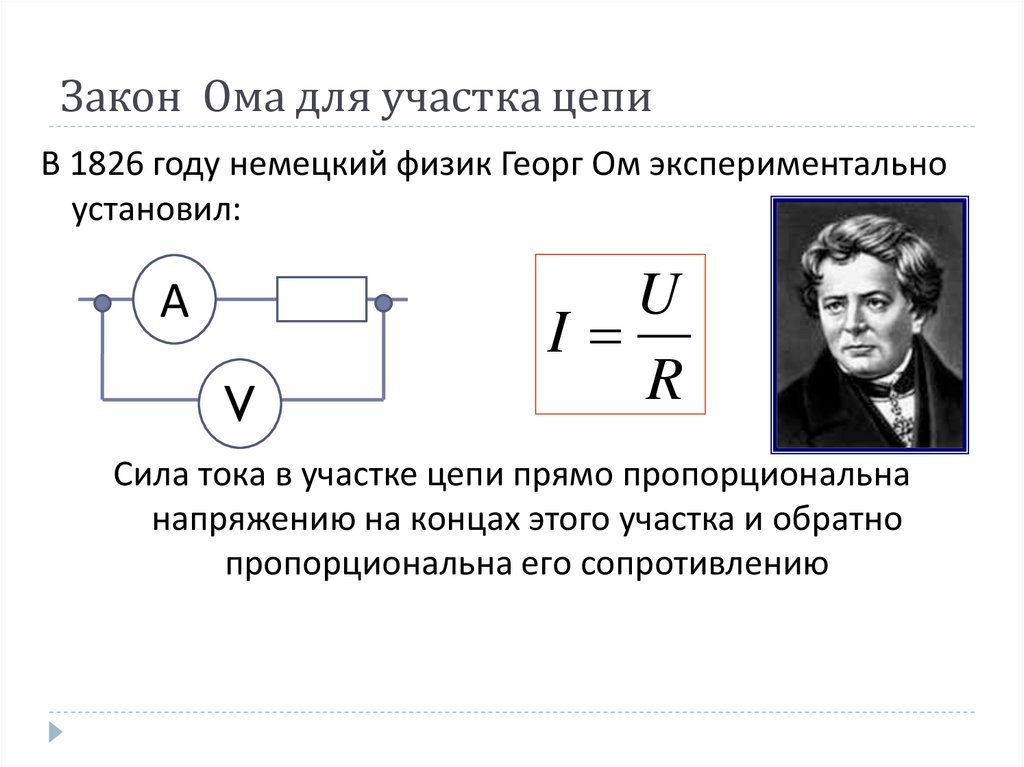
 .. США), пинта сухая (США), кварта сухая (США), пек (США), пек (Великобритания), бушель (США), бушель (Великобритания), кор (библейский), гомер (библейский), ефа (библейский), сеах (библейский), омер (библейский), каб (библейский), бревно (библейский), кубический метр.
.. США), пинта сухая (США), кварта сухая (США), пек (США), пек (Великобритания), бушель (США), бушель (Великобритания), кор (библейский), гомер (библейский), ефа (библейский), сеах (библейский), омер (библейский), каб (библейский), бревно (библейский), кубический метр. ..
.. ..
.. ..
.. ..
.. ..
.. ..
..
 ..
.. )/фут³, CHU/фут³, метр³/джоуль, литр/джоуль, галлон (США)/лошадиная сила-час, галлон (США)/лошадиная сила (метрическая )-час.
)/фут³, CHU/фут³, метр³/джоуль, литр/джоуль, галлон (США)/лошадиная сила-час, галлон (США)/лошадиная сила (метрическая )-час.

 ..
..







 В этой таблице перечислены размеры и сопротивления AWG для медных проводников. Используйте закон Ома для расчета падения напряжения на проводнике.
В этой таблице перечислены размеры и сопротивления AWG для медных проводников. Используйте закон Ома для расчета падения напряжения на проводнике.

 ..
.. Некоторые группы имеют имена, а также номера. Например, все элементы 1-й группы, кроме водорода, являются щелочными металлами, а элементы 18-й группы — благородными газами, которые ранее назывались инертными газами. Различные строки таблицы называются периодами, потому что такое расположение отражает периодическое повторение сходных химических и физических свойств химических элементов по мере увеличения их атомного номера. Элементы одного периода имеют одинаковое количество электронных оболочек.
Некоторые группы имеют имена, а также номера. Например, все элементы 1-й группы, кроме водорода, являются щелочными металлами, а элементы 18-й группы — благородными газами, которые ранее назывались инертными газами. Различные строки таблицы называются периодами, потому что такое расположение отражает периодическое повторение сходных химических и физических свойств химических элементов по мере увеличения их атомного номера. Элементы одного периода имеют одинаковое количество электронных оболочек.