Какие бывают интегралы: WolframAlpha по-русски: Несобственные интегралы в Wolfram|Alpha - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Несобственные интегралы примеры решения сложные. Несобственные интегралы. Примеры решений

Несобственный интеграл с бесконечным пределом интегрирования

Иногда такой несобственный интеграл еще называют несобственным интегралом первого рода..gif”>.

Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: .

Мы рассмотрим самый популярный случай https://pandia.ru/text/80/057/images/image005_1.gif”>? Нет, не всегда. Подынтегральная функция https://pandia.ru/text/80/057/images/image007_0.gif”>

Изобразим на чертеже график подынтегральной функции . Типовой график и криволинейная трапеция для данного случая выглядит так:

Несобственный интеграл https://pandia.ru/text/80/057/images/image009_0.gif”>», иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что, что несобственный интеграл расходится .

2) Но . Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: .. Во втором случае несобственный интеграл сходится .

А что будет, если бесконечная криволинейная трапеция расположена ниже оси?.gif”>.

: .

Пример 1

Подынтегральная функция https://pandia.ru/text/80/057/images/image017_0.gif”>, значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.

Применение нашей формулы https://pandia.ru/text/80/057/images/image018_0.gif”>

То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.

При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!

Пример 2

Вычислить несобственный интеграл или установить его расходимость.

Выполним чертеж:

Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд..gif”>

(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.

(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.

(3) Указываем, что https://pandia.ru/text/80/057/images/image024.gif”> (Господа, это уже давно нужно понимать) и упрощаем ответ.

Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.

Пример 3

Вычислить несобственный интеграл или установить его расходимость.

Подынтегральная функция непрерывна на .

Сначала попытаемся найти первообразную функцию (неопределенный интеграл).

На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.

Проведем замену:

Всегда полезно выполнить проверку, то есть продифференцировать полученный результат:

Теперь находим несобственный интеграл:

(1) Записываем решение в соответствии с формулой . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.

(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница..gif”>? Смотрите график арктангенса в уже неоднократно рекомендованной статье.

(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.

Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:

“

Подынтегральная функция непрерывна на https://pandia.ru/text/80/057/images/image041.gif”>
“

Пример 4

Вычислить несобственный интеграл или установить его расходимость.

! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата.

Пример 5

Вычислить несобственный интеграл или установить его расходимость.

Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала..

Несобственные интегралы от неограниченных функций

Иногда такие несобственные интегралы называют несобственными интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: ..gif”>, 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.

Сразу пример, чтобы было понятно: https://pandia.ru/text/80/057/images/image048.gif”>, то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!

Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования . .jpg” alt=”Несобственный интеграл, точка разрыва в нижнем пределе интегрирования”>

Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).

Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению https://pandia.ru/text/80/057/images/image052.gif”> справа .

Пример 6

Вычислить несобственный интеграл или установить его расходимость.

Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)

Сначала вычислим неопределенный интеграл:

Замена:

Вычислим несобственный интеграл:

(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.

(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.

(3) Разбираемся с https://pandia.ru/text/80/057/images/image058.gif”>. Как определить, куда стремиться выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.

В данном случае несобственный интеграл равен отрицательному числу.

Пример 7

Вычислить несобственный интеграл или установить его расходимость.

Пример 8

Вычислить несобственный интеграл или установить его расходимость.

Если подынтегральной функции не существует в точке

Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом:

Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению

https://pandia. ru/text/80/057/images/image052.gif”> мы должны бесконечно близко приблизиться к точке разрыва слева .

Несобственные интегралы первого рода: распространение понятия определённого интеграла на случаи интегралов с бесконечным верхним или нижними пределами интегрирования, или оба предела интегрирования бесконечны.

Несобственные интегралы второго рода: распространение понятия определённого интеграла на случаи интегралов от неограниченных функций, подынтегральная функция в конечном числе точек конечного отрезка интегрирования не существует, обращаясь в бесконечность.

Для сравнения. При введении понятия определённого интеграла предполагалось, что функция f (x ) непрерывна на отрезке [a , b ], а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений. Так появляются несобственные интегралы.

y = f (x ) , осью абсцисс и ординатами x = a , x = b . В свою очередь несобственный интеграл выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями y = f (x ) (на рисунке ниже – красного цвета), x = a и осью абсцисс.

Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:

Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный интеграл называется сходящимся. Площадь может быть и бесконечностью и в этом случае несобственный интеграл называется расходящимся.

Использование предела интеграла вместо самого несобственного интеграла. Для того, чтобы вычислить несобственный интеграл, нужно использовать предел определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то несобственный интеграл называется сходящимся, а в противном случае – расходящимся. К чему стремится переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода или второго рода. Узнаем об этом сейчас же.

Несобственные интегралы первого рода – с бесконечными пределами и их сходимость

Несобственные интегралы с бесконечным верхним пределом

Итак, запись несобственного интеграла как отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.

Определение. Несобственным интегралом с бесконечным верхним пределом интегрирования от непрерывной функции f (x ) на промежутке от a до ∞ называется предел интеграла этой функции с верхним пределом интегрирования b и нижним пределом интегрирования a при условии, что верхний предел интегрирования неограниченно растёт , т. е.

Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся , а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся и ему не приписывается никакого значения.

Пример 1. Вычислить несобственный интеграл (если он сходится).

Решение. На основании определения несобственного интеграла находим

Так как предел существует и равен 1, то и данный несобственный интеграл сходится и равен 1.

В следующем примере подынтегральная функция почти как в примере 1, только степень икса – не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость. То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится, а при каких расходится?

Пример 2. Исследовать на сходимость несобственный интеграл (нижний предел интегрирования больше нуля).

Решение. Предположим сначала, что , тогда

В полученном выражении перейдём к пределу при :

Нетрудно видеть, что предел в правой части существует и равен нулю, когда , то есть , и не существует, когда , то есть .

В первом случае, то есть при имеет место . Если , то и не существует.

Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .

Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница , можно вывести следующую очень похожую на неё формулу:

Это обобщённая формула Ньютона-Лейбница.

Пример 3. Вычислить несобственный интеграл (если он сходится).

Предел этого интеграла существует:

Второй интеграл, составляющий сумму, выражающую исходный интеграл:

Предел этого интеграла также существует:

Находим сумму двух интегралов, являющуюся и значением исходного несобственного интеграла с двумя бесконечными пределами:

Несобственные интегралы второго рода – от неограниченных функций и их сходимость

Пусть функция f (x ) задана на отрезке от a до b и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b , в то время как во всех остальных точках отрезка она непрерывна.

Определение. Несобственным интегралом функции f (x ) на отрезке от a до b называется предел интеграла этой функции с верхним пределом интегрирования c , если при стремлении c к b функция неограниченно возрастает, а в точке x = b функция не определена , т.е.

Если этот предел существует, то несобственный интеграл второго рода называется сходящимся, в противном случае – расходящимся.

Используя формулу Ньютона-Лейбница, выводим.

Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….

Итак, начнем-с. Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного интеграла есть очень хороший геометрический смысл.

Что значит вычислить несобственный интеграл?

Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).

Несобственные интегралы бывают двух видов.

Несобственный интеграл с бесконечным пределом (ами) интегрирования

Иногда такой несобственный интеграл называют несобственным интегралом первого рода . В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: . В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .

Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: , и их мы рассмотрим позже – когда войдёте во вкус:)

Ну а сейчас разберём самый популярный случай . В подавляющем большинстве примеров подынтегральная функция непрерывна на промежутке , и этот важный факт следует проверять в первую очередь! Ибо если есть разрывы, то есть дополнительные нюансы. Для определённости предположим, что и тогда типичная криволинейная трапеция будет выглядеть так:

Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл численно равен её площади . При этом возможны следующие варианты:

1) Первая мысль, которая приходит в голову: «раз фигура бесконечная, то », иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что несобственный интеграл расходится .

2) Но . Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: . Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится .

3) О третьем варианте чуть позже.

В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции , и конкретные примеры мы очень скоро рассмотрим.

А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл (расходится) либо равен конечному отрицательному числу.

Таким образом, несобственный интеграл может быть отрицательным .

Важно! Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно . Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.

Коль скоро, несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: . На самом деле формула применима и к несобственным интегралам, только ее нужно немного модифицировать. В чем отличие? В бесконечном верхнем пределе интегрирования: . Наверное, многие догадались, что это уже попахивает применением теории пределов, и формула запишется так: .

В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию (неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела. У кого с ними плохо, изучите урок Пределы функций. Примеры решений , ибо лучше поздно, чем в армии.

Рассмотрим два классических примера:

Пример 1

Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно .

Подынтегральная функция непрерывна на полуинтервале , значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.

Применение нашей формулы и решение задачи выглядит так:

В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применятся эта формула под знаком предела. Вместо привычной буквы «динамической» переменной выступает буква «бэ». Это не должно смущать или ставить в тупик, потому что любая буква ничем не хуже стандартного «икса».

Если Вам не понятно почему при , то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. Во втором случае посетите урок Графики и свойства элементарных функций .

При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!

Чистовое оформление задания должно выглядеть примерно так:

“

! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией – непрерывна она на промежутке интегрирования или нет . Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.

Пример 2

Вычислить несобственный интеграл или установить его расходимость.

Выполним чертеж:

Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд. Решаем с помощью формулы :

(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.

(3) Указываем, что при (Господа, это уже давно нужно понимать) и упрощаем ответ.

Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.

Чистовое оформление примера должно выглядеть примерно так:

“

Подынтегральная функция непрерывна на

“

Что делать, если вам встретится интеграл наподобие – с точкой разрыва на интервале интегрирования? Это говорит о том, что в примере опечатка (вероятнее всего) , либо о продвинутом уровне обучения. В последнем случае, в силу свойства аддитивности , следует рассмотреть два несобственных интеграла на промежутках и и затем разобраться с суммой.

Иногда вследствие опечатки либо умысла несобственного интеграла может вовсе не существовать , так, например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть промежутка интегрирования вообще не войдёт в область определения подынтегральной функции.

Более того, несобственного интеграла может не существовать даже при всём «видимом благополучии». Классический пример: . Несмотря на определённость и непрерывность косинуса, такого несобственного интеграла не существует! Почему? Всё очень просто, потому что:
– не существует соответствующего предела .

И такие примеры пусть редко, но встречаются на практике! Таким образом, помимо сходимости и расходимости, есть ещё и третий исход решения с полноправным ответом: «несобственного интеграла не существует».

Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе. Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:

Пример 3

Вычислить несобственный интеграл или установить его расходимость.

Сначала попытаемся найти первообразную функцию (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.

Проведем замену:

Неопределенный интеграл найден, константу в данном случае добавлять не имеет смысла.

На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:

Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.

Теперь находим несобственный интеграл:

(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему при ? Смотрите график арктангенса в уже неоднократно рекомендованной статье.

(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.

“

Подынтегральная функция непрерывна на .

“

Пример 4

Вычислить несобственный интеграл или установить его расходимость.

! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей .

Пример 5

Вычислить несобственный интеграл или установить его расходимость.

Полные решения и ответы в конце урока.

Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов . Там же разобран случай, когда оба предела интегрирования бесконечны.

Несобственные интегралы от неограниченных функций

Или несобственные интегралами второго рода . Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: Но, в отличие от определенного интеграла, подынтегральная функция терпит бесконечный разрыв (не существует): 1) в точке , 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.

Сразу пример, чтобы было понятно: . Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!

Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования . В этой связи проверим и верхний предел: . Здесь всё хорошо.

Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:

Здесь почти всё так же, как в интеграле первого рода.

Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).

* по умолчанию привычно полагаем, что несобственный интеграл существует

Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению справа. Легко проследить по чертежу: по оси мы должны бесконечно близко приблизиться к точке разрыва справа .

Посмотрим, как это реализуется на практике.

Пример 6

Вычислить несобственный интеграл или установить его расходимость.

Сначала вычислим неопределенный интеграл:

Замена:

У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле .

Вычислим несобственный интеграл:

(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом . В данном случае у нас правосторонний предел .

(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.

(3) Разбираемся с при . Как определить, куда стремится выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.

В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью .

А сейчас два примера для самостоятельного решения.

Пример 7

Вычислить несобственный интеграл или установить его расходимость.

Пример 8

Вычислить несобственный интеграл или установить его расходимость.

Если подынтегральной функции не существует в точке

Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом.

Определенный интеграл как предел интегральной суммы

может существовать (т.е. иметь определенное конечное значение) лишь при выполнении условий

Если хотя бы одно из этих условий нарушено, то определение теряет смысл. Действительно, в случае бесконечного отрезка, например [a ; ) его нельзя разбить на п частей конечной длины
, которая к тому же с увеличением количества отрезков стремилась бы к нулю. В случае же неограниченной в некоторой точкес [a ; b ] нарушается требование произвольного выбора точки на частичных отрезках – нельзя выбрать=с , поскольку значение функции в этой точке не определено. Однако и для этих случаев можно обобщить понятие определенного интеграла, введя еще один предельный переход. Интегралы по бесконечным промежуткам и от разрывных (неограниченных) функций называют несобственными .

Определение.

Пусть функция
определена на промежутке [a ; ) и интегрируема на любом конечном отрезке [a ; b ], т.е. существует
для любого b > a . Предел вида
называютнесобственным интегралом первого рода (или несобственным интегралом по бесконечному промежутку) и обозначают
.

Таким образом, по определению,
=
.

Если предел справа существует и конечен, то несобственный интеграл
называютсходящимся . Если этот предел бесконечен, или не существует вообще, то говорят, что несобственный интеграл расходится .

Аналогично можно ввести понятие несобственного интеграла от функции
по промежутку (–; b ]:

=
.

А несобственный интеграл от функции
по промежутку (–; +) определяется как сумма введенных выше интегралов:

=
+
,

где а – произвольная точка. Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно из слагаемых.

С геометрической точки зрения, интеграл
,
, определяет численное значение площади бесконечной криволинейной трапеции, ограниченной сверху графиком функции
, слева – прямой
, снизу – осью ОХ. Сходимость интеграла означает существование конечной площади такой трапеции и равенство ее пределу площади криволинейной трапеции с подвижной правой стенкой
.

На случай интеграла с бесконечным пределом можно обобщить и формулу Ньютона-Лейбница :

=
=F(+ ) – F(a ),

где F(+ ) =
. Если этот предел существует, то интеграл сходится, в противном случае – расходится.

Мы рассмотрели обобщение понятия определенного интеграла на случай бесконечного промежутка.

Рассмотрим теперь обобщение для случая неограниченной функции.

Определение

Пусть функция
определена на промежутке [a ; b ), неограниченна в некоторой окрестности точки b , и непрерывна на любом отрезке
, где>0 (и, следовательно, интегрируема на этом отрезке, т.е.
существует). Предел вида
называетсянесобственным интегралом второго рода (или несобственным интегралом от неограниченной функции) и обозначается
.

Таким образом, несобственный интеграл от неограниченной в точке b функции есть по определению

=
.

Если предел справа существует и конечен, то интеграл называется сходящимся . Если конечного предела не существует, то несобственный интеграл называется расходящимся.

Аналогично можно определить несобственный интеграл от функции
имеющей бесконечный разрыв в точкеа :

=
.

Если функция
имеет бесконечный разрыв во внутренней точкес 
, то несобственный интеграл определяется следующим образом

=
+
=
+
.

Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно слагаемое.

С геометрической точки зрения, несобственный интеграл от неограниченной функции также характеризует площадь неограниченной криволинейной трапеции:

Поскольку несобственный интеграл выводится путем предельного перехода из определенного интеграла, то все свойства определенного интеграла могут быть перенесены (с соответствующими уточнениями) на несобственные интеграла первого и второго рода.

Во многих задачах, приводящих к несобственным интегралам, не обязательно знать, чему равен этот интеграл, достаточно лишь убедиться в его сходимости или расходимости. Для этого используют признаки сходимости . Признаки сходимости несобственных интегралов:

1) Признак сравнения .

Пусть для всех х 

. Тогда, если
сходится, то сходится и
, причем

. Если
расходится, то расходится и
.

2) Если сходится
, то сходится и
(последний интеграл в этом случае называетсяабсолютно сходящимся ).

Признаки сходимости и расходимости несобственных интегралов от неограниченных функций аналогичны сформулированным выше.

Примеры решения задач.

Пример 1.

а)
; б)
; в)

г)
; д)
.

Решение.

а) По определению имеем:

б) Аналогично

Следовательно, данный интеграл сходится и равен .

в) По определению
=
+
, причем,а – произвольное число. Положим в нашем случае
, тогда получим:

Данный интеграл сходится.

Значит, данный интеграл расходится.

д) Рассмотрим
. Чтобы найти первообразную подынтегральной функции, необходимо применить метод интегрирования по частям. Тогда получим:

Поскольку ни
, ни
не существуют, то не существует и

Следовательно, данный интеграл расходится.

Пример 2.

Исследовать сходимость интеграла в зависимости от п .

Решение.

При
имеем:

Если
, то
и. Следовательно, интеграл расходится.

Если
, то
, а
, тогда

Следовательно, интеграл сходится.

Если
, то

следовательно, интеграл расходится.

Таким образом,

Пример 3.

Вычислить несобственный интеграл или установить его расходимость:

а)
; б)
; в)
.

Решение.

а) Интеграл
является несобственным интегралом второго рода, поскольку подынтегральная функция
не ограничена в точке

. Тогда, по определению,

Интеграл сходится и равен .

б) Рассмотрим
. Здесь также подынтегральная функция не ограничена в точке
. Поэтому, данный интеграл – несобственный второго рода и по определению,

Следовательно, интеграл расходится.

в) Рассмотрим
. Подынтегральная функция
терпит бесконечный разрыв в двух точках:
и
, первая из которых принадлежит промежутку интегрирования
. Следовательно, данный интеграл – несобственный второго рода. Тогда, по определению

=

=

Следовательно, интеграл сходится и равен
.

Несобственные интегралы и их расходимость. Несобственные интегралы. Примеры решений

Определенные интегралы онлайн на сайт для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн – определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн – определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно. Если все-таки получится вычислить определенный интеграл онлайн с решением бесплатно, то, пожалуйста, напишите адрес сайт всем желающим им воспользоваться. Как говорится, поделишься полезной ссылкой – и тебя отблагодарят добрые люди за даром. Очень интересным будет вопрос разбора задачки, в которой определенный интеграл будет калькулятор решать самостоятельно, а не за счет траты вашего драгоценного времени. На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса. Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B. Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре. . Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов. которыми студенты пользуются повседневно, один из них как раз есть определенный интеграл онлайн с решением в полном виде. В этом же разделе можно вычислить несобственный интеграл онлайн с подробным решением для дальнейших применений ответа как в институте, так и в инженерных работах. Казалось бы, всем определить определенный интеграл онлайн дело нехитрое, если заранее решить такой пример без верхней и нижней границы, то есть не интеграл Лейбница, а неопределенный интеграл. Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам. Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница. Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес Math34 – это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах. Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку “Решение”. Неправда ли – это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира. Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни. А кто такой студент? В первую очередь – это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию – сайт – самая полезная для молодежи решалка в режиме онлайн. Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения. Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта сайт перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением.

Определенный интеграл как предел интегральной суммы

может существовать (т.е. иметь определенное конечное значение) лишь при выполнении условий

Определение.

Пусть функция
определена на промежутке [a ; ) и интегрируема на любом конечном отрезке [a ; b ], т. е. существует
для любого b > a . Предел вида
называютнесобственным интегралом первого рода (или несобственным интегралом по бесконечному промежутку) и обозначают
.

Таким образом, по определению,
=
.

Аналогично можно ввести понятие несобственного интеграла от функции
по промежутку (–; b ]:

=
.

=
+
,

На случай интеграла с бесконечным пределом можно обобщить и формулу Ньютона-Лейбница :

=
=F(+ ) – F(a ),

где F(+ ) =
. Если этот предел существует, то интеграл сходится, в противном случае – расходится.

Мы рассмотрели обобщение понятия определенного интеграла на случай бесконечного промежутка.

Рассмотрим теперь обобщение для случая неограниченной функции.

Определение

Таким образом, несобственный интеграл от неограниченной в точке b функции есть по определению

=
.

Аналогично можно определить несобственный интеграл от функции
имеющей бесконечный разрыв в точкеа :

=
.

=
+
=
+
.

Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно слагаемое.

1) Признак сравнения .

Пусть для всех х 

. Тогда, если
сходится, то сходится и
, причем

. Если
расходится, то расходится и
.

2) Если сходится
, то сходится и
(последний интеграл в этом случае называетсяабсолютно сходящимся ).

Примеры решения задач.

Пример 1.

а)
; б)
; в)

г)
; д)
.

Решение.

а) По определению имеем:

б) Аналогично

Следовательно, данный интеграл сходится и равен .

в) По определению
=
+
, причем,а – произвольное число. Положим в нашем случае
, тогда получим:

Данный интеграл сходится.

Значит, данный интеграл расходится.

Поскольку ни
, ни
не существуют, то не существует и

Следовательно, данный интеграл расходится.

Пример 2.

Исследовать сходимость интеграла в зависимости от п .

Решение.

При
имеем:

Если
, то
и. Следовательно, интеграл расходится.

Если
, то
, а
, тогда

Следовательно, интеграл сходится.

Если
, то

следовательно, интеграл расходится.

Таким образом,

Пример 3.

Вычислить несобственный интеграл или установить его расходимость:

а)
; б)
; в)
.

Решение.

Интеграл сходится и равен .

Следовательно, интеграл расходится.

=

=

Следовательно, интеграл сходится и равен
.

Геометрический смысл несобственного интеграла выясняется довольно просто. В случае, когда график функции y = f (x ) находится выше оси Ox , определённый интеграл выражает площадь криволинейной трапеции, ограниченной кривой y = f (x ) , осью абсцисс и ординатами x = a , x = b . В свою очередь несобственный интеграл выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями y = f (x ) (на рисунке ниже – красного цвета), x = a и осью абсцисс.

Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:

Несобственные интегралы первого рода – с бесконечными пределами и их сходимость

Несобственные интегралы с бесконечным верхним пределом

Пример 1. Вычислить несобственный интеграл (если он сходится).

Решение. На основании определения несобственного интеграла находим

Так как предел существует и равен 1, то и данный несобственный интеграл сходится и равен 1.

Пример 2. Исследовать на сходимость несобственный интеграл (нижний предел интегрирования больше нуля).

Решение. Предположим сначала, что , тогда

В полученном выражении перейдём к пределу при :

В первом случае, то есть при имеет место . Если , то и не существует.

Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .

Это обобщённая формула Ньютона-Лейбница.

Пример 3. Вычислить несобственный интеграл (если он сходится).

Предел этого интеграла существует:

Второй интеграл, составляющий сумму, выражающую исходный интеграл:

Предел этого интеграла также существует:

Несобственные интегралы второго рода – от неограниченных функций и их сходимость

Используя формулу Ньютона-Лейбница, выводим.

Что значит вычислить несобственный интеграл?

Несобственные интегралы бывают двух видов.

Несобственный интеграл с бесконечным пределом (ами) интегрирования

3) О третьем варианте чуть позже.

Таким образом, несобственный интеграл может быть отрицательным .

Рассмотрим два классических примера:

Пример 1

Применение нашей формулы и решение задачи выглядит так:

При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!

Чистовое оформление задания должно выглядеть примерно так:

“

Пример 2

Вычислить несобственный интеграл или установить его расходимость.

Выполним чертеж:

(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.

(3) Указываем, что при (Господа, это уже давно нужно понимать) и упрощаем ответ.

Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.

Чистовое оформление примера должно выглядеть примерно так:

“

Подынтегральная функция непрерывна на

“

Пример 3

Вычислить несобственный интеграл или установить его расходимость.

Проведем замену:

Неопределенный интеграл найден, константу в данном случае добавлять не имеет смысла.

На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:

Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.

Теперь находим несобственный интеграл:

(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.

“

Подынтегральная функция непрерывна на .

“

Пример 4

Вычислить несобственный интеграл или установить его расходимость.

Пример 5

Вычислить несобственный интеграл или установить его расходимость.

Полные решения и ответы в конце урока.

Несобственные интегралы от неограниченных функций

Здесь почти всё так же, как в интеграле первого рода.

* по умолчанию привычно полагаем, что несобственный интеграл существует

Посмотрим, как это реализуется на практике.

Пример 6

Вычислить несобственный интеграл или установить его расходимость.

Сначала вычислим неопределенный интеграл:

Замена:

У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле .

Вычислим несобственный интеграл:

(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом . В данном случае у нас правосторонний предел .

(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.

В данном случае несобственный интеграл равен отрицательному числу. 3+1}. \]

Криволинейный интеграл 1 рода для чайников. МА

Теоретический минимум
Криволинейные и поверхностные интегралы часто встречаются в физике. Они бывают двух видов, первый из которых рассматривается здесь. Этот
тип интегралов строится согласно общей схеме, по которой вводятся определённые, двойные и тройные интегралы. Коротко напомним эту схему.
Имеется некоторый объект, по которому проводится интегрирование (одномерный, двумерный или трёхмерный). Этот объект разбивается на малые части,
в каждой из частей выбирается точка. В каждой из этих точек вычисляется значение подынтегральной функции и умножается на меру той части, которой
принадлежит данная точка (длину отрезка, площадь или объём частичной области). Затем все такие произведения суммируются, и выполняется предельный
переход к разбиению объекта на бесконечно малые части. Получающийся предел и называется интегралом.
1. Определение криволинейного интеграла первого рода
Рассмотрим функцию , определённую на кривой . Кривая предполагается спрямляемой. Напомним, что это означает, грубо говоря,
что в кривую можно вписать ломаную со сколь угодно малыми звеньями, причём в пределе бесконечно большого числа звеньев длина ломаной должна оставаться
конечной. Кривая разбивается на частичные дуги длиной и на каждой из дуг выбирается точка . Составляется произведение ,
проводится суммирование по всем частичным дугам . Затем осуществляется предельный переход с устремлением длины наибольшей
из частичных дуг к нулю. Предел является криволинейным интегралом первого рода
.
Важной особенностью этого интеграла, прямо следующей из его определения, является независимость от направления интегрирования, т.е.
.
2. Определение поверхностного интеграла первого рода
Рассмотрим функцию , определённую на гладкой или кусочно-гладкой поверхности . Поверхность разбивается на частичные области
с площадями , в каждой такой области выбирается точка . Составляется произведение , проводится суммирование
по всем частичным областям . Затем осуществляется предельный переход с устремлением диаметра наибольшей из всех частичных
областей к нулю. Предел является поверхностным интегралом первого рода
.
3. Вычисление криволинейного интеграла первого рода
Методика вычисления криволинейного интеграла первого рода просматривается уже из формальной его записи, а фактически следует непосредственно из
определения. Интеграл сводится к определённому, только нужно записать дифференциал дуги кривой, вдоль которой проводится интегрирование.
Начнём с простого случая интегрирования вдоль плоской кривой, заданной явным уравнением . В этом случае дифференциал дуги
.
Затем в подынтегральной функции выполняется замена переменной , и интеграл принимает вид
,
где отрезок отвечает изменению переменной вдоль той части кривой, по которой проводится интегрирование.
Очень часто кривая задаётся параметрически, т.е. уравнениями вида . Тогда дифференциал дуги
.
Формула эта очень просто обосновывается. По сути, это теорема Пифагора. Дифференциал дуги – фактически длина бесконечно малой части кривой.
Если кривая гладкая, то её бесконечно малую часть можно считать прямолинейной. Для прямой имеет место соотношение
.
Чтобы оно выполнялось для малой дуги кривой, следует от конечных приращений перейти к дифференциалам:
.
Если кривая задана параметрически, то дифференциалы просто вычисляются:
и т.д.
Соответственно, после замены переменных в подынтегральной функции криволинейный интеграл вычисляется следующим образом:
,
где части кривой, по которой проводится интегрирование соответствует отрезок изменения параметра .
Несколько сложнее обстоит дело в случае, когда кривая задаётся в криволинейных координатах. Этот вопрос обычно обсуждается в рамках дифференциальной
геометрии. Приведём формулу для вычисления интеграла вдоль кривой, заданной в полярных координатах уравнением :
.
Приведём обоснование и для дифференциала дуги в полярных координатах. Подробное обсуждение построения координатной сетки полярной системы координат
см. . Выделим малую дугу кривой, расположенную по отношению к координатным линиям так, как показано на рис. 1. В силу малости всех фигурирующих
дуг снова можно применить теорему Пифагора и записать:
.
Отсюда и следует искомое выражение для дифференциала дуги.
С чисто теоретической точки зрения достаточно просто понять, что криволинейный интеграл первого рода должен сводиться к своему частному случаю –
определённому интегралу. Действительно, выполняя замену, которая диктуется параметризацией кривой, вдоль которой вычисляется интеграл, мы устанавливаем
взаимно-однозначное отображение между частью данной кривой и отрезком изменения параметра . А это и есть сведение к интегралу
вдоль прямой, совпадающей с координатной осью – определённому интегралу.
4. Вычисление поверхностного интеграла первого рода
После предыдущего пункта должно быть ясно, что одна из основных частей вычисления поверхностного интеграла первого рода – запись элемента поверхности ,
по которой выполняется интегрирование. Опять-таки начнём с простого случая поверхности, заданной явным уравнением . Тогда
.
Выполняется замена в подынтегральной функции, и поверхностный интеграл сводится к двойному:
,
где – область плоскости , в которую проектируется часть поверхности, по которой проводится интегрирование.
Однако часто задать поверхность явным уравнением невозможно, и тогда она задаётся параметрически, т.е. уравнениями вида
.
Элемент поверхности в этом случае записывается уже сложнее:
.
Соответствующим образом записывается и поверхностный интеграл:
,
где – область изменения параметров, соответствующая части поверхности , по которой проводится интегрирование.
5. Физический смысл криволинейного и поверхностного интегралов первого рода
Обсуждаемые интегралы обладают очень простым и наглядным физическим смыслом. Пусть имеется некоторая кривая, линейная плотность которой не является
константой, а представляет собой функцию точки . Найдём массу этой кривой. Разобьём кривую на множество малых элементов,
в пределах которых её плотность можно приближённо считать константой. Если длина маленького кусочка кривой равна , то его масса
, где – любая точка выбранного кусочка кривой (любая, так как плотность в пределах
этого кусочка приближённо предполагается постоянной). Соответственно, масса всей кривой получится суммированием масс отдельных её частей:
.
Чтобы равенство стало точным, следует перейти к пределу разбиения кривой на бесконечно малые части, но это и есть криволинейный интеграл первого рода.

Аналогично разрешается вопрос о полном заряде кривой, если известна линейная плотность заряда .
Эти рассуждения легко переносятся на случай неравномерно заряженной поверхности с поверхностной плотностью заряда . Тогда
заряд поверхности есть поверхностный интеграл первого рода
.
Замечание . Громоздкая формула для элемента поверхности, заданной параметрически, неудобна для запоминания. Другое выражение получается в дифференциальной геометрии,
оно использует т. н. первую квадратичную форму поверхности.
Примеры вычисления криволинейных интегралов первого рода
Пример 1. Интеграл вдоль прямой .
Вычислить интеграл
вдоль отрезка прямой, проходящей через точки и .
Сначала запишем уравнение прямой, вдоль которой проводится интегрирование: . Найдём выражение для :
.
Вычисляем интеграл:
Пример 2. Интеграл вдоль кривой на плоскости .
Вычислить интеграл
по дуге параболы от точки до точки .
Заданные точки и позволяют выразить переменную из уравнения параболы: .

Вычисляем интеграл:
.
Однако можно было проводить вычисления и иначе, пользуясь тем, что кривая задана уравнением, разрешённым относительно переменной .
Если принять переменную за параметр, то это приведёт к небольшому изменению выражения для дифференциала дуги:
.
Соответственно, интеграл несколько изменится:
.
Этот интеграл легко вычисляется подведением переменной под дифференциал. Получится такой же интеграл, как и в первом способе вычисления.
Пример 3. Интеграл вдоль кривой на плоскости (использование параметризации) .
Вычислить интеграл
вдоль верхней половины окружности .
Можно, конечно, выразить из уравнения окружности одну из переменных, а затем провести остальные вычисления стандартно. Но можно использовать и
параметрическое задание кривой. Как известно, окружность можно задать уравнениями . Верхней полуокружности
отвечает изменение параметра в пределах . Вычислим дифференциал дуги:
.
Таким образом,
Пример 4. Интеграл вдоль кривой на плоскости, заданной в полярных координатах .
Вычислить интеграл

вдоль правого лепестка лемнискаты .

На чертеже выше изображена лемниската. Вдоль её правого лепестка нужно проводить интегрирование. Найдём дифференциал дуги для кривой :
.
Следующий шаг – определение пределов интегрирования по полярному углу. Ясно, что должно выполняться неравенство , а потому
.
Вычисляем интеграл:
Пример 5. Интеграл вдоль кривой в пространстве .
Вычислить интеграл
вдоль витка винтовой линии , соответствующего пределам изменения параметра

Задача о массе кривой. Пусть в каждой точке кусочно-гладкой материальной кривойL: (AB) задана ее плотность . Определить массу кривой.

Поступим так же, как мы поступали при определении массы плоской области (двойной интеграл) и пространственного тела (тройной интеграл).

1. Организуем разбиение области- дуги Lна элементы – элементарные дугитак, чтобы эти элементы не имели общих внутренних точек и
(условие А )

2. Отметим на элементах разбиения «отмеченные точки» M i и вычислим в них значения функции

3. Построим интегральную сумму
, где- длина дуги(обычно вводятся одни и те же обозначения для дуги и ее длины). Это – приблизительное значение массы кривой. Упрощение состоит в том, что мы предположили плотность дуги постоянной на каждом элементе и взяли конечное число элементов.

Переходя к пределу при условии
(условие В ), получим криволинейный интеграл первого рода как предел интегральных сумм:

Теорема существования 10 .

Пусть функция
непрерывна на кусочно-гладкой дугеL 11 . Тогда криволинейный интеграл первого рода существует как предел интегральных сумм.

Замечание. Предел этот не зависит от

способа выбора разбиения, лишь бы выполнялось условие А

выбора «отмеченных точек» на элементах разбиения,

способа измельчения разбиения, лишь бы выполнялось условие В

Свойства криволинейного интеграла первого рода.

1. Линейность а) свойство суперпозиции

б) свойство однородности
.

Доказательство. Запишем интегральные суммы для интегралов в левых частях равенств. Так как в интегральной сумме число слагаемых конечно, перейдем к интегральным суммам для правых частей равенств. Затем перейдем к пределу, по теореме о предельном переходе в равенстве получим желаемый результат.

2. Аддитивность. Если
, то
=
+

Доказательство. Выберем разбиение области Lтак, чтобы ни один из элементов разбиения (первоначально и при измельчении разбиения) не содержал одновременно как элементыL 1 , так и элементыL 2 . Это можно сделать по теореме существования (замечание к теореме). Далее проводится доказательство через интегральные суммы, как в п.1.

3.
.Здесь – длина дуги .

4. Если на дуге выполнено неравенство, то

Доказательство. Запишем неравенство для интегральных сумм и перейдем к пределу.

Заметим, что, в частности, возможно

5. Теорема об оценке.

Если существуют константы
, что, то

Доказательство. Интегрируя неравенство
(свойство 4), получим
. По свойству 1 константы
можно вынести из-под интегралов. Используя свойство 3, получим искомый результат.

6. Теорема о среднем (значении интеграла).

Существует точка
, что

Доказательство. At+i произвольную точку Mk и составим сумму где Alt – длина дуги и назовем ее интегральной суммой для функции f(M) по длине дуги кривой. Пусть Д / – наибольшая издлин частичных дуг, т. е. Свойства криволинейных интегралов 1-го рода для пространственных кривых Криволинейные интегралы 2-го рода Вычисление криволинейного интеграла Свойства Связь между Определе нив. Если при интегральная сумма (I) имеет конечный предел, не зависящий ни от способа разбиения кривой АВ на части, ни от выбора точек на каждой из дуг разбиения, то этот предел называется криволинейным интегралом \ -го рода от функции f(M) по кривой АВ (интеграл по длине дуги кривой) и обозначается символом В этом случае функция /(М) называется интегрируемой вдоль кривой АВУ кривая А В называется контуром интегрирования, А – начальной, В – конечной точками интегрирования. Таким образом, по определению, Пример 1. Пусть вдоль некоторой гладкой кривой L распределена масса с переменной линейной плотностью J(M). Найти массу т кривой L. (2) Разобьем кривую L на п произвольных частей) и вычислим приближен- но массу каждой части, предполагая, что на каждой из частей плотность постоянна и равна плотности в какой-нибудь из ее точек, например, в крайней левой точке /(Af*). Тогда сумма кшо где Д/д – длина Дг-ой части, будет приближенным значением массы т. Ясно, что погрешность будет тем меньше, чем мельче разбиение кривой L. В пределе при Ы -* 0 (Д / = max Л/») получим точное значение массы всей кривой L, т.е. Но предел справа есть криволинейный интеграл 1-го рода. Значит, 1.1. Существование криволинейного интеграла 1-го рода Примем на кривой АВ за параметр длину дуги I, отсчитываемую от начальной точки А (рис.2). Тогда кривую АВ можно описать уравнениями (3) где L – длина кривой АВ. Уравнения (3) называются натуральными уравнениями кривой АВ. При переходе к натуральным уравнениям функция f(x} у), заданная на кривой АВ, сведется к функции переменной I: / (х(1)} у(1)). Обозначив через значение параметра I, отвечающее точке Мку перепишем интегральную сумму (I) в виде Это – интегральная сумма, отвечающая определенному интегралу Поскольку интегральные суммы (1) и (4) равны междусобой, то равны и отвечающие им интегралы. Таким образом, (5) Теорема 1. Если функция /(М) непрерывна вдоль гладкой кривой АВ, то существует криволинейный интеграл (поскольку при этих условиях существует определенный интеграл, стоящий в равенстве (5) справа). 1.2. Свойства криволинейных интегралов 1-го рода 1. Из вида интегральной суммы (1) следует, что т.е. величина криволинейного интеграла 1-го рода не зависит ог направления интегрирования. 2. Линейность. Если для каждой из функций /() существует криволинейный интеграл по кривой ABt то для функции а/, где а и /3 – любые постоянные, также существует криволинейный интеграл по кривой АВ> причем 3. Аддитивность. Если кривая АВ состоит из двух кусков и для функции /(М) существует криволинейный интеграл по АВУ то существуют интегралы причем 4. Если 0 на кривой АВ, то 5. Если функция интегрируема на кривой АВ, то функция || также интегрируема на А В, и при этом б. Формула среднего значения. Если функция / непрерывна вдоль кривой АВ, то на этой кривой найдется точка Мс такая, что где L – длина кривой АВ. 1.3. Вычисление криволинейного интеграла 1-го рода Пусть кривая АВ задана параметрическими уравнениями причем точке А соответствует значение t = to, а точке В – значение. Будем предполагать, что функции) непрерывны на вместе со своими производными и выполнено неравенство Тогда дифференциал дуги кривой вычисляется по формуле В частности, если кривая АВ задана явным уравнением непрерывно дифференцируема на [а, Ь] и точке А соответствует значение х = а, а точке В – значение х = 6, то, принимая х за параметр, получаем 1.4. Криволинейные интегралы 1-го рода для пространственных кривых Определение криволинейного интеграла 1-го рода, сформулированное выше для плоской кривой, дословно переносится на случай, когда функция f(M) задана вдоль некоторой пространственной кривой АВ. Пусть кривая АВ задана параметрическими уравнениями Свойства криволинейных интегралов 1-го рода для пространственных кривых Криволинейные интегралы 2-го рода Вычисление криволинейного интеграла Свойства Связь между Тогда криволинейный интеграл взятый вдоль этой кривой, можно свести к определенному интегралу при помоши следующей формулы: Пример 2. Вычислитькриволинейный интеграл где L – контур треугольнике с вершинами в точка* (рис.3). По свойству аддитивности имеем Вычислим каждый из интегралов в отдельности. Так как на отрезке OA имеем: , то На отрезке АН имеем, откуда причем тогда Рис. Наконец, Следовательно, Замечание. При вычислении интегралов мы воспользовались свойством 1, согласно которому. Криволинейные интегралы 2-го рода Пусть А В – гладкая или кусочно-гладкая ориентированная кривая на плоскости хОу и пусть – вектор-функция, определенная в некоторой области D, содержащей кривую АВ. Разобьем кривую АВ на части точками координаты которых обозначим соответственно через (рис. 4). На каждой из элементарныхдуг АкАк+\ возьмем произвольно точку и составим сумму Пусть Д/ – длина наибольшей из дуг Определение. Если при сумма (1) имеет конечный предел, не зависящий ни от способа разбиения кривой АВ, ни от выбора точек rjk) на элементарных дугах, то этот предел называется криволинейным интегралом 2-города от вектор-функции по кривой АВ и обозначается символом Так что по определению Теорема 2. Если в некоторой области D, содержащей кривую АВ, функции непрерывны, то криволинейный интеграл 2-города существует. Пусть – радиус-вектор точки М(х, у). Тогда и подынтегральное выражение в формуле (2) можно представить в виде скалярного произведения векторов F(M) и dr. Так что интеграл 2-го рода от вектор-функции по кривой АВ можно записать коротко так: 2.1. Вычисление криволинейного интеграла 2-го рода Пусть кривая АВ задана параметрическими уравнениями, где функции непрерывны вместе с производными на отрезке, причем изменению параметра t от t0 до t\ соответствует движение точки по кривой АВ отточки А к точке В. Если в некоторой области D, содержащей кривую АВ, функции непрерывны, то криволинейный интеграл 2-го рода сводится к следующему определенному интегралу: Таким образом, вычисление криволинейного интеграла 2-го рода также может быть сведено к вычислению определенного интеграла. О) Пример 1. Вычислить интеграл вдоль прямолинейного отрезка, соединяющего точки 2) вдоль параболы, соединяющей те же тонки) Уравнение линии параметр, откуда Так что 2) Уравнение линии AB: Отсюда поэтому Рассмотренный пример помазывает, что величина криволинейного интеграла 2-го рода, вообще говоря, зависитот формы пути интегрирования.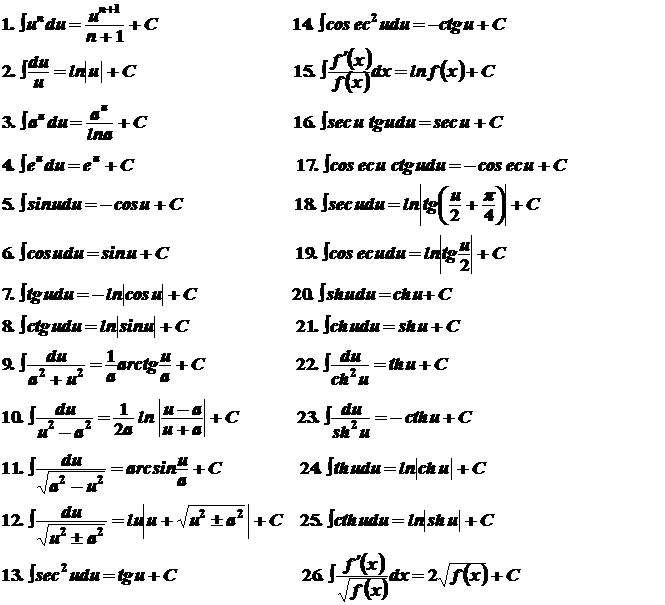 2.2. Свойства криволинейного интеграл а 2-го рода 1. Линейность. Если существуют Свойства криволинейных интегралов 1-го рода для пространственных кривых Криволинейные интегралы 2-го рода Вычисление криволинейного интеграла Свойства Связь между то при любых действительных а и /5 существует и интеграл причем 2. Аддитеностъ. Если кривая АВ разбита на части АС и СБ и криволинейный интеграл существует, то существуют и нтегралы Последнее свойство соитвггггнусг физической интерпретации криволинейного интеграла 2-го рода ках работы силового поля F вдоль некоторого путь: при изменении направления дешкения по кривой работа силового поля вдоль этой кривой меняет знак на противоположный. 2.3. Связь между криволинейными интегралами 1-го и 2-го рода Рассмотрим криволинейный интеграл 2-го рода где ориентированная кривая АВ (А – начальная точка, В – конечная точка) задана векгорным уравнением (здесь I – длина кривой, отсчитываемая в том направлении, в котором ориентирована кривая АВ) (рис. 6). Тогда dr или где г = т(1) – единичный вектор касательной к кривой АВ в точке М(1). Тогда Заметим, что последний интеграл в этой формуле – криволинейный интеграл 1-го рода. При изменении ориентации кривой АВ единичный вектор касательной г заменяется на противоположный вектор (-г), что влечет изменение знака его подынтегрального выражения и, значит, знака самого интеграла.

Лекция 5 Криволинейные интегралы 1 и 2 рода, их свойства..

Задача о массе кривой. Криволинейный интеграл 1 рода.

Задача о массе кривой. Пусть в каждой точке кусочно-гладкой материальной кривой L: (AB) задана ее плотность . Определить массу кривой.

1. Организуем разбиение области- дуги L на элементы – элементарные дуги так, чтобы эти элементы не имели общих внутренних точек и(условие А )

3. Построим интегральную сумму , где – длина дуги (обычно вводятся одни и те же обозначения для дуги и ее длины). Это – приблизительное значение массы кривой. Упрощение состоит в том, что мы предположили плотность дуги постоянной на каждом элементе и взяли конечное число элементов.

Переходя к пределу при условии (условие В ), получим криволинейный интеграл первого рода как предел интегральных сумм:

Теорема существования.

Пусть функция непрерывна на кусочно-гладкой дуге L. Тогда криволинейный интеграл первого рода существует как предел интегральных сумм.

Замечание. Предел этот не зависит от

Свойства криволинейного интеграла первого рода.

1. Линейность
а) свойство суперпозиции

б) свойство однородности .

2. Аддитивность.
Если, то = +

3. .Здесь – длина дуги .

4. Если на дуге выполнено неравенство , то

Доказательство. Запишем неравенство для интегральных сумм и перейдем к пределу.

Заметим, что, в частности, возможно

5. Теорема об оценке.

Если существуют константы , что , то

Доказательство. Интегрируя неравенство (свойство 4), получим . По свойству 1 константы можно вынести из-под интегралов. Используя свойство 3, получим искомый результат.

6. Теорема о среднем (значении интеграла).

Существует точка , что

Доказательство. Так как функция непрерывна на замкнутом ограниченном множестве , то существует ее нижняя грань и верхняя грань . Выполнено неравенство . Деля обе части на L, получим . Но число заключено между нижней и верхней гранью функции. Так как функция непрерывна на замкнутом ограниченном множестве L, то в некоторой точке функция должна принимать это значение. Следовательно, .

Вычисление криволинейного интеграла первого рода.

Параметризуем дугу L: AB x = x(t), y = y(t), z =z (t). Пусть t 0 соответствует точке A, а t 1 соответствует точке B. Тогда криволинейный интеграл первого рода сводится к определенному интегралу ( – известная из 1 семестра формула для вычисления дифференциала длины дуги):

Пример. Вычислить массу одного витка однородной (плотность равна k) винтовой линии: .

Криволинейный интеграл 2 рода.

Задача о работе силы.

Какую работу производит сила F (M ) при перемещении точки M по дуге AB ?

Если бы дуга AB была отрезком прямой, а сила была бы постоянной по величине и направлению при перемещении точки M по дуге AB, то работу можно было бы вычислить по формуле , где – угол между векторами. В общем случае эту формулу можно использовать для построения интегральной суммы, предполагая силу постоянной на элементе дуги достаточно малой длины. Вместо длины малого элемента дуги можно взять длину стягивающей ее хорды , так как эти величины – эквивалентные бесконечно малые величины при условии (первый семестр).

1. Организуем разбиение области- дуги AB на элементы – элементарные дуги так, чтобы эти элементы не имели общих внутренних точек и(условие А )

2. Отметим на элементах разбиения «отмеченные точки» M i и вычислим в них значения функции

3. Построим интегральную сумму , где вектор, направленный по хорде, стягивающей -дугу .

4. Переходя к пределу при условии (условие В ), получим криволинейный интеграл второго рода как предел интегральных сумм (и работу силы):

. Часто обозначают

Теорема существования.

Пусть вектор – функция непрерывна на кусочно-гладкой дуге L. Тогда криволинейный интеграл второго рода существует как предел интегральных сумм.

Замечание. Предел этот не зависит от

Способа выбора разбиения, лишь бы выполнялось условие А

Выбора «отмеченных точек» на элементах разбиения,

Способа измельчения разбиения, лишь бы выполнялось условие В

Свойства криволинейного интеграла 2 рода.

1. Линейность
а) свойство суперпозиции

б) свойство однородности .

Доказательство. Запишем интегральные суммы для интегралов в левых частях равенств. Так как в интегральной сумме число слагаемых конечно, используя свойство скалярного произведения, перейдем к интегральным суммам для правых частей равенств. Затем перейдем к пределу, по теореме о предельном переходе в равенстве получим желаемый результат.

2. Аддитивность.
Если, то = + .

Доказательство. Выберем разбиение области L так, чтобы ни один из элементов разбиения (первоначально и при измельчении разбиения) не содержал одновременно как элементы L 1 , так и элементы L 2 .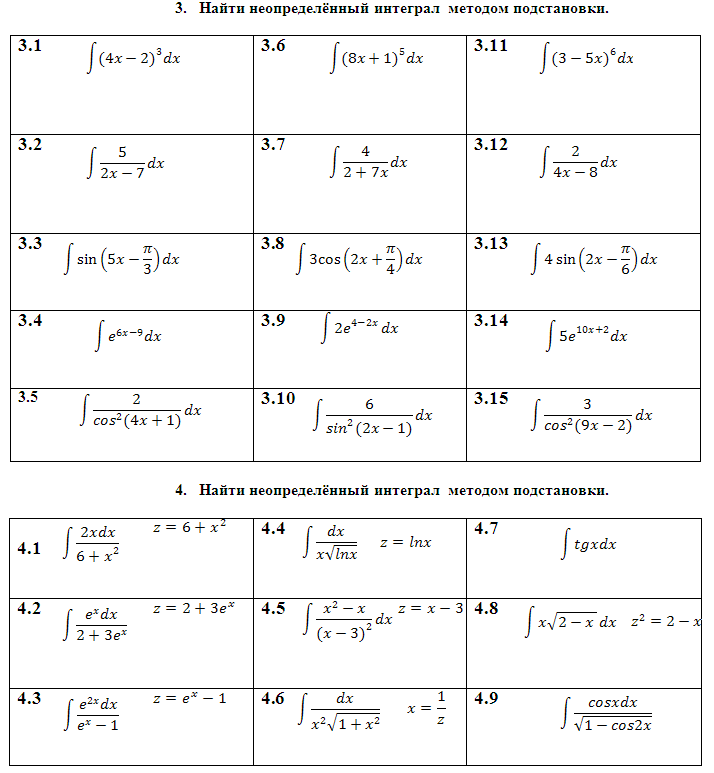 Это можно сделать по теореме существования (замечание к теореме). Далее проводится доказательство через интегральные суммы, как в п.1.

3. Ориентируемость.

= –

Доказательство. Интеграл по дуге –L, т..е. в отрицательном направлении обхода дуги есть предел интегральных сумм, в слагаемых которых вместо стоит (). Вынося «минус» из скалярного произведения и из суммы конечного числа слагаемых, переходя к пределу, получим требуемый результат.

На случай, когда областью интегрирования является отрезок некоторой кривой, лежащий в плоскости. Общая запись криволинейного интеграла следующая:

где f (x , y ) – функция двух переменных, а L – кривая, по отрезку AB которой происходит интегрирование. Если подынтегральная функция равна единице, то криволинейный интеграл равен длине дуги AB .

Как всегда в интегральном исчислении, криволинейный интеграл понимается как предел интегральных сумм каких-то очень маленьких частей чего-то очень большого. Что же суммируется в случае криволинейных интегралов?

Пусть на плоскости расположен отрезок AB некоторой кривой L , а функция двух переменных f (x , y ) определена в точках кривой L . Пусть мы выполняем с этим отрезком кривой следующий алгоритм.

Разделить кривую AB на части точками (рисунки ниже).
В каждой части свободно выбрать точку M .
Найти значение функции в выбранных точках.
Значения функции умножить на
- длины частей в случае криволинейного интеграла первого рода ;
- проекции частей на ось координат в случае криволинейного интеграла второго рода .
Найти сумму всех произведений.
Найти предел найденной интегральной суммы при условии, что длина самой длинной части кривой стремится к нулю.

Если упомянутый предел существует, то этот предел интегральной суммы и называется криволинейным интегралом от функции f (x , y ) по кривой AB .

первого рода

Случай криволинейного интеграла
второго рода

Введём следующие ообозначения.

M i (ζ i ; η i ) – выбранная на каждом участке точка с координатами.

f i (ζ i ; η i ) – значение функции f (x , y ) в выбранной точке.

Δs i – длина части отрезка кривой (в случае криволинейного интеграла первого рода).

Δx i – проекция части отрезка кривой на ось Ox (в случае криволинейного интеграла второго рода).

d = maxΔs i – длина самой длинной части отрезка кривой.

Криволинейные интегралы первого рода

Исходя из вышеизложенного о пределе интегральных сумм, криволинейный интеграл первого рода записывается так:

Криволинейный интеграл первого рода обладает всеми свойствами, которыми обладает определённый интеграл . Однако есть одно важное различие. У определённого интеграла при перемене местами пределов интегрирования знак меняется на противоположный:

В случае же криволинейного интеграла первого рода не имеет значения, какую из точек кривой AB (A или B ) считать началом отрезка, а какую концом, то есть

Криволинейные интегралы второго рода

Исходя из изложенного о пределе интегральных сумм, криволинейный интеграл второго рода записывается так:

В случае криволинейного интеграла второго рода при перемене местами начала и конца отрезка кривой знак интеграла меняется:

При составлении интегральной суммы криволинейного интеграла второго рода значения функции f i (ζ i ; η i ) можно умножать также на проекции частей отрезка кривой на ось Oy . Тогда получим интеграл

На практике обычно используется объединение криволинейных интегралов второго рода, то есть две функции f = P (x , y ) и f = Q (x , y ) и интегралы

а сумма этих интегралов

называется общим криволинейным интегралом второго рода .

Вычисление криволинейных интегралов первого рода

Вычисление криволинейных интегралов первого рода сводится к вычислению определённых интегралов. Рассмотрим два случая.

Пусть на плоскости задана кривая y = y (x ) и отрезку кривой AB соответствует изменение переменной x от a до b . Тогда в точках кривой подынтегральная функция f (x , y ) = f (x , y (x )) (“игрек” должен быть выражен через “икс”), а дифференциал дуги и криволинейный интеграл можно вычислить по формуле

Если интеграл проще интегрировать по y , то из уравнения кривой нужно выразить x = x (y ) (“икс” через “игрек”), где и интеграл вычисляем по формуле

Пример 1.

где AB – отрезок прямой между точками A (1; −1) и B (2; 1) .

Решение. Составим уравнение прямой AB , используя формулу (уравнение прямой, проходящей через две данные точки A (x 1 ; y 1 ) и B (x 2 ; y 2 ) ):

Из уравнения прямой выразим y через x :

Тогда и теперь можем вычислять интеграл, так как у нас остались одни “иксы”:

Пусть в пространстве задана кривая

Тогда в точках кривой функцию нужно выразить через параметр t () а дифференциал дуги , поэтому криволинейный интеграл можно вычислить по формуле

Аналогично, если на плоскости задана кривая

то криволинейный интеграл вычисляется по формуле

Пример 2. Вычислить криволинейный интеграл

где L – часть линии окружности

находящаяся в первом октанте.

Решение. Данная кривая – четверть линии окружности, расположенная в плоскости z = 3 . Она соответствует значениям параметра . Так как

то дифференциал дуги

Подынтегральную функцию выразим через параметр t :

Теперь, когда у нас всё выражено через параметр t , можем свести вычисление данного криволинейного интеграла к определённому интегралу:

Вычисление криволинейных интегралов второго рода

Так же, как и в случае криволинейных интегралов первого рода, вычисление интегралов второго рода сводится к вычислению определённых интегралов.

Кривая дана в декартовых прямоугольных координатах

Пусть дана кривая на плоскости уравнением функции “игрек”, выраженной через “икс”: y = y (x ) и дуге кривой AB соответствует изменение x от a до b . Тогда в подынтегральную функцию подставим выражение “игрека” через “икс” и определим дифференциал этого выражения “игрека” по “иксу”: . Теперь, когда всё выражено через “икс”, криволинейный интеграл второго рода вычисляется как определённый интеграл:

Аналогично вычисляется криволинейный интеграл второго рода, когда кривая дана уравнением функции “икс”, выраженной через “игрек”: x = x (y ) , . В этом случае формула для вычисления интеграла следующая:

Пример 3. Вычислить криволинейный интеграл

, если

а) L – отрезок прямой OA , где О (0; 0) , A (1; −1) ;

б) L – дуга параболы y = x ² от О (0; 0) до A (1; −1) .

а) Вычислим криволинейный интеграл по отрезку прямой (на рисунке – синяя). Напишем уравнение прямой и выразим “игрек” через “икс”:

Получаем dy = dx . Решаем данный криволинейный интеграл:

б) если L – дуга параболы y = x ² , получим dy = 2xdx .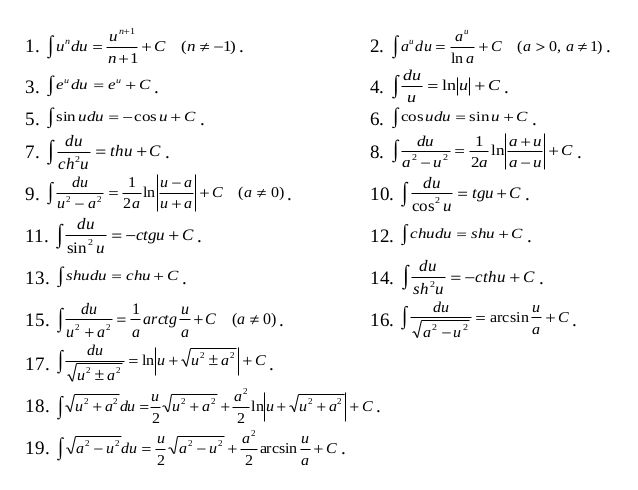 Вычисляем интеграл:

В только что решённом примере получили в двух случаях один и тот же результат. И это не совпадение, а результат закономерности, так как данный интеграл удовлетворяет условиям следующей теоремы.

Теорема . Если функции P (x ,y ) , Q (x ,y ) и их частные производные , – непрерывные в области D функции и в точках этой области частные производные равны, то криволинейный интеграл не зависит от пути интегрирования по линии L , находящейся в области D .

Кривая дана в параметрической форме

Пусть в пространстве дана кривая

а в подынтегральные функции подставим

выражения этих функций через параметр t . Получаем формулу для вычисления криволинейного интеграла:

Пример 4. Вычислить криволинейный интеграл

если L – часть эллипса

отвечающая условию y ≥ 0 .

Решение. Данная кривая – часть эллипса, находящаяся в плоскости z = 2 . Она соответствует значению параметра .

можем представить криволинейный интеграл в виде определённого интеграла и вычислить его:

Если дан криволинейный интеграл и L – замкнутая линия, то такой интеграл называется интегралом по замкнутому контуру и его проще вычислить по формуле Грина .

Больше примеров вычисления криволинейных интегралов

Пример 5. Вычислить криволинейный интеграл

где L – отрезок прямой между точками её пересечения с осями координат.

Решение. Определим точки пересечения прямой с осями координат. Подставив в уравнение прямой y = 0 , получим , . Подставив x = 0 , получим , . Таким образом, точка пересечения с осью Ox – A (2; 0) , с осью Oy – B (0; −3) .

Из уравнения прямой выразим y :

, .

Теперь можем представить криволинейный интеграл в виде определённого интеграла и начать вычислять его:

В подынтегральном выражении выделяем множитель , выносим его за знак интеграла. В получившемся после этого подынтегральном выражении применяем подведение под знак дифференциала и окончательно получаем.

Несобственный интеграл с бесконечным верхним пределом. Несобственные интегралы от неограниченных функций. Если подынтегральной функции не существует в точке

Несобственный интеграл с бесконечным пределом интегрирования

Иногда такой несобственный интеграл еще называют несобственным интегралом первого рода..gif”>.

Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: .

Несобственный интеграл https://pandia. ru/text/80/057/images/image009_0.gif”>», иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что, что несобственный интеграл расходится .

А что будет, если бесконечная криволинейная трапеция расположена ниже оси?.gif”>.

: .

Пример 1

Применение нашей формулы https://pandia.ru/text/80/057/images/image018_0.gif”>

При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!

Пример 2

Вычислить несобственный интеграл или установить его расходимость.

Выполним чертеж:

Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд..gif”>

(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.

(3) Указываем, что https://pandia.ru/text/80/057/images/image024.gif”> (Господа, это уже давно нужно понимать) и упрощаем ответ.

Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.

Пример 3

Вычислить несобственный интеграл или установить его расходимость.

Подынтегральная функция непрерывна на .

Сначала попытаемся найти первообразную функцию (неопределенный интеграл).

Проведем замену:

Всегда полезно выполнить проверку, то есть продифференцировать полученный результат:

Теперь находим несобственный интеграл:

(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.

“

Подынтегральная функция непрерывна на https://pandia. ru/text/80/057/images/image041.gif”>
“

Пример 4

Вычислить несобственный интеграл или установить его расходимость.

Пример 5

Вычислить несобственный интеграл или установить его расходимость.

Несобственные интегралы от неограниченных функций

Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования ..jpg” alt=”Несобственный интеграл, точка разрыва в нижнем пределе интегрирования”>

Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению https://pandia. ru/text/80/057/images/image052.gif”> справа .

Пример 6

Вычислить несобственный интеграл или установить его расходимость.

Сначала вычислим неопределенный интеграл:

Замена:

Вычислим несобственный интеграл:

(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.

В данном случае несобственный интеграл равен отрицательному числу.

Пример 7

Вычислить несобственный интеграл или установить его расходимость.

Пример 8

Вычислить несобственный интеграл или установить его расходимость.

Если подынтегральной функции не существует в точке

Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению https://pandia.ru/text/80/057/images/image052.gif”> мы должны бесконечно близко приблизиться к точке разрыва слева .

Иногда такие несобственные интегралы называют несобственными интегралами второго рода . Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: .

Но, в отличие от определенного интеграла, подынтегральная функция терпит бесконечный разрыв (не существует):

1) в точке ,

2) точке ,

3) в обеих точках сразу,

4) или даже на отрезке интегрирования.

Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.

Рассмотрим сразу пример, чтобы было понятно:

Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, так как если мы подставим в подынтегральную функцию, то значение нижнего предела

тогда знаменатель у нас обращается в ноль, то есть подынтегральной функции в этой точке просто не существует!

При анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования . В этой связи проверим и верхний предел:

Здесь всё хорошо. Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:

Здесь почти всё так же, как в интеграле первого рода. Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна), либо несобственный интеграл равен конченому числу (когда площадь бесконечной фигуры – конечна!).

Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значениюсправа. Легко проследить по чертежу, что по оси OX справа .

Посмотрим, как это реализуется на практике.

Пример 6

(не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!). Сначала вычислим неопределенный интеграл:

У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле .

Вычислим несобственный интеграл:

(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела:

Добавка +0 обозначает, что мы стремимся к значению ¾ справа, что логично (см. график). Такой предел в теории пределов называют односторонним пределом . В данном случае у нас правосторонний предел .

(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.

В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью OX . А сейчас примеры для самостоятельного решения.

Пример 7

Вычислить несобственный интеграл или установить его расходимость.

Пример 8

Вычислить несобственный интеграл или установить его расходимость.

Если подынтегральной функции не существует в точке

Здесь всё абсолютно делаем так же, за исключением того, что предел у нас стремится к значению b слева. По оси OX мы должны бесконечно близко приблизиться к точке разрыва слева .

Пример 9

Вычислить несобственный интеграл или установить его расходимость.

Подынтегральная функция терпит бесконечный разрыв в точке b = 3 (устно проверяем, что с другим пределом интегрирования всё нормально!).

Для разнообразия решим этот предел сразу – методом подведения функции под знак дифференциала. Те, кому трудно, могут сначала найти неопределенный интеграл по уже рассмотренной схеме.

Добавка (-0) обозначает, что предел у нас левосторонний , и к точке b = 3 мы приближаемся по оси OX слева .

Разбираемся, почему дробь

(это лучше делать устно или на черновике).

Подставляем под корень предельное значение b = 3 – 0.

Окончательно:

Несобственный интеграл расходится.

Знак минус обозначает, что соответствующая криволинейная трапеция расположена под осьюOX . Будьте очень внимательны в знаках.

Да, конечно, несобственный интеграл расходится, но и – это разные вещи, разные жанры, и если Вы недосмотрите за знаками, то, строго говоря, допустите серьезную ошибку.

И заключительные два примера для самостоятельного рассмотрения:

Пример 10

Вычислить несобственный интеграл или установить его расходимость.

Пример 11

Вычислить несобственный интеграл или установить его расходимость.

Разбор ситуации, когда оба предела интегрирования «плохие», или точка разрыва содержится прямо на отрезке интегрирования, можно найти в статье Эффективные методы решения определённых и несобственных интегралов .

Решения и ответы:

Пример 4: Решение:

Пример 5: Решение:

Подынтегральная функция непрерывна на .

Пример 7: Решение:
Подынтегральная функция терпит бесконечный разрыв в точке

Несобственный интеграл расходится.

Примечание: с пределом выражения

Определенный интеграл как предел интегральной суммы

может существовать (т.е. иметь определенное конечное значение) лишь при выполнении условий

Если хотя бы одно из этих условий нарушено, то определение теряет смысл. Действительно, в случае бесконечного отрезка, например [a ; ) его нельзя разбить на п частей конечной длины
, которая к тому же с увеличением количества отрезков стремилась бы к нулю. В случае же неограниченной в некоторой точке с [a ; b ] нарушается требование произвольного выбора точки на частичных отрезках – нельзя выбрать =с , поскольку значение функции в этой точке не определено. Однако и для этих случаев можно обобщить понятие определенного интеграла, введя еще один предельный переход. Интегралы по бесконечным промежуткам и от разрывных (неограниченных) функций называют несобственными .

Определение.

Пусть функция
определена на промежутке [a ; ) и интегрируема на любом конечном отрезке [a ; b ], т.е. существует
для любого b > a . Предел вида
называют несобственным интегралом первого рода (или несобственным интегралом по бесконечному промежутку) и обозначают
.

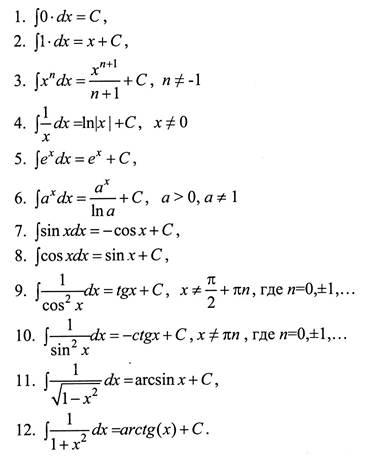
Таким образом, по определению,
=
.

Если предел справа существует и конечен, то несобственный интеграл
называют сходящимся . Если этот предел бесконечен, или не существует вообще, то говорят, что несобственный интеграл расходится .

Аналогично можно ввести понятие несобственного интеграла от функции
по промежутку (–; b ]:

=
.

А несобственный интеграл от функции
по промежутку (–; +) определяется как сумма введенных выше интегралов:

=
+
,

где а – произвольная точка. Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно из слагаемых.

С геометрической точки зрения, интеграл
,
, определяет численное значение площади бесконечной криволинейной трапеции, ограниченной сверху графиком функции
, слева – прямой
, снизу – осью ОХ. Сходимость интеграла означает существование конечной площади такой трапеции и равенство ее пределу площади криволинейной трапеции с подвижной правой стенкой
.

На случай интеграла с бесконечным пределом можно обобщить и формулу Ньютона-Лейбница :

=
= F(+ ) – F(a ),

где F(+ ) =
. Если этот предел существует, то интеграл сходится, в противном случае – расходится.

Мы рассмотрели обобщение понятия определенного интеграла на случай бесконечного промежутка.

Рассмотрим теперь обобщение для случая неограниченной функции.

Определение

Пусть функция
определена на промежутке [a ; b ), неограниченна в некоторой окрестности точки b , и непрерывна на любом отрезке
, где >0 (и, следовательно, интегрируема на этом отрезке, т.е.
существует). Предел вида
называется несобственным интегралом второго рода (или несобственным интегралом от неограниченной функции) и обозначается
.

Таким образом, несобственный интеграл от неограниченной в точке b функции есть по определению

=
.

Если предел справа существует и конечен, то интеграл называется сходящимся . Если конечного предела не существует, то несобственный интеграл называется расходящимся.

Аналогично можно определить несобственный интеграл от функции
имеющей бесконечный разрыв в точке а :

=
.

Если функция
имеет бесконечный разрыв во внутренней точке с 
, то несобственный интеграл определяется следующим образом

=
+
=
+
.

Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно слагаемое.

С геометрической точки зрения, несобственный интеграл от неограниченной функции также характеризует площадь неограниченной криволинейной трапеции:

Поскольку несобственный интеграл выводится путем предельного перехода из определенного интеграла, то все свойства определенного интеграла могут быть перенесены (с соответствующими уточнениями) на несобственные интеграла первого и второго рода.

Во многих задачах, приводящих к несобственным интегралам, не обязательно знать, чему равен этот интеграл, достаточно лишь убедиться в его сходимости или расходимости. Для этого используют признаки сходимости . Признаки сходимости несобственных интегралов:

1) Признак сравнения .

Пусть для всех х 

. Тогда, если
сходится, то сходится и
, причем

. Если
расходится, то расходится и
.

2) Если сходится
, то сходится и
(последний интеграл в этом случае называется абсолютно сходящимся ).

Признаки сходимости и расходимости несобственных интегралов от неограниченных функций аналогичны сформулированным выше.

Примеры решения задач.

Пример 1.

а)
; б)
; в)

г)
; д)
.

Решение.

а) По определению имеем:

.

б) Аналогично

Следовательно, данный интеграл сходится и равен .

в) По определению
=
+
, причем, а – произвольное число. Положим в нашем случае
, тогда получим:

Данный интеграл сходится.

Значит, данный интеграл расходится.

д) Рассмотрим
. Чтобы найти первообразную подынтегральной функции, необходимо применить метод интегрирования по частям. Тогда получим:

Поскольку ни
, ни
не существуют, то не существует и

Следовательно, данный интеграл расходится.

Пример 2.

Исследовать сходимость интеграла в зависимости от п .

Решение.

При
имеем:

Если
, то
и . Следовательно, интеграл расходится.

Если
, то
, а
, тогда

= ,

Следовательно, интеграл сходится.

Если
, то

следовательно, интеграл расходится.

Таким образом,

Пример 3.

Вычислить несобственный интеграл или установить его расходимость:

а)
; б)
; в)
.

Решение.

а) Интеграл
является несобственным интегралом второго рода, поскольку подынтегральная функция
не ограничена в точке

. Тогда, по определению,

.

Интеграл сходится и равен .

б) Рассмотрим
. Здесь также подынтегральная функция не ограничена в точке
. Поэтому, данный интеграл – несобственный второго рода и по определению,

Следовательно, интеграл расходится.

в) Рассмотрим
. Подынтегральная функция
терпит бесконечный разрыв в двух точках:
и
, первая из которых принадлежит промежутку интегрирования
. Следовательно, данный интеграл – несобственный второго рода. Тогда, по определению

=

=

.

Следовательно, интеграл сходится и равен
.

Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….

Итак, начнем-с. Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного интеграла есть очень хороший геометрический смысл.

Что значит вычислить несобственный интеграл?

Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).

Несобственные интегралы бывают двух видов.

Несобственный интеграл с бесконечным пределом (ами) интегрирования
Иногда такой несобственный интеграл называют несобственным интегралом первого рода . В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: . В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .

Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: , и их мы рассмотрим позже – когда войдёте во вкус:)

Ну а сейчас разберём самый популярный случай . В подавляющем большинстве примеров подынтегральная функция непрерывна на промежутке , и этот важный факт следует проверять в первую очередь! Ибо если есть разрывы, то есть дополнительные нюансы. Для определённости предположим, что и тогда типичная криволинейная трапеция будет выглядеть так:

Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл численно равен её площади . При этом возможны следующие варианты:

1) Первая мысль, которая приходит в голову: «раз фигура бесконечная, то », иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что несобственный интеграл расходится .

2) Но . Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: . Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится .

3) О третьем варианте чуть позже.

В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции , и конкретные примеры мы очень скоро рассмотрим.

А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл (расходится) либо равен конечному отрицательному числу.

Таким образом, несобственный интеграл может быть отрицательным .

Важно! Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно . Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.

Коль скоро, несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: . На самом деле формула применима и к несобственным интегралам, только ее нужно немного модифицировать. В чем отличие? В бесконечном верхнем пределе интегрирования: . Наверное, многие догадались, что это уже попахивает применением теории пределов, и формула запишется так: .

В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию (неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела. У кого с ними плохо, изучите урок Пределы функций. Примеры решений , ибо лучше поздно, чем в армии.

Рассмотрим два классических примера:

Пример 1

Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно .

Подынтегральная функция непрерывна на полуинтервале , значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.

Применение нашей формулы и решение задачи выглядит так:

То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.

В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применятся эта формула под знаком предела. Вместо привычной буквы «динамической» переменной выступает буква «бэ». Это не должно смущать или ставить в тупик, потому что любая буква ничем не хуже стандартного «икса».

Если Вам не понятно почему при , то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. Во втором случае посетите урок Графики и свойства элементарных функций .

При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!

Чистовое оформление задания должно выглядеть примерно так:

“

! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией – непрерывна она на промежутке интегрирования или нет . Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.

Пример 2

Вычислить несобственный интеграл или установить его расходимость.

Выполним чертеж:

Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд. Решаем с помощью формулы :

(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.

(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.

(3) Указываем, что при (Господа, это уже давно нужно понимать) и упрощаем ответ.

Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.

Чистовое оформление примера должно выглядеть примерно так:

“
Подынтегральная функция непрерывна на
“

Что делать, если вам встретится интеграл наподобие – с точкой разрыва на интервале интегрирования? Это говорит о том, что в примере опечатка (вероятнее всего) , либо о продвинутом уровне обучения. В последнем случае, в силу свойства аддитивности , следует рассмотреть два несобственных интеграла на промежутках и и затем разобраться с суммой.

Иногда вследствие опечатки либо умысла несобственного интеграла может вовсе не существовать , так, например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть промежутка интегрирования вообще не войдёт в область определения подынтегральной функции.

Более того, несобственного интеграла может не существовать даже при всём «видимом благополучии». Классический пример: . Несмотря на определённость и непрерывность косинуса, такого несобственного интеграла не существует! Почему? Всё очень просто, потому что:
– не существует соответствующего предела .

И такие примеры пусть редко, но встречаются на практике! Таким образом, помимо сходимости и расходимости, есть ещё и третий исход решения с полноправным ответом: «несобственного интеграла не существует».

Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе. Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:

Пример 3

Вычислить несобственный интеграл или установить его расходимость.

Сначала попытаемся найти первообразную функцию (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.

На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.

Проведем замену:

Неопределенный интеграл найден, константу в данном случае добавлять не имеет смысла.

На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:

Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.

Теперь находим несобственный интеграл:

(1) Записываем решение в соответствии с формулой . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.

(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему при ? Смотрите график арктангенса в уже неоднократно рекомендованной статье.

(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.

Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:

“
Подынтегральная функция непрерывна на .

“

Пример 4

Вычислить несобственный интеграл или установить его расходимость.

! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей .

Пример 5

Вычислить несобственный интеграл или установить его расходимость.

Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала. У кого какая математическая подготовка.

Полные решения и ответы в конце урока.

Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов . Там же разобран случай, когда оба предела интегрирования бесконечны.

Несобственные интегралы от неограниченных функций
Или несобственные интегралами второго рода . Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: Но, в отличие от определенного интеграла, подынтегральная функция терпит бесконечный разрыв (не существует): 1) в точке , 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.

Сразу пример, чтобы было понятно: . Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!

Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования . В этой связи проверим и верхний предел: . Здесь всё хорошо.

Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:

Здесь почти всё так же, как в интеграле первого рода.

Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).

* по умолчанию привычно полагаем, что несобственный интеграл существует

Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению справа. Легко проследить по чертежу: по оси мы должны бесконечно близко приблизиться к точке разрыва справа .

Посмотрим, как это реализуется на практике.

Пример 6

Вычислить несобственный интеграл или установить его расходимость.

Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)

Сначала вычислим неопределенный интеграл:

Замена:

У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле .

Вычислим несобственный интеграл:

(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом . В данном случае у нас правосторонний предел .

(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.

(3) Разбираемся с при . Как определить, куда стремится выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.

В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью .

А сейчас два примера для самостоятельного решения.

Пример 7

Вычислить несобственный интеграл или установить его расходимость.

Пример 8

Вычислить несобственный интеграл или установить его расходимость.

Если подынтегральной функции не существует в точке

Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом.

Несобственные интегралы первого рода. По сути это тот же определённый интеграл, но в случаях, когда интегралы имеют бесконечный верхний или нижний пределы интегрирования, или оба предела интегрирования бесконечны.

Несобственные интегралы второго рода. По сути это тот же определённый интеграл, но в случаях, когда интеграл берётся от неограниченных функций, подынтегральная функция в конечном числе точек конечного отрезка интегрирования не имеет, обращаясь в бесконечность.

Для сравнения. При введении понятия определённого интеграла предполагалось, что функция f (x ) непрерывна на отрезке [a , b ], а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений. Так появляются несобственные интегралы.

Геометрический смысл несобственного интеграла выясняется довольно просто. В случае, когда график функции y = f (x ) находится выше оси Ox , определённый интеграл выражает площадь криволинейной трапеции, ограниченной кривой y = f (x ) , осью абсцисс и ординатами x = a , x = b . В свою очередь несобственный интеграл выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями y = f (x ) (на рисунке ниже – красного цвета), x = a и осью абсцисс.

Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:

Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный интеграл называется сходящимся. Площадь может быть и бесконечностью и в этом случае несобственный интеграл называется расходящимся.

Использование предела интеграла вместо самого несобственного интеграла. Для того, чтобы вычислить несобственный интеграл, нужно использовать предел определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то несобственный интеграл называется сходящимся, а в противном случае – расходящимся. К чему стремится переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода или второго рода. Узнаем об этом сейчас же.

Несобственные интегралы первого рода – с бесконечными пределами и их сходимость

Несобственные интегралы с бесконечным верхним пределом

Итак, запись несобственного интеграла как отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.

Определение. Несобственным интегралом с бесконечным верхним пределом интегрирования от непрерывной функции f (x ) на промежутке от a до ∞ называется предел интеграла этой функции с верхним пределом интегрирования b и нижним пределом интегрирования a при условии, что верхний предел интегрирования неограниченно растёт , т.е.

.

Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся , а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся и ему не приписывается никакого значения.

Пример 1. Вычислить несобственный интеграл (если он сходится).

Решение. На основании определения несобственного интеграла находим

Так как предел существует и равен 1, то и данный несобственный интеграл сходится и равен 1.

В следующем примере подынтегральная функция почти как в примере 1, только степень икса – не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость. То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится, а при каких расходится?

Пример 2. Исследовать на сходимость несобственный интеграл (нижний предел интегрирования больше нуля).

Решение. Предположим сначала, что , тогда

В полученном выражении перейдём к пределу при :

Нетрудно видеть, что предел в правой части существует и равен нулю, когда , то есть , и не существует, когда , то есть .

В первом случае, то есть при имеет место . Если , то и не существует.

Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .

Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница , можно вывести следующую очень похожую на неё формулу:

.

Это обобщённая формула Ньютона-Лейбница.

Пример 3. Вычислить несобственный интеграл (если он сходится).

Предел этого интеграла существует:

Второй интеграл, составляющий сумму, выражающую исходный интеграл:

Предел этого интеграла также существует:

.

Находим сумму двух интегралов, являющуюся и значением исходного несобственного интеграла с двумя бесконечными пределами:

Несобственные интегралы второго рода – от неограниченных функций и их сходимость

Пусть функция f (x ) задана на отрезке от a до b и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b , в то время как во всех остальных точках отрезка она непрерывна.

Определение. Несобственным интегралом функции f (x ) на отрезке от a до b называется предел интеграла этой функции с верхним пределом интегрирования c , если при стремлении c к b функция неограниченно возрастает, а в точке x = b функция не определена , т.е.

.

Если этот предел существует, то несобственный интеграл второго рода называется сходящимся, в противном случае – расходящимся.

Используя формулу Ньютона-Лейбница, выводим.

Читайте также…

Неопределенный и Определенный интегралы Основная теорема интегрального

Неопределенный и Определенный интегралы

Основная теорема интегрального исчисления. Теорема (основная теорема интегрального исчисления). Если F 1(x) и F 2(x) – любые первообразные для f(x) на X, то F 1(x) – F 2(x) = const на промежутке X. Доказательство: Введем обозначение: F(x) = F 1(x) – F 2(x). Требуется доказать, что F(x) = const на X. Этот факт будет доказан позже, и тогда эта теорема будет доказана. Следствие. Если F(x) – какая-то первообразная для f(x) на X, то любую другую первообразную Ф(x) можно представить в виде: Ф(х) = F(x)+C, где C – некоторая постоянная.

Неопределенный интеграл. Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением: F(x) + C. Записывают: ∫ f(x)dx = F(x) + C. f(x) называется подынтегральной функцией. f(x)dx называется подынтегральным выражением. Отметим, что подынтегральное выражение является дифференциалом любой первообразной функции f(x): d. F(x) = F'(x) = f(x)dx. (1) Результат примера 2 можно записать в виде:

Свойства неопределенного интеграла: 1. Производная от неопределенного интеграла равна подинтегральной функции (∫ f(x)dx) = (F(x) + C)’ = f(x) 2. Дифференциал от неопределенного интеграла равен подинтегральному выражению d(∫ f(x)dx)= f(x)dx. 3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: ∫ d. F(x) = F(x) + C.

Произвольная постоянная При практическом вычислении неопределенных интегралов часто приходится использовать свойство линейности, что приводит к необходимости складывать произвольные постоянные или умножать их на некоторое (фиксированное) число. Если С 1 и С 2 – постоянные, которые могут принимать любое значение из R, α Ο R – фиксированное число, α≠ 0, то С 1+ С 2 = С, αС = С. На практике при нахождении первообразных произвольную постоянную на промежуточных этапах не записывают, а добавляют лишь в конце вычислений. Пример 3: ∫(x 2 – 2 sinx + 1)dx = ∫ x 2 dx – 2∫ sinxdx + ∫dx = =

Нахождение значения неопределенного интеграла связано главным образом с нахождением первообразной функции. Для удобства значения неопределенных интегралов большинства элементарных функций собраны в специальные таблицы интегралов, которые бывают иногда весьма объемными. В них включены различные наиболее часто встречающиеся комбинации функций. Но большинство представленных в этих таблицах формул являются следствиями друга, поэтому ниже приведем таблицу основных интегралов, с помощью которой можно получить значения неопределенных интегралов различных функций.

Таблица интегралов элементарных функций

Некоторые формулы интегрирования

Элементарные методы интегрирования Метод подстановки (замены переменных): Теорема: Если требуется найти интеграл , но сложно отыскать первообразную, то с помощью замены x =и dx = получается: Доказательство: Продифференцируем предлагаемое равенство: По рассмотренному выше свойству 2 неопределенного интеграла: что с учетом введенных обозначений и является исходным предположением. Теорема доказана.

Свойства определенного интеграла 1. При перестановке пределов интегрирования определенный интеграл меняет знак: 2. Для любого значения а справедливо равенство: 3. Для любых значений а, b и с верно равенство:

Свойства определенного интеграла 4. Интеграл от суммы функций равен сумме интегралов слагаемых 5. Постоянный множитель можно вынести за знак интеграла:

Применение интеграла с использованием презентации Microsoft Office PowerPoint

Цели урока:

Применение интеграла в решении задач, ориентированных на многообразие связей между физическими и математическими величинами;

Углубить и систематизировать теоретические знания, развивать познавательный интерес, мышление, речь, творчество;

Воспитывать коллективизм, интерес к предмету.

Тип урока – урок повторения и обобщения знаний.

Форма урока – урок-игра, презентация.

Методы обучения – проблемно-поисковые, наглядно-иллюстративные, коллективные.

Оборудование – компьютер, мультимедийный проектор, игральный стол, волчок, плакаты с заданиями.

Ход урока.

1. Организационный момент
– Добрый день, ребята! Мы изучили материал по теме «Интеграл». Сегодня на уроке систематизируем знания по этой теме и остановимся на задачах, в решении которых используется интеграл. Задачи ориентированы на обнаружении и изучении многообразия связей между физическими и математическими величинами. И поэтому сегодняшний урок я предлагаю провести в форме игры «Что? Где? Когда?» под девизом «Единство в многообразии» (слайд № 1 Приложения 1).

Эпиграфом урока являются слова Пафнутия Львовича Чебышева: «Сближение теории с практикой даёт самые благотворные результаты, и не одна только практика от этого выигрывает, сами науки развиваются под её влиянием, она открывает им новые предметы для исследования или новые стороны в предметах давно известных» (слайд № 2).

2. Актуализация опорных знаний учащихся.
Повторение теоретического материала по данной теме.

– Объясните, что такое интеграл? (Слайд № 3)

– Как обозначается интеграл? (Слайд № 4)

– Какие бывают интегралы? (Слайд № 5)

– Перечислите свойства интеграла. (Слайд № 6)

– В чем заключается геометрический смысл интеграла? Какую фигуру называют криволинейной трапецией? Запишите формулу для вычисления площади криволинейной трапеции. Какие ученые вывели эту формулу? (Слайд № 7)

– Назовите несколько примеров применения определенного интеграла в геометрии и физике.

3. Закрепление материала по формированию практических умений и навыков учащихся.
– Итак, мы повторили теоретический материал и теперь рассмотрим применение интеграла в решении задач. Этот этап урока мы проведем в форме игры «Что? Где? Когда?» (слайд № 8).

– Представляю команду знатоков и капитана команды.

Ведущая:

– У нас в гостях присутствует и команда зрителей. Поприветствуем друг друга!

Правила игры:

Игра состоит из 11 раундов.

В каждом раунде знатокам предлагается вопрос из сектора, выпавшего на игровом столе.

После обдумывания капитан называет игрока, который будет давать ответ.

Если команда отвечает сразу, то одна минута остается в запасе и ее можно взять дополнительно в любом раунде.

Если команда дает правильный ответ, то ей засчитывается одно очко.

В случае неправильного ответа на вопрос в игре могут принять участие зрители.

– Играем до 6 очков!

– Итак, начинаем 1 раунд, разыгрываем 1 очко. (Крутится волчок на игральном столе, останавливается на одном из секторов. На экране высвечивается табло, на котором выбирается номер выпавшего сектора (слайд 8 Приложения 1)).

4. Подведение итогов.
Объявляется счет игры в пользу знатоков/ зрителей. Награждение.

– Спасибо всем! Игра закончена! До новых встреч!

5. Задание на дом.
Подготовить мини-проекты на следующие темы (по выбору учащегося):

Объем тела и интеграл.

Перемещение и интеграл.

Работа и интеграл.

Давление жидкости и интеграл.

Нужны ли интегралы и логарифмы, если есть компьютеры? — Российская газета

На эти вопросы “РГ” отвечает директор знаменитой физматшколы имени академика Андрея Колмогорова при МГУ Анатолий Часовских.

Российская газета | Дети стали плохо знать математику. Без калькулятора не способны сказать, сколько будет “дважды два”. Плохо учат в школе или учебники негодные?

Анатолий Часовских | Причина, я думаю, не в учебниках. Просто учат сейчас другому. Помню, как нас муштровали на таблицу умножения. Требовали, чтобы мы умели считать в уме и без бумажки. В XXI веке меньше учат счету, больше смекалке, сообразительности. На этом основаны и учебники Петерсона.

Мне кажется, что ничего плохого в том, что нынешние дети умеют пользоваться калькулятором, нет. И для этого мозги нужны. Зачем искусственно усложнять жизнь, если можно нудные вычисления поручить машине. Если человек знает алгоритм деления столбиком, может быть, и не надо его заставлять повторять это тысячу раз. Лучше пусть в это время учится другим алгоритмам. Другое дело, стало труднее задачки составлять: ведь в них теперь нужно нивелировать эффект калькулятора. Эта машинка должна давать импульс к творческому решению задач. На вступительных экзаменах на мехмат МГУ пользоваться калькуляторами не разрешается только потому, что они бывают разные: одни только считают, а другие могут и графики строить.

РГ | Многие с ностальгией вспоминают учебник Киселева – четкий и ясный. Действительно, старшее поколение неплохо помнит основные алгебраические действия и формулы.

Часовских | Это старый учебник. Математика представлена там незыблемой и не зависимой от времени наукой. Но в 70-х годах прошлого века обходиться только этим учебником стало трудно. Просто появились новые разделы: комбинаторика и дифференциальное, интегральное исчисление.

Конечно, математическое образование меньше подвержено изменениям, чем, скажем, историческое или филологическое. Но кругозор математиков должен расширяться в зависимости от развития науки. А оно всегда есть.

РГ | Известно письмо академика Арнольда, который возмущался предложениями убрать из учебного стандарта по математике синусы, степенные функции и стереометрию. А действительно, зачем нужны логарифмы и интегралы, если есть компьютеры?

Часовских | В компьютере заложен зачастую только приближенный алгоритм решения трудной задачи. Ученый знает, какими действиями нужно искать ответ. Без интегралов вы не сможете подойти к решению, и компьютер ничем не поможет. Ведь это лишь инструмент. Впрочем, может быть, когда-нибудь человек и придумает машину, которая будет сама себе ставить задачи и творчески решать их.

РГ | Может быть, освободить от утомительных “косинусов-синусов” хотя бы будущих литературоведов и историков?

Часовских | Без математики гуманитариям не обойтись уже потому, что она учит объективности. Ведь решение задачи не устаревает, нельзя менять аксиоматику в зависимости от политической конъюнктуры. То, что было доказано сто лет назад, корректировке не подлежит. С другой стороны, математика приучает к логике. А она никому, в том числе и гуманитарию, не помешает. Противоречивых суждений в нашей жизни и так хватает.

РГ | А самим математикам так ли уж нужна литература или история? Согласитесь, среди юных “физиков” очень часто встречается снисходительное отношение к “лирикам”?

Часовских | Без гуманитарного взгляда на вещи, мне кажется, не разберешься даже в правилах дорожного движения. А некая элитарность в наших учащихся есть, вы правы. Когда в нашей школе открылся химический класс, математики поначалу смотрели на “пришельцев” свысока. “Химия не наука!” – появились и такие надписи на стенах. Со временем надменное отношение к другим предметам ушло. Ведь понятно же, что из математических формул не узнаешь, что такое любовь к родине, дружба, – все те идеалы, о которых теперь немодно говорить, но которые никуда не делись.

РГ | А вот, скажем, цветок. Математик его видит каким-то особенным образом?

Часовских | В МГУ недавно открыли факультет биоинженерии и биоинформатики. А у нас – соответствующий класс. Школьники-биологи как раз и демонстрируют этот самый математический взгляд на живое. К примеру, стремятся к стройному и формальному описанию структуры ДНК. Математик, в отличие от художника, должен проникнуть в сущность явления и попытаться найти его математическую модель. Условно, без подробностей. Главное знать общие свойства описываемой системы. Он умеет формализовать ситуацию, выделять главное и не обращать внимание на мелочи.

РГ | Это качество, наверное, очень помогает в семейной жизни?

Часовских | Не могу не согласиться. К тому же, математики обычно бережно относятся к прекрасному полу. В отличие от филфака, который называют факультетом невест, мехмат – это факультет жен. Потому что к концу учебы все девушки там уже замужем.

РГ | Что вы думаете о едином экзамене по математике?

Часовских | У нас, в отличие от западных стран, другая культура проверки знаний: мы сочиняем задачки, в которых предполагается решение. По нему можно проследить ход мыслей. А по ответам на тест – вряд ли. Там возможно случайное попадание.

РГ | Котируется ли современное российское математическое образование в мире?

Часовских | Иностранцы, в частности, корейцы и китайцы, очень интересуются нашей системой. Приезжали к нам, чтобы перенять методы преподавания. В городе Пусан в Южной Корее открыли точно такое же учебное заведение. Конкурс там – 20 человек на место. Есть и еще более объективные показатели. На международных олимпиадах у нас пока первые места. Кстати, профильное образование (спецшколы и факультативы), тоже по-прежнему на высоте. В стране возникла система математических соревнований: в течение всего года в разных городах идут “замеры знаний” среди школьников. Есть заочные школы при университетах.

РГ | Кто-то из наших ученых сказал, что для российских математиков главный вопрос: “Почему?”, а, допустим, для американских – “Как?”

Часовских | Я не вполне согласен. Вопрос “Почему?” должен задавать себе любой ученый, занимающийся фундаментальной наукой. “Как?” – это сфера интересов инженеров. Другое дело, в США масса хороших специалистов, которых не очень интересует доказательная часть. А вот в переосмыслении готовых решений помощь россиян, которых много сейчас за рубежом, неоценима. И вырастить фундаментального ученого стоит гораздо дороже, чем прикладника.

РГ | А заработать на математике сейчас можно?

Часовских | Лучше говорить не “заработать”, а “зарабатывать”. Потому что математика быстрого дохода не дает. А возможность иметь стабильный кусок хлеба есть. Особенно если учесть, что спрос на математиков и физиков будет только расти.

РГ | Сначала в вашу школу принципиально принимали лишь способных ребят из провинции. Положа руку на сердце: сейчас можно отыскать самородка где-нибудь в деревне, где нет ни одного компьютера и учителей грамотных тоже почти не осталось?

Часовских | Начнем с того, что в Москве нет ни одного победителя последней международной олимпиады школьников по математике и информатике. Все они из регионов. Это Санкт-Петербург, Юг России, Урал, Сибирь. И еще хочу подчеркнуть: в школе постоянный приток способных ребят как раз не из университетских городов. Однако сельским школьникам часто не под силу у нас учиться по финансовым соображениям. Ведь на каникулы все разъезжаются по домам, а значит, нужны деньги на дорогу. Мы добираем москвичей в основном потому, что наши общежития, которые строились по санитарным нормам 60-х годов, не вмещают теперь 350-400 человек, которых должна готовить школа. Кто умнее? Это не зависит от места жительства. Одно скажу, у москвичей, конечно, больше возможностей.

РГ | Известно, что Капица критиковал методику Колмогорова. Что не устраивало нобелевского лауреата?

Часовских | Петр Леонидович считал, что нельзя обескровливать обычные школы, забирая оттуда талантливых детей. Потому что в любом коллективе должны быть маяки, за которыми тянутся остальные. А Андрей Николаевич предлагал собирать талантливых детей, чтобы они “варились” в интеллектуальном бульоне, а потом отдавали полученные знания обществу. На мой взгляд, истина посредине.

РГ | Вы можете сделать обобщенный психологический портрет вашего ученика?

Часовских | Прежде всего это творческая личность. И на веру ничего не воспринимает. Отмахнуться от себя не позволит: все объясни с доказательствами и примерами. Как и любой подросток, стремится к самоутверждению. Но к внешним эффектам для этого не прибегает. Абсолютно равнодушен к “шмоткам-тряпкам”. В этой связи иногда даже приходится проводить разъяснительную работу, куда и как одеться.

РГ | В общем, со странностями ребята?

Часовских | Недавно одна учительница возмущалась: захожу, говорит, на урок математики и вижу, что на первой парте стоит перевернутый стул. И никто этого не замечает. Поглощены решением задачи.

РГ | То есть сплошные “ботаны”? И шпаргалками не пользуются?

Часовских | Ну почему же? И у нас бывают “проколы”. Не то чтобы списывают внаглую, а просто много чего интересного “выясняют” в разговоре с коллегой на перемене. После этого можно уже и не искать самостоятельного решения. Только ведь мы готовим ученых, которые сами должны докопаться до истины.

Интегральные границы / пределы интегрирования

Что такое границы интеграла?

Границы интеграла , также называемые границами интегрирования , определяют область, которую вы будете интегрировать.

Пределы интегрирования для этого графика (0,2).

Верхние и нижние границы

Интеграл имеет две границы : нижнюю границу и верхнюю границу. Если вам дан интеграл, вы будете интегрировать между этими двумя границами.

Нижняя граница – это место, где вы начинаете интегрирование. Вы найдете его под интегральным символом:

Верхняя граница — это линия, на которой вы прекращаете интегрирование. Он находится над символом интеграла:

В приведенном выше примере можно сказать, что границы интегрирования равны 0 и 2.

Как найти пределы интегрирования

Если вам дан ряд функций и вас попросили найти ограниченную область (которую содержат функции), самый простой способ найти пределы интегрирования — построить графики функций.

Например, допустим, вас попросили найти ограниченную область:

у = 5 – х

у = х

у = 4 – 3х

На графике функции выглядят так:

Пределы интегрирования (черные точки) легко увидеть, если построить графики функций.

Вы можете использовать свой графический калькулятор (я использовал онлайн-калькулятор графиков в HRW), чтобы увеличить точку пересечения линий. Обратите внимание, что в этом примере область ограничена тремя функциями, поэтому вам потребуется выполнить более одного интегрирования, чтобы найти решение.Вы можете увидеть простой пример этой концепции здесь: Площадь между двумя кривыми.
Определенные интегралы и границы

Интегральные ограничения применяются только к определенным интегралам.

Если у вас есть непрерывная функция (т. е. такая, которая простирается до бесконечности), вы должны установить границы функции, чтобы интегрировать ее. Когда вы размещаете эти нижнюю и верхнюю границы, это становится определенным интегралом . Интеграл без границ называется неопределенным интегралом.

Как найти верхний предел интеграла

Когда вы находите верхний предел интеграла, вы находите определенный интеграл с верхней границей.

Интеграл с нижним пределом -1 и верхним пределом 1.

Шаги

Шаг 1: Идентифицируйте рассматриваемую функцию . В интеграле это значение между символом интеграла и константой интегрирования (обычно обозначается как «dx» или, возможно, «dy»). В качестве примера мы назовем функцию чем-то простым, например, «f(x) = 4x».
Шаг 2: Определите пределы исчисления интеграла. Эти значения обычно обозначаются вверху и внизу знака интеграла.Верхняя граница — это значение вверху, а нижняя граница — это значение внизу символа. Допустим, что верхняя граница равна 2, а нижняя граница равна 1.
Шаг 3: Выполните интегрирование функции с использованием неопределенных интегральных правил. Для f(x) = 4x увеличьте степень переменной на единицу и разделите всю функцию на новый показатель степени переменной. Например, интеграл f(x) = 4x становится 2x ² .
Шаг 4: Вставьте верхнюю границу интеграла во вновь интегрированную функцию .Мы заменяем нашу переменную ранее определенной верхней границей (которую мы оценили в 2). Тогда наша интегрированная функция принимает вид f(x) = 2(2) ² , где значение в скобках — это верхняя граница, заменившая переменную.
Шаг 5: Выполните математические вычисления. Не забывайте порядок действий — ваш ответ может привести к совершенно другому результату, если вы не выполните этот шаг!
f(x) = 2(2) ² = 2(4) = 8. Таким образом, для функции f(x) = 4x ее интегрирование с верхней границей 2 даст значение 8.

Вот и все!
Наверх

Проблемы

Даже если интеграл имеет границы, это не всегда означает, что у интеграла есть аналитическое решение. Например, между нижней границей и верхней границей может быть существенный разрыв. Всегда полезно изобразить функцию в виде графика, прежде чем пытаться ее интегрировать; в большинстве случаев этой проблемы можно избежать. Тем не менее, непрерывные функции с хорошим поведением обычно интегрируемы (King & Mody, 2010).

Ссылки

Кинг, М. и Моди, Н. (2010). Численные и статистические методы биоинженерии: приложения в MATLAB. Издательство Кембриджского университета.
————————————————– ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Интегрирование и взятие интеграла

Интегрирование — это алгебраический метод нахождения интеграла функции в любой точке графика.
Нахождение интеграла
функции по х означает нахождение площади по оси х по кривой.
Интеграл обычно называют антипроизводной
, потому что интегрирование — это процесс, обратный дифференцированию.
Основная теорема математического анализа показывает, что антидифференцирование — это то же
, что и интегрирование.

Физическое понятие интеграла аналогично производной.
Для производной мотивацией было найти скорость в любой момент времени
при заданном положении объекта.Если мы знаем скорость объекта в определенное время
раз, интеграл даст нам положение объекта в это время.
Точно так же, как производная дает мгновенную скорость изменения, интеграл
дает общее расстояние в любой момент времени.

Интеграл получается не только при попытке найти процесс, обратный взятию производной
, но и при попытке решить задачу о площади . Точно так же, как процесс
дифференцирования используется для нахождения наклона в любой точке графика, процесс
интегрирования находит площадь кривой до любой точки графика.

Интеграция Римана

До того, как была разработана интеграция, мы могли только аппроксимировать площадь функций
, разделив пространство на прямоугольники и добавив площади.

Мы можем приблизить площадь к оси x, увеличив количество прямоугольников
под кривой. Площадь этих прямоугольников была рассчитана путем умножения длины на
ширины, или х умноженных на изменение х .После вычисления площади сумма
прямоугольников будет аппроксимировать площадь. По мере увеличения количества прямоугольников,
, тем лучше будет аппроксимация. Это формула для суммы Римана,
, где i — любое начальное значение x, а n — количество прямоугольников:

Это был утомительный процесс и никогда не давал точной площади кривой. К счастью,
Ньютон и Лейбниц разработали метод интегрирования, который позволил им найти
точную площадь кривой в любой точке.

Подобно тому, как процесс дифференцирования находит функцию наклона
, когда расстояние между двумя точками становится бесконечно малым, процесс интегрирования
находит площадь под кривой, когда количество разбиений прямоугольников под кривой
становится бесконечно большим. .

Определение интеграла от f(x) из [a,b]

Интеграл функции x от a до b представляет собой сумму прямоугольников кривой
на каждом интервале изменения x по мере того, как число прямоугольников стремится к бесконечности.

Обозначения в левой части обозначают определенный интеграл от f(x)
от a до b. Когда мы вычисляем интеграл из интервала [a,b], мы подставляем a к
интегральной функции и вычитаем его из b в интегральной функции:

где F обозначает интегрированную функцию. Это точно вычисляет площадь под
любой непрерывной функцией.

Общее правило мощности для интеграции

Для проведения интегрирования важно знать общее правило мощности. Это
полная противоположность степенному правилу дифференцирования.

Давайте посмотрим на общую функцию

Когда мы берем интеграл от функции, мы сначала прибавляем 1 к показателю степени, а затем
делим член на сумму показателя степени и 1.

После того, как мы сделали это с каждым термином, мы добавляем константу в конце.Напомним, что
, взяв производную от константы, уберет ее, поэтому взятие интеграла от
функции даст нам константу. Мы помечаем его C, потому что константа
неизвестна — это может быть любое число! Поскольку у нас может быть бесконечно много возможных функций
для интеграла, мы называем его неопределенным интегралом.

Сделаем пример.

Найдите интеграл от
.

Начнем с первого термина.Мы смотрим на показатель степени 2 и увеличиваем его на 1,
, затем делим член на полученный показатель степени 3.

Затем мы смотрим на следующий член и делаем то же самое. Поскольку его показатель степени равен
1, результирующий показатель степени будет равен 2, поэтому мы делим весь член на 2.

Последний член имеет значение x, но мы его просто не видим. Мы можем представить последний член
как -3x ⁰ . Это эквивалентно -3(1).Если мы воспользуемся степенным правилом интегрирования
, мы добавим 1 к показателю степени, чтобы возвести его в первую степень, а затем разделим член
на 1.

Все, что нам нужно сделать, это добавить константу в конце, и все готово.

Эта формула степени для интегрирования работает для всех значений n , кроме для n = -1 (поскольку
нельзя делить на 0). Мы можем взять обратную производную от логарифмической функции
, чтобы решить эти случаи.

В общем

Сводка по интеграции

Мы должны понять

Определенный интеграл как предел сумм Римана

Определенный интеграл как изменение количества над интегралом

как интегралы представляются графически, численно и аналитически

как они интерпретируются как положение объекта при заданной скорости.

Напомним, что интеграл — это функция, определяющая площадь под кривой для любого
заданного интервала.Взятие интеграла от производной функции даст
исходную функцию. Интеграл также может сообщить нам положение объекта в
раз в любой момент времени, учитывая по крайней мере две точки скорости объекта.

6: Приложения интеграции – Mathematics LibreTexts

Последнее обновление

Сохранить как PDF

Авторы и авторы

В этой главе мы используем определенные интегралы для расчета силы, действующей на плотину, когда водохранилище заполнено, и исследуем, как изменение уровня воды влияет на эту силу.Гидростатическая сила — лишь одно из многих применений определенных интегралов, которые мы исследуем в этой главе. От геометрических приложений, таких как площадь поверхности и объем, до физических приложений, таких как масса и работа, до моделей роста и распада, определенные интегралы являются мощным инструментом, помогающим нам понять и смоделировать мир вокруг нас.

6.0: Прелюдия к приложениям интеграции

Плотина Гувера — чудо инженерной мысли. Когда озеро Мид, водохранилище за плотиной, заполнено, плотина выдерживает большую нагрузку.Однако уровень воды в озере значительно колеблется в результате засух и различных потребностей в воде.

6.1: Площади между кривыми

Точно так же, как определенные интегралы можно использовать для нахождения площади под кривой, их также можно использовать для нахождения площади между двумя кривыми. Чтобы найти площадь между двумя кривыми, заданными функциями, проинтегрируйте разность функций. Если графики функций пересекаются или область сложная, используйте абсолютное значение разности функций.В этом случае может потребоваться вычисление двух или более интегралов.

6.2: Определение объемов путем разрезания

В этом разделе мы используем определенные интегралы для нахождения объемов трехмерных тел. Мы рассматриваем три подхода — срезы, диски и шайбы — для нахождения этих объемов в зависимости от характеристик твердого тела.

6.3: Объемы вращения – цилиндрические оболочки

В этом разделе мы исследуем метод цилиндрических оболочек, последний метод нахождения объема тела вращения.Мы можем использовать этот метод для тех же типов твердых тел, что и метод диска или метод шайбы; однако при использовании метода диска и шайбы мы интегрируем по оси координат, параллельной оси вращения. При методе цилиндрических оболочек интегрируем по оси координат, перпендикулярной оси вращения.

6.4: Длина дуги кривой и площадь поверхности

Длину дуги кривой можно рассчитать с помощью определенного интеграла.Длина дуги сначала аппроксимируется с использованием отрезков прямой, что приводит к сумме Римана. Принятие предела дает нам формулу определенного интеграла. Тот же процесс можно применить к функциям от y. Понятия, используемые для расчета длины дуги, можно обобщить, чтобы найти площадь поверхности вращения. Интегралы, полученные по формулам длины дуги и площади поверхности, часто трудно оценить.

6.5: Физические приложения интеграции

В этом разделе мы рассмотрим некоторые физические приложения интеграции.Несколько физических приложений определенного интеграла распространены в технике и физике. Определенные интегралы можно использовать для определения массы объекта, если известна его функция плотности. Работу также можно рассчитать путем интегрирования силовой функции или при противодействии силе тяжести, как в задаче о насосе. Определенные интегралы также можно использовать для расчета силы, действующей на объект, погруженный в жидкость.

6.6: Моменты и центры масс

В этом разделе мы рассматриваем центры масс (также называемые центроидами при определенных условиях) и моменты.Основная идея центра масс — это понятие точки баланса. Многие из нас видели исполнителей, которые крутят тарелки на концах палочек. Артисты стараются, чтобы несколько из них вращались, не позволяя ни одному из них упасть. Математически эта точка наилучшего восприятия называется центром масс тарелки.

6.7: Интегралы, показательные функции и логарифмы

Мы уже рассматривали показательные функции и логарифмы в предыдущих главах.Тем не менее, мы упустили некоторые ключевые детали в предыдущих обсуждениях. Например, мы не изучали, как обращаться с экспоненциальными функциями с иррациональными показателями. Определение числа e — еще одна область, в которой предыдущее развитие было несколько неполным. Теперь у нас есть инструменты для более строгой математической обработки этих концепций, и мы делаем это в этом разделе.

6.8: Экспоненциальный рост и затухание

Одно из наиболее распространенных применений экспоненциальных функций включает модели роста и затухания.Экспоненциальный рост и затухание проявляются во множестве естественных приложений. От роста населения и постоянного начисления процентов до радиоактивного распада и закона охлаждения Ньютона — экспоненциальные функции встречаются в природе повсеместно. В этом разделе мы исследуем экспоненциальный рост и затухание в контексте некоторых из этих приложений.

6.9: Вычисление гиперболических функций

Мы познакомились с гиперболическими функциями во Введении в функции и графики, наряду с некоторыми их основными свойствами.В этом разделе мы рассмотрим формулы дифференцирования и интегрирования для гиперболических функций и их обратных функций.

6R: Упражнения на обзор главы 6

Миниатюра: область между двумя функциями.

Авторы и авторство

Гилберт Странг (MIT) и Эдвин «Джед» Херман (Харви Мадд) со многими авторами. Этот контент от OpenStax имеет лицензию CC-BY-SA-NC 4.0 лицензия. Скачать бесплатно на http://cnx.org.

Определение, правила, примеры и решение

Площадь под прямой на графике можно найти по разным формулам. Но задумывались ли вы когда-нибудь, как найти площадь под кривой? Потому что если да, не беспокойтесь, мы на одной волне.

Мы уже знаем, что можем вычислить наклон кривой посредством дифференцирования. Теперь попробуем вычислить формулу площади под кривой.

Для лучшего понимания рассмотрим этот график.

Как можно рассчитать площадь под кривой от точки 0 до 3 на оси x и выше?

Согласно Риману, сумма площадей определенных прямоугольников под линией кривой дает приблизительную площадь под этой кривой. Что-то вроде этого:

Но это не удовлетворяет достаточно. Как насчет уменьшения ширины прямоугольных плит. И еще немного и еще.Может быть так:

Эта область будет относительно более точной, чем предыдущая. Но что, если… мы уменьшим его еще немного. Настолько, что почти ноль! Что-то щелкнуло в вашем сознании?

ДА, производные! Производные используются для расчета мгновенного наклона. Мы собираемся использовать эту концепцию, чтобы найти площадь под этой кривой. Это понятие называется интегралом.

Давайте узнаем, что такое интегралы? Каковы правила интегралов и как их решить?

Что такое интегралы?

Интегрирование — это процесс нахождения интегралов.Интегралы имеют множество применений, например, для нахождения объемов, массы и т. д. Но в этой статье мы обсудим площадь под кривой.

Определение интеграла:

«Если производная функции равна f’(x), то ее интеграл равен ∫f(x).dx + c».

Это можно объяснить на примере. Рассмотрим функцию и ее производную, т. е. f'(x) = 3. Но какова ее первообразная? Мы можем сделать некоторые предположения.

Если подумать, мы получим постоянный член как производную для функции с одним X.То есть:

= 3x

Итак, антидифференцированием мы получаем исходную функцию 3x .

Коэффициент интегрирования
Посмотрите на эти уравнения:

Производная всех этих уравнений также равна 3x . Поэтому, чтобы исправить любую ошибку, мы пишем:

= 3x + C , где c может быть любым постоянным числом

Вот почему интеграл имеет все возможные первообразные этой функции.

Теперь, когда вы знаете, что такое интеграл, мы теперь изучим целочисленное обозначение.

Интегральная запись

У каждой операции есть свой оператор, символ. Для производных у нас есть обозначение d/dx. Точно так же для интегралов мы используем причудливое s .

∫ fx.dx + c

Интегралы и производные

Вы можете задаться вопросом: «Теперь я знаю, что такое интеграл, но как он связан с производными?».

Если быть точным, то первообразные (обратное дифференцирование) и неопределенные интегралы — это почти одно и то же. Но есть большая разница между определенными интегралами и первообразными.

Когда мы находим производные, мы уменьшаем разницу между двумя точками настолько, что она становится бесконечно малой. Но в интегралах мы делаем так много мелких деталей, что число этих достигает бесконечности.

Проще говоря, в производных мы применяем предел приблизительно нулевого значения, а в интегрировании применяем предел до бесконечности. Таким образом, мы можем сказать, что интегралы являются обратными производными.

Правила вычисления интегралов

Есть несколько правил, которые помогают решать интегралы так же, как мы используем правила дифференцирования.Правила интегралов очень похожи на правила, которые мы используем для решения производных.

Степенное правило
Когда функция возведена в некоторую степень, то для интегрирования используется следующее правило:

∫ fx.dx = (xn+1)/n+1                     дифференциация. Давайте сначала докажем, что это правило является обратным степенному правилу дифференцирования.

Пример

Производная функции равна 6×2.Давайте пересмотрим процесс дифференциации и поступим наоборот.

Единица вычитается из степени функции, поэтому, чтобы найти ее обратную, мы прибавляем единицу к степени, т.е. 6×2+1 = 6×3.

Коэффициент такой же, как мощность, поэтому, чтобы обратить его, мы разделим на то же число, т.е. 6×3/3 = 2×3.

Таким образом, интеграл от 6×2 равен 2×3 (исходная функция). Чтобы проверить, равна ли производная 2×3 6×2, воспользуйтесь калькулятором производной.

Умножение на константу
Когда мы видим функцию, которая находится в умножении на некоторое постоянное число, мы применяем правило. Согласно этому правилу при интегрировании постоянный член выносится за интегральную запись. Пример Вы видите постоянные числа 6 и 12. Возьмем 6 обычных.

= 6 ( у ² + 2 года)

Применить интегрирование:

∫ 6 лет ² + 12 лет .dy = 6 ∫ y ² + 2y .dy

Применяя степенное правило:

= 6 ∫ y ² + 2y .dy

= 6) { (y ^{8+1 0+1 ^{1 + 1}/1 + 1}}

= 6 {y ³/3 + Y ²}

= 2y ³ + 6y ² + 6y ² + C

Sum
Когда две функции являются дополнительными, то при интеграции их можно интегрировать отдельно, а затем добавить позже.

∫ (fx + gx).dx = ∫ fx.dx + ∫ gx.dx

Пример

Найдите интеграл от u ⁵ + 2u.

Решение:

∫U ⁵ + 2U.du = ∫U ⁵ .du + ∫2u.du

= (U ^{5 + 1}/5 + 1) + 2∫ U.du

= U ⁶
= U ⁶/6 + 2U ^{1 + 1}/2

= U ⁶
= U ⁶/6 + U ² + C

Разница
к правилу сумм, когда функции находятся в вычитании, они могут быть интегрированы отдельно.

∫ (fx – gx).dx = ∫ fx.dx – ∫ gx.dx

Пример

Найдите интеграл от u ⁵ – 2u.

Решение:

∫U ⁵ + 2U.du = ∫U ⁵ .du – ∫2u.du

= (U ^{5 + 1}/5 + 1) – 2∫ 1U.DU

= U ⁶
= U ⁶/6 – 2U ^{1 + 1}/2

= U ⁶/6 – U ² + C
Вы можете увидеть из примера выше , единственная разница между правилом суммы и правила разности заключается в символе знака.

Интегрирование по частям
Это обратное правило дифференцирования произведения. Выведем его формулу.

Правило продукта:

(uv)’ = uv’ + u’v

Применить интегрирование с обеих сторон.

∫(uv)’.dx = ∫ uv’.dx + ∫ u’v.dx

uv = ∫ uv’.dx + ∫ u’v.dx

∫ uv’.dx = uv – ∫ u ‘v.dx

Пример

Вычислить ∫ x.cosx .dx

Решение:

Определить u и v’.

u = x

v’ = cosx

Найдите значения u’ и v.

u = x

u’ = 1

Для v найдите интеграл от v’.

v = cosx

∫v.dx = ∫ cosx.dx = sinx

Решить.

∫xcosx.dx = x.sinx – ∫1.sinx.dx

= x.sinx – cosx

Добавить константу.

= x.sinx – cosx + c

Правило подстановки
Это правило также известно как правило обратной цепочки . Это правило применяется в особых случаях. Иногда функцию можно настроить таким образом, чтобы можно было применить правило подстановки.

Правило:

∫ f((gx)).g’(x).dx = ∫f(u).du

Чтобы понять эту формулу, посмотрите на задействованные операции.

g'(x) = d/dx g(x)

Для удобства пусть

u = g(x) тогда du = g'(x)

Следует отметить, что эта формула применима только когда в интегрируемой функции есть и и, и и’.

Пример

Найдите интеграл от (x + 1) ² .

Решение:

Понимая функцию, мы видим, что производная x + 1 равна 1 .Это означает, что мы можем умножить 1, чтобы использовать правило подстановки.

∫(x + 1) ² .dx = ∫(x + 1) ² .1dx

Теперь у нас есть u и u’, равные x + 1 и 1 соответственно. Используя формулу:

∫(x + 1) ² .1dx = ∫ u ² . du

= ∫ u ²⁺¹ / 3

= ∫u ³ /3

Возврат значения u:

= ∫(x+3) Some 90 31 0085 3 90 90 Правила

Функция

Интеграл

∫cos(x).dx

SINX + C

∫sin (x) .dx

-COSX + C

9005 Tanx + C

∫(1/x).dx

ln|x| + c

∫ex . DX

EX + C

∫ln (x) .dx

x ln (x) – x + c

Типы интегралов: неопределенные и определенные интегралы

Существует два типа интегралов.Оба решаются по-разному и имеют разные приложения.

Неопределенные интегралы
Это обратная производная. Он вычисляет всю площадь под графиком кривой линии. Все примеры, которые вы видели в этой статье, относятся к неопределенной интеграции.

В этих интегралах нижняя, ни верхняя границы не применяются. Более того, в конце добавляется константа c , чтобы указать, что ответ включает в себя все возможные первообразные функции.

Давайте рассмотрим пример пула. Считайте, что вы наполняете бассейн с помощью водопроводной трубы. Поток воды время от времени меняется по какой-то причине.

Теперь, если бы скорость потока была постоянной, было бы легко вычислить объем воды в бассейне через некоторое время t .

Но проблема в том, что расход постоянно меняется и его нельзя измерить только в одной точке. Необходимо найти скорость потока в каждой точке, чтобы знать точный объем.

Для этого используем неопределенные интегралы. Скорость потока рассчитывается по производным и показывает, с какой скоростью бассейн заполняется в момент времени t .

d/d (x ² ) = 2x (расход)

Интегрирование показывает, каков объем воды в бассейне через время t .

∫2x.dx = x ² (объем)

Это также подтверждает тот факт, что интегралы являются первообразными.

А что, если в бассейне уже было немного воды c ? Это означает, что наш расчетный объем не является «чистым объемом». Чтобы получить правильный ответ, добавьте в ответ c .

= x ² + c

Определенные интегралы
Определенный интеграл находит объем за определенный интервал времени. Например, вы хотите рассчитать объем, накопленный между точками a и b на оси x.

Чтобы вычислить площадь от 1 до 3 по оси x, мы применяем верхнюю и нижнюю границы. Таким образом, вы найдете точно определенную область выделенной части.

Продолжая пример с бассейном, предположим, что мы хотим найти объем воды, добавленной в бассейн между 5 и 8 минутами. Мы напишем:

После интегрирования функции поместите значения в и b соответственно и вычесть значение b из значения a.

= [(8) ² – (5) ² ]

= 64 – 25

= 39

Калькулятор первообразных может находить как определенные, так и неопределенные интегралы для заданных функций.

Подведение итогов

Интегралы используются для нахождения площади под кривой. Он представлен стильным символом S . Интегральные правила помогают в процессе интеграции. Интегралы могут быть определенными и неопределенными (первообразные).

Линейный интеграл | Блестящая математика и естественные науки вики

Теперь о реальной проблеме, которую нужно исследовать:

Предположим, есть грабитель банка, который хочет найти ключ, а затем использовать его, чтобы открыть сейф.

Хитрость заключается в том, что когда он получает ключ, он активирует сигнал тревоги, который запускает радиационную бомбу, испускающую излучение с постоянной скоростью, пока он не откроет сейф, после чего излучение больше не излучается.

Теперь он хочет оптимизировать свой маршрут, чтобы получить минимально возможную дозу радиации.

Предположим, что ключ находится в точке (0,1)(0,1)(0,1). Сейф находится на уровне (1,0)(1,0)(1,0), а интенсивность излучения составляет
.
I=1r2.2}.(Общее излучение)=R2T.

Итак, теперь вопрос… Какой из следующих путей позволит грабителю схватить ключ и открыть сейф с наименьшим радиационным облучением? (Предположим, что какой бы путь он ни выбрал, он будет двигаться с постоянной скоростью.)

Рассмотрим эти три варианта:

A. Дуга окружности с центром в (1,1)(1,1)(1,1)
B. Прямой маршрут из (0,1)(0,1)(0,1) в (1,0)(1,0)(1,0)
С. Дуга окружности с центром в точке (0,0)(0,0)(0,0).

Очевидно, перед грабителем встает вопрос, как провести наименьшее количество времени под воздействием радиации, но при этом оставаться достаточно далеко от источника радиации.

Интуитивно понятно, что A отсутствует, так как это не только более длинный маршрут, чем B , но и приближает его к излучению.2} = T,EC=R2T=12T=T,

, где ТТТ — это общее время, за которое он доберется туда.Поскольку WLOG его скорость можно принять равной 1, это просто длина дуги, или π2:\frac{\pi}{2}:2π:

EC=π2.E_C = \frac{\pi}{2}.EC=2π.

Теперь для пути B…

Для этого потребуется линейный интеграл , поскольку грабитель находится на разном расстоянии от излучения и, следовательно, получает разное количество излучения в разных точках своего пути.

Ясно, что в точке (12,12)\big(\frac{1}{2},\frac{1}{2}\big)(21,21) излучение будет максимальным, и при (0,1)(0,1)(0,1) и (1,0)(1,0)(1,0) лучевая нагрузка будет минимальной (для данного конкретного пути).\circ45∘ угол траектории.

Это дает

x(t)=t2,y(t)=1−t2.x(t) = \frac{t}{\sqrt{2}},\quad y(t) = 1 – \frac{t}{ \sqrt{2}}.x(t)=2t,y(t)=1−2t.

Итак,

dxdt=12,dydt=−12.\frac{dx}{dt} = \frac{1}{\sqrt{2}},\quad \frac{dy}{dt} = – \frac{1}{ \sqrt{2}}.dtdx=21,dtdy=−21.

Наконец, линейный интеграл можно использовать для определения радиационного облучения вдоль пути B , EB:E_B:EB:

EB=∫BI dS=∫t=0t=2I(x(t),y(t))(dxdt)2+(dydt)2 dt=∫t=0t=2(1r2)(12)2+( −12)2 dt=∫t=0t=2(1×2+y2)12+12 dt=∫t=0t=21(t2)2+(1−t2)2 dt=∫021t22+(1−2t2+t22) dt=∫02dtt2−2t+1.{\ гидроразрыва {1} {\ sqrt {2}}} \\ &= \sqrt2\big(\arctan(1) – \arctan(-1)\big)\\ &= \frac{\sqrt2\pi}{2}. \end{align}EB=∫−2121u2+21du=2arctan(2u)∣∣∣−2121= 2(arctan(1)−arctan(−1))=22π.

Следовательно, EB>ECE_B > E_CEB>EC. Его лучший выбор — Путь C\boxed{\text{Путь C}}Путь C.

функций, определяемых интегралами, часть 1
функций, определяемых интегралами, часть 1

Функции, определяемые интегралами

Часть 1: Функция
F(x) и ее производная
Многие полезные функции естественным образом описываются интегрированием известных функций.Иногда эти недавно определенные функции оказываются функциями, которые мы уже знаем в каком-то другом контексте, а иногда они действительно новые. В этой части мы определяем функцию F(x) путем интегрирования заданной непрерывной функции f(x) , а затем изучаем производную новой функции F(x) .
Для нашего первоначального примера мы начинаем с функции
.
график которого представляет собой четверть окружности радиуса 5 :

Мы определяем новую функцию F(x) , установив ее значение в виде положительного числа x как интеграл от f от 0 до x :

Обратите внимание, что поскольку x используется для представления независимой переменной для функции F , другая переменная t используется для переменной интегрирования.

Что означает это определение функции? Поскольку определенный интеграл положительной функции f представляет собой площадь под графиком f , мы можем думать о F(x) как о площади под графиком f(t) между t = 0 и t = x . Проиллюстрируем это на следующем рисунке.

Чтобы увидеть построение функции F в динамике, щелкните одну из следующих анимаций.Но сначала прочтите эти инструкции.

Каждая анимация появляется в новом окне браузера. Чтобы вернуться на эту страницу, закройте окно анимации.

Чтобы запустить анимацию, щелкните в любом месте окна. Вы можете делать это столько раз, сколько захотите.

Если у мыши есть правая кнопка, щелчок правой кнопкой мыши вызовет параметры для приостановки анимации, покадрового перемещения и т. д.

Если ваш компьютер подключен к Интернету напрямую, выберите самую плавную анимацию.Если вы используете коммутируемый доступ, обратите внимание на размеры файлов — время загрузки пропорционально размеру файла.

Горизонтальные масштабы графиков f и F одинаковы: от x = 0 до x = 5 . Но обратите внимание, что вертикальные масштабы разные.

Варианты анимации F(x): Наименее гладкий (93K), более гладкий (316K), самый гладкий (762K).

Используйте определение F(x) в своем рабочем листе, чтобы построить собственный график F(x) .Изучите график и объясните, почему он имеет именно такую форму.

Составьте таблицу значений F(x) для x в диапазоне от 0 до 5 . (Не ограничивайтесь только целочисленными значениями x .) Убедитесь, что полученные значения соответствуют вашему графику F(x) .

Обратимся теперь сначала к оценке, а затем к вычислению производной F(x) . В целях оценки мы рассчитаем коэффициенты разности

с разницей = 0.001 . (Подойдет любое разумно маленькое значение – вы можете поэкспериментировать с другими значениями в своем рабочем листе.)

Вычислите приближенную производную F (разностное частное) и соответствующее значение f для каждого из x значений, указанных на вашем листе. Заполняйте таблицу в своем рабочем листе по ходу дела.

Ваши результаты на шаге 3 должны убедительно свидетельствовать о связи между F'(x) и f(x) .Однако горстки примерно равных пар чисел недостаточно для установления равенства. Теперь мы рассмотрим, почему это кажущееся равенство на самом деле может быть истинным .

Сначала мы рассмотрим изменение в значениях функции F , когда x увеличивается на:

по определению F и свойству определенных интегралов. Таким образом, изменение F представляет собой площадь под графиком f между x и x + .[Примечание: мы неявно используем тот факт, что f(x) неотрицательно, когда мы ссылаемся на площадь. Однако вывод остается верным для любой непрерывной функции, если мы используем понятие «площадь со знаком».]

О каком свойстве интегралов говорится в предыдущем абзаце?

Опишите в геометрических терминах, почему изменение F составляет указанную площадь. [Подсказка: интерпретируйте определение F с точки зрения площади.]

Мы иллюстрируем площадную интерпретацию изменения F на следующей паре рисунков, используя x = 3 и = 0.001 . На левом рисунке показана область под графиком f между 3 и 3,001 , заштрихованная зеленым цветом. Поскольку интервал настолько мал, заштрихованная область больше похожа на линию. На правом рисунке мы оставили прежним масштаб по вертикали, но значительно расширили масштаб по горизонтали. Опять же, область под графиком f между 3 и 3,001 заштрихована зеленым цветом.

Почему график f на [3, 3.001] выглядят как горизонтальной линией?

Дайте быструю оценку заштрихованной области.

Для произвольного x и произвольного (маленького) дайте быструю оценку площади под графиком f на интервале [x, x + ] .

Объясните оценку разностного отношения:

Обратите внимание, что ваша оценка разностного отношения

улучшает по мере уменьшения, а

является независимым от .

Объясните следующий расчет мгновенной скорости изменения F :

Для нашего конкретного примера
используйте вспомогательное приложение, чтобы подтвердить формулу на шаге 10. То есть запросите у системы компьютерной алгебры символьную формулу для F(x) . Затем запросите производную этой формулы и подтвердите, что результат эквивалентен формуле для f(x) .

(необязательно) Объясните, почему F является решением задачи о начальных значениях

| Главная | Материалы | Интегральное исчисление | Содержание модуля | Назад | Вперед |

Определенные интегралы – Интегрирование – Высшая математика Редакция

Функция	Интеграл
∫cos(x).dx	SINX + C
∫sin (x) .dx	-COSX + C
	9005 Tanx + C
∫(1/x).dx	ln\|x\| + c
∫ex . DX	EX + C
∫ln (x) .dx	x ln (x) – x + c

Несобственные интегралы примеры решения сложные. Несобственные интегралы. Примеры решений

Несобственные интегралы первого рода – с бесконечными пределами и их сходимость

Несобственные интегралы с бесконечным верхним пределом

Несобственные интегралы второго рода – от неограниченных функций и их сходимость

Что значит вычислить несобственный интеграл?

Определение

Несобственные интегралы и их расходимость. Несобственные интегралы. Примеры решений

Определение

Несобственные интегралы первого рода – с бесконечными пределами и их сходимость

Несобственные интегралы с бесконечным верхним пределом

Несобственные интегралы второго рода – от неограниченных функций и их сходимость

Что значит вычислить несобственный интеграл?

Криволинейный интеграл 1 рода для чайников. МА

Криволинейные интегралы первого рода

Криволинейные интегралы второго рода

Вычисление криволинейных интегралов первого рода

Вычисление криволинейных интегралов второго рода

Кривая дана в декартовых прямоугольных координатах

Кривая дана в параметрической форме

Больше примеров вычисления криволинейных интегралов

Несобственный интеграл с бесконечным верхним пределом. Несобственные интегралы от неограниченных функций. Если подынтегральной функции не существует в точке

Определение

Что значит вычислить несобственный интеграл?

Несобственные интегралы первого рода – с бесконечными пределами и их сходимость

Несобственные интегралы с бесконечным верхним пределом

Несобственные интегралы второго рода – от неограниченных функций и их сходимость

Читайте также…

Неопределенный и Определенный интегралы Основная теорема интегрального

Применение интеграла с использованием презентации Microsoft Office PowerPoint

Нужны ли интегралы и логарифмы, если есть компьютеры? — Российская газета

Интегральные границы / пределы интегрирования

Что такое границы интеграла?

Верхние и нижние границы

Как найти пределы интегрирования

Определенные интегралы и границы

Как найти верхний предел интеграла

Шаги

Проблемы

Ссылки

Интегрирование и взятие интеграла

Интеграция Римана

Общее правило мощности для интеграции

Сводка по интеграции

6: Приложения интеграции – Mathematics LibreTexts

Авторы и авторство

Определение, правила, примеры и решение

Что такое интегралы?

Интегральная запись

Интегралы и производные

Правила вычисления интегралов

Типы интегралов: неопределенные и определенные интегралы

Подведение итогов

Линейный интеграл | Блестящая математика и естественные науки вики

функций, определяемых интегралами, часть 1

Функции, определяемые интегралами

Часть 1: Функция

Определенные интегралы – Интегрирование – Высшая математика Редакция

Оставить комментарий Отменить ответ