Равнодействующая сила, обозначение сил, нахождение проекций на оси
Физика->Динамика->равнодействующая сила->
Тестирование онлайн
Равнодействующая сила. Основные понятия
Равнодействующая сила
Равнодействующая сила. Движение по окружности, наклонной плоскости
Домашняя работа
Системы и блоки. Основные понятия
Системы и блоки
Системы и блоки. Домашняя работа
Система тел, которая движется с ускорением.
Определение
Это векторная сумма всех сил, действующих на тело.
Велосипедист наклоняется в сторону поворота. Сила тяжести и сила реакции опоры со стороны земли дают равнодействующую силу, сообщающую центростремительное ускорение, необходимое для движения по окружности
Взаимосвязь со вторым законом Ньютона
Вспомним закон Ньютона:
Равнодействующая сила может быть равна нулю в том случае, когда одна сила компенсируется другой, такой же силой, но противоположной по направлению.
В этом случае тело находится в покое или движется равномерно.
Сила Архимеда уравновешивается силой тяжести, тело равномерно перемещается в жидкости вниз. | Сила тяжести уравновешивается силой упругости. Книга покоится |
Если равнодействующая сила НЕ равна нулю, то тело движется равноускоренно. Собственно именно эта сила является причиной неравномерного движения. Направление равнодействующей силы всегда совпадает по направлению с вектором ускорения.
Когда требуется изобразить силы, действующие на тело, при этом тело движется равноускоренно, значит в направлении ускорения действующая сила длиннее противоположной. Если тело движется равномерно или покоится длина векторов сил одинаковая.
Сила реакции опоры (сила, направленная вверх) длиннее силы тяжести, так как шарик движется по окружности, центростремительное ускорение направлено вверх | Сила реакции опоры (сила, направленная вверх) короче силы тяжести, так как шарик движется по окружности, центростремительное ускорение направлено вниз. |
Вектор силы тяжести, направленный вниз, длиннее.Нахождение равнодействующей силы
Для того, чтобы найти равнодействующую силу, необходимо: во-первых, верно обозначить все силы, действующие на тело; затем изобразить координатные оси, выбрать их направления; на третьем шаге необходимо определить проекции векторов на оси; записать уравнения. Кратко: 1) обозначить силы; 2) выбрать оси, их направления; 3) найти проекции сил на оси; 4) записать уравнения.
Как записать уравнения? Если в некотором направлении тело двигается равномерно или покоится, то алгебраическая сумма (с учетом знаков) проекций сил равна нулю. Если в некотором направлении тело движется равноускоренно, то алгебраическая сумма проекций сил равна произведению массы на ускорение, согласно второму закону Ньютона.
Примеры
На движущееся равномерно по горизонтальной поверхности тело, действуют сила тяжести, сила реакции опоры, сила трения и сила, под действием которой тело движется.
Обозначим силы, выберем координатные оси
Найдем проекции
Записываем уравнения
Тело, которое прижимают к вертикальной стенке, равноускоренно движется вниз. На тело действуют сила тяжести, сила трения, реакция опоры и сила, с которой прижимают тело. Вектор ускорения направлен вертикально вниз. Равнодействующая сила направлена вертикально вниз.
Тело равноускоренно движется по клину, наклон которого альфа. На тело действуют сила тяжести, сила реакции опоры, сила трения.
Главное запомнить
1) Если тело покоится или движется равномерно, то равнодействующая сила равна нулю и ускорение равно нулю;
2) Если тело движется равноускоренно, значит равнодействующая сила не нулевая;
3) Направление вектора равнодействующей силы всегда совпадает с направлением ускорения;
4) Уметь записывать уравнения проекций действующих на тело сил
Виды сил вокруг нас
В окружающем нас мире бесчисленное множество тел, которые взаимодействуют друг с другом.
Но, несмотря на это многообразие сил, несколько их видов принято выделять особо.
Силой упругости называют силу, которая возникает в теле при изменении его формы или размеров. Это происходит, если тело сжимают, растягивают, изгибают или скручивают. Например, сила упругости возникла в пружине в результате её сжатия и действует на кирпич.
Сила упругости всегда направлена противоположно той силе, которая вызвала изменение формы или размеров тела. В нашем примере упавший кирпич сжал пружину, то есть подействовал на неё с силой, направленной вниз. В результате в пружине возникла сила упругости, направленная в противоположную сторону, то есть вверх. Мы можем это утверждать, наблюдая отскок кирпича.
Силой тяготения называют силу, с которой все тела в мире притягиваются друг к другу (см.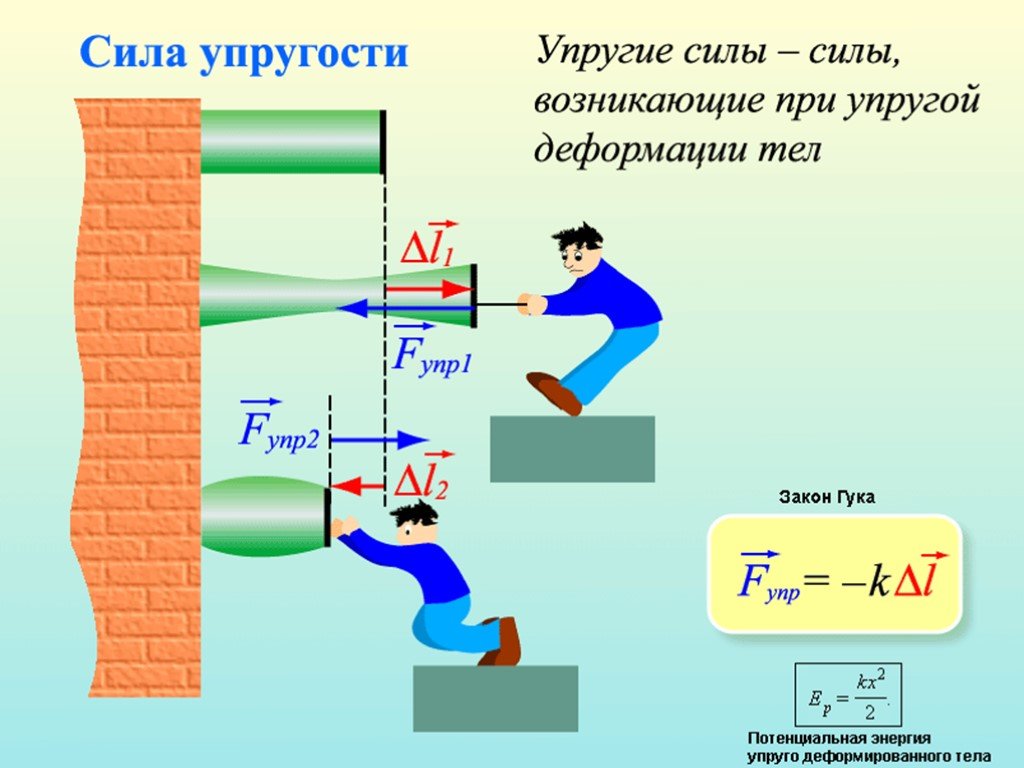
§ 2-а). Разновидностью силы тяготения является сила тяжести – сила, с которой тело, находящееся вблизи какой-либо планеты, притягивается к ней. Например, на ракету, стоящую на Марсе, тоже действует сила тяжести.
Сила тяжести всегда направлена к центру планеты. На рисунке показано, что Земля притягивает мальчика и мяч с силами, направленными вниз, то есть к центру планеты. Как видите, направление «вниз» различно для различных мест на планете. Это будет справедливо и для других планет и космических тел. Более подробно силу тяжести мы изучим в § 3-г.
Силой трения называют силу, препятствующую проскальзыванию одного тела по поверхности другого. Рассмотрим рисунок. Резкое торможение автомобиля всегда сопровождается «визгом тормозов». Этот звук возникает из-за проскальзывания шин по асфальту. При этом шины сильно стираются, так как между колёсами и дорогой действует сила трения, препятствующая проскальзыванию.
Сила трения всегда направлена противоположно направлению (возможного) проскальзывания рассматриваемого тела по поверхности другого.
Например, при резком торможении автомобиля его колёса проскальзывают вперёд, значит, действующая на них сила трения о дорогу направлена в противоположную сторону, то есть назад.
Сила трения возникает не только при скольжении одного тела по поверхности другого. Существует также сила трения покоя. Например, отталкиваясь ботинком от дороги, мы не наблюдаем его проскальзывания. При этом возникает сила трения покоя, благодаря которой мы движемся вперёд. В отсутствие этой силы мы бы не смогли сделать и шага, как, например, на льду.
Силой Архимеда (или выталкивающей силой) называют силу, с которой жидкость или газ действуют на погруженное в них тело – выталкивают его. На рисунке показано, что вода действует на пузырьки выдыхаемого рыбой воздуха – выталкивает их на поверхность. Вода также действует на рыбу и камни – она уменьшает их вес (силу, с которой камни давят на дно).
Архимедова сила обычно направлена вверх, противоположно силе тяжести. Более подробно она будет изучена в § 3-е.
Опубликовано в разделах: 7 класс, Силы в природеСил | Определение и формула
force
Посмотреть все СМИ
- Ключевые люди:
- Исаак Ньютон Христиан Гюйгенс Сэр Чарльз Вернон Бойз
- Похожие темы:
- электромагнетизм сила тяжести фундаментальная сила носить трение
Просмотреть весь связанный контент →
сила , в механике любое действие, которое имеет тенденцию поддерживать или изменять движение тела или искажать его. Понятие силы обычно объясняется с точки зрения трех законов движения Исаака Ньютона, изложенных в его Principia Mathematica (1687). Согласно первому принципу Ньютона, тело, находящееся в состоянии покоя или движущееся равномерно и прямолинейно, будет оставаться в этом состоянии до тех пор, пока к нему не будет приложена какая-либо сила.
Поскольку сила имеет как величину, так и направление, она является векторной величиной. Представление сил векторами предполагает, что они сосредоточены либо в одной точке, либо вдоль одной линии. Однако это физически невозможно. Например, на нагруженный компонент конструкции приложенная сила создает внутреннюю силу или напряжение, которое распределяется по поперечному сечению компонента.
Сила тяжести неизменно распределена по всему объему тела. Тем не менее, когда основное внимание уделяется равновесию тела, обычно справедливо и удобно предполагать, что силы сосредоточены в одной точке. В случае гравитационной силы можно предположить, что весь вес тела сосредоточен в его центре тяжести (
Физики используют ньютон, единицу Международной системы (СИ), для измерения силы. Ньютон — это сила, необходимая для ускорения тела массой один килограмм на один метр в секунду за секунду. Формула F = ма используется для расчета количества ньютонов, необходимого для увеличения или уменьшения скорости данного тела. В странах, до сих пор использующих английскую систему измерения, инженеры обычно измеряют силу в фунтах. Сила в один фунт сообщает объекту весом в один фунт ускорение 32,17 фута в секунду в квадрате.
Редакторы Британской энциклопедии
Эта статья была недавно пересмотрена и обновлена Эриком Грегерсеном.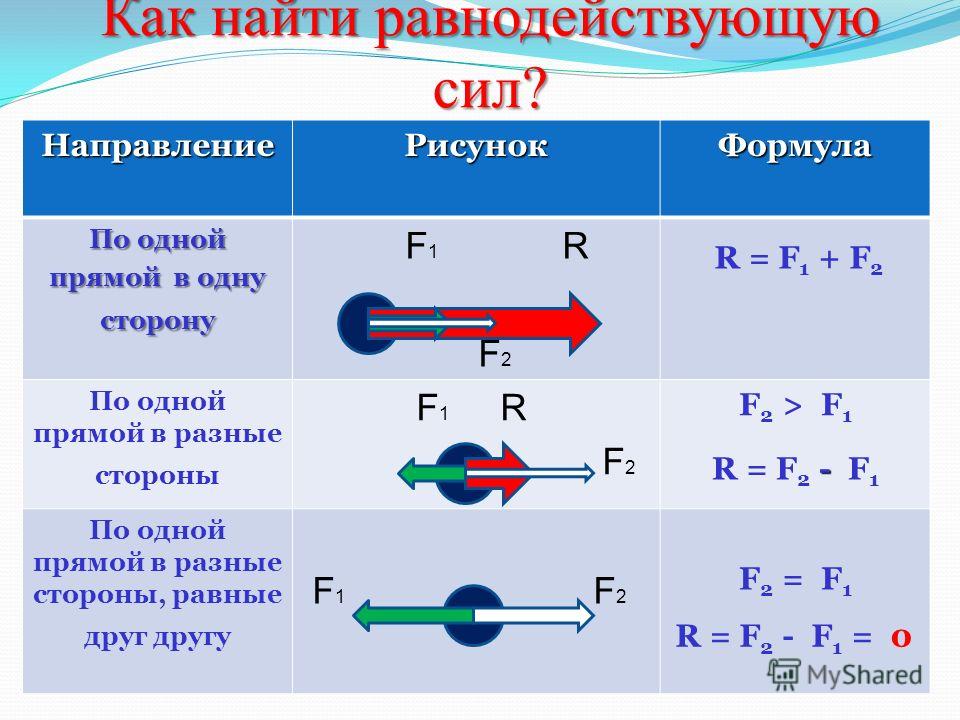
2.3: Типы сил – Физика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 16297
- Том Вайдеман
- Калифорнийский университет, Дэвис
Гравитация
Мы уже знаем кое-что о гравитации из нашего изучения свободного падения и движения снаряда. Мы знаем, что ускорение одинаково для тел разной массы. Хотя мы использовали это в качестве модели, было бы большим шагом утверждать, что гравитация в основном следует этому правилу. Мы знаем, что перо испытает такое же ускорение под действием силы тяжести, как и камень, если убрать сопротивление воздуха. Теперь, как мы вернем сопротивление воздуха в нашу модель, чтобы уменьшенное ускорение пера имело смысл?
Эффект уменьшения ускорения легко показать с помощью FBD двух объектов, которые идентичны, за исключением массы и падают в воздухе с одинаковой скоростью.
Для этих двух объектов силы сопротивления воздуха равны, а сила тяжести больше на более тяжелом объекте. Таким образом, результирующие силы, действующие на два объекта, различны, что дает следующие ускорения:
\[ \left. \begin{array}{l} a_{\left(heavy\right)} = \dfrac{F_{гравитация \; \left(тяжелая \правая)} – F_{воздух} }{m_{\left(тяжелая \правая)}} \\ a_{\left(легкая \правая)}= \dfrac{F_{гравитация \; \left(light \right) } – F_{air} }{m_{ \left(light \right) }} \\ g = \dfrac{F_{гравитация} }{ m }\\ \end{array} \right \} \;\;\; \Правая стрелка \;\;\; \begin{array}{l} a_{\left(тяжелый\правый)} = g -\dfrac{F_{воздух}} }{m _{\left(тяжелый \правый)}} \\ a _{\left( свет \справа)} = г – \dfrac{ F_{воздух} }{м_{\влево(свет \справа)} } \конец{массив} \]
Таким образом, причина, по которой более тяжелая масса ускоряется больше, заключается просто в том, что сила сопротивления воздуха оказывает на нее меньшее влияние. Следует проявлять осторожность, чтобы не делать поспешных выводов, потому что можно сделать неверный вывод об одной силе, не обращая внимания на другую присутствующую силу.
В случае свободного падения без сопротивления воздуха получается один простой результат:
\[ F_{гравитация} = ma, \ a=g \ \Rightarrow F_{гравитация} = mg \]
Предупреждение
92}\)! Когда на объект не действует никакая другая сила, кроме гравитации, ускорение объекта просто равно этой константе, но константа присутствует независимо от состояния ускорения объекта.
Натяжение
Когда мы моделируем задачи, связанные с силами натяжения струн или веревок, мы обычно предполагаем, что струна или веревка не имеют массы. Если этого не делать, возникают некоторые сложные (но интересные!) осложнения, которые обычно не являются предметом этой проблемы. Например, представьте, что два человека соревнуются в перетягивании каната, где один выигрывает и, следовательно, ускоряет другого. FBD только веревки показывает две силы на ней (если мы игнорируем гравитацию), по одной в каждом направлении. Когда выигрывает один из людей, ускоряются не только оба человека, но и веревка.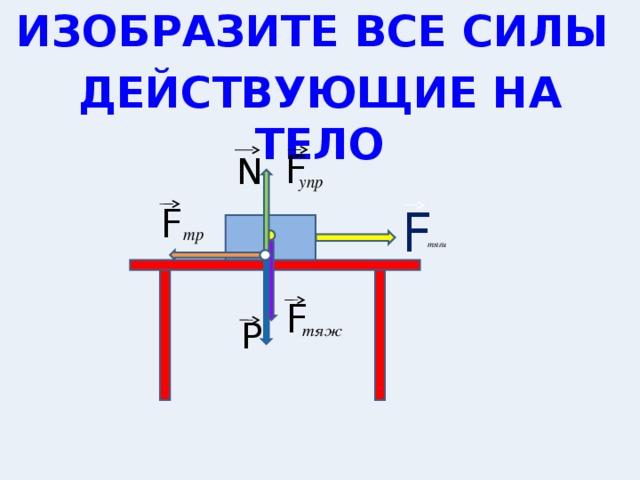
Это означает, что на веревку действует результирующая сила, и поэтому один человек тянет веревку сильнее, чем другой.
Если предположить, что веревка невесома, то масса, умноженная на ускорение веревки, равна нулю, а это означает, что на веревку не действует результирующая сила, несмотря на то, что она ускоряется. Без чистой силы на нем два бойца тянут его с одинаковой силой, а это означает, что сила, которую один человек прикладывает к нему, передается через веревку, чтобы воздействовать на другого человека. То есть веревка ничем не отличается от случая, когда два человека берутся за руки и тянут друг друга. Это позволяет нам использовать веревки как идеализированное средство, позволяющее объекту «рядом» воздействовать силой «на» другой объект на расстоянии. Без этого устройства нам пришлось бы либо неуклюже придумывать примеры, либо чрезмерно усложнять задачи, включая ускоряющие массивные веревки.
Предупреждение
Иногда веревки будут использоваться в качестве канала для выражения пар по третьему закону («сила натяжения на А на В», где ни А, ни В не являются веревкой), но это опасно, потому что веревки также могут передавать сила вокруг шкива, и в этом случае пара сил третьего закона Ньютона явно не имеет противоположных направлений.
Шкивы — еще один аспект натяжения, о котором следует сказать несколько слов. Если шкив при вращении испытывает трение или имеет некоторую массу (так что для его вращения требуется ускорение некоторой массы), то сила натяжения не передается вокруг него беспрепятственно. На самом деле мы рассмотрим случай шкивов с массой позже в курсе, но сейчас мы идеализируем их, как веревки — без трения и без массы.
Нормальная (контактная) сила
Что отличает контактную силу от некоторых других, так это то, что она является не чем иным, как «балансиром». Это означает, что его величина определяется не независимыми критериями, а деталями контакта. Например, если блок лежит на ровной столешнице, то нулевое ускорение блока означает, что результирующая сила, действующая на блок, равна нулю. Земля воздействует на блок силой тяжести вниз, поэтому должна быть уравновешивающая сила вверх, чтобы результирующая сила равнялась нулю. Единственная другая сила, доступная здесь, — это контактная сила, поэтому ее величина подстраивается так, чтобы равняться силе тяжести, действующей на блок.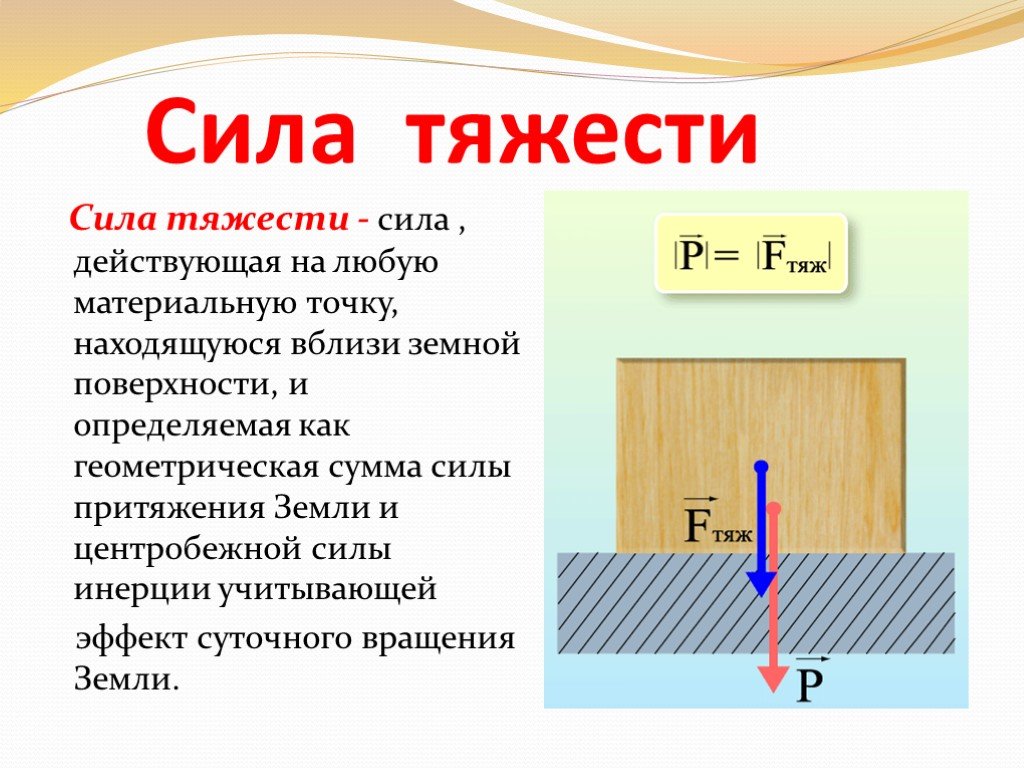
Если теперь мы привяжем к блоку веревку и потянем за него с силой, меньшей веса блока, он сохранит контакт со столешницей и все еще останется неподвижным. На этот раз, чтобы силы уравновесились, количество контактной силы, необходимой для создания баланса, уменьшается на величину силы натяжения, которую обеспечивает струна.
В первую очередь эта особенность контактной силы возникает в задачах, когда используются весы (например, те, на которых вы стоите в своей ванной). Мы привыкли думать о весах как о чем-то, что измеряет вес, но это не так — они измеряют контактную силу! Для доказательства просто представьте, что вы прислоняете весы к вертикальной стене, а не стоите на ней.
Кинетическое трение
Вероятно, самой сложной и трудной для понимания силой, о которой мы упоминали, является трение. Микроскопический механизм даже не так хорошо понят, отчасти потому, что он имеет два разных режима. Этот первый из этих режимов возникает из-за того, что две поверхности могут быть очень неровными. Второй способ включает адгезионные связи, которые образуются между поверхностными молекулами для каждого из задействованных объектов. Обратите внимание, что фундаментальная сила, участвующая в обоих случаях, имеет электрическую природу, но в первом случае она отталкивающая, а во втором — притягивающая.
Оба эти режима приводят к двум различным формам трения. Первый, который мы обсудим, включает в себя трение двух поверхностей друг о друга. Это называется кинетическим трением . Можно представить себе ряд факторов, влияющих на величину силы трения, которая может существовать между двумя объектами, но для нашей макроскопической модели мы сводим эти факторы всего к двум. Первая — это другая сила — нормальная сила между поверхностями. Чем сильнее поверхности прижимаются друг к другу, тем глубже зацепляются неровности поверхности и тем больше молекул сближается. Экспериментально мы находим, что сила трения растет примерно линейно с этой нормальной силой. Все остальные факторы мы объединяем в одну безразмерную константу, умножающую величину нормальной силы, известную как коэффициент кинетического трения:
\[ f_k = \mu_kN \]
Важно отметить, что движение двух объектов во время контакта не гарантирует возникновения кинетического трения – поверхности должны скользить друг по другу . Например, мяч, катящийся по полу, который никоим образом не скользит, не испытывает кинетического трения.
Статическое трение
Вторую форму трения немного сложнее понять, хотя мы все о ней знаем. Вместо того, чтобы быть силой, которая существует, когда две поверхности скользят друг по другу, этот тип трения представляет собой силу реакции, которая пытается предотвращает скольжение двух поверхностей друг относительно друга. Эта сила, известная как статическое трение , отвечает за явление, которое мы испытываем, когда пытаемся что-то скользить и терпите неудачу, пока не приложим достаточно усилий, чтобы заставить это скользить — с любой меньшей силой объект остается на месте.
Статическое трение очень похоже на контактную силу, поскольку оно является просто балансиром. Если вы нажимаете на что-то достаточно сильно, чтобы оно начало скользить, то статическое трение больше не действует, но если оно не начинает скользить, то это происходит потому, что сила статического трения уравновешивает это давление, что приводит к нулевому ускорению. Однако, в отличие от контактной силы, статическое трение имеет максимум – если другие силы достаточно велики, начнется скольжение, и сила трения сместится со статической на кинетическую. Этот максимум также сводится к константе, но соотношение между силой трения и контактной силой теперь представляет собой неравенство:
\[ f_s \leq \mu_s N\]
Чаще всего мы сталкиваемся с трением (кинетическим или статическим) в отношении объекта на горизонтальной плоскости, такого как стол на полу или тарелка на столе. Когда поверхность горизонтальна, нулевое вертикальное ускорение означает, что контактная сила равна весу, а это означает, что сила трения прямо пропорциональна весу. Другими словами, «тяжелые предметы трудно скользить по полу». Но этот прыжок делать нехорошо, так как не все поверхности горизонтальны (и ускорение не всегда равно нулю, например, в лифте). Величина (или максимальная величина) силы трения определяется контактной силой, а не силой гравитации и уж точно не массой объекта.
Явление, с которым мы все знакомы, заключается в том, что для одних и тех же двух поверхностей, находящихся в контакте, коэффициент статического трения больше, чем коэффициент кинетического трения. То есть заставить объект скользить по поверхности сложнее, чем заставить его скользить по ней. Это можно понять концептуально, если подумать о двух микроскопических модах, которые мы обсуждали ранее. Когда поверхности скользят друг по другу, неровности не успевают встроиться друг в друга, а молекулярные связи разрываются и переформируются, а в период до переформирования силы нет.
Это явление является главной причиной того, что многие ошибочно называют «инерцией». Используемые физические понятия коварно тонки: кто-то толкает объект по полу, ускоряя его из состояния покоя, и замечает, что его труднее заставить двигаться, чем поддерживать. Затем они пытаются подтолкнуть более крупный объект и им еще труднее начать работу. Они делают вывод, что большая масса второго объекта означает, что ему «нужно преодолеть большую инерцию», чтобы заставить его двигаться. Действительно, эти люди могли даже слышать о «законе инерции» и знать, что масса связана с инерцией.
Теперь у нас есть инструменты, чтобы опровергнуть этот анализ. «Закон инерции» — первый закон Ньютона. Этот закон гласит, что толкаемый объект «хочет» оставаться неподвижным, но закон не предусматривает минимальной силы, необходимой для преодоления «желания» объекта оставаться на месте. Влияние толчка на объект определяется вторым законом Ньютона, и независимо от того, насколько велика масса или насколько мала результирующая сила, результатом будет ненулевое ускорение. Правильное объяснение этого кажущегося явления инерции таково: для объекта на горизонтальной поверхности нормальная сила равна силе тяжести. Сила тяжести пропорциональна массе объекта (она равна \(мг\)), поэтому нормальная сила пропорциональна массе. Максимальная статическая сила трения пропорциональна нормальной силе, поэтому она также пропорциональна массе. Следовательно, сила, необходимая для того, чтобы что-то скользило по горизонтальной поверхности, оказывается пропорциональной массе объекта. Но это не внутреннее свойство массы — между количеством массы и тем, что люди называют «инерцией», есть много важных ступеней. Опасно делать поспешные выводы без тщательного анализа.
Применение: антиблокировочная система тормозов
Тот факт, что коэффициент кинетического трения больше, чем коэффициент статического трения для тех же поверхностей, находит самое широкое применение в изобретении под названием «антиблокировочная система тормозов». Когда шина идеально катится по поверхности дороги, поверхность шины не скользит по поверхности дороги, а это означает, что если и возникает какое-либо трение, то это статическое трение. Если вы задействуете тормоза, вращение шин будет замедляться до тех пор, пока не будет превышено максимальное статическое трение, после чего шины перестанут вращаться и покатятся по дорожному полотну. При этом сила трения на шинах снижается, потому что кинетическое трение меньше, чем максимальное статическое трение. Таким образом, система ABS автоматически отключает тормоза на короткое время, так что шины снова поворачиваются, восстанавливая идеальное качение и позволяя восстановить статическое трение. Это похоже на попытку толкать тяжелую картонную коробку по полу очень короткими рывками — как только коробка начинает скользить (и ее становится легче толкать), вы останавливаетесь и начинаете сначала. До изобретения систем ABS водителям говорили «слегка нажимать на тормоза» на скользкой дороге, чтобы создать тот же эффект. Системы ABS качают за нас с гораздо большей частотой, чем мы могли бы управлять, и с большим эффектом.
Сопротивление воздуха (сопротивление)
Сопротивление воздуха иногда называют «воздушным трением», но, хотя оно обладает диссипативными свойствами, подобными трению (как мы увидим при изучении энергии), механизм его действия совсем другое. Сопротивление воздуха возникает из-за бесчисленных столкновений между микроскопическими частицами, составляющими атмосферу, и движущимся в ней макроскопическим объектом. Не может быть столкновений без движения, поэтому, в отличие от трения, не существует «статического сопротивления воздуха». В этом классе мы действительно не будем рассматривать сопротивление воздуха строгим математическим способом, прежде всего потому, что гидродинамика — особенно сложный предмет (поэтому мы упрощаем задачи о снарядах, предполагая отсутствие сопротивления воздуха).
- площадь поперечного сечения — Любой, кто когда-либо высовывал руку из окна движущегося автомобиля, знает, что воздух отталкивает ее с большей силой, когда ладонь смотрит вперед, чем когда она смотрит вниз. Разница заключается в площади поперечного сечения, и это важно, потому что чем больше это значение, тем больше атмосферных частиц в секунду может попасть на руку. Очевидно, что если площадь удвоится, количество частиц, сталкивающихся с объектом в секунду, удвоится, поэтому сила сопротивления прямо пропорциональна площади поперечного сечения.
Предупреждение
- скорость – Возвращаясь к обычному опыту вытягивания руки из окна движущегося автомобиля, мы знаем, что чем быстрее движется автомобиль, тем больше сила действует на нашу руку. В этом случае точное математическое соотношение не столь очевидно, как для площади поперечного сечения. На самом деле, она может по-разному зависеть от относительной скорости воздуха для разных скоростей воздуха (или, точнее, от того, является ли воздушный поток упорядоченным или турбулентным).
- плотность воздуха. Плотность — это мера того, сколько частиц вы найдете в данной небольшой области пространства. Если воздух очень плотный, то на площадь поперечного сечения может попасть больше частиц, чем если бы воздух был менее плотным. Таким образом, сила сопротивления прямо пропорциональна плотности воздуха.
Мы не будем записывать или использовать конкретное уравнение сопротивления воздуха, но мы можем использовать приведенные выше факты, чтобы сделать некоторые выводы. Представьте, что вы только что выпрыгнули из самолета, и гравитация Земли начинает ускорять вас вниз. Это ускорение приводит к тому, что ваша скорость становится все больше и больше, и вместе с этим увеличивается сила сопротивления воздуха вверх, действующая на ваше тело. Конечно, ваше нисходящее ускорение определяется не только гравитацией, но и результирующей силой, действующей на ваше тело, которая уменьшается по мере роста сопротивления воздуха (противодействующего гравитации). В конце концов вы движетесь достаточно быстро, чтобы сила сопротивления воздуха сравнялась с вашим весом, и вы перестаете ускоряться. Скорость, с которой это происходит, известна как
Эластичная (пружинная) сила
Чтобы закрыть раздел, посвященный деталям сил, мы рассмотрим еще один, еще не упомянутый. На самом деле она может подпадать под категории как напряжения, так и контактной силы (и, следовательно, является одновременно и притягивающей, и отталкивающей), но у нее есть приятная особенность, заключающаяся в том, что мы можем обрабатывать ее более точно математически. Это называется сила упругости или пружины . Характерной особенностью этой силы является то, что она действует восстанавливающим образом (и, следовательно, является типом восстанавливающей силы ), что означает, что существует состояние равновесия, и любое отклонение от этого равновесия приводит к силе, действующей для возврата объекта. к равновесному состоянию.
0022
В частности, сила упругости пропорциональна удалению объекта от положения равновесия:
\[ |F_{elastic} | = к |\Дельта х | \]
Эта сила всегда направлена от точки, в которую перемещается объект, обратно к точке равновесия. Константа \(k\) известна как жесткость пружины и имеет единицы измерения ньютона на метр . Это мера того, насколько «жесткой» является пружина (т. е. насколько трудно ее растянуть или сжать). Как всегда, важно иметь в виду, что это модель силы пружины. Реальные пружины обычно отличаются от этого поведения, в некоторых случаях значительно. Но полезность этой модели в физике невозможно переоценить. Действительно, эта модель нашла применение буквально во всех уголках физической теории.
Хотя уравнение 2.3.5 хорошо описывает силу упругости, на самом деле существует хороший способ компактно выразить ее в виде векторного уравнения. Рассматривая смещение от положения равновесия как вектор, мы видим, что направление силы прямо противоположно независимо от того, растянута или растянута пружина. Соответственно, мы можем написать:
\[ \overrightarrow F_{elastic} = -k\Delta \overrightarrow x \]
Это уравнение широко известно как закон Гука .