Магнитное поле. Тема 7 – презентация онлайн
Тема 7
Магнитное поле
1
ПЛАН ЛЕКЦИИ
1.Магнитное поле. Вектор магнитной индукции.
Поток вектора магнитной индукции.
2. Закон Ампера. Контур с током в магнитном
поле.
3. Напряженность магнитного поля. Закон Био—
Савара— Лапласа.
4. Применение закона Био—Савара— Лапласа к
расчету магнитного поля.
5. Закон полного тока.
6. Действие магнитного поля на движущийся
заряд. Сила Лоренца.
7. Эффект Холла.
2
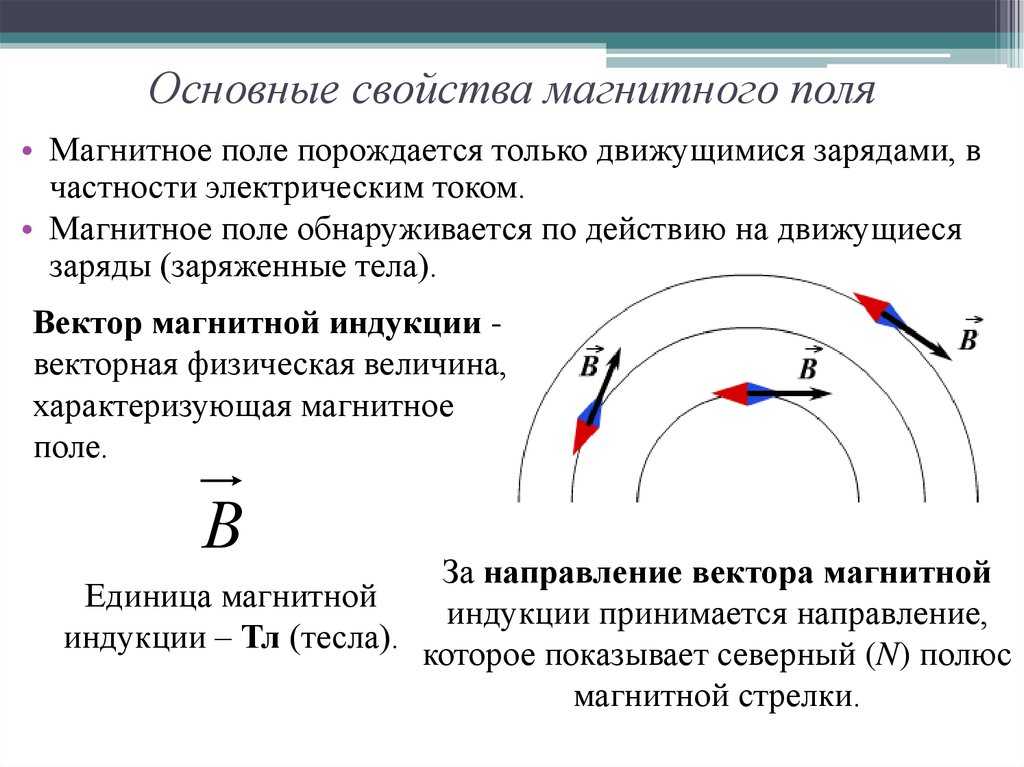
Вектор магнитной индукции
Магнитным полем называют вид материи, через которую передается силовое
воздействие на движущиеся электрические заряды и тела, обладающие
магнитным моментом.
Величину IS называют магнитным моментом контура pm.
Положительное направление нормали совпадает с
направлением перемещения буравчика с правой нарезкой,
вращаемого в направлении тока.
Магнитная индукция — это векторная физическая
величина, являющаяся силовой характеристикой в данной точке
магнитного поля:
M max
B
pm
Линии магнитной индукции – линии, касательные к
которым в данной точке совпадают по направлению с
вектором В в этой точке.
Направление силовых линий магнитного поля, создаваемого
проводником с током, определяется по правилу правого винта
(буравчика): если правовинтовой буравчик ввинчивать по
направлению тока, то направление вращения рукоятки
буравчика будет совпадать с направлением линий магнитной
3
Линии магнитной индукции прямого проводника с током представляют
концентрические окружности, лежащие в плоскости, перпендикулярной току.
Центр этих окружностей находится на оси проводника.
Линии магнитной индукции всегда замкнуты и охватывают проводники с
токами. Это отличает их от линий напряженности электрического поля.
Замкнутость линий магнитной индукции говорит о том, что в природе не
существует магнитных зарядов, на которых бы они начинались или кончались.
Такие поля называют соленоидальными или вихревыми.
Циркуляция вектора магнитной индукции по любому замкнутому контуру
не равна нулю:
(2)
⃗
∮ В d r⃗ ≠ 0
В отличие от потенциального, каким является электростатическое поле
∮ E r dr =0
Магнитное поле называют однородным, если векторы магнитной индукции во
всех его точках одинаковы:
В=const.
(3)
Примером однородного магнитного поля может служить поле внутри
соленоида, т.е. катушки, длина которой много больше ее диаметра. Линии
магнитной индукции однородного поля параллельны, и их густота везде
одинакова.
Поток вектора магнитной индукции
Магнитным потоком (потоком вектора магнитной
индукции), пронизывающим площадку S, называют
величину
Ф=BSо.
Из рис. следует, что Sо=Scos , откуда Ф=BS cos или
Ф=ВnS, где Bn = Bcos – проекция вектора В на
направление нормали к площадке. Магнитный поток величина скалярная.
В зависимости от того, какой знак имеет cos , магнитный поток может быть
положительным (Ф>0) и отрицательным (Ф<0). Знак cos зависит от выбора
положительного направления нормали. Положительное направление нормали
связано с направлением тока.
Теорема Остроградского – Гаусса для магнитного поля свидетельствует об
отсутствии в природе магнитных зарядов, т.е. замкнутости магнитных силовых
линий:
Ф ВndS=0.
S
5
Закон Ампера
Ампером было установлено, что на проводник с током, помещенный в
однородное магнитное поле, индукция которого В, действует сила,
пропорциональная силе тока и индукции магнитного поля:
FА=BIlsin ,
где – угол между направлением тока и индукцией магнитного поля.
В векторной форме
dFА =I [dl, B],
где dl – малый участок проводника, имеющий
направление, совпадающее с направлением тока.
Произведение Idl называют элементом тока.
Сила Ампера направлена перпендикулярно плоскости,
в которой лежат векторы dl и В (рис.).
Для определения направления силы, действующей на проводник с током,
помещенный в магнитное поле, применяется правило левой руки: если левую
руку расположить так, чтобы линии магнитной индукции входили в ладонь, а
вытянутые четыре пальца совпадали с направлением тока в проводнике, то
отогнутый большой палец укажет направление силы, действующей на
проводник с током, помещенный в магнитное поле (рис.
).
6
Контур с током в магнитном поле
Контур с током, имеющий стороны а и l, помещен
в магнитное поле (рис.). На каждую сторону
контура
действует
сила
Ампера.
На
горизонтальные стороны l контура действуют
силы, которые растягивают или сжимают контур,
не поворачивая его. На каждую из вертикальных
сторон а действует сила F=IBa.
Эти силы создают пару сил, момент которой
M = Fl cos ,
где — угол между вектором В и стороной контура l.
Момент сил стремится повернуть контур так, чтобы поток Ф, пронизывающий
контур, был максимальным.
Подставляя выражение для силы в формулу для момента силы:
М = IBal cos ,
где al=S, IS=pm, cos =cos( 2 ) sin , тогда M = Bpm sin .
Механический момент М, действующий на контур с током в однородном
магнитном поле, пропорционален магнитному моменту pm, контура, индукции
В магнитного поля и синусу угла между направлением векторов pm и В.
В векторной форме соотношение имеет вид: М=[pm, В].
7
Напряженность магнитного поля.
Закон Био – Савара – Лапласа
Величина, показывающая, во сколько раз магнитная индукция в данной
однородной изотропной среде больше или меньше, чем в вакууме, называется
относительной магнитной проницаемостью среды: В
Во
Магнитное поле в вакууме принято характеризовать не индукцией Во, а
напряженностью Н магнитного
поля. Эти две физические величины связаны
Bo или
между собой:
H
Bo o H , где o=4 10-7 Гн/м – магнитная
o
постоянная.
Обобщая экспериментальные данные французских физиков
Био и Савара, Лаплас (французский математик) предложил
формулу, по которой можно вычислять напряженность поля,
создаваемого элементом тока в точке М, расположенной от
этого элемента на расстоянии r :
Idl sin
dH
4 r
2
.
Напряженность Н в любой точке магнитного поля проводника с
током I равна векторной сумме напряженностей dH,
элементарных полей, создаваемых всеми участками проводника
(принцип суперпозиции полей): n
H H i
i 1
8
Применение закона Био – Савара – Лапласа
к расчету магнитного поля
1.
Магнитное поле прямолинейного бесконечно длинного
проводника с током
Из рис. видно, что
dl sin dl cos dS
d ,
r
r
r
r
ro
cos
Подставляя эти выражения в формулу Био – Савара Лапласа,
находим,
напряженность,
создаваемая
элементом тока Idl:
dH
Idl sin
I
cos d
2
4 r
4 ro
Чтобы определить напряженность магнитного поля, создаваемого бесконечно
длинным прямолинейным проводником с током, нужно проинтегрировать
последнее выражение в пределах от – /2 до + /2:
I
H
4 ro
/2
cos d
/2
I
4 ro
9
Применение закона Био – Савара – Лапласа
к расчету магнитного поля
2. Магнитное поле в центре кругового тока
Пусть ток протекает по окружности. В этом случае все
элементы проводника перпендикулярны радиусу – вектору
r и sin =l. Расстояние всех элементов проводника до
центра одинаково и равно r. Поэтому напряженность поля
в центре кругового проводника: dH Idl
4 r 2
Так как все элементы тока создают поле, напряженность которого одинаково
направлена, то напряженность поля в центре кругового проводника:
I
H
4 r 2
2 r
dl
0
I
I
2
r
2r
4 r 2 o
3.
Магнитное поле движущегося заряда
Рассмотрим отрезок проводника длиной dl с током I. Он создает в некоторой
точке, удаленной на расстояние r, поле напряженностью
Idl sin
dH
Напряженность поля, создаваемого одной заряженной
4 r 2
частицей:
e [⃗υ r⃗ ]
e sin
⃗
H=
H
3
2
4
πr
10
4 r
Закон полного тока
Циркуляцией вектора Н по замкнутому контуру называется интеграл
Hdl H e dl ,
L
L
где dl – вектор элементарной длины контура, направленной вдоль обхода контура,
Не=Нcos – составляющая вектора Н в направлении касательной к контуру, угол между векторами В и dl.
Выберем в магнитном поле бесконечно прямолинейного проводника с током I
произвольный контур, совпадающий с одной из силовых линий, охватывающих
ток. Силовые линии бесконечно длинного прямолинейного проводника
представляют собой концентрические окружности.
В каждой точке этого контура вектор Н одинаков по модулю, следовательно,
2 ro
циркуляция вектора Н:
I
I
Hdl 2 r
L
L
o
dl
2 ro
dl I ,
0
I
где ro — радиус выбранной силовой линии, т.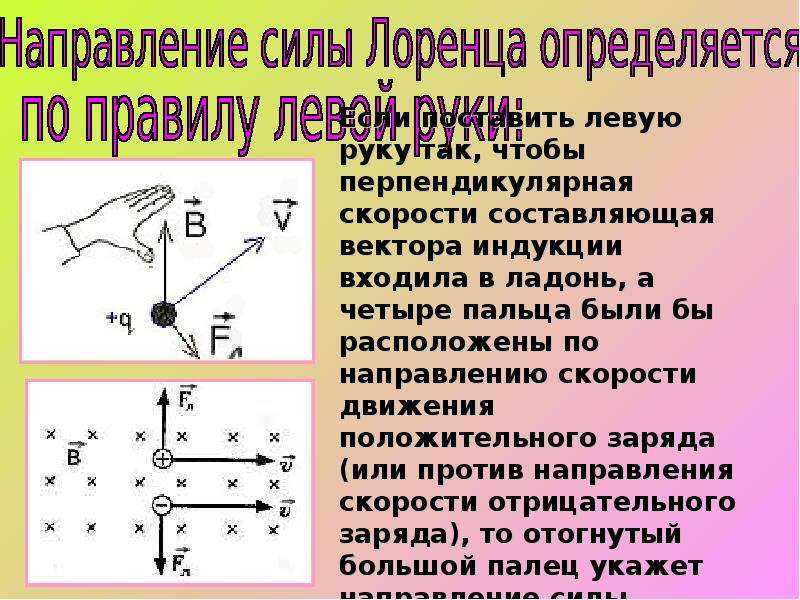
е. окружности:
2 ro
Соотношение связывает циркуляцию вектора напряженности магнитного поля и
ток и называется законом полного тока.
n
Циркуляция вектора напряженности магнитного
Hdl I i
поля по контуру равна алгебраической сумме токов,
11
i 1
L
охватываемых этим контуром:
H
Положительным считается ток, направление которого
связано с направлением обхода по контуру правилом
правого винта; ток противоположного направления
считается отрицательным. Используя закон полного
тока,
определим
напряженность
однородного
магнитного поля внутри соленоида длиной l.
Соленоид имеет N витков, где п=N/l – число витков,
приходящихся на единицу длины соленоида.
Рассчитываем циркуляцию вектора Н для произвольно
выбранного контура L.
Участок 1-2 контура L совпадает с силовой линией внутри
соленоида.
Участки 2-3 и 4-1 на всем протяжении перпендикулярны
линиям. Участок 3-4, проходящий достаточно далеко от
соленоида, совпадает с линией, где напряженность
магнитного поля мала.
Циркуляцию вектора Н по контуру
можно представить четырьмя интегралами:
Hdl= 12 Hdl+ 32 Hdl+ 43 Hdl+ 14
Hdl.
На участках 2-3 и 4-1 H и dl перпендикулярны, поэтому
второй и четвертый интегралы равны нулю. На участке 34 напряженность Н мала, поэтому третьим интегралом
можно пренебречь.
Действие магнитного поля на движущийся заряд.
Сила Лоренца
13
Действие магнитного поля на движущийся заряд.
Сила Лоренца
14
15
Действие магнитного поля на движущийся заряд.
Сила Лоренца
16
Действие магнитного поля на движущийся заряд.
Сила Лоренца
17
18
19
Эффект Холла
Американский
ученый
Э.
Холл
обнаружил,
что
в
проводнике,
помещенном
в
магнитное
поле,
возникает
разность
потенциалов
(поперечная)
в
направлении,
перпендикулярном вектору магнитной
индукции В и току I, вследствие
действия силы Лоренца на заряды,
движущиеся в этом проводнике.
Опыт показывает, что поперечная разность потенциалов пропорциональна
плотности тока j, магнитной индукции и расстоянию а между электродами:
U=RаjB,
где R — постоянная Холла, зависящая от рода вещества,
R=1/пе.
Постоянная Холла зависит от концентрации
электронов. Поэтому, измеряя постоянную R,
можно определить концентрацию электронов
внутри проводника.
20
Закон Ампера или влияние магнитного поля на проводник с током
Из глубокой древности известны магнитные свойства некоторых железных руд, которые получили свое применение более чем за тысячу лет до нашей эры в устройстве магнитного компаса (устройства, в котором магнитная стрелка свободно вращается вокруг своей оси и показывает направление север — юг).
Практические опыты убеждают, что магниты (куски железных руд) способны создавать вокруг себя особое магнитное поле, которое способно влиять на другой находящийся в данном поле магнит.
Магнитные силы прямого магнита (прямолинейный стержень) сосредоточены в основном на его концах, которые называют полюсами магнита.
Например, магнитная стрелка будет поворачиваться около концов магнита (направление вращения стрелки зависит от полюса), но будет оставаться неподвижной, если помещена у средней части магнита.
В магнитном поле магнит будет вести себя точно также как и электрический диполь в электростатическом поле – будет стремиться повернуться по полю. Но есть важный нюанс – если диполь можно разделить на положительный и отрицательный заряды, то при разломе магнита пополам получится
В 1820 году Эрстедом было установлено, что проводники, по которым проходят токи, также взаимодействуют с магнитной стрелкой. Положение магнитной стрелки, которую поместили рядом с проводником с током, также изменяется вместе с изменением величины и направления тока, но при этом стрелка совершенно не реагирует на неподвижные электрические заряды. Из этого явления был сделан вывод, что создавать магнитное поле могут лишь движущиеся электрические заряды (электрический ток), а вокруг неподвижных зарядов существует лишь электростатическое поле.
Магнитное поле, возникающее рядом с проводником с током, как и электрическое поле, обусловленное неподвижными электрическими зарядами, является одним из видов материи. У него имеются определенные физические свойства, такие как инерция, и характеризуется энергией.
Магнитное поле взаимодействует не только с магнитами, но и с электрическими зарядами, находящимися в движении, поскольку они способны сами создавать магнитное поле. Именно поэтому проводники, по которым протекает электрический ток, отталкиваются или притягиваются в зависимости от направления протекающего тока.
Вектор магнитной индукции В является основной характеристикой магнитного поля. Данная величина пропорциональна силе, которая действует на северный конец бесконечно маленькой магнитной стрелки, которая помещена в данную точку магнитного поля. В разных точках поля по направлению и величине индукция имеет различные значения.
Действия магнитного поля на проводник с током было исследовано Ампером.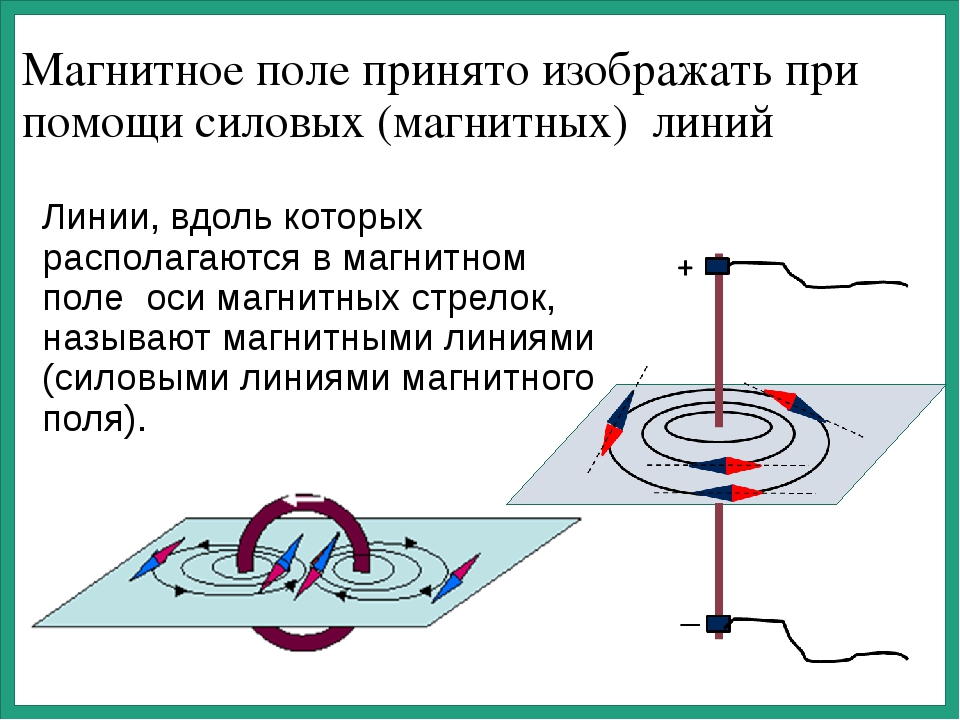
Отсюда и название – закон Ампера.
Если проводник с током помещен во внешнее магнитное поле, например между полюсами магнита, на этот проводник начнет действовать сила F (рисунок ниже), которую можно измерить:
Направление силы F, указанное на рисунке выше, соответствует тому случаю, когда вектор B направлен так, как указывают стрелки, а ток течет перпендикулярно «на нас». При этом было обнаружено, что действующая на прямолинейный проводник с током сила F, прямо пропорциональна силе тока I в проводнике, его длине l, sin α (в данном случае α это угол между вектором В и направлением тока) и магнитной индукции В:
В данном случае k – коэффициент пропорциональности, который зависит от выбранной системы единиц.
Данная формула справедлива для случая однородного поля (в котором вектор В постоянен) и прямолинейного проводника.
В случае, когда поле неоднородно и проводник имеет произвольную форму, формула (1) примет вид:
Данное выражение носит название закон Ампера.
В системе СИ закон Ампера для прямолинейного проводника конечной длины l и однородного поля записывается в виде:
А для системы СГС выражение будет иметь вид:
Здесь с – электродинамическая постоянная, имеющая значение 3·1010 см/с, α – угол между вектором В и направлениями тока в проводнике.
Направление вектора В или силы F определяют с использованием правила левой руки (рисунок ниже):
Правило левой руки звучит так: если указательный палец левой руки направить по полю, а средний по направлению тока, то отогнутый большой палец покажет направление силы, которая действует на проводник с током.
Подтверждением закона Ампера может служить следующий опыт. По свободно провисающему между двумя изоляторами проводнику протекает электрический ток (рисунок ниже):
Когда к проводнику подносят постоянный магнит, то он по мере приближения магнита отклоняется в сторону. Магнит действует на проводник с током с силой F. Проводник также действует на постоянный магнит с
силой F, но направленной противоположно и приложенной в данном случае к северному полюсу магнита.
Так же как и электрическое поле, магнитное поле можно отображать графически с магнитных силовых линий или линий магнитной индукции.
Кривые, касательные к которым в каждой точке совпадают с направлением вектора В в этих точках называют линиями магнитной индукции (линии поля В). В отличии от силовых линий электростатического поля линии магнитной индукции всегда замкнуты. Они выходят из северного полюса магнита, входят в южный, и замыкаются внутри магнита.
Линии поля магнита Вмагн.
Направление данных линий определяют с помощью правила буравчика – если по направлению тока ввинчивать буравчик (винт справа), то вращение рукоятки буравчика покажет направление линий B.
Магнитные силы
Магнитные силыМагнитное поле B определяется по закону силы Лоренца, и конкретно от магнитной силы на движущийся заряд: Значение этого выражения включает: 1. Сила перпендикулярна как скорости v заряда q, так и магнитное поле Б. 2. Величина силы равна F = qvB sinθ, где θ — угол 3. Направление силы определяется правилом правой руки. Приведенное выше соотношение сил представлено в виде векторного произведения. Когда отношение магнитной силы применяется к проводнику с током, можно использовать правило правой руки для определения направления силы на проводе. Из приведенного выше соотношения сил можно сделать вывод, что единицами магнитного поля являются ньютон-секунды/(кулон-метр) или ньютоны на ампер-метр. Эта единица называется Тесла. Это большая единица, а меньшая единица Гаусс используется для небольших полей, таких как магнитное поле Земли.
| Индекс Электромагнитная сила Концепции магнитного поля | ||||||||
| RAVE
Правило правой руки — полезная мнемоника для визуализации направления магнитной силы, заданного законом силы Лоренца. Диаграммы выше представляют собой две формы, используемые для визуализации силы, действующей на движущийся положительный заряд. Сила действует в противоположном направлении для отрицательного заряда, движущегося в указанном направлении. Один факт, который следует иметь в виду, заключается в том, что магнитная сила перпендикулярна как магнитному полю, так и скорости заряда, но это оставляет две возможности. Для применений к токонесущим проводам обычное направление электрического тока может быть заменено скоростью заряда v на приведенной выше диграмме.
| Указатель Магнитная сила Концепции магнитного поля | ||
| Назад |
Магнитные поля: линии, направление и Лоренц
Магнитное поле — это часть пространства, в каждой точке которой действует сила. Эта сила исходит из источника, который может иметь различную природу.
В случае магнитных полей они бывают электрическими или магнитными.
Линии магнитного поля
Если подложить магнит под тонкую поверхность и бросить сверху металлические осколки, появится форма, подобная показанной на рисунке 1. Причина этого в том, что, подобно стрелке компаса, каждый осколок выравнивается по линиям магнитного поля, создаваемого магнитом. Эти линии представляют векторы силы поля. Чем плотнее они в области пространства, тем сильнее поле в этой области.
Линии, создаваемые магнитом, воздействующим на частицы железа
Следует отметить, что каждая линия представляет собой замкнутый контур, идущий от одного полюса к другому, и это свойство делает поле соленоидальным. Оно отличается от электрического поля отсутствием магнитного монополя и строго связано с ним тем, что магнитное и электрическое поля порождают друг друга посредством движения зарядов. Чтобы понять связь между этими двумя полями, мы должны рассмотреть силу Лоренца.
Направление магнитного поля: сила Лоренца
Рассмотрим электрическое поле, магнитное поле и электрически заряженную частицу, проходящую через них.
На эту частицу будет действовать сила, зависящая от обоих полей и перпендикулярная магнитному полю. Эти три физические величины вместе всегда образуют упорядоченную тройку, подобную декартовой оси. Чтобы визуализировать эту связь, вы можете использовать правило левой руки Флеминга. Если двигаться против часовой стрелки, у вас есть два вектора и их векторное произведение соответственно.
Правило левой руки Флеминга говорит нам направление векторного произведения относительно направления векторов. Сила Лоренца F имеет направление векторного произведения между скоростью v и магнитным полем B.
Правило левой руки Флеминга, Камачо – StudySmarter Originals
Выражение для силы Лоренца: заряд, E — электрическое поле, v — скорость частицы, B — магнитное поле.
Применив это к силе Лоренца, она имеет направление большого пальца, когда скорость соответствует среднему пальцу, а магнитное поле параллельно указательному пальцу. Существует также полезное правило, называемое правилом правой руки, чтобы увидеть магнитное поле провода под напряжением, указав большим пальцем в направлении тока, в то время как другие пальцы, хватающие провод, представляют магнитное поле.
Магнитные поля: в чем разница между H и B?
При рассмотрении вакуума как области, где присутствует поле, примерно то же самое можно сказать о напряженности магнитного поля или плотности потока магнитного поля, поскольку эти величины пропорциональны. Но внутри материала мы можем наблюдать разницу между ними. Поток — это часть поля, проходящая через поверхность каждую секунду.
Плотность магнитного потока
Термин магнитное поле используется для описания двух разных (но тесно связанных) величин. H — напряженность магнитного поля, а B — плотность магнитного потока. Эти величины в вакууме пропорциональны из-за проницаемости вакуума .
Вместо этого внутри материала намагниченность M вычитается из члена, вычисляющего поле B . Его еще называют плотность магнитного потока :
Намагничивание учитывает влияние магнитной поляризации в материале, концепция, двойственная по отношению к электрической поляризации и придающая симметрию формулам, описывающим электромагнитное поле.
Что такое электромагнитная индукция?
Электрические и магнитные поля генерируют друг друга, но как это происходит? Объяснением является электромагнитная индукция, которая представляет собой явление, вызывающее генерацию тока в проводнике благодаря магнитному полю.
Создание электродвижущей силы с помощью магнитного поля (закон Фарадея)
Закон Ленца гласит, что (индуцируемое) магнитное поле, создаваемое индукционным током в материале внешним магнитным полем, противодействует этому последнему. Это имеет смысл, поскольку в противном случае магнитное поле внутри материала будет увеличиваться экспоненциально.
Фарадей изучал влияние магнитного поля на электрическую цепь и обнаружил, что перемещение магнита с цепью, погруженной в его поле, или перемещение магнита в петлю, образованную цепью, вызывает протекание тока в самой цепи . Причем этот ток пропорционален скорости движения, которая представлена производной по времени d / dt потока магнитного поля ΦB:
ЭДС здесь электродвижущая сила, измеренная в вольтах.
Магнитные поля: переменный ток
Изобретение, работающее по принципу индукции и использующее магнитное поле для генерирования тока, представляет собой асинхронный двигатель, производящий переменный ток. Он состоит из магнитно заряженного якоря, называемого статором, который содержит подвижную часть, называемую ротором. Ротор подключен к цепи проводами, которые воспринимают магнитное поле, которое всегда направлено в одном направлении, но создает ток, который изменяется по мере движения ротора.
Создается переменный ток, который имеет синусоидальную форму волны и выражается в виде:
Движение медной катушки (в медном цвете) внутри магнита (слева) создает переменный во времени ток ( Правильно).
Следует отметить, что инвертируя функции статора и ротора в магнитном поле, генерирующем ток, вы получаете цепь, генерирующую механическое движение.
Магнитные поля: индуктивность и потокосцепление
Петли взаимодействуют с магнитным полем.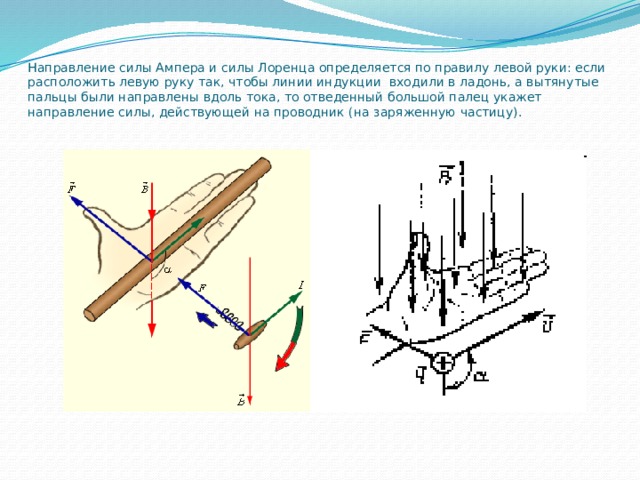
Таким образом, элементом, который наследует это качество в электрической цепи, является индуктор. Чтобы понять, как это работает, давайте сделаем некоторые определения. Потокосцепление , которое в основном используется в инженерных приложениях, определяется как общий поток, проходящий через катушку. Это получается путем умножения магнитного потока на число контуров N:
Индуктивность, обозначенная буквой L, определяется как магнитная связь объекта, деленная на ток, вызывающий этот поток:
Когда ток, вызывающий потокосцепление, также является током, соединяющим катушку (нет токов, внешних по отношению к катушке), это уравнение упрощается, так как больше нет необходимости в нижних индексах. Затем он получает название самоиндукции .
Представьте, что у вас есть катушка с 500 витками, через которую проходит ток 10А, создающий магнитное поле 10мВб. Какая ЭДС будет сгенерирована через 10 мс?
Используя обе формулы: L = 500 ⋅ 0,01Wb / 10A = 0,5H
Таким образом, ЭДС = 0,5 Гн ⋅ 10 А / 0,01 с = 500 В
Магнитные поля (только для A2) — ключевые выводы
- Магнитное поле тесно связано с электрическим полем.
