Какое свойство тела выражает момент инерции
Момент инерции для чайников: определение, формулы, примеры решения задач
Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».
Определение момента инерции
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.
Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:
Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
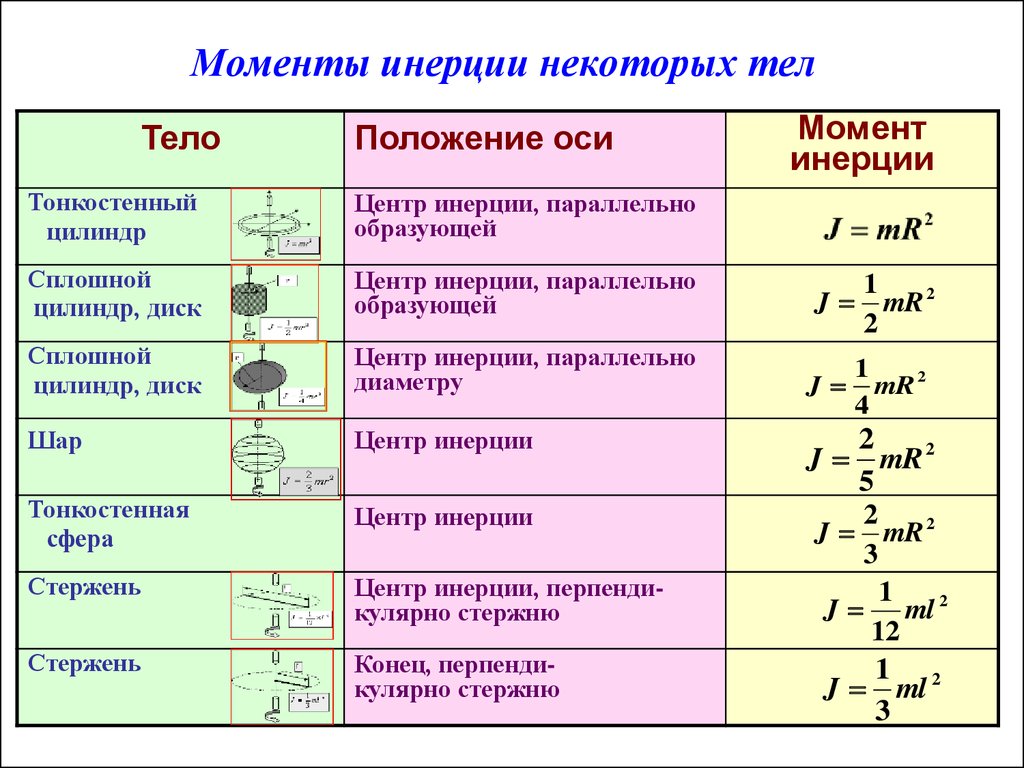
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:
Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
какое свойство тела выражает момент инерции и как он вычисляется для материальной точки и системы материальных точек!?
Момент инерции — скалярная физическая величина, характеризующая распределение масс в теле.
и являющаяся наряду с массой мерой инертности тела при непоступательном движении.
Момент инерции тела относительно оси вращения зависит от массы тела и от распределения этой массы. Чем больше масса тела и чем дальше она отстоит от воображаемой оси, тем большим моментом инерции обладает тело.
Физический смысл момента инерции
Когда тело продолжает двигаться при отсутствии на него воздействия каких-либо сил, говорят о проявлении инерции. Именно ею объясняются трудности удержаться на ногах при резком торможении автобуса или усидеть в седле велосипеда, когда под колеса резко выбегает кот. Кроме инерции, проявляющейся при движении тел по прямой, аналогичное явление бывает при вращении вокруг оси. В таком случае в физике говорят о моменте инерции – скалярной величине, измеряющей инертность тела при осевом вращении.
Именно ею объясняются трудности удержаться на ногах при резком торможении автобуса или усидеть в седле велосипеда, когда под колеса резко выбегает кот. Кроме инерции, проявляющейся при движении тел по прямой, аналогичное явление бывает при вращении вокруг оси. В таком случае в физике говорят о моменте инерции – скалярной величине, измеряющей инертность тела при осевом вращении.
Момент инерции и его физический смысл
Обеспечить поступательное движение предмета при его толкании будет тем тяжелее, чем больше он весит. Аналогичные эксперименты предусматривались школьной программой и относились к прямо направленному действию.
Было понятно, что именно масса тела характеризует степень его инертности и является ее мерой.
При совершении предметом вращательных движений наблюдается иной вид зависимости. В данном случае мерой инертности выступает момент инерции.
Момент инерции – скалярная измеряемая характеристика инертности тела в момент совершения осевого вращения.
Задачи по определению величины момента инерции решаются с помощью теоремы Гюйгенса-Штейнера, смысл которой заключается в следующем:
МИ для тела, вращающегося вокруг какой-либо оси, равна сумме слагаемых единиц: момент инерции предмета, который вращается вокруг оси, параллельной данной, и проходящей через центр масс, а также произведения массы на расстояние между осями, возведенное в квадрат.
В приведенной формуле используются следующие обозначения: d – расстояние между осями, m – масса тела, Iz – момент инерции относительно рассматриваемой оси, а Ic – относительно оси, которая проходит через центр масс. В профильной литературе и учебниках буква I может заменяться J.
Формулировка способа количественного измерения момента инерции при осевом вращении предмета стала возможной в результате работы двух ученых-математиков: Гюйгенса и Штейнера. Теорема дает возможность быстрого решения задач на определение инерции предмета любой формы, для которого уже просчитана центробежная сила.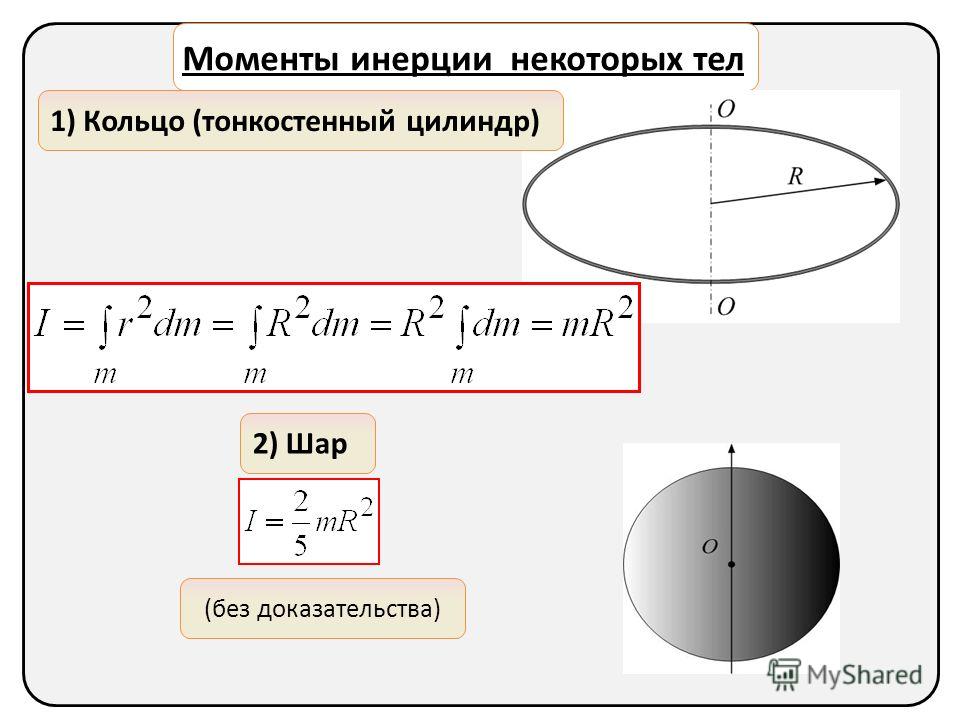 Формула Штейнера позволяет вычислить момент инерции этого предмета относительно выбранной оси, проходящей параллельно прямой, следующей через центр фигуры.
Формула Штейнера позволяет вычислить момент инерции этого предмета относительно выбранной оси, проходящей параллельно прямой, следующей через центр фигуры.
Единицы измерения в системе СИ
Единицей измерения момента инерции, принятой в системе СИ, является кг, умноженный на метр в квадрате — кг·м². В еще одной системе измерения (СГС) единицей измерения является грамм на квадратный сантиметр — г·см².
Как рассчитать момент инерции, формула
Измерение значения момента инерции можно произвести теоретически, согласно формуле. Для этого условно движущийся предмет разбивается на мелкие составляющие, масса которых обозначается dm. В конечном итоге момент инерции (МИ) равняется сумме произведений всех образовавшихся масс на расстояние до оси, возведенное в квадрат.
Исходя из этой формулы, момент инерции, кроме массы тела, определяется положением оси, вокруг которой предмет вращается, а также его формой и габаритами.
Возможность рассчитать моменты инерции полезна, к примеру, при исследованиях свойств и структуры элементов Солнечной системы. Это так называемый безразмерный момент инерции. Высчитанная по формуле величина дает представление о распределении массы по глубине.
Это так называемый безразмерный момент инерции. Высчитанная по формуле величина дает представление о распределении массы по глубине.
Виды моментов инерции
Кроме безразмерного момента инерции, в физике существуют понятия:
- центробежный МИ;
- главный МИ;
- геометрический МИ;
- МИ относительно плоскости;
- центральный МИ;
- тензор инерции;
- эллипсоид инерции.
Центробежными МИ относительно прямоугольных осей координат (декартовой системы) считаются Jxy, Jxz, Jyz. Ось ОХ является главной, когда центробежные моменты инерций Jxy и Jxz равняются нулям.
Любая точка тела может являться центром трех главных осей инерции. Они характеризуются взаимной перпендикулярностью. МИ относительно них считается главным для данного предмета. Главные оси, которые пролегают через центр масс, — являются главными центральными осями инерции предмета. МИ относительно них – главные центральные МИ. Для однородного тела ось симметрии всегда является главной центральной осью инерции.
Для геометрических МИ существуют формулы, основывающиеся на объеме относительно оси и площади относительно оси.
Твердое тело может иметь МИ относительно плоскости. Тогда это – скалярная величина, которая рассчитывается суммированием произведений массы каждой точки предмета и расстояния от нее до плоскости, возведенного в квадрат.
Понятие «Центрального МИ» связано с точкой О, МИ относительно полюса либо полярным МИ.
Момент инерции тела относительно оси вращения
МИ служит единицей измерения инерции тела, которое вращается вокруг оси, подобно тому, как масса является мерой при поступательном движении.
Определить МИ предметов касательно оси вращения позволяет формула Штейнера.
Пример:
Наглядное подтверждение применения формулы Штейнера – расчет МИ стержня, ось вращения которого проходит через конец.
Моменты инерции простейших объектов
Момент инерции некоторых однородных тел, имеющих простую форму, в зависимости от характеристик осей вращения можно определить по следующим формулам:
- МИ точечного предмета либо полого цилиндра с тонкими стенками (с массой m и радиусом r) = mr 2
- МИ диска или сплошного цилиндра = 1/2 mr 2
- МИ цилиндра с толстыми стенками, у которого внешний радиус обозначен r2, а внутренний – r1, :
Примеры решения задач
Применение на практике приведенных формул происходит, например, для решения следующих задач.
Пример №1
Задано найти МИ однородного диска с известными массой и радиусом. Из дополнительных сведений: ось вращения – через центр диска.
Для решения диск разбивается на тонкие кольца, радиусы которых равняются от 0 до R. Взяв одно из них и обозначив его радиус буквой \(r\) , а массу – \(dm\) , формула для расчета МИ (согласно теореме Гюйгенса-Штейнера) выглядит следующим образом: \(dJ=dmr2.\)
С учетом подстановки в конечную формулу для определения МИ формулы для массы кольца получаем:
Пример № 2
Задано найти у того же диска МИ относительно оси, которая проходит через середину радиуса.
Из предшествующего задания используем найденную величину МИ относительно оси, которая проходит через центр масс. Используя формулу Штейнера, решаем задачу.
Если решать аналогичные задачи нет желания или времени, а контрольную работу нужно сдать в срок, на помощь придут сотрудники Феникс.Хелп.
Открытая Физика.
 Вращение твердого тела
Вращение твердого телаДля кинематического описания вращения твердого тела удобно использовать угловые величины: угловое перемещение Δφ, угловую скорость ω ω=ΔφΔt; (Δt→0), и угловое ускорение ε ε=ΔωΔt; (Δt→0).
В этих формулах углы выражаются в радианах. При вращении твердого тела относительно неподвижной оси все его точки движутся с одинаковыми угловыми скоростями и одинаковыми угловыми ускорениями. За положительное направление вращения обычно принимают направление против часовой стрелки.
При малых угловых перемещениях Δφ модуль вектора Δs→ линейного перемещения некоторого элемента массы Δm вращающегося твердого тела выражается соотношением: Δs = rΔφ, где r – модуль радиус-вектора r→ (рис. 1.23.1). Отсюда следует связь между модулями линейной и угловой скоростей: υ = rω, и между модулями линейного и углового ускорения:

Векторы υ→ и a→=a→τ направлены по касательной к окружности радиуса r. Следует вспомнить, что при движении тела по окружности возникает также нормальное или центростремительное ускорение, модуль которого есть an=υ2r=ω2r.
Разобьем вращающееся тело на малые элементы Δmi. Расстояния до оси вращения обозначим через ri, модули линейных скоростей – через υi. Тогда кинетическую энергию вращающегося тела можно записать в виде: Ek=∑iΔmυi22=∑iΔm(riω)22=ω22∑iΔmiri2.
Физическая величина ∑iΔmiri2 зависит от распределения масс вращающегося тела относительно оси вращения. Она называется моментом инерции I тела относительно данной оси: I=∑iΔmiri2.
В пределе при Δm → 0 эта сумма переходит в интеграл. Единица измерения момента инерции в СИ – килограмм-метр в квадрате (кгċм2). Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде
Ek=Iω22.
Эта формула очень похожа на выражение для кинетической энергии поступательно движущегося тела mυ22, только теперь вместо массы
Момент инерции в динамике вращательного движения играет ту же роль, что и масса тела в динамике поступательного движения. Но есть и принципиальная разница. Если масса – внутреннее свойство данного тела, не зависящее от его движения, то момент инерции тела зависит от того, вокруг какой оси оно вращается. Для разных осей вращения моменты инерции одного и того же тела различны.
Во многих задачах рассматривается случай, когда ось вращения твердого тела проходит через его центр массы. Положение xC, yC
 1.23.2), определяется выражениями:
xC=m1x1+m2x2m1+m2; yC=m1y1+m2y2m1+m2.
1.23.2), определяется выражениями:
xC=m1x1+m2x2m1+m2; yC=m1y1+m2y2m1+m2.В векторной форме это соотношение принимает вид: r→C=m1r→1+m2r→2m1+m2.
Аналогично, для системы из многих частиц радиус-вектор r→C центра масс определяется выражением r→C=∑mir→i∑mi.
Для сплошного тела суммы в выражении для r→C заменяются интегралами. Легко видеть, что в однородном поле тяготения центр масс совпадает с центром тяжести. Если в однородном поле тяготения твердое тело сложной формы подвесить за центр масс, то оно будет находиться в безразличном состоянии равновесия. Поэтому положение центра масс тела сложной формы можно практически определить путем последовательного подвешивания его за несколько точек и отмечая по отвесу вертикальные линии (рис. 1.23.3).
Равнодействующая сил тяжести в однородном поле тяготения приложена к центру масс тела. Если тело подвешено за центр масс, то оно находится в состоянии безразличного равновесия (см. §1.14).
Если тело подвешено за центр масс, то оно находится в состоянии безразличного равновесия (см. §1.14).
Любое движение твердого тела можно представить как сумму двух движений: поступательного движения со скоростью центра масс тела и вращения относительно оси, проходящей через центр масс. Примером может служить колесо, которое катится без проскальзывания по горизонтальной поверхности (рис. 1.23.4). При качении колеса все его точки движутся в плоскостях, параллельных плоскости рисунка. Такое движение называется плоским.
В механике доказывается теорема о движении центра масс: под действием внешних сил центр масс любого тела или системы взаимодействующих тел движется как материальная точка, в которой сосредоточена вся масса системы

Иллюстрацией этого утверждения может служить рис. 1.23.5, на котором изображено движение тела под действием силы тяжести. Центр масс тела движется по параболической траектории как материальная точка, в то время как все другие точки движутся по более сложным траекториям.
Если твердое тело вращается относительно некоторой неподвижной оси, то его момент инерции
Рассмотрим сечение твердого тела произвольной формы, изображенное на рис. 1.23.6. Выберем координатную систему XY с началом координат O в центре масс C тела. Пусть одна из осей вращения проходит через центр масс C, а другая через произвольную точку P, расположенную на расстоянии d от начала координат.
Выражение для IP можно переписать в виде: IP=∑Δmi(xi2+yi2)+∑Δmi(a2+b2)-2a∑Δmixi-2b∑Δmiyi.
Поскольку начало координат совпадает с центром масс C, последние два члена обращаются в нуль. Это следует из определения центра масс. Следовательно, IP = IC + md2, где m – полная масса тела. Этот результат называют теоремой Штейнера (теоремой о параллельном переносе оси вращения).
На рис. 1.23.7 изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.
Второй закон Ньютона может быть обобщен на случай вращения твердого тела относительно неподвижной оси. На рис. 1.23.8 изображено некоторое твердое тело, вращающееся относительно оси, перпендикулярной плоскости рисунка и проходящей через точку O. Выделим произвольный малый элемент массы Δmi
На рис. 1.23.8 изображено некоторое твердое тело, вращающееся относительно оси, перпендикулярной плоскости рисунка и проходящей через точку O. Выделим произвольный малый элемент массы Δmi
Касательная составляющая F→iτ вызывает тангенциальное ускорение a→iτ массы Δmi. Второй закон Ньютона, записанный в скалярной форме, дает Δmiaiτ = Fiτ = Fi sin θ или Δmiriε = Fi sin θ
Если обе части написанного выше уравнения умножить на ri, то мы получим:
Δmiri2ε=Firisinθ=Fili=Mi.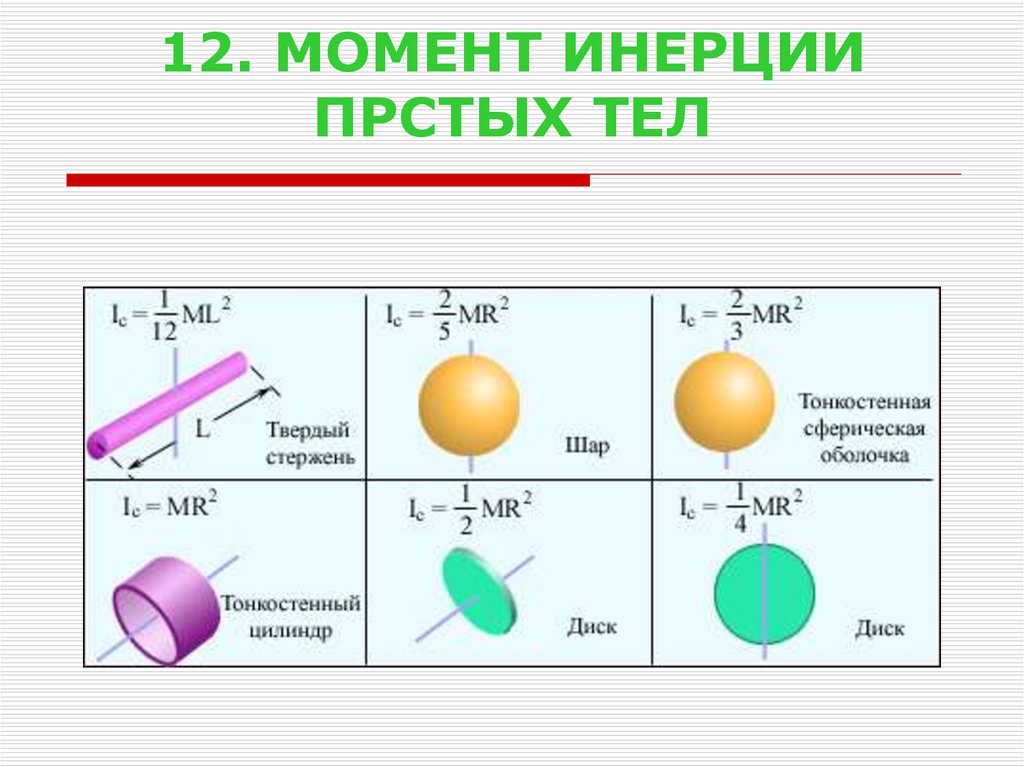
Здесь li – плечо силы F→i, Mi – момент силы.
Теперь нужно аналогичные соотношения записать для всех элементов массы Δmi вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает: ∑Δmiri2ε=∑Mi.
Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил. ∑M=∑(Miвнешн)+∑(Miвнутр).
Но сумма моментов всех внутренних сил согласно третьему закону Ньютона равна нулю, поэтому в правой части остается только сумма моментов всех внешних сил, которые мы будем обозначать через M. В итоге: Iε = M.
Это и есть основное уравнение динамики вращательного движения твердого тела. Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими. Обычно за положительное направление вращения принимают направление против часовой стрелки.
Возможна и векторная форма записи основного уравнения динамики вращательного движения, при которой величины ω→, ε→, M→ определяются как векторы, направленные по оси вращения.
При изучении поступательного движения тел вводится понятие импульса тела p→ (см. §1.16). Аналогично, при изучении вращательного движения вводится понятие момента импульса.
Моментом импульса вращающегося тела называют физическую величину, равную произведению момента инерции тела I на угловую скорость ω его вращения. Момент импульса обозначается буквой L: L = Iω.
Поскольку ε=ΔωΔt; (Δt→0), уравнение вращательного движения можно представить в виде: M=Iε=IΔωΔt или MΔt=IΔω=ΔL.
Окончательно будем иметь: M=ΔLΔt; (Δt→0).
Это уравнение, полученное здесь для случая, когда I = const, справедливо и в общем случае, когда момент инерции тела изменяется в процессе движения.
Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L = Iω относительно данной оси сохраняется:
ΔL = 0, если M = 0.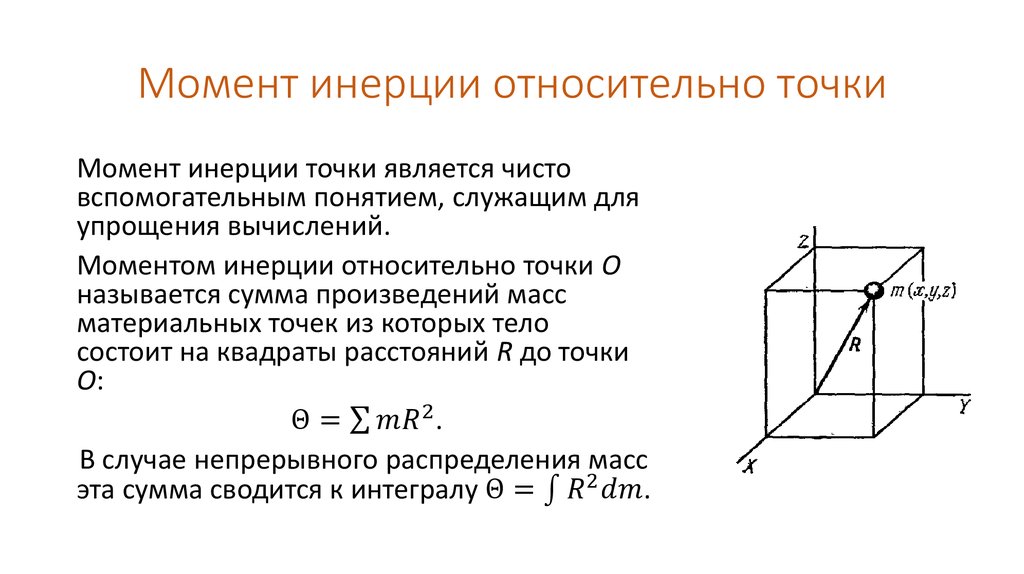
Следовательно, L = Iω = const.
Это и есть закон сохранения момента импульса. Иллюстрацией этого закона может служить неупругое вращательное столкновение двух дисков, насажанных на общую ось (рис. 1.23.9).
Закон сохранения момента импульса справедлив для любой замкнутой системы тел. Он выполняется, например, при движении планет по эллиптическим орбитам вокруг Солнца (второй закон Кеплера).
Уравнение вращательного движения тела можно записывать не только относительно неподвижной или равномерно движущейся оси, но и относительно оси, движущейся с ускорением.
Основное уравнение динамики вращательного движения не изменяет своего вида и в случае ускоренно движущихся осей при условии, что ось вращения проходит через центр массы тела и что ее направление в пространстве остается неизменным. Примером может служить качение тела (обруч, цилиндр, шар) по наклонной плоскости с трением (рис. 1.23.10).
Примером может служить качение тела (обруч, цилиндр, шар) по наклонной плоскости с трением (рис. 1.23.10).
Ось вращения O проходит через центр масс тела. Моменты силы тяжести mg→ и силы реакции N→ относительно оси O равны нулю. Момент M создает только сила трения: M = FтрR.
Уравнение вращательного движения: ICε=ICaR=M=FтрR, где ε – угловое ускорение катящегося тела, a – линейное ускорение его центра масс, IC – момент инерции относительно оси O, проходящей через центр масс.
Второй закон Ньютона для поступательного движения центра масс записывается в виде: ma = mg sin α – Fтр.
Исключая из этих уравнений Fтр, получим окончательно: a=mgsinθ(ICR2+m).
Из этого выражения видно, что быстрее будет скатываться с наклонной плоскости тело, обладающее меньшим моментом инерции. Например, у шара IC=25mR2, а у сплошного однородного цилиндра IC=12mR2. Следовательно, шар будет скатываться быстрее цилиндра.
Например, у шара IC=25mR2, а у сплошного однородного цилиндра IC=12mR2. Следовательно, шар будет скатываться быстрее цилиндра.
При рассмотрений обязательных упражнений мы встречались с разновидностями опорных вращательных движений. Мы знаем, что вращательные движения, например повороты, обусловлены главным образом встречным поворотом верхней части тела относительно нижней и не связаны с длительным и быстрым вращением всего тела. Напротив, в произвольном катании наиболее характерными являются движения, связанные с вращением всего тела вокруг продольной оси в 2; 2,5; 3; 3,5 и более оборотов в полете в прыжках, а во вращениях достигают нескольких десятков оборотов. Именно стремительные вращения вокруг вертикальной оси, пожалуй, являются наиболее ярким олицетворением движений произвольного катания. Основы механики вращенийВ связи с особой важностью вращательных движении в общем комплексе упражнений произвольного катания рассмотрим коротко основные понятия и терминологию механики вращательного движения тела вокруг вертикальной оси. Характеристики вращательных движений. В качестве пример, вращающегося тела рассмотрим тело фигуриста, выполняющего пируэт на одной ноге (рис. 19, а). Будем условно считать, что вращение его тела происходит вокруг неподвижной оси. Вращательным движением твердого тела относительно неподвижной оси называется такое движение, при котором две его точки остаются неподвижными. Ось, проходящая через эти точки, называется осью вращения. Вращение тела характеризуется угловой скоростью тела. Величина угловой скорости определяется отношением угла поворота тела к времени, за которое произошел этот поворот: Угловая скорость характеризуется не только величиной, но и направлением в пространстве, т. Если угловая скорость всех точек напряженного тела одинакова, то линейная скорость для каждой точки разная. Зависимость между угловой и линейной скоростями точки выражается формулой: где R — расстояние точки от оси вращения. Эта простая зависимость имеет во вращениях важное значение, так как при одной и той же угловой скорости тела со линейные скорости точек тела разные; чем дальше они остоят от оси вращения, тем их линейная скорость больше (рис. 19, б). Рассмотрим ускорения точки вращающегося тела (рис. 20). Скорость точки является величиной векторной, т. е. может изменяться по величине и направлению в пространстве. Ускорение, вызванное изменением величины вектора скорости, называется касательным или тангенциальным; оно направлено по касательной к траектории движения точки, совпадает с направлением вектора скорости при ускоренном движении и противоположно вектору скорости при замедленном движении. При движении точки по окружности ,где – угловое ускорение тела, имеющее размерность Ускорение, вызванное изменением направления вектора скорости точки, называется нормальным. Оно направлено по нормали в сторону вогнутости траектории и равно при движении точки по окружности . Ускорение точки имеет размерность м/с2. На рис. 20 приведены векторы касательного и нормального ускорений точки кисти руки фигуриста в пируэте. Таким образом, если вектор скорости изменяется и по величине, и по направлению, то движущаяся точка имеет ускорение, состоящее из касательного и нормального. Геометрическая сумма этих ускорений называется полным ускорением и направлена по диагонали прямоугольника, построенного на векторах касательного и нормального ускорений. Мерой инертности тела при. поступательном движении является его масса, измеряемая в килограммах. Во вращательном движении особое значение приобретает распределение массы тела относительно оси вращения: удаление массы тела от оси вращения увеличивает инертность тела во вращательном движении вокруг этой оси, а приближение к оси уменьшает.
Мерой инертности тела во вращательном движении является момент инерции, равный сумме произведений масс частей тела на квадраты их расстояний до оси вращения: где m — массы частей тела; r — расстояние масс тела до оси вращения. Следует подчеркнуть, что в выражение для величины момента инерции входят расстояния масс частей тела до оси вращения во второй степени, что объясняет значительное изменение момента инерции тела с постоянной массой при перераспределении масс частей тела относительно оси вращения. Одной из важных характеристик вращающегося тела является количество запасенного им вращательного движения. Она носит название момента количества движения* или кинетического момента тела К. Величина кинетического момента вращающегося тела измеряется произведением момента инерции тела относительно оси I и угловой скорости, вращения тела вокруг этой оси : Величина кинетического момента вращающегося тела измеряется произведением момента инерции тела относительно оси I и угловой скорости, вращения тела вокруг этой оси :
Кинетический момент является характеристикой, свойственной вращательному движению. Закон сохранения момента количества движения Для анализа вращательных движений фигуриста очень важно знать закон сохранения кинетического момента. Одним из свойств вращающегося тела является стремление сохранить количество приобретенного вращательного движения, или, другими словами, величину кинетического момента. Для рассматриваемого нами случая закон сохранения кинетического момента может быть упрощенно сформулирован следующим образом: «Кинетический момент тела относительно оси постоянен, если сумма моментов внешних сил относительно оси равна нулю»: Пренебрегая сопротивлением воздуха и трением конька о лед, можно считать, что при выполнении вращения на тело фигуриста действуют две внешние силы: сила веса и вертикальная составляющая реакции опоры. Во вращательном движении при выполнении пируэта зависимость проявляется в постоянной взаимосвязи между величинами момента инерции тела и его угловой скоростью вращения. Другими словами, уменьшение одного множителя вызывает увеличение другого настолько, что их произведение остается неизменным. Именно поэтому приближение звеньев тела к оси вращения в процессе группировки, т. е. уменьшение момента инерции, обусловливает увеличение скорости вращения тела и наоборот. Сравнение моментов инерции тела в различных положениях позволяет, в частности, установить, что группировка рук из положения в стороны может увеличить скорость вращения тела почти вдвое, а переход из положения ласточки в положение стоя с руками вдоль тела—более чем в семь раз. Эти данные не учитывают сил сопротивления, испытываемых телом при вращении, поэтому реальное увеличение угловой скорости всегда меньше и зависит от характера контакта конька со льдом. Силы инерции при вращениях Для определения динамической структуры вращательного движения рассмотрим силы инерции, действующие на звенья тела фигуриста при выполнении пируэта. При анализе ускорений, действующих на точки вращающегося тела, было определено, что в общем случае таких ускорений два: нормальное и касательное. Отсюда на точки вращающегося тела действуют также две силы инерции: нормальная и касательная. Возьмем систему координат хОу с началом в центре тяжести тела. Ось Oz направим по оси вращения. При равномерном вращении тела вокруг оси Oz с угловой скоростью w на две симметрично расположенные точки A и B будут действовать только нормальные силы инерции, равные по величине направленные противоположно центростремительному ускорению (рис. При изменении угловой скорости появляются угловое ускорение и касательные силы инерции, равные по величине и направленные по касательной к траектории точек А и В в стороны, противоположные касательным ускорениям (рис. 21,б). Касательные силы инерции образуют пару сил, лежащую в плоскости, параллельной плоскости хОу. Эта пара сил препятствует вращению фигуриста вокруг оси Oz. Причины изменения скорости вращения В различных вращательных движениях и пируэтах фигурист меняет угловую скорость вращения своего тела в значительных пределах. В соответствии с законом сохранения кинетического момента изменение скорости вращения сопровождается изменением момента инерции тела— группировкой или раз-группировкой. Причиной изменения скорости являются определенные силы. Какие же силы вызывают изменение скорости вращения фигуриста? Пренебрегая силами трения, можно сказать, что внешние силы, как мы уже говорили, не создают значительных моментов относительно оси вращения, т. Рассматривая эти силы, легко убедиться, что линии их действия при группировке и разгруппировке направлены к оси вращения или от нее, т. е., грубо говоря, они не поворачивают тело вокруг оси. Какие же силы непосредственно ускоряют или замедляют вращение тела? Это силы инерции Кориолиса, или, говоря точнее, моменты этих сил. Рассмотрим физическую сущность возникновения сил инерции Кориолиса, определим направление их действия и формулу для определения величины этих сил (рис.22). В пируэте при группировке и разгруппировке имеют место два движения: вращение тела, которое будем называть переносным, и движение рук и свободной ноги вдоль радиуса к оси или от нее, которое будем называть относительным. Когда руки притягиваются к оси вращения (относительное движение), линейные скорости их частей станут меньше, т. Итак, в процессе вращения тела фигуриста, перемещения рук и свободной ноги к оси вращения или от нее возникают силы инерции Кориолиса, которые ускоряют вращение при группировке и замедляют его при разгруппировке. Кориоли-совы силы инерции зависят от величины угловой скорости вращения тела , линейной скорости частей тела при группировке и замедляют его при разгруппировке. Кориолисовы силы инерции зависят от величины угловой скорости вращения тела со, линейной скорости частей тела при группировке и разгруппировке — V, а также от синуса угла между векторами . На рис.23 приведена совокупность всех сил инерции, действующих на точки А и В вращающегося тела. Необходимо учитывать, что в действительности на каждую из точек тела действует результирующая сила инерции, равная векторной сумме перечисленных сил инерции: нормальной,касательной и кориоли-совой.
Прецессия оси вращения Анализируя вращательное движение, мы говорили, что в процессе вращения о. ц. т. тела находится точно над точкой опоры. В практике фигурного катания встречаются случаи, когда проекция о. ц. г. не совпадает с точкой опоры. В этом случае продольная ось тела z1, проходящая через точку опоры и о. где: l-расстояние от точки опоры до о.ц.т. тела; – момент инерции фигуриста относительно оси вращения z1; Р-вес тела фигуриста; — угловая скорость фигуриста вокруг оси z1; —угловая скорость прецессии оси z1. Прецессионное движение оси вращения нежелательно и с точки зрения качественной оценки пируэта, и, что, пожалуй, главное, с точки зрения управления движением, поскольку ориентация спортсмена, сохранение равновесия резко осложняются. Из формулы видно, что угловая скорость прецессии обратно пропорциональна угловой скорости вращения фигуриста: чем больше угловая скорость вращения фигуриста, тем меньше угловая скорость прецессии , и наоборот. На устойчивость оси вращения положительно влияет также увеличение момента инерции тела относительно оси вращения . Однако наиболее важную роль в устойчивости оси вращения играет положение центра тяжести. Момент силы тяжести относительно точки опоры определяет угловую скорость прецессии. Для уменьшения угловой скорости прецессии следует уменьшить величину этого момента, т. е. стремиться к такому положению, при котором о.ц.т. тела находится над точкой опоры. Устойчивость вращения к прецессии связана с расстоянием l от о.ц.т. до неподвижной точки вращения. Чем оно меньше, тем при прочих равных условиях меньше угловая скорость прецессии. Не удивительно поэтому, что наиболее устойчивым вращением является волчок —пируэт, в котором расстояние l минимально. Интересно отметить, что устранение момента силы тяжести приводит к мгновенному устранению прецессии. На практике встречаются две основные причины возникновения прецессии в пируэтах. В первом случае несовпадение точки опоры и проекции силы тяжести вызвано несовершенным въездом во вращение, неправильным определением центра вращения. Здесь резкое торможение, раннее начало вращения, неточное маховое движение порождают инерционные силы, отклоняющие о.ц.т. тела от вертикали. В другом случае смещение о.ц.т. вызвано неправильным перемещением частей тела при смене позы. Влияние положения тела фигуриста при вращениях на частоту сердечных сокращений* Влияние положения тела фигуриста на характер кровообращения и частоту сердечных сокращений при вращениях наиболее ярко прослеживается при выполнении таких элементов, как вращение в ласточке, в ласточке со сменой ног, прыжок во вращение ласточка. В это время частота сердечных сокращений оказывается наиболее низка. Интересна пульсограмма вращения в ласточке. Этот интересный факт требует более глубокого исследования. Однако уже на основании проведенных опытов было высказано предположение, что данное явление может быть объяснено антиортостатической реакцией организма. Имеется в виду практически горизонтальное положение верхней части тела и свободной ноги при вращении. Возможно, что урежение пульса действительно является следствием реакции барорецепторов скаротидных синусов на увеличение венозного возврата крови, вызванного центробежными силами инерции.
Исследования автора, проведенные под руководством профессора А. Необходимо также учитывать эмоциональную сторону упражнения. В этом плане следует отметить, во-первых, сравнительную комфортность положения тела при вращении в ласточке и, во-вторых, наиболее низкую из всех вращений угловую скорость, которая и обусловливает относительно спокойный эмоциональный фон упражнения. Другие же сходные по биомеханической структуре элементы: вращение в ласточке со сменой ног и прыжок во вращение ласточка —вызывают более выраженную ответную пульсовую реакцию, и феномен уменьшения частоты сердечных сокращений проявляется в меньшей степени. Этот факт связан с тем, что наряду с менее благоприятным эмоциональным фоном при выполнении данных двух элементов фигурист затрачивает дополнительную энергию на отталкивание и смену ног при вращении, что, естественно, увеличивает частоту сердечных сокращений. Феномен уменьшения частоты сердечных сокращений при простом вращении в положении ласточка может быть использован при составлении произвольных программ. Рационально включать вращения в ласточке в те места программы, после которых необходим промежуточный отдых, расслабление, снижение эмоционального фона, успокоение. Анализ техники вращенийБлагодаря кривизне лезвия конька в арсенале фигуриста может быть большое количество вращательных движений, возникающих естественно и выполняемых сравнительно легко. Пируэт представляет собой длительное вращательное движение тела вокруг вертикальной оси без заметного перемещения точки опоры. В зависимости от направления вращения различают пируэты вперед (вращение происходит в сторону опорной ноги) и назад (вращение выполняется в сторону свободной ноги). С точки зрения позы, в которой выполняется пируэт, можно выделить три основные группы: пируэты стоя, пируэты в приседе (волчки) и пируэты в положении ласточка. Различают простые пируэты, в которых вращение происходит в относительно неизменной позе, и сложные —со сменой позы (например, с переходом из положения стоя в положение сидя). Пируэты могут выполняться на одной и обеих ногах. В последнем случае понятие «направление вращения» (вперед или назад) теряет смысл, так как обе ноги являются опорными. Пируэт состоит из подхода, въезда, вращения и выезда. На рис. 25 приведены следы, оставленные при выполнении пируэта вперед. Дуги 1, 2, 3 и 4 соответствуют подходу, дуга 5 —въезду, точка 6—вращению, а дуги .7 и 8 —выезду. Подход. Существует несколько вариантов подходов. Наиболее удобным и поэтому целесообразным для начального обучения является сочетание тройки вперед-наружу с перебежкой назад. Используют подходы в виде тройки вперед-внутрь—назад-наружу, а также ходом вперед-наружу, подходе важно сохранять плавность скольжения, хорошу осанку, чтобы вращение было естественным, а приготовление к нему — незаметным. Въезд. Это наиболее сложная и ответственная часть пируэта. Именно здесь возникает вращение. Как правило, если фигурист сообщил телу устойчивое вращение, то сохранять и поддерживать его не составляет большой сложности. Вращение телу можно придать двумя способами: толчком ногой при переходе с последней дуги подхода на въездную дугу, а также круговым маховым движением свободной ноги и руки при въезде. Во вращении стоя и в волчках следует использовать оба способа. При вращениях в ласточке маховое движение не всегда эффективно. Здесь оно приводит к выведению свободной ноги вперед, и для принятия положения ласточки фигурист вынужден в конце въезда резко отводить свободную ногу назад. Это движение часто вызывает потерю равновесия. Более простым и надежным является въезд с отведенной назад свободной ногой и одноименной рукой. Напротив, при въезде в волчок круговое маховое движение весьма целесообразно и эффективно. Необходимо во время подхода сделать сильный мах руками и свободной ногой назад. Въезд во вращение стоя, по существу, не отличается от въезда в волчок. Здесь только опорная нога более выпрямлена. Не следует, однако, выпрямлять ее полностью: это может привести к нарушению равновесия. Для устойчивости вращения очень важно, как выполнен конечный участок дуги въезда. В пируэтах вперед в конце въезда, когда дуга достигла максимальной кривизны, следует поворот тройкой вперед-наружу, после чего —окружность диаметром 30—40 см, выполняемая ходом назад-внутрь, и только затем начинается вращение.
Вращение. В простых пируэтах группировка отсутствует и положение, принятое в начале вращения, сохраняется почти неизменным. Поэтому здесь, как и при выполнении спиралей, важна точность положения тела, стабильность удержания его. В ласточке необходимо вращаться на плоскости конька, не касаясь льда зубцами. Начинающие фигуристы часто теряют равновесие уже в начале вращения, так как чрезмерно перемещают центр тяжести тела вперед. Чтобы избежать этого, необходимо на протяжении всего вращения, особенно в начале его, оттягивать свободную ногу назад. Она должна быть выпрямлена, развернута, голова направлена вперед, а вытянутые руки на одной линии, находящейся в одной плоскости с опорной и свободной ногами. В волчке вращение происходит на передней трети конька. Для повышения устойчивости в начале вращения допустимо легкое касание льда зубцами. Наиболее распространенная ошибка здесь—падение назад. Чтобы предотвратить ее, развернутая свободная нога и руки должны быть прямыми и вытянутыми вперед. Опорная нога при этом согнута, голова подтянута, плечи опущены. Вращение стоя также происходит на передней трети конька с легким касанием льда зубцами. В сложных пируэтах происходит группировка. Ее можно выполнять в двух вариантах: в первом варианте приближение рук и свободной ноги к оси вращения происходит при неизменном основном положении тела (например, стоя или в приседе), во втором поза меняется —части тела приближаются к оси вращения (например, переход из ласточки в волчок или из волчка в положение стоя). При этом скорость вращения тела возрастает. Рассмотрим пример группировки в пируэте стоя, называемом винтом. Из положения, когда нога вытянута вперед, правую ногу, не опуская, выводят вперед, сгибают в колене и скрещивают с левой, на которой происходит вращение. Затем правую ногу опускают, скользя задней поверхностью голени по левой. Это движение сопровождается группировкой рук одновременно с группировкой ног или несколько позже. В заключительной фазе руки плотно прижимают к телу, а слегка согнутую опорную ногу выпрямляют, что дает дополнительное увеличение скорости вращения. Необходимо следить за симметрией группировки, ибо неодинаковое движение рук вызывает нарушение равновесия. Выезд. Выполнению всегда предшествует движение, обратное группировке,— разгруппировка. Делается это для уменьшения скорости вращения, что облегчает выполнение выезда. Здесь важно, чтобы разгруппировка заканчивалась небольшим сгибанием опорной ноги. Обычно выезд выполняют со сменой ноги: ранее свободная ном становится опорной, и вращение завершается тол-ком, аналогичным толчку в обязательной фигуре № 3, с последующим скольжением назад-наружу. Данный вариант выезда наиболее распространен; его рекомендуют при разучивании пируэтов. В программах мастеров встречаются более сложные выезды (например, вперед-наружу со сменой ноги, назад-внутрь без смены ноги, въезд в остановку, в прыжок). При любом варианте следует стремиться к слитности всех движений, к такому выполнению, при котором выезд является естественным продолжением вращения. Заклоны. Особой разновидностью пируэтов являются так называемые заклоны. Прежде чем осваивать данную группу пируэтов, фигурист должен научиться уверенно принимать эту позу без коньков. Подход и въезд делают как в обычных вращениях. Положение заклона принимают в тот момент, когда начинается вращение. Далее прогиб рекомендуется увеличить и вместе с тем по возможности (незаметно для наблюдателя) выполнять группировку. Опытные фигуристы иногда поднимают одну руку вверх или опускают вниз, чтобы ее положение совпадало с положением оси вращения: это обеспечивает дополнительную группировку, что вызывает увеличение скорости вращения. С заклонами весьма схожи паузы с захватом свободной ноги одной или двумя руками. Пируэты назад. При обучении вращениям назад рекомендуется выполнять подход (рис. 26) в виде крутой дуги вперед-внутрь (дута 1). Въезд представляет собой дугу вперед-внутрь на другой ноге (дуга 2), описывая которую фигурист делает энергичное вращательное движение свободной ноги и рук. Вращение (точка 3) может выполняться в любом положении (в ласточке, волчке, стоя), а также в промежуточных положениях. Выезд (дуга 4) лучше всего разучивать на той же ноге, на которой происходило вращение: это помогает совершенствовать выезд из многооборотных прыжков. Освоение пируэтов вперед и назад открывает большие возможности для выполнения различных комбинаций: это волчок со сменой ноги, вращение в ласточке со сменой ноги, варианты смены положения тела и ноги. Для успешного овладения пируэтами важно определить удобную для спортсмена сторону вращения. Большинство фигуристов быстрее овладевают вращениями влево и лучше их переносят. Наиболее простой и верный способ определения «своего» направления вращения —выполнение пируэта назад с выездом без смены ноги. Если этот, пируэт и выезд увереннее и легче получаются на правой ноге, следует лучшие варианты своих вращений планировать влево, и наоборот. Разучивание пируэтов вперед и назад в различных позах помогает подготовить организм фигуриста к вращательным нагрузкам, которые он постоянно испытывает во время катания. Специальные упражнения для совершенствования вращенийОдним из важных направлений в тренировке вращений вне льда является работа над гибкостью. При этом необходимо сочетать традиционные способы развития пассивной гибкости с помощью различных растягиваний, шпагатов, махов и т. п. с развитием активной гибкости. Например, одной из наиболее сложных поз, особенно для мальчиков, является вращение в ласточке. Для ее совершенствования целесообразно применять утяжелитель, прикрепляемый к стопе свободной ноги. Он позволяет добиваться хорошего эффекта при развитии как пассивной гибкости (выполнение махов назад), так и активной (удержание свободной ноги с грузом в требуемой позе).
Этот же способ эффективен и в занятиях вне льда. Лучшим способом совершенствования положения тела во вращении ласточка, на наш взгляд, является разучивание так называемой качающейся ласточки—поочередно на обеих нoгax. Целесообразно использовать тренажер «Грация» для совершенствования точности позы и чувства равновесия. В тренировках на льду основное внимание следует уделять поиску оптимального варианта въезда во вращение и оптимального контакта конька со льдом во время вращения. Следует анализировать характер следов на льду, обращая главное внимание на отсутствие скоблений, касания льда зубцами. Хорошим средством совершенствования качества въезда во вращения, повышения стабильности их выполнения являются тренировки с выключением зрения. Надевая специальные непрозрачные очки, фигурист выполняет требуемое вращение. При этом обостряется деятельность двигательного, вестибулярного, тактильного и слухового анализаторов. Опыты показали, что такие упражнения повышают устойчивость навыка, делают выполнение вращений более уверенными, стабильными. | ||||||||||||||||
| Мишин А.Н. Биомеханика движений фигуриста. — М: Физкультура и спорт, 1981. — 144 с, ил. |
Момент инерции бейсбольных бит
Момент инерции бейсбольных бит| Физика и акустика бейсбольных и софтбольных бит Дэниел А. Рассел, доктор философии. Прикладная физика, Университет Кеттеринга, Флинт, Мичиган 48504-4898 Содержание этой страницы © 2008 Daniel A. Russell |

Инерция — это мера того, насколько сложно изменить скорость объекта путем приложения силы, и обычно выражается в единицах массы. Чем больше инерция объекта ( т.е. , чем больше масса объекта), тем труднее изменить его скорость. Масса отличается от вес , хотя эти два термина часто используются взаимозаменяемо.
| |
| Вращательная инерция или момент инерции (MOI) является мерой того, насколько сложно изменить скорость вращения объекта, который вращается вокруг точки вращения. Чем больше момент инерции, тем сложнее изменить скорость вращения объекта. Значение MOI зависит от общей массы объекта, а также от того, как эта масса распределяется вокруг точки поворота. Рассмотрим сначала точечную массу м (маленький шар), который вращается параллельно земле на расстоянии x от фиксированной точки вращения, как показано на изображении вверху справа. | Масса с одной точкой, вращающаяся на фиксированном расстоянии от точки вращения. |
| Если есть несколько точечных объектов, вращающихся вокруг одной и той же точки вращения, но на разных расстояниях от точки вращения, то общий момент инерции системы представляет собой просто сумму отдельных моментов инерции. | Несколько точечных масс, вращающихся на разных расстояниях от точки вращения. |
В нашем случае вращающимся объектом является летучая мышь, масса которой распределена по всей ее длине. Чтобы решить эту более сложную задачу, мы предположим, что летучая мышь состоит из очень большого количества очень маленьких кусочков, каждый из которых имеет свою собственную приращенную массу дм и каждый находится на расстоянии x от точки вращения. Если бы мы знали, как масса dm варьировались в зависимости от положения, мы могли сложить все отдельные моменты инерции вместе, чтобы получить общую инерцию летучей мыши. Если бы мы знали, как масса dm варьировались в зависимости от положения, мы могли сложить все отдельные моменты инерции вместе, чтобы получить общую инерцию летучей мыши. | Протяженный объект (летучая мышь), вращающийся вокруг фиксированной оси, может быть разбит на множество мелких частей с различной массой и разным расстоянием от точки вращения. |
Вес и точка равновесияЧтобы измерить вес летучей мыши, вы можете просто положить ее на весы и напрямую записать вес. Чтобы найти точку баланса, вы можете использовать лезвие ножа и найти место, где летучая мышь точно балансирует. Это немного сложно, но работает очень хорошо. Или вы можете следовать процедуре измерения веса и точки равновесия, как указано в стандарте ASTM F239.8-04 «Метод испытаний для измерения момента инерции и центра удара бейсбольного мяча или софтбольной биты», которым занимаются производители бит и управляющие ассоциации. Этот стандарт испытаний требует использования двух весов, одна из которых поддерживает биту в точке на расстоянии 6 дюймов от конца ручки, а другая поддерживает ствол летучей мыши на расстоянии 24 дюйма от ручки. Вес летучей мыши представляет собой сумму двух показаний весов Это немного сложно, но работает очень хорошо. Или вы можете следовать процедуре измерения веса и точки равновесия, как указано в стандарте ASTM F239.8-04 «Метод испытаний для измерения момента инерции и центра удара бейсбольного мяча или софтбольной биты», которым занимаются производители бит и управляющие ассоциации. Этот стандарт испытаний требует использования двух весов, одна из которых поддерживает биту в точке на расстоянии 6 дюймов от конца ручки, а другая поддерживает ствол летучей мыши на расстоянии 24 дюйма от ручки. Вес летучей мыши представляет собой сумму двух показаний весов |
Важно знать расположение точки баланса. Момент инерции всегда рассчитывается или измеряется относительно заданной точки поворота. В соответствии со стандартной практикой [1] , используемой производителями, испытательными лабораториями и руководящими органами, точка поворота находится на рукоятке в 6 дюймах от конца биты с выступом. В лабораторных тестах по измерению производительности летучей мыши летучая мышь захватывается за 6-дюймовую точку на рукоятке, поэтому момент инерции в этом месте имеет значение для испытаний. Однако в нескольких полевых исследованиях скорости поворота летучей мыши использовался момент инерции летучей мыши по отношению к точке поворота на ручке. Значения MOI для двух опорных точек сильно различаются. Тем не менее, можно преобразовать одно в другое, если вы знаете одно из значений MOI и положение оси вращения, вес летучей мыши и положение точки баланса (центра масс). Теорема о параллельной оси утверждает, что момент инерции относительно оси, проходящей через центр масс (I см ), и момент инерции относительно другой оси, которая параллельна оси, проходящей через центр масс. В соответствии со стандартной практикой [1] , используемой производителями, испытательными лабораториями и руководящими органами, точка поворота находится на рукоятке в 6 дюймах от конца биты с выступом. В лабораторных тестах по измерению производительности летучей мыши летучая мышь захватывается за 6-дюймовую точку на рукоятке, поэтому момент инерции в этом месте имеет значение для испытаний. Однако в нескольких полевых исследованиях скорости поворота летучей мыши использовался момент инерции летучей мыши по отношению к точке поворота на ручке. Значения MOI для двух опорных точек сильно различаются. Тем не менее, можно преобразовать одно в другое, если вы знаете одно из значений MOI и положение оси вращения, вес летучей мыши и положение точки баланса (центра масс). Теорема о параллельной оси утверждает, что момент инерции относительно оси, проходящей через центр масс (I см ), и момент инерции относительно другой оси, которая параллельна оси, проходящей через центр масс. массы связаны соотношением: массы связаны соотношением:Таким образом, если вы измерите MOI для точки поворота на расстоянии 6 дюймов от конца ручки, вы можете использовать теорему о параллельной оси для расчета I см . Затем можно снова использовать значение I см и теорему о параллельной оси, чтобы вычислить момент инерции относительно какой-либо другой оси (скажем, относительно ручки). | Центр масс или точка равновесия. |
Наряду с моментом инерции часто упоминается еще одна дополнительная величина — радиус вращения . Радиус вращения — это расстояние R от точки вращения, где находится точечная масса (маленький шарик) с массой, равной общей массе M летучей мыши будет располагаться так, чтобы момент инерции этого шара с точечной массой был таким же, как момент инерции настоящей летучей мыши. | Радиус вращения по сравнению с точкой равновесия. |
| Стандартные отраслевые лабораторные тесты, которые в настоящее время используются для регулирования характеристик биты, требуют, чтобы момент инерции софтбольной или бейсбольной биты измерялся относительно точки поворота на рукоятке, находящейся в 6 дюймах от ручки. конец биты. Летучая мышь зажата в 6-дюймовой точке шарнирной опоры, которая позволяет летучей мыши раскачиваться вперед и назад, как маятник. Период (время одного полного колебания маятника) тщательно измеряется с помощью синхронизирующего инфракрасного механизма. Зная период T , масса m , ускорение свободного падения g и расстояние d между точкой вращения и точкой равновесия, затем момент инерции рассчитывается из |
Каталожные номера
Стандарт ASTM F2398-04 Метод испытаний для измерения момента инерции и центра удара бейсбольного мяча или софтбольной битыНазад к Физика и акустика бейсбольных и софтбольных бит
Основные оси
Главные моменты инерции Как показано в [6] в Inertia Тензор, угловой момент твердого тела относительно начала локальной система отсчета выражается как
Если случайно все недиагональные члены тензора инерции показанные в [1], становятся равными нулю, [1] можно упростить до
Это может произойти при выравнивании осей локальной ссылки
каркас таким образом, чтобы масса корпуса равномерно распределялась вокруг осей, таким образом,
все члены произведения инерции исчезают. Топ Главные оси Как показано в [1], нет гарантии что вектор углового момента имеет то же направление, что и вектор угловой скорости вектор. Это вызывает проблему: если направление углового момента продолжает меняться, развивает крутящий момент, который в конечном итоге заставляет ось вращения двигаться. это главное Причина, вызывающая износ и вибрацию в машинах с вращающимися частями. Но в некоторых особых случаях может выполняться следующее условие, так что векторы углового момента и скорости показывают одно и то же направление:
, где I = эквивалентный скалярный момент инерции
тело вокруг оси вращения. Любая ось вращения тела, которая достаточна [3], называется главной осью .
[3] в основном говорит, что инерция тензор можно заменить одним скалярным моментом инерции, когда ось вращения главная ось. Топ Диагонализация тензора инерции Из [3]:
Или [4] можно упростить до
, где 1 = единичная матрица. I , показанное в [5], называется собственным значением, а w — собственным вектором. [5] — собственное значение уравнение. Чтобы [5] имело нетривиальное решение, определитель коэффициентов должен исчезнуть:
[6] ведет к светскому уравнение , которое в основном является кубическим, дает три корня (собственные значения): я 1 , I 2 и I 3 .
Когда собственные значения известны, можно вычислить главные оси. Пусть
, где n = единичный вектор главной оси, таким образом,
Из [4] и [8]:
Для каждого собственного значения можно вычислить соответствующее n x , n y и n z из [9] & [10]. Следует обратить внимание на направление собственный вектор в этом процессе. При анализе движения можно получить главные моменты инерции
от инерционных свойств сегментов тела. Топ
Кинетическая энергия вращения | безграничная физика |Кинетическая энергия вращения: работа, энергия и мощностьКинетическая энергия вращения представляет собой кинетическую энергию, обусловленную вращением объекта, и является частью его полной кинетической энергии. Цели обученияВыразите кинетическую энергию вращения как функцию угловой скорости и момента инерции и свяжите ее с полной кинетической энергией 9{2}Эротационное=21Iω2, гдеω\omegaω — угловая скорость, аI\text{I}I — момент инерции вокруг оси вращения.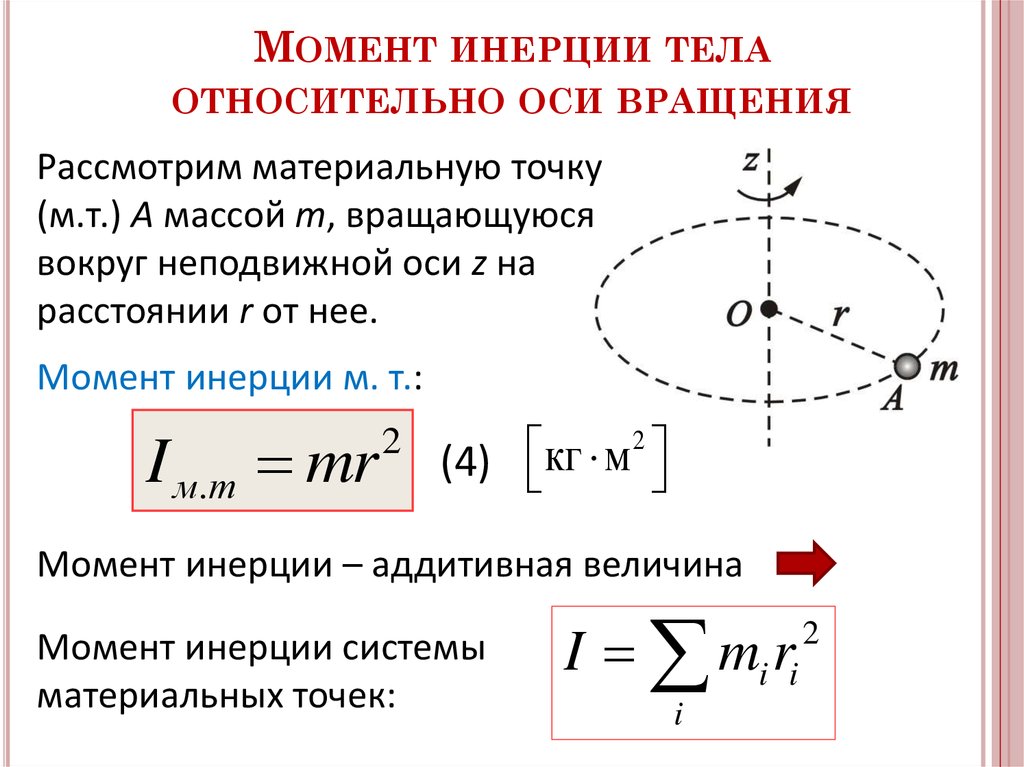 W=τθ\text{W} = \tau \thetaW=τθ .P=τω\text{P} = \tau \omegaP=τω .Ключевые термины
Кинетическая энергия вращения — это кинетическая энергия, обусловленная вращением объекта и являющаяся частью его общей кинетической энергии. Рассмотрение энергии вращения отдельно вокруг оси вращения объекта дает следующую зависимость от момента инерции объекта: Кинетическая энергия вращения : Предметы, которые катятся без скольжения, имеют некоторую часть своей энергии как поступательную кинетическую, а остальную часть как вращательная кинетика. Отношение зависит от момента инерции объекта, который катится. 9{2}Erotational=21Iω2 , , где ω\omegaω — угловая скорость, а I\text{I}I — момент инерции вокруг оси вращения. Механическая работа, приложенная во время вращения, равна крутящему моменту ( τ\tauτ ), умноженному на угол поворота ( θ\thetaθ ): W=τθ\text{W} = \tau \thetaW= τθ . Мгновенная мощность тела с угловым ускорением равна произведению крутящего момента на угловую скорость: 9{2}Etranslational=21mv2 . Во вращающейся системе момент инерции играет роль массы, а угловая скорость — линейной скорости. В качестве примера рассчитаем кинетическую энергию вращения Земли (анимировано на рис. 1). Поскольку у Земли период около 23,93 часа, она имеет угловую скорость 7,29×10 −5 рад/с. Земля имеет момент инерции I = 8,04×10 37 кг·м2. Следовательно, он имеет кинетическую энергию вращения 2,138×10 29 J. Вращение Земли : Вращение Земли является ярким примером кинетической энергии вращения. Это можно частично использовать с помощью приливной энергии. Дополнительное трение двух глобальных приливных волн создает энергию физическим образом, бесконечно замедляя угловую скорость Земли. Благодаря сохранению углового момента этот процесс передает угловой момент орбитальному движению Луны, увеличивая ее расстояние от Земли и период обращения. Момент инерцииМомент инерции — это свойство массы, которое измеряет ее сопротивление ускорению вращения вокруг одной или нескольких осей. Цели обученияОпределите свойство массы, описываемое моментом инерции Ключевые выводыКлючевые моменты
Ключевые термины
Момент инерцииМомент инерции — это свойство распределения массы в пространстве, которое измеряет сопротивление массы ускорению вращения вокруг одной или нескольких осей. Первый закон Ньютона, описывающий инерцию тела при прямолинейном движении, можно распространить на инерцию тела, вращающегося вокруг оси, используя момент инерции. То есть объект, вращающийся с постоянной угловой скоростью, будет продолжать вращаться, если на него не действует внешний крутящий момент. Таким образом, момент инерции играет ту же роль в динамике вращения, что и масса в линейной динамике: он описывает взаимосвязь между угловым моментом и угловой скоростью, а также крутящим моментом и угловым ускорением. Момент инерции : Краткое введение в момент инерции (вращательная инерция) для студентов, изучающих физику. Момент инерции I объекта можно определить как сумму mr 2 для всех точечных масс, из которых он состоит, где m — масса, r — расстояние массы от центра масс . Математически это можно выразить так: I = ∑mr 2 . Здесь I аналогично 92. Вся масса m находится на расстоянии r от центра. Момент инерции также зависит от оси, вокруг которой вы вращаете объект. Объекты обычно вращаются вокруг своего центра масс, но их можно заставить вращаться вокруг любой оси. Момент инерции в случае вращения вокруг оси, отличной от центра масс, определяется теоремой о параллельных осях. Теорема утверждает, что момент инерции тела, вращающегося вокруг другой оси, параллельной оси, проходящей через центр масс, равен 92Icm+mr2 , где r — теперь расстояние между двумя осями, а Icm\text{I}_{\text{cm}}Icm — момент инерции при вращении вокруг центра масс, который вы научились считать в предыдущем абзаце. Общее соотношение между крутящим моментом, моментом инерции и угловым ускорением: net τ = I α или α = (net τ)/ I. Net τ — это суммарный крутящий момент от всех сил относительно выбранная ось. Такие крутящие моменты бывают положительными или отрицательными и складываются как обычные числа. Соотношение в τ = Iα является вращательным аналогом второго закона Ньютона и очень применимо. Это уравнение действительно справедливо для любого крутящего момента, приложенного к любому объекту и относительно любой оси. Как и следовало ожидать, чем больше крутящий момент, тем больше угловое ускорение. Например, чем сильнее ребенок толкает карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением состоит в том, что чем больше момент инерции, тем меньше угловое ускорение. Момент инерции зависит не только от массы объекта, но и от распределения его массы относительно оси, вокруг которой он вращается. Момент инерции карусели : Отец толкает игровую карусель за ее край и перпендикулярно ее радиусу для достижения максимального крутящего момента. Лицензии и атрибуцииКонтент под лицензией CC, совместно используемый ранее
Лицензионный контент CC, конкретное указание авторства
|


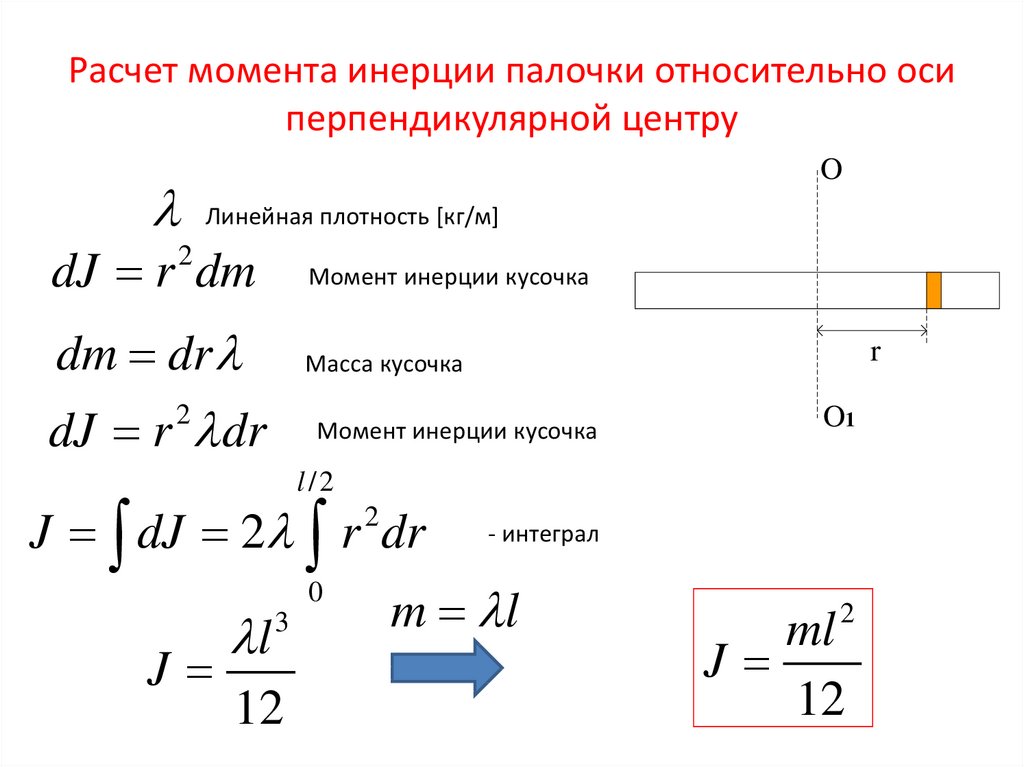 е. является вектором, направленным по оси вращения в ту сторону, откуда вращение наблюдается против часовой стрелки. Различают среднюю угловую скорость, измеряемую в течение нескольких оборотов, и мгновенную угловую скорость тела в данный момент.
е. является вектором, направленным по оси вращения в ту сторону, откуда вращение наблюдается против часовой стрелки. Различают среднюю угловую скорость, измеряемую в течение нескольких оборотов, и мгновенную угловую скорость тела в данный момент.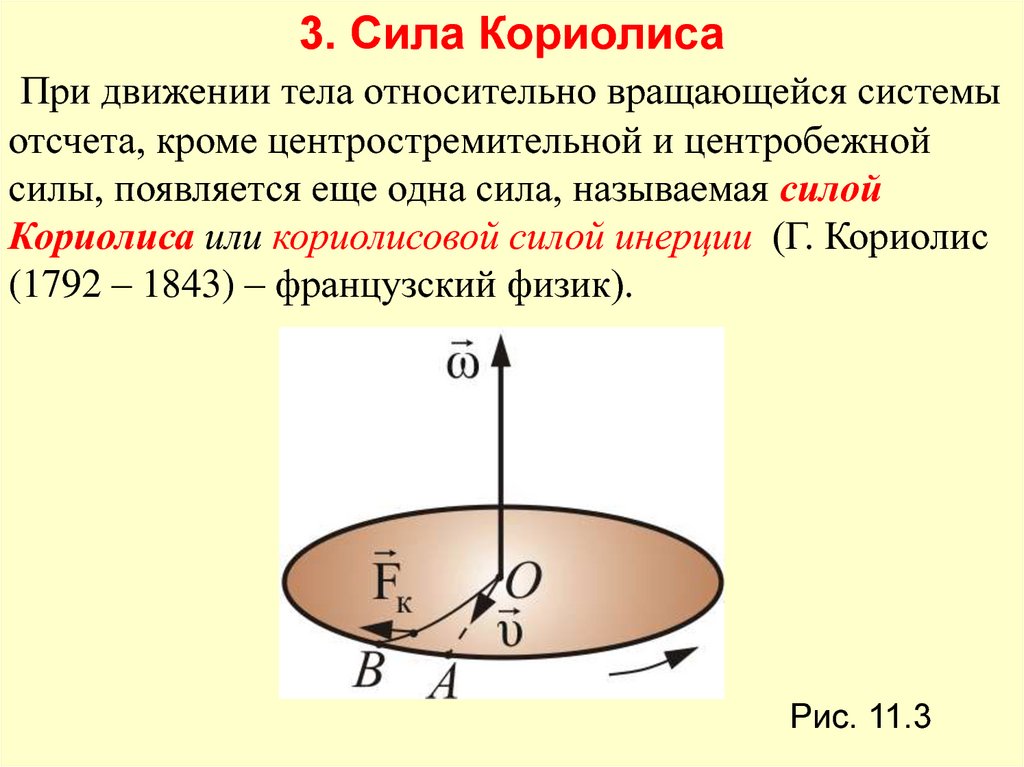 Оно равно:
Оно равно:
 При хорошем выполнении пируэта эти силы совпадают с осью вращения, поэтому не создают моментов сил относительно оси.
При хорошем выполнении пируэта эти силы совпадают с осью вращения, поэтому не создают моментов сил относительно оси. С этой точки зрения выгодны опора на переднюю треть конька без касания льда зубцами и отсутствие так называемого скобления ребром конька о лед. Наименьшее сопротивление оказывается в случае, если конец опорной ноги во время вращения выполняет петли небольшого размера (3—5 см).
С этой точки зрения выгодны опора на переднюю треть конька без касания льда зубцами и отсутствие так называемого скобления ребром конька о лед. Наименьшее сопротивление оказывается в случае, если конец опорной ноги во время вращения выполняет петли небольшого размера (3—5 см). 21, а). И) формулы видно, что величина этих сил прямо пропорциональна массе точки т, квадрату угловой скорости w и расстоянию r точки от оси вращения.
21, а). И) формулы видно, что величина этих сил прямо пропорциональна массе точки т, квадрату угловой скорости w и расстоянию r точки от оси вращения. е. не являются причиной изменений скорости вращения. Следовательно, изменение скорости вращения вызывают силы внутренние —группировки и разгруппировки, т. е. силы активного действия, обусловленные мышечной деятельностью человека.
е. не являются причиной изменений скорости вращения. Следовательно, изменение скорости вращения вызывают силы внутренние —группировки и разгруппировки, т. е. силы активного действия, обусловленные мышечной деятельностью человека. е. звенья тела, участвующие в относительном движении, приобретут отрицательное ускорение (кориолисово). Иными словами —ускорение, направленное против вращения. Так-как всякая сила инерции всегда направлена в сторону, противоположную ускорению, то силы инерции Кориолиса будут направлены по ходу вращения. Они приложены к частям тела, выполняющим группировку, направлены в сторону вращения и увеличивают его угловую скорость.
е. звенья тела, участвующие в относительном движении, приобретут отрицательное ускорение (кориолисово). Иными словами —ускорение, направленное против вращения. Так-как всякая сила инерции всегда направлена в сторону, противоположную ускорению, то силы инерции Кориолиса будут направлены по ходу вращения. Они приложены к частям тела, выполняющим группировку, направлены в сторону вращения и увеличивают его угловую скорость. Величина этих сил определяется по формуле:
Величина этих сил определяется по формуле: ц. т., начинает вращаться вокруг вертикальной оси z2 с угловой скоростью (рис. 24). Такое движение оси вращающегося тела называют прецессией, а угловую скорость вращательного движения оси — угловой скоростью прецессии. Угловая скорость прецессии может быть определена из следующего выражения:
ц. т., начинает вращаться вокруг вертикальной оси z2 с угловой скоростью (рис. 24). Такое движение оси вращающегося тела называют прецессией, а угловую скорость вращательного движения оси — угловой скоростью прецессии. Угловая скорость прецессии может быть определена из следующего выражения: Отсюда вытекает важный практический вывод: чем больше скорость вращения тела фигуриста в пируэте, тем устойчивее положение оси вращения.
Отсюда вытекает важный практический вывод: чем больше скорость вращения тела фигуриста в пируэте, тем устойчивее положение оси вращения. Дру-гими словами, прецессия не обладает инерцией.
Дру-гими словами, прецессия не обладает инерцией. При выполнении данного элемента отмечено заметное уменьшение частоты сердечных сокращений —6—12 уд/мин по сравнению с исходным — фоновым.
При выполнении данного элемента отмечено заметное уменьшение частоты сердечных сокращений —6—12 уд/мин по сравнению с исходным — фоновым. Б. Гандельсмана, позволяют предположить более сложную природу такого явления. Не отрицая возможности влияния центробежных сил на характер передвижения масс крови, хочется обратить внимание на два обстоятельства. Вращение в ласточке является пируэтом, в котором, пожалуй, в наибольшей степени выражен статический компонент движения. Вот почему энергетика этого упражнения весьма низкая. Кроме того, характер въезда во вращение и выезда из него не связан с необходимостью глубокого приседания и подъема, как в волчке, или группировки, как во вращении винт. Это также свидетельствует о наиболее низкой энергетической стоимости вращения в простой ласточке. Таким образом, можно предположить, что одной из причин урежения сердечного ритма при вращении в простой ласточке является именно низкая энергетика этого упражнения—более низкая, чем энергетика комплекса различных движений, при которых измеряется фоновый пульс.
Б. Гандельсмана, позволяют предположить более сложную природу такого явления. Не отрицая возможности влияния центробежных сил на характер передвижения масс крови, хочется обратить внимание на два обстоятельства. Вращение в ласточке является пируэтом, в котором, пожалуй, в наибольшей степени выражен статический компонент движения. Вот почему энергетика этого упражнения весьма низкая. Кроме того, характер въезда во вращение и выезда из него не связан с необходимостью глубокого приседания и подъема, как в волчке, или группировки, как во вращении винт. Это также свидетельствует о наиболее низкой энергетической стоимости вращения в простой ласточке. Таким образом, можно предположить, что одной из причин урежения сердечного ритма при вращении в простой ласточке является именно низкая энергетика этого упражнения—более низкая, чем энергетика комплекса различных движений, при которых измеряется фоновый пульс.
 Такими движениями являются опорные вращения — пируэты. Они разнообразят произвольную программу, позволяют спортсмену продемонстрировать способность сохранять равновесие в сложной позиции при быстром вращении.
Такими движениями являются опорные вращения — пируэты. Они разнообразят произвольную программу, позволяют спортсмену продемонстрировать способность сохранять равновесие в сложной позиции при быстром вращении. Поэтому здесь указывают лишь сторону вращения. В произвольных программах сейчас, как правило, встречаются сложные пируэты, состоящие из комбинаций перечисленных пируэтов.
Поэтому здесь указывают лишь сторону вращения. В произвольных программах сейчас, как правило, встречаются сложные пируэты, состоящие из комбинаций перечисленных пируэтов. След, оставляемый коньком при въезде, представляет собой кривую с плавно меняющейся кривизной. Выполняют въезд на согнутой ноге и не выпрямляют ее до тех пор, пока не возникнет устойчивое вращение.
След, оставляемый коньком при въезде, представляет собой кривую с плавно меняющейся кривизной. Выполняют въезд на согнутой ноге и не выпрямляют ее до тех пор, пока не возникнет устойчивое вращение. Мах, т. е. выведение рук и ноги вперед, следует начинать только тогда, когда дуга достигнет максимальной кривизны.
Мах, т. е. выведение рук и ноги вперед, следует начинать только тогда, когда дуга достигнет максимальной кривизны. Малейшая погрешность, допускаемая на протяжении пяти, шести и более оборотов, портит впечатление.
Малейшая погрешность, допускаемая на протяжении пяти, шести и более оборотов, портит впечатление.
 В этом пируэте скорость вращения наибольшая—до 4 и более оборотов в секунду.
В этом пируэте скорость вращения наибольшая—до 4 и более оборотов в секунду. Их выполняют со значительным прогибом назад или в сторону и с откинутой головой. Вращение с необычным положением головы усложняет пространственную ориентировку, вызывает нарушение координации движений, порой сопровождается головокружением. В то же время заклоны —очень ценное упражнение для совершенствования равновесия.
Их выполняют со значительным прогибом назад или в сторону и с откинутой головой. Вращение с необычным положением головы усложняет пространственную ориентировку, вызывает нарушение координации движений, порой сопровождается головокружением. В то же время заклоны —очень ценное упражнение для совершенствования равновесия.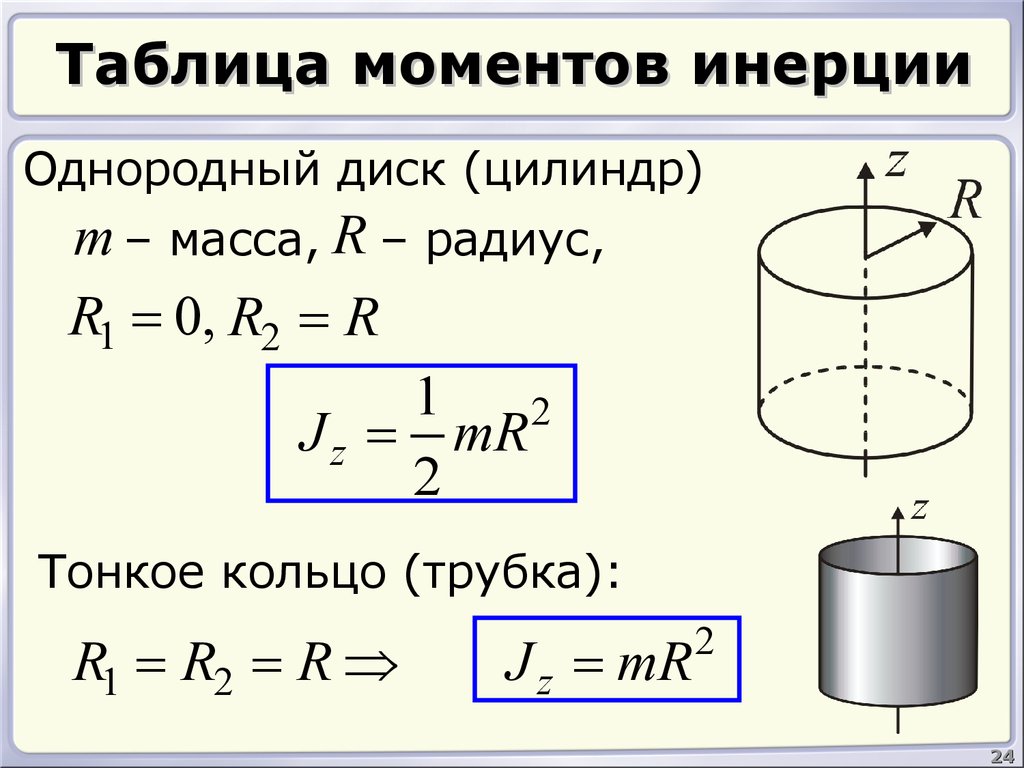 Исключительно ценными для дальнейшего овладения прыжками являются пируэты назад. Их выполняют в тех же позах, что и пируэты вперед. Но есть у них некоторые особенности. Так, несмотря на то, что направление общего вращения тела в пируэте назад и вперед может быть одно и то же, ощущения, испытываемые фигуристом, различны. Пируэты назад наиболее точно имитируют движения тела в полете при выполнении прыжков, поэтому важны как подготовительные упражнения. Они красивы; включают их в различные комбинации.
Исключительно ценными для дальнейшего овладения прыжками являются пируэты назад. Их выполняют в тех же позах, что и пируэты вперед. Но есть у них некоторые особенности. Так, несмотря на то, что направление общего вращения тела в пируэте назад и вперед может быть одно и то же, ощущения, испытываемые фигуристом, различны. Пируэты назад наиболее точно имитируют движения тела в полете при выполнении прыжков, поэтому важны как подготовительные упражнения. Они красивы; включают их в различные комбинации.
 Для совершенствования общей выносливости фигуриста к вращательным нагрузкам весьма эффективны специальные тренажеры в виде вращающихся платформ с электроприводом и плавной регулировкой скорости вращения в пределах от ноля до 5 и более оборотов в секунду.
Для совершенствования общей выносливости фигуриста к вращательным нагрузкам весьма эффективны специальные тренажеры в виде вращающихся платформ с электроприводом и плавной регулировкой скорости вращения в пределах от ноля до 5 и более оборотов в секунду.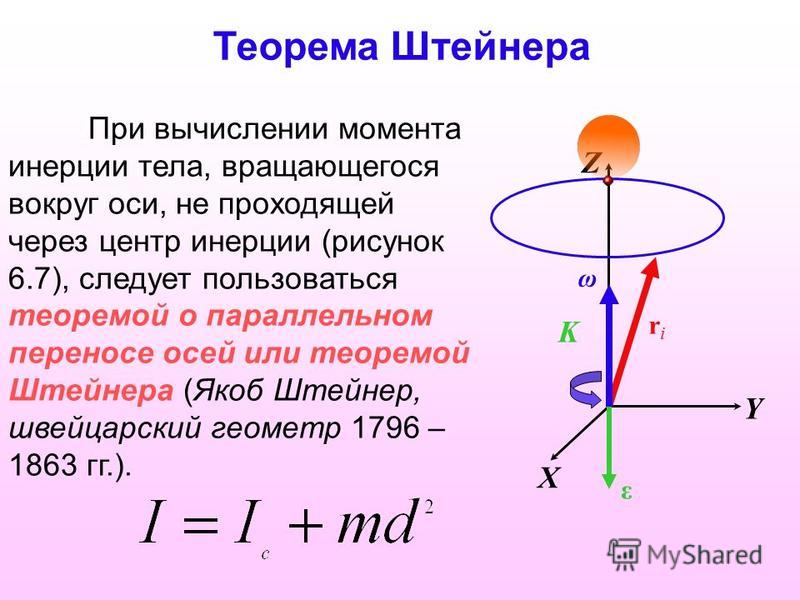 Практика показала, что у одних фигуристов принятие требуемой позы происходит с участием зрительного анализатора, выключение зрения у них нарушает точность позы; у других же это происходит практически без участия зрительного анализатора. Сравнение стабильности и качества выполнения вращений показало, что обеспечение позы в основном с помощью двигательного анализатора более совершенно.
Практика показала, что у одних фигуристов принятие требуемой позы происходит с участием зрительного анализатора, выключение зрения у них нарушает точность позы; у других же это происходит практически без участия зрительного анализатора. Сравнение стабильности и качества выполнения вращений показало, что обеспечение позы в основном с помощью двигательного анализатора более совершенно. Сила гравитационного поля зависит от массы объекта, создающего поле, а также от квадрата расстояния от этого объекта. Гравитационное поле Луны составляет всего около 1/6 земного. Таким образом, в то время как шар для боулинга имеет ту же массу на Земле, что и на Луне (и, следовательно, его скорость было бы так же трудно изменить в обоих местах), вес шара на Луне будет составлять 1/6 его веса. на земле.]
Сила гравитационного поля зависит от массы объекта, создающего поле, а также от квадрата расстояния от этого объекта. Гравитационное поле Луны составляет всего около 1/6 земного. Таким образом, в то время как шар для боулинга имеет ту же массу на Земле, что и на Луне (и, следовательно, его скорость было бы так же трудно изменить в обоих местах), вес шара на Луне будет составлять 1/6 его веса. на земле.]  MOI точечной массы является произведением массы и квадрата расстояния от точки вращения:
MOI точечной массы является произведением массы и квадрата расстояния от точки вращения: Ненулевые диагональные члены тензора инерции
показанные в [2], называются основные моменты
инерция объекта.
Ненулевые диагональные члены тензора инерции
показанные в [2], называются основные моменты
инерция объекта. Есть группа
главных осей (теоретически 3) в трехмерном теле. Например, есть
три перпендикулярные главные оси для системы, показанной на рис. 1.
Есть группа
главных осей (теоретически 3) в трехмерном теле. Например, есть
три перпендикулярные главные оси для системы, показанной на рис. 1. Каждому корню соответствует момент
инерция относительно главной оси. На самом деле три корня являются главными моментами
инерция твердого тела, введенная в [2]:
Каждому корню соответствует момент
инерция относительно главной оси. На самом деле три корня являются главными моментами
инерция твердого тела, введенная в [2]: я 1 , я 2 & I 3 каждого сегмента общеизвестны. Данные доступны
в виде отношений радиусов инерции (отношение радиуса инерции к
длина сегмента), уравнения регрессии и коэффициенты масштабирования. Можно также вычислить
главные моменты инерции сегментов тела путем моделирования с использованием некоторых геометрических
формы. См. Индивидуальную оценку BSP для
Детали.
я 1 , я 2 & I 3 каждого сегмента общеизвестны. Данные доступны
в виде отношений радиусов инерции (отношение радиуса инерции к
длина сегмента), уравнения регрессии и коэффициенты масштабирования. Можно также вычислить
главные моменты инерции сегментов тела путем моделирования с использованием некоторых геометрических
формы. См. Индивидуальную оценку BSP для
Детали.





 Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять на внешнем краю.
Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять на внешнем краю.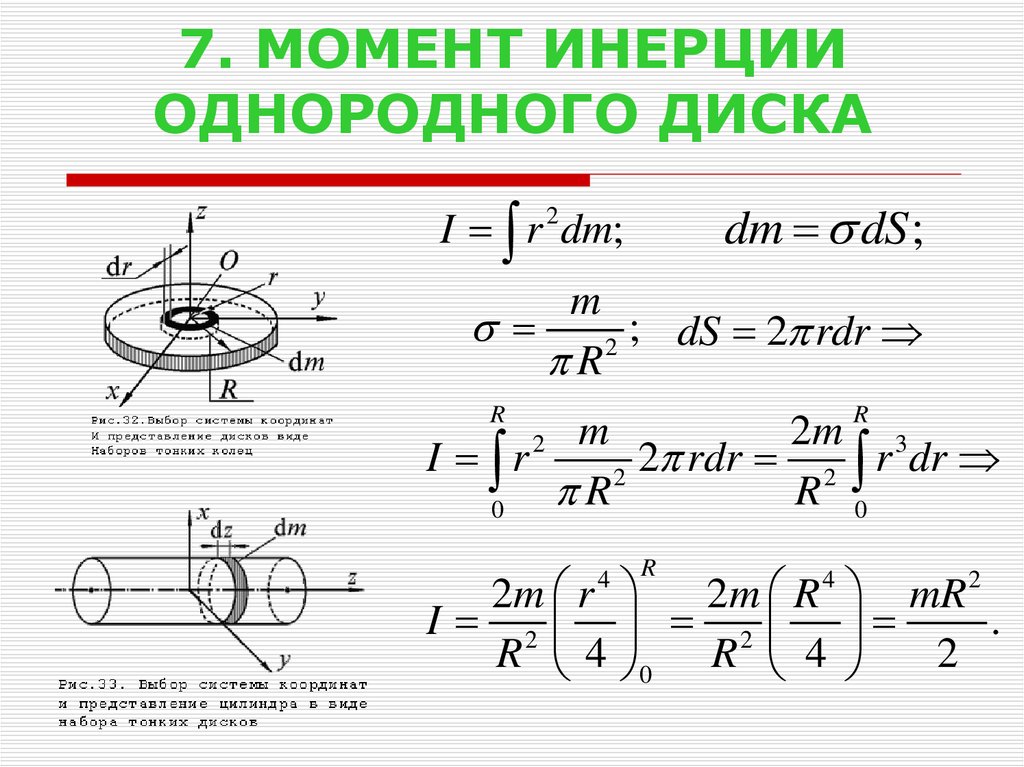 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike