Урок 4. равномерное движение точки по окружности – Физика – 10 класс
Физика, 10 класс
Урок 04.Равномерное движение точки по окружности
Перечень вопросов, рассматриваемых на уроке:
- Равномерное движение точки по окружности и его характеристики.
- Центростремительное ускорение.
Глоссарий по теме
Криволинейное движение – это движение по дугам окружностей разных радиусов.
Ускорение – это векторная величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло, при ∆t → 0
Равномерное движение точки по окружности – движение точки с постоянной по модулю скоростью (ν = const) по траектории, представляющей собой окружность.
Ключевые слова
Криволинейное движение; движение по окружности; скорость; радиус кривизны; изменение скорости; центростремительное ускорение.
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016. С.55-56
Марон Е.А., Марон А.Е. Сборник качественных задач по физике. М., Просвещение, 2006
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.-С.20-22
Открытые электронные ресурсы:
http://kvant.mccme.ru/1986/11/kinematika_vrashchatelnogo_dvi.htm
Теоретический материал для самостоятельного изучения
1. Мы уже знакомы с равноускоренным движением. Как же меняются скорость и ускорение при криволинейном движении? Сегодня рассмотрим равномерное движение по окружности, узнаем, что такое центростремительное ускорение.
Если траектория движения тела прямая линия, то движение прямолинейное; если траектория кривая линия – криволинейное движение. Напомним, что траектория – это линия, вдоль которой двигалось тело.
При изучении равноускоренного движения мы заметили, что в некоторых случаях тело движется по прямой, например свободное падение тел, а в некоторых по кривой – тело, брошенное под углом к горизонту.
Рассмотрим движение тела, брошенного под углом к горизонту. Траекторией является парабола.
Возьмем разные точки на линии и нарисуем векторы скорости . Вектор скорости направлен по касательной, а ускорение свободного падения направлен вниз.
Векторы и не лежат на одной прямой, угол между ними не равен нулю.
Это естественно, так как, если ускорение образует угол со скоростью, то изменение скорости направлено не так, как скорость. Это приводит к изменению направления скорости. Изменение скорости направлено как ускорение. Скорость через некоторый промежуток времени образует некоторый угол с Итак, сформулируем первый вывод: если угол между векторами скорости и ускорения не равен нулю, то движение будет криволинейным.
2.Может ли быть движение одновременно равномерным и криволинейным? Да, например, движение по окружности.
Равномерное движение точки по окружности – это движение точки с постоянной по модулю скоростью (
Сформулируем второй важный вывод: любое криволинейное движение является движением с ускорением, потому что меняется направление вектора скорости.
Решим задачу: найдем ускорение тела, равномерно движущегося по окружности.
Рассмотрим равномерное движение тела по окружности с центром в точке О. В какой-то момент времени, скорость тела в точке А была
Модули скоростей равны:
но вектора скоростей не равны.
Поэтому построим вектор для тела, движущегося по окружности. Перенесем вектор в начало вектораи найдем разность векторов.
направлен в сторону.
Вспомним, что векторнаправлен по касательной, а касательная перпендикулярна радиусу окружности. Проведем радиусы к обеим точкам и обозначим угол между ними через ?.
Что можно сказать об угле между векторами ? Он равен малому углу, как углы с взаимно перпендикулярными сторонами.
Рассмотрим равнобедренный треугольник со сторонами , . Углы у основания равны.
Если угол φ стремится к нулю, то углы у основания совпадут и станут равными 900
Вектор будет перпендикулярен вектору в пределе, а значит вектор ускорения тоже перпендикулярен т.е направлен по радиусу к центру окружности. Поэтому часто его называют центростремительным ускорением
Теперь следующая задача: как найти модуль вектора ускорения. Давайте рассмотрим два треугольника: треугольник, образованный векторами и треугольник, образованный радиусами и хордой. У этих треугольников углы при вершинах равны, они равнобедренные. Треугольники подобны и, следовательно, выполняются соотношения подобия.
Промежуток времени мал, поэтому очень мал и угол при вершине, в пределе он стремится к нулю. Тогда можно сказать, что длина хорды s равна длине дуги АВ при
Длина дуги АВ это путь, пройденный точкой от А до В,
тогда запишем:
Умножим наи получим:
В левой части мы получили отношение изменения скорости за некоторый промежуток времени к этому промежутку времени т.е. ускорение:
Равномерное движение точки по окружности является движением с переменным ускорением и переменной скоростью. Модули скорости и ускорения остаются постоянными
- Криволинейное движение – это движение по дугам окружностей разных радиусов
А если меняется радиус, то меняется и центростремительное ускорение. Чем меньше радиус, тем больше ускорение при одинаковой скорости.
Всегда при равномерном криволинейном движении вектор ускорения перпендикулярен вектору скорости, поэтому центростремительное ускорение иногда называют нормальным ускорением, от слова нормаль, т. е. перпендикуляр.
е. перпендикуляр.
Основные выводы:
– движение криволинейное, так как траекторией является окружность;
– движение равномерное, так как модуль скорости не меняется;
– вектор скорости направлен по касательной к окружности;
-вектор ускорения направлен к центру окружности;
– модуль центростремительного ускорения равен:
Примеры и разбор решения заданий
1. Велосипедист движется по закруглению дороги радиусом 50 м со скоростью 36 км/ч. С каким ускорением он проходит закругление?
При движении по окружности линейная скорость и центростремительное ускорение связаны соотношением
где R = 50 м; υ= км/ч = 10 м/с.
Тогда ac = (10 м/с)2 / 50 м = 2 м/с2.
Ответ: 2 м/с2
2. Две материальные точки движутся по окружностям радиусами R1
Дано:
R1 =10см = 0,10 м
R2 = 30см = 0,30 м
Найти –
Задано два объекта:
1) материальная точка, которая движется по окружности R1;
2) материальная точка, которая движется по окружности R2.
При движении по окружности центростремительное ускорение и линейная скорость связаны соотношением
Для тела 1 уравнение (1) примет вид:
для тела 2:
Тогда
Центростремительное ускорение тела (2) меньше ускорения тела (1) в 3 раза.
ускорение
им. Н. Г. ЧЕРНЫШЕВСКОГО
Реферат на тему:
«Ускорение».
Выполнил:
Студент I курса
физического
факультета
121 группы
Васюнин
Н.
Преподаватель:
Шаповалов А.С.
Саратов
2014
Содержание:
Ускорение
Рабочая формула
Ускорение точки при прямолинейном движении
Ускорение точки при движении по окружности
Ускорение точки при движении по кривой
Единицы измерения ускорения
Примеры ускорений
1.Ускоре́ние— быстрота изменения скорости, то есть первая производная от скорости по времени, векторная величина, показывающая, на сколько изменяется вектор скорости v⃗ тела при его движении за единицу времени.
2. a⃗ =dv⃗/ dt.
3.Ускорение точки при прямолинейном движении Важным частным случаем движения с ускорением является прямолинейное движение, когда ускорение в любой момент времени коллинеарно скорости (например, случай падения тела с вертикальной начальной скоростью). В случае прямолинейного движения можно выбрать одну из координатных осей вдоль направления движения и заменить радиус-вектор и векторы ускорения и скорости на скаляры. При постоянном ускорении из приведённых выше формул вытекает, что v2=u2+2as. Здесь u и v — начальная и конечная скорость тела, a — его ускорение, s — пройденный телом путь.
4.
Ускорение
точки при движении по окружности
Равномерное
движение по окружности. Ускорение всегда
перпендикулярно скорости и направлено
к центру.
Пример неравномерного
движения по окружности (математический
маятник). Ускорение, складывающееся из
тангенциальной и центростремительной
компонент, в разные моменты изменяется
от полностью касательного до полностью
нормального к траектории.
Вектор
ускорения
a = dv/ dt
при движении точки
по окружности можно разложить на два
слагаемых (компоненты):
a = a τ+a
n. Тангенциальное или касательное
ускорение a направлено по касательной
к траектории. Является составляющей
вектора ускорения a, коллинеарной вектору
мгновенной скорости. Характеризует
изменение скорости по модулю.
a τ=v |v
|d|v |dt.
Центростремительное или нормальное
ускорение a возникает всегда при движении
точки не только по окружности, но и по
любой траектории с ненулевой кривизной.
Является составляющей вектора ускорения
a, перпендикулярной вектору мгновенной
скорости. Характеризует изменение
скорости по направлению. Вектор
нормального ускорения всегда направлен
к мгновенной оси вращения,
a n=|v |d/dtv |v
|,
а модуль равен
|a n|=ω2r=v2r,
где ω —
угловая скорость относительно центра
вращения, а r — радиус окружности.
Кроме
этих двух компонент, используется также
понятие угловое ускорение, показывающее,
на сколько изменилась угловая скорость
за единицу времени, и, аналогично
линейному ускорению, вычисляемое
следующим образом:
ε =dω dt.
Направление
вектора здесь показывает, увеличивается
или уменьшается модуль скорости. Если
векторы углового ускорения и угловой
скорости сонаправлены (или хотя бы их
скалярное произведение положительно),
значение скорости растёт, и наоборот.
В
частном случае равномерного движения
по окружности векторы углового ускорения
и тангенциального ускорения равны нулю,
а центростремительное ускорение
постоянно по модулю.
Тангенциальное или касательное
ускорение a направлено по касательной
к траектории. Является составляющей
вектора ускорения a, коллинеарной вектору
мгновенной скорости. Характеризует
изменение скорости по модулю.
a τ=v |v
|d|v |dt.
Центростремительное или нормальное
ускорение a возникает всегда при движении
точки не только по окружности, но и по
любой траектории с ненулевой кривизной.
Является составляющей вектора ускорения
a, перпендикулярной вектору мгновенной
скорости. Характеризует изменение
скорости по направлению. Вектор
нормального ускорения всегда направлен
к мгновенной оси вращения,
a n=|v |d/dtv |v
|,
а модуль равен
|a n|=ω2r=v2r,
где ω —
угловая скорость относительно центра
вращения, а r — радиус окружности.
Кроме
этих двух компонент, используется также
понятие угловое ускорение, показывающее,
на сколько изменилась угловая скорость
за единицу времени, и, аналогично
линейному ускорению, вычисляемое
следующим образом:
ε =dω dt.
Направление
вектора здесь показывает, увеличивается
или уменьшается модуль скорости. Если
векторы углового ускорения и угловой
скорости сонаправлены (или хотя бы их
скалярное произведение положительно),
значение скорости растёт, и наоборот.
В
частном случае равномерного движения
по окружности векторы углового ускорения
и тангенциального ускорения равны нулю,
а центростремительное ускорение
постоянно по модулю.
5.Ускорение
точки при движении по кривой
Разложение
ускорения по сопутствующему базису для
движения в плоскости.
Вектор ускорения
a можно разложить по сопутствующему
базису {τ ,n ,b }:
a =aττ +ann +abb =dvdtτ +v2Rn +abb
,
где
v — величина скорости,τ =v /|v | — единичный
касательный к траектории вектор,
направленный вдоль скорости,n — орт
главной нормали к траектории, который
можно определить как единичный вектор
в направлении dτ /dl,b — орт бинормали к
траектории, перпендикулярный одновременно
ортам τ и n (то есть ортогональный к
мгновенной плоскости траектории),R —
радиус кривизны траектории.
Слагаемое
abb , называемое бинормальным ускорением,
всегда равно нулю. Это можно считать
прямым следствием определения векторов
n ,b : можно сказать, что они выбираются
именно так, чтобы первый всегда совпадал
с нормальным ускорением, второй же был
ортогонален первому.
Векторы aττ и ann
называются касательным (тангенциальным)
и нормальным ускорениями соответственно.
Итак,
учитывая сказанное выше, вектор ускорения
при движении по любой траектории можно
записать как:
a =aττ +ann =dvdtτ +v2Rn .
Это можно считать
прямым следствием определения векторов
n ,b : можно сказать, что они выбираются
именно так, чтобы первый всегда совпадал
с нормальным ускорением, второй же был
ортогонален первому.
Векторы aττ и ann
называются касательным (тангенциальным)
и нормальным ускорениями соответственно.
Итак,
учитывая сказанное выше, вектор ускорения
при движении по любой траектории можно
записать как:
a =aττ +ann =dvdtτ +v2Rn .
6. Единицы измерения ускорения метр на секунду в квадрате (метр в секунду за секунду), м/с², производная единица системы СИ; сантиметр на секунду в квадрате (сантиметр в секунду за секунду), см/с², производная единица системы СГС, имеет также собственное наименование гал, или галилео; g (произносится «же»), стандартное ускорение свободного падения на поверхности Земли, равное по определению 9,80665 м/с². В технических расчётах, не требующих точности выше 2 %, часто используется приближение g ≈ 10 м/с². Преобразования между различными единицами ускорения м/с2 фут/с2 g
3
Российские и зарубежные ученые обсудили на базе НГАСУ (Сибстрин) вопросы экологии урбанизированных территорий 31 марта 2021 года на базе кафедры ЮНЕСКО Новосибирского государственного архитектурно-строительного университета (Сибстрин) состоялся англоязычный круглый стол «Природоохранные технологии урбанизированных территорий» в рамках XIV Международной научно-технической конференции «Актуальные вопросы архитектуры и строительства». Приветственное слово на английском языке прозвучало из уст ректора НГАСУ (Сибстрин), руководителя кафедры ЮНЕСКО Юрия Леонидовича Сколубовича и партнеров университета – профессора кафедры ЮНЕСКО Университета Белграда (Сербия) Марко Иветича, профессора, советника по международным вопросам ректора Коньянского технического университета (Турция) Эсры Йел. |
НГАСУ (Россия) и КазГАСА (Казахстан) проведут масштабный международный онлайн-форум по архитектуре, строительству и дизайну 15-16 апреля 2021 года Новосибирский государственный архитектурно-строительный университет (Сибстрин) и Казахская головная архитектурно-строительная академия (г. Алматы, Казахстан) проведут X Международный фестиваль архитектурно-строительных и дизайнерских школ Евразии. Фестиваль пройдет в дистанционном формате и соберет студентов, магистрантов и преподавателей ведущих архитектурно-строительных вузов евразийского континента. Планируется, что в нем примут участие представители России, Казахстана, Киргизии, Узбекистана, Таджикистана, Украины, Молдовы, Венгрии, Италии и других стран. В программе мероприятия – официальные церемонии открытия и закрытия X Международного фестиваля архитектурно-строительных и дизайнерских школ Евразии с участием почетных гостей и ректоров вузов, мастер-классы и вебинары по архитектуре, строительству и геодезии от экспертов… |
Команда НГАСУ (Сибстрин) стала лучшей на Региональном конкурсе по начертательной геометрии, инженерной и компьютерной графике 23 марта 2021 года на базе кафедры Инженерной и компьютерной графики НГАСУ (Сибстрин) в дистанционном режиме прошел XХVII Региональный конкурс по начертательной геометрии, инженерной и компьютерной графике. Региональный конкурс проводится ежегодно среди студентов вузов при поддержке компании «Аскон» – ведущего российского разработчика программного обеспечения систем автоматизированного проектирования. Конкурс проходит по трем номинациям: «Начертательная геометрия», «Инженерная графика» и «Компьютерная графика». В этом году на участие в нем зарегистрировалось 43 студента из НГАСУ (Сибстрин), НГТУ, НГПУ, СГУПСа (все – г. Новосибирск), СибГУ им. М.Ф. Решетнева (г. Красноярск), СФУ (г. Красноярск), ТИУ (г. Тюмень). |
Студентов приглашают на беговой онлайн-челлендж «Космический пульс России» С 12 по 25 апреля 2021 года пройдет Всероссийский онлайн-челлендж «Космический пульс России». Его цель – привлечь студенческую молодежь к систематическим занятиям спортом и занятием физкультурой на свежем воздухе. Беговой онлайн-челлендж посвящен Дню космонавтики, который отмечается 12 апреля. В забеге могут принять участие молодые люди от 16 до 35 лет. Число участников не ограничено, участие бесплатное. Турнир проводится в личном и командном зачетах в 5 номинациях: Космическая десятка – пробежка на 10 км; Бескрайняя Вселенная – на самую дальнюю пробежку; Выше звезд, где учитывается суммарный рейтинг; Большая медведица – командный рейтинг по количеству участников; Звездный экипаж… |
Физические основы механики
Представим себе материальную точку, движущуюся по некоторой криволинейной траектории . Запишем скорость в виде
и заметим, что вектор
— это единичный вектор, касательный к траектории и совпадающий по направлению с вектором скорости. Продифференцируем вектор скорости, записанный в данном представлении, и получим
Мы представили ускорение в виде двух слагаемых. Заметим прежде всего, что слагаемые ортогональны друг другу. Действительно, поскольку вектор — единичный, то
Дифференцируя это скалярное произведение, получаем
то есть
по свойству скалярного произведения.
Таким образом, мы разложили ускорение на сумму двух взаимно ортогональных составляющих, обозначем их и :
Обсудим физический смысл каждого слагаемого. Слагаемое
— это тангенциальное ускорение, которое характеризует быстроту изменения модуля скорости. Эта часть полного ускорения направлена либо по скорости, когда производная dv/dt > 0, то есть движение ускоренное, либо в сторону противоположную скорости, когда эта производная dv/dt < 0, то есть движение замедленное. Если движение равномерное dv/dt = 0, то есть скорость, если и меняется, то лишь по направлению, то тангенциальная часть ускорения равна нулю:
Эта часть полного ускорения направлена либо по скорости, когда производная dv/dt > 0, то есть движение ускоренное, либо в сторону противоположную скорости, когда эта производная dv/dt < 0, то есть движение замедленное. Если движение равномерное dv/dt = 0, то есть скорость, если и меняется, то лишь по направлению, то тангенциальная часть ускорения равна нулю:
Слагаемое
направлено по нормали к траектории — перпендикулярно касательной к траектории и называется нормальным ускорением. Если тангенциальное ускорение определяет скорость, с которой меняется модуль вектора скорости, то нормальное ускорение определяет скорость, с которой меняется направление вектора скорости.
Рис. 2.10. К определению кривизны траектории
Рассмотрим «достаточно гладкую», в остальном произвольную плоскую криволинейную траекторию. Плоскую, то есть все точки траектории лежат в некоторой плоскости, — исключительно для упрощения выкладок, получаемый в рамках этого предположения, результат годится и для любой «достаточно гладкой» пространственной кривой, чьи точки уложить в одну плоскость невозможно. Последнее обстоятельство мы здесь рассматривать не будем, оно строго доказывается методами аналитической геометрии. Слова «достаточно гладкая» означают, что кривая описывается непрерывной функцией, имеющей непрерывные первую и вторую производные. С точки зрения физических приложений, требование существования непрерывных первых двух производных фактически не является ограничением на форму траектории, так как практически всегда выполнено. Проще говоря, на траектории не должно быть “углов” типа показанного на рисунке 2.11.
Рис. 2.11.
Такую «гладкую» кривую на любом её бесконечно малом участке можно заменить (рис. 2.12) участком окружности некоторого радиуса. Радиус этой окружности, аппроксимирующей траекторию на её бесконечно малом участке в окрестности некоторой точки, принято называть радиусом кривизны траектории в этой точке.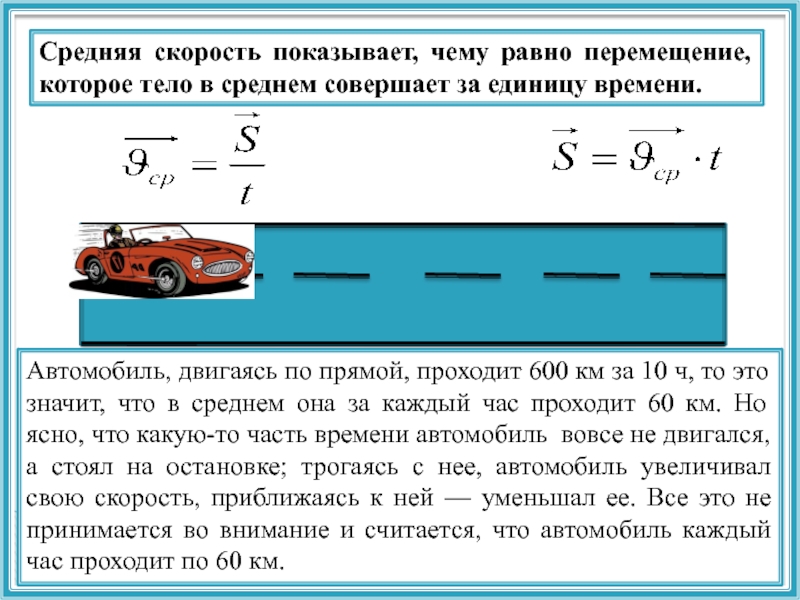 Центр этой окружности принято называть центром кривизны траектории в данной точке. Кривизной траектории называется величина C = 1/R. Подчеркнем, что радиус кривизны, как и центр кривизны траектории — её локальные характеристика: каждой точке траектории соответствует свой радиус кривизны и свой центр кривизны. Исключениями являются: 1) окружность, её радиус кривизны во всех её точках один и тот же и равен радиусу окружности, центр кривизны «один на всех» и совпадает с центром окружности, и 2) прямая, для любой точки прямой радиус кривизны бесконечен, а центр кривизны находится в бесконечно удаленной от прямой точке. Это легко понять: давайте увеличивать радиус окружности, чем больше радиус окружности, тем ближе любой её конечный участок к участку прямой. На равнине, лучше всего на пляже, с высоты человеческого роста до горизонта не более пяти километров, — в этих пределах Земля плоская.
Центр этой окружности принято называть центром кривизны траектории в данной точке. Кривизной траектории называется величина C = 1/R. Подчеркнем, что радиус кривизны, как и центр кривизны траектории — её локальные характеристика: каждой точке траектории соответствует свой радиус кривизны и свой центр кривизны. Исключениями являются: 1) окружность, её радиус кривизны во всех её точках один и тот же и равен радиусу окружности, центр кривизны «один на всех» и совпадает с центром окружности, и 2) прямая, для любой точки прямой радиус кривизны бесконечен, а центр кривизны находится в бесконечно удаленной от прямой точке. Это легко понять: давайте увеличивать радиус окружности, чем больше радиус окружности, тем ближе любой её конечный участок к участку прямой. На равнине, лучше всего на пляже, с высоты человеческого роста до горизонта не более пяти километров, — в этих пределах Земля плоская.
Рис. 2.12. К определению радиуса кривизны траектории
Вычислим модуль производной , входящей в выражение для нормального ускорения. Направлен вектор по нормали к траектории к центру к центру кривизны, что поясняет рис. 2.13.
Рис. 2.13. Графическое определение радиуса кривизны траектории
Для этого прежде всего перейдем от дифференцирования по времени к дифференцированию по «пути»: , имеем:
По определению производная кривизне кривой C, а величина ей обратная равна радиусу кривизны кривой R. Собирая всё вместе, для нормального ускорения окончательно получаем:
,
где нормаль перпендикулярна к касательной и всегда направлена к центру кривизны, см. рис. 11.
Приведем некоторое дополнительное пояснение к рисунку 11. Возьмем неподалеку от точки 1 точку 2. Построим в этих точках касательные единичные векторы 1 и 2. Перпендикуляры к этим касательным пересекутся в некоторой точке O2. Заметим, что для кривой, не являющейся окружностью, расстояния R1 и R2 будут немного отличаться друг от друга. Если теперь точку 2 приближать к точке 1, пересечение перпендикуляров O2 будет перемещаться вдоль прямой O21 и в пределе окажется в некоторой точке O1. Расстояния R1 и R2 будут стремиться к общему пределу R, равному радиусу кривизны, а точка O1 и будет центром кривизны для точки 1. Действительно, окружность радиусом R с центром в 0 проходит через точку 1 и касается траектории (так как радиус ортогонален орту 1). Кроме того, по построению бесконечно близкая точка 2 также лежит на этой окружности. Таким образом, построенная окружность действительно «сливается» с траекторией в точке 1.
Заметим, что для кривой, не являющейся окружностью, расстояния R1 и R2 будут немного отличаться друг от друга. Если теперь точку 2 приближать к точке 1, пересечение перпендикуляров O2 будет перемещаться вдоль прямой O21 и в пределе окажется в некоторой точке O1. Расстояния R1 и R2 будут стремиться к общему пределу R, равному радиусу кривизны, а точка O1 и будет центром кривизны для точки 1. Действительно, окружность радиусом R с центром в 0 проходит через точку 1 и касается траектории (так как радиус ортогонален орту 1). Кроме того, по построению бесконечно близкая точка 2 также лежит на этой окружности. Таким образом, построенная окружность действительно «сливается» с траекторией в точке 1.
Итак, в общем случае ускорение имеет две составляющие — тангенциальную
направленную вдоль касательной и определяющую скорость изменения модуля вектора скорости нормальную
направленную перпендикулярно скорости к центру кривизны траектории и пропорциональную угловой скорости вращения вектора скорости при движении частицы вдоль криволинейной траектории (рис. 2.14).
Рис. 2.14. Тангенциальное и нормальное ускорения при ускоренном криволинейном движении.
Действительно , где и есть угловая скорость вращения вектора скорости .
Полное ускорение
определяется по правилу параллелограмма. Модуль полного ускорения в соответствии с теоремой Пифагора равен
Выпишем без вывода формулы, связывающие радиус кривизны плоской траектории с координатами траектории. Если известна зависимость y = y(x), то
Если же траектория задана в параметрическом виде, x = x(t), y = y(t), то
Пример криволинейного движения с постоянным ускорением (тело, брошенное под углом к горизонту) приведен на следующем рисунке:
Рис. 2.15. Движение тела, брошенного под углом к горизонту
2.15. Движение тела, брошенного под углом к горизонту
Разгон
Как упоминалось ранее в Уроке 1, объект, движущийся равномерно по кругу, движется по кругу с постоянной или постоянной скоростью. Вектор скорости постоянен по величине, но меняется по направлению. Поскольку скорость такого движения постоянна, многие студенты ошибочно полагают, что ускорения нет. «В конце концов, – могут сказать они, – если бы я вел машину по кругу с постоянной скоростью 20 миль / ч, тогда скорость не уменьшалась и не увеличивалась, поэтому не должно быть ускорения.”В основе этого распространенного заблуждения студентов лежит неправильное представление о том, что ускорение связано со скоростью, а не со скоростью. Но факт в том, что ускоряющийся объект – это объект, который меняет свою скорость. А поскольку скорость – это вектор, который имеет как по величине, так и по направлению, изменение величины или направления представляет собой изменение скорости. По этой причине можно с уверенностью заключить, что объект, движущийся по кругу с постоянной скоростью, действительно ускоряется. Он ускоряется, потому что направление вектора скорости меняется.
Геометрический
Доказательство внутреннего ускоренияЧтобы понять это на более глубоком уровне, нам придется объединить определение ускорения с обзором некоторых основных векторных принципов. Напомним, из раздела 1 Физического класса, что ускорение как величина определялось как скорость, с которой изменяется скорость объекта. Таким образом, он рассчитывается с использованием следующего уравнения:
, где v i представляет начальную скорость, а v f представляет конечную скорость через некоторое время t .Числитель уравнения находится путем вычитания одного вектора ( v i ) из второго вектора ( v f ). Но сложение и вычитание векторов друг из друга выполняется иначе, чем сложение и вычитание скалярных величин.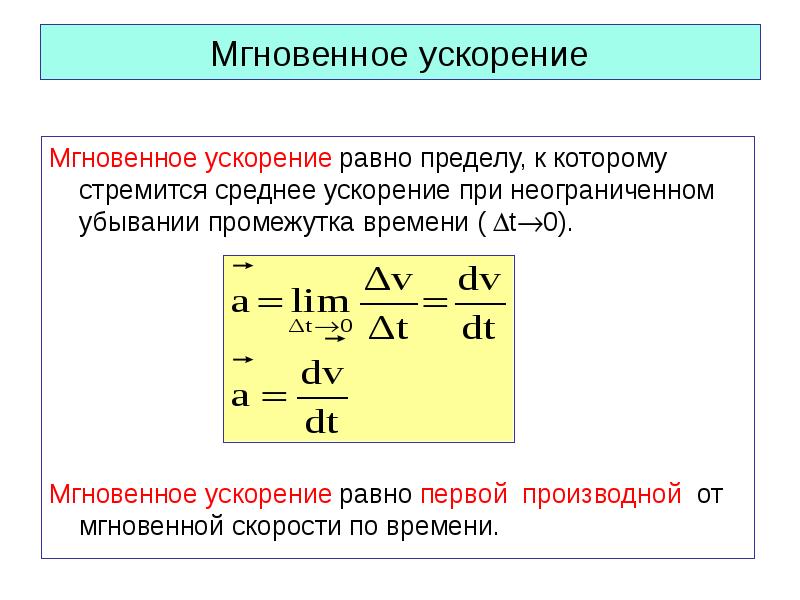 Рассмотрим случай, когда объект движется по окружности вокруг точки C, как показано на диаграмме ниже. За время t секунд объект переместился из точки A в точку B. За это время скорость изменилась с v i на v f .Процесс вычитания v i из v f показан на векторной диаграмме; этот процесс приводит к изменению скорости.
Рассмотрим случай, когда объект движется по окружности вокруг точки C, как показано на диаграмме ниже. За время t секунд объект переместился из точки A в точку B. За это время скорость изменилась с v i на v f .Процесс вычитания v i из v f показан на векторной диаграмме; этот процесс приводит к изменению скорости.
Направление вектора ускорения
Обратите внимание на диаграмму выше, что есть изменение скорости для объекта, движущегося по кругу с постоянной скоростью. Тщательный осмотр вектора изменения скорости на приведенной выше диаграмме показывает, что он указывает вниз и влево.В средней точке дуги, соединяющей точки A и B, изменение скорости направлено в сторону точки C – центра окружности. Ускорение объекта зависит от этого изменения скорости и находится в том же направлении, что и это изменение скорости. Ускорение объекта совпадает с направлением вектора изменения скорости; ускорение также направлено в сторону точки C – центра окружности. Объекты, движущиеся по кругу с постоянной скоростью, ускоряются к центру круга.
Ускорение объекта часто измеряется с помощью устройства, известного как акселерометр. Простой акселерометр состоит из объекта, погруженного в жидкость, например воду. Рассмотрим герметичную банку, наполненную водой. Пробка, прикрепленная к крышке шнурком, может служить акселерометром. Чтобы проверить направление ускорения объекта, движущегося по кругу, банку можно перевернуть и прикрепить к концу короткой секции деревянного 2х4. Второй акселерометр, сконструированный таким же образом, может быть прикреплен к противоположному концу 2×4.Если 2×4 и акселерометры закреплены на вращающейся платформе и вращаются по кругу, направление ускорения можно четко определить по направлению наклона пробок. Когда смесь пробки и воды вращается по кругу, пробка наклоняется к центру круга. Наименее массивный из двух объектов всегда наклоняется в направлении ускорения. В случае пробки и воды пробка менее массивна (в расчете на миллилитр) и, следовательно, испытывает большее ускорение. Имея меньшую инерцию (благодаря меньшей массе на 1 мл), пробка меньше всего сопротивляется ускорению, и, таким образом, наклоняется на внутрь банки к центру круга.Это очевидное свидетельство того, что объект, движущийся по кругу с постоянной скоростью, испытывает ускорение, направленное к центру круга.
Наименее массивный из двух объектов всегда наклоняется в направлении ускорения. В случае пробки и воды пробка менее массивна (в расчете на миллилитр) и, следовательно, испытывает большее ускорение. Имея меньшую инерцию (благодаря меньшей массе на 1 мл), пробка меньше всего сопротивляется ускорению, и, таким образом, наклоняется на внутрь банки к центру круга.Это очевидное свидетельство того, что объект, движущийся по кругу с постоянной скоростью, испытывает ускорение, направленное к центру круга.
Другой простой самодельный акселерометр – это зажженная свеча, расположенная вертикально по центру открытого стакана. Если стакан держать ровно и неподвижно (так, чтобы не было ускорения), то пламя свечи распространяется вверх. Однако, если вы держите систему стекло-свеча вытянутой рукой и вращаете по кругу с постоянной скоростью (так, чтобы пламя испытывало ускорение), то пламя свечи больше не будет распространяться вертикально вверх.Вместо этого пламя отклоняется от вертикального положения. Это означает, что есть ускорение, когда пламя движется по круговой траектории с постоянной скоростью. Отклонение пламени будет в сторону ускорения. Это можно объяснить, утверждая, что горячие газы пламени менее массивны (в расчете на миллилитр) и, следовательно, имеют меньшую инерцию, чем более холодные газы, которые его окружают. Впоследствии более горячие и легкие газы пламени испытывают большее ускорение и наклоняются в направлении ускорения.Тщательное изучение пламени показывает, что пламя направлено к центру круга, указывая, таким образом, на то, что есть не только ускорение; но есть внутреннее ускорение. Это еще одно наблюдаемое свидетельство того, что объекты, движущиеся по кругу с постоянной скоростью, испытывают ускорение, направленное к центру круга.
До сих пор мы видели геометрическое доказательство и две реальных демонстрации этого внутреннего ускорения.На этом этапе ученик принимает решение верить или не верить. Разве разумно, что объект, движущийся по кругу, испытывает ускорение, направленное к центру круга? Можете ли вы придумать логическую причину, чтобы верить в отсутствие ускорения или даже внешнего ускорения, испытываемого объектом, движущимся в равномерном круговом движении? В следующей части Урока 1 будут представлены дополнительные логические доказательства в поддержку концепции внутренней силы для объекта, движущегося по кругу.
1. Начальная и конечная скорости мяча в два разных момента времени показаны ниже. Направление мяча указано стрелкой. Для каждого случая укажите, есть ли ускорение. Объясните, почему да или почему нет. Укажите направление ускорения.
| а. | |
| Ускорение: да или нет? Объяснять. | Если есть ускорение, то в каком оно направлении? |
| б. | |
| Ускорение: да или нет? Объяснять. | Если есть ускорение, то в каком оно направлении? |
| c. | |
| Ускорение: да или нет? Объяснять. | Если есть ускорение, то в каком оно направлении? |
| d. | |
| Ускорение: да или нет? Объяснять. | Если есть ускорение, то в каком оно направлении? |
е. | |
| Ускорение: да или нет? Объяснять. | Если есть ускорение, то в каком оно направлении? |
2.Объясните связь между вашими ответами на вышеуказанные вопросы и аргументацией, использованной для объяснения того, почему можно сказать, что объект, движущийся по кругу с постоянной скоростью, испытывает ускорение.
3. Диззи Смит и Гектор Вектор все еще обсуждают № 1e. Диззи говорит, что мяч не ускоряется, потому что его скорость не меняется. Гектор говорит, что, поскольку мяч изменил свое направление, происходит ускорение.С кем ты согласен? Обсудите свою позицию, объяснив несоответствие в аргументах другого ученика.
4. Определите три элемента управления автомобилем, которые позволяют автомобилю ускоряться.
Для вопросов № 5- № 8: Объект движется в направлении по часовой стрелке и по кругу с постоянной скоростью.Используйте свое понимание концепций скорости и ускорения, чтобы ответить на следующие четыре вопроса. Используйте диаграмму, показанную справа.
5. Какой вектор ниже представляет направление вектора скорости, когда объект находится в точке B на окружности?
6. Какой вектор ниже представляет направление вектора ускорения, когда объект находится в точке C на окружности?
7.Какой вектор ниже представляет направление вектора скорости, когда объект находится в точке C на окружности?
8. Какой вектор ниже представляет направление вектора ускорения, когда объект находится в точке A на окружности?
Веб-сайт класса физики
Равномерное круговое движение
Равномерное круговое движение можно описать как движение объекта по кругу с постоянной скоростью. Когда объект движется по кругу, он постоянно меняет свое направление. Во всех случаях объект движется по касательной к окружности. Поскольку направление вектора скорости совпадает с направлением движения объекта, вектор скорости также направлен по касательной к окружности. Анимация справа изображает это с помощью векторной стрелки.
Когда объект движется по кругу, он постоянно меняет свое направление. Во всех случаях объект движется по касательной к окружности. Поскольку направление вектора скорости совпадает с направлением движения объекта, вектор скорости также направлен по касательной к окружности. Анимация справа изображает это с помощью векторной стрелки.
Объект, движущийся по кругу, ускоряется. Ускоряющиеся объекты – это объекты, которые изменяют свою скорость – либо скорость (т.е., величина вектора скорости) или направление. Объект, совершающий равномерное круговое движение, движется с постоянной скоростью. Тем не менее, он ускоряется из-за изменения направления. Направление ускорения внутрь. Анимация справа изображает это с помощью векторной стрелки.
Последней характеристикой движения объекта, совершающего равномерное круговое движение, является чистая сила. Чистая сила, действующая на такой объект, направлена к центру круга.Чистая сила считается направленной внутрь или центростремительной силой . Без такой внутренней силы объект продолжал бы движение по прямой линии, никогда не отклоняясь от своего направления. Тем не менее, с внутренней чистой силой, направленной перпендикулярно вектору скорости, объект всегда меняет свое направление и испытывает внутреннее ускорение.
Для получения дополнительной информации о физических описаниях движения посетите The Physics Classroom Tutorial. Доступна подробная информация по следующим темам:
СкоростьУскорение
Чистая сила и ускорение
Круговое движение и тангенциальная скорость
Круговое движение и ускорение
Требование центростремительной силы
4.4 Равномерное круговое движение – Университетская физика, том 1
Цели обучения
К концу этого раздела вы сможете:
- Найдите центростремительное ускорение объекта, движущегося по круговой траектории.

- Используйте уравнения кругового движения, чтобы найти положение, скорость и ускорение частицы, совершающей круговое движение.
- Объясните разницу между центростремительным ускорением и тангенциальным ускорением, возникающим в результате неравномерного кругового движения.
- Оцените центростремительное и тангенциальное ускорение при неравномерном круговом движении и найдите вектор полного ускорения.
Равномерное круговое движение – это особый тип движения, при котором объект движется по кругу с постоянной скоростью. Например, любая точка пропеллера, вращающегося с постоянной скоростью, совершает равномерное круговое движение. Другими примерами являются секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах действительно ускоряются, хотя скорость вращения постоянна.Чтобы увидеть это, мы должны проанализировать движение в терминах векторов.
Центростремительное ускорение
В одномерной кинематике объекты с постоянной скоростью имеют нулевое ускорение. Однако в двух- и трехмерной кинематике, даже если скорость постоянна, частица может иметь ускорение, если она движется по криволинейной траектории, такой как окружность. В этом случае вектор скорости меняется, или
Это показано на (Рисунок). Поскольку частица движется против часовой стрелки во времени
по круговой траектории, его вектор положения перемещается из
Спо
Вектор скорости имеет постоянную величину и касается пути, поскольку он изменяется от
. Спо
только меняет направление.Поскольку вектор скорости
перпендикулярно вектору положения
треугольников, образованных векторами положения и
и векторы скорости и
похожи. Кроме того, с
и
два равнобедренных треугольника. Из этих фактов мы можем сделать утверждение
или
Рисунок 4. 18 (a) Частица движется по кругу с постоянной скоростью, временами имея векторы положения и скорости.
18 (a) Частица движется по кругу с постоянной скоростью, временами имея векторы положения и скорости.и
(b) Векторы скорости, образующие треугольник. Два треугольника на рисунке похожи. Вектор
указывает на центр круга в пределах
Величину ускорения можно найти из
Направление ускорения также можно найти, отметив, что как
и, следовательно,
приближаются к нулю, вектор
приближается к направлению, перпендикулярному
В пределе
перпендикулярно
С
касается окружности, ускорение
указывает на центр круга.Таким образом, частица, движущаяся по кругу с постоянной скоростью, имеет ускорение с величиной
.Направление вектора ускорения – к центру круга ((Рисунок)). Это радиальное ускорение и называется центростремительным ускорением , поэтому мы даем ему индекс c. Слово центростремительный происходит от латинских слов centrum (что означает «центр») и petere (означает искать ») и, таким образом, принимает значение« поиск центра ».”
Рис. 4.19. Вектор центростремительного ускорения указывает на центр круговой траектории движения и представляет собой ускорение в радиальном направлении. Также показан вектор скорости, касающийся окружности.Давайте рассмотрим несколько примеров, которые иллюстрируют относительные величины скорости, радиуса и центростремительного ускорения.
Пример
Создание ускорения 1
gСамолет летит со скоростью 134,1 м / с по прямой и делает разворот по круговой траектории на уровне земли.Каким должен быть радиус окружности для создания центростремительного ускорения 1 g на пилоте и самолете по направлению к центру круговой траектории?
Стратегия
Учитывая скорость струи, мы можем найти радиус окружности в выражении для центростремительного ускорения.
Решение
Установите центростремительное ускорение равным ускорению свободного падения:
Решая для радиуса, находим
Значение
Чтобы создать у пилота большее ускорение, чем g , реактивному двигателю придется либо уменьшить радиус своей круговой траектории, либо увеличить скорость на существующей траектории, либо и то, и другое.
Проверьте свое понимание
Радиус маховика 20,0 см. Какова скорость точки на краю маховика, если она испытывает центростремительное ускорение
?[показывать-ответ q = ”fs-id116516
09 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id116516
09 ″]
134,0 см / с
[/ hidden-answer]
Центростремительное ускорение может иметь широкий диапазон значений в зависимости от скорости и радиуса кривизны круговой траектории.Типичные центростремительные ускорения приведены в следующей таблице.
| Объект | Центростремительное ускорение (м / с 2 или коэффициент g ) |
|---|---|
| Земля вокруг Солнца | |
| Луна вокруг Земли | |
| Спутник на геостационарной орбите | 0. 233 233 |
| Внешний край компакт-диска при воспроизведении | |
| Струя в бочке рулона | (2–3 г ) |
| Американские горки | (5 г ) |
| Электрон, вращающийся вокруг протона в простой модели атома Бора |
Уравнения движения для равномерного кругового движения
Частица, совершающая круговое движение, может быть описана ее вектором положения
(рисунок) показывает частицу, совершающую круговое движение против часовой стрелки.Когда частица движется по окружности, ее вектор положения выметает угол
.с осью x- . Вектор
образующий угол
с осью x- показан с его компонентами вдоль осей x и y . Величина вектора положения
., а также радиус круга, так что с точки зрения его составляющих
Здесь,
– это константа, называемая угловой частотой частицы.Угловая частота измеряется в радианах (рад) в секунду и представляет собой просто количество радианов угловой меры, через которую проходит частица за секунду. Уголок
, которое имеет вектор положения в любой конкретный момент времени, равно
..
Если T – это период движения или время для завершения одного оборота (
рад), затем
Рис. 4.20. Вектор положения частицы, движущейся по кругу, с ее компонентами по осям x и y.Частица движется против часовой стрелки. Угол– угловая частота
в радианах в секунду, умноженное на t.
Скорость и ускорение могут быть получены из функции положения путем дифференцирования:
Из (Рисунок) можно показать, что вектор скорости тангенциальный к окружности в месте нахождения частицы с величиной
.
Аналогично, вектор ускорения находится путем дифференцирования скорости:
Из этого уравнения мы видим, что вектор ускорения имеет величину
.и направлен против вектора положения, к началу координат, потому что
Пример
Круговое движение протона
Протон имеет скорость
и движется по окружности в плоскости xy радиуса r = 0.175 м. Каково его положение в плоскости xy в момент времени
При t = 0 положение протона
и вращается против часовой стрелки. Набросайте траекторию.
Решение
По приведенным данным протон имеет период и угловую частоту:
Положение частицы в
с A = 0.175 м –
Из этого результата мы видим, что протон расположен немного ниже оси x . Это показано на (Рисунок).
Рисунок 4.21 Вектор положения протона наПоказана траектория протона. Угол, под которым протон движется по окружности, составляет 5,712 рад, что немного меньше одного полного оборота.
Значение
Мы выбрали начальное положение частицы на оси x-.Это было совершенно произвольно. Если бы была дана другая начальная позиция, у нас было бы другое конечное положение при t = 200 нс.
Неравномерное круговое движение
Круговое движение не обязательно должно иметь постоянную скорость. Частица может двигаться по кругу и ускоряться или замедляться, показывая ускорение в направлении движения.
При равномерном круговом движении частица, совершающая круговое движение, имеет постоянную скорость, а круг имеет фиксированный радиус.Если скорость частицы тоже меняется, то мы вводим дополнительное ускорение в направлении, касательном к окружности. Такие ускорения происходят в точке на вершине, которая изменяет скорость вращения, или в любом ускоряющем роторе.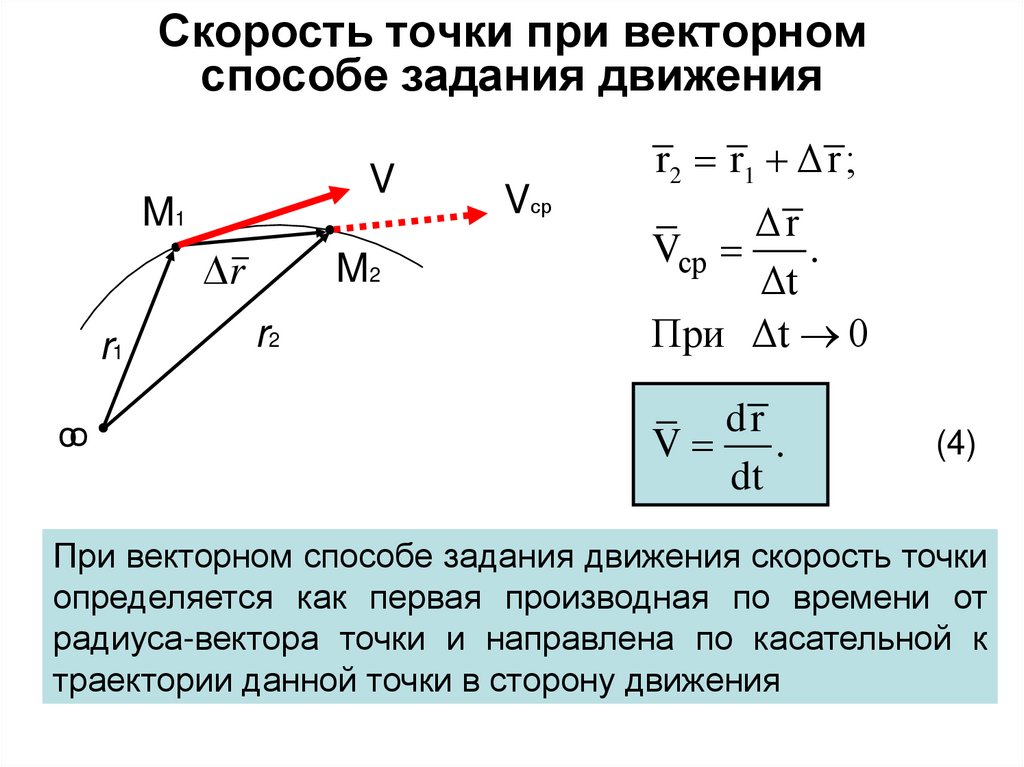 В работе «Векторы смещения и скорости» мы показали, что центростремительное ускорение – это скорость изменения направления вектора скорости во времени. Если скорость частицы изменяется, то она имеет тангенциальное ускорение , , то есть скорость изменения величины скорости во времени:
В работе «Векторы смещения и скорости» мы показали, что центростремительное ускорение – это скорость изменения направления вектора скорости во времени. Если скорость частицы изменяется, то она имеет тангенциальное ускорение , , то есть скорость изменения величины скорости во времени:
Направление тангенциального ускорения касается окружности, тогда как направление центростремительного ускорения радиально внутрь к центру окружности.Таким образом, частица, движущаяся по кругу с тангенциальным ускорением, имеет общее ускорение , которое является векторной суммой центростремительного и тангенциального ускорений:
Векторы ускорения показаны на (Рисунок). Обратите внимание, что два вектора ускорения
и
перпендикулярны друг другу, при этом
в радиальном направлении и
в тангенциальном направлении.Общее ускорение
точек под углом между
и
Рис. 4.22 Центростремительное ускорение указывает на центр круга. Тангенциальное ускорение является касательным к окружности в месте расположения частицы. Общее ускорение – это векторная сумма тангенциального и центростремительного ускорений, которые перпендикулярны.Пример
Полное ускорение при круговом движении
Частица движется по окружности радиуса r = 2.0 мин. В интервале времени от t = 1,5 с до t = 4,0 с его скорость изменяется со временем в соответствии с
.Каково полное ускорение частицы при т = 2,0 с?
Стратегия
Нам даны скорость частицы и радиус круга, поэтому мы можем легко вычислить центростремительное ускорение. Направление центростремительного ускорения – к центру круга. Мы находим величину тангенциального ускорения, взяв производную по времени
., используя (рисунок) и оценив его как t = 2. 0 с. Мы используем это и величину центростремительного ускорения, чтобы найти полное ускорение.
0 с. Мы используем это и величину центростремительного ускорения, чтобы найти полное ускорение.
Решение
Центростремительное ускорение
направлен к центру круга. Касательное ускорение
Суммарное ускорение
и
от касательной к окружности. См. (Рисунок).
Рис. 4.23 Векторы тангенциального и центростремительного ускорения.Чистое ускорение– это векторная сумма двух ускорений.
Значение
Направления центростремительного и тангенциального ускорений можно описать более удобно в терминах полярной системы координат с единичными векторами в радиальном и тангенциальном направлениях. Эта система координат, которая используется для движения по криволинейным траекториям, подробно обсуждается позже в книге.
Сводка
- Равномерное круговое движение – это движение по окружности с постоянной скоростью.
- Центростремительное ускорение
– это ускорение, которое должна иметь частица, чтобы двигаться по круговой траектории. Центростремительное ускорение всегда направлено к центру вращения и имеет величину
. - Неравномерное круговое движение возникает, когда есть тангенциальное ускорение объекта, выполняющего круговое движение, так что скорость объекта изменяется. Это ускорение называется тангенциальным ускорением.
Величина тангенциального ускорения – это скорость изменения величины скорости во времени.Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности. Общее ускорение – это векторная сумма тангенциального и центростремительного ускорений.
- Объект, выполняющий равномерное круговое движение, можно описать уравнениями движения. Вектор положения объекта
, где A – величина
., который также является радиусом круга, и
– угловая частота.

Концептуальные вопросы
Может ли центростремительное ускорение изменить скорость частицы, совершающей круговое движение?
Может ли тангенциальное ускорение изменить скорость частицы, совершающей круговое движение?
[показывать-ответ q = ”fs-id1165169156423 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165169156423 ″]
да
[/ hidden-answer]
Проблемы
Маховик вращается со скоростью 30 об / с.Каков полный угол в радианах, на который точка на маховике поворачивается за 40 с?
Частица движется по кругу радиусом 10 м с постоянной скоростью 20 м / с. Какая величина ускорения?
[show-answer q = ”fs-id1165168
5 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165168
5 ″]
[/ hidden-answer]
Кэм Ньютон из Carolina Panthers бросает идеальную футбольную спираль на отметке 8.0 об / с. Радиус профессионального футбола составляет 8,5 см по середине короткой стороны. Что такое центростремительное ускорение шнурков на футбольном мяче?
Выставочный аттракцион раскручивает своих пассажиров внутри контейнера в форме летающей тарелки. Если горизонтальный круговой путь, по которому следуют гонщики, имеет радиус 8,00 м, при скольких оборотах в минуту гонщики подвергаются центростремительному ускорению, равному ускорению силы тяжести?
[показывать-ответ q = ”fs-id116516
61 ″] Показать решение [/ показывать-ответ][скрытый-ответ a = ”fs-id116516
61 ″], что равно
[/ hidden-answer]
Бегун, участвующий в забеге на 200 м, должен обойти конец трассы, имеющей дугу окружности с радиусом кривизны 30.0 мин. Бегун начинает забег с постоянной скоростью. Если она преодолевает 200-метровый рывок за 23,2 с и бежит с постоянной скоростью на протяжении всей гонки, каково ее центростремительное ускорение при прохождении криволинейной части трассы?
Каково ускорение Венеры по направлению к Солнцу, если принять круговую орбиту?
[показывать-ответ q = ”fs-id11651611 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id11651611 ″]
Венера находится на расстоянии 108,2 миллиона км от Солнца и имеет период обращения 0. 6152 г.
6152 г.
[/ hidden-answer]
Экспериментальная реактивная ракета движется вокруг Земли вдоль экватора прямо над ее поверхностью. С какой скоростью должен двигаться реактивный двигатель, если величина его ускорения g ?
Вентилятор вращается с постоянной скоростью 360,0 об / мин. Какова величина ускорения точки на одной из лопастей на расстоянии 10,0 см от оси вращения?
[показывать-ответ q = ”fs-id1165168934870 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165168934870 ″]
[/ hidden-answer]
Точка, расположенная на секундной стрелке больших часов, имеет радиальное ускорение
.Как далеко точка от оси вращения секундной стрелки?
Глоссарий
- угловая частота
скорость изменения угла, с которым объект движется по круговой траектории
- центростремительное ускорение
- Компонент ускорения объекта, движущегося по окружности, радиально направленной внутрь к центру окружности
- тангенциальное ускорение
- величина которой является временной скоростью изменения скорости.Его направление касается окружности.
- общее ускорение
- векторная сумма центростремительного и тангенциального ускорений
Скорость, ускорение и сила | Безграничная физика
Угол вращения и угловая скорость
Угол поворота – это мера того, как далеко вращается объект, а угловая скорость – это скорость его вращения.
Цели обучения
Выразите взаимосвязь между углом поворота и расстоянием
Основные выводы
Ключевые моменты
- Когда объект вращается вокруг оси, точки на краю объекта перемещаются по дугам.
- Угол, выходящий за пределы этих дуг, называется углом поворота и обычно обозначается символом theta .

- Мера того, насколько быстро объект вращается относительно времени, называется угловой скоростью. Обычно он представлен греческим символом омега . Как и его аналог линейной скорости, это вектор.
Ключевые термины
- радиан : угол, образуемый в центре окружности дугой той же длины, что и радиус окружности.
Угол вращения и угловая скорость
Когда объект вращается вокруг оси, как в случае с шиной автомобиля или записью на поворотной платформе, движение можно описать двумя способами. Точка на краю вращающегося объекта будет иметь некоторую скорость и будет перенесена по дуге на вращающемся объекте. Точка пройдет расстояние [latex] \ Delta \ text {S} [/ latex], но часто удобнее говорить о степени поворота объекта. Величина поворота объекта называется углом поворота и может измеряться в градусах или радианах.Поскольку угол поворота связан с расстоянием [latex] \ Delta \ text {S} [/ latex] и с радиусом [latex] \ text {r} [/ latex] уравнением [latex] \ Delta \ theta = \ frac {\ Delta \ text {S}} {\ text {R}} [/ latex], обычно удобнее использовать радианы.
Угол θ и длина дуги s : Радиус круга поворачивается на угол [латекс] \ дельта \ тета [/ латекс]. Длина дуги [латекс] \ Delta \ text {s} [/ latex] указывается на окружности.
Скорость вращения объекта определяется угловой скоростью, которая представляет собой скорость изменения угла поворота во времени.Хотя сам угол не является векторной величиной, угловая скорость – это вектор. Направление вектора угловой скорости перпендикулярно плоскости вращения в направлении, которое обычно задается правилом правой руки. Угловое ускорение дает скорость изменения угловой скорости. Угол, угловая скорость и угловое ускорение очень полезны при описании вращательного движения объекта.
Направление угловой скорости : Угловая скорость описывает скорость вращения и ориентацию мгновенной оси, вокруг которой происходит вращение. Направление угловой скорости будет вдоль оси вращения. В этом случае (вращение против часовой стрелки) вектор направлен вверх.
Направление угловой скорости будет вдоль оси вращения. В этом случае (вращение против часовой стрелки) вектор направлен вверх.
Когда ось вращения перпендикулярна вектору положения, угловую скорость можно вычислить, взяв линейную скорость [latex] \ text {v} [/ latex] точки на краю вращающегося объекта и разделив на радиус. Это даст угловую скорость, обычно обозначаемую [latex] \ omega [/ latex], в радианах в секунду.
Угловая скорость : Муха на краю вращающегося объекта фиксирует постоянную скорость [latex] \ text {v} [/ latex]. Объект вращается с угловой скоростью, равной [latex] \ frac {\ text {v}} {\ text {r}} [/ latex].
Центробежное ускорение
Центростремительное ускорение – это постоянное изменение скорости, необходимое объекту для поддержания круговой траектории.
Цели обучения
Выразите центростремительное ускорение через скорость вращения
Основные выводы
Ключевые моменты
- Для того, чтобы объект сохранял круговое движение, он должен постоянно менять направление.
- Поскольку скорость является вектором, изменения направления представляют собой изменения скорости.
- Изменение скорости называется ускорением. Изменение скорости из-за кругового движения известно как центростремительное ускорение.
- Центростремительное ускорение можно рассчитать, разделив квадрат линейной скорости на радиус круга, по которому движется объект.
Ключевые термины
- ускорение : величина, на которую увеличивается скорость или скорость (и, следовательно, скалярная величина или векторная величина).
- круговое движение : движение таким образом, что выбранная траектория представляет собой круговую траекторию.
- скорость : векторная величина, которая обозначает скорость изменения положения относительно времени или скорость с направленным компонентом.

Обзор
Как упоминалось в предыдущих разделах по кинематике, любое изменение скорости определяется ускорением. Часто изменения скорости являются изменениями по величине. Когда объект ускоряется или замедляется, это изменение скорости объекта.Изменения в величине скорости соответствуют нашему интуитивному и повседневному использованию термина «ускорение». Однако, поскольку скорость является вектором, у нее также есть направление. Следовательно, любое изменение направления движения объекта также должно сопровождаться ускорением.
Равномерное круговое движение означает, что объект движется по круговой траектории с постоянной скоростью. Поскольку скорость постоянна, обычно не думается, что объект ускоряется. Однако направление постоянно меняется, когда объект пересекает круг.Таким образом, говорят, что он ускоряется. Это ускорение можно почувствовать, катаясь на американских горках. Даже если скорость постоянна, быстрый поворот вызовет у гонщика чувство силы. Это ощущение ускорения.
Центростремительное ускорение : Краткий обзор центростремительного ускорения для школьников-физиков.
Расчет центростремительного ускорения
Чтобы вычислить центростремительное ускорение объекта, совершающего равномерное круговое движение, необходимо иметь скорость, с которой движется объект, и радиус круга, вокруг которого происходит движение.2 \ text {r} [/ latex]
, где омега – это скорость вращения, заданная [latex] \ frac {\ text {v}} {\ text {r}} [/ latex].
Центростремительное ускорение : Когда объект движется по окружности, направление вектора скорости постоянно меняется.
Центростремительная сила
Сила, которая вызывает движение по криволинейной траектории, называется центростремительной силой (равномерное круговое движение является примером центростремительной силы).
Цели обучения
Выразите уравнения для центростремительной силы и ускорения
Основные выводы
Ключевые моменты
- Когда объект находится в равномерном круговом движении, он постоянно меняет направление и, следовательно, ускоряется.Это угловое ускорение.
- Сила, действующая на объект при равномерном круговом движении (называемая центростремительной силой), действует на объект из центра круга.
Ключевые термины
- центростремительный : направлен или движется к центру.
- угловая скорость : векторная величина, описывающая объект в круговом движении; его величина равна скорости частицы, а направление перпендикулярно плоскости ее кругового движения.
Сила, вызывающая движение по криволинейной траектории, называется центростремительной силой. Равномерное круговое движение является примером действия центростремительной силы. Это можно увидеть на орбите спутников вокруг Земли, натяжении веревки в игре с тросом, в петле-петле на американских горках или в ведре, вращающемся вокруг тела.
Обзор центростремительной силы : Краткий обзор центростремительной силы.
Ранее мы узнали, что любое изменение скорости – это ускорение.По мере того, как объект движется по круговой траектории, он постоянно меняет направление и, следовательно, ускоряется, вызывая постоянное воздействие на объект силы. Эта центростремительная сила действует по направлению к центру кривизны, по направлению к оси вращения. Поскольку объект движется перпендикулярно силе, путь, по которому он движется, является круговым. Именно эта сила удерживает мяч от выпадения из ведра, если вы непрерывно раскачиваете его по кругу.
Центростремительная сила : Когда объект движется по круговой траектории с постоянной скоростью, он испытывает центростремительную силу, ускоряющую его к центру.2 [/ латекс]
6.2 Равномерное круговое движение | Техасский шлюз
Центростремительная сила
Поскольку объект в равномерном круговом движении испытывает постоянное ускорение (за счет изменения направления), мы знаем из второго закона движения Ньютона, что на объект должна действовать постоянная чистая внешняя сила.
Любая сила или комбинация сил могут вызвать центростремительное ускорение. Вот лишь несколько примеров: натяжение веревки на тросе, сила притяжения Земли на Луне, трение между дорогой и шинами автомобиля при движении по кривой или нормальная сила американских горок. следите за тележкой во время петли.
Любая чистая сила, вызывающая равномерное круговое движение, называется центростремительной силой. Направление центростремительной силы – к центру вращения, такое же, как и для центростремительного ускорения. Согласно второму закону движения Ньютона, чистая сила вызывает ускорение массы согласно F net = м a . Для равномерного кругового движения ускорение является центростремительным: a = a c . Следовательно, величина центростремительной силы F c равна Fc = macFc = mac.
Используя две разные формы уравнения для величины центростремительного ускорения, ac = v2 / rac = v2 / r и ac = rω2ac = rω2, мы получаем два выражения, включающих величину центростремительной силы F c . Первое выражение относится к тангенциальной скорости, второе – к угловой скорости: Fc = mv2rFc = mv2r и Fc = mrω2Fc = mrω2.
Обе формы уравнения зависят от массы, скорости и радиуса круговой траектории. Вы можете использовать любое более удобное выражение для центростремительной силы. Второй закон Ньютона также гласит, что объект будет ускоряться в том же направлении, что и чистая сила. По определению центростремительная сила направлена к центру вращения, поэтому объект также будет ускоряться к центру. Прямая линия, проведенная от круговой траектории к центру круга, всегда будет перпендикулярна тангенциальной скорости. Обратите внимание, что если вы решите первое выражение для r , вы получите
Второй закон Ньютона также гласит, что объект будет ускоряться в том же направлении, что и чистая сила. По определению центростремительная сила направлена к центру вращения, поэтому объект также будет ускоряться к центру. Прямая линия, проведенная от круговой траектории к центру круга, всегда будет перпендикулярна тангенциальной скорости. Обратите внимание, что если вы решите первое выражение для r , вы получите
Из этого выражения мы видим, что для данной массы и скорости большая центростремительная сила вызывает малый радиус кривизны, то есть резкую кривую.
Рисунок 6.9 На этом рисунке сила трения f служит центростремительной силой F c . Центростремительная сила перпендикулярна тангенциальной скорости и вызывает равномерное круговое движение. Чем больше центростремительная сила F c , тем меньше радиус кривизны r и тем круче кривизна. Нижняя кривая имеет ту же скорость v , но большая центростремительная сила F c дает меньший радиус r’r ‘.Watch Physics
Центростремительная сила и ускорение Intuition
В этом видео объясняется, почему центростремительная сила создает центростремительное ускорение и равномерное круговое движение. Он также охватывает разницу между скоростью и скоростью и показывает примеры равномерного кругового движения.
Проверка захвата
Представьте, что вы качаете йойо по вертикальному кругу по часовой стрелке перед собой, перпендикулярно направлению, в которое вы смотрите. Теперь представьте, что струна рвется, когда йойо достигает своего самого нижнего положения, ближайшего к полу.Что из следующего описывает путь йо-йо после разрыва струны?
- Йо-йо полетит вверх в направлении центростремительной силы.

- Йо-йо полетит вниз в направлении центростремительной силы.
- Йо-йо полетит влево в направлении тангенциальной скорости.
- Йо-йо полетит вправо в направлении тангенциальной скорости.
Ускоряется ли объект при равномерном круговом движении?
Чтобы избежать путаницы, давайте посмотрим на определение ускорения: скорость изменения скорости во времени. Всякий раз, когда изменяется скорость, должно быть соответствующее ускорение.
Автомобиль в равномерном круговом движении по тупику.
Путаница возникает из-за разницы между скоростью в одном измерении и скоростью в нескольких измерениях.В одном измерении скорость имеет величину (например, 5 м / с \ SI [per-mode = symbol] {5} {\ meter \ per \ second} 5 м / с) и направление (например, на северо-восток). Однако, поскольку направление может быть только влево или вправо, невозможно плавно, изменять направление скорости – как в случае с круговым движением – мы можем иметь только дискретные сдвиги. Такое движение обычно не встречается, за исключением столкновений, когда мало кто сомневается в существовании значительного ускорения.
В измерениях d> 1d \ gt 1d> 1 скорость является полноценной векторной величиной, и ее направление может изменяться естественным образом.Одним из таких случаев является равномерное круговое движение, при котором направление скорости плавно изменяется по мере того, как мы движемся по кругу. Несмотря на постоянство скорости, направление движения меняется, и поэтому скорость изменения скорости во времени отлична от нуля, что составляет ускорение.
В каком направлении ускоряется объект?
Поскольку его скорость неизменна, ускорение должно быть перпендикулярно направлению движения и, следовательно, к центру круга.
Его величина может быть найдена несколькими способами, и она определяется как acent = v2 / R, \ mathbf {a} _ \ textrm {cent} = v ^ 2 / R, acent = v2 / R, где RRR – это радиус круга.
См. Общие опровержения
Опровержение : В случае равномерного кругового движения, каков угол между скоростью и ускорением?
Ответ : Если скорость остается постоянной, то составляющая ускорения, параллельная скорости, равна нулю. Эта составляющая называется тангенциальным ускорением. Направление меняется из-за центростремительного ускорения, направленного радиально внутрь. Таким образом, чистое ускорение в случае равномерного кругового движения перпендикулярно скорости.Опровержение : Можно ли в случае равномерного кругового движения записать величину ускорения равной скорости изменения скорости?
Ответ : Нет, скорость изменения скорости полностью отличается от скорости изменения скорости. Ускорение определяется как скорость изменения скорости.
Только (a) и (b) верны Только (a), (b) и (c) верны Только (c) и (d) верны Все варианты верны
Частица движется по круговой дорожке с постоянной ненулевой скоростью.\ circ 90∘.
См. Также
Заряженная частица в магнитном поле
Заряженная частица в магнитном полеследующий: Эффект Холла Up: Магнетизм Предыдущая: Сила Лоренца Предположим, что частица массы движется по круговой орбите радиус с постоянной скоростью.
 Как известно, ускорение
частица имеет величину, и всегда
направлен к центру орбиты.Отсюда следует, что
ускорение всегда перпендикулярно мгновенному
направление движения.
Как известно, ускорение
частица имеет величину, и всегда
направлен к центру орбиты.Отсюда следует, что
ускорение всегда перпендикулярно мгновенному
направление движения. Мы видели, что сила, действующая на заряженную частицу со стороны магнитного
поле всегда перпендикулярно его мгновенному направлению движения.
Означает ли это, что поле заставляет частицу совершать круговое движение?
орбита? Рассмотрим случай, показанный на рис. 24. Предположим, что a
частица с положительным зарядом и массой движется в плоскости, перпендикулярной
к однородному магнитному полю.На рисунке поле указывает на
самолет бумаги. Предположим, что частица движется в
против часовой стрелки, с постоянным
скорость (помните, что магнитное поле не может воздействовать на
частица, поэтому она не может повлиять на ее скорость) по круговой орбите с радиусом.
Магнитная сила, действующая на частицу, равна
величины и, согласно формуле. (158) эта сила всегда
направлен к центру орбиты. Таким образом, если
| (166) |
тогда у нас есть непротиворечивая картина.Следует, что
| (167) |
Угловая частота вращения частицы ( т.е. , число радиан, через которые частица вращается за одну секунду)
| (168) |
Обратите внимание, что эта частота, известная как частота Лармора , не зависят от скорости частицы. Для отрицательно заряженной частицы картина в точности такая же, как описано выше, за исключением того, что частица движется в орбита по часовой стрелке.
Это ясно, из уравнения. (168), угловая частота вращения заряженного частица в известном магнитном поле может быть использована для определения ее заряда до соотношение масс. Кроме того, если скорость частицы известна, то радиус орбиты также можно использовать для определения с помощью уравнения. (167). Этот метод используется в физике высоких энергий для идентификации частиц из фотографии следов, которые они оставляют в камерах намагничивания или пузырях камеры.Конечно, легко отличить положительно заряженные частицы. от отрицательно заряженных, используя направление отклонения частицы в магнитном поле.
Мы видели, что заряженная частица, помещенная в магнитное поле, выполняет круговая орбита в плоскости, перпендикулярной направлению поля. Является ли это наиболее общим движением заряженной частицы в магнитном поле? Не совсем. Мы также можем добавить произвольный дрейф по направлению магнитного поля.Это следует потому, что сила действующее на частицу зависит только от составляющей скорости частицы что на перпендикулярно направлению магнитного поля (крест произведение двух параллельных векторов всегда равно нулю, потому что угол они подчиняются нулю). Сочетание кругового движения в плоскости, перпендикулярной магнитному полю, и равномерное движение по направление поле, вызывает спираль траектории заряженной частицы в магнитное поле, где поле образует ось спирали – см. рис.25.
следующий: Эффект Холла Up: Магнетизм Предыдущая: Сила Лоренца Ричард Фицпатрик 2007-07-14 .







