Какими буквами обозначают скорость расстояние и время. Скорость движения
Цель : продолжить формировать представление о новой величине «скорость, время, расстояние» и единицах ее измерения.
Задачи :
- Создать условия для осознания детьми зависимости между величинами, характеризующими движение тел – скоростью, временем и расстоянием.
- Познакомить детей с понятием скорости и единицами её измерения.
- Отрабатывать вычислительные навыки, обучать детей работе с графическими моделями.
- Развивать познавательную активность детей, способности к самооценке и самоконтролю, формировать коммуникативные умения.
Оборудование : карточки, карточки для работы в парах, интерактивная доска, название единиц времени на карточках, рабочая тетрадь, компьютер, проектор, экран
учебник.
Тип урока: урок закрепления и развития знаний, умений и навыков.
Методы : формы познавательной деятельности учащихся на уроке, индивидуальная работа, работа в парах.
Планируемые достижения учащихся на уроке:
- знать понятие скорости, времени и расстоянии как новой единицы измерения, уметь решать задачи на нахождение скорости движения по известным расстоянию и времени движения;
- закрепить табличные и внетабличные случаи умножения и деления, знание единиц длины и времени.
Ход урока
Организационный момент
Психологический настрой
Прозвенел заливистый школьный звонок.
Начинается новый урок.
Мы готовы считать и задачи решать.
Учитель : Я улыбнулась вам, и вы улыбнитесь друг другу, и подумайте, как хорошо, что мы сегодня все вместе. Мы спокойны, добры и приветливы. Глубоко вдохните и выдохните. Выдохните вчерашнюю обиду и злость, беспокойство. Забудьте о них. Я желаю вам хорошего настроения.
Сообщение темы и цели урока
Сегодня на уроке мы с вами вспомним о величинах, с которыми познакомились на предыдущих уроках и решали с ними задачи на движение и ставить свои ответы на листах самооценки.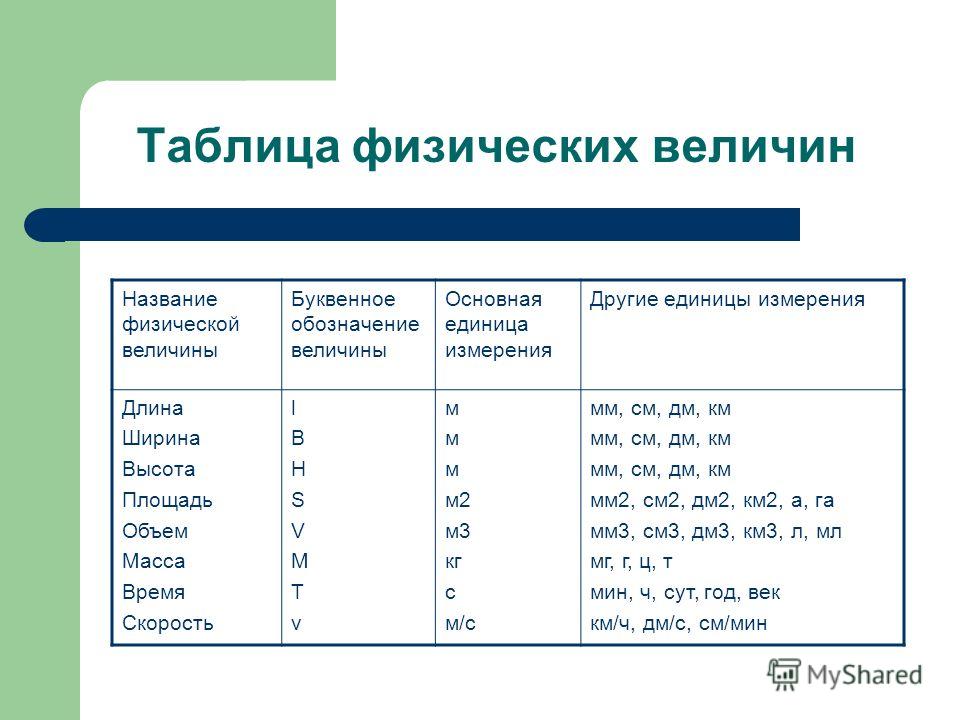
(Ответы учащихся) Верно, это скорость, время, расстояние. Какими латинскими буквами они обозначаются. (s, v, t).
Слайд № 1
Девиз нашего урока: «Один за всех, все за одного»
Работа в парах
На партах карточки с примерами:
Увеличь произведение чисел 805 и 5 на 1025 (5050)
Из 10000 вычти частное число 40025 и 5 (1995)
Увеличь частное чисел 4025 и 5 в 100 раз (80500)
Прибавь к числу 1207 частное чисел 51300 и 9 (6907)
Из произведения чисел 480 и 7 вычти число 1406 (1954)
Произведение чисел 4070 и 6 уменьши на 4420 (20000)
Записать ответы в порядке возрастания
(ответ записан на интерактивной доске)
Минутка чистописания
Слайд № 2
2 4 6 8 10 (образец в тетради)
Прочитайте числа. Какие это числа? В каком порядке они расположены? Как они увеличиваются? Прочитайте число целиком. Сколько цифр использовано? В обратном направлении можем прочитать? Прочитайте. Запишите числа в порядке возрастания, через клеточку в порядке убывания. Прочитайте их, сравните. Запишите еще раз в порядке возрастания, найдите сумму этих четных чисел. Как вы это сделали?
Прочитайте их, сравните. Запишите еще раз в порядке возрастания, найдите сумму этих четных чисел. Как вы это сделали?
Индивидуальная работа по карточкам
(4 ученика решают № 7)
Устная работа с остальными учениками:
В саду растут груши и ивы. На груше росло 69 груш, а на иве на 100 груш больше. Сколько груш росло на иве?
Мама варила одно яйцо 5 минут. Сколько времени будет варить 3 яйца?
Масса 1 мешка сахара 50 кг. Сколько кг в 4 таких мешках?
За 1 с человек делает 2 шага. Сколько шагов он сделает за 5 с.? За 10 с?
Слайд № 3
Физминутка
Слайд № 4
Качу, лечу во весь опор. (Выполняют ходьбу на месте.)
Я сам – шофер (Имитируют управление автомобильным рулем.)
И сам – мотор. (Круговые движения плечами вперед-назад.)
Нажимаю на педаль, (Имитируют нажимание на педаль.)
И машина мчится вдаль! (Бег на месте.)
Первичное закрепление
Слайд № 5
Орел летел со скоростью 20 км/ч. За сколько часов он пролетит 80 км?
Cкорость полета космического спутника 8 км/сек.
Слайд № 6
Решение задачи № 2
Автобус
S – 90 км 90: 45= 2 часа
T – ?
V – 45 км/ч
Легковая машина
S – 270 км 270: 90 = 3 часа
T – ?
V – 90 км/ч
Самостоятельная работа по учебнику
Итог урока
Давайте подведем итог урока
Чем занимались на уроке?
Что запомнили?
Рефлексия
Окрасьте сегодняшний урок (Дети рисуют сердечко своего настроения от урока) Учитель объясняет значении выбранного цвета.
- Красный – радость
- Жёлтый – приятное
- Зелёный – спокойное
- Синий – грустное
- Фиолетовый – тревожный
- Оранжевый – удовлетворение
И на память об уроке солнышко дарит вам частичку своего тепла и хорошего настроения.
Наш закончен урок –
Спасибо за внимание,
Будем рады новой встрече,
Всем Вам до свидания!
Скорость численно равна пути (путь обозначается S), пройденного телом за единицу времени (время обозначается t).
Единица измерения скорость – это метр в секунду (м/с).
Скорость в физической науке обозначается латинской буквой “V”.
Основной его расшифровкой служит определение: Скорость – это отношение пройденного пути (расстояния) за определенный промежуток времени. То есть: V=S/t
Основной единицей измерения скорости, как можно понять из формулы, служит отношение км/ч (иногда м/с). А вообще, данную единицу измерения скорости можно переформулировать в зависимости от процесса и науки, в котором ее измеряют!
Обычно в физике скорость обозначается латинской буквой v. Иногда эту букву пишут прописной, иногда строчной.
Однако есть одно исключение. Скорость обозначается буквой с, если равна скорости света.
111111 222222 333333 444444
Поскольку скорость света в вакууме – величина постоянная, в расчетах она принимается за константу. Для того, чтобы отличить скорость света от переменной скорости, эти скорости обозначаются разными буквами.
Скорость в физике, алгебре и других науках принято обозначать латинской буквой v (английская буква в).
Скорость это величина, которая характеризует быстроту перемещения объекта относительно выбранной системы отсчета. Скорость обычно обозначается английской буквой “V”. Как правило в физике и математике рассматривается скорость какого-либо тела.
В физике скорость обозначают латинской “V”. Еще с уроков математики помню формулу:
Скорость равна: расстояние разделить на затраченное время.
Бесплатная юридическая консультация:
Вот так выглядят эти формулы:
Измеряется скорость обычно в км/ч, хотя иногда измеряют в м/с.
Скорость в физики имеет символ от латинской буквы “V”, только прописной и в некоторых случаях со стрелкой сверху, которая смотрит направо, к сожалению редактор не поддерживает прописную букву, поэтому приходится на картинке показать:
В физике, как впрочем и в математике, скорость обозначается латинской буквой “V”.
Все мы прекрасно помним еще со школы, чтобы найти Скорость (V), нужно Расстояние (S) разделить на Время (t), которое затратили на преодоление этого расстояния (пути).
Бесплатная юридическая консультация:
Скорость движущихся объектов может измеряться в км/ч или м/с.
Насколько мне известно, в настоящее время в физике скорость обозначается буквой “V”. Вообще, существует ещё скорость света, которая является постоянной величиной, и обозначается буквой “C”. Кстати, скорость всегда равняется отношению пройденного расстояния в единицу времени.
Скорость обозначается буквой –
Скорость величина векторая, так что зачастую требуется указывать направление скорость.
Самая простая формула скорость, это длина деленная на расстояние.
Бесплатная юридическая консультация:
Очень часто люди путают скорость с ускорением, что приводит плохим последствиям.
Латинской буквой V. Такое обозначение используется и в математике, и в физике.
Список обозначений в физике
Список обозначений в физике включает обозначения понятий в физике из школьного и университетского курсов. Также включены и общие математические понятия и операции для того, чтобы сделать возможным полное прочтение физических формул.
Также включены и общие математические понятия и операции для того, чтобы сделать возможным полное прочтение физических формул.
Для обозначения физических величин и понятий в физике используются буквы латинского и греческого алфавитов, а также несколько специальных символов и диакритических знаков. Поскольку количество физических величин больше количества букв в латинском и греческом алфавитах, одни и те же буквы используются для обозначения различных величин. Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики.
Бесплатная юридическая консультация:
В печатном тексте математические обозначения, использующие латиницу, принято писать курсивом. Названия функций, а также цифры и греческие буквы оставляют прямыми. Буквы также могут быть записаны различными шрифтами для того, чтобы различать природу величин или математических операций. В частности принято обозначать жирным шрифтом векторные величины, а тензорные величины – рубленым шрифтом. Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные – заглавными буквами.
Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные – заглавными буквами.
В силу исторических причин, многие из обозначений используют латинские буквы – от первой буквы слова, обозначающего понятие на иностранном языке (преимущественно латинском, английском, французском и немецком). Когда такая связь существует, это обозначено в скобках. Среди латинских букв для обозначения физических величин практически не используется буква O .
Обозначения с несколькими буквами
Для обозначения некоторых величин иногда используют несколько букв или и отдельные слова или аббревиатуры. Так, постоянная величина в формуле обозначается часто как const. Дифференциал обозначается малой буквой d перед названием величины, например dx.
Латинские названия математических функций и операций, которые часто используются в физике:
Крупные греческие буквы, которые в написании похожи на латинские (A , B , E , Z , H , I , K , M , N , O , P , T , Υ , X ,\mathrm ,\mathrm ,\mathrm
,\mathrm ,\Upsilon ,\mathrm >) используются очень редко.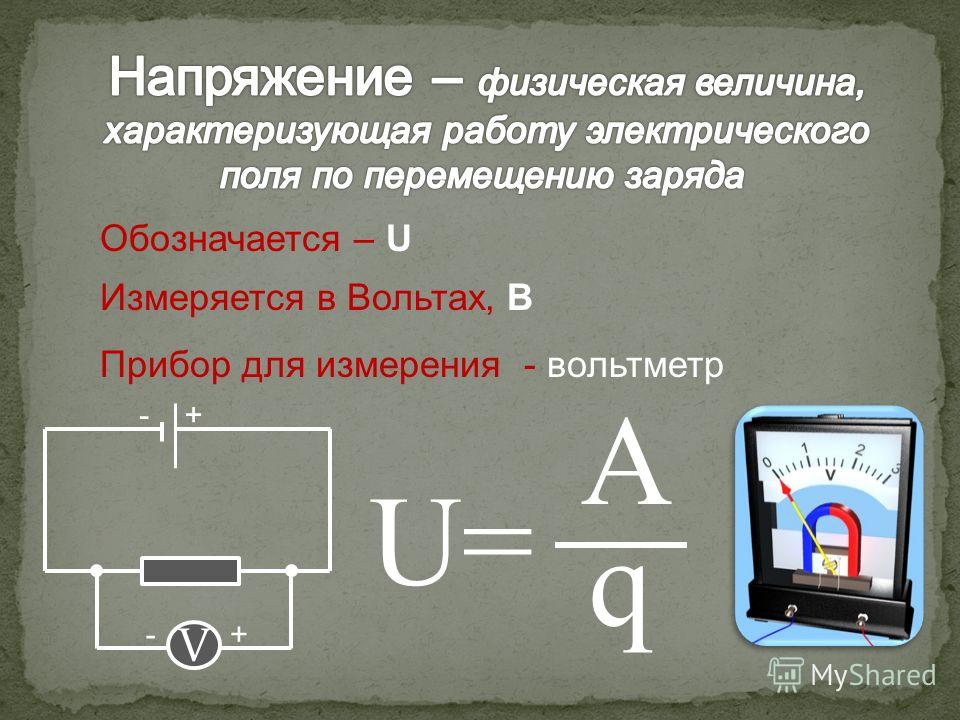
Кириллические буквы сейчас очень редко используются для обозначения физических величин, хотя частично применялись в русскоязычной научной традиции. Одним примером использования кириллической буквы в современной международной научной литературе есть обозначения инварианта Лагранжа буквой Ж . Гребень Дирака иногда обозначают буквой Ш , так как график функции визуально схож с формой буквы.
В круглых скобках указывается одна или несколько переменных, от которых зависит физическая величина. Например, f(x, y) означает, что величина f является функцией x и y.
Диакритические знаки добавляются к символу физической величины для обозначения определённых различий. Ниже диакритические знаки добавлены для примера к букве x .
Обозначения физических величин часто имеют нижний, верхний, или оба индекса. Обычно нижний индекс обозначает характерный признак величины, например её порядковый номер, тип, проекцию и т. п. Верхний индекс обозначает степень, кроме случаев, когда величина является тензором.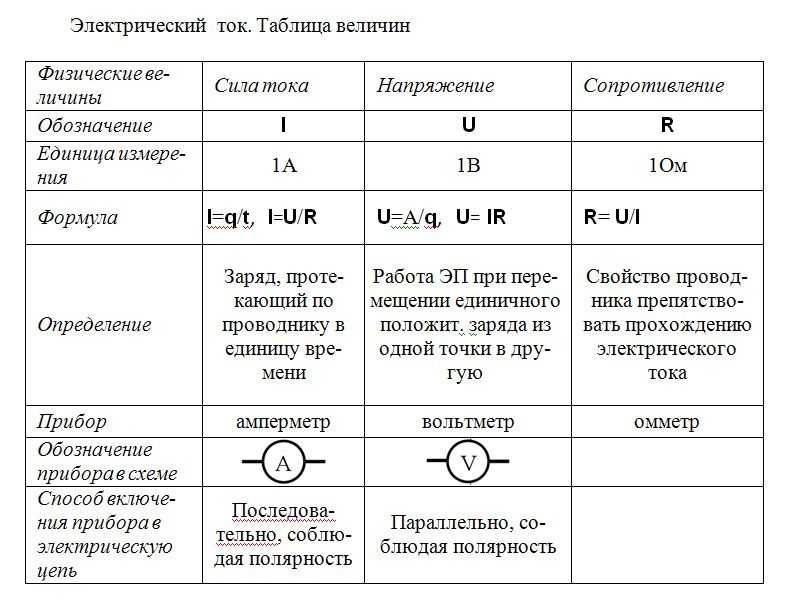
Для наглядного обозначения физических процессов и математических операций используются графические обозначения: Фейнмановские диаграммы, спиновые сети и графические обозначения Пенроуза.
обозначение скорости
2.33 обозначение скорости:
2.33.1. Буква алфавита, указывающая скорость, на которой шина может использоваться при нагрузке, о которой свидетельствует соответствующий индекс нагрузки;
2.33.2. Обозначения скорости и соответствующие им максимальные значения приведены в таблице 2.
Словарь-справочник терминов нормативно-технической документации. academic.ru . 2015 .
Смотреть что такое «обозначение скорости» в других словарях:
Обозначение – сопряжения, контролируемого размера, поверхности или зоны контроля, номер сварного шва или обозначение пересечения сварных швов, указываемого номерами сварных швов, через тире, например № 1 2, и других параметров. Источник … Словарь-справочник терминов нормативно-технической документации
коэффициент скорости реактивного сопла – коэффициент скорости сопла Отношение средней по массе скорости газа в выходном сечении реактивного сопла ГТД к идеальной скорости, соответствующей расширению потока газа до давления в окружающей среде. Обозначение φс [ГОСТ] Тематики… … Справочник технического переводчика
Обозначение φс [ГОСТ] Тематики… … Справочник технического переводчика
ГОСТ Р7: Инструмент абразивный. Акустический метод определения твердости и звуковых индексов по скорости распространения акустических волн – Терминология ГОСТ Р7: Инструмент абразивный. Акустический метод определения твердости и звуковых индексов по скорости распространения акустических волн оригинал документа: 3.2 звуковой индекс абразивного инструмента; ЗИ: Условное… … Словарь-справочник терминов нормативно-технической документации
категория скорости пневматической шины – категория скорости шины Условное обозначение, определяющее максимальную скорость качения пневматической шины. [ГОСТ] Тематики шины пневматические Обобщающие термины конструктивные обозначения пневматических шин Синонимы категория… … Справочник технического переводчика
категория скорости массивной шины – Условное обозначение, определяющее максимальную скорость качения массивной шины. [ГОСТ] Тематики шины пневматические Обобщающие термины показатели функциональной и технической эффективности массивных шин EN speed category FR catégorié de … Справочник технического переводчика
ГОСТ Р 41.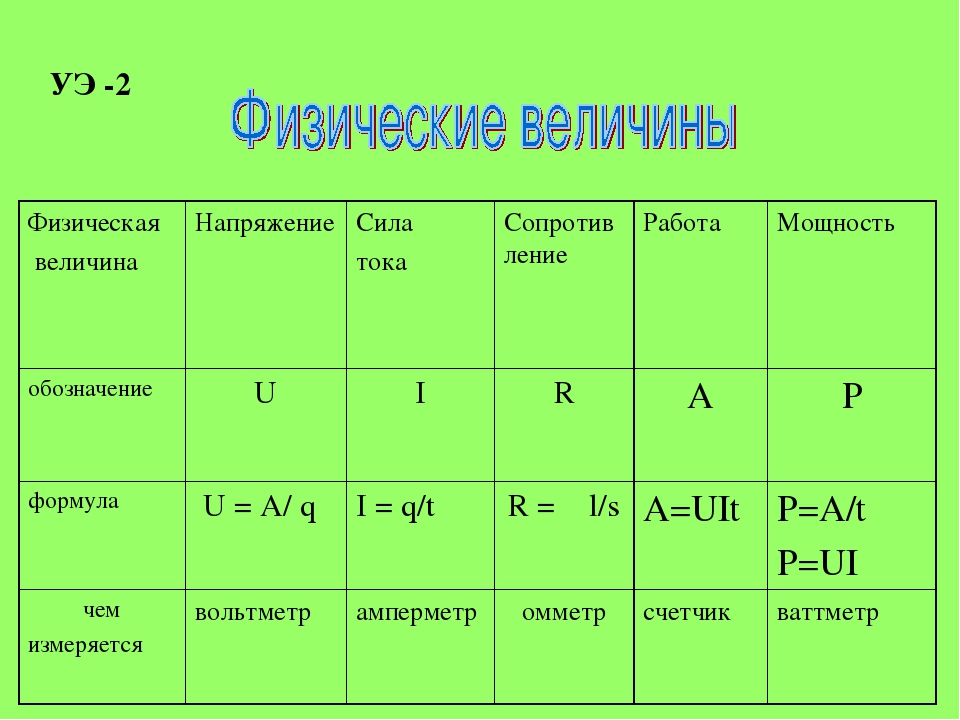 109-99: Единообразные предписания, касающиеся официального утверждения в отношении производства шин с восстановленным протектором для транспортных средств неиндивидуального пользования и их прицепов – Терминология ГОСТ Р 41.109 99: Единообразные предписания, касающиеся официального утверждения в отношении производства шин с восстановленным протектором для транспортных средств неиндивидуального пользования и их прицепов оригинал документа: 2.38 … Словарь-справочник терминов нормативно-технической документации
109-99: Единообразные предписания, касающиеся официального утверждения в отношении производства шин с восстановленным протектором для транспортных средств неиндивидуального пользования и их прицепов – Терминология ГОСТ Р 41.109 99: Единообразные предписания, касающиеся официального утверждения в отношении производства шин с восстановленным протектором для транспортных средств неиндивидуального пользования и их прицепов оригинал документа: 2.38 … Словарь-справочник терминов нормативно-технической документации
Индекс – 6. Индекс Кодированная импульсная последовательность, записанная на сервоповерхности вида: dddddododdo, где d означает: для сервозоны пару дибитов, для защитных зон одиночный дибит; о означает: для сервозоны отсутствующую пару дибитов, для… … Словарь-справочник терминов нормативно-технической документации
индекс нагрузки – 2.32 индекс нагрузки: Цифровая кодировка, свидетельствующая о нагрузке, которую может выдержать шина при скорости, на которую указывает соответствующее обозначение скорости, и в рабочем режиме, соответствующем условиям эксплуатации, указанным… … Словарь-справочник терминов нормативно-технической документации
Трель – Обозначение трели Трель (итал. trillare дребезжать) один из наиболее употребительных мелизмов; быстрое чередование двух соседних нот, отстоящих на секунду, большую или малую. Первая нота называется главной и по отношению к… … Википедия
trillare дребезжать) один из наиболее употребительных мелизмов; быстрое чередование двух соседних нот, отстоящих на секунду, большую или малую. Первая нота называется главной и по отношению к… … Википедия
Симистор – Обозначение на схемах Эквивалентная схема симистора … Википедия
Книги
- Угол атаки, Джесси Рассел. Эта книга будет изготовлена в соответствии с Вашим заказом по технологии Print-on-Demand. High Quality Content by WIKIPEDIA articles! Угол атаки (общепринятое обозначение – буква… ПодробнееКупить за 743 руб
Мы используем куки для наилучшего представления нашего сайта. Продолжая использовать данный сайт, вы соглашаетесь с этим. Хорошо
Как обозначается скорость
Цель: продолжить формировать представление о новой величине «скорость, время, расстояние» и единицах ее измерения.
- Создать условия для осознания детьми зависимости между величинами, характеризующими движение тел – скоростью, временем и расстоянием.
- Познакомить детей с понятием скорости и единицами её измерения.

- Отрабатывать вычислительные навыки, обучать детей работе с графическими моделями.
- Развивать познавательную активность детей, способности к самооценке и самоконтролю, формировать коммуникативные умения.
Оборудование: карточки, карточки для работы в парах, интерактивная доска, название единиц времени на карточках, рабочая тетрадь, компьютер, проектор, экран
Тип урока: урок закрепления и развития знаний, умений и навыков.
Методы: формы познавательной деятельности учащихся на уроке, индивидуальная работа, работа в парах.
Планируемые достижения учащихся на уроке:
- знать понятие скорости, времени и расстоянии как новой единицы измерения, уметь решать задачи на нахождение скорости движения по известным расстоянию и времени движения;
- закрепить табличные и внетабличные случаи умножения и деления, знание единиц длины и времени.
Ход урока
Организационный момент
Прозвенел заливистый школьный звонок.
Учитель: Я улыбнулась вам, и вы улыбнитесь друг другу, и подумайте, как хорошо, что мы сегодня все вместе. Мы спокойны, добры и приветливы. Глубоко вдохните и выдохните. Выдохните вчерашнюю обиду и злость, беспокойство. Забудьте о них. Я желаю вам хорошего настроения.
Мы спокойны, добры и приветливы. Глубоко вдохните и выдохните. Выдохните вчерашнюю обиду и злость, беспокойство. Забудьте о них. Я желаю вам хорошего настроения.
Сообщение темы и цели урока
Сегодня на уроке мы с вами вспомним о величинах, с которыми познакомились на предыдущих уроках и решали с ними задачи на движение и ставить свои ответы на листах самооценки.
(Ответы учащихся) Верно, это скорость, время, расстояние. Какими латинскими буквами они обозначаются. (s, v, t).
Девиз нашего урока: «Один за всех, все за одного»
Работа в парах
На партах карточки с примерами:
Увеличь произведение чисел 805 и 5 на 1025 (5050)
Извычти частное числои 5 (1995)
Увеличь частное чисел 4025 и 5 в 100 раз (80500)
Прибавь к числу 1207 частное чисели 9 (6907)
Из произведения чисел 480 и 7 вычти число 1406 (1954)
Произведение чисел 4070 и 6 уменьши на 4420 (20000)
Записать ответы в порядке возрастания
(ответ записан на интерактивной доске)
Минутка чистописания
(образец в тетради)
Прочитайте числа. Какие это числа? В каком порядке они расположены? Как они увеличиваются? Прочитайте число целиком. Сколько цифр использовано? В обратном направлении можем прочитать? Прочитайте. Запишите числа в порядке возрастания, через клеточку в порядке убывания. Прочитайте их, сравните. Запишите еще раз в порядке возрастания, найдите сумму этих четных чисел. Как вы это сделали?
Какие это числа? В каком порядке они расположены? Как они увеличиваются? Прочитайте число целиком. Сколько цифр использовано? В обратном направлении можем прочитать? Прочитайте. Запишите числа в порядке возрастания, через клеточку в порядке убывания. Прочитайте их, сравните. Запишите еще раз в порядке возрастания, найдите сумму этих четных чисел. Как вы это сделали?
Индивидуальная работа по карточкам
(4 ученика решают № 7)
Устная работа с остальными учениками:
В саду растут груши и ивы. На груше росло 69 груш, а на иве на 100 груш больше. Сколько груш росло на иве?
Мама варила одно яйцо 5 минут. Сколько времени будет варить 3 яйца?
Масса 1 мешка сахара 50 кг. Сколько кг в 4 таких мешках?
За 1 с человек делает 2 шага. Сколько шагов он сделает за 5 с.? За 10 с?
Физминутка
Качу, лечу во весь опор. (Выполняют ходьбу на месте.)
Я сам – шофер (Имитируют управление автомобильным рулем.)
И сам – мотор. (Круговые движения плечами вперед-назад. )
)
Нажимаю на педаль, (Имитируют нажимание на педаль.)
И машина мчится вдаль! (Бег на месте.)
Первичное закрепление
Орел летел со скоростью 20 км/ч. За сколько часов он пролетит 80 км?
Cкорость полета космического спутника 8 км/сек. Сколько км он пролетит за 10 сек?
Решение задачи № 2
S – 90 км 90: 45= 2 часа
Sкм 270: 90 = 3 часа
Самостоятельная работа по учебнику
Итог урока
Давайте подведем итог урока
Чем занимались на уроке?
Рефлексия
Окрасьте сегодняшний урок (Дети рисуют сердечко своего настроения от урока) Учитель объясняет значении выбранного цвета.
- Красный – радость
- Жёлтый – приятное
- Зелёный – спокойное
- Синий – грустное
- Фиолетовый – тревожный
- Оранжевый – удовлетворение
- Чёрный – неудовлетворение
И на память об уроке солнышко дарит вам частичку своего тепла и хорошего настроения.
Наш закончен урок –
Спасибо за внимание,
Будем рады новой встрече,
Всем Вам до свидания!
Понятие скорости широко используется в науке: математике, физике, механике. Школьники начинают знакомиться с ним уже в третьем классе. Более подробно это происходит в 7-8 классах. В общепринятом смысле скорость – это величина, которая характеризует, насколько быстро предмет перемещается в пространстве за единицу времени. В зависимости от области применения, скорость обозначается разными символами.
Школьники начинают знакомиться с ним уже в третьем классе. Более подробно это происходит в 7-8 классах. В общепринятом смысле скорость – это величина, которая характеризует, насколько быстро предмет перемещается в пространстве за единицу времени. В зависимости от области применения, скорость обозначается разными символами.
Как обозначается скорость в математике
В учебниках по математике принято использовать строчную прописную латинскую букву v. Скорость взаимосвязана с пройденным путем и временем, за который оно пройдено.
При равномерном движении величина v=S/t, где:
Как обозначается скорость в физике
В разделе физики, именуемом механикой, также изучается скорость. Обозначение скорости зависит от того, векторная это величина или обычная. В первом случае над буквой v ставится стрелочка, направленная вправо →. Если же нет необходимости учитывать направление, то применяют обычный символ v.
Единицы измерения скорости
В международной системе единиц измерения принято оперировать метрами в секунду (м/с). В то же время общепризнанными единицами измерения являются километр в час (км/ч), узел (морская миля в час).
В то же время общепризнанными единицами измерения являются километр в час (км/ч), узел (морская миля в час).
Как обозначается скорость света и звука
Учеными доказано, что скорость света является абсолютной величиной, с которой могут перемещаться информация и энергия. Этот показатель постоянен и равен58 ± 1,2 м/с. Его символом выбрали латинскую букву с.
Скорость звука зависит от плотности и упругости среды, в которой распространяются звуковые волны. Ее измеряют в Махах. Например, сверхзвуковая скорость находится в границах от 1,2 до 5 Махов. А все что выше, называют гиперзвуковой скоростью.
Очевидно, что символ, которым обозначается скорость, зависит от математического или физического смысла, которым наполняется данное понятие.
Как известно, масса тела равна его объему, умноженному на плотность. Обычно это утверждение записывается в виде формулы, посредством общепринятых условных обозначений.
Как обозначается объём
И в математике, и в физике объём обозначается буквой V. Произносится это обозначение так же, как и обозначение скорости, т.е. [вэ], но визуально обозначения различны. Скорость обозначается строчной (т.е. маленькой) буквой v, а объём обозначается заглавной (т.е. большой) буквой V.
Произносится это обозначение так же, как и обозначение скорости, т.е. [вэ], но визуально обозначения различны. Скорость обозначается строчной (т.е. маленькой) буквой v, а объём обозначается заглавной (т.е. большой) буквой V.
Как обозначается плотность
Плотность обозначается греческой буквой «ро». Этой буквой обозначается плотность любого вещества (газа, воды или любой другой жидкости, воздуха, металла, льда и прочего). При необходимости, если требуется в рамках одной задачи обозначить плотность нескольких веществ, используются нижние индексы (буквенные, числовые или буквенно-числовые). Поскольку буквенные индексы имеют преимущество – смысловой оттенок, их использование предпочтительнее, чем числовых. Например, плотность льда можно обозначить как р л, а плотность воды – как р в. Такие обозначения, со смысловым оттенком, удобнее, чем р 1 и р 2 . Но, если необходимо обозначить, к примеру, плотность нескольких жидкостей, будут удобны числовые индексы: р 1, р 2 , р 3 , р 4 , р 5 . Если нужно обозначить плотности нескольких жидкостей и нескольких газов, целесообразно использовать буквенно-числовые индексы: р ж1, р ж2 , р ж3 , р ж4 , р ж5 для жидкостей и р г1, р г2 , р г3 , р г4 , р г5 для газов.
Если нужно обозначить плотности нескольких жидкостей и нескольких газов, целесообразно использовать буквенно-числовые индексы: р ж1, р ж2 , р ж3 , р ж4 , р ж5 для жидкостей и р г1, р г2 , р г3 , р г4 , р г5 для газов.
Как обозначается масса тела
Масса тела обозначается буквой «m» (читается: [эм]). При необходимости, в обозначении массы используются нижние буквенные, числовые или буквенно-числовые символы. Например, массу шара и массу куба можно обозначить в одной задаче как m ш m к (в данном случае буквенные индексы использовать удобнее, так как они несут смысловую нагрузку). Если же нужно обозначить массы, например, десяти коробок, то удобнее пользоваться числовыми индексами (m 1 , m 2 , m 3 и т.д.)
Как обозначается вес тела
В физике часто приходится обозначать буквой вес тела. Для этого используют буквы G (читается: [жэ]) или Р (читается: [пэ]). Когда речь идёт о собственном весе тела, обычно используют букву G. Когда речь идёт о весе тел, создающих внешнюю нагрузку на рассматриваемое тело, их вес обозначается обычно буквой Р, но может использоваться и G. При необходимости, к этим обозначениям добавляют нижний индекс (числовой, буквенный или буквенно-числовой). Например, рассматривается балка массой m. Её собственный вес G = m*g. На этой балке расположены грузы массой m 1 , m 2 , m 3 , m 4 , m 5 . По отношению к этой балке они создают внешнюю нагрузку, поэтому их вес обычно обозначается не буквой G, а буквой Р (Р 1 , Р 2 , Р 3 , Р 4 , Р 5). Если же речь шла бы не о балке, а непосредственно об этих пяти грузах, для обозначения их веса была бы выбрана буква G (т.е. G 1 , G 2 , G 3 , G 4 , G 5). Бывает, что при обозначении веса удобно использовать не числовые, а буквенные или буквенно-числовые индексы. Например, если в одной задаче нужно обозначить вес шара и вес цилиндра, в качестве индекса лучше использовать не «1» и «2», а несущие смысловой оттенок «ш» и «ц». Если же в одной задаче нужно обозначить, например, вес двух шаров и трех цилиндров, лучше использовать буквенно-числовые нижние индексы: G ш1 , G ш2 , G ц1 , G ц2 , G ц3 .
При необходимости, к этим обозначениям добавляют нижний индекс (числовой, буквенный или буквенно-числовой). Например, рассматривается балка массой m. Её собственный вес G = m*g. На этой балке расположены грузы массой m 1 , m 2 , m 3 , m 4 , m 5 . По отношению к этой балке они создают внешнюю нагрузку, поэтому их вес обычно обозначается не буквой G, а буквой Р (Р 1 , Р 2 , Р 3 , Р 4 , Р 5). Если же речь шла бы не о балке, а непосредственно об этих пяти грузах, для обозначения их веса была бы выбрана буква G (т.е. G 1 , G 2 , G 3 , G 4 , G 5). Бывает, что при обозначении веса удобно использовать не числовые, а буквенные или буквенно-числовые индексы. Например, если в одной задаче нужно обозначить вес шара и вес цилиндра, в качестве индекса лучше использовать не «1» и «2», а несущие смысловой оттенок «ш» и «ц». Если же в одной задаче нужно обозначить, например, вес двух шаров и трех цилиндров, лучше использовать буквенно-числовые нижние индексы: G ш1 , G ш2 , G ц1 , G ц2 , G ц3 .
Читайте также.

Как устроиться на работу в полицию
Как научиться делать шпагат – хорошая растяжка без возрастных ограничений
Как самому изготовить защитную сетку от насекомых – видео
Как послушнику в монастыре живется
Работа со сводными таблицами в экселе
Как сделать морфологический разбор
Выбираем самые модные и актуальные платья
Вполне может быть, что за этим также скрывается какая-нибудь серьёзная легенда о том, что данный амулет будет защищать вас «до гроба», а то и дольше
Делаем короб для сабвуфера своими руками
Карта скидок. Что она даёт? Как получить? Нужна ли от «Икеа Фэмили» карта? Как получить, и что она дает?
Как научиться рисовать: советы для начинающих
Большая Энциклопедия Нефти и Газа
Обозначение – скорость
Обозначения скоростей и углов см. фиг.
Припишем обозначениям скорости и эффективной массы отсутствующих электронов индекс О и определим отсутствующий электрон (или дырку) как гипотетическую частицу, представляющую собой совокупность электронов заполненной зоны, в которой отсутствует только один электрон.
Индекс 1 принят для обозначения скоростей и углов на входе в рабочее колесо, индекс 2 – на выходе из него.
Индекс 1 принят для обозначения скоростей жидкости на входе в рабочее колесо, индекс 2 – на выходе из него.
Введем также индекс 1 для обозначения скоростей и углов на входе в рабочее колесо и индекс 2 – на выходе из него.
Введем также индекс 1 для обозначения скоростей и углов на входе в рабочее колесо и индекс 2 для обозначения тех же величин на выходе из него.
XII-XIV мы используем U для обозначения скорости свободного потока вместо (обычно не существующего) потенциала скорости.
Около ручек управления на шильдиках нанесены обозначения скорости вращения диска, включения и выключения ЭПУ, включенного и выключенного положения автостопа.
Около ручек управления на шильдиках нанесены обозначения скоростей вращения диска, включения и выключения ЭПУ, включенного и выключенного положения автостопа.
Дорожки 2, 8 и 4 служат для обозначения скорости вращения шпинделя, при которой выполняется данный этап технологического цикла.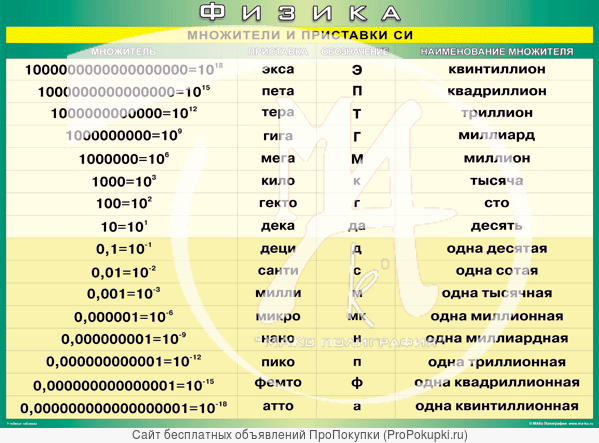
Эта тема будет полезна не только учащимся средней школы, но даже взрослым. Кроме того, статья будет интересна родителям, желающим объяснить своим детям простые вещи из естественных наук. Среди очень важных тем – это скорость в физике.
Довольно часто ученики не могут разобраться в решении задач, отличить имеющиеся виды скоростей, а еще сложнее понять научные определения. Здесь мы рассмотрим все на более доступном языке, чтобы было не только все ясно, но даже интересно. А вот запомнить некоторые вещи все же придется, так как технические науки (физика и математика) требуют заучивать наизусть формулы, единицы измерения и, конечно же, значения символов в каждой формуле.
Где встречается?
Для начала вспомним, что данная тема относится к такому разделу физики как механика, подразделу «Кинематика». Кроме того, изучение скорости на этом не заканчивается, оно будет и в последующих разделах:
- оптика,
- колебания и волны,
- термодинамика,
- квантовая физика и так далее.

Также понятие скорость встречается в химии, биологии, географии, информатике. В физике тема «скорость» встречается чаще всего и изучается углубленно.
Кроме того, данное слово употребляется в повседневной жизни всеми нами, особенно среди автомобилистов, водителей транспортной техники. Даже опытные кулинары иногда используют фразу, например, «взбить яичные белки миксером на средней скорости».
Что такое скорость?
Скорость в физике – это кинематическая величина. Означает расстояние, которое преодолевается телом за какой-то промежуток времени. Допустим, молодой человек движется от дома к магазину, преодолевая двести метров за одну минуту. Напротив, его старенькая бабушка пройдет тем же маршрутом за шесть минут мелкими шажками. То есть парень перемещается намного быстрее своей пожилой родственницы, так как развивает скорость гораздо больше, делая очень быстрые длинные шаги.
То же самое стоит сказать про автомобиль: одна машина едет быстрее, а другая медленнее, потому что скорости движения разные. Позднее мы рассмотрим многочисленные примеры, связанные с этим понятием.
Позднее мы рассмотрим многочисленные примеры, связанные с этим понятием.
Формула
На уроке в школе обязательно рассматривается формула скорости в физике для того, чтобы было удобно решать задачи.
- V – это, соответственно, скорость движения;
- S – расстояние, которое преодолевается телом при перемещении от одной точки в пространстве до другой;
- t – время перемещения.
Следует запомнить формулу, потому что она пригодится в будущем при решении множества задач и не только. Например, вам может стать интересно, с какой скоростью дойдете от дома до работы или места учебы. Но вы заранее можете узнать расстояние по карте в смартфоне или на компьютере, либо по бумажному варианту, зная масштаб и имея при себе линейку. Далее вы засекаете время, перед тем, как начать движение. Придя на место назначения, смотрите, сколько минут или часов потребовалось пройти без остановки.
В чем измеряется?
Скорость чаще всего измеряется по системе единиц СИ.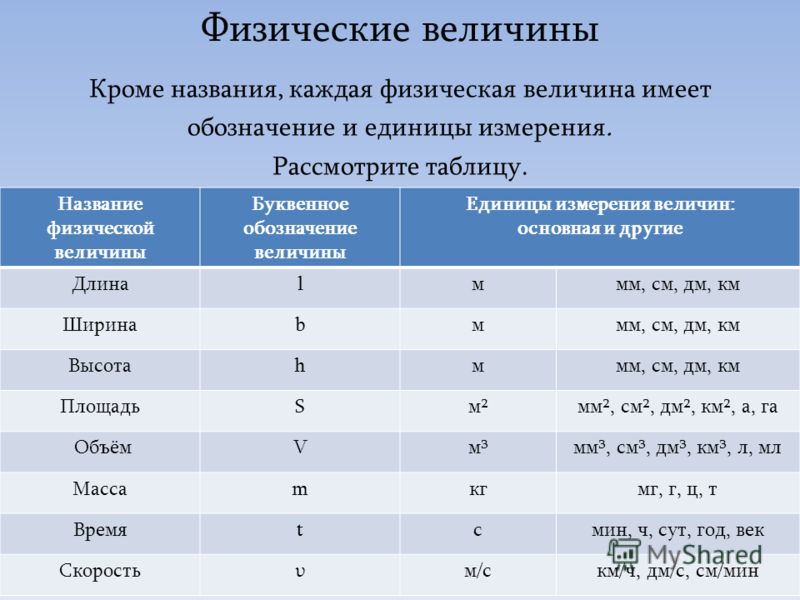 Ниже представлены не только единицы, но и примеры того, где они применяются:
Ниже представлены не только единицы, но и примеры того, где они применяются:
- км/ч (километр в час) – транспорт;
- м/с (метр в секунду) – ветер;
- км/с (километр в секунду) – космические объекты, ракеты;
- мм/ч (миллиметр в час) – жидкости.
Давайте для начала разберемся, откуда взялась дробная черта и почему единица измерения именно такая. Обратите внимание по физике на формулу скорости. Что вы видите? В числителе стоит S (расстояние, путь). В чем измеряется расстояние? В километрах, метрах, миллиметрах. В знаменателе, соответственно, t (время) – часы, минуты, секунды. Отсюда и единицы измерения величины именно такие, как представлены в начале данного раздела.
Закрепим с вами изучение формулы скорости в физике следующим образом: какое расстояние преодолеет тело за конкретный промежуток времени? Например, человек пройдет 5 километров за 1 час. Итого: скорость движения человека – 5 км/ч.
От чего зависит?
Нередко учителя задают ученикам вопрос: “От чего зависит скорость?”. Школьники часто теряются и не знают, что сказать. На самом деле, все очень просто. Достаточно посмотреть на формулу, чтобы всплыла подсказка. Скорость тела в физике зависит от времени движения и расстояния. Если неизвестен хотя бы один из этих параметров, решить задачу будет невозможно. Кроме того, в примере можно встретить другие виды скоростей, о которых речь пойдет в следующих разделах этой статьи.
Школьники часто теряются и не знают, что сказать. На самом деле, все очень просто. Достаточно посмотреть на формулу, чтобы всплыла подсказка. Скорость тела в физике зависит от времени движения и расстояния. Если неизвестен хотя бы один из этих параметров, решить задачу будет невозможно. Кроме того, в примере можно встретить другие виды скоростей, о которых речь пойдет в следующих разделах этой статьи.
Во многих задачах по кинематике приходится строить графики зависимости, где по оси Х – время, а по оси Y – расстояние, путь. По таким изображениям можно легко оценить характер скорости движения. Стоит отметить, что во многих профессиях, связанных с транспортом, электрическими машинами часто применяются графики. Например, на железной дороге.
В нужный момент измеряем скорость
Есть еще одна тема, которая пугает учеников средней школы, – мгновенная скорость. В физике это понятие встречается как определение величины скорости в мгновенный промежуток времени.
Давайте рассмотрим простой пример: машинист ведет поезд, его помощник наблюдает за скоростью движения время от времени. Вдалеке виднеется Следует проконтролировать, с какой скоростью движется поезд именно сейчас. Помощник машиниста сообщает в 16 часов 00 минут, что скорость равна 117 км/ч. Это и есть мгновенная скорость, зафиксированная ровно в 4 часа вечера. Через три минуты скорость стала 98 км/ч. Это тоже мгновенная скорость относительно 16 часов 03 минут.
Вдалеке виднеется Следует проконтролировать, с какой скоростью движется поезд именно сейчас. Помощник машиниста сообщает в 16 часов 00 минут, что скорость равна 117 км/ч. Это и есть мгновенная скорость, зафиксированная ровно в 4 часа вечера. Через три минуты скорость стала 98 км/ч. Это тоже мгновенная скорость относительно 16 часов 03 минут.
Начало движения
Без начальной скорости физика не представляет практически ни одно движение транспортной техники. Что это за параметр? Это скорость, с которой начинает движение объект. Допустим, машина не может начинать движение моментально со скоростью 50 км/ч. Ей нужно разогнаться. Когда водитель нажимает педаль, автомобиль плавно начинает движение, например, со скоростью сначала 5 км/ч, потом постепенно 10 км/ч, 20 км/ч и так далее (5 км/ч и есть начальная скорость).
Конечно, можно совершить резкий старт, какой бывает у бегунов-спортсменов, при ударе теннисного мяча ракеткой, но все равно всегда существует начальная скорость. Ее нет по нашим меркам только у звезд, планет и спутников нашей Галактики, так как мы не знаем, когда началось движение и каким образом. Ведь до самой смерти космические объекты не могут останавливаться, они всегда в движении.
Ее нет по нашим меркам только у звезд, планет и спутников нашей Галактики, так как мы не знаем, когда началось движение и каким образом. Ведь до самой смерти космические объекты не могут останавливаться, они всегда в движении.
Равномерная скорость
Скорость в физике – это совокупность отдельных явлений и характеристик. Различают также равномерное и неравномерное движение, криволинейное и прямолинейное. Давайте приведем пример: человек идет по прямой дороге с одинаковой скоростью преодолевая из точки А в точку В расстояние 100 метров.
С одной стороны, это можно назвать прямолинейной и равномерной скоростью. Но если присоединить человеку очень точные датчики скорости, маршрута, то можно заметить, что разница все же есть. Неравномерная скорость – это когда скорость регулярно или постоянно меняется.
В быту и технике
Скорость движения в физике существует всюду. Даже микроорганизмы перемещаются, пусть и с очень медленной скоростью. Стоит отметить, что существует вращение, которое характеризуется также скоростью, но имеет единицу измерения – об/мин (обороты в минуту).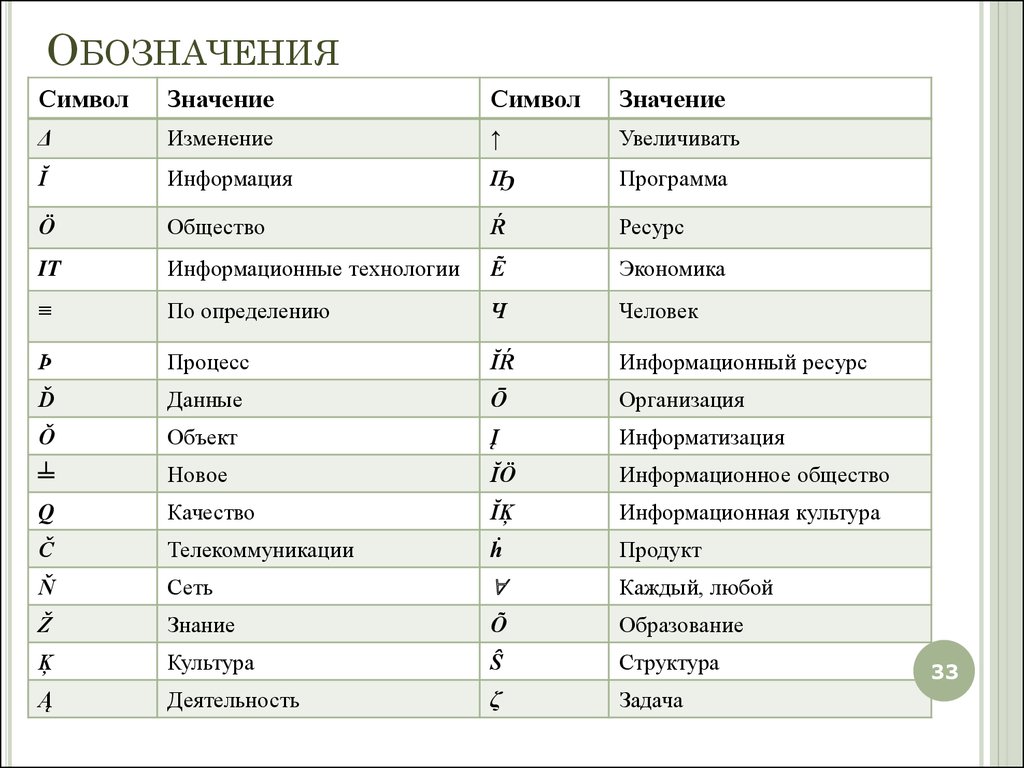 Например, скорость вращения барабана в стиральной машине. Данная единица измерения употребляется всюду, где есть механизмы и машины (двигатели, моторы).
Например, скорость вращения барабана в стиральной машине. Данная единица измерения употребляется всюду, где есть механизмы и машины (двигатели, моторы).
В географии и химии
Даже вода имеет скорость движения. Физика всего лишь является дочерней наукой в сфере процессов, происходящих в природе. Допустим, скорость ветра, волны в море – это все измеряется привычными физическими параметрами, величинами.
Наверняка, многие из вас знакомы с фразой «скорость химической реакции». Только в химии это имеет иное значение, так как имеется в виду, за какое время произойдет тот или иной процесс. Например, марганцовка быстрее растворится в воде, если взболтать сосуд.
Скорость-невидимка
Существуют невидимые явления. Например, мы не можем видеть, как перемещаются частицы света, различных излучений, как распространяется звук. Но если бы не было движения их частиц, то никакое бы из этих явлений не существовало в природе.
Информатика
Практически каждый современный человек сталкивается с понятием «скорость» во время работы на компьютере:
- скорость Интернета;
- скорость загрузки страниц;
- быстрота загрузки процессора и так далее.

Примеров скорости движения в физике можно привести огромное множество.
Внимательно прочитав статью , вы познакомились с понятием скорости, узнали, что она из себя представляет. Пусть данный материал поможет вам углубленно изучить раздел «Механика», проявить к нему интерес и побороть страх при ответах на уроках. Ведь скорость в физике – это часто встречающееся понятие, которое легко запомнить.
Скорость является одной из основных характеристик . Она выражает саму суть движения, т.е. определяет то отличие, которое имеется между телом неподвижным и телом движущимся.
Единицей измерения скорости в системе СИ является м/с .
Важно помнить, что скорость – величина векторная. Направление вектора скорости определяется по движения. Вектор скорости всегда направлен по касательной к траектории в той точке, через которую проходит движущееся тело (рис.1).
К примеру, рассмотрим колесо движущегося автомобиля. Колесо вращается и все точки колеса движутся по окружностям. Брызги, разлетающиеся от колеса, будут лететь по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек колеса.
Брызги, разлетающиеся от колеса, будут лететь по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек колеса.
Таким образом, скорость характеризует направление движения тела (направление вектора скорости) и быстроту его перемещения (модуль вектора скорости).
Отрицательная скорость
Может ли скорость тела быть отрицательной? Да, может. Если скорость тела отрицательна, это значит, что тело движется в направлении, противоположном направлению оси координат в выбранной системе отсчета. На рис.2 изображено движение автобуса и автомобиля. Скорость автомобиля отрицательна, а скорость автобуса положительна. Следует помнить, что говоря о знаке скорости, мы имеем ввиду проекцию вектора скорости на координатную ось.
Равномерное и неравномерно движение
В общем случае скорость зависит от времени. По характеру зависимости скорости от времени, движение бывает равномерное и неравномерно.
ОПРЕДЕЛЕНИЕ
Равномерное движение – это движение с постоянной по модулю скоростью.
В случае неравномерного движения говорят о :
Примеры решения задач по теме «Скорость»
ПРИМЕР 1
| Задание | Автомобиль прошел первую половину пути между двумя населенными пунктами со скоростью 90 км/ч, а вторую половину – со скоростью 54 км/ч. Определите среднюю скорость автомобиля. |
| Решение | Было бы неверным вычислять среднюю скорость автомобиля как среднее арифметическое двух указанных скоростей. Воспользуемся определением средней скорости: Так как предполагается прямолинейное равномерное движение, знаки векторов можно опустить. Время, потраченное автомобилем на прохождение всего отрезка пути: где — время, затраченное на прохождение первой половины пути, а — время, затраченное на прохождение второй половины пути. Суммарное перемещение равно расстоянию между населенными пунктами, т.е. . Подставив эти соотношения в формулу для средней скорости, получим: Переведем скорости на отдельных участках в систему СИ: Тогда средняя скорость автомобиля: (м/с) |
| Ответ | Средняя скорость автомобиля равна 18,8 м/с |
ПРИМЕР 2
| Задание | Автомобиль проехал 10 секунд со скоростью 10 м/с, а затем ехал еще 2 минуты со скоростью 25 м/с. Определить среднюю скорость автомобиля. Определить среднюю скорость автомобиля. |
| Решение | Сделаем рисунок. |
Как вы думаете, кто двигается быстрее агроном Васечкин, автомобиль Renault или самолет Боинг? Кто из них быстрее доберется от Москвы до Краснодара? Ответ очевиден Renault быстрее Васечкина, но медленнее Боинга.
То есть мы не только знаем, как двигаются разные объекты, но и можем сравнить их скорости. А что такое скорость в физике? Как найти скорость тела, и что такое единицы измерения скорости?
Скорость в физике: как найти скорость?
В 7 классе на уроках физики вводят понятие скорости. Без сомнения, все школьники к этому моменту уже знакомы с этим словом и представляют, что оно означает.
- А также знают, что скорость измеряется в км/ч и обозначается буквой V.
Но объяснить, что же такое скорость в физике, каковы единицы скорости, связно вряд ли смогут. Именно потому это простое, казалось бы, понятие требует пояснений и разбора.
В физике быстроту движения Васечкина, Renault и Боинга называют скоростью их движения. И скорость эта характеризует, какой путь преодолевает каждый из участников этого путешествия за единицу времени. И если в полете расстояние в 1350 километров между Москвой и Краснодаром мы преодолеем за два часа, на машине нам потребуется никак не меньше 15 часов, то пешком бесшабашный Васечкин сможет в бодром темпе как раз прошагать весь свой отпуск и прибыть на место лишь для того, чтобы поцеловать тещу, отведать блинов и сесть на самолет до Москвы, дабы успеть на работу в понедельник.
Соответственно, за единицу времени за час самолет пролетит 670 километров, машина проедет 90 километров, а турист Васечкин отмахает аж целых пять километров дороги. И тогда говорят, что скорость самолета 670 километров в час, машины 90 км в час, а пешехода 5 км/ч. То есть, скорость определяется делением пройденного пути на единицу времени на час, на минуту или на секунду.
Единицы измерения скорости
На практике применяются такие единицы, как км/ч, м/с и некоторые другие. Обозначают скорость буквой v, расстояние буквой s, а время буквой t. Формула для нахождения скорости в физике выглядит так:
Обозначают скорость буквой v, расстояние буквой s, а время буквой t. Формула для нахождения скорости в физике выглядит так:
- V = s / t,
Где s – пройденный путь
t – время, затраченное на преодоление этого пути
А если нам надо пересчитать скорость не в километрах в час, а в метрах за секунду, то пересчет происходит следующим образом. Так как 1 км=1000 м, а 1 ч = 60 мин = 3600 с, то можно записать: 1 км/ч=(1000 м)/(3600 с). И тогда скорость самолета будет равна: 670 км/ч=670×(1000 м)/(3600 с)=186м/с
Кроме своего числового значения, скорость имеет еще и направление, поэтому на рисунках скорость обозначают стрелкой и называют векторной величиной.
Средняя скорость в физике
Отметим еще один момент. В нашем примере водитель машины вел машину со скоростью 90 км/ч. По шоссе он мог ехать равномерно с такой скоростью долгое время. А вот проезжая по пути разные города, он то останавливался на светофорах, то полз в пробках, то короткими урывками набирал хорошую скорость.
Т.е. его скорость на разных участках пути была неравномерной. В таком случае вводят понятие средней скорости. Средняя скорость в физике обозначается V_ср и считается также как и скорость при равномерном движении. Только берут общее расстояние пути и делят на общее время.
Урок математики: «Скорость. Время
Тема посвящена тем учащимся, у кого физика только первый год. Здесь мы поговорим не только о том, как обозначается расстояние в физике, но и о других интересных вещах. Пусть этот предмет будет интересным по всем разделам и темам.
Какое же оно – расстояние?
В физике у каждой имеется свой символ (обозначение или на латинице, или греческой буквой). Все это сделано для того, чтобы было проще и не путаться. Согласитесь, можно замучиться при написании в тетрадь примерно такой фразы: расстояние = скорость х время. А в физике очень и очень много различных формул с множеством параметров. Причем встречаются и квадратные, и кубические величины. Так какой буквой обозначается расстояние в физике? Сразу оговоримся, что встречаются двух видов обозначения, так как расстояние и длина имеют одинаковые величины и одни и те же единицы измерения. Итак, «S» – это то самое обозначение. Встретите такую букву в задачках или формулах из раздела «Механика».
Итак, «S» – это то самое обозначение. Встретите такую букву в задачках или формулах из раздела «Механика».
Поверьте, в решении задач нет ничего сложного. Но при условии, что вы знаете математику и успеваете по ней. Вам понадобятся знания по операциям с дробями, умение считать, раскрывать скобки, решать уравнения. Без таких навыков по физике будет очень сложно.
Примеры из жизни
Что же такое расстояние? Как обозначается расстояние в физике, мы уже уяснили. Теперь разберемся с понятием.
Представьте себе, что вы сейчас стоите возле своего дома. Ваша задача – дойти до школы. Дорога все время прямая. Идти от силы около двух минут. От дверей подъезда до школьных дверей 200 метров. Это и есть расстояние. Как будет выглядеть описание вашей прогулки от дома до школы?
Почему мы не написали «метров», а ограничились только буквой? Потому что такое вот сокращенное буквенное обозначение. Чуть позже познакомимся и с другими параметрами, которые связаны с расстоянием.
А теперь представьте, что путь от дома до магазина извилистый. Если посмотрите на карту своего района, то увидите, что до магазина от дома расстояние такое же, как до школы. Но почему же путь такой длинный? Потому что дорога не прямая. Приходится переходить у светофора, обходить огромный жилой дом и только уже вы попадаете в магазин. В таком случае фактическое расстояние будет намного больше. В геометрии и физике это обозначает «кривой путь». А прямая линия – это всего лишь чистое расстояние, будто идете сквозь стену большого дома. Можно еще привести пример и с мужчиной, который едет на работу.
Если посмотрите на карту своего района, то увидите, что до магазина от дома расстояние такое же, как до школы. Но почему же путь такой длинный? Потому что дорога не прямая. Приходится переходить у светофора, обходить огромный жилой дом и только уже вы попадаете в магазин. В таком случае фактическое расстояние будет намного больше. В геометрии и физике это обозначает «кривой путь». А прямая линия – это всего лишь чистое расстояние, будто идете сквозь стену большого дома. Можно еще привести пример и с мужчиной, который едет на работу.
С чем связано расстояние?
Понятие “расстояние” не может существовать само по себе, оно должно играть какую-то роль. Например, вы едете на велосипеде в школу, а не идете пешком, потому что опаздываете. Как мы говорили ранее, наш путь до школы прямой. Можно спокойно ехать по тротуару. Естественно, если перемещаться пешком, то получится дольше, чем проделать путь на велосипеде. В чем же здесь дело? Речь, разумеется, идет о скорости, с которой перемещаетесь. Позже мы увидим формулы, которые подскажут, Физика – это такая наука, в которой приходится что-то вычислять. Согласитесь, интересно же, с какой скоростью вы едете на велосипеде? Если вы знаете точно расстояние до школы и время перемещения, то найдете и скорость.
Позже мы увидим формулы, которые подскажут, Физика – это такая наука, в которой приходится что-то вычислять. Согласитесь, интересно же, с какой скоростью вы едете на велосипеде? Если вы знаете точно расстояние до школы и время перемещения, то найдете и скорость.
Итак, у нас появились еще два параметра:
v – скорость.
Все будет намного интереснее, если научитесь работать с формулами и находить неизвестное с помощью дробей. Напомним лишь только правило из математики: все, что находится рядом с неизвестным, идет в знаменатель (то есть вниз дроби). Например, формула расстояния (физика) – это произведение времени и скорости. А в других случаях – дроби. Посмотрите на картинку, в которой изображено, как находить расстояние, скорость и время. Обязательно потренируйтесь и разберитесь, как получаются такие формулы. Все следует только из законов математики, ничего выдуманного в этих формулах нет. Давайте-ка потренируемся (не подглядывайте): какой буквой обозначается расстояние в физике?
В чем измеряются?
Будем надеяться, что вы запомнили обозначение основных величин, их обозначения. Пришла пора изучать единицы измерений. Здесь тоже придется тренировать память, запоминать. Важно знать, не только как обозначается расстояние в физике, но и время, скорость. А ведь это только маленькая тема. Дальше будет сложнее. Давайте приступим:
Пришла пора изучать единицы измерений. Здесь тоже придется тренировать память, запоминать. Важно знать, не только как обозначается расстояние в физике, но и время, скорость. А ведь это только маленькая тема. Дальше будет сложнее. Давайте приступим:
S – расстояние – метр, километр [м], [км];
v – скорость – метров в секунду, километров в час [м/с], [км/ч] (в случае может применяться километр в секунду;
t – время – секунда, минута, час [с], [мин],[ч].
Обратите внимание, как обозначается скорость. Правильно, дробью. А теперь представьте вот что: S/t=м/с или S/t=км/ч. Вот откуда появились дроби. В системе международных единиц СИ эти параметры имеют величины метр, секунда, метр в секунду.
Мы разобрались, как обозначается расстояние в физике, рассмотрели время и скорость, которые неразрывно связаны с ним.
Цели урока:
- ввести понятие скорости как новой единицы измерения; установить зависимости между величинами – скорость, время, расстояние; учить решать задачи на нахождение скорости по известным расстоянию и времени движения используя формулу движения;
- повторить табличные и внетабличные случаи умножения и деления, формировать вычислительные навыки, закрепить знание единиц времени и длины;
- способствовать развитию логического мышления, внимания, речи, самостоятельности;
- прививать интерес к физкультуре и спорту.

Планируемые достижения учащихся на уроке:
- знать понятие скорости как новой единицы измерения, уметь решать задачи на нахождение скорости движения по известным расстоянию и времени движения;
- закрепить табличные и внетабличные случаи умножения и деления, знание единиц длины и времени.
Оборудование: Петерсон Л.Г. Математика, 3кл., III часть; рабочая тетрадь по математике, сигнальные карты, таблицы с дифференцированными заданиями для самостоятельной работы, название единиц длины и единиц времени на карточках, индивидуальные карточки для учащихся, нарисованные герои “Улицы Сезам” (Зелибоба, Кубик, Бусинка).
ХОД УРОКА
- Самоопределение к деятельности.
Урок я хочу начать словами французского философа Ж.Ж. Руссо (1712-1778гг.):
“Вы – талантливые дети! Когда-нибудь вы сами приятно поразитесь, какие вы умные,
как много и хорошо умеете, если будете постоянно работать над собой, ставить
новые цели и стремиться к их достижению…” Я желаю вам уже сегодня на уроке
убедиться в этих словах, ведь вас ждёт открытие новых знаний при решении задач.
- Актуализация знаний.
- Узнав о том, что вы любите смотреть детские телепрограммы, я пригласила героев одной телепередачи к нам на урок. А они появятся здесь, как только вы назовёте эту передачу. Но слова зашифрованы. Что же делать?
- Правильно, надо решить примеры и расшифровать слова. Для этого вам необходимо вспомнить табличные и внетабличные случаи умножения и деления.
- Приготовьте сигнальные карты, контролируем правильность решения примеров.
(Два ученика работают индивидуально на карточках.)
Индивидуальные задания на карточках
- Почему некоторые ребята допускали ошибки? Как этого избежать?
- Что мы им посоветуем?
- Прочитайте слова, расставляя ответы в порядке убывания.
I вариант – первое слово (1 столбик)
II вариант – второе слово (2 столбик)
- Кто готов? (Улица, Сезам)
- Молодцы, ваши знания помогли вам расшифровать названия передачи.
 У нас в
гостях “Улица Сезам”.
У нас в
гостях “Улица Сезам”. - Назовите героев этой передачи. (Зелибоба, Бусинка и Кубик)
- Наши друзья ведут здоровый образ жизни, учатся правильно питаться, занимаются спортом. Увлекаясь ходьбой на лыжах, Зелибоба и Кубик решили всерьёз заняться лыжным спортом и готовиться к Зимним Олимпийским играм, которые пройдут в г. Сочи в 2014 году.
Бусинка объявила старт. Соперники преодолели путь 24 метра. Зелибоба пришёл к финишу через 3 минуты, а Кубик через 4 минуты.
Проблемный вопрос: Почему так произошло? (Один быстрее двигался, а другой медленнее)
- Да, они двигались с разной скоростью.
- Где вы встречались с понятием “скорость”? (В машине спидометр измеряет скорость)
- Как измерить скорость движущихся тел, у которых нет спидометра?
- Назовите тему урока.
- Что будем учиться измерять на уроке?
- Постановка темы урока
- Чтобы точнее сформулировать тему и цели урока, найдём опорные слова.
 Они
необходимы для определения скорости. Для этого, работая в парах, расположите
данные вас единицы измерения в порядке возрастания.
Они
необходимы для определения скорости. Для этого, работая в парах, расположите
данные вас единицы измерения в порядке возрастания. - Какие единицы измерения у I и III ряда? (Длины)
- У II ряда? (Времени)
Кто готов назвать их в порядке возрастания? (Ученики называют и выкладывают на наборное полотно.)
мм, см, дм, м, км
с, мин, ч, сут, мес
Проверьте правильность выполнения, переверните каждую карточку и прочитайте слово. (I и III ряды: расстояние; II ряд: время)
Расстояние – это промежуток между двумя пунктами, точками, между
чем-нибудь. В чём измеряется расстояние? (В единицах длины).
Время – это продолжительность, длительность чего-нибудь. В чём измеряется время? (В единицах времени).
Проблемный вопрос:
- А что называется скоростью?
- В чём измеряется скорость движения?
- Уточните тему нашего урока. (Скорость. Время. Расстояние.)
- Чему будем учиться на уроке? (Ответы детей).

Сегодня нам предстоит узнать как скорость движения связана со временем движения и расстоянием, научиться решать задачи на нахождение скорости движения.
- Открытие новых знаний.
- Что называют скоростью? Где найти ответ на наш вопрос? (В учебнике)
- Откройте учебник с. 1, найдите выделенное слово “скоростью”. Прочитаем определение скорости. (Скоростью называют расстояние, пройденное в единицу времени.)
- Так что же называют скоростью?
- Какими величинами будем пользоваться для определения скорости? (Расстоянием и временем)
- И в качестве единиц измерения скорости мы будем пользоваться и единицами длины и единицами времени.
- Обычно используют такие единицы скорости, как метр в секунду, метр в минуту, километр в час, а записывают так: м/с, м/мин, км/ч. Обратите внимание, что предлог “в” в математике заменили чёрточкой “ / ”.
- Прочитайте единицы скорости км/с м/мин км/ч м/с
- Из каких единиц измерения образуются названия единиц скорости? (Из единиц
длины и единиц времени).

Физминутка.
Руки ставим все вразлёт,
Появился самолёт.
Мах крылом туда-сюда,
Делай раз и делай два.
Отпустите руки вниз
И на место все садитесь.
Работа с учебником
- Интересно, а какая скорость у самолёта?
- Объясните смысл предложений, записанных в задании № 1, стр.2. (Самолёт летит со скоростью 800 км/ч, т.е. за 1 ч самолёт преодолевает расстояние 800 км)
Молодцы. Откройте тетради, запишите число, классная работа. Следите за осанкой. Мы будем учиться решать задачи на нахождение скорости движения по данному расстоянию и времени. Зелибоба и Кубик очень хотят узнать свою скорость движения. Поможем им. Решим задачу.
Задача 1. Зелибоба прошёл на лыжах расстояние, равное 24 метрам за 3 минуты. С какой скоростью он шёл?
Что нам известно?
- Расстояние – 24 м
- Время – 3 мин.
Что нужно узнать? Скорость Зелибобы, т. е. расстояние, которое проходил Зелибоба за 1 мин.
е. расстояние, которое проходил Зелибоба за 1 мин.
Сделаем чертёж к задаче
Чертим отрезок. Чему равно расстояние? Обозначим время на отрезке. Весь путь, который прошёл Зелибоба, мы может разделить на 3 равные части, потому что в каждую минуту Зелибоба проходил одинаковое расстояние.
- Кто из вас догадался, с какой скоростью двигался Зелибоба?
- Как узнать скорость его движения?
Запись в тетради: 24 ׃ 3 = 8 (м/мин) скорость Зелибобы.
Т.е. за 1 мин Зелибоба проходил 8 м.
Напишем ответ задачи. Ответ: 8 м/мин.
- Первичное закрепление.
Закрепим умение решать задачи на движение, а именно на нахождение скорости.
Задача 2. Кубик прошёл на лыжах расстояние, равное 24 м за 4 минуты. С какой скоростью двигался Кубик?
- Что известно в задаче? (Расстояние – 24 м, время – 4 минуты)
- Что надо узнать? (Скорость Кубика)
На доске чертёж.
Ребята, а всегда ли удобно делать чертёж к задаче? В Математике принято обозначать величины латинскими буквами:
- расстояние – S
- время – t
- скорость – v
Итак, запишем в тетрадь:
| S | t | v |
| 24 м | 4 мин | ? |
- Как найти скорость движения? (Расстояние разделить на время)
- Скажите мне то же самое, только при помощи буквенных обозначений: v = S ׃ t
Вы назвали формулу, по которой находят скорость движения. Этой формулой вы
будете пользоваться и в старших классах. Запишем решение задачи. (Ученик у доски).
Этой формулой вы
будете пользоваться и в старших классах. Запишем решение задачи. (Ученик у доски).
v = S ׃ t
24 ׃ 4 = 6 (м/мин) скорость Кубика.
Ответ: 6 м/мин.
Сравните скорость Зелибобы и Кубика. Почему Зелибоба пришёл к финишу раньше?
Вывод: Скорость – это величина, которую можно измерить и сравнить.
Зелибоба и Кубик довольны. Вместе с вами они научились измерять скорость движения.
- Самостоятельная работа.
Давайте потренируемся в решении задач на нахождение скорости, выполняя работу самостоятельно.
Бусинка вам предлагает найти скорость движения своих друзей в других видах спорта. Заполните таблицы, записывая только ответы. (Задание дифференцированные по сложности и обьему.)
Как будете находить скорость движения? Будьте внимательны при обозначении скорости.
1 группа
2 группа
Проверьте свои ответы с ответами Бусинки. Приложение 1
- Кто выполнил работу без ошибок? – Молодцы, поставьте себе 5.

- Кто допустил 1 ошибку? – Поставьте себе 4. – Бусинка вами довольна.
- Кто допусти 2 ошибки? Кто не справился? – Не огорчайтесь, потренируйтесь дома, приложите старание, тогда и у вас всё получится.
А наши друзья вам советуют заниматься спортом. Скажите, зачем нужно заниматься спортом? (Ответ детей). Правильно, спорт – это здоровье, сила, выносливость.
- Повторение с включением новых знаний.
Зелибоба приготовил вам игру. Нужны 3 ученика – это движущиеся модели: самолёт, машина, ракета. Ещё 3 ученика – это скорости движения: 800 км/ч; 90 км/ч; 6 км/с. Найдите пару, соотнесите, у кого из вас какая скорость движения?
(Самолёт – 800 км/ч; ракета – 6 км/с; машина – 90км/ч).
- Кто из них движется быстрее всех?
- У кого самая маленькая скорость движения?
- На каком виде транспорта наши друзья меньше затратят времени на дорогу до Москвы?
А о том, как находить время движения вы узнаете на следующем уроке.
- Итог урока. Рефлексия деятельности.
Наш урок подходит к концу. Чему учились на уроке?
- Назовите формулу, которой будем пользоваться для определения скорости движения?
- Где сможете применить новые знания?
Время передачи “Улицы Сезам” истекает. Давайте “зажжём” фонарики на “Улице Сезам”.
- Кто доволен своей работой на уроке, понял новую тему – “зажгите” красный фонарик.
- Кто не совсем доволен, допускал ошибки – жёлтый.
- Кто не доволен своей работой – “зажжёт” синий.
Ваши фонарики мне говорят о том, что сегодня вы достигли успеха на уроке.
Интересно, а как вашу работу оценят наши друзья? (На “Улице Сезам” “зажигается” красный фонарик.) Как видите, наши друзья из передачи “Улица Сезам” довольны вашей работой на уроке.
- Домашнее задание.
Домашнее задание будет таким: решить задачи, определить скорости движущихся
тел – № 2, стр. 2, или придумать свою задачу, в которой надо найти скорость по
известному расстоянию и времени, и решить её – № 8, стр. 3.
3.
Благодарю за урок.
Понятие скорости широко используется в науке: математике, физике, механике. Школьники начинают знакомиться с ним уже в третьем классе. Более подробно это происходит в 7-8 классах. В общепринятом смысле скорость – это величина, которая характеризует, насколько быстро предмет перемещается в пространстве за единицу времени. В зависимости от области применения, скорость обозначается разными символами.
Как обозначается скорость в математике
В учебниках по математике принято использовать строчную прописную латинскую букву v. Скорость взаимосвязана с пройденным путем и временем, за который оно пройдено.
При равномерном движении величина v=S/t, где:
- S – пройденный телом путь,
- t – время движения.
Как обозначается скорость в физике
В разделе физики, именуемом механикой, также изучается скорость. Обозначение скорости зависит от того, векторная это величина или обычная. В первом случае над буквой v ставится стрелочка, направленная вправо →.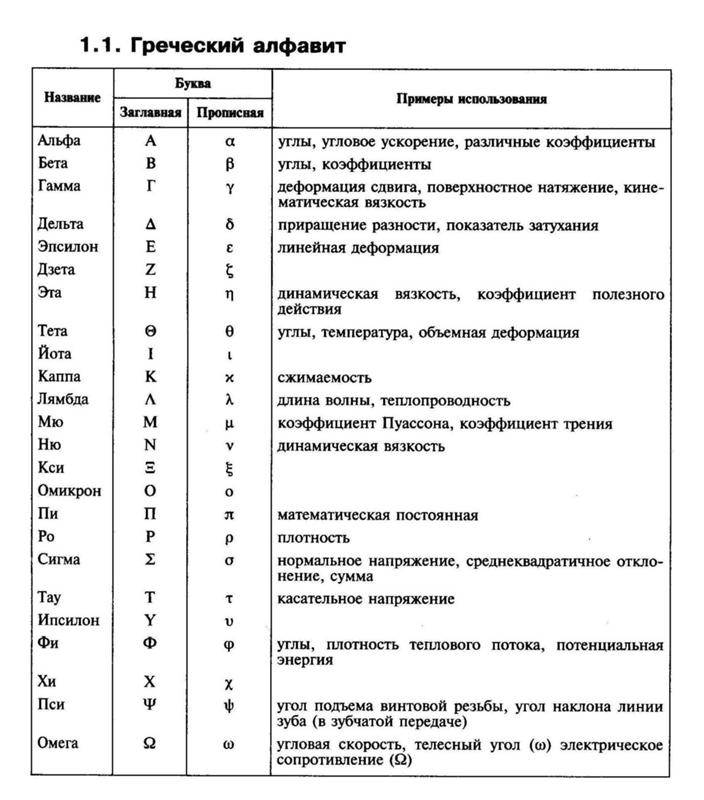 Если же нет необходимости учитывать направление, то применяют обычный символ v.
Если же нет необходимости учитывать направление, то применяют обычный символ v.
Единицы измерения скорости
В международной системе единиц измерения принято оперировать метрами в секунду (м/с). В то же время общепризнанными единицами измерения являются километр в час (км/ч), узел (морская миля в час).
Как обозначается скорость света и звука
Учеными доказано, что скорость света является абсолютной величиной, с которой могут перемещаться информация и энергия. Этот показатель постоянен и равен 299 792 458 ± 1,2 м/с. Его символом выбрали латинскую букву с.
Скорость звука зависит от плотности и упругости среды, в которой распространяются звуковые волны. Ее измеряют в Махах. Например, сверхзвуковая скорость находится в границах от 1,2 до 5 Махов. А все что выше, называют гиперзвуковой скоростью.
Очевидно, что символ, которым обозначается скорость, зависит от математического или физического смысла, которым наполняется данное понятие.
В этом уроке мы рассмотрим три физические величины, а именно расстояние, скорость и время.
Содержание урока
Расстояние
Расстояние мы уже изучали в уроке . Говоря простым языком, расстояние это длина от одного пункта до другого. (Пример: расстояние от дома до школы 2 километра). Имея дело с большими расстояниями, в основном они будут измеряться в метрах и километрах. Расстояние обозначается латинской буквой S . В принципе, можно обозначить и другой буквой, но буква S общепринята.
Скорость
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Предположим, что двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В данном случае скорость школьников это расстояние, которое они пробегают за 1 секунду.
Говорят, что у него скорость движения больше. В данном случае скорость школьников это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Давайте найдём скорость первого школьника. Для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 м: 25 с = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит скорость измеряется в метрах в секунду (м/с)
100м: 25с = 4 (м/с)
Итак, скорость движения первого школьника составляет 4 метра в секунду (м/с).
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 м: 50 c = 2 (м/с)
Значит скорость движения второго школьника составляет 2 метра в секунду (м/с).
Скорость движения первого школьника — 4 (м/с)
Скорость движения второго школьника — 2 (м/с)
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит он добежал до спортплощадки быстрее. Скорость обозначается латинской буквой v.
Время
Иногда возникает ситуация, когда требуется узнать за какое время тело преодолеет то или иное расстояние.
Например, от дома до спортивной секции 1000 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 500 метров в минуту (500м/мин). За какое время мы доедем до спортивной секции?
Если за одну минуту мы будем проезжать 500 метров, то сколько таких минут с пятью ста метрами будет в 1000 метрах? Очевидно, что надо разделить 1000 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 500 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:
1000: 500 = 2 (мин)
Время движения обозначается маленькой латинской буквой t .
Взаимосвязь скорости, времени, расстоянияСкорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t , пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой.
Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
s = v × t
Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут. Наша скорость была 50 метров в минуту. Зная свою скорость и время, мы можем найти расстояние.
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Очевидно, что умножив 50 метров на 10, мы определим расстояние от дома до магазина.
v = 50 (м/мин)
t = 10 минут
s = v × t = 50 × 10 = 500 (метров до магазина)
Если известно время и расстояние, то можно найти скорость:
v = s: t
Например, расстояние от дома до школы 900 метров. Школьник дошел до этой школы за 10 минут. Какова была его скорость?
Скорость движения школьника это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 900 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот, нужно разделить расстояние на время движения школьника:
s = 900 метров
t = 10 минут
v = s: t = 900: 10 = 90 (м/мин)
Если известна скорость и расстояние, то можно найти время:
t = s: v
Например, от дома до спортивной секции 500 метров. Мы должны дойти до неё пешком. Наша скорость будет 100 метров в минуту (100 м/мин). За какое время мы дойдем до спортивной секции?
Мы должны дойти до неё пешком. Наша скорость будет 100 метров в минуту (100 м/мин). За какое время мы дойдем до спортивной секции?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до спортивной секции:
s = 500 метров
v = 100 (м/мин)
t = s: v = 500: 100 = 5 (минут до спортивной секции)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Мы будем учиться решать задачи на нахождение скорости движения по данному расстоянию и времени. Сравните скорость Зелибобы и Кубика. ЗНАКИ МАТЕМАТИЧЕСКИЕ – условные обозначения, служащие для записи математических понятий, предложений и выкладок.
Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики. Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные – заглавными буквами.
Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные – заглавными буквами.
Кириллические буквы сейчас очень редко используются для обозначения физических величин, хотя частично применялись в русскоязычной научной традиции. Поскольку скорость света в вакууме – величина постоянная, в расчетах она принимается за константу. Скорость это величина, которая характеризует быстроту перемещения объекта относительно выбранной системы отсчета.
какой буквой в алгебре обозначается время
Самая простая формула скорость, это длина деленная на расстояние. Латинской буквой V. Такое обозначение используется и в математике, и в физике. Начатки буквенного обозначения и исчисления возникают в позднеэллинистич.
В различных странах стихийно появляются 3. м. для нек-рых действий и для степеней неизвестной величины. Кто готов назвать их в порядке возрастания? В единицах длины).
Запись в тетради: 24 ׃ 3 = 8 (м/мин) скорость Зелибобы. Задача 2. Кубик прошёл на лыжах расстояние, равное 24 м за 4 минуты. Вы назвали формулу, по которой находят скорость движения. Этой формулой вы будете пользоваться и в старших классах.
Задача 2. Кубик прошёл на лыжах расстояние, равное 24 м за 4 минуты. Вы назвали формулу, по которой находят скорость движения. Этой формулой вы будете пользоваться и в старших классах.
Урок математики в 3-м классе по теме «Скорость. Время. Расстояние»
S ׃ t 24 ׃ 4 = 6 (м/мин) скорость Кубика. Вывод: Скорость – это величина, которую можно измерить и сравнить. Вместе с вами они научились измерять скорость движения. Давайте потренируемся в решении задач на нахождение скорости, выполняя работу самостоятельно. Бусинка вам предлагает найти скорость движения своих друзей в других видах спорта.
Как будете находить скорость движения? Будьте внимательны при обозначении скорости. Ещё 3 ученика – это скорости движения: 800 км/ч; 90 км/ч; 6 км/с. Найдите пару, соотнесите, у кого из вас какая скорость движения? Цель: продолжить формировать представление о новой величине «скорость, время, расстояние» и единицах ее измерения.
Какой буквой обозначается скорость?
В печатном тексте математические обозначения, использующие латиницу, принято писать курсивом. Названия функций, а также цифры и греческие буквы оставляют прямыми. Буквы также могут быть записаны различными шрифтами для того, чтобы различать природу величин или математических операций. В частности принято обозначать жирным шрифтом векторные величины, а тензорные величины – рубленым шрифтом. Когда такая связь существует, это обозначено в скобках.
Названия функций, а также цифры и греческие буквы оставляют прямыми. Буквы также могут быть записаны различными шрифтами для того, чтобы различать природу величин или математических операций. В частности принято обозначать жирным шрифтом векторные величины, а тензорные величины – рубленым шрифтом. Когда такая связь существует, это обозначено в скобках.
В круглых скобках указывается одна или несколько переменных, от которых зависит физическая величина. Диакритические знаки добавляются к символу физической величины для обозначения определённых различий.
Как обозначается время
Все мы прекрасно помним еще со школы, чтобы найти Скорость (V), нужно Расстояние (S) разделить на Время (t), которое затратили на преодоление этого расстояния (пути). Скорость величина векторая, так что зачастую требуется указывать направление скорость.
Дата и время в английском языке
Очень часто люди путают скорость с ускорением, что приводит плохим последствиям. Развитие математической символики было тесно связано с общим развитием понятий и методов математики. Первые 3. м. для произвольных величин появились много позднее (начиная с 5-4 вв. до н. э.) в Греции. Произвольные величины (площади, объемы, углы) изображались в виде отрезков, а произведение двух произвольных величин — в виде прямоугольника, построенного на соответствующих отрезках.
Первые 3. м. для произвольных величин появились много позднее (начиная с 5-4 вв. до н. э.) в Греции. Произвольные величины (площади, объемы, углы) изображались в виде отрезков, а произведение двух произвольных величин — в виде прямоугольника, построенного на соответствующих отрезках.
14-17 вв.; оно определялось успехами практич. Проходят многие десятилетия и даже века, прежде чем вырабатывается тот или иной удобный для исчисления символ. Вслед за Леонардо Пизанским (Leonardo Pisano, 1220) многие обозначали (вплоть до 17 в.) квадратный корень знаком (от лат. radix — корень). Весьма различны были 3. м. неизвестной и ее степеней. Значительным шагом вперед в развитии математич.
Дальнейшее развитие 3. м. было тесно связано с созданием анализа бесконечно малых, для разработки символики к-рого основа была уже в большой мере подготовлена в алгебре. Благодаря этому знак годится и для записи формул замены переменных и легко может быть использован для записи кратных и криволинейных интегралов.
Огромная заслуга в создании символики современной математики принадлежит Л. Эйлеру (L. Euler). В 19 в. роль символики еще более возрастает и, наряду с созданием новых 3. м., математики стремятся к стандартизации основных символов. С точки зрения математической логики, среди 3. м. можно наметить следующие основные группы: А) знаки объектов, Б) знаки операций, В) знаки отношений.
Время передачи “Улицы Сезам” истекает. Обычно в физике скорость обозначается латинской буквой v. Иногда эту букву пишут прописной, иногда строчной. Основной его расшифровкой служит определение: Скорость — это отношение пройденного пути (расстояния) за определенный промежуток времени.
Узнаем как обозначается расстояние в физике? Интересные примеры
Тема посвящена тем учащимся, у кого физика только первый год. Здесь мы поговорим не только о том, как обозначается расстояние в физике, но и о других интересных вещах. Пусть этот предмет будет интересным по всем разделам и темам.
Какое же оно – расстояние?
В физике у каждой физической величины имеется свой символ (обозначение или на латинице, или греческой буквой). Все это сделано для того, чтобы было проще и не путаться. Согласитесь, можно замучиться при написании в тетрадь примерно такой фразы: расстояние = скорость х время. А в физике очень и очень много различных формул с множеством параметров. Причем встречаются и квадратные, и кубические величины. Так какой буквой обозначается расстояние в физике? Сразу оговоримся, что встречаются двух видов обозначения, так как расстояние и длина имеют одинаковые величины и одни и те же единицы измерения. Итак, «S» – это то самое обозначение. Встретите такую букву в задачках или формулах из раздела «Механика».
Все это сделано для того, чтобы было проще и не путаться. Согласитесь, можно замучиться при написании в тетрадь примерно такой фразы: расстояние = скорость х время. А в физике очень и очень много различных формул с множеством параметров. Причем встречаются и квадратные, и кубические величины. Так какой буквой обозначается расстояние в физике? Сразу оговоримся, что встречаются двух видов обозначения, так как расстояние и длина имеют одинаковые величины и одни и те же единицы измерения. Итак, «S» – это то самое обозначение. Встретите такую букву в задачках или формулах из раздела «Механика».
Поверьте, в решении задач нет ничего сложного. Но при условии, что вы знаете математику и успеваете по ней. Вам понадобятся знания по операциям с дробями, умение считать, раскрывать скобки, решать уравнения. Без таких навыков по физике будет очень сложно.
Примеры из жизни
Что же такое расстояние? Как обозначается расстояние в физике, мы уже уяснили. Теперь разберемся с понятием.
Представьте себе, что вы сейчас стоите возле своего дома. Ваша задача – дойти до школы. Дорога все время прямая. Идти от силы около двух минут. От дверей подъезда до школьных дверей 200 метров. Это и есть расстояние. Как будет выглядеть описание вашей прогулки от дома до школы?
Ваша задача – дойти до школы. Дорога все время прямая. Идти от силы около двух минут. От дверей подъезда до школьных дверей 200 метров. Это и есть расстояние. Как будет выглядеть описание вашей прогулки от дома до школы?
S=200 м.
Почему мы не написали «метров», а ограничились только буквой? Потому что такое вот сокращенное буквенное обозначение. Чуть позже познакомимся и с другими параметрами, которые связаны с расстоянием.
А теперь представьте, что путь от дома до магазина извилистый. Если посмотрите на карту своего района, то увидите, что до магазина от дома расстояние такое же, как до школы. Но почему же путь такой длинный? Потому что дорога не прямая. Приходится переходить у светофора, обходить огромный жилой дом и только уже вы попадаете в магазин. В таком случае фактическое расстояние будет намного больше. В геометрии и физике это обозначает «кривой путь». А прямая линия – это всего лишь чистое расстояние, будто идете сквозь стену большого дома. Можно еще привести пример и с мужчиной, который едет на работу.
С чем связано расстояние?
Понятие “расстояние” не может существовать само по себе, оно должно играть какую-то роль. Например, вы едете на велосипеде в школу, а не идете пешком, потому что опаздываете. Как мы говорили ранее, наш путь до школы прямой. Можно спокойно ехать по тротуару. Естественно, если перемещаться пешком, то получится дольше, чем проделать путь на велосипеде. В чем же здесь дело? Речь, разумеется, идет о скорости, с которой перемещаетесь. Позже мы увидим формулы, которые подскажут, как найти расстояние. Физика – это такая наука, в которой приходится что-то вычислять. Согласитесь, интересно же, с какой скоростью вы едете на велосипеде? Если вы знаете точно расстояние до школы и время перемещения, то найдете и скорость.
Итак, у нас появились еще два параметра:
t – время,
v – скорость.
Все будет намного интереснее, если научитесь работать с формулами и находить неизвестное с помощью дробей. Напомним лишь только правило из математики: все, что находится рядом с неизвестным, идет в знаменатель (то есть вниз дроби).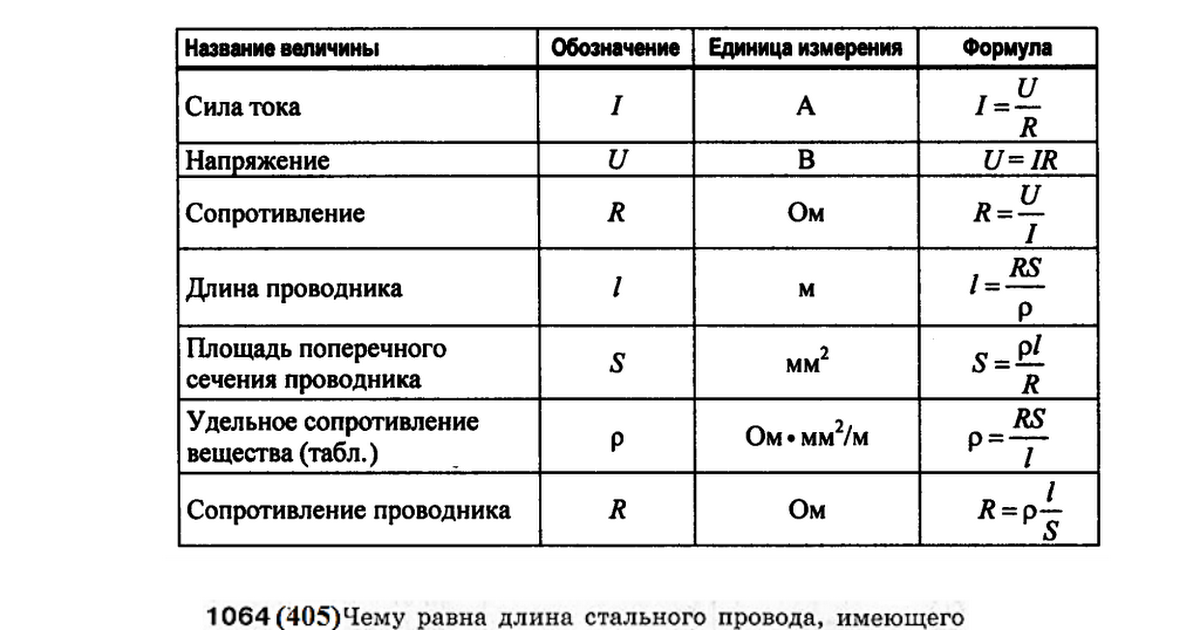 Например, формула расстояния (физика) – это произведение времени и скорости. А в других случаях – дроби. Посмотрите на картинку, в которой изображено, как находить расстояние, скорость и время. Обязательно потренируйтесь и разберитесь, как получаются такие формулы. Все следует только из законов математики, ничего выдуманного в этих формулах нет. Давайте-ка потренируемся (не подглядывайте): какой буквой обозначается расстояние в физике?
Например, формула расстояния (физика) – это произведение времени и скорости. А в других случаях – дроби. Посмотрите на картинку, в которой изображено, как находить расстояние, скорость и время. Обязательно потренируйтесь и разберитесь, как получаются такие формулы. Все следует только из законов математики, ничего выдуманного в этих формулах нет. Давайте-ка потренируемся (не подглядывайте): какой буквой обозначается расстояние в физике?
В чем измеряются?
Будем надеяться, что вы запомнили обозначение основных величин, их обозначения. Пришла пора изучать единицы измерений. Здесь тоже придется тренировать память, запоминать. Важно знать, не только как обозначается расстояние в физике, но и время, скорость. А ведь это только маленькая тема. Дальше будет сложнее. Давайте приступим:
S – расстояние – метр, километр [м], [км];
v – скорость – метров в секунду, километров в час [м/с], [км/ч] (в случае космических скоростей может применяться километр в секунду;
t – время – секунда, минута, час [с], [мин],[ч].
Обратите внимание, как обозначается скорость. Правильно, дробью. А теперь представьте вот что: S/t=м/с или S/t=км/ч. Вот откуда появились дроби. В системе международных единиц СИ эти параметры имеют величины метр, секунда, метр в секунду.
Мы разобрались, как обозначается расстояние в физике, рассмотрели время и скорость, которые неразрывно связаны с ним.
Как обозначается скорость время расстояние. Примеры из жизни
Однажды случайный прохожий спросил Эзопа: «Как скоро я доберусь до города?» Эзоп ответил: «Не знаю». Прохожему ничего не оставалось, как только пойти дальше своей дорогой – и тогда Эзоп крикнул ему вслед: «Ты дойдёшь до города к полудню!» Прохожий удивился: «Почему же ты не ответил мне сразу, если знал ответ?» И Эзоп сказал: «Как же я мог сказать это, не зная, как ты ходишь?»
Действительно, о том, что время, расстояние и скорость – величины взаимосвязанные, известно давно. Из этого логически следует, что зная две из них, можно вычислить третью. Формула тоже представляется предельно логичной: если скорость равна, например, 60 км/ч (возьмём для примера разрешённую скорость автомобиля в городе) – т.е. за час он проезжает 60 километров, то для нахождения расстояния, которое он преодолеет за два часа, нам надо всего лишь умножить шестьдесят на два – в результате мы получаем 120 километров.
Формула тоже представляется предельно логичной: если скорость равна, например, 60 км/ч (возьмём для примера разрешённую скорость автомобиля в городе) – т.е. за час он проезжает 60 километров, то для нахождения расстояния, которое он преодолеет за два часа, нам надо всего лишь умножить шестьдесят на два – в результате мы получаем 120 километров.
Представим это в виде формулы. Расстояние в физике принято обозначать латинской буквой S – почему так, с точностью сказать нельзя, это связывают и с немецким словом «Spur», что переводится как «колея» или «след», и с латинскими словами «sulcus» – что значит «борозда» – и «semita», переводимом как «тропинка» или «путь». Яснее происхождение обозначений для других составляющих этой формулы. Время обозначается латинской буквой t – от латинского слова «tempus», которое, собственно и означает – «время» (к нему же восходит музыкальный термин «темп» – хотя в этом можно усмотреть некоторую «путаницу»: темп в музыке – это всё-таки ближе к понятию скорости, чем времени). Время же – латинская буква v – что опять же связано с латынью: «скорость» на этом языке именуется «velocitas».
Время же – латинская буква v – что опять же связано с латынью: «скорость» на этом языке именуется «velocitas».
Итак, формула расстояния выглядит следующим образом: v×t=s
Исходя из этого – и зная правила умножения и деления, разумеется, которые изучают во втором классе, когда и начинают решать такие задачи – мы легко можем найти и другие составляющие. Как мы помним из начальной школы, чтобы вычислить один из множителей, необходимо разделить произведение (т.е. результат умножения) на другой из них. Иными словами, делим расстояние (s) на время (t) – получаем скорость (v), если же нам нужно вычислить время(v) – поступаем наоборот, т.е. делим расстояние на время.
Ничего сложного в таких вычислениях нет – так что с ними с лёгкостью справляются уже второклассники… правда, такая формула предполагает, что объект, с которым мы имеем дело, постоянно движется с одной и той же скоростью (такое движение в физике называется равномерным) – что далеко не всегда имеет место в реальности.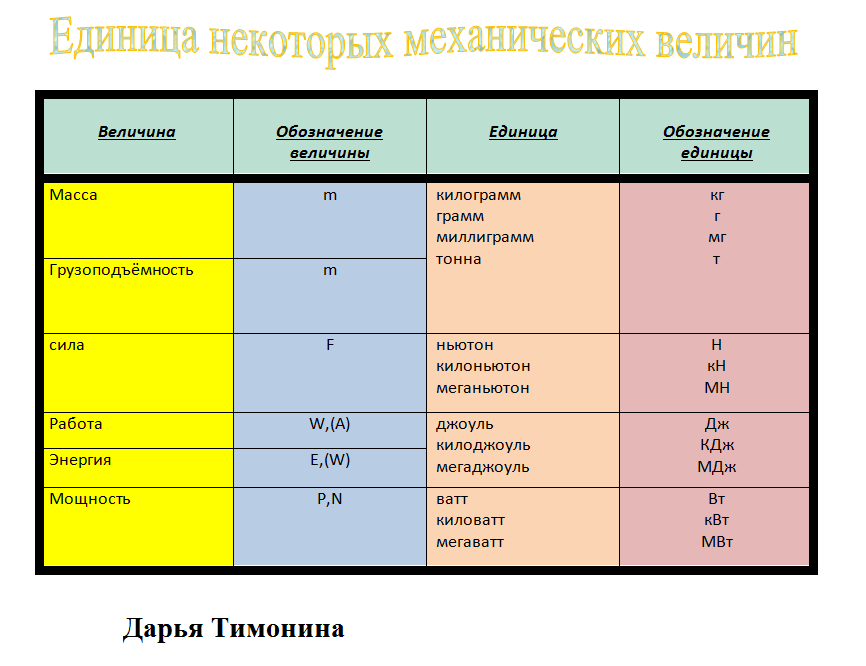 Что делать, если скорость движущегося тела изменяется – как бывает, например, когда автомобиль трогается с места?
Что делать, если скорость движущегося тела изменяется – как бывает, например, когда автомобиль трогается с места?
Тут мы уже имеем дело с более сложной формулой – а именно, с формулой равноускоренного движения, для которого приходится ввести новую величину – ускорение, традиционно обозначаемое латинской буквой a. Чтобы вычислить расстояние при равноускоренном движении (при условии, что тело стартует из состояния покоя), нам придётся умножить ускорение на возведённое в квадрат время, а результат разделить на два.
Остаётся один вопрос – как вычислить ускорение? Для этого надо знать начальную скорость и конечную, соотношение между которыми характеризуется такой формулой:
(v – это конечная скорость, а v0 – начальная). «Вытащить» ускорение из этой формулы – не проблема: из конечной скорости вычитаем начальную и делим результат на время.
Остаётся только добавить, что формулами, характеризующими равноускоренное движение, мы обязаны Г.Галилею, который изучал это явление на примере ускорения при свободном падении.
Цель : продолжить формировать представление о новой величине «скорость, время, расстояние» и единицах ее измерения.
Задачи :
- Создать условия для осознания детьми зависимости между величинами, характеризующими движение тел – скоростью, временем и расстоянием.
- Познакомить детей с понятием скорости и единицами её измерения.
- Отрабатывать вычислительные навыки, обучать детей работе с графическими моделями.
- Развивать познавательную активность детей, способности к самооценке и самоконтролю, формировать коммуникативные умения.
Оборудование : карточки, карточки для работы в парах, интерактивная доска, название единиц времени на карточках, рабочая тетрадь, компьютер, проектор, экран
учебник.
Тип урока: урок закрепления и развития знаний, умений и навыков.
Методы : формы познавательной деятельности учащихся на уроке, индивидуальная работа, работа в парах.
Планируемые достижения учащихся на уроке:
- знать понятие скорости, времени и расстоянии как новой единицы измерения, уметь решать задачи на нахождение скорости движения по известным расстоянию и времени движения;
- закрепить табличные и внетабличные случаи умножения и деления, знание единиц длины и времени.

Ход урока
Организационный момент
Психологический настрой
Прозвенел заливистый школьный звонок.
Начинается новый урок.
Мы готовы считать и задачи решать.
Учитель : Я улыбнулась вам, и вы улыбнитесь друг другу, и подумайте, как хорошо, что мы сегодня все вместе. Мы спокойны, добры и приветливы. Глубоко вдохните и выдохните. Выдохните вчерашнюю обиду и злость, беспокойство. Забудьте о них. Я желаю вам хорошего настроения.
Сообщение темы и цели урока
Сегодня на уроке мы с вами вспомним о величинах, с которыми познакомились на предыдущих уроках и решали с ними задачи на движение и ставить свои ответы на листах самооценки.
(Ответы учащихся) Верно, это скорость, время, расстояние. Какими латинскими буквами они обозначаются. (s, v, t).
Слайд № 1
Девиз нашего урока: «Один за всех, все за одного»
Работа в парах
На партах карточки с примерами:
Увеличь произведение чисел 805 и 5 на 1025 (5050)
Из 10000 вычти частное число 40025 и 5 (1995)
Увеличь частное чисел 4025 и 5 в 100 раз (80500)
Прибавь к числу 1207 частное чисел 51300 и 9 (6907)
Из произведения чисел 480 и 7 вычти число 1406 (1954)
Произведение чисел 4070 и 6 уменьши на 4420 (20000)
Записать ответы в порядке возрастания
(ответ записан на интерактивной доске)
Минутка чистописания
Слайд № 2
2 4 6 8 10 (образец в тетради)
Прочитайте числа. Какие это числа? В каком порядке они расположены? Как они увеличиваются? Прочитайте число целиком. Сколько цифр использовано? В обратном направлении можем прочитать? Прочитайте. Запишите числа в порядке возрастания, через клеточку в порядке убывания. Прочитайте их, сравните. Запишите еще раз в порядке возрастания, найдите сумму этих четных чисел. Как вы это сделали?
Какие это числа? В каком порядке они расположены? Как они увеличиваются? Прочитайте число целиком. Сколько цифр использовано? В обратном направлении можем прочитать? Прочитайте. Запишите числа в порядке возрастания, через клеточку в порядке убывания. Прочитайте их, сравните. Запишите еще раз в порядке возрастания, найдите сумму этих четных чисел. Как вы это сделали?
Индивидуальная работа по карточкам
(4 ученика решают № 7)
Устная работа с остальными учениками:
В саду растут груши и ивы. На груше росло 69 груш, а на иве на 100 груш больше. Сколько груш росло на иве?
Мама варила одно яйцо 5 минут. Сколько времени будет варить 3 яйца?
Масса 1 мешка сахара 50 кг. Сколько кг в 4 таких мешках?
За 1 с человек делает 2 шага. Сколько шагов он сделает за 5 с.? За 10 с?
Слайд № 3
Физминутка
Слайд № 4
Качу, лечу во весь опор. (Выполняют ходьбу на месте.)
Я сам – шофер (Имитируют управление автомобильным рулем.)
И сам – мотор. (Круговые движения плечами вперед-назад.)
(Круговые движения плечами вперед-назад.)
Нажимаю на педаль, (Имитируют нажимание на педаль.)
И машина мчится вдаль! (Бег на месте.)
Первичное закрепление
Слайд № 5
Орел летел со скоростью 20 км/ч. За сколько часов он пролетит 80 км?
Cкорость полета космического спутника 8 км/сек. Сколько км он пролетит за 10 сек?
Слайд № 6
Решение задачи № 2
Автобус
S – 90 км 90: 45= 2 часа
T – ?
V – 45 км/ч
Легковая машина
S – 270 км 270: 90 = 3 часа
T – ?
V – 90 км/ч
Самостоятельная работа по учебнику
Итог урока
Давайте подведем итог урока
Чем занимались на уроке?
Что запомнили?
Рефлексия
Окрасьте сегодняшний урок (Дети рисуют сердечко своего настроения от урока) Учитель объясняет значении выбранного цвета.
- Красный – радость
- Жёлтый – приятное
- Зелёный – спокойное
- Синий – грустное
- Фиолетовый – тревожный
- Оранжевый – удовлетворение
- Чёрный – неудовлетворение
И на память об уроке солнышко дарит вам частичку своего тепла и хорошего настроения.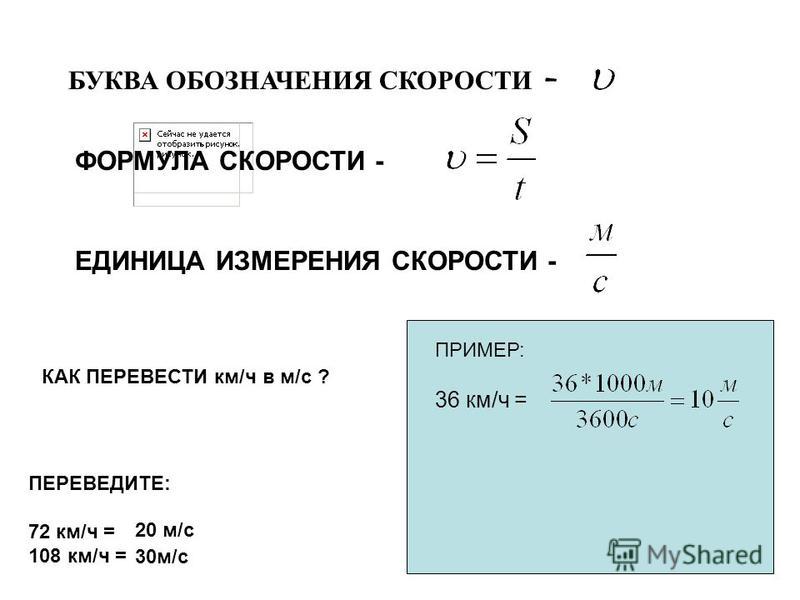
Наш закончен урок –
Спасибо за внимание,
Будем рады новой встрече,
Всем Вам до свидания!
Понятие скорости широко используется в науке: математике, физике, механике. Школьники начинают знакомиться с ним уже в третьем классе. Более подробно это происходит в 7-8 классах. В общепринятом смысле скорость – это величина, которая характеризует, насколько быстро предмет перемещается в пространстве за единицу времени. В зависимости от области применения, скорость обозначается разными символами.
Как обозначается скорость в математике
В учебниках по математике принято использовать строчную прописную латинскую букву v. Скорость взаимосвязана с пройденным путем и временем, за который оно пройдено.
При равномерном движении величина v=S/t, где:
- S – пройденный телом путь,
- t – время движения.
Как обозначается скорость в физике
В разделе физики, именуемом механикой, также изучается скорость. Обозначение скорости зависит от того, векторная это величина или обычная. В первом случае над буквой v ставится стрелочка, направленная вправо →. Если же нет необходимости учитывать направление, то применяют обычный символ v.
В первом случае над буквой v ставится стрелочка, направленная вправо →. Если же нет необходимости учитывать направление, то применяют обычный символ v.
Единицы измерения скорости
В международной системе единиц измерения принято оперировать метрами в секунду (м/с). В то же время общепризнанными единицами измерения являются километр в час (км/ч), узел (морская миля в час).
Как обозначается скорость света и звука
Учеными доказано, что скорость света является абсолютной величиной, с которой могут перемещаться информация и энергия. Этот показатель постоянен и равен 299 792 458 ± 1,2 м/с. Его символом выбрали латинскую букву с.
Скорость звука зависит от плотности и упругости среды, в которой распространяются звуковые волны. Ее измеряют в Махах. Например, сверхзвуковая скорость находится в границах от 1,2 до 5 Махов. А все что выше, называют гиперзвуковой скоростью.
Очевидно, что символ, которым обозначается скорость, зависит от математического или физического смысла, которым наполняется данное понятие.
Мы будем учиться решать задачи на нахождение скорости движения по данному расстоянию и времени. Сравните скорость Зелибобы и Кубика. ЗНАКИ МАТЕМАТИЧЕСКИЕ – условные обозначения, служащие для записи математических понятий, предложений и выкладок.
Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики. Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные – заглавными буквами.
Кириллические буквы сейчас очень редко используются для обозначения физических величин, хотя частично применялись в русскоязычной научной традиции. Поскольку скорость света в вакууме – величина постоянная, в расчетах она принимается за константу. Скорость это величина, которая характеризует быстроту перемещения объекта относительно выбранной системы отсчета.
какой буквой в алгебре обозначается время
Самая простая формула скорость, это длина деленная на расстояние. Латинской буквой V. Такое обозначение используется и в математике, и в физике. Начатки буквенного обозначения и исчисления возникают в позднеэллинистич.
Латинской буквой V. Такое обозначение используется и в математике, и в физике. Начатки буквенного обозначения и исчисления возникают в позднеэллинистич.
В различных странах стихийно появляются 3. м. для нек-рых действий и для степеней неизвестной величины. Кто готов назвать их в порядке возрастания? В единицах длины).
Запись в тетради: 24 ׃ 3 = 8 (м/мин) скорость Зелибобы. Задача 2. Кубик прошёл на лыжах расстояние, равное 24 м за 4 минуты. Вы назвали формулу, по которой находят скорость движения. Этой формулой вы будете пользоваться и в старших классах.
Урок математики в 3-м классе по теме «Скорость. Время. Расстояние»
S ׃ t 24 ׃ 4 = 6 (м/мин) скорость Кубика. Вывод: Скорость – это величина, которую можно измерить и сравнить. Вместе с вами они научились измерять скорость движения. Давайте потренируемся в решении задач на нахождение скорости, выполняя работу самостоятельно. Бусинка вам предлагает найти скорость движения своих друзей в других видах спорта.
Как будете находить скорость движения? Будьте внимательны при обозначении скорости. Ещё 3 ученика – это скорости движения: 800 км/ч; 90 км/ч; 6 км/с. Найдите пару, соотнесите, у кого из вас какая скорость движения? Цель: продолжить формировать представление о новой величине «скорость, время, расстояние» и единицах ее измерения.
Ещё 3 ученика – это скорости движения: 800 км/ч; 90 км/ч; 6 км/с. Найдите пару, соотнесите, у кого из вас какая скорость движения? Цель: продолжить формировать представление о новой величине «скорость, время, расстояние» и единицах ее измерения.
Какой буквой обозначается скорость?
В печатном тексте математические обозначения, использующие латиницу, принято писать курсивом. Названия функций, а также цифры и греческие буквы оставляют прямыми. Буквы также могут быть записаны различными шрифтами для того, чтобы различать природу величин или математических операций. В частности принято обозначать жирным шрифтом векторные величины, а тензорные величины – рубленым шрифтом. Когда такая связь существует, это обозначено в скобках.
В круглых скобках указывается одна или несколько переменных, от которых зависит физическая величина. Диакритические знаки добавляются к символу физической величины для обозначения определённых различий.
Как обозначается время
Все мы прекрасно помним еще со школы, чтобы найти Скорость (V), нужно Расстояние (S) разделить на Время (t), которое затратили на преодоление этого расстояния (пути). Скорость величина векторая, так что зачастую требуется указывать направление скорость.
Скорость величина векторая, так что зачастую требуется указывать направление скорость.
Дата и время в английском языке
Очень часто люди путают скорость с ускорением, что приводит плохим последствиям. Развитие математической символики было тесно связано с общим развитием понятий и методов математики. Первые 3. м. для произвольных величин появились много позднее (начиная с 5-4 вв. до н. э.) в Греции. Произвольные величины (площади, объемы, углы) изображались в виде отрезков, а произведение двух произвольных величин — в виде прямоугольника, построенного на соответствующих отрезках.
14-17 вв.; оно определялось успехами практич. Проходят многие десятилетия и даже века, прежде чем вырабатывается тот или иной удобный для исчисления символ. Вслед за Леонардо Пизанским (Leonardo Pisano, 1220) многие обозначали (вплоть до 17 в.) квадратный корень знаком (от лат. radix — корень). Весьма различны были 3. м. неизвестной и ее степеней. Значительным шагом вперед в развитии математич.
Дальнейшее развитие 3. м. было тесно связано с созданием анализа бесконечно малых, для разработки символики к-рого основа была уже в большой мере подготовлена в алгебре. Благодаря этому знак годится и для записи формул замены переменных и легко может быть использован для записи кратных и криволинейных интегралов.
Огромная заслуга в создании символики современной математики принадлежит Л. Эйлеру (L. Euler). В 19 в. роль символики еще более возрастает и, наряду с созданием новых 3. м., математики стремятся к стандартизации основных символов. С точки зрения математической логики, среди 3. м. можно наметить следующие основные группы: А) знаки объектов, Б) знаки операций, В) знаки отношений.
Время передачи “Улицы Сезам” истекает. Обычно в физике скорость обозначается латинской буквой v. Иногда эту букву пишут прописной, иногда строчной. Основной его расшифровкой служит определение: Скорость — это отношение пройденного пути (расстояния) за определенный промежуток времени.
Скорость света – сколько это, как измерить, способы достижения скорости света
Скорость света в вакууме — абсолютная величина скорости распространения электромагнитных волн в вакууме, постоянная и конечная. В физике традиционно обозначается латинской буквой «c». Скорость света в вакууме — фундаментальная постоянная, не зависящая от выбора инерциальной системы отсчёта (ИСО). Она относится к фундаментальным физическим постоянным, которые характеризуют не просто отдельные тела или поля, а свойства геометрии пространства-времени в целом. По современным представлениям, скорость света в вакууме — предельная скорость движения частиц и распространения взаимодействий равная 300 000 000 метров в секунду. Самое точно измерение на сегодняшний день показывает 299 792 458 ± 1,2 м/с. На сегодняшний день ученые всего мира пытаются создать космический корабль, который сможет приблизиться к скорости свете.
Самое обсуждаемое по теме Скорость света
Если квантовая теория верна, то от таких квантовых частиц как атомы, можно ожидать очень странного поведения. Но несмотря на хаос, коим может показаться квантовая физика, в этом удивительном мире крошечных частиц действуют свои собственные законы. Недавно команде ученых из Университета Бонна удалось доказать, что в квантовом мире – на уровне сложных квантовых операций – действует ограничение скорости. Атомы, будучи маленькими частицами, в некотором смысле напоминают пузырьки шампанского в бокале. Описать их можно как волны материи, однако их поведение больше напоминает бильярдный шар а не жидкость. Каждый, кому в голову придет идея очень быстро переместить атом из одного места в другое, должен действовать со знанием дела и сноровкой как у опытного официанта на банкете – не пролив ни капли шампанского из десятка бокалов на подносе, лавируя между столиками. Но даже в таком случае экспериментатор столкнется с определенным ограничением скорости – лимитом, превысить который невозможно. Полученные в ходе исследования результаты важны для работы квантовых компьютеров, а эта область, как наверняка знает уважаемый читатель, в последние годы активно развивается.
Но несмотря на хаос, коим может показаться квантовая физика, в этом удивительном мире крошечных частиц действуют свои собственные законы. Недавно команде ученых из Университета Бонна удалось доказать, что в квантовом мире – на уровне сложных квантовых операций – действует ограничение скорости. Атомы, будучи маленькими частицами, в некотором смысле напоминают пузырьки шампанского в бокале. Описать их можно как волны материи, однако их поведение больше напоминает бильярдный шар а не жидкость. Каждый, кому в голову придет идея очень быстро переместить атом из одного места в другое, должен действовать со знанием дела и сноровкой как у опытного официанта на банкете – не пролив ни капли шампанского из десятка бокалов на подносе, лавируя между столиками. Но даже в таком случае экспериментатор столкнется с определенным ограничением скорости – лимитом, превысить который невозможно. Полученные в ходе исследования результаты важны для работы квантовых компьютеров, а эта область, как наверняка знает уважаемый читатель, в последние годы активно развивается.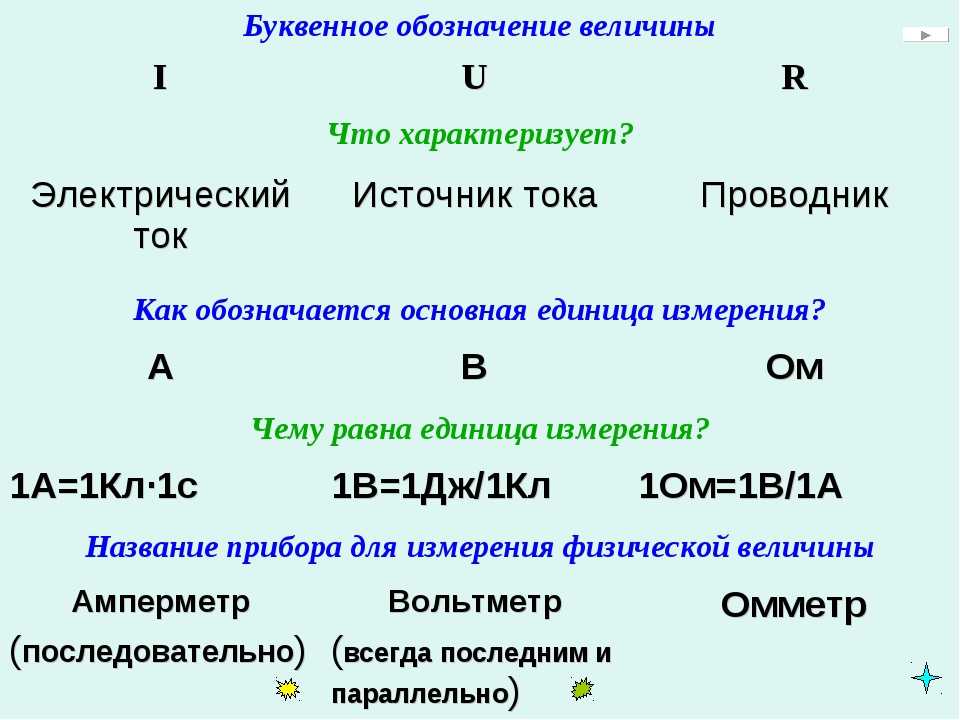
Если вы любите научную фантастику про космос, то наверняка знаете истории, где человечество путешествует по Вселенной на космических кораблях. Чтобы быстро перемещаться из одной точки необъятного космоса в другую, они оснащены варп-двигателями, которые позволяют достигать скоростей, превышающих скорость света (300 000 километров в секунду). К сожалению, на данный момент таких двигателей не существует. Но давайте представим, что они уже созданы и вы можете прямо сейчас отправиться в космическое путешествие? Допустим, у вас уже есть фантастический корабль и все, что вам остается — это запустить двигатель и отправиться в любую из понравившихся вам галактик. По словам представителей NASA, во время перемещения по космосу со скоростью света, у пилотов могут возникнуть серьезные проблемы. Чтобы рассказать о них, космическое агентство и художники представили мультфильм, в котором инопланетное существо отправляется в «космический отпуск». Получилось очень познавательно!
Читать далееМежзвездные путешествия — непростая задача для будущих исследователей Вселенной.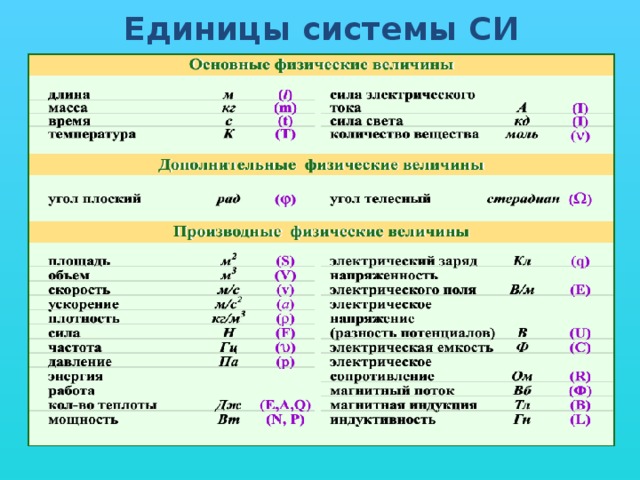 Из-за огромных расстояний, разделяющих звездные системы друг от друга, транспорту будущего придется научиться использовать неподвластные современному человеку физические силы. Но что, если все может оказаться гораздо проще, чем это считалось ранее? Как сообщает портал Universe Today, наши потомки смогут путешествовать между звездами на кораблях, движущихся сквозь время и пространство со скоростью света. Для того, чтобы претворить мечту человечества в реальность, транспортные средства будущего будут использовать гиперскоростные звезды и метеоры, ускоренные взрывами сверхновых. Так неужели мечта человечества о покорении Вселенной может однажды осуществиться?
Из-за огромных расстояний, разделяющих звездные системы друг от друга, транспорту будущего придется научиться использовать неподвластные современному человеку физические силы. Но что, если все может оказаться гораздо проще, чем это считалось ранее? Как сообщает портал Universe Today, наши потомки смогут путешествовать между звездами на кораблях, движущихся сквозь время и пространство со скоростью света. Для того, чтобы претворить мечту человечества в реальность, транспортные средства будущего будут использовать гиперскоростные звезды и метеоры, ускоренные взрывами сверхновых. Так неужели мечта человечества о покорении Вселенной может однажды осуществиться?
Феномен замедления времени в космосе долгое время волновал умы писателей-фантастов со всего мира. Вместе с тем, вопрос о том, как сильно воздействует перемещение астронавта со скоростью света на его биологические часы, впервые был описан в так называемом “парадоксе близнецов”, в котором астронавт совершает путешествие в космос на скоростной ракете, а его брат-близнец остается на Земле.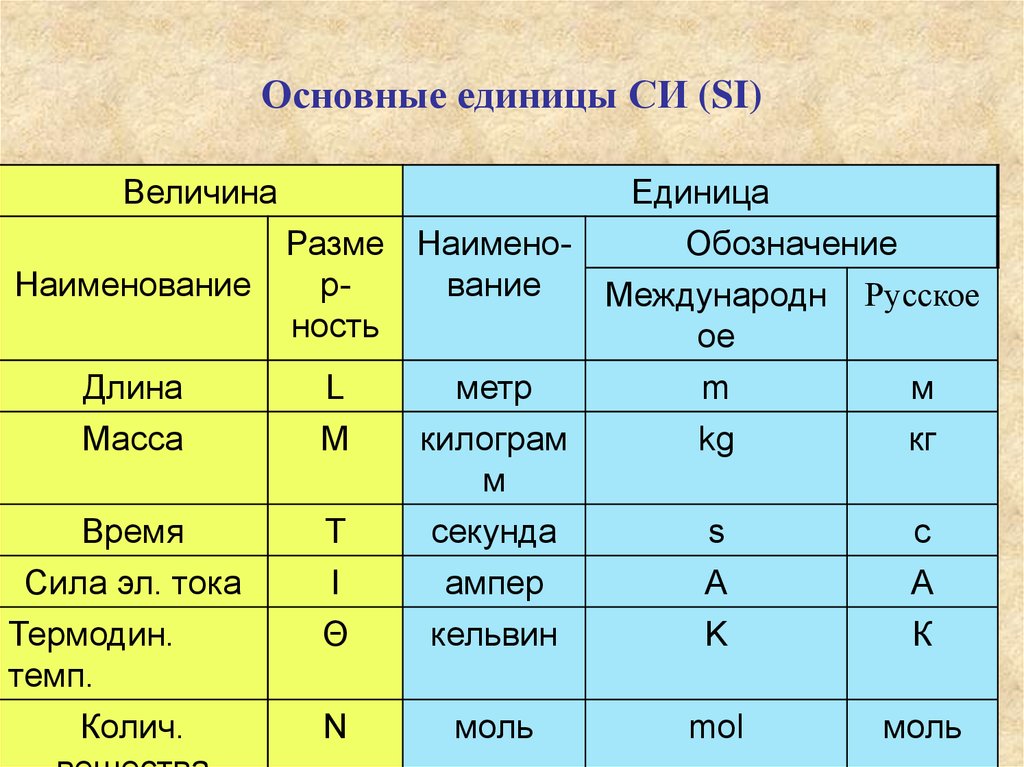 Считается, что по возвращению на голубую планету, астронавт обнаружит своего близнеца постаревшим, в то время как внешний вид самого космического путешественника останется едва ли не прежним.
Считается, что по возвращению на голубую планету, астронавт обнаружит своего близнеца постаревшим, в то время как внешний вид самого космического путешественника останется едва ли не прежним.
Скорость света – это предел, с которым может двигаться материальный объект в пространстве, если, конечно, не брать в расчет гипотетические кротовые норы, с помощью которых, согласно предположениям, объекты могут перемещаться в пространстве еще быстрее. В идеальном вакууме частица света, фотон, может двигаться со скоростью 299 792 километра в секунду или примерно 1,079 миллиарда километров в час. На первый взгляд может показаться, что это удивительно быстро. Нет, это на самом деле быстро. Но в масштабах космоса такая скорость может быть мучительно медленной, особенно, если речь идет о радиосообщениях и полетах на другие планеты, в частности, находящиеся за пределами нашей Солнечной системы.
Читать далееСкорость света является одной из важнейших констант в физике. Впервые оценку скорости света дал датский астроном Олаф Рёмер в 1676 году. Однако ученым, который установил, что именно свет задает верхний предел достижимой скорости в нашей Вселенной, равняющийся почти 300 000 километрам в секунду, был именно Альберт Эйнштейн. И все же, согласно той же теории Эйнштейна, все в этой Вселенной относительно, включая движение. Это, в свою очередь, заставляет задать вполне логичный вопрос: какова же скорость полной противоположности света – тьмы?
Однако ученым, который установил, что именно свет задает верхний предел достижимой скорости в нашей Вселенной, равняющийся почти 300 000 километрам в секунду, был именно Альберт Эйнштейн. И все же, согласно той же теории Эйнштейна, все в этой Вселенной относительно, включая движение. Это, в свою очередь, заставляет задать вполне логичный вопрос: какова же скорость полной противоположности света – тьмы?
Когда варп-двигатель впервые был представлен людям — вместе с дебютом «Звездного пути» пятьдесят лет назад — наше понимание Вселенной принципиально отличалось от нынешнего. С одной стороны, варп-двигатель был просто сюжетным устройством, которое позволяло добираться до далеких звезд весьма быстро; казалось, он нарушает принцип относительности Эйнштейна и физически невозможен. С другой стороны, казалось, что гравитация стягивает далекие галактики между собой, и если двигаться достаточно близко к скорости света, можно достичь чего угодно. Тогда мы не знали о темной энергии.
Группа ученых из МГУ имени М. В. Ломоносова и Технологического университета Тойохаши (что в Японии) разработала метод управления поворотом поляризации света. Как утверждают физики, это сможет открыть новые горизонты для развития систем оптической обработки информации, а также поможет в создании нового типа сверхбыстрых компьютеров, в которых вместо электронов работают фотоны.
Читать далее Если посмотреть на Солнце через 150 миллионов километров космоса, который разделяет наш мир от ближайшей звезды, свет, который вы видите, не показывает Солнце на текущий момент, а каким оно было 8 минут и 20 секунд назад. Это потому что свет движется не мгновенно (а со скоростью света, хаха): его скорость составляет 299 792,458 километра в секунду (подробности этого невероятного факта здесь). Именно такое время нужно свету, чтобы преодолеть путь от фотосферы Солнца до нашей планеты. Но силе тяжести не обязательно нужно вести себя так же; возможно, как предсказывала теория Ньютона, гравитационная сила представляет собой мгновенное явление и ощущается всеми объектами с массой во Вселенной, через все эти огромные космические расстояния, одновременно.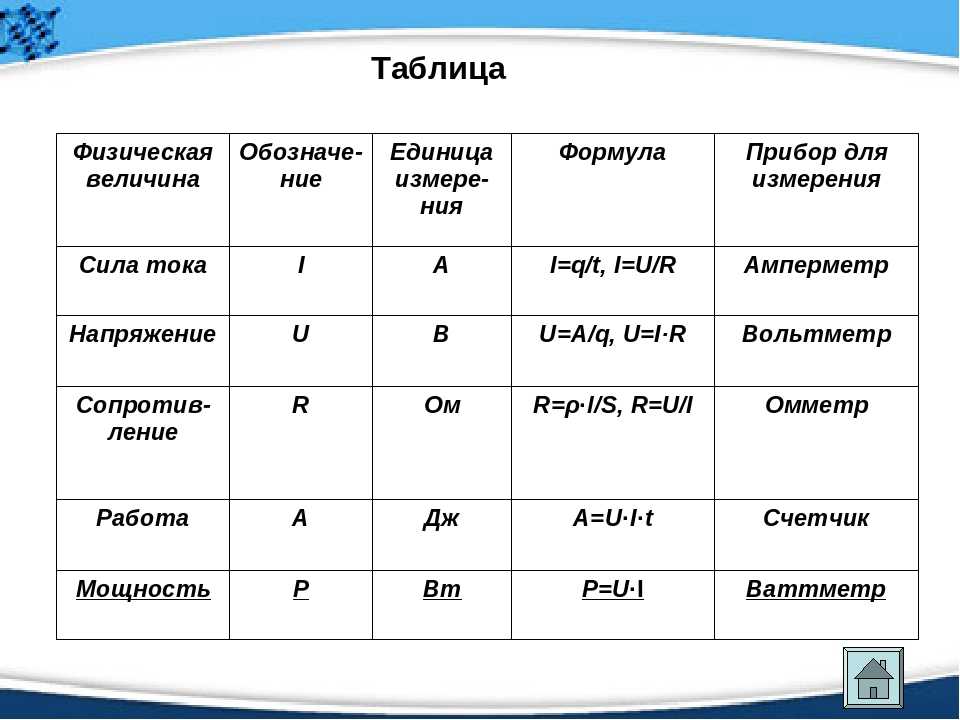
Исследователи из Гарвардского университета заявили о создании способа управления светом на наноуровне, который может привести к созданию фотонных телекоммуникаций (вместо современных электронных). Как сообщается, команда исследователей разработала метаматериал из кремниевых опор, заключённых в полимер и обёрнутых золотой плёнкой, которая снижает коэффициент преломления до нуля. Говоря русским языком, это означает, что световая волна может проходить этот материал со скоростью, стремящейся к бесконечности, при этом не нарушая известные законы физики.
Читать далееТренажёр по формулам по физике. (7 класс)
Похожие презентации:
Введение. Механика – раздел курса общей физики
Плотность вещества. 7 класс
Разделы физики
Физика. Механика
Путешествие в мир физики
Динамика материальной точки и поступательного движения твердого тела
Семифизик. Обобщающий урок по курсу физики 7 класса
Давление. Физика, 7 класс
Давление. (7 класс)
(7 класс)
Законы Ньютона. Масса и силы
1. Тренажёр по формулам физика 7 класс
Учитель физики«Беловской СОШ» филиала
МКОУ «Уйская СОШ»
Халикова З.А.
2. Выбери формулу для вычисления давления твёрдого тела
Ты неp=F*S
прав!
Умница!
p=F/S
дальше
Не
p=F+S
верно!
12.02.2017
Подумай
p=F*m
ещё!
Только в физике соль…
3. Выбери формулу для вычисления скорости тела
Ты неs=v*t
прав!
Умница!
v=s/t
дальше
Не
s=v/t
верно!
12.02.2017
Подумай
v=s*t
ещё!
Только в физике соль…
4. Выбери формулу для вычисления пройденного пути телом за время t
Подумайv=s/t
ещё!
Ты не
v=s*t
прав!
дальше
Не
s=v/t
верно!
12.02.2017
Умница!
s=v*t
Только в физике соль…
5. Выбери формулу для вычисления времени движения
Подумайt=s*v
ещё!
Ты не
s=v/t
прав!
дальше
Не
s=v/t
верно!
12.
 02.2017
02.2017Умница!
t=s/v
Только в физике соль…
6. Выбери формулу для вычисления силы тяжести
Ты неF=-kx
прав!
Умница!
F=m*g
дальше
Не
F=g/m
верно!
Подумай
F=m/g
ещё!
12.02.2017
Только в физике соль…
7. Выбери формулу для вычисления силы упругости
Ты неF=m*g
прав!
Умница!
F=-kx
дальше
Не
F=g/m
верно!
Подумай
F=m/g
ещё!
12.02.2017
Только в физике соль…
8. выбери формулу для расчёта массы тела
m *VВсё правильно
Вас
m
постигла
V
неудача
!
12.02.2017
Только в физике соль…
m
V
Стоит
подумать!
дальше
9. выбери формулу для расчёта объёма тела
m *Vm
V
Стоит
подумать!
Ой, Ой,Ой!
m
Умница!!!
V
12.02.2017
Только в физике соль…
дальше
10. выбери формулу для расчёта плотности вещества
m *VСтоит
подумать!
Подумай
ещё!
12.
 02.2017
02.2017Только в физике соль…
m
V
Отлично !
дальше
11. Какой буквой обозначается высота?
P.v
t
s.
S.
m
F
9,8Н/кг
ρ
p.
12.02.2017
V
g
h
k
Только в физике соль…
дальше
12. Какой буквой обозначается площадь?
P.S.
v
t
s.
m
F
9,8Н/кг
g
h
ρ
p.
12.02.2017
V
k
Только в физике соль…
дальше
13. Какой буквой обозначается время?
tP.
v
s.
S.
m
F
9,8Н/кг
ρ
p.
12.02.2017
V
g
h
k
Только в физике соль…
дальше
14. Какой буквой обозначается масса?
P.v
t
s.
S.
m
F
9,8Н/кг
ρ
p.
12.02.2017
V
g
h
k
Только в физике соль…
дальше
15. Какой буквой обозначается путь?
P.v
t
S.
s.
m
F
9,8Н/кг
g
h
ρ
p.
12.02.2017
V
k
Только в физике соль.
 ..
..дальше
16. Какой буквой обозначается скорость?
vP.
t
s.
S.
m
F
9,8Н/кг
ρ
p.
12.02.2017
V
g
h
k
Только в физике соль…
дальше
17. Какой буквой обозначается вес тела?
P.v
t
s.
S.
m
F
9,8Н/кг
ρ
p.
12.02.2017
V
g
h
k
Только в физике соль…
дальше
18. Какой буквой обозначается сила?
P.v
t
s.
S.
m
F
9,8Н/кг
ρ
p.
12.02.2017
V
g
h
k
Только в физике соль…
дальше
19. Какой буквой обозначается объём тела?
P.v
t
s.
S.
V
m
F
g
9,8Н/кг
ρ
p.
12.02.2017
h
k
Только в физике соль…
дальше
20. Какой буквой обозначается ускорение свободного падения?
vt
s.
S.
P.
m
F
9,8Н/кг
ρ
p.
12.02.2017
V
g
h
k
Только в физике соль…
дальше
21.
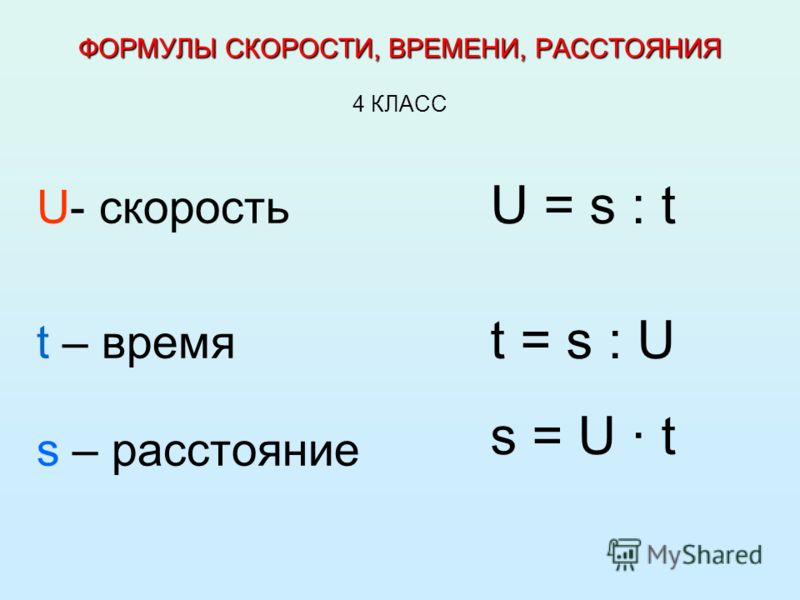 Какой буквой обозначается плотность вещества?P.
Какой буквой обозначается плотность вещества?P.v
t
s.
S.
m
F
ρ
12.02.2017
9,8Н/кг
p.
V
g
h
k
Только в физике соль…
дальше
22. Какой буквой обозначается давление?
P.v
t
s.
S.
m
F
ρ
12.02.2017
9,8Н/кг
p.
V
g
h
k
Только в физике соль…
дальше
23. Какой буквой обозначается жёсткость?
P.v
t
s.
S.
m
F
ρ
12.02.2017
9,8Н/кг
p.
k
Только в физике соль…
V
g
h
дальше
24. Чему равно ускорение свободного падения на Земле?
P.v
t
s.
S.
m
F
ρ
V
9,8Н/кг
p.
k
g
h
дальше
12.02.2017
Только в физике соль…
25. Единица измерения силы…
м/cc
Па
кг
м
Н
(Ньютон)
Дж
3
м
2
м
Н/кг
Н/м
3
кг/м
дальше
12.02.2017
Только в физике соль.
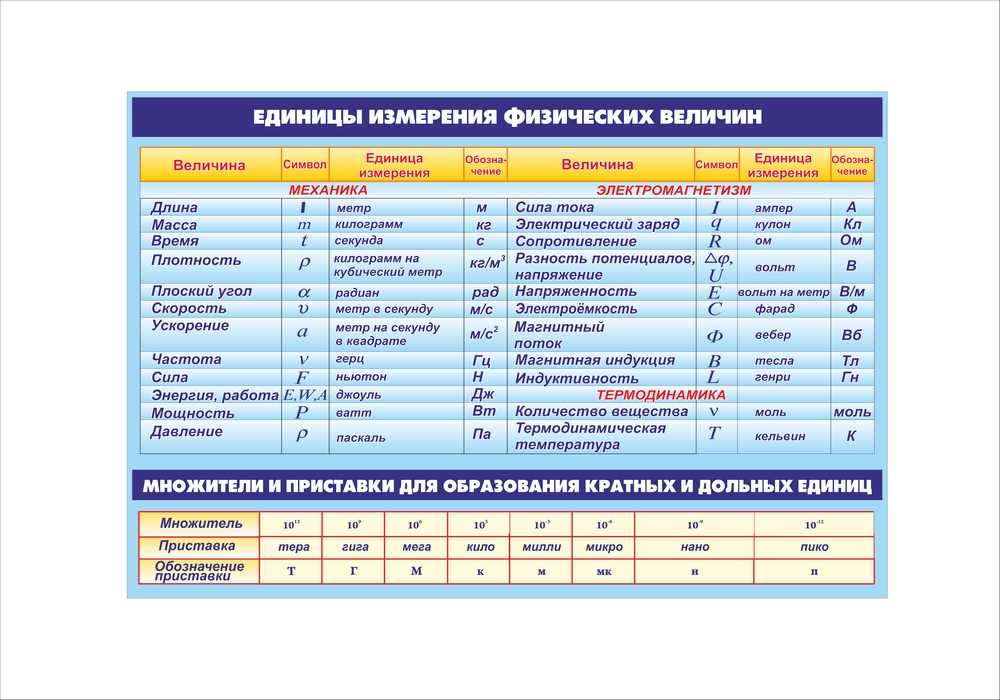 ..
..26. Единица измерения скорости…
cм/c
Па
кг
м
Н
(Ньютон)
Дж
3
м
2
м
Н/кг
Н/м
3
кг/м
дальше
12.02.2017
Только в физике соль…
27. Единица измерения времени…
м/cc
Па
кг
м
Н
(Ньютон)
Дж
3
м
2
м
Н/кг
Н/м
3
кг/м
дальше
12.02.2017
Только в физике соль…
28. Единица измерения объёма…
м/cc
Па
кг
м
Н
(Ньютон)
Дж
2
м
м3
Н/кг
Н/м
3
кг/м
дальше
12.02.2017
Только в физике соль…
29. Единица измерения плотности…
м/cc
Па
кг
м
Н
(Ньютон)
3
кг/м
Дж
3
м
2
м
Н/кг
Н/м
дальше
12.02.2017
Только в физике соль…
30. Единица измерения массы…
м/cПа
c
кг
м
Н
(Ньютон)
Дж
3
м
2
м
Н/кг
Н/м
3
кг/м
дальше
12.
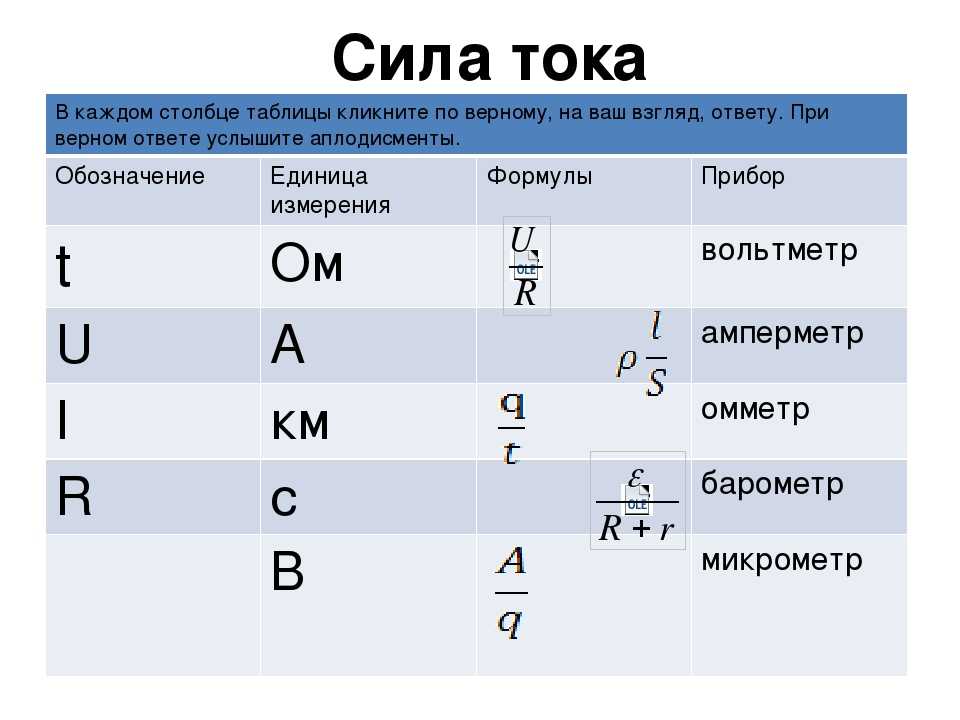 02.2017
02.2017Только в физике соль…
31. Единица измерения давления…
м/cПа
c
кг
м
Н
(Ньютон)
Дж
3
м
2
м
Н/кг
Н/м
3
кг/м
дальше
12.02.2017
Только в физике соль…
32. Единица измерения жёсткости…
м/cc
Па
кг
м
Н
(Ньютон)
Дж
3
м
2
м
Н/кг
Н/м
3
кг/м
дальше
12.02.2017
Только в физике соль…
33. Единица измерения площади…
м/cc
Па
кг
м
Н
(Ньютон)
Дж
3
м
м2
Н/кг
Н/м
3
кг/м
дальше
12.02.2017
Только в физике соль…
34. Единица измерения g…
м/cc
Па
кг
м
Н
(Ньютон)
Дж
2
м
3
м
Н/кг
Н/м
3
кг/м
дальше
12.02.2017
Только в физике соль…
35. Единица измерения энергии…
м/cc
Па
кг
м
Н
(Ньютон)
Дж
3
м
2
м
Н/кг
Н/м
3
кг/м
дальше
12.
 02.2017
02.2017Только в физике соль…
36. Единица измерения работы…
м/cc
Па
кг
м
Н
(Ньютон)
Дж
3
м
2
м
Н/кг
Н/м
3
кг/м
дальше
12.02.2017
Только в физике соль…
37. Единица измерения веса тела…
м/cc
Па
кг
м
Н
(Ньютон)
Дж
3
м
2
м
Н/кг
Н/м
3
кг/м
дальше
12.02.2017
Только в физике соль…
38. Выбери формулу для вычисления работы
Ты неN=A/t
прав!
Умница!
A=F*s
дальше
Неmv
Ек
верно!2
12.02.2017
2
Подумай
Е р mgh
ещё!
Только в физике соль…
39. Выбери формулу для вычисления мощности
Ты неA=F*s
прав!
Умница!
N=A/t
дальше
Неmv
Ек
верно!2
12.02.2017
2
Подумай
Е р mgh
ещё!
Только в физике соль…
40. Выбери формулу для вычисления кинетической энергии
НеA=F*s
верно!
Ты не
N=A/t
прав!
дальше
mv
Е
Умница!
к
2
12.
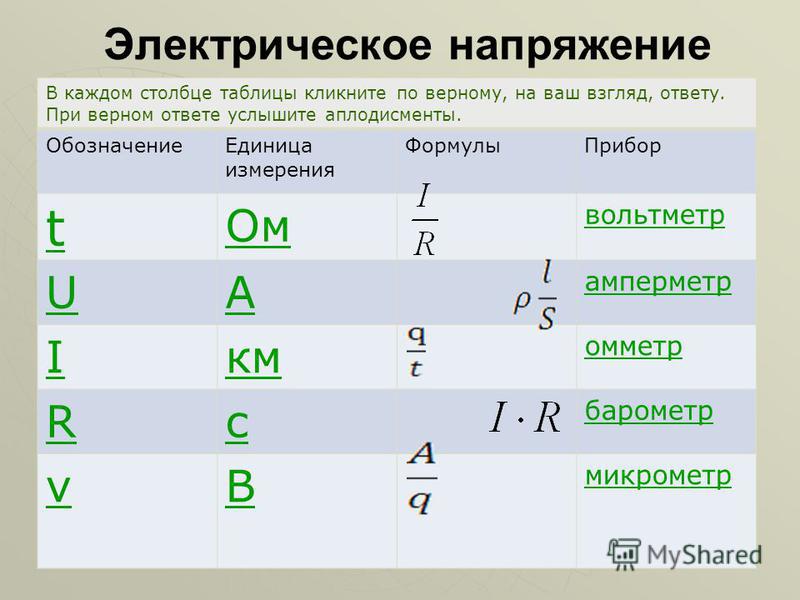 02.2017
02.20172
Подумай
Е р mgh
ещё!
Только в физике соль…
41. Выбери формулу для вычисления потенциальной энергии
ПодумайA=F*s
ещё!
Ты не
N=A/t
прав!
дальше
Неmv 2
Еверно!
к
Е рУмница!
mgh
2
12.02.2017
Только в физике соль…
42. Выбери формулу для вычисления работы
Ты неN=A/t
прав!
Умница!
A=N*t
дальше
Неmv
Ек
верно!2
12.02.2017
2
Подумай
Е р mgh
ещё!
Только в физике соль…
43. Выбери формулу для вычисления мощности
Ты неA=F*s
прав!
Умница!
N=F*v
дальше
Неmv
Ек
верно!2
12.02.2017
2
Подумай
Е р mgh
ещё!
Только в физике соль…
44. Выбери формулу для вычисления давления жидкости на дно сосуда
Ты неFa= ρжgVт
прав!
Умница!
P=ρgh
дальше
Ап
Подумай
ещё!100%
А
Не
M=Fl
верно!
12.02.2017
з
Только в физике соль.
 ..
..45. Выбери формулу для вычисления момента силы
Ты неFa= ρжgVт
прав!
Не
P=ρgh
верно!
дальше
Ап
Подумай
ещё!100%
А
M=Fl
Умница!
з
12.02.2017
Только в физике соль…
46. Выбери формулу для вычисления силы Архимеда
Ты неP=ρgh
прав!
FУмница!
a= ρжgVт
дальше
Ап
Подумай
ещё!100%
А
Не
M=Fl
верно!
12.02.2017
з
Только в физике соль…
47. Выбери формулу для вычисления КПД
Ты неFa= ρжgVт
прав!
Подумай
P=ρgh
ещё!
дальше
Ап
Умница!
100%
Аз
Не
M=Fl
верно!
12.02.2017
Только в физике соль…
English Русский Правила
символов в физике | NSTA
В математических науках важна способность умело использовать символы для представления понятий и процессов. Подвижность либо одного символа, используемого для представления нескольких понятий, либо нескольких символов, используемых для представления одного и того же понятия, требует гибкости мышления от практиков, чтобы контекстуально определять правильное значение символа каждый раз, когда он встречается.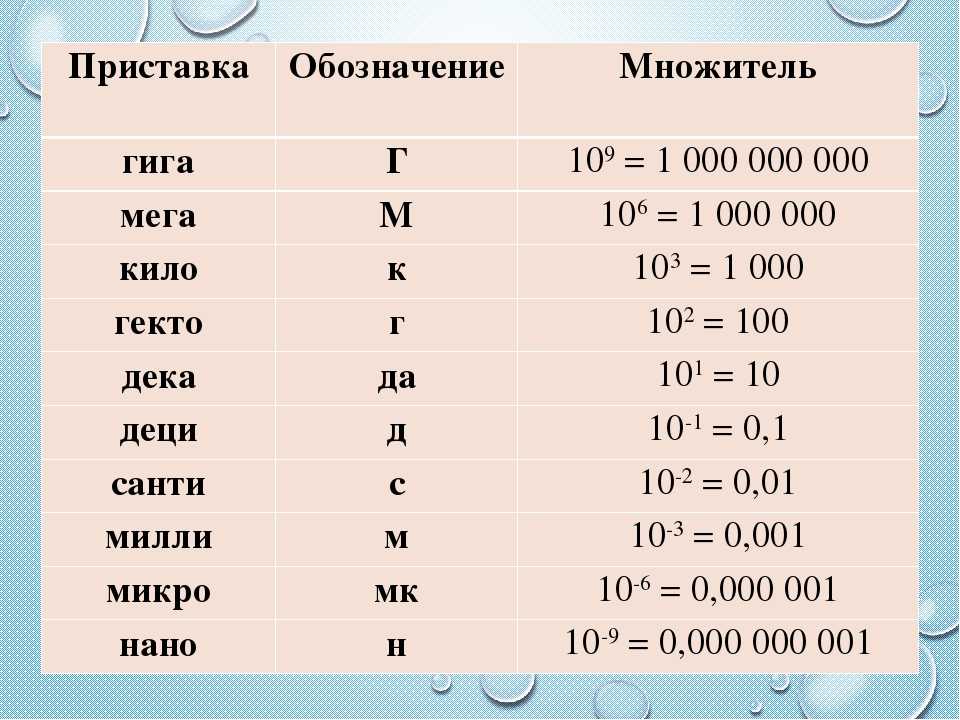 Кроме того, шрифт и стиль, применяемые к аналогичным обозначениям, могут различаться в зависимости от средства коммуникации. Бардини и Пирс (2015) обратили внимание на проблему, с которой учащиеся изучают математику при переходе от средней школы к изучению математики в университете, где вводятся новые символы, а знакомые символы могут использоваться с измененными или расширенными значениями. В этой статье исследуются трудности, с которыми сталкиваются студенты-физики, ориентируясь в этом символически насыщенном и потенциально запутанном языке. Мы исследовали, воспринимают ли студенты первого курса бакалавриата, изучающие физику, какие-либо трудности или различия, связанные с использованием символов при переходе в университет. Испытывают ли они трудности с разнообразием и/или дублированием символов, используемых в их исследованиях физики или между математикой и физикой? Как эти студенты справляются с этими трудностями? Во-первых, мы рассматриваем ключевую связанную литературу.
Кроме того, шрифт и стиль, применяемые к аналогичным обозначениям, могут различаться в зависимости от средства коммуникации. Бардини и Пирс (2015) обратили внимание на проблему, с которой учащиеся изучают математику при переходе от средней школы к изучению математики в университете, где вводятся новые символы, а знакомые символы могут использоваться с измененными или расширенными значениями. В этой статье исследуются трудности, с которыми сталкиваются студенты-физики, ориентируясь в этом символически насыщенном и потенциально запутанном языке. Мы исследовали, воспринимают ли студенты первого курса бакалавриата, изучающие физику, какие-либо трудности или различия, связанные с использованием символов при переходе в университет. Испытывают ли они трудности с разнообразием и/или дублированием символов, используемых в их исследованиях физики или между математикой и физикой? Как эти студенты справляются с этими трудностями? Во-первых, мы рассматриваем ключевую связанную литературу.
Литература
Сила математики в значительной степени зависит от использования символов (Arcavi, 2005), но исследования, проведенные в течение длительного периода времени, показали, что их краткость и абстракция могут стать препятствием для обучения (MacGregor & Stacey, 1997; Pierce et al. , 2010). Символы также играют важную роль в физике, их использование и важность на высшем уровне возрастают. В исследовании с участием студентов-первокурсников университетов-физиков (Torigoe & Gladding, 2007) было обнаружено, что успеваемость студентов тесно связана с их пониманием символов. В этой статье основное внимание уделяется пониманию и интерпретации учащимися символических выражений, которые используются на первом курсе бакалавриата по физике, в том числе тех, которые являются уникальными для физики, а также символических выражений, которые пересекаются с математикой, которую студенты ранее изучали или изучают. учусь по совместительству. Мы не сосредотачиваемся на навыках учащихся в вычислении или манипулировании символическими выражениями.
, 2010). Символы также играют важную роль в физике, их использование и важность на высшем уровне возрастают. В исследовании с участием студентов-первокурсников университетов-физиков (Torigoe & Gladding, 2007) было обнаружено, что успеваемость студентов тесно связана с их пониманием символов. В этой статье основное внимание уделяется пониманию и интерпретации учащимися символических выражений, которые используются на первом курсе бакалавриата по физике, в том числе тех, которые являются уникальными для физики, а также символических выражений, которые пересекаются с математикой, которую студенты ранее изучали или изучают. учусь по совместительству. Мы не сосредотачиваемся на навыках учащихся в вычислении или манипулировании символическими выражениями.
Предыдущее опубликованное исследование выявило четыре ключевые проблемы в этом отношении: трудности учащихся при работе с количеством и разнообразием символов; необходимость знать о неписаных условностях; преимущество распознавания значения в общих шаблонах символов; и необходимость осознавать эпистемологическую разницу в работе с символами и их интерпретации в математике и физике.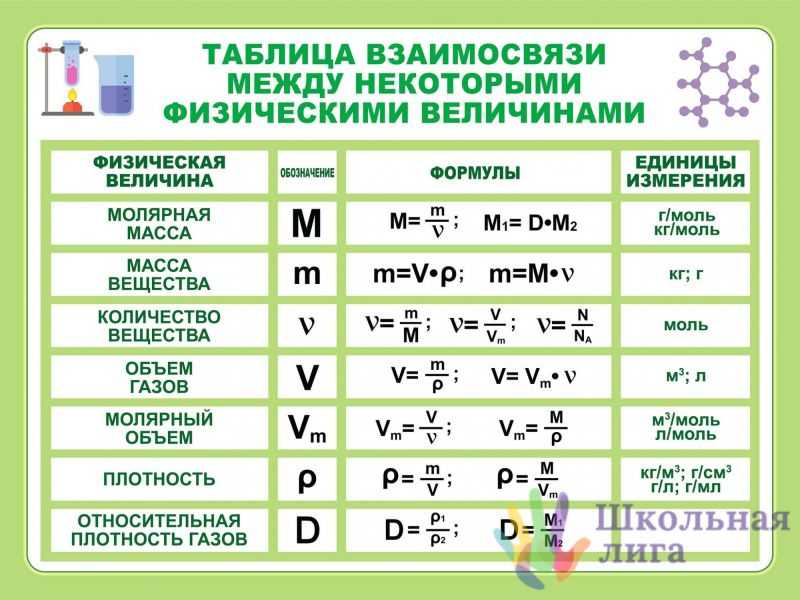
Во-первых, как указывает Бейли (1999), в физике используется множество символов. Римские и греческие буквы используются как в нижнем, так и в верхнем регистре и имеют разные значения. Студенты не только должны быть внимательны к этой детали, но и одна и та же буква может использоваться в разных значениях, например, как местоимение для обозначения количества и как сокращение для единицы измерения. Типичным примером является использование m для количества массы и m для метров. Здесь намек на другое значение дается курсивом для переменной величины. Бейли (1999) предполагает, что учащимся можно помочь, предоставив им список символов с их соответствующими значениями и объяснив учащимся, что им нужно будет работать над запоминанием символов по мере того, как они вводятся в течение курса.
Ториго и Глэддинг (2006; 2007) сообщают о своем исследовании числовых вычислений студентов-физиков в сравнении с символическим представлением. На начальном этапе своего исследования, когда они давали студентам параллельные числовые и символьные версии экзаменационных вопросов, они обнаружили, что средний балл по числовым вопросам был на 50% выше, чем по соответствующим символическим вопросам. Основываясь на своем первом исследовании, Ториго и Глэддинг предположили, что расхождение было связано с непониманием учащимися переменных, а не с навыками вычислений. Их расширенное исследование с использованием дополнительных параллельных вопросов дало дополнительные сведения: работа с числами означает, что каждый шаг может быть сведен к одному значению, в то время как символические выражения должны переноситься от шага к шагу. Затем Ториго и Глэддинг (2007) предположили, что работа с символами приводит к большей когнитивной нагрузке, особенно в многоэтапных задачах.
Основываясь на своем первом исследовании, Ториго и Глэддинг предположили, что расхождение было связано с непониманием учащимися переменных, а не с навыками вычислений. Их расширенное исследование с использованием дополнительных параллельных вопросов дало дополнительные сведения: работа с числами означает, что каждый шаг может быть сведен к одному значению, в то время как символические выражения должны переноситься от шага к шагу. Затем Ториго и Глэддинг (2007) предположили, что работа с символами приводит к большей когнитивной нагрузке, особенно в многоэтапных задачах.
Джаммарино (2000), студент, пишущий от имени группы студентов, озвучивает тревогу, которую они испытывают, когда сталкиваются с тем, что они воспринимают как разные символические обозначения, представляющие одни и те же переменные. Он отмечает разнообразие от учителя к учителю и от учебника к учебнику. Студенты беспокоятся о том, какой символ использовать и с какими из них они столкнутся на экзаменах. В то время как другие авторы подчеркивают необходимость для учащихся быть гибкими, эти студенты призывают к большей последовательности.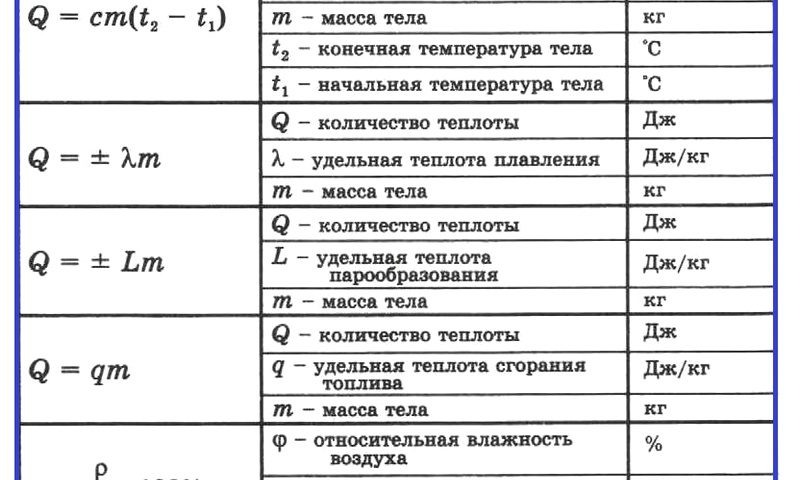
При построении и записи символьных уравнений необходимо соблюдать определенные неписаные соглашения. Эти соглашения упрощают распознавание шаблонов в выражениях и, следовательно, помогают в интерпретации. Bailey (1999), De Lozano and Cardenas (2002) и Moelter and Jackson (2012) обращают внимание на эти тонкости. Как упоминалось выше, курсив обычно используется для переменных и латинских букв для единиц измерения. Константы, параметры и переменные записываются в том порядке, в котором они перемножаются в выражении; там, где есть дроби, этот порядок соблюдается отдельно в числителе и в знаменателе.
Дальнейший шаг в рассмотрении изложения символических выражений был предложен Шерином (2001) и продолжен Редиш и Куо (2015). Шерин подчеркивает важность того, что он называет «символическими формами», и их интерпретации или, наоборот, при моделировании определение того, что физическое явление может быть абстрактно представлено определенной символической формой. Например, если «целое» состоит из частей, то символически оно может быть представлено выражением, которое примет вид □+□+□… или, если одна переменная пропорциональна другой, то соответствующая форма будет пропорциональна другой. […/(….х….)] (Шерин, 2001, с. 590).
[…/(….х….)] (Шерин, 2001, с. 590).
Выбор подходящих символических форм требует от учащегося рассмотрения не только переменных и констант, но также математических процессов и их значения в конкретном контексте. Студенты должны думать, например, о реальном влиянии сложения, а не умножения, сложения, а не вычитания и т. д. Они должны сделать осознанный, вдумчивый выбор, а не просто надеяться правильно запомнить формулу.
Де Лозано и Карденас (2002) поднимают тему эпистемологической линзы, через которую следует рассматривать символы в математике и физике. Они утверждают, что математика является теоретической, построенной пошагово из аксиом, с упором на логическую непротиворечивость. Физику, с другой стороны, всегда следует рассматривать и интерпретировать в свете ограничений реального мира, которые могут быть явными, а могут и не быть. Они предполагают, что в то время как в математике «=» указывает на отношение, обладающее свойствами симметрии, рефлексивности и транзитивности, в физике его можно использовать для более свободного обозначения «соответствует».
Методология
Студенты первого курса, изучающие физику, математику или статистику, были набраны из двух австралийских университетов, с которыми исследователи сотрудничали. Участниками, на которых мы сосредоточились в этом отчете, были преподаватели физики первого курса (которые также были координаторами предмета) и 187 студентов-первокурсников-физиков, набранных с помощью объявлений, размещенных на досках объявлений системы онлайн-обучения их предмета. Сорок три (24%) из этих студентов были зачислены на инженерные курсы, а физика составляла элемент курса. Остальные 134 (76%) были зачислены на различные курсы бакалавриата с одним и двумя дипломами, при этом решение о том, станет ли физика основным направлением бакалавриата на последнем курсе их курса, еще предстоит принять. Из них 19 студентовсогласился встретиться с нами индивидуально для 30–40-минутного полуструктурированного аудиозапись интервью, в дополнение к ответу на онлайн-опрос. Ответы на опросы были классифицированы по общим шаблонам ответов, а стенограммы интервью проанализированы для выявления повторяющихся тем в комментариях студентов.
Выводы и обсуждение
Ощущают ли студенты-первокурсники, изучающие физику, какие-либо трудности или различия, связанные с использованием символов при переходе в университет?
Изменение условного обозначения символов. Символы, которые используются для представления физических или математических понятий в средней школе, могут для учащегося, плохо знакомого с университетской физикой (проиллюстрировано S13 ниже), измениться неожиданно и без объяснения причин, с новым символическим представлением, включающим незнакомый синтаксис, такой как нижние индексы и надстрочные индексы.
S13: Я только что нашел, что это действительно очень отталкивает в начале… Например, s мы использовали в специалисте [12-й класс математики] — теперь это дельта x. Вместо u и v для начальной и конечной скоростей имеем v i [ v i ] и v f [ v f ]. Я имею в виду, что физические обозначения более логичны и ясны, они лучше, но почему они вообще разные?
Студенты упомянули ряд изменений в обозначениях (в отличие от новой терминологии) по сравнению с предыдущими исследованиями после посещения семинедельных занятий по физике на первом курсе бакалавриата. Они были сведены в Таблицу 1. Интересно отметить, что трудности, отмеченные учащимися в связи с изменением обозначений единичных векторов с î, ĵ и k ̂ на x̂, ŷ и ẑ, наблюдались Лектором 1 в обратном порядке, где они используют î, ĵ и k̂ в физике на первом курсе, но заметили студентов, уже имевших опыт использования x̂, ŷ и ẑ. Лектор 2 отметил, что «у вас есть люди i, j, k, и я предполагаю, что одна из вещей… вероятно, между учеными, не будет большой согласованности, потому что они из разных слоев общества. ” Это иллюстрирует трудности, которые могут возникнуть как у студентов, так и у преподавателей при письменном общении друг с другом.
Они были сведены в Таблицу 1. Интересно отметить, что трудности, отмеченные учащимися в связи с изменением обозначений единичных векторов с î, ĵ и k ̂ на x̂, ŷ и ẑ, наблюдались Лектором 1 в обратном порядке, где они используют î, ĵ и k̂ в физике на первом курсе, но заметили студентов, уже имевших опыт использования x̂, ŷ и ẑ. Лектор 2 отметил, что «у вас есть люди i, j, k, и я предполагаю, что одна из вещей… вероятно, между учеными, не будет большой согласованности, потому что они из разных слоев общества. ” Это иллюстрирует трудности, которые могут возникнуть как у студентов, так и у преподавателей при письменном общении друг с другом.
Одним из факторов, способствовавших замешательству студентов, примером которого является S21 ниже, является то, что изменения в обозначениях из средних учебных заведений не всегда явно подчеркивались лекторами или наставниками, оставляя студентам возможность расшифровать эквивалентность используемых символов. Студенты интерпретировали это молчание как означающее, что их преподаватели не знали об изменениях в обозначениях, и, например, прокомментировали:
Студент S21: Я не думаю, что они поняли, потому что я просто сидел в одном из семинаров, а у девушки рядом со мной были s, и я такой, я никогда раньше не видел это уравнение, я не узнаю его как что-то такое, что я видел раньше, а потом она говорит: «Означает смещение».
В предмете физики используется широкий спектр того, что мы называем «символическими синонимами» (т. е. несколько символов, используемых для представления одного понятия). Международные стандарты обозначений в физике, основанные на Système International (Международная система единиц) , публикуются с 1961 г. (см. Cohen, 1987), однако они не всегда используются или соблюдаются даже в общепринятых учебниках (например, , Уокер и др., 2011).
Преподаватели физики, с которыми мы беседовали, знали о непоследовательности обозначений в физике и о том, как это может повлиять на понимание студентами. Каждый из них стремился к согласованности в своих учебных материалах. Например:
Лектор 2: Я намеренно изменил все символы, и я уверен, что когда мы меняли учебники или мы меняли ссылки, я использую те же символы, что и в учебнике… [потому что] когда они на в начале, это становится барьером для входа в тему в первую очередь, если ты путаешь их со смесью символов.
Однако это было предпринято изолированно, и еще предстоит разработать политику для обеспечения согласованности обозначений на факультетах физики (особенно с учетом того, что студентов могут обучать несколько преподавателей физики в течение каждого года) или с австралийской школьной программой.
Испытывают ли учащиеся трудности с разнообразием и/или дублированием символов, используемых при изучении физики или между математикой и физикой?
Физика использует очень широкий спектр символов для представления констант, параметров и переменных в уравнениях, при этом количество и разнообразие символов, используемых во время обучения в бакалавриате, увеличивается. Это неоднократно отмечалось в интервью:
S02: Типа… особенно потому, что у них почти закончились символы, так что они просто бросаются в нас греческими буквами…
S06: В этом году будет гораздо больше разнообразных символов и вещей. В старших классах они были строгими, что это так, и я думаю, что и с физикой это просто потому, что там больше уравнений для использования, больше символов и переменных.
Студенты (например, см. S20 ниже) отметили, что некоторые символы используются для представления нескольких понятий (которые мы описываем как «символические омонимы») как из недавно введенных понятий в университете, так и для понятий, встречающихся в школе.
S20: Да ладно, даже с точки зрения физики омега — это три разных вещи. Это угловая скорость… [и] это также и угловая частота… Итак, они одинаковы для круга, я думаю, поэтому у него может быть один и тот же символ, но разные для всего остального, что раздражает.
Большое количество терминов, требующих символического представления в физике, может сделать это неизбежным, но различные значения одного символа добавили слой расшифровки, который иногда вызывал трудности у студентов. Коэн (1987) указывает, что в стандартных соглашениях символ, выделенный S20, строчная омега (ω) используется для обозначения телесного угла, угловой частоты и угловой скорости, все в области механики, с пятью дополнительными применениями.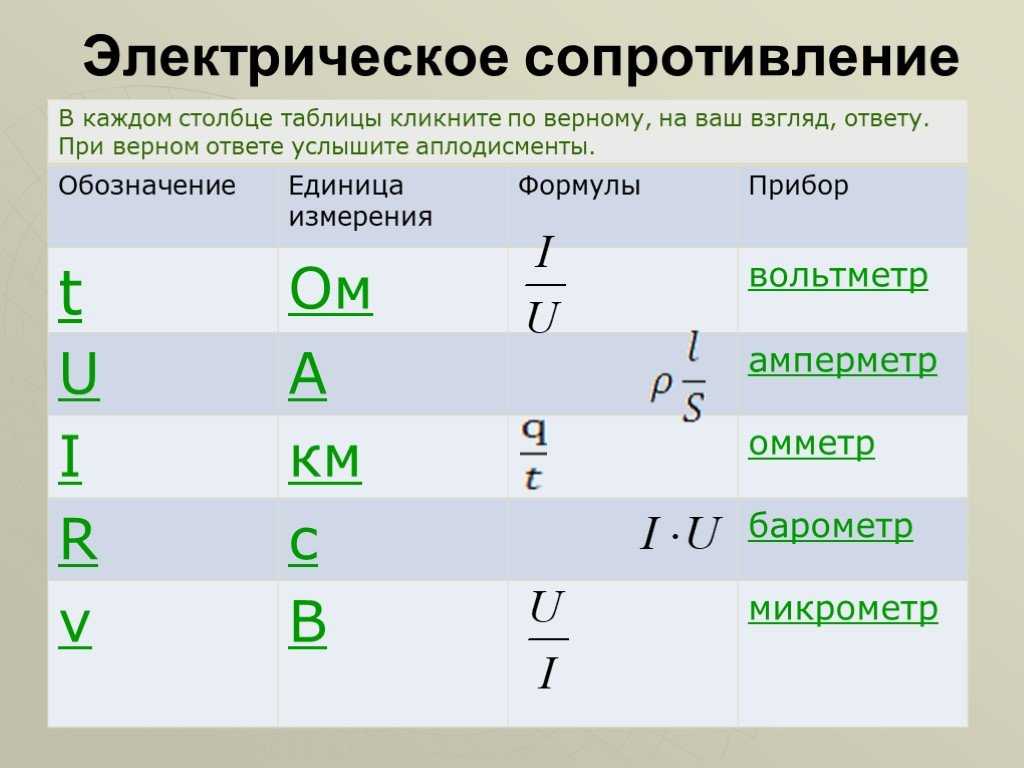 строчных букв омеги, перечисленных с использованием нижних индексов в различных разделах физики. Нетрудно понять, как это может сбить с толку студентов.
строчных букв омеги, перечисленных с использованием нижних индексов в различных разделах физики. Нетрудно понять, как это может сбить с толку студентов.
И наоборот, в рамках бакалавриата по физике студенты также сталкиваются с ситуациями, когда несколько символов использовались для представления одного понятия.
S05: Получается, что у нас три разные системы, и иногда это действительно хаотично. Потому что я перешел на ту версию, которая используется в учебнике, но все мои друзья используют ту, что в старшей школе, а лектор использует другую.
Преподаватели физики признали разнообразие и сложность символического аспекта предмета, подчеркнув даже то, что «условные обозначения на самом деле также меняются в зависимости от ситуации или контекста» (лектор 2), причем временами для акцента используются специальные обозначения.
Учащиеся также сталкиваются с дублированием или изменением соглашений между физикой и математикой, например:
S22: В физике часто используется буква k, а в математике часто используется буква c, хотя, знаете ли, я видел кое-что, когда одно заимствует другое» [относительно общих констант].
S13: В физике будет использоваться дельта t в формуле постоянного ускорения, которая лучше, чем d [в математике], потому что этот вид указывает на изменение во временном интервале.
Другие темы, в которых учащиеся подчеркнули, что символические синонимы широко распространены между предметами, включают векторы ( i , j и k по сравнению с x , y и z, и тильда по сравнению со стрелками или полужирным шрифтом), движение ( с , 10012 – начальная скорость, 10110 – скорость , v – конечная скорость , a – ускорение, t – время: механические обозначения, известные как формулы Сувата по сравнению с другими обозначениями), сил ( N против R для нормальных сил реакции) и различные соглашения с единицы СИ.
Преподаватели физики также прокомментировали различия в обозначениях между своим предметом и математикой, например, лектор 1 заявил, что «я бы сказал, что использование одного и того же символа для разных вещей является самым большим [сложность символа]. Это разница в том, как представлены определенные математические понятия. Например, дифференциалы представлены различными способами».
Это разница в том, как представлены определенные математические понятия. Например, дифференциалы представлены различными способами».
Согласование учебных программ по физике и математике
К этому добавляется сложность в планировании времени изучения тем по физике, чтобы гарантировать, что необходимые университетские математические знания уже изучены их студентами, о чем свидетельствует следующая обратная связь:
S02: Ах, физика, да… Еще одна вещь, как… векторы появились в ней [физике] очень рано, и я только занимаюсь [вводным курсом по математическому анализу на первом курсе], и мы только что закончили с векторами. . Так что сейчас все это имеет смысл, но тогда это было… что происходит?
Как первокурсники-физики справляются с трудностями с символами?
На вопрос о том, вызвали ли несоответствия и различия трудности, учащиеся сказали, что они могут приспособиться к изменениям, но было отмечено, что связанная с этим дополнительная нагрузка усложняет задания.
S02: …Но, как и… работа над этим меня немного смутила. Я получаю немного больше знаний, повторяя все это несколько раз, но да, это намного сложнее понять в первый раз, чем мне в школе.
Некоторые студенты также беспокоились о том, будут ли экзаменаторы понятны нотации, которые они выучили на предыдущих занятиях. Это побудило их изменить номенклатуру (таково было разъединение в использовании обозначений от вторичных к третичным исследованиям физики). Например:
S05: На самом деле, меня тоже очень беспокоило использование символов. Я не был уверен, что мой… преподаватель, который оценивает мои задания, поймет мои… символы, которые я использовал в старшей школе. Вот почему я перешел на новый, и у меня были проблемы в начале .
Некоторые студенты отметили, как и следовало ожидать, что они поняли значение символа, используя контекст ситуации. Однако у других студентов было больше трудностей; они решили выполнять расчеты, используя символы, знакомые со школы, а затем «перевели» их на символы, используемые на уроках физики в университете.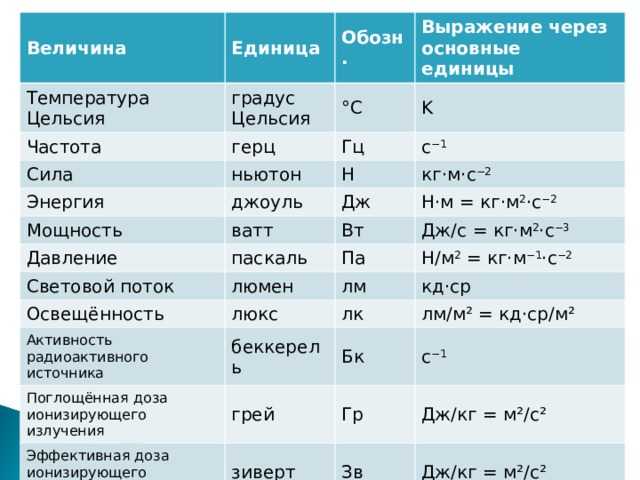
S13: В основном [это] просто замедляло меня. … Я размышляю… следует ли мне использовать его запись или мою запись? … Мне кажется странным, когда лектор читает лекцию в определенной нотации, использовать другую нотацию, когда я ее пишу… На самом деле я пытаюсь писать в своей собственной нотации. Но тогда ваш мозг будет одновременно пытаться слушать его, и тогда вы в конечном итоге просто будете писать то, что он пишет, и это будет как половина в одной половине в другой….
Этот подверженный ошибкам метод добавляет сложности и когнитивной нагрузки для этих учащихся. Тем не менее, некоторые студенты чувствовали себя более уверенно при таком подходе, чем при работе с новой системой обозначений.
Обсуждение и значение для обучения
Наши результаты и более ранняя исследовательская литература, обсуждавшаяся выше, предполагают, что студенты могут испытывать трудности, справляясь с возросшим разнообразием, дублированием и зависимостью от символических обозначений в физике бакалавриата. Они пытаются осмыслить вновь встречающиеся символы или контексты, отчасти используя предшествующие концепции, которые приходят им на ум, когда они видят знакомый символ, и отчасти пытаясь сопоставить новые обозначения, символизирующие знакомый контекст.
Они пытаются осмыслить вновь встречающиеся символы или контексты, отчасти используя предшествующие концепции, которые приходят им на ум, когда они видят знакомый символ, и отчасти пытаясь сопоставить новые обозначения, символизирующие знакомый контекст.
Трудности, о которых сообщали студенты, столкнувшиеся с неожиданными и порой необъяснимыми изменениями в обозначениях при переходе от изучения физики в средней школе к бакалавриату, не были непредвиденными опытными преподавателями физики. Тем не менее, эти высокопоставленные сотрудники были рады результатам исследований, которыми они могли поделиться со своими коллегами. Учитывая различия в символических стандартах в рамках предмета, разрыв в использовании символов может показаться почти неизбежным для некоторых студентов, когда они переходят к изучению физики в университете. Мы выступаем за то, чтобы лекторы и преподаватели знакомились с содержанием и условными обозначениями общеобразовательной программы средней школы, но, возможно, полезным подходом для преподавателей было бы попросить учащихся прочитать вслух символические утверждения, а затем объяснить, что означают обозначения. Это будет определять как знание, так и предубеждения. Различия или изменения в обозначениях должны быть явно указаны.
Это будет определять как знание, так и предубеждения. Различия или изменения в обозначениях должны быть явно указаны.
В дополнение к наблюдению и явному выделению многих символических синонимов и омонимов, с которыми студенты сталкиваются после перехода к изучению физики и математики в университете, могут быть приняты дополнительные меры для повышения компетентности студента в использовании символического языка физики. Например:
- Принимая к сведению и специально выделяя форму символа, отмечая, выделен ли он курсивом, заглавным или строчным, из какого он алфавита, есть ли надстрочные или нижние индексы и что они означают. Например, переход от s to x i в теме механики символически сложнее из-за индекса, но x i несет дополнительную важную информацию.
- Также может быть полезным явное преподавание соглашений, таких как порядок символов в уравнениях с константами сначала, затем с параметрами, а затем с переменными, как это было предложено Moelter and Jackson (2012).

- Постановка задач для улучшения знакомства учащихся с различными символами, с которыми они сталкиваются, независимо от контекста. Например, греческие буквы широко распространены в этой области, но многие студенты имеют небольшой или не связанный с ними опыт работы с ними. Знакомство учащихся со всем греческим алфавитом, включая регистр, фонетику и способы их написания, может помочь сделать эти символы меньшим препятствием для учащихся, когда они сталкиваются с ними в формулах.
- Преподаватели опрашивают учащихся, чтобы определить новое, измененное или конфликтующее использование символов внутри и между предметами, которые они изучают.
Несмотря на международные опубликованные стандарты, несоответствия в обозначениях в области физики, хотя и не новые (Bailey, 1999), остаются препятствием, мешающим обучению некоторых учащихся. Этой сложности нельзя — и, возможно, не следует — избегать со студентами, если они хотят успешно ориентироваться в своих занятиях по физике. Студентам необходимо развивать гибкое мышление в отношении физических обозначений. Тем не менее, лекторы и наставники должны быть готовы к вероятным областям путаницы. Преподаватели физики и математики должны знать о широком междисциплинарном использовании одних и тех же символов и о возможности путаницы, которую может вызвать у учащихся различное использование символов как внутри предметов, так и между ними, особенно в связи с форматом и информацией, передаваемой каждым символом. усложняется по мере обучения. Рассмотрение точки зрения новичка может повлиять на педагогические приемы, чтобы помочь улучшить опыт и успехи учащегося в предмете.
Студентам необходимо развивать гибкое мышление в отношении физических обозначений. Тем не менее, лекторы и наставники должны быть готовы к вероятным областям путаницы. Преподаватели физики и математики должны знать о широком междисциплинарном использовании одних и тех же символов и о возможности путаницы, которую может вызвать у учащихся различное использование символов как внутри предметов, так и между ними, особенно в связи с форматом и информацией, передаваемой каждым символом. усложняется по мере обучения. Рассмотрение точки зрения новичка может повлиять на педагогические приемы, чтобы помочь улучшить опыт и успехи учащегося в предмете.
Благодарности
Авторы хотели бы поблагодарить доктора Кэролайн Бардини за разработку этого исследовательского проекта, а также преподавателей физики, которые щедро уделили нам свое время и рассказали о проблемах, с которыми приходится сталкиваться при обучении физике в бакалавриате. Авторы также хотели бы поблагодарить студентов, преподавателей и преподавателей из нескольких университетов, которые пожертвовали своим временем, знаниями и учебными материалами для пользы этого исследования.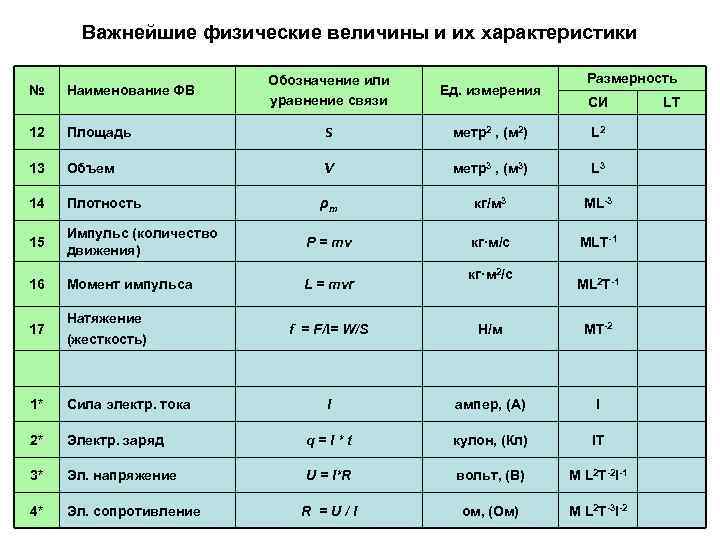 Это исследование финансировалось Австралийским исследовательским советом: DP150103315.
Это исследование финансировалось Австралийским исследовательским советом: DP150103315.
97% людей не могут назвать все эти физические символы. Не могли бы вы?
Автор: Жаклин Самару
Расчетное время выполнения3-минутный тест
- Поделиться контентом в Твиттере
- Делитесь контентом на Facebook
- Делитесь контентом по электронной почте
“”
Изображение: Исходное изображение
Хватит ли у вас энергии, чтобы выбить правильные ответы из этой викторины?
Физика может быть очень сложной, запутанной и часто трудной для полного понимания. На самом деле физика считается одной из самых фундаментальных научных дисциплин. В результате этого неудивительно, что физика и концепции, с которыми она имеет дело, образуют основу, на которой строятся другие научные области.
Физика — большая и постоянно расширяющаяся наука, поэтому она имеет дело с широким спектром физических величин, понятий и идей, которые представлены различными символами. Символы в этой викторине состоят из 40 самых знаковых символов в физике, о которых слышали даже люди, не являющиеся учеными!
Символы в этой викторине состоят из 40 самых знаковых символов в физике, о которых слышали даже люди, не являющиеся учеными!
Одна из причин, по которой сегодня используется так много разных физических символов, заключается в том, что физика на самом деле является одной из древнейших наук и академических дисциплин в мире! Эти символы обычно бывают в виде прописных или строчных букв латинского алфавита (a, b, c и т. д.) или греческого алфавита (омега, каппа, сигма и т. д.).
Итак, готовы ли вы найти правильные ответы в этой викторине? Наденьте лабораторный халат и приступим!
“”
Оригинал
Какой символ физики изображен на этом изображении?
электропроводность
В физике электропроводность чаще всего обозначается символом σ. Электропроводность относится к тому, насколько сильно данный материал сопротивляется прохождению электрического тока.
светимость
емкость
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
импульс
угловое ускорение
В физике сила чаще всего обозначается символом F.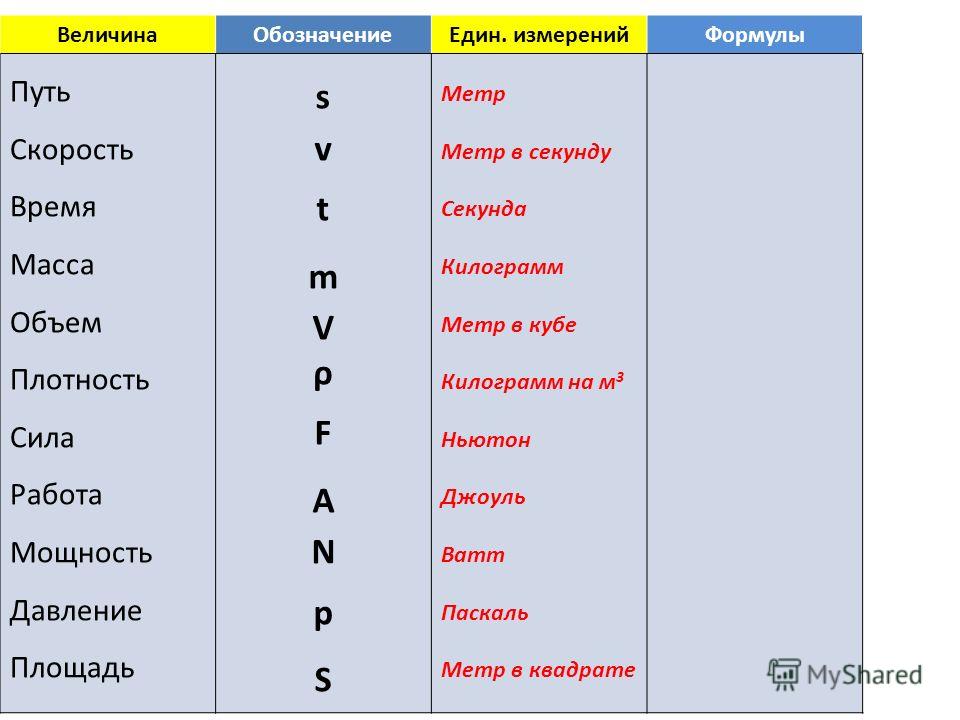 Сила относится к любому взаимодействию, которое, если ему не противостоять, изменяет движение объекта.
Сила относится к любому взаимодействию, которое, если ему не противостоять, изменяет движение объекта.
электрический потенциал
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
энергия
напряженность магнитного поля
В физике напряженность магнитного поля чаще всего обозначается символом H. Напряженность магнитного поля относится к силовому полю, которое создается движущимися электрическими зарядами и магнитными диполями.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
удельное сопротивление
температура
ускорение
В физике ускорение чаще всего обозначается символом a. Ускорение относится к скорости изменения скорости объекта по отношению ко времени.
плотность магнитного потока
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
плотность
потенциальная энергия
В физике потенциальная энергия чаще всего представлена символом U. Потенциальная энергия относится к энергии, которой обладает объект из-за его положения относительно других объектов, внутренних напряжений, его электрического заряда или другие факторы.
энтропия
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
диэлектрическая проницаемость
длина волны
Длина волны в физике чаще всего обозначается символом λ. Длина волны относится к расстоянию, на котором форма волны повторяется.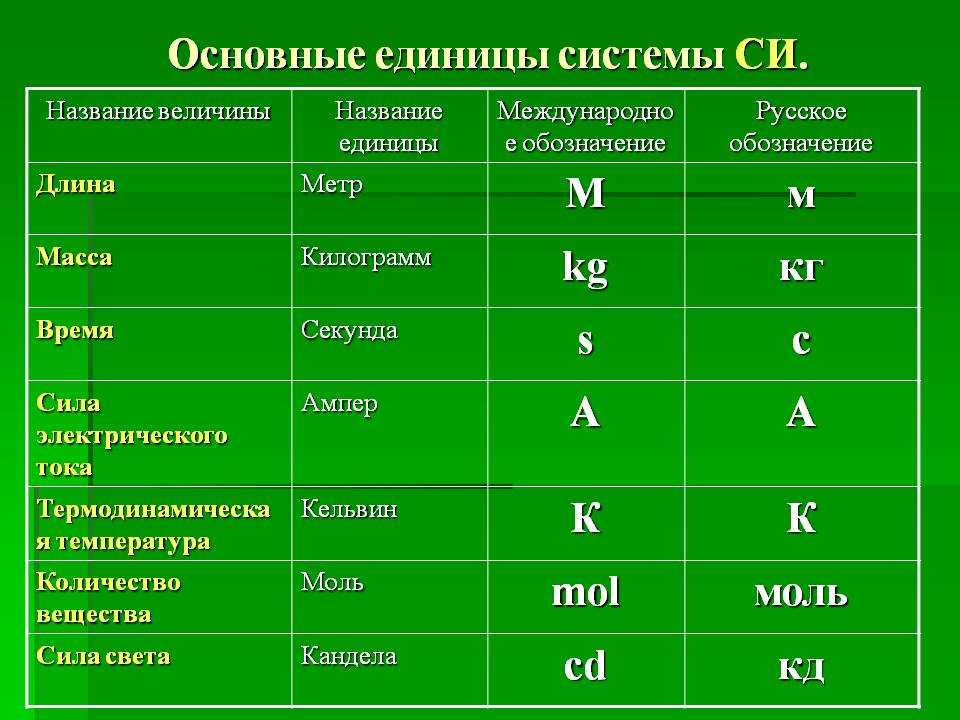
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
гравитационная постоянная
торсионный коэффициент
В физике торсионный коэффициент чаще всего обозначается символом Κ. Коэффициент кручения представляет собой способность стержня или балки сопротивляться кручению (скручиванию).
электрический потенциал
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
момент инерции
В физике момент инерции чаще всего обозначается символом I. Момент инерции относится к тенденции тела сопротивляться угловому ускорению, он также известен как угловая масса или инерция вращения.
Коэффициент демпфирования
Энергия
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
плотность магнитного потока
атомный номер
В физике атомный номер чаще всего обозначается символом N.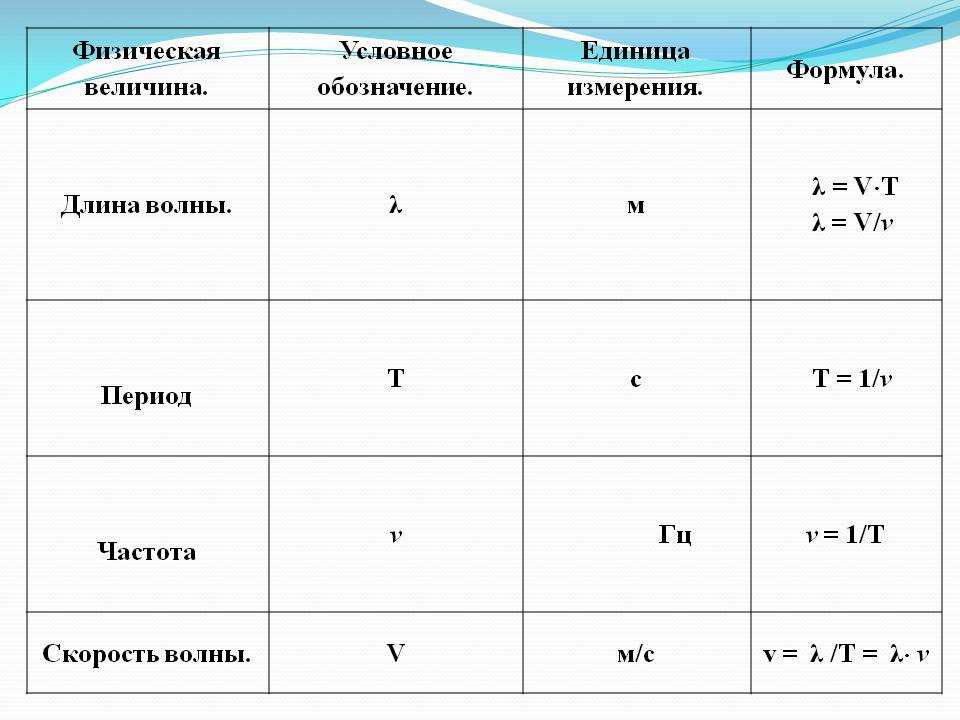 Атомный номер относится к числу протонов в ядре атома химического элемента. Он используется в качестве идентификатора элементов периодической таблицы.
Атомный номер относится к числу протонов в ядре атома химического элемента. Он используется в качестве идентификатора элементов периодической таблицы.
энтропия
удельное сопротивление
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
электрическое поле
импульс
частота
В физике частота чаще всего обозначается символом v. Частота относится к количеству повторений повторяющегося события в единицу времени.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
ускорение свободного падения
гамма-излучение
В физике гамма-излучение чаще всего обозначается символом γ. Гамма-излучение относится к электромагнитному излучению, возникающему в результате радиоактивного распада атомных ядер.
электропроводность
светимость
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
волновая функция
В физике волновая функция чаще всего обозначается символом ψ. Волновая функция относится к функции, которая описывает волновые свойства частицы.
кинетическая энергия
электрическое поле
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
атомный номер
электрическое сопротивление
расстояние
В физике расстояние чаще всего обозначается символом d. Расстояние относится к любому числовому измерению того, насколько далеко объекты находятся друг от друга.
гравитационная постоянная
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
Постоянная Планка
В физике постоянная Планка чаще всего обозначается символом h. Постоянная Планка относится к физической константе, которая является квантом действия, центральным в квантовой механике. Он назван в честь Макса Планка, немецкого физика, который впервые обнаружил его.
Постоянная Планка относится к физической константе, которая является квантом действия, центральным в квантовой механике. Он назван в честь Макса Планка, немецкого физика, который впервые обнаружил его.
ускорение
коэффициент демпфирования
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
оригинал
Какой символ физики изображен на этом изображении?
потенциальная энергия
момент силы
В физике момент силы чаще всего обозначается символом M. Момент силы относится к поворотному эффекту силы. Он рассчитывается с использованием силы и расстояния от перпендикулярной точки отсчета.
диэлектрическая проницаемость
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
длина волны
гамма-излучение
электрическое сопротивление
скорость звука
В физике скорость звука чаще всего обозначается символом c. Скорость звука относится именно к тому, как имя «звучит». Это расстояние, которое за единицу времени проходит звуковая волна.
Скорость звука относится именно к тому, как имя «звучит». Это расстояние, которое за единицу времени проходит звуковая волна.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
температура
коэффициент кручения
В физике ширина чаще всего обозначается символом w. Ширина относится к расстоянию от стороны до стороны объекта, расположенного под прямым углом к длине.
постоянная Планка
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
оригинал
Какой символ физики изображен на этом изображении?
электрическое сопротивление
В физике электрическое сопротивление чаще всего обозначается символом Ω. Электрическое сопротивление относится к тому, как устройство или материал уменьшает протекающий через него электрический ток.
момент инерции
расстояние
скорость звука
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
напряженность магнитного поля
волновая функция
угловое ускорение
кинетическая энергия
В физике кинетическая энергия чаще всего обозначается символом K. Кинетическая энергия относится к энергии, которой объект обладает благодаря своему движению.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
ускорение свободного падения
В физике ускорение свободного падения чаще всего обозначается символом g. Ускорение под действием силы тяжести относится к ускорению объекта в вакууме вблизи поверхности Земли.
частота
момент силы
емкость
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
ускорение свободного падения
волновая функция
емкость
В физике емкость чаще всего обозначается символом C. Емкость относится к отношению изменения электрического заряда в системе к соответствующему изменение электрического потенциала системы.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
электрический потенциал
угловое ускорение
В физике угловое ускорение чаще всего обозначается символом α. Угловое ускорение просто относится к скорости изменения угловой скорости.
коэффициент кручения
кинетическая энергия
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
оригинал
Какой символ физики изображен на этом изображении?
атомный номер
момент инерции
В физике время чаще всего обозначается символом t. Время часто определяется просто как «то, что часы показывают/читают». Время иногда называют четвертым измерением.
Время часто определяется просто как «то, что часы показывают/читают». Время иногда называют четвертым измерением.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
напряженность магнитного поля
температура
В физике температура чаще всего обозначается символом T. Температура относится к физической величине, выражающей тепло и холод.
плотность магнитного потока
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
плотность
В физике плотность чаще всего обозначается символом D. Плотность относится к массе на единицу объема вещества.
частота
энтропия
скорость звука
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
электропроводность
диэлектрическая проницаемость
В физике диэлектрическая проницаемость чаще всего обозначается символом ϵ. Диэлектрическая проницаемость относится к мере сопротивления, возникающего при формировании электрического поля в конкретной среде.
Диэлектрическая проницаемость относится к мере сопротивления, возникающего при формировании электрического поля в конкретной среде.
момент силы
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
импульс
коэффициент затухания
В физике коэффициент затухания чаще всего обозначается символом ζ. Коэффициент демпфирования относится к мере того, как колебания затухают после наблюдаемого возмущения.
постоянная Планка
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
расстояние
гравитационная постоянная
В физике гравитационная постоянная чаще всего обозначается символом G. Гравитационная постоянная относится к физической постоянной (6,674×10-11 м3⋅кг-1⋅с-2), которая используется при расчете гравитационных эффектов.
плотность
энергия
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
электрическое поле
В физике электрическое поле чаще всего обозначается символом E. Электрическое поле просто относится к полю, которое окружает электрические заряды.
ускорение
длина волны
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
гамма-излучение
удельное сопротивление
светимость
В физике светимость чаще всего обозначается символом L. Светимость относится к общему количеству энергии, излучаемой объектом в единицу времени.
потенциальная энергия
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
частота
импульс
В физике импульс чаще всего обозначается символом J.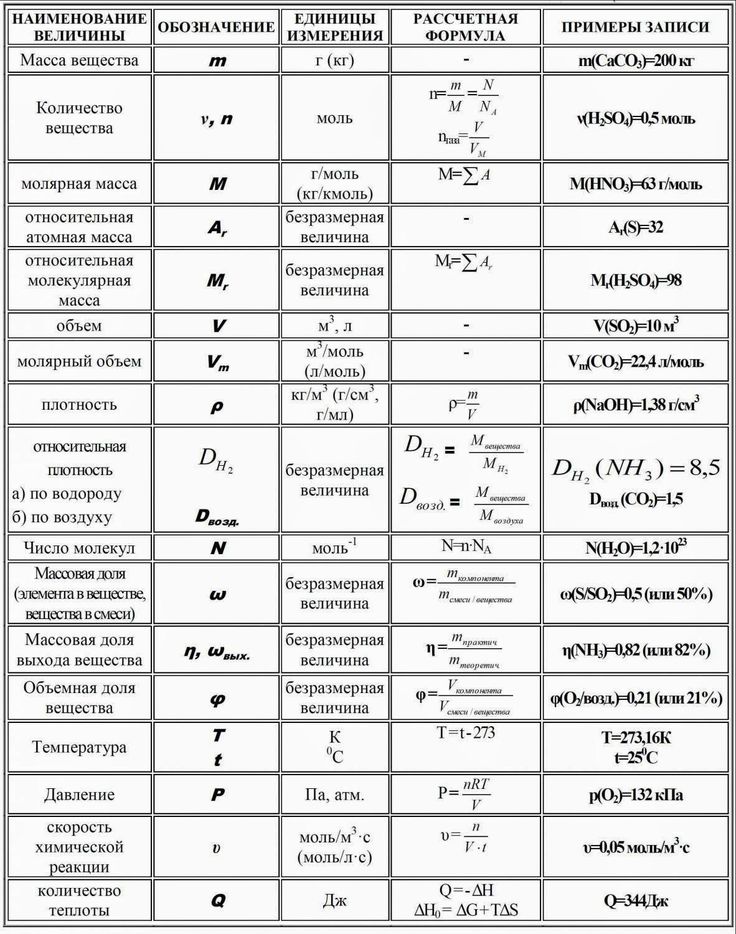 Импульс относится к интегралу силы за интервал времени, в течение которого она действует.
Импульс относится к интегралу силы за интервал времени, в течение которого она действует.
коэффициент демпфирования
ускорение свободного падения
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
кинетическая энергия
электрическое поле
напряженность магнитного поля
энергия
В физике энергия чаще всего обозначается символом E. Энергия относится к способности выполнять работу. Закон сохранения энергии гласит, что энергия не может быть создана или уничтожена, ее можно только преобразовать из одной формы в другую.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
момент инерции
светимость
удельное сопротивление
В физике удельное сопротивление чаще всего обозначается символом ρ. Сопротивление относится к тому, насколько сильно данный материал сопротивляется потоку электрического тока.
Сопротивление относится к тому, насколько сильно данный материал сопротивляется потоку электрического тока.
атомный номер
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
коэффициент кручения
гравитационная постоянная
В физике площадь чаще всего обозначается символом A. Площадь относится к двумерному размеру формы или объекта.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
длина волны
В физике число пи чаще всего обозначается символом π, обозначающим отношение длины окружности к ее диаметру; примерно 3,14159.
скорость звука
диэлектрическая проницаемость
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
потенциальная энергия
электрическое сопротивление
момент силы
энтропия
В физике энтропия чаще всего обозначается символом S. Энтропия относится к мере числа возможных расположений атомов в системе.
Энтропия относится к мере числа возможных расположений атомов в системе.
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
плотность магнитного потока
В физике плотность магнитного потока чаще всего обозначается символом B. Плотность магнитного потока относится к мере силы магнитного поля в данной точке.
постоянная Планка
температура
ускорение
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
плотность
В физике тепло чаще всего обозначается символом Q. Теплота относится к энергии, которая передается от более теплого вещества или тела к более холодному.
расстояние
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
электрический потенциал
В физике электрический потенциал чаще всего обозначается символом ϕ.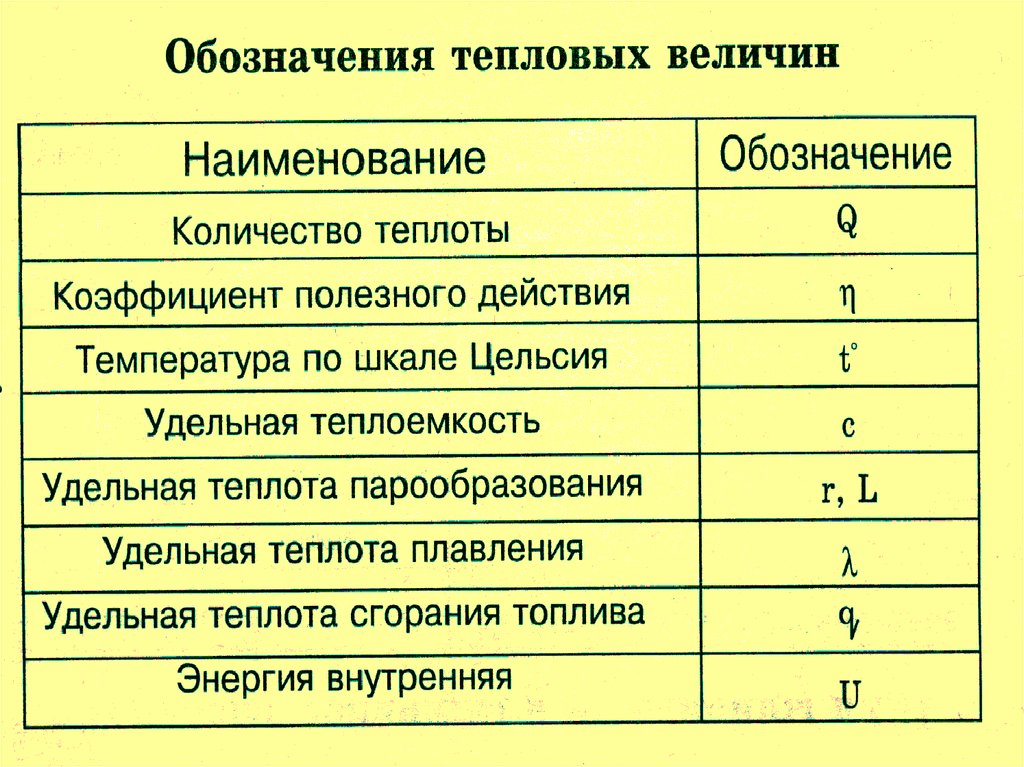 Электрический потенциал относится к количеству работы, необходимой для перемещения заряда из контрольной точки в заданную точку.
Электрический потенциал относится к количеству работы, необходимой для перемещения заряда из контрольной точки в заданную точку.
волновая функция
угловое ускорение
ПРОКРУТИТЕ К СЛЕДУЮЩЕМУ ВОПРОСУ
Реклама
Реклама
“”
Оригинал
Какой символ физики изображен на этом изображении?
электропроводность
емкость
В физике мощность чаще всего обозначается символом P. Мощность относится к скорости выполнения работы; т. е. количество энергии, передаваемой в единицу времени.
гамма-излучение
ЗАВЕРШЕНИЕ ВИКТОРИНЫ
Реклама
Реклама
Вы получили:
/40
Оригинал
Физические символы и их названия
by Veerendra
Физические символы : Все физические символы и их названия Pdf описаны на этой странице, мы также предоставляем греческие символы по физике, а также их единицы и количество.
Список физических символов и их названий
Символы, используемые для обозначения физических величин, связанных с пространством и временем:
| Symbol | Quantity/ Coefficients | S.I Unit | ||
| r | Radius, the radius of curvature | Meter | ||
| s | Displacement | Meter | ||
| d | Расстояние | Радиан | ||
| θ, φ | Угловое смещение, угловой разнос, угол поворота | Meter | ||
| x, y, z | Cartesian coordinates | Unitless | ||
| î, ĵ, k̂ | Cartesian unit vectors | Unitless | ||
| r, θ, φ | Spherical coordinates | Meter/Radian | ||
| r̂, θ̂, φ̂ | Spherical unit vectors | Unitless | ||
| r, θ, z | Cylindrical coordinates | Meter/Radian | ||
| r̂, θ̂, ẑ | Cylindrical unit vectors | Unitless | ||
| n̂ | Normal unit vector | Unitless | ||
| t̂ | Tangential unit vector | Unitless | ||
| h | Height, Глубина | Метр | ||
| ℓ, L | Длина | Метр | ||
| T | Время | Второй | ||
| D | Second | |||
| D | . 9 9 | Diameter | Meter | |
| C | Circumference | Meter | ||
| A, A | Area | Square meter | ||
| V | Volume | Cubic meter | ||
| t | Время, продолжительность | Секунда | ||
| T | Периодическое время | Секунда | ||
| τ | Постоянная времени | Секунда 1095f | Frequency | Hertz |
| ω | Angular frequency | Radian per second |
Symbols used to denote physical quantities related to Mechanics:
| Symbol | Количество/Коэффициенты | Единица S.I |
| v | Скорость, скорость | метр в секунду |
| A | Ускорение | метра в секунду квадрат |
| A C | Centripetal Squaltal/Centrifugal Acceleration | метра на второй квадрат. |
| м | Масса | Килограмм |
| F | Сила | Ньютон |
| Force due to gravity/Weight | Newton | |
| F n , N | Normal force, normal | Newton |
| F f | Force of friction | Newton |
| µ | Коэффициент трения | Безразмерный |
| p | Импульс | Килограмм метр в секунду |
| Дж | Импульс1099 | |
| E | Energy | Joule |
| K | Kinetic energy | Joule |
| U | Potential energy | Joule |
| V g | Gravitational potential | Joule на килограмм |
| η | Эффективность | Безразмерная |
| P | Мощность | Вт | Скорость вращения, скорость вращения | Радиан в секунду |
| α | . | Килограмм-метр в квадрате |
| L | Угловой момент | Килограмм-метр в квадрате в секунду |
| H | Angular impulse | Newton meter second |
| k | Spring constant | Newton per meter |
| p | Pressure | Pascal |
| σ | Stress | Pascal |
| τ | Напряжение сдвига | Паскаль |
| ρ | Плотность, объемная массовая плотность | Килограмм на кубический метр |
| σ | Area mass density | Kilogram per square meter |
| λ | Linear mass density | Kilogram per meter |
| F B , B | Buoyancy | Newton |
| q m | Массовый расход | Килограмм в секунду |
| q V | Объемный расход | Кубический метр в секунду |
| Drag or air resistance | Newton | |
| C D | Drag coefficient | Unitless |
| η | Viscosi | Pascal-second |
| ν | Kinematic viscosity | Square meter в секунду |
| Ма | Число Маха | Безразмерное |
| Re | Число Рейнольдса | Безразмерное | 5 | Fr | Froude number | Unitless |
| E | Young’s modulus of elasticity | Pascal |
| G | Shear modulus of rigidity | Pascal |
| K | Bulk modulus of compression | Паскаль |
| ε | Линейная деформация | Безразмерная |
| γ | Деформация сдвига | Безразмерная |
| θ | ТОЛОВНАЯ ДАМАНИЯ | БЕСПЛАТНАЯ |
| γ | NEWTON PER SYMER |
Символы, используемые с помощью Denote Физические кванты. Символы, используемые для обозначения физических количеств, связанных с электричеством и магнитизмом 9005 9 Магнитная сила1099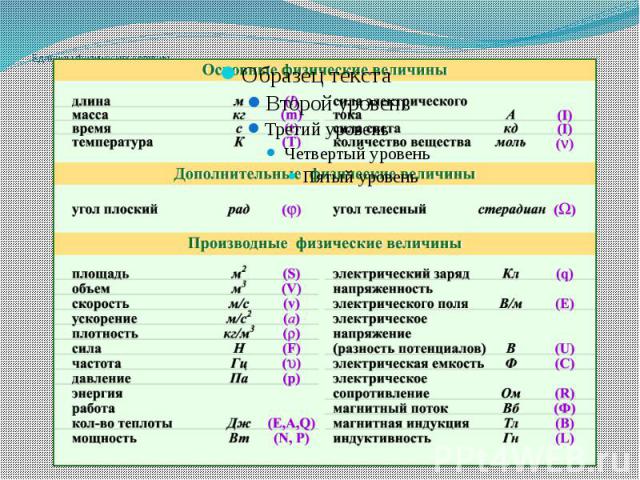
Количество/коэффициенты S.I Unit COP Коэффициент производительности Безразмерный w Ways, number of identical microstates Unitless S Entropy Joule per kelvin U Internal energy Joule ε Emissivity Безразмерный k Теплопроводность Ватт на метр по Кельвину P Тепловой поток Ватт N Number of particles Unitless n Amount of substance Mole L Latent heat/specific latent heat Joule per kilogram c Удельная теплоемкость Джоуль на килограмм-кельвин Q Теплота Джоуль Β Объемное тепловое расширение, коэффициент объемного теплового расширения1099 Обратный Kelvin α Линейная экспансия, коэффициент термического расширения .  :
: Символ Количество/коэффициенты Единица S.I M Magnification Unitless f Focal length Meter n Index of refraction Unitless L Level Decibel, decineper I Интенсивность Ватт на квадратный метр v, c Скорость волны Метр в секунду λ Длина волны метра P Мощность объектива 9000 2 .
 Количество/Коэффициенты
Количество/Коэффициенты Единица S.I S Вектор Пойнтинга, интенсивность Вт на квадратный метр η Energy density Joule per cubic meter n Turns per unit length Inverse meter N Number of turns Unitless Φ B Магнитный поток Вебер B Магнитное поле Тесла F B Newton σ Conductivity Siemens per meter G Conductance Siemens ρ Resistivity Ohm-meter R, r Electric сопротивление/внутреннее сопротивление Ом I Электрический ток Ампер ϵ Диэлектрическая проницаемость Unitless C Capacitance Farad ℰ Electromotive force (emf) Volt V voltage, electric potential Volt U E Электрическая потенциальная энергия Джоуль Φ E Электрический поток Ньютон-метр в квадрате на кулон E Electric field Newton per coulomb/volt per meter F E Electrostatic force Newton λ Linear charge density Kilogram per meter σ Поверхностная плотность заряда Килограмм на квадратный метр ρ Объемная плотность заряда Килограмм на кубический метр q, Q Electric charge Coulomb
Symbols used in modern physics:
| Symbol | Quantity/Coefficients | S.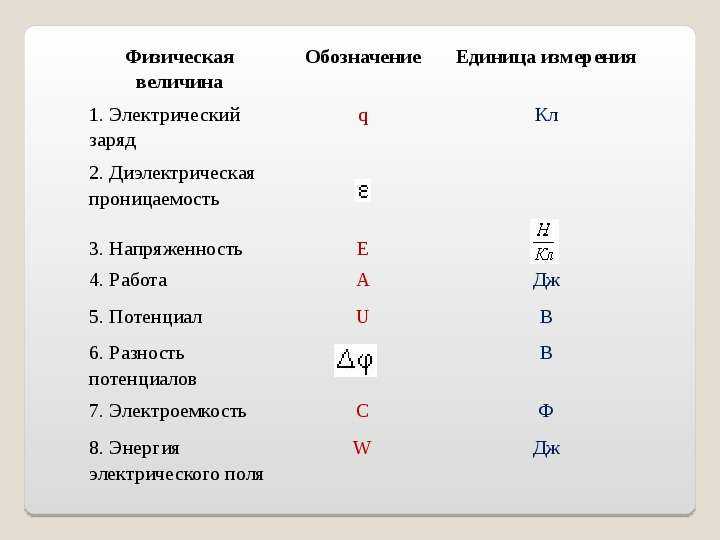 I Unit I Unit |
| D | Доза/поглощенная доза | серый |
| Период полураспада | Секунда | |
| 1099 | Unitless | |
| Φ | Work function | Joule |
| H | Effective dose | Sievert |
| Γ | Lorentz factor/Lorentz gamma | Unitless |
Filed Under: Физика
Определения, изображения и символы (ЧАСТЬ-1)
UTPAL SHARMA Воскресенье, 7 июня 2020 г.
ВВЕДЕНИЕ: –В физике используется множество терминов, и без этих терминов мы не можем выразить свои мысли. Для лучшего понимания мы обсудим разные полезные слова физики с картинками.
Это расширит наш словарный запас. Мы изучим различные ключевые слова физики, такие как Сила, Работа, Скорость, Импульс, Поверхностное натяжение и т. д.
д.
Сила
Сила — это внешний эффект, вызывающий движение объекта, или эффект, который может остановить объект. Символ силы — F.
РаботаКогда мы воздействуем силой на объект и смещаем его, это называется Работа. Символ работы W.
OR
На рисунке ниже показано, когда мы применяем внешнюю силу к объекту, и он перемещается со своего места, поэтому это называется работой.
Мощность
Скорость выполнения работы называется мощностью. Символ мощности — P.
ИЛИ
Когда мы выполняем какую-то работу над объектом, то сколько работы выполняется в единицу времени (за один час, одну секунду или одну минуту и т. д.), называется мощностью. .
ЭнергияСпособность выполнять работу называется энергией. Символом энергии является E.
Согласно приведенному выше рисунку, когда человек А выполняет больше работы, его возможности высоки, и мы можем сказать, что человек А обладает высокой энергией.
Таким образом, согласно этой энергии человек Б имеет низкую энергию из-за меньшего количества работы.
Трение
Сила, противодействующая движению, называется трением.
На приведенном выше рисунке показано, что когда мы прикладываем к объекту внешнюю силу, то сила, противодействующая объекту снизу, называется трением.
Тяга
Сила, действующая на поверхность объекта перпендикулярно или под углом девяносто градусов, известна как тяга.
It means when we apply thrust on per unit area like per meter square or per centimeter square etc.
The property of an object which tries to оставаться в состоянии покоя или в состоянии движения называется его инерцией. Символом инерции является I.
- Изображение выше показано, когда мы применяем тормоза в транспортном средстве (автобусе). затем наше тело движется вперед.
- Потому что наше тело и автобус имеют одинаковую скорость, когда автобус движется в дороге, после остановки, скорость автобуса равна нулю, но мы в движение до сих пор.
- Итак, мы движемся в направлении движения.
- Как и прежде, автобус едет, автобус и наше тело отдыхают, после запуска автобуса автобус находится в движении, но мы находимся в состоянии покоя, поэтому наше тело движется в обратном направлении.
Количество вещества в любом объекте называется его массой.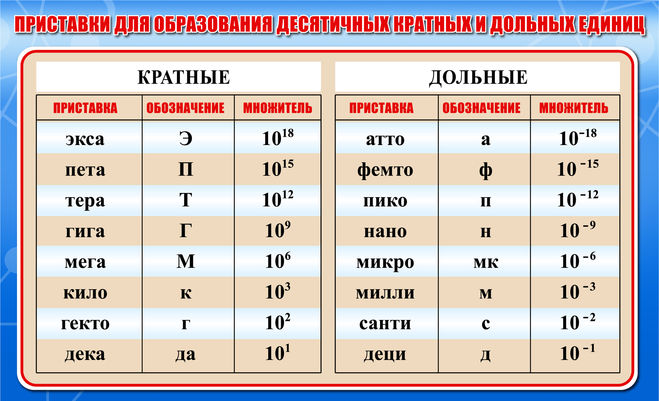 Символ массы m.
Символ массы m.
ИЛИ
Это означает, что если количество вещества в объекте меньше, то его масса меньше. Ведь чем больше количество вещества, тем больше его масса.Вес
Произведение массы в этом месте и силы тяжести. Это означает, что если масса меньше, то его вес меньше, и наоборот. Символ веса W.
Длина пути, пройденного объектом, называется расстоянием. Символ расстояния — s.
Кратчайшая длина или расстояние, пройденное объектом, называется перемещением от начальной точки B до конечной точки A.
Расстояние, пройденное объектом в единицу времени, называется скоростью.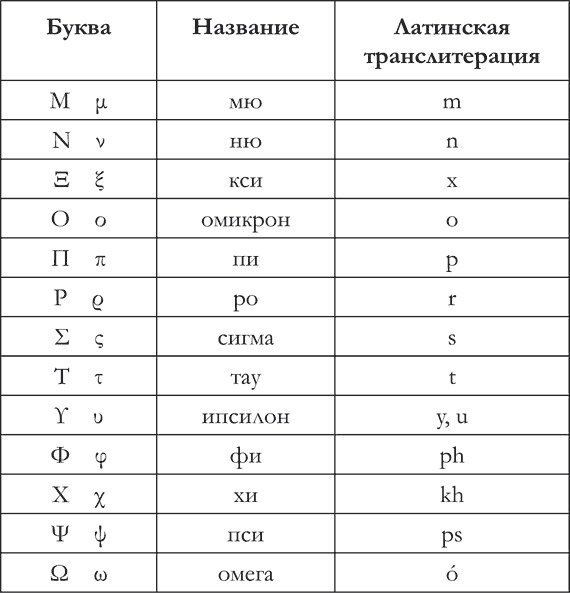 Символом скорости является v.
Символом скорости является v.
Изменение скорости во времени называется ускорением. Символ ускорения – это а.
Произведение массы и скорости объекта называется его импульсом. Символ импульса p.
На приведенном выше рисунке показано, что импульс трактора зависит от его массы и скорости. Поскольку импульс ракеты высок, потому что у нее больше массы и скорости.
Поверхностное натяжение
Свойство свободной поверхности жидкости стремиться занять минимальную площадь поверхности известно как поверхностное натяжение жидкости.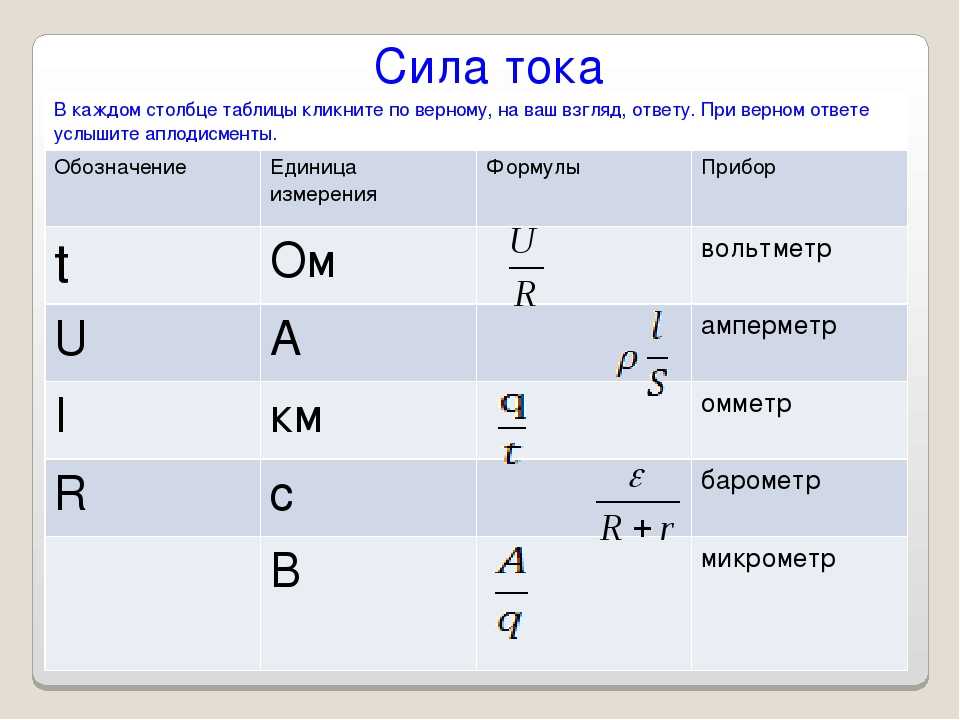 Символ поверхностного натяжения – σ (сигма).
Символ поверхностного натяжения – σ (сигма).
На приведенном выше рисунке открытая поверхность воды имеет верхний слой, который также известен как поверхностное натяжение воды.
Мы можем видеть, как капля воды пытается уменьшить свой размер, когда мы распыляем воду в воздухе. Он показывает его поверхностное натяжение.
ЗАКЛЮЧЕНИЕ:-
В этом блоге мы узнали определения силы, мощности, работы, трения, энергии и т. д. В следующей части глоссария по физике мы узнаем больше полезных терминов.
Физика символов: Преодоление эпистемологического разреза
Физика символов: Преодоление эпистемологического разреза HH Pattee
Отдел системоведения и промышленной инженерии
Школа инженерии и прикладных наук им. Т. Дж. Уотсона
State University at Binghamton, NY 13902-6000 (США)
Abstract :Эволюция требует различия между генотипом и фенотипом, первобытного эпистемического разреза, который отделяет энергетически вырожденные, не зависящие от скорости генетические символы от зависящей от скорости динамики конструкции, которую они
контроль. Это различение символа-материи или субъекта-объекта происходит на всех более высоких уровнях, где символы
связанный с референтом произвольным кодом. Противоположностью управления является измерение, в котором динамическое состояние, зависящее от скорости, кодируется в символах покоя. Неинтегрируемые ограничения являются одним из необходимых
условия преодоления эпистемического разреза посредством измерения, контроля и кодирования. Дополнительные свойства
гетерополимерные ограничения необходимы для биологической эволюции.
Это различение символа-материи или субъекта-объекта происходит на всех более высоких уровнях, где символы
связанный с референтом произвольным кодом. Противоположностью управления является измерение, в котором динамическое состояние, зависящее от скорости, кодируется в символах покоя. Неинтегрируемые ограничения являются одним из необходимых
условия преодоления эпистемического разреза посредством измерения, контроля и кодирования. Дополнительные свойства
гетерополимерные ограничения необходимы для биологической эволюции.
Ключевые слова : ссылка на символ, измерение и контроль, неинтегрируемые ограничения, субъект-объект
“Как же, спрашивается, можем ли мы отличить живое от безжизненными, если мы можем концептуально описать и то, и другое движением неорганических корпускул?”
Карл Пирсон Грамматика науки
1. Краткая история проблемы
В конце девятнадцатого века ученые мало интересовались дуалистическими и виталистическими
взгляды на жизнь.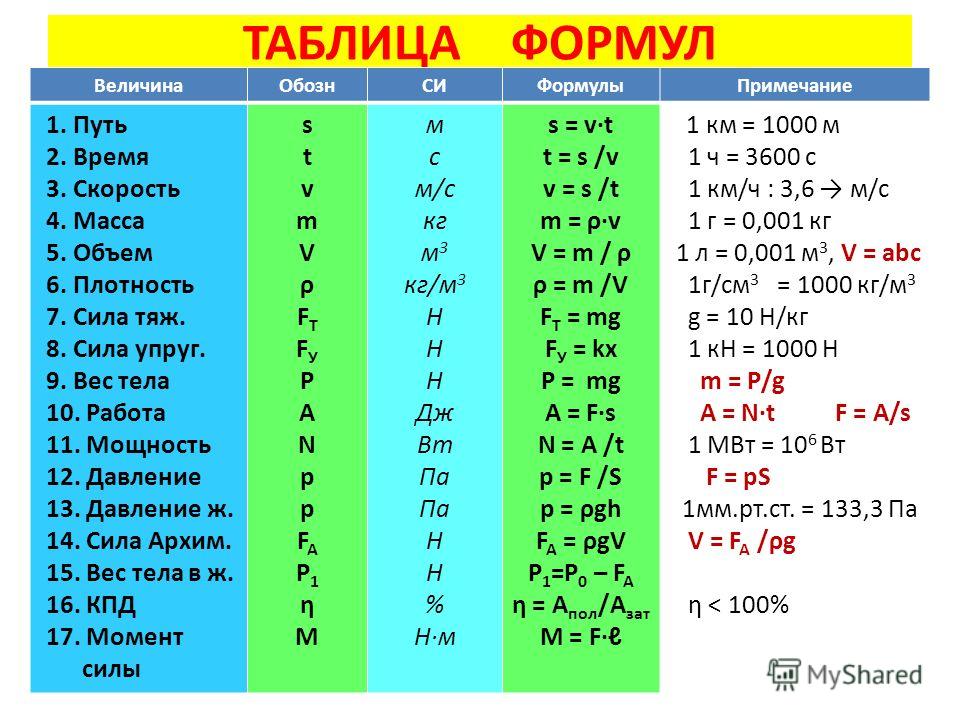 Именно потому, что Карл Пирсон (1937) считал жизнь полностью физическим процессом, он
заставили задаться вопросом (в 1892 г.), что физически отличает живое от неживого. Он предположил, что
органические молекулы имеют «вторичные характеристики», но могут ли эти характеристики быть получены
из фундаментальных неорганических законов «в настоящее время у нас нет средств для определения». В начале этого
века, во многом благодаря квантовой теории, у многих физиков возникло ощущение, что
все еще некоторая важная загадка жизни, которая может потребовать серьезного переосмысления физики. Например, в
1949 Макс Дельбрюк под влиянием более ранних рассуждений Бора (1933) 1 писал: «Может оказаться, что некоторые
особенности живой клетки, включая, возможно, репликацию, находятся во взаимоисключающем отношении к
строгое применение квантовой механики, и что новый концептуальный язык должен быть разработан для
принять эту ситуацию.» Гюнтер Стент (1966) описал ситуацию в 1940-х следующим образом:
«Таким образом, это была романтическая идея, что «другие законы физики» (Шредингер) могут быть открыты путем изучения
ген, который действительно очаровал физиков.
Именно потому, что Карл Пирсон (1937) считал жизнь полностью физическим процессом, он
заставили задаться вопросом (в 1892 г.), что физически отличает живое от неживого. Он предположил, что
органические молекулы имеют «вторичные характеристики», но могут ли эти характеристики быть получены
из фундаментальных неорганических законов «в настоящее время у нас нет средств для определения». В начале этого
века, во многом благодаря квантовой теории, у многих физиков возникло ощущение, что
все еще некоторая важная загадка жизни, которая может потребовать серьезного переосмысления физики. Например, в
1949 Макс Дельбрюк под влиянием более ранних рассуждений Бора (1933) 1 писал: «Может оказаться, что некоторые
особенности живой клетки, включая, возможно, репликацию, находятся во взаимоисключающем отношении к
строгое применение квантовой механики, и что новый концептуальный язык должен быть разработан для
принять эту ситуацию.» Гюнтер Стент (1966) описал ситуацию в 1940-х следующим образом:
«Таким образом, это была романтическая идея, что «другие законы физики» (Шредингер) могут быть открыты путем изучения
ген, который действительно очаровал физиков. Этот поиск физического парадокса, эта донкихотская надежда, что
генетика оказалась бы непостижимой в рамках обычных физических знаний,
оставался важным элементом психологической инфраструктуры создателей молекулярной биологии».0003
Этот поиск физического парадокса, эта донкихотская надежда, что
генетика оказалась бы непостижимой в рамках обычных физических знаний,
оставался важным элементом психологической инфраструктуры создателей молекулярной биологии».0003
Затем в начале 1950-х начался взрывной рост молекулярной биологии и экспериментов по происхождению жизни, последний начался в 1953 году с абиогенного синтеза аминокислот Миллером и Юри. Одинаковый году Уотсон и Крик объявили о двойной спирали ДНК. Некоторыми из других крупных достижений были использование дифракции рентгеновских лучей для получения структуры миоглобина и гемоглобина Перутцем и Кендрю, а также выделение ДНК-полимеразы Корнбергом. За этим последовали в 1960-х годов с поломкой генетический код Ниренбергом и Хораной, открытие регуляции генов Якобом и Моно, открытие информационной РНК Бреннером, Джейкобом и Мезельсоном, секвенирование транспортной РНК Холли, и открытие плазмид Ледербергом.
К 1970 году уже не было большого интереса к возможным парадоксам или пересмотру физических теорий для
разместить живые системы. Ничего нового оказалось не нужно. Кендрю (1967) резюмировал
позиция молекулярных биологов в журнале Scientific American: «… до настоящего времени обычные, нормальные
законов физики и химии было достаточно».
биологи 2 . Но этот редукционистский взгляд на самом деле является лишь ответом на дуализм и витализм. Это представление делает
даже не адресовать вопрос Пирсона. Если бы это было указано как «ответ», это было бы в общей сложности non sequitur : Life
отличается от безжизненного тем, что следует условным, нормальным законам физики и
химия неживой материи.
Ничего нового оказалось не нужно. Кендрю (1967) резюмировал
позиция молекулярных биологов в журнале Scientific American: «… до настоящего времени обычные, нормальные
законов физики и химии было достаточно».
биологи 2 . Но этот редукционистский взгляд на самом деле является лишь ответом на дуализм и витализм. Это представление делает
даже не адресовать вопрос Пирсона. Если бы это было указано как «ответ», это было бы в общей сложности non sequitur : Life
отличается от безжизненного тем, что следует условным, нормальным законам физики и
химия неживой материи.
В отличие от этого господствующего редукционистского взгляда на молекулярную биологию, по-прежнему существовало меньшинство
более скептические и холистически настроенные мыслители, которые считали, что физические законы неполны или
неприменимы в их нынешнем виде (например, Вигнер, 1961; Бургеры, 1965; Эльзассер, 1975 год; Розен, 1991) 3 .
Также по-прежнему существует много предположений о том, можно ли адекватно объяснить жизнь
классические модели без учета квантовой динамики.
2. Модели без физики – Искусственная жизнь
В последнее десятилетие в дополнение к этим противоположным школам физических редукционистов и физические скептики , третья школа, моделирующая жизнь и эволюцию без учета элементарных физических законов. вообще. Некоторыми хорошо известными примерами являются болезнь Лэнгтона (1989) репликация клеточных автоматов, Рэй (1992). Программа Tierra, эхо-модель Холланда (1995) с использованием генетических алгоритмов, случайных булевых сетей Кауфмана (1993), алгоритмической химии Фонтаны (1992) и многих компьютерных симуляций искусственной жизни. Фон Неймана (1966) часто называют основателем исследований искусственной жизни из-за его логической теории самовоспроизведение, но важно подчеркнуть, что он не считал, что такие свободные от физики модели ответил бы: «Самый интригующий, захватывающий и важный вопрос о том, почему молекулы… типа того они 4 .
Многие другие абстрактные описания жизни теперь подпадают под название теории сложности. Это поле
преобладают математические подходы, нелинейная динамика, эргодическая теория, случайные многообразия, самоорганизованная критичность, информация и теория игр (например, Cowan, Pines, and Meltzer, 1994).
Теоретики сложности ищут универсальные принципы сложных систем, применимые на всех уровнях, от
вращать стаканы и песочницы в клетки и общества. Отношение этих моделей к биологии и даже к
физики, часто является спорным вопросом. Возможности компьютеров для имитации моделей самовоспроизведения,
развитие, эволюция и экология привели ко многим интересным формам поведения. Вычисление также
позволяет изучать нелинейную динамику, которая порождает бесконечную формальную сложность. Однако из-за
высокая степень абстракции, эти симуляции часто трудно интерпретировать, и их применимость к
биология сомнительна. Для таких абстрактных моделей трудно найти прямое эмпирическое обоснование. В любом случае,
поскольку эти модели напрямую не связаны с какими-либо микроскопическими физическими законами и применимы как к живому, так и к
безжизненные системы они не отвечают на вопрос Пирсона.
Это поле
преобладают математические подходы, нелинейная динамика, эргодическая теория, случайные многообразия, самоорганизованная критичность, информация и теория игр (например, Cowan, Pines, and Meltzer, 1994).
Теоретики сложности ищут универсальные принципы сложных систем, применимые на всех уровнях, от
вращать стаканы и песочницы в клетки и общества. Отношение этих моделей к биологии и даже к
физики, часто является спорным вопросом. Возможности компьютеров для имитации моделей самовоспроизведения,
развитие, эволюция и экология привели ко многим интересным формам поведения. Вычисление также
позволяет изучать нелинейную динамику, которая порождает бесконечную формальную сложность. Однако из-за
высокая степень абстракции, эти симуляции часто трудно интерпретировать, и их применимость к
биология сомнительна. Для таких абстрактных моделей трудно найти прямое эмпирическое обоснование. В любом случае,
поскольку эти модели напрямую не связаны с какими-либо микроскопическими физическими законами и применимы как к живому, так и к
безжизненные системы они не отвечают на вопрос Пирсона. Если задать вопрос Пирсона, свободный от физики
Модельер ответил бы, что существенные свойства жизни отличаются абстрактными отношениями, которые
не зависит от какой-либо конкретной физической реализации.
Если задать вопрос Пирсона, свободный от физики
Модельер ответил бы, что существенные свойства жизни отличаются абстрактными отношениями, которые
не зависит от какой-либо конкретной физической реализации.
3. Безмодельная физика – Автономные агенты и ситуационная робототехника
В последнее время наблюдается большой интерес к управляемым компьютером роботам, размещенным в реальной физической среде.
Компьютерное управление часто представляет собой искусственную нейронную сеть, а адаптивное обучение может включать генетические
алгоритмы (например, Varela et al. , 1991; Brooks, 1992; Brooks and Maes, 1994; Clark, 1997). Эти модели
обычно предпочитают последовательную динамическую интерпретацию контроля, а не символическую, основанную на правилах.
«представления» старых моделей искусственного интеллекта. Поскольку среда реальна, нет необходимости
моделировать любую физику. Понятие символа обычно рассматривается как артефакт, порожденный лежащим в его основе
динамика. Физический мир состоит только из тех аспектов окружающей среды, которые робот может
на самом деле обнаружить.
Физический мир состоит только из тех аспектов окружающей среды, которые робот может
на самом деле обнаружить.
Этот тип динамического контроля сенсомоторного поведения кажется вероятной моделью, которая поможет
для учета скорости и сложности реакций организма с относительно сложной сенсомоторной
поведение и маленькие мозги (хотя пока этого не произошло). Любая форма символического представления или вычисления на основе правил на скорости нейронов просто слишком медленна и требует гораздо большего мозга. Насекомое
поведение, такое как облет препятствий, приземление на ветку или спаривание в полете при порывистом ветре, не
разрешить любое решение, кроме какой-либо формы когерентной динамики в реальном времени. Если задать вопрос Пирсона,
робототехник, вероятно, заявил бы, что в отношении сенсомоторного контроля не существует фундаментального физического
различие между живым организмом и адаптивными динамически управляемыми роботами, даже если они
согласитесь, что в настоящее время существует огромный разрыв между самыми сложными роботами и простейшими насекомыми.
Проблема с этой точкой зрения состоит в том, что динамика сенсомоторного контроля и обучения — это только один аспект. жизни. Проблема надежного самовоспроизведения, происхождения новых органов чувств и двигательных структур, т.е. эволюция с открытым концом, пока еще не имеет модели, основанной исключительно на временной динамике. Даже если познание и функция мозга должна оказаться описанной как временно закодированная динамика без статического символа. структуры, которые не будут адекватно описывать покоящиеся молекулярные структуры, формирующие геном и ограничения кодирования, которые контролировали синтез белка в течение миллиардов лет.
4. Взгляды биологов на отношение биологии к физике
Многие биологи считают физические законы, искусственную жизнь, робототехнику и даже теоретическую биологию в значительной степени
не имеет значения для их исследования. В 1970-х годах один видный молекулярный генетик спросил меня: «Зачем нам нужны
теорию, когда у нас есть все факты?» В то время я отклонил этот вопрос как глупый, поскольку большинство физиков
бы. Однако он не так глуп, как обратный вопрос: зачем нам факты, когда у нас есть все
теории? На самом деле это интересные философские вопросы, которые показывают, почему попытки связать биологию с
физика редко представляет интерес для биологов, хотя она представляет большой интерес для физиков. Опрос
Важность теории звучит эксцентрично для физиков, для которых общие теории — это все, чем занимается физика.
Следовательно, физики, как и скептики, о которых я упоминал выше, обеспокоены, когда узнают факты жизни.
что их теории кажутся неспособными обратиться. С другой стороны, биологи, когда у них есть
фактов, не нужно беспокоиться о физических теориях, которые не обращаются к их фактам и не изменяют их. Эрнст Майр (1997)
считает, что это различие достаточно велико, чтобы разделить физические и биологические модели: «Да, биология, как и
физика и химия, наука. Но биология не такая наука, как физика и химия; это скорее
автономная наука наравне с столь же автономными физическими науками».
Однако он не так глуп, как обратный вопрос: зачем нам факты, когда у нас есть все
теории? На самом деле это интересные философские вопросы, которые показывают, почему попытки связать биологию с
физика редко представляет интерес для биологов, хотя она представляет большой интерес для физиков. Опрос
Важность теории звучит эксцентрично для физиков, для которых общие теории — это все, чем занимается физика.
Следовательно, физики, как и скептики, о которых я упоминал выше, обеспокоены, когда узнают факты жизни.
что их теории кажутся неспособными обратиться. С другой стороны, биологи, когда у них есть
фактов, не нужно беспокоиться о физических теориях, которые не обращаются к их фактам и не изменяют их. Эрнст Майр (1997)
считает, что это различие достаточно велико, чтобы разделить физические и биологические модели: «Да, биология, как и
физика и химия, наука. Но биология не такая наука, как физика и химия; это скорее
автономная наука наравне с столь же автономными физическими науками».
Существуют фундаментальные причины, по которым физика и биология требуют разных уровней моделей, наиболее
очевидным является то, что физическая теория описывается зависящими от скорости динамическими законами, которые не имеют памяти,
в то время как эволюция зависит, по крайней мере, до некоторой степени, от управления динамикой с помощью памяти, не зависящей от частоты
структуры. Менее очевидная причина заключается в том, что «корпускулы» Пирсона теперь описываются квантовой теорией.
в то время как биологические объекты требуют классического описания, поскольку они функционируют как наблюдатели. Этот факт
остается фундаментальной проблемой для интерпретации квантовых измерений, и, как я упоминаю ниже, это может
до сих пор оказываются существенными для отличия реальной жизни от макроскопических классических симулякров. я согласен с
Майра, что физика и биология требуют разных моделей, но я не согласен с тем, что они автономны.
модели. Физические системы требуют многих уровней моделей, некоторые из которых формально несводимы друг к другу, но
мы все еще должны понимать, как связаны уровни. Эволюция также создает иерархии организации.
от ячеек к обществам, каждый уровень требует разных моделей, но более высокие уровни иерархии должны
вышли из более низких уровней. Жизнь должна была возникнуть из физического мира. Это появление должно
быть понятым, если наше знание не выродится (более чем уже выродилось) в набор непересекающихся
профильные дисциплины.
Эволюция также создает иерархии организации.
от ячеек к обществам, каждый уровень требует разных моделей, но более высокие уровни иерархии должны
вышли из более низких уровней. Жизнь должна была возникнуть из физического мира. Это появление должно
быть понятым, если наше знание не выродится (более чем уже выродилось) в набор непересекающихся
профильные дисциплины.
5. Личная история проблемы
Я впервые узнал о вопросе Карла Пирсона о 1939 году, когда учился в 8-м классе. мой директор
и учитель естественных наук, доктор П.Л.К. Гросс, дал мне книгу «Грамматика
Science (первое издание вышло в 1892 г.). Большая часть книги была выше моего понимания, но я
думал, что понял главу о жизни с подзаголовком «Отношение биологии к физике». Чтобы сделать
Коротко о моем образовании: десятилетие спустя, работая над докторской диссертацией по физике, я перешел в Hermann
Вейла (1949), столь же глубокий, но более современный, Философия математики и естествознания , который завершается приложениями «Физика и биология» и «Морфе и эволюция». Это стало
моя книга по философии науки. В то время физика и математика были неразделимы в моем
разум. Я не отличал четко формальные символические модели от реальности. Как отмечает Вейль, «возможно,
философски наиболее значимой чертой современной науки является появление абстрактных символических структур.
как твердая сердцевина объективности, стоящая, как выразился Эддингтон, за красочным рассказом о субъективном рассказчике.
ум.”
Это стало
моя книга по философии науки. В то время физика и математика были неразделимы в моем
разум. Я не отличал четко формальные символические модели от реальности. Как отмечает Вейль, «возможно,
философски наиболее значимой чертой современной науки является появление абстрактных символических структур.
как твердая сердцевина объективности, стоящая, как выразился Эддингтон, за красочным рассказом о субъективном рассказчике.
ум.”
В 1960-х годах я впервые серьезно задумался об отношении абстрактных структур символов к физическим законам.
которые они представляют, открыл мне физик Макс Борн (1969) в статье, озаглавленной «Символы и
Реальность», в которой он вспоминает о своем шоке, когда он был молодым студентом, когда до него дошло, что все наши
восприятие и мысленные образы, «все без исключения», совершенно субъективны, и то только
с помощью символов мы можем передать какие-либо объективные компоненты нашего субъективного личного опыта.
Условием Борна для объективного использования символов является «разрешимость», термин, который он ввел для выражения
функция эксперимента. Если символьному выражению не хватает эмпирической разрешимости, потенциально доступной для всех
наблюдателям оно не имеет необходимого отношения к какой-либо объективной реальности. Я также был заинтригован Юджином Вигнером.
(1960) статья «О неразумной эффективности математики в естественных науках», в которой ставится вопрос
многие фундаментальные вопросы о природе математических символов 5 . Таким образом, вслед за Борном мои усилия
к ответу на вопрос: как физика связана с биологией? был дополнен вопросом: как
связаны ли физические законы с математическими символами, от которых зависит их представление? я теперь часто
сформулируйте те же вопросы в более общем виде: как соотносятся универсальные, неумолимые естественные законы с местными,
произвольные символы?
Если символьному выражению не хватает эмпирической разрешимости, потенциально доступной для всех
наблюдателям оно не имеет необходимого отношения к какой-либо объективной реальности. Я также был заинтригован Юджином Вигнером.
(1960) статья «О неразумной эффективности математики в естественных науках», в которой ставится вопрос
многие фундаментальные вопросы о природе математических символов 5 . Таким образом, вслед за Борном мои усилия
к ответу на вопрос: как физика связана с биологией? был дополнен вопросом: как
связаны ли физические законы с математическими символами, от которых зависит их представление? я теперь часто
сформулируйте те же вопросы в более общем виде: как соотносятся универсальные, неумолимые естественные законы с местными,
произвольные символы?
Мое первое побуждение к пониманию отношения символов к живым организмам возникло раньше из
Проблема происхождения жизни. В 1954 году я защитил докторскую диссертацию по рентгеновской оптике, используемой для изучения
биологические структуры. Открытие физической структуры нуклеиновых кислот и белков было тогда главной задачей.
Проблема новой молекулярной биологии. Я понял, однако, что самовоспроизведение такого сложного
структур — это совершенно другой и более сложный тип проблемы. Я думал, это очевидно, что
надежное самовоспроизведение потребует объективной связи любой структуры, которая воспроизводится. В
Другими словами, чтобы эволюция была возможной, любое описание «я» должно быть объективно сообщено
все клетки-потомки, независимо от того, какое конкретное «я» реплицируется. Здесь объективность просто означает, что
одни и те же инструкции будут давать одинаковые результаты для всех потомков.
Открытие физической структуры нуклеиновых кислот и белков было тогда главной задачей.
Проблема новой молекулярной биологии. Я понял, однако, что самовоспроизведение такого сложного
структур — это совершенно другой и более сложный тип проблемы. Я думал, это очевидно, что
надежное самовоспроизведение потребует объективной связи любой структуры, которая воспроизводится. В
Другими словами, чтобы эволюция была возможной, любое описание «я» должно быть объективно сообщено
все клетки-потомки, независимо от того, какое конкретное «я» реплицируется. Здесь объективность просто означает, что
одни и те же инструкции будут давать одинаковые результаты для всех потомков.
Я попробовал несколько самоорганизующихся схем с использованием моделей автоматов для создания и воспроизведения симулированных
последовательностей сополимеров (Pattee, 1961, 1965), но стало ясно, что эволюционный потенциал всех этих
моделей было очень мало. В конце концов я осознал фундаментальную проблему всех таких схем самоорганизации, основанных на правилах, а именно: поскольку организация зависит от внутренних фиксированных правил,
структуры будут иметь ограниченную потенциальную сложность, и поскольку любая новая организация возникает из
вне среды новые структуры не имеют возможности надежного воспроизведения без символического
память, которая могла бы реконструировать новую организацию. Первая компьютерная симуляция, по моему мнению, имела некоторые
интересный эволюционный потенциал был развит Майклом Конрадом (1969) в котором генетические, клеточные,
были представлены население и экологические уровни. Однако, помимо абстрактного сохранения
принципы, это была свободная от физики модель, которая не касалась вопроса Пирсона или природы символов.
в процессах измерения и контроля. (Конрад и Патти, 1970).
Первая компьютерная симуляция, по моему мнению, имела некоторые
интересный эволюционный потенциал был развит Майклом Конрадом (1969) в котором генетические, клеточные,
были представлены население и экологические уровни. Однако, помимо абстрактного сохранения
принципы, это была свободная от физики модель, которая не касалась вопроса Пирсона или природы символов.
в процессах измерения и контроля. (Конрад и Патти, 1970).
К 1970-м годам я полагал, что у меня есть некоторое понимание вопроса Пирсона. Эти идеи, которые я резюмирую
ниже, были представлены в четырех томах Уоддингтона (1968-72) Белладжио конференции по теоретической
биология. Мой первый вопрос тогда был: как мы можем описать на физическом языке самые элементарные
наследственные символы? Оказалось, что даже для простейшего известного случая — гена — адекватная
описание требует двух неприводимо дополняющих друг друга понятий динамических законов и неинтегрируемых
ограничения, не вытекающие из законов. Это первобытное различие между локальным
символические ограничения, впервые появившиеся при зарождении жизни, и объективные универсальные законы вновь проявляются в
много форм на более высоких уровнях. 6 От фон Неймана (1955) я узнал, что такое же эпистемическое разрезание происходит в
физики в процессе измерения, т. е. тот факт, что динамические законы не могут описать измерение
функция определения начальных условий.
6 От фон Неймана (1955) я узнал, что такое же эпистемическое разрезание происходит в
физики в процессе измерения, т. е. тот факт, что динамические законы не могут описать измерение
функция определения начальных условий.
Позднее я рассматривал их как частные случаи общей эпистемологической проблемы: как преодолеть разделение между наблюдатель и наблюдаемое, контролер и контролируемое, знающий и известное, и даже ум и мозг. Это пресловутое эпистемическое сокращение на протяжении тысячелетий служило поводом для философских споров. особенно проблема сознания, к которой только недавно стали относиться как к возможно эмпирически разрешимая проблема (например, Shear, 1997; Тейлор, 1999). Мой второй вопрос заключался в том, Преодоление эпистемического разреза можно было бы даже решить с точки зрения физических законов.
Конечно, мои ответы на вопрос Пирсона не были полными и не представляли большого интереса для биологов. я имел
лишь сформулировал некоторые необходимые, но ни в коем случае не достаточные условия для физического описания символических
контроль. Это была легкая часть вопроса. Моя концепция того, что символическое поведение должно также влечь за собой
была значительно расширена Эрнстом Кассирером (1957) Философия символических форм . Позже в Белладжио
встречах, философ Марджори Грене (1974) познакомила меня с взглядами Майкла Поланьи на
неспособность всех наших символических выражений, особенно формальных математических выражений, достичь идеального
объективности. Антиредукционистские аргументы Поланьи (1964) показывают, как все наши явные символические
описания должны основываться на резервуаре невыразимых структур и дополнительных знаний. Но больше
важной для меня в то время была его статья «Нередуцируемая структура жизни» (Полани, 1968) потому что это сделало
тот же самый существенный момент, который я сделал, что структурная сложность, которую мы связываем с жизнью, может быть только
описывается на языке физики как специальные ограничения или машиноподобные «граничные условия», которые
«упряжь» законы, но формально не выводимые из физических законов 7 .
Это была легкая часть вопроса. Моя концепция того, что символическое поведение должно также влечь за собой
была значительно расширена Эрнстом Кассирером (1957) Философия символических форм . Позже в Белладжио
встречах, философ Марджори Грене (1974) познакомила меня с взглядами Майкла Поланьи на
неспособность всех наших символических выражений, особенно формальных математических выражений, достичь идеального
объективности. Антиредукционистские аргументы Поланьи (1964) показывают, как все наши явные символические
описания должны основываться на резервуаре невыразимых структур и дополнительных знаний. Но больше
важной для меня в то время была его статья «Нередуцируемая структура жизни» (Полани, 1968) потому что это сделало
тот же самый существенный момент, который я сделал, что структурная сложность, которую мы связываем с жизнью, может быть только
описывается на языке физики как специальные ограничения или машиноподобные «граничные условия», которые
«упряжь» законы, но формально не выводимые из физических законов 7 . Поланьи также признавал
несводимость всех высших развитых функциональных иерархических уровней к более низким уровням, с которых они
эволюционировали (Патти, 1969а).
Поланьи также признавал
несводимость всех высших развитых функциональных иерархических уровней к более низким уровням, с которых они
эволюционировали (Патти, 1969а).
Наибольшее историческое влияние оказал Джон фон Нейман. Его обсуждение в 1966 году самовоспроизводящихся автоматы предположили, что эффективное управление динамической конструкцией требует нединамического «спокойного состояния». описание», и это я интерпретировал как эквивалент эпистемического разреза между объективными динамическими законами и субъективные нединамические символические ограничения, описывающие «я». Фон Нейман также спросил вопрос, который, как я обнаружил, тесно связан с вопросом Пирсона: почему основные макромолекулы организмы, настолько большие, чем фундаментальные частицы физической теории? 4
Не менее влиятельным было обсуждение фон Нейманом (1955) необходимости эпистемического разреза в любом
процесс измерения (см. раздел 9), показывающий, что функция измерения обязательно несводима к
динамика измерительного прибора. Эта логика тесно связана с необходимым разделением символов.
и динамику для управления самовоспроизведением, поскольку измерение и управление являются обратными процессами, т.е.
измерение преобразует физические состояния в символы в памяти, в то время как хранящиеся в памяти элементы управления преобразуют
символы к физическим состояниям.
Эта логика тесно связана с необходимым разделением символов.
и динамику для управления самовоспроизведением, поскольку измерение и управление являются обратными процессами, т.е.
измерение преобразует физические состояния в символы в памяти, в то время как хранящиеся в памяти элементы управления преобразуют
символы к физическим состояниям.
6. Динамические законы – проблема детерминизма
«Опять же, если всякое движение взаимосвязано, то новое, возникающее из старого в определенном порядке, если атомы никогда не отклонятся так, чтобы вызвать какое-то новое движение, которое сломает узы судьбы, вечная череда причин и следствий, что является источником свободного будут одержимы живыми существами по всей земле?» [Лукреций, О природе Вещи ].
Если жизнь отличается хранимыми в памяти элементами управления, и если память и управление подразумевают альтернативные
движений, то чтобы ответить на вопрос Пирсона, мы должны сначала ответить на вопрос Лукреция. Как
рвем узы неумолимых динамических законов, не допускающих новых альтернативных движений? К
Чтобы понять проблему, важно сосредоточиться на том, как физические законы на самом деле описываются в их
математическая форма. «Необоснованная эффективность» этого типа формального описания в значительной степени
результатом точности его выполнения (которую я не буду дублировать здесь). Эта формулировка имеет
история развития, что тоже немаловажно. Ньютоновская динамика началась с движения точечных масс под
законы силы тяготения или вообще законы, вытекающие из потенциальной и кинетической энергии
система. Эти законы выражаются в виде дифференциальных уравнений во времени (уравнений движения), которые определяют
бесконечное семейство возможных орбит в пространстве состояний (фазовом пространстве).
Как
рвем узы неумолимых динамических законов, не допускающих новых альтернативных движений? К
Чтобы понять проблему, важно сосредоточиться на том, как физические законы на самом деле описываются в их
математическая форма. «Необоснованная эффективность» этого типа формального описания в значительной степени
результатом точности его выполнения (которую я не буду дублировать здесь). Эта формулировка имеет
история развития, что тоже немаловажно. Ньютоновская динамика началась с движения точечных масс под
законы силы тяготения или вообще законы, вытекающие из потенциальной и кинетической энергии
система. Эти законы выражаются в виде дифференциальных уравнений во времени (уравнений движения), которые определяют
бесконечное семейство возможных орбит в пространстве состояний (фазовом пространстве).
Три тесно связанных эпистемологических условия являются фундаментальными для этого типа динамического описания и
необходимо подчеркнуть: (1) Чтобы начать описание этого типа, мир должен быть разделен на состояния
и законы, меняющие штаты. Подробные (микроскопические) законы выражаются как зависящие от скорости
дифференциальные уравнения, определяющие семейства орбит в пространстве состояний. Это означает, что пути из состояний
состояния однозначно детерминированы и обратимы. (2) Только когда конкретная система расположена в
это пространство актом измерения (определение его начальных условий, т. е. положений и скоростей
все частицы в определенное время) приводят ли уравнения к каким-либо наблюдаемым следствиям и позволяют ли
орбиту вычисляют путем интегрирования уравнений движения. (3) Наконец, что наиболее важно, эта форма
описание может претендовать на объективность только в том случае, если акт измерения не влияет на форму
законов, и если законы не влияют на акт измерения.
Подробные (микроскопические) законы выражаются как зависящие от скорости
дифференциальные уравнения, определяющие семейства орбит в пространстве состояний. Это означает, что пути из состояний
состояния однозначно детерминированы и обратимы. (2) Только когда конкретная система расположена в
это пространство актом измерения (определение его начальных условий, т. е. положений и скоростей
все частицы в определенное время) приводят ли уравнения к каким-либо наблюдаемым следствиям и позволяют ли
орбиту вычисляют путем интегрирования уравнений движения. (3) Наконец, что наиболее важно, эта форма
описание может претендовать на объективность только в том случае, если акт измерения не влияет на форму
законов, и если законы не влияют на акт измерения.
Первое расширение этой модели было связано с твердыми телами, которые можно изобразить как множество удерживаемых точечных масс.
вместе фиксированными (нединамическими) силами. Природа этих сил была загадкой для Ньютона. Мы сейчас
приписать их электромагнитным, квантовым силам или силам фундаментальных частиц, которые в принципе также могут быть
более подробно описывается динамическими законами. Обычно эти внутренние силы не совершают работы и поэтому играют
никакой роли в динамических законах твердого тела. Их можно интерпретировать как фиксированные, что значительно
уменьшение числа переменных (степеней свободы), входящих в уравнения движения. Эти
внутренние (реактивные или геометрические) силы называются силами связи. То, что мы называем более или менее жестким
структуры, от природных молекул, кристаллов и камней до искусственных столов, зданий и мостов, удерживаются
вместе силами принуждения.
Обычно эти внутренние силы не совершают работы и поэтому играют
никакой роли в динамических законах твердого тела. Их можно интерпретировать как фиксированные, что значительно
уменьшение числа переменных (степеней свободы), входящих в уравнения движения. Эти
внутренние (реактивные или геометрические) силы называются силами связи. То, что мы называем более или менее жестким
структуры, от природных молекул, кристаллов и камней до искусственных столов, зданий и мостов, удерживаются
вместе силами принуждения.
Однако существуют и гибкие силы принуждения, удерживающие воедино бесчисленные сочлененные сборки жестких структур, которые мы называем машинами, а также лабильные сборки не очень жестких структур, таких как биополимеры, которые выполняют процессы измерения и контроля в организмах. это физическое описания этих гибких и сформулированных ограничений, которые необходимо объяснить более подробно, чтобы чтобы начать отвечать на вопросы Лукреция и Пирсона.
7.
 Эпистемический разрез требуется для всех динамических законов
Эпистемический разрез требуется для всех динамических законов Перед определением этих гибких ограничений мне нужно подчеркнуть общность динамики, которую они могут
контроль. Часто считается, что ньютоновская или классическая картина была заменена теорией относительности и
квантовой теории, но это несправедливая оценка ньютоновской динамики. Во-первых, классические законы все еще
справедливо для гравитационных сил и скоростей, малых по сравнению со скоростью света. Во-вторых, результаты
все измерения как релятивистских, так и квантово-механических систем должны быть выражены в этом классическом
язык. Верно, что формы этих современных динамических законов отличаются от ньютоновских, и что
понятие государства определяется совершенно иначе, но три фундаментальных эпистемологических условия должны
по-прежнему верны для всех динамических законов, чтобы иметь объективный смысл. По-прежнему требуется, чтобы (1) законы и исходные
условия должны быть четко разделены, (2) начальные условия должны быть определены измерениями, и (3)
измерения и законы не должны влиять друг на друга 8 .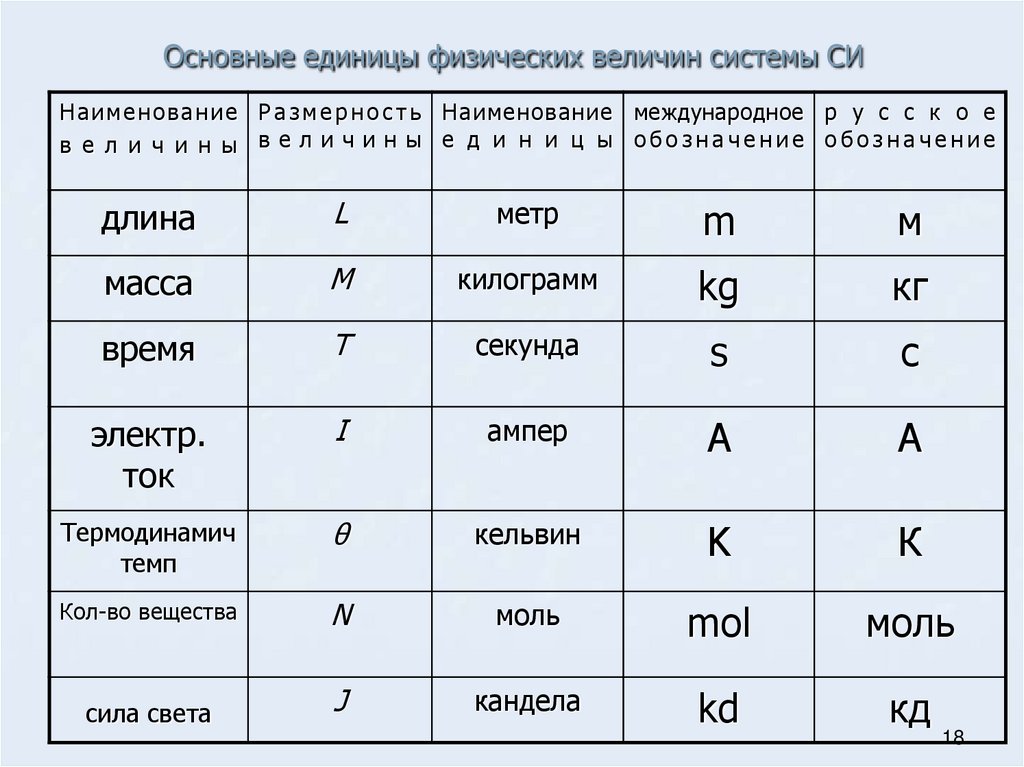 Именно по этой причине Юджин Вигнер (1982)
считал величайшим открытием Ньютона не его законы, а скорее «его резкое разделение начальных условий
и законы природы.”
Именно по этой причине Юджин Вигнер (1982)
считал величайшим открытием Ньютона не его законы, а скорее «его резкое разделение начальных условий
и законы природы.”
Это высокоразвитое интеллектуальное различение начальных условий и законов есть форма эпистемологического
разрез, но я хочу отметить, что этот разрез имеет примитивное происхождение и встречается во всех живых организмах. Это
является просто крайним случаем различия, проводимого даже первыми клетками между стимулами, которые не могут быть
коррелированные и стимулы, которые могут быть коррелированы или следуют узнаваемому образцу. С точки зрения информации
хранения, мы говорим, что некоторые записи событий могут иметь сжатое описание (например, законы) из-за
внутренние корреляции, в то время как другие записи (например, начальные условия) имеют не более короткое описание, чем
записывает себя. Динамические законы выражают максимальное сжатие всех событий определенного типа,
а именно, на орбитах, определяемых одним набором начальных условий. Учитывая начальные условия, все прошлые
и будущие события определяются законами (кроме сингулярностей). Исторически такое поведение привело к
идеал лапласовского детерминизма. Сегодня это более скромно называют поведением, детерминированным состоянием.
Тем не менее, рассматриваемые как формальное описание, все динамические законы остаются синтаксически детерминированными, даже
если их интерпретировал как вероятности. Кроме того, наше восприятие, а также наши естественные языки
поддерживать детерминистский логический синтаксис «или-или» и каузальную семантику, соответствующие классической
динамика. Именно по этой причине интерпретация квантовой теории в значительной степени невыразима.
Учитывая начальные условия, все прошлые
и будущие события определяются законами (кроме сингулярностей). Исторически такое поведение привело к
идеал лапласовского детерминизма. Сегодня это более скромно называют поведением, детерминированным состоянием.
Тем не менее, рассматриваемые как формальное описание, все динамические законы остаются синтаксически детерминированными, даже
если их интерпретировал как вероятности. Кроме того, наше восприятие, а также наши естественные языки
поддерживать детерминистский логический синтаксис «или-или» и каузальную семантику, соответствующие классической
динамика. Именно по этой причине интерпретация квантовой теории в значительной степени невыразима.
Это максимальное сжатие событий динамическими законами действительно оказалось необоснованно эффективным в
описывающих все основные законы микроскопии. Но мы знаем из повседневного принятия решений, что все
наш опыт нельзя полностью сжать, и что наша жизнь не определяется состоянием. Как любой может
непосредственно наблюдаем, между этими крайностями универсальных и максимально сжимаемых законов и
локальные несжимаемые начальные условия множество промежуточных уровней естественных и искусственных локальных ограничений
структуры, выполняющие функции измерения и контроля и демонстрирующие различную степень местного и
частично сжимаемое поведение. Как Гелл-Манн (1994) заметил: «эффективная сложность [
вселенная] получает лишь небольшой вклад от фундаментальных законов. Остальное поступает из
многочисленные закономерности, возникающие в результате «замороженных случайностей». Я бы добавил, что для эффективности в эволюции эти
закономерности из замороженных случайных ограничений должны быть наследственными. Это означает, что они должны быть реконструируемыми.
из памяти. И машины, и организмы характеризуются такими ограничениями. Вопрос
остается: как можно описать такие ограничения специального назначения в точных физических терминах?
Как любой может
непосредственно наблюдаем, между этими крайностями универсальных и максимально сжимаемых законов и
локальные несжимаемые начальные условия множество промежуточных уровней естественных и искусственных локальных ограничений
структуры, выполняющие функции измерения и контроля и демонстрирующие различную степень местного и
частично сжимаемое поведение. Как Гелл-Манн (1994) заметил: «эффективная сложность [
вселенная] получает лишь небольшой вклад от фундаментальных законов. Остальное поступает из
многочисленные закономерности, возникающие в результате «замороженных случайностей». Я бы добавил, что для эффективности в эволюции эти
закономерности из замороженных случайных ограничений должны быть наследственными. Это означает, что они должны быть реконструируемыми.
из памяти. И машины, и организмы характеризуются такими ограничениями. Вопрос
остается: как можно описать такие ограничения специального назначения в точных физических терминах?
8. Неинтегрируемое условие перекрытия эпистемического разреза
Поскольку мы знаем, что наследуемая генетическая память является необходимым условием жизни, мой подход к
Проблема детерминизма началась с выражения точных требований к ограничению, удовлетворяющему
Условия наследственности.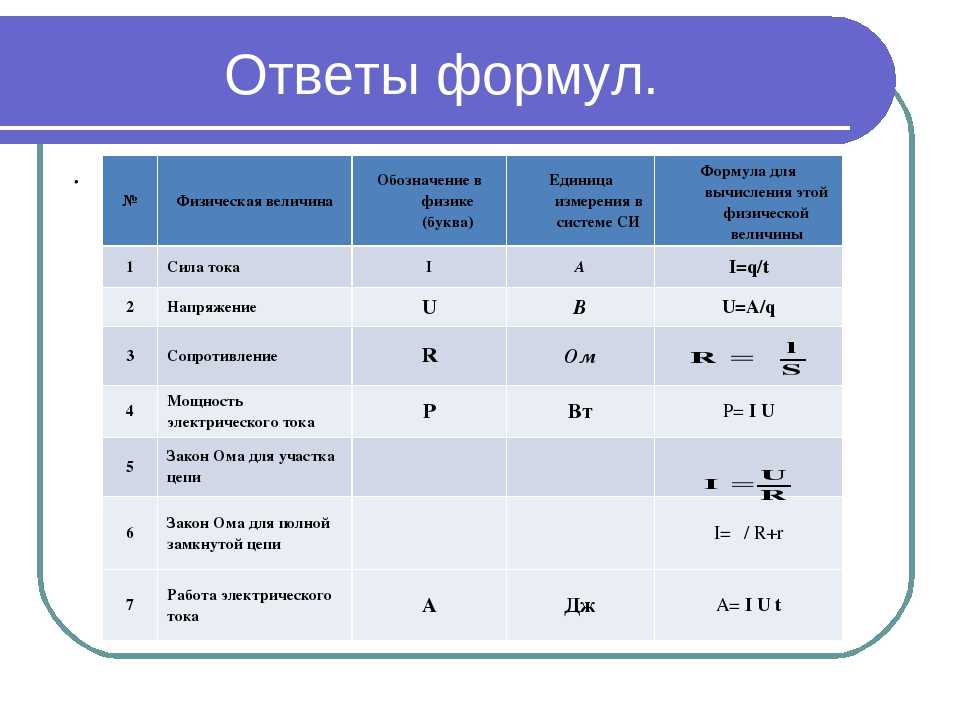 Я не могу сделать ничего лучше, чем переформулировать свой ранний аргумент (Патти, 1969b):
Я не могу сделать ничего лучше, чем переформулировать свой ранний аргумент (Патти, 1969b):
«Физическая система определяется числом степеней свободы, которые представлены
как переменные в уравнениях движения. После того, как заданы начальные условия для данного
времени уравнения движения дают детерминированную процедуру нахождения состояния систем
в любое другое время. Поскольку в этом описании нет места альтернативам,
нет места наследственным процессам. . . Единственное полезное описание памяти или наследственности в
физическая система требует введения возможности альтернативных путей или траекторий для
системы, наряду с «генетическим» механизмом, заставляющим систему следовать тому или иному
эти возможные альтернативы в зависимости от состояния генетического механизма. Это означает, что
генетический механизм должен быть способен описывать или представлять все альтернативы
пути, даже если только один путь фактически соблюдается во времени. Другими словами, должен быть
иметь больше степеней свободы для описания всей системы, чем для следующего
его фактическое движение. . . Такие связи называются неголономными .
. . Такие связи называются неголономными .
В более распространенной терминологии этот тип ограничения представляет собой структуру, которая, как мы говорим, управляет динамикой. К
управления динамическими системами подразумевает, что существуют управляющие переменные, которые отделены от динамических
системные переменные, однако они должны быть описаны вместе с динамическими переменными. Они контролируют
переменные должны обеспечивать дополнительные степени свободы или гибкости для системной динамики. В то же
время типичные системы управления не удаляют степени свободы из динамической системы, хотя
они изменяют скорости или диапазоны системных переменных. Многие искусственные машины зависят от такого контроля.
ограничения в виде рычажных механизмов, спусковых механизмов, переключателей и регуляторов. В живых системах ферменты
и другие аллостерические макромолекулы выполняют такие контрольные функции. Характерное свойство всех
этих неголономных структур заключается в том, что их нельзя с пользой отделить от динамической системы, которую они
контроль. Они существенно нелинейны в том смысле, что ни динамика, ни ограничения управления
можно рассматривать отдельно.
Они существенно нелинейны в том смысле, что ни динамика, ни ограничения управления
можно рассматривать отдельно.
Этот тип ограничения, который я предпочитаю называть неинтегрируемым , решает две проблемы. Во-первых, он отвечает
Вопрос Лукреция. Эти гибкие ограничения буквально заставляют «атомы отклоняться и создавать новые
движение» в описательных рамках детерминированной в других отношениях динамики (это все еще
путь от свободы воли). Они также учитывают чтение покоящейся, независимой от скорости памяти, чтобы
контролировать динамику, зависящую от скорости, тем самым преодолевая эпистемологический разрыв между контролером и
контролируемый. Поскольку законопослушная динамика основана на энергии, помимо неинтегрируемой памяти чтение ,
память память требует альтернативных состояний с одинаковой энергией (энергетическое вырождение). Эти гибкие,
аллостерические или изменяющие конфигурацию структуры неинтегрируемы, потому что их движения не полностью
определяются до тех пор, пока они не связывают явную структуру памяти с законами, зависящими от скорости (удаление
вырождение).
Ключевым условием здесь является то, что ограничение действует на динамические траектории, не снимая альтернативные конфигурации. Таким образом, количество координат, необходимое для задания конфигурации ограниченная система всегда больше, чем число динамических степеней свободы, оставляя некоторые конфигурационные альтернативы, доступные для «чтения» структур памяти. Это, в свою очередь, требует, чтобы силы не все ограничения являются жесткими, т. е. должно быть некоторое вырождение, чтобы обеспечить гибкость. Таким образом, внутренний силы и формы неинтегрируемых структур должны изменяться во времени отчасти из-за памяти структур и отчасти в результате управляемой ими динамики. Другими словами, уравнения ограничение не может быть решено отдельно, потому что они находятся на той же формальной основе, что и законы сами по себе, а орбиты системы неустранимо зависят от обоих (Уиттакер, 1944; Зоммерфельд, 1956 год; Гольдштейн, 1953; Неймарк, Фуфаев, 1972).
Исторически удивительно то, что этот распространенный тип ограничения не был официально признан
физиков до конца прошлого века (Герц, 1894).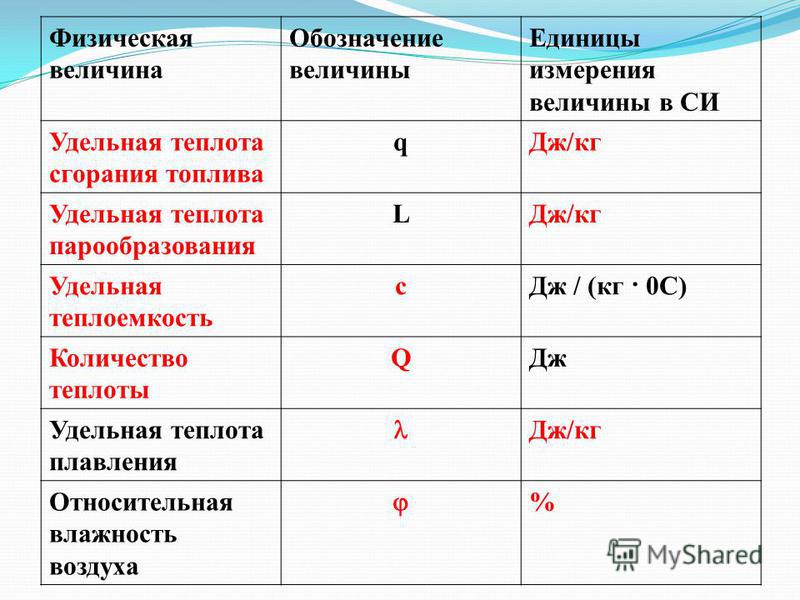 Такие структуры встречаются на многих уровнях. Они
соединяет все эпистемологические разрезы между контролирующим и контролируемым, классификатором и классифицируемым,
наблюдатель и наблюдаемое. Существует бесчисленное множество типов неинтегрируемых ограничений, встречающихся во всех
механические устройства в виде защелок и спусковых механизмов, электрические устройства в виде затворов и
переключателях и во многих биологических аллостерических макромолекулах, таких как ферменты, белки мембранных каналов,
цилиарные и мышечные белки. Они функционируют как структуры кодирования и декодирования во всех символах.
манипулятивные системы.
Такие структуры встречаются на многих уровнях. Они
соединяет все эпистемологические разрезы между контролирующим и контролируемым, классификатором и классифицируемым,
наблюдатель и наблюдаемое. Существует бесчисленное множество типов неинтегрируемых ограничений, встречающихся во всех
механические устройства в виде защелок и спусковых механизмов, электрические устройства в виде затворов и
переключателях и во многих биологических аллостерических макромолекулах, таких как ферменты, белки мембранных каналов,
цилиарные и мышечные белки. Они функционируют как структуры кодирования и декодирования во всех символах.
манипулятивные системы.
Существует значительная разница между тем, как обрабатываются неинтегрируемые ограничения в классическом и
квантовая механика. Описание неинтегрируемых ограничений в квантовой теории ограничивает волновую функцию
как будто производится какое-то измерение (Eden 1951). Это привело меня к предположению, что неинтегрируемая
ограничения молекулы фермента выполняют функцию квантового измерения и контроля скорости с
специфичность и скорость, с которыми не может сравниться ни одно классическое устройство измерения и контроля. (Патти, 19 лет67).
(Патти, 19 лет67).
9. Нередуцируемость эпистемического разреза
Понятие связи не считается фундаментальным в физике, поскольку (внутреннее, геометрическое реактивные) силы принуждения, в принципе, могут быть сведены к активным приложенным силам, подчиняющимся основанным на энергии микроскопическим динамическим законам. Так называемые фиксированные геометрические силы — это всего лишь стационарные состояния более быстрая, более детальная динамика. Эта сводимость к микроскопической динамике в принципе возможна для структуры, даже если это вычислительно совершенно непрактично. Однако, описывая любой мост через эпистемический разрез единым динамическим описанием невозможен даже в принципе.
Самый убедительный общий аргумент в пользу этой неприводимой дополнительности динамических законов и
Функция измерения снова исходит от фон Неймана (1955, стр. 352). Он называет систему существом
измеряемый, S, и измерительный прибор, M, который должен обеспечить начальные условия для динамических законов
из S.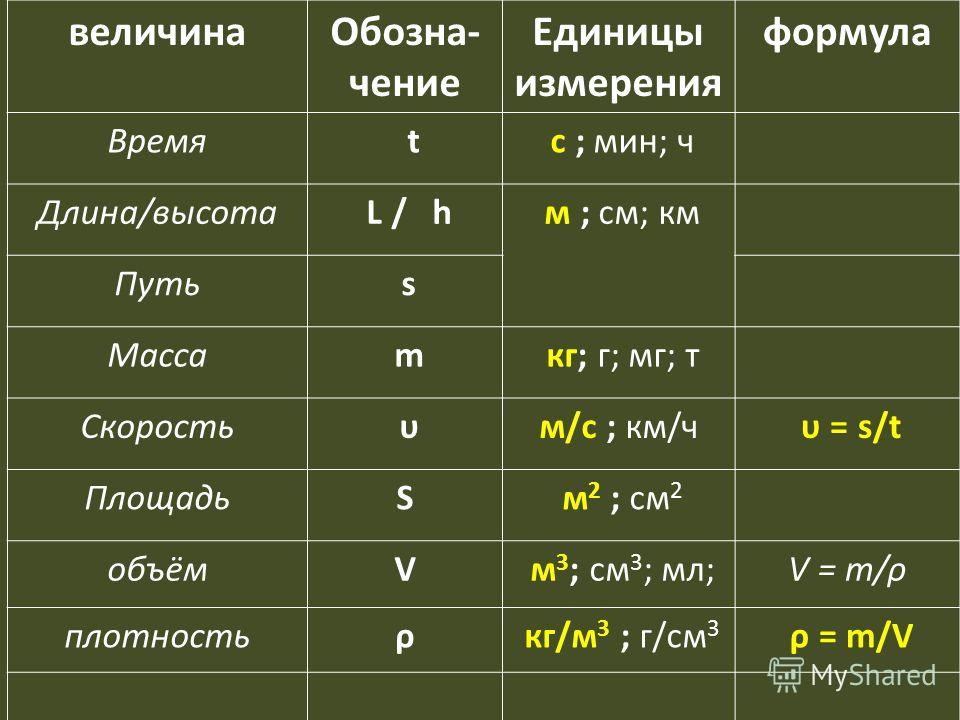 Поскольку неинтегрируемое ограничение M также является физической системой, подчиняющейся тем же законам, что и S, мы
можно попробовать унифицированное описание, рассмотрев комбинированную физическую систему (S + M). Но тогда мы будем
нужен новый измерительный прибор М’, чтобы обеспечить начальные условия для более крупной системы (S + M). Этот
ведет к бесконечному регрессу; но главное в том, что хоть любое ограничение, как измерительный прибор,
М, в принципе можно описать более подробными универсальными законами, дело в том, что если вы решите это сделать
ты потеряешь функция М как измерительного прибора. Это показывает, что законы не могут описать прагматическая функция измерения, даже если они могут правильно и полностью описать подробное
динамика измерительных ограничений.
Поскольку неинтегрируемое ограничение M также является физической системой, подчиняющейся тем же законам, что и S, мы
можно попробовать унифицированное описание, рассмотрев комбинированную физическую систему (S + M). Но тогда мы будем
нужен новый измерительный прибор М’, чтобы обеспечить начальные условия для более крупной системы (S + M). Этот
ведет к бесконечному регрессу; но главное в том, что хоть любое ограничение, как измерительный прибор,
М, в принципе можно описать более подробными универсальными законами, дело в том, что если вы решите это сделать
ты потеряешь функция М как измерительного прибора. Это показывает, что законы не могут описать прагматическая функция измерения, даже если они могут правильно и полностью описать подробное
динамика измерительных ограничений.
Этот же аргумент справедлив и для контрольных функций, включающих генетический контроль над белками.
строительство. Если мы назовем управляемую систему S, а ограничения управления С, то мы также можем посмотреть на
комбинированная система (S + C) в этом случае функция управления просто исчезает в динамике. Эта эпистемическая несводимость не подразумевает никакого онтологического дуализма. Оно возникает всякий раз, когда различие должно
быть проведено между субъектом и объектом, или в семиотических терминах, когда необходимо провести различие между
символ и его референт или между синтаксисом и прагматикой. Без этого эпистемического разреза любое использование
концепции измерения начальных условий и символического контроля конструкции были бы излишними.
Эта эпистемическая несводимость не подразумевает никакого онтологического дуализма. Оно возникает всякий раз, когда различие должно
быть проведено между субъектом и объектом, или в семиотических терминах, когда необходимо провести различие между
символ и его референт или между синтаксисом и прагматикой. Без этого эпистемического разреза любое использование
концепции измерения начальных условий и символического контроля конструкции были бы излишними.
“То есть мы всегда должны делить мир на две части, одна из которых является наблюдаемой системой, а другая
другой наблюдатель. В первом случае мы можем проследить все физические процессы (по крайней мере, в принципе)
произвольно точно. В последнем это бессмысленно. Граница между ними произвольна
очень большая степень. . . но это не меняет того факта, что в каждом способе описания
где-то должна быть проведена граница, если метод не будет действовать бессодержательно, т. е. если
сравнение с экспериментом должно быть возможным» (фон Нейман, 19 лет). 55, стр.419)
55, стр.419)
10. Первобытный эпистемологический разрез
Эпистемический разрез или различие между субъектом и объектом обычно ассоциируется с
эволюционировали субъекты с мозгом и их моделями внешнего мира, как в случае измерения. Как фон
Нейман утверждает, что место, где мы размещаем разрез, кажется в значительной степени произвольным. Сам разрез представляет собой
эпистемологическая необходимость, а не онтологическое условие. То есть надо сделать резкий срез, дизъюнкт, как раз в
для того, чтобы говорить о знании как о чем-то или как о чем-то, к чему оно относится. Что такое
происходящее онтологически на разрезе (или то, что мы видим, если решим рассмотреть самую детальную физику) — это
очень сложный процесс. Кажущаяся произвольность размещения эпистемического разреза возникает отчасти
поскольку процесс не может быть полностью или однозначно описан объективными динамическими законами,
поскольку для выполнения измерения испытуемый должен контролировать конструкцию
измерительный прибор. Только предметная сторона разреза может измерять или контролировать.
Только предметная сторона разреза может измерять или контролировать.
Понятие эпистемического разреза должно сначала возникнуть на интерфейсе управления генотип-фенотип. Воображение
такое различие между субъектом и объектом до существования жизни было бы совершенно беспочвенным и ограничивало бы контроль только
к высшим организмам было бы произвольным. Проблема происхождения до сих пор остается загадкой. Что самое простое
эпистемическое событие? Одним из необходимых условий является то, что различение проводится субъектом, который не является различением.
производным от объекта. На физическом языке это означает, что субъект должен создать некоторую форму различия.
или классификация между физическими состояниями, которая не производится самими законами (т.е. измерение
конкретное начальное условие, снимающее вырождение или нарушающее симметрию). В случае с клеткой,
последовательности гена не различаются по физическим законам, так как энергетически вырождены.
Где впервые появляется новое различие? Именно здесь это вырождение памяти частично устраняется, и
этого не происходит до тех пор, пока не начнется процесс сворачивания белка. Процессы транскрипции, трансляции и копирования
относиться ко всем последовательностям одинаково и, следовательно, не проводить новых различий, но, конечно, они существенны для
построение линейных ограничений белка, которые частично объясняют способ его сворачивания. Сложенный
белок устраняет вырождение носителя символа, но все еще имеет много вырожденных состояний (много конформаций)
которые необходимы для того, чтобы он функционировал как неинтегрируемое ограничение.
Процессы транскрипции, трансляции и копирования
относиться ко всем последовательностям одинаково и, следовательно, не проводить новых различий, но, конечно, они существенны для
построение линейных ограничений белка, которые частично объясняют способ его сворачивания. Сложенный
белок устраняет вырождение носителя символа, но все еще имеет много вырожденных состояний (много конформаций)
которые необходимы для того, чтобы он функционировал как неинтегрируемое ограничение.
Важно признать, что детали построения и складывания на этом первобытном эпистемологическом срезе делают
никакого смысла, кроме как в контексте целой самовоспроизводящейся клетки. Один свернутый белок не выполняет никакой функции.
если только он не является компонентом более крупной единицы, сохраняющей свою индивидуальность посредством генетической памяти.
Мы говорим о генах, контролирующих синтез белка, но для этого они должны опираться на ранее
синтезированные и организованные ферменты и РНК. Это дополнительное самореферентное условие для того, чтобы быть
предметная часть эпистемического разреза, который я назвал семантическое (или семиотическое) замыкание (Патти, 1982, 1995). Это
молекулярное замыкание куриного яйца, которое делает проблему происхождения жизни такой сложной.
Это
молекулярное замыкание куриного яйца, которое делает проблему происхождения жизни такой сложной.
11. Ответ на вопрос Пирсона
Теперь мы можем дать прямой ответ на вопрос Пирсона: а не возможно отличить живое от живого. безжизненными только благодаря детальнейшему «движению неорганических частиц». Логика этого ответа в том, что жизнь влечет за собой эпистемический разрез, не различимый по микроскопическим (корпускулярным) законам. Как у фон Неймана аргумент показывает, что любое различие между субъектом и объектом требует описания ограничений, которые выполнять процессы измерения и контроля; и такое функциональное описание несводимо к динамика, которая измеряется или контролируется. 9
Это еще далеко не полный ответ. Эволюционируемость — это нечто большее, чем наследственная изменчивость и естественная
выбор и контроль динамических законов по памяти и неинтегрируемым ограничениям. это совсем не очевидно
почему такие локальные структуры управления должны сохраняться в реальном мире, полном некоррелированных нерегулярных событий. Управление предсказуемыми физическими законами — это только часть проблемы выживания. Есть дополнительные
физические условия эволюционируемости. Это не абстрактные принципы, а конкретные требования о том, как
эффективно эпистемический разрез фактически перекрывается. Я упомяну только три из этих условий. Эволюция
в решающей степени зависит от (1) того, насколько легко можно найти последовательности генов, соответствующие функциональным белкам,
(2) насколько надежно эти последовательности могут контролировать построение белков, и (3) насколько гладко или
постепенное изменение последовательностей может привести к адаптации функции. Иными словами, эволюционируемость
зависит от многих физических и статистических деталей того, как фактически эпистемологический мост от символов к
динамика выполнена
Управление предсказуемыми физическими законами — это только часть проблемы выживания. Есть дополнительные
физические условия эволюционируемости. Это не абстрактные принципы, а конкретные требования о том, как
эффективно эпистемический разрез фактически перекрывается. Я упомяну только три из этих условий. Эволюция
в решающей степени зависит от (1) того, насколько легко можно найти последовательности генов, соответствующие функциональным белкам,
(2) насколько надежно эти последовательности могут контролировать построение белков, и (3) насколько гладко или
постепенное изменение последовательностей может привести к адаптации функции. Иными словами, эволюционируемость
зависит от многих физических и статистических деталей того, как фактически эпистемологический мост от символов к
динамика выполнена
12. Иллюзия автономных систем символов
Здесь настоящий концептуальный блокпост. В нашем обычном повседневном использовании языков само понятие
“физика символов” совершенно чужда. Мы пришли к мысли, что системы символов не имеют
отношение к физическим законам. Эта кажущаяся независимость символов и физических законов является характерной чертой
все высокоразвитые языки, будь то естественные или формальные. Они эволюционировали так далеко от происхождения жизни
и системы генетических символов, которые практика и изучение семиотики, по-видимому, не имеют никакого значения.
необходимой связи с физическими законами. В роли Хоффмейера и Эммече (1991) подчеркни, это
общепринято, что « Ни один закон природы не ограничивает пространство возможностей письменного (или устного) текста. » или
по словам Кулла (1998): «Семиотические взаимодействия не происходят по физической необходимости». Добавляя к этому
Иллюзией строгой автономии символического выражения является современное принятие абстрактных символов в
наука как «жесткое ядро объективности», упомянутое Вейлем. Эта изоляция символов и есть то, что Розен
(1987) назвал «синтаксизацией» наших моделей мира, а также примером того, что
Эммече (1994) охарактеризовал как культурную тенденцию «постмодернистской науки», в которой материальные формы
подверглась «дереализации».
Мы пришли к мысли, что системы символов не имеют
отношение к физическим законам. Эта кажущаяся независимость символов и физических законов является характерной чертой
все высокоразвитые языки, будь то естественные или формальные. Они эволюционировали так далеко от происхождения жизни
и системы генетических символов, которые практика и изучение семиотики, по-видимому, не имеют никакого значения.
необходимой связи с физическими законами. В роли Хоффмейера и Эммече (1991) подчеркни, это
общепринято, что « Ни один закон природы не ограничивает пространство возможностей письменного (или устного) текста. » или
по словам Кулла (1998): «Семиотические взаимодействия не происходят по физической необходимости». Добавляя к этому
Иллюзией строгой автономии символического выражения является современное принятие абстрактных символов в
наука как «жесткое ядро объективности», упомянутое Вейлем. Эта изоляция символов и есть то, что Розен
(1987) назвал «синтаксизацией» наших моделей мира, а также примером того, что
Эммече (1994) охарактеризовал как культурную тенденцию «постмодернистской науки», в которой материальные формы
подверглась «дереализации».
Другим прекрасным примером является наша самая популярная искусственная совокупность неинтегрируемых ограничений,
программируемый компьютер. Программируемый компьютер с хранимой в памяти памятью — крайний случай полного символического
управление явным неинтегрируемым аппаратным обеспечением (ограничения чтения, записи и переключения), так что его
вычислительная траектория, определяемая программой, однозначна и в то же время не зависит от
физические законы (кроме законов, поддерживающих силы нормальных конструкционных связей, которые не входят в
динамика, неспецифический энергетический потенциал для перевода компьютера из одного ограниченного состояния в другое,
и термопоглотитель). Для пользователя компьютерная функция может быть операционально описана как свободная от физики
машина или, альтернативно, как символически управляемая, основанная на правилах (синтаксическая) машина. Его поведение
обычно интерпретировал как манипулирование значимыми символами, но это уже другая проблема. Компьютер — это
ярким примером того, как внешне не связанная с физикой функция или манипуляция дискретными данными на основе памяти
системы символов могут легко создать иллюзию строгой изоляции от физической динамики.
Компьютер — это
ярким примером того, как внешне не связанная с физикой функция или манипуляция дискретными данными на основе памяти
системы символов могут легко создать иллюзию строгой изоляции от физической динамики.
Эта иллюзия обособленности символов от материи может также возникнуть из-за кажущегося произвола
эпистемический разрез. Существенная функция символа состоит в том, чтобы «обозначать» что-то — его референт, т. е.
определение, на другой стороне разреза. Это необходимое различие, которое, по-видимому, изолирует системы символов
из физических законов, управляющих материей и энергией, позволяет представить геометрические и математические
структуры, а также физические структуры и даже сама жизнь, как абстрактные отношения и платоновские формы. я
Полагаю, это концептуальная основа картезианского дуализма разума и материи. Эта кажущаяся изоляция символического
выражение из физики рождается из эпистемологической необходимости, но онтологически это все еще иллюзия . В других
словами, проведение четкого разграничения — это не то же самое, что изоляция от всех отношений. Мы четко разделяем
генотип от фенотипа, но мы, конечно, не думаем о них как об изолированных или независимых друг от друга
Другой. Эти необходимые неинтегрируемые уравнения ограничений, которые соединяют эпистемологический разрез и тем самым
памяти, измерения и управления находятся на той же формальной основе, что и физические уравнения
движение. Они называются неинтегрируемыми именно потому, что их нельзя решить или проинтегрировать
независимо от законопослушной динамики. Следовательно, идея о том, что мы могли бы с пользой изучать жизнь
без учета естественных физических требований, обеспечивающих эффективное символическое управление, означает упустить
существенная проблема жизни: как символические структуры управляют динамикой.
В других
словами, проведение четкого разграничения — это не то же самое, что изоляция от всех отношений. Мы четко разделяем
генотип от фенотипа, но мы, конечно, не думаем о них как об изолированных или независимых друг от друга
Другой. Эти необходимые неинтегрируемые уравнения ограничений, которые соединяют эпистемологический разрез и тем самым
памяти, измерения и управления находятся на той же формальной основе, что и физические уравнения
движение. Они называются неинтегрируемыми именно потому, что их нельзя решить или проинтегрировать
независимо от законопослушной динамики. Следовательно, идея о том, что мы могли бы с пользой изучать жизнь
без учета естественных физических требований, обеспечивающих эффективное символическое управление, означает упустить
существенная проблема жизни: как символические структуры управляют динамикой.
13. Реальные условия преодоления эпистемического разреза
Наконец, я резюмирую некоторые физические требования для успешного преодоления эпистемического разреза. По сути, мы отвечаем на «самый интригующий, захватывающий и важный вопрос фон Неймана о том, почему
молекулы. . . такие вещи, какими они являются». Во-первых, это проблема поиска. Это была проблема для Дарвина,
и с открытием спирали ДНК и кода, который точно сопоставляет последовательности оснований с белками
последовательностей проблема поиска оказалась хуже. Предполагая, что молекулярные детали имеют значение, мы видим
пространство базовой последовательности, которое безнадежно велико для любого детального поиска. Но пока это предположение верно
для символической стороны разреза мы теперь знаем, что предположение неверно для функции на другом
сторона разреза. Преодоление эпистемологических разрезов подразумевает выполнение классификации физических деталей, а
Качество классификаций определяет качество функции. Мы знаем, что белковые последовательности
функционально сильно избыточны, и что многие замены аминокислот существенно не изменяют
функция. Мы также знаем, что многие псевдонимы последовательностей оснований могут конструировать белки с практически одинаковыми свойствами.
По сути, мы отвечаем на «самый интригующий, захватывающий и важный вопрос фон Неймана о том, почему
молекулы. . . такие вещи, какими они являются». Во-первых, это проблема поиска. Это была проблема для Дарвина,
и с открытием спирали ДНК и кода, который точно сопоставляет последовательности оснований с белками
последовательностей проблема поиска оказалась хуже. Предполагая, что молекулярные детали имеют значение, мы видим
пространство базовой последовательности, которое безнадежно велико для любого детального поиска. Но пока это предположение верно
для символической стороны разреза мы теперь знаем, что предположение неверно для функции на другом
сторона разреза. Преодоление эпистемологических разрезов подразумевает выполнение классификации физических деталей, а
Качество классификаций определяет качество функции. Мы знаем, что белковые последовательности
функционально сильно избыточны, и что многие замены аминокислот существенно не изменяют
функция. Мы также знаем, что многие псевдонимы последовательностей оснований могут конструировать белки с практически одинаковыми свойствами. форма. Кроме того, упрощенные модели вторичной укладки РНК предполагают, что поиск не похож на поиск
конкретная иголка в бесконечном стоге сена, но ищущая любая иголка в стоге сена, полном иголок, которые
распределены равномерно (например, Schuster, 1994). Есть также доказательства того, что поиск гораздо более эффективен.
чем классическая слепая вариация. Искусственные генетические алгоритмы продемонстрировали неожиданный успех в обнаружении
приемлемые решения для многих типов поисковых задач, возникающих логически или алгоритмически
неразрешимый.
форма. Кроме того, упрощенные модели вторичной укладки РНК предполагают, что поиск не похож на поиск
конкретная иголка в бесконечном стоге сена, но ищущая любая иголка в стоге сена, полном иголок, которые
распределены равномерно (например, Schuster, 1994). Есть также доказательства того, что поиск гораздо более эффективен.
чем классическая слепая вариация. Искусственные генетические алгоритмы продемонстрировали неожиданный успех в обнаружении
приемлемые решения для многих типов поисковых задач, возникающих логически или алгоритмически
неразрешимый.
Второе требование для надежной саморепликации. Это сложный адаптивный баланс между
противоречивые требования на многих уровнях. С одной стороны, полная надежность не позволила бы
поиск, изменение или эволюция вообще. С другой стороны, слишком низкая надежность приведет к исчезновению
ошибка катастрофа. На уровне сворачивания, где частично снимается вырожденность последовательностей оснований,
должен быть баланс между стабильным энергетическим ландшафтом, обеспечивающим быстрое складывание и постоянство, и
сложные конформационные вырождения, необходимые для гибкого специфического связывания и быстрого катализа. процесс складывания уникален во многих отношениях. Это трансформация во всех трех пространственных
измерениях во временных масштабах, охватывающих многие порядки величины и включающих прочные связи и
много более слабых сил в когерентных сильно нелинейных взаимодействиях. Сложность любого подробного квантового
механическое описание таких неинтегрируемых ограничений означает, что такие задачи складывания могут быть
обработаны статистически. Даже формулировка микроскопического описания кажется неразрешимой. это даже не очевидно
что линейная последовательность из нескольких сотен аминокислот или любого подобного гетерополимера должна надежно складываться
в определенную шаровидную форму. Что такие гибкие глобулы должны быть в состоянии выполнять высокоскоростные, высоко
специфический катализ еще менее очевиден. Тем не менее, мы знаем, что это так, и обычно принимаем эти невероятные
функции как нечто само собой разумеющееся (например, Frauenfelder and Wolynes, 1994).
процесс складывания уникален во многих отношениях. Это трансформация во всех трех пространственных
измерениях во временных масштабах, охватывающих многие порядки величины и включающих прочные связи и
много более слабых сил в когерентных сильно нелинейных взаимодействиях. Сложность любого подробного квантового
механическое описание таких неинтегрируемых ограничений означает, что такие задачи складывания могут быть
обработаны статистически. Даже формулировка микроскопического описания кажется неразрешимой. это даже не очевидно
что линейная последовательность из нескольких сотен аминокислот или любого подобного гетерополимера должна надежно складываться
в определенную шаровидную форму. Что такие гибкие глобулы должны быть в состоянии выполнять высокоскоростные, высоко
специфический катализ еще менее очевиден. Тем не менее, мы знаем, что это так, и обычно принимаем эти невероятные
функции как нечто само собой разумеющееся (например, Frauenfelder and Wolynes, 1994).
Последнее требование, которое я упомянул, заключалось в том, насколько плавно вариации в генетических последовательностях могут производить
адаптация в функциях. Здесь снова должен быть баланс между конфликтующими требованиями. Стремительный
сворачивание и стабильность белка требуют крутых энергетических ландшафтов, в то время как оптимизация функции
требует тонкой настройки свернутой формы белка путем небольших изменений в генетических последовательностях. Этот
требует относительно ровного энергетического ландшафта. Балансировка этих требований облегчается достаточно большим
молекул, так что основные условия фолдинга защищены от локальных изменений тонкой настройки в последовательностях (например,
Конрад, 19 лет90). Степень, в которой эти и другие требования удовлетворяются естественным отбором на
с другой стороны, и принципами неселективного упорядочивания, с другой стороны, будет решаться только путем эмпирического изучения
молекулярные детали.
Здесь снова должен быть баланс между конфликтующими требованиями. Стремительный
сворачивание и стабильность белка требуют крутых энергетических ландшафтов, в то время как оптимизация функции
требует тонкой настройки свернутой формы белка путем небольших изменений в генетических последовательностях. Этот
требует относительно ровного энергетического ландшафта. Балансировка этих требований облегчается достаточно большим
молекул, так что основные условия фолдинга защищены от локальных изменений тонкой настройки в последовательностях (например,
Конрад, 19 лет90). Степень, в которой эти и другие требования удовлетворяются естественным отбором на
с другой стороны, и принципами неселективного упорядочивания, с другой стороны, будет решаться только путем эмпирического изучения
молекулярные детали.
14. Заключение
Вопрос Пирсона касается понимания природы жизни. Понимание будет частично зависеть от
объективные критерии, такие как согласие с фактами. Но есть и субъективные критерии, такие как уровень
абстракции, которую можно найти интересной, и степень общности, которую можно допустить в аналогиях и
метафоры. Например, законы Ньютона абстрагируют Землю до простой точки массы, абстракции слишком много.
крайне интересны большинству биологов. Тем не менее жизнь не могла обойти эти законы, и ход
они оказывают глубокое влияние на эволюцию, как Холдейн (1927) указывал в своем эссе «О том, чтобы быть правильным
Размер». С другой стороны, квантовая теория слишком детализирована, чтобы заинтересовать большинство биологов, но жизнь может
не уклоняются от этих законов и могут фактически зависеть от них существенными способами, которые мы еще не осознаем.
Эволюция путем наследственных вариаций и отбора привела ко многим странным структурам и поведению, но
все они без исключения подчиняются гравитационным, электродинамическим, квантовым и статистическим динамическим
законы. Модели искусственной жизни, теория сложности и исследования сложных адаптивных систем мотивированы
надежда открыть больше этих абстрактных и общих законов, которым должна следовать жизнь.
Например, законы Ньютона абстрагируют Землю до простой точки массы, абстракции слишком много.
крайне интересны большинству биологов. Тем не менее жизнь не могла обойти эти законы, и ход
они оказывают глубокое влияние на эволюцию, как Холдейн (1927) указывал в своем эссе «О том, чтобы быть правильным
Размер». С другой стороны, квантовая теория слишком детализирована, чтобы заинтересовать большинство биологов, но жизнь может
не уклоняются от этих законов и могут фактически зависеть от них существенными способами, которые мы еще не осознаем.
Эволюция путем наследственных вариаций и отбора привела ко многим странным структурам и поведению, но
все они без исключения подчиняются гравитационным, электродинамическим, квантовым и статистическим динамическим
законы. Модели искусственной жизни, теория сложности и исследования сложных адаптивных систем мотивированы
надежда открыть больше этих абстрактных и общих законов, которым должна следовать жизнь.
Но есть еще один тип субъективного ощущения понимания жизни, которое мотивировало вопрос Пирсона,
то же самое, я думаю, мотивировало вопросы Лукреция и фон Неймана. Это чувство парадокса, т.
то же чувство, которое двигало Бором, Вигнером, Поланьи, скептиками и, по иронии судьбы, основателями
то, что сейчас является редукционистской молекулярной биологией, как Дельбрюк. Все они верили, что жизнь следует законам, но
из их концепции закона они не могли понять, почему жизнь так разительно отличается от не-жизни. Так
Я нахожу другой способ задать этот тип вопроса: Что именно означает наш взгляд на универсальную динамическую
законы абстрагируются от жизни, так что поразительные различия между живым и неживым становятся
неясно и, по-видимому, парадоксально?
Это чувство парадокса, т.
то же чувство, которое двигало Бором, Вигнером, Поланьи, скептиками и, по иронии судьбы, основателями
то, что сейчас является редукционистской молекулярной биологией, как Дельбрюк. Все они верили, что жизнь следует законам, но
из их концепции закона они не могли понять, почему жизнь так разительно отличается от не-жизни. Так
Я нахожу другой способ задать этот тип вопроса: Что именно означает наш взгляд на универсальную динамическую
законы абстрагируются от жизни, так что поразительные различия между живым и неживым становятся
неясно и, по-видимому, парадоксально?
Мой первый ответ состоит в том, что динамический язык абстрагируется от предметной стороны эпистемического разреза.
Необходимое разделение законов и начальных условий является явным принципом в физике и стало
основа (и предвзятость) объективности во всех науках. Идеал физики состоит в устранении субъективного
наблюдатель полностью. Оказалось, что на квантовом уровне это принципиально невозможно, но что
идеал не изменился. Физика в значительной степени игнорирует исключительные эффекты индивидуальных (субъективных)
ограничений и граничных условий и фокусируется на общей динамике законов. Это потому что
ограничения предполагаются сводимыми к законам (хотя мы знаем, что они не сводимы к эпистемологическим
сокращения), а также потому, что математика сложных ограничений часто неуправляема. Философы
представили бесчисленные неразрешимые метафизические модели разреза разум-мозг, и физики
представил более точные, но все еще неразрешимые математические модели квантовых измерений. Но на
первобытный уровень, где все началось, разрез генотип-фенотип теперь воспринимается как должное, как обычное
химия.
Физика в значительной степени игнорирует исключительные эффекты индивидуальных (субъективных)
ограничений и граничных условий и фокусируется на общей динамике законов. Это потому что
ограничения предполагаются сводимыми к законам (хотя мы знаем, что они не сводимы к эпистемологическим
сокращения), а также потому, что математика сложных ограничений часто неуправляема. Философы
представили бесчисленные неразрешимые метафизические модели разреза разум-мозг, и физики
представил более точные, но все еще неразрешимые математические модели квантовых измерений. Но на
первобытный уровень, где все началось, разрез генотип-фенотип теперь воспринимается как должное, как обычное
химия.
Мой второй ответ заключается в том, что если абстрагироваться от деталей взаимодействия субъекта и объекта,
«специфический диапазон» размеров и поведения аллостерических полимеров, связывающих субъект и объект,
Контролируемая памятью конструкция полипептидов, складывание в высокоспецифичные ферменты и др. функциональные макромолекулы, отображение последовательностей в структуры «многие ко многим», самосборка и
много зависимых от конформации элементов управления – другими словами, если вы игнорируете фактическую физику, связанную с этими
молекулы, соединяющие эпистемологический разрез, то маловероятно, что вы когда-нибудь сможете различить
живые организмы по динамическим законам «неорганических корпускул» или из любого числа крупнозернистых
искусственные симуляции и симулякры жизни. Разве не правдоподобно, что жизнь была впервые отделена от неживой материи не какой-то модификацией физики, какой-то сложной нелинейной динамикой или какой-то универсальной
законы сложности, а локальные и уникальные гетерополимерные ограничения, которые демонстрируют подробное поведение
в отличие от поведения любых других известных форм материи во Вселенной?
функциональные макромолекулы, отображение последовательностей в структуры «многие ко многим», самосборка и
много зависимых от конформации элементов управления – другими словами, если вы игнорируете фактическую физику, связанную с этими
молекулы, соединяющие эпистемологический разрез, то маловероятно, что вы когда-нибудь сможете различить
живые организмы по динамическим законам «неорганических корпускул» или из любого числа крупнозернистых
искусственные симуляции и симулякры жизни. Разве не правдоподобно, что жизнь была впервые отделена от неживой материи не какой-то модификацией физики, какой-то сложной нелинейной динамикой или какой-то универсальной
законы сложности, а локальные и уникальные гетерополимерные ограничения, которые демонстрируют подробное поведение
в отличие от поведения любых других известных форм материи во Вселенной?
ПРИМЕЧАНИЯ
1. Взгляды Бора трудно сокращать без искажения: In Light and Life Bohr (1933)
начинается: «С одной стороны, удивительные черты, постоянно обнаруживающиеся в физиологических
исследований, которые так заметно отличаются от того, что известно о неорганической материи, привели биологов
к убеждению, что правильное понимание существенных аспектов жизни невозможно в чисто физическом
условия. С другой стороны, воззрение, известное как витализм, вряд ли может быть однозначно выражено
предположение, что вся органическая жизнь управляется особой жизненной силой, неизвестной физике. Действительно, я думаю, мы
все согласны с Ньютоном в том, что конечной основой науки является ожидание того, что природа проявит то же самое.
эффекты в тех же условиях. Если, следовательно, мы смогли продвинуть анализ механизма
живых организмов вплоть до атомных явлений, мы не должны ожидать найти какие-либо черты, чуждые
неорганическое вещество». Затем он продолжает: «. . .напрашивается мысль, что минимальную свободу мы должны допустить
организм будет достаточно большим, чтобы позволить ему, так сказать, скрывать от нас свои секреты. С этой точки зрения,
само существование жизни должно быть в биологии. . . [подобно кванту действия], взятому за базовый факт, который не может
быть выведены из обычной механической физики».0003
С другой стороны, воззрение, известное как витализм, вряд ли может быть однозначно выражено
предположение, что вся органическая жизнь управляется особой жизненной силой, неизвестной физике. Действительно, я думаю, мы
все согласны с Ньютоном в том, что конечной основой науки является ожидание того, что природа проявит то же самое.
эффекты в тех же условиях. Если, следовательно, мы смогли продвинуть анализ механизма
живых организмов вплоть до атомных явлений, мы не должны ожидать найти какие-либо черты, чуждые
неорганическое вещество». Затем он продолжает: «. . .напрашивается мысль, что минимальную свободу мы должны допустить
организм будет достаточно большим, чтобы позволить ему, так сказать, скрывать от нас свои секреты. С этой точки зрения,
само существование жизни должно быть в биологии. . . [подобно кванту действия], взятому за базовый факт, который не может
быть выведены из обычной механической физики».0003
2. Консенсус среди биологов 1970-х годов можно найти в Biology and the Future of Man под редакцией
Филип Хэндлер, отчет комитета Национальной академии наук, которому поручено представить «
полный обзор основных моментов современного понимания наук о жизни». Предисловие Хендлера
утверждает: «Тема этой презентации состоит в том, что жизнь может быть понята с точки зрения законов, которые управляют и
явления, характеризующие неодушевленную, физическую вселенную и действительно то, что по своей сути жизнь может
понять только на языке химии».0003
Предисловие Хендлера
утверждает: «Тема этой презентации состоит в том, что жизнь может быть понята с точки зрения законов, которые управляют и
явления, характеризующие неодушевленную, физическую вселенную и действительно то, что по своей сути жизнь может
понять только на языке химии».0003
3. Необходимо обратиться к их обширным трудам для адекватного взгляда на эти идеи. Юджин Вигнер
(1961) не могли приспособить самовоспроизведение, используя линейные законы квантовой теории. Дж. М. Бургерс
(1965), вслед за философом А. Н. Уайтхедом, считал: «Существуют существенные черты жизни, которые
не имеют однозначного отношения к состояниям материи или полям, которые можно объективно охарактеризовать
[по обычной физике и математике]. Их объяснение требует ссылки на субъективные особенности».
Бюргерс рассматривал эти особенности как форму памяти, присущую добиотической вселенной, но возникающую и
постепенно усиливаясь в ходе эволюции. Уолтер Эльзассер (1975) принял квантовую теорию как
правильно применительно к жизни в принципе, но считал, что существуют и «биотонические» законы, управляющие
«непостижимая сложность», которая делала жизнь непоправимо нелинейной. Эльзассер и Бюргерс чувствовали, что жизнь
Хранит некоторые формы информации не только «механическими средствами». Роберт Розен (1991) утверждает, что
«это самое разделение на независимые категории причинности», которое мешает ньютоновской картине
описывая характерные для жизни отношения «повлечений» и «связей». Он сосредоточился на классе
формальные структуры, моделирующие эти отношения.
Эльзассер и Бюргерс чувствовали, что жизнь
Хранит некоторые формы информации не только «механическими средствами». Роберт Розен (1991) утверждает, что
«это самое разделение на независимые категории причинности», которое мешает ньютоновской картине
описывая характерные для жизни отношения «повлечений» и «связей». Он сосредоточился на классе
формальные структуры, моделирующие эти отношения.
4. «Таким образом аксиоматизируя автоматы, можно выбросить половину проблемы в окно, и
быть более важной половиной. Смирился с тем, чтобы не объяснять, как эти части состоят из реальных
вещи, в частности, как эти части состоят из реальных элементарных частиц или даже из высших
химические молекулы. Никто не задается самым интригующим, захватывающим и важным вопросом о том, почему
молекулы или агрегаты, которые в природе действительно встречаются в этих частях, являются такими вещами, почему они
в одних случаях они представляют собой очень большие молекулы, а в других — большие агрегаты, почему они
всегда лежат в диапазоне, начинающемся с нескольких микрон и заканчивающемся несколькими дециметрами. Это очень своеобразно
диапазон для элементарного объекта, так как даже в линейной шкале он, по крайней мере, в пяти десятых степенях отстоит от
размеров действительно элементарных объектов» (фон Нейман, 1966, с. 77)
Это очень своеобразно
диапазон для элементарного объекта, так как даже в линейной шкале он, по крайней мере, в пяти десятых степенях отстоит от
размеров действительно элементарных объектов» (фон Нейман, 1966, с. 77)
5. Вигнер (1960) задал тон своей статье цитатой из К. С. Пирса: «… и вполне вероятно, что здесь есть какой-то секрет, который еще предстоит раскрыть». формализм, такой как матрицы, комплексные числа и бесконечномерное гильбертово пространство, не может быть выведен из физических наблюдений или физических законов, или даже из здравого смысла. Тем не менее, они кажутся совершенно подходит, если не существенно, для квантовой теории. В заключение Вигнер высказал предположение о том, что жизнь может быть конфликтом между законами наследственности и квантовой теорией (см. также Wigner, 1961).
6. Я определяю символ с точки зрения его структуры и функции. Во-первых, символ может существовать только в контексте
живой организм или его артефакты. Жизнь возникла из символической памяти, а символы возникли из жизни. я
считаю неуместным использовать понятие символа, даже метафорически, в физических системах, где нет
функция есть. Символы не существуют изолированно, а являются частью семиотической или лингвистической системы (Патти,
1969а). Семиотические системы состоят из (1) дискретного набора символьных структур (символических носителей), которые могут
существуют в неактивном, независимом от скорости (нединамическом) состоянии, как и в большинстве хранилищ памяти, (2) набор
интерпретирующие структуры (неинтегрируемые ограничения, коды) и (3) организм или система, в которой
символы имеют функцию (Патти, 1986). Во многих иерархических структурах существует бесчисленное множество символьных функций.
уровнях, но контроль над строительством стоял на первом месте.
Жизнь возникла из символической памяти, а символы возникли из жизни. я
считаю неуместным использовать понятие символа, даже метафорически, в физических системах, где нет
функция есть. Символы не существуют изолированно, а являются частью семиотической или лингвистической системы (Патти,
1969а). Семиотические системы состоят из (1) дискретного набора символьных структур (символических носителей), которые могут
существуют в неактивном, независимом от скорости (нединамическом) состоянии, как и в большинстве хранилищ памяти, (2) набор
интерпретирующие структуры (неинтегрируемые ограничения, коды) и (3) организм или система, в которой
символы имеют функцию (Патти, 1986). Во многих иерархических структурах существует бесчисленное множество символьных функций.
уровнях, но контроль над строительством стоял на первом месте.
7. Поланьи (1968) может быть включен в список других нередукционистов (примечание 3). Однако я считаю, что логика
его аргумент против редукционизма может быть сделан в рамках обычной физической теории и не требует
постулирование некоторого отклонения, модификации или расширения физического языка или понятий. Он утверждает только
эмерджентная иерархия физических структур «граничных условий», подчиняющаяся всем нормальным законам, но
приобретая сложность, которая требует новых наблюдаемых и новых моделей. Появление, концепция, которую когда-то избегали
философами и физиками, теперь принято в искусственной жизни, теории сложности, неврологии,
философии и физики (например, Рэй, 1992; Кариани, 1992 год; Андерсон, 1972, 1997).
Он утверждает только
эмерджентная иерархия физических структур «граничных условий», подчиняющаяся всем нормальным законам, но
приобретая сложность, которая требует новых наблюдаемых и новых моделей. Появление, концепция, которую когда-то избегали
философами и физиками, теперь принято в искусственной жизни, теории сложности, неврологии,
философии и физики (например, Рэй, 1992; Кариани, 1992 год; Андерсон, 1972, 1997).
8. Явное признание того, что эти условия являются существенным требованием объективности, возникло только
постепенно, достигнув кульминации в этом столетии с тем, что сейчас называется принципами инвариантности или симметрии (например,
Вигнер, 1964). Все теории-кандидаты должны сначала соответствовать этим принципам. В идеале объективность
вера в то, что точно такие же события произойдут независимо от того, наблюдались они на самом деле или нет. За исключением
очень редкий случай «квантового неразрушающего», этот идеал недостижим, поскольку измерение в квантовых
теория изменяет состояние системы (но не законы). Постмодернистские философы утверждают, что этот идеал
объективность также недостижима из-за культурных влияний. Даже объективность фундаментальных
частицы подвергались критике на культурных основаниях (например, Пикеринг, 1984). Конечно, многие аспекты
наши физические теории являются общепринятыми социальными построениями, но другие аспекты кажутся неумолимо объективными и
выдержали гораздо более суровые и серьезные вызовы со стороны скептической и конкурентной физики
сообщества, чем предлагали социальные конструктивисты.
Постмодернистские философы утверждают, что этот идеал
объективность также недостижима из-за культурных влияний. Даже объективность фундаментальных
частицы подвергались критике на культурных основаниях (например, Пикеринг, 1984). Конечно, многие аспекты
наши физические теории являются общепринятыми социальными построениями, но другие аспекты кажутся неумолимо объективными и
выдержали гораздо более суровые и серьезные вызовы со стороны скептической и конкурентной физики
сообщества, чем предлагали социальные конструктивисты.
9. Некоторые специалисты по моделированию динамики считают, что естественный отбор может происходить как чисто динамический процесс без
необходимость ограничения символической памяти. Например, Гудвин (1994) утверждает: «Из этого становится ясно, что
что в естественном отборе нет ничего особенно биологического: это просто термин, используемый биологами
для описания того, как одна форма заменяет другую в результате их различных динамических свойств. .
. Мы могли бы, если бы захотели, просто заменить термин естественный отбор термином динамическая стабилизация ,
появление устойчивых состояний в динамической системе». Точно так же Келсо (1995) утверждает: «Таким образом, отбор и
самоорганизация идут рука об руку, как хлеб с маслом. Действительно, язык отбора именно в
те же термины, что и основная динамика паттерна». По многим причинам, приведенным выше, я не согласен с тем, что
Сама по себе динамика — достаточно богатый язык для описания жизни. В частности, естественный отбор
больше, чем распределение населения со статистической динамикой. Единицы, образующие совокупность, должны
воспроизводиться с контролем своих индивидуальных вариаций.
.
. Мы могли бы, если бы захотели, просто заменить термин естественный отбор термином динамическая стабилизация ,
появление устойчивых состояний в динамической системе». Точно так же Келсо (1995) утверждает: «Таким образом, отбор и
самоорганизация идут рука об руку, как хлеб с маслом. Действительно, язык отбора именно в
те же термины, что и основная динамика паттерна». По многим причинам, приведенным выше, я не согласен с тем, что
Сама по себе динамика — достаточно богатый язык для описания жизни. В частности, естественный отбор
больше, чем распределение населения со статистической динамикой. Единицы, образующие совокупность, должны
воспроизводиться с контролем своих индивидуальных вариаций.
Каталожные номера
Андерсон, П.В., 1972, «Больше другое». Наука 177, 393-396.
Андерсон, П. В., 1997, «Является ли само измерение эмерджентным свойством?» Сложность 3(1), 14-16.
Бор, Нильс, 1933, «Свет и жизнь». Nature 131, 421. Перепечатано в Bohr, N., Atomic Physics and
Человеческие знания (Джон Уайли, Нью-Йорк) с. 3.
Nature 131, 421. Перепечатано в Bohr, N., Atomic Physics and
Человеческие знания (Джон Уайли, Нью-Йорк) с. 3.
Родился, Макс, 19 лет69, «Символ и реальность», в: Physics in My Generation (Springer-Verlag, NY), стр. 132- 146.
Брукс, Р. А., 1992, «Искусственная жизнь и настоящие роботы», в: К практике автономных систем, F. Дж. Варела и П. Бургин (редакторы) (MIT Press, Кембридж, Массачусетс), стр. 3–10.
Брукс, Р. А. и Мэйс, П. (ред.) 1994, Artificial Life 4 (MIT Press, Кембридж, Массачусетс).
Бургерс, Дж. М., 1965, Опыт и концептуальная деятельность (MIT Press, Кембридж, Массачусетс).
Кариани, П., 1992, «Появление и искусственная жизнь», в: Искусственная жизнь II , К. Лэнгтон, К. Тейлор, Дж. Фармер, С. Расмуссен, (ред.) (Аддисон-Уэсли, Редвуд-Сити, Калифорния), стр. 775-797.
Кассирер, Э., 1957, Философия символических форм, Vol. 3 , Феноменология познания
(Издательство Йельского университета, Нью-Хейвен, Коннектикут).
3 , Феноменология познания
(Издательство Йельского университета, Нью-Хейвен, Коннектикут).
Кларк А., 1997, Быть там (MIT Press, Кембридж, Массачусетс).
Конрад М., 1969, Компьютерные эксперименты по эволюции коадаптации в примитивной экосистеме , Кандидатская диссертация, программа биофизики, Стэнфордский университет, Стэнфорд, Калифорния.
Конрад, М. и Патти, Х. Х., «Эксперименты по эволюции с искусственной экосистемой». J. Теоретическая Биология 28, 393-409.
Конрад, М., 1990, «Геометрия эволюции». БиоСистемс 24, 61-81.
Коуэн, Г. А., Пайнс, Д., и Мельцер, Д. (ред.), 1994, Сложность, метафоры, модели и реальность (Аддисон-Уэсли, Рединг, Массачусетс).
Дельбрюк, Макс, 1949, Академия искусств и наук Коннектикута 38, 173.
Иден, Р. Дж., 1951, «Квантовая механика неголономных систем». Труды Королевского
Общество (Лондон) 205A, 583-595.
Elsasser, W.M., 1975, Главное изложение биологии (Северная Голландия, Амстердам, The Нидерланды).
Emmeche, C., 1994, The Garden in the Machine (Princeton University Press, Принстон, Нью-Джерси) с. 158.
Фонтана, В., 1992, “Алгоритмическая химия”, в: Искусственная жизнь II, К. Лэнгтон, К. Тейлор, Дж. Фармер, С. Расмуссен, (ред.) (Аддисон-Уэсли, Редвуд-Сити, Калифорния), стр. 159–209.
Frauenfelder H. and Wolynes, P.G., 1994, «Биомолекулы: где физика сложности и встреча с простотой ». Physics Today , февраль 1994 г., стр. 58–64.
.Гелл-Манн, М., 1994, The Quark and the Jaguar (WH Freeman, NY), с. 134.
Гольдштейн, Х., 1953, Классическая механика (Аддисон-Уэсли, Кембридж, Массачусетс).
Гудвин, Б., 1994, Как леопард изменил свои пятна (Саймон и Шустер, Нью-Йорк) с. 53.
Грене, М., 1974, Знающий и известный (Калифорнийский университет Press, Беркли, Калифорния).
Холдейн, JBS, 1927, «О правильном размере», в: Возможные миры и другие эссе (Chatto & Виндус, Лондон). Перепечатано в: О правильном размере, Дж. М. Смит (ред.) (Oxford University Press, 1985)
Hertz, H., 1894, Die Principien der Mechanik in neuem Zusammenhange dargestellt (Лейпциг). Английский перевод: Принципы механики (Довер, Нью-Йорк, 1956 г.).
Хоффмайер, Дж. и Эммече, К., 1991, «Двойственность кода и семиотика природы», в: О семиотике. Моделирование , М. Андерсон и Ф. Меррелл (ред.) Берлин: Mouton de Gruyter, стр. 117-166.
Холланд, Дж., 1995, Скрытый Орден (Аддисон-Уэсли, Рединг, Массачусетс).
Кауфман С., 1993, The Origins of Order (Oxford University Press), стр. 25, 36.
Кендрю, Дж. К., 19 лет67, обзор Фаг и истоки молекулярной биологии . Научный американец 216, 142.
Kelso, JAS, 1995, Dynamic Patterns (MIT Press, Cambridge, MA) p. 183.
183.
Кулл, К., 1998, «О семиозисе, Умвельте и семиосфере». Семиотика 120, 3-4, 299-310.
Лэнгтон, К., 1989, «Искусственная жизнь», в: Искусственная жизнь , К. Лэнгтон (ред.) (Аддисон-Уэсли, Редвуд Город, Калифорния) с. 15.
Неймарк И.И., Фуфаев Н.А., 1972, Динамика неголономных систем (Переводы математические монографии, т. 33, Американское математическое общество).
Mayr, E., 1997, This Is Biology (издательство Гарвардского университета, Кембридж, Массачусетс) с. 32.
Pattee, HH, 1961, «О происхождении макромолекулярных последовательностей». Биофизический журнал 1,683-710.
Патти, Х. Х., 19 лет65, «Распознавание наследуемого порядка в примитивных химических системах», в: The Origins of Prebiological Systems , S. Fox (ed.) (Academic Press, NY).
Патти, HH, 1967, «Квантовая механика и происхождение жизни». J. Теоретическая биология 17, 410-420.
Патти, 1969a, “Как молекула становится сообщением?” Приложение по биологии развития 3, 1- 16.
Pattee, HH, 1969b, «Физические проблемы наследственности и эволюции», в На пути к теоретической биологии 2 , CH Waddington (ed.) (Edinburgh University Press), p. 274.
Патти, Х. Х., 1982, «Клеточная психология: эволюционный подход к проблеме символьной материи». Познание и теория мозга 5(4), 325-341.
Патти, Х. Х., 1986, “Универсальные принципы измерения и языковые функции в развитии”. систем», в: Сложность, язык и жизнь , Дж. Л. Касти и А. Карлквист (ред.) (Springer- Верлаг, Берлин), стр. 579.-581.
Pattee, HH, 1995, «Развитие самореференции: материальные символы и семантическое завершение». Связь и Познание Искусственный интеллект 12(1-2), 9-27.
Пирсон, К., 1937, Грамматика науки (Дж. М. Дент и сыновья, Лондон) с. 287. [Первые издания
опубликовано в 1892 г.]
[Первые издания
опубликовано в 1892 г.]
Пикеринг, А., 1984, Конструирование кварков: социологическая история физики элементарных частиц (Эдинбург Университетское издательство).
Поланьи, М., 1964, Личные знания (Харпер, Нью-Йорк).
Поланьи, М., 1968, “Непреодолимая структура жизни”. Наука 160:1308-1312.
Рэй, Т., 1992, «Подход к синтезу жизни», в: Artificial Life II , C. Langton, C. Taylor, J. Фармер, С. Расмуссен (ред.) (Аддисон-Уэсли, Редвуд-Сити, Калифорния), стр. 371-408.
Розен, Р., 1991, Сама жизнь (издательство Колумбийского университета, Нью-Йорк).
Розен, Р., 1987, «О возможностях синтаксиса в математике и естественных науках: машинная метафора», в: Настоящие мозги, искусственные разумы , Дж. Л. Касти и А. Карлквист (ред.) (Северная Голландия, Нью-Йорк), стр. 1- 23.
Шустер, П., 1994, «Как молекулы ДНК и вирусы исследуют свои миры?», в: Коуэн, Г. А.,
Пайнс, Д., и Мельцер, Д. (ред.), 199.4, Сложность, метафоры, модели и реальность (Аддисон-Уэсли, Рединг, Массачусетс), стр. 383–414.
А.,
Пайнс, Д., и Мельцер, Д. (ред.), 199.4, Сложность, метафоры, модели и реальность (Аддисон-Уэсли, Рединг, Массачусетс), стр. 383–414.
Shear, J., 1997, Объяснение сознания: сложная проблема (MIT Press, Кембридж, Массачусетс).
Зоммерфельд А., 1956, Механика . (Академическое издательство, Нью-Йорк) с. 80.
Stent, G.S., 1966, в: Phage and the Origin of Molecular Biology , J. Cairns, G.S. Stent, and J.D. Томпсон (ред.) (Лаборатория количественной биологии Колд-Спрингс-Харбор, 1966) с. 4.
Тейлор, Дж. Г., 1999, Гонка за сознание (MIT Press, Кембридж, Массачусетс).
Варела Ф.Дж., Томпсон Э. и Рош Э., 1991, Воплощенный разум (MIT Press, Кембридж, Массачусетс).
фон Нейман, Дж., Теория самовоспроизводящихся автоматов , А. В. Беркс (редактор) (Университет Иллинойса Пресс, 1966).
фон Нейман, Дж., 1955, Математические основы квантовой механики (Принстонский университет Press, Принстон, Нью-Джерси)
Waddington, CH (ed. ), 1968-72, Towards a Theoretical Biology, vol. 1, Пролегомена, 1968; об. 2,
Эскизы, 1969; об. 3, Черновики, 1970; об. 4, Очерки, 1972, Эдинбург: издательство Эдинбургского университета,
1970 г.; об. 4, Очерки, 1972, Эдинбург: Издательство Эдинбургского университета.
), 1968-72, Towards a Theoretical Biology, vol. 1, Пролегомена, 1968; об. 2,
Эскизы, 1969; об. 3, Черновики, 1970; об. 4, Очерки, 1972, Эдинбург: издательство Эдинбургского университета,
1970 г.; об. 4, Очерки, 1972, Эдинбург: Издательство Эдинбургского университета.
Weyl, H., 1949, Философия математики и естествознания (Princeton University Press), с. 237.
Вигнер, Э.П., 1960, «Необоснованная эффективность математики в естественных науках». Сообщения по чистым и прикладным наукам 13, 1-14.
Вигнер, Э. П., 1961, «О невозможности самовоспроизведения», в: Логика личного знания (Кеган Пол, Лондон) с. 231.
Вигнер, EP, 1964, «События, законы и принципы инвариантности». Наука 145, 995-999.
Вигнер, EP, 1982, «Ограничения достоверности современной физики», в: Mind in Nature .
Нобелевская конференция XVII (Harper & Row, Сан-Франциско, Калифорния) с. 119.
Whittaker, ET, 1944, Трактат по аналитической динамике частиц и твердых тел , 4-е изд. (Довер, Нью-Йорк) с. 33 и Глава VIII.
Измерение скорости передачи информации | Факультет физики
Мы разработали новую методику измерения скорости передачи информации v i на основе теоретико-информационных идей. Мы делаем это, сначала создавая алфавит символов, каждый из которых представляет собой отдельную форму импульса. Затем мы посылаем символы через вакуум и тестовую среду, которая имеет либо очень высокую, либо очень медленную групповую скорость. Измеряя точность, с которой можно различить символы в зависимости от времени, мы можем определить скорость распространения информации.
Создание алфавита
| Два символа в нашем алфавите. Передние кромки идентичны. |
Наша техника начинается с создания алфавита форм символов. Алфавит, который мы используем, двоичный, состоит из двух символов, но в принципе может иметь любое количество символов. Мы разработали наши символы так, чтобы их было легко отличить друг от друга, , но не сразу . Передние края символов идентичны.
Мы разработали наши символы так, чтобы их было легко отличить друг от друга, , но не сразу . Передние края символов идентичны.
Этот выбор форм символов имеет ряд привлекательных особенностей. Во-первых, когда символы становятся различимыми, отношение сигнал/шум велико. Другая привлекательность заключается в том, что мы можем наблюдать, как символы ведут себя, когда они похожи, и когда они различны.
Количественная оценка обнаруженной информации
Представьте, что вы отправляете информацию о своем друге с помощью этих символов. Пока не беспокойтесь о быстром свете или скоростях. Допустим, вы сидите рядом друг с другом. Каждую минуту вы отправляете один из этих символов, чтобы сообщить ей, счастливы ли вы (1) или грустны (0).
Когда придет время, вы начнете отправлять символ. В момент времени -100 нс ваша подруга ясно видит приближающийся символ, но может ли она сказать, счастливы вы или грустны? Нет! Она еще не знает, потому что в этот момент символы те же. Поэтому она не получила никакой информации 1 .
Поэтому она не получила никакой информации 1 .
Более тонкий вопрос: действительно ли вы отправляли какую-либо информацию? Ответ снова нет. Причина в том, что вы все еще можете передумать. В момент времени -100 нс вы еще не зафиксировались, и вам не нужно это делать до времени 0 [1]! Только тогда вы должны зафиксировать, и только тогда вы отправляете информацию.
А как насчет вашего друга? В момент времени 100 нс вы фиксируете символ, и она может легко определить, в каком вы настроении. В этом случае время отправки и время получения информации почти совпадают, потому что вы и ваш друг так близки. друг другу, но если бы вы были на большом расстоянии друг от друга, она бы получила информацию намного позже, чем вы ее отправили. Эта разница во времени вместе с расстоянием говорит нам о скорости передачи информации.
Задержка обнаружения
Более реалистичные формы символов. Они имеют неидеальные разрывы и добавляют шум. Они имеют неидеальные разрывы и добавляют шум. |
Но есть одна загвоздка! Формы символов, использованные выше, идеальны. В реальном мире мы не можем делать такие идеальные прыжки или такие плавные формы. Устройства, которые мы используем, имеют шум и склонны фильтровать или сглаживать скачки. В результате символы, показанные справа, стали немного более реалистичными.
Что, если это то, что видит ваш друг? Допустим, она снова сидит прямо напротив вас за столом. Когда она улавливает информацию? Вы все еще сделали свой выбор в момент времени 0, но теперь она не может сказать, что вы отправили, до некоторого времени спустя. Мы называем эту задержку задержкой обнаружения , и она не имеет ничего общего со скоростью передачи информации. Это фундаментальная часть отправки и обнаружения информации, и это то, что мы должны учитывать в наших измерениях.
Частота битовых ошибок
Обнаружив реалистичные символы, показанные выше, когда ваш друг может быть полностью уверен, какой символ вы отправили? Настоящий ответ никогда! Если шум сильный, всегда есть шанс, что то, что она видит только , выглядит как 0, но на самом деле было 1. Однако в какой-то момент она может быть уверена на 90% или на 99% и т. д.
Однако в какой-то момент она может быть уверена на 90% или на 99% и т. д.
В в мире теории информации и коммуникаций мы количественно определяем такую достоверность с помощью коэффициента битовых ошибок, или BER. BER — это всего лишь доля неверных идентификаций символов. Таким образом, BER, равный 1/2, является наихудшим из возможных; это то, что вы получите, если вы даже не посмотрите на символы и просто угадайте. Чем лучше ваше обнаружение, тем ниже будет этот BER. BER, равный 0,1, означает, что вы правы в 9 случаях из 10.
BER удобен тем, что дает нам способ количественного определения обнаруженной информации в заданное время. Если мы скажем вашей подруге, что она должна идентифицировать символ, который она получает во время -100 нс, и повторять тест снова и снова, она получит BER 1/2. Она будет гадать, потому что это все, что она может сделать. Теперь, если мы сделаем то же самое во время 100 нс, ее BER, вероятно, будет довольно хорошим, потому что это легко тогда различать символы. Все, что нам нужно сделать, это найти время, когда BER впервые отклоняется от 1/2.
Все, что нам нужно сделать, это найти время, когда BER впервые отклоняется от 1/2.
И снова нам мешает задержка обнаружения. Шум в импульсах приводит к шуму в BER, поэтому сразу не ясно, когда BER выходит за пределы 1/2. Мы должны выбрать некоторый порог BER, при котором, по нашему мнению, мы обнаруживаем информацию. Например, ваш друг может проверить 1000 символов и обнаружить, что он прав в 9 случаях из 10, когда он идентифицирует символ в момент времени 50 нс. С BER, равным 0,1, она может быть уверена, что обнаруживает какая-то информация.
Измерение скорости передачи информации
В соответствии с этой системой мы сказали бы, что вы отправили информацию в момент времени 0, ваш друг обнаружил ее в момент времени 50 нс, и (поскольку вы находитесь рядом друг с другом и не было время распространения) задержка обнаружения составляет 50 нс.
Проблема лишь немного усложняется, когда вы отправляете символы через какой-либо носитель. Часто бывает трудно точно узнать, когда информация покинула отправляющее устройство, потому что устройства могут быть довольно сложными. Однако, если мы отправим символы через одинаковую длину вакуума (где скорость информации равна с), мы сможем выяснить, когда информация была отправлена. Также трудно понять, какова задержка обнаружения. Однако мы можем оценить его, теоретически моделируя наш эксперимент. Преимущество теоретической модели в том, что вы можете знать ровно , когда информация была закодирована.
Однако, если мы отправим символы через одинаковую длину вакуума (где скорость информации равна с), мы сможем выяснить, когда информация была отправлена. Также трудно понять, какова задержка обнаружения. Однако мы можем оценить его, теоретически моделируя наш эксперимент. Преимущество теоретической модели в том, что вы можете знать ровно , когда информация была закодирована.
Комбинируя все эти инструменты, мы можем измерить скорость передачи информации через любой носитель!
Наши результаты
Итак, что мы видим? Когда мы измеряем информационную скорость в нашей системе, которая имеет очень быструю групповую скорость 3 , мы обнаруживаем, что информационная скорость v i ≈ 0,4(+ 0,7 – 0,2) с. Почему так медленно? Что ж, наш диапазон неопределенности включает с, но мы думаем, что причина, по которой мы получили 0,4 с, так же проста, как шум, несовершенная теоретическая модель и разные шумы в вакууме по сравнению с быстрыми случаями. Мы надеемся, что будущие эксперименты с лучшим оборудованием помогут приблизиться к реальному ответу!
Мы надеемся, что будущие эксперименты с лучшим оборудованием помогут приблизиться к реальному ответу!
Приложение: Идентификация символов
Может показаться, что идентифицировать символы, показанные выше, довольно легко, но для того, чтобы провести этот эксперимент хорошо, важно использовать наилучшую доступную технику. Мы используем схему идентификации, называемую согласованным фильтром.
Основная идея заключается в том, что каждый входящий символ сравнивается с двумя эталонными символами; идеальные формы символов для 0 и 1. Сравнение выполняется путем интегрирования произведения каждого эталонного символа с тестовым символом (включая некоторую нормализацию) до времени идентификации. Если тестовый символ подобен эталону, интеграл будет большим. В противном случае интеграл будет мал. Если один из этих интегралов вычесть из другого, полученное число говорит нам, какой символ мы думаем, что это .
Более полное описание см. в нашем недавнем письме.

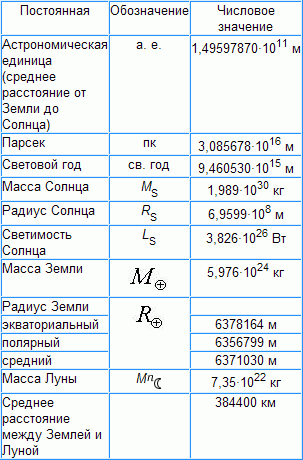
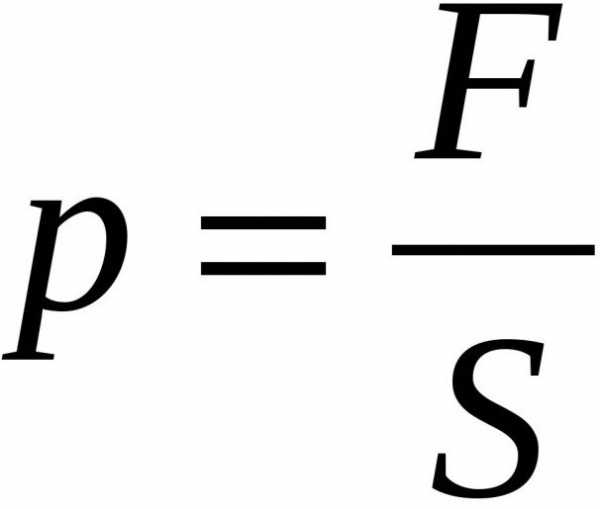
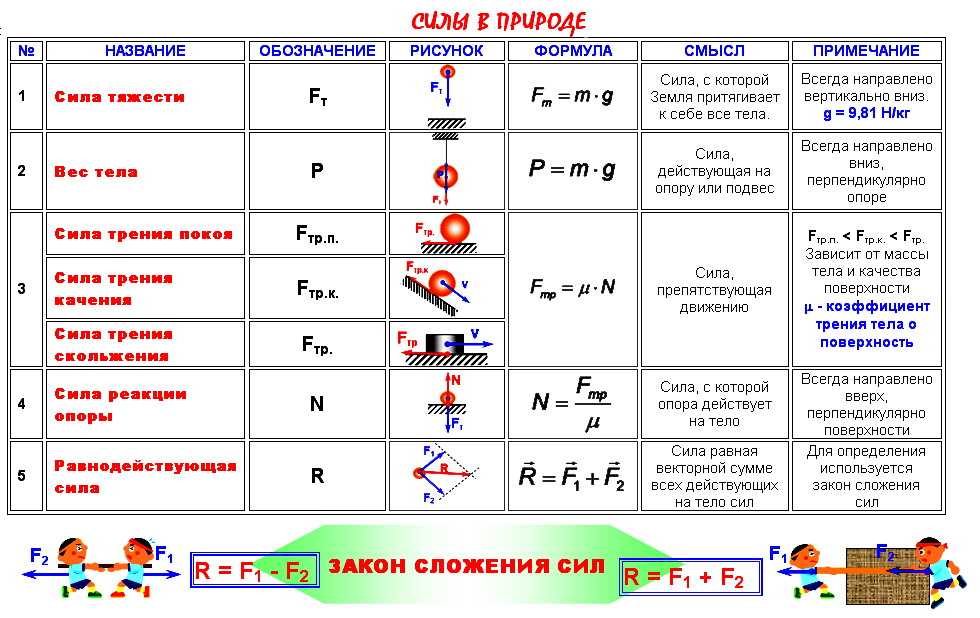

 У нас в
гостях “Улица Сезам”.
У нас в
гостях “Улица Сезам”.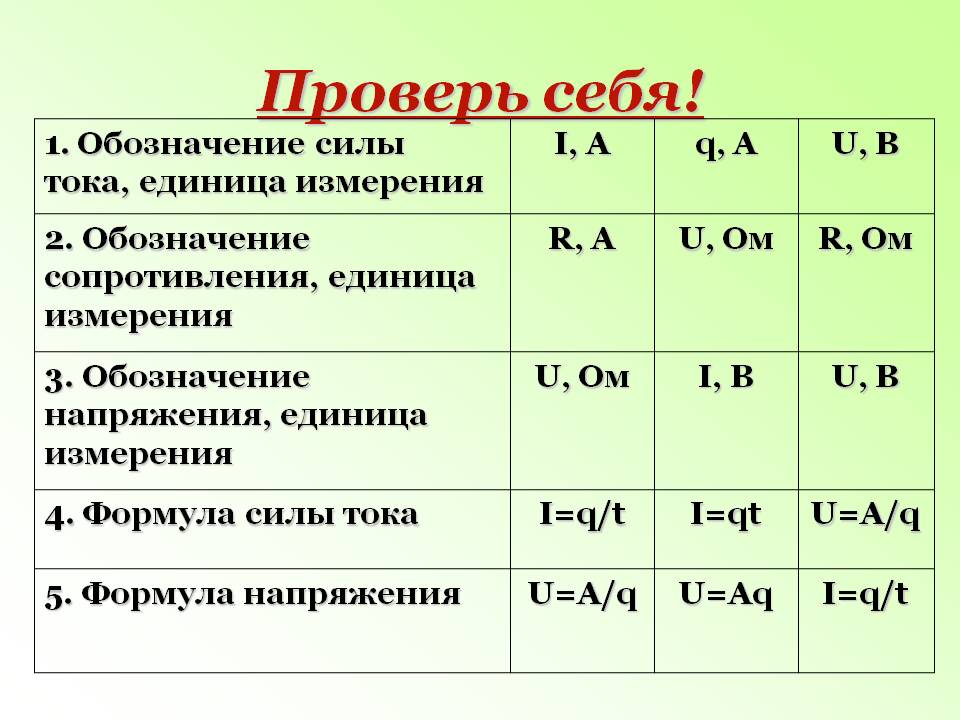 Они
необходимы для определения скорости. Для этого, работая в парах, расположите
данные вас единицы измерения в порядке возрастания.
Они
необходимы для определения скорости. Для этого, работая в парах, расположите
данные вас единицы измерения в порядке возрастания.