Каков физический смысл уравнения бернулли: 7.Физический смысл уравнения Бернулли . - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

7.Физический смысл уравнения Бернулли .

Уравнение Бернулли дает связь между давлением (P) , средней скоростью (v) ,

И геометрической высотой в различных сечениях (z) , является основным уравнением для практических расчетов в гидродинамике. Оно записывается для двух сечений потока 1-1 и 2-2 :

Где H – полная высота или полный напор.

Геометрическая высота , характеризует потенциальную энергию положения.

пьезометрическая высота , характеризует потенциальную энергию давления .

скоростная высота характеризует кинетическую энергию жидкости .

потерянная высота.

коэффициент неравномерности скорости по потоку .

Геометрический смысл :

При установившемся движении жидкости сумма четырёх высот в каждом живом сечении есть величина постоянная и равна полной высоте (H) (полному напору )

Физический смысл:

При установившемся движении жидкости сумма четырех удельных энергий неизменна вдоль потока и равна общему запасу удельной энергии .

8.Уравнение Бернулли для потока вязкой жидкости.

Вязкая жидкость –это жидкость в которой при движении возникают касательные напряжения .

Уравнение Бернулли выражает закон сохранения механической энергии .

H – полный напор –это удельная механическая энергия .

Z- геометрический напор(удельная потенциальная энергия положения ) .

пьезометрический напор (удельная потенциальная энергия давления).

скоростной напор (удельная кинетическая энергия ).

потери напора (для идеальной жидкости равно 0-ю).

Для вязкой несжимаемой жидкости :

давление в сечениях 1-1 и2-2.

средние скорости.

коэффициенты учитывающие неоднородность распределения скоростей.

координаты сечений.

9.Применение уравнения Бернулли при решении технических задач.

Мощность насоса.

Уравнение Бернулли –это основное уравнение гидродинамики , с помощью которого производят расчеты течения жидкости в трубопроводах , насосах , турбинах , приборах.

Геометрическая высота , характеризует потенциальную энергию положения.

пьезометрическая высота , характеризует потенциальную энергию давления .

H- полный напор.

коэффициенты учитывающие неоднородность распределения скоростей.

скоростная высота характеризует кинетическую энергию жидкости .

Пример.

Продолжение 9

Жидкость поступает из А по В (всасывающей трубке) в насос (Н) где энергия от двигателя передается жидкости , поступающей в нагнетательную линию (С).В сечении 1-1 установлен вакуумметр (P) .За насосом установлен манометр (P).

Удельная энергия в сечении 1-1 и 2-2 :

абсолютное давление.

т.к. жидкость приобретает дополнительную энергию .

Тогда :

Мощность насоса равна N :

т.е.N = расходу (Q) умноженному на разность давлений .

10.Расходометр Вентури .

Р.В.служит для измерения расхода жидкости (Q) в трубопроводах. Р.в. состоит из 2х участков : широкого и узкого .

Этот расходометр с горизонтальной осью. Проведем сечение 1-1 в широкой части и2-2 в узкой . Запишем уравнение неразрывности:

(Расход)

скорости.

площадь сечений .

Уравнение Бернулли будет :

т.к. труба горизонтальная то пренебрегаем.

Примем (коэффициент неравномерности скоростей).

исключаем из уравнения т.к. очень узкий проход 2, получаем :

находим измеряем манометрамии,

плотность ртути . Расход

Физический смысл уравнения Бернулли.

Рассмотрим частицу жидкости массой dm, которая движется по линии тока. Определим величину полной энергии, которой обладает частица в сечениях 1–1 и 2–2.

Полная энергия представляет собой сумму кинетической и потенциальной

энергии. Кинетическая энергия в сечении 1–1 равна u2dm/2. Потенциальная энергия относительно плоскости сравнения 0–0 равна произведению

веса частицы на высоту ее подъема над этой плоскостью z1gdm . В сечении 1–1 частица будет поднята на высоту z1 + p1/ρg, где p1/ρg – высота, соответствующая давлению, которое поднимет эту частицу, например, в

пьезометрической трубке. В сечении 2–2 частица будет поднята на высоту z2 + p2/ρg. Таким образом, в сечении 1–1 частица обладает потенциальной

энергией gdm (z1 + p1/ρg). Аналогично в сечении 2–2 gdm (z2 + p2/ρg).

Тогда полная энергия dE в сечениях будет равна:

(9)

Разделив почленно уравнения (9) на вес gdm, определим полную энергию жидкости, отнесенную к единице ее веса, т.е. удельную энергию de.

(10)

В (10) u12/2g и u22/2g – удельная кинетическая энергия; p1/ρg и p2/ρg

– удельная потенциальная энергия давления; z1 и z2 – удельная потенциальная энергия положения частицы в сечениях 1–1 и 2–2 соответственно.

Согласно уравнению Бернулли сумма трех указанных величин является постоянной, что приводит к равенству: de1= de2.

Сечения 1–1 и 2–2 взяты произвольно, поэтому

Внимание!

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас.

Бесплатные корректировки и доработки. Узнайте стоимость своей работы.

Расчет стоимостиГарантииОтзывы

(11)

Итак, сумма трех членов уравнения Бернулли есть сумма трех удельных энергий: удельной кинетической энергии, удельной потенциальной

энергии давления и удельной потенциальной энергии положения. Для

идеальной жидкости сумма трех удельных энергий по длине элементарной струйки – постоянна.

В общем, уравнение Бернулли является специальным выражением ос-

новного физического закона сохранения энергии.

Поможем написать любую работу на аналогичную тему

Реферат
Физический смысл уравнения Бернулли.
От 250 руб
Контрольная работа
Физический смысл уравнения Бернулли.
От 250 руб

Курсовая работа
Физический смысл уравнения Бернулли.
От 700 руб

Получить выполненную работу или консультацию специалиста по вашему учебному проекту

Узнать стоимость

Уравнение Бернулли | безграничная физика |

Применение уравнения Бернулли: давление и скорость

Для «идеального» течения вдоль линии тока без изменения высоты увеличение скорости происходит в результате уменьшения статического давления.

Цели обучения

Адаптируйте уравнение Бернулли для нестационарных или сжимаемых течений

Ключевые выводы

Ключевые моменты

Простейшая форма уравнения Бернулли (стационарное и несжимаемое течение) утверждает, что сумма механической энергии, потенциальной энергии и кинетической энергии вдоль поток постоянен. Следовательно, любое увеличение одной формы приводит к уменьшению другой.
Уравнение Бернулли учитывает только силы давления и гравитации, действующие на частицы жидкости. Следовательно, если вдоль линии тока нет изменения высоты, уравнение Бернулли становится балансом между статическим давлением и скоростью.
Стационарное уравнение Бернулли для несжимаемой жидкости может быть получено путем интегрирования 2-го закона Ньютона вдоль линии тока.

Ключевые термины

вязкость : Величина, выражающая величину внутреннего трения в жидкости, измеряемая силой на единицу площади, препятствующей равномерному потоку.
Ideal Fluid : Невязкая и несжимаемая жидкость
несжимаемый : Не поддается сжатию или конденсации.

Применение уравнения Бернулли

Связь между давлением и скоростью в идеальных жидкостях количественно описывается уравнением Бернулли, названным в честь его первооткрывателя, швейцарского ученого Даниэля Бернулли (1700–1782).

Уравнение Бернулли утверждает, что для несжимаемой и невязкой жидкости полная механическая энергия жидкости постоянна. (Невязкая жидкость считается идеальной жидкостью без вязкости.) 9221ρV2

, где \rho — плотность жидкости в (единица СИ: кг/м ³ ), а V — скорость жидкости (единица СИ: м/с). Единицей статического и динамического давления в системе СИ является паскаль.

Перекачка : Перекачка жидкости между двумя резервуарами. Выходной расход можно определить, проведя линию тока из точки (А) в точку (С).

Статическое давление — это просто давление в данной точке жидкости, динамическое давление — это кинетическая энергия на единицу объема жидкой частицы. Таким образом, жидкость не будет иметь динамического давления, если она не движется. Следовательно, если потенциальная энергия вдоль линии тока не изменяется, уравнение Бернулли подразумевает, что полная энергия вдоль этой линии тока постоянна и представляет собой баланс между статическим и динамическим давлением.

2 + \rho \text{g}\Delta \text{h} = \text{константа}ps+21ρV2+ρgΔh=константа

Вывод уравнения Бернулли

Уравнение Бернулли можно получить, интегрируя 2-й закон Ньютона вдоль линии тока с силами гравитации и давления как единственными силами, действующими на жидкий элемент. Учитывая, что любой обмен энергией является результатом консервативных сил, полная энергия вдоль линии тока постоянна и просто обменивается между потенциальной и кинетической.

Применение уравнения Бернулли

Уравнение Бернулли можно применять при перекачивании жидкости между двумя резервуарами. Еще одним полезным применением уравнения Бернулли является вывод закона Торричелли для потока из отверстия с острыми краями в резервуаре. Линия тока может быть проведена от верхней части резервуара, где известна полная энергия, до точки выхода, где известны статическое давление и потенциальная энергия, но неизвестно динамическое давление (скорость исходящего потока).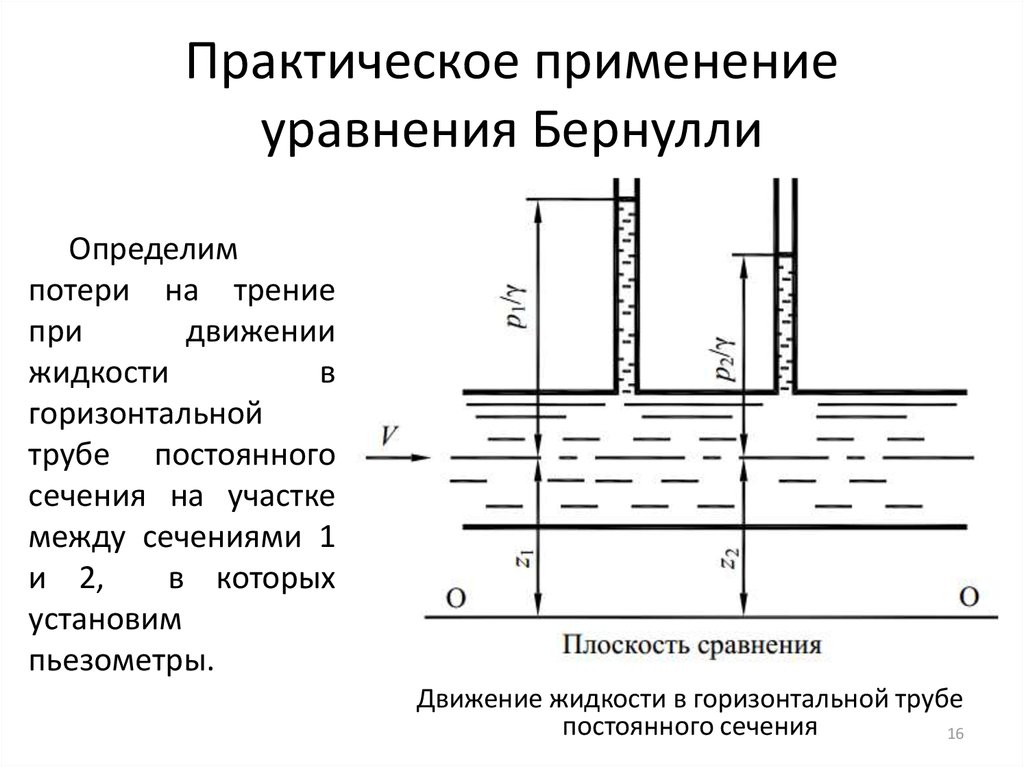

Адаптация уравнения Бернулли

Уравнение Бернулли может быть адаптировано к потокам, которые являются как нестационарными, так и сжимаемыми. Однако предположение о невязком течении сохраняется как в нестационарной, так и в сжимаемой версиях уравнения. Эффекты сжимаемости зависят от скорости потока относительно скорости звука в жидкости. Это определяется безразмерной величиной, известной как число Маха. Число Маха представляет собой отношение скорости объекта, движущегося в среде, к скорости звука в среде.