Резонансная частота LC контура. График. Калькулятор.
Резонансная частота LC контура. График. Калькулятор.Авторский сайт ТехСтоп Екб Ру
Стандарт лучшей рекламы … Проверить полномочия … Статичное размещение … Нравится – смотрите, иначе – листайте дальше … Никаких проблем …
# … mvideo.ru, Холодильники и морозильные камеры.
а также плиты газовые и электрические, посудомоечные машины, кулеры для воды, миксеры, блендеры и мясорубки, мультиварки … Кухонная техника, посуда и аксессуары, кофемолки и кофеварки …
# … eldorado.ru, Игры, софт и развлечения, интернет-магазин N1 в России, где всегда дешево.
# … ya.cc, Встраиваемая техника.
Встраиваемая техника для кухни, встроенное оборудование. Кухонная для кухни. Комплекты. Отзывы. Цены. Electrolux. С фото. Рейтинг. Шкафы. Bosch. Выбрать из каталога на сайте. Розетки. Бытовая электроника. Встройка соло. Подключить устройство. Интехника. Быттехника. Интерактивное оборудование. Кухонное и техническое. Приспособления для кухни. Доступное для встройки : холодильник, электрический духовой шкаф, микроволновая печь СВЧ, вытяжка, варочная панель, посудомоечная машина. Bosch. Electrolux. GEFEST. Gorenje. Hansa.
Интехника. Быттехника. Интерактивное оборудование. Кухонное и техническое. Приспособления для кухни. Доступное для встройки : холодильник, электрический духовой шкаф, микроволновая печь СВЧ, вытяжка, варочная панель, посудомоечная машина. Bosch. Electrolux. GEFEST. Gorenje. Hansa.
Официальный сайт, интернет магазин товаров – работает для вас, умея ценить ваши покупки и эмоции … Очень нужно каждому свое … Детские игрушки для девочек … Женские аксессуары для женщин … Бытовая техника … Обувь для юношей … Внешние аккумуляторы powerbank …
Калькуляторы параметров параллельной или последовательной LC цепи контура (включая RLC calc), в том числе : рассчитывают импеданс, фазовый сдвиг для соединения катушки индуктивности и конденсатора … Вычисляются, также : угловая частота ; емкостное реактивное сопротивление XC ; индуктивное реактивное сопротивление XL ; резонансная частота контура … При расчетах используется мнимая единица j …
Измерение частоты f и резонансной f0 в герцах (Гц), L индуктивности в генри (Гн) и C емкости в фарадах (Ф) – иногда бывает затруднительно : из-за неиспользуемых больших значений, которые нужно конвертировать в более привычные единицы . .. Но, одним из главных неудобств, для людей, незнакомых с поведением частоты и ее зависимости в LC контуре – является отсутствие наглядности, в виде простого и понятного графика взаимного влияния параметров частотной цепи – друг на друга …
.. Но, одним из главных неудобств, для людей, незнакомых с поведением частоты и ее зависимости в LC контуре – является отсутствие наглядности, в виде простого и понятного графика взаимного влияния параметров частотной цепи – друг на друга …
В первую очередь, это связано с отсутствием внятных инструментов рисования в HTML, тем более для интерактивного взаимодействия с калькулятором параметров цепи LC контура, чтобы методом прямого перебора подобрать оптимальные значения … Подключение технологий рисования в виде Canvas, SVG или иных, взаимодействующих с расчетами на JavaScript – также может оказаться затруднительным делом … В частности, лично я – не смог подобрать оптимального решения для онлайн рисования графика резонансной частоты и частотной зависимости, при изменении номиналов компонентов LC контура … И, поэтому – пошел по пути наименьшего сопротивления – в программную среду Excel, Microsoft Office …
В результате некоторых экспериментов – были разработаны однотипные калькуляторы, предоставляющие наглядный способ визуального наблюдения за поведением резонансной частоты LC контура – при изменении номиналов, составляющих его схему : катушки индуктивности и емкости конденсатора . .. Простая формула, на основе встроенных математических функций Excel Microsoft Office – полностью соответствует формуле расчета резонансной частоты LC контура …
.. Простая формула, на основе встроенных математических функций Excel Microsoft Office – полностью соответствует формуле расчета резонансной частоты LC контура …
Калькулятор резонансной частоты LC контура с графиком, расчет зависимости от емкости.
Калькулятор резонансной частоты LC контура с графиком, расчет зависимости от индуктивности.
При определенном, возникшем интересе – калькулятор графика резонансной частоты LC контура можно скачать и поэкспериментировать самому, лично … В поля, подсвеченные желтым фоном – можно вводить значения емкости (пФ) и индуктивности (мкГн), чтобы наглядно, на графике – отслеживать изменения и взаимные влияния параметров контура цепи …
Калькулятор, график, частота LC контура. Новый формат, XLSX, Excel, Microsoft Office …
Калькулятор, график, частота LC контура. Старый формат, XLS, Excel, Microsoft Office … Некоторые свойства книги Excel формата XSLX – не поддерживаются более ранними версиями XLS … Предупреждение относится к несущественной потере точности .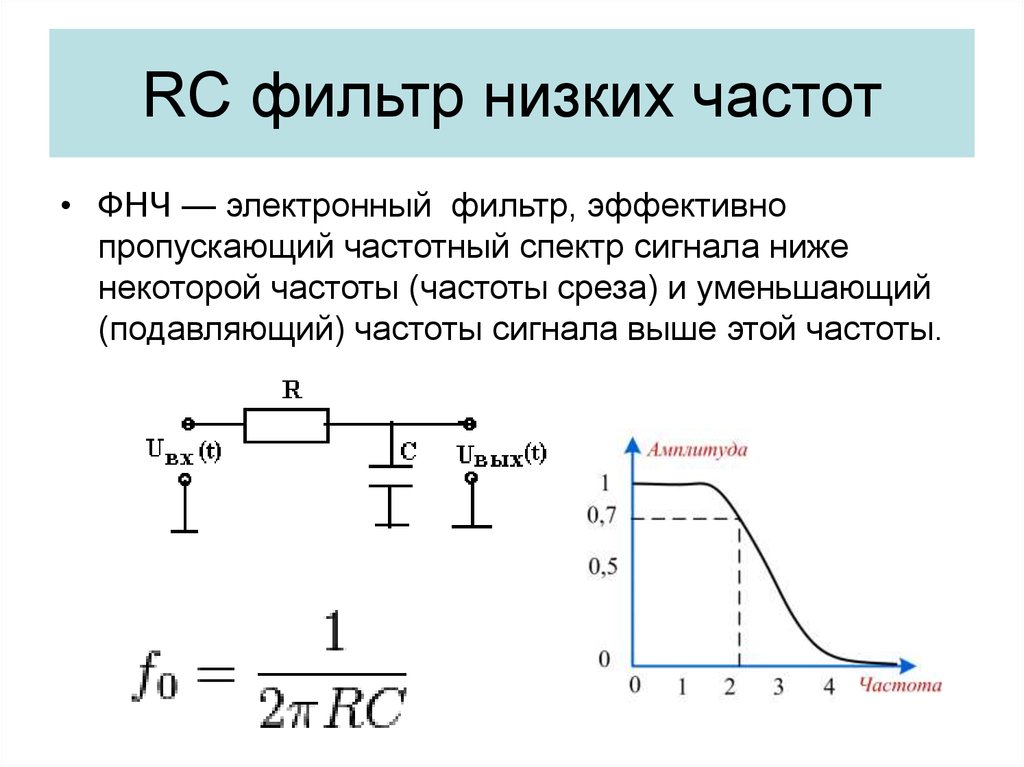
Исследование графика и параметров LC контура.
Что показали первичные исследования ? … Частота контура параллельной или последовательной LC цепи, в принципе ничем не отличаются, так как формула расчета частоты – не содержит никаких переменных или зависимых значений, кроме взаимного влияния емкости и индуктивности друг на друга … Эта особенность LC контура – широко используется в разработке конструкций ФВЧ и ФНЧ LC фильтров … Г-образные звенья, образованные последовательным соединением емкости и индуктивности (или – наоборот : катушки и конденсатора) – собираются вместе, чтобы получить Т-образное или П-образное звено LC фильтра третьего порядка – с более крутой АЧХ (амплитудно / частотной характеристикой) …
# … vpayaem.ru, Расчет LC фильтров. Онлайн калькулятор ПФ, ФВЧ, ФНЧ.
…
При этом, при соединении Г последовательных LC контуров в Т или П звенья – ближайшие друг к другу : емкости или индуктивности – удваиваются . ..
..
ФНЧ (фильтр нижних частот, пропускает ниже частоты среза и задерживает выше) … Сигнал – через катушку ; конденсатор – на массу … Более предпочитают схему П звеньев – с меньшим содержанием катушек индуктивности …
ФНЧ (фильтр верхних частот, пропускает выше частоты среза и задерживает ниже) … Сигнал – через конденсатор ; катушка – на массу … Более предпочитают схему Т звеньев – с меньшим содержанием катушек индуктивности …
Широкополосные полосовые LC фильтры получают каскадным соединением ФНЧ и ФВЧ …
Резонансная частота LC контура. График асинхронного влияния номиналов компонентов.
Судя по кривой графика резонансной частоты LC контура – далеко неочевидно, почему на симметричной частотной зависимости : слева – должен быть ФВЧ, а справа – ФНЧ … Более того : здесь, даже – нет места ФВЧ фильтру, так как, это – зеркальный график самого себя, выше некоторой точки частоты . .. Единственное что здесь различается, справа и слева, это – реактивное сопротивление (импеданс) и, соответственно – амплитуда резонансного тока в контуре …
.. Единственное что здесь различается, справа и слева, это – реактивное сопротивление (импеданс) и, соответственно – амплитуда резонансного тока в контуре …
На следующей картинке – ситуация несколько проясняется : для ФВЧ – кривая частоты лежит несколько выше номиналов LC фильтра (то, есть – верхняя частота) … Для ФНЧ – наоборот, график в области нижних частот … Я бы, даже сказал, что срез фильтра – изначально нормируется с отклонением от резонансной частоты, чтобы способствовать улучшенному прохождению радио частот в полосе резонанса контура …
Резонансная частота LC контура. График синхронного влияния номиналов компонентов.
Из первого постулата автоматически проистекает – второй : взаимное изменение номиналов компонентов – не влияет на частоту … 25 пкФ и 13 мкГн, на резонансной частоте : около 15 мГц – это примерно то же самое, что и 13 пкФ и 25 мкГн … Что-то, типа : от перемены мест слагаемых, сумма – не меняется … Поэтому большинство авто расчетов емкости конденсатора и индуктивности катушки для LC контура – будут предлагать их одинаковые значения .
Конечно, все эти примеры – применимы для общего понимания частотных зависимостей LC контура, без учета влияния сопротивлений, порядка фильтра, добротности его компонентов и рабочей полосы частот … Несмотря на теоретические выкладки взаимозаменяемости номиналов L и C компонентов, из-за реактивного сопротивления переменной частоте – амплитуда резонансного тока – будет различной … (Включены расчеты для примера : 15 мГц) …
 -12) … То, есть 2,5 мкГн и 25 пкФ – должно быть : оптимальным соотношением … Проверка : XC = 316 Ом, XL= 316 Ом, ZLC = 308 кОм … Не так, чтобы уж очень много … При резонансе возникает бесконечно большой импеданс … Емкостное и индуктивное реактивные сопротивления – равны по величине, но противоположны по знаку и, поэтому – взаимно нейтрализуются … Токи в конденсаторе и катушке индуктивности – равны и противоположны … Собственно, импеданс – стремится к бесконечности … Ток от источника питания – не потребляется … Фазовый сдвиг – равен нулю (0) …
-12) … То, есть 2,5 мкГн и 25 пкФ – должно быть : оптимальным соотношением … Проверка : XC = 316 Ом, XL= 316 Ом, ZLC = 308 кОм … Не так, чтобы уж очень много … При резонансе возникает бесконечно большой импеданс … Емкостное и индуктивное реактивные сопротивления – равны по величине, но противоположны по знаку и, поэтому – взаимно нейтрализуются … Токи в конденсаторе и катушке индуктивности – равны и противоположны … Собственно, импеданс – стремится к бесконечности … Ток от источника питания – не потребляется … Фазовый сдвиг – равен нулю (0) …Фазовый сдвиг в колебательном контуре.
Фазовый сдвиг – один из самых непонятных параметров LC контура … Само, по себе, определение – понятно : временное смещение одного сигнала относительно другого, в каких то определенных точках измерения … Время связано с периодом … Период с частотой … Частота – с угловой частотой … Угловая частота – с Пи и кругом … Здесь будет не лишним вспомнить углы через Пи .. . Пи / 2 = 90 градусов … Пи = 180 градусов … 3 * Пи / 2 = 270 градусов … Нелогичная связь между временем и кругом – вполне определенная : чтобы повернуть круг на некоторый угол – нужно затратить какое-то количество времени …
. Пи / 2 = 90 градусов … Пи = 180 градусов … 3 * Пи / 2 = 270 градусов … Нелогичная связь между временем и кругом – вполне определенная : чтобы повернуть круг на некоторый угол – нужно затратить какое-то количество времени …
Непонятно, какое влияние оказывает сдвиг фаз на колебательный контур … Вернее, об этом много написано, но (часто) – не указано характерное конкретное применение … А, также – с учетом влияния сдвига фаз на различие типа резонанса (по току ; по напряжению) … Глобальное понимание сути вопроса – могли бы значительно облегчить утверждения, типа : токовый резонанс открывает биполярный транзистор … Или : резонанс напряжений – управляет полевым транзистором … А, так, в общем случае – считается, что резонанс помогает настроиться на волну радиостанции … А, какой, там – резонанс : токов, напряжений, синфазный или еще какой – в радио / технической литературе об этом, обычно – не упоминается …
Фазовый сдвиг со знаком плюс : цепь имеет индуктивный характер, напряжение опережает ток . .. Такую реакцию, при подаче электрического сигнала – проявляет катушка индуктивности … Ток сигнала – дважды испытывает ЭДС индукции : при накоплении и при отдаче энергии, поэтому напряжение опережает отстающий ток на угол Пи / 2 … В свою очередь, ток, сам и порождая ЭДС индукции – опережает ее на угол Пи / 2 …
.. Такую реакцию, при подаче электрического сигнала – проявляет катушка индуктивности … Ток сигнала – дважды испытывает ЭДС индукции : при накоплении и при отдаче энергии, поэтому напряжение опережает отстающий ток на угол Пи / 2 … В свою очередь, ток, сам и порождая ЭДС индукции – опережает ее на угол Пи / 2 …
Индуктивный характер преобладает … при частоте, выше резонансной – для последовательного LC контура … при частоте, ниже резонансной – для параллельного LC контура …
Фазовый сдвиг со знаком минус : цепь имеет емкостный характер, ток опережает напряжение … Такую реакцию проявляет конденсатор, при подаче на него электрического сигнала … Ток сигнала опережает напряжение сигнала на угол Пи / 2 … Образующаяся противодействующая (со знаком минус) ЭДС емкости – опережает ток сигнала – на угол Пи / 2 …
Емкостный характер преобладает … при частоте, ниже резонансной – для последовательного LC контура … при частоте, выше резонансной – для параллельного LC контура . ..
..
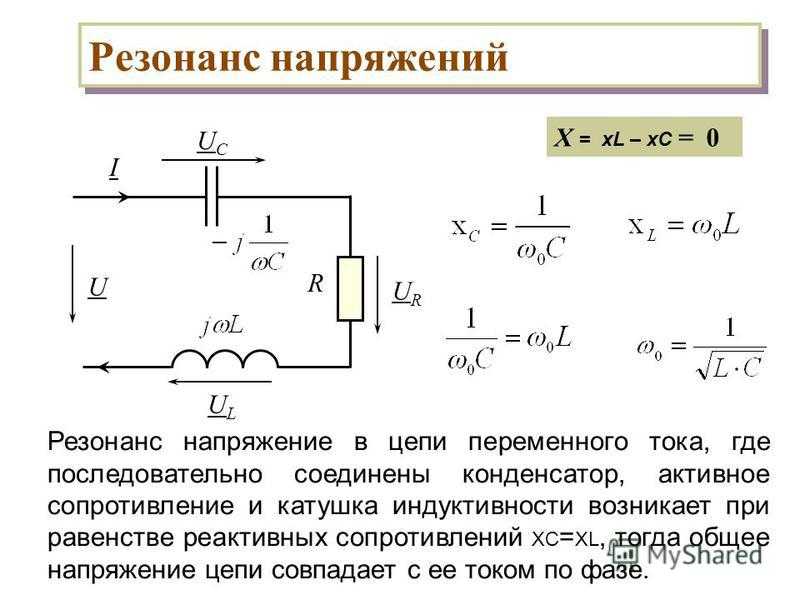
Фазовый сдвиг = 0 : такое состояние наблюдается в цепи с одним активным R сопротивлением, а также в момент резонанса колебательного контура … В момент резонанса напряжения в контуре – противофазны (сдвиг на угол Пи) и их сумма : UL + (-UC) = 0, при этом : их индивидуальные значения – могут значительно превышать входной сигнальный уровень напряжений … Фазочастотные ФЧХ характеристики последовательного и параллельного LC контуров – зеркально противоположны … Последовательный LC – это контур резонанса напряжений … Параллельный LC – это контур резонанса токов …
# … elar.urfu.ru, Резонансные свойства RLC цепей. Учебно-методическое пособие. Формат PDF.
… Рекомендовано в программах подготовки по направлениям : радиофизика, нанотехнология, стандартизация и метрология, инноватика … Уральский Федеральный Университет (УрФУ), Министерство образования и науки Российской Федерации …
Фазовый сдвиг : практическое применение … Несмотря на многочисленные примеры и пояснения, практическая роль фазового сдвига – все еще может оставаться, не окончательно понятной – среди практикующих и, особенно, начинающих радио любителей . .. В электротехнике, сдвиг фаз между напряжением и током – определяет коэффициент мощности в цепях переменного тока … В радио технике, это – фазовые детекторы и фазовращатели … Программные системы и вычислительные методы : алгоритм Герцеля для спектрального анализа сигналов (для определения сдвига фаз между двумя синусоидальными
сигналами) … Алгоритм Герцеля позволяет эффективно рассчитывать фиксированные спектральные отсчеты и имеет ряд преимуществ перед стандартным Быстрым преобразованием Фурье (БПФ) … Моделирование и практическая реализация алгоритма Герцеля, с помощью которой удалось рассчитать сдвиг фаз между сигналами входа и выхода … Фазовый сдвиг позволяет вычислять активную составляющую комплексного сопротивления Z фильтра – без его непосредственного измерения …
.. В электротехнике, сдвиг фаз между напряжением и током – определяет коэффициент мощности в цепях переменного тока … В радио технике, это – фазовые детекторы и фазовращатели … Программные системы и вычислительные методы : алгоритм Герцеля для спектрального анализа сигналов (для определения сдвига фаз между двумя синусоидальными
сигналами) … Алгоритм Герцеля позволяет эффективно рассчитывать фиксированные спектральные отсчеты и имеет ряд преимуществ перед стандартным Быстрым преобразованием Фурье (БПФ) … Моделирование и практическая реализация алгоритма Герцеля, с помощью которой удалось рассчитать сдвиг фаз между сигналами входа и выхода … Фазовый сдвиг позволяет вычислять активную составляющую комплексного сопротивления Z фильтра – без его непосредственного измерения …
Практически : наиболее просто – измерить сдвиг фаз между двумя напряжениями, используя двух / канальный осциллограф … Более сложно : на одно / канальном осциллографе в режиме синхронизации собственно самим измеряемым сигналом . .. По методу эллипса / по анализу фигур Лиссажу (с систематической ошибкой и явной неоднозначностью) … Со снятием и измерением осциллограмм переменного тока, дела обстоят – еще хуже … Трудности с подключением … Высокоскоростные переменные частоты … Необходимость специального оборудования : шунты, токовые клещи, токовые петли, необходимость пересчетов и согласования … Все, это – отбивает желание связываться со снятием осциллограмм тока …
.. По методу эллипса / по анализу фигур Лиссажу (с систематической ошибкой и явной неоднозначностью) … Со снятием и измерением осциллограмм переменного тока, дела обстоят – еще хуже … Трудности с подключением … Высокоскоростные переменные частоты … Необходимость специального оборудования : шунты, токовые клещи, токовые петли, необходимость пересчетов и согласования … Все, это – отбивает желание связываться со снятием осциллограмм тока …
Смотреть список всех страниц, раздел radio …
techstop-ekb.ru QR Code Link, ссылка, сканировать и прочитать куар код кюар онлайн на русском …
Ссылки на самые популярные страницы интернет сайта, случайные и бесплатные прямые ссылки онлайн …
Cookie для пользователя. Зачем и для чего они … Веб безопасность посетителя, его конфиденциальные данные и выбор действий – охраняются зак …
Delphi на Андроид. На планшет или смартфон. D … Delphi на Андроид. На планшет или смартфон. Где скачать и как запустить Делфи DS150E. RDP …
RDP …
Расчет л ч топлива двигателя по оборотам и во … Работа мотора, связь воздуха, топлива, параметры расчета, оборотов, нагрузки трудно понять …
М-2 прогноз погоды дорогой на трассе по маршр … Погода в городе Москва, Подольск, Тула, Орел, Курск, Белгород, Харьков по М 2, метео обста …
Игрушки и настольные игры для детей. … Игры настольные, головоломки и toys детские игрушки. Отзывы, скидки. Игровые наборы. Попул …
кратчайшие рассказы, невероятный мир …
# … groups.io, Группа наблюдения Земли, GEO, любительский спутниковый мониторинг.
… Цель Группы по наблюдению Земли – обеспечить любительский прием метеорологических спутников и спутников для получения изображений Земли, которые находятся на орбите или планируются к запуску в ближайшем будущем … Членство в GEO является бесплатным …
там где хорошо, лента новостей …
# … tass.ru, Ютюб заработает на вас, если вы не хотите заработать с Youtube.
. ..
YouTube с июня будет вставлять рекламу в видео – без согласия разместивших ролик … Весь доход от рекламных вставок в ролики на каналах, которые недостаточно популярны или не стремятся к получению прибыли от своего контента – будет идти в бюджет видеохостинга …
..
YouTube с июня будет вставлять рекламу в видео – без согласия разместивших ролик … Весь доход от рекламных вставок в ролики на каналах, которые недостаточно популярны или не стремятся к получению прибыли от своего контента – будет идти в бюджет видеохостинга …
краткое содержание, краткая история …
# … kod.ru, Приложение для слежки за друзьями стало одним из самых популярных в России.
… Французская социальная сеть Zenly внезапно стала одним из самых популярных приложений в России, уступив только Telegram и TikTok, и обогнав WhatsApp, Instagram, GetContact, StateService и другие …
главная страница … быстрый поиск … в России и мире … карта сайта … как почистить кеш …
Быстро и просто вкусно, а в целом – относительно аскетично. © 2022 ТехСтоп Екатеринбург.
С 2016++ техническая остановка, с вами и для вас, бесплатно и доступно …
Политика конфиденциальности Cookie
Расчёт LC – фильтров. Онлайн калькулятор ПФ, ФВЧ, ФНЧ.
Калькуляторы ФНЧ, ФВЧ, резонансных, полосовых LC – фильтров, а также фильтров для акустических систем
LC – фильтры я оставил на десерт, подобно бутылке благородного вина, покрытой слоем вековой пыли.
Это антиквариат, причём наиболее древним из семейства фильтров, построенных при помощи индуктивностей и ёмкостей, является
параллельный LC колебательный контур, изображённый на Рис.1.
Частотная зависимость коэффициента передачи такого LC контура соответствует характеристике резонансного полосового фильтра.
Именно с этого самого простого LC-фильтра мы и начнём расчёт.
Как уже было сказано – LC контур, включённый по схеме, приведённой на Рис.1, представляет собой узкополосный полосовой резонансный фильтр,
настроенный на частоту:
fо= 1/(2π√LС).
На резонансной частоте сопротивление контура равно:
Rо = pQ, где р –
это характеристическое сопротивление колебательного контура, численно равное:
р = √L/C, а
Q = fо/Δf – это параметр добротности LC контура, определяющий полосу пропускания
фильтра по уровню 3 дБ.
Рис.1
А рассчитать добротность контура можно по формуле
Q = p/Rпот = (√L/C)/Rпот,
где
Rпот – это сумма сопротивлений потерь:
а) в катушке индуктивности (в первом приближении = активному сопротивлению катушки) и
б) в конденсаторе (сопротивление потерь в диэлектрике).
На низких частотах конденсаторы практически не вносят потерь, поэтому добротность контура равна добротности катушки
индуктивности, величина которой напрямую зависит от активного сопротивления катушки. Чем ниже частота, тем больше витков и тоньше
провод, тем проще его измерить активное сопротивление тестером.
На радиочастотах значение активного сопротивления катушки может составлять доли ома. Поэтому для расчёта добротности надо: либо
найти сопротивление катушки в Омах по формуле R= 4ρ*L/(πd²), где ρ — удельное сопротивление меди, равное 0,017 Ом•мм²/м,
L – длина в метрах, d – диаметр провода в мм. Либо (и лучше) – вооружиться генератором сигналов, каким-либо измерителем уровня выходного
сигнала с высоким внутренним сопротивлением, и определить добротность контура экспериментально.
Либо (и лучше) – вооружиться генератором сигналов, каким-либо измерителем уровня выходного
сигнала с высоким внутренним сопротивлением, и определить добротность контура экспериментально.
Это решение является более правильным в связи с тем, что на высоких частотах на сопротивление потерь начинают влиять и другие факторы,
в частности потери в конденсаторе, особенно если он окажется варикапом.
Нарисуем табличку с расчётом фильтра для низкочастотных приложений.
ТАБЛИЦА ДЛЯ LC- РЕЗОНАНСНОГО (ПОЛОСОВОГО) ФИЛЬТРА ДЛЯ НЧ.
|
Индуктивность катушки L1 (миллигенри) |
|
| Активное сопротивление катушки R (Ом) | |
| Ёмкость конденсатора С1 (нФ) | |
Резонансная частота фильтра Fр. (Гц) (Гц) |
|
| Добротность фильтра Q | |
| Характеристическое сопротивление ρ (Ом) | |
| Полоса пропускания фильтра (Гц) |
Если параметр активного сопротивления катушки R опущен, его значение принимается равным 100 Омам.
Необходимо отметить, что все полученные в таблице данные верны и для последовательного колебательного контура.
При этом, если мы хотим использовать свойства контура полностью, т. е. получить острую резонансную кривую, соответствующую
конструктивной добротности, то параллельный контур надо нагружать слабо, выбирая R1 и Rн намного больше Rо (на практике
десятки-сотни кОм), для последовательного же контура, сопротивление генератора R1 наоборот должно быть на порядки меньше
характеристического сопротивления ρ.
Теперь, нарисуем таблицу для расчёта высокочастотных резонансных контуров.
Тут на добротность влияет не только активное сопротивление катушек, но и другие факторы, такие как – потери в ферритах, наличие экрана,
эффект близости витков и т. д.
Поэтому вводить этот параметр в качестве входного я не
стану – будем считать, что добротность катушки вы измерили, или подсмотрели в документации на готовые катушки. Естественным образом
значение добротности катушки должно измеряться на резонансной частоте контура, ввиду прямой зависимости этой величины от рабочей
частоты (Q=2πfL/R).
К тому же я добавлю сюда параметр добротности конденсатора, особенно актуальный в случае применения варикапов.
По умолчанию (для желающих оставить эти параметры без внимания), добротность катушки примем равной 100, конденсатора – 1000, а для
испытывающих стремление измерить эти параметры в радиолюбительских условиях, рекомендую посетить страницу
ссылка на страницу .
ТАБЛИЦА ДЛЯ LC- РЕЗОНАНСНОГО (ПОЛОСОВОГО) ФИЛЬТРА ДЛЯ ВЧ.
|
Индуктивность катушки L1 (микрогенри) |
|
| Добротность катушки Q1 | |
| Ёмкость конденсатора С1 (пф) | |
| Добротность конденсатора Q2 | |
| Резонансная частота фильтра Fр. (кГц) | |
| Добротность фильтра Q | |
| Характеристическое сопротивление ρ (Ом) | |
| Сопротивление контура на резонансной частоте (Ом) | |
| Полоса пропускания фильтра (кГц) |
Теперь плавно переходим к LC фильтрам верхних и нижних частот (ФВЧ и ФНЧ).
Рис.2
В полосе пропускания коэффициент передачи по напряжению данных фильтров близок к единице при условии R1 Однако оптимальные параметры, с точки зрения равномерности АЧХ и передачи максимальной мощности в нагрузку, обеспечиваются при R1 = Rн = ρ. В этом случае фильтр является согласованным, правда коэффициент передачи в полосе пропускания становится равным К=0.5.
Номиналы элементов и параметры ФВЧ и ФНЧ вычислим для согласованных LC фильтров. За частоту среза, как водится, примем частоту, на которой
ослабление сигнала составляет 3дБ.
Крутизна спада АЧХ в полосе подавления таких фильтров составляет 12 дБ/октаву.
Ну да ладно, ближе к делу.
ТАБЛИЦА LC- ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ.
| Характеристика фильтра |   ФНЧ ФВЧ | |
| Индуктивность катушки L1 | Миллигенри Микрогенри | |
| Ёмкость конденсатора С1 | МикрофарадНанофарадПикофарад | |
Частота среза фильтра Fср. |
||
| Характеристическое сопротивление ρ (Ом) |
А если надо рассчитать L и C при известных значениях Fср и ρ?
ТАБЛИЦА РАСЧЁТА ЭЛЕМЕНТОВ LC- ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ.
| Характеристика фильтра |   ФНЧ ФВЧ | |
| Частота среза фильтра Fср. | Герц Килогерц Мегагерц | |
| Характеристическое сопротивление ρ (Ом) | ||
| Индуктивность катушки L1 | ||
| Ёмкость конденсатора С1 |
В последнее время мне на почту приходит всё большее количество вопросов по поводу LC-фильтров для акустических систем. Т. е. фильтров, для которых входным источником является усилитель с практически нулевым внутренним сопротивлением, а нагрузкой –
динамическая головка, обладающая неким (условно примем) активным импедансом.
Т. е. фильтров, для которых входным источником является усилитель с практически нулевым внутренним сопротивлением, а нагрузкой –
динамическая головка, обладающая неким (условно примем) активным импедансом.
Естественно, что расчёт элементов, выполненный с помощью приведённых выше калькуляторов для согласованных цепей, ожидаемых результатов
не даст ни с точки зрения частоты среза фильтра, ни с точки зрения – равномерности его АЧХ. Поэтому вдогонку размещу-ка я и калькулятор для
расчёта НЧ-ВЧ фильтров для акустики, либо каких иных приложений, где величина сопротивления источника имеет величину
значительно меньшую, чем Rн.
Плюсом этих фильтров является близкий к единице коэффициент передачи сигнала, минусом – меньшая (чем у согласованных) крутизна
спада АЧХ в полосе подавления, которая составляет 10 против 12 дБ/октаву.
РАСЧЁТ ЭЛЕМЕНТОВ LC- ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ для АКУСТИКИ и прочего.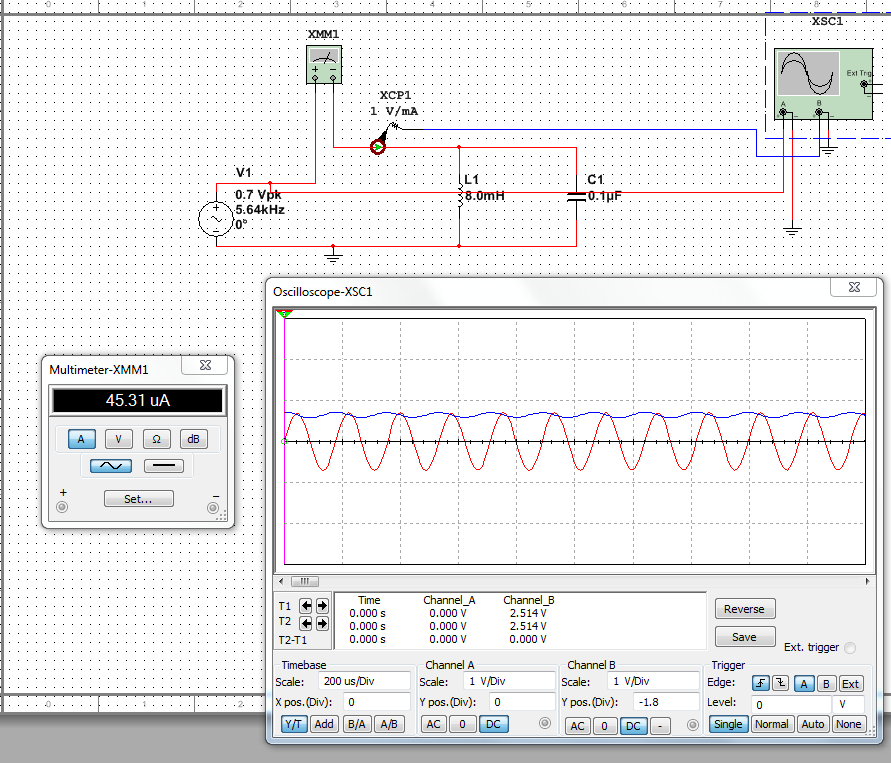
| Характеристика фильтра |   ФНЧ ФВЧ | |
| Частота среза фильтра Fср. | Герц Килогерц Мегагерц | |
| Сопротивление нагрузки Rн (Ом) | ||
| Индуктивность катушки L1 | ||
| Ёмкость конденсатора С1 |
Фильтры, посчитанные на последнем калькуляторе, являются фильтрами Баттерворта 2-го порядка. А желающим рассчитать акустические
ФВЧ, ФНЧ и ПФ различных типов и порядков предлагаю посетить страницу: ссылка на страницу.
А желающим рассчитать акустические
ФВЧ, ФНЧ и ПФ различных типов и порядков предлагаю посетить страницу: ссылка на страницу.
Приведённые выше ФВЧ и ФНЧ называются Г-образными.
Для получения более крутых скатов АЧХ используют два или более согласованных Г-образных звеньев, соединяя их последовательно,
чтобы образовать Т-образное звено (на Рис.3 сверху), или П-образное звено (на Рис.3 снизу).
При этом получаются ФНЧ третьего порядка. Обычно, ввиду меньшего количества катушек, предпочитают П-образные звенья.
Рис.3
ФВЧ конструируют подобным же образом, лишь катушки заменяются конденсаторами, а конденсаторы – катушками.
Широкополосные полосовые LC – фильтры получают каскадным соединением ФНЧ и ФВЧ.
Что касается многозвенных LC-фильтров высоких порядков, то более грамотным решением (по сравнению с последовательным
соединением фильтров низших порядков) будет построение подобных устройств с использованием полиномов товарищей Чебышева или Баттерворта.
Именно такие фильтры 3-го, 5-го и 7-го порядков мы и рассмотрим на следующей странице.
Онлайн расчет lc контура
В статье расскажем что такое колебательный контур. Последовательный и параллельный колебательный контур. Разделяется на два типа в зависимости от соединения элементов: последовательный и параллельный. Основная радиоэлементная база колебательного контура : Конденсатор, источник питания и катушка индуктивности.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Калькулятор
- Расчет частоты колебательного контура
- Расчет колебательного контура
- Резонансная частота контура
- Колебательный контур LC
- Резонансная частота: формула
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Исследование параллельного колебательного контура
youtube.com/embed/i6EpdyyB7_g” frameborder=”0″ allowfullscreen=””/>Калькулятор
Последовательный колебательный контур — это цепь, состоящая их катушки индуктивности и конденсатора, которые соединяются последовательно. На схемах идеальный последовательный колебательный контур обозначается вот так:. Реальный колебательный контур имеет сопротивление потерь катушки и конденсатора. Это суммарное суммарное сопротивление потерь обозначается буквой R. В результате, реальный последовательный колебательный контур будет иметь такой вид:.
L — собственно сама индуктивность катушки. С — собственно сама емкость конденсатора. Давайте проведем классический эксперимент, который есть в каждом учебнике по электронике. Для этого соберем вот такую схему:. Генератор у нас будет выдавать синус. Для того, чтобы снять осциллограмму силы тока через последовательный колебательный контур, мы подключим в схему шунтовый резистор с малым сопротивлением в 0,5 Ом и с него уже будем снимать напряжение.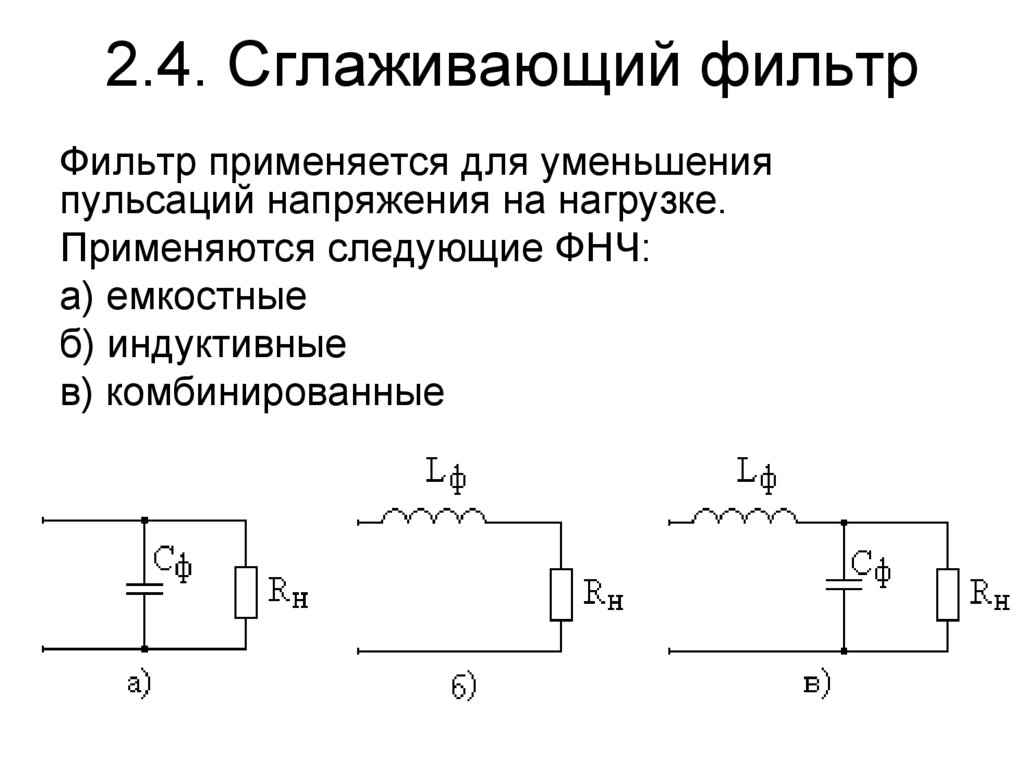
То есть в данном случае мы шунт используем для наблюдения силы тока в цепи. А вот и сама схема в реальности:. Слева-направо: шунтовый резистор, катушка индуктивности и конденсатор. Как вы уже поняли, сопротивление R — это суммарное сопротивление потерь катушки и конденсатора, так как нет идеальных радиоэлементов. Теперь нам осталось подцепить эту схему к генератору частоты и осциллографу , и прогнать по некоторым частотам, снимая осциллограмму с шунта U ш , а также снимая осциллограмму с самого генератора U ГЕН.
С шунта мы будем снимать напряжение , которое у нас отображает поведение силы тока в цепи, а с генератора собственно сам сигнал генератора. Давайте прогоним нашу схемку по некоторым частотам и глянем что есть что. В схеме я взял конденсатор на 1мкФ и катушку индуктивности на 1 мГн.
На генераторе настраиваю синус размахом в 4 Вольта. Вспоминаем правило: если в цепи соединение радиоэлементов идет последовательно друг за другом, значит, через них течет одинаковая сила тока. Красная осциллограмма — это напряжение с генератора частоты, а желтая осциллограмма — отображение силы тока через напряжение на шунтовом резисторе.
Красная осциллограмма — это напряжение с генератора частоты, а желтая осциллограмма — отображение силы тока через напряжение на шунтовом резисторе.
Частота Герц с копейками:. Как мы видим, при такой частоте ток в этой цепи есть, но очень слабый. Добавляем частоту. Здесь мы уже отчетливо видим, что сила тока возросла, а также видим, что осциллограмма силы тока опережает напряжение. Попахивает реактивным сопротивлением конденсатора. Сила тока стала еще больше. Сила тока увеличилась.
Заметьте также, что сдвиг фаз стал уменьшаться. Осциллограммы почти уже сливаются в одну. Сдвиг фаз между напряжением и силой тока становится почти незаметным. И вот на какой-то частоте у нас сила тока стала максимальной, а сдвиг фаз стал равен нулю. Запомните этот момент. Для нас он будет очень важен. Ну а давайте далее будем увеличивать частоту. Смотрим, что получается в итоге. Еще совсем недавно ток опережал напряжение, а сейчас уже стал запаздывать после того, как выровнялся с ним по фазе.
Так как ток уже отстает от напряжения, здесь уже попахивает реактивным сопротивлением катушки индуктивности. Увеличиваем частоту еще больше. Сила тока начинает падать, а сдвиг фаз увеличивается. Как вы видите, с увеличением частоты, сдвиг приближается к 90 градусов, а сила тока становится все меньше и меньше. Давайте подробнее рассмотрим тот самый момент, когда сдвиг фаз был равен нулю и сила тока, проходящая через последовательный колебательный, контур была максимальна:. Это явление носит название резонанса.
Увеличиваем частоту еще больше. Сила тока начинает падать, а сдвиг фаз увеличивается. Как вы видите, с увеличением частоты, сдвиг приближается к 90 градусов, а сила тока становится все меньше и меньше. Давайте подробнее рассмотрим тот самый момент, когда сдвиг фаз был равен нулю и сила тока, проходящая через последовательный колебательный, контур была максимальна:. Это явление носит название резонанса.
Дело в том, что в этот самый момент реактивное сопротивление катушки и конденсатора становятся равными, но противоположными по знаку. Поэтому, эти реактивные сопротивления как-бы вычитаются друг из друга, что в сумме дает ноль, и в цепи остается только активная составляющая сопротивления, то есть то самое паразитное сопротивление катушки и конденсатора, или иначе, сопротивление потерь R. Если генератор мощный, то напряжение на нем не меняется, а сопротивление становится пренебрежимо малым и вуаля!
Ток растет как грибы после дождя, что мы и увидели, посмотрев на желтую осциллограмму при резонансе. Итак, реактивное сопротивление катушки у нас выражается формулой:. Реактивное сопротивление конденсатора вычисляется по формуле:. Приравниваем обе части и вычисляем отсюда F :. В данном случае мы получили формулу резонансной частоты.
Итак, реактивное сопротивление катушки у нас выражается формулой:. Реактивное сопротивление конденсатора вычисляется по формуле:. Приравниваем обе части и вычисляем отсюда F :. В данном случае мы получили формулу резонансной частоты.
Это формула по другому называется формулой Томсона , как вы поняли, в честь ученого, который ее вывел. Давайте по формуле Томсона посчитаем резонансную частоту нашего последовательного колебательного контура. Для этого я буду использовать свой RLC-транзисторметр. Замеряем индуктивность катушки:.
И замеряем нашу емкость:. Высчитываем по формуле нашу резонансную частоту:. У меня получилось 5, 09 Килогерц. Спишем погрешность в с копейками Герц на погрешность измерений приборов. Как вы видите, формула Томпсона работает.
Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-. Беру катушку индуктивности с индуктивностью в 22 микрогенри:.
Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее. Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R.
Поступлю более хитрее. Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R.
В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор — это не есть хорошо, но что не сделаешь ради науки! Ну что же, приступим ;-. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту.
У меня получилось 1, Мегагерц. Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:. Размах амплитуды 4 Вольта. Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1, Мегагерц. Теперь небольшой прикол ;-. Вот этот сигнал мы подаем на наш последовательный колебательный контур:. Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.
Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:. Смотрим напряжение на конденсаторе:.
Размах амплитуды 20 Вольт 5х4! Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта! Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:. Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке.
Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Как видите — полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии. Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока — увы! Поэтому последовательный колебательный контур носит также название узкополосного резонансного усилителя напряжения , а не мощности!
Расчет частоты колебательного контура
Последовательный колебательный контур — это цепь, состоящая их катушки индуктивности и конденсатора, которые соединяются последовательно. На схемах идеальный последовательный колебательный контур обозначается вот так:. Реальный колебательный контур имеет сопротивление потерь катушки и конденсатора. Это суммарное суммарное сопротивление потерь обозначается буквой R. В результате, реальный последовательный колебательный контур будет иметь такой вид:.
На схемах идеальный последовательный колебательный контур обозначается вот так:. Реальный колебательный контур имеет сопротивление потерь катушки и конденсатора. Это суммарное суммарное сопротивление потерь обозначается буквой R. В результате, реальный последовательный колебательный контур будет иметь такой вид:.
Онлайн калькулятор для Расчёта резонансной частоты контура.
Расчет колебательного контура
Random converter. Калькулятор определяет импеданс и фазовый сдвиг для соединенных последовательно идеальной катушки индуктивности и идеального конденсатора для заданной частоты синусоидального сигнала. Определяется также угловая частота. Рассчитать импеданс катушки индуктивности мГн и конденсатора нФ на частоте Гц. Калькулятор показывает импеданс около 0,9 Ом. Это почти резонанс. Можно проверить импеданс при почти полном резонансе, если ввести , Гц вместо Гц. При этой частоте импеданс получается индуктивным. Однако, если ввести чуть большую частоту , Гц, импеданс станет емкостным, и вы увидите, что фазовый угол, который был чуть меньше нуля, стал положительным.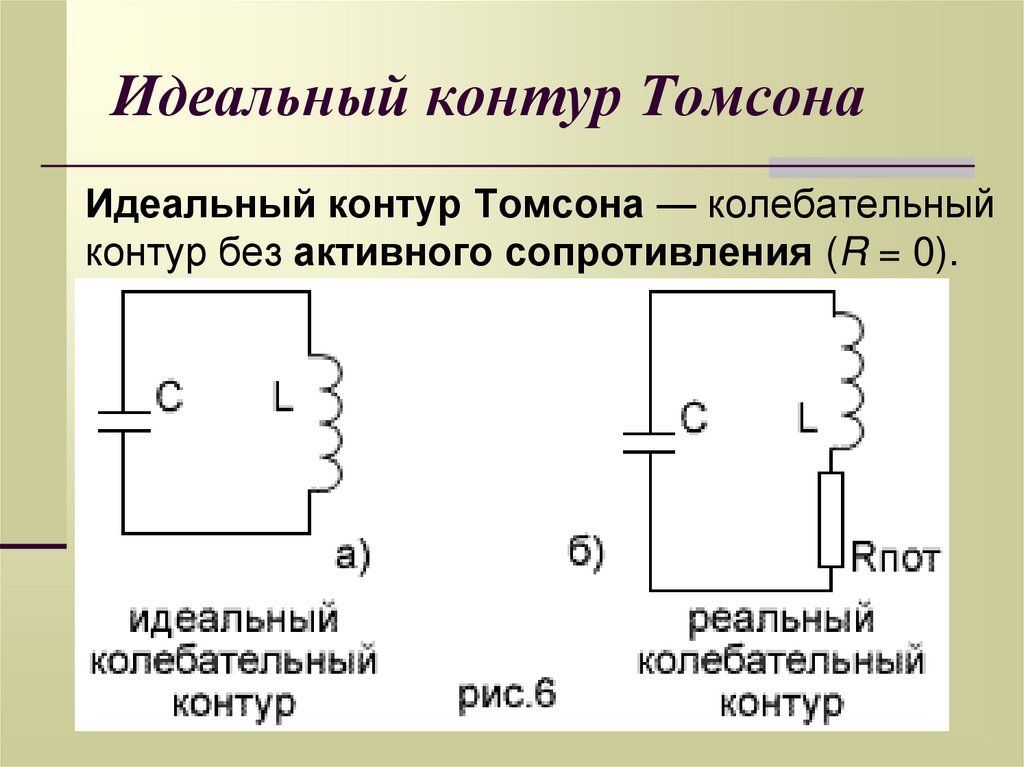 Нажмите ссылку для установки резонансной частоты в качестве входного параметра и расчета всех выходных величин для этой частоты.
Нажмите ссылку для установки резонансной частоты в качестве входного параметра и расчета всех выходных величин для этой частоты.
Резонансная частота контура
Колебательный контур — электрическая цепь, содержащая катушку индуктивности, конденсатор и источник электрической энергии. Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания. Резонансная частота контура определяется так называемой формулой Томсона:. При слишком малой индуктивности и большой емкости будет падать резонансное сопротивление контура, что приведет к ухудшению его избирательных свойств, а в схеме резонансного усилителя упадет усиление каскада. При слишком малой емкости и большой индуктивности катушка будет содержать большое количество витков, добротность ее будет уменьшаться, а собственная емкость расти, в результате она может сравняться с емкостью контурного конденсатора, что не допустимо.
Данный справочник собран из разных источников.
Колебательный контур LC
Колебательный контур — электрическая цепь, содержащая катушку индуктивности, конденсатор и источник электрической энергии. Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания. Резонансная частота контура определяется так называемой формулой Томсона:. При слишком малой индуктивности и большой емкости будет падать резонансное сопротивление контура, что приведет к ухудшению его избирательных свойств, а в схеме резонансного усилителя упадет усиление каскада. При слишком малой емкости и большой индуктивности катушка будет содержать большое количество витков, добротность ее будет уменьшаться, а собственная емкость расти, в результате она может сравняться с емкостью контурного конденсатора, что не допустимо.
Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания. Резонансная частота контура определяется так называемой формулой Томсона:. При слишком малой индуктивности и большой емкости будет падать резонансное сопротивление контура, что приведет к ухудшению его избирательных свойств, а в схеме резонансного усилителя упадет усиление каскада. При слишком малой емкости и большой индуктивности катушка будет содержать большое количество витков, добротность ее будет уменьшаться, а собственная емкость расти, в результате она может сравняться с емкостью контурного конденсатора, что не допустимо.
Резонансная частота: формула
Расчёт фильтров для ШИМ. В статье речь пойдёт про расчёт простейших фильтрующих цепей для сглаживания широтно-импульсной модуляции. Что такое ШИМ, где он применяется и как его реализовать читайте в отдельной статье. Первое, на чём следует заострить внимание – это назначение цепи, для которой вы собрались строить фильтр. Строго говоря, в источниках питания сам сигнал ШИМ тоже используется в сигнальной цепи управление транзисторами и на выходе таких источников сигнал повторяет форму управляющих сигналов, однако имеет более высокую мощность, потому они требуют фильтров позволяющих пропускать большие мощности.
Строго говоря, в источниках питания сам сигнал ШИМ тоже используется в сигнальной цепи управление транзисторами и на выходе таких источников сигнал повторяет форму управляющих сигналов, однако имеет более высокую мощность, потому они требуют фильтров позволяющих пропускать большие мощности.
Формулы расчета резонансной частоты колебательного контура. и емкости можно сделать на онлайн калькуляторе, подставив конкретные значения. LC-цепи используются либо для генерации сигналов на определенной.
Практический расчет последовательного или параллельного LC контура. Доброго дня уважаемые радиолюбители! Некоторые из вас могут спросить, а на черта нам это нужно? Ну, во-первых, лишние знания никогда не помешают, а во-вторых, бывают в жизни моменты, когда вам знание этих расчетов может понадобиться.
Русский: English:. Бесплатный архив статей статей в Архиве. Справочник бесплатно. Параметры радиодеталей бесплатно. Даташиты бесплатно.
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
LC – фильтры я оставил на десерт, подобно бутылке благородного вина, покрытой слоем вековой пыли. Это антиквариат, который на Сотбисе не купишь! Как ни крути, а не получил бы Александр Степаныч наш Попов звание почётного инженера-электрика, не направь он искровой разряд напрямик в колебательный контур для обретения благословения свыше и резонанса с передающей антенной. И заскучала бы братва копателей свободной энергии эфира, не изобрети Никола Тесла свой резонансный трансформатор и электрический автомобиль с неведомой коробочкой. А то и вовсе, заширялась бы в подъездах, лишённая идей вселенского масштаба.
Портал QRZ. RU существует только за счет рекламы, поэтому мы были бы Вам благодарны если Вы внесете сайт в список исключений. Мы стараемся размещать только релевантную рекламу, которая будет интересна не только рекламодателям, но и нашим читателям.
Расчет lc контура
Программа “Калькулятор” представляет собой электротехнический калькулятор, позволяющий рассчитывать параметры колебательных контуров, определять индуктивности обособленных проводников и катушек различных типов, а также производить вычисления активных и реактивных сопротивлений.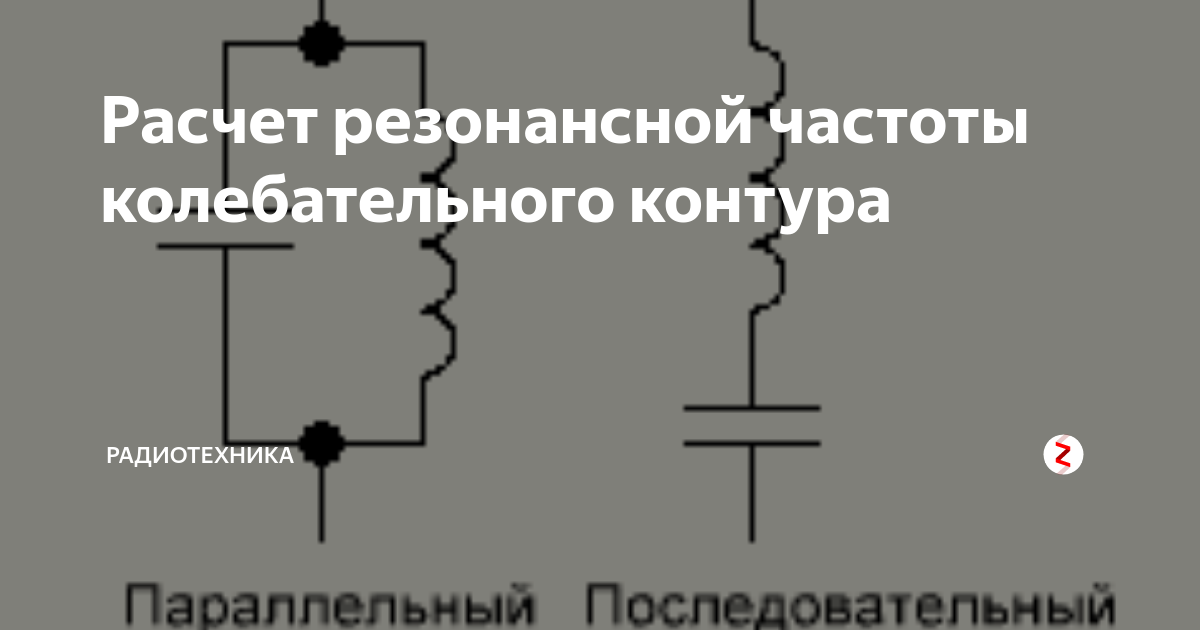 Помимо этого, в программу интегрирован поиск аналогов отечественных и зарубежных транзисторов и микросхем, а также модуль, содержащий справочные данные по SMD транзисторам и дающий возможность определять по цветовой маркировке номинал и класс точности резисторов и дросселей. В каждом из них, в свою очередь, можно выбрать необходимый шаблон для вычислений. Шаблон для расчёта последовательного и параллельного колебательных контуров позволяет при задании резонансной частоты и ёмкости либо индуктивности определить недостающий параметр. При выборе расширенного режима расчёта контура дополнительно появляется возможность задать параметры волны, а также рассчитать физические параметры катушки индуктивности. К примеру, в последнем случае задаются два из трёх параметров — длина проводника, диаметр его сечения и индуктивность, а третий рассчитывается автоматически.
Помимо этого, в программу интегрирован поиск аналогов отечественных и зарубежных транзисторов и микросхем, а также модуль, содержащий справочные данные по SMD транзисторам и дающий возможность определять по цветовой маркировке номинал и класс точности резисторов и дросселей. В каждом из них, в свою очередь, можно выбрать необходимый шаблон для вычислений. Шаблон для расчёта последовательного и параллельного колебательных контуров позволяет при задании резонансной частоты и ёмкости либо индуктивности определить недостающий параметр. При выборе расширенного режима расчёта контура дополнительно появляется возможность задать параметры волны, а также рассчитать физические параметры катушки индуктивности. К примеру, в последнем случае задаются два из трёх параметров — длина проводника, диаметр его сечения и индуктивность, а третий рассчитывается автоматически.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Колебательный контур
- Частота резонанса в колебательном контуре, онлайн расчет
- Расчет контуров
- Резонансная частота: формула
- Резонансный контур lc – Расчёт частоты резонанса колебательного контура
- Расчет колебательного контура
- Расчет колебательного контура
- Резонансная частота контура
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Частотные характеристики последовательного контура
youtube.com/embed/R23kUTUV3kQ” frameborder=”0″ allowfullscreen=””/>Колебательный контур
Колебательный контур — электрическая цепь, содержащая катушку индуктивности, конденсатор и источник электрической энергии. Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания. Резонансная частота контура определяется так называемой формулой Томсона:. При слишком малой индуктивности и большой емкости будет падать резонансное сопротивление контура, что приведет к ухудшению его избирательных свойств, а в схеме резонансного усилителя упадет усиление каскада.
При слишком малой емкости и большой индуктивности катушка будет содержать большое количество витков, добротность ее будет уменьшаться, а собственная емкость расти, в результате она может сравняться с емкостью контурного конденсатора, что не допустимо. Также на настройку контура будет влиять емкость монтажа, ведь она соизмерима со значением С.
Исходя из вышеуказанного, рекомендую выбирать соотношение емкости к индуктивности примерно как : 1 в абсолютном значении, что подходит для большинства контуров. Для расчета частоты резонанса колебательного контура LC заполните предложенную форму:. Для отправки комментария вам необходимо авторизоваться. Ваш IP: Расчет резонансной частоты колебательного контура. Радиотехнические калькуляторы LC метр – приставка к частотомеру – На рисунке показана схема приставки к частотомеру позволяющая измерять индуктивность от нГн до мГн и емкость конденсаторов от 1 пФ до 0,1 мкФ с достаточно большой точностью.
Схема собрана на компараторе LM и нескольких пассивных элементах. Для работы с приставкой Вам понадобится Схема приемника который может быть перестроен в диапазоне Реальная чувствительность приемника около 0,3 мкВ, напряжение питания 9 В. Следует заметить, что напряжение питания МС – Задающий генератор с кварцевой стабилизацией частоты на T1, при этом последовательно с кварцем включен варикап с помощью которого производится частотная модуляция. Начальное смещение на варикап задается делителем R8 R9.
Начальное смещение на варикап задается делителем R8 R9.
Кварцевый резонатор на частоту Перестраиваемый малошумящий антенный усилитель – Данный усилитель обеспечивает усиление в зависимости от частоты – 18 50МГц до 14 МГц дБ.
В нем применен малошумящий полевой транзистор, что обеспечивает высокую чувствительность. Входной контур образован индуктивностью L1 и емкостями варикапов, диодов и транзистора, обеспечивает частотную Коротковолновый усилитель мощности – Применение автоматической регулировки тока покоя лампы по огибающей однополосного сигнала позволяет значительно снизить его и приблизить режим работы усилителя к идеальному.
Вторым, не менее важным, узлом в усилителе является стабилизатор напряжения экранной сетки, которому в любительском Добавить комментарий Отменить ответ Для отправки комментария вам необходимо авторизоваться.
Войти с помощью:. Случайные статьи Сторожевые уст-ва В случае проникновения на объект постороннего сторожевые уст-ва способны подать звуковой или иной сигнал. На рисунке показана схема сторожевого уст-ва с механическим контактом геркон или кнопочный выключатель.
На рисунке показана схема сторожевого уст-ва с механическим контактом геркон или кнопочный выключатель.
Основа уст-ва это компараторы на элементах DD1. Реле времени позволяет коммутировать 4 реле, для этого необходимо указать для каждого реле время включения и время выключения.
Такое устройство может применяться как индикатор выходного сигнала УЗЧ при наличии детектора. Индикатор выполнен на 2-х микросхемах LM, каждая микросхема содержит 4-е … Подробнее На рисунке показаны схемы светодиодных светильников состоящих из 16 и 46 светодиодов.
Питаются светодиоды от бестрансформаторного источника питания. Светодиоды могут иметь рабочее напряжение от 3 до 3,6В и ток потребления от 10 до 30 мА каждый.
Приемник предназначен для приема сигналов в диапазоне ДВ кГц…кГц. Главная особенность приемника в антенне, которая имеет большую индуктивность чем обычная магнитная антенна. Что позволяет применить емкость подстроечного конденсатора в пределах 4…20пФ, а так же такой приемник обладает приемлемой чувствительностью и небольшом усилении тракта РЧ.
Работает приемник на головные телефоны наушники , питается … Подробнее Аудиопроцессор … Подробнее На рисунке показана схема простого усилителя для наушников с сверхнизким коэффициентом нелинейных искажений.
Выходная мощность усилителя мВт на нагрузке … Подробнее Панель управления сайтом Регистрация Войти.
Частота резонанса в колебательном контуре, онлайн расчет
Доброго дня уважаемые радиолюбители! Сегодня мы с вами рассмотрим порядок расчета LC контура. Некоторые из вас могут спросить, а на черта нам это нужно? Ну, во первых, лишние знания никогда не помешают, а во вторых, бывают в жизни моменты, когда вам знание этих расчетов может понадобиться. К примеру, очень многие начинающие радиолюбители естественно, в основном молодые , увлекаются сборкой так называемых жучков устройств позволяющих на расстоянии прослушивать что нибудь.
Что такое LC контур (колебательный контур). Расчет, колебания, резонансная частота, добротность. – Zaochnik.
Расчет контуров
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи. Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно. Все калькуляторы. Конвертеры Обратная связь Приложения. Учеба и наука — Математика — Красота и здоровье — Внешность — Компьютерная техника — Железо —
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно. Все калькуляторы. Конвертеры Обратная связь Приложения. Учеба и наука — Математика — Красота и здоровье — Внешность — Компьютерная техника — Железо —
Резонансная частота: формула
Для работы калькулятора необходимо включить JavaScript в вашем браузере! В сети на разных сайтах можно найти, в основном, одну и ту же версию такого калькулятора. Здесь предлагается совершенно другой вариант Справка по расчету здесь.
При последовательном соединении элементов цепи колебательный контур называется последовательным, при параллельном — параллельным [1].
Резонансный контур lc – Расчёт частоты резонанса колебательного контура
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи. Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.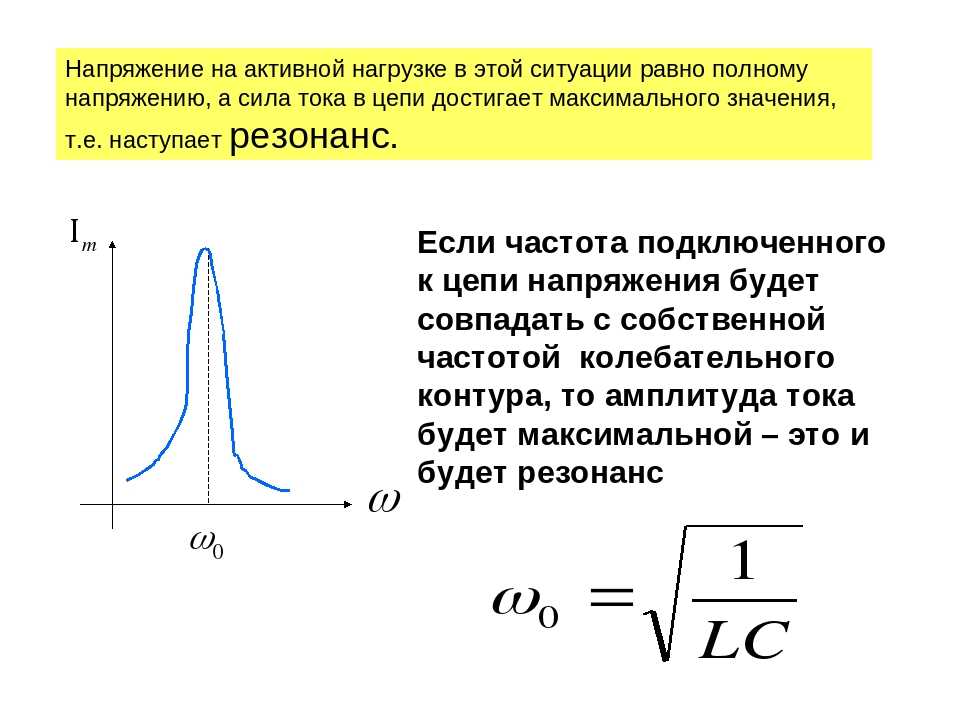 Обладает способностью накапливать и отдавать электрическую энергию. Обладает способностью накапливать и отдавать магнитную энергию. Если конденсатор ёмкостью C заряжен до напряжения U , потенциальная энергия его заряда составит.
Обладает способностью накапливать и отдавать электрическую энергию. Обладает способностью накапливать и отдавать магнитную энергию. Если конденсатор ёмкостью C заряжен до напряжения U , потенциальная энергия его заряда составит.
Расчет колебательного контура
Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока и напряжения. Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания. Резонансная частота контура определяется так называемой формулой Томсона:. В таблице ниже приведен онлайн-расчет колебательного контура по формуле Томпсона, в которой можно произвольным образом выбрать единицы измерения параметров F, L, C. Расчёт резонансной частоты колебательного контура site:radioaktiv. Онлайн расчет сопротивления конденсатора Xc и индуктивности Xl переменному току.
Для повышения мощности можно использовать резонанс LC на трансформаторе. Расчет емкости и индуктивности для контура по мощности.
Расчет емкости и индуктивности для контура по мощности.
Расчет колебательного контура
Применение и расчет резонанса на трансформаторе Для повышения мощности можно использовать резонанс LC на трансформаторе. Есть три вида резонанса LC – параллельный, последовательный и комбинированный. При параллельном резонансе в колебательном контуре повышаются амперы, но напряжение обычно сохраняется.
Резонансная частота контура
ВИДЕО ПО ТЕМЕ: Часть 4 2 Малыш FM2 Емкость для LC контура
Для генерации высокочастотных волн часто применяются схемы на основе колебательного контура. Подобрав параметры элементов цепи, можно производить частоты свыше МГц. Схемы используются в ВЧ-генераторах, высокочастотном нагреве, телевизионных и радиоприемниках. Колебательный контур — это последовательное или параллельное соединение индуктивных и конденсаторных элементов, генерирующих электромагнитные колебания любой заданной частоты.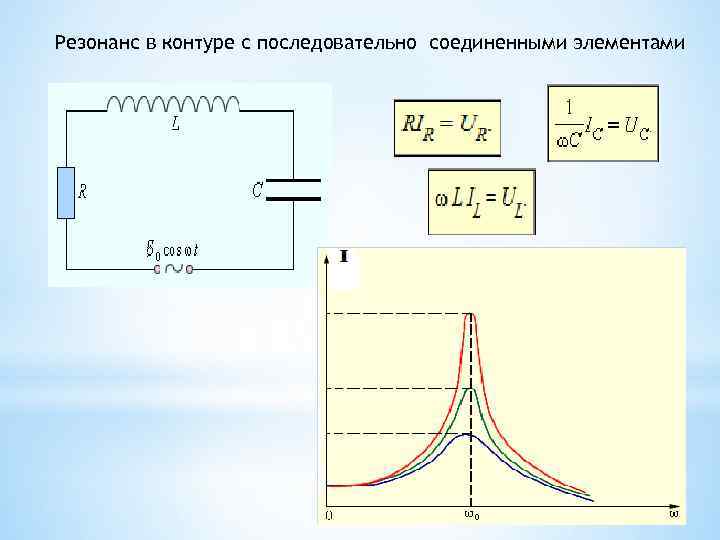 Оба компонента схемы способны хранить энергию.
Оба компонента схемы способны хранить энергию.
LC – фильтры я оставил на десерт, подобно бутылке благородного вина, покрытой слоем вековой пыли. Это антиквариат, который на Сотбисе не купишь!
Колебательный контур — электрическая цепь, содержащая катушку индуктивности, конденсатор и источник электрической энергии. Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания. Резонансная частота контура определяется так называемой формулой Томсона:. При слишком малой индуктивности и большой емкости будет падать резонансное сопротивление контура, что приведет к ухудшению его избирательных свойств, а в схеме резонансного усилителя упадет усиление каскада. При слишком малой емкости и большой индуктивности катушка будет содержать большое количество витков, добротность ее будет уменьшаться, а собственная емкость расти, в результате она может сравняться с емкостью контурного конденсатора, что не допустимо. Также на настройку контура будет влиять емкость монтажа, ведь она соизмерима со значением С. Исходя из вышеуказанного, рекомендую выбирать соотношение емкости к индуктивности примерно как : 1 в абсолютном значении, что подходит для большинства контуров.
Исходя из вышеуказанного, рекомендую выбирать соотношение емкости к индуктивности примерно как : 1 в абсолютном значении, что подходит для большинства контуров.
Практический расчет последовательного или параллельного LC контура. Доброго дня уважаемые радиолюбители! Некоторые из вас могут спросить, а на черта нам это нужно? Ну, во-первых, лишние знания никогда не помешают, а во-вторых, бывают в жизни моменты, когда вам знание этих расчетов может понадобиться.
Калькулятор резонанса колебательного контура — Строй Обзор
Содержание
- Свободные электрические колебания в параллельном контуре.
- Расчёт частоты резонанса LC-контура:
- Расчёт ёмкости:
- Расчёт индуктивности:
- Сайт для радиолюбителей
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.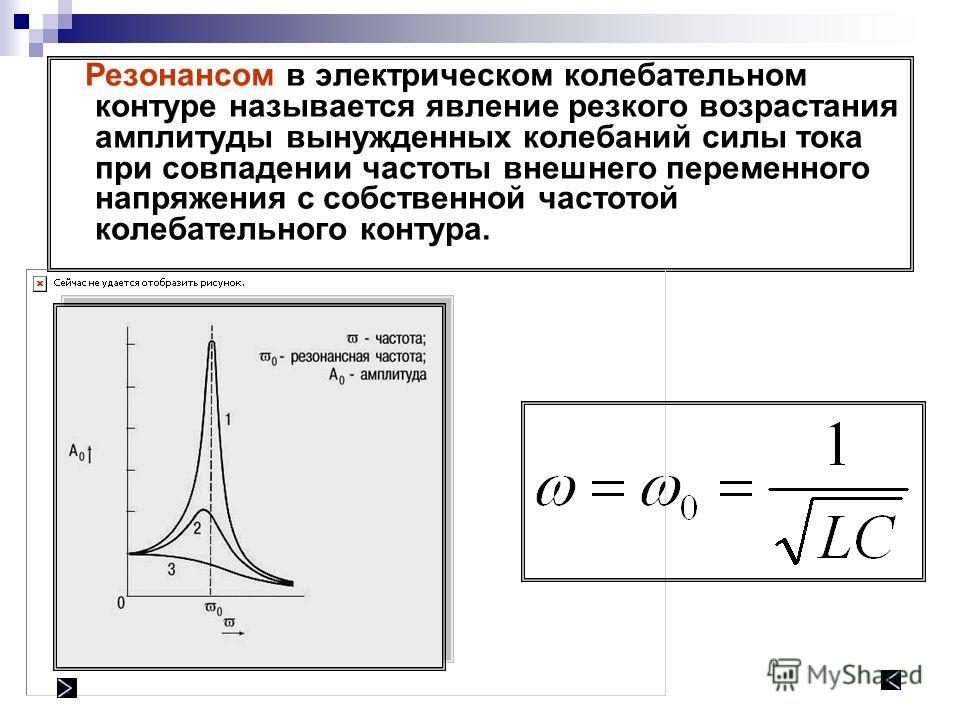
— Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
— Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.
Основные свойства индуктивности:
— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией .
— Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.
Период свободных колебаний контура LC можно описать следующим образом:
Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит.
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток его разряда, создавая магнитное поле в катушке.
Магнитный поток, увеличиваясь от нуля, создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в цепи, поэтому конденсатор разрядится не мгновенно, а через время t1, которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t1 = .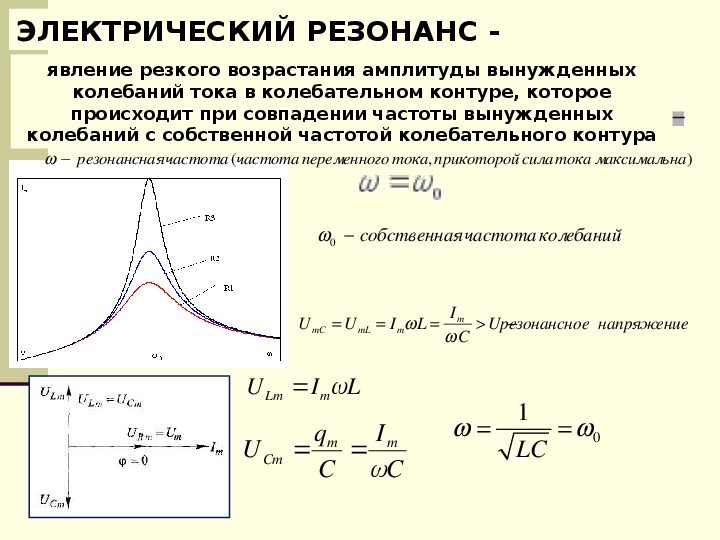
По истечении времени t1, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, EC будет равна EL. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.
Изменение (уменьшение) магнитного потока накопленной энергии катушки создаст в ней ЭДС, которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t2 = t1, он перезарядит конденсатор от нуля до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.
Описанные интервалы t1 и t2 составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени t3, сменив полярность полюсов.
В течении заключительного этапа колебания (t4), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U (в случае отсутствия потерь) и процесс колебания повторится.
В реальности, при наличии потерь энергии на активном сопротивлении проводников, фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t1 + t2 + t3 + t4 составит период колебаний .
Частота свободных колебаний контура ƒ = 1 / T
Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности XL=2πfL равно реактивному сопротивлению ёмкости XC=1/(2πfC).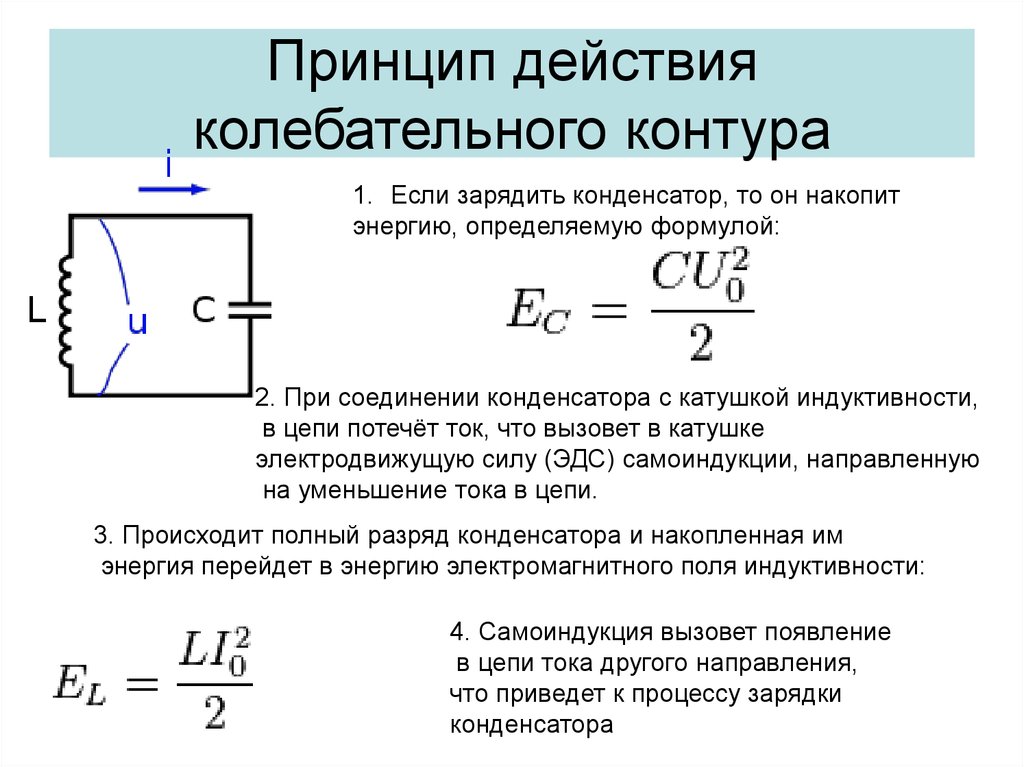
Расчёт частоты резонанса
LC-контура:Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Расчёт ёмкости:
Расчёт индуктивности:
Похожие страницы с расчётами:
Замечания и предложения принимаются и приветствуются!
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно. — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при совпадении частоты внешнего воздействия с некоторыми значениями (резонансными частотами), определяемыми свойствами системы.
F=1/(2π×√L×C), где
F — Резонансная частота, Гц)
L — Индуктивность, (Гн)
C — Ёмкость, (Ф)
Сайт для радиолюбителей
Колебательный контур — электрическая цепь, содержащая катушку индуктивности, конденсатор и источник электрической энергии. При последовательном соединении элементов цепи колебательный контур называется последовательным, при параллельном − параллельным.
При последовательном соединении элементов цепи колебательный контур называется последовательным, при параллельном − параллельным.
Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания.
Резонансная частота контура определяется так называемой формулой Томсона:
При слишком малой индуктивности и большой емкости будет падать резонансное сопротивление контура, что приведет к ухудшению его избирательных свойств, а в схеме резонансного усилителя упадет усиление каскада. При слишком малой емкости и большой индуктивности катушка будет содержать большое количество витков, добротность ее будет уменьшаться, а собственная емкость расти, в результате она может сравняться с емкостью контурного конденсатора, что не допустимо. Также на настройку контура будет влиять емкость монтажа, ведь она соизмерима со значением С. Исходя из вышеуказанного, рекомендую выбирать соотношение емкости к индуктивности примерно как 100000 : 1 в абсолютном значении, что подходит для большинства контуров.
Например, для частоты 10,7 МГц оптимальным будет С=47 пФ и L= 4,7 мкГн, а для частоты 465 кГц оптимальные С=1000пФ и L=117мкГн.
Исходя из всего выше сказанного, онлайн калькулятор позволяет подобрать значения емкости и индуктивности в пределах ±20% от оптимального значения.
Для расчета частоты резонанса колебательного контура LC заполните предложенную форму:
Расчёт ёмкости для колебательного контура LC
Расчёт индуктивности для колебательного контура LC
Расчёт частоты резонанса колебательного контура
Колебательный контур LC
Колебательный контур
— электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.
— Конденсатор C
– реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию. — Катушка индуктивности
— Катушка индуктивности
L
– реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.
Рассмотрим, как возникают и поддерживаются свободные электрические колебания в параллельном контуре LC
.
Основные свойства индуктивности
— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией . — Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.
Природа электромагнитных колебаний в контуре
Период свободных колебаний контура LC
можно описать следующим образом:
Если конденсатор ёмкостью C
заряжен до напряжения
U
, потенциальная энергия его заряда составит. Если параллельно заряженному конденсатору подключить катушку индуктивности
L
, в цепи пойдёт ток разряда конденсатора, создавая магнитное поле в катушке.
Внешний магнитный поток создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в каждом витке, поэтому конденсатор разрядится не мгновенно, а через время t
1, которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта
t
1 = . По истечении времени
По истечении времени
t
1, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны. Накопленная катушкой магнитная энергия в этот момент составит. В идеальном рассмотрении, при полном отсутствии потерь в контуре,
EC
будет равна
EL
. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.
Далее изменение (уменьшение от максимума) магнитного потока накопленной энергии катушки будет создавать в ней ЭДС, которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t
2 =
t
1, он перезарядит конденсатор от нулевого до максимального отрицательного значения (
-U
). Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.
Описанные интервалы t
1 и
t
2 составят половину периода полного колебания в контуре. Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени
t
3, сменив полярность полюсов.
В течении заключительного этапа колебания (t
4), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения
U
(в случае отсутствия потерь) и процесс колебания повторится.
В реальности, при наличии потерь энергии на активном сопротивлении проводников, фазовых и магнитных потерь, колебания будут затухающими по амплитуде. Время t
1 +
t
2 +
t
3 +
t
4 составит период колебаний . Частота свободных колебаний контура ƒ = 1 /
T
Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности XL=2πfL
равно реактивному сопротивлению ёмкости
XC=1/(2πfC)
.
Расчёт частоты резонанса LC-контура:
Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.
Необходимо вписать значения и кликнуть мышкой в таблице. При переключении множителей автоматически происходит пересчёт результата.
Наверх
Расчёт частоты:
| Частота резонанса колебательного контура LC. ƒ = 1/(2π√(LC)) |
Расчёт ёмкости:
| Ёмкость для колебательного контура LC C = 1/(4𲃲L) |
Расчёт индуктивности:
| Индуктивность для колебательного контура LC L = 1/(4𲃲C) |
Похожие страницы с расчётами:
Рассчитать импеданс.
Рассчитать реактивное сопротивление.
Рассчитать реактивную мощность и компенсацию.
Как работает контур колебаний
Работа контура колебаний основана на циклическом преобразовании энергии индуктивности в качественный показатель эффективности конденсатора и наоборот. Допустим, что конденсатор полностью заряжен и энергия, запасенная в нем, максимальна. При подключении его к катушке индуктивности, он начинает разряжаться. При этом, через индуктивность начинает протекать ток, вызывающий появление ЭДС самоиндукции, направленную на уменьшение протекающего тока. Это означает, что начинается процесс перезарядки конденсатора. В тот момент, когда энергия прибора становится равной нулю, та же величина для катушки максимальна.
При подключении его к катушке индуктивности, он начинает разряжаться. При этом, через индуктивность начинает протекать ток, вызывающий появление ЭДС самоиндукции, направленную на уменьшение протекающего тока. Это означает, что начинается процесс перезарядки конденсатора. В тот момент, когда энергия прибора становится равной нулю, та же величина для катушки максимальна.
Далее, энергия индуктивности снижается, расходуясь на заряд емкости с противоположной полярностью. После уменьшения показателя коэффициента самоиндукции до нуля, на конденсаторе она опять имеет максимальное значение.
Вам это будет интересно Как узнать ампераж
Процессы в системе
Важно! В идеальном случае, данный процесс способен протекать бесконечно. В реальных устройствах колебание затухает со скоростью, пропорциональной потерям в цепи проводников.
Вне зависимости от величины энергии, наличия потерь, частота колебаний постоянна и зависит только от значений параметров коэффициента самоиндукции и емкости. Данная величина называется резонансной. Формула резонанса учитывает значение величины емкости и индуктивности контура колебаний.
Данная величина называется резонансной. Формула резонанса учитывает значение величины емкости и индуктивности контура колебаний.
Осциллограмма
При воздействии на электрическую цепь с катушкой внешним сигналом с частотой, равной резонансной, амплитуда изменения положения частиц резко возрастает. Резонанс отсутствует при несовпадении частот. Из-за предельных значений электрическую цепь с катушкой индуктивности часто называют резонансной.
Потери в цепи с катушкой индуктивности (потери в диэлектрике конденсатора, сопротивление самого устройства, соединительных проводов) ограничивают величину предельных изменений направления частиц. В следствие этого, введена характеристика электроцепи, именуемая добротностью. Добротность обратно пропорциональна предельной величине потерь.
Зависимость предельной частоты от добротности
Важно! Снижение добротности приводит к тому, что предел изменения направлений наступает не только на основной частоте, но и на некотором приближении к ней, то есть, в некоторой полосе частот, где резонансное значение находится посередине. Чем выше добротность, тем более узкой становится полоса частот.
Чем выше добротность, тем более узкой становится полоса частот.
Формула Томсона (резонанса) для последовательного колебательного контура
Если при резонансе у нас реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора XL=XC , то можно уравнять их реактивные сопротивления и уже отсюда вычислить частоту, на которой произошел резонанс. Итак, реактивное сопротивление катушки у нас выражается формулой:
Реактивное сопротивление конденсатора вычисляется по формуле:
Приравниваем обе части и вычисляем отсюда F:
В данном случае мы получили формулу резонансной частоты. Это формула по другому называется формулой Томсона, как вы поняли, в честь ученого, который ее вывел.
Давайте по формуле Томсона посчитаем резонансную частоту нашего последовательного колебательного контура. Для этого я буду использовать свой RLC-транзисторметр.
Замеряем индуктивность катушки:
И замеряем нашу емкость:
Высчитываем по формуле нашу резонансную частоту:
У меня получилось 5, 09 Килогерц.
С помощью регулировки частоты и осциллографа я поймал резонанс на частоте 4,78 Килогерц (написано в нижнем левом углу)
Спишем погрешность в 200 с копейками Герц на погрешность измерений приборов. Как вы видите, формула Томпсона работает.
Последовательный колебательный контур обозначение на схеме
Последовательный колебательный контур – это цепь, состоящая их катушки индуктивности и конденсатора, которые соединяются последовательно.
Идеальный последовательный колебательный контур
На схемах идеальный последовательный колебательный контур обозначается вот так:
где
L – индуктивность, Гн
С – емкость, Ф
Реальный последовательный колебательный контур
Реальный колебательный контур имеет сопротивление потерь катушки и конденсатора. Это суммарное суммарное сопротивление потерь обозначается буквой R. В результате, реальный последовательный колебательный контур будет иметь такой вид:
R – это суммарное сопротивление потерь катушки и конденсатора
L – собственно сама индуктивность катушки
С – собственно сама емкость конденсатора
Формула индуктивности
Расчет резонанса колебательного контура производится на основании значений емкости и индуктивности. Как правило, емкость конденсатора является постоянной величиной, за исключением случаев использования переменных устройств в перестраиваемых электроцепях. Коэффициент самоиндукции катушки зависит от многих факторов:
Как правило, емкость конденсатора является постоянной величиной, за исключением случаев использования переменных устройств в перестраиваемых электроцепях. Коэффициент самоиндукции катушки зависит от многих факторов:
- Количество и расположение витков обмотки;
- Наличие или отсутствие сердечника;
- Материал сердечника.
Общей формулы для определения индуктивности катушки колебательного контура не существует. Для расчетов используют формулы, соответствующие форме катушки. К сожалению, все формулы определения качественной величины электрической цепи с подсоединённой к ней катушкой индуктивности позволяют производить только приблизительные расчеты.
Вам это будет интересно Описание распределительной коробки
Приборы индуктивности различных типов
Важно! Для того, чтобы получить катушку с заданными параметрами, приходится принимать дополнительные меры, например, производить подстройку коэффициента самоиндукции путем изменения длины сердечника или корректировки расстояния между витками в однорядных катушках.
Общие сведения
Колебательным контуром называется электрическая цепь, состоящая из конденсатора и катушки индуктивности, применяемой для генерации свободных электромагнитных колебаний в радиоприемниках и радиопередатчиках. Это устройство используется в качестве различных фильтров (полосовых и режекторных). Для подстройки сигналов в сторону увеличения или уменьшения амплитуды используется этот радиоэлемент. Основная функция контура — фильтрация частот.
Широкое распространение устройство получило в военной сфере. В радиолокационных станциях применяются фильтры шумоподавления. Противник использует различные постановщики помех, блокирующие обнаружение цели. В состав техники входит специальное устройство, состоящее из обыкновенных контуров, но с сердечником из специального сплава. Помехи «фильтруются», и оператор радиолокационной станции получает полную картину воздушной обстановки.
Устройство можно применять и для автоматизации. Например, в состав самолетов включен блок для регулировки частоты. Основными его элементами являются два контура, которые настроены только на две частоты — 760 и 840 Гц. На них приходит напряжение с частотой 790 Гц от специального генератора. Последний издает всего 395 Гц. Если частота отклоняется от номинального значения в меньшую сторону, то реактивное сопротивление одного из контуров уменьшается.
Основными его элементами являются два контура, которые настроены только на две частоты — 760 и 840 Гц. На них приходит напряжение с частотой 790 Гц от специального генератора. Последний издает всего 395 Гц. Если частота отклоняется от номинального значения в меньшую сторону, то реактивное сопротивление одного из контуров уменьшается.
После этого активируется электроника блока, и выдается сигнал на увеличение оборотов генератора. Когда величина частоты превышает номинальное значение, реактивное сопротивление другого контура увеличивается. В результате этого срабатывает автоматика, и поступает другой тип сигнала на уменьшение оборотов генератора.
Резонанс напряжений
Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:
и конденсатор в 1000 пФ
Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.
Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.
Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор – это не есть хорошо, но что не сделаешь ради науки!
Ну что же, приступим ;-). Давайте сначала посчитаем резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.
Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:
Размах амплитуды 4 Вольта
Хотя на генераторе частоты размах более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.
И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.
Теперь небольшой прикол
Вот этот сигнал мы подаем на наш последовательный колебательный контур:
Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.
Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:
Смотрим напряжение на конденсаторе:
Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!
Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:
Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!
Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке.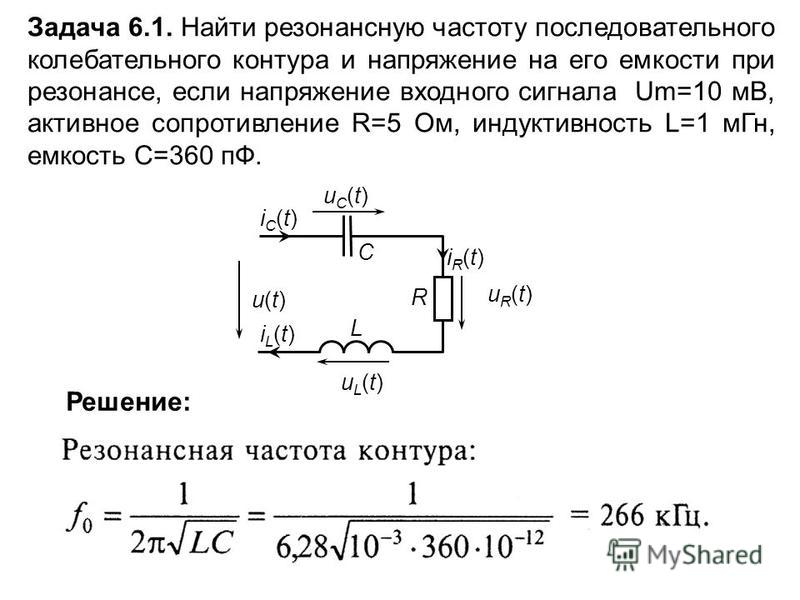 Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14, и цепляю поочередно к ним лампочку:
Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14, и цепляю поочередно к ним лампочку:
Как видите – полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока – увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!
Объяснение резонанса напряжения
При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.
Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.
При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение UL = IXL , а на конденсаторе UC = IXC . А так как при резонансе у нас XL = XC , то получаем что UL = UC , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.
Преобразователь случайных чисел |
Калькулятор импеданса LC-цепи Калькулятор импеданса LC-цепи серии определяет импеданс и угол разности фаз идеальной катушки индуктивности и идеального конденсатора, соединенных последовательно для заданной частоты синусоидального сигнала. Пример: Рассчитайте импеданс катушки индуктивности 100 мГн и конденсатора 800 нФ при частоте 562 Гц. Этот пример показывает очень низкий, близкий к резонансу импеданс около 0,9 Ом. Если вы хотите проверить импеданс почти при точном резонансе, введите 562,6977 Гц вместо 562 Гц. На этой частоте импеданс немного индуктивный. Если вы введете чуть более низкую частоту 562,6976 Гц, импеданс изменится на слегка емкостный, и вы заметите, что угол разности фаз изменился с 9от 0° до –90°. Вход Индуктивность, л генри (Гн) миллигенри (мГн) микрогенри (мкГн) наногенри (нГн) пикогенри (pH) (нФ)пФ (пФ) Частота, f герц (Гц)миллигерц (мГц)килогерц (кГц)мегагерц (МГц)гигагерц (ГГц) Доля Выход Угловая Частота рад/сЕмкостное реактивное сопротивление X C = Ом Индуктивное сопротивление X L = Ом Полное сопротивление LC |Z LC | = ω Разница в фазах φ = ° = RAD Резонансная частота F 0 = HZ ω 0 = RAD/S Вычисляйте по частоте RESONSANT . Введите значения емкости, индуктивности и частоты, выберите единицы измерения и нажмите или коснитесь кнопки Рассчитать . Попробуйте ввести нулевые или бесконечно большие значения, чтобы увидеть, как ведет себя эта схема. Бесконечная частота не поддерживается. Чтобы ввести значение Infinity , просто введите inf в поле ввода. Для расчета используются следующие формулы: φ = 90 °, если 1/2 πfc <2 πfl φ = –90 ° IF 1/2 πFC > 2 πFL φ111110 πfl φ111 = 0 ° 10 φ111 = 0 ° 1109 φ111 = 0 ° a 110 πfl a 110. πfc = 2 πfl , где Z LC – это схема LC в Ом (ω), ω = 2πf 1 – это угловая частота. f – частота в герцах (Гц), L — индуктивность в генри (Гн), C — емкость в фарадах (Ф), ω 0 = резонансная угловая частота в радианах в секунду (рад/с), 4 f 0 = резонансная частота в герцах (Гн),X C — реактивное сопротивление конденсатора в Ом (Ом), X L — реактивное сопротивление индуктивности в Ом , φ — фазовый сдвиг между полным напряжением В Т и полный ток I Т , а j — мнимая единица. Для расчета введите индуктивность, емкость и частоту, выберите единицы измерения, и результат для импеданса LC будет показан в омах, а для разности фаз — в градусах. Также будут рассчитаны реактивные сопротивления C и L и резонансная частота. Нажмите или коснитесь Рассчитать на резонансной частоте , чтобы увидеть, что произойдет при резонансе. Последовательная LC-цепь состоит из катушки индуктивности L и конденсатора C, соединенных последовательно. LC-контур может резонировать на резонансной частоте. Резонанс возникает на частоте, при которой полное сопротивление цепи минимально, то есть если в цепи нет реактивного сопротивления. Это явление возникает, когда реактивные сопротивления катушки индуктивности и конденсатора равны и из-за противоположных знаков они компенсируют друг друга (компенсацию можно наблюдать на правой векторной диаграмме ниже). Несколько графиков импеданса последовательного LC-контура Z LC в зависимости от частоты f для заданных индуктивности и емкости показывают нулевой импеданс на резонансных частотах. Когда частота увеличивается, реактивное сопротивление катушки индуктивности увеличивается, а реактивное сопротивление конденсатора уменьшается. Однако если частота приближается к нулю (или постоянному току), реактивное сопротивление катушки индуктивности уменьшается до нуля, а реактивное сопротивление конденсатора увеличивается до бесконечности. Калькулятор определяет резонансную частоту LC-контура, и вы можете ввести эту частоту или значение немного выше или ниже ее, чтобы увидеть, что произойдет с другими рассчитанными значениями при резонансе. Векторная диаграмма теоретически идеальной последовательной LC-цепи. Слева — емкостное сопротивление, то есть схема действует как конденсатор; центр — индуктивное сопротивление, то есть контур действует как индуктор; справа — нулевое реактивное сопротивление при резонансе, и схема действует как короткое замыкание. В последовательной цепи через катушку индуктивности и конденсатор протекает один и тот же ток, но отдельные напряжения на конденсаторе и катушке индуктивности различны. На векторной диаграмме показано напряжение V T идеального источника синусоидального напряжения. Поскольку сопротивление отсутствует, на резисторе нет падения напряжения в фазе с током, протекающим через цепь. На резонансной частоте емкостное и индуктивное сопротивления равны, и если мы посмотрим на уравнение для |Z| выше мы увидим, что эффективное сопротивление равно нулю, потому что два противоположных напряжения просто компенсируют друг друга. Ток, протекающий через катушку индуктивности и конденсатор, одинаков, а напряжения на них равны и противоположны. Таким образом, при резонансной частоте ток, потребляемый от источника, становится теоретически бесконечным, и идеальная последовательная LC-цепь на резонансной частоте, подключенная к источнику напряжения, действует как короткое замыкание. Резонансная частота последовательного LC-контура определяется с учетом того, что Умножив обе части уравнения на частоту f , получим Разделив обе части на 1 0 2 90 квадратный корень из обеих частей уравнения и упростив, получим резонансную частоту: Катушки индуктивности в ВЧ модуле телевизионного приемника Виды отказовЧто, если что-то пойдет не так в этой цепи? Click or tap a corresponding link to view the calculator in various failure modes:
Специальные режимыЩелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных специальных режимах: Различные режимы постоянного тока Короткая замыкания Открытая цепи Чисто контурная цепь Схема резонанса Чисто индуктивная цепь Индуктивная схема Примечания
Эта статья написана Анатолием Золотковым Вас могут заинтересовать другие калькуляторы из группы Калькуляторы для электротехники, ВЧ и электроники:Калькулятор резисторно-конденсаторных (RC) цепей Калькулятор параллельного сопротивления Калькулятор конденсации калькулятор конденсации . Калькулятор импеданса параллельной LC-цепи Параллельный калькулятор импеданса RL с цепью Параллельный калькулятор импедантного импеданса с цепи RLC СЕРИЧЕСКИЙ СКОРОСТЬ ИМЕННЫЙ КАЛКОТОР СКИРОВА СЕРИЯ RL CUMDANCE CULCUTUTUTURE СЕРИЯ RLC CUMPEDANCE CULCEUTUTURE Энергия батареи батареи DRON -Калькулятор индуктивности многослойной катушки NFC/RFID Калькулятор индуктивности плоской спиральной катушки Калькулятор коаксиального кабеля Калькулятор светодиодов. Расчет токоограничивающих резисторов для одиночного светодиода и светодиодных матриц Калькулятор цветового кода резистора Калькулятор максимальной дальности РЛС Калькулятор максимальной однозначной дальности РЛС и частоты повторения импульсов Калькулятор радиолокационного горизонта и видимости цели Радиолиния прямой видимости Калькулятор расстояния Калькулятор эффективной апертуры антенны Калькулятор дипольной антенны Калькулятор частоты наложения частот DC Power Calculator Калькулятор мощности переменного тока VA к калькулятору ватт Трехфазный калькулятор мощности переменного тока (сбалансированная нагрузка) Обращение фазора: прямоугольный-полосовой Калькулятор времени передачи данных Калькулятор внутреннего сопротивления батареи Калькуляторы Электрические, радиочастотные и электронные калькуляторы | |||||||||
LC-контур (он же бак или резонансный контур)
LC-цепь состоит из катушки и конденсатора, которые резонируют. друг с другом, передавая энергию туда и обратно между ними (цепь показано ниже). Этот происходит на определенной частоте, называемой резонансной частотой. L — это символ индуктивности, которая является свойством катушки. C – это символ емкости, которая является свойством конденсатора. Примеры на фотографиях ниже показывают кристаллические радиоприемники, каждый со своим катушка и конденсатор соединены параллельно.
Схема цепи LC.
LC-цепь в кварцевом радиоприемнике с цилиндрическим конденсатором.
LC-цепь в кварцевом радиоприемнике с плоским конденсатором.
Цепи LC используются для ряда вещей, таких как генерация сигналов на резонансной частоте и для выделения конкретной частота (резонансная частота) от цепи со многими частотами. Выделение определенной частоты — вот что происходит в кристаллическом радиоприемнике. где катушка и конденсатор соединены параллельно.
На самом деле сопротивление тоже играет роль, но часто при выполнении расчетах сопротивлением пренебрегаем. При включении сопротивления, вместо этого мы говорим о цепи RLC, где R представляет собой сопротивление.
Принцип работы LC-цепи
Индуктивность катушки (L) и емкость конденсатора (C) равны
выбираются таким образом, чтобы они резонировали на определенной частоте. Формула
дается раздел ниже, показывающий, как это сделать. Как показано
в анимации они обмениваются энергией туда и обратно на этой частоте.
В то время, когда ток течет через катушку, либо
увеличиваясь или уменьшаясь, вокруг него создается магнитное поле. По мере увеличения тока увеличивается напряженность магнитного поля.
По мере уменьшения тока магнитное поле ослабевает.
Когда нет больше тока, больше нет магнитного поля.
Конденсатор действует противоположно току.
Пока ток увеличивается, конденсатор разряжается.
Пока ток уменьшается, конденсатор заряжается.
Когда тока больше нет, конденсатор полностью заряжен.
По мере увеличения тока увеличивается напряженность магнитного поля.
По мере уменьшения тока магнитное поле ослабевает.
Когда нет больше тока, больше нет магнитного поля.
Конденсатор действует противоположно току.
Пока ток увеличивается, конденсатор разряжается.
Пока ток уменьшается, конденсатор заряжается.
Когда тока больше нет, конденсатор полностью заряжен.
LC-контур резонирует.
Кривые заряда/разряда конденсатора.
Все это имеет смысл. Если ток все еще течет, то конденсатор
не будет полностью заряжен – его заряд будет меняться.
Но как только он заряжен, ничто не держит его заряженным, и поэтому
этот заряд циркулирует обратно по цепи, обеспечивая ток.
Конденсатор не разряжается с постоянной скоростью (см. график).
Это начинается
разрядка медленно и быстро ускоряется, что означает, что ток также
начинается медленно и быстро ускоряется.
Ток, проходящий через катушку, создает
магнитное поле, поэтому пока конденсатор разряжается,
магнитное поле увеличивается в силе.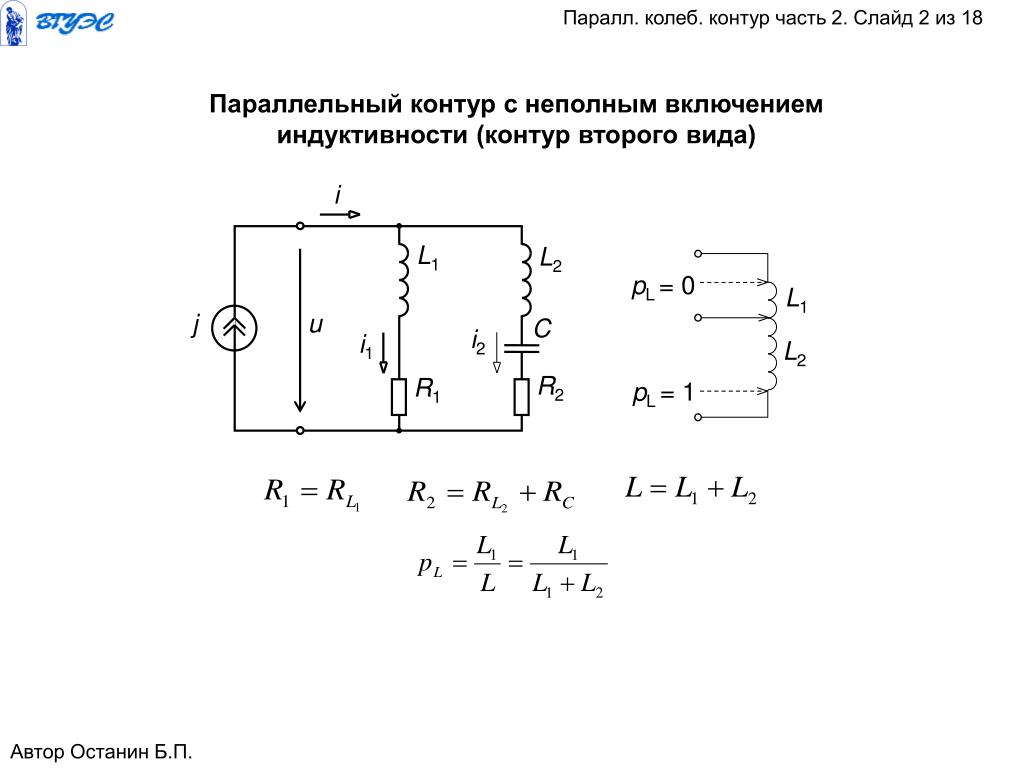 Но когда больше нет заряда
на конденсаторе тока больше нет, а значит магнитный
поле схлопывается. Изменяющееся магнитное поле индуцирует ток
течет по контуру, и пока поле схлопывается, оно меняется.
И так в цепи течет ток. Этот ток заряжает
конденсатор снова, и мы начинаем снова.
Но когда больше нет заряда
на конденсаторе тока больше нет, а значит магнитный
поле схлопывается. Изменяющееся магнитное поле индуцирует ток
течет по контуру, и пока поле схлопывается, оно меняется.
И так в цепи течет ток. Этот ток заряжает
конденсатор снова, и мы начинаем снова.
Калькулятор резонансной частоты LC и варианты
Вот калькулятор для расчета резонансной частоты. формулы ниже, если вам интересно.
Заполните следующие поля и нажмите кнопку «Рассчитать»…Если вы не знаете индуктивность и вам нужно вычислить ее, вы можете использовать калькулятор индуктивности, или формула на этой странице.
Если вы не знаете емкость и вам нужно вычислить ее, вы можете используйте калькулятор емкости, или формула на этой странице.
Индуктивность (л): Генримиллигенримикрогенри
Емкость (С): Фарадмиллифарадмикрофараднанофарадпикофарад
Результат:
Резонансная частота
Гц
Однако иногда вы знаете, какая частота вам нужна, и либо не знаете,
знать, что емкость или индуктивность вам нужно, чтобы получить эту частоту. Поэтому ниже приведены калькуляторы для этих двух.
Поэтому ниже приведены калькуляторы для этих двух.
Если вы не знаете емкость и вам нужно вычислить ее, вы можете используйте калькулятор емкости, или формула на этой странице.
Частота (f):
Гц (Герц) или циклов в секунду
Емкость (С): Фарадмиллифарадмикрофараднанофарадпикофарад
Результат:
Индуктивность
микрогенри
Чтобы получить емкость, заполните следующее и нажмите кнопку «Рассчитать»…
Если вы не знаете индуктивность и вам нужно вычислить ее, вы можете использовать калькулятор индуктивности, или формула на этой странице.
Частота (f):
Гц (Герц) или циклов в секунду
Индуктивность (л): Генримиллигенримикрогенри
Результат:
Емкость
микрофарады
Расчет резонансной частоты ЖК
Формула, необходимая для расчета резонансной частоты параллельная LC-цепь выглядит следующим образом:
L в приведенной выше формуле резонансной частоты представляет собой индуктивность
катушка. Если вы не знаете индуктивность, вы можете ее рассчитать
с помощью онлайн-калькулятора или формулы на
эта страница о конструкции катушки и
индукция.
Если вы не знаете индуктивность, вы можете ее рассчитать
с помощью онлайн-калькулятора или формулы на
эта страница о конструкции катушки и
индукция.
C в приведенной выше формуле резонансной частоты представляет собой емкость конденсатор. Трудно дать формулу для этого, так как есть много форм для конденсаторов, и каждая из них имеет разные формулы, но вы можете найти онлайн-калькуляторы и формулы для некоторых из них на эта страница о емкости.
Видео — схема LC (параллельная): выбор катушки и конденсатора
Это видео показывает магнитное поле катушки и заряд конденсаторов. в действии, объясняя все это. Он также проходит через пример используя формулы и калькуляторы для выбора индуктивности и емкость, чтобы получить желаемый диапазон резонансных частот для LC-цепи. Используемый пример относится к хрустальное радио.
Преобразователь случайных чисел |
Калькулятор импеданса LC-цепи Калькулятор импеданса LC-цепи определяет импеданс и угол разности фаз идеальной катушки индуктивности и идеального конденсатора, соединенных последовательно, для заданной частоты синусоидальный сигнал. Пример: Рассчитайте импеданс катушки индуктивности 100 мГн и конденсатора 800 нФ при частоте 562 Гц. Этот пример показывает очень низкий, близкий к резонансу импеданс около 0,9 Ом. Если вы хотите проверить импеданс почти при точном резонансе, введите 562,6977 Гц вместо 562 Гц. На этой частоте импеданс немного индуктивный. Если вы введете чуть более низкую частоту 562,6976 Гц, импеданс изменится на слегка емкостный, и вы заметите, что угол разности фаз изменился с 9от 0° до –90°. Вход Индуктивность, л генри (Гн) миллигенри (мГн) микрогенри (мкГн) наногенри (нГн) пикогенри (pH) (нФ)пикофарад (пФ) Частота, f герц (Гц)миллигерц (мГц)килогерц (кГц)мегагерц (МГц)гигагерц (ГГц) Багикан Выход Выход рад/с Емкостное реактивное сопротивление X C = Ом Индуктивное сопротивление X L = Ом Полное сопротивление LC |Z LC | = ω Разница в фазах φ = ° = RAD Резонансная частота F 0 = HZ ω 0 = RAD/S Вычисляйте по частоте RESONSANT . Введите значения емкости, индуктивности и частоты, выберите единицы измерения и нажмите или коснитесь кнопки Рассчитать . Попробуйте ввести нулевые или бесконечно большие значения, чтобы увидеть, как ведет себя эта схема. Бесконечная частота не поддерживается. Чтобы ввести значение Infinity , просто введите inf в поле ввода. Для расчета используются следующие формулы: φ = 90 °, если 1/2 πfc <2 πfl φ = –90 ° IF 1/2 πFC > 2 πFL φ111110 πfl φ111 = 0 ° 10 φ111 = 0 ° 1109 φ111 = 0 ° a 110 πfl a 110. πfc = 2 πfl , где Z LC – это схема LC в Ом (ω), ω = 2πf 1 – это угловая частота. f – частота в герцах (Гц), L — индуктивность в генри (Гн), C — емкость в фарадах (Ф), ω 0 = резонансная угловая частота в радианах в секунду (рад/с), 4 f 0 = резонансная частота в герцах (Гн),X C — реактивное сопротивление конденсатора в Ом (Ом), X L — реактивное сопротивление индуктивности в Ом , φ — фазовый сдвиг между полным напряжением В Т и полный ток I Т , а j — мнимая единица. Для расчета введите индуктивность, емкость и частоту, выберите единицы измерения, и результат для импеданса LC будет показан в омах, а для разности фаз — в градусах. Также будут рассчитаны реактивные сопротивления C и L и резонансная частота. Нажмите или коснитесь Рассчитать на резонансной частоте , чтобы увидеть, что произойдет при резонансе. Последовательная LC-цепь состоит из катушки индуктивности L и конденсатора C, соединенных последовательно. LC-контур может резонировать на резонансной частоте. Резонанс возникает на частоте, при которой полное сопротивление цепи минимально, то есть если в цепи нет реактивного сопротивления. Это явление возникает, когда реактивные сопротивления катушки индуктивности и конденсатора равны и из-за противоположных знаков они компенсируют друг друга (компенсацию можно наблюдать на правой векторной диаграмме ниже). Несколько графиков импеданса последовательного LC-контура Z LC в зависимости от частоты f для заданных индуктивности и емкости показывают нулевой импеданс на резонансных частотах. Когда частота увеличивается, реактивное сопротивление катушки индуктивности увеличивается, а реактивное сопротивление конденсатора уменьшается. Однако если частота приближается к нулю (или постоянному току), реактивное сопротивление катушки индуктивности уменьшается до нуля, а реактивное сопротивление конденсатора увеличивается до бесконечности. Калькулятор определяет резонансную частоту LC-контура, и вы можете ввести эту частоту или значение немного выше или ниже ее, чтобы увидеть, что произойдет с другими рассчитанными значениями при резонансе. Векторная диаграмма теоретически идеальной последовательной LC-цепи. Слева — емкостное сопротивление, то есть схема действует как конденсатор; центр — индуктивное сопротивление, то есть контур действует как индуктор; справа — нулевое реактивное сопротивление при резонансе, и схема действует как короткое замыкание. В последовательной цепи через катушку индуктивности и конденсатор протекает один и тот же ток, но отдельные напряжения на конденсаторе и катушке индуктивности различны. На векторной диаграмме показано напряжение V T идеального источника синусоидального напряжения. Поскольку сопротивление отсутствует, на резисторе нет падения напряжения в фазе с током, протекающим через цепь. На резонансной частоте емкостное и индуктивное сопротивления равны, и если мы посмотрим на уравнение для |Z| выше мы увидим, что эффективное сопротивление равно нулю, потому что два противоположных напряжения просто компенсируют друг друга. Ток, протекающий через катушку индуктивности и конденсатор, одинаков, а напряжения на них равны и противоположны. Таким образом, при резонансной частоте ток, потребляемый от источника, становится теоретически бесконечным, и идеальная последовательная LC-цепь на резонансной частоте, подключенная к источнику напряжения, действует как короткое замыкание. Резонансная частота последовательного LC-контура определяется с учетом того, что Умножив обе части уравнения на частоту f , получим Разделив обе части на 1 0 2 90 квадратный корень из обеих частей уравнения и упростив, получим резонансную частоту: Катушки индуктивности в ВЧ модуле телевизионного приемника Виды отказовЧто, если что-то пойдет не так в этой цепи? Click or tap a corresponding link to view the calculator in various failure modes:
Специальные режимыЩелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных специальных режимах: Различные режимы постоянного тока Короткая замыкания Открытая цепи Чисто контурная цепь Схема резонанса Чисто индуктивная цепь Индуктивная схема Примечания
Artikel ini ditulis oleh Анатолий Золотков. Вас могут заинтересовать другие калькуляторы из группы Калькулятор RF dan Elektronik:Калькулятор резисторно-конденсаторных (RC) цепей Калькулятор параллельного сопротивления Калькулятор конденсации калькулятор индуктивности . Калькулятор импеданса по конденсациям Калькулятор индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивного индуктивность . Калькулятор полного сопротивления цепи Калькулятор полного сопротивления параллельной LC-цепи Калькулятор полного сопротивления параллельной RL-цепи Параллельный калькулятор RLC-цепного схемы серии RC Калькулятор схемы. Калькулятор индуктивности плоской спиральной катушки NFC/RFID Калькулятор коаксиального кабеля Калькулятор светодиодов. Расчет токоограничивающих резисторов для одиночного светодиода и светодиодных матриц Цветочный код резистора Калькулятор Калькулятор максимального диапазона радара Максимальный радар -максимальный диапазон и калькулятор с частотой пульса Радар -горизонт и калькулятор визвижности целевого визита Радиоколдельный калькулятор расстояния. Калькулятор частоты наложения частот Калькулятор мощности постоянного тока Калькулятор мощности переменного тока Калькулятор ВА в Вт Калькулятор трехфазной мощности переменного тока (сбалансированная нагрузка) Преобразование вектора: прямоугольный–полярный Калькулятор полного гармонического искажения (THD) Калькулятор закона Ома Калькулятор времени передачи данных 0007 Сопротивление батареи Kalkulator Kalkulator RF dan Elektronik | |||||||||
Калькулятор резонансной частоты и импеданса RLC
Попробуйте этот новый инструмент
Калькулятор резонансной частоты и импеданса RLC Sierra Circuits вычисляет резонансную частоту и импеданс последовательных и параллельных цепей RLC. Резонансная частота — это частота, при которой возникает самый высокий колебательный отклик цепи. Это можно увидеть в цепях с конденсаторами и катушками индуктивности. Обычно в резонансные цепи вводят резистор для затухания колебаний. Этот процесс известен как демпфирование. Цепи RLC (резистор, катушка индуктивности и конденсатор) являются одними из самых основных схем, используемых в разводках печатных плат. Следовательно, разработчику платы важно знать о резонансной частоте и импедансе цепи RLC.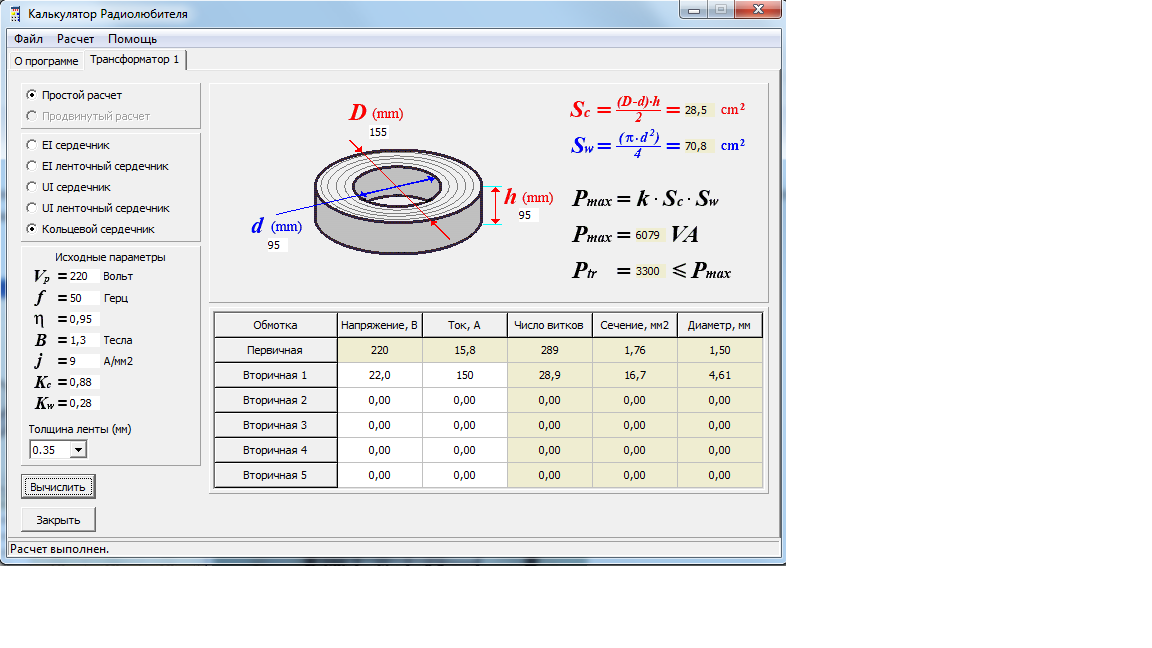
Калькулятор резонанса и импеданса RLC определяет емкостное реактивное сопротивление, индуктивное реактивное сопротивление, резонансную частоту, импеданс (параллельный/последовательный) и добротность без необходимости вводить слишком много входных параметров.
Характеристики инструмента
- Расчет емкостного сопротивления, индуктивного сопротивления, резонансной частоты, импеданса (параллельного/последовательного) и добротности
- Позволяет выбирать между последовательными и параллельными комбинациями RLC
- Единицы входов и выходов можно изменить с помощью соответствующих раскрывающихся списков
- Краткое описание каждого параметра можно просмотреть, нажав на кнопку справки
Сначала выберите нужное соединение RLC (параллельное/последовательное) . Далее введите следующие параметры:
Далее введите следующие параметры:
- Частота (f)
- Сопротивление (R)
- Емкость (Кл)
- Индуктивность (л)
Единицы этих параметров можно изменить с помощью соответствующих раскрывающихся списков.
После того, как вы введете значения всех обязательных полей, нажмите , вычислите . Теперь инструмент отображает значения следующих выходных параметров:
- Емкостное реактивное сопротивление (X C )
- Индуктивное сопротивление (X L )
- Резонансная частота (f r )
- Последовательный импеданс (Z S ) или параллельный импеданс (Z P )
- Серийный коэффициент качества (Q S ) или параллельный коэффициент качества (Q P )
Если вы хотите узнать больше о каком-либо из этих входных/выходных параметров, нажмите соответствующую кнопку справки.
Цепи RLC широко используются в низкоскоростных, высокоскоростных и радиочастотных приложениях, таких как фильтры, сети подачи питания (PDN) и сети согласования импеданса.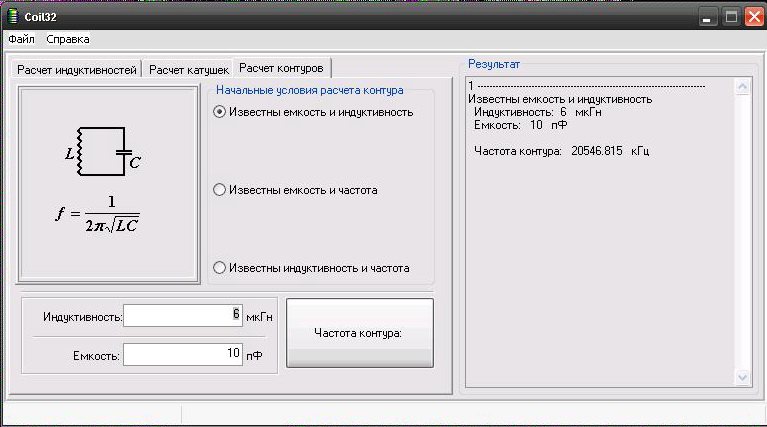 Для анализа поведения конденсаторов и катушек индуктивности важно рассчитать емкостные и индуктивные реактивные сопротивления . Иногда это может быть сложной и трудоемкой задачей для разработчиков, работающих с радиочастотными и высокоскоростными приложениями. Чтобы ускорить этот процесс, вы можете использовать калькулятор резонансной частоты и импеданса RLC .
Для анализа поведения конденсаторов и катушек индуктивности важно рассчитать емкостные и индуктивные реактивные сопротивления . Иногда это может быть сложной и трудоемкой задачей для разработчиков, работающих с радиочастотными и высокоскоростными приложениями. Чтобы ускорить этот процесс, вы можете использовать калькулятор резонансной частоты и импеданса RLC .
Платы PRO под ключ
Загрузите свою спецификацию, чтобы начать расчет
Начните мгновенное предложение
Посмотреть демонстрацию инструмента:
Компания Sierra Circuits разработала простые в использовании инструменты для проектировщиков печатных плат и инженеров-электриков на каждом этапе разработки печатных плат.
Печатные платы под ключ
Изготовление, закупка и сборка. печатных платы полностью собраны всего за 5 дней.
- Объединены в единый онлайн-процесс
- Проверено и протестировано инженерами
- Проверки DFA и DFM при каждом заказе
- Доставка из Кремниевой долины всего за 5 дней
Начать мгновенную онлайн-расценку
Стандартные печатные платы
Изготовление. Приобретение и сборка по желанию. Гибкость и прозрачность для продвинутых авторов.
- Жесткие печатные платы , изготовленные в соответствии со спецификациями IPC-6012 Class 2
- 2 мил (0,002″) след/пробел
- DFM проверяет каждый заказ
- 24-часовое время работы
Начать мгновенную онлайн-расценку
Расширенные печатные платы
Сложная технология с выделенным CAM-инженером.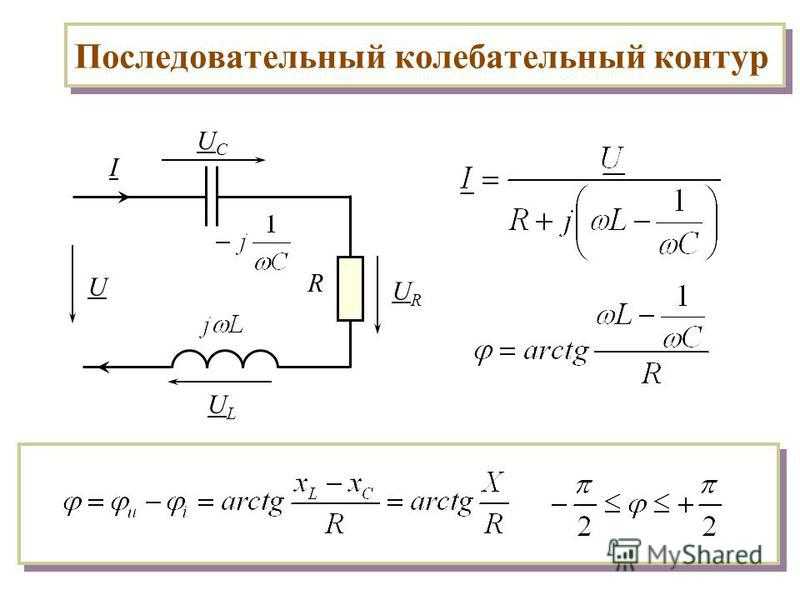 Включена помощь в укладке.
Включена помощь в укладке.
- Сложные требования к печатным платам
- Mil-Spec и класс 3 с функциями HDI
- Слепые и погребенные Виас
- Пластины Flex & Rigid-Flex
Стартовый номер +1 800-763-7503
Калькулятор контура бака | Техническая поддержка Do Supply
bydosupply
Емкость конденсатора
пикоФарад (пФ) наноФарад (нФ) микроФарад (мкФ) миллиФарад (мФ) Фарад (Ф)
Емкость катушки индуктивности
наноГенри (нГн) микроГенри (мкГн) миллиГенри (мГн) Генри (Гн)
Результаты
| Резонансная частота (МГц) |
Контур резервуара также называют LC-контуром, резонансным контуром или настроенным контуром. Это идеализированная электрическая цепь RLC с нулевым сопротивлением. Он состоит только из катушки индуктивности (L) и конденсатора (C), соединенных последовательно или параллельно; отсюда и название LC-схемы. Контурные схемы особенно полезны из-за их резонансных свойств. Они реализованы в различных электрических приложениях, таких как тюнеры частоты, фильтры и генераторы.
Это идеализированная электрическая цепь RLC с нулевым сопротивлением. Он состоит только из катушки индуктивности (L) и конденсатора (C), соединенных последовательно или параллельно; отсюда и название LC-схемы. Контурные схемы особенно полезны из-за их резонансных свойств. Они реализованы в различных электрических приложениях, таких как тюнеры частоты, фильтры и генераторы.
В любой цепи переменного тока (переменного тока), содержащей элементы сопротивления (R), емкости (C) и индуктивности (L), фаза напряжения в цепи и фаза тока в цепи обычно отличаются. Но если вы отрегулируете значения параметров компонентов L или C или частоту источника питания, вы можете сделать напряжение и ток одинаковыми по фазе, и вся цепь переменного тока будет казаться чисто резистивной. Когда схема достигает этого состояния, говорят, что она находится в резонансе, отсюда и название резонансной цепи.
Работа этой схемы аналогична работе резервуара в жидкостной системе, в которой размеры резервуара определяют наблюдаемую собственную частоту; всякий раз, когда жидкость пульсирует через бак.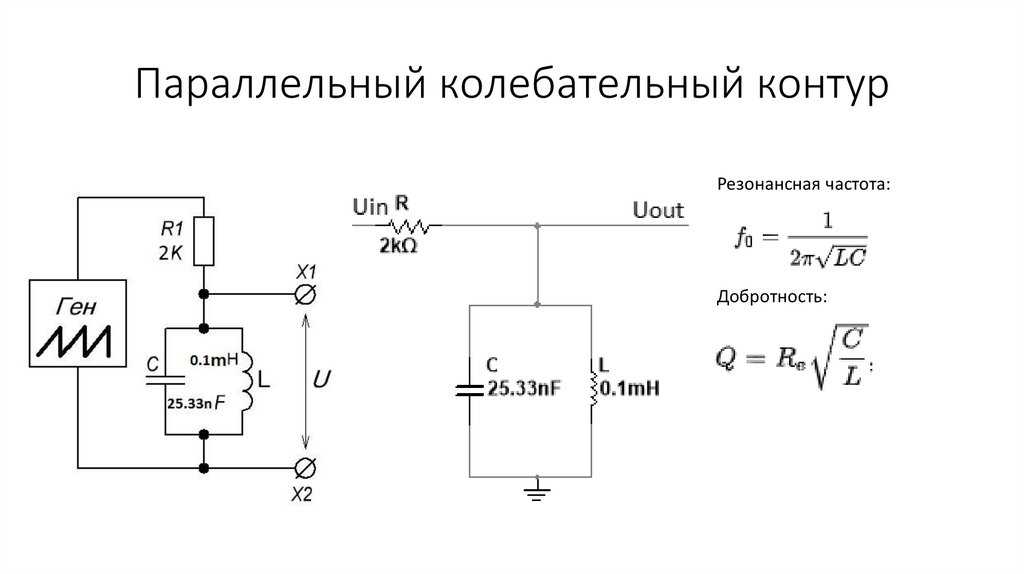 Точно так же контур резервуара накапливает энергию, колеблющуюся на своей резонансной частоте. Это объясняется тем, что электроды конденсатора накапливают электростатическую энергию в соответствии с изменениями напряжения в цепи. В то время как электромагнитная энергия, хранящаяся в магнитном поле индуктора, изменяется в соответствии с током, протекающим через индуктор.
Точно так же контур резервуара накапливает энергию, колеблющуюся на своей резонансной частоте. Это объясняется тем, что электроды конденсатора накапливают электростатическую энергию в соответствии с изменениями напряжения в цепи. В то время как электромагнитная энергия, хранящаяся в магнитном поле индуктора, изменяется в соответствии с током, протекающим через индуктор.
Принципиальная схема цепи бака с катушкой индуктивности и конденсатором в параллельной конфигурации показана справа.
Катушки индуктивности накапливают электрическую энергию в магнитных полях, и накопленная энергия пропорциональна квадрату силы тока в цепи. В то время как конденсаторы накапливают электрическую энергию в электрических полях, накопленная энергия пропорциональна квадрату напряжения в цепи. Таким образом, когда катушка индуктивности и конденсатор соединены вместе, их взаимодополняющие режимы накопления энергии вызывают передачу электрической энергии между индуктивностью и емкостью: при синусоидальных колебаниях тока и напряжения. Этот циклический обмен энергией называется резонансом. А простейшая резонансная цепь — это колебательная схема, состоящая из одного конденсатора, соединенного с одной индуктивностью, как показано выше.
Этот циклический обмен энергией называется резонансом. А простейшая резонансная цепь — это колебательная схема, состоящая из одного конденсатора, соединенного с одной индуктивностью, как показано выше.
Обратите внимание, что в емкостных цепях не используются электролитические конденсаторы, поскольку обе стороны конденсатора должны быть заряжены, вместо этого они используют керамические конденсаторы. Это связано с тем, что выводы керамических конденсаторов не поляризуются, поэтому зарядка может происходить на обоих выводах конденсатора. Однако у электролитических конденсаторов выводы поляризуются, и зарядка может происходить только с одной стороны.
Полностью заряженный конденсатор цепи бакаЧтобы понять, как работает накопительная цепь, давайте предположим, что конденсатор уже заряжен от источника постоянного тока, и его полярность соответствует показанной на схеме справа.
Верхняя пластина конденсатора заряжена положительно по отношению к нижней пластине. Это означает, что конденсатор обладает электростатической энергией и напряжение на его клеммах. Когда переключатель SW на рис. 2 замкнут (или источник питания на рис. 1 отключен), конденсатор начнет разряжаться, а заряд будет проходить между его электродами через катушку индуктора. Направление тока показано на рисунке слева.
Это означает, что конденсатор обладает электростатической энергией и напряжение на его клеммах. Когда переключатель SW на рис. 2 замкнут (или источник питания на рис. 1 отключен), конденсатор начнет разряжаться, а заряд будет проходить между его электродами через катушку индуктора. Направление тока показано на рисунке слева.
Верхняя пластина конденсатора заряжена положительно по отношению к нижней пластине. Это означает, что конденсатор обладает электростатической энергией и напряжение на его клеммах. Когда переключатель SW на рис. 2 замкнут (или источник питания на рис. 1 отключен), конденсатор начнет разряжаться по ходу заряда, потому что катушка индуктивности на самом деле имеет внутреннее сопротивление, она не пропускает весь ток мгновенно. . Вместо этого ток будет постепенно увеличиваться до максимального значения. Этот постепенный поток тока создает магнитное поле, тем самым генерируя электромагнитное поле вокруг катушки индуктора.
В конце концов, вся электростатическая энергия, накопленная в конденсаторе, высвобождается и преобразуется в электромагнитную энергию, которая накапливается вокруг катушки индуктивности. Таким образом, как только конденсатор полностью разрядится, так что напряжение на катушке индуктивности станет больше, чем напряжение на конденсаторе, магнитное поле катушки индуктивности начнет разрушаться. Это создает встречную ЭДС, и, согласно закону Ленца, встречная ЭДС будет поддерживать протекание тока. Учитывая, что функция катушки индуктивности в цепи бака состоит в том, чтобы предотвращать изменения тока, извлекать электромагнитную энергию из генерируемого магнитного поля и пытаться сделать ток как можно более постоянным.
Зарядка конденсатора в противоположной полярности По мере того, как катушка индуктивности рассеивает свою энергию на конденсаторе, ток постепенно накапливается в конденсаторе, и он заряжается в противоположной полярности, чем раньше. Как показано на рисунке справа: лин между его электродами через катушку индуктивности. Направление тока показано на рисунке справа.
Направление тока показано на рисунке справа.
Когда магнитное поле вокруг индуктора исчезает, ток прекращается, и конденсатор возвращается в исходное заряженное состояние, несмотря на то, что напряжение подается с противоположной полярностью, чем раньше. При полной зарядке конденсатор снова начнет разряжаться через катушку индуктивности. Весь этот процесс непрерывно повторяется до тех пор, пока вся энергия не рассеется на сопротивлении в контуре бака.
Баковые цепи имеют множество важных применений в области электротехники, в том числе:
- В радиотехнике: Движение электрической энергии вперед и назад через конденсатор и катушку индуктивности создает электромагнитную частоту. Эта частота очень полезна в телекоммуникационных технологиях, особенно в радиопередатчиках и приемниках. Например, простейший радиопередатчик состоит из усилителя класса C, имеющего колебательную схему на стороне нагрузки. Таким образом, когда на схему усилителя подается питание, схема резервуара генерирует достаточно энергии для передачи радиосигнала от усилителя на передающую антенну, которая, в свою очередь, излучает сигнал в космос.

- Аналогично, колебательная схема используется в радиоприемниках при приеме сигнала. В таких приложениях, как только контур резервуара заряжается, он генерирует точную частоту, которая настраивает радиоприемник на частоту принимаемого сигнала. Этот точный резонанс полезен для фильтрации других частот (путем их блокировки), поэтому могут воспроизводиться только выбранные радиостанции. Технология применима ко всем устройствам связи, таким как рации, радиомачты и т. д.
- В электронике: Резервуарные схемы используются либо для выбора заданного сигнала на определенной частоте из более сложной полосы пропускания сигнала (например, полосовые фильтры), либо для генерации сигналов на определенной частоте (в качестве генераторов сигналов). В таких приложениях они играют ключевую роль в работе многих электронных устройств, включая радиооборудование, и используются в различных электрических схемах, таких как смесители частоты, генераторы, фильтры и тюнеры.
Это инструмент, разработанный и созданный для расчета резонансной частоты контура резервуара, когда известны значения индуктивности (L) и емкости (C).
Как указывалось ранее, накопительный контур является наиболее распространенным типом резонансного контура. И вообще резонансный контур поглощает максимальную мощность на резонансной частоте. Итак, прежде чем погрузиться в расчет резонансной частоты контура резервуара, давайте сначала разберемся с явлением резонанса и тем, как возникает формула резонансной частоты.
Резонанс возникает, когда емкостное сопротивление ( X C ) и индуктивное сопротивление ( X L ) бакового контура имеют одинаковую величину. Итак, в резонансе X C = X L 5 90. Это явление заставляет электрическую энергию колебаться между электрическим полем конденсатора и магнитным полем катушки индуктивности. Однако контур резервуара не может резонировать сам по себе, и должен присутствовать источник питания переменного тока или аналогичный источник питания, например радиоволны.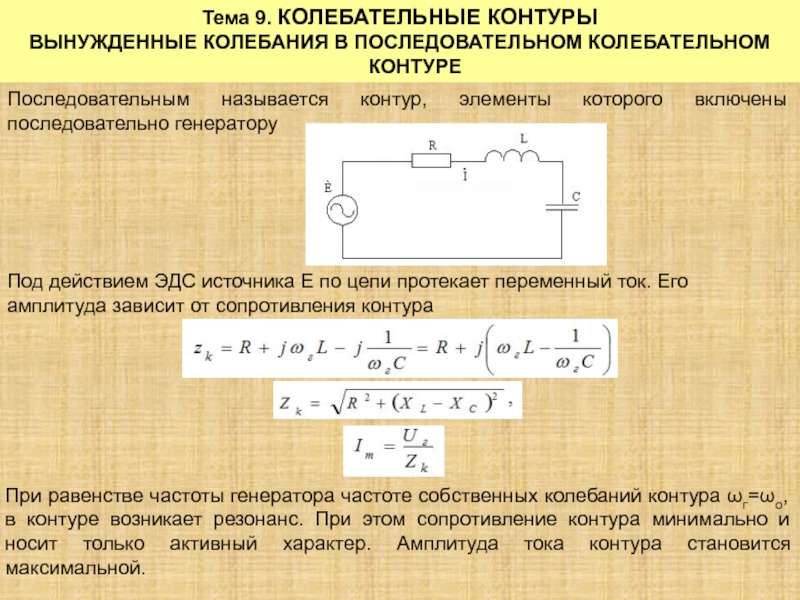
Примечание: Резонанс в цепях резервуара возникает из-за того, что разрушающееся магнитное поле индуктора создает электрический ток в его обмотках, который заряжает конденсатор, а разряжающийся конденсатор создает электрическое поле, которое создает магнитное поле в индукторе — этот процесс постоянно повторяется.
Также важно отметить, что при резонансе импеданс последовательной цепи бака (когда компоненты L и C соединены последовательно) минимален, а параллельный импеданс максимален.
- Наиболее типичным применением резонанса в контурах резервуаров является регулировка сигнала. Например, всякий раз, когда вы настраиваете свое радио на определенную вещательную станцию, контур резонатора резонирует на несущей частоте этой вещательной станции.
- Цепь последовательного бака увеличивает напряжение. По этой причине резонансные контуры серии используются в качестве фильтрующих или ситовых цепей. В таких приложениях последовательный колебательный контур будет пропускать частоты, близкие к резонансной частоте.

- Параллельная цепь бака увеличивает ток. Таким образом, параллельные резонансные схемы в основном используются в качестве полосовых режекторных фильтров или ловушек для фильтрации определенных частот.
- Цепь параллельного резервуара может использоваться в выходной цепи ВЧ (радиочастотного) усилителя в качестве импеданса нагрузки.
- Параллельные резонансные контуры также широко используются для индукционного нагрева
Резонансная или резонансная частота — это частота, при которой значения индуктивности и емкостного сопротивления контура резервуара равны. В общем случае резонансная частота — это собственная и незатухающая частота системы. Всякий раз, когда применяется резонансная частота, колебания достигают максимальной амплитуды, и даже относительно меньшие силы могут создавать большие амплитуды.
Однако, если вы выберете другую частоту, отличную от резонансной, этот высокоамплитудный сигнал будет заглушен. Существует множество различных типов резонансов, включая механические и акустические, электрические, орбитальные, оптические и молекулярные резонансы.
Для контуров резервуара резонансная частота определяется значениями индуктивности (L) и емкости (C). По этой причине, когда компоненты индуктора и конденсатора соединены последовательно или параллельно, они имеют резонансную частоту. И, как было сказано ранее, резонанс в цепях резервуара возникает, когда 9. Это связано с тем, что индуктивная реактивная способность ( x L ) увеличивается с увеличением частоты, тогда как емкостная реактивность ( x C 9018 C 9018 C 9018 C 9018
7 C 9018 . частота, при которой два реактивных сопротивления могут быть равны, что является резонансной частотой.
Уравнения для определения индуктивного и емкостного сопротивления на заданной частоте следующие:
X L = 2πfL ……… (i)
X C = (1) / (2πfC) ……… (ii)
При резонансе X L = X С
Затем мы можем приравнять два уравнения и решить их алгебраически для резонансной частоты. Следовательно,
Следовательно,
2πfL = (1) / (2πfC) ………(iii)
Решая f, мы получаем,
f 2 = (1) / (4π 2 LC)
f = [1] / [2π √(L×C)]
Таким образом, резонансная частота (fr) контура резервуара вычисляется с использованием следующего уравнения:
f r = [1] / [2π √(L×C)] ………(iv)
Где:
f r = Резонансная частота контура резервуара, указанная в Гц (Герцах)
Л = Индуктивность в Генри (Гн)
C = емкость в фарадах (Ф)
Обратите внимание, формула для расчета резонансной частоты колебательного контура универсальна как для последовательного, так и для параллельного резонансного контура. Это связано с тем, что в обоих случаях при резонансе напряжение и ток совпадают по фазе с омическим сопротивлением. И фазовый сдвиг =0°. Это приводит к резонансной частоте, определяемой формулой в уравнении (iv).
Это связано с тем, что в обоих случаях при резонансе напряжение и ток совпадают по фазе с омическим сопротивлением. И фазовый сдвиг =0°. Это приводит к резонансной частоте, определяемой формулой в уравнении (iv).
Однако импеданс Z последовательной цепи бака наименьший на резонансной частоте, когда 9. Принимая во внимание, что импеданс Z параллельного контура бака максимален на резонансной частоте, когда
Кроме того, импеданс цепи резервуара при резонансе может быть выражен как: Z = √ [ R 2 + ( X L − X C ) 2 ]
R = сопротивление в контуре бака
Так как фазы напряжения на цепи противоположны и Х С = Х Л ; два значения реактивности компенсируются, и применяется следующее: Z = R
Пример 1: Значения индуктивности и емкости баковой цепи равны 35 мГн и 10 мкФ соответственно. Определить резонансную частоту контура?
Определить резонансную частоту контура?
Решение: Учитывая это,
L = 35 мH = 35 × 10 −3 H
C = 10 мкФ = 10 × 10 −6 F
И формула резонансной частоты:
f r = [ 1 ] / [ 2π √(L×C) ] ………(iv)
Тогда
ж р = [ 1 ] / [ 2π √(LC) ] = ( 1 ) / ( 2π √[(35 × 10 −3 H ) × (10 × 10 −6 F )] ) = 269,0210 Гц
Таким образом, резонансная частота контура резервуара будет равна f r = 269,02 Гц
Пример 2: Допустим, вы хотите определить резонансную частоту LC-контура, имеющего катушку индуктивности 3 мГн и конденсатор емкостью 4 мкФ.
Решение: Резонансная частота ( f r ) цепи вычисляется следующим образом:
Д = 3 мГн
C = 4 мкФ = 4 × 10 −3 мФ
Следовательно,
f r = [ 1 ] / [ 2π √(L×C) ] = × [ 1 ] / [ 2π √( (9 ) 1 ) 11018 −3 мФ) )] = 1,4529 Гц
Следовательно, резонансная частота LC-контура будет ≈ 1,45 Гц
Примечание. Всякий раз, когда вы вручную вычисляете резонансную частоту контура резервуара (без использования калькулятора резонансной частоты), убедитесь, что вы конвертируете единицы заданных параметров в единицы СИ Генри и Фарады или убедитесь, что данные значения имеют общий Переменная единицы измерения СИ, такая как микро (µ), милли (м), нано (n) и т. д. В противном случае результаты f r будут неточными.
д. В противном случае результаты f r будут неточными.
Пример 3: Параметры электрической цепи бака даны как: индуктивность 50 мГн и емкость 8 мкФ. Рассчитайте резонансную частоту этого контура в МГц?
Решение:
Заданные параметры в этой задаче:
Д = 50 мГн = 50 × 10 −3 Н
C = 8 мкФ = 8 × 10 −6 F
Формула резонансной частоты:
f r = [1] / [2π√(L × C)]
Подставляя значения индуктивности и емкости в приведенную выше формулу,
f r = ( 1 ) / ( 2π√[(50 × 10 −3 H ) × (8 × 10 −6 F)] ) = 251,6461 Гц
Следовательно, резонансная частота колебательного контура в МГц будет:
f r = 251,6461 Гц × 10 −6 = 0,0002516 МГц
f r = 2. 516 × 10 −4 MHz
516 × 10 −4 MHz
Этот калькулятор использует значения индуктивности (L) и емкости (C) накопительного контура (в последовательной или параллельной конфигурации) для расчета резонансной частоты контура ( ф р ). Его принцип работы основан на следующей формуле: f r = (1) / (2π√[L × C])
Калькулятор предоставляет значение резонансной частоты в терагерцах (ТГц), гигагерцах (ГГц), мегагерцах (МГц), килогерцах (кГц) или герцах (Гц).
Шаги по использованию калькулятора:
Вы можете использовать калькулятор, просто выполнив следующие три шага:
- Введите указанные значения конденсатора (C) и катушки индуктивности (L).
- Выберите единицы измерения для заданных параметров и единицу измерения резонансной частоты, которую вы хотите использовать.

- Нажмите кнопку «Рассчитать», и значение резонансной частоты будет рассчитано мгновенно.
Пример: Используя калькулятор резонанса резервуара (показан выше), определите резонансную частоту контура резервуара, индуктивность (L) которого равна 65 мГн и Емкость (C) 10 мкФ?
Используя приведенный выше калькулятор, полученная резонансная частота цепи резервуара: F R = 0,0001974 МГц , который также может быть выраженным как:
974 МГц
, который также может быть выражен в74 МГц , который также может быть выражен:74 МГц , который также может быть выражен в = 0,0001974 МГц , который также может быть выражен. r = 197,4 Гц Примечание. При использовании калькулятора резонанса контура резервуара вам не нужно менять единицы измерения заданных значений индуктивности и емкости на общепринятые префиксы единиц СИ.
Пример: Учитывая, что контур резервуара имеет резонансную частоту 300 Гц, а его емкость составляет 6 мкФ. Каково значение индуктивности цепи?
Решение 1. Вычисления вручную,
Указанные параметры:
f r = 300 Гц
C = 6 × 10 −6 Ф
А так как формула для резонансной частоты: f r = ( 1 ) / ( 2π√[L×C] ) 4 Чтобы получить значение индуктивности, мы можем сделать L субъектом в приведенном выше уравнении, f r 2 = (1) / (4π 2 × Д × В) L = (1) / (4π 2 × C × f р 2 ) Подставляя данные значения в приведенную выше формулу индуктивности, L = (1) / (4π 2 × C × f r 2 ) = (1) / (4π 2 × [6 × 10 −6 0F] × 30 0,04691 Н Следовательно, индуктивность этой цепи бака будет ≈ 46,91 мГн (миллиГенри) Решение 2. Вы можете просто определить значение индуктивности с помощью калькулятора: (i) введя значения конденсатора и резонансной частоты; (ii) Выбор соответствующих единиц измерения. VK4ADC LC Calculator 24 февраля 2011 г. Кажется, мне часто нужно узнать резонансную частоту LC-контура, и в прошлом я использовал электронную таблицу на основе Excel. В связи с моим нынешним участием в синтезаторах частоты, использующих варикапные диоды, я подумал, что пришло время упростить задачу и написать специальное программное обеспечение. Вас могут интересовать не ГУН, а диапазон настройки, который вы могли бы ожидать, например, с подстроечным конденсатором 4-20 пФ на катушке индуктивности 100 нГн, которую вы планируете использовать в двухметровом входном каскаде преобразователя (ответ: от 107 до 206 МГц). с 2 пФ паразитных C/входной емкости устройства в соответствии с этим программным обеспечением. Программное обеспечение основано на стандартной формуле для резонансной частоты: 1 / (2*Pi*SQRT(L*C)) и позволяет пользователю учитывать любые значения паразитной емкости цепи (включая входную или выходную емкость активного устройства). значения) – этот последний «компонент» является наиболее важным при работе с верхним пределом диапазона настройки, в большей степени, чем с нижним. Обратите внимание, что формула последовательного и параллельного резонанса одинакова, поэтому независимо от того, хотите ли вы построить последовательную резонансную ловушку или стандартную параллельную резонансную схему, используется одна и та же формула, и, следовательно, этот калькулятор применим. Просто предупреждение, хотя : отображаемые значения с точностью до нескольких знаков после запятой. Точность этих десятичных знаков зависит от таких вещей, как длина ваших выводов, насколько точно вы оценили мощность паразитных цепей и т. Если вам интересно, как вы можете узнать эти минимальные и максимальные частоты на практике, подключите параллельную настроенную схему LC к 2-контактному ВЧ генератору/устройству и используйте частотомер (хороший метод) или измерьте их с помощью -meter” {чревато неточностями калибровки}. При расчете не учитывается добротность катушки индуктивности. Он всегда считается высоким из-за метода построения. Катушки индуктивности с низкой добротностью в любом случае обычно используются в параллельных цепях LC….. Программное обеспечение, которое я написал, не выглядит слишком красивым, но оно функционально: Наведите указатель мыши, чтобы увидеть увеличенное изображение Объяснить поля, которые пользователь может заполнить деталями: Фиксированная индуктивность:  Использование калькулятора контура бака
Использование калькулятора контура бака VK4ADC LC Calculator
 … Измените это паразитное/входное значение на 5 пФ, и оно упадет до 100–167 МГц.).
… Измените это паразитное/входное значение на 5 пФ, и оно упадет до 100–167 МГц.). д. Я бы просто проигнорировал почти все десятичные знаки в любом отображаемом значении (за исключением, может быть, расчетной индуктивности). из-за вовлеченных физических неточностей, а не из-за процесса расчета.
д. Я бы просто проигнорировал почти все десятичные знаки в любом отображаемом значении (за исключением, может быть, расчетной индуктивности). из-за вовлеченных физических неточностей, а не из-за процесса расчета. Стандарт измеряется в микрогенри (мкГн), хотя калькулятор работает со значениями наногенри (нГн) или миллгенри (мГн) при выборе из раскрывающегося списка (версии 1/3/11 и более поздние версии). Если известно измерение верхней частоты и минимальной емкости LC-цепи, можно рассчитать значение индуктивности (L).
Стандарт измеряется в микрогенри (мкГн), хотя калькулятор работает со значениями наногенри (нГн) или миллгенри (мГн) при выборе из раскрывающегося списка (версии 1/3/11 и более поздние версии). Если известно измерение верхней частоты и минимальной емкости LC-цепи, можно рассчитать значение индуктивности (L).
Оценка паразитного рассеяния C : Физическая компоновка электронной схемы вносит некоторую паразитную емкость в резонансный контур. Это приводит к снижению верхнего предела частоты, на который может настроиться LC-схема с переменным конденсатором. Вместо того, чтобы игнорировать его, пользователь может заменить его номинальным значением (например) 10 пФ. Это значение соответствует как минимальным, так и максимальным значениям конденсатора (CMin и CMax) при расчете резонанса. Если используется известная индуктивность и измеряется верхняя частота с известной (минимальной) емкостью, можно рассчитать паразитную емкость цепи.
Максимум C : Это максимальное значение емкости физического подстроечного конденсатора (например, 415 пФ для 10-415, 250 пФ для 10-250) или варикапа (например, 85 пФ для BB200, как указано в поле данных). ). Значение MaxC может быть рассчитано для известного L и измеренного верхнего и нижнего пределов частоты.
). Значение MaxC может быть рассчитано для известного L и измеренного верхнего и нижнего пределов частоты.
Минимум C : Это минимальное значение емкости физического подстроечного конденсатора (например, 10 пФ для 10-415, 10 пФ для 10-250) или варикапа (например, 11 пФ для BB200, как указано в поле данных). для синтезатора, работающего от источника питания 5 В). Значение MinC может быть рассчитано для известного L и измеренного верхнего и нижнего пределов частоты.
Min Freq : Это минимальная или нижняя граница частотного диапазона, на которую данное значение индуктивности (L) будет настроено при максимальном значении способности настройки (Maximum C) с параллельным значением паразитного C. Если измеряется фактическое значение, его можно ввести в это поле для расчета значений L или Максимум C в зависимости от того, какие фактические значения неизвестны.
Max Freq : Это максимальная или верхняя граница частотного диапазона, на который будет настроено заданное значение индуктивности (L) при минимальном значении емкости настройки (Минимум C) с параллельным значением паразитного C. Если измерено фактическое значение, его можно ввести в это поле для расчета значений L, минимального C или паразитного C в зависимости от того, какие фактические значения неизвестны.
Если измерено фактическое значение, его можно ввести в это поле для расчета значений L, минимального C или паразитного C в зависимости от того, какие фактические значения неизвестны.
На следующих изображениях показано, какие значения используются в доступных режимах расчета. Значения, выделенные голубым фоном, являются входными (или введенными пользователем) значениями. Значение/с, выделенное желтым цветом, является выходным расчетом. Кнопка, нажатая для достижения результата, очевидна по вставке в виде «нажатой кнопки» на изображении. Обратите внимание, что фактическое программное обеспечение устанавливает синий цвет фона текста для всех полей, необходимых для этого конкретного расчета/функции, с выделенными желтыми результатами, чтобы было легче увидеть, в каком поле (или полях) содержатся результаты..
Расчет нижнего и верхнего пределов частоты с известной индуктивностью, расчетной паразитной емкостью, известными максимальным и минимальным значениями основной подстроечной емкости. В этом примере показана катушка индуктивности 10 мкГн, переменный конденсатор 10-415 пФ и расчетная емкость паразитной цепи 10 пФ.
В этом примере показана катушка индуктивности 10 мкГн, переменный конденсатор 10-415 пФ и расчетная емкость паразитной цепи 10 пФ.
Расчет максимального и минимального значений емкости с известными нижним и верхним частотными пределами с известными значениями индуктивности и расчетными значениями паразитной емкости. Этот пример показывает, что мы знаем, что значение индуктивности составляет 10 мкГн, а диапазон настройки составляет от 3 до 12 МГц, опять же, паразитная емкость 10 пФ. Переменный конденсатор, вероятно, составляет от 10 до 250 пФ с указанной точностью частоты.
Расчет индуктивности с известным значением верхней частоты и минимальной основной настроечной емкостью. Расчетная паразитная емкость влияет на точность расчетного значения индуктивности. Это показывает, что значение индуктивности 3,9 мкГн требуется для резонанса с 45 пФ (35 пФ мин. + 10 пФ паразитных) на частоте 12 МГц.
Расчет емкости паразитной индуктивности с известным значением верхней частоты, минимальной основной настроечной емкостью и известной индуктивностью. Если мы точно знаем значения индуктивности и минимального конденсатора и измерили верхнюю частоту, то мы можем рассчитать фактическую паразитную емкость…
Если мы точно знаем значения индуктивности и минимального конденсатора и измерили верхнюю частоту, то мы можем рассчитать фактическую паразитную емкость…
Начиная с версии 1, в правом нижнем углу была добавлена дополнительная кнопка «Очистить все значения данных», которая позволяет пользователю очистить все поля данных одновременно, чтобы можно было использовать совершенно новый набор значений.
Начиная с версии 2, для компонента Inductance добавлен раскрывающийся список единиц измерения. Стандартная единица измерения – мкГн, альтернативно – нГн и мГн. см. изображение ниже.
Имейте в виду, что если вы не введете значения во все обязательные поля, появится сообщение об ошибке, в котором говорится, что вам нужно добавить дополнительные сведения, чтобы все поля были выделены цветом Aqua ( /светло-синий) содержат действительные данные.
Это единственные доступные режимы расчета.
Вы можете использовать его для определения параллельной резонансной частоты LC компонентов, которые у вас есть. Допустим, у вас есть настроечный конденсатор 10-415 пФ и катушка индуктивности 10 мкГн (она отмечена на самой катушке индуктивности). Если вы установите параметр Stray C равным 0 пФ (ноль), диапазон частот будет составлять от 2,47 до 15,91 МГц. С учетом 5 пФ паразитного C (достаточно разумное значение для некоторых физических макетов), эти пределы меняются на 2,45 и 12,99 МГц – так что всего 5 пФ неучтенной емкости схемы изменяют верхний предел почти на 4 МГц !!!!
Допустим, у вас есть настроечный конденсатор 10-415 пФ и катушка индуктивности 10 мкГн (она отмечена на самой катушке индуктивности). Если вы установите параметр Stray C равным 0 пФ (ноль), диапазон частот будет составлять от 2,47 до 15,91 МГц. С учетом 5 пФ паразитного C (достаточно разумное значение для некоторых физических макетов), эти пределы меняются на 2,45 и 12,99 МГц – так что всего 5 пФ неучтенной емкости схемы изменяют верхний предел почти на 4 МГц !!!!
Может тоже попробовать понизить до 1.8МГц – у вас получится??? Да, если вы добавите 470 пФ к настроечному конденсатору, но это уменьшит диапазон настройки до 1,7–2,3 МГц. Как я это узнал? Я просто попробовал разные стандартные значения C в поле Stray C, оставив значения L, MaxC и MinC в покое до тех пор, пока у меня не было MinF ниже 1,8 МГц.
Где это программное обеспечение? Прямо здесь: ZIP-файл { 167Kb }
Процесс установки не требуется, просто разархивируйте один LCFreqs. exe в папку или на рабочий стол Windows и запустите его. Никаких дополнительных файлов не требуется и не создается.
exe в папку или на рабочий стол Windows и запустите его. Никаких дополнительных файлов не требуется и не создается.
Авторские права заявлены. Не распространяйте файл на другие веб-сайты, просто дайте ссылку на эту веб-страницу.
Программное обеспечение должно работать в любой 32- или 64-разрядной версии Windows, и все функции находятся в одном EXE-файле. Он был написан на Delphi 5 (производная от Pascal для Windows), относительно старой версии в наши дни… но у меня есть последняя версия.
Обратите внимание, что программное обеспечение может быть обновлено, если в нем будут обнаружены какие-либо ошибки, но последняя версия всегда будет доступна по ссылке выше. Он уже был обновлен один раз с момента первоначальной публикации на сайте.
Версии программного обеспечения : (видно по дате в верхней части приложения)
Первоначальный выпуск: 24 февраля 2011 г. (без даты файла) кнопка плюс текстовое поле добавлено синее выделение.


 Также определяется угловая частота.
Также определяется угловая частота. установить резонансную частоту и рассчитать для нее все выходные значения.
установить резонансную частоту и рассчитать для нее все выходные значения.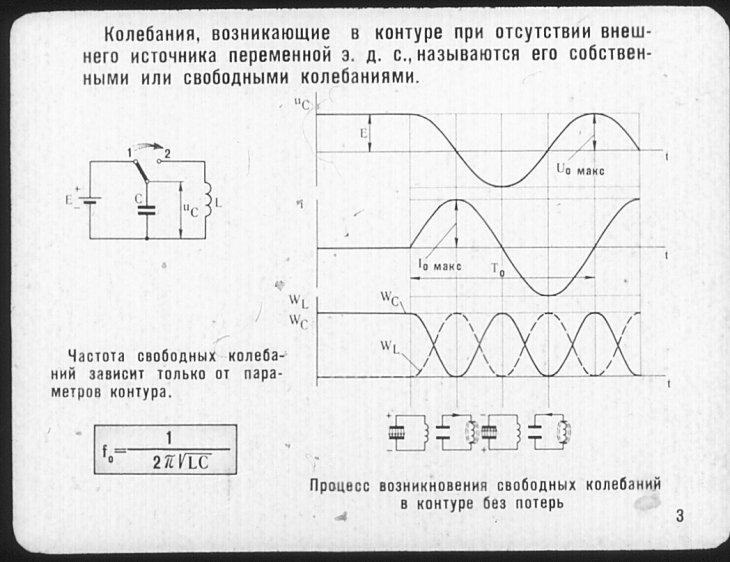

 При нулевой частоте последовательная LC-цепь действует как разомкнутая цепь. Обратите внимание, что импеданс справа от резонанса индуктивный, а слева от резонанса емкостной
При нулевой частоте последовательная LC-цепь действует как разомкнутая цепь. Обратите внимание, что импеданс справа от резонанса индуктивный, а слева от резонанса емкостной Вектор напряжения индуктивности V L отстает от тока в векторе индуктивности на 90°, поэтому он рисуется при +90°. Вектор напряжения емкости V C опережает вектор тока в конденсаторе на 90° и оттягивается при –90°. Векторная сумма двух противоположных векторов может быть направлена вниз или вверх в зависимости от падения напряжения на катушке индуктивности и конденсаторе.
Вектор напряжения индуктивности V L отстает от тока в векторе индуктивности на 90°, поэтому он рисуется при +90°. Вектор напряжения емкости V C опережает вектор тока в конденсаторе на 90° и оттягивается при –90°. Векторная сумма двух противоположных векторов может быть направлена вниз или вверх в зависимости от падения напряжения на катушке индуктивности и конденсаторе. В реальной жизни катушки индуктивности всегда имеют некоторое сопротивление, ограничивающее ток. Реальные источники питания также не могут обеспечивать бесконечно большой ток, поскольку он ограничен внутренним сопротивлением источника питания.
В реальной жизни катушки индуктивности всегда имеют некоторое сопротивление, ограничивающее ток. Реальные источники питания также не могут обеспечивать бесконечно большой ток, поскольку он ограничен внутренним сопротивлением источника питания.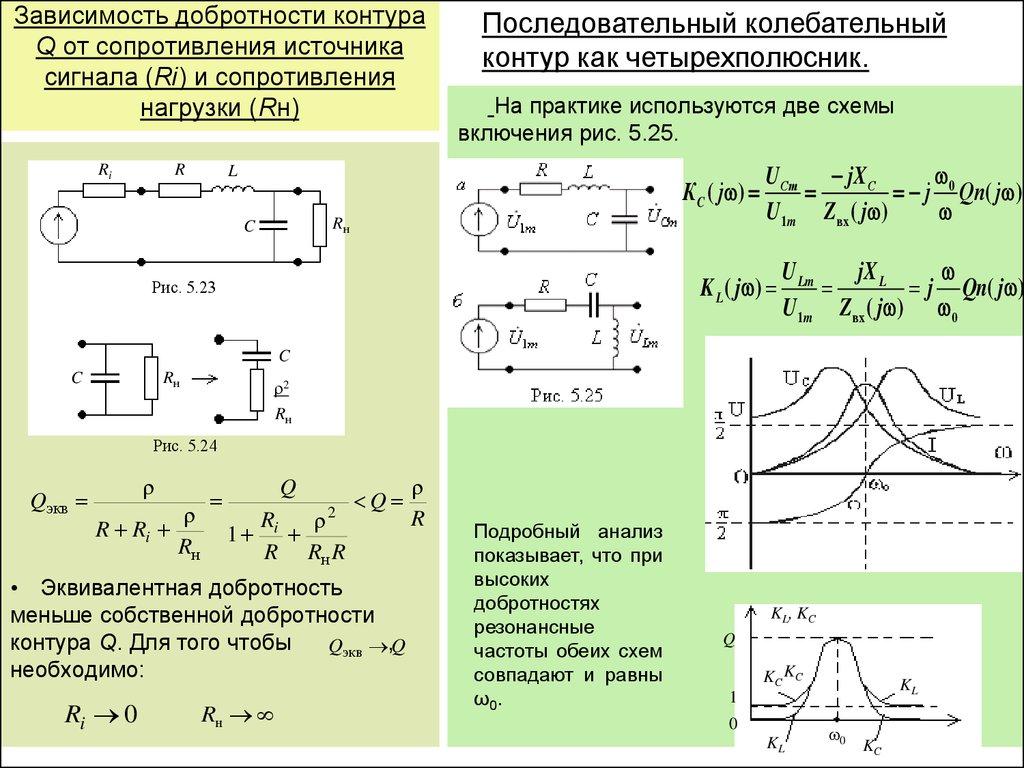 . Если f = 0, мы предполагаем, что цепь подключена к идеальному источнику постоянного напряжения.
. Если f = 0, мы предполагаем, что цепь подключена к идеальному источнику постоянного напряжения. Калькулятор импеданса RC-цепи
Калькулятор импеданса RC-цепи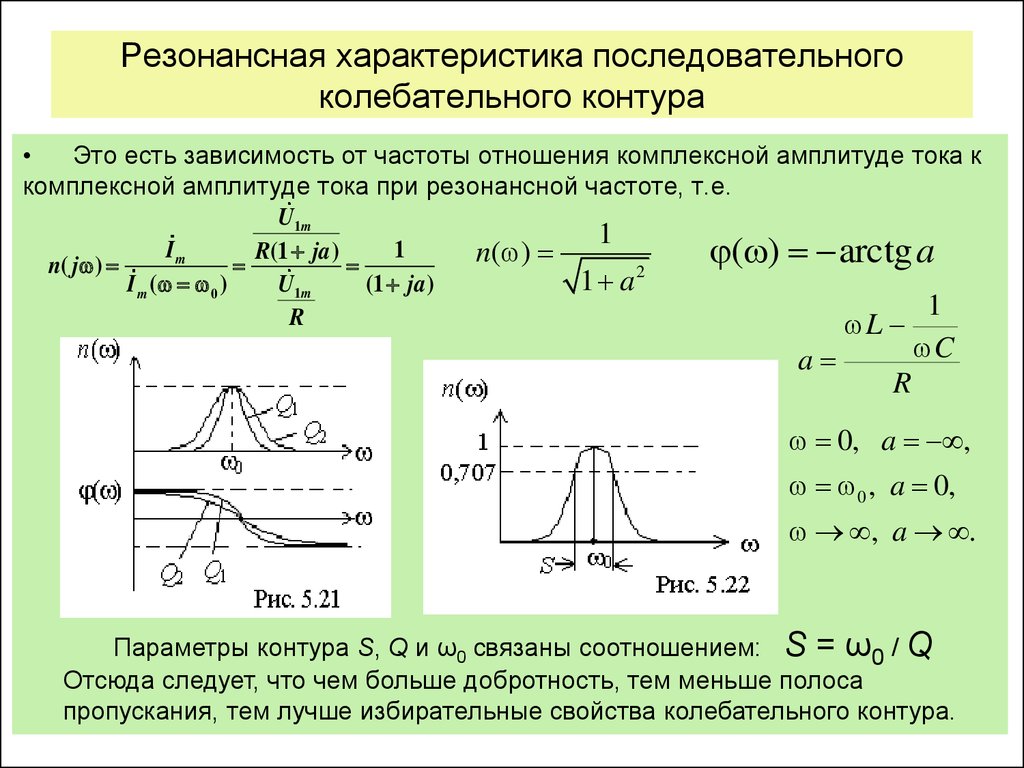
 com, были правильными. Однако мы не гарантируем, что наши конвертеры и калькуляторы не содержат ошибок. Весь контент предоставляется «как есть», без каких-либо гарантий. Условия и положения.
com, были правильными. Однако мы не гарантируем, что наши конвертеры и калькуляторы не содержат ошибок. Весь контент предоставляется «как есть», без каких-либо гарантий. Условия и положения. Также определяется угловая частота.
Также определяется угловая частота.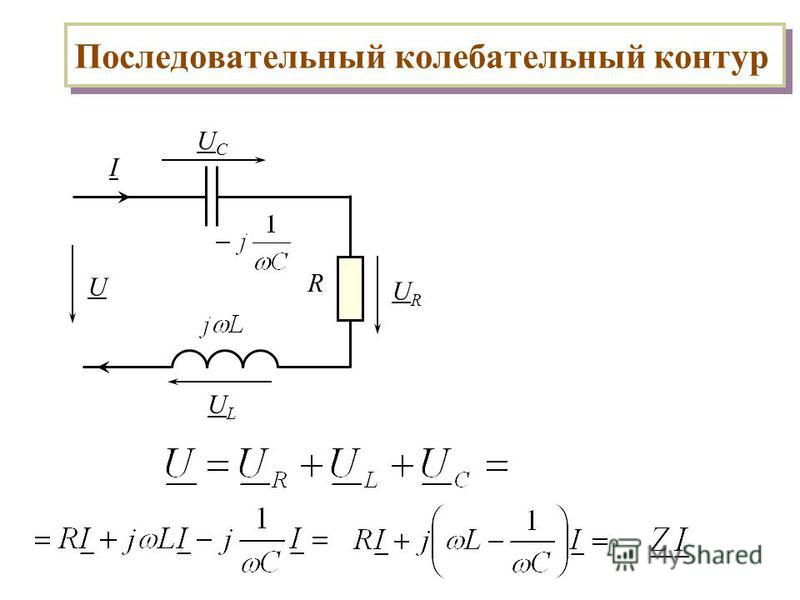 установить резонансную частоту и рассчитать для нее все выходные значения.
установить резонансную частоту и рассчитать для нее все выходные значения.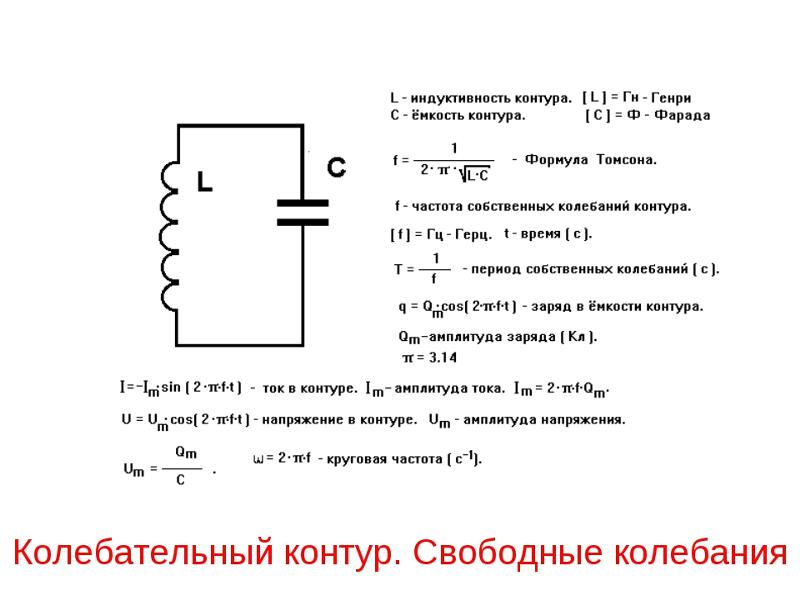

 При нулевой частоте последовательная LC-цепь действует как разомкнутая цепь. Обратите внимание, что импеданс справа от резонанса индуктивный, а слева от резонанса емкостной
При нулевой частоте последовательная LC-цепь действует как разомкнутая цепь. Обратите внимание, что импеданс справа от резонанса индуктивный, а слева от резонанса емкостной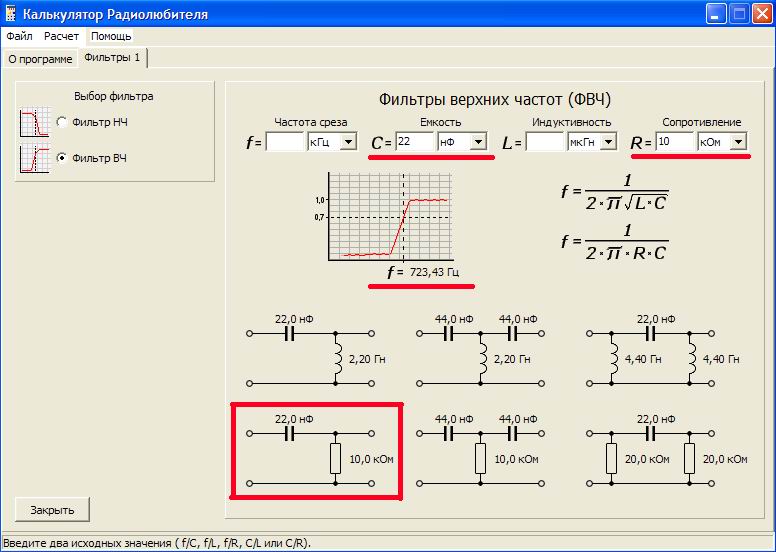 Вектор напряжения индуктивности V L отстает от тока в векторе индуктивности на 90°, поэтому он рисуется при +90°. Вектор напряжения емкости V C опережает вектор тока в конденсаторе на 90° и оттягивается при –90°. Векторная сумма двух противоположных векторов может быть направлена вниз или вверх в зависимости от падения напряжения на катушке индуктивности и конденсаторе.
Вектор напряжения индуктивности V L отстает от тока в векторе индуктивности на 90°, поэтому он рисуется при +90°. Вектор напряжения емкости V C опережает вектор тока в конденсаторе на 90° и оттягивается при –90°. Векторная сумма двух противоположных векторов может быть направлена вниз или вверх в зависимости от падения напряжения на катушке индуктивности и конденсаторе.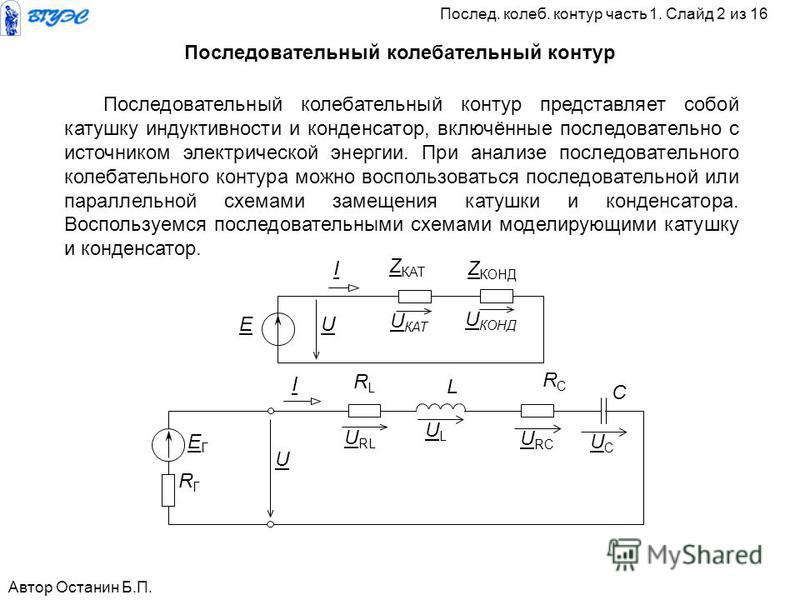 В реальной жизни катушки индуктивности всегда имеют некоторое сопротивление, ограничивающее ток. Реальные источники питания также не могут обеспечивать бесконечно большой ток, поскольку он ограничен внутренним сопротивлением источника питания.
В реальной жизни катушки индуктивности всегда имеют некоторое сопротивление, ограничивающее ток. Реальные источники питания также не могут обеспечивать бесконечно большой ток, поскольку он ограничен внутренним сопротивлением источника питания. . Если f = 0, мы предполагаем, что цепь подключена к идеальному источнику постоянного напряжения.
. Если f = 0, мы предполагаем, что цепь подключена к идеальному источнику постоянного напряжения. Калькулятор конденсатора
Калькулятор конденсатора
 Contoh дари perangkat ини adalah ponsel, маршрутизатор, komputer, радио dua-arah, kartu kredit, penerima Satelit, телевидение, дан peralatan лаин янь mengirim дан menerima gelombang радио.
Contoh дари perangkat ини adalah ponsel, маршрутизатор, komputer, радио dua-arah, kartu kredit, penerima Satelit, телевидение, дан peralatan лаин янь mengirim дан menerima gelombang радио.  Сярат дан Кетентуан.
Сярат дан Кетентуан.
