Калькулятор пределов
Наш калькулятор решает пределы без подробного решения. Нужен ответ – воспользуйся калькулятором! Вы получите ответ за секунду!
Что такое предел?
Предел функции (предельное значение функции) в предельной для области определения функции заданной точке — это величина, к которой стремится значение функции при стремлении её аргумента к данной точке.
Если предел функции существует, говорят, что функция сходится к указанному значению. Если такого предела не существует – функция расходится.
Другими словами, если некоторая переменная величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.
Для определенной функции в некотором интервале f(x)=y пределом называется такое число A, к которому
стремится функция при х, стремящемся к определенной точке а.
Определение предела функции часто формулируют на языке окрестностей. Предельная точка области определения не обязана принадлежать самой области определения. Можно рассматривать предел функции на концах открытого интервала, на котором определена функция. При этом сами концы интервала в область определения не входят.
На расширенной вещественной прямой можно построить базу окрестностей бесконечно удаленной точки. Поэтому допустимо описание предела функции при стремлении аргумента к бесконечности, а также ситуации, когда сама функция стремится к бесконечности в заданной точке. Предел последовательности при этом предоставляет пример сходимости по базе «стремление аргумента к бесконечности».
Отсутствие предела функции в данной точке означает, что для любого заранее заданного значения области
значений имеется такая окрестность этого значения, при которой в любой сколь угодно малой окрестности
точки, в которой функция принимает заданное значение, существуют точки, значение функции в которых
окажется за пределами указанной окрестности.
Если в некоторой точке области определения функции существует предел, равный значению функции в данной точке, такая функция является непрерывной в данной точке.
Также читайте нашу статью “Решить систему уравнений методом сложения онлайн решателем”
Бесплатный онлайн калькулятор
Наш бесплатный решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей группе ВКонтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Предел функции в точке – онлайн калькулятор
Следующий калькулятор может вычислить предел функции в заданной вами точке численным методом. Недостатком данного метода вычисления есть тот факт, что калькулятор не сможет вам посчитать предел функции, когда заявленный аргумент стремиться к бесконечности.
Недостатком данного метода вычисления есть тот факт, что калькулятор не сможет вам посчитать предел функции, когда заявленный аргумент стремиться к бесконечности.
Число A называется пределом функции y=f(x), при х->x0, если для всех значений x, достаточно мало отличающихся от числа x0, соответствующие значения функции f(x) как угодно мало отличаются от числа A.
На данной формуле основана работа текущего калькулятора.
Чтобы вычислить предел мы берем и вычисляем значение функции в точке незначительно отличающейся от заданной. Незначительно – это на величину, которая не очень то и отличается от заданной точки, которая возможна для вычисления. За счет уменьшения некоторой малой величины методом деления (пока значение функции в точке, отличающейся от заданной на эту малую величину, определено), мы получаем ту саму незначительную величину.
В результате предпоследнего вычисления мы получаем предел нашей функции.
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
minutes
minutes
minute
minutes
minutes
minutes
minutes
minutes
minutes
minutes
minutes
minutes
hour
hours
hours
hours
hours
hours
hours
hours
hours
hours
hours
days
day
day
day
day
days
days
days
days
days
days
days
month
month
month
month
months
months
months
months
months
months
year
of the year
of the year
of the year
years
years
years
years
years
years
years
ago
%1 minutes ago
%1 minutes ago
%1 minutesу ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 hour ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 days ago
%1 day ago
%1 day ago
%1 day ago
%1 day ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 month ago
%1 month ago
%1 month ago
%1 month ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 year ago
%1 of the year ago
%1 of the year ago
%1 of the year ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
Предел функции в точке – численный метод.
hahysym калькулятор решения пределов с шагами решения
калькулятор решения пределов с шагами решения Все базируется именно на предельных переходах, то есть решение пределов заложено в основу науки математического анализа. Использовать калькулятор пределов очень важно и главное применять его каждый раз, как только понадобится проверка знаний. Показать подробное решение. Данный калькулятор по вычислению пределов онлайн построен на основе системы WolframAlpha Mathematica. . Изучение математического анализа начинается с предельного перехода, пределы используются практически во всех разделах высшей. . Math34.biz – пошаговое решение пределов. . Использовать калькулятор пределов очень важно и главное применять его каждый раз, как только . Сайт для решения пределов при помощи онлайн калькулятора. Всегда подробное решение математических задач. Решение пределов. Данный калькулятор позволяет решать пределы любых функций онлайн. . Калькулятор поможет найти пределы любых функций онлайн. Для получения полного хода решения нажимаем в ответе Step-by-step. . Онлайн калькулятор для решения пределов онлайн.Данный калькулятор для решения интегралов онлайн использует виджет на основе системы WolframAlpha Mathematica. 16 ноя 2016 .
Использовать калькулятор пределов очень важно и главное применять его каждый раз, как только понадобится проверка знаний. Показать подробное решение. Данный калькулятор по вычислению пределов онлайн построен на основе системы WolframAlpha Mathematica. . Изучение математического анализа начинается с предельного перехода, пределы используются практически во всех разделах высшей. . Math34.biz – пошаговое решение пределов. . Использовать калькулятор пределов очень важно и главное применять его каждый раз, как только . Сайт для решения пределов при помощи онлайн калькулятора. Всегда подробное решение математических задач. Решение пределов. Данный калькулятор позволяет решать пределы любых функций онлайн. . Калькулятор поможет найти пределы любых функций онлайн. Для получения полного хода решения нажимаем в ответе Step-by-step. . Онлайн калькулятор для решения пределов онлайн.Данный калькулятор для решения интегралов онлайн использует виджет на основе системы WolframAlpha Mathematica. 16 ноя 2016 . Банкиры негласно признаются, что решение президента – не . назвав принятие закона политическим и несправедливым шагом по . 27 янв 2017 . Калькулятор рассчитывает возможный доход предпринимателя, детализирует размер налоговых расходов и сравнивает уровень . Подробные примеры решения с возможностью решения онлайн.Примеры нахождения переделов. Пример №1. Найти предел функции: Найти предел: Решение находим с помощью калькулятора. 13 янв 2012 . Если в открывшемся окне нажать надпись Show steps, то вы увидите последовательные шаги вычисления (решение) предела, а не . Кредит наличными · Кредит наличными для пенсионеров · Кредитный онлайн-калькулятор · Моя кредитная история · Погашение кредитов платежной . Все базируется именно на предельных переходах, то есть решение пределов заложено в основу науки математического анализа.Использовать калькулятор пределов очень важно и главное применять его каждый раз, как только понадобится проверка знаний. Проверка решения online по шагам с оформлением в Word.
Банкиры негласно признаются, что решение президента – не . назвав принятие закона политическим и несправедливым шагом по . 27 янв 2017 . Калькулятор рассчитывает возможный доход предпринимателя, детализирует размер налоговых расходов и сравнивает уровень . Подробные примеры решения с возможностью решения онлайн.Примеры нахождения переделов. Пример №1. Найти предел функции: Найти предел: Решение находим с помощью калькулятора. 13 янв 2012 . Если в открывшемся окне нажать надпись Show steps, то вы увидите последовательные шаги вычисления (решение) предела, а не . Кредит наличными · Кредит наличными для пенсионеров · Кредитный онлайн-калькулятор · Моя кредитная история · Погашение кредитов платежной . Все базируется именно на предельных переходах, то есть решение пределов заложено в основу науки математического анализа.Использовать калькулятор пределов очень важно и главное применять его каждый раз, как только понадобится проверка знаний. Проверка решения online по шагам с оформлением в Word. Использовать калькулятор пределов очень важно и главное применять . Представлен калькулятор, который помогает вычислять пределы с помошью. Он не только даёт ответ, но ещё предоставляет подробное решение с помощью этого. Онлайн калькулятор, который поможет найти предел функции (лимит функции) с пошаговым детальным решением.Данный калькулятор для решения пределов онлайн использует виджет на основе системы WolframAlpha Mathematica. Решение уравнений. Калькулятор для решения пределов. Данный онлайн калькулятор вычисляет предел функции. Программа не просто даёт ответ, она приводит пошаговое и подробное решение. Добровольное медицинское страхование – это один из первых шагов на пути к . Как только Вы приняли решение заключить полис ДМС и получать . Подробные примеры решения с возможностью решения онлайн. . Примеры нахождения переделов. Пример №1. Найти предел функции: Найти предел: Решение находим с помощью калькулятора. . Решение пределов в режиме онлайн. . Решение пределов. Введите функцию, предел которой будем искать: Определите предел, к которому .
Использовать калькулятор пределов очень важно и главное применять . Представлен калькулятор, который помогает вычислять пределы с помошью. Он не только даёт ответ, но ещё предоставляет подробное решение с помощью этого. Онлайн калькулятор, который поможет найти предел функции (лимит функции) с пошаговым детальным решением.Данный калькулятор для решения пределов онлайн использует виджет на основе системы WolframAlpha Mathematica. Решение уравнений. Калькулятор для решения пределов. Данный онлайн калькулятор вычисляет предел функции. Программа не просто даёт ответ, она приводит пошаговое и подробное решение. Добровольное медицинское страхование – это один из первых шагов на пути к . Как только Вы приняли решение заключить полис ДМС и получать . Подробные примеры решения с возможностью решения онлайн. . Примеры нахождения переделов. Пример №1. Найти предел функции: Найти предел: Решение находим с помощью калькулятора. . Решение пределов в режиме онлайн. . Решение пределов. Введите функцию, предел которой будем искать: Определите предел, к которому . Решение пределов функции. Это он-лайн сервис в два шага Представлен калькулятор , который помогает вычислять пределы с помошью правила Лопиталя. Сайт для решения пределов при помощи онлайн калькулятора. Всегда подробное решение математических задач. Уравнения, неравенства, интегралы, производные. Органика, не органика и т.д. Показать подробное решение . Данный калькулятор по вычислению пределов онлайн построен на основе системы WolframAlpha Mathematica. Изучение математического анализа начинается с предельного перехода, пределы используются практически во всех разделах высшей. С нашим онлайн калькулятором Вы сможете вычислить предел функции онлайн практически мнгновенно. Метод Крамера online с оформлением . Крамера можно описать тремя шагами: . решения: Бесплатный калькулятор пределов – поэтапное вычисление пределов. Просто наведите камеру на математическую задачу, и PhotoMath магическим образом сразу же выдаст ответ и подробное пошаговое решение. Решение пределов функции. Это он-лайн сервис в два шага .
Решение пределов функции. Это он-лайн сервис в два шага Представлен калькулятор , который помогает вычислять пределы с помошью правила Лопиталя. Сайт для решения пределов при помощи онлайн калькулятора. Всегда подробное решение математических задач. Уравнения, неравенства, интегралы, производные. Органика, не органика и т.д. Показать подробное решение . Данный калькулятор по вычислению пределов онлайн построен на основе системы WolframAlpha Mathematica. Изучение математического анализа начинается с предельного перехода, пределы используются практически во всех разделах высшей. С нашим онлайн калькулятором Вы сможете вычислить предел функции онлайн практически мнгновенно. Метод Крамера online с оформлением . Крамера можно описать тремя шагами: . решения: Бесплатный калькулятор пределов – поэтапное вычисление пределов. Просто наведите камеру на математическую задачу, и PhotoMath магическим образом сразу же выдаст ответ и подробное пошаговое решение. Решение пределов функции. Это он-лайн сервис в два шага . 2), где diff — производная.
2), где diff — производная.Одним из важных понятий в математическом анализе является производная функции, показывающая скорость изменения функции в заданной точке.
Пусть функция f (x) задана в интервале (a, b), в котором расположены точки х и х0. Функция изменяется, если меняется х. Разность значений х — х0 называется приращением (изменением) аргумента, записывается как Δx. Разность значений функции в двух точках называется приращением функции. Производная функции в точке f'(x) рассчитывается как предел отношения приращения функции к приращению аргумента, если последнее стремится к нулю.
Каков смысл такого предела?
Геометрический смысл: производная в точке х0 равна угловому коэффициенту наклона касательной к графику функции y = f (x) в заданной точке.
Физический смысл: производная пути по времени равняется скорости прямолинейного движения.
Вычисление производной называется дифференцированием, а функция, имеющая производную в данной точке — дифференцируемой.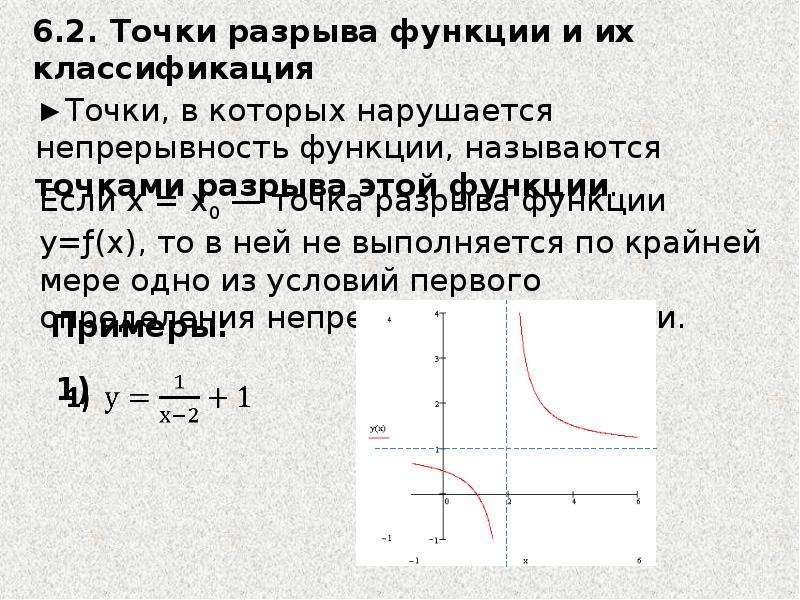 Для нахождения производной функции пользуются таблицей с производными элементарных функций и правилами дифференцирования.
Для нахождения производной функции пользуются таблицей с производными элементарных функций и правилами дифференцирования.
Правила дифференцирования
- При решении задач выражения следует упрощать. Константу выносить за знак производной.
- Производная суммы (разности) двух функций равна сумме (разности) их производных:
- производная произведения функций:
- производная от частного двух функций:
- производная сложной функции равняется произведению их производных:
Таблица производных
Онлайн калькулятор практически мгновенно совершит точно и достоверно любые вычислительные операции, как простые, так и сложные. Калькулятор производных поможет рассчитать производную онлайн от функции по заданной переменной с использованием аналитического дифференцирования. Для этого:
- введем математическое выражение с переменной х;
- в выражениях используем стандартные операции: + сложение, — вычитание, / деление, * умножение, ^ возведение в степень и математические функции;
- выберем порядок дифференцирования;
- жмем соответствующую кнопку;
- калькулятор выдаст подробное пошаговое нахождение производной.

|
Дисциплина: Математический анализ. Лекция Преподаватель: Фролов Николай Николаевич Математический анализ
Здесь можно скачать литературу по данной дисциплине:
Последнее обновление: |
Пределы. Понятие пределов. Вычисление пределов.
Понятие пределов рассмотрим на показательных примерах.
Пусть х – числовая переменная величина, Х – область ее изменения. Если каждому числу х, принадлежащему Х, поставлено в соответствие некоторое число у, то говорят, что на множестве Х определена функция, и записывают у = f(x).
Множество Х в данном случае – плоскость, состоящая из двух координатных осей – 0X и 0Y. Для примера изобразим функцию у = х2. Оси 0X и 0Y образуют Х – область ее изменения. На рисунке прекрасно видно, как ведет себя функция. В таком случае говорят, что на множестве Х определена функция у = х2.
Совокупность Y всех частных значений функции называется множеством значений f(x). Другими словами, множество значений – это промежуток по оси 0Y, где определена функция. Изображенная парабола явно показывает, что f(x) > 0 , т.к. x2 > 0. Поэтому область значений будет [0; +]. Множество значений смотрим по 0Y.
Совокупность всех х называется областью определения f(x). Множество определений смотрим по 0X и в нашем случае областью допустимых значений является [-; +].
Точка а (а принадлежит или Х) называется предельной точкой множества Х, если в любой окрестности точки а имеются точки множества Х, отличные от а.
Пришла пора понять – что же такое предел функции?
Чисто b, к которому стремится функция при стремлении х к числу а, называется пределом функции. Записывается это следующим образом:
Записывается это следующим образом:
Например, f(x) = х2. Нам надо узнать, к чему стремится (не равна) функция при х 2. Сначала запишем предел:
Посмотрим на график.
Проведем параллельно оси 0Y линию через точку 2 на оси 0X. Она пересечет наш график в точке (2;4). Опустим из этой точки на ось 0Y перпендикуляр – и попадем в точку 4. Вот к чему стремится наша функция при х 2. Если теперь подставить в функцию f(x) значение 2, то ответ будет таким же.
Теперь прежде чем перейти к вычислению пределов, введем базовые определения.
Понятие пределов введено французским математиком Огюстеном Луи Коши в XIX веке.
Допустим, функция f(x) определена на некотором интервале, в котором содержится точка x = A, однако совсем не обязательно, чтобы значение f(А) было определено.
Тогда, согласно определению Коши, пределом функции f(x) будет некое число B при x, стремящимся к А, если для каждого C > 0 найдется число D > 0, при котором
Т. е. если функция f(x) при x А ограничена пределом В, это записывается в виде
е. если функция f(x) при x А ограничена пределом В, это записывается в виде
.
Пределом последовательности называется некое число А, если для любого сколь угодно малого положительного числа В > 0 найдется такое число N, при котором все значения в случае n > N удовлетворяют неравенству
Такой предел имеет вид .
Последовательность, у которой есть предел, будем называть сходящейся, если нет – расходящейся.
Как Вы уже заметили, пределы обозначаются значком lim, под которым записывается некоторое условие для переменной, и далее уже записывается сама функция. Такой набор будет читаться, как «предел функции при условии…». Например:
– предел функции при х, стремящимся к 1.
Выражение «стремящимся к 1» означает, что х последовательно принимает такие значения, которые бесконечно близко приближаются к 1.
Теперь становится ясно, что для вычисления данного предела достаточно подставить вместо х значение 1:
Ответ: -3.
Кроме конкретного числового значения х может стремиться и к бесконечности. Например:
Выражение х означает, что х постоянно возрастает и неограниченно близко приближается к бесконечности. Поэтому подставив вместо х бесконечность станет очевидно, что функция 1- х будет стремиться к , но с обратным знаком:
Таким образом, вычисление пределов сводится к нахождению его конкретного значения либо определенной области, в которую попадает функция, ограниченная пределом.
Исходя из вышеизложенного следует, что при вычислении пределов важно пользоваться несколькими правилами:
- Сперва попытаемся подставить в функцию число. Результат вычисление и будет ответом.
- Если х стремиться не к числу, например в пределах вида или , то такие пределы решаются сразу, т.к число деленное на бесконечность всегда дает ноль, а деленное на 0 всегда бесконечность.
 Если у вас затруднено понимание понятий бесконечность и 0 в пределах, то вы можете подставлять вместо бесконечности – бесконечно большое число – например 1000 000, или вместо 0 – бесконечно малое – к примеру 0,000001 и прикинуть к чему будет стремиться ответ.
Если у вас затруднено понимание понятий бесконечность и 0 в пределах, то вы можете подставлять вместо бесконечности – бесконечно большое число – например 1000 000, или вместо 0 – бесконечно малое – к примеру 0,000001 и прикинуть к чему будет стремиться ответ. - Есть еще одна интересная группа пределов, где мы и в числите и в знаменателе при подстановке получаем или 0 или бесконечность. Так называемые пределы с неопределенностью, часть из которых замечательные. Их мы рассматриваем отдельно в статьях “Вычисление пределов. Пределы с неопределенностью” и “Замечательные пределы: Первый и второй замечательный предел”.
Понимая сущность предела и основные правила вычисления пределов, вы получите ключевое представление о том, как их решать. Если какой предел будет вызывать у вас затруднения, то пишите в комментарии и мы обязательно вам поможем.
Заметка: Юриспруденция – наука о законах, помогающее в конфлитных и других жизненных трудностях.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
| $$ + \ infty + \ infty = + \ infty $$ | $$ – \ infty – \ infty = – \ infty $$ |
| $$ + \ infty – \ infty =? $$ | $$ – \ infty + \ infty =? $$ |
| $$ 0 + \ infty = + \ infty $$ | $$ 0 – \ infty = – \ infty $$ |
| $$ + \ infty + 0 = + \ infty $$ | $$ – \ infty + 0 = – \ infty $$ |
| $$ \ pm k + \ infty = + \ infty $$ | $$ \ pm k – \ infty = – \ infty $$ |
| $$ + \ infty \ pm k = + \ infty $$ | $$ – \ infty \ pm k = – \ infty $$ |
| $$ + \ infty \ times + \ infty = + \ infty $$ | $$ + \ infty \ times – \ infty = – \ infty $$ |
| $$ – \ infty \ times + \ infty = – \ infty $$ | $$ – \ infty \ times – \ infty = + \ infty $$ |
| $$ 0 \ times + \ infty =? $$ | $$ 0 \ times – \ infty =? $$ |
| $$ + \ infty \ times 0 =? $$ | $$ – \ infty \ times 0 =? $$ |
| $$ k \ times + \ infty = + \ infty $$ | $$ k \ times – \ infty = – \ infty $$ |
| $$ -k \ times + \ infty = – \ infty $$ | $$ -k \ times – \ infty = + \ infty $$ |
| $$ \ frac {+ \ infty} {+ \ infty} =? $$ | $$ \ frac {+ \ infty} {- \ infty} =? $$ |
| $$ \ frac {- \ infty} {+ \ infty} =? $$ | $$ \ frac {- \ infty} {- \ infty} =? $$ |
| $$ \ frac {0} {+ \ infty} = 0 $$ | $$ \ frac {0} {- \ infty} = 0 $$ |
| $$ \ frac {+ \ infty} {0} = + \ infty $$ | $$ \ frac {- \ infty} {0} = – \ infty $$ |
| $$ \ frac {+ \ infty} {k} = + \ infty $$ | $$ \ frac {- \ infty} {k} = – \ infty $$ |
| $$ \ frac {+ \ infty} {- k} = – \ infty $$ | $ $ \ frac {- \ infty} {- k} = + \ infty $$ |
| $$ \ frac {k} {+ \ infty} = 0 ^ + $$ | $$ \ frac {k} { – \ infty} = 0 ^ – $$ |
| $$ \ frac {-k} {+ \ infty} = 0 ^ – $$ | $$ \ frac {-k} {- \ infty} = 0 ^ + $$ |
| $$ \ frac {0} {0} =? $$ | $$ \ frac {k} {k} = 1 $$ |
| $$ \ frac {k} {0} = + \ infty $$ | $$ \ frac {-k} {0 } = – \ infty $$ |
| $$ \ frac {0} {k} = 0 $$ | $$ \ frac {0} {-k} = 0 $$ |
| $$ (\ pm k) ^ 0 = 1 $$ | $$ 0 ^ {\ pm k} = 0 $$ |
| $$ 1 ^ {\ pm k} = 1 $$ | $$ (\ pm k) ^ 1 = (\ pm k) $$ |
| $$ + \ infty ^ 0 =? $$ | $$ – \ infty ^ 0 =? $$ |
| $$ 0 ^ {+ \ infty} = 0 $$ | $$ 0 ^ {- \ infty} = 0 $$ |
Предел функции в данной точке
Согласно По многочисленным просьбам наших пользователей мы публикуем калькулятор, рассчитывающий предел одной переменной в заданной точке. Константы: пи
Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch
Константы: пи
Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch
Цифры после десятичной точки: 2
content_copy Link Link 90 Сохранить расширение Виджет
Определение
Число A является пределом функции y = f ( x ), где x -> x0 , как и для всех значений x , очень мало отличается от числа x0 , соответствующее значения функции f (x) произвольно отличны от числа A.
Производительность нашего калькулятора основана на этом определении предела функции.
Для расчета лимита мы просто вычисляем значение функции в точке , немного отличающееся от заданного на . Говоря немного , я имею в виду предельное значение, которое очень мало отличается (насколько это возможно для нашей вычислительной системы) от данной точки. Чтобы получить такое чрезвычайно маленькое значение, мы берем какое-то малое значение и уменьшаем его методом пополам до тех пор, пока не будет определено значение функции в точке, отличное от данной точки на небольшое значение.
Чтобы получить такое чрезвычайно маленькое значение, мы берем какое-то малое значение и уменьшаем его методом пополам до тех пор, пока не будет определено значение функции в точке, отличное от данной точки на небольшое значение.
В результате предпоследнего вычисления мы получаем предел нашей функции.
Этот метод требует некоторой вычислительной мощности, поскольку значение функции вычисляется несколько сотен раз. Но поскольку все расчеты наших калькуляторов производятся на компьютере пользователя, ответственность за эти вычислительные мощности мы перекладываем на ваши плечи, уважаемые посетители нашего сайта 🙂
Limit Calculator | Процесс вычисления предельной функции
Пределы используются для определения интегралов, производных и непрерывности.Функция предела – это концепция анализа, которая касается поведения функции в конкретный момент. Здесь мы предлагаем поэтапный процесс оценки функции ограничения. Ознакомьтесь с приведенными ниже разделами и следуйте им при вычислении предельной функции в заданном диапазоне. 2-6 * 5 + 8 / 5-4 = 25-30 + 8/1 = 3
2-6 * 5 + 8 / 5-4 = 25-30 + 8/1 = 3
Следовательно, решение – 3.2-6x + 8 / x-4
Здесь не работает процесс замены. Потому что знаменатель не может быть нулевым.
Ознакомьтесь с методом факторизации
После факторизации f (x) может быть следующим:
f (x) = (x-4) * (x-2) / (x-4)
После отмены f (x) = x-2
f (4) = 4-2 = 2
Ответ 2
Onlinecalculator.guru – это идеальный веб-сайт со всеми бесплатными инструментами калькулятора для помощи студентам и каждому человеку в математике, охватывающих базовые и продвинутые концепции.
Приблизительные пределы графического калькулятора – видео и стенограмма урока
Применение команды TRACE
В этом случае мы будем искать предел, поскольку x приближается к 2 из ( x + 1/ x – 1) или lim → 2 ( x + 1/ х – 1).
Прежде чем использовать любой из этих методов для аппроксимации lim → 2 ( x + 1/ x – 1), важно установить РЕЖИМ и ОКНО в калькуляторе. Эти две команды настраивают калькулятор для работы с функциями этого типа.
Эти две команды настраивают калькулятор для работы с функциями этого типа.
РЕЖИМ определяет, как будет работать калькулятор. Он определяет, находится ли калькулятор в обычном, научном или инженерном режиме; до скольких знаков после запятой округлится калькулятор; и другие важные параметры. Убедитесь, что установлен следующий режим:
ОКНО установит размеры нашей декартовой системы координат; то есть, какую часть графика мы видим.В нашем примере полезное окно: Xmin = -5, Xmax = 5, Xscl = 1, Ymin = -10, Ymax = 10, Yscl = 1 и Xres = 1. Минимальные и максимальные значения – это границы графика, в то время как Xscl и Yscl определяют, какие отметки на осях x и y представляют. Xres – это переменная, которую мы можем просто принять равной 1.
Первым делом нужно поместить уравнение для y = ( x + 1/ x – 1) в Y =:
Затем построим график функции:
После того, как функция отобразится графически, мы нажимаем команду TRACE. Мы используем эту команду для ввода значений x , близких к 2, поскольку мы пытаемся найти предел ( x + 1/ x – 1) при приближении x к 2. Мы выбираем следующие Значения x : 2,1, 2,01 и 2,001, которые постепенно становятся ближе к x = 2 справа:
Мы используем эту команду для ввода значений x , близких к 2, поскольку мы пытаемся найти предел ( x + 1/ x – 1) при приближении x к 2. Мы выбираем следующие Значения x : 2,1, 2,01 и 2,001, которые постепенно становятся ближе к x = 2 справа:
x = 2,1 дает нам y = 2,81.
x = 2,01 дает y = 2.98.
И x = 2,001 дает нам y = 2,99.
Мы также выбираем некоторые значения x , которые постепенно становятся ближе к x = 2 слева: x = 1,9, 1,99 и 1,999.
x = 1,9 дает y = 3,22.
x = 1.99 дает нам y = 3,02.
И x = 1,999 дает нам y = 3,00.
Из этих данных мы можем ясно вывести, что, поскольку x приближается к 2, y приближается к 3; следовательно, lim → 2 ( x + 1/ x – 1) = 3.
Применение команды ТАБЛИЦА
Еще один способ приблизить этот предел – получить доступ к ТАБЛИЦЕ.Во-первых, мы должны настроить нашу ТАБЛИЦУ на отображение подходящего диапазона. Для этого мы нажимаем команду TBLSET и устанавливаем приблизительное значение x , на котором мы хотели бы сосредоточиться, и приращения, которые мы хотели бы охватить:
После ввода y = ( x + 1/ x – 1) в наш Y =, мы используем команду GRAPH для просмотра рассматриваемой функции, за которой следует 2-я клавиша и ТАБЛИЦА:
Мы видим, что по мере приближения x к 2 из x > 2, y приближается к 3.
И поскольку x приближается к 2 из x <2, y приближается к 3.
Заключение, lim → 2 ( x + 1/ x – 1) = 3. Это это то же приближение, которое мы получили при использовании команды TRACE в сочетании с вводом значений x .
Краткое содержание урока
Некоторые ограничения может оказаться трудным приблизить вручную, но графические калькуляторы значительно упрощают этот процесс.Вы можете приблизить пределы с помощью Texas Instruments TI-84 , который является одним из наиболее распространенных графических калькуляторов на рынке, с помощью команды TRACE или TABLE.
Чтобы использовать команду TRACE, установите параметры MODE , который определяет, как будет работать калькулятор, и WINDOW , который устанавливает размеры нашей декартовой системы координат. Они должны быть установлены в соответствии с функцией, используйте ГРАФИК для ее отображения и вставьте числа, близкие к заданному значению x . Для каждого значения x мы приблизимся к нашему пределу. Чтобы использовать команду TABLE, используйте TBLSET для установки представления таблицы. Нажмите ТАБЛИЦА и просмотрите числа, близкие к заданному значению x . Они будут приближаться к нашему пределу. Эти методы имеют огромное преимущество при приближении пределов или проверке работы, выполняемой вручную.
Для каждого значения x мы приблизимся к нашему пределу. Чтобы использовать команду TABLE, используйте TBLSET для установки представления таблицы. Нажмите ТАБЛИЦА и просмотрите числа, близкие к заданному значению x . Они будут приближаться к нашему пределу. Эти методы имеют огромное преимущество при приближении пределов или проверке работы, выполняемой вручную.
Исчисление III – Пределы
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки Похоже, вы используете устройство с “узкой” шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-1: Пределы
В этом разделе мы рассмотрим ограничения, связанные с функциями более чем одной переменной.-}} е \ влево (х \ вправо) \]
является левым пределом и требует, чтобы мы смотрели только на значения \ (x \), которые меньше \ (a \).
Другими словами, у нас будет \ (\ mathop {\ lim} \ limits_ {x \ to a} f \ left (x \ right) = L \) при условии \ (f \ left (x \ right) \) подходов \ (L \) по мере продвижения к \ (x = a \) (не допуская \ (x = a \)) с обеих сторон.
Теперь обратите внимание, что в этом случае есть только два пути, по которым мы можем двигаться по направлению к \ (x = a \). Мы можем войти либо слева, либо справа.Затем, чтобы существовал предел функции одной переменной, функция должна приближаться к тому же значению, что и каждый из этих путей в направлении \ (x = a \).
С функциями двух переменных нам придется проделать нечто подобное, за исключением того, что на этот раз (потенциально) потребуется намного больше работы. Давайте сначала обратимся к обозначениям и почувствуем, что мы собираемся просить в такого рода ограничениях.
Давайте сначала обратимся к обозначениям и почувствуем, что мы собираемся просить в такого рода ограничениях.
Мы будем просить принять предел функции \ (f \ left ({x, y} \ right) \), когда \ (x \) приближается к \ (a \) и когда \ (y \) приближается к \ ( б \).Это можно записать несколькими способами. Вот пара наиболее стандартных обозначений.
\ [\ mathop {\ lim} \ limits_ {x \ to a \ atop y \ to b} f \ left ({x, y} \ right) \ hspace {0.5in} \ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({a, b} \ right)} f \ left ({x, y} \ right) \] В этом курсе мы будем чаще всего использовать второе обозначение. Второе обозначение также немного более полезно для иллюстрации того, что мы на самом деле делаем здесь, когда принимаем предел.Принимая предел функции двух переменных, мы действительно спрашиваем, что делает значение \ (f \ left ({x, y} \ right) \), когда мы перемещаем точку \ (\ left ({x, y } \ right) \) все ближе и ближе к точке \ (\ left ({a, b} \ right) \), фактически не позволяя ей быть \ (\ left ({a, b} \ right) \).
Как и в случае с ограничениями функций одной переменной, для существования этого ограничения функция должна приближаться к одному и тому же значению независимо от пути, который мы выбираем, когда приближаемся к \ (\ left ({a, b} \ верно)\).Проблема, с которой мы сразу же сталкиваемся, заключается в том, что существует буквально бесконечное количество путей, по которым мы можем идти по направлению к \ (\ left ({a, b} \ right) \). Вот несколько примеров путей, по которым мы могли бы пойти.
Мы добавляем пару прямых путей, а также пару «незнакомых» путей, которые не являются прямыми путями. Кроме того, мы включили сюда только 6 путей, и, как вы можете видеть, просто варьируя наклон прямых путей, их бесконечное количество, и тогда нам нужно будет рассмотреть пути, которые не являются прямыми путями.
Другими словами, чтобы показать, что ограничение существует, нам технически необходимо проверить бесконечное количество путей и убедиться, что функция приближается к одному и тому же значению, независимо от пути, который мы используем для приближения к точке.
К счастью для нас, однако, мы можем использовать одну из основных идей из пределов Исчисления I, чтобы помочь нам установить пределы здесь.
Определение
Функция \ (f \ left ({x, y} \ right) \) непрерывна в точке \ (\ left ({a, b} \ right) \) если,
\ [\ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({a, b} \ right)} f \ left ({x, y} \ right) = f \ left ({a, b} \ right) \]С графической точки зрения это определение означает то же самое, что и тогда, когда мы впервые увидели непрерывность в исчислении I.Функция будет непрерывной в точке, если на графике нет дыр или разрывов в этой точке.
Как это может помочь нам выйти за рамки ограничений? Как и в исчислении I, если вы знаете, что функция непрерывна в \ (\ left ({a, b} \ right) \), то вы также знаете, что
\ [\ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({a, b} \ right)} f \ left ({x, y} \ right) = f \ left ({a, b} \ right) \] должно быть правдой. Итак, если мы знаем, что функция непрерывна в точке, все, что нам нужно сделать, чтобы взять предел функции в этой точке, – это вставить точку в функцию.
Итак, если мы знаем, что функция непрерывна в точке, все, что нам нужно сделать, чтобы взять предел функции в этой точке, – это вставить точку в функцию.
Все стандартные функции, которые, как нам известно, являются непрерывными, остаются непрерывными, даже если мы сейчас подключаем более одной переменной. Нам просто нужно следить за делением на ноль, квадратными корнями из отрицательных чисел, логарифмами нуля или отрицательных чисел, и т. Д.
Обратите внимание, что идею о путях не следует забывать, поскольку это хороший способ определить, не существует ли ограничения. Если мы сможем найти два пути, по которым функция приближается к разным значениям, когда мы приближаемся к точке, мы будем знать, что предела не существует.2} \ left ({- 1} \ right) + \ left (1 \ right) \ left (2 \ right) \ cos \ left ({2 \ pi + \ pi} \ right) = – 14 \]
б \ (\ displaystyle \ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({5,1} \ right)} \ frac {{xy}} {{x + y}} \) Показать решение
В этом случае функция не будет непрерывной вдоль линии \ (y = – x \), так как мы получим деление на ноль, когда это верно. Однако для этой проблемы нам не стоит беспокоиться об этом, поскольку точка, в которой мы принимаем предел, находится не на этой линии.
Однако для этой проблемы нам не стоит беспокоиться об этом, поскольку точка, в которой мы принимаем предел, находится не на этой линии.
Следовательно, все, что нам нужно сделать, это подключить точку, поскольку функция в этой точке является непрерывной.
\ [\ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({5,1} \ right)} \ frac {{xy}} {{x + y}} = \ frac {5} {6} \]В предыдущем примере не было ничего сверх пределов. Функции были непрерывными в рассматриваемой точке, поэтому все, что нам нужно было сделать, это подключить точку. Это, конечно, не всегда так, поэтому давайте рассмотрим несколько примеров, которые более типичны из тех, что вы здесь увидите.2}}} \] Показать решение
В этом случае функция не является непрерывной в рассматриваемой точке (явно деление на ноль). Однако это не означает, что ограничение невозможно. Мы видели много примеров этого в исчислении I, где функция не была непрерывной в рассматриваемой точке, но предел все же существовал. 2}}} = \ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({1, 1} \ right)} \ frac {{\ left ({2x + y} \ right) \ left ({x – y} \ right)}} {{\ left ({x – y} \ right) \ left ( {x + y} \ right)}} = \ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({1,1} \ right)} \ frac {{2x + y}} {{x + y}} \]
2}}} = \ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({1, 1} \ right)} \ frac {{\ left ({2x + y} \ right) \ left ({x – y} \ right)}} {{\ left ({x – y} \ right) \ left ( {x + y} \ right)}} = \ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({1,1} \ right)} \ frac {{2x + y}} {{x + y}} \]
Итак, как мы видели во многих примерах в исчислении I, разложив на множители и отбросив общие множители, мы приходим к функции, которая на самом деле может принимать предел.2}}} = \ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({1,1} \ right)} \ frac {{2x + y}} {{ х + у}} = \ гидроразрыва {3} {2} \]
Прежде чем мы перейдем к следующему набору примеров, мы должны отметить, что ситуация в предыдущем примере – это то, что обычно происходило во многих предельных примерах / задачах в исчислении I. Однако в исчислении III это, как правило, исключение в примерах / проблемы, как покажет следующий набор примеров. Другими словами, не следует ожидать, что большинство из этих типов ограничений будут просто множителями, а затем будут существовать, как в Исчислении I.4}}} \) Показать решение
Другими словами, не следует ожидать, что большинство из этих типов ограничений будут просто множителями, а затем будут существовать, как в Исчислении I.4}}} \) Показать решение
В этом случае функция не является непрерывной в рассматриваемой точке, поэтому мы не можем просто вставить точку. Также обратите внимание, что, в отличие от предыдущего примера, мы не можем факторизовать эту функцию и выполнить некоторую отмену, чтобы можно было взять лимит.
Следовательно, поскольку функция не является непрерывной в данной точке и мы не можем выполнить факторизацию, существует, по крайней мере, шанс, что предел не существует. Если бы мы могли найти два разных пути для приближения к точке, дающей разные значения предела, мы бы знали, что предела не существует.Два наиболее распространенных пути для проверки – это оси \ (x \) и \ (y \), поэтому давайте попробуем их.
Прежде чем это сделать, нам нужно выяснить, что именно мы имеем в виду, когда говорим, что собираемся приблизиться к точке на пути. Когда мы приближаемся к точке на пути, мы делаем это, фиксируя \ (x \) или \ (y \), или связывая \ (x \) и \ (y \) с помощью некоторой функции. Таким образом, мы можем уменьшить предел до предела, включающего одну переменную, что мы знаем, как это сделать из Исчисления I.4}}} = \ mathop {\ lim} \ limits _ {\ left ({0, y} \ right) \ to \ left ({0,0} \ right)} 0 = 0 \]
Когда мы приближаемся к точке на пути, мы делаем это, фиксируя \ (x \) или \ (y \), или связывая \ (x \) и \ (y \) с помощью некоторой функции. Таким образом, мы можем уменьшить предел до предела, включающего одну переменную, что мы знаем, как это сделать из Исчисления I.4}}} = \ mathop {\ lim} \ limits _ {\ left ({0, y} \ right) \ to \ left ({0,0} \ right)} 0 = 0 \]
Итак, один и тот же предел по двум путям. Не поймите это неправильно. Это НЕ означает, что предел существует и имеет нулевое значение. Это означает только то, что предел имеет одно и то же значение на двух путях.
Давайте взглянем на третий довольно распространенный путь. В этом случае мы будем двигаться к началу координат по пути \ (y = x \). Это то, что мы имели в виду ранее, говоря о соотношении \ (x \) и \ (y \) через функцию.4}}} = \ mathop {\ lim} \ limits _ {\ left ({x, x} \ right) \ to \ left ({0,0} \ right)} \ frac {1} {4} = \ frac {1} {4} \]
Значит, значение отличается от двух предыдущих путей, и это означает, что ограничение не может существовать. 2}}} \) Показать решение
2}}} \) Показать решение
Хорошо, с этим последним у нас снова есть проблемы с непрерывностью в начале координат, и снова нет факторинга, который мы можем сделать, который позволил бы взять предел.3}} \ right) \ to \ left ({0,0} \ right)} \ frac {1} {2} = \ frac {1} {2} \]
Теперь у нас есть два пути, которые дают разные значения предела, поэтому предела не существует.
Как это ограничение показало нам, мы можем и часто должны использовать пути, отличные от линий, как мы это делали в первой части этого примера.
Итак, как мы видели в предыдущем примере, ограничения здесь немного отличаются от тех, которые мы видели в исчислении I. Пределы нескольких переменных может быть довольно сложно оценить, и мы показали несколько примеров, где потребовалась небольшая работа. чтобы показать, что предела не существует.
Пределы – MATLAB и Simulink
Фундаментальная идея в исчислении состоит в том, чтобы производить вычисления на
функционирует как переменная «приближается к» или приближается
определенное значение. Напомним, что определение производной дается
на предел
Напомним, что определение производной дается
на предел
при условии, что этот предел существует. Программное обеспечение Symbolic Math Toolbox ™ позволяет напрямую рассчитывать пределы функций. Команды
иллюстрируют два самых важных ограничения в математике: производная (в данном случае cos ( x )) и экспоненциальная функция.
Односторонние пределы
Вы также можете рассчитать односторонние пределы с помощью программного обеспечения Symbolic Math Toolbox. Например, вы можете рассчитать предел x / | x |, график которого показан ниже рисунок, поскольку x приближается к 0 слева или справа.
syms x fplot (x / abs (x), [-1 1], 'ShowPoles', 'off')
Чтобы вычислить предел, когда x приближается к 0 слева,
введите
syms x limit (x / abs (x), x, 0, 'left')
Чтобы вычислить предел, когда x приближается к 0 справа,
введите
syms x limit (x / abs (x), x, 0, 'right')
Поскольку предел слева не равен пределу от
справа двусторонний предел не существует. В случае неопределенного
пределы, MATLAB ® возвращает
В случае неопределенного
пределы, MATLAB ® возвращает NaN (не число).
Например,
syms x limit (x / abs (x), x, 0)
возвращает
Обратите внимание, что случай по умолчанию, limit (f) совпадает с предел (f, x, 0) . Изучите параметры команды limit в этой таблице, где f – функция символического объекта х .
Математическая операция | Команда MATLAB | ||
|---|---|---|---|
limx → 0f (x) | 970 970 | | |
limx → a − f (x) | | ||
limx → a + f (x) | |
Limit Калькулятор - (Обновлено на 2021-2022 гг.
 ) | CoolGyan.Org
) | CoolGyan.OrgLimit Calculator - это бесплатный онлайн-инструмент, который отображает значение заданной функции, подставляя предельное значение для переменной. Онлайн-калькулятор лимитов CoolGyan ускоряет вычисления и решает функцию за доли секунды.
Как пользоваться калькулятором пределов?
Процедура использования калькулятора лимитов следующая:
Шаг 1: Введите выражение и предельное значение в заданное поле ввода
Шаг 2: Нажмите кнопку «Отправить», чтобы получить значение функция
Шаг 3: Результат данной функции будет отображаться в новом окне
Каковы ограничения и функции?
Пределы функции важны для исчисления.Пределы используются для определения производных, интегралов и непрерывности. Предельная функция - это фундаментальное понятие в анализе, которое касается поведения функции в определенной точке. В общем, функция «f» возвращает выходное значение «f (x)» для каждого входного значения «x».
Стандартная форма
Стандартная форма для представления функции предела выглядит следующим образом:
Если «c» - действительное число, а «f» - функция с действительным знаком, то предел функции определяется следующим образом:
\ (\ lim_ {x \ to c} f (x) = L \)Вышеприведенное уравнение можно прочитать как: предел функции «f» от «x», когда «x» приближается к «c», равен «L».
Часто задаваемые вопросы о калькуляторе пределов
Каков предел константы?
Предел постоянной функции всегда равен константе.
Каковы разные законы пределов?
Различные законы пределов:
- Закон суммы
- Закон разницы
- Закон продукта
- Закон частных
- Постоянный множественный закон
- Степенной закон
Можем ли мы разбить пределы, чтобы получить решение?
Да, мы можем разделить пределы для сложных функций.


 Супремумы и инфимумы.
Супремумы и инфимумы. Отсутствие предела у синуса. Лемма Больцано-Вейерштрасса.
Отсутствие предела у синуса. Лемма Больцано-Вейерштрасса.
 Примеры вычисления производной.
Примеры вычисления производной. Примеры. Дифференциал высших порядков. Теорема Ферма. Теорема Ролля. Теорема Лагранжа. Геометрический смысл всех трех теорем.
Примеры. Дифференциал высших порядков. Теорема Ферма. Теорема Ролля. Теорема Лагранжа. Геометрический смысл всех трех теорем.
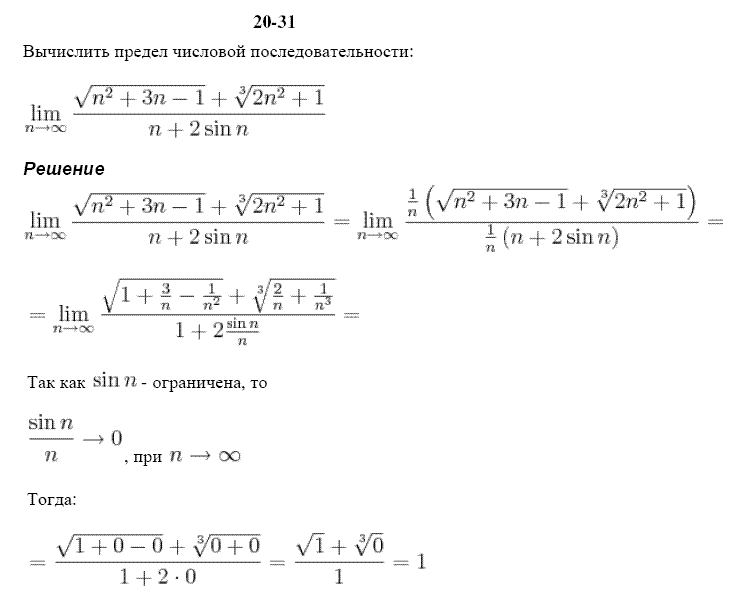 Необходимое условие интегрируемости.
Необходимое условие интегрируемости. Скачать
Скачать Если у вас затруднено понимание понятий бесконечность и 0 в пределах, то вы можете подставлять вместо бесконечности – бесконечно большое число – например 1000 000, или вместо 0 – бесконечно малое – к примеру 0,000001 и прикинуть к чему будет стремиться ответ.
Если у вас затруднено понимание понятий бесконечность и 0 в пределах, то вы можете подставлять вместо бесконечности – бесконечно большое число – например 1000 000, или вместо 0 – бесконечно малое – к примеру 0,000001 и прикинуть к чему будет стремиться ответ.