Калькулятор определителя: Wolfram|Alpha
О-о! Wolfram|Alpha не работает без JavaScript.
Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha.
Wolframalpha
Возьмите детерминанту матриц с Wolfram | Alpha
123321213
Vectors & Matrices- 9.
- Детерминанты »
- определитель {{2, 3}, {4, 7}}
- определитель {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}
- найти определитель матрицы ((a, 3), (5, -7))
- |{{2/3, -5/7}, {-3, 4/9}}|
- определитель [[2, 3], [5, 6]]
- Посмотреть другие примеры »
- Пошаговые решения »
- Генератор задач Wolfram »
24
Больше, чем просто онлайн-калькулятор определителей
Wolfram|Alpha — идеальный ресурс для вычисления определителей матриц.
Он также может вычислять матричные произведения, ранг, недействительность, сокращение строк, диагонализацию, собственные значения, собственные векторы и многое другое.
Узнайте больше о:
Советы по вводу запросов
Для ввода запросов используйте простой английский или общепринятый математический синтаксис. Чтобы ввести матрицу, разделяйте элементы запятыми, а строки — фигурными скобками, скобками или круглыми скобками.
Доступ к средствам мгновенного обучения
Получите немедленную обратную связь и рекомендации с помощью пошаговых решений и Генератора проблем Wolfram
Узнать больше о:
База знаний об определителях
Определитель — это свойство квадратной матрицы.
Значение определителя имеет много значений для матрицы. Определитель, равный 0, означает, что матрица сингулярна и, следовательно, необратима. Систему линейных уравнений можно решить, создав матрицу из коэффициентов и взяв определитель; этот метод называется правилом Крамера и может использоваться только в том случае, если определитель не равен 0. Геометрически определитель представляет собой площадь параллелограмма со знаком, образованную векторами-столбцами, принятыми в качестве декартовых координат.
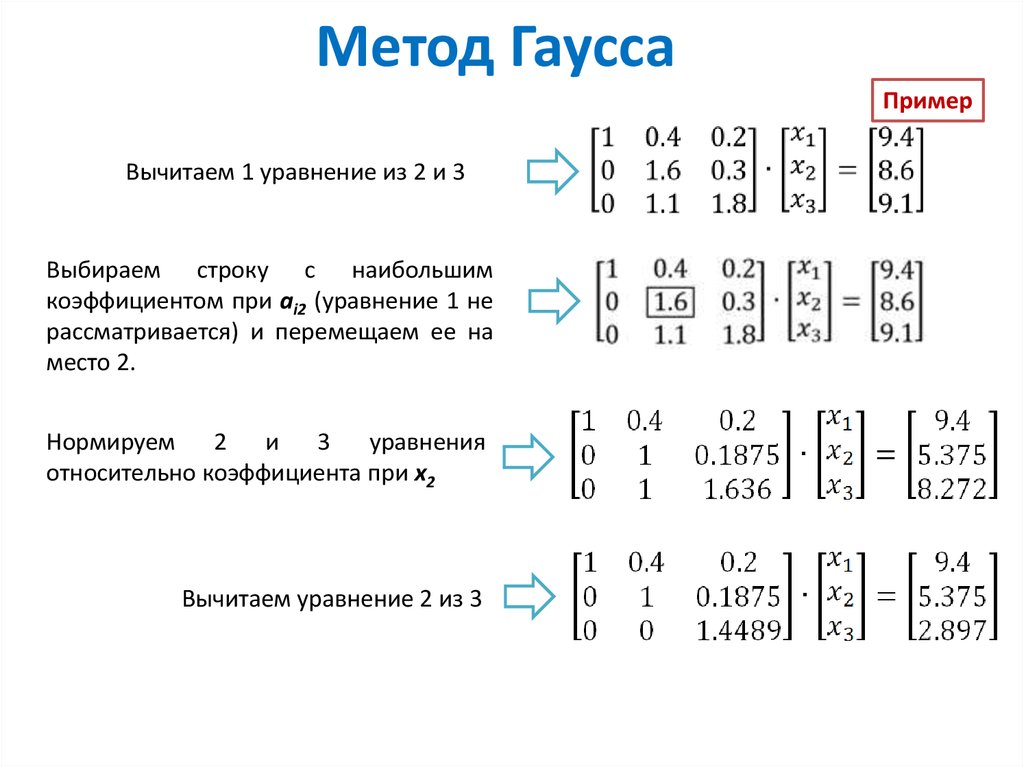
Для вычисления определителя используется множество методов. Определения некоторых матриц, таких как диагональные или треугольные матрицы, можно вычислить, взяв произведение элементов на главной диагонали. Для матрицы 2 на 2 определитель вычисляется путем вычитания обратной диагонали из главной диагонали, что известно как формула Лейбница. Определитель произведения матриц равен произведению определителей этих матриц, поэтому может быть полезно разложить матрицу на более простые матрицы, вычислить отдельные определители, а затем умножить результаты.
Некоторые полезные методы разложения включают QR, LU и разложение Холецкого. Для более сложных матриц для вычисления определителя необходимо использовать формулу Лапласа (разложение кофакторов), исключение Гаусса или другие алгоритмы.
Калькулятор исключения Гаусса
Что говорят наши клиенты…
Тысячи пользователей используют наше программное обеспечение, чтобы справиться со своими домашними заданиями по алгебре. Вот некоторые из их опытов:
Я ценю, что это основа. Это очень помогло мне
Рик Паркер, Миссури
Я был так горд, когда мой сын решил сдать экзамен с отличием по алгебре, но я был обескуражен, когда понял, что могу не помогать ему с домашним заданием. Я не изучал алгебру со школы и просто не помнил, как выполнять некоторые проекты. Алгебратор позволил нам пройти каждый шаг вместе. Спасибо за создание программы, которая позволяет мне помочь моему сыну!
Джим Хендри, Коннектикут.
Существует так много программ по алгебре.
Я не знаю, как я застрял с вашим, но академически говоря, это лучшее, что когда-либо случалось со мной!
Сара Джонс, Калифорния
Я учусь в 9-м классе, и мне всегда было интересно, как некоторые ученики всегда получают хорошие оценки по математике, но никогда не могли представить, что я буду одним из них. Снимаю шляпу перед Алгебратором! Теперь я хорошо разбираюсь в алгебре, и мой подход к решению задач стал более методичным.
Alexis Stratton, FL
Больше всего мне нравится в этом программном обеспечении возможность настройки в соответствии с требованиями пользователя. Сопоставьте свой ответ или проверьте свои шаги или обратитесь за объяснением – это ваша собственная воля. Это дает вам практическое и четкое понимание проблемы.
Алекс Мартин, NH
Поисковые фразы, использованные 27 мая 2011 г.:
Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение может спасти им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт.