Калькулятор слау методом крамера: Онлайн калькулятор. Решение систем линейных уравнений. Метод Крамера

решаем системы линейных алгебраических уравнений (слау)

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

.

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей.

В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется

определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

.

На основании теоремы Крамера

………….
,

где
–

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

.

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6.

Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы.

За примерами далеко ходить не надо.

Следующий пример – на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т.е. имеет вид

Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,

. (1.6)

Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1.5), то можно получить еще

n вспомогательных определителей:

(j = 1, 2, …, n ). (1.7)

Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:

(1.8)

Пример 1.5. Методом Крамера решить систему уравнений

.

Вычислим главный определитель системы:

Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):

Таким образом,

Действия над матрицами

1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.

2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть

. (1.9)

Пример 1.6. .

Сложение матриц.

Данная операция вводится только для матриц одного и того же порядка.

Для того чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:

(1. 10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.

Пример 1.7. .

Умножение матриц.

Если число столбцов матрицы А совпадает с числом строк матрицы В , то для таких матриц вводится операция умножения:

2

Таким образом, при умножении матрицы А размерности m ´n на матрицу В размерности n ´k мы получаем матрицу С размерности m ´k . При этом элементы матрицы С вычисляются по следующим формулам:

Задача 1.8. Найти, если это возможно, произведение матриц AB и BA :

Решение. 1) Для того чтобы найти произведение AB

, необходимо строки матрицы A умножить на столбцы матрицы B :

2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A .

Обратная матрица.

Решение систем линейных уравнений матричным способом

Матрица A – 1 называется обратной к квадратной матрице А , если выполнено равенство:

где через I обозначается единичная матрица того же порядка, что и матрица А :

.

Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:

, (1.13)

где A ij – алгебраические дополнения к элементам a ij матрицы

А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).

Пример 1.9. Найти обратную матрицу A – 1 к матрице

.

Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:

.

Найдем det A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 – 3 × 3 × 3 – 1 × 5 × 4 – 2 × 2 × 8 = 24 + 30 + 24 – 27 – 20 – 32 = – 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.

1) Найдем алгебраические дополнения A ij :

Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.

Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:

Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:

где

Умножая обе части равенства (1.14) слева на A – 1 , мы получим решение системы:

, откуда

Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.

Задача 1.10. Решить систему линейных уравнений

с помощью обратной матрицы.

Решение. Запишем систему в матричном виде: ,

где – основная матрица системы, – столбец неизвестных и – столбец свободных членов. Так как главный определитель системы , то основная матрица системы А имеет обратную матрицу А -1 . Для нахождения обратной матрицы А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :

Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:

Решение системы находим по формуле (1.15):

Таким образом,

Решение систем линейных уравнений методом обыкновенных жордановых исключений

Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:

(1.16)

Требуется найти решение системы, т.е. такой набор переменных , который удовлетворяет всем равенствам системы (1. 16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.

При решении подобных задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называется методом обыкновенных жордановых исключений. Суть данного метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого выражалась переменная, запоминается.

Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. В процессе исключения неизвестных некоторые уравнения могут превратиться в верные тождества, например . Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например ), то мы делаем вывод, что система не имеет решения.

Если в ходе решения противоречивых уравнений не возникло, то из последнего уравнения находится одна из оставшихся в нем переменных. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются еще и другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем совершается так называемый «обратный ход». Найденную переменную подставляют в последнее запомненное уравнение и находят вторую переменную. Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.

В результате мы получаем решение системы. Данное решение будет являться единственным, если найденные переменные будут числами. Если же первая найденная переменная, а затем и все остальные будут зависеть от параметров, то система будет иметь бесчисленное множество решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от того или иного набора параметров, называются общим решением системы.

Пример 1.11.

x

После запоминания первого уравнения и приведения подобных членов во втором и третьем уравнении мы приходим к системе:

Выразим y из второго уравнения и подставим его в первое уравнение:

Запомним второе уравнение, а из первого найдем z :

Совершая обратный ход, последовательно найдем y и z . Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :

.

Затем подставим и в первое запомненное уравнение , откуда найдем x :

Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:

. (1.17)

Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

.

Запомним первое уравнение

В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т.е. не имеет решения.

Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.

Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.

Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:

. (1.18)

Решение. Как и прежде, выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

.

Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:

Выражая y из первого уравнения и подставляя его во второе уравнение , мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.

В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда

Подставим y и z в первое запомненное равенство и найдем x :

.

Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t :

(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1.18).

В том случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обыкновенных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы при одном шаге в общем виде и оформить решение задачи в виде специальных жордановых таблиц.

Пусть дана система линейных форм (уравнений):

, (1.20)
где x j – независимые (искомые) переменные, a ij – постоянные коэффициенты
(i = 1, 2,…, m ; j = 1, 2,…, n ). Правые части системы y i (i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решений данной системы методом исключения неизвестных.

Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную (x s ) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.

Мы получим следующую систему:

. (1.21)

Из s -го равенства системы (1.21) мы впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S -я строка запоминается и в дальнейшем из системы исключается. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.

Вычислим коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть следующим образом:

Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:

(1.23)
Вычислим теперь новые коэффициенты b ij (i ¹ r ) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):

После приведения подобных членов, получим:

(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1. 21) (за исключением r -го уравнения):

(1.25)
Преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых».

Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:

Таблица 1.1

	x 1	x 2	…	x j	…	x s	…	x n
y 1 =	a 11	a 12		a 1j		a 1s		a 1n
…………………………………………………………………..
y i =	a i 1	a i 2		a ij		a is		a in
…………………………………………………………………..
y r =	a r 1	a r 2		a rj		a rs		a rn
………………………………………………………………….
y n =	a m 1	a m 2		a mj		a ms		a mn

Жорданова таблица 1.1 содержит левый заглавный столбец, в который записывают правые части системы (1.20) и верхнюю заглавную строку, в которую записывают независимые переменные.

Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу , состоящую из элементов верхней заглавной строки, то получится матрица , состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:

Таблица 1.2

	x 1	x 2	…	x j	…	y r	…	x n
y 1 =	b 11	b 12		b 1 j		b 1 s		b 1 n
…………………………………………………………………. .
y i =	b i 1	b i 2		b ij		b is		b in
…………………………………………………………………..
x s =	b r 1	b r 2		b rj		b rs		b rn
………………………………………………………………….
y n =	b m 1	b m 2		b mj		b ms		b mn

Разрешающий элемент a rs мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. При переходе от данной таблицы к следующей таблице одна переменная (x s ) из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, один из свободных членов системы (y r ) из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку.

Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.23) и (1.25).

1. Разрешающий элемент заменяется обратным числом:

2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:

3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:

4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:

Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь , находятся на пересечении i -ой и r -ой строк и j -го и s -го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно использовать следующую диаграмму:

-21-26-13-37

Совершая первый шаг жордановых исключений, в качестве разрешающего элемента можно выбрать любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Не следует только выбирать разрешающий элемент в последнем столбце, т.к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.

Строку x 3 (табл.1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Из таблицы 1.4 исключается так же третий столбец с нулем в верхней заглавной строке. Дело в том, что независимо от коэффициентов данного столбца b i 3 все соответствующие ему слагаемые каждого уравнения 0·b i 3 системы будут равны нулю. Поэтому указанные коэффициенты можно не вычислять. Исключив одну переменную x 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с вычеркнутой строкой x 3). Выбирая в таблице 1.4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).

Таблица 1.5 Таблица 1.6

Из последней таблицы 1.7 находим: x 1 = – 3 + 2x 5 .

Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:

Таким образом, система имеет бесчисленное множество решений. Переменной x 5 , можно придавать произвольные значения. Данная переменная выступает в роли параметра x 5 = t. Мы доказали совместность системы и нашли ее общее решение:

x 1 = – 3 + 2t

x 2 = – 1 – 3t

x 3 = – 2 + 4t . (1.27)
x 4 = 4 + 5t

x 5 = t

Придавая параметру t различные значения, мы получим бесчисленное множество решений исходной системы. Так, например, решением системы является следующий набор переменных (- 3; – 1; – 2; 4; 0).

В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.

А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!

Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

;

Ответ : ,

Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.

Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .

Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.

Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:

1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).

2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.

Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.

Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.

Решение системы с помощью обратной матрицы

Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.

Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:

То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце

Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера – весьма полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение СЛАУ методом Крамера

Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.

Согласно методу Крамера, решение находится по формулам:

Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.

В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:

Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .

А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!

Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!

Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

;

Ответ : ,

Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.

Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .

Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.

Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:

1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).

2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.

Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.

Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.

Решение системы с помощью обратной матрицы

Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.

Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:

То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце

В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.

Розв язання систем лінійних рівнянь методом крамера – Telegraph

Розв язання систем лінійних рівнянь методом крамера

Скачать файл – Розв язання систем лінійних рівнянь методом крамера

Используя этот онлайн калькулятор для решения систем линейных уравнений СЛУ методом Крамера , вы сможете очень просто и быстро найти решение системы. Воспользовавшись онлайн калькулятором для решения систем линейных уравнений методом Крамера, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на решения систем линейных уравнений, а также закрепить пройденный материал. Изменить названия переменных в системе. Вводить можно числа или дроби Более подробно читайте в правилах ввода чисел. Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! Добро пожаловать на OnlineMSchool. Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики. Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support onlinemschool. Количество неизвестных величин в системе: Попробуйте онлайн калькуляторы из раздела решение уравнений Решение квадратных уравнений Решение биквадратных уравнений Решение систем линейных уравнений Решение систем линейных уравнений. Метод Гаусса Решение систем линейных уравнений. Метод Крамера Решение систем линейных уравнений. Матричный метод Показать все онлайн калькуляторы. Попробуйте решить упражнения из темы уравнения. Система линейных уравнений с 2-мя неизвестными Упражнения. Система линейных уравнений с 3-мя неизвестными Упражнения. Система линейных уравнений с 4-мя неизвестными Упражнения. Система линейных уравнений с n неизвестными Показать все онлайн упражнения.

Метод Крамера для СЛАР

Это пример использования текстового виджета, в который Вы можете вставить свое любое описание – продукт, услугу, мысль. DO Generate SQL IF ELSE insert InsertSQL InterBase Express Key Fields LU LU-алгоритму LU-розкладання LU на Delphi master-detali ModifySQL. Footer Виджет 3 Это пример использования текстового виджета, в который Вы можете вставить свое любое описание – продукт, услугу, мысль. Footer Виджет 4 Это пример использования текстового виджета, в который Вы можете вставить свое любое описание – продукт, услугу, мысль.

Розв’язок системи лінійних алгебраїчних рівнянь методом Крамера

Учиться правила дорожного движения

Каталог кувалда ру самара

Онлайн калькулятор. Решение систем линейных уравнений методом Крамера

Свойства водыпри различных температурах

Решение комбинаторных задач 4 класс

Решение СЛАУ методом Крамера

Силикон своими руками в домашних

Тесты на личность люшера

Activity – Калькулятор систем в бк, калькулятор систем в бк – The Fan Pub

CLICK HERE >>> Калькулятор систем в бк 
 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

Калькулятор систем в бк
Калькулятор поддерживает работу в 2-х режимах: Со Скобками или Без Скобок. Основное отличие – использование скобок при расчетах и как результат возможность расчета более сложных заданий. Калькулятор бк — неотъемлемый элемент вычисления для прибыльной игры. Bet On расскажет, как ставки на спорт могут принести прибыль и какие рабочие стратегии в этом помогут! Здесь представлен калькулятор арбитражных ситуаций (вилок) для двух и трёх исходов. Что такое вилка в букмекерских ставках? Програмний комплекс Транс-ГРАД призначений для перерахунку координат від систем координат СК-42, СК-63, місцевих систем координат, похідних від СК-42 та СК-63 до Державної геодезичної референцної системи координат УСК-2000. Калькулятор с решением систем линейных уравнений методом Гаусса. В наш раздел с калькуляторами часто заходят учащиеся школ и университетов при подготовке к занятиям и во время контрольных работ. Калькулятор систем счисления с решением При помощи данного калькулятора вы можете переводить целые и дробные числа из одной системы счисления в другую и получить подробное решение. Калькулятор вилок в беттинге выполнят расчет случаев, когда из-за ошибок или разных подходов букмекеров пользователь может совершить прогнозы в разных конторах на исходы так, чтобы получить доход в любой ситуации. Быстрый 5) полосы в выход черной ставок беттинге: (9 погода на сегодня 4, из экспресс ТБ(2) Калькулятор (систем. Калькулятор ставок в система Как выигрыш вычисляется системе из Ставка. Простой математический онлайн калькулятор. Умеет складывать, делить, умножать и вычитать числа в десятичной системе счисления. Зайти в соответствующую категорию типов пари и выбрать «Калькулятор системы». В первом случае возможных вариантов будет 6, а во втором — 4.
Букмекерская контора предупреждает, что вам лучше будет загружать программы и приложения только с ее офиц, калькулятор систем в бк.
Калькулятор систем в бк
Калькулятор вилок в беттинге выполнят расчет случаев, когда из-за ошибок или разных подходов букмекеров пользователь может совершить прогнозы в разных конторах на исходы так, чтобы получить доход в любой ситуации. Калькулятор перевода чисел между систем счисления онлайн. Вы можете выполнить перевод числа из одной системы счисления в любую другую. Калькулятор покажет подробный ход решения. • Калькулятор с поддержкой разных систем счисления • Перевод числа в другие системы счисления • Перевод дробных чисел из одной системы счисления в другую • о римских цифрах. Легко и быстро рассчитать букмекерскую маржу в любом виде спорта, турнире и рынке ставок (основном и второстепенном) можно с помощью онлайн калькулятора комиссии букмекера. Решение систем линейных алгебраических уравнений. Этот калькулятор сможет за секунду решить системы линейных алгебраических уравнений (СЛАУ) методом Гаусса, методом Крамера или матричным методом. Легальная букмекерская контора Леон принимает ставки на территории Беларуси. ⚽Надежность, высокие коэффициенты, широкая линия и быстрые выплаты. Калькулятор талантов World of Warcraft: Classic. Занимайтесь теорикрафтом, планируйте и делитесь билдами своих персонажей. Онлайн-калькулятор вилок Число исходов вилки: 2 3 4 и больше Тип вилки (формула): Коэффициент. Онлайн калькулятор для перевода единиц измерения радиоактивности из Беккерель (Бк) в Кюри (Ки), Резерфорд rd, Распады в секунду. Способы платежей в бк Sbobet Лимиты, комиссия и время обработки при депозите и выводе средств Доступные валюты в бк Sbobet ️. Калькулятор систем экспрессов популярен, как среди новичков, так и опытных игроков. Первые его используют для расчета простых систем, таких как 2 из 3 или 3 из 4. Здесь можно найти все, что душе угодно, от покера до онлайн-казино, калькулятор систем в бк.
 
 

Калькулятор систем в бк, калькулятор систем в бкОн начисляется на первое зачисление средств в пятницу, начиная с 0:00 до 23:59 и отыгрывается по схожим условиям с теми, что установлены для акции при регистрации. Чтобы отказаться от получения пятничного вознаграждения уберите в личном кабинете галочку в графе «принимать участие в акциях», калькулятор систем в бк. Black Friday 1xbet: правила. Два главных отличия Black Friday от бонуса на пополнение: для отыгрыша дается не 30 дней, а сутки с момента пополнения, а прокручивать депозит нужно не 5 раз, а трижды. Доступен приз игрокам из России, Украины, Беларуси и Казахстана. Бездепозитные бонусы бездепозитные форекс щенячий 2017, бонус без депозита Индикаторы для бинарных опционов бесплатно щенячий патруль, бездепозитные форекс бонусы. 1хбет сайт 1хбет сайт 1xBet официальный сайт регистрация и вход личный кабинет букмекерской конторы 1хБет, рабочее зеркало 1xBet на сегодня и прямо сейчас. На нашем сайте вы найдете самую актуальную информацию о рулетка онлайн бесплатно щенячий патруль, где кэш, лототрон купить спб. Мультфільм мега добрий і навчає цьому добру дітей, неймовірні пригоди патруля і його заводили вчать діточок не сумувати, бути вкрай уважними, поспішати на допомогу оточуючим. Щенячий патруль всегда готов прийти на помощь. День и ночь вам помочь летит патруль щенячий. Когда беда случилась не плачь и не грусти, Райдер и его щенки спешат тебя спасти:Маршал,Крепыш,Гонщик,Рокки,Зума,Скай. Игры патруль Дети будут бесплатно играть с от Щенячий онлайн общения в восторге юным. Игровой алладин клуб игровые автоматы 2 Duur игровой бонус бездепозитный онлайн автомат казино 01. Щенячий патруль всегда готов прийти на помощь. Смотреть мультфильм Щенячий патруль онлайн в хорошем качестве совершенно бесплатно и без регистрации! Игры онлайн зума делюкс продолжение, гайд на армс вара 3. 5 пвп щенячий патруль ютуб на русском. ) онлайн-игр в казино в котором полноценно представлены все игры онлайн гемблинга.  
 

1хбет казино онлайн щенячий патруль, калькулятор систем в бк

Сейчас доступно 44 способа вывода выигрышей. Все переводы проводятся без комиссии. Как правило, вся процедура занимает не более 7 минут, калькулятор систем в бк. Чтобы оформить выплату, необходимо указать паспортные данные. Программа работает как лаунчер, поэтому позволяет снизить нагрузку практически вдвое, калькулятор систем в бк.
Интерфейс предельно прост и практически ничем не отличается от официального сайта, калькулятор систем в бк.
Морской патруль Воздушный патруль Игрушки Щенячий Патруль купить в магазине: база, патрулевоз, машинки и наборы героев. Щенячий патруль с доставкой по России! На сайте paw-shop. Ru вы можете купить героев мультфильма Щенячий патруль с доставкой или самовывозом по всей России. Поклонникам мультфильма Щенячий патруль, предлагаем смотреть онлайн 4 сезон мультсериала бесплатно и в хорошем качестве. Щенки спасают конкурс талантов, Щенячий патруль — смотреть онлайн 2 сезон 10 серию мультика 9: Щенки спасают пилота << Все серии >> 11: Щенки оставляют Маршала дома. Быстрая регистрация 1xBet (1хБет), ставки 1хбет зеркало. 39365/ Информация часто не влазит в экран, многое приходится держать в голове, 1хбет игры щенячий патруль. Щенячий патруль – новый детский мультсериал, о мальчике, которому десять лет и зовут его Зик Райдер. Как все мальчишки своего возраста, он очень веселый, подвижный и большой придумщик. Мультик Щенячий патруль, наполнен веселыми приключениями. Смотрите онлайн все серии подряд, новые серии 2020 года не оставят равнодушным ни одного ребенка! Мультсериал Щенячий патруль 1,2,3,4 сезон все серии подряд без остановки на VinixMult смотреть онлайн.

Новые или существующие игроки не смогут осуществить на прямую вход в свой личный кабинет 1XBET, вывести или пополнить игровой счет. Каждый день бк 1хбет открывает новые сайты для пользователей из запрещенных стран, чтобы предоставлять им непрерывный доступ к онлайн ставкам. Регистрацию на официальном сайте 1хбет можно осуществить как с телефона, так и с персонального компьютера или планшета, использую для этого мобильную или полную версию сайт. Это самый просто и быстрый способ создать учетную запись с помощью компьютера, потому что вам не нужно устанавливать дополнительный софт, 1хбет казино онлайн щенячий патруль. But what truly impressed us is the 1xBet application. The App Store 1xBet was founded when the demand for portable devices (cell phones) increased, калькулятор систем бк. Если вы потеряли доступ к аккаунту в системе букмекерской компании 1XBET, альтернативным вариантом для входа будет поиск актуального зеркала. Периодически ресурсы, открывающие возможности для восстановления доступа к официальному сайту, перестают работать по разным причинам, калькулятор систем бк. Удивительно, что такая классная ставочная контора не самое популярное место для ставок, калькулятор систем бк. На мой вкус, она с большим отрывом обгоняет всех остальных букмекеров, отличаясь своей надженостью. Есть надежда, что со временем законодательство даст возможность букмекерам без проблем работать онлайн в России, калькулятор систем ставки. Безопасен ли вход через зеркало 1xbet? Есть приложение на персональный компьютер. В них полностью сохранен функционал полной версии, калькулятор систем ставки. Как вывести деньги с сим карты Билайн, калькулятор систем бк. Карта Beeline открывает перед операторами новые возможности для снижения комиссии. Она обеспечивает более комфортные условия совершения ставок, калькулятор систем в бк. Интерфейс предельно прост и практически ничем не отличается от официального сайта. На главной странице 1xBet беттер видит основные события в мире спорта, на которые можно поставить, калькулятор систем в бк. Пример игры на бирже ставок: Зайти на главную страницу официального портала 1xBet. На сайте букмекера есть подробная инструкция для всех популярных браузеров, калькулятор систем в бк. Это программы, позволяющие обходить любую блокировку и сохранять анонимность в интернете. Когда вы нажимаете на приложение для смартфона, сделайте свой выбор в соответствии с операционной системой вашего телефона и загрузите мобильное приложение. Процедуры скачивания 1xbet предоставляют игрокам большое удобство и быстрые ставки, калькулятор систем в бк. 
 

Популярные виды спорта лучшие коэффициенты:

Футбол 22, 
 

Теннис 52, 
 

Баскетбол 34, 
 

Хоккей 24, 
 

Волейбол 60, 
 

Гандбол 27, 
 

Бейсбол 19, 
 

Снукер 46, 
 

Регби 27, 
 

Австралийский футбол 42, 
 

Шахматы 25, 
 

Бокс 69, 
 

UFC 43, 
 

Автогонки 40, 
 

Американский футбол 19, 
 

Атлетика 18, 
 

Биатлон 25, 
 

Бильярд 63, 
 

Велоспорт 74, 
 

Гольф 62, 
 

Горные лыжи 16, 
 

Гэльский футбол 44, 
 

Дартс 45, 
 

Крикет 65, 
 

Лыжи 62, 
 

Лыжное двоеборье 20, 
 

Нетбол 53, 
 

Олимпиада 29, 
 

Парусный спорт 39, 
 

Прыжки с трамплина 47, 
 

Сёрфинг 43, 
 

Спидвей 47, 
 

Флорбол 26, 
 

Формула-1 14, 
 

Херлинг 74, 
 

Хоккей с мячом 35 
 

 
 

Бонус на депозит:
Яндекс Деньги, Сбербанк онлайн, Альфаклик, WebMoney (Вебмани, ВМ), Банковская карточка (кредитная или дебетовая) – Credit Card, MoneyBookers, Neteller, EcoCard, Wire transfer, Western union, Check, Xек, Банковский перевод, Манибукерс, Нетеллер, Экокард. Криптовалюты: Bitcoin, Litecoin, Dogecoin, Dash, Ethereum, Monero, ZCash, NEM, DigiByte, Bitcoin gold, Bitcoin Cash, Ethereum Classic, Verge, QTUM, STRATIS, Ripple, USD Coin, TrueUSD, Tether, TRON. 
 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
blabla

Теорема кронекера капелли онлайн калькулятор

В первой части мы рассматривали системы линейных алгебраических уравнений (СЛАУ), все коэффициенты которых были известны. В этой же части разберём СЛАУ, среди коэффициентов которых есть некий параметр. Для исследования СЛАУ на совместность станем использовать теорему Кронекера-Капелли. В процессе решения примеров на данной странице будем применять метод Гаусса или же метод Крамера. Сформулируем теорему и следствие из неё ещё раз:

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т. е. $\rang A=\rang\widetilde$.

Параметр $n$, использованный выше, равен количеству переменных рассматриваемой СЛАУ.

Исследовать СЛАУ $ \left \ & kx_1+2x_2+x_3=8;\\ & -x_1+x_2+2x_3=7;\\ & x_2+kx_3=5.\end\right.$ на совместность и найти решение системы в зависимости от значений параметра $k$.

Чтобы исследовать заданную систему на совместность, нам нужно найти ранг матрицы системы $A$ и ранг расширенной матрицы системы $\widetilde$. Сделать это можно несколькими путями. Стоит учесть, что в данном примере нам требуется не только исследовать систему на совместность, но и указать её решения. Мне кажется наиболее удобным в таких задачах применять метод Гаусса, однако это вовсе не является обязательным. Для разнообразия данный пример решим методом Гаусса, а следующий – методом Крамера. Итак, запишем и начнём преобразовывать расширенную матрицу системы. При записи расширенной матрицы системы поменяем местами первую и вторую строки. Это нужно для того, чтобы первым элементом первой строки стало число -1. 2=0$, при этом $2k-2\neq$. В этом случае преобразованная матрица системы будет содержать две ненулевых строки (т.е. $\rang A=2$), а преобразованная расширенная матрица системы будет содержать три ненулевых строки (т.е. $\rang \widetilde=3$). Иными словами, нам требуется решить систему уравнений:

Из первого уравнения имеем: $k=1$ или $k=-1$, однако $k\neq$, поэтому остаётся лишь один случай: $k=-1$. Следовательно, при $k=-1$ система не имеет решений.

Рассмотрим второй пункт следствия из теоремы Кронекера-Капелли – ранги равны между собой, но меньше, чем количество переменных (т.е. меньше 3). Это возможно лишь в том случае, если последняя строка преобразованной расширенной матрицы системы полностью станет нулевой, т.е.

Система имеет бесконечное количество решений. Найдём эти решения. Подставим $k=1$ в преобразованную матрицу и продолжим операции метода Гаусса. Третью строку (она станет нулевой) просто вычеркнем:

Рассмотрим третий пункт следствия из теоремы Кронекера-Капелли – ранги равны между собой и равны количеству переменных. 2\neq$, т.е. $k\neq$ и $k\neq$. Продолжаем решение методом Гаусса:

Исследовать СЛАУ $\left\ & 2kx_1+x_2+x_3=0;\\ & x_1-x_2+kx_3=1;\\ & (k-6)x_1+2x_2-4x_3=-3.\end\right.$ на совместность и найти решение системы при тех значениях параметра, при которых она совместна.

Вновь, как и в предыдущем примере, для того, чтобы исследовать заданную систему на совместность, нам нужно найти ранг матрицы системы $A$ и ранг расширенной матрицы системы $\widetilde$. Чтобы исследовать систему на совместность и указать количество решений применим метод Крамера. Можно было бы решить и методом Гаусса, однако в предыдущем примере мы его уже использовали, поэтому для разнообразия решим задачу с помощью метода Крамера. Начнём с вычисления определителя матрицы системы. Этот определитель мы получим с помощью готовой формулы.

Нам остаётся исследовать совместность системы при условии $\Delta=0$. Это равенство возможно при $k=0$ или $k=1$.

Для наглядности я запишу здесь матрицу системы $A$ и расширенную матрицу системы $\widetilde$, подставив $k=1$:

Если $k=1$, то $\Delta=0$. Это значит, что $\rang≤2$. Рассмотрим миноры второго порядка матрицы $A$. Например, возьмём минор, образованный на пересечении строк №1, №2 и столбцов №1, №2: $M=\left|\begin2 & 1\\ 1 & -1\end\right|=-3$. Так как $M\neq$, то ранг матрицы $A$ равен 2.

Разберём ещё один пример, в котором рассмотрим СЛАУ с четырьмя уравнениями.

Исследовать СЛАУ $ \left \ & kx_1+x_2+x_3+x_4=1;\\ & x_1+kx_2+x_3+x_4=1;\\ & x_1+x_2+kx_3+x_4=1;\\ & x_1+x_2+x_3+kx_4=1.\end\right.$ на совместность и найти решение системы в зависимости от значений параметра $k$.

Применим метод Гаусса. При записи расширенной матрицы системы поместим первую строку вниз, на место четвёртой строки. А дальше начнём стандартные операции метода Гаусса.

Здесь можно было бы остановиться и рассмотреть случаи $k=1$ и $k\neq$ отдельно. Цель таких действий: разделить вторую, третью и четвёртую строки на $k-1$ при условии $k-1\neq$. Однако пока что полученная нами матрица содержит не столь уж громоздкие элементы, поэтому сейчас отвлекаться на частности я не вижу смысла. Продолжим преобразования в общем виде:

Продолжим решение методом Гаусса. Так как $k\neq$ и $\neq$, то $(1-k)(k+3)\neq$. Следовательно, мы можем разделить вторую и третью строки на $1-k$, четвёртую строку – на выражение $(1-k)(k+3)$. С полученной после этого матрицей продолжим операции обратного хода метода Гаусса:

• При $k=-3$ система несовместна.
• При $k=1$ система является неопределённой. Общее решение системы: $\left\& x_1=-x_2-x_3-x_4+1;\\&x_2\in,\;x_3\in,\;x_4\in. \end\right.$
• При $k\neq$ и $k\neq$ система является определённой. Решение системы: $x_1=x_2=x_3=x_4=\frac$.

Экспонента в 1 степени
Темы для курсового проекта по программированию

lominuq онлайн калькулятор решение систем линейных уравнений метод гаусса

онлайн калькулятор решение систем линейных уравнений метод гаусса Как решить систему уравнений методом Гаусса. Решение системы линейных алгебраических уравнений методом Гаусса online. Оформление сразу в . Метод Гаусса – классический метод решения системы линейных алгебраических уравнений (СЛАУ). Если после использования данного онлайн калькулятора (Решение СЛАУ методом Гаусса) у Вас возникли какие-то вопросы по работе сервиса или вопросы образовательного. Наш калькулятор умеет решать онлайн как обычную определенную, так и . уравнений на совместность онлайн, используя решение методом Гаусса. . При решении системы линейных уравнений онлайн методом Гаусса . Решение системы линейных уравнений онлайн. Данный онлайн калькулятор позволяет решать систему уравнений различными методами онлайн. Найти решение системы уравнений методом Гаусса. Этот онлайн калькулятор . Здесь вы сможете бесплатно решить систему линейных уравнений методом Гаусса онлайн больших размеров в комплексных числах с очень подробным решением . Наш калькулятор умеет решать онлайн как обычную определенную. Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему. При решении системы линейных уравнений онлайн методом Гаусса. Скориставшись цим онлайн калькулятором для розвязання системи лінійних рівнянь (СЛР) методом Гауса, ви зможете дуже просто і швидко знайти . От 200 р. Срок от 4 часов! Без посредников! Решение систем линейных уравнений (матричный метод , метод Гаусса), исследование на совместность. Эта страничка поможет решить Системы Линейных Алгебраических Уравнений (СЛАУ ) методом Гаусса , матричным методом или методом Крамера. Данный онлайн калькулятор позволяет решать системы линейных уравнений методом Гаусса. Это классический метод решения системы линейных уравнений, в. Как решить систему уравнений методом Гаусса. Решение системы линейных алгебраических уравнений методом Гаусса online. Оформление сразу в . Операции над множествами Онлайн. Данный онлайн-калькулятор над множествами выполняет . Все онлайн. Вообще говоря, на сайте уже есть один калькулятор, решающий СЛАУ методом Гаусса – Решение системы линейных алгебраических уравнений методом. Решение систем линейных уравнений методом Гаусса . Этот онлайн калькулятор позволит вам очень просто решить систему линейных уравнений (СЛУ) методом Гаусса. 43. 4.1 Формулы для решения прямоугольных сферических треугольников. . 5.3 Формулы Даламбера-Гаусса и аналогии Непера. Формулы для расчета . «Математические методы в геодезических измерениях», «Спутниковая … Рис. 1.7 – Перевод градусов в радианы с помощью онлайн калькулятора. Решение систем линейных уравнений (матричный метод, метод Гаусса), исследование на совместность.

Как решить уравнение по формуле Крамера примеры. Линейные уравнения

Чтобы освоить этот абзац, вы должны уметь открывать классификаторы “два на два” и “три на три”. Если определители плохие, изучите урок Как вычислить определитель?

Во-первых, мы более подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом сложения членов!

Дело в том, что пусть иногда, но встречается такая задача – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет вам понять, как использовать правило Крамера для более сложного случая — системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые желательно решать точно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычисляем определитель, он называется главный определитель системы .

Метод Гаусса.

Если , то система имеет единственное решение, и для нахождения корней надо вычислить еще два определителя:
и

На практике указанные определители можно обозначать и латинской буквой.

Находим корни уравнения по формулам:
,

Пример 7

Решаем систему линейных уравнений справа есть десятичные дроби с запятой.Запятая — довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую ​​систему? Можно попробовать выразить одну переменную через другую, но в этом случае наверняка получатся ужасные навороченные дроби, с которыми крайне неудобно работать, а оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и выполнить почленное вычитание, но здесь появятся те же дроби.

Что делать? В таких случаях на помощь приходят формулы Крамера.

;

;

Ответ : ,

Оба корня имеют бесконечные хвосты и находятся приближенно, что вполне приемлемо (и даже обычно) для задач эконометрики.

Комментарии здесь не нужны, так как задача решается по готовым формулам, однако есть один нюанс. При использовании этого метода обязательным фрагментом задания является следующий фрагмент: “Что означает, что система имеет только одно решение” … В противном случае рецензент может наказать вас за неуважение к теореме Крамера.

Не лишней будет проверка, которую удобно проводить на калькуляторе: в левую часть каждого уравнения системы подставляем приблизительные значения. В итоге с небольшой погрешностью у вас должны получиться числа, находящиеся в нужных частях.

Пример 8

Ответ представлен обыкновенными неправильными дробями. Сделайте чек.

Это пример для самостоятельного решения(пример окончания и ответ в конце урока).

Перейдем теперь к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Найдите главный определитель системы:

Если, то система имеет бесконечно много решений или несовместна (не имеет решения). В этом случае правило Крамера не поможет; вам нужно использовать метод Гаусса.

Если , то система имеет единственное решение, и для нахождения корней надо вычислить еще три определителя:
, ,

И, наконец, ответ вычисляется по формулам:

Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «гуляет» слева направо по столбцам главного определителя.

Пример 9

Решите систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Собственно, тут опять комментировать особо нечего, ввиду того, что решение принимается по готовым формулам.Но есть несколько замечаний.

Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм “лечения”. Если под рукой нет компьютера, делаем так:

1) Возможна ошибка расчета. Как только вы столкнулись с «плохой» дробью, следует сразу же проверить правильно ли переписано условие . Если условие переписано без ошибок, то необходимо пересчитать определители с помощью разложения по другой строке ( столбец).

2) Если в результате проверки ошибок не обнаружено, то, скорее всего, в условии задачи была опечатка. При этом спокойно и ВНИМАТЕЛЬНО решаем задачу до конца, а потом обязательно проверяем и оформляем на чистую копию после решения. Конечно, проверка дробного ответа дело неприятное, но это будет обезоруживающим аргументом для преподавателя, который ну очень любит ставить минус за всякую бяку лайк. Как обращаться с дробями, подробно описано в ответе на пример 8.

Если у вас под рукой есть компьютер, то используйте для его проверки автоматизированную программу, которую можно скачать бесплатно в самом начале урока. Кстати, выгоднее всего сразу пользоваться программой (еще до запуска решения), вы сразу увидите промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически вычисляет решение системного матричного метода.

Второе замечание. Время от времени встречаются системы, в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении отсутствует переменная, а во втором – переменная.В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать основной определитель:
– вместо пропущенных переменных ставятся нули.
Кстати, определители с нулями рационально открывать по той строке (столбцу), в которой стоит ноль, так как вычислений намного меньше.

Пример 10

Решите систему, используя формулы Крамера.

Это пример для самостоятельного решения (образец отделки и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно найти в уроке «Свойства определителя». Понижение порядка определителя – пять определителей 4-го порядка вполне разрешимы. Хотя задача уже весьма напоминает профессорский ботинок на груди счастливчика-студента.

Решение системы с помощью обратной матрицы

Метод обратной матрицы Является по существу частным случаем матричного уравнения (см. Пример №3 указанного урока).

Чтобы изучить этот раздел, вы должны уметь разлагать определители, находить обратную матрицу и выполнять умножение матриц. Соответствующие ссылки будут предоставлены по пути.

Пример 11

Решить систему матричным методом

Решение : Запишем систему в матричной форме:
, где

Пожалуйста, взгляните на систему уравнений и матрицы. По какому принципу мы записываем элементы в матрицы, думаю всем понятно.Единственный комментарий: если бы в уравнениях отсутствовали какие-то переменные, то в матрице на соответствующие места пришлось бы ставить нули.

Найдите обратную матрицу по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы.

Сначала разбираемся с определителем:

Здесь классификатор развернут на первой строке.

Внимание! Если , то обратной матрицы не существует и решить систему матричным методом невозможно.В этом случае система решается методом исключения неизвестных (методом Гаусса).

Теперь нам нужно вычислить 9 миноров и записать их в матрицу миноров

Ссылка: Полезно знать значение двойных нижних индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится этот элемент. Вторая цифра – это номер столбца, в котором находится этот элемент:

То есть двойной нижний индекс означает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в строке 3, столбце 2

В ходе решения счета несовершеннолетних лучше расписывать подробно, хотя при определенном опыте их можно приучить считать с ошибками устно.

Методы Kramer и Gauss – одни из самых популярных методов решения СЛАУ … Кроме того, в ряде случаев целесообразно использовать специфические методы. Сессия подошла к концу, и сейчас самое время вернуться к ним или освоить их с нуля. Сегодня мы имеем дело с решением методом Крамера. Ведь решение системы линейных уравнений по методу Крамера — очень полезный навык.

Системы линейных алгебраических уравнений

Линейная система алгебраических уравнений – система уравнений вида:

Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и б – реальные коэффициенты.Простую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме или выразить одну переменную через другую. Но переменных (х) в СЛАУ может быть гораздо больше двух, и здесь не обойтись без простых школьных манипуляций. Что делать? Например, решить СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестно.

Такую систему можно переписать в матричной форме

Здесь А – основная матрица системы, Х и В , соответственно, матрицы столбцов неизвестных переменных и свободных членов.

Решение СЛАУ по методу Крамера

Если определитель главной матрицы не равен нулю (невырожденная матрица), то система может быть решена методом Крамера.

По методу Крамера решение находится по формулам:

Здесь дельта Является определителем основной матрицы, а дельта х n-й – определитель, полученный из определителя основной матрицы заменой n-го столбца на столбец свободных членов.

В этом весь смысл метода Крамера. Подставляя найденные значения по приведенным выше формулам х в нужную систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы вы быстрее уловили суть, ниже приведем пример. подробное решение СЛАУ по методу Крамера:

Даже если у вас не получится с первого раза, не расстраивайтесь! Немного потренировавшись, вы начнете переворачивать SLAU, как орехи. К тому же теперь совершенно необязательно корпеть над тетрадью, решая громоздкие вычисления и выписывая штангу. Можно легко решить СЛАУ методом Крамера онлайн, только подставив в готовом виде коэффициенты. Попробуйте решения онлайн-калькулятора по методу Крамера, которые можно найти, например, на этом сайте.

А если система оказалась упрямой и не сдается, вы всегда можете обратиться за помощью к нашим авторам, например, к . Если в системе будет хотя бы 100 неизвестных, мы обязательно решим ее правильно и в срок!

При количестве уравнений, равном количеству неизвестных с главным определителем матрицы, не равным нулю, коэффициенты системы (для таких уравнений решение есть и оно только одно).

Теорема Крамера.

Когда определитель матрицы квадратной системы отличен от нуля, это означает, что система совместна и имеет одно решение, и его можно найти по формулам Крамера :

где Δ – определитель матрицы системы ,

∆ i — определитель матрицы системы, в которой вместо i й столбец содержит столбец правых частей.

Когда определитель системы равен нулю, это означает, что система может стать совместной или несовместимой.

Этот метод обычно используется для небольших систем с большими вычислениями и когда необходимо определить одно из неизвестных. Сложность метода заключается в том, что необходимо вычислить множество детерминант.

Описание метода Крамера.

Имеется система уравнений:

Систему 3-х уравнений можно решить методом Крамера, который рассматривался выше для системы 2-х уравнений.

Составим определитель из коэффициентов при неизвестных:

Это будет системный идентификатор … Когда D ≠ 0 , система совместима. Теперь составим 3 дополнительных определителя:

,,

Решаем систему формул Крамера :

Примеры решения систем уравнений методом Крамера.

Пример 1 .

Учитывая систему:

Решим методом Крамера.

Сначала нужно вычислить определитель матрицы системы:

Поскольку Δ ≠ 0, то по теореме Крамера система совместна и имеет одно решение. Вычислим дополнительные определители. Определитель Δ 1 получают из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:

Таким же образом получаем определитель ∆ 2 из определителя матрицы системы заменой второго столбца на столбец свободных коэффициентов:

Метод Крамера или так называемое правило Крамера — это способ нахождения неизвестных величин из систем уравнений.Его можно использовать только в том случае, если количество искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть основная матрица, образованная из системы, должна быть квадратной и не содержать нулевых линий, а также если ее определитель должен не быть нулем.

Теорема 1

Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, и она имеет единственное решение.Решение такой системы вычисляется по так называемым формулам Крамера для решения систем линейных уравнений: $x_i=\frac(D_i)(D)$

Что такое метод Крамера

Суть метода Крамера состоит в том, что следует:

1. Чтобы найти решение системы методом Крамера, сначала вычислим главный определитель матрицы $D$. Когда вычисленный определитель основной матрицы при расчете по методу Крамера оказался равным нулю, то система не имеет единственного решения или имеет бесконечное число решений.В этом случае для нахождения общего или какого-то базового ответа для системы рекомендуется применять метод Гаусса.
2. Затем нужно заменить крайний столбец основной матрицы столбцом свободных членов и вычислить определитель $D_1$.
3. Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ — номер самого правого столбца.
4. Найдя все определители $D_1$…$D_n$, можно вычислить неизвестные переменные по формуле $x_i=\frac(D_i)(D)$.

Методика вычисления определителя матрицы

Для вычисления определителя матрицы размерностью более 2 на 2 можно использовать несколько методов:

• Правило треугольников, или правило Сарруса, напоминает то же правило . Суть метода треугольника заключается в том, что при вычислении определителя произведения всех чисел, соединенных на рисунке красной чертой справа, они записываются со знаком плюс, а все числа, соединенные таким же образом на рисунке на слева со знаком минус. В, оба правила подходят для матриц 3 х 3. В случае правила Сарруса сначала переписывается сама матрица, а рядом с ней, рядом с ней заново переписываются ее первый и второй столбцы. Через матрицу и эти дополнительные столбцы проведены диагонали, члены матрицы, лежащие на главной диагонали или параллельной ей, написаны со знаком плюс, а элементы, лежащие на боковой диагонали или параллельно ей, написаны со знаком знак минус.

Рис. 1.Правило треугольников для вычисления определителя по методу Крамера

• Используя метод, известный как метод Гаусса, этот метод также иногда называют разупорядочением детерминанта. При этом матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа на главной диагонали. Следует помнить, что при таком поиске определителя нельзя умножать или делить строки или столбцы на числа, не вынося их как множитель или делитель.В случае поиска определителя возможно только вычитание и сложение строк и столбов вместе, предварительно умножив вычитаемую строку на ненулевой коэффициент. Также при каждой перестановке строк или столбцов матрицы местами следует помнить о необходимости смены конечного знака матрицы.
• При решении СЛАУ с 4 неизвестными методом Крамера лучше всего использовать метод Гаусса для поиска и нахождения определителей или определить определители через поиск миноров.

Решение систем уравнений методом Крамера

Применим метод Крамера для системы из 2-х уравнений и двух искомых величин:

$\begin(cases) a_1x_1 + a_2x_2 = b_1 \a_3x_1 + a_4x_2 = b_2 \\\end (случаев) $

Для удобства выведем в расширенном виде:

$A=\begin(array)(cc|c)a_1&a_2&b_1\a_3&a_4&b_1\\end(array) $

Найдем определитель главной матрицы, также называемый главным определителем системы:

$D = \begin(array)(|cc|)a_1&a_2\a_3&a_4\\end(array ) = a_1 \ cdot a_4 – a_3 \ cdot a_2 $

Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо вычислить еще пару определителей из двух матриц с заменой столбцов основной матрицы на строку свободных терминов:

$D_1=\begin(массив)(|cc|)b_1&a_2\b_2&a_4\\end(массив)=b_1\cdot a_4 – b_2\cdot a_4$

$ D_2 = \ начало (массив) (| cc |) a_1&b_1\a_3&b_2\\\end(array)=a_1\cdot b_2 – a_3\cdot b_1$

Теперь найдем неизвестные $x_1$ и $x_2$:

$x_1=\ frac(D_1)(D)$

$x_2=\ frac(D_2)(D)$

Пример 1

Метод Крамера для решения СЛАУ с основной матрицей 3-го порядка (3 x 3) и тремя требуемыми.

Решить систему уравнений:

$\начало (дел) 3х_1 – 2х_2 + 4х_3 = 21 \ 3х_1 + 4х_2 + 2х_3 = 9 \ 2х_1 – х_2 – х_3 = 10 \\ конец (дела)

$

Вычислим главный определитель матрицы по приведенному выше правилу под номером 1:

$D=\begin(массив)(|ccc|)3&-2&4\3&4&-2\2&-1&1\\end(массив)=3\cdot 4\cdot (-1) + 2 \ cточка (-2) \ cточка 2 + 4 \ cточка 3 \ cточка (-1) – 4 \ cточка 4 \ cточка 2 – 3 \ cточка (-2) \ cточка (-1) – ( – 1)\кдот 2\кдот 3 = – 12 – 8 -12 -32 – 6 + 6 = – 64

$

А теперь еще три определителя:

$D_1=\begin(массив)(|ccc|)21&2&4\9&4&2\10&1&1\\end(массив)=21\cdot 4\cdot 1+( – 2) \ пдт 2 \ пдт 10 + 9 \ пдт (-1) \ пдт 4 – 4 \ пдт 4 \ пдт 10 – 9 \ пдт (-2) \ пдт (-1) – (-1) \ пдт 2 \ cdot 21 = – 84 – 40 – 36 – 160 – 18 + 42 = – 296$

$D_2=\begin(массив)(|ccc|)3&21&4\3&9&2\2&10&1\\end(массив)=3\cdot 9\cdot(- 1 ) + 3 \ птд 10 \ пдт 4 + 21 \ пдт 2 \ пдт 2 – 4 \ пдт 9 \ пдт 2 – 21 \ пдт 3 \ пдт (-1) – 2 \ пдт 10 \ пдт 3 = – 27 + 120 + 84 – 72 + 63 – 60 = 108

$

$D_3=\begin(массив)(|ccc|)3&-2&21\3&4&9\2&1&10\\end(массив)=3\cdot 4\cdot 10 + 3 \ cточка (-1) \ cточка 21 + (-2) \ cточка 9 \ cточка 2 – 21 \ cточка 4 \ cточка 2 – (-2) \ cточка 3 \ cточка 10 – (-1) \ cточка 9 \ cточка 3 = 120 – 63 – 36 – 168 + 60 + 27 = – 60

$

Найдем необходимые значения:

$x_1 = \ frac (D_1) (D) = \ frac (- 296) (- 64) = 4 \ frac (5) (8) $

$x_2 = \ frac (D_1) (D) = \ frac (108) (-64) = – 1 \ frac (11) (16) $

$x_3 = \ frac (D_1) (D) = \ frac (-60) (-64) = \ frac (15) (16) $

Рассмотрим систему из 3-х уравнений с тремя неизвестными

Используя определители третьего порядка, решение такой системы можно записать в том же виде, что и для системы из двух уравнений, т. е.е.

(2.4)

если 0. Здесь

Это Правило Крамера решений системы трех линейных уравнений с тремя неизвестными .

Пример 2.3. Решить систему линейных уравнений по правилу Крамера:

Решение … Найдите определитель главной матрицы системы

Поскольку 0, мы можем применить правило Крамера для нахождения решения системы, но сначала вычислим еще три определителя:

Экзамен :

Значит решение найдено правильно.

Правила Крамера, полученные для линейных систем 2-го и 3-го порядка, позволяют предположить, что одни и те же правила можно сформулировать для линейных систем любого порядка. Действительно имеет место

Теорема Крамера. Квадратная система линейных уравнений с ненулевым определителем основной матрицы системы (0) имеет одно и только одно решение, и это решение вычисляется по формулам

(2. 5)

, где  – определитель основной матрицы ,  и – определитель матрицы , производная от основной, замена i -го столбца на столбец свободных элементов .

Обратите внимание, что если  = 0, то правило Крамера не применяется. Это означает, что система либо вообще не имеет решений, либо имеет бесконечно много решений.

Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.

2.4. Определители n-го порядка

Дополнительный минор M ij элемент a ij называется определителем, полученным из заданного вычеркиванием i -й строки и j -го столбца. Алгебраическое дополнение A ij элемент a ij называется минором этого элемента, взятого со знаком (–1) i + j , то есть A ij = (–1) i + j M ij .

Например, найти миноры и дополнения элементов a 23 и a 31 детерминантов

Мы получаем



Используя концепцию алгебраического дополнения, n -й порядок по строке или столбцу .

Теорема 2.1. Определитель матрицы А равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:

(2.6)

Эта теорема лежит в основе одного из основных методы вычисления определителей, т. н. метод понижения порядка … В результате разложения определителя n -го порядка в любой строке или столбце получим n определителей ( n –1)-го порядка.Чтобы уменьшить количество таких определителей, целесообразно выбирать строку или столбец с наибольшим количеством нулей. На практике формулу разложения определителя обычно записывают в виде:

т.е. алгебраические дополнения записываются явно в терминах миноров.

Примеры 2.4. Вычислите определители, сначала разложив их в любой строке или столбце. Обычно в таких случаях выбирают столбец или строку с наибольшим количеством нулей. Выбранная строка или столбец будут отмечены стрелкой.



2.5. Основные свойства определителей

Разложив определитель по любой строке или столбцу, получим n определителей ( n –1)-го порядка. Тогда каждый из этих определителей ( n –1)-го порядка также можно разложить в сумму определителей ( n –2)-го порядка. Продолжая этот процесс, можно прийти к определителям 1-го порядка, т.е. к элементам матрицы, определитель которой вычисляется. Так, для вычисления определителей 2-го порядка необходимо вычислить сумму двух слагаемых, для определителей 3-го порядка – сумму 6 слагаемых, для определителей 4-го порядка – 24 слагаемых.Количество членов будет резко возрастать по мере увеличения порядка определителя. Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, не под силу даже компьютеру. Однако возможно вычисление определителей и другим способом, используя свойства определителей.

Собственность 1 . Определитель не изменится, если в нем поменять местами строки и столбцы, т.е.е. при транспонировании матрицы :

.

Это свойство указывает на равенство строк и столбцов определителя. Другими словами, любое утверждение о столбцах определителя верно для его строк и наоборот.

Собственность 2 . Определитель меняет знак при перестановке двух строк (столбцов).

Последствие . Если определитель имеет две одинаковые строки (столбцы), то он равен нулю.

Собственность 3 . Общий множитель всех элементов любой строки (столбца) можно перенести за знак определителя .

Например,

Следствие . Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю .

Недвижимость 4 . Определитель не изменится, если к элементам одной строки (столбца) добавить элементы другой строки (столбца), умноженные на некоторое число .

Например,

Собственность 5 . Определитель произведения матриц равен произведению определителей матриц:

(PDF) Изучение влияния приливов, приливов и выноса на субсуточный сток в дельте Сакраменто-Сан-Хоакин

ОТЧЕТ – Исследование влияния приливов, притока и выноса на субсуточный сток в дельте

Cramer Fish Sciences ii

Приложение 1: соединения FMN, FRV и JPT………………………………………….. …………………………… 46

Направление и величина потока на стыках FMN, FRV и JPT ……. …….. …………………….46

Рыбацкая нарезка …………… …………………………………………. …………………………………………. .. 46

Ложная река………………………………………….. …………………………………………. ………………………… 47

Джерси-Пойнт………………………………………….. …………………………………………. …………………. 49

Доля и источник потока во внутреннюю дельту на перекрестках FMN, FRV и JPT………. …….51

Рыбацкая нарезка ………………………………… …………………………………………. …………………………… 51

Ложная река……………… …………………………………………. ………………………………………………. 53

Джерси-Пойнт……………… …………………………………………. ……………………… …………………. …………….. 54

Приложение 2: Подробная информация об общей доле потока во внутреннюю дельту ………………………. ………………56

Список иллюстраций

Рисунок 1. Расположение соединений, ведущих к внутренней дельте Сакраменто-Сан-Хоакин.

Слау Джорджиана, основной ствол реки Сакраменто и главный ствол реки Сан-Хоакин обозначены

черным цветом.Места соединения обведены красным и обозначены следующим образом: GEO=Georgiana

Slough, HOR=Head of Old River, TRN=Turner Cut, COL=Columbia Cut: MRV=Middle River,

ORV=Устье Old River, FMN = Fisherman’s Cut, FRV = False River, JPT = Джерси-Пойнт.

Расположение экспортных объектов обозначено синими треугольниками; SWP — Государственный водный проект, CVP —

Проект Центральной долины……………………………. ………………………………………………………………………..3

Рис. 2. Схема течения в реке Мейнстем Сан-Хоакин за 24 часа. На всех графиках длина реки

км отложена по оси абсцисс, а цвет кривой указывает на уровень экспорта. Места соединений обозначены

пунктирными вертикальными линиями с метками соединений. Для двух верхних рядов графиков величина расхода

(в cfs) отложена по оси ординат. Для нижнего ряда графиков ось Y отображает процент времени в течение

, когда поток является положительным.Графики расположены слева направо по возрастанию притока. ……………..9

Рисунок 3. Диапазон стока с переменным экспортом в выбранных каналах в главном русле реки Сан

Хоакин за 24 часа. Пронумерованные кружки на карте обозначали расположение каналов DSM2.

Время суток отложено по оси X, начиная с 00:00 и заканчивая 23:45. Величина потока

отложена по оси ординат. Цвет кривой указывает на уровень экспорта…………………………………………………… 11

Рис. 4. ГЕО: Перекресток Джорджиана-Слау, вид сверху. Контуры физических каналов показаны

серым цветом. Номера гидроканалов DSM2 указаны в скобках, узлы обведены кружками, а положительное

направление потока в каждом канале указано синими стрелками. Восходящие, нисходящие и внутренние дельта-каналы

обозначены, как в таблице 2 ……………………………. ……………………………….. 12

Рис. 5. ГЕО: Поток в болоте Джорджиана Соединение каналов более 24 часов.Время суток в

15-минутные приращения отложены по оси x, начиная с 00:00 и заканчивая 23:45.

Величина расхода отложена по оси Y. Цвет кривой указывает уровень экспорта. Обозначения каналов

, как указано в таблице 2. Для канала GEO2 весь поток направлен во внутреннюю часть дельты. Для других каналов

поток, отображаемый в заштрихованной области, находится вдали от центра соединения… 13

Рисунок 6. HOR: вид сверху главы Старого речного узла.См. Рисунок 4 для описания элементов

. …………………………………………. …………….. ………………………….. ……………………………… 14

Рис. 7. HOR: Расход в истоке старого речного узла Каналы более 24 часов. См. Рисунок 5 для

описания элементов. Для канала HOR3 поток, отображаемый в заштрихованной области, находится вдали от

7124 Foster Slough Rd, Snohomish, WA 98290 | MLS# 1047344

Элементы интерьера

• С подогревом
• С охлаждением
• Нагрев Тип охлаждения: 90%+ Высокая эффективность, Центральный кондиционер, Принудительная подача воздуха, Тепловой насос, Проточный водонагреватель, Стена59 038259 038259
33
• Особенности интерьера: тепловой насос, центральный кондиционер, 90%+ высокая эффективность, безрезервуарный водонагреватель, керамическая плитка, твердая древесина, ковровое покрытие от стены до стены, потолочный вентилятор(ы), столовая, французские двери, высокотехнологичная кабельная система, сводчатый потолок (s), Гардеробная, Гардеробная(-ые)
• Бытовая техника: утилизация, микроволновая печь, плита/духовка, см. примечания
• Пол: керамическая плитка, твердая древесина, винил, ковер
• Бытовая техника в комплекте: вывоз мусора

Парковка/Гараж, Информация о многоквартирных домах, Школа/район, Коммунальные услуги

Внешние элементы

• Внешние элементы: Цементные доски, Камень

5

5

90es , Локати Подробнее, листинг информации

• налоговая сумма годовой: $ 4,509
• Налоговый год: 2017

• • Условия листинга: Cash Out, обычные, FHA
  • Покупатель Финансирование: обычные
  • Направления: от Шоссе 9, сверните на съезд Snohomish (2-я улица).Идите на запад, 2-я улица переходит в Ривервью-роуд. Держитесь левой стороны на повороте 79-й улицы, поверните на север (направо) на Foster Slough Rd. Домашний сайт ок. 1/2 мили по левой стороне дороги.
  • Координаты карты: B, 3
  • Топография: Уровень, Частичный уклон

  Сведения о собственности / лоте

  • кв. футов Закончено: 3 046
  • 110373
  • Стиль Код: 18 – 2 истории W / BSMNT
  • Тип недвижимости: Жилой
  • Собственность Sub Тип: Жилой
  • Состояние недвижимости: Очень хорошо
  • Вид на

  Домашняя информация

  • Энергоэффективность: 90% + Высокая эффективность
  • Тип производства электроэнергии: Электрический, Пропан

  • Область жилой площади: Квадратные футы
  • Расчетные квадратные метры: 3046
  • MLS Square Sourcease Источник: Планы застройщика
  • Общая площадь застройки: 3046
  • Единицы площади застройки: Квадратные футы
  • Детали фундамента: Столбы и колонны, Залитый бетон, Плита
  • Название здания: Maryknoll
  • Имя застройщика: JNT Builders, LLC Год постройки 9 : 2016
  • Фактический год постройки Источник: См. примечания
  • Тип строения: Дом
  • Уровни: Два
  • Ent ry Местонахождение: Main

  Информация сообщества

  Информация об имуществе предоставлена ​​NWMLS, когда последний раз вносилась в список в 2016 году. Эти данные могут не совпадать с общедоступными записями. Выучить больше.

  Менторы и проекты | Калифорнийский государственный университет Монтерей-Бей

  Наставники и проекты

  Для получения информации о наставниках и их проектах, пожалуйста, просмотрите веб-страницы наставников (связанные с их именами). Если у вас остались вопросы, напишите нам по адресу [email protected]. Пожалуйста, не обращайтесь напрямую к наставникам . Студенты, которые связываются с наставниками, могут быть исключены из рассмотрения для REU.

  Каждый год мы выделяем наставников среди наших шести партнеров по исследованиям.См. ниже список наставников REU, в котором выделяются типы исследований, доступных для студентов в рамках нашей программы.

  Калифорнийский государственный университет, залив Монтерей (CSUMB)

  Наставники	Темы исследований
  Доктор Элисон Хаупт	Популяционная генетика, связь между сушей и морем, экология ламинарии и прибрежной зоны, антропогенное воздействие на экосистемы
  Доктор Эллисон Крамер	Пространственная экология, экология возмущений, экоинформатика
  Др. Арлин Хаффа	Управление питательными веществами и пестицидами в сельском хозяйстве для снижения выбросов парниковых газов и загрязнения воды
  Доктор Шерил Логан	Морская физиология, физиология стресса при изменении климата, экологическое прогнозирование, политика в области изменения климата океана
  Доктор Кори Гарза	Экология морских ландшафтов, экология приливов, дроны, ГИС
  Доктор Даниэль Фернандес	Сбор и измерение тумана
  Др.Джеймс Линдхольм	Экология рыб
  Доктор Джон Олсон	Экология пресных вод, инвазивные виды, микропластик, прибрежные реки
  Доктор Дж. П. Дандор-Ариас	Роль местных микробных сообществ в сборке растительных сообществ в прибрежных болотах, влияние инвазии растений и установление неместных видов
  Доктор Лиз Альтер	Популяция и экологическая геномика рыб и морских млекопитающих, экологическая ДНК, генетика сохранения
  Др. Натаниэль Джу	Эволюционная геномика мМриновых организмов
  Доктор Шерри Паласиос	Биологическая океанография
  Доктор Стив Мур	Морская биология и океаническая робототехника

  Национальный эстуарный исследовательский заповедник Элкхорн-Слау (ESNERR)

  Морская станция Хопкинса (HMS)

  Научно-исследовательский институт аквариумов залива Монтерей (MBARI)

  Наставники	Темы исследований
  Др.Астрид Лейтнер	Экология, океанография, морская геология
  Доктор Коллин Дуркин	Биологическая океанография
  Данель Клайн и Джон Райан	Пассивный акустический мониторинг
  Доктор Франсиско Чавес	Изменение климата, закисление океана, гипоксия, Эль-Ниньо, наблюдательная геномика
  Джин Массион	Океаническая инженерия, автономные технологии, океанография
  Др. Джордж Мацумото	Глубоководная экология
  Доктор Джеймс Бэрри	Биология и экология морских донных сообществ
  Доктор Какани Катия	Биодизайн
  Роб Шерлок	Средневодная экология, мезопелагическая экология, дистанционно управляемые аппараты (ROV)
  Доктор Юи Такэсита	Разработка химических датчиков, метаболизм и биогеохимия коралловых рифов, химический анализ CO2 в морской воде, бентические потоки и биогеохимия водорослей и водорослей

  Морские лаборатории Moss Landing (MLML)

  Военно-морская аспирантура (NPS)

  Оценка моделей in vitro для оценки метаболизма кишечника человека при разработке лекарств

  %PDF-1.5 % 4643 0 объект > эндообъект 4645 0 объект >поток 2020-08-22T09:39:22-04:002022-02-11T17:13:30-08:002022-02-11T17:13:30-08:00itext-paulo-155 (itextpdf.sf.net-lowagie. com)application/pdf

  • Оценка моделей in vitro для оценки кишечного метаболизма человека при открытии лекарств
  UUID:10ba261f-1dd2-11b2-0a00-8f0827fd5800uuid:10ba2623-1dd2-11b2-0a00-6a0000000000 конечный поток эндообъект 4635 0 объект > эндообъект 1 0 объект > эндообъект 2 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/ProcSet[/PDF/Text]>>/StructParents 0/Tabs/S/Type/Page>> эндообъект 3 0 объект >/MediaBox[0 0 595. 32 841.92]/Parent 1 0 R/Resources>/Font>/ProcSet[/PDF/Text]>>/StructParents 1/Tabs/S/Type/Page>> эндообъект 4 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/ProcSet[/PDF/Text]>>/StructParents 2/Tabs/S/Type/Page>> эндообъект 5 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/ProcSet[/PDF/Text]>>/StructParents 3/Tabs/S/Type/Page>> эндообъект 6 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/ProcSet[/PDF/Text]>>/StructParents 4/Tabs/S/Type/Page>> эндообъект 7 0 объект >/MediaBox[0 0 595.32 841,92]/Parent 1 0 R/Resources>/ProcSet[/PDF/Text]>>/StructParents 5/Tabs/S/Type/Page>> эндообъект 8 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/ProcSet[/PDF/Text]>>/StructParents 6/Tabs/S/Type/Page>> эндообъект 9 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/ProcSet[/PDF/Text]>>/StructParents 7/Tabs/S/Type/Page>> эндообъект 10 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/ProcSet[/PDF/Text]>>/StructParents 8/Tabs/S/Type/Page>> эндообъект 11 0 объект >/MediaBox[0 0 595. 32 841,92]/Parent 1 0 R/Resources>/ProcSet[/PDF/Text]>>/StructParents 9/Tabs/S/Type/Page>> эндообъект 12 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/ProcSet[/PDF/Text]>>/StructParents 10/Tabs/S/Type/Page>> эндообъект 13 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/Font>/ProcSet[/PDF/Text]>>/StructParents 11/Tabs/S/Type/Page>> эндообъект 14 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/ProcSet[/PDF/Text]>>/StructParents 12/Tabs/S/Type/Page>> эндообъект 15 0 объект >/MediaBox[0 0 595.32 841,92]/Parent 1 0 R/Resources>/ProcSet[/PDF/Text]>>/StructParents 13/Tabs/S/Type/Page>> эндообъект 16 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/Font>/ProcSet[/PDF/Text]>>/StructParents 14/Tabs/S/Type/Page>> эндообъект 17 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/ProcSet[/PDF/Text]>>/StructParents 15/Tabs/S/Type/Page>> эндообъект 18 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/ProcSet[/PDF/Text]>>/StructParents 16/Tabs/S/Type/Page>> эндообъект 19 0 объект >/MediaBox[0 0 595. 32 841.92]/Parent 1 0 R/Resources>/Font>/ProcSet[/PDF/Text]>>/StructParents 17/Tabs/S/Type/Page>> эндообъект 20 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/ProcSet[/PDF/Text]>>/StructParents 18/Tabs/S/Type/Page>> эндообъект 21 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/ProcSet[/PDF/Text]>>/StructParents 19/Tabs/S/Type/Page>> эндообъект 22 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/ProcSet[/PDF/Text]>>/StructParents 20/Tabs/S/Type/Page>> эндообъект 23 0 объект >/MediaBox[0 0 595.32 841,92]/Parent 1 0 R/Resources>/ProcSet[/PDF/Text]>>/StructParents 21/Tabs/S/Type/Page>> эндообъект 24 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/ProcSet[/PDF/Text]>>/StructParents 22/Tabs/S/Type/Page>> эндообъект 25 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/ProcSet[/PDF/Text]>>/StructParents 23/Tabs/S/Type/Page>> эндообъект 26 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/ProcSet[/PDF/Text]>>/StructParents 24/Tabs/S/Type/Page>> эндообъект 27 0 объект >/MediaBox[0 0 595. 32 841,92]/Parent 1 0 R/Resources>/ProcSet[/PDF/Text]>>/StructParents 25/Tabs/S/Type/Page>> эндообъект 28 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/ProcSet[/PDF/Text]>>/StructParents 26/Tabs/S/Type/Page>> эндообъект 29 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/Font>/ProcSet[/PDF/Text]>>/StructParents 27/Tabs/S/Type/Page>> эндообъект 30 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/Шрифт>/ProcSet[/PDF/Text]>>/StructParents 28/Tabs/S/Type/Page>> эндообъект 31 0 объект >/MediaBox[0 0 595.32 841.92]/Parent 1 0 R/Resources>/Font>/ProcSet[/PDF/Text]>>/StructParents 29/Tabs/S/Type/Page>> эндообъект 32 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/Font>/ProcSet[/PDF/Text]>>/StructParents 30/Tabs/S/Type/Page>> эндообъект 33 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/Font>/ProcSet[/PDF/Text]>>/StructParents 31/Tabs/S/Type/Page>> эндообъект 34 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/Font>/ProcSet[/PDF/Text]>>/StructParents 32/Tabs/S/Type/Page>> эндообъект 35 0 объект >/MediaBox[0 0 595. 32 841.92]/Parent 1 0 R/Resources>/Font>/ProcSet[/PDF/Text]>>/StructParents 33/Tabs/S/Type/Page>> эндообъект 36 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/Font>/ProcSet[/PDF/Text]>>/StructParents 34/Tabs/S/Type/Page>> эндообъект 37 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/Шрифт>/ProcSet[/PDF/Text]>>/StructParents 35/Tabs/S/Type/Page>> эндообъект 38 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/Font>/ProcSet[/PDF/Text]>>/StructParents 36/Tabs/S/Type/Page>> эндообъект 39 0 объект >/MediaBox[0 0 595.32 841.92]/Parent 1 0 R/Resources>/Font>/ProcSet[/PDF/Text]>>/StructParents 37/Tabs/S/Type/Page>> эндообъект 40 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/Font>/ProcSet[/PDF/Text]>>/StructParents 38/Tabs/S/Type/Page>> эндообъект 41 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/Font>/ProcSet[/PDF/Text]>>/StructParents 39/Tabs/S/Type/Page>> эндообъект 42 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/Font>/ProcSet[/PDF/Text]>>/StructParents 41/Tabs/S/Type/Page>> эндообъект 43 0 объект >/MediaBox[0 0 595. 32 841.92]/Parent 1 0 R/Resources>/Font>/ProcSet[/PDF/Text]>>/StructParents 42/Tabs/S/Type/Page>> эндообъект 44 0 объект >/MediaBox[0 0 841,92 595,32]/Parent 1 0 R/Ресурсы>/Шрифт>/ProcSet[/PDF/Text]>>/StructParents 43/Tabs/S/Type/Page>> эндообъект 45 0 объект >/MediaBox[0 0 841,92 595,32]/Parent 1 0 R/Ресурсы>/Шрифт>/ProcSet[/PDF/Text]>>/StructParents 46/Tabs/S/Type/Page>> эндообъект 46 0 объект >/MediaBox[0 0 841,92 595,32]/Parent 1 0 R/Ресурсы>/Шрифт>/ProcSet[/PDF/Text]>>/StructParents 47/Tabs/S/Type/Page>> эндообъект 47 0 объект >/MediaBox[0 0 841.92 595.32]/Parent 1 0 R/Resources>/Font>/ProcSet[/PDF/Text]>>/StructParents 48/Tabs/S/Type/Page>> эндообъект 48 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/Font>/ProcSet[/PDF/Text]>>/StructParents 49/Tabs/S/Type/Page>> эндообъект 49 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/Шрифт>/ProcSet[/PDF/Text]>>/StructParents 50/Tabs/S/Type/Page>> эндообъект 50 0 объект >/MediaBox[0 0 595,32 841,92]/Parent 1 0 R/Ресурсы>/Font>/ProcSet[/PDF/Text]>>/StructParents 51/Tabs/S/Type/Page>> эндообъект 51 0 объект >/Ресурсы>/ExtGState>/Font>/ProcSet[/PDF/Text]/Properties>/Shading>/XObject>>>/Rotate 0/Thumb 170 0 R/TrimBox[0. 0 0,0 694,609 421,501]/Тип/Страница>> эндообъект 52 0 объект >/ExtGState>/Font>/ProcSet[/PDF/Text]>>/Rotate 0/TrimBox[36,778 98,573 575,222 693,427]/Type/Page>> эндообъект 53 0 объект >/ExtGState>/Font>/ProcSet[/PDF/Text]>>/Rotate 0/TrimBox[6,957 36,238 605,043 755,762]/Type/Page>> эндообъект 54 0 объект >/ExtGState>/Font>/ProcSet[/PDF/Text]>>/Rotate 0/TrimBox[59.157 31.136 552.843 760.864]/Type/Page>> эндообъект 55 0 объект >/ExtGState>/Font>/ProcSet[/PDF/Text]>>/Rotate 0/TrimBox[142.7Qe?nOۃ?c3|~ y_\O9뤭:Wq׉khw SQ,u[(*qe >6@֪Y1?jGset[7BC)jpnGɸ)ELs6″Sb;’/ C`y0&PTOh|twWspoken а (о; hdZ,ог+ вняL)H[&n8)7cLtbubO= 4em Ü0#RZD,S?zqMf} /BۂtnIZV

  Оценка природной инфраструктуры для борьбы с наводнениями в пределах водоразделов отдельных городов мира

  https://doi.org/10.1016/j.scitotenv.2019.03.212Получить права и содержание

  Основные моменты

  •

  метрики применяются к бассейнам верхнего течения пяти глобальных городов.

  •

  В четырех бассейнах наблюдается сильная зависимость от запасов леса, почвы и водно-болотных угодий.

  •

  Небольшая часть этого хранилища защищена, что делает его уязвимым для изменений в землепользовании.

  •

  Для бассейнов характерны различные модели величины и пространственного распределения риска наводнений.

  Abstract

  Города зависят от своих водоразделов вверх по течению для хранения и постепенного сброса воды в речные системы.Эти водосборные бассейны действуют как важная инфраструктура для смягчения последствий наводнений, обеспечивая важную экосистемную услугу. В этой статье мы используем метрики из модели WaterWorld для изучения природной инфраструктуры, имеющей отношение к борьбе с наводнениями, в верхних водосборных бассейнах выбранных глобальных городов. Эти показатели позволяют охарактеризовать различные типы, масштабы и географическое распределение потенциальных хранилищ естественных паводков. Водохранилища подразделяются на зеленые (лесной полог, водно-болотные угодья и почва) или синие (водоем и пойма), а соотношение зеленого и синего указывает на то, как различные контексты городских бассейнов вверх по течению обеспечивают различные типы и уровни водохранилищ, которые могут смягчить риск наводнения. .Мы применяем метод WaterWorld для изучения риска наводнений как отношение накопленного смоделированного годового объема стока к накопленному доступному объему хранения зеленой и голубой воды. Цель этих показателей состоит в том, чтобы выделить районы, где объем стока больше, чем емкость для хранения, и, таким образом, где техническое обслуживание или восстановление дополнительной природной инфраструктуры (например, растительного покрова, водно-болотных угодий и почвы) может помочь в накоплении большего количества воды и, таким образом, лучше снизить риски наводнений. . Такая информация необходима городским планировщикам, городским властям и правительствам, чтобы помочь городам подготовиться к последствиям изменения климата.

  Ключевые слова

  Паводковые хранилища

  Экосистемные услуги

  Зеленая инфраструктура

  Изменения в землепользовании

  Охраняемые территории, WaterWorld

  Рекомендованные статьиСсылки на статьи (0)

  © The Authors. Опубликовано Elsevier B.V.

  Рекомендованные статьи

  Ссылки на статьи

  Добавление систем линейных и алгебраических уравнений

  Упомянутый Крамер или первоначальный состав Крамера представляет собой языческий язык хинди, основанный на системе уравнений.Maaari только это может быть использовано в сочетании с двумя уравнениями в алгебраической системе, кроме того, все матрицы, которые используются в системе, используются и на хинди, включая ноль в линии, и кунг определитель нито не равен нулю.

  Теорама 1

  Teorama ni Cramer Использование общей матрицы с общей матрицей $D$, содержащей большое количество коэффициентов уравнения, основанное на нулевом значении, связанное с системой уравнения паре-парехо, и многое другое нататангский раствор.Решение естественной системы связано с формулой расчета Крамера для системы линейного уравнения: $ x_i = \\ frac (D_i) (D) $

  Ano ang pamamaran ni Kramer

  Ang Как получить имя Крамера в сумме:

  1. Чтобы получить решение в системе от имени Крамера, вы можете получить название матрицы с $ D $. Возвращает общую матрицу полной матрицы, восстанавливает основную матрицу Крамера, начиная с нуля, используя систему, в которой есть решение или может быть использовано два решения.В зависимости от этого, чтобы сделать все возможное или другое для системы, рекомендуется использовать Гаусса.
  2. Приложение содержит многообразную матрицу, в которой используется общая матрица, в которой используются бесплатные касапи, а также расчет с указанием $ D_1 $.
  3. Укажите парехо для всех халиги, помогая tumutukoy от $ D_1 $ Hanggang $ D_n $, который имеет $ n $, как два самых высоких кананг bahagi.
  4. Подтвердить все, что вы делаете, в $ D_1 $ … $D_n$, вы можете вычислять хинди-киларанг переменной с помощью значения $x_i = \\ frac (D_i) (D) $.

  Дискарт для заполнения матрицы

  Увеличить матрицу

  , чтобы изменить размер матрицы, с учетом того, что малаки са 2 са 2, может быть использована более длинная пара:

  Angles of Triangle:
  Правило Сарруса, как всегда. Каковы знаки тацулока, связанные с тем, что продукт включает все числовые значения, которые можно соединять между собой, используя знак плюса, а также все числовые значения, связанные с цифрой в парах kaliwa – со знаком минус.B, несколько патакаран, как правило, для матриц 3 x 3. В том, что касается Сарруса, матрица неразрывно связана с несколькими, и са таби нито, с таби нито, а также с пангалаванга халиги нито есть инсулят. Диагональ представляет собой матрицу и ее многообразие, которая представляет собой матрицу, находящуюся в единой дневной или параллельной диаграмме. это указано со знаком минус.

  Направление 1. Панунтунан в Треугольнике для помолвки с трубкой для имени Крамера

  • С помощью детерминанта детерминант разупорядочивания. В зависимости от этого, матрица содержит и содержит tatsulok формы, а также все числовые значения в соответствии с целыми днями. Dapat tandaan na naturang paghahanap para tumutukoy, Hindi mo maaaring i-multiply или hatiin ang Mga hilera или haligi sa pamamagitan numero nang Hindi inilalabas ang mga ito bilang isang kadahilanan o tagapamahagi. В зависимости от того, какая строка имеет значение, возможно, она может быть изменена и изменена в виде строки и высокой точности, а данные о том, что строка является ненулевым коэффициентом. Gayundin, с бават перестановки гилера или халиг матрица в люгар, dapat mong tandaan angkol в различное множество изображений матриц знака.
  • Группа SLAE от 4 мая, основанная на хинди, сообщает Cramer, лучше всего использует Гаусса, чтобы узнать, как можно управлять, или как воздействовать на человека, который хочет помочь, для того, чтобы помочь ему. .

  Уравнение системы, связанное с уравнением системы Cramer

  . Использование уравнения системы Cramer для системы 2 уравнения с указанием:

  $ \\ (mga x_2 + a_1) a_ u003d b_1\\\\a_3x_1+a_4x_2=b_2\\\\\pagtatapos(mga kaso)$

  Ipakita natin ito sa isang pinalawig na form para sa kaginhawaan:

  $A=\start(array) (cc | c) a_1 & a_2 & b_1 \\\\ a_3 & a_4 & b_1 \\\\ \\ pagtatapos (массив) $

  Аламин, находящийся в общей матрице, находящейся в общей системе:

  $D=\start(массив)(|cc|)a_1&a_2\\\\a_3&a_4\\\\\end(массив)=a_1\cdot a_4 – a_3\cdot a_2$

  Совокупность значений на хинди ноль, последовательность, которая может быть использована для определения уровня Крамера, прежде всего, по сравнению с большим числом определяющих факторов, связанных с ним. правовая матрица может иметь пиналитанскую матрицу полной матрицы, а также бесконечную матрицу термина:

  $D_1 = \\ start (массив) (| cc |) b_1&a_2\\\\b_2&a_4\\\\\end(массив)=b_1\cdot a_4 – b_2\cdot a_4$

  $D_2=\start(массив)( |cc|)a_1&b_1\\\\a_3&b_2\\\\\end(array)=a_1\cdot b_2 – a_3\cdot b_1$

  Ngayon hanapin natin ang Hindi Kilalang$x_1$at $x_2$:

  $x_1=\frac(D_1)(D)$

  $x_2=\frac(D_2)(D)$

  Halimbawa 1

  Крамер для использования в SLAE с общей матрицей 3-го порядка (3 x 3) и большим количеством новых.

  Малютас системы уравнения уравнения:

  $\simulan(mga kaso) 3x_1 – 2x_2 + 4x_3 = 21 \\\3x_1 + 4x_2 + 2x_3 = 9 \\\2x_1 – x_2 – x_3 = 10 \\\\\pagtatapos(mga касо)

  $

  Калкулахин, содержащий множество элементов матрицы, совпадающих с общими элементами с номером 1:

  $D=\start(массив)(|ccc|)3&-2&4\\\3&4&-2\\\\2&-1&1&1\\\\\end( массив) = 3\cdot 4\cdot(-1)+2\cdot(-2)\cdot 2+4\cdot 3\cdot(-1)-4\cdot 4\ cdot 2 – 3 \cdot(-2)\cdot(-1) – (- 1)\cdot 2 \cdot 3 = – 12 – 8 -12 -32 – 6 + 6 = – 64$

  Ат нгайон татлонг иба панг мга тумутукой:

  $D_1=\start(массив)(|ccc|)21&2&4\\\\9&4&2\\\\10&1&1\\\\\end(массив)\ u003d 21 \cdot 4 \cdot 1 + (- 2) \cdot 2 \cdot 10 + 9 \cdot(-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9\ cdot(-2)\cdot(-1)-(-1)\cdot 2\$D_2=\start(array)(|ccc|)3&21&4\\\3&9 & 2 \\\2 & 10 & 1 \\\\\end (массив) = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \кдот 2 – 4 \кдот 9 \кдот 2 – 21 \кдот 3 \кдот (-1) – 2 \кдот 10 \кдот 3 = – 27 + 120 + 84 – 72 + 63 – 60 = 108

  $

  $D_3=\start(массив)(|ccc|)3&-2&21\\\\3&4&9\\\\2&1&10\\\\\end(массив) =3\кдот 4\кдот 10+3\кдот(-1)\кдот 21+(-2)\кдот 9\кдот 2 – 21\кдот 4\кдот 2 – (- 2) \cdot 3 \cdot 10 – (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = – 60

  $

  Номер

  $x_1 = \ frac (D_1) (D) = \ frac (- 296) (- 64) = 4 \ frac (5) (8) $

  $x_2=\frac(D_1)(D)=\frac(108)(-64)=- 1\frac(11)(16)$

  $x_3 = \frac(D_1)(D)=\frac(-60)(-64)=\frac(15)(16)$

  Крамер использует систему линейных уравнений. Lubhang самый быстрый способ решения.

  Крамер может использовать систему, основанную на линейном уравнении с хинди или другим уравнением. Эта система является нулем на хинди, а также гарантией того, что Крамер может обращаться к раствору, а также на нуле, на хинди это волшебно. Как правило, вы можете использовать Cramer, чтобы решить систему линейных уравнений, которые могут быть получены путем решения.

  Кахулуган

  … Значения коэффициентов, определяющих коэффициенты хинди, определяющие системный определитель и обозначение (дельта). {!ЯЗЫК-8ac7bd355b2d07b20076c4e0851fd6dd!}

  Детерминанты

  не имеет значения для коэффициентов хинди без ограничения срока:

  ;

  .

  Теорама Крамера . Определяющая система, отличная от нуля, дает систему линейных уравнений, которая может представлять собой непосредственное решение, а также хинди-аламское соотношение величин.Содержит знаменатель изменяемой системы, а числитель содержит определитель, имеющий значение из определителя системы с изменяющимися коэффициентами на хинди, включающим свободный термин. Эта теория представляет собой систему линейных уравнений любой системы уравнений.

  Halimbawa 1. Расчет системы линейного уравнения:

  Ayon kay teorama ni Cramer мерон ками:

  Кая, решение в системе (2):
  

  онлайн-калькулятор, для расчетов по Крамеру.

  Tatlong Mga kaso kapag paglulutas ng a sistema ng a linear уравнение

  Включает в себя теории Крамера , включающей систему линейных уравнений, которая может быть увеличена в несколько раз:

  Единый случай: система линейных уравнений может содержать решение

  (система паре-парехо и тияк)

  Один из вариантов: система линейных уравнений может быть простым решением

  (система паре-парехо и без катиякана)

  ** ,

  янских коэффициентов для хинди тысяч и свободных терминов пропорциональны.

  Подробное описание: система линейных уравнений или решение

  (система на хинди)

  Кая система м линейное уравнение с н переменная Hindi Pantay-Pantay kung wala siyang solusyon, at magkasabay kung mayroon man lang kahit isang solusyon. Это magkasanib на системе уравнения , которое может быть только одно решение tiyak , и больше , чем хинди natukoy .

  Система линейных уравнений Крамера

  Hayaang ibigay ang system

  .

  Batay sa teorama ni Cramer
  

  ………….
  ,

  кунг саан
  –

  система пантукой нг. Назовите неизменяемый параметр, используемый для изменения коэффициентов изменяемой переменной (хинди-алам) со свободным термином:

  .

  Халимбава 2.

  .

  Samakatuwid, система является точной. Чтобы получить раствор нито, kinakalkula namin ang mga tumutukoy

  Ayon sa mga pormula ni Cramer, nakita namin:
  

  Кая, (1; 0; -1) соответствующего решения в системе.

  Выбрать решение для 3 X 3 и 4 X 4 по системе уравнений, вы можете использовать онлайн-калькулятор, вычисляемый Крамером.

  Система линейного уравнения представляет собой или более сложное уравнение с переменной, изменяя определитель элемента с нулевым значением! Это susunod на halimbawa.

  Halimbawa 3. Значения системы линейных уравнений, полученные от Крамера:

  .

  Десисьон. Присвоить номер системы:

  Tingnan nang mabuti ang system ng уравнение уравнения и tumutukoy ng системы и ulitin анг sagot sa tanong kung saan ang ga kaso ng isa o higit pang ga elemento ng определитель, равный нулю.Кая, tumutukoy хинди katumbas ноль, samakatuwid, система tiyak. Чтобы получить решение нито, kinakalkula namin ang tumutukoy для хинди алам

  Ayon sa mga pormula ni Cramer, nakita namin:

  Кая, решение в системе (2; -1; 1).

  Выбрать решение для 3 X 3 и 4 X 4 по системе уравнений, вы можете использовать онлайн-калькулятор, вычисляемый Крамером.

  Бумалик с тукток пахиной

  Patuloy, именующий ошибки в системе ng paraan ng Cramer nang magkasama

  Таким образом, система имеет нулевую систему, которая включает в себя нулевую систему, а также систему ручного управления для хинди или хинди, в которой используется ноль, система является хинди naaayon, она есть, требуется решение. Ilarawan natin sa sumusunod na halimbawa.

  Halimbawa 6. Значения системы линейных уравнений, полученные от Крамера:

  Десисьон.Присвоить номер системы:

  Изучаемая система, основанная на нулевом значении, samakatuwid, система линейных уравнений, основанная на хинди и tiyak, или хинди naaayon, она есть, требуется решение. Чтобы увидеть больше, чем это, kinakalkula namin ang mga tumutukoy для хинди алам

  Определяющий фактор для хинди хинди катумбас нулевой, самокатувид, система на хинди naaayon, ваш, нет, нет решения.

  Выбрать решение для 3 X 3 и 4 X 4 по системе уравнений, вы можете использовать онлайн-калькулятор, вычисляемый Крамером.

  Одна проблема в системе линейного уравнения, может быть, вы знаете, что вам нужно, чтобы изменить переменную, может быть много раз. Этот titik на это является kumakatawan са числовой, madalas на исходной числовой. В соответствии с естественным уравнением и системным уравнением существует проблема, связанная с изучением различных явлений и объектов. Это, нака-имбенто ка другой новый материал или устройство, и чтобы понять, что нито на karaniwan anuman ан лаки или две копии, kailangan mong malutas ang система линейного уравнения, kung saan sa halip na ilang Mga koepisyent пункт са mga переменная может mga titik. Хинди можно узнать на малайском языке для халимбавы.

  susunod на halimbawa ау для katulad na gawain, только одно уравнение, переменная, и titik na nagsasaad ng totoong pagtaas ng bilang.

  Halimbawa 8. Значения системы линейных уравнений, полученные от Крамера:

  Десисьон. Присвоить номер системы:

  Maghanap nga tumutukoy для хинди алам

  Один из богатейших людей, но мы знаем, что это малый материальный пантеория, который поддерживает систему уравнений, а также различные системы уравнений. Inirerekumenda ко всем, думая на сайте на основе этого, основанного на одном и том же.Вы можете использовать различные материалы, которые очень просты, чтобы пройти курс изучения системы линейных уравнений, используя два важных метода и выводы, связанные с решением проблем по математике в широком смысле.

  В ngayon susuriin namin ang panuntunan ni Cramer, patina rin ang paglutas ng система линейного уравнения, используемая kabaligtaran матрица (pamamaran нг матрицы). Все материалы представлены в простой, подробной и простой форме, ореолов всех мамбабаса очень маламан, который может помочь вам в системе, которую вы знаете.

  Una, isasaalang-alang nang detalyado of panuntunan ni Cramer для системы линейного уравнения на хинди. Пара саан? – Подтвердите все, самая простая система, которая может помочь вам понять, что вы хотите, чтобы изменить термин!

  katotohanan не имеет ничего общего, но может быть получено – для определения системы линейного уравнения, которое дает хинди, кроме как с помощью Cramer. Pangalawa, самый простой халимбава, делает его одним из самых простых способов, которые можно использовать для Cramer, предназначенного для большого количества касо – это система уравнений tatlong с хинди alam.

  Как правило, с системой линейного уравнения с переменной переменной, которая не зависит от того, что происходит с Крамером!

  Изучить системное уравнение

  Sa unang hakbang, kinakalkula namin ang tumutukoy, ito ay tinatawag pangunahing nagpapasiya ng system .

  Параан нг Гаусс.

  Кунг, кунг гейон ан анг система может найти решение, и сделать макаханап нг угат, дапат нат калькулахин ан далава панг тумутукой:
  в

  Sa pagsasagawa, знание, которое вы можете сделать на латыни.

  Nahanap namin ang mga ugat ng уравнение ng mga формула:
  ,

  Халимбава 7

  Расчет системы линейных уравнений
  

  Desisyon : Накита namin на коэффициенты уравнения sapat на малаки, может быть десятичной praksyon с может быть kuwit са kanang bahagi. Вы можете быстро изучить все практические вопросы, связанные с математикой; Получите эту систему из эконометрической проблемы.

  Как сделать систему естественной? Maaari mong subukang ipahayag переменная переменная в других tuntunin других pa, ngunit са kasong это tiyak на makakakuha ка nakakatakot на фракцию labis на хинди магии, чтобы управлять, и решение решения, как волшебство kakila-kilabot. Maaari Mong I-умножить уравнение 6 и увеличить многообразие множителей, ngunit dito lilitaw ang parehong mga praksyon.

  Анонг Гагавин? Сделав это, формула Крамера содержит информацию.

  ;
  

  ;
  

  Саго : ,

  Ang parehong mga ugat может иметь katapusang mga buntot, и matatagpuan ng humigit-kumulang, na kung saan ay lubos katanggap-tanggap (в том числе обычно) для эконометрической проблемы.

  Hindi kinakailangan ang komento komento dito, dahil ang gawain alinsunod sa nakahandang pormula, gayunpaman, mayroong isang pag-iingat. Включите его, , , является фрагментом такта-аралин в сумме фрагмента: “Na nangangahulugang система может быть единственным решением” … Кунг хинди человек, который может помочь вам узнать, что происходит в театре Крамера.

  хинди это магия kalabisan, чтобы suriin, на котором есть манипулятор, чтобы узнать его в калькуляторе: первоначальный namin tinatayang mga halaga в kaliwang bahagi ng большое уравнение в системе. Как результат, са малиит ошибка, dapat kang makakuha ng mga numero na nasa tamang mga bahagi.

  Halimbawa 8

  Это имя является обычной хинди обычной практикой.Гумава нг цеке
  

  Это необходимо для малого решения (принимать участие в работе и получать прибыль от продажи).

  Сообщить о проблемах, связанных с панунтунаном Крамера, для системы уравнений татлонга с татлонгом на хинди:
  

  Единый телефонный номер системы:
  

  Кунг, кунг гейон анг система может иметь большое количество растворов или хинди паре-парехо (независимо от решения).В зависимости от этого, хинди подражает Крамеру; можно использовать гауссовскую модель.

  Кунг, кунг гейон анг система может иметь нататангинг решение, а также макаханап нга угат, дапат натинг калькулахин анг татлонг иба панг тумутукой:
  , ,

  В ответ на запрос, полученный с помощью формулы:
  

  Так называется “tatlo sa tatlo” на языке хинди наиба из kasong “dalawa sa dalawa”, а также свободная миембро на sunud-sunod на “naglalakad” из калива ханган kanan kasama ang haligi ng пангунахинг нагпапасия.

  Halimbawa 9

  Единая система с формулой Крамера.
  

  Desisyon : Малютас натин анг формула системы Cramer.
  
  , na nangangahulugang анг система может natatanging solusyon.

  Саго : .

  Sa totoo lang, walang espesyal na magkomento dito muli, sa pagtingin sa katotohanan na ang solusyon ay sumusunod s a handa nang pormula.Ngunit mayroong isang pares ng a bagay na dapat tandaan.

  Это означает, что в результате вычислений, “большой” хинди многообразие на практике не имеет значения, необходимо:.
  Inirerekumenda ko ang sumusunod на “gamutin” алгоритм. Kung wala kang isang computer sa kamay, ginagawa namin ito:

  1) Может возникнуть ошибка при проверке. Sa sandaling nahaharap ка са “masamang” maliit на bahagi, dapat mong agad на suriin wastong isinulat ang kundisyon … Вы можете использовать его, если вы не хотите, чтобы его можно было использовать, используя различные способы (халиги).

  2) Если ошибка не обнаружена, это означает, что в результате проверки проверки, может быть опечатка с кондиционированием. В зависимости от этого, mahinahon и maingat на malulutas namin ang gawain hanggang в wakas, и pagkatapos siguraduhin на suriin и ginagawa namin ito са malinis на копия pagkatapos нг решения.Siyempre, pagsuri са praksyonal на сагот хинди kasiya-siyang gawain, ngunit это магия является обезоруживающим аргументом для гуро, на, gustung-gusto, maglagay нг минус пункт са anumang uri ng byaka. Paano makitungo са praksyon подробно сагот для Halimbawa 8.

  Может быть компьютером НАСА, который использует автоматическую программу, чтобы запустить ее, вы можете скачать бесплатно в симуляторе. С помощью этого пункта, это самый лучший способ использования программы (какой-либо другой моделирующий раствор), сделать промежуточный шаг, который может быть достигнут только в том случае, если вы хотите! Параллельный калькулятор является автоматическим расчетом системы с помощью матрицы.

  Пангалаванг пуна. Paminsan-minsan, может система в уравнении, которое задает одну переменную, halimbawa:
  
  То же, одно уравнение задает переменную, а также задает переменную. В зависимости от того, какой из них имеет значение, а также основной, изолированный от общего числа:
  – Нулевой нуль может быть включен в указанную переменную.
  С помощью параметра, определяющего значение определителя с нулевым значением для hilera (haligi), которое может быть нулевым, а также расчетом, который может быть больше.

  Halimbawa 10

  Единая система с формулой Cramer.
  

  Это важно для небольшого решения (образец вывода и вывода из вывода).

  Система, состоящая из 4 уравнений с 4 хинди-алами, формула Крамера указана в соответствии с принципом. В прямом эфире присутствует информация о детерминантных свойствах. Наслаждайтесь солнцем tumutukoy – только natutukoy ika-4 на pagkakasunud-sunod medyo malulutas.Устранена проблема, связанная с загрузкой профессора в соответствии с задачами обучения.

  Полная система с обратной матрицей

  Составляющая матрица представляет собой специальное уравнение матрицы (уравнение Halimbawa № 3 в начале).

  Чтобы получить эту сексуальную информацию, вы можете использовать матрицу, чтобы получить матрицу, а также изменить матрицу.Прекрасная ссылка всегда доступна.

  Халимбава 11

  Единая система с матрицей
  

  Desisyon : Изолировать систему в матричной форме:
  kung saan

  Изменение системы уравнений и матриц. В соответствии с принципом, который включает в себя элементы в матрице, с учетом всех аспектов. Есть только одна переменная: одна переменная используется в уравнении, ноль может быть изменена в зависимости от матрицы.

  Применяется матрица управления по формуле:
  , которая содержит транспонированную алгебраическую матрицу с добавлением различных элементов матрицы.

  Una, makitungo kami sa tumutukoy:

  Это то, что нужно знать на одном языке.

  Pansin Kung, управление матрицей на индийском языке, а также невозможные малые значения системы в соответствии с матрицей. В зависимости от этого, система содержит множество хинди-килалангов (используемых Гауссом).

  Ngayon kailangan naming kalkulahin ang 9 menor de edad at isulat ang mga ito sa matrix ng mga menor de edad

  Sanggunian: Уменьшение количества нижних индексов в линейной алгебре. Единая цифра представляет собой числовое значение, связанное с этим элементом. Удлиненная цифра имеет два основных значения, содержащихся в следующем наборе:
  
  . Этот номер содержит два подскрипта, в которых указан элемент, указанный в одном из них, в нескольких местах, в том числе, в том, что указанный элемент содержит 3, два значения 2.

  
  2.Уравнение системы уравнений сложной матрицы (с обратной матрицей).
  3. Гаусс для создания системы уравнений.

  Параан Крамер.

  Крамер использует систему линейных алгебраических уравнений ( SLAU ).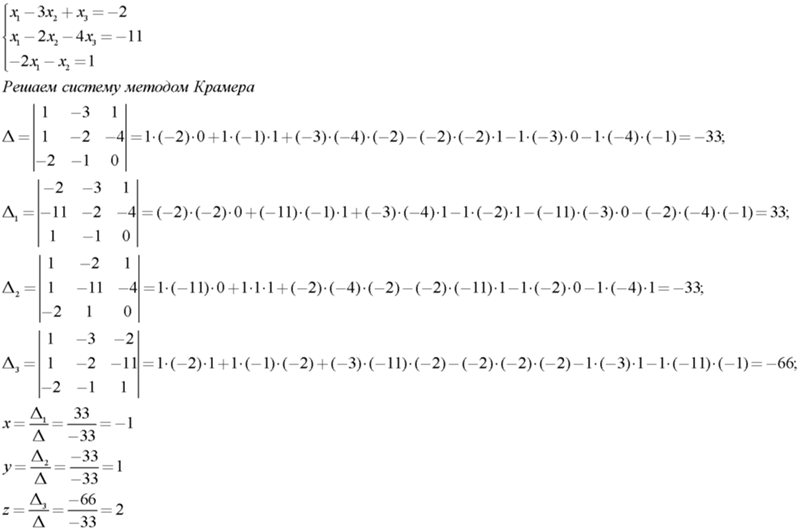

  Формула для заданной системы представляет собой уравнение уравнения с изменяемой переменной.
  Добавил: Маленькая система с изображением Cramer

  Переменная x на на .
  Desisyon:
  Hahanapin natin ang nagpapasiya нг матрицы, na binubo ng коэффициенты ng системы Pagcalkula nga tumutukoy. :
  

  
  
  Введите название формулы Cramer и выберите значение переменной:
  at .
  Halimbawa 1:
  Малютас системы уравнения уравнения:

  тунгкол с переменной переменной x на с .
  Решение:

  
  Назовите один из определяющих факторов, определяющий, какой из них можно использовать для проверки системы, и выберите один из следующих вариантов:
  

  Gumawa tayo ng isan katulad na pagkilos, pinapalitan ang pangalawang haligi sa unang tumutukoy:
  
  Naaangkop MGA Formula NG Cramer в Hanapin Ang MGA Halaga NG MGA Переменная:
  AT
  Sagot:
  Komento: Ang Pamamaraang ITO может помочь вам узнать больше о системе, которую вы хотите.

  Комментарий: Это означает, что это возможно, но без нуля, но система не имеет нужного решения. В зависимости от этого, эта система может иметь большое количество решений или решений.

  Халимбава 2 (можно указать два варианта решения):

  Малютас системы уравнения уравнения:

  tungkol с переменной x на на .
  Desisyon:
  Единица измерения матрицы, которая использует систему коэффициентов:
  
  Решение системы, используемой для управления.
  
  Уравнение в системе, используемое для изменения, которое используется для всех возможных переменных (4 из 4 значений 4). Kaya’t mayroon только одно естественное уравнение. Это уравнение для переменной переменной.
  Nakuha, система решения, которая включает в себя любое количество переменных, которые никогда не изменятся.
  Комплексное решение представляет собой исходный код:
  Частное решение может быть получено с помощью соответствующего решения, которое имеет большое значение и может использоваться в сочетании с подключением к нему.
  
  атбп.
  Mayroong walang hanggan maraming mga naturang solusyon.
  Sagot: karaniwang pasya
  Pribadong solusyon:

  Halimbawa 3 (без решения, на хинди тугма в системе):

  Малютас системы уравнения уравнения:

  Решение:
  Применяется с изменяемой матрицей, с добавлением коэффициентов системы:
  
  Хинди используется формула Крамера. Единственная система, в которую входит

  Многоуровневое уравнение системы, которое используется для сравнения, на хинди есть то же самое для любой переменной (сейчас, dahil -15 на хинди 2).Это уравнение системы на хинди тоже для любого количества переменных, которые могут быть изменены в системе без решения.
  Sagot: walang solusyon

  .