Калькулятор сложных производных функций: Вторая и третья производные функции

Калькулятор Частичных Производных – Mathcracker.Com

Инструкции: Используйте этот калькулятор частичных производных для нахождения производной функции более чем одной переменной, которую вы задаете относительно конкретной переменной, показывая все этапы процесса. Пожалуйста, введите функцию, для которой вы хотите вычислить производную, в поле ниже.

О частичной производной

Этот калькулятор позволит вам вычислить частную производную любой действительной дифференцируемой функции, которую вы предоставите, относительно заданной переменной.

Функция, которую вы предоставляете, должна сопровождаться определением функции, например f(x, y) = x^3 + y^2.

2 без полного определения, будет считаться, что предоставлена функция двух переменных x и y.

Как только вы зададите действительную дифференцируемую функцию и действительную переменную, следующим шагом будет нажатие на кнопку “Вычислить”, после чего будут показаны все этапы процесса, со всеми используемые производные правила , прямо указано.

Деривативы и их естественное расширение до частных производных по нескольким переменным являются одними из самых важных предметов изучения в математике. Это связано с тем, что они имеют дело со скоростью изменения и течением многих моделей, которые часто появляются в приложениях.

Что такое частичная производная?

Проще говоря, частичная производная состоит в том, чтобы провести то же самое, что и обычное дифференцирование относительно одной переменной, предполагая, что остальные переменные постоянны.

Если бы мы хотели формально определить частичную производную, давайте упростим задачу и сделаем это для функции двух переменных, \(x\) и \(y\). Частная производная по отношению к \(x\) в точке \((x_0, y_0)\) имеет вид

\[\frac{\partial f}{\partial x}(x_0, y_0) = \displaystyle \lim_{h \to 0} \frac{f(x_0 + h, y_0) – f(x_0, y_0)}{h} \]

Итак, как мы видим, по сути это то же самое, что и определение обычной производной, только здесь есть еще одна переменная, но она остается постоянной в процессе вычисления.

Аналогично, частная производная по отношению к \(y\) в точке \((x_0, y_0)\) равна

\[\frac{\partial f}{\partial y}(x_0, y_0) = \displaystyle \lim_{h \to 0} \frac{f(x_0, y_0 + h) – f(x_0, y_0)}{h} \]

Вектор всех частных производных называется градиентом. Если вам нужно действительно получить все частные производные, вы можете использовать следующее градиентный калькулятор .

Шаги для вычисления частных производных

• Шаг 1: Определите функцию, частную производную которой вы хотите вычислить. Не забудьте сначала упростить ее
• Шаг 2: Обратите внимание, что не все функции дифференцируемы, поэтому вам нужно убедиться, что функция, о которой идет речь, действительно дифференцируема
• Шаг 3: Используйте все соответствующие правила производной для функции и дифференцируйте функцию, как обычно, по дифференцируемой переменной, а любую другую переменную считайте постоянной

Таким образом, когда мы выполняем частичную производную по x для чего-то вроде ‘x^2+y^2’, в процессе частичного дифференцирования по x переменная y рассматривается как константа. 2)}{\partial x} = 0\), поскольку y предполагается постоянным относительно x.

Зачем использовать калькулятор частных производных

Вычисление частных производных может быть относительно простым упражнением, но это не значит, что оно обязательно будет легким. Важно быть очень систематичным во время применения соответствующего Правила производных .

Использование калькулятора частичных производных с шагами может помочь вам, по крайней мере, проверить результат и точно увидеть, какие шаги являются правильными и какие правила вычисления производных необходимо использовать.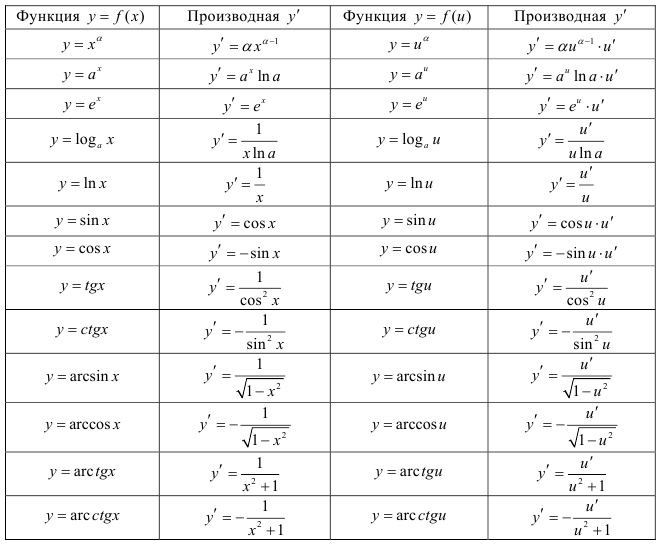

Особенно в сложных задачах, с алгебраически сложными выражениями калькулятор действительно может пригодиться.

Каковы правила производных для частичных производных?

Они точно такие же, как и для обычных производных. Для частных производных у нас есть линейность, а также Правило Продукта , Правило цепи и Правило квоты . Как правило, для более сложных примеров производных вы в конечном итоге будете использовать комбинацию всех этих правил.

Что такое неявная дифференциация

Существует ситуация, когда задействовано более одной переменной, в которой мы не предполагаем, например, что y изменяется с x, как это делается в частных производных. В некоторых случаях, когда есть уравнение, связывающее переменные, мы предполагаем наличие неявной зависимости между y и x, и пишем y = y(x).

Это контекст неявное дифференцирование это своего рода гибрид между частичной и обычной дифференциацией.

И есть одна вещь, которую невозможно переоценить: Частичные производные действительно являются одним из основных инструментов, используемых в инженерии, физике и экономике. 2}\)

Другие калькуляторы calculus

Понятие производной находится в центре Calculus, а использование производный калькулятор может значительно помочь вам во многих различных приложениях Calculus, включая оптимизацию, одну из самых “больших”.

Идея производной естественно распространяется на случай функции со многими переменными, где a Калькулятор частичных производных будет делать то же самое, что и обычная производная, но теперь предполагается, что изменяется только одна переменная, в то время как другие переменные принимаются фиксированными.

Часто бывает так, что известно, что \(y\) зависит от \(x\), но не явно, а скорее неявно, с помощью уравнения связи, в этом случае можно использовать неявное дифференцирование использовать правила производных, чтобы получить выражение, для которого затем можно решить производную \(\frac{d f}{d x}\) .

9 лучших научных калькуляторов для Android

Трудно представить себе мир без математики. Каждый день наполнен числами, и поэтому мы обычно попадаем в ситуации сложения, вычитания, умножения и деления, которые мы можем выполнить с помощью только ума и за несколько секунд и чуть больше, но в других случаях мы сталкиваемся с гораздо более трудными и сложными вычислениями, выполнить которые мы не можем без помощи научного калькулятора.

Поэтому в этой статье мы собрали 9 лучших приложений научного калькулятора для Android, которые доступны бесплатно в Google Play Store, имеют хорошую репутацию и миллионы загрузок, а также являются самыми популярными и всеобъемлющими для выполнения базовых и сложных расчетов.

Вот 9 наиболее полных и продвинутых приложений для научных вычислений для Android, которые вы можете найти в настоящее время в Google Play Store.

Научный калькулятор 991 плюс

Мы начинаем эту подборку с одного из самых интересных научных калькуляторов в Play Store, поскольку именно он практически превращает ваш телефон Android в калькулятор Casio.

И это потому, что он поставляется не только с типичными базовыми функциями, которые мы можем найти в любом другом калькуляторе, но и со всем тем, что предлагают нам научные калькуляторы, такие как Casio 82 is plus и 991 is plus, среди прочих, оставляя нам сотни функций для вычисления того, что нам предлагается.

Это приложение также предлагает графики, что не всем пользователям доступно. Он также может вычислять корни, проценты, производные, интегралы, степени, тригонометрические операции, расширенные уравнения (квадратные, кубические и системы уравнений), логарифмы, операции линейной алгебры, дроби, многочлены и т. д.

Помимо прочего, он также поддерживает полярные, параметрические и неявные функции, а также вычисление простых чисел.

Скачать в Google Play.

Научный калькулятор HiPER

Если вы ищете научный калькулятор с красивым и понятным дизайном, HiPER Scientific Calculator – один из лучших для Android, с более чем 10 миллионами загрузок в Play Store и рейтингом 4,7 звезды на основе более чем 180 отзывов. Еще одной изюминкой является его размер, который составляет около 8 МБ, поэтому он также очень легкий.

Это еще один научный калькулятор, способный строить графики. Он также поддерживает множество базовых и расширенных функций, что делает его идеальным для учащихся начальной и средней школы, а также студентов колледжей.

Вы можете выполнять простые и сложные арифметические операции, включая проценты, модуль и отрицание. Также графические функции и интегральные площади, вычисление комплексных чисел, преобразование из декартовых в полярные и наоборот, поддержка гониометрических и гиперболических функций, отображение истории результатов, более 90 физических констант, преобразование между 200 единицами, выполнение вычислений степеней, корней и логарифмов, а также, среди прочего, с интегральными и производными вычислениями. Это, без сомнения, один из самых полных инструментов, а также хороший инструмент для инженеров.

Скачать в Google Play.

Калькулятор Photomathie

Вполне вероятно, что в какой-то момент вам порекомендовали это приложение или, по крайней мере, вы слышали, как кто-то о нем говорил. И именно этот калькулятор выделяется среди других не только тем, что предлагает функции продвинутого научного калькулятора, но и тем, что сканирует документы, тексты и листы для решения уравнений и операций, которые вы положите перед ним.

Photomath не только предоставит вам результат этой операции или задачи, но и покажет процедуру ее решения, что делает ее идеальной для учащихся начальной и средней школы, а также студентов колледжей. Другое дело, что он позволяет выбрать метод решения проблем.

Это особенно полезно для решения уравнений с помощью таких методов, как факторизация и квадратичная формула. Хорошо и то, что для решения вычислений не требуется подключение к Интернету, и он доступен на более чем 30 языках.

Скачать в Google Play.

Бесплатный научный калькулятор

Это приложение для научных вычислений – еще одно легкое приложение, размер которого не превышает 6 МБ. Его репутация предшествует ему как еще одной отличной альтернативе для студентов от начального уровня до продвинутых профессий, таких как бухгалтерский учет, инженерное дело и многие другие, чтобы иметь достаточно полный каталог функций вычисления.

Его интерфейс делает его простым и несложным в использовании, что очень важно для приложений такого типа, поскольку они поставляются с большим количеством символов, которые могут легко запутать пользователя. Здесь можно найти все: базовую арифметику, перевод единиц, решение дробей, логарифмы, линейные уравнения и гиперболические операции, тригонометрические функции и даже матричные графики, и многое другое. Также поддерживаются предопределенные научные константы и 10 переменных.

Скачать в Google Play.

Инженерный Калькулятор

Опять же, перед нами еще одно научное вычислительное приложение, способное строить графики. Программа превращает ваш мобильный телефон Android в инструмент, способный выполнять практически любые вычисления, что делает ее одним из лучших решений для студентов начального и продвинутого уровней.

Некоторые из его многочисленных функций включают в себя следующее: цветная графика с деталями для ясной и краткой интерпретации, вычисление полиномов, дробей, линейных уравнений, алгоритмов, основных арифметических операций (сложение, вычитание, умножение и деление), процентов, двоичных операций, десятичных и шестнадцатеричных чисел. . Он также поддерживает комплексные числа и основные статистические функции.

Как и предыдущее приложение, оно не весит даже 6 МБ, но его репутация в 4,6 звезды, основанная на более чем 1 миллионе загрузок и 120+ отзывах, многое говорит о его вычислительных возможностях.

Скачать в Google Play.

Научный калькулятор TechCalc

Это приложение научного калькулятора является одним из наиболее полных, и его использование особенно предназначено для продвинутых исследований, включающих такие профессии, как инженерные и другие, схожие с математической и физической природой, поскольку это высокопроизводительное приложение для сложных вычислений.

Для базовых и сложных вычислений он поддерживает алгебраические и арифметические функции, а также обратную польскую запись. Он также поддерживает решение комплексных чисел, уравнений, производных, определенных и неопределенных интегралов и рядов Тейлора.

С помощью научного калькулятора TechCalc мы также можем решать функции степеней и корней, а также всевозможные дроби. Он также поддерживает преобразования, константы для расширенных вычислений, перестановки и комбинации, тригонометрические функции в радианах, градусах и градиентах, факториальные функции, модули и случайные числа.

Как будто этого недостаточно, он также включает справочный раздел в виде каталога, в котором можно найти функции и инструменты для физических законов, тригонометрические тождества, элементарную и матричную алгебру, правила дифференцирования и интегрирования, уравновешивание химических уравнений, математические векторы, математические формулы, последовательности чисел и многое другое. В свою очередь, есть и другие внутренние калькуляторы, такие как эмпирическая формула, соотношение высоты и ширины, футы и дюймы, барометрическая формула, давление в шинах велосипеда и многое другое.

Скачать в Google Play.

Научный калькулятор He-580

Еще одно приложение для базовых и расширенных расчетов, очень полезное для студентов и пользователей для целей линейного программирования. Более 1000 математических формул, которыми он снабжен, делают его одним из самых интересных инструментов этой подборки, поэтому вам не придется запоминать каждую из них для решения различных операций; просто просмотрев их каталог, вы обязательно найдете ту, которая вам нужна. Кроме того, в этом смысле они сопровождаются пояснениями с рисунками, которые облегчают их понимание.

Хотя он имеет большинство функций, которые мы можем найти в любом продвинутом портативном научном калькуляторе, он особенно предназначен для студентов-физиков, чтобы иметь функции и инструменты для 7 категорий или ветвей одного и того же, которые являются механикой, теплофизикой, атомной физикой, периодическим движением, электричеством, константами и параметрами.

Он также способен строить графики функций с особыми точками, в дополнение к решению квадратичных, линейных, кубических уравнений и систем уравнений. В свою очередь, для химиков он способен решать химические уравнения с одной или несколькими переменными.

Другие функции включают преобразование различных единиц измерения, начиная от температуры, валюты, длины, массы/веса, объема, скорости, площади и давления до времени, мощности, энергии, цифровой емкости и расхода топлива.

Скачать в Google Play.

Научный калькулятор Panecal

Если вы ищете научный калькулятор, который показывает, проверяет и корректирует математические формулы, это может быть наиболее практичным вариантом для вас и ваших исследований и расчетов. Его специализация – математические формулы, возможность редактировать и изменять уже введенные в качестве корректировки.

Среди других его основных функций, что неудивительно, решение основных и расширенных арифметических и алгебраических операций, тригонометрических и логарифмических функций, угловых единиц, вычисление и преобразование числа по основанию N.

Скачать в Google Play.

Научный калькулятор

Его название может быть самым общим из всех, но это один из самых популярных научных калькуляторов в Android Play Store, поскольку он является одним из самых полных и используемых, с более чем 5 миллионами загрузок.

Первое, что следует отметить, это то, что он весит всего 2 МБ, являясь одним из самых легких из всех уже перечисленных. Он способен решать простые и сложные арифметические и алгебраические операции, а также тригонометрические операции, среди многих других. Он также позволяет применять законы тангенса, синуса и косинуса, поддерживает операции с логарифмами, экспонентами и уравнениями.

Скачать в Google Play.

Калькулятор частных производных – MathCracker.com

Инструкции: Используйте этот калькулятор частных производных, чтобы найти производную функции более чем одной переменной, которая вы предоставляете в отношении конкретной переменной, показывая все этапы процесса. Пожалуйста, введите функцию, для которой вы хотите вычислить производную, в поле ниже. 92, без полное определение, будет предполагаться, что задана функция двух переменных x и y.

После того, как вы предоставите допустимую дифференцируемую функцию и допустимую переменную, следующим шагом будет нажатие кнопки «Рассчитать», чтобы просмотреть все этапы процесса, со всеми используемыми производными правилами, явно указанными.

Производные и их естественное распространение на частные производные с несколькими переменными являются одними из наиболее важных предметов изучения математики, и точка. Это связано с тем, что они имеют дело со скоростью изменения и потоком многих моделей, которые часто появляются в приложениях.

Что такое частная производная?

Проще говоря, частная производная состоит из проведения того же, что и регулярное дифференцирование по одной переменной, при условии, что остальные переменные постоянны.

Если бы нам нужно было формально определить частную производную, давайте сделаем это проще и сделаем это для функции двух переменных, \(x\) и \(y\). Частная производная относительно \(x\) в точке \((x_0, y_0)\) равно

\[\ frac {\ partial f} {\ partial x} (x_0, y_0) = \ displaystyle \ lim_ {h \ to 0} \ frac {f (x_0 + h, y_0) – f (x_0, y_0)} { ч} \]

Таким образом, как мы видим, это по существу то же самое, что и определение правильной производной, только есть еще одна переменная, но она остается постоянной в процесс расчета.

Аналогично, частная производная относительно \(y\) в точке \((x_0, y_0)\) равно

\[\ frac {\ partial f} {\ partial y} (x_0, y_0) = \ displaystyle \ lim_ {h \ to 0} \ frac {f (x_0, y_0 + h) – f (x_0, y_0)} { ч} \]

Вектор всех частных производных называется градиентом. Если вам действительно нужно получить все частные производные, вы можете использовать это калькулятор градиента.

Шаги для вычисления частных производных

• Шаг 1: Определите функцию, для которой вы хотите вычислить частную производную. Обязательно сначала упростите его
• Шаг 2: Обратите внимание, что не все функции дифференцируемы, поэтому вам нужно убедиться, что задействованная функция действительно дифференцируема
• Шаг 3: Используйте все соответствующие производные правила для функции и дифференцируйте функцию, как обычно, по отношению к дифференцируемая переменная, а любую другую переменную рассматривать как константу 92)}{\partial x} = 0\), потому что y считается постоянным по отношению к x.

  Зачем использовать калькулятор частных производных

  Вычисление частных производных может быть относительно простым упражнением, но это не обязательно легко. Важно быть очень систематически во время применения соответствующих производных правил.

  Использование калькулятора частных производных с шагами может помочь вам, по крайней мере, проверить ваш результат и увидеть, какие именно шаги являются правильными и какие производные правила необходимо использовать.

  В частности, в сложных задачах с алгебраически сложными выражениями калькулятор действительно может пригодиться.

  Какие производные правила для частных производных?

  Точно такие же, как и у обычных производных. Для частных производных у нас есть линейность, правило произведения, цепное правило и частное правило. Как правило, вы в конечном итоге будете использовать комбинацию всех этих правил для более сложных производных примеров.

  Что такое неявное дифференцирование

  Существует ситуация, когда задействовано более одной переменной, в которой мы не предполагаем, например, что y изменяется вместе с x, как мы это делаем в частные производные. В некоторых случаях, когда есть уравнение, связывающее переменные, мы предполагаем, что существует неявная связь между y и x, и мы пишем y = y(x).

  Это контекст неявной дифференциации, которая является своего рода гибридом частичной дифференциации и регулярная дифференциация. 2\) 92}\)

  Другие калькуляторы исчисления

  Концепция производной находится в центре исчисления, и использование калькулятора производной может значительно поможет вам во многих различных приложениях исчисления, включая оптимизацию, одну из «больших».

  Идея производной естественным образом распространяется на случай функции со многими переменными, когда калькулятор частных производных будет делать то же самое, что и обычная производная, но теперь предполагается, что изменяется только одна переменная, а остальные переменные считаются фиксированными.

  Часто вы знаете, что \(y\) зависит от \(x\), но не явно, а неявно, посредством уравнения связи, и в этом случае вы можно использовать неявное дифференцирование, чтобы использовать правила производных, чтобы получить выражение, для которого вы можете затем найти производную \(\frac{d f}{d x}\) .

  Калькулятор и решатель логарифмического дифференцирования

  Получите подробные решения ваших математических задач с помощью нашего пошагового калькулятора

  Логарифмического дифференцирования . Практикуйте свои математические навыки и учитесь шаг за шагом с помощью нашего математического решателя. Проверьте все наши онлайн-калькуляторы здесь!

  1

  2

  3

  4

  5

  6

  7

  8

  9 0002 9

  9 5

  б

  в

  г

  е

  г

  м

  n

  u

  v

  w

  x

  y

  z

  .

  (◻)

  +

  –

  ×

  ◻/◻

  /

  ÷

  ◻ ² 5 ◻

  316

  √◻

  √

  ^◻ √◻

  ^◻ √

  ∞

  e

  π

  ln

  бревно

  бревно _◻

  900/

  lim 9000 05

  D ^□ _x

  ∫

  ∫ ^◻

  |◻|

  θ

  =

  >

  <

  >=

  <=

  sin

  cos

  tan 2 0

  2

  5

  2

  csc

  asin

  acos

  atan

  acot

  asec

  acsc

  sinh

  cosh

  tanh

  coth

  sech

  csch

  000co 9002 asinh 90 5

  атан

  акот

  асеч 9n)=n\cdot\log_a(x)$

  $\ln\left(y\right)=x\ln\left(x\right)$

  5

  Вывести обе части равенства относительно $x$

  $\frac{d}{dx}\left(\ln\left(y\right)\right)=\frac{d}{dx}\ влево(x\ln\влево(x\вправо)\вправо)$

  6

  Применение правила произведения для дифференцирования: $(f\cdot g)’=f’\cdot g+f\cdot g’$, где $f=x$ и $g=\ln\left(x\right) $

  $\frac{d}{dx}\left(\ln\left(y\right)\right)=\frac{d}{dx}\left(x\right)\ln\left(x\ вправо)+x\frac{d}{dx}\left(\ln\left(x\right)\right)$

  Промежуточные шаги

  Производная линейной функции равна $1$

  $\frac{d}{dx}\left(\ln\left(y\right)\right)=1\ln\left (x\right)+x\frac{d}{dx}\left(\ln\left(x\right)\right)$

  Любое выражение, умноженное на $1$, равно самому себе

  $\frac{d }{dx}\left(\ln\left(y\right)\right)=\ln\left(x\right)+x\frac{d}{dx}\left(\ln\left(x\right) )\справа)$

  7

  Производная линейной функции равна $1$

  $\frac{d}{dx}\left(\ln\left(y\right)\right)=\ln\left(x\right)+x\frac{d}{dx}\left(\ ln\влево(х\вправо)\вправо)$

  8

  Производная натурального логарифма функции равна производной функции, деленной на эту функцию.