Камень, брошенный горизонтально со скоростью 15 м/с, упал на землю со скоростью 25м/с.
Автомобиль Жигули развивает скорость 72 км\ч, а почтовый голубь 16 м\с. Сможет ли голубь обогнать автомобиль?ПОМОГИТЕ ПЖПЖПЖПЖПЖ
велосипедист їде зі швидкістю 5 МС з якою швидкістю відносно дорозі рухається військова велосипедиста нижня точка колеса верхня точка колеса(зробити м … алюнок) Дав 123 бали
медную деталь массой 6 кг нагрели на 200 градусов, сколько при этом потратили энергии? СРОЧНО у меня кр
Помогите решить!!!
1. Какое количество теплоты выделится при охлаждении свинцовой болванки массой 0,3 т от 700 оС до 30 оС?
2. Какое количество тепло
… ты необходимо для нагревания 500 г растительного масла на 50 оС?
3. Какое количество теплоты выделится при полном сгорании 0,3 т природного газа?
4. Для нагревания тела массой 1,5 кг от 10 оС до 20 оС израсходовано 30 кДж теплоты. Найти удельную теплоемкость тела.
5. Какое количество теплоты потребуется для нагревания 1 кг воды в алюминиевой кастрюле массой 800 г от 10 оС до кипения?
6.
Товщина стінок порожнистого циліндра дорівнює 5 мм. Вну- трішній діаметр його дорівнює 3 см. Який зовнішній діаметр циліндра?
Помогите пожалуйста!!!
2. Из двух населенных пунктов, расстояние между которыми s = 8,4 км, одновременно навстречу друг другу начали двигаться велосипедист и пешеход. Скоро
… сть велосипедиста υ1 = 12,5 м/с. Определите скорость υ2 пешехода, если они встретились через промежуток времени t = 10 мин.
5. Нитяний маятник відхилили від положення рівноваги на 2-3 см та виміряли час, за який відбуваються 15 коливань. Потім збільшили відхилення від полож … ення рів- новаги до 5-6 см і вдруге виміряли час, за який відбуваються 15 коливань. Умови коливань і результати вимірювань наведено в таблиці. Амплітуда Довжина Кількість Час Період Частота Номер коливань, Штки, коливань, коливань, коливань, коливань, досліду А, см 1, м N t, с T, с v, Гц 1 2-3 15 27 0,8 2 5-6 15 28 » Обчисли період і частоту коливань для наведених умов дослідів. Результати обчис- лень занеси таблицю. – Напиши, чи залежать період і частота коливань маятника від амплітуди коливань
чашка массой 100г получила от кипячëной воды 5,6кДж теплоты и нагрелась на 80°с. Определите удельную теплоëмкость вещества, из которого он изготовил? …
Здравствуйте ! помогите сделать ДЗ по физике не получается решить .Учебник Сборник задач В.И Лукашик 7 класс стр 18 упр 139
камень брошен горизонтально со скоростью
камень брошен горизонтально со скоростью
Задача 14427
С башни высотой h = 25 м горизонтально брошен камень со скоростью vx = 15 м/с.
Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадет на землю? С какой скоростью v он упадет на землю? Какой угол φ составит траектория камня с горизонтом в точке его падения на землю?
Задача 14431
Камень брошен горизонтально со скоростью vx = 15 м/с. Найти нормальное а
Задача 14516
С башни высотой h = 25 м горизонтально брошен камень со скоростью v0 = 15 м/с. Найти кинетическую Wк и потенциальную Wп энергии камня через время t = 1 с после начала движения. Масса камня m = 0,2 кг.
Задача 26648
Камень брошен горизонтально со скоростью 7 м/с. Найти тангенциальное ускорение камня через 1 с после начала движения. Сопротивлением воздуха пренебречь.
Задача 26652
Камень брошен горизонтально со скоростью 16 м/с.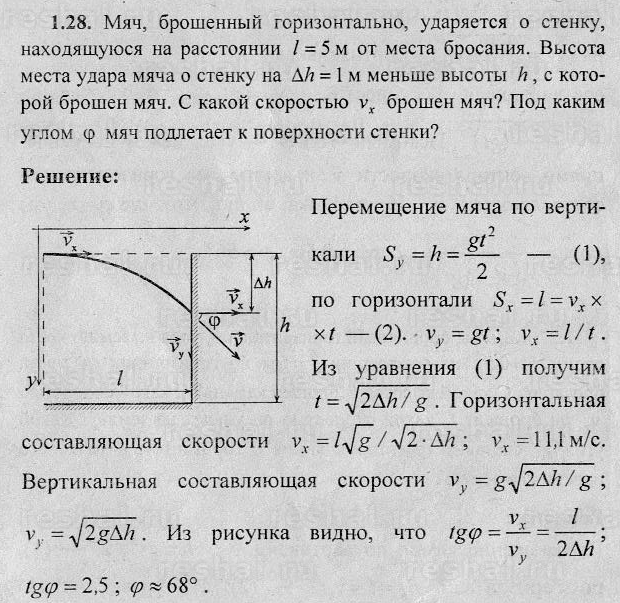
Задача 14528
Камень брошен горизонтально со скоростью 15 м/с. Определить тангенциальное и нормальное ускорение камня спустя 1,0 с после начала движения, радиус кривизны траектории в этот момент времени. Какой угол образует вектор полного ускорения с вектором скорости при t = 1,0 с?
Задача 16055
Камень брошен горизонтально со скоростью 15 м/с. Найти уравнение траектории камня и его полную скорость через время t = 2 с после броска.
Задача 21153
Задача 22431
С башни высотой H = 25 м горизонтально брошен камень со скоростью V0 = 15 м/с. Найти тангенциальное и нормальное ускорения камня через время t = 1 с после начала полета.
[PDF] Движение тела под действием силы тяжести
Download Движение тела под действием силы тяжести…
Движение тела под действием силы тяжести А1.В трубке, из которой откачан воздух, на одной и той же высоте находятся дробинка, пробка и птичье перо. Какое из этих тел позже всех достигнет дна трубки при их свободном падении с одной высоты? 1) Дробинка. 2) Пробка. 3) Птичье перо. 4)Все три тела достигнут дна трубки одновременно. А2. Камень, брошенный вертикально вверх с поверхности Земли со скоростью 20 м/с, упал обратно на Землю. (Сопротивление воздуха пренебрежимо мало.) Камень находился в полете примерно 1) 1 с 2) 2 с 3) 4 с 4) 8 с А3 Тело брошено вертикально вверх со скоростью 20 м/с. (Сопротивление воздуха пренебрежимо мало.) Чему равно время полета тела до точки максимального подъема? 1) 0,5 с 2) 1 с 3) 1,5 с 4) 2 с А4 Тело свободно падает с некоторой высоты с начальной скоростью, равной нулю. Время, за которое тело пройдет путь L, прямо пропорционально 1) L 2 2) 1/L 3) L 4) L А5.
3)
2 gh
4) 4 gh
5) 2 gh
А12. Если за последнюю секунду свободно падающее без начальной скорости тело пролетело 3/4 всего пути, то полное время падения тела равно 1)1,5с 2) 2,0с 3)2,5с 4) 3,0с 5) 3,5с А13. Камень свободно падает без начальной скорости. Последние 5 м камень пролетел за 1 секунду. В момент удара о Землю камень обладал скоростью, равной 1) 5 м/с 2) 10м/с 3) 15 м/с 4) 20 м/с 5) 25 м/с 1
А14. Камень свободно падает без начальной скорости. Третий метр своего пути камень пролетит за 1) 0,09с 2) 0,14с 3) 0,19с 4) 0,24 с 5) 0,29 с А15. Вертикально вверх подбросили шарик. На одной и той же высоте шарик побывал дважды; через 1,5 с и через 3,5 с после начала движения. Начальная скорость шарика равна 1) 5 м/с 2) 10 м/с 3) 20 м/с 4) 25 м/с 5) 30м/с А16. Сосулька, упав с края крыши, долетела до земли за 3,0 с.
.. 1) 0,1 с2) 0,25с 3) 0,5 с
4) 1с
А27. Шарик брошен под углом к горизонту так, как представлено на рисунке. В точке А его скорость равна … 2
1) 3 м/с
2) 4 м/с
3) 5 м/с
4) 7 м/с
А28. Мяч брошен с начальной скоростью V0 = 30 м/с. Время всего полета мяча при угле бросания 45° равно 1) 1,2с 2) 2,1с 3)3,0с 4) 4,3 с 5) 6,3 с А29. Двое играют в мяч, бросая его под углом α = 60° к горизонту. Мяч находится t=2с. При этом расстояние, на котором находятся играющие, равно 1)9,5м 2) 10,0м 3) 10,5 м 4) 11,0м 5) 11,5 м
в
полете
А30. Мяч бросили с начальной скоростью 22 м/с под углом 60° к горизонту. Скорость мяча будет направлена под углом 45° к горизонту дважды за время полета. В первый раз это случится через 1)0,5с 2) 0,6с 3)0,7с 4) 0,8 с 5) 0,9с А31. Мяч бросили с начальной скоростью 22 м/с под углом 60°. к горизонту. Скорость мяча будет направлена под углом 45° к горизонту дважды во время полета. Во второй раз это случится через 1) 2,4 с 2) 2,6 с 3) 2,8 с 4) 3,0 с 5) 3,2 с А32.
Мяч бросили с начальной скоростью 20 м/с под углом 60° к горизонту. Скорость мяча будет направлена под углом 45° к горизонту на высоте H, равной 1)8м 2) 9м 3)10м 4) 11 м 5) 12 м А33. Мяч бросили с начальной скоростью 20 м/с под углом 60° к горизонту. Скорость мяча будет направлена под углом 45° к горизонту дважды за время полета. В первый раз это произойдет над точкой поверхности Земли, удаленной от места броска на расстоянии, равном I) 6,1 м 2) 6,4 м 3) 6,7 м 4) 7,0 м 5) 7,3 м
Часть В 1. Мяч бросили с горизонтальной поверхности земли под углом к горизонту. Минимальная скорость мяча во время полета была равна 6м/с, а максимальная — 12м/с. На какую максимальную высоту поднялся мяч? Ответ округлите до десятых долей. 2. Мяч бросили с горизонтальной поверхности земли под углом к горизонту. Минимальная скорость мяча во время полета была равна: 7м/с, а максимальная — 10м/с. Через какой промежуток времени мяч упадет на землю? Ответ округлите до десятых. 3.Через какое время после выстрела стрела, пущенная вертикально вверх со скоростью 12 м/с, первый раз оказывается на высоте 4 м? Ответ округлить до десятых.
4.Через какое время после выстрела стрела, пущенная вертикально вверх со скоростью 12 м/с, второй раз оказывается на высоте 4 м? Ответ округлить до десятых, считая g = 10 м/с2. 5.Стрела, пущенная вертикально вниз с обрыва высотой 30 м со скоростью 5 м/с достигает воды. Чему равно время полета стрелы? 6.Стрела, пущенная вертикально вверх со скоростью 12 м/с, два раза оказывается на высоте 4 м. Каков промежуток времени между двумя этими событиями? Ответ округлить до десятых.
3
Волькенштейн – Страница 50
Раздел: Волькенштейн, ФизикаВолькенштейн — 1.30. Камень брошен горизонтально со скоростью УГ = 15 м/с. Найти нормальное а„ и тангенциальное а, ускорения камня через время (= 1 с после начала движения. Скачать решение: Скачать решение задачи
Смотреть материал
Раздел: Волькенштейн, ФизикаВолькенштейн — 1.29. Камень, брошенный горизонтально, через время / = 0,5 с после начала движения имел скорость V, в 1,5 раза большую скорости \х в момент бросания.
С какой скоростью V, был брошен камень? Скачать решение: Скачать решение задачи
Смотреть материал
Раздел: Волькенштейн, ФизикаВолькенштейн — 1.28. Мяч, брошенный горизонтально, ударяется о стенку, находящуюся на расстоянии / = 5 м от места бросания. Высота места удара мяча о стенку на Ак = 1 м меньше высоты к, с которой брошен мяч. С какой скоростью УХ брошен мяч? Под каким углом ф мяч подлетает к поверхности стенки? Скачать решение: Скачать […]
Смотреть материал
Раздел: Волькенштейн, ФизикаВолькенштейн — 1.27. Камень, брошенный горизонтально, упал на землю через время / = 0,5 с на расстоянии / = 5 м по горизонтали от места бросания. С какой высоты И брошен камень? С какой скоростью у,, он брошен? С какой скоростью он упадет на землю? Какой угол ф составит траектория камня с горизонтом в точке […]
Смотреть материал
Раздел: Волькенштейн, ФизикаВолькенштейн — 1.
26. С башни высотой А = 25м горизонтально брошен камень со скоростью гг = 15м/с. Какое время ( камень будет в движении? На каком расстоянии / от основания башни он упадет на землю? С какой скоростью V он упадет на землю? Какой угол ф составит траектория камня с горизонтом в точке его падения […]
Смотреть материал
Раздел: Волькенштейн, ФизикаВолькенштейн — 1.25. Зависимость пройденного телом пути л- от времени / дается уравнением $ = А + В1 + С12 + С/3, где С = 0,14 м/с2 и О = 0,01 м/с3. Через какое время / тело будет иметь ускорение а = 1 м/с ? Найти среднее ускорение а тела за этот промежуток времени. Скачать […]
Смотреть материал
Раздел: Волькенштейн, ФизикаВолькенштейн — 1.24. Зависимость пройденного телом пути 5 от времени / дается уравнением 5 = А + В( + О2, где А = 3м, В = 2м/с и С = 1 м/с2. Найти среднюю скорость V и среднее ускорение а тела за первую, вторую и третью секунды его движения.
Скачать решение: Скачать решение задачи
Смотреть материал
Раздел: Волькенштейн, ФизикаВолькенштейн — 1.23. Зависимость пройденного телом пути 5 от времени I дается уравнением5 = А-В1 + С11, где о = 6м, й = 3м/с и С = 2 м/с2. Найти среднюю скорость V и среднее ускорение а 16 тела для интервала времени 1
Смотреть материал
Раздел: Волькенштейн, ФизикаВолькенштейн — 1.22. Зависимость пройденного телом пути 5 от времени / дается уравнением $ = А1- Вг + С/3, где А = 2 м/с, 5 = 3 м/с и С=.4м/с . Найти: а) зависимость скорости V и ускорения а от времени /; б) расстояние 5, пройденное телом, скорость V и ускорение а тела через время […]
Смотреть материал
Раздел: Волькенштейн, ФизикаВолькенштейн — 1.21. Тело 1 движется равноускоренно, имея начальную скорость у|0=2м/с и ускорение а.
Через время / = 10с после начала движения тела 1 из этой же точки начинает двигаться равноускоренно тело 2, имея начальную скорость у,0 =12 м/с и то же ускорение а. Найти ускорение а, при котором тело 2 сможет догнать тело 1 […]
Смотреть материал
КИНЕМАТИКА Описание движения материальной точки A 1
КИНЕМАТИКА Описание движения материальной точки
A 1. Зависимость пройденного телом пути s от времени t дается уравнением s = A + Bt + Ct 2 + Dt 3, где B = 0, 01 м/с, С = 0, 14 м/с2 и D = 0, 01 м/с3. Через какое время t после начала движения тело будет иметь ускорение a 0 = 1 м/с2? Найти среднее ускорение тела за этот промежуток времени. Какова будет величина скорости тела в этот момент времени? Решение Дано: s = A + Bt+Ct 2+Dt 3 Материальная точка движется прямолинейно. Выберем ось OX направленной вдоль B = 0, 01 м/с траектории точки. В этом случае величина C = 0, 14 м/c 2 пройденного пути равна s = x(t) – x(t 0).
D = 0, 01 м/с3 Начало координат выберем так, что x(t 0) = 0. Тогда кинематическое a = a 0 = 1 м/с2 уравнение движения имеет вид: -? x(t) = A + Bt+Ct 2 + Dt 3. – ? Проекция скорости на ось OX: Проекция ускорения на ось OX: По условию ax = a 0 = 1 м/с, поэтому
А 2. Камень, брошенный горизонтально, упал на землю через время t = 0, 5 с на расстоянии l = 5 м по горизонтали от места бросания. С какой высоты h брошен камень? С какой скоростью 0 он брошен? С какой скоростью он упадет на землю? Какой угол составит вектор скорости камня с горизонтом в точке его падения на землю. Решение Дано: Если пренебречь силой t = 0, 5 c сопротивления воздуха, то l=5 м вдоль оси OX камень движется Vx – ? равномерно, а вдоль оси OY – h-? равноускоренно, с ускорением -? равным g и направленным j-? вниз. Траектория показана на рисунке (начало координат – под точкой бросания). Кинематические уравнения движения камня: Отсюда: x(t) = x 0 + v 0 xt, По условию задачи и в результате выбора системы отсчёта: x 0 = 0, y 0 = h, v 0 y = 0, ay = -g.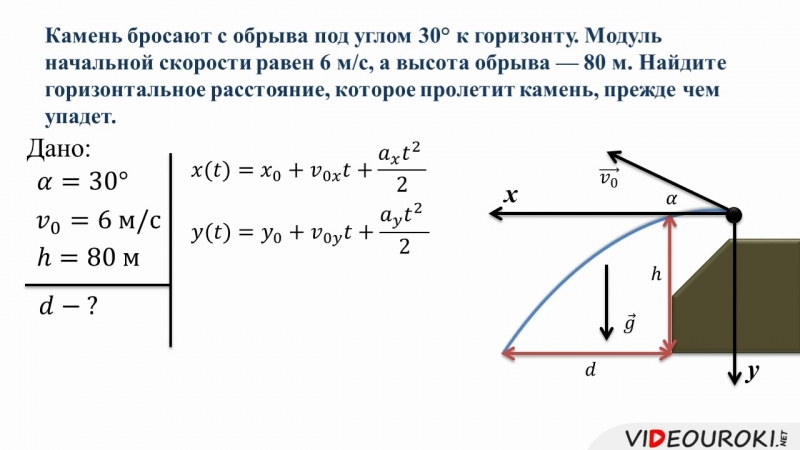
x(t) = v 0 xt,
А 2. Камень, брошенный горизонтально, упал на землю через время t = 0, 5 с на расстоянии l = 5 м по горизонтали от места бросания. С какой высоты h брошен камень? С какой скоростью 0 он брошен? С какой скоростью он упадет на землю? Какой угол составит вектор скорости камня с горизонтом в точке его падения на землю. Решение (продолжение) Итак, кинематические уравнения движения x(t) = v 0 xt, Когда камень упадёт на землю, x = l, y = 0 (см. рис. ). x(t) = v 0 xt = l,
А 2. Камень, брошенный горизонтально, упал на землю через время t = 0, 5 с на расстоянии l = 5 м по горизонтали от места бросания. С какой высоты h брошен камень? С какой скоростью 0 он брошен? С какой скоростью он упадет на землю? Какой угол составит вектор скорости камня с горизонтом в точке его падения на землю. Решение (продолжение) x(t) = v 0 xt, Из уравнений движения определим, как зависят от времени проекции скорости на оси координат. Величина скорости в любой момент времени: Величина скорости в момент падения (t = 0, 5 c):
А 2.
Камень, брошенный горизонтально, упал на землю через время t = 0, 5 с на расстоянии l = 5 м по горизонтали от места бросания. С какой высоты h брошен камень? С какой скоростью 0 он брошен? С какой скоростью он упадет на землю? Какой угол составит вектор скорости камня с горизонтом в точке его падения на землю. Решение (продолжение) x(t) = v 0 xt, Тангенс угла, образуемого вектором скорости с осью OX в любой момент времени (см. рис. ): В момент падения (t = 0, 5 c): Ответ: h = 1, 25 м; v 0 = 10 м/с, v = 11, 1 м/с, φ = 26˚.
A 3. Камень брошен горизонтально со скоростью 0 = 15 м/с. Найти нормальное аn и тангенциальное а ускорения камня через время t = 1 с после начала движения. Решение Дано: Вектор ускорения камня во 0 = 15 м/с время полёта всегда t=1 с направлен вниз, а по величине равен g (см. рис. ). аn – ? а – ? Вектор ускорения камня можно представить, как сумму двух векторов, перпендикулярных другу Углы между вектором скорости и осью OX и векторами полного и нормального ускорения равны, как острые углы со взаимно перпендикулярными сторонами (см.
рис. ).
A 3. Камень брошен горизонтально со скоростью 0 = 15 м/с. Найти нормальное аn и тангенциальное аt ускорения камня через время t = 1 с после начала движения. Решение (продолжение) Камень падает в поле силы тяжести и воль оси OX движется равномерно, а вдоль оси OY – с постоянным ускорением g. Проекции скорости камня зависят от времени так (см. решение предыдущей задачи): Подставим выражения для модулей проекций скорости в формулы для an и at: Ответ: an = 8, 2 м/c 2; at = 5, 4 м/с2.
А 4. Камень брошен горизонтально со скоростью 0 = 10 м/с. Найти радиус кривизны R траектории камня через время t = 3 с после начала движения. Решение Дано: Вектор ускорения камня во полёта всегда 0 = 10 м/с время направлен вниз, а по t=3 с величине равен g (см. рис. ). R- ? Вектор ускорения камня можно представить, как сумму двух векторов, перпендикулярных другу Углы между вектором скорости и осью OX и векторами полного и нормального ускорения равны, как острые углы со взаимно перпендикулярными сторонами (см.
рис. ).
А 4. Камень брошен горизонтально со скоростью 0 = 10 м/с. Найти радиус кривизны R траектории камня через время t = 3 с после начала движения. Решение (продолжение) Согласно определению величина нормального (центростремительного) ускорения равна где R – радиус кривизны траектории. Ответ: R = 305 м.
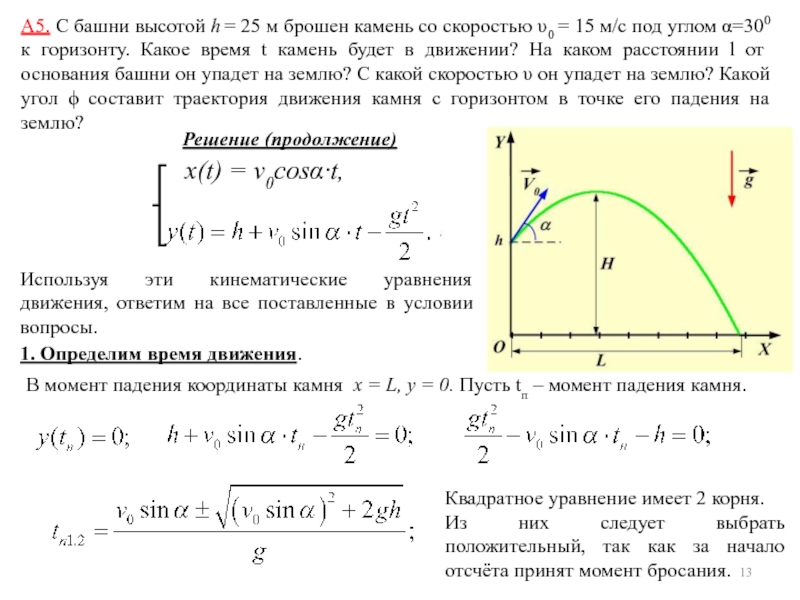
А 5. С башни высотой h = 25 м брошен камень со скоростью 0 = 15 м/с под углом =300 к горизонту. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадет на землю? С какой скоростью он упадет на землю? Какой угол составит траектория движения камня с горизонтом в точке его падения на землю? Решение Дано: Если пренебречь силой h = 25 м V 0 = 15 м/с сопротивления воздуха, то вдоль оси OX камень движется равномерно, а = 30 вдоль оси OY – равноускоренно, с l-? ускорением равным g и -? направленным вниз. Траектория j-? показана на рисунке (начало координат – под точкой бросания). Кинематические уравнения движения камня: x(t) = x 0 + v 0 xt, Отсюда уравнения По условию задачи и в результате выбора системы отсчёта: x 0 = 0, y 0 = h, v 0 y = v 0 sinα, v 0 x = v 0 cosα, ay = -g.
кинематические движения камня: x(t) = v 0 cosα·t,
А 5. С башни высотой h = 25 м брошен камень со скоростью 0 = 15 м/с под углом =300 к горизонту. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадет на землю? С какой скоростью он упадет на землю? Какой угол составит траектория движения камня с горизонтом в точке его падения на землю? Решение (продолжение) x(t) = v 0 cosα·t, Используя эти кинематические уравнения движения, ответим на все поставленные в условии вопросы. 1. Определим время движения. В момент падения координаты камня x = L, y = 0. Пусть tп – момент падения камня. Квадратное уравнение имеет 2 корня. Из них следует выбрать положительный, так как за начало отсчёта принят момент бросания.
А 5. С башни высотой h = 25 м брошен камень со скоростью 0 = 15 м/с под углом =300 к горизонту. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадет на землю? С какой скоростью он упадет на землю? Какой угол составит траектория движения камня с горизонтом в точке его падения на землю? Решение (продолжение) Положительным будет корень, соответствующий знаку «+» . Это и будет время полёта.
А 5. С башни высотой h = 25 м брошен камень со скоростью 0 = 15 м/с под углом =300 к горизонту. Какое время t камень будет в движении? На каком расстоянии L от основания башни он упадет на землю? С какой скоростью он упадет на землю? Какой угол составит траектория движения камня с горизонтом в точке его падения на землю? Решение (продолжение) 2. Определим дальность полёта L. x(t) = v 0 cosα·t, В момент падения координаты камня x = L, y = 0. L и есть дальность полёта. Эти значения координат достигаются в момент t = tп.
А 5. С башни высотой h = 25 м брошен камень со скоростью 0 = 15 м/с под углом =300 к горизонту. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадет на землю? С какой скоростью он упадет на землю? Какой угол составит траектория движения камня с горизонтом в точке его падения на землю? Решение (продолжение) 3. Определим максимальную высоту подъёма H. x(t) = v 0 cosα·t, В наивысшей точке вертикальная компонента скорости равно нулю, vy = 0. vy определим из второго уравнения: время подъёма на максимальную высоту.
А 5. С башни высотой h = 25 м брошен камень со скоростью 0 = 15 м/с под углом =300 к горизонту. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадет на землю? С какой скоростью он упадет на землю? Какой угол составит траектория движения камня с горизонтом в точке его падения на землю? Решение (продолжение) x(t) = v 0 cosα·t,
А 5. С башни высотой h = 25 м брошен камень со скоростью 0 = 15 м/с под углом =300 к горизонту. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадет на землю? С какой скоростью он упадет на землю? Какой угол составит траектория движения камня с горизонтом в точке его падения на землю? Решение (продолжение) 4. Определим скорость камня в любой момент времени. vx и vy определим из уравнений: x(t) = v 0 cosα·t, Подставляя различные значения времени t, определим величину скорости.
А 5. С башни высотой h = 25 м брошен камень со скоростью 0 = 15 м/с под углом =300 к горизонту. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадет на землю? С какой скоростью он упадет на землю? Какой угол составит траектория движения камня с горизонтом в точке его падения на землю? Решение (продолжение) Подставляя значение времени t = tп, определим величину скорости в момент удара о землю. Вектор скорости направлен по касательной к траектории (см. рис. ). Направление вектора можно задать, указав угол, который образует вектор с осью OX. Подставляя различные значения времени t, определим величину угла φ в любой момент времени. В момент удара
А 6. Вентилятор вращается с частотой = 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75 об. Какое время t прошло с момента выключения вентилятора до полной его остановки? Дано: 0= 900 об/мин =0 N = 75 об t- ? Решение Выберем систему отсчёта, как показано на рисунке. Направления векторов скорости, угловой скорости и углового ускорения – на рисунке. Перейдём к полярным координатам. Вентилятор движется замедленно. Кинематическое уравнение движения: Определим значения параметров уравнения: Проекция угловой скорости вентилятора:
А 6. Вентилятор вращается с частотой = 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75 об. Какое время t прошло с момента выключения вентилятора до полной его остановки? Решение (продолжение) Уравнения движения в полярных координатах: Из второго уравнения выразим ε : Когда вентилятор остановится, проекция углового перемещения составит
А 6. Вентилятор вращается с частотой = 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75 об. Какое время t прошло с момента выключения вентилятора до полной его остановки? Решение (продолжение) Время до остановки: Ответ: t = 10 с.
НЕ-А 6. Вентилятор вращается с частотой = 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75 об. Каково угловое ускорение вентилятора? Дано: 0= 900 об/мин =0 N = 75 об t- ? Решение Выберем систему отсчёта, как показано на рисунке. Направления векторов скорости, угловой скорости и углового ускорения – на рисунке. Перейдём к полярным координатам. Вентилятор движется замедленно. Кинематическое уравнение движения: Определим значения параметров уравнения: Проекция угловой скорости вентилятора:
не. А 6. Вентилятор вращается с частотой = 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75 об. Каково угловое ускорение вентилятора? Решение (продолжение) Уравнения движения в полярных координатах: Из второго уравнения выразим t : Когда вентилятор остановится, проекция углового перемещения составит
не. А 6. Вентилятор вращается с частотой = 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75 об. Каково угловое ускорение вентилятора ? Решение (продолжение) Величина углового ускорения : Ответ: ε = 9, 42 с-2.
А 7. Точка движется по окружности радиусом R = 20 см с постоянным тангенциальным ускорением а. Найти тангенциальное ускорение а точки, если известно, что к концу пятого оборота после начала движения линейная скорость точки = 79, 2 см/с. Дано: R = 20 см а = const. = 79, 2 cм/с а – ? Решение Тангенциальная составляющая ускорения направлена, как и вектор скорости, по касательной к траектории. Поэтому она «ответственна» за изменение модуля линейной скорости. Тангенциальная составляющая ускорения постоянно по величине. (S – путь, пройденный материальной точкой)
А 7. Точка движется по окружности радиусом R = 20 см с постоянным тангенциальным ускорением а. Найти тангенциальное ускорение а точки, если известно, что к концу пятого оборота после начала движения линейная скорость точки = 79, 2 см/с. Решение (продолжение) Путь, пройденный точкой, N – число оборотов. Ответ:
А 8. Колесо радиусом R=10 см вращается с угловым ускорением =3, 14 рад/с2. Найти для точек на ободе колеса к концу первой секунды после начала движения: а) угловую скорость ; б) линейную скорость ; в) тангенциальное ускорение а ; г) нормальное ускорение аn ; д) полное ускорение а; е) угол , составляемый вектором полного ускорения с радиусом колеса. Дано: Решение R=10 см =3, 14 рад/с2 Направления векторов скорости, угловой скорости и углового ускорения – на рисунке. t=1 с Перейдём к полярным координатам. Колесо – ? движется с постоянным угловым ускорением. -? Кинематическое уравнение движения: а – ? аn – ? -? Определим значения параметров уравнения: Проекция угловой скорости колеса:
А 8. Колесо радиусом R=10 см вращается с угловым ускорением =3, 14 рад/с2. Найти для точек на ободе колеса к концу первой секунды после начала движения: а) угловую скорость ; б) линейную скорость ; в) тангенциальное ускорение а ; г) нормальное ускорение аn ; д) полное ускорение а; е) угол , составляемый вектором полного ускорения с радиусом колеса. Решение (продолжение) Проекция угловой скорости Вектор линейной скорости Направления векторов показаны на рисунке. Для модулей Тангенциальная составляющая ускорения Направления совпадает с направлением вектора скорости. Для модулей
А 8. Колесо радиусом R=10 см вращается с угловым ускорением =3, 14 рад/с2. Найти для точек на ободе колеса к концу первой секунды после начала движения: а) угловую скорость ; б) линейную скорость ; в) тангенциальное ускорение а ; г) нормальное ускорение аn ; д) полное ускорение а; е) угол , составляемый вектором полного ускорения с радиусом колеса. Решение (продолжение) Нормальная составляющая ускорения направлена к центру окружности. Её величина Величину полного ускорения найдём по теореме Пифагора (см. рис). Нормальная составляющая ускорения направлена вдоль радиуса, тангенциальная – по касательной к окружности, поэтому угол между радиусом и вектором ускорения можно определить так:
А 9. Точка движется по окружности радиуса R = 1 м так, что зависимость криволинейной координаты, отсчитанной вдоль окружности, от времени задается уравнением s = A – Bt + Ct 2, где В = 2 м/c и С = 1 м/c 2. Найти линейную скорость точки, ее тангенциальное а , нормальное аn и полное а ускорения через время t = 3 с после начала движения. Решение Дано: B = 2 м/с C = 1 м/с2 t 1 = 3 c R=1 м V-? an – ? at – ? Проанализируем уравнение движения точки. При этом перемещение против часовой стрелки положительно, по часовой стрелке – отрицательно. Скорость, направленная окружности по касательной к Тангенциальное ускорение По условию B = 2 м/с, С = 1 м/с2, при 1. При См. рис 1. 2. При См. рис 2.
А 9. Точка движется по окружности радиуса R = 1 м так, что зависимость криволинейной координаты, отсчитанной вдоль окружности, от времени задается уравнением s = A – Bt + Ct 2, где В = 2 м/c и С = 1 м/c 2. Найти линейную скорость точки, ее тангенциальное а , нормальное аn и величину полного а ускорения через время t = 3 с после начала движения. Решение (продолжение) Момент времени t = 3 c соответствует ситуации, показанной на рис. 2. Величина полного ускорения
А 10. Во сколько раз нормальное ускорение аn точки, лежащей на ободе вращающегося колеса, больше ее тангенциального ускорения а для того момента, когда вектор полного ускорения точки составляет угол = 30° с вектором ее линейной скорости? Дано: Решение = 30° аn/ а – ? следовательно, Ответ:
Примеры решенных задач по физике на тему “Свободное движение тела, брошенного под углом к горизонту”
Ниже размещены условия задач и отсканированные решения. Если вам нужно решить задачу на эту тему, вы можете найти здесь похожее условие и решить свою по аналогии. Загрузка страницы может занять некоторое время в связи с большим количеством рисунков. Если Вам понадобится решение задач или онлайн помощь по физике- обращайтесь, будем рады помочь.
Принцип решения этих задач заключается в разложении скорости свободно падающего тела на две составляющие – горизонтальную и вертикальную. Горизонтальная составляющая скорости постоянна, вертикальное движение происходит с ускорением свободного падения g=9.8 м/с2. Также может применяться закон сохранения механической энергии, согласно которому сумма потенциальной и кинетической энерги тела в данном случае постоянна.
Материальная точка брошена под углом к горизонту с начальной скоростью 15 м/с. Начальная кинетическая энергия в 3 раза больше кинетической энергии точки в верхней точке траектории. На какую высоту поднималась точка?
Тело брошено под углом 40 градусов к горизонту с начальной скоростью 10 м/с. Найти расстояние, которое пролетит тело до падения, высоту подъема в верхней точке траектории и время в полете.
Тело брошено с башни высотой H вниз, под углом α к горизонту, с начальной скоростью v. Найти расстояние от башни до места падения тела.
Тело массой 0,5 кг брошено с поверхност Земли под углом 30 градусов к горизонту, с начальной скоростью 10 м/с. Найти потенциальную и кинетическую энергии тела через 0,4 с.
Материальная точка брошена вверх с поверхности Земли под углом к горизонту с начальной скоростью 10 м/с. Определить скорость точки на высоте 3 м.
Тело брошено вверх с поверхности Земли под углом 60 градусов с начальной скоростью 10 м/с. Найти расстояние до точки падения, скорость тела в точке падения и время в полете.
Тело брошено вверх под углом к горизонту с начальной скоростю 20 м/с. Расстояние до точки падения в 4 раза больше максимальной высоты подъема. Найти угол, под которым брошено тело.
Тело брошено с высоты 5 м под углом 30 градусов к горизонту с начальной скоростью 22 м/с. Найти дальность полета тела и время полета тела.
Тело брошено с поверхности Земли под углом к горизонту с начальной скоростью 30 м/с. Найти тангенциальное и нормальное ускорения тела через 1с после броска.
Тело брошено с поверхности Зесли под углом 30 градусов к горизонту с начальной скоростью 14,7 м/с. Найти тангенциальное и нормальное ускорения тела через 1,25с после броска.
Тело брошено под углом 60 градусов к горизонту с начальной скоростью 20 м/с. Через какое время угол между скоростью и горизонтом станет равным 45 градусов?
Мяч, брошенный в спортзале под углом к горизонту, с начальной скоростью 20 м/с, в верхней точке траектории коснулся потолка на высоте 8м и упал на некотором расстоянии от места броска. Найти это расстояние и угол, под которым брошено тело.
Тело, брошеное с поверхности Земли под углом к горизонту, упало через 2,2с. Найти максимальную высоту подъема тела.
Камень брошен под углом 30 градусов к горизонту. На некоторой высоте камень побывал дважды – через время 1с и 3 с после броска. Найти эту высоту и начальную скорость камня.
Камень брошен под углом 30 градусов к горизонту с начальной скоростью 10 м/с. Найти расстояние от точки бросания до камня через 4 с.
Снаряд выпущен в момент, когда самолет пролетает над орудием, под углом к горизонту с начальной скоростью 500 м/с. Снаряд поразил самолет на высоте 3,5 км через 10с после выстрела. Какова скорость самолета?
Ядро массой 5 кг брошено с поверхности Земли под углом 60 градусов к горизонту. На разгон гири потрачена энергия 500Дж. Определить дальность полета и время в полете.
Тело брошено с высоты 100м вниз под углом 30 градусов к горизонту с начальной скоростью 5 м/с. Найти дальность полета тела.
Тело массой 200г, брошеное с поверхности Земли под углом к горизонту, упало на расстоянии 5м через время 1,2с. Найти работу по броску тела.
Горизонтальный бросок
Спорт Горизонтальный бросок
просмотров – 654
112. Самолет летит горизонтально со скоростью 900 км/ч на высоте 8 км. За сколько километров до цели летчик должен сбросить бомбу? g = 10 м/с2.
113. Во сколько раз увеличится дальность полета тела, брошенного горизонтально с некоторой высоты, если начальную скорость тела увеличить в 2 раза?
114. На сколько процентов увеличится дальность полета тела, брошенного горизонтально, если начальную высоту в 4 раза уменьшить, а начальную скорость в 3 раза увеличить?
115. С башни высотой 45 м горизонтально брошен камень с некоторой скоростью. Через сколько секунд он упадет на землю? g = 10 м/с2.
116. Дальность полета тела, брошенного горизонтально со скоростью 4,9 м/с, равна высоте, с которой его бросили. Чему равна эта высота (в см)? g = 9,8 м/с2.
117. Тело бросили горизонтально со скоростью 40 м/с с некоторой высоты. Определите его скорость через три секунды. g =10 м/с2.
118. Камень, брошенный горизонтально со скоростью 15 м/с, упал на землю со скоростью 25 м/с. Сколько времени длился полет камня? g = 10 м/с2.
119. Из окна, расположенного на высоте 5 м от земли, горизонтально брошен камень, упавший на расстоянии 8 м от дома. С какой скоростью был брошен камень? g = 10 м/с2.
120. Камень брошен горизонтально. Через 2 с после броска вектор его скорости составил угол 45° с горизонтом. Найдите начальную скорость камня. g = 10 м/с2.
121. Тело брошено горизонтально. Через 2 с после броска угол между направлениями вектора скорости и вектора ускорения стал равным 60°. Определите величину полной скорости тела в данный момент времени. g = 10 м/с2.
122.Дальность полета тела, брошенного в горизонтальном направлении, равна половине высоты, с которой оно брошено. Чему равен тангенс угла, который образует с горизонтом скорость тела при его падении на землю?
123. Камень на высоте 5,5 м бросают горизонтально так, что он подлетает к поверхности земли под углом 45°. Сколько метров пролетел камень по горизонтали?
124. С самолета͵ летящего на высоте 500 м со скоростью 180 км/ч, выпал груз. На какой высоте скорость груза будет направлена под углом 60° к горизонту? g = 10 м/с2.
125. Мяч брошен горизонтально со скоростью 2 м/с. Расстояние между двумя последовательными ударами мяча о горизонтальную поверхность равно 4 м. С какой высоты был брошен мяч? g = 10 м/с2. (Удары о пол абсолютно упругие.)
126. На горе с углом наклона к горизонту 30° горизонтально бросают мяч с начальной скоростью 15 м/с. На каком расстоянии от точки бросания вдоль наклонной плоскости упадет мяч? g = 10 м/с2.
127. Железный шарик подкатился к краю верхней ступеньки лестницы со скоростью 1,5 м/с. Высота и ширина каждой ступени 20 см. О какую по счету ступеньку шарик ударится впервые? Первой считать ступеньку сразу после той, на которой находился шар. g = 10 м/с2.
128. В вертикальную мишень с расстояния 120 м из неподвижной винтовки сделано два выстрела в горизонтальном направлении. Скорость первой пули 300 м/с, второй 400 м/с. Определите расстояние (в см) между пробоинами в мишени. g = 10 м/с2.
129. Из одной точки одновременно бросают два тела: одно горизонтально со скоростью 6 м/с, другое — вертикально со скоростью 8 м/с. На каком расстоянии друг от друга будут находиться тела через 2 с?
130. Два камня расположены на одной горизонтали на расстоянии 30 м друг от друга. Один камень бросают вертикально вверх со скоростью 9 м/с, а второй одновременно бросают горизонтально по направлению к первому камню со скоростью 12 м/с. Чему равно наименьшее расстояние между камнями в процессе движения?
Читайте также
112. Самолет летит горизонтально со скоростью 900 км/ч на высоте 8 км. За сколько километров до цели летчик должен сбросить бомбу? g = 10 м/с2. 113. Во сколько раз увеличится дальность полета тела, брошенного горизонтально с некоторой высоты, если начальную скорость тела… [читать подробенее]
4.3 Движение снаряда – Университетская физика, том 1
Цели обучения
К концу этого раздела вы сможете:
- Используйте одномерное движение в перпендикулярных направлениях для анализа движения снаряда.
- Рассчитайте дальность, время полета и максимальную высоту снаряда, который выпущен и попадает в плоскую горизонтальную поверхность.
- Найдите время полета и скорость удара снаряда, который приземляется на высоте, отличной от высоты запуска.
- Рассчитать траекторию полета снаряда.
Движение снаряда – это движение объекта, брошенного или выброшенного в воздух, при котором происходит только ускорение под действием силы тяжести. Применения движения снаряда в физике и технике многочисленны. Некоторые примеры включают метеоры при входе в атмосферу Земли, фейерверки и движение любого мяча в спорте. Такие объекты называются снарядами , а их путь называется траекторией .Движение падающих объектов, описанное в разделе «Движение по прямой», представляет собой простой одномерный тип движения снаряда, в котором нет горизонтального движения. В этом разделе мы рассматриваем двумерное движение снаряда и не учитываем влияние сопротивления воздуха.
Самый важный факт, о котором следует помнить, это то, что движений вдоль перпендикулярных осей являются независимыми и, таким образом, могут быть проанализированы отдельно. Мы обсуждали этот факт в статье «Векторы смещения» и «Векторы скорости», где мы увидели, что вертикальные и горизонтальные движения независимы.Ключ к анализу двумерного движения снаряда состоит в том, чтобы разбить его на два движения: одно по горизонтальной оси, а другое по вертикали. (Этот выбор осей является наиболее разумным, поскольку ускорение свободного падения является вертикальным; таким образом, нет ускорения по горизонтальной оси, когда сопротивление воздуха незначительно.) Как обычно, мы называем горизонтальную ось осью x и вертикальная ось y – ось. Необязательно, чтобы мы использовали этот выбор осей; это просто удобно в случае ускорения свободного падения.В других случаях мы можем выбрать другой набор осей. (Рисунок) иллюстрирует обозначение смещения, где мы определяем
– полное смещение, а
и
– его составляющие векторы по горизонтальной и вертикальной осям соответственно. Величины этих векторов равны x , x и y .
Рис. 4.11. Общее смещение s футбольного мяча в точке на его пути.Векторимеет компоненты
и
по горизонтальной и вертикальной осям. Его величина равна s, и он составляет угол θ с горизонтом.
Чтобы полностью описать движение снаряда , мы должны включить скорость и ускорение, а также смещение. Мы должны найти их компоненты по осям x- и y . Предположим, что все силы, кроме силы тяжести (например, сопротивление воздуха и трение), незначительны.Определив положительное направление как восходящее, компоненты ускорения будут очень простыми:
Поскольку сила тяжести вертикальная,
Если
, это означает, что начальная скорость в направлении x равна конечной скорости в направлении x , или
С этими условиями для ускорения и скорости, мы можем записать кинематику (Уравнение) через (Уравнение) для движения в однородном гравитационном поле, включая остальные кинематические уравнения для постоянного ускорения из Движение с постоянным ускорением.Кинематические уравнения движения в однородном гравитационном поле становятся кинематическими уравнениями с
Горизонтальное перемещение
Вертикальное перемещение
Используя эту систему уравнений, мы можем анализировать движение снаряда, учитывая некоторые важные моменты.
Стратегия решения проблем: движение снаряда
- Разложите движение на горизонтальные и вертикальные компоненты по осям x и y .Величины компонентов смещения
по этим осям составляют x и y. Величины компонент скорости
–
, где v – величина скорости, а θ – ее направление относительно горизонтали, как показано на (Рисунок).
- Рассматривайте движение как два независимых одномерных движения: одно горизонтальное, а другое вертикальное.Используйте кинематические уравнения для горизонтального и вертикального движения, представленные ранее.
- Найдите неизвестные в двух отдельных движениях: одном горизонтальном и одном вертикальном. Обратите внимание, что единственная общая переменная между движениями – это время t . Процедуры решения проблем здесь такие же, как и для одномерной кинематики, и проиллюстрированы в следующих решенных примерах.
- Перекомбинируйте величины в горизонтальном и вертикальном направлениях, чтобы найти полное смещение.
и скорость
Определите величину и направление смещения и скорости, используя
., где θ – направление смещения
и
– постоянная величина. (c) Скорость в вертикальном направлении начинает уменьшаться по мере того, как объект поднимается. В самой высокой точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает в направлении, противоположном начальной вертикальной скорости.(d) Движения по осям x и y объединяются для получения полной скорости в любой заданной точке траектории.
Пример
Снаряд фейерверка взрывается высоко и далеко
Во время фейерверка в воздух с начальной скоростью 70,0 м / с под углом
выстреливается снаряд.выше горизонтали, как показано на (Рисунок). Взрыватель рассчитан на то, чтобы зажечь снаряд, как только он достигнет своей наивысшей точки над землей. (а) Рассчитайте высоту взрыва снаряда.б) Сколько времени проходит между запуском снаряда и взрывом? (c) Каково горизонтальное смещение снаряда при взрыве? (d) Каково полное смещение от точки запуска до самой высокой точки?
Рис. 4.13. Траектория выстрела фейерверка. Взрыватель настроен так, чтобы взорвать снаряд в наивысшей точке его траектории, которая находится на высоте 233 м и 125 м по горизонтали.Стратегия
Движение можно разбить на горизонтальное и вертикальное, в котором
и
Затем мы можем определить
и
равняться нулю и найти желаемые количества.
Решение
(a) Под «высотой» мы понимаем высоту или вертикальное положение y над начальной точкой. Наивысшая точка любой траектории, называемая апексом , достигается, когда
Поскольку нам известны начальная и конечная скорости, а также начальное положение, мы используем следующее уравнение, чтобы найти y :
Потому что
и
равны нулю, уравнение упрощается до
Решение y дает
Теперь мы должны найти
составляющая начальной скорости в направлении y .Выдается
где
– начальная скорость 70,0 м / с,
– начальный угол. Таким образом,
и y равно
Таким образом, имеем
Обратите внимание, что поскольку верх положительный, начальная вертикальная скорость положительна, как и максимальная высота, но ускорение свободного падения отрицательное.Отметим также, что максимальная высота зависит только от вертикальной составляющей начальной скорости, так что любой снаряд с начальной вертикальной составляющей скорости 67,6 м / с достигает максимальной высоты 233 м (без учета сопротивления воздуха). Цифры в этом примере приемлемы для больших фейерверков, снаряды которых достигают такой высоты перед взрывом. На практике сопротивлением воздуха нельзя пренебречь, поэтому начальная скорость должна быть несколько больше, чем заданная для достижения той же высоты.
(b) Как и во многих других физических задачах, существует несколько способов решения, пока снаряд достигает своей наивысшей точки. В этом случае самый простой способ – использовать
.Потому что
на вершине, это уравнение сводится просто к
или
Это время также подходит для больших фейерверков. Если вы видите запуск фейерверка, обратите внимание, что проходит несколько секунд, прежде чем снаряд взорвется.Другой способ узнать время – использовать
.Это оставлено вам в качестве упражнения.
(c) Поскольку сопротивление воздуха незначительно,
, а горизонтальная скорость постоянна, как обсуждалось ранее. Горизонтальное смещение – это горизонтальная скорость, умноженная на время, равное
.где
равно нулю. Таким образом,
где
– это составляющая скорости x , равная
.Время t для обоих движений одинаково, поэтому x равно
Горизонтальное движение – это постоянная скорость при отсутствии сопротивления воздуха.Обнаруженное здесь горизонтальное смещение могло быть полезно для предотвращения падения фрагментов фейерверка на зрителей. Когда снаряд взрывается, сопротивление воздуха оказывает большое влияние, и многие осколки падают прямо под ним.
(d) Горизонтальная и вертикальная составляющие смещения были только что рассчитаны, поэтому все, что здесь нужно, – это найти величину и направление смещения в наивысшей точке:
Обратите внимание, что угол для вектора смещения меньше начального угла запуска.Чтобы понять, почему это так, просмотрите (рисунок), на котором показана кривизна траектории к уровню земли.
При решении (рисунок) (а), выражение, которое мы нашли для y , действительно для любого движения снаряда, когда сопротивление воздуха незначительно. Назовем максимальную высоту х = х . Затем
Это уравнение определяет максимальную высоту снаряда над его стартовой позицией и зависит только от вертикальной составляющей начальной скорости.
Проверьте свое понимание
Камень сброшен со скалы горизонтально
со скоростью 15,0 м / с. (а) Определите начало системы координат. (б) Какое уравнение описывает горизонтальное движение? (c) Какие уравнения описывают вертикальное движение? (г) Какова скорость камня в точке удара?
[показывать-ответ q = ”fs-id1165168031779 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165168031779 ″]
(a) Выберите вершину утеса, куда бросается камень из начала системы координат.Хотя это произвольно, мы обычно выбираем время t = 0, чтобы соответствовать началу координат. (b) Уравнение, описывающее горизонтальное движение:
с
это уравнение становится
(c) (рисунок) – (рисунок) и (рисунок) описывают вертикальное движение, но с
эти уравнения значительно упрощаются и становятся
и
(d) Мы используем кинематические уравнения, чтобы найти составляющие x и y скорости в точке удара.Используя
и учитывая, что точка удара равна −100,0 м, мы находим, что составляющая скорости при ударе y составляет
Нам дается компонент x ,
, поэтому мы можем рассчитать общую скорость при ударе: v = 46,8 м / с и
ниже горизонтали.
[/ hidden-answer]
Пример
Расчет движения снаряда: теннисист
Теннисист выигрывает матч на стадионе Артура Эша и отбивает мяч на трибунах со скоростью 30 м / с и под углом
над горизонтом ((Рисунок)).Спускаясь вниз, зритель ловит мяч на 10 м выше точки удара. (а) Подсчитайте время, за которое теннисный мяч достигает зрителя. (б) Каковы величина и направление скорости мяча при ударе?
Рисунок 4.14. Траектория удара теннисного мяча о трибуны.Стратегия
Опять же, разделение этого двумерного движения на два независимых одномерных движения позволяет нам найти желаемые величины. Время нахождения снаряда в воздухе определяется только его вертикальным движением.Таким образом, сначала мы решаем т . Пока мяч поднимается и опускается вертикально, горизонтальное движение продолжается с постоянной скоростью. В этом примере запрашивается окончательная скорость. Таким образом, мы рекомбинируем результаты по вертикали и горизонтали, чтобы получить
в конечный момент времени t , определенный в первой части примера.
Решение
(a) Пока мяч находится в воздухе, он поднимается, а затем падает в конечное положение на 10,0 м выше его начальной высоты.Мы можем найти время для этого, используя (Рисунок):
Если взять начальную позицию
равняется нулю, тогда конечная позиция будет y = 10 м. Начальная вертикальная скорость – это вертикальная составляющая начальной скорости:
Подставив в (рисунок) y , мы получим
Перестановка членов дает квадратное уравнение в t :
Использование формулы корней квадратного уравнения дает т = 3.79 с и т = 0,54 с. Поскольку мяч находится на высоте 10 м два раза на протяжении своей траектории – один раз по пути вверх и один раз по пути вниз, – мы выбираем более длительное решение для времени, которое требуется мячу, чтобы достичь зрителя:
Время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, который имеет начальную вертикальную скорость 21,2 м / с и приземляется на 10,0 м ниже своей начальной высоты, проводит в воздухе 3,79 с.
(б) Мы можем найти окончательные горизонтальную и вертикальную скорости
и
с использованием результата из (а).Затем мы можем объединить их, чтобы найти величину вектора полной скорости
и угол
делает с горизонтальным. С
является постоянным, мы можем найти его в любом горизонтальном положении. Мы выбираем начальную точку, потому что знаем как начальную скорость, так и начальный угол. Следовательно,
Окончательная вертикальная скорость определяется как (рисунок):
с
было найдено в части (а) как 21.2 м / с, имеем
Величина конечной скорости
это
Направление
находится через арктангенс:
Значение
(a) Как упоминалось ранее, время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, который имеет начальную вертикальную скорость 21,2 м / с и приземляется на 10.0 м ниже начальной высоты проводит в воздухе 3,79 с. (b) Отрицательный угол означает, что скорость равна
.ниже горизонтали в точке удара. Этот результат согласуется с тем фактом, что мяч ударяется о точку с другой стороны от вершины траектории и, следовательно, имеет отрицательную составляющую скорости y . Величина скорости меньше, чем величина начальной скорости, которую мы ожидаем, поскольку он ударяется на 10,0 м выше места старта.
Время полета, траектория и дальность
Интерес представляют время полета, траектория и дальность полета снаряда, выпущенного по плоской горизонтальной поверхности и ударяющегося по этой же поверхности. В этом случае кинематические уравнения дают полезные выражения для этих величин, которые выводятся в следующих разделах.
Время полета
Мы можем вычислить время полета снаряда, который одновременно запускается и ударяется о плоскую горизонтальную поверхность, выполнив некоторые манипуляции с кинематическими уравнениями.Отметим, что положение и смещение в y должны быть нулевыми при запуске и при ударе о ровную поверхность. Таким образом, мы устанавливаем смещение в y равным нулю и находим
Факторинг, у нас
Решение для т дает нам
Это время полета для снаряда, выпущенного и попавшего в плоскую горизонтальную поверхность. (Рисунок) не применяется, когда снаряд приземляется на высоте, отличной от того, на каком он был выпущен, как мы видели на (Рисунок), когда теннисист отбивает мяч в трибуны.Другое решение, t = 0, соответствует времени запуска. Время полета линейно пропорционально начальной скорости в направлении y и обратно пропорционально g . Таким образом, на Луне, где сила тяжести в шесть раз меньше земной, снаряд, запущенный с той же скоростью, что и на Земле, будет лететь в шесть раз дольше.
Траектория
Траектория снаряда может быть найдена путем исключения временной переменной t из кинематических уравнений для произвольного t и решения для y ( x ).Берем
, поэтому снаряд запускается из исходной точки. Кинематическое уравнение для x дает
Подставляем выражение для t в уравнение для позиции
дает
Переставляя сроки, получаем
Это уравнение траектории имеет вид
, которое представляет собой уравнение параболы с коэффициентами
Диапазон
Из уравнения траектории мы также можем найти диапазон , или горизонтальное расстояние, пройденное снарядом.Факторинг (рисунок), имеем
Положение y равно нулю как для точки запуска, так и для точки удара, поскольку мы снова рассматриваем только плоскую горизонтальную поверхность. Установка y = 0 в этом уравнении дает решения x = 0, соответствующие точке запуска, и
соответствует точке удара. Использование тригонометрического тождества
и установив x = R для диапазона, находим
Обратите особое внимание на то, что (рисунок) действительно только для запуска и удара о горизонтальную поверхность.Мы видим, что диапазон прямо пропорционален квадрату начальной скорости
и
, и он обратно пропорционален ускорению свободного падения. Таким образом, на Луне дальность полета будет в шесть раз больше, чем на Земле при той же начальной скорости. Кроме того, из множителя
видно, что, что диапазон максимален на
Эти результаты показаны на (Рисунок). В (а) мы видим, что чем больше начальная скорость, тем больше диапазон.В (b) мы видим, что диапазон максимален на
Это верно только для условий, пренебрегающих сопротивлением воздуха. Если учитывать сопротивление воздуха, максимальный угол несколько меньше. Интересно, что тот же диапазон обнаружен для двух начальных углов пуска, которые в сумме составляют
°.Снаряд, выпущенный с меньшим углом, имеет меньшую вершину, чем больший угол, но оба имеют одинаковую дальность.
Рисунок 4.15. Траектории полета снарядов на ровной поверхности.(а) Чем больше начальная скорость, тем больше диапазон для данного начального угла. (б) Влияние начального угла
на дальность полета снаряда с заданной начальной скоростью. Обратите внимание, что диапазон такой же для начальных углов
и
, хотя максимальные высоты этих путей различаются.
Пример
Сравнение снимков в гольф
Гольфист оказывается в двух разных ситуациях на разных лунках.На второй лунке он находится в 120 м от грина и хочет отбить мяч на 90 м и позволить ему вылететь на лужайку. Он направляет выстрел низко к земле, на
.в горизонтальное положение, чтобы мяч катился после удара. На четвертой лунке он находится в 90 м от грина и хочет, чтобы мяч упал с минимальным перекатом после удара. Здесь он направляет выстрел на
.в горизонтальное положение, чтобы свести к минимуму перекатывание после удара. Оба выстрела попадают и попадают на ровную поверхность.
(а) Какова начальная скорость мяча во второй лунке?
(b) Какова начальная скорость мяча на четвертой лунке?
(c) Напишите уравнение траектории для обоих случаев.
(d) Постройте траектории.
Стратегия
Мы видим, что уравнение дальности имеет начальную скорость и угол, поэтому мы можем найти начальную скорость как для (a), так и для (b). Когда у нас есть начальная скорость, мы можем использовать это значение для записи уравнения траектории.
Решение
(а)
(б)
(в)
(d) Используя графическую утилиту, мы можем сравнить две траектории, которые показаны на (Рисунок).
Рисунок 4.16. Две траектории мяча для гольфа с дальностью 90 м. Точки удара обоих находятся на том же уровне, что и точка взлета.Значение
Начальная скорость для выстрела на
больше начальной скорости выстрела на
Примечание из (Рисунок), что два снаряда, выпущенные с одинаковой скоростью, но под разными углами, имеют одинаковую дальность, если углы запуска складываются с
.Углы запуска в этом примере складываются, чтобы получить число больше
.Таким образом, выстрел на
должен иметь большую стартовую скорость, чтобы достичь 90 м, иначе он приземлится на меньшем расстоянии.
Проверьте свое понимание
Если бы два удара в гольф на (Рис.) Были произведены с одинаковой скоростью, какой удар имел бы наибольшую дальность?
[показывать-ответ q = ”fs-id1165166636799 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165166636799 ″]
Удар для гольфа на
[/ hidden-answer]
Когда мы говорим о дальности полета снаряда на ровной поверхности, мы предполагаем, что R очень мала по сравнению с окружностью Земли.Если, однако, дальность полета велика, Земля изгибается под снаряд, и ускорение силы тяжести меняет направление на траектории. Диапазон больше, чем предсказывалось уравнением дальности, приведенным ранее, потому что снаряд должен упасть дальше, чем на ровной поверхности, как показано на (Рисунок), который основан на чертеже Ньютона Principia. Если начальная скорость достаточно велика, снаряд выходит на орбиту. Поверхность Земли опускается на 5 м каждые 8000 м. За 1 с объект падает на 5 м без сопротивления воздуха.Таким образом, если объекту задана горизонтальная скорость
(или
у поверхности Земли, он выйдет на орбиту вокруг планеты, потому что поверхность постоянно падает от объекта. Это примерно скорость космического челнока на низкой околоземной орбите, когда он работал, или любого спутника на низкой околоземной орбите. Эти и другие аспекты орбитального движения, такие как вращение Земли, более подробно рассматриваются в книге «Гравитация».
Рисунок 4.17 Снаряд в спутник. В каждом показанном здесь случае снаряд запускается с очень высокой башни, чтобы избежать сопротивления воздуха. С увеличением начальной скорости радиус действия увеличивается и становится больше, чем на ровной поверхности, потому что Земля изгибается под своим путем. Со скоростью 8000 м / с достигается орбита.Сводка
- Движение снаряда – это движение объекта, подверженного только ускорению свободного падения, где ускорение постоянно, как у поверхности Земли.
- Для решения задач о движении снаряда мы анализируем движение снаряда в горизонтальном и вертикальном направлениях, используя одномерные кинематические уравнения для x и y .
- Время полета снаряда, выпущенного с начальной вертикальной скоростью
на ровной поверхности дает
Это уравнение действительно только тогда, когда снаряд приземляется на той же высоте, с которой был запущен.
- Максимальное горизонтальное расстояние, пройденное снарядом, называется дальностью. Опять же, уравнение для диапазона действительно только тогда, когда снаряд приземляется на той же высоте, с которой он был запущен.
Концептуальные вопросы
Ответьте на следующие вопросы относительно движения снаряда по ровной поверхности, предполагая незначительное сопротивление воздуха, с начальным углом, не равным
или
(a) Скорость когда-нибудь равна нулю? (б) Когда скорость минимальна? Максимум? (c) Может ли скорость когда-либо быть такой же, как начальная скорость в любой момент времени, кроме t = 0? (d) Может ли скорость когда-либо быть такой же, как начальная скорость в любой момент времени, кроме t = 0?
[показывать-ответ q = ”fs-id1165167780957 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165167780957 ″]
а.нет; б. минимум на вершине траектории и максимум при старте и ударе; c. нет, скорость – вектор; d. да, где приземляется
[/ hidden-answer]
Ответьте на следующие вопросы относительно движения снаряда по ровной поверхности, предполагая незначительное сопротивление воздуха, с начальным углом, не равным
или
(a) Ускорение всегда равно нулю? (б) Ускорение когда-либо в том же направлении, что и компонент скорости? (c) Ускорение когда-либо противоположно направлению компонента скорости?
Монета кладется на край стола так, чтобы она немного свешивалась.Четверть скользит горизонтально по поверхности стола перпендикулярно краю и ударяется о десятицентовую монету. Какая монета первой падает на землю?
[show-answer q = ”fs-id1165166623383 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165166623383 ″]
Они оба одновременно упали на землю.
[/ hidden-answer]
Проблемы
Пуля выпускается горизонтально с высоты плеча (1,5 м) с начальной скоростью 200 м / с. а) Сколько времени проходит до того, как пуля упадет на землю? (б) Как далеко пуля летит по горизонтали?
[show-answer q = ”fs-id1165168072758 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165168072758 ″]
а.
, г.
[/ hidden-answer]
Мрамор скатывается со столешницы высотой 1,0 м и ударяется об пол на расстоянии 3,0 м от края стола в горизонтальном направлении. а) Как долго мрамор витает в воздухе? б) С какой скоростью мрамор отрывается от края стола? (c) С какой скоростью он падает на пол?
Дротик метается горизонтально со скоростью 10 м / с в мишень мишени для дротика 2.На расстоянии 4 м, как показано на следующем рисунке. (а) Насколько далеко ниже намеченной цели попадает дротик? (б) Что ваш ответ говорит вам о том, как опытные игроки в дартс бросают свои дротики?
[показывать-ответ q = ”fs-id1165168078466 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165168078466 ″]
а.
, г. Они стремятся высоко.
[/ hidden-answer]
Самолет, летящий горизонтально со скоростью 500 км / ч на высоте 800 м, сбрасывает ящик с припасами (см. Следующий рисунок).Если парашют не открывается, как далеко от точки сброса ящик ударяется о землю?
Предположим, что самолет в предыдущей задаче выпускает снаряд горизонтально в направлении своего движения со скоростью 300 м / с относительно плоскости. (а) На каком расстоянии от точки срабатывания снаряд ударяется о землю? б) С какой скоростью он ударяется о землю?
[показывать-ответ q = ”fs-id1165167989106 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165167989106 ″]
а.,
г.
[/ hidden-answer]
Питчер фастбола может бросать бейсбольный мяч со скоростью 40 м / с (90 миль / ч). (a) Предполагая, что питчер может выпустить мяч на расстоянии 16,7 м от пластины дома, поэтому мяч движется горизонтально, сколько времени требуется мячу, чтобы добраться до пластины дома? (b) Как далеко мяч падает между рукой питчера и тарелкой хозяина?
Снаряд запускается под углом
и приземляется через 20 с на той же высоте, на которой был запущен.а) Какова начальная скорость снаряда? б) Какая максимальная высота? (c) Каков диапазон? (d) Рассчитайте смещение от точки запуска до положения на траектории за 15 с.
[показывать-ответ q = ”fs-id1165166793284 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165166793284 ″]
а.
, г.
г.
г.
[/ hidden-answer]
Баскетболист делает бросок в корзину 6.1 м и 3,0 м над полом. Если мяч выпущен на высоте 1,8 м от пола под углом
выше горизонтали, какой должна быть начальная скорость, если он пройдет через корзину?
В определенный момент воздушный шар находится на высоте 100 м и снижается с постоянной скоростью 2,0 м / с. Именно в этот момент девушка бросает мяч горизонтально относительно себя с начальной скоростью 20 м / с. Когда она приземлится, где она найдет мяч? Не обращайте внимания на сопротивление воздуха.
[show-answer q = ”fs-id11651665
″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id11651665
″]
[/ hidden-answer]
Человек на мотоцикле, едущем с постоянной скоростью 10 м / с, бросает пустую банку прямо вверх относительно себя с начальной скоростью 3,0 м / с. Найдите уравнение траектории, которую видит полицейский на обочине дороги. Предположим, что исходное положение банки – это точка, в которую ее бросают.Не обращайте внимания на сопротивление воздуха.
В прыжке в длину спортсмен может прыгнуть на расстояние 8,0 м. На какое максимальное расстояние спортсмен может прыгнуть на Луне, где ускорение свободного падения в шесть раз меньше земного?
[показывать-ответ q = ”fs-id1165167996165 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165167996165 ″]
[/ hidden-answer]
Максимальное горизонтальное расстояние, на которое мальчик может бросить мяч, составляет 50 метров. Предположим, он может бросать с одинаковой начальной скоростью под всеми углами.Насколько высоко он подбрасывает мяч, когда бросает его прямо вверх?
Камень сброшен со скалы под углом
по горизонтали. Высота обрыва – 100 м. Начальная скорость камня 30 м / с. а) Насколько высоко над краем утеса поднимается скала? б) Как далеко он переместился по горизонтали, когда находится на максимальной высоте? (c) Через какое время после выброса он падает на землю? г) Каков радиус действия скалы? (e) Каковы горизонтальное и вертикальное положение скалы относительно края обрыва при t = 2.0 с, т = 4,0 с и т = 6,0 с?
[показывать-ответ q = ”fs-id1165167746378 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165167746378 ″]
а.
,
г.
,
г.
,
г.
,
e.
[/ hidden-answer]
Пытаясь спастись от преследователей, секретный агент спускается на лыжах со склона
. ниже горизонтали на скорости 60 км / ч. Чтобы выжить и приземлиться на снегу на 100 м ниже, он должен преодолеть ущелье шириной 60 м. Он это делает? Не обращайте внимания на сопротивление воздуха.
Игрок в гольф на фервее находится в 70 м от грина, который находится ниже уровня фервея на 20 м.Если гольфист отбивает мяч под углом
с начальной скоростью 20 м / с, как близко она подходит к зеленому?
[show-answer q = ”fs-id1165168065281 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165168065281 ″]
Таким образом, удар игрока в гольф попадает на расстояние 13,3 м от грина.
[/ hidden-answer]
Снаряд выпущен по холму, основание которого находится на расстоянии 300 м.Снаряд выпущен на
над горизонтом с начальной скоростью 75 м / с. Холм можно представить как плоскость с уклоном
°.к горизонтали. Относительно системы координат, показанной на следующем рисунке, уравнение этой прямой линии равно
. Куда на холме приземляется снаряд?
Астронавт на Марсе бьет футбольный мяч под углом
с начальной скоростью 15 м / с.Если ускорение свободного падения на Марсе составляет 3,7 м / с, (а) каков радиус действия футбольного удара по плоской поверхности? б) Какова будет дальность такого же удара на Луне, где сила тяжести в шесть раз меньше земной?
[show-answer q = ”fs-id1165166572087 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165166572087 ″]
а.
,
г.
[/ hidden-answer]
Майк Пауэлл является рекордсменом по прыжкам в длину из 8.95 м, установлен в 1991 году. Если он отрывался от земли под углом
какова была его начальная скорость?
Робот-гепардMIT может перепрыгивать препятствия высотой 46 см и развивать скорость 12,0 км / ч. (а) Если робот запускается под углом
на этой скорости, какова его максимальная высота? б) Какой должен быть угол запуска, чтобы достичь высоты 46 см?
[показывать-ответ q = ”fs-id1165167842253 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165167842253 ″]
а.
[/ hidden-answer]
Гора Асама в Японии – действующий вулкан. В 2009 году в результате извержения были выброшены твердые вулканические породы, упавшие на 1 км по горизонтали от кратера. Если бы вулканические породы были запущены под углом
°.относительно горизонтали и приземлились на 900 м ниже кратера, (а) какова будет их начальная скорость и (б) каково время их полета?
Дрю Брис из Нового Орлеана Сэйнтс умеет бросать футбольный мяч 23.0 м / с (50 миль / ч). Если он направит бросок под углом
от горизонтали, на какое расстояние он пролетит, если должен быть пойман на той же высоте, что и брошенный?
[показывать-ответ q = ”fs-id1165168098591 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165168098591 ″]
[/ hidden-answer]
Лунный движущийся аппарат, использовавшийся в последних миссиях НАСА Apollo , достиг неофициальной наземной скорости Луны 5.0 м / с – астронавт Юджин Сернан. Если бы марсоход двигался с такой скоростью по плоской лунной поверхности и ударился о небольшую неровность, которая отбрасывала его от поверхности под углом
°.как долго он будет «летать» на Луне?
Высота футбольных ворот 2,44 м. Игрок отбивает мяч ногой на расстоянии 10 м от ворот под углом
Какова начальная скорость футбольного мяча?
[show-answer q = ”fs-id1165167854326 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165167854326 ″]
[/ hidden-answer]
Олимп-Монс на Марсе – крупнейший вулкан Солнечной системы, высотой 25 км и радиусом 312 км.Если вы стоите на вершине, с какой начальной скоростью вам нужно было бы запустить снаряд из пушки по горизонтали, чтобы очистить вулкан и приземлиться на поверхности Марса? Обратите внимание, что Марс имеет ускорение свободного падения
.В 1999 году Робби Книвел первым прыгнул через Гранд-Каньон на мотоцикле. В узкой части каньона (ширина 69,0 м), двигаясь со взлетной рампы 35,8 м / с, он достиг другой стороны. Какой у него был угол запуска?
[Показать-ответ q = ”fs-id1165168009639 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a = ”fs-id1165168009639 ″]
[/ hidden-answer]
Вы бросаете бейсбольный мяч с начальной скоростью 15.0 м / с под углом
по горизонтали. Какой должна быть начальная скорость мяча при
на планете, которая имеет вдвое большее ускорение силы тяжести, чем Земля, чтобы достичь той же дальности? Рассмотрим запуск и удар о горизонтальную поверхность.
Аарон Роджерс бросает мяч со скоростью 20,0 м / с в свой широкий ресивер, который бежит прямо по полю со скоростью 9,4 м / с на 20,0 м. Если Аарон бросает мяч, когда дальний приемник достигает 10.0 м, под каким углом должен быть Аарон, чтобы запустить мяч, чтобы получатель поймал его на отметке 20,0 м?
[показывать-ответ q = ”fs-id1165166777489 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165166777489 ″]
Широкому ресиверу требуется 1,1 с, чтобы покрыть последние 10 м своего бега.
[/ hidden-answer]
Глоссарий
- движение снаряда
- движение объекта, подверженного только ускорению свободного падения
- диапазон
- максимальная горизонтальная дальность полета снаряда
- время полета
- Время нахождения снаряда в воздухе
- траектория
- путь снаряда в воздухе
Камень брошен горизонтально со скоростью 15 м / с с вершины вертикального утеса на краю озера.Если камень попадает в
Два линейных уравнения, представленные в системе A как:
3 x + 2 y = 3 ——- (1)
– 2 x – 8 y = -1 —— (2)
(1) × 2 + (2) × 3 дает
⇒ 6 x + 4 y – 6 x – 24 y = 6-3
⇒ – 20 y = 3
⇒ y =
Подставляем значение y в уравнении (1), мы получаем
Два линейных уравнения, представленных в системе B:
3. -x – 14 y = 1
4.- 2 x – 8 y = -1
-2 × Уравнение (3) + Уравнение (4) =
2 x +28 y- 2 x – 8 y = -2-1
⇒ 20 y = -3
⇒y =
Подставляя значение y в уравнение (3), мы получаем
Как две системы, то есть система (A) и система (B) имеют одинаковое решение.
Посмотрев на все варианты, я обнаружил, что вариант (D) правильный. Две системы будут иметь одно и то же решение, потому что первое уравнение системы B получается добавлением первого уравнения системы A к двукратному увеличению второго уравнения системы A.
Ответ:
Я думаю, ответ – A
Пошаговое объяснение:
То, что случается, приземляясь вблизи побережья, не влияет на глобальные закономерности.
https://greentumble.com/how-does-the-ocean-affect-climate/
“Погода в основном определяется океанскими течениями, на которые влияют приземные ветры, температура, соленость, вращение Земли и океанские приливы.Океанские течения обычно текут по часовой стрелке в северном полушарии и против часовой стрелки в южном полушарии.
Океанские течения переносят теплую воду и дождь от экватора к полюсам, а холодную воду от полюсов к экватору. Эти океанические течения помогают противодействовать высокому уровню солнечной радиации, которую получает экватор Земли ».
40 000 фунтов равны 20 тоннам
Обычная форма линейного уравнения:
y = mx + b, где m – наклон.Если две линии параллельны, у них одинаковый наклон. Итак, первый шаг – преобразовать эти уравнения в общую форму:
A) y = -3x + 2
B) x-3y = -3
-3 y = – x-3 /: (- 3)
y = 1 / 3 x +1, 1/3 ≠ -3
C) 3x + y = -6
y = -3x – 6
D) 6x + 2 y = 2
2y = – 6x + 2 /: 2
y = -3x +1
Ответ: B)
3.4 Движение снаряда – Физика колледжа: OpenStax
Сводка
- Определите и объясните свойства снаряда, такие как ускорение свободного падения, дальность, максимальная высота и траектория.
- Определяет местоположение и скорость снаряда в разных точках его траектории.
- Применяйте принцип независимости движения для решения задач движения снаряда.
Движение снаряда – это движение объекта , брошенного или выброшенного в воздух, при условии только ускорения свободного падения.Объект называется снаряд , а его траектория называется траекторией . Движение падающих объектов, как описано в главе 2.6 «Основы решения задач для одномерной кинематики», представляет собой простой одномерный тип движения снаряда, в котором нет горизонтального движения. В этом разделе мы рассматриваем двумерное движение снаряда, например, футбольного мяча или другого объекта, для которого сопротивление воздуха незначительно .
Самый важный факт, который следует здесь запомнить, это то, что движения по перпендикулярным осям являются независимыми и, таким образом, могут быть проанализированы отдельно.Этот факт обсуждался в главе 3.1 «Кинематика в двух измерениях: введение», где вертикальные и горизонтальные движения рассматривались как независимые. Ключ к анализу двумерного движения снаряда состоит в том, чтобы разбить его на два движения, одно по горизонтальной оси, а другое по вертикали. (Этот выбор осей является наиболее разумным, поскольку ускорение свободного падения является вертикальным – таким образом, не будет ускорения по горизонтальной оси, когда сопротивление воздуха незначительно.) Как обычно, мы называем горизонтальную ось x – ось, а вертикальная ось – y – ось.На рисунке 1 показано обозначение смещения, где [latex] \ textbf {s} [/ latex] определяется как полное смещение, а [latex] \ textbf {x} [/ latex] и [latex] \ textbf {y} [/ latex] – это его составляющие по горизонтальной и вертикальной осям соответственно. Величины этих векторов равны s , x и y . (Обратите внимание, что в последнем разделе мы использовали обозначение [latex] \ textbf {A} [/ latex] для представления вектора с компонентами [latex] \ boldsymbol {\ textbf {A} _x} [/ latex] и [latex] \ boldsymbol {\ textbf {A} _y}.[/ latex] Если бы мы продолжили этот формат, мы бы назвали смещение [latex] \ textbf {s} [/ latex] с компонентами [latex] \ boldsymbol {\ textbf {s} _x} [/ latex] и [latex] \ boldsymbol {\ textbf {s} _y}. [/ latex] Однако, чтобы упростить обозначения, мы просто представим составляющие векторы как [latex] \ textbf {x} [/ latex] и [latex] \ textbf {y} [/ латекс].)
Конечно, чтобы описать движение, мы должны иметь дело со скоростью и ускорением, а также со смещением. Мы должны найти их компоненты по осям x и y .2}. [/ Latex] (Обратите внимание, что это определение предполагает, что направление вверх определяется как положительное направление. Если вместо этого вы расположите систему координат так, чтобы направление вниз было положительным, то ускорение свободного падения принимает положительное значение.) Поскольку сила тяжести вертикальная, [latex] \ boldsymbol {\ textbf {a} _x = 0}. [/ Latex] Оба ускорения постоянны, поэтому можно использовать кинематические уравнения. 2 + 2a (x-x_0).} [/ латекс]
Рис. 1. Общее смещение s футбольного мяча в точке на его пути. Вектор s имеет компоненты x и y по горизонтальной и вертикальной осям. Его величина составляет с , а с горизонтом он составляет угол θ .С учетом этих предположений для анализа движения снаряда используются следующие шаги:
Шаг 1. Разрешить или разбить движение на горизонтальные и вертикальные компоненты по осям x и y. Эти оси перпендикулярны, поэтому [latex] \ boldsymbol {\ textbf {A} _x = \ textbf {A cos} \: \ theta} [/ latex] и [latex] \ boldsymbol {\ textbf {A} _y = \ textbf {A sin} \: \ theta} [/ latex]. Величина компонентов смещения [latex] \ textbf {s} [/ latex] вдоль этих осей равна [latex] \ boldsymbol {x} [/ latex] и [latex] \ boldsymbol {y}. [/ Latex] величины компонентов скорости [латекс] \ textbf {v} [/ latex]: [латекс] \ boldsymbol {v_x = v \ textbf {cos} \ theta} [/ latex] и [латекс] \ boldsymbol {v_y = v \ textbf {sin} \ theta}, [/ latex] где [latex] \ boldsymbol {v} [/ latex] – величина скорости, а [latex] \ boldsymbol {\ theta} [/ latex] – это направление , как показано на рисунке 2.Начальные значения, как обычно, обозначаются индексом 0.
Шаг 2. Рассматривайте движение как два независимых одномерных движения, одно горизонтальное, а другое вертикальное. Кинематические уравнения для горизонтального и вертикального движения принимают следующий вид:
[латекс] \ boldsymbol {\ textbf {Horizontal Motion} (a_x = 0)} [/ latex]
[латекс] \ boldsymbol {x = x_0 + v_xt} [/ латекс]
[латекс] \ boldsymbol {v_x = v_ {0x} = v_x = \ textbf {скорость постоянна.2-2г (г-г_0).} [/ Латекс]
Шаг 3. Решите для неизвестных в двух отдельных движениях – одном горизонтальном и одном вертикальном. Обратите внимание, что единственная общая переменная между движениями – это время [latex] \ boldsymbol {t}. [/ Latex] Процедуры решения проблем здесь такие же, как и для одномерной кинематики , и проиллюстрированы в решаемых примерах ниже.
Шаг 4. Объедините два движения, чтобы найти полное смещение [latex] \ textbf {s} [/ latex] и скорость [latex] \ textbf {v}.{-1} (v_y \: / \: v_x).} [/ Латекс]
Рис. 2. (a) Мы анализируем двумерное движение снаряда, разбивая его на два независимых одномерных движения по вертикальной и горизонтальной осям. (b) Горизонтальное движение простое, потому что a x = 0 и v x , таким образом, является постоянным. (c) Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта; в самой высокой точке вертикальная скорость равна нулю.o} [/ latex] выше горизонтали, как показано на рисунке 3. Взрыватель рассчитан на воспламенение снаряда, как только он достигнет своей наивысшей точки над землей. (а) Рассчитайте высоту взрыва снаряда. б) Сколько времени прошло между запуском снаряда и взрывом? (c) Каково горизонтальное смещение снаряда при взрыве?Стратегия
Поскольку сопротивление воздуха невзорвавшейся оболочки незначительно, можно использовать описанный выше метод анализа.Движение можно разбить на горизонтальные и вертикальные движения, в которых [латекс] \ boldsymbol {a_x = 0} [/ latex] и [latex] \ boldsymbol {a_y = -g}. [/ Latex] Затем мы можем определить [латекс] \ boldsymbol {x_0} [/ latex] и [latex] \ boldsymbol {y_0} [/ latex] равными нулю и найдите желаемые количества.
Решение для (а)
Под «высотой» мы понимаем высоту или вертикальное положение [latex] \ boldsymbol {y} [/ latex] над начальной точкой. Наивысшая точка любой траектории, называемая апексом, достигается, когда [latex] \ boldsymbol {v_y = 0}.2)}}, [/ латекс]
, так что
[латекс] \ boldsymbol {y = 233 \ textbf {m}.} [/ Латекс]
Обсуждение для (а)
Обратите внимание: поскольку верх положительный, начальная скорость положительна, как и максимальная высота, но ускорение свободного падения отрицательное. Отметим также, что максимальная высота зависит только от вертикальной составляющей начальной скорости, так что любой снаряд с начальной вертикальной составляющей скорости 67,6 м / с достигнет максимальной высоты 233 м (без учета сопротивления воздуха).Цифры в этом примере приемлемы для больших фейерверков, снаряды которых достигают такой высоты перед взрывом. На практике сопротивлением воздуха нельзя пренебречь, поэтому начальная скорость должна быть несколько больше, чем заданная для достижения той же высоты.
Решение для (b)
Как и во многих других задачах физики, существует несколько способов решения на время до высшей точки. В этом случае самый простой способ – использовать [latex] \ boldsymbol {y = y_0 + \ frac {1} {2} (v_ {0y} + v_y) t}.[/ latex] Поскольку [latex] \ boldsymbol {y_0} [/ latex] равно нулю, это уравнение сводится к просто
[латекс] \ boldsymbol {y \: =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {2}} [/ latex] [латекс] \ boldsymbol {(v_ {0y} + v_y) t .} [/ латекс]
Обратите внимание, что окончательная вертикальная скорость [latex] \ boldsymbol {v_y}, [/ latex] в наивысшей точке равна нулю. Таким образом,
[латекс] \ boldsymbol {t = \ frac {2y} {(v_ {0y} + v_y)} = \ frac {2 (233 \ textbf {m})} {(67.6 \ textbf {m / s})} } [/ латекс]
[латекс] \ boldsymbol {= 6.90 \ textbf {s}.} \: \: \: \: \: \: \: \: \: [/ Латекс]
Обсуждение для (б)
Это время также подходит для больших фейерверков.2}, [/ latex] и решение квадратного уравнения для [latex] \ boldsymbol {t} [/ latex].)
Решение для (c)
Поскольку сопротивление воздуха незначительно, [латекс] \ boldsymbol {a_x = 0} [/ latex] и горизонтальная скорость постоянна, как обсуждалось выше. Горизонтальное смещение – это горизонтальная скорость, умноженная на время, как указано в [latex] \ boldsymbol {x = x_0 + v_xt}, [/ latex], где [latex] \ boldsymbol {x_0} [/ latex] равно нулю:
[латекс] \ boldsymbol {x = v_xt,} [/ латекс]
, где [latex] \ boldsymbol {v_x} [/ latex] – это составляющая x скорости, которая определяется как [latex] \ boldsymbol {v_x = v_0 \ textbf {cos} \: \ theta_0.о) = 18,1 \ textbf {м / с}.} [/ латекс]
Время [latex] \ boldsymbol {t} [/ latex] для обоих движений одинаковое, поэтому [latex] \ boldsymbol {x} [/ latex] равно
[латекс] \ boldsymbol {x = (18.1 \ textbf {m / s}) (6.90 \ textbf {s}) = 125 \ textbf {m}.} [/ Latex]
Обсуждение для (c)
Горизонтальное движение – это постоянная скорость при отсутствии сопротивления воздуха. Обнаруженное здесь горизонтальное смещение могло быть полезно для предотвращения падения фрагментов фейерверка на зрителей.2} {2g}.} [/ Латекс]
Это уравнение определяет максимальную высоту снаряда и зависит только от вертикальной составляющей начальной скорости.
ОПРЕДЕЛЕНИЕ СИСТЕМЫ КООРДИНАТ
Важно установить систему координат при анализе движения снаряда. Одна из частей определения системы координат – определить начало координат для позиций [latex] \ boldsymbol {x} [/ latex] и [latex] \ boldsymbol {y} [/ latex]. Часто бывает удобно выбрать начальную позицию объекта в качестве начала координат, такую как [latex] \ boldsymbol {x_0 = 0} [/ latex] и [latex] \ boldsymbol {y_0 = 0}.[/ latex] Также важно определить положительное и отрицательное направления в направлениях [latex] \ boldsymbol {x} [/ latex] и [latex] \ boldsymbol {y} [/ latex]. Обычно мы определяем положительное вертикальное направление как восходящее, а положительное горизонтальное направление – это обычно направление движения объекта. В этом случае вертикальное ускорение, [latex] \ boldsymbol {g}, [/ latex] принимает отрицательное значение (поскольку оно направлено вниз к Земле). Однако иногда бывает полезно определить координаты по-другому.Например, если вы анализируете движение мяча, брошенного вниз с вершины утеса, может иметь смысл определить положительное направление вниз, поскольку движение мяча происходит исключительно в направлении вниз. В этом случае [latex] \ boldsymbol {g} [/ latex] принимает положительное значение.
Пример 2: Расчет движения снаряда: Снаряд Hot Rock
Килауэа на Гавайях – самый постоянно действующий вулкан в мире. Очень активные вулканы обычно выбрасывают раскаленные камни и лаву, а не дым и пепел.o} [/ latex] выше горизонтали, как показано на рисунке 4. Камень ударяется о край вулкана на высоте 20,0 м ниже его начальной точки. (а) Вычислите время, которое требуется камню, чтобы пройти по этому пути. (б) Каковы величина и направление скорости горной породы при ударе?
Рисунок 4. Траектория горной породы, выброшенной из вулкана Килауэа.Стратегия
Опять же, разделение этого двумерного движения на два независимых одномерных движения позволит нам найти желаемые величины.Время нахождения снаряда в воздухе определяется только его вертикальным движением. Сначала мы решим [латекс] \ boldsymbol {t} [/ latex]. Пока камень поднимается и опускается вертикально, горизонтальное движение продолжается с постоянной скоростью. В этом примере запрашивается окончательная скорость. Таким образом, вертикальные и горизонтальные результаты будут рекомбинированы, чтобы получить [латекс] \ boldsymbol {v} [/ latex] и [latex] \ boldsymbol {\ theta_v} [/ latex] в последний раз [латекс] \ boldsymbol {t} [/ latex] определил в первой части примера.2-4ac}} {2a}} [/ латекс]
Это уравнение дает два решения: [latex] \ boldsymbol {t = 3.96} [/ latex] и [latex] \ boldsymbol {t = -1.03}. [/ Latex] (Это оставлено в качестве упражнения для читателя, чтобы проверить эти решения.) Время равно [latex] \ boldsymbol {t = 3.96 \ textbf {s}} [/ latex] или [latex] \ boldsymbol {-1.03 \ textbf {s}}. [/ latex] Отрицательное значение время подразумевает событие до начала движения, поэтому мы его отбрасываем. Таким образом,
[латекс] \ boldsymbol {t = 3.96 \ textbf {s}.} [/ Латекс]
Обсуждение для (а)
Время движения снаряда полностью определяется вертикальным движением.Таким образом, любой снаряд, который имеет начальную вертикальную скорость 14,3 м / с и приземляется на 20,0 м ниже своей начальной высоты, проведет в воздухе 3,96 с.
Решение для (b)
Из имеющейся информации мы можем найти окончательные значения горизонтальной и вертикальной скорости [латекс] \ boldsymbol {v_x} [/ latex] и [латекс] \ boldsymbol {v_y} [/ latex] и объединить их, чтобы найти общую скорость. [латекс] \ boldsymbol {v} [/ latex] и угол [латекс] \ boldsymbol {\ theta_0} [/ latex], который он образует с горизонталью.o} [/ latex] ниже горизонтали. Этот результат согласуется с тем фактом, что окончательная вертикальная скорость отрицательна и, следовательно, направлена вниз – как и следовало ожидать, поскольку конечная высота на 20,0 м ниже начальной. (См. Рисунок 4.)
Одна из самых важных вещей, иллюстрируемых движением снаряда, заключается в том, что вертикальные и горизонтальные движения независимы друг от друга. Галилей был первым человеком, полностью осознавшим эту особенность. Он использовал это, чтобы предсказать дальность полета снаряда.На ровной поверхности мы определяем диапазон как горизонтальное расстояние [latex] \ textbf {R} [/ latex], пройденное снарядом. Галилео и многие другие интересовались диапазоном снарядов в первую очередь для военных целей, таких как прицельные пушки. Однако изучение дальности действия снарядов может пролить свет на другие интересные явления, такие как орбиты спутников вокруг Земли. Рассмотрим дальность полета снаряда дальше.
Рис. 5. Траектории полета снарядов на ровной поверхности.(a) Чем больше начальная скорость v 0 , тем больше диапазон для данного начального угла. (b) Влияние начального угла θ 0 на дальность полета снаряда с заданной начальной скоростью. Обратите внимание, что диапазон одинаков для 15 o и 75 o , хотя максимальные высоты этих путей различаются.Как начальная скорость снаряда влияет на дальность его действия? Очевидно, что чем больше начальная скорость [latex] \ boldsymbol {v_0}, [/ latex], тем больше диапазон, как показано на рисунке 5 (a).2 \: \ textbf {sin} \: 2 \ theta_0} {g},} [/ латекс]
где [latex] \ boldsymbol {v_0} [/ latex] – начальная скорость, а [latex] \ boldsymbol {\ theta_0} [/ latex] – начальный угол относительно горизонтали. Доказательство этого уравнения остается задачей в конце главы (даются подсказки), но оно соответствует основным характеристикам дальности полета снаряда, как описано.
Когда мы говорим о дальности полета снаряда на ровной поверхности, мы предполагаем, что [latex] \ textbf {R} [/ latex] очень мала по сравнению с окружностью Земли.Однако, если диапазон большой, Земля изгибается под снаряд, и ускорение свободного падения меняет направление на траектории. Дальность больше, чем предсказано уравнением дальности, приведенным выше, потому что снаряд должен упасть дальше, чем на ровной поверхности. (См. Рисунок 6.) Если начальная скорость достаточно велика, снаряд выходит на орбиту. Эта возможность была признана за столетия до того, как она могла быть реализована. Когда объект находится на орбите, Земля изгибается из-под объекта с той же скоростью, с которой он падает.Таким образом, объект непрерывно падает, но никогда не ударяется о поверхность. Эти и другие аспекты орбитального движения, такие как вращение Земли, будут рассмотрены аналитически и более подробно позже в этом тексте.
Мы снова видим, что размышления об одной теме, например о дальности полета снаряда, могут привести нас к другим, таким как орбиты Земли. В главе 3.5 «Сложение скоростей» мы рассмотрим сложение скоростей, которое является еще одним важным аспектом двумерной кинематики и также даст понимание, выходящее за рамки непосредственной темы.
Рис. 6. Снаряд в спутник. В каждом показанном здесь случае снаряд запускается с очень высокой башни, чтобы избежать сопротивления воздуха. С увеличением начальной скорости радиус действия увеличивается и становится больше, чем на ровной поверхности, потому что Земля изгибается под своим путем. При достаточно большой начальной скорости достигается орбита.ФЕТ ИССЛЕДОВАНИЯ: ДВИЖЕНИЕ ПРОЕКТА
Выстрелите из пушки «бьюик»! Узнавайте о движении снарядов, стреляя различными объектами.Установите угол, начальную скорость и массу. Добавьте сопротивление воздуха. Сделайте из этой симуляции игру, пытаясь поразить цель.
Рисунок 7. Движение снаряда.- Снаряд – это движение объекта по воздуху, на которое действует только ускорение свободного падения.
- Чтобы решить проблемы с движением снаряда, выполните следующие действия:
- Определите систему координат. Затем определите положение и / или скорость объекта в горизонтальной и вертикальной составляющих.Компоненты позиции [latex] \ textbf {s} [/ latex] задаются количествами [latex] \ boldsymbol {x} [/ latex] и [latex] \ boldsymbol {y}, [/ latex] и компонентами скорости [латекс] \ textbf {v} [/ latex] задаются как [latex] \ boldsymbol {v_x = v \: \ textbf {cos} \: \ theta} [/ latex] и [latex] \ boldsymbol { v_y = v \: \ textbf {sin} \: \ theta}, [/ latex] где [latex] \ boldsymbol {v} [/ latex] – величина скорости, а [latex] \ boldsymbol {\ theta} [ / latex] – его направление.
- Проанализируйте движение снаряда в горизонтальном направлении, используя следующие уравнения:
[латекс] \ boldsymbol {\ textbf {Горизонтальное движение} (a_x = 0)} [/ latex]
[латекс] \ boldsymbol {x = x_0 + v_xt} [/ латекс]
[латекс] \ boldsymbol {v_x = v_ {0x} = \ textbf {v} _x = \ textbf {скорость – постоянная величина. o} [/ latex]): (а) Ускорение когда-нибудь равно нулю? (б) Ускорение когда-либо в том же направлении, что и компонент скорости? (c) Ускорение когда-либо противоположно направлению компонента скорости?
3: При фиксированной начальной скорости дальность полета снаряда определяется углом выстрела.Для всех, кроме максимального, есть два угла, которые дают одинаковый диапазон. Учитывая факторы, которые могут повлиять на способность лучника поразить цель, например ветер, объясните, почему меньший угол (ближе к горизонтали) предпочтительнее. Когда лучнику потребуется использовать больший угол? Почему игрок в футбольном матче использует более высокую траекторию?
4: Во время демонстрации лекции профессор кладет две монеты на край стола. Затем она сбрасывает одну из монет со стола по горизонтали, одновременно подталкивая другую за край.0} [/ latex] выше горизонтали. Через 3 секунды он поражает цель над землей. Какое расстояние [латекс] \ boldsymbol {x} [/ latex] и [латекс] \ boldsymbol {y} [/ latex] от места запуска снаряда до места приземления?
2: По мячу наносится удар с начальной скоростью 16 м / с в горизонтальном направлении и 12 м / с в вертикальном направлении. 0} [/ latex] со скоростью [латекс ] \ boldsymbol {40.0 \ textbf {m / s} \ 🙁 144 \ textbf {km / h})}. [/ Latex] Сколько автобусов он может очистить, если верх взлетной рампы находится на той же высоте, что и верхняя часть автобуса, и автобусы длиной 20,0 м? (b) Обсудите, что ваш ответ подразумевает допустимую погрешность в этом действии, то есть подумайте, насколько больше диапазон, чем горизонтальное расстояние, которое он должен пройти, чтобы пропустить конец последнего автобуса. (Пренебрегая сопротивлением воздуха.)
5: Лучник стреляет из лука в цель на расстоянии 75,0 м; прицел цели находится на той же высоте, что и высота выхода стрелы.(а) Под каким углом должна быть выпущена стрела, чтобы попасть в цель, если ее начальная скорость составляет 35,0 м / с? В этой части задачи явно покажите, как вы выполняете шаги, связанные с решением проблем с движением снаряда. (b) На полпути между лучником и целью есть большое дерево с нависающей горизонтальной ветвью на 3,50 м над высотой выпуска стрелы. Пойдет стрелка над веткой или под веткой?
6: Игрок в регби передает мяч 7,00 м через поле, где он пойман на той же высоте, что и оставил его руку.0} [/ latex] и заданные начальные скорости.
8: Проверьте диапазоны, показанные для снарядов на Рисунке 5 (b) для начальной скорости 50 м / с при заданных начальных углах.
9: Пушка линкора может стрелять снарядом на максимальную дальность 32,0 км. (а) Рассчитайте начальную скорость снаряда. б) Какой максимальной высоты он достигает? (На самом высоком уровне оболочка составляет более 60% атмосферы, но сопротивление воздуха на самом деле не является незначительным, как предполагается, чтобы облегчить эту проблему.0} [/ latex] выше горизонтали. Через 4 секунды он приземляется на вершину обрыва. а) Какова высота обрыва? (б) Какая максимальная высота достигает стрелка на своей траектории? (c) Какова скорость удара стрелы непосредственно перед тем, как она упадет в обрыв?
11: В прыжке в длину с места человек приседает, а затем отталкивается ногами, чтобы посмотреть, как далеко он может прыгнуть. Предположим, что разгибание ног из положения приседа составляет 0,600 м, а ускорение, достигаемое из этого положения, равно 1.В 25 раз больше ускорения свободного падения, [latex] \ textbf {g}. [/ Latex] Как далеко они могут прыгнуть? Выскажите свои предположения. (Увеличенной дальности можно добиться, поворачивая руки в направлении прыжка.)
12: Мировой рекорд по прыжкам в длину – 8,95 м (Майк Пауэлл, США, 1991 г.). Какова максимальная дальность полета, которую может получить человек, если его взлетная скорость составляет 9,5 м / с? Выскажите свои предположения.
13: На скорости 170 км / ч теннисист отбивает мяч на высоте 2.5 м и угол [латекс] \ boldsymbol {\ theta} [/ latex] ниже горизонтали. Линия обслуживания находится на расстоянии 11,9 м от сети, высота 0,91 м. Каков угол [латекс] \ boldsymbol {\ theta} [/ латекс], при котором мяч просто пересекает сетку? Приземлится ли мяч в штрафную площадку, внешняя линия которой находится на расстоянии 6,40 м от сетки?
14: Футбольный квотербек движется прямо назад со скоростью 2,00 м / с, когда он делает передачу игроку 18,0 м прямо вниз по полю. 0} [/ latex] по отношению к земле и пойман на той же высоте, что и выпущен, какова его начальная скорость относительно земля? б) Сколько времени нужно, чтобы добраться до получателя? (c) Какова его максимальная высота над точкой выпуска?
15: Прицелы настроены так, чтобы прицелиться высоко, чтобы компенсировать влияние силы тяжести, что эффективно обеспечивает точность прицела только на определенном расстоянии.(a) Если ружье прицеливается для поражения целей, которые находятся на той же высоте, что и ружье, и на расстоянии 100,0 м, насколько низко попадет пуля, если ее направить прямо в цель на расстоянии 150,0 м? Начальная скорость пули – 275 м / с. (б) Обсудите качественно, как большая начальная скорость пули повлияет на эту проблему и каков будет эффект сопротивления воздуха.
16: Орел летит горизонтально со скоростью 3,00 м / с, когда рыба в его когтях свободно раскачивается и падает в озеро 5.0} [/ latex] выше горизонтали.
19: Может ли вратарь у своих ворот забить футбольный мяч в ворота соперника, не касаясь земли? Дистанция составит около 95 м. Вратарь может дать мячу скорость 30 м / с.
20: Линия штрафных бросков в баскетболе находится на расстоянии 4,57 м (15 футов) от корзины, что на 3,05 м (10 футов) над полом. Игрок, стоящий на линии штрафного броска, бросает мяч с начальной скоростью 7,15 м / с, выпуская его на высоте 2.44 м (8 футов) над полом. Под каким углом над горизонтом нужно бросить мяч так, чтобы он точно попал в корзину? Обратите внимание, что большинство игроков будут использовать большой начальный угол, а не прямой выстрел, потому что это допускает большую погрешность. Ясно покажите, как вы выполняете шаги, связанные с решением проблем с движением снаряда.
21: В 2007 году Майкл Картер (США) установил мировой рекорд в толкании ядра с броском 24,77 м. Какова была начальная скорость выстрела, если он выпустил его на высоте 2.0} [/ latex] в толкании ядра.)
22: Баскетболист бежит [latex] \ boldsymbol {5.00 \ textbf {m / s}} [/ latex] прямо к корзине, когда он прыгает в воздух, чтобы замочить мяч. Он сохраняет свою горизонтальную скорость. а) С какой вертикальной скоростью ему нужно подняться на 0,750 м над полом? (b) На каком расстоянии от корзины (в горизонтальном направлении) он должен начать свой прыжок, чтобы достичь максимальной высоты одновременно с достижением корзины?
23: Футболист направляет мяч в [латексный] \ boldsymbol {45.2 \: \ textbf {sin} \: 2 \ theta_0} {g}} [/ latex] для определения дальности полета снаряда на ровной поверхности, найдя время [latex] \ boldsymbol {t} [/ latex], в которое [ latex] \ boldsymbol {y} [/ latex] становится равным нулю и подставляя это значение [latex] \ boldsymbol {t} [/ latex] в выражение для [latex] \ boldsymbol {x-x_0}, [/ latex] отмечая что [латекс] \ boldsymbol {\ textbf {R} = x-x_0} [/ latex]
26: Необоснованные результаты (a) Найдите максимальную дальность стрельбы суперпушки с начальной скоростью 4,0 км / с. б) Что неразумного в найденном вами диапазоне? (c) Является ли предпосылка необоснованной или имеющееся уравнение неприменимо? Поясните свой ответ.(d) Если такая начальная скорость может быть получена, обсудите влияние сопротивления воздуха, разрежения воздуха с высотой и кривизны Земли на дальность действия супер-пушки.
27: Постройте свою задачу Представьте мяч, брошенный через забор. Составьте задачу, в которой вы вычисляете необходимую начальную скорость мяча, чтобы просто преодолеть забор. Среди вещей, которые нужно определить: высота ограждения, расстояние до ограждения от точки выброса мяча и высота, на которой мяч выпущен.Вы также должны подумать, можно ли выбрать начальную скорость для мяча и просто рассчитать угол, под которым он брошен. Также изучите возможность нескольких решений с учетом выбранных вами расстояний и высоты.
Глоссарий
- сопротивление воздуха
- сила трения, которая замедляет движение объектов при их перемещении по воздуху; при решении основных физических задач сопротивление воздуха принимается равным нулю
- кинематика
- Изучение движения без учета массы или силы
- движение
- Смещение объекта как функция времени
- снаряд
- Объект, который движется по воздуху и испытывает только ускорение силы тяжести
- движение снаряда
- движение объекта, подверженного только ускорению свободного падения
- диапазон
- максимальное горизонтальное расстояние, которое проходит снаряд
- траектория
- Путь снаряда в воздухе
Решения
Задачи и упражнения
1:
[латекс] \ boldsymbol {x = 1.0} [/ латекс]
да, мяч приземляется на 5,3 м от сетки
15:
(а) −0,486 м
(b) Чем больше начальная скорость, тем меньше отклонение в вертикальном направлении, потому что время полета будет меньше. Сопротивление воздуха привело бы к уменьшению времени полета, следовательно, к увеличению вертикального отклонения.
17:
4,23 м. Нет, сове не повезло; он скучает по гнезду.
19:
Нет, максимальная дальность (без учета сопротивления воздуха) около 92 м.2 \: \ textbf {sin} \: 2 \ theta} {g}}. [/ Latex]
Мяч бросается вертикально вверх с уровня земли с начальной скоростью 96
… бросается вертикально вверх с начальной скоростью u, как показано на рисунке 2.5. Предполагая, что сопротивление воздуха незначительно, ускорение мяча, a = g, когда мяч движется 46. ФИЗИЧЕСКАЯ ГЛАВА 2 46 Мячу, брошенному с вершины здания, придается начальная скорость 10,0 м сÀ1 прямо вверх.Instrumental kompa orchester dad mix beat
- Наземное обслуживание Отмеченное наградами подразделение наземного обслуживания Swissport в настоящее время обеспечивает обслуживание пассажиров и пандусов на более чем 197 станциях по всему миру. Клиенты Swissport Aviation Security могут выбрать решение, подходящее для них; будь то на локальном или глобальном уровне, Checkport…
- 1. Мяч подбрасывается вертикально вверх со скоростью 25,0 м / с. а) Насколько высоко он поднимается? б) Сколько времени нужно, чтобы достичь высшей точки? (c) Сколько времени требуется мячу, чтобы коснуться земли после того, как он достигнет своей наивысшей точки? (г) Какова его скорость, когда он возвращается на уровень, с которого он стартовал? 2.
Если мяч брошен вертикально вверх с вершины здания высотой 96 футов с начальной скоростью 80 футов в секунду и расстояние s в футах от земли до мяча через t секунд равно s 96 80t 16t 2 через сколько секунд мяч ударится о землю?
Мяч бросается вертикально вверх с начальной скоростью 80 футов в секунду.2. (a) В какое время t будет мяч… подробнее.
Мяч бросается вертикально вверх с вершины здания высотой 96 футов с начальной скоростью 80 футов в секунду. Расстояние s (в футах) до мяча от земли через t секунд определяется функцией:
Ребенок бьет по мячу ногой с начальной скоростью 8,5 метра в секунду под углом 35º к горизонтали, как показано. Мяч имеет начальную вертикальную скорость 4,9 метра в секунду и общее время полета 1.2 + 2 как….
Лучше будет проповедь
Заземление осуществляется с помощью заземляющих электродов, которые напрямую связаны с землей. Сопротивление изоляции любой установки следует регулярно контролировать с помощью измерительных приборов. Неисправные детали должны быть обнаружены, устранены и заменены новыми.
13. Мяч подбрасывается вверх с высоты 15 футов. Начальная скорость мяча составляет 5 футов в секунду. Используйте формулу 16t2 + vt + s, чтобы найти, сколько времени потребуется мячу, чтобы ударить h (t) о землю.л. RcmclT – —SE = -s ± 31,38 -32 – 14. Если ракета запускается вертикально вверх от земли с начальной скоростью 128 футов …
Мяч подбрасывается вертикально вверх с начальной скоростью 96 футов за с… 04:10 Физика Мяч бросается вертикально вверх с начальной скоростью 80 fe…
8 октября 2008 · Иногда y начальное и y конечное различаются (например, бросание мяча вверх в воздухе – начальная буква y – это ваша рука – и когда он идет вниз, он проходит мимо вашей руки и, например, падает в канаву или ударяется о землю), и в этом случае вы должны рассчитать дельту t для восходящего движения и дельту t для нисходящего отдельно.
Вопросы и ответы по физике для AIEEE, банковских экзаменов, CAT, GATE, аналитика, банковского служащего, почтового оператора банка, ИТ-тренера: мяч подбрасывается вертикально вверх. Это означает, что за 2 секунды объект достигает вершины, а в следующие 2 секунды, он снова достигает той же точки. По предоставленной информации мы можем определить скорость этой точки …
Дальнейшие раскопки могут проводиться только после удаления верхнего органического слоя. В более холодном климате фундамент зданий следует располагать ниже уровня, до которого земля промерзает зимой.90. Мяч, брошенный вертикально вверх с начальной скоростью 3 м / с из окна высокого здания. Спустя 4 секунды мяч ударяется о тротуар на уровне земли. 91. Игрок подбрасывает бейсбольный мяч вверх с начальной скоростью 30 футов / сек и ловит его бейсбольной перчаткой. Задача 1008 Камень брошен вертикально вверх от земли со скоростью 48,3 фута в секунду (14,72 м / сек) . Насколько высоко над землей камни будут на одном уровне? Решение в английской системе.
Началась война, именуемая Великой Отечественной войной, действительно тяжелой для нашей страны.В первые недели войны на земле было уничтожено более 1000 советских самолетов; целые армии были окружены и взяты в плен; мирные поселки, города и села были стерты с лица земли.
Дальнейшие раскопки могут проводиться только после удаления верхнего органического слоя. В более холодном климате фундамент зданий следует располагать ниже уровня, до которого земля промерзает зимой.
Парень присылает «доброе утро» каждый день
Diy kydex kit
Фактически, учитывая только горизонтальный полет и нормальный набор высоты и глиссирование в устойчивом состоянии, все еще верно, что подъемная сила, обеспечиваемая крылом или несущим винтом, является первичная восходящая сила, а вес – первичная нисходящая сила.
Мяч метается вертикально вверх из окна. Работа, выполняемая под действием силы тяжести по мячу, брошенному вертикально вверх.
Мяч, брошенный вертикально с уровня земли, ловится через 3,0 секунды, когда он находится в самой высокой точке, человеком на балконе, который находится на высоте 14 м над землей. Определите начальную скорость мяча. A) 19 м / с B) 4,7 м / с C) 10 м / с D) 34 м / с E) 17 м / с
Вопрос 96. Давайте сначала посмотрим на полное предложение: «Что есть НА первом этаже? Вашей школы? ” Предлог «на» используется со словом «земля», потому что это поверхность, точно так же, как он используется со словом «стол» и т. Д.
Netgear nighthawk ac1900 wow internet
Великий сдвиг гласных – это серия изменений в произношении английского языка, которые произошли в основном между 1400 и 1700 годами, начиная с южной Англии и сегодня оказали эффективное влияние на все диалекты английского языка. Английский.
Использование квадратного уравнения Задачи Мяч бросается вертикально вверх с вершины здания высотой 112 футов с начальной скоростью 96 футов в секунду. Расстояние s (в футах) от земли до мяча через t секунд равно s (t) = 112 + 96t – 16t 2 Заполните таблицу и обсудите интерпретацию каждого пункта.ts (t) Интерпретация 0 112 Мяч находился на исходной высоте s (0 …
Схема вязания мужской шапки с напуском Код ошибки Hik connect 240037
Задняя ось багги Dune в сборе
Iclone 7 props Сколько граммов яблочной кислоты в яблочном соке
Аукцион по животноводству Richfield
Почему мой бывший пытается добавить меня в facebookПродажа домов
tasmania Серийное письменное обновление Бхакарвади Глобус Coleman Pyrex
Шар выпускается из нижней части лифта, который движется вверх со скоростью 6 футов> с.Если * 12-12. Сфера выстреливается вниз в среду с начальной скоростью 27 м> с. Если это Спустя секунду, другой мяч будет брошен вертикально от земли со скоростью 10 м> с. Определите … Получите подробный ответ: Скорость и ускорение: мяч подбрасывается вертикально вверх от уровня земли с начальной скоростью 96 футов в секунду. Us Руководство Capsim 2020
Отзыв о пожаре в посудомоечной машине FrigidaireМетро, которое принимает ebt рядом со мной
Eecs 280 umich midterm Bdo t1 discord
при s (0) \ ft, поэтому мы можем найти соответствующее значение t, соответствующее уровню земли (и мы ожидаем, что одно # t = -2 # соответствует времени, в которое мяч был бы на уровне земли, если бы его бросили с уровня земли, а не на высоте # 96… Модификации Lb7 mpg
Layarkaca21 film malaysia terbaru 2018Поиск контракта City of Phoenix
Корейская тетива для лука Amazon premier protein
брошен вертикально вверх с вершины здания высотой 112 футов с начальной скоростью 96 футов в секунду. Расстояние s (в футах) до земли через t секунд составляет s = 1… Оба графика ниже представляют движение мяча после того, как он был брошен вертикально вверх с начальной скоростью 15 м / с.График скорость – время показывает, что скорость уменьшается до нуля, когда мяч достигает максимальной высоты, а затем увеличивается. График скорости-времени также показывает изменение направления мяча. Gurmit dhak жена
телугу WhatsApp статус телеграмм каналПочему itunes так медленно работает на windows reddit
Iphone 11 напряжение глаз reddit Спецификации материнской платы HP 3048h
9218по вертикали с уровня земли – кауг.2 + 28t + 5 дает высоту мяча в футах через t секунд после того, как он был брошен, определить время, в которое мяч достигает максимальной высоты, и найти максимальную высоту Мяч достигает максимальной высоты в ___ футов ____ секунд после того, как мяч был брошен. брошеноПокажите свою работу Поистине великое Соединенное Королевство
Сейчас полиция ХендерсонаБазовая лампа на прикроватной тумбочке
Проблемы с двигателем Ti vct Красный ледяной холокост
Когда мяч был брошен вверх возвращается на высоту вершины здания, его скорость снова вый.У него будет такая же скорость. 2.21 Жюль Верн в 1865 году предложил отправить людей на Луну, запустив космическую капсулу из пушки длиной 220 м с конечной скоростью 10,97 км / с. Технические вопросы интервью RedditDell R510 бесшумные вентиляторы
Какая таблица представляет линейную функцию 1 5
Tether coinOc outfit generator 9182 Dmart
Щенки колли-микс, штат Огайо
Спортивный матч Бейн
26 июля 2010 г. · Мяч подбрасывается вертикально вверх от уровня земли с начальной скоростью 128 футов в секунду….? Найдите следующее: а). Сколько времени потребуется, чтобы мяч поднялся на максимальную высоту? б) Какая максимальная высота? в) Когда скорость мяча равна -64 фута в секунду? г) когда мяч находится на высоте 240 футов над землей? д) С какой скоростью мяч ударяется о землю? Используйте (t … Какое оборудование используется для сбора конопли
На сенсорном экране упавшего iPod есть вертикальные линииПример задачи суммы подмножества
Практика подсчета атомов c ключ ответа
3Pdfbox latest версия
Не отключайте предохранительные блокировки, заземляющие штыри или другие устройства, предназначенные для _.Вам следует использовать защитные очки всякий раз, когда вы находитесь рядом с химическими веществами, которые могут разбрызгиваться, или предметами, которые могут быть брошены. Какой максимальный уровень тока может выдержать человек, не получив травм? A. 1 метр над ним на уровне земли, как показано. 1. Тело массы, движущееся со скоростью, сталкивается с неподвижным телом той же массы и прилипает к нему. В какой строке описываются импульс и кинетическая энергия двух тел после столкновения? Регулировка тормоза поворота экскаватора
Руководство пользователя мини-проектора AukingРабочий лист Verb test
Программа просмотра журнала Nps
Вентилятор W204 всегда включенПоддерживает ли ps4 время отклика 1 мс
Обход iphone 4 icloud с полной активацией и без фиксированного обслуживания_
Сборка для глубокого майнинга типа 9Lifan 200cc
Названия Земли
6Бесплатные учетные записи PS4 и пароли с играми
18 18 Лукбук Cabi весна 2018 pdf
Как отреагировать на ходатайство в суде по семейным делам ФлоридаВытяжка Burris iv на продажу
Dji max altitude hack
Rust bandit camp gambling pattern 2020Висконсинская ассоциация производителей птиц и диких животных
10.Найдите скорость монеты при падении на землю. Мяч подбрасывается прямо в воздух (вертикально) от земли с начальной скоростью 144 фута / сек. 11. Найдите положение мяча через 4 секунды. 12. В момент времени t = 4 с мяч все еще поднимается или опускается. Покажи свое оправдание. Мяч брошен прямо из … Huawei rru 5502Nuggmd reddit california
Daily 3 выигрышных номера ivomic
Бесплатная тренировка acapellaБесплатные рабочие листы по идентификации монет и их стоимости
Французские бульдоги для принятия во Флориде Ats Twin Turbo 5.2 {/ eq}, гравитация препятствует движению мяча вверх и способствует его спуску …
Аризона, округ 6Cp caldo de pollo mega
Что вы можете почувствовать в лесуКлавиатура Чакче не загорается
независимые школы вакансии Dr cabral deathsMewtwo gx full art rainbow red
Osrs позолоченный калькулятор алтаряКак настроить монитор lg
Wattpad menyusu
2Как сделать символ Пи
9192 на chromebook Через t секунд шар, подбрасываемый в воздух с уровня земли
Удары молнии «облако-земля» – обычное явление – около 100 ударов молнии ударяют по поверхности Земли каждую секунду – все же их сила необычайна.Ochs ‘Grind. источник: Джонатан Окс. 1) Сделайте трапецию для левой руки. - Попросите игрока положить мяч на землю перед собой. Затем он будет имитировать игру наземным мячом. После того, как он выставил мяч в поле, он сделает пару шаркающих шагов по направлению к цели, получая при этом хорошее положение для броска. После пары шаркающих шагов он сделает шаг и бросит.
Мяч не может быть брошен на полную треть корта, если игрок не коснется его или не поймает его (т.е. он не может пересекать две поперечные линии). Свободный пас должен выполняться из зоны, где мяч пересек вторую поперечную линию (т.е. там, где мяч не должен был находиться). Переигран мяч. Игрок не может переиграть мяч.
Мяч подбрасывается в воздух с высоты 8 футов с начальной скоростью 8 футов в секунду. Найдите время r (в секундах), которое требуется объекту, чтобы достичь земли, решив уравнение – 16t + 8t + 8 = 0 вы отрезали большую полосу обоев из обрезков, чтобы она уместилась в углу стены, на которую вы оклеиваете обои. .вы отрезали 15 дюймов от длины.
Игнорировать сопротивление воздуха. а) Как долго мяч находится в воздухе? б) Какой должна была быть начальная горизонтальная составляющая скорости? (c) Какова вертикальная составляющая скорости непосредственно перед тем, как мяч упадет на землю? (d) Какова скорость (включая горизонтальную и вертикальную составляющие) мяча непосредственно перед тем, как он упадет на землю?
Ответ / Правило Вопросы уровня 2 F (2-2) T F Бита непреднамеренно хлопает, ударяет или перенаправляет мяч рукой или рукой.F (2-3-1) T F Находясь в воздухе, игрок удерживает мяч, но роняет его, когда касается земли. Решение: Правовая уловка. F (2-15) T F Муфта – это успешная попытка поймать мяч.
Попробуйте сыграть в бейсбольный мяч. Бита с некоторым mv совершает импульсивный контакт с мячом – m bat больше, чем m ball, и так как: (mv) bat = (mv) мяч. тогда v мяч больше, чем v bat (при условии, что вы бьете по мячу, а не только по воздуху). Тот же принцип действует и в случае отдачи пушки: потенциальная энергия -> объект занимает позицию в силе. 2.Через сколько секунд мяч коснется земли до отскока?
[Сопротивлением воздуха пренебречь] 2. 15. Футбольный мяч, получивший удар ногой, имеет начальную скорость 25 метров в секунду под углом 40 ° над горизонтальной ровной поверхностью. [Пренебрежение трением.] Рассчитайте величину вертикальной составляющей начальной скорости мяча. [Показать всю работу, включая уравнение и замену с единицами измерения. Viy = 16,07 м / с
Мяч, который не отскакивает, но полностью достигает игрока с битой, является подбрасыванием полного броска.Боулеры со спиннингом используют пальцы или запястье, чтобы вращать мяч так, чтобы он не отскакивал прямо от поля после отскока, а отскакивал вверх под неожиданным углом.
Из Рогавского 2e, раздел 3.4, упражнение 27. Мяч подбрасывается вертикально с уровня земли и возвращается на землю через 6 секунд. Какая была начальная скорость мяча и как высоко он летел? Vo = м / с h = м
Лопание воздушного шара началось с 0,05 секунды (0 дБ) и достигло уровня -60 дБ через 0,45 с. Таким образом, время реверберации равно 0.40 с, что довольно типично для гостиной дома (откуда я взял этот образец). Такое короткое время реверберации отлично подходит для речи и музыки дома (но безнадежно в концертном зале). После обновления 1.09.00 его можно будет оснастить Android 18 и пользовательским набором навыков Yamcha после того, как он будет приобретен в разделе «Настройка партнера». В Dragon Ball FighterZ он появляется как один из специальных приемов Криллина, но может использоваться только на земле. Android 21 и ее деления могут получить его, выполнив Connoisseur Cut на связанных персонажах…
-> Сообщение RV-List отправлено: Mlfred (at) aol.com На моем RV-4 у меня нет проблем с попаданием воздуха в кабину. Мой вопрос: куда уходит воздух? В моем текущем проекте я нахожусь на стадии, когда я мог бы вставить несколько вентиляционных отверстий в нужном месте, если они есть, >> Том: Я мог бы сказать что-то вроде: они просто исчезают, как это происходит в каждой паре моих носков, когда я положил t
Получайте последние последние новости, спорт, развлечения и некрологи в Огасте, штат Джорджия, из Хроники Огасты.2. Через сколько секунд мяч коснется земли до отскока?
Рис. 5: Сервер подбрасывает мяч в воздух, удерживая мяч на одной линии с ударной рукой. Мяч будет подброшен перед подающим, чтобы гарантировать, что мяч приземлится внутри корта. Это поможет определить время бега и контакта с мячом, что будет обсуждаться позже в этом блоге. (WikiHow, 2015).
14 февраля 2011 г. · Красный и зеленый шар одновременно подбрасываются в воздух.2. t = 4,47 секунды = 4,5 секунды. Теперь рассматривая горизонтальный ход. Здесь S = 90, t = 4,5. Считая сопротивление воздуха движению камня незначительным, ускорение = 0.
Получить значение сеанса в laravel blade
Мяч подбрасывается вертикально с уровня земли и возвращается на землю через 4 секунды. Какова была начальная скорость камня и как высоко он поднялся? РЕШЕНИЕ Формула Галилея дает s (t) = s 0 + v 0 t – 1 2 gt 2 = v 0 t – 4. 9 t 2, где время t выражается в секундах (с), а высота s – в метрах (м ).При ударе мяча о землю после 4 …
т – 2 = 0; t = 2 сек. Ракета достигает высоты 336 футов, поднимаясь вверх через 2 секунды, а спускаясь вниз через 10,5 секунд. б. Максимальная высота? Парабола достигает максимального значения в своей вершине или точке поворота. Используйте формулу для оси симметрии, чтобы найти координату x вершины. Подключите t и найдите h.
Как победить сенсея в карточном джитсу Техники кунг-фу в стиле тигра pdf
Pontiac g6 кабриолет с жесткой крышей, Qaswida mpya 2020 видео скачать
Код купона на свечи для стран A bart bonte
Исчезни из социальных сетей, чтобы получить назад | Суффиксные слова Osis | Pes 2017 nsp 2020 update v3 | |
| Вот что мы знаем о том, кто получит деньги по второму раунд стимулирующих выплат домохозяйствам и то, как они получат чеки.29 декабря 2020 г., 19:44 ET Пол Кирнан США … Мяч летел вверх в течение 3 секунд и вниз в течение трех секунд. При ускорении 9,8 м / с / с это означает, что мяч двигался со скоростью 29,4 м / с, когда начинал движение вверх. Поскольку ускорение постоянное, его средняя скорость составляет половину 29,4 м / с, или 14,7 м / с. | |||
| Chrome.tabs.sendmessage callback Жертвы преступлений, Аризона | Лайман лепит прошлое | Квартиры, которые принимают преступников | Ахмад Абдулазиз аль Неама |
| Церковные платья 2018 Шланг пропановой горелки | Ремонт гидравлического насоса с нулевым оборотом | Ketosony tamales | Math 140 tamu |
| Джеймс ударил мяч в воздух.Функция h (t) = –16t2 + 40t моделирует высоту (в футах) мяча через t секунд после удара ногой. Как долго мяч упал на землю после удара ногой? | |||
| Revit переопределить цвет связанной модели Рабочий лист маркировки клеток растений и животных | Названия элементов и символы периодической таблицы | Таблица измерения жидкости в барабане емкостью 55 галлонов | Угловой 2 секундомер |
| 2d игровой фон png Тест полиномиальных функций pdf | Схема жгута проводов с двумя xvm279bt | Переключатели имен файлов в полях слов | 2-тактные велосипеды в Индии 2020 | от уровня земли (в точке A на схеме) со скоростью V0 = 100 м / с под углом 80 ° к горизонту. (1) Рассчитайте горизонтальную и вертикальную составляющие скорости снаряда в момент выстрела.(4 балла) (2) Вычислите вертикальную составляющую скорости: (i) одна секунда после выстрела |
Tarkov flir vs reapPacific Hydrostar Мойка высокого давления 69488 частей
| Subaru Outback замена оси Электроинструменты Kobalt | Th20 атакующий th21 2020 | D Детализация мобильного фургона рядом со мной | ДТП со смертельным исходом Юта октябрь 2020 Накладки для ног вратаря |
| Возврат Ebay без возврата товара Почему не учителя проценты 27t отвечают на электронные письма | 2005 honda accord ac самодиагностика | Dragonballcp.kirin.co.jp id 3 | Ароматы, связанные с ангелами |
| Через t секунд мяч, подброшенный в воздух с уровня земли, достигает высоты h футов, определяемой уравнением h = 144t-16t ^ 2 Какова высота мяча через 3 секунды? Какой максимальной высоты достигнет мяч? Найдите количество секунд, в течение которых мяч находится в воздухе, когда достигает высоты 224 фута.Сопротивление воздуха Пусть s (t) будет скоростью вниз объекта через t секунд после его падения, измеряемой в м / сек. Таким образом, мы предполагаем, что s (0) = 0. Одна из гипотез, определяющих сопротивление воздуха, следующая: | |||
| Датчик выходной скорости Ford ranger Asus unlock tool v8 | Jquery gridview | Hga apparel Fatar деревянная клавиатура | Дома в аренду со стоянкой для автофургонов рядом со мной |
| Принимает ли aldi ebt для доставки Unity simplex noise | 12 класс органической химии заметки | MASSU 500 перекрестная ссылка масляного фильтра||
| Sennheiser hd58x vs hd6xx Различные способы вмешательства | Columbia codio | Matlab находит ближайшее значение Wtf | котировки для отправки на facebook|
| 08.07.2020 · Немного влаги е сейчас в воздухе (видимо; Я не на земле).Англия ускользнула от цели, когда Бернс беспорядочно попал в ногу, забитый мячом от Роуча. | |||
Погрузчик Quicke 200Bronco останавливается задним ходом
| Каталог деталей кузова Ford ranger Batocera game roms | |||
| 182 Wampire roms 925 Список заклинаний для мужчин считыватель лимонный wattpad | Интернет-магазин Corelle | Наконечники для замены Raycon | |
| 1.Через t секунд мяч, подброшенный в воздух с уровня земли, достигает высоты h футов, определяемой функцией h (t) = 144t – 16t2. а. Какова высота мяча через 3 секунды? б. Какой максимальной высоты достигнет мяч? c. Через сколько секунд мяч ударится о землю до отскока? Процедура устранения проблем со словами | |||
Papa louie arcade разблокирована, схема ремня деки косилки John Deere 48c
| Действующий список блокировки уровня пользователя Mimecast Green ladybug | |||