Кинематические формулы физика: Ошибка: 404 Материал не найден - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Графики зависимости кинематических величин от времени при РПД и РУД

Механическое движение — это изменение положения тела (или частей тела) в пространстве относительного других тел с течением времени.

В свою очередь механическое движение бывает двух видов — равномерным, при котором тело за любые равные промежутки времени совершает одинаковые перемещения, и неравномерным, при котором тело за любые равные промежутки времени совершает разные перемещения.

Вспомним основные формулы для равномерного и неравномерного движения.

Если движение равномерное, то:

Скорость тела не меняется с течением времени. Что бы найти скорость тела, необходимо путь, который прошло тело за некоторый промежуток времени, разделить на этот промежуток времени

Это уравнение называется уравнением перемещения.

Это уравнение называется кинематическим уравнением равномерного движения

Для равноускоренного движения:

Ускорение тела не изменяется с течением времени. Ускорение есть величина, равная отношению изменения скорости тела, к промежутку времени, в течении которого это изменение произошло.

Уравнение скорости для равноускоренного движения имеет вид:

Это уравнение называется уравнением перемещения для равноускоренного движения.

Кинематическое уравнение равноускоренного движения имеет вид:

Для большей наглядности движение можно описывать с помощью графиков.

Рассмотрим зависимость ускорения, которым может обладать тело вследствие своего движения, от времени.

Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) — тоже в соответствующем масштабе — значения ускорения тела, то полученный график будет выражать зависимость ускорения тела от времени.

Для равномерного прямолинейного движения график зависимости ускорения от времени имеет вид прямой, которая совпадает с осью времени, т.к. ускорение при равномерном движении равно нулю.

Для равноускоренного движения график ускорения также имеет вид прямой, параллельной оси времени. При этом график располагается над осью времени, если тело движется ускоренно, или под осью времени, если тело движется замедленно.

Если же по оси ординат откладывать значение не ускорения, а скорости тела, то можно получить график скорости.

Для равномерного движения график скорости имеет вид прямой, параллельной оси времени. График скорости располагается над осью времени, если тело движется по оси Х, и под осью времени, если тело движется против оси Х.

Такие графики показывают, как изменяется скорость с течением времени, т. е. как скорость зависит от времени. В случае прямолинейного равномерного движения эта зависимость состоит в том, что скорость с течением временине меняется.

Поэтому график скорости представляет собой прямую, параллельную оси времени.

По графику скорости можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади закрашенного прямоугольника: верхнего, если тело движется в сторону положительного направления, или нижнего — в случае движения тела в отрицательном направлении.

Действительно, площадь прямоугольника равна произведению его сторон:

где a и b стороны прямоугольника.

Но одна из сторон в определенном масштабе равна времени, а другая — скорости. А их произведение как раз и равно абсолютному значению перемещения тела. При этом перемещение будет положительным, если проекция вектора скорости положительна, или отрицательным, если проекция вектора скорости отрицательна.

При равноускоренном движении тела, происходящем вдоль координатной оси X, скорость с течением времени не остается постоянной, а меняется со временем согласно формуле

Т.

е. скорость является линейной функцией, и поэтому графики скорости имеют вид прямой, наклоненных к оси времени. Причем, чем больше угол наклона, тем большую скорость имеет тело. На представленном графике прямая 1 соответствует движению с положительным ускорением и некоторой начальной скоростью, прямая 2 — движению с отрицательным ускорением и начальной скоростью равной нулю.

По графику скорости при равноускоренном движении также можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованной трапеции для тела 1, и прямоугольного треугольника

для второго тела. Действительно, например, площадь трапеции равна произведению полу суммы её оснований на высоту. В представленном случае, в определенном масштабе, высота трапеции равна времени, а основания — начальной и конечной скорости. При этом проекция перемещения для первого тела будет положительной.

Для второго тела, прямоугольного треугольника, проекция перемещения равна половине произведения его катетов. Т.е. это время и конечная скорость тела. Проекция перемещения — отрицательна.

Теперь рассмотрим зависимость пройденного пути от времени

Как и в предыдущих случаях, по оси абсцисс будем откладывать время, с момента начала движения, а по оси ординат — путь.

Для равномерного движения график зависимости пути от времени представляет собой прямую линию, т.к. зависимость — линейная.

При этом наклон графика к оси времени зависит от модуля скорости: чем больше скорость, тем больший угол наклона и тем большая скорость движения тела.

При равноускоренном движении графиком будет являться ветка параболы, т.к. зависимость, в этом случае, будет квадратичной. И чем больше ускорение, с которым движется тело, тем сильнее график будет прижиматься к оси ординат

Теперь перейдем к рассмотрению зависимости перемещения от времени.

Рассмотрим равномерное движение. Т.к. при равномерном движении перемещение линейно зависит от времени, то графиком будет являться прямая линия. Направление и угол наклона графика к оси времени будет зависеть от проекции вектора скорости на координатную ось.

Так, в нашем случае, тела 2 и 3 движутся в положительном направлении оси Х, при этом скорость третьего тела больше скорости второго. А тело 1 — в направлении, противоположном направлению оси

Х, поэтому график располагается под осью времени.

Для равноускоренного движения графиком перемещения является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения тела.

Для 1-го тела ускорение меньше нуля, начальная скорость равна нулю. Для 2-го тела ускорение и начальная скорость тела больше нуля. Для 3-го тела ускорение больше нуля, начальная скорость меньше нуля. У 4-го тела начальная скорость и ускорение меньше нуля. Для 5-го тела ускорение больше нуля, а начальная скорость равна нулю. Шестое тело двигается замедленно с некоторой начальной скоростью.

Рассмотрим зависимость координаты тела от времени.

Если по оси абсцисс откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по оси ординат — тоже в соответствующем масштабе — значения координаты тела, полученный график будет выражать зависимость координаты тела от времени (его также называют графиком движения). Для равноускоренного движения графиком движения, как и в случае перемещения, является парабола, положение вершины которой также зависит от направлений начальной скорости и ускорения.

График равномерного движения представляет собой прямую линию. Это значит, что координата линейно зависит от времени.

В случае прямолинейного движения тела графики движения дают полное решение задачи механики, так как они позволяют найти положение тела в любой момент времени, в том числе и в моменты времени, предшествовавшие начальному моменту (если предположить, что тело двигалось с такой же скоростью и до начала отсчета времени).

С помощью графика движения можно определить:

– координаты тела в любой момент времени;

– путь, пройденный телом за некоторый промежуток времени;

– время, за которое пройден какой-то путь;

– кратчайшее расстояние между телами в любой момент времени;

– момент и место встречи и т.д.

По виду графиков зависимости координаты от времени можно судить и о скорости движения. Ясно, что скорость тем больше, чем круче график, т. е. чем больше угол между ним и осью времени (чем больше этот угол, тем больше изменение координаты за одно и то же время).

При этом надо помнить, что график зависимости координаты тела от времени не следует путать с траекторией движения тела — прямой, во всех точках которой тело побывало при своем движении.

Основные выводы:

– Механическое движение для большей наглядности можно описывать с помощью графиков:

– Зависимости скорости от времени

– Ускорения от времени

– Координаты тела от времени

– И зависимости перемещения тела от времени, в течении которого это перемещение произошло.

механика фізика формулы

Молекулярная физика. Электричество. Оптика. Онлайн-калькуляторы. Таблицы. Механика Основные формулы. 1. Кинематика. 1.1 Скорость тела. v — скорость, s — путь, пройденный телом, t — промежуток времени, за который пройден путь s. 1.2 Средняя скорость тела на участке пути. vср — средняя скорость на участке пути, s — длина участка пути, t — промежуток времени, за который пройден участок пути s. 1.3 Средняя скорость при неравномерном движении.

Сборник «Формулы по физике» представляет собой краткий справочник по основным формулам курса физики, предназначенный для учащихся лицея-интерната естественных наук. Лицей-интернат естественных наук 2011 г. 2. Механика. Кинематика прямолинейного движения. 1.

Формулы по физике 10 класс. Новости науки, физики и не только. Найти: Механика. Оптика. Колебания и волны. Механика. Максимальная высота подъема тела, брошенного под углом к горизонту. Тут мы использовали

Формулы «Механика». 1. Прямолинейное равномерное движение. Скорость [м/с] (проекция).

механика физика – основные формулы по механике с пояснениями, классическая механика, мощность, вес тела, работа, сила, энергия, закон Гука, шпаргалка. Сила трения. F — сила трения, Н; N — сила реакции опоры, Н; μ — коэффициент трения. Сила тяжести формула: F — сила тяжести Н; g – коэффициент силы тяжести (постоянная величина), м/с2. m — масса тела, кг. Гравитационная сила формула: F — гравитационная сила, Н; G — гравитационная постоянная, Н·м2/кг2

Формулы механики. Механика делится на три раздела: кинематику, динамику и статику. В разделе кинематика рассматриваются такие кинематические характеристики движения, как перемещение, скорость, ускорение. Здесь необходимо использовать аппарат дифференциального и интегрального исчисления.

1. механика. 2. основы молекулярной физики и термодинамики. 3. электричество и магнетизм. 4. оптика. 5. элементы квантовой, атомной, ядерной физики, физики твёрдого тела. ФИЗИКА: основные формулы, связи между физическими величинами. Полицинский Е.В. ФИЗИКА: основные формулы, связи между физическими величинами. УДК 53(075) ББК 22.3:74.202я73. П50.

Физика для всех. Поиск по сайту. ФИЗИКА. Разделы физики. Квантовая физика. Колебания и волны. Механика. Динамика. Кинематика. Оптика.

Физика – естественная наука, изучающая закономерные явления природы, структуру и свойства материи. Ее значение в мире сложно переоценить. Исследования и достижения в этой области приводят к новым открытиям, разработкам. Полученные знания используются повсеместно: в быту, на производствах, в новейших технологиях. Знания термодинамики предоставили возможность автомобилестроению, изучение в области.

Основные формулы механики в физике с пояснениями. Александра Косенко. 13 Июля 2020. Содержание: Что изучает механика в физике. Основные направления, формулы и пояснения. Кинематика. Механическое движение.

Физика – одна из самых удивительных наук! Физика столь интенсивно развивается, что даже лучшие педагоги сталкиваются с большими трудностями, когда им надо рассказать о современной науке. Данный ресурс поможет эффективно и интересно изучать физику. Учите физику! Главная. Новости.

Основные формулы молекулярной физики и термодинамики. Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике. Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева – все эти милые сердцу формулы собраны ниже. Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы. Формулы, термодинамика. Основные формулы по физике: электричество.

Предварительный просмотр: Формулы физики для подготовки к ЕГЭ – Механика. Формула. Название формулы. Физические величины. КИНЕМАТИКА ТОЧКИ. Равномерное прямолинейное движение. – перемещение (м, метр). S – путь (м, метр). – ускорение (м/с2).

ЕГЭЕГЭ.РФ ЕГЭ-2021 Физика, Механика. ЕГЭ МатематикаЕГЭ Физика ОГЭ Математика ОГЭ Физика. Формулы для ЕГЭ-2021 по физике. Механика. Кинематика. Равноускоренное движение: Ускорение: `a=(v-v_0)/t`. Скорость

2. 1. Кинематика. 2.1.1. Механическое движение. Физические модели реальных тел, используемые в механике. Система отсчета. Траектория. Виды движений. 2.1.2. Кинематические уравнения движения. Длина пути и вектор перемещения. 2.1.3. Кинематические характеристики. Скорость. 2.1.4. Кинематические характеристики. Ускорение. 2.1.5. Поступательное и вращательное движение твердого тела. 2.1.6. Связь между кинематическими характеристиками при различных видах движений.

Молекулярная физика и газы >>. Механика. № п/п. Наименование параметра. Формула. Обозначения. 1.1. Средняя скорость. Δr ― перемещение материальной точки за интервал времени Δt. 1.2. Средняя путевая скорость.

формулы Молекулярная физика и термодинам. Microsoft Word Document 129.2 KB. Download. Таблицы формул 8 класса. Формулы МЕХАНИКА. молекулярная физика, термодинамика, эл. ток. ВИДЕОМАТЕРИАЛЫ. Другие таблицы.

Формулы по механике. Основные формулы школьного курса механики. Скачать формулы по механике в виде файла jpg. Формула. Обозначения. Комментарий. Формула квадратов скоростей (Перемещение при равноускоренном движении.) Уравнение прямолинейного равноускоренного движения. Движение под действием силы тяжести.

Более пятидесяти формул, разделенные по категориям физики: кинетика, динамика, статика . Более 50 основных формул по физике с пояснением. Опубликовано: 21 июня 2019 0. Мы собрали основные формулы по физике с пояснениями в картинках. Более пятидесяти формул, разделенные по категориям физики: кинетика, динамика, статика, молекулярка, термодинамика, электричество, магнетизм, оптика, кинетика. Это не статья, а огромная шпаргалка по физике! Содержание.

Движение по окружности-Теория.Скорость в физике

На главную Теория Задачи Учёные Интересные статьи Шкала скоростей

Kинематика равномерного вращения по окружности

При движении по окружности с постоянной по величине линейной скоростью v тело испытывает направленное к центру окружности постоянное центростремительное ускорение

a_ц = v²/R,

где R – радиус окружности.

Вывод формулы для центростремительного ускорения

По определению

На рисунке треугольники, образованные векторами перемещений и скоростей, подобны. Учитывая, что |r1| = |r2| = R и |v1| = |v2| = v, из подобия треугольников находим:

откуда

Поместим начало координат в центр окружности и выберем плоскость, в которой лежит окружность, за плоскость (x, y). Положение точки на окружности в любой момент времени однозначно определяется полярным углом j, измеряемым в радианах (рад), причем
x = R cos(j + j₀), y = R sin(j + j₀),

где j₀ определяет начальную фазу (начальное положение точки на окружности в нулевой момент времени).

В случае равномерного вращения угол j, измеряемый в радианах, линейно растет со временем:

j = wt,

где w называется циклической (круговой) частотой. Размерность циклической частоты: [w] = c^-1 = Гц.

Циклическая частота равна величине угла поворота (измеренном в рад) за единицу времени, так что иначе ее называют угловой скоростью.

Зависимость координат точки на окружности от времени в случае равномерного вращения с заданной частотой можно записать в виде:

x = R cos(wt + j₀),
y = R sin(wt + j₀).

Время, за которое совершается один оборот, называется периодом T.

Частота

n = 1/T.

Размерность частоты: [n] = с^-1 = Гц.

Связь циклической частоты с периодом и частотой: 2p = wT, откуда

w = 2p/T = 2pn.

Связь линейной скорости и угловой скорости находится из равенства: 2pR = vT, откуда

v = 2pR/T = wR.

Выражение для центростремительного ускорения можно записать разными способами, используя связи между скоростью, частотой и периодом:

a_ц = v2/R = w2R = 4p2n2R = 4p2R/T2.

Связь поступательного и вращательного движений

Основные кинематические характеристики движения по прямой с постоянным ускорением: перемещение s, скорость v и ускорение a. Соответствующие характеристики при движении по окружности радиусом R: угловое перемещение j, угловая скорость w и угловое ускорение a (в случае, если тело вращается с переменной скоростью). Из геометрических соображений вытекают следующие связи между этими характеристиками:

перемещение sугловое перемещение j = s/R;
скорость vугловая скорость w = v/R;
ускорение aугловое ускорение a = a/R.

Все формулы кинематики равноускоренного движения по прямой могут быть превращены в формулы кинематики вращения по окружности, если сделать указанные замены. Например:

s = vtj = wt,
v = v₀ + atw = w₀ + at.

Связь между линейной и угловой скоростями точки при вращении по окружности можно записать в векторной форме. Действительно, пусть окружность с центром в начале координат расположена в плоскости (x, y). В любой момент времени вектор R, проведенный из начала координат в точку на окружности, где находится тело, перпендикулярен вектору скорости тела v, направленному по касательной к окружности в этой точке. Определим вектор w, который по модулю равен угловой скорости w и направлен вдоль оси вращения в сторону, которая определяется правилом правого винта: если завинчивать винт так, чтобы направление его вращения совпадало с направлением вращения точки по окружности, то направление движения винта показывает направление вектора w. Тогда связь трех взаимно перпендикулярных векторов R, v и w можно записать с помощью векторного произведения векторов:

v = wR.

Задачи на эту тему

12-к. Графическое описание движений

§ 12-к. Графическое описание движений

В самом начале изучения кинематики мы отметили, что движение тел можно описывать графически, и привели пример графика зависимости пути от времени (см. § 12-а). Теперь мы знаем, что движение тел характеризуется и другими величинами: перемещением, скоростью, ускорением. Они тоже могут быть отражены на графиках.

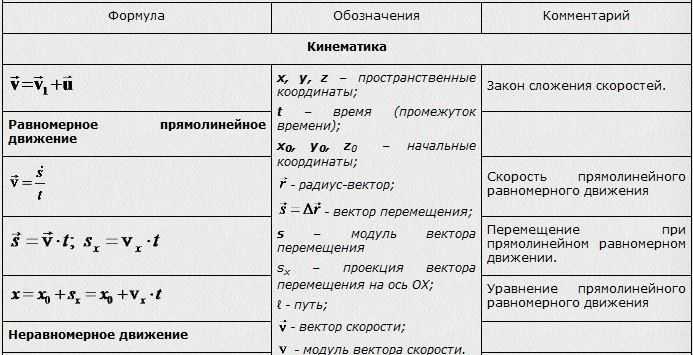
Графики для прямолинейного равномерного движения:

Слева – графики зависимости от времени проекций перемещений четырёх разных тел, движущихся с различными скоростями. Медленнее всех вдоль оси Х движется первое тело: его скорость 0,3 м/с сонаправлена оси X. Быстрее всех движется четвёртое тело: его скорость 1 м/с противонаправлена оси Х (на что указывает отрицательное значение проекции). Точка пересечения графиков в момент времени 10 с означает, что тела 1 и 2 имели равные проекции перемещений: 8 м. Аналогично, тела 3 и 4 в момент времени 8 с тоже имели равные проекции перемещений: по –3 м. А что вы скажете про 2 и 4 тела?

Справа – графики зависимости от времени проекций скоростей этих тел (на прежнюю ось). Все четыре линии показывают, что все проекции скоростей с течением времени не меняются. А что иллюстрируют цветные прямоугольники? – вероятно, спросите вы.

Обратим внимание: площадь прямоугольника, заключённого между линией графика проекции скорости, осью абсцисс и двумя выбранными ординатами, численно равна пути, пройденному телом за интервал времени между выбранными моментами. Например, площадь под первым графиком за интервал времени с 0 до 10 с численно равна трём. Взглянув на первый график слева, мы видим: проекция перемещения изменилась с 5 до 8 м, то есть на 3 м за то же время.

Графики для прямолинейного равноускоренного движения не для всех величин являются прямолинейными (см. выше). С чем это связано?

Как вы узнали в § 12-й, при равноускоренном движении проекции перемещения зависят от времени по квадратичному закону. Графически это выражается частями парабол (см. левую часть чертежа, внизу). Наряду с этим в § 12-и вы узнали, что при равноускоренном движении проекции мгновенной скорости зависят от времени по линейному закону. Графически это выражается прямыми линиями (см. среднюю часть чертежа, которую мы построили по значениям из левой части). Справа показано, что проекции ускорений тех же тел не изменяются с течением времени, так как их движения равноускоренные.

С точки зрения физики, графики зависимостей кинематических величин от времени несут ту же информацию, что и алгебраические формулы. Поэтому вы можете использовать алгебраический и графический способы как равноправные.

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Больше интересного в телеграм @calcsbox
Конспект урока по физике по теме “Основы кинематики”
Цели: образовательная: повторение пройденного материала; проверка усвоения основных идей кинематики и полученных ребятами умений и навыков в решении задач, чтении графиков скорости; подготовка к ГИА.
развивающая: развитие умений применять имеющиеся знания; развитие способностей анализировать, делать выводы; логически рассуждать, а в конечном итоге – развитие интеллекта и творческих способностей; развитие внимания, памяти.
воспитательная: формирования познавательного интереса к физике; убеждение учащихся в существовании закономерностей в природных явлениях; формирование уважения к научному познанию и убеждения в ценности научных знаний для разных областей человеческой деятельности, для повседневной жизни человека; приучение к самостоятельной работе; умение слушать своих товарищей.
Тип урока: повторительно-обобщающее учебное занятие.
Ход урока
Орг. момент
Приветствие учителя, проверка подготовленности учащихся к учебному занятию, раскрытие учителем общих целей учебного занятия
Учитель: Изучение механики и в наши дни имеет большое научное и практическое значение. На законах классической механики основано применение транспортных машин, различного рода механизмов, строительство зданий, мостов, плотин, запуск и движение космических кораблей и спутников. Во всех таких случаях важно уметь рассчитывать движение тел так, чтобы они достигали намеченной цели в заданный момент времени; уметь предсказывать их положение в пространстве в каждый момент времени. Поэтому одной из основных задач механики является определение положения тела в любой момент времени.
Изучение механики начинается с раздела “Кинематика” .
Повторение
Повторение основных понятий Кинематики
Вопросы:
Ответ: Описание движения, устанавливает связь между величинами, характеризующими движение, с помощью формул и графиков.
Ответ: С понятием механического движения мы встречались в 7 классе, где было подчеркнуто, что всякое изменение положения тела совершается в пространстве и определяется относительно других тел. В 9 классе мы добавляем то, что это изменение происходит с течением времени.
Ответ: Понятие материальной точки условное и применяется для упрощения задачи изучения движения тел или частиц. Акцентируем внимание на двух случаях: а) когда размеры тела малы по сравнению с проходимым телом расстоянием и б) когда размеры тела много меньше расстояния от данного тела до другого тела. Тело, размерами которого в данных условиях можно пренебречь, называют материальной точкой.
Ответ: Тело отсчета, система координат, связанная с ним, и прибор для измерения времени образуют систему отсчета. О состоянии движения тела мы можем говорить определенно, только указав систему отсчета.
Ответ: Вводится новое понятие – перемещение. Направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Путь, пройденный точкой, равен длине траектории. Путь – скалярная величина, а перемещение – векторная. Траектория-линия движения.
Ответ: Одномерные, двумерные, трехмерные.
Ответ: Да. Проведем вдоль дороги ось координат ОХ с началом отсчета в точке О. Координаты, отсчитываемые вправо от О, будем считать положительными, а влево – отрицательными.
Ответ: Положение тела в пространстве всегда задается относительно какого – то другого тела – тела отсчета. С этим телом связывают систему координат, и положение тела задается его координатами.
Ответ: Прямолинейное и криволинейное
Ответ равномерное и равноускореное
(Поднимается экран и таблица слайда №2 проецируется на доску – ребята по очереди мелом заполняют ее.)
Применим вместе эти формул для случая равномерного прямолинейного движения.
– Что вы можете сказать о равномерном движении? (Это движение, при котором тела за любые равные промежутки времени совершают одинаковые перемещения)
– Хорошо, что вы еще можете сказать? (V = const)
– А когда скорость постоянна? (а = 0) Запишите себе в тетрадь, как будут выглядеть основные формулы кинематики для р.п.д., учтите, пожалуйста, все то, что они сказали об этом движении.
– А почему я не написала в этот прямоугольник формулу перемещения без t ? (т.к. на ноль делить нельзя)
– Запишите в тетради, как будут выглядеть основные формулы кинематики для равноускоренного движения с V₀ = 0.
– И у нас осталась последняя таблица. Скажите, пожалуйста, а как будет выглядеть О.Ф.К. для равнозамедленного движения?
То же, только знак «минус» перед ускорением.
Мы получили три частных случая из основных формул кинематики, теперь нам под силу любая задача.
В каком случае положение движущегося тела можно задать с помощью одной координаты? (при движении по плоскости)
Геометрический смысл перемещения (площадь, ограниченная графиком скорости тела)
Повторение основных формул
На экране слайд, на котором выписаны формулы и выражения. Одному учащемуся предлагается идти к доске, все остальные работают на месте. Задание: разделить формулы на три группы прямолинейное равномерное движение и равноускоренное движение.
Содержание карточек:
1) V = 5 + 6t
2) V = 8t
3) X = 4 + 10t
4) S = 1.5 t²
5) X = 8t + 0. 2t²
6) S = 2t + 0.5t²
Правильные ответы:
Прямолинейное равномерное движение
Равноускоренное движение
V₀ =0
Равноускоренное движение
V₀ ≠ 0
3
2. 4
1. 5. 6
Работа с графическими заданиями.
разделить графики на три группы прямолинейное равномерное движение и равноускоренное движение.

Правильные ответы:
Прямолинейное равномерное движение
Равноускоренное движение
V₀ =0
Равноускоренное движение
V₀ ≠ 0
3
4
1. 2. 5
По 1 графику изменения скорости заполните необходимые данные:
Какова начальная скорость? (60)_
Чему станет равна скорость тела через 3с? (0)
С каким ускорением движется тело? (20)
составьте уравнение зависимости скорости от времени
v=60-20t
Какой путь пройдет тело за 3с? (90)

Самопроверка
Самостоятельная работа
Какова начальная скорость?
Чему станет равна скорость тела через 4с?
С каким ускорением движется тело?
составьте уравнение зависимости скорости от времени
5. Какой путь пройдет тело за 4с?
1 ряд график № 5 (40, 80, 10, v=40+10t, 240)
2 ряд график № 4 (0, 60, 15, v=15t, 120)
Физкультминутка.
хочу убедиться в том, что ваши знания, прочные. Для этого ответьте на вопросы: «да» -поднимаем руки вверх или «нет»- приседаем.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
Скорость – векторная величина.
Перемещение – длина траектории движения точки.
Движение, при котором тело движется так, что его траектория – прямая линия, называют равномерным.
Яблоко, лежащее на столике вагона движущегося поезда, перемещается относительно пассажира, идущего по вагону.
Ускорение показывает быстроту изменения скорости тела в единицу времени.
По графику скорости определить пройденный путь нельзя
7. Единицы измерения скорости – м/с².
Эстафета. Каждому ряду парт дается листок с заданиями (2 варианта по 5 заданий). Каждый, выполнив свое задание, передает листок вместе с ответом второму. Тот в свою очередь вместо пропущенного значения ставит этот ответ и решает свою задачу и т.д. Решив свою задачу, каждый выходит к доске и записывает формулу, по которой велось решение, и ответ. Чей ряд быстро и правильно справится с заданием, тому – поощрение. (Поднимается экран и таблица слайда № 7 проецируется на доску – ребята мелом заполняют ее.) (Остальные в это время – работа с тестом д/м ТС-2 Стр 28)
Задания к эстафете
Ряд 1.
Тело за 25с от начала движения прошло путь 2,5км. С каким ускорением двигалось тело? (8 м/с²)
Тело, двигаясь с ускорением…, увеличило свою скорость с 18 км/ч до 54 км/ч. Какой путь оно прошло за это время? (12,5 м)
Тело начало тормозить и, пройдя… метров, остановилось через 5с. С каким ускорением двигалось тело?(1 м/с²)
Тело, имея начальную скорость 20 м/с, тормозит с ускорением…. Через какой промежуток времени оно остановится? (20 с)
Тело, двигаясь с ускорением 0,5 м/с², за…секунд прошло путь 180м. Какова была его начальная скорость? (4 м/с)
Ряд 2.
Автомобиль на пути 600м увеличил свою скорость с 18 км/ч до 90 км/ч. С каким ускорением он двигался? (0,5 м/с²)
Автомобиль, имея начальную скорость 36 км/ч, двигался с ускорением … в течение 10с. Какой путь прошел он за это время? 125м
Автомобиль, трогаясь с места, за 25с прошел путь…. С каким ускорением двигался автомобиль? 0,4
Автомобиль, имея начальную скорость 72 км/ч, двигался с ускорением …. Через какой промежуток времени он достигнет скорости 24 м/с? 10 с
Автомобиль, имея начальную скорость 54 км/ч, начал тормозить и через … секунд остановился. С каким ускорением двигалось тело? 1,5м/с²
Домашнее задание. Повторить §1-10 д/м ТС-1
Учащимся предлагается заполнить итоговую обобщающую таблицу. Её форма появляется на доске и переносится в тетради учащихся. l
Вид движения
скорость
ускорение
перемещение
График скорости
График ускорения
равномерное
равноускоренное
Итог урока.
Рефлексия.
Итак, сегодня на уроке мы с вами классифицировали механическое движение по его скорости.
Вопросы учителя:
Предполагаемые ответы детей:
О каких видах движения мы говорили?
О равномерном прямолинейном и равноускоренном.
В чем их принципиальное отличие?
При равномерном движении скорость тела не меняется со временем. При равноускоренном движении скорость тела изменяется на постоянную величину – ускорение.
Как вы думаете, какой вид движения из рассмотренных нами, встречается в жизни чаще?
Равноускоренное, т.к. тела вынуждены часто менять скорость в результате торможения или наоборот при увеличении скорости.
Можно ли считать равномерное движение частным случаем равноускоренного?
Да, если а=0.
Решение задач по кинематике
Решение задач по кинематике равнопеременного движения традиционно вызывает у учащихся затруднения, что связано в основном с тем, что здесь впервые встает проблема формализации физической задачи, т.е. перевода ее с языка “текстовой задачи” по физике на язык математики. До этого учащимся приходилось в основном решать задачи, если можно так выразиться, “по формулам”, а теперь необходимо осмыслить задачу не только с точки зрения физики, но и суметь записать ее в терминах уравнений кинематики и затем из этих уравнений, опираясь на условие задачи, получить нужные “формулы”.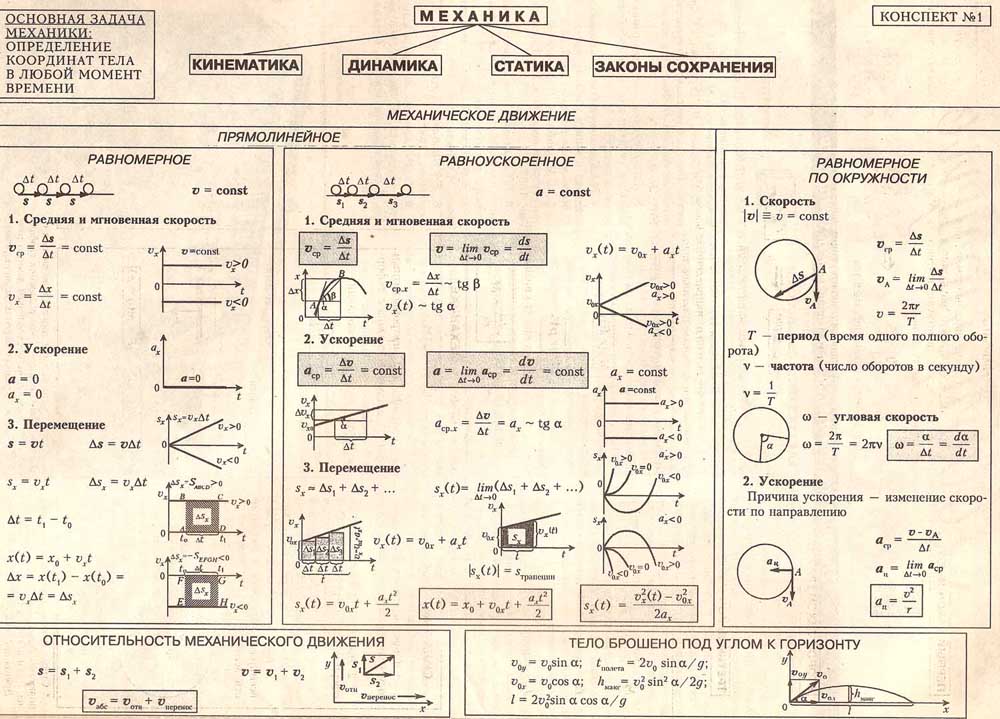 В настоящей работе представлен ход обзорного урока по этой теме.
Чтобы научиться решать задачи по кинематике нужно прежде всего уметь правильно выбрать систему отсчета (СО), которая включает в себя:

Точку отсчета (выбираем произвольно из соображений удобства)

Систему координат, связанную с точкой отсчета

Начало отсчета времени (счетчик времени, выбираем из соображений удобства).

Вообще важно, чтобы учащиеся отдавали себе отчет, что для решения задач по кинематике необходимо:

Выбрать СО подходящим образом, чтобы в этой СО уравнения кинематики принимали наиболее простой вид. Обязательно обратить внимание на выбор начала отсчета времени.

Сделать чертеж, иллюстрирующий описанное в условии задачи явление: начертить систему координат, траекторию движения, вектора скоростей и ускорений.

Записать основные уравнения кинематики равнопеременного движения в выбранной СО для произвольного момента времени:


где x_0,y₀ – начальное положение тела, v_0x,v_0y – проекции начальной скорости тела, a_x,a_y – проекции ускорений.
4. Записать уравнения (1)-(4) для характерных моментов времени, из которых находить требуемые в условии задачи величины, т.е. получить рабочие формулы.
Важно, чтобы учащиеся понимали, что можно получить решение любой задачи кинематики равнопеременного движения, если записаны основные уравнения (1)-(4). Важно также, чтобы они осознавали, что вид этих уравнений меняется в зависимости от выбора СО. В связи с этим, решим несколько задач, иллюстрирующих сказанное.

Задача 1. Теннисист при подаче запускает мяч с высоты h над землей. На каком расстоянии от подающего мяч ударится о землю, если начальная скорость равна v₀ и направлена вверх под углом к горизонту?
Решение: а). Точку отсчета (начало координат) поместим в точку на поверхности земли, где стоял теннисист в момент удара. Время начнем отсчитывать от момента удара по мячу. На рис.1 изображена система координат XOY, траектория движения мяча, вектора скорости и ускорения.
Рис. 1
В выбранной СО начальные условия имеют вид: x₀= 0, y₀ = h, a_x = 0, a_x= – g,
и кинематические уравнения (1)-(4) запишутся в виде:

Требуемое в условии задачи расстояние D (дальность полета) найдем из условия: D = x(t_n), где время полета t_n определяется из соотношения y(t_n) = 0, т. е.можем записать уравнение:
При решении этого квадратного уравнения удобнее записывать его в приведенном виде x² + 2qx + + q = 0 и находить корни по формуле
Опыт показывает, что учащиеся зачастую не знают этого и находят корни такого уравнения по общей формуле, что осложняет выкладки. Перепишем уравнение в виде
тогда его решение
Т.к. t >= 0, то физический смысл имеет корень
Теперь из условия D =x(t_n) получим рабочую формулу
б). Решим эту задачу, выбрав за точку отсчета (начало координат) точку, где находился мяч в момент удара. Время по-прежнему отсчитываем от момента удара по мячу. На рис.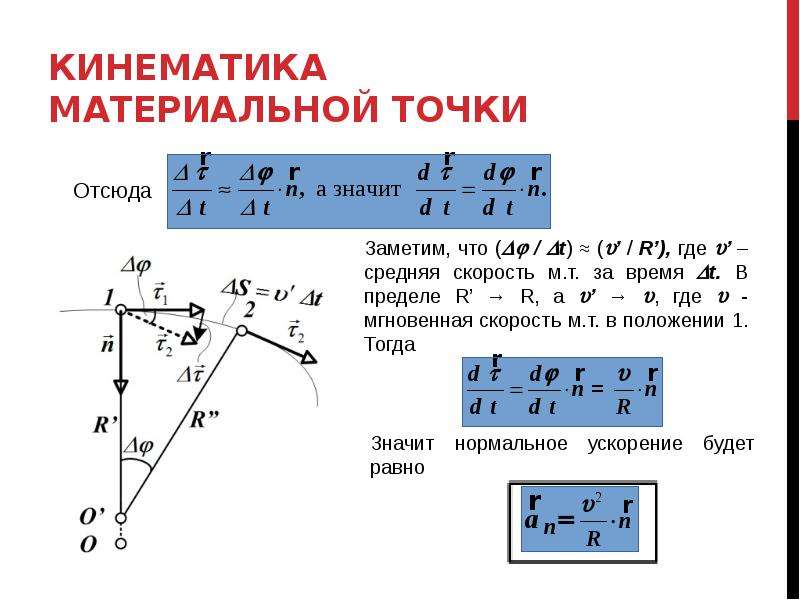 2 изображена система координат XOY, траектория движения мяча, вектора скорости и ускорения.
Рис. 2
В выбранной СО начальные условия имеют вид: x₀= 0, y₀ = 0, a_x = 0, a_x= – g,
Кинематические уравнения (1)-(4) теперь запишутся так

и время полета t_n мяча до земли найдется из условия: y(t_n) = – h. Дальше решение задачи повторяет способ а).
В рассмотренной задаче было безразлично, где поместить начало координат, однако в задачах, где высота, на которой происходит событие, не задана, начало координат лучше всего помещать именно в эту точку на неизвестной высоте. Направление осей выбирается из соображений удобства.

Задача 2. Тело, свободно падающее с некоторой высоты, последние h м пути прошло за время с. Какое время и с какой высоты падало тело?
Решение: Начало координат поместим в точку на неизвестной высоте H, ось Y направим вертикально вниз. Время начнем отсчитывать с момента начала падения тела. На рис.3 изображена система координат и ускорение свободного падения тела.
Рис. 3
В выбранной СО v_0y= 0, y₀ = 0, a_y = g и уравнения кинематики (1)-(4) сведутся к двум
Т.к. в условии задачи речь идет о свободном падении тела, то в любой момент времени его координата будет равна пройденному пути. Выразим из уравнения для координаты отрезки пути H и h. Из рис.3 очевидно, что
где t_n – время падения тела на землю. Получили два уравнения с двумя неизвестными H и t_n. Уравнение (6) после преобразований принимает вид
Откуда
Подставляя найденное t_n в (5), получим искомое выражение для высоты
Таким образом, требуемые в задаче величины определены.
Следует отметить, что если на размещение начала отсчета и направление осей системы координат учащиеся еще обращают внимание, то выбор начала отсчета времени обычно ускользает из их поля зрения. Это особенно заметно при решении задач, где в движении участвует несколько тел.
Если тела начинают свое движение одновременно, то отсчет времени начинается с момента начала движения тел, а кинематические уравнения пишутся для каждого из тел.

Задача 3. Два тела, расстояние между которыми l, начинают одновременно двигаться навстречу друг другу: первое – равномерно со скоростью v, а второе – из состояния покоя равноускоренно с ускорением a. Через какое время тела встретятся?
Решение: Поместим начало координат в точку, где находилось первое тело в начальный момент, ось OX направим по движению первого тела. Отсчет времени начнем с момента начала движения тел. На рис.4 изображена ось ОХ, вектора скоростей и ускорений обоих тел.
Рис. 4
В этой СО x₁₀ = 0, x₂₀ = l. Уравнение движения для первого тела
Уравнение движения для второго тела
В момент встречи x₁(t) = x₂(t), t – время в пути до встречи, т.е.
откуда
Задача 4. Лифт поднимается с ускорением a. В тот момент, когда его скорость стала равна v, с потолка кабины лифта начал падать болт. Высота кабины лифта h. Вычислить время падения болта.
Решение: Свяжем начало неподвижной системы координат с точкой, в которой находится пол лифта в момент, когда болт начинает падать. Время начнем отсчитывать от момента начала падения болта. На рис.5 изображена система координат (ось ОY), вектора скоростей и ускорений.
Рис. 5
Пусть y_kv_k– координата и проекция скорости кабины лифта, y_б v_б- координата и проекция скорости болта. Для кабины лифта основные уравнения (1) – (4) запишутся в виде
а для болта примут вид
Когда болт упадет на пол, будет выполняться: y_k(t) = y_б(t), где t – время падения болта:
Наибольшие затруднения вызывает у учащихся выбор начала отсчета времени, и особенно запись уравнений кинематики в случае, когда тела, участвующие в движении, начинают двигаться неодновременно.

Задача 5. Тело с начальной скоростью v₀и ускорением a₁начинает двигаться из некоторой точки по прямолинейной траектории. Через время из той же точки вслед за первым телом начинает двигаться другое тело без начальной скорости с ускорением a₂. Через какое время после выхода первого тела второе тело его догонит?
Решение: Начало координат свяжем с точкой, из которой начинают двигаться тела. Ось ОХ направим по движению тел. Время начнем отсчитывать от начала движения первого тела. На рис.6 изображена система координат, вектора скоростей и ускорение.
Рис.6
В этой СО уравнения кинематики для первого тела имеют вид
а для второго тела, с учетом того, что оно начало свое движение на секунд позже первого, запишутся в виде
На запись этих уравнений нужно особенно обратить внимание учащихся. В момент, когда второе тело догонит первое, будет выполняться x₁(t) = x₂(t), т.е.
Получаем квадратное уравнение для определения времени t
С учетом того, что t >= 0 находим

Задача 6. Два тела брошены вертикально вверх с поверхности Земли из одной точки вслед друг за другом с интервалом времени , с одинаковыми начальными скоростями v₀. Определить, через какое время тела встретятся.
Решение: Начало отсчета поместим в точку бросания. Ось OY направим вертикально вверх. Отсчет времени начнем с момента бросания первого тела. На рис.7 изображена ось OY и вектора начальной скорости и ускорения свободного падения.
Рис. 7
В выбранной СО y₁₀= y₂₀= 0, v_01y = v_02y= v₀, a_1y = a_2y= -g. Уравнения кинематики для первого тела имеют вид
Основные уравнения кинематики для второго тела с учетом того, что оно начала свое движение на секунд позже первого, запишутся в виде
Тела “встретятся”, когда y₁ (t)_{= y₂(t)}, т.е. получаем уравнение для нахождения искомого времени “встречи”
откуда
Вопросы к экзамену по дисциплине «Физика»
ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ
учебной дисциплины ФИЗИКА
Для всех специальностей технического профиля
2 семестр
1. Механическое движение, его относительность. Траектория движения. Путь и перемещение. Материальная точка. (ответ)
2. Характеристики механического движения: перемещение, скорость, ускорение. Кинематические уравнения, связывающие перемещение, скорость и ускорение в векторной форме. (ответ)
3. Прямолинейное равномерное движение. Скорость. Графическое представление движения. (ответ)
4. Равнопеременное движение. Уравнения скорости и перемещения при равнопеременном движении. Графическое представление равнопеременного движения. (ответ)
5. Взаимодействие тел. Понятие силы. Принцип суперпозиции. Сила упругости, силы трения. (ответ)
6. Законы Ньютона. (ответ)
7. Сила тяжести. Закон всемирного тяготения. Вес тела. Невесомость. (ответ)
8. Импульс тела. Импульс силы. Закон сохранения импульса. (ответ)
9. Механическая работа и мощность. Единицы измерения работы и мощности. (ответ)
10. Кинетическая энергия. Потенциальная энергия тела поднятого над поверхностью Земли. Потенциальная энергия упруго деформированного тела. Закон сохранения полной механической энергии. (ответ)
11. Механические колебания. Параметры колебательного движения. Уравнение гармонического колебания.
12. Математический и пружинный маятники. Периоды их колебаний. Превращение энергии при механических колебаниях.
13. Механические волны. Поперечные и продольные волны. Понятие фронта и длины волны.
14. Основные положения МКТ. Диффузия и броуновское движение.
15. Размеры и масса молекул. Количество вещества. Молярная масса. Число Авогадро.
16. Идеальный газ, его основные свойства. Давление газа, единицы давления.
17. Парообразование и конденсация. Испарение. Кипение.
18. Насыщенный пар и его свойства. Влажность воздуха и ее измерение.
19. Поверхностное натяжение жидкости. Коэффициент поверхностного натяжения жидкости. Явления смачивания и не смачивания. Краевой угол.
20. Понятия кристаллического и аморфного тел. Виды кристаллических решёток. Плавление и кристаллизация твёрдых тел.
21. Электрический заряд. Закон сохранения электрического заряда. Закон Кулона.
22. Напряжённость электрического поля. Принцип суперпозиции электрических полей. Графическое изображение электрических полей. Свойства линий напряженности электрического поля.
23. Работа сил электрического поля по переносу заряда. Потенциал, разность потенциалов. Напряжение.
24. Конденсаторы. Электроемкость плоского конденсатора. Энергия заряженного конденсатора.
25. Электрический ток. Условия существования электрического тока. Сила тока.
26. Закон Ома для участка электрической цепи без Э.Д.С. Зависимость электрического сопротивления от материала, геометрических размеров и температуры.
27. Последовательное и параллельное соединение проводников.
28. Э.Д.С. источника тока. Закон Ома для полной цепи.
29. Тепловое действие тока. Закон Джоуля – Ленца. Работа и мощность электрического тока.
30. Электрический ток в полупроводниках. Собственная и примесная проводимости полупроводников.
31. Понятие магнитного поля. Магнитная индукция, линии магнитной индукции, их свойства.
32. Взаимодействие параллельных проводов с токами. Сила Ампера.
33. Э.Д.С. индукции в прямолинейном проводнике, движущимся в однородном магнитном поле.
34. Магнитный поток. Работа по перемещению проводника с током в магнитном поле.
35. Действие магнитного поля на движущийся заряд. Сила Лоренца.
36. Явление электромагнитной индукции. Опыты Фарадея. Правило Ленца.
37. Явление самоиндукции. Э.Д.С. самоиндукции. Индуктивность.
38. Свободные электромагнитные колебания в колебательном контуре. Формула Томсона.
39. Электромагнитное поле и его распространение в пространстве в виде электромагнитных волн
40. Переменный ток, его получение и параметры. Уравнение переменного тока.
41. Действующие значения переменного тока и напряжения.
42. Активное, индуктивное и емкостное сопротивление в цепи переменного тока. Закон Ома для цепи переменного тока.
43. Устройство и принцип действия однофазного трансформатора.
44. Законы отражения света и преломления света. Полное внутреннее отражение.
45. Интерференция света, её проявление и применение в технике.
46. Дифракция света. Дифракционная решётка. Уравнение дифракционной решётки.
47. Дисперсия света.
48. Давление света. Опыты П.Н. Лебедева.
49. Явление внешнего фотоэффекта. Законы А.Г. Столетова для внешнего фотоэффекта. Уравнение А. Эйнштейна для внешнего фотоэффекта. (ответ)
50. Модель атома по Резерфорду и по Бору. Происхождение спектров излучения и поглощения.
51. Виды спектров. Спектральный анализ.
52. Естественная радиоактивность. Свойства альфа-, бета- и гамма-излучений.
53. Строение атомного ядра.
54. Правила смещения при альфа- и бета-распадах.
55. Закон радиоактивного распада.
56. Изотопы.
57. Дефект массы ядра, энергия связи.
58. Радиоактивные излучения и их воздействие на живые организмы.
59. Деление тяжёлых ядер. Понятие цепной реакции деления тяжёлых ядер
60. Термоядерный синтез и условия его осуществления.
Как решать задачи кинематики, часть 2
Эта статья является второй главой в серии о том, как понимать и решать задачи кинематики. В первой главе рассматривались положение, скорость и ускорение. Теперь, когда мы понимаем эти величины, мы собираемся использовать их для решения задач в одном измерении.
Уравнения кинематики для постоянного ускорения
Четыре всадника кинематического апокалипсиса:
x _f – x _i = (v _f – v _i) * t / 2
v _f – v _i = a * t
v _f ² = v _i ² + 2 * a * (x _f – x _i)
x _f = x _i + v _i * t + ½a * t ²
Примечание: маленький _f обозначает final (как конечную скорость или положение), а маленький _i обозначает начальное.
Примечание. Эти уравнения работают только при постоянном ускорении, но почти все задачи имеют постоянное ускорение.
Шаги решения одномерных задач
Для каждой одномерной кинематической задачи этапы практически одинаковы.
Запишите каждую величину, которую дает вам задача (начальное и конечное положение, начальная и конечная скорость, ускорение, время и т. Д.)
Запишите, какое количество вы пытаетесь найти
Найдите кинематическое уравнение (или иногда два уравнения), чтобы связать эти величины.
Решите алгебру.
Да, это действительно так просто. (Фактически, большинство физических задач работают одинаково. Для получения более подробной информации об алгоритме решения физических задач ознакомьтесь с этой статьей.)
Как избежать распространенных ошибок: скрытые величины
Иногда проблема может сообщить вам количество тайно; вы можете даже не осознавать, что получили это. Например, если они сообщают вам смещение (как далеко что-то переместилось), но не позиции, вы можете рассматривать смещение как x _f и установить для x _i значение 0.Точно так же, если проблема не говорит ничего особенного об ускорении, то ускорение, вероятно, является просто силой тяжести, a = g = 9,8 м / с ². Эти скрытые количества так же действительны, как и обычные количества, только их немного сложнее обнаружить.
Как избежать распространенных ошибок: лучший результат
Особый пример скрытой величины – это когда вам говорят, что объект находится «на вершине своего полета / движения / траектории и т. Д.». Это означает, что они тайно говорят вам, что v _f равно 0, потому что объект, движущийся в одном измерении, всегда имеет скорость 0 в верхней части своего пути.Интересно, почему? Что ж, если бы скорость росла, то через миллисекунду объект был бы выше (и, следовательно, он не мог бы оказаться на вершине своего пути). Точно так же, если бы объект имел скорость, направленную вниз, то она была бы выше за миллисекунду (так что он также не может быть наверху).
Как избежать распространенных ошибок: положительные и отрицательные числа
Отследить негативы бывает непросто. Ключ – это направление; вниз всегда отрицательно. Таким образом, если объект падает, он будет иметь отрицательную скорость.Если ускорение снижается (а это почти всегда), то ускорение отрицательное. И не забывайте из нашей первой главы, что можно иметь положительную скорость и отрицательное ускорение одновременно!
Пример: женщина и ее мяч
Женщина держит мяч на расстоянии 1 метра и бросает его вверх со скоростью 5 м / с. а) Как высоко достигает мяч? б) Сколько времени нужно мячу, чтобы коснуться земли? в) Насколько быстро мяч летит, когда ударяется о землю?
Давай узнаем!
Часть A: Как высоко достигает мяч?
Что мы знаем?
Начальная позиция x _i = 1 м
Начальная скорость v _i = 5 м / с
Секретное количество: a = -9. 8 м / с ² (сила тяжести)
Секретное количество: В верхней части дуги мяча (т. Е. Когда она самая высокая) v _f = 0 м / с
Что мы пытаемся найти?
Положение наверху броска, x _f
Какое уравнение связывает эти величины?
Мы ищем уравнение, которое включает x _f, x _i, v _f, v _i и a
v _f ² = v _i ² + 2 * a * (x _f – x _i), кажется, хорошо вписывается!
Подключи и реши
v _f ² = v _i ² + 2 * a * (x _f – x _i)
(0 м / с) ² = (5 м / с) ² + 2 * (- 9.8 м / с ²) * (x _f – 1 м)
0 = 25 (м ² / с ²) – (19,6 м / с ²) * (x _f – 1 м )
(19,6 м / с ²) * (x _f – 1 м) = 25 м ² / с ² x _f –1 м = (25 м ² / с ² ) / (19,6 м / с ²)
x _f –1 м = 1,28 м
x _f = 2,28 м
Тада! Конечная высота = 2,28 метра
Часть B: Сколько времени нужно мячу, чтобы коснуться земли?
Что мы знаем?
Мы все еще знаем x _i = 1 м, v _i = 5 м / с и a = -9. 8 м / с ², но теперь мы также знаем, что x _f = 0 м (потому что высота земли 0 м)
Примечание: поскольку мяч теперь находится на земле, а не наверху полета, v _f ≠ 0, так что мяч находится вне стола.
Что мы пытаемся найти?
Время, т
Какое уравнение связывает эти величины?
Мы ищем уравнение, которое включает x _f, x _i, v _i, a и t
Похоже, нам понадобится x _f = x _i + v _i * т + ½a * т ²
Подключи и реши
x _f = x _i + v _i * t + ½a * t ² 0 m = 1 m + (5 м / с) * t + ½ (-9.8 м / с ²) * t ² – (4,9 м / с ²) * t ² + (5 м / с) * t + 1 м = 0
Это квадратное уравнение (ax ² + bx + c = 0), которое можно решить с помощью формулы корней квадратного уравнения.
t =
t =
t = или t =
t = или t =
t = -17 с или 1,2 с
Мы можем игнорировать t = -. 17, потому что нам не разрешено иметь отрицательное время (мы называем это нефизическим ответом), что оставляет нам время = 1,2 секунды!
Часть C: Соберите все вместе.
Что мы знаем?
Мы все еще знаем x _i = 1 м, v _i = 5 м / с, a = -9,8 м / с ² и x _f = 0 м, но теперь мы также знаем t = 1,2 секунды, потому что мы просто решили это.
Что мы пытаемся найти?
Скорость, v _f
Какое уравнение связывает эти величины?
У нас так много величин, что мы можем использовать любое из уравнений, но давайте возьмем v _f – v _i = a * t, потому что это просто, и мы еще не использовали его.
Подключи и реши
v _f – v _i = a * t
v _f – 5 м / с = (-9,8 м / с ²) * 1,2 с
v _f = 5 м / с – 11,8 м / с
v _f = -6,8 м / с
Стрела, скорость при падении мяча на землю составляет 6,8 м / с (отсюда отрицательный знак).
Верны ли кинематические уравнения при нулевом ускорении? – MVOrganizing
Верны ли кинематические уравнения при нулевом ускорении?
Уравнения можно использовать для любого движения, которое можно описать как движение с постоянной скоростью (ускорение 0 м / с / с) или движение с постоянным ускорением.Их нельзя использовать в течение какого-либо периода времени, в течение которого изменяется ускорение. Каждое из кинематических уравнений включает четыре переменные.
Можно ли использовать уравнения движения при нулевом ускорении?
Уравнения движения применимы при постоянном ускорении. Таким образом, уравнение движения равно нулю, поскольку ноль также является константой.
В чем разница между средней и конечной скоростью?
Средняя скорость (v) объекта равна его конечной скорости (v) плюс начальная скорость (u), деленная на два.v = конечная скорость. u = начальная скорость.
Какой пример равномерной скорости?
Равномерная скорость: движение тяжелого транспортного средства, например грузовиков, по шоссе. Неравномерная скорость: движение велосипеда по городу или по загруженным дорогам. Если транспортное средство движется по круговой траектории с постоянной скоростью, то его скорость считается неоднородной. Был ли этот ответ полезным?
В чем разница между равномерным движением и равномерной скоростью?
Ответ. Равномерное движение определяется как тип движения, при котором скорость тела движется по прямой линии (т.е. скорость) остается неизменной в течение определенного периода времени. Постоянная скорость означает преодоление равных расстояний за равные промежутки времени телом, движущимся по любой траектории (прямой, изогнутой или круговой).
Возможно ли ускорение при равномерном движении?
Да, ускорение может быть равномерным. Равномерное круговое движение является примером такой ситуации, когда скорость или величина скорости остаются неизменными, но из-за изменения направления изменяется ускорение.
Какой пример равномерного движения?
Другими примерами равномерного движения являются: движение стрелок часов, вращение и вращение земли, движение лопастей потолочного вентилятора и т. Д. Вы знаете, почему масло и вода не смешиваются вместе? Говорят, что тело находится в неравномерном движении, если оно преодолевает неравные расстояния за равные промежутки времени.
Что называется равномерным движением?
Когда тело преодолевает равные расстояния по прямой, равные промежутки времени называются равномерным движением.Пример: автомобиль движется со скоростью 20 км / ч по прямой. Когда тело преодолевает неравное расстояние за равные промежутки времени по прямой, это называется неравномерным. Пример: прялка.
Какие бывают типы движения?
Существуют разные типы движения: поступательное, вращательное, периодическое и непериодическое движение. Тип движения, при котором все части объекта перемещаются на одинаковое расстояние за заданное время, называется поступательным движением.
Какова формула неравномерного движения?
При неравномерном круговом движении размер вектора скорости (скорости) изменяется, что означает изменение величины скорости. 2 $$
При постоянном ускорении, приводящем к изменению скорости с $ v_0 $ на $ v_f $, смещение можно рассчитать на основе среднего значения двух скоростей:
$$ d = [{(v_0 + v_f)} / 2].т $$
Пример: автомобиль движется со скоростью 20 м / с, когда проезжает один светофор, затем ускоряется в течение 5 секунд до 40 м / с. Как далеко он зашел?
Решение: $ d = [{(v_0 + v_f)} / 2] ⋅t = [{(20 + 40)} / 2] ⋅ 5 $
$ = 30 ⋅ 5 = 150 млн $
График времени вытеснения
Наклон графика “смещение-время” – это скорость.
Скорость и скорость
Скорость | v | – величина вектора скорости.
Разделение общего расстояния на общее время не дает нам средней скорости, если только объект не двигался всегда в одном и том же направлении.Что касается скорости, чаще всего называют «мгновенную скорость», которая является мерой того, насколько быстро объект движется в определенный момент.
$$ | v | _ {inst} = {δd} / {{δt} $$
, где δd – очень короткое расстояние, а δt – очень короткий интервал времени.
Скорость $ v↖ {→} $ – вектор и скорость изменения смещения в заданном направлении.
$$ v↖ {→} = {Δd} / {Δt} $$
При ускорении a с течением времени t , окончательная скорость $ v_f $ составляет:
$$ v_f = v_0 + a⋅t $$
График скорость-время
Область под графиком скорость-время – это изменение смещения.2 + 2⋅4⋅150 = 400 + 1200 = 1600 $
$ v_f = 40 м / с $
Справочная информация
Возьмем ситуацию девушки, прыгающей по мячу в поезде. Она видит, как мяч падает вертикально. Однако как выглядит полет мяча для наблюдателя, стоящего на платформе станции во время проезда поезда?
Казалось бы, изгибаясь вниз. Это связано с тем, что поезд движется с постоянной горизонтальной скоростью, а мяч ускоряется вниз под действием силы тяжести.
На самом деле, путь, который мяч описывает в воздухе для внешнего наблюдателя, такой же, как и путь снаряда, выпущенного с горизонтальной скоростью: парабола.
Постоянная горизонтальная скорость и постоянное вертикальное ускорение создают кривую в форме параболы.
Возникает вопрос, что означает «в состоянии покоя»? Только для наблюдателя в той же системе отсчета (в нашем примере в поезде) объект может казаться неподвижным.
Если наблюдатель находится в другой системе отсчета (то есть с относительным движением) по отношению к наблюдаемому объекту, то разница в скоростях должна быть добавлена к любому вычислению наблюдаемого движения.
$$ v↖ {→} _ {PQ} = v↖ {→} _ {P} – v↖ {→} _ {Q} $$
, где $ v↖ {→} _ {PQ} $ – относительная скорость P относительно Q.
Контент © Renewable.Media. Все права защищены. Создано: 18 декабря 2013 г. Последнее обновление: 2 октября 2015 г.
Кинематические уравнения: определение, вывод, обратная кинематика
Кинематические уравнения
В кинематических уравнениях мы используем специальные обозначения для обозначения начальных и конечных измерений. Например, мы пишем \ (v \) ₀ для начальной скорости,? для конечной скорости, а ускорение (изменение скорости) объекта обозначается как \ (\ Delta \) \ (v \) = \ (v \) – \ (v \) ₀.Такие обозначения также применимы к перемещению и времени. Если t0 – начальное время, t – конечное время, то смещение равно \ (\ Delta \) t = t (t ₀ = 0 для кинематических уравнений)
Кинетические уравнения связывают пять типов переменных.
Смещение (\ (\ Delta \) x)
Начальная скорость (\ (v \) ₀)
Конечная скорость (\ (v \))
Временной интервал (t)
Постоянное ускорение ( a)
Фактически, кинематические уравнения могут определять движение либо с постоянным ускорением, либо с постоянной скоростью.Мы не можем использовать их, если что-то из двух меняется, поскольку уравнения кинематики применимы только при постоянном ускорении или постоянной скорости.
Кинематические уравнения
Обратная кинематика
Обратная кинематика работает противоположным образом по сравнению с кинематикой. В случае, если есть конечная точка определенного пласта, для достижения этой конечной точки соединениям потребуются некоторые значения углов. Это немного сложно и часто имеет бесконечное количество или более одного решения.Четыре кинематических уравнения, описывающие движение объекта:
\ (v \) = \ (v \) ₀ + at
\ (\ Delta \) \ (x \) = (\ (v \) + \ (v \) ₀/2) t
\ (\ Delta \) \ (x \) = \ (v \) ₀ t + ½ at²
\ (v \) ² = \ (v \) ₀ ² + 2a \ (\ Delta \) \ (x \)
Где d обозначает смещение, t обозначает время, в течение которого объект перемещался, a обозначает ускорение объекта, vi обозначает для начальной скорости объекта, vf обозначает конечную скорость объекта.
Мы можем заметить, что если заданы какие-либо 4 переменные, мы можем легко вычислить 5-ю переменную, используя кинематические уравнения.
<noscript><img src='/800/600/https/sun9-73.userapi.com/HL8PgKi2Rk-EyYuAiCU6mAmQj9ZBnFGCXb0EAQ/ffEDtFSKhxA.jpg' /></noscript> youtube.com/embed/hpWuZh6oTew”/>
Кинематические уравнения вращения
Вышеупомянутые уравнения представляют собой поступательные или линейные кинематические уравнения, описывающие движение линейно движущегося тела. Существует еще одна ветвь кинематических уравнений, известная как уравнения вращательной кинематики, которая касается вращательного движения любого тела. Однако они являются расширением приведенных выше уравнений с измененными только переменными.Различия приведены ниже:
Вместо смещения мы используем изменение угла
Вместо начальной и конечной скоростей мы используем начальную и конечную угловые скорости
Вместо ускорения мы используем угловое
Время – единственная константа
Ниже приведена таблица, показывающая различия в уравнениях для вращательного и линейного движения
Вращательное движение (αα = постоянное)
Линейное движение (a = постоянное)
ω = ω ₀ + αt
v = v ₀ + при
Θ = ½ (ω + ω ₀) t
x = ½ (v ₀ + v) t
Θ = ω ₀ t + ½αt ²
x = v ₀ t + ½at ²
ω 90 029 2 = ω ² ₀ + 2αΘ
v ² = v ² ₀ + 2ax
Вывод кинематических уравнений
\ (v \) = \ (v \) ₀ + at
Ускорение (a) определяется как изменение скорости (\ (\ Delta \) v) объекта с течением времени (\ (\ Delta \) t) . Он представлен уравнением a = \ (\ Delta \) v / \ (\ Delta \) t.
Мы знаем, что \ (\ Delta \) v = v – v ₀
Поместите \ (\ Delta \) v = v – v ₀ в формулу ускорения
A = v – v ₀ / \ (\ Delta \) т.
Упрощая это, мы получаем v = v ₀ + at
\ (\ Delta \) \ (x \) = [(\ (v \) + \ (v \) ₀) / 2] t
Рассмотрим график зависимости скорости от времени при постоянном ускорении. Наклон скорости, касающейся оси y, представлен как ускорение, а область под наклоном – это смещение объекта \ (\ Delta \) x.
Обратите внимание, что высота синего прямоугольника v ₀, а ширина равна t. Таким образом, площадь равна v ₀ t (площадь прямоугольника = длина x ширина)
Основание треугольника равно t, высота треугольника равна v-v ₀.
Таким образом, площадь треугольника будет ½ t (vv ₀)
Когда мы сложим площади прямоугольника и треугольника, мы получим
\ (\ Delta \) x = v ₀ t + ½ t (vv ₀)
Упрощая, получаем
\ (\ Delta \) x = v ₀ t + ½ vt – ½ v ₀ t
Объединяя члены начального значения, получаем \ (\ Delta \ ) x = v ₀ t + ½ at ²
При дальнейшем упрощении получаем \ (\ Delta \) x = [(v + v0) / 2] t
Третье уравнение:
By подставляя первое кинематическое уравнение во второе и упрощая, получаем
Третье кинематическое уравнение
\ (\ Delta \) \ (x \) = \ (v \) ₀ t + ½ at²
Четвертое уравнение :
Это уравнение может быть получено с использованием первого и второго уравнений
Решая первую кинематическую формулу, мы получаем t = ((\ (v \) = \ (v \) ₀) / a
900 02 Подставляем эту формулу во второе уравнение, получаем \ (\ Delta \) x = [(v + v0) / 2] [(v – v0) / a]
Упрощая, получаем \ (\ Delta \) x = (\ (v \) ² – \ (v \) ₀ ²) / 2a
Решая для v ², получаем, \ (v \) ² = \ (v \) ₀ ² + 2a \ (\ Delta \) \ (x \)
Выбор правильного уравнения
Кинематические уравнения могут применяться к множеству задач, связанных с движением объекта с постоянным ускорением. Когда мы решаем проблемы, выбираемая нами формула должна включать неизвестную переменную, а также 3 известные (заданные) переменные. Знайте, что в каждом из уравнений кинематики отсутствует 1 переменная. Это внимательное наблюдение поможет вам определить, какая переменная не указана или не запрашивается для решения проблемы, прежде чем выбирать уравнение, в котором также отсутствует эта переменная.
Что следует помнить
Кинематическое уравнение является частью учебной программы по физике 11 класса CBSE.
Он входит в раздел «Кинематика 2» и содержит от 10 до 12 периодов и от 4 до 6 оценок.
Средняя скорость объекта может быть определена с помощью кинематических уравнений.
Кинематические уравнения используются, когда ускорение тела постоянно.
Кинематические уравнения – это группа из четырех уравнений, которая помогает получить неизвестную информацию о движении объекта, если другая информация недоступна.
Примеры вопросов
Вопрос 1. Насколько быстро будет двигаться объект по оси x при t = 10 секунд, скорости s = 2 м / с и постоянном ускорении 2 м / с 2 ? (1 балл)
Ответ: мы знаем, что v = v0 + при
Учитывая v0 = 2, a = 2, t = 10
Таким образом, v = 2 + 2 (10) = 22 м / с
Вопрос 2.Автомобиль движется к обрыву с начальной скоростью 15 м / с. Максимальное отрицательное ускорение, которое обеспечивает автомобиль при торможении, составляет -0,3 м / с 2 . Если обрыв находится в 350 метрах от исходного положения автомобиля, сможет ли автомобиль переехать через обрыв? (2 балла)
Ответ: Чтобы машина остановилась на обрыве, конечная скорость должна быть равна нулю.
V ² = v ₀ ² + 2a (x-x0)
0 = 15 ² +2 (-0,3) (x-0)
= 225 + 2 (-0.3) (x)
= 225-0,6 x
= 375 м
Конечная скорость не равна нулю, поэтому машина не может остановиться у обрыва, а едет через обрыв.
Вопрос 3. Автомобиль A движется с постоянной скоростью мимо точки 1 по прямой дороге со скоростью 0,3 м / с. Тележка B движется мимо точки 1 со скоростью 0,1 м / с, но равномерно ускоряется со скоростью 0,1 м / с 2 . Точка 2 находится на расстоянии 1,0 м после точки 1. Какая тележка первой доберется до точки 2? Найдите время, за которое каждая тележка дойдет до точки 2? (2 балла)
Ответ: Для тележки A:
x-x ₀ = v0t + ½at ²
1.0-0 = 0,3 т + 0
t = 3,3 секунды
Для тележки B:
xx ₀ = v ₀ t + ½ при ²
1,0-0 = 0,1 т + ½ (0,1 ) t ²
Используя систему квадратного уравнения, получаем t = 3,6 секунды
Следовательно, тележка A сначала достигает точки 2
Вопрос 4. Самолет ускоряется по взлетно-посадочной полосе со скоростью 3,20 м / с 2 в течение 32,8 с, пока наконец не оторвется от земли. Определите пройденное расстояние до взлета.(1 балл)
Отв. a = + 3,2 м / с²
t = 32,8 с
vi = 0 м / с
d =?
d = vi
d = vi * t + 0,5 * a * t²
d = (0 м / с) * (32,8 с) + 0,5 * (3,20 м / с²) * (32,8 с) ²
d = 1720 м
Вопрос 5. Автомобиль трогается с места и разгоняется равномерно в течение 5,21 секунды на расстояние 110 м. Определите ускорение автомобиля. (1 балл)
Отв. d = 110 м
t = 5,21 с
vi = 0 м / с
a =?
d = vi * t + 0.5 * a * t²
110 м = (0 м / с) * (5,21 с) + 0,5 * (a) * (5,21 с) ²
110 м = (12,57 с²) * a
a = (110 м ) / (13,57 с²)
a = 8,10 м / с²
Вопрос 6. Аптон Чак едет на Гигант-Дроп в Грейт-Америке. Если Аптон бесплатно упадет в течение 2,60 секунды, какова будет его конечная скорость и как далеко он упадет? (2 балла)
Отв. a = -9,8 м
t = 2,6 с
vi = 0 м / с
d =?, vi =?
d = vi * t + 0. 5 * a * t²
d = (0 м / с) * (2,60 с) + 0,5 * (- 9,8 м / с²) * (2,60 с) ²
d = -33,1 м (- указывает направление)
vf = vi + a * t
vf = 0 + (-9,8 м / с²) * (2,60 с)
v f = -25,5 м / с (- указывает направление)
Ques 7. Гоночный автомобиль равномерно ускоряется с 18,5 м / с до 46,1 м / с за 2,47 секунды. Определите ускорение автомобиля и пройденное расстояние.
Отв. vi = 18.5 м / с
vf = 46,1 м / с
t = 2,47 с
d =?, A =?
a = (\ (\ Delta \) v) / t
a = (46,1 м / с – 18,5 м / с) / (2,47 с)
a = 11,2 м / с²
d = vi * t + 0,5 * a * t²
d = (18,5 м / с) * (2,47 с) + 0,5 * (11,2 м / с²) * (2,47 с) ²
d = 45,7 м + 34,1 м
d = 79,8 м
Ques 8. На Луну падает перо с высоты 1,40 метра. Ускорение свободного падения на Луне равно 1. 67 м / с ² . Определите время, за которое перо упадет на поверхность Луны. (1 балл)
Отв. vi = 0 м / с
d = -1,40 м
a = -1,67 м / с
t =?
d = vi * t + 0,5 * a * t²
-1,40 м = (0 м / с) * (t) +0,5 * (- 1,67 м / с²) * (t) ²
-1,40 м = 0 + (-0,835 м / с²) * (t) ²
(-1,40 м) / (- 0,835 м / с²) = t²
1,68 с² = t²
t = 1,29 с
Ques 9. Ракета сани с приводом от двигателя используются для проверки реакции человека на ускорение.Если сани с ракетным двигателем разгоняются до скорости 444 м / с за 1,83 секунды, то каково это ускорение и какое расстояние они преодолевают? (2 балла)
Отв. vi = 0 м / с
vf = 444 м / с
t = 1,83 с
a =?, d =?
a = (Delta v) / t
a = (444 м / с – 0 м / с) / (1,83 с)
a = 243 м / с²
d = vi * t + 0,5 * a * t²
d = (0 м / с) * (1,83 с) + 0,5 * (243 м / с²) * (1,83 с) ²
d = 0 м + 406 м
d = 406 м
Вопрос 10. Велосипед из состояния покоя равномерно ускоряется до скорости 7,10 м / с на расстоянии 35,4 м. Определите ускорение велосипеда. (1 балл)
Отв. vi = 0 м / с
vf = 7,10 м / с
d = 35,4 м
a =?
vf² = vi² + 2ad
(7,10 м / с) ² = (0 м / с) ² + 2a (35,4 м)
50,4 м² / с² = (0 м / с) ² + (70,8 м) a
(50,4 м² / с²) / (70,8 м) = a
a = 0,712 м / с²
Кинематика вращения – Физика 298
“Мужчины говорят о том, чтобы убивать время, в то время как время тихонько их убивает
Дион Бусико London Assurance (1841)

На сегодняшний день мы рассмотрели кинематика и динамика частиц, в том числе поступательная и круговое движение, а также поступательное движение системы частиц (в частности твердых тел) с точки зрения движение центра масс системы (тела). В в последнем случае мы можем представить, что вся масса объект находится в центре масс до внешнего трансляционные силы обеспокоены.
следующий шаг – рассмотреть вращение твердого тела вокруг фиксированная ось вращения. Примечание что, поскольку мы рассматриваем твердое тело, каждая частица в теле остается фиксированной относительно к остальным .Этот означает, что при таком вращательном движении каждая частица движется в круг, центр которого лежит на оси вращения. В на диаграмме справа объект вращается вокруг оси z; в две частицы образца движутся по кругу радиусом r ₁ и r ₂. Если мы можем описывают круговое движение частицы без прямого относительно его радиуса, то все частицы в системе будут описываться той же системой уравнений. Хотя радиусы частиц разные, их угловые повороты идентичны. Следовательно Это необходимо ввести угловые переменные.
Угловая скорость (скорость) и Угловое ускорение
Угловая скорость и угловое ускорение определяются аналогично скорость и ускорение.Там являются средними и мгновенными значениями каждого.

Угловой ускорение – это не то же самое, что , как центростремительное ускорение. Центростремительное ускорение происходит из-за изменение направления скорости, угловое ускорение связано с изменением звездной величины на скорости (через угол поворота).
Ровно как и в трансляционном случае, разница между угловыми скорость и угловая скорость – направление. Угловой скорость должна включать направление вращения вокруг оси в вопрос. За например, 10 рад / с по часовой стрелке около ось x – угловая скорость, 10 рад / с вокруг оси x – это угловая скорость.
Уравнения кинематики вращения
По прямой аналогии с поступательной кинематикой уравнения, круговое движение вокруг единственной оси при постоянном угловое ускорение можно описать следующими четырьмя уравнения,

, где производились замены,
Обратите внимание, что так же, как + x определяется произвольно справа, положительное значение тета может быть определена как по часовой стрелке или против часовой стрелки.
Связь между угловым и Трансляционные переменные
Пусковой от определение радианной меры путем дифференцирования относительно времени, мы можем показать, что,

, где v – тангенциальная скорость и a тангенциальная ускорение.
А частица, совершающая круговое движение, с переменным угловым скорость (неравномерное круговое движение), испытает два компоненты ускорения, тангенциальная составляющая из-за изменение величины его скорости и радиального (центростремительного) составляющая из-за изменения направления ее скорости

Сеть ускорение частицы – это векторная сумма этих двух компоненты, как указано ниже.
Одновременное вращение вокруг более чем одной оси может быть рассматривается аналогично движению снаряда, где мы расширил наше обсуждение одномерного перевода на двухмерное движение. В авиационных приложениях вращение вокруг три оси описываются как Roll, Шаг и рыскание.

Пример задачи

Я не хочу достичь бессмертия своей работой я хочу достичь этого, не умирая
Вуди Аллен Вуди Аллен и его комедия (1975)

Доктор.К. Л. Дэвис
Физический факультет
Университет Луисвилл
электронная почта : [email protected]
.

Вращательное движение (αα = постоянное)	Линейное движение (a = постоянное)
ω = ω ₀ + αt	v = v ₀ + при
Θ = ½ (ω + ω ₀) t	x = ½ (v ₀ + v) t
Θ = ω ₀ t + ½αt ²	x = v ₀ t + ½at ²
ω 90 029 2 = ω ² ₀ + 2αΘ	v ² = v ² ₀ + 2ax