Основные понятия и уравнения кинематики равноускоренного движения тела
Ознакомление учащимся целями и критериям оценивание
Если нам дано график зависимости скорости от времени как мы найдем перемешение через график?
Механи́ческимдвиже́нием тела называется изменение его положения в пространстве относительно других тел с течением времени. Равномерное движение — механическое движение, при котором тело за любые равные промежутки времени проходит одно и то же расстояние. При равномерном движении величина скорости точки остаётся неизменной.Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Рассмотрим график перемешении от времени при равномерном движении. Проанализируйте данный график?
Обсуждая
изменение скорости от времени при равнопеременном движении находя градиент то
есть тангенс угла найдем ускорение.
Ускорением движущегося тела называют величину, равную отношению изменения скорости тела к промежутку времени, в течение которого это изменение произошло
единица измерения м/с2
Найдем перемещение через график. Показывая график ученики должны придти что площадь данного фигуры дает перемешение тела.
По данному графику площадь тарпеции будет равна если учитовать что ускорение , тоотсюда перемешение будет равна:
Если мы хоти преминить график или уровнение координаты от времени, то мы должны определить по какому осьи надо учитывать. Например по оси ОХ перемешение или по ОУ , то наша уравнение будет таком формате:
Объяснение кинематических уровнении и графиков
Закрепление
Групповая работа
Уровень А
1.Каково ускорение велосипедиста, если его скорость за 5 секунд изменилась от 7 до 2 м/с?
2.На рисунке дано
изменение скорости от времени. Какой из них подходит на равнозамедленному
двужению?
Какой из них подходит на равнозамедленному
двужению?
Уровень В
3.Материальная точка движется по уравнению х═2t+5t². Какова начальная скорость данного материального движения?
4.Используя уравнение и ,постройте график зависимосьти перемешении от времени. Найдите координату и время пересичение.
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
Вопросы для закрепления
1.
2.При каком условии ускорение тела будет положительным?
3. используя график V(t) постройте график a(t)?
Узнаем что это – ускорение в физике. Понятие о полном ускорении и его компонентах. Равноускоренное прямолинейное движение
Механическое движение окружает нас с самого рождения. Каждый день мы видим, как движутся по дорогам машины, по морям и рекам корабли, летают самолеты, даже наша планета движется, пересекая космическое пространство. Важной характеристикой для всех без исключения видов движения является ускорение. Это физическая величина, типы и основные характеристики которой будут рассмотрены в данной статье.
Физическое понятие об ускорении
Многим термин “ускорение” интуитивно знаком. В физике ускорение – это величина, характеризующая любое изменение во времени скорости. Соответствующая математическая формулировка имеет вид:
a¯ = dv¯/ dt
Черта над символом в формуле означает, что эта величина векторная. Таким образом, ускорение a¯ является вектором и описывает оно изменение также векторной величины — скорости v¯. Это ускорение называется полным, оно измеряется в метрах в секунду квадратную. Например, если тело увеличивает за каждую секунду своего движения скорость на 1 м/с, то соответствующее ускорение равно 1 м/с2.
Таким образом, ускорение a¯ является вектором и описывает оно изменение также векторной величины — скорости v¯. Это ускорение называется полным, оно измеряется в метрах в секунду квадратную. Например, если тело увеличивает за каждую секунду своего движения скорость на 1 м/с, то соответствующее ускорение равно 1 м/с2.
Откуда возникает ускорение и куда оно направлено?
Мы разобрались с определением, что это ускорение. Также было выяснено, что речь идет о величине векторной. Куда направлен этот вектор?
Чтобы дать правильный ответ на поставленный выше вопрос, следует вспомнить второй закон Ньютона. В общепринятой форме он записывается следующим образом:
F¯ = m*a¯
Словами можно прочитать это равенство так: действующая на тело массой m сила F¯ любой природы приводит к появлению у этого тела ускорения a¯. Поскольку масса — это скалярная величина, то получается, что вектора силы и ускорения будут направленными вдоль одной и той же прямой. Иными словами, ускорение всегда направлено в сторону действия силы и совершенно не зависит от вектора скорости v¯. Последний направлен вдоль касательной к траектории движения.
Иными словами, ускорение всегда направлено в сторону действия силы и совершенно не зависит от вектора скорости v¯. Последний направлен вдоль касательной к траектории движения.
Криволинейное движение и компоненты полного ускорения
В природе мы часто встречаемся с движением тел по криволинейным траекториям. Рассмотрим, как можно описать ускорение в этом случае. Для этого предположим, что скорость материальной точки в рассматриваемой части траектории может быть записана в виде:
v¯ = v*ut¯
Скорость v¯ является произведением его абсолютной величины v на единичный вектор ut¯, направленный вдоль касательной к траектории (тангенциальная составляющая).
Согласно определению, ускорение — это производная скорости по времени. Имеем:
a¯ = dv¯/dt = d(v*ut¯)/dt = dv/dt*ut¯ + v*d(ut¯)/dt
Первое слагаемое в правой части записанного равенства называется тангенциальным ускорением. Так же, как и скорость, оно направлено вдоль касательной и характеризует изменение абсолютной величины v¯. Второе слагаемое — это ускорение нормальное (центростремительное), оно направлено перпендикулярно к касательной и характеризует изменение вектора величины v¯.
Так же, как и скорость, оно направлено вдоль касательной и характеризует изменение абсолютной величины v¯. Второе слагаемое — это ускорение нормальное (центростремительное), оно направлено перпендикулярно к касательной и характеризует изменение вектора величины v¯.
Таким образом, если радиус кривизны траектории равен бесконечности (прямая линия), то вектор скорости в процессе перемещения тела не меняет своего направления. Последнее означает, что нормальная составляющая полного ускорения равна нулю.
В случае движения материальной точки по окружности равномерно, модуль скорости остается постоянным, то есть тангенциальная компонента полного ускорения равна нулю. Нормальная же составляющая направлена к центру окружности и вычисляется по формуле:
an = v2/r
Здесь r — радиус. Причиной появления центростремительного ускорения является действие на тело некоторой внутренней силы, которая направлена к центру окружности. Например, для движения планет вокруг Солнца этой силой является гравитационное притяжение.
Формула, которая связывает модули полного ускорения и его компонент at (касательная), an (нормальная), имеет вид:
a = √(at2 + an2)
Равноускоренное перемещение по прямой линии
Движение по прямой с постоянным ускорением часто встречается в быту, например это перемещение автомобиля по дороге. Этот вид движения описывается следующим уравнением для скорости:
v = v0 + a*t
Здесь v0 — некоторая скорость, которой тело обладало до возникновения у него ускорения a.
Если изобразить график функции v(t), то мы получим прямую линию, которая ось y пересекает в точке с координатами (0; v0), а тангенс угла наклона к оси x равен модулю ускорения a.
Взяв интеграл от функции v(t), мы получим формулу для пути L:
L = v0*t + a*t2/2
График функции L(t) – это правая ветвь параболы, которая начинается в точке (0; 0).
Приведенные формулы являются основными уравнениями кинематики ускоренного перемещения по прямой.
Если тело, имея начальную скорость v0, начинает замедлять свое движение с ускорением постоянным, то говорят о равнозамедленном перемещении. Для него справедливы следующие формулы:
v = v0 – a*t;
L = v0*t – a*t2/2
Решение задачи на вычисление ускорения
Находясь в неподвижном состоянии, автомобиль начинает движение. При этом за 20 первых секунд он проходит расстояние 200 метров. Чему равно ускорение автомобиля?
Сначала запишем общее кинематическое уравнение для пути L:
L = v0*t + a*t2/2
Поскольку в нашем случае транспортное средство находилось в состоянии покоя, то его скорость v0 была равна нулю. Получаем формулу для ускорения:
L = a*t2/2 =>
a = 2*L/t2
Подставляем значение пройденного пути L = 200 м за промежуток времени t = 20 с и записываем ответ на вопрос задачи: a = 1 м/с2.
Кинематика. Основные кинематические характеристики прямолинейного и криволинейного движения
Лекция 11. Механика
1.1. Кинематика
Основные кинематические характеристики
прямолинейного и криволинейного движения: путь,
перемещение, скорость и ускорение. Нормальное,
тангенциальное и полное ускорения. Кинематика
вращательного движения: угловой путь, угловая
скорость и угловое ускорение, их связь с линейными
величинами. Период и частота вращения.
Механика
Механическое движение
Механическим движением тела называется изменение его
положения в пространстве относительно других тел с течением
Система отсчета
Тело, которое считается неподвижным, и по отношению к которому
определяется положение других тел, называют телом отсчета. Тело
отсчета вместе со связанной с ним системой координат образуют
систему отсчета.
Относительность механического движения
Зависимость характера движения от выбора тела, относительно
которого это движение определяется, называется
относительностью движения.
 Всякое движение, и покой в
Всякое движение, и покой вчастности, является относительным.
Кинематика
Абсолютно твердое тело
Абсолютно твердым называется тело, деформацией которого
неизменно во времени.
Поступательное движение тела
Движение тела, при котором все его точки движутся одинаково,
называется поступательным. При таком движении любая прямая,
жестко связанная с телом, перемещается в пространстве,
оставаясь параллельной самой себе.
Материальная точка
Тело, размерами которого в данных условиях можно пренебречь
(по сравнению с масштабом движения), называется материальной
точкой.
Траектория движения
Траекторией движения материальной точки называется линия,
которую эта точка описывает в пространстве при своем движении.
Путь
Путь — скалярная физическая величина, численно равная длине
отрезка траектории, пройденного телом за время движения.
S S (t )
S S (t2 ) S (t1 )
t t2 t1
Перемещение
Перемещением тела (материальной точки) называется
направленный отрезок прямой (вектор), соединяющий начальное и
конечное положение тела.

r r r
2
z
r1
Прямолинейное движение
S
A
r
B
r2
y
x
1
Движение называется прямолинейным,
если его траектория представляет
собой прямую линию.
При прямолинейном движении путь и
перемещение совпадают: r S
При криволинейном движении они
совпадают в пределе для бесконечно
малого перемещения:
dr dS
Линейная скорость
Линейной скоростью перемещения тела называют векторную
физическую величину, характеризующую процесс изменения
пространственного положения тела относительно выбранной
системы отсчета, численно равную перемещению тела в единицу
времени и совпадающую по направлению с этим перемещением.
Единица скорости
За единицу скорости (м/сек) принимают скорость такого движения,
при котором тело за 1 сек перемещается на расстояние 1 м.
r
v
t
vA
z
A
r
B
vB
y
x
Мгновенная скорость:
r
d
r
v lim
t 0 t
dt
d
r
dS
v v
dt
dt
Мгновенная скорость
Мгновенная скорость, или скорость в данной точке, равна
отношению достаточно малого перемещения на участке
траектории, включающем эту точку, к малому промежутку времени,
в течение которого это перемещение совершается.
 Направлена по
Направлена покасательной к траектории в данной точке.
Равномерное прямолинейное движение
Равномерным прямолинейным называется такое прямолинейное
движение, при котором тело (материальная точка) за любые
равные промежутки времени проходит одинаковый путь.
Средняя скорость
Средней скоростью движения на данном участке пути называется
отношение длины этого участка пути к промежутку времени, за
которой этот участок пройден.
Средняя скорость есть скорость такого равномерного движения,
при котором тело прошло бы данный участок пути за тот же
промежуток времени.
S ( S S )
v ср v v
t
2
1
(t 2 t1 )
Принцип независимости движений
Если тело участвует одновременно в нескольких движениях, то
каждое из них совершается независимо от остальных.
n
r r1 r2 rn rn
i 1
Сложение скоростей
Скорость тела относительно неподвижной системы координат
равна геометрической (векторной) сумме скорости тела
относительно подвижной системы координат и скорости подвижной
системы координат относительно неподвижной.
n
drn
dr dr1 dr2
v
v1 v 2 v n v n
dt dt dt
dt
i 1
При движении вдоль одной прямой скорости направленные по
направлению движения берутся со знаком “+”, против движения со
знаком “–”.
Линейное ускорение
Линейное ускорение — векторная физическая величина,
характеризующая процесс изменения линейной скорости с
течением времени, численно равная изменению скорости в единицу
времени и совпадающая по направлению с направлением этого
изменения.
v
Единица ускорения
a
t
За единицу ускорения (м/сек2) в системе СИ принимают ускорение
такого движения, при котором тело за 1 сек изменяет свою скорость
на 1 м/сек.
Мгновенное ускорение
Мгновенное ускорение, или ускорение в данной точке, равно
отношению достаточно малого изменения скорости на участке
траектории, включающем эту точку, к малому промежутку времени,
в течении которого это изменение совершается.
v d v
a lim
t 0 t
dt
d 2 r
d 2S
dv
a a
2 2
dt
dt
dt
A
Тангенциальное ускорение
vА
v
B
Тангенциальным (касательным) ускорением называется
составляющая ускорения, обусловленная изменением
модуля вектора скорости.
dv
vB
a
Нормальное ускорение
vA
A
Нормальным (центростремительным) ускорением
называется составляющая ускорения, обусловленная
изменение направления вектора скорости.
a
an
a
vA
r
О
dt
B
v
vB
v AB
v
АO
v r v t
v
R
R
v v 2
t
R
v2
an
R
v v 2
an lim
t 0 t
R
dv v
2
2
a a a an
dt R
2
2
2
Частные случаи криволинейного движения
1.
a 0
an 0
Равномерное прямолинейное движение
2.
a const
an 0
Равнопеременное прямолинейное движение
3.
a 0
an const
Равномерное движение по окружности
4. a const
an const
Равнопеременное движение по окружности
Кинематические уравнения и графики
Равномерное движение
v const
S v t
a 0
При равномерном движении график зависимости пути от времени
есть прямая линия, проходящая через начало системы координат.

При равномерном движении график зависимости скорости от
времени есть прямая линия, проходящая параллельно оси
времени.
При равномерном движении ускорение тела равно нулю.
v
v
S
t
t
t1
t2
t
Равнопеременное движение
a t2
S v0 t
2
v v0 a t
a const
При равнопеременном движении график зависимости скорости от
времени есть прямая линия.
При равнопеременном движении график зависимости ускорения от
времени есть прямая, параллельная оси времени.
a
v
S
a 0
a 0
a 0
a 0
t
t
t
Вращательное движение
Вращательным движением твердого тела вокруг неподвижной оси
называется такое движение, при котором все точки тела двигаются
по окружности, центры которых лежат на одной прямой,
называемой осью вращения. Ось вращения перпендикулярна
плоскости, в которой лежат эти окружности.
Вращение тела
Радиусы-векторы, соединяющие все точки твердого тела с
центрами описываемых ими окружностей, поворачиваются за один
и тот же промежуток времени на одинаковый угол, т.
 е. описывают
е. описываютодинаковый угловой путь.
Угловой путь
Угловой путь тела — векторная физическая величина,
характеризующая вращение тела вокруг неподвижной оси,
численно равная углу поворота за определенный промежуток
времени и направленная вдоль оси вращения так, что из конца
вектора вращение видно происходящим против часовой стрелки.
Единица угла поворота
За единицу угла поворота в системе СИ принимают
1 радиан (рад) — такой угол, длина дуги которого
равна радиусу. В полном обороте 2 радиан.
Угловая скорость
Угловой скоростью вращения тела называют векторную
физическую величину, характеризующую быстроту вращения тела
вокруг неподвижной оси, численно равную угловому пути в единицу
времени и направленную вдоль оси вращения. Направление
угловой скорости вдоль оси вращения определяется по правилу
“буравчика”, т.е. таким образом, чтобы получился правый винт.
d
dt
Единица угловой скорости
За единицу угловой скорости рад/сек в системе СИ принимают
угловую скорость такого вращения, при котором тело за 1 сек
поворачивается на угол равный 1 рад.

Угловое ускорение
Угловым ускорением вращения тела называют векторную
физическую величину, характеризующую быстроту изменения
угловой скорости и численно равную изменению угловой скорости в
единицу времени. Вектор углового ускорения направлен по оси
вращения либо в сторону угловой скорости (при ускоренном
вращении), либо противоположно ей (при замедленном вращении).
d d 2
2
dt
dt
Единица углового ускорения
За единицу углового ускорения рад/сек2 в системе СИ принимают
угловое ускорение такого вращения, при котором угловая скорость
вращения тела за 1 сек изменяется 1 рад/сек.
Равномерное вращение
Равномерным вращением твердого тела называется такое
вращение, при котором тело за любые равные промежутки
поворачивается на одинаковый угол поворота.
Период обращения
Периодом обращения называют скалярную физическую величину,
численно равную промежутку времени, в течение которого тело
совершает полный оборот,
2
2
T
т.
 е. поворачивается на угол 2 .
е. поворачивается на угол 2 .t
Частота обращения
T
Частотой обращения называют скалярную физическую величину,
численно равную числу оборотов, совершаемых за единицу
времени.
N 1
t
T
2
2
Связь между линейными и угловыми единицами
Вращательное движение
Поступательное движение
Путь S
S R
Угол поворота
v R
Угловая скорость
Угловое ускорение
Тангенциальное ускорение a R
2
v
Нормальное ускорение
an
2 R
R
Линейная скорость v
Кинематические уравнения и графики
Равномерное вращение
t
const
0
При равномерном вращении график зависимости угла поворота от
времени есть прямая линия, проходящая через начало системы
координат.
При равномерном вращении график зависимости угловой скорости
от времени есть прямая линия, проходящая параллельно оси
времени.
При равномерном вращении угловое ускорение тела равно нулю.

t
t
t1
t2
t
Равнопеременное вращение
0 t
t2
0 t
2
const
При равнопеременном вращении график зависимости угловой
скорости от времени есть прямая линия.
При равнопеременном вращении график зависимости углового
ускорения от времени есть прямая, параллельная оси времени.
0
0
0
0
t
t
t
Графику скорости построить график перемещения. Определение кинематических характеристик движения с помощью графиков. Пример решения задачи
1) Аналитический способ.Считаем шоссе прямолинейным. Запишем уравнение движения велосипедиста. Так как велосипедист двигался равномерно, то его уравнение движения:
(начало координат помещаем в точку старта, поэтому начальная координата велосипедиста равна нулю).
Мотоциклист двигался равноускоренно. Он также начал движение с места старта, поэтому его начальная координата равна нулю, начальная скорость мотоциклиста также равна нулю (мотоциклист начал двигаться из состояния покоя).
Учитывая, что мотоциклист начал движение на позже, уравнение движения мотоциклиста:
При этом скорость мотоциклиста изменялась по закону:
В момент, когда мотоциклист догнал велосипедиста их координаты равны, т.е. или:
Решая это уравнение относительно , находим время встречи:
Это квадратное уравнение. Определяем дискриминант:
Определяем корни:
Подставим в формулы числовые значения и вычислим:
Второй корень отбрасываем как несоответствующий физическим условиям задачи: мотоциклист не мог догнать велосипедиста через 0,37 с после начала движения велосипедиста, так как сам покинул точку старта только через 2 с после того, как стартовал велосипедист.
Таким образом, время, когда мотоциклист догнал велосипедиста:
Подставим это значение времени в формулу закона изменения скорости мотоциклиста и найдем значение его скорости в этот момент:
2) Графический способ.
На одной координатной плоскости строим графики изменения со временем координат велосипедиста и мотоциклиста (график для координаты велосипедиста — красным цветом, для мотоциклиста — зеленым). Видно, что зависимость координаты от времени для велосипедиста — линейная функция, и график этой функции — прямая (случай равномерного прямолинейного движения). Мотоциклист двигался равноускоренно, поэтому зависимость координаты мотоциклиста от времени — квадратичная функция, графиком которой является парабола.
Видно, что зависимость координаты от времени для велосипедиста — линейная функция, и график этой функции — прямая (случай равномерного прямолинейного движения). Мотоциклист двигался равноускоренно, поэтому зависимость координаты мотоциклиста от времени — квадратичная функция, графиком которой является парабола.
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций . Обозначают
Графики равномерного движения
Зависимость ускорения от времени . Так как при равномерном движении ускорение равно нулю, то зависимость a(t) – прямая линия, которая лежит на оси времени.
Зависимость скорости от времени. Скорость со временем не изменяется, график v(t) – прямая линия, параллельная оси времени.
Численное значение перемещения (пути) – это площадь прямоугольника под графиком скорости.
Зависимость пути от времени. График s(t) – наклонная линия.
Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.
Графики равноускоренного движения
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) – прямая линия, параллельная оси времени.
Зависимость скорости от времени . При равномерном движении путь изменяется, согласно линейной зависимости . В координатах . Графиком является наклонная линия.
Правило определения пути по графику v(t): Путь тела – это площадь треугольника (или трапеции) под графиком скорости.
Правило определения ускорения по графику v(t): Ускорение тела – это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.
Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно
Цели урока:
обучающая: рассмотреть и сформировать навыки построения графиков зависимости кинематических величин от времени при равномерном и равноускоренном движении; научить учащихся анализировать эти графики; путем решения задач закрепить полученные знания на практике;
развивающая: развитие умения наблюдать, анализировать конкретные ситуации; выделять определенные признаки;
воспитывающая: воспитание дисциплины и норм поведения, творческого отношения к изучаемому предмету; стимулировать активность учащихся.
Методы:
словесный – беседа;
наглядный – видеоурок, записи на доске;
контролирующий – тестирование или устный (письменный) опрос, решение задач).
Связи:
межпредметные : математика – линейная зависимость, график линейной функции; квадратичная функция и ее график;
внутрипредметные : равномерное и равноускоренное движение.
Ход урока :
1. Организационный этап.
Добрый день. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.
2. Актуализация знаний.
3. Объяснение нового материала.
Мы с вами знаем, что механическое движение – это изменение положения тела (или частей тела) в пространстве относительного других тел с течением времени.
В свою очередь механическое движение бывает двух видов – равномерное, при котором тело за любые равные промежутки времени совершает одинаковые перемещения, и неравномерным, при котором тело за любые равные промежутки времени совершает разные перемещения.
Давайте вспомним основные формулы, которые мы выучили для равномерного и неравномерного движения.
Если движение равномерное, то:
1. Скорость тела не меняется с течением времени;
2. Что бы найти скорость тела, необходимо путь, который прошло тело за некоторый промежуток времени, разделить на этот промежуток времени;
3. Уравнение перемещения имеет вид:
4. И – кинематическое уравнение равномерного движения.
Для равноускоренного:
1. Ускорение тела не изменяется с течением времени;
2. Ускорение есть величина, равная отношению изменения скорости тела, к промежутку времени, в течении которого это изменение произошло
3. Уравнение скорости для равноускоренного движения имеет вид:
4. – уравнение перемещения для равноускоренного движения;
5. – кинематическое уравнение равноускоренного движения.
Для большей наглядности движение можно описывать с помощью графиков.
Рассмотрим зависимость ускорения, которым может обладать тело вследствие своего движения, от времени.
Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) – тоже в соответствующем масштабе – значения ускорения тела, полученный график будет выражать зависимость ускорения тела от времени.
Для равномерного прямолинейного движения график зависимости ускорения от времени имеет вид прямой, которая совпадает с осью времени, т.к. ускорение при равномерном движении равно нулю.
Для равноускоренного движения график ускорения также имеет вид прямой, параллельной оси времени. При этом график располагается над осью времени, если тело движется ускоренно, и под осью времени, если тело движется замедленно.
Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, а по вертикальной оси ординат – тоже в соответствующем масштабе – значения скорости тела, то мы получим график скорости.
Для равномерного движения график скорости имеет вид прямой, параллельной оси времени. При этом график скорости располагается над осью времени, если тело движется по оси Х , и под осью времени, если тело движется против оси Х .
При этом график скорости располагается над осью времени, если тело движется по оси Х , и под осью времени, если тело движется против оси Х .
Такие графики показывают, как изменяется скорость с течением времени, т. е. как скорость зависит от времени. В случае прямолинейного равномерного движения эта «зависимость» состоит в том, что скорость с течением времени не меняется. Поэтому график скорости представляет собой прямую, параллельную оси времени.
По графику скорости тоже можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованного прямоугольника: верхнего, если тело движется в сторону положительного направления, и нижнего – в случае движения тела в отрицательном направлении.
Действительно, площадь прямоугольника равна произведению его сторон: S=ab, где a и b стороны прямоугольника.
Но одна из сторон в определенном масштабе равна времени, а другая – скорости. А их произведение как раз и равно абсолютному значению перемещения тела. При этом перемещение будет положительным, если проекция вектора скорости положительна, и отрицательным, если проекция вектора скорости отрицательна.
А их произведение как раз и равно абсолютному значению перемещения тела. При этом перемещение будет положительным, если проекция вектора скорости положительна, и отрицательным, если проекция вектора скорости отрицательна.
При равноускоренном движении тела, происходящем вдоль координатной оси X, скорость с течением времени не остается постоянной, а меняется со временем согласно формуле v = v 0+ at , т. е. скорость является линейной функцией, и поэтому графики скорости имеют вид прямой, наклоненную к оси времени. Причем, чем больше угол наклона, те большую скорость имеет тело. На нашем графике прямая 1 соответствует движению с положительным ускорением (скорость увеличивается) и некоторой начальной скоростью, прямая 2 – движению с отрицательным ускорением (скорость убывает) и начальной скоростью равной нулю.
По графику скорости при равноускоренном движении также можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованной трапеции для тела 1, и прямоугольного треугольника – в противоположном случае. Действительно, например, площадь трапеции равна произведению полу суммы её оснований на высоту. В нашем случае, в определенном масштабе, высота трапеции равна времени, а основания – начальной и конечной скорости.
Действительно, например, площадь трапеции равна произведению полу суммы её оснований на высоту. В нашем случае, в определенном масштабе, высота трапеции равна времени, а основания – начальной и конечной скорости.
При этом проекция перемещения для первого тела будет положительной.
Для второго тела, прямоугольного треугольника – половине произведения его катетов. В нашем случае, катеты – это время и конечная скорость тела.
Проекция перемещения – отрицательна.
Теперь рассмотрим зависимость пройденного пути от времени.
Как и в предыдущих случаях, по оси абсцисс мы будем откладывать время, с момента начала движения, а по оси ординат – путь.
Для равномерного движения график зависимости пути от времени представляет собой прямую линию, т.к. зависимость – линейная.
При этом наклон графика к оси времени зависит от модуля скорости: чем больше скорость, тем больший угол наклона и тем больше скорость движения тела.
При равноускоренном движении графиком будет являться ветка параболы, т. к. зависимость, в этом случае, будет квадратичной. И чем больше ускорение, с которым движется тело, тем сильнее график будет прижиматься к оси ординат.
к. зависимость, в этом случае, будет квадратичной. И чем больше ускорение, с которым движется тело, тем сильнее график будет прижиматься к оси ординат.
Теперь перейдем к рассмотрению зависимости перемещения от времени.
Рассмотрим равномерное движение.
Т.к. при равномерном движении перемещение линейно зависит от времени (sx = υx t ), то графиком будет являться прямая линия. Направление и угол наклона графика к оси времени будет зависеть от проекции вектора скорости на координатную ось.
Так, в нашем случае, тела 2 и 3 движутся в положительном направлении оси Х , при этом скорость третьего тела больше скорости второго.
А тело 1 – в направлении, противоположном направлению оси Х , поэтому график располагается под осью времени.
Для равноускоренного движения графиком перемещения является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения.
Для 1-го тела ускорение меньше нуля, начальная скорость равна нулю.
Для 2-го тела ускорение и начальная скорость тела больше нуля.
Для 3-го тела ускорение больше нуля, начальная скорость меньше нуля.
У 4-го тела начальная скорость и ускорение меньше нуля.
Для 5-го тела ускорение больше нуля, а начальная скорость равна нулю.
И, наконец, 6-ое тело двигается замедленно, но с некоторой начальной скоростью.
И последнее, что мы с вами рассмотрим – это зависимость координаты тела от времени.
Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) – тоже в соответствующем масштабе – значения координаты тела, полученный график будет выражать зависимость координаты тела от времени (его также называют графиком движения).
Для равноускоренного движения графиком движения, как и в случае перемещения, является парабола, положение вершины которой также зависит от направлений начальной скорости и ускорения.
График равномерного движения представляет собой прямую линию.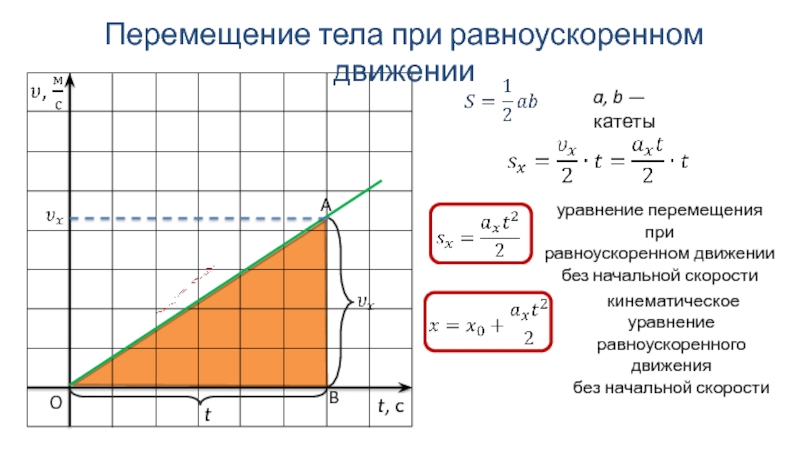 Это значит, что координата линейно зависит от времени.
Это значит, что координата линейно зависит от времени.
В случае прямолинейного движения тела графики движения дают полное решение задачи механики, так как они позволяют найти положение тела в любой момент времени, в том числе и в моменты времени, предшествовавшие начальному моменту (если предположить, что тело двигалось с такой же скоростью и до начала отсчета времени).
С помощью графика движения можно определить:
1. координаты тела в любой момент времени;
2. путь, пройденный телом за некоторый промежуток времени;
3. время, за которое пройден какой-то путь;
4. кратчайшее расстояние м/у телами в любой момент времени;
5. момент и место встречи и т.д.
По виду графиков зависимости координаты от времени можно судить и о скорости движения. Ясно, что скорость тем больше, чем круче график, т. е. чем больше угол между ним и осью времени (чем больше этот угол, тем больше изменение координаты за одно и то же время).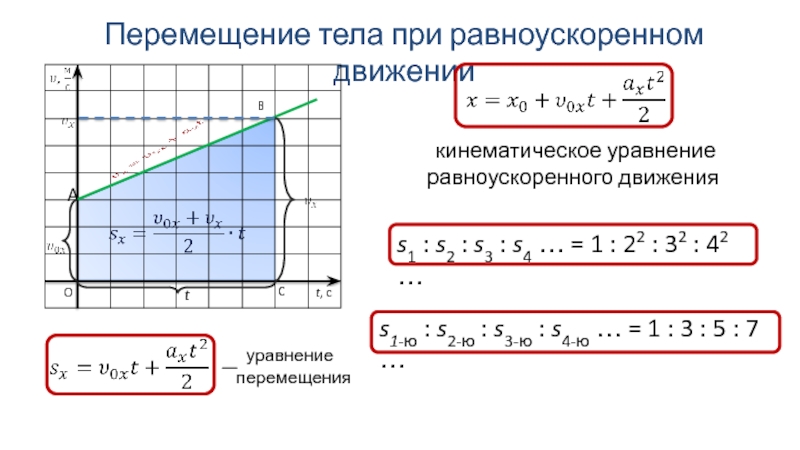
При этом надо помнить, что график зависимости координаты тела от времени не следует путать с траекторией движения тела – прямой, во всех точках которой тело побывало при своем движении.
4. Этап обобщения и закрепления нового материала
И так, сделаем главный вывод.
Механическое движение для большей наглядности можно описывать с помощью графиков:
1) Зависимости скорости от времени;
2) Зависимости ускорения от времени;
3) Зависимость координаты тела от времени;
4) И зависимости перемещения тела от времени, в течении которого это перемещение произошло.
5. Рефлексия
Хотелось бы услышать ваши отзывы о сегодняшнем уроке: что вам понравилось, что не понравилось, чем бы хотелось узнать еще.
6. Домашнее задание.
План-конспект урока по теме « »
Дата:
Тема: Графики пути и скорости при равномерном прямолинейном движении
Цели:
Образовательная: формирование знаний и представлений графиках пути и скорости при равномерном прямолинейном движении;
Развивающая: развитие и формирование практических умений пользоваться физическими понятиями и величинами для описания равномерного прямолинейного движения; развивать познавательный интерес;
Воспитательная: прививать культуру умственного труда, аккуратность, учить видеть практическую пользу знаний, продолжить формирование коммуникативных умений, воспитывать внимательность, наблюдательность.
Тип урока: урок усвоения новых знаний
Оборудование и источники информации:
Исаченкова, Л. А. Физика: учеб. для 7 кл. учреждений общ. сред. образования с рус. яз. обучения / Л. А. Исаченкова, Г. В. Пальчик, А. А. Сокольский; под ред. А. А. Сокольского. Минск: Народная асвета, 2017.
Структура урока:
Организационный момент(5 мин)
Актуализация опорных знаний(5мин)
Изучение нового материала (14 мин)
Физкультминутка (3 мин)
Закрепление знаний (13мин)
Итоги урока(5 мин)
Содержание урока
Организационный момент (проверка присутствующих в классе, проверка выполнения домашнего задания, озвучивание темы и основных целей урока)
Актуализация опорных знаний
№ 1. Закончите фразы.
Скорость при равномерном прямолинейном движении с течением времени __________________________________________________________________
Скорость в СИ измеряется ________________________________________
Пройденный путь при равномерном движении с течением времени _______________________________________________________________
№ 2. Есть способ получения формул с помощью «треугольника памяти» (рис. 1). Если закрыть символ величины, которую нужно определить, то в треугольнике (открытой части) остается формула для ее вычисления. Получите и запишите формулы для вычисления пути
s , скорости и промежутка времени
t .
Есть способ получения формул с помощью «треугольника памяти» (рис. 1). Если закрыть символ величины, которую нужно определить, то в треугольнике (открытой части) остается формула для ее вычисления. Получите и запишите формулы для вычисления пути
s , скорости и промежутка времени
t .
Изучение нового материала
Можно ли выразить связь пути s и времени t не через формулы, а каким-либо другим способом? Для этого используются графики.
Поясним суть графического метода на конкретном примере. Пусть самолет движется равномерно и прямолинейно со скоростью v = 900 (рис. 96). Опишем движение самолета графически, т. е. построим графики зависимости пути и скорости движения самолета от времени движения.
Путь s от начального момента времени t 0 до момента времени t равен v ( t – t 0 ). Начальный момент времени t 0 примем за нуль ( t 0 = 0). Тогда формула пути упростится: s = vt .
Тогда формула пути упростится: s = vt .
Найдем значения пути для различных значений промежутка времени и занесем их в таблицу 1.
Теперь построим график зависимости пути от времени. По оси абсцисс в определенном масштабе (например, 1 см – 1ч) будем откладывать промежутки времени движения, а по оси ординат (в масштабе 1 см – 900 км) – путь (рис. 97).
Прямая I выражает графическую зависимость пути от времени равномерного движения самолета. Эту прямую называют графиком пути. График пути напоминает известный вам из математики график функции у = kx , выражающей прямую пропорциональную зависимость у от х.
Ценность графика пути в том, что он, как и соотношение s = vt , позволяет решить главную задачу – найти путь s , пройденный телом за произвольный промежуток времени t .
Например, нас интересует путь самолета за промежуток времени t = 4 ч. Для этого из точки на горизонтальной оси, соответствующей времени t = 4 ч (см. рис. 97), проводим перпендикуляр до пересечения с графиком (точка К). Из найденной точки К опускаем перпендикуляр на ось ординат и получаем ответ без вычислений. Путь s = 3600 км.
Для этого из точки на горизонтальной оси, соответствующей времени t = 4 ч (см. рис. 97), проводим перпендикуляр до пересечения с графиком (точка К). Из найденной точки К опускаем перпендикуляр на ось ординат и получаем ответ без вычислений. Путь s = 3600 км.
А что представляет собой график скорости ? Он выражает зависимость скорости от времени. Так как скорость с течением времени не изменяется, то различным моментам времени соответствует одно и то же значение скорости. Составим таблицу 2 и построим прямую, выражающую зависимость скорости от времени, откладывая по оси абсцисс время, а по оси ординат – скорость (рис. 98).
График скорости равномерного прямолинейного движения – прямая, параллельная оси времени.
Прямая II изображает график скорости движения самолета. Что дает график скорости? Он не только показывает значение скорости, но и позволяет найти пройденный путь. Рассчитаем путь самолета за промежуток времени t = 2 ч. Согласно формуле s = vt этот путь s = 900 2 ч = 1800 км. Посмотрим на это произведение с точки зрения геометрии. Первый множитель (900 выражает одну сторону закрашенного прямоугольника (см. рис. 98), второй (2 ч) – другую. Из математики вы уже знаете, что перемножением сторон а и b находят площадь S прямоугольника (рис. 99).
Согласно формуле s = vt этот путь s = 900 2 ч = 1800 км. Посмотрим на это произведение с точки зрения геометрии. Первый множитель (900 выражает одну сторону закрашенного прямоугольника (см. рис. 98), второй (2 ч) – другую. Из математики вы уже знаете, что перемножением сторон а и b находят площадь S прямоугольника (рис. 99).
Конечно, площадь не есть путь, речь идет только о численном равенстве. Пройденный путь численно равен площади фигуры под графиком скорости.
Площадью фигуры под графиком скорости определяется путь не только при равномерном прямолинейном, но и при любом другом движении. Например, путь за промежуток времени (см. рис.) численно равен площади закрашенной фигуры:
s =
Физкультминутка
Закрепление знаний
А сейчас поработаем с карточками по теме «Графики пути и скорости при равномерном прямолинейном движении» (приложение 1)
№ 1.
Ответ: в 4 движении на прохождение одного и того же пути затрачено больше времени.
№ 2.
Ответ: в движении 1 пройден больший путь за один и тот же промежуток времени, т.к. s = v / t (в 1 движении скорость больше, чем в случае 2, поэтому и путь будет больше в случае 1)
№ 3. t = 2,0 ч?
Ответ:
автобус проехал путь 10 км за 15 мин;
15 мин автобус ехал без остановок, а затем совершил остановку продолжительностью: 1ч 15 мин – 30 мин = 40 мин;
до остановки автобус двигался со скоростью :
а после остановки ехал со скоростью: .
За время 2 ч автобус проехал путь 60 км.
№ 4. За промежуток времени t
Ответ:
а) график 1 соответствует движению Нади;
б)
Следовательно, скорость движения Нади в раза меньше, чем у Игоря.
№ 5.
Ответ:
а) жук сначала двигался, потом отдыхал, а затем снова двигался;
б) в конце 3-й секунды скорость движения равна 2 , а в конце 11-й секунды скорость движения равна 3 ;
в) s = v * t = 3 = 36 м.
Нет, т.к. жук двигается медленнее
№ 6. t = 4 с?
Ответ:
Движение велосипедиста было равномерным прямолинейный. Он двигался со скорость 8 . s = v * t = 8 * 4 c = 32 м.
№ 7.
Ответ:
Движение равномерное прямолинейное. За все время движения легкоатлет пробежал путь s = 6 км. За 15 мин он пробежал путь .
Итоги урока
Итак, подведем итоги:
График пути выражает зависимость пройденного пути от времени движения тела.
Путь при равномерном прямолинейном движении можно определить по формуле s = vt , по графику пути или с помощью графика скорости.
Организация домашнего задания
§17,ответить на контрольные вопросы.
Рефлексия
Продолжите фразы:
Сегодня на уроке я узнал…
Было интересно…
Знания, которые я получил на уроке, пригодятся.
Приложение 1
Карточка по теме «Графики пути и скорости при равномерном прямолинейном движении»
Выполните задания и решите задачи
№ 1. В каком из движений (рис. 2.) на прохождение одного и того же пути затрачено больше времени?
№ 2. В каком из движений, графики скорости которых представлены на рисунке 3, пройден больший путь за один и тот же промежуток времени?
№ 3. По графику (рис. 4) зависимости пути от времени движения автобуса определите, какой путь прошел автобус за промежуток времени. Определите промежуток времени движения автобуса до остановки и время остановки. С какой скоростью двигался автобус до и после остановки? Какой путь проехал автобус за время t = 2,0 ч?
№ 4. За промежуток времени t = 4 с Надя проехала на велосипеде путь а Игорь за этот же промежуток времени – путь Определите:
а) какой из графиков зависимости пути от времени (рис. 5) соответствует движению Нади;
5) соответствует движению Нади;
б) во сколько раз отличаются скорости движения Нади и Игоря.
№ 5. Дан график скорости движения жука. По графику (рис. 6) определите:
а) характер движения; б) скорость жука в конце 3-й и 11-й секунд движения; в) путь, пройденный жуком за время t = 12 с. Может ли график описывать реальное движение жука?
№ 6. На рисунке 7 представлен график зависимости скорости движения велосипедиста на прямолинейном участке дороги от времени. Каким было движение велосипедиста? С какой скоростью он двигался? Какой путь проехал велосипедист за время t = 4 с?
№ 7. По графику (рис.8) зависимости пути от времени определите скорость и время движения легкоатлета. Какое это движение? Какой путь пробежал легкоатлет за все время движения? За какое время он пробежал путь
Постройте график зависимости скорости движения спортсмена от времени.
Задачи по физике – это просто!
Не забываем , что решать задачи надо всегда в системе СИ!
А теперь к задачам!
Элементарные задачи из курса школьной физики по кинематике.
Задача на составление описания движения и составление уравнения движения по заданному графику движения
Дано: график движения тела
Найти :
1.
составить описание движения
2. составить
уравнение движения тела.
Проекцию вектора скорости определяем по графику, выбрав любой удобный для рассмотрения отрезок времени.
Здесь удобно взять t=4c
Составляем уравнение движения тела:
Записываем формулу уравнения прямолинейного равномерного движения.
Подставляем в нее найденный коэффициент V x (не забываем о минусе!).
Начальная координата тела (X о) соответствует началу графика, тогда X о =3
Составляем описание движения тела:
Желательно сделать чертеж, это поможет не ошибиться!
Не забываем, что все физические величины имеют единицы измерения, их необходимо указывать!
Тело движется прямолинейно и равномерно из начальной точки X о =3м со скоростью 0,75 м/с противоположно направлению оси X.
Задача на определение места и времени встречи двух движущихся тел (при прямолинейном равномерном движении)
Движение тел задано уравнениями движения для каждого тела.
Дано:
1.
уравнение движения первого тела
2. уравнение движения второго тела
Найти:
1. координату места встречи
2. момент время (после начала движения), когда произойдет встреча тел
По заданным уравнениям движения строим графики движения для каждого тела в одной системе координат.
Точка пересечения двух графиков движения определяет:
1.
на оси t – время встречи (через сколько времени после начала движения произойдет встреча)
2. на оси X – координату места встречи (относительно начала координат)
В результате:
Два тела встретятся в точке с координатой -1,75 м через 1,25 секунд после начала движения.
Для проверки полученных графическим способом ответов можно решить систему уравнений из двух заданных
уравнений движения:
Все было верно!
Для тех, кто почему-то забыл , как построить график прямолинейного равномерного движения:
График движения – это линейная зависимость (прямая), строится по двум точкам.
Выбираем два любых удобных для простоты расчета значения t 1 и t 2 .
Для этих значений t подсчитываем соответствующие значения координат X 1 и X 2 .
Откладываем 2 точки
с координатами (t 1 , X 1) и (t 2 , X 2) и соединяем их прямой – график готов!
Задачи на составление описания движения тела и построение графиков движения по заданному уравнению прямолинейного равномерного движения
Задача 1
Дано: уравнение движения тела
Найти:
Заданное уравнение сравниваем с формулой и определяем коэффициенты.
Не забываем делать чертеж, чтобы еще раз обратить внимание на направление вектора скорости.
Задача 2
Дано: уравнение движения тела
Найти:
1. составить описание движения
2. построить график движения
Задача 3
Дано: уравнение движения тела
Найти:
1. составить описание движения
2. построить график движения
Задача 4
Дано: уравнение движения тела
Найти:
1. составить описание движения
составить описание движения
2. построить график движения
Описание движения:
Тело находится в состоянии покоя в точке с координатой X=4м (состояние покоя – это частный случай движения, когда скорость тела равна нулю).
Задача 5
Дано:
начальная координата движущейся точки xo=-3 м
проекция вектора скорости Vx=-2 м/с
Найти:
1. записать уравнение движения
2. построить график движения
3. показать на чертеже векторы скорости и перемещения
4. найти координату точки через 10 секунд после начала движения
Физические основы механики
ЦЕЛЬ РАБОТЫ
Изучение равнопеременного и равномерного прямолинейных движений в поле земного тяготения. Определение ускорения свободного падения.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Основные законы динамики материальных точек – это законы Ньютона. В частности, второй закон Ньютона, математическая запись которого, как известно, имеет вид:
|
|
(1) |
называют основным уравнением динамики.
Эскиз машины Атвуда показан на рис. 1.
Рис. 1. Эскиз машины Атвуда
Два одинаковых груза с массами М соединены нитью, перекинутой через неподвижный блок. Если на один из грузов положить перегрузок массой m (в виде шайбы), то система приходит в ускоренное движение. Каждый из грузов натягивает участок нити, который, стараясь сократиться, действует на соответствующий груз с силой натяжения Т1 или Т2, а на блок – с силами Т’1 и Т’2. Тогда на каждый груз действует сила тяжести и сила натяжения нити.
Основное уравнение динамики для груза с перегрузком имеет вид:
|
|
(2) |
а для другого груза (без перегрузка):
|
|
(3) |
Основное уравнение динамики вращательного движения неподвижного блока имеет вид:
|
|
(4) |
где SMk – алгебраическая сумма моментов сил, действующих на блок, относительно оси вращения; I – момент инерции блока относительно оси вращения; e – его угловое ускорение.
Если вращение по часовой стрелке считать положительным, то, согласно рис. 1, получим
|
|
(4а) |
где: R – радиус блока; Мтр – момент силы трения.
Будет считать, что нить невесомая, нерастяжимая и не скользит по блоку. Из условия невесомости нити следует:
|
|
(5) |
Из условия нерастяжимости нити следуют равенства модулей перемещений, скоростей и ускорений грузов и нити:
|
|
(6) |
Наконец, в отсутствие скольжения нити по блоку, ускорение грузов и нити а равно модулю тангенциального ускорения точек обода блока:
или
|
|
(7) |
Проецируя уравнения (2) и (3) на ось у, направленную вертикально вверх, получим с учетом формул (5), (6) и (7) систему уравнений, к которой присоединим уравнение (4а):
|
|
(8) |
Умножая первое из уравнений (8) на (-1), и складывая все уравнения (8), получим
|
|
(9) |
В данной лабораторной установке момент сил трения настолько мал, что выполняется неравенство
|
|
(10) |
Кроме того, в лабораторной установке величина момента инерции I блока такова, что справедливо другое неравенство:
|
|
(11) |
Пренебрегая малыми величинами, из уравнения (9) получим формулу для расчёта ускорения а системы грузов под действием перегрузка массой m:
|
|
(12) |
а модули сил натяжения нити Т1 и Т2 по обе стороны блока равны:
|
|
(13) |
Можно сказать, что равенство (13) выполняется при двух предположениях (10) и (11).
Равноускоренное движение системы грузов вдоль оси у описывается уравнениями движения произвольной точки системы:
где у1, v1 – начальные параметры.
Исключая из этих уравнений время t, при условии v1=0, получим
|
|
(14) |
Система грузов перемещается на величину sy=L1, двигаясь равноускоренно под действием перегрузка массой m с ускорением, которое определяется формулой (12).
В точке с координатой у2 и скоростью v2 перегрузок подхватывается столиком, и система грузов движется равномерно, перемещаясь на величину L2 за время t, измеряемое миллисекундомером экспериментальной установки. Подставляя в равенство (14) формулу
Подставляя в равенство (14) формулу
получим
|
|
(15) |
При изменении L2 меняется время t, измеряемое секундомером, но ускорение а должно оставаться неизменным.
С помощью формулы (15) найдём расчётную формулу для величины ускорения а грузов с перегрузком:
|
|
(16) |
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
К основанию 1 экспериментальной установки (см. рис. 2), которая стоит на ножках 2, прикреплена вертикальная стойка 3. К стойке крепится кронштейн 4, который может перемещаться вдоль стойки. На кронштейне находится столик для снятия перегрузка.
рис. 2), которая стоит на ножках 2, прикреплена вертикальная стойка 3. К стойке крепится кронштейн 4, который может перемещаться вдоль стойки. На кронштейне находится столик для снятия перегрузка.
Рис. 2. Схема экспериментальной установки
На верхнем конце стойки находится неподвижный блок 5. Для наблюдения ускоренного движения грузов на правый груз 6 помещают перегрузок 7 и поднимают их в верхнее положение путем нажатия кнопок «+» или «-». Значение массы перегрузка показывается в окне «масса После нажатия кнопки «ПУСК» начинается ускоренное движение грузов и перегрузка до того момента, когда столик 4 подхватит перегрузок. Одновременно включается миллисекундомер, измеряющий время равномерного движения грузов до остановки. Итак, во время равноускоренного движения грузы проходят расстояние L1 (см. рис. 1) и приобретают скорость v2, с которой, двигаясь равномерно, проходят расстояние L2 за время t, измеренное миллисекундомером в секундах и показанное в окне «время».
Для подготовки прибора к следующему измерению нажимают кнопку «СБРОС».
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Упражнение 1. ИЗМЕРЕНИЕ УСКОРЕНИЯ ГРУЗОВ
1. Измерьте расстояние L с помощью линейки и занесите результат в таблицу измерений 1. Цена деления линейки 1 см.
Обратите внимание на необходимость записывать данные в системе СИ, то есть, в метрах.
Таблица 1
|
m=… кг |
L=… м |
L2=… м |
|
|
№ наблюдения |
Время ti, с |
||
|
1 |
|||
|
2 |
|||
|
3 |
|||
|
4 |
|||
|
5 |
|||
2. Выберите значение массы перегрузка m и занесите ее значение в таблицу 1. Выбор производится мышкой с помощью нажатия ей на кнопки со значками «+» или «-». Значение массы перегрузка показывается в окне «масса». Оптимальным для выбора является значение массы от 5 до 10 г. Учтите, что масса в данной работе определена при взвешивании тел на весах с точностью, равной половине цены деления весов. Приборная погрешность весов составляла 0.1 г.
Выберите значение массы перегрузка m и занесите ее значение в таблицу 1. Выбор производится мышкой с помощью нажатия ей на кнопки со значками «+» или «-». Значение массы перегрузка показывается в окне «масса». Оптимальным для выбора является значение массы от 5 до 10 г. Учтите, что масса в данной работе определена при взвешивании тел на весах с точностью, равной половине цены деления весов. Приборная погрешность весов составляла 0.1 г.
Обратите внимание на необходимость записывать данные в системе СИ, то есть, в килограммах.
3. Установите, взяв мышкой, кронштейн со столиком на некотором расстоянии L2 от нижнего фиксатора расстояний. Возможные пределы варьирования расстояния от 12 до 25 см. Измерьте установленное расстояние L2 по линейке, взяв отсчёт по красной черте. Результаты измерения запишите в таблицу 1 результатов измерений 1. Цена деления линейки 1 см.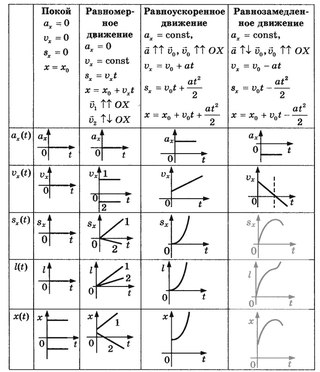
Обратите внимание на необходимость записывать данные в системе СИ, то есть, в метрах.
4. Нажмите кнопку «ПУСК».
5. После остановки грузов запишите в таблицу 1 время t равномерного движения грузов, измеренное миллисекундомером и показанное на табло «время». Время необходимо записывать в системе СИ, то есть в секундах. Погрешность миллисекундомера составляет 0.001 с.
6. Нажмите кнопку «СБРОС».
7. Повторите пункты 3 – 5 ещё четыре раза, не меняя расстояние L2.
8. Вычислите среднее значение времени <t>. Результат занесите в таблицу расчетов 2.
Таблица 2
|
№ наблюдения |
ti |
ti-<t> |
(ti-<t>)2 |
|
1 |
|||
|
2 |
|||
|
3 |
|||
|
4 |
|||
|
5 |
|||
|
Суммы |
Sti=… |
S(ti-<t>)2 |
|
|
<t>=… |
s=… |
||
|
E= |
9. Найдите отклонения каждого из пяти измерений ti от среднего значения времени <t>.
Найдите отклонения каждого из пяти измерений ti от среднего значения времени <t>.
10. Возведите в квадрат каждое отклонение и просуммируйте квадраты отклонений.
11. Рассчитайте среднее квадратичное отклонение s, применив для его расчёта формулу для выборочной оценки S(<t>) стандартного отклонения результата измерения по формуле из теории погрешностей
12. Умножив это значение среднего квадратичного отклонения на коэффициент Стьюдента, найдём полуширину доверительного интервала в определении времени
где tP(n) – коэффициент Стьюдента, соответствующий вероятности Р и числу степеней свободы n=n-1.
Для n=5 измерений при рекомендуемой доверительной вероятности P=0.9 имеем из таблицы коэффициентов Стьюдента t0.9(5-1)=2.13.
13. Приборная погрешность в определении времени в нашем случае значительно меньше случайной, поэтому приборная погрешность в определении времени в данном случае не учитывается.
Приборная погрешность в определении времени в нашем случае значительно меньше случайной, поэтому приборная погрешность в определении времени в данном случае не учитывается.
Тогда результат измерения времени t запишем в виде
14. Произведите расчет относительной погрешности в определении времени Et (в процентах) по формуле:
15. Приборная погрешность в определении расстояний уже не может быть отброшена, так как случайной погрешности здесь нет, Тогда для расстояний L и L2 имеем приборные погрешности, равные половине цены деления линейки
16. Ускорение грузов а рассчитывается по формуле (16), в которую подставляется среднее значение времени <t> и измеренные линейкой значения расстояний L и L2.
17. Относительная погрешность в определении ускорения найдётся по формуле:
18. Результат измерения ускорения а запишется в виде
Результат измерения ускорения а запишется в виде
Упражнение 2. ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ
19. Определите величину ускорения свободного падения g по формуле
При этом значение массы грузов принять равным M=90 г.
20. Полуширину доверительного интервала Dg найдите с помощью формулы
Значения погрешностей в определении масс в данной работе принять равными приборной погрешности при их взвешивании:
21. Оформите отчёт по работе.
ВЫПОЛНЕНИЕ ЛАБОРАТОРНОЙ РАБОТЫ
На рис.3 представлена реальная лабораторная установка, используемая для выполнения данной работы.
Рис.3. Лабораторная установка “Машина Атвуда”
После ознакомления с принципом работы установки необходимо проделать работу на виртуальной лабораторной установке, представленной в правом окне. В процессе выполнения измерений можно свернуть-развернуть окно с описанием лабораторной работы либо свернуть-развернуть окно с лабораторной установкой.
В процессе выполнения измерений можно свернуть-развернуть окно с описанием лабораторной работы либо свернуть-развернуть окно с лабораторной установкой.
После окончания измерений следует сохранить результаты работы. Для этого необходимо нажать на клавишу или. После этого будет предложено сохранить результаты в файле, имя которого – название лабораторной работы (имя файла изменять не рекомендуется), месторасположение – рабочий стол (можно изменить место сохранения файла). Так как результаты сохраняются в формате html, в дальнейшем вы можете просмотреть результаты, открыв сохраненный файл, а также можете отправить файл на проверку правильности выполнения лабораторной работы преподавателю.
РЕКОМЕНДАЦИИ
по оформлению отчета по лабораторным работам (физика)
1. Отчет оформляют в электронном виде в редакторе Word
2. Объем отчета составляет 2-3 страницы.
3. В отчете необходимо указать:
3.1 Фамилию, имя, отчество студента;
3. 2 Номер группы;
2 Номер группы;
3.3 Дисциплину;
3.4 Фамилию, имя, отчество преподавателя;
4. Рекомендуемая структура отчета:
4.1 Название работы;
4.2 Цель работы;
4.3 Таблицы измерений и таблицы расчетов, сохраненные в виде отдельного файла.
4.5 Формулы и законы, используемые для расчетов;
4.6 Результаты расчетов, не вошедшие в таблицу расчётов;
4.7 Выводы, которые можно сделать из работы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется системой отсчета?
2. Дайте определение материальной точки.
3. Сравните понятия пути и перемещения.
4. Дайте определения средней и мгновенной скоростей.
5. Дайте определения среднего и мгновенного ускорений.
6. Укажите формулы, связывающие кинематические величины при равноускоренном прямолинейном движении.
7. Дайте определение силы.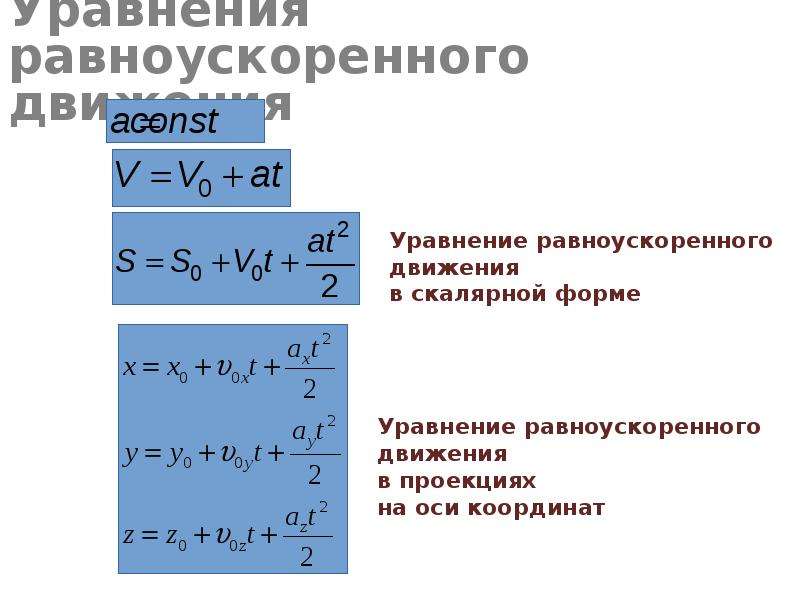
8. Что характеризует масса тела?
9. Сформулируйте основные законы динамики – законы Ньютона.
10. Какая система тел называется изолированной?
11. Сформулируйте законы сохранения импульса и полной механической энергии системы.
12. Какое движение тела называется свободным падением?
13. Как изменится ускорение свободного падения при подъеме с уровня моря на высоту h=10 км? Радиус Земли R3=6 370 км.
14. При каком условии ускорения тел, используемых в машине Атвуда, одинаковы по модулю?
Кинематические уравнения: равноускоренное движение Примечания | Изучайте физику, класс 11
Кинематические уравнения движения
Если объект начинает движение со скоростью «u», а через некоторое время «t» его скорость изменяется на v, если равномерное ускорение равно a и пройденное расстояние во времени (t) равно s, то получаем следующие кинематические уравнения равноускоренного движения.
Уравнения движения кинематики описывают основную концепцию движения объекта, такую как положение, скорость или ускорение объекта в различные моменты времени.Эти три уравнения движения управляют движением объекта в 1D, 2D и 3D. Вывод уравнений движения — одна из важнейших тем физики. В этой статье мы покажем вам, как вывести первое, второе и третье уравнения движения графическим методом, алгебраическим методом и методом исчисления.
Определение уравнений движения
Уравнения движения в физике определяются как уравнения, описывающие поведение физической системы в терминах ее движения как функции времени.
Существуют три уравнения движения, которые можно использовать для получения компонентов, таких как перемещение(я), скорость (начальная и конечная), время(t) и ускорение(а). Ниже приведены три уравнения движения:
- Первое уравнение движения: v = u + at
- Второе уравнение движения: s = ut + 1/2at 2
- 9000 Третье уравнение движения Вывод уравнения движения
- Вывод уравнений движения графическим методом
- Вывод уравнений движения математическим методом
В следующих нескольких разделах уравнения движения выводятся всеми тремя методами простым и легким понять способ.
Вывод первого уравнения движения
Для вывода рассмотрим тело, движущееся прямолинейно с постоянным ускорением. Тогда пусть начальная скорость равна u , ускорение обозначено как a , период времени обозначен как t , скорость обозначена как v , а пройденное расстояние обозначено как s .
Вывод первого уравнения движения алгебраическим методом
Мы знаем, что ускорение тела определяется как скорость изменения скорости.
Математически ускорение представляется следующим образом:
где v — конечная скорость, а u — начальная скорость.
Преобразовывая приведенное выше уравнение, мы приходим к первому уравнению движения следующим образом:
v = u + at
Вывод первого уравнения движения графическим методом
Первое уравнение движения может быть получено с использованием скорости -временной график для движущегося объекта с начальной скоростью u , конечной скоростью u и ускорением u .
На приведенном выше графике
- Скорость тела изменяется от A до B за время t с постоянной скоростью.
- BC – конечная скорость и OC – общее время t .
- Из B в OC проведен перпендикуляр, из A в D проведена параллельная линия, а из B в OE проведена параллельная линия (обозначены пунктирными линиями).
Следующие детали получены из приведенного выше графика:
Начальная скорость тела, u = OA
Конечная скорость тела, v = BC
Из графика мы знаем, что
BC = BD + DC
Следовательно, v = BD + DC
v = BD + OA (так как DC = OA)
Наконец,
v = BD + u (так как 0A0 = 4 u 9 0A0 Уравнение 1)
Теперь, поскольку наклон графика скорость-время равен ускорению a ,
Итак,
a = наклон линии AB
a = BD/AD
Так как AD = AC = t приведенное выше уравнение принимает вид:
BD = at (Уравнение 2)
Теперь, объединяя уравнения 1 и 2, получаем следующее:
v = u + at
Метод
Поскольку ускорение представляет собой скорость изменения скорости, его можно математически записать en как:
a = dv/dt
Преобразовывая приведенное выше уравнение, мы получаем
adt = dv
Интегрируя обе части, мы получаем
at = v − u
Преобразовывая, мы получаем
v = u + at
Вывод второго уравнения движения
Для вывода второго уравнения движения рассмотрим те же переменные, которые использовались для вывода первого уравнения движения.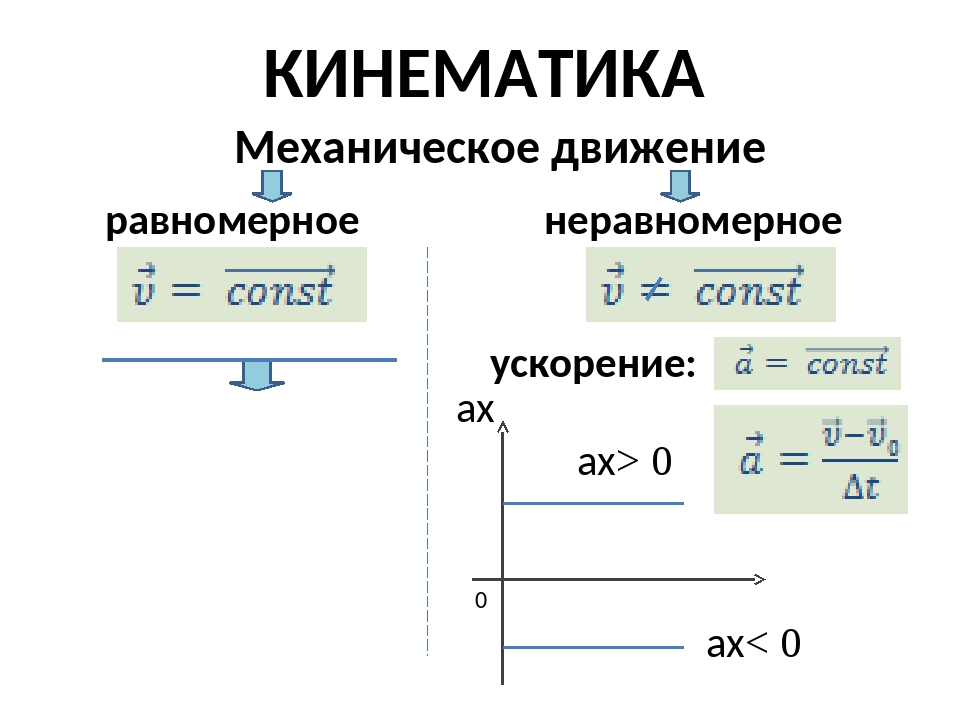
Вывод второго уравнения движения алгебраическим методом
Скорость определяется как скорость изменения перемещения. Это математически представляется как:
Скорость = Перемещение/Время
Переставляя, мы получаем
Перемещение = Скорость × Время
Если скорость непостоянна, то в приведенном выше уравнении мы можем использовать среднюю скорость вместо скорости и переписать уравнение следующим образом:
Перемещение = × Время
Подставляя вышеприведенные уравнения обозначениями, использованными при выводе первого уравнения движения, получаем
s = u+v/2 × t
Из первого уравнения движения получаем знаем, что v = u + at.Подставляя это значение v в приведенное выше уравнение, мы получаем
. При дальнейшем упрощении уравнение принимает следующий вид:
Из приведенного выше графика можно сказать, что
Пройденное расстояние (с) = Площадь фигуры OABC = Площадь прямоугольника OADC + Площадь треугольника ABD
с = (1/2AB × BD)+(OA × OC)
Поскольку BD = EA , приведенное выше уравнение принимает вид
s = (1/2AB × EA) + (u × t)
Поскольку EA = at , уравнение принимает вид
s = 1/2 × at × t + ut
При дальнейшем упрощении уравнение принимает вид
s = ut + 1/2at 2
Вывод второго уравнения движения методом исчисления
Скорость – это скорость изменения перемещения.
Математически это выражается как
v = ds/dt
Преобразовывая уравнение, мы получаем
ds = vdt
Подставляя первое уравнение движения в приведенное выше уравнение, мы получаем
ds = (u + at)dt
ds = (u + at)dt = (udt + atdt)
При дальнейшем упрощении уравнение принимает вид: Вывод третьего уравнения движения алгебраическим методом
Мы знаем, что смещение — это скорость изменения положения объекта.Математически это можно представить как:
Перемещение = × t
Подставляя стандартные обозначения, приведенное выше уравнение принимает вид
s = × t
Из первого уравнения движения мы знаем, что
v = u + at
выше формулы, мы получаем
t = v – u/a
Подставляя значение t в формулу водоизмещения, мы получаем
2as = v 2 – u 2
v 2 = u 2 + 2as
Вывод третьего уравнения движения графическим методом
Из графика можно сказать, что
Общее пройденное расстояние, с 900 трапеции OABC.
Следовательно,
S = ½ (сумма параллельных сторон) × высота
S = (OA+CB) × OC
Поскольку OA = u, CB = v и OC = t
Выше уравнение принимает вид
S= ½ (u+v) × t
Теперь, поскольку t = (v – u)/a
Вышеупомянутое уравнение может быть записано как:
S= ½ ((u+v) × (vu))/a
Преобразовывая уравнение, получаем
S = ½ (v+u) × (vu)/a
S = (v 2 – u 2 )/2a
Третье уравнение движения: получается путем решения приведенного выше уравнения:
v 2 = u 2 + 2aS
Вывод третьего уравнения движения математическим методом
Мы знаем, что ускорение представляет собой скорость изменения скорости и может быть представлено в виде :
a = dv/dt (1)
Мы также знаем, что скорость есть скорость изменения смещения и может быть представлена как:
v = ds/dt (2)
Перемножив (1) и (2), получаем
v 2 = u 2 + 2as
Решаемые Примеры:
Q. Автомобиль, движущийся со скоростью 60 км/ч, может затормозить, чтобы остановиться на расстоянии 20 м. Если автомобиль движется в два раза быстрее, т. е. со скоростью 120 км/ч, тормозной путь составит
Автомобиль, движущийся со скоростью 60 км/ч, может затормозить, чтобы остановиться на расстоянии 20 м. Если автомобиль движется в два раза быстрее, т. е. со скоростью 120 км/ч, тормозной путь составит
A. 60 м
B. 40 м.
C. 20 м
D. 80 м
Ответ: D
Q2. Тележка, которая может свободно двигаться в одном измерении, движется в положительном направлении и замедляется под влиянием постоянного обратного притяжения, пока тележка не остановится на мгновение и не изменит направление. Каковы знаки скорости и ускорения тележки в момент ее остановки?
А.скорость : 0 ускорение : +
B. ускорение : 0 скорость : +
C. скорость : 0 ускорение : –
Ответ: C. Поскольку тележка в данный момент остановилась, скорость и скорость тележки равны нулю. Следовательно, тележка достигает отрицательной скорости, что означает, что она должна ускоряться в отрицательном направлении, чтобы увеличить скорость от нуля до конечного значения в отрицательном направлении.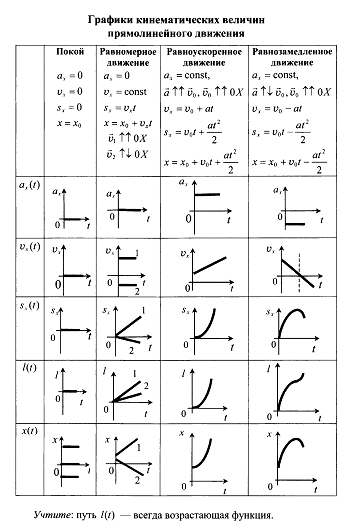
Движение под действием силы тяжести (свободное падение)
Ускорение, создаваемое телом под действием силы тяжести, называется ускорением свободного падения.Обозначается символом g.
Величина g=9,8 м/с 2 = 980 см/с 2 = 32 фут/с 2
Установлено, что в отсутствие воздуха все тела (независимо от размера, веса или состава) падают с одинаковым ускорением у поверхности земли. Это движение тела, падающего на землю с малой высоты (h << земного радиуса), называется движением под действием силы тяжести. Свободное падение означает, что ускорение тела равно ускорению свободного падения.
Если тело спроецировано вертикально вверх
Положительное/отрицательное направления – вопрос выбора. Вы можете выбрать другой вариант.
(i) Уравнения движения: Принимая начальное положение в качестве источника и направление движения (т.е. вертикально вверх) как положительное a = – g [Поскольку ускорение направлено вниз, а движение вверх] скорость u и через время t достигает высоты h тогда
v = u – gt, h = ut – 1/2gt 2
v 2 = u 2 – 2gh, h n th = u – g/2(2n – 1)
(ii) Для максимальной высоты v = 0
Таким образом, из приведенного выше уравнения u = gt
называется временем подъема (t 1 ) = u/g
В случае движения под действием силы тяжести, время подъема вверх равно времени падения на то же расстояние. Время снижения (t 2 ) = время подъема (t 1 ) = u/g
Время снижения (t 2 ) = время подъема (t 1 ) = u/g
∴ Общее время полета T = t1 + t2 = 2u/g
и u2 = 2gh ⇒ H = u 2 /2g
Если тело брошено вертикально вниз с некоторой начальной скоростью с некоторой высоты
Уравнения движения: у нас есть
Формулы и примеры равномерно-ускоренного движения | Большая пятерка кинематических уравнений — видео и расшифровка урока
Пять величин для уравнений равномерного ускорения
Пять величин или переменных, обычно встречающихся в уравнениях UAM, — это перемещение, время, начальная скорость, конечная скорость и постоянное ускорение.Различия между каждой величиной обсуждаются ниже:
- Смещение , {eq}\Delta x {/eq} или {eq}x-x_0 {/eq} — смещение относится к изменению положения объекта. Он также описывается как кратчайшее прямолинейное расстояние между начальным и конечным положениями объекта.
 Это векторная величина, что означает, что она имеет как величину, так и направление. Его единица СИ находится в метрах (м), но также используются другие единицы измерения расстояния, такие как километры (км), мили (ми) и футы (футы).
Это векторная величина, что означает, что она имеет как величину, так и направление. Его единица СИ находится в метрах (м), но также используются другие единицы измерения расстояния, такие как километры (км), мили (ми) и футы (футы).
- Время , t – Время, прошедшее время или временной интервал – это время, которое проходит в течение выбранного периода наблюдения. Его единицей СИ является секунда (с). Другие единицы времени, такие как минуты (мин) или часы (ч), также используются для выражения времени.
- Начальная скорость , v {eq}_0 {/eq} — начальная скорость определяет, насколько быстро объект движется в определенном направлении в начале прошедшего времени. Это векторная величина, однако в некоторых случаях рассматривается только ее величина (скорость).Единицей скорости в системе СИ является метр в секунду (м/с). Другими используемыми единицами скорости являются километры в час (км/ч) и мили в час (миль в час).
- Конечная скорость , v – Конечная скорость описывает скорость движения объекта или тела в конце прошедшего времени.
 Как и начальная скорость, это векторная величина, описываемая величиной и направлением. Она имеет те же единицы измерения, что и начальная скорость: м/с, км/ч и мили в час.
Как и начальная скорость, это векторная величина, описываемая величиной и направлением. Она имеет те же единицы измерения, что и начальная скорость: м/с, км/ч и мили в час. - Постоянное ускорение , a – Ускорение относится к изменению скорости объекта за интервал времени.2 экв.}.
Уравнения большой пятерки
Существуют уравнения большой пятерки, используемые для решения задач, связанных с равноускоренным движением. Эти большие 5 кинематических уравнений требуют одной неизвестной величины и по крайней мере трех известных величин, чтобы иметь возможность решить проблему.
Первое кинематическое уравнение имеет вид {eq}v=v_0 + at {/eq}, где v — конечная скорость, v {eq}_0 {/eq} — начальная скорость, a – постоянное ускорение, а t – время. 2 {/eq}, где {eq}\Delta {/eq} 90 484 x 90 485 — перемещение, v {eq}_0 {/eq} — начальная скорость, t — время, a — постоянное ускорение.2+2a\Delta x {/eq}, где v — конечная скорость, v {eq}_0 {/eq} — начальная скорость, a — постоянное ускорение, а {eq}\Delta {/eq} 90 484 x 90 485 — это смещение. Он используется для определения конечной скорости объекта, когда известны начальная скорость, ускорение и перемещение. Уравнение показывает, что на конечную скорость влияет величина ускорения и расстояние или изменение положения объекта.
2 {/eq}, где {eq}\Delta {/eq} 90 484 x 90 485 — перемещение, v {eq}_0 {/eq} — начальная скорость, t — время, a — постоянное ускорение.2+2a\Delta x {/eq}, где v — конечная скорость, v {eq}_0 {/eq} — начальная скорость, a — постоянное ускорение, а {eq}\Delta {/eq} 90 484 x 90 485 — это смещение. Он используется для определения конечной скорости объекта, когда известны начальная скорость, ускорение и перемещение. Уравнение показывает, что на конечную скорость влияет величина ускорения и расстояние или изменение положения объекта.
Пятое кинематическое уравнение можно использовать для определения изменения положения с учетом начальной скорости, конечной скорости и времени.Он выражается как {eq}\Delta x = (\frac{v+v_0}{2})t {/eq}, где {eq}\Delta {/eq} 90 484 x 90 485 – смещение, 90 484 v 90 485 – конечная скорость, v {eq}_0 {/eq} — начальная скорость, а t — время. Он показывает, что когда объект движется с постоянным ускорением, средняя скорость {eq}\frac{v+v_0}{2} {/eq} находится посередине между начальной и конечной скоростями. Это применимо только тогда, когда ускорение является постоянным или равномерным.
Это применимо только тогда, когда ускорение является постоянным или равномерным.
Примеры уравнений UAM
Попрактикуйтесь в использовании уравнений равномерного ускорения или уравнений UAM, используя следующие примеры задач.Выбирая, какое уравнение использовать, всегда оценивайте, присутствуют ли в уравнении заданные величины и неизвестные величины.
Пример 1
Космический аппарат равномерно ускоряется с 70 м/с до 185 м/с в течение 8 с. Каково ускорение автомобиля?
- Шаг 1
- Определите данные величины.
Даны величины v{eq}_0 {/eq} = 70 м/с, v = 185 м/с и t = 8 с.
- Шаг 2
- Определите неизвестную величину.
Неизвестная величина – ускорение, а.
- Шаг 3
- Определите наилучшее уравнение для использования.
Наиболее подходящим уравнением является первое кинематическое уравнение: {eq}v=v_0+at {/eq}.
- Шаг 4
- Решите для неизвестной величины.

Преобразуйте уравнение, чтобы найти выражение для ускорения из уравнения.
{eq}v=v_0+at \rightarrow a=\frac{v-v_0}{t} {/eq}
Подставим неизвестные величины в уравнение:
{eq}a=\frac{185 \ text{ м/с} – 70 \text{ м/с}}{8 \text{ с}}=14.2) (500 \text { м})}=122,47 \text { м/с} {/eq}
Конечная скорость автомобиля 122,47 м/с.
Пример 4
Спринтер, стартующий из состояния покоя, может развить скорость 10 м/с через 25 м. Если она бежит с постоянным ускорением, сколько времени потребуется спринтеру, чтобы достичь указанной скорости?
- Шаг 1
- Определите данные величины.
Даны величины v{eq}_0 {/eq} = 0, v = 10 м/с и {eq}\Delta {/eq}x = 25 м.
- Шаг 2
- Определите неизвестную величину.
Найти время, за которое спринтер достигнет конечной скорости, т. н.
- Шаг 3
- Определите наилучшее уравнение для использования.

Преобразуйте пятое уравнение кинематики, чтобы найти выражение для времени:
{eq}\Delta x =(\frac{v+v_0}{2})t \rightarrow t=\frac{\Delta x}{\frac {v+v_0}{2}} {/экв}
- Шаг 4
- Решите для неизвестной величины.
Подставим неизвестные величины в уравнение:
{eq}t=\frac{25 \text{ м}}{\frac{10 \text{ м/с} +0}{2}}=5\text { s} {/eq}
Спринтеру потребуется 5 с, чтобы достичь скорости 10 м/с.
Краткий обзор урока
Кинематика — раздел классической механики, описывающий «геометрию движения». Он рассматривает движение и положение объекта без учета его причин (например, силы). Одним из важнейших понятий кинематики является равномерно ускоренное движение (УАМ) , которое описывает движение объекта, движущегося с постоянным или равномерным ускорением.2 +2а\Дельта х {/экв}; и (5) {eq}\Delta x =(\frac{v+v_0}{2})t {/eq}. При использовании этих уравнений важно сначала идентифицировать заданные и неизвестные величины, прежде чем выбирать наиболее подходящее уравнение для использования среди пяти кинематических уравнений.
Напишите три уравнения равномерно ускоренного движения 11 класс физики CBSE
Подсказка: Все три уравнения равномерно ускоренного движения можно вывести, используя выражения для скорости, смещения и ускорения и интегрируя их.Первое уравнение — это просто переставленная формула ускорения. И два других могут быть производными от него. Полный пошаговый ответ:
В вопросе дано, что для тела, обладающего равноускоренным движением,
Начальная скорость представлена как, $u$
Конечная скорость представлена как, $v$
Ускорение представлено $a$
, а его перемещение представлено $S$.
Тогда три уравнения движения могут быть получены следующим образом-
Вывод $v = u + at$
Мы знаем, что ускорение тела определяется величиной изменения его скорости в данный интервал времени-
$a = \dfrac{{dv}}{{dt}}$
Переставляя это,
$ \Rightarrow adt = dv$
Если объект меняет свою скорость с $u$ на $v$ за заданный интервал времени $t$. 2} + 2а с$……….$(3)$
2} + 2а с$……….$(3)$
Выведены все три уравнения движения.
Примечание: Этот вывод основан на расчетном методе вывода уравнений движения равномерно ускоряющегося тела. Два других подхода — графический и алгебраический — также могут быть использованы для вывода этих уравнений.
Описание движения вдоль линии — OpenLearn
Уравнения 22, 23 и 24 дают полное описание равномерно ускоренного движения. Соответствующим образом комбинируя их, можно решать широкий класс задач кинематики равноускоренного движения.Тем не менее, эти конкретные уравнения не всегда являются лучшей отправной точкой для наиболее распространенных задач. Например, часто бывает так, что мы хотим узнать смещение от начального положения после некоторого заданного периода постоянного ускорения, а не конечное положение x . В таких обстоятельствах полезно вычесть x 0 из обеих частей уравнения 22 и использовать определение как
Что еще более важно, часто бывает так, что нам нужно найти конечную скорость v x , когда все, что нам дано, это (постоянное) ускорение a x , начальная скорость u x и перемещение s x . Задачу можно решить с помощью уравнений 23 и 25, но для этого нужно найти продолжительность движения t , что не требуется как часть ответа. Было бы удобнее использовать уравнение, которое связано V x – a x , u x × отработать т всего. К счастью, такое уравнение можно найти, используя стандартную математическую процедуру, называемую исключением .
Задачу можно решить с помощью уравнений 23 и 25, но для этого нужно найти продолжительность движения t , что не требуется как часть ответа. Было бы удобнее использовать уравнение, которое связано V x – a x , u x × отработать т всего. К счастью, такое уравнение можно найти, используя стандартную математическую процедуру, называемую исключением .
Первым шагом в этом процессе является определение набора уравнений, содержащих переменные, которые мы хотим связать, а также хотя бы одну переменную, которую мы можем исключить. В этом случае мы хотим исключить t из уравнений 23 и 25. Второй шаг обычно включает перестановку одного из уравнений таким образом, чтобы нежелательная переменная была изолирована в левой части, таким образом становясь предметом этого уравнения. В этом случае мы можем вычесть u x из обеих частей уравнения 23, разделить обе части на a x и затем поменять местами две стороны, чтобы получить
Получив это соотношение из одного уравнений, третий шаг состоит в том, чтобы использовать его для исключения нежелательной переменной из всех других уравнений. В нашем случае это означает замена t by v x – u x 85
В нашем случае это означает замена t by v x – u x 85
Таким образом, после небольшой алгебры мы получаем
, которые можно преобразовать, чтобы получить результат
Уравнения 23, 25 и 27 являются наиболее часто используемыми уравнениями равноускоренного движения и обычно называются постоянным ускорением уравнения (или уравнения равномерного ускорения).
Уравнения постоянного (или равномерного) ускорения
Из этих уравнений следует, что
Помните, что это не универсальные уравнения, которые описывают все формы движения. Они применяют только к ситуациям, в которых ускорение a x является постоянным .
Вопрос 20
Исходя из уравнений постоянного ускорения, используйте процедуру исключения для получения уравнения 28d.
Ответ
В этом случае мы хотим исключить a x из уравнений 28a и 28b. Один из способов состоит в том, чтобы изменить уравнение 28b (вычитая u x с обеих сторон и разделив обе стороны на t ), чтобы получить:
Один из способов состоит в том, чтобы изменить уравнение 28b (вычитая u x с обеих сторон и разделив обе стороны на t ), чтобы получить:
Подставляя это в уравнение 28a, получаем
28г в терминах площади под графиком скорость-время для случая равноускоренного движения.
Ответ
Графически, s x – область со знаком под графиком скорость-время между заданными моментами времени.В этом случае эти моменты времени равны t = 0, когда начальная скорость равна u x , и несколько более позднее время t , когда скорость равна v x x . Поскольку график зависимости скорости от времени для равномерно ускоренного движения представляет собой прямую линию с фиксированным градиентом, требуемая площадь всегда будет либо трапецией (над или под осью), либо парой треугольников. (На рисунке 37 показан конкретный случай.)
Рисунок 37: График зависимости скорости от времени для вопроса самооценки 19
Вопрос 22
Конечная скорость объекта равна 30.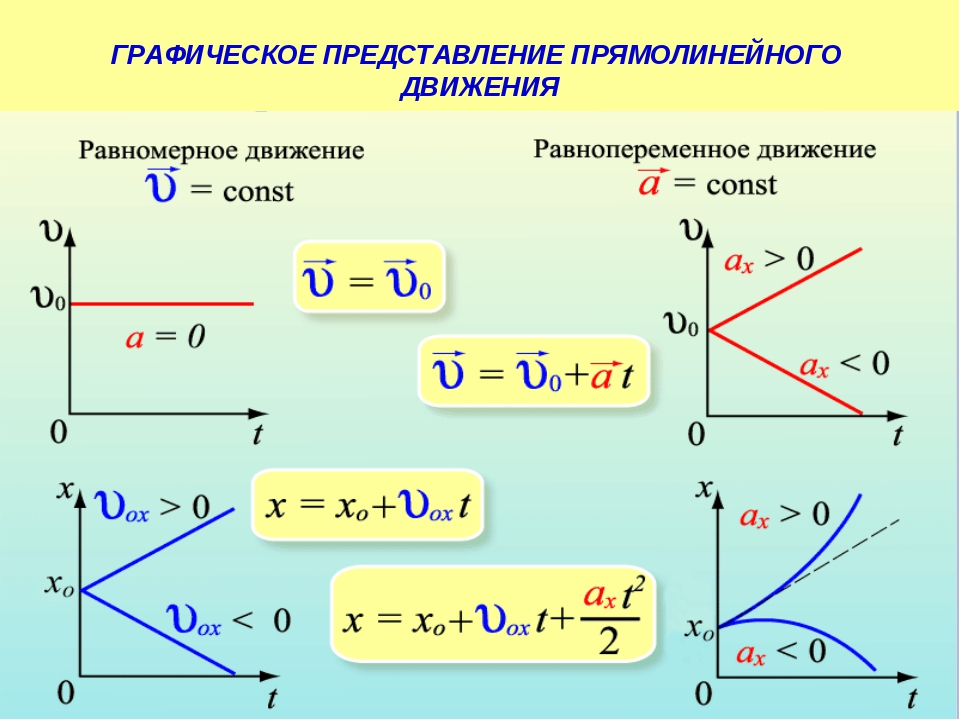 0 м с −1 , после равномерного ускорения 2,00 м с −2 при перемещении 20,0 м. а) Какова была начальная скорость тела? б) Как долго тело ускорялось?
0 м с −1 , после равномерного ускорения 2,00 м с −2 при перемещении 20,0 м. а) Какова была начальная скорость тела? б) Как долго тело ускорялось?
Ответ
(а) в этом случае мы знаем S x = 20 м, и -1 и A x = 2 мс -2 и нам нужно найти u x . В качестве первого шага мы должны сделать u x предметом уравнения, которое включает известные величины.Преобразование уравнения 28c дает
Извлечение квадратного корня из каждой стороны
Подставляя заданные значения,
(b) Продолжительность ускорения определяется уравнением 26 как x ) /a x , что само по себе было получено перестановкой уравнений постоянного ускорения. Подстановка соответствующих значений дает
Вопрос 23
Поезд равномерно ускоряется по прямому пути в 2.00 м с −2 от начальной скорости 4,00 м с −1 до конечной скорости 16,00 м с −1 .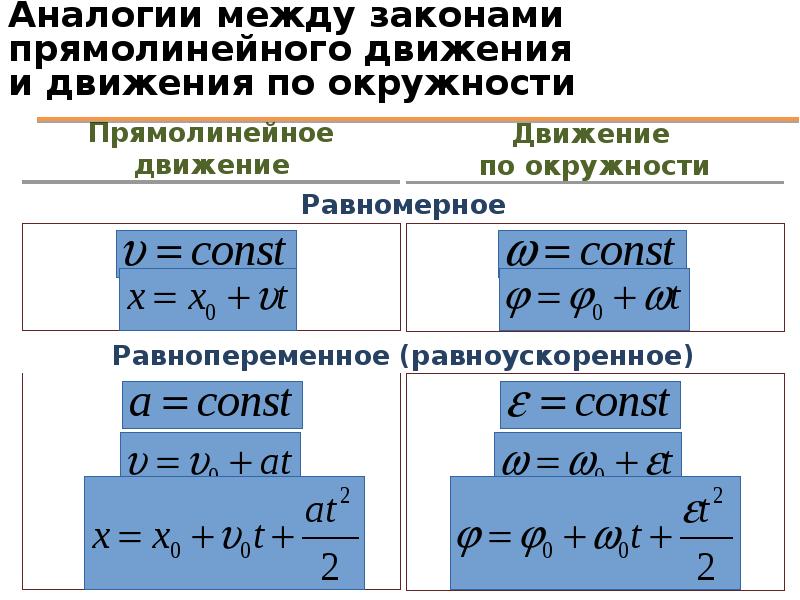 Каково смещение поезда от его начального положения в конце этого интервала?
Каково смещение поезда от его начального положения в конце этого интервала?
ответ
с использованием уравнения 28C
с u x = 4,00 мс -1 , 4 v x 9048-160436 , получим после перестановки
Что такое кинематическое уравнение равноускоренного движения? – Первый законкомик.ком
Что такое кинематическое уравнение равноускоренного движения?
с=ut+12at2. C. v2=u2+2as. Подсказка: все три уравнения равномерно ускоренного движения можно вывести, используя выражения для скорости, перемещения и ускорения и интегрируя их.
Что такое равноускоренное прямолинейное движение?
Равномерное прямолинейное движение: Когда объект движется с постоянной скоростью с нулевым ускорением, это называется равномерным прямолинейным движением.Равномерно ускоренное прямолинейное движение: когда объект движется с постоянным ускорением, это называется равноускоренным прямолинейным движением.
Какие 5 уравнений равноускоренного движения?
Это: a = ускорение, принимаемое за постоянное, t = количество времени, в течение которого объект ускорялся, vo = начальная скорость объекта, vf = скорость объекта в момент времени t позже, и Δx = перемещение объекта за промежуток времени.+ 2а∆х.
Какие три уравнения равноускоренного движения?
Три уравнения: v = u + at. v² = u² + 2ас. с = ut + ½at²
Какое из следующих уравнений можно использовать для равноускоренного движения?
в=у+ат.
Какое из следующих уравнений можно использовать для равноускоренного вращающегося тела?
Мы используем уравнение ω = d θ d t ; ω знак равно d θ d т ; поскольку производная угла по времени является угловой скоростью, мы можем найти угловое смещение, интегрируя угловую скорость, что на рисунке означает взятие площади под графиком угловой скорости.
Что такое уравнение равномерного движения?
Формула равномерного движения: d = rt, что означает, что расстояние равно скорости, умноженной на время.
Как вы решаете равномерно ускоренное движение?
Уравнения равномерно ускоренного движения
- s=12(v+u)t.
- в=у+ат.
- v2=u2+2as.
- с=ут+12ат2.
Какие 4 уравнения кинематики?
Существует четыре кинематических уравнения, когда начальное исходное положение является исходной точкой, а ускорение постоянно:
- v=v0+at.v = v 0 + ат.
- d=12(v0+v)t d = 1 2 ( v 0 + v ) t или альтернативно vaverage=dt. v среднее = d t.
- д=v0t+(at22)
- v2=v20+2ad.
Какова формула равномерного движения?
Какая из следующих ситуаций является примером равноускоренного движения?
Некоторые примеры равномерного ускоренного движения включают мяч, катящийся по склону, парашютист, выпрыгивающий из самолета, мяч, упавший с вершины лестницы, и велосипед, тормоза которого включены.
youtube.com/embed/OwiO4hi5YBM?feature=oembed” frameborder=”0″ allow=”accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture” allowfullscreen=””/>
кинематических уравнений для равноускоренного движения – MyRank
Для представления движения любого объекта используются различные представления, такие как графическое изображение, графическое изображение, словесное представление и т. д. Раздел механики, изучающий движение объекта, называется кинематикой. Он описывает концепцию движения с графическим представлением его основных терминов, таких как перемещение, скорость, скорость, ускорение и т. д. , а также уравнение движения, которое дает связь между этими основными терминами
Ускоренное движение: Скорость автомобиля на дороге никогда не бывает одинаковой.Его скорость увеличивается и уменьшается случайным образом. Поскольку скорость транспортного средства на дороге продолжает меняться, говорят, что оно имеет ускоренное движение.
Скорость изменения скорости объекта во времени называется ускорением объекта.
Равномерно ускоренное движение: Ускорение — это изменение скорости в каждую единицу времени. В случае, когда изменение скорости в каждую единицу времени постоянно, говорят, что объект движется с постоянным ускорением, и такое движение называется «равномерно ускоренным движением».
Движение с неравномерным ускорением: Если изменение скорости в каждую единицу времени непостоянно, говорят, что объект движется с переменным ускорением, и такое движение называется «движением с неравномерным ускорением».
В общем случае движение транспортного средства по дороге неравномерно ускорено, так как оно ускоряется и замедляется случайным образом.
Кинематические уравнения: Эти кинематические уравнения используются для обнаружения неизвестного значения или переменной с использованием известной информации о переменных.Эти уравнения описывают движение либо с постоянной скоростью, либо с постоянным ускорением.
Первое уравнение движения: Рассмотрим частицу, движущуюся по прямой линии с равномерным ускорением «а». При t = 0 пусть частица находится в точке A, а u — ее начальная скорость, а когда t = t, v — ее конечная скорость. \(Acceleration=\frac{change\,\,in\,\,velocity}{time }=\frac{vu}{t}\)
\(a=\frac{v-u}{t}\)
v – u = at
v = u + at
Второе уравнение движения:
Средняя скорость = \(\frac{Всего\,расстояний\,пройденных}}{Всего\,времени\,взятых}\)
Средняя скорость = \(\frac{S}{t}\) … (1)
Средняя скорость также может быть записана как \(\frac{v+u}{2}\)
Средняя скорость = \(\frac{v+u}{2}\) … (2)
Из уравнений (1) и (2):
\(\frac{S}{t}=\frac{v+u}{2}\) … (3)
Первое уравнение движения v = u + at
Подстановка значения v в уравнение (3),
Получаем
\(\frac{S}{t}=\frac{u+u+at}{2}=\frac{(u+u+at)t}{2}\)
\(=\frac{(2u+at)t}{2}\)
\(=\frac{2ut+a{{t}^{2}}}{2}\)
\(=\frac{2ut}{2}+\frac{a{{t}^{2}}}{2}\)
S = ut + ½ at²
Третье уравнение движения: Первое уравнение движения v = u + at
v – u = при … (1)
Средняя скорость = \(\frac{S}{t}\) … (2)
Средняя скорость = \(\frac{v+u}{2}\) … (3)
Из уравнений (2) и (3) получаем
\(\frac{v+u}{2}\,=\,\frac{S}{t}\) … (4)
Умножая уравнения (1) и (4), получаем
v² – u² = 2 как
(v – u) (v + u) = 2as [∵ (a – b) (a + b) = a² – b²]
v² – u² = 2 как
Пример: Автомобиль движется по прямому шоссе со скоростью 126 км/ч и останавливается на расстоянии 200 м, то за какое время автомобиль проехал?
Сол: Здесь, пройденное расстояние, S = 200 м
Начальная скорость автомобиля, u = 126 км/ч
= 126 х (1000 м) х (60 х 60 с)¯¹
= 35 м/с
Конечная скорость автомобиля, v = 0
Пусть a будет Замедление автомобиля
Мы знаем, что:
v² – u² = 2 как
(0)² – (35)² = 2a x 200
\(a\,=\,-\,\frac{{{(35)}^{2}}}{2\times 200}=3. 06м/\сек \)
06м/\сек \)
Сейчас,
v = u + at (или) \(0\,=\,35\,+\,\left(-\,\frac{49}{16} \right)t\)
\(t\,=\,\frac{35\times 16}{49}=\frac{80}{7}=11,43\,\sec \).
250+ ЛУЧШИХ MCQ по кинематическим уравнениям равномерно ускоренного движения
Вопросы и ответы по физике с несколькими вариантами ответов по теме «Кинематические уравнения равномерно ускоренного движения».
1. Автомобиль движется за 60 с, преодолев расстояние 3600 м с нулевой начальной скоростью. Чему равно ускорение в м/с 2 ?
а) 2
б) 2.5
c) 3
d) 4.5
Ответ: a
Уточнение: Здесь мы будем использовать второе уравнение движения, s = ut + (1/2)at 2 . Здесь u = 0, s = 3600, t = 60 с. При решении получим a = 2 м/с 2 .
2. Количество первичных уравнений движения ___
а) 1
б) 2
в) 3
г) 4
Ответ: а
Пояснение: Есть в основном 3 уравнения движения. Это v = u + at, s = ut + (1/2)at 2 и v 2 = u 2 + 2as.
3. Автомобиль движется с нулевой начальной скоростью до скорости 5 м/с с ускорением 10 м/с 2 . Пройденное расстояние равно ___
а) 1,25 м
б) 1,5 м
в) 1,6 м
г) 0 м
Ответ: а
Уточнение: Здесь мы будем использовать третье уравнение движения. Третье уравнение движения имеет вид v 2 = u 2 + 2as, u = 0, a = 10, v = 5. Следовательно, при решении получаем s = 1,25m.
4. Мяч брошен вверх с начальной скоростью 20 м/с и через некоторое время возвращается обратно.Какая максимальная высота достигнута? Возьмем g = 10 м/с 2 .
а) 80 м
б) 20 м
в) 70 м
г) 40 м
Ответ: б
Уточнение: Здесь мы будем использовать третье уравнение движения. Третье уравнение движения: v 2 = u 2 + 2as. На максимальной высоте скорость мяча будет равна нулю, поэтому v = 0, u = 20, a = -g = -10. При решении получим s = 20m.
5. Гусеница начинает двигаться со скоростью 1 м/ч.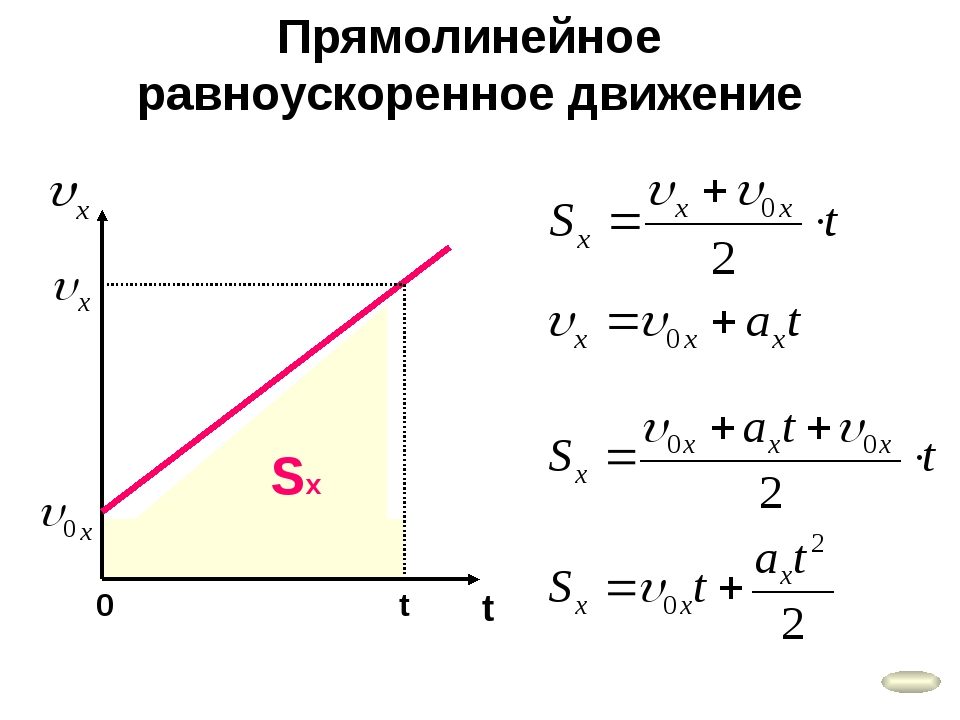 Если скорость изменения скорости равна 0.1 м/ч 2 , какова конечная скорость через 10 часов?
Если скорость изменения скорости равна 0.1 м/ч 2 , какова конечная скорость через 10 часов?
а) 2 м/ч
б) 1 м/ч
в) 0,5 м/ч
г) 5 м/ч
Ответ: а
Уточнение: здесь можно использовать первое уравнение движения. В первом уравнении v = u + at, здесь u = 1 м/ч, t = 10 часов, a = 0,1 м/ч 2 . Подставив все значения в уравнение, мы получим v = 2 м/ч.
6. В первые 10 с движения тела скорость изменяется от 10 м/с до 20 м/с. В течение следующих 30 с скорость изменяется от 20 м/с до 50 м/с.Каково среднее ускорение в м/с 2 ?
а) 1
б) 2
в) 3
г) 0,5
Ответ: а
Пояснение: Среднее ускорение – это полное изменение скорости на полное изменение во времени. Здесь общее изменение скорости = 50-10 = 40 м/с, а общее изменение во времени = 30+10 = 40 с. Следовательно, среднее ускорение = 1 м/с 2 .
7. Тело проходит расстояние 15 м за 15 мин с начальной скоростью 0 м/мин. Чему равна конечная скорость в м/мин?
а) 2
б) 8
в) 5
г) 6
Ответ: а
Пояснение: Используйте второе уравнение движения, чтобы найти ускорение. s = ut + (1/2)at 2 , u = 0, t =15, s=15, следовательно, a = 2/15 м/мин 2 . Теперь используйте первое уравнение, чтобы найти конечную скорость. v = u + at, u = 0, t = 15 мин, a = 2/15, следовательно, v = 2 м/мин.
s = ut + (1/2)at 2 , u = 0, t =15, s=15, следовательно, a = 2/15 м/мин 2 . Теперь используйте первое уравнение, чтобы найти конечную скорость. v = u + at, u = 0, t = 15 мин, a = 2/15, следовательно, v = 2 м/мин.
8. 15 м/с можно записать в км/ч как ______
а) 54
б) 44
в) 45
г) 56
Ответ: а
Пояснение: Формула для перевода, км/ч = ( 18/5) х м/с. Следовательно, 15 м/с = 15 х (18/5) = 54 км/ч.
9. Монету и мешок с камнями бросают в невесомой среде с одинаковой начальной скоростью.Какое из следующих утверждений верно относительно ситуации?
а) Мешок будет двигаться быстрее
б) Монета будет двигаться быстрее
в) Оба будут двигаться с одинаковой скоростью
г) Мешок не будет двигаться
Ответ: в
Пояснение: При отсутствии внешней силы, такой как сила тяжести, ускорение равно нулю. Следовательно, оба тела будут двигаться с одинаковой начальной скоростью.
10. Автобус проходит первые несколько метров пути с ускорением 5 м/с 2 за 10 с, а следующие несколько метров с ускорением 15 м/с 2 за 20 с. Какова конечная скорость в м/с, если он стартует из состояния покоя?
Какова конечная скорость в м/с, если он стартует из состояния покоя?
а) 100
б) 350
в) 450
г) 400
Ответ: б
Уточнение: Примените первое уравнение движения к обеим частям. Для первой части v 1 = u + a 1 t 1 = 0 + 5×10 = 50 м/с. Для второй части v 2 = u 2 (= v 1 ) + a 2 t 2 = 50 + 15×20 = 350 м/с.
11. Для какого из следующих видов движения справедливы уравнения движения?
а) Постоянная энергия
б) Равноускоренный
в) Неравномерно ускоренный
г) Движение по кривой
Ответ: б
Пояснение: Три уравнения движения справедливы для равноускоренного движения.Уравнения не работают в ситуациях, когда ускорение неравномерно. В этом случае лучше работать с дифференциальными формами скорости и ускорения.
12. Сколько переменных требуется для полного описания системы при равномерно ускоренном движении?
а) 1
б) 3
в) 4
г) 2
Ответ: б
Уточнение: При равноускоренном движении для полного определения системы требуется не менее трех переменных Это также можно выяснить, используя уравнения движение.

 Это векторная величина, что означает, что она имеет как величину, так и направление. Его единица СИ находится в метрах (м), но также используются другие единицы измерения расстояния, такие как километры (км), мили (ми) и футы (футы).
Это векторная величина, что означает, что она имеет как величину, так и направление. Его единица СИ находится в метрах (м), но также используются другие единицы измерения расстояния, такие как километры (км), мили (ми) и футы (футы). Как и начальная скорость, это векторная величина, описываемая величиной и направлением. Она имеет те же единицы измерения, что и начальная скорость: м/с, км/ч и мили в час.
Как и начальная скорость, это векторная величина, описываемая величиной и направлением. Она имеет те же единицы измерения, что и начальная скорость: м/с, км/ч и мили в час.
