404 Not Found
404 Not Found
|
|
Основные формулы по физике | Студенческая жизнь
In естественные наукиТэги правила, физика, формулыПросмотров: 4K
Окружающий мир уже довольно плотно изучен и, в какой-то степени, предсказуем.
Происходящие в макромире процессы описывают основные формулы по физике, которые помогают определить характеристики — скорость, температуру, высоту, агрегатное состояние, массу объекта в любой момент времени. А также помогают описать взаимодействие разных сил и предметов.
Посмотрим, почему так сложны определения из учебника по сравнению с тем, что они описывают.
Формулы, допущения и основные правила. На примере прямолинейного движения
Самое простое — инерциальные системы и движение тела в пространстве. Это изучает механика, а конкретнее — кинематика объекта. Упрощенно называют «прямолинейного движения», однако любое тело в современном мире испытывает воздействия сил в разном направлении.
Основные формулы по физике движения тела применялись еще в начальной школе. «Поезд вышел из города А и двигался в город В три часа. Где он оказался, если его скорость составляла…». Все помнят подобные задачки. Это простое изложение формулы для определения координат материальной точки в любой момент времени, если она двигается прямолинейно и равномерно.
Звучит формула как «координата равна начальной координате плюс приращение, равное произведению скорости вдоль оси координат, умноженной на время, прошедшее после начала отсчета».
Сложные допущения
Хотя основные формулы по физике могут быть пояснены «на пальцах», они включают в себя множество допущений и ограничений. Это связано с тем, что поведение объекта исследуется в трех измерениях одновременно.
- Вводится понятие «материальной точки». Для глобального анализа многих параметров, включая температуру и излучение, масса объекта, материал, форма — не важны. Физика упрощает оперирование для более прозрачного расчета.
- Глобальное время. Для всех объектов внутри исследуемого пространства, грубо, существует одно время — прошедшее с момента начала наблюдения. Даже если материальная точка «родилась» в результате взаимодействия других, для нее вносится поправка параметра. Но основные формулы по физике оперируют только понятием «время после начала отсчета».
- «Ось координат» — существенный параметр всех формул.
- линейные координаты. Это, грубо, стандартное описание трехмерного пространства. «Длина — ширина — высота». Оси Х — Y – Z;
- полярная система. На ее основе работают некоторые основные формулы физики, относящиеся к различным полям и излучениям, а также силами взаимного притяжения или отталкивания;
- локальная система координат. Очень редко используется в случае анализа поведения одного объекта. Начало координат и направление оси принимается в зависимости от характеристик исследуемой материальной точки. Локальная система служит обычно для сравнительного анализа поведения материальной точки и определения отклонений от заранее просчитанных параметров.
Заключение
Приведенные выше основные понятия, принципы и терминология относится ко всем основным формулам в физике. Они помогают применять элементарные и четкие правила для расчета и понимания процессов в очень сложных системах. Так и построен окружающий мир — все сложное состоит из простых кусочков.
Физика на кончиках пальцев — видео
Кинематика – одно направление | Репетиторство в Читауне
Перейти к содержимому Кинематика — это наука о движении без учета сил. Есть четыре основных уравнения для движения в одном направлении. Они охватывают рассмотренные ранее векторные величины – перемещение, скорость и ускорение.
Уравнение 1: d = v i * t + ½ * a * t 2
Здесь d — смещение, v i — начальная скорость, a — ускорение и t — время.
Это уравнение можно использовать для определения смещения движущегося объекта с известными начальной скоростью, ускорением и временем. Кроме того, любая из вышеуказанных величин может быть определена, если присутствуют другие.
Уравнение 2: v f 2 = v i 2 + 2 * a * d
Это уравнение обычно используется для определения конечной скорости или преобразуется для определения смещения.
Уравнение 3: v f =v i + a * t
Конечная скорость равна сумме начальной скорости и ускорения, умноженной на затраченное время.
Может использоваться для определения конечной скорости. Это уравнение обычно перестраивается, чтобы найти ускорение.
Уравнение 4: d = (v i + v f ) / 2 * t
Это уравнение вычисляет среднюю скорость и умножает ее на время, чтобы получить перемещение.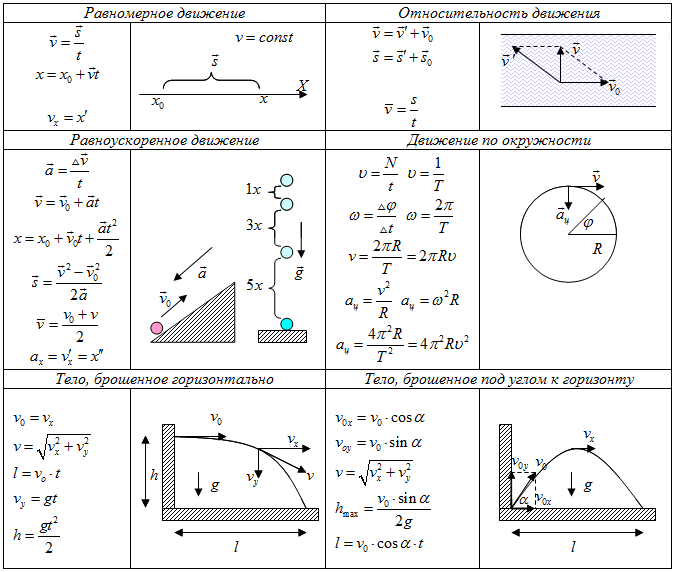
Кинематика может быть решена в направлении X или Y, в зависимости от задачи.
Особые случаи:
Если проблема связана с движением в направлении Y,
- Ускорение = g = -9,81 м/с2
- Если мяч подброшен в воздух вертикально, а затем падает на землю,
- Начальная скорость (скорость в начале запуска) = конечная скорость (скорость непосредственно перед достижением земли)
- Движение можно разделить пополам, поэтому первая половина движения (когда оно достигает высшей точки) совпадает со второй половиной (от высшей точки до земли)
- Скорость в высшей точке равна нулю. В высшей точке объект на мгновение останавливается. Следовательно, скорость в этой точке равна нулю.
Рекомендуемые шаги:
1. Нарисуйте схему ситуации. Это поможет вам визуализировать начальное и конечное положение, а также направление движущегося объекта.
2. Запишите данные переменные. Сделайте предположения, основанные на деталях проблемы.
3. Перечислите переменную, которую необходимо решить.
4. Найдите уравнение(я), связывающее все переменные вместе.
а. Необходимо выбрать уравнение, в котором должны быть известны все переменные, кроме одной. Если вы выбираете уравнение, в котором 2 или более переменных неизвестны, то необходимо выбрать другое уравнение.
5. Найдите отсутствующую переменную.
а. Совет: Сначала изолируйте переменную, которую необходимо решить, а затем подставьте известные значения.
Пример: Майкл ждет на светофоре. Когда он, наконец, становится зеленым, Майкл ускоряется из состояния покоя со скоростью 6,00 м/с2 за время 4,10 секунды. Определите водоизмещение автомобиля Михаила за этот период времени. 92
= 0 + 3* 16,81
= 50,43 м
Практические задачи
1. Самолет движется по взлетно-посадочной полосе со скоростью 3,20 м/с2 в течение 32,8 с, пока, наконец, не оторвется от земли. Определить расстояние, пройденное до взлета.
Решение:
1.
Запишите данные переменные. Делайте предположения.
Дано:
a = 3,20 м/с 2
t = 32,8 с
v i = 0 (объект стартует из состояния покоя)
) Предположения:
м (начальное положение =м)0005
2. Запишите переменную, которую необходимо решить.
Решите для: d
3. Найдите уравнения, связывающие переменные вместе.
Используйте уравнение 1: d = v i * t + ½ * a * t 2
4. Подставьте переменные в уравнение и найдите отсутствующую переменную.
d = v i * t + ½ * a * t 2
d = 0 * (32,8) + ½ * (3,20) * (32,8) 2
d = 1721,304 м 90 A автомобиль трогается с места и равномерно разгоняется за время 5,21 секунды на расстояние 110 м. Определить ускорение автомобиля.
Решение:
1. Запишите данные переменные. Делайте предположения.
Дано:
t = 5,21 с
v i = 0 (объект стартует из состояния покоя)
d = 110 м
Предположения:
Начальная позиция = 0 м (исходная точка)
5 9,0 необходимо решить
Решить для: a
3.
Найдите уравнения, связывающие переменные вместе.
Используйте уравнение 1: d = v i * t + ½ * a * t 2
4. Подставьте переменные в уравнение и найдите отсутствующую переменную. (5.21) s 2
3. Гоночный автомобиль равномерно ускоряется с 18,5 м/с до 46,1 м/с за 2,47 секунды. Определить ускорение автомобиля и пройденный путь.
Решение:
1. Запишите данные переменные. Делайте предположения.
Дано:
t = 2,47 с
v i = 18,5 м/с
v f = 46,1 м/с
Предположения:
Начальная позиция = 0 м (исходная точка) необходимо решить.
Решите для:
a
d
3. Найдите уравнения, связывающие переменные вместе. Замените известные переменные и найдите отсутствующую переменную.
Уравнение 3: a = (V f – V i )/ время = (46,1 – 18,5) / 2,47 = 11,174 м/с 2
Уравнение 4: d = (v i + v f ) / 2 * t
d = (v i + v f ) / 2 * t
3 d = (5,18.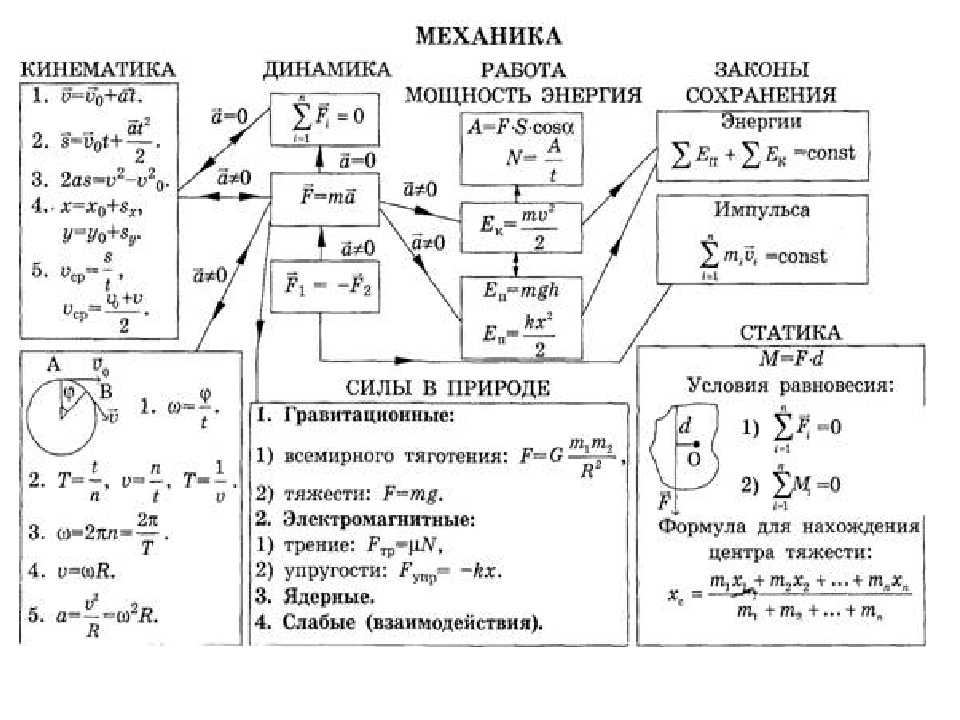
1 d )/2 * 2,47 d = 79,781 м
Ссылка
https://www.physicsclassroom.com/class/1DKin/Lesson-6/Kinematic-Equations-and-Free-Fall
Перейти к началу
Уравнение кинематики
Уравнения кинематики определяют, как входное движение в одном или нескольких суставах определяет конфигурацию устройства для достижения рабочего положения или положения рабочего органа в механической системе, такой как робот-манипулятор. От четырехзвенных звеньев до последовательных и параллельных роботов уравнения кинематики используются для оценки и разработки шарнирных систем. Эти уравнения можно использовать для любого движения, которое можно классифицировать как с постоянной скоростью или с постоянным ускорением. Их нельзя использовать в любой период, когда ускорение меняется.
Уравнения кинематики
Существует четыре формулы кинематики:
Переменные уравнения кинематики В каждой из кинематических формулировок есть четыре переменные.
Если известны значения первых трех переменных, можно вычислить значение четвертой переменной.
Δx Водоизмещение
vo Начальная скорость
v Конечная скорость
t временной интервал
a ускорение
Как выбрать и использовать кинематическую формулу?
Мы выбираем кинематическую формулу, которая содержит и неизвестную переменную, и три уже известные нам кинематические переменные. Таким образом, мы можем найти искомое неизвестное, которое будет единственным неизвестным в формулах.
Например, предположим, что мы знаем, что книга, лежащая на земле, двигалась вперед с начальной скоростью v0=5 м/с, после чего книга скользила на расстояние x=8 м за интервал времени t=3 с. Поскольку мы знали все остальные переменные в формуле, кроме a, мы могли бы использовать кинематическую формулу для алгебраического решения неизвестного ускорения a книги (при условии, что ускорение было постоянным).
Что такое снаряд?
Может показаться, что тот факт, что кинематические формулы работают только для интервалов времени с постоянным ускорением, сильно ограничивает их применимость. Постоянное ускорение оказывается одним из самых распространенных видов движения, свободного падения. Независимо от их массы, все свободно летающие объекты — также известные как снаряды — на Земле имеют непрерывное нисходящее ускорение величиной 9,81 м/сек 2 из-за гравитации. Любой объект, который ускоряется исключительно за счет силы тяжести, называется свободно летящим объектом. Любой объект, который падает, швыряется или иным образом свободно летит по воздуху, обычно считается свободно летящим снарядом с постоянным нисходящим ускорением величиной g = 9.0,81 м/с 2 .
Примеры уравнения кинематики
Маленький мальчик едет на велосипеде с начальной скоростью 2 м/с. Через 3 секунды он прибывает в пункт назначения с конечной скоростью 10 м/с.
Вычислите его ускорение, вызванное движением.
Ниже приведены предоставленные параметры:
v0=2 м/с Начальная скорость
v=10 м/с — конечная скорость.
t = 3 секунды — период времени.
Для расчета ускорения воспользуемся следующей формулой:
v=v0+at
Ускорение:
a=(v-v0)/t
a=(10-2)/3
Ускорение 2,76 м/с 2
2 Вращательное k Большинство уравнений имеют дело с уравнениями линейной или поступательной кинематики, которые могут быть связаны с движением тела. Однако в области физики, известной как уравнения вращательной кинематики, есть и другая возможность. Разница лишь в том, что изменились переменные. Переменные в уравнениях вращательной кинематики перечислены ниже- В этом уравнении вместо ускорения используется угловое, в отличие от уравнений линейной кинематики.
- Вместо смещения используется изменение угла.
