Кинематика. Формулы
Кинематика. Формулы| Номер | Название формулы | Запись формулы | Примечание |
| (1) | Закон равноускоренного криволинейного движения | vS0 — модуль начальной скорости; aS — ускорение | |
| (2) | Скорость равномерного прямолинейного движения | ||
| (3) | Скорость | ||
| (4) | Ускорение | ||
| (5) | Касательное ускорение | dv = dl/dt, т.е. путевая скорость вдоль рассматриваемой траектории | |
| (6) | Нормальное ускорение | ||
| (7) | Скорость свободного падения тела | ||
| (8) | Время тела при свободном падении | ||
| (9) | Время при равномерном движении по окружности | ||
| (10) | Скорость равномерного движения по окружности | ||
| (11) | Угловая (мгновенная) скорость равномерного движения по окружности | Единица измерения угловой скорости — радианы в секунду | |
| (12) | Скорость равноускоренного движения по окружности | ||
| (13) | Угловая (мгновенная) скорость равноускоренного движения по окружности |
— версия для печати
- Определение
- Кинематикой называется раздел физики, занимающийся исследованием законов движения идеальных тел
- Пояснение
- Под чертой вверху буквы подразумевается знак вектора.

| Если у вас есть мысли или идеи по поводу данной таблицы или, например, вы считаете, что полезно было бы создать определенную вспомогательную памятку, то мы обязательно рассмотрим ваше предложение, которое можно изложить по ссылке (где вы также можете поделиться с нами любыми мыслями по поводу сайта scolaire.ru). Мы готовы устранить любые неудобства, связанные с использованием данной таблицы, или ей подобных, которые можно найти в разделе «Физика». |
© Школяр. Лингвистика (при поддержке «Ветвистого древа») 2009—2016
Формулы кинематики с пояснениями по физике / Блог :: Бингоскул
Кинематика — раздел физики, занимающийся исследованием законов движения идеальных тел.
Основные формулы с пояснениями, которые помогут в решении заданий ЕГЭ по физике: движение, скорость, ускорение.
Путь, время, скорость
S=v *t
- S – путь
- v – скорость
- t – время
Равномерное движение
x=x_0 + v*t
- x – координата
- x0 – начальная координата
- v – скорость
- t – время
Равномерно ускоренное движение: ускорение
a=\frac { v – v_0 } { t }
- a – ускорение
- v – скорость
- v0 – начальная скорость
- t – время
Равномерно ускоренное движение: скорость
v=v_0 + at
- v – скорость
- v0 – начальная скорость
- a – ускорение
- t – время
Равномерно ускоренное движение: путь
S=vt + \frac { at^2 } { 2 }
- s – путь
- v – скорость
- t – время
- a – ускорение
Равномерно ускоренное движение: координата
x=x_0 + vt + \frac { at^2 } { 2 }
- x – координата
- x0 – начальная координата
- v – скорость
- t – время
- a – ускорение
Высота тела, брошенного вертикально вверх (вниз)
h=h_0 + v_ { 0 } t – \frac { gt^2 } { 2 }
- h – высота
- h0 – начальная высота
- v0 – начальная скорость
- t – время
- g – ускорение свободного падения
Скорость тела, брошенного вертикально вверх (вниз)
v=v_0 – gt
- v – скорость
- v0 – начальная скорость
- g – ускорение свободного падения
- t – время
Скорость, ускорение, время
v=at
- v – скорость
- a – ускорение
- t – время
Скорость свободно падающего тела
v=gt
- v – скорость
- g – ускорение свободного падения
- t – время
Центростремительное ускорение
a=\frac { v^2 } { R }
- a – центростремительное ускорение
- v – скорость
- R – радиус
Угловая скорость
\omega=\frac { \phi } { t }
- ω – угловая скорость
- φ – угол
- t – время
Равномерное круговое движение
l=R\phi
- l – длина дуги окружности
- R – радиус
- φ – угол
Равномерное круговое движение: линейная скорость
v=R \omega
- v – линейная скорость
- R – радиус
- ω – угловая скорость
Период вращения
T=\frac { t } { N }
- T – период
- t – время
- N – число вращений
T=\frac { 2 \pi R } { v }
- T – период
- R – радиус
- v – линейная скорость
T=\frac { 2 \pi } { \omega }
- T – период
- ω – угловая скорость
Центростремительное ускорение
a=\frac { 4 \pi^ { 2 } R } { T^2 }
- a – центростремительное ускорение
- R – радиус
- T – период вращения
a=4 \pi^ { 2 } Rn^2
- a – центростремительное ускорение
- R – радиус
- n – частота вращения
Частота вращения
n=\frac { 1 } { T }
- n – частота вращения
- T – период вращения
Центростремительное ускорение
a=\omega ^ { 2 } R
- a – центростремительное ускорение
- ω – угловая скорость
- R – радиус
Дальность броска тела, брошенного под углом к горизонту
x=v_0t \cos(\alpha)
- x – координата (дальность)
- v0 – начальная скорость
- t – время
- α – угол
Высота подъема тела, брошенного под углом к горизонту
y=v_0t \sin (\alpha) – \frac { gt^2 } { 2 }
- y – координата (высота подъема )
- v0 – начальная скорость
- t – время
- g – ускорение свободного падения
- α – угол
Вертикальная скорость тела, брошенного под углом к горизонту
v_y=v_0* \sin (\alpha) – gt
- vy – вертикальная скорость
- v0 – начальная скорость
- α – угол
- g – ускорение свободного падения
- t – время
Максимальная высота подъема тела, брошенного под углом к горизонту
h_max =\frac { v_0^2* \sin (\alpha)^ { 2 } } { 2g }
- hмакс – максимальная высота
- v0 – начальная скорость
- α – угол
- g – ускорение свободного падения
Общее время движения тела, брошенного под углом к горизонту
t=\frac { 2v_0 * \sin (\alpha) } { g }
- t – время
- v0 – начальная скорость
- α – угол
- g – ускорение свободного падения
Дальность броска тела, брошенного горизонтально
x=x_0 + vt
- x – координата (дальность)
- x0 – начальная координата
- v – скорость
- t – время
Высота подъема тела, брошенного горизонтально
y=y_0 – \frac { gt^2 } { 2 }
- y – координата (высота подъема)
- y0 – начальная координата (высота)
- g – ускорение свободного падения
- t – время
Общее время движения тела, брошенного горизонтально
t_max=\sqrt { \frac { 2h } { g } }
- tмакс – максимальное время
- h – высота
- g – ускорение свободного падения
Смотри также:
Глава 7. Вращательное движение. Кинематика и динамика
Вращательное движение. Кинематика и динамика
Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел
(7.1) |
В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан – безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7.
(7.2) |
Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.
Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим
(7.3) |
Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.
Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна
(7.4) |
Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах
(7.5) |
Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине
Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине
(7.6) |
Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.
Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.
Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»).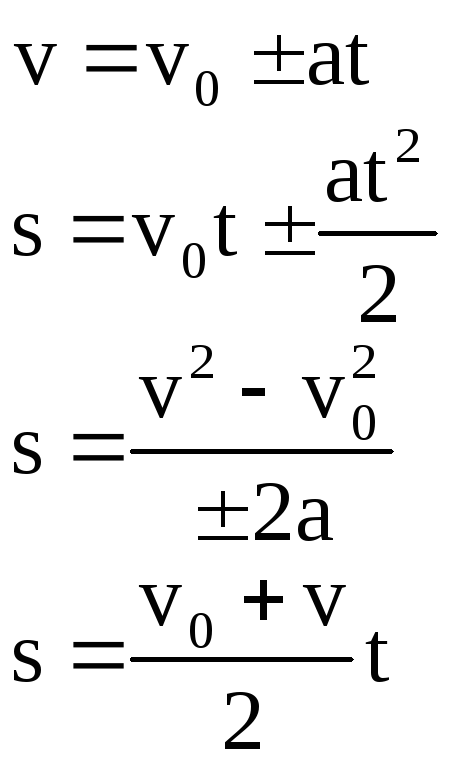 Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).
Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).
Для нахождения линейной скорости конца секундной стрелки часов (задача 7.1.2
(правильный ответ – 2).
Применяя определение угловой скорости к колесу (задача 7.1.3), получаем
(правильный ответ 1).
Из формулы (7.2) имеем
(задача 7.1.4 – правильный ответ 4).
Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.1.5), из формулы (7.5) находим квадрат угловой скорости диска
А теперь по формуле (7.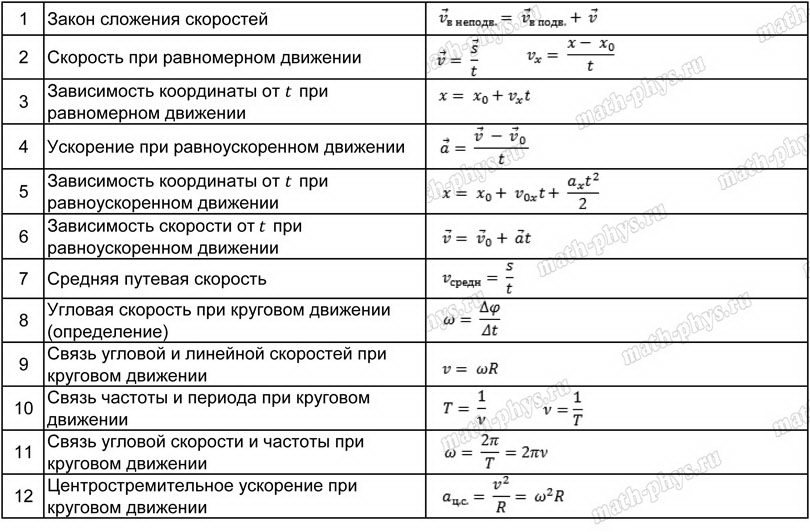 5) для второй точки получаем
5) для второй точки получаем
(ответ 2).
Поскольку скорость автомобиля в задаче 7.1.6 не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7.4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ – 3).
Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно
(ответ 4).
Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (
 Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).
Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).
Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с2, получим для равнодействующей =2 Н (ответ 2).
Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из задачи 7.2.1
(ответ 1).
Для сравнения центростремительных ускорений материальных точек в задаче 7. 2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем
2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем
(ответ 3).
Для сравнения центростремительных ускорений тел в задаче 7.2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим
(7.5) |
Поэтому
(ответ 1).
Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)
где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем
Учитывая, что , получаем
(ответ 2).
Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7.2.5), центростремительное ускорение сообщается силой трения
Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства
(ответ 4).
В задаче 7. 2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем
2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем
(ответ 3).
В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает
(1) |
На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем
Подставляя в эту формулу силу из формулы (1), находим (ответ 2).
В задаче 7. 2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем
2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем
где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим
(ответ 3).
Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):
где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно
(задача 7.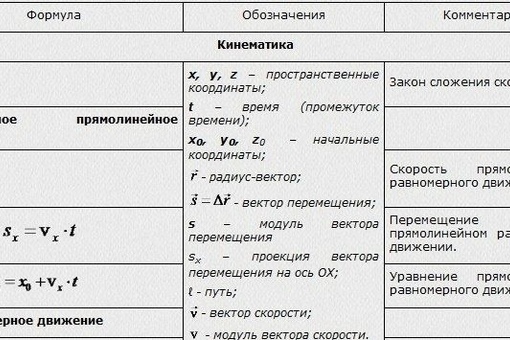 2.9 – ответ 1).
2.9 – ответ 1).
Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7.2.10 – ответ 2).
формулы, определения, методы решения задач
Кинематика — это специальный раздел теоретической механики. Направление сформировалось несколько позднее, чем статика и динамика: во второй половине XIX столетия. Первые исследования в области кинематики были посвящены огнестрельному оружию. Ученые стремились понять процесс полета снаряда, производили расчет траектории его движения. В дальнейшем кинематика как научное направление получило широкое распространение и существенно повлияло на развитие технического прогресса.
Кинематика — описание
Кинематика является разделом механики, цель которого — изучение механического движения тел с пренебрежением к причинам, вызывающим это движение.
Механика представляет собой научную область физики, которой посвящены исследования механического движения тел. Основной целью данного направления служит определение точного положения тела в пространстве в любой момент времени. Важным понятием этого раздела является материальная точка в виде тела с определенной массой и размерами, которыми можно пренебречь для решения задачи при наличии следующих условий:
- Путь, который преодолевает тело, существенно больше, чем его размеры.
- Расстояние между телами значительно превышает их размеры.
- Объект совершает поступательное движение.
Движение тела рассматривают в системе отсчета, состоящей из системы координат и прибора, измеряющего время. Траекторией называют линию, которую объект описывает, совершая движение. Путь является скалярной величиной, определяемой как длина траектории. Перемещением обозначают вектор, который соединяет начальное и конечное положение тела, преодолеваемое им в течение определенного промежутка времени.
Совершая движение, тело может только увеличивать пройденный путь, при этом перемещение увеличивается или уменьшается. К примеру, уменьшение перемещения наблюдается во время обратного движения тела. Если объект движется прямолинейно в одном направлении, то путь определяется модулем перемещения. В случае криволинейного движения — путь превышает перемещение. При рассмотрении замкнутой траектории перемещение будет равно нулю.
Теория и формулы
Благодаря многолетним исследованиям в области кинематики ученым удалось вывести определенные закономерности движения тела. С помощью справедливых уравнений представляется возможным ответить на многие вопросы о разных характеристиках, которые изменяются либо остаются постоянными во время движения объектов.
Путь, время, скорость
Расстояние представляет собой удаленность одной точки положения тела от другой. Тело преодолевает путь, который представляет собой важную характеристику механического движения. Общепринятым обозначением пути является латинская буква s. Данный параметр измеряют метрами и километрами, если речь идет о больших расстояниях.
Тело преодолевает путь, который представляет собой важную характеристику механического движения. Общепринятым обозначением пути является латинская буква s. Данный параметр измеряют метрами и километрами, если речь идет о больших расстояниях.
Скорость представляет собой путь, который тело преодолело в течение единицы времени. В качестве единицы времени часто используют 1 час, 1 минуту, 1 секунду. Для расчета скорости необходимо определить отношение пути к времени движения. В случае, когда в условиях задачи расстояние измеряется в метрах, а время пути — в секундах, то скорость следует рассчитывать в метрах в секунду (м/с). Для обозначения скорости используют латинскую букву \(v\).
Нередко требуется определить время пути. Данный параметр обозначают с помощью латинской буквы \(t\).
Важно отметить, что скорость, путь и время взаимосвязаны. При известных характеристиках скорости и времени можно определить расстояние, которое преодолело тело. Путь в данном случае равен произведению скорости и времени, рассчитывается по формуле:
\(s=v\times t\)
При известных величинах времени и расстояния достаточно просто определить скорость движения тела, руководствуясь следующим уравнением:
\(v=\frac{s}{t}\)
Равномерное движение
Равномерным движением называют движение тела, которое совершает равные перемещения в течение любых равных промежутков времени.
Скорость при равномерном движении определяется как отношение перемещения ко времени, в течение которого данное перемещение было совершено. Уравнение имеет следующий вид:
\(\vec{v}=\frac{\vec{s}}{t}\)
\(\vec{v}=const\)
Проекция вектора скорости на ось ОХ выглядит таким образом:
\(v_{x}=\frac{s_{x}}{t}\)
\(v_{x}=const\)
Если вектор скорости спроецировать на ось координат, то она будет равна быстроте изменения данной координаты:
\(v_{x}=\frac{x-x_{0}}{t}\)
Прямолинейное равноускоренное движение
Прямолинейным равноускоренным движением называют движение по прямой траектории, для которого характерно постоянное ускорение.
Ускорение для прямолинейного равноускоренного движения обозначают следующим образом:
\(\vec{a}=const\)
При таком движении можно наблюдать увеличение или уменьшение скорости. Чтобы определить скорость, необходимо выполнить следующий расчет:
\(\vec{v}=\vec{v}_{0}+\vec{a}t\)
Если тело разгоняется в проекции оси ОХ, то скорость можно определить по формуле:
\(v_{x}=v_{0x}+a_{x}t\)
a>0, движение является равноускоренным.
Во время торможения в проекции на ось ОХ скорость рассчитывают следующим образом:
\(v_{x}=v_{0x}-a_{x}t\)
а<0, движение является равнозамедленным.
Источник: fizi4ka.ruГрафически зависимость ускорения от времени, то есть график ускорения во время равноускоренного движения тела, можно представить в виде:
Источник: fizi4ka.ruГрафик ускорения, характеризующий равноускоренное движение тела, представляет собой прямую, которая параллельна оси времени:
- график 1 находится над осью t, тело совершает разгон, ах>0;
- график 2 размещен под осью t, тело тормозит, ах<0.
Графически скорость или проекция скорости изображается в виде зависимости скорости от времени:
Источник: fizi4ka.ruГрафически скорость, характерная для равноускоренного движения тела, имеет вид прямой. График 1 направлен вверх, тело будет совершать равноускоренное движение в положительном направлении оси ОХ:
\(v_{0x}>0\)
\(a_x>0\)
\(a_{1x} = tg α \)
График 2 направлен вниз, тело будет двигаться равнозамедленно в положительном направлении оси ОХ:
\(v_{0x}>0\)
\(a_x<0\)
\(a_{2x} = tg α \)
График 3 направлен вниз, тело свершает равноускоренное движение против оси ОХ:
\(v_{0x}<0\)
\(a_x<0\)
Исходя из графика зависимости скорости от времени, определяют перемещение, которое тело преодолело в течение определенного промежутка времени \(t_2-t_1\). {2}}{-2g}\)
{2}}{-2g}\)
В максимальной верхней точке тело, брошенное вверх, будет обладать нулевой скоростью, \(v=0\). Для расчета времени подъема можно воспользоваться формулой:
\(t=\frac{v_{0}}{g}\)
Свободно падающее тело
Свободным падением называют движение тела в условиях безвоздушного пространства под действием силы тяжести.
В условиях свободного падения ускорения тел с разной массой будут равны. Данный параметр называют ускорением свободного падения. Оно всегда направлено к центру нашей планеты, то есть вертикально вниз. Величина обозначается латинской буквой g, а единицами измерения являются м/с2.
Ускорение свободного падения равно 9,8 м/с2. В задачах по физике допускается использовать значение g=10 м/с2.
Движение по окружности с постоянной по модулю скоростью
Движением по окружности при постоянной по модулю скоростью называют простейшим видом криволинейного движения. {-1}\) (Гц).
{-1}\) (Гц).
\(\nu=\frac{N}{t}\)
Период и частота являются взаимно обратными величинами:
\(T=\frac{1}{\nu}\)
\(\nu =\frac{1}{T}\)
Линейная скорость представляет собой скорость движения тела по окружности. Параметр обозначают латинской буквой v, единицами измерения являются м/с. Линейная скорость направлена по касательной к окружности и рассчитывается по формуле:
\(v=\frac{2\pi \times R}{T}\)
\(R\) является радиусом окружности.
Угловой скоростью называют физическую величину, которая определяется как отношение угла поворота и времени, за которое тело совершает этот поворот. Обозначают параметр как ω. Единицами измерения угловой скорости являются рад/с. Угловая скорость определяется по формуле:
\(\omega =\frac{\varphi }{t}\)
\(\varphi\) представляет собой угол поворота.
Источник: fizi4ka.ruНаправление угловой скорости определяют с помощью правила правого винта или буравчика. В случае, когда вращательное движение винта соотносится с направлением движения тела по окружности, то поступательное движение винта и направление угловой скорости совпадают. {2}R\)
{2}R\)
\(\omega = \frac{2\pi }{T}\)
\(\omega = 2\pi v\)
Во время равномерного движения тела по окружности точки, расположенные на радиусе, перемещаются с равной угловой скоростью, так как радиус за одно и то же время поворачивается на одинаковый угол. В это время линейная скорость разных точек радиуса отличается в зависимости от того, насколько близко или далеко от центра они размещены:
\(v_{1}=\omega r\)
\(v_{2}=\omega R\)
\(\frac{v_{1}}{v_{2}}=\frac{r}{R}\)
Источник: fizi4ka.ruПри рассмотрении равномерного движения двух соединенных тел можно наблюдать отсутствие отличий в линейных скоростях, но при этом угловые скорости тел будут различны в зависимости от радиуса тела:
\(\omega _{1}=\frac{v}{R_{1}}\)
\(\omega _{2}=\frac{v}{R_{2}}\)
\(\frac{\omega _{1}}{\omega _{2}}=\frac{R_{1}}{R_{2}}\)
Источник: fizi4ka.ruДвижение тела, брошенного под углом к горизонту
Движение тела, которое бросили под углом к горизонту, можно представить в виде суперпозиции двух движений:
- Равномерного горизонтального перемещения.
 {2}}\)
{2}}\)Дальность полета тела соответствует уравнению:
\(l=v_{0x}t=v_{0x}\sqrt{\frac{2h_{0}}{g}}\)
Вычислить угол между вектором скорости и осью ОХ можно с помощью формулы:
\(\tan \beta =\frac{v_{y}}{v_{x}}=\frac{-gt}{v_{0x}}\)
Задачи по кинематике, их решение
Задача 1
Рассмотрим путь велосипедиста из одного населенного пункта в другой. Половина расстояния была преодолена со скоростью 12 км/ч (\(v_1\)). Далее половину оставшегося времени он ехал со скоростью 6 км/ч (\(v_2\)). Остаток расстояния путник преодолел пешком со скоростью 4км/ч (\(v_3\)). Необходимо рассчитать среднюю скорость на всем пути следования велосипедиста.
Решение
Данный пример относится к теме равномерного прямолинейного движения одного тела. Процесс можно изобразить схематично:
Источник: pandia.ru\(S = S_1 + S_2 + S_3\)
\(t = t_1 + t_2 + t_3\)
На каждый отрезок пути необходимо составить уравнение движения:
\(S_1 = v_1t_1\)
\(S_2 = v_2t_2\)
\(S_3 = v_3t_3\)
Далее можно представить дополнительные условия задачи:
\(S_1 = S_2 + S_3\)
\(t_2 = t_3\)
\(v_{sr}=\frac{S}{t}=\frac{S_{1}+S_{2}+S_{3}}{t_{1}+t_{2}+t_{3}}\)
Следует преобразить формулу и подставить числовые значения:
\(v_{sr}=\frac{2S_{1}}{\frac{S_{1}}{v_{1}}+\frac{2S_{1}}{v_{2}+v_{3}}}=\frac{2v_{1}\left(v_{2}+v_{3} \right)}{2v_{1}+v_{2}+v_{3}}\)
\(v_{sr}=\frac{2\times 12\left(6+4 \right)}{2\times 12+6+4}=7\)
Ответ: средняя скорость составляет \(7\) км/ч.
 {2}}=\frac{9,81}{0,17}=57,7\)
{2}}=\frac{9,81}{0,17}=57,7\)Ответ: камень упал с высоты \(57,7\) м.
Решение задач по кинематике основано на простых формулах. Успешность результата зависит от умения грамотно применять справедливые уравнения в том или ином случае. Бывают ситуации, когда в процессе изучения физики возникают некоторые трудности. Простым решением будет обратиться к порталу Феникс.Хелп.
Кинематика. Формулы ЕГЭ — Репетитор по физике (Краснодар)
1.1.1 Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.
Относительность механического движения — зависимость механического движения тела от системы отсчёта, относительно которой рассматривается движение.
Система отсчета — это совокупность неподвижных относительно друг друга тел (тело отсчёта), по отношению к которым рассматривается движение.
1.1.2 Материальная точка — тело, размерами которого можно пренебречь при проведении расчетов в данных условиях.

Радиус-вектор — вектор идущий из начала координат в рассматриваемую точку:
Траектория (м) — линия в пространстве по которой двигалась материальная точка (совокупность точек пространства в которых находилась материальная точка в заданный промежуток времени).
Перемещение (м) — вектор проведенный из точки начала движения в конец:
Сложение перемещений:
1.1.3 Скорость материальной точки (м/c) — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта:Сложение скоростей:
1.1.4 Ускорение материальной точки (м/c2) — векторная физическая величина, характеризующая быстроту изменения скорости материальной точки:
аналогично
1.1.5 Равномерное прямолинейное движение — это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения:
1.
 1.6 Равноускоренное прямолинейное движение -это движение, при котором тело движется вдоль прямой линии, а его скорость за любые равные промежутки времени меняется на одно и ту же величину:
1.6 Равноускоренное прямолинейное движение -это движение, при котором тело движется вдоль прямой линии, а его скорость за любые равные промежутки времени меняется на одно и ту же величину:1.1.7 Свободное падение — равнопеременное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют, скомпенсированы, либо пренебрежимо малы.
Ускорение свободного падения — ускорение, придаваемое телу силой тяжести, при исключении из рассмотрения других сил (g = 9,80665 м/с²).
Движение тела, брошенного под углом α к горизонту:
1.1.8 Движение точки по окружности.
Угловая скорость (рад/c) — физическая величина, равная отношению угла поворота к интервалу времени, в течение которого этот поворот произошел и линейная скорость точки (м/c) — скорость точки, направленная по касательной к окружности:
Центростремительное ускорение (м/с²) — ускорение движущегося по окружности тела, направленное к центру:
Кинематика.
 Движение
Движение
{Тут текста просто дохуя}
{Тут формул просто дохуя}
[sqrt –это обозначение корня]Кинематика – это такой раздел физики, который изучает механическое движение, но без причин, его начавших. То есть, когда едет машина – она едет за счёт спуска с горы, двигателя, божественной силы или ее притягивает чёрная дыра – неважно, главное – ее движение.
Существует несколько видов движения:
• Равномерное прямолинейное – движение по прямой с постоянной скоростью.
• Равноускоренное прямолинейное – движение с постоянным ускорением по прямой.
• Разноускоренное прямолинейное – движение с непостоянными ускорением по прямой
• Криволинейное – движение по окружности с ускорением (всегда с ускорением!)Наверное, я должен здесь объяснять все буквы, которые будут использоваться, но хуй там.
— Итак, равномерное прямолинейное. Тут все просто, обычная функция:
• S[перемещение]=v[скорость]*t[время]
За некоторое время объект проходит какое-то расстояние. 2)/2.
2)/2.
Лайфачек: чтобы найти расстояние, которое проходит тело, можно воспользоваться соотношением 1, 3, 5, 7.., то есть за 1 секунду тело проходит Х метров, за вторую 3Х, за две – 4Х, и дальше по аналогии.— Разноускоренное движение.
Тут все элементарно, мы разбиваем путь на расстояния, где ускорение одинаковое, находим, что нам нужно, и складываем.— Криволинейное движение.
Если нам необходимо высчитать, как какая-то хуетень будет двигаться по окружности, то нам нужно знать несколько правил:
1. Не сосатб. Когда видишь задачу с криволинейным движением, помни – она решается очень легко.
2. Криволинейное движение, если оно равномерное, ВСЕГДА равноускоренное.
3. Скорость ВсЕгДа направлена по касательной к окружности в точке касания нахождения этого объекта. Тип вот наш объект движется по окружности, он – точка касания его скорости (т.к. скорость – вектор) и окружности.
4. Все измеряется в радианах. Нахуй градусы. 2*sin2α)/g
2*sin2α)/g
Исходя из этого, максимальный путь тело проделывает, если его бросить под углом 45°.Безусловно, это далеко не все, что вы можете узнать о кинематике – в ней просто дохуища всего, но это вы уже сделаете сами, а то я заебался.
Спасибо за то, что вы с нами.
С любовью, Рителлинг favoriteТест на тему “Кинематика”
Автор –учитель высшей категории МОУ «Гимназия №2»
Радкевич Валентина Степановна
Глава 1 «Кинематика».
Тема 1: Наука о движении тел.Ускорение,скорость и путь при равноускоренном прямолинейном движении.
Задание 1.
Проверочная работа по определениям, понятиям и формулам темы:
1 вариант:
Что такое механическое движение?
Что такое ускорение? /формула с расшифровкой/.
Формула средней скорости /с расшифровкой/.

Формула для расчета пути при р/у движении /с расшифровкой/.
График зависимости U(t) при р/у движении тела.
2 вариант:
1. В чем состоит относительность механического движения?
2. Формула для расчета скорости при р/у движении / с расшифровкой/.
3. Что такое мгновенная скорость?
4. Формула для расчета пути при р/у движении по известному ускорению тела/с расшифровкой/.
5. График зависимости U(t) при р/з движении тела.
Задание 2.
Самостоятельная работа:
Уровень 1.
/Задания оцениваются по 1 баллу/.
О какой скорости – средней или мгновенной – идет речь в следующих случаях: а/ пуля вылетает из винтовки со скоростью 800 м/с; б/ скорость движения Земли вокруг Солнца 30 км/ч; в/ спидометр автомобиля показывает скорость 85 км/ч ?
Поезд через 10 с после начала движения приобретает скорость 0.6 м/с. Чему равно ускорение поезда?
Какой должна быть длина взлетной полосы, если известно, что самолет для взлета должен приобрести скорость 60 м/с, а время разгона равно 30 с ?
Определите вид движения тел, если их скорости изменяются со временем, как показано на рисунке.

Уровень 2.
/Задания оцениваются по 2 балла/.
Первый участок пути поезд прошел со скоростью 54 км/ч за 2 ч, остаток пути, равный 216 км, – за 3 ч. Какую среднюю скорость развил поезд на всем пути ?
Через сколько времени останавливается автобус, если его начальная скорость 20 м/с, а ускорение 1.25 м/с(2) ?
По графику зависимости скорости движения тела от времени определить: а/ ускорение тела на каждом участке; б/ путь, пройденный телом на каждом участке.
Уровень 3.
/Задания оцениваются по 3 балла/.
Поезд через 10 с после начала движения приобретает скорость 0,6 м/с. Через сколько времени от начала движения скорость поезда станет равна 3 м/с ?
Шарик, скатываясь с наклонного желоба из состояния покоя, за первую секунду прошел путь 10 см. Какой путь он пройдет за 3 с ?
По графику зависимости скорости движения тел от времени определить: а/ ускорения тел; б/ путь, пройденный телами за все время движения.

1*. Через сколько времени от начала движения велосипедист проходит путь 20 м при ускорении 0.4 м/с(2) ?
Тема 2: Движение по окружности. Период и частота обращения.
Задание 3.
Проверочная работа по определениям, понятиям и формулам темы:
1 вариант:
1. Как направлена скорость тела при движении по окружности ?
2. Что характеризует ускорение при движении по окружности ?
3. Что такое период обращения ?
4. Формула для расчета периода /с расшифровкой/ .
5. Формула связи частоты с периодом обращения ?
2 вариант:
1. Как направлено ускорение тела при движении по окружности ? Как оно называется ?
2. Формула для расчета центростремительного ускорения /с расшифровкой/ .
3. Что такое частота обращения ?
4. Формула для расчета частоты /с расшифровкой/ .
5. Формула для расчета периода обращения по известной скорости движения тела.
Задание 4.

Самостоятельная работа:
Уровень 1.
/Задания оцениваются по 1 баллу/ .
Показать на рисунке направления скорости и ускорения тела в точках А и В.
Период обращения круга равен 14 с. Как это понимать?
Частота обращения колеса 10 с(-1). Как это понимать?
Определите период вала токарного станка, если частота его вращения 125 с(-1).
Чему равно центростремительное ускорение автомобиля, движущегося по выпуклому мосту, радиус кривизны которого 35 м, со скоростью 15 м/с. Куда оно направлено?
Уровень 2.
/Задания оцениваются по 2 балла/ .
Колесо велосипеда имеет радиус 25 см. С какой скоростью едет велосипедист, если колесо вращается с частотой 1 с(-1) ?
Каков радиус закругления дороги, если по ней автомобиль движется с центростремительным ускорением 1 м/с(2) при скорости 10 м/с ?
Уровень 3.
/Задания оцениваются по 3 балла/ .

Шкив диаметром 16 см делает 300 оборотов за 3 мин. Какова скорость равномерного движения точек обода этого шкива?
Секундная стрелка часов делает полный оборот за 1 мин. Радиус стрелки равен 10 см. Каково центростремительное ускорение конца стрелки?
Минутная стрелка часов на Спасской башне Кремля имеет длину 3.5 м. Какой путь совершит конец этой стрелки за 15 мин?
1*. Минутная стрелка часов в 3 раза длиннее секундной. Найти отношение скоростей концов стрелок.
Задание 5.
Повторение темы «Кинематика» /подготовка к контрольной работе/ :
1. Ряд формул в физике служит определением физических величин. Какая из следующих формул является определением ускорения?
А. S=at(2)/2. Б. a=U/t. В. Uср=U/2
2. Скорость и ускорение движущегося шарика совпадает по направлению. Как изменяется скорость движения шарика в этом случае?
А. Увеличивается Б. Уменьшается В. Не изменяется
3. Искусственный спутник движется по окружности вокруг Земли с постоянной по модулю скоростью из точки К в точку М.
 В точке А траектории показаны три вектора: АВ, АС и АД. Какой из этих векторов является направлением скорости, а какой ускорения?
В точке А траектории показаны три вектора: АВ, АС и АД. Какой из этих векторов является направлением скорости, а какой ускорения?А. Скорость АВ, ускорение АД. Б. Скорость АС, ускорение АД. В. Скорость АД, ускорение АС
4. Ускорение шарика 1 м/с(2). Чему равна скорость шарика в момент времени 2 с ?
А. 2.5 м/с Б. – 1.5 м/с В. 2 м/с
5. Шарик движется из состояния покоя равноускоренно. Путь шарика равен 0.6 м, время движения 1 с. Чему равно ускорение шара?
А. 1.2 м/с(2) Б. 0.6 м/с(2) В. 1 м/с(2)
6. Картинг движется по закруглению дороги радиусом 100 м. С каким центростремительным ускорением движется картинг?
А. 1 м/с(2) Б. 0.1 м/с(2) В. 10 м/с(2)
7. Точильный круг радиусом 10 см имеет период вращения 0.2 с. Какова частота вращения круга?
А. 5 с(-1) Б. 15 с(-1) В. 0.5 с(-1)
8. На рисунке изображен график зависимости скорости прямолинейного движения автомобиля от времени . Чему равно ускорение автомобиля?
А. 2 м/с(2) Б.
 0.5 м/с(2) В. 1 м/с(2)
0.5 м/с(2) В. 1 м/с(2)9. На рисунке изображен график зависимости скорости прямолинейного движения тела от времени. Чему равен путь за 3 с ?
А. 6 м Б. 36 м В. 9 м
10. Какая величина характеризует быстроту движения тела?
А. Ускорение Б. Скорость В. Время
Задание 6.
Контрольная работа по теме «Кинематика» :
Уровень 1.
/Задания оцениваются по 1 баллу/ .
Определите тормозной путь автомобиля, если его торможение длилось 10 с при ускорении 4 м/с(2)
По графикам зависимости скорости движения двух тел от времени, определите какое из тел двигалось с большим по модулю ускорением. Почему?
С каким ускорением двигался автобус, если, трогаясь с места стоянки, он развил скорость 15 м/с за 50 с ?
Тело движется по окружности радиусом 1.2 м с постоянной по модулю скоростью, равной 3 м/с. Чему равно центростремительное ускорение тела? Покажите на чертеже направления скорости и ускорения тела.

Уровень 2.
/Задания оцениваются по 2 балла/ .
По графику зависимости скорости движения тела от времени определить: а/ ускорение тела на каждом участке; б/ путь, пройденный телом на каждом участке.
Велосипедист движется по закруглению дороги некоторого радиуса со скоростью 10 м/с. Чему равен радиус закругления дороги, если центростремительное ускорение велосипедиста равно 1 м/с(2) ?
Определите время полета груза с высоты 500 м, если во время удара о землю его скорость была равна 50 м/с, а ускорение 10 м/с(2).
Уровень 3.
/Задания оцениваются по 3 балла/ .
Двигаясь со скоростью 72 км/ч, мотоциклист притормозил и его скорость уменьшилась до 36 км/ч . Ускорение мотоциклиста было равно 1.8 м/с(2). Сколько времени длилось торможение?
По графику зависимости скорости движения тела от времени определите: а/ ускорение тела на каждом участке пути; б/ путь, пройденный телом на каждом участке.

Определите скорость равномерного движения конца секундной стрелки своих часов. Какова частота вращения этой стрелки?
Кинематика. Формулы
Кинематика. ФормулыНомер Название формулы Запись формулы Примечание (1) Закон равноускоренного криволинейного движения v S 0 – модуль начальной скорости; a S – ускорение (2) Скорость равномерного прямолинейного движения (3) Скорость (4) Ускорение 03
03 5)
Касательное ускорение dv = dl / dt, т.е. путевая скорость вдоль рассматриваемой траектории (6) Нормальное ускорение (7) Скорость свободного падения тела (8) Время тела при свободном падении (9) Время при равномерном движении по окружности (10) Скорость равномерного движения по окружности (11) Угловая (мгновенная) скорость равномерного движения по окружности Единица измерения угловой – радианы в секунду (12) Скорость равноускоренного движения по окружности (13) Угловая скорость (мгновенная) скорость равноускоренного движения по окружности
– версия для печ ати- Определение
- Кинематика называется раздел физики, занимающийся изучением движения идеальных тел
- Пояснение
- Под чертой вверху буквы подразумевается знак события.

Если у вас есть мысли по поводу данной таблицы или, например, вы считаете, что полезно бы создать определенную Мы обязательно рассмотрим ваше предложение, которое можно изложить по ссылке (где вы также можете поделиться с нами любыми мыслями по поводу сайта scolaire.ru ). Мы готовы устранить неудобства, связанные с использованием данной таблицы, или ей подобных, можно найти в разделе данной таблицы. «Физика». © Школяр . Лингвистика (при поддержке «Ветвистого древа») 2009-2016
Формулы кинематики с пояснениями по физике / Блог :: Бингоскул
Кинематика – раздел физики, занимающийся исследованием движения идеальных тел.
Основные формулы с пояснениями, которые используются в решении заданий ЕГЭ по физике: движение, скорость, ускорение.
Путь, время, скорость
S = v * t
- S – путь
- v – скорость
- t – время
Равномерное движениеx = x_0 + v * t
- x – координата
- x 0 – начальная координата
- v – скорость
- t – время
- a – ускорение
- v – скорость
- v 0 – начальная скорость
- t – время
- v – скорость 2 v 0 – начальная скорость
- a – ускорение
- t – время
- v – скорость
- t – время
- a – ускорение
- x – координата
- x 0 – начальная координата
- v – скорость
- t – время
- a – ускорение
- h – высота
- h 0 – начальная высота
- v 0 – начальная скорость
- t – время
- g – ускорение свободного падения
- v – скорость
- v 0 – начальная скорость
- g – ускорение свободного падения
- t – время
- v – скорость
- a – ускорение
- t – время
- v – скорость – ускорение свободного падения
- t – время
- a – центростремительное ускорение
- v – скорость
- R – радиус
- ω – угловая скорость
- φ – угол
- t – время
- R – радиус
- φ – угол
- R – радиус
- ω – угловая скорость
- T – период
- t – время
- N – число вращений
- T – период
- R – радиус
- v – линейная скорость
- T – период
- ω – угловая скорость
- a – центростремительное ускорение
- R – радиус
- T – период вращения
- a – центростремительное ускорение
- R – радиус
- n – частота вращения
- n – частота вращения
- T – период вращения
- a – центростремительное ускорение
- ω – угловая скорость
- R – радиус
- x – координата (дальность)
- v 0 – начальная скорость
- t – время
- α – угол
- y – координата (высота подъема)
- v 0 – начальная скорость
- t – время
- g – ускорение свободного падения
- α – угол
- v y – вертикальная скорость
- v 0 – начальная скорость
- α – угол
- g – ускорение свободного падения
- t – время
- h макс – максимальная высота
- v 0 – начальная скорость
- α – угол
- g – ускорение свободного падения
- t – время
- v 0 – начальная скорость
- α – угол
- g – ускорение свободного падения
- x – координата (дальность) 901 83
- x 0 – начальная координата
- v – скорость
- t – время
- y – координата (высота подъема)
- y 0 – начальная координата (высота)
- g – ускорение свободного падения
- t – время
- t макс – максимальное время
- h – высота
- g – ускорение свободного падения
- Путь, который преодолевает, крупнее, чем его размеры.

- Расстояние между телами значительно превышает их размеры.
- Объект совершает поступательное движение.
- график 1 находится над осью t, тело совершает разгон, ах> 0;
- график 2 размещен под осью t, тормозит, ах <тело.

- Равномерное горизонтальное движение со скоростью v0 = v0x.{2}} \)
Дальность полета тела соответствует уравнению:
\ (l = v_ {0x} t = v_ {0x} \ sqrt {\ frac {2h_ {0}} {g}} \)
Вычислить угол между вектором скорости и осью ОХ можно с помощью формулы:
\ (\ tan \ beta = \ frac {v_ {y}} {v_ {x}} = \ frac {-gt} {v_ {0x}} \)
Задачи по кинематике, их решение
Задача 1
Рассмотрим путь велосипедиста из одного пункта в другой. Половина расстояния была преодолена со скоростью 12 км / ч (\ (v_1 \)).Далее половину оставшегося времени он ехал со скоростью 6 км / ч (\ (v_2 \)). Остаток расстояния путник преодолел пешком со скоростью 4км / ч (\ (v_3 \)). Необходимо рассчитать среднюю скорость на всем пути следования велосипедиста.

Решение
данный пример относится к теме равномерного прямолинейного движения одного тела. Процесс можно изобразить схематично:
Источник: pandia.ru\ (S = S_1 + S_2 + S_3 \)
\ (t = t_1 + t_2 + t_3 \)
На каждый отрезок пути необходимо составить уравнение движения:
\ (S_1 = v_1t_1 \)
\ (S_2 = v_2t_2 \)
\ (S_3 = v_3t_3 \)
Далее можно выполнить дополнительные условия задачи:
\ (S_1 = S_2 + S_3 \)
\ (t_2 = t_3 \)
\ (v_ {sr} = \ frac {S} {t} = \ frac {S_ {1} + S_ {2} + S_ {3}} {t_ {1} + t_ {2} + t_ {3}) } \)
Следует преобразить формулу и подставить числовые значения:
\ (v_ {sr} = \ frac {2S_ {1}} {\ frac {S_ {1}} {v_ {1}} + \ frac {2S_ {1}} {v_ {2} + v_ {3}) }} = \ frac {2v_ {1} \ left (v_ {2} + v_ {3} \ right)} {2v_ {1} + v_ {2} + v_ {3}} \)
\ (v_ {sr} = \ frac {2 \ times 12 \ left (6 + 4 \ right)} {2 \ times 12 + 6 + 4} = 7 \)
Ответ: средняя скорость составляет \ (7 \) км / ч.

Задача 2
Тело подбросили вертикально вверх. Начальная скорость при этом составила 3,13 м / с (\ (v_0 \)). В момент, когда данное тело достигло максимальной высоты полета, из начального пункта подбросили второе тело с такой же начальной скоростью, как у первого. Необходимо определить на каком расстоянии от точки бросания встретятся тела. Сопротивлением воздуха при решении можно не учитывать.
Решение
Схематично перемещение тел можно следующим образом:
Источник: пандиа.{2}} {2 * 9,8} = 0,37 \)Ответ: тела встретятся на высоте \ (0,37 \) м.
Задача 3
Камень, находясь в свободном падении, вторую часть пути преодолел за 1 секунду. Необходимо вычислить высоту \ (h \), с которой упал камень.
Решение
Ось Y системы координат, в которой падает камень, направлена вертикально вниз. В качестве начала координат можно принять точку, из которой камень упал.
 {2}} = \ frac {9,81} {0,17} = 57,7 \)
{2}} = \ frac {9,81} {0,17} = 57,7 \)Ответ: камень упал с высоты \ (57,7 \) м.
Решение задач по кинематике основано на простых формулах. Успешность результата зависит от умения грамотно справедливые уравнения в том или ином случае. Бывают ситуации, когда в процессе изучения физики возникают некоторые трудности. Простым решением будет обратиться к порталу Феникс.Хелп.
Формула скорости свободного падения в физике
Задание. Одно тело бросили вертикально вверх с начальной скоростью равной $ v_0.$ В этот же момент времени вертикально вниз с начальной скоростью $ v_0 $ бросили второе тело. Высота, с которой бросили это тело равной высоты подъема первого тела. Какова скорость первого и второго тел в момент встречи этих двух тел? Тела считающими материальными точками, сопротивление воздуха не учитывать.
Решение. Сделаем рисунок.
За основу решения примем уравнения для скорости движения тела в поле тяжести Земли:
\ [\ overline {v} \ left (t \ right) = {\ overline {v}} _ 0+ \ overline {g} t \ \ left (2. 2} {2} \ to 0 = h-2v_0t ‘\ to t’ = \ frac {h} {2v_0} \ left (2.7 \ right). \]
2} {2} \ to 0 = h-2v_0t ‘\ to t’ = \ frac {h} {2v_0} \ left (2.7 \ right). \]Подставим время $ t ‘$ в уравнение (2.2) получим скорость первого тела в момент встречи:
\ [v_1 = v_0-g \ frac {h} {2v_0} \ left (2.8 \ right). \]Найдем высоту $ h $, на которую способно подняться первое тело. Для этого найдем время подъема тела, зная, что в верхней точке подъема скорость тела равна нулю:
\ [v_1 = v_0-gt = 0 \ to t_ {pod} = \ frac {v_0} {g} \ left (2.9 \ right). \]Высота подъема, она же высота с которой бросили второе тело найдётся из уравнения (2.2_0} {2g} = v_0 + \ frac {v_0} {4} = \ frac {5} {4} v_0. \]
Ответ. $ v_1 = \ frac {3} {4} v_0, $ $ v_2 = \ frac {5} {4} v_0 $
Кинематика. Формулы ЕГЭ – Репетитор по физике (Краснодар)
1.1.1 Механическое движение – изменение положения тела в отношении другого тел с течением времени.
Относительность механического движения – зависимость механического движения тела от системы отсчёта.

Система отсчета – это совокупность неподвижных относительно друг друга тел (тело отсчёта), по отношению к рассматриваемому движению.
1.1.2 Материальная точка – тело, размерами которого можно пренебречь при проведении расчетов в данных условиях.
Радиус-вектор – вектор идущий из начала в рассматриваемую точку:
Траектория (м) – линия в пространстве по которой двигалась материальная точка (совокупность точек пространства в находилась материальная точка в заданном промежутке времени).
Перемещение (м) – вектор проведенный из точки начала движения в конец:
Сложение перемещений:
1.1.3 Скорость материальной точки (м / c) – скорость физической величины, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта:Сложение скоростей:
1.
 1.4 Ускорение материальной точки (м / c 2 ) – скорость физической величины, характеризующая быстроту изменения скорости материальной точки:
1.4 Ускорение материальной точки (м / c 2 ) – скорость физической величины, характеризующая быстроту изменения скорости материальной точки:аналогично
1.1.5 Равномерное прямолинейное движение – это движение, при котором за любые промежутки времени совершает одинаковые перемещения:
1.1.6 Равноускоренное прямолинейное движение -это движение, при котором тело движется вдоль прямой линии, а его скорость за любые равные промежутки времени меняется на одно и ту же роль:
1.1.7 Свободное падение – равнопеременное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют, скомпенсированы, либо пренебрежимо малы.
Ускорение свободного падения – ускорение, придаваемое телу силой тяжести, при исключении рассмотрения из других сил ( г = 9,80665 м / с² ).
Движение тела, брошенного под углом к горизонту:
1.
 1.8 Движение точки по окружности.
1.8 Движение точки по окружности.Угловая скорость (рад / c) – физическая величина, равная относительно угла поворота к интервалу времени, в течение которого этот поворот произошел и линейная скорость точки (м / c) – скорость точки, направленная по касательной к окружности:
Центростремительное ускорение (м / с²) – ускорение движущегося по окружности тела, направленное к центру:
Кинематика.Движение
{Тут текста просто дохуя}
{Тут формул просто дохуя}
[sqrt –это обозначение корня]Кинематика – это такой раздел физики, который изучает механическое движение, но без его начавших. То есть, когда едет машина – она едет за счёт спуска с горы, двигателя, божественной силы или ее притягивает чёрная дыра – неважно, главное – ее движение.
Существует несколько видов движения:
• Равномерное прямолинейное – движение по прямой с постоянной скоростью.
• Равноускоренное прямолинейное – движение с постоянным ускорением по прямому.
• Разноускоренное прямолинейное – движение с непостоянными ускорением по прямому
• Криволинейное – движение по окружности с ускорением (всегда с ускорением!)Наверное, я должен здесь объяснять все буквы, которые будут работать, но хуй там.
– Итак, равномерное прямолинейное. Тут все просто, обычная функция:
• S [перемещение] = v [скорость] * t [время]
За некоторое время объект проходит какое-то расстояние.– Равноускоренное прямолинейное движение. Тут уже сложнее – появляется нормальное ускорение (дальше – ускорение) (а). Ускорение – это когда тело стоит и такое вжжжжжж и поехало, или сначала ехало, а потом начало останавливаться. Набираение скорости в единицу времени – это и есть ускорение. Ускорение находится как:
• а [ускорение] = (v [скорость в конце движения] -v0 [скорость в начале движения]) / t
Чтобы найти скорость, нам нужно действовать так:
• v = v0 + при
Скорость – от какой начальной скорости и сколько тело находилось под (спидами) ускорением. 2) / 2.
2) / 2.
Лайфачек: чтобы найти расстояние, которое проходит, можно воспользоваться 1, 3, 5, 7 .., то есть за 1 второе тело Х метров, за вторую 3Х, за две – 4Х, и дальше по аналогии.– Разноускоренное движение.
Тут все элементарно, мы разбиваем путь на расстояние, где ускорение одинаковое, находим, что нам нужно, и складываем.– Криволинейное движение.
Если нам необходимо высчитать, как какая-то хуетень будет двигаться по окружности, то нам нужно знать несколько правил:
1.Не сосатб. Когда видишь задачу с криволинейным движением, помни – она решается очень легко.
2. Криволинейное движение, если оно равномерное, ВСЕГДА равноускоренное.
3. Скорость ВсЕгДа направлена по касательной к окружности в точке касания нахождения этого объекта. Тип вот наш объект движется по окружности, он – точка касания его скорости (т.к. скорость – вектор) и окружности.
4. Все измеряется в радианах. Нахуй градусы.
Ну, а теперь к формулам. 2) / 2
2) / 2
Скорость (v) тут находится так же, как и в ДТБГ.2 * sin2α) / г
Исходя из этого, максимальный путь тело проделывает, если его бросить под углом 45 °.Безусловно, это далеко не все, что вы можете узнать о кинематике – в ней просто дохуища всего, но это вы уже сделаете сами, а то я заебался.
Спасибо за то, что вы с нами.
С любовью, Рителлинг избранноеУрок 2. равномерное прямолинейное движение материальной точки – Физика – 10 класс
Физика, 10 класс
Урок 2.Равномерное прямолинейное движение материальной точки
Перечень вопросов, рассматриваемых в теме: 1) основная задача механики; 2) относительность механического движения; 3) система отсчёта, материальная точка, перемещение, траектория, скорость; 4) кинематическое уравнение.
Глоссарий по теме:
Раздел механики причин, в котором изучается движение тел без изннения, вызывающего данное движение, называют кинематикой .

Механическим движением тела называется изменение положения тела в отношении других тел с течением времени.
Материальной точкой называют тело, размерами и формой которого в условиях рассматриваемой задачи можно пренебречь. Тело, относительно которого рассматривается движение, называется телом отсчета . Совокупность тела отсчета часов, с ним системы отсчета и называют системой отсчета.
Траектория – линия, по которой движется точка в пространстве.
Длину траектории, по которой двигалось в течение какого-то промежутка времени, называют путем, пройденным за этот промежуток времени.
Перемещением тела (материальной точки) вектор называется соединяющий начальное положение тела с его последующим положением.
Равномерное прямолинейное движение – это движение, при котором за любые равные промежутки времени совершает равные перемещения.
Скорость равномерного прямолинейного движения точки – величина, равная перемещение к промежутку времени, в течение которого это перемещение произошло.

Относительно механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н .. Физика.10 класс. Учебник для общеобразовательных организаций М .: Просвещение, 2016.– С.10-30.
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М .: Дрофа, 2009.
Открытые электронные ресурсы по теме урока:
http://kvant.mccme.ru/1974/12/byvaet_li_ravnomernoe_dvizheni.htm.
Теоретический материал для самостоятельного изучения
Основная задача классической механики – определить положение тела в изображении в любой момент времени.По характеру решаемых задач классическую механику делят на кинематику, динамику и статику. В кинематике описывают движение тел, без причин, вызывающих данное движение. Раздел механики, в котором изучаются причины движения, называют динамикой.
 Статика – раздел механики, в котором изучаются условия равновесия абсолютно твердый тел. Законы сохранения энергии и энергии происходят следствиями заката Ньютонов.
Статика – раздел механики, в котором изучаются условия равновесия абсолютно твердый тел. Законы сохранения энергии и энергии происходят следствиями заката Ньютонов.Механическим движением тела называется изменение положения тела в отношении других тел с течением времени.Сформулируем закон относительности движения : характер движения тела зависит от того, относительно каких тел мы рассматриваем движение. Нет абсолютно неподвижных тел.
Рассмотрим самое простое движение – прямолинейное равномерное движение. Описать движение тела – это значит, указать способ его положения в любой момент времени.
Для описания движения нужно некоторые понятия: материальная точка, траектория, путь, перемещение, координата, момент времени, промежуток времени, скорость. Материальной точкой называют размерами которого в условиях рассматриваемой задачи можно пренебречь. Это первая физическая модель реального тел. Практически всякое тело можно рассматривать как материальную точку в тех случаях, когда расстояния, проходимые точками тела, очень велики по с его размерами.
 Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении разных точек любой планеты, вызванные ее суточным вращением, не влияют на величины, описывающие годовое движение.Но при решении задач, связанных с суточным вращением планет (например, при определении времени восхода в разных местах поверхности земного шара), считать планету материальной точки нельзя, так как результат зависит от размеров этой планеты и скорости движения точек её поверхности.
Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении разных точек любой планеты, вызванные ее суточным вращением, не влияют на величины, описывающие годовое движение.Но при решении задач, связанных с суточным вращением планет (например, при определении времени восхода в разных местах поверхности земного шара), считать планету материальной точки нельзя, так как результат зависит от размеров этой планеты и скорости движения точек её поверхности.Тело, движущееся поступательно, можно принимать за материальную точку даже в том случае, если его размеры соизмеримы с проходимыми им расстояниями. Поступательным называется такое движение абсолютно твердого тела, при любом отрезке, соединяя любые две точки тела, остается параллельным себе.
Что нужно знать для того, чтобы в любой момент времени указать положение тела? Надо, во-первых, знать, где оно было в начальный момент времени; во-вторых, каков вектор перемещения в любой момент времени.
 Мы уже знаем, что движение любого тела относительно. Поэтому, изучая движение тела, мы обязательно указываем, относительно какого тела это движение. Тело, относительно которого рассматривается движение, называется телом отсчета. Чтобы рассчитать положение материальной точки относительно выбранной точки отсчета, надо связать с ним систему координат и измерить время.Совокупность тела отсчета часов, используемая с ним системы координат и называется системой отсчета.
Мы уже знаем, что движение любого тела относительно. Поэтому, изучая движение тела, мы обязательно указываем, относительно какого тела это движение. Тело, относительно которого рассматривается движение, называется телом отсчета. Чтобы рассчитать положение материальной точки относительно выбранной точки отсчета, надо связать с ним систему координат и измерить время.Совокупность тела отсчета часов, используемая с ним системы координат и называется системой отсчета.Рассмотрим два наиболее часто используемых метода описания тел: координатный и вектор. В координатном пространстве задается координатами, которые с течением времени меняются.
Рассмотрим движение материальной точки М с координатами (х, y, z) в момент времени t.
Математически это принято записывать в виде:
Количество координат зависит от условий задачи: на прямой – одна, в плоскости – две, в пространстве – три.
В векторном способе используется радиус-вектор. Радиус-вектор – это направленный отрезок, проведенный из начала в данную точку.
 Закон (или уравнение) движения в векторной форме – зависимость радиуса-вектора от времени:
Закон (или уравнение) движения в векторной форме – зависимость радиуса-вектора от времени:Итак, для задания движения материальной точки необходимо указать функциональную зависимость всех трех координат от времени, либо зависимость от времени геометрической точки. точки.
Три скалярных уравнения или эквивалентное им одно цифровое уравнение называются кинематическими уравнениями движения материальной точки.
Двигаясь, материальная точка занимает положение в положении относительно выбранной системы отсчета. При этом она «изображена» в пространстве какую-то линию. Линия, по которой движется точка в пространстве, называется траекторией . По траектории все движения делятся на прямолинейные и криволинейные. Траектория движения указывает все положения, которые занимала точка, но, зная траекторию, ничего нельзя о том, быстро или медленно проходила точка отдельные участки траектории.Длину траектории, по которой двигалось в течение какого-то промежутка времени, называют путём , пройденным за этот промежуток времени, его обозначают буквой S.
 Путь – скалярная величина.
Путь – скалярная величина.Для описания движения тела нужно указать, как меняется положение точек с течением времени. Если участки криволинейные, то изменение координат описывают с помощью такого понятия как перемещение. Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.Обозначается на чертежах, как направленный отрезок, соединяющий начальное и конечное положение тела в пространстве:
Путь и модуль перемещения совпадают по значению, только в том случае, если тело движется вдоль одного прямого в одном направлении.
Важной величиной, характеризующей движение тела, является его скоростью. Скорость – величина величина. Она заданной, если указан ее модуль и направление. Скорость равномерного прямогоолинейного движения точки – равная величина перемещения к промежутку времени, в течение которого это перемещение произошло.Пусть радиус-вектор задает положение точки в начальный момент времени t 0 , а радиус-вектор- в момент времени t. Тогда промежуток времени:
,
и перемещение:
.
Подставляя выражение для скорости, получим:
Если начальный момент времени t 0 принять равным нулю, то скорость равна:
Выразим отсюда вектор-вектор:
Это и есть ение равномерного прямолинейного движения точки, записанное в векторной форме .Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известна скорость точки и радиус-вектор, задает ее положение в начальный момент времени. В проекциях на ось ОХ уравнение можно записать в виде:
х = х 0 + v х т.
Это уравнение есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме. Оно позволяет найти координаты тела при этом движении в любой момент времени, если известны проекция его скорости на ось ОX и его начальные координаты х 0 .
Путь S, пройденная точка при движении вдоль оси ОХ, равенство модулю изменения ее координаты:
Его можно найти, зная модуль скорости
Строго говоря, равномерного прямолинейного движения не существует. На протяжении не слишком большого промежутка времени движение автомобиля можно равномерным и прямолинейным с достаточной точностью для практических целей. Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения.
Полученные результаты можно изобразить наглядно с помощью графиков. Для прямолинейного равномерного движения график зависимости проекции скорости от времени очень прост. Это прямая, параллельная оси времени.
Как мы уже знаем, зависимость тела от времени описывается формулой х = х 0 + 𝞾 х т. График движения представляет собой прямую линию:
Из второго рисунка видим, что углы наклона прямые разные. Угол наклона второй прямой больше угол наклона первой прямой, т.е за одно и тоже время тело, движущееся со скоростью, проходит большее расстояние, чем при движении со скоростью А значит А что же в случае 3, когда угол α <0? В случае 3 тело движется в сторону, противоположную ось ОХ. Проекция скорости в случае 3 имеет отрицательное значение и проходит ниже оси ОХ. Проекция скорости определяет угол наклона прямой х (t) к оси t и численно равна тангенсу угла
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.В рамках классической механики время есть величина, то есть протекающее во всех системах отсчета одинаково.
Примеры и разбор решения заданий
1. Тело движется равномерно и прямолинейно в положительном направлении оси ОХ. Координата тела в начальный момент времени равна x о = -10м. Найдите координату тела через 5с, если модуль её скорости равен ʋ = 2 м / с. Какой путь проделало тело за это время?
Дано: x о = – 10 м, t = 5 c, ʋ = 2 м / с.
Равномерно ускоренное движение: ускорение
a = \ frac {v – v_0} {t}
Равномерно ускоренное движение: скорость
v = v_0 + at
Равномерно ускоренное движение: путь
S = vt + \ frac {at ^ 2} {2}
- 9018 2 с – путь
Равномерно ускоренное движение: координата
x = x_0 + vt + \ frac {at ^ 2} {2}
Высота тела, брошенного вверх (вниз)
h = h_0 + v_ {0} t – \ frac {gt ^ 2} {2}
Скорость тела, брошенного вертикально вверх (вниз)
v = v_0 – gt
Скорость, ускорение, время
v = at
свободно Скорость падающего тела
v = gt
Центростремительное ускорение
a = \ frac {v ^ 2} {R}
Угловая скорость
\ omega = \ frac {\ phi} {t}
Равномерное круговое движение
l = R \ phi
l – длина дуги окружности
Равное круговое движение: линейная скорость
v = R \ omega
9018 2 v – линейная скорость
Период вращения
T = \ frac {t} {N}
T = \ frac {2 \ pi R} {v}
T = \ frac {2 \ pi} {\ omega}
Центростремительное ускорение
a = \ frac {4 \ pi ^ {2} R} {T ^ 2}
a = 4 \ pi ^ {2} Rn ^ 2
Частота вращения
n = \ frac {1} {T}
Центростремительное ускорение
a = \ omega ^ {2} R
Дальность броска тела, брошенного под углом к горизонту
Равномерное круговое движение
- l – длина дуги окружности
Равное круговое движение: линейная скорость
v = R \ omega
- 9018 2 v – линейная скорость
Период вращения
T = \ frac {t} {N}
T = \ frac {2 \ pi R} {v}
T = \ frac {2 \ pi} {\ omega}
Центростремительное ускорение
a = \ frac {4 \ pi ^ {2} R} {T ^ 2}
a = 4 \ pi ^ {2} Rn ^ 2
Частота вращения
n = \ frac {1} {T}
Центростремительное ускорение
a = \ omega ^ {2} R
x = v_0t \ cos (\ alpha)
Высота подъема тела, брошенного под углом к горизонту
y = v_0t \ sin (\ alpha) – \ frac {gt ^ 2} {2}
Вертикальная скорость тела, брошенного под углом к горизонту
v_y = v_0 * \ sin (\ alpha) – gt 90 164
Максимальная высота подъема тела, брошенного под углом к горизонту
h_max = \ frac {v_0 ^ 2 * \ sin (\ alpha) ^ {2}} {2g}
Общее время движения тела, брошенного под углом к горизонту
t = \ frac {2v_0 * \ sin (\ alpha)} {g}
Дальность броска тела, брошенного горизонтально
x = x_0 + vt
Высота подъема тела, брошенного горизонтально
y = y_0 – \ frac {gt ^ 2} {2}
Общее время движения тела, брошенного горизонтально
t_max = \ sqrt {\ frac { 2h} {g}}
Смотри также:
формулы, определения, методы решения задач
Кинематика – это специальный раздел теоретической механики.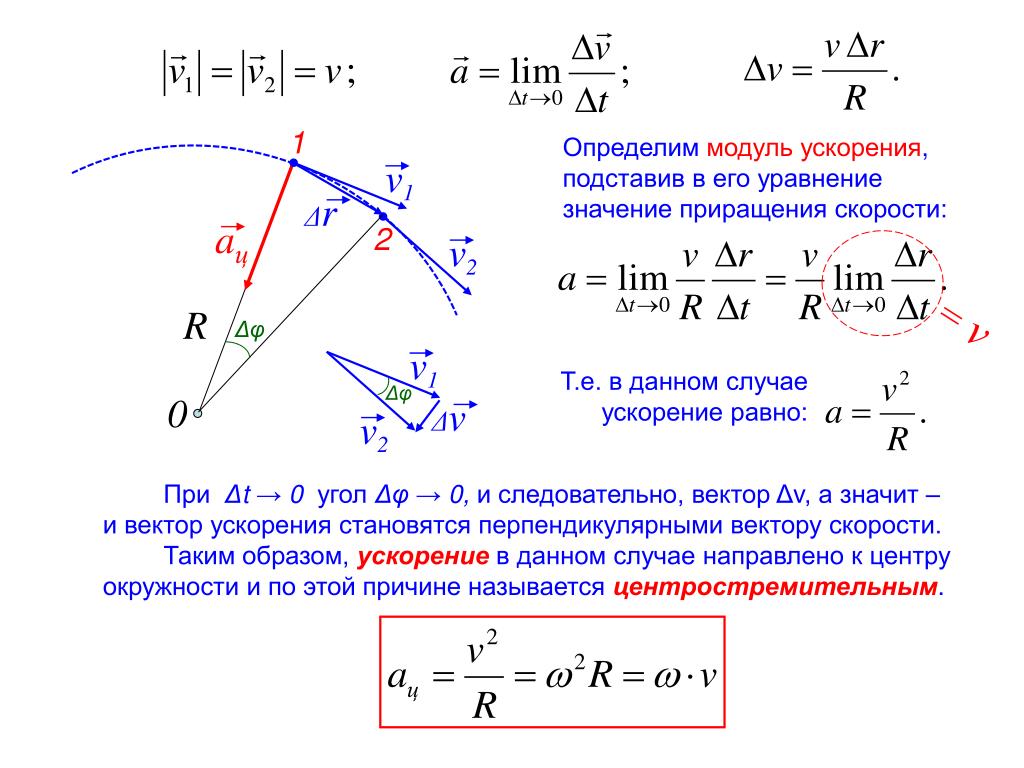 Направление сформировано несколько позднее, чем статика и динамика: во второй половине XIX столетия. Первые исследования в области кинематики были посвящены огнестрельному оружию. Ученые стремились понять процесс полета снаряда, производили расчет траектории его движения. В дальнейшем кинематика как научное направление получило широкое распространение и значительное повлияло на развитие технического прогресса.
Направление сформировано несколько позднее, чем статика и динамика: во второй половине XIX столетия. Первые исследования в области кинематики были посвящены огнестрельному оружию. Ученые стремились понять процесс полета снаряда, производили расчет траектории его движения. В дальнейшем кинематика как научное направление получило широкое распространение и значительное повлияло на развитие технического прогресса.
Кинематика – описание
Кинематика является разделом механики, цель которого – изучение механического движения тел с пренебрежением к вызывающим это движение.
Механика представляет собой научную область физики, которой посвящены исследования механического движения тел. Основной целью данного направления является определение точного положения тела в любой момент времени. Важным понятием этого раздела является материальная точка в виде материала с массой и размерами, которые можно пренебречь для решения задачи при наличии следующих условий:
Движение тела рассматривают в системе отсчета, состоящей из системы координат и прибора, измеряющего время. Траекторией называют линию, данный объект, совершая движение. Путь является скалярной величиной, определяемой как длина траектории. Перемещением обозначают вектор, который соединяет начальное и конечное положение тела.
Совершая движение, может только увеличивать пройденный путь, при этом увеличивается или уменьшается. К примеру, уменьшение перемещения наблюдается во время обратного движения тела. Если объект движется в одном направлении, то путь модулем прямое перемещение. В случае криволинейного движения – путь перемещения. При рассмотрении замкнутой траектории перемещение будет равно нулю.
youtube.com/embed/eZy2wp5XINY”/>
Теория и формулы
Благодаря многолетним исследованиям в области кинематики ученым удалось вывести закономерности движения тела.С помощью справедливых решений можно ответить на многие вопросы о разных характеристиках, которые остаются постоянными во время движения объектов.
Путь, время, скорость
Расстояние представляет собой удаленность одной точки положения тела от другого. Тело преодолевает путь. Общепринятым обозначением пути является латинская буква s. Данный параметр измеряют метрами и километрами, если речь идет о больших расстояниях.
Скорость представляет собой путь, который проходит через течение в течение единицы времени. В качестве единицы времени используют 1 час, 1 минуту, 1 секунду. Для расчета скорости необходимо определить отношение пути к времени движения. В случае, когда в условиях измеряется расстояние в метрах, а время пути – в секундах, то скорость следует в метрах в секунду (м / с). Для обозначения скорости использовать латинскую букву \ (v \).
Для обозначения скорости использовать латинскую букву \ (v \).
Нередко требуется определить время пути.Данный параметр обозначают с помощью латинской буквы \ (t \).
Важно отметить, что скорость, путь и время взаимосвязаны. При характеристиках скорости и времени можно определить расстояние, проходящее через тело. Путь в данном случае равенство скорости и времени, рассчитывается по формуле:
\ (s = v \ раз t \)
При известных величинах времени и расстоянии просто определить скорость движения тела, руководствуясь следующим уравнением:
\ (v = \ frac {s} {t} \)
Равномерное движение
Равномерным движением представляет движение тела, которое совершает перемещение в любых промежутках времени.
Источник: goodfon.ruСкорость при равномерном движении, в котором движение было совершено. Уравнение имеет следующий вид:
\ (\ vec {v} = \ frac {\ vec {s}} {t} \)
\ (\ vec {v} = const \)
Проекция вектора скорости на ось ОХ выглядит таким образом:
\ (v_ {x} = \ frac {s_ {x}} {t} \)
\ (v_ {x} = const \)
Если вектор скорости спроецировать на ось координат, то она будет равна быстроте данной координаты:
\ (v_ {x} = \ frac {x-x_ {0}} {t} \)
Прямолинейное равноускоренное движение
Прямолинейным равноускоренным движением называют движение по прямой траектории, для которого характерно постоянное ускорение.
Ускорение для прямолинейного равноускоренного движения обозначают следующим образом:
\ (\ vec {a} = const \)
При таком движении можно наблюдать увеличение или уменьшение скорости. Чтобы определить скорость, выполнить следующий расчет:
\ (\ vec {v} = \ vec {v} _ {0} + \ vec {a} t \)
Если тело разгоняется в проекции оси ОХ, то скорость можно определить по формуле:
\ (v_ {x} = v_ {0x} + a_ {x} t \)
a> 0, движение является равноускоренным.
Источник: fizi4ka.ruВо время торможения в проекции на ось ОХ скорость следующим образом:
\ (v_ {x} = v_ {0x} -a_ {x} t \)
а <0, движение является равнозамедленным.
Источник: fizi4ka.ruГрафически зависимость ускорения от времени, то есть график ускорения во время равноускоренного движения тела, можно представить в виде:
Источник: fizi4ka.ruГрафик ускорения, характеризующий равноускоренное движение тела, представляет собой прямую, параллельна оси времени:
Графически скорость или проекция скорости изображается в виде зависимости скорости от времени:
Источник: fizi4ka.ruГрафически скорость, характерная для равноускоренного движения тела, имеет вид. График 1 направлен вверх, тело будет совершать равноускоренное движение в положительном направлении оси ОХ:
\ (v_ {0x}> 0 \)
\ (a_x> 0 \)
\ (a_ {1x} = tg α \)
График 2 направлен вниз, тело будет двигаться равнозамедленно в положительном направлении оси ОХ:
\ (v_ {0x}> 0 \)
\ (a_x <0 \)
\ (a_ {2x} = tg α \)
График 3 направлен вниз, тело свершает равноускоренное движение против оси ОХ:
\ (v_ {0x} <0 \)
\ (a_x <0 \)
Исходя из графика зависимости скорости от времени, перемещение через границу тела в течение промежутка времени \ (t_2-t_1 \).{2}} {- 2g} \)
В верхней точке тела, брошенное вверх, будет обладать нулевой скоростью, \ (v = 0 \). Для расчета времени подъема можно использовать формулой:
Для расчета времени подъема можно использовать формулой:
\ (t = \ frac {v_ {0}} {g} \)
Свободно падающее тело
Свободным падением называют движение тела в условиях безвоздушного пространства под силой тяжести.
В условиях свободного падения ускорения тел с разной массой будут равны. Данный параметр называют ускорением свободного падения.Оно всегда направлено к центру нашей планеты, то есть вертикально вниз. Величина обозначается латинской буквой g, а единицами измерения являются м / с 2 .
Ускорение свободного падения равно 9,8 м / с 2 . В задаче по физике использовать значение g = 10 м / с 2 .
Движение по окружности с постоянной по модулю скоростью
Движением по окружности при постоянной по модулю скорости называют простейшим видом криволинейного движения.
Траектория такого движения будет представлена в виде окружности.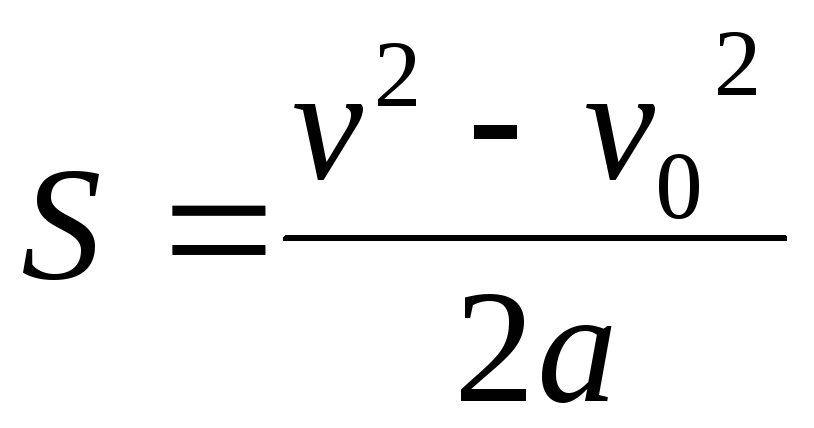 Вектор скорости тела приобретает направление по касательной к окружности. Модуль скорости тела при изменении времени остается постоянным, а направление движения в каждой точке изменяется. Из этого можно сделать вывод, что движение по окружности представляет собой движение с ускорением. В свою очередь ускорение, изменяющее направление скорости, носит название центростремительного.
Вектор скорости тела приобретает направление по касательной к окружности. Модуль скорости тела при изменении времени остается постоянным, а направление движения в каждой точке изменяется. Из этого можно сделать вывод, что движение по окружности представляет собой движение с ускорением. В свою очередь ускорение, изменяющее направление скорости, носит название центростремительного.
Центростремительное ускорение направлено по радиусу окружности к ее центру.{2}} {R} \)
Движение тела по окружности при постоянной по модулю скорости называют период движением. Таким образом, его координата будет повторяться через одинаковые периоды времени. Периодом называют время, в течение которого тело совершает один полный оборот. Обозначается величина как Т. Единицами измерения периода являются секунды, с. Для расчета справедливо равенство:
\ (T = \ frac {t} {N} \)
\ (N \) является первым оборотов, \ (t \) – временем, которое является совершает обороты.{-1} \) (Гц).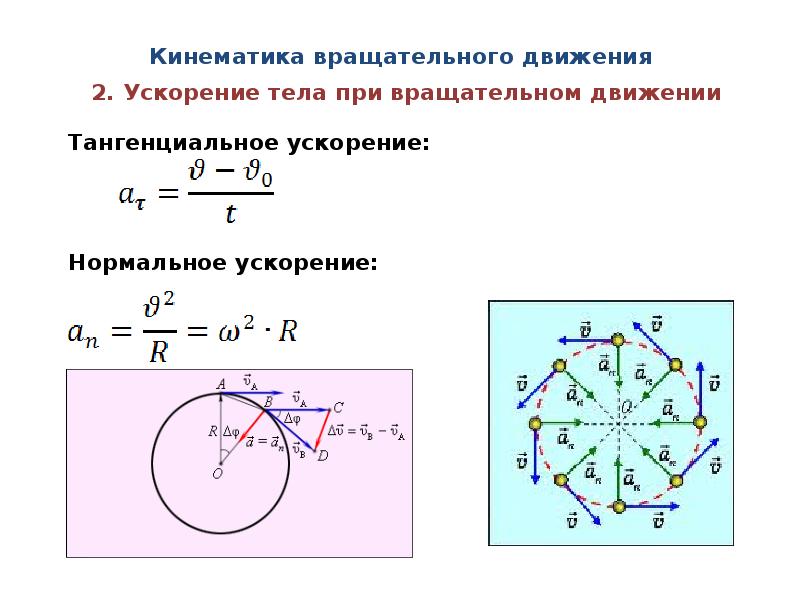
\ (\ nu = \ frac {N} {t} \)
Период и частота частоты взаимно обратными величинами:
\ (T = \ frac {1} {\ nu} \)
\ (\ nu = \ frac {1} {T} \)
Линейная скорость представляет собой скорость движения тела по окружности. Параметр обозначают латинской буквой v, единицами измерения являются м / с. Линейная скорость направлена по касательной к окружности и рассчитывается по формуле:
\ (v = \ frac {2 \ pi \ times R} {T} \)
\ (R \) является радиусом окружности.
Угловой скоростью называют физическое совершение, которое определяется как отношение угла поворота и времени. Обозначают параметр как ω. Единицами измерения угловой скорости являются рад / с. Угловая скорость определяет по формуле:
\ (\ omega = \ frac {\ varphi} {t} \)
\ (\ varphi \) представляет собой угол поворота.
Источник: fizi4ka.ru Направление угловой скорости определяет с помощью правил правого винта или буравчика. {2} Р \)
{2} Р \)
\ (\ omega = \ frac {2 \ pi} {T} \)
\ (\ omega = 2 \ pi v \)
Во время равномерного движения тела по окружности точки, расположенные на радиусе, перемещается с равной угловой скоростью, так как движение за одно и то же время поворачивается на одинаковый угол. В это время линейная скорость разных точек радиуса отличается в зависимости от того, насколько близко или далеко от центра они размещены:
\ (v_ {1} = \ omega r \)
\ (v_ {2} = \ omega R \)
\ (\ frac {v_ {1}} {v_ {2}} = \ frac {r} {R} \)
Источник: fizi4ka.ruПри рассмотрении равномерного движения двух соединенных тел можно наблюдать отсутствие отличий в линейных скоростях, но при этом угловые скорости тел будут различны в зависимости от радиуса тела:
\ (\ omega _ {1} = \ frac {v} {R_ {1}} \)
\ (\ omega _ {2} = \ frac {v} {R_ {2}} \)
\ (\ frac {\ omega _ {1}} {\ omega _ {2}} = \ frac {R_ {1}} {R_ {2}} \)
Источник: fizi4ka. {2} \ sin 2 \ alpha} {g} \)
{2} \ sin 2 \ alpha} {g} \)Движение тела, брошенного горизонтально
Движение тела, которое бросили горизонтально, представлено в виде суперпозиции двух движений:


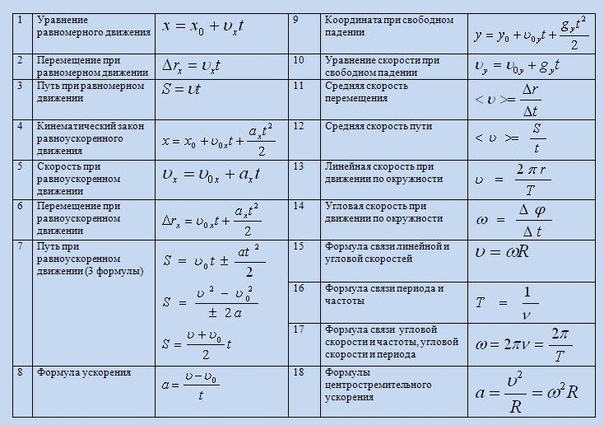 Вращательное движение. Кинематика и динамика
Вращательное движение. Кинематика и динамика {2}}\)
{2}}\)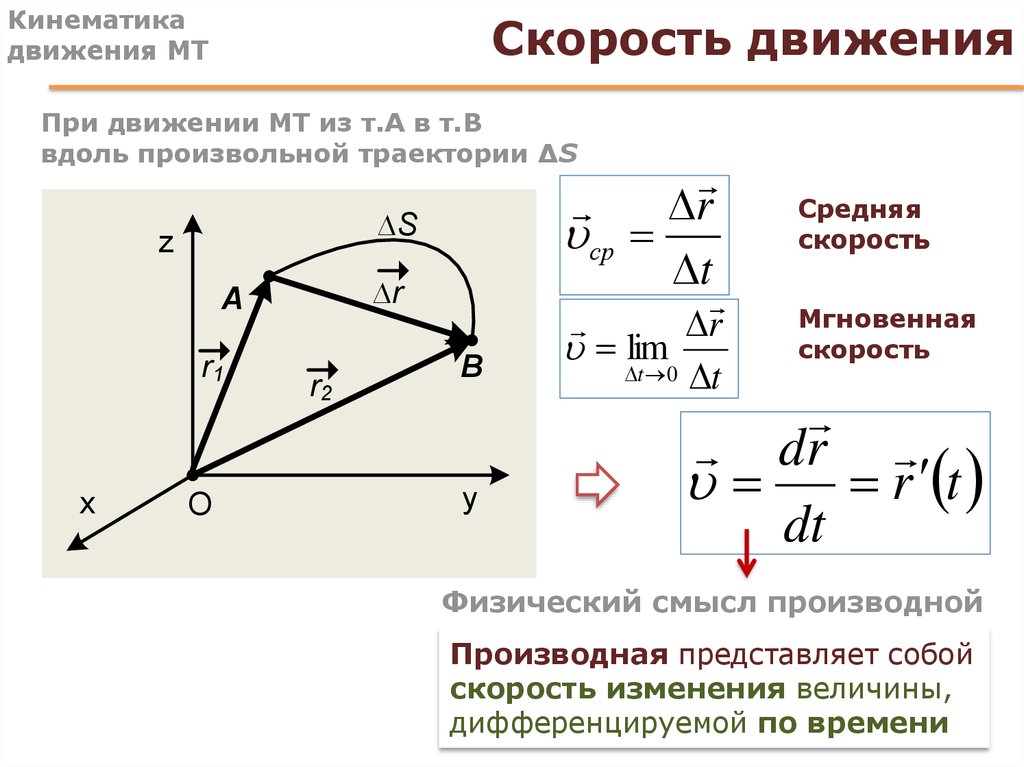 {2}}=\frac{9,81}{0,17}=57,7\)
{2}}=\frac{9,81}{0,17}=57,7\)
 1.6 Равноускоренное прямолинейное движение -это движение, при котором тело движется вдоль прямой линии, а его скорость за любые равные промежутки времени меняется на одно и ту же величину:
1.6 Равноускоренное прямолинейное движение -это движение, при котором тело движется вдоль прямой линии, а его скорость за любые равные промежутки времени меняется на одно и ту же величину: Движение
Движение 2)/2.
2)/2. 2*sin2α)/g
2*sin2α)/g




 В точке А траектории показаны три вектора: АВ, АС и АД. Какой из этих векторов является направлением скорости, а какой ускорения?
В точке А траектории показаны три вектора: АВ, АС и АД. Какой из этих векторов является направлением скорости, а какой ускорения? 0.5 м/с(2) В. 1 м/с(2)
0.5 м/с(2) В. 1 м/с(2)






 {2}} = \ frac {9,81} {0,17} = 57,7 \)
{2}} = \ frac {9,81} {0,17} = 57,7 \) 2} {2} \ to 0 = h-2v_0t ‘\ to t’ = \ frac {h} {2v_0} \ left (2.7 \ right). \]
2} {2} \ to 0 = h-2v_0t ‘\ to t’ = \ frac {h} {2v_0} \ left (2.7 \ right). \]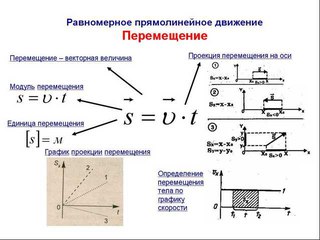
 1.4 Ускорение материальной точки (м / c 2 ) – скорость физической величины, характеризующая быстроту изменения скорости материальной точки:
1.4 Ускорение материальной точки (м / c 2 ) – скорость физической величины, характеризующая быстроту изменения скорости материальной точки: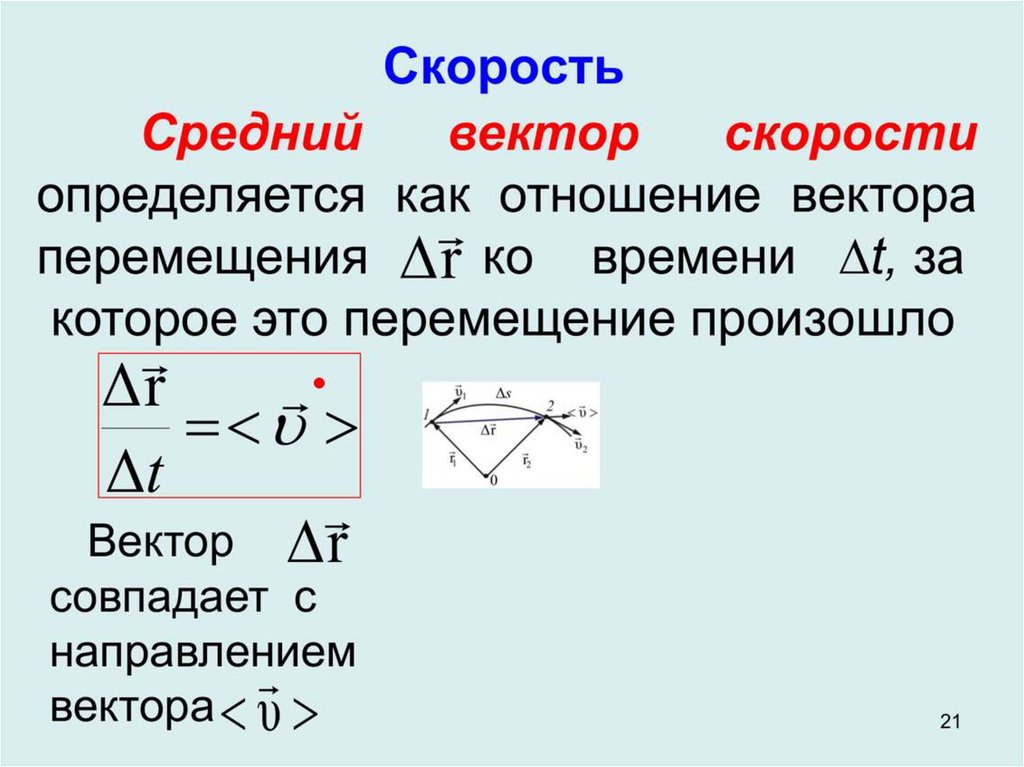 1.8 Движение точки по окружности.
1.8 Движение точки по окружности.
 2) / 2.
2) / 2. 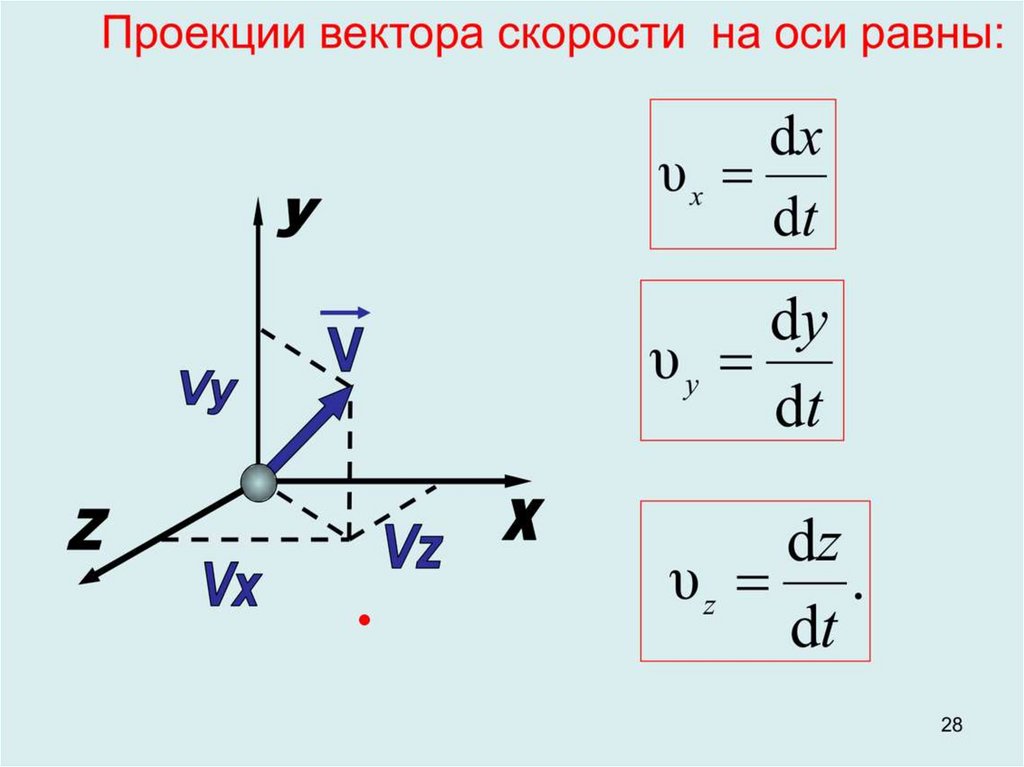 2) / 2
2) / 2 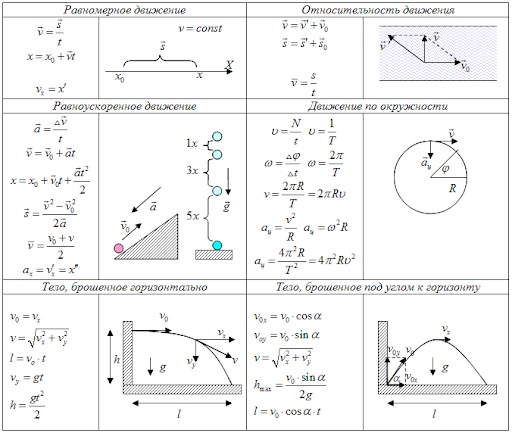

 Статика – раздел механики, в котором изучаются условия равновесия абсолютно твердый тел. Законы сохранения энергии и энергии происходят следствиями заката Ньютонов.
Статика – раздел механики, в котором изучаются условия равновесия абсолютно твердый тел. Законы сохранения энергии и энергии происходят следствиями заката Ньютонов. Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении разных точек любой планеты, вызванные ее суточным вращением, не влияют на величины, описывающие годовое движение.Но при решении задач, связанных с суточным вращением планет (например, при определении времени восхода в разных местах поверхности земного шара), считать планету материальной точки нельзя, так как результат зависит от размеров этой планеты и скорости движения точек её поверхности.
Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении разных точек любой планеты, вызванные ее суточным вращением, не влияют на величины, описывающие годовое движение.Но при решении задач, связанных с суточным вращением планет (например, при определении времени восхода в разных местах поверхности земного шара), считать планету материальной точки нельзя, так как результат зависит от размеров этой планеты и скорости движения точек её поверхности. Мы уже знаем, что движение любого тела относительно. Поэтому, изучая движение тела, мы обязательно указываем, относительно какого тела это движение. Тело, относительно которого рассматривается движение, называется телом отсчета. Чтобы рассчитать положение материальной точки относительно выбранной точки отсчета, надо связать с ним систему координат и измерить время.Совокупность тела отсчета часов, используемая с ним системы координат и называется системой отсчета.
Мы уже знаем, что движение любого тела относительно. Поэтому, изучая движение тела, мы обязательно указываем, относительно какого тела это движение. Тело, относительно которого рассматривается движение, называется телом отсчета. Чтобы рассчитать положение материальной точки относительно выбранной точки отсчета, надо связать с ним систему координат и измерить время.Совокупность тела отсчета часов, используемая с ним системы координат и называется системой отсчета. Закон (или уравнение) движения в векторной форме – зависимость радиуса-вектора от времени:
Закон (или уравнение) движения в векторной форме – зависимость радиуса-вектора от времени: Путь – скалярная величина.
Путь – скалярная величина.