Кинематика формулы динамика формулы: Основные формулы кинематики

Классическая механика | Открытые видеолекции учебных курсов МГУ

Курс классической механики для студентов 4-го курса отделения математики механико-математического факультета МГУ имени М.В.Ломоносова. Читается в 7-ом семестре.

Список всех тем лекций

Лекция 1. Введение в курс, кинематика точки и начала кинематики твердого тела.
Предисловие к курсу Рекомендуемые учебники О предмете курса Объекты механики Три раздела механики Кинематика точки Движение точки по окружности Движение точки по кривой Кинематика твердого тела Теорема Шаля о конечных движениях твердого тела Мгновенная угловая скорость твердого тела

Лекция 2. Мгновенная угловая скорость твердого тела, формулы Эйлера и Ривальса, мгновенно-винтовое и поступательное движение.
Мгновенная угловая скорость твердого тела (повторение и продолжение) Формула Эйлера о распределении скоростей в твердом теле Пример: угловая скорость твёрдого тела, вращающегося вокруг неподвижной оси Формула Ривальса о распределении ускорений в твердом теле Мгновенная ось винта Плоско-параллельное движение твердого тела

Лекция 3. Относительное движение, углы Эйлера.
Плоско-параллельное движение твердого тела (повторение и продолжение) Относительное движение (сложное движение) Теорема о сложении скоростей Теорема о сложении ускорений Сложение угловых скоростей Углы Эйлера

Лекция 4. Ориентация твердого тела с неподвижной точкой в пространстве, углы Эйлера.
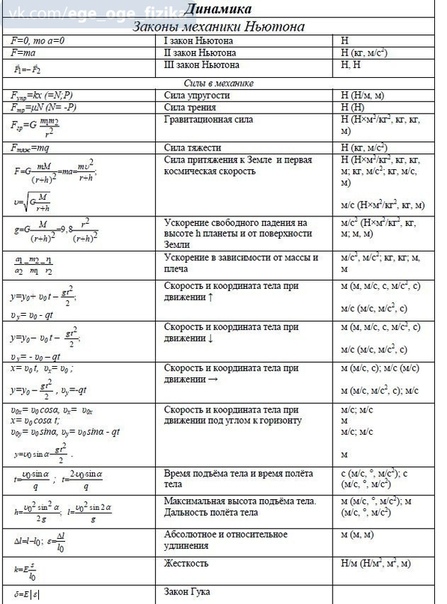
Углы Эйлера в подвижной системе координат Кинематические формулы Эйлера Проекции угловой скорости Основные формулы Кинематики Ньютонова механика Принцип суперпозиции сил Принцип относительности Внутренние и внешние силы Динамика материальной точки в инерциальной системе координат (анонс следующей темы)

Лекция 5. Динамика материальной точки в инерциальной системе координат.

Динамика материальной точки в инерциальной системе координат Импульс (количество движения) Момент импульса Кинетическая энергия точки Основные законы динамики точки I закон-теорема об изменении импульса II закон-теорема об изменении кинетического момента III закон-теорема об изменении кинетической энергии Движение точки по прямой под действием силы, зависящей только от положения точки Закон сохранения энергии Интегрирование уравнений движения Область возможности движения Формула для периода колебания Фазовый портрет гармонического осциллятора Положение равновесия Линеаризация уравнений движения в окрестности состояния равновесия

Лекция 6.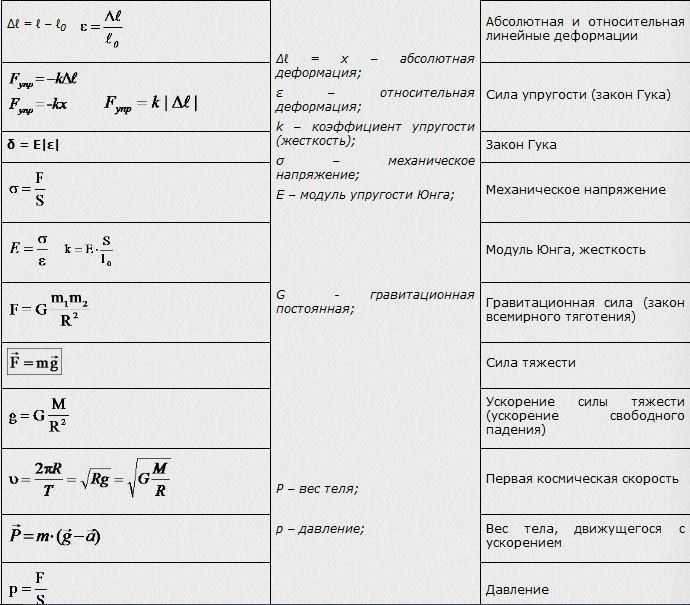 Динамика материальной точки в инерциальной системе координат (продолжение).

Уравнение движения точки по прямой Асимптотика периода колебаний в окрестности невырожденного устойчивого равновесия Лемма Адамара Лемма Морса Фазовые портреты в нелинейных случаях Фазовый портрет в окрестности невырожденного положения равновесия Понятие о фазовом портрете в общем случае Фазовый портрет математического маятника Учение о связях

Лекция 7. Связи в механике.

Виды связи Связи в дифференциальной форме общего вида Пример: конек Чаплыгина Понятие стационарной связи Виртуальные перемещения Число степеней свободы Элементарная работа реакции связей на элементарном перемещении Понятие идеальных связей Принцип Даламбера-Лагранжа

Лекция 8.

Виртуальные перемещения.
Принцип Даламбера-Лагранжа Лемма о множителях Лагранжа Свободное твёрдое тело Частные случаи перемещения твёрдого тела Внутренние силы Основные теоремы динамики для систем с идеальными связями Теорема об изменении импульса Теорема об изменении кинетического момента

Лекция 9. Общие теоремы динамики в относительном движении.

Теорема об изменении кинетического момента Теорема об изменении кинетической энергии системы Оси Кёнига Формулы Кёнига Теорема об изменении кинетического момента Теорема об изменении кинетической энергии Динамика и статика свободного твёрдого тела Момент инерции твёрдого тела относительно оси

Лекция 10.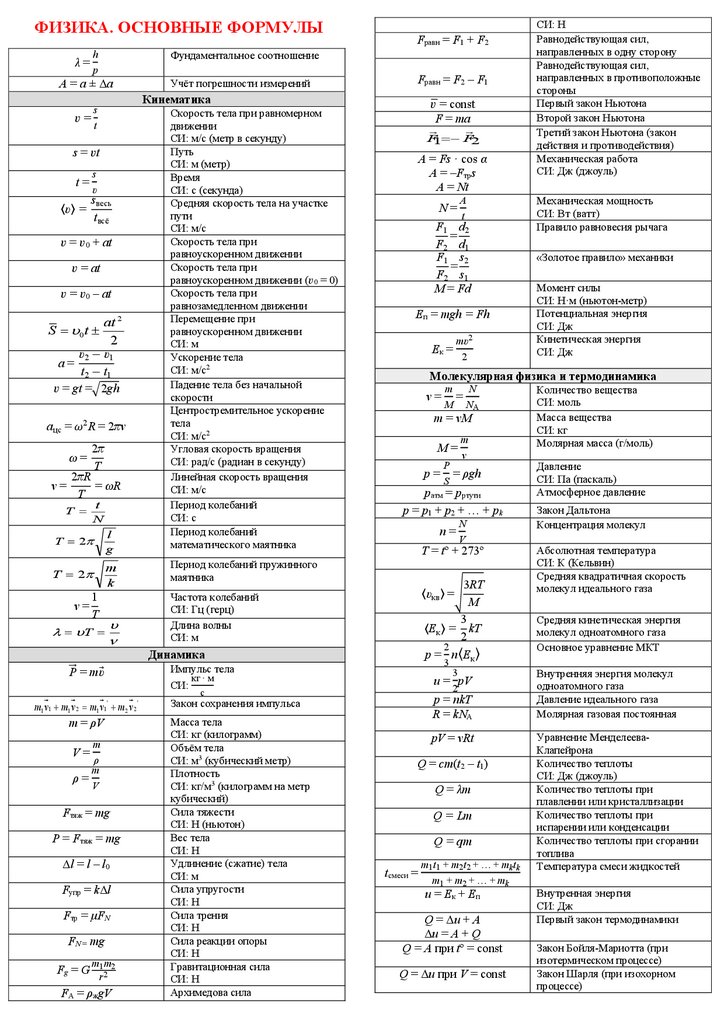

Динамика и статика свободного твёрдого тела.
Момент инерции твёрдого тела относительно оси Теорема Гюйгенса-Штейнера Вычисление кинетического момента и кинетической энергии в общем случае Матрица в координатной записи Свойства тензора инерции Главные оси инерции Уравнение движения свободного твёрдого тела Эквивалентность систем сил Условия равновесия Пример (тело в однородном поле тяжести)

Лекция 11. Законы Кеплера.
Понятие небесной механики Центральные силы Силы, зависящие только от расстояния до центра Закон сохранения энергии Интегрирование уравнения движения Законы Кеплера закон (Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце) закон (Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, заметает собой равные площади) закон (Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей орбит планет) Вывод формулы для гравитационной силы Задача Кеплера

Лекция 12. Задача Кеплера.
Задача Кеплера Интеграл Лапласа Классификация орбит Задача двух тел Задача n тел Устойчивость по Якоби

Лекция 13. Динамика относительного движения.
Теорема о необходимой устойчивости по Якоби Динамика относительного движения Теорема об изменении кинетической энергии точки относительно движения Переносные силы инерции Закон сохранения энергии Равномерно вращающаяся система координат Задача трёх тел

Лекция 14. Движение материальной точки около поверхности Земли.
Задача трёх тел Относительное равновесие (точки либрации) случай (у равен 0) случай (у не равен 0) Движение материальной точки около поверхности Земли Угловая скорость Уравнение движение материальной точки около поверхности Земли

Лекция 15. Маятник Фуко.
Движение материальной точки около поверхности Земли Маятник Фуко Задача (гармонический осциллятор на плоскости) Линеаризованное уравнение движения маятника

Лекция 16. Маятник Фуко. Окончание.
Маятник Фуко Уравнения в координатной форме Гармонический осциллятор на плоскости

Тесты по физике по теме “Динамика” онлайн

1. Онлайн тесты
2. Физика
3. Динамика

• Формулы динамика, статика, законы сохранения

  29. 12.2018 5268 0

  Тест предназначен для проверки базовых формул по динамике 10-11 класс. Подойдет как для подготовки к ЕГЭ, так и для систематического курса физики. Создан не по кодификатору, но с оглядкой на него.

• Зачетная работа по теме “Динамика”

  29.09.2014 12071 0

  Данный тест предназначен для проведения зачета по теме “Кинематика” для учащихся 10 класса, изучающих физику на базовом уровне

• 1.2.1 Инерциальные системы отсчета. Первый закон Ньютона. Принцип относительности Галилея. Задание 2.

  06.09.2015 2062 0

  Тест предназначен для проверки базовых знаний и умений по динамике полной школы при подготовке к ЕГЭ. Коды по кодификатору 2016 года: 1.2.1

• Основы динамики

  02.02.2020 4909 0

  Тест по динамике имеет 10 заданий с выбором правильного ответа. Применяется в 9 классе посмсле прохождения темы “Динамика”. Можно применять и при подготовке к ГИА по физике.

• 1.2.5 Третий закон Ньютона для материальных точек.

  07.09.2015 1821 0

  Тест предназначен для проверки базовых знаний и умений по динамике полной школы при подготовке к ЕГЭ. Коды по кодификатору 2020 года: 1.2.5.

• Простые задачи по физике (динамика)

  09. 06.2020 54 0

  Простейшие задачи по физике раздела “Динамика” с использованием трёх законов Ньютона и закона всемирного тяготения.

• Тест для проверки знаний по теме “Динамика”

  09.07.2018 1254 0

  Тест составлен в соответствии со структурой ЕГЭ по физике. Предназначен для проверки знаний по теме “Динамика”

• Сила. Второй закон Ньютона

  01.11.2019 2340 0

  В данном тесте проверяются знания второго закона Ньютона. Правило нахождения равнодействующей силы. Особенности второго закона Ньютона. Вычисление кинематических величин при использовании второго закона Ньютона

• Законы Ньютона

  31.05.2022 1052 0

  Тест предназначен для проверки базовых знаний и умений по динамике. В данном тесте проверяются знания законов Ньютона. 

• 1.2.3 Сила. Принцип суперпозиции сил.

  07.09.2015 235 0

  Тест предназначен для проверки базовых знаний и умений по динамике полной школы при подготовке к ЕГЭ. Коды по кодификатору 2016-2019  года: 1.2.3

• 1.

  2.4 Второй закон Ньютона: для материальной точки в ИСО.

  07.09.2015 412 0

  Тест предназначен для проверки базовых знаний и умений по динамике полной школы при подготовке к ЕГЭ. Коды по кодификатору 2019 года: 1.2.4

• 1.2.6 Закон всемирного тяготения. Сила тяжести. 1.2.7 Движение небесных тел и их искусственных спутников. Первая космическая скорость.Вторая космическая скорость

  07.09.2015 5370

  Тест предназначен для проверки базовых знаний и умений по динамике полной школы при подготовке к ЕГЭ. Код по кодификатору 2016-2019 гг: 1.2.6.-1.2.7

• Физика.

  11 класс. Тема 2.2. Динамика колебательного движения.

  17.11.2015 1198

  Среди предлагаемых утверждений могут верные и неверные. Неверные утверждения построены так, что они содержат фактические ошибки, нарушают логические связи между элементами теории, искажающие суть физических законов и закономерностей. Высказывание считается ошибочным, если в нем содержится неполная формулировка. Если в утверждении по умолчанию подразумеваются случаи, когда физический закон или теория неприменимы, оно тоже не может быть признано верным. Как правило, неверное утверждение содержит одну ошибку, неверными могут быть одно-два слова, возможно, ошибочные слова нужно поменять местами.

• Выходная диагностика по динамике

  15.12.2019 9 0

  Тест проверяет знания трех законов Ньютона. Применение законов Ньтона в стандартных ситуациях. 

• Формулы динамики

  07.06.2020 33 0

  Вспоминаем основные формулы физики для решения задач на тему “Динамика”

• Задачи по динамике

  11.06.2020 20 0

  Типичные задания по динамике для подготовки к экзамену достаточного уровня.

• физика тест Динамика материальной точки

  04.05.2022 181 0

  Контрольная работа ” Динамика материальной точки” состоит из 4 задач по следующим темам: 2 закон Ньютона, криволинейное движение, закон всемирного тяготения, закон сохранения импульса.  

Кинематика и динамика

Кинематика и динамика

Если объект вращается вокруг фиксированной оси Z с постоянным угловым ускорение α, имеем Δω = αΔt,

ω _f = ω _i + α(t _f – t _i ).

Угловое смещение θ относительно оси z определяется как

θ _f = θ _i + ω _i (t _f – t _i ) +  ½α(t _ф -т _и ) ² .

Эти уравнения имеют тот же вид, что и уравнения линейного движения с постоянным ускорением a.
Для движения по оси абсцисс имеем

v _f = v _i + a(t _f – t _i ),
x _f – x _i = v _xi ∆t + ½a _x (t _f – т _и ) ² .

Если мы заменим x на θ и a на α, то кинематическая уравнения линейного движения вдоль оси x преобразуются в кинематические уравнения для вращательного движения вокруг оси z.

С нашими определениями углового положения, скорости и ускорения мы имеем кинематические уравнения для вращательных движений, которые имеют тот же вид, что и кинематические уравнения поступательного движения. И те же уравнения имеют те же растворы. Решаем их точно так же. Но решения описывают различные физические ситуации. Например, в то время как θ _f может принимать любое значение, значение, которое не лежит между 0 и 2π радиан, просто говорит нам о том, что объект совершил более одного оборота.

Проблема:

Авиалайнер прибывает в терминал, двигатели выключены выключенный. Ротор одного из двигателей имеет начальный поворот по часовой стрелке угловая скорость 2000 рад/с. Вращение двигателей замедляется с угловое ускорение величиной 80 рад/с ² .
(a) Определите угловую скорость через 10 с.
(b) Сколько времени требуется ротору, чтобы остановиться?

Решение:

• Рассуждение:
  В этой задаче начальная угловая скорость ω _i и угловое ускорение α . Если выбираем направление начального углового ускорения быть направлением z, тогда
  ω _f = ω _i – α(t _f – t _i ),
  , так как α находится в отрицательном направлении z.
• Детали расчетов
  (а) При t = 0 ω _i = 2000/с.
  При t = 10 с имеем ω _f  = 2000/с – (80/с ² )(10 с) = 1200/с.
  (b) Настройка ω _f = ω _i – α(t _f – t _i ) = 0 мы можем найти время, за которое ротор придет отдыхать.
  2000/с – (80/с ² )t = 0, t = (2000/80) с = 25 с — это время, необходимое ротору для остановки.

Проблема:

Вращающемуся колесу требуется 3 с, чтобы сделать 37 оборотов. Его угловатый скорость в конце 3-секундного интервала равна 98 рад/с. Что постоянное угловое ускорение колеса?

Решение:

• Обоснование:
  Дано: Δθ = θ _f – θ _i = 37 оборотов, Δt = 3 с, ω _f = 98 рад/с.
  С использованием θ _f – θ _i = ω _i (t _f – t _i ) + ½α(t _f – t _i ) ² и ω _f = ω _i + α(t _f – t _i ), у нас есть два уравнения, которые мы можем решить для двух неизвестных, ω _i и α.
• Детали расчета:
  Использование θ _f = θ _i + ω _i (t _f – t _i ) + ½α(t _f – t _i ) ² с θ _i = 0, имеем 37*2π = ω _i *(3 с) + ½α(3 с) ² .
  Использование ω _f = ω _i + α(t _f – t _i ) имеем 98/с = ω _i + α(3 с).
  Решим это уравнение для ω _i  ω _i = 98 с – α(3 с), и вставить его в первое уравнение.
  37*2π = (98/с)(3 с) – α(3 с) ² + ½α(3 с) ² , 74π = 294 – α*(9 с ² ) ^{+ α*(4,5 с 2 ),
  (4,5 с 2 )*α = 294 – 74π, α = 13,67/с 2 постоянный ускорение колеса.}

---

Когда колесо вращается вокруг оси Z, каждая точка колеса имеет одинаковый угол скорость. Однако линейная скорость v точки P зависит от ее расстояния от оси вращения.
Когда точка P проходит угловое смещение 2π, тогда его пройденный путь равен 2πr.
Когда точка P проходит угловое смещение π, то пройденное им расстояние равно πr.
Когда точка P проходит угловое смещение θ, то его пройденный путь равен θr.
По угловой скорости ω скорость v точки P поэтому v = ωr, если r постоянно; v — тангенциальная скорость точки P.

Внешняя ссылка: Тангенциальная и угловая скорость (Youtube)

тангенциальное ускорение a точки P, движущейся по круговой траектории, дано в с точки зрения его углового ускорения на _t = rα.
радиальное или центростремительное ускорение равно _r = v ² /р = рω ² .
Общее ускорение равно
a = (a _t ² + a _r ² ) ^½ = (r ² α ² + r ² ω ⁴ ) ^½ = r(α ² + ω ⁴ 1 ) 32093 .

Проблема:

Если колеса автомобиля заменить на колеса большего диаметра, показания спидометра изменились? Объяснять!

Решение:

• Обоснование:
  Датчик спидометра определяет угловую скорость колеса. Используя v _ном. = r _ном. ω, спидометр отображает правильную скорость, если шины имеют номинальный радиус. Если вы положите шины вашего автомобиля больше, чем ваша фактическая скорость v _{фактическая} = r _{фактическая} ω больше отображаемой скорости v _{номинально} = r _{номинально} ω.

Проблема:

Автомобиль равномерно ускоряется из состояния покоя и достигает скорости 22 м/с в 9 с. Если диаметр шины 58 см, найдите
(а) число оборотов, которое шина делает во время этого движения, при условии, что нет проскальзывание и
(b) конечная скорость вращения шины в оборотах в секунду.

Решение:

• Обоснование:
  Задано равномерное ускорение автомобиля a = Δv/Δt. Мы можем использовать кинематические уравнения для линейного движения, чтобы найти расстояние, которое он проходит в интервал времени Δt.
  Разделив это расстояние на длину окружности шины, находим число сделанной революции. Конечная угловая скорость определяется как ω _f = v _f /r _шина .
• Детали расчета:
  (a) Ускорение автомобиля равно a = Δv/Δt = (22 м/с)/(9 с) = 2,44 м/с ² .
  Расстояние d = ½at ² = (½*2,44*81) м = 99 м.
  Окружность шины равна π*0,58 м = 1,82 м.
  Число оборотов, совершаемых колесом, равно 99/1,82 = 54,3.
  (b) Конечная линейная скорость шины v = 22 м/с. Используя v = ωr, ω = v/r, конечная угловая скорость составляет ω = 75,9/с. Число оборотов в секунду ω/2π = 12/с.

---

Встроенный вопрос 1

Кинематические уравнения движения с постоянным линейным ускорением и движение с постоянным угловым ускорением имеют такой же вид. Сравнивать движение с постоянной скоростью с движением с постоянной угловой скоростью.

Обсудите это со своими сокурсниками на форуме!

---

Что вызывает угловое ускорение?

Предположим, вы хотите изменить вращающийся угловая скорость колеса. Для увеличения угловой скорости вероятно, приложит силу к ободу, касательную к ободу, и в направление мгновенной скорости сечения обода на которым вы прикладываете силу.

Если вы хотите уменьшить угловую скорость, вы измените направление направление силы.

Предположим, вы хотите войти в здание с вращающейся дверью. В двери четыре панели, и вы толкаете на одном из них, перпендикулярно поверхности панели.
Скорость, при которой угловая скорость двери изменения, то есть угловое ускорение α , тем больше, чем дальше от оси вращения вы применяете сила.

Угловое ускорение относительно точки является результатом крутящего момента вокруг этой точки. А крутящий момент – продукт рычага плечо и сила, приложенная перпендикулярно плечу рычага. рычаг или моментный рычаг — расстояние по перпендикуляру от центра вращения, т. е. от точка поворота, точка приложения силы.

Крутящий момент всегда определяется относительно точки вращения.

Чем больше крутящий момент, тем больше угловое ускорение. Вы можете получить больший крутящий момент, приложив большее усилие или используя более длинный рычаг. Пишем

крутящий момент = плечо рычага × усилие,
τ = r × F .

Крутящий момент является вектором. это векторный продукт или перекрестное произведение из R и F . Единицами крутящего момента в СИ являются Нм.
Крутящий момент имеет величину и направление. Его направление задается правило правой руки .

Пусть пальцы правой руки указывают от оси вращение до точки приложения силы. Сверните их в направление F . Ваш большой палец указывает в направлении вектор крутящего момента.

Величина крутящего момента τ τ = rFsinθ, где θ – наименьший угол между направлениями векторов р и Ф .
Мы также можем написать τ = r _perp F = rF _perp , где r _perp — компонент плечо рычага перпендикулярно F, или где F _perp — это составляющая F, перпендикулярная плечу рычага.

Если сила F действует на объект, то крутящий момент, создаваемый этой силой относительно a точка поворота τ = r × F , где р — вектор смещения от точки поворота до точки, где применяется сила. Если на тело действуют две или более сил, то суммарный крутящий момент равен векторная сумма крутящие моменты, создаваемые отдельными силами. (Для вращения вокруг одной оси два крутящих момента могут быть направлены в одном направлении или в противоположных направлений и поэтому может складывать или вычитать. )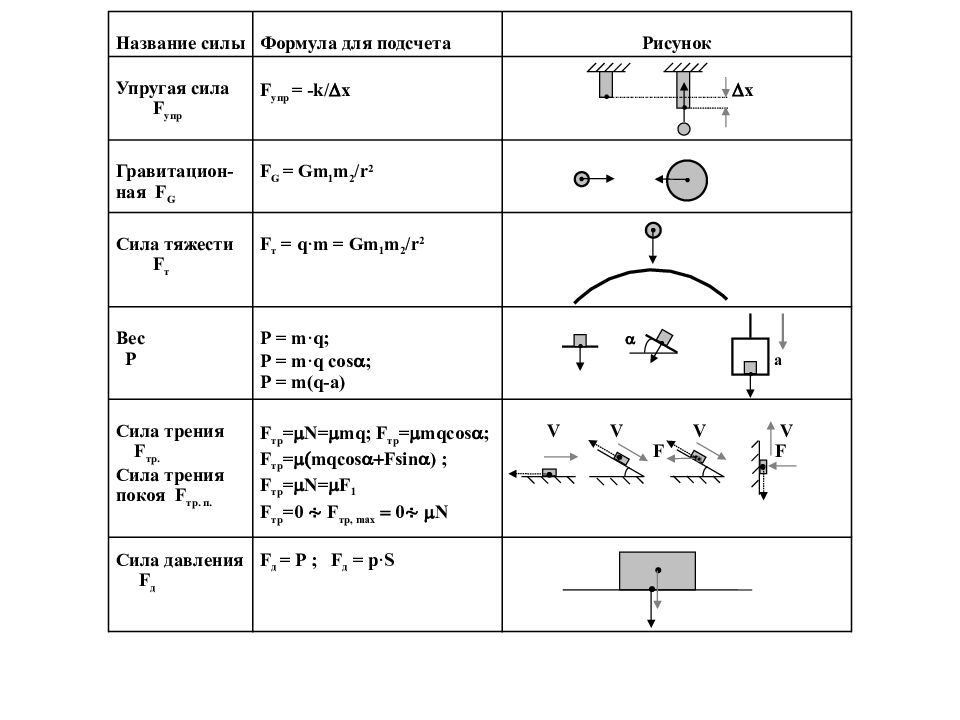

---

Итог

Вращения – самый сложный предмет курса для большинства студентов. Векторная природа величин, описывающих вращение, противоречит здравому смыслу. изначально, но математика вращения – это векторное перекрестное произведение.

Вращение определяется вокруг оси. Чтобы начать вращать объект вокруг ось, т.е. чтобы придать ей угловое ускорение, нужна сила. Но не любой старый сила сделает. Это зависит от того, где вы толкаете или тянете, и в какой направление.

Предположим, вы хотите запустить вращение колеса. Пусть красные стрелки укажите направление силы, которую вы прикладываете. Какая стрела совершит это? Нельзя давить прямо на ось, это не сработает. Ты нужен рычаг. Вы также не можете толкать к оси, даже если у вас есть плечо рычага. Сила должна иметь тангенциальную составляющую. Все это входит в понятие крутящего момента.

крутящий момент = плечо рычага × усилие,
τ = r × F .

Здесь r — плечо рычага, направленное от оси вращения к точка приложения силы, F — это сила. nПерекрестное произведение говорит, что они не могут быть выровнены, поскольку величина крутящего момента равна τ = rFsinθ, где θ — наименьший угол между направлениями векторов r и F . Перекрестное произведение — это математический способ выражения того, что необходимо для получить угловое ускорение.

---

Проблема:

На рисунке справа найдите сеть крутящий момент на колесе относительно оси, проходящей через центр, если a = 10 см и b = 25 см.

Решение:

• Обоснование:
  Пусть ось Z выходит из страницы. Используйте τ = rFsinθ для величины и правило правой руки для направления т .
• Детали расчета:
  Тогда крутящий момент, создаваемый силой 10 Н, равен τ = -(10 Н * 0,25 м) к = -(2,5 Нм) к .
  Крутящий момент, создаваемый силой 9 Н, равен τ = -(9 Н * 0,25 м) к = -(2,25 Нм) к .
  Крутящий момент, создаваемый силой 12 Н, равен τ = (12 Н * 0,1 м) к = (1,2 Нм) к .
  (Обратите внимание, что эта сила также применяется перпендикулярно плечу рычага.)
  Общий крутящий момент составляет τ = -(3,55 Нм) к .

---

Второй закон Ньютона, когда применительно к вращательному движению утверждает, что крутящий момент равен произведение массы вращения или момент инерции I и угловое ускорение α .

крутящий момент = момент инерции × угловое ускорение
τ = I α

Момент инерции является мерой инерции вращения объекта. Это зависит от массы объекта и от того, как эта масса распределена относительно оси вращение. Чем дальше основная часть массы от оси вращения, тем больше инерция вращения (момент инерции) объекта. Момент инерции зависит от массы, и как она распределенный. это не зависит от того, какую силу или крутящий момент вы прикладываете. Если вы прикладываете больший крутящий момент к твердому объекту, вы получаете большее угловое ускорение, но момент инерции не меняется.

Момент инерции системы относительно оси вращения можно найти, умножив массу m _на каждого частицы в системе на квадрат ее перпендикулярного расстояния r _я от оси вращения, и суммируя все эти произведения, I = ∑m _i r _i ² .

 

Проблема:

Четыре частицы на рисунке справа соединены жесткими стержнями. Начало находится в центре прямоугольника. Вычислите момент инерции системы относительно оси z.

Решение:

• Обоснование:
  Момент инерции I = ∑m _и р _я ² . Здесь r _i — перпендикулярное расстояние частицы i от ось Z.
• Детали расчета:
  Каждая частица – это расстояние r = (9 + 4) ^½ м = (13) ^½ м от ось вращения.
  I = (3 кг + 2 кг + 4 кг + 2 кг)*13 м ² = 143 кг м ² .

Момент инерции объекта является мерой его сопротивления угловому ускорению. Из-за его инерции вам нужен крутящий момент, чтобы изменить угловую скорость. объект. Если на объект не действует чистый крутящий момент, его угловая скорость не изменится. Если он изначально не крутится, то и не начнет крутиться. Если он вращается с заданным угловая скорость, эта угловая скорость не изменится. Как его угловая скорость, так и ориентация его оси вращения останется прежней.

постоянная угловая скорость <--> без угловой ускорение <--> нет полезного крутящего момента

Когда на два объекта воздействует одинаковый крутящий момент, объект с большим моментом инерции имеет меньший угловой ускорение. Единицы момента инерции единицы массы, умноженной на квадрат расстояния, например, кгм ² .

Представьте себе два колеса одинаковой массы. Одно сплошное колесо с его масса равномерно распределена по всей конструкции, а другая имеет большая часть массы сосредоточена у края.

Колесо с массой у обода имеет больший момент инерция.

Момент инерции определяется относительно оси вращения.

Например, момент инерции круглого диска, вращающегося вокруг оси через его центр перпендикулярно плоскости диска отличается от момент инерции диска, вращающегося вокруг оси через центр в плоскости диска.

Внешняя ссылка: Список моментов инерции

---

Качели

Двое детей играют на качелях, раскачиваются взад-вперед. Центр качели зафиксированы. Поступательного движения нет. Мы наблюдаем вращение движение относительно центра. При движении качелей практически нет крутящий момент на качелях, и они вращаются с равномерной угловой скоростью. Вес каждого ребенка, умноженное на плечо рычага от центра до места, где сидит ребенок создает крутящий момент, но два крутящих момента имеют одинаковую величину и точку в противоположных направлениях и, следовательно, отменить. Если один ребенок тяжелее, он сидит ближе к центру, чем более светлый ребенок. Это уменьшает плечо рычага. В таким образом, разные веса могут создавать крутящие моменты одинаковой величины.

Когда ступни одного ребенка касаются пола, пол отталкивается и производит крутящий момент направлен противоположно угловой скорости. Этот крутящий момент уменьшит угловой скорости до нуля за короткий промежуток времени. Качели теперь остановлены. Затем ребенок отталкивается, а земля отталкивается назад. Направление крутящий момент остается прежним. Крутящий момент создает угловое ускорение, в результате чего с угловой скоростью, противоположной первоначальному направлению. качели достигает своей конечной угловой скорости, когда ребенок прекращает тужиться. Теперь он держит при вращении с постоянной угловой скоростью до тех пор, пока ноги другого ребенка не коснутся этаж.

Все, что вам нужно знать — Shemmassian Academic Consulting

17 февраля 2021 г. 17 февраля 2021 г. / Викрам Шоу, М.С. (начальник службы репетиторства)

Изучите основные понятия MCAT о кинематике, а также практические вопросы и ответы

(Примечание. Это руководство является частью серии MCAT Physics . )

Часть 1. Введение в кинематику

Часть 2. Перемещение, скорость и ускорение

ускорение  

Часть 4. Движение снаряда с постоянным ускорением

Часть 5. Круговое движение

Часть 6. Наклонные плоскости Часть 9 9 80232

Часть 8: Уравнения кинематики и высокодоходные термины

Часть 9: Практика Kinematics. наука о том, как движутся объекты, и это часто первый модуль в вводном классе физики, потому что это такая повседневная тема. Любой ученик, который когда-либо бросал что-то в воздух, будет иметь хоть какое-то представление о кинематике!

В MCAT кинематика – это малоэффективная тема, и вам нужно ознакомиться с ней только в биологическом контексте. Тем не менее, кинематика — это тема физики, наиболее часто используемая в повседневной жизни. Понимание этого может быть важным первым шагом в понимании более сложных тем в физике.

В приведенном ниже руководстве наиболее важные термины выделены жирным шрифтом. Увидев его, попробуйте определить его своими словами и использовать для создания собственных примеров.  Это отличный способ проверить, как вы понимаете и формулируете термины  таким образом, который имеет для вас наибольший смысл  и сделает обучение намного проще (и намного эффективнее!) в долгосрочной перспективе.

В конце этого руководства есть практический отрывок в стиле MCAT и отдельные вопросы, которые не только проверят ваши знания о силе, энергии и работе, но и покажут вам, как AAMC любит задавать вопросы.

Часть 2. Перемещение, скорость и ускорение 

Перемещение, скорость, ускорение и время являются основными переменными в кинематике. Большинство вопросов дадут вам информацию о некоторой комбинации этих переменных и попросят вас решить другую. Для этого вы будете использовать уравнения и определения, связанные с каждым из них.

а) Определение терминов

Сначала давайте определим каждый термин, начиная со смещения. Перемещение — это изменение положения, определяемое как:

$$\Дельта х=х-х_0$$ $$\mbox{где} \Delta x \mbox{ = смещение,}$$ $$x \mbox{ = конечная позиция,}$$ $$x_0 \mbox{ = начальная позиция}$$

Смещение измеряет, насколько далеко что-то перемещается и в каком направлении. Обычно дается в стандартных единицах метров (м). Перемещение часто путают с расстоянием, но это , а не  то же самое. Смещение должно иметь как расстояние , так и направление. Например, «5 метров на восток» — это смещение, а «5 метров» — нет.

Другой способ думать об этом состоит в том, что смещение касается только разницы между начальной и конечной точками. Итак, если вы возвращаетесь домой после поездки по пересеченной местности, пройденное вами расстояние может составлять тысячи миль, но ваше смещение будет равно нулю, потому что вы закончили в том же месте, где и начали.

Скорость — это изменение положения за изменение времени, выраженное как:

$$v =\frac{\Delta x}{\Delta t}$$ $$\mbox{где } v \mbox{ = скорость,}$$ $$\Delta x=x_2-x_1\mbox{ = смещение,}$$ $$\Delta t=t_2-t_1\mbox{ = изменение во времени}$$

Скорость показывает, насколько быстро и в каком направлении изменяется позиция. Его стандартная единица измерения – метры в секунду (м/с). Подобно смещению и расстоянию, скорость часто отождествляют со скоростью . Опять же, разница в том, что скорость должна указывать направление.

Скорость, рассчитанная с использованием приведенного выше уравнения, обычно представляет собой среднюю скорость , или вычисленное среднее значение всех скоростей за определенный период времени. Период времени может быть таким коротким, как секунды или миллисекунды.

Напротив, мгновенная скорость относится к скорости, измеренной в один момент времени. Мгновенная скорость не может быть измерена и должна быть рассчитана с использованием производных и интегралов. Поскольку исчисление не проверяется на MCAT, мгновенная скорость выходит за рамки экзамена. Тем не менее, средняя скорость по-прежнему является справедливой игрой, и вас могут попросить рассчитать скорость, используя таблицу значений.

Наконец, ускорение — это изменение скорости во времени, которое записывается как:

$$a =\frac{\Delta v}{\Delta t}$$ $$\mbox{где } a \mbox{ = ускорение,}$$ $$\Delta v=v_2-v_1\mbox{ = изменение скорости,}$$ $$\Delta t=t_2-t_1\mbox{ = изменение во времени}$$

Как и два предыдущих термина, ускорение измеряет величину изменения, а также его направление. Стандартной единицей измерения является метр на секунду в квадрате (м/с²).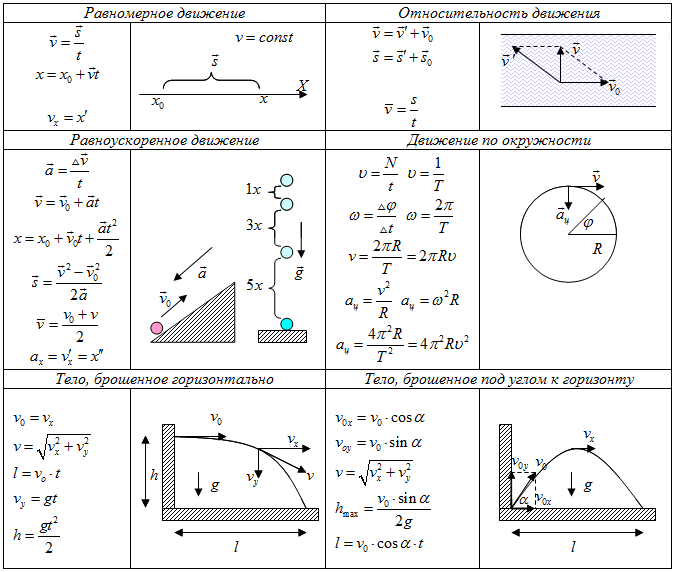 Примечание: даже если скорость объекта остается той же величины, может иметь место ускорение, если объект меняет направление.

Вы могли заметить, как много мы подчеркивали направление в каждом из этих определений. Мы включили направление, потому что смещение, скорость, ускорение — все это векторы , что означает, что они имеют величину и направление. У каждого должно быть и то, и другое! Хороший способ думать о векторах — представлять их в виде стрелок. Стрелка должна иметь некоторую длину и указывать в каком-то направлении (иначе это не стрелка!)

Рисунок 1. Добавление вектора

Векторы также можно комбинировать. Например, последовательные смещения в одном и том же направлении приведут к большему смещению, а смещения в противоположных направлениях будут уравновешены (как показано в правой части рисунка 1).

b) Определение условных обозначений

Большинство задач кинематики существуют в одном или двух измерениях. Обычно наиболее удобно использовать вертикальную ось Y и горизонтальную ось X для определения направления. Соглашение определяет вверх и вправо как положительные, а вниз и влево – как отрицательные.

Итак, если кто-то проходит 10 метров вправо, мы говорим Δx=+10 м. Точно так же, если кто-то проходит 10 метров влево за 10 секунд, v = -1 м/с.

c) Графическая интерпретация

Умение интерпретировать графики зависимости перемещения, скорости и ускорения от времени является важным навыком в начальной физике. В дополнение к базовым навыкам интерпретации графиков, есть пара отношений, специфичных для кинематических графиков.

Сначала рассмотрим наклон графика зависимости смещения от времени. Уклон определяется как подъем по отношению к пробегу или изменение вертикальной оси относительно изменения горизонтальной оси.

Рис. 2. Наклон графика зависимости смещения от времени

В этом случае наклон равен Δx/Δt. Возможно, вы тоже узнаете это уравнение — это определение скорости! Оказывается, наклон графика зависимости смещения от времени — это скорость, а наклон графика зависимости скорости от времени — ускорение.

Далее рассмотрим график зависимости скорости от времени только с постоянной скоростью. Какова площадь под этой линией?

Рисунок 3 . Площадь под кривой зависимости скорости от времени

Фигура представляет собой прямоугольник, поэтому его площадь определяется как ширина, умноженная на высоту. В этом случае ширина — это изменение во времени, а высота — постоянная скорость. Преобразование приведенного выше уравнения скорости говорит нам, что эта площадь должна равняться смещению! Другими словами, площадь под кривой на графике зависимости скорости от времени представляет собой смещение, а площадь под кривой на графике зависимости ускорения от времени представляет собой изменение скорости.