Главная
Кинематика формулы по физике 9 класс: Ошибка: 404 Материал не найден

Кинематика формулы по физике 9 класс: Ошибка: 404 Материал не найден

Содержание

Физика 9 класс

  • Главная
  • Справочник
  • Физика
  • Книги, лекции и конспекты по физике
  • Физика 9 класс

Физика 9 класс

  • Введение в кинематику

  • Введение в динамику

  • Введение в квантовую физику

  • Введение в оптику

  • 12-а. Что такое кинематика

    Введение в кинематику Формулы Физика Теория 9 класс

  • 12-б. Относительность движения

    Введение в кинематику Формулы Физика Теория 9 класс

  • 12-в. Путь и перемещение тела

    Введение в кинематику Формулы Физика Теория 9 класс

  • 12-г. Сложение и вычитание векторов

    Введение в кинематику Формулы Физика Теория 9 класс

  • 12-д. Две скорости равномерного движения

    Введение в кинематику Формулы Физика Теория 9 класс

  • 12-е. Проекции векторов на координатные оси

    Введение в кинематику Формулы Физика Теория 9 класс

  • 12-ж. Равномерное движение по прямой

    Введение в кинематику Формулы Физика Теория 9 класс

  • 12-з. Мгновенная скорость и ее изменение

    Введение в кинематику Формулы Физика Теория 9 класс

  • 12-и. Мгновенное ускорение и его постоянство

    Введение в кинематику Формулы Физика Теория 9 класс

  • 12-й. Движение с постоянным ускорением

    Введение в кинематику Формулы Физика Теория 9 класс

  • 12-к. Графическое описание движений

    Введение в кинематику Формулы Физика Теория 9 класс

  • 12-л. Равномерное движение по окружности

    Введение в кинематику Формулы Физика Теория 9 класс

  • 13-а. Что такое динамика

    Введение в динамику Формулы Физика Теория 9 класс

  • 13-б. Первый закон Ньютона

    Введение в динамику Формулы Физика Теория 9 класс

  • 13-в. Второй закон Ньютона

    Введение в динамику Формулы Физика Теория 9 класс

  • 13-г. Третий закон Ньютона

    Введение в динамику Формулы Физика Теория 9 класс

  • 13-д. Закон всемирного тяготения

    Введение в динамику Формулы Физика Теория 9 класс

  • 13-е. Вес и невесомость

    Введение в динамику Формулы Физика Теория 9 класс

  • 13-ж. Закон Гука

    Введение в динамику Формулы Физика Теория 9 класс

  • 13-з. Закон Амонтона-Кулона

    Введение в динамику Формулы Физика Теория 9 класс

  • 13-и. Закон сохранения импульса

    Введение в динамику Формулы Физика Теория 9 класс

  • 13-й. Реактивное движение

    Введение в динамику Формулы Физика Теория 9 класс

  • 13-к. Кинетическая энергия

    Введение в динамику Формулы Физика Теория 9 класс

  • 13-л. Потенциальная энергия

    Введение в динамику Формулы Физика Теория 9 класс

  • 13-м. Механическая энергия

    Введение в динамику Формулы Физика Теория 9 класс

  • 14-а. Что такое оптика

    Введение в оптику Формулы Физика Теория 9 класс

  • 14-б. Прямолинейное распространение света

    Введение в оптику Формулы Физика Теория 9 класс

  • 14-в. Отражение света

    Введение в оптику Формулы Физика Теория 9 класс

  • 14-г. Плоские и сферические зеркала

    Введение в оптику Формулы Физика Теория 9 класс

  • 14-д. Преломление света

    Введение в оптику Формулы Физика Теория 9 класс

  • 14-е. Собирающие и рассеивающие линзы

    Введение в оптику Формулы Физика Теория 9 класс

  • 14-ж. Формула тонкой линзы

    Введение в оптику Формулы Физика Теория 9 класс

  • 14-з. Оптические приборы

    Введение в оптику Формулы Физика Теория 9 класс

  • 14-и. Дисперсия света и цвета тел

    Введение в оптику Формулы Физика Теория 9 класс

  • 14-й. Спектры и спектральный анализ

    Введение в оптику Формулы Физика Теория 9 класс

  • 15-а. Из истории квантовой физики

    Введение в квантовую физику Формулы Физика Теория 9 класс

  • 15-б. Радиоактивность и сложное строение атомов

    Введение в квантовую физику Формулы Физика Теория 9 класс

  • 15-в. Строение атома и атомного ядра

    Введение в квантовую физику Формулы Физика Теория 9 класс

  • 15-г. Ядерные реакции

    Введение в квантовую физику Формулы Физика Теория 9 класс

  • 15-д. Энергия ядерных реакций

    Введение в квантовую физику Формулы Физика Теория 9 класс

  • 15-е. Методы изучения субатомных частиц

    Введение в квантовую физику Формулы Физика Теория 9 класс

  • 15-ж. Закон радиоактивного распада

    Введение в квантовую физику Формулы Физика Теория 9 класс

  • 15-з. Влияние радиации на живые организмы

    Введение в квантовую физику Формулы Физика Теория 9 класс

  • 15-и. Ядерная энергетика

    Введение в квантовую физику Формулы Физика Теория 9 класс

Формулы физика 9 – Справочник

Формулы физика 9

Физика 9 класс. Все формулы и определения

«Физика 9 класс. Все формулы и определения» — это Справочник по физике в 9 классе, доступный для скачивания в 2-х форматах: КРУПНО (формат PDF, на 7-ми страницах) и МЕЛКО (формат JPG, на 2-х страницах). Смотрите также справочные материалы по физике за другие классы:

Физика 9 Все формулы КРУПНО

Физика 9. Все формулы МЕЛКО. Стр 1

Физика 9. Все формулы МЕЛКО. Стр 2

В пособии «Физика 9 класс. Все формулы и определения» представлено 45 формул :

Физика 9 класс. Все формулы и определения в разделе «КИНЕМАТИКА»

I. Равномерное прямолинейное движение

1. Скорость
2. Проекция скорости на координатную ось
3. Перемещение
4. Проекция перемещения на координатную ось

II. Равноускоренное прямолинейное движение

5. Средняя скорость при неравномерном прямолинейном движении
6. Ускорение
7. Скорость
8. Перемещение
9. Координата тела
10. Ускорение свободного падения

III. Равномерное движение по окружности

11. Угловая скорость
12. Частота обращения
13. Период обращения
14. Линейная скорость
15. Центростремительное ускорение

Физика 9 класс. Все формулы и определения в разделе «ДИНАМИКА»

IV Законы Ньютона

16. Первый закон Ньютона
17. Второй закон Ньютона
18. Третий закон Ньютона

V Силы в природе

19. Закон Гука
20. Закон всемирного тяготения
21. Гравитационная постоянная
22. Сила тяжести
23. Ускорение свободного падения
24. Вес покоящихся и движущихся тел.

VI. Движение тела под действием силы тяжести

25. Движение тела под углом к горизонту.
26. Горизонтально брошенное тело.
27. Скорость искусственного спутника Земли.

VII. Силы трения

28. Трение покоя.
29. Трение скольжения.
30. Коэффициент трения.
31. Движение тела под действием силы трения.

VIII. Движение тела под действием нескольких сил

32. Условие равновесия тела (как материальной точки)
33. Движение тела по наклонной плоскости.
34. Движение связанных тел через неподвижный блок.

IX. Законы сохранения в механике

36. Импульс тела
37. Импульс силы
38. Закон сохранения импульса
39. Механическая работа силы
40. Теорема о кинетической энергии
41. Потенциальная энергия поднятого тела
42. Работа силы тяжести
43. Потенциальная энергия деформированного тела
44. Закон сохранения полной механической энергии

X. Движение жидкостей и газов по трубам

45. Закон Бернулли

Дополнительные материалы

Девять самых необходимых (самых востребованных) формул по физике в 9 классе.

Таблицы физических величин

Вы смотрели «Физика 9 класс. Все формулы». Смотрите также справочные материалы по физике за другие классы:

«Физика 9 класс. Все формулы и определения» — это Справочник по физике в 9 классе, доступный для скачивания в 2-х форматах: КРУПНО (формат PDF, на 7-ми страницах) и МЕЛКО (формат JPG, на 2-х страницах). Смотрите также справочные материалы по физике за другие классы:

Физика 9 Все формулы КРУПНО.

Uchitel. pro

20.05.2017 16:37:35

2017-05-20 16:37:35

Источники:

Https://uchitel. pro/%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0-9-%D0%BA%D0%BB%D0%B0%D1%81%D1%81-%D0%B2%D1%81%D0%B5-%D1%84%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D1%8B/

Основни формули във физиката за 9 клас. Всичко, което трябва да знаете! » /> » /> .keyword { color: red; }

Формулы физика 9

Физиката е строга техническа наука. Понякога не всички успяват да завършат тази дисциплина през учебните години. Нещо повече, не всеки ученик има логично и техническо мислене и всеки е принуден да преподава физика в училище. Учебните формули може да не се вписват в главата. В тази статия ще разгледаме основните формули във физиката за клас 9 в механиката.

Механика

Струва си да се започне с най-основните и прости закони във физиката. Както е известно, такава обширна тема като механиката се състои от три части:

Статика. Dynamics. Кинематика.

Кинематиката се изучава в 10 клас, така че няма да го разглеждаме в тази статия.

Статика

Трябва да се изследва последователно, като се започне с прости статични формули. А именно, с формулите на натиск, момента на инерцията на телата на революцията и момента на силата. Формули за физика клас 9 с обяснения ще бъдат ясно представени по-долу.

Налягането е мярка за сила, действаща върху повърхността на тялото, измерена в паскали. Налягането се изчислява чрез отношението на силата към областта, така че формулата ще изглежда възможно най-проста:

Моментът на инерция на телата на оборота е мярка за инерция по време на въртеливо движение тела около себе си, или, строго погледнато, продуктът на телесна маса по радиуса му на квадрат.

Съответстваща формула:

Моментът на сила (или, както мнозина го наричат, въртящ момент) е силата, приложена към твърдо тяло и създаваща въртене. Това е така векторно количество който може също да има отрицателен знак, измерен в метри, умножен по Нютон. В каноничното представяне, формулата предполага произведението на силата, приложена към тялото и разстоянието (силата на рамото), формулата:

Динамика

По динамике — наш следующий этап. Формули за физика 7-9 клас с обяснения за динамиката — следващият ни етап. Всъщност това е най-голямата и най-значима част от механиката. Всички тела са обект на движение, дори и да са в покой, някои сили действат върху тях, предизвиквайки движение. Важни понятия, които трябва да бъдат изследвани преди разбирането на динамиката — пътя, скоростта, ускорението и масата.

Първото нещо, разбира се, е да изучаваме законите на Нютон.

Първият закон на Нютон е определение без формули. Той казва, че тялото или е в покой, или се движи, но само след като всички сили, концентрирани върху него, са балансирани.

Вторият и най-известен закон на Нютон е ускорението на тялото в зависимост от приложената към него сила. Формулата включва също масата на обекта, към който се прилага силата.

Моля, обърнете внимание, че горната формула е написана в скаларна форма — силата и ускорението във вектора могат да имат отрицателен знак, това трябва да се вземе под внимание.

Третият закон на Нютон: силата на действие е равна на силата на съпротивата. Всичко, което трябва да бъде известно от този закон, е, че всяка сила има противопоставяне на една и съща сила, насочена само в обратната посока, като по този начин се наблюдава равновесието на нашата планета.

Сега разгледайте другите сили, действащи в рамките на динамиката, и това на силата на гравитацията, еластичност, триене и сила на триене при търкаляне. Всички те са базирани на вектор и могат да бъдат изпращани във всяка посока, а също и като цяло могат да формират системи: събират и изваждат, умножават или споделят. Ако силите не са насочени успоредно един на друг, тогава изчислението ще трябва да използва косинуса на ъгъла между тях.

Формулите на физиката на 9-ти клас включват в своята програма и закона на световната ширина и космическите скорости, които всеки ученик трябва да знае.

Законът на света е закон, който вече ни е известен Исак Нютон в класическата му теория. Всъщност се оказа революционно: законът гласи, че всяко тяло, разположено в гравитационното поле на Земята, е привлечено от ядрото му. И това е вярно.

Космически скорости

Първата космическа скорост е необходима, за да влезе в орбита на Земята (числено равна на 7.9 km / s), а втората космическа скорост е необходима, за да се преодолее гравитационното привличане, да излезе извън орбитата, но също така и да позволи на обекта да се движи по кръгова пътека. Той е равен съответно на 11,2 km / s. Важно е, че и двете космически скорости са преодолени от човечеството и благодарение на тях днес са възможни полети в космоса. Формулите за физика в 9 клас не предполагат трета и четвърта космически скорости, но те също съществуват.

Заключение

В тази статия бяха разгледани основните формули за физика в 9 клас. Проучването им дава възможност на ученика да научи по-сложно раздели на физиката, електричество, магнетизъм, звук или молекулярна теория. Без да познаваме механиката, не е възможно да разберем останалата част от физиката, механиката е фундаментална част от тази наука днес. Формули по физика за 9 клас са също необходими за полагане на държавния изпит по НГЕ по физика, а всеки 9-ти клас, постъпил в техническия колеж, трябва да знае обобщението и писмеността си. Запомни ги не е трудно.

Физиката е строга техническа наука. Понякога не всички успяват да завършат тази дисциплина през учебните години. Нещо повече, не всеки ученик има логично и техническо мислене и всеки е принуден да преподава физика в училище. Учебните формули може да не се вписват в главата. В тази статия ще разгледаме основните формули във физиката за клас 9 в механиката.

Струва си да се започне с най-основните и прости закони във физиката. Както е известно, такава обширна тема като механиката се състои от три части:

Статика. Dynamics. Кинематика.

Кинематиката се изучава в 10 клас, така че няма да го разглеждаме в тази статия.

Динамика

Той е равен съответно на 11,2 km s.

Bg. puntomarinero. com

28.07.2019 13:06:15

2019-07-28 13:06:15

Источники:

Https://bg. puntomarinero. com/basic-formulas-in-physics-for/

Физика 9 класс. Законы, правила, формулы | Задачи по физике » /> » /> .keyword { color: red; }

Формулы физика 9

    Силы трения Трение покоя
    Максимальная сила трения покоя (Fтр)max пропорциональна силе нормального давления (N) и зависит от характера взаимодействия соприкасающихся поверхностей тел, определяемого коэффициентом трения (μ)
    (Fтр)max=μ×N
    СИ: Н Трение скольжения
    Сила трения скольжения (Fтр) пропорциональна силе давления (N), коэффициенту трения (μ) и направлена противоположно направлению движения тела. 2/*g>» />, (g — ускорение свободного падения).
    2) Время (t) движения тела под действием силы трения до момента полной остановки (время торможения) прямо пропорционально начальной скорости (v0) и обратно пропорционально коэффициенту трения (μ): *g>» />
    СИ: м, с
    Движение тела под действием нескольких сил Условие равновесия тела (как материальной точки).
    Тело находится в равновесии (в покое или движется равномерно и прямолинейно), если сумма проекций всех сил (, vec. vec» />), действующих на тело, на любую ось (ОХ, ОY, O, …) равна нулю.
    0″ />;
    0″ />;
    0″ />
    СИ: Н Движение тела по наклонной плоскости
    Ускорение тела, скользящего вниз по наклонной плоскости с углом наклона (α) и коэффициентом трения тела о плоскость (μ), не зависит от массы тела и равно: -*cos)» />, (g — ускорение свободного падения)
    СИ: м/с 2 Движение связанных тел через неподвижный блок
    Ускорение двух тел, массами m1 и m2, связанных нитью, перекинутой через неподвижный блок, равно:
    />*g» />, (g — ускорение свободного падения)
    СИ: м/с 2

Давление жидкости, текущей в трубе, больше в тех частях трубы, где скорость её движения меньше, и наоборот, в тех частях, где скорость больше, давление меньше. 2>/2=const» />,
Где p1, v1, h2 — давление, скорость и вертикальная координата жидкости в одном сечении трубы; p2, v2, h3 — давление, скорость и вертикальная координата жидкости в другом сечении трубы;
Ρ — плотность жидкости; g — ускорение свободного падения.
СИ: Па

    Силы трения Трение покоя
    Максимальная сила трения покоя (Fтр)max пропорциональна силе нормального давления (N) и зависит от характера взаимодействия соприкасающихся поверхностей тел, определяемого коэффициентом трения (μ)
    (Fтр)max=μ×N
    СИ: Н Трение скольжения
    Сила трения скольжения (Fтр) пропорциональна силе давления (N), коэффициенту трения (μ) и направлена противоположно направлению движения тела.
    Fтр=μ×N
    СИ: Н Коэффициент трения
    Коэффициент трения (μ) вычисляют как отношение модулей силы трения (Fтр) и силы давления (N).
    Μ=Fтр/N Движение тела под действием силы трения
    1) Путь (l), пройденный движущимся телом под действием силы трения до полной остановки (тормозной путь), прямо пропорционален квадрату начальной скорости (v0) и обратно пропорционален коэффициенту трения (μ): ^2/*g>» />, (g — ускорение свободного падения).
    2) Время (t) движения тела под действием силы трения до момента полной остановки (время торможения) прямо пропорционально начальной скорости (v0) и обратно пропорционально коэффициенту трения (μ): *g>» />
    СИ: м, с
    Движение тела под действием нескольких сил Условие равновесия тела (как материальной точки).
    Тело находится в равновесии (в покое или движется равномерно и прямолинейно), если сумма проекций всех сил (, vec. vec» />), действующих на тело, на любую ось (ОХ, ОY, O, …) равна нулю.
    0″ />;
    0″ />;
    0″ />
    СИ: Н Движение тела по наклонной плоскости
    Ускорение тела, скользящего вниз по наклонной плоскости с углом наклона (α) и коэффициентом трения тела о плоскость (μ), не зависит от массы тела и равно: -*cos)» />, (g — ускорение свободного падения)
    СИ: м/с 2 Движение связанных тел через неподвижный блок
    Ускорение двух тел, массами m1 и m2, связанных нитью, перекинутой через неподвижный блок, равно:
    />*g» />, (g — ускорение свободного падения)
    СИ: м/с 2

Давление жидкости, текущей в трубе, больше в тех частях трубы, где скорость её движения меньше, и наоборот, в тех частях, где скорость больше, давление меньше. 2>/2=const» />,
Где p1, v1, h2 — давление, скорость и вертикальная координата жидкости в одном сечении трубы; p2, v2, h3 — давление, скорость и вертикальная координата жидкости в другом сечении трубы;
Ρ — плотность жидкости; g — ускорение свободного падения.
СИ: Па

Силы трения.

Zadachi-po-fizike. ru

01.03.2017 11:00:41

2017-03-01 11:00:41

Источники:

Https://zadachi-po-fizike. ru/9-klass/

Основные формулы по физике по 9 класс. Все, что нужно знать

Формулы за 9 класс по физике

Физика — строгая техническая наука. Порой не у всех получается успевать в этой дисциплине в школьные годы. Тем более, что не каждый школьник обладает логическим и техническим складом ума, а физику в школе принуждают учить абсолютно каждого. Формулы из учебника могут не укладываться в голове. В данной статье мы рассмотрим основные формулы по физике по 9 класс по механике.

Механика

Начать стоит с самых основных и простейших законов в физике.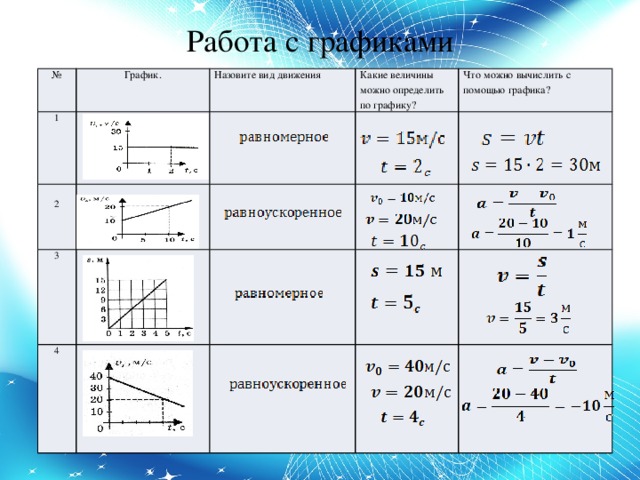 Как известно, такая обширная тема, как механика состоит из трех параграфов:

Статика. Динамика. Кинематика.

Кинематика изучается в 10 классе, поэтому рассматривать ее в рамках данной статьи мы не будем.

Статика

Ее следует изучать последовательно, начиная с простых формул статики. А именно с формул давления, момента инерции тел вращения и момента силы. Формулы по физике 9 класса с пояснениями будут наглядно представлены ниже.

Давление — мера силы, действующая на площадь поверхности тела, измеряется в Паскалях. Давление рассчитывается отношением силы к площади, поэтому формула будет выглядеть максимально просто:

Момент инерции тел вращения — это мера инертности во вращательном движении тела вокруг себя самого, или, строго говоря, произведение массы тела на его радиус, возведенный в квадрат. Соответствующая формула:

Моментом силы (или как многие называют — вращательным моментом) называют силу, приложенную к твердому телу и создающую вращение. Это векторная величина, которая также может иметь отрицательный знак, измеряется в метрах умноженных на Ньютон. В каноничном представлении формула подразумевает собой произведение силы, приложенной к телу и расстояния (плечо силы), формула:

Динамика

Формулы по физике 7-9 класса с пояснениями по динамике — наш следующий этап. Собственно, это самый большой и самый значимый раздел механики. Все тела подвержены движению, даже находясь в состоянии покоя на них действуют некоторые силы, провоцируя на движение. Важные понятия, которые следует изучить перед вниканием в динамику — путь, скорость, ускорение и масса.

Первым делом, конечно же, стоит изучить законы Ньютона.

Первый закон Ньютона — это определение, не имеющее формулы. Он гласит, что тело либо находится в состоянии покоя, либо же движется, но только лишь после того, как все силы, сконцентрированные на нем, будут сбалансированы.

Второй и самый известный закон Ньютона гласит об ускорении тела в зависимости от приложенной к нему силе. В формуле также фигурирует масса объекта, к которому приложена сила.

Обратите внимание, что формула выше записана в скалярном виде — сила и ускорение в векторном могут иметь отрицательный знак, это нужно учитывать.

Третий закон Ньютона: сила действия равна силе противодействия. Все, что нужно знать из этого закона, это то, что каждая сила имеет в противовес такую же силу, только направленную в обратную сторону, таким образом соблюдается баланс на нашей планете.

Теперь же рассмотрим другие силы, действующие в рамках динамики, а это сила тяжести, упругости, трения и сила трения качения. Все они являются векторными и могут быть направлены в любые стороны, также в совокупности способны образовывать системы: складываться и вычитаться, умножаться или делиться. Если силы, направленные не параллельно друг другу, то в вычисления нужно будет использовать косинус угла между ними.

Формулы по физике 9 класса включают в свою программу также закон всемирного тяготения и космические скорости, которые каждый школьник должен знать.

Закон всемирного тяготения — это закон уже небезызвестного нам Исаака Ньютона, фигурирующий в его классической теории. По сути, он оказался революционным: закон утверждает, что любое тело, находящееся в гравитационном поле Земли, притягивается к его ядру. И это действительно так.

Космические скорости

Первая космическая скорость необходима для выхода на орбиту Земли (численно равна 7,9 км/с), а вторая космическая скорость нужна для преодоления гравитационного притяжения, чтобы выйти не только за орбиту, но и позволить объекту двигаться не по круговой траектории. Она равна 11,2 км/с соответственно. Важно, что обе космические скорости были преодолены человечеством, и благодаря им сегодня возможны полеты в космос. Формулы по физике по 9 класс не предполагают третью и четвертую космические скорости, однако они также существуют.

Вывод

В этой статье были рассмотрены основные формулы по физике по 9 класс. Их изучение открывает возможности школьнику познавать более сложные разделы физики, такие как электричество, магнетизм, звук или молекулярную теорию.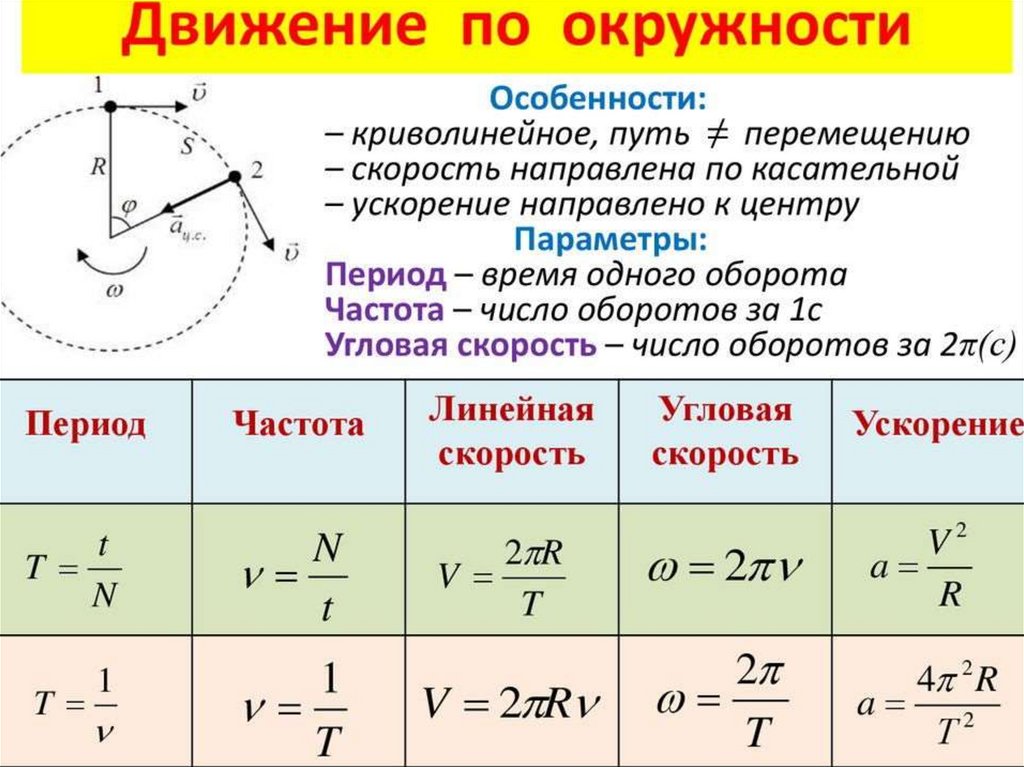 Не зная механику, невозможно понять остальную физику, механика является основополагающей частью этой науки на сегодняшний день. Формулы по физике по 9 класс также необходимы для прохождения государственного экзамена ОГЭ по физике, их краткое содержание и написание обязан знать каждый выпускник 9-го класса, поступающий в технический колледж. Запомнить их не составляет труда.

Все, что нужно знать.

Www. syl. ru

03.03.2017 11:12:02

2017-03-03 11:12:02

Источники:

Https://www. syl. ru/article/391425/osnovnyie-formulyi-po-fizike-po-klass-vse-chto-nujno-znat

Все ⚠️ формулы по физике за 9 класс: определения, пояснения » /> » /> .keyword { color: red; }

Формулы за 9 класс по физике

Программа обучения по предмету физика в 9 классе включает в себя несколько разделов: кинематика и динамика, которые в свою очередь состоят из подразделов. Таким образом ученики старшей школы изучают механические колебания и волны, законы взаимодействия и движения тел, электромагнитные явления, строение атомов и их ядер, основные законы механики. В школьную программу девятого года обучения также входят основные свойства света: интерференция, преломление и дисперсия.

Кинематика

Кинематика — один из разделов механики. Кинематика изучает механическое движение тел и способы его описания, независимо от причин этого движения. В данном случае под механическим движением подразумевается любое изменение положения какого-либо тела полностью или частично относительно других тел, случившееся с течением времени.

В Кинематике изучают простые виды движения.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Равномерное прямолинейное движение

Понятие равномерного прямолинейного движения заключается в том, что тело движется по прямой с одинаковой скоростью, то есть за равные промежутки времени тело перемещается на одинаковое расстояние. В таком случае скорость тела остается постоянной, однако является векторной величиной.

Скорость может быть как положительной, так и отрицательной. Все зависит от того, в каком направлении оси X (положительном или отрицательно) направлен вектор скорости. Если тело находится в покое, то его скорость равняется нулю, а координата не меняется в течение времени.

При равномерном прямолинейном движении координата тела вычисляется по следующей формуле:

В этой формуле x0 – начальная координата, x – конечная координата, v – скорость, t – время.

Если начальная координата — это начало движения и x0 = 0, то формулу можно сократить до x1 = v · t.

Если x0 = 0, то пройденный путь S будет равен координате x. Из этого утверждения можно получить формулу прямолинейного равномерного движения относительно пройденного телом расстояния:

Из этого можно вывести формулы относительно скорости и времени:

Скорость и время также можно выразить из полной формулы для тех случаев, когда x0 не равно 0:

Равноускоренное прямолинейное движение

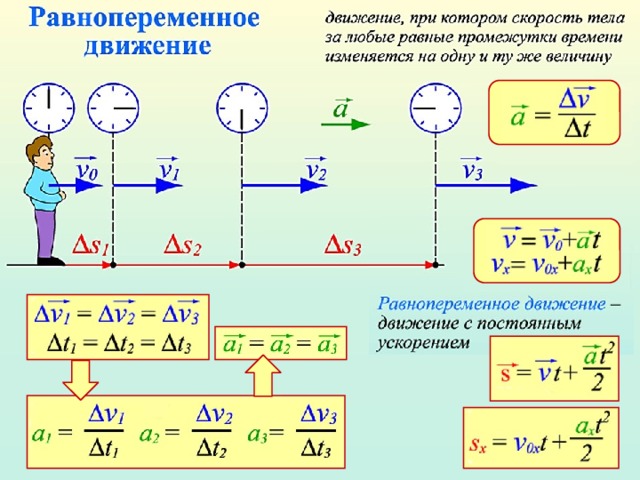
В случае равноускоренного прямолинейного движения тело изменяет скорость своего движения на одинаковую величину за любые равные промежутки времени.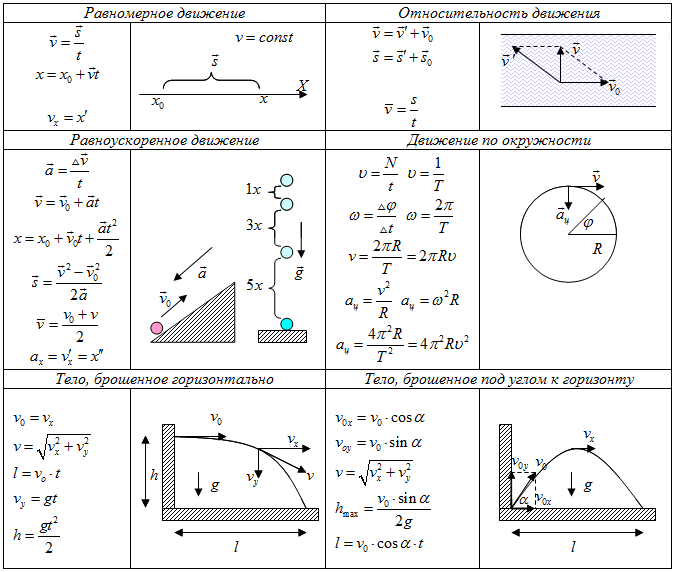 Под ускорением в контексте данного определения понимается изменение значения скорости за единицу времени.

Скорость тела вычисляется по формуле:

В данной формуле v – конечная скорость, v0 – начальная скорость, a – ускорение, t – время.

В равноускоренном прямолинейном движении постоянной величиной является ускорение, а не скорость. Ускорение может быть больше или меньше нуля. В случае увеличения скорость, значение ускорения будет больше нуля, а в случае уменьшения — меньше.

Рассмотрим случай, если начальная скорость тела равно 0. Тогда его скорость через какое-либо время t будет равна произведению ускорения и этого времени:

Допустим, что нам известны текущая скорость тела и время, за которое тело развило указанную скорость из состояния покоя. Тогда мы можем определить ускорение:

В том случае, если начальная скорость тела не равна нулю, мы можем рассчитать конечную скорость тела по следующей формуле:

Взглянем на случаи, когда вектор скорости направлен в противоположном направлении (например, подброшенный камень, его скорость направлена в противоположную сторону от ускорения свободного падения) или в случае торможения. Тогда формула будет выглядеть следующим образом:

В случае свободного ускорения остальные формулы будут записываться так:

At = v – v0, a = (v – v)/t

А говоря о торможении, мы используем эти формулы:

Если тело останавливается, то нам следует использовать эту формулу:

А если необходимо узнать, через какой отрезок времени тело остановится, то мы запишем формулу так:

Обратимся к формуле, которая поможет найти путь, которое тело проходит при прямолинейном ускорении. Если при равномерном движении, оси времени и расстояния параллельны, то в случае равноускоренного движения ось движения либо возрастает, либо убывает. Тогда вместо прямоугольника, чью площадь мы вычисляли при равномерном движении, необходимо вычислить площадь трапеции.

Площадь трапеции равна полусумме оснований на высоту, таким образом мы получаем:

Пройденный путь определяется по формуле:

Путь торможения рассчитывается с помощью этой формулы:

Равномерное движение по окружности

Говоря о равномерном движении по окружности, нужно понимать, что в этом случае вектор скорости тела изменяется (скорость направлена по касательным к окружности), а модуль скорости тела (числовое значение) остается постоянным.

Предположим, что необходимо вычислить модуль скорости за один оборот тела по окружности. Обозначим оборот как S, а время, за которое тело его совершило, как t. Тогда формула будет записываться следующим образом: v = s/t.

Однако, если мы говорим об одном обороте, то это называется период. То есть время, за которое тело совершает один оборот вокруг окружности. Он обозначается как T. И тогда формула одного оборота будет выглядеть так: v = s/T

Если S в данном случае это длина окружности (l), то формула принимает вид v = 2πR/T, в соответствии с формулой окружности l = 2\piR

Если необходимо найти период при известном модуле скорости, то формула примет вид T = 2\piR/v

Аналогично радиус можно найти через формулу R = ½ vT/\pi

Динамика

Динамика — раздел механики, изучающий предпосылки изменения в характере движения. Например, возникновение движения. Именно этот раздел изучает три закона Ньютона. В задачах динамики содержится решение таких вопросов как определение действующих на тело сил по характеру его движения и наоборот.

Законы Ньютона

Первый закон Ньютона гласит, что существуют такие системы отсчета, относительно которых тело движется прямолинейно и равномерно, или покоится, если на него не действуют другие тела или их действия скомпенсированы.

Введем основные величины:

Инерциальными называются системы отсчета, которые движутся равномерно прямолинейно относительно Земли. Все системы отсчета, которые движутся прямолинейно и равномерно относительно инерциальной, также являются таковыми. Если система отсчета движется с ускорением, то она — неинерциальная.

Сила — это физическая величина, которая характеризует действие одного тела на второе. В результате этого действия второе тело получает ускорение в инерциальной системе отсчета. Измеряется в ньютонах.

Масса — это физическая величина, которая количественно характеризует инертность тела. Измеряется в килограммах.

Взглянем на тело, на которое действует сила с модулем равным 1 Н. Так как изначально тело массой 1 кг находилось в покое в инерциальной системе, модуль его ускорения будет равен 1 м/с 2 .

В соответствии со вторым законом Ньютона сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение. Это основной закон динамики.

Для выведения второго закона Ньютона и формулы, где F = ma, необходимо обобщить два факта:

    если на два тела, масса которых различна, подействовать равной силой, то ускорения, которые приобретут тела, будут обратно пропорциональны массам; если на одно и то же тело действуют силы разной величины, то ускорения тела будут прямо пропорциональны приложенным силам.

Благодаря этому закону, возможно вычислить не только силу, действующую на тело, но и ускорение. Для этого нужно использовать формулу \[w = \frac\]

В векторной форме второй закон Ньютона записывается как ma = mg + N + Fтр

Третий закон Ньютона гласит, что силы, с которыми две материальные точки воздействуют друг на друга, всегда равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти точки.

Выразить закон формулой можно следующим образом F1 = — F2

В случае взаимодействия тел силы имеют одинаковую природу, однако, они приложены к разным телам. Таким образом эти силы не могут уравновешивать друг друга, а складывать можно только силы, приложенные к одному телу.

Силы в природе

В соответствии с законом Гука, при деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Природа этой силы состоит в электромагнитном взаимодействии между атомами и молекулами вещества. Эта сила называется упругость.

В данном случае коэффициент k — жесткость тела, она измеряется в ньютонах на метр (Н/м).

Физике свойственен другой способ записи закона Гука. В его записи используются понятия относительной деформации и напряжения. Относительная деформация ε = x / l, а напряжение — это отношение силы к площади поперечного сечения деформированного тела δ = F / S = — Fупр / S.

Исходя из этого, закон Гука можно сформулировать так \[ε = \frac\]

Коэффициент Е — это модуль Юнга. Он зависит исключительно от свойств материала. Размеры и форма не имеют значения.

Если говорить о случаях сложных деформациях, например в случае деформации изгиба, в формуле появляется сила N — сила реакции опоры. Эта сила направлена перпендикулярно поверхности соприкосновения. N = — mg

Сила всемирного тяготения

Закон всемирного тяготения говорит, что все тела притягиваются друг к другу с силами, прямо пропорциональными их массам и обратно пропорциональна квадрату расстояния между ними.

Эту силу можно вычислить по формуле F = G\fracMR3 2 m = mg

G в данном случае — ускорение свободного падения, о котором говорилось выше. В данном случае g = G\fracMR3 2 . Среднее значение ускорения свободного падения равно 9,81 м/с 2 .

R3 — это радиус Земли. Он равен 6,38·10 6 м.

G в формуле обозначает гравитационную постоянную. Она равна 6,67·10 –11 Н·м 2 /кг 2 .

Движение тела под действием силы тяжести

Ускорение свободного падение является частным случаем равноускоренного прямолинейного движения. В этом случае ускорение всегда будет равно 9,8 м/с 2 и обозначается буквой g. Таким образом g — это ускорение свободного падения.

Ускорение свободного падения можно вычислить по следующей формуле: g = GM3/(R3+H) 2

В данном случае H — это гравитационная постоянная, M — масса земли, R — радиус земли, а H — высота падения тела.

Скорость тела под действием силы тяжести можно вычислить по формуле: v = gt

Высоту, с которой падает тело, можно вычислить по формуле H=gt 2 /2

Силы трения

Силой трения называют силу, характеризующую взаимодействие, возникающее в месте соприкосновения тел и препятствующее их относительному движению. Сила трения имеет электромагнитную природу.

Трение можно разделить на три вида: трение покоя, трение скольжения и трение качения.

Трение покоя — это трение, которое возникает при отсутствии перемещения соприкасающихся тел относительно друг друга.

Можно сказать, что эта сила не позволяет одному телу двигаться относительно другого. Эта сила направлена противоположно силе, приложенной извне параллельно поверхности соприкосновения. Сила трения покоя возрастает вместе с силой, которая стремится сдвинуть тело с места.

Трение скольжения возникает при действии на тело силе, превышающей максимальную силу трения покоя.

Это тело сдвигается с места и начинает дальнейшее движение. Сила трения скольжения всегда направлена в противоположную сторону от относительной скорости соприкасающихся тел.

Трение качения возникает в случае, если тело не скользит по другому телу, а катится наподобие колеса или цилиндра. Трение качения — это трение, которое возникает на месте их соприкосновения.

В виде формулы сила трения выглядит следующим образом: Fтр = μmg

В данном случае μ – коэффициент трения, m – масса тела, а g — ускорение свободного падения (постоянная величина 9,81 м/с 2 ).

Движение тела под действием нескольких сил

Если на тело действуют несколько сил одновременно, то необходимо найти равнодействующую всех сил по формуле F = F1 + F2 + F3

Равнодействующая сила может быть равна нулю. В таком случае тело находится в состоянии покоя.

Закон сохранения в механике

Закон сохранения импульса гласит, что геометрическая сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых движениях и взаимодействиях тел системы.

В виде формулы закон сохранения импульса выглядит следующим образом: p1 + p2 = p1’ + p2’ m1v + m2u = m1v’ + m2u’

В свою очередь импульсом тела называют величину, которая равна произведению массы тела на его скорость: p = mv.

Изменение импульса тела равно импульсу силы, который в свою очередь вычисляется по формуле P = Ft

Кинетическая энергия равна половине произведения массы тела и квадрата его скорости: Ek = mv2/2

Кинетическая энергия — это физическая величина, которая характеризует движущиеся тела. Выражается в Дж.

Закон сохранения энергии состоит в том, что полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения или силами упругости, остается неизменной при любых движениях тел системы.

Мощность — это величина, которая равна отношению совершенной работы к промежутку времени, за который она совершена. Выражается в Вт.

Вычисляется по формуле N = A/t

Коэффициент полезного действия (КПД) — это название величины, равной отношению полезной работы ко всей совершенной работе. Выражается в Дж.

КПД демонстрирует эффективность использования затраченной энергии. Коэффициент не может быть больше единицы, однако его можно выразить в процентах.

Вычисляется КПД по формуле η = Aп/Aз

Для выражения в процентах применяется формула η = Aп/Aз ∙ 100%

Движение жидкостей и газов по трубам

Закон Бернулли гласит, что давление жидкости, текущей в трубе, больше в тех частях трубы, где скорость ее движения меньше, и наоборот, в тех частях трубы, где скорость больше, давление меньше.

Уравнение Бернулли для горизонтальной трубы выглядит следующим образом \(\[p_ + \frac = p_ +\frac\]\)

В этом уравнении p1 и p2 — статические давления, а \rho — плотность жидкости. В данном случае статическое давление равно отношению силы давления одной части жидкости на другую к площади соприкосновения, когда скорость их относительного движения равна нулю.

Если труба не горизонтальная, то уравнение Бернулли примет следующую форму:

Примеры задач

На рисунке представлены графики зависимости координаты двух тел от времени.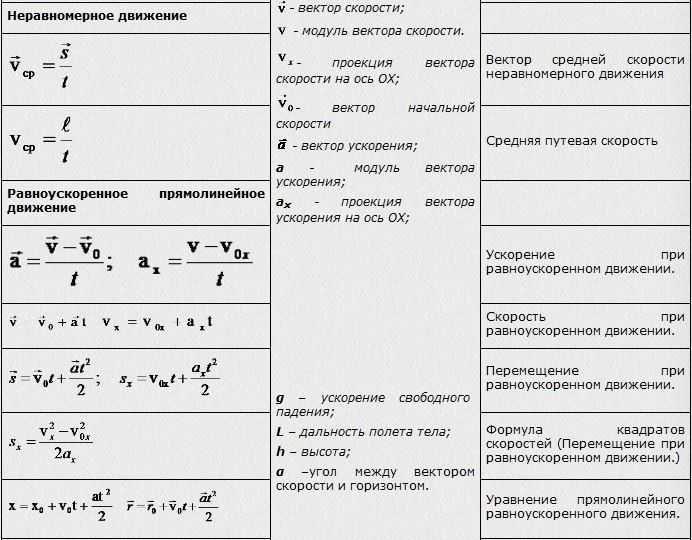 Графики каких зависимостей показаны? Какой вид имеют графики зависимости скорости и пути пройденного телом, от времени?

На рисунке показаны графики равномерного движения тел.

В начальный момент времени t = 0 первое тело имеет начальную координату хо1 = 1 м, второе тело — координату хо2 = 0. Оба тела движутся в направлении оси Х, так как координата возрастает с течением времени. Уравнение движения для равномерного прямолинейного движения имеет вид: x=xо+vхt.

Тогда для первого, второго тела соответственно:

Определим скорости первого и второго тела:

Шар подвешен на невесомой нерастяжимой нити длиной l = 0,5 м. Какую минимальную горизонтально направленную скорость vo надо сообщить шару, чтобы он сделал полный оборот в вертикальной плоскости?

Воспользуемся законом сохранения механической энергии при переходе шарика из нижнего положения в верхнее:

В верхней точке на шарик будут действовать 2 силы: сила тяжести mg (направлена вниз) и сила натяжения нити T (также направлена вниз). Эти силы сообщают шарику центростремительное ускорение, направленное вниз — к точке подвеса, где l — длина подвеса или нерастяжимой нити.

Поскольку шарик достиг верхней точки (T = 0, условие задачи), то \(\[ \frac = mg \]\) , отсюда v 2 = gl

Сделаем подстановку и получим \(\[ \frac = 2mgl + \frac\]\)

Vo 2 = g4l + gl = 5gl

Выполнив вычисления, получим: vo = √(5×10×0,5) = 5 (м/с).

Ответ: если шарик подвешен на нерастяжимой нити, его скорость должна составлять не менее 5 м/с.

Экваториальный радиус Земли равен 6370 км. Определить линейную и угловую скорости движения точек экватора при вращении Земли вокруг оси.

Программа обучения по предмету физика в 9 классе включает в себя несколько разделов: кинематика и динамика, которые в свою очередь состоят из подразделов. Таким образом ученики старшей школы изучают механические колебания и волны, законы взаимодействия и движения тел, электромагнитные явления, строение атомов и их ядер, основные законы механики. В школьную программу девятого года обучения также входят основные свойства света: интерференция, преломление и дисперсия.

Кинематика — один из разделов механики. Кинематика изучает механическое движение тел и способы его описания, независимо от причин этого движения. В данном случае под механическим движением подразумевается любое изменение положения какого-либо тела полностью или частично относительно других тел, случившееся с течением времени.

В Кинематике изучают простые виды движения.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Равномерное прямолинейное движение

Понятие равномерного прямолинейного движения заключается в том, что тело движется по прямой с одинаковой скоростью, то есть за равные промежутки времени тело перемещается на одинаковое расстояние. В таком случае скорость тела остается постоянной, однако является векторной величиной.

Скорость может быть как положительной, так и отрицательной. Все зависит от того, в каком направлении оси X (положительном или отрицательно) направлен вектор скорости. Если тело находится в покое, то его скорость равняется нулю, а координата не меняется в течение времени.

При равномерном прямолинейном движении координата тела вычисляется по следующей формуле:

В этой формуле x0 – начальная координата, x – конечная координата, v – скорость, t – время.

Если начальная координата — это начало движения и x0 = 0, то формулу можно сократить до x1 = v · t.

Если x0 = 0, то пройденный путь S будет равен координате x. Из этого утверждения можно получить формулу прямолинейного равномерного движения относительно пройденного телом расстояния:

Из этого можно вывести формулы относительно скорости и времени:

Скорость и время также можно выразить из полной формулы для тех случаев, когда x0 не равно 0:

Равноускоренное прямолинейное движение

В случае равноускоренного прямолинейного движения тело изменяет скорость своего движения на одинаковую величину за любые равные промежутки времени. Под ускорением в контексте данного определения понимается изменение значения скорости за единицу времени.

Скорость тела вычисляется по формуле:

В данной формуле v – конечная скорость, v0 – начальная скорость, a – ускорение, t – время.

В равноускоренном прямолинейном движении постоянной величиной является ускорение, а не скорость. Ускорение может быть больше или меньше нуля. В случае увеличения скорость, значение ускорения будет больше нуля, а в случае уменьшения — меньше.

Рассмотрим случай, если начальная скорость тела равно 0. Тогда его скорость через какое-либо время t будет равна произведению ускорения и этого времени:

Допустим, что нам известны текущая скорость тела и время, за которое тело развило указанную скорость из состояния покоя. Тогда мы можем определить ускорение:

В том случае, если начальная скорость тела не равна нулю, мы можем рассчитать конечную скорость тела по следующей формуле:

Взглянем на случаи, когда вектор скорости направлен в противоположном направлении (например, подброшенный камень, его скорость направлена в противоположную сторону от ускорения свободного падения) или в случае торможения. Тогда формула будет выглядеть следующим образом:

В случае свободного ускорения остальные формулы будут записываться так:

At = v – v0, a = (v – v)/t

А говоря о торможении, мы используем эти формулы:

Если тело останавливается, то нам следует использовать эту формулу:

А если необходимо узнать, через какой отрезок времени тело остановится, то мы запишем формулу так:

Обратимся к формуле, которая поможет найти путь, которое тело проходит при прямолинейном ускорении. Если при равномерном движении, оси времени и расстояния параллельны, то в случае равноускоренного движения ось движения либо возрастает, либо убывает. Тогда вместо прямоугольника, чью площадь мы вычисляли при равномерном движении, необходимо вычислить площадь трапеции.

Площадь трапеции равна полусумме оснований на высоту, таким образом мы получаем:

Пройденный путь определяется по формуле:

Путь торможения рассчитывается с помощью этой формулы:

Равномерное движение по окружности

Говоря о равномерном движении по окружности, нужно понимать, что в этом случае вектор скорости тела изменяется (скорость направлена по касательным к окружности), а модуль скорости тела (числовое значение) остается постоянным.

Предположим, что необходимо вычислить модуль скорости за один оборот тела по окружности. Обозначим оборот как S, а время, за которое тело его совершило, как t. Тогда формула будет записываться следующим образом: v = s/t.

Однако, если мы говорим об одном обороте, то это называется период. То есть время, за которое тело совершает один оборот вокруг окружности. Он обозначается как T. И тогда формула одного оборота будет выглядеть так: v = s/T

Если S в данном случае это длина окружности (l), то формула принимает вид v = 2πR/T, в соответствии с формулой окружности l = 2\piR

Если необходимо найти период при известном модуле скорости, то формула примет вид T = 2\piR/v

Аналогично радиус можно найти через формулу R = ½ vT/\pi

Равномерное движение по окружности.

Wiki. fenix. help

25.06.2019 20:03:39

2019-06-25 20:03:39

Источники:

Https://wiki. fenix. help/fizika/vse-formuly-po-fizike-za-9-klass

Физика 9 класс. Все формулы и определения. Скачать в PDF и JPEG » /> » /> .keyword { color: red; }

Формулы за 9 класс по физике

Физика 9 класс. Все формулы и определения

«Физика 9 класс. Все формулы и определения» — это Справочник по физике в 9 классе, доступный для скачивания в 2-х форматах: КРУПНО (формат PDF, на 7-ми страницах) и МЕЛКО (формат JPG, на 2-х страницах). Смотрите также справочные материалы по физике за другие классы:

Физика 9 Все формулы КРУПНО

Физика 9. Все формулы МЕЛКО. Стр 1

Физика 9. Все формулы МЕЛКО. Стр 2

В пособии «Физика 9 класс. Все формулы и определения» представлено 45 формул :

Физика 9 класс. Все формулы и определения в разделе «КИНЕМАТИКА»

I. Равномерное прямолинейное движение

1. Скорость
2. Проекция скорости на координатную ось
3. Перемещение
4. Проекция перемещения на координатную ось

II. Равноускоренное прямолинейное движение

5. Средняя скорость при неравномерном прямолинейном движении
6. Ускорение
7. Скорость
8. Перемещение
9. Координата тела
10. Ускорение свободного падения

III. Равномерное движение по окружности

11. Угловая скорость
12. Частота обращения
13. Период обращения
14. Линейная скорость
15. Центростремительное ускорение

Физика 9 класс. Все формулы и определения в разделе «ДИНАМИКА»

IV Законы Ньютона

16. Первый закон Ньютона
17. Второй закон Ньютона
18. Третий закон Ньютона

V Силы в природе

19. Закон Гука
20. Закон всемирного тяготения
21. Гравитационная постоянная
22. Сила тяжести
23. Ускорение свободного падения
24. Вес покоящихся и движущихся тел.

VI. Движение тела под действием силы тяжести

25. Движение тела под углом к горизонту.
26. Горизонтально брошенное тело.
27. Скорость искусственного спутника Земли.

VII. Силы трения

28. Трение покоя.
29. Трение скольжения.
30. Коэффициент трения.
31. Движение тела под действием силы трения.

VIII. Движение тела под действием нескольких сил

32. Условие равновесия тела (как материальной точки)
33. Движение тела по наклонной плоскости.
34. Движение связанных тел через неподвижный блок.

IX. Законы сохранения в механике

36. Импульс тела
37. Импульс силы
38. Закон сохранения импульса
39. Механическая работа силы
40. Теорема о кинетической энергии
41. Потенциальная энергия поднятого тела
42. Работа силы тяжести
43. Потенциальная энергия деформированного тела
44. Закон сохранения полной механической энергии

X. Движение жидкостей и газов по трубам

45. Закон Бернулли

Дополнительные материалы

Девять самых необходимых (самых востребованных) формул по физике в 9 классе.

Таблицы физических величин

Вы смотрели «Физика 9 класс. Все формулы». Смотрите также справочные материалы по физике за другие классы:

«Физика 9 класс. Все формулы и определения» — это Справочник по физике в 9 классе, доступный для скачивания в 2-х форматах: КРУПНО (формат PDF, на 7-ми страницах) и МЕЛКО (формат JPG, на 2-х страницах). Смотрите также справочные материалы по физике за другие классы:

Закон Бернулли.

Uchitel. pro

04.09.2020 23:58:12

2020-09-04 23:58:12

Источники:

Https://uchitel. pro/%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0-9-%D0%BA%D0%BB%D0%B0%D1%81%D1%81-%D0%B2%D1%81%D0%B5-%D1%84%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D1%8B/

Математический вывод уравнения движения Класс 9

При прямолинейном движении тела с равноускорением можно установить связь между скоростью тела, ускорением тела и расстоянием, пройденным телом за определенное время, с помощью системы уравнений. Эти уравнения называются уравнениями движения.

Три уравнения:

  1. Первое уравнение движения: v = u + at
  2. Второй Уравнение движения: с = ut + 1/2at 2
  3. Третье уравнение движения: v 2 – u 2 = 2as

Где u = начальная скорость тела

v = конечная скорость тела

а = равномерное ускорение тела

t = затраченное время

с = пройденное расстояние

v = u + at

Рассмотрим тело, имеющее начальную скорость «u». Предположим, что он подвергается равномерному ускорению «а», так что через время «t» его конечная скорость становится «v». Теперь мы сейчас,

Ускорение = изменение скорости/времени

а= v-u/t

или v = u + at или v = at + u …..(i)

Это уравнение известно как первое уравнение движения.

ВТОРОЕ УРАВНЕНИЕ ДВИЖЕНИЯ

s = ut + 1/2at 2

Предположим, что тело имеет начальную скорость «u» и равномерное ускорение «a» в течение времени «t», так что его конечная скорость становится «v». Расстояние, пройденное движущимся телом за время «t», равно «S», тогда средняя скорость = (v + u)/2. Пройденное расстояние = средняя скорость × время

S = ut + 1/2at 2

Это второе уравнение движения.

ТРЕТЬЕ УРАВНЕНИЕ ДВИЖЕНИЯ

в 2 – у 2 = 2 как

Из второго уравнения движения имеем

s = ut + 1/2at 2 …(i)

Из первого уравнения движения имеем

v = u + at

⇒ at = v – u

⇒ t = v – u/a

Поместив это значение «t» в уравнение … (i)

У нас есть

или v 2 = u 2 + 2as

или в 2 – у 2 = 2 как

Это третье уравнение движения

Где v = конечная скорость

u = начальная скорость

а = ускорение

с = пройденное расстояние

Расстояние, пройденное за энную секунду:

S = ut + 1/2 at 2 — расстояние, пройденное телом за t s.

……..(в)

[расстояние, пройденное телом по прямой за n секунд.

…….(vi)

[расстояние, пройденное телом по прямой за (n-1) с]

Путь, пройденный телом за n-ю секунду, будет равен –

S n й = S n – S n -1

Для решения числовых задач:

  • Если тело падает с высоты, то его начальная скорость u = 0, но имеет ускорение (действующее). Если тело стартует из состояния покоя, его начальная скорость u = 0,
    • .
  • Если тело останавливается, то его конечная скорость v = 0 или, если тело достигло высшей точки после броска вверх, его конечная скорость v = 0, но имеет ускорение (действующее).
  • Если тело движется с равномерной скоростью, его ускорение равно нулю, т.е. a = 0,
    • .
  • Движение тела называется свободным падением, если только сила, действующая на него, есть сила тяжести (т. е. земное притяжение).

ДВИЖЕНИЕ ПОД СИЛОЙ ТЯЖЕСТИ

  • Движение под действием силы тяжести означает, что объект движется в пространстве только под действием силы тяжести.
  • Движение под действием силы тяжести есть равноускоренное движение. Таким образом, можно использовать уравнения движения для равноускоренного движения, которые имеют вид
    • .

  • Здесь ускорение будет ускорением силы тяжести.

В единицах СИ g = 9,8 м/с 2

В с.г.с. ед. g = 980 см/с 2

  • Когда объект брошен вверх или вниз, в обоих случаях объект будет испытывать одинаковое ускорение g, действующее в направлении вниз.
  • Здесь пренебрегают сопротивлением воздуха. В реальном эксперименте сопротивлением воздуха пренебречь нельзя. Это идеальный случай. Такое движение называется свободным падением.

Случай 1:

Когда объект брошен вверх (принимая положительное значение) в пространстве с начальной скоростью v0.

Ускорение = –g (в направлении вниз)

Итак, уравнение движения будет

v = v 0 – гт

h = v 0 t – 1/2 gt2

v2 – 2 гх

Случай 2:

Когда объект брошен вниз (принимая положительное значение) в пространстве с начальной скоростью v0.

Ускорение = +g (в направлении вниз)

Итак, уравнение движения будет

v = v 0 +gt

s = v 0 t + 1/2 gt2

v 2 = v 0 2 + 2гх

Случай 3:

Когда предмет брошен в пространство таким образом, что сначала он поднимается, а затем опускается.

Для решения таких типов задач используется следующее соглашение о знаках: –

Соглашение о знаках

Величины движения в направлении вверх принимаются положительными.

Движущиеся величины, направленные вниз, считаются отрицательными.

Пусть начальная скорость v 0 направлена ​​вертикально вверх и в конце концов достигает земли, как показано на рисунке.

Начальная скорость = +v 0 (в восходящем направлении)

Рабочий объем = –h (в направлении вниз)

Ускорение = –g (в направлении вниз)

Итак, используя уравнение движения, s = мы имеем

– h = v 2

Q1.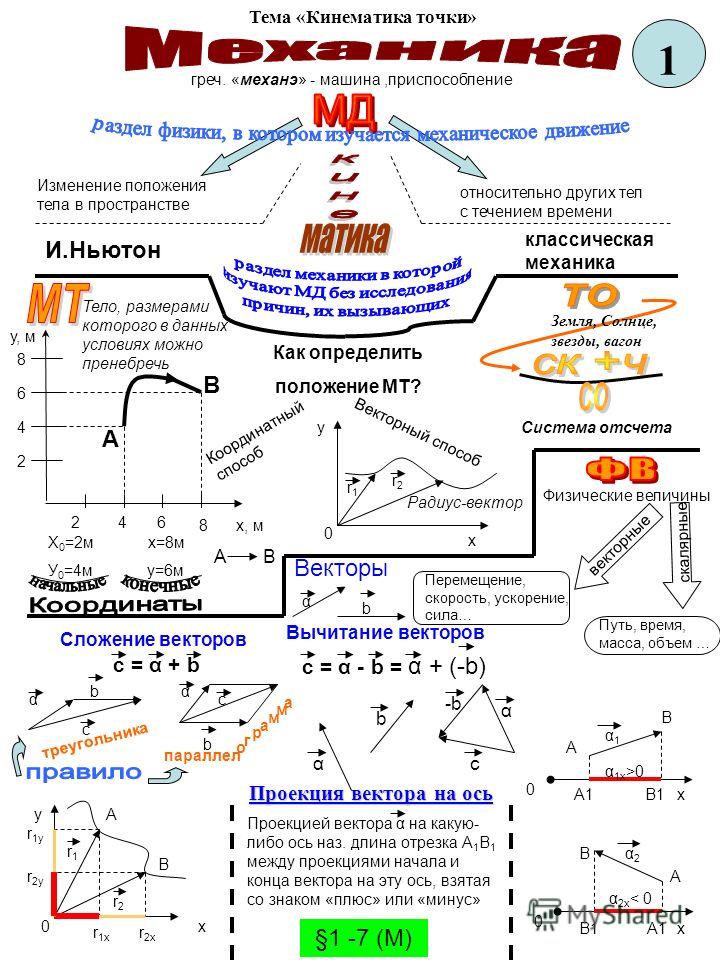 Автомобиль движется со скоростью 50 км/ч. Через две секунды он движется со скоростью 60 км/ч. Вычислите ускорение автомобиля.

Ответ. Здесь u = 50 км/ч = 50 × 5/18 м/с = 250/18 м/с

и v = 60 км/ч = 60 × 5/18 = 300/18 м/с

С

Q2 . Автомобиль развивает скорость 54 км/ч через 20 с после старта. Найдите ускорение автомобиля.

Ответ. u = 0 (поскольку автомобиль трогается с места)

v = 54 км/ч = 54 × 5/18 = 15 м/с

Как,

Q 3. Мяч брошен вертикально вверх со скоростью 20 м/с. Как высоко поднялся мяч? (примем g = 9,8 м/с2.

Ответ. u = 20 м/с, a = – g = – 9,8 м/с2 (движение против силы тяжести)

с = ? v = 0 (в высшей точке)

v 2 – u 2 = 2as

(o)2 – (20)2 = 2(-g) с

–400 = 2 (–9,8) с

–400 = –19,6 с

= с ⇒ с = 20,4 м.

РАССТОЯНИЕ (СМЕЩЕНИЕ) ОТ СКОРОСТИ (СКОРОСТИ) ГРАФИК ВРЕМЕНИ:

Расстояние (перемещение = скорость (скорость) x время, поэтому расстояние (перемещение) можно рассчитать (вычислить) с помощью графика скорость (скорость) – время.

Случай (i): Когда скорость (скорость) постоянна (постоянна):

На рисунке показан график скорость-время автомобиля, движущегося с равномерной скоростью 50 км/ч. Это прямая линия, параллельная оси X (оси времени). Расстояние, пройденное этим такси с момента времени t1 = 4 часа в точке P до момента времени t2 = 8 часов в точке S, определяется как расстояние = 50 × (t 2 – t 1 )

= 50 (8 – 4)

= 50 × 4 = 200 км

На рисунке PQ = 50, SP = (t 1 – т 1 )

Отсюда расстояние = PQ × SP = площадь прямоугольника PSRQ

Случай (ii): Когда скорость (скорость), а также ускорение неравномерны (переменные)

На рисунке показана зависимость скорости от времени тела, движущегося с переменной скоростью и ускорением. На небольшом интервале времени скорость можно считать постоянной. Для этого небольшого промежутка времени расстояние ΔS = vΔt = Площадь зачерненной полосы.

За весь промежуток времени между t 1 и t 2

Расстояние = сумма площадей всех полос между t 1 и t 2 = площадь заштрихованной фигуры PQRS.

ГРАФИЧЕСКИЙ ВЫВОД УРАВНЕНИЙ ДВИЖЕНИЯ

ПОЛУЧИТЬ v = u + at ГРАФИЧЕСКИМ МЕТОДОМ

Предположим, что тело, движущееся с равномерным ускорением «а», имеющее начальную скорость «u», достигает конечной скорости v за время «t», преодолевая расстояние «s», как показано на графике.

На данном графике скорость-время

Начальная скорость, u = OA …(i)

Конечная скорость, v =BC …(ii)

Из графика ВС = BD + DC

⇒ v = BD + OA(DC = OA)

⇒ v = BD + u …(iii)

Чтобы найти значение BD,

Ускорение, a = наклон линии AB

или а = BD/AD

⇒ а = BD/t (AD = OC = t)

⇒ BD = at …(iv)

Подставляя BD = at в уравнении (iii)

Получаем v=at+u

или v = u + at

ПОЛУЧИТЬ S = ut + 1/2at 2 ГРАФИЧЕСКИМ МЕТОДОМ

Предположим, что тело, движущееся с равномерным ускорением «а», имеющее начальную скорость «u», достигает конечной скорости «v» за время «t», преодолевая расстояние s, как показано на графике 8. 1 (а).

Тогда из графика:

Расстояние, пройденное телом = Площадь под графиком скорости от времени

Пройденное расстояние = площадь фигуры OABC = площадь прямоугольника OADC + площадь треугольника ABD

⇒ S = (OA x OC) + (1/2 AD x BD)

⇒ S = u x t + 1/2t x BD …(i)

Чтобы найти значение BD,

Ускорение, a= наклон линии AB

или а = BD/AD

⇒ а = BD/t (AD = OC = t)

⇒ БД = по адресу

Подставляя BD = at в уравнение (i), получаем

S = ut + 1/2at 2

ПОЛУЧИТЬ v 2 – u 2 = 2as ГРАФИЧЕСКИМ МЕТОДОМ

Рассмотрим тело, движущееся с равномерным ускорением «а», имеющее начальную скорость «u» и достигшее конечной скорости «v». За время «t» преодолев расстояние s, как показано на графике 8.1 (а).

Тогда из графика:

Пройденное расстояние, ‘s’ = площадь под графиком скорость-время

т. е. пройденное расстояние, s = площадь трапеции OABC

сумма параллельных сторон x высота/2

= (OA + CD) x ОС/2

s = (u + v) x t/2….(i)

Чтобы исключить «t» из приведенного выше уравнения

Мы знаем, v = u + at

⇒ v – u = ат

⇒ t = (v – u/a)…(ii)

Подставив это значение в уравнение (i),

Получаем, s = (u + v)(v-u)/2a

⇒ v 2 = u 2 + 2as

⇒ v 2 – у 2 = 2ас

  • Наклон графика расстояние-время/перемещение-время дает скорость/скорость.
  • Наклон графика скорость-время/скорость-время дает ускорение.
  • Площадь под графиком скорость-время/скорость-время дает расстояние/перемещение.
  • Площадь под графиком ускорение-время дает изменение скорости.

КРУГОВОЕ ДВИЖЕНИЕ:

Определение:

Движение частицы (маленького тела) по окружности (круговой траектории) называется круговым движением. Если тело проходит равные расстояния по окружности за равные промежутки времени, то движение называется равномерным круговым движением.

Равномерное круговое движение – это движение, при котором скорость остается постоянной, но изменяется направление скорости.

Объяснение:

Рассмотрим мальчика, бегущего по правильной шестиугольной дорожке (дорожке), как показано на рисунке. Поскольку мальчик бежит вдоль стороны шестиугольника с постоянной скоростью, он должен поворачивать на каждом углу, меняя направление, но сохраняя скорость. В одном раунде он должен сделать шесть ходов через равные промежутки времени.

Если тот же мальчик будет бежать по обочине правильной восьмиугольной дорожки с одинаковой скоростью, то ему придется сделать восемь поворотов за один раунд через равные промежутки времени, но интервал станет меньше.

Увеличивая количество сторон правильного многоугольника, мы обнаруживаем, что число оборотов за виток становится больше, а интервал между двумя витками становится еще короче. Окружность — это предельный случай многоугольника с бесконечным числом сторон. На кольцевой трассе поворот становится непрерывным процессом без каких-либо промежуточных промежутков.

Мальчик, бегущий по сторонам такой дорожки, будет совершать круговые движения. Следовательно, круговое движение есть движение тела по сторонам бесконечного числа сторон многоугольника с постоянной скоростью, направление которого непрерывно меняется.

Пример равномерного кругового движения:

  • Движение Луны вокруг Земли.
  • Движение спутника вокруг своей планеты.

Характер кругового движения:

Круговое движение – это движение с ускорением. Так как при круговом движении скорость изменяется только в направлении, то движение называется ускоренным.

РАЗНИЦА МЕЖДУ РАВНОМЕРНЫМ ЛИНЕЙНЫМ ДВИЖЕНИЕМ И РАВНОМЕРНЫМ КРУГОВЫМ ДВИЖЕНИЕМ:

Равномерное линейное движение

Равномерное круговое движение

1. Направление движения не меняется

1. Направление движения постоянно меняется.

2. Движение неускоренное.

2. Движение ускоряется.

РАДИАН – (ЕДИНИЦА ПЛОСКОГО УГЛА):

Определение:

Угол в радианах равен длине дуги, стягивающей угол, деленной на радиус окружности.

то есть

т. е. θ (в радианах) = l/r

Где θ = угол в радианах

l = длина дуги

r = радиус окружности

если l = r

∴ θ = l/l = 1 радиан

т. е. θ = 1 радиан

Следовательно, один радиан — это угол, который в центре окружности опирается на дугу, длина которой равна радиусу окружности.

(1 радиан = 57°2616)

ЛИНЕЙНАЯ СКОРОСТЬ И УГЛОВАЯ СКОРОСТЬ:

Пусть тело движется по окружности радиуса «r» с равномерной линейной скоростью «v», когда тело движется из точки А в точку В, преодолевая расстояние «s» за время «t».

Тогда линейная скорость v определяется как:

Линейная скорость = Пройденное расстояние/Время

т. е. v = с/т

Когда тело движется по окружности из А в В за время t. Он также движется на угол θ, известный как угловое смещение тела.

УГЛОВАЯ СКОРОСТЬ:

Он определяется как угловое перемещение в единицу времени

т. е. угловая скорость = угловое смещение / затраченное время

или (Омега)

где ω = угловая скорость

θ = угол в радианах, под которым движется тело.

Единицей угловой скорости в системе СИ является рад с1.

СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНОЙ СКОРОСТЬЮ И УГЛОВОЙ СКОРОСТЬЮ:

Когда тело движется с равномерной линейной скоростью «v», преодолевая расстояние «s» за время «t» по круговой траектории радиуса «r», образуя угол θ в центре.

Тогда у нас есть

Угол в радианах, θ = s/r …(i)

Линейная скорость v = с/т

с = v х т

Поместив это в уравнение (i)

У нас есть

θ = v x t/r

θ/t = v/r…(ii)

Мы знаем, Угловая скорость,

Поместив это в уравнение (ii)

Получаем (ω) = v/r

v = ωr

т. е. линейная скорость = угловая скорость × радиус кругового пути

Также проверьте

  • Расстояние и перемещение
  • Типы движения

Что такое кинематика? Заметки, книги, формулы, уравнения по физике кинематики

  1. Главная
  2. Физика
  3. Кинематика

Что такое кинематика

Кинематика — одна из самых основных глав механики, и после прочтения этой статьи вы также обнаружите, что кинематика широко используется в нашей повседневной жизни. Большую часть нашей жизни мы ходим пешком, путешествуем отсюда туда, и поэтому нас также беспокоит, сколько времени потребуется для перехода из одного места в другое. Кинематика занимается всеми этими процессами и облегчает нашу повседневную жизнь.

В Индии большинство из нас являются поклонниками крикета, и если вы когда-нибудь замечали, когда боулер подает мяч, на табло также отображается скорость мяча, а иногда повторы также показывают возможную траекторию мяча, которую можно определить для этапа «Лег до калитки». (НМТ) тест. Это возможно, потому что кинематика помогает понять «движение» мяча. Движение есть не что иное, как изменение положения. В этой главе вы поймете некоторые основные термины, такие как расстояние, перемещение, скорость, скорость, ускорение и т. д. Вам следует очень внимательно прочитать эту главу, потому что вопросы из этой главы задаются не только на экзаменах 10+2, но и на различных других государственных экзаменах. в разделе «Общие способности».

Использование DRS для проверки для LBW

Темы кинематики

Справочная кадра, движение по прямой линейной скорости и скорости, однородное и неопроверженное движение, средняя скорость и скорость и скорость и скорость и скорость и скорость, средняя скорость и скорость и скорость и скорость. мгновенная скорость, равноускоренное движение, положение-время, графики скорость-время, соотношения для равноускоренного движения. Скаляры и векторы, нулевые векторные, скалярные и векторные произведения, единичный вектор, скорость, разрешение вектора, векторное сложение и вычитание. Движение в плоскости, относительная скорость, движение снаряда, равномерное круговое движение.

 

Обзор кинематики

В кинематике нас не интересует причина движения, нас интересует только движение объекта, проще говоря, нас не волнует, какой импульс передается объекту. мяч котелком, нас интересует только движение мяча после того, как он потерял контакт с рукой игрока. Движение объекта может быть одномерным, двухмерным или даже трехмерным.

 

Движение объекта также может быть линейным или круговым. В этой главе вы познакомитесь с 3 уравнениями движения. Вы можете решить большинство вопросов кинематики, используя только эти три уравнения движения. Но прежде чем двигаться дальше в этой главе, я бы посоветовал вам сначала развить некоторые базовые математические навыки, такие как дифференцирование, интегрирование, а также векторы. Я уверен, что вы изучали разницу между скалярными и векторными величинами в школьных учебниках. В этой главе вы познакомитесь с системой отсчета. Система отсчета представляет собой систему координат. Существует множество используемых систем координат, но наиболее распространена декартова система координат, состоящая из трех взаимно перпендикулярных осей. На самом деле ничто не является стационарным, понятие стационарности используется с системой отсчета. Например, здание неподвижно, только если вы наблюдаете его с Земли, но если вы видите это здание с Луны, оно не является неподвижным, поскольку Земля также вращается. Звучит интересно? Теперь вы можете разыграть своих одноклассников с помощью этой основы системы отсчета.

 

В начале вы будете часто делать ошибки или вычитание величин, например, если мяч будет брошен вертикально вниз из здания со скоростью «u», то какой будет конечная скорость через время t? Будет ли он равен «u+gt» или «u-gt»? Таким образом, чтобы свести к минимуму путаницу такого типа, вы всегда должны использовать вектор в векторных величинах. Вопросы из этой главы сложны, когда они представлены в графической форме. Вы должны ознакомиться с основными уравнениями линии, параболы, чтобы получить решение.

Предположим, ваш школьный автобус отправляется в 7:00. Какое расстояние он проедет до 7:45?

Solution :

Given

 

Formulas for Kinematics

Уравнения движения

Как подготовить Кинематику?

Прежде чем решать вопросы, вы должны хорошо владеть основами исчисления, уметь различать и объединять функции. Чтобы хорошо усвоить концепции, вы должны сначала решить вопрос об одномерном движении, а затем решить только двухмерное движение. Кроме того, изучите основы построения графиков. После прочтения темы пройдите несколько имитационных тестов по этой конкретной теме, чтобы набраться сил в этой теме. Иногда вопросы относительно относительного движения, движения снаряда и задачи о реке сложны, поэтому больше практикуйтесь в этих темах.

 

Примечания по кинематике

  • С помощью дифференцирования и интегрирования всегда можно найти функции x,v, a из одной заданной функции. Посмотрите на диаграмму ниже, чтобы понять это. Этот трюк очень важен, потому что он будет использоваться во многих вопросах.

 

  • Самостоятельно составьте графики для различных уравнений, с которыми вы сталкиваетесь при решении вопросов. Например. график x-t, график v-t, график a-t, график v-x, график a-x и т. д.

  • Используйте векторную запись в векторных величинах, направления очень важны, чтобы избежать глупых ошибок.

  • Не только заучивайте формулы, сначала докажите их сами.

  • Для движения в 2-D или 3-D всегда разбивайте (разделяйте) движение на компоненты по осям.

  • Существует общий совет для всех типов вопросов. При отработке вопросов всегда пишите, какие количества даны в вопросе и что вам нужно найти.

Книги по кинематике

В книгах NCERT вы найдете простые для модерации вопросы. Сначала решите их. Затем вы можете ответить на вопросы из книги «Понимание физики» Д.К. Панди или Х.К. Верма. В обеих этих книгах есть вопросы хорошего качества. Но помимо этих книг, вы также должны проводить пробные онлайн-тесты по темам. Наша платформа предоставит вам видеоролики по всем темам, статьи на простом языке, чтобы облегчить обучение, и разнообразные вопросы в пробных тестах.

 

Примечания по главам физики для технических и медицинских экзаменов

Темы из кинематики

  • Движение по прямой: график положение-время, скорость и скорость. [REST_COUNT]+ Еще’> ( JEE Главная ) (18 концепций)
  • Система отсчета. [REST_COUNT]+ Еще’> ( JEE Главная ) (1 концепт)
  • Движение в самолете [REST_COUNT]+ Еще’> ( JEE Главная ) (1 концепт)
  • Скаляры и векторы, векторное сложение и вычитание, нулевой вектор, скалярное и векторное произведение, единичный вектор, разрешение вектора. [REST_COUNT]+ Еще’> ( JEE Главная ) (22 концепции)
  • Равномерное и неравномерное движение, средняя скорость и мгновенная скорость [REST_COUNT]+ Еще’> ( JEE Главная ) (6 концепций)
  • Относительная скорость [REST_COUNT]+ Еще’> ( JEE Главная ) (10 концепций)
  • Равноускоренное движение, графики скорость-время, положение-время, соотношения для равноускоренного движения. [REST_COUNT]+ Еще’> ( JEE Главная ) (13 концепций)
  • Равномерное круговое движение [REST_COUNT]+ Еще’> ( JEE Главная ) (8 концепций)
  • Движение снаряда [REST_COUNT]+ Еще’> ( JEE Главная ) (21 концепт)
  • Основы кинематики [REST_COUNT]+ Еще’> ( JEE Главная ) (5 концепций)
  • 2D-движение [REST_COUNT]+ Еще’> ( JEE Главная ) (9концепции)
  • Физические величины в кинематике [REST_COUNT]+ Еще’> ( JEE Главная ) (5 концепций)

Частые сомнения из-за кинематики

  • Если тело, движущееся по круговой траектории, сохраняет постоянную скорость 10 мс -1 , то что из следующего правильно описывает связь между ускорением и радиусом?

    • Опция 1)

    • Вариант 2)

    • Вариант 3)

    • Вариант 4)

     

  • Вектор поворачивается на небольшой угол в радианах    для получения нового вектора. В этом случае   :

    • Опция 1)

    • Вариант 2)

    • Вариант 3)

    • Вариант 4)

     

  • С края обрыва высотой 240 м одновременно брошены два камня с начальной скоростью 10 м/с и 40 м/с соответственно. Какой из следующих графиков лучше всего представляет изменение во времени относительного положения второго камня по отношению к первому? (Предположим, что камни не отскакивают после удара о землю и пренебрегают сопротивлением воздуха, примем g = 10 м/с 2

     

    • Опция 1)

    • Вариант 2)

    • Вариант 3)

    • Вариант 4)

     

Просмотреть все

Важные книги по кинематике

Статьи

Вопросы

Напишите свой вопрос

Ваш ответ

Как решать задачи кинематики, часть 2

Эта статья является второй главой в серии о том, как понимать задачи кинематики и подходить к ним. В первой главе рассматривались положение, скорость и ускорение. Теперь, когда мы понимаем эти величины, мы собираемся использовать их для решения задач в одном измерении.

Четыре всадника апокалипсиса кинематики это:

x f – x I = (V F – V I )*T/2

V F – V I = A*T

V F 2 = V . + 2*a*(x f – x i )

x f = x i + v i *t + ½a*t 2 10 30 маленький 900 означает окончательную (например, конечную скорость или положение), а маленькая цифра i означает начальную.

Примечание. Эти уравнения работают только для постоянного ускорения, но почти все задачи имеют постоянное ускорение.

Этапы решения одномерных задач

Для каждой одномерной кинематической задачи шаги практически одинаковы.

  • Запишите все величины, которые дает вам задача (начальное и конечное положение, начальная и конечная скорость, ускорение, время и т. д.)
  • Запишите, какое количество вы пытаетесь найти
  • Найдите кинематическое уравнение (или иногда два уравнения), чтобы связать эти величины.
  • Решите алгебру.

Да, это действительно так просто. (На самом деле, большинство задач по физике работают одинаково. Чтобы узнать больше об алгоритме решения задач по физике, ознакомьтесь с этой статьей.)

Как избежать распространенных ошибок: скрытые величины

Иногда задача может тайно подсказать вам величину; вы можете даже не осознавать, что получили это. Например, если они сообщают вам смещение (как далеко что-то пройдено), но не позиции, вы можете рассматривать смещение как x f и установите x i равным 0. Точно так же, если задача не говорит ничего особенного об ускорении, то ускорение, вероятно, является просто силой тяжести, a = g = 9,8 м/с 2 . Эти скрытые количества так же действительны, как и обычные количества, просто их немного сложнее обнаружить.

Как избежать распространенных ошибок: вершина полета

Особый пример скрытой величины — когда вам говорят, что объект находится «на вершине своего полета/движения/траектории/и т. д.». Это означает, что они тайно говорят вам, что v f равно 0, потому что объект, движущийся в одном измерении, всегда имеет скорость 0 в начале своего пути. Интересно, почему? Что ж, если бы скорость росла, то через миллисекунду объект был бы выше (и, следовательно, он не мог бы находиться в верхней части своего пути). Точно так же, если бы объект имел скорость, направленную вниз, то на миллисекунду раньше она была бы выше (поэтому он не может быть и наверху).

Как избежать распространенных ошибок: положительные и отрицательные числа

Уследить за отрицательными числами может быть сложно. Ключ — это направление; вниз всегда отрицательно.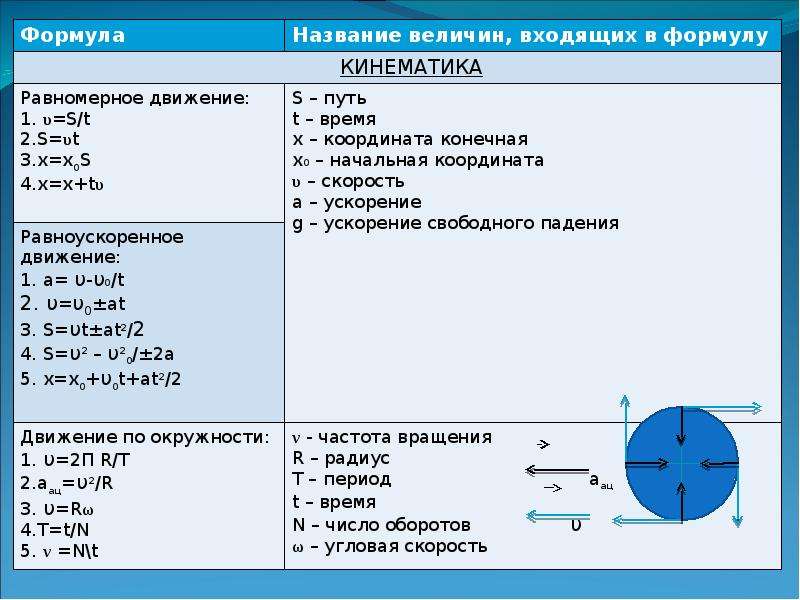 Итак, если объект падает, его скорость будет отрицательной. Если ускорение уменьшается (что почти всегда бывает), то ускорение отрицательное. И не забывайте из нашей первой главы, что возможно иметь положительную скорость и отрицательное ускорение одновременно!

Пример: Женщина и ее мяч

Женщина держит мяч на высоте 1 метр и бросает его вверх со скоростью 5 м/с. а) До какой высоты долетит мяч? б) Через какое время мяч упадет на землю? в) С какой скоростью движется мяч в момент удара о землю?

Давайте узнаем!

Часть A: Как высоко поднимается мяч?

Что мы знаем?

Начальное положение x i = 1 м
Начальная скорость v i = 5 м/с
Секретное количество: a = -9,8 м/с 2 (гравитация)
Секретное количество: В верхней части дуги мяча (т. мы пытаемся найти?

Положение в верхней части броска, x f

Какое уравнение связывает эти величины?

Мы ищем уравнение, которое включает x f , x i , v f , v i и a
v f 2 = v i 2 + 2*a*(x f – x i ) отлично подходит!

Подключите и решайте

V F 2 = V I 2 + 2*A*(x F – x I )
(0 M/S) – x I )
(0 M/S) – x I )
(0 M. – x I ) = (5 м/с) 2 + 2*(-9,8 м/с 2 )*(х f – 1 м)
0 = 25 (м 2 /с 2 ) – ( 19,6 м/с 2 )*(x f – 1 м)
(19,6 м/с 2 )*(x f – 1 м) = 25 м 2 /с 2
x f –1 м = (25 м 27) /(19,6 м/с 2 )
x f –1 м = 1,28 м
x f = 2,28 м

Тада! Окончательная высота = 2,28 метра

Часть B: Сколько времени потребуется мячу, чтобы коснуться земли?

Что мы знаем?

Мы все еще знаем x i = 1 м, v i = 5 м/с и a = -90,8 м/с 2 но теперь мы также знаем, что x f = 0 м (поскольку высота земли равна 0 м)

полет, v f ≠ 0, так что это исключено.

Что мы пытаемся найти?

Время, т

Какое уравнение связывает эти величины?

Мы ищем уравнение, которое включает x f , x i , v i , a и t
Похоже, нам понадобится x f = x i + v i *t + ½a*t 2

f

3 x

0

= x i + v i *t + ½a*t 2
0 м = 1 м + (5 м/с)*t + ½ (-9,8 м/с 2 )* t 2
-(4,9 м/с 2 )* t 2 + (5 м/с)*t + 1 м = 0

Это квадратное уравнение (ax 2 + bx + c = 0 ) и может быть решена с помощью квадратичной формулы.

Оставить комментарий