Кинематика. Основные понятия кинематики: механическое движение, материальная точка
Содержание и основные понятия кинематики. Чтобы обработать деталь на металлорежущем станке, необходимо предварительно настроить станок. В коробке скоростей и в механизмах подачи детали, передающие вращение от электродвигателя, соединяют так, что обеспечиваются вполне определенные перемещения детали и инструмента в течении некоторого времени. Перемещение одних тел или частей тела относительно других называется механическим движением. Раздел механики, изучающий механическое движение на основании законов геометрии, называют кинематикой. При этом не принимаются во внимание ни свойства движущихся тел, ни силы, под воздействием которых происходит движение. Так как при движении тела различные его точки могут двигаться по- разному, то в кинематике сначала изучается движение более простого объекта, а именно материальной точки.
Материальной точкой называют такое тело, размерами и формой которого можно пренебречь в данной задаче.
Введение понятия материальной точки вносит значительное упрощение в исследование движения тел. Для решения задач о движении тела в целом достаточно знать движение одной или двух его точек.
Движущееся тело всегда проходит определенный путь в пространстве от начальной до конечной точки движения, на что затрачивается определенное время.
Пространство и время являются такими же необходимыми условиями существования окружающего нас мира, как и движение.
Изучая движение в пространстве и во времени, устанавливают геометрические показатели движения — пройденный путь и траекторию движения. В то же время определяют качественные зависимости движения — быстроту движения и интенсивность ее изменения. Рассматривая тело в движении, отмечают начало и конец движения, и на этом отрезке определяют особенности движения.
Рассматривая тело в движении, отмечают начало и конец движения, и на этом отрезке определяют особенности движения.
В материальном мире покой и движение относительны. Наблюдаемые нами неподвижные тела (здания, сооружения, неработающие машины) находятся лишь в относительном покое, то есть в покое относительно Земли. В действительности они осуществляют сложное движение вместе с Землей в мировом пространстве.
В относительном покое можно рассматривать и некоторые подвижные тела. К примеру, неподвижный пассажир в движущемся вагоне находится в движении лишь по отношению к Земле, а по отношению к вагону он в покое.
Отсюда следует, что всякое движение относительно, так как рассматривается по отношению к определенным телам. Принцип относительности движения позволяет установить особенности его различных видов. Так, конец педали велосипеда по отношению к раме описывает окружность, а по отношению к Земле — сложную кривую.
Используя принцип относительности, можно неподвижное тело принять за подвижное, если рассматривать его относительно движущегося тела.
Именно такой эффект можно наблюдать из неподвижного вагона в тот момент, когда рядом расположенный состав находится в движении: нам кажется, что состав неподвижен, а в движении находится вагон, в котором мы находимся.
Таким образом, всякий покой и движение относительны, и рассматривать механическое движение необходимо в каждом случае с учетом конкретных условий движения и времени.
К основным понятиям кинематики относятся: траектория движения, его продолжительность, пройденный путь, скорость, ускорение.
Траекторией называют линию, которую описывает движущаяся точка в пространстве (рис. 15). Траектории весьма разнообразны: они могут иметь вид прямой линии, окружности, эллипса, параболы (I), циклоиды (II) и других кривых. Длина траектории при движении материальной точки характеризует пройденный путь. При движении по прямой от одной точки пространства к другой пройденный путь равен расстоянию между точками, при движении по другим траекториям путь получается больше расстояния.
Рис. 15
Величина пути и продолжительность движения во времени определяют скорость движения.
Скорость есть быстрота перемещения тел от одной точки пространства к другой, которая определяется величиной пути, проходимого за единицу времени.
Движение тела с постоянной скоростью называют равномерным, движение с переменной скоростью — переменным.
Величина, определяющая изменение скорости с течением времени, называется ускорением.
Рис. 16
Из рассмотрения основных понятий кинематики следует, что между кинематическими величинами механического движения существует тесная связь.
Пройденный путь, скорость и ускорение зависят от времени: с течением времени путь возрастает, а скорость и ускорение могут оставаться постоянными или меняться в большую или меньшую сторону.
Закон движения точки может быть выражен графически прямой или кривой линией в координатных осях пути и времени. На рис, 16, I график движения представлен кривой AB, каждая точка которой соответствует определенному пути и времени. Например, точка а показывает, что к концу 4-й секунды движения пройден путь 35 м.
На рис, 16, I график движения представлен кривой AB, каждая точка которой соответствует определенному пути и времени. Например, точка а показывает, что к концу 4-й секунды движения пройден путь 35 м.
Используя графический метод, можно построить график пути в зависимости от скорости и времени (рис. 16, II), график ускорения в зависимости от времени, график скорости в зависимости от времени и ускорения (рис. 16, III и IV). Следует иметь в виду, что график движения определяет не форму траектории, а зависимость между указанными величинами.
Кинематика имеет большое прикладное значение. На ее основе изучается движение звеньев механизмов и рабочих органов машин, делаются выводы, которые используются при проектировании новых механизмов, машин, приборов и других механических устройств.
Простейшие движения твердого тела.
 д. Движение, при котором тело перемещается по прямой и за равные отрезки времени проходит одинаковые пути, называется равномерным прямолинейным (рис. 17, I).
д. Движение, при котором тело перемещается по прямой и за равные отрезки времени проходит одинаковые пути, называется равномерным прямолинейным (рис. 17, I).
Рис. 17
Скорость равномерного движения определяется отношением пройденного пути ко времени движения. Единицы скорости устанавливаются по единицам пути и времени. Если, например, путь выражен в метрах, а время в секундах, то скорость получается в м/с. В таких единицах измеряют скорость течения воды по трубам, движение воздуха под действием вентилятора и т. д. Скорость резания металла на станках измеряют в м/мин, а скорость транспортных машин — в км/ч.
В движении тело может совершать различные перемещения с различными скоростями и ускорениями. Одно из таких перемещений — прямолинейное возвратно-поступательное движение (рис. 17, II). Наиболее типичный пример такого движения — поршень механизма двигателя внутреннего сгорания. Но в отличие от равномерного движения тела в первом примере, поршень движется неравномерно, так как при повороте кривошипа (коленчатого вала), с которым он сочленен, на равные углы, поршень проходит неравные пути.
Движение, при котором за равные отрезки времени тело проходит неравные пути, называют переменным или неравномерным. Такое движение происходит во время разбега машин или торможения.
В переменном движении скорость изменяется непрерывно, ее величина различна в каждый момент времени. Поэтому такую скорость называют мгновенной.
Движение, при котором скорость возрастает, называют ускоренны м, а прирост скорости за единицу времени называют ускорением. Численная величина ускорения определяется отношением разности мгновенных скоростей между рассматриваемыми точками пути ко времени, в течении которого происходило изменение скорости.
Движение тела по отношению к неподвижной системе отсчета называется абсолютным движением. Движение тела по отношению к движущейся системе отсчета называется относительным движением (рис. 17, III).
Криволинейное движение является одним из самых распространенных видов движения в механизмах многих машин. В криволинейном движении тело также занимает последовательные положения на траектории и в каждый момент времени имеет определенную мгновенную скорость.
В криволинейном движении тело также занимает последовательные положения на траектории и в каждый момент времени имеет определенную мгновенную скорость.
Криволинейным (рис. 17, IV) принято называть такое движение, при котором тело при перемещении описывает кривую линию — траекторию относительно выбранной системы отсчета.
Рассматривая положения тела через бесконечно малые отрезки времени, можно считать, что вектор скорости совпадает с направлением движения. Но так как направление в криволинейном движении непрерывно меняется, то и вектор скорости тела при переходе его в каждое новое положение изменяет свое направление по отношению к предыдущему направлению.
Таким образом, вектор скорости тела в криволинейном движении непрерывно изменяет свое направление соответственно форме траектории, оставаясь все время касательным к ней.
Этот вывод подтверждается многочисленными примерами из практики: раскаленные частицы камня и металла отлетают от точильного круга при его вращении по касательным; потоки воды в работающем центробежном насосе устремляются из колеса по касательным к ее окружностям; частицы при отрыве от общей массы тела на криволинейной траектории также отлетают по касательной к траектории в месте отрыва.
3.3. Поступательное и вращательное движения твердого тела. Поступательным называют такое движение, при котором все точки тела имеют одинаковые траектории. Если соединить две любые точки поступательно движущегося тела прямой линией, то эта прямая остается все время параллельна самой себе (рис. 18).
Рис. 18
Сохранение параллельности прямых во всех положениях тела — главный признак поступательного движения.
В большинстве случаев точки поступательно движущегося тела имеют прямолинейные траектории (рис. 18, I). В таком движении находятся, например, поршни компрессоров и насосов, транспортные машины на прямом участке пути и т. п.
Но могут быть случаи криволинейного поступательного движения (рис. 18, II). Так движется, например, рычаг, соединяющий ведущие колеса паровоза. Он прикреплен к колесам шарнирно на равном расстоянии от осей.
Благодаря этому при перекатывании колес по рельсам рычаг остается параллельным самому себе, а все точки (см. рис. 18) описывают в пространстве кривые векторного переноса (одинаковые кривые со сдвигом).
рис. 18) описывают в пространстве кривые векторного переноса (одинаковые кривые со сдвигом).
Сохранение параллельности линий движущегося тела возможно в том случае, когда все точки этих линий, перемещаясь из одного положения в другое, проходят одинаковый путь. Отсюда следует, что в поступательном движении все точки тела имеют одинаковые скорости и ускорения, поэтому для характеристики поступательно движущегося тела достаточно знать скорость и ускорение какой-либо одной его точки.
Вращательное движение широко распространено в природе и технике. Планеты Солнечной системы вращаются вокруг своей оси. Во многих механизмах и машинах так движутся валы, шкивы, зубчатые колеса, маховики и другие детали.
Вращательное движение характеризуется тем, что все точки тела описывают концентрические окружности относительно неподвижной оси, расположенной в пределах тела. Осью вращения называется геометрическое место точек, остающихся неподвижными при вращении тела (рис. 19).
19).
Рис. 19
Кинематическими параметрами вращающегося тела являются угловое перемещение, угловая скорость и угловое ускорение. Угловое перемещение измеряется величиной угла, на который поворачивается тело за время вращения. За единицу углового перемещения принят радиан — центральный угол, длина дуги которого равна радиусу этой дуги. 1 рад = 57,3°. Центральный угол содержит 360°: 57,3° = 6,28 или 2п рад.
Вращательное движение может быть равномерным и неравномерным. Равномерным называют такое вращение, при котором за равные промежутки времени тело поворачивается на равные углы. Величина поворота тела за единицу времени определяет угловую скорость.
Численная величина угловой скорости в равномерном вращательном движении определяется отношением углового перемещения ко времени, в течении которого происходит это перемещение.
В практических расчетах угловая скорость обычно выражается числом оборотов тела за одну минуту времени.
Рекомендуемая литература по курсу физики
Электронные версии изданий доступны тем, кто зарегистрирован на сайте ntb.mai.ru
а) основная литература:
Литература из электронного каталога:
- Савельев И. В. Курс общей физики Механика. Молекулярная физика Учеб. Пособие в 3-х тт/ Лань, 2007. — 432 с.
- Савельев И. В. Курс общей физики в 3 т. Т. 2: Электричество и магнетизм. Волны. Оптика/ Лань, 2007. — 496 с.
- Савельев И. В. Курс общей физики в 3 т. Т. 3: Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц / Лань, 2006. — 317 с.
4*. Анисимов В.М., Данилова И.Н., Пронина В.С., Солохина Г. Э. Лабораторные работы по физике Механика. Молекулярная физика и термодинамика Учеб. пособие для втузов. ВВИА им. Н. Е. Жуковского, 2008. — 226 с.
5*. Анисимов В.М., Третьякова О. Н. Практический курс физики. Механика Учеб. пособие для студентов вузов, обучающихся по техн. направлениям и специальностям. ВВИА им. Н. Е. Жуковского, 2008. — 168 с.
6*. Лаушкина Л.А., Солохина Г.Э., Хохлачева Г. М. Практический курс физики. Электричество Учеб. пособие для студентов вузов, обучающихся по направлениям подготовки и специальностям в области техники и технологии. ВВИА им. Н. Е. Жуковского, 2008. — 182 с.
7*. Лаушкина Л.А., Солохина Г.Э., Черкасова М. В. Практический курс физики. Молекулярная физика и термодинамика Учеб пособие для студентов вузов, обучающихся по направлениям и специальностям в обл. техники и технологии. Б.и., 2008. — 155 с.
8*. Анисимов В.М., Данилова И.Н., Пронина В.С., Солохина Г. Э. Лабораторные работы по физике Электричество. Оптика. Атомная физика. Физика твердого тела Учеб. пособие для втузов. ВВИА им. Н. Е. Жуковского, 2008. — 220 с.
9*. Соколова Е.Ю., Рудакова Л. И. Практический курс физики. Волновая оптика [Пособие для самостоят. работы студентов]. ВВИА им. Н. Е. Жуковского, 2008. — 135 с.
10*. Соколова Е.Ю., Мартыненко Т.П., Одинцова Г.А., Пронина В. С. Практический курс физики. Квантовая физика. Элементы физики твердого тела и ядерной физики Учеб. пособие для студентов вузов, обучающихся по техн. направлениям подготовки и специальностям в области техники и технологии. ВВИА им. Н. Е. Жуковского, 2008. — 209 с.
11. Бобошина С.Б., Измайлов Г. Н. Тепловые процессы Учеб. пособие. МАИ, 2016. — 97 с. http://elibrary.mai.ru/MegaPro/Download/ToView/1548?idb=NewMAI2014
12. Измайлов Г.Н., Озолин В. В. Лекции по курсу общей физики. Квантовая физика учеб. пособие для вузов по техн. направлениям подготовки и специальностям. МАИ, 2015. — 187 с. http://elibrary.mai.ru/MegaPro/Download/ToView/1409?idb=NewMAI2014
13. Бобошина С. Б., Измайлов Г. Н. Физические основы механики с приложениями к аэрокосмическим задачам Учеб. пособие. МАИ, 2017. — 111 с.
http://elibrary.mai.ru/MegaPro/Download/ToView/1961?idb=NewMAI2014
Б., Измайлов Г. Н. Физические основы механики с приложениями к аэрокосмическим задачам Учеб. пособие. МАИ, 2017. — 111 с.
http://elibrary.mai.ru/MegaPro/Download/ToView/1961?idb=NewMAI2014
14. Суров О.И., Демков В. П. Физика. Механика. Кинематика. Динамика. Законы сохранения. Учеб. пособие. МАИ, 2017. — 134 с. http://elibrary.mai.ru/MegaPro/Download/ToView/5321?idb=NewMAI2014
15.Демков В.П., Суров О. И. Физика. Механика. Вращательное движение. Механические колебания и волны. Специальная теория относительности. МАИ, 2018. http://elibrary.mai.ru/MegaPro/Download/ToView/10566?idb=NewMAI2014
16. Браун А.Г., Левитина И. Г. Атомная и ядерная физика. Элементы квантовой механики Практикум: учебное пособие для вузов по техн. направлениям подготовки и спец. ИНФРА-М, 2016. — 87 с. http://znanium.com/catalog.php?bookinfo=502451
17. Браун А.Г., Левитина И. Г. Элементы квантовой механики и физики атомного ядра Учебное пособие для вузов по техническим направлениям подготовки и спец. ИНФРА-М, 2015. — 84 с.
http://znanium.com/catalog.php?bookinfo=486392
ИНФРА-М, 2015. — 84 с.
http://znanium.com/catalog.php?bookinfo=486392
18. Демков В.П., Суров О.И., Ципенко А. В. Физика. Молекулярная физика. Тепловые явления Учеб. пособие. МАИ, 2019. — 155 с. http://elibrary.mai.ru/MegaPro/Download/ToView/21479?idb=NewMAI2014
19. Гаврилова А.Ю., Кули-Заде М.Е., Решетникова О.Ф., Скороход Е.П., Ципенко А. В. Основы механики. Физика для информатиков Учеб. пособие. МАИ, 2019. — 83 с. http://elibrary.mai.ru/MegaPro/Download/ToView/20733?idb=NewMAI2014
20. Решетникова О.Ф., Скороход Е.П., Ципенко А.В., Гаврилова А.Ю., Кули-ЗадеМ. Е. Основы теории поля и электричество. Физика для информатиков Учеб. пособие. МАИ, 2019. — 100 с. http://elibrary.mai.ru/MegaPro/Download/ToView/21465?idb=NewMAI2014
21. Гаврилова А.Ю., Кули-Заде М.Е., Решетникова О.Ф., Скороход Е.П., Ципенко А. В. Колебания и волновые процессы. Физика для информатиков Учеб. пособие. МАИ, 2019. — 74 с.
http://elibrary.mai.ru/MegaPro/Download/ToView/21471?idb=NewMAI2014
Физика для информатиков Учеб. пособие. МАИ, 2019. — 74 с.
http://elibrary.mai.ru/MegaPro/Download/ToView/21471?idb=NewMAI2014
*Пособия кафедры под номерами 4–10 в бумажном издании и в электронном (на странице кафедры) могут отличаться.
б) дополнительная литература:
Нет в каталоге:
- Матвеев А. Н. Механика и теория относительности. М., 2003 — 432с.
- Матвеев А. Н. Молекулярная физика. М.: Высшая школа, 1981.
- Матвеев А. Н. Электромагнетизм. М.: Высшая школа, 1985.
- Матвеев А. Н. Атомная физика. М.: Высшая школа, 1989.
Литература из электронного каталога:
- Иродов И. Е. Механика Основные законы: Учеб. пособие для вузов. Физматлит, 2000. — 320 с.
- Иродов И. Е. Электромагнетизм: Основные законы Учеб. пособие для вузов. Физматлит, 2000. — 351 с.
- Иродов И.
 Е. Квантовая физика: основные законы: учеб. пособие / М. : БИНОМ. Лаб. знаний, 2010. — 256 с.
Е. Квантовая физика: основные законы: учеб. пособие / М. : БИНОМ. Лаб. знаний, 2010. — 256 с. - Иродов И. Е. Задачи по общей физике учеб. пособие для вузов по естественнонаучным, педагог. и техн. направлениям и спец. Лань, 2016. — 416 с. https://e.lanbook.com/book/111196
- Воробьев А.А., Чертов А. Г. Задачник по физике. Физматлит, 2002. — 636 с.
- Бабецкий В.И., Третьякова О. Н. Прикладная физика. Механика. Электромагнетизм учеб. пособие для вузов по инженерно-технич. и естественнонаучным направления, а также для студентов, изучающих курс общей физики. Юрайт, 2017. — 335 с. https://biblio-online.ru/book/7AAD2FE1-315E-44FE-B45A-84E44FCAA49F?idb=NewMAI2014
- Бабецкий В.И., Третьякова О. Н. Механика в примерах и задачах учеб. пособие для академического бакалавриата вузов по инженерно-технич. и естественнонауч. направлениям, а также для студентов младших курсов, изучающих курс общей физики.
 Юрайт, 2017. — 92 с.
Юрайт, 2017. — 92 с. - Бондарев Б.В., Калашников Н.П., Спирин Г. Г. Курс общей физики: В 3-х кн. Механика Учеб. пособие для втузов. Высш.шк., 2005. — 352 с.
- Бондарев Б.В., Калашников Н.П., Спирин Г. Г. Курс общей физики Электромагнетизм. Волновая оптика. Квантовая физика Учеб. пособие для втузов: В 3-х кн. Высш.шк., 2005. — 438 с.
- Бондарев Б.В., Калашников Н.П., Спирин Г. Г. Курс общей физики: В 3-х кн. Термодинамика. Статистическая физика. Строение вещества Учеб. пособие для втузов. Высш. шк., 2005. — 366 с.
- Браун А.Г., Левитина И. Г. Основы статистической физики: учеб. пособие для вузов М. : ИНФРА-М, 2015. — 120 с. http://znanium.com/catalog.php?bookinfo=478437
- Детлаф А.А., Яворский Б. М. Курс физики Учеб. пособие для вузов. Высш. шк., 2002. — 718 с.
- Анисимов В.М., Лаушкина Л.А., Третьякова О. Н. Физика в задачах Учеб. пособие для втузов. Вузовская книга, 2007. — 239 с.
- Сивухин Д.
 В. Общий курс физики Термодинамика и молекулярная физика Учеб. пособие для вузов: в 5 т. Физматлит, 2011. — 543 с.
В. Общий курс физики Термодинамика и молекулярная физика Учеб. пособие для вузов: в 5 т. Физматлит, 2011. — 543 с. - Сивухин Д. В. Механика Общий курс физики Учеб. пособие для вузов: в 5 т. Физматлит, 2010. — 560 с.
- Сивухин Д. В. Общий курс физики Электричество учеб. пособие для студентов физ. спец. вузов. Физматлит, 2009. — 654 с.
- Сивухин Д. В. Атомная и ядерная физика Общий курс физики Учеб.пособие для физ.спец.вузов. Физматлит МФТИ, 2002. — 782 с.
- Сивухин Д. В. Общий курс физики Оптика Учеб. пособие для физ.спец.вузов. Физматлит МФТИ, 2002. — 791 с.
- Калашников С. Г. Электричество учеб. пособие для физ. спец. вузов. Физматлит, 2008. — 624 с.
- Ландсберг Г. С. Электричество. Магнетизм Элементарный учебник физики В 3-х т. Физматлит, 2000. — 480 с.
- Ландсберг Г. С. Колебания и волны. Оптика. Атомная и ядерная физика Элементарный учебник физики В 3-х т. Физматлит, 2000. — 656 с.
- Ландсберг Г.
 С. Оптика учеб. пособие для физ. спец. вузов. Физматлит, 2006. — 848 с.
С. Оптика учеб. пособие для физ. спец. вузов. Физматлит, 2006. — 848 с. - Кикоин А.К., Кикоин И. К. Молекулярная физика учеб. пособие для физ. спец. вузов. Наука, 1976. — 480 с.
Кинематика (скорость, ускорение, путь). Формулы, примеры решения
В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.
Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.
Траектория, радиус-вектор, закон движения тела
Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.
Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.
Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.
Радиус-вектор – вектор, задающий положение точки в пространстве.
Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.
Перемещение и путь
Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.
В системе СИ перемещение и длина пути измеряются в метрах.
Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.
Скорость и ускорение
Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло
А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.
Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.
Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.
В системе СИ скорость измеряется в метрах в секунду
Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.
Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости
Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.
Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории
Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.
Здесь R – радиус окружности, по которой движется тело.
Закон равноускоренного движения
Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.
Здесь – x нулевое- начальная координата. v нулевое – начальная скорость. Продифференцируем по времени, и получим скорость
Производная по скорости от времени даст значение ускорения a, которое является константой.
Пример решения задачи
Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. 2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.
2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.
Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.
Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.
Учебная работа (кафедра Теоретической механики)
Учебная работа
Кафедра традиционно преподает дисциплину «Теоретическая механика» для студентов НГАСУ (Сибстрин). Механика – одна из важнейших дисциплин, изучаемых в техническом ВУЗе. Она, будучи научной основой практически всех направлений развития современной техники, является хорошо отработанной замкнутой аксиоматической фундаментальной наукой, развивающей в том числе и логику мышления. На знаниях, полученных при изучении теоретической механики, базируется большая часть изучаемых на старших курсах технических дисциплин.
На знаниях, полученных при изучении теоретической механики, базируется большая часть изучаемых на старших курсах технических дисциплин.
Значимость дисциплины диктует уровень требований, предъявляемых ее профессорско-преподавательским составом к знаниям студентов. В то же время кафедра делает все, чтобы обеспечить студента необходимым учебно-методическим материалом. Только за последние десять лет были изданы учебник «Лекции по теоретической механике» (В.Я. Рудяк, В.А. Юдин), более десяти учебных пособий, необходимые методические указания. Эта литература позволила обеспечить планомерный переход к системе «бакалавриат – магистратура». На кафедре разработан мультимедийный курсы теоретической механики, который все преподаватели используют при проведении занятий. Кафедра первой в Университете ввела в учебный процесс рейтинговую систему оценку знаний, мотивирующую студента к регулярному изучению дисциплины. В настоящее время ведется работа над интерактивными учебными пособиями.
Особое внимание преподаватели кафедры уделяют индивидуальной работе с студентами, не боящимися решать задачи нестандартные, требующие не только отличного знания предмета, но и смекалки, фантазии, умения найти оптимальный путь к решению. Студентам доступны задачи повышенной сложности и реферативный материал. Под руководством В.А. Юдина работает специализированная учебная группа, проводятся Олимпиады по ТМ.
Одной из целей кафедры является расширение перечня преподаваемых дисциплин, созданию актуальных и востребованных учебных программ, С 2019 года ППС кафедры ТМ преподает дисциплины «Основы строительной механики» (П.В. Александров, Е.Г. Борд), «Основы научных исследований» (В.Я. Рудяк, А.А. Белкин).
Кафедра теоретической механики в 2020-21 учебном году
предлагает студентам НГАСУ (Сибстрин) следующие
темы научно-исследовательской работы:
-
Моделирование методом молекулярной динамики вязкости и теплопроводности наножидкостей на основе воды (руководитель Краснолуцкий С.
 Л.).
Л.). -
Молекулярно-динамическое моделирование вязкости жидкости в наноканалах (руководитель Белкин А.А.).
-
Стохастический алгоритм моделирования процесса диффузии наночастицы в разреженном газе (руководитель Лежнев Е.В.).
-
Изучение структуры наножидкостей (руководитель Белкин А.А.).
-
Устойчивость обводненных оснований в условиях циклического теплообмена (руководитель Борд Е.Г.).
На кафедре в 2020-21 учебном году работают два научных студенческих кружка:
-
Кружок углубленного изучения теоретической механики. На занятиях решаются нестандартные задачи, задачи повышенной сложности, помогающие студенту лучше освоить курс механики, формируются и готовятся команды для участия в Олимпиадах по ТМ.
 Руководит занятиями доктор физ.-мат. наук профессор В.А. Юдин.
Руководит занятиями доктор физ.-мат. наук профессор В.А. Юдин. -
Научно-исследовательский кружок по изучению свойств переноса в газах, жидкостях и наножидкостях. Руководит занятиями доктор физ.-мат. наук, завкафедрой А.А. Белкин. Время занятий может изменяться, информация размещается на странице https://vk.com/club171787929.
В 2020-21 учебном году планируется участие студентов в следующих мероприятиях:
-
Международная и Всероссийская олимпиады по теоретической механике.
-
Региональная олимпиада по теоретической механике.
-
Олимпиады НГАСУ (Сибстрин) по теоретической механике.
-
Научно техническая студенческая конференция НГАСУ (Сибстрин).
Планируется участие студентов в грантах РФФИ и НГАСУ (Сибстрин), публикация по крайней мере одной совместной со студентами статьи в изданиях из списка ВАК и три публикации в материалах конференции НГАСУ (Сибстрин).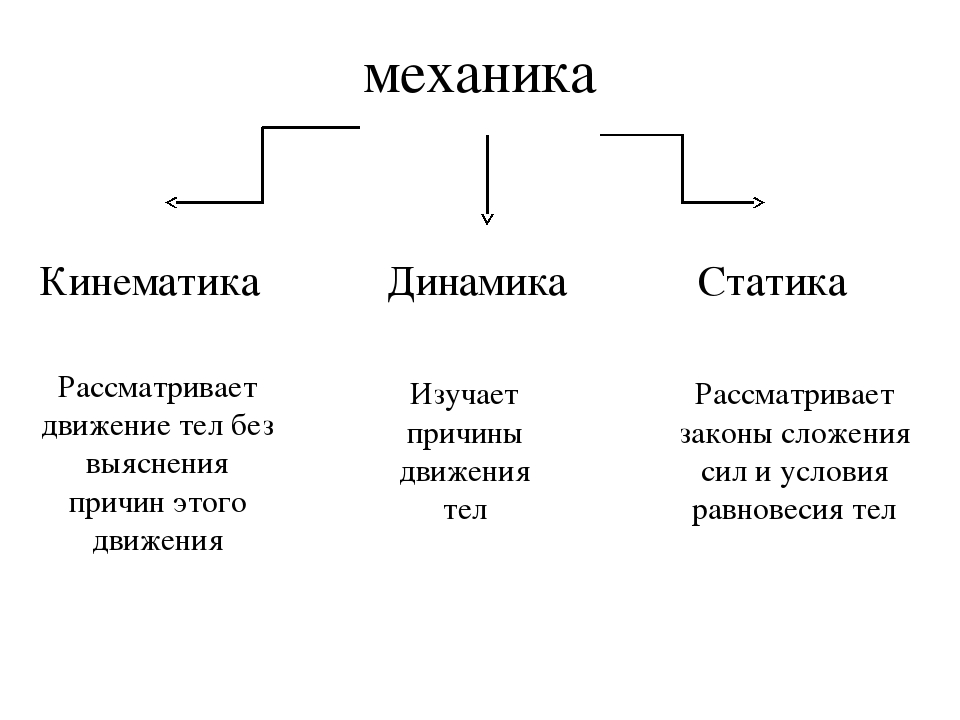
читать .pdf файл
Памятка для студентов первого курса всех специальностей дневной формы обучения.
Памятка для студентов второго курса 3 сем СУЗС.
Памятка для студентов второго курса 3 семестр прикладной бакалавриат. Строительство.
Памятка для студентов второго курса 3 семестр академический баклавриат. ПиВ.
Памятка для студентов второго курса 3 семестр академический бакалавриат. Строительство.
- ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ. СТАТИКА. Лекция 1 – Лекция 4.
- ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ. СТАТИКА. Лекция 5 – Лекция 8.
- СБОРНИК ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
 СТАТИКА. 2004.
СТАТИКА. 2004. - СБОРНИК ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ. СТАТИКА. 2018.
- ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ. 2007.
- ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ. КИНЕМАТИКА. ЛЕКЦИЯ 9 – ЛЕКЦИЯ 12.
- ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ. КИНЕМАТИКА. ЛЕКЦИЯ 13 – ЛЕКЦИЯ 14.
- СБОРНИК ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ. КИНЕМАТИКА. 2007.
- ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. 2013.
- СБОРНИК ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ. ДИНАМИКА.
- СБОРНИК ТЕСТОВЫХ ЗАДАНИЙ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ. ДИНАМИКА ТОЧКИ. 2015.
- ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ. 2016.
- КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ. 2017.
- ЛЕКЦИИ ПО ДИНАМИКЕ ТОЧКИ. 2014.
- ЛЕКЦИИ ПО ОБЩИМ ТЕОРЕМАМ ДИНАМИКИ МЕХАНИЧЕСКИХ СИСТЕМ. 2015.
- ДОПОЛНИТЕЛЬНЫЕ ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ. 2017.
- ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА.
 2013.
2013. - В.А.Юдин ЛЕКЦИИ ПО АНАЛИТИЧЕСКОЙ МЕХАНИКЕ, 2016
- В.А.Юдин, Е.В.Лежнев Задачи для углубленного изучения теоретической механики. Статика, 2018
- В.А.Юдин, Е.В.Лежнев Задачи для углубленного изучения теоретической механики. Кинематика, 2019
- В.А.Юдин, Т.А.Перегутова Задачи для углубленного изучения теоретической механики. Динамика, 2021
Кинематика (физика) – это… Что такое Кинематика (физика)?
У этого термина существуют и другие значения, см. Кинематика.Кинема́тика (греч. κινειν — двигаться) в физике — раздел механики, изучающий математическое описание (средствами геометрии, алгебры, математического анализа…) движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т. д.). Исходные понятия кинематики — пространство и время. Например, если тело движется по окружности, то кинематика предсказывает необходимость существования центростремительного ускорения без уточнения того, какую природу имеет сила, его порождающая. Причинами возникновения механического движения занимается другой раздел механики — динамика.
Причинами возникновения механического движения занимается другой раздел механики — динамика.
Различают классическую кинематику, в которой пространственные (длины отрезков) и временные (промежутки времени) характеристики движения считаются абсолютными, то есть не зависящими от выбора системы отсчёта, и релятивистскую. В последней длины отрезков и промежутки времени между двумя событиями могут изменяться при переходе от одной системы отсчёта к другой. Относительной становится также одновременность. В релятивистской механике вместо отдельных понятий пространство и время вводится понятие пространства-времени, в котором инвариантным относительно преобразований Лоренца является величина, называемая интервалом.
История кинематики
Долгое время понятия о кинематике были основаны на работах Аристотеля, в которых утверждалось, что скорость падения пропорциональна весу тела, а движение в отсутствие сил невозможно. Только в конце XVI века этим вопросом подробно занялся Галилео Галилей. Изучая свободное падение (знаменитые опыты на Пизанской башне) и инерцию тел, он доказал неправильность идей Аристотеля. Итоги своей работы по данной теме он изложил в книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению»[1].
Изучая свободное падение (знаменитые опыты на Пизанской башне) и инерцию тел, он доказал неправильность идей Аристотеля. Итоги своей работы по данной теме он изложил в книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению»[1].
Рождением современной кинематики можно считать выступление Пьера Вариньона перед Французской Академией наук 20 января 1700 года. Тогда впервые были даны понятия скорости и ускорения в дифференциальном виде.
В XVIII веке Ампер первый использовал вариационное исчисление в кинематике.
После создания СТО, показывающей, что время и пространство не абсолютны и скорость имеет принципиальное ограничение, кинематика вошла в новый этап развития в рамках релятивистской механики (см. Релятивистская кинематика).
Основные понятия кинематики
Задачи кинематики
Главной задачей кинематики является математическое (уравнениями, графиками, таблицами и т. п.) определение положения и характеристик движения точек или тел во времени. Любое движение рассматривается в определённой системе отсчёта. Также кинематика занимается изучением составных движений (движений в двух взаимно перемещающихся системах отсчёта).
п.) определение положения и характеристик движения точек или тел во времени. Любое движение рассматривается в определённой системе отсчёта. Также кинематика занимается изучением составных движений (движений в двух взаимно перемещающихся системах отсчёта).
Положение точки (или тела) относительно заданной системы отсчёта определяется некоторым количеством взаимно независимых функций координат:
- ,
где определяется количеством степеней свободы. Так как точка не может быть в нескольких местах одновременно, все функции должны быть однозначными. Также в классической механике выдвигается требование их дифференцируемости на промежутках. Производные этих функций определяют скорость тела[2].
Скорость движения определяется как производная координат по времени:
- ,
где — единичные векторы, направленные вдоль соответствующих координат.
Ускорение определяется как производная скорости по времени:
Следовательно, характер движения можно определить, зная зависимость скорости и ускорения от времени. А если кроме этого известны ещё и значения скорости/координат в определённый момент времени, то движение полностью задано.
А если кроме этого известны ещё и значения скорости/координат в определённый момент времени, то движение полностью задано.
Деление кинематики по типам объекта исследования
В зависимости от свойств изучаемого объекта, кинематика делится на кинематику точки, кинематику твёрдого тела, кинематику деформируемого тела, кинематику газа, кинематику жидкости и т. д.
Кинематика точки
Основная статья: Кинематика точки
Кинематика точки изучает движение материальных точек — тел, размерами которых можно пренебречь по сравнению с характерными размерами изучаемого явления. Поэтому в кинематике точки скорость, ускорение, координаты всех точек тела считаются равными.
Частные случаи движения в кинематике точки:
- Если ускорение равно нулю, движение прямолинейное (траектория представляет собой прямую) и равномерное (скорость постоянна).
- ,
где — длина пути траектории за промежуток времени от до , — проекции на соответствующие оси координат.
- Если ускорение постоянно и лежит в одной прямой со скоростью, движение прямолинейное, равнопеременное (равноускоренное, если ускорение и скорость направлены в одном направлении; равнозамедленное — если в разные).
- ,
где — длина пути траектории за промежуток времени от до , — проекции на соответствующие оси координат, — проекции на соответствующие оси координат.
- Если ускорение постоянно и перпендикулярно скорости, движение происходит по окружности — вращательное движение.
- ,
где — радиус окружности, по которой движется тело.
Если выбрать систему декартовых координат xyz так, чтобы центр координат был в центре окружности, по которой движется точка, оси y и x лежали в плоскости этой окружности, так чтобы движение осуществлялось против часовой стрелки, то значения координат можно вычислить по формулам:
Для перехода в другие системы координат используются преобразования Галилея для скоростей намного меньших скорости света, и преобразования Лоренца для скоростей, сравнимых со скоростью света.
- Если ускорение постоянно и не лежит на одной прямой с начальной скоростью, движение параболическое.
Если выбрать систему декартовых координат xyz так, чтобы ускорение и начальная скорость лежали в плоскости xy и ускорение было сонаправленно с осью y, то значения координат можно вычислить по формулам:
- ,
где и — проекции на соответствующие оси.
Для перехода в другие системы координат используются преобразования Галилея для скоростей намного меньших скорости света, и преобразования Лоренца для скоростей, сравнимых со скоростью света.
- Если тело выполняет разные движения в разных направлениях, то эти движения могут рассчитываться отдельно и складываться по принципу суперпозиции. Например, если в одной плоскости тело совершает вращательное движение, а по оси, перпендикулярной этой плоскости — равномерное поступательное, то вид движения — винтовая линия с постоянным шагом.

- В общем виде скорость, ускорение и координаты вычисляются по общим формулам (см. задачи кинематики), путь вычисляется по формуле:
Кинематика твёрдого тела
Кинематика твёрдого тела изучает движение абсолютно твёрдых тел (тел, расстояние между двумя любыми точками которого не может изменяться).
Так как любое тело ненулевого объёма имеет бесконечное число точек, и соответственно бесконечное число фиксированных связей между ними, тело имеет 6 степеней свободы и его положение в пространстве определяется шестью координатами (если нет дополнительных условий).
Связь скорости двух точек твердого тела выражается через формулу Эйлера:
- ,
где — вектор угловой скорости тела.
Кинематика деформируемого тела, Кинематика жидкости
Основные статьи: Кинематика деформируемого тела, Кинематика жидкости
Кинематика деформируемого тела и кинематика жидкости относятся к кинематике непрерывной среды.
Кинематика газа
Основная статья: Кинематика газа
Кинематика газа изучает деление газа на скопления при движении и описывает движение этих скоплений. В рамках кинематики газа описываются не только основные параметры движения, но и типы движения газа.
Примечания
Литература
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. — М.: Изд-во Физического факультета МГУ, 1997.
- Матвеев. А. Н. Механика и теория относительности. — М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
- Павленко Ю. Г. Лекции по теоретической механике. — М.: ФИЗМАТЛИТ, 2002. — 392 с.
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. — М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560с.
- Стрелков С. П. Механика. — М.: Наука, 1975.
- Яворский Б. М., Детлаф А. А. Справочник по физике для инженеров и студентов вузов (4-е изд.
 ). — М.: Наука, 1968.
). — М.: Наука, 1968.
Техническая механика – Тема 1.6. Основные понятия кинематики
Рис.3. Координаты точки М
Материальная точка – тело, размерами которого в данных условиях можно пренебречь.
Этой моделью пользуются в тех случаях, когда линейные размеры рассматриваемых тел много меньше всех прочих расстояний в данной задаче или когда тело движется поступательно.
Основной задачей кинематики точки является изучение законов движения точки. Зависимость между произвольными положениями движущейся точки в пространстве и времени определяет закон ее движения. Закон движения точки считают известным, если можно определить положение точки в пространстве в произвольный момент времени. Положение точки рассматривается по отношению к выбранной системе координат.
Поступательным называется движение тела, при котором прямая, проходящая через любые две точки тела, перемещается, оставаясь параллельной самой себе. При поступательном движении все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки.
При поступательном движении все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки.
В дальнейшем под словом “тело” будем понимать “материальная точка”.
Линия, которую описывает движущееся тело в определенной системе отсчета, называется траекторией. Вид траектории зависит от выбора системы отсчета.
В зависимости от вида траектории различают прямолинейное и криволинейное движение.
Путь s – скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Путь всегда положителен: s> 0.Единицы измерения в системе СИ: м (метр).
Перемещение тела за определенный промежуток времени – направленный отрезок прямой, соединяющий начальное (точка М0) и конечное (точка М) положение тела (см. рис. 2):
рис. 2):
,
где и — радиус-векторы тела в эти моменты времени.Единицы измерения в системе СИ: м (метр).
Проекция перемещения на ось Ох: ∆rx =∆х = х-х0, где x0 и x – координаты тела в начальный и конечный моменты времени.
Модуль перемещения не может быть больше пути: ≤s.
Знак равенства относится к случаю прямолинейного движения, если направление движения не изменяется.
Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:
Вступительное испытание – Физика
СОДЕРЖАНИЕ ПРОГРАММЫ
Механика
Кинематика. Механическое движение. Относительность движения. Система отсчета. Материальная точка. Траектория. Путь и перемещение. Скорость. Ускорение.
Равномерное и равноускоренное прямолинейное движение. Свободное падение тел. Ускорение свободного падения. Уравнение прямолинейного равноускоренного движения.
Криволинейное движение точки на примере движения по окружности с постоянной по модули скоростью. Центростремительное ускорение.
Центростремительное ускорение.
Основы динамики. Инерция. Первый закон Ньютона. Инерциальные системы отсчета.
Взаимодействие тел. Масса. Импульс. Сила. Второй закон Ньютона.
Силы в природе. Сила тяготения. Закон всемирного тяготения. Вес тела. Невесомость. Первая космическая скорость. Сила упругости. Закон Гука. Сила трения. Коэффициент трения.
Третий закон Ньютона.
Момент силы. Условие равновесия тел.
Законы сохранения в механике. Закон сохранения импульса. Механическая работа. Мощность. Кинетическая энергия. Потенциальная энергия. Закон сохранения энергии в механике.
Молекулярная физика. Термодинамика
Основы молекулярно-кинетической теории. Опытное обоснование основных положений молекулярно-кинетической теории. Масса и размер молекул. Измерение скорости молекул. Опыт Штерна. Количество вещества. Моль. Постоянная Авогадро. Взаимодействие молекул.
Основы термодинамики. Тепловое равновесие. Температура и её измерение. Абсолютная температурная шкала. Внутренняя энергия. Количество теплоты. Теплоемкость вещества. Работа в термодинамике. Первый закон термодинамики. Изотермический, изохорный и изобарный процессы. Адиабатный процесс.
Температура и её измерение. Абсолютная температурная шкала. Внутренняя энергия. Количество теплоты. Теплоемкость вещества. Работа в термодинамике. Первый закон термодинамики. Изотермический, изохорный и изобарный процессы. Адиабатный процесс.
Преобразование энергии в тепловых двигателях. КПД теплового двигателя.
Идеальный газ. Связь между давлением и средней кинетической энергией молекул идеального газа.. Связь температуры со средней кинетической энергией частиц газа.
Уравнение Клапейрона-Менделеева. Универсальная газовая постоянная.
Основы электродинамики
Электростатика. Электризация тел. Электрический заряд. Взаимодействие зарядов. Элементарный электрический заряд. Закон сохранения электрического заряда. Закон Кулона.
Электрическое поле. Напряженность электрического поля. Электрическое поле точечного заряда. Потенциальность электростатического поля. Разность потенциалов. Принцип суперпозиции полей.
Проводники в электрическом поле. Электрическая ёмкость. Конденсатор. Емкость плоского конденсатора.
Электрическая ёмкость. Конденсатор. Емкость плоского конденсатора.
Диэлектрики в электрическом поле. Диэлектрическая проницаемость. Энергия электрического поля плоского конденсатора.
Постоянный электрический ток. Электрический ток. Сила тока. Напряжение. Носители свободных электрических зарядов в металлах, жидкостях и газах. Сопротивление проводников. Закон Ома для участка цепи. Последовательное и параллельное соединение проводников. Электродвижущая сила. Закон Ома для полной цепи. Работа и мощность тока. Закон Джоуля-Ленца.
Магнитное поле. Электромагнитная индукция. Взаимодействие магнитов. Взаимодействие проводников с током. Магнитное поле. Действие магнитного поля на электрические заряды. Индукции магнитного поля. Сила Ампера. Сила Лоренца. Магнитный поток.
Электромагнитная индукция. Закон электромагнитной индукции Фарадея. Самоиндукция. Индуктивность. Энергия магнитного поля.
Колебания и волны
Механические колебания и волны. Гармонические колебания. Амплитуда, период и частота колебаний. Свободные колебания. Математический маятник. Период колебаний математического маятника.
Гармонические колебания. Амплитуда, период и частота колебаний. Свободные колебания. Математический маятник. Период колебаний математического маятника.
Превращение энергии при гармонических колебаниях. Вынужденные колебания. Резонанс.
Механические волны. Скорость распространения волны. Длина волны. Поперечные и продольные волны. Звук.
Электромагнитные колебания и волны. Колебательный контур. Свободные электромагнитные колебания в контуре. Превращение энергии в колебательном контуре. Собственная частота колебаний в контуре.
Электромагнитные волны. Скорость распространения электромагнитных волн. Шкала электромагнитных волн.
Оптика
Законы отражения и преломления света. Показатель преломления. Полное отражение. Предельный угол полного отражения. Собирающая и рассеивающая линзы. Формула тонкой линзы. Построение изображений в линзах.
Интерференция света. Дифракция света. Дифракционная решетка.
Квантовая физика
Постоянная Планка. Фотоэффект. Опыты Столетова. Уравнение Эйнштейна для фотоэффекта.
Фотоэффект. Опыты Столетова. Уравнение Эйнштейна для фотоэффекта.
Радиоактивность. Альфа-, бета-, гамма-излучения.
Опыт Резерфорда по рассеянию a-частиц. Планетарная модель атома.
Закон радиоактивного распада. Заряд ядра. Массовое число ядра. Энергия связи частиц в ядре. Деление ядер. Синтез ядер. Ядерные реакции. Сохранение заряда и массового числа при ядерных реакциях. Выделение энергии при делении и синтезе ядер.
Основы кинематики | Безграничная физика
Определение кинематики
Кинематика – это исследование движения точек, объектов и групп объектов без учета причин их движения.
Цели обучения
Определить кинематику
Основные выводы
Ключевые моменты
- Для описания движения кинематика изучает траектории точек, линий и других геометрических объектов.
- Изучение кинематики можно абстрагировать в чисто математических выражениях.
- Кинематические уравнения могут использоваться для расчета различных аспектов движения, таких как скорость, ускорение, смещение и время.

Ключевые термины
- кинематика : Раздел механики, имеющий отношение к движущимся объектам, но не к задействованным силам.
Кинематика – это раздел классической механики, который описывает движение точек, объектов и систем групп объектов без ссылки на причины движения (т.е., силы). Изучение кинематики часто называют «геометрией движения».
Объекты вращаются вокруг нас. Все, от теннисного матча до полета космического зонда над планетой Нептун, связано с движением. Когда вы отдыхаете, ваше сердце перемещает кровь по венам. Даже в неодушевленных предметах есть непрерывное движение в колебаниях атомов и молекул. Могут возникнуть интересные вопросы о движении: сколько времени потребуется космическому зонду, чтобы добраться до Марса? Куда приземлится футбольный мяч, если его бросить под определенным углом? Однако понимание движения также является ключом к пониманию других концепций физики.Например, понимание ускорения имеет решающее значение для изучения силы.
Для описания движения кинематика изучает траектории точек, линий и других геометрических объектов, а также их дифференциальные свойства (такие как скорость и ускорение). Кинематика используется в астрофизике для описания движения небесных тел и систем; и в машиностроении, робототехнике и биомеханике для описания движения систем, состоящих из соединенных частей (таких как двигатель, роботизированная рука или скелет человеческого тела).
Формальное изучение физики начинается с кинематики. Слово «кинематика» происходит от греческого слова «kinesis», означающего движение, и связано с другими английскими словами, такими как «cinema» (фильмы) и «kinesiology» (изучение движения человека). Кинематический анализ – это процесс измерения кинематических величин, используемых для описания движения. Изучение кинематики можно абстрагировать в чисто математических выражениях, которые можно использовать для расчета различных аспектов движения, таких как скорость, ускорение, смещение, время и траектория.
Кинематика траектории частицы : кинематические уравнения могут использоваться для расчета траектории частиц или объектов. Физические величины, относящиеся к движению частицы, включают: массу m, положение r, скорость v, ускорение a.
Системы отсчета и смещение
Чтобы описать движение объекта, необходимо указать его положение относительно удобной системы отсчета.
Цели обучения
Оценить смещение в системе координат.
Основные выводы
Ключевые моменты
- Выбор системы отсчета требует решения, где находится исходное положение объекта и какое направление будет считаться положительным.
- Допустимые системы отсчета могут отличаться друг от друга перемещением друг относительно друга.
- Опорные рамки особенно важны при описании смещения объекта.
- Смещение – это изменение положения объекта относительно его системы отсчета.
Ключевые термины
- смещение : векторная величина, которая обозначает расстояние с направленным компонентом.

- рамка отсчета : система координат или набор осей, в пределах которых можно измерить положение, ориентацию и другие свойства объектов в ней.
Чтобы описать движение объекта, вы должны сначала описать его положение – где он находится в любой конкретный момент времени. Точнее, нужно указать его положение относительно удобной системы отсчета.Земля часто используется в качестве системы отсчета, и мы часто описываем положение объектов, связанных с их положением на Землю или от нее. Математически положение объекта обычно представлено переменной x .
Справочная информация
Есть два варианта, которые вы должны сделать, чтобы определить переменную положения x . Вы должны решить, где поставить x = 0 и какое направление будет положительным. Это называется выбором системы координат или выбором системы отсчета.Пока вы последовательны, любой фрейм одинаково действителен. Но вы не хотите менять систему координат во время расчета. Представьте, что вы сидите в поезде на станции и вдруг замечаете, что станция движется назад. Большинство людей сказали бы, что они просто не заметили, что поезд движется – только казался , как движение станции. Но это показывает, что существует третий и произвольный выбор, связанный с выбором системы координат: действительные системы отсчета могут отличаться друг от друга, перемещаясь друг относительно друга.Может показаться странным использовать систему координат, движущуюся относительно земли, но, например, система координат, движущаяся вместе с поездом, может быть гораздо более удобной для описания вещей, происходящих внутри поезда. Рамки отсчета особенно важны при описании смещения объекта.
Представьте, что вы сидите в поезде на станции и вдруг замечаете, что станция движется назад. Большинство людей сказали бы, что они просто не заметили, что поезд движется – только казался , как движение станции. Но это показывает, что существует третий и произвольный выбор, связанный с выбором системы координат: действительные системы отсчета могут отличаться друг от друга, перемещаясь друг относительно друга.Может показаться странным использовать систему координат, движущуюся относительно земли, но, например, система координат, движущаяся вместе с поездом, может быть гораздо более удобной для описания вещей, происходящих внутри поезда. Рамки отсчета особенно важны при описании смещения объекта.
СПРАВОЧНИКИ профессора Хьюма и профессора Дональда Айви из Университета Торонто
В этом классическом фильме профессора Хьюм и Айви умело иллюстрируют системы отсчета и различают фиксированные и подвижные системы отсчета.
youtube.com/embed/b4xmHNgiYtA?feature=oembed&rel=0″ frameborder=”0″ allow=”accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture” allowfullscreen=””/>
Frames of Reference (1960) Обучающий фильм : Frames of Reference – образовательный фильм 1960 года, созданный Комитетом по изучению физических наук. Фильм предназначен для показа на курсах физики в средней школе. В фильме профессора физики Университета Торонто Паттерсон Хьюм и Дональд Айви объясняют различие между инерциальной и неинтерциальной системами отсчета, демонстрируя эти концепции с помощью юмористических трюков с камерой. Например, фильм открывается с Доктора.Хьюм, который кажется перевернутым, обвиняет доктора Айви в том, что он перевернут. Только когда пара подбрасывает монету, становится очевидно, что доктор Айви – и камера – действительно перевернуты. Юмор фильма служит как для заинтересованности студентов, так и для демонстрации обсуждаемых концепций. В этом фильме PSSC используется увлекательный набор, состоящий из вращающегося стола и мебели, занимающих неожиданно непредсказуемые места в зоне просмотра. Прекрасная кинематография Авраама Морочника и забавное повествование профессоров Университета Торонто Дональда Айви и Паттерсона Хьюма – прекрасный пример того, как творческая группа кинематографистов может весело провести время с предметом, который другие, менее творческие люди могут найти в прохожих.Продюсер: Ричард Ликок Продюсерская компания: Educational Development Corp. Спонсор: Эрик Престамон
Прекрасная кинематография Авраама Морочника и забавное повествование профессоров Университета Торонто Дональда Айви и Паттерсона Хьюма – прекрасный пример того, как творческая группа кинематографистов может весело провести время с предметом, который другие, менее творческие люди могут найти в прохожих.Продюсер: Ричард Ликок Продюсерская компания: Educational Development Corp. Спонсор: Эрик Престамон
Рабочий объем
Смещение – это изменение положения объекта относительно его системы отсчета. Например, если автомобиль движется из дома в продуктовый магазин, его перемещение – это относительное расстояние продуктового магазина до системы отсчета или дома. Слово «смещение» означает, что объект переместился или был перемещен. Смещение – это изменение положения объекта, которое математически можно представить следующим образом:
[латекс] \ Delta \ text {x} = \ text {x} _ \ text {f} – \ text {x} _0 [/ latex]
, где Δ x – смещение, x f – конечное положение, а x 0 – начальное положение.
показывает важность использования системы координат при описании перемещения пассажира в самолете.
Смещение в системе ведения : Пассажир перемещается со своего места на заднюю часть самолета. Его расположение относительно самолета указано x. Смещение пассажира на -4,0 м относительно самолета показано стрелкой в направлении задней части самолета. Обратите внимание, что стрелка, обозначающая его перемещение, вдвое длиннее стрелки, обозначающей перемещение профессора (он перемещается вдвое дальше).
Введение в скаляры и векторы
Вектор – это любая величина, имеющая как величину, так и направление, тогда как скаляр имеет только величину.
Цели обучения
Определите разницу между скалярами и векторами
Основные выводы
Ключевые моменты
- Вектор – это любая величина, имеющая величину и направление.
- Скаляр – это любая величина, которая имеет величину, но не имеет направления.

- Смещение и скорость – это векторы, а расстояние и скорость – скаляры.
Ключевые термины
- скаляр : величина, имеющая величину, но не направление; сравнить вектор.
- вектор : Направленная величина, имеющая как величину, так и направление; между двумя точками.
В чем разница между расстоянием и смещением? В то время как смещение определяется как направлением, так и величиной, расстояние определяется только величиной. Смещение – это пример векторной величины. Расстояние – это пример скалярной величины.Вектор – это любая величина, имеющая как величину, так и направление. Другие примеры векторов включают скорость 90 км / ч на восток и силу 500 ньютонов прямо вниз.
Скаляры и векторы : Г-н Андерсен объясняет различия между скалярными и векторными величинами. Он также использует демонстрацию, чтобы показать важность векторов и сложения векторов.
Он также использует демонстрацию, чтобы показать важность векторов и сложения векторов.
В математике, физике и технике вектор – это геометрический объект, который имеет величину (или длину) и направление и может быть добавлен к другим векторам в соответствии с векторной алгеброй.Направление вектора в одномерном движении задается просто знаком плюс (+) или минус (-). Вектор часто представлен отрезком линии с определенным направлением или графически в виде стрелки, соединяющей начальную точку A с конечной точкой B, как показано на.
Векторное представление : Вектор часто представляется отрезком линии с определенным направлением или графически в виде стрелки, соединяющей начальную точку A с конечной точкой B.
Некоторые физические величины, например расстояние, либо не имеют направления, либо не имеют определенного направления.В физике скаляр – это простая физическая величина, которая не изменяется при поворотах или перемещениях системы координат. Это любая величина, которая может быть выражена одним числом и имеет величину, но не направление. Например, температура 20ºC, 250 килокалорий (250 калорий) энергии в шоколадном батончике, ограничение скорости 90 км / ч, рост человека 1,8 м и расстояние 2,0 м – все это скаляры или количества, не указанные. направление. Обратите внимание, однако, что скаляр может быть отрицательным, например, температура –20ºC.В этом случае знак минус указывает точку на шкале, а не направление. Скаляры никогда не изображаются стрелками. (Сравнение скаляров и векторов показано на.)
Это любая величина, которая может быть выражена одним числом и имеет величину, но не направление. Например, температура 20ºC, 250 килокалорий (250 калорий) энергии в шоколадном батончике, ограничение скорости 90 км / ч, рост человека 1,8 м и расстояние 2,0 м – все это скаляры или количества, не указанные. направление. Обратите внимание, однако, что скаляр может быть отрицательным, например, температура –20ºC.В этом случае знак минус указывает точку на шкале, а не направление. Скаляры никогда не изображаются стрелками. (Сравнение скаляров и векторов показано на.)
Скаляры и векторы : Краткий список величин, которые являются либо скалярами, либо векторами.
Кинематика | физика | Britannica
Kinematics , раздел физики и подраздел классической механики, занимающийся геометрически возможным движением тела или системы тел без учета задействованных сил ( i.е., причин и следствий движений).
Британская викторина
Викторина “Все о физике”
Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какая единица измерения для циклов в секунду? Проверьте свою физическую хватку с помощью этой викторины.
Далее следует краткое описание кинематики.Для полного обращения см. Механику .
Кинематика предназначена для описания пространственного положения тел или систем материальных частиц, скорости движения частиц (скорости) и скорости изменения их скорости (ускорения). Если пренебречь причинными силами, описание движения возможно только для частиц, имеющих ограниченное движение – , то есть , движущихся по определенным траекториям. В неограниченном или свободном движении силы определяют форму траектории.
Для частицы, движущейся по прямому пути, список положений и соответствующих моментов времени мог бы составить подходящую схему для описания движения частицы. Для непрерывного описания потребуется математическая формула, выражающая положение во времени.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас Когда частица движется по криволинейной траектории, описание ее положения становится более сложным и требует двух или трех измерений. В таких случаях невозможно непрерывное описание в виде единого графика или математической формулы. Положение частицы, движущейся по кругу, например, можно описать радиусом вращения круга, как у спицы колеса, один конец которого закреплен в центре круга, а другой конец прикреплен к частице. Радиус вращения известен как вектор положения частицы, и, если угол между ним и фиксированным радиусом известен как функция времени, можно вычислить величину скорости и ускорения частицы.Однако скорость и ускорение имеют не только величину, но и направление; скорость всегда касается пути, в то время как ускорение состоит из двух компонентов: одна касается пути, а другая – перпендикулярна касательной.
В таких случаях невозможно непрерывное описание в виде единого графика или математической формулы. Положение частицы, движущейся по кругу, например, можно описать радиусом вращения круга, как у спицы колеса, один конец которого закреплен в центре круга, а другой конец прикреплен к частице. Радиус вращения известен как вектор положения частицы, и, если угол между ним и фиксированным радиусом известен как функция времени, можно вычислить величину скорости и ускорения частицы.Однако скорость и ускорение имеют не только величину, но и направление; скорость всегда касается пути, в то время как ускорение состоит из двух компонентов: одна касается пути, а другая – перпендикулярна касательной.
Франция | История, карта, флаг, столица и факты
Франция , официально Французская Республика , Франция Франция или République Française , страна северо-западной Европы. В историческом и культурном плане Франция входит в число наиболее важных стран западного мира, а также играет очень важную роль в международных делах, имея бывшие колонии во всех уголках земного шара. Ограниченная Атлантическим океаном и Средиземным морем, Альпами и Пиренеями, Франция долгое время служила географическим, экономическим и лингвистическим мостом, соединяющим северную и южную Европу. Это крупнейший в Европе производитель сельскохозяйственной продукции и одна из ведущих промышленных держав мира.
Ограниченная Атлантическим океаном и Средиземным морем, Альпами и Пиренеями, Франция долгое время служила географическим, экономическим и лингвистическим мостом, соединяющим северную и южную Европу. Это крупнейший в Европе производитель сельскохозяйственной продукции и одна из ведущих промышленных держав мира.
Британская викторина
Викторина “Найди страну в ее полушарии”
Эта викторина представит вам название страны.Вы должны решить, в северном или южном полушарии. (Не будет никаких обманов со странами, которые касаются экватора.)
Франция – одна из старейших наций земного шара, продукт союза герцогств и княжеств под одним правителем в средние века. Сегодня, как и в ту эпоху, центральная власть принадлежит государству, хотя в последние десятилетия регионам и была предоставлена определенная автономия. Французы смотрят на государство как на главного стража свободы, а государство, в свою очередь, предоставляет своим гражданам щедрую программу удобств, от бесплатного образования до здравоохранения и пенсионных планов. Даже в этом случае эта централистская тенденция часто противоречит другой давней теме французской нации: настойчивости на превосходстве личности. По этому поводу историк Жюль Мишле заметил: «Англия – это империя, Германия – это нация, раса, Франция – это личность». Государственный деятель Шарль де Голль тоже жаловался: «Только опасность может сплотить французов.Нельзя внезапно навязать единство стране, имеющей 265 видов сыра ».
Французы смотрят на государство как на главного стража свободы, а государство, в свою очередь, предоставляет своим гражданам щедрую программу удобств, от бесплатного образования до здравоохранения и пенсионных планов. Даже в этом случае эта централистская тенденция часто противоречит другой давней теме французской нации: настойчивости на превосходстве личности. По этому поводу историк Жюль Мишле заметил: «Англия – это империя, Германия – это нация, раса, Франция – это личность». Государственный деятель Шарль де Голль тоже жаловался: «Только опасность может сплотить французов.Нельзя внезапно навязать единство стране, имеющей 265 видов сыра ».
Эта тенденция к индивидуализму сочетается с плюралистическим мировоззрением и большим интересом к большему миру. Несмотря на то, что его империалистическая стадия была вызвана импульсом к цивилизации этого мира в соответствии с французскими стандартами ( la mission civilisatrice ), французы до сих пор одобрительно отмечают слова писателя Гюстава Флобера:
Я не более современен, чем я древний.
не больше французского, чем китайского; и идея la patrie , отечества, то есть обязанность жить на клочке земли, окрашенном в красный или синий цвет на карте, и ненавидеть другие части, окрашенные в зеленый или черный цвет, всегда казалась мне узкой, ограниченный и безумно глупый.
Одновременно универсальная и особенная, французская культура широко распространилась и оказала большое влияние на развитие искусства и науки, особенно антропологии, философии и социологии.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас Франция также оказала влияние в правительственных и гражданских делах, дав миру важные демократические идеалы в эпоху Просвещения и Французской революции и вдохновляя рост реформистских и даже революционных движений на протяжении поколений.Однако нынешняя Пятая республика обладает заметной стабильностью с момента ее провозглашения 28 сентября 1958 года, отмеченного колоссальным ростом частной инициативы и подъемом центристской политики. Хотя Франция была вовлечена в давние споры с другими европейскими державами (и, время от времени, с Соединенными Штатами, их давним союзником), она стала ведущим членом Европейского Союза (ЕС) и его предшественников. С 1966 по 1995 год Франция не участвовала в интегрированной военной структуре Организации Североатлантического договора (НАТО), сохраняя полный контроль над собственными воздушными, наземными и военно-морскими силами; Однако начиная с 1995 года Франция была представлена в Военном комитете НАТО, а в 2009 году президент Франции Николя Саркози объявил, что страна вновь присоединится к военному командованию организации.Как один из пяти постоянных членов Совета Безопасности ООН – вместе с Соединенными Штатами, Россией, Соединенным Королевством и Китаем – Франция имеет право наложить вето на решения Совета.
Хотя Франция была вовлечена в давние споры с другими европейскими державами (и, время от времени, с Соединенными Штатами, их давним союзником), она стала ведущим членом Европейского Союза (ЕС) и его предшественников. С 1966 по 1995 год Франция не участвовала в интегрированной военной структуре Организации Североатлантического договора (НАТО), сохраняя полный контроль над собственными воздушными, наземными и военно-морскими силами; Однако начиная с 1995 года Франция была представлена в Военном комитете НАТО, а в 2009 году президент Франции Николя Саркози объявил, что страна вновь присоединится к военному командованию организации.Как один из пяти постоянных членов Совета Безопасности ООН – вместе с Соединенными Штатами, Россией, Соединенным Королевством и Китаем – Франция имеет право наложить вето на решения Совета.
Столица и самый важный город Франции – Париж, один из выдающихся мировых культурных и коммерческих центров. Величественный город, известный как ville lumière , или «город света», Париж часто переделывали, особенно в середине 19 века под командованием Жоржа-Эжена, барона Османа, который был приверженцем видения Наполеона III. современного города, свободного от холерических болот и переполненных старых переулков, с широкими проспектами и правильной планировкой.Сейчас Париж превратился в огромный мегаполис, один из крупнейших мегаполисов Европы, но его историческое сердце все еще можно пройти за вечернюю прогулку. Уверенные в том, что их город находится в самом центре мира, парижане когда-то привыкли называть свою страну двумя частями: Парижем и le désert , пустошью за его пределами. Метрополитен Париж теперь распространился далеко за пределы своих древних пригородов в сельскую местность, и почти каждый французский город и деревня теперь насчитывает одного или двух пенсионеров, вынужденных покинуть город из-за высокой стоимости жизни, так что, в некотором смысле, Париж пришел к нам. Обнять пустыню и пустынный Париж.
современного города, свободного от холерических болот и переполненных старых переулков, с широкими проспектами и правильной планировкой.Сейчас Париж превратился в огромный мегаполис, один из крупнейших мегаполисов Европы, но его историческое сердце все еще можно пройти за вечернюю прогулку. Уверенные в том, что их город находится в самом центре мира, парижане когда-то привыкли называть свою страну двумя частями: Парижем и le désert , пустошью за его пределами. Метрополитен Париж теперь распространился далеко за пределы своих древних пригородов в сельскую местность, и почти каждый французский город и деревня теперь насчитывает одного или двух пенсионеров, вынужденных покинуть город из-за высокой стоимости жизни, так что, в некотором смысле, Париж пришел к нам. Обнять пустыню и пустынный Париж.
Париж на фоне заката.
© Digital Vision / Getty Images Среди других крупных городов Франции – Лион, расположенный вдоль древнего торгового пути в долине Роны, соединяющего Северное море и Средиземное море; Марсель, многонациональный порт на Средиземном море, основанный как перевалочная база для греческих и карфагенских торговцев в VI веке до нашей эры; Нант, промышленный центр и глубоководная гавань на побережье Атлантического океана; и Бордо, расположенный на юго-западе Франции вдоль реки Гаронна.
Кинематика – документация SymPy 0.7.4.1
В механике кинематика относится к движению тел (или частиц). Это «а» в «f = ma». Этот документ даст некоторые математические основы. к описанию кинематики системы, а также к тому, как представлять кинематику в механике.
Введение в кинематику
Первая тема – кинематика жесткого движения. Твердое тело – это идеализированный представление физического объекта, имеющего инерцию массы и вращения.Очевидно, твердые тела не гибкие. Мы можем сломать движение твердого тела в поступательное движение и вращательное движение (когда мы имеем дело с частицами, мы есть только поступательное движение). Вращательное движение можно далее разбить на простые вращения и общие вращения.
Перенос твердого тела определяется как движение, при котором ориентация
тело не меняется при движении; или во время движения любой отрезок линии
будет параллельно самому себе в начале движения.{\ mathbf {B}} \), или угловая скорость
\ (\ mathbf {B} \) в \ (\ mathbf {N} \), который является вектором. {\ mathbf {B}} = w_x \ mathbf {\ hat {b} _x} +
w_y \ mathbf {\ hat {b} _y} + w_z \ mathbf {\ hat {b} _z} \]
{\ mathbf {B}} = w_x \ mathbf {\ hat {b} _x} +
w_y \ mathbf {\ hat {b} _y} + w_z \ mathbf {\ hat {b} _z} \]
Есть несколько дополнительных важных моментов, касающихся угловой скорости.{\ mathbf {D}} & = \ dot {q_1} \ mathbf {\ hat {a} _x} – \ dot {q_2} \ mathbf {\ hat {b} _z} + \ dot {q_3} \ mathbf {\ hat {c} _y} \\\ end {split} \]
Обратите внимание на знаки, используемые в определениях угловой скорости, которые относятся к как в этом случае определяется угол смещения.
Эта теорема значительно затрудняет определение угловых скоростей многотельных систем. проще, так как угловая скорость тела в цепочке нужно только определить к предыдущему телу, чтобы быть полностью определенным (а первое тело нуждается в быть определенным в желаемой системе отсчета).{\ mathbf {B}} \ times \ mathbf {v} \]
Вектор \ (\ mathbf {v} \) может быть любой векторной величиной: вектором положения,
вектор скорости, вектор угловой скорости и т. д. Вместо того, чтобы брать время
производная вектора в \ (\ mathbf {N} \), берем ее в
\ (\ mathbf {B} \), где \ (\ mathbf {B} \) может быть любой системой отсчета или
тело, обычно такое, в котором легко взять производную от
\ (\ mathbf {v} \) в (\ (\ mathbf {v} \) обычно состоит только из базиса
векторный набор, принадлежащий \ (\ mathbf {B} \)). {\ mathbf {B}} \) и наша векторная величина
\ (\ mathbf {v} \).{\ mathbf {B}} & = \ dot {w_x} \ mathbf {\ hat {b} _x} +
\ dot {w_y} \ mathbf {\ hat {b} _y} + \ dot {w_z} \ mathbf {\ hat {b} _z} \\\ end {split} \]
{\ mathbf {B}} \) и наша векторная величина
\ (\ mathbf {v} \).{\ mathbf {B}} & = \ dot {w_x} \ mathbf {\ hat {b} _x} +
\ dot {w_y} \ mathbf {\ hat {b} _y} + \ dot {w_z} \ mathbf {\ hat {b} _z} \\\ end {split} \]
Опять же, это только для случая, когда угловая скорость тела равна определены в фиксированных компонентах кузова.
Скорость точки и ускорение
Рассмотрим точку \ (P \): мы можем определить некоторые характеристики точки. Во-первых, мы можем определить вектор положения из некоторой другой точки в \ (P \). Во-вторых, мы можем определить вектор скорости \ (P \) в системе отсчета наш выбор.P & = \ ddot {q} _x \ mathbf {\ hat {n} _x} + \ ddot {q} _y \ mathbf {\ hat {n} _y} \\\ end {split} \]
В приведенном выше примере важно понимать, что точка \ (O \)
фиксируется в системе отсчета \ (\ mathbf {N} \). Нет теоремы сложения
для поступательных скоростей; альтернативы будут обсуждены позже.
Также обратите внимание, что положение каждой точки может не
всегда нужно определять для формирования динамических уравнений движения.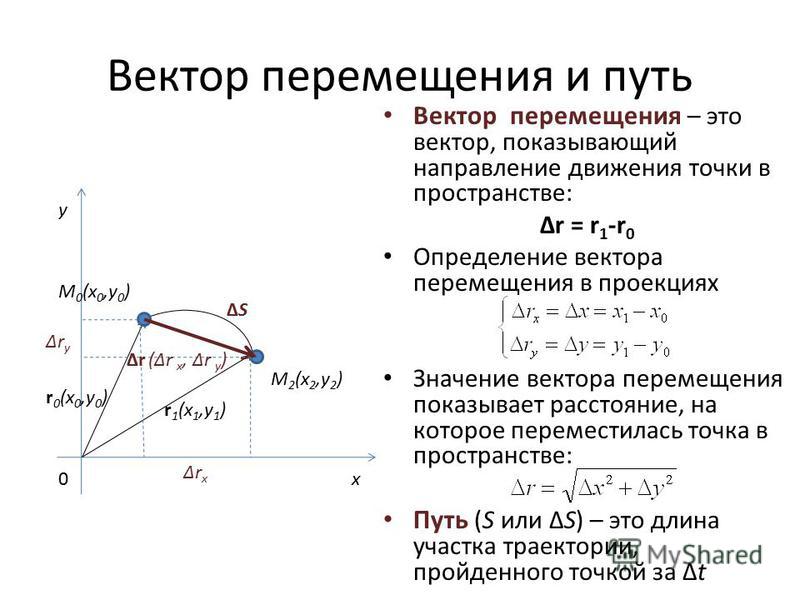 {SP}) \\\ end {split} \]
{SP}) \\\ end {split} \]
Когда на теле закреплена только одна из двух точек, используется теорема об 1 балле. вместо.P & = – R u_2 sin (q_2) \ mathbf {\ hat {c} _x} + (R u_2 cos (q_2) + u_1 l) \ mathbf {\ hat {c} _y} + R u_1 sin (q_2) \ mathbf {\ hat {c} _z} \\\ end {split} \]
Последняя тема в описании скоростей точек – это качение, или скорее катится без пробуксовки. Говорят, что два тела катятся без проскальзывания, если и только если точка контакта каждого тела имеет одинаковую скорость в другом Рамка. См. Следующий рисунок:
Обычно используется для определения скорости точки на одном объекте, катящемся по другой фиксированный объект, например, в следующем примере:
Кинематика в механике SymPy
К настоящему времени должно быть ясно, что тема кинематики здесь в основном
описание правильного способа манипулирования векторами для представления
скорости точек.В механике есть удобные методы для
сохранение этих скоростей, связанных с кадрами и точками. Теперь мы вернемся к
приведенные выше примеры и покажите, как их представить в sympy.
Теперь мы вернемся к
приведенные выше примеры и покажите, как их представить в sympy.
Тема создания системы координат уже освещена. Когда ReferenceFrame создается, он автоматически вычисляет угловой скорости кадра с использованием производной по времени DCM и углового определение скорости.
>>> из sympy import Symbol, sin, cos
>>> от симпы.Physics.mechanics импорт *
>>> Mechanics_printing ()
>>> N = ReferenceFrame ('N')
>>> q1 = динамические символы ('q1')
>>> A = N.orientnew ('A', 'Axis', [q1, N.x])
>>> A.ang_vel_in (N)
q1 '* N.x
Обратите внимание, что угловая скорость может быть определена другим способом:
>>> B = опорный кадр ('B')
>>> u1 = динамические символы ('u1')
>>> B.set_ang_vel (N, u1 * B.y)
>>> B.ang_vel_in (N)
u1 * B.y
>>> N.ang_vel_in (B)
- u1 * B.у
Как при создании кадра во время orientnew, так и при вызове set_ang_vel, угловая скорость устанавливается в обоих задействованных кадрах, как показано выше.
Здесь у нас есть несколько тел с угловыми скоростями, определенными относительно каждого
Другие. Это кодируется как:
Это кодируется как:
>>> N = опорный кадр ('N')
>>> A = ReferenceFrame ('A')
>>> B = ReferenceFrame ('B')
>>> C = ReferenceFrame ('C')
>>> D = ReferenceFrame ('D')
>>> u1, u2, u3 = динамические символы ('u1 u2 u3')
>>> А.set_ang_vel (N, 0)
>>> B.set_ang_vel (A, u1 * A.x)
>>> C.set_ang_vel (B, -u2 * B.z)
>>> D.set_ang_vel (C, u3 * C.y)
>>> D.ang_vel_in (N)
u3 * C.y - u2 * B.z + u1 * A.x
В механике при нахождении используется кратчайший путь между двумя кадрами. угловая скорость. Это означало бы, если бы мы вернулись и установили:
>>> D.set_ang_vel (N, 0) >>> D.ang_vel_in (N) 0
Используется только что определенный путь. Однако это может вызвать проблемы, так как теперь угловой определения скорости противоречивы.Рекомендуется избегать делая это.
точки являются трансляционным аналогом вращающейся опорной рамки. Создать точку можно двумя способами, например ReferenceFrame:
. >>> O = точка ('O')
>>> P = O.locatenew ('P', 3 * N. x + N.y)
>>> P.pos_from (O)
3 * Н.x + Н.у
>>> Q = точка ('Q')
>>> Q.set_pos (P, N.z)
>>> Q.pos_from (P)
N.z
>>> Q.pos_from (O)
3 * N.x + N.y + N.z
x + N.y)
>>> P.pos_from (O)
3 * Н.x + Н.у
>>> Q = точка ('Q')
>>> Q.set_pos (P, N.z)
>>> Q.pos_from (P)
N.z
>>> Q.pos_from (O)
3 * N.x + N.y + N.z
Подобно ReferenceFrame, находится вектор положения между двумя точками. по кратчайшему пути (количеству промежуточных точек) между ними.в отличие вращательное движение, нет теоремы сложения для скорости точек. В чтобы иметь скорость точки в ReferenceFrame, вы должны установить значение.
>>> O = точка ('O')
>>> O.set_vel (N, u1 * N.x)
>>> O.vel (N)
u1 * N.x
Значение как для поступательного, так и для вращательного ускорения вычисляется по формуле взяв производную по времени от соответствующей скорости, если пользователь не устанавливает ее иначе.
>>> O.acc (N) и1 '* Н.Икс >>> O.set_acc (N, u2 * u1 * N.y) >>> O.acc (N) u1 * u2 * N.y
Далее следует описание теорем о 2 и 1 баллах, используемых в сочувствующий.
Во-первых, это поступательный вращающийся диск.
>>> N = опорный кадр ('N')
>>> u1, u2, u3 = динамические символы ('u1 u2 u3')
>>> R = символ ('R')
>>> B = ReferenceFrame ('B')
>>> O = точка ('O')
>>> O. set_vel (N, u1 * N.x + u2 * N.y)
>>> P = O.locatenew ('P', R * B.Икс)
>>> B.set_ang_vel (N, u3 * B.z)
>>> P.v2pt_theory (O, N, B)
u1 * N.x + u2 * N.y + R * u3 * B.y
>>> P.a2pt_theory (O, N, B)
u1 '* N.x + u2' * N.y - R * u3 ** 2 * B.x + R * u3 '* B.y
set_vel (N, u1 * N.x + u2 * N.y)
>>> P = O.locatenew ('P', R * B.Икс)
>>> B.set_ang_vel (N, u3 * B.z)
>>> P.v2pt_theory (O, N, B)
u1 * N.x + u2 * N.y + R * u3 * B.y
>>> P.a2pt_theory (O, N, B)
u1 '* N.x + u2' * N.y - R * u3 ** 2 * B.x + R * u3 '* B.y
Мы также рассмотрим реализацию теоремы об одном балле.
Это снова частица, движущаяся по кольцу.
>>> N = опорный кадр ('N')
>>> u1, u2 = динамические символы ('u1 u2')
>>> q1, q2 = динамические символы ('q1 q2')
>>> l = символ ('l')
>>> R = символ ('R')
>>> C = N.orientnew ('C', 'Ось', [q1, N.x])
>>> C.set_ang_vel (N, u1 * N.x)
>>> O = точка ('O')
>>> O.set_vel (N, 0)
>>> Q = O.locatenew ('Q', -l * C.z)
>>> P = Q.locatenew ('P', R * (cos (q2) * C.x + sin (q2) * C.y))
>>> P.set_vel (C, R * u2 * (-sin (q2) * C.x + cos (q2) * C.y))
>>> Q.v2pt_theory (O, N, C)
l * u1 * C.y
>>> P.v1pt_theory (Q, N, C)
- R * u2 * sin (q2) * C.x + (R * u2 * cos (q2) + l * u1) * C.y + R * u1 * sin (q2) * C.z
Механика против кинематики – в чем разница?
В контексте | Physics | lang = en terms разница между механикой и кинематикой
заключается в том, что механика (физика) является разделом физики, который имеет дело с действием сил на материальные объекты с массой, а кинематика (физика) раздел механики, имеющий отношение к движущимся объектам, но не к задействованным силам.
Как существительные, разница между механикой
и кинематикой состоит в том, что механика (физика) является разделом физики, который имеет дело с действием сил на материальные объекты с массой, а кинематика (физика) является ветвью физики. механика связана с движущимися объектами, но не с задействованными силами.Другие сравнения: в чем разница?
Английскийсуществительное(–)
Производные термины( Производные термины ) * аэромеханика * аналитическая механика * биомеханика * кузовная механика * небесная механика * классическая механика * электромеханика * механика жидкости * газовая механика * наследственная механика * гидромеханика * магнитомеханика * матричная механика * микромеханика * молекулярная механика * Ньютоновская механика * неквантовая механика * нерелятивистская механика * механика частиц * квантовая механика * рациональная механика * релятивистская механика * механика горных пород * механика грунтов * статистическая механика * волновая механикаАнаграммы* | wiktionary.org/wiki/kinematics”>Существительное(–)Связанные термины* кинематическаяСм. Также* динамика |
Теория кинематики | Механика | Физические упражнения
Кинематика – это раздел классической механики, который описывает движение тел (объектов) и систем (групп объектов) без учета сил, вызывающих движение.
Когда мы изучаем движение тела, мы всегда должны делать это в соответствии с Системой отсчета, которая представляет собой точку или набор точек, через которые мы описываем движение тела.
Мы говорим, что тело движется относительно Системы отсчета, когда оно меняет свое положение с течением времени; если оно не меняется, мы скажем, что оно находится в состоянии покоя. Движение относительное, то есть оно будет зависеть от выбранной нами системы отсчета.
Если мы соединим все точки, где проходит тело, мы получим кривую под названием траектория , на которой мы можем определить положение точки, которая после соединения ее с осями OX и OY, мы получим в результате вектор, называемый положением . вектор .
Bioprofe | Теория кинематики | 01
Длина или модуль этого вектора положения вычисляется по формуле:
Bioprofe | Теория кинематики | 02
ОБЗОР ФОРМУЛЫ:
Скалярная средняя скорость
Bioprofe | Теория кинематики | 03
Скалярная мгновенная скорость
Bioprofe | Теория кинематики | 04
Средняя векторная скорость
Bioprofe | Теория кинематики | 05
Векторная мгновенная скорость
Bioprofe | Теория кинематики | 06
Среднее ускорение
Bioprofe | Теория кинематики | 07
Мгновенное ускорение
Bioprofe | Теория кинематики | 08
Касательное ускорение
Bioprofe | Теория кинематики | 09
Нормальное ускорение
Bioprofe | Теория кинематики | 10
Прямолинейное равномерное движение
Bioprofe | Теория кинематики | 11
Прямолинейное равномерно переменное движение
Bioprofe | Теория кинематики | 12
Свободное падение
Bioprofe | Теория кинематики | 13
Угловые величины
Bioprofe | Теория кинематики | 14
Угловая скорость
Bioprofe | Теория кинематики | 15
Угловое ускорение
Bioprofe | Теория кинематики | 16
Равномерное круговое движение (T = период; f = частота)
Bioprofe | Теория кинематики | 17
Bioprofe | Теория кинематики | 18
Равномерное круговое переменное движение
Bioprofe | Теория кинематики | 19
Вибрационное гармоническое движение (s = удлинение; A = амплитуда; ω = пульсация)
Bioprofe | Теория кинематики | 20
СОСТАВ ДВИЖЕНИЙ
Пуск снарядов вертикальный
Bioprofe | Теория кинематики | 21
Пуск снарядов горизонтальный
Bioprofe | Теория кинематики | 22
Пуск снарядов под углом
Уравнение траектории
Bioprofe | Теория кинематики | 23
Максимальная высота
Bioprofe | Теория кинематики | 24
Окончательный объем
Bioprofe | Теория кинематики | 25
Кинематика и статика (Достижения механики и математики, 28): Аврейцевич, январь: 9781461437901: Amazon.
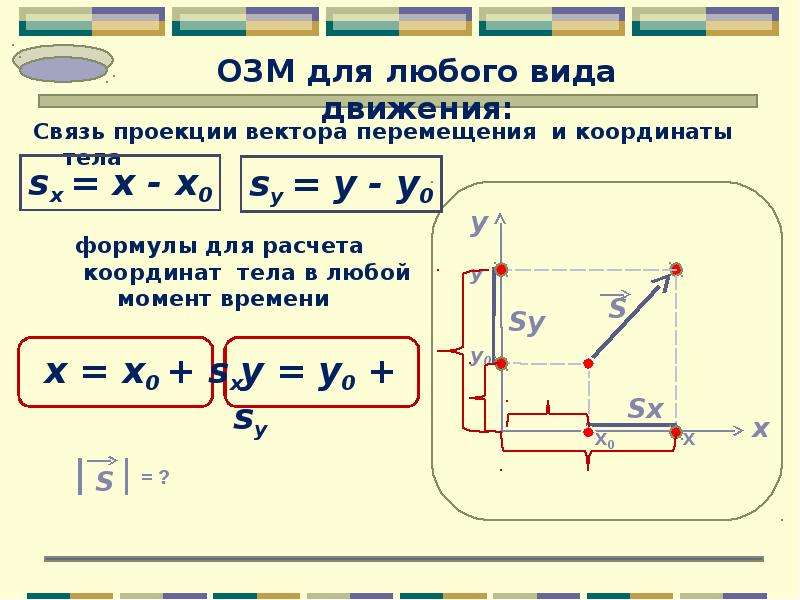 com: Книги
com: КнигиИз обзоров:
«Эта книга представляет классическую механику, включая кинематику и статику, и может быть рекомендована в качестве учебного пособия для студентов и аспирантов в области машиностроения, гражданского строительства и прикладной физики. … Эта прекрасная книга объединяет различные подходы к предмету в английской, русской, польской и немецкой литературе ». (Василе Маринка, zbMATH, том 1268, 2013 г.)Это первый том из трех книг одного автора, полностью посвященных классической механике.Триада работ охватывает разные темы классической механики и создает связь между ними, выводя темы из одного корня. Кроме того, автор объединяет различные подходы из английской, русской, польской и немецкой литературы, посвященной классической механике. Особое внимание уделяется изучению электромагнетомеханических систем.
Классическая механика: кинематика и статика адресован широкому кругу студентов и аспирантов, аспирантов, исследователей и преподавателей из областей машиностроения и гражданского строительства.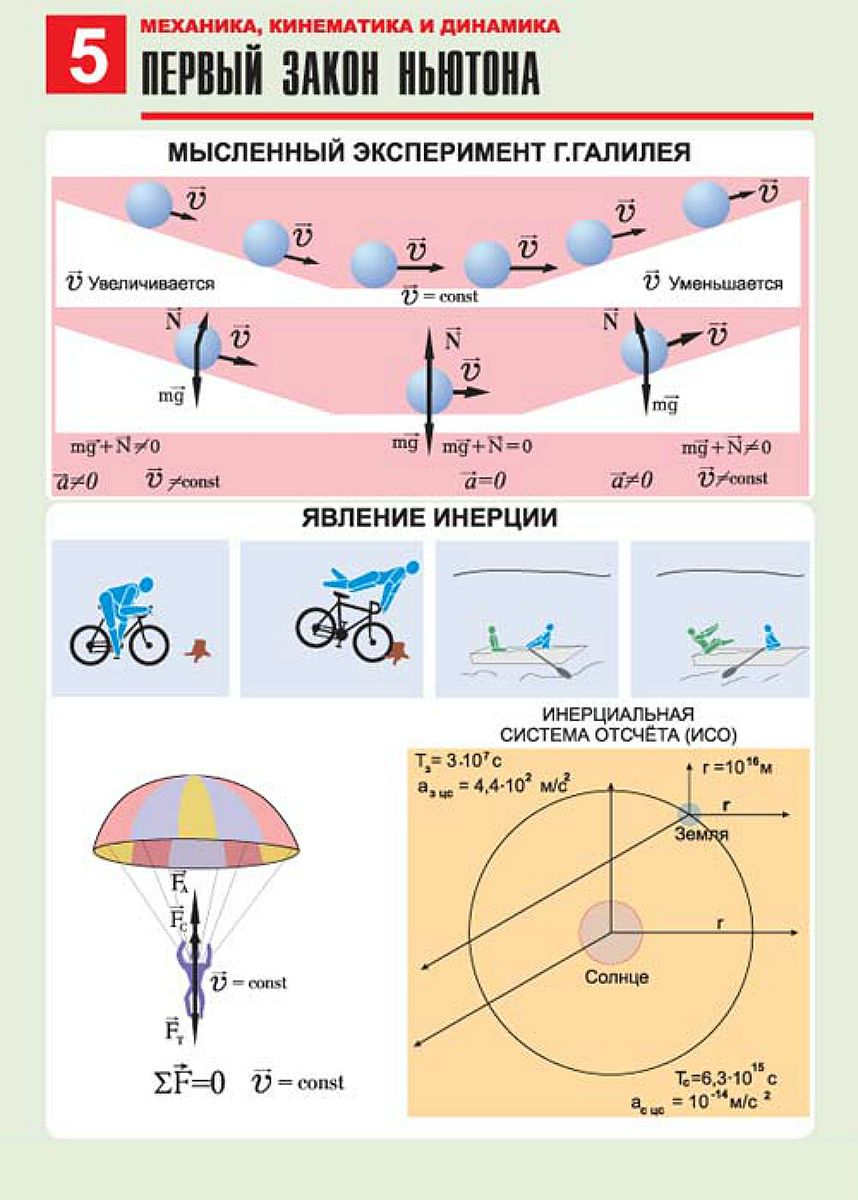 Этот том, который включает множество проработанных примеров и приложений, также предназначен для использования в качестве самостоятельного справочника для исследователей в области прикладной математики и физических наук. Его также рекомендуется использовать в качестве дополнительного учебника для старших курсов бакалавриата и магистратуры.
Этот том, который включает множество проработанных примеров и приложений, также предназначен для использования в качестве самостоятельного справочника для исследователей в области прикладной математики и физических наук. Его также рекомендуется использовать в качестве дополнительного учебника для старших курсов бакалавриата и магистратуры.
В главе 1 сформулированы, проиллюстрированы и обсуждаются фундаментальные принципы механики. Глава 2 посвящена статике, а глава 3 представляет геометрию масс. Кинематика частицы, криволинейные и нормальные координаты, а также кинематические пары и цепочки – это основное внимание главы 4.В главе 5 изучается кинематика твердого тела и составное движение частицы. Глава 6 завершает текст кинематикой деформируемого тела.
Об авторе
Ян Аврейцевич – лауреат Премии Гумбольдта 2011 года. Эта награда вручается Фондом Александра фон Гумбольдта в Германии. Премия основана на всех достижениях исследователя на сегодняшний день, чьи фундаментальные открытия, новые теории или идеи оказали значительное влияние на их собственную дисциплину и который, как ожидается, продолжит создавать передовые достижения в будущем.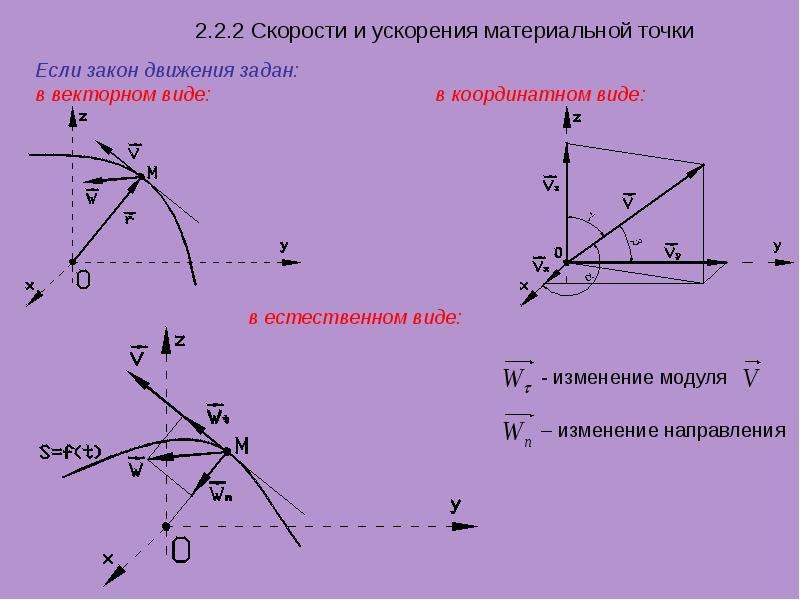

 Е. Квантовая физика: основные законы: учеб. пособие / М. : БИНОМ. Лаб. знаний, 2010. — 256 с.
Е. Квантовая физика: основные законы: учеб. пособие / М. : БИНОМ. Лаб. знаний, 2010. — 256 с. Юрайт, 2017. — 92 с.
Юрайт, 2017. — 92 с. В. Общий курс физики Термодинамика и молекулярная физика Учеб. пособие для вузов: в 5 т. Физматлит, 2011. — 543 с.
В. Общий курс физики Термодинамика и молекулярная физика Учеб. пособие для вузов: в 5 т. Физматлит, 2011. — 543 с. С. Оптика учеб. пособие для физ. спец. вузов. Физматлит, 2006. — 848 с.
С. Оптика учеб. пособие для физ. спец. вузов. Физматлит, 2006. — 848 с. Л.).
Л.).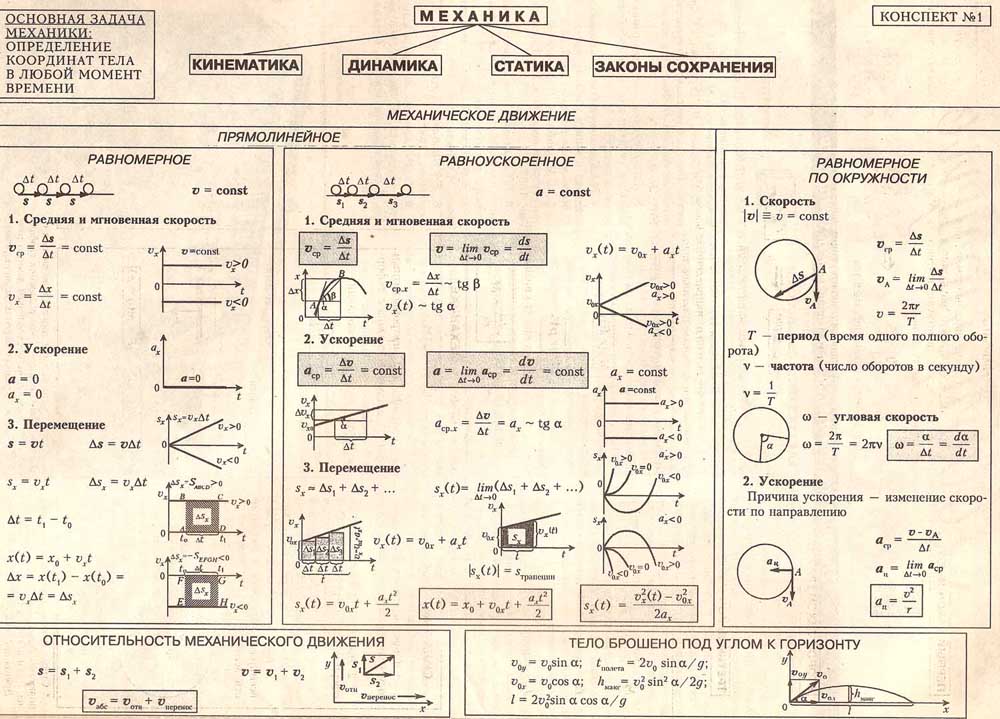 Руководит занятиями доктор физ.-мат. наук профессор В.А. Юдин.
Руководит занятиями доктор физ.-мат. наук профессор В.А. Юдин. СТАТИКА. 2004.
СТАТИКА. 2004. 2013.
2013.
 ). — М.: Наука, 1968.
). — М.: Наука, 1968.


 не больше французского, чем китайского; и идея la patrie , отечества, то есть обязанность жить на клочке земли, окрашенном в красный или синий цвет на карте, и ненавидеть другие части, окрашенные в зеленый или черный цвет, всегда казалась мне узкой, ограниченный и безумно глупый.
не больше французского, чем китайского; и идея la patrie , отечества, то есть обязанность жить на клочке земли, окрашенном в красный или синий цвет на карте, и ненавидеть другие части, окрашенные в зеленый или черный цвет, всегда казалась мне узкой, ограниченный и безумно глупый.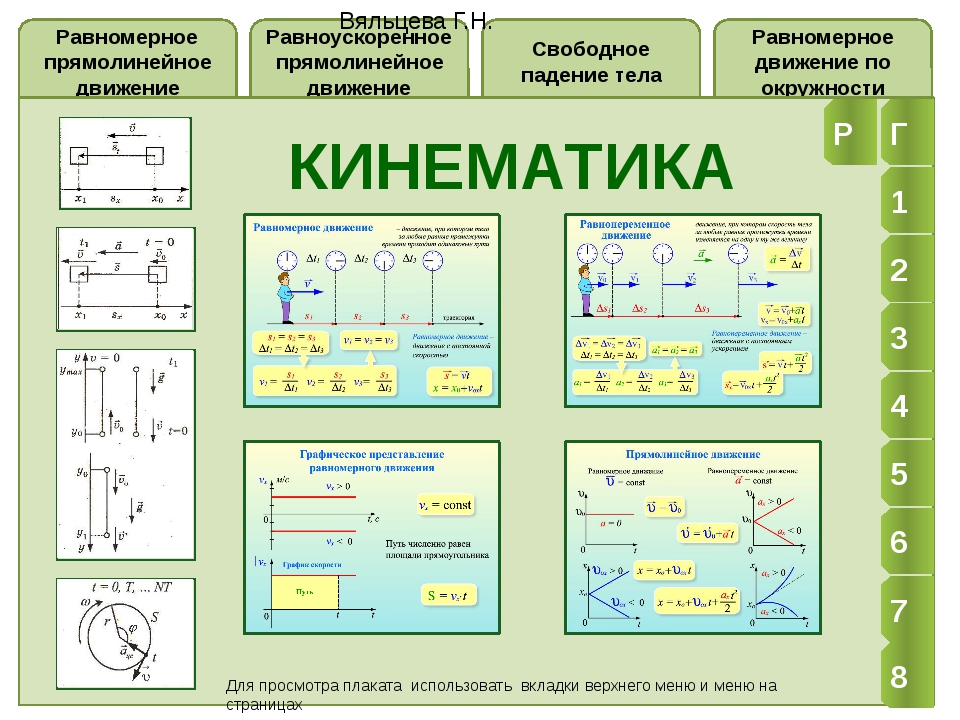 x + N.y)
>>> P.pos_from (O)
3 * Н.x + Н.у
>>> Q = точка ('Q')
>>> Q.set_pos (P, N.z)
>>> Q.pos_from (P)
N.z
>>> Q.pos_from (O)
3 * N.x + N.y + N.z
x + N.y)
>>> P.pos_from (O)
3 * Н.x + Н.у
>>> Q = точка ('Q')
>>> Q.set_pos (P, N.z)
>>> Q.pos_from (P)
N.z
>>> Q.pos_from (O)
3 * N.x + N.y + N.z
 set_vel (N, u1 * N.x + u2 * N.y)
>>> P = O.locatenew ('P', R * B.Икс)
>>> B.set_ang_vel (N, u3 * B.z)
>>> P.v2pt_theory (O, N, B)
u1 * N.x + u2 * N.y + R * u3 * B.y
>>> P.a2pt_theory (O, N, B)
u1 '* N.x + u2' * N.y - R * u3 ** 2 * B.x + R * u3 '* B.y
set_vel (N, u1 * N.x + u2 * N.y)
>>> P = O.locatenew ('P', R * B.Икс)
>>> B.set_ang_vel (N, u3 * B.z)
>>> P.v2pt_theory (O, N, B)
u1 * N.x + u2 * N.y + R * u3 * B.y
>>> P.a2pt_theory (O, N, B)
u1 '* N.x + u2' * N.y - R * u3 ** 2 * B.x + R * u3 '* B.y