Кинематика определение в физике: Ошибка: 404 Материал не найден

Основные понятия кинематики

Определение 1

Кинематика − это раздел механики, который рассматривает движение тел без объяснения вызывающих его причин. 

Определение 2

Механическое движение тела − это изменение положения данного тела в пространстве относительно других тел во времени. 

Как мы сказали, механическое движение тела относительно. Движение одного и того же тела относительно разных тел может быть разным.

Определение 3

Для характеристики движения тела указывается, по отношению к какому из тел рассматривается это движение. Это будет тело отсчета.

Определение 4

Система отсчета − система координат, которая связана с телом отсчета и временем для отсчета. Она позволяет определить положение передвигающегося тела в любой отрезок времени.

В СИ единицей длины выступает метр, а единицей времени – секунда.

У каждого тела есть определенные размеры. Разные части тела расположены в разных пространственных местах. Но в большинстве задач механики не нужно указывать положение отдельных частей тела. Если размеры тела маленькие в сравнении с расстояниями до остальных тел, тогда заданное тело считается его материальной точкой. Таким образом поступают при изучении перемещения планет вокруг Солнца.

Определение 5

Механическое движение называют поступательным, в случае если все части тела перемещаются одинаково.

Пример 1

Поступательное движение наблюдается у кабин в аттракционе «Колесо обозрения» или у автомобиля на прямолинейном участке пути.

При поступательном движении тела его также рассматривают в качестве материальной точки.

Определение 6

Материальная точка − это тело, размерами которого при заданных условиях можно пренебречь. 

Материальная точка в механике

Термин “материальная точка” имеет важное значение в механике.

Определение 7

Траектория движения тела − некоторая линия, которую тело или материальная точка описывает, перемещаясь во времени от одной точки до другой.

Местонахождение материальной точки в пространстве в любой временной отрезок (закон движения) определяют, используя зависимость координат от времени x=x(t), y=y(t), z=z(t) или зависимость от времени радиус-вектора r→=r→(t), проведенного от начала координат до заданной точки. Наглядно это представлено на рисунке 1.1.1.

Рисунок 1.1.1. Определение положения точки при помощи координат x=x (t), y=y (t) и z=z (t) и радиус-вектора r→(t), r0→ – радиус-вектор положения точки в начальный момент времени.

Определение 8

Перемещение тела s→=∆r→=r→-r0→ – это направленный отрезок прямой, который соединяет начальное положение тела с его дальнейшим положением. Перемещение является векторной величиной.

Пройденный путь l равняется длине дуги траектории, преодоленной телом за определенное время t.

Путь является скалярной величиной.

Если движение тела рассматривается в течение довольно короткого отрезка времени, тогда вектор перемещения оказывается направленным по касательной к траектории в заданной точке, а его длина равняется преодоленному пути.

В случае небольшого промежутка времени Δt преодоленный телом путь Δl практически совпадает с модулем вектора перемещения ∆s→. При перемещении тела по криволинейной траектории модуль вектора движения все время меньше пройденного пути (рисунок 1.1.2).

Рисунок 1.1.2. Пройденный путь l и вектор перемещения ∆s→ при криволинейном движении тела.
a и b – это начальная и конечная точки пути.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Определение средней и мгновенной скорости движения тела. Основные формулы кинематики

Для описания движения в физике введено понятие средней скорости: υ→=∆s→∆t=∆r→∆t.

Физиков больше интересует формула не средней, а мгновенной скорости, которая рассчитывается как предел, к которому стремится средняя скорость на бесконечно маленьком промежутке времени Δt, то есть υ→=∆s→∆t=∆r→∆t; ∆t→0.

В математике данный предел называется производная и обозначается dr→dt или r→˙.

Мгновенная скорость υ→ тела в каждой точке криволинейной траектории направлена по касательной к траектории в заданной точке. Отличие между средней и мгновенной скоростями демонстрирует рисунок 1.1.3.

Рисунок 1.1.3. Средняя и мгновенная скорости. ∆s1→, ∆s2→, ∆s3→ – перемещения за время ∆t1<∆t2<∆t3 соответственно. При t→0, υ→ср→υ→.

При перемещении тела по криволинейной траектории скорость υ→ меняется по модулю и по направлению. Изменение вектора скорости υ→ за какой-то маленький промежуток времени Δt задается при помощи вектора ∆υ→ (рисунок 1.1.4).

Вектор изменения скорости ∆υ→=υ2→-υ1→ за короткий промежуток времени Δt раскладывается на 2 составляющие: ∆υr→, которая направлена вдоль вектора υ→ (касательная составляющая) и ∆υn→, которая направлена перпендикулярно вектору υ→ (нормальная составляющая).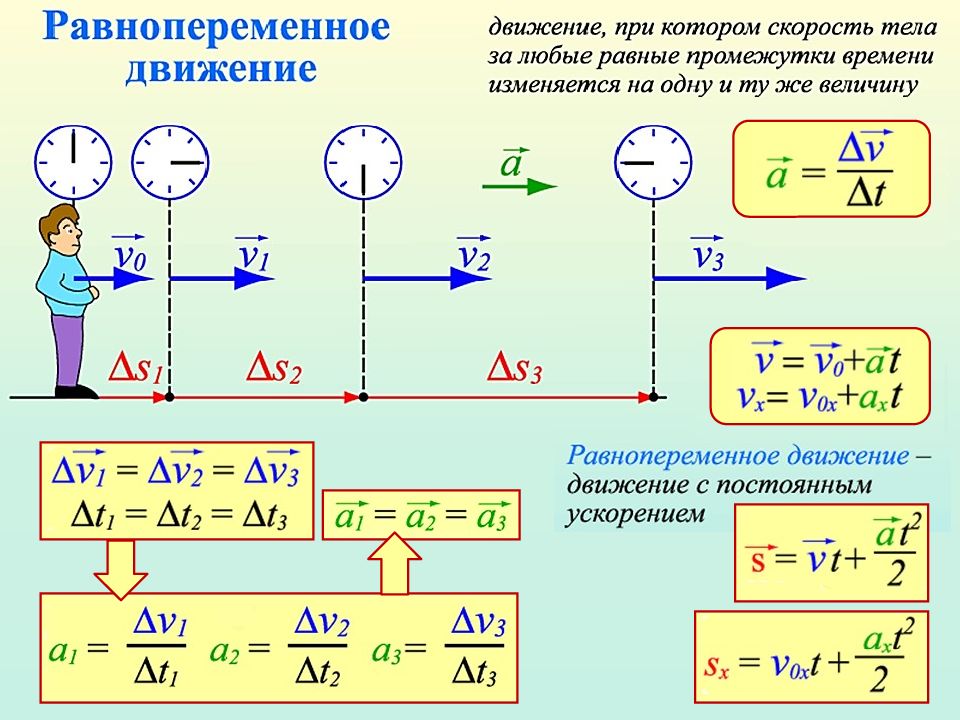

Рисунок 1.1.4. Изменение вектора скорости по величине и по направлению. ∆υ→=∆υ→r+∆υ→n – изменение вектора скорости за промежуток времени Δt.

Определение 9

Мгновенное ускорение тела a→ – это предел отношения небольшого изменения скорости ∆υ→ к короткому отрезку времени Δt, в течение которого изменялась скорость: a→=∆υ→∆t=∆υ→τ∆t+∆υ→n∆t; (∆t→0).

Направление вектора ускорения a→, при криволинейном движении, не совпадает с направлением вектора скорости υ→. Составляющие вектора ускорения a→ – это касательные (тангенциальные) a→τ и нормальные a→n ускорения (рисунок 1.1.5).

 Рисунок 1.1.5.Касательное и нормальное ускорения. 

Касательное ускорение показывает, как быстро меняется скорость тела по модулю: aτ=∆υ∆t; ∆t→0.

Вектор a→τ направлен по касательной к траектории.

Нормальное ускорение показывает, как быстро скорость тела меняется по направлению.

Пример 2

Представим криволинейное движение, как движение по дугам окружностей (рисунок 1.

1.6).

Рисунок 1.1.6. Движение по дугам окружностей.

Нормальное ускорение находится в зависимости от модуля скорости υ и радиуса R окружности, по дуге которой тело перемещается в определенный момент времени: an=υ2R.

Вектор an→ все время направлен к центру окружности.

По рисунку 1.1.5 видно, модуль полного ускорения равен a=aτ2+an2.

Итак, основные физические величины в кинематике материальной точки – это пройденный путь l, перемещение s→, скорость υ→ и ускорение a→.

Путь l – скалярная величина.

Перемещение s→, скорость υ→ и ускорение a→ – векторные величины.

Для того чтобы задать какую-нибудь векторную величину, необходимо задать ее модуль и определить направление. Вектора подчиняются математическим правилам: их можно проектировать на координатные оси, складывать, вычитать и др.

Кинематика | Физика

Наблюдая вокруг себя самые разнообразные объекты: облака, звезды и планеты, автомобили, летящую птицу, мы говорим, что тот или иной объект движется. Что же имеют в виду, произнося слово «движение»? В русском языке слово «движение» означает любое изменение, в отличие от состояния неподвижности, покоя. Например, говорят о «душевном движении», «общественном движении» и т. п. Мы же, изучая механику, будем использовать понятие «механическое движение», при этом часто ради краткости будем говорить просто «движение», опуская прилагательное «механическое».

Дать определение механическому движению ученые смогли, лишь обобщив все накопленные за многие века знания. В настоящее время говорят:

механическое движение — это изменение положения тела или его частей относительно других тел с течением времени.

Попробуем разобраться в этом определении, чтобы научиться правильного его использовать.

Ясно, что любое реальное тело имеет определенные размеры. Чтобы описать изменение его положения при механическом движении относительно других тел, мы должны рассматривать, как движутся все части этого тела. В ряде случаев, например при объезде автомобилем крупного препятствия на дороге, размеры и форма тел играют решающую роль.

Однако вначале мы будем изучать наиболее простые виды движения. При этом мы будем рассматривать движение тел, размерами которых пренебрегают. Такие тела называют точечными телами. О точечном теле можно говорить, что в данный момент времени оно находится в некоторой точке пространства.

Очевидно, что реальное тело можно считать точечным лишь тогда, когда нас не интересует различие в движении или положении отдельных частей этого тела. Например, если нас интересует только время движения поезда, выехавшего из Москвы до Владивосток, то этот поезд разумно считать точкой. Если же нас интересует время, за которое этот поезд проследует мимо километрового столба, то очевидно, что нам нельзя рассматривать поезд как точку, иначе мы не ответим на вопрос задачи. Также нельзя считать этот поезд точкой, если нас интересует, например, движение разных частей колеса этого поезда.

Следовательно, можно ли принять все тело за точку, зависит от поставленной задачи.

Мы начнем изучение механики с изучения движения точечного тела, т. е. будем рассматривать ситуации, когда реальное тело можно принять за точку.

Изучение механики традиционно начинают с кинематики.

Кинематика — раздел механики, в котором рассматривают способы описания механического движения тел без выяснения причин изменения характера их движения. Сами причины мы рассмотрим в других разделах механики, а здесь попытаемся ответить на вопрос: «Как описать движение тела?» Для этого прежде всего необходимо научиться отвечать на два важнейших вопроса: «Где (в какой точке пространства) и когда (в какой момент времени) находилось, находится и будет находится тело в процессе своего движения?». Начнем с ответа на первый вопрос — выясним, как можно описать положение тела в пространстве.

формулы, определения, методы решения задач

Кинематика — это специальный раздел теоретической механики. Направление сформировалось несколько позднее, чем статика и динамика: во второй половине XIX столетия. Первые исследования в области кинематики были посвящены огнестрельному оружию. Ученые стремились понять процесс полета снаряда, производили расчет траектории его движения. В дальнейшем кинематика как научное направление получило широкое распространение и существенно повлияло на развитие технического прогресса.

Кинематика — описание

Кинематика является разделом механики, цель которого — изучение механического движения тел с пренебрежением к причинам, вызывающим это движение.

Механика представляет собой научную область физики, которой посвящены исследования механического движения тел. Основной целью данного направления служит определение точного положения тела в пространстве в любой момент времени. Важным понятием этого раздела является материальная точка в виде тела с определенной массой и размерами, которыми можно пренебречь для решения задачи при наличии следующих условий:

1. Путь, который преодолевает тело, существенно больше, чем его размеры.
2. Расстояние между телами значительно превышает их размеры.
3. Объект совершает поступательное движение.

Движение тела рассматривают в системе отсчета, состоящей из системы координат и прибора, измеряющего время. Траекторией называют линию, которую объект описывает, совершая движение. Путь является скалярной величиной, определяемой как длина траектории. Перемещением обозначают вектор, который соединяет начальное и конечное положение тела, преодолеваемое им в течение определенного промежутка времени.

Совершая движение, тело может только увеличивать пройденный путь, при этом перемещение увеличивается или уменьшается. К примеру, уменьшение перемещения наблюдается во время обратного движения тела. Если объект движется прямолинейно в одном направлении, то путь определяется модулем перемещения. В случае криволинейного движения — путь превышает перемещение. При рассмотрении замкнутой траектории перемещение будет равно нулю.

Теория и формулы

Благодаря многолетним исследованиям в области кинематики ученым удалось вывести определенные закономерности движения тела. С помощью справедливых уравнений представляется возможным ответить на многие вопросы о разных характеристиках, которые изменяются либо остаются постоянными во время движения объектов.

Путь, время, скорость

Расстояние представляет собой удаленность одной точки положения тела от другой. Тело преодолевает путь, который представляет собой важную характеристику механического движения. Общепринятым обозначением пути является латинская буква s. Данный параметр измеряют метрами и километрами, если речь идет о больших расстояниях.

Скорость представляет собой путь, который тело преодолело в течение единицы времени. В качестве единицы времени часто используют 1 час, 1 минуту, 1 секунду. Для расчета скорости необходимо определить отношение пути к времени движения. В случае, когда в условиях задачи расстояние измеряется в метрах, а время пути — в секундах, то скорость следует рассчитывать в метрах в секунду (м/с). Для обозначения скорости используют латинскую букву \(v\).

Нередко требуется определить время пути. Данный параметр обозначают с помощью латинской буквы \(t\).

Важно отметить, что скорость, путь и время взаимосвязаны. При известных характеристиках скорости и времени можно определить расстояние, которое преодолело тело. Путь в данном случае равен произведению скорости и времени, рассчитывается по формуле:

\(s=v\times t\)

При известных величинах времени и расстояния достаточно просто определить скорость движения тела, руководствуясь следующим уравнением:

\(v=\frac{s}{t}\)

Равномерное движение

Равномерным движением называют движение тела, которое совершает равные перемещения в течение любых равных промежутков времени.

Источник: goodfon.ru

Скорость при равномерном движении определяется как отношение перемещения ко времени, в течение которого данное перемещение было совершено. Уравнение имеет следующий вид:

\(\vec{v}=\frac{\vec{s}}{t}\)

\(\vec{v}=const\)

Проекция вектора скорости на ось ОХ выглядит таким образом:

\(v_{x}=\frac{s_{x}}{t}\)

\(v_{x}=const\)

Если вектор скорости спроецировать на ось координат, то она будет равна быстроте изменения данной координаты:

\(v_{x}=\frac{x-x_{0}}{t}\)

Прямолинейное равноускоренное движение

Прямолинейным равноускоренным движением называют движение по прямой траектории, для которого характерно постоянное ускорение.

Ускорение для прямолинейного равноускоренного движения обозначают следующим образом:

\(\vec{a}=const\)

При таком движении можно наблюдать увеличение или уменьшение скорости. Чтобы определить скорость, необходимо выполнить следующий расчет:

\(\vec{v}=\vec{v}_{0}+\vec{a}t\)

Если тело разгоняется в проекции оси ОХ, то скорость можно определить по формуле:

\(v_{x}=v_{0x}+a_{x}t\)

a>0, движение является равноускоренным.

Источник: fizi4ka.ru

Во время торможения в проекции на ось ОХ скорость рассчитывают следующим образом:

\(v_{x}=v_{0x}-a_{x}t\)

а<0, движение является равнозамедленным.

Источник: fizi4ka.ru

Графически зависимость ускорения от времени, то есть график ускорения во время равноускоренного движения тела, можно представить в виде:

Источник: fizi4ka.ru

График ускорения, характеризующий равноускоренное движение тела, представляет собой прямую, которая параллельна оси времени:

• график 1 находится над осью t, тело совершает разгон, ах>0;
• график 2 размещен под осью t, тело тормозит, ах<0.

Графически скорость или проекция скорости изображается в виде зависимости скорости от времени:

Источник: fizi4ka.ru

Графически скорость, характерная для равноускоренного движения тела, имеет вид прямой. График 1 направлен вверх, тело будет совершать равноускоренное движение в положительном направлении оси ОХ:

\(v_{0x}>0\)

\(a_x>0\)

\(a_{1x} = tg α \)

График 2 направлен вниз, тело будет двигаться равнозамедленно в положительном направлении оси ОХ:

\(v_{0x}>0\)

\(a_x<0\)

\(a_{2x} = tg α \)

График 3 направлен вниз, тело свершает равноускоренное движение против оси ОХ:

\(v_{0x}<0\)

\(a_x<0\)

Исходя из графика зависимости скорости от времени, определяют перемещение, которое тело преодолело в течение определенного промежутка времени \(t_2-t_1\). {2}}{-2g}\)

В максимальной верхней точке тело, брошенное вверх, будет обладать нулевой скоростью, \(v=0\). Для расчета времени подъема можно воспользоваться формулой:

\(t=\frac{v_{0}}{g}\)

Свободно падающее тело

Свободным падением называют движение тела в условиях безвоздушного пространства под действием силы тяжести.

В условиях свободного падения ускорения тел с разной массой будут равны. Данный параметр называют ускорением свободного падения. Оно всегда направлено к центру нашей планеты, то есть вертикально вниз. Величина обозначается латинской буквой g, а единицами измерения являются м/с².

Ускорение свободного падения равно 9,8 м/с². В задачах по физике допускается использовать значение g=10 м/с².

Движение по окружности с постоянной по модулю скоростью

Движением по окружности при постоянной по модулю скоростью называют простейшим видом криволинейного движения.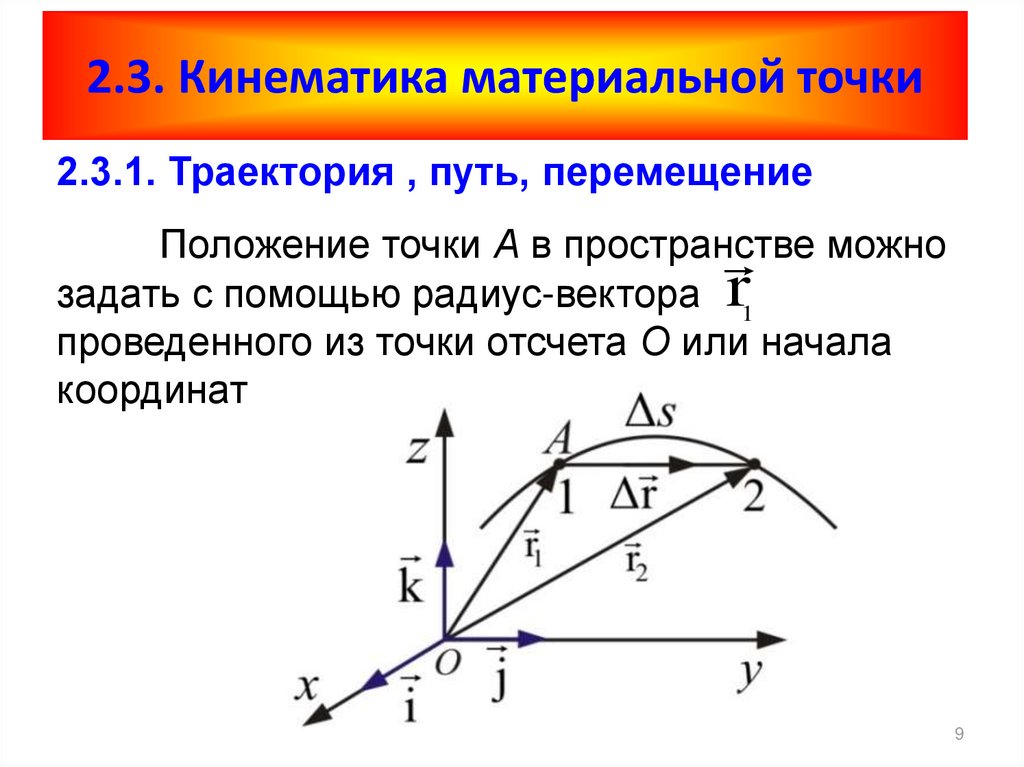 {-1}\) (Гц).

\(\nu=\frac{N}{t}\)

Период и частота являются взаимно обратными величинами:

\(T=\frac{1}{\nu}\)

\(\nu =\frac{1}{T}\)

Линейная скорость представляет собой скорость движения тела по окружности. Параметр обозначают латинской буквой v, единицами измерения являются м/с. Линейная скорость направлена по касательной к окружности и рассчитывается по формуле:

\(v=\frac{2\pi \times R}{T}\)

\(R\) является радиусом окружности.

Угловой скоростью называют физическую величину, которая определяется как отношение угла поворота и времени, за которое тело совершает этот поворот. Обозначают параметр как ω. Единицами измерения угловой скорости являются рад/с. Угловая скорость определяется по формуле:

\(\omega =\frac{\varphi }{t}\)

\(\varphi\) представляет собой угол поворота.

Источник: fizi4ka.ru

Направление угловой скорости определяют с помощью правила правого винта или буравчика. В случае, когда вращательное движение винта соотносится с направлением движения тела по окружности, то поступательное движение винта и направление угловой скорости совпадают. {2}R\)

\(\omega = \frac{2\pi }{T}\)

\(\omega = 2\pi v\)

Во время равномерного движения тела по окружности точки, расположенные на радиусе, перемещаются с равной угловой скоростью, так как радиус за одно и то же время поворачивается на одинаковый угол. В это время линейная скорость разных точек радиуса отличается в зависимости от того, насколько близко или далеко от центра они размещены:

\(v_{1}=\omega r\)

\(v_{2}=\omega R\)

\(\frac{v_{1}}{v_{2}}=\frac{r}{R}\)

Источник: fizi4ka.ru

При рассмотрении равномерного движения двух соединенных тел можно наблюдать отсутствие отличий в линейных скоростях, но при этом угловые скорости тел будут различны в зависимости от радиуса тела:

\(\omega _{1}=\frac{v}{R_{1}}\)

\(\omega _{2}=\frac{v}{R_{2}}\)

\(\frac{\omega _{1}}{\omega _{2}}=\frac{R_{1}}{R_{2}}\)

Источник: fizi4ka.ru

Движение тела, брошенного под углом к горизонту

Движение тела, которое бросили под углом к горизонту, можно представить в виде суперпозиции двух движений:

1. Равномерного горизонтального перемещения. 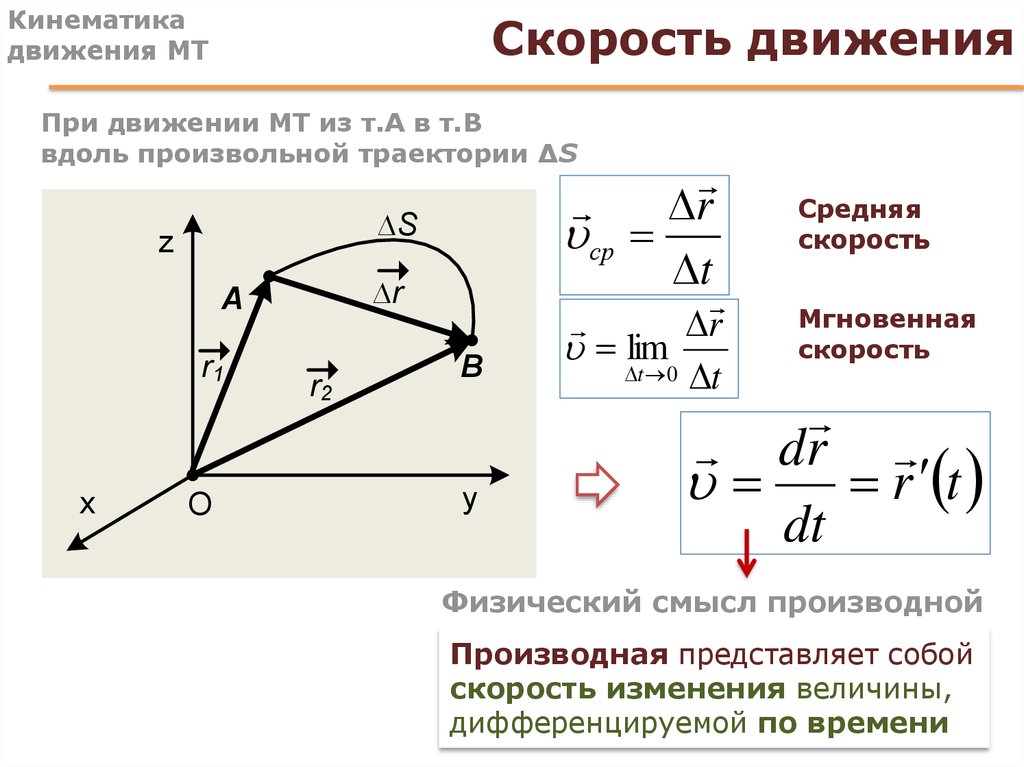{2}}\)

   Дальность полета тела соответствует уравнению:

   \(l=v_{0x}t=v_{0x}\sqrt{\frac{2h_{0}}{g}}\)

   Вычислить угол между вектором скорости и осью ОХ можно с помощью формулы:

   \(\tan \beta =\frac{v_{y}}{v_{x}}=\frac{-gt}{v_{0x}}\)

   Задачи по кинематике, их решение

   Задача 1

   Рассмотрим путь велосипедиста из одного населенного пункта в другой. Половина расстояния была преодолена со скоростью 12 км/ч (\(v_1\)). Далее половину оставшегося времени он ехал со скоростью 6 км/ч (\(v_2\)). Остаток расстояния путник преодолел пешком со скоростью 4км/ч (\(v_3\)). Необходимо рассчитать среднюю скорость на всем пути следования велосипедиста.

   Решение

   Данный пример относится к теме равномерного прямолинейного движения одного тела. Процесс можно изобразить схематично:

   Источник: pandia.ru

   \(S = S_1 + S_2 + S_3\)

   \(t = t_1 + t_2 + t_3\)

   На каждый отрезок пути необходимо составить уравнение движения:

   \(S_1 = v_1t_1\)

   \(S_2 = v_2t_2\)

   \(S_3 = v_3t_3\)

   Далее можно представить дополнительные условия задачи:

   \(S_1 = S_2 + S_3\)

   \(t_2 = t_3\)

   \(v_{sr}=\frac{S}{t}=\frac{S_{1}+S_{2}+S_{3}}{t_{1}+t_{2}+t_{3}}\)

   Следует преобразить формулу и подставить числовые значения:

   \(v_{sr}=\frac{2S_{1}}{\frac{S_{1}}{v_{1}}+\frac{2S_{1}}{v_{2}+v_{3}}}=\frac{2v_{1}\left(v_{2}+v_{3} \right)}{2v_{1}+v_{2}+v_{3}}\)

   \(v_{sr}=\frac{2\times 12\left(6+4 \right)}{2\times 12+6+4}=7\)

   Ответ: средняя скорость составляет \(7\) км/ч. {2}}=\frac{9,81}{0,17}=57,7\)

   Ответ: камень упал с высоты \(57,7\) м.

   Решение задач по кинематике основано на простых формулах. Успешность результата зависит от умения грамотно применять справедливые уравнения в том или ином случае. Бывают ситуации, когда в процессе изучения физики возникают некоторые трудности. Простым решением будет обратиться к порталу Феникс.Хелп.

   основные формулы с пояснениями или определения по физике в 10 классе, какие законы динамики или механики для ЕГЭ

   Описать можно все что угодно: картину в галерее, уличного хулигана в кабинете участкового и даже свои душевные переживания на приеме у психотерапевта. Достаточно вооружиться бумагой, ручкой и вперед.

   Но что необходимо, чтобы описать движение? На этот вопрос нам поможет ответить кинематика, раздел механики, который как раз и занимается описанием механического движения.

   Физика простыми словами | Кинематика

   Как описать движение?

   Давайте разберемся с терминологией и введем основные понятия, без которых нам никак не обойтись. Итак, движением мы будем называть любое изменение положения тела в пространстве с течением времени.

   К слову сразу отметим, что время в физике принято мерить секундами, а само движущееся тело не всегда рассматривается целиком. Зачастую его размерами и формой можно пренебречь и рассматривать как точку, имеющую массу.

   В механике вы можете услышать такие понятия как точечное тело или материальная точка. Так вот знайте, речь идет как раз об этом.

   К примеру, какие бы габариты не имела ваша машина, если вы едете по трасе из Ростова в Москву, то она в любом случае очень мала в сравнении с расстоянием, а значит мы можем рассматривать её как материальную точку. А вот если, приехав в столицу нашей необъятной родины, вы ищете свободное место где припарковаться, то тут размерами и формой автомобиля пренебречь уже не получится.

   Положение тела или материальной точки в пространстве рассматривается с помощью системы координат, за начало которой мы принимаем тело отсчета, относительно которого  происходит движение. В зависимости от сложности этого движения мы можем иметь дело с одномерным, двухмерным, или трехмерным пространством.

   Соответственно, наша система координат может иметь одну, две или три оси. Как правило трехмерные пространства в школьной физике практически не встречаются, поэтому мы ограничимся двухмерным с координатными осями х и у.

   Чтобы определить координаты нашей материальной точки, необходимо построить её проекции на соответствующие  координатные оси, опустив на них перпендикуляры.

   Теперь если наблюдая за движущейся материальной точкой, построить линию, по которой она движется, мы получим траекторию движения. Измерив длину траектории можно определить пройденный путь, а если построить вектор, соединяющий начальное и конечное положение точки, это будет  перемещение.

   Так как единицей длинны в международной системе единиц был принят метр, то путь, пройденный телом, и длина вектора перемещения, или, как еще говорят, его модуль,  так же будут измерятся в метрах. Отметим, что модуль перемещения всегда будет меньше, ну или в крайнем случае равен пути, но никак не больше.

   Все просто,  вектора кривыми не бывают, и перемещение не является исключением. А вот что касается траектории, то её мы можем  гнуть как угодно.

   Исходя из этого, можно выделить два вида механического движения: прямолинейное — когда траектория прямая линия и криволинейное — когда тело движется по кривой, ну, к примеру, параболе или окружности.

   Прямолинейное движение

   Давайте представим, что мы едем в автобусе, а для простоты будем считать, что траектория нашего движения — прямая линия. Если разделить весь путь (s), который мы проедем на затраченное время (t), мы получим скорость (v). То есть величину, которая характеризует быстроту движения. Измеряется она в метрах в секунду м/с.

   v=s/t

   Так как движение относительно, то относительной будет и скорость. К примеру, если наш автобус едет со скоростью v1, ну скажем, равной 20 м/с, а мы, находясь в автобусе, идем в направлении водителя со скоростью v2, равной 1 м/с, то наша скорость относительно  дороги будет определятся как сумма двух этих скоростей. То есть 21 м/с.

   v=v1+v2

   Ну а если  мы будем идти от водителя, то наша скорость относительно дороги будет уже равна 19 м/с. И казалось бы, ничего не поменялось, и значения скоростей v1 и v2 остались прежними, но изменилось направление нашего движения, а значит, чтобы найти скорость, с которой мы движемся относительно дороги, нам нужно вычесть v2 из v1 .

   v=v1-v2

   В рассмотренных примерах мы условно принимали движение как равномерное, то есть движение с постоянной скоростью. Но в реальности, автобус то и дело будет останавливаться на светофорах и остановках, а потом опять разгоняться. Обгонять неторопливых автолюбителей.

   Да и у нас не получится ходить по нему с постоянной скоростью, тем более если ехать в час пик, когда автобус забит под завязку. В реальности движение будет неравномерным, и скорость будет постоянно меняться.

   При неравномерном движении отношение всего пройденного пути ко времени называется средней скоростью.

   vср=s/t

   И хотя в некоторых случаях она бывает очень удобна, но все же не всегда приемлема при описании движения. Думаю, будет очень трудно доказать сотруднику гос автоинспекции, остановившему вас за превышение скорости, что ваша средняя скорость на всем пути была в пределах нормы.

   Тут речь пойдет о мгновенной скорости, или скорости в какой-то определенный момент времени. Если посмотреть на спидометр движущегося автомобиля, то мы как раз её увидим.

   И стоит нам по сильнее  нажать на педаль газа, как  в то же мгновение стрелка спидометра начинает ползти вверх, оповещая нас об изменении скорости.

   И здесь необходимо ввести понятие ускорения, величины, которая будет  характеризовать изменение скорости движения за какой то промежуток времени (t). Её принято обозначать маленькой буквой a и измерять в м/с2.

   а=(V-V0)/t

   Ускорение, так же как и скорость, величина векторная, а значит будет иметь свое направление. Причем, если направление вектора ускорения будет совпадать с направлением скорости, то скорость будет возрастать.

   Такое движение называют ускоренным. И напротив, снижение скорости, при замедленном движении, будет свидетельствовать о том что вектора ускорения и скорости смотрят в разные стороны. Выразим скорость и перемещение для движения с ускорением:

   Если объединить эти уравнения в одно, мы получим формулу разности квадратов скоростей :

   Итак, мы ввели основные понятия и величины кинематики и вывели основные уравнения, связывающие их. Но для простоты мы брали прямолинейное движение.

   Если же говорить о движении по кривой, то нам придется уже рассматривать его в двухмерном или даже трехмерном пространстве.

   Для этого необходимо будет построить проекции векторов скорости, перемещения и ускорения на соответствующие координатные оси, а при работе с проекциями мы опять получим уже знакомые уравнения для прямолинейного движения, которые примут следующий вид:

   1. Sx=  V0x t +(axt2) /2
      Sy= V0у t +(aуt2) /2
      vx=v0x+axt
      vy=v0y+ayt

   Или для определения координат движущейся материальной точки:

   1. x= x 0 + V0x t +(axt2) /2
      y= y 0 + V0у t +(aуt2) /2

   Где х0, у0 — координаты начального положения точки в пространстве, а х, у — координаты её конечного положения.
   Для описания движения в трехмерном пространстве у нас добавится третья ось z, и, соответственно, проекции скорости, ускорения и перемещения на эту ось.

   Принцип разложения движения на простые составляющие лежит в основе многих устройств.  Так первые компьютерные  мыши были оснащены шариком, вращение которого приводило во вращение два перпендикулярно расположенных друг к другу колесика со специальными датчиками, они то  и  раскладывали сложные движения мыши на горизонтальные и вертикальные составляющие.

   Стоило одному из этих колесиков покрыться толстым слоем грязи, как оно переставало вращаться, и указатель на экране начинал двигаться только по прямой, горизонтальной или вертикальной.

   Современные оптические мыши лишены этого недостатка, так как в них шарик и колесики, заменены на лазерные датчики, но тем не менее принцип разложения движения они унаследовали от своих прародительниц.

   Источник: https://physicsline.ru/teoriya/fizika-prostymi-slovami/fizika-prostymi-slovami-kinematika/

   Основные формулы по физике: кинематика, динамика, статика

   Итак, как говорится, от элементарного к сложному. Начнём с кинетических формул:

   Также давайте вспомним движение по кругу:

   Медленно, но уверенно мы перешли более сложной теме – к динамике:

   Уже после динамики можно перейти к статике, то есть к условиям равновесия тел относительно оси вращения:

   После статики можно рассмотреть и гидростатику:

   Куда же без темы “Работа, энергия и мощность”. Именно по ней даются много интересных, но сложных задач. Поэтому без формул здесь не обойтись:

   Основные формулы термодинамики и молекулярной физики

   Последняя тема в механике – это “Колебания и волны”:

   Теперь можно смело переходить к молекулярной физике:

   Плавно переходим в категорию, которая изучает общие свойства макроскопических систем. Это термодинамика:

   Основные формулы электричества

   Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:

   • Переходим к постоянному электрическому току:
   • Далее добавляем формулы по теме: “Магнитное поле электрического тока”
   • Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:
   • Ну и, конечно, куда же без электромагнитных колебаний:

   Это были основные формулы физики

   В статье мы подготовили 50 формул, которые понадобятся на экзамене в 99 случая из 100.

   Совет: распечатайте все формулы и возьмите их с собой. Во время печати, вы так или иначе будете смотреть на формулы, запоминая их. К тому же, с основными формулами по физике в кармане, вы будете чувствовать себя на экзамене намного увереннее, чем без них.

   Надеемся, что подборка формул вам понравилась!

   Источник: https://NauchnieStati.ru/spravka/bolee-50-osnovnyh-formul-po-fizike/

   100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА

   Код и классификация направлений подготовки	Код группы образовательной программы	Наименование групп образовательных программ	Количество мест
   8D01 Педагогические науки
   8D011 Педагогика и психология	D001	Педагогика и психология	45
   8D012 Педагогика дошкольного воспитания и обучения	D002	Дошкольное обучение и воспитание	5
   8D013 Подготовка педагогов без предметной специализации	D003	Подготовка педагогов без предметной специализации	22
   8D014 Подготовка педагогов с предметной специализацией общего развития	D005	Подготовка педагогов физической культуры	7
   8D015 Подготовка педагогов по естественнонаучным предметам	D010	Подготовка педагогов математики	30
   	D011	Подготовка педагогов физики (казахский, русский, английский языки)	23
   	D012	Подготовка педагогов информатики (казахский, русский, английский языки)	35
   	D013	Подготовка педагогов химии (казахский, русский, английский языки)	22
   	D014	Подготовка педагогов биологии (казахский, русский, английский языки)	18
   	D015	Подготовка педагогов географии	18
   8D016 Подготовка педагогов по гуманитарным предметам	D016	Подготовка педагогов истории	17
   8D017 Подготовка педагогов по языкам и литературе	D017	Подготовка педагогов казахского языка и литературы	37
   	D018	Подготовка педагогов русского языка и литературы	24
   	D019	Подготовка педагогов иностранного языка	37
   8D018 Подготовка специалистов по социальной педагогике и самопознанию	D020	Подготовка кадров по социальной педагогике и самопознанию	10
   8D019 Cпециальная педагогика	D021	Cпециальная педагогика	20
   		Всего	370
   8D02 Искусство и гуманитарные науки
   8D022 Гуманитарные науки	D050	Философия и этика	20
   	D051	Религия и теология	11
   	D052	Исламоведение	6
   	D053	История и археология	33
   	D054	Тюркология	7
   	D055	Востоковедение	10
   8D023 Языки и литература	D056	Переводческое дело, синхронный перевод	16
   	D057	Лингвистика	15
   	D058	Литература	26
   	D059	Иностранная филология	19
   	D060	Филология	42
   		Всего	205
   8D03 Социальные науки, журналистика и информация
   8D031 Социальные науки	D061	Социология	20
   	D062	Культурология	12
   	D063	Политология и конфликтология	25
   	D064	Международные отношения	13
   	D065	Регионоведение	16
   	D066	Психология	17
   8D032 Журналистика и информация	D067	Журналистика и репортерское дело	12
   	D069	Библиотечное дело, обработка информации и архивное дело	3
   		Всего	118
   8D04 Бизнес, управление и право
   8D041 Бизнес и управление	D070	Экономика	39
   	D071	Государственное и местное управление	28
   	D072	Менеджмент и управление	12
   	D073	Аудит и налогообложение	8
   	D074	Финансы, банковское и страховое дело	21
   	D075	Маркетинг и реклама	7
   8D042 Право	D078	Право	30
   		Всего	145
   8D05 Естественные науки, математика и статистика
   8D051 Биологические и смежные науки	D080	Биология	40
   	D081	Генетика	4
   	D082	Биотехнология	19
   	D083	Геоботаника	10
   8D052 Окружающая среда	D084	География	10
   	D085	Гидрология	8
   	D086	Метеорология	5
   	D087	Технология охраны окружающей среды	15
   	D088	Гидрогеология и инженерная геология	7
   8D053 Физические и химические науки	D089	Химия	50
   	D090	Физика	70
   8D054 Математика и статистика	D092	Математика и статистика	50
   	D093	Механика	4
   		Всего	292
   8D06 Информационно-коммуникационные технологии
   8D061 Информационно-коммуникационные технологии	D094	Информационные технологии	80
   8D062 Телекоммуникации	D096	Коммуникации и коммуникационные технологии	14
   8D063 Информационная безопасность	D095	Информационная безопасность	26
   		Всего	120
   8D07 Инженерные, обрабатывающие и строительные отрасли
   8D071 Инженерия и инженерное дело	D097	Химическая инженерия и процессы	46
   	D098	Теплоэнергетика	22
   	D099	Энергетика и электротехника	28
   	D100	Автоматизация и управление	32
   	D101	Материаловедение и технология новых материалов	10
   	D102	Робототехника и мехатроника	13
   	D103	Механика и металлообработка	35
   	D104	Транспорт, транспортная техника и технологии	18
   	D105	Авиационная техника и технологии	3
   	D107	Космическая инженерия	6
   	D108	Наноматериалы и нанотехнологии	21
   	D109	Нефтяная и рудная геофизика	6
   8D072 Производственные и обрабатывающие отрасли	D111	Производство продуктов питания	20
   	D114	Текстиль: одежда, обувь и кожаные изделия	9
   	D115	Нефтяная инженерия	15
   	D116	Горная инженерия	19
   	D117	Металлургическая инженерия	20
   	D119	Технология фармацевтического производства	13
   	D121	Геология	24
   8D073 Архитектура и строительство	D122	Архитектура	15
   	D123	Геодезия	16
   	D124	Строительство	12
   	D125	Производство строительных материалов, изделий и конструкций	13
   	D128	Землеустройство	14
   8D074 Водное хозяйство	D129	Гидротехническое строительство	5
   8D075 Стандартизация, сертификация и метрология (по отраслям)	D130	Стандартизация, сертификация и метрология (по отраслям)	11
   		Всего	446
   8D08 Сельское хозяйство и биоресурсы
   8D081 Агрономия	D131	Растениеводство	22
   8D082 Животноводство	D132	Животноводство	12
   8D083 Лесное хозяйство	D133	Лесное хозяйство	6
   8D084 Рыбное хозяйство	D134	Рыбное хозяйство	4
   8D087 Агроинженерия	D135	Энергообеспечение сельского хозяйства	5
   	D136	Автотранспортные средства	3
   8D086 Водные ресурсы и водопользование	D137	Водные ресурсы и водопользования	11
   		Всего	63
   8D09 Ветеринария
   8D091 Ветеринария	D138	Ветеринария	21
   		Всего	21
   8D11 Услуги
   8D111 Сфера обслуживания	D143	Туризм	11
   8D112 Гигиена и охрана труда на производстве	D146	Санитарно-профилактические мероприятия	5
   8D113 Транспортные услуги	D147	Транспортные услуги	5
   	D148	Логистика (по отраслям)	4
   8D114 Социальное обеспечение	D142	Социальная работа	10
   		Всего	35
   		Итого	1815
   		АОО “Назарбаев Университет”	65
   		Стипендиальная программа на обучение иностранных граждан, в том числе лиц казахской национальности, не являющихся гражданами Республики Казахстан	10
   		Всего	1890

   Основные понятия и формулы кинематики по физике – тест от Skills4u

   Одним из важных разделов физики, изучаемых в школьной программе, является кинематика – формулы помогают вычислить скорость движения и пройденный путь, определить координаты тела. Для успешной сдачи итогового экзамена очень важно не только хорошо знать формулы кинематики по физике, но и уметь правильно их применять. На экзамене часто не хватает времени на размышления – нужно безошибочно выбирать правильный ответ. Наш тренажер помогает выработать стойкий учебный навык находить верные решения за кратчайшее время.

   Движение, скорость и ускорение изучает именно кинематика – формулы для ЕГЭ можно быстро повторить с помощью нашего теста. Каждый может пройти его бесплатно и определить, насколько хорошо он знает азы школьной программы. Тест состоит примерно из 20 вопросов, на его выполнение уйдет не более 5-10 минут.

   Вам предстоит выбрать один из 4 вариантов ответа, показанных на экране. Если ответ верный, загорается зеленый свет, а ошибка подсвечивается красным. При составлении заданий учтены все основные понятия и формулы кинематики. Вам придется вспомнить их, чтобы успешно пройти тестирование. По его итогам система сформирует рейтинг и предложит продолжить занятия, чтобы добиться 100% результата.

   Очень важно, что вы всегда можете видеть верный ответ. Это позволяет сэкономить время и понять, что следует повторить перед экзаменом. Так, например, если вам плохо даются формулы движения – кинематика основана на них – вам следует вновь пройти тест через несколько часов, а затем регулярно тренироваться в течение последующих 4-5 дней. За это время сформируется стойкий учебный навык нахождения правильных ответов. Теперь, если вам попадется задача по кинематике, вы с блеском справитесь с ней.

   Один раз тест предоставляется бесплатно, но для того, чтобы получить возможность заниматься на тренажерах и изучать основные формулы кинематики на конкретных примерах, следует зарегистрироваться на сайте образовательной платформы Skills4u и оплатить доступ на месяц, полугодие или полный учебный год. Выбирайте подходящий план занятий и присоединяйтесь к нам! Занятия на интерактивных тренажерах – очень быстрый и эффективный способ подготовиться к ЕГЭ и успешно сдать итоговый экзамен.

   Чат-бот для решения задач по физике по теме «Кинематика»

   Актуальность

   В самом общем смысле чат-бот – это компьютерная программа, которая интерактивно имитирует человеческую речь (устную или письменную) и позволяет общаться с цифровыми устройствами так, как если бы они были живыми людьми. Чат-боты могут быть очень простыми, как элементарные программы, отвечающие на простой запрос однострочным ответом, или сложными, как цифровые помощники, которые обучаются и развиваются по мере сбора и обработки информации, тем самым повышая свой уровень персонализации.

   Большинство школьников сталкиваются с проблемой непонимания задач, например, из курса физики раздела «Механика». Этот бот поможет разобраться с решением задач по теме «Кинематика» и проверить полученные решения в режиме онлайн.

   Цель

   Разработать обучающую программу для решения задач по физике из раздела «Кинематика», а также создать чат-бот для социальной сети ВКонтакте для повышения доступности и удобства использования программы.

   Задачи

   1. Изучить язык программирования Python и проанализировать существующие решения.
   2. Составить алгоритм программы на языке Python, позволяющий решать задачи по физике из темы «Кинематика» (базовый уровень).
   3. Изучить принципы работы VK_API с целью создания чат-бота и дальнейшего его продвижения.
   4. Провести бета-тест чат-бота на уроке физики в классе, получить обратную связь посредством сервиса, интегрированного в чат-бот.

   Оснащение и оборудование, использованное при создании работы

   • Персональный компьютер с установленным ПО (pycharm Community Edition 2020.2.3, Python)
   • Смартфон с установленным ПО и выходом в интернет

   Описание

   Первый этап работы. Большинство школьников сталкиваются с проблемой непонимания некоторых задач по физике. В интернете есть много онлайн-помощников. Но большинство связано лишь с математическими уравнениями/функциями. Всё, что мы нашли в сфере физики, либо было заброшено, либо не работало.

   Следующим этапом было выявление возможности разработки программы для решения задач по физике из раздела «Механика», а также создания чат-бота по решению задач из курса физики базового уровня. Далее – визуализация алгоритма работы. Для этого нам не нужны были знания программирования, надо было просто составить блок-схему из последовательных шагов. Алгоритм работы чат-бота удобно представлять в виде mind map. Это инструмент визуализации, который позволяет конвертировать идею в схему из готовых блоков.

   Определены формулы для решения задач по кинематике и значения, при  которых уравнения не решаются. Формулы записаны на языке Python, введены переменные, размерности физических величин в системе СИ. Для удобства использования бота сделаны специальные кнопки быстрой клавиатуры, благодаря которым не придётся писать долгий текст о том, что нужно сделать. Достаточно будет нажать на кнопку и получить результат.

   Результаты работы/выводы

   Автор изучил язык программирования Python, написал базовый алгоритм программы, изучил принципы VK_API, провёл бета-тест чат-бота на уроке физики.

   Создан чат-бот, выдающий алгоритм решения задачи, формулы и основные определения из раздела «Механика» по теме кинематика.

   Перспективы использования результатов работы

   С помощью бота вы сможете подготовиться к самостоятельной или контрольной работе по данному разделу физики. Наш чат-бот содержит полный список формул по разделу «Механика», в его функции входит решение задач с предоставлением формулы из списка формул, с помощью которой производился расчёт, показ расчёта единиц измерений физических величин, перевод в систему СИ.

   Сотрудничество с вузом/учреждением при создании работы

   Инженерная академия РУДН

   Награды/достижения (в каких конкурсах и с какими результатами выставлялась ранее эта работа)

   Призер конференции Инженерной академии РУДН

   Мнение автора

   «Участие в проекте «Инженерный класс в московской школе» помогло представить результаты выполненного проекта на конкурсе проектов и исследований Открытой городской научно-практической конференции «Инженеры будущего». Было замечательно почувствовать себя разработчиком программного контента и научиться представлять результаты работы. Обмен мнениями во время представления проекта поможет его усовершенствовать и представить на следующей конференции!»

   Что такое кинематика? Простые ответы по физике

   Как пользоваться этим руководством

   Этот пост в блоге является первым из серии о том, как понимать и решать проблемы кинематики. Он призван дополнить ваш класс и учебник. Я сосредоточусь на практических приложениях, способах решения проблем и типичных ошибках, которые делают студенты. Если вы хотите изучить основы кинематики, я рекомендую учебник, но если вы хотите получить более глубокое понимание, избежать путаницы и научиться решать проблемы, примите красную таблетку и присоединяйтесь к нам!

   Что такое кинематика?

   Кинематика – это просто изучение движения.Буквально это слово означает: кинезис (движение) + тики (изучение. Подумайте о математике, политике, пиццатике). На более практическом уровне кинематика, которую вы изучаете на вводном уроке физики, – это изучение положения, скорости и импульса. На самом практическом уровне кинематика – это изучение того, что происходит, когда вы подбрасываете мяч. Это означает, что если вы можете подбрасывать мяч, вы можете изучить кинематику – к вашему сведению, любой, кто когда-либо видел, как я занимаюсь спортом, знает, обратное неверно.

   Положение, скорость и ускорение

   Итак, кинематика – это изучение трех вещей, но что именно это за три вещи?

   Позиция :

   Где находится объект.Его месторасположение. В физических задачах это обозначается как x, y, z p, r или d. У каждого учителя есть свои предпочтения, поэтому изучите свои, но для этого блога мы будем использовать x и y. Нас также часто интересует изменение положения, известное как смещение, которое обозначается как Δx, Δy, Δp, Δd или иногда просто x, y или d, чтобы запутать вещи. Положение и перемещение обычно измеряются в метрах или м.

   Скорость :

   Как быстро объект движется и в каком направлении: то есть как расстояние меняется с течением времени.В физических задачах скорость почти всегда обозначается буквой v. Скорость обычно измеряется в метрах в секунду или м / с. Когда скорость постоянна, это можно описать уравнением v = Δx / Δt (изменение положения, деленное на изменение во времени).

   Разгон :

   Как меняется скорость объекта. Если Ferrari разгоняется до 100 км / ч за 2,4 секунды, значит, он ускоряется. Если водитель пугается и врезается в стену, которая останавливает автомобиль, значит, он также разогнался.Ускорение всегда обозначается буквой a и измеряется в метрах в секунду в секунду или м / с ² .

   Когда ускорение постоянное, его можно описать уравнением a = Δv / Δt (изменение положения, деленное на изменение во времени). Вы могли заметить, что это уравнение очень похоже на уравнение для скорости. Это не совпадение: оно отражает фундаментальную физику, которая определяет все в мире.

   Избегайте распространенных ошибок: положение, расстояние и смещение

   Положение, смещение и расстояние легко спутать, и учителя физики часто проводят тесты, чтобы убедиться, что вы понимаете разницу.Положение измеряется от некоторой исходной точки и определяет местоположение объекта – в кинематике мы часто определяем исходную точку как начальное местоположение объекта, чтобы упростить задачу. Расстояние измеряет общее расстояние, пройденное объектом. Смещение измеряет, как далеко находится объект от того места, где он начался.

   Чтобы понять разницу, представьте сценарий, в котором вы начинаете на 3 метра вправо от исходной точки и идете на 2 метра влево, а затем на 4 метра вправо. Ваша позиция в начале – 3 метра, а в конце – 5 метров.Ваше расстояние составляет 6 метров, потому что именно столько вы прошли. Однако ваше смещение в конце составляет 2 метра, потому что вы находитесь всего в 2 метрах от того места, откуда начали.

   Избегайте распространенных ошибок: скорость и скорость

   В обычной жизни мы используем слова скорость и скорость как синонимы, но в физике мы никогда не используем их. Скорость – это то, насколько быстро что-то движется, скорость – это насколько быстро оно движется И в каком направлении (мы называем это понятие величины + направления вектором).Это означает, что объект может изменять скорость без изменения скорости, например, автомобиль, движущийся по круговой трассе. Это также означает, что скорость может увеличиваться, а скорость снижаться. Если скорость отрицательная, а ускорение отрицательное, то скорость будет все более и более отрицательным числом, поэтому скорость будет уменьшаться (с -60 м / с до -120 м / с), но скорость увеличится (с 60 м / с. до 120 м / с).

   Избегайте распространенных ошибок: ускорение и скорость

   Студенты, плохо знакомые с физикой, часто озадачены идеей, что ускорение и скорость могут идти в разных направлениях.Когда объект ускоряется, он должен лететь быстрее, верно? Не обязательно. Например, если вы подбрасываете объект в воздух, он начинает с положительной восходящей скорости, но ускорение отрицательное и нисходящее. В конце концов, объект перестает подниматься и падает обратно на землю, при этом ускорение и скорость идут в одном направлении. Однако в любой момент ускорение может быть в любом направлении – ускорение определяет изменение скорости, а НЕ саму скорость.

   Заключение

   Итак, теперь мы понимаем основы кинематики, но как их использовать? В моем следующем блоге я расскажу о стандартных уравнениях кинематики и о том, как их использовать для решения задач в одномерном измерении.

   Кинематика – обзор | Темы ScienceDirect

   2.1 ОБЗОР

   Кинематика – это исследование движения системы тел без прямого учета сил или потенциальных полей, влияющих на движение. Другими словами, кинематика изучает, как импульс и энергия распределяются между взаимодействующими телами. Многие из взаимодействий, обсуждаемых в главе 1, представляют собой взаимодействия двух тел в том смысле, что в них участвуют две взаимодействующие сущности: снаряд по цели. Одним из важных следствий взаимодействия двух тел является то, что существует одна плоскость , которая содержит две взаимодействующие частицы.Таким образом, не будет компонента импульса вне плоскости взаимодействия. Следовательно, два тела, возникающие в результате взаимодействия, также должны находиться в одной плоскости. Следовательно, взаимодействия двух тел двумерны и . Кроме того, имея всего два тела, можно легко определить центр масс , вокруг которого будут вращаться падающие и вылетающие частицы. Центр масс таков, что общий момент массы (масса X на расстоянии от центра масс) равен нулю.Следовательно, центр масс также таков, что общий импульс (масса × скорость) также равен нулю . Это значительно облегчает выполнение баланса импульса. Таким образом, кинематический анализ выполняется в центре масс. В разделе 2.2 мы обсуждаем взаимосвязь между системой отсчета центра масс и лабораторной системой отсчета (в которой записываются наблюдения). Помимо сохранения энергии и импульса, взаимодействия должны также подчиняться некоторым стехиометрическим и внутренним принципам сохранения, которые кратко изложены в разделе 2.4.

   При работе с частицами излучения малый размер частицы может привести к величине скоростей, близких к скорости света. Фотоны всегда движутся со скоростью света. Эти высокие скорости вызывают особые релятивистские эффекты, которые необходимо учитывать. Поэтому в разделе 2.3 рассматривается специальная теория относительности с особым вниманием к ее влиянию на сохранение энергии и импульса. Конечно, во многих случаях релятивистские эффекты не важны.Тем не менее, использование релятивистского кинематического анализа приведет к результатам, которые действительны как для высоких, так и для низких скоростей. По сути, классическая кинематика – это частный случай (приближение первого порядка) релятивистской механики, что демонстрируется некоторыми примерами в этой главе. Подробный математический анализ кинематики релятивистских частиц приведен в [18]. Релятивистская кинематика, часто называемая кинематикой Эйнштейна, обсуждается в разделе 2.5, а нерелятивистская классическая кинематика Ньютона рассматривается в разделе 2.6. В разделе 2.7 кинематический анализ применяется к тем взаимодействиям, которые обсуждались в главе 1, на которые не влияют электромагнитные поля.

   В большинстве случаев кинематика взаимодействия излучения касается взаимодействия одного снаряда с единственной мишенью, в отличие от взаимодействия молекул газа, где рассматривается коллективное движение газа. Газовая динамика требует общего анализа движения молекул газа, поскольку эти молекулы взаимодействуют друг с другом.В случае излучения плотность поля обычно довольно мала, и взаимодействие между частицами излучения маловероятно и просто игнорируется. Поэтому радиационные взаимодействия рассматриваются как процесс один-на-один (удар по цели), в котором падающее излучение передает энергию цели, но не получает от нее энергию. Однако, когда частицы излучения находятся в тепловом равновесии с атомами среды, частицы могут получать энергию от атомов мишени; процесс, который очень похож на газовый.Однако коллективный момент радиационных частиц рассматривается вероятностным образом, как обсуждалось в разделе 3.3.7 для теплового равновесия нейтронов.

   Как было показано в главе 1, существуют некоторые взаимодействия излучения, которые регулируются поведением электромагнитных волн, а не корпускулярной природой излучения. Кинематика этих волновых взаимодействий обсуждается в разделе 2.8.

   Кинематика: определение и графическое представление

   Графики движения

   Есть три основных графика движения, которые обычно исследуются в кинематике: графики смещения-времени, графики скорости-времени и графики ускорения-времени.Смещение во многом похоже на расстояние – если быть точным, это то, как далеко вы находитесь от своей исходной позиции. Скорость похожа на скорость, но с направлением. Например, 5 миль в час – это скорость, 5 миль в час на север – это скорость. А ускорение – это скорость, с которой изменяется скорость.

   Вот пример графика смещения-времени :

   График расстояние-время

   На нем показано, как объект движется с постоянной скоростью от своего исходного положения, а затем замедляется до полной остановки.

   Чтобы построить график скорости-времени этого движения, мы можем либо концептуально подумать о том, что происходит, либо найти наклон графика смещения-времени. Наклон графика смещения-времени показывает скорость. График скорость-время того же движения выглядит так:

   График скорости-времени

   Сначала мы видим постоянную скорость, а затем объект замедляется до полной остановки. Или, другими словами, у нас есть положительная скорость, когда наклон графика смещения был положительным, и скорость, уменьшающаяся до нуля, когда наклон графика смещения сглаживается до нуля.

   Теперь, чтобы перейти к графику “ускорение-время”, мы можем сделать то же самое снова – подумать о том, как скорость меняется концептуально, или найти наклон графика “скорость-время”. Наклон графика зависимости скорости от времени показывает ускорение. А график ускорение-время того же движения выглядит так:

   График времени ускорения

   Сначала нет ускорения, потому что объект двигался с постоянной скоростью.Тогда есть отрицательное ускорение, потому что скорость становилась все более отрицательной. Или, другими словами, нулевое ускорение, когда график скорости имел нулевой наклон (где он был пологим), и отрицательное ускорение, когда наклон был отрицательным.

   Краткое содержание урока

   Кинематика – это исследование движения без ссылки на силы, вызывающие движение. Он включает такие понятия, как расстояние или смещение, скорость или скорость и ускорение, и смотрит, как эти значения меняются с течением времени.Кинематику можно изучать в одном, двух или трех измерениях.

   Кинематика связана с множеством уравнений, но иногда проще использовать графики для понимания движения. Есть три основных кинематических графика: графики смещения-времени, графики скорости-времени и графики ускорения-времени. Смещение во многом похоже на расстояние – если быть точным, это то, как далеко вы находитесь от своей исходной позиции. Скорость похожа на скорость, но с направлением. А ускорение – это скорость, с которой изменяется скорость, или насколько скорость изменяется каждую секунду.

   Кинетика против кинематики: в чем разница и почему это важно движение. Вместе они помогают физику понять вопросы «что» и «почему», связанные с движущимися объектами.

   TL; DR (слишком долго; не читал)

   Кинетика – это исследование сил, вызывающих движение, в то время как кинематика – это математическое описание движения, которое не относится к силам.

   Другие заметные различия между кинетикой и кинематикой включают:

   • Кинематика не учитывает массу любого объекта в системе для описания его движения, тогда как кинетика учитывает.
   • Кинематику можно считать разделом математики. По сути, это касается применения системы уравнений движения для решения различных физических задач.
   • Кинетика имеет дело с законами движения , тогда как кинематика имеет дело с уравнениями движения.

   Кинетика

   Раздел физики, известный как кинетика, специально занимается анализом сил, действующих на объект (или, когда речь идет о вращательном движении, их аналог: крутящих моментов ). Таким образом, физик, изучающий кинетику, использует законы движения Ньютона для изучения движения объектов.

   При изучении кинетики физик обычно рисует силовых диаграмм (также известных как диаграмм свободного тела ) и с помощью векторной математики находит такие значения, как чистая сила и направление ускорения.

   Кинетика относится к подкатегории классической механики, известной как сил .

   Кинематика

   Раздел физики, известный как кинематика, связан с использованием математических описаний – набора уравнений движения – и определений для объяснения того, как движутся объекты реального мира.

   Таким образом, кинематика требует глубокого понимания математических понятий, таких как векторы, скаляры и сложение векторов, а также физических измерений, таких как скорость, скорость, расстояние, смещение и ускорение.

   Физики средней школы часто изучают кинематику в одном измерении (линейное движение, как яблоко, падающее с дерева) или в двух измерениях (например, движение снаряда, как пушечное ядро, покидающее пушка по диагонали и образующее дугу в небе) . Для движения в двух измерениях им нужно будет разделить задачу на две части: одну для вертикального движения объекта и одну для его горизонтального движения.

   Кинематика относится к подкатегории классической механики, известной как движение .

   Пример кинетики и кинематики

   Рассмотрим классическую ситуацию движения снаряда: бейсболист бросает мяч в воздух. Физик, анализирующий движение мяча с помощью кинематики, вычислит такие факторы, как конечная скорость, время в воздухе и конечное положение.

   Кинетический взгляд на то же самое может быть для определения того, как второй закон Ньютона применим к мячу, путем количественной оценки чистой силы на мяч от броска игрока и силы тяжести.

   Как кинетика и кинематика вписываются в классическую механику

   Другой способ проанализировать тот же сценарий движения бейсбольного мяча по воздуху – применить понимание сохранения энергии, чтобы объяснить, почему мяч в конечном итоге останавливается.Однако этот анализ относится к подкатегории классической механики, известной как энергия .

   В целом, три основные категории изучения классической механики – это сил, движения и энергии.

   Почему это важно

   И кинетика, и кинематика являются важными разделами классической механики. Они позволяют физикам по-разному понимать природу движения и вычислять разные значения в зависимости от того, что они изучают.

   Таким образом, два поля дополняют друг друга. Кинематика могла бы ответить на большее количество вопросов «что», которые конкретно описывают движение объекта: его скорость, ускорение, положение, время и тому подобное.

   Но без кинетики физики также не смогли бы ответить на вопросы «почему», например, что в первую очередь заставило объект начать движение и почему это движение не продолжается вечно? Откуда взялось ускорение, тянущее брошенный шар обратно к Земле? Чтобы ответить на все эти вопросы, физику нужны уравнения и , которые дают твердое представление о силах.

   кинематика – определение и значение

2. Затем они провели комплексные сравнения характеристик движения, известные как кинематика , у собак с отсутствующими конечностями, а также с «нормальным» движением четвероногих собак.

   Ежедневные новости и аналитика

3. Затем они провели комплексные сравнения характеристик движения, известные как кинематика , у собак с отсутствующими конечностями, а также с «нормальным» движением четвероногих собак.

   Интернет-газета The Earth Times

4. 56 АЛЬБЕРТ ЭЙНШТЕЙН логическое согласование путем внесения изменений в кинематику , то есть в доктрину физических законов пространства и времени.

   Из моих последних лет

5. Но еще менее признана теоретическая система обозначений конструкции машин, известная как « кинематика », которая проложила путь для сложных машин.

   неопределенный

6. «Исследователи отмечают, что компьютер развивает эти законы без каких-либо предварительных знаний в области физики, кинематики или геометрии».

   Разрушая законы природы?

7. Кинематика этой машины более несортированная, чем мой ящик для носков.

   Nissan на выставке CrossPurposes With Competence

8. Эту проблему недавно рассмотрели Дэвид Виано и его коллеги, которые работают в ProBiomechanics LLC, фирме из Мичигана, специализирующейся на кинематике водителя и пассажира и причинно-следственных связях, опубликованных в прошлом месяце в журнале Traffic Injury Prevention.

   Заметки доктора Шармы об ожирении »Архив блога» Оценка травм, полученных в результате дорожно-транспортных происшествий

9. Г-н Деннис видит в McLaren услугу «летающего доктора технологий», предлагающую индивидуальные решения компаниям, имеющим неотложные проблемы в таких сложных областях, как электроника, пневматика, гидродинамика, кинематика , и материаловедение.

   Новая формула McLaren

10. Горячая точка Йеллоустоуна и мантийный шлейф: сейсмические и GPS-изображения, кинематика , и мантийный поток, J.Volcanol.

    Научные статьи о Йеллоустоне

11. Если вы думали, что спутник Hipparcos, который также был ESA в 1991 году, был хорош, этот спутник предоставит динамическое знание нашей части Млечного Пути и информацию о кинематике всей галактики!

    Обама представит «амбициозный» план для НАСА | Вселенная сегодня

Физика – Кинематика – Мартин Бейкер

Кинематика: Изучение и описание движения без учета его причин, например, мы можем вычислить конечную точку манипулятора робота из углов все его суставы.В качестве альтернативы, учитывая конечную точку манипулятора робота, мы могли бы рассчитать углы и параметры всех его стыков, необходимых для его установки (обратная кинематика – И.К.). Кинематику можно изучать без учета массы или физические величины, зависящие от массы.

О динамике поговорим позже. Один из способов подумать о разнице между кинематика и динамика заключается в том, что динамика является причиной движения и кинематики это эффект.

Кинематика включает в себя положение, скорость и ускорение (и их вращательное эквиваленты).

• Позиция – это точка в пространстве, которую занимает объект, это должно быть определенный в некоторой координате система.
• Скорость – это скорость изменения положения во времени.
• Ускорение – это скорость изменения скорости во времени.

Хотя я оставляю динамику на потом, здесь стоит упомянуть, что, если на объект не действуют результирующие силы, то он будет иметь постоянную скорость.Также, если на объект действует постоянная чистая сила, например сила тяжести например, тогда он будет иметь постоянное ускорение. Итак, эти частные случаи постоянной скорости и постоянного ускорения заслуживают рассмотрения в более деталь.

Движение в одном измерении

Если объект движется по прямой, и если мы измеряем его положение по эта линия, то ее положение, скорость и ускорение могут быть представлены скалярными величинами.Это значительно упрощает анализ, так что давайте начнем с этого.

Постоянная скорость (без чистой силы)

Скорость – это скорость при смене позиции:

v = dp / dt

где:
символ	описание	тип	шт.
v	скорость	вектор	м / с
п.	позиция, расстояние от заданной точки	вектор	м
т	время	скаляр	с
г… / dt	скорость изменения

Таким образом, интеграция обеих сторон дает:

p = ∫v dt

, поэтому, если v постоянно:

p = p ₀ + v t

где:
символ	описание	тип	шт.
v	скорость	вектор	м / с
п.	позиция, расстояние от заданной точки	вектор	м
т	время	скаляр	с
п. 0	позиция в момент времени t = 0	вектор	м

Постоянное ускорение (постоянная сила)

Скорость – это скорость при смене позиции:

а = дв / дт

Таким образом, интеграция обеих сторон дает:

v = ∫a dt

, поэтому, если a постоянно:

v = v ₀ + a * t

где:
символ	описание	тип	шт.
v	скорость	вектор	м / с
	ускорение (дв / дт)	вектор	м
т	время	скаляр	с
v 0 или u	скорость в момент времени t = 0 (иногда пишется u)	вектор	м / с

Итак, интегрирование ускорения дает скорость, чтобы получить положение, в котором мы нужно снова интегрировать:

p = ∫v dt

p = ∫ (v ₀ + a * t) dt

p = p ₀ + v ₀ t + ½ a t ²

Переменное ускорение – приблизительные методы

Если у нас есть уравнение для ускорения как функции времени, мы можем применить интегрирование, чтобы найти скорость и положение, если мы этого не сделаем, мы можем использовать приближенные методы, такие как метод конечных разностей, метод Эйлера или Рунге-Кутта Метод.Если мы оживляем компьютерное моделирование, то это может быть очень хорошим методом, потому что нам нужно в любом случае сгенерировать позицию для каждого кадра, так что сгенерировать намного проще следующий кадр из кадра перед ним.

v _{n + 1} = v _n + a * dt

где:
символ	описание	тип	шт.
v n + 1	скорость на кадре n + 1	вектор	м / с
v n	скорость на кадре n	вектор	м / с
	ускорение	вектор	м / с 2
дт	время между кадром n и кадром n + 1	скаляр	с

и снова суммируя:

p _{n + 1} = p _n + v _n * dt

где:
символ	описание	тип	шт.
п. п + 1	позиция в кадре n + 1	вектор	м / с
p n	позиция в кадре n	вектор	м / с
v n	скорость на кадре n	вектор	м / с
дт	время между кадром n и кадром n + 1	скаляр	с

Эти приближения можно сделать более точными, используя метод Эйлера или Рунге-Кутта. Метод

Положение в трех измерениях (расположение и ориентация)

Когда мы работаем в трехмерном пространстве, скалярные величины в одномерном случае p, v и необходимость в замене трехмерными векторами,, и .Также, чтобы определить положение объекта в трех измерениях, нам необходимо знать как его местоположение, так и его ориентацию. Это дает максимум 6 градусов. свободы (6DOF) 3 для линейного перемещения, 3 для вращения.

Итак, следующий вектор состояния полностью определяет позицию, используя 6 скалярных величин. количества.

Примечание: здесь смешанные единицы, верхние 3 – радианы, нижние 3 – метры.

Если объект ограничен, например, он может быть связан с другими объектами шарниром или другим типом соединения, то он может иметь менее 6 градусов Свобода.

Может быть полезно представить местоположение и ориентацию как один вектор, особенно когда мы переходим к уравнениям ускорения и динамики, это не так полезно для позиции, потому что мы не можем использовать векторное сложение для представления вращения. Я добавил его сюда, чтобы начать знакомство с пространственным вектором Featherstone. обозначение (см. http://www.syseng.anu.edu.au/~roy/technical.html) Спасибо Майклу Шанцу, рассказавшему мне об этом (см. Файл hybridgdc.pdf на http: // michaelshantz.com).

Когда мы определяем положение твердого объекта, нам нужно сделать это относительно некоторая точка на объекте, также это точка, вокруг которой объект вращается. Итак, нам нужно определить локальную систему координат на теле. Если взять планетарный Например, в случае с Землей мы могли бы выбрать измерение относительно середины ядра Земли, или места на поверхности, или любого другого Другое место. Теперь, когда Земля движется, и перевод, и ориентация являются функциями времени.

Если мы выберем измерение локальной системы координат относительно точки на поверхность, то перевод будет сложной функцией времени, но если мы измеряем местную систему координат относительно центра Земли тогда перевод будет менее сложной функцией времени. Итак, в этом случае лучше, но не обязательно, иметь местную систему координат относительно к центру земли. Ориентация как функция времени не зависит местной опорной точки, в случае Земли, один оборот в день.

Преобразование

Матрицы

могут использоваться для выполнения различных операций с объектами, таких как перевод, вращение, масштабирование и отвес. Когда мы представляем твердые объекты, мы хотим чтобы ограничить наши преобразования только перемещениями и поворотами, поэтому матрица 4×4 содержит избыточную информацию, и мы должны быть осторожны, чтобы не делать никаких других операции на нем.

Сложные сочлененные объекты, например рука робота, могут быть представлены в виде иерархии. групп преобразований, подробнее см. здесь.

Теоретически мы могли бы указать наше перемещение / вращение с помощью одного 6-мерного вектор, однако, как объяснялось в разделе «Вращение», это не так полезно, как могло бы кажется, что множественные преобразования не могут быть представлены простыми арифметическими операциями на векторах.

Примечание: здесь смешанные единицы, верхние 3 – радианы, нижние 3 – метры.

Множественные преобразования могут быть представлены только сложением их векторов, если преобразования бесконечно малы.Это означает, что 6-мерные векторы полезны для комбинирования скоростей и ускорений.

---

Равномерная угловая скорость

Хотя векторное сложение не может использоваться для углов, оно начинает приближать правильное значение по мере уменьшения угла, для вектора бесконечно малых вращений Можно использовать алгебру, поэтому можно использовать векторную алгебру для объединения вращений. Вектор вращения [w] содержит 3 значения: вращение вокруг x, вращение вокруг y и вращение вокруг z.

6d Вектор скорости

Может быть полезно иметь один вектор состояния, который может представлять угловой и линейные скорости. Так что операции с этой скоростью можно представить одним уравнением, которое включает как линейные, так и вращательные эффекты.

Примечание: здесь смешанные единицы измерения, верхние 3 – радиан / сек, нижние 3 – метры / сек.

Например, если объект двигался в рамках системы отсчета и системы отсчета сам двигался, мы могли вычислить вектор, представляющий абсолютную скорость путем сложения векторов, представляющих скорость системы отсчета и относительная скорость.Однако здесь нужно быть очень осторожными, это работает. Хорошо для линейной составляющей (при условии, что мы используем ньютоновскую теорию относительности и не относительность Эйнштейна), но с вращательной частью мы должны быть осторожны если вращения не в одной и той же точке, в этом случае движение может может быть какое-то сложное спиральное или планетарное движение, но сложение все еще может работать для мгновенных значений.

Равномерное угловое ускорение

Вектор углового ускорения – это скорость изменения угловой скорости.

6D вектор ускорения

Единый вектор состояния, представляющий как угловое, так и линейное ускорение. Это может быть очень полезно в динамике (см. здесь), например, это единственное уравнение связывает крутящие моменты, силы и ускорение объекта.

Моделирование программой

Я определил предлагаемый узел кинематики для представления поведения кинематики, поскольку VRML и Java3D еще нет такого узла.

Эти уравнения для равномерного ускорения можно решить аналитически и получить:

• v = v ₀ + a * t
• p = p ₀ + v ₀ t + ½ a t ²
• v ² = v0 ² + 2 * a * p

где v0 = начальная скорость и s = дельта x (т.е. пройденное расстояние)

Однако при моделировании в реальном времени быстрее выполнять интегрирование численно, это делается программой в kinematicsBean, алгоритм для этого объясняется здесь.

кинематических переменных – Nexus Wiki

Ключевая идея в описании движения – где и когда. Если мы настроим систему координат, чтобы иметь возможность описывать положение и можем указать положение с помощью вектора, тогда все, что нам нужно сделать для описания движения, – это сказать, где что-то находится (его положение) в зависимости от того, когда мы на это смотрим ( время). Мы записываем это в 2D с вектором, где и вектор, и координаты заданной позиции зависят от времени (являются функциями). Запишем это так:

$$ \ overrightarrow {r} = x (t) \ hat {i} + y (t) \ hat {j} $$

Это дает нам значение позиции.Теперь нам нужно изучить, как он меняется и с какой скоростью.

Положение, изменение положения и различные скорости изменения положения (его производные) называются кинематическими переменными , поскольку «кинематика» означает «изучение движения» от греческого слова «движение», Кинезис .

Рабочий объем

Основная концепция – смена позиции. Это называется смещением . Как обычно, мы будем записывать изменение количества маркером изменения Δ.Таким образом, смещение объекта с момента времени t ₁ до момента времени t ₂ задается выражением $ \ Delta \ overrightarrow {r} = \ overrightarrow {r} (t_2) – \ overrightarrow {r} ( t_1) $.

Если это записать в терминах координат и перегруппировать, мы можем увидеть, как это представлено в терминах координат x и y:

$$ \ Delta \ overrightarrow {r} = \ overrightarrow {r} (t_2) – \ overrightarrow {r} (t_1) $$

$$ \ Delta (x \ hat {i} + y \ hat {j}) = (x (t_2) \ hat {i} + y (t_2) \ hat {j}) – (x (t_1) \ hat {i} + y (t_1)) \ hat {j} $$

$$ (\ Delta x) \ hat {i} + (\ Delta y) \ hat {j} = (x (t_2) – x (t_1)) \ hat {i} – (y (t_2) -y ( t_1)) \ hat {j} $$

Поскольку $ \ hat {i} $ и j $ \ hat {j} $ указывают в разных направлениях, если у нас есть уравнение, в котором есть как i, так и j, коэффициенты i должны быть равны, а коэффициенты j должны быть равны.Смещение в направлении x никогда не может отменить смещение в направлении y. Таким образом, мы можем заключить, что вещи, умножающие i, должны быть равны, а вещи, умножающие j, должны быть равны:

$$ \ Delta x = x (t_2) – x (t_1) $$

$$ \ Delta y = y (t_2) – y (t_1) $$

Такой вид алгебраической перегруппировки чрезвычайно ценен в физике. Причина, по которой мы переставляем, заключается в том, что в разных аранжировках мы фокусируемся на разных способах определения физического смысла.Когда мы пишем это в терминах всего вектора, мы думаем о переходе от начальной позиции к конечной. Когда мы разбиваем его на координаты, мы сосредотачиваемся на том, как меняется каждая координата. Конечно, результат полного смещения будет таким же, но анализ координат дает нам дополнительное понимание конструкции.

Обратите внимание, что вектор положения можно рассматривать как смещение относительно опорной точки (начала координат) системы координат.Но поскольку мы не можем указать положение без начала координат или точки отсчета, мы склонны говорить о «положении» и «смещении» по-разному.

Скорость

Теперь мы можем посмотреть, как быстро происходит изменение. Разделение смещения на время, необходимое для его выполнения, говорит нам не только об изменении, но и о скорости изменения . Это намного полезнее. От того, насколько быстро вы путешествуете, может иметь значение, опоздаете ли вы на концерт или, возможно, пропустите его совсем.Скорость, с которой происходит химическая реакция, может иметь значение, будет ли клетка жить или умирает.

Скорость изменения положения называется скоростью . Есть несколько сложных аспектов размышлений о скорости, поэтому прочтите следующую страницу с подробностями.

Разгон

Как только мы изменим положение, мы можем получить скорость. Но теперь скорость может измениться, поэтому мы можем посмотреть на скорость изменения скорости. Это называется ускорением .Это оказывается чрезвычайно важным в физике из-за принципа, который связывает движение с факторами, которые приводят к изменениям в движении объекта – силами.