Кинематика основные формулы и понятия: Ошибка: 404 Материал не найден - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Раздел “Кинематика” теоретической механики

Кинематика — это раздел теоретической механики, в котором изучается движение механических систем с геометрической точки зрения, без учета причин (сил), вызывающих это движение и изменение движения.

Положение тела, его движение в пространстве может быть определено относительно другого неизменяемого тела. С ним связывают выбранную систему отсчёта — систему координат, в которой и определяют параметры движения.

Установление способов, с помощью которых может быть задано движение точек или тел по отношению к выбранной системе отсчёта, позволит определить кинематические характеристики движения (траектории точек, их скорости, ускорения, угловые параметры тел.)

Движение любой механической системы относительно выбранной системы отсчёта будет известно, если известно движение каждой точки этой системы. Поэтому изучение раздела «Кинематика» начинается с темы «Кинематика точки», далее рассматривается тема «Кинематика твёрдого тела».

Данное учебно-методическое пособие поможет студентам при выполнении контрольных работ по разделу «Кинематика».

В пособии кратко изложена теория, даны основные формулы, приведены примеры решения типовых задач.

Краткость изложения теории предполагает предварительное изучение курса по учебникам, в которых даны подробные обоснования определений, выводы, доказательства теорем.

Методическое пособие может быть рекомендовано и на практических занятиях и при выполнении расчётно-графических работ.

Содержание

Кинематика точки

Способы задания закона движения точки

Векторный
Координатный
Естественный

Кинематика твердого тела

Поступательное движение
Вращательное движение твердого тела

Вращение твердого тела вокруг неподвижной оси
Угловая скорость и угловое ускорение
Скорости и ускорения точек вращающегося твердого тела
Передаточные механизмы

Плоскопараллельное движение твердого тела

Определение скоростей точек в плоскопараллельном движении
Теорема о скоростях точек в ППД
Следствие из теоремы о скоростях точек
Мгновенный центр скоростей

Определение МЦС

Ускорение точки в плоскопараллельном движении
Мгновенный центр ускорений
Частные случаи МЦУ

Сложное движение точки

Определение скоростей и ускорений точек в сложном движении
Ускорение Кориолиса

Сферическое движение

Теорема о конечном перемещении твердого тела, имеющего одну неподвижную точку
Угловая скорость и угловое ускорение при вращении тела вокруг неподвижной точки
Скорости и ускорения точек при вращении тела вокруг неподвижной точки

Кинематика (скорость, ускорение, путь).

Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.

Траектория, радиус-вектор, закон движения тела

Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.

Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.

Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.

Радиус-вектор – вектор, задающий положение точки в пространстве.

Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.

Перемещение и путь

Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории

В системе СИ перемещение и длина пути измеряются в метрах.

Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.

Скорость и ускорение

Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло

А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной.

Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.

В системе СИ скорость измеряется в метрах в секунду

Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.

Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости

Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.

Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории

Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.

Здесь R – радиус окружности, по которой движется тело.

Закон равноускоренного движения

Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.

Здесь – x нулевое- начальная координата. v нулевое – начальная скорость. Продифференцируем по времени, и получим скорость

Производная по скорости от времени даст значение ускорения a, которое является константой.

Пример решения задачи

Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. 2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.

Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.

Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.

Теоретическая механика и кинематика

Механика – это наука о простейших формах движения материи, которые сводятся к простым перемещениям или переходам физических тел с одного положения или состояния в пространстве и времени в другое, в результате взаимодействия между ними.

Теоретическая механика

Механика охватывает целый комплекс дисциплин, изучающих движение и взаимодействие различных материальных тел, например, прикладная механика, гидромеханика, аэромеханическая, небесная механика, биомеханика и др. Изучение наиболее общих свойств движения и взаимодействия всех тел является предметом специальной дисциплины, которую называют теоретическая механика.

Итак, теоретическая механика изучает наиболее общие законы движения и взаимодействия тел, считая своей главной задачей познания количественных и качественных закономерностей, наблюдаемых в природе. С определения теоретической механики следует, что она принадлежит к фундаментальным естественным наукам.

История развития теоретической механики убеждает в том, что она является одной из научных основ техники и технологии, поскольку существует взаимосвязь между проблемами теоретической механики, проблемами техники и технологии.

Теоретическая механика широко применяет такие методы:

абстракции;
обобщение;
математические методы;
методы формальной логики.

Критерием истинности наших знаний является опыт и практика. Таким образом, теоретическая механика имеет дело не с самими материальными объектами, а с их моделями.

Теоретическая механика – это важная наука для подготовки инженерных кадров. Она является основой для изучения таких дисциплин, как:

теория колебаний, гидравлика;
сопротивление материалов;
теория машин, механизмов и тому подобное.

Знание законов теоретической механики, отражающие объективно существующие взаимосвязи, взаимообусловленности механических движений и преобразования энергии, позволяет научно предсказать ход процессов в новых задачах, возникающих при развитии науки, техники и технологии.

Замечание 1

Статикой называется раздел теоретической механики, в котором изучают методы преобразования одних систем сил в другие, эквивалентные им, а также условия равновесия различных систем сил, действующих на твердое тело.

Одним из основных понятий в статике, как и во всей механике, является понятие о силе. Величина, являющаяся мерой механического взаимодействия материальных тел, называется силой. Сила, действующая на тело, является вектором. Она характеризуется точкой приложения, направлением и величиной. В теоретической механике силу принято обозначать $\vec {F} $ cила, $A$- точка приложения силы, прямая $AB$ – линия действия силы.

Рисунок 1. Сила $\vec {F} $. Автор24 — интернет-биржа студенческих работ

В Международной системе единиц (СИ) за единицу силы принимают один ньютон (1Н). Ньютон – это такая сила, которая массе в 1 кг оказывает ускорение в 1 $мс_2$ (1Н = 1кг • м • с-2).

Основные понятия теоретической механики

К основным понятиям теоретической механики, прежде всего, относятся понятия материальной точки и абсолютно твердого тела. Они являются идеальными моделями материальных тел с той или иной степенью абстракции конкретных свойств реальных физических тел.

Определение 1

Материальной точкой называется геометрическая точка, которой приписана определенная масса.

Например, изучая движение планет вокруг Солнца, их рассматривают как материальные точки, в каждой из которых сосредоточена вся масса соответствующей планеты, абстрагируясь при этом от размеров планет.

С понятием материальной точки тесно связано понятие о системе материальных точек.

Определение 2

Абсолютно твердым телом называется тело, которое состоит из системы материальных точек, которые непрерывно заполняют определенную часть пространства таким образом, что расстояние между любыми двумя его точками остается неизменной.

Отметим, что абстракция абсолютно твердого тела позволяет изучать механическое движение тел, не связанных с существующим изменением их формы, в частности с деформацией. Изучение механических движений тел, зависит от их деформируемости, а также движения жидкости и газов, которые приводят к новой абстракции в виде понятие сплошной среды.

Раздел кинематика

Замечание 2

Кинематикой называется раздел теоретической механики, в котором изучается движение системы материальных точек с геометрической точки зрения. Кинематику называют также геометрией движения, поскольку в ней рассматриваются геометрические свойства движения.

Механические движения, что изучаются в кинематике, осуществляются в пространстве и времени. Отметим, что в теоретической механике пространство, в котором происходит движение тел, рассматривается как трехмерное, и все измерения выполняются на основании методов евклидовой геометрии. В механике время считается одинаковым в любых системах отсчета (системах координат) и не зависит от движения этих систем относительно друг друга. Время сказывается буквой $t$ и рассматривается как непрерывная переменная величина, которая применяется в качестве аргумента.

Изучая движение тела, всегда следует знать, в отношении какого другого тела, которое называется телом отсчета, рассматривается это движение. Совокупность тела отсчета, с которым связана система координат, и часов называют системой отсчета. Эта система может быть как подвижной, так и условно неподвижной. Точки тела, постоянно движущиеся, осуществляют в общем случае различные движения. Поэтому, в первую очередь, возникает необходимость изучить движение отдельных точек тела.

Поскольку движение геометрического образа тела будет известным, когда станет известен закон движения всех его точек, определение движения любого геометрического образа предшествует изучению движения одной его точки.

Эта логика лежит в основе разделения кинематики на такие разделы, как кинематика точки и кинематика твердого тела. Для определения положения точки в пространстве выбирают некоторую систему отсчета (систему координат).

Определение 3

Линия, которую описывает точка при своем движении, называется траекторией. Если траектория точки прямая линия, то движение точки называется прямолинейным, если траектория точки кривая, то – криволинейным.

Движение точки относительно выбранной системы отсчета считается заданным, если известно, с помощью которого способа можно определить положение точки в любой момент времени. Основными пространственно-временными (кинематическими) характеристиками движения точки является ее положение, скорость и ускорение.

Исходя из этого, основная задача кинематики точки заключается в нахождении способов задания ее положения и методов определения скорости и ускорения. Движение точки можно определить тремя способами: векторным, координатным и натуральным.

Векторный. Положение точки можно определить с помощью радиус-вектора $\vec {r}$, проведенного с некоторой заданной неподвижной точки $О$ в данную точку $М$. При движении точки радиус-вектор $\vec {r} $меняется по величине и направлению. Каждому моменту времени $t$ соответствует определенное значение $\vec {r}$. Следовательно, $\vec {r}$ является функцией времени $t$, т.е. $\vec {r} = \vec {r} (t) $. Функцию $\vec {r} (t) $ считают однозначной и непрерывной функцией.

Уравнение $\vec {r} = \vec {r} (t) $ называется кинематической уравнением движения точки в векторной форме. Это уравнение выражает закон движения точки, а также уравнение траектории точки в векторной форме.

Замечание 3

Кривую, которую описывает конец любого вектора при условии, что начало его находится все время в одной и той же точке, называют годографом вектора. 2}$

Основы кинематики (8-й класс)

Цель урока: повторение, обобщение и закрепление знаний и основных понятий по теме “Основы кинематики”; совершенствование навыков постановки опытов, решения экспериментальных задач, развитие навыков расчета скорости, ускорения, перемещения; развитие аналитического мышления, умения анализировать и делать выводы при проведении опытов, развитие устной речи.

Оборудование: штативы, желоба, игрушечный автомобиль, линейка, проградуированная в секундах; мяч, секундомер, сантиметровая лента, плакаты с частями формул кинематики, компьютер, мультимедийный проектор.

План урока:

Организационный момент;
Повторение основных кинематических величин и формул;
Самостоятельная работа;
Демонстрация опытов и решение задач по экспериментальным данным;
Задание на дом;
Подведение итогов.

Ход урока

Учитель (У): Здравствуйте, ребята. Садитесь, пожалуйста. Сегодня на уроке нам предстоит повторить и систематизировать основные сведения и знания по кинематике.

В руках у меня линейка, которая позволяет определять время реакции человека.

Время реакции – промежуток времени от начала сигнала до реакции организма человека на этот сигнал. Оно зависит от возраста, тренированности, самочувствия человека.

Ребята, как вы думаете, зачем нужно знать время реакции?

Ученики предлагают свои версии ответа на вопрос.

У: Совершенно верно. А кто из вас знает свое время реакции? Кто хочет его определить?

Выходят 2 ученика.

У: Я отпускаю линейку, а вы должны ее поймать. Время реакции у одного ученика – 0,202 с, у другого – 0,197 с. (линейка проградуирована в секундах). Ребята, как вы думаете, какой принцип лежит в основе создания этого прибора?

Ученик: линейка свободно падает под действием силы тяжести.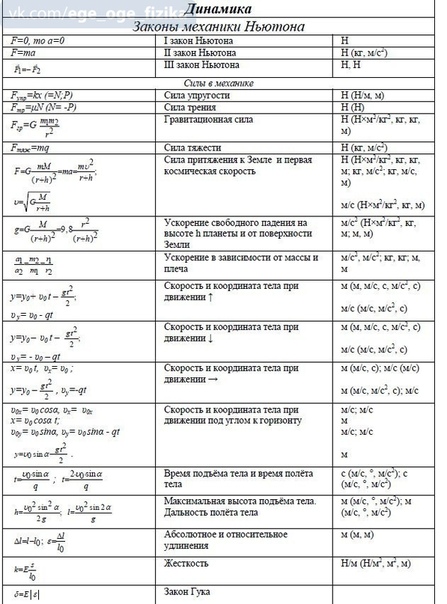 Ее движение – равноускоренное, с ускорением свободного падения 9,81 м/с².

У: Правильно! К этому прибору мы еще вернемся. А сейчас повторим основные понятия и формулы кинематики.

Проводится фронтальный опрос.

Что такое механика? Что она изучает?
Что называется механическим движением?
Почему механическое движение относительно?
Что такое система отсчета и как она выбирается?
Какие системы координат вы знаете?
Что такое тело отсчета?
Какие физические величины характеризуют механическое движение?
В чем заключается основная задача механики?
Какова классификация механического движения?
Что такое равноускоренное движение?
Что называется ускорением и в каких единицах оно измеряется?
Что называется свободным падением?
Чему равно ускорение свободного падения на полюсе и на экваторе и почему эти величины различны?
Что называется перемещением?

Ученики отвечают на вопросы правильно.

У: Отлично! А теперь вспомним формулы для расчета равноускоренного движения. На доске представлены отдельные части формул. Необходимо правильно их собрать и прокомментировать.

Выходит 1 ученик, собирает правильно формулы на магнитной доске и рассказывает, в каких случаях и для расчета чего служит каждая формула.

; ; S=; ;

; ;

У: Молодцы! Вы показали хорошее знание теории, а сейчас посмотрим, как вы умеете применять эти знания на практике. Приготовили по половинке листочка, подписали свой вариант.

На экране представлены графики зависимости скорости от времени. Написано, что необходимо определить: 5 вопросов – 5 правильных ответов – 5 баллов (рис.1). На выполнение работы отводится 6 мин. Кто выполнит работу раньше, поднимает руку, я подойду и возьму работу.

Вариант 1.

Вариант 2.

Определить:

Начальную скорость
Конечную скорость
Время движения
Ускорение
Перемещение

Учащиеся выполняют самостоятельную работу.

У: Отложили, пожалуйста, ручки. Передаем работы по рядам. На экране представлены ответы, вы можете себя проверить и оценить свою работу, а оценки я скажу на следующем уроке. А теперь применим свои знания для решения экспериментальных задач.

Задача № 1 “Движение автомобиля по наклонной плоскости из состояния покоя”.

Вызываются 2 инженера – экспериментатора, а инженерами – теоретиками будет весь класс. Ребята, что мы можем измерить при проведении эксперимента, а какие характеристики можем рассчитать?

Ученики: Измерить можем расстояние S, пройденное автомобилем, время t, затраченное на движение, высоту наклонной плоскости h, рассчитать – ускорение а, конечную скорость ?.

У: Мы будем изменять высоту наклонной плоскости и записывать полученные данные в зависимости от угла наклона.

Инженеры-экспериментаторы запускают автомобиль, измеряя время движения, пройденный путь, высоту наклонной плоскости. Данные заносятся в таблицу 1 на экране.

Таблица 1

№ опыта	1	2	3
Перемещение Ѕ, м
Время t, с
Высота h, м
Ускорение a, м/с²
Конечная скорость ?, м/с

Ученики рассчитывают по полученным измерениям ускорение а, конечную скорость ? и заполняют таблицу 1.

У: Ребята, какой вывод можно сделать, анализируя полученные значения?
Ученик: Скорость и ускорение зависят от угла наклона: чем больше угол наклона, тем больше скорость и ускорение. Эти знания можно использовать при катании с горок.
У: Молодец! А при решении задач динамики мы еще раз подтвердим этот вывод. С первой задачей мы справились.

Задача № 2 “Движение мяча по вертикали с начальной скоростью под действием силы тяжести”.

У: Какие физические величины мы можем измерить, а какие – рассчитать?

Ученик: Можем измерить время и высоту подъема, а определить начальную скорость.

Вызываются 2 инженера – экспериментатора и 1 теоретик. Они подбрасывают мяч, измеряют высоту подъема мяча, время движения мяча вверх и вниз. Данные заносятся в таблицу 2 на экране.

Таблица 2

№ опыта	1	2	3
Высота H ,м
Время t, с
Начальная скорость ,м/с

Ученики рассчитывают по полученным измерениям начальную скорость .

У: Если мяч брошен с начальной скоростью вверх, то каким будет движение мяча?

Ученик: Мяч будет двигаться под действием силы тяжести равноускоренно. Так движение по вертикали обратимо, то можем для расчета исследовать движение мяча вниз и рассчитать начальную скорость по формуле

Можно проверить свои расчеты, применив формулу

У: Очень хорошо! А теперь вернемся к нашему прибору для определения времени реакции. Кто объяснит принцип его действия?

Ученик: Линейка падает свободно, без начальной скорости. Следовательно, расстояние, пройденное линейкой, определяется по формуле . Зная Н, можно определить t. Это и есть время реакции.

У: Молодец! Ставлю оценку “5”. Ребята, вы поняли, как сделать такой прибор? Ваше домашнее задание – изготовить прибор для измерения времени реакции человека и измерить время реакции у своих родственников и друзей.

Мы повторили основные понятия по кинематике и решили экспериментальные задачи. У вас есть вопросы? Спасибо за работу на уроке. До свидания.

Литература:

Громов С.В., Родина Н.А. Физика. 8 класс. – М.: Просвещение, 2006.
Урок физики в современной школе. Творческий поиск учителей. – М.: Просвещение, 1993.

Лекции по курсу “Теория механизмов и машин”

Лекция 1 Основные понятия и определения. Основные виды рычажных механизмов.

Лекция 2 Анализ рычажных механизмов. Определение числа степеней свободы рычажных механизмов. Кинематический анализ рычажных механизмов.

Лекция 3 Анализ машинного агрегата. Силы и моменты, действующие в машинном агрегате. Понятие о механических характеристиках. Понятие о расчетной схеме машинного агрегата и переход от нее к динамической модели. Приведение сил и масс к одномассовой динамической модели.

Лекция 4 Вывод формулы для определения закона движения звена приведения в форме кинетической энергии. Режимы работы машинного агрегата.

Лекция 5 Определение реакций в кинематических парах рычажных механизмов без учета трения. Учет трения при определении реакций в кинематических парах.

Лекция 6 Краткие сведения по определению КПД машинного агрегата. Основные сведения о виброзащите машинного агрегата. Статическое уравновешивание рычажных механизмов. Балансировка ротора.

Лекция 7 Статическая неуравновешенность ротора и способы ее устранения. Моментная неуравновешенность ротора и способы ее устранения. Динамическая неуравновешенность ротора и способы ее устранения. Механизмы с высшей кинематической парой. Условие существования высшей КП. Кинематика высшей КП.

Лекция 8 Сопряженные поверхности. Эвольвента и ее свойства. Элементы эвольвентного зубчатого колеса. Эвольвентная зубчатая передача и ее свойства. Свойства эвольвентного зацепления.

Лекция 9 Основные расчетные зависимости для определения основных параметров эвольвентных зубчатых передач. Способы изготовления зубчатых колес.

Лекция 10 Специальные передаточные (планетарные) механизмы. Сравнительный анализ передачи с неподвижными осями планетарной передачи. Определение передаточного отношения планетарных механизмов различных схем.

Лекция 11 Синтез (проектирование) планетарных механизмов.

Лекция 12 Кулачковые механизмы. Основные схемы кулачковых механизмов.

Лекция 13 Основные параметры кулачковых механизмов. Построение графика перемещений толкателя при заданном профиле кулачка. Понятие об угле давления.

Лекция 14 Синтез (проектирование) кулачковых механизмов по заданному закону движения толкателя.

Лекция 15 Построение профиля кулачка.

В «МЭШ» собраны лучшие приложения по физике ко дню рождения Льва Ландау

«Московская электронная школа» («МЭШ») предлагает узнать, что такое молекулярная физика, повторить способы уменьшения силы сопротивления и вспомнить точные понятия физических терминов. Ко дню рождения лауреата Нобелевской премии Льва Ландау «МЭШ» собрала самые интересные приложения по физике.

Советский физик-теоретик родился 22 января 1908 года. Уже к 21 году он стал знаменитым ученым, в лучших европейских университетах мечтали, чтобы он работал у них. Но Лев Ландау до последнего был уверен, что лучшая наука может быть только в родной стране. Любимый ученик Нильса Бора вывел простую формулу счастья: наука, любовь и общение с людьми, и на первом месте для него стояла именно наука. С помощью специального приложения «МЭШ» школьники могут познакомиться с биографией физика.

Из видеосюжета пользователи узнают, какую роль Ландау сыграл в освоении космоса. Активно оно началось в 1970-е годы, когда ученые уже обладали определенными данными. Американский физик Кип Торн и польский астроном Анна Житков предположили, что в космосе могут возникать гибриды красных сверхгигантов и нейтронных звезд. Такие гипотетические звездные объекты стали называть объектами Торна — Житков. Но иногда добавляют и фамилию Ландау, который еще в 1932-м говорил о существовании звезд с нейтронным ядром.

Решив кроссворд по теме «Кинематика», можно узнать, какие существуют виды траекторий, как называется изменение положения тела в пространстве относительно других с течением времени и какой раздел механики изучает движение тела без учета причин движения.

Ближе познакомиться с молекулярной физикой школьники могут в интерактивном приложении «Основные формулы МКТ». Наука изучает физические свойства тел в разных агрегатных состояниях на основе их молекулярного строения, и приложение поможет вспомнить основные ее формулы, определить среднюю кинетическую энергию и многое другое.

Все эти сервисы можно найти в библиотеке проекта «Московская электронная школа». Сегодня в нее входят более 50 тысяч сценариев уроков и более восьми тысяч видеоуроков, свыше 1600 электронных пособий, 381 учебник, более 130 тысяч образовательных интерактивных приложений, восемь уникальных виртуальных лабораторий, 245 произведений художественной литературы, а также огромное количество тестовых заданий.

Формула кинематических уравнений

Кинематика – это исследование движущихся объектов и их взаимосвязей. Есть четыре (4) кинематических уравнения, которые относятся к смещению D, скорости v, времени t и ускорению a.

a) D = v _i t + 1/2 при ² b) (v _i + v _f) / 2 = D / t

c) a = (v _f – v _i) / t d) v _f ² = v _i ² + 2aD

D = смещение

a = ускорение

t = время

v _f = конечная скорость

v _i = начальная скорость

Вопросы по формулам кинематических уравнений.

1) Боб едет на велосипеде в магазин со скоростью 4 м / с, когда перед ним выбегает кошка. Он быстро тормозит до полной остановки, с ускорением – 2м / с ². Какое у него перемещение?

Ответ: Поскольку Боб остановлен, конечная скорость v _f = 0. Его начальная скорость v _i = 4 м / с. Ускорение, a = -2 м / с ². Время не указано, поэтому используйте уравнение (d) для смещения D, потому что оно не зависит от времени.

v _f ² = v _i ² + 2aD

(0) ² = (4 м / с) ² +2 (- 2 м / с ²) D

0 = 16 м ² / с ² + (- 4 м / с ²) D

-16 м ² / с ² = (- 4 м / с ²) D

16 м ² / с ² = 4 м / с ²) D

(16 м ² / с ²) / (4 м / с ²) = D

Водоизмещение полное 4 м.

2) Вы путешествуете с постоянной скоростью 11 м / с в течение 5 минут. Как далеко ты проехал?

Ответ: При постоянной скорости v _i = v _f = 11 м / с. Время t = 5 мин или t = (60 сек / мин x 5 мин) = 300 сек. Теперь используйте уравнение (b), чтобы найти смещение D.

(v _i + v _f) / 2 = D / t

D = [(v _i + v _f) / 2] t

D = [(11 м / с + 11 м / с) / 2] x 300 с

D = (22 м / с) / 2 x 300 сек

D = 11 м / с x 300 с

D = 3300 м Водоизмещение полное 3,300 м.

3) Каково ускорение автомобиля, который разгоняется с 11 до 40 м / с за 10 секунд?

Ответ: V _i = 11 м / с. V _f = 40 м / с. Время, t = 10 с. Используйте кинематическое уравнение c), чтобы найти ускорение.

a = (v _f – v _i) / t

a = (40 м / с – 11 м / с) / 10 с

a = (29 м / с) / 10 с = 2,9 м / с ²

4) Если автомобиль разгоняется на 3.0 м / с ² от полной остановки, сколько времени потребуется, чтобы проехать 3000 м?

Ответ: Ускорение a = 2,9 м / с ² и перемещение D = 3000 м. Автомобиль был неподвижен, поэтому v _i = 0. Используйте уравнение a), чтобы найти время.

D = v _i t + 1/2 при ²

3000 м = 0т + 1/2 (3,0 м / с ²) т ²

3000 м = 1/2 (3,0 м / с ²) / т ²

3000 м / 1.5 м / с ² = t ²

2000 с ² = t ²

t = 44,72 сек

Формула кинематических законов. Кинематика Основные понятия, законы и формулы. Свободное падение по вертикали

Чтобы понять, что изучает механика, необходимо рассмотреть, что означает движение в самом общем смысле. Значение этого слова подразумевает изменение чего-либо. Например, политическое движение выступает за равенство разных слоев населения независимо от их расовой принадлежности.Раньше этого не было, потом что-то изменилось, и теперь все люди равноправны. Это движение цивилизации вперед. Другой пример – экология. Раньше, выбирая на природе, никто не задумывался о том, что оставляет после себя мусор. Сегодня любой цивилизованный человек заберет его с собой и отнесет в специально отведенное место для дальнейшей утилизации.

Примерно так можно наблюдать в механике. При механическом движении положение тела со временем меняется в пространстве относительно других предметов.Основная задача механики – указать, где находится объект в любой момент, учитывая даже тот, который еще не пришел. То есть, чтобы предсказать положение тела в указанное время, а не просто узнать, где оно было в прошлом.

Кинематика – это раздел механики, изучающий движение тела без анализа его причин. Это значит, что она учит не объяснять, а описывать. То есть придумать способ, с помощью которого можно было бы в любой момент задать положение тела.Основные понятия кинематики включают скорость, ускорение, расстояние, время и движение.

Сложность в описании механизма

Первая проблема, с которой сталкивается кинематика, заключается в том, что каждое тело имеет определенный размер. Предположим, необходимо описать движение некоторого объекта. Это означает, что вы научитесь определять свою должность в любое время. Но каждый предмет занимает какое-то место в космосе. То есть все части этого объекта в один и тот же момент времени занимают разное положение.

Какой момент в данном случае нужно брать, чтобы описать местонахождение всего объекта? Если рассматривать каждую, то расчеты будут слишком сложными. Поэтому решение ответить на этот вопрос можно легко упростить. Если все точки одного тела движутся в одном направлении, достаточно описать движение, которое это тело содержит.

Типы движения в кинематике

Есть три типа:

Есть поступательное движение, при котором любое прямое, проведенное в теле, остается параллельно самому себе.Например, такое движение совершает машина, которая движется по шоссе.
Вращением называется такое движение тела, при котором все его точки движутся по окружностям с центрами, лежащими на одной прямой, называемой осью вращения. Например, вращение Земли относительно своей оси.
Колебательное движение – это движение, при котором тело повторяет свою траекторию в течение определенного периода времени. Например, движение маятника.

Основные понятия кинематики – материальная точка

Любое сложное движение можно описать как сочетание двух простых видов – поступательного и вращательного.Например, колесо транспортного средства или юла, стоя непосредственно на движущемся, одновременно участвуют в этих двух типах движения.

А что, если движение тела нельзя представить как комбинацию? Например, если машина едет по ухабистой дороге, ее положение будет очень сложно изменить. Если посчитать только тот факт, что этот транспорт движется из одного города в другой, то в такой ситуации не имеет значения, какого размера тело движется из точки А в точку б и ими можно пренебречь.В этом случае важно только, за какое время машина прошла определенное расстояние и с какой скоростью двигалась.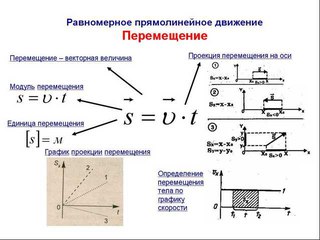

Однако следует учитывать, что пренебрежение размером не допускается в каждой задаче. Например, если вы рассчитываете движение на парковке, то игнорирование величины этого тела приведет к пагубным последствиям. Поэтому только в тех ситуациях, когда в рамках конкретной задачи габаритами движущегося объекта можно пренебречь, такое тело называют материальной точкой.

Формулы кинематики

Числа, с помощью которых задается положение точки в пространстве, называются координатами. Чтобы определить это по прямой, просто одно число, если говорить о поверхности, затем два, о пробеле – три. Больше чисел в трехмерном мире (для описания положения материальной точки) не требуется.

Есть три основных уравнения для концепции кинематики, как раздел о движении тел:

v = U + AT.
S = UT + 1 / 2AT 2.
v 2 = U 2 + 2as.

v = предельная скорость,

u = начальная скорость

a = ускорение

s = пройденное телом расстояние

Формулы кинематики в одномерном пространстве:

X – XO = V + 1 / 2A T2

V 2 = VO 1 + 2A (X – XO)

X – XO = 1 \ 2 (VO + V) T
Где,

V – конечная скорость (м / с),

V o – начальная скорость (м / с),

a – ускорение (м / с 2),

t – время (с),

X – конечное положение (м),

Формулы кинематики в двухмерном пространстве

Поскольку следующие уравнения используются для описания материальной точки на плоскости, стоит рассмотреть оси X и Y.

С учетом направления x:

a x =. константа.

V fx = vix + ax Δt

X f = xi + vix Δt + 1 / 2a x Δt 2

ΔT = V FX -V IX / AX

V FX 2 = V ix 2 + 2AX ΔX

X f = xi + 1/2 (v fx + v ix) Δ t.
А с учетом Y:

a y =. константа.

V FY = V IY + AY ΔT

yf = yi + v Δt + 1/2 ax Δt 2

Δt = V FY – V IY / AY

V FY 2 = V IY 2 + 2 AY Δ Y

yf = yi +1/2 (V FY + V IY) ΔT.

V f – конечная скорость (м / с),

V i – начальная скорость (м / с),

a – ускорение (M / C 2),

t – время (с),

X – конечное положение (м),

X 0 – исходное положение (M).

Перемещение брошенного снаряда – лучший пример для описания движения объекта в двух измерениях. Здесь тело движется как в вертикальном положении y, так и в горизонтальном положении x, поэтому мы можем сказать, что объект имеет две скорости.

Примеры кинематических задач

Задача 1. : Начальная скорость грузовика равна нулю. Изначально этот объект покоится. Он начинает действовать равномерно в течение 5,21 секунды. Расстояние, пройденное грузовиком – 110 м. Найдите ускорение.

Решение:
Расстояние s = 110 м пройдено
Начальная скорость v i = 0,
Время T = 5,21 с,
Разгон а =?
Используя основное понятие и формулу кинематики, можно сделать вывод, что
s = V I T + 1/2 A T 2,
110 м = (0) × (5.21) + 1/2 × A (5.21) 2,
a = 8,10 м / с 2.

Задача 2: Точка движется по оси x (в см), через t секунд хода она можно представить с помощью уравнения x = 14t 2 – T + 10. Необходимо найти среднюю точку точки при условии, что t = 3S?

Решение:
Положение точки при Т = 0 x = 10 см.
При t = 3s, x = 133 см.
Средняя скорость, V AV = ΔX / ΔT = 133-10 / 3-0 = 41 см / с.

Что является точкой отсчета

О движении можно сказать только в том случае, если есть что-то, относительно чего учитывается изменение положения изучаемого объекта. Такой объект называется эталонным телом и всегда считается фиксированным.

Если задача не указана, в какой системе отчетов перемещается материальная точка, земля по умолчанию считается телом по умолчанию. Однако это не означает, что за фиксированное время в данный момент времени объект, относительно которого совершается движение, ни какой другой удобный для расчета не может быть взят.Например, для эталонного тела, вы можете взять движущийся поезд, вращающийся автомобиль и так далее.

Система отсчета и ее значение в кинематике

Для описания движения необходимы три компонента:

Система координат.
Ориентир.
Устройство для измерения времени.

Эталонное тело, связанная с ним система координат и устройство для измерения времени образуют систему отсчета. Бессмысленно говорить о движении, если оно не уточняет.Правильно подобранная система отсчета позволяет упростить описание движения и, наоборот, усложнить, если оно выбрано.

Именно по этой причине человечество считало, что Солнце движется вокруг Земли и находится в центре Вселенной. Такое сложное движение светил связано с тем, что земные наблюдатели находятся в системе отсчета, которая движется очень замысловато. Земля вращается вокруг своей оси и одновременно вокруг Солнца.На самом деле, если поменять систему отсчета, то все движения небесных тел легко описываются. Одно время это сделал Коперник. Он предложил собственное описание мироустройства, в котором солнце неподвижно. В связи с этим описать движение планет намного проще, чем если бы телом была Земля.

Основные понятия кинематики – путь и траектория

Пусть некоторая точка сначала находилась в позиции A, а через некоторое время оказалась в позиции V.Между ними можно провести одну строчку. Но для того, чтобы эта прямая не несла больше информации о движении, то есть было ясно, откуда и куда двигалось тело, это должен быть не просто сегмент, а направление, обычно обозначаемое буквой S. называется вектор, проводимый от начальной позиции предмета в конечном.

Если тело изначально находилось в точке A, а затем оказалось в точке B, это не означает, что оно двигалось только по прямой.Из одной позиции в другую можно попасть бесконечным количеством способов. Линия, по которой движется тело, – это еще одно базовое понятие кинематики – траектория. А его длина называется путем, который обычно обозначают буквами L или L.

Приближается занятие, и нам пора переходить от теории к практике. На выходных мы сели и подумали, что у многих студентов должна быть под рукой хорошая физическая формула. Сухие формулы с пояснением: коротко, лаконично, ничего лишнего.Знаете, очень полезная штука при решении задач. Да и на экзамене, когда он может «выскочить» из головы, ровно то, что накануне пролез, такая подборка сослужит отличную службу.

Большинство задач обычно задают по трем наиболее популярным разделам физики. это механика , термодинамика и молекулярная физика , электричество . И возьми их!

Основные формулы для физики, динамики, кинематики, статики

Начнем с самого простого.Давно-добрый любимец прямое и равномерное движение.

Кинематические формулы:

Конечно, не будем забывать о движении по кругу, а затем перейдем к динамике и законам Ньютона.

После динамики пора рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику

А теперь представим основные формулы по теме «Работа и энергия». Куда мы без них!

Основные формулы молекулярной физики и термодинамики

Закончим раздел механики формулами флуктуаций и волн и перейдем к молекулярной физике и термодинамике.

Коэффициент полезного, Закон Гей-Лурсака, уравнение Клапаирона-Менделеева – все эти милые сердцевины формулы собраны ниже.

Кстати! Для всех наших читателей теперь действует скидка 10% на любой вид работы .

Основные формулы для физики: электричество

Пора переходить к электричеству, хоть оно и меньше любит термодинамику. Начнем с электростатики.

А под дробью барабана закончить формулы закона Ома, электромагнитной индукции и электромагнитных колебаний.

Вот и все. Конечно, можно было бы привести всю формулу горы, но это еще ничего. Когда формул становится слишком много, можно легко запутаться, и там они могут растопить мозг. Надеемся, что наша шпаргалка по основным формулам физики поможет решать любимые задачи быстрее и эффективнее. А если вы хотите что-то уточнить или не нашли нужной формулы: спросите у специалистов студенческой службы . Наши авторы держат в голове сотни формул и щелкают по задачам как орехи.Обращайтесь, и скоро любое задание будет вам «по зубам».

Прежде всего, следует отметить, что речь пойдет о геометрической точке, то есть о площади пространства, не имеющей размеров. Именно для этого абстрактного изображения (модели) и всех приведенных ниже определений и формул. Однако для краткости я продолжу рассказывать о движении тела , объекта или частиц . Я такой лишь для того, чтобы вам было легче читать. Но всегда помните, что речь идет о геометрической точке.

Радиус-вектор Точки – это вектор, начало которого совпадает с началом системы координат, а конец находится в этой точке. Радиус-вектор обозначается, как правило, буквой р. . К сожалению, некоторые авторы обозначают его буквой с. . Настоятельно советую не использовать Обозначение s. Для радиус-вектора. Дело в том, что подавляющее большинство авторов (как отечественных, так и зарубежных) используют букву S для обозначения пути, который является скаляром и к радиус-вектору, как правило, отношения не имеет.Если обозначить радиус-вектор как с. Можно легко запутаться. Еще раз, мы, как и все нормальные люди, будем использовать следующие обозначения: r. – Радиус-вектор точки, S – путь, пройденный точкой.

Вектор движения (часто говорят просто – ход ) – это вектор , начало которого совпадает с точкой траектории, где находилось тело, когда мы начали изучать это движение, и конец этого вектора. совпадает с точкой траектории, по которой мы изучали это исследование.Обозначим этот вектор Δ r. . Использование символа Δ очевидно: Δ р. – это разница между радиус-вектором r. Конечная точка исследуемого отрезка траектории и радиус-вектор r. 0 точек начала этого отрезка (рис.1), то есть Δ r =. г. – р. 0.

Траектория – это линия, по которой движется тело.

Путь – это сумма длин всех участков траектории, последовательно проходимых телом при движении.Обозначается либо ΔS, если речь идет о участке траектории, либо S, если речь идет о всей траектории наблюдаемого движения. Иногда (редко) путь обозначают другой буквой, например, L (только не указывайте его как R, об этом мы уже говорили). Помнить! Путь положительный скаляр ! Путь в процессе движения может увеличиться, только .

Средняя скорость передвижения v. ср.

в. ср = Δ. г. / Δt.

Мгновенная скорость перемещения V – это вектор, определяемый выражением

v. = D. r. / DT.

Средняя скорость пути V ср – скаляр, определяемый выражением

V cp = ΔS / Δt.

Часто встречаются и другие обозначения, например,.

Мгновенная скорость пути v – скаляр, определяемый выражением

Модуль мгновенной скорости движения и мгновенной скорости пути одинаковы, поскольку DR = DS.

Среднее ускорение a.

а. ср = Δ. v. / Δt.

Мгновенное ускорение (или просто ускорение ) a. – это вектор, определяемый выражением

a. = D. v. / DT.

Тангенциальное (тангенциальное) ускорение a τ (нижний индекс – греческая строчная буква Тау) – это вектор , , то есть проекция вектора Мгновенное ускорение по касательной оси.

Нормальное (центростремительное) ускорение A n – это вектор , то есть проекция вектора Мгновенное ускорение на оси нормали.

Модуль ускорения Таннера

| а. τ | = dv / dt,

То есть это производный модуль мгновенной скорости.

Модуль нормального ускорения

| а. N | = V 2 / R,

где R – величина радиуса кривизны траектории в точке нахождения тела.

Важно! Хочу обратить внимание на следующее. Не путайте с обозначениями касательного и нормального ускорений! Дело в том, что в литературе по этому поводу наблюдалась полная листовка.

Помните!

а. τ – это вектор тангенциальное ускорение

a. n – тот вектор Нормальное ускорение.

а. т I. а. n – вектор Проекции полного ускорения , но на касательную ось и ось нормали, соответственно,

A τ – проекция (скаляр!) Ускорения Таннера на касательную ось,

A n – проекция (скаляр!) Нормальное ускорение по главной оси,

| а. τ | – это модуль вектор тангенциальное ускорение

| а. N | – это модуль вектор Нормальное ускорение.

Особенно не удивлюсь, если, читая литературу по криволинейному (в частности, вращательному) движению, вы обнаружите, что автор под τ понимает и вектор, и его проекцию, и его модуль. То же самое и с n. Все, как говорится, «в одном флаконе». И это, к сожалению, полностью и рядом. Даже учебники для вузов не исключение, во многих из них (поверьте – в большинстве!) По этому поводу царит полная неразбериха.

Итак, не зная азовской векторной алгебры или пренебрегая ею, очень легко полностью запутаться при изучении и анализе физических процессов.Следовательно, знание векторной алгебры является самым успешным условием успеха при изучении механики. И не только механика. В дальнейшем, изучая другие разделы физики, вы неоднократно в этом убедитесь.

Мгновенная угловая скорость (или просто угловая скорость ) ω – это вектор, определяемый выражением

ω = D. φ / dt,

Где D. φ – бесконечно малое изменение угловой координаты (D φ – Вектор!).

Мгновенное угловое ускорение (или просто угловое ускорение ) ε – это вектор, определяемый выражением

ε = D. ω / DT.

Связь между и , ω и р. :

v. = ω × р. .

Связь Между V, Ω и R:

Связь Между | а. τ |, ε и r:

| а. τ | = ε · r.

Теперь перейдите к K. кинематические уравнения конкретных типов движения. Эти уравнения необходимо выучить наизусть .

Кинематическое уравнение равномерного и прямолинейного движения Имеет вид:

р. = р. 0 + в. т,

Где р. – объект радиус-вектор в момент времени t, r. 0 то же самое в начальный момент времени T 0 (в момент начала наблюдений).

Кинематическое уравнение постоянного ускорения Имеет вид:

r. = р. 0 + v. 0 t +. а. t 2/2, где v. 0 Скорость объекта в момент времени T 0.

Уравнение для скорости тела при движении с постоянным ускорением Оно имеет вид:

v. = v . 0 + а. т.

Кинематографическое уравнение равномерного движения по окружности в полярных координатах Имеет вид:

φ = φ 0 + ω zt,

где φ – угловая координата тела в момент времени, φ 0 – угловая координата тела в момент начала наблюдения (в начальный момент времени), Ω z – проекция угловой скорости ω По оси z (обычно эту ось выбирают перпендикулярно плоскости вращения).

Кинематическое уравнение окружности с постоянным ускорением в полярных координатах Имеет вид:

φ = φ 0 + ω 0z T + ε Z T 2/2.

Кинематическое уравнение гармонических колебаний по оси X Имеет вид:

X = a cos (ω t + φ 0),

где A – амплитуда колебаний, ω – циклическая частота, φ 0 – начальная фаза колебаний.

Проекция точки скорости, колеблющейся вдоль оси X, на эту ось равна:

V x = – ω · a · sin (ω t + φ 0).

Проекция ускорения точки, колеблющейся вдоль оси X, на эту ось равна:

А x = – ω 2 · a · cos (ω t + φ 0).

Связь Между циклической частотой ω, обычной частотой ƒ и периодом колебаний T:

ω = 2 πƒƒ = 2 π / T (π = 3,14 – число Пи).

Математический маятник Имеет период колебаний Т, определяемый выражением:

В числителе питающего выражения – длина нити маятника, в знаменателе – ускорение свободного падения

Связь между абсолютным v. ABS, родственник v. Rels и переносной v. По скоростям:

v. abs = v. Rev +. v. Per.

Здесь, пожалуй, все определения и формулы, которые могут понадобиться при решении задач кинематики. Приведенная выше информация носит справочный характер и не может заменить электронную книгу, где она доступна, в деталях и, я надеюсь, увлекательная теория этого раздела механики.

Основные единицы измерения величин в системе СИ Такие:

единица длины – метр (1 м),
раз – секунда (1 с),
масс – килограмм (1 кг),
количество вещества моль (1 моль),
температур – Кельвина (1 К),
сил электрического тока – ампер (1 А),
Ссылка: Световые силы – кандела (1 кд, при решении школьных задач практически не используется).

При расчетах в системе углы измеряются в радианах.

Если в задаче по физике не указано, в каких единицах нужно ответить, ее нужно задавать в единицах системы СИ или производных от них, значения, соответствующие физическому размеру которых задаются в задаче. . Например, если в задаче нужно найти скорость и не сказано, что нужно выразить, ответ должен быть дан в м / с.

Для удобства задач по физике часто приходится использовать доллары (уменьшение) и несколько (увеличение) приставок.Их можно применять к любому физическому размеру. Например, MM – миллиметр, CT – килотонна, нс – наносекунда, mg – мегаграммы, mmol – миллимоль, MCA – микроампер. Помните, что в физике не бывает двойных консолей. Например, ICG – это микрограмм, а не милликилограмм. Обратите внимание, что при сложении и вычитании значений вы можете оперировать только значениями одного и того же измерения. Например, килограммы можно складывать только килограммами, вы можете вычитать миллиметры из миллиметров и так далее.При передаче значений используйте следующую таблицу.

Путь и движение

Кинематика Так называется раздел механики, в котором рассматривается движение тел без выяснения причин этого движения.

Механическое движение Тело называют изменением своего положения в пространстве относительно других тел с течением времени.

Каждое тело имеет определенные размеры. Однако во многих задачах механики нет необходимости указывать положение отдельных частей тела.Если размеры тела малы по сравнению с расстояниями до других тел, то это тело можно считать материальной точкой . Так что при перемещении машины на большие расстояния можно долго пренебрегать ею, поскольку длина машины мала по сравнению с расстояниями, которые она проезжает.

Интуитивно понятно, что характеристики движения (скорость, траектория и т. Д.) Зависят от того, где мы на это смотрим. Поэтому для описания движения вводится понятие системы отсчета. Базовая система (СО) – Сочетание опорного тела (считается абсолютно твердое вещество), привязаны к нему в системе координат, линейка (измерительный прибор), часы и время синхронизатора.

Перемещаясь во времени из одной точки в другую, тело (материальная точка) описывает заданной линией траекторию движения тела .

Смещение тела Они называют направленной линией разреза, соединяющей начальное положение тела с его конечным положением. Перемещение есть вектор величины. Перемещение может увеличиваться в процессе движения, уменьшаться и становиться нулевым.

Пройдено путь, равняется длине траектории, пройденной телом за некоторое время.Путь – это скалярное значение. Путь не может быть сокращен. Путь только увеличивается или остается постоянным (если тело не двигается). При движении тела по криволинейной траектории модуль (длина) вектора движения всегда меньше пройденного пути.

Для равномерного (при постоянной скорости) путь движения л. Можно найти по формуле:

где: v. – скорость кузова, т. – Время, на которое он переместился. При решении кинематических задач движение обычно осуществляется из геометрических соображений.Часто геометрические соображения относительно местоположения хода требуют знания теоремы Пифагора.

средняя скорость

Скорость – векторная величина, характеризующая скорость перемещения тела в пространстве. Скорость быстрая средняя и мгновенная. Мгновенная скорость описывает движение в этой конкретной точке в этой конкретной точке пространства, а средняя скорость характеризует все движение в целом, в целом, без описания деталей движения в каждом конкретном месте.

Средняя скорость пути – Это отношение всего пути ко всему времени движения:

где: л. полный – весь путь, который прошел кузов, т. Full – все время движения.

Средняя скорость движения – Это отношение всего движения ко всему времени движения:

Это значение направлено так же, как и полное движение тела (то есть от начальной точки движения до конечной точки).В то же время не забывайте, что полное движение не всегда равно алгебраическому количеству движений на определенных этапах движения. Полный вектор движения равен векторной сумме перемещений на отдельных этапах движения.

При решении задач по кинематике не допускайте очень частых ошибок. Средняя скорость обычно не равна средней арифметической скорости тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
Более того, средняя скорость не равна одной из скоростей, с которыми движется тело во время движения, даже если эта скорость имела примерно промежуточное значение по сравнению с другими скоростями, с которыми двигалось тело.

Равно-заданный прямой ход

Ускорение – Векторная физическая величина, определяющая скорость изменения тела тела. Ускорением тела называют отношение изменения скорости к периоду, в течение которого произошло изменение скорости:

где: v. 0 – начальная скорость тела, v. – конечная скорость тела (т.е. через промежуток времени т. ).

Далее, если в условии задачи не указано иное, мы полагаем, что если тело движется с ускорением, это ускорение остается постоянным. Такое движение тела называется равным (или равным). При равновесном движении скорость тела изменяется на одно и то же значение в течение любых равных периодов времени.

Равноправное движение фактически ускоряется, когда тело увеличивает скорость, и замедляется, когда скорость уменьшается.Для простоты задания удобно брать ускорение со знаком «-».

Из предыдущей формулы должна быть описана другая более общая формула изменение скорости во времени При равновесном движении:

Двигаться (но не в сторону) При уравнительном движении формулы рассчитываются по формулам:

В последней формуле использовалась одна особенность эквивалентного механизма. При равновесном движении среднюю скорость можно рассчитать как среднее арифметическое и конечную скорость (это свойство очень удобно использовать при решении некоторых задач):

С расчетом пути все сложнее.Если тело не изменило направление движения, то при уравновешенном прямом движении путь численно равен движению. А если изменилось – надо отдельно читать путь до остановки (момент поворота) и путь после остановки (момент разворота). И просто временное сопротивление в формуле движения в этом случае приведет к типичной ошибке.

Координата При движении равновесия, изменяется по закону:

Скорость проецирования При равновесном движении она изменяется по такому закону:

Аналогичные формулы получены для остальных координатных осей.

Свободное падение по вертикали

На все тела на земле действует сила тяжести. В отсутствие опоры или подвески эта сила заставляет тела падать на поверхность Земли. Если пренебречь сопротивлением воздуха, то движение тела только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одно и то же ускорение, называемое ускорением свободного падения. У поверхности Земли ускорение свободного падения Количество:

Это означает, что свободное падение всех тел у поверхности Земли эквивалентно (но не обязательно прямолинейному) движению.Сначала рассмотрим простейший случай свободного падения, когда тело движется строго вертикально. Такое движение является равновесным прямолинейным движением, поэтому все ранее изученные закономерности и фокусы такого движения подходят для свободного падения. Только ускорение всегда равно ускорению свободного падения.

Традиционно при свободном падении используется направленная вертикально ось Oy. Здесь нет ничего страшного. Просто нужно во всех формулах вместо индекса « ч. » написать « ч.». »Значение этого индекса и правила определения знаков сохранены. Куда направить ось Oy – выбор на ваш выбор в зависимости от удобства решения задачи. Варианты 2: вверх или вниз.

Приведем несколько формул, решающих некоторые конкретные кинематические задачи для свободного падения по вертикали. Например, скорость падения тела с высоты ч. Без начальной скорости:

Время падения тела с высоты ч. Без начальной скорости:

Максимальная высота, на которую поднимется корпус, оставленный вертикально вверх с начальной скоростью v. 0, время подъема этого корпуса на максимальную высоту и полное время полета (до возвращения в исходную точку):

Горизонтальный бросок

При горизонтальном броске с начальной скоростью v. 0 Движение тела удобно рассматривать как два движения: равномерное по оси oh (по оси oh нет силы препятствовать или помогать движению) и равновесие движение по оси Oy.

Скорость в любой момент определяется траекторией.Его можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна v. x =. v. 0. А вертикаль увеличивается по законам ускоренного движения v. y =. gT. . При этом полная скорость тела Можно найти по формулам:

Важно понимать, что время падения тела на землю не зависит от того, с какой горизонтальной скоростью оно было брошено, а определяется только высотой, с которой тело было брошено.Время падения тела на землю рассчитывается по формуле:

Пока тело падает, оно одновременно движется по горизонтальной оси. Следовательно, дальность полета тела или расстояние, на которое тело может пролететь вдоль оси ОН, будет равно:

Угол каждого горизонта и скорость тела легко найти из соотношения:

Иногда иногда в задачах может спросить о времени, в которое полная скорость тела будет наклонена под определенным углом к вертикали .Тогда этот угол будет из соотношения:

Важно понимать, какой угол фигурирует в задаче (вертикальный или горизонтальный). Это поможет вам выбрать правильную формулу. Если решить эту задачу координатным методом, то общая формула закона изменения координаты при равновесном движении:

Преобразуется в следующий закон движения по оси Oy для тела покинутой горизонтали:

С ее помощью мы в любой момент сможем найти высоту, на которой будет находиться тело.При этом в момент падения тела на землю координата тела по оси Oy будет равна нулю. Очевидно, что по оси О тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменится по закону:

Бросок под углом к горизонту (от земли к земле)

Максимальная высота подъема при метании под углом к горизонту (относительно начального уровня):

Время подъема на максимальную высоту при броске под углом к горизонту:

Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте, с которой тело было брошено, например, с земли на землю):

Минимальная скорость тела, брошенного под углом к горизонту, находится в наивысшей точке подъема и равна:

Максимальная скорость брошенного тела под углом к горизонту в моменты броска и падения на землю равна начальной.Это утверждение верно только для метания с Земли на Землю. Если тело продолжает лететь ниже уровня, с которого оно было брошено, оно будет там, чтобы приобретать все большую и большую скорость.

Сложение скоростей

Тел. Движение может быть описано в различных системах отсчета. С точки зрения кинематики все системы отсчета равны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах различны. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называются относительными.Таким образом, покой и движение тела относительны.

Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в фиксированной системе отсчета равна векторной величине скорости тела в подвижной системе отсчета, а скорость подвижной системы отсчета относительно фиксирована.

Равномерное движение по кругу

Движение тела по окружности – частный случай криволинейного движения.Этот тип движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит при движении по кругу (см. Рисунок). Равномерное движение тела по окружности характеризуется рядом значений.

Период – Время, за которое тело, двигаясь по окружности, делает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:

Частота – Число оборотов, которые совершило тело при перемещении по окружности за единицу времени.Единица измерения – 1 об / с или 1 Гц. Частота рассчитывается по формуле:

В обеих формулах: Н. – количество оборотов за время т. . Как видно из приведенных выше формул, период и частота величины интерпретации:

Для с равномерной скоростью вращения Тела будут определены следующим образом:

где: л. – Длина круга или пути, пройденного телом за равный период т.. При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряется в радианах. Угловая скорость ω Тела в этой точке называются отношением малого углового перемещения Δ φ на небольшой промежуток времени Δ т. . Очевидно, за равный период T. Тело пройдет угол, равный 2 π. Следовательно, при равномерном движении по окружности выполняются формулы:

Угловая скорость измеряется в рад / с.Не забудьте перевести углы из градусов в радианы. Дуги Длина л. связано с углом поворота соотношением:

Связь между модулем линейной скорости v. и угловой скоростью ω :

Когда тело движется по окружности с постоянным модулем, изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной скоростью по скорости является движением с ускорением (но не равным) , так как направление скорости меняется.В этом случае ускорение направлено по радиусу к центру окружности. Это называется нормальным, или центростремительным ускорением, Так как вектор ускорения в любой точке окружности направлен к ее центру (см. Рисунок).

Модуль центростремительного ускорения Linear привязан к этому сайту v. Для этого нужно все, что угодно, а именно посвятить подготовку к КТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день.Дело в том, что КТ – это экзамен, где мало знания физики или математики, нужно уметь быстро и без сбоев решать большое количество задач разной тематики и разной сложности. Вы можете только научиться решать тысячи задач.

Выучить все формулы и законы физики, а также формулы и методы математики. На самом деле выполнить это тоже очень просто, необходимых формул в физике всего около 200 штук, а в математике даже чуть меньше.В каждом из этих пунктов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже можно хорошо изучить, а значит полностью на машине и без труда решить в нужный момент большую часть Центральных Ц. . После этого вы будете просто думать о самых сложных задачах.
Пройдите все три репетиционных этапа тестирования по физике и математике. Каждый RT можно посетить дважды, чтобы сломать оба варианта. Опять же, на КТ, помимо умения быстро и качественно решать задачи, и знания формул и методов, также необходимо уметь правильно планировать время, распределять силы, а главное правильно заполнять форма ответа, не путая количество ответов и задач, без фамилии.Также в Республике Татарстан важно привыкнуть к вопросу постановки вопросов в задачах, которые на КТ могут показаться очень необычным человеком.

Успешное, кропотливое и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов позволят вам показать КТ отличный результат, максимум того, на что вы способны.

Нашли ошибку?

Если вы считаете, что допустили ошибку в учебных материалах, напишите об этом по электронной почте ().В письме укажите предмет (физика или математика), название или номер темы или теста, номер задачи или место в тексте (странице), где, по вашему мнению, есть ошибка. Также опишите, какова предполагаемая погрешность. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо вы объясните, почему это не ошибка.

Как решать кинематические задачи: часть II

Эта статья является второй главой в серии о том, как понимать и решать проблемы кинематики.Первая глава посвящена положению, скорости и ускорению. Теперь, когда мы понимаем эти величины, мы собираемся использовать их для решения задач в одном измерении.

Четыре всадника кинематического апокалипсиса:

x _f – x _i = (v _f – v _i) * t / 2

v _f – v _i = a * t

v _f ² = v _i ² + 2 * a * (x _f – x _i)

x _f = x _i + v _i * t + ½a * t ²

Примечание: маленькое _f обозначает final (как конечную скорость или положение), а маленькое _i обозначает начальное.

Примечание. Эти уравнения работают только при постоянном ускорении, но почти все задачи имеют постоянное ускорение.

Для каждой одномерной кинематической задачи этапы практически одинаковы.

Запишите каждую величину, которую дает вам задача (начальное и конечное положение, начальная и конечная скорость, ускорение, время и т. Д.)
Запишите, какое количество вы пытаетесь найти
Найдите кинематическое уравнение (или иногда два уравнения), чтобы связать эти величины.
Решите алгебру.

Да, это действительно так просто. (На самом деле, большинство физических задач работают одинаково. Подробнее об алгоритме решения физических задач читайте в этой статье.)

Как избежать распространенных ошибок: скрытые величины

Иногда проблема может сообщить вам количество тайно; вы можете даже не осознавать, что получили это. Например, если они сообщают вам смещение (как далеко что-то переместилось), но не позиции, вы можете рассматривать смещение как x _f и установить x _i равным 0.Точно так же, если проблема не говорит ничего особенного об ускорении, то ускорение, вероятно, просто гравитационное, a = g = 9,8 м / с ². Эти скрытые количества так же действительны, как и обычные количества, только их немного труднее обнаружить.

Как избежать распространенных ошибок: лучший результат

Особый пример скрытой величины – это когда вам говорят, что объект находится «на вершине своего полета / движения / траектории и т. Д.». Это означает, что они тайно говорят вам, что v _f равно 0, потому что объект, движущийся в одном измерении, всегда имеет скорость 0 в верхней части своего пути.Интересно, почему? Что ж, если бы скорость росла, то через миллисекунду объект был бы выше (и, следовательно, он не мог бы оказаться на вершине своего пути). Точно так же, если бы объект имел скорость, направленную вниз, то она была бы выше за миллисекунду (так что он также не может быть наверху).

Как избежать распространенных ошибок: положительные и отрицательные числа

Отследить негативы бывает непросто. Ключ – это направление; вниз всегда отрицательно. Итак, если объект падает, он будет иметь отрицательную скорость.Если ускорение снижается (а это почти всегда), то ускорение отрицательное. И не забывайте из нашей первой главы, что можно иметь положительную скорость и отрицательное ускорение одновременно!

Пример: женщина и ее мяч

Женщина держит мяч на расстоянии 1 метра и бросает его вверх со скоростью 5 м / с. а) Как высоко достигает мяч? б) Сколько времени нужно мячу, чтобы коснуться земли? в) Насколько быстро мяч летит, когда ударяется о землю?

Давай узнаем!

Часть A: Как высоко достигает мяч?

Что мы знаем?

Начальная позиция x _i = 1 м
Начальная скорость v _i = 5 м / с
Секретное количество: a = -9.8 м / с ² (гравитация)
Секретное количество: В верхней части дуги мяча (т. Е. Когда она самая высокая) v _f = 0 м / с

Что мы пытаемся найти?

Положение наверху броска, x _f

Какое уравнение связывает эти величины?

Мы ищем уравнение, которое включает x _f, x _i, v _f, v _i и
v _f ² = v _i ² + 2 * a * (x _f – x _i), кажется, хорошо вписывается!

Подключи и реши

v _f ² = v _i ² + 2 * a * (x _f – x _i)
(0 м / с) ² = (5 м / с) ² + 2 * (- 9.8 м / с ²) * (x _f – 1 м)
0 = 25 (м ² / с ²) – (19,6 м / с ²) * (x _f – 1 м )
(19,6 м / с ²) * (x _f – 1 м) = 25 м ² / с ² x _f –1 м = (25 м ² / с ² ) / (19,6 м / с ²)
x _f –1 м = 1,28 м
x _f = 2,28 м

Тада! Конечная высота = 2,28 метра

Часть B: Сколько времени нужно мячу, чтобы коснуться земли?

Что мы знаем?

Мы все еще знаем x _i = 1 м, v _i = 5 м / с и a = -9.8 м / с ², но теперь мы также знаем, что x _f = 0 м (потому что высота земли 0 м)

Примечание. Поскольку мяч теперь находится на земле, а не наверху полета, v _f ≠ 0, так что мяч находится вне стола.

Что мы пытаемся найти?

Время, т

Какое уравнение связывает эти величины?

Мы ищем уравнение, которое включает x _f, x _i, v _i, a и t
Похоже, нам понадобится x _f = x _i + v _i * т + ½a * т ²

Подключи и реши

x _f = x _i + v _i * t + ½a * t ² 0 m = 1 m + (5 м / с) * t + ½ (-9.8 м / с ²) * t ² – (4,9 м / с ²) * t ² + (5 м / с) * t + 1 м = 0

Это квадратное уравнение (ax ² + bx + c = 0), которое можно решить с помощью формулы корней квадратного уравнения.

t =
t =
t = или t =
t = или t =
t = -17 с или 1,2 с

Мы можем игнорировать t = -. 17, потому что нам не разрешено иметь отрицательное время (мы называем это нефизическим ответом), что оставляет нам время = 1,2 секунды!

Часть C)

Что мы знаем?

Мы все еще знаем x _i = 1 м, v _i = 5 м / с, a = -9.8 м / с ² и x _f = 0 м, но теперь мы также знаем, что t = 1,2 секунды, потому что мы только что решили это.

Что мы пытаемся найти?

Скорость, v _f

Какое уравнение связывает эти величины?

У нас так много величин, что мы можем использовать любое из уравнений, но давайте возьмем v _f – v _i = a * t, потому что это просто, и мы еще не использовали его.

Подключи и реши

v _f – v _i = a * t
v _f – 5 м / с = (-9.8 м / с ²) * 1,2 с
v _f = 5 м / с – 11,8 м / с
v _f = -6,8 м / с

Стрела, скорость при падении мяча на землю составляет 6,8 м / с (отсюда отрицательный знак)

Теперь мы знаем, как использовать наши кинематические уравнения для решения задач в одном измерении. В нашем следующем блоге мы обсудим, как «вырезать» векторы при подготовке к кинематике в двух измерениях.

Следите за обновлениями! То же время летучей мыши, тот же канал летучей мыши.

Вы заинтересованы в работе с Джейкобом – в Нью-Йорке или в Интернете – над своими физическими работами?

Для более релевантного чтения ознакомьтесь с другими сообщениями в блогах, написанными нашими преподавателями физики в Нью-Йорке и Бостоне:

уравнений движения | Блестящая вики по математике и науке

Графики очень интерактивны и помогают суммировать различные вещи в одном месте.Следовательно, они полезны для идентификации, отслеживания и моделирования движения объекта. Следующие типы графиков могут быть полезны в кинематике: графики положения-времени и графики скорости-времени.

График положения-времени:

Графики положения-времени – это самые простые графики в кинематике. Они позволяют описывать движение объекта как по положению, так и по времени. Ось yyy этих графиков представляет смещение объекта, а ось xxx представляет время.Таким образом, наклон графика «положение-время» дает скорость объекта.

Найдите скорость частицы в интервале (1,2) (1,2) (1,2).
Можно видеть, что наклон графика положение-время дает нам скорость за период времени. Таким образом,
v = s2 − s1t2 − t1 = 10−7,52−1 = 2,5 м / с. \ Begin {align} v & = \ dfrac {s_2-s_1} {t_2-t_1} \\ & = \ dfrac {10-7.5} {2-1} \\ & = 2,5 \ текст {м / с}. \ end {align} v = t2 −t1 s2 −s1 = 2−110−7,5 = 2,5 м / с.
Также можно видеть, что смещение этого объекта задается функцией s (t) = 2,5t + 5s (t) = 2,5t + 5s (t) = 2,5t + 5. Таким образом, можно найти скорость этой функции, которая есть не что иное, как ее производная:
v (t) = ddt (2,5t + 5) = 2,5 м / зв (t) = \ dfrac {d} {dt} (2,5t + 5) = 2,5 \ text {m / s} .v (t) = dtd (2,5t + 5) = 2,5 м / с.

Отправьте свой ответ

Позиционно-временной график объекта

Найдите скорость объекта в интервале (2,4) (2,4) (2,4).

График скорости-времени:

Эти графики позволяют вычислить скорость объекта в данный момент времени. Ось yyy представляет скорость, а ось xxx – время. В основном они могут помочь в вычислении двух вещей:

смещение объекта на интервале,
ускорение объекта на интервале.

Из приведенного выше графика видно, что наклон графика скорость-время дает ускорение:

(Наклон графика скорости и времени) = a = v2 − v1t2 − t1.2. \ end {align} a = t2 −t1 v2 −v1 = 4−210−6 = 2 м / с2.

Площадь под графиком показывает смещение, которое является площадью трапеции:

s = h (a + b) 2 = 2 (6 + 10) 2 = 16 м. \ Begin {align} s & = \ dfrac {h (a + b)} 2 \\ & = \ dfrac {2 (6 + 10)} {2} \\ & = 16 \ текст {м}. \ end {align} s = 2h (a + b) = 22 (6 + 10) = 16 м.

Также можно сделать вывод, что график задается функцией: v (t) = 2t + 2v (t) = 2t + 2v (t) = 2t + 2. Таким образом, ускорение будет производной

a = ddt (2t + 2) = 2 м / с2.2 + 4 \ вправо) \\ & = 16 \ текст {м}. \ end {align} s = ∫24 2t + 2dt = [t2 + 2t] 24 = 42 + 8− (22 + 4) = 16 м.

Выше приведен график скорости бега от времени. Как далеко проходит этот бегун за 1616 16 секунд?

Вертикальный масштаб фигуры установлен на vs = 8,0 м / с.v_ {s} = 8.0 \ text {м / с.} vs = 8.0 м / с.

Отправьте свой ответ

Скорость ракеты определяется следующей функцией:

v (t) = 3t2−2t − 1.2-2t-1.v (t) = 3t2−2t − 1.

Найти смещение ракеты за интервал времени (1,3) (1,3) (1,3).

Изображение предоставлено Wikimedia Commons.

Хотя использование графиков может показаться более запутанным, чем использование простых уравнений для решения вопросов, оно может дать важную интуицию при решении физических проблем и дать подсказки относительно того, как вывести уравнения движения в сложных случаях. В следующих разделах графики скорости-времени используются для получения фундаментальных уравнений, управляющих движением объектов.

по кинематике | askIITians

Инерциальная система отсчета: – Система отсчета, в которой действует ньютоновская механика, называется инерциальной системой отсчета или инерциальной системой отсчета. Система отсчета, в которой не работает ньютоновская механика, называется неинерциальной системой отсчета или неинерциальной системой отсчета.
Средняя скорость v _av и средняя скорость тела за промежуток времени? т определяется как,

v _av = средняя скорость

=? с /? т

Примечание:

(a) Изменение скорости или направления движения приводит к изменению скорости

(b) Частица, которая совершает один оборот по круговой траектории с постоянной скоростью, считается обладающей нулевой скоростью и ненулевой скоростью.

Среднее ускорение определяется как изменение скорости за интервал времени? т .

Мгновенное ускорение частицы – это скорость, с которой ее скорость изменяется в данный момент.

Три уравнения движения для объекта с постоянным ускорением приведены ниже.

(а) v = u + при

(б) s = ut + 1/2 при ²

Здесь u – начальная скорость, v – конечная скорость, a – ускорение, s – перемещение тела и t – время.

Примечание: примите знак «+ ve», когда тело ускоряется, и знак «–ve», когда тело замедляется.

Смещение корпусом в n ^th секундах определяется как,

с _n = u + a /2 (2 n -1)

Время позиционирования ( x против t ), скорость-время ( v против t ) и время ускорения ( a против t ) график для движения в одном измерении:

(i) Изменение смещения (x), скорости (v) и ускорения (a) во времени для различных типов движения.

	Рабочий объем (x)	Скорость (v)	Разгон (а)
(а) В состоянии покоя
(б) Движение с постоянной скоростью
(c) Движение с постоянным ускорением
(d) Движение с постоянным замедлением

Скалярные величины: – Скалярные величины – это те величины, которые требуют только величины для их полной спецификации.(например, масса, длина, объем, плотность)
Векторные величины: – Векторные величины – это те величины, которые требуют как величины, так и направления для их полной спецификации. (например, перемещение, скорость, ускорение, сила)
Нулевой вектор (нулевые векторы): – Это вектор с нулевой величиной и произвольным направлением.

Когда нулевой вектор добавляется или вычитается из заданного вектора, результирующий вектор совпадает с заданным вектором.

Точечное произведение нулевого вектора с любым произвольным всегда равно нулю. Перекрестное произведение нулевого вектора с любым другим вектором также является нулевым вектором.

Коллинеарный вектор: – Векторы, имеющие общую линию действия, называются коллинеарными векторами. Есть два типа.

Параллельный вектор ( θ = 0 °): – Два вектора, действующих в одном направлении, называются параллельными векторами.

Антипараллельный вектор ( θ = 180 °): – Два вектора, направленные в противоположных направлениях, называются антипараллельными векторами.

Копланарные векторы – Векторы, расположенные в одной плоскости, независимо от их направления, называются копланарными векторами.
Сложение вектора: –

Сложение вектора коммутативно –

Сложение векторов ассоциативно –

Векторное сложение распределительное –

Треугольники Закон сложения векторов: – Если два вектора представлены двумя сторонами треугольника, взятыми в одном порядке, то их результат представлен третьей стороной треугольника, взятой в противоположном порядке.

Величина результирующего вектора: –

R = √ ( A ² + B ² +2 AB cos θ )

Здесь θ – угол между и.

Если β – угол между и,

тогда,

Если три вектора, действующих одновременно на частицу, можно представить тремя сторонами треугольника, взятыми в одном порядке, то частица останется в равновесии.

Итак,

Параллелограммный закон сложения векторов: –

R = √ ( A ² + B ² +2 AB cos θ ),

Случаи 1: – Когда, θ = 0 °, тогда

R = A + B (максимум), β = 0 °

Случаи 2: – Когда, θ = 180 °, тогда

R = A – B (минимум), β = 0 °

Случаи 3: – Когда, θ = 90 °, тогда

R = √ ( A ² + B ²), β = tan ^-1 (B / A)

Процесс вычитания одного вектора из другого эквивалентен векторному сложению отрицательного значения вычитаемого вектора.

Итак,

(a) Точечное произведение или скалярное произведение: –

Здесь A – величина, B, – величина, а θ, – угол между и.

(i) Перпендикулярный вектор: –

(ii) Коллинеарный вектор: –

Когда, Параллельный вектор (θ = 0 °),

Когда, Антипараллельный вектор (θ = 180 °),

(b) Перекрестное произведение или векторное произведение: –

Или,

Здесь A – величина, B – величина, θ – угол между и и – единичный вектор в направлении, перпендикулярном плоскости, содержащей и.

(i) Перпендикулярный вектор (θ = 90 °): –

(ii) Коллинеарный вектор: –

Когда, Параллельный вектор (θ = 0 °), (нулевой вектор)

Когда, θ = 180 °, (нулевой вектор)

В трех измерениях,

Площадь треугольника: –

Площадь параллелограмма: –

Объем параллелепипеда: –

(i) Перпендикулярный вектор: – В верхней части наклонной плоскости ( t = 0, u = 0 и a = g sin q ) уравнение движения будет иметь вид

(а) v = (g sinθ) t

(б) s = ½ (g sinθ) t ²

(в) v ² = 2 (g sinθ) с

(ii) Если время, необходимое телу для достижения дна, составляет t , то с = ½ ( г sin θ ) t ²

t = √ (2s / g sin θ )

Но sin θ = ч / с или с = ч / sin θ

Итак, t = (1 / sin θ ) √ (2 h / g )

(iii) Скорость тела на дне

v = g (sin θ ) t

= √2 гх

Относительная скорость объекта A относительно объекта B определяется как

V _AB = V _A – V _B

Здесь, V 91 346 91 347 В называется ссылкой скорость объекта.

Изменение массы: – В соответствии с формулой изменения массы Эйнштейна релятивистская масса тела определяется как,

м = м ₀ / √ (1- v ²/ c ²)

Здесь m ₀ – масса покоя тела, v – скорость тела и c – скорость света.

Движение снаряда в плоскости: – Если частица с начальной скоростью u проецируется под углом θ (угол проекции) с осью x , то

Время полета, T = (2 u sin α ) / g

Диапазон по горизонтали, R = u ² sin2 α / g

Максимальная высота, H = u ² sin ² α /2 g

Уравнение траектории, y = x tan α – ( gx ²/2 u ² cos ² α )

(a) При падении: – Период времени, t = √ (2h / g) и скорость, v = √ (2gh

(b) При подбрасывании: – Период времени, t = u / g и высота, h = u ² / 2g

Состояние равновесия: –

(а)

(b) | F ₁ + F ₂ | ≥ | F ₃ | ≥ | F ₁ -F ₂ |

Возможно, вам понравится:

CBSE класс 7 по математике | CBSE, класс 7, естественные науки | CBSE класс 11 по химии

2: Кинематика – Физика LibreTexts

Последнее обновление
Сохранить как PDF

Авторы и авторство

Объекты находятся в движении, куда бы мы ни посмотрели.Все, от игры в теннис до полета космического зонда над планетой Нептун, связано с движением. Когда вы отдыхаете, ваше сердце перемещает кровь по венам. И даже в неодушевленных предметах есть непрерывное движение в колебаниях атомов и молекул. Вопросы о движении интересны сами по себе: Сколько времени потребуется космическому зонду, чтобы добраться до Марса? Куда приземлится футбол, если его бросить под определенным углом? Но понимание движения также является ключом к пониманию других концепций физики.Например, понимание ускорения имеет решающее значение для изучения силы. Кинематика – это раздел классической механики, который описывает движение точек, тел и систем тел без учета масс этих объектов и сил, которые могли вызвать движение.

2.0: прелюдия к одномерной кинематике
Наше формальное изучение физики начинается с кинематики, которая определяется как изучение движения без учета его причин.В одномерной кинематике и двумерной кинематике мы будем изучать только движение футбольного мяча, например, не беспокоясь о том, какие силы вызывают или изменяют его движение. Подобные рассуждения рассматриваются в других главах. В этой главе мы исследуем простейший тип движения, а именно движение по прямой или одномерное движение.
2.1: Смещение
Кинематика – это исследование движения без учета его причин. В этой главе оно ограничивается движением по прямой линии, называемым одномерным движением.Смещение – это изменение положения объекта.
2.2: Векторы, скаляры и системы координат
Вектор – это любая величина, имеющая величину и направление. Скаляр – это любая величина, которая имеет величину, но не имеет направления. Смещение и скорость – это векторы, а расстояние и скорость – скаляры. В одномерном движении направление указывается знаком плюс или минус для обозначения влево или вправо, вверх или вниз и т.п.
2.3: Время, скорость и скорость
Движение – это нечто большее, чем расстояние и смещение. Такие вопросы, как: «Сколько времени занимает пешая гонка?» и “Какая была скорость бегуна?” невозможно ответить без понимания других концепций. В этом разделе мы добавляем определения времени, скорости и скорости, чтобы расширить наше описание движения.
2.4: Ускорение
Ускорение – это скорость, с которой изменяется скорость. В символах среднее ускорение a = Δv / Δt.Единица измерения ускорения в системе СИ – м / с². Ускорение – это вектор, поэтому он имеет как величину, так и направление. Ускорение может быть вызвано изменением величины или направления скорости. Мгновенное ускорение a – это ускорение в определенный момент времени. Замедление – это ускорение с направлением, противоположным направлению скорости.
2.5: Уравнения движения для постоянного ускорения в одном измерении
Мы могли бы знать, что чем больше ускорение, скажем, у автомобиля, удаляющегося от знака «стоп», тем больше смещение за данный момент времени.Но мы не разработали конкретное уравнение, связывающее ускорение и смещение. В этом разделе мы разработаем некоторые удобные уравнения кинематических отношений, начиная с уже рассмотренных определений перемещения, скорости и ускорения.
2.6: Основы решения проблем для одномерной кинематики
Способность применять общие физические принципы, обычно представленные уравнениями, к конкретным ситуациям – очень мощная форма знания.Это намного эффективнее, чем запоминание списка фактов. Аналитические навыки и способность решать проблемы могут быть применены к новым ситуациям, тогда как список фактов не может быть достаточно длинным, чтобы содержать все возможные обстоятельства. Такие аналитические навыки полезны как для решения задач в этом тексте, так и для применения физики.
2.7: Падающие объекты
Объект в свободном падении испытывает постоянное ускорение, если сопротивление воздуха незначительно. На Земле все свободно падающие объекты имеют ускорение силы тяжести g, которое в среднем составляет g = 9.80 м / с2. Следует ли принимать ускорение a как + g или -g, определяется вашим выбором системы координат. Поскольку ускорение является постоянным, приведенные выше кинематические уравнения могут быть применены с соответствующими + g или -g, замененными на a. Для объектов, падающих в свободном падении, обычно считается положительным.
2.8: Графический анализ одномерного движения
Графики движения могут использоваться для анализа движения. Графические решения дают идентичные решения математическим методам вывода уравнений движения.Наклон графика зависимости смещения x от времени t – это скорость v. Наклон графика графика зависимости скорости v от времени t – это ускорение a. Среднюю скорость, мгновенную скорость и ускорение можно получить, анализируя графики.
2.E: Кинематика (упражнения)

Эскиз: кинематика классической частицы массы \ (m \), положения \ (r \), скорости \ (v \), ускорение \ (а \). (Общественное достояние; Машен).

Авторы и авторство

Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрикс (Государственный университет Нью-Йорка, колледж в Освего) с участвующими авторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет).Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

Уравнения движения с постоянной скоростью

Движение с постоянной скоростью , также известное как равномерное прямолинейное движение (urm) , это движение с постоянной скоростью , т. Е. Траектория является прямой, а скорость равна постоянный. В этом разделе мы собираемся объяснить:

Определение движения с постоянной скоростью

Хотя нахождение прямолинейного равномерного движения или движения с постоянной скоростью в природе встречается довольно редко, его легче всего изучать, и оно будет полезно при изучении других, более сложных движений.Равномерное прямолинейное движение имеет следующие свойства:

Ускорение равно нулю ( a = 0 ), потому что ни величина, ни направление не меняются
С другой стороны, начальная, средняя и мгновенная скорости всегда имеют одинаковые значения

Тело имеет движение с постоянной скоростью или равномерное прямолинейное движение , когда его траектория представляет собой прямую линию , а его скорость постоянна .Это означает, что он преодолевает равные расстояния за равное время .

Уравнения движения с постоянной скоростью

Прямолинейное и равномерное движение

Равное время тратится на путешествие на равные расстояния. Средняя скорость постоянна и равна величине скорости.

уравнений движения с постоянной скоростью :

Где:

x , x ₀ : Позиция тела в данный момент времени ( x ) и в начальный момент времени ( x ₀ ).Единицей измерения в Международной системе (S.I.) является метр (м)
v , v ₀ : Скорость тела в данный момент времени ( v ) и в начальный момент времени ( v ₀ ). Его единица измерения в Международной системе (S.I.) – метр в секунду (м / с)
a : Разгон кузова. Единицей измерения в Международной системе (S.I.) является метр на секунду в квадрате (м / с ²)

Вывести уравнений равномерного прямолинейного движения u.среднеквадратичное значение следует учитывать, что:

Средняя скорость совпадает с мгновенной скоростью
Нет разгона

С этими ограничениями получаем:

vavg = vvavg = ΔxΔt = x-x0t-t0 = ⏟t0 = 0x-x0t → x-x0 = v⋅t → x = x0 + v⋅t

Пример

Два мраморных игрока смотрят друг на друга со своими шариками в руках.

Раздел “Кинематика” теоретической механики

Содержание

Кинематика (скорость, ускорение, путь).

Траектория, радиус-вектор, закон движения тела

Перемещение и путь

Скорость и ускорение

Закон равноускоренного движения

Пример решения задачи

Теоретическая механика и кинематика

Теоретическая механика

Основные понятия теоретической механики

Раздел кинематика

Основы кинематики (8-й класс)

Лекции по курсу “Теория механизмов и машин”

В «МЭШ» собраны лучшие приложения по физике ко дню рождения Льва Ландау

Формула кинематических уравнений

Формула кинематических законов. Кинематика Основные понятия, законы и формулы. Свободное падение по вертикали

Сложность в описании механизма

Типы движения в кинематике

Основные понятия кинематики – материальная точка

Формулы кинематики

Формулы кинематики в двухмерном пространстве

Примеры кинематических задач

Что является точкой отсчета

Система отсчета и ее значение в кинематике

Основные понятия кинематики – путь и траектория

Основные формулы для физики, динамики, кинематики, статики

Основные формулы молекулярной физики и термодинамики

Основные формулы для физики: электричество

Путь и движение

средняя скорость

Равно-заданный прямой ход

Свободное падение по вертикали

Горизонтальный бросок

Бросок под углом к ​​горизонту (от земли к земле)

Сложение скоростей

Равномерное движение по кругу

Нашли ошибку?

Как решать кинематические задачи: часть II

уравнений движения | Блестящая вики по математике и науке

Изображение предоставлено Wikimedia Commons.

по кинематике | askIITians

2: Кинематика – Физика LibreTexts

Авторы и авторство

Уравнения движения с постоянной скоростью

Определение движения с постоянной скоростью

Уравнения движения с постоянной скоростью

Оставить комментарий Отменить ответ

Бросок под углом к горизонту (от земли к земле)