Кинематика основные понятия и формулы: Кинематика – основные определения и формулы

Повторение: основные понятия и уравнения кинематики

1. Повторение: основные понятия и уравнения кинематики.

Цель: повторить и
систематизировать основные
понятия и формулы нескольких
видов движения для решения
задач.

2. Ваша цель:

• Я буду знать……
• Я буду уметь…..
• Я смогу: назвать, применить и
объяснить…..
сравнить…… по следующим
критериям…..
успешно выполнить тест….
объяснить смысл терминов…..
правильно записать слова…..
правильно ответить на ключевой
вопрос….
Буду обращать внимание на знание следующих вопросов:
1. Что изучает механика? Её основная задача.
2. Кинематика. Основные понятия и формулы:
A.
B.
C.
D.
E.
F.
G.
тело отсчета, система координат, система отсчета
материальная точка , абсолютно твердое тело
Поступательное, вращательное движение
Равномерное, равноускоренное, равнозамедленное движение;
траектория, путь, перемещение
скорость
ускорение
3. Классификация механических движений.
4. Графики движений.

4. Что изучает механика? Её основная задача.

• Раздел физики – механика занимается
изучением механического движения тел.
Механическим движением называется
изменение
положения
тела
(в
пространстве) относительно других тел с
течением времени.
• Основная задача механики заключается в
определении положения тела в любой
момент времени.

5. Кинематика. Основные понятия:

• Механика состоит из двух основных
разделов: кинематики и динамики.
Раздел, который не рассматривает причин
возникновения механического движения и
описывает только его геометрические
свойства называется кинематикой. В
кинематике используются такие понятия
как траектория, путь и перемещение,
скорость и ускорение.

6. Относительность движения. Система отсчета.

ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ. СИСТЕМА ОТСЧЕТА.
• Чтобы описать механическое движение тела (точки),
нужно знать его координаты в любой момент времени.
Для определения координат следует выбрать тело
отсчета и связать с ним систему координат. Часто
телом отсчета служит Земля, с которой связывается
прямоугольная декартова система координат. Для
определения положения точки в любой момент времени
необходимо также задать начало отсчета времени.
• Система координат, тело отсчета, с которым она связана,
и прибор для измерения времени образуют систему
отсчета, относительно которой рассматривается
движение тела

7. Материальная точка и абсолютно твердое тело.

МАТЕРИАЛЬНАЯ ТОЧКА И АБСОЛЮТНО
ТВЕРДОЕ ТЕЛО.
• Тело, размерами которого в данных условиях
движения
можно
пренебречь,
называют
материальной точкой. Тело можно рассматривать
как материальную точку, если его размеры малы по
сравнению с расстоянием, которое оно проходит, или
по сравнению с расстояниями от него до других тел.
• Абсолютно твердым телом называется тело,
расстояние между любыми двумя точками которого
остается постоянным при его движении. Эти модели
позволяют исключить деформацию тел при
движении.

8. Поступательное и вращательное движение.

• Поступательным называется движение, при котором отрезок,
соединяющий любые две точки твердого тела, перемещается при
движении параллельно самому себе. Из этого следует, что все
точки тела при поступательном движении движутся одинаково,
т.е. с одинаковыми скоростями и ускорениями.
• Вращательным называется движение, при котором все точки
абсолютно твёрдого тела движутся по окружностям, центры
которых лежат на одной прямой, называемой осью вращения,
причем эти окружности лежат в плоскостях, перпендикулярных
оси вращения. Пользуясь законом независимости движений,
сложное движение твёрдого тела можно рассматривать как
сумму поступательного и вращательных движений.

9. Поступательное движение

Выберите верное утверждение о поступательном
движении:
1. Поступательное движение – это движение тела, при
котором отрезок прямой, соединяющий две любые точки,
принадлежащие этому телу, перемещается, оставаясь
параллельным самому себе.
2. При поступательном движении все точки твердого тела
движутся одинаково, описывают одинаковые траектории
и в каждый момент времени имеют одинаковые скорости
и ускорения.
3. Движение парашютиста вниз
поступательного движения.
является
4. Луна вокруг Земли движется поступательно.
примером

10. Траектория, путь, перемещение

ТРАЕКТОРИЯ, ПУТЬ, ПЕРЕМЕЩЕНИЕ
• Траекторией движения называется линия, вдоль которой
движется тело. Длина траектории называется пройденным
путем. Путь – скалярная физическая величина, сумма длин
отрезков траектории, может быть только положительным.
• Перемещением называется вектор, соединяющий начальную
и конечную точки траектории.
ПРИМЕРЫ:
пройденный путь –
вектор перемещения – S
a и b – начальная и конечная точки пути
при криволинейном движении тела.
S
С
D
Рис. 1
N
E
S
Рис. 2
ACDENB – траектория
вектор перемещения – S

11. Скорость

• Характер движения тела определяется его скоростью. Если
скорость постоянна, то движение называют равномерным
и уравнение движения выглядит следующим образом:
[м/с2]
s
t
x y
• Модуль скорости равен:
• Если скорость увеличивается на одинаковую величину за
одинаковые
промежутки времени, то движение
называется равноускоренным.
• Если скорость уменьшается на одинаковую величину за
одинаковые
промежутки времени, то движение
называется равнозамедленным. Такие виды движений
называют равнопеременным движением.
2
2

12. Ускорение

• Величина изменения скорости за единицу времени есть
ускорение:
a
t
2 1
t 2 t1
• В процессе движения скорость может измениться,
отсутствие изменения скорости приводит к отсутствию
ускорения.
• Неподвижное тело, либо тело движущее с постоянной
скоростью обладает нулевым ускорением.
• Ускорение определяет на сколько скорость увеличилась
при
равноускоренном
движении,
и
насколько
уменьшилась при равнозамедленном движении за 1
секунду.

13. Например:

• Велосипедист движется с ускорением
а=5м/с2, тогда через каждую секунду его
скорость будет принимать значения:
a * t 5 *1 5 м / с
a * t 5 * 2 10 м / с
a * t 5 * 3 15 м / с

14. Классификация механических движений

Прямолинейное
неравномерное
равномерное
Равно
Равно
ускоренное
замедленное
Криволинейное
(движение по окружности)
равномерное
неравномерное

15. Основные уравнения.

СКОРОСТЬ
РАВНОМЕРНОЕ
РАВНОЗАМЕДЛЕННОЕ
РАВНОУСКОРЕННОЕ
ДВИЖЕНИЕ
s
t
const
УСКОРЕНИЕ
a 0
0 at a 0
t
2 02 2aS
0 at
0
a
2
2
0 2aS
t
ПРОЙДЕННЫЙ
ПУТЬ
КООРДИНАТЫ
х х0 t
S t
2
at 2
at
S 0t
х х0 0t
2
2
S 0t
2
at
2
at 2
х х0 0t
2

16. Равномерное движение График зависимости х от t

• Уравнение прямой в координатах х, t в общем случае имеет
вид:
у=b+kt
• b – это отрезок на оси OX, отсекаемой прямой;
• k – тангенс угла наклона прямой к оси Оt
X(м)
Пример:
По графику можно
записать уравнение
движения тела.
5
1
2
3
t (c)
-5
x0

17. Равномерное движение График зависимости S от t

Пример
По
графику
можно
определить:
1. Скорость движения,
которая определяется
тангенсом угла наклона
прямой к оси Оt –
S (м)
12
9
6
S
3ì / ñ
t
3
1 2 3 4
t (c)
2. Путь, пройденный телом за определенный интервал времени.
Например путь, пройденный велосипедистом за интервал времени от
t1=1с до t2=4с равен S=S2-S1=12-3=9м

18. График зависимости от t

Ра в н о м е р н о е д в и ж е н и е
График зависимости от t
(м)
const
S1 1 *t1
a 0
S2 2 *t2
1
t2 t1
2
t (c)
Пример:
По графику можно определить проекцию перемещения S1, S2. В 1м случае
проекция на ось положительна, во втором отрицательна. В обоих случаях
проекция перемещения численно равна площади прямоугольников.

19. Равноускоренное движение Скорость

0 at
• График при a 0
• График при a 0
(м)
(м)
0
0
0
0
t (c)
t (c)

20.

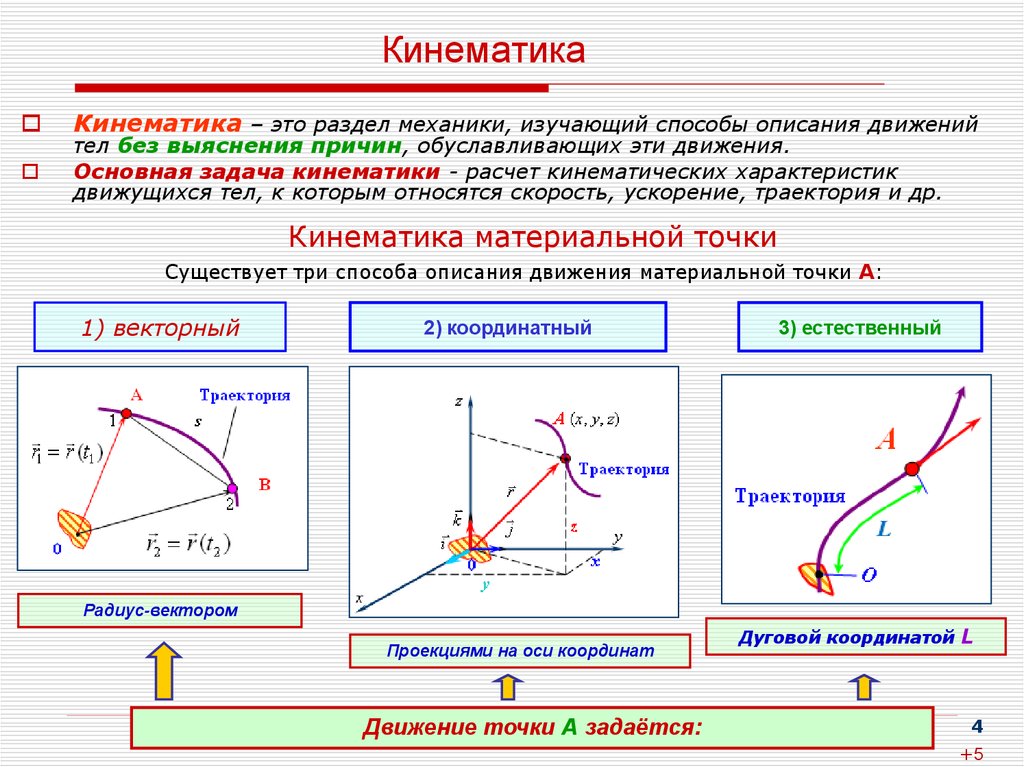Равноускоренное движение УскорениеРавноускоренное движение
0
Ускорение a
• График при a 0
t
• График при a 0
а (м/с2)
а (м/с2)
0
0
t (c)
t (c)

21. Равноускоренное движение Перемещение

Равноускоренное движение
2
at
Перемещение S 0t 2
• График при a 0
S (м)
• График при a 0
S (м)
0
0
t (c)
t (c)

22. Равноускоренное движение Координата

Равноускоренное движение
at
Координата х х t 2
2
• График при a 0
0
0
• График при a 0
х (м)
х(м)
х0
х0
0
0
t (c)
t (c)

23. Задание №1 (уровни)

1. Двигаясь по шоссе, велосипедист проехал 900м со
скоростью 15 м/с, а затем по плохой дороге 400м со
скорость10м/с. С какой средней скоростью он проехал
весь путь?
2. На горизонтальном участке пути автомобиль ехал со
скоростью 72 км/ч в течении 10 мин, а затем проехал
подъем со скоростью 36 км/ч за 20 мин. Чему равна
средняя скорость на всем пути?
3. Первую половину пути автомобиль прошел со скоростью
20 км/ч, а вторую – 30 км/ч. Найти среднюю скорость на
всем участке.

24. Задание №2 (уровни)

1. Через 25 с после начала движения спидометр
автомобиля показал скорость движения 36 км/с.
С каким ускорением двигался автомобиль?
2. При равнозамедленном движении автомобиля в
течении 5 с его скорость уменьшилась с 15 до 10
м/с. Чему равен модуль ускорения?
3. Скорость поезда, движущегося на подъеме с
ускорением 0,1 м/с 2 , уменьшается от 54 до 36
км/ч. Определите время подъема.

25. Задание №3

1. Расстояние между пунктами А и В по прямой
линии 5 км. Человек проходит это расстояние
туда и обратно за 2 ч. Чему будут равны путь и
перемещение человека за 1 ч, за 2ч?
2. Ускорение автомобиля, начавшего движение 0,5
м/с2 . Какой путь пройдет автомобиль за 4 с,
двигаясь с этим ускорением?

26. Задание №4

1. Автомобиль берет подъем длиной 1,95 км в
течении 5 мин, и к концу подъема его скорость
равна 18 км/ч. Принимая, что ускорение с
которым движется автомобиль , постоянно,
определить его значение.
2. Автомобиль тормозит с ускорением, которое во
все время можно считать неизменным и равным
-4м/сек2. Какой путь пройдет он за это
времяторможения, если начнет тормозить при
скорости 16 м/с?

27. Задание №5

• Запишите уравнение координаты тела
X(м)
6
1
2
3
t (c)
-6

28. Задание №6

S (м)
По графику
определите:
1. Вид движения
2. Скорость
движения
16
12
8
4
1 2 3 4
t (c)
3. Путь, пройденный
велосипедистом за
интервал
времени
от t1=1с до t 2=3с
(м/с)
Задание №7
5
4
3
2
1
1 2 3 4 5 6
t (c)
Определите проекцию перемещения S1
за 6 с.
(м/с)
Задание №8
5
4
3
2
1
1 2 3 4 5 6
t (c)
Определите проекцию перемещения
(путь) S2, пройденный телом за 6 с.

31. Задание №9.

(м/с)
1. Какой из графиков соответствует
равномерному движению?
0
2. Какой из графиков соответствует
равнопеременному движению,
при котором вектор ускорения
направлен
противоположно
вектору скорости?
0
3. Какой из графиков соответствует
t (c) равноускоренному движению,
при
котором
направление
вектора ускорения совпадает с
направлением
вектора
скорости?

32. Задание №10. Прочитайте график изображенный на рисунке

(м/с)
1. Какой вид
движения?
2. Как
изменяется
скорость в
течении
каждой
секунды?
3
2
1
0
1
2
3
4
5
t (cек) 3. Чему равно
ускорение?

Тема 1.7. Основные понятия кинематики.

Кинематика как наука о механическом движении , изучаемом с точки зрения геометрии. Покой и движение; относительность этих понятий. Основные понятия кинематики: траектория, перемещение, время, скорость и ускорение.

Тема 1.8.Кинематика точки.

Способы задания движения точки : естественный и координатный. Уравнение движения точки по заданной криволинейной траектории. Средняя скорость и скорость в данный момент времени. Ускорение нормальное ( центростремительное ) , касательное

( тангенциальное) и полное. Виды движения в зависимости от ускорения.

Частные случаи поступательного движения точки : равномерное и равнопеременное.

Равномерное движение точки : уравнение движения, основные формулы. Равноперемен-ное движение точки: уравнение движения, основные и вспомогательные формулы. Кине –

матические графики и связь между ними.

Тема 1.9. Простейшие движения твердого тела.

Поступательное движение твердого тела и его свойства. Вращательное движение твердого тела вокруг неподвижной оси. Угловое перемещение. Уравнение вращательного движения. Средняя угловая скорость и угловая скорость в данный момент времени. Частота вращения. Единицы угловой скорости и частоты вращения, связь между ними.

Угловое ускорение.

Равномерное вращение: уравнение движения, основные формулы. Равнопеременное вращение: уравнение движения, основные и вспомогательные формулы .

Линейные скорости и ускорения точек вращающегося тела. Выражение линейной (окружной ) скорости, касательного , нормального и полного ускорений точек вращающе-гося тела через его угловую скорость , угловое ускорение и расстояние точки до оси вращения.

Тема. 1.10. Сложное движение точки.

Переносное, относительное и абсолютное движение точки. Теорема сложения скоростей.

Тема 1.11. Сложное движение твердого тела.

Плоскопараллельное движение тела. Разложение плоскопараллельного движения на поступательное и вращательное. Определение абсолютной скорости любой точки тела при плоскопараллельном движении по теореме сложения скоростей.

Мгновенный центр скоростей ( МЦС) .

Основные способы определения мгновенного центра скоростей. Определение абсолютной скорости любой точки тела с помощью МЦС.

Сложение вращений вокруг параллельных и пересекающихся осей.

Динамика.

Тема 1.12. Основные понятия и аксиомы динамики.

Предмет динамики; понятие о двух основных задачах динамики. Первая аксиома

динамики – принцип инерции.

Вторая аксиома – основной закон динамики точки. Системы единиц физических величин. Масса материальной точки и ее единицы. Зависимость между массой точки и силой тяжести.

Третья аксиома динамики – закон независимости действия сил. Четвертая аксиома –

Закон равенства действия и противодействия.

Тема 1.13.Движение материальной точки.

Метод кинетостатики. Понятие о свободной и несвободной точке. Сила инерции.

Силы инерции при прямолинейном и криволинейном движении материальной точки.

Принцип Даламбера; метод кинетостатики.

Тема. 1.14.Работа и мощность.

Работа постоянной силы при прямолинейном движении. Единицы работы. Работа равнодействующей системы сил. Понятие о работе переменной силы. Работа силы тяжести.

Мощность, единицы мощности. Понятие о механическом КПД ( коэффициент полезного действия ).

Работа и мощность при вращательном движении. Окружная сила , вращающий момент. Зависимость вращающего момента от угловой скорости ( частоты вращения) и

величины передаваемой мощности.

Работа при качении тела по негладкой поверхности ; коэффициент трения качения, его размерность.

Тема. 1.15. Общие теоремы динамики.

Импульс силы, количество движения точки, Теорема об изменении количества движения точки.

Кинетическая энергия точки. Теорема об изменении кинетической энергии точки.

Система материальных точек. Внешние и внутренние силы системы.

Основное уравнение динамики для вращательного движения тела.

Момент инерции

тела. Формулы для определения моментов инерции тел простейшей формы (без вывода).

Кинетическая энергия тела при поступательном, вращательном и плоскопараллель-

мом движениях. Теорема кинетической энергии для системы.

Примечания по кинематике | JEE Главная | JEE Advanced

Кинематика Примечания | JEE Главная | JEE Расширенный

Вот примечания по кинематике ( сводка понятий ), которые вы должны использовать для своей доработки. И, если вы только начинаете изучать эту главу в 11-м классе, она даст вам хорошее представление о том, чего ожидать и на каких концепциях следует сосредоточиться.

Итак, приступим!

Примечания по концепциям кинематики были разделены на четыре группы, как указано ниже. (Обратите внимание, что для каждого раздела есть аудиозапись заметок, сделанная Викасом Сэром (выпускником ИИТ Дели), которую вы не должны пропустить)

1. Одномерное движение (понятия)

2 Векторы (понятия)

3 Двухмерное движение (понятия)

4 Двухмерное движение | Снаряды | Круговое движение | Относительная скорость (понятия)

Примечания по кинематике | Одномерное движение (концепции)

Script

Добро пожаловать в этот подкаст о кинематике одномерного движения, где мы рассмотрим ключевые концепции движения частицы или объекта в одном измерении или направлении.

Здесь мы вернемся к определению перемещения, мгновенной скорости и мгновенной скорости, средней скорости и средней скорости, мгновенного и среднего ускорения.

Далее мы кратко поговорим об одномерном движении с постоянным ускорением, т.е. сценарии, в котором частица движется с постоянным ускорением

И закончим кратким обзором сценариев, где ускорение непостоянно и поговорим о подходе к нахождению желаемое неизвестное.

Таким образом, начиная со смещения, перемещение определяется как конечное положение минус начальное положение и является векторной величиной. Таким образом, в случае одномерного движения смещение может быть положительным или отрицательным в зависимости от того, где находится конечное положение по отношению к начальному положению, и обратите внимание, что смещение не зависит от выбора начала координат. Если вы не поняли последнее утверждение, подумайте над этим, я уверен, что вы его поймете.

Теперь, прежде чем двигаться дальше, обратите внимание, что расстояние, пройденное частицей при переходе из начального положения в конечное, может совпадать или не совпадать со смещением. Обратите внимание, что они не будут одинаковыми, если частица поменяет направление в какой-то момент времени при переходе из начального положения в конечное положение 9.0007

Переходим к средней скорости и средней скорости. Средняя скорость, скалярная величина, определяется как пройденное расстояние, деленное на время, затраченное на переход из начального положения в конечное. Средняя скорость, векторная величина с величиной и направлением, с другой стороны, определяется как смещение, т.е. конечное положение минус начальное положение, деленное на продолжительность времени. И по причинам, упомянутым ранее, величина двух может быть или не быть одинаковой в зависимости от того, совпадает ли пройденное расстояние со смещением. Другими словами, средняя скорость будет такой же, как и средняя скорость, по величине, если частица не изменит свое направление на противоположное. Итак, можете ли вы сказать, какова будет средняя скорость теннисного мяча, брошенного вертикально вверх со скоростью v, между стартом и приземлением, т. е. когда он вернется обратно на землю, и будет ли она такой же, как средняя скорость? Если сомневаетесь, пингуйте нас.

Итак, теперь давайте поговорим о мгновенной скорости и мгновенной скорости в некоторый момент времени «t». Мгновенная скорость, скалярная величина, определяется как расстояние, пройденное за очень малое или дифференциальное время dt, деленное на dt, а мгновенная скорость, векторная величина, определяется как перемещение за очень малое или дифференциальное время dt, деленное на dt. И насколько мала «dt», теоретически она должна быть достаточно мала, чтобы скорость или скорость не менялись значительно в течение этого времени. И, как вы можете догадаться, дифференциальное расстояние, пройденное частицей за такое короткое время, будет равно по величине дифференциальному смещению, и, следовательно, мгновенная скорость и мгновенная скорость одинаковы по модулю 9.0007

И прежде чем мы перейдем к краткому обсуждению ускорения, обратите внимание, что вы должны освоиться с графиком зависимости положения от времени, где наклон кривой зависимости положения от времени, представляющий движение частицы, дает нам мгновенную скорость.

Теперь перейдем к среднему и мгновенному ускорению.

Таким образом, среднее ускорение, векторная величина, определяется как конечная скорость минус начальная скорость, деленная на продолжительность времени. Это так просто и понятно. А теперь давайте проверим наше понимание. Итак, для частицы, движущейся по круговой траектории с постоянной скоростью, каково будет ее среднее ускорение за один оборот. Ну, как вы уже догадались, это будет ноль.

Итак, как мы определяем мгновенное ускорение в некоторый момент времени t, то есть оно определяется как изменение скорости, т. время.

Теперь, прежде чем мы перейдем к кинематическим уравнениям для частицы, движущейся с постоянным ускорением, важно отметить, что график зависимости скорости от времени весьма удобен для описания движения частицы, и поэтому вы должны освоиться с ним. . Обратите внимание, что наклон графика «v» и «t» в некоторый момент времени «t» дает нам мгновенное ускорение в это время, а площадь под кривой дает нам смещение, если вы присвоите отрицательный знак площади с отрицательной скоростью. и это дает нам пройденное расстояние, если взять сумму абсолютных значений площадей под кривой

Кстати, обратите внимание, что на графике зависимости ускорения от времени t площадь под кривой даст нам изменение скорости, вспомним, что a = dv/dt или dv = a dt, поэтому, если бы мы суммировали или, скорее, интегрировали dt в течение интересующей нас продолжительности мы получим дельту v или изменение скорости.

При этом поговорим о кинематических уравнениях движения частицы, движущейся с постоянным ускорением.

Я надеюсь, что вы сможете сослаться на любой стандартный текст, чтобы понять вывод этих кинематических уравнений для движения с постоянным ускорением, где уравнения будут получены либо графически с использованием графика «v» против «t», либо алгебраически путем интегрирования dv = a dt и dx = v dt. 92

s = 1/2(v+u) t

Теперь важно отметить, что существует только 2 независимых уравнения, это означает, что вы можете вывести остальные 3 из любых двух из этих уравнений. Более того, вы можете определить только две неизвестные переменные. Еще раз вы можете определить только два неизвестных из этих уравнений.

Итак, сколько переменных. Ну, их 5: начальная скорость u, конечная скорость v, смещение s, которое представляет собой просто конечное положение минус начальное положение, ускорение «а» и продолжительность времени «t» 9+ 2 ас.

Итак, что еще важно, пока вы учитесь применять эти уравнения. Что ж, выберите начало координат и координатные оси и придерживайтесь их. Например, для частицы, брошенной вертикально вверх с высоты, вы можете выбрать положительную ось Y, чтобы она была направлена ​​вверх или вниз, и вы можете выбрать свое начало на земле или в точке запуска, это не имеет большого значения. , но как только вы сделаете выбор, обязательно внимательно запишите знаки начальной скорости u, ускорения a и внимательно запишите выражение для перемещения. После этого остальное будет простой математикой.

Надеюсь, это помогло, но ключевым моментом будет регулярное использование разных типов вопросов. Поэтому убедитесь, что вы охватили все типы вопросов и связанные с ними практические вопросы на платформе AceJEE.

С наилучшими пожеланиями

Примечания по кинематике | Векторы (концепты)

Скрипт

Добро пожаловать. В этом подкасте мы кратко поговорим о векторах, физических величинах с величиной и направлением, которые подчиняются законам векторной алгебры.

Обратите внимание, что в этом подкасте векторы рассматриваются с точки зрения физики, что поможет нам применить физические концепции к двух- или трехмерным ситуациям.

Итак, для начала, что мы подразумеваем под законами векторной алгебры. Итак, под законами векторной алгебры мы подразумеваем законы, касающиеся сложения векторов, их умножения на скаляр и умножения одного вектора на другой.

Хорошо, теперь, прежде чем мы погрузимся в векторную алгебру, давайте быстро поговорим об единичной векторной записи вектора. Таким образом, мы можем выразить любой трехмерный вектор через единичные векторы i, j и k вдоль трех перпендикулярных декартовых координатных осей x, y и z. ​​2, и если вы хотите узнать угол, который этот вектор составляет, скажем, с осью x, он является обратным компоненту вектора вдоль эта ось, т. е. Ax, деленная на длину или величину вектора A.

Хорошо, а теперь, когда мы использовали единичный вектор фразы, что это такое. Well — это просто вектор величины 1 в интересующем направлении. Итак, каков будет единичный вектор вдоль направления вектора А. Ну, это будет вектор А, деленный на его величину.

Теперь давайте поговорим о векторной алгебре и обратимся к сделанному в начале утверждению о том, что вектор — это физическая величина с величиной и направлением, подчиняющаяся законам векторной алгебры. Итак, можете ли вы представить себе физическую величину, которая имеет величину и направление, но НЕ является вектором. Что ж, угловое смещение — одна из таких величин. Таким образом, угловое смещение имеет величину, оно имеет направление, то есть в 2D оно может быть по часовой стрелке или против часовой стрелки, но все же это не вектор, потому что оно не следует коммутативному закону сложения векторов. т. е. вектор A + вектор B не равен вектору B + вектору A в случае углового смещения. Не убежден. Ну возьмите толстую книгу и поверните ее на 90 градусов по одному из его краев, а затем поверните его на 90 градусов по одному из других краев. Запишите конечное положение книги. Теперь верните книгу в исходное положение и измените порядок вращения вокруг двух краев, и вы увидите, что конечное положение книги изменилось.

Хорошо. прежде чем мы двинемся дальше и поговорим о двух разных способах умножения векторов, т. е. о скалярном произведении и векторном произведении, обратите внимание, что, хотя угловое перемещение не является вектором, угловая скорость и угловое ускорение являются таковыми.

Итак, давайте быстро поговорим о скалярном произведении и векторном произведении.

Скалярное произведение, как следует из названия, дает скалярный результат при умножении двух векторов. И мы можем записать результат скалярного произведения между двумя векторами, скажем, A и B, двумя способами. AB \cos\theta, где A и B — их величины, а theta — угол между двумя векторами, или мы можем выразить скалярное произведение через их компоненты x, y и z как AxBx + AyBy + AzBz. Эти два определения вместе позволяют нам алгебраически вывести угол между двумя векторами, обозначения единичных векторов которых известны. Теперь интересным вариантом использования с точки зрения экзамена является нахождение угла между двумя векторами, для которых не задано обозначение единичного вектора, а задано некоторое отношение между их величинами. Например, при условии, что вектор P плюс вектор Q равен вектору R и при условии, что величина P и результирующий вектор R равны. Чему равен угол между векторами (2P+Q) и Q. В таких случаях используют отношение квадрата величины вектора A, равное скалярному произведению A на самого себя, т.е. A.A

Теперь давайте быстро поговорим о перекрестном или векторном произведении двух векторов, результатом которого является вектор. И снова мы можем выразить результат A x B как AB sin theta n cap, где n cap — это единичный вектор, перпендикулярный плоскости A и B, а его направление задается правилом большого пальца правой руки. Его также можно выразить через компоненты векторов A и B, как указано в примечаниях.

На этом краткий обзор векторов заканчивается. Еще раз я бы порекомендовал вам пройтись по разным типам вопросов по векторам для лучшего понимания и подготовки к экзамену.

До свидания и берегите себя

Примечания по кинематике | Двухмерное движение (концепции)

Script

В этом подкасте мы расширим обсуждение перемещения, скорости и ускорения в одном измерении до двух измерений. И в качестве предупреждения вы можете ссылаться на заметки в блоге, так как вам помогут диаграммы или визуальные представления.

Но прежде чем мы начнем обсуждение смещения, которое представляет собой векторную величину, определяемую как конечное положение минус начальное положение, давайте быстро поговорим о векторе положения в 2 или 3 измерениях.

Итак, вектор положения — это вектор от начала координат до положения частицы в момент времени t, и допустим, что координаты этой точки равны x, y и z. Таким образом, вектор положения в записи единичного вектора будет x i + y j + z k,

. Теперь вектор смещения — это просто вектор от начального положения до конечного положения. Таким образом, с точки зрения векторов положения мы можем записать это как r_f минус r_i, где r_f — вектор положения конечного положения, а r_i — вектор положения начального положения.

Как для средней, так и для мгновенной скорости. Средняя скорость определяется как чистое смещение, т. е. конечный вектор положения минус начальный вектор положения, разделенный на продолжительность времени

. Мгновенная скорость определяется просто как dr/dt или скорость изменения вектора положения.

Обратите внимание, что это может показаться сложным, но если вы потратите некоторое время на это, это будет довольно прямолинейно, и если вы боретесь с векторами, убедитесь, что вы достаточно комфортно себя чувствуете с векторами, особенно с графическим представлением суммы или разности двух векторов. . 92 для каждого отдельного направления и определить координаты положения в момент времени t = 2 секунды.

Итак, мы закончим обсуждение здесь и обсудим движение снаряда в следующем подкасте. И если у вас есть какие-либо вопросы, не стесняйтесь пинговать нас.

Двумерное движение | Движение снаряда | Круговое движение | Относительное движение (концептуальные заметки)

Script

Добро пожаловать на подкаст о движении снарядов и относительной скорости, где мы рассмотрим основы и ключевые концепции. Чтобы лучше понять эти темы, обратитесь к блогам о движении снарядов и относительном движении, ссылка на которые указана в описании подкаста 9.0007

Итак, начнем с движения снаряда, точнее наклонного движения снаряда, когда снаряд брошен под углом к ​​горизонту.

В таком сценарии частица движется по горизонтали или, скажем, по оси x, а также по вертикали или по оси y. В горизонтальном направлении нет силы или ускорения, поэтому снаряд движется через пространство с постоянной горизонтальной скоростью, но в вертикальном направлении он испытывает гравитационное притяжение mg или, можно сказать, гравитационное ускорение «g», направленное вертикально вниз. Другими словами, можно сказать, что оно в вертикальном направлении движется с постоянным ускорением. 92 – 2gy

Хорошо, а теперь какая информация об этом движении снаряда обычно интересует экзаменаторов. Ну, максимальная высота, дальность и время полета будут основной информацией, которую вы должны помнить или знать, как рассчитать. Но интересующие сценарии могут включать максимальную дальность, которая в случае, если точка запуска и приземления находятся на одной высоте, составляет 45 градусов. Обратите внимание, что, другими словами, для того, чтобы снаряд имел желаемую дальность, необходимая скорость выброса будет минимальной при 45 градусах 92, вас могут попросить определить начальную скорость, угол проекции, максимальную высоту, дальность полета и время полета

или вам могут дать два снаряда и попросить определить точку их пересечения

или вам может быть дано, что снаряд запускается с движущейся платформы, и вам будут заданы скорость и угол выброса по отношению к движущейся платформе, и вам нужно будет определить начальную скорость и угол выброса по отношению к земле, чтобы определить неизвестное.

или вам могут сообщить, что снаряд запускается с высоты, и вас могут попросить определить время полета и горизонтальное расстояние, которое он проходит до удара о землю

, или вам могут сообщить, что снаряд запускается вдоль наклон и вам будет предложено определить дальность, время полета и максимальную высоту от наклона. В этом сценарии альтернативным способом было бы выбрать ось X, чтобы она была направлена ​​вверх вдоль наклона, а ось Y — перпендикулярно наклону. В этом случае ваше ускорение по оси x будет равно – g sin theta, а ваше ускорение по оси y будет – g cos theta 9.0007

Теперь, прежде чем мы перейдем к краткому обсуждению относительного движения, я настоятельно рекомендую вам изучить все эти различные типы вопросов на платформе acejee и прослушать поясняющее видео, чтобы понять, как подходить к ним, если у вас возникнут трудности

Хорошо, переходим к относительному движению, то есть к движению одной частицы, наблюдаемому другой частицей или наблюдателем. Здесь вы должны быть в состоянии определить относительное положение и относительную скорость.

Относительное положение, скажем, A относительно B в некоторый момент времени t будет просто равно r_a – r_b, где r_a — вектор положения A в момент времени t, а r_b — вектор положения B в момент времени t. Таким образом, пока вы можете определить векторы положения A и B в интересующий момент, вы можете легко определить их относительное положение

Что касается относительной скорости, то я настоятельно рекомендую вам прочитать блог, ссылка на который дана в описании, но в целом, прежде всего, вам нужно освоиться с определением относительной скорости одного объекта относительно к другому в одном измерении, то есть в сценарии, когда обе частицы движутся в одном измерении, скажем, вдоль оси x. Здесь, если вам даны их скорости относительно земли, тогда относительная скорость A относительно B будет просто V_A – V_B. И если вам дана относительная скорость, скажем, человека относительно, скажем, поезда, движущегося с некоторой скоростью, тогда скорость человека относительно земли будет равна v_train + v_man_rel_train

Теперь давайте перейдем к 2 измерениям, и для начала давайте поговорим о задачах о человеке дождя и задачах, скажем, о пловце в реке

В задачах о человеке дождя вам будет дано, что наблюдатель движется по земле с некоторой скоростью и дождь падает под некоторым углом к ​​вертикали, и вас могут попросить определить скорость капель дождя по отношению к человеку или угол, который скорость капель дождя составляет с вертикалью, как ее видит наблюдатель. Пожалуйста, обратитесь к блогу о том, как подходить к таким проблемам

Что касается пловца в реке, вам будет задана скорость пловца относительно воды и скорость реки, а затем вас могут попросить определить минимальное время пересечения реки или точку приземления пловца. или время, затраченное пловцом, если он должен приземлиться прямо напротив своей начальной точки, или вас могут попросить определить минимальную скорость, с которой он достигнет назначенной точки приземления

Двигаемся дальше, в другом сценарии вам может быть дано два движущихся объекта с постоянными скоростями в 2 измерениях, и вас могут попросить определить минимальное расстояние между двумя

Или вам могут быть даны два объекта, которые движутся с постоянным ускорением в двух измерениях, и вас попросят определить время, через которое они встретятся или столкнутся.

На этом мы завершаем краткий обзор ключевых понятий и навыков решения проблем, которые вы должны развить, чтобы овладеть этой темой.

С наилучшими пожеланиями

 

Основные понятия кинематики и уравнения

Каковы основные понятия кинематики? Что это за наука и что она изучает? Сегодня мы поговорим о том, что такое кинематика, какие основные понятия кинематики имеют место в задачах и что они означают. Кроме того, поговорим о значениях, с которыми чаще всего приходится иметь дело.

Кинематика. Основные понятия и определения

Для начала поговорим о том, что это такое. Одним из наиболее изучаемых разделов физики в школьном курсе является механика. В неопределенном порядке следуют молекулярная физика, электричество, оптика и некоторые другие разделы, такие как, например, ядерная и атомная физика. Но давайте подробнее рассмотрим механику. Этот раздел физики занимается изучением механического движения тел. Он устанавливает определенные закономерности и изучает свои методы.

Кинематика как часть механики

Последняя делится на три части: кинематика, динамика и статика. Эти три поднауки, если их можно так назвать, имеют некоторые особенности. Например, статика изучает законы равновесия механических систем. Сразу приходит на ум ассоциация с весами. Динамика изучает закономерности движения тел, но в то же время обращает внимание на действующие на них силы. А вот кинематика занимается тем же, только в счет силы не принимаются. Следовательно, массы одних и тех же тел в задачах не учитываются.

Основные понятия кинематики. Механическое движение

Предметом этой науки является материальная точка. Имеется в виду тело, размерами которого по сравнению с некоторой механической системой можно пренебречь. Это так называемое идеализированное тело, родственное идеальному газу, которое рассматривается в разделе молекулярной физики. Вообще понятие материальной точки как в механике вообще, так и в кинематике в частности играет довольно важную роль. Чаще всего рассматривают так называемое поступательное движение.

Что это значит и как это может быть?

Обычно движения делят на вращательные и поступательные. Основные понятия кинематики поступательного движения связаны главным образом с величинами, используемыми в формулах. О них мы поговорим позже, а пока вернемся к типу движения. Понятно, что если речь идет о вращательном, то тело вращается. Соответственно поступательным движением будем называть перемещение тела в плоскости или прямолинейно.

Теоретические основы решения задач

Кинематика, основные понятия и формулы которой мы сейчас рассматриваем, имеет огромное количество задач. Это достигается с помощью обычной комбинаторики. Одним из способов разнообразия здесь является изменение неизвестных условий. Одну и ту же проблему можно представить в ином свете, просто изменив цель ее решения. Требуется найти расстояние, скорость, время, ускорение. Как видите, вариантов целое море. Если подключить сюда условия свободного падения, космос становится просто невообразимым.

Значения и формулы

Прежде всего, сделаем одну оговорку. Как известно, величины могут иметь двоякую природу. С одной стороны, конкретному значению может соответствовать определенное числовое значение. Но с другой стороны, он может иметь направление распространения. Например, волна. В оптике мы сталкиваемся с таким понятием, как длина волны. Но если есть когерентный источник света (тот же лазер), то мы имеем дело с пучком плоскополяризованных волн. Таким образом, волне будет соответствовать не только числовое значение, указывающее на ее длину, но и заданное направление распространения.

Классический пример

Такие случаи аналогия в механике. Допустим, перед нами телега. По характеру движения можно определить векторные характеристики его скорости и ускорения. Сделать это при поступательном движении (например, на ровном полу) будет немного сложнее, поэтому рассмотрим два случая: когда тележка катится вверх и когда она скользит вниз.

Итак, давайте представим, что тележка поднимается по небольшому склону. В этом случае он будет тормозиться, если на него не действуют внешние силы. Но в обратной ситуации, а именно, когда тележка скользит сверху вниз, она будет ускоряться. Скорость в двух случаях направлена ​​туда, куда движется объект. Это следует принять за правило. Но ускорение может изменить вектор. При торможении она направлена ​​в сторону, противоположную вектору скорости. Это объясняет замедление. Аналогичную логическую цепочку можно применить и ко второй ситуации.

Остальные значения

Мы только что говорили о том, что в кинематике мы оперируем не только скалярными величинами, но и векторными величинами. Теперь мы сделаем еще один шаг вперед. Помимо скорости и ускорения при решении задач применяются такие характеристики, как расстояние и время. Кстати, скорость делится на начальную и мгновенную. Первое из них является частным случаем второго. Мгновенная скорость – это скорость, которую можно найти в любой момент времени. А с начальным, наверное, все понятно.

Задача

Значительная часть теории была изучена нами ранее в предыдущих параграфах.