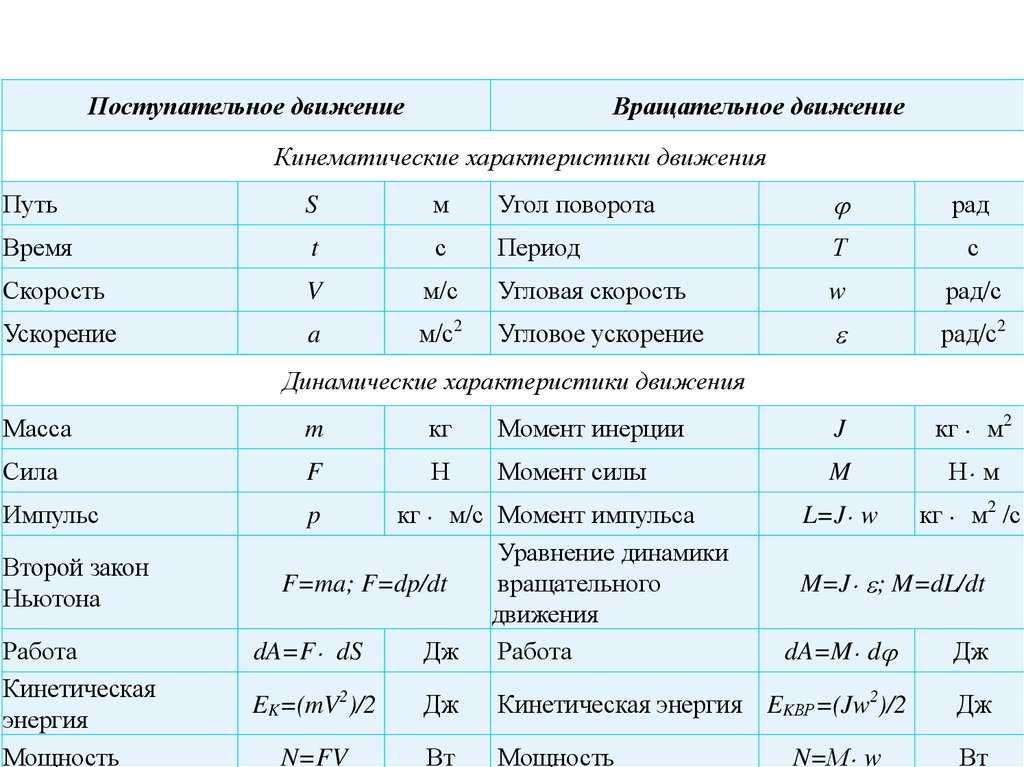
Кинематика таблица формул: Таблица формул по физике. Кинематика. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Что такое кинематика

Вокруг нас множество движущихся тел. Их движение можно описать по-разному. Рассмотрим, например, словесное описание движения поезда. Выехав из пункта А, поезд 2 часа ехал со скоростью 100 км/ч, затем 1 час стоял, и в пункт Б прибыл через 3 часа после возобновления движения, всё это время поддерживая скорость 50 км/ч.

Движение этого же поезда можно описать при помощи таблицы:

Время t, ч	0	1	2	3	4	5	6
Путь l, км	0	100	200	200	250	300	350

По данным таблицы построим график, и мы получим описание движения при помощи графика. На нём три этапа: от 0 до 2 часов (движение со скоростью 100 км/ч), от 2 до 3 часов (стоянка) и от 3 до 6 часов (движение со скоростью 50 км/ч).

Каждый этап движения поезда на графике отражён прямой линией, которой в алгебре соответствует линейная функция y = kx + b, где k и b – числа. Применительно к нашей задаче про поезд, вместо y будем писать l, а вместо x будем писать t. Тогда мы получим описание движения формулами:

Этап движения на графике	Интервал времени	Формула линии графика
I. (красный)	если 0 < t < 2 , то	l = 100 · t + 0
II.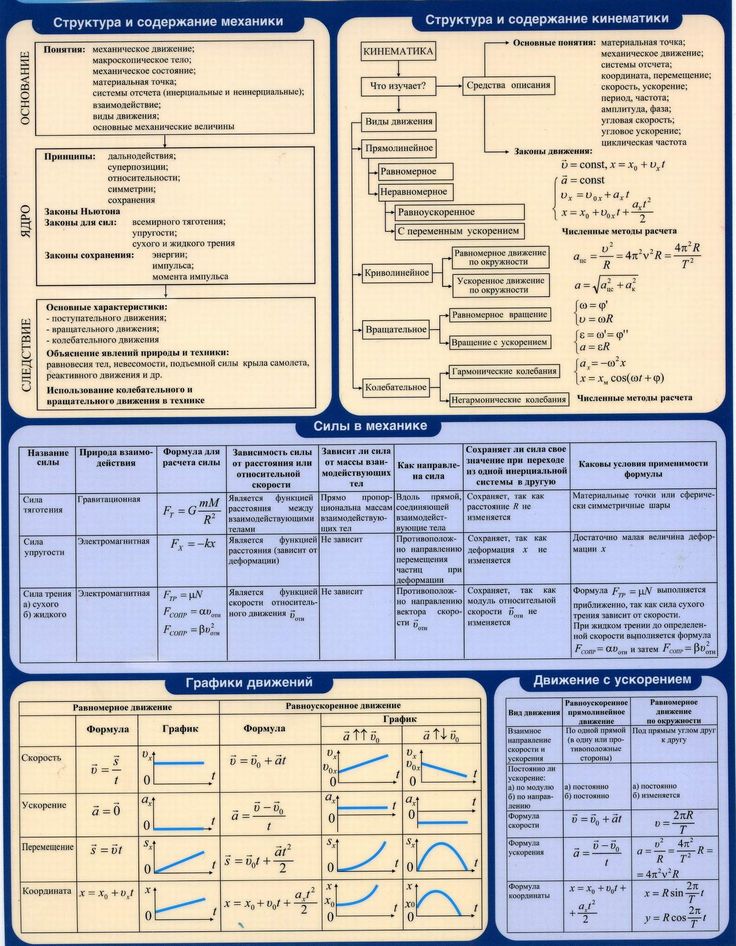 (чёрный)	если 2 < t < 3 , то	l = 0 · t + 200
III. (синий)	если 3 < t < 6 , то	l = 50 · t + 50

Как получаются эти формулы, мы изучим при решении задач, а пока убедимся, что они верные, например последняя. Значение t должно лежать в интервале от 3 до 6 часов. Возьмём значение 4 и подставим в формулу: l = 50 · 4 + 50. Вычисляем: 250 километров. В верхней таблице мы тоже видим, что за 4 часа поезд проехал 250 км. Взгляните и на график: для момента времени t = 4 ч получается путь l = 250 км.

Обобщим сказанное: рассмотренные способы описания движения – словесный, табличный, графический и формулами – равноправны. В зависимости от ситуации мы будем выбирать более удобный способ.

Кинематика (от греч. «кинематос» – движение) – раздел физики, изучающий способы математического описания движения тел без выяснения причин, вызвавших движение. Кинематика не интересуется тем, почему тело движется так, а не иначе. Она лишь отвечает на вопросы: как движение описать математически и что нового из такого описания можно почерпнуть?

Тело, собственными размерами которого в данных условиях можно пренебречь, называют материальной точкой. Например, если самолёт совершает перелёт по маршруту Москва–Сочи, диспетчер вполне может считать самолёт точкой (именно так он и отображается на экране радара). Однако тот же самолёт, выруливающий на взлётную полосу, точкой считать нельзя – надо учитывать, например, размах крыльев, чтобы не повредить другие самолёты или мачты освещения на месте стоянки.

В физике линию, которую «описывает» материальная точка при движении в пространстве, называют траекторией. Траектория может быть видимой или невидимой. Например, линия движения самолёта в небе часто видна (см. рисунок), а линия движения автомобиля по шоссе не видна. Заметим, что с точки зрения геометрии линия не имеет ширины.

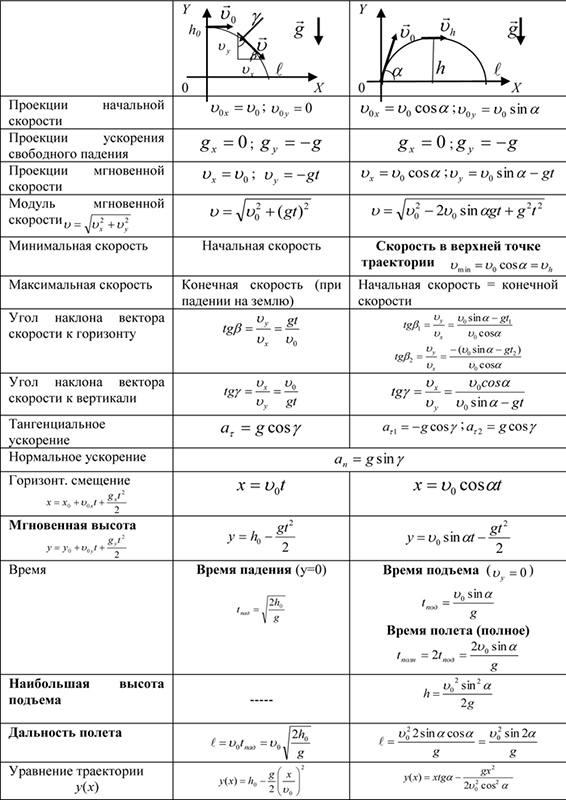
2}{2} \\ \overline{v}\left(t\right)={\overline{v}}_0+\overline{g}t \end{array} \right.\left(3\right).\]

Первое уравнение системы (3) записано для перемещения тела в поле тяжести Земли (${\overline{s}}_0$ – смещение тела из начала отсчета в момент начала наблюдения ($t=0c$)). Второе уравнение системы (3) показывает изменение вектора скорости (${\overline{v}}_0$ – начальная скорость движения тела).

Используя эти уравнения, и зная начальные условия движения тела можно найти скорость и положение тела относительно избранной системы отсчета для любого момента времени.

Тело, брошенное под углом к горизонту

Так, если нам заданы начальные условия в виде и сказано, что тело свободно движется в поле силы тяжести Земли:

\[\left\{ \begin{array}{c} x\left(t=0\ \right)=0, \\ y\left(t=0\ \right)=h, \\ v_x\left(t=0\ \right){=v}_{0x}=v_0{\cos \alpha ,\ } \\ v_y\left(t=0\ \right){=v}_{0y}=v_0{\sin \alpha .\ } \end{array} \right.\left(4\right)\]

это означает, что тело бросили под углом $\alpha $ к горизонту с начальной скоростью ${\overline{v}}_0$ с высоты $h$, оси координат выбраны так, что в момент броска смещения по оси X нет. 2}{2} \\ v_y=-gt \end{array} \right.(9)\]

Время падения тела равно:

\[t_{pad}=\sqrt{\frac{2h}{g}}\left(10\right).\]

Скорость тела в момент падения составляет:

\[v_{pad}=-\sqrt{2gh}\left(11\right).\]

Знак минус в формуле (11) означает, что скорость падения направлена против нашей оси Y.

Примеры задач с решением

Пример 1

Задание. Какова глубина шахты, если камень, брошенный в нее, упал на дно спустя 1 секунду после начала движения по ней?

Решение. В этой задаче мы имеем свободное вертикальное падение тела без начальной скорости (рис.2). Систему отсчета свяжем с Землей. Начало отсчета пусть находится на дне шахты (точка 0).

В качестве основы для решения задачи воспользуемся системой уравнений, полученной для подобного движения в теоретической части статьи:

\[\left\{ \begin{array}{c} y=h-\frac{gt^2}{2} \\ v_y=-gt \end{array} \right.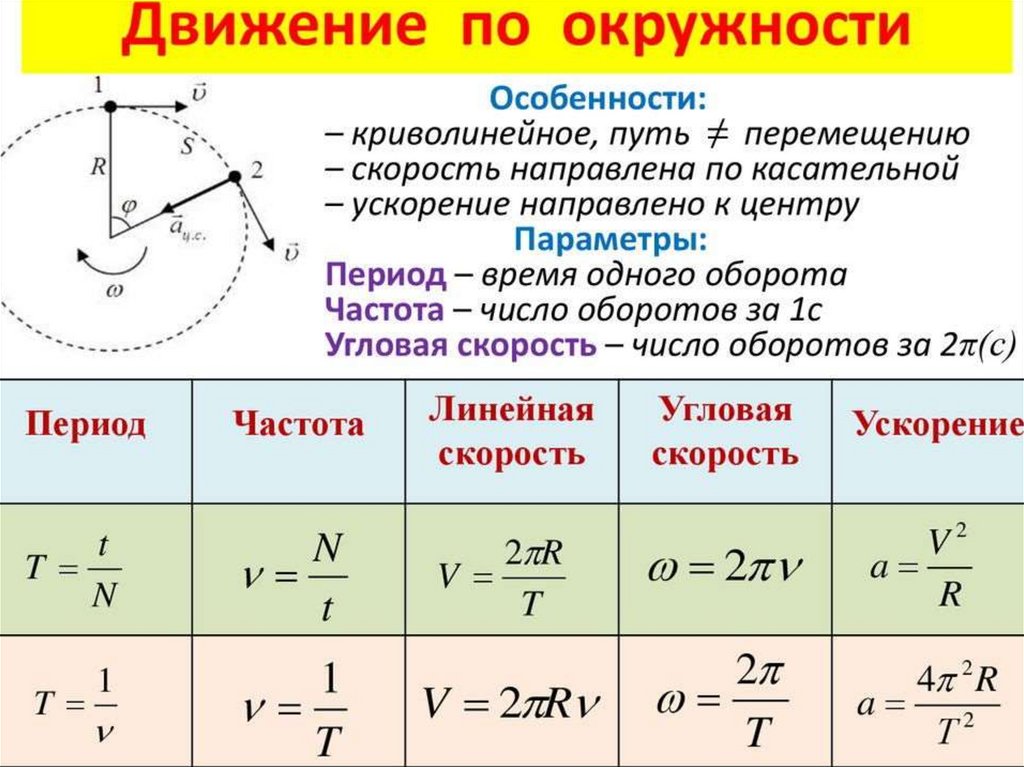 2}\to t_{pad}=\frac{v_0}{g}\ \left(2.7\right).\]

Сравниваем выражения (2.3) и (2.7), получаем:

\[t_{pad}=t_{pod}.\]

Время подъема равно времени падения.

Читать дальше: формулы эффекта Доплера.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Электронная таблица кинематики

Введение:

Традиционный способ решения числовых задач кинематики состоит в том, чтобы выучите набор формул кинематики, а затем научитесь складывать правильные значения в правильных местах в этих формулах. Это кажется очень сложная и запутанная для начинающих физиков.

Как вы видели, табличный подход решает почти все проблема кинематики, с которой вы столкнетесь в физике, и это намного менее сложно. Электронная таблица — это удобный способ автоматизировать табличное решение и позволяет (а) решать рутинные задачи легко, (б) решить некоторые довольно сложные проблемы без большого количества заморачиваться, и (в), главное, экспериментировать с различными комбинации ускорений и скоростей, чтобы увидеть, что происходит.

Вот подробные пошаговые инструкции по созданию Электронная таблица (ClarisWorks), которая решит многие числовые задачи кинематики проблемы, с которыми вы столкнетесь в этом курсе.

Процедура:

Вот значения и формулы, которые вам нужно ввести в таблицу кинематики.
Откройте новую электронную таблицу ClarisWorks.
В ячейке A1 введите заголовок электронной таблицы «Электронная таблица кинематики». от __you__”.
В ячейке A3 введите метку ускорения “acc (м/с/с)”. =”
В ячейке A4 введите метку временного интервала “time int (s) = “.
В ячейку B3 введите текущее значение ускорения, “10”.
В ячейку B4 введите текущее значение временного интервала, “1”.
В ячейке A6 введите заголовок для столбца времени, “время (с)”.
В ячейке A7 введите значение времени начала “0”.
Вы можете ввести «1» в ячейку A8 и т. д., но не делайте этого. Мы хотим увеличить время на временной интервал, который не всегда может быть 1. Будет удобнее использовать формулу в ячейке A8, которая будет “=A7 +$B$4”. Это говорит о добавлении значения в ячейке A7 (последний раз) к значение в ячейке B7 (интервал времени). Знаки доллара (“$”) сообщают электронной таблице, чтобы не изменять ячейку временного интервала, когда это формула копируется. Значение, которое должно появиться в ячейке A8 после вы набрали формулу “1”.
Щелкните и перетащите мышь, чтобы выбрать ячейки с A8 по A32 (или так). Затем в меню «Расчет» выберите «Заполнить». Бум!
Измените значение в ячейке B4, скажем, на «0,1», и обратите внимание, что все значения времени изменяются для отсчета времени на десятые доли секунды. Круто, нет? Теперь измените B4 обратно на «1».
В ячейке B6 введите заголовок столбца для мгновенного скорость, “скорость (м/с)”
В ячейке B7 введите значение начальной скорости “0”
Изменение скорости за каждый интервал времени равно ускорение объекта, умноженное на прошедшее время. Формула для ячейки B8 равно “=B7+$B$4*$B$3”.
Нажмите и перетащите мышь, чтобы выбрать ячейки с B8 по B32 (или так). Затем в меню «Расчет» выберите «Заполнить».
Измените значение ускорения в ячейке B3 и обратите внимание, что все скорости изменяются автоматически.
В ячейке C6 введите заголовок столбца средней скорости, “ср v (м/с)”.
Ячейка C7 пуста, так как средняя скорость отсутствует до тех пор, пока конец первого временного интервала.
Ячейка C8 содержит среднее значение скоростей в ячейках B7 и Б8. Формула “=($B$7+B8)/2”.
Снова выделите остальную часть столбца средней скорости и «Заполнить».
В ячейке D6 введите заголовок столбца пройденного расстояния столбец, “расст. (м).
В ячейке D7 введите значение начальной позиции «0».
Пройденное расстояние равно произведению средней скорости на пройденное время. Формула для ячейки D8: “=$D$7+C8*(A8-$A$7)”.
Используйте «Заполнить вниз», чтобы заполнить оставшуюся часть расстояния. столбец.

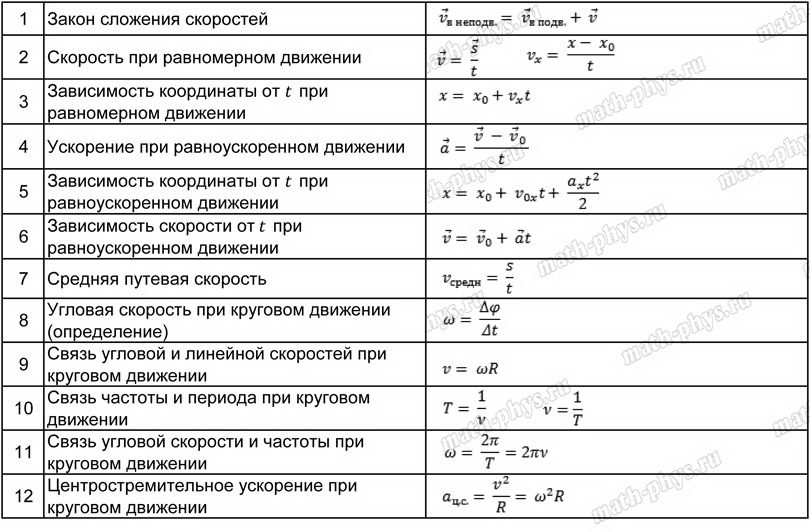Вот так должен выглядеть “готовый продукт” нравиться.

Расширения:

Вы можете легко построить элементарную зависимость скорости от времени или положения зависимости от времени, выделив соответствующие значения и выбрав (линия график) из диалогового окна, которое появляется, когда вы выбираете «Создать диаграмму» из меню «Параметры».

Скорость выборки в зависимости от времени (в середине) и положение в зависимости от времени графики (справа) для примера электронной таблицы.

Использование электронной таблицы:

Для решения типовой задачи кинематики (с постоянной ускорение), вам может потребоваться изменить начальную скорость (ячейка B7) или ускорение (ячейка B3) и найдите в таблице ценить. Вам также может понадобиться изменить временной интервал (ячейка B4) на повысить точность или, возможно, использовать «Заполнить вниз», чтобы увеличить размер Таблица. Вот некоторые примеры.

последнее обновление 14 сентября 2000 г., JL Стэнбро

Уравнения кинематики – быстрый расчет уравнений движения

Последнее обновление: 20 мая 2021 г., 04:34

Здесь мы перечислили важные уравнения (или наборы формул), относящиеся к кинематике. Вы получите уравнения кинематики на положения, перемещение, полное перемещение, среднюю скорость, мгновенную скорость, среднюю скорость, мгновенную скорость, среднее ускорение, мгновенное ускорение, скорость из ускорения, положение из скорости, уравнения свободного падения, и т.д.

Уравнения кинематики – шпаргалка

Уравнения кинематики для равномерно ускоренного движения (6 уравнений)

Если ускорение объекта равномерное, то к его движению применяются следующие уравнения:

средняя скорость = ( V + U)/ 2 и S = [ U = [ U 7779 U 779 U 9. U .0135 t

acceleration, a =( v – u)/t or v = u + at

s = ut +(1/2) at ²
v ² = u ² + 2 as

where u is the initial velocity, v конечная скорость, a ускорение, t затраченное время и s смещение.

Числовые вопросы – решены

Пример (1 )

Драгстер стартует с места и разгоняется до 25 м/с ² на 4 с.
Рассчитайте:
(а) конечную скорость
(б) пройденное расстояние.

Ответ:

(a) v = u + at = 0 + (25×4) = 100 м/с

(b) s = ut +(1/2)at Пример (2) направлении со скоростью 35 м/с. Если мяч находился в контакте с битой 0,02 с, вычислить:
(а) ускорение мяча во время удара
(б) расстояние, пройденное мячом во время удара.