Кинематика термех для чайников: Краткий курс теории по теоретической механике

Подробные решения задач по теоретической механике с ответами

Здесь собраны основные примеры задач с решениями по теоретической механике. Рядом с условием задачи приводится ссылка на страницу с ее подробным решением и ответом. Задачи охватывают следующие разделы технической и теоретической механики: статика, кинематика, динамика материальной точки и системы тел.

Здесь приводятся условия задач по теоретической механике, имеющие подробные решения с ответами. Задачи сгруппированы по основным разделам теоретической механики: статика, кинематика и динамика. Чтобы посмотреть решение, нажмите на соответствующую ссылку в конце условия.

Статика

Условия задач

Найти графическим способом реакции опор балки AB, на которую действует сила P, приложенная в точке C.
Дано: P = 55 kH,   AB = 10 м,   AC = 7 м,   BC = 3 м.

Решение

Найти реакции опор для того способа закрепления, при котором момент M_A в опоре A имеет наименьшее значение.
Решение

Найти реакции опор балки.
Решение

Найти реакции опор составной конструкции.
Решение

Определить реакции стержней, поддерживающих тонкую однородную прямоугольную плиту в трехмерном пространстве.
Решение

Кинематика

Кинематика материальной точки

Определение скорости и ускорения точки по заданным уравнениям ее движения

Дано:   Уравнения движения точки:   x = 12 sin(πt/6), см;   y = 6 cos²(πt/6), см.

Установить вид ее траектории и для момента времени t = 1 с найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.

Решение задачи

Поступательное и вращательное движение твердого тела

Дано:
t = 2 с; r₁ = 2 см, R₁ = 4 см; r₂ = 6 см, R₂ = 8 см; r₃ = 12 см, R₃ = 16 см; s₅ = t³ – 6t (см).

Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.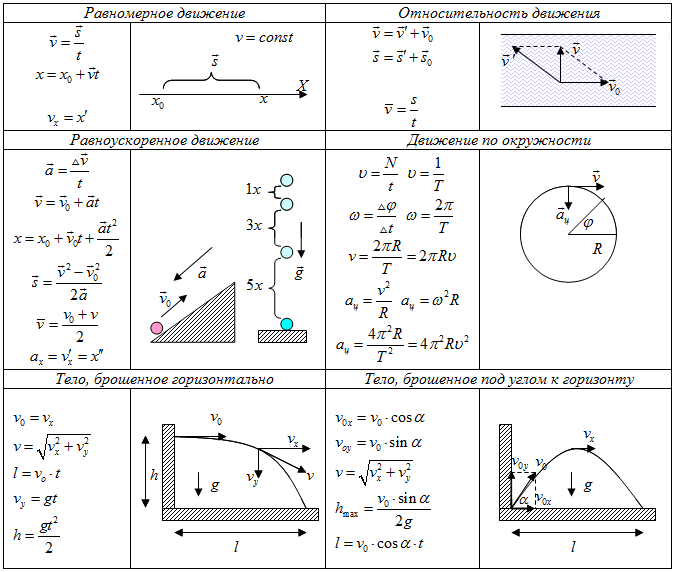

Решение

Кинематический анализ плоского механизма

Дано:
R₁, R₂, L, AB, ω₁.
Найти: ω₂.

Решение с помощью
теоремы о проекциях скоростей

Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна E. Стержни соединены с помощью цилиндрических шарниров. Точка D расположена в середине стержня AB.
Дано: ω₁, ε₁.
Найти: скорости V_A, V_B, V_D и V_E; угловые скорости ω₂, ω₃ и ω₄; ускорение a_B; угловое ускорение ε_AB звена AB; положения мгновенных центров скоростей P₂ и P₃ звеньев 2 и 3 механизма.

Решение

Определение абсолютной скорости и абсолютного ускорения точки

Прямоугольная пластина вращается вокруг неподвижной оси по закону   φ = 6t ² – 3t ³ . Положительное направление отсчета угла φ показано на рисунках дуговой стрелкой. Ось вращения OO ₁ лежит в плоскости пластины (пластина вращается в пространстве).

По пластине вдоль прямой BD движется точка M . Задан закон ее относительного движения, т. е. зависимость   s = AM = 40(t – 2t ³) – 40   (s – в сантиметрах, t – в секундах). Расстояние b = 20 см. На рисунке точка M показана в положении, при котором   s = AM > 0 (при   s < 0 точка M находится по другую сторону от точки A).

Найти абсолютную скорость и абсолютное ускорение точки M в момент времени   t ₁ = 1 с.

Решение задачи

Динамика

Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил

Рисунок к условию задачи.

Груз S, рассматриваемый как материальная точка массы m = 5кг, движется по шероховатой поверхности от точки A до точки B, в которой отрывается от поверхности и продолжает движение в воздухе до падения на наклонную поверхность в точке C. Движение происходит в плоскости рисунка.

В точке A, груз имел скорость v_A = 1 м/с. Скорость в точке B: v_B = 4 м/с. Участок AB представляет собой плоскую поверхность с углом наклона α = 30° к горизонту. На участке AB, кроме силы тяжести и силы трения, на груз действует постоянная сила Q = 10 Н, направленная под углом φ = 45° к поверхности. Коэффициент трения f = 0,1.

На участке BC, груз движется под действием только силы тяжести. Сопротивлением воздуха пренебречь. Поверхность, на которую падает груз, является плоской с углом наклона β = 15° к горизонту (см. рисунок). Точка D расположена ниже точки B на расстояние |BD| = h = 1 м.

Найти: Время движения t_AB на участке AB; длину этого участка; время падения t_BC от точки B к точке C; расстояние |DC|; уравнение траектории BC.

Решение задачи

Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил

Рисунок к условию задачи.

Груз D массой m, получив в точке A начальную скорость V₀, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости. На участке AB, длина которого l, на груз действует постоянная сила T(ее направление показано на рисунке) и сила R сопротивления среды (модуль этой силы R = μV², вектор R направлен противоположно скорости V груза).

Груз, закончив движение на участке AB, в точке B трубы, не изменяя значения модуля своей скорости, переходит на участок BC. На участке BC на груз действует переменная сила F, проекция F_x которой на ось x задана.

Считая груз материальной точкой, найти закон его движения на участке BC, т.е. x = f(t), где x = BD. Трением груза о трубу пренебречь.

Решение задачи

Теорема о движении центра масс системы

Найти перемещение плиты и реакцию направляющих.

Механическая система состоит из грузов D₁, D₂ и прямоугольной вертикальной плиты, движущейся вдоль горизонтальных направляющих. В момент времени t₀=0, когда система находилась в покое, под действием внутренних сил грузы начинают двигаться по желобам, представляющим собой окружности.

Считая грузы материальными точками, и пренебрегая всеми сопротивлениями, определить закон движения плиты x₃=f₃(t) и полной нормальной реакции направляющих N=f(t).

Решение

В кривошипно-шатунном механизме кривошип OA и шатун AB представляют собой однородные стержни массой m₁ и длиной l. Ползун B массой m₂ движется в вертикальных направляющих. Определить вертикальную составляющую реакции шарнира O в функции угла φ, если кривошип вращается с постоянной угловой скоростью ω. Трением в направляющих ползуна пренебречь.

Решение

Теорема об изменении кинетической энергии механической системы

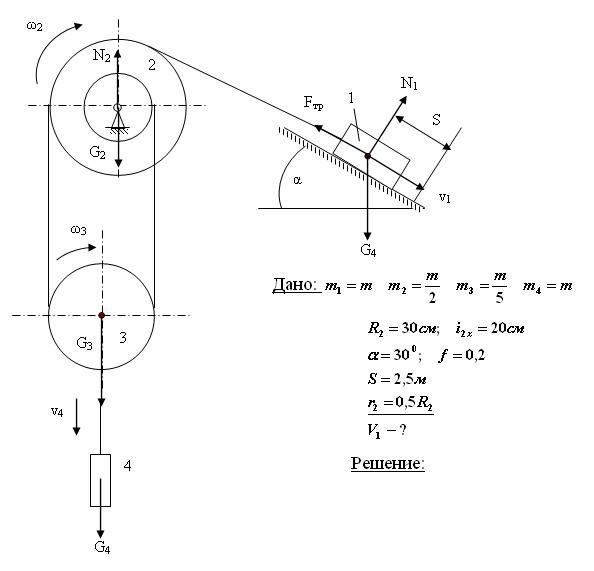
Рисунок к условию задачи.

Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3, блока 4 и подвижного блока 5. Заданы радиусы ступеней и радиусы инерции шкива 3 и блока 4. Блок 5 считать сплошным однородным цилиндром. Коэффициент трения груза 2 о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3. Участки нитей параллельны соответствующим плоскостям. К подвижному блоку 5 прикреплена пружина с коэффициентом жесткости с.

Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя. Деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент M сил сопротивления (от трения в подшипниках).

Заданы массы тел m₁, m₂, m₃ , m₄, m₅, коэффициент жесткости пружины c, зависимость силы от перемещения F = f(s), величина момента M.

Определить значение центра масс тела 5 V_C5 в тот момент времени, когда перемещение s груза 1 станет равным s₁ = 0,2 м.

Решение задачи

Применение общего уравнения динамики к исследованию движения механической системы

Механическая система

Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3-6, прикрепленных к этим нитям, и невесомого блока.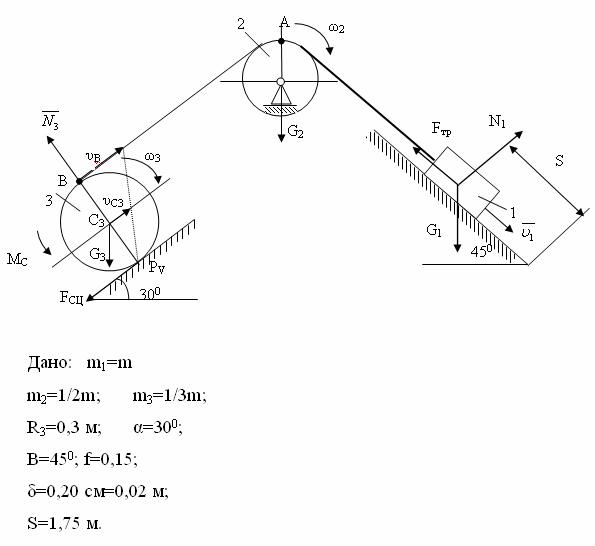 Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом M = 10 Н·м, приложенной к шкиву 1. Заданы радиусы ступеней шкивов, их радиусы инерции относительно осей вращения, а также веса шкивов и грузов. Грузы, веса которых равны нулю, на чертеже не изображать.

Пренебрегая трением, определить ускорение груза 5.

Решение

Применение принципа Даламбера к определению реакций опор вращающегося тела

Рисунок к условию задачи.

Вертикальный вал AK, вращающийся равномерно с угловой скоростью ω = 10 с^-1, закреплен подпятником в точке A и цилиндрическим подшипником в точке K.

К валу жестко прикреплены невесомый стержень 1 длиной l₁ = 0,3 м, на свободном конце которого расположен груз массой m₁ = 4 кг, и однородный стержень 2 длиной l₂ = 0,6 м, имеющий массу m₂ = 8 кг. Оба стержня лежат в одной вертикальной плоскости. Точки прикрепления стержней к валу, а также углы α и β заданы. Размеры AB=BD=DE=EK=b, где b = 0,4 м. Груз принять за материальную точку.

Пренебрегая массой вала, определить реакции подпятника и подшипника.

Решение

 

---

Динамика – раздел теоретической механики.



Основные понятия и аксиомы динамики

Динамика есть часть теоретической механики, изучающая механическое движение тел в зависимости от сил, влияющих на это движение.

Основы динамики заложил итальянский ученый Галилео Галилей (1564-1642), который опроверг существовавшее в науке со времен Аристотеля (IV в. до н.э.) заблуждение о том, что из двух тел, падающих на Землю, более тяжелое движется быстрее. Галилей установил, что причиной изменения скорости тела является сила, т. е. любое ускорение или замедление вызывается силовым воздействием.
На основе выводов Г. Галилея англичанин И. Ньютон сформулировал основные аксиомы (законы) движения, ставшие фундаментом, на который сотни лет опирается классическая физика, в том числе и современная.

Динамика основывается на ряде положений, которые являются аксиомами и называются законами динамики.

Прежде чем перейти к рассмотрению этих законов, необходимо раскрыть сущность понятий материальной точки и изолированной материальной точки.
Под материальной точкой подразумевают некое тело, имеющее определенную массу (т. е. содержащее некоторое количество материи), но не имеющее линейных размеров (бесконечно малый объем пространства).
Изолированной считается материальная точка, на которую не оказывают действие другие материальные точки.
В реальном мире изолированных материальных точек, как и изолированных тел, не существует, это понятие является условным.

***

Первый закон Ньютона (первый закон динамики)

Первый закон динамики, называемый аксиомой инерции, формулируется в применении к материальной точке так: изолированная материальная точка либо находится в покое, либо движется прямолинейно и равномерно.

В кинематике было установлено, что прямолинейное равномерное движение является единственным видом движения, при котором ускорение равно нулю, поэтому аксиому инерции можно сформулировать следующим образом: ускорение изолированной материальной точки равно нулю.

Итак, изолированная от влияния окружающих тел материальная точка не может сама себе сообщить ускорение. Это свойство тел называют инерцией или инертностью, т. е. инертность (инерция) – свойство тел сохранять скорость по модулю и направлению (в т. ч. и покой – состояние, при котором скорость равна нулю). Изменить скорость, т. е. сообщить материальной точке ускорение способна только приложенная к ней сила.

***

Второй закон Ньютона (второй закон динамики)

Зависимость между силой и сообщаемым ею ускорением устанавливает второй закон Ньютона, который гласит, что ускорение, сообщаемое материальной точке силой, имеет направление силы и пропорционально ее модулю.

Если сила F₁ сообщает материальной точке ускорение a₁, а сила F₂ сообщает этой же точке ускорение a₂, то на основании второго закона Ньютона можно записать:

F₁/F₂ = a₁/a₂   или   F₁/a₁ = F₂/a₂.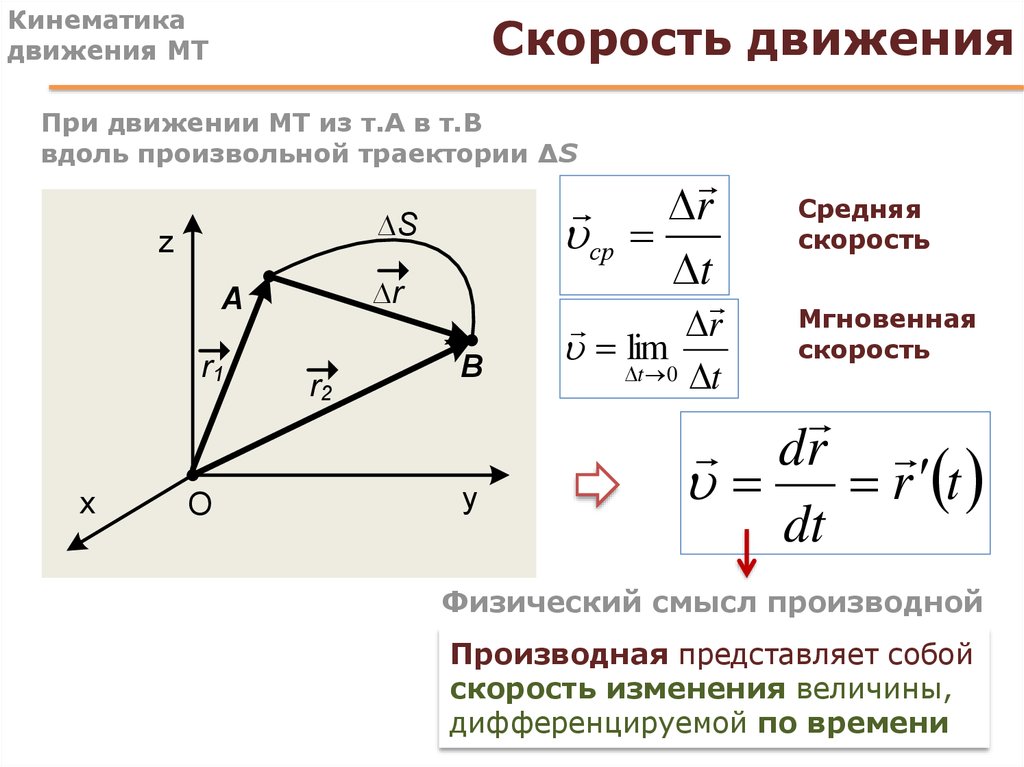

Следовательно, для данной материальной точки отношение любой силы к вызываемому ею ускорению есть величина постоянная. Эту величину (отношение силы к ускорению) называют массой материальной точки, и обозначают ее m:

F/a = m = const.

На основании этого равенства можно сделать выводы:
– две материальные точки, имеющие одинаковые массы, получат от одной и той же силы одинаковые ускорения;
– чем больше масса точки, тем большую силу необходимо приложить, чтобы придать данной точке требуемое ускорение.

***



Что такое масса тела

Масса – одна из основных характеристик любого материального объекта, определяющая его инертные и гравитационные свойства. Ньютон называл массой количество материи, заключенной в теле, считая массу каждого тела величиной постоянной.

Современное представление о мире, после открытий, совершенных А. Эйнштейном, опровергает этот вывод И. Ньютона – масса не является постоянной величиной для тела, она зависит от скорости, с которой это тело движется. Так, например, наблюдения за движением заряженных частиц в ускорителях показали, что инертность частицы (т. е. способность сохранять свою скорость) возрастает с увеличением ее скорости.

Теория относительности устанавливает следующую зависимость между массой тела, находящегося в покое, и массой движущегося тела:

m = m₀/√(1 – v²/c²),

где m – масса движущегося тела, m₀ – масса покоящегося тела (масса покоя), v = скорость движения тела, c – скорость света.

Из этой формулы видно, что чем больше скорость движения тела, тем больше его масса и, следовательно, тем труднее сообщить ему дальнейшее ускорение. При скоростях близких к скорости света масса тела стремится к бесконечности, и для дальнейшего ускорения такого тела требуется сила бесконечной величины.
Очевидно, что материальное тело не может двигаться со скоростью света, поскольку не существует реальная сила, способная ускорить его до такого состояния.

На основании теории относительности современная наука дает массе такое определение: масса есть мера инертности тела.
Однако заметное изменение массы (инертности) тела наблюдается лишь при очень больших скоростях, близких к скорости света, поэтому в классической физике массу принимают величиной постоянной, при этом погрешности, возникающие в расчетах, являются ничтожно малыми.

Второй закон Ньютона выражается равенством:

F = ma,

которое называется основным уравнением динамики и читается так: сила есть вектор, равный произведению массы точки на ее ускорение.

Основное уравнение динамики является уравнением движения материальной точки в векторной форме.

Ускорение свободного падения

Опытным путем установлено, что под действием притяжения Земли в вакууме тела падают с одинаковым ускорением, которое называется ускорением свободного падения.

Следует отметить, что это явление будет верным для конкретного географического места на поверхности планеты или над ее поверхностью – ускорение свободного падения не является постоянной величиной и зависит, в частности, от расстояния между центром тяжести тела и центром тяжести нашей планеты, а также от существования центробежной силы инерции, вызываемой вращением Земли.

Так, на полюсах ускорение свободного падения g ≈ 9,83 м/с², а на экваторе g ≈ 9,78 м/с². Но в приближенных расчетах принимают среднее значение, равное примерно g ≈ 9,81 м/с², при этом погрешности результатов незначительны.

Итак, сила тяжести тела равна его массе, умноженной на ускорение свободного падения. Если сила тяжести одного тела G₁ = m₁/g, а второго тела – G₂ = m₂/g, то

G₁/G₂ = (m₁g)/(m₂g) = m₁

/m₂,

т. е. силы тяжести тел пропорциональны их массам, что позволяет сравнивать массы различных тел путем взвешивания (сравнивания их сил тяжести при помощи весов).

Из второго закона Ньютона следует, что под действием постоянной силы находившаяся в покое свободная материальная точка движется прямолинейно равнопеременно (с постоянным ускорением).

Движение под действием постоянной силы может быть и прямолинейным и криволинейным (в последнем случае материальная точка имеет начальную скорость, вектор которой не совпадает с вектором силы). Пример движения под действием постоянной силы – свободное падение тел.

***

Третий закон Ньютона

К основным законам динамики относится и рассмотренная в Статике аксиома взаимодействия, или третий закон Ньютона.
Применительно к материальной точке закон формулируется так: силы взаимодействия двух материальных точек по модулю равны между собой и направлены в противоположные стороны (действие равно противодействию).

На основании этого закона можно сделать вывод, что сила, как мера взаимодействия между телами, не может проявляться без пары, т. е. если возникает какое-либо силовое воздействие, то существует и “двойник” этого силового воздействия, равный по модулю и противоположный по вектору.

***

Дифференциальные уравнения движения материальной точки



Главная страница

• Страничка абитуриента

Дистанционное образование

• Группа ТО-81
• Группа М-81
• Группа ТО-71
  

Специальности

• Ветеринария
• Механизация сельского хозяйства
• Коммерция
• Техническое обслуживание и ремонт автотранспорта

Учебные дисциплины

• Инженерная графика
• МДК. 01.01. «Устройство автомобилей»
•    Карта раздела
•       Общее устройство автомобиля
•       Автомобильный двигатель
•       Трансмиссия автомобиля
•       Рулевое управление
•       Тормозная система
•       Подвеска
•       Колеса
•       Кузов
•       Электрооборудование автомобиля
•       Основы теории автомобиля
•       Основы технической диагностики
• Основы гидравлики и теплотехники
• Метрология и стандартизация
• Сельскохозяйственные машины
• Основы агрономии
• Перевозка опасных грузов
• Материаловедение
• Менеджмент
• Техническая механика
• Советы дипломнику

Олимпиады и тесты

• «Инженерная графика»
• «Техническая механика»
• «Двигатель и его системы»
• «Шасси автомобиля»
• «Электрооборудование автомобиля»

Правильные ответы на тестовые вопросы по разделу “Динамика”:
Тест №1     2-3-2-1-1
Тест №2     4-2-4-3-1
Тест №3     3-1-1-2-4
Тест №4     4-2-1-2-3
Тест №5     1-1-4-3-2
Тест №6     1-3-3-2-4
Тест №7     2-2-4-1-3

Обзор кинематики: термины кинематики

Условия

Кинематика

Кинематика занимается описанием того, как движутся объекты.

смещение

Полное изменение положения объектов. Если человек пробегает по овалу 400 метров след, остановившись в том же месте, где он начал, хотя он пробежал расстояние 400 метров, его полное водоизмещение равнялось 0.

Динамика

Динамика фокусируется на понимании того, почему объекты движутся именно так, а не иначе.

Система отсчета

Система координат, относительно которой описывается движение.

Скорость

Мера того, насколько быстро движется объект.

Средняя скорость

Среднее значение функции скорости за указанный интервал времени. (См. формулу ниже.)

Мгновенная скорость

Значение функции скорости в конкретный момент времени. (Видеть формула ниже.)

Гравитационное ускорение

Гравитационное ускорение объектов вблизи земной поверхности одинаково для всех объектов независимо от массы и дается числом г = 9,8 м/с ² .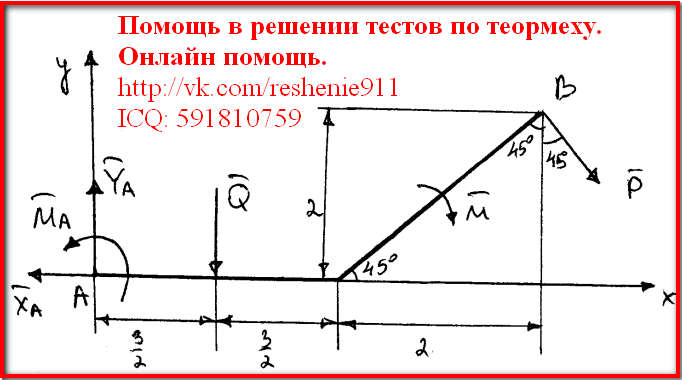

Скалярнозначная функция

Функция, которая выводит скаляры (обычные числа). Наиболее распространенные функции, с которыми вы, вероятно, знакомы, скалярнозначные функции.

Вектор-функция

Функция, которая выводит векторы. Это означает, что а область определения функции может состоять из скаляры, все значения в диапазоне являются векторами.

Функция положения

Функция положения может быть как скалярнозначной (для движения в одном размерность) или векторные (для движения в двух или трех измерениях). В каждый момент времени его значение представляет положение объекта в это время.

Функция скорости

Эта функция является производной по времени от функции положения, и дает скорость объекта в каждый момент времени.

Функция ускорения

Эта функция является производной по времени от функции скорости, и вторая производная по времени от функции положения. Он дает значение ускорение тела в каждый момент времени.

Производная по времени

Производная функции по времени равна новая функция , значение которой в каждом точка представляет скорость изменения исходной функции относительно ко времени.

Простые гармонические колебания

Периодическое движение, которое может быть описано специальными типами функций положения. Примеры простого гармонического движения включают объект, движущийся по кругу, и мяч подпрыгивает на пружине.

Кинематические формулы

 

Средняя скорость для объекта с функцией положения x ( t ) по временной интервал ( t 0 , t 1 ).

v среднее =

 

Мгновенная скорость в момент времени t для объекта с функцией положения х ( т ).

v ( т ) =

Николас Орем | Французский епископ, ученый и экономист

Дата рождения:

около 1320 г. Франция

Умер:

11 июля 1382 г. Лизьё Франция

Предметы изучения:

монета

Посмотреть весь связанный контент →

Николь Оресм , француз Николь Оресм , (род. ок. 1320, Нормандия — умерла 11 июля 1382, Лизье, Франция), французский римско-католический епископ, философ-схоласт, экономист и математик, чьи работа послужила некоторой основой для развития современной математики и естественных наук, а также французской прозы, особенно ее научной лексики.

Известно, что Орем был нормандцем по происхождению, хотя точное место и год его рождения неизвестны. Точно так же неизвестны подробности его раннего образования. В 1348 году его имя фигурирует в списке стипендиатов бакалавриата по богословию в Наваррском колледже Парижского университета. Поскольку Орем стал гроссмейстером колледжа в 1356 году, он должен был получить докторскую степень по богословию до этой даты. Орем был назначен каноником (1362 г.) и деканом (1364 г.) Руанского собора, а также каноником Сент-Шапель в Париже (1363 г.). Примерно с 1370 года по указанию французского короля Карла V Орем перевел 9 Аристотеля.0183 Этика , Политика и На Небесах , а также псевдоаристотелевская Экономика , с латыни на французский. Его влияние на французский язык можно увидеть в создании им французских эквивалентов для многих латинских научных и философских терминов. Орем был избран епископом Лизье в 1377 г. и был рукоположен в 1378 г.

Britannica Quiz

Числа и математика

A-B-C, 1-2-3… Если вы считаете, что считать числа — это то же самое, что читать алфавит, проверьте, насколько свободно вы владеете языком математики в этом тесте.

Оресм представил свои экономические идеи в комментариях к Этике , Политике и Экономике , а также к более раннему трактату De origine, natura, jure et Mutationibus monetarum (ок. 1360; , природа, юридический статус и варианты чеканки»). Орем утверждал, что чеканка монет принадлежит публике, а не князю, который не имеет права произвольно изменять содержание или вес. Его отвращение к последствиям обесценивания валюты повлияло на денежную и налоговую политику Чарльза. Орем считается величайшим средневековым экономистом.

Орем также считается одним из самых выдающихся философов-схоластов, известным своим независимым мышлением и критикой нескольких аристотелевских догматов. Он отверг аристотелевское определение места тела как внутренней границы окружающей среды в пользу определения места как пространства, занимаемого телом. Точно так же он отверг аристотелевское определение времени как меры движения, выступая вместо этого за определение времени как последовательной длительности вещей, независимой от движения.

В Livre du ciel et du monde (1377; «Книга о небе и мире») Орем блестяще выступил против любых доказательств аристотелевской теории неподвижной Земли и вращающейся сферы неподвижных звезд. Хотя Орем показал возможность ежедневного осевого вращения Земли, он закончил тем, что подтвердил свою веру в стационарную Землю. Как и некоторые другие философы-схоласты, Орем приводил доводы в пользу существования бесконечной пустоты за пределами мира, которую он отождествлял с Богом, точно так же, как он отождествлял с Богом вечность, в которой нет отдельных прошлого, настоящего и будущего.

Орем был решительным противником астрологии, которую он критиковал по религиозным и научным соображениям. В De Proportibus Proportum («О соотношениях отношений») Орем впервые исследовал возведение рациональных чисел в рациональные степени, прежде чем расширить свою работу, включив в нее иррациональные степени. Результаты обеих операций он назвал иррациональными отношениями , хотя первый тип считал соизмеримым с рациональными числами, а второй — нет. Его мотивацией для этого исследования было предложение теолога-математика Томаса Брэдвардина (ок. 129 г.).0–1349), что зависимость между силами ( F ), сопротивлениями ( R ) и скоростями ( V ) является экспоненциальной. Говоря современным языком: ^{F ₂} / _{R 2}  = ( ^{F ₁} / _{R 1} ) ^{V ₂ / _{V 1}} . Затем Орем утверждал, что отношение любых двух небесных движений, вероятно, несоизмеримо. Это исключает точные предсказания последовательно повторяющихся соединений, оппозиций и других астрономических аспектов, и впоследствии он утверждал в Ad pauca respicientes (название происходит от вступительного предложения «Относительно некоторых вопросов…»), тем самым была опровергнута астрология. Как и в случае с астрологией, он боролся с широко распространенной верой в оккультные и «чудесные» явления, объясняя их с точки зрения естественных причин в Livre de divinacions («Книга гаданий»).

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Основной вклад Орема в математику содержится в его Tractatus de configurationibus qualitatum et motuum («Трактат о конфигурациях качеств и движений»). В этой работе Орем задумал использовать прямоугольные координаты ( широты и долготы ) и полученные геометрические фигуры для различения равномерного и неравномерного распределения различных величин, даже расширив свое определение, включив в него трехмерные фигуры. Таким образом, Орем помог заложить фундамент, который впоследствии привел к открытию Рене Декартом аналитической геометрии (159 г.6–1650). Кроме того, он использовал свои рисунки, чтобы дать первое доказательство теоремы Мертона: расстояние, пройденное за любой данный период телом, движущимся с равноускоренным ускорением, такое же, как если бы тело двигалось с равномерной скоростью, равной его скорости в середине Период. Некоторые ученые считают, что графическое представление скоростей Оремом оказало большое влияние на дальнейшее развитие кинематики, затронув, в частности, работы Галилея (1564–1642).