Кинематика термех решение задач: Примеры решения задач теоретической механики

Примеры решения задач теоретической механики

Примеры решения задач и РГР по теоретической, инженерной и технической механике с необходимыми графическими построениями и пояснениями выполняемых действий.

Сохранить и поделиться с друзьями

Выберите раздел теоретической механики:
Кинематика   |   Статика   |   Динамика

Здесь рассмотрены решения задач по разделу «Кинематика» на расчет скоростей, ускорений, траекторий и других кинематических параметров движения точек и твердых тел при различных способах задания движения.

Расчет угловой скорости и радиуса диска

Задача

Точка, лежащая на ободе равномерно вращающегося диска движется со скоростью v=1,6 м/с и нормальным ускорением a_n=8 м/с².

Требуется определить радиус диска r и величину его угловой скорости ω.

Пример решения

Радиус диска определяется по формуле радиуса кривизны траектории движения точки

где
v – скорость точки;

a_n – её нормальное ускорение.

Далее, зная радиус диска, рассчитаем его угловую скорость, которая определяется отношением полной скорости точки к расстоянию от оси вращения диска до самой точки

в данном случае, это радиус r окружности обода диска.

Ответ: Радиус диска r=32 см, угловая скорость составляет ω = 5 оборотов в секунду.

Помощь с решением задач

Далее показаны другие примеры решения задач кинематики (теоретическая, инженерная и техническая механика) по соответствующим подразделам.

Кинематика точки

Примеры расчетов:

1. положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, радиус кривизны траектории
2. траектория движения точки, скорость и ускорение, путь, пройденный точкой
3. модуль полного ускорения и угол с вектором скорости
4. параметры движения точки
5. вид траектории, скорость точки, полное, касательное, нормальное ускорения и радиус кривизны траектории
6. угол между вектором ускорения и радиусом
7. Расчет скорости и ускорения точки кривошипа

Другие видео

Кинематика твердого тела

1. сколько оборотов сделает колесо
2. скорость и ускорение точки обода и груза
3. угловая скорость вала
4. скорость точки на ободе диска, её ускорение и угол между вектором ускорения и радиусом диска
5. скорость и ускорение точки

Плоскопараллельное движение твердого тела

Примеры расчетов скорости и ускорения точек при плоскопараллельном движении твердого тела (ППД)

1. пример 1
2. пример 2
3. пример 3
4. пример 4
5. ускорение точки

Сложное движение точки

Решение задач по определению абсолютной скорости и абсолютного ускорения точки при сложном движении точек

1. пример 1
2. пример 2
3. пример 3

Сферическое движение

1. угловая скорость и угловое ускорение, скорости и ускорения точек тела.

---

См. также:

• Лекции по теормеху
• Задачи на скорость
• Задачи на ускорение

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.

---

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

– Рамки A4 для учебных работ
– Миллиметровки разного цвета
– Шрифты чертежные ГОСТ
– Листы в клетку и в линейку

Сохранить или поделиться с друзьями

---

Заказать решение

---

Поиск формул и решений задач

Решение задач статики. Техмех, теормех и инженерная механика

Задачи с решениями по разделу «Статика» теоретической, технической и инженерной механики.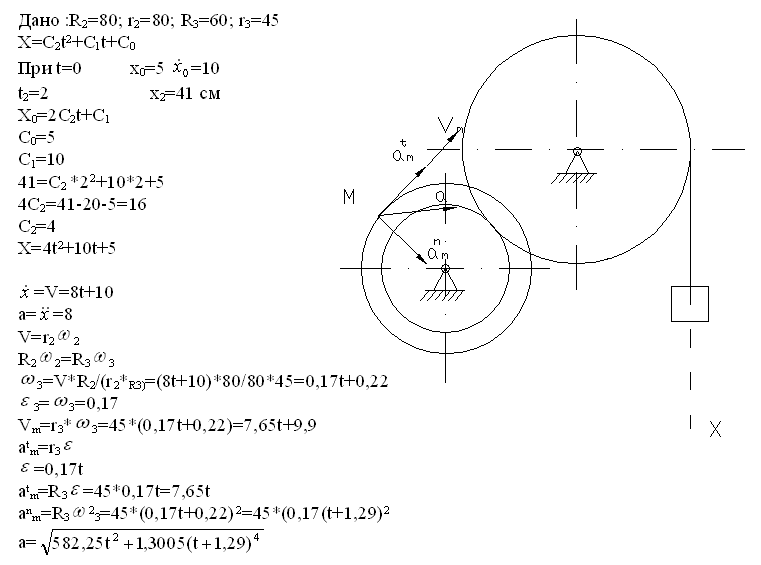

Сохранить и поделиться с друзьями

Выберите раздел теоретической механики:
Кинематика   |   Статика   |   Динамика

Здесь рассмотрены примеры решения задач на расчет реакций связей и опор при равновесии тел и составных конструкций под действием произвольной системы сил, определение центов тяжести плоских фигур и твердых тел и другие задачи статики.

Определение реакций стержней под действием груза

Задача

Стержневая система из двух стержней AB и BC соединенных между собой и закрепленных в опоре шарнирно, удерживают на нерастяжимой нити груз весом F = 40 кН.

Углы наклона стержня 1 — 30°, стержня 2 — 50°.
Требуется определить величину и направление реакций стержней, под действием груза.

Пример решения

Все элементы заданной системы неподвижны, т.е. находятся в состоянии статического равновесия.
Рассмотрим равновесие шарнира В.
Для этого освобождаем шарнир В от связей и изображаем действующие на него вдоль стержней 1 и 2 и нити удерживающей груз F активные силы и реакции связей.

Выбираем положение системы координат X-Y. Начало координат совмещаем с точкой В.

Ось Х совместим с направлением линии действия одной из неизвестных реакций, например R₁, а ось Y направим перпендикулярно оси X и определим углы между усилиями и осями.

Составляем уравнения равновесия для системы сил, действующих на шарнир В.
Для равновесия точки B, обе суммы проекций всех сил на оси X и Y должны быть равны нулю.

Определяем реакции стержней R₁ и R₂, решая полученную систему уравнений.
Из уравнения (2) определяем величину R₂:

Затем подставляем полученное значение R₂ в уравнение (1) и находим R₁:

Знак минус перед значением R ₂ указывает на то, что первоначально выбранное направление реакции неверное – следует изменить направление реакции R₂ в противоположную сторону, то есть к шарниру В.

Проверка геометрическим способом

Выполним геометрическую проверку значений найденных реакций с помощью построения силового многоугольника.

Для этого, задав определенный масштаб, переносим силу и реакции опор в заданном положении (сохраняя величину и угол наклона вектора усилий).

При этом каждый следующий вектор откладываем от стрелки предыдущего. Последовательность векторов значения не имеет.

Стрелка последнего вектора совпала с началом первого.
Следовательно, величина и направление реакций были определены правильно.

Ответ: R₁ = 31,11 кН и R₂ = 20,31 кН. Стержень №1 (AB) — растягивается, стержень №2 (BC) — сжимается.

Помощь с решением задач

Пример определения координат центра тяжести сложной фигуры в нашем коротком видео:

Другие видео

Далее рассмотрены примеры решения задач статики по соответствующим подразделам механики.

Порядок решения задач на равновесие системы сил

Задачи на равновесие тела под действием произвольной плоской системы сил

1. Составление уравнений суммы моментов сил относительно точки
2. Определение реакции шарнира и опоры
3. Определение реакций связей аналитическим и графическим способом
4. Определение реакций стержней треугольной системы, удерживающей два груза
5. Определение реакций опор балки, когда сила приложена под углом
6. Определение опорных реакций для разных способов нагружения

Задачи на равновесие составных конструкций под действием плоской системы сил

1. реакции в шарнирах
2. реакции опор и шарнира

Задачи на равновесие твердого тела при наличии трения

1. вес груза для равновесия тела
2. коэффициент трения обеспечивающий равновесие
3. угол наклона плоскости при котором цилиндр начнет скатываться

Задачи на расчет пространственной системы сил

1. вес противовеса и реакции шарниров
2. величина груза для равновесия и реакции подшипников
3. Определение реакций подшипников пространственно нагруженного вала

Задачи на определение центра тяжести

Расчет координат центра тяжести:

1. пространственной фигуры
2. сложной несимметричной фигуры
3. тонкой однородной симметричной пластинки (плоской фигуры)
4. сложного сечения
5. объемного тела

Другие примеры расчета равновесия системы сил

1. Определение усилий в стержнях
2. Натяжение троса и реакция опоры
3. Реакции опор в точках системы
4. Опорные реакции невесомой конструкции
5. Опорные реакции в скользящей заделке
6. Давление в шарнире и реакции в бискользящей заделке
7. Реакции в скользящей заделке
8. Натяжение бесконечного ремня
9. Расчет усилия в стержне
10. Равновесие тела на шероховатой наклонной плоскости
11. Расчет силы для равновесия тела

---

Конспект лекций по теормеху

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.