Кинематика ускорение: 1.1. Основные понятия кинематики

Кинематика. Ускорение – презентация онлайн

Похожие презентации:

Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов

Газовая хроматография

Геофизические исследования скважин

Искусственные алмазы

Трансформаторы тока и напряжения

Транзисторы

Воздушные и кабельные линии электропередач

Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса

Магнитные аномалии

Нанотехнологии

УСКОРЕНИЕ
Ускорение
характеризует быстроту
изменения вектора скорости со
временем.
Среднее ускорение равно отношению
изменения вектора скорости к
промежутку времени, за который это
изменение произошло.
r
r Dv
a =
Dt
Мгновенное ускорение
равно производной вектора скорости по
времени.
r
r
Dv
a = lim
Dt ®0 Dt
r
r dv r&
a=
=v
dt
r

r dr r&
Так как v =
= r , то
dt
r
r d r &
r&
a= 2 =r
dt
2
Ускорение равно второй производной
радиус-вектора по времени.
é мù
[ a] = ê с2 ú
ë û
Компоненты ускорения
Представим вектор скорости как
r
r
v = vt .
Вычислим ускорение
r
r
r d v d ( vt )
a=
=
dt
dt
r
r dv r
dt
a= t +v
dt
dt
r
r
(v ­ ­ t )
Первое слагаемое в формуле
r
r dv r
dt
a= t +v
dt
dt
дает вектор, направленный по касательной к
траектории. Его называют
касательным или тангенциальным
ускорением.
r dv r
at = t
dt
По величине тангенциальное ускорение

равно производной модуля скорости по
времени
dv
at =
dt
и показывает, как быстро
величина скорости
меняется со временем.
Тело
разгоняется
r r
at v
r r
v at
r
r
at ­ ­ v
at > 0
Тело
тормозит
r
r
at v
r r
at v
r
at
r
v
r r
at v
r
r
at ­ ¯ v
at < 0
Второе слагаемое в формуле
r
r dv r
dt
a= t +v
dt
dt
дает нормальную компоненту ускорения
r
r
dt
an = v
dt
Проведем окружность, дуга которой совпадает
с некоторым участком траектории. v
Нормальное ускорение
2
r v r
an = n
R
По модулю
2
v
an =
R
Вектор нормального
ускорения направлен к
центру кривизны
траектории и характеризует
быстроту изменения
скорости по направлению.
r
Вектор полного ускорения a
является векторной суммой
r
тангенциального ускорения at
r
и нормального ускорения an .
r
at
r
r a
an
O
r r r
a = at + an
По модулю
a=
2
at
2
+ an
2
æ dv ö æ v ö
a = ç ÷ +ç ÷
è dt ø è R ø
2
2
ВИДЫ ДВИЖЕНИЯ
1. Равномерное движение
Равномерным называют движение с постоянной по
модулю скоростью.
По определению
При равномерном движении тангенциального ускорения нет!
Если движение криволинейное, нормальное ускорение есть.
Полное ускорение равно нормальному.
2. Равномерное прямолинейное движение
Вектор мгновенной скорости остается постоянным не
только по модулю, но и по направлению.
По определению
3. Движение по произвольной траектории с
постоянной тангенциальной составляющей вектора
ускорения aτ
По определению
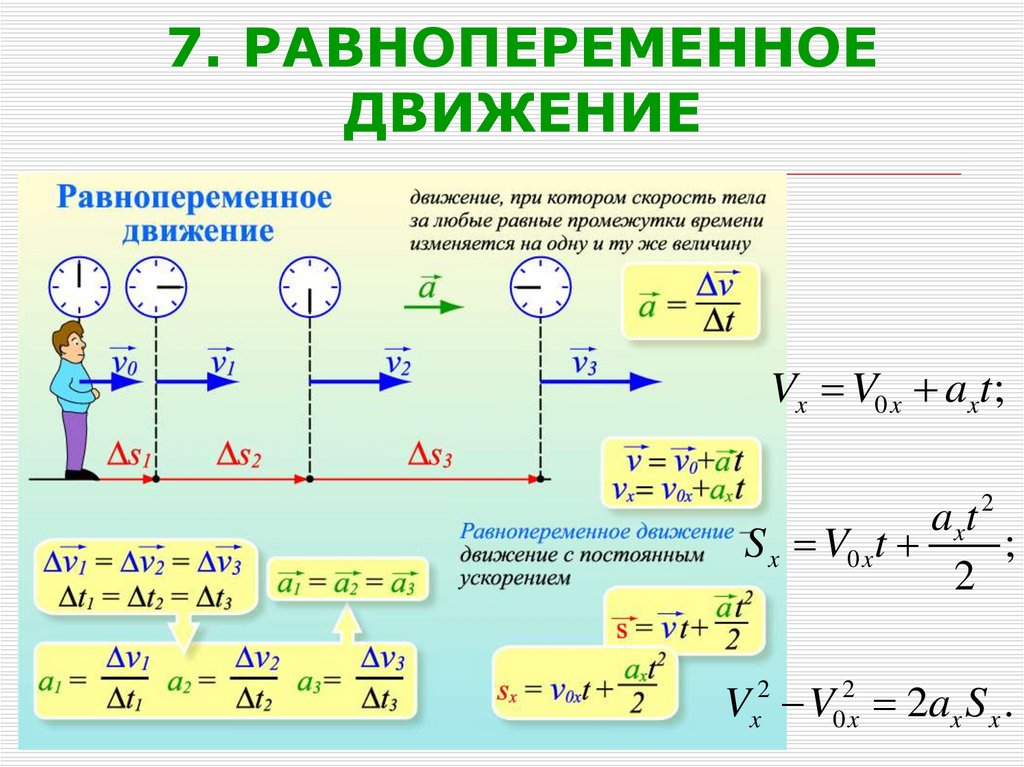
4. Равнопеременное движение
Движение называют равнопеременным, если оно
происходит с постоянным вектором полного
ускорения
y
r
v
r A
at r r
a r
r
B v
r
a
r r
a=g
Cr
at r
r
v
a
x
По определению
По определению
5. Прямолинейное равнопеременное движение
В случае прямолинейного движения радиус кривизны
траектории R стремится к бесконечности, тогда
– движение
равноускоренное
– движение
равнозамедленное
ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
r
r
O
j
x
Движение точки по окружности задается
зависимостью φ (t).
φ – угол между радиус-вектором точки и осью х.
R
Dj
O
Dj = 1рад.
Ds
x
Углом в 1 радиан называют такой
центральный угол, длина дуги которого Δs
равна её радиусу R.
Для произвольного угла поворота Δφ
Ds
Dj =
R
Ds = R × Dj
Угол в 1 оборот равен 2 радиан.
Вектор углового пути
Вектор углового пути по модулю равен
углу поворота.
Его направление определяется
правилом правого винта.
r
dj
r
r
dj
dj
r
dj
Угловая скорость
Угловая скорость характеризует быстроту
движения материальной точки по окружности.
Это векторная величина равная
производной вектора углового пути по
времени.
r
r dj
é рад. ù

w=
w] = ê
[
ú
dt
ë с û
r r&
w =j
Направление вектора угловой скорости
также находят по правилу правого винта.
r
w
r
w
Угловое ускорение
Угловое ускорение характеризует быстроту
изменения угловой скорости со временем.
Это векторная величина равная
производной угловой скорости по времени.
r
r dw
e=
é рад. ù
dt [ e ] = êë с úû
r r&
e =w
2
Векторы углового пути, угловой скорости,
углового ускорения
направлены вдоль оси вращения.
Если ω увеличивается, то
r
w
r
e
r
an
Если ω уменьшается, то
r
r v
at
r
w
r
an
r
e
r
v
r
at
Связь линейных и угловых характеристик движения
Свяжем линейный и угловой пути
ds = R × dj
Возьмем производную по времени
ds
dj
= R×
dt
dt
Получим связь линейной и угловой скоростей
v = wR
Заметив, что векторы линейной и
угловой скоростей, а также радиусвектор взаимно перпендикулярны и
связаны правилом правого винта,
можно записать векторное равенство:
r
r r
v = [ w ,r ]
Снова возьмем производную по времени:
dv
dw
=R
dt
dt
Получим
at = e R
Теперь найдем нормальное ускорение
v w Rv
an = =
= wv
R
R
2
или
w R
an =
R
2
2
an = w R
2
Характеристики равномерного вращения
Период Т равен времени, за которое
происходит один оборот.
Частота вращения ν равна числу
оборотов в единицу времени.
1
1
T = иn =
n
T
Угловая скорость при равномерном вращении:
j об 2
w=
=
= 2 n
tоб
T

English     Русский Правила

Кинематика – FIZI4KA

ЕГЭ 2018 по физике ›

Механика — это раздел физики, изучающий механическое движение тел.

Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.

Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если

• расстояние, которое проходит тело, много больше его размера;
• расстояние от данного тела до другого тела много больше его размера;
• тело движется поступательно.

Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.

Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.

Важно! 
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.

Основная задача механики — определить положение тела в пространстве в любой момент времени.

Содержание

• Механическое движение и его виды
• Относительность механического движения
  • Правило сложения перемещений
  • Правило сложения скоростей
  • Относительная скорость
• Скорость
• Ускорение
• Равномерное движение
  • График скорости (проекции скорости)
  • График перемещения (проекции перемещения)
• Прямолинейное равноускоренное движение
• Свободное падение (ускорение свободного падения)
  • Движение тела по вертикали
  • Движение тела, брошенного горизонтально
  • Движение тела, брошенного под углом к горизонту (баллистическое движение)
• Движение по окружности с постоянной по модулю скоростью
• Основные формулы по теме «Кинематика»

Механическое движение и его виды

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение может быть:
1. по характеру движения

• поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
• вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
• колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;

2. по виду траектории

• прямолинейным — это движение, траектория которого прямая линия;
• криволинейным — это движение, траектория которого кривая линия;

3. по скорости

• равномерным — движение, при котором скорость тела с течением времени не изменяется;
• неравномерным — это движение, при котором скорость тела с течением времени изменяется;

4. по ускорению

• равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
• равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.

Относительность механического движения

Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.

Правило сложения перемещений

Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ​\( S \)​ — перемещение тела относительно неподвижной системы отсчета;
​\( S_1 \)​ — перемещение тела относительно подвижной системы отсчета;
​\( S_2 \)​ — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.

Правило сложения скоростей

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ​\( v \)​ — скорость тела относительно неподвижной системы отсчета;
​\( v_1 \)​ — скорость тела относительно подвижной системы отсчета;
​\( v_2 \)​ — скорость подвижной системы отсчета относительно неподвижной системы отсчета.

Относительная скорость

Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.

Пусть \( v_1 \) — скорость первого тела, а \( v_2 \) — скорость второго тела.
Определим скорость первого тела относительно второго \( v_{12} \):

Определим скорость второго тела относительно первого \( v_{21} \):

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.

Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:

Если скорости направлены под углом ​\( \alpha \)​ друг к другу, то относительная скорость рассчитывается по теореме косинусов:

Скорость

Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.

Обозначение — ​\( v \)​, единицы измерения — ​м/с (км/ч)​.

Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:

Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:

Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.

Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.

Ускорение

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.

Обозначение — ​\( a \)​, единица измерения — м/с².
В векторном виде:

где ​\( v \)​ – конечная скорость; ​\( v_0 \)​ – начальная скорость;
​\( t \)​ – промежуток времени, за который произошло изменение скорости.

В проекциях на ось ОХ:

где ​\( a_n \)​ – нормальное ускорение, ​\( a_{\tau} \)​ – тангенциальное ускорение.

Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.

Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если \( a_{\tau} \) ≠ 0, \( a_n \) = 0, то тело движется по прямой;
если \( a_{\tau} \) = 0, \( a_n \) = 0, ​\( v \)​ ≠ 0, то тело движется равномерно по прямой;
если \( a_{\tau} \) = 0, \( a_n \) ≠ 0, тело движется равномерно по кривой;
если \( a_{\tau} \) = 0, \( a_n \) = const, то тело движется равномерно по окружности;
если \( a_{\tau} \) ≠ 0, \( a_n \) ≠ 0, то тело движется неравномерно по окружности.

Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ​\( t \)​, тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ​\( t \)​, тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью \( t \), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью \( t \), тело движется против оси ОХ.

По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время \( t \). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ​\( x=x(t) \)​.

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Прямолинейное равноускоренное движение

Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:

При движении с ускорением скорость может как увеличиваться, так и уменьшаться.

Скорость тела при равноускоренном движении рассчитывается по формуле:

При разгоне (в проекциях на ось ОХ):

При торможении (в проекциях на ось ОХ):

График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:

График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ​\( a_x \)​ > 0.
График 2 лежит под осью t, тело тормозит, \( a_x \) < 0.

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ​\( v_{0x} \)​ > 0, ​\( a_x \)​ > 0.

График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, \( v_{0x} \) > 0, \( a_x \) < 0,

График 3 направлен вниз, тело движется равноускоренно против оси ОХ, \( v_{0x} \) < 0, \( a_x \) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ​\( t_2-t_1 \)​. Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Перемещение при равноускоренном движении рассчитывается по формулам:

Перемещение в ​\( n \)​-ую секунду при равноускоренном движении рассчитывается по формуле:

Координата тела при равноускоренном движении рассчитывается по формуле:

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – ​\( g \)​, единицы измерения – м/с².

Важно! \( g \) = 9,8 м/с², но при решении задач считается, что \( g \) = 10 м/с².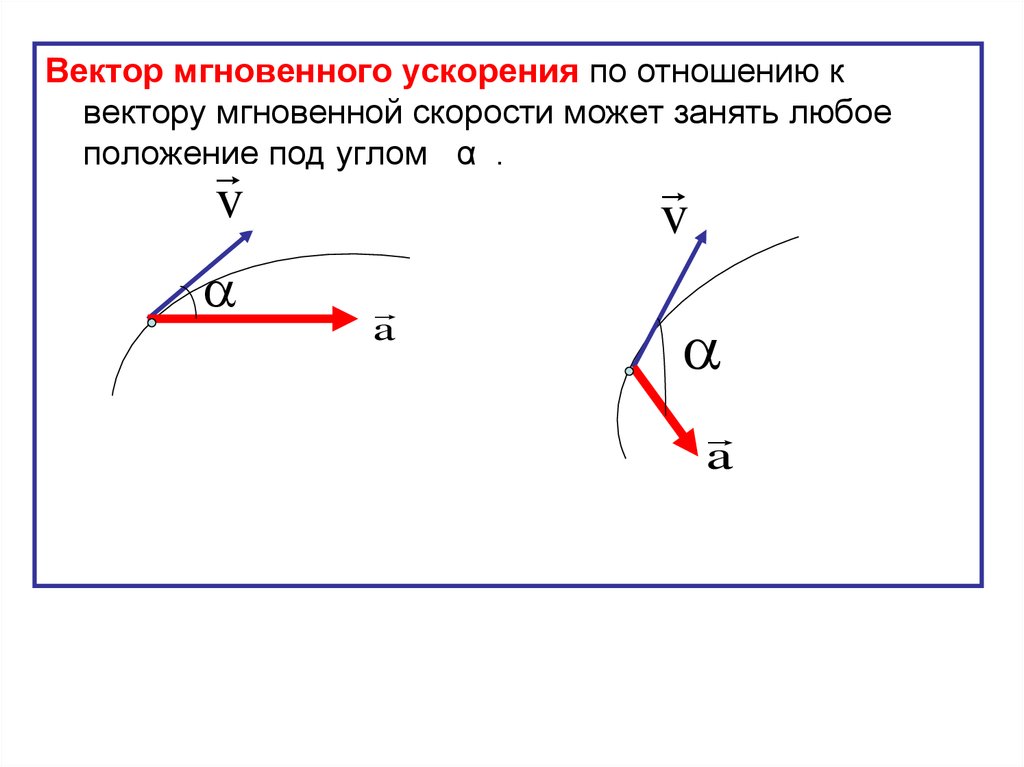

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ​\( v_0 \)​ = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ​\( v \)​ = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали со скоростью ​\( v_0=v_{0x} \)​;
2. равноускоренного движения по вертикали с ускорением свободного падения ​\( g \)​ и без начальной скорости ​\( v_{0y}=0 \)​.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Дальность полета:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали;
2. равноускоренного движения по вертикали с ускорением свободного падения.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Время полета:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ​\( v_0 \)​, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ​\( \alpha \)​, под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ​\( a_{цс} \)​, единицы измерения – ​м/с^2​.

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ​\( T \)​, единицы измерения – с.

где ​\( N \)​ – количество оборотов, ​\( t \)​ – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ​\( \nu \)​, единицы измерения – с^–1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ​\( v \)​, единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ​\( \omega \)​, единицы измерения – рад/с .

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ​\( v_1 \)​, и все точки обода колеса движутся относительно его центра с такой же линейной скоростью \( v_1 \), то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ​\( (m) \)​ равна нулю, мгновенная скорость в верхней точке ​\( (n) \)​ равна удвоенной скорости ​\( v_1 \)​, мгновенная скорость точки ​\( (p) \)​, лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ​\( (c) \)​ – по теореме косинусов.

Основные формулы по теме «Кинематика»

 

Динамика →

← ПРИМЕР ВАРИАНТА КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫХ МАТЕРИАЛОВ ОГЭ (ГИА)

Почему кинематические уравнения работают только с постоянным ускорением?

$\begingroup$

Люди говорят, что уравнения получены при постоянном ускорении. Я просто не понимаю, как это происходит. (Я новичок в исчислении.)

• кинематика
• ускорение
• исчисление

$\endgroup$

2

$\begingroup$ 92}{2}\;, $$ где – обычное кинематическое уравнение с постоянным ускорением.

$\endgroup$

0

$\begingroup$

Кинематические уравнения, одно из которых $v=u+at$, выводятся в предположении, что ускорение $a$ является постоянным. t_0 v \,dt$, которую вам нужно было бы использовать, если ускорение зависит от времени. 9{2}}=\vec{F},$$ где $\vec{F}$ — любая сила. Вы не можете сказать больше о движении массы, не зная деталей силы $\vec{F}$, действующей на нее. Различные законы силы дадут разные решения.

Кинематические уравнения, по существу, являются решением дифференциального уравнения, когда закон силы принимает простую форму константы: $\vec{F}=-m\vec{g}$ (для гравитационного ускорения $-\vec{g}$, но та же математика применима к любой силе, производящей постоянное ускорение). Дифференциальное уравнение (второй закон Ньютона) имеет второй порядок по времени, поэтому для него требуются два начальных условия: положение в начальный момент времени (принятое равным $t=0$), $\vec{x}(t=0)= \vec{x}_{0}$ и первая производная позиции в начальный момент времени, $\frac{d\vec{x}}{dt}(0)=\vec{v}(0)=\ vec{v}_{0}$. Как только эти исходные данные заданы, существует единственное решение, $$\vec{x}(t)=\vec{x}_{0}+\vec{v}_{0}t-\frac{1}{2}\vec{g}t^{2} .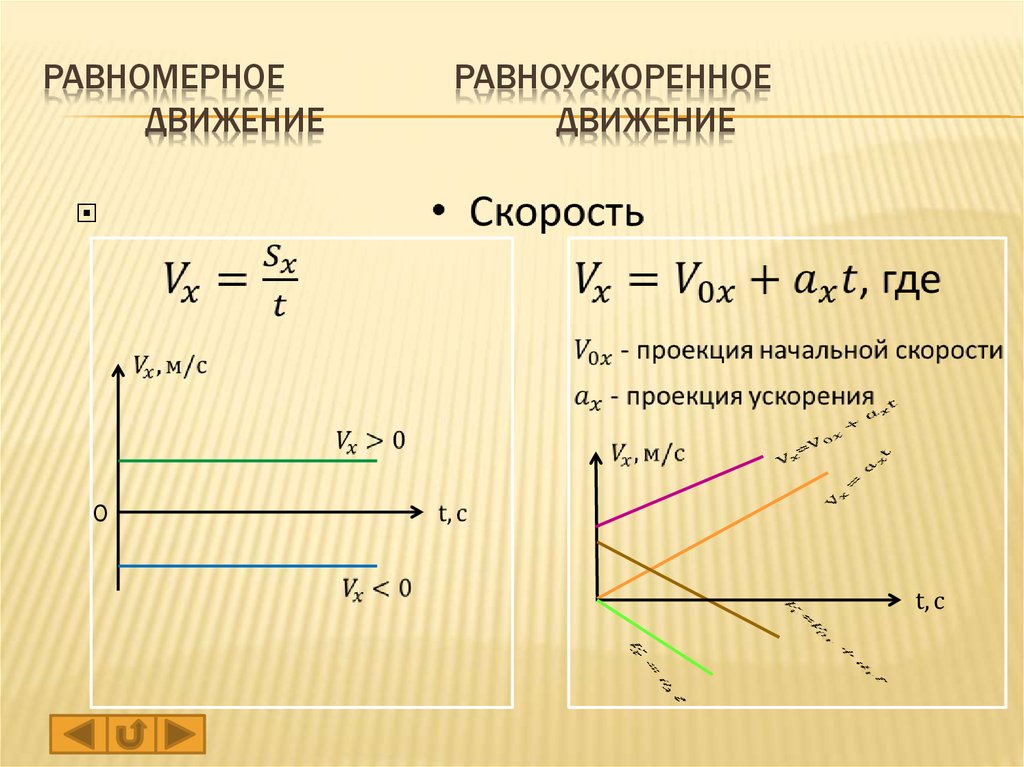 $$ 9{2}_{0}+m\vec{g}\cdot\vec{x}_{0},$$ что представляет собой просто сохранение энергии (постоянство $K+U$) с потенциальной энергией $U(\vec{x})=m\vec{g}\cdot\vec{x}$. При другом силовом законе (то есть другом $U$ и, следовательно, другом $\vec{F}=-\vec{\nabla}U$) явный вид уравнения сохранения энергии должен был бы быть другим.

$\endgroup$

$\begingroup$

У вас могут быть кинематические уравнения для различных типов переменного ускорения. Просто уравнения, полученные для случая постоянного ускорения, недействительны, когда ускорение непостоянно. Что и следовало ожидать. Уравнения, рассматриваемые в начале вводного курса физики, ограничены случаем постоянного ускорения, поскольку это простейший случай ускоренного движения. Это не значит, что это единственный случай и это не “НАСТОЯЩИЕ” кинематические уравнения. Только один набор уравнений, справедливый для конкретного случая – постоянное ускорение. Если вы изучите простой гармонический осциллятор, вы узнаете о другом наборе кинематических уравнений, которые выражают положение, скорость и ускорение как функции времени (с функциями синуса и косинуса). Это пример кинематических уравнений для непостоянного ускорения.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Введение в кинематику | Великолепная математика и естественные науки Wiki

Шравант С., Мэтт ДеКросс, Рам Мохит, а также

способствовал

Содержимое

• Должность
• Скорость
• Ускорение
• Скорость против ускорения

Позиция

Положение объекта — это любой способ однозначно установить его положение в пространстве относительно точки отсчета. Это может быть выполнено с использованием системы координат, такой как декартова сетка, сферическая система координат или любой другой обобщенный набор координат.

Короче говоря, положение объекта — это просто его положение в некоторой системе координат. Можно рассмотреть график положение-время или график смещения-времени объекта, в котором ось xxx представляет время, а ось yyy представляет смещение. Такой график показывает, как меняется позиция в зависимости от времени, x(t)x(t)x(t).

Перемещение — понятие, несколько отличающееся от расстояния или положения. В отличие от расстояния, перемещение является векторной величиной. Он дает чистое изменение положения по сравнению с фиксированным начальным положением в отличие от общего пройденного расстояния. Например, если объект находится в точке x1x_1x1​ в момент времени t1t_1t1​ и в точке x2x_2x2​ в момент времени t2t_2t2​, то смещение будет равно

d=x2−x1=x(t1+Δt)−x(t1) ,d=x_2-x_1=x(t_1+\Delta t)-x(t_1),d=x2​−x1​=x(t1​+Δt)−x(t1​),

, где Δt=t2−t1 \Дельта t = t_2-t_1Δt=t2​−t1​.

Обратите внимание, что «скорость изменения yyy по отношению к xxx» относится к производной yyy по отношению к xxx, dydx\frac{dy}{dx}dxdy​ или наклону функции yyy в данной точке .

Вы начинаете в точке AAA и проходите 4 км4\text{ км}4 км на юг, а затем 3 км3\text{ км}3 км на восток, наконец, достигая C.C.C. Найдите полное расстояние и перемещение, пройденное вами.

---

Вы всегда должны помнить, что пройденное расстояние — это фактически пройденный путь, а перемещение — это кратчайший возможный путь. Вопрос можно визуализировать на диаграмме, как показано ниже: 92} = 5∣AC∣=42+32​=5.

-2 4 8 10

Частица, ограниченная одним измерением, начинается в точке x=0x=0x=0, движется вправо в точку x=4x=4x=4, а затем движется влево в точку x=−2x=-2x=− 2. Если aaa — смещение частицы после этого процесса, а bbb — пройденное расстояние, найти a+ba+ba+b.

Скорость

Скорость объекта — это скорость, с которой объект меняет свое положение. Направление скорости объекта в любой момент времени параллельно касательному вектору кривой, представляющей траекторию объекта.

Из определения производная функции положения дает функцию скорости: x1Δt.v (t) = \ dfrac {dx} {dt} = \ displaystyle \ lim _ {\ Delta t \ rightarrow 0} \ dfrac {x (t + \ Delta t) -x (t)} {\ Delta t} = \displaystyle\lim_{\Delta t\rightarrow 0}\dfrac{x_2-x_1}{\Delta t}. v(t)=dtdx​=Δt→0lim​Δtx(t+Δt)−x(t)​=Δt→0lim​Δtx2​−x1​​.

Часто вместо скорости используется термин скорость . Скорость объекта является нормой скорости, т. е. дает величину, но не направление скорости.

Таким образом, функция скорости имеет вид

|\dfrac{dx}{dt}\right|=\left|\displaystyle\lim_{\Delta t\rightarrow 0}\dfrac{x(t+\Delta t)-x(t)}{\Delta t}\ right|. ∣v(t)∣=∣∣∣∣​dtdx​∣∣∣∣​=∣∣∣∣​Δt→0lim​Δtx(t+Δt)−x(t)​∣∣∣∣​.

Поскольку скорость частицы является производной от ее положения, мы можем пойти наоборот, чтобы получить смещение, интегрируя функцию скорости; то есть 92-2t-1\big)=6t-2.v(t)=dtd​(3t2−2t−1)=6t−2.

Следовательно, функция скорости будет ∣v(t)∣=∣6t−2∣\big|v(t)\big|=|6t-2|∣∣​v(t)∣∣​=∣6t− 2∣. В результате скорость и скорость при t=3t=3t=3 равны

v(3)=6(3)−2=16 м/с∣v(3)∣=∣16∣=16 м/с,\begin{выровнено} v(3)=6(3)-2&=16 \text{ м/с} \\ \big|v(3)\big|=|16|&=16\text{ м/с}, \end{выровнено}v(3)=6(3)−2∣∣​v(3)∣∣​=∣16∣​=16 м/с=16 м/с,​

и при t=5t=5t=5

v(5)=6(5)−2=28 м/с∣v(5)∣=∣28∣=28 м/с. □\begin{выровнено} v(5)=6(5)-2&=28\text{ м/с}\\ \big|v(5)\big|=|28|&=28\text{ м/с}.\ _\квадрат \end{выровнено}v(5)=6(5)−2∣∣​v(5)∣∣​=∣28∣​=28 м/с=28 м/с. □​​ 92s=15t−21 gp t2 метров ттт секунд после пуска. Если мяч достиг максимальной высоты через 202020 секунд, каково было значение gp?g_p?gp​?

---

Попробуйте мой набор Gravity, если хотите решить больше таких задач!

Ускорение

Ускорение объекта определяется скоростью изменения скорости объекта. Если тело движется с постоянной скоростью, то его ускорение равно нулю. Если объект меняет свою скорость или направление своей скорости, то он имеет ненулевое ускорение. 92\справа)= -gt.v(t)=dtdx​=dtd​(−21​gt2)=−gt.

Следовательно, v(2)=−9,8(2)=−19,6 м/с.v(2)= -9,8(2)=-19,6 \text{ м/с}.v(2)=−9,8(2)= −19,6 м/с.

Скорость – это абсолютное значение v(t)v(t)v(t), поэтому скорость=∣v(t)∣=19,6 м/с.\text{скорость}=\big|v(t)\ big|=19,6 \text{ м}/\text{с}.скорость=∣∣​v(t)∣∣​=19,6 м/с.

Наконец, ускорение есть производная от функции скорости, поэтому

a(t)=dvdt=ddt(-gt)=-g,a(t)= \dfrac{dv}{dt} =\dfrac{d}{dt}(-gt)=-g,a(t )=dtdv​=dtd​(-gt)=-g, 92а(2)=-9,8 м/с2. □_\квадрат□​

Важно понимать, что ускорение объекта дает только скорость изменения скорости и не коррелирует со скоростью объекта. Объект может двигаться очень медленно, быстро или вообще не двигаться и иметь любое ускорение.

Графически ускорение представляет собой наклон касательной к графику зависимости скорости от времени. Скорость может быть очень большой и отрицательной, с очень большим и положительным наклоном. В этом случае объект будет быстро двигаться назад, но замедляться и менять направление за короткий промежуток времени.

Распространенное заблуждение состоит в том, что ускорение всегда представляет собой изменение скорости. Это , а не . Поскольку ускорение является векторной величиной, изменения в направлении скоростей также представляют собой ускорения. Следовательно, объект, движущийся по кругу с постоянной скоростью, также постоянно ускоряется, потому что направление вектора скорости меняется в каждый момент времени.

Золотая кривая Синяя кривая Эти двое равны. Недостаточно информации

На приведенном ниже графике представлены две кривые, представляющие зависимость скорости от времени для двух разных частиц.